Формула мощность передачи теплоты: Тепловой расчет теплообменника - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Тепловой расчет теплообменника

На главную

Блог

Все о теплообменниках и теплотехническом оборудовании

Рубрики

Мы в соцсетях

Подписка на статьи

Фильтр по статьям

Содержание статьи

Введение
Основы теплового расчета теплообменных аппаратов
Пример расчета
Выводы

Введение

Теплообменный аппарат – это устройство, обеспечивающее передачу тепла между средами, разнящимися по температуре. Для обеспечения тепловых потоков различного количества конструируются разные теплообменные устройства. Они могут иметь разные формы и размеры в зависимости от требуемой производительности, но основным критерием выбора агрегата является площадь его рабочей поверхности. Она определяется с помощью теплового расчета теплообменника при его создании или эксплуатации.

Расчет может нести в себе проектный (конструкторский) или проверочный характер.

Конечным результатом конструкторского расчета является определение площади поверхности теплообмена, необходимой для обеспечения заданных тепловых потоков.

Проверочный расчет, напротив, служит для установления конечных температур рабочих теплоносителей, то есть тепловых потоков при имеющейся площади поверхности теплообмена.

Соответственно, при создании устройства проводится конструкторский расчет, а при эксплуатации – проверочный. Оба расчета идентичны и, по сути, являются взаимообратными.

Основы теплового расчета теплообменных аппаратов

Основой для расчета теплообменников являются уравнения теплопередачи и теплового баланса.

Уравнение теплопередачи имеет следующий вид:

Q = F‧k‧Δt, где:

Q – размер теплового потока, Вт;
F – площадь рабочей поверхности, м2;
k – коэффициент передачи тепла;
Δt – разница между температурами носителей на выходе в аппарат и на выходе из него. Также величина называется температурным напором.

Как можно заметить, величина F, являющаяся целью расчета, определяется именно через уравнение теплопередачи. Выведем формулу определения F:

F = Q/ k‧Δt

Уравнение теплового баланса учитывает конструкцию самого аппарата. Рассматривая его можно определить значения t1 и t2 для дальнейшего вычисления F. Уравнение выглядит следующим образом:

Q = G₁c_p₁(t₁^вх-t₁^вых) = G₂c_p₂(t₂^вых-t₂^вх), где:

G₁и G₂ – расходы масс греющего и нагреваемого носителей соответственно, кг/ч;
c_p

₁и c_p₂ – удельные теплоемкости (принимаются по нормативным данным), кДж/кг‧ ºС.

В процессе обмена тепловой энергией носители изменяют свои температуры, то есть в устройство каждый из них входит с одной температурой, а выходит – с другой. Эти величины (t₁^вх;t₁^вых и t₂^вх;t₂^вых) являются результатом проверочного расчета, с которым сравниваются фактические температурные показатели теплоносителей.

Вместе с тем большое значение имеют коэффициенты теплоотдачи несущих сред, а также особенности конструкции агрегата. При детальных конструкторских расчетах составляются схемы теплообменных аппаратов, отдельным элементом которых являются схемы движения теплоносителей. Сложность расчета зависит от изменения коэффициентов теплопередачи

k на рабочей поверхности.

Для учета этих изменений уравнение теплопередачи принимает дифференциальный вид:

Такие данные, как коэффициенты теплоотдачи носителей, а также типовые размеры элементов при конструировании аппарата или при проверочном расчете, учитываются в соответствующих нормативных документах (ГОСТ 27590).

Пример расчета

Для большей наглядности представим пример конструкторского расчета теплообмена.

Этот расчет имеет упрощенный вид, и не учитывает потерь теплоты и особенностей конструкции теплообменного аппарата.

Исходные данные:

Температура греющего носителя при входе t₁^вх = 14 ºС;
Температура греющего носителя при выходе t₁^вых = 9 ºС;
Температура нагреваемого носителя при входе t₂^вх = 8 ºС;
Температура нагреваемого носителя при выходе t₂^вых = 12 ºС;
Расход массы греющего носителя G₁= 14000 кг/ч;
Расход массы нагреваемого носителя G₂= 17500 кг/ч;
Нормативное значение удельной теплоемкости с_р =4,2 кДж/кг‧ ºС;
Коэффициент теплопередачи k = 6,3 кВт/м².

1) Определим мощность теплообменного аппарата с помощью уравнения теплового баланса:

Q^вх = 14000‧4,2‧(14 – 9) = 294000 кДж/ч

Q^вых = 17500‧4,2‧(12 – 8) = 294000 кДж/ч

Qвх = Qвых. Условия теплового баланса выполняются. Переведем полученную величину в единицу измерения Вт. При условии, что 1 Вт = 3,6 кДж/ч, Q = Qвх = Qвых = 294000/3,6 = 81666,7 Вт = 81,7 кВт.

2) Определим значение напора t. Он определяется по формуле:

3) Определим площадь поверхности теплообмена с помощью уравнения теплопередачи:

F = 81,7/6,3‧1,4 = 9,26 м2.

Как правило, при проведении расчета не все идет гладко, ведь необходимо учитывать всевозможные внешние и внутренние факторы, влияющие на процесс обмена теплом:

особенности конструкции и работы аппарата;
потери энергии при работе устройства;
коэффициенты теплоотдачи тепловых носителей;
различия в работе на разных участках поверхности (дифференциальный характер) и т.д.

Вы можете самостоятельно провести тепловой расчет на основе уравнений выше и получить результат в pdf-формате (в полях «Допустимые потери», «Давление расч.» и «Tmax» можно указать произвольные данные, единственное ограничение: Tmax > t1).

Греющая сторона

Среда: Вода

м3/чт/чкПабармвс Гкал/чккал/чкВтМВт

Давление расч., кгс/см2

Введите мощность или один из расходов

Температура должна быть от 1 до 200, при этом t1 должна быть больше t4, а t2 должна быть больше t3

t1 должна быть больше t2, а t4 должна быть больше t3

Разность температур t1 и t4 не должна быть равна разности температур t2 и t3

Допустимые потери должны быть в пределах: мвс: от 0 до 10, бар: от 0 до 1, кПа: от 0 до 100

Максимальная температура должна быть от 1 до 200

Максимальная температура должна быть больше или равна t1

Мощность должна быть больше 0

Расход должен быть больше 0

Нагреваемая сторона

Среда: Вода

м3/чт/чкПабармвс

ВАЖНО: Для наиболее точного и достоверного расчета инженер должен понимать сущность процесса передачи тепла от одного тела к другому. Также он должен быть максимально обеспечен необходимой нормативной и научной литературой, поскольку в расчете на множество величин составлены соответствующие нормы, которых специалист обязан придерживаться.

Выводы

Что мы получаем в результате расчета и в чем его конкретное применение?

Допустим, что на предприятие поступил заказ. Необходимо изготовить тепловой аппарат с заданной поверхностью теплообмена и производительностью. То есть перед предприятием не стоит вопрос размеров аппарата, но стоит вопрос материалов, которые обеспечат нужную производительность с заданной рабочей площадью.

Для решения данного вопроса производится тепловой расчет, то есть определяются температуры теплоносителей на входе и выходе из аппарата. Исходя из этих данных выбираются материалы для изготовления элементов устройства.

В конечном итоге, можно сказать, что рабочая площадь и температура носителей на входе и выходе из аппарата – основные взаимосвязанные показатели качества работы теплообменника. Определив их путем теплового расчета инженер сможет разработать основные решения для конструирования, ремонта, контроля и поддержания работы теплообменников.

В следующей статье мы рассмотрим назначение и особенности механического расчета теплообменника, поэтому подписывайтесь на нашу e-mail рассылку и новости в соц сетях, чтобы не пропустить анонс.

Расчет мощности теплового насоса для дома: методика и формула

Использование тепловых насосов обеспечивает экономию на горячей воде, отоплении, кондиционировании при задействовании температуры внешней среды в качестве источника тепла. Оптимальной энергоэффективности можно добиться, если правильно рассчитать мощность теплового насоса. Тип объекта, оснащенного подобной отопительной системой при этом не имеет значения. Теплонасос будет эффективен при работе в здании любого назначения будь то частный дом, квартира, промышленные сооружения или загородный коттедж. Важным моментом при создании энергосберегающих контуров ГВС, охлаждения и обогрева помещений является грамотный расчет мощности в соответствии с видом ТН.

Виды тепло насосов

Принцип работы всех типов ТН состоит в отборе тепла от низкотемпературного источника, преобразовании его и передаче потребителю. Классификации тепловых приборов по источнику тепловой энергии подразделяет их на:

воздушные – энергия извлекается из атмосферы;
геотермальные – обеспечение энергией происходит из воды или грунта;
использующие вторичное тепло – энергия пополняется из воды, воздуха и даже канализационных стоков.

На абсорбционные и компрессионные ТН подразделяются по виду передачи энергии. Разделение происходит и по теплоносителю контура, который делит их на оборудование типа воздух-воздух, грунт-вода, вода-вода, воздух-вода, вода-воздух.

В чем особенность деления тепло насосов

Прежде чем приступать к расчету теплового насоса, стоит понимать, какие еще разновидности приборов существуют.

Так, воздушное оборудование разнится и по конструкции – есть моноблочные ТН и сплит-системы, включающие внутренний и наружный блоки и автоматику управления. Геотермальные по типу установки коллектора делятся на вертикальные, которые погружаются в специальную скважину, созданную бурением, и горизонтальные — прокладываемые ниже глубины промерзания под слоем грунта. Выбор коллектора осуществляется, принимая во внимание особенности участка земли. Прежде чем монтировать ТН, необходимо рассчитать его эффективность исходя из основных характеристик.

Формула расчета

Потенциальным потребителям стоит понимать, что знание всех особенностей типов оборудования и их преимуществ не всегда является гарантией выбора наиболее эффективного. К основным параметрам, характеризующие эффективность относятся коэффициенты – полезного действия (КПД) — отражает соотношение потраченной на выработку энергии и полученной, эффективности трансформации. Всегда лучше обратиться за помощью к специалистам.

Однако тем, кто чувствует в себе способность справиться с задачей самостоятельно, может помочь калькулятор теплового насоса. Еще один способ предварительного расчета мощности – использование программ, которые предоставляет производитель ТН.

Методика и значения

Для определения мощности ТН можно воспользоваться формулой для расчетов вручную – R = (k x V x T) / 860. В ней символы имеют следующие значения:

R — размер потребляемых энергоресурсов в киловаттах и кКал/ч;
k — усредненный коэффициент теплопотерь здания;
V — объемы отапливаемых площадей;
T — перепад температур с учетом минимальных показателей внутри и снаружи помещения.

Коэффициент теплопотерь, влияющий на конечный результат, зависит от материала изготовления особняка или дачи, качества утепления и означает:

тщательное утепление – 0,6-1;
2-х слойное кирпичное сооружение – 1-2;
однослойная кирпичная кладка – 2-3;
дерево – 3-4.

Для получения показателя мощности в кВт/ч значение делят на 860.

Расчет мощности геотермальных насосов

Универсальной формулы, которая бы подходила для того, чтобы рассчитать мощность теплового насоса любого типа, не существует. Каждый вид оборудования имеет свои нюансы. Так, чтобы выбрать геотермальный прибор нужной мощности можно использовать калькулятор. Методика расчета для геотермальных насосов учитывает длину наружного контура, который размещается в грунте или водоеме. Помимо этого в расчет принимается длина труб, площадь участка для горизонтального геотермального контура. При использовании вертикальных находят длину скважин с размещенными в них геотермальными зондами. Если схема подключения открытая из скважины в скважину, определяют подходящий дебет для подбора погружного насоса.

Расчет мощности воздушных насосов

При использовании воздушных аппаратов вначале рассчитывают теплонагрузку, для снабжения дома ГВС и подогрева помещений. Алгоритм вычислений следующий:

Рпод. = 0,050х300= 15 кВт, где 0,050 кВт / м2 – норма теплопотерь дома с утеплением; 300 – его площадь.
Ргвс = 0,25х6=1,5 кВт, где 0,25 – тепло мощность на 1 чел. для ГВС; 6 –число жильцов.
Робщ.=15+1,5=16,5 кВт.
Расчетное значение с учетом точки бивалентности и разницы температур:
Ртн =(15+1,5)х (20-(-7))/(20-(-22))= 16,5х27/42=10,56 кВт,
где +20, -7, -22 – величины температур воздуха в помещении, точки бивалентности и наружной.

Аналогично определяется нужная мощность при работе ТН в качестве кондиционера.

Расчет мощности ТН, использующих вторичное тепло

Обычно ТН, использующие вторичное тепло, применяются на промышленных предприятиях с паразитными теплоисточниками по принципу «утилизация тепла». Их температурные характеристики, обеспечивающие высокую эффективность, постоянны. Проекты с использованием подобного тепла требуют тщательных расчетов. К примеру, при работе со сточными водами нужно принимать во внимание промежуточный теплообменник с высокой коррозионной стойкостью. Возможна установка геотермальных коллекторов прямо в отстойниках для стоков. При расчете теплового насоса, использующего альтернативные источники тепла типа вентиляционного воздуха или выделяемого серверами в дата-центрах, требуется учитывать их специфику.

Как подобрать тепло насос для отопления дома

Выбрать модель ТН для нагрева помещений в доме с подходящими параметрами, позволит корректное определение теплопотерь объекта. При подборе, кроме расчета теплового насоса, стоит учитывать климат региона, место расположения строения и его площадь. Например, геотермальный насос – не лучшее решение при размещении дома на небольшом каменистом участке. Важны и нюансы эксплуатации объекта. Так, для обогрева бассейна или работы отеля требуется много горячей воды. В этих случаях отлично подойдет ТН «воздух-вода». Лучшими объектами для установки прибора«воздух-воздух» станут квартиры, а «вода-вода» – дома, находящиеся рядом с водоемом, или имеющие нужный дебет подземных вод.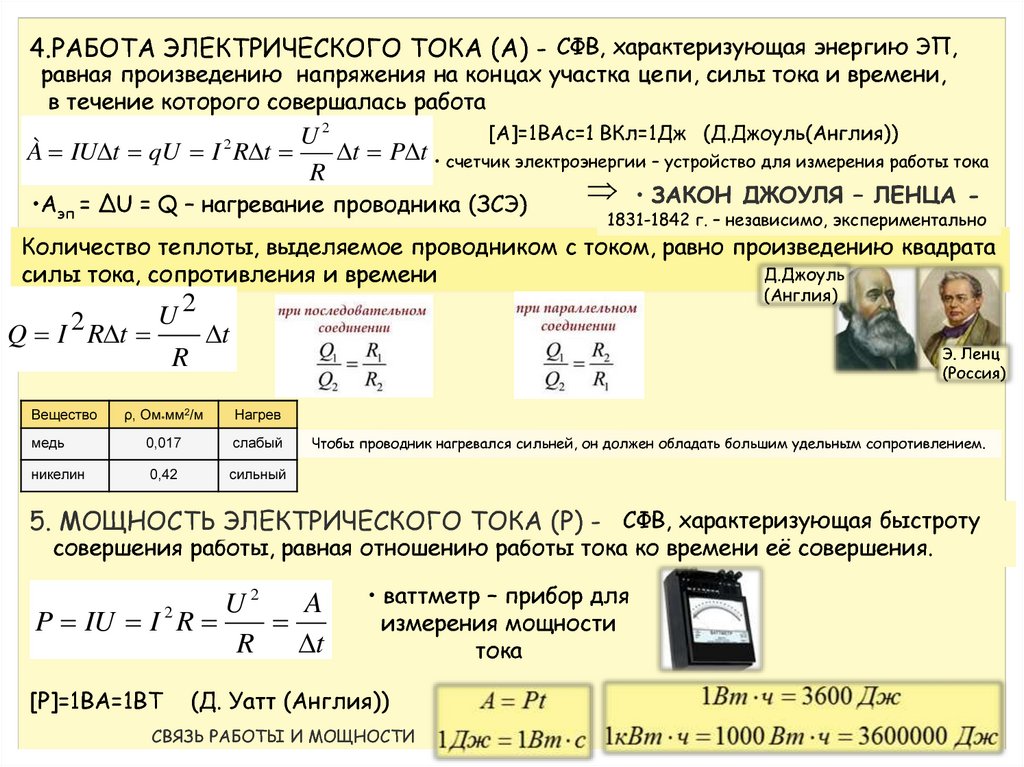

Молекулярная физика и термодинамика

Помимо цикла Карно и технических циклов, используемых в различных двигателях, представляет интерес так называемая внутреннеобратимая тепловая машина (смысл названия станет ясен позже). Дело в том, что максимальный КПД, соответствующий циклу Карно, никогда не достигается на практике. Более того, если бы это было даже возможно, далеко не очевидно, что такую машину стоило бы создавать. Помимо КПД в реальной жизни немаловажную роль играют также простота устройства и управления, стоимость установки, ее надежность, скорость работы и тому подобные требования, которые зачастую конфликтуют между собой. В цикле Карно контакты рабочего тела с тепловыми резервуарами происходят при одинаковой температуре. Это значит, что тепло перетекает бесконечно медленно, что, конечно, очень непрактично. Представление о реальной производительности используемых установок можно получить, рассматривая внутреннеобратимую тепловую машину.

Предположим снова, что мы имеем два тепловых резервуара при температурах Т_maх и T_min. Предположим также, что работа производится циклом Карно, функционирующим при температурах нагревателя T₁ и холодильника Т₂. Имеется в виду, что выполняется следующая цепочка неравенств: T_mах > T₁ > Т₂ > T_min. Иными словами, мы рассматриваем необратимый в целом процесс, внутри которого есть обратимый цикл. Тепло подается к рабочему телу при постоянной разности температур Т_mах – T₁ и отводится от него при постоянной разности температур Т₂ – Т_min(см. схему на рис. 5.13).

Рис. 5.13. Цикл внутреннеобратимой тепловой машины, имитирующий реальные энергетические установки

В этом и заключается главное отличие от стандартного идеального цикла Карно, где соответствующие разности температур равны нулю.

Предположим, что скорость теплообмена между рабочим телом и тепловыми резервуарами пропорциональна разности температур между ними:

(1)

где Q₊, t₊ — получаемое количество теплоты и время его передачи рабочему телу при контакте с нагревателем, a Q_–, t_– — количество теплоты, отдаваемой холодильнику, и время этого процесса. Величины с₊и с_–— соответствующие коэффициенты теплопередачи. Тогда полное время t теплообмена равно

(2)

Время, затрачиваемое машиной на внутренний цикл Карно, определяется временем установления равновесия в рабочем теле, которое существенно меньше, чем время передачи тепла t. Поэтому t можно считать временем совершения полного цикла.

Как обычно, мы предполагаем, что отсутствуют потери тепла на трение и тому подобные процессы. Количества теплоты Q₊и Q_–, а также совершенная работа А связаны между собой соотношениями, найденными нами при изучении цикла Карно:

(3)

Подставляя (3) в (2), находим для времени осуществления цикла выражение

(4)

Мощность рассматриваемой машины равна A/t. Представим себе, что мы проектируем такую машину. У нас имеется возможность выбрать оптимальным образом температуры Т₁, Т₂, при которых функционирует внутренний цикл Карно. Выбирая их равными Т_mах и Т_min соответственно, мы добьемся максимального КПД. Но из формулы (4) следует, что при этом

и выходная мощность машины стремится к нулю. Более практично выбрать температуры таким образом, чтобы максимума достигла выходная мощность. Приравнивая нулю производные по Т₁ и Т₂от выражения (4) для t/A, находим уравнения для этих температур. Опуская детали, приведем лишь конечный результат: максимальная выходная мощность при этих условиях равна

(5)

Достигается это значение при температурах внутреннего цикла Карно

(6)

где параметр Т₀, имеющий смысл некой средней температуры системы, определен соотношением

(7)

Очевидно, что КПД нашей машины равен КПД внутреннего цикла Карно

Поскольку отношение температур внутреннего цикла равно квадратному корню из отношения температур нагревателя и холодильника, находим КПД внутреннеобратимой машины:

(8)

Легко убедиться, что КПД меньше максимально возможного

но зато мы выиграли в выходной мощности. Любопытно, что КПД оптимизированной по мощности внутреннеобратимой машины не зависит от коэффициентов с₊и с_–: как и в цикле Карно, он определяется лишь отношением температур нагревателя и холодильника. Авторы концепции внутреннеобратимой машины (F.L. Curzon and В. Ahlborn, Amer. J. Phys. 43, 22, 1975) приводят следующую таблицу, где сравниваются несколько крупных электростанций. Видно, что формула (8) гораздо лучше соответствует практике, нежели КПД идеального цикла Карно.

Таблица

Сравнение наблюдаемых КПД нескольких электростанций разных типов с КПД цикла Карно h_С и цикла внутреннеобратимой машины h_ВОМ

Местонахождение и тип электростанции	Т*_min*, °С	*T_max,* °С	h_С	h_ВОМ	Наблюдаемый КПД
West Thurrock, Великобритания (угольная)	25	565	0,64	0,40	0,36
CANDU, Канада (ядерная)	25	300	0,48	0,28	0,30
Larderello, Италия (геотермальная)	80	250	0,33	0,18	0,16

В заключение этого параграфа приведем численный пример.

Пример. Пусть коэффициенты теплопередачи с₊ одинаковы и таковы, что при разнице температур DТ = 10 К мощность теплового потока между тепловыми резервуарами и рабочим телом составляет 1 кВт. Иными словами,

Пусть далее температуры резервуаров составляют Т_mах = 50 °С = 823 К и Т_min = 20 °С = 293 К. Найдем максимальную выходную мощность внутреннеобратимой тепловой машины и температуры T₁ и Т₂, при которых должно функционировать рабочее тело, использующее цикл Карно.

Из формулы (5.29) следует, что при равенстве коэффициентов теплопроводности «средняя» температура Т₀ определяется как

Используя соотношения (5.28), находим оптимальные температуры

КПД такой установки равен h_BOM = 0,403 (ср. h_С = 0,644). При таким образом выбранных температурах рабочего тела достигается максимальная выходная мощность, определяемая по формуле (5):

Видео 5.1. Двигатель Стирлинга, в котором — в отличие от традиционных двигателей внутреннего сгорания — рабочее тело не расходуется.

Дополнительная информация

http://eqworld.ipmnet.ru/ru/library/physics/thermodynamics.htm — Второе начало термодинамики. Сборник работ. Составитель А.К. Тимирязев. ГТТБ, 1934 г. Стр. 16–62, Сади Карно «Размышления о движущей силе огня и о машинах, способных развивать эту силу»;

http://www.femto.com.ua/articles/part_2/4051.html — Физическая энциклопедия. Статья о термодинамике: история возникновения, основные понятия и законы;

http://kvant.mirror1.mccme.ru/1995/05/vechnyj_dvigatel_demony_i_info.htm — Журнал Квант, 1995 г. № 5, стр.14–16, М. Альперин, А. Герега, Вечный двигатель, демоны и информация — о законах термодинамики в работах Сади Карно.

Правила расчета мощности обогрева трубопроводов

Системы кабельного электрообогрева широко используются в промышленности и строительстве. Применение систем кабельного электрообогрева позволяет решать такие задачи как:
• поддержание технологической температуры трубопровода;
• разогрев трубопровода вместе с содержащимся в нем продуктом.

Принцип действия систем электрообогрева, предназначенных для поддержания технологической температуры, состоит в компенсации тепловых потерь трубопровода. В отдельных случаях подобную систему используют для разогрева трубопроводов с целью повышения температуры содержащейся в них жидкости, одновременно с компенсацией тепловых потерь, имеющих место в данном процессе. Оба этих варианта могут иметь место как для трубопроводов в режиме останова, так и для трубопроводов с постоянной прокачкой продукта.

Несмотря на то, что системы электрообогрева прочно заняли свое место в российской промышленности, вопросы проектирования систем электрообогрева, в частности, расчет тепловых потерь обогреваемого объекта, практически не освещен в нормативных документах, действующих на территории РФ. В проектных организациях обычно базируются на строительных нормах и правилах, но специальный СНиП, в котором бы давались рекомендации по расчету характеристик систем обогрева для трубопроводов, отсутствует. Некоторые соображения можно позаимствовать из документов касающихся проектирования тепловой изоляции: СП 41-103- 2000, СНиП 41-03-2003. Однако в них нет четких рекомендаций к расчету и нормированию тепловых потерь обогреваемых трубопроводов. В данной статье приводятся основные рекомендации по расчету тепловых потерь трубопроводов, которые применяются при проектировании систем электрообогрева. При этом мы базировались на стандарт ГОСТ Р МЭК 62086-2-2005 «Нагреватели сетевые электрические резистивные. Требования по проектированию, установке и обслуживанию». Рекомендации по расчету разогрева трубопроводов будут даны нами в следующих публикациях.

Процесс передачи тепла от трубопровода в окружающую среду осуществляется теплопроводностью через стенку трубопровода, теплоизоляцию и защитную оболочку и далее конвекцией в окружающую среду (рис. 1).

Рис.1. Процесс передачи тепла от трубопровода в окружающую среду

На рисунке показано, что тепло от жидкости внутри трубы рассеивается в окружающую среду, причем интенсивность теплового потока тем меньше, а градиент температуры тем больше, чем больше термическое сопротивление тепловой изоляции. Согласно гОСТ Р МЭК 62086-2-2005 расчет потерь тепла следует выполнять по формуле (1):

где T_p – требуемая температура поддержания, °С T_a – минимальная расчетная температура окружающей среды, °С R₁ – термическое сопротивление трубопровода, (м∙К)/Вт R₂ – термическое сопротивление теплоизоляции, (м∙К)/Вт R₃ – термическое сопротивление защитной оболочки, (м∙К)/Вт R₄ – термическое сопротивление конвективной теплоотдачи в окружающую среду, (м∙К)/Вт Термическое сопротивление отдельных слоев: стенки трубопровода, тепловой изоляции, защитной оболочки рассчитывается по формуле для цилиндрической стенки:

где D_{н_i} – наружный диаметр трубопровода /теплоизоляции/ защитной оболочки, мм d_{вн_i} – внутренний диаметр трубопровода /теплоизоляции/ защитной оболочки, мм λ_i – теплопроводность трубопровода /теплоизоляции/ защитной оболочки, Вт/(м∙К) Термическое сопротивление конвективной теплоотдачи поверхности трубопровода в окружающую среду:
где α – коэффициент конвективной теплопередачи, Вт/(м2 ∙К). D – наружный диаметр защитного покрытия, мм.
Очевидно, что термическое сопротивление стальной стенки трубопровода и стальной защитной оболочки крайне мало и в расчетах ими можно пренебречь. Но в случае выполнения трубопровода и защитной оболочки из пластиков следует учитывать их термическое сопротивление. Существенное влияние на величину тепловых потерь оказывает термическое сопротивление теплоизоляции, то есть ее толщина и теплопроводность. Основная функция теплоизоляции – снижение большей части тепловых потерь от трубопровода. Оставшуюся часть тепловых потерь должна скомпенсировать система электрообогрева. Соответственно, чем больше толщина теплоизоляции и меньше ее теплопроводность, тем меньше тепловые потери и экономичнее система электрообогрева. Однако, при чрезмерном увеличении толщины теплоизоляции, затраты на нее окажутся несоизмеримо больше затрат на электроэнергию. На рис. 2 приведен график соотношения тепловых потерь и массы теплоизоляции на примере трубопровода диаметром 108 мм, теплоизоляция – минеральная вата. На рисунке видно, что применение теплоизоляции толщиной более 80 мм становится неэффективным.
Рис. 2. Соотношение тепловых потерь и толщины теплоизоляции на примере трубопровода диаметром 108 мм
Согласно СНиП 41-03-2003 в качестве минимальной расчетной температуры окружающей среды следует принимать среднюю температуру наиболее холодной пятидневки обеспеченностью 0.92 для данного региона (для оборудования и трубопроводов, расположенных на открытом воздухе и имеющих поверхности с положительными температурами). В то же время ряд проектных организаций за минимальную температуру окружающего воздуха принимают абсолютную минимальную температуру. Как показано в работе [2] оптимальным является следующее решение: Для труб малых диаметров (менее 100 мм) в качестве минимальной температуры окружающей среды принимать абсолютную минимальную температуру.
Для труб диаметром более 100 мм в качестве минимальной температуры окружающей среды принимать температуру наиболее холодной пятидневки обеспеченностью 0. 92. В теоретическом расчете тепловых потерь, как правило, не учитываются недостатки, связанные с фактической работой системы электрообогрева, например разрушение и ухудшение свойств теплоизоляции в процессе эксплуатации, колебания и падение напряжения питания, качество монтажа теплоизоляции. Для нивелирования данных факторов к рассчитанному значению тепловых потерь добавляется коэффициент запаса. Согласно рекомендациям гОСТ Р МЭК 62086-2- 2005 значение коэффициента запаса лежит в диапазоне 10% – 25%. Основываясь на многолетнем опыте проектирования и монтажа систем электрообогрева, ООО «ССТ» допускает увеличение коэффициента запаса до 36%. Однако коэффициент запаса не решает всех проблем при проектировании систем обогрева. Для корректного учета потерь тепла через крупногабаритные опоры и прочие фитинги необходимо проводить специальные расчеты и экспериментальные исследования. (Примечание редакции: В данном номере журнала публикуется статья И. Чернова об обследовании тепловых потоков на неподвижных опорах и противопожарных вставках. ) В действующем на данный момент гОСТ Р МЭК 62086-2- 2005 нет четких рекомендаций по данному вопросу. Инженеры компании «ССТ» широко используют методы математического моделирования, позволяющие с высокой степенью точности определить тепловые потери того или иного объекта. Одна из наиболее часто встречающихся задач – определение тепловых потерь резервуара на седловых нетеплоизолированных опорах. На рис.3 показано температурное поле резервуара диаметром 1400 мм.
Рис. 3. Температурное поле резервуара на седловой опоре
В данном случае потери через нетеплоизолированную опору составили 350 Вт. Выбор нагревательного кабеля представляет собой многофакторную задачу. С одной стороны, нагревательный кабель должен скомпенсировать тепловые потери трубопровода. С другой стороны, необходимо обеспечить термическую устойчивость системы электрообогрева. грамотно спроектированная система электрообогрева не должна превысить максимально допустимую температуру трубопровода и содержащегося в нем продукта. Это особенно важно при обогреве трубопроводов, расположенных во взрывоопасных зонах. Согласно рекомендациям гОСТ Р МЭК 62086-2-2005 максимальная температура металлического трубопровода может быть определена по формуле:
где P_hc – выходная мощность нагревательного кабеля, Вт/м Необходимо отметить, что нагревательный кабель также должен быть защищен от перегрева и воздействия температуры, превышающей максимальную допустимую температуру его применения. То есть максимальная технологическая температура трубопровода не должна превышать максимально допустимую температуру нагревательного кабеля. Под максимальной технологической температурой понимается наивысшая температура, которую иногда может приобретать трубопровод. Воздействие такой температуры, как правило, носит кратковременный характер, например при пропарке трубопровода. В остальное время на трубопроводе требуется поддержать относительно невысокую температуру. В некоторых случаях вместо применения более температуростойкого нагревательного кабеля целесообразно использовать двухслойную изоляцию с размещением кабеля не на трубе, а по первому слою тепловой изоляции. На рис. 4 показан случай, когда нагревательный кабель помещают между двумя слоями теплоизоляции, покрывающей трубу.
Рис.4. Обогреваемый трубопровод в двухслойной теплоизоляции и схема размещения нагревательного кабеля
При правильном сочетании толщин теплоизоляций и их типов, температура на поверхности контакта нагревательного кабеля и внутренней теплоизоляции не превысит допустимого значения. Компания «ССТ» широко использует данный метод при обогреве коротких импульсных линий с высокой максимальной технологической температурой. За счет малой длины трубопроводов (до 2 м) наиболее оптимальным вариантом нагревательного элемента будет саморегулирующийся кабель. Однако максимальная температура применения саморегулирующихся кабелей составляет 230 ºС. Применение двухслойной изоляции позволяет применять саморегулирующиеся кабели при температуре воздействия свыше 500 ºС. В гОСТ Р 62086-2-2005 описан такой способ обогрева трубопроводов, однако нет четких указаний по расчетам теплоизоляции и нагревательного кабеля. Инженеры компании «ССТ» разработали методику расчета трубопроводов с двойной теплоизоляцией, основанную на методах математического моделирования. При выполнении подобных расчетов необходимо уделять пристальное внимание температурным режимам нагревательного кабеля. Так как передаче тепла от кабеля в продукт будет препятствовать внутренний слой теплоизоляции, то мощность кабеля и его расход должны быть завышены по сравнению с обычным трубопроводом. В то же время, конструкция двухслойной теплоизоляции обеспечивает работу нагревательного кабеля при повышенных температурах. На рис. 5а и 5б показано распределение температуры трубопровода диаметром 18 мм, толщина внутренней теплоизоляции – 20 мм, внешней теплоизоляции – 20 мм; требуемая температура поддержания +5 ºС. Максимальная температура воздействия составляет +300 ºС. Для обеспечения требуемого температурного режима в данном случае используется саморегулирующийся нагревательный кабель 15 ВТХ2- ВР мощностью 15 Вт/м при температуре +10 ºС. Как видно из рис.5а, выбранная марка кабеля обеспечивает поддержание температуры +5 ºС, и в то же время, температура кабеля не превышает максимально допустимую для него температуру 230 ºС.
Рис.5а. Температурное поле трубопровода ø18 мм
Рис.5б. График распределения температуры по радиусу трубопровода
Описанный выше подход к методике расчета мощности обогрева типовых трубопроводов используется в программе «Тепломаг», разработанной специалистами компании «ССТ». Программа позволяет не только рассчитать тепловые потери трубопроводов, но и автоматически выбрать оптимальную марку кабеля для конкретного трубопровода, а также составить спецификацию оборудования. Программа проста в использовании и не требует длительного обучения.
Рис.6. Внешний вид программы «Тепломаг»

Выводы
Имеющейся на данный момент нормативной документации недостаточно для полноценного проектирования систем электрообогрева. Несмотря на это, накопленный опыт позволяет специалистам компании «ССТ» решать самые разнообразные задачи. Разработанные нами методики расчета тепловых потерь фитингов, методики расчета трубопроводов с двухслойной теплоизоляцией, а также исследования по расчету мощности обеспечивают качественное проектирование систем электрообогрева.

Источник:
Журнал «Промышленный электрообогрев и электроотопление», № 1 / 2011
Автор:
– Дегтярева Е. О., начальник отдела техподдержки ООО «ССТ»
Литература:
ОСТ 62086-2-2005 «Электрооборудование для взрывоопасных сред. Нагреватели сетевые электрические резистивные. Часть 2. Требования по проектированию, установке и обслуживанию».

М.Л. Струпинский, Н.Н. Хренков. Расчет мощности систем обогрева трубопроводов. «Территория Нефтегаз», 2008, №4.

41-103-2000 «Проектирование тепловой изоляции оборудования и трубопроводов».

Теплотехника: Учебн. для вузов/ В.Н. Луканин, М.Г. Шатров, Г.М. Камфер и др.; Под ред. В.Н. Луканина. – М.: Высш. шк., 1999.

Вернуться к списку
Как рассчитать тепловую мощность воздухонагревателя
Читайте также
Рейтинг мотоблоков 2021 – 2022
К выбору тепловой пушки нужно подходить ответственно. Слабый обогреватель не справится с отоплением на большой площади, а слишком мощный будет расходовать лишнюю энергию. Заранее вычислите, какая тепловая мощность воздухонагревателя в кВт нужна для вашего помещения.
Как определить мощность тепловой пушки
Формула для расчета минимальной тепловой мощности выглядит так:
V * T * k / 860 ккал/ч = Q
Чтобы определить минимальную тепловую мощность нагревателя, нужно знать следующие значения:
Q — необходимая тепловая мощность (кВт).

V — объем помещения (м³). Рассчитывается как произведение длины, ширины и высоты.

T — разница между температурой воздуха на улице и желательной температурой в помещении (C°).

k — коэффициент рассеяния тепла, зависящий от типа конструкции и теплоизоляции помещения.

Коэффициент рассеяния тепла, k

Тип помещения

3,0–4,0

Конструкция из дерева или профлиста.

Отсутствие теплоизоляции.

2,0–2,9

Упрощенная конструкция.

Кирпичные стены одиночной кладки.

Стандартное число окон, одинарные рамы.

Слабая теплоизоляция кровли.

1,0–1,9

Стандартная конструкция.

Кирпичные стены двойной кладки.

Мало окон или одинарные рамы.

Кровля со стандартной теплоизоляцией.

0,6–0,9

Утепленная конструкция.

Кирпичные стены с двухслойной изоляцией.

Мало окон, окна с двойными рамами.

Толстая основа пола.

Кровля с качественной теплоизоляцией.

Читайте также
Выбор снегоуборщика – вопросы, ответы и рекомендации
Пример расчета мощности воздухонагревателя
Расскажем, как найти тепловую мощность пушки для комнаты площадью 15 метров, с высотой потолков 2,5 метров. Перемножаем значения, получаем объем комнаты 35,5 м³. Предположим, комната находится в новостройке. Возьмем средний коэффициент рассеяния тепла для утепленной квартиры — 1,5. Допустим, при температуре окружающей среды -15 °C мы хотим достичь температуры в комнате 20 °C. Итого разница температур — 35 °C.
С этими показателями расчет тепловой мощности будет выглядеть так:
35,5*35*1,5/860=2,16 кВт
Технические специалисты «ТМК» рекомендуют выбирать воздухонагреватели с небольшим запасом. Таким образом, для нашего помещения подойдут тепловые пушки мощностью 3 кВт.
Читайте рейтинг электрических тепловых пушек за 2017–2018 года.

Читайте также
Рейтинг лучших аккумуляторных триммеров для травы: топ-5 моделей 2018-2019
Воздухонагреватель электрический RedVerg RD-EHR9/380TR – переносной электрический воздухонагреватель с тепловой мощностью 9 кВт. Отличается компактными габаритами. Поддерживает три режима работы. Не распространяет посторонних запахов при эксплуатации. Термостат фиксирует температуру воздуха на входе и в дальнейшем контролирует температуру в помещении. Термовыключатель с самовозвратом отключает устройство при перегреве в целях обеспечения безопасности. Нагревательный элемент изготовлен из нержавеющей стали. Выключатель выбора режимов нагрева. Удобная рукоятка для транспортировки. Корпус из листовой стали покрыт огнеупорной краской. Предназначен для работы от сети 380 В. Вес товара 12 кг.
6 490c
Воздухонагреватель электрический Master B 22 EPA/EPB может использоваться как для обогрева офисных и складских помещений, так и для просушки поверхностей после отделочных работ. Широчайший спектр применения делает это оборудование востребованным среди специалистов множества сфер. Электрический воздухонагреватель Master безопасен и неприхотлив в эксплуатации. Он не производит шумов и вредных выхлопов, что позволяет включать его даже в местах, где постоянно находятся люди. Питание от электрической сети даст вам возможность не беспокоиться о заполнении топливного бака и спокойно оставлять технику работать. Современные системы защиты отключат ее самостоятельно при появлении первых признаков неполадок.
Лучшая цена
45 990c 52 300c
19 000c
Воздухонагреватель электрический RedVerg RD-EHS2 безопасен для людей. Компактные размеры и небольшой вес позволяют без труда транспортировать его и располагать в помещениях любой площади. Термостат даст вам возможность контролировать рабочие параметры оборудования и настраивать его так, чтобы добиться максимальной эффективности при обогреве. Техника RedVerg станет превосходным выбором для вашего дома и предприятия.
2 270c

расчет теплообменников, методика расчета теплообменников, тепловой расчет теплообменников
Когда проводится расчет теплообменников, используются базовые знания о законах теплообмена, открытые на сегодняшний день.
В частности используются такие понятия как удельная теплоемкость и теплосодержание (энтальпия), а также удельная теплота химических превращений (и фазовых превращений).
Под удельной теплоемкость понимается количество тепла, которое необходимо для нагрева одного килограмма вещества ровно на один градус. На основании данных о теплоемкости можно судить об интенсивности аккумулирования тепла.
При тепловых расчетах используются средняя теплоемкость, исчисляемую в заданном температурном интервале.
Под понятием удельной энтальпии понимается количество тепла, которое потребуется для нагрева одного килограмма от нуля до заданной температуры.
Под удельной теплотой химических превращений понимается то количество тепла, которое будет выделяться при химической трансформации одной единицы массы данного вещества.
Под удельной теплотой фазовых превращений понимается то количество тепла, которое будет поглощаться или выделяться при изменении агрегатного состояния единицы массы данного вещества.
Расчет теплообменников и различные методы составления теплового баланса
При расчете теплообменников могут использоваться внутренний и внешний методы составления теплового баланса. При внутреннем методе используются величины теплоемкостей. При внешнем методе используются величины удельных энтальпий.
При применении внутреннего метода тепловая нагрузка рассчитывается по разным формулам, в зависимости от характера протекания теплообменных процессов.
Если теплообмен происходит без каких-либо химических и фазовых превращений, а соответственно и без выделений или поглощений тепла.
Соответственно тепловая нагрузка рассчитывается по формуле
Если в процессе теплообмена происходит конденсация пара или испарение жидкости, протекают какие-либо химические реакции, то используется другая форму для вычисления теплового баланса.
При использовании внешнего метода расчет теплового баланса ведется на основании того, что в теплообменный аппарат за какую-то единицу времени поступает и выходит равное количество тепла.
Если при внутреннем методе используются данные о теплообменных процессах в самом агрегате, то при внешнем методе используются данные внешних показателей.
Для расчета теплового баланса по внешнему методу используется формула
.
Под Q1 подразумевается то количество тепла, которое поступает в агрегат и ходит из него за единицу времени.
Под подразумевается энтальпия веществ, которые входит в агрегат и выходят из него.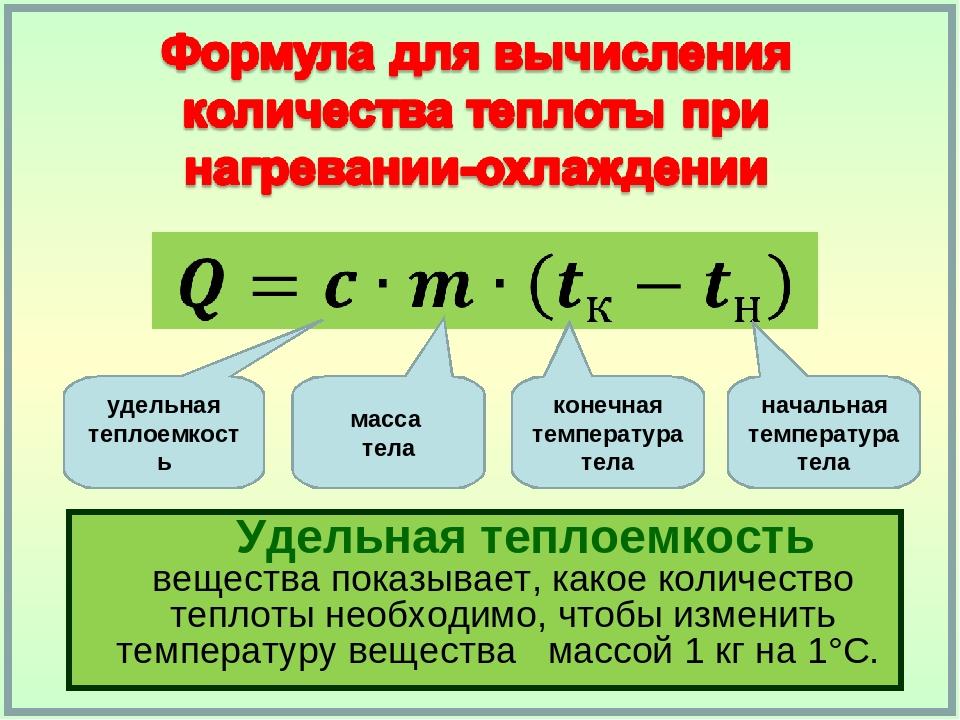
Можно также вычислить разность энтальпий для того, чтобы установить то количество тепла, которое было передано между разными средами. Для этого используется формула .
Если же в процессе теплообмена происходили какие-либо химические или фазовые превращения, используется формула.
Механизмы теплопередачи в расчете теплообменников
Теплообмен осуществляется посредством трех основных видов теплопередачи. Это конвекция, теплопроводность и излучение.
При теплообменных процессах, которые протекают по принципам механизма теплопроводности передача тепла происходит как перенос энергии упругих колебаний молекул и атомов. Данная энергия переходит от одних атомов к другим в направлении уменьшения.
При проведении расчетов параметров передачи тепла по принципу теплопроводности используется закон Фурье:.
Для вычисления количества тепла используются данные о времени прохождения потока, площади поверхности, градиенте температуры, а также о коэффициенте теплопроводности. Под градиентом температуры понимается ее изменение в направлении теплопередачи на одну единицу длины.
Под коэффициентом теплопроводности понимается скорость теплообмена, то есть то количество тепла, которое проходит через одну единицу поверхности в единицу времени.
При любых тепловых расчетах учитывается, что самый большой коэффициент теплопроводности имеют металлы. Различные твердые тела имеют гораздо меньший коэффициент. А у жидкостей этот показатель, как правило, ниже, чем у любого из твердых тел.
При расчете теплообменников, где передача тепла от одной среды к другой идет через стенку, также используется уравнение Фурье для получения данных о количестве передаваемого тепла. Оно вычисляется как количество тепла, которое проходит через плоскость с бесконечно малой толщиной:
.
Если проинтегрировать показатели температурных изменений по толщине стенки, получится
Исход из этого получается, что температура внутри стенки падает по закону прямой линии.
Конвекционный механизм передачи тепла: расчеты
Еще один механизм передачи тепла – конвекция. Это передача тепла объемами среды посредством их взаимного перемещения. При этом передача тепла от среды к стенке и наоборот, от стенке к рабочей среде называется теплоотдачей. Чтобы определить количество тепла, которое передается, используется закон Ньютона
В данной формуле a — это коэффициент теплоотдачи. При турбулентном движении рабочей среды этот коэффициент зависит от многих дополнительных величин:
физических параметров текучей среды, в частности теплоемкости, теплопроводности, плотности, вязкости;
условий омывания газом или жидкостью теплоотдающей поверхности, в частности скорости текучей среды, ее направления;
пространственных условий, которые ограничивают поток (длина, диаметр, форма поверхности, ее шероховатости).
Следовательно, коэффициент теплоотдачи — функция многих величин, что показано в формуле
Метод анализа размерностей позволяет вывести функциональную связь критериев подобия, которые характеризуют теплоотдачу при турбулентном характере движения потока в гладких, прямых и длинных трубах.
Это вычисляется по формуле
.
Коэффициент теплоотдачи в расчете теплообменников
В химической технологии нередко встречаются случаи обмена тепловой энергией между двумя текучими средами через разделяющую стенку. Теплообменный процесс проходит три стадии. Тепловой поток для установившегося процесса остается неизменным.
Проводится расчет теплового потока, проходящего от первой рабочей среды к стенке, затем через стенку теплопередающей поверхности и затем от стенки ко второй рабочей среде.
Соответственно для проведения расчетов используется три формулы:

В результате совместного решения уравнений получаем
Величина
и есть коэффициент теплопередачи.
Расчет средней разности температур
Когда при помощи теплового баланса определено необходимое количество тепла, необходимо провести расчет поверхности теплообмена (F).
При расчете необходимой теплообменной поверхности используется то же уравнение, что и при предыдущих расчетах:
В большинстве случаев температура рабочих сред будет меняться в процессе протекания теплообменных процессов. Значит вдоль теплообменной поверхности будет меняться разность температур. Поэтому проводится расчет средней разности температур. А в связи с тем, что изменение температур не линейно, рассчитывают логарифмическую разность
. В отличие от прямоточного потока, при противоточном движении рабочих сред необходимая площадь теплообменной поверхности должна быть меньше. Если в одном и том же ходу теплообменника используется и прямоточный, и противоточный потоки, разность температур определяется, исходя из соотношения
.
Учебное пособие по физике
На предыдущих страницах этого урока мы узнали, что тепло — это форма передачи энергии из места с высокой температурой в место с низкой температурой. Три основных метода передачи тепла — теплопроводность, конвекция и излучение — подробно обсуждались на предыдущей странице. Теперь мы исследуем тему скорости теплопередачи. Эта тема имеет большое значение из-за частой необходимости либо увеличивать, либо уменьшать скорость, с которой тепло перемещается между двумя точками. Например, те из нас, кто живет в более холодном зимнем климате, постоянно ищут способы согреть свои дома, не тратя слишком много денег. Тепло уходит из дома с более высокой температурой на улицу с более низкой температурой через стены, потолки, окна и двери. Мы прилагаем усилия, чтобы уменьшить эту потерю тепла, улучшая изоляцию стен и чердаков, заделывая окна и двери и покупая высокоэффективные окна и двери. В качестве другого примера рассмотрим производство электроэнергии. Бытовая электроэнергия чаще всего изготовлено с использованием ископаемого топлива или ядерного топлива . Способ включает выделение тепла в реакторе. Тепло передается воде, и вода переносит тепло к паровой турбине (или другому типу электрогенератора), где производится электричество . Задача состоит в том, чтобы эффективно передать тепло воде и паровой турбине с минимальными потерями. Следует обратить внимание на увеличение скоростей теплообмена в реакторе и турбине и уменьшение скоростей теплообмена в трубах между реактором и турбиной.
Итак, какие переменные влияют на скорость теплопередачи? Как можно регулировать скорость теплопередачи? Это вопросы, которые будут обсуждаться на этой странице Урока 1. Наше обсуждение будет ограничено переменными, влияющими на скорость теплопередачи путем теплопроводности . После обсуждения переменных, влияющих на скорость теплопередачи, мы рассмотрим математическое уравнение, выражающее зависимость скорости от этих переменных.

Разница температур
При теплопроводности тепло передается от места с высокой температурой к месту с низкой температурой. Передача тепла будет продолжаться до тех пор, пока существует разница температур между двумя точками. Как только в двух точках достигается одинаковая температура, устанавливается тепловое равновесие, и теплопередача прекращается. Ранее в этом уроке мы обсуждали передачу тепла в ситуации, когда металлическая банка с водой высокой температуры была помещена в чашку из пенопласта с водой низкой температуры. Если две пробы воды снабжены датчиками температуры, регистрирующими изменения температуры во времени, то получаются следующие графики.
На приведенных выше графиках наклон линии представляет собой скорость изменения температуры каждой отдельной пробы воды. Температура меняется из-за теплопередачи от горячей воды к холодной. Горячая вода теряет энергию, поэтому ее наклон отрицателен. Холодная вода набирает энергию, поэтому ее наклон положительный. Скорость изменения температуры пропорциональна скорости передачи тепла. Температура образца изменяется быстрее, если тепло передается с высокой скоростью, и медленнее, если тепло передается с низкой скоростью. Когда два образца достигают теплового равновесия, теплопередача прекращается и наклон равен нулю. Таким образом, мы можем рассматривать уклоны как меру скорости теплопередачи. С течением времени скорость теплопередачи уменьшается. Первоначально тепло передается с высокой скоростью, что отражается в более крутых склонах. И с течением времени наклоны линий становятся менее крутыми и более пологими.
Какая переменная способствует этому уменьшению скорости теплопередачи с течением времени? Ответ: разница температур двух емкостей с водой. Первоначально, когда скорость теплопередачи высока, горячая вода имеет температуру 70°C, а холодная вода имеет температуру 5°C. Два контейнера имеют разницу температур в 65°C. По мере того как горячая вода начинает остывать, а холодная вода начинает нагреваться, разница в их температурах уменьшается и скорость теплообмена уменьшается. По мере приближения к тепловому равновесию их температуры приближаются к одному и тому же значению. При приближении разности температур к нулю скорость теплообмена приближается к нулю. В заключение, на скорость кондуктивной теплопередачи между двумя точками влияет разница температур между двумя точками.

Материал
Первая переменная, которую мы определили как влияющую на скорость кондуктивной теплопередачи, — это разница температур между двумя точками. Второй важной переменной являются материалы, участвующие в передаче. В предыдущем обсуждаемом сценарии металлическая банка с водой высокой температуры была помещена в чашку из пенопласта с водой низкой температуры. Тепло передавалось от воды через металл к воде. Важными материалами были вода, металл и вода. Что произойдет, если передать теплоту от горячей воды через стекло к холодной воде? Что произойдет, если теплота будет передаваться от горячей воды через пенопласт к холодной воде? Ответ: скорость теплообмена была бы другой. Замена внутренней металлической банки стеклянной банкой или чашкой из пенопласта изменит скорость теплопередачи. Скорость теплопередачи зависит от материала, через который передается тепло.
Влияние материала на скорость теплопередачи часто выражается числом, известным как теплопроводность. Значения теплопроводности представляют собой числовые значения, которые определяются экспериментальным путем. Чем выше это значение для конкретного материала, тем быстрее тепло будет передаваться через этот материал. Материалы с относительно высокой теплопроводностью называют теплопроводниками. Материалы с относительно низкими значениями теплопроводности называются теплоизоляторами. В таблице ниже приведены значения теплопроводности (k) для различных материалов в единицах Вт/м/°C.
Материал

к

Материал
к
Алюминий(и)

237

Песок(и)
0,06
Латунь(и)

110

Целлюлоза (ы)
0,039
Медь(и)

398

Стекловата(и)
0,040
Золото (а)

315

Вата (вата)
0,029
Чугун(ы)

55

Овечья шерсть(и)
0,038
Лид(ы)

35,2

Целлюлоза (ы)
0,039
Серебро (ы)

427

Пенополистирол (ы)
0,03
Цинк

113

Древесина (и)
0,13
Полиэтилен (HDPE) (s)

0,5

Ацетон (л)
0,16
Поливинилхлорид (ПВХ)

0,19

Вода (л)
0,58
Плотный кирпич (и)

1,6

Воздух (г)
0,024
Бетон (низкой плотности) (s)

0,2

Аргон (г)
0,016
Бетон (высокой плотности) (s)

1,5

Гелий (г)
0,142
Лед (ы)

2,18

Кислород (г)
0,024
Фарфор(ы)

1,05

Азот (г)
0,024
Источник: http://www. roymech.co.uk/Related/Thermos/Thermos_HeatTransfer.html
Как видно из таблицы, теплопроводность обычно передается со значительно большей скоростью через твердые тела (вещества) в сравнение с жидкостями (l) и газами (g). Теплопередача происходит с наивысшей скоростью для металлов (первые восемь элементов в левой колонке), потому что механизм проводимости включает подвижные электроны (как обсуждалось на предыдущей странице). Некоторые твердые вещества в правой колонке имеют очень низкие значения теплопроводности и считаются изоляторами. Структура этих твердых тел характеризуется карманами захваченного воздуха, перемежающимися между волокнами твердого тела. Поскольку воздух является отличным изолятором, воздушные карманы, расположенные между этими твердыми волокнами, придают этим твердым телам низкие значения теплопроводности. Одним из таких твердых изоляторов является пенополистирол, материал, используемый в изделиях из пенополистирола. Такие изделия из пенополистирола изготавливаются путем вдувания инертного газа под высоким давлением в полистирол перед впрыскиванием в форму. Газ заставляет полистирол расширяться, оставляя заполненные воздухом карманы, которые способствуют изолирующей способности готового продукта. Пенополистирол используется в кулерах, изоляторах для банок, термосах и даже пенопластовых плитах для домашней изоляции. Еще одним твердым изолятором является целлюлоза. Целлюлозный утеплитель используется для утепления чердаков и стен в домах. Он изолирует дома от потерь тепла, а также от проникновения звука. Его часто задувает на чердаки как сыпучий целлюлозный утеплитель . Он также применяется в виде стекловолоконных плит (длинных листов бумаги с изоляцией) для заполнения зазоров между стойками 2×4 наружных (а иногда и внутренних) стен домов.
Площадь
Другой переменной, влияющей на скорость кондуктивной теплопередачи, является площадь, через которую передается тепло. Например, передача тепла через окна домов зависит от размера окна. Через большое окно из дома будет теряться больше тепла, чем через меньшее окно того же состава и толщины. Через большую крышу дом будет терять больше тепла, чем через меньшую крышу с такими же изоляционными характеристиками. Каждая отдельная частица на поверхности объекта участвует в процессе теплопроводности. Объект с большей площадью имеет больше поверхностных частиц, работающих для проведения тепла. Таким образом, скорость теплопередачи прямо пропорциональна площади поверхности, через которую проходит тепло.
Толщина или расстояние
Последней переменной, влияющей на скорость кондуктивной теплопередачи, является расстояние, на которое должно передаваться тепло. Тепло, выходящее через чашку из пенопласта, будет выходить быстрее через чашку с тонкими стенками, чем через чашку с толстыми стенками. Скорость теплопередачи обратно пропорциональна толщине чашки. Аналогичное утверждение можно сделать и для тепла, проводимого через слой целлюлозной изоляции в стене дома. Чем толще изоляция, тем ниже скорость теплопередачи. Те из нас, кто живет в более холодном зимнем климате, хорошо знают этот принцип. Нам говорят одеваться слоями перед выходом на улицу. Это увеличивает толщину материалов, через которые передается тепло, а также задерживает воздушные карманы (с высокой изоляционной способностью) между отдельными слоями.

Математическое уравнение
Итак, мы узнали о четырех переменных, влияющих на скорость теплопередачи между двумя точками. Переменными являются разница температур между двумя точками, материал, присутствующий между двумя точками, площадь, через которую будет передаваться тепло, и расстояние, на которое оно должно быть передано. Как это часто бывает в физике, математическая связь между этими переменными и скоростью теплопередачи может быть выражена в виде уравнения. Рассмотрим передачу тепла через стеклянное окно изнутри дома с температурой Т ₁ снаружи дома с температурой T ₂ . Окно имеет площадь поверхности А и толщину d. Значение теплопроводности оконного стекла равно k. Уравнение, связывающее скорость теплопередачи с этими переменными, имеет вид ватт. Это уравнение применимо к любой ситуации, когда тепло передается в одном и том же направлении через плоский прямоугольник 9.0003 стена . Оно применимо к проводимости через окна, плоские стены, наклонные крыши (без кривизны) и т. д. Немного другое уравнение применимо к проводимости через изогнутые стены, такие как стены банок, чашек, стаканов и труб. Мы не будем обсуждать это уравнение здесь.
Пример задачи
Чтобы проиллюстрировать использование приведенного выше уравнения, рассчитаем скорость теплопередачи в холодный день через прямоугольное окно шириной 1,2 м и высотой 1,8 м, толщиной 6,2 мм, значение теплопроводности 0,27 Вт/м/°C. Температура внутри дома 21°С, снаружи дома -4°С.
Чтобы решить эту задачу, нам нужно знать площадь поверхности окна. Будучи прямоугольником, мы можем вычислить площадь как ширина • высота.
Площадь = (1,2 м)•(1,8 м) = 2,16 м ² .
Нам также необходимо обратить внимание на единицу толщины (d). Дается в единицах см; нам нужно будет преобразовать единицы в метры, чтобы единицы соответствовали единицам k и A.
d = 6,2 мм = 0,0062 м
Теперь мы готовы рассчитать скорость теплопередачи путем подстановки известных значений в приведенное выше уравнение.
Скорость = (0,27 Вт/м/°C)•(2,16 м ² )•(21°C – -4°C)/(0,0062 м)
Норма = 2400 Вт (округлено от 2352 Вт)
Полезно отметить, что значение теплопроводности окна дома намного ниже, чем значение теплопроводности самого стекла. Теплопроводность стекла составляет около 0,96 Вт/м/°С. Стеклянные окна изготавливаются в виде двойных и тройных окон со слоем инертного газа низкого давления между стеклами. Кроме того, на окна наносят покрытия для повышения эффективности. В результате получается ряд веществ, через которые должно последовательно проходить тепло, чтобы быть переданным из дома (или в него). Подобно последовательно соединенным электрическим резисторам, ряд теплоизоляционных материалов оказывает аддитивное влияние на общее сопротивление, оказываемое тепловому потоку. Суммарный эффект различных слоев материалов в окне приводит к тому, что общая проводимость намного меньше, чем у одного стекла без покрытия.

Урок 1 этой главы по теплофизике был посвящен значению температуры и тепла. Особое внимание уделялось разработке модели частиц материалов, способной объяснить макроскопические наблюдения. Были предприняты усилия для разработки прочного концептуального понимания темы в отсутствие математических формул. Это прочное концептуальное понимание сослужит вам хорошую службу по мере приближения к Уроку 2. Глава станет немного более математической, поскольку мы будем исследовать вопрос: как можно измерить количество тепла, выделяемого или получаемого системой? Урок 2 будет относиться к науке калориметрии.

Проверьте свое понимание
1. Предскажите влияние следующих изменений на скорость, с которой тепло передается через прямоугольный объект, заполнив пропуски.
а. Если площадь, через которую передается теплота, увеличить в 2 раза, то скорость теплопередачи ________________ (увеличилась, уменьшилась) в _________ раз (число).
б. Если толщину материала, через который передается тепло, увеличить в 2 раза, то скорость теплопередачи составит ________________ в _________ раз.
в. Если толщину материала, через который передается тепло, уменьшить в 3 раза, то скорость теплопередачи будет ________________ в _________ раз.
д. Если теплопроводность материала, через который передается теплота, увеличить в 5 раз, то скорость теплопередачи будет ________________ в _________ раз.
эл. Если теплопроводность материала, через который передается тепло, уменьшить в 10 раз, то скорость теплопередачи будет ________________ в _________ раз.
ф. Если разность температур на противоположных сторонах материала, через который передается теплота, увеличить в 2 раза, то скорость теплопередачи будет ________________ в _________ раз.
2. Используйте информацию на этой странице, чтобы объяснить, почему слой жира толщиной 2–4 дюйма помогает согревать белых медведей в холодную арктическую погоду.
3. Рассмотрим приведенный выше пример задачи. Предположим, что место, где расположено окно, заменено стеной с толстым утеплителем. Теплопроводность той же площади уменьшится до 0,0039.Вт/м/°C и толщина будет увеличена до 16 см. Определить скорость теплопередачи через эту площадь 2,16 м ² .

Перейти к следующему уроку:
Кондуктивный теплообмен | Инженерная библиотека
На этой странице представлена глава о кондуктивной теплопередаче из «Справочника по основам Министерства энергетики: термодинамика, теплопередача и поток жидкости», DOE-HDBK-1012/2-92, Министерство энергетики США, 19 июня.92.
Другие связанные главы из «Справочника по основам Министерства энергетики: термодинамика, теплопередача и поток жидкости» можно увидеть справа.
Кондуктивный теплообмен — это передача тепловой энергии за счет взаимодействий между соседними атомами и молекулами твердого тела.
Проводка
Теплопроводность включает передачу тепла за счет взаимодействия между соседними молекулами материала. Теплопередача за счет теплопроводности зависит от движущей «силы» разницы температур и сопротивления теплопередаче. Сопротивление теплопередаче зависит от природы и размеров теплоносителя. Все проблемы теплообмена связаны с разностью температур, геометрией и физическими свойствами изучаемого объекта.
В задачах о кондуктивном теплообмене объектом исследования обычно является твердое тело. Проблемы конвекции связаны с жидкой средой. Проблемы теплопередачи излучением связаны с твердыми или жидкими поверхностями, разделенными газом, паром или вакуумом. Существует несколько способов соотнести геометрию, физические свойства и разность температур объекта со скоростью теплопередачи через объект. В кондуктивной теплопередаче наиболее распространенным средством корреляции является закон проводимости Фурье. Закон в форме уравнения чаще всего используется в прямоугольной или цилиндрической форме (трубы и цилиндры), обе из которых представлены ниже.
Прямоугольный $$ \dot{Q} = k ~A \left({ \Delta T \over \Delta x }\right) $$
(2-4)
Цилиндрический $$ \dot{Q} = k ~A \left({ \Delta T \over \Delta r }\right) $$
(2-5)
куда:
$ \точка{Q} $ = скорость теплопередачи (БТЕ/ч)
А = площадь поперечного сечения теплопередачи (фут ² )
Δx = толщина плиты (футы)
Δr = толщина цилиндрической стенки (футы)
ΔТ = разница температур (°F)
к = теплопроводность плиты (БТЕ/фут-час-°F)
Использование уравнений 2-4 и 2-5 для определения количества тепла, передаваемого теплопроводностью, продемонстрировано в следующих примерах.
Прямоугольные координаты проводимости
Пример:
1000 БТЕ/час проходит через участок изоляционного материала, показанный на рисунке 1, площадь поперечного сечения которого составляет 1 фут ². 2 } \end{эквнаррай} $$ 92) \номер\\ &=& 28 800 ~{\text{Btu} \over \text{hr}} \end{эквнаррай} $$
Метод эквивалентного сопротивления
Теплопередачу можно сравнить с протеканием тока в электрических цепях. Скорость теплопередачи можно рассматривать как ток, а комбинацию теплопроводности, толщины материала и площади как сопротивление этому потоку. Разность температур представляет собой потенциальную или движущую функцию для теплового потока, в результате чего уравнение Фурье записывается в форме, аналогичной закону Ома теории электрических цепей. Если член теплового сопротивления Δx/k записать как член сопротивления, где сопротивление является обратной величиной теплопроводности, деленной на толщину материала, результатом будет уравнение проводимости, аналогичное электрическим системам или сетям. Электрическая аналогия может использоваться для решения сложных задач, связанных как с последовательными, так и с параллельными тепловыми сопротивлениями. Ученик обращается к рисунку 2, на котором показана схема эквивалентного сопротивления. Типичная задача проводимости в ее аналогичной электрической форме дается в следующем примере, где «электрическое» уравнение Фурье может быть записано следующим образом.
$$ \dot{Q}” = { \Delta T \over R_{th} } $$
(2-6)
куда:
$\точка{Q}”$ = Тепловой поток ($ \dot{Q}/A $) (Btu/hr-ft ² )
ΔТ = Разница температур (°F)
Р _й = Термическое сопротивление (Δx/k) (час-фут ² -°F/Btu)
Рисунок 2: Эквивалентное сопротивление
Электрическая аналогия
Пример:
Композитная защитная стена состоит из медной пластины толщиной 1 дюйм, слоя асбеста толщиной 1/8 дюйма и слоя стекловолокна толщиной 2 дюйма. Теплопроводность материалов в единицах БТЕ/час-фут-°F следующая: k _Cu = 240, k _asb = 0,048 и k _fib = 0,022. Общая разница температур по всей стене составляет 500°F. Рассчитайте термическое сопротивление каждого слоя стены и скорость теплопередачи на единицу площади (тепловой поток) через композитную конструкцию. 92} \end{эквнаррай} $$
Кондуктивные цилиндрические координаты
Теплопередача через прямоугольное твердое тело является наиболее прямым применением закона Фурье. Теплопередачу через трубу или стенку трубы теплообменника оценить сложнее. Через цилиндрическую стенку площадь поверхности теплопередачи постоянно увеличивается или уменьшается. Фиг.3 представляет собой сечение трубы, изготовленной из однородного материала.
Рисунок 3: Площадь поперечного сечения цилиндрической трубы
Площадь поверхности (A) для передачи тепла по трубе (без учета концов трубы) прямо пропорциональна радиусу (r) трубы и длине (L) трубы.
А = 2πrL
По мере увеличения радиуса от внутренней стенки к внешней увеличивается площадь теплообмена.
Разработка уравнения, оценивающего теплопередачу через объект цилиндрической геометрии, начинается с закона Фурье (уравнение 2-5).
$$ \dot{Q} = k ~A \left({ \Delta T \over \Delta r }\right) $$
Из приведенного выше обсуждения видно, что никакое простое выражение для площади не является точным. Ни площадь внутренней поверхности, ни площадь внешней поверхности сами по себе не могут использоваться в уравнении. Для задачи с цилиндрической геометрией необходимо определить среднелогарифмическую площадь поперечного сечения (A _lm ).
$$ A_{lm} = { A_{внешний} – A_{внутренний} \over \ln \left({ A_{внешний} \over A_{внутренний} }\right) } $$
(2-7)
Подстановка выражения 2πrL для площади в уравнении 2-7 позволяет вычислить среднелогарифмическую площадь по внутреннему и внешнему радиусу без предварительного вычисления внутренней и внешней площади.
$$ \begin{выравнивание} A_{lm} &=& { 2 \pi ~r_{внешняя} L – 2 \pi ~r_{внутренняя} L \over \ln \left({ 2 \pi ~r_{внешняя} L \over 2 \pi ~ r_{внутренний} L }\right) } \nonumber \\ &=& 2 \pi ~L \left({ r_{внешний} – r_{внутренний} \over \ln{ r_{внешний} \over r_{внутренний} } }\right) \end{эквнаррай} $$
Это выражение для логарифмической средней площади можно подставить в уравнение 2-5, что позволит нам рассчитать скорость теплопередачи для цилиндрических геометрий.
$$ \begin{выравнивание} \dot{Q} &=& k ~A_{lm} \left({ \Delta T \over \Delta r }\right) \nonumber \\ &=& k \left[ 2 \pi ~L \left({ r_o – r_i \over \ln{ r_o \over r_i } }\right) \right] \left({ T_o – T_i \over r_o – r_i }\ справа) \номер\\ \dot{Q} &=& { 2 \pi ~k ~L ~(\Delta T) \over \ln (r_o / r_i) } \end{эквнаррай} $$
(2-8)
куда:
Л = длина трубы (фут)
р _и = внутренний радиус трубы (футы)
р _или = Внешний радиус трубы (футы)
Пример:
Труба из нержавеющей стали длиной 35 футов имеет внутренний диаметр 0,92 фута и внешний диаметр 1,08 фута. Температура внутренней поверхности трубы составляет 122°F, а температура внешней поверхности составляет 118°F. Теплопроводность нержавеющей стали составляет 108 БТЕ/час-фут-°F. 92 } \end{эквнаррай} $$
Пример:
Труба длиной 10 футов с внутренним радиусом 1 дюйм и внешним радиусом 1,25 дюйма имеет температуру внешней поверхности 250°F. {\circ}\text{F} \end{эквнаррай} $$
Оценка теплопередачи через цилиндрическую стенку может быть распространена на составное тело, состоящее из нескольких концентрических цилиндрических слоев, как показано на рисунке 4.
Рисунок 4: Составные цилиндрические слои
Пример:
Толстостенная труба ядерного теплоносителя (k _s = 12,5 БТЕ/час-фут-°F) с внутренним диаметром 10 дюймов (ID) и наружным диаметром 12 дюймов (OD) покрыта 3-дюймовым слоем асбестовая изоляция (k _a = 0,14 БТЕ/час-фут-°F), как показано на рис. 5. Если температура внутренней стенки трубы поддерживается на уровне 550°F, рассчитайте потери тепла на фут длины. Наружная температура составляет 100°F. 9{\circ}\text{F}} } \right] } \nonumber \\ &=& 971 ~{ \text{Btu} \over \text{hr-ft} } \end{эквнаррай} $$
Проведение:
Проведение:
S3.4 Моделирование процесса лазерной обработки (1)

Лазерная обработка — это термический процесс, при котором материал удаляется посредством фазовых переходов (плавление, испарение). Прежде чем мы познакомим читателей с моделями, используемыми в LMP, необходимо сделать краткий обзор связанных с ними тепловых процессов. К ним относятся кондуктивный, конвекционный и радиационный теплообмен. Знание гидромеханики также необходимо для чтения литературы по LMP. Мы также поговорим об энергии, связанной с изменением состояния материалов.

Обзор теплопередачи:
Теплопередача – это передача энергии за счет разницы температур. Теплопроводность, конвекция и излучение являются тремя основными механизмами теплопередачи.
Кондуктивный теплообмен:
Проводимость – передача энергии от более энергичных к менее энергичным частицам вещества за счет взаимодействия между частицами. В газе и жидкостях теплопроводность осуществляется за счет беспорядочных молекулярных движений (диффузии), в твердых телах теплопроводность — за счет решеточных волн, индуцированных движениями атомов. В непроводниках передача энергии осуществляется исключительно через такие волны решетки, в проводниках движение свободных электронов также способствует теплопроводности.

Закон Фурье представляет собой уравнение скорости, основанное на экспериментальных данных. Этот закон гласит, что поток тепла на нормали к поверхности пропорционален градиенту температуры.
Рисунок 3.16: 1D теплопередача
Для одномерной теплопроводности в направлении x:
q”=-k dT/dx
Где k — теплопроводность (Вт/м·K), T — температура (K), q” — тепловой поток в направлении x.
Общая форма закона Фурье:
q” = – k Ñ T(x,y,z,t) = -k(i T/ x + j T/ y + k T/ z)
Теплопроводность k является свойством материала, она может меняться в зависимости от температуры и давления. При лазерной обработке, в которой обычно используются твердые тела, следует учитывать зависимость от температуры. Это делает k функцией температуры k(T), такие функциональные соотношения находятся путем интерполяции экспериментальных результатов при различных температурах.
Используя соотношение энергетического баланса, т. е. увеличение запасенной энергии в объеме материала = энергия на входе + производство энергии в этом объеме – энергия на выходе, мы можем вывести общую дифференциальную форму трехмерного уравнения теплопроводности. Короче:
Ein + Eg – Eout = D Est
Общее уравнение теплопроводности:
(k T/ x)/ x + (k T/ y)/ y + (k T/ z)/ z + dq/dt =r c _p ( T/ t)
Т = Т (х, у, г, т). Установившееся состояние: ( T/ t)=0
Если материал имеет постоянные свойства, мы можем вытащить k и мы получим:
² T/ x ² + ² T/ y ² + ^{² T/ z ² + (dq/dt)/k = (r c 904) /т) =1/а ( т/т)}
a = k/(r c _p ) – коэффициент температуропроводности.

В цилиндрических координатах имеем:
Закон Фурье: q” = – k Ñ T(r,f ,z,t) = -k(i T/ r + j(1/r) T/ f + k T/ z)
Общее уравнение теплопроводности:
(1/r) (k T/ r)/ r +(1/r ² ) (k T/ f )/ f + (k T/ z)/ z + dq/dt =r c _p ( т/т)
Где r — радиальное направление, f — окружное направление, z — осевое направление.
Когда мы предполагаем осесимметричный перенос тепла, что часто происходит при моделировании лазерного бурения, мы имеем в виду, что изменение температуры в направлении f равно нулю. Тогда приведенное выше уравнение принимает вид:
(1/r) (k T/ r)/ r + (k T/ z)/ z + dq/dt =r c _p ( T/ t)

Аналогично в сферических координатах:
q” = – k Ñ T(r,q ,f ,t) = -k(i T/ r + j(1/r) T/ q + k(1/r sinq ) T/ f )
(1/р ² ) (^{крон 2} Т/ r)/ r + (1/r ² sin ² ^д ) (к Тл/ ф )/ f + (1/r ² sinq ) (k sinq Т/ к )/ q + dq/dt = г с _р ( Т/ т)
Эти уравнения сложны, но они по-прежнему утверждают закон сохранения энергии.

Конвекционная теплопередача:
Конвекция обычно относится к передаче энергии между твердой поверхностью и соседним движущимся газом или жидкостью. Конвекционная теплопередача представляет собой комбинацию диффузионного или молекулярного движения внутри жидкости и объемного или макроскопического движения жидкости.
Скорость передачи энергии от системы к жидкости количественно определяется законом охлаждения Ньютона:
q” = h(T _{жидкость} – T _s )
где q” — конвективный тепловой поток (Вт/м ² ), h — коэффициент конвективной теплопередачи (Вт/м2К), T _s — температура поверхности (К) и
T _{жидкость} – температура жидкости вдали от поверхности (K).
Коэффициент теплопередачи, h, является эмпирическим параметром, который охватывает эффекты потока жидкости у поверхности, свойства жидкости и геометрию поверхности. Решение h является важнейшей задачей при анализе конвекционного теплообмена. Выдвинуто много эмпирических формулировок, за подробной информацией читатель может обратиться к учебнику по теплопередаче. Конвективный теплообмен связан с гидродинамикой системы. На следующем рисунке показано развитие пограничного слоя однородного потока вдоль плоской пластины.
Рисунок 3.17: Иллюстрация пограничного слоя и конвекционного тепла передача
Радиационный теплообмен:
В отличие от теплопроводности и конвекции, для распространения излучения не требуется наличие среды. На самом деле излучение наиболее эффективно переносит тепловую энергию в вакууме. Энергия излучения переносится электромагнитными волнами. Тепловое излучение — это энергия, излучаемая веществом при конечной температуре в результате изменения электронных конфигураций атомов или молекул. Как правило, радиационный анализ теплопередачи сосредоточен на твердых поверхностях, но излучение может также происходить от жидкостей и газов.
Закон Стефана-Больцмана гласит, что излучательная способность поверхности E пропорциональна T ⁴ :
E=e s T _s ⁴ ,
Где e — коэффициент излучения поверхности; s =5,67*10 ^-8 Вт/м ² . K ⁴ – постоянная Больцмана.
Энергия, поглощаемая поверхностью:
G _абс =a G=a s T _sur ⁴ ,
где а — поглощательная способность; G – излучение из окружающей среды.
Таким образом, чистая теплопередача энергии излучения от конечной поверхности к бесконечному окружению равна:
q” _рад =E-G _абс =es s T _s ⁴ -as T _sur ⁴
Где T _s и T _sur — температура поверхности и окружающей среды.

Рисунок 3.18: Обмен энергией излучения между поверхностью и окрестности
Реальный анализ радиационного энергообмена гораздо сложнее, чем то, что мы видим здесь. Излучение связано с направлением, площадью, длиной волны, состоянием поверхности и т. д. Мы также видим, что излучение увеличивается с четвертой степенью температуры, поэтому при высокой температуре следует учитывать перенос тепла излучением.
Обзор гидромеханики:
Подробное обсуждение конвективного теплообмена основано на механике жидкости. Поэтому необходимо дать краткий обзор некоторых основных понятий и соотношений в механике жидкости. К ним относятся:
1. Эйлерово и лагранжево описание:
Существуют две основные системы координат, которые можно использовать в механике. В рамках Эйлера независимыми переменными являются пространственные координаты x, y, z и время t. Внимание сосредоточено на жидкости, которая проходит через контрольный объем, который неподвижен в пространстве, жидкость внутри контрольного объема в любой момент времени будет состоять из частиц жидкости, отличных от той, которая была там в какой-то предыдущий момент времени. В лагранжевом подходе внимание сосредоточено на конкретной массе жидкости во время ее течения, в этой системе отсчета x,y,z,t больше не являются независимыми переменными, независимыми переменными являются x ₀ , y ₀ , z ₀ в момент времени t ₀ и время t. Все положения рассматриваемой нами массы можно вычислить, если известно поле скоростей.
Пусть F будет любой переменной поля, такой как плотность или температура, F=F(x,y,z,t) в эйлеровом описании или F= F(x ₀ ,y ₀ ,z ₀ ,t) в лагранжевом описании. Тогда производная по времени от F равна DF/Dt, и мы имеем:
, где u, v, w — скорости в направлениях x, y, z.
2. Сохранение массы
Рассмотрим конкретную массу жидкости, объем V которой выбран произвольно. За этой жидкой массой следует движение, ее форма и размер могут меняться со временем, но ее масса останется неизменной, если только не существует какого-либо механизма образования/исчезновения массы (например, ядерной реакции). Таким образом, закон сохранения массы утверждает, что лагранжева производная массы жидкости внутри объема равна нулю. В математической форме:
(Интеграция форма)
Форма сохранения массы PDE:
где x _k и u _k координаты и скорость в k=1,2,3 направления.
Если жидкость несжимаема, то имеем:
Объединив это соотношение с общим законом сохранения массы, мы получим хорошо известное уравнение неразрывности для несжимаемых потоков:
3. Сохранение импульса
Принцип сохранения количества движения является приложением второго закона Ньютона. закон движения элемента жидкости. Учитывая заданную массу жидкости в лагранжевой системе отсчета этот закон гласит, что скорость, с которой импульс масса жидкости изменяется, равна суммарной внешней силе, действующей на масса. Внешние силы могут быть классифицированы как объемные силы (такие как гравитационное или электромагнитные силы) и поверхностные силы (например, силы давления или силы вязкости). Таким образом имеем:
После многих манипуляций с использованием соотношения непрерывности и транспорта Ренольдса Теорема, и свяжите поверхностную силу с тензором напряжений и нормаль к поверхности n _i , (i=1,2,3 , j=1,2,3). Мы получили уравнения импульса:
Здесь мы использовали правило суммирования. Приведенное выше уравнение на самом деле состоит из трех уравнений. У нас нет места, чтобы объяснять все детали вывода и правила суммирования. Важно понимать физический смысл этих уравнений.
Определяющие соотношения связывают тензор напряжений с полем давления и скорости жидкости путем введения некоторых материальных коэффициентов. Предполагая ньютоновскую жидкость, мы имеем:
, где p – давление, м динамическая вязкость, л – еще один материальный коэффициент.
Принимая это соотношение в уравнение сохранения импульса, мы получаем знаменитое уравнение Навье-Стокса:

Опять же, это уравнение использует правило суммирования и представляет собой три скалярных уравнения.
При условии несжимаемого потока и постоянной динамической вязкости уравнение Навье-Стокса принимает вид:
Если пренебречь вязкостью, мы получим уравнения Эйлера:
4. Сохранение энергии
Применим первый закон термодинамики к жидкому элементу, получим принцип Закон сохранения энергии в механике жидкости. Рассмотрим любую произвольную массу жидкости объемом V и следить за ней в лагранжевой системе отсчета по мере ее течения. Полная энергия этой массы в единице объема есть сумма внутренних энергия и кинетическая энергия, . Скорость изменения энергии массы, за которой мы следим, уравновешивается работа, совершаемая внешними силами, за вычетом энергии, которую масса отдает наружу. В интегральной форме это соотношение имеет вид:
Применяя соотношение неразрывности и количества движения, получаем уравнение сохранения тепловой энергии:
Это уравнение представляет собой баланс только тепловой энергии, оно получается путем вычитания механической энергии из исходного соотношения баланса энергии. Но его обычно называют энергетическим уравнением.
Принимая отношение напряжения к приведенному выше уравнению, мы имеем:
, где T — температура, k — коэффициент теплопроводности, функция диссипации определяется как:
Для несжимаемой жидкости в декартовой системе координат .
5. Уравнения состояния материалов
Два уравнения состояния необходимы, чтобы сделать приведенные выше соотношения автономными.
Мы знаем, что для идеального газа P=r RT и внутренней энергии e=C _v T, где C _v — постоянная объемная удельная теплоемкость.
Иногда в уравнении энергии используется энтальпия, энтальпия определяется как:
Из обсуждения 2, 3, 4 и 5 мы показали семь скалярных уравнений с 7 переменных (предположим, что k, l и m известны). Для наиболее общего случая эти отношения являются связанными. Но обычно мы можем упростить их как для одномерного, так и для двумерного потока, или принять некоторые особые условия. Предположим, что несжимаемый поток или пренебрежение вязким потоком могут упростить уравнение. Если в уравнении энергии пренебречь скоростью, то можно получить теплопроводность уравнение. Предположим, что безвихревой поток приводит к анализу потенциального потока.
Модель может стать более сложной при учете турбулентности. Турбулентность, безусловно, имеет место в реальных приложениях, но у нас нет времени рассказывать об этом здесь. Еще одна сложность возникает из-за ударной волны, которая характерна для высокоэнергетической лазерной обработки. Мы увидим некоторые обсуждения в следующих разделах.
Вам надоела эта математическая каша? Я думаю, вам нужно понять их, чтобы читать литературу в этой области. Я не могу взять задание по гидромеханике, если вы не смогли понять смысл этих соотношений, вам предлагается обратиться за книгой по гидромеханике. Если вы чувствуете себя комфортно в этом разделе, то вы будете чувствовать себя комфортно и в следующих разделах.
Пограничные слои и потенциальные течения широко обсуждаются в гидромеханике. Давайте покажем вам несколько картинок в дополнение к скучным уравнениям.
Схема течения диполя
Обтекание цилиндра
Обтекание аэродинамического профиля
Рисунок 3. 19 Некоторые модели поля жидкости (с разрешения UNIVERSITY ГЕНУИ, ГИДРАВЛИЧЕСКИЙ ИНСТИТУТ)
Теплообмен | Спиракс Сарко
Дом / Узнать о паре /
Теплопередача
Содержимое
Инженерные единицы
Что такое пар?
Перегретый пар
Качество пара
Теплопередача
Методы оценки расхода пара
Измерение потребления пара
Тепловой рейтинг
Энергопотребление резервуаров и чанов
Отопление с помощью змеевиков и кожухов
Обогрев чанов и резервуаров с помощью впрыска пара
Потребление пара трубами и воздухонагревателями
Потребление пара теплообменниками
Потребление пара растительными предметами
Энтропия – основное понимание
Энтропия – ее практическое применение
Вернуться к информации о паре
Теплопередача
Пар часто генерируется для обеспечения теплопередачи в процессе. Объясняются режимы теплопередачи (проводимость, конвекция, излучение) внутри среды или между средами, а также расчеты и другие вопросы, такие как барьеры теплопередачи.
В системе парового отопления единственной целью производства и распределения пара является обеспечение тепла на поверхности теплопередачи технологического процесса. Если известны требуемый расход теплоты и давление пара, то можно определить необходимый расход пара. Это позволит установить размер котла и систему распределения пара.
Способы теплопередачи
Всякий раз, когда существует температурный градиент внутри среды или между средами, происходит передача тепла. Это может принимать форму проводимости, конвекции или излучения.
Теплопроводность
Когда существует градиент температуры либо в твердой, либо в стационарной жидкой среде, происходящая теплопередача называется теплопроводностью. Когда соседние молекулы в жидкости сталкиваются, энергия передается от более энергичных молекул к менее энергичным. Поскольку более высокие температуры связаны с более высокими молекулярными энергиями, проводимость должна происходить в направлении снижения температуры.
Это явление наблюдается как в жидкостях, так и в газах. Однако в жидкостях молекулярные взаимодействия тем сильнее и чаще, чем ближе друг к другу молекулы. В твердых телах проводимость вызвана атомной активностью колебаний решетки, как объясняется в Модуле 2.2.
Уравнение, используемое для выражения теплопередачи теплопроводностью, известно как закон Фурье. Там, где существует линейное распределение температуры в стационарных условиях, для одномерной плоской стенки это может быть записано как:
Пример 2.5.1
Рассмотрим плоскую стену, изготовленную из твердого железа с теплопроводностью 70 Вт/м °C и толщиной 25 мм. Он имеет площадь поверхности 0,3 м на 0,5 м, с температурой 150 ° C с одной стороны и 80 ° C с другой.
Теплопроводность является характеристикой материала стены и зависит от температуры. В таблице 2.5.1 показано изменение теплопроводности в зависимости от температуры для различных распространенных металлов.
Таблица 2.5.1 Теплопроводность (Вт/м °C)
Материал
Теплопроводность (Вт/м °C)
При 25°С При 125 °С При 225 °С
Железо 80 68 60
Низкоуглеродистая сталь 54 51 47
Нержавеющая сталь 16 17,5 19
Вольфрам 180 160 150
Платина 70 71 72
Алюминий 250 255 250
Золото 310 312 310
Серебро 420 418 415
Медь 401 400 398

Учитывая механизм теплопередачи при теплопроводности, в общем случае теплопроводность твердого тела будет намного больше, чем жидкости, а теплопроводность жидкости будет больше, чем газа. Воздух имеет особенно низкую теплопроводность, поэтому изоляционные материалы часто имеют много воздушных пространств.
Конвекция
Передача тепловой энергии между поверхностью и движущейся жидкостью при различных температурах называется конвекцией. На самом деле это комбинация механизмов диффузии и объемного движения молекул.
Вблизи поверхности, где скорость жидкости мала, преобладает диффузия (или беспорядочное молекулярное движение).
Однако по мере удаления от поверхности объемное движение оказывает все большее влияние. Конвективный теплообмен может принимать форму принудительной конвекции или естественной конвекции. Принудительная конвекция возникает, когда поток жидкости вызывается внешней силой, такой как насос или мешалка.
И наоборот, естественная конвекция вызывается силами плавучести из-за различий в плотности, возникающих из-за колебаний температуры жидкости.
Перенос тепловой энергии, вызванный фазовым переходом, таким как кипение или конденсация, также называют процессом конвективной теплопередачи.
Уравнение конвекции выражается уравнением 2.5.2, которое является производным от закона охлаждения Ньютона:
Пример 2.5.2
Рассмотрим плоскую поверхность размером 0,4 м на 0,9 м при температуре 20 °C.
По поверхности течет жидкость с объемной температурой 50 °C.
Коэффициент конвективной теплопередачи (h) составляет 1 600 Вт/м² °C.
Излучение
Теплопередача за счет излучения энергии от поверхностей в форме электромагнитных волн известна как тепловое излучение. В отсутствие промежуточной среды существует чистый теплообмен между двумя поверхностями с разными температурами. Эта форма теплопередачи не зависит от материальной среды и на самом деле наиболее эффективна в вакууме.
Общее уравнение теплопередачи
В большинстве практических ситуаций очень необычно, чтобы вся энергия передавалась только одним видом теплопередачи. Общий процесс теплопередачи обычно представляет собой комбинацию двух или более различных механизмов.
Общее уравнение, используемое для расчета теплопередачи через поверхность, используемое в процедуре расчета и являющееся частью теории теплообмена:
Общий коэффициент теплопередачи (U)
Учитывает как кондуктивное, так и конвективное сопротивление между двумя жидкостями, разделенными сплошной стенкой. Общий коэффициент теплопередачи является обратной величиной общего сопротивления теплопередаче, которое представляет собой сумму отдельных сопротивлений.
Общий коэффициент теплопередачи может также учитывать степень загрязнения в процессе теплопередачи. Отложение пленки или накипи на поверхности теплопередачи значительно снижает скорость теплопередачи. Фактор загрязнения представляет собой дополнительное тепловое сопротивление, вызванное примесями жидкости, образованием ржавчины или другими реакциями между жидкостью и стенкой.
Величина отдельных коэффициентов будет зависеть от природы процесса теплопередачи, физических свойств жидкостей, расходов жидкости и физического расположения поверхности теплопередачи.
Поскольку физическое расположение не может быть установлено до тех пор, пока не будет определена площадь теплопередачи, проектирование теплообменника по необходимости представляет собой итеративную процедуру. Отправной точкой для этой процедуры обычно является выбор типичных значений общего коэффициента теплопередачи различных типов теплообменников.
Точный расчет индивидуальных коэффициентов теплопередачи является сложной процедурой, и во многих случаях это невозможно из-за того, что некоторые параметры неизвестны. Поэтому для практических целей целесообразно использовать установленные типовые значения общего коэффициента теплоотдачи.
Разность температур (ΔT)
Закон охлаждения Ньютона гласит, что скорость теплопередачи связана с мгновенной разностью температур между горячей и холодной средой. В процессе теплопередачи эта разность температур будет меняться либо в зависимости от положения, либо во времени. Таким образом, общее уравнение теплопередачи было разработано как дополнение к закону охлаждения Ньютона, где средняя разность температур используется для определения площади теплопередачи, необходимой для данной тепловой нагрузки.
Средняя разность температур (ΔTM)
Определение средней разности температур в процессах проточного типа, таких как теплообменник, будет зависеть от направления потока. Первичная и вторичная жидкости могут течь в одном направлении (параллельный поток/прямоточный поток), в противоположном направлении (противоточный поток) или перпендикулярно друг другу (поперечный поток). При использовании насыщенного пара температуру первичной жидкости можно принять за постоянную, так как тепло передается только в результате фазового перехода. В результате температурный профиль больше не зависит от направления потока.
Однако по мере того, как вторичная жидкость проходит над поверхностью теплопередачи, самая высокая скорость теплопередачи возникает на входе и постепенно снижается по мере ее движения к выходу. Это просто потому, что разница температур между паром и вторичной жидкостью уменьшается с повышением вторичной температуры.
Результирующий температурный профиль пара и вторичной жидкости обычно показан на рисунке 2. 5.1.
Повышение вторичной температуры нелинейно и лучше всего представлено логарифмическим вычислением. Для этой цели выбранная средняя разность температур называется средней логарифмической разностью температур, или LMTD, или ΔTLM.
Более простой (но менее точный) способ расчета средней разницы температур состоит в том, чтобы рассмотреть среднеарифметическую разницу температур, или AMTD, или ΔT _AM . Это учитывает линейное увеличение температуры вторичной жидкости и для быстрых ручных расчетов обычно дает удовлетворительную аппроксимацию средней разности температур, используемую в уравнении 2.5.3. Температурный профиль AMTD показан на рисунке 2.5.2.
Среднеарифметическая разность температур (AMTD):
Для пара, где температура первичной жидкости (пара) остается постоянной, это уравнение можно упростить до:
Поскольку температура на стороне пара не изменяется, AMTD обычно обеспечивает удовлетворительный анализ процесса теплопередачи, которым легко управлять при расчетах вручную.
Однако можно также использовать среднелогарифмическую разность температур, которая учитывает нелинейное изменение температуры вторичной жидкости.
Среднелогарифмическая разность температур (LMTD):
В обоих уравнениях 2.5.4 и 2.5.5 предполагается, что удельная теплоемкость или общий коэффициент теплопередачи не изменяются, а потери тепла отсутствуют.
В действительности удельная теплоемкость может изменяться в результате колебаний температуры. Общий коэффициент теплопередачи также может изменяться из-за различий в свойствах жидкости и условиях потока. Однако в большинстве приложений отклонения будут почти незначительными, и вполне допустимо использование средних значений.
Во многих случаях теплообменное оборудование должно быть изолировано от окружающей среды, но изоляция не будет эффективной на 100%. Следовательно, энергия, передаваемая между паром и вторичной жидкостью, может не отражать все потери тепла от первичной жидкости.
Пример 2.
5.3
Пар при давлении 2 бар изб. используется для нагрева воды с 20 °C до 50 °C.
Температура насыщения пара при 2 бар изб. составляет 134 °C.
Определение арифметической и среднелогарифмической разницы температур:
В этом примере AMTD и LMTD имеют одинаковое значение. Это связано с тем, что повышение температуры вторичной жидкости мало по сравнению с разницей температур между двумя жидкостями.
Пример 2.5.4
Рассмотрим резервуар с технологической жидкостью под давлением, который нагревается с 10 °C до 120 °C с помощью пара под давлением 4,0 бар изб. Температура насыщения пара при 4,0 бар изб. составляет 152 °С.
Определение средней арифметической и логарифмической разницы температур:
Поскольку повышение температуры вторичной жидкости велико по сравнению с разницей температур между двумя жидкостями, расхождение между двумя результатами является более значительным.
При использовании AMTD вместо LMTD расчетная площадь теплопередачи будет почти на 15 % меньше требуемой.
Барьеры для теплопередачи
Металлическая стенка может быть не единственным барьером в процессе теплопередачи. На стороне пара может быть пленка воздуха, конденсата и накипи. Со стороны продукта также может быть пригоревший продукт или накипь, а также застойная пленка продукта.
Встряхивание продукта может устранить эффект застойной пленки, в то время как регулярная очистка со стороны продукта должна уменьшить накипь.
Регулярная очистка поверхности со стороны пара также может увеличить скорость теплопередачи за счет уменьшения толщины любого слоя накипи, однако это не всегда возможно. Этот слой также можно уменьшить, уделяя особое внимание правильной работе котла и удаляя капли воды, несущие загрязнения из котла.
Пленочная конденсация
Удаление пленки конденсата не так просто. Когда пар конденсируется, теряя свою энтальпию испарения, на поверхности теплообмена могут образовываться капли воды. Затем они могут сливаться вместе, образуя непрерывную пленку конденсата. Пленка конденсата может быть в 100–150 раз более устойчивой к теплопередаче, чем стальная поверхность нагрева, и в 500–600 раз более устойчивой, чем медная.
Капельная конденсация
Если капли воды на поверхности теплообмена не сливаются сразу и не образуется сплошная пленка конденсата, происходит «капельная» конденсация. Скорости теплопередачи, достигаемые при капельной конденсации, обычно намного выше, чем при пленочной конденсации.
Поскольку при капельной конденсации открывается большая часть поверхности теплопередачи, коэффициенты теплопередачи могут быть в десять раз выше, чем при пленочной конденсации.
В конструкции теплообменников, в которых поощряется капельная конденсация, тепловое сопротивление, которое она создает, часто незначительно по сравнению с другими барьерами теплопередачи. Однако оказалось очень трудно достичь подходящих условий для капельной конденсации.
Если поверхность покрыта веществом, препятствующим смачиванию, можно поддерживать капельную конденсацию в течение определенного периода времени. С этой целью на поверхности теплообменника, на котором должна происходить конденсация, иногда наносят ряд поверхностных покрытий, таких как силиконы, ПТФЭ и набор восков и жирных кислот. Однако эти покрытия постепенно теряют свою эффективность из-за таких процессов, как окисление или загрязнение, и в конечном итоге преобладает пленочная конденсация.
Поскольку воздух является таким хорошим изолятором, он обеспечивает еще большее сопротивление теплопередаче. Воздух может быть в 1 500–3 000 раз более устойчивым к тепловому потоку, чем сталь, и в 8 000–16 000 раз более устойчивым, чем медь. Это означает, что воздушная пленка толщиной всего 0,025 мм может противостоять такой же теплопередаче, как медная стена толщиной 400 мм! Конечно, все эти сравнительные отношения зависят от профилей температуры в каждом слое.
Определение общего коэффициента теплопередачи (значение U)
Пять основных общеупотребительных терминов, связанных с предметом теплопередачи :
Теплопроводность k (Вт/м °C)
Удельное тепловое сопротивление r (м °C/Вт)
Термическое сопротивление R (м2 °C/Вт)
Коэффициент теплопередачи U (Вт/м2 °C)
Следующий текст в этом модуле описывает их и то, как они связаны друг с другом.
Традиционный метод расчета теплопередачи через плоскую стену предполагает использование общего коэффициента теплопередачи «U» или, точнее, общего коэффициента теплопередачи между одной стороной стены и другой.
Значения U указаны для широкого диапазона и комбинации материалов и жидкостей и обычно зависят от эмпирических данных и опыта эксплуатации. Вышеупомянутые пленки конденсата, воздуха, окалины и продукта по обе стороны от металлической стенки могут оказывать значительное влияние на общую теплопроводность, и поэтому стоит рассмотреть весь вопрос теплопередачи через простую плоскую стенку и затем многослойный барьер.

Теплопередача путем теплопроводности через простую плоскую стенку
Для начала можно рассмотреть простейший возможный случай — металлическую стену с однородными тепловыми свойствами и заданной температурой поверхности.
T ₁ и T ₂ _{— температуры поверхности по обе стороны от металлической стенки толщиной L; а разница температур между двумя поверхностями – ΔT.}
Если не учитывать возможное сопротивление тепловому потоку на двух поверхностях, процесс теплового потока через стену можно вывести из закона проводимости Фурье, как показано в уравнении 2.5.1.
Термин «барьер» относится к термостойкой пленке или металлической стенке теплообменника.
Из их определений в уравнении 2.5.6 видно, что χ/k представляет собой толщину барьера, деленную на присущее ему свойство теплопроводности. Простая арифметика подсказывает, что если длина (χ) барьера увеличивается, значение χ/k будет увеличиваться, а если значение проводимости барьера (k) увеличивается, то значение χ/k уменьшается. Характеристикой, которая будет вести себя таким образом, является тепловое сопротивление.
Если длина барьера увеличивается, сопротивление тепловому потоку увеличивается; и если проводимость материала барьера увеличивается, сопротивление тепловому потоку уменьшается. Можно сделать вывод, что член χ/k в уравнении 2.5.6 относится к тепловому сопротивлению барьера известной длины.
Результаты простой теории электричества аналогичны уравнениям, относящимся к тепловому потоку. В частности, возможна концепция последовательного добавления сопротивлений, которая является полезным инструментом при анализе теплопередачи через многослойный барьер, как будет показано в следующем разделе этого модуля.
Уравнение 2.5.6 теперь можно переформулировать в терминах теплового сопротивления, где:
, как показано в уравнении 2.5.7
Термическое сопротивление обозначает характеристику конкретного барьера и будет меняться в зависимости от его толщины и проводимости.
Напротив, способность барьера сопротивляться тепловому потоку не меняется, так как это физическое свойство материала барьера. Это свойство называется «удельное тепловое сопротивление»; это обратная величина теплопроводности, показанная в уравнении 2.5.8.
Отношение общего сопротивления к общему значению U
Обычной проблемой, которую необходимо решить в приложениях для теплопередачи, является скорость теплопередачи, и это видно из общей формулы теплопередачи, уравнение 2. 5.3.
Тепловой поток через многослойный барьер
Как видно на рис. 2.5.4, практическим применением может быть металлическая стенка трубы или пластины теплообменника, в которой пар используется с одной стороны для нагрева воды с другой. Также видно, что существуют различные другие барьеры, замедляющие поток тепла, такие как воздушная пленка, пленка конденсата, пленка накипи и неподвижная пленка вторичной воды, непосредственно примыкающая к нагреваемой поверхности.
Эти пленки можно рассматривать как «загрязняющие» поток тепла через барьер, и, следовательно, эти сопротивления рассматриваются разработчиками теплообменников как «факторы загрязнения».
Все эти пленки, в дополнение к сопротивлению металлической стенки, создают сопротивление тепловому потоку, и, как и в электрической цепи, эти сопротивления могут быть добавлены для формирования общего сопротивления.
Следовательно:
Поскольку сопротивление равно χ/k, как показано в уравнении 2. 5.6, то уравнение 2.5.10 можно переписать как уравнение 2.5.11:
Теплопроводность зависит от материала пленки (и температуры). Например, сопротивление тепловому потоку воздуха примерно в тридцать раз больше, чем у воды. По этой причине более важно удалять воздух из подачи пара до того, как он достигнет теплообменника, чем удалять воду в виде влажного пара. Конечно, в то же время имеет смысл удалять влажный пар.
Сопротивление воздуха стали примерно в две тысячи раз больше, а сопротивление воздуха меди примерно в двадцать тысяч раз больше. Из-за высокого сопротивления воздуха и воды по сравнению со сталью и медью влияние небольших толщин воздуха и воды на общее сопротивление тепловому потоку может быть относительно большим.
Нет смысла менять стальную систему теплообмена на медную, если еще присутствуют воздушная и водяная пленки; производительность улучшится незначительно, как будет показано в примере 2. 5.5.
Воздушная и водяная пленки на стороне пара могут быть устранены с помощью надлежащей инженерной практики путем простой установки сепаратора и поплавковой ловушки в линии подачи пара перед регулирующим клапаном. Пленки накипи на стороне пара также можно уменьшить, установив сетчатые фильтры на той же линии.
Накипь на стороне продукта поддается обработке немного сложнее, но регулярная очистка теплообменников иногда является одним из решений этой проблемы. Еще один способ уменьшить образование накипи – использовать теплообменники при более низком давлении пара; это снижает температуру пара и тенденцию к образованию накипи на продукте, особенно если продукт представляет собой раствор, подобный молоку.
Пример 2.5.5
Рассмотрим пароводяной теплообменник, в котором воздушная пленка, пленка конденсата и накипь на стороне пара имеют толщину 0,2 мм; со стороны воды толщина пленки воды и накипи составляет 0,05 мм и 0,1 мм соответственно.
Толщина нагревательной поверхности со стальными стенками 6 мм.
Таблица 2.5.3 Прочность ограждений, включая стальную трубу
Материал Толщина ‘x’ мм
Электропроводность «k» (Вт/м °C)
Сопротивление R = x/k (Вт/м °C)
Воздух 0,2 0,025 0,008
Конденсат 0,2 0,4 0,000 5
Накипь со стороны пара 0,2 0,5 0,000 4
Стальная трубка 6,0 50,0 0,000 12
Вода 0,05 0,6 0,000 08
Накипь со стороны воды 0,1 0,5 0,000 2

Из уравнения 2. 5.6:
1. Рассчитайте общее значение U (U1) из условий, показанных в таблице 2.5.3
2. Удаление воздуха и конденсата из системы подачи пара
Теперь рассмотрим тот же теплообменник, в котором воздух и конденсат удалены сепаратором системы подачи пара.
Рассчитать U ₂
Из U ₂ видно, что при установке сепаратора на линии подачи пара к этому теплообменнику и допущении, что из пара удален весь воздух и конденсат, коэффициент теплопередачи более чем в 11 раз превышает исходный ценность.
3. Удалите накипь на стороне пара и воды
Теперь рассмотрите возможность уменьшения накипи на стороне пара, установив сетчатый фильтр на паропроводе, и уменьшить накипь на стороне воды, работая при более низком давлении пара .
Рассчитать U ₃
Благодаря удалению накипи коэффициент теплопередачи увеличился еще в четыре раза.
4. Вернитесь к исходным условиям, но замените стальную трубу медной трубой той же толщины.
Таблица 2.5.4 Сопротивление барьеров, включая медную трубку
Материал Толщина ‘x’ мм
Электропроводность ‘k’
(Вт/м°C)
Сопротивление R = ^x /k
(м ² °С/Вт)
Воздух 0,2 0,025 0,008
Конденсат 0,2 0,4 0,000 5
Шкала на паровой стороне 0,2 0,5 0,000 4
Медная трубка 6 400 0,000 015
Вода 0,05 0,6 0,000 08
Накипь со стороны воды 0,1 0,5 0,000 2

Рассчитать U ₄
Можно видеть, что большая проводимость меди по сравнению со сталью очень мало повлияла на общую теплопроводность теплообменника из-за преобладающего влияния воздуха и других факторов загрязнения .
Обратите внимание, что на практике на общее значение U будут влиять другие факторы, такие как скорость пара и воды, проходящих через трубы или пластины теплообменника, а также сочетание теплопередачи конвекцией и излучением.
Также маловероятно, что установка сепаратора и сетчатого фильтра полностью устранит присутствие воздуха, влажного пара и накипи внутри теплообменника. Приведенные выше расчеты показаны только для того, чтобы подчеркнуть их влияние на теплопередачу. Однако любая попытка удалить такие барьеры из системы, как правило, оказывается успешной и практически гарантированно увеличивает теплопередачу в паровых отопительных установках и оборудовании, как только это будет сделано.
Вместо расчета отдельных сопротивлений пленочных барьеров существуют таблицы, показывающие общие значения U для различных типов применения теплообмена, таких как нагрев воды или масла паровым змеевиком. Они описаны в Модуле 2.10 «Отопление с помощью змеевиков и кожухов».
Значения U для теплообменников значительно различаются в зависимости от таких факторов, как конструкция («кожухотрубная» или «пластинчатая рама»), материал конструкции и тип жидкости, участвующей в функции теплопередачи.
Начало страницы
Предыдущая – Качество пара Далее – Методы оценки расхода пара
Механизмы теплопередачи – Энергетическое образование
Energy Education
Меню навигации
ИСТОЧНИКИ ЭНЕРГИИ
ЭНЕРГОПОТРЕБЛЕНИЕ
ЭНЕРГЕТИЧЕСКОЕ ВОЗДЕЙСТВИЕ
Поиск
Рисунок 1. На фотографии выше показан аэрогель, чрезвычайно хороший теплоизолятор, между паяльной лампой и спичками. Аэрогель блокирует все тепло от паяльной лампы и предотвращает возгорание спичек. ^[1]
Механизмы теплопередачи — это способы, которыми тепловая энергия может передаваться между объектами, и все они основаны на основном принципе, согласно которому кинетическая энергия или тепло должны быть в равновесии или в равных энергетических состояниях . Существует три различных способа передачи тепла: теплопроводность, конвекция и лучистое тепло (часто называемое излучением, но это более общий термин, включающий множество других явлений). ^[2] Существует родственное явление, связанное с передачей скрытого тепла, называемое эвапотранспирацией.
Теплопроводность
Основная статья
Теплопроводность — это простейшая модель теплопередачи с точки зрения возможности математического объяснения происходящего. Это движение кинетической энергии в материалах из областей с более высокой температурой в области с более низкой температурой через вещество. ^[3] Молекулы будут просто отдавать свою энергию соседним молекулам, пока не будет достигнуто равновесие. Модели проводимости не имеют дело с движением частиц внутри материала.
Конвекция
Рис. 2. Воздух над сушей нагревается быстрее, чем воздух над водой, что приводит к конвекции, которая ощущается как прохладный океанский бриз. ^[4]
основная статья
Конвекция — это передача тепла посредством движения жидкости (например, воздуха или воды). Разница между проводимостью и конвекцией заключается в движении материального носителя; конвекция – это движение тепловой энергии за счет движения горячей жидкости (в отличие от нагревания другого материала за счет шевеления атомов). Обычно это движение происходит в результате различий в плотности. Более теплые частицы менее плотны, поэтому частицы с более высокой температурой будут перемещаться в области с более низкой температурой, а частицы с более низкой температурой – в области с более высокой температурой. Жидкость будет оставаться в движении, пока не будет достигнуто равновесие.
Излучение
Рисунок 1: Костры излучают лучистую «энергию» и ощущаются как «лучистое тепло». ^[5]
основной артикул
Тепло, передаваемое излучением, называется лучистым теплом. Подобно свету, лучистое тепло является лучистой энергией, и для его переноса не обязательно требуется среда. Этой форме передачи энергии способствует электромагнитное излучение. ^[6] Все движущиеся заряженные частицы излучают электромагнитное излучение. Эта излучаемая волна будет двигаться, пока не столкнется с другой частицей. Частица, получившая это излучение, получит его в виде кинетической энергии. Частицы будут получать и излучать излучение даже после того, как все будет иметь одинаковую температуру, но этого не замечают из-за того, что в этот момент материал находится в равновесии.
Этот тип теплопередачи особенно важен при установлении температуры Земли. Излучение, как передача тепла, — это то, как Земля получает энергию от солнца. Радиация также важна для парникового эффекта.
Эвапотранспирация
Рисунок 1. Круговорот воды зависит от эвапотранспирации. ^[7]
основная статья
Эвапотранспирация — это энергия, переносимая фазовыми переходами, такими как испарение или сублимация. ^[8] Вода требует достаточного количества энергии для изменения фазы, поэтому этот процесс подтверждает, что водяной пар имеет достаточное количество энергии, связанной с ним. Этот тип механизма передачи энергии часто не указывается среди различных типов механизмов передачи, так как его сложнее понять.
Для дополнительной информации
Эвапотранспирация
Радиация
Теплопроводность
Конвекция
Или просмотрите случайную страницу
Ссылки
↑ Wikimedia Commons. (30 июля 2015 г.). Аэрогель [Онлайн]. Доступно: https://upload.wikimedia.org/wikipedia/commons/b/b4/Aerogel_matches.jpg
↑ Гиперфизика, Теплопередача [Онлайн], Доступно: http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/heatra.html
↑ Гиперфизика, Теплопроводность [Онлайн], Доступно: http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/heatra.html#c2
↑ «Свойства выбора чтения материи: плотность создает течения». [Онлайн]. Доступно: http://www.propertiesofmatter.si.edu/Density_Creates.html
↑ Wikimedia Commons [в сети], доступно: http://commons.wikimedia.org/wiki/File:Fire_from_brazier.jpg
↑ Р. Чабай и Б. Шервуд, «Энергия и импульс в излучении», в Matter & Interactions, 3rd ed., Hoboken, NJ: Wiley, 2011, ch.24, sec.5, pp. 1002-1003
↑ Wikimedia Commons [в сети], доступно: http://en.wikipedia.org/wiki/Evapotranspiration#/media/File:Surface_water_cycle.svg
↑ Геологическая служба США, Эвапотранспирация — круговорот воды [онлайн], доступно: http://water.usgs.gov/edu/watercycleevapotranspiration.html
7.6 Основы теплопередачи – руководство по использованию CubeSat и конструкции шины
7. Термоконтроль
Механизмы теплопередачи
На изображении выше показано, как все три метода теплопередачи (теплопроводность, конвекция и излучение) работают в одной и той же среде. Изображение предоставлено НАСА.
Проводка
Теплопроводность — это прямая передача тепла между материалами, которые 1) имеют физический контакт и 2) имеют относительную разницу температур. «Проводимость имеет место во всех фазах: твердой, жидкой и газообразной. Скорость, с которой энергия передается в виде тепла между двумя телами, зависит от разницы температур (и, следовательно, градиента температуры) между двумя телами и свойств проводящего интерфейса, через который передается тепло» [Википедия].
Диаграмма, показывающая передачу тепловой энергии посредством проводимости. Изображение предоставлено Boundless.
Теплопроводность — это основной механизм теплопередачи внутри космического корабля. Тепло переходит от горячего (высокая температура) к холодному (низкая температура) до тех пор, пока не будет достигнуто равновесие. Основной закон одномерной теплопроводности был сформулирован Фурье в 1822 г. Величина переноса тепла пропорциональна теплопроводности, площади и градиенту температуры.
.
Теплопроводность может быть определена с точки зрения теплового потока через разность температур. Изображение Maxwell Molecule.
Теплопроводность – это свойство материала с единицами измерения. Теплопроводность уподобляется электрическому сопротивлению в том смысле, что оба свойства представляют собой легкость, с которой энергия передается через материал. Общие материалы в конструкциях космических кораблей и их теплопроводность [Википедия]:
Материал Теплопроводность Использование космического корабля
Алюминий 237[6] Структура
Медь (чистая) 401[4][12][13] Электрические интерфейсы и плоскости заземления
Силикатный аэрогель 0,02[4] Изоляция
Вода 0,5918[15] Терморегуляция или топливо
Поликарбонат 0,2 Материал печатной платы
Если бы мы хотели изучить систему более внимательно, чтобы понять, как тепло «течет» в твердом теле, нам нужно общее дифференциальное уравнение, описывающее, как тепло распространяется в пространстве во времени:
Где
q(r,t)=внутренне выделяемое тепло
ρ=плотность (кг/м3)
c=удельная теплоемкость (Дж/кг°K)
Это уравнение используется в тепловых моделях диффузия , составляющая основу конечно-элементного анализа распределения температуры по телу с течением времени.
Конвекция
Моментальные снимки температурного поля в двухмерном моделировании конвекции Рэлея-Бенара. (Вверху) При достаточно слабых перепадах температуры ΔT жидкость остается в состоянии покоя и передает тепло посредством теплопроводности. (В центре) Достаточно большое ΔT дестабилизирует состояние проводимости, а когерентные конвекционные валы активно увеличивают тепловой поток. (Внизу) Конвективная турбулентность начинается при большем ΔT. Изображение PNAS.
Конвекция – это передача тепла посредством движения жидкостей. Конвекция обычно является доминирующей формой теплопередачи в жидкостях и газах. Жидкости используют гравитацию для циркуляции. У нас не так много гравитации или жидкостей в космосе, поэтому мы не будем касаться физики.
Моделирование тепловой конвекции. Красные оттенки обозначают горячие области, а синие — холодные. Горячий, менее плотный нижний пограничный слой направляет шлейфы горячего материала вверх, и точно так же холодный материал сверху движется вниз. Эта иллюстрация взята из модели конвекции в мантии Земли. Изображение предоставлено Харрошмелингом.
Излучение
«Тепловое излучение — это излучение электромагнитных волн от всего вещества, имеющего температуру выше абсолютного нуля. Тепловое излучение отражает преобразование тепловой энергии в электромагнитную энергию. Тепловая энергия – это кинетическая энергия случайных движений атомов и молекул в веществе. Вся материя с ненулевой температурой состоит из частиц с кинетической энергией» [Википедия]. «Тепловое излучение может исходить от объектов на любой длине волны, и при очень высоких температурах такое излучение связано со спектрами далеко за пределами инфракрасного, простирающимися в видимый, ультрафиолетовый и даже рентгеновский диапазоны (например, солнечная корона). Таким образом, популярная ассоциация инфракрасного излучения с тепловым излучением является лишь совпадением, основанным на типичных (сравнительно низких) температурах, часто встречающихся вблизи поверхности планеты Земля» [Википедия].
Короче говоря, тепловое излучение работает через электромагнитные поля и не нуждается в транспортной среде, поэтому излучение работает в вакууме. Излучение — это единственный механизм теплового взаимодействия космического корабля с космической средой, который мы используем для сброса или отвода внешнего тепла от космического корабля на орбите.
Материалы с более высоким коэффициентом излучения кажутся более горячими. На этом тепловом изображении керамический цилиндр кажется более холодным, чем его кубический контейнер (из карбида кремния), хотя на самом деле они имеют одинаковую температуру. Изображение от Bancquo.
Излучение является основным внешним по отношению к космическому кораблю механизмом передачи тепла. Тепло течет от горячего (высокая температура) к холодному (низкая температура) до тех пор, пока не будет достигнуто равновесие, как и при теплопроводности. Скорость передачи тепла испускаемым излучением определяется законом Стефана-Больцмана для излучения. Количество передаваемого тепла пропорционально коэффициенту излучения, площади поверхности и абсолютной температуре в градусах Кельвина. постоянная Стефана-Больцмана, имеющая значение
Полная форма уравнения Стефана-Больцмана:
где = температура окружающей среды (=3°К для пространства)
Два тела в тепловом равновесии внутри полости, изолированной от окружающей среды. Стрелки изображают сияющие силы. Буквы e и буква обозначают испускаемое и поглощаемое излучение белого тела.CC BY-NC-SA 2.0. Изображение предоставлено SEOS.
Коэффициент излучения — это свойство материала, которое указывает на излучение тепла телом. Коэффициент излучения варьируется от 0 (белое тело, отражающее излучение) до 1 (черное тело, поглощающее все тепло). Значения от 0 до 1 означают «серое» тело, которое частично отражает и поглощает в некотором отношении; коэффициент излучения является безразмерной величиной. Более формально, «коэффициент излучения — это отношение теплового излучения от поверхности к излучению от идеально черной поверхности при той же температуре, что и согласно закону Стефана-Больцмана» [Википедия]. Вот некоторые распространенные материалы, используемые в космосе, и их коэффициенты излучения [EngineeringToolbox]:
Материал Коэффициент излучения Использование космического корабля
Алюминий (полированный) 0,039 – 0,057 Структура
Алюминий (анодированный) 0,77 Структура
Аморфный кремний 0,45 – 0,8 Стандартный материал для солнечных элементов
Медь (гальваническая, полированная) 0,03 – 0,06 Электрические интерфейсы и плоскости заземления
Силикатный аэрогель 0,79 Изоляция
Вода 0,95 – 0,96 Терморегуляция или топливо
Поликарбонат 0,90 – 0,97 Материал печатной платы
Поглощающая способность поверхности материала – это его способность поглощать лучистую энергию. Для данной длины волны коэффициент поглощения равен коэффициенту излучения:
Однако существуют некоторые материалы, которые поглощают на другой длине волны, чем излучают, коэффициенты излучения и поглощения отличаются:
Различные материалы с различными коэффициентами излучения и поглощения приведены ниже:
Материал Соотношение
Алюминий 0,09 0,03 3,00
Белая краска 0,2 0,92 0,22
Черная краска 0,92 0,89 1,03
Серебряный тефлон 0,08 0,8 0,1
Каптон с алюминиевым покрытием 0,38 0,67 0,56
Эти материалы можно использовать для достижения общего согревающего или охлаждающего эффекта. Отношение больше 1 способствует потеплению, а отношение меньше 1 способствует охлаждению. Некоторые распространенные стратегии:
Используйте серебряный тефлон, чтобы свести к минимуму поглощение солнечного света, но максимально увеличить излучение (например, для зеркал телескопа)
Используйте черную краску для максимальной передачи энергии, как поглощения, так и излучения (внутри)
Используйте металлы (например, алюминий) для минимизации как поглощения, так и излучения (солнцезащитный экран прибора)
Объединяйте эти поверхности, чтобы получить почти все, что захотите
Взаимодействие излучений
Тепловое излучение в космос
Вспомните уравнение Стефана-Больцмана:
Где — температура в градусах Кельвина,
— площадь поверхности, спроецированная в пространство в ,
— постоянная Стефана-Больцмана, а
— коэффициент излучения поверхности, который зависит от длины волны .
Обратите внимание, что коэффициенты излучения для разных длин волн не эквивалентны: . Но также и то, что излучение испускается на всех длинах волн, так как же нам определить, какое значение коэффициента излучения использовать? Мы используем закон Вина, чтобы определить преобладающую длину волны.
Излучение черного тела как функция длины волны при различных температурах. Каждая температурная кривая имеет пик на своей длине волны, и закон Вина описывает сдвиг этого пика. СС BY-SA 3.0. Изображение Курва Планк.
В качестве быстрого примера, для космического корабля с коэффициентом излучения поверхности 0,8, температурой 330K и проекцией площади поверхности 1 тепло, излучаемое в космос, составляет 538 Вт!
Solar Irradiance
Solar Radiation Spectrum.Creative Commons Attribution-Share Alike 3.0 Неперенесенная лицензия. Изображение Роберта А. Роде.
«Солнце излучает свет с распределением, подобным тому, что можно было бы ожидать от черного тела с температурой 5525 К (5250 ° C), что приблизительно соответствует температуре поверхности Солнца. Эти кривые основаны на данных NREL над атмосферой и на уровне моря, которые являются стандартами, принятыми фотоэлектрической промышленностью для обеспечения согласованных условий испытаний и аналогичны свету, который можно ожидать в Северной Америке». [Википедия].
Например, возьмем белую краску, коэффициент излучения которой равен 0,8, а коэффициент поглощения равен 0,4. Приходящая мощность солнечного излучения определяется по формуле:
где площадь, перпендикулярная вектору Солнца, и солнечное излучение вокруг Земли; видите некоторое сходство с уравнением мощности солнечных батарей? Входящая мощность по этим параметрам составляет 26,9 Ватт.
Последнее замечание о влиянии солнечной радиации, выделяющей частицы отложений на поверхности, что увеличивает поглощающую способность, но почти не влияет на излучательную способность.
Спектральное поглощение/излучение некоторых материалов и покрытий. Изображение Кейвана Ниаки.
Альбедо
Использование реального альбедо Земли и потока ИК-излучения Земли для теплового анализа космических аппаратов

Пример ежедневных данных альбедо (CERES). Изображение Ромена Пейру-Логи.
Отраженный солнечный свет от планетарных тел имеет форму альбедо. Альбедо — это доля солнечного излучения, отраженного от поверхности планетарного тела, чаще всего рассчитываемая для Земли. Альбедо зависит от орбиты и положения космического корабля. Значения для Земли колеблются от 0,2 до 0,6. это площадь проекта на Землю.
Иллюстрация эффективного альбедо в любой момент, воспринимаемого космическим кораблем на околоземной орбите. Пейру-Лауга, Ромен. «Использование реального альбедо Земли и потока ИК-излучения Земли для теплового анализа космического корабля». 47-я Международная конференция по экологическим системам, 2017 г. Изображение Ромена Пейру-Лога.
Для расчета результирующего тепла, исходящего от альбедо:
Где R — коэффициент альбедо. Давайте проведем пример расчета, включив в него некоторые примерные значения, где коэффициент поглощения, альбедо и . Результирующее тепло от альбедо составляет 26,9.Вт.
Тепловое излучение Земли
Радиационный баланс Земли – поступающее излучение на Землю должно равняться исходящему излучению. Поглощенное солнечное излучение (коротковолновое) повышает температуру Земли, а испускаемое длинноволновое излучение (тепло) понижает температуру. Изображение UMaine.edu.
Земля не только отражает солнечный свет, но и излучает тепло как источник излучения. Земля поглощает солнечное тепло, а также генерирует собственное тепло из своего динамичного расплавленного ядра. Это тепло излучается ближайшими космическими аппаратами со следующей зависимостью:
Где F — геометрический фактор, называемый коэффициентом обзора. Фактор обзора — это безразмерный коэффициент от 0 до 1, который определяет, какая часть поверхности видна другой поверхности, и является чисто геометрическим свойством [Klobuchar]. Где F — геометрический фактор, называемый коэффициентом обзора, коэффициент излучения Земли, коэффициент поглощения космического корабля в инфракрасном диапазоне. Для взаимодействия между космическим кораблем и Землей метод Nusselt Unit Sphere вычисляет коэффициент обзора между сферой и плоской поверхностью.
Для примера расчета, где высота составляет 500 км, а угол между нормалями к поверхностям областей составляет 90 градусов, коэффициент обзора равен 0,28. Излучательная способность Земли составляет около 1, почти идеально для черного тела. Температура около 255 Кельвинов. Площадь излучения — это площадь космического корабля, перпендикулярная Земле, которую мы будем использовать 1 . Излучательная способность Земли составляет 26,9 Вт.
Тепловое равновесие
При тепловом равновесии количество поступающей тепловой энергии равно ее исходящей. Этот результат вытекает из первого закона термодинамики: «закон сохранения энергии утверждает, что полная энергия изолированной системы постоянна; энергия может быть преобразована из одной формы в другую, но не может быть ни создана, ни уничтожена» [Википедия]. Изменение внутренней энергии замкнутой системы представляет собой разницу количества тепла, поступающего в систему, и количества термодинамической работы, совершаемой системой:
Для космического корабля поступающее тепло представляет собой поглощенную падающую энергию. Уходящее тепло является излучаемой энергией. Работа, выполненная внутри, представляет собой используемую внутреннюю мощность (отрицательная работа в этом смысле – добавляет к общему теплу в системе).
Окружающая среда
Давайте рассмотрим конкретный случай для космического корабля, ориентированного на Землю, чтобы продемонстрировать, как найти равновесную температуру.
Теплообмен между спутником и космической средой. Открытый доступ Abdelkhalek, Hamdy Soltan, et al. «Моделирование и прогнозирование спутниковых датчиков температуры на основе искусственной нейронной сети». Журнал аэрокосмических технологий и менеджмента 11 (2019 г.)).Изображение от Scielo.
Энергия, поступающая в систему, является результатом прямого солнечного излучения, отраженного солнечного света (альбедо), теплового излучения Земли и внутренних источников тепла (таких как электроника и люди):
Энергия, выходящая из системы, единый сток: излучение в космос, которое зависит от температуры поверхности. Уравнение теплового баланса тогда:
Одно уравнение и одно неизвестное приводят к единственному решению. Это уравнение теплового баланса решает равновесную температуру для одного узла, которым является космический корабль. Это решение представляет собой среднюю температуру всего космического корабля и не учитывает разницу температур между различными компонентами внутри космического корабля.
Влияние расстояния на равновесную температуру. Аналогично ENAE 483/788D – Принципы проектирования космических систем Конспекты лекций.
Свойства поверхности
Давайте немного почувствуем, как равновесная температура меняется в зависимости от свойств поверхности, которыми мы можем управлять, таких как геометрия спутника и коэффициент поглощения/излучательной способности. Форма поглощает энергию только через освещенные грани, но форма излучает энергию через всю площадь поверхности. Основное сделанное предположение состоит в том, что черные тела по своей природе изотермические (совершенная и мгновенная проводимость тепла внутрь ко всем граням). Хотя баланс включает в себя эффекты солнца, альбедо, Земли и внутренних компонентов, давайте упростим баланс, включив в него только мощность солнечного света и излучаемую мощность:
Где
И
Новый баланс со всеми переменными включает:
Выделив слева температуру, мы получим: варьироваться, 2) отношение поглощающей способности и излучательной способности, которые мы можем изменить поверхностные покрытия, и 3) отношение освещенной солнцем площади к излучающей площади. Отношение освещенной солнцем площади к излучающей площади для различных геометрий приведено ниже:
Геометрия Поглощающая зона Зона излучения Коэффициент площади
Двусторонняя стенка 1 1 1/2
Сфера 1/4
Цилиндр
Куб 1 6 1/6
Вы заметите, что чем компактнее объем космического корабля, тем меньше отношение площадей, тем ниже равновесная температура.
Влияние формы на температуру черного тела. Аналог ENAE 483/788D – Принципы проектирования космических систем Конспекты лекций.
Внутреннее электроснабжение
Радиатор с прямым оребрением размером 60×60×10 мм с тепловым профилем и закручивающимися анимированными траекториями принудительной конвекции от осевого трубчатого вентилятора, спрогнозированные с помощью пакета анализа CFD. СС BY-SA 3.0. Изображение Изофильм.
До сих пор мы говорили только об идеальных взаимодействиях теплопередачи. Нам нужно включить неидеальные эффекты, которые лучше отражают реальность, такие как выработка энергии внутри космического корабля. Авионика космического корабля будет выделять тепло из-за неэффективного использования или передачи энергии, например, когда ток протекает через резистор в электрической цепи [Renesas]. Космический корабль также может иметь встроенные нагреватели, которые преднамеренно или целенаправленно вырабатывают энергию. Эта генерируемая мощность находится в левой части уравнения как часть тепла, поступающего в систему.
Когда полупроводник проводит ток, на нем возникает ненулевое падение напряжения. Это приводит к потерям, которые почти полностью преобразуются в тепло. Рассмотрим следующую упрощенную структуру типичного варианта использования кремниевой микросхемы IGBT и кремниевой микросхемы диода, смонтированных на корпусе, который крепится к радиатору. Как для IGBT, так и для диода тепловая мощность возникает в переходе, где ее значение наибольшее. Мгновенное значение мощности равно сопротивлению (I x V) IGBT или диода. Тепло проходит через тепловой импеданс конструкции и рассеивается в окружающей среде. Чем ниже тепловой импеданс, тем меньше превышение температуры кремния над окружающей средой. Изображение My Electronic Days.
Чтобы рассчитать приблизительное количество вырабатываемой энергии, измерьте общую мощность, потребляемую электроникой, и умножьте ее на полезный КПД. Потери мощности превращаются в тепло за счет теплопроводности, нагревая компонент:
Где — КПД электронной части, а
— общая мощность, потребляемая электронными компонентами
Для нагревателей это же уравнение можно использовать, установив .

Коэффициент рассеяния тепла, k	Тип помещения
3,0–4,0	Конструкция из дерева или профлиста. Отсутствие теплоизоляции.
2,0–2,9	Упрощенная конструкция. Кирпичные стены одиночной кладки. Стандартное число окон, одинарные рамы. Слабая теплоизоляция кровли.
1,0–1,9	Стандартная конструкция. Кирпичные стены двойной кладки. Мало окон или одинарные рамы. Кровля со стандартной теплоизоляцией.
0,6–0,9	Утепленная конструкция. Кирпичные стены с двухслойной изоляцией. Мало окон, окна с двойными рамами. Толстая основа пола. Кровля с качественной теплоизоляцией.

Материал	к	Материал	к
Алюминий(и)	237	Песок(и)	0,06
Латунь(и)	110	Целлюлоза (ы)	0,039
Медь(и)	398	Стекловата(и)	0,040
Золото (а)	315	Вата (вата)	0,029
Чугун(ы)	55	Овечья шерсть(и)	0,038
Лид(ы)	35,2	Целлюлоза (ы)	0,039
Серебро (ы)	427	Пенополистирол (ы)	0,03
Цинк	113	Древесина (и)	0,13
Полиэтилен (HDPE) (s)	0,5	Ацетон (л)	0,16
Поливинилхлорид (ПВХ)	0,19	Вода (л)	0,58
Плотный кирпич (и)	1,6	Воздух (г)	0,024
Бетон (низкой плотности) (s)	0,2	Аргон (г)	0,016
Бетон (высокой плотности) (s)	1,5	Гелий (г)	0,142
Лед (ы)	2,18	Кислород (г)	0,024
Фарфор(ы)	1,05	Азот (г)	0,024

\( \точка{Q} \)	=	скорость теплопередачи (БТЕ/ч)
А	=	площадь поперечного сечения теплопередачи (фут ² )
Δx	=	толщина плиты (футы)
Δr	=	толщина цилиндрической стенки (футы)
ΔТ	=	разница температур (°F)
к	=	теплопроводность плиты (БТЕ/фут-час-°F)

\(\точка{Q}”\)	=	Тепловой поток (\( \dot{Q}/A \)) (Btu/hr-ft ² )
ΔТ	=	Разница температур (°F)
Р _й	=	Термическое сопротивление (Δx/k) (час-фут ² -°F/Btu)

Л	=	длина трубы (фут)
р _и	=	внутренний радиус трубы (футы)
р _или	=	Внешний радиус трубы (футы)

Материал	Теплопроводность (Вт/м °C)
Материал	При 25°С	При 125 °С	При 225 °С
Железо	80	68	60
Низкоуглеродистая сталь	54	51	47
Нержавеющая сталь	16	17,5	19
Вольфрам	180	160	150
Платина	70	71	72
Алюминий	250	255	250
Золото	310	312	310
Серебро	420	418	415
Медь	401	400	398

Материал	Толщина ‘x’ мм	Электропроводность «k» (Вт/м °C)	Сопротивление R = x/k (Вт/м °C)
Воздух	0,2	0,025	0,008
Конденсат	0,2	0,4	0,000 5
Накипь со стороны пара	0,2	0,5	0,000 4
Стальная трубка	6,0	50,0	0,000 12
Вода	0,05	0,6	0,000 08
Накипь со стороны воды	0,1	0,5	0,000 2

Материал	Толщина ‘x’ мм	Электропроводность ‘k’ (Вт/м°C)	Сопротивление R = ^x /k (м ² °С/Вт)
Воздух	0,2	0,025	0,008
Конденсат	0,2	0,4	0,000 5
Шкала на паровой стороне	0,2	0,5	0,000 4
Медная трубка	6	400	0,000 015
Вода	0,05	0,6	0,000 08
Накипь со стороны воды	0,1	0,5	0,000 2

Материал	Теплопроводность	Использование космического корабля
Алюминий	237[6]	Структура
Медь (чистая)	401[4][12][13]	Электрические интерфейсы и плоскости заземления
Силикатный аэрогель	0,02[4]	Изоляция
Вода	0,5918[15]	Терморегуляция или топливо
Поликарбонат	0,2	Материал печатной платы

Материал	Коэффициент излучения	Использование космического корабля
Алюминий (полированный)	0,039 – 0,057	Структура
Алюминий (анодированный)	0,77	Структура
Аморфный кремний	0,45 – 0,8	Стандартный материал для солнечных элементов
Медь (гальваническая, полированная)	0,03 – 0,06	Электрические интерфейсы и плоскости заземления
Силикатный аэрогель	0,79	Изоляция
Вода	0,95 – 0,96	Терморегуляция или топливо
Поликарбонат	0,90 – 0,97	Материал печатной платы

Материал			Соотношение
Алюминий	0,09	0,03	3,00
Белая краска	0,2	0,92	0,22
Черная краска	0,92	0,89	1,03
Серебряный тефлон	0,08	0,8	0,1
Каптон с алюминиевым покрытием	0,38	0,67	0,56

Геометрия	Поглощающая зона	Зона излучения	Коэффициент площади
Двусторонняя стенка	1	1	1/2
Сфера			1/4
Цилиндр
Куб	1	6	1/6

Тепловой расчет теплообменника

Введение

Основы теплового расчета теплообменных аппаратов

Пример расчета

Выводы

Расчет мощности теплового насоса для дома: методика и формула

Виды тепло насосов

В чем особенность деления тепло насосов

Формула расчета

Методика и значения

Расчет мощности геотермальных насосов

Расчет мощности воздушных насосов

Расчет мощности ТН, использующих вторичное тепло

Как подобрать тепло насос для отопления дома

Молекулярная физика и термодинамика

Правила расчета мощности обогрева трубопроводов

Как рассчитать тепловую мощность воздухонагревателя

Как определить мощность тепловой пушки

Пример расчета мощности воздухонагревателя

расчет теплообменников, методика расчета теплообменников, тепловой расчет теплообменников

Расчет теплообменников и различные методы составления теплового баланса

Механизмы теплопередачи в расчете теплообменников

Конвекционный механизм передачи тепла: расчеты

Коэффициент теплоотдачи в расчете теплообменников

Расчет средней разности температур

Учебное пособие по физике

Площадь

Математическое уравнение

Кондуктивный теплообмен | Инженерная библиотека

Проводка

Прямоугольные координаты проводимости

Метод эквивалентного сопротивления

Электрическая аналогия

Кондуктивные цилиндрические координаты

Проведение:

Теплообмен | Спиракс Сарко

Содержимое

Теплопередача

Способы теплопередачи

Теплопроводность

Пример 2.5.1

Конвекция

Пример 2.5.2

Излучение

Общее уравнение теплопередачи

Общий коэффициент теплопередачи (U)

Разность температур (ΔT)

Средняя разность температур (ΔTM)

Среднеарифметическая разность температур (AMTD):

Среднелогарифмическая разность температур (LMTD):​

Пример 2.

Пример 2.5.4

Барьеры для теплопередачи

Пленочная конденсация

Капельная конденсация

Определение общего коэффициента теплопередачи (значение U)

Теплопередача путем теплопроводности через простую плоскую стенку

Отношение общего сопротивления к общему значению U

Тепловой поток через многослойный барьер

Пример 2.5.5

Механизмы теплопередачи – Энергетическое образование

Меню навигации

Поиск

Теплопроводность

Конвекция

Излучение

Эвапотранспирация

Для дополнительной информации

Ссылки

7.6 Основы теплопередачи – руководство по использованию CubeSat и конструкции шины

Проводка

Излучение

Взаимодействие излучений

Тепловое излучение в космос

Solar Irradiance

Тепловое равновесие

Окружающая среда

Свойства поверхности

Оставить комментарий Отменить ответ

Среднелогарифмическая разность температур (LMTD):