формулы расчетов скорости, высоты и времени падения
Свободное падение тела — это его равнопеременное движение, которое происходит под действием силы тяжести. В этот момент другие силы, которые могут воздействовать на тело либо отсутствуют, либо настолько малы, что их влияние не учитывается. Например, когда парашютист прыгает из самолета, первые несколько секунд после прыжка он падает в свободном состоянии. Этот короткий отрезок времени характеризуется ощущением невесомости, сходным с тедж.м, что испытывают космонавты на борту космического корабля.
Содержание:
- История открытия явления
- Формулы для расчетов
- Интересные факты
- Видео
История открытия явления
О свободном падении тела ученые узнали еще в Средневековье: Альберт Саксонский и Николай Орем изучали это явление, но некоторые их выводы были ошибочными. Например, они утверждали, что скорость падающего тяжелого предмета возрастает прямо пропорционально пройденному расстоянию. В 1545 году поправку этой ошибки сделал испанский ученый Д. Сото, установивший факт, что скорость падающего тела увеличивается пропорционально времени, которое проходит от начала падения этого предмета.
В 1545 году поправку этой ошибки сделал испанский ученый Д. Сото, установивший факт, что скорость падающего тела увеличивается пропорционально времени, которое проходит от начала падения этого предмета.
В 1590 г. итальянский физик Галилео Галилей сформулировал закон, который устанавливает четкую зависимость пройденного падающим предметом пути от времени. Также ученым было доказано, что при отсутствии воздушного сопротивления все предметы на Земле падают с одинаковым ускорением, хотя до его открытия было принято считать, что тяжелые предметы падают быстрее.
Была открыта новая величина — ускорение свободного падения, которое состоит из двух составляющих: гравитационного и центробежного ускорений. Обозначается ускорение свободного падения буквой g и имеет различное значение для разных точек земного шара: от 9,78 м/с2 (показатель для экватора) до 9,83 м/с2 (значение ускорения на полюсах). На точность показателей влияют долгота, широта, время суток и некоторые другие факторы.
Стандартное значение g принято считать равным 9,80665 м/с2. В физических расчетах, которые не требуют соблюдения высокой точности, значение ускорения принимают за 9,81 м/с2. Для облегчения расчетов допускается принимать значение g равным 10 м/с2.
Для того чтобы продемонстрировать, как предмет падает в соответствии с открытием Галилея, ученые устраивают такой опыт: в длинную стеклянную трубку помещают предметы с различной массой, из трубки выкачивают воздух. После этого трубку переворачивают, все предметы под действием силы тяжести падают одновременно на дно трубки, независимо от их массы.
Когда эти же предметы помещены в какую-либо среду, одновременно с силой тяжести на них действует сила сопротивления, поэтому предметы в зависимости от своей массы, формы и плотности будут падать в разное время.
Формулы для расчетов
Существуют формулы, с помощью которых можно рассчитывать различные показатели, связанные со свободным падением. В них используются такие условные обозначения:
В них используются такие условные обозначения:
- u — конечная скорость, с которой перемещается исследуемое тело, м/с;
- h — высота, с которой перемещается исследуемое тело, м;
- t — время перемещения исследуемого тела, с;
- g — ускорение (постоянная величина, равная 9,8 м/с2).
Формула для определения расстояния, пройденного падающим предметом при известной конечной скорости и времени падения: h = ut /2.
Формула для расчета расстояния, пройденного падающим предметом по постоянной величине g и времени: h = gt 2/2.
Формула для определения скорости падающего предмета в конце падения при известном времени падения: u = gt .
Формула для расчета скорости предмета в конце падения, если известна высота, с которой падает исследуемый предмет: u = √2 gh.
Интересные факты
Если не углубляться в научные знания, бытовое определение свободного перемещения подразумевает передвижение какого-либо тела в земной атмосфере, когда на него не воздействуют никакие посторонние факторы, кроме сопротивления окружающего воздуха и силы тяжести.
В различное время добровольцы соревнуются между собой, пытаясь установить личный рекорд. В 1962 г. испытатель-парашютист из СССР Евгений Андреев установил рекорд, который был занесен в Книгу рекордов Гиннеса: при прыжке с парашютом в свободном падении он преодолел расстояние в 24500 м, во время прыжка не был использован тормозной парашют.
В 1960 г. американец Д. Киттингер совершил парашютный прыжок с высоты 31 тыс. м, но с использованием парашютно-тормозной установки.
В 2005 г. была зафиксирована рекордная скорость при свободном падении — 553 км/ч, а через семь лет установлен новый рекорд — эта скорость была увеличена до 1342 км/ч. Этот рекорд принадлежит австрийскому парашютисту Феликсу Баумгартнеру, который известен во всем мире своими опасными трюками.
Видео
Посмотрите интересное и познавательное видео, которое расскажет вам о скорости падения тел.
Обзор формул
Если вы не знакомы с Excel в Интернете, скоро вы обнаружите, что это не просто сетка, в которую вы вводите числа в столбцах или строках. Да, можно использовать Excel в Интернете для поиска итогов по столбцу или строке чисел, но можно также вычислить платеж по кредиту, решить математические или технические задачи или найти оптимальный сценарий на основе переменных чисел, которые вы подключали.
Да, можно использовать Excel в Интернете для поиска итогов по столбцу или строке чисел, но можно также вычислить платеж по кредиту, решить математические или технические задачи или найти оптимальный сценарий на основе переменных чисел, которые вы подключали.
Excel в Интернете делает это с помощью формул в ячейках. Формула выполняет вычисления или другие действия с данными на листе. Формула всегда начинается со знака равенства (=), за которым могут следовать числа, математические операторы (например, знак “плюс” или “минус”) и функции, которые значительно расширяют возможности формулы.
Ниже приведен пример формулы, умножающей 2 на 3 и прибавляющей к результату 5, чтобы получить 11.
=2*3+5
Следующая формула использует функцию ПЛТ для вычисления платежа по ипотеке (1 073,64 долларов США) с 5% ставкой (5% разделить на 12 месяцев равняется ежемесячному проценту) на период в 30 лет (360 месяцев) с займом на сумму 200 000 долларов:
=ПЛТ(0,05/12;360;200000)

-
=A1+A2+A3 Вычисляет сумму значений в ячейках A1, A2 и A3.
-
=КОРЕНЬ(A1) Использует функцию КОРЕНЬ для возврата значения квадратного корня числа в ячейке A1.
=СЕГОДНЯ() Возвращает текущую дату.
-
=ПРОПИСН(“привет”) Преобразует текст “привет” в “ПРИВЕТ” с помощью функции ПРОПИСН.
(“крышка”) применяется для возведения числа в степень, а оператор * (“звездочка”) — для умножения. -
Трехмерные ссылки нельзя использовать в формулах массива.
-
Трехмерные ссылки нельзя использовать вместе с оператор пересечения (один пробел), а также в формулах с неявное пересечение.
-
Вставка или копирование . Если вставить или скопировать листы между листами 2 и 6 (в этом примере это конечные точки), Excel в Интернете содержит все значения в ячейках A2–A5 из добавленных листов в вычислениях.
-
Удаление . При удалении листов между листами 2 и 6 Excel в Интернете удаляет их значения из вычисления.
-
Перемещение .
 При перемещении листов между листами 2 и 6 в расположение за пределами указанного диапазона листов Excel в Интернете удаляет их значения из вычисления.
При перемещении листов между листами 2 и 6 в расположение за пределами указанного диапазона листов Excel в Интернете удаляет их значения из вычисления. -
Перемещение конечного листа . При перемещении листа 2 или листа 6 в другое место в той же книге Excel в Интернете корректирует вычисление в соответствии с новым диапазоном листов между ними.
-
Удаление конечного листа . При удалении sheet2 или Sheet6 Excel в Интернете корректирует вычисление в соответствии с диапазоном листов между ними.
-
Ввода Введите имя, например, в качестве аргумента формулы.
-
<c0>Автозавершение формул</c0>. Используйте раскрывающийся список автозавершения формул, в котором автоматически выводятся допустимые имена.
-
Константы заключены в фигурные скобки ( { } ).
-
Столбцы разделены запятыми (,). Например, чтобы представить значения 10, 20, 30 и 40, введите {10,20,30,40}. Эта константа массива является матрицей размерности 1 на 4 и соответствует ссылке на одну строку и четыре столбца.

-
Значения ячеек из разных строк разделены точками с запятой (;). Например, чтобы представить значения 10, 20, 30, 40 и 50, 60, 70, 80, находящиеся в расположенных друг под другом ячейках, можно создать константу массива с размерностью 2 на 4: {10,20,30,40;50,60,70,80}.
Александр Коновалов
10/10
- 1 Общие сведения
- 2 Работы Ньютона
- 3 Эксперимент Кавендиша
- 4 Измерение гравитационной постоянной
- 5 Материалы по теме
- m1 и m2 — тела, взаимодействующие посредством гравитации
- F1 и F2 – векторы силы гравитационного притяжения, направленные к противоположному телу
- r – расстояние между телами
- G – гравитационная постоянная
G – универсальная гравитационная постоянная G = 6,674 x 10 -11 м 3 кг -1 с -2 .

M – масса тела, измеренная в кг.
R — массовый радиус тела, измеренный в м.
g ускорение свободного падения, определяемое м/с 2 .
Поскольку Земля представляет собой эллипсоид, расстояние от центра точки на поверхности уменьшается с широтой, увеличивая g.
Вращение планеты создает антигравитационный центробежный эффект, который максимален на экваторе и равен нулю на полюсах.
Высота над уровнем моря
- Что такое ускорение под действием силы тяжести?
- Формула ускорения свободного падения
- Как рассчитать ускорение свободного падения на Земле
- Как использовать калькулятор ускорения свободного падения
- Другие подобные калькуляторы
- Часто задаваемые вопросы
Введите массу Земли как 5,972 e24.
Введите радиус Земли как 6371 км или 6371000 м.
Инструмент рассчитает модуль ускорения силы тяжести на поверхности Земли как 9,8 м/с 2 .
- Калькулятор гравитационной силы;
- Калькулятор ускорения с использованием силы и массы; и Калькулятор перегрузки
- .

Возьмите квадрат радиуса Марса (3390 км или 3,390 × 10⁶ м). Вы получите 1,1492 × 10¹³ м².
Разделите массу Марса (6,4185 x 10²³ кг) на квадрат его радиуса в метрах.
Умножьте результат на G , то есть на постоянную всемирного тяготения.
Вы получите значение ускорения свободного падения на Марсе, то есть 3,7 м/с² .
Разделите массу Луны (7,346 x 10²² кг) на квадрат ее радиуса (1737,4 км).

Умножьте на результат шага 1 на 6,674×10⁻¹¹ м³/кг с², т. е. на значение G.
Поздравляем! Вы рассчитали ускорение под действием силы тяжести на поверхности Луны как 1,6 м/с² .
- Вес самолета:
- силы на модели ракеты:
- Домашняя страница руководства для начинающих
- 4 403344 403344 403344 403344 403344 403344 403344 403344 403344 403344 FIR
- 4 FIS
- 4 FIS 44 FIS344 FIS344 Fi G /M
- The force of attraction between any two unit masses separated by a unit distance is called the Universal Gravitational Constant denoted by G measured in Nm 2 /кг 2 .
- Это эмпирическая физическая константа, используемая в гравитационной физике. Ее также называют постоянной Ньютона .
- Повсюду в космосе гравитационная постоянная имеет то же значение .
- G — это не то же самое, что g, так как последнее представляет ускорение под действием силы тяжести.
- Единица F → Ньютон(Н)
- Единица массы → кг
- Единица R → м
- Единица G → Нм ² кг ²
- Значение гравитационной постоянной остается неизменным на Луне, Марсе или где-либо еще во Вселенной, что делает его инвариантным объектом.
- Согласно общей гипотезе Большого Взрыва и некоторым астрономам, по мере расширения Вселенной значение G в конечном итоге будет уменьшаться. . Вот некоторые из методов измерения гравитационной постоянной –
- В первом методе исследователи создали пластину с металлическим покрытием из кремнезема , которая была подвешена в воздухе на проволоке.
 Гравитационное притяжение обеспечивают два стальных шарика . Сила тяжести была рассчитана путем определения того, насколько сильно скручена проволока .
Гравитационное притяжение обеспечивают два стальных шарика . Сила тяжести была рассчитана путем определения того, насколько сильно скручена проволока . - Второй метод был идентичен первому, но пластина подвешивалась к вращающемуся поворотному столу , который удерживал провод на месте. Гравитационная сила была измерена с использованием этого подхода путем наблюдения за вращением поворотного стола . Используя сейсмические характеристики в обоих методах, исследователи смогли избежать влияния окружающих объектов и возмущений.
- гравитационная сила 903:45 между двумя планетами можно точно определить.
- Его можно использовать для определения гравитационной силы для объектов вблизи земли , таких как спутники .

- Солнечные и лунные затмения также можно предсказать с помощью этой гравитационной постоянной.
- Значение G полезно при расчете траекторий астрономических тел и их движения .
- Ускорение измеряется в метрах в секунду в квадрате (м/с 2 ) в единицах СИ или равным образом в ньютонов на килограмм (Н/кг или Н.кг -1 ).
- гравитационное ускорение вблизи поверхности Земли составляет примерно 9,81 м/с 2 .

- Скорость свободно падающего объекта будет увеличиваться на 9,81 метра в секунду каждый раз .
- Ускорение свободного падения обозначается ‘g ’.
- Гравитационная постоянная — это эмпирическая физическая постоянная , используемая в законе универсальной постоянной Ньютона для расчета гравитационных эффектов.

- Значение g или значение гравитационной постоянной в любой точке этой вселенной. G = 6,67408×10 -11 Н·м 2 /кг 2 .
- Размерная формула для гравитационной постоянной [L] 3 [M] -1 [T] -2
- The SI unit of gravitational constant is Nm 2 / kg 2
- What should be the radius for earth стать черной дырой? [NEET 2014]
- Соотношение периодов времени планет. [NEET 1994]
- Рассчитайте отношение скоростей убегания, если радиус планеты удвоится. [НЕТ 2013]
- Какая минимальная скорость проецирования. [NEET 2013]
- Сортировка кинетической энергии планеты в разных положениях.
 [NEET 2018]
[NEET 2018] - Минимальное значение скорости, при котором частица не может вернуться. [NEET 2011]
- Скорость частицы для высоты, равной радиусу. [NEET 2001]
- Рассчитайте радиус геостационарного спутника. [NEET 1992]
- Скорость убегания при изменении массы и радиуса Земли. [НЕТ 1997]
- Вычислите расстояние двух планет от Солнца. [NEET 1997]
- Убегающая скорость планеты с половиной радиуса Земли. [NEET 2000]
- Для чего требуется гравитационная сила? [NEET 2000]
- Гравитационная сила, действующая на тело на поверхности земли. [NEET 2000]
- Сколько будет весить тело в центре Земли. [NEET 2019]
- Величина гравитационного потенциала. [NEET 2011]
- Найдите коэффициент линейной скорости. [NEET 2011]
- Найдите ускорение спутника.
 [NEET 1994]
[NEET 1994] - Изменение потенциальной энергии объекта на высоте от поверхности земли. [NEET 2019]
- Рассчитайте орбитальную скорость. [NEET 1994]
- Выберите правильную гравитационную постоянную. [NEET 2018]
- масса=плотность×объем (m=ρV) . Плотность — это мера массы на единицу объема, поэтому массу объекта можно определить, умножив плотность на объем.
- масса=сила÷ускорение (m=F/a) . Согласно второму закону Ньютона (F=ma), ускорение тела прямо пропорционально приложенной к нему силе. Следовательно, величина ускорения, сопровождающего приложение постоянной силы, обратно пропорциональна массе.
- масса=вес÷ускорение свободного падения (м=Вт/г). Вес есть произведение ускорения массы в гравитационном поле.
 В зависимости от силы гравитационного ускорения вес будет разным.
В зависимости от силы гравитационного ускорения вес будет разным.
Использование констант в формулах
Константа представляет собой готовое (не вычисляемое) значение, которое всегда остается неизменным. Например, дата 09.10.2008, число 210 и текст «Прибыль за квартал» являются константами. выражение или его значение константами не являются. Если формула в ячейке содержит константы, но не ссылки на другие ячейки (например, имеет вид =30+70+110), значение в такой ячейке изменяется только после изменения формулы.
Использование операторов в формулах
Операторы определяют операции, которые необходимо выполнить над элементами формулы. Вычисления выполняются в стандартном порядке (соответствующем основным правилам арифметики), однако его можно изменить с помощью скобок.
Типы операторов
Приложение Microsoft Excel поддерживает четыре типа операторов: арифметические, текстовые, операторы сравнения и операторы ссылок.
Арифметические операторы
Арифметические операторы служат для выполнения базовых арифметических операций, таких как сложение, вычитание, умножение, деление или объединение чисел. Результатом операций являются числа. Арифметические операторы приведены ниже.
|
Арифметический оператор |
Значение |
Пример |
|
+ (знак «плюс») |
Сложение |
3+3 |
|
– (знак «минус») |
Вычитание |
3–1 |
|
|
Умножение |
3*3 |
|
/ (косая черта) |
Деление |
3/3 |
|
|
Доля |
20% |
|
^ (крышка) |
Возведение в степень |
3^2 |
Операторы сравнения
Операторы сравнения используются для сравнения двух значений. Результатом сравнения является логическое значение: ИСТИНА либо ЛОЖЬ.
Результатом сравнения является логическое значение: ИСТИНА либо ЛОЖЬ.
|
Оператор сравнения |
Значение |
Пример |
|
= (знак равенства) |
Равно |
A1=B1 |
|
> (знак «больше») |
Больше |
A1>B1 |
|
< (знак «меньше») |
Меньше |
A1<B1 |
|
>= (знак «больше или равно») |
Больше или равно |
A1>=B1 |
|
<= (знак «меньше или равно») |
Меньше или равно |
A1<=B1 |
|
<> (знак «не равно») |
Не равно |
A1<>B1 |
Текстовый оператор конкатенации
Амперсанд (&) используется для объединения (соединения) одной или нескольких текстовых строк в одну.
|
Текстовый оператор |
Значение |
Пример |
|
& (амперсанд) |
Соединение или объединение последовательностей знаков в одну последовательность |
Выражение «Северный»&«ветер» дает результат «Северный ветер». |
Операторы ссылок
Для определения ссылок на диапазоны ячеек можно использовать операторы, указанные ниже.
|
Оператор ссылки |
Значение |
Пример |
|
: (двоеточие) |
Оператор диапазона, который образует одну ссылку на все ячейки, находящиеся между первой и последней ячейками диапазона, включая эти ячейки. |
B5:B15 |
|
; (точка с запятой) |
Оператор объединения. Объединяет несколько ссылок в одну ссылку. |
СУММ(B5:B15,D5:D15) |
|
(пробел) |
Оператор пересечения множеств, используется для ссылки на общие ячейки двух диапазонов. |
B7:D7 C6:C8 |
Порядок выполнения Excel в Интернете в формулах
В некоторых случаях порядок вычисления может повлиять на возвращаемое формулой значение, поэтому для получения нужных результатов важно понимать стандартный порядок вычислений и знать, как можно его изменить.
Порядок вычислений
Формулы вычисляют значения в определенном порядке. Формула всегда начинается со знака равенства (=). Excel в Интернете интерпретирует символы, которые следуют знаку равенства, как формулу. После знака равенства вычисляются элементы (операнды), такие как константы или ссылки на ячейки. Они разделяются операторами вычислений. Excel в Интернете вычисляет формулу слева направо в соответствии с определенным порядком для каждого оператора в формуле.
Приоритет операторов
Если объединить несколько операторов в одну формулу, Excel в Интернете выполняет операции в порядке, показанном в следующей таблице. Если формула содержит операторы с одинаковым приоритетом (например, если формула содержит оператор умножения и деления), Excel в Интернете вычисляет операторы слева направо.
|
Оператор |
Описание |
|
: (двоеточие) (один пробел) , (запятая) |
Операторы ссылок |
|
– |
Знак «минус» |
|
% |
Процент |
|
^ |
Возведение в степень |
|
* и / |
Умножение и деление |
|
+ и – |
Сложение и вычитание |
|
& |
Объединение двух текстовых строк в одну |
|
= |
Сравнение |
Использование круглых скобок
Чтобы изменить порядок вычисления формулы, заключите ее часть, которая должна быть выполнена первой, в скобки. Например, приведенная ниже формула возвращает значение 11, так как Excel в Интернете выполняет умножение перед добавлением. В этой формуле число 2 умножается на 3, а затем к результату прибавляется число 5.
Например, приведенная ниже формула возвращает значение 11, так как Excel в Интернете выполняет умножение перед добавлением. В этой формуле число 2 умножается на 3, а затем к результату прибавляется число 5.
=5+2*3
В отличие от этого, если для изменения синтаксиса используются круглые скобки, Excel в Интернете 5 и 2, а затем умножает результат на 3, чтобы получить 21.
=(5+2)*3
В следующем примере скобки, которые заключают первую часть формулы, принудительно Excel в Интернете сначала вычислить B4+25, а затем разделить результат на сумму значений в ячейках D5, E5 и F5.
=(B4+25)/СУММ(D5:F5)
Использование функций и вложенных функций в формулах
Функции — это заранее определенные формулы, которые выполняют вычисления по заданным величинам, называемым аргументами, и в указанном порядке. Эти функции позволяют выполнять как простые, так и сложные вычисления.
Эти функции позволяют выполнять как простые, так и сложные вычисления.
Синтаксис функций
Приведенный ниже пример функции ОКРУГЛ, округляющей число в ячейке A10, демонстрирует синтаксис функции.
1. Структура. Структура функции начинается со знака равенства (=), за которым следует имя функции, открывающая скобка, аргументы функции, разделенные запятыми, и закрывающая скобка.
2. Имя функции. Чтобы отобразить список доступных функций, щелкните любую ячейку и нажмите клавиши SHIFT+F3.
3. Аргументы. Существуют различные типы аргументов: числа, текст, логические значения (ИСТИНА и ЛОЖЬ), массивы, значения ошибок (например #Н/Д) или ссылки на ячейки. Используемый аргумент должен возвращать значение, допустимое для данного аргумента. В качестве аргументов также используются константы, формулы и другие функции.
4. Всплывающая подсказка аргумента. При вводе функции появляется всплывающая подсказка с синтаксисом и аргументами. Например, всплывающая подсказка появляется после ввода выражения =ОКРУГЛ(. Всплывающие подсказки отображаются только для встроенных функций.
Всплывающая подсказка аргумента. При вводе функции появляется всплывающая подсказка с синтаксисом и аргументами. Например, всплывающая подсказка появляется после ввода выражения =ОКРУГЛ(. Всплывающие подсказки отображаются только для встроенных функций.
Ввод функций
Диалоговое окно Вставить функцию упрощает ввод функций при создании формул, в которых они содержатся. При вводе функции в формулу в диалоговом окне Вставить функцию отображаются имя функции, все ее аргументы, описание функции и каждого из аргументов, текущий результат функции и всей формулы.
Чтобы упростить создание и редактирование формул и свести к минимуму количество опечаток и синтаксических ошибок, пользуйтесь автозавершением формул. После ввода знака = (знак равенства) и начальных букв или триггера отображения Excel в Интернете под ячейкой отображается динамический раскрывающийся список допустимых функций, аргументов и имен, соответствующих буквам или триггеру. После этого элемент из раскрывающегося списка можно вставить в формулу.
После этого элемент из раскрывающегося списка можно вставить в формулу.
Вложенные функции
В некоторых случаях может потребоваться использовать функцию в качестве одного из аргументов другой функции. Например, в приведенной ниже формуле для сравнения результата со значением 50 используется вложенная функция СРЗНАЧ.
1. Функции СРЗНАЧ и СУММ вложены в функцию ЕСЛИ.
Допустимые типы вычисляемых значений Вложенная функция, используемая в качестве аргумента, должна возвращать соответствующий ему тип данных. Например, если аргумент должен быть логическим, т. е. Если это не так, Excel в Интернете отображает #VALUE! В противном случае TE102825393 выдаст ошибку «#ЗНАЧ!».
<c0>Предельное количество уровней вложенности функций</c0>. В формулах можно использовать до семи уровней вложенных функций. Если функция Б является аргументом функции А, функция Б находится на втором уровне вложенности. Например, в приведенном выше примере функции СРЗНАЧ и СУММ являются функциями второго уровня, поскольку обе они являются аргументами функции ЕСЛИ. Функция, вложенная в качестве аргумента в функцию СРЗНАЧ, будет функцией третьего уровня, и т. д.
В формулах можно использовать до семи уровней вложенных функций. Если функция Б является аргументом функции А, функция Б находится на втором уровне вложенности. Например, в приведенном выше примере функции СРЗНАЧ и СУММ являются функциями второго уровня, поскольку обе они являются аргументами функции ЕСЛИ. Функция, вложенная в качестве аргумента в функцию СРЗНАЧ, будет функцией третьего уровня, и т. д.
Использование ссылок в формулах
Ссылка определяет ячейку или диапазон ячеек на листе и сообщает Excel в Интернете где искать значения или данные, которые нужно использовать в формуле. С помощью ссылок можно использовать в одной формуле данные, находящиеся в разных частях листа, а также использовать значение одной ячейки в нескольких формулах. Вы также можете задавать ссылки на ячейки разных листов одной книги либо на ячейки из других книг. Ссылки на ячейки других книг называются связями или внешними ссылками.
Стиль ссылок A1
Стиль ссылок по умолчанию По умолчанию в Excel в Интернете используется ссылочный стиль A1, который ссылается на столбцы с буквами (A–XFD, всего 16 384 столбца) и ссылается на строки с числами (от 1 до 1 048 576). Эти буквы и номера называются заголовками строк и столбцов. Для ссылки на ячейку введите букву столбца, и затем — номер строки. Например, ссылка B2 указывает на ячейку, расположенную на пересечении столбца B и строки 2.
|
Ячейка или диапазон |
Использование |
|
Ячейка на пересечении столбца A и строки 10 |
A10 |
|
Диапазон ячеек: столбец А, строки 10-20. |
A10:A20 |
|
Диапазон ячеек: строка 15, столбцы B-E |
B15:E15 |
|
Все ячейки в строке 5 |
5:5 |
|
Все ячейки в строках с 5 по 10 |
5:10 |
|
Все ячейки в столбце H |
H:H |
|
Все ячейки в столбцах с H по J |
H:J |
|
Диапазон ячеек: столбцы А-E, строки 10-20 |
A10:E20 |
<c0>Ссылка на другой лист</c0>. В приведенном ниже примере функция СРЗНАЧ используется для расчета среднего значения диапазона B1:B10 на листе «Маркетинг» той же книги.
В приведенном ниже примере функция СРЗНАЧ используется для расчета среднего значения диапазона B1:B10 на листе «Маркетинг» той же книги.
1. Ссылка на лист «Маркетинг».
2. Ссылка на диапазон ячеек с B1 по B10 включительно.
3. Ссылка на лист, отделенная от ссылки на диапазон значений.
Различия между абсолютными, относительными и смешанными ссылками
Относительные ссылки . Относительная ссылка в формуле, например A1, основана на относительной позиции ячейки, содержащей формулу, и ячейки, на которую указывает ссылка. При изменении позиции ячейки, содержащей формулу, изменяется и ссылка. При копировании или заполнении формулы вдоль строк и вдоль столбцов ссылка автоматически корректируется. По умолчанию в новых формулах используются относительные ссылки. Например, при копировании или заполнении относительной ссылки из ячейки B2 в ячейку B3 она автоматически изменяется с =A1 на =A2.
Абсолютные ссылки . Абсолютная ссылка на ячейку в формуле, например $A$1, всегда ссылается на ячейку, расположенную в определенном месте. При изменении позиции ячейки, содержащей формулу, абсолютная ссылка не изменяется. При копировании или заполнении формулы по строкам и столбцам абсолютная ссылка не корректируется. По умолчанию в новых формулах используются относительные ссылки, а для использования абсолютных ссылок надо активировать соответствующий параметр. Например, при копировании или заполнении абсолютной ссылки из ячейки B2 в ячейку B3 она остается прежней в обеих ячейках: =$A$1.
Смешанные ссылки . Смешанная ссылка содержит либо абсолютный столбец и относительную строку, либо абсолютную строку и относительный столбец. Абсолютная ссылка на столбец имеет вид $A1, $B1 и т. д. Абсолютная ссылка на строку имеет вид A$1, B$1 и т. д. Если положение ячейки с формулой изменяется, относительная ссылка меняется, а абсолютная — нет.
Стиль трехмерных ссылок
Удобный способ для ссылки на несколько листов . Трехмерные ссылки используются для анализа данных из одной и той же ячейки или диапазона ячеек на нескольких листах одной книги. Трехмерная ссылка содержит ссылку на ячейку или диапазон, перед которой указываются имена листов. Excel в Интернете использует все листы, хранящиеся между начальным и конечным именами ссылки. Например, формула =СУММ(Лист2:Лист13!B5) суммирует все значения, содержащиеся в ячейке B5 на всех листах в диапазоне от Лист2 до Лист13 включительно.
- org/ListItem”>
При помощи трехмерных ссылок можно создавать ссылки на ячейки на других листах, определять имена и создавать формулы с использованием следующих функций: СУММ, СРЗНАЧ, СРЗНАЧА, СЧЁТ, СЧЁТЗ, МАКС, МАКСА, МИН, МИНА, ПРОИЗВЕД, СТАНДОТКЛОН.Г, СТАНДОТКЛОН.В, СТАНДОТКЛОНА, СТАНДОТКЛОНПА, ДИСПР, ДИСП.В, ДИСПА и ДИСППА.
Что происходит при перемещении, копировании, вставке или удалении листов . Нижеследующие примеры поясняют, какие изменения происходят в трехмерных ссылках при перемещении, копировании, вставке и удалении листов, на которые такие ссылки указывают. В примерах используется формула =СУММ(Лист2:Лист6!A2:A5) для суммирования значений в ячейках с A2 по A5 на листах со второго по шестой.
В примерах используется формула =СУММ(Лист2:Лист6!A2:A5) для суммирования значений в ячейках с A2 по A5 на листах со второго по шестой.
Стиль ссылок R1C1
Можно использовать такой стиль ссылок, при котором нумеруются и строки, и столбцы. Стиль ссылок R1C1 удобен для вычисления положения столбцов и строк в макросах. В стиле R1C1 Excel в Интернете указывает расположение ячейки с “R”, за которым следует номер строки и “C”, за которым следует номер столбца.
Стиль ссылок R1C1 удобен для вычисления положения столбцов и строк в макросах. В стиле R1C1 Excel в Интернете указывает расположение ячейки с “R”, за которым следует номер строки и “C”, за которым следует номер столбца.
|
Ссылка |
Значение |
|
R[-2]C |
относительная ссылка на ячейку, расположенную на две строки выше в том же столбце |
|
R[2]C[2] |
Относительная ссылка на ячейку, расположенную на две строки ниже и на два столбца правее |
|
R2C2 |
Абсолютная ссылка на ячейку, расположенную во второй строке второго столбца |
|
R[-1] |
Относительная ссылка на строку, расположенную выше текущей ячейки |
|
R |
Абсолютная ссылка на текущую строку |
При записи макроса Excel в Интернете некоторые команды с помощью ссылочного стиля R1C1. Например, если вы записываете команду, например нажатие кнопки “ Автосчет”, чтобы вставить формулу, которая добавляет диапазон ячеек, Excel в Интернете формулу с помощью стиля R1C1, а не стиля A1, ссылок.
Например, если вы записываете команду, например нажатие кнопки “ Автосчет”, чтобы вставить формулу, которая добавляет диапазон ячеек, Excel в Интернете формулу с помощью стиля R1C1, а не стиля A1, ссылок.
Использование имен в формулах
Можно создать определенные имена для представления ячеек, диапазонов ячеек, формул, констант или Excel в Интернете таблиц. Имя — это значимое краткое обозначение, поясняющее предназначение ссылки на ячейку, константы, формулы или таблицы, так как понять их суть с первого взгляда бывает непросто. Ниже приведены примеры имен и показано, как их использование упрощает понимание формул.
|
Тип примера |
Пример использования диапазонов вместо имен |
Пример с использованием имен |
|
Ссылка |
=СУММ(A16:A20) |
=СУММ(Продажи) |
|
Константа |
=ПРОИЗВЕД(A12,9. |
=ПРОИЗВЕД(Цена,НСП) |
|
Формула |
=ТЕКСТ(ВПР(MAX(A16,A20),A16:B20,2,FALSE),”дд.мм.гггг”) |
=ТЕКСТ(ВПР(МАКС(Продажи),ИнформацияОПродажах,2,ЛОЖЬ),”дд.мм.гггг”) |
|
Таблица |
A22:B25 |
=ПРОИЗВЕД(Price,Table1[@Tax Rate]) |
Типы имен
Существует несколько типов имен, которые можно создавать и использовать.
Определенное имя Имя, используемое для представления ячейки, диапазона ячеек, формулы или константы. Вы можете создавать собственные определенные имена. Кроме того, Excel в Интернете иногда создает определенное имя, например при настройке области печати.
Имя таблицы Имя таблицы Excel в Интернете, которая представляет собой коллекцию данных об определенной теме, которая хранится в записях (строках) и полях (столбцах). Excel в Интернете создает имя таблицы Excel в Интернете “Table1”, “Table2” и т. д. при каждой вставке таблицы Excel в Интернете, но вы можете изменить эти имена, чтобы сделать их более значимыми.
Создание и ввод имен
Имя создается с помощью команды “Создать имя” из выделенного фрагмента. Можно удобно создавать имена из существующих имен строк и столбцов с помощью фрагмента, выделенного на листе.
Примечание: По умолчанию в именах используются абсолютные ссылки на ячейки.
Имя можно ввести указанными ниже способами.
Использование формул массива и констант массива
Excel в Интернете не поддерживает создание формул массива. Вы можете просматривать результаты формул массива, созданных в классическом приложении Excel, но не сможете изменить или пересчитать их. Если на вашем компьютере установлено классическое приложение Excel, нажмите кнопку Открыть в Excel, чтобы перейти к работе с массивами.
Если на вашем компьютере установлено классическое приложение Excel, нажмите кнопку Открыть в Excel, чтобы перейти к работе с массивами.
В примере формулы массива ниже вычисляется итоговое значение цен на акции; строки ячеек не используются при вычислении и отображении отдельных значений для каждой акции.
При вводе формулы «={СУММ(B2:D2*B3:D3)}» в качестве формулы массива сначала вычисляется значение «Акции» и «Цена» для каждой биржи, а затем — сумма всех результатов.
<c0>Вычисление нескольких значений</c0>. Некоторые функции возвращают массивы значений или требуют массив значений в качестве аргумента. Для вычисления нескольких значений с помощью формулы массива необходимо ввести массив в диапазон ячеек, состоящий из того же числа строк или столбцов, что и аргументы массива.
Например, по заданному ряду из трех значений продаж (в столбце B) для трех месяцев (в столбце A) функция ТЕНДЕНЦИЯ определяет продолжение линейного ряда объемов продаж. Чтобы можно было отобразить все результаты формулы, она вводится в три ячейки столбца C (C1:C3).
Чтобы можно было отобразить все результаты формулы, она вводится в три ячейки столбца C (C1:C3).
Формула «=ТЕНДЕНЦИЯ(B1:B3;A1:A3)», введенная как формула массива, возвращает три значения (22 196, 17 079 и 11 962), вычисленные по трем объемам продаж за три месяца.
Использование констант массива
В обычную формулу можно ввести ссылку на ячейку со значением или на само значение, также называемое константой. Подобным образом в формулу массива можно ввести ссылку на массив либо массив значений, содержащихся в ячейках (его иногда называют константой массива). Формулы массива принимают константы так же, как и другие формулы, однако константы массива необходимо вводить в определенном формате.
Константы массива могут содержать числа, текст, логические значения, например ИСТИНА или ЛОЖЬ, либо значения ошибок, такие как «#Н/Д». В одной константе массива могут присутствовать значения различных типов, например {1,3,4;ИСТИНА,ЛОЖЬ,ИСТИНА}. Числа в константах массива могут быть целыми, десятичными или иметь экспоненциальный формат. Текст должен быть заключен в двойные кавычки, например «Вторник».
Числа в константах массива могут быть целыми, десятичными или иметь экспоненциальный формат. Текст должен быть заключен в двойные кавычки, например «Вторник».
Константы массива не могут содержать ссылки на ячейку, столбцы или строки разной длины, формулы и специальные знаки: $ (знак доллара), круглые скобки или % (знак процента).
При форматировании констант массива убедитесь, что выполняются указанные ниже требования.
ПАДЕНИЕ ТЕЛА • Большая российская энциклопедия
Авторы: А. В. Гуденко
ПАДЕ́НИЕ ТЕ́ЛА, движение тела, вызванное гравитационным притяжением Земли, без начальной скорости тела относительно Земли. Падают, напр., камень со скалы, капли дождя из облака, листья с деревьев. Протяжённое тело может упасть из-за потери устойчивости, продолжая взаимодействовать с опорой в процессе падения. Так, в частности, падает дерево в лесу, человек на скользкой дороге.
П. т. под действием только силы тяжести называется свободным падением. На рубеже 16–17 вв. Г. Галилей установил, что при отсутствии сопротивления воздуха тела разной массы падают с одинаковой высоты за одно и то же время. Позднее И. Ньютон доказал, что ускорение, приобретаемое телом в гравитац. поле, не зависит от массы тела.
Пренебрегая вращением Земли и её несферичностью, можно считать, что центр тяжести свободно падающего тела движется с ускорением свободного падения $\boldsymbol g$ по прямой, направленной к центру Земли. При свободном П. т. с высоты $h$, малой по сравнению с радиусом Земли (напр., при падении сосульки с крыши), можно пренебречь зависимостью $g$ от расстояния до центра Земли и считать движение равноускоренным. Тогда время П. т. $t=\sqrt{2h/g_0}$, а конечная скорость $v=\sqrt{2g_0 h}$, где $g_0$ – ускорение свободного падения у поверхности Земли. 2$, где $R$ – радиус Земли. Скорость, которую приобретает тело при падении с такой высоты, $v=\sqrt{2g_0Rh/(R+h)}$. В соответствии с этой формулой при входе в плотные слои атмосферы тело, падающее на Землю с высоты $h=R$, будет иметь скорость, близкую к первой космич. скорости $v_1=\sqrt{g_0R}≈7,9$ км/с, а при падении с высоты $h≫R$ – ко второй космич. скорости $v_2=\sqrt{2g_0R}≈11,2$ км/с.
2$, где $R$ – радиус Земли. Скорость, которую приобретает тело при падении с такой высоты, $v=\sqrt{2g_0Rh/(R+h)}$. В соответствии с этой формулой при входе в плотные слои атмосферы тело, падающее на Землю с высоты $h=R$, будет иметь скорость, близкую к первой космич. скорости $v_1=\sqrt{g_0R}≈7,9$ км/с, а при падении с высоты $h≫R$ – ко второй космич. скорости $v_2=\sqrt{2g_0R}≈11,2$ км/с.
П. т. в воздухе определяется не только гравитац. силой, но и силой сопротивления воздуха, зависящей от плотности воздуха, скорости движения, формы и размеров тела. Напр., падение капель дождя нельзя считать свободным: сила сопротивления воздуха оказывается значительной из-за большой скорости движения капель. Это приводит к тому, что у поверхности Земли дождевые капли падают практически с постоянной скоростью, зависящей от размеров капель и составляющей ок. 10 м/с. 2 φ$ . Кориолиса сила приводит к дополнит. отклонению свободно падающего тела к востоку от вертикали (т. е. от направления вектора $\boldsymbol g$). Величина этого отклонения $S_{вост}$ в первом приближении составляет: $$S_{вост}=(2/3)\omega\sqrt{2h/g_0}h\cos \varphi.$$ Этот эффект невелик, однако его удалось с уверенностью наблюдать уже в сер. 19 в. в опытах с падением тел в глубокие шахты. Для широты Москвы при свободном падении тела с высоты Останкинской телевизионной башни отклонение к востоку составляет ок. 14 см.
2 φ$ . Кориолиса сила приводит к дополнит. отклонению свободно падающего тела к востоку от вертикали (т. е. от направления вектора $\boldsymbol g$). Величина этого отклонения $S_{вост}$ в первом приближении составляет: $$S_{вост}=(2/3)\omega\sqrt{2h/g_0}h\cos \varphi.$$ Этот эффект невелик, однако его удалось с уверенностью наблюдать уже в сер. 19 в. в опытах с падением тел в глубокие шахты. Для широты Москвы при свободном падении тела с высоты Останкинской телевизионной башни отклонение к востоку составляет ок. 14 см.
Падение (опрокидывание) протяжённого тела, находящегося на опоре, происходит, если вертикальная линия, проходящая через центр тяжести тела, не пересекает площадь опоры. В этом случае тело падает, поворачиваясь вокруг своего основания. При таком П. т. конечная скорость верхней части протяжённого тела высотой $h$ превышает скорость небольшого тела, упавшего с высоты $h$. Напр., при падении фабричной трубы высотой $h$ конечная скорость, приобретаемая вершиной трубы, составляет $v=\sqrt{3gh}$. Примером равновесия тела на опоре может служить «падающая» башня в Пизе. Башня имеет форму цилиндра высотой 55 м и радиусом 7 м. У своей вершины башня отклонена от вертикали на 4,5 м, а линия действия силы тяжести проходит на расстоянии 2,3 м от центра её основания. Наклон башни постепенно увеличивается. Расчёты показывают, что равновесие нарушится и башня упадёт, когда отклонение её вершины от вертикали достигнет 14 м.
Напр., при падении фабричной трубы высотой $h$ конечная скорость, приобретаемая вершиной трубы, составляет $v=\sqrt{3gh}$. Примером равновесия тела на опоре может служить «падающая» башня в Пизе. Башня имеет форму цилиндра высотой 55 м и радиусом 7 м. У своей вершины башня отклонена от вертикали на 4,5 м, а линия действия силы тяжести проходит на расстоянии 2,3 м от центра её основания. Наклон башни постепенно увеличивается. Расчёты показывают, что равновесие нарушится и башня упадёт, когда отклонение её вершины от вертикали достигнет 14 м.
Сила тяжести – формула, определение, обозначение
4.6
Средняя оценка: 4.6
Всего получено оценок: 93.
4.6
Средняя оценка: 4.6
Всего получено оценок: 93.
Большинство задач классической механики рассматриваются в поле тяготения Земли, поэтому определение силы тяжести, действующей на тело в этом поле – необходимость.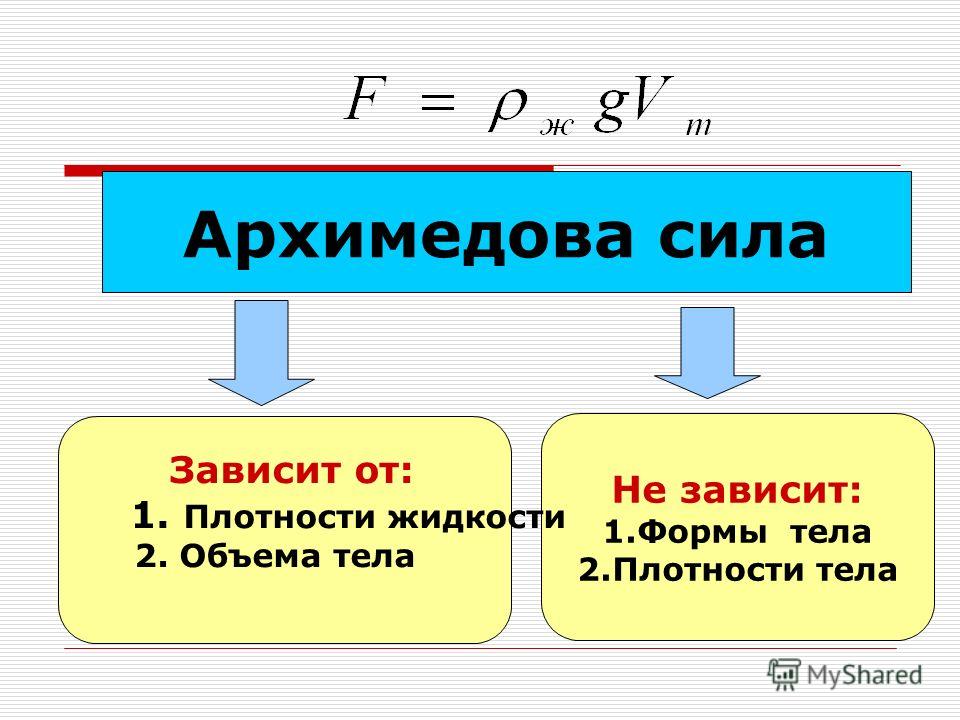 3} \vec r$ – (2)
3} \vec r$ – (2)
Из формулы (2) видно, что ускорение тела не зависит от его массы. Ему дали название – ускорение свободного падения, и ввели специальное обозначение – g.
Величину $\varphi = \gamma {m \over r}$ – называют потенциалом поля тяжести объекта массой m. Геометрическое место точек, удаленное от объекта на расстояние r – сфера, значение потенциала на любой ее точке одно и тоже. Такую поверхность называют эквипотенциальной. Потенциал, умноженный на массу тела, помещенного в гравитационное поле объекта, называют потенциальной энергией тела в поле объекта.
Рис. 2. Эквипотенциальная поверхность.Сила притяжения земли
Если в формулу (2) подставить значения массы Земли и ее радиуса, то получим ускорение свободного падения на Земле. В силу того, что наша планеты приплюснута с боков, то значение g будет наибольшим на полюсах и наименьшим на экваторе. Влияет также и вращение планеты вокруг собственной оси, что создает инерциальные силы. В целом g принимают равным 9,8 м/с2, что является средним значением на поверхности Земли. 2} = 15,6 Н$ – сила тяжести, действующая на космонавта на Луне.
2} = 15,6 Н$ – сила тяжести, действующая на космонавта на Луне.
$F_1 – F_2 = 552,4 Н$
Что мы узнали?
В ходе урока был разобран закон всемирного тяготения, выведена формула для расчета ускорения свободного падения и введено понятие потенциала гравитационного поля. После чего было рассмотрено ускорение свободного падение на Земле и приведена формула силы тяжести, действующей на тела в гравитационном поле нашей планеты. В завершении урока были разобраны две задачи на пройденную тему.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 93.
А какая ваша оценка?
Парадоксы сверхмассивных черных дыр | Астрономические мероприятия, наблюдения звездного неба в Крыму!
1. Мы привыкли по отношению к черным дырам употреблять прилагательное “сверхплотная”. А, оказывается, средняя плотность сверхмассивной чёрной дыры (вычисляемая путём деления общей массы чёрной дыры на объём ее сферы Шварцшильда) может быть даже меньше плотности комнатного воздуха! Не верите? Смотрите расчеты
А, оказывается, средняя плотность сверхмассивной чёрной дыры (вычисляемая путём деления общей массы чёрной дыры на объём ее сферы Шварцшильда) может быть даже меньше плотности комнатного воздуха! Не верите? Смотрите расчеты
Расчет средней плотности черной дыры
Рассмотрим подробнее первый миф. Математически легко рассчитать среднюю плотность черной дыры (ЧД), если знать ее массу и принять ее радиус равным радиусу Шварцшильда. Допустим, у нас есть сверхмассивная черная дыра массой в миллиард солнечных масс. Вполне реальный пример, существуют даже более массивные черные дыры. Выразим в килограммах: М=109*2*1030=2*1039кг.
Плотность = масса/объем
Дело за объемом. Черная дыра в простейшем случае – шар. Объем шара = (4/3)*Пи*R3.
Какой же размер дыры ?
Размер вычисляем из формулы второй космической скорости: R=(2*G*М)/c2
Все цифры известны, подставляем в формулу:
R= (2*6. 67*10-11*2*1039)/9*1016
67*10-11*2*1039)/9*1016
Отсюда R=3*1012м
Переходим к расчету объема. Считаем примерно – Пи с тройкой нагло сокращаются.
Объем=4*R3 = 4*27*1036 = 108*1036 м3
Теперь считаю плотность. Плотность = масса/объем.
Масса=2*1039кг.
Объем = 108*1036м3
В результате, средняя плотность черной дыры в данном случае равна примерно 18.5 килограмм на метр кубический – для массы черной дыры в миллиард солнечных масс. Это всего на порядок выше плотности воздуха и гораздо меньше плотности воды. Можно аналогичным образом посчитать плотности для черных дыр любой массы.
Интересно, что наблюдается следующая нелинейная зависимость: чем тяжелеее черная дыра, тем она менее плотная. Причем при изменении массы на 11 порядков, плотность меняется на 22 порядка. И при массах черных дыр от 10ти и выше миллиардов солнечных масс их средняя плотность становится меньше плотности комнатного воздуха (1. 27т), а плотность обратно пропорциональна радиусу в кубе. Отсюда следует, что при увеличении массы средняя плотность ЧД быстро падает.
27т), а плотность обратно пропорциональна радиусу в кубе. Отсюда следует, что при увеличении массы средняя плотность ЧД быстро падает.
Отсюда следует важный вывод, что черную дыру можно получить не только сжатием вещества, но и путем накопления большого количества материала в определенном объеме.
P.S. Радиус Шварцшильда – радиус простейшей невращающейся ЧД без заряда и вращения.
***
2. Включение маршевых двигателей, красиво показанное в фильмах, увеличивает время падения на черную дыру, то есть замедляет падение. На самом деле это не так.
Обоснование.
Чтобы просуществовать максимально долгое время, космический корабль должен осуществить следующий маневр. При падении в черную дыру нужно включить на полную мощность двигатель при подлете к горизонту так, чтобы почти остановиться у самого горизонта. После этого необходимо выключить двигатель и дать кораблю свободно падать от горизонта до сингулярности. Время такого падения и будет максимальным временем существования. Любые попытки космонавтов как-то затормозить с помощью включения двигателя падение внутрь черной дыры или попытки направить корабль в орбитальное движение приведут только к тому, что корабль упадет в сингулярность за более короткий промежуток времени (по часам космонавта).
Любые попытки космонавтов как-то затормозить с помощью включения двигателя падение внутрь черной дыры или попытки направить корабль в орбитальное движение приведут только к тому, что корабль упадет в сингулярность за более короткий промежуток времени (по часам космонавта).
Как же так может быть? Хорошо, согласимся, что работа двигателей не в состоянии побороть огромную силу тяготения внутри черной дыры и остановить ракету, но все же торможение должно хоть немного замедлить падение, сделать его более продолжительным? И уж тем более это торможение не ускорит падения!
И тем не менее внутри черной дыры это возможно. Дело в том, что, включая двигатели, космонавт разгоняет свою ракету (назовем ее А} по отношению к свободно падающей ракете с выключенными двигателями (ракета Б). Но на разгоняющейся ракете время течет медленнее. А внутри черной дыры этот фактор оказывается решающим. Ракета А все равно падает в сингулярность. Но из-за того, что часы на ней шли существенно медленнее с точки зрения ракеты Б, то и весь процесс падения занял по часам А меньше времени. Идя медленнее, часы А “нати-кают” меньше секунд (или долей секунды), то есть с точки зрения ракеты А падение было менее продолжительным!
Идя медленнее, часы А “нати-кают” меньше секунд (или долей секунды), то есть с точки зрения ракеты А падение было менее продолжительным!
Напомню, что эта ситуация реальна именно для сверхмассивной черной дыры, поскольку у горизонта событий черной дыры звездной массы разность гравитационных потенциалов для двух соседних точек будет значительно превышать предел прочности любого реального тела.
***
3. Ускорение свободного падения (один из показателей гравитации) на горизонте событий сверхмассивной черной дыры значительно БОЛЬШЕ такового на горизонте событий черной дыры звездной массы. Это тоже заблуждение.
Расчет:
Ускорение свободного падения считается по известной формуле: g=(G*M)/R2. Где G – гравитационная постоянная, M – масса черной дыры, R – радиус горизонта событий.
а) Считаем для ЧД с массой Солнца. Известно, что ее горизонт событий равен 3000 м, массу тоже можем взять из энциклопедии 2*1030 кг, G=6. 67*10-11. В результате g=15*109 м/с2
67*10-11. В результате g=15*109 м/с2
б) Считаем для сверхмассивной ЧД с массой 10 млрд солнечных. Ее горизонт событий (который линейно зависит от массы) равен 3*1013 м, масса соответственно 2*1040 кг, G=6.67*10-11. В результате g=1500 м/с2
в) И для сравнения выполним расчет для нашего Солнца. Его радиус равен 7*108 м, масса 2*1030 кг, G=6.67*10-11. В результате g=272 м/с2
Вывод: Ускорение свободного падения на горизонте сверхмассивных черных дыр сравнимо с ускорением на поверхности Солнца.
***
4. Мы не можем жить в черной дыре – нас сразу разорвет и засосет. Кто разорвет и куда засосет? 🙂 Можем, если дыра достаточно большая, например размером со Вселенную!
Расчет:
Размер черной дыры (с небольшой погрешностью можно сказать – он же радиус горизонта событий, радиус Шварцшильда, гравитационный радиус) считается по формуле: R=2*G*М/c2. Подставляем значения констант, получаем R=М(кг)*1,48*10-27 (м). То есть радиус ЧД напрямую, линейно, зависит от ее массы, и только от нее! Зная массу, получаем размер горизонта ЧД. То зная размер и массу любого тела мы можем проверить является ли тело черной дырой: если его размер больше горизонта событий, то не является, меньше – является.
Подставляем значения констант, получаем R=М(кг)*1,48*10-27 (м). То есть радиус ЧД напрямую, линейно, зависит от ее массы, и только от нее! Зная массу, получаем размер горизонта ЧД. То зная размер и массу любого тела мы можем проверить является ли тело черной дырой: если его размер больше горизонта событий, то не является, меньше – является.
Подставляем, например, Землю: радиус горизонта около 1см, значит оно ЧД не является. Солнце: радиус горизонта 3км, не является. Что же будет если мы будем брать все большие по размеру тела?
Дело в том, что при сохранении постоянной плотности масса тела напрямую зависит от его объема. А объем пропорционален кубу радиуса тела (V шара = (4/3)*Пи*R3).
То есть когда мы берем, скажем, Солнце и добавляем ему размер в два раза, то его масса вырастет примерно в 8 раз, а при увеличении массы в 8 раз радиус его горизонта событий тоже вырастет в 8 раз. То есть для такого объекта радиус горизонта событий становится в 4 раза ближе к его настоящему размеру.
Получается, что при подборе все большего и большего объекта может наступить такой момент, когда радиус горизонта событий догонит его настоящий радиус и объект станет черной дырой!
Самый крупный объект, известный человеку – это Вселенная. Размер ее оценивается в 46-47 млрд св. лет (около 1026 м), а масса 1053-1054 кг. Подставляем в формулу грав-радиуса (в начале этой главы) и получаем ответ 1027 м. Что больше принятого на сегодня размера Вселенной! => Вывод
МЫ ЖИВЕМ В ЧЕРНОЙ ДЫРЕ!
Литература:
1. o8ode.ru/article/timy/coza/black/vnutri_4ernoi_dyry.htm
2. en.wikipedia.org/wiki/Observable_universe
3. ru.wikipedia.org/wiki/Космология_чёрной_дыры
Назаров С.В.
Астробиблиотека
Словарик терминов
Если Вас заинтересовала эта тема и Вы хотите самостоятельно во всем разобраться, рекомендуем посетить Астроканикулы!
Гравитационная постоянная
Значение гравитационной постоянной
Содержание:
Общие сведения
Гравитационная постоянная или иначе – постоянная Ньютона – одна из основных констант, используемых в астрофизике. Фундаментальная физическая постоянная определяет силу гравитационного взаимодействия. Как известно, силу, с которой каждое из двух тел, взаимодействующих посредством гравитации, притягивается можно высчитать из современной формы записи закона всемирного тяготения Ньютона:
Фундаментальная физическая постоянная определяет силу гравитационного взаимодействия. Как известно, силу, с которой каждое из двух тел, взаимодействующих посредством гравитации, притягивается можно высчитать из современной формы записи закона всемирного тяготения Ньютона:
Гравитационное взаимодействие двух тел
Здесь:
Данный коэффициент пропорциональности равен модулю силы тяготения первого тела, которая действует на точечное второе тело единичной массы, при единичном расстоянии между этими телами.
G = 6,67408(31)·10−11 м3·с−2·кг−1, или Н·м²·кг−2.
Очевидно, что данная формула широко применима в области астрофизики и позволяет рассчитать гравитационное возмущение двух массивных космических тел, для определения дальнейшего их поведения.
Работы Ньютона
Примечательно, что в трудах Ньютона (1684—1686) гравитационная постоянная в явном виде отсутствовала, как и в записях других ученых аж до конца XVIII-го века.
Исаак Ньютон (1643 — 1727)
Ранее использовался так называемый гравитационный параметр, который равнялся произведению гравитационной постоянной на массу тела. Нахождение такого параметра в то время было более доступно, поэтому на сегодняшний день значение гравитационного параметра различных космических тел (в основном Солнечной системы) более точно известно, нежели порознь значение гравитационной постоянной и массы тела.
µ = GM
Здесь: µ — гравитационный параметр, G – гравитационная постоянная, а M — масса объекта.
Размерность гравитационного параметра — м3с−2.
Следует отметить тот факт, что значение гравитационной постоянной несколько варьируется даже до сегодняшнего дня, а чистое значение масс космических тел в то время было определить довольно сложно, поэтому гравитационный параметр нашел более широкое применение.
Эксперимент Кавендиша
Эксперимент по определению точного значения гравитационной постоянной впервые предложил английский естествоиспытатель Джон Мичелл, который сконструировал крутильные весы. Однако, не успев провести эксперимент, в 1793-м году Джон Мичелл умер, а его установка перешла в руки Генри Кавендишу – британскому физику. Генри Кавендиш улучшил полученное устройство и провел опыты, результаты которых были опубликованы в 1798-м году в научном журнале под названием «Философские труды Королевского общества».
Генри Кавендиш (1731 — 1810)
Установка для проведения эксперимента состояла из нескольких элементов. Прежде всего она включала 1,8-метровое коромысло, к концам которого крепились свинцовые шарики с массой 775 г и диаметром 5 см. Коромысло было подвешено на медной 1-метровой нити. Несколько выше крепления нити, ровно над ее осью вращения устанавливалась еще одна поворотная штанга, к концам которой жестко крепились два шара массой 49,5 кг и диаметром 20 см. Центры всех четырех шаров должны были лежать в одной плоскости. В результате гравитационного взаимодействия притяжение малых шаров к большим должно быть заметно. При таком притяжении нить коромысла закручивается до некоторого момента, и ее сила упругости должна равняться силе тяготения шаров. Генри Кавендиш измерял силу тяготения посредством измерения угла отклонения плеча коромысла.
Центры всех четырех шаров должны были лежать в одной плоскости. В результате гравитационного взаимодействия притяжение малых шаров к большим должно быть заметно. При таком притяжении нить коромысла закручивается до некоторого момента, и ее сила упругости должна равняться силе тяготения шаров. Генри Кавендиш измерял силу тяготения посредством измерения угла отклонения плеча коромысла.
Установка Генри Кавендиша
Более наглядное описание эксперимента доступно в видео ниже:
Для получения точного значения константы Кавендишу пришлось прибегнуть к ряду мер, снижающих влияние сторонних физических факторов на точность эксперимента. В действительности Генри Кавендиша проводил эксперимент не для того, чтобы выяснить значение гравитационной постоянной, а для расчета средней плотности Земли. Для этого он сравнивал колебания тела, вызванные гравитационным возмущением шара известной массы, и колебания, вызванные тяготением Земли.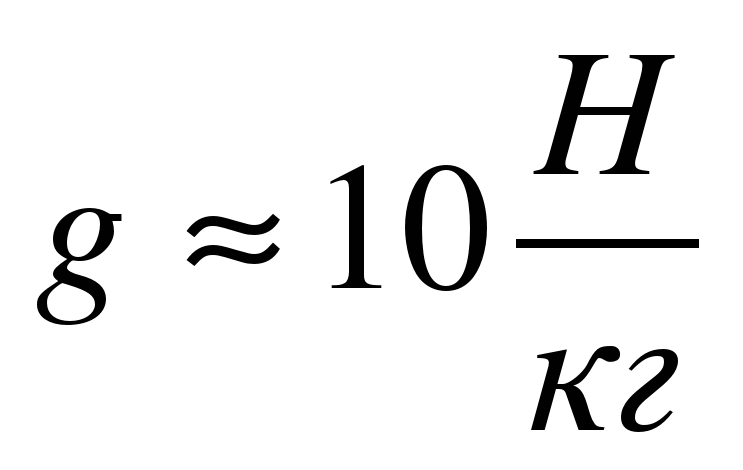 Он достаточно точно вычислил значение плотности Земли – 5,47 г/см3 (сегодня более точные расчеты дают 5,52 г/см3). Согласно различным источникам, значение гравитационной постоянной, высчитанное из гравитационного параметра с учетом плотности Земли, полученной Кавердишем, составило G=6,754·10−11 м³/(кг·с²), G = 6,71·10−11м³/(кг·с²) или G = (6,6 ± 0,04)·10−11м³/(кг·с²). До сих пор неизвестно, кто впервые получил численное значение постоянной Ньютона из работ Генри Кавердиша.
Он достаточно точно вычислил значение плотности Земли – 5,47 г/см3 (сегодня более точные расчеты дают 5,52 г/см3). Согласно различным источникам, значение гравитационной постоянной, высчитанное из гравитационного параметра с учетом плотности Земли, полученной Кавердишем, составило G=6,754·10−11 м³/(кг·с²), G = 6,71·10−11м³/(кг·с²) или G = (6,6 ± 0,04)·10−11м³/(кг·с²). До сих пор неизвестно, кто впервые получил численное значение постоянной Ньютона из работ Генри Кавердиша.
Измерение гравитационной постоянной
Наиболее раннее упоминание гравитационной постоянной, как отдельной константы, определяющей гравитационное взаимодействие, найдено в «Трактате по механике», написанном в 1811-м году французским физиком и математиком — Симеоном Дени Пуассоном.
Материалы по теме
Измерение гравитационной постоянной проводится различными группами ученых и по сей день. При этом, несмотря на обилие доступных исследователям технологий, результаты экспериментов дают различные значения данной константы. Из этого можно было бы сделать вывод, что, возможно, гравитационная постоянная на самом деле непостоянная, а способна менять свое значение, с течением времени или от места к месту. Однако, если значения константы по результатам экспериментов разнятся, то неизменность этих значений в рамках этих экспериментов уже проверена с точностью до 10-17. Кроме того, согласно астрономическим данным постоянная G не изменилась в значительной степени за несколько последних сотен миллионов лет. Если постоянная Ньютона и способна меняться, то ее изменение не превысило б отклонение на число 10-11 – 10-12 в год.
Из этого можно было бы сделать вывод, что, возможно, гравитационная постоянная на самом деле непостоянная, а способна менять свое значение, с течением времени или от места к месту. Однако, если значения константы по результатам экспериментов разнятся, то неизменность этих значений в рамках этих экспериментов уже проверена с точностью до 10-17. Кроме того, согласно астрономическим данным постоянная G не изменилась в значительной степени за несколько последних сотен миллионов лет. Если постоянная Ньютона и способна меняться, то ее изменение не превысило б отклонение на число 10-11 – 10-12 в год.
Примечательно, что летом 2014-го года совместно группа итальянских и нидерландских физиков провели эксперимент по измерению гравитационной постоянной совсем иного вида. В эксперименте использовались атомные интерферометры, которые позволяют отследить влияние земной гравитации на атомы. Значение константы, полученное таким образом, имеет погрешность 0,015% и равняется G = 6. 67191(99) × 10−11 м3·с−2·кг−1.
67191(99) × 10−11 м3·с−2·кг−1.
Понравилась запись? Расскажи о ней друзьям!
Просмотров записи: 35148
Запись опубликована: 16.04.2017
Автор: Владимир Соловьев
Величина g — Расчет и уравнение
Величина g в кадрах в секунду
Ускорение, ощущаемое свободно падающим объектом из-за силы тяжести массы тела, называется ускорением свободного падения и выражается в g, рассчитанном с использованием единицы СИ м/ с 2 . Величина g зависит от массы тела и его размера, и ее значение варьируется от тела к телу. Значение g на Луне постоянно.
Ускорение под действием силы тяжести Луны
Ускорение под действием силы тяжести Луны или величина g на Луне составляет 1625 м/с 2 .
Рассчитайте ускорение, вызванное гравитацией Луны
Ускорение, вызванное формулой гравитации, указано как
G = GM / R 2
Где
Масса Луны 7,35 × 10 22 кг.
Радиус Луны 1,74×10 6 м
Подставляя значения в формулу получаем-
g= 6,67×10 −11 ×7,35×10 22 6 6 ) 2
Таким образом, значение g на Луне равно g=1,625 м/с 2 .
Ускорение свободного падения также соответствует единице ускорения
Закон всемирного тяготения Ньютона применительно к Земле равен F = G m M / r 2 , где F — сила тяжести, действующая на тело массой m, G — универсальная гравитационная постоянная, M — масса Луны, r — расстояние тела от центра Солнца. g — коэффициент в уравнении F = m g, поэтому g определяется следующим образом:
g — коэффициент в уравнении F = m g, поэтому g определяется следующим образом:
g = G M / r 2
Обе G и M являются эмпирическими константами, а g имеет обратную квадратичную зависимость от r, расстояния от центра земной массы.
Отсюда два следствия:
Эти два эффекта совместно вызывают увеличение широты. Их величины легко определяются простой геометрией.
Влияние широты рассчитывается на основе стандартной поверхности геоида, который представляет собой сфероид на уровне моря. Точки над уровнем моря постепенно удаляются от центра Земли, поэтому g уменьшается с высотой предсказуемым образом.
Точки над уровнем моря постепенно удаляются от центра Земли, поэтому g уменьшается с высотой предсказуемым образом.
На практике значение g несколько отличается от геометрически предсказанного значения в зависимости от широты и высоты. Положительное отклонение обусловлено следующим:
Компоненты структуры Земли имеют разную плотность. Геометрическая модель гравитации представляет Землю как набор слоев луковичной шелухи, каждый из которых имеет одинаковую плотность (и это почти так). Каждый отдельный лист из-за его однородной плотности имеет свой центр масс, соответствующий центру масс Земли. Тем не менее, если слой имеет небольшой участок материала с более высокой плотностью, центр массы смещается в сторону участка, уменьшая r и тем самым увеличивая g.
В таблице ниже показано значение g в различных местах от центра Земли.
| . 6,38 x 106 м | 9,8 | |
1000 км над поверхностью | 7. | 7.33 |
2000 km above surface | 8.38 x 106 m | 5.68 |
3000 km above surface | 9.38 x 106 m | 4.53 |
4000 km above surface | 1.04 x 107 m | 3.70 |
5000 km above surface | 1.14 x 107 m | 3.08 |
8000 km above surface | 1.44 x 107 m | 1.93 |
9000 km above surface | 1.54 x 107 m | 1.69 |
10000 km above surface | 1. | 1.49 |
50000 км над поверхностью | 5,64 x 107 м | 0,13 |
Земля. Фактически изменение g с расстоянием следует закону обратных квадратов, где g обратно пропорционально расстоянию от центра Земли. Это уравнение обратного квадрата означает, что при увеличении зазора вдвое значение g уменьшается в 4 раза. При утроении расстояния значение g уменьшается в 9 раз.. И так далее. Эта обратная квадратичная зависимость показана на правом графике.
Величина G, равная гравитации, является основной концепцией, изучаемой на уроках естествознания. Учащиеся узнают о гравитации в более ранних классах, начиная с шестого класса.
В этой статье подробно объясняется значение G в FPS, ускорение под действием силы тяжести Луны, ускорение под действием силы тяжести также соответствует единице ускорения, а также приводится значение G в различных местах от центра Земли. Это очень информативная статья, и студенты, которые хотят получить хороший балл и получить четкое представление о концепции значения G, обязательно должны прочитать и изучить эту статью подробно.
Это очень информативная статья, и студенты, которые хотят получить хороший балл и получить четкое представление о концепции значения G, обязательно должны прочитать и изучить эту статью подробно.
Эта статья подготовлена группой экспертов Веданту с целью упростить концепции, которые могут показаться трудными для некоторых учащихся. Этот учебный материал доступен на веб-сайте Vedantu. Ссылка легкодоступна и доступна для бесплатной загрузки в формате PDF. Студенты могут загрузить бесплатный PDF-файл и учиться в офлайн-среде, что поможет им больше сосредоточиться на учебе и не будет загромождать мозг ненужной информацией.
Учебный материал по значению G ориентирован в основном на конкретную тему и не включает в себя какую-либо ненужную информацию, которая не нужна при изучении этой темы.
Все мы знаем, что гравитация — это невидимая притягивающая сила, которая притягивает предметы к центру объекта. Сила гравитации изучается как неотъемлемо связанная с массой. Все мы знаем, что существует гравитационная сила притяжения, которая присутствует между каждым объектом. Сила гравитации пропорциональна массе объекта и по мере увеличения расстояния между ними сила ослабевает. Оба объекта продолжают оказывать друг на друга равную и притягивающую силу. Падающий предмет притягивает землю с той же силой, с какой земля притягивает его.
Все мы знаем, что существует гравитационная сила притяжения, которая присутствует между каждым объектом. Сила гравитации пропорциональна массе объекта и по мере увеличения расстояния между ними сила ослабевает. Оба объекта продолжают оказывать друг на друга равную и притягивающую силу. Падающий предмет притягивает землю с той же силой, с какой земля притягивает его.
Ускорение силы тяжести на Земле также известно как значение g на Земле, равное 9,8 м/с2. Это указывает на то, что если объект падает свободно, скорость этого объекта будет увеличиваться на 9,8 каждую секунду.
Ускорение силы тяжести на Луне, также известное как величина g на Луне, составляет 1625 м/с2. Формула силы тяжести обозначается как G = GM / R 2 . Масса Луны 7,35×10 22 кг.
Радиус Луны 1,74×10 6 M
Заменить значения в формуле, которую мы получаем-
G = 6,67 × 10 −11 × 7,35 × 10 22 / (1,74 × 100005 6 ) 2 9
Таким значение g на Луне равно g=1,625 м/с 2 .
Калькулятор ускорения под действием силы тяжести
Создано Purnima Singh, PhD
Отзыв от Madhu Raman
Последнее обновление: 17 мая 2022 г.
Содержание:падающие объекты будут вести себя на разных планетах , наш калькулятор ускорения под действием силы тяжести поможет вам это выяснить.
Продолжайте читать, чтобы узнать , чему равно ускорение свободного падения и как рассчитать его значение на любом небесном теле. Вы также найдете пример расчета величины ускорения свободного падения с помощью нашего инструмента.
Каково ускорение свободного падения?
Как следует из названия, ускорение свободного падения — это ускорение, испытываемое телом при свободном падении под действием только силы тяжести . Мы используем символ ggg для его обозначения. Единицей единиц СИ ggg является м/с 2 92}
\end{align*}g=R2G M=(6,371×106 м)26,674×10−11 м3кг−1с−2×5,972×1024 кг=9,8 м/с2
Мы используем символ ggg для его обозначения. Единицей единиц СИ ggg является м/с 2 92}
\end{align*}g=R2G M=(6,371×106 м)26,674×10−11 м3кг−1с−2×5,972×1024 кг=9,8 м/с2
Следовательно, величина ускорения к силе тяжести на поверхности Земли составляет 9,8 м/с 2 . В следующем разделе вы увидите, как определить значение ggg с помощью нашего калькулятора гравитационного ускорения.
Как использовать калькулятор ускорения под действием силы тяжести
Теперь давайте вычислим ту же задачу, что и выше, используя калькулятор ускорения под действием силы тяжести:
Другие подобные калькуляторы
Если вам понравился этот калькулятор гравитационного ускорения, обязательно ознакомьтесь с другими нашими инструментами по гравитации, а именно:
Часто задаваемые вопросы
Как рассчитать ускорение свободного падения на Марсе?
Чтобы рассчитать ускорение свободного падения на поверхности Марса, выполните указанные шаги:
Как рассчитать ускорение свободного падения на Луне?
Чтобы рассчитать ускорение свободного падения на Луне, выполните следующие действия:
Пурнима Сингх, доктор философии
МАСС (M)
Радиус (R)
Ускорение из -за гравитации (G)
Проверьте 82 аналогичные калькуляторы механики ⚙
. Эта страница предназначена для учащихся колледжа, старшей или средней школы.
Для младших школьников более простое объяснение информации на этой странице
доступно на
Детская страница. |
Вес – это сила порождается гравитационным притяжением земли к какому-либо объекту. Вес в принципе отличается от аэродинамических сил, поднять и перетащить. Аэродинамические силы составляют 90 544 механических сил 90 545, и объект должен быть в физическом контакте с воздухом, который создает силу. гравитационная сила равна силе поля ; источник силы делает не должен быть в физическом контакте с объектом.
Природа гравитационной силы была изучена учеными на протяжении многих лет и до сих пор исследуется физики-теоретики. Для объекта размером с летящий самолет около земли, описания, данные триста лет назад сэром Исаак Ньютон работает очень хорошо. Ньютон опубликовал свою теорию гравитация с его законами движения в 1686. Гравитационная сила F между двумя частицами равна универсальная константа, 92
Если у вас есть много частиц, действующих на одну частицу, вы
необходимо сложить вклад всех отдельных частиц.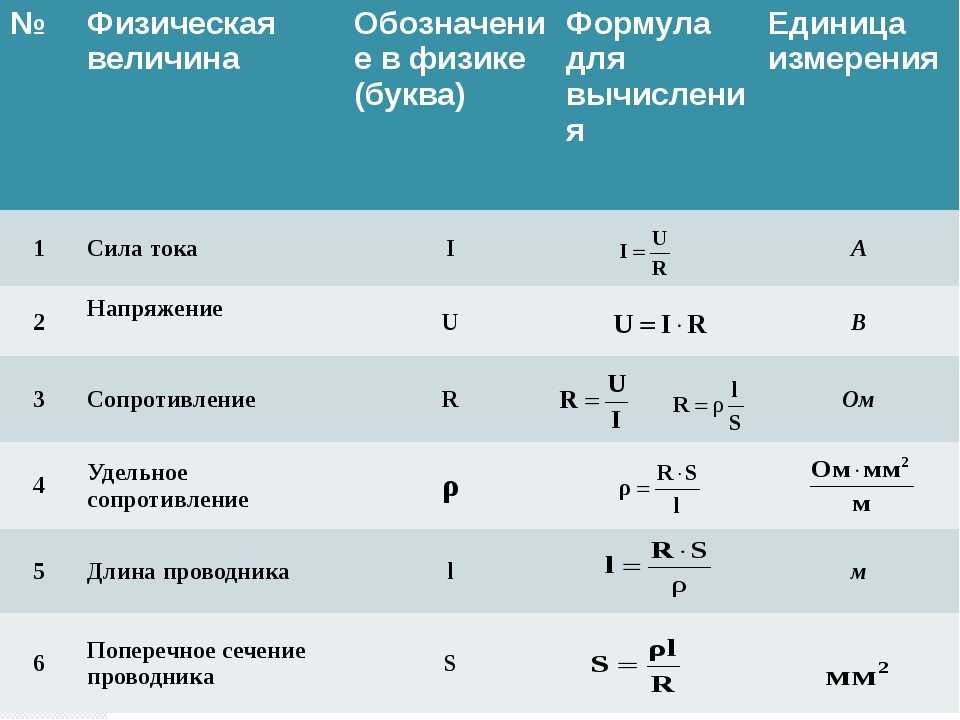 За
объектов вблизи Земли сумма масс всех частиц равна
просто масса земли, а расстояние затем измеряется от
центр земли. На поверхности земли расстояние равно
около 4000 миль. Ученые объединили универсальное
гравитационная постоянная, масса Земли и квадрат
радиус земли, чтобы сформировать ускорение свободного падения, 92
За
объектов вблизи Земли сумма масс всех частиц равна
просто масса земли, а расстояние затем измеряется от
центр земли. На поверхности земли расстояние равно
около 4000 миль. Ученые объединили универсальное
гравитационная постоянная, масса Земли и квадрат
радиус земли, чтобы сформировать ускорение свободного падения, 92
Вес Вт или гравитационная сила, то это просто масса объекта, умноженная на гравитационное ускорение.
Вт = м * г
Поскольку гравитационная постоянная (g) зависит от квадрата расстояние от центра земли, т. вес объекта уменьшается с высотой.
Давайте сделаем
тестовая задача, чтобы увидеть, насколько изменится вес самолета
с высотой. Если самолет будет
полет на высоте 35000 футов (около 7 миль) расстояние до центра
Земля составляет около 4007 миль. Мы можем рассчитать соотношение
гравитационная постоянная к значению на поверхности
земля как квадрат (4000/4007), что равно
. 9983 * 0,9983 = 0,9965. Если самолет весит 10000 фунтов на поверхности
земля, он весит 9965 фунтов на высоте 35000 футов; он потерял 35 фунтов,
очень маленькая сумма по сравнению с 10000 фунтов стерлингов.
9983 * 0,9983 = 0,9965. Если самолет весит 10000 фунтов на поверхности
земля, он весит 9965 фунтов на высоте 35000 футов; он потерял 35 фунтов,
очень маленькая сумма по сравнению с 10000 фунтов стерлингов.
Давайте решим другую задачу и вычислим вес Спейс Шаттл на низкой околоземной орбите. На земле орбитальный аппарат весит около 250 000 фунтов. На орбите шаттл находится на высоте около 200 миль над поверхность земли. Как и прежде, отношение гравитационной постоянной равно квадрат (4000/4200), что равно 0,9523 * 0,9523 = 0,907. На орбите шаттл весит 250 000 * 0,907 = 226 757 фунтов. Примечание: вес не нуль. Шаттл не невесомый на орбите . “Невесомость” это из-за скорости шаттла на орбите. Шаттл притягивается к земле под действием силы тяжести. Но высокая орбитальная скорость, касательной к поверхности земли, вызывает падение к поверхности точно соответствовать кривизне земли вдали от шаттла. По сути, шаттл постоянно падает по всей земле.
Вы можете просмотреть короткий
кино
из «Орвилл и Уилбур Райт», обсуждая силу веса
и как это повлияло на полет их самолетов. Файл фильма может
сохранять на свой компьютер и просматривать как подкаст на проигрывателе подкастов.
Файл фильма может
сохранять на свой компьютер и просматривать как подкаст на проигрывателе подкастов.
Деятельность:
Экскурсии с гидом
Навигация ..
Несколько подходов и примеров задач – Lambda Geeks
В статье обсуждается несколько подходов к поиску гравитационного ускорения.
Гравитационное ускорение — это ускорение свободного падения объекта в вакууме с постоянной скоростью, несмотря на его массу, из-за силы тяжести. С помощью законов Ньютона, описывающих силу тяжести, мы можем обнаружить ускорение свободного падения или ускорение под действием силы тяжести.
Как найти гравитационное ускорение g? Гравитационное ускорение зависит от гравитирующего тела большой массы M, но не зависит от тела малой массы m. Поэтому тела малой массы падают вниз к гравитирующему телу, несмотря на его массу. Поэтому ускорение свободного падения называется ускорение свободного падения или ускорение свободного падения , обозначаемое как «g».
Поэтому тела малой массы падают вниз к гравитирующему телу, несмотря на его массу. Поэтому ускорение свободного падения называется ускорение свободного падения или ускорение свободного падения , обозначаемое как «g».
Поскольку сила создает такое ускорение, мы можем определить значение g несколькими способами, используя законы движения Ньютона .
Читать Как рассчитать массу по гравитационной силе .
Как найти гравитационное ускорение, используя законы НьютонаДавайте рассчитаем значение g, используя второй закон Ньютона и закон всемирного тяготения.
Второй закон движения Ньютона определяет силу гравитации между объектом и землей, тогда как закон всемирного тяготения определяет силу гравитации между двумя объектами. Когда мы сравниваем обе силы гравитации, мы получаем значение ускорения свободного падения g.
Законы Ньютона для нахождения значения gСила тяжести F g определяется с помощью второго закона Ньютона is,
F g =… мг. ……
……
Сила тяжести F g определяется через закон всемирного тяготения is,
F g =GMm/r 2
расстояние между центром масс объекта и земли.
А G – константа гравитационной пропорциональности.
Сравнение обеих сил гравитации F г в уравнениях (1) и (2),
мг=ГМм/р 2
г=ГМм/мр 2
g=Gm/r 2
Выше приведена стандартная формула для расчета ускорения свободного падения g .
Как вы заметили, масса падающего объекта m аннулируется при определении g, так как ускорение свободного падения зависит только от силы притяжения массы земли M.
Подробнее о законах Ньютона.
Рассчитайте ускорение свободного падения мяча, падающего на земная поверхность. Масса Земли равна 6 х 10 24 кг, а расстояние между объектом и Землей равно 6,38 х 10 6 м. (G = 6,67 x 10-11 нм 2 /кг 2 )
(G = 6,67 x 10-11 нм 2 /кг 2 ) Дано :
M = 6 x 10 0005 24 кг
R = 6,38 x 1000066 6 2 6 40006 40006 40006 40006 40006 40006 40006 40006 40006 40006 40006 40006 40006 40006 40006 40006 40006 400066 6 400067 6 6 6 0006 400067 6 7 6 6 0006.
G = 6,67 x 10 -11 Н·м 2 /кг 2
Найти : g=?
Formula :
F G = Mg
Решение :
Сила тяжести из -за Второй законы Newton
Замена Закон гравитации Формула (2) в вышеупомянутое уравнение,
G = GMM/MR 2
G = GM/R 2
. = 9,86
= 9,86
Ускорение свободного падения шара, падающего на поверхность земли, равно 9,86 м/с 2 .
Сила тяжести – это сила веса, которая различна для разных масс M. Следовательно, значение g также немного различается для других планет из-за разных масс .
Различные значения g для различных массПрочтите Как вычислить массу по силе и расстоянию .
Луна имеет массу 7,35 X 10 22 кг, а расстояние между центрами масс 1,74 X 10 6 м. Вычислите гравитационное ускорение космонавта, идущего по Луне.Given :
M = 7.35 X 10 22 kg
r = 1.74 X 10 6 m
G = 6.67 x 10 -11 Nm 2 /kg 2
Найти: г=?
Формула :
g = GM/R 2
Решение :
Гравитационное ускорение на космонавте рассчитывается с использованием Законы Ньютона ,
G = GM/R 2 2 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3,,, 3, 3,, 9033.
г = 1,619
Гравитационное ускорение космонавта на Луне составляет 1,619 м/с 2 .
Если объект перемещается на определенной высоте h от гравитирующей поверхности; как спутник вращается на высоте h от земли, радиус между ними становится R (r + h). Следовательно, значение ускорения свободного падения g также изменяется из-за изменения радиуса r.
Различные значения g для различных радиусовПодробнее о наклонной плоскости .
Если спутник движется по орбите на высоте около 280 км над земной поверхностью, какое гравитационное ускорение он испытает?Given :
M = 6 x 10 24 kg
G = 6.67 x 10 -11 Nm 2 /kg 2
r = 6.38 X 10 6 м
H = 280 км = 0,28 x 10 6 M
R = (R + H) = (6,38 x 10 6 + 0,28 x 10 6 ) = 6,66 x 10 0005 6 M
07. Чтобы найти : g=?
Чтобы найти : g=?
Формула :
g = GM/R 2
Решение :
. ГРУБИТАЦИОННЫЕ АВЕТА.
Подстановка всех значений,
g = 9,02
Гравитационное ускорение спутника, вращающегося над Землей, равно 9,02 м/с 2 .
Как найти гравитационное ускорение, используя третий закон КеплераДавайте рассчитаем значение g, используя третий закон Кеплера, следующим образом: к его большой полуоси. Период времени планеты получается путем сравнения как центростремительной силы, так и силы гравитации, обусловленной законом гравитации.
Законы Кеплера, чтобы найти G Значение(кредит: Shutterstock)
Центрипетальная сила ( ( FIRSERSE
F C . ) с уравнением закона всемирного тяготения (2),
mv 2 /r=GMm/r 2
v 2 =GM/r
033 Скорость = 9034 / Время 9034 / Время планета, когда она движется по орбите = 2πr
V = 2πr /T
V 2 = 4π 2 R 2
Замена выше уравнения в уравнение (5),
4* 2 R 2 /T
2 = GM = GM 2 R 2 /T 2 = GM = GM = GM 2 R 2 /T 9000 2 = GM = GM 2 R 2 /T 9000 2 = GM = GM 2 R 2 /T 9000 2 = GM /rT 2 =4π 2 r 3 /GM
Вышеупомянутое уравнение представляет собой период времени обращения планеты.
Выведем формулу гравитационного ускорения через период времени.
Используя уравнение (3), M=gr 2 /g
Значение замены M на уравнение (6),
T 2 = 4π 2 R 3 /GR 2
G = 4π95 2
R /T 2 2Вот как мы можем рассчитать значение g, используя период времени обращения объекта по орбите T.
Спутнику, вращающемуся на расстоянии около 500 км, требуется 90 минут, чтобы совершить один оборот вокруг Земли. Каким будет гравитационное ускорение, которое он испытывает?Дано :
R = 6,38 x 10 6 M
H = 500 км
R = (R+H) = 9,88 x 10 0005 6 M
T = 90 мин. = 5,4 X 10 3 сек
Найти : g=?
Формула :
g = 4π 2 R/T 2
Раствор :
. ГРЕЙТАТИЧЕСКИ0003
ГРЕЙТАТИЧЕСКИ0003
g=4π 2 r/T 2
Substituting all values,
g = 9.28
The gravitational acceleration on an orbiting satellite by earth is 9.28 m/s 2
Read подробнее об угловом движении .
Как найти ускорение свободного падения с помощью сферически симметричных телРассчитаем значение g с использованием сферически симметричных тел следующим образом:
Гравитационно притягивающие тела обладают сферически симметричным распределением масс, так как вся их масса сосредоточена в его центре. Следовательно, мы можем получить гравитационное ускорение для симметричных тел, используя закон всемирного тяготения Ньютона.
Сферически симметричное тело(кредит: Physicsbootcamp)
Поскольку масса = плотность / объем
Когда тела имеют симметричное распределение массы,
в Уравнение закона тяготения Ньютона (2),
Подставляя Уравнение второго закона Ньютона (1) в приведенное выше уравнение,
Вот как мы можем рассчитать значение g, используя плотность объекта ρ 0 .
Given :
G = 6.67 x 10 -11 Nm 2 /kg 2
r = 6.38 X 10 6 m
ρ 0 = 17 kg/cm 3 = 17 X 10 3 г/см 3
Чтобы найти : g=?
Formula :
Решение :
Гравитационное ускорение на шарике рассчитывается,
Заместитель.
g =9,64
Ускорение свободного падения при падении мяча на землю равно 9,64 м/с0354 [Щелкните здесь, чтобы просмотреть примеры вопросов] В соответствии с законом Ньютона любые два объекта, имеющие массы м1 и м2 (в килограммах), центры которых разделены расстоянием r (в метрах), будут иметь Гравитационная Сила F (в Ньютоне). Gravitational Constant Ускорение свободного падения на Земле или значение g на Земле составляет 9,8 м/с 2 . Таким образом, скорость тела, находящегося в свободном падении, увеличивается на 9,8 каждую секунду. Подробнее: Кинетическая энергия [Щелкните здесь, чтобы просмотреть примеры вопросов] Значение гравитационной постоянной G во Универсальном законе гравитации может быть установлено эмпирически. Рассмотрим два тела массами м 1 и м 2 . Пусть r — расстояние между центрами этих тел и обратно пропорционально квадрату расстояния между ними. сила Между двумя телами дается, F ∝ M 1 .M 2 / R 2 или, F = G.M 0 1 9061. М . 2 Здесь G — константа пропорциональности, называемая универсальной гравитационной постоянной . Пусть, m 1 = m 2 =1 и r =1 Тогда уравнение принимает вид: → F = G*1*1/1 → F = G гравитационная постоянная равна силе притяжения, действующей между двумя телами с единичной массой , когда их центры находятся на расстоянии единицы друг от друга. В настоящее время принятое значение G равно G = 6,67×10 -11 Н·м 2 /кг 2 Читать дальше: Потенциальная энергия [Click Here Hare Hare Hare Champe. это строчная буква g это ускорение свободного падения и заглавная буква G это универсальная гравитационная постоянная.  /р 2
/р 2 Ускорение свободного падения на Земле
 Это ускорение является результатом гравитации Земли.
Это ускорение является результатом гравитации Земли. Гравитационная постоянная – вывод

Значение G
Расчет гравитационной постоянной
Применение гравитационной постоянной
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Некоторые из приложений значения G включают –
Ускорение свободного падения
[Щелкните здесь, чтобы просмотреть примеры вопросов]
Суммарное ускорение , которое передается объектам из-за комбинированного действия гравитации (от распределения масс внутри Земли) и центробежной силы (от вращения Земли), представляет собой ускорение, обусловленное сила тяжести. Он указан как г на Земле .
Ускорение свободного падения на Земле
Расчет массы объекта на поверхности Земли
Различия между G и g
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Различия между универсальной гравитационной постоянной, G и ускорением свободного падения, представленным g, следующие:
G vs g Различия
| Универсальная гравитационная постоянная ‘G’ | Ускорение под действием силы тяжести ‘g ‘ |
|---|---|
g — ускорение свободного падения. | |
Универсальная гравитационная постоянная описывает гравитационную силу между двумя телами с единичной массой, разделенными единичным расстоянием. | Ускорение, возникающее в свободно падающем теле благодаря гравитационному притяжению, известно как гравитационное ускорение. |
Величина G постоянна везде на Земле и во всем космосе. | Значение «g» зависит от того, где вы находитесь на планете. |
Изменения высоты и глубины от земной поверхности не влияют на значение G. | Значение g уменьшается по мере того, как мы продвигаемся вглубь Земли или выше от ее поверхности. |
Значение G не равно нулю в центре Земли или где-либо еще. | Значение g в ядре Земли равно нулю. |
Значение G равно 6,6734 × 10 -11 Н·м 2 /кг 2 по всей Вселенной. | Значение 9,8 м/с 2 на поверхности Земли. |
Its SI unit is N m 2 /kg 2 | The SI unit is m/s 2 |
Things to Remember
[Click Here for Примеры вопросов]
Also Check Out:
Previous Year Questions on Gravitational Constant
Примеры вопросов
Вопросы. Предположим, что наша галактика состоит из 2,5 х 10 11 звезд каждая с массой в одну солнечную. За какое время звезда, находящаяся на расстоянии 50 000 световых лет от центра Галактики, совершит один оборот? Примем диаметр Млечного Пути равным 100 000 90 345 90 344 световых лет. (3 балла)
Отв. Здесь r = 50000 световых лет = 50000 x 9,46 x 10 15 m = 4,73 x 10 20 m
M = 2,5 x 10 11 масса Солнца = 2,9 x 10{1/2}\)
= 1,12 х 10 16 с.
Вопрос. Зависит ли скорость отрыва тела от Земли от (а) массы тела, (б) места, откуда оно выбрасывается, (в) направления выброса, (г) высоты места, откуда запускается тело? (3 балла)
Ответ. Скорость убегания v es = \(\sqrt{\frac{2GM}{R}}\) = \(\sqrt{2gR}\) . Отсюда
Скорость убегания v es = \(\sqrt{\frac{2GM}{R}}\) = \(\sqrt{2gR}\) . Отсюда
а) Скорость отрыва тела от Земли не зависит от массы тела.
(б) Скорость убегания не зависит от места, откуда выбрасывается тело.
(в) Скорость убегания не зависит от направления выброса тела.
(d) Скорость убегания тела зависит от высоты места, откуда тело выбрасывается, потому что скорость убегания зависит от гравитационного потенциала в точке, из которой оно выбрасывается, а этот потенциал также зависит от высоты.
Вопросы. В следующих двух упражнениях выберите правильный ответ из предложенных: Напряженность гравитации в центре полусферической оболочки однородной плотности массы имеет направление, указанное стрелкой (см. рис.) (3 балла)
(i) a, (ii) b, (iii) c, (iv) 0.
Ответ. Во всех точках внутри полой сферической оболочки потенциал одинаков. Итак, гравитационная интенсивность, которая отрицательна градиенту гравитационного потенциала, равна нулю. Из-за нулевой гравитационной напряженности гравитационные силы, действующие на любую частицу в любой точке внутри сферической оболочки, будут расположены симметрично. Отсюда следует, что если убрать верхнюю полусферическую оболочку, то результирующая гравитационная сила, действующая на частицу в точке P, будет направлена вниз. Поскольку интенсивность гравитации – это сила гравитации на единицу массы, поэтому направление интенсивности гравитации будет вдоль c. Итак, вариант (iii) правильный.
Из-за нулевой гравитационной напряженности гравитационные силы, действующие на любую частицу в любой точке внутри сферической оболочки, будут расположены симметрично. Отсюда следует, что если убрать верхнюю полусферическую оболочку, то результирующая гравитационная сила, действующая на частицу в точке P, будет направлена вниз. Поскольку интенсивность гравитации – это сила гравитации на единицу массы, поэтому направление интенсивности гравитации будет вдоль c. Итак, вариант (iii) правильный.
Вопрос. Ракета запускается с земли по направлению к солнцу. На каком расстоянии от центра Земли сила тяжести на ракете равна нулю? Масса Солнца = 2 х 10 30 кг, масса Земли = 6 х 10 24 кг. Влиянием других планет и т. д. пренебречь (радиус орбиты = 1,5 x 10 11 м). (3 балла)
Ответ. Масса Солнца, М = 2 х 10 30 кг; Масса Земли, м = 6 х 10 93} \)= 2,6 х 10 8 м.
Вопросы. Как вы будете «взвешивать солнце», то есть оценивать его массу? Средний радиус обращения Земли вокруг Солнца равен 1,5 x 10 8 км (3 балла)
Ответ. Средний радиус обращения Земли вокруг Солнца. Солнца будет М, а Земли будет М.
92}\)= 2,009 х 10 30 кг = 2,0 х 10 30 кг.
Вопросы. Ракета запускается вертикально со скоростью 5 км с – ¹ от поверхности земли. Какое расстояние от земли пролетит ракета, прежде чем вернуться на землю? Масса Земли = 6,0 х 10 24 кг; средний радиус Земли = 6,4 х 10 8 м; G = 6,67 x 10-11 Н·м 2 кг -2 (3 балла)
Ответ. Начальная кинетическая энергия ракеты = 1/2 мВ 2 = 1/2 x м x (5000) 2 = 1,25 x 10 7 мДж
На расстоянии r от центра Земли кинетическая энергия становится равной 9 нулю, 003
. •. Изменение кинетической энергии = 1,25 x 10 7 – 0 = 1,25 x 10 7 м Дж
•. Изменение кинетической энергии = 1,25 x 10 7 – 0 = 1,25 x 10 7 м Дж
Эта энергия превращается в потенциальную энергию.
Начальная потенциальная энергия на поверхности земли = GM 97} м\)= 8х 10 16 м.
Вопросы. Убегающая скорость снаряда по поверхности Земли составляет 11,2 км с -1 . Тело выбрасывается с утроенной скоростью. Какова скорость тела вдали от Земли? Игнорировать присутствие Солнца и других планет. (3 балла)
Ответ. Пусть ves будет скоростью отрыва от поверхности земли, имеющей значение ves = 11,2 кг с -1 ]
= 11,2 x 10 3 м.с -1 . По определению 92}\)
= 11,2 x 10 3 x \(\sqrt{8}\)
= 31,7 x 10 3 мс -1 или 31,7 км с -6
Вопросы. Два тяжелых шара массой 100 кг каждый и радиусом 0,10 расположены на расстоянии 1,0 м друг от друга на горизонтальном столе. Каково гравитационное поле и потенциал в средней точке линии, соединяющей центры сфер? Находится ли в этой точке предмет в равновесии? Если да, то является ли равновесие устойчивым или неустойчивым? (3 балла)
Каково гравитационное поле и потенциал в средней точке линии, соединяющей центры сфер? Находится ли в этой точке предмет в равновесии? Если да, то является ли равновесие устойчивым или неустойчивым? (3 балла)
Ответ. Здесь значение G = 6,67 x 10 -11 Нм 2 кг -2 , M = 100 кг , R = 0,1 м, расстояние между двумя сферами, d = 1,0 м
Предположим, что расстояние любая сфера из середины линии, соединяющей их центр, равна r. Тогда r=d/2=0,5 м. Гравитационное поле в средней точке из-за двух сфер будет равным и противоположным.
Следовательно, результирующее гравитационное поле в точке рассогласования =0
Гравитационный потенциал в средней точке = ( – \(\frac{GM}{r} \)) x 2 9{-11} * 100 * 2}{0,5} \)= – 2,668 x 10 -8 Дж кг -1 .
Объект, помещенный в эту точку, будет находиться в устойчивом равновесии.
Вопросы. Геостационарный спутник вращается вокруг Земли на высоте почти 36 000 км от поверхности Земли. Каков потенциал из-за земного притяжения в месте нахождения этого спутника? (Возьмем потенциальную энергию на бесконечности равной нулю). Масса Земли = 6,0 х 10 24 кг, радиус = 6400 км. (3 балла)
Каков потенциал из-за земного притяжения в месте нахождения этого спутника? (Возьмем потенциальную энергию на бесконечности равной нулю). Масса Земли = 6,0 х 10 24 кг, радиус = 6400 км. (3 балла)
Вопрос. Звезда в 2,5 раза массивнее Солнца и сжавшаяся до размеров 12 км вращается со скоростью 1,2 об/мин. в секунду. Будет ли объект, помещенный на его экваторе, оставаться прилипшим к его поверхности из-за гравитации? (масса солнца = 2 x 10 30 кг).(3 балла)
Ответ. Ускорение свободного падения звезды, g = GM/R 2 …………(i)
Здесь M — масса, R — радиус звезды. 92\)
= m x 1,06 x 10 6 N
Поскольку внутренняя сила гравитации, действующая на тело на экваторе звезды, примерно в 2,2 миллиона раз больше внешней центробежной силы, тело останется прилипшим к поверхность звезды.
Также проверьте:
Что такое формула для массы?
Масса — это свойство физических объектов и мера устойчивости тела к ускорению. Можно рассматривать массу объекта как меру того, сколько физического «вещества» составляет этот объект.
Можно рассматривать массу объекта как меру того, сколько физического «вещества» составляет этот объект.
В отличие от относительных свойств, таких как положение, скорость или потенциальная энергия, которые всегда должны определяться по отношению к другому объекту или контрольной точке, масса является внутренним свойством, которым объект обладает независимо от его отношения к другим вещам. Массу объекта можно рассчитать несколькими способами:
Все три формулы являются способом определения массы объекта. Поскольку масса является фундаментальным свойством, она не определяется в терминах других единиц, как джоуль (Дж) Ньютона (Н). Существуют и другие способы расчета массы объекта, но эти три формулы являются наиболее распространенными.
m=ρV
m=Вт/г
m=F/a
Единицы массы
0345 (кг). Килограмм является единственной базовой единицей СИ с приставкой в названии (кило-). Первоначально один килограмм определялся как масса одного кубического децилитра (дл) воды при температуре ее плавления. С 1889 года килограмм был переопределен как масса Международного прототипа килограмма (IPK), физического артефакта, предназначенного для универсальной эталонной массы килограмма. Первоначально ИПК представлял собой чугунную гирю. В настоящее время принятым ИПК является цилиндр высотой 39 мм, изготовленный из специального платинового сплава.
«Слова тоже имеют подлинную субстанцию — массу, вес и удельный вес». — Тим О’Брайен
По состоянию на 2018 год килограмм является единственной единицей СИ, в которой физический объект является исходным значением. Все остальные единицы СИ были переопределены с точки зрения фундаментальных физических констант, таких как скорость света или постоянная Планка. В ноябре 2018 года Генеральная конференция мер и весов (GCPM) проголосовала за новое определение килограмма с точки зрения фундаментальных физических констант, и это изменение вступит в силу 20 мая 2019 года..
Способы вычисления массы
Из плотности и объема
Плотность объекта, иногда обозначаемая греческой буквой «ρ», является мерой массы на единицу объема. По сути, плотность говорит вам, насколько плотно упакована масса объекта. Чем плотнее объект, тем больше его масса на единицу объема.
Например, вода имеет плотность 977 кг/м 3 при стандартной температуре и давлении. То есть один кубический метр воды имеет массу 977 кг. Если мы знаем плотность и объем вещества, мы также можем вычислить массу этого вещества. Скажем, у нас есть 0,7 м 3 пробы воды. Какова масса этого образца?
То есть один кубический метр воды имеет массу 977 кг. Если мы знаем плотность и объем вещества, мы также можем вычислить массу этого вещества. Скажем, у нас есть 0,7 м 3 пробы воды. Какова масса этого образца?
Решение для массы дает нам:
m=ρV
m=(0,7 м 3 )(977 кг/м 3 ) = 683 кг
кубических метров при стандартной температуре воды и давлении воды 0. иметь массу 683 кг.
Некоторые объекты невероятно плотные. Нейтронная звезда, например, имеет среднюю плотность 1,1 х 10 18 кг/м 3 . Одна чайная ложка нейтронной звезды на Земле весила бы около 100 миллионов тонн.
«Масса становится неподвижной; он не может маневрировать и, следовательно, не может одерживать победы, он может только сокрушать своим весом». — Ганс фон Сект
Из «Силы и ускорения»
Свойство массы понимается также как мера сопротивления физического объекта ускорению под действием внешней силы. Это понятие массы иногда называют инерционная масса . Инерция — это тенденция движущегося тела продолжать находиться в постоянном состоянии движения, поэтому инерционная масса — это мера того, насколько сильно инерционно обладает тело и насколько трудно изменить состояние своего движения. Связь между массой, силой и ускорением выражается вторым законом Ньютона F=ma. Это математическое соотношение говорит нам о том, что перед лицом постоянной силы более массивное тело будет ускоряться медленнее. Измеряя силу, приложенную к телу, и измеряя наблюдаемое ускорение, мы можем вычислить массу тела.
Это понятие массы иногда называют инерционная масса . Инерция — это тенденция движущегося тела продолжать находиться в постоянном состоянии движения, поэтому инерционная масса — это мера того, насколько сильно инерционно обладает тело и насколько трудно изменить состояние своего движения. Связь между массой, силой и ускорением выражается вторым законом Ньютона F=ma. Это математическое соотношение говорит нам о том, что перед лицом постоянной силы более массивное тело будет ускоряться медленнее. Измеряя силу, приложенную к телу, и измеряя наблюдаемое ускорение, мы можем вычислить массу тела.
Например, допустим, что мы прикладываем силу 748 Н к металлическому кубу и измеряем его ускорение как 21 м/с 2 . Какова масса металлического куба? Мы можем вычислить массу, разделив величину силы на величину ускорения так:
м=F/a
м=(748 Н)/(21 м/с 2 ) ≈ 35,62 кг
Итак, мы знаем, что металлический куб должен иметь массу 35,62 кг.
From Weight
Строго говоря, вес и масса — разные вещи. В английском языке два слова «вес» и «масса» являются синонимами, однако в физических науках они имеют разные значения. Масса — это неизменное свойство, которое не меняется от места к месту. Вес является мерой силы гравитационного поля, действующего на массивное тело. Поскольку напряженность гравитационного поля может различаться, т. Е. Луна имеет более слабую напряженность гравитационного поля, чем Земля, вес объекта может различаться в разных средах.
Соотношение между массой и весом выражается формулой W = mg, где g — мера ускорения свободного падения. Точное значение g зависит от местоположения. На Земле g имеет значение примерно 9,81 м/с 2 , а на Луне g составляет около 1,6 м/с 2 . Выражение W=mg дает вес в ньютонах, в то время как повседневное понимание веса дается в фунтах (lbs) коэффициент преобразования из ньютонов в фунты составляет около 1 N=0,22 фунта.
Например, на поверхности Земли где г=90,81 м/с 2 , 50-килограммовый объект будет иметь вес в фунтах:
W=(50kg)(9,81м/с 2 )=490,5N
Преобразование ньютонов в фунты дает нам:
490,5 Н(0,22 фунта/1 Н)≈ 108 фунтов
И наоборот, на Луне, где g имеет значение 1,6 м/с 2 , объект массой 50 кг будет весить:
W=50(кг) (1,6 м/с 2 )(0,22 фунта/1 Н) ≈ 18 фунтов
Тот же 50-килограммовый объект весит 108 фунтов на Земле и 18 фунтов на Луне.
Точно так же, если мы знаем вес объекта, мы можем вычислить его массу в обратном направлении. Скажем, объект весит 160 фунтов Земли. мы можем рассчитать массу объекта как: 2 )≈ 83,4 кг
Итак, 180-фунтовое тело на Земле имеет массу около 84,3 кг.
Массово-энергетическая эквивалентность
Очень долгое время ученые считали, что массу объекта можно считать полностью независимой от других его свойств. Однако в начале 20 века специальная теория относительности Эйнштейна показала, что масса и энергия на самом деле являются двумя разными названиями одной и той же физической величины. В частности, масса объекта и его полная энергия связаны знаменитым уравнением Эйнштейна E=mc 2 , где c — скорость света в вакууме.
E=mc 2 говорит нам, что полная энергия неподвижного тела прямо пропорциональна его массе с коэффициентом c 2 . Поскольку c=3 000 000 м/с, c 2 является чрезвычайно большим фактором. Следовательно, даже крошечный кусочек массы содержит подавляющее количество внутренней энергии. Для сравнения, общее количество энергии от полного преобразования 1 грамма вещества в энергию примерно равно 21,5 килотоннам тротила — мощности атомной бомбы, сброшенной на Хиросиму.
Следовательно, даже крошечный кусочек массы содержит подавляющее количество внутренней энергии. Для сравнения, общее количество энергии от полного преобразования 1 грамма вещества в энергию примерно равно 21,5 килотоннам тротила — мощности атомной бомбы, сброшенной на Хиросиму.
«Любой дурак может знать. Суть в том, чтобы понять». — Альберт Эйнштейн
В некоторых физических процессах, таких как деление ядер или движение тела в сильном гравитационном поле, материя преобразуется в энергию и высвобождается в виде большого количества света и тепла. В частности, уравнение Эйнштейна говорит нам, как мы можем рассчитать количество энергии, высвобождаемой во время таких реакций.
Допустим, 30 кг урана (Ur) помещают в ядерный реактор. При делении примерно 0,1% этой массы полностью превращается в энергию. Сколько энергии получается?
0,1% от 30 кг равно 0,3 кг. Подключение этого к уравнению Эйнштейна дает нам:
E = (0,3 кг) (3000 000) 2 = (0,3) (8,98755179 × 10 16 ) = 2,69626554 × 100005 16 J
323554 × 100005 16 J
2323333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333н3н3н3н 313323333. 0 16 6. кг (0,6 фунта) вещества в энерговыделение 2,69626554 × 10 16 Дж энергии. Это количество примерно равно взрыву более 6 млн тонн тротила (12 млрд фунтов), чего достаточно, чтобы полностью сровнять с землей даже самые крупные города.
0 16 6. кг (0,6 фунта) вещества в энерговыделение 2,69626554 × 10 16 Дж энергии. Это количество примерно равно взрыву более 6 млн тонн тротила (12 млрд фунтов), чего достаточно, чтобы полностью сровнять с землей даже самые крупные города.
Мы также можем работать в обратном направлении от некоторого количества энергии, чтобы определить количество преобразованной массы. Скажем, какая-то реакция деления высвобождает 1,6178 × 10 16 джоулей энергии. Какое количество массы перешло в энергию при этом процессе? Используя нашу удобную формулу массовой энергии, мы можем определить:
1,6178 × 10 16 j = M (8,98755179 × 10 16 )
(1,6178 × 10 0005 16 ) /8,98555179 × 10000666666666666666666666666666196666666996669 66666699000 16.1 16) /8.98555179996619969996619966199000 16.1). )=m
m ≈ 0,18 кг
Итак, около 0,18 кг массы было преобразовано в энергию.
Почему объекты имеют массу?
Только недавно ученые начали открывать ответ на вопрос, почему частицы вообще имеют массу. В 1960-х годах несколько ученых заметили некоторые проблемы с их уравнениями, описывающими поведение элементарных частиц. В частности, их уравнения предсказывали, что некоторые частицы, генерируемые во время высокоскоростных столкновений, не будут иметь массы. Однако экспериментальное наблюдение показало, что эти частицы действительно имели ненулевую массу.
В 1960-х годах несколько ученых заметили некоторые проблемы с их уравнениями, описывающими поведение элементарных частиц. В частности, их уравнения предсказывали, что некоторые частицы, генерируемые во время высокоскоростных столкновений, не будут иметь массы. Однако экспериментальное наблюдение показало, что эти частицы действительно имели ненулевую массу.
Ученые предположили, что масса бозона может генерироваться взаимодействием между этими бозонами и всепроникающим полем, называемым полем Хиггса (в честь одного из его теоретиков Питера Хиггса). Когда безмассовые бозоны движутся против этого поля, их импульс замедляется, и они теряют часть энергии. Поле Хиггса преобразует эту энергию в энергию массы, которая проявляется как свойство массы, которое мы измеряем. Было предсказано, что это взаимодействие между бозонами и полем Хиггса создаст новую частицу, крошечный бозон, названный бозоном Хиггса. Ускоритель частиц в ЦЕРНе наконец продемонстрировал существование частицы Хиггса в 2013 году, а 8 октября 2013 года Питер Хиггс и Франсуа Энглер были удостоены Нобелевской премии по физике за свою теоретическую работу над частицей.




 При перемещении листов между листами 2 и 6 в расположение за пределами указанного диапазона листов Excel в Интернете удаляет их значения из вычисления.
При перемещении листов между листами 2 и 6 в расположение за пределами указанного диапазона листов Excel в Интернете удаляет их значения из вычисления. 5%)
5%)

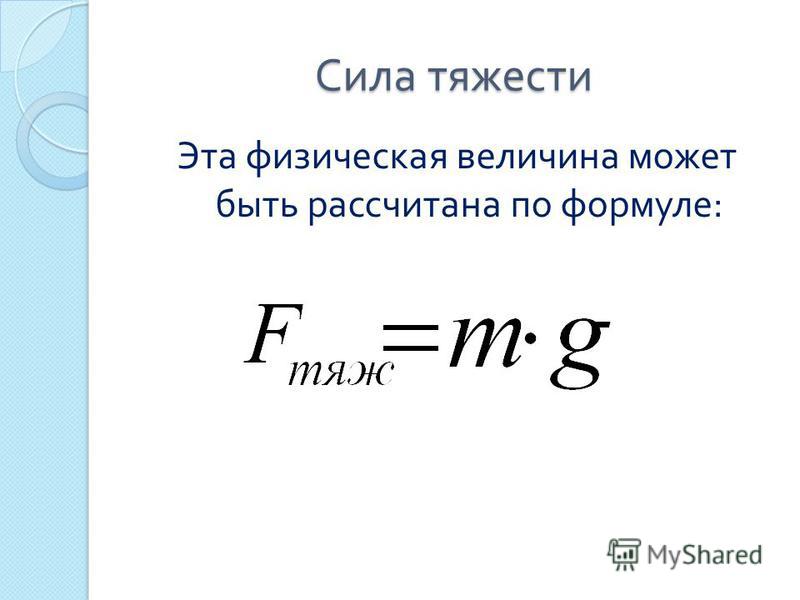 38 x 106 m
38 x 106 m 64 x 107 m
64 x 107 m

 Гравитационное притяжение обеспечивают два стальных шарика . Сила тяжести была рассчитана путем определения того, насколько сильно скручена проволока .
Гравитационное притяжение обеспечивают два стальных шарика . Сила тяжести была рассчитана путем определения того, насколько сильно скручена проволока .



 [NEET 2018]
[NEET 2018]  [NEET 1994]
[NEET 1994]  В зависимости от силы гравитационного ускорения вес будет разным.
В зависимости от силы гравитационного ускорения вес будет разным.