Как рассчитать мгновенную скорость, формула мгновенной скорости –
Мгновенная скорость сообщает нам о движении частицы в определенный момент времени в любом месте на ее пути.
Мгновенная скорость принимается за предел средней скорости при стремлении времени к нулю. Вычислять Vинст мы можем использовать график смещения-времени / формулу мгновенной скорости. т.е. производная смещения (s) по времени (t), взятая.
Чтобы узнать, как рассчитать мгновенную скорость объекта, нам нужно выполнить следующие действия.. Давайте посмотрим на это на примере.
Рассмотрим уравнение скорости в терминах положения / смещения.Вычислять мгновенная скорость, мы должны рассмотреть уравнение это говорит нам о его должность ‘s’ в определенный время ‘t’.
Это означает, что уравнение должно содержать переменную ‘s‘с одной стороны и’t‘ с другой стороны,
s = -2т2 + 10т +5 при t = 2 секунды.
В этом уравнении переменными являются:
Смещение = s, измеряется в метрах.
Время = t, измеряется в секундах.
Рассмотрим производную данного уравнения.Чтобы найти производную данного уравнения перемещения, дифференцировать функцию по времени,
Подставьте данное значение «t» в уравнение производной, чтобы найти мгновенную скорость.ds / dt = – (2) 2т (2-1) + (1) 10 т1 – 1 + (0) 5 т0
ds / dt = -4т1 + 10т0
ds / dt = -4t + 10
Найдите мгновенная скорость при t = 2 подставить “2” для t в производной ds / dt = -4t + 10.
Тогда мы можем решить уравнение
ds / dt = -4t + 10
ds / dt = -4 (2) + 10
ds / dt = -8 + 10
ds / dt = -2 метра в секунду
Здесь «метры / секунда» – это единица измерения мгновенной скорости в системе СИ.
Мгновенная скорость в любой конкретный момент времени определяется наклоном касательной, проведенной к графику положения-времени в этой точке.
- Постройте график расстояние против времени.
- Отметьте точку, в которой вам нужно найти мгновенную скорость, скажем A.
- Определите точку на графике, соответствующую времени t1и t2.
- Вычислить vсредний и проведем касательную в точке A.
- На графике vинст в точке A находится по касательной, проведенной в этой точке
- Чем длиннее тангенс, тем точнее будут значения.
- На показанном изображении Синяя линия это график зависимости положения от времени, А Красная линия – приблизительный наклон линии при t = 2.5 секунды.
- Если мы продолжаем выбирать точки, которые все ближе и ближе друг к другу, линия начнет приближаться к наклону линии, касательной к одной точке.
- Если мы возьмем предел функции в этой точке, мы получим значение наклона касательной в этой точке.
- Расстояние составляет примерно 140 м, а временной интервал – 4.3 с. Следовательно, приблизительный уклон составляет 32.55 м / с.
Для вычисления мгновенной скорости по графику положения-времени.
Постройте график зависимости смещения от времени.- Используйте оси X и Y для представления время и перемещение.
- Затем нанесите на график значения времени и смещения.
- Линия смещения содержит точки (3,6) и (5,8).
- В этом примере, если мы хотим найти наклон в точке (3,6), мы можем установить А = (3,6) и B = (5,8)
Найдите наклон линии, соединяющей две точки, т. Е. Между точками A и B.
Найдите среднюю скорость между этими двумя временными интервалами, т. Е.
где K – наклон между двумя точками.
Здесь наклон между A и B равен:
Slope = k= (8-6)/(5-3)=1
Повторите несколько раз, чтобы найти уклон, перемещая B ближе к A.- Продолжайте выбирать точки ближе друг к другу; затем он начнет приближаться к наклону касательной.
- Если мы рассмотрим предел функции в этой точке, мы получим значение наклона в этой точке.
- Здесь мы можем использовать точки (4,7.7), (3.5, 6.90) и (3.25, 6.49) для B и исходную точку (3,6) для A.
- При B = (4,7. 7)
7) - При B = (3.5; 6.90)
- При B = (3.25; 6.49)
В этом примере, когда мы приближаем B к A, мы получаем значения 1.7, 1.8 и 1.96 для K. Поскольку эти числа примерно равны 2, можно сказать, что 2 – наклон А.
Здесь, мгновенная скорость 2 м / с.
С математической точки зрения мы можем написать формула мгновенной скорости в виде,
Instantaneous Velocity= Change in position/ Time Interval
Здесь, ds / dt – это производная смещения (с) по времени (t).
Приведенные выше производная имеет конечное значение когда и знаменатель, и числитель стремятся к нулю.
Используя вычисления, всегда можно вычислить скорость объекта в любой момент на его пути. Это называется мгновенной скоростью. и задается уравнением v = ds / dt.
Мгновенная скорость = предел, поскольку изменение во времени приближается к нулю (изменение положения / изменение во времени) = производная смещения по времени
| Формула | Символ | Определение | |
| Средняя скорость | sf= Окончательный смещение si = Начальное смещение tf = Последний раз ti = Начальное время | Средняя скорость is общее расстояние деленное на общее затраченное время. | |
| Мгновенная скорость | Скорость при любом момент времени. |
Компания мгновенная угловая скорость скорость, с которой частица движется по круговой траектории в определенный момент времени.
Компания мгновенная угловая скорость вращающегося объекта определяется выражением
dθ/dt = производная углового положения θ по времени, найденное предельным переходом Δ t → 0 в средняя угловая скорость.
Компания направление угловой скорости на круговой траектории – вдоль оси вращения и указывает от вас на вращающееся тело по часовой стрелке и к вам для тела, вращающегося против часовой стрелки. В математике это обычно описывается правило правой руки.
Формула мгновенной скорости
Формула мгновенной скорости
Instantaneous Speed=ds/dt
Разница между мгновенной скоростью и мгновенной скоростью.
| Мгновенная скорость | Мгновенная скорость |
| Это скорость движущейся частицы в определенный момент t. | Вход в музей Мадам Тюссо мера скорости частицы в определенный момент t. |
| Мгновенная скорость определяет, насколько быстро и в каком направлении движется объект. | Мгновенная скорость измеряет, насколько быстро частица движется. |
| Количество векторов | Скалярная величина |
Мгновенная скорость описывается как скорость движущегося объекта.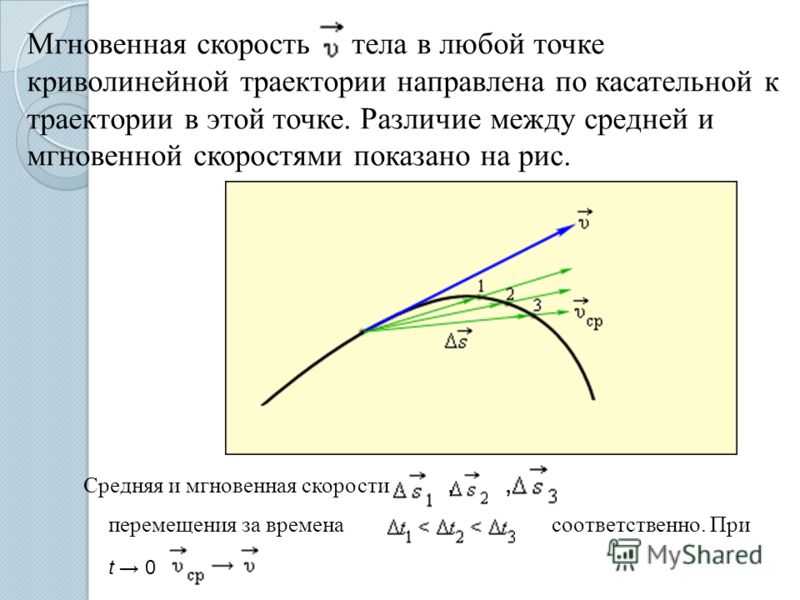
Мы можем найти его, используя среднюю скорость, но мы должны сузить время, чтобы приблизиться к нулю.
Итого можно сказать, что мгновенная скорость – это скорость движущейся частицы в определенный момент времени.
Формула мгновенной скоростиДля любого уравнения движения s(t), для мгновенная скорость когда t приближается к нулю, мы можем записать формула в виде,
Мгновенная скорость любого объекта – это предел средней скорости, когда время приближается к нулю..
Вставьте значения t1= t и t2 = t + Δt в уравнение для средней скорости и переходя к пределу при Δt → 0, находим формула предела мгновенной скорости
Мгновенная скорость равна наклону касательной на графике положение-время.
Мгновенноs Интерпретация скорости из графика st- Мгновенная скорость равна наклону касательной на графике положение-время.
- Интерпретация мгновенной скорости по графику st
- Наклон фиолетовой линии (касательной) на графике смещения v / s дает мгновенную скорость.
- Если фиолетовая линия образует угол с положительной осью абсцисс.
Vinst= наклон фиолетовой линии = tanθ
Для того, чтобы найти мгновенная скорость в точке, мы должны сначала найти среднюю скорость в этой точке.
Вы можете найти мгновенную скорость при t = a с помощью вычисление средней скорости графика зависимости положения от времени путем взятия меньшего и большего приращения точки, в которой вы хотите определить Vinst.
Во время езды на велосипеде велосипедист меняет свою скорость в зависимости от расстояния и времени, которое он проходит.
Велосипедисты катаются на велосипеде, Изображение предоставлено: Автор изображения pxfuel.
com
Если мы хотим найти скорость в одной конкретной точке, мы должны использовать мгновенную скорость.
Покажи нам пример,
а). Определить мгновенную скорость частицы, движущейся по прямому пути за t = 2 секунды, с функцией положения «s», определенной как 4t² + 2t + 3?Решение:
Данный с = 4т² + 2т + 3
Дифференцируя данную функцию по времени, мы вычисляем мгновенную скорость следующим образом:
Подставляя значение t = 2, мы получаем мгновенную скорость как,
Vмоментальный =ds/dt
Подставляя функцию s,
vинст =d(4t2 +2t +3)/dt
vинст =8t+2
vинст = (8 * 2)+2vинст =18 ms-1
Таким образом, мгновенная скорость для вышеуказанной функции составляет 18 м / с.
Некоторые проблемы с мгновенной скоростью,Проблема 1:Движение тележки задается функцией s = 3t2 + 10t + 5.
Вычислите его мгновенную скорость в момент времени t = 4 с.Решение:
Данная функция s = 3t2 + 10т + 5.
Продифференцируя указанную выше функцию по времени, получим
Vмоментальный =ds/dt=d(3t2 +10t +5)/dt
Подставляя функцию s,
Vмоментальный = v(t)=6t+10
Подставляя значение t = 4 с, мы получаем мгновенную скорость как,
v(4)= 6(4)+10
v(4) =34ms-1
Для данной функции мгновенная скорость составляет 34 м / с.
Проблема 2:Выстреленная пуля движется по прямой траектории, и ее уравнение движения имеет вид S (t) = 3t + 5t.2. Так, например, если он летит за 12 секунд до удара, найдите мгновенную скорость при t = 7 с.Решение: Мы знаем уравнение движения:
s(t) = 3t + 5t2
Vмоментальный =ds/dt=d(3t + 5t2)/dt=3+10t
Vмоментальный at (t = 7) = 3 + (10 * 7)
Vмоментальный = 73 м / с
Проблема 3:Объект выпускается с определенной высоты, чтобы он мог свободно падать под действием силы тяжести.
Уравнение движения для перемещения s (t) = 5.1 т.2. Какой будет мгновенная скорость объекта в момент времени t = 6 с после выпуска?Изображение предоставлено PXHere.com Решение:
Уравнение движения:
s (t) = 5.1 т2
Мгновенная скорость при t = 6 с
Проблема 4:Найдите скорость при t = 2, учитывая уравнение перемещения s = 3t3 – 3т2 + 2т + 7.Решение:
Это похоже на предыдущие задачи, за исключением того, что они дали кубическое уравнение вместо квадратного уравнения, чтобы решить его таким же образом.
Уравнение движения:
s (t) = 3t3 – 3т2 + 2т + 7.
Мгновенная скорость при t = 7 с
vинст = 9 (7)2 – 6(7) +2
vинст = 441 – 42 +2
vинст = 401 м / с
Проблема 5:Положение человека, движущегося по прямой, определяется выражением s (t) = 7t.
2+ 3t + 19, где t – время (секунды). Найдите уравнение для мгновенной скорости v (t) частицы в момент времени t.Решение:
Дано: s (t) = 7t2+ 3т + 19
vинст = ds/dt =d(7t2 + 3t+19)/dt
vинст = 14t + 3
vинст = v (t) = (14t + 3) м / с – уравнение для мгновенной скорости.
Предположим, что если принять t = 3s, то
vинст = v(t)= 14(3) + 3 = 45m/s
Проблема 6:Движение автомобиля описывается уравнением движения s = gt2 + b, где b = 20 м и g = 12 м. Следовательно, найдите мгновенную скорость при t = 4 с.Решение:
s (t) = gt2 + b
v (t) = 2gt + 0
v (t) = 2gt
Здесь g = 12 и t = 4s,
v (4) = [2 x 12 x 4] = 96 м / с.
v (т) = 96 м / с.
Проблема 7:Стол, упавший со здания 1145 футов, имеет высоту (в футах) над землей, определяемую как s (t) = 1145-12 т.
2. Затем вычислите мгновенную скорость стола на 3 с?Решение:
Мгновенная скорость при t = 3 с составляет -72 м / с.
Проблема 8:Функция положения частиц определяется выражением s = (3t2)i – (4т)k + 2. какова его мгновенная скорость при t = 2? Каково его мгновенное ускорение как функция времени?
Решение:
s (t) = (3т2)i – (4т)k +2
v (t) = (6t)i -4k………… .. (Уравнение 1)
v (2) = (6 * 2)i -4k
v (2) = 12i -4k м/с
Чтобы вычислить мгновенное ускорение как функцию времени
а (т) = v1(Т)
дифференцируя уравнение 1 по t, получаем
а (т) = 6i м/с
Проблема 9:Положение насекомого определяется как s = 44 + 20t – 3t.
3, где t в секундах, а s в метрах.а. Найдите среднюю скорость объекта между t = 0 и t = 4. s.б. В какое время между 0 и 4 мгновенная скорость равна нулю.решение:
Для расчета средней скоростиЧтобы найти время, при котором мгновенная скорость равна нулю.vинст =ds/dt=20-9t2
20-9t2=0
t=(20/9)½
т=1.49 с
Проблема 10:Частица движется с функцией смещения s = t2 + 3.Найдите положение при t = 2.Найдите среднюю скорость от t = 2 до t = 3.Найти его мгновенную скорость при t = 2.Решение:
Чтобы найти позицию при t = 2s (t) = t2 + 3
с (2) = (2)2 + 3
с (2) = 7
Для того, чтобы найти Средняя скорость.
Чтобы найти мгновенную скоростьvинст = ds / dt
vинст =2t
При t = 2 с
vинст =2(2)=4m/s
| Мгновенная скорость | Средняя скорость |
| Компания мгновенная скорость – средняя скорость между двумя точками. | Средняя скорость это соотношение изменения дистасть относительно времени за период. |
| Мгновенная скорость рассказывает о движении между двумя точками на пройденном пути. | Средняя скорость не дает информации о движении между точками. Путь может быть прямым / изогнутым, а движение может быть постоянным / переменным. |
Мгновенная скорость равен наклону касательной к смещение (с) в зависимости от графика времени. | Он равен наклону секущая линия of граф st. |
| вектор | вектор |
Wмы можем найти мгновенную скорость приближением по график зависимости смещения от времени без исчисления в определенной точке. Нам нужно провести касательную в точке вдоль изогнутой линии и оценить наклон, где вам нужно найти мгновенную скорость.
| Мгновенная скорость | Мгновенное ускорение | |
| Из формулы | Для расчета мгновенной скорости, возьмем предел изменения расстояния по времени, когда время приближается к нулю. т. е. взяв первая производная функции смещения. | к рассчитать мгновенное ускорение, принять предел изменения скорости по времени, когда изменение во времени приближается к нулю. т.е. взяв вторая производная функции смещения. |
| Из графика | Равно наклон касательной к графику st. | Равно наклон касательной графика vt. |
Решение: Мы знаем уравнение движения: s (t) = 2t + 4t2
vинст = ds/dt= 2t + 4t2/dt=2+8t
vинст at t=7
v(t=7)=2+((8X3)
vинст = 26 м / с
a(t)=dv/dt=d(2+8t)/dt=8
a(t)=8m/s
Мгновенная скорость задается как величина мгновенной скорости.
Если известно перемещение как функция времени, мы можем найти мгновенная скорость в любое время.
Давайте разберемся в этом на примере.
12 задачи:Уравнение движения s (t) = 3t3
Instantaneous Speed= ds/dt
sинст =d3t3/dt=9t2
Рассмотрим t = 2s
sинст = 9 (2)2= 36 м / с
Уравнения кинематики можно использовать только при постоянном ускорении объекта.
В случае переменные ускорения, Уравнения кинематики будут разными в зависимости от функции, которую принимает ускорение; в то время; мы должны использовать Комплексный подход вычислять мгновенная скорость. Что будет немного сложно.
Компания мгновенная скорость дан кем-то,
Чем меньше значение «t», Тем точнее будет наклон касательной, т.
е. мгновенная скорость.
Когда ты хочешь рассчитать скорость в определенное время вам нужно сначала рассчитать средние скорости взяв небольшие промежутки времени. Если эти средние скорости дают одно и то же значение, тогда это будет требуемый мгновенная скорость.
Мгновенная скорость отличается от скорости.
Скорость обычно известен как скорость изменения положения во времени. Напротив, в мгновенная скорость, временной интервал сужается, чтобы приблизиться к нулю, чтобы получить скорость в конкретный момент времени.
Например,
Частица движение по кругу имеет нулевые смещения, и требуется знать скорость частицы. В этом случае мы можем вычислить мгновенную скорость, потому что она имеет тангенциальная скорость в любой момент времени.
Реальные примеры мгновенной скорости
Если мы рассмотрим пример мяча для сквоша, мяч возвращается в исходную точку; на тот момент полное водоизмещение и средняя скорость будет равна нулю.
В таких случаях движение рассчитывается по формуле мгновенная скорость.
- Спидометр автомобиля дает информацию о мгновенная скорость / скорость средство передвижения. Он показывает скорость в определенный момент времени.
Спидометр, Изображение предоставлено: Автор изображения pxfuel.com
- Во время гонки фотографы делают снимки бегунов, их средняя скорость не меняется, но меняется их мгновенная скорость, зафиксированная на «снимках». Так что это будет пример мгновенной скорости.
- Если вы находитесь рядом с магазином, и перед вами проехал автомобиль на отметке «t«Во-вторых, и вы начинаете думать о его скорости на конкретном время, здесь вы имели бы в виду мгновенная скорость транспортного средства.
Является ли мгновенная скорость вектором
Мгновенная скорость – это векторная величина.
Мгновенная скорость – это вектор, потому что он имеет как величину, так и направление. Он показывает как скорость (относится к величине), так и направление. участникале Имеет размер LT-1Мы можем определить это, взяв наклон графика расстояние-время..
Как найти мгновенную скорость только с графиком положения и времени и без заданного уравненияМы можем определить мгновенную скорость, взяв наклон графика положения-времени.
- Постройте график смещения во времени.
- Выберите точку A и другую точку B, которая находится рядом с точкой A на линии.
- Найдите угол наклона между A и B, рассчитайте несколько раз, перемещая A ближе к B.
- Рассчитайте наклон для бесконечно малого интервала на прямой.
- Полученный наклон представляет собой мгновенную скорость.
Невозможно вызвать мгновенное изменение скорости, так как для этого потребуется бесконечное ускорение.
Как правило, ускорение является результатом F = ma
a=F/m=Force over a mass
а скорость является результатом ускорения (от интегрирования). Если изменение скорости является ступенчатой функцией и когда время приближается к нулю, потребуется бесконечное ускорение и сила, чтобы мгновенно изменить скорость массы.
Как я могу рассчитать смещение, если ускорение является функцией мгновенной скорости Задана начальная скоростьМы можем вычислить смещение двумя способами, когда задана начальная скорость.
От происхожденияЗдесь ускорение является функцией мгновенной скорости,
а=дв/дт
Начальная скорость
v=дс/дт
a=d(ds)/dt2
d(ds)=adt2
Интегрируя,
Используя эту форму, вы можете получить ds смещения.
Используя приведенное ниже кинематическое уравнение, мы можем найти смещение,
[S = ut + 1/2(at2)]
Что такое средний и мгновенная скорость
Средняя скорость и мгновенная скорость выражаются следующим образом:
| Средняя скорость | Мгновенная скорость |
| Средняя скорость для определенного временного интервала – это полное смещение, деленное на общее время. | И временной интервал, и смещение в какой-то момент приближаются к нулю. Но предел производной смещения по общему интервалу времени отличен от нуля и называется мгновенной скоростью. |
| Средняя скорость это скорость всего пути в движении | а мгновенная скорость скорость частицы в определенный момент времени |
vavg = s/t | vinst = ds/dt |
Мгновенное ускорение тела всегда перпендикулярно мгновенной скорости.
При круговом движении мгновенная ускорение тела всегда перпендикулярно мгновенной скорости, и это ускорение называется центростремительным. ускорение. Скорость остается неизменной; изменяется только направление, поскольку перпендикулярное ускорение изменяет траекторию тела.
чему равна, как найти начальную и среднюю, какой буквой обозначается
Скорость в физике — что это такое
Скорость — векторная физическая величина, которая характеризуется направлением и быстротой перемещения материальной точки.
В международной системе единиц (СИ) единица измерения скорости обозначается как метр в секунду (мс).
На практике зачастую используют внесистемные единицы измерения скорости. Например: километр в час (кмч).
В физике понятие скорости встречается в разделе «Кинематика», в котором дается описание механического движения, а это основа изучения скорости как векторной физической величины.
Скорость может характеризоваться быстротой перемещения не только материальной точки, но и еще элементарных частиц и волн.
Скорость звука — это величина, которая показывает, на какое расстояние может распространиться звуковая волна за единицу времени.
Скорость света — абсолютная величина, которая показывает скорость распространения электромагнитных волн.
Виды скорости в физике, основные характеристики
В физике существуют такие виды скорости, как: начальная скорость, равномерная скорость, средняя скорость, мгновенная скорость.
- Начальная скорость — это скорость в течении начального момента времени. Начальная скорость подразумевается какой-то момент времени, в который начинается измерение скорости (обычно t = t0).
- Равномерная скорость — это скорость при равномерном движении, численно равная отношению пути, пройденного телом, ко времени, затраченному на прохождение этого пути.
- Средняя скорость — это отношение всего пройденного пути к затраченному на это движение времени.
- Мгновенная скорость — это векторная величина, равная отношению перемещения к малому промежутку времени, за которое это перемещение производится.
Скорость принято записывать буквой ϑ, в СИ она обозначается как мс.
Как писалось выше, скорость равна отношению пути S ко времени t.
Формулы скорости при движении разных видов
Нахождение начальной скорости зависит от задачи и от исходных данных. Ее можно найти по конечной скорости, ускорению и времени: ϑн=ϑ0-(α∙t), где:
ϑн — начальная скорость;
ϑ0 — конечная скорость;
α — ускорение;
t — время.
Равномерная — находится по обычной формуле скорости: ϑ = St, где:
ϑ — скорость;
S — путь;
t — время.
Формула средней скорости: ϑср=Sобщtобщ.
Формула мгновенной скорости:ϑ⇀ = ∆S⇀∆t.
Примеры задач с решением
Задача 1На автомобиле за 3 часа проехали 180 км с одной и той же скоростью. Чему равна скорость автомобиля?
Решение:
Скорость — это расстояние, пройденное телом за единицу времени. Чтобы определить скорость, нужно пройденное расстояние разделить на время движения.
Если за 3 часа автомобиль проехал 180 километров с одной и той же скоростью, то разделив 180 км на 3 часа мы определим расстояние, которое проезжал автомобиль за один час. А это и есть скорость движения.
ϑ = St
ϑ = 1803 = 60 кмч
Ответ: скорость автомобиля составляет 60 км/ч.
Задача 2Первый час автомобиль ехал со скоростью 100 км/ч, следующие два часа — со скоростью 90 км/ч, а затем два часа — со скоростью 80 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
В условии сказано о трех участках пути.
ϑср=Sобщtобщ
ϑср=S1+S2+S3t1+t2+t3
Участки пути нам не даны, но мы можем без труда их вычислить:
Первый участок пути составил 1∙100 = 100 километров.
Второй участок пути составил 2∙90 = 180 километров.
Третий участок пути составил 2∙80 = 160 километров.
Вычисляем скорость:
ϑср=100+180+1601+2+2/=4405=88кмч
Ответ: средняя скорость составляет 88 км/ч.
Конечная скорость после 2 секунд движения с ускорением 0,2 м/с², равна 3 м/с. Найти начальную скорость.
ϑн=ϑ0-(α∙t)
ϑн=3-(0,2∙2)=2,6мс
Ответ: начальная скорость составляет 2,6 м/с.
Мгновенная скорость: значение, формулы и примеры
Что означает мгновенная скорость? Какова его связанная формула? Как вы решаете задачи, связанные с этой концепцией физики? В этой статье мы ответим вам на все эти вопросы.
Найти уравнение движения
Уметь вычислять скорость объекта в любой момент , его уравнение движения ( уравнение, устанавливающее связь смещения со временем ) необходимо выяснить.
Скорость — это векторная величина, которая формально определяется как скорость изменения положения или смещения во времени . Говоря о любом векторе, таком как скорость объекта, мы говорим не только о величине, но и о направлении. Вот почему скорость и скорость это разные вещи. Скорость — это скаляр ( — чистое число, указанное по величине, без направления ), а скорость — это вектор.
Проще говоря, скорость – это величина скорости. Говоря о скорости, мы указываем ее в соответствии с некоторой фиксированной системой отсчета, и ее единицей является метров в секунду . Его можно измерить двумя способами. Один находится в форме средней скорости, а другой – мгновенной скорости. Формула для первого выглядит следующим образом.
Средняя скорость = ΔS/ΔT
Здесь ΔS — пройденное расстояние, а ΔT — период времени в пути.
Формула мгновенной скорости
Средняя скорость не может сказать вам, как изменилась скорость объекта в определенные моменты времени. Мгновенная скорость, как следует из самого названия, — это скорость движущегося объекта в конкретный момент времени. В математических терминах это можно определить следующим образом.
Мгновенная скорость = Lim ΔT → 0 ΔS/ΔT = dS/dT
Это скорость объекта, рассчитанная в кратчайший возможный момент времени ( рассчитанная при стремлении временного интервала ΔT к нулю ).
dS/dT — производная вектора смещения «S» по отношению к «T». Мгновенная скорость в определенный момент вычисляется путем подстановки соответствующего значения переменной времени в первую производную уравнения смещения по времени.
Во время вождения автомобиля стрелка спидометра или значение цифрового дисплея ( , показывающее скорость в километрах в час ) на приборной панели колеблется в каждый момент времени в зависимости от достигнутой им скорости. Эта величина вместе с направлением движения, меняющимся в каждое мгновение, и есть мгновенная скорость автомобиля. Теоретически он должен быть измерен в кратчайший отрезок времени. Вот почему производная вычисляется, предполагая, что ΔT стремится к нулю.
Из общего количества времени, затраченного на автомобильную поездку, и пройденного расстояния можно рассчитать среднюю скорость, но мгновенное значение будет учитываться при поездке. То есть в среднем ваш автомобиль может двигаться со скоростью 50 км/ч, но в любой момент она может достигать значений в диапазоне 30 км/ч, 40 км/ч или даже 60 км/ч в разные моменты времени.
.
Концепцию можно также понять с точки зрения двумерного графика времени (по оси X) относительно смещения (по оси Y). С точки зрения графика, мгновенная скорость в данный момент равна наклон касательной , проведенной в точке кривой, соответствующей этому конкретному моменту.
Исчисление, разработанное сэром Исааком Ньютоном и Лейбницем, может вычислять небольшие изменения во времени, включая понятия предела и производной. Приведенное выше уравнение требует, чтобы вы знали, как рассчитать производную. Позвольте мне проиллюстрировать использование формулы несколькими примерами.
Понятия физики никогда не могут быть правильно поняты, если вы не решаете проблемы и не запускаете математический механизм, лежащий в основе всего этого. Давайте решим некоторые задачи.
Задача 1:
Пуля, выпущенная в космосе, движется прямолинейно, уравнение ее движения S(t) = 4t + 6t 2 . Если он движется за 15 секунд до удара, найдите мгновенную скорость в 10 -й -й секунде.
Решение : Мы знаем уравнение движения:
S(t) = 4t + 6t 2
(S — перемещение или пройденное расстояние d/dt =
8 .)
3 . /дт (4т + 6т 2 ) = 4 + 12t Следовательно, V Мгновенное при (t = 10) = 4 + (12 x 10) = 124 м/с.
Судя по всему, эта пуля летит с феноменальной скоростью.
Задача 2:
Тело падает под действием силы тяжести. Его приблизительное уравнение движения определяется как S(t) = 4,9 t 2 . Какова будет мгновенная скорость тела на пятой секунде после освобождения?
Решение : В этом случае уравнение движения:
S(t) = 4,8 t 2
Мгновенная скорость при t = 5 с определяется по формуле:
В 2 )] t=5
= [4,9 x 2 x t] t=5 = 4,9 x 2 x 5 = 49 м/с
Здесь используется правило производной d/dx(x n ) = nx n-1 .
Вот краткое описание того, как решать эти проблемы. Чтобы найти мгновенную скорость, сначала уравнение движения ( связь смещения с переменными времени и расстояния ) должна быть построена или известна. Взяв его первую производную, вы получите уравнение для скорости. Подставив значение переменной времени, вы получите искомое значение скорости в этот момент.
Как найти: мгновенная скорость против средней скорости без использования исчисления?
Подготовка к экзаменам по физике
София П.
спросил 12.10.22 Предположим, вы держите мяч над обрывом и отпускаете. как найти мгновенную скорость через 10 секунд и среднюю скорость через 10 секунд?
Я думал, что вы можете просто найти смещение x за 10 секунд, а затем разделить смещение x на 10 секунд.
Я ошибаюсь?
Подписаться
І
2
Подробнее
Отчет
1 ответ эксперта
Лучший
Новейшие
Самый старый Автор:
Лучшие новыеСамые старые
София А. ответил 12.10.22
Репетитор
5,0
(76)
Дружелюбный и поддерживающий репетитор по физике AP
Об этом репетиторе ›
Об этом репетиторе ›
Привет, София,
Вы не ошиблись, вы определенно можете найти среднюю скорость, разделив перемещение на время или среднюю скорость, разделив пройденное расстояние на время. Этот универсальный метод работает для любого движения. Однако для движения с постоянным ускорением (кстати, постоянное ускорение может быть и нулевым) есть полезные «ярлыки», а именно кинематические уравнения, не требующие исчисления.
Чтобы найти мгновенную скорость (или ее величину, мгновенную скорость) мы можем использовать уравнение
v(t) = v 0 + at
9 v в вашем случае 3 3 0 = 0 м/с A = 10 м/с 2
T = 10 S
V = 0/S + 0/S + 0/M/S + 0/S + 0/S + 0/S + 0/M/S + 0,0/S + 0/S + 0/S + 0,0000 (10/м/с. /с 2 )(10 с) = 100 м/с
Чтобы найти среднюю скорость (значение которой в вашем случае является средней скоростью), вы можете использовать формулу
v среднее = (v 0 9003
In your example
v 0 = 0 m/s
v = 100 m/s
Therefore the average speed is
v average = (0 м/с + 100 м/с) / 2 = 50 м/с
Теперь давайте проверим наш ответ. Через 10 секунд наш объект прошел расстояние
x = V 0 T + 1/2 A T 2
= (0,5) (10 м/с 9 266668 2 668.
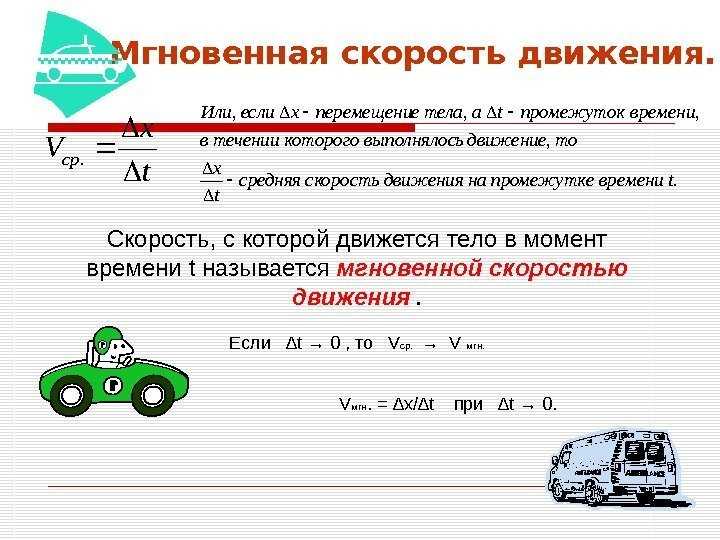Чтобы найти мгновенную скорость, сначала уравнение движения ( связь смещения с переменными времени и расстояния ) должна быть построена или известна. Взяв его первую производную, вы получите уравнение для скорости. Подставив значение переменной времени, вы получите искомое значение скорости в этот момент.
ответил 12.10.22
/с 2 )(10 с) = 100 м/с 