Формула нахождения ускорения в физике: Ускорение (видео) | Прямолинейное движение

Acceleration — Key Stage Wiki

Содержание

• 1 Key Stage 3
  • 1.1 Значение
  • 1.2 Об ускорении
  • 1.3 Уравнение ускорения
  • 1.4 Пример расчета
• 2 Ключевой этап 4
  • 2.1 Значение
  • 2.2 Об ускорении
  • 2.3 Сила и ускорение
  • 2.4 Типовые ускорения
  • 2.5 Примеры
  • 2.6 Уравнения
    • 2.6.1 Ускорение, скорость и время
    • 2.6.2 Ускорение, масса и сила
  • 2.7 Пример расчета
    • 2.7.1 Определение ускорения по изменению скорости и времени
    • 2.7.2 Определение ускорения с учетом массы и силы
    • 2.7.3 Определение изменения скорости с учетом ускорения и времени
    • 2.7.4 Определение времени, затрачиваемого на ускорение и изменение скорости
  • 2.8 Ссылки
    • 2.8.1 АКК
    • 2.8.2 Edexcel
    • 2.8.3 ОКР

Ключевой этап 3

Значение

Ускорение — увеличение скорости.

Существительное: Ускорение

Глагол: Ускорять

Об ускорении

Противоположностью ускорения является замедление, то есть замедление.

Ускорение происходит, когда на объект воздействуют неуравновешенные силы.

Уравнение ускорения

\(а = {\ гидроразрыва {vu} {t}} \)

Где:

а = ускорение

v = конечная скорость

u = начальная скорость

t = время

Пример расчета

Человек начинает движение в состоянии покоя и разгоняется до скорости 8 м/с за 0,8 секунды. Вычислите ускорение человека.	Гоночный автомобиль проходит поворот со скоростью 20 м/с и за 1,5 секунды разгоняется до скорости 80 м/с. Рассчитайте ускорение гоночного автомобиля.
конечная скорость = 8 м/с начальная скорость = 0 м/с время = 0,8 с \(а = {\ гидроразрыва {vu} {t}} \) \(а = {\ гидроразрыва {8-0} {0,8}} \) \(а = {\ гидроразрыва {8} {0,8}} \) \(а = 10 м/с/с \)	конечная скорость = 80 м/с начальная скорость = 20 м/с время = 1,5 с \(а = {\ гидроразрыва {vu} {t}} \) \(а = {\ гидроразрыва {80-20} {1,5}} \) \(а = {\ гидроразрыва {60} {1,5}} \) \(а = 40 м/с/с \)
Лошадь начинает двигаться рысью со скоростью 3,0 м/с и разгоняется до 11 м/с за 2,0 секунды. Вычислите ускорение лошади.	Космический зонд движется со скоростью 18 000 м/с и использует двигатель в течение 250 секунд, чтобы снизить скорость до 6 000 м/с. Вычислите ускорение космического зонда.
конечная скорость = 11 м/с начальная скорость = 3,0 м/с время = 2,0 с \(а = {\ гидроразрыва {vu} {t}} \) \(а = {\ гидроразрыва {11-3.0} {2.0}} \) \(а = {\ гидроразрыва {8,0} {2,0}} \) \(а = 4 м/с/с \)	конечная скорость = 18000 м/с начальная скорость = 6000 м/с время = 250 с \(а = {\ гидроразрыва {vu} {t}} \) \(а = {\ гидроразрыва {6000-18000} {250}} \) \(а = {\ гидроразрыва {-12 000} {250}} \) \(а = -48 м/с/с \)

Ключевой этап 4

Значение

Ускорение — векторная величина, описывающая скорость изменения скорости.

Об ускорении

Ускорение является вектором, поскольку оно имеет величину и направление.

Единицы СИ ускорения и метры в секунду в секунду (м/с/с).

Ускорение может означать:

• Увеличение скорости – Величина скорости увеличивается.
• Уменьшение скорости – Величина скорости уменьшается, также известная как замедление.
• Изменение направления – Величина скорости остается постоянной (постоянная скорость), но объект меняет направление движения.

Первый закон Ньютона указывает на то, что ускорение возникает из-за неуравновешенных сил, действующих на объект:

Движущийся объект стремится оставаться в движении по прямой линии, а покоящийся объект стремится оставаться в покое, если только на него действует неуравновешенная сила.

Сила и ускорение

Второй закон Ньютона указывает, что ускорение объекта прямо пропорционально результирующей силе, действующей на объект, но обратно пропорционально его массе.

Типичные ускорения

Вы должны быть в состоянии оценить ускорение для следующих событий:

Событие	Ускорение в м/с/с
Падающий предмет	9,8
Начать работу	3. 0
Автомобиль ускоряется	4.0
Взлет пассажирского самолета	5.0
Взлет истребителя	60

Примеры

Эта анимация показывает линейное ускорение, когда объекты катятся вниз по склону.	Эта анимация показывает ускорение из-за смены направления.

В этой анимации есть линейное ускорение и замедление при изменении скорости автомобилей, а также ускорение при изменении направления. Пассажиры замечают это ускорение, потому что им кажется, что на них действует сила: Когда автомобиль замедляется перед кольцевой развязкой, пассажиры ощущают силу ремня безопасности, замедляющую их. Когда автомобиль набирает скорость, пассажиры чувствуют силу спинки кресла разгоняет им. Когда машина быстро поворачивает, пассажиры чувствуют, как боковая дверь меняет направление движения.

Уравнения

Ускорение, скорость и время

NB: Вы должны запомнить это уравнение.

Это уравнение применимо к линейному ускорению, но не к изменению направления.

ускорение = (изменение скорости)/(время)

\(a = {\frac{\Delta v}{t}} \)

Где

\(a\) = Ускорение объекта.

\(\Delta v\) = изменение величины скорости: разница между конечной скоростью (v) и начальной скоростью (u) (v-u)

\(t\)= Время, необходимое для изменения скорости.

Ускорение, масса и сила

NB: Вы должны запомнить это уравнение.

\(а = {\ гидроразрыва {F} {м}} \)

Где:

Сила = Масса x Ускорение

\(F=ma\)

Где

\(F\) = Результирующая сила, действующая на объект.

\(m\) = масса объекта.

\(a\) = Ускорение объекта.

Примеры расчетов

Определение ускорения с учетом изменения скорости и времени

Человек начинает движение в состоянии покоя и разгоняется до скорости 7,8 м/с за 0,64 секунды.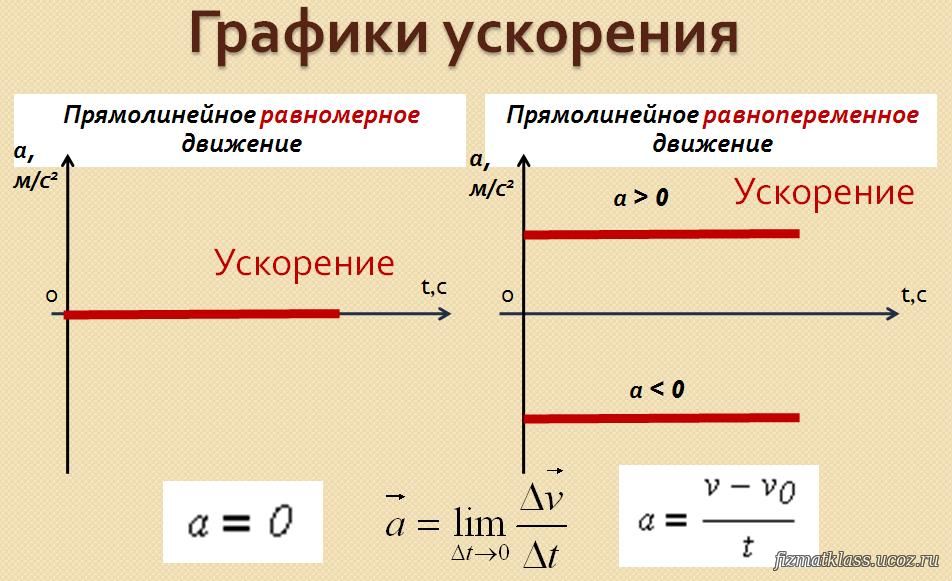 Вычислите ускорение человека с точностью до двух значащих цифр.	Гоночный автомобиль проходит поворот со скоростью 25 м/с и за 1,4 секунды разгоняется до скорости 73 м/с. Рассчитайте ускорение гоночного автомобиля с точностью до двух значащих цифр.
1. Укажите известные количества \(\Дельта v\) = 7,8 – 0 = 7,8 м/с время = 0,64 с	1. Укажите известные количества \(\Дельта v\) = 73 – 25 = 48 м/с время = 1,5 с
2. Подставьте числа в уравнение и решите. \(а = {\ гидроразрыва {\ Delta v} {t}} \) \(а = {\ гидроразрыва {7,8} {0,64}} \) \(а = 12,1875 м/с/с \) \(a \около 12 м/с/с\)	2. Подставьте числа в уравнение и решите. \(а = {\ гидроразрыва {\ Delta v} {t}} \) \(а = {\ гидроразрыва {48} {1,5}} \) \(а = 32 м/с/с \)

Лошадь начинает двигаться рысью со скоростью 3,2 м/с и разгоняется до 11 м/с за 1,8 секунды. Вычислите ускорение лошади с точностью до двух значащих цифр.	Космический зонд движется со скоростью 18 100 м/с и использует двигатель в течение 4,25 минут, чтобы замедлить скорость до 6 200 м/с. Рассчитайте ускорение космического зонда с точностью до двух значащих цифр.
1. Укажите известные количества \(\Дельта v\) = 11 – 3,2 = 7,8 м/с время = 1,8 с	1. Укажите известные количества \(\Дельта v\) = 6 200 – 18 100 = -11900 м/с время = 4,25 мин = 255 с
2. Подставьте числа в уравнение и решите. \(а = {\ гидроразрыва {\ Delta v} {t}} \) \(а = {\ гидроразрыва {7,8} {1,8}} \) \(а = 4,333 м/с/с \) \(a \примерно 4,3 м/с/с\)	2. Подставьте числа в уравнение и решите. \(а = {\ гидроразрыва {\ Delta v} {t}} \) \(а = {\ гидроразрыва {-11900} {255}} \) \(а = -46,67 м/с/с \) \(a \приблизительно -47 м/с/с\)

Определение ускорения с учетом массы и силы

На объект массой 7 кг действует равнодействующая сила 53 Н. Вычислите ускорение объекта с точностью до двух значащих цифр.	Снукерный шар массой 160 г испытывает результирующую силу 12 Н. Вычислите ускорение бильярдного шара с точностью до двух значащих цифр.
1. Укажите известные количества м = 7 кг Ф = 53Н	1. Укажите известные количества м = 160 г = 0,16 кг Ф = 12Н
2. Подставьте числа и оцените. \(F=ма\) \(53=7а\)	2. Подставьте цифры и оцените. \(F=ма\) \(12=0,16а\)
3. Переформулируйте уравнение и решите. \(а = \фракция{53}{7}\) \(а = 7,571 м/с/с\) \(a \около 7,6 м/с/с\)	3. Переформулируйте уравнение и решите. \(а = \фракция{12}{0,16}\) \(а = 75 м/с/с\)

Определение изменения скорости с учетом ускорения и времени

Автомобиль трогается с места и разгоняется со скоростью 4,5 м/с/с в течение 23 секунд. Рассчитайте изменение скорости автомобиля с точностью до двух значащих цифр.	Человек на Луне роняет мяч вертикально. Ускорение свободного падения на Луне составляет 1,6 м/с/с. Рассчитайте изменение скорости мяча через 5,3 секунды, исправьте до двух значащих цифр.
1. Укажите известные количества а = 4,5 м/с/с т = 23 с	1. Укажите известные количества а = 1,6 м/с/с t = 5,3 с
2. Подставьте числа и оцените. \(а = {\ гидроразрыва {\ Delta v} {t}} \) \(4,5 = {\frac{\Delta v}{23}} \)	2. Подставьте цифры и оцените. \(а = {\ гидроразрыва {\ Delta v} {t}} \) \(1,6 = {\frac{\Delta v}{5,3}} \)
3. Переформулируйте уравнение и решите. \(\Дельта v = 4,5 \умножить на 23\) \(\Дельта v = 103,5 м/с\) \(\Дельта v \около 100 м/с\)	3. Переформулируйте уравнение и решите. \(\Дельта v = 1,6 \умножить на 5,3\) \(\Дельта v = 8,48 м/с\) \(\Дельта v \около 8,5 м/с\)

Нахождение затраченного времени с учетом ускорения и изменения скорости

Паром, движущийся со скоростью 5 м/с, замедляет движение к гавани со скоростью 0,02 м/с/с. Вычислите время, за которое паром замедлится до скорости 0,1 м/с, с точностью до двух значащих цифр.	Заряженная частица ускоряется из состояния покоя со скоростью 1300 м/с/с в электрическом поле. Рассчитайте время, необходимое для разгона до 1 500 000 м/с, с точностью до двух значащих цифр.
1. Укажите известные количества \(\Дельта v\) = 0,1 – 5 = -4,9 м/с а = -0,02 м/с/с	1. Укажите известные количества \(\Дельта v\) = 1 500 000 – 0 = 1 500 000 м/с а = 1300 м/с/с
2. Подставьте цифры и оцените. \(а = {\ гидроразрыва {\ Delta v} {t}} \) \(-0,02 = {\frac{-4,9}{t}} \)	2. Подставьте цифры и оцените. \(а = {\ гидроразрыва {\ Delta v} {t}} \) \(1300 = {\frac{1500000}{t}} \)
3. Переформулируйте уравнение и решите. \(-0,002 = {\frac{-4,9}{t}} \) \(-0,002t = -4,9\) \(т = {\ гидроразрыва {-4,9} {-0,02}} \) \(t = 245 с\) \(т \около 250 с\)	3. Переформулируйте уравнение и решите. \(1300 = {\frac{1500000}{t}} \) \(1300т = 1500000\) \(т = {\ гидроразрыва {1500000} {1300}} \) \(t = 1153,85 с \) \(т \около 1200 с\)

Список литературы

AQA

Ускорение, стр. 136-138, 140-141, 144-147, GCSE Physics; Третье издание, Oxford University Press, AQA

Ускорение, стр. 140-1, 145-51, 158-61, GCSE Physics; Студенческая книга, Коллинз, AQA

Ускорение, стр. 150, 151, комбинированная научная трилогия GCSE; Физика, CGP, AQA

Ускорение, страницы 152-3, GCSE Physics, Hodder, AQA

Ускорение, стр. 181, 182, 196, GCSE Physics; Полный курс 9-1 для AQA, CGP, AQA

Acceleration, страницы 209, 212, 214, GCSE Combined Science; Руководство по пересмотру, CGP, AQA

Ускорение, страницы 228, 230, GCSE Combined Science Trilogy 2, Hodder, AQA

Ускорение, страницы 61, 64, 66, GCSE Physics; Руководство по пересмотру, CGP, AQA

Ускорение; Расчет скорости-времени’

Ускорение; определение, стр. 146, GCSE Physics; Студенческая книга, Коллинз, AQA

Ускорение; из-за гравитации, стр. 151, комбинированная научная трилогия GCSE; Физика, CGP, AQA

Ускорение; из-за гравитации, стр. 182, GCSE Physics; Полный курс 9-1 для AQA, CGP, AQA

Ускорение; из-за гравитации, страницы 146, 291, GCSE Physics; Студенческая книга, Коллинз, AQA

Ускорение; оценка, стр. 209, GCSE Combined Science; Руководство по пересмотру, CGP, AQA

Ускорение; Графики, страницы 230-1, GCSE Combined Science Trilogy 2, Hodder, AQA

Ускорение; расследование, страницы 160-3, GCSE Physics; Учебник, Коллинз, AQA

Ускорение; расследование, страницы 167, 168, Комбинированная научная трилогия GCSE; Физика, CGP, AQA

Ускорение; расследование, страницы 199, 200, GCSE Physics; Полный курс 9-1 для AQA, CGP, AQA

Ускорение; исследование связи с силой, страницы 160-1, GCSE Physics, Hodder, AQA

Ускорение; Исследование, страницы 238-9, GCSE Combined Science Trilogy 2, Hodder, AQA

Ускорение; Второй закон движения Ньютона, страницы 236-7, GCSE Combined Science Trilogy 2, Hodder, AQA

Ускорение; Второй закон движения Ньютона, страницы 158-9, GCSE Physics, Hodder, AQA

Ускорение; на графиках расстояние-время, стр. 152, 153, Комбинированная научная трилогия GCSE; Физика, CGP, AQA

Ускорение; на графиках расстояние-время, стр. 183, 184, GCSE Physics; Полный курс 9-1 для AQA, CGP, AQA

Ускорение; на графиках скорость-время, стр. 155, 156, Комбинированная научная трилогия GCSE; Физика, CGP, AQA

Ускорение; на графиках скорость-время, страницы 186, 187, GCSE Physics; Полный курс 9-1 для AQA, CGP, AQA

Ускорение; орбиты, стр. 101, GCSE Physics; The Revision Guide, CGP, AQA

Edexcel

Ускорение, стр. 25, GCSE Physics, CGP, Edexcel

Ускорение, стр. 13, 15, 16, 106, GCSE Физика; Руководство по редакции, CGP, Edexcel

Acceleration, стр. 146, 148, 149, 210, GCSE Combined Science; Руководство по редакции, CGP, Edexcel

Acceleration, страницы 287, 290-291, 296, 308, GCSE Combined Science, Pearson Edexcel

Ускорение, страницы 3, 6-7, 12, 24, GCSE Physics, Pearson Edexcel

Ускорение; опасности, стр. 53, GCSE Physics, CGP, Edexcel

Ускорение; графики расстояние/время, стр. 27, GCSE Physics, CGP, Edexcel

Ускорение; из-за гравитации, стр. 26, GCSE Physics, CGP, Edexcel

Ускорение; Второй закон Ньютона, стр. 35, GCSE Physics, CGP, Edexcel

Ускорение; униформа, стр. 26, GCSE Physics, CGP, Edexcel

Ускорение; графики скорость/время, стр. 31, GCSE Physics, CGP, Edexcel

OCR

Ускорение, страницы 159–162, Gateway GCSE Combined Science; Руководство по редакции, CGP, OCR

Ускорение, страницы 22-25, 28, 29, 89, Gateway GCSE Physics; Руководство по редакции, CGP, OCR

Ускорение, страницы 51–52, 217, 222–223, 254–254, Gateway GCSE Physics, Оксфорд, OCR

Ускорение; расчеты, страницы 52–53, 56–57, 69, 255, Gateway GCSE Physics, Оксфорд, OCR

Ускорение; из-за гравитации, стр. 83, Gateway GCSE Physics, Oxford, OCR

Калькулятор ускорения (простой в использовании)

Похожие материалы

сообщите об этом объявлении

сообщите об этом объявлении

Какие известные параметры?

Начальная скорость, конечная скорость, время
Начальная скорость, конечная скорость, расстояние
Начальная скорость, расстояние, время
Сила и масса

Начальная скорость (v 9

Расстояние (x – x ₀ ) = mkmftmi

Время (t) = secminms

Сила (F) = NkNlbf

Масса (м) = kgglboz

Единицы ответа: м ⁄ с 2 футов ⁄ с 2 g-force

Урок ускорения

Содержание урока

Как вручную рассчитать ускорение

Ускорение определяется как скорость изменения скорости объекта. В простейшей форме уравнение для ускорения имеет вид:
a = ^Δv ⁄ _t
Где a — ускорение объекта, Δv — изменение скорости, t t . это количество времени, которое требуется для изменения скорости.

Конечно, мы не всегда знаем изменение скорости и прошедшее время, поэтому иногда мы должны использовать другие уравнения для решения для ускорения. Эти уравнения известны как кинематические уравнения. Есть четыре кинематических уравнения, но только три из них можно использовать для решения ускорения. После перестановки членов в этих трех уравнениях, чтобы найти ускорение, они задаются следующим образом:
1.) a = ^{(V – V ₀ )} ⁄ _T
2.) A = ^{(V 2 – V ₀ 2 )} 3333333333333333 гг. a = ^{2(x – x ₀ – v ₀ t)} ⁄ _{t ²}

Выбираем кинематическое уравнение, исходя из уже известных нам параметров.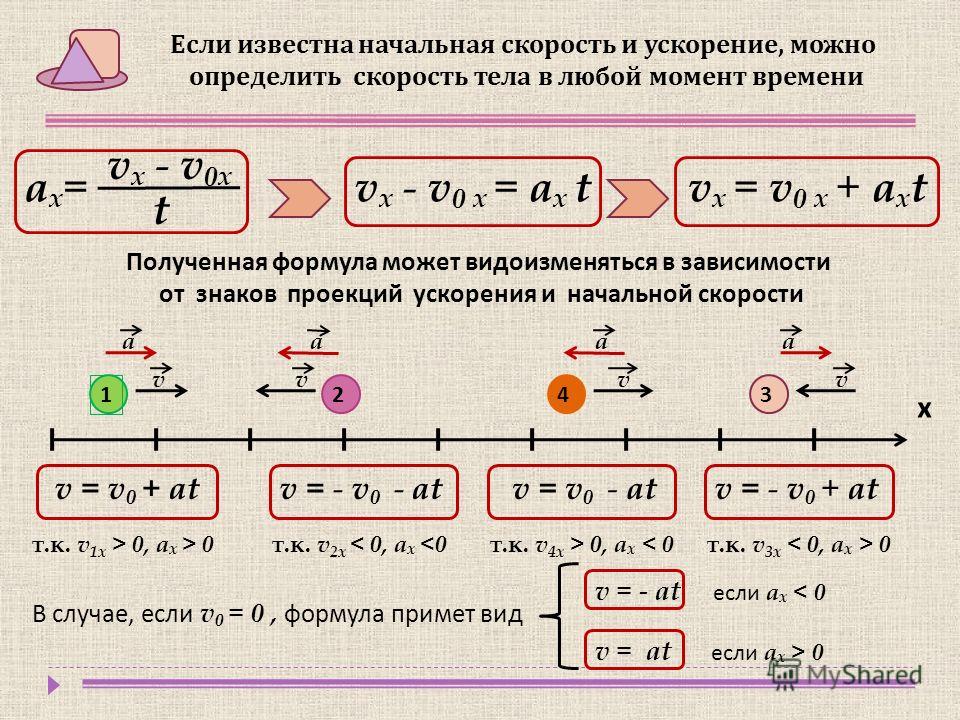 Например, если нам даны значения начальной скорости (v ₀ ), конечной скорости (v) и расстояния (Δx), мы будем использовать уравнение 2. Если нам дано время вместо расстояния, мы будем использовать уравнение 1.

Как работает калькулятор

Калькулятор на этой странице написан на языке программирования  JavaScript . Интернет-браузеры имеют встроенный механизм JavaScript, который может запускать этот калькулятор внутри браузера. Это позволяет почти мгновенно рассчитать решение.

При нажатии кнопки «Рассчитать» запускается функция  ускорения . Эта функция использует все уравнения, перечисленные в уроке выше. Он берет введенные числа, применяет их к применимой формуле, а затем округляет ответ до пятого знака после запятой. Функция также заботится обо всех преобразованиях единиц измерения для входов и выходов.

Код также содержит логику для отлова ошибок. Если решение не является конечным числом, оно выдаст ошибку и попросит пользователя проверить свои входные данные.