Определение напряжения на участке цепи. Напряжение на участке цепи
Когда электрическая цепь создана, свободные заряды (электроны) получают возможность двигаться. Это движение называется электрическим током, или иначе, потоком электричества. Такое движение подобно движению жидкости внутри полой трубы, но не во всём сохраняется такое подобие, есть и существенные различия.
Сила движения свободных зарядов определяется напряжением, которое является специфическим показателем потенциальной энергии. Напряжение всегда характеризуется двумя точками в электрической цепи, и потому правильнее говорить не о напряжении, а о падении напряжения между двумя точками цепи. Обычно слово падение опускают, подразумевая под обозначением «напряжение» – падение напряжения на определённом участке электрической цепи. Это значит, что употребляя термин «напряжение» всегда подразумеваются две точки участка цепи, начальная и конечная. Для одной точки понятие падения напряжения не имеет смысла, всегда две точки и конкретный участок цепи .
Свободные заряды, а в проводниках первого рода (металлы и сплавы) ими являются электроны, имеют свойство двигаться через проводник с некоторой степенью трения, оказывая сопротивление к своему движению под действие источника тока (ЭДС). Это противостояние так и называется – сопротивление .
Величина тока в цепи зависит от величины напряжения, которое разгоняет свободные электроны, и от величины сопротивления участка цепи. Точно так же как и падение напряжения (напряжение), сопротивление является величиной характеризующей участок цепи, то есть сопротивление – это всегда между двумя точками цепи.
Ток существует в электрической цепи, а падение напряжения и сопротивление – это всегда участок цепи, всегда между двумя точками.
Для того, чтобы работать с этими параметрами электрической цепи, надо иметь возможность описать их количественно, точно так же как описывается масса, объем, длина и другие физические величины.
Вот стандартные единицы измерения для электрического тока, напряжения и сопротивления:
«Символ» – это обозначение физической величины в алгебраических уравнениях, на схемах, таблицах, технической документации, в дисциплинах физики и инженерии.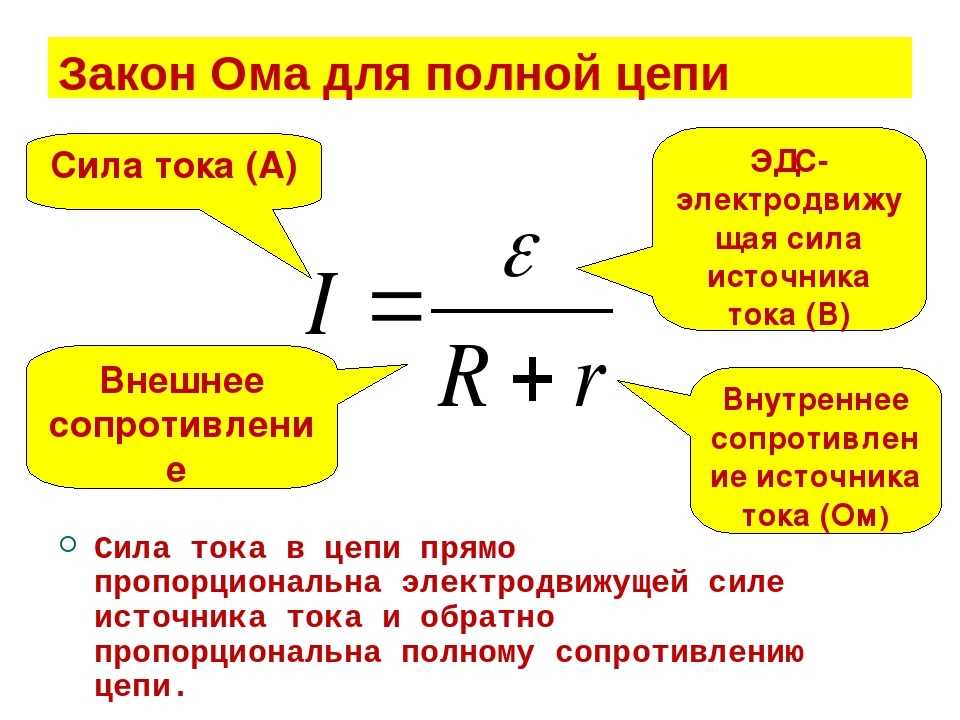 Эти обозначения являются общепризнанными на международном уровне.
Эти обозначения являются общепризнанными на международном уровне.
«Аббревиатура» – представляет собой алфавитный символ, который используется для сокращённой записи количества в единицах измерения. Своеобразная подкова
Каждая единица измерения названа в честь известного исследователя электричества. Сила тока в честь француза Андре Мари Ампера, напряжение в честь Алессандро Вольта, и сопротивление в честь немецкого исследователя – Георга Симона Ома.
Закон Ома – взаимосвязь трёх величин
Все три величины: напряжение, ток и сопротивление, взаимосвязаны. Такую взаимосвязь обнаружил Георг Симон Ом и опубликовал в статье в 1827 году. Он математически исследовал гальваническую электрическую цепь.
Основным открытием Ома было то, что величина силы тока, проходящего через металлический проводник прямо пропорциональна напряжению, что и выразил он в виде математической записи – уравнения (формулы).
В этом алгебраическом выражении напряжение (V ) равно величине силе тока (I ) умноженной на сопротивление (R ). Используя алгебраические методы, мы можем манипулировать этим уравнением и записать его ещё в двух вариантах, для I и для R соответственно:
Формулировка Закона Ома для участка цепи имеет следующее содержание:
Сила тока, протекающего в участке цепи, прямо пропорциональна падению напряжения на этом участке, и обратно пропорциональна сопротивлению этого участка.
Важно помнить, что сила тока всегда в участке цепи (ветви), а падение напряжения и сопротивление – это всегда на участке цепи.
Не может быть силы тока на участке цепи, или падения напряжения и сопротивления в участке цепи, потому как это нелогично, абсурдно. Неверное употребление в речи и письме предлогов «в» и «на» говорит об отсутствии понимания сути основных электрических величин: напряжения, тока и сопротивления говорящим или пишущим.
Без правильного понимания сути физических явлений и величин, которые характеризуют электрическую цепь, невозможно профессионально выполнять электротехнические работы, и тем более выполнять инженерные расчёты.
Прямая пропорциональность говорит о том, что при увеличении напряжения V в n раз, сила тока I увеличится также в n раз, то же самое касается уменьшения величины напряжения.
Под напряжением на некотором участке электрической цепи понимают разность потенциалов между крайними точками этого участка.
На рис. 1-13 изображен участок цепи, на котором есть резистор сопротивлением и нет ЭДС. Крайние точки этого участка обозначены буквами a и b
Рис. 1-13. Участок электрической цепи
На участке без ЭДС ток течет от более высокого потенциала к более низкому. Следовательно, потенциал точки a выше потенциала точки b на величину, равную произведению тока на сопротивление :
.
В соответствии с определением, напряжение между точками a и b
. (1-8)
Другими словами, напряжение на резисторе равно произведению тока, протекающего по резистору, на величину сопротивления этого резистора.
В электротехнике разность потенциалов на концах резистора принято называть либо «напряжением на резисторе», либо «падением напряжения». В литературе встречаются оба этих определения.
Рассмотрим теперь вопрос о напряжении на участке цепи, содержащем не только резистор, но и источник ЭДС.
На рис. 1-14 а и б показаны участки некоторых цепей, по которым протекает ток . . Найдем напряжение между точками a и c для этих участков.
а) б)
Рис. 1-14. Участки электрической цепи
По определению
. (1-9)
Выразим потенциал точки a
 1-14,а )
идем встречно ЭДС ,
поэтому потенциал точки b оказывается меньше, чем потенциал точки c на величину ЭДС ,
т.е.
1-14,а )
идем встречно ЭДС ,
поэтому потенциал точки b оказывается меньше, чем потенциал точки c на величину ЭДС ,
т.е.. (1-10)
На рис. 1-14,б при перемещении от точки c к точке b идем согласно ЭДС и потому потенциал точки b оказывается больше, чем потенциал точки c на величину ЭДС , т.е.
. (1-11)
Ранее говорилось, что на участке цепи без ЭДС ток течет от более высокого потенциала к более низкому. Поэтому в обеих схемах рис. 1-14 потенциал точки
. (1-12)
Таким образом, для рис. 1-14,а имеем
, или
. (1-13)
И для рис. 1-14, б имеем
, или
. (1-14)
Положительное
направление напряжения указывают на
схемах стрелкой. Стрелка должна быть
направлена от первой буквы индекса ко
второй. Так, положительное направление
напряжения
изобразится
стрелкой, направленной от
Так, положительное направление
напряжения
изобразится
стрелкой, направленной от
Из самого определения напряжения следует также, что . Поэтому . Другими словами, изменение чередования индексов равносильно изменению знака этого напряжения. Из изложенного ясно, что напряжение может быть и положительной, и отрицательной величиной.
Закон ома для участка цепи, не содержащего эдс
Закон Ома устанавливает связь между током и напряжением на некотором участке цепи. Так, применительно к участку цепи, изображенному на рис. 1-13 имеем
.(1-15)
Под напряжением на некотором участке электрической цепи понимают разность потенциалов между крайними точками этого участка.
На рис. 13 изображен участок цепи, на котором есть резистор сопротивлением и нет ЭДС. Крайние точки этого участка обозначены буквами

Рис. 13. Участок электрической цепи
На участке без ЭДС ток течет от более высокого потенциала к более низкому. Следовательно, потенциал точки a выше потенциала точки b на величину, равную произведению тока на сопротивление :
.
В соответствии с определением, напряжение между точками a и b
Другими словами, напряжение на резисторе равно произведению тока, протекающего по резистору, на величину сопротивления этого резистора.
В электротехнике разность потенциалов на концах резистора принято называть либо «напряжением на резисторе», либо «падением напряжения». В литературе встречаются оба этих определения.
Рассмотрим теперь вопрос о напряжении на участке цепи, содержащем не только резистор, но и источник ЭДС.
На
рис. 14 а и б показаны участки некоторых цепей, по
которым протекает ток . .
Найдем напряжение между точками a и c для этих участков.
а) б)
Рис. 14. Участки электрической цепи
По определению
. (9)
Выразим потенциал точки a через потенциал точки c . При перемещении от точки c к точке b (рис. 14,а ) идем встречно ЭДС , поэтому потенциал точки b оказывается меньше, чем потенциал точки c на величину ЭДС , т.е.
. (10)
На рис. 14,б при перемещении от точки c к точке b идем согласно ЭДС и потому потенциал точки b оказывается больше, чем потенциал точки c на величину ЭДС , т.е.
. (11)
Ранее говорилось, что на участке цепи без ЭДС ток течет от более высокого потенциала к более низкому. Поэтому в обеих схемах рис. 14 потенциал точки a выше, чем потенциал точки b на величину падения напряжения на резисторе сопротивлением :
. (12)
(12)
Таким образом, для рис. 14,а имеем
, или
. (13)
И для рис. 14, б имеем
, или
. (14)
Положительное направление напряжения указывают на схемах стрелкой. Стрелка должна быть направлена от первой буквы индекса ко второй. Так, положительное направление напряжения изобразится стрелкой, направленной от a к c .
Из самого определения напряжения следует также, что . Поэтому . Другими словами, изменение чередования индексов равносильно изменению знака этого напряжения. Из изложенного ясно, что напряжение может быть и положительной, и отрицательной величиной.
Закон Ома для участка цепи, не содержащего эдс.
Закон Ома устанавливает связь между током и напряжением на некотором участке цепи. Так, применительно к участку цепи, изображенному на рис. 13 имеем
.(15)
Закон Ома для участка цепи, содержащего эдс.
Закон
Ома для участка цепи, содержащего ЭДС,
позволяет найти ток этого участка по
известной разности потенциалов на
концах этого участка и имеющейся на
этом участке ЭДС . Так из уравнения (13) имеем для схемы рис.
14, а
Так из уравнения (13) имеем для схемы рис.
14, а
.(16)
Аналогично из уравнения (14) для схемы рис. 14, б следует
.(17)
Уравнения (16) и (17) выражают собой закон Ома для участка цепи, содержащего ЭДС, для разных случаев включения ЭДС .
Приступая к определению численного выражения напряжения тока, следует определиться с терминологией. Напряжение на участке электрической цепи характеризует выполняемую по переносу положительного единичного заряда работу (или же энергию, которая выделяется при перемещении оного заряда) из одной точки в другую. Начальная и конечная точки отличаются потенциалом, вследствие чего напряжение еще именуют разностью потенциалов или электродвижущей силой. Величина обозначается буквой U, ее измерение осуществляется в вольтах (B). Определить напряжение, имея в руках вольтметр, не составит труда. Однако, если данного прибора нет, то знание взаимосвязей между прочими характеристиками электрической схемы и напряжением помогут установить искомую величину.
Узнать напряжение тока через закон Ома
Имея числовые данные силы тока (I) и сопротивления (R), найти неизвестную составляющую, напряжение, поможет закон Ома. Его формула I=U/R. Она отражает прямо пропорциональную взаимосвязь напряжение-сила тока, и обратно пропорциональное соотношение напряжение-сопротивление на определенном участке цепи. Установленная закономерность справедлива для участков как постоянного, так и переменного тока. Взаимосвязь U=I*R – не фундаментальный закон. Она лишь показывает эмпирическое соотношение между величинами в определенных условиях.
Не всегда работает закон в таких случаях:
- В некоторых гетерогенных приборах (диоды, транзисторы).
- В случаях высоких частот.
- При низких температурах (для сверхпроводников).
- При явном нагреве элемента в процессе прохождения по нему тока (как в случае лампы накаливания).
- В электронных лампах, содержащих вакуум или газ (люминесцентные лампы).
- Касания проводника или диэлектрика высоким напряжением, повлекшее возникновение пробоя.

Физическая расшифровка закона Ома, чтобы узнать напряжение
«Классическое» представление закона не учитывает некоторых свойств проводящего материала, поэтому оно корректно лишь с математической точки зрения. Учесть физические характеристики проводника позволяет другая интерпретация закона: U=I*ℓ*ρ/S, где
I – сила тока,
ρ – удельное сопротивление проводника,
ℓ – длина,
S – поперечное сечение материала (площадь).
Определение напряжения, используя знание величины мощности
Георг Симон Ом установил следующую взаимосвязь между сопротивлением и мощностью: R=P/I 2 и R=U 2 /P, поэтому P=I*U. Из этого следует, что U=P/I.
Взаимосвязь с работой (A)
Исходя из определения напряжения, определить его численное выражение возможно, зная величину работы. Связь этих характеристик выражается в виде формулы U=A/q. Она определяет отношение работы тока к заряду, прошедшему по данному участку цепи.
Все характеристики, необходимые для вычисления напряжения, можно получить или из инструкций к электроприборам, или с помощью соответствующих измерительных приборов.
Закон ома для участка цепи: формула, объяснение простыми словами
Основой прикладной электротехники безусловно является закон Ома для участка цепи. Не зная его основных положений, можно допустить серьезные ошибки в практической работе. О самом физическом явлении всем известно еще со школы. Но с помощью базовых положений может формулироваться много других вариантов, так или иначе затрагивающих особенности применения закона в реальных условиях. Именно здесь возникают сложности, требующие точных знаний и навыков оперирования физическими величинами.
Содержание
Как звучит закон Ома для участка цепи
Ток в проводнике возникает в электрическом поле, которое, в свою очередь, появляется при наличии разности потенциалов или напряжения. Движение тока направлено в сторону меньшего потенциала. Условно считается, что в этом направлении двигаются положительные заряды, а в обратную сторону происходит движение свободных электронов.
На участке металлического проводника данный процесс будет выглядеть следующим образом. На каждом конце присутствует потенциал – ϕ1 и ϕ2, при этом ϕ1 > ϕ2. Следовательно, напряжение в этом месте равно U = ϕ1 – ϕ2. Немецкий ученый Ом практически установил зависимость, при которой с увеличением напряжения, возрастает и сила тока, протекающего через неполный участок.
На каждом конце присутствует потенциал – ϕ1 и ϕ2, при этом ϕ1 > ϕ2. Следовательно, напряжение в этом месте равно U = ϕ1 – ϕ2. Немецкий ученый Ом практически установил зависимость, при которой с увеличением напряжения, возрастает и сила тока, протекающего через неполный участок.
Для каждого из проводников, отличающихся материалами, был построен свой график, отражающий зависимость силы тока от напряжения. В дальнейшем, эти графики стали известны, как вольт-амперные характеристики. В результате, было установлено наличие линейной связи между обеими величинами – силой тока и напряжением. То есть, они находятся в прямой пропорциональной зависимости.
Но, как показывают графики, все проводники обладают разными коэффициентами пропорциональности. Следовательно, у них разная степень проводимости, получившая название электрического сопротивления (R). Поэтому, чем ниже будет сопротивление проводника, тем выше сила тока, проходящего через него. При том, что напряжение для всех проводников будет одинаковым.
После всех опытов ученый смог окончательно сформулировать свой закон для участка цепи:
Сила тока в однородном проводнике на отдельном участке, находится в прямой пропорции с напряжением на этом же участке и в обратной пропорциональной зависимости с сопротивлением данного проводника.
Принятые единицы измерения
При использовании закона Ома для практических расчетов все математические вычисления выполняются в установленных единицах измерений для всех 3-х величин:
- Сила тока – в амперах (А).
- Напряжение – в вольтах (В/V).
- Сопротивление – в омах (Ом).
Исходные данные и другие параметры, представленные в единицах, должны переводиться в общепринятые значения.
Действие основных единиц и физическое соблюдение закона Ома невозможно в следующих ситуациях:
- Наличие высоких частот, при которых электрическое поле изменяется с большой скоростью.
- Низкотемпературный режим и сверхпроводимость.

- Сильно разогретые спирали ламп накаливания, когда отсутствует линейность напряжения.
- Пробой проводника или диэлектрика, вызванный высоким напряжением.
- Электронные и вакуумные лампы, заполненные газами.
- Полупроводники с р-п-переходами, в том числе, диоды и транзисторы.
Сила тока
Сила тока возникает при наличии частиц со свободными зарядами. Они перемещаются через поперечное сечение проводника из одной точки в другую. Источник питания создает электрическое поле, под действием которого электроны начинают двигаться упорядоченно.
Таким образом, сила тока является количеством электричества, проходящего через определенное сечение за единицу времени. Увеличить этот показатель можно путем увеличения мощности источника тока или изъятия из цепи резистивных элементов.
Международная единица СИ для тока – ампер. Это довольно большая величина, поскольку для человека смертельно опасными считаются всего 0,1 А. В электротехнике малые величины могут выражаться в микро- и миллиамперах.
Определение силы тока можно окончательно сформировать в виде формулы I = q/t, в которой q является зарядом, проходящим через сечение, t – отрезок времени, затраченный на перемещение этого заряда.
Кроме того, сила тока может записываться с помощью основной формулы, когда известны значения напряжения и сопротивления. В числом виде она будет гласить следующее:
- I = U/R
Сопротивление
Рассматривая закон ома для участка цепи, нельзя забывать о таком понятии, как сопротивление. Данная величина считается основной характеристикой проводника, поскольку именно сопротивление влияет на качество проводимости. Разные материалы проводят ток лучше или хуже. Это объясняется неоднородностью их структуры, различиями в кристаллических решетках. Поэтому в одних случаях электроны движутся с большей скоростью, а в других – с меньшей.
Собственным электрическим сопротивлением обладают все проводники, находящиеся в твердом, жидком, газообразном и плазменном состоянии. У каждого из них своя характеристика, называемая удельным сопротивлением. Данная величина отражает способность каждого материала к сопротивлению. За эталон принимается проводник длиной 1 м с поперечным сечением 1 м².
У каждого из них своя характеристика, называемая удельным сопротивлением. Данная величина отражает способность каждого материала к сопротивлению. За эталон принимается проводник длиной 1 м с поперечным сечением 1 м².
Чтобы найти сопротивление проводника из данного материала нужно воспользоваться формулой: R = ρ x (l/S). В ней l является длиной проводника, S – площадью его поперечного сечения, ρ – удельным сопротивлением.
По закону Ома на участке цепи эта величина определяется: R = U/I.
Напряжение
Напряжение относится к важным характеристикам электрического тока, протекающего в проводнике. С физической точки зрения, это работа электрического поля, которое перемещает заряд на какое-то расстояние. В электротехнике напряжением считается разность потенциалов между двумя точками участка цепи. На практике эта величина служит для определения возможности подключения к сети потребителей электроэнергии, продолжительность их работы в этом состоянии.
В электрической цепи напряжение возникает следующим образом:
- Вначале цепь подключается к источнику тока путем соединения с двумя полюсами. Это может быть генератор или батарея.
- На одном полюсе или клемме – избыточное количество электроном, а на другом – их недостает. Первый условно считается положительным, второй – отрицательным.
- Электрическое поле источника энергии воздействуют на электроны положительного полюса и самого проводника, заставляя их двигаться в сторону отрицательного полюса и притягиваться к нему. Такое притяжение происходит из-за положительного заряда на этом полюсе, поскольку электроны здесь отсутствуют.
- Между обеими клеммами возникает разность потенциалов с определенным значением, что приводит к упорядоченному движению электронов в проводниках и подключенных нагрузках. Постепенно избыток электронов положительного полюса уменьшается, соответственно, снижается и потенциал. Характерным примером служит аккумуляторная батарея.
 При подключении нагрузки, ее потенциал будет падать, вплоть до полной разрядки. Для восстановления первоначальных свойств, потребуется подзарядка от постороннего источника тока.
При подключении нагрузки, ее потенциал будет падать, вплоть до полной разрядки. Для восстановления первоначальных свойств, потребуется подзарядка от постороннего источника тока.
При неизменной мощности источника энергии, значение напряжения может быть разным под действием следующих факторов:
- Материал соединительных проводников. У каждого свой вольтамперный график.
- Количество потребителей, подключенных к сети.
- Температура окружающей среды.
- Качество монтажа самой сети.
Закон Ома для участка цепи — расчет цепей
Простейший вариант наглядно представлен на рисунке. Это однородный участок цепи открытого типа.
Для его описания применяется известная формула, которая будет иметь следующую форму:
- I = U/R, где I является силой тока, U – напряжением, R – сопротивлением.
Данная формула является интегральной. С ее помощью хорошо видно, как при возрастании напряжения, увеличивается и сила тока. Но, если увеличить сопротивление, то сила тока, наоборот, будет понижаться.
На схеме изображен всего один элемент, обладающий сопротивлением. На практике, их может быть любое количество. Они могут соединяться последовательно, параллельно и смешанным способом.
Неоднородный участок цепи постоянного тока
Неоднородную структуру имеет такой участок цепи, где помимо проводников и элементов, присутствует источник тока. Его ЭДС необходимо учитывать при расчетах общей силы тока на данном участке.
Существует формула, которая дает определение основным параметрам и процессам неоднородного участка: q = q0 x n x V. Ее показатели характеризуются следующим образом:
- В процессе перемещения зарядов (q) они приобретают определенную плотность. Ее показатели зависят от силы тока и площади поперечного сечения проводника (S).
- В условиях определенной концентрации (n) можно точно указать численность единичных зарядов (q0), которые были перемещены за единичный отрезок времени.
- Для расчетов проводник условно считается цилиндрическим участком, имеющим какой-то объем (V).

При подключении проводника к аккумулятору, последний через некоторое время будет разряжен. То есть, движение электронов постепенно замедляется и, в конце концов, прекратится совсем. Этому способствует молекулярная решетка проводника, оказывающая противодействие, столкновения электронов между собой и другие факторы. Для преодоления такого сопротивления следует дополнительно приложить определенные сторонние силы.
Во время расчетов эти силы суммируются с кулоновскими. Кроме того, для перенесения единичного заряда q из 1-й точки во 2-ю потребуется выполнение работы А1-2 или просто А12. С этой целью создается разница потенциалов (ϕ1 – ϕ2). Под действием источника постоянного тока возникает ЭДС, перемещающая заряды по цепи. Величина общего напряжения будет состоять из всех сил, отмеченных выше.
Полярность подключения к источнику постоянного тока нужно учитывать в расчетах. При изменении клемм будет меняться и ЭДС, ускоряющая или замедляющая перемещение зарядов.
Формулировка закона Ома для полной цепи
Закон Ома для полной цепи выражается поведением основных величин, был выведен опытным экспериментальным путем. Результатом стало выявление связей, объединяющих силу тока (I), электродвижущую силу – ЭДС (Е), внешнее (R) и внутреннее (r) сопротивления в цепи.
В теоретических расчетах с точки зрения чистой физики, в цепях предполагался так называемый идеальный источник постоянного тока. После того, как были проведены реальные исследования, выяснилось, что источник тока обладает собственным сопротивлением.
Формулировка закона Ома для полной цепи приобрела следующий вид: Сила тока находится в прямой пропорции с суммой ЭДС цепи, и в обратной пропорции с суммой сопротивлений самой цепи и источника тока.
Следует сразу же выяснить, что такое электродвижущая сила. По сути, она является физической величиной, характеризующей действие внешних сил источника ЭДС. Например, в простой батарейке перемещение зарядов происходит в результате химической реакции. То есть, данная сила двигает заряд, обеспечивая общее течение электрического тока.
То есть, данная сила двигает заряд, обеспечивая общее течение электрического тока.
Формулу закона Ома можно записать по-другому. ЭДС источника тока полной цепи представляет собой суммарные падения напряжений у самого источника и во внешней цепи:
- E = Ir + IR = Ur + UR
Переменный ток
В отличие от цепей, по которым течет постоянный ток, в цепи переменного тока кроме активной нагрузки в виде потребителей, входят элементы с реактивным сопротивлением. Это различные типы катушек и конденсаторов, обладающих индуктивностью и емкостью.
С увеличением напряжения будет расти и сила тока. Однако, к активному сопротивлению здесь добавляются реактивные. С связи с этим, полный расклад для такой цепи будет выглядеть так:
- I = U/Z, где I и U – это сила тока и напряжение, а Z – является полным сопротивлением цепи.
Показатель Z следует рассмотреть более подробно. Прежде всего, это сумма, включающая активное, индуктивное и емкостное сопротивления. То есть, на электрический ток оказывает влияние не только обычная омическая нагрузка, но также емкость (С) и индуктивность (L).
То есть, на электрический ток оказывает влияние не только обычная омическая нагрузка, но также емкость (С) и индуктивность (L).
В результате, краткая формула полного сопротивления примет следующий вид:
Опытным путем было установлено, что в цепях переменного тока наблюдается несовпадение по фазе колебаний тока и напряжения. Величина этих несовпадений она же разница фаз находится под непосредственным влиянием индуктивности и емкости.
Использование на практике
Закон Ома лежит в основе всех расчетов производимых в электронике и электротехнике. Будущих специалистов с первых дней учат, как использовать так называемый треугольник. Чтобы найти какую-то искомую величину, должны выполняться простые арифметические действия. Если два оставшихся параметра находятся в одной строке – они перемножаются. Если на разных уровнях, то верхний всегда делится на нижний.
Практически данная схема выглядит так:
- U = I x R, I = U/R, R = U/I.
Самые простые вычисления производятся на основе данных измерительных приборов.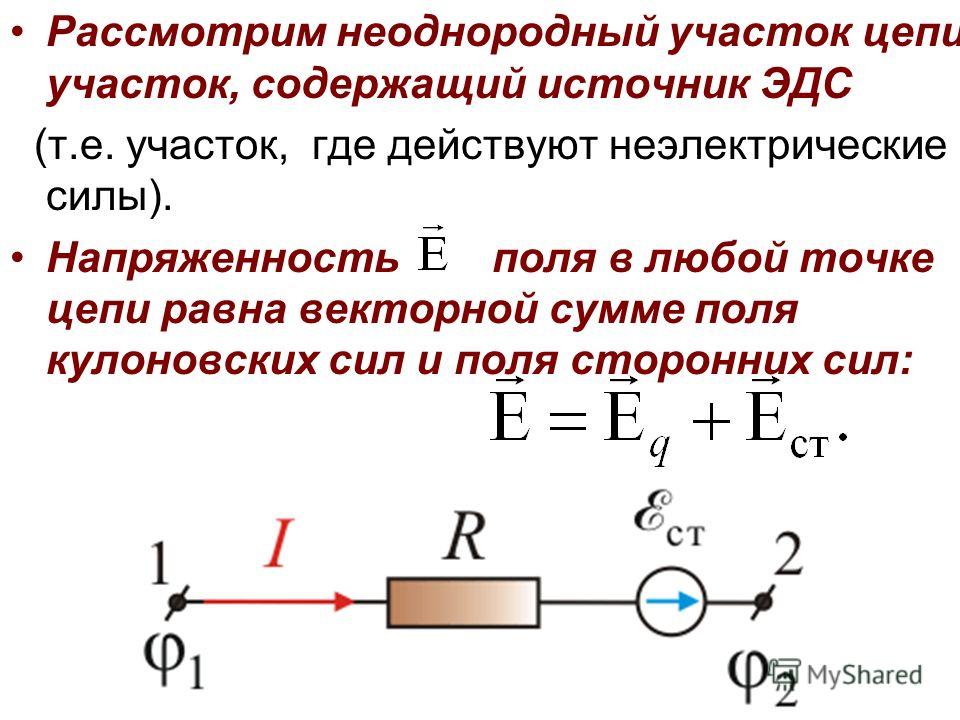 На участке цепи измерение тока выполняется амперметром, а напряжения – вольтметром. После этого найти сопротивление математическим путем не составит труда.
На участке цепи измерение тока выполняется амперметром, а напряжения – вольтметром. После этого найти сопротивление математическим путем не составит труда.
Для замеров сопротивления тоже есть прибор – омметр. Полученное выражение, подставляется в одну из формул, после чего находятся величины силы тока или напряжения. Точность омметра зависит от стабильности напряжения, подаваемого источником тока. Стабилизация проводится путем добавления резистора, выполняющего функцию регулятора.
Иногда требуется исключить из схемы какой-нибудь элемент без демонтажа. С этой целью проводится шунтирование, когда приходится устанавливать проводник на входных клеммах ненужного резистора. Ток начинает идти через шунт с меньшим сопротивлением, а напряжение на резисторе падает до нуля.
Закон Ома используется в защитных системах. Это делается с помощью уставок, обеспечивающих нормальную работу и отключающих питание лишь в аварийных ситуациях.
Формулы для закона Ома
Представленные на рисунке формулы, начали формироваться из основных формул для полной цепи и отдельного участка.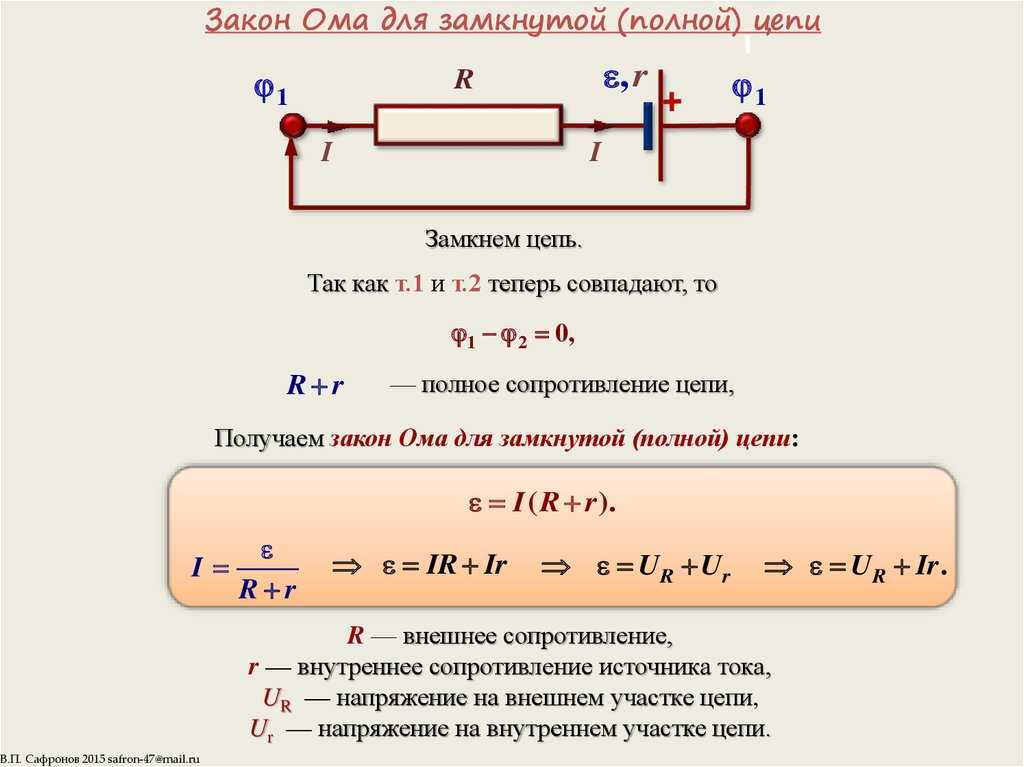 С их помощью можно выполнять все основные расчеты, при составлении проектов и в других ситуациях. Формулы полностью пригодны для работы с цепями как постоянного, так и переменного тока.
С их помощью можно выполнять все основные расчеты, при составлении проектов и в других ситуациях. Формулы полностью пригодны для работы с цепями как постоянного, так и переменного тока.
Видеоинструкция
Электрическое сопротивление участка цепи
Электрическое сопротивление для участка цепи определяется при помощи закона Ома. Для того, чтобы понять процессы, происходящие в элементах электрической цепи постоянного тока, необходимо дать общее определение закона Ома.
Закон Ома
Сила тока на участке цепи всегда прямо пропорциональна напряжению на данном участке и обратно пропорциональна сопротивлению участка.
Подобное определение будет верно также для растворов электролитов. Общий закон Ома характерен при описании однородного участка цепи, который не содержит источников тока.
Общий закон Ома характерен при описании однородного участка цепи, который не содержит источников тока.
При составлении формул вводятся дополнительные характеристики. Среди них коэффициент пропорциональности. Его записывают в виде $1=R$. Отсюда следует, что $I = \frac{U}{R}$.
$R$ – сопротивление проводника.
Сопротивление принято измерять в омах (Ом).
Закон Ома является главным законом в электротехнике. С помощью его:
- изучаются и рассчитываются электрические цепи;
- устанавливается логическое соотношение между сопротивлением и напряжением.
Определение 1
Вольтамперная характеристика – функциональная зависимость элемента участка цепи. Она является очень важной величиной электрических свойств элемента. Такую зависимость можно представить в виде $I = I(U)$.
Подобные характеристики в зависимости от ситуации могут приобретать различные формы и выражения. Наиболее простой вид вольтамперной характеристики выразил в формуле Георг Ом, в честь которого была названа единица сопротивления тока. Ученый подтвердил свою теорию многочисленными экспериментами, применяя опыты к металлическому проводнику.
Ученый подтвердил свою теорию многочисленными экспериментами, применяя опыты к металлическому проводнику.
Закон Ома необходимо понимать на теоретическом и практическом уровне, чтобы решать различные задачи. Если неправильно применять основные параметры закона, то результат приобретает неправильные черты, поэтому допускаются многочисленные ошибки.
Применение закона Ома для участка цепи
Каждый участок электрической цепи можно описать с помощью трех основных величин:
- сопротивления;
- напряжения;
- тока.
Такое сочетание также называют «треугольником Ома», поскольку величины характеризуют все процессы электротехники.
Все производимые расчеты имеют смысл только в тех случаях, когда напряжение на участке цепи выражается в вольтах (В), сопротивление – в омах (Ом), а ток – в амперах (А). При использовании иных единиц измерений или их кратных значений необходимо осуществлять дополнительный ряд действий, чтобы искомый результат полностью соответствовал задачам и целям расчетов.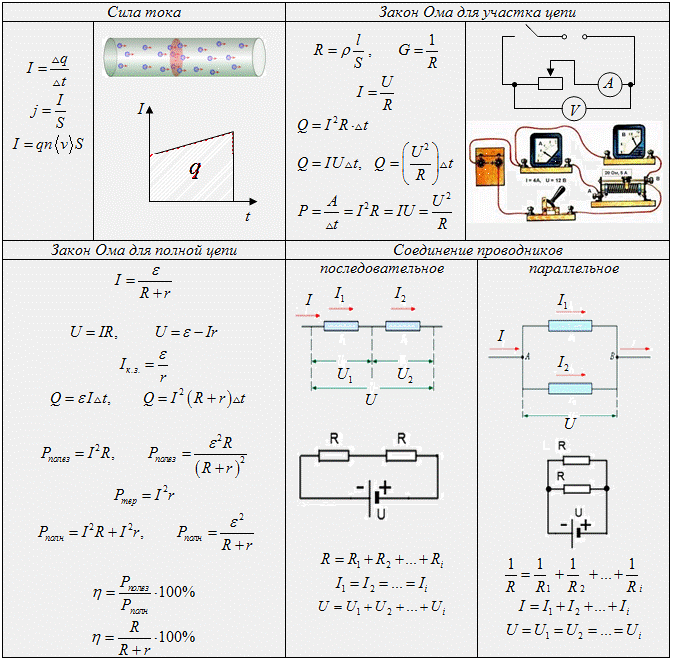 Для этого кратные единицы используемых величин переводят в традиционные величины.
Для этого кратные единицы используемых величин переводят в традиционные величины.
Кратные единицы измерений:
- милливольты;
- миллиамперы;
- мегаомы.
При произведении расчетов в кратных единицах измерений величин напряжение всегда выражается в вольтах.
Для расчета сопротивления на участке цепи по закону Ома необходимо сначала определить ток на заданном участке цепи. Напряжение при этом делят на сопротивление конкретного участка цепи. Эти действия можно производить на любом участке без погрешности.
Для определения напряжения в цепи используют формулу $U = IR$.
Согласно указанной формуле, напряжение на обоих концах участка электрической цепи прямо пропорционально сопротивлению и току. Иными словами, если не стремиться все время изменять сопротивление на данном участке, то при увеличении тока применяется способ увеличения напряжения.
Значительному напряжению в цепи будет соответствовать больший ток. Эти правила действуют при постоянном сопротивлении.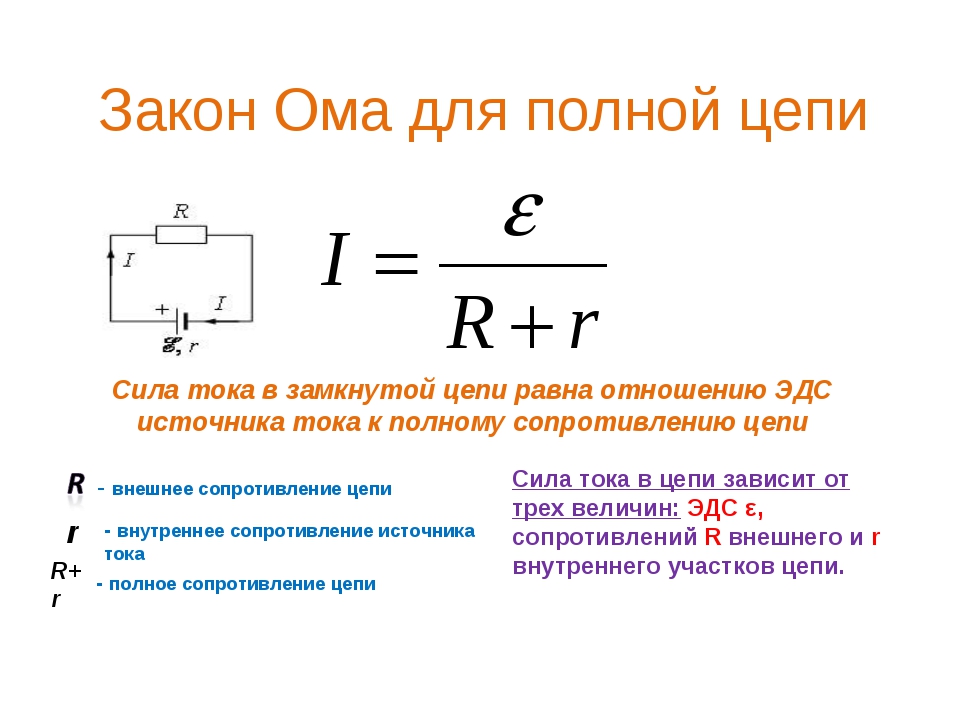 Для получении одинакового тока при различных сопротивлениях большее напряжение должно соответствовать большему сопротивлению.
Для получении одинакового тока при различных сопротивлениях большее напряжение должно соответствовать большему сопротивлению.
Падение напряжения – это напряжение на определенном участке цепи. Это означает, что напряжение и падение напряжения – идентичные понятия, а слово «падение» никак не связано с потерей некоторого количества напряжения в цепи. Потерю напряжения следует различать от падения напряжения.
Расчет сопротивления
Сопротивление на участке цепи рассчитывается по классической формуле $R = \frac{U}{I}$. Для этого необходимо установить значения напряжения и тока. Сопротивление – отношение напряжения к току.
При многократном увеличении или уменьшении напряжения ток также изменяется в несколько раз в ту или иную сторону. Отношение напряжения к току, которое равно сопротивлению, всегда остается на неизменном уровне.
Сопротивление определенного проводника не зависит от напряжения и тока. Оно будет лежать в зависимости от материала проводника, его длины и площади сечения. Формула для расчета сопротивления на участке цепи очень похожа на формулу для определения тока, однако существует между ними принципиальное различие.
Формула для расчета сопротивления на участке цепи очень похожа на формулу для определения тока, однако существует между ними принципиальное различие.
Оно состоит в том, что ток на конкретном участке цепи зависит от напряжения и сопротивления, поэтому изменяется таким же образом. Сопротивление на данном участке цепи – постоянная величина. Она не зависит от изменения значений тока и напряжения, однако равно отношению этих величин.
Вольтамперная характеристика
Закон Ома представляют в виде вольтамперной характеристики. Зависимость между двумя пропорциональными величинами выражается прямой линией на графике. Она проходит через начало координат. Подобную прямую пропорциональную зависимость величин также называют линейной зависимостью.
В графическом выражении закона Ома для участка цепи при отрицательных значениях напряжения и тока также рисуют прямую линию. Это означает, что ток в цепи проходит в разных направлениях одинаково. При большем сопротивлении меньшее значение имеет ток с таким же напряжением.
Вольтамперную характеристику составляют при помощи специальных приборов. Линейными называют такие приборы, у которых характеристика выражается прямой линией, и она проходит через начало координат.
Специалисты при составлении вольтамперной характеристики применяют также понятия линейные сопротивления и линейные цепи.
Определение 2
Нелинейными называют приборы, у которых сопротивление меняется при изменении тока или напряжения. Для таких случаев уже не действует закон Ома.
Закон Ома для участка цепи. Последовательное и параллельное соединение проводников. 10 класс. Физика. – Объяснение нового материала.
Комментарии преподавателяЗакон Ома для участка цепиСила тока на участке цепи прямо пропорциональна напряжению на этом участке и обратно пропорциональна сопротивлению участка.
Закон Ома оказался справедливым не только для металлов, но и для растворов электролитов. Сформулированный закон имеет место для так называемого однородного участка цепи – участка, не содержащего источников тока.
Математическая запись закона Ома проста, как и его формулировка, но экспериментально подтвердить эту зависимость очень трудно. Сила тока, протекающая по участку цепи, мала. Поэтому используют достаточно чувствительные приборы. Г. Ом изготовил чувствительный прибор для измерения силы тока, а в качестве источника тока использовал термопару. Действие амперметра и вольтметра основано на применение закона Ома для участка цепи. Угол поворота стрелки прибора пропорционален силе тока.
Из математической записи закона Ома:
можно выразить напряжение :
и сопротивление проводника:
.
Таким образом, закон Ома связывает три параметра, характеризующих постоянный электрический ток, проходящий по проводнику, и позволяет находить любой из них, если известны два других.
Закон Ома имеет границы применимости и выполняется только в том случае, когда при прохождении тока температура заметно не меняется. На вольт–амперной характеристике лампы накаливания видно, что график сильно искривляется при напряжении выше 10В, значит, закон Ома выше этого напряжения применять нельзя.
Также нельзя говорить, что сопротивление проводника зависит от напряжения и силы тока в цепи. Сопротивление участка цепи зависит от свойств проводника: длины, площади поперечного сечения и материала, из которого состоит проводник.
где l-длина проводника, s-его площадь поперечного сечения.
ρ –удельное сопротивление проводника – это физическая величина, характеризующая зависимость сопротивления проводника от материала, из которого он изготовлен.
Удельное сопротивление показывает, каким сопротивлением обладает сделанный из этого вещества проводник длиной 1м и площадью поперечного сечения 1м2 .
Из формулы видно, что единицей измерения в системе СИ является Ом·м. Но так как площадь поперечного сечения проводника достаточно мала, используют единицы измерения
при вычислении площадь поперечного сечения проводника следует выражать в мм2.
В заключении хочется заметить, что Ом начал свои опыты, когда был учителем физики в гимназии. В своих экспериментах Ом брал куски проволоки одинакового диаметра, но разного материала и изменял их длину таким образом, чтобы в цепи сила тока имела одинаковое значение. Находящаяся рядом магнитная стрелка отклонялась при прохождении тока в цепи. Установив связь между напряжением и силой тока, Г. Ом вывел один из основных законов постоянного тока.
В своих экспериментах Ом брал куски проволоки одинакового диаметра, но разного материала и изменял их длину таким образом, чтобы в цепи сила тока имела одинаковое значение. Находящаяся рядом магнитная стрелка отклонялась при прохождении тока в цепи. Установив связь между напряжением и силой тока, Г. Ом вывел один из основных законов постоянного тока.
Электрические цепи, с которыми приходится иметь дело на практике, обычно состоят не из одного приёмника электрического тока, а из нескольких различных, которые могут быть соединены между собой по-разному. Зная сопротивление каждого и способ их соединения, можно рассчитать общее сопротивление цепи.
На рисунке а изображена цепь последовательного соединения двух электрических ламп, а на рисунке б — схема такого соединения. Если выключать одну лампу, то цепь разомкнётся и другая лампа погаснет.
Рис. Последовательное включение лампочек и источников питания
Мы уже знаем, что при последовательном соединении сила тока в любых частях цепи одна и та же, т. е.
е.
I = I1 = I2
А чему равно сопротивление последовательно соединённых проводников?
Соединяя проводники последовательно, мы как бы увеличиваем длину проводника. Поэтому сопротивление цепи становится больше сопротивления одного проводника.
Последовательное соединение проводников
Общее сопротивление цепи при последовательном соединении равно сумме сопротивлений отдельных проводников (или отдельных участков цепи):
R = R1 + R2
Напряжение на концах отдельных участков цепи рассчитывается на основе закона Ома:
U1 = IR1, U2 = IR2.
Из приведённых равенств видно, что напряжение будет большим на проводнике с наибольшим сопротивлением, так как сила тока везде одинакова.
Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи:
U = U1 + U2.
Это равенство вытекает из закона сохранения энергии. Электрическое напряжение на участке цепи измеряется работой электрического тока, совершающейся при прохождении по участку цепи электрического заряда в 1 Кл. Эта работа совершается за счёт энергии электрического поля, и энергия, израсходованная на всём участке цепи, равна сумме энергий, которые расходуются на отдельных проводниках, составляющих участок этой цепи.
Эта работа совершается за счёт энергии электрического поля, и энергия, израсходованная на всём участке цепи, равна сумме энергий, которые расходуются на отдельных проводниках, составляющих участок этой цепи.
Все приведённые закономерности справедливы для любого числа последовательно соединённых проводников.
Пример 1. Два проводника сопротивлением R1 = 2 Ом, R2 = 3 Ом соединены последовательно. Сила тока в цепи I = 1 А. Определить сопротивление цепи, напряжение на каждом проводнике и полное напряжение всего участка цепи.
Запишем условие задачи и решим её.
Расчет параметров электрической цепи
при параллельном соединении сопротивлений:
1. сила тока в неразветвленном участке цепи равна сумме сил токов
во всех параллельно соединенных участках
2. напряжение на всех параллельно соединенных участках цепи одинаково
3. при параллельном соединении сопротивлений складываются величины, обратные сопротивлению :
при параллельном соединении сопротивлений складываются величины, обратные сопротивлению :
( R – сопротивление проводника,
1/R – электрическая проводимость проводника)
Если в цепь включены параллельно только два сопротивления, то:
( при параллельном соединении общее сопротивление цепи меньше меньшего из включенных сопротивлений )
4. работа электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме работ на отдельных участках:
A=A1+A2
5. мощность электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме мощностей на отдельных участках:
P=P1+P2
Для двух сопротивлений:
т.е. чем больше сопротивление, тем меньше в нём сила тока.
Домашняя работа.Задание 1. Ответить на вопросы.
- Какое соединение проводников называют последовательным? Изобразите его на схеме.

- Какая электрическая величина одинакова для всех проводников, соединённых последовательно?
- Как найти общее сопротивление цепи, зная сопротивление отдельных проводников, при последовательном соединении?
- Как найти напряжение участка цепи, состоящего из последовательно соединённых проводников, зная напряжение на каждом?
- Какое соединение проводников называют параллельным? Изобразите его на схеме.
- Какая из электрических величин одинакова для всех проводников, соединённых параллельно?
- Как выражается сила тока в цепи до её разветвления через силы токов в отдельных ветвях разветвления?
- Как изменяется общее сопротивление разветвления после увеличения числа проводников в разветвлении?
- Какое соединение проводников применяется в жилых помещениях? Какие напряжения используются для бытовых нужд?
Задание 2.Решите задачи.
1. Две лампочки соединены последовательно. Сила тока на первой лампочке 2А. Найдите общее напряжение и напряжение на каждой из ламп, если сопротивление на первой лампе 3Ом, а на второй 4Ом.
Сила тока на первой лампочке 2А. Найдите общее напряжение и напряжение на каждой из ламп, если сопротивление на первой лампе 3Ом, а на второй 4Ом.
2. Две лампочки соединены параллельно. Напряжение на второй лампочке10В. Найдите силу тока в цепи и на каждой из ламп, если сопротивление на первой лампе 1Ом, а на второй 2Ом.
К занятию прикреплен файл «Это интересно». Вы можете скачать файл в любое удобное для вас время.
Использованные источники:
- http://www.tepka.ru/
- http://class-fizika.narod.ru
- http://www.youtube.com/watch?v=cVKE9NItreo
- http://znaika.ru/catalog/10-klass/physics/
- http://www.youtube.com/watch?v=NB7hOVYe7h0
- https://www.youtube.com/watch?v=cVKE9NItreo
- https://www.youtube.com/watch?v=0hFWeR8ybxs
- http://www.youtube.com/watch?v=EDI8DzWSSWY
- http://www.youtube.com/watch?v=bH_-qGnjJqc
Как найти напряжение через ЭДС и сопротивление?
Закон Ома для замкнутой цепи
Если к источнику питания подключить внешнюю цепь сопротивлением R, в цепи пойдёт ток с учётом внутреннего сопротивления источника:
I – Сила тока в цепи.
– Электродвижущая сила (ЭДС) – величина напряжения источника питания не зависящая от внешней цепи (без нагрузки). Характеризуется потенциальной энергией источника. r – Внутреннее сопротивление источника питания.
Для электродвижущей силы внешнеее сопротивление R и внутреннее r соединены последовательно, значит величина тока в цепи определится значением ЭДС и суммой сопротивлений: I = /(R+r) .
Напряжение на выводах внешней цепи определится исходя из силы тока и сопротивления R соотношением, которое уже рассматривалось выше: U = IR. Напряжение U, при подключении нагрузки R, всегда будет меньше чем ЭДС на величину произведения I*r, которую называют падением напряжения на внутреннем сопротивлении источника питания. С этим явлением мы сталкиваемся достаточно часто, когда видим в работе частично разряженные батарейки или аккумуляторы. По мере разряда, увеличивается их внутреннее сопротивление, следовательно, увеличивается падение напряжение внутри источника, значит уменьшается внешнее напряжение U = – I*r.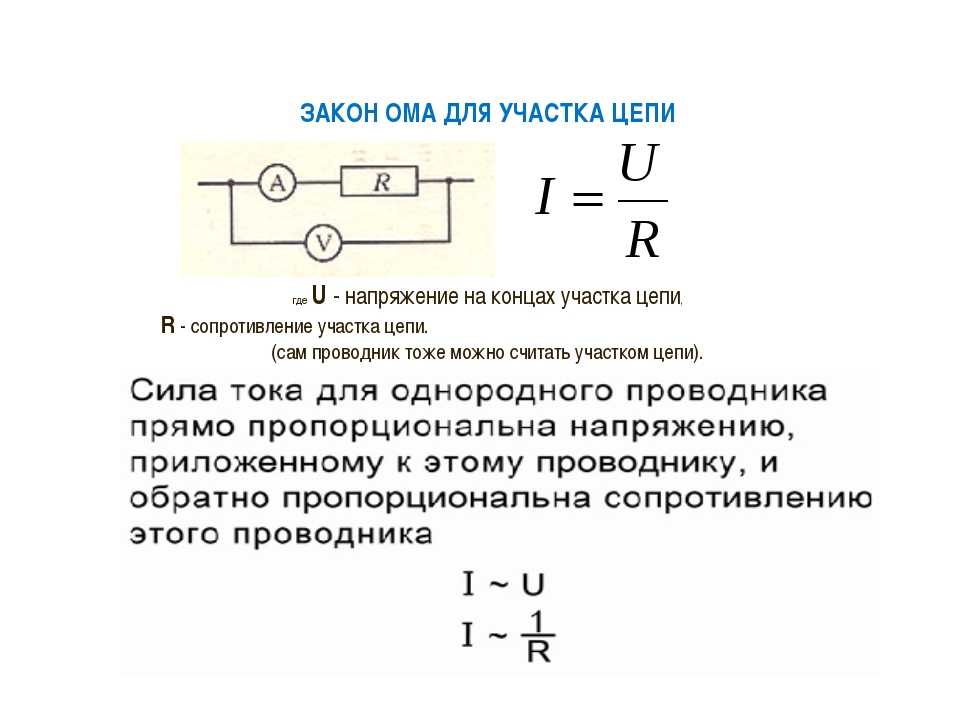 Чем меньше ток и внутреннее сопротивление источника, тем ближе по значению его ЭДС и напряжение на его выводах U. Если ток в цепи равен нулю, следовательно, = U. Цепь разомкнута, ЭДС источника равна напряжению на его выводах.
Чем меньше ток и внутреннее сопротивление источника, тем ближе по значению его ЭДС и напряжение на его выводах U. Если ток в цепи равен нулю, следовательно, = U. Цепь разомкнута, ЭДС источника равна напряжению на его выводах.
В случаях, когда внутренним сопротивлением источника можно пренебречь (r ≈ 0), напряжение на выводах источника будет равно ЭДС ( ≈ U ) независимо от сопротивления внешней цепи R. Такой источник питания называют источником напряжения.
Разомкнутая электрическая цепь
При отсутствии потока электронов необходимое напряжение источника цепи проявляется на концах точек. В этом случае происходит процесс ожидания момента соединения концов точек, чтобы возобновился поток электронов. Подобную цепь принято называть разомкнутой.
Замечание 1При связывании концов проводов, где существует разрыв, непрерывность всей цепи восстановится. Это основная разница между замкнутой и разомкнутой цепью.
При включении и выключении электрического освещения (лампы) требуется постоянно осуществлять похожие процессы. Для удобства были созданы специальные устройства. Их называют выключателями или рубильниками. Они в автоматическом режиме по сигналу управляют потоками электронов в цепи, контролируя начало и завершение работы электрооборудования.
Для удобства были созданы специальные устройства. Их называют выключателями или рубильниками. Они в автоматическом режиме по сигналу управляют потоками электронов в цепи, контролируя начало и завершение работы электрооборудования.
Рубильники практически идеально подходят для демонстрации принципов работы выключателей и переключателей. Однако при использовании их в больших электрических цепях существует немало проблем, связанных с безопасной эксплуатацией. Так как некоторые части рубильников открыты, то существует вероятность воспламенения горючих материалов. В современных выключателях применяются подвижные и неподвижные контакты, которые защищены изоляционным корпусом.
Простейшая электрическая цепь представляет собой нагрузку, подключенную к источнику питания. Для управления цепью в нее последовательно включают замыкающее устройство (ключ). При замкнутом ключе в цепи возникает электрический ток, а при разомкнутом – ток отсутствует. Именно от положения ключа (замкнутый/разомкнутый) напрямую зависит – какую электрическую цепь называют замкнутой и разомкнутой.
[custom_ads_shortcode1]
Закон Ома для переменного тока
При наличии индуктивности или ёмкости в цепи переменного тока необходимо учитывать их реактивное сопротивление. В таком случае запись Закона Ома будет иметь вид:
I = U/Z
Здесь Z – полное (комплексное) сопротивление цепи – импеданс. В него входит активная R и реактивная X составляющие. Реактивное сопротивление зависит от номиналов реактивных элементов, от частоты и формы тока в цепи. Более подробно ознакомится с комплексным сопротивлением можно на страничке импеданс.
С учётом сдвига фаз φ, созданного реактивными элементами, для синусоидального переменного тока обычно записывают Закон Ома в комплексной форме:
Элементы электрической цепи
Электрическую цепь разделяют на 2 участка – внутренний и внешний. Внутренним участком считается источник питания постоянного или переменного напряжения, а внешним – система, состоящая из нагрузки, приборов и соединительных элементов (проводов). Кроме обязательных элементов – источника и нагрузки, электрическая цепь может включать выключатели, реостаты, предохранительные плавкие или автоматические устройства, приборы контроля и индикации. Нагрузка также может состоять из различных потребителей, подключенных в цепь параллельно или последовательно.
Нагрузка также может состоять из различных потребителей, подключенных в цепь параллельно или последовательно.
[custom_ads_shortcode2]
Нелинейные элементы и цепи
Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях, например, для большинства проводников. Его невозможно использовать для расчёта напряжения и тока в полупроводниковых или электровакуумных приборах, где эта зависимость не является пропорциональной и её можно определять только с помощью вольтамперной характеристики (ВАХ). К данной категории элементов относятся все полупроводниковые приборы (диоды, транзисторы, стабилитроны, тиристоры, варикапы и т.д.) и электронные лампы. Такие элементы и цепи, в которых они используются, называют нелинейными.
Напряжение, ток и сопротивление
Электрическая цепь образуется, когда создается проводящий путь, позволяющий электрическому заряду непрерывно перемещаться. Это непрерывное движение электрического заряда по проводникам цепи называется током, и о нем часто говорят как о «потоке», как о потоке жидкости через полую трубу.
Сила, побуждающая носители заряда «течь» по цепи, называется напряжением. Напряжение – это особая мера потенциальной энергии, которая всегда относительна между двумя точками. Когда мы говорим об определенной величине напряжения, присутствующего в цепи, мы имеем в виду измерение потенциальной энергии для перемещения носителей заряда из одной конкретной точки этой цепи в другую конкретную точку. Без упоминания двух конкретных точек термин «напряжение» не имеет значения.
Ток, как правило, проходит через проводники с некоторой степенью трения или противодействия движению. Это противодействие движению правильнее называть сопротивлением. Величина тока в цепи зависит от величины напряжения и величины сопротивления в цепи, препятствующего прохождению тока. Как и напряжение, сопротивление – это величина, измеряемая между двумя точками. По этой причине величины напряжения и сопротивления часто указываются как «между» двумя точками в цепи.
Идеальный источник ЭДС
Электродвижущая сила (E) – физическая величина, определяющая степень воздействия внешних сил на перемещение в замкнутой цепи носителей заряда. Иными словами, от ЭДС будет зависеть то, как сильно ток стремится течь по проводнику.
Иными словами, от ЭДС будет зависеть то, как сильно ток стремится течь по проводнику.
При объяснении подобных непонятных явлений отечественные школьные учителя любят обращаться к методу гидравлических аналогий. Если проводник – это труба, а электрический ток – это количество протекающей по ней воды, то ЭДС – это давление, которое развивает насос, чтобы качать жидкость.
Термин электродвижущая сила родственен такому понятию, как напряжение. Она, ЭДС, так же измеряется в вольтах (ед. изм. – «В»). Каждый источник питания, будь то батарейка, генератор или солнечная панель, обладает своей собственной электродвижущей силой. Зачастую эта ЭДС близка к выходному напряжению (U), но всегда немного меньше его. Вызвано это внутренним сопротивлением источника, на котором неизбежно падает часть вольтажа.
Советуем изучить — Закалка стали
По этой причине идеальный источник ЭДС – это скорее абстрактное понятие или физическая модель, не имеющая места в реальном мире, ведь внутреннее сопротивление элемента питания Rвн хоть и весьма низкое, но всё же отлично от абсолютного нуля.
Идеальный и реальный источник ЭДС
Кулон и электрический заряд
Одна из основных единиц электрических измерений, которую часто преподают в начале курсов электроники, но нечасто используют впоследствии, – это кулон – единица измерения электрического заряда, пропорциональная количеству электронов в несбалансированном состоянии. Один кулон заряда соответствует 6 250 000 000 000 000 000 электронов. Символом количества электрического заряда является заглавная буква «Q», а единица измерения кулонов обозначается «Кл». Единица измерения тока, ампер, равна 1 кулону заряда, проходящему через заданную точку в цепи за 1 секунду. В этом смысле, ток – это скорость движения электрического заряда через проводник.
Как указывалось ранее, напряжение – это мера потенциальной энергии на единицу заряда, доступная для стимулирования протекания тока из одной точки в другую. Прежде чем мы сможем точно определить, что такое «вольт», мы должны понять, как измерить эту величину, которую мы называем «потенциальной энергией». Общей метрической единицей измерения энергии любого вида является джоуль, равный количеству работы, совершаемой силой в 1 ньютон при движении на 1 метр (в том же направлении). В этих научных терминах 1 вольт равен 1 джоулю электрической потенциальной энергии на (деленному на) 1 кулон заряда. Таким образом, 9-вольтовая батарея выделяет 9 джоулей энергии на каждый кулон заряда, проходящего через цепь.
Общей метрической единицей измерения энергии любого вида является джоуль, равный количеству работы, совершаемой силой в 1 ньютон при движении на 1 метр (в том же направлении). В этих научных терминах 1 вольт равен 1 джоулю электрической потенциальной энергии на (деленному на) 1 кулон заряда. Таким образом, 9-вольтовая батарея выделяет 9 джоулей энергии на каждый кулон заряда, проходящего через цепь.
Эти единицы и символы электрических величин станут очень важны, когда мы начнем исследовать отношения между ними в цепях.
Формула закона Ома
Основное открытие Ома заключалось в том, что величина электрического тока, протекающего через металлический проводник в цепи, при любой заданной температуре прямо пропорциональна напряжению, приложенному к нему. Ом выразил свое открытие в виде простого уравнения, описывающего взаимосвязь напряжения, тока и сопротивления:
[E=IR]
В этом алгебраическом выражении напряжение (E) равно току (I), умноженному на сопротивление (R). Используя алгебру, мы можем преобразовать это уравнение в других два варианта, решая его для I и R соответственно:
Используя алгебру, мы можем преобразовать это уравнение в других два варианта, решая его для I и R соответственно:
Метода треугольника закона Ома
Закон Ома – очень простой и полезный инструмент для анализа электрических цепей. Он так часто используется при изучении электричества и электроники, что студент должен запомнить его. Если вы не очень хорошо умеете работать с формулами, то для его запоминания существует простой прием, помогающий использовать его для любой величины, зная две других. Сначала расположите буквы E, I и R в виде треугольника следующим образом:
Рисунок 5 – Треугольник закона Ома
Если вы знаете E и I и хотите определить R, просто удалите R с картинки и посмотрите, что осталось:
Рисунок 6 – Закон Ома для определения R
Если вы знаете E и R и хотите определить I, удалите I и посмотрите, что осталось:
Рисунок 7 – Закон Ома для определения I
Наконец, если вы знаете I и R и хотите определить E, удалите E и посмотрите, что осталось:
Рисунок 8 – Закон Ома для определения E
В конце концов, вам придется научиться работать с формулами, чтобы серьезно изучать электричество и электронику, но этот совет может облегчить запоминание ваших первых вычислений. Если вам удобно работать с формулами, всё, что вам нужно сделать, это зафиксировать в памяти E = IR и вывести из нее две другие формулы, когда они вам понадобятся!
Если вам удобно работать с формулами, всё, что вам нужно сделать, это зафиксировать в памяти E = IR и вывести из нее две другие формулы, когда они вам понадобятся!
Что нам дает параллельное и последовательное соединение?
Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа. Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:
В общем, это наиболее распространенные варианты использования этих соединений.
Работа и мощность электрического тока
Электрическое поле, создавая упорядоченное движение заряженных частиц в проводнике, выполняет работу, которую принято называть работой тока.
Работа электрического тока А — физическая величина, характеризующая: изменение электрической энергии тока — превращение ее в другие виды. Единица работы электрического тока — джоуль, 1 Дж. В быту и технике используют также внесистемная единица — киловатт-час (кВт • ч), 1 кВт • ч = 3,6 • 106 Дж.
В быту и технике используют также внесистемная единица — киловатт-час (кВт • ч), 1 кВт • ч = 3,6 • 106 Дж.
Советуем изучить — Статическое и астатическое регулирование
Если рассматривать внешний участок электрической цепи, то работа тока определяется как А = qU = UIt, где q — заряд, прошедший через поперечное сечение проводника за время t, U — электрическое напряжение на участке цепи, I — сила тока.
Если на участке цепи, по которой проходит ток, не выполняется механическая работа и не происходят химические реакции, то результатом работы электрического тока будет только нагрев проводников. Нагретый проводник вследствие теплообмена отдает полученную энергию в окружающую среду. Согласно закону сохранения энергии, количество выделенной теплоты равна работе тока: Q = А и вычисляется по закону Джоуля — Ленца: количество теплоты Q, выделяемой за время t в проводнике с сопротивлением R во время прохождения по нему тока силой I, равна Q = I2Rt.
Воспользовавшись законом Ома I = U/R, математически можно получить и такие формулы закона Джоуля — Ленца: Q =U2t/R и Q = UIt. Однако, если в цепи выполняется механическая работа или происходят химические реакции, эти формулы использовать нельзя.
Однако, если в цепи выполняется механическая работа или происходят химические реакции, эти формулы использовать нельзя.
Мощность электрического тока Р — физическая величина, характеризующая способность электрического тока выполнять определенную работу и измеряется работой, выполненной в единицу времени, Р = A/t, здесь А — работа электрического тока, t — время, за которое эта работа выполнена. Мощность во внешнем участке электрической цепи можно определить по формулам Р = UI, Р = I2R, Р = U2/R, где U — электрическое напряжение, I — сила тока, R — электрическое сопротивление участка цепи. Единица мощности — ватт, 1 Вт = 1.
Если цепь состоит из нескольких потребителей, то при параллельном их соединения общая мощность тока во всей цепи равна сумме мощностей отдельных потребителей
Это стоит принять во внимание. В быту мы пользуемся мощными электрическими приборами
Если одновременно их включить, то общая мощность может превышать ту, на которую рассчитана электрическая сеть в помещении.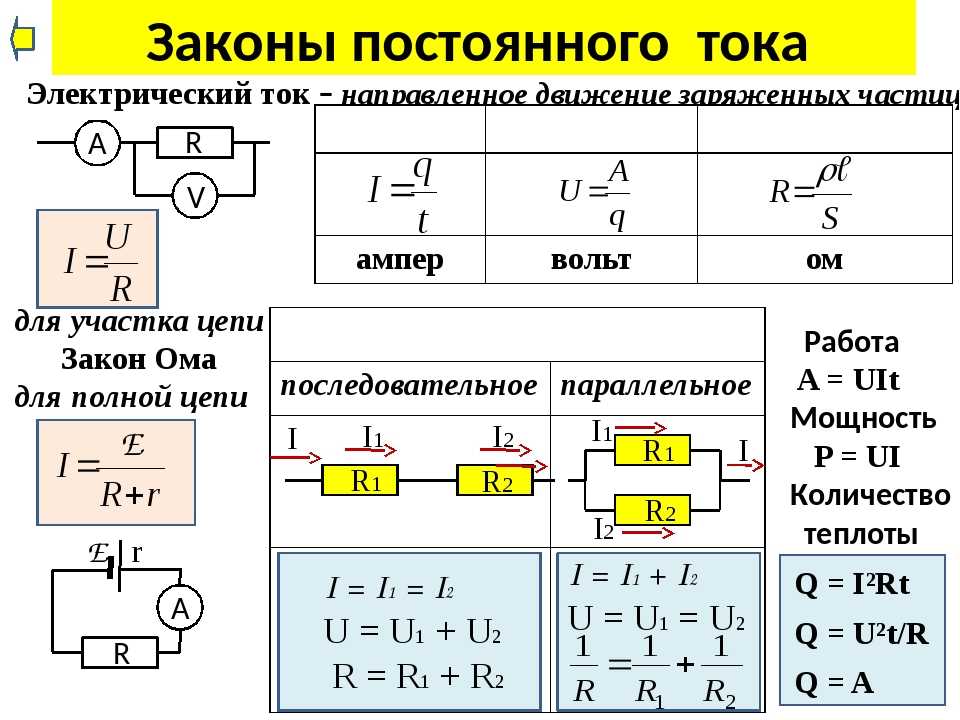
Выясним, в каком случае в электрической цепи выделяется максимальная мощность. Для этого запишем закон Ома для полной цепи в таком виде: ε = IR + Ir. Умножив обе части уравнения на I, получим: εI = I 2 R + I 2 r, где εI — полная мощность, которую развивает источник тока, I2R — мощность потребителей внешней участка цепи, I2г — мощность, которую потребляет внутренняя часть круга. Итак, потребляемая мощность внешней частью цепи, составляет: P = εI – I 2 r.
График зависимости потребляемой мощности во внешней части цепи от силы тока
Графиком зависимости Р (I) является парабола, вершина которой имеет координаты {ε/2r;ε2/4r}. Из графика видно, что максимальная мощность потребляется во внешнем цепи при силе тока I = ε/2r.
Параллельное и последовательное соединение
В электрике элементы соединяются либо последовательно — один за другим, либо параллельно — это когда к одной точке подключены несколько входов, к другой — выходы от тех же элементов.
Закон Ома для параллельного и последовательного соединения
Параллельное соединение
Параллельное соединение — это когда начала проводников/элементов сходятся в одной точке, а в другой — соединены их концы. Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.
Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.
Теперь относительно напряжения. Если напряжение — это работа по перемещению заряда, тоо работа, которая необходима на перемещение одного заряда будет одинакова на любом элементе. То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.
Законы для параллельного соединения
Для сопротивления все несколько сложнее. Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.
В формуле это выглядит так: G = 1/R.
Закон Ома для полной цепи и для участка цепи: формулы, описание и объяснение
Закон Ома — мощность
Когда через резистор протекает электрический ток, он рассеивает определенную часть мощности в виде тепла.
Мощность является функцией протекающего тока I (А) и приложенного напряжения V (В):
где
Р — мощность в ваттах (В)
В сочетании с законом Ома для участка цепи, формулу можно преобразовать в следующий вид:
или
Идеальный резистор рассеивает всю энергию и не сохраняет электрическую или магнитную энергию. Каждый резистор имеет предел мощности, которая может быть рассеяна, не оказывая повреждение резистору. Это мощность называется номинальной.
Окружающие условия могут снизить или повысить это значение. Например, если окружающий воздух горячий, то способность рассеять излишнее тепло у резистора снижается, и на оборот, при низкой температуре окружающего воздух рассеиваемая способность резистора возрастает.
На практике, резисторы редко имеют обозначение номинальной мощности. Тем не менее, большинство из резисторов рассчитаны на 1/4 или 1/8 Вт.
Ниже приведена круговая диаграмма, которая поможет вам быстро определить связь между мощностью, силой тока, напряжением и сопротивлением. Для каждого из четырех параметров показано, как вычислить свое значение.
Параллельное и последовательное соединение
В электрике элементы соединяются либо последовательно — один за другим, либо параллельно — это когда к одной точке подключены несколько входов, к другой — выходы от тех же элементов.
Закон Ома для параллельного и последовательного соединения
Последовательное соединение
Как работает закон Ома для этих случаев? При последовательном соединении сила тока, протекающая через цепочку элементов, будет одинаковой. Напряжение участка цепи с последовательно подключенными элементами считается как сумма напряжений на каждом участке. Как можно это объяснить? Протекание тока через элемент — это перенос части заряда с одной его части в другую. То есть, это определенная работа. Величина этой работы и есть напряжение. Это физический смысл напряжения. Если с этим понятно, двигаемся дальше.
То есть, это определенная работа. Величина этой работы и есть напряжение. Это физический смысл напряжения. Если с этим понятно, двигаемся дальше.
Последовательное соединение и параметры этого участка цепи
При последовательном соединении приходится переносить заряд по очереди через каждый элемент. И на каждом элементе это определенный «объем» работы. А чтобы найти объем работы на всем участке цепи, надо работу на каждом элементе сложить. Вот и получается, что общее напряжение — это сумма напряжений на каждом из элементов.
Точно так же — при помощи сложения — находится и общее сопротивление участка цепи. Как можно это себе представить? Ток, протекая по цепочке элементов, последовательно преодолевает все сопротивления. Одно за другим. То есть чтобы найти сопротивление, которое он преодолел, надо сопротивления сложить. Примерно так. Математический вывод более сложен, а так понять механизм действия этого закона проще.
Параллельное соединение
Параллельное соединение — это когда начала проводников/элементов сходятся в одной точке, а в другой — соединены их концы.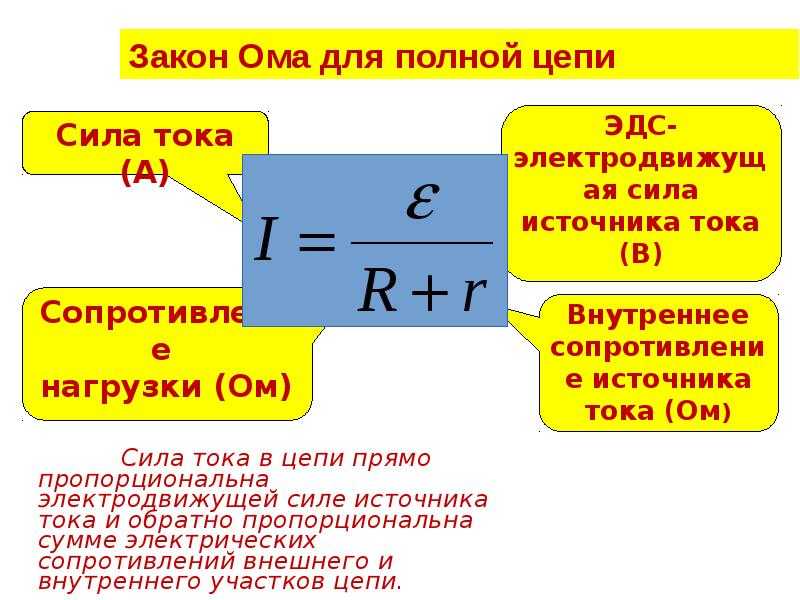 Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.
Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.
Теперь относительно напряжения. Если напряжение — это работа по перемещению заряда, тоо работа, которая необходима на перемещение одного заряда будет одинакова на любом элементе. То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.
Законы для параллельного соединения
Для сопротивления все несколько сложнее. Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.
В формуле это выглядит так: G = 1/R.
Для чего мы говорили о проводимости? Потому что общая проводимость участка с параллельным соединением элементов равна сумме проводимости для каждого из участков. G = G1 + G2 + G3 — понять несложно. Насколько легко току будет преодолеть этот узел из параллельных элементов, зависит от проводимости каждого из элементов. Вот и получается, что их надо складывать.
Теперь можем перейти к сопротивлению. Так как проводимость — обратная к сопротивлению величина, можем получить следующую формулу: 1/R = 1/R1 + 1/R2 + 1/R3.
Что нам дает параллельное и последовательное соединение?
Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа. Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:
Если в наличии нет резистора большого номинала, но есть несколько более «мелких», нужное сопротивление можно получить соединив последовательно несколько резисторов. Как видите, это полезный прием.
Как видите, это полезный прием.
Для продления срока жизни батареек, их можно соединять параллельно. Напряжение при этом, согласно закону Ома, останется прежним (можно убедиться, измерив напряжение мультиметром). А «срок жизни» сдвоенного элемента питания будет значительно больше, нежели у двух элементов, которые сменят друг друга
Только обратите внимание: параллельно соединять можно только источники питания с одинаковым потенциалом. То есть, севшую и новую батарейки соединять нельзя
Если все-таки соединить, та батарейка которая имеет больший заряд, будет стремиться зарядить менее заряженную. В результате общий их заряд упадет до низкого значения.
В общем, это наиболее распространенные варианты использования этих соединений.
Параметры постоянного тока
Как и всякая физическая величина, постоянный электрический ток характеризуется целым рядом параметров, имеющих непосредственное к нему отношение и отношение к взаимосвязанным с ним величинам.
Величина постоянного тока (сила тока)
Прежде чем говорить о силе тока, определимся с таким понятием, как электрический заряд, выражающий способность тел участвовать в электромагнитных явлениях типа создания электромагнитного поля и электромагнитного взаимодействия.
Впервые это понятие было введено в конце XVIII века французским учёным Шарлем Кулоном, сформулировавшим тогда же свой знаменитый закон о силе взаимодействия между точечными зарядами в зависимости от разделяющего их расстояния. В честь него единица измерения электрического заряда (количества электричества) стала называться «Кулон» (Кл).
Только опираясь на понятие электрического заряда, можно говорить о величине (силе) тока, формула расчёта которого (для равномерного движения зарядов) выглядит следующим образом:
I = Q/t
Что можно выразить следующими словами: сила тока прямо пропорциональна количеству зарядов, проходящих через поперечное сечение проводника за единицу времени. Здесь:
- I – ток, измеряемый в амперах (Андре Мари-Ампер – ещё один французский физик, внёсший значительный вклад в теорию электромагнетизма).
- Q – электрический заряд, измеряемый в кулонах или ампер-часах (А·ч). 1 А·ч = 3600 Кл.
- t – единица времени.
Для измерения силы тока используются амперметры, включаемые последовательно с источником электрического тока.
Плотность тока
Ещё одно важное понятие, необходимое в целях правильного выбора токопроводящего сечения линий электропередачи. Плотность тока это:. j = I/S
j = I/S
Где: I – сила тока в амперах. S – площадь поперечного сечения в м2. J – плотность тока в А/м2 или А/мм2.
Электродвижущая сила (ЭДС)
Электродвижущая сила (ЭДС) – это величина, характеризующая работу первичного источника электрической энергии по созданию постоянного электрического тока.
E = A/Q
E – электродвижущая сила (ЭДС), измеряемая в вольтах (Алессандро Вольта – известнейший итальянский физик). A – работа, измеряемая в джоулях (Джеймс Прескотт Джоуль – английский физик, внёсший значительный вклад в развитие термодинамики).
Электрическое напряжение
Электрическое напряжение – это величина, показывающая работу эффективного электрического поля, затраченную на перенос единичного пробного заряда из точки A в точку B.
UAB = φA – φB + EAB
φA – φB – разница потенциалов между точками A и B. EAB – электродвижущая сила, возникающая на искомом участке цепи постоянного тока. Здесь все величины измеряются в вольтах. Для определения величины напряжения применяются вольтметры, подключаемые параллельно участку измерения напряжения.
EAB – электродвижущая сила, возникающая на искомом участке цепи постоянного тока. Здесь все величины измеряются в вольтах. Для определения величины напряжения применяются вольтметры, подключаемые параллельно участку измерения напряжения.
Использование на практике
Закон Ома лежит в основе всех расчетов производимых в электронике и электротехнике. Будущих специалистов с первых дней учат, как использовать так называемый треугольник. Чтобы найти какую-то искомую величину, должны выполняться простые арифметические действия. Если два оставшихся параметра находятся в одной строке – они перемножаются. Если на разных уровнях, то верхний всегда делится на нижний.
Самые простые вычисления производятся на основе данных измерительных приборов. На участке цепи измерение тока выполняется амперметром, а напряжения – вольтметром. После этого найти сопротивление математическим путем не составит труда.
Для замеров сопротивления тоже есть прибор – омметр. Полученное выражение, подставляется в одну из формул, после чего находятся величины силы тока или напряжения. Точность омметра зависит от стабильности напряжения, подаваемого источником тока. Стабилизация проводится путем добавления резистора, выполняющего функцию регулятора.
Точность омметра зависит от стабильности напряжения, подаваемого источником тока. Стабилизация проводится путем добавления резистора, выполняющего функцию регулятора.
Иногда требуется исключить из схемы какой-нибудь элемент без демонтажа. С этой целью проводится шунтирование, когда приходится устанавливать проводник на входных клеммах ненужного резистора. Ток начинает идти через шунт с меньшим сопротивлением, а напряжение на резисторе падает до нуля.
Закон Ома используется в защитных системах. Это делается с помощью уставок, обеспечивающих нормальную работу и отключающих питание лишь в аварийных ситуациях.
Неоднородный участок цепи постоянного тока
Неоднородную структуру имеет такой участок цепи, где помимо проводников и элементов, присутствует источник тока. Его ЭДС необходимо учитывать при расчетах общей силы тока на данном участке.
Существует формула, которая дает определение основным параметрам и процессам неоднородного участка: q = q0 x n x V. Ее показатели характеризуются следующим образом:
- В процессе перемещения зарядов (q) они приобретают определенную плотность.
 Ее показатели зависят от силы тока и площади поперечного сечения проводника (S).
Ее показатели зависят от силы тока и площади поперечного сечения проводника (S). - В условиях определенной концентрации (n) можно точно указать численность единичных зарядов (q0), которые были перемещены за единичный отрезок времени.
- Для расчетов проводник условно считается цилиндрическим участком, имеющим какой-то объем (V).
При подключении проводника к аккумулятору, последний через некоторое время будет разряжен. То есть, движение электронов постепенно замедляется и, в конце концов, прекратится совсем. Этому способствует молекулярная решетка проводника, оказывающая противодействие, столкновения электронов между собой и другие факторы. Для преодоления такого сопротивления следует дополнительно приложить определенные сторонние силы.
Во время расчетов эти силы суммируются с кулоновскими. Кроме того, для перенесения единичного заряда q из 1-й точки во 2-ю потребуется выполнение работы А1-2 или просто А12. С этой целью создается разница потенциалов (ϕ1 – ϕ2). Под действием источника постоянного тока возникает ЭДС, перемещающая заряды по цепи. Величина общего напряжения будет состоять из всех сил, отмеченных выше.
Под действием источника постоянного тока возникает ЭДС, перемещающая заряды по цепи. Величина общего напряжения будет состоять из всех сил, отмеченных выше.
Полярность подключения к источнику постоянного тока нужно учитывать в расчетах. При изменении клемм будет меняться и ЭДС, ускоряющая или замедляющая перемещение зарядов.
Закон Ома для переменного тока
При наличии индуктивности или ёмкости в цепи переменного тока необходимо учитывать их реактивное сопротивление.В таком случае запись Закона Ома будет иметь вид:
I = U/Z
Здесь Z — полное (комплексное) сопротивление цепи — импеданс. В него входит активная R и реактивная X составляющие.Реактивное сопротивление зависит от номиналов реактивных элементов, от частоты и формы тока в цепи.Более подробно ознакомится с комплексным сопротивлением можно на страничке импеданс.
С учётом сдвига фаз φ, созданного реактивными элементами, для синусоидального переменного тока обычно записывают Закон Ома в комплексной форме:— комплексная амплитуда тока. = Iampe jφ— комплексная амплитуда напряжения. = Uampe jφ— комплексное сопротивление. Импеданс.φ — угол сдвига фаз между током и напряжением.e — константа, основание натурального логарифма.j — мнимая единица.Iamp , Uamp — амплитудные значения синусоидального тока и напряжения.
= Iampe jφ— комплексная амплитуда напряжения. = Uampe jφ— комплексное сопротивление. Импеданс.φ — угол сдвига фаз между током и напряжением.e — константа, основание натурального логарифма.j — мнимая единица.Iamp , Uamp — амплитудные значения синусоидального тока и напряжения.
Для ЭДС
Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.
Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.
Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.
Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.
Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:
То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:
I = U / (R + r)
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
Как найти с помощью формулы напряжение
Людей, интересующихся электричеством и физикой, всегда волнует вопрос, как найти напряжения, если известны другие характеристики. Его можно найти через многие формулы: в соответствии с законом Ома, через работу тока, путём сложения всех напряжений в электрической цепи и практическим способом – с помощью вольтметра. Как вычислить показатель с помощью последнего способа было описано выше.
Его можно найти через многие формулы: в соответствии с законом Ома, через работу тока, путём сложения всех напряжений в электрической цепи и практическим способом – с помощью вольтметра. Как вычислить показатель с помощью последнего способа было описано выше.
Важно! В цепях с последовательным соединением общее напряжение – сумма значений каждой нагрузки. При параллельном соединении общее напряжение равно значению каждой лампочки, у которых оно также эквивалентно
Вам это будет интересно WAGO соединители
Измерение напряжения
По каким формулам вычисляется напряжение через работу и сама сила тока, рассказывают на уроках физики, так как эти величины считаются базовыми. Работа тока равна произведению напряжения и заряда: A = U*q. Также, из этой формулы выводится A = U*I*t, так как заряд – произведение силы тока и времени. Из них следует, что U = A/q или U = A/(I*t). Кроме того, одной из основных является формула напряжения, выведенная из закона Ома: U = R/I.
Важно! Определить напряжение можно и через мощность электрического тока. Мощность равна A/t, и, так как A = U*I*t, конечная формула выглядит, как P = (U*I*t)/t
Мощность равна A/t, и, так как A = U*I*t, конечная формула выглядит, как P = (U*I*t)/t
Здесь t сократится, и останется P = U*I, из которой следует, что U = P/I.
Отдельный участок и полная электрическая цепь
Закон Ома, применительно к участку или всей цепи, может рассматриваться в двух вариантах расчетов:
- Отдельный краткий участок. Является частью схемы без источника ЭДС.
- Полная цепь, состоящая из одного или нескольких участков. Сюда же входит источник ЭДС со своим внутренним сопротивлением.
Расчет тока участка электрической схемы
В этом случае применяется основная формула I = U/R, в которой I является силой тока, U – напряжением, R – сопротивлением. По ней можно сформулировать общепринятую трактовку закона Ома:
Данная формулировка является основой для многих других формул, представленных на так называемой «ромашке» в графическом исполнении. В секторе Р – определяется мощность, в секторах I, U и R – проводятся действия, связанные с силой тока, напряжением и сопротивлением.
Каждое выражение – и основное и дополнительные, позволяют рассчитать точные параметры элементов, предназначенных для использования в схеме.
Специалисты, работающие с электрическими цепями, выполняют быстрое определение любого из параметров по методике треугольников, изображенных на рисунке.
В расчетах следует учитывать сопротивление проводников, соединяющих между собой элементы участка. Поскольку они изготавливаются из разных материалов, данный параметр будет отличаться в каждом случае. Если же потребуется сформировать полную схему, то основная формула дополняется параметрами источника напряжения, например, аккумуляторной батареи.
Вариант расчета для полной цепи
Полная цепь состоит из отдельно взятых участков, объединенных в единое целое вместе с источником напряжения (ЭДС). Таким образом, существующее сопротивление участков дополняется внутренним сопротивлением подключенного источника. Следовательно, основная трактовка, рассмотренная ранее, будет читаться следующим образом: I = U / (R + r). Здесь уже добавлен резистивный показатель (r) источника ЭДС.
Здесь уже добавлен резистивный показатель (r) источника ЭДС.
С точки зрения чистой физики этот показатель считается очень малой величиной. Однако, на практике, рассчитывая сложные схемы и цепи, специалисты вынуждены его учитывать, поскольку дополнительное сопротивление оказывает влияние на точность работы. Кроме того, структура каждого источника очень разнородная, в результате, сопротивление в отдельных случаях может выражаться достаточно высокими показателями.
Приведенные расчеты выполняются применительно к цепям постоянного тока. Действия и расчеты с переменным током производятся уже по другой схеме.
Действие закона к переменной величине
При переменном токе сопротивление цепи будет представлять из себя так называемый импеданс, состоящий из активного сопротивления и реактивной резистивной нагрузки. Это объясняется наличием элементов с индуктивными свойствами и синусоидальной величиной тока. Напряжение также является переменной величиной, действующей по своим коммутационным законам.
Следовательно, схема цепи переменного тока по закону Ома рассчитывается с учетом специфических эффектов: опережения или отставания величины тока от напряжения, а также наличия активной и реактивной мощности. В свою очередь, реактивное сопротивление включает в себя индуктивную или емкостную составляющие.
Все этим явлениям будет соответствовать формула Z = U / I или Z = R + J * (XL – XC), в которой Z является импедансом; R – активной нагрузкой; XL , XC – индуктивной и емкостной нагрузками; J – поправочный коэффициент.
Закон Джоуля-Ленца
Закон Джоуля-Ленца устанавливает связь между током «бегающему» по проводнику, его сопротивлению и теплом которое при этом выделяется.
В математическом символизме закон Джоуля-Ленца выглядит так:
Q=I2×R×t,где Q это количество выделяемого тепла в проводнике, в Джоулях;I-сила тока;R-сопротивление проводника;t-время прохождения тока в секундах.
В качестве информации: Ленц это русский физик Эмилий Христианович Ленц. Русский физик, электротехник, физический географ.1804-1865 года жизни.
Русский физик, электротехник, физический географ.1804-1865 года жизни.
Говоря о практическом применении закона Джоуля-Ленца, трудно назвать в какой части электрики он не проявляется. Электрические обогреватели, электрические водонагреватели, тепловые завесы, выбор автоматов защиты, тепловые реле в автоматике и многое другое.
Конечно это не все основные законы электрики. На по своему значению эти законы имеют фундаментальное значение.
Другие статьи сайта
- Автоматы защиты
- Виды опор линий электропередачи по материалу
- Виды опор по назначению
- Воздушные линии электропередачи проводами СИП
- Деревянные опоры воздушных линий электропередачи
- Железобетонные опоры линий электропередачи
- Железобетонные опоры линий электропередачи
- Защита человека от поражения электрическим током, прямое и косвенное прикосновение
- Как получает электроэнергию потребитель низкого напряжения 380 Вольт
- Колодцы кабельной сети этапы установки
Единицы измерения: вольт, ампер и ом
Чтобы иметь возможность делать осмысленные утверждения об этих величинах в цепях, нам нужно уметь описывать их количества так же, как мы могли бы количественно определить массу, температуру, объем, длину или любые другие физические величины. Для массы мы можем использовать единицы «килограмм» или «грамм». Для температуры мы можем использовать градусы Фаренгейта или градусы Цельсия. В таблице ниже приведены стандартные единицы измерения электрического тока, напряжения и сопротивления:
Для массы мы можем использовать единицы «килограмм» или «грамм». Для температуры мы можем использовать градусы Фаренгейта или градусы Цельсия. В таблице ниже приведены стандартные единицы измерения электрического тока, напряжения и сопротивления:
Единицы измерения тока, напряжения, сопротивления в таблице:
| Величина | Символ | Единица измерения | Сокращение единицы измерения |
| Ток | I | Ампер | А |
| Напряжение | V | Вольт | В |
| Сопротивление | R | Ом | Ом |
«Символ», присвоенный каждой величине, представляет собой стандартную букву латинского алфавита, используемую для представления этой величины в формулах. Подобные стандартизированные буквы распространены во всех физических и технических дисциплинах и признаны во всем мире. «Сокращение единицы измерения» для каждой величины представляет собой алфавитный символ(ы), используемый в качестве сокращенного обозначения конкретной единицы измерения.
Каждая единица измерения названа в честь известного экспериментатора в области электричества: ампер в честь француза Андре М. Ампера, вольт в честь итальянца Алессандро Вольта, а ом в честь немца Георга Симона Ома.
Математический символ для каждой величины также имеет значение. «R» для сопротивления и «V» для напряжения говорят сами за себя («Resistance» и «Voltage», соответственно), тогда как «I» для тока кажется немного странным. Предполагается, что буква «I» должна представлять «интенсивность» («Intensity»)(потока заряда). Судя по исследованиям, которые мне удалось провести, кажется, что есть некоторые разногласия по поводу значения слова «I». Другой символ напряжения, «E», означает «электродвижущую силу» («Electromotive force»). Символы «E» и «V» по большей части взаимозаменяемы, хотя в некоторых текстах «E» зарезервировано для обозначения напряжения на источнике (таком как батарея или генератор), а «V»– для обозначения напряжения на любом другом элементе.
Все эти символы выражаются заглавными буквами, за исключением случаев, когда величина (особенно напряжение или ток) описывается в терминах короткого периода времени (так называемые «мгновенные» значения). Например, напряжение батареи, которое стабильно в течение длительного периода времени, будет обозначаться заглавной буквой «E», тогда как пиковое напряжения при ударе молнии в тот самый момент, когда она попадает в линию электропередачи, скорее всего, будет обозначаться строчной буквой «е» (или строчной буквой «v»), чтобы отметить это значение как имеющееся в один момент времени. Это же соглашение о нижнем регистре справедливо и для тока: строчная буква «i» представляет ток в некоторый момент времени. Однако большинство измерений в цепях постоянного тока, которые стабильны во времени, будут обозначаться заглавными буквами.
Например, напряжение батареи, которое стабильно в течение длительного периода времени, будет обозначаться заглавной буквой «E», тогда как пиковое напряжения при ударе молнии в тот самый момент, когда она попадает в линию электропередачи, скорее всего, будет обозначаться строчной буквой «е» (или строчной буквой «v»), чтобы отметить это значение как имеющееся в один момент времени. Это же соглашение о нижнем регистре справедливо и для тока: строчная буква «i» представляет ток в некоторый момент времени. Однако большинство измерений в цепях постоянного тока, которые стабильны во времени, будут обозначаться заглавными буквами.
Источник ЭДС в полной цепи
Для возникновения электрического тока в замкнутой цепи, эта цепь должна содержать хотя бы один особый элемент, в котором будет происходить работа по переносу зарядов между его полюсами. Силы, переносящие заряды внутри этого элемента, делают это против электрического поля, а значит, их природа должна быть отлична от электрической. Поэтому такие силы называются сторонними.
Поэтому такие силы называются сторонними.
Рис. 1. Сторонние силы в физике.
Элемент электрической цепи, в котором происходит работа сторонних сил по переносу зарядов против действия электрического поля, называется источником тока. Главная его характеристика – это величина сторонних сил. Для ее характеристики вводится специальная мера – Электродвижущая Сила (ЭДС), она обозначается буквой $\mathscr{E}$.
Значение ЭДС источника тока равно отношению сторонних сил по переносу заряда к величине этого заряда:
$$\mathscr{E}={A_{ст}\over q}$$
Поскольку смысл ЭДС очень близок к смыслу электрического напряжения (напомним, напряжение – это отношение работы, совершаемой электрическим полем, переносящим заряд, к величине этого заряда), то ЭДС так же, как и напряжение, измеряется в Вольтах:
$$1В={Дж\overКл}$$
Второй важнейшей электрической характеристикой реального источника тока является его внутреннее сопротивление. При переносе зарядов между клеммами происходит их взаимодействие с веществом источника ЭДС, а поэтому, источник для электрического тока также представляет некоторое сопротивление. Внутреннее сопротивление, как и обычное сопротивление, измеряется в Омах, но обозначается малой латинской буквой $r$.
Внутреннее сопротивление, как и обычное сопротивление, измеряется в Омах, но обозначается малой латинской буквой $r$.
Рис. 2. Примеры источников тока.
Просадка напряжения
Итак, знакомьтесь, автомобильный аккумулятор!
Для дальнейшего его использования, припаяем к нему два провода: красный на плюс, черный на минус
Наш подопечный готов к бою.
Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на “ближний” свет.
Первым делом давайте замеряем напряжение на клеммах аккумулятора
12,09 вольт. Вполне нормально, так как наш аккумулятор выдает именно 12 вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.
Подключаем галогенную лампу к аккумулятору и снова замеряем напряжение:
Видели да? Напряжение на клеммах аккумулятора просело до 11,79 Вольт!
А давайте замеряем, сколько потребляет тока наша лампа в Амперах. Для этого составляем вот такую схемку:
Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр – силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.
Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.
Смотрим на показания приборов:
Как мы видим, наша лампа потребляет 4,35 Ампер. Напряжение просело до 11,79 Вольт.
Давайте вместо галогенной лампы поставим простую лампочку накаливания на 12 Вольт от мотоцикла
Смотрим показания:
Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.
Какие выводы можно сделать? Чем больше нагрузка потребляет силу тока, тем больше просаживается напряжение на аккумуляторе.
ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ
Расчет параметров электрической цепи
при параллельном соединении сопротивлений:
1. сила тока в неразветвленном участке цепи равна сумме сил токов
во всех параллельно соединенных участках
2. напряжение на всех параллельно соединенных участках цепи одинаково
3. при параллельном соединении сопротивлений складываются величины, обратные сопротивлению :
( R — сопротивление проводника,
1/R — электрическая проводимость проводника)
Если в цепь включены параллельно только два сопротивления, то:
( при параллельном соединении общее сопротивление цепи меньше меньшего из включенных сопротивлений )
4. работа электрического тока в цепи, состоящей из параллельно соединенных участков,
работа электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме работ на отдельных участках:A=A1+A2
5. мощность электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме мощностей на отдельных участках:P=P1+P2
Для двух сопротивлений:
т.е. чем больше сопротивление, тем меньше в нём сила тока.
Домашняя работа.
Задание 1. Ответить на вопросы.
- Какое соединение проводников называют последовательным? Изобразите его на схеме.
- Какая электрическая величина одинакова для всех проводников, соединённых последовательно?
- Как найти общее сопротивление цепи, зная сопротивление отдельных проводников, при последовательном соединении?
- Как найти напряжение участка цепи, состоящего из последовательно соединённых проводников, зная напряжение на каждом?
- Какое соединение проводников называют параллельным? Изобразите его на схеме.
- Какая из электрических величин одинакова для всех проводников, соединённых параллельно?
- Как выражается сила тока в цепи до её разветвления через силы токов в отдельных ветвях разветвления?
- Как изменяется общее сопротивление разветвления после увеличения числа проводников в разветвлении?
- Какое соединение проводников применяется в жилых помещениях? Какие напряжения используются для бытовых нужд?
Задание 2. Решите задачи.
Решите задачи.
1. Две лампочки соединены последовательно. Сила тока на первой лампочке 2А. Найдите общее напряжение и напряжение на каждой из ламп, если сопротивление на первой лампе 3Ом, а на второй 4Ом.
2. Две лампочки соединены параллельно. Напряжение на второй лампочке10В. Найдите силу тока в цепи и на каждой из ламп, если сопротивление на первой лампе 1Ом, а на второй 2Ом.
- http://www.tepka.ru/
- http://class-fizika.narod.ru
- http://znaika.ru/catalog/10-klass/physics/
- https://www.youtube.com/watch?v=NB7hOVYe7h0
- https://www.youtube.com/watch?v=cVKE9NItreo
- https://www.youtube.com/watch?v=0hFWeR8ybxs
- https://www.youtube.com/watch?v=EDI8DzWSSWY
- https://www.youtube.com/watch?v=bH_-qGnjJqc
Электродвижущая сила источника тока
Двигая разноименные частицы к противоположным полюсам ИТ, сторонние силы преодолевают сопротивление электростатического поля. Следовательно, они совершают некую работу Ас. Она пропорциональна заряду q, перемещаемому за тот же промежуток времени вдоль электроцепи.
Она пропорциональна заряду q, перемещаемому за тот же промежуток времени вдоль электроцепи.
Что такое электродвижущая сила
Иными словами, Ас/q остается постоянным при любом значении данных величин, а следовательно, это соотношение может выступать характеристикой ИТ. Называют ее электродвижущей силой (ЭДС) и обозначают литерой Ԑ = Ас / q
Важно понимать условность данного термина. ЭДС – это не механическая сила, а энергетический параметр ИТ
ЭДС измеряется в тех же единицах, что и разность потенциалов (напряжение) – в вольтах (В). Например, у пальчиковой батарейки с полным зарядом, Ԑ составляет 1,5 В.
Формулировка для полной цепи
Трактовка для полной цепи будет несколько иной, чем для участка, поскольку в законе, составленном Омом, еще учитывает параметр «r», это сопротивление источника ЭДС. На рисунке ниже проиллюстрирована подобная схема.
Схема с подключенным с источником
Учитывая «r» ЭДС, формула предстанет в следующем виде:
Заметим, если «R» сделать равным 0, то появляется возможность рассчитать «I», возникающий во время короткого замыкания.
Напряжение будет меньше ЭДС, определить его можно по формуле:
Собственно, падение напряжения характеризуется параметром «I*r». Это свойство характерно многим гальваническим источникам питания.
Просадка напряжения
Итак, знакомьтесь, автомобильный аккумулятор!
Для дальнейшего его использования, припаяем к нему два провода: красный на плюс, черный на минус
Наш подопечный готов к бою.
Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на «ближний» свет.
Первым делом давайте замеряем напряжение на клеммах аккумулятора
12,09 вольт. Вполне нормально, так как наш аккумулятор выдает именно 12 вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.
Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.
Подключаем галогенную лампу к аккумулятору и снова замеряем напряжение:
Видели да? Напряжение на клеммах аккумулятора просело до 11,79 Вольт!
А давайте замеряем, сколько потребляет тока наша лампа в Амперах. Для этого составляем вот такую схемку:
Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр — силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.
Смотрим на показания приборов:
Как мы видим, наша лампа потребляет 4,35 Ампер. Напряжение просело до 11,79 Вольт.
Давайте вместо галогенной лампы поставим простую лампочку накаливания на 12 Вольт от мотоцикла
Смотрим показания:
Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.
Какие выводы можно сделать? Чем больше нагрузка потребляет силу тока, тем больше просаживается напряжение на аккумуляторе.
Переменный ток
Мы уже рассмотрели закон Ома для всей цепи для постоянного тока. Как же изменится формула при переменном токе? Прежде чем мы это узнаем, давайте охарактеризуем само понятие. Переменный ток – это движение электрически заряженных частиц, направление и значение которых изменяется с течением времени. В отличие от постоянного он сопровождается дополнительными факторами, порождающими новый вид сопротивления (реактивного). Свойственно оно конденсаторам и катушкам индуктивности.
Закон Ома для полной цепи для переменного тока имеет вид:
I = U / Z,
где Z – комплексное сопротивление, состоящее из активных и реактивных.
Цепи постоянного тока серии— Цепи постоянного тока
Цепи постоянного тока
Цепь серии определяется как цепь, содержащая только один путь для текущего потока. Чтобы сравнить базовую схему и более
сложная последовательная цепь, на рисунке ниже показаны две цепи. Основная схема имеет
только одна лампа, а в последовательной цепи три лампы соединены последовательно.
Сравнение основных и последовательных схем.
Сопротивление в последовательной цепи
Ссылаясь на рисунок выше, ток в последовательной цепи должен протекать через каждая лампа для завершения электрического пути в цепи. Каждая дополнительная лампа оказывает дополнительное сопротивление. В последовательной цепи полное сопротивление цепи R t равно сумме индивидуальные сопротивления .
В виде уравнения:
Примечание. Нижний индекс n обозначает любое количество дополнительных сопротивлений, может быть в уравнении.
Пример: На рисунке ниже последовательная цепь, состоящая из трех резисторов: показаны один из 10 Ом, один из 15 Ом и один из 30 Ом. Источник напряжения дает 110 В. Чему равно полное сопротивление?
Расчет полного сопротивления в последовательной цепи.
Дано:
R 1 = 10 Ом, R 2 = 15 Ом, R 3 = 30 Ом
Решение:
В некоторых схемах общее сопротивление известно, а значение
необходимо определить один из резисторов цепи. Уравнение R t = R 1 + R 2 + R 3 можно транспонировать, чтобы найти значение неизвестного сопротивления.
Уравнение R t = R 1 + R 2 + R 3 можно транспонировать, чтобы найти значение неизвестного сопротивления.
Пример:
На рисунке ниже полное сопротивление цепи
с тремя резисторами составляет 40 Ом. Два резистора цепи
10 Ом каждый. Рассчитайте значение третьего резистора ( R 3 ).
Расчет значения одного сопротивления в последовательной цепи.
Дано:
R t = 40 Ом, R 1 = 10 Ом, R 2 = 10 Ом, Ч 3 = ?
Решение:
Вычитание ( R 1 + R 2 ) с обеих сторон уравнение
Ток в последовательной цепи
Так как в последовательной цепи ток проходит только один путь, то один и тот же ток
должен протекать через каждый компонент цепи. Чтобы определить ток в
последовательной цепи, только ток через один из
компоненты должны быть известны.
Тот факт, что один и тот же ток протекает через каждый компонент серии цепь можно проверить, вставив счетчики в цепь в различных точках, как показано на рисунке ниже. Если бы это было сделано, каждый метр окажется, что они указывают на одно и то же значение тока.
Ток в последовательной цепи.
Напряжение в последовательной цепи
Падение напряжения на резисторе в цепи, состоящей из одного резистор и источник напряжения – это общее напряжение в цепи, равное равно приложенному напряжению. Полное напряжение в последовательной цепи, которое состоит из более чем одного резистора и равно приложенному напряжению, но состоит из суммы падений напряжения на отдельных резисторах. В любой серии цепи сумма падений напряжения на резисторе должна равняться напряжению источника. Это утверждение может быть подтверждено исследованием схемы, показанной на рис. рисунок ниже.
Расчет отдельных падений напряжения в последовательной цепи.
В этой цепи сброшен потенциал источника ( В t ) 20 В. через последовательную цепь, состоящую из двух резисторов по 5 Ом. Общая
сопротивление цепи ( R t ) равно сумме
два отдельных сопротивления или 10 Ом. По закону Ома схема
ток можно рассчитать следующим образом:
через последовательную цепь, состоящую из двух резисторов по 5 Ом. Общая
сопротивление цепи ( R t ) равно сумме
два отдельных сопротивления или 10 Ом. По закону Ома схема
ток можно рассчитать следующим образом:
Дано: В t = 20 В, R t = 10 Ом
Решение:
Поскольку известно, что номинал резисторов равен 5 Ом каждый, а ток через резисторы равен 2 А, напряжение на них падает резисторы можно рассчитать. Напряжение ( В 1 ) через R 1 поэтому:
Дано: I 1 = 2 А, R 1 = 5 Ом
Решение:
Осмотрев схему, можно увидеть, что R 2 то же
омическое значение как R 1 и проводит такой же ток. Напряжение
падение на R 2 поэтому также равно 10 В.
Сложение этих двух 10-вольтовых падений вместе дает общее падение 20 В, точно
равно приложенному напряжению. Тогда для последовательной цепи:
Тогда для последовательной цепи:
Пример: Последовательная цепь состоит из трех резисторов со значениями 20 Ом, 30 Ом и 50 Ом соответственно. Найдите прикладной напряжение, если ток через резистор 30 Ом равен 2 А.
Для решения задачи сначала рисуется и маркируется принципиальная схема (рисунок ниже).
Расчет приложенного напряжения в последовательной цепи.
Дано: R 1 = 20 Ом, R 2 = 30 Ом, R 3 = 50 Ом, I = 2 А
Решение: поскольку задействованная цепь представляет собой последовательную цепь, те же 2 А ток течет через каждый резистор. По закону Ома напряжение падает на каждый из трех резисторов может быть рассчитан и составляет:
Когда известны отдельные капли, их можно сложить, чтобы найти общее количество. или приложенное напряжение:
Примечание. Когда вы используете закон Ома, величины для уравнения должны быть равны . взято из той же части схемы. В приведенном выше примере
напряжение на R 2 было рассчитано с использованием тока
через R 2 и сопротивление R 2 .
взято из той же части схемы. В приведенном выше примере
напряжение на R 2 было рассчитано с использованием тока
через R 2 и сопротивление R 2 .
Величина падения напряжения на резисторе определяется приложенным напряжения и пропорциональна сопротивлениям цепи. Напряжение падает которые возникают в последовательной цепи, прямо пропорциональны сопротивлениям. Это результат того, что через каждый резистор протекает одинаковый ток. чем больше омическое сопротивление резистора, тем больше падение напряжения на нем.
Напряжение холостого хода | PVEducation
Напряжение холостого хода, В OC , является максимальным напряжением, доступным от солнечного элемента, и это происходит при нулевом токе. Напряжение холостого хода соответствует величине прямого смещения на солнечном элементе из-за смещения перехода солнечного элемента с генерируемым светом током. Напряжение холостого хода показано на ВАХ ниже.
ВАХ солнечного элемента, показывающая напряжение холостого хода.
Уравнение для V oc находится путем установки чистого тока равным нулю в уравнении солнечного элемента, чтобы получить:
$$V_{OC}=\frac{n k T}{q} \ln \left( \frac{I_{L}}{I_{0}}+1\right)$$
Беглый взгляд на приведенное выше уравнение может показать, что V OC линейно возрастает с температурой. Однако это не так, так как I 0 быстро увеличивается с температурой, главным образом из-за изменений собственной концентрации носителей заряда n i . Влияние температуры является сложным и варьируется в зависимости от клеточной технологии. Подробнее см. на странице «Влияние температуры»
В OC уменьшается с температурой. При изменении температуры I 0 также меняется.
Калькулятор напряжения разомкнутой цепи 1Темновой ток насыщения, I 0 = Световой ток, I L = Коэффициент идеальности, n = Температура, T = K
Напряжение разомкнутой цепи, В OC = В
Приведенное выше уравнение показывает, что V oc зависит от тока насыщения солнечного элемента и тока, генерируемого светом. Пока я sc обычно имеет небольшую вариацию, ключевым эффектом является ток насыщения, так как он может варьироваться на порядки величины. Ток насыщения I 0 зависит от рекомбинации в солнечном элементе. Тогда напряжение холостого хода является мерой количества рекомбинации в устройстве. Кремниевые солнечные элементы на высококачественном монокристаллическом материале имеют напряжение холостого хода до 764 мВ в условиях одного солнца и AM1,51, в то время как коммерческие кремниевые устройства обычно имеют напряжение холостого хода около 69 мВ.{2}}\right]$$
Пока я sc обычно имеет небольшую вариацию, ключевым эффектом является ток насыщения, так как он может варьироваться на порядки величины. Ток насыщения I 0 зависит от рекомбинации в солнечном элементе. Тогда напряжение холостого хода является мерой количества рекомбинации в устройстве. Кремниевые солнечные элементы на высококачественном монокристаллическом материале имеют напряжение холостого хода до 764 мВ в условиях одного солнца и AM1,51, в то время как коммерческие кремниевые устройства обычно имеют напряжение холостого хода около 69 мВ.{2}}\right]$$
где kT/q — тепловое напряжение, N A — концентрация легирующих примесей, Δn — концентрация избыточных носителей заряда, а n i — собственная концентрация носителей заряда. Определение V OC по концентрации носителя также называется предполагаемым V OC .
Калькулятор напряжения разомкнутой цепи 2Концентрация допинга, N A = см -3 Концентрация избыточного носителя, Δn = см -3 Температура, T =K Концентрация собственного носителя, n i = см -3
Напряжение разомкнутой цепи, В OC = В
Voc как функция ширины запрещенной зоны, E
G Там, где ток короткого замыкания (I SC ) уменьшается с увеличением ширины запрещенной зоны, напряжение холостого хода увеличивается по мере увеличения ширины запрещенной зоны. В идеальном устройстве V OC ограничивается излучательной рекомбинацией, и в анализе используется принцип детального баланса для определения минимально возможного значения J 9{x}-1} d x$$,
В идеальном устройстве V OC ограничивается излучательной рекомбинацией, и в анализе используется принцип детального баланса для определения минимально возможного значения J 9{x}-1} d x$$,
, где q — заряд электрона, σ — постоянная Стефана–Больцмана, k — постоянная Больцмана, T — температура и
$$u=\frac{E_{G} }{k T}$$
Вычисление интеграла в приведенном выше уравнении довольно сложно. На приведенном ниже графике используется метод, описанный в 4
. Ток насыщения диода как функция ширины запрещенной зоны. Значения определяются на основе детального баланса и ограничивают напряжение холостого хода солнечной батареи.
Рассчитанное выше значение J 0 можно напрямую подставить в стандартное уравнение солнечного элемента, приведенное в верхней части страницы, для определения V OC , если напряжение меньше ширины запрещенной зоны, как в случае с одним солнечное освещение.
V OC как функция ширины запрещенной зоны для ячейки с AM 0 и AM 1,5. V OC увеличивается с шириной запрещенной зоны по мере падения тока рекомбинации. В V OC наблюдается спад при очень больших ширинах запрещенной зоны из-за очень низкого I СК .
V OC увеличивается с шириной запрещенной зоны по мере падения тока рекомбинации. В V OC наблюдается спад при очень больших ширинах запрещенной зоны из-за очень низкого I СК .
- 1. A. Augusto, Herasimenka, S.Y., King, R.R., Bowden, S.G., and Honsberg, C., «Анализ механизмов рекомбинации кремниевого солнечного элемента с малым смещением ширины запрещенной зоны», Journal of Applied Physics , том. 121, нет. 20, с. 205704, 2017.
- 2. Р. А. Синтон и Куэвас, А., “Бесконтактное определение вольт-амперных характеристик и времени жизни неосновных носителей в полупроводниках на основе данных о квазистационарной фотопроводимости”, Письма по прикладной физике, том. 69, стр. 2510-2512, 1996.
- 3. П. Барух, Де Вос, А., Ландсберг, П. Т., и Парротт, Дж. Э., «О некоторых термодинамических аспектах фотоэлектрического преобразования солнечной энергии», Материалы солнечной энергии и солнечные элементы, том. 36, стр. 201-222, 1995.
- 4.
 М. Ю. Леви и Хонсберг, С. Б., «Быстрые и точные расчеты энергии и потока частиц для детального баланса фотоэлектрических приложений», Твердотельная электроника, том. 50, стр. 1400-1405, 2006.
М. Ю. Леви и Хонсберг, С. Б., «Быстрые и точные расчеты энергии и потока частиц для детального баланса фотоэлектрических приложений», Твердотельная электроника, том. 50, стр. 1400-1405, 2006.
RC-цепи
РЦ Цепи
Цепь RC это просто схема с резистором и конденсатором. Эту комбинацию полезно изучать, потому что конденсаторы можно использовать для хранения энергии и резистора, расположенного вдоль с конденсатором может контролировать скорость, с которой энергия освобождается от конденсатора.
Мы будем Ограничим наши исследования следующим типом RC-цепи.
Переключатель может быть перемещены из позиции в в позиция б . Прежде чем мы пойдем далее, давайте рассмотрим некоторые факты о конденсаторах:
заряд на конденсаторе не может измениться мгновенно .
 С момента изменения в
заряд D Q = I D t , там
всегда должно быть ненулевое время перед зарядом
может измениться на ненулевую сумму, если только не было
бесконечный ток.
С момента изменения в
заряд D Q = I D t , там
всегда должно быть ненулевое время перед зарядом
может измениться на ненулевую сумму, если только не было
бесконечный ток.Есть отсутствует ток через конденсатор в установившемся режиме . Поскольку заряд накапливается на конденсаторе, а не протекая через него, ток может нарастать до тех пор, пока момент, когда напряжение В=Q/C будет балансировать внешнее напряжение, толкающее заряд на конденсаторе.
При наличии конденсатора емкостью C последовательно с батареей напряжением В б и резистор сопротивления R , падение напряжения должно быть:
,
, который является заявлением
что напряжение, полученное на аккумуляторе, должно
равно падению напряжения на конденсаторе плюс
падение напряжения на резисторе. Уравнение, в котором
скорость изменения количества (Д В/ Д т )
пропорционально количеству (D Q) всегда будет
имеют показательное решение. Рассматриваем два экземпляра:
Уравнение, в котором
скорость изменения количества (Д В/ Д т )
пропорционально количеству (D Q) всегда будет
имеют показательное решение. Рассматриваем два экземпляра:
Разгрузка конденсатор : Конденсатор изначально подключен (переключатель в положении и ) долгое время, а затем отключается ставлю переключатель на б в момент времени т = 0 . затем конденсатор разряжается, оставляя конденсатор без заряда или напряжения после длительного времени.
Зарядка конденсатор : Переключатель в положении b в течение длительного времени, позволяя конденсатор не должен иметь заряда.
 По времени т
= 0 , переключатель изменен на a и конденсатор заряжается.
По времени т
= 0 , переключатель изменен на a и конденсатор заряжается.
| Разгрузка | Зарядка | |
| Плата | ||
| Текущий | ||
| Напряжение |
Здесь, Q 0 , В 0 и I 0 ток и напряжение заряда
конденсатор в тот момент, когда переключатель брошен. Время t — характерное время распада, т = РК . Когда
столкнувшись с проблемой RC , лучший
стратегия следующая:
Время t — характерное время распада, т = РК . Когда
столкнувшись с проблемой RC , лучший
стратегия следующая:
Решите, что заряд на конденсаторе был непосредственно перед переключатель был брошен. Так как заряд не может изменить мгновенно, это заряд сразу после переключатель брошен.
Решите, что заряд долго после того, как переключатель брошен.
Выберите экспоненциальная форма заряда Q(t) , чтобы удовлетворить правильный начальный и конечный обвинения.
Напряжение через конденсатор можно найти через, В = К/К .
 Напряжения на
другие элементы можно найти с помощью Кирхгофа
первый закон.
Напряжения на
другие элементы можно найти с помощью Кирхгофа
первый закон.Текущий через конденсатор всегда должен распадаться и заканчиваться на нуле, так как заряд не может течь непрерывно через конденсатор. Начальный ток может обычно определяют с помощью Ома закон, V=R I .
Характерное время t = RC сообщает, что зарядка/разрядка медленнее с большим резистором или конденсатор. Это имеет смысл, потому что больший резистор препятствует протеканию тока; тем самым замедляя зарядка/разрядка, а больший конденсатор вмещает больше обвинение; поэтому требуется больше времени для зарядки.
У всех должно быть хорошее самочувствие
для показательных функций. Ниже представлены эскизы
заряд Q(t) для зарядки
и разрядка конденсаторов.
Ниже представлены эскизы
заряд Q(t) для зарядки
и разрядка конденсаторов.
айглкайла
Примеры Кирхгофа законы / Указатель цепи RC
Подробные факты – Lambda Geeks
В этой статье разъясняется, что такое падение напряжения и как рассчитать падение напряжения в последовательной цепи. Всякий раз, когда напряжение встречает какой-либо резистивный элемент в цепи, значение уменьшается или «падает».
В последовательной цепи имеется несколько сопротивлений или импедансов. Каждый раз, когда через них проходит ток, напряжение уменьшается. Итак, нам нужно знать значение определенного сопротивления и тока, проходящего через него, чтобы вычислить падение напряжения на нем. Падение напряжения – это ток, умноженный на сопротивление.
Что такое падение напряжения? Предположим, мы соединяем батарею с резистором через провод. Электроны имеют тенденцию течь от отрицательной стороны батареи к положительной. Это похоже на электрический заряд, идущий от положительного к отрицательному выводу.
Электроны имеют тенденцию течь от отрицательной стороны батареи к положительной. Это похоже на электрический заряд, идущий от положительного к отрицательному выводу.
Когда одна единица заряда сталкивается с резистором, он на некоторое время останавливается. Когда он проходит резистор, приходит другая единица заряда и останавливается. В любой момент времени заряд на конце резистора меньше, чем заряд на начале резистора. Это явление создает «падение потенциала или напряжения».
Подробнее…..Постоянно ли напряжение в последовательной цепи: полная информация и часто задаваемые вопросы
Как рассчитать общее падение напряжения в последовательной цепи?Полное падение напряжения в последовательной цепи представляет собой сумму всех отдельных падений напряжения, вызванных параметрами импеданса. Кроме того, сумма равна общему напряжению, подаваемому на цепь, или напряжению до любого «падения».
Рассмотрим явления с помощью схемы. В схеме ниже есть два резистора, R 1 на 100 Ом и R 2 на 200 Ом, подключенные к источнику питания V 30 вольт. Текущий [латекс] i = \frac {V} {R_{1} + R_{2}} = \frac {30} {100+200} = 0,1 \; [/латекс]. Следовательно, падение напряжения на R 1 [Latex] = i \times R_{1} = 0,1 \times 100 = 10 \; V [/Latex] и через R2 [Latex] = i \times R_{2} = 0,1 \times 200 = 20 \; В[/латекс].
В схеме ниже есть два резистора, R 1 на 100 Ом и R 2 на 200 Ом, подключенные к источнику питания V 30 вольт. Текущий [латекс] i = \frac {V} {R_{1} + R_{2}} = \frac {30} {100+200} = 0,1 \; [/латекс]. Следовательно, падение напряжения на R 1 [Latex] = i \times R_{1} = 0,1 \times 100 = 10 \; V [/Latex] и через R2 [Latex] = i \times R_{2} = 0,1 \times 200 = 20 \; В[/латекс].
Цепи переменного или переменного тока представляют собой электрические цепи с напряжением питания переменного тока. Последовательная цепь переменного тока состоит из любой комбинации резистора, катушки индуктивности и конденсатора, соединенных последовательно.
Точно так же, как и при постоянном токе, мы можем вычислить полное сопротивление последовательной цепи переменного тока, складывая их. Аналогичным образом можно найти и падение напряжения. Падение напряжения на любом элементе последовательной цепи переменного тока равно V = iZ, где Z — полное сопротивление цепи, а i — полный ток, протекающий через нее.
Падение напряжения на любом элементе последовательной цепи переменного тока равно V = iZ, где Z — полное сопротивление цепи, а i — полный ток, протекающий через нее.
Подробнее о…..Как рассчитать напряжение в последовательной цепи: подробные факты
Падение напряжения в последовательной цепи RLC:Цепь RLC является частным случаем цепей переменного тока. Цепь RLC состоит из резисторов, конденсаторов и катушек индуктивности, соединенных последовательно. Давайте разберемся с падением напряжения в последовательной цепи RLC на примере.
Схема состоит из трех компонентов, изображенных ниже: резистор ом, индуктор L Генри и конденсатор C фарад. Ранее мы знали, что падение напряжения на любом из них = импеданс × ток. Итак,
Падение напряжения на резисторе = iR, индуктивности = iXL и конденсаторе = iXC, где XL = 2πfL и XC = 1/2πfC
Как рассчитать падение напряжения в последовательной цепи. Q1. Три резистора соединены последовательно со значениями R 1 = 4 Ом, R 2 = 5 Ом и R 3 = 6 Ом. Цепь соединена с источником питания 15 В. Найдите падение напряжения на резисторах.
Q1. Три резистора соединены последовательно со значениями R 1 = 4 Ом, R 2 = 5 Ом и R 3 = 6 Ом. Цепь соединена с источником питания 15 В. Найдите падение напряжения на резисторах. Для расчета падения потенциала на R 1 , R 2 и R 3 сначала необходимо получить ток в цепи. Мы знаем, [Latex] current = \frac {net \; напряжение} {эквивалентное \; сопротивление} [/Latex]
Эквивалентное сопротивление [Latex] R_{eq} = R_{1} + R_{2} + R_{3} = 4 + 5 + 6 = 15 \; \Omega [/Latex]
Следовательно, общий ток [Latex] = \frac { 15 \: V} {15 \: \Omega } = 1\: A [/Latex]
Теперь мы можем использовать закон Ома ( V = IR) для каждого резистора и найти падения напряжения на них.
Итак, [Латекс] V_{1} = I \times R_{1} = 1 \times 4 = 4 \; V [/Latex] ,
[Latex] V_{2} = I \times R_{2} = 1 \times 5 = 5 \; V [/Latex]
[Latex] V_{3} = I \times R_{3} = 1 \times 6 = 6 \; V[/Latex]
Q2. Для приведенной ниже схемы падение напряжения на резисторе 6 Ом составляет 12 В. Найдите другие падения напряжения и рассчитайте общее падение напряжения или напряжение питания.
Для приведенной ниже схемы падение напряжения на резисторе 6 Ом составляет 12 В. Найдите другие падения напряжения и рассчитайте общее падение напряжения или напряжение питания. Мы знаем, что падение напряжения на любом резисторе в последовательной цепи = сопротивление × общий ток
Если в цепи протекает ток i, падение напряжения на резисторе 6 Ом равно 6i.
6i = 12 или i = 2 ампера
Следовательно, падение напряжения на резисторе 2 Ом = 2 x 2 = 4 В
Падение напряжения на резисторе 4 Ом = 2 x 4 = 8 В
Таким образом, чистое напряжение падение напряжения питания = (12 + 4 + 8) = 24 В
Q3. На изображении ниже показана цепь серии RLC со следующими компонентами: Источник питания переменного тока 120 В, 50 Гц , Резистор 100 Ом , Конденсатор 20 мкФ , Катушка индуктивности 420 мГн. Рассчитайте падение напряжения на всех трех импедансах.
Ранее мы знали, как рассчитать падение напряжения для последовательной цепи RLC. Ток, умноженный на импеданс (R или X L или X C ), дает нам падение напряжения. Сначала найдем X L и X C .
X L = 2πfL (f — частота сети переменного тока)
9{\ круг} \; A [/Latex]Следовательно, [Latex] V_{R} = iR = 1,16\угол -15,22 \times 100\угол 0 = 116\угол -15,22\; V [/Latex]
Здесь ток опережает напряжение как X C > X L .
[Латекс] V_{C} = iX_{C} = 1,16\угол -15,22\умножить на 159,15\угол 90 = 184,61\угол 74,78\; V [/Latex]
[Latex] V_{L} = iX_{L} = 1,16\угол -15,22\умножить на 131,95\угол -90 = 153,06\угол -105,22\; V [/Latex]
Подробнее… Что такое напряжение в последовательной цепи: подробные факты
Как рассчитать падение напряжения на резисторе в параллельной цепи
Обновлено 28 декабря 2020 г.
Автор: S. Hussain Ather Прочтите)
Hussain Ather Прочтите)
На приведенной выше схеме параллельных цепей падение напряжения можно найти путем суммирования сопротивлений каждого резистора и определения того, какое напряжение получается из тока в этой конфигурации. Эти примеры параллельных цепей иллюстрируют концепции тока и напряжения в разных ветвях.
На схеме параллельной цепи падение напряжения на резисторе в параллельной цепи одинаково на всех резисторах в каждой ветви параллельной цепи. Напряжение, выраженное в вольтах, измеряет электродвижущую силу или разность потенциалов, которая управляет цепью.
Когда у вас есть цепь с известной величиной тока потока электрического заряда, вы можете рассчитать падение напряжения в схемах параллельных цепей по:
- Определить комбинированный сопротивление или противодействие потоку заряда параллельных резисторов. Суммируйте их как 1/R всего = 1/R 1 + 1/R 2 .
 .. для каждого резистора. Для приведенной выше параллельной цепи общее сопротивление можно найти как:
.. для каждого резистора. Для приведенной выше параллельной цепи общее сопротивление можно найти как:- 1/R всего = 1/5 Ом + 1/6 Ом + 1/10 Ом
- 1/R всего = 6/30 Ом + 5/30 Ом + 3/30 Ом
- 1/R всего = 14/30 Ом
- R всего = 30/14 Ом = 15/7 Ом
- 1/R всего = 1/5 Ом + 1/6 Ом + 1/10 Ом
- , чтобы получить падение напряжения 2,
- Закон Ома
Если мы сравним ток, входящий в три ветви параллельной цепи, он должен быть равен общему току, выходящему из ветвей. Поскольку падение напряжения остается постоянным на каждом параллельном резисторе, это падение напряжения, вы можете суммировать сопротивление каждого резистора, чтобы получить общее сопротивление и определить напряжение из этого значения. Примеры параллельных цепей показывают это.
Поскольку падение напряжения остается постоянным на каждом параллельном резисторе, это падение напряжения, вы можете суммировать сопротивление каждого резистора, чтобы получить общее сопротивление и определить напряжение из этого значения. Примеры параллельных цепей показывают это.
Падение напряжения в последовательной цепи
••• Syed Hussain Ather
С другой стороны, в последовательной цепи можно рассчитать падение напряжения на каждом резисторе, зная, что в последовательной цепи ток постоянен. через. Это означает, что падение напряжения на каждом резисторе разное и зависит от сопротивления в соответствии с законом Ома В = IR . В приведенном выше примере падение напряжения на каждом резисторе составляет:
V_1=R_1I=3\times 3 = 9\text{ V}\\ V_2=R_2I=10\times 3 = 30\text{ V}\\ V_3=R_3I=5\times 3 = 15\text{ V}
Сумма каждого падения напряжения должна быть равна к напряжению батареи в последовательной цепи. Это означает, что наша батарея имеет напряжение 54 В.
Это означает, что наша батарея имеет напряжение 54 В.
Этот метод решения уравнений работает, потому что падения напряжения, поступающие на все резисторы, расположенные последовательно, должны суммироваться с общим напряжением последовательной цепи. Это происходит из-за закона напряжения Кирхгофа , который гласит, что «направленная сумма разностей потенциалов (напряжений) вокруг любого замкнутого контура равна нулю». Это означает, что в любой заданной точке замкнутой последовательной цепи падения напряжения на каждом резисторе должны суммироваться с общим напряжением цепи. Поскольку ток в последовательной цепи постоянный, падение напряжения на каждом резисторе должно быть разным.
Параллельные и последовательные цепи
В параллельной цепи все компоненты цепи соединены между одними и теми же точками цепи. Это дает им их разветвленную структуру, в которой ток делится на каждую ветвь, но падение напряжения на каждой ветви остается одинаковым. Сумма каждого резистора дает общее сопротивление, основанное на инверсии каждого сопротивления ( 1/R всего = 1/R 1 + 1/R 2 … для каждого резистора).
Сумма каждого резистора дает общее сопротивление, основанное на инверсии каждого сопротивления ( 1/R всего = 1/R 1 + 1/R 2 … для каждого резистора).
В последовательной цепи, напротив, есть только один путь для протекания тока. Это означает, что ток остается постоянным, а падение напряжения на каждом резисторе разное. Сумма каждого резистора дает общее сопротивление при линейном суммировании ( R всего = R 1 + R 2 … для каждого резистора).
Последовательно-параллельные цепи
Вы можете использовать оба закона Кирхгофа для любой точки или контура любой цепи и применять их для определения напряжения и тока. Законы Кирхгофа дают вам метод определения тока и напряжения в ситуациях, когда характер цепи как последовательной и параллельной может быть не таким простым.
Как правило, для цепей, которые имеют как последовательные, так и параллельные компоненты, вы можете рассматривать отдельные части схемы как последовательные или параллельные и комбинировать их соответствующим образом.
Эти сложные последовательно-параллельные схемы можно решить несколькими способами. Обработка их частей как параллельных или последовательных — это один из методов. Еще одним методом является использование законов Кирхгофа для определения обобщенных решений, использующих систему уравнений. Калькулятор последовательно-параллельных цепей будет учитывать различную природу цепей.
••• Syed Hussain Ather
В приведенном выше примере текущая точка отправления A должна совпадать с текущей точкой отправления A. Это означает, что вы можете написать:
(1). I_1=I_2+I_3\text{ или }I_1-I_2-I_3=0
Если вы рассматриваете верхний контур как замкнутую последовательную цепь и рассматриваете падение напряжения на каждом резисторе, используя закон Ома с соответствующим сопротивлением, вы можете написать:
(2). V_1-R_1I_1-R_2I_2=0
и, делая то же самое для нижнего контура, вы можете рассматривать каждое падение напряжения в направлении тока как зависящее от тока и сопротивления, чтобы записать:
(3). V_1+V_2+R_3I_3-R_2I_2=0
V_1+V_2+R_3I_3-R_2I_2=0
Это дает вам три уравнения, которые можно решить несколькими способами. Вы можете переписать каждое из уравнений (1) – (3) так, чтобы напряжение было на одной стороне, а ток и сопротивление – на другой. Таким образом, вы можете рассматривать три уравнения как зависящие от трех переменных I 1 , I 2 и I 3 с коэффициентами комбинаций R 1 , R 2 и R 3 .
\begin{выровнено}&(1). I_1-I_2-I_3=0\\ &(2). R_1I_1+R_2I_2+0\times I_3=V_1\\ &(3). 0\раз I_1+R_2I_2-R_3I_3=V_1+V_2\конец{выровнено}
Эти три уравнения показывают, как напряжение в каждой точке цепи каким-то образом зависит от тока и сопротивления. Если вы помните законы Кирхгофа, вы можете создать эти обобщенные решения для проблем со схемами и использовать для их решения матричную запись. Таким образом, вы можете подставить значения для двух величин (напряжение, ток, сопротивление), чтобы найти третью.
Отдел цепей и напряжения серииЭлементы цепи включены последовательно, если они проводят одинаковый ток.
 Эквивалентное сопротивление последовательно соединенных резисторов равно сумме сопротивлений отдельных резисторов.
Эквивалентное сопротивление последовательно соединенных резисторов равно сумме сопротивлений отдельных резисторов.
Пример 1: Найдите полное эквивалентное сопротивление в следующей цепи
Раствор |
Пример 2: Для следующей цепи:
- Найти общее сопротивление
- Найти текущий i
- Найти напряжение на резисторе 10 Ом
Раствор
|
Пример 3: Для следующей цепи:
- Найдите общее значение сопротивления R T
- Найти текущий i
- Найти напряжение на отдельных резисторах
- Проверка закона напряжения Кирхгофа
Раствор
|
Пример 4: Для следующей схемы:
- Найти V 1
- Найти V 2
- Проверка закона напряжения Кирхгофа для замкнутого контура
Решение |
Разделение по напряжению :
В следующей цепи ток через все последовательные резисторы равен Чтобы найти падение напряжения v i на резисторе R i , мы используем ток и номинал резистора Правая часть уравнения дает нам уравнение деления напряжения. |
Примеры:
Пример 5: Для следующей цепи
- Найти общее значение сопротивления R T
- Найти текущий i
- Найти напряжение на резисторах
- Проверка закона напряжения Кирхгофа
Решение
|
Пример 6: Найти ток для следующей цепи
|
Практические задачи :
(Щелкните изображение, чтобы просмотреть решение)
Задача 1: Найдите следующую схему.


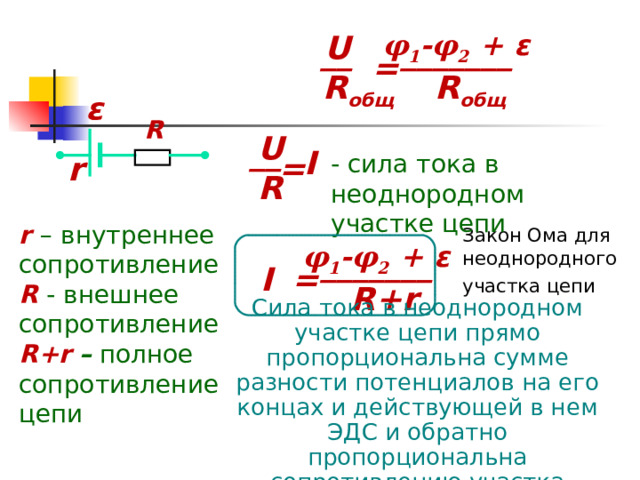
 При подключении нагрузки, ее потенциал будет падать, вплоть до полной разрядки. Для восстановления первоначальных свойств, потребуется подзарядка от постороннего источника тока.
При подключении нагрузки, ее потенциал будет падать, вплоть до полной разрядки. Для восстановления первоначальных свойств, потребуется подзарядка от постороннего источника тока.
