Формула Ньютона-Лейбница презентация, доклад, проект
Тема:
Формула Ньютона-Лейбница
Работу выполнили:
Павшинцев И.С.
Чижков А.А.
Работу приняла:
Плешакова О.В.
2010 год
план
1-Ньютон и Лейбниц
2- теорема
3- интеграл
4- применение интеграла
5-историческое значение и философский смысл формулы
6- список используемой литературы интернет ресурсы
7- конец!☺
Ньютон
Лейбниц
Ньютон и Лейбниц
Из сохранившихся документов историки науки выяснили, что дифференциальное и интегральное исчислениеИз сохранившихся документов историки науки выяснили, что дифференциальное и интегральное исчисление Ньютон открыл ещё в 1665Из сохранившихся документов историки науки выяснили, что дифференциальное и интегральное исчисление Ньютон открыл ещё в 1665-1666 годыИз сохранившихся документов историки науки выяснили, что дифференциальное и интегральное исчисление Ньютон открыл ещё в 1665-1666 годы, однако не публиковал его до 1704 года.
Вняв уговорам друзей, взывавших к его патриотизму, Ньютон во 2-й книге своих «Начал» (1687) сообщил:[71]
В письмах, которыми около десяти лет тому назад я обменивался с весьма искусным математиком г-ном Лейбницем, я ему сообщал, что обладаю методом для определения максимумов и минимумов, проведения касательных и решения тому подобных вопросов, одинаково приложимых как для членов рациональных, так и для иррациональных, причем я метод скрыл, переставив буквы следующего предложения: «когда задано уравнение, содержащее любое число текущих количеств, найти флюксии[14] и обратно».
В 1693 году, когда Ньютон наконец опубликовал первое краткое изложение своей версии анализа, он обменялся с Лейбницем дружескими письмами. Ньютон сообщил:[72]
Наш Валлис присоединил к своей «Алгебре», только что появившейся, некоторые из писем, которые я писал к тебе в своё время. При этом он потребовал от меня, чтобы я изложил открыто тот метод, который я в то время скрыл от тебя переставлением букв; я сделал это коротко, насколько мог. Надеюсь, что я при этом не написал ничего, что было 6ы тебе неприятно, если же это случилось, то прошу сообщить, потому что друзья мне дороже математических открытий.
После появления первой подробной публикации ньютонова анализа (математическое приложение к «Оптике», 1704После появления первой подробной публикации ньютонова анализа (математическое приложение к «Оптике», 1704) в журнале Лейбница «Acta eruditorum» появилась анонимная рецензия с оскорбительными намёками в адрес Ньютона.
Рецензия ясно указывала, что автором нового исчисления является Лейбниц. Сам Лейбниц решительно отрицал, что рецензия составлена им, но историки сумели найти черновик, написанный его почерком.[70] Ньютон проигнорировал статью Лейбница, но его ученики возмущённо ответили, после чего разгорелась общеевропейская приоритетная война, «наиболее постыдная склока во всей истории математики».[46]
31 января31 января 1713 года Королевское общество получило письмо от Лейбница, содержащее примирительную формулировку: он согласен, что Ньютон пришёл к анализу самостоятельно, «на общих принципах, подобных нашим». Рассерженный Ньютон потребовал создать международную комиссию для прояснения приоритета. Комиссии не понадобилось много времени: спустя полтора месяца, изучив переписку Ньютона с Ольденбургом и другие документы, она единогласно признала приоритет Ньютона, причём в формулировке, на этот раз оскорбительной в отношении Лейбница.
В ответ с лета 1713 года Европу наводнили анонимные брошюры, которые отстаивали приоритет Лейбница и утверждали, что «Ньютон присваивает себе честь, принадлежащую другому». Брошюры также обвиняли Ньютона в краже результатов Гука и Флемстида.[70] Друзья Ньютона, со своей стороны, обвинили в плагиате самого Лейбница; по их версии, во время пребывания в Лондоне (1676) Лейбниц в Королевском обществе ознакомился с неопубликованными работами и письмами Ньютона, после чего изложенные там идеи Лейбниц опубликовал и выдал за свои.[73]
теорема
Теорема
Если f непрерывна на отрезке a,b и Ф — ее любая первообразная на этом отрезке, то имеет место равенство
Доказательство
Пусть на отрезке (a,b) задана интегрируемая функция ʄ Начнем с того, что отметим, что
то есть не имеет никакого значения, какая буква ( x или u ) стоит под знаком ʄ в определенном интеграле по отрезку (a,b)
Зададим произвольное значение x € (a.
b) и определим новую функцию
Она определена для всех значений x € (a.b) , потому что мы знаем, что если существует интеграл от ʄ на (a,b) , то существует также интеграл от ʄ на (a,b) , где
Напомним, что мы считаем по определению
Заметим, что
Покажем, что F непрерывна на отрезке (a,b) В самом деле, пусть
и если , то
Таким образом , F непрерывна на (a,b) независимо от того, имеет или не имеет ʄ разрывы; важно, что ʄ интегрируема на (a,b)
На рисунке изображен график ʄ . Площадь переменной фигуры aABx равна F (X) Ее приращение F (X+h)-F(x) равно площади фигуры xBC(x+h) , которая в силу
Ограниченности ʄ очевидно, стремится к нулю при h→ 0 независимо от того, будет ли x точкой непрерывности или разрыва ʄ например точкой x-d
Пусть теперь функция ʄ не только интегрируема на (a,x) , но непрерывна в точке
В самом деле, для указанной точки x
Мы положили
а так как ʄ (x) постоянная относительно t ,TO
Далее, в силу непрерывности ʄ в точке x для всякого ε ˃0 можно указать такое δ что
для
Поэтому
что доказывает, что левая часть этого неравенства есть о(1) при h→0
Переход к пределу в при h→0 показывает существование производной от F в точке и справедливость равенства .
Если функция ʄ непрерывна на (a,b) , то на основании доказанного выше соответствующая ей функция
имеет производную, равную
Следовательно, функция F(x) есть первообразная для ʄ (a,b)
Мы доказали, что произвольная непрерывная на отрезке (a,b) функция ʄ имеет на этом отрезке первообразную, определенную равенством. Этим доказано существование первообразной для всякой непрерывной на отрезке функции.
Пусть теперь есть произвольная первообразная функции ʄ(x) на (a,b) . Мы знаем, что
Где C — некоторая постоянная. Полагая в этом равенстве x=a и учитывая, что F(a)=0 получим
Поэтому
Интеграл
Интеграл функции — естественный аналог суммы последовательности.
Согласно основной теореме анализа — естественный аналог суммы последовательности. Согласно основной теореме анализа, интегрирование — операция, обратная к дифференцированию. Процесс нахождения интеграла называется интегрированием.
Существует несколько различных определений операции интегрирования, отличающиеся в технических деталях. Однако все они совместимы, то есть любые два способа интегрирования, если их можно применить к данной функции, дадут один и тот же результат.
Типы интегралов
Определённый интеграл
Неопределённый интеграл
Интеграл РиманаИнтеграл Римана и Римана — Стилтьеса
Интеграл ЛебегаИнтеграл Лебега и Лебега — Стилтьеса
Интеграл Даниэля
Кратный интеграл
Криволинейный интеграл
Поверхностный интеграл
Эллиптический интеграл
История
Знаки интеграла ʃ дифференцирования dx были впервые использованы Лейбницембыли впервые использованы Лейбницем в конце XVII векабыли впервые использованы Лейбницем в конце XVII века.
Символ интеграла образовался из буквы Sбыли впервые использованы Лейбницем в конце XVII века. Символ интеграла образовался из буквы S — сокращения слова лат. summa (сумма).
Интеграл в древности
Интегрирование прослеживается ещё в древнем Египте, примерно в 1800 до н. э., Московский математический папирус в 1800 до н. э., Московский математический папирус демонстрирует знание формулы объёма усечённой пирамиды в 1800 до н. э., Московский математический папирус демонстрирует знание формулы объёма усечённой пирамиды. Первым известным методом для расчёта интегралов является метод исчерпывания в 1800 до н. э., Московский математический папирус демонстрирует знание формулы объёма усечённой пирамиды. Первым известным методом для расчёта интегралов является метод исчерпывания Евдокса (примерно 370 до н. э.), который пытался найти площади и объёмы, разрывая их на бесконечное множество частей, для которых площадь или объём уже известны. Этот метод был подхвачен и развит Архимедом 370 до н.
э.), который пытался найти площади и объёмы, разрывая их на бесконечное множество частей, для которых площадь или объём уже известны. Этот метод был подхвачен и развит Архимедом, и использовался для расчёта площадей парабол и приближенного расчёта площади круга. Аналогичные методы были разработаны независимо в Китае в 3-м веке н.э Лю Хуэйем 370 до н. э.), который пытался найти площади и объёмы, разрывая их на бесконечное множество частей, для которых площадь или объём уже известны. Этот метод был подхвачен и развит Архимедом, и использовался для расчёта площадей парабол и приближенного расчёта площади круга. Аналогичные методы были разработаны независимо в Китае в 3-м веке н.э Лю Хуэйем, который использовал их для нахождения площади круга. Этот метод был впоследствии использован Дзю Чонгши для нахождения объёма шара.
Историческое значение и философский смысл
формулы Ньютона-Лейбница
Одним из важнейших исследовательских инструментов этого ряда является формула Ньютона-Лейбница, и стоящий за ней метод нахождения первообразной функции путем интегрирования ее производной.
Историческое значение формулы в использовании бесконечно малых величин и абсолютно точном ответе на поставленный вопрос. Общеизвестны преимущества применения этого метода для решения математических, физических и прочих естественнонаучных задач, например, классической задачи о квадратуре круга – построении квадрата равновеликого заданному кругу. Философский смысл – в возможности получения информации о целом по его бесконечно малой части, замеченный ранее – наглядно реализуется в медицине и биологии, примером чему могут служить успехи генной инженерии в клонировании – создании взаимоподобных живых существ. Редким исключением в перечне наук, воспользовавшихся формулой Ньютона-Лейбница, остается история. Невозможность представления информации исторических источников в виде цифр – аргументов формулы – традиционна. Таким образом, до сих пор философский смысл формулы является не совсем философским, так как реализуется лишь в естественнонаучном знании, оставляя социально-гуманитарное знание без столь мощного инструмента.
Хотя, если придерживаться традиционных особенностей социально-гуманитарного знания, его так сказать, слабостей, то и по делом ему.
Но дальнейший научный анализ дает в наше время новую, иную картину происходящего процесса. Ныне господствующие в науке атомистические воззрения разлагают материю на кучу мельчайших частиц или правильно расположенных центров сил, находящихся в вечных разнообразных движениях. Точно так же и проникающий материю эфир постоянно возбуждается и волнообразно колеблется. Все эти движения материи и эфира находятся в теснейшей и непрерывной связи с бесконечным для нас мировым пространством. Такое представление, недоступное нашему конкретному воображению, вытекает из данных физики .
Даже мистические и магические течения должны считаться с этим положением, хотя они могут, придав иной смысл понятию времени, совершенно уничтожить значение этого факта в общем миросозерцании.
Таким образом, пока вопрос касается явлений, воспринимаемых органами чувств, даже эти наиболее далекие от точного знания области философии и религии должны считаться с научно доказанным фактом, как они должны считаться с тем, что дважды два – четыре в той области, которая подлежит ведению чувств и разума .
Вместе с тем объема накопленных человечеством знаний уже вполне достаточно для того, что бы эту традицию нарушить. В самом деле, нет необходимости на пифагорейский лад искать цифровое соответствие высказываниям «Петр I посетил Венецию во время Великого посольства» и «Петр I не был в Венеции во время Великого посольства», когда сами эти выражения легко могут служить аргументами алгебры логики Джорджа Буля . Результат каждого исторического исследования по сути и есть набор таких аргументов. Таким образом, оправдано, на мой взгляд, использование в качестве подинтегральной функции набора исторических исследований, представленных в виде аргументов алгебры логики, с целью соответствующего получения в качестве первообразной – наиболее вероятной реконструкции исследуемого исторического события.
На этом пути есть много проблем. В частности: представление конкретного исторического исследования – производной реконструируемого события – в виде набора логических выражений – операция заведомо более сложная, чем, например, электронная каталогизация простого библиотечного архива. Однако информационный прорыв конца XX – начала XXI века (чрезвычайно высокая степень интегрированности элементной базы и увеличение мощности информационных ) делают выполнение такой задачи вполне реальным.
В свете вышесказанного, на современном этапе исторический анализ представляет собой математический анализ с теорией вероятности и алгеброй логики, а искомая первообразная функция – вероятность исторического события, что в целом вполне соответствует и даже дополняет представление о науке на современном этапе, ибо замена понятия сущность понятием функция – главное в понимании науки в Новое время – дополняется оценкой этой функции.
Следовательно, современное историческое значение формулы в возможности претворения в жизнь мечты Лейбница «о том времени, когда два философа вместо бесконечных споров будут подобно двум математикам брать перья в руки и, засаживаясь за стол, заменять спор вычислением» .
Каждое историческое исследование – заключение имеет право на существование, отражает реально происходившее событие и дополняет информационную историческую картину. Опасность вырождения исторической науки в набор бесцветных фраз-утверждений – результата применения предлагаемого метода, не больше опасности вырождения музыки в набор звуков, а живописи в набор красок на современном этапе развития человечества. Таким видится мне новый философский смысл формулы Ньютона-Лейбница, приведенной впервые в конце XVII – начале XVIII вв.
Собственно же формулу, ввиду особенности восприятия математических символов носителями социально-гуманитарного знания, выражающуюся в панической боязни этими носителями любого представления таковых знаков, приведем в словесной форме: определенный интеграл производной функции есть первообразная этой функции . Некоторое формальное отличие приводимого примера задачи о квадратуре круга от обычного учебно-математического примера вычисления площади, расположенной под произвольной кривой в декартовой системе координат, не меняет, естественно, сути.
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА:
1. Бродский И.А. Сочинения в четырех томах. Т.3. СПб., 1994.
2. Вернадский В.И. Биосфера и ноосфера. М., 2003.
3. Вундт, Вильгельм. Введение в философию. М., 2001.
4. Гайденко П.П. Эволюция понятия науки. М., 1980.
5. Декарт, Рене. Размышления о первоначальной философии. СПб., 1995.
6. Карпов Г.М. Великое посольство Петра I. Калининград, 1998.
7. Кунцман П., Буркард Ф.-П., Видман Ф. Философия: dtv-Atlas. М., 2002.
8. Малаховский В.С. Избранные главы истории математики. Калининград, 2002.
9. Натансон И.П. Краткий курс высшей математики. СПб., 2001.
10. Энгельс Ф. Анти-Дюринг. М., 1988.
11. Шереметевский В.П. Очерки по истории математики. М., 2004
Интернет ресурсы
http://ru.wikipedia.org
Конец ☺
Скачать презентацию
Теги
- формула
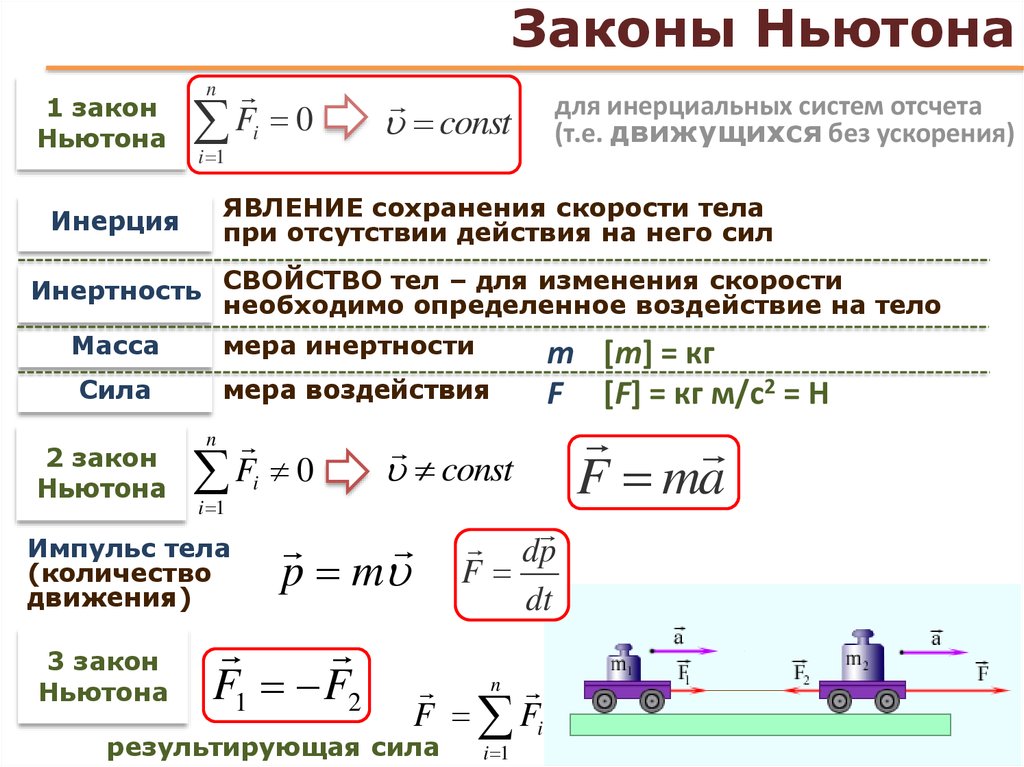
Законы Ньютона.
Второй закон Ньютона. Законы НьютонаИзучение явлений природы на основании эксперимента возможно только при условии соблюдения всех этапов: наблюдение, гипотеза, эксперимент, теория. Наблюдение позволит выявить и сопоставить факты, гипотеза дает возможность дать им подробное научное пояснение, требующее экспериментального подтверждения. Проведение наблюдения за движением тел привело к интересному выводу: изменение скорости тела возможно только под действием другого тела.
К примеру, если быстро бежать по лестнице, то на повороте просто необходимо ухватиться за перила (изменение направления движения), либо приостановиться (изменением величины скорости), чтобы не столкнуться с противоположной стеной.
Наблюдения за аналогичными явлениями привело к созданию раздела физики, изучающего причины изменения скорости тел или их деформации.
Основы динамики
Ответить на сакраментальный вопрос о том, почему физическое тело движется тем или иным образом или покоится, призвана динамика.
Рассмотрим состояние покоя. Исходя из понятия относительности движения, можно сделать вывод: нет и не может быть абсолютно неподвижных тел. Любой предмет, будучи неподвижным по отношению к одному телу отсчета, движется относительно другого. К примеру, книга, лежащая на столе, неподвижна относительно стола, но если рассмотреть ее положение по отношению к проходящему человеку, то делаем естественный вывод: книга движется.
Поэтому законы движения тел рассматриваются в инерциальных системах отсчета. Что это такое?
Инерциальной называется система отсчета, в которой тело покоится или выполняет равномерное и прямолинейное движение при условии отсутствия воздействия на него иных предметов или объектов.
В приведенном выше примере система отсчета, связанная со столом, может быть названа инерциальной. Человек, движущийся равномерно и прямолинейно, может служить телом отсчета ИСО. Если его движение будет ускоренным, то связать с ним инерциальную СО нельзя.
По сути, такую систему можно соотнести с телами, жестко закрепленными на поверхности Земли.
Однако сама планета не может служить телом отсчета для ИСО, так как равномерно вращается вокруг собственной оси. Тела на поверхности имеют центростремительное ускорение.
Что такое инерция?
Явление инерции напрямую связано с ИСО. Вспомните, что происходит, если движущийся автомобиль резко останавливается? Пассажиры подвергаются опасности, поскольку продолжают свое движение. Остановить его может кресло впереди либо ремни безопасности. Поясняют этот процесс инерцией пассажира. Так ли это?
Инерция – явление, предполагающее сохранение постоянной скорости тела при отсутствии воздействия на него других тел. Пассажир находится под действием ремней или кресел. Явление инерции здесь не наблюдается.
Объяснение кроется в свойстве тела, и, согласно ему, мгновенно изменить скорость того или иного предмета невозможно. Это – инертность. К примеру, инертность ртути в термометре позволяет опустить столбик, если мы встряхнем градусник.
Мерой инертности называют массу тела.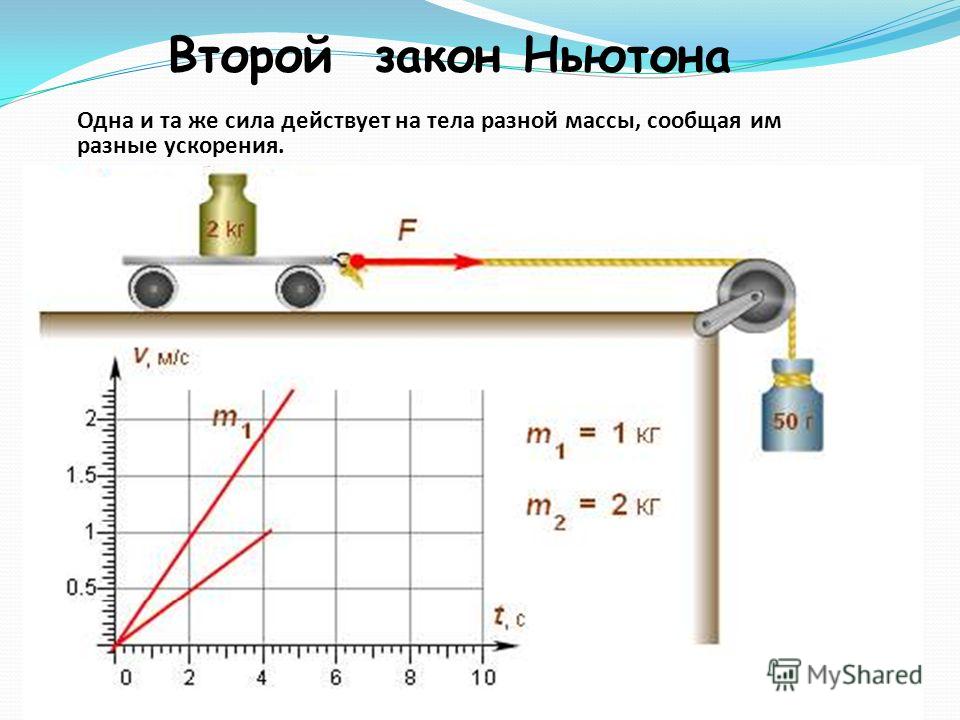
При взаимодействии скорость быстрее меняется у тел с меньшей массой. Столкновение автомобиля с бетонной стеной для последней протекает практически бесследно. Автомобиль чаще всего претерпевает необратимые изменения: меняется скорость, происходит значительная деформация. Получается, что инертность бетонной стены значительно превышает инертность автомобиля.
Возможно ли в природе встретиться с явлением инерции? Условие, при котором тело находится без взаимосвязи с другими телами – глубокий космос, в котором движется космический корабль с выключенными двигателями. Но даже в этом случае гравитационный момент присутствует.
Основные величины
Изучение динамики на экспериментальном уровне предполагает проведение опыта с измерениями физических величин. Наиболее интересны:
- ускорение как мера быстроты изменения скорости тел; обозначают ее буквой а, измеряют в м/с2;
- масса как мера инертности; обозначена литерой m, измеряется в кг;
- сила как мера взаимного действия тел; обозначается чаще всего буквой F, измеряется в Н (ньютонах).
Взаимосвязь этих величин изложена в трех закономерностях, выведенных величайшим английским физиком. Законы Ньютона призваны объяснить сложности взаимодействия различных тел. А также процессы, ими управляющие. Именно понятия “ускорение”, “сила”, “масса” законы Ньютона связывают математическими соотношениями. Попробуем разобраться, что же это значит.
Действие только одной силы – явление исключительное. К примеру, искусственный спутник, движущийся по орбите вокруг Земли, находится под действием только силы притяжения.
Равнодействующая
Действие нескольких сил можно заменить одной силой.
Геометрическая сумма сил, воздействующих на тело, именуется равнодействующей.
Речь идет именно о геометрической сумме, поскольку сила – векторная величина, которая зависит не только от точки приложения, но и от направления действия.
К примеру, если необходимо передвинуть достаточно массивный шкаф, то можно пригласить друзей. Совместными усилиями достигается желаемый результат.
Но можно пригласить только одного, очень сильного человека. Его усилие равно действию всех друзей. Сила, приложенная богатырем, может быть названа равнодействующей.
Законы движения Ньютона формулируются на основании понятия «равнодействующая».
Закон инерции
Начинают изучать законы Ньютона с наиболее часто встречающегося явления. Первый закон обычно называют законом инерции, поскольку он устанавливает причины равномерного прямолинейного движения или состояния покоя тел.
Тело перемещается равномерно и прямолинейно или покоится, если на него не осуществляют действия силы, либо это действие скомпенсировано.
Можно утверждать, что равнодействующая в этом случае равна нулю. В таком состоянии находится, к примеру, движущийся с постоянной скоростью автомобиль на прямолинейном участке дороги. Действие силы притяжения скомпенсировано силой реакции опоры, а сила тяги двигателя по модулю равна силе сопротивления движению.
Люстра на потолке покоится, так как сила тяжести скомпенсирована силой натяжения ее креплений.
Скомпенсированными могут быть только те силы, которые приложены к одному телу.
Второй закон Ньютона
Идем далее. Причины, вызывающие изменение скорости тел, рассматривает второй закон Ньютона. О чем он говорит?
Равнодействующая сил, воздействующих на тело, определяется как произведение массы тела на приобретаемое под действием сил ускорение.
2 закон Ньютона (формула: F=ma), к сожалению, не устанавливает причинно-следственных связей между основными понятиями кинематики и динамики. Он не может с точностью указать, что является причиной появления ускорения тел.
Сформулируем иначе: ускорение, получаемое телом, прямо пропорционально равнодействующей сил и обратно пропорционально массе тела.
Так, можно установить, что изменение скорости происходит только в зависимости от силы, приложенной к нему, и массы тела.
2 закон Ньютона, формула которого может быть и такой: a = F/m, в векторном виде считают основополагающим, поскольку он дает возможность установить связь между разделами физики.
Здесь, a – вектор ускорения тела, F – равнодействующая сил, m – масса тела.
Ускоренное движение автомобиля возможно, если сила тяги двигателей превышает силу сопротивления движению. С увеличением силы тяги возрастает и ускорение. Грузовые автомобили снабжаются двигателями большой мощности, ведь их масса значительно превышает массу легкового авто.
Болиды, созданные для скоростных гонок, облегчаются таким образом, что на них закрепляется минимум необходимых деталей, а мощность двигателей увеличивается до возможных пределов. Одной из важнейших характеристик спортивных авто является время разгона до 100 км/ч. Чем меньшее этот интервал времени, тем лучше скоростные свойства болида.
Закон взаимодействия
Законы Ньютона, основанные на силах природы, утверждают, что любое взаимодействие сопровождается появлением пары сил. Если шар висит на нити, то испытывает ее действие. При этом нить также растягивается под действием шара.
Завершает законы Ньютона формулировка третьей закономерности.
Вкратце это звучит так: действие равно противодействию. Что это значит?
Силы, с которыми тела воздействуют друг на друга, равны по величине, противоположны по направлению и направлены вдоль линии, соединяющей центры тел. Интересно, что скомпенсированными их назвать нельзя, ведь действуют они на разные тела.
Применение законов
Знаменитая задача «Конь и телега» может поставить в тупик. Конь, запряженный в упомянутую повозку, сдвигает ее с места. В соответствии с третьим законом Ньютона, эти два объекта действуют друг на друга с равными по модулю силами, но на практике лошадь может сдвинуть телегу, что не укладывается в основы закономерности.
Решение найдется, если учесть, что эта система тел не замкнута. Дорога оказывает свое действие на оба тела. Сила трения покоя, действующая на копыта коня, превышает по значению силу трения качения колес телеги. Ведь момент движения начинается с попытки сдвинуть повозку. Если положение изменится, то конь ни при каких условиях не сдвинет её с места.
Его копыта будут проскальзывать по дороге, и движения не будет.
В детстве, катая друг друга на санках, каждый мог столкнуться с таким примером. Если на санки сядут два-три ребенка, то усилий одного явно недостаточно, чтобы сдвинуть их с места.
Падение тел на поверхность земли, объясняемое Аристотелем («Каждое тело знает свое место») можно опровергнуть на основании вышеизложенного. Предмет движется к земле под действием такой же силы, что и Земля к нему. Сравнив их параметры (масса Земли намного больше массы тела), в соответствии со вторым законом Ньютона, утверждаем, что ускорение предмета во столько же раз больше ускорения Земли. Мы наблюдаем именно изменение скорости тела, Земля не смещается с орбиты.
Границы применимости
Современная физика законы Ньютона не отрицает, а лишь устанавливает границы их применимости. До начала XX века физики не сомневались в том, что эти законы объясняют все явления природы.
1, 2, 3 закон Ньютона полностью выявляет причины поведения макроскопических тел.
Движение объектов с незначительными скоростями полностью описывается этими постулатами.
Попытка пояснить на их основании движение тел со скоростями, близкими к скорости света, обречена на провал. Полное изменение свойств пространства и времени при этих скоростях не позволяет использовать динамику Ньютона. Кроме того, законы меняют свой вид в неинерциальных СО. Для их применения вводится понятие силы инерции.
Пояснить движение астрономических тел, правила их расположения и взаимодействия могут законы Ньютона. Закон всемирного тяготения вводится с этой целью. Увидеть же результат притяжения малых тел невозможно, ведь сила мизерна.
Взаимное притяжение
Известна легенда, согласно которой господина Ньютона, сидевшего в саду и наблюдавшего падение яблок, посетила гениальная идея: объяснить движение предметов вблизи поверхности Земли и движение космических тел на основании взаимного притяжения. Это не так далеко от истины. Наблюдения и точный расчет касались не только падения яблок, но и перемещения Луны.
Закономерности этого движения приводят к выводам, что сила притяжения возрастает с увеличением масс взаимодействующих тел и уменьшается с увеличением расстояния между ними.
Опираясь на второй и третий законы Ньютона, закон всемирного тяготения формулируют следующим образом: все тела во вселенной притягиваются друг к другу с силой, направленной вдоль линии, соединяющей центры тел, пропорциональной массам тел и обратно пропорциональной квадрату расстояния между центрами тел.
Математическая запись: F = GMm/r2, где F – сила притяжения, M, m – массы взаимодействующих тел, r – расстояние между ними. Коэффициент пропорциональности (G = 6.62 х 10-11 Нм2/кг2) получил название гравитационной постоянной.
Физический смысл: эта постоянная равна силе притяжения между двумя телами массами по 1 кг на расстоянии 1 м. Понятно, что для тел небольших масс сила столь незначительна, что ею можно пренебречь. Для планет, звезд, галактик сила притяжения настолько огромна, что полностью определяет их движение.
Именно закон притяжения Ньютона утверждает, что для запуска ракет необходимо топливо, способное создать такую реактивную тягу, чтобы преодолеть влияние Земли. Скорость, необходимая для этого – первая космическая скорость, равная 8 км/с.
Современная технология изготовления ракет позволяет запускать беспилотные станции как искусственные спутники Солнца к другим планетам, чтобы их исследовать. Скорость, развиваемая таким аппаратом, – вторая космическая скорость, равная 11 км/с.
Алгоритм применения законов
Решение задач динамики подчиняется определенной последовательности действий:
- Провести анализ задачи, выявить данные, вид движения.
- Выполнить рисунок с указанием всех сил, действующих на тело, и направления ускорения (при его наличии). Выбрать систему координат.
- Записать первый или второй законы, в зависимости от наличия ускорения тела, в векторной форме. Учесть все силы (равнодействующая сила, законы Ньютона: первый, если скорость тела не меняется, второй, если есть ускорение).
- Уравнение переписать в проекциях на выбранные оси координат.
- Если полученной системы уравнений недостаточно, то записать иные: определения сил, уравнения кинематики и т. п.
- Решить систему уравнений относительно искомой величины.
- Выполнить проверку размерностей, чтобы определиться с правильностью полученной формулы.
- Вычислить.
Обычно этих действий вполне достаточно для решения любой стандартной задачи.
Второй ⚠️ закон Ньютона: определение простыми словами, формулировка
Содержание:
- Второй закон Ньютона: определение и формула
- Равнодействующая сила
-
Пояснение на конкретных примерах
- Второй закон Ньютона в классической механике
- Второй закон за пределами классической механики
Содержание
- Второй закон Ньютона: определение и формула
- Равнодействующая сила
-
Пояснение на конкретных примерах
- Второй закон Ньютона в классической механике
- Второй закон за пределами классической механики
Второй закон Ньютона: определение и формула
Определение
Второй закон Ньютона: под действием силы тело приобретает такое ускорение, что его произведение на массу тела равно действующий силе.
Это одна из возможных формулировок открытия Ньютона. В виде формулы данная связь массы, силы и ускорения представлена так:
\(\vec F=m\times\vec a\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Где \(\vec F\) — это сила, которая оказывает воздействие на тело, m — масса этого тела, \(\vec a\) — ускорение, которое приобрело тело.
Из этого уравнения легко можем получить формулу для определения ускорения:
\(\vec a=\frac{\vec F}m\)
Другой формой этого закона является его дифференциальный вид:
\(\vec F=\frac{d\vec p}{dt}\)
Где dt — небольшой промежуток времени, \(\vec F\) — сила, оказывающая воздействие на тело, \(d\vec p\) — производная импульса тела.
Равнодействующая сила
Определение
При условии, что на тело воздействует одновременно несколько сил, в данную формулу вместо силы подставляется векторная сумма всех сил, которая называется равнодействующей силой.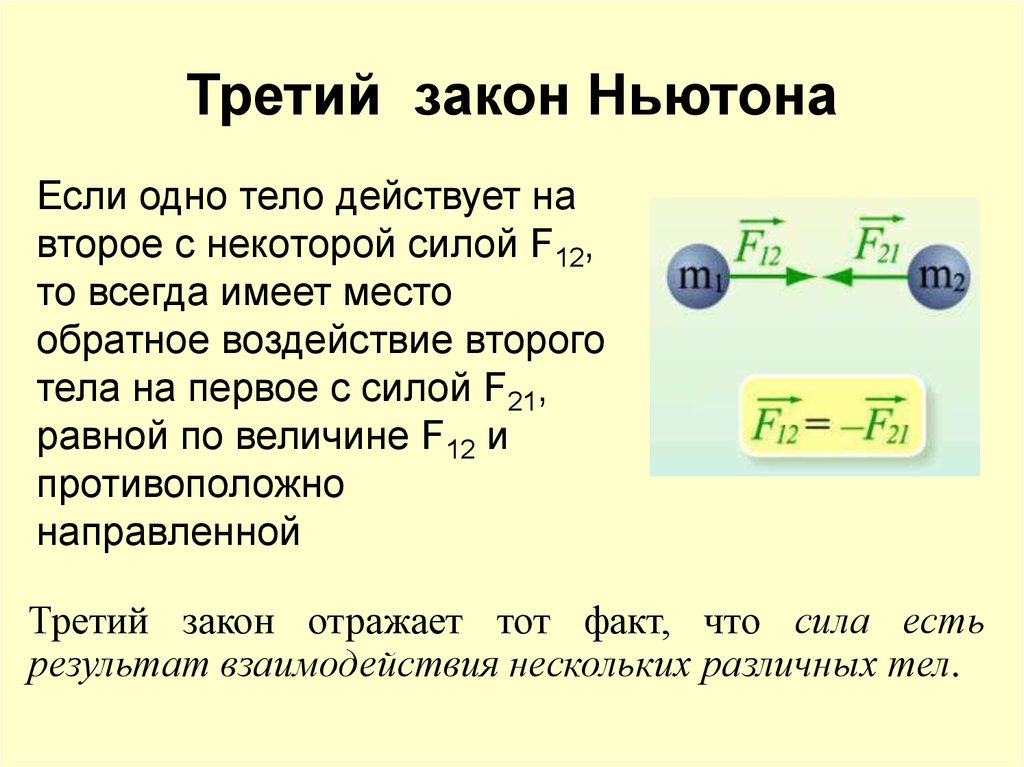
Формула приобретает следующий вид:
\(\vec a=\frac{\sum\vec F}m\)
В зависимости от направления сил, действующих на тело, расчет равнодействующей может осуществляться тремя способами:
- Если силы, действующие на тело, направлены по одной прямой и в одну сторону, то направление равнодействующей будет совпадать с направлениями этих сил, и вычисляться она будет по формуле: \(\vec R=\vec F_1+\vec F_2\)
- Если силы, воздействующие на тело, направлены по одной прямой в противоположные стороны, то равнодействующая сила будет направлена в сторону силы, большей по модулю и вычисляться будет по формуле: \(\vec R=\vec F_2-\vec F_1\)
- Если силы, действующие на тело, равны по модулю и противоположны по направлению, то равнодействующая всех сил будет равна нулю.
Пояснение на конкретных примерах
Второй закон Ньютона в классической механике
Определение
Классическая механика — раздел физики, в котором рассматриваются взаимодействия тел, обладающих гораздо меньшими в сравнении со скоростью света скоростями.
Примерами демонстрации второго закона Ньютона могут служить:
- Удар ногой по мячу. Ударяя по мячу, мы прикладываем силу, которая задает его направление и ускорение. Чем сильнее будет удар, тем быстрее полетит мяч.
- Толкание тележки в супермаркете. Это хороший пример, чтобы продемонстрировать, как вес влияет на ньютоновскую закономерность. Попробуйте толкнуть пустую и груженую тележку. Во втором случае понадобится гораздо большая сила, чтобы придать тележке такое же ускорение, как в первом случае.
- Игра в гольф — наглядный пример закона Ньютона в действии.
Второй закон за пределами классической механики
Второй закон Ньютона используется не только в классической механике, его используют для решения задач в релятивистской динамике и квантовой механике.
В релятивистской динамике уравнение Исаака Ньютона принимает следующий вид:
\(\vec Phi=\frac{dP}{d\tau}\)
Где P — производная четырехимпульса, \(\tau\) — собственное время, \(\Phi\) — четырехсила.
Уравнение Ньютона используют для квантовомеханического описания движения электронов, находящихся в кристаллической решетке.
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Второй закон Ньютона: концепция системы | Физика |
Цели обучения
К концу этого раздела вы сможете:
- Определить результирующую силу, внешнюю силу и систему.
- Поймите второй закон движения Ньютона.
- Примените второй закон Ньютона для определения веса объекта.
Второй закон движения Ньютона тесно связан с первым законом движения Ньютона. Он математически устанавливает причинно-следственную связь между силой и изменениями в движении. Второй закон Ньютона носит более количественный характер и широко используется для расчета того, что происходит в ситуациях, связанных с силой.
Прежде чем мы сможем записать второй закон Ньютона в виде простого уравнения, определяющего точное соотношение между силой, массой и ускорением, нам нужно уточнить некоторые уже упомянутые идеи.
Во-первых, что мы подразумеваем под изменением движения? Ответ заключается в том, что изменение движения эквивалентно изменению скорости. Изменение скорости означает, по определению, что существует ускорение . Первый закон Ньютона гласит, что результирующая внешняя сила вызывает изменение движения; таким образом, мы видим, что суммарная внешняя сила вызывает ускорение .
Сразу возникает другой вопрос. Что мы понимаем под внешней силой? Интуитивное представление о внешнем верно — внешняя сила действует снаружи системы интереса. Например, на рис. 1(а) интересующей нас системой является повозка плюс ребенок в ней. Две силы, действующие со стороны других детей, являются внешними силами. Между элементами системы действует внутренняя сила. Снова взглянув на рисунок 1 (а), сила, которую ребенок в тележке прилагает, чтобы повиснуть на тележке, является внутренней силой между элементами интересующей системы.
Только внешние силы влияют на движение системы в соответствии с первым законом Ньютона. (Внутренние силы на самом деле компенсируются, как мы увидим в следующем разделе.) Вы должны определить границы системы, прежде чем сможете определить, какие силы являются внешними . Иногда система очевидна, тогда как в других случаях определение границ системы является более тонким. Понятие системы является фундаментальным для многих областей физики, как и правильное применение законов Ньютона. К этой концепции мы будем возвращаться много раз в нашем путешествии по физике.
Рис. 1. Различные силы, действующие на одну и ту же массу, вызывают различные ускорения. а) Двое детей толкают тележку с ребенком. Показаны стрелки, представляющие все внешние силы. Система интереса — это повозка и ее всадник. Вес w системы и опоры земли N также показаны для полноты и предполагаются аннулирующими. Вектор f представляет трение, действующее на вагон, и он действует слева, противодействуя движению вагона.
(b) Все внешние силы, действующие на систему, складываются вместе, чтобы создать результирующую силу F net . Диаграмма свободного тела показывает все силы, действующие на интересующую систему. Точка представляет собой центр масс системы. Каждый вектор силы простирается от этой точки. Поскольку справа действуют две силы, мы рисуем векторы коллинеарно. (c) Большая результирующая внешняя сила производит большее ускорение ( a′ > a ), когда взрослый толкает ребенка.
Теперь кажется разумным, что ускорение должно быть прямо пропорционально и направлено в том же направлении, что и чистая (полная) внешняя сила, действующая на систему. Это предположение было подтверждено экспериментально и показано на рис. 1. В части (а) меньшая сила вызывает меньшее ускорение, чем большая сила, показанная в части (в). Для полноты показаны также вертикальные силы; предполагается, что они компенсируются, поскольку ускорение в вертикальном направлении отсутствует.
Вертикальные силы – это вес w и опора на землю N , а горизонтальная сила f представляет собой силу трения. Они будут обсуждаться более подробно в последующих разделах. Сейчас мы определим трение как силу, противодействующую движению соприкасающихся объектов друг относительно друга. На рис. 1(b) показано, как векторы, представляющие внешние силы, складываются вместе, чтобы получить результирующую силу
F net .
Чтобы получить уравнение для второго закона Ньютона, мы сначала запишем отношение ускорения и чистой внешней силы в виде пропорциональности
a∝Fnet\text{a}\propto{\text{F}_{net}}\\a∝Fnet
где символ ∝ означает «пропорционально», а F net — это чистая внешняя сила . (Чистая внешняя сила представляет собой векторную сумму всех внешних сил и может быть определена графически, используя метод «голова к хвосту», или аналитически, используя компоненты.
Методы такие же, как и для добавления других векторов, и рассматриваются в двумерной кинематике.) Эта пропорциональность выражает то, что мы сказали словами — ускорение прямо пропорционально чистой внешней силе . После выбора интересующей системы важно определить внешние силы и игнорировать внутренние. Не учитывать многочисленные внутренние силы, действующие между объектами внутри системы, такие как мышечные силы в теле ребенка, не говоря уже о бесчисленных силах между атомами в объектах, — это огромное упрощение, но, делая это, мы можем легко решить некоторые очень сложные проблемы с минимальной ошибкой из-за нашего упрощения.
Теперь также кажется разумным, что ускорение должно быть обратно пропорционально массе системы. Другими словами, чем больше масса (инерция), тем меньше ускорение, создаваемое данной силой. И действительно, как показано на рис. 2, та же внешняя сила, приложенная к автомобилю, создает гораздо меньшее ускорение, чем при приложении к баскетбольному мячу.
Пропорциональность записывается как
a∝1m\text{a}\propto{\frac{1}{m}}\\a∝m1
где м – масса системы. Эксперименты показали, что ускорение точно обратно пропорционально массе, так же как оно точно линейно пропорционально суммарной внешней силе.
Рис. 2. Одна и та же сила, действующая на системы с разной массой, создает разные ускорения. а) Баскетболист толкает мяч, чтобы сделать передачу. (Влияние силы тяжести на мяч игнорируется.) (b) Тот же игрок прикладывает такую же силу к заглохшему внедорожнику и создает гораздо меньшее ускорение (даже если трением можно пренебречь). (c) Диаграммы свободного тела идентичны, что позволяет проводить прямое сравнение двух ситуаций. Ряд паттернов для диаграммы свободного тела появится по мере того, как вы будете решать больше задач.
Было обнаружено, что ускорение объекта зависит только от суммарной внешней силы и массы объекта.
Сочетание двух только что приведенных пропорций дает второй закон движения Ньютона.
Второй закон движения Ньютона
Ускорение системы прямо пропорционально внешней силе, действующей на систему, и направлено в том же направлении, что и обратно пропорционально ее массе. В форме уравнения второй закон Ньютона равен 9.0005
a=Fnetm{\text{a}}=\frac{{{\text{F}}}_{\text{net}}}{m}\\a=mFnet
. Это часто записывается в более знакомой форме
F нетто = м a .
Когда учитываются только величина силы и ускорения, это уравнение выглядит просто как
F net = ma.
Хотя эти два последних уравнения на самом деле одинаковы, первое дает более полное представление о том, что означает второй закон Ньютона. Закон причинно-следственная связь между тремя величинами, которая не просто основана на их определениях.
Справедливость второго закона полностью основана на экспериментальной проверке.
Единицы силы
F нетто = м a используется для определения единиц силы с точки зрения трех основных единиц массы, длины и времени. Единица силы в СИ называется ньютонов (сокращенно Н) и представляет собой силу, необходимую для ускорения системы массой 1 кг со скоростью 1 м/с 2 . То есть, поскольку F net = м a ,
1 N = 1 кг ⋅ м/с 2 .
В то время как почти во всем мире в качестве единицы силы используется ньютон, в Соединенных Штатах наиболее распространенной единицей силы является фунт (фунт), где 1 Н = 0,225 фунта.
Вес и гравитационная сила
Когда объект падает, он ускоряется к центру Земли. Второй закон Ньютона гласит, что результирующая сила, действующая на объект, отвечает за его ускорение.
Если сопротивлением воздуха можно пренебречь, результирующая сила, действующая на падающий объект, представляет собой гравитационную силу, обычно называемую ее вес ш. Вес можно обозначить как вектор w, потому что он имеет направление; вниз — это, по определению, направление силы тяжести, и, следовательно, вес — это направленная вниз сила. Величина веса обозначается как w . Галилей доказал, что в отсутствие сопротивления воздуха все тела падают с одинаковым ускорением g . Используя результат Галилея и второй закон Ньютона, мы можем вывести уравнение для веса.
Рассмотрим объект массой м падает вниз к Земле. На него действует только направленная вниз сила тяжести, величина которой составляет w . Второй закон Ньютона гласит, что величина чистой внешней силы, действующей на объект, равна F нетто = мА . Поскольку на объект действует только направленная вниз сила тяжести, F net = w .
Мы знаем, что ускорение объекта под действием силы тяжести составляет g , или a = g . Подстановка их во второй закон Ньютона дает
w = mg
Поскольку g = 9,80 м/с 2 на Земле, вес объекта массой 1,0 кг на Земле равен 9,8 Н, как мы видим:w = mg = (1,0 кг)(9,80 м/с 2 )=9,8 №
Напомним, что g может принимать положительное или отрицательное значение в зависимости от положительного направления в системе координат. Обязательно учитывайте это при решении задач с весом. Когда чистая внешняя сила, действующая на объект, равна его весу, мы говорим, что он находится в свободном падении . То есть единственная сила, действующая на объект, — это сила тяжести. В реальном мире, когда объекты падают вниз к Земле, они никогда не находятся в состоянии свободного падения, потому что на объект всегда действует восходящая сила воздуха.
Ускорение свободного падения g незначительно варьируется по поверхности Земли, поэтому вес объекта зависит от местоположения и не является неотъемлемым свойством объекта. Вес резко меняется, если человек покидает поверхность Земли. На Луне, например, ускорение свободного падения составляет всего 1,67 м/с9.0131 2 . Таким образом, масса в 1,0 кг имеет вес 9,8 Н на Земле и всего около 1,7 Н на Луне.
Самое широкое определение веса в этом смысле состоит в том, что вес объекта — это гравитационная сила, действующая на него со стороны ближайшего крупного тела , такого как Земля, Луна, Солнце и так далее. Это наиболее распространенное и полезное определение веса в физике. Однако оно резко отличается от определения веса, используемого НАСА и популярными средствами массовой информации в связи с космическими путешествиями и исследованиями. Когда они говорят о «невесомости» и «микрогравитации», они на самом деле имеют в виду явление, которое в физике называется «свободным падением».
Мы воспользуемся приведенным выше определением веса и проведем тщательное различие между свободным падением и фактической невесомостью.
Важно помнить, что вес и масса — очень разные физические величины, хотя и тесно связанные между собой. Масса — это количество материи (сколько «вещества») и не меняется в классической физике, тогда как вес — это гравитационная сила, которая зависит от гравитации. Заманчиво приравнять их, поскольку большинство наших примеров происходят на Земле, где вес объекта лишь немного зависит от местоположения объекта. Кроме того, термы масса и вес взаимозаменяемы в повседневном языке; например, наши медицинские записи часто показывают наш «вес» в килограммах, но никогда в правильных единицах измерения — ньютонах.
Распространенные заблуждения: масса и вес В повседневном языке масса и вес часто используются как синонимы. Однако в науке эти термины резко отличаются друг от друга. Масса — это мера того, сколько материи содержится в объекте.
Типичной мерой массы является килограмм (или «слаг» в английских единицах измерения). Вес, с другой стороны, является мерой силы тяжести, действующей на объект. Вес равен массе объекта (m), умноженной на ускорение свободного падения (g). Как и любая другая сила, вес измеряется в ньютонах (или фунтах в английских единицах измерения). Если предположить, что масса объекта остается неизменной, она останется неизменной, независимо от его местоположения. Однако, поскольку вес зависит от ускорения свободного падения, вес объекта может измениться на , когда объект входит в область с более сильной или более слабой гравитацией. Например, ускорение свободного падения на Луне составляет 1,67 м/с 2 (что намного меньше ускорения свободного падения на Земле, 9,80 м/с 2 ). Если вы измерите свой вес на Земле, а затем измерите свой вес на Луне, вы обнаружите, что «весите» намного меньше, даже если вы не выглядите стройнее. Это связано с тем, что на Луне сила гравитации слабее.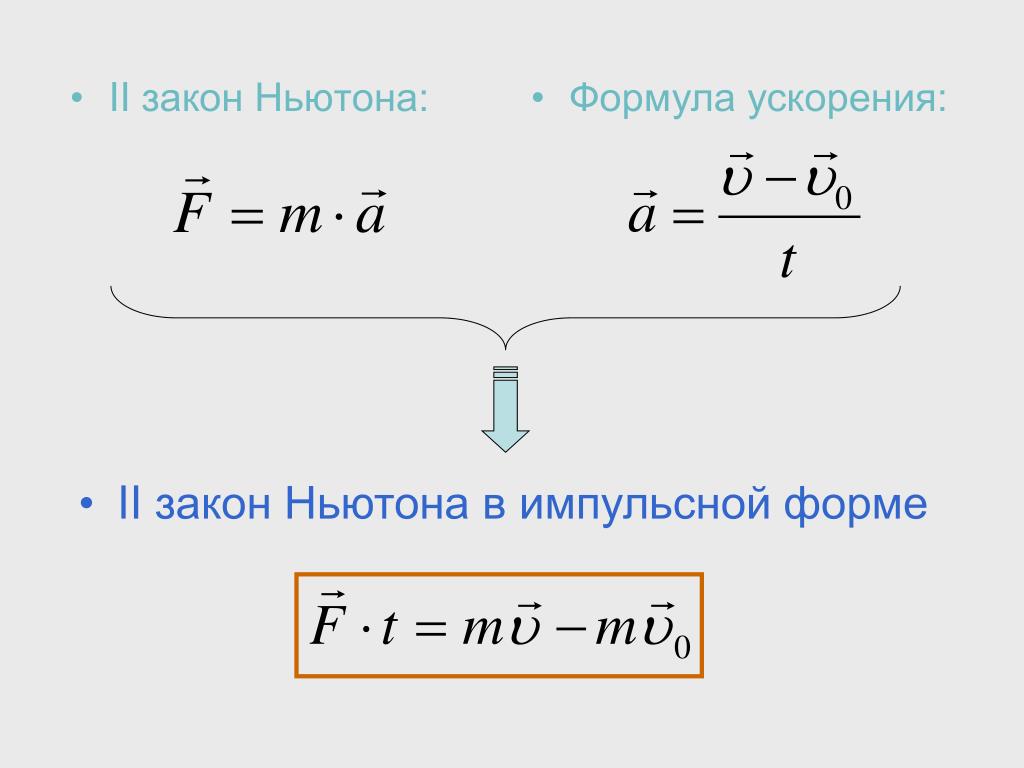
На самом деле, когда люди говорят, что они «худеют», они на самом деле имеют в виду, что теряют «массу» (что, в свою очередь, заставляет их весить меньше).Эксперимент на вынос: масса и вес
Что измеряют напольные весы? Когда вы встаете на напольные весы, что происходит с весами? Это слегка угнетает. Весы содержат пружины, которые сжимаются пропорционально вашему весу, подобно резиновым лентам, которые растягиваются при натяжении. Пружины обеспечивают меру вашего веса (для объекта, который не ускоряется). Это сила в ньютонах (или фунтах). В большинстве стран измерение делится на 9,80, чтобы получить показание в единицах массы килограммов. Весы измеряют вес, но откалиброваны для предоставления информации о массе. Стоя на весах в ванной, нажмите на стол рядом с вами. Что происходит с чтением? Почему? Измерят ли ваши весы ту же «массу» на Земле, что и на Луне?
Пример 1. Какое ускорение может создать человек, толкая газонокосилку?
Предположим, что чистая внешняя сила (толчок минус трение), действующая на газонокосилку, равна 51 Н (около 11 фунтов) параллельно земле.
Масса косилки 24 кг. Каково его ускорение?Рисунок 3. Чистая сила, действующая на газонокосилку, направлена вправо 51 Н. С какой скоростью газонокосилка ускоряется вправо?
Стратегия Поскольку F net и m заданы, ускорение можно рассчитать непосредственно из второго закона Ньютона, как указано в 9.{2}\\a=24 кг51 кг⋅м/с2=2,1 м/с2.
Обсуждение Направление ускорения совпадает с направлением чистой силы, которая параллельна земле. В этом примере нет информации об отдельных внешних силах, действующих на систему, но мы можем кое-что сказать об их относительных величинах. Например, сила, действующая на человека, толкающего косилку, должна быть больше, чем трение, противодействующее движению (поскольку мы знаем, что косилка движется вперед), а вертикальные силы должны уравновешиваться, если не должно быть ускорения в вертикальном направлении (ускорение в вертикальном направлении).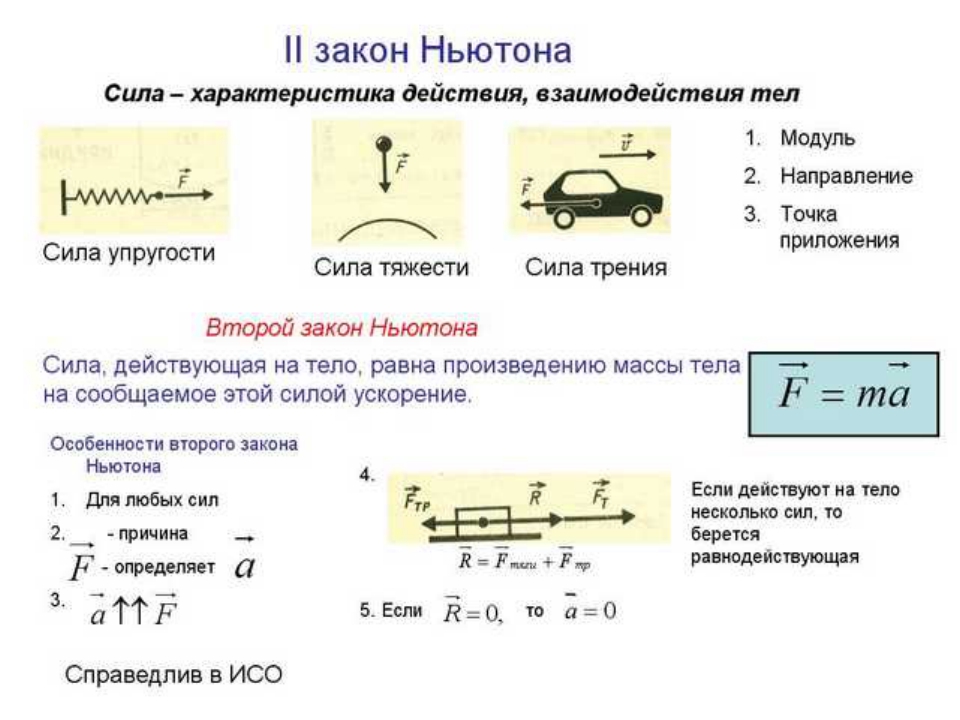
косилка движется только горизонтально). Найденное ускорение достаточно мало, чтобы быть приемлемым для человека, толкающего косилку. Такое усилие не продлится слишком долго, потому что человек скоро достигнет максимальной скорости.Пример 2. Какая ракетная тяга ускоряет эти сани?
До пилотируемых космических полетов ракетные сани использовались для испытаний самолетов, ракетного оборудования и физиологических воздействий на людей на высоких скоростях. Они состояли из платформы, установленной на одном или двух рельсах и приводившейся в движение несколькими ракетами. Рассчитайте величину силы, действующей на каждую ракету, называемую ее тягой Т, для четырехракетной двигательной установки, показанной на рис. 4. Начальное ускорение саней 49 м/с2, масса системы 2100 кг, сила трения противодействующее движению, как известно, составляет 650 Н. Рис. 4. На сани действует реактивная тяга, которая ускоряет их вправо. Каждая ракета создает одинаковую тягу Т.
Как и в других ситуациях, когда есть только горизонтальное ускорение, вертикальные силы компенсируются. Земля воздействует на систему направленной вверх силой N, равной по величине и противоположной по направлению ее весу w. Система здесь — это сани, их ракеты и всадник, поэтому никакие силы между этими объектами не учитываются. Стрелка, обозначающая трение (f), нарисована больше масштаба.
Поэтому начинаем сF нетто = ма,
где F нетто — результирующая сила в горизонтальном направлении. Из рис. 4 видно, что тяга двигателя добавляется, а трение противодействует тяге. В форме уравнения чистая внешняя сила равнаF нетто = 4 T−f .
Подставив это во второй закон Ньютона, мы получимF нетто = ma = 4 T−f .
Используя немного алгебры, находим полную тягу 4 9{4}\text{N}\\T=41,0×105N=2,6×104N.
Обсуждение Цифры довольно большие, поэтому результат может вас удивить. Подобные эксперименты проводились в начале 1960-х годов для проверки пределов человеческой выносливости и установки, предназначенной для защиты людей при аварийном катапультировании реактивного истребителя. Были получены скорости 1000 км/ч с ускорениями 45g. (Вспомним, что g, ускорение свободного падения, равно 9,80 м/с 2 .
Когда мы говорим, что ускорение равно 45 g, это 45×90,80 м/с 2 , что примерно равно 440 м/с 2 .) Хотя живые объекты больше не используются, на ракетных салазках была получена наземная скорость 10 000 км/ч. В этом примере, как и в предыдущем, интересующая система очевидна. В последующих примерах мы увидим, что выбор интересующей системы имеет решающее значение, и этот выбор не всегда очевиден.Второй закон движения Ньютона — это больше, чем определение; это отношение между ускорением, силой и массой. Это может помочь нам делать прогнозы. Каждая из этих физических величин может быть определена независимо, поэтому второй закон говорит нам нечто основное и универсальное о природе. В следующем разделе представлен третий и последний закон движения.
Резюме раздела
Концептуальные вопросы
1. Какое утверждение верно? а) Суммарная сила вызывает движение. (b) Суммарная сила вызывает изменение движения. Объясните свой ответ и приведите пример.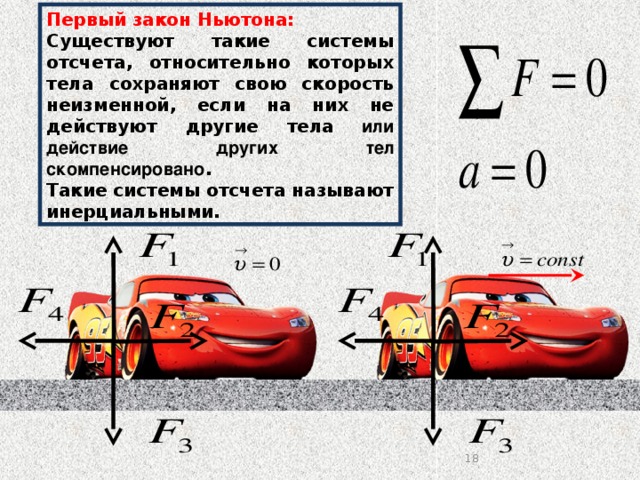
2. Почему мы можем пренебречь силами, такими как те, которые удерживают тело вместе, когда мы применяем второй закон движения Ньютона?
3. Объясните, как выбор «исследуемой системы» влияет на то, какие силы необходимо учитывать при применении второго закона Ньютона.
4. Опишите ситуацию, в которой результирующая внешняя сила, действующая на систему, отлична от нуля, но ее скорость остается постоянной.
5. Система может иметь ненулевую скорость, в то время как результирующая внешняя сила, действующая на нее , равна нулю. Опишите такую ситуацию.
6. Камень брошен прямо вверх. Какова чистая внешняя сила, действующая на камень, когда он находится в верхней части своей траектории?
7. (a) Приведите пример различных суммарных внешних сил, действующих на одну и ту же систему и создающих различные ускорения. (b) Приведите пример, когда одна и та же результирующая внешняя сила действует на системы с разными массами, создавая разные ускорения.
в) Какой закон точно описывает оба эффекта? Сформулируйте это словами и в виде уравнения.
8. Если ускорение системы равно нулю, то не действуют ли на нее внешние силы? А внутренние силы? Объясните свои ответы.
9. Если к объекту приложена постоянная ненулевая сила, что можно сказать о скорости и ускорении объекта?
10. Сила тяжести, действующая на баскетбольный мяч на рисунке 2, не учитывается. Если принять во внимание гравитацию и , каково направление чистой внешней силы, действующей на баскетбольный мяч — выше горизонтали, ниже горизонтали или все еще горизонтально?
Задачи и упражнения
Вы можете предположить, что данные, взятые из иллюстраций, точны до трех цифр.
1. Спринтер массой 63,0 кг начинает гонку с ускорением 4,20 м/с 2 . Какова чистая внешняя сила, действующая на него?
2. Если спринтер из предыдущей задачи разгоняется с такой скоростью на протяжении 20 м, а затем сохраняет эту скорость до конца бега на 100 м, каково будет его время в забеге?
3.
Уборщик толкает тележку для белья массой 4,50 кг так, что результирующая внешняя сила, действующая на нее, равна 60,0 Н. Вычислите величину ее ускорения.
4. Поскольку астронавты на орбите, по-видимому, не имеют веса, необходим умный метод измерения их массы, чтобы контролировать их прирост или потерю массы для корректировки диеты. Один из способов сделать это — приложить к космонавту известную силу и измерить вызванное им ускорение. Предположим, что действует чистая внешняя сила 50,0 Н, и измеренное ускорение космонавта равно 0,893 м/с 2 . а) Вычислите ее массу. (b) Воздействуя на космонавта силой, транспортное средство, в котором они вращаются, испытывает равную и противоположную силу. Обсудите, как это повлияет на измерение ускорения космонавта. Предложите способ предотвращения отдачи автомобиля.
5. На рисунке 3 чистая внешняя сила, действующая на косилку массой 24 кг, равна 51 Н. Если сила трения, противодействующая движению, равна 24 Н, какую силу F (в ньютонах) оказывает человек, воздействующий на косилка? Предположим, косилка движется со скоростью 1,5 м/с, когда сила F устранена.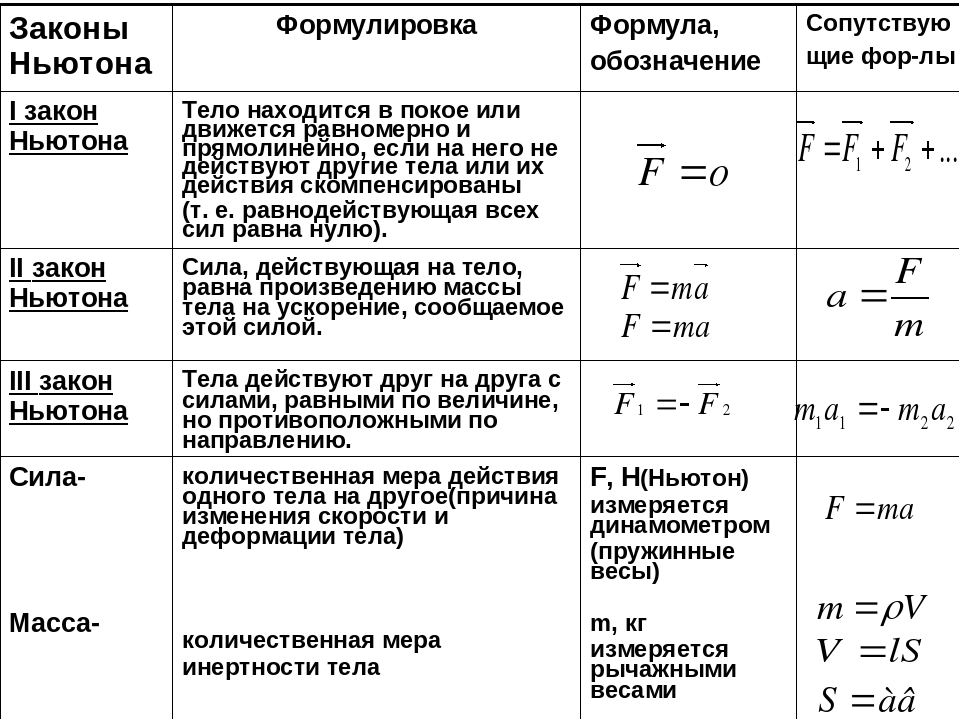
Какое расстояние пройдет косилка до остановки?
6. Те же ракетные салазки, изображенные на рис. 5, тормозятся со скоростью 196 м/с 2 . Какая сила необходима для создания этого торможения? Предположим, что ракеты выключены. Масса системы 2100 кг.
Рис. 5.
7. (a) Если ракетные салазки, показанные на рис. 6, стартуют с горящей только одной ракетой, какова величина ее ускорения? Предположим, что масса системы равна 2100 кг, тяга T равна 2,4 × 10 4 Н, а сила трения, противодействующая движению, известна и равна 650 Н. (б) Почему ускорение не составляет 1/4 от что это со всеми горящими ракетами?
Рис. 6.
8. Чему равно торможение салазок ракеты, если они остановятся за 1,1 с со скорости 1000 км/ч? (Такое замедление привело к тому, что один испытуемый потерял сознание и временно ослеп.)
9. Предположим, что двое детей толкают горизонтально, но точно в противоположных направлениях, третьего ребенка в тележке.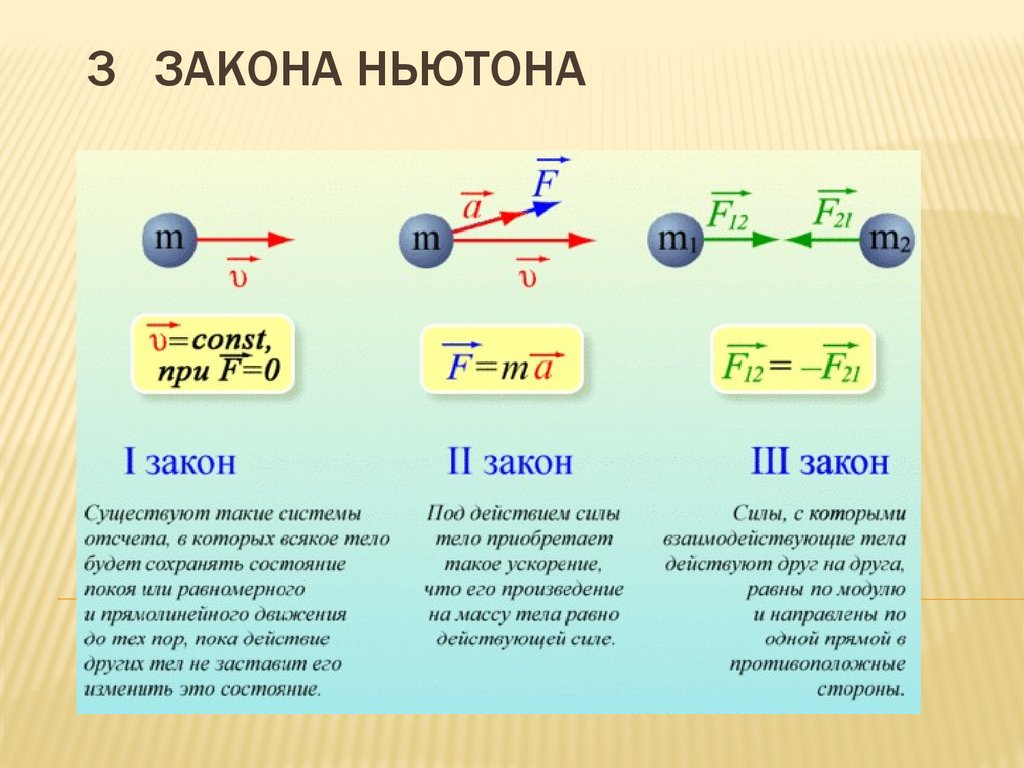
На первого ребенка действует сила 75,0 Н, на второго — 90,0 Н, сила трения — 12,0 Н, а масса третьего ребенка вместе с тележкой — 23,0 кг. а) Какова система процентов, если нужно рассчитать ускорение ребенка в тележке? (b) Нарисуйте диаграмму свободного тела, включая все силы, действующие на систему. в) Рассчитайте ускорение. г) Каким было бы ускорение, если бы трение было равно 15,0 Н? 9{2}\\3,50 м/с2
при движении со скоростью 90,0 км/ч. При этой скорости силы, препятствующие движению, включая трение и сопротивление воздуха, составляют в сумме 400 Н. (Сопротивление воздуха аналогично трению воздуха. Оно всегда противодействует движению объекта.) чтобы произвести его ускорение, если масса мотоцикла с водителем 245 кг?
11. Ракетные салазки, показанные на рисунке 8, разгоняются со скоростью 49,0 м/с 2 . Его пассажир имеет массу 75,0 кг. а) Рассчитайте горизонтальную составляющую силы, с которой сиденье действует на его тело. Сравните это с его весом, используя соотношение.
(b) Рассчитайте направление и величину общей силы, с которой сиденье действует на его тело.
Рис. 8.
12. Повторите предыдущую задачу для ситуации, когда салазки ракеты замедляются со скоростью 201 м/с 2 . В этой задаче силы действуют на ремни безопасности и ремни безопасности.
13. Вес космонавта плюс его скафандр на Луне всего 250 Н. Сколько они весят на Земле? Какова масса Луны? На земле?
14. Предположим, что масса полностью загруженного модуля, в котором космонавты взлетают с Луны, составляет 10 000 кг. Тяга его двигателей 30 000 Н. а) Рассчитайте величину его ускорения при вертикальном взлете с Луны. б) Мог ли он взлететь с Земли? Если нет, то почему? Если бы он мог, рассчитайте величину его ускорения.
Глоссарий
- ускорение:
- скорость изменения скорости объекта в течение определенного периода времени
- свободное падение:
- ситуация, в которой единственной силой, действующей на объект, является сила тяжести
- трение:
- сила, приложенная друг к другу соприкасающимися объектами; примеры включают шероховатые поверхности и сопротивление воздуха
- результирующая внешняя сила:
- векторная сумма всех внешних сил, действующих на объект или систему; заставляет массу двигаться с ускорением
- Второй закон Ньютона:
- результирующая внешняя сила F net действующая на объект с массой m пропорциональна и направлена в том же направлении, что и ускорение объекта, a , и обратно пропорциональна к массе; определяется математически как
a=Fnetm\mathbf{\text{a}}=\frac{{\mathbf{\text{F}}}_{\text{net}}}{m}\\a=mFnet
- система
- определяется границами объекта или совокупности наблюдаемых объектов; все силы, исходящие извне системы, считаются внешними силами
- вес
- сила w под действием силы тяжести, действующей на объект массой
ммм
; определяется математически как: w = mg , где g является величиной и направлением ускорения свободного падения
Избранные решения задач и упражнений
1.
265 N
3. 13,3 м/с 2
7. (a) 12 м/с 2 (b) Ускорение не составляет 1/4 от того, что было при горении всех ракет из-за трения сила все еще такая же большая, как и при сжигании всех ракет.
9. (a) Система – это ребенок в повозке плюс повозка.
Рисунок 9
(б)
(в) а = 0,130 м/с 2 в направлении толчка второго ребенка.
(г) а = 0,00 м/с 2
11. (a) 3,68 × 10 3 Н. Эта сила в 5,00 раз больше его веса. (б) 3750 Н; 11,3º над горизонталью
13. 1,5 × 10 3 Н, 150 кг, 150 кг
Лицензии и атрибуты
Контент, лицензированный CC, ранее опубликованный
- College Physics. Автор: : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/college-physics/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units. Лицензия : CC BY: Attribution . Условия лицензии : Находится в лицензии
Лицензия : CC BY: Attribution . Условия лицензии : Находится в лицензииУравнение движения Ньютона: вывод, определение, формула, примеры
Уравнение движения Ньютона является основой классической механики. Для всех макроскопических тел, движущихся со скоростью, значительно меньшей скорости света, анализ движения проводится с помощью уравнения движения Ньютона. В этой статье мы узнаем об этих законах и их выводах, а также о практических проблемах. 92+2as \end{align}\)
Где V — конечная скорость, u — начальная скорость, S — смещение, a — ускорение, t — затраченное время.
Посмотрим, как мы их получили.
Чтобы получить подробную информацию о кинетической теории газов, кандидаты могут посетить статью по ссылке.
Содержание
- Вывод уравнения движения расчетным методом
- Первое уравнение движения
- Второе уравнение движения
- Третье уравнение движения
- Вывод уравнения движения с помощью алгебрического метода
- Первое уравнение движения
- Второе уравнение движения
- Третье уравнение движения
- Вывод уравнения движения с помощью графического метода
- Первое уравнение движения движения
- второе уравнение движения
- третье уравнение движения0606
Давайте посмотрим на вывод уравнения движения методом исчисления.
2) \над 2а}\)V2 – u2 = 2 a S
Ознакомьтесь со статьей о равномерном круговом движении здесь.
Вывод уравнения движения алгебраическим методомРассмотрим вывод уравнения движения алгебраическим методом.
Первое уравнение движенияМы знаем, что ускорение тела определяется как скорость изменения скорости за период времени, который может быть задан как
\(\text {Ускорение (a) }={(v-u)\over{t}}\)
где v = конечная скорость, u = начальная скорость и t = затраченное время
Преобразовав приведенное выше уравнение, мы получили первое уравнение движения: деталь.
Второе уравнение движенияРассмотрим тело, движущееся с начальной скоростью «u» под действием постоянного ускорения «a». Через время «t» скорость тела становится «v», а перемещение — «s».
Мы знаем, что скорость определяется как скорость изменения смещения.
Математически это представляется как:
\({\text{Скорость}}={\text{Смещение}\over{\text{время}}}\)
После перестановки получаем смещение (с) , который является произведением скорости и периода времени (t), когда скорость постоянна.
Перемещение = скорость x время Если скорость непостоянна, то мы можем использовать среднюю скорость вместо скорости в приведенном выше уравнении и переписать уравнение следующим образом: 92\)
Проверьте питание в цепи переменного тока, чтобы узнать подробности здесь.
Третье уравнение движенияМы знаем, что смещение — это скорость изменения положения объекта {t}\)
Теперь из первого уравнения движения мы знаем, что-
v=u+at Преобразовывая вышеприведенную формулу,
получаем \(t={v-u\over{a}}\)
Теперь, подставив это значение ‘t’ в формулу перемещения, мы получим следующее уравнение: 92+2as\)
Прочитайте об атоме и ядрах здесь.
Вывод уравнения движения графическим методомРассмотрим вывод уравнения движения графическим методом.
Первое уравнение движенияс графика
V = BD + DC
DC = OA
V = BD + OA
OA = U
V = BD + UA
AA = U
V = BD + UA
AA = U
V = BD + UA
AA = U
V = BD + UA
AA = U
V = BD + UA
AA = U
V = BD + UA
AA = U
V = BD + UA
.
наклон линии ABa = BD/AD
92\) Третье уравнение движенияИз графика
Перемещение, с определяется площадью трапеции OABC.
Следовательно,
\(s={1\over2}\text{(Сумма параллельных сторон)}\times{Высота}\)
s=(OA+CB)×OC
Из графика OA = u, CB = v и OC = t
\(\следовательно{s={1\over2}(u+v)\times{t}}\)
\(t={(v–u) \over{a}}\)
\(\следовательно{s={1\over2}(u+v)\times{{(v–u)\over{a}}}}\)
После перестановки получаем, 92\)
Приведенные выше три уравнения движения справедливы только для постоянного ускорения частицы. Если есть переменное ускорение, то мы не можем использовать эти уравнения для расчетов.
Надеюсь, эта статья помогла вам понять три закона движения Ньютона. Для получения дополнительных практических задач попробуйте наше бесплатное приложение Testbook. Скачать сейчас.
Часто задаваемые вопросы об уравнении движения Ньютона
В.
1 Что такое уравнения движения Ньютона? 92+2as\)Q.5 Каковы ограничения уравнения движения Ньютона?
Ответ 5 Их нельзя использовать для микроскопических тел. Они неприменимы для тел, имеющих скорость, близкую к скорости света.
Скачать публикацию в формате PDFЕще на testbook.com
Векторная алгебра: изучите определения, свойства, формулы и приложения на примерах! Горные породы Примечания: значение, типы – магматические, осадочные и метаморфические породы Внутренняя структура Земли: кора, мантия и ядро Отношения и функции: изучите типы, свойства, операции, сопоставления на примерах! Компьютерные сети: TCP/UDP и контроль перегрузки сокетов связывать движение с силами, его вызывающими. Обратите внимание, что слово «сила» не всегда используется явно в постановке задачи. Вы знаете много сил, таких как гравитация, напряжение и нормальная сила, которые присутствуют, даже если они не указаны в задаче. Примеры проблем
1Д
- Объект на веревке
- Видимый вес в лифте
2Д
- Коробка с трением
- Объект на склоне без трения
- Объект на склоне
- Восхождение по лестнице
Несколько объектов
- Ящики штабелированные с трением
- Два блока, связанных вместе
- Подвесной светильник
Циркуляр
- Объект в горизонтальном круге
- Автомобиль на вираже
Выталкивающая сила
- Кажущийся вес в жидкости
- Лодка с грузом
Составной
- Тормозной путь
- Вертикальный круг
- Горная дорога
- Ускоряющая карусель
Электричество и магнетизм
- Задача об электричестве: заряд пробкового шарика
- Задача о магнитной силе: движение заряда в магнитном поле
Как решить проблемы с силой
1.
Определите проблемуЛюбая задача, требующая соотнесения силы и движения, является задачей второго закона Ньютона, независимо от того, что было дано или запрошено в задаче . В некоторых случаях второй закон Ньютона легко определить — например, в задаче вас могут попросить указать значение определенной силы.
В других случаях труднее распознать проблемы со 2-м законом. Вы можете знать силы, которые присутствуют, но никогда не упоминали силу в задаче, и вас могут спросить о таких вещах, как скорость движения объекта по кругу или какая часть объекта находится под водой. Понимание того, как подходить к этим проблемам, приходит с опытом — уделение времени ответу на вопрос «откуда я узнал, что это проблема 2-го закона» для каждого отдельного примера силы, с которым вы работаете, поможет развить ту интуицию, которая понадобится вам на выпускном экзамене. .
2. Нарисуй картинку
Когда вы подходите к силовым задачам, диаграмма свободного тела позволит вам представить себе происходящее и напрямую отразить эту картину в уравнении.
Вся физика делается в процессе рисования диаграммы — после этого шага остается только алгебра.Первое, что вам нужно сделать, это определить какие объекты будут в центре внимания диаграммы, другими словами, какую систему вам нужно рассмотреть, чтобы ответить на вопрос. В некоторых случаях потребуется рассматривать несколько объектов как отдельные системы. В этих случаях вы будете рисовать бесплатные диаграммы тела и составлять уравнения для каждого объекта отдельно. Скорее всего, вы воспользуетесь третьим законом Ньютона, чтобы связать силы, действующие на два объекта.
После того, как вы идентифицировали свою систему, подумайте обо всех силах в этой системе, отбросьте те, которые слишком малы, чтобы иметь значение. Только заставляет воздействовать на объект, так как вы пытаетесь понять, что вызывает движение объекта. Диаграмма свободного тела отображается непосредственно в левой части ∑F=ma. Ускорение — это результат, а не причина — если вы хотите нарисовать ускорение, убедитесь, что вы делаете это сбоку, а не на рисунке сил.
Поскольку второй закон Ньютона представляет собой векторное уравнение, вам потребуется разделить все силы на их x- и y-компоненты, чтобы работать с уравнением. Математика всегда проще всего, если вы выберете одну ось вдоль направления ускорения . Таким образом, один компонент a будет равен нулю, и у вас будет меньше связанных уравнений.
3. Выберите связь
Все задачи о силе начинаются с соотношения ∑F=ma. Это верно независимо от того, что вас просят найти. Если потребуется какая-либо дополнительная информация, она станет очевидной по мере решения проблемы.
4. Решить проблему
∑F=ma является векторным уравнением, поэтому задается отдельно в направлениях x и y. Тщательно подумайте о направлении каждой силы и включите соответствующий знак. После того, как вы вложили свои силы в эти уравнения, у вас осталась только алгебра, и вы можете решать уравнения любым удобным для вас способом. В общем, проще всего сначала решить уравнение, в котором a=0, так как иногда вам понадобятся эти значения в другом выражении.
5. Понимание результатов
После того, как вы решите задачу, посмотрите на нее еще раз. Ваш ответ имеет смысл? Дало ли это поведение, которое вы интуитивно ожидали найти? Можете ли вы теперь сделать шаги, которые раньше вызывали у вас проблемы? Можете ли вы объяснить словами, что происходит? Если вы распознали это как проблему 2-го закона только из-за заголовка раздела в вашем учебнике, определите информацию, которую вы использовали бы, чтобы распознать подобную задачу на выпускном экзамене.
Помогите! Я не могу найти пример, похожий на проблему, с которой мне нужно работать!
Вы уверены, что ваша проблема относится ко второму закону Ньютона?
Одна из самых распространенных ошибок — слишком много думать. Если вам говорят о чистой силе и просят об ускорении или наоборот, вам не нужно проходить все этапы решения задачи второго закона Ньютона. Проверьте проблемы с определением и соотношением, чтобы увидеть, сможете ли вы найти полезный пример.
Также возможно, что вашу задачу лучше решить с помощью кинематики (описание движения) или энергии и импульса. Можете ли вы ясно объяснить себе, что ваша проблема требует от вас соотнесения причины движения (сил) с действием этих сил (ускорение или изменение скорости?)
Да, моя проблема определенно относится ко второму закону Ньютона.
В таком случае подумайте шире о том, что делает пример полезным. Помните, вам дали задание на практикуйте подход к решению проблем не потому, что ответы на ваши проблемы особенно интересны. Пример, в котором вы просто заменяете числа в задаче своими числами, даст вам возможность попрактиковаться в вводе чисел на калькуляторе, но ничему не научит вас по физике, и когда вы будете сдавать экзамен, каждая задача на нем будет казаться вам новой и необычной. Поэтому подумайте о своем примере как о поддержке, которая поможет вам практиковать подход к решению проблем.
И каждая отдельная проблема в этом разделе использует один и тот же подход, поэтому любая проблема является подходящим примером, который поможет вам решить вашу проблему.
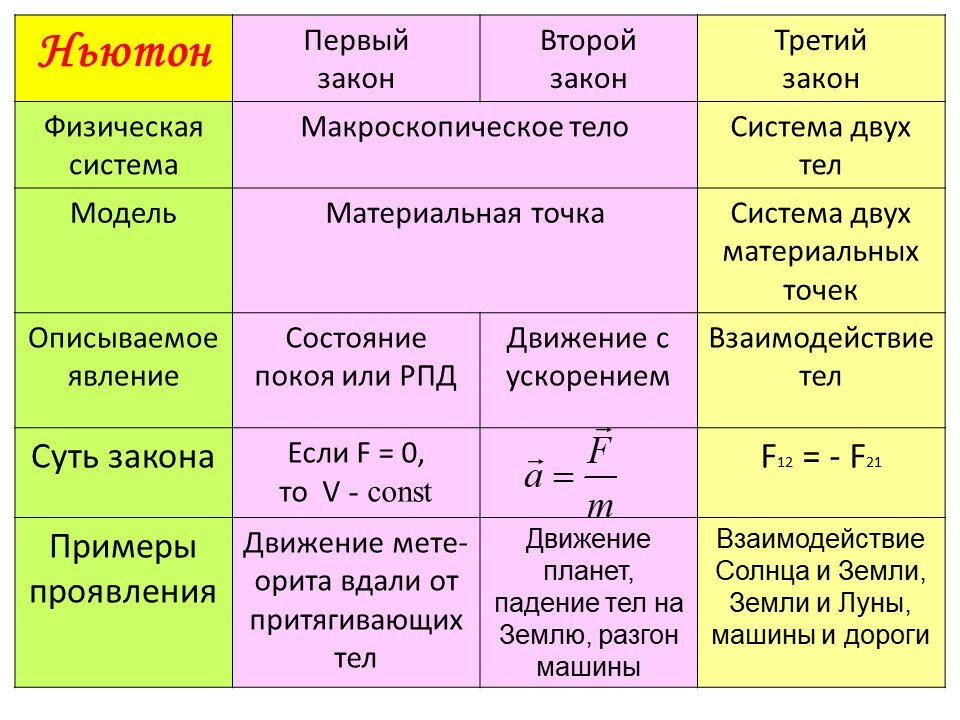2) \над 2а}\)
наклон линии AB
1 Что такое уравнения движения Ньютона? 92+2as\)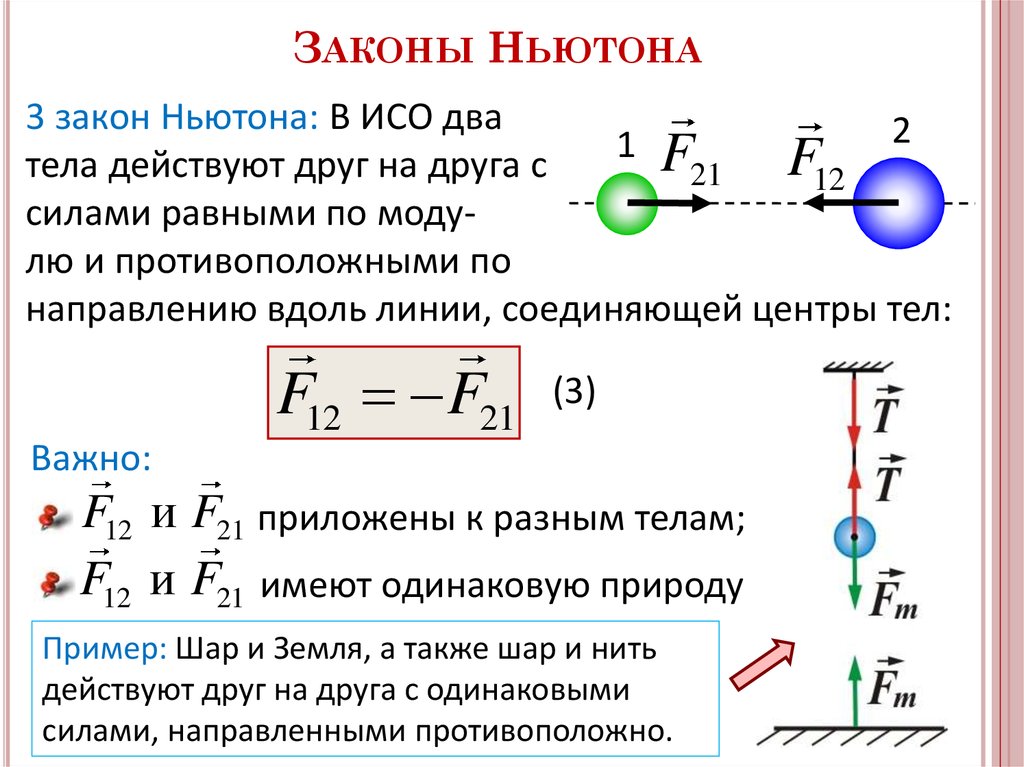
Определите проблему
Вся физика делается в процессе рисования диаграммы — после этого шага остается только алгебра.
