Формула ньютона лейбница вычисления определенного интеграла. Определённый интеграл и методы его вычисления
Определённым интегралом от непрерывной функции f (x ) на конечном отрезке [a , b ] (где ) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись
Как видно на графиках внизу (приращение первообразной функции обозначено ), определённый интеграл может быть как положительным, так и отрицательным числом (Вычисляется как разность между значением первообразной в верхнем пределе и её же значением в нижнем пределе, т. е. как F (b ) – F (a )).
Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a , b ] – отрезком интегрирования.
Таким образом, если F (x ) – какая-нибудь первообразная функция для f (x ), то, согласно определению,
(38)
Равенство (38) называется
 Разность F (b ) – F (a ) кратко записывают так:
Разность F (b ) – F (a ) кратко записывают так:Поэтому формулу Ньютона-Лейбница будем записывать и так:
(39)
Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F (x ) и Ф(х ) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х ) = F (x ) + C . Поэтому
Тем самым установлено, что на отрезке [
Таким образом, для вычисления
определённого интеграла необходимо найти любую первообразную подынтегральной
функции, т.е. сначала следует найти неопределённый интеграл. Постоянная С из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница:
в первообразную функцию подставляется значение верхнего предела b , далее – значение
нижнего предела a и вычисляется разность F(b) – F(a) . Полученное число и будет
определённым интегралом.
.
Полученное число и будет
определённым интегралом.
.
При a = b по определению принимается
Пример 1.
Решение. Сначала найдём неопределённый интеграл:
Применяя формулу Ньютона-Лейбница к первообразной
(при С = 0), получим
Однако при вычислении определённого интеграла лучше не находить отдельно первообразную, а сразу записывать интеграл в виде (39).
Пример 2. Вычислить определённый интеграл
Решение. Используя формулу
Свойства определённого интеграла
Теорема 2. Величина определённого интеграла не зависит от обозначения переменной интегрирования , т.е.
(40)
Пусть F (x ) – первообразная для f (x ). Для f (t ) первообразной служит та же функция
На основании формулы (39) последнее равенство означает равенство интегралов
Теорема 3. Постоянный множитель можно выносить за знак определённого интеграла , т.е.
Постоянный множитель можно выносить за знак определённого интеграла , т.е.
(41)
Теорема 4. Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций , т.е.
(42)
Теорема 5. Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям
(43)
Теорема 6. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак , т.е.
(44)
Теорема 7 (теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке внутри его , т.е.
(45)
Теорема 8. Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.
Теорема 9. Если верхний предел интегрирования больше нижнего и функции и непрерывны, то неравенство
можно почленно интегрировать , т.е.
(46)
Свойства определённого интеграла позволяют упрощать непосредственное вычисление интегралов.
Пример 5. Вычислить определённый интеграл
Используя теоремы 4 и 3, а при нахождении первообразных – табличные интегралы (7) и (6), получим
Определённый интеграл с переменным верхним пределом
Пусть f (x ) – непрерывная на отрезке [a , b ] функция, а F (x ) – её первообразная. Рассмотрим определённый интеграл
(47)
а через
 е.
е.(48)
Докажем, что функция Ф (х ) является первообразной для f (x ) = f (t ). Действительно, дифференцируя Ф (х ), получим
так как F (x ) – первообразная для f (x ), а F (a ) – постояная величина.
Функция Ф (
Вычисление определённых интегралов методом интегрирования по частям и методом замены переменной
где, по определению, F (x ) – первообразная для f (x ). Если в подынтегральном выражении произвести замену переменной
то в соответствии с формулой (16) можно записать
В этом выражении
первообразная функция для
В самом деле, её производная, согласно правилу дифференцирования сложной функции , равна
Пусть α и β – значения переменной
принимает соответственно значения a и b , т. е.
е.
Но, согласно формуле Ньютона-Лейбница, разность F (b ) – F (a ) есть
1 из 30
№ слайда 1
Описание слайда:
№ слайда 2
Описание слайда:
№ слайда 3
Описание слайда:
№ слайда 4
Описание слайда:
Ньютон и Лейбниц Из сохранившихся документов историки науки выяснили, что дифференциальное и интегральное исчисление Ньютон открыл ещё в 1665-1666 годы, однако не публиковал его до 1704 года. Лейбниц разработал свой вариант анализа независимо (с 1675 года), хотя первоначальный толчок, вероятно, его мысль получила из слухов о том, что такое исчисление у Ньютона уже имеется, а также благодаря научным беседам в Англии и переписке с Ньютоном. В отличие от Ньютона, Лейбниц сразу опубликовал свою версию, и в дальнейшем, вместе с Якобом и Иоганном Бернулли, широко пропагандировал это эпохальное открытие по всей Европе. Большинство учёных на континенте не сомневались, что анализ открыл Лейбниц.
Лейбниц разработал свой вариант анализа независимо (с 1675 года), хотя первоначальный толчок, вероятно, его мысль получила из слухов о том, что такое исчисление у Ньютона уже имеется, а также благодаря научным беседам в Англии и переписке с Ньютоном. В отличие от Ньютона, Лейбниц сразу опубликовал свою версию, и в дальнейшем, вместе с Якобом и Иоганном Бернулли, широко пропагандировал это эпохальное открытие по всей Европе. Большинство учёных на континенте не сомневались, что анализ открыл Лейбниц.
№ слайда 5
Описание слайда:
Вняв уговорам друзей, взывавших к его патриотизму, Ньютон во 2-й книге своих «Начал» (1687) сообщил:В письмах, которыми около десяти лет тому назад я обменивался с весьма искусным математиком г-ном Лейбницем, я ему сообщал, что обладаю методом для определения максимумов и минимумов, проведения касательных и решения тому подобных вопросов, одинаково приложимых как для членов рациональных, так и для иррациональных, причем я метод скрыл, переставив буквы следующего предложения: «когда задано уравнение, содержащее любое число текущих количеств, найти флюксии и обратно».
№ слайда 6
Описание слайда:
В 1693 году, когда Ньютон наконец опубликовал первое краткое изложение своей версии анализа, он обменялся с Лейбницем дружескими письмами. Ньютон сообщил:Наш Валлис присоединил к своей «Алгебре», только что появившейся, некоторые из писем, которые я писал к тебе в своё время. При этом он потребовал от меня, чтобы я изложил открыто тот метод, который я в то время скрыл от тебя переставлением букв; я сделал это коротко, насколько мог. Надеюсь, что я при этом не написал ничего, что было 6ы тебе неприятно, если же это случилось, то прошу сообщить, потому что друзья мне дороже математических открытий.
№ слайда 7
Описание слайда:
После появления первой подробной публикации ньютонова анализа (математическое приложение к «Оптике», 1704) в журнале Лейбница «Acta eruditorum» появилась анонимная рецензия с оскорбительными намёками в адрес Ньютона. Рецензия ясно указывала, что автором нового исчисления является Лейбниц. Сам Лейбниц решительно отрицал, что рецензия составлена им, но историки сумели найти черновик, написанный его почерком. Ньютон проигнорировал статью Лейбница, но его ученики возмущённо ответили, после чего разгорелась общеевропейская приоритетная война, «наиболее постыдная склока во всей истории математики».
Рецензия ясно указывала, что автором нового исчисления является Лейбниц. Сам Лейбниц решительно отрицал, что рецензия составлена им, но историки сумели найти черновик, написанный его почерком. Ньютон проигнорировал статью Лейбница, но его ученики возмущённо ответили, после чего разгорелась общеевропейская приоритетная война, «наиболее постыдная склока во всей истории математики».
№ слайда 8
Описание слайда:
31 января 1713 года Королевское общество получило письмо от Лейбница, содержащее примирительную формулировку: он согласен, что Ньютон пришёл к анализу самостоятельно, «на общих принципах, подобных нашим». Рассерженный Ньютон потребовал создать международную комиссию для прояснения приоритета. Комиссии не понадобилось много времени: спустя полтора месяца, изучив переписку Ньютона с Ольденбургом и другие документы, она единогласно признала приоритет Ньютона, причём в формулировке, на этот раз оскорбительной в отношении Лейбница. Решение комиссии было напечатано в трудах Общества с приложением всех подтверждающих документов
№ слайда 9
Описание слайда:
В ответ с лета 1713 года Европу наводнили анонимные брошюры, которые отстаивали приоритет Лейбница и утверждали, что «Ньютон присваивает себе честь, принадлежащую другому». Брошюры также обвиняли Ньютона в краже результатов Гука и Флемстида. Друзья Ньютона, со своей стороны, обвинили в плагиате самого Лейбница; по их версии, во время пребывания в Лондоне (1676) Лейбниц в Королевском обществе ознакомился с неопубликованными работами и письмами Ньютона, после чего изложенные там идеи Лейбниц опубликовал и выдал за свои.Война не ослабевала до декабря 1716 года, когда аббат Конти сообщил Ньютону: «Лейбниц умер – диспут окончен
Брошюры также обвиняли Ньютона в краже результатов Гука и Флемстида. Друзья Ньютона, со своей стороны, обвинили в плагиате самого Лейбница; по их версии, во время пребывания в Лондоне (1676) Лейбниц в Королевском обществе ознакомился с неопубликованными работами и письмами Ньютона, после чего изложенные там идеи Лейбниц опубликовал и выдал за свои.Война не ослабевала до декабря 1716 года, когда аббат Конти сообщил Ньютону: «Лейбниц умер – диспут окончен
№ слайда 10
Описание слайда:
№ слайда 11
Описание слайда:
№ слайда 12
Описание слайда:
Зададим произвольное значение x € (a.b) и определим новую функцию Она определена для всех значений x € (a.b) , потому что мы знаем, что если существует интеграл от ʄ на (a,b) , то существует также интеграл от ʄ на (a,b) , где Напомним, что мы считаем по определению
№ слайда 13
Описание слайда:
№ слайда 14
Описание слайда:
Таким образом, F непрерывна на (a,b) независимо от того, имеет или не имеет ʄ разрывы; важно, что ʄ интегрируема на (a,b)На рисунке изображен график ʄ . Площадь переменной фигуры aABx равна F (X) Ее приращение F (X+h)-F(x) равно площади фигуры xBC(x+h) , которая в силу Ограниченности ʄ очевидно, стремится к нулю при h→ 0 независимо от того, будет ли x точкой непрерывности или разрыва ʄ например точкой x-d
Площадь переменной фигуры aABx равна F (X) Ее приращение F (X+h)-F(x) равно площади фигуры xBC(x+h) , которая в силу Ограниченности ʄ очевидно, стремится к нулю при h→ 0 независимо от того, будет ли x точкой непрерывности или разрыва ʄ например точкой x-d
№ слайда 15
Описание слайда:
№ слайда 16
Описание слайда:
№ слайда 17
Описание слайда:
Переход к пределу в при h→0 показывает существование производной от F в точке и справедливость равенства. При x=a,b речь здесь идет соответственно о правой и левой производной. Если функция ʄ непрерывна на (a,b) , то на основании доказанного выше соответствующая ей функция имеет производную, равнуюСледовательно, функция F(x) есть первообразная для ʄ (a,b)
№ слайда 18
Описание слайда:
Мы доказали, что произвольная непрерывная на отрезке (a,b) функция ʄ имеет на этом отрезке первообразную, определенную равенством.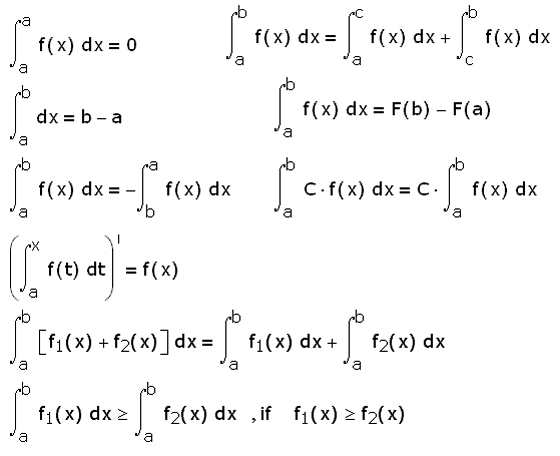 Этим доказано существование первообразной для всякой непрерывной на отрезке функции. Пусть теперь есть произвольная первообразная функции ʄ(x) на (a,b) . Мы знаем, что Где C – некоторая постоянная. Полагая в этом равенстве x=a и учитывая, что F(a)=0 получим Ф(a)=C Таким образом, Но
Этим доказано существование первообразной для всякой непрерывной на отрезке функции. Пусть теперь есть произвольная первообразная функции ʄ(x) на (a,b) . Мы знаем, что Где C – некоторая постоянная. Полагая в этом равенстве x=a и учитывая, что F(a)=0 получим Ф(a)=C Таким образом, Но
№ слайда 19
Описание слайда:
№ слайда 20
Описание слайда:
Интеграл Интеграл функции – естественный аналог суммы последовательности. Согласно основной теореме анализа, интегрирование – операция, обратная к дифференцированию. Процесс нахождения интеграла называется интегрированием.Существует несколько различных определений операции интегрирования, отличающиеся в технических деталях. Однако все они совместимы, то есть любые два способа интегрирования, если их можно применить к данной функции, дадут один и тот же результат.
№ слайда 21
Описание слайда:
№ слайда 22
Описание слайда:
История Знаки интеграла ʃ дифференцирования dx были впервые использованы Лейбницем в конце XVII века. Символ интеграла образовался из буквы S – сокращения слова лат. summa (сумма). Интеграл в древностиИнтегрирование прослеживается ещё в древнем Египте, примерно в 1800 до н. э., Московский математический папирус демонстрирует знание формулы объёма усечённой пирамиды. Первым известным методом для расчёта интегралов является метод исчерпывания Евдокса (примерно 370 до н. э.), который пытался найти площади и объёмы, разрывая их на бесконечное множество частей, для которых площадь или объём уже известны. Этот метод был подхвачен и развит Архимедом, и использовался для расчёта площадей парабол и приближенного расчёта площади круга. Аналогичные методы были разработаны независимо в Китае в 3-м веке н.э Лю Хуэйем, который использовал их для нахождения площади круга. Этот метод был впоследствии использован Дзю Чонгши для нахождения объёма шара.
Символ интеграла образовался из буквы S – сокращения слова лат. summa (сумма). Интеграл в древностиИнтегрирование прослеживается ещё в древнем Египте, примерно в 1800 до н. э., Московский математический папирус демонстрирует знание формулы объёма усечённой пирамиды. Первым известным методом для расчёта интегралов является метод исчерпывания Евдокса (примерно 370 до н. э.), который пытался найти площади и объёмы, разрывая их на бесконечное множество частей, для которых площадь или объём уже известны. Этот метод был подхвачен и развит Архимедом, и использовался для расчёта площадей парабол и приближенного расчёта площади круга. Аналогичные методы были разработаны независимо в Китае в 3-м веке н.э Лю Хуэйем, который использовал их для нахождения площади круга. Этот метод был впоследствии использован Дзю Чонгши для нахождения объёма шара.
№ слайда 23
Описание слайда:
Историческое значение и философский смысл формулы Ньютона-Лейбница Одним из важнейших исследовательских инструментов этого ряда является формула Ньютона-Лейбница, и стоящий за ней метод нахождения первообразной функции путем интегрирования ее производной. Историческое значение формулы в использовании бесконечно малых величин и абсолютно точном ответе на поставленный вопрос. Общеизвестны преимущества применения этого метода для решения математических, физических и прочих естественнонаучных задач, например, классической задачи о квадратуре круга – построении квадрата равновеликого заданному кругу. Философский смысл – в возможности получения информации о целом по его бесконечно малой части, замеченный ранее – наглядно реализуется в медицине и биологии, примером чему могут служить успехи генной инженерии в клонировании – создании взаимоподобных живых существ. Редким исключением в перечне наук, воспользовавшихся формулой Ньютона-Лейбница, остается история. Невозможность представления информации исторических источников в виде цифр – аргументов формулы – традиционна. Таким образом, до сих пор философский смысл формулы является не совсем философским, так как реализуется лишь в естественнонаучном знании, оставляя социально-гуманитарное знание без столь мощного инструмента.
Историческое значение формулы в использовании бесконечно малых величин и абсолютно точном ответе на поставленный вопрос. Общеизвестны преимущества применения этого метода для решения математических, физических и прочих естественнонаучных задач, например, классической задачи о квадратуре круга – построении квадрата равновеликого заданному кругу. Философский смысл – в возможности получения информации о целом по его бесконечно малой части, замеченный ранее – наглядно реализуется в медицине и биологии, примером чему могут служить успехи генной инженерии в клонировании – создании взаимоподобных живых существ. Редким исключением в перечне наук, воспользовавшихся формулой Ньютона-Лейбница, остается история. Невозможность представления информации исторических источников в виде цифр – аргументов формулы – традиционна. Таким образом, до сих пор философский смысл формулы является не совсем философским, так как реализуется лишь в естественнонаучном знании, оставляя социально-гуманитарное знание без столь мощного инструмента. Хотя, если придерживаться традиционных особенностей социально-гуманитарного знания, его так сказать, слабостей, то и по делом ему.
Хотя, если придерживаться традиционных особенностей социально-гуманитарного знания, его так сказать, слабостей, то и по делом ему.
№ слайда 24
Описание слайда:
Но дальнейший научный анализ дает в наше время новую, иную картину происходящего процесса. Ныне господствующие в науке атомистические воззрения разлагают материю на кучу мельчайших частиц или правильно расположенных центров сил, находящихся в вечных разнообразных движениях. Точно так же и проникающий материю эфир постоянно возбуждается и волнообразно колеблется. Все эти движения материи и эфира находятся в теснейшей и непрерывной связи с бесконечным для нас мировым пространством. Такое представление, недоступное нашему конкретному воображению, вытекает из данных физики.
№ слайда 25
Описание слайда:
Даже мистические и магические течения должны считаться с этим положением, хотя они могут, придав иной смысл понятию времени, совершенно уничтожить значение этого факта в общем миросозерцании. Таким образом, пока вопрос касается явлений, воспринимаемых органами чувств, даже эти наиболее далекие от точного знания области философии и религии должны считаться с научно доказанным фактом, как они должны считаться с тем, что дважды два – четыре в той области, которая подлежит ведению чувств и разума.
Таким образом, пока вопрос касается явлений, воспринимаемых органами чувств, даже эти наиболее далекие от точного знания области философии и религии должны считаться с научно доказанным фактом, как они должны считаться с тем, что дважды два – четыре в той области, которая подлежит ведению чувств и разума.
№ слайда 26
Описание слайда:
Вместе с тем объема накопленных человечеством знаний уже вполне достаточно для того, что бы эту традицию нарушить. В самом деле, нет необходимости на пифагорейский лад искать цифровое соответствие высказываниям «Петр I посетил Венецию во время Великого посольства» и «Петр I не был в Венеции во время Великого посольства», когда сами эти выражения легко могут служить аргументами алгебры логики Джорджа Буля. Результат каждого исторического исследования по сути и есть набор таких аргументов. Таким образом, оправдано, на мой взгляд, использование в качестве подинтегральной функции набора исторических исследований, представленных в виде аргументов алгебры логики, с целью соответствующего получения в качестве первообразной – наиболее вероятной реконструкции исследуемого исторического события. На этом пути есть много проблем. В частности: представление конкретного исторического исследования – производной реконструируемого события – в виде набора логических выражений – операция заведомо более сложная, чем, например, электронная каталогизация простого библиотечного архива. Однако информационный прорыв конца XX – начала XXI века (чрезвычайно высокая степень интегрированности элементной базы и увеличение мощности информационных) делают выполнение такой задачи вполне реальным.
На этом пути есть много проблем. В частности: представление конкретного исторического исследования – производной реконструируемого события – в виде набора логических выражений – операция заведомо более сложная, чем, например, электронная каталогизация простого библиотечного архива. Однако информационный прорыв конца XX – начала XXI века (чрезвычайно высокая степень интегрированности элементной базы и увеличение мощности информационных) делают выполнение такой задачи вполне реальным.
№ слайда 27
Описание слайда:
В свете вышесказанного, на современном этапе исторический анализ представляет собой математический анализ с теорией вероятности и алгеброй логики, а искомая первообразная функция – вероятность исторического события, что в целом вполне соответствует и даже дополняет представление о науке на современном этапе, ибо замена понятия сущность понятием функция – главное в понимании науки в Новое время – дополняется оценкой этой функции. Следовательно, современное историческое значение формулы в возможности претворения в жизнь мечты Лейбница «о том времени, когда два философа вместо бесконечных споров будут подобно двум математикам брать перья в руки и, засаживаясь за стол, заменять спор вычислением» . Каждое историческое исследование – заключение имеет право на существование, отражает реально происходившее событие и дополняет информационную историческую картину. Опасность вырождения исторической науки в набор бесцветных фраз-утверждений – результата применения предлагаемого метода, не больше опасности вырождения музыки в набор звуков, а живописи в набор красок на современном этапе развития человечества. Таким видится мне новый философский смысл формулы Ньютона-Лейбница, приведенной впервые в конце XVII – начале XVIII вв.
Каждое историческое исследование – заключение имеет право на существование, отражает реально происходившее событие и дополняет информационную историческую картину. Опасность вырождения исторической науки в набор бесцветных фраз-утверждений – результата применения предлагаемого метода, не больше опасности вырождения музыки в набор звуков, а живописи в набор красок на современном этапе развития человечества. Таким видится мне новый философский смысл формулы Ньютона-Лейбница, приведенной впервые в конце XVII – начале XVIII вв.
№ слайда 28
Описание слайда:
Собственно же формулу, ввиду особенности восприятия математических символов носителями социально-гуманитарного знания, выражающуюся в панической боязни этими носителями любого представления таковых знаков, приведем в словесной форме: определенный интеграл производной функции есть первообразная этой функции. Некоторое формальное отличие приводимого примера задачи о квадратуре круга от обычного учебно-математического примера вычисления площади, расположенной под произвольной кривой в декартовой системе координат, не меняет, естественно, сути.
№ слайда 29
Описание слайда:
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА: 1. Бродский И.А. Сочинения в четырех томах. Т.3. СПб., 1994. 2. Вернадский В.И. Биосфера и ноосфера. М., 2003. 3. Вундт, Вильгельм. Введение в философию. М., 2001. 4. Гайденко П.П. Эволюция понятия науки. М., 1980. 5. Декарт, Рене. Размышления о первоначальной философии. СПб., 1995. 6. Карпов Г.М. Великое посольство Петра I. Калининград, 1998. 7. Кунцман П., Буркард Ф.-П., Видман Ф. Философия: dtv-Atlas. М., 2002. 8. Малаховский В.С. Избранные главы истории математики. Калининград, 2002. 9. Натансон И.П. Краткий курс высшей математики. СПб., 2001. 10. Энгельс Ф. Анти-Дюринг. М., 1988. 11. Шереметевский В.П. Очерки по истории математики. М., 2004 Интернет ресурсы http://ru.wikipedia.org
№ слайда 30
Описание слайда:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts. google.com
google.com
Подписи к слайдам:
Интеграл. Формула Ньютона – Лейбница. составитель: преподаватель математики ГОУНПО ПУ № 27 п. Щельяюр Семяшкина Ирина Васильевна
Цель урока: Ввести понятие интеграла и его вычисление по формуле Ньютона – Лейбница, используя знания о первообразной и правила её вычисления; Проиллюстрировать практическое применение интеграла на примерах нахождения площади криволинейной трапеции; Закрепить изученное в ходе выполнения упражнений.
Определение: Пусть дана положительная функция f(x) , определенная на конечном отрезке [ a;b ] . Интегралом от функции f(x) на [ a;b ] называется площадь её криволинейной трапеции. y=f(x) b a 0 x y
Обозначение: «интеграл от a до b эф от икс дэ икс »
Историческая справка: Обозначение интеграла Лейбниц произвёл от первой буквы слова «Сумма» (Summa). Ньютон в своих работах не предложил альтернативной символики интеграла, хотя пробовал различные варианты. Сам термин интеграл придумал Якоб Бернулли. S umma Исаак Ньютон Готфрид Вильгельм фон Лейбниц Якоб Бернулли
S umma Исаак Ньютон Готфрид Вильгельм фон Лейбниц Якоб Бернулли
Обозначение неопределённого интеграла ввёл Эйлер. Жан Батист Жозеф Фурье Леонард Эйлер Оформление определённого интеграла в привычном нам виде придумал Фурье.
Формула Ньютона – Лейбница
Пример 1. Вычислить определённый интеграл: = Решение:
Пример 2. Вычислите определённые интегралы: 5 9 1
Пример 3 . S y x Вычислить площадь фигуры, ограниченной линиями и осью абсцисс. Для начала найдем точки пересечения оси абсцисс с графиком функции. Для этого решим уравнение. = Решение: S =
y x S A B D C Пример 4 . Вычислить площадь фигуры, ограниченной линиями и Найдём точки пересечения (абсциссы) этих линий, решив уравнение S=S BADC – S BAC S BADC = = S BAC = S = 9 – 4,5 = 4,5 смотри пример 1 Решение:
ПРАВИЛА СИНКВЕЙНА 1строка – тема синквейна 1 слово 2строка – 2 прилагательных, описывающих признаки и свойства темы 3строка – 3 глагола описывающие характер действия 4строка – короткое предложение из 4 слов, показывающее Ваше личное отношение к теме 5строка – 1 слово, синоним или Ваша ассоциация тема предмета.
Интеграл 2. Определённый, положительный Считают, прибавляют, умножают 4. Вычисляют формулой Ньютона – Лейбница 5. Площадь
Список используемой литературы: учебник Колмагорова А.Н. и др. Алгебра и начала анализа 10 – 11 кл.
Спасибо за внимание! « ТАЛАНТ – это 99% труда и 1% способности» народная мудрость
Пример 1. Вычислить определённый интеграл: = Решение: пример 4
Предварительный просмотр:
Предмет: математика (алгебра и начала анализа), класс: 11 класс.
Тема урока: «Интеграл. Формула Ньютона-Лейбница».
Тип урока: Изучение нового материала.
Продолжительность занятия: 45 минут.
Цели урока: ввести понятие интеграла и его вычисление по формуле Ньютона-Лейбница, используя знания о первообразной и правила ее вычисления; проиллюстрировать практическое применение интеграла на примерах нахождения площади криволинейной трапеции; закрепить изученное в ходе выполнения упражнений.
Задачи урока:
Образовательные:
- сформировать понятие интеграла;
- формирование навыков вычисления определенного интеграла;
- формирование умений практического применения интеграла для нахождения площади криволинейной трапеции.

Развивающие:
- развитие познавательного интереса учащихся, развивать математическую речь, умения наблюдать, сравнивать, делать выводы;
- развивать интерес к предмету с помощью ИКТ.
Воспитательные:
- активизировать интерес к получению новых знаний, формирование точности и аккуратности при вычислении интеграла и выполнении чертежей.
Оснащение: ПК, операционная система Microsoft Windows 2000/XP, программа MS Office 2007: Power Point, Microsoft Word; мультимедийный проектор, экран.
Литература: учебник Колмагорова А.Н. и др. Алгебра и начала анализа 10-11 кл.
Технологии: ИКТ , индивидуального обучения.
ХОД УРОКА
Этап урока | Деятельность учителя | Деятельность учащихся | Время | |
Вводная часть | ||||
Организационный момент | Приветствует, проверяет готовность учащихся к уроку, организует внимание. Раздает опорный конспект. | Слушают, записывают дату. | 3 мин | |
Сообщение темы и целей урока | Актуализация опорных знаний и субъектного опыта с выходом на цели урока. | Слушают, записывают тему урока в тетради.
Активно включаются в мыслительную деятельность. Анализируют, сравнивают, делают выводы с выходом на цели занятия. | Презентация ИКТ 3 мин | |
Основная часть урока Изложение нового материала с попутной проверкой знаний прошлых тем. | ||||
Определение интеграла (слайд 3) | Даёт определение. ИКТ Что такое криволинейная трапеция? | Фигуру, ограниченная графиком функции, отрезком и прямыми x=a и x=b. | 10 мин | |
Обозначение интеграла (слайд 4) | Вводит обозначение интеграла и то, как он читается. | Слушают, записывают. | ||
История интеграла (слайды 5 и 6) | Рассказывает историю термина «интеграл». | Слушают, коротко записывают. | ||
Формула Ньютона – Лейбница (слайд 7) | Дает формулу Ньютона – Лейбница. Что в формуле обозначает F? | Слушают, записывают, отвечают на вопросы преподавателя. Первообразная. | ||
Заключительная часть урока. | ||||
Закрепление материала. Решение примеров с применением изученного материала | ||||
Пример 1 (слайд 8) | Разбирает решение примера, задавая вопросы по нахождению первообразных для подынтегральных функций. | Слушают, записывают, показывают знание таблицы первообразных. | 20 мин | |
Пример 2 (слайд 9). | Контролирует решение примеров. | Выполняют задание по очереди, комментируя (технология индивидуального обучения ), слушают друг друга, записывают, показывают знание прошлых тем. | ||
Пример 3 (слайд 10) | Разбирает решение примера. Как найти точки пересечения оси абсцисс с графиком функции? | Слушают, отвечают на вопросы, показывают знание прошлых тем, записывают. Подынтегральную функцию приравнять к 0 и решить уравнение. | ||
Пример 4 (слайд 11) | Разбирает решение примера. Как найти точки пересечения (абсциссы) графиков функций? Определите вид треугольника ABC. Как находиться площадь прямоугольного треугольника? | Слушают, отвечают на вопросы. Приравнять функции друг к другу и решить получившееся уравнение. Прямоугольный. где a и b- катеты прямоугольного треугольника. | ||
Подведение итогов урока (слайды 12 и 13) | Организует работу по составлению синквейна. | Участвуют в составлении синквейна. Анализируют, сравнивают, делают выводы по теме. | 5 мин. | |
Задание на дом по уровню сложности. | Дает задание на дом, объясняет. | Слушают, записывают. | 1 мин. | |
Оценивание работы обучающихся на уроке. | Оценивает работу обучающихся на уроке, анализирует. | Слушают. | 1 мин |
Предварительный просмотр:
Опорный конспект по теме «Интеграл. Формула Ньютона-Лейбница».
Определение:
Пусть дана положительная функция
f(x)
, определенная на конечном отрезке . | ||
Обозначение: Читается: «интеграл от a до b эф от икс дэ икс» | ||
Формула Ньютона – Лейбница | ||
Пример 1. Вычислить определённый интеграл: Решение: | ||
Пример 3. и осью абсцисс. Решение: | ||
Пример 3. Вычислить площадь фигуры, ограниченной линиями и . |
Решение прикладных задач сводится к вычислению интеграла, но не всегда это возможно сделать точно. Иногда необходимо знать значение определенного интеграла с некоторой степенью точности, к примеру, до тысячной.
Существуют задачи, когда следовало бы найти приближенное значение определенного интеграла с необходимой точностью, тогда применяют численное интегрирование такое, как метод Симпосна, трапеций, прямоугольников. Не все случаи позволяют вычислить его с определенной точностью.
Не все случаи позволяют вычислить его с определенной точностью.
Данная статья рассматривает применение формулы Ньютона-Лейбница. Это необходимо для точного вычисления определенного интеграла. Будут приведены подробные примеры, рассмотрены замены переменной в определенном интеграле и найдем значения определенного интеграла при интегрировании по частям.
Yandex.RTB R-A-339285-1
Формула Ньютона-Лейбница
Определение 1Когда функция y = y (x) является непрерывной из отрезка [ a ; b ] ,а F (x) является одной из первообразных функции этого отрезка, тогда формула Ньютона-Лейбница считается справедливой. Запишем ее так ∫ a b f (x) d x = F (b) – F (a) .
Данную формулу считают основной формулой интегрального исчисления.
Чтобы произвести доказательство этой формулы, необходимо использовать понятие интеграла с имеющимся переменным верхним пределом.
Когда функция y = f (x) непрерывна из отрезка [ a ; b ] , тогда значение аргумента x ∈ a ; b , а интеграл имеет вид ∫ a x f (t) d t и считается функцией верхнего предела. Необходимо принять обозначение функции примет вид ∫ a x f (t) d t = Φ (x) , она является непрерывной, причем для нее справедливо неравенство вида ∫ a x f (t) d t ” = Φ ” (x) = f (x) .
Необходимо принять обозначение функции примет вид ∫ a x f (t) d t = Φ (x) , она является непрерывной, причем для нее справедливо неравенство вида ∫ a x f (t) d t ” = Φ ” (x) = f (x) .
Зафиксируем, что приращении функции Φ (x) соответствует приращению аргумента ∆ x , необходимо воспользоваться пятым основным свойством определенного интеграла и получим
Φ (x + ∆ x) – Φ x = ∫ a x + ∆ x f (t) d t – ∫ a x f (t) d t = = ∫ a x + ∆ x f (t) d t = f (c) · x + ∆ x – x = f (c) · ∆ x
где значение c ∈ x ; x + ∆ x .
Зафиксируем равенство в виде Φ (x + ∆ x) – Φ (x) ∆ x = f (c) . По определению производной функции необходимо переходить к пределу при ∆ x → 0 , тогда получаем формулу вида Φ ” (x) = f (x) . Получаем, что Φ (x) является одной из первообразных для функции вида y = f (x) , расположенной на [ a ; b ] . Иначе выражение можно записать
F (x) = Φ (x) + C = ∫ a x f (t) d t + C , где значение C является постоянной.
Произведем вычисление F (a) с использованием первого свойства определенного интеграла. Тогда получаем, что
Тогда получаем, что
F (a) = Φ (a) + C = ∫ a a f (t) d t + C = 0 + C = C , отсюда получаем, что C = F (a) . Результат применим при вычислении F (b) и получим:
F (b) = Φ (b) + C = ∫ a b f (t) d t + C = ∫ a b f (t) d t + F (a) , иначе говоря, F (b) = ∫ a b f (t) d t + F (a) . Равенство доказывает формулу Ньютона-Лейбница ∫ a b f (x) d x + F (b) – F (a) .
Приращение функции принимаем как F x a b = F (b) – F (a) . С помощью обозначения формулу Ньютона-Лейбница принимает вид ∫ a b f (x) d x = F x a b = F (b) – F (a) .
Чтобы применить формулу, обязательно необходимо знать одну из первообразных y = F (x) подынтегральной функции y = f (x) из отрезка [ a ; b ] , произвести вычисление приращения первообразной из этого отрезка. Рассмотрим несколько примером вычисления, используя формулу Ньютона-Лейбница.
Пример 1
Произвести вычисление определенного интеграла ∫ 1 3 x 2 d x по формуле Ньютона-Лейбница.
Решение
Рассмотрим, что подынтегральная функция вида y = x 2 является непрерывной из отрезка [ 1 ; 3 ] , тогда и интегрируема на этом отрезке. По таблице неопределенных интегралов видим, что функция y = x 2 имеет множество первообразных для всех действительных значений x , значит, x ∈ 1 ; 3 запишется как F (x) = ∫ x 2 d x = x 3 3 + C . Необходимо взять первообразную с С = 0 , тогда получаем, что F (x) = x 3 3 .
По таблице неопределенных интегралов видим, что функция y = x 2 имеет множество первообразных для всех действительных значений x , значит, x ∈ 1 ; 3 запишется как F (x) = ∫ x 2 d x = x 3 3 + C . Необходимо взять первообразную с С = 0 , тогда получаем, что F (x) = x 3 3 .
Воспользуемся формулой Ньютона-Лейбница и получим, что вычисление определенного интеграла примет вид ∫ 1 3 x 2 d x = x 3 3 1 3 = 3 3 3 – 1 3 3 = 26 3 .
Ответ: ∫ 1 3 x 2 d x = 26 3
Пример 2
Произвести вычисление определенного интеграла ∫ – 1 2 x · e x 2 + 1 d x по формуле Ньютона-Лейбница.
Решение
Заданная функция непрерывна из отрезка [ – 1 ; 2 ] , значит, на нем интегрируема. Необходимо найти значение неопределенного интеграла ∫ x · e x 2 + 1 d x при помощи метода подведения под знак дифференциала, тогда получаем ∫ x · e x 2 + 1 d x = 1 2 ∫ e x 2 + 1 d (x 2 + 1) = 1 2 e x 2 + 1 + C .
Отсюда имеем множество первообразных функции y = x · e x 2 + 1 , которые действительны для всех x , x ∈ – 1 ; 2 .
Необходимо взять первообразную при С = 0 и применить формулу Ньютона-Лейбница. Тогда получим выражение вида
∫ – 1 2 x · e x 2 + 1 d x = 1 2 e x 2 + 1 – 1 2 = = 1 2 e 2 2 + 1 – 1 2 e (- 1) 2 + 1 = 1 2 e (- 1) 2 + 1 = 1 2 e 2 (e 3 – 1)
Ответ: ∫ – 1 2 x · e x 2 + 1 d x = 1 2 e 2 (e 3 – 1)
Пример 3
Произвести вычисление интегралов ∫ – 4 – 1 2 4 x 3 + 2 x 2 d x и ∫ – 1 1 4 x 3 + 2 x 2 d x .
Решение
Отрезок – 4 ; – 1 2 говорит о том, что функция, находящаяся под знаком интеграла, является непрерывной, значит, она интегрируема. Отсюда найдем множество первообразных функции y = 4 x 3 + 2 x 2 . Получаем, что
∫ 4 x 3 + 2 x 2 d x = 4 ∫ x d x + 2 ∫ x – 2 d x = 2 x 2 – 2 x + C
Необходимо взять первообразную F (x) = 2 x 2 – 2 x , тогда, применив формулу Ньютона-Лейбница, получаем интеграл, который вычисляем:
∫ – 4 – 1 2 4 x 3 + 2 x 2 d x = 2 x 2 – 2 x – 4 – 1 2 = 2 – 1 2 2 – 2 – 1 2 – 2 – 4 2 – 2 – 4 = 1 2 + 4 – 32 – 1 2 = – 28
Производим переход к вычислению второго интеграла.
Из отрезка [ – 1 ; 1 ] имеем, что подынтегральная функция считается неограниченной, потому как lim x → 0 4 x 3 + 2 x 2 = + ∞ , тогда отсюда следует, что необходимым условием интегрируемости из отрезка. Тогда F (x) = 2 x 2 – 2 x не является первообразной для y = 4 x 3 + 2 x 2 из отрезка [ – 1 ; 1 ] , так как точка O принадлежит отрезку, но не входит в область определения. Значит, что имеется определенный интеграл Римана и Ньютона-Лейбница для функции y = 4 x 3 + 2 x 2 из отрезка [ – 1 ; 1 ] .
Ответ: ∫ – 4 – 1 2 4 x 3 + 2 x 2 d x = – 28 , имеется определенный интеграл Римана и Ньютона-Лейбница для функции y = 4 x 3 + 2 x 2 из отрезка [ – 1 ; 1 ] .
Перед использованием формулы Ньютона-Лейбница нужно точно знать о существовании определенного интеграла.
Замена переменной в определенном интеграле
Когда функция y = f (x) является определенной и непрерывной из отрезка [ a ; b ] , тогда имеющееся множество [ a ; b ] считается областью значений функции x = g (z) , определенной на отрезке α ; β с имеющейся непрерывной производной, где g (α) = a и g β = b , отсюда получаем, что ∫ a b f (x) d x = ∫ α β f (g (z)) · g ” (z) d z .
Данную формулу применяют тогда, когда нужно вычислять интеграл ∫ a b f (x) d x , где неопределенный интеграл имеет вид ∫ f (x) d x , вычисляем при помощи метода подстановки.
Пример 4
Произвести вычисление определенного интеграла вида ∫ 9 18 1 x 2 x – 9 d x .
Решение
Подынтегральная функция считается непрерывной на отрезке интегрирования, значит определенный интеграл имеет место на существование. Дадим обозначение, что 2 x – 9 = z ⇒ x = g (z) = z 2 + 9 2 . Значение х = 9 , значит, что z = 2 · 9 – 9 = 9 = 3 , а при х = 18 получаем, что z = 2 · 18 – 9 = 27 = 3 3 , тогда g α = g (3) = 9 , g β = g 3 3 = 18 . При подстановке полученных значений в формулу ∫ a b f (x) d x = ∫ α β f (g (z)) · g ” (z) d z получаем, что
∫ 9 18 1 x 2 x – 9 d x = ∫ 3 3 3 1 z 2 + 9 2 · z · z 2 + 9 2 ” d z = = ∫ 3 3 3 1 z 2 + 9 2 · z · z d z = ∫ 3 3 3 2 z 2 + 9 d z
По таблице неопределенных интегралов имеем, что одна из первообразных функции 2 z 2 + 9 принимает значение 2 3 a r c t g z 3 . Тогда при применении формулы Ньютона-Лейбница получаем, что
Тогда при применении формулы Ньютона-Лейбница получаем, что
∫ 3 3 3 2 z 2 + 9 d z = 2 3 a r c t g z 3 3 3 3 = 2 3 a r c t g 3 3 3 – 2 3 a r c t g 3 3 = 2 3 a r c t g 3 – a r c t g 1 = 2 3 π 3 – π 4 = π 18
Нахождение можно было производить, не используя формулу ∫ a b f (x) d x = ∫ α β f (g (z)) · g ” (z) d z .
Если при методе замены использовать интеграл вида ∫ 1 x 2 x – 9 d x , то можно прийти к результату ∫ 1 x 2 x – 9 d x = 2 3 a r c t g 2 x – 9 3 + C .
Отсюда произведем вычисления по формуле Ньютона-Лейбница и вычислим определенный интеграл. Получаем, что
∫ 9 18 2 z 2 + 9 d z = 2 3 a r c t g z 3 9 18 = = 2 3 a r c t g 2 · 18 – 9 3 – a r c t g 2 · 9 – 9 3 = = 2 3 a r c t g 3 – a r c t g 1 = 2 3 π 3 – π 4 = π 18
Результаты совпали.
Ответ: ∫ 9 18 2 x 2 x – 9 d x = π 18
Интегрирование по частям при вычислении определенного интеграла
Если на отрезке [ a ; b ] определены и непрерывны функции u (x) и v (x) , тогда их производные первого порядка v ” (x) · u (x) являются интегрируемыми, таким образом из этого отрезка для интегрируемой функции u ” (x) · v (x) равенство ∫ a b v ” (x) · u (x) d x = (u (x) · v (x)) a b – ∫ a b u ” (x) · v (x) d x справедливо.
Формулу можно использовать тогда, необходимо вычислять интеграл ∫ a b f (x) d x , причем ∫ f (x) d x необходимо было искать его при помощи интегрирования по частям.
Пример 5
Произвести вычисление определенного интеграла ∫ – π 2 3 π 2 x · sin x 3 + π 6 d x .
Решение
Функция x · sin x 3 + π 6 интегрируема на отрезке – π 2 ; 3 π 2 , значит она непрерывна.
Пусть u (x) = х, тогда d (v (x)) = v ” (x) d x = sin x 3 + π 6 d x , причем d (u (x)) = u ” (x) d x = d x , а v (x) = – 3 cos π 3 + π 6 . Из формулы ∫ a b v ” (x) · u (x) d x = (u (x) · v (x)) a b – ∫ a b u ” (x) · v (x) d x получим, что
∫ – π 2 3 π 2 x · sin x 3 + π 6 d x = – 3 x · cos x 3 + π 6 – π 2 3 π 2 – ∫ – π 2 3 π 2 – 3 cos x 3 + π 6 d x = = – 3 · 3 π 2 · cos π 2 + π 6 – – 3 · – π 2 · cos – π 6 + π 6 + 9 sin x 3 + π 6 – π 2 3 π 2 = 9 π 4 – 3 π 2 + 9 sin π 2 + π 6 – sin – π 6 + π 6 = 9 π 4 – 3 π 2 + 9 3 2 = 3 π 4 + 9 3 2
Решение примера можно выполнить другим образом.
Найти множество первообразных функции x · sin x 3 + π 6 при помощи интегрирования по частям с применением формулы Ньютона-Лейбница:
∫ x · sin x x 3 + π 6 d x = u = x , d v = sin x 3 + π 6 d x ⇒ d u = d x , v = – 3 cos x 3 + π 6 = = – 3 cos x 3 + π 6 + 3 ∫ cos x 3 + π 6 d x = = – 3 x cos x 3 + π 6 + 9 sin x 3 + π 6 + C ⇒ ∫ – π 2 3 π 2 x · sin x 3 + π 6 d x = – 3 cos x 3 + π 6 + 9 sincos x 3 + π 6 – – – 3 · – π 2 · cos – π 6 + π 6 + 9 sin – π 6 + π 6 = = 9 π 4 + 9 3 2 – 3 π 2 – 0 = 3 π 4 + 9 3 2
Ответ: ∫ x · sin x x 3 + π 6 d x = 3 π 4 + 9 3 2
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Формулы и уравнения определенных интегралов
Формулы и уравнения определенных интегралов- Формула Ньютона-Лейбница:
, где - Формула интегрирования по частям в определенном интеграле:
- Замена переменной в определенном интеграле:
Если функция f(x) непрерывна на отрезке [a;b], а функция x=ϕ(t) непрерывно дифференцируема на отрезке [α;β], где a=ϕ(α), b=ϕ(β), то - Интегралы с бесконечными пределами:
- Признаки сходимости интегралов с бесконечными пределами (признаки сравнения):
1. Если a≤x≤+∞, 0≤f(x)≤g(x), то из сходимости
Если a≤x≤+∞, 0≤f(x)≤g(x), то из сходимости
сходимость
≤
из расходимости расходимость
2. Если при a≤x≤+∞, f(x)>0, g(x)>0 и существует конечный предел ≠0, то интегралы сходятся или расходятся одновременно.
Эталоном сравнения служит интеграл:
он сходится при p>1 и расходится при p≤1. - Интегралы от неограниченных функций:
Если функция f(x) непрерывна при a≤x<b и
, то
. - Признаки сходимости несобственных интегралов от неограниченных функций:
Аналогичны признакам сходимости интегралов с бесконечными пределами. Эталоном сравнения служит интеграл он сходится при 0<p<1 и расходится при p>1.
- Приложения определенного интеграла
- Площадь плоской фигуры
1.1. Фигура ограничена графиком функции y=f(x)(f(x)≥0), прямыми x=a, x=b и осью Ox:
.
1.2. Фигура ограничена графиками функций y=f1(x) и y=f2(x), f1(x)≤2f2(x), и прямыми x=a, x=b:
.
1.3. Фигура ограничена кривой, имеющей параметрические уравнения x=x(t), y=y(t), прямыми x=a, x=b и осью Ox:
, где f=x(t1), b=x(t2), y(t)≥0 на отрезке [t1; t2].
1.4. Площадь криволинейного сектора, ограниченного графиком непрерывной функции ρ=ρ(ϕ), лучами ϕ=α, ϕ=β, где ϕ и ρ — полярные координаты:
. - Длина дуги кривой
2.1. Гладкая кривая задана явно, y=f(x), a≤x≤b:
.
2.2. Кривая задана параметрически, x=x(t), y=y(t), z=z(t), t1≤t≤t2:
(для плоской кривой z(t)≡0).
2.3. Кривая задана в полярных координатах, ρ=ρ(ϕ), α≤ϕ≤β:
. - Площадь поверхности вращения, образованной вращением вокруг оси Ox дуги кривой
3.1. Дуга задана явно, y=f(x), a≤x≤b:
.
3. 2. Дуга задана параметрически, x=x(t), y=y(t), t1≤t≤t2:
2. Дуга задана параметрически, x=x(t), y=y(t), t1≤t≤t2:
.
3.3. Дуга задана в полярных координатах, ρ=ρ(ϕ), α≤ϕ≤β:
. - Объем тела
4.1. Тело заключено между плоскостями x=a и x=b, площадь сечения тела плоскостью, перпендикулярной оси Ox – известная функция S=f(x), непрерывная на отрезке [a; b], f(x)≥0:
.
4.2. Криволинейная трапеция, ограниченная кривой y=f(x), a≤x≤b вращается вокруг оси Ox:
.
4.3. Криволинейная трапеция, ограниченная кривой x=g(y), c≤y≤d вращается вокруг оси Oy:
.
Формулы, уравнения, теоремы, примеры решения задач
Определенный интеграл. Формула Ньютона-Лейбница
Будьте внимательны! У Вас есть 10 минут на прохождение теста. Система оценивания – 5 балльная. Разбалловка теста – 3,4,5 баллов, в зависимости от сложности вопроса. Порядок заданий и вариантов ответов в тесте случайный. С допущенными ошибками и верными ответами можно будет ознакомиться после прохождения теста. Удачи!
Система оценивания – 5 балльная. Разбалловка теста – 3,4,5 баллов, в зависимости от сложности вопроса. Порядок заданий и вариантов ответов в тесте случайный. С допущенными ошибками и верными ответами можно будет ознакомиться после прохождения теста. Удачи!Список вопросов теста
Вопрос 1
Какая из нижеприведенных формул называется формулой Ньютона-Лейбница:
Варианты ответов
Вопрос 2
Выберите верную формулу:
Варианты ответов
Вопрос 3
Укажите верные свойства определенного интеграла:
Варианты ответов
Вопрос 4
Укажите не верные свойства определенного интеграла:
Варианты ответов
Вопрос 5
Вопрос 6
Варианты ответов
Вопрос 7
Вопрос 8
Варианты ответов
0
1
Вопрос 9
Укажите утверждение, которое показывает геометрический смысл определенного интеграла:
Варианты ответов
- угол наклона касательной к графику функции в точке с абсциссой x1
- закон перемещения материальной точки на промежутке а,b
- площадь криволинейной трапеции
Вопрос 10
Укажите утверждение, которое показывает физический смысл определенного интеграла:
Варианты ответов
- угол наклона касательной к графику функции в точке с абсциссой x1
- закон перемещения материальной точки на промежутке а,b
- площадь криволинейной трапеции
Определенный интеграл.
 Формула Ньютона-Лейбница
Формула Ньютона-ЛейбницаВопросы занятия:
• показать геометрический смысл определённого интеграла;
• показать физический смысл определённого интеграла;
• рассказать историю интегрального исчисления;
• ввести формулу Ньютона-Лейбница.
Материал урока
Давайте рассмотрим задачу.
Пусть в декартовой прямоугольной системе координат дана фигура:
Такую фигуру мы назовем криволинейной трапецией. Требуется вычислить площадь криволинейной трапеции.
Рассмотрим еще одну задачу.
Пусть дан прямолинейный неоднородный стержень.
Нам надо найти массу стержня.
Рассмотрим еще одну задачу.
Пусть по прямой
неравномерно движется материальная точка. Зависимость скорости от времени
выражается формулой v
= v(t). Надо найти
перемещение точки за промежуток времени [a; b].
Надо найти
перемещение точки за промежуток времени [a; b].
Итак, при решении каждой задачи, мы получали одну и ту же математическую модель. Задач, которые приводятся к этой же математической модели довольно много. Поэтому возникла необходимость специально изучить данную математическую модель, то есть присвоить ей новый термин, ввести для нее обозначение, научится с ней работать.
Давайте еще раз дадим математическое описание той модели, которую мы использовали в задачах:
В курсе математического анализа доказано, что этот предел в случае непрерывной (или кусочно-непрерывной) функции существует. Его обозначают так
Числа a и b называют пределами интегрирования (соответственно верхним и нижним). Здесь dx – замена Δx, длин кусочков из которых состоит целое.
Согласно интернет энциклопедии
Википедии интегрирование прослеживалось еще в Древнем Египте, примерно в 1800
году до нашей эры. Первым известным методом для расчета интегралов является
метод исчерпывания Евдокса, который пытался найти
площади и объемы, разрывая их на бесконечное множество частей, для которых
площадь или объем уже известны. Это метод был подхвачен и развит Архимедом.
Аналогичные методы были разработаны независимо в Китае в третьем веке нашей
эры.
Первым известным методом для расчета интегралов является
метод исчерпывания Евдокса, который пытался найти
площади и объемы, разрывая их на бесконечное множество частей, для которых
площадь или объем уже известны. Это метод был подхвачен и развит Архимедом.
Аналогичные методы были разработаны независимо в Китае в третьем веке нашей
эры.
Следующий шаг в исчислении интегралов был сделан в Ираке в одиннадцатом веке математиком Ибн аль-Хайсамом. В своей работе «Об измерении параболического тела» он приходит к уравнению четвертой степени. Решая эту проблему, он проводит вычисления, равносильные вычислению определенного интеграла, чтобы найти объем параболоида.
Следующий значительный прогресс в исчислении
интегралов появился в шестнадцатом веке. В работах Кавальери с его методом
неделимых, а также в работах Ферма, были заложены основы современного
интегрального исчисления. Дальнейшие шаги были сделаны в начале семнадцатого
века Барроу и Торичелли,
которые представили первые намеки на связь между интегрированием и
дифференцированием.
В качестве символа интегрирования, Ньютон использовал значок квадрата перед обозначением функции или вокруг него, но эти обозначения не получили широкого распространения. Современное обозначение было введено Лейбницем в 1675 году. Он образовал интегральный символ из длинной буквы S – сокращения латинского слова сумма. Современное обозначение определенного интеграла, с указанием пределов интегрирования, были впервые предложены Жаном Батистом Жозефом Фурье в 1820.
Введя понятие определенного интеграла, мы можем переписать формулы, полученные при решении наших задач.
Площадь криволинейной трапеции можно найти так:
В этом состоит геометрический смысл определенного интеграла.
Определение массы прямолинейного неоднородного стержня с плотностью ро от икс можно вычислить так:
В этом заключается физический смысл определенного интеграла.
Определение перемещения материальной точки, движущейся по прямой со скоростью v(t), за промежуток времени [a; b] можно записать так:
Это еще одно физическое истолкование
определенного интеграла.
Давайте еще раз вернемся к третьей задаче.
Мы записали, что перемещение точки, которая движется со скоростью v(t), за промежуток времени [a; b] вычисляется по формуле:
С другой стороны, координата движущейся точки – это первообразная для скорости:
В курсе математического анализа доказана следующая теорема:
В 1708 году вспыхнул печально известный спор Лейбница с Ньютоном о научном приоритете открытия дифференциального исчисления. Известно, что Лейбниц и Ньютон работали над дифференциальным исчислением. Известно также, что Ньютон создал свою версию математического анализа, «метода флюксий», хоть и опубликовал свои результаты лишь много лет спустя; Лейбниц же первым опубликовал исчисление бесконечно малых и разработал символику, которая оказалась настолько удобной, что ее используют и на сегодняшний день.
Поэтому эту формулу называют формулой
Ньютона – Лейбница. На практике вместо разности пишут так:
На практике вместо разности пишут так:
Такую запись иногда называют двойной подстановкой.
Рассмотрим пример.
Рассмотрим еще один пример.
Давайте попробуем найти некоторые свойства определенного интеграла.
Свойство 1. Интеграл от суммы функций равен сумме интегралов.
Докажем это свойство.
Рассмотрим пример.
Свойство 2.
Постоянный множитель можно вынести за знак интеграла.
Рассмотрим пример.
Определенный интеграл. Площадь криволинейной трапеции. Формула Ньютона-Лейбница. Задание 7
В этой статье мы будем учиться решать задачи на нахождение площади криволинейной трапеции.
Как всегда, начнем с теории. Как вы помните, неопределенный интеграл от функции – это множество всех первообразных :
∫
В неопределенном интеграле не заданы границы интегрирования, и в результате нахождения неопределенного интеграла от функции мы получаем множество первообразных, отличающихся друг от друга на постоянную величину С.
Если заданы границы интегрирования, то мы получаем определенный интеграл:
Здесь число – нижний предел интегрирования, число – верхний предел интегрирования. Определенный интеграл – это ЧИСЛО, значение которого вычисляется по формуле Ньютона – Лейбница:
.
– это значение первообразной функции в точке , и, соответственно, – это значение первообразной функции в точке .
Для нас с точки зрения решения задач важное значение имеет геометрический смысл определенного интеграла.
Рассмотрим фигуру, изображенную на рисунке:
Зеленая фигура, ограниченая сверху графиком функции , слева прямой , справа прямой , и снизу осью ОХ называется криволинейной трапецией.
Геометрический смысл определенного интеграла:
Определенный интеграл – это число, равное площади криволинейной трапеции – фигуры, ограниченой сверху графиком положительной на отрезке функции , слева прямой , справа прямой , и снизу осью ОХ.
Решим задачу из Открытого банка заданий для подготовки к ЕГЭ по математике.
Прототип Задания 7 (№ 323080)
На рисунке изображён график некоторой функции . Функция — одна из первообразных функции . Найдите площадь закрашенной фигуры.
Закрашенная фигура представляет собой криволинейную трапецию, ограниченную сверху графиком функции , слева прямой , справа прямой , и снизу осью ОХ.
Площадь этой криволинейной трапеции вычисляется по формуле:
, где – первообразная функции .
По условию задачи , поэтому, чтобы найти площадь фигуры, нам нужно найти значение первообразной в точке -8, в точке -10, и затем из первого вычесть второе.
Замечу, что в этих задачах очень часто возникают ошибки именно в вычислениях, поэтому советую аккуратно и подробно их записывать, и ничего не считать “в уме”.
=
=
Ответ: 4
Посмотрите небольшую видеолекцию, в которой решены все типы задач на первообразную:
youtube.com/embed/-yqBjcnG7vs?rel=0″ frameborder=”0″ allowfullscreen=””/>
И.В. Фельдман, репетитор по математике.
Определенный интеграл. Основные свойства и теоремы. Формула Ньютона-Лейбница. (Семинар 17)
1. Семинар 17. Определенный интеграл. Основные свойства и теоремы. Формула Ньютона Лейбница
nПредел S интегральной суммы S n
k 1
f ( x k’ ) x k
для функции y=f(x)
на отрезке [a,b], когда число n отрезков неограниченно возрастает, а
наибольшая длина отрезка xk 0 называют определенным интегралом
от функции y=f(x) на отрезке [a,b].
Обозначение
b
f ( x)dx lim
a
n
xk
k 1
f ( x k’ ) x k
a– нижний предел интегрирования;
b – верхний предел интегрирования;
[a,b] – отрезок интегрирования;
f(x) – подынтегральная функция;
x – переменная интегрирования.
Формула Ньютона-Лейбница
Вычисление интеграла основано на применении формулы НьютонаЛейбница
Пусть f(x) – интегрируема на отрезке [a,b] и F(x) – одна из первообразных
функции f(x), то есть f(x)=F’(x).
 Тогда приращение первообразной на
Тогда приращение первообразной наотрезке [a,b], то есть F(b)-F(a) равно
значению определенного интеграла
b
b
b
f
(
x
)
dx
F
(
x
)
f
(
x
)
dx
F
(
b
)
F
(
a
)
Другая
форма
a -двойная подстановка
a
a
от a до b
Основные свойства определенного интеграла
При выводе основных свойств определенного интеграла исходим из
формулы Ньютона-Лейбница
b
f ( x)dx F (b) F (a) (1), где f(x) – непрерывна на отрезке [a,b] , f(x)=F’(x).
a
I. Величина определенного интеграла не зависит от обозначения
переменной интегрирования, то есть
b
b
b
a
a
a
f ( x)dx = f ( y)dy =…= f (u)du
II. Определенный интеграл с одинаковыми пределами
a
интегрирования равен 0, то есть
f ( x)dx =F(a)-F(a)=0
a
III. При перестановке пределов интегрирования определенный
интеграл меняет свой знак на обратный.

Действительно,
переставляя пределы интегрирования,
в силу формулы
a
b
(1), получим f ( x)dx F (a) F (b) [ F (b) F (a)] f ( x)dx (2)
b
a
IV. Если отрезок интегрирования [a,b] разбить на конечное число
частичных отрезков, то определенный интеграл, взятый по отрезку
[a,b] равен сумме определенных интегралов, взятых по всем
частичным отрезкам.
Пусть [a, b, ] [a, c] [c, b] , где
a c b . Полагая F’(x)=f(x)
a
c
b
b
a
c
f ( x)dx F (a) F (b) [ F (с) F (a)] [ F (b) F (c)] f ( x)dx f ( x)dx
(3)
V. Постоянный множитель можно выносить за знак интеграла
a
Af ( x)dx AF ( x) |
b
b
a
AF (b) AF (a) A[ F (b) F (a)] A f ( x)dx
b
a
VI. Определенный интеграл от алгебраической суммы конечного
числа непрерывных функций равен такой же алгебраической сумме
определенных интегралов от этих функций.
b
b
b
b
a
a
a
a
[ f ( x) g ( x) h( x)]dx f ( x)dx g ( x)dx h( x)dx
VII.
 Если подынтегральная функция определенного интеграла
Если подынтегральная функция определенного интеграланепрерывна и неотрицательна, а верхний предел интегрирования
больше нижнего или равен ему, то определенный интеграл также
неотрицателен.
Пусть f ( x) 0 при a x b Так как F’(x)=f(x) 0, то F(x) – неубывающая
b
функция. В таком случае при b 0 имеем f ( x)dx F (b) F (a) 0
a
VIII. Неравенство между непрерывными функциями можно
интегрировать поэлементно при условии, что верхний предел
интегрирования больше нижнего.
Пусть f ( x) g ( x) при a x b , f(x),g(x) – непрерывные функции на
отрезке [a,b].
Так как g ( x) f ( x) 0, то в силу свойств VI и VIII имеем
b
b
b
a
a
a
b
b
[ g ( x) f ( x)]dx g ( x)dx f ( x)dx 0 , отсюда a f ( x)dx a g ( x)dx
Примеры с решениями
1) Вычислить интеграл
1
2
x
dx как предел интегральной суммы.
0
Решение
Здесь f ( x) x 2 , a 0, b 1; Разделим отрезок [0;1] на n конгруэнтных
частей, тогда xk (b a) / n 1 / n, и выберем k x k
1
2
n
x
0
,
x
,
x
,.
 ..,
..,x
1;
1
2
n
Имеем 0
n
n
n
2
2
2
2
1
2
n
k 1
f ( 1 ) ; f ( 2 ) ;…., f ( n ) ; f ( k ) x k
n
n
n
n n
, следовательно,
1 1 / n (2 1 / n) 1
1 2 2 32 … n 2
n(n 1)( 2n 1)
x
dx
lim
lim
lim
0
n
n
n
6
3
n3
6n 3
1
2
(Здесь использована формула суммы квадратов натуральных чисел)
2) Вычислить
4
dx по формуле Ньютона-Лейбница
2
cos x
6
dx
3
/4
tgx
|
tg
tg
1
Решение. Имеем
/6
2
4
6
3
cos x
4
6
18
3)Оценить интеграл
cos xdx
10
1 x4
Решение. Так как | cos x | 1 , то при x>10 получим неравенство
18
Следовательно,
10
cos xdx
1 x4
8 10 2 10 1 0,1.
cos x
1 x4
10 2
Примеры для самостоятельного решения
1
1.
 Вычислить интеграл
Вычислить интегралкак предел интегральной суммы.
xdx
0
1
2. Вычислить интеграл
x
e
dx как предел интегральной суммы.
0
1
2
x
(
1
x
)
dx
3. Оценить интеграл
0
sin x
/2 x
4. Оценить интеграл
5. Вычислить интегралы
1
2
3
/3
/4
xdx
e1 / x
3
2
3
1)
;..
2
)
;..
3
)
x
x
1
dx
;..
4
)
cos
x sin 2 xdx;..
4
2
0 1 x
1 x
1
0
0
x sin x
dx
1 cos x
Урок 23. площадь криволинейной трапеции. интеграл и его свойства – Алгебра и начала математического анализа – 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №23.Площадь криволинейной трапеции. Интеграл и его свойства.
Перечень вопросов, рассматриваемых в теме
1) Нахождение определенного интеграла
2) Нахождение площади криволинейной трапеции с помощью формулы Ньютона – Лейбница
3) Решение задач, с помощью формулы Ньютона – Лейбница
Формула Ньютона – Лейбница
Основная литература:
Колягин Ю. М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
ОрловаЕ. А., СеврюковП. Ф., СидельниковВ. И., СмоляковА.Н.Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющей на отрезке [а;b] знака функции f(х), прямыми х=а, x=b и отрезком [а;b].
Отрезок [a;b] называют основанием этой криволинейной трапеции
формула Ньютона – Лейбница
Если в задаче требуется вычислить площадь криволинейной трапеции, то ответ всегда будет положительный. Если требуется, используя чертеж, вычислить интеграл, то его значение может быть любым(зависит от расположения криволинейной трапеции).
Примеры и разбор решения заданий тренировочного модуля
№1.Найти площадь криволинейной трапеции, изображенной на рисунке
Решение
Для вычисления площади криволинейной трапеции воспользуемся формулой Ньютона – Лейбница.
Ответ:
№2. Вычислить определенный интеграл:
Решение: Воспользуемся формулой Ньютона-Лейбница.
Сначала находим первообразную функцию F(x) . Далее подставляем значение верхнего предела в первообразную функцию: F(b) .
Затем подставляем значение нижнего предела в первообразную функцию: F(а).
Рассчитываем разность F(b) – F(а), это и будет ответ.
№3. Найти площадь криволинейной трапеции (х-1)2, ограниченной линиями х=2 и х=1, осью 0х
Решение:
Воспользуемся формулой Ньютона-Лейбница.
Сначала находим первообразную функцию F(x). Далее подставляем значение верхнего предела в первообразную функцию: F(b) .
Затем подставляем значение нижнего предела в первообразную функцию: F(а).
Рассчитываем разность F(b) – F(а), это и будет ответ.
b_af(x)dx\). Интегрирование представляет собой сумму площадей, и для нахождения площади в определенных пределах используются определенные интегралы.Изучение интегрирования началось в третьем веке до нашей эры с его использованием для нахождения площади окружности, параболы, эллипса. Давайте узнаем больше об определенных интегралах и свойствах определенных интегралов.
Что такое определенный интеграл?
Определенный интеграл – это площадь под кривой между двумя фиксированными пределами.b_af(x)dx\), где a — нижний предел, а b — верхний предел для функции f(x), определенной относительно оси x. Чтобы найти площадь под кривой между двумя пределами, мы делим площадь на прямоугольники и суммируем их. Чем больше прямоугольников, тем точнее площадь. Итак, мы делим площадь на бесконечное количество прямоугольников одинакового (очень маленького) размера и складываем все площади. Это фундаментальная теория, которая лежит в основе определенных интегралов.
Это фундаментальная теория, которая лежит в основе определенных интегралов.
Определенная интегральная формула
Формулы определенных интегралов используются для вычисления определенного интеграла.2dx\) = (1 3 /3 + С) – (0 3 /3 + С) = 1/3.
Постоянная интегрирования C всегда отменяется при применении пределов. Поэтому мы всегда игнорируем C при вычислении определенного интеграла.
Свойства определенного интеграла
Свойства определенного интеграла помогают найти интеграл для функции, умноженной на константу, для суммы функций, а также для четных и нечетных функций. Проверим следующие свойства определенных интегралов, которые помогают решать задачи об определенных интегралах.a_{-a}f(x).dx = 0\), если f(x) — нечетная функция (т. е. f(-x) = -f(x)).
Применение определенного интеграла
Определенные интегралы в основном используются для нахождения площадей плоских фигур, таких как окружности, параболы, эллипсы. Проверим подробно применение определенных интегралов для нахождения площадей каждой из этих фигур.
Проверим подробно применение определенных интегралов для нахождения площадей каждой из этих фигур.
Площадь круга с помощью определенного интеграла
Площадь круга рассчитывается путем вычисления площади части круга в первом квадранте.Здесь уравнение окружности x 2 + y 2 = a 2 заменяется уравнением кривой вида y = √(a 2 – x 2 ). Здесь мы используем понятие определенного интеграла, чтобы найти уравнение кривой относительно оси x и пределы от 0 до a.
Площадь круга в четыре раза больше площади квадранта круга. Площадь квадранта вычисляется путем интегрирования уравнения кривой через пределы в первом квадранте.а_0\)
= 4[((a/2)× 0 + (a 2 /2)sin -1 1) – 0]
= 4(а 2 /2)(π/2)
= πa 2
Следовательно, площадь круга равна πa 2 квадратных единиц.
Площадь параболы с использованием определенного интеграла
Парабола имеет ось, которая делит параболу на две симметричные части. Здесь мы берем параболу, симметричную относительно оси x и имеющую уравнение y 2 = 4ax. Это можно преобразовать как y = √(4ax).2}{3}\) квадратных единиц.
Здесь мы берем параболу, симметричную относительно оси x и имеющую уравнение y 2 = 4ax. Это можно преобразовать как y = √(4ax).2}{3}\) квадратных единиц.
Площадь эллипса с помощью определенного интеграла
Уравнение эллипса с большой осью длиной 2а и малой осью 2b имеет вид как y = b/a .√(a 2 – x 2 ). Здесь мы используем понятие определенного интеграла для вычисления площади, ограниченной эллипсом по первой координате и относительно оси x. Далее его умножают на 4, чтобы получить площадь эллипса.2}{2}.\frac{\pi}{2}\\&=\pi ab\end{align}\)
Следовательно, площадь эллипса равна πab кв.
Похожие темы
Следующие темы помогут лучше понять определенный интеграл.
Часто задаваемые вопросы по Definite Integral
Что такое определение определенного интеграла?
Определенный интеграл используется для нахождения площади кривой и представляется как \(\int^b_af(x). b _a f(a + b – x).dx \)
b _a f(a + b – x).dx \)
Как вычислить определенный интеграл?
Чтобы вычислить определенный интеграл:
- Вычисление неопределенного интеграла (т. е. без ограничений)
- Замените верхний предел, а затем нижний предел в ответе на предыдущем шаге.
- Вычесть оба результата по порядку.
Как вычислить определенные интегралы четных функций?
Определенные интегралы четной функции также следуют тому же процессу, что и любая другая функция.Ь_а = Ь — а\).
Что такое определенный интеграл и неопределенный интеграл?
| Определенный интеграл | Неопределенный интеграл |
|---|---|
| Определенные интегралы определяются для интегралов с пределами. | Неопределенные интегралы не имеют пределов. |
| Ответ определенного интеграла представляет собой простое числовое значение. | Для неопределенного интеграла результирующий ответ в основном является выражением.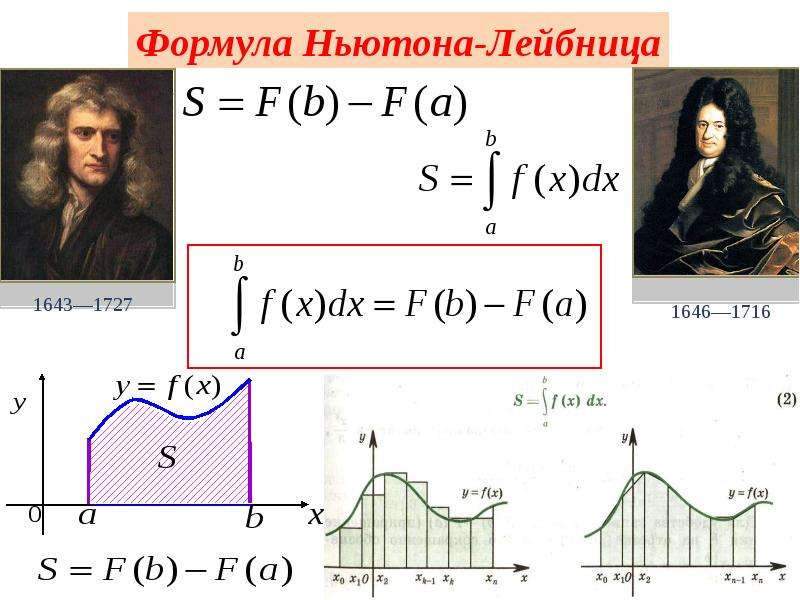 |
| Не будет константы интегрирования ‘C’. | Мы всегда используем константу интегрирования ‘C’ в ответе. |
Все формулы неопределенных интегралов можно использовать с определенными интегралами вместе с применением ограничений к формуле.
Каково практическое применение определенного интеграла?
Определенные интегралы можно использовать для нахождения площади кривых, таких как круг, эллипс, парабола.В основном формулы интегрирования используются для нахождения площади неправильных форм. В определенных интегралах площадь небольшого пространства вычисляется путем применения ограничений, а затем манипулируется, чтобы найти площадь всего пространства. Площадь круга рассчитывается путем его интегрирования по оси x в первом квадранте с ограничениями от начала координат до его радиуса, а затем умножается на 4, чтобы получить площадь всего круга.
Результаты и формулы определенных интегралов
1) $$\int\limits_a^b {F'(x)dx = F(a) – F(b)} $$ называется Основной теоремой интегрального исчисления.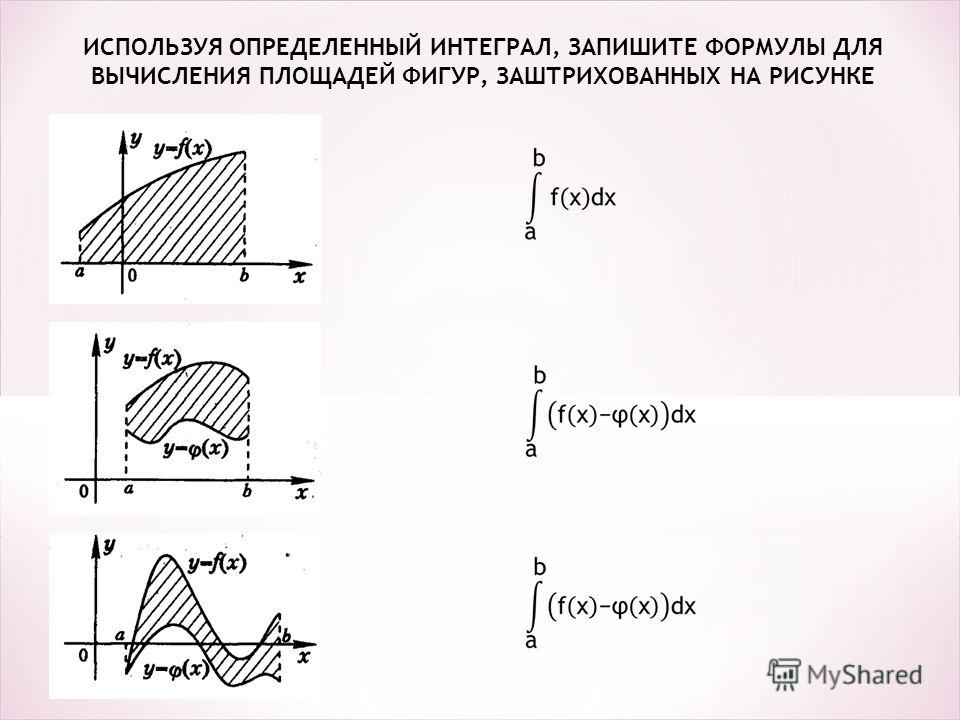 {\ frac {\ pi} {2}} {\ ln \ csc xdx = \ frac {\ pi} {2}} \ ln 2 = – \ frac {\ pi} {2} \ ln \ frac {1} 2}\]
{\ frac {\ pi} {2}} {\ ln \ csc xdx = \ frac {\ pi} {2}} \ ln 2 = – \ frac {\ pi} {2} \ ln \ frac {1} 2}\]
определенных интегралов | Определение, формулы, примеры
Определенные интегралы обобщают правило нахождения площадей под кривыми с помощью интегралов. В прошлом мы научились работать с первообразными и неопределенными интегралами непрерывных функций. Теперь пришло время изучить, как установить правила и свойства, когда определены ограничения и установлены границы для входных значений.
В этой статье мы покажем вам основные свойства и формулы, необходимые для вычисления и применения определенных интегралов. К концу нашего обсуждения мы хотим, чтобы вы чувствовали себя уверенно при работе с определенными интегралами и их приложениями.
Что такое определенные интегралы?
Определенные интегралы представляют собой площади, найденные под кривой, ограниченной определенными интервалами. Математически мы определяем определенный интеграл f (x) для интервала x \ in [a, b], как показано ниже. {b} f(x) \phantom{x}dx}\end{выровнено}
{b} f(x) \phantom{x}dx}\end{выровнено}
Мы вернулись к области под кривой, но на этот раз у нас есть интервал [a, b]. Мы можем оценить площадь кривой, разделив ее на прямоугольники одинаковой ширины, h = \dfrac{b – a}{n}. Добавление этих сумм приведет к площади кривой — аналогично тому, как мы используем сумму Римана для оценки неопределенных интегралов.
Это означает, что когда нас просят вычислить площадь под кривой функции y = f(x), ограниченной пределами, x = a и x = b, мы просто вычисляем определенный интеграл от f(x) между интервал x \in [a, b].{n} f(x_i)h\end{выровнено}
Конечно, это математическое определение наиболее полезно, когда вычисление неопределенного интеграла функции является сложной задачей. Численные аппроксимации определенных интегралов сильно зависят от формул этих аппроксимаций для вычисления сложных определенных интегралов.
Формула определенного интеграла (основная теорема исчисления)
Теперь давайте сосредоточимся на формуле, которую нам легче запомнить и с которой работать. Сняв ограничения на то, чтобы наша функция была непрерывной, а также положительной, мы теперь можем установить математическое определение определенного интеграла функции.{b}\\&= [F(b) + C] – [F(a) + C]\\&= F(b) + \cancel{C}- F(a) – \cancel{C}\ \&= F(b) -F(a)\end{выровнено}
Сняв ограничения на то, чтобы наша функция была непрерывной, а также положительной, мы теперь можем установить математическое определение определенного интеграла функции.{b}\\&= [F(b) + C] – [F(a) + C]\\&= F(b) + \cancel{C}- F(a) – \cancel{C}\ \&= F(b) -F(a)\end{выровнено}
Конечно, если мы записываем таким образом вычисления определенных интегралов, со временем это становится утомительным. Вот почему двигаться вперед; мы можем пренебречь произвольной константой, когда имеем дело с определенными интегралами.
Определенные интегральные свойства и формула
Прежде чем мы приступим к более сложным примерам, мы хотим показать вам некоторые важные свойства определенных интегралов, которые следует запомнить.{b}f(x)\,dx}.
- Знак интеграла ∫ обозначает интегрирование.
- Символ dx, называемый дифференциалом переменной x, указывает, что переменной интегрирования является x.
- Интегрируемая функция f ( x ) называется подынтегральной функцией.

- Символ dx отделяется от подынтегральной функции пробелом (как показано). Если функция имеет интеграл, то говорят, что она интегрируема. Точки a и b называются пределами интеграла.Интеграл, пределы которого указаны, называется определенным интегралом.
- Говорят, что интеграл находится на интервале [ a , b ].
Основная теорема исчисления является важной частью исчисления, поскольку она связывает понятие производной с понятием интеграла. В результате мы можем использовать наши знания о производных для нахождения площади под кривой, что зачастую быстрее и проще, чем использование определения интеграла.{b}\!f(x)\,dx=F(b)-F(a).}
Теорема о среднем значении для интегрирования[править | править источник]
Нам понадобится следующая теорема при обсуждении основной теоремы исчисления.
Шаблон:Расчет/Определ.
Доказательство теоремы о среднем значении для интегрирования[править | править источник]
f (x) {\ displaystyle f (x)} удовлетворяет требованиям теоремы об экстремальных значениях, поэтому оно имеет минимум m {\ displaystyle m} и максимум M {\ displaystyle M} в [a, b] {\ стиль отображения [a,b]} . {x} f (t) dt \ quad {\ text {for}} x \ in [a, b]}
{x} f (t) dt \ quad {\ text {for}} x \ in [a, b]}
Шаблон: Исчисление / Def
Когда у нас есть такие функции F {\ displaystyle F} и f {\ displaystyle f}, где F ‘(x) = f (x) {\ displaystyle F ‘(x) = f (x)} для каждого x {\ displaystyle x} в некотором интервале мы говорим, что F {\ displaystyle F} является первообразной f {\ displaystyle f} на I {\ displaystyle I}.
Шаблон:Расчет/Определ.
Примечание: меньшинство математиков называют первую часть двумя, а вторую — одной.{x+\Delta x}f(t)dt=f(c)\cdot \Delta x}
Обратите внимание, что c{\displaystyle c} зависит от Δx{\displaystyle \Delta x} . Во всяком случае, мы показали, что
- F (x + Δx) − F (x) = f (c) ⋅ Δx {\ displaystyle F (x + \ Delta x) -F (x) = f (c) \ cdot \ Delta x}
и деление обеих сторон на Δx {\ displaystyle \ Delta x} дает
- F (x + Δx) − F (x) Δx = f (c) {\ displaystyle {\ frac {F (x + \ Delta x) -F (x)} {\ Delta x}} = f (c) }
Возьмем предел как Δx→0{\displaystyle \Delta x\to 0}, мы получим определение производной F{\displaystyle F} в точке x{\displaystyle x}, поэтому мы имеем
- F′(x)=limΔx→0F(x+Δx)−F(x)Δx=limΔx→0f(c){\displaystyle F'(x)=\lim _{\Delta x\to 0}{ \frac {F(x+\Delta x)-F(x)}{\Delta x}}=\lim _{\Delta x\to 0}f(c)}
Чтобы найти другой предел, мы используйте теорему сжатия . c∈[x,x+Δx]{\displaystyle c\in [x,x+\Delta x]} , поэтому x≤c≤x+Δx{\displaystyle x\leq c\leq x+\Delta x} . Следовательно,
c∈[x,x+Δx]{\displaystyle c\in [x,x+\Delta x]} , поэтому x≤c≤x+Δx{\displaystyle x\leq c\leq x+\Delta x} . Следовательно,
- limΔx→0[x+Δx]=x⇒limΔx→0c=x{\displaystyle \lim _{\Delta x\to 0}{\Big [}x+\Delta x{\Big]}=x\quad \Rightarrow \quad \lim _{\Delta x\to 0}c=x}
Поскольку f{\displaystyle f} непрерывно, мы имеем
- F′(x)=limΔx→0f(c)=f(limΔx→0c)=f(x){\displaystyle F'(x)=\lim _{\Delta x\to 0}f(c) =f\left(\lim _{\Delta x\to 0}c\right)=f(x)}
, что завершает доказательство.{x}f(t)dt} . Тогда по основной теореме исчисления, часть I, мы знаем, что P {\ displaystyle P} дифференцируемо на (a, b) {\ displaystyle (a, b)} и для всех x∈ (a, b) {\ displaystyle x \ в (а, б)}
- P′(x)=f(x){\displaystyle P'(x)=f(x)}
Таким образом, P{\displaystyle P} является производной от f{\displaystyle f} . Поскольку мы предполагали, что F {\ displaystyle F} также является первообразной для всех x∈ (a, b) {\ displaystyle x \ in (a, b)},
- P′(x)=F′(x)P′(x)−F′(x)=0(P(x)−F(x))′=0 {\ displaystyle {\ begin {align} & P ‘(x)=F'(x)\\&P'(x)-F'(x)=0\\&{\Big (}P(x)-F(x){\Big)}’=0 \end{выровнено}}}
Пусть g (x) = P (x) − F (x) {\ displaystyle g (x) = P (x) -F (x)} . Теорема о среднем значении применяется к г (х) {\ displaystyle g (x)} на [a, ξ] {\ displaystyle [a, \ xi]} с a <ξ
Теорема о среднем значении применяется к г (х) {\ displaystyle g (x)} на [a, ξ] {\ displaystyle [a, \ xi]} с a <ξ
для некоторого c {\ displaystyle c} in (a, ξ) {\ displaystyle (a, \ xi)} . Но поскольку г ‘(х) = 0 {\ displaystyle g ‘(x) = 0} для всех x {\ displaystyle x} в [a, b] {\ displaystyle [a, b]}, g (ξ) {\ displaystyle g (\ xi )} должен быть равен g (a) {\ displaystyle g (a)} для всех ξ {\ displaystyle \ xi} в (a, b) {\ displaystyle (a, b)}, т.е.е. g(x) постоянно на (a,b){\displaystyle (a,b)} .
Это означает, что существует константа. -F(a)} такой, что для всех x∈(a,b){\displaystyle x\in (a,b)} ,
- P (x) = F (x) + C {\ displaystyle P (x) = F (x) + C}
и, поскольку g {\ displaystyle g} является непрерывным, мы видим, что это выполняется, когда x = a { \displaystyle x=a} и x=b{\displaystyle x=b}. {b} f (t) dx = P (b) = F (b) + C = F (b) -F (a)}
{b} f (t) dx = P (b) = F (b) + C = F (b) -F (a)}
◼ {\ displaystyle \ blacksquare}
Обозначения для вычисления определенных интегралов[править | править источник]
Вторая часть основной теоремы исчисления дает нам способ вычисления определенных интегралов.{n+1}}{n+1}}} является производной от f{\displaystyle f} . Если 0∉[a,b]{\displaystyle 0\notin [a,b]}, то F{\displaystyle F} непрерывно на [a,b]{\displaystyle [a,b]} и, применяя фундаментальный Теорема исчисления, мы можем вычислить интеграл f {\ displaystyle f}, чтобы получить следующее правило.
Шаблон:Расчет/Определ.
Обратите внимание, что мы допускаем все значения n{\displaystyle n} , даже отрицательные или дробные. Если n>0{\displaystyle n>0}, то это работает, даже если [a,b]{\displaystyle [a,b]} включает 0{\displaystyle 0} .{2}+2\cdot 3-0=27+18+6=51}
Интеграл Римана, рациональное или иррациональное выражение
Интегрирование — одна из наиболее важных частей математических вычислений, и оно также имеет множество приложений в математике, физике и химии. Интеграция соответствует объединению, суммированию, суммированию или сбору различных частей уравнения для получения полного значения. Интегрирование представлено знаком ( ∫ ). В частности, есть два типа интегрирования: определенный интеграл и неопределенный интеграл.Здесь мы узнаем об определенных интегралах, их свойствах и некоторых важных формулах.
Интеграция соответствует объединению, суммированию, суммированию или сбору различных частей уравнения для получения полного значения. Интегрирование представлено знаком ( ∫ ). В частности, есть два типа интегрирования: определенный интеграл и неопределенный интеграл.Здесь мы узнаем об определенных интегралах, их свойствах и некоторых важных формулах.
Читайте также: Условная вероятность
Определенные интегралы
Когда интегрирование происходит в пределах двух конкретных точек, то оно называется определенным интегралом. У них есть постоянные верхний и нижний пределы, и предполагается, что константы используются для получения фактического значения интегрирования между этими пределами. Определенные интегралы действуют только в терминах неопределенных интегралов.Одно из основных применений определенных интегралов состоит в том, что они сообщают нам площадь, покрываемую кривой функции над осью x.
Концепция, стоящая за определенным интегралом
Давайте проверим, какая реальная концепция стоит за определенным интегралом. Определенный интеграл подобен соседу первообразной и неопределенного интеграла данной функции. Рассмотрим заданную функцию f(x), которая непрерывна на замкнутом интервале (a,b), и пусть этот интервал разделен на подынтервалы, считая за n.Эти подынтервалы могут иметь или не иметь одинаковую длину. Возьмем произвольное значение домена xi в каждом подинтервале и вычислим его соответствующую длину подынтервала. Эти «n» произведений добавляются для вычисления их сумм. Сумма известна как сумма Римана, которая может быть положительной, отрицательной и даже нулевой в зависимости от поведения функции на замкнутом интервале. Несмотря на то, что определенный интеграл дает площадь над осью x, а площадь всегда положительна, значение определенного интеграла может быть положительным, отрицательным или нулевым.
Определенный интеграл подобен соседу первообразной и неопределенного интеграла данной функции. Рассмотрим заданную функцию f(x), которая непрерывна на замкнутом интервале (a,b), и пусть этот интервал разделен на подынтервалы, считая за n.Эти подынтервалы могут иметь или не иметь одинаковую длину. Возьмем произвольное значение домена xi в каждом подинтервале и вычислим его соответствующую длину подынтервала. Эти «n» произведений добавляются для вычисления их сумм. Сумма известна как сумма Римана, которая может быть положительной, отрицательной и даже нулевой в зависимости от поведения функции на замкнутом интервале. Несмотря на то, что определенный интеграл дает площадь над осью x, а площадь всегда положительна, значение определенного интеграла может быть положительным, отрицательным или нулевым.
У нас есть несколько свойств определенных интегралов, которые мы широко используем для решений, которые помогают легко решать задачи.
Формула определенного интеграла
Формула определенного интеграла приведена ниже-
Здесь «a» и «b» — верхний и нижний пределы. F(a) — верхнее предельное значение, а F(b) — нижнее предельное значение интегрирования.
F(a) — верхнее предельное значение, а F(b) — нижнее предельное значение интегрирования.
Предел «a» и «b» представляет собой интервал. Нет необходимости, чтобы нижний предел был меньше, а верхний предел был больше нижнего.Вы можете назвать «a» и «b» интервалом интегрирования.
Определенный интеграл также известен как интеграл Римана , когда «x» ограничен вещественной прямой.
Определенная формула интегрирования по частям
Формула определенного интегрирования по частям обычно используется для интегрирования произведения двух функций. Формула определенного интегрирования по частям имеет вид:
∫ pq dx = p ∫ q dx – ∫ p’ ( ∫ q dx ) dx
, где
p – функция p(x),
q – функция q (x), а
p’ — производная функции p(x).
Свойства формулы определенного интеграла
Определенный интеграл имеет некоторые свойства, которые мы собираемся изучить. Некоторые из этих свойств были получены из других. Они также помогают нам легко получить решение с меньшим количеством шагов.
Они также помогают нам легко получить решение с меньшим количеством шагов.
Свойства определенных интегральных формулы приведены ниже:
Формулы для рациональных и иррациональных выражений
Формулы для рациональных и иррациональных выражений
Применение определенного интеграла
Определенные интегралы могут быть обычно применяемыми и используется для поверхностных интегралов, линейных интегралов и контурных интегралов.В математике вы можете найти длину и площадь, используя определенные интегралы. Давайте узнаем об этом подробнее –
Площадь поверхности
Уже обсуждалось, как мы можем найти площадь поверхности фигуры, используя определенные интегралы. Даже если форма неправильная, мы можем использовать определенные интегралы, чтобы найти площадь поверхности, используя двойное интегрирование (что не входит в вашу программу).
Площадь, ограниченная двумя кривыми
Одним из основных применений определенного интеграла является нахождение площади кривой над осью x. Точно так же мы можем найти площадь между двумя кривыми, заданными функциями. Если графики функций пересекаются. Найти замкнутую площадь можно в основном путем вычитания меньшей площади из большей над осью x. Возможно, вам придется вычислить два или более интеграла.
Точно так же мы можем найти площадь между двумя кривыми, заданными функциями. Если графики функций пересекаются. Найти замкнутую площадь можно в основном путем вычитания меньшей площади из большей над осью x. Возможно, вам придется вычислить два или более интеграла.
Объем трехмерных фигур
Определенные интегралы можно использовать не только для определения площади поверхности, но и для определения объема формы. Вам нужно будет поместить их в единичные ломтики, а затем узнать площадь одного ломтика и умножить ее на количество ломтиков.Трехмерный объем можно получить срезами, дисками и шайбами. Тип трехмерной формы играет важную роль в процедуре.
Длина дуги кривых
Еще одним применением определенного интеграла является нахождение длины дуги кривой. Во-первых, длина дуги должна быть аппроксимирована с помощью отрезков прямой, и, следовательно, будет сгенерирована сумма Римана. Возьмите предел, затем подставьте его в формулу определенного интеграла.
Объем вращения
Когда кривая вращается вокруг оси, то объем твердого тела, образованного ее вращением вокруг оси, может быть получен как интуитивное расширение площади поверхности вращения. Формула площади и объема цилиндра аналогична вращающемуся твердому телу.
Формула площади и объема цилиндра аналогична вращающемуся твердому телу.
Физические приложения
Физические приложения интеграции очень распространены в области техники и физики. Если у вас есть функция плотности объекта, то вы можете легко найти массу этого объекта, используя определенные интегралы. Вы также можете рассчитать проделанную работу, интегрируя известную силовую функцию. Более того, используя определенные интегралы, можно вычислить силу, действующую на предмет, погруженный в жидкость.
Нахождение центра масс и моментов
Моменты и центр масс объекта можно вычислить с помощью определенного интегрирования. Концепция центра масс – это то, где находится точка баланса.
Что нужно помнить
- Интегрирование, являющееся одной из важнейших частей математики, соответствует процессу, в котором происходит вычисление интегралов. В математике интегралы можно широко использовать для нахождения таких величин, как площади, объемы, смещения и т.
 д.Термин интеграл обычно относится к определенным интегралам, в то время как неопределенные интегралы можно увидеть, что они используются для первообразных. Интеграция – важная тема в исчислении.
д.Термин интеграл обычно относится к определенным интегралам, в то время как неопределенные интегралы можно увидеть, что они используются для первообразных. Интеграция – важная тема в исчислении. - Как мы все уже знаем, дифференцирование — это процесс, в котором мы находим производную функции, тогда как интегрирование — это процесс нахождения первообразной функции. Вы можете ясно видеть, что оба эти процесса обратны друг другу. Следовательно, можно сказать, что интеграция есть обратный процесс дифференциации или наоборот.Интеграцию также можно назвать антидифференцировкой.
- Когда интеграл имеет верхний и нижний пределы, он называется определенным интегралом. В основном он обеспечивает закрытый интервал, в пределах которого должно быть найдено значение интегрирования. Определенный интеграл также называют интегралом Римана. Например,
здесь функция f(x) интегрируется с в интервале (a,b)
- Формула определенного интеграла приведена здесь-
- Есть несколько свойств определенных интегралов, приведенных выше.
 Проверьте их и запомните, так как они очень полезны для будущего использования. Мы будем использовать все свойства при решении вопросов в конце этой статьи.
Проверьте их и запомните, так как они очень полезны для будущего использования. Мы будем использовать все свойства при решении вопросов в конце этой статьи. - Применение определенных интегралов включает в себя множество полезных тем. Некоторые из них заключаются в нахождении площади поверхности, площади поверхности, заключенной в две кривые, вычислении объема трехмерных фигур, измерении длины дуги кривых, определении объема вращения формы и определении центра масс и моментов объекта. .5\) (5x 4 -4x 3 +2x) dx
Сначала нужно проинтегрировать все слагаемые / 2] 1 2
= [x5 – x4 + x2] 1 2
= [(1) 5 – (1) 4 + (1) 2 – {(2) 5 – (2) 4 + (2) 2 }]
= [ 1 – 1 + 1 – {32 – 16 + 4}]
= [1 – 20]
=[-19]
= -19
Вопросы: Решить \(\int\limits_{-3}^{-1}\)10x 4 dx
баллов (3)
Ответ: Здесь у нас есть интеграция-
\(\int\limits_{-3}^{-1}\) 10x 4 dx = [10x 5 /5] -1 -3 = [2x 5 ] -3 -1 = 2[(-1) 5 – (-3) 5 ]
=
-243 )] = 2 [- 1 + 243]
= 2 [242]
= 484
Вопросы: Решите \(\int\limits_{1}^{2}\){x / (x² + 2 )}dx (4 балла)Ответ: Нам дали интегрирование как-
\(\int\limits_{1}^{2}\) {x / (x² + 2 )}dx
Мы собираемся использовать для этого метод подстановки-
Возьмем знаменатель равным
u =x 2 + 2
du = 2x dx
xdx = 0 du
лимиты тоже изменятся.
 {2}\) e x dx
{2}\) e x dxI = [ex] 0 2 = e2 – e0
I = e2 -1
Вопросы: Каковы основные применения определенных интегралов? (3 балла)
Ответ: Определенные интегралы в основном применяются в финансах, экономике, технике и физике.Его можно использовать для операций с такими функциями, как вычисление дуги, длины, площади поверхности, объема и т. д. Определенный интеграл также может определять площадь под кривой над осью x, а также площадь, заключенную между двумя кривыми.Решено: Как набрать определенный интеграл для исчисления?
@mgillespie ,
Высшее образование не имеет специального редактора формул в Canvas, которого нет у вас.
Если вы собираетесь преподавать математику для старших классов, изучите LaTeX.Это своего рода стандарт для форматирования математики, и вы не пожалеете. Он (начиная с TeX) существует в той или иной форме с 1978 года, и для него доступно много помощи в Интернете.
 Он был написан не только для математики, и некоторые университеты требуют, чтобы диссертации были написаны на нем, а некоторые журналы требуют, чтобы документы были в формате TeX. Тем не менее, он имеет самое полное форматирование математики из всего, что я когда-либо видел.
Он был написан не только для математики, и некоторые университеты требуют, чтобы диссертации были написаны на нем, а некоторые журналы требуют, чтобы документы были в формате TeX. Тем не менее, он имеет самое полное форматирование математики из всего, что я когда-либо видел.Тем не менее, это можно набрать с основного экрана, но это больно.{g(x)} f(t)dt\right]=f(g(x))g'(x)
Редактор уравнений Basic предназначен для базовых задач. Если вам нужны дополнительные материалы, вам нужно перейти в расширенный вид и ввести их.
Вы можете начать с Базового и переключиться на Расширенный, и он сохранится, но если вы делаете что-то продвинутое, вы не сможете вернуться к базовому. Первый пример перешел бы от Advanced к Basic, а второй — нет.
Другим вариантом является использование онлайн-редактора математических уравнений, такого как Code Cogs, который предоставляет дополнительные шаблоны на выбор.Вы даже можете скопировать код LaTeX и вставить его в редактор холста, чтобы вам не пришлось вводить его заново.

Если вы преподаете математику, вы также можете быть знакомы с MathType от Design Science. Хотя это коммерческий продукт, он имеет разумную цену для ученых, и я использовал и обновлял его в течение многих лет, прежде чем научился создавать документы в TeX, потому что он дал мне WYSIWYG-редактор, и вы можете настроить его для копирования/вставки с использованием TeX. . Затем вы можете скопировать / вставить его оттуда в Canvas.
Посмотреть решение в исходном сообщении
Как изменить пределы определенных интегралов — видео и расшифровка урока
U -ПодстановкаПри вычислении интеграла с использованием u -подстановка выражение, включающее исходную переменную, заменяется новой переменной.Конечным результатом является более простой интеграл.
Когда мы используем u -подстановку для вычисления определенного интеграла, мы должны изменить каждую часть интеграла, чтобы использовать новую переменную (обычно u ) вместо старой переменной (часто x ).
 Необходимо изменить три элемента:
Необходимо изменить три элемента:- Саму функцию (изменить выражение, включающее x , на u )
- Дифференциал (изменить dx на выражение, включающее du )
- Границы (изменить границы интегрирования со значений для x на значения для и )
Надеюсь, первые два вам знакомы.Мы сосредоточимся на третьем шаге. Чтобы изменить границы, используйте выражение, связывающее 90 529 x 90 530 и 90 529 u 90 530. Подставьте исходную нижнюю границу для x и найдите u . Это дает новую нижнюю границу. Затем подставьте исходную верхнюю границу для x и решите u , чтобы найти новую верхнюю границу.
Первый пример
Вычислите определенный интеграл ∫ √(4 x +1) dx от 0 до 2.
Что вы делаете в первую очередь? Как и в случае с большинством определенных интегралов, вы должны сначала игнорировать границы (0 и 2) и сосредоточиться на том, как найти первообразную функции внутри интеграла.
 Нам нужна первообразная √(4 x +1).
Нам нужна первообразная √(4 x +1).Это достаточно просто, чтобы вы могли сделать это без использования u -замены, но особенно для начинающих студентов, может быть проще заменить u = 4 x + 1. Затем возьмите производную, чтобы увидеть, что du = 4 dx , и решить для dx , чтобы получить dx = 1/4 * du .
Вот новая часть. Мы заменили все выражения, включающие x , на выражения, включающие u .Помните, что границы 0 и 2 интеграла были границами для x , а не u ! Так что теперь мы можем изменить и их.
Помните, что х = 4 х + 1. Это означает, что когда х = 0, х = 4(0) + 1 = 1, а когда х = 2, 0 х 4(2) + 1 = 9. Таким образом, в то время как старые границы для x были равны 0 и 2, новые границы для u равны 1 и 9. Соединяя все эти части вместе, исходный интеграл переписывается следующим образом:
∫ √(4 x +1) dx от 0 до 2 = ∫ √ u * 1/4 * du от 1 до 9.

Видите, как все, что говорило о x (само x , dx и границы), превратилось в разговоры о u ? Это означает, что теперь мы можем полностью забыть о x и просто вычислить интеграл, используя переменную u .
Завершая, первообразная для √ u равна 2/3* u 3/2, поэтому мы можем закончить:
- ∫ √ u * 1/4 * du
- = 2/3 * u 3/2 * 1/4 оценивается от 1 до 9
- = 1/6(93/2 – 13/2)
- = 1/6(27 – 1)
- = 13/3
Второй пример
Вычислить определенный интеграл ∫ sin3 x cos x dx от π/3 до π/2.
Вы должны заметить, что функция sin3 x cos x довольно сложная, поэтому будет полезно попробовать u -подстановку, чтобы упростить выражение.
Возьмем u = sin x . Тогда 90 529 du 90 530 = cos 90 529 x 90 530 90 529 d x 90 530 , так что теперь интеграл содержит 90 529 u 90 530 3 90 529 du 90 530, и остается только изменить границы.

Так как u = sin x , когда x = π/3, u = sin(π/3) = √(3)/2.Кроме того, когда x = π/2, u = sin(π/2) = 1. Наш интеграл переписывается следующим образом:
- ∫ sin3 x cos x dx из π/3 до π/2
- = ∫ u 3 du от √(3)/2 до 1
Теперь решим как обычно, используя переменную u и забыв, что переменная x когда-либо существовала.
- = u 4/4 оценивается от √(3)/2 до 1
- = (1)4/4 – (√(3)/2)4/4
- = 1/4 – 9/64
- = 7/64
Тригонометрическая замена
Другим типом замены, часто используемым для решения интегралов, является тригонометрическая замена .В этом типе замены мы заменяем 90 529 x 90 530 тригонометрической функцией 90 529 θ 90 530. Эта замена упрощает интеграл до того, с чем мы можем справиться. Этот метод является одним из самых сложных в интегральном исчислении, поэтому, если вы немного запутались, вы не одиноки!
Пример
Вычислить определенный интеграл ∫ ( dx / √( x 2 + 9) ) от 0 до √3.

Обратите внимание, что мы не можем использовать какие-либо «простые» методы для нахождения первообразной этой функции, поэтому у нас нет другого выбора, кроме как использовать более сложный метод.Исходя из того, что в этом интеграле мы видим х 2 + 9, воспользуемся заменой х = 3tan θ .
Чтобы найти dx , мы берем производную от x = 3tan θ , чтобы получить dx = 3sec2 θ dθ . Нам также нужно упростить выражение квадратного корня внутри интеграла:
- √( x 2 + 9)
- = √((3tan θ )2 + 9)
- = √(9tan2 θ + 9)
- = √( 9(tan2 θ + 1))
- = √(9сек2 θ )
- = 3 с θ
С этим упрощением и выражением, которое мы находим для dx , выражение внутри интеграла упрощается до:
- dx / √( x 2 + 9)
- = 3сек2 θ dθ / (3сек θ )
- = сек θ dθ
Гораздо проще! Это сила тригонометрической замены!
Теперь нам нужно беспокоиться только об изменении пределов.
 Мы делаем это, используя начальное соотношение 90 529 x 90 530 = 3tan 90 529 θ 90 530 и начальные пределы для 90 529 x 90 530 : 0 и √3. Во-первых, мы подставляем 0 для x и находим θ , используя функцию арктангенса:
Мы делаем это, используя начальное соотношение 90 529 x 90 530 = 3tan 90 529 θ 90 530 и начальные пределы для 90 529 x 90 530 : 0 и √3. Во-первых, мы подставляем 0 для x и находим θ , используя функцию арктангенса:- 0 = 3tan θ
- 0 = коричневый θ
- θ = арктангенс (0)
- θ = 0
Теперь подставьте √3 и найдите θ :
- √3 = 3tan θ
- √(3)/3 = тангенс θ
- θ = арктангенс( √(3)/3 )
- θ = π/6
Собрав все воедино, мы перепишем исходный интеграл и решим его, используя новую переменную θ .Обратите внимание, что мы изменили саму функцию, dx и пределы интегрирования на выражения для θ , а не x , так что мы можем забыть о x , когда мы фактически интегрируем.
- ∫ ( dx / √( x 2 + 9)) от 0 до √3
- = ∫ сек θ dθ от 0 до π/6
- = ln |сек θ + тангенс θ | оценивается от 0 до π/6
- = пер |сек(π/6) + тангенс(π/6)| – ln | сек (0) + тангенс (0) |
- = пер |2/√3 + 1/√3| – пер |1 + 0|
- = пер(3/√3) – пер(1)
- = пер(√3) – 0
- = пер(√3)
Резюме урока
При решении определенного интеграла с использованием либо u -подстановки , либо тригонометрической подстановки , мы можем изменить границы интегрирования.





 Примеры для самостоятельного решения обучающимися.
Примеры для самостоятельного решения обучающимися.
 Интегралом от функции f(x) на
называется площадь её криволинейной трапеции.
Интегралом от функции f(x) на
называется площадь её криволинейной трапеции. Если a≤x≤+∞, 0≤f(x)≤g(x), то из сходимости
Если a≤x≤+∞, 0≤f(x)≤g(x), то из сходимости
 2. Дуга задана параметрически, x=x(t), y=y(t), t1≤t≤t2:
2. Дуга задана параметрически, x=x(t), y=y(t), t1≤t≤t2:
 д.Термин интеграл обычно относится к определенным интегралам, в то время как неопределенные интегралы можно увидеть, что они используются для первообразных. Интеграция – важная тема в исчислении.
д.Термин интеграл обычно относится к определенным интегралам, в то время как неопределенные интегралы можно увидеть, что они используются для первообразных. Интеграция – важная тема в исчислении. Проверьте их и запомните, так как они очень полезны для будущего использования. Мы будем использовать все свойства при решении вопросов в конце этой статьи.
Проверьте их и запомните, так как они очень полезны для будущего использования. Мы будем использовать все свойства при решении вопросов в конце этой статьи.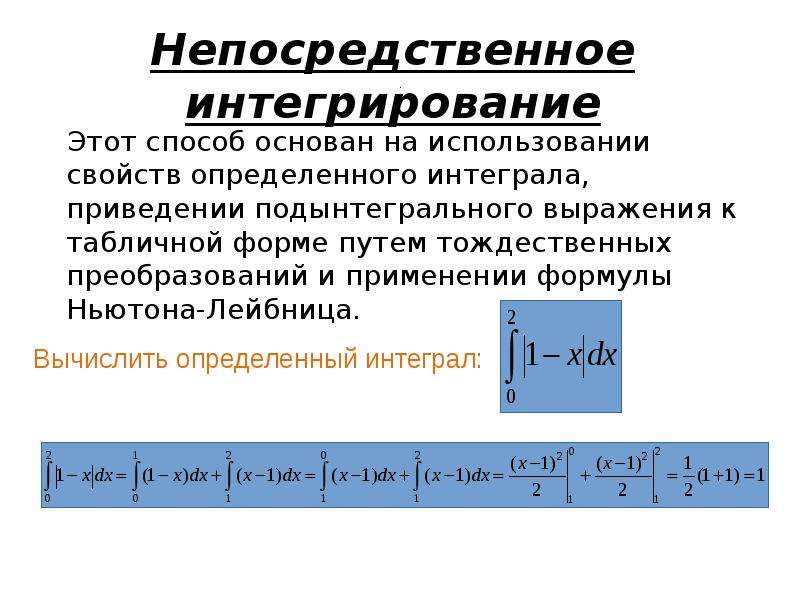 {2}\) e x dx
{2}\) e x dx Он был написан не только для математики, и некоторые университеты требуют, чтобы диссертации были написаны на нем, а некоторые журналы требуют, чтобы документы были в формате TeX. Тем не менее, он имеет самое полное форматирование математики из всего, что я когда-либо видел.
Он был написан не только для математики, и некоторые университеты требуют, чтобы диссертации были написаны на нем, а некоторые журналы требуют, чтобы документы были в формате TeX. Тем не менее, он имеет самое полное форматирование математики из всего, что я когда-либо видел.
 Необходимо изменить три элемента:
Необходимо изменить три элемента: Нам нужна первообразная √(4 x +1).
Нам нужна первообразная √(4 x +1).


 Мы делаем это, используя начальное соотношение 90 529 x 90 530 = 3tan 90 529 θ 90 530 и начальные пределы для 90 529 x 90 530 : 0 и √3. Во-первых, мы подставляем 0 для x и находим θ , используя функцию арктангенса:
Мы делаем это, используя начальное соотношение 90 529 x 90 530 = 3tan 90 529 θ 90 530 и начальные пределы для 90 529 x 90 530 : 0 и √3. Во-первых, мы подставляем 0 для x и находим θ , используя функцию арктангенса: