4.2. Вывод основного закона электромагнитной индукции из закона сохранения и превращения энергии
Основной закон электромагнитной индукции (закон Фарадея) можно вывести из закона сохранения и превращения энергии, что и было сделано Гельмгольцем (1847 г.).
Пусть имеется замкнутая цепь (контур с током), содержащая источник ЭДС, величина которой , и пусть полное сопротивление этой цепи равно R. Обозначим силу тока в цепи через I. Количество энергии, затрачиваемое источником ЭДС за время dt, как известно, равно
.
Если внешнее магнитное поле отсутствует или контур неподвижен, то вся эта энергия превращается в тепло, количество которого определяется законом Джоуля-Ленца:
.
Имеем
.
Откуда после сокращения на dt получим закон Ома для замкнутой (полной) цепи в интегральной форме:
и
.
(4. 11)
11)
При перемещении такого контура с источником ЭДС (с током) в магнитном поле часть энергии источника тока будет расходоваться против перемещения контура в магнитном поле, а часть выделяться в контуре в виде тепла. Расходование энергии источника тока против перемещения контура с током в магнитном поле связано с тем, что для получения индукционных токов методом перемещения проводника в магнитном поле необходимо совершить работу, так как сила, действующая на индукционный ток, препятствует перемещению проводника.
Известно, что работа по перемещению проводника с током в магнитном поле dA = IdФ, где dФ – величина изменения магнитного потока, сцепленного с данным контуром.
Так как при таком перемещении магнитное поле остается неизменным, то эта работа может совершаться лишь за счет энергии источника тока.
На основании закона сохранения и превращения энергии будем иметь
или
.
Откуда
. (4.12)
Решая уравнение (4.12) относительно силы тока, найдем
. (4.13)
Принимая равенство (4.13) за математическое выражение закона Ома и сравнивая его с полученным ранее для этого же контура в отсутствие магнитного поля, можно установить, что благодаря изменению потока магнитной индукции к имевшейся в цепи ЭДС источника прибавилась ЭДС:
. (4.14)
Как видно, величина ЭДС электромагнитной индукции не зависит от величины источника тока и, значит, сохранит свое значение и при = 0, т.е. будет возникать вне зависимости от всяких других ЭДС, действующих в той же цепи.
Знак «минус» служит математическим выражением правила (закона) Ленца.
Таким образом,
формула (4.14) является математическим
выражением основного закона электромагнитной
индукции (в формулировке Максвелла).
Аналогично можно получить вывод этого закона и для отрезка проводника (в формулировке Фарадея).
4.3. Явление самоиндукции. Магнитное поле бесконечно длинного соленоида. Коэффициенты индуктивности и взаимной индуктивности
Известно, что вокруг любого проводника с током возникает магнитное поле. Следовательно, с любым контуром тока всегда связан поток магнитной индукции. Этот поток будет изменяться при изменении силы тока в контуре, а также формы контура или магнитной проницаемости окружающей среды. Изменение же магнитного потока, согласно закону электромагнитной индукции, возбудит в контуре ЭДС. ЭДС электромагнитной индукции, которая возникает в каком-либо контуре вследствие изменения магнитного потока, создаваемого электрическим током этого контура, называют ЭДС самоиндукции (рис. 4.4).
Величина ЭДС самоиндукции может быть определена по общей формуле, выражающей основной закон электромагнитной индукции:
.
Рассчитаем ЭДС самоиндукции, возникающую в бесконечно длинном соленоиде, магнитное поле которого однородно находится внутри объема соленоида, заполненного средой с магнитной проницаемостью .
Магнитный поток Ф1, пронизывающий каждый виток соленоида сечением S,
При изменении тока в соленоиде в каждом витке возникает ЭДС самоиндукции:
. (4.16)
В N последовательно соединенных витках соленоида возникает ЭДС самоиндукции:
(4.17)
где – коэффициент самоиндукции или индуктивность.
Индуктивность L зависит от формы, размеров проводника и магнитной проницаемости среды, окружающей проводник.
При
с
= L,
т.е. индуктивность (коэффициент
самоиндукции) – это физическая величина,
численно равная ЭДС самоиндукции,
возникающей в проводнике при скорости
изменения тока в нем, равной 1 А/с.
Один Гн (генри) – это индуктивность такого проводника, в котором при скорости изменения тока в 1 А/с индуцируется ЭДС самоиндукции, равная 1 В.
Если L = const,
. (4.18)
Следовательно, ЭДС самоиндукции прямо пропорциональна скорости изменения тока в проводнике. Оказывается, что данное утверждение справедливо для любых проводников.
Если L const, что возможно при = f(H),
. (4.19)
То есть при наличии ферромагнетиков и в переменных магнитных полях коэффициент пропорциональности в выражении для ЭДС самоиндукции не равен L.
Таким образом, в проводниках с переменным током существуют одновременно две ЭДС – источника тока и самоиндукции.
При возрастании
тока
,с<0,
а это означает, что ЭДС самоиндукции
«тормозит» движение зарядов в проводнике,
совершая отрицательную работу, т. е.
уменьшает ток в проводнике.
е.
уменьшает ток в проводнике.
Если ток в проводнике
убывает
,
Следовательно, с противодействует причине, которая порождает ее (препятствует изменению тока в проводнике).
Сравнивая выражения идля магнитного потока, имеем
Ф = LI. (4.20)
4.3.1. Взаимная индукция. Коэффициент взаимной индукции
Взаимная индукция, явление, в котором обнаруживается магнитная связь двух или более электрических цепей. Благодаря этой связи возникает ЭДС индукции в одном из контуров при изменении тока в другом. Количественной характеристикой магнитной связи электрических цепей является взаимная индуктивность.
Если два контура
(два замкнутых проводника) находятся в
магнитных полях друг друга, то при всяком
изменении тока в одном из них происходит
изменение магнитного потока, пронизывающего
(сцепленного) другой контур, что вызывает
в нем появление ЭДС индукции (рис. 4.5).
4.5).
Магнитный поток через первый контур с током I1 частично пронизывает площадь, ограниченную вторым контуром. Причем магнитный поток Ф12 через контур два прямо пропорционален току I1:
, (4.21)
где М12
Если ток I2 течет в контуре “два”, то магнитный поток Ф21 через контур «один» также пропорционален току I2:
. (4.22)
Согласно закону электромагнитной индукции,
; (4.23)
, (4.24)
где 2 и 1 – возникающие во втором и в первом контурах ЭДС индукции;
и
– скорости изменения магнитных потоков
через соответствующие контуры.
Взаимная индукция лежит в основе действия трансформаторов.
19.2. Основной закон электромагнитной индукции
Математическая формула основного закона электромагнитной индукции имеет следующий вид:
.
ЭДС индукции равна скорости изменения магнитного потока, взятой со знаком минус. Этот закон называют основным законом электромагнитной индукции или законом Фарадея-Ленца.
Основной закон электромагнитной индукции можно вывести из закона сохранения энергии.
Р ассмотрим проводник длиной , подключенный к источнику тока с ЭДС (рис. 19.2.1).
Вектор индукции магнитного поля перпендикулярен горизонтальной плоскости, в которой находится проводник. При замыкании цепи проводник движется под действием силы Ампера.
За время источник тока совершает работу
,
где I – сила тока в
проводнике.
Энергия источника тока расходуется на работу магнитного поля по перемещению проводника
и на работу по нагреванию проводника, которая определяется законом Джоуля-Ленца
.
В соответствии с законом сохранения энергии можно записать
или .
Из полученного выражения можно определить силу тока
.
Очевидно, что второе слагаемое в числителе является ЭДС и равно
.
Минус в формуле связан с направлением индукционного тока, которое определяется по правилу Ленца: индукционный ток направлен так, что мешает (препятствует) изменению магнитного потока.
Например, при
внесении магнита в катушку северным
магнитным полюсом в катушке, соединенной
с гальванометром, возникает индукционный
ток, который создает магнитное поле,
направленное противоположно полю
магнита (рис. 19.2.2), т.е. северным полюсом
к магниту. Значит, магнитное поле
индукционного тока препятствует движению
магнита, т.е. мешает изменению магнитного
потока.
19.2.2), т.е. северным полюсом
к магниту. Значит, магнитное поле
индукционного тока препятствует движению
магнита, т.е. мешает изменению магнитного
потока.
При удалении магнита из катушки (рис. 19.2.3) в ней возникает индукционный ток, магнитное поле которого опять препятствует движению проводника (мешает изменению магнитного потока), т.е. направлено южным полюсом к магниту. Индукционный ток во втором случае направлен противоположно индукционному току в первом случае, что подтверждается отклонением стрелки гальванометра в противоположную сторону.
Среднее значение ЭДС индукции для закона Фарадея-Ленца можно записать в виде
.
Если в катушке содержится N витков, то в каждом витке появляется ЭДС индукции. Витки соединены последовательно, потому общая ЭДС индукции в N раз больше, чем в одном витке
.
Внесем число витков под дифференциал
.
Введем обозначение
,
где – ψ называется потокосцеплением.
Закон Фарадея-Ленца для катушки записывается в следующем виде:
.
В однородном магнитном поле равномерно вращается рамка (рис. 19.3.1) так, что угол между вектором магнитной индукции и нормалью к плоскости рамки меняется по закону
,
здесь – круговая частота вращения рамки;
t – время вращения рамки.
Магнитное поле создается постоянными магнитами и не изменяется, как и площадь рамки. Подставим в закон Фарадея-Ленца
формулу магнитного потока
,
получим
.
Вычислим производную, подставив значение угла,
,
тогда .
ЭДС в рамке изменяется по гармоническому закону:
,
где – амплитудное значение ЭДС индукции в
рамке.
ЭДС индукции будет равна нулю, если = принимает значения 0,и т.д., т.е. когда плоскость рамки перпендикулярна вектору магнитной индукции. Силу тока, возникающего в рамке, можно определить по закону Ома
.
Сила тока изменяется синфазно с ЭДС
,
здесь является амплитудным значением силы тока.
Если рамка состоит из N витков, то ЭДС индукции равна
.
Рассмотренное явление применяют для получения переменного тока в генераторах небольшой мощности. Переменное напряжение снимают с помощью щеток, которые схематически представлены на рис. 19.3.1.
При токе большой мощности в щетках возникают сильные искры, что может привести к большим потерям энергии и аварии. Поэтому на электростанциях большой мощности вращается электромагнит, а рамка остается неподвижной.
Значение, термины, законы и примеры
Законы термодинамики
Законы термодинамики: Законы термодинамики представляют собой группу физических величин, таких как температура, энергия, работа, теплота и энтропия, которые характеризуют термодинамические системы в термодинамике. равновесие. Законы также используют различные параметры для термодинамических процессов, чтобы установить отношения между ними. Термодинамика — это раздел физики, который занимается понятиями, касающимися тепла и температуры, а также взаимопревращениями тепла и других форм энергии. Термодинамика является частью макроскопической науки. Он имеет дело только с объемными системами и не вдается в подробности о молекулярном строении материи. В этой статье мы подробно обсудим законы термодинамики.
равновесие. Законы также используют различные параметры для термодинамических процессов, чтобы установить отношения между ними. Термодинамика — это раздел физики, который занимается понятиями, касающимися тепла и температуры, а также взаимопревращениями тепла и других форм энергии. Термодинамика является частью макроскопической науки. Он имеет дело только с объемными системами и не вдается в подробности о молекулярном строении материи. В этой статье мы подробно обсудим законы термодинамики.
Термины, относящиеся к законам термодинамики
Есть некоторые термины, которые будут часто использоваться при формулировании законов термодинамики. Поэтому вам необходимо ознакомиться с этим термином. Таким образом, некоторые термины, относящиеся к законам термодинамики: энергия не меняется со временем.
Термодинамическая система: Термодинамическая система — это система, в которой материя заключена в стенах, отделяющих систему от окружающей среды. Термодинамические системы могут быть трех типов:
- Изолированная термодинамическая система: В изолированной системе между системой и окружающей средой не происходит обмена энергией или веществом.
 Изолированный сосуд является примером изолированной системы.
Изолированный сосуд является примером изолированной системы. - Замкнутая термодинамическая система: В замкнутой системе не происходит обмена веществом, но возможен обмен энергией между системой и окружающей средой. Медь или сталь являются примером закрытой системы.
- Открытая термодинамика Система: В открытой системе происходит перенос как массы, так и энергии между системой и окружающей средой.
Окружение: Включает в себя все, кроме системы. Вселенная вместе включает в себя как системы, так и окружающую среду.
Термодинамический процесс: Процесс, при котором термодинамическое состояние системы изменяется за счет изменения тепла, давления и внутренней энергии. Четыре типа термодинамических процессов:
- Адиабатический процесс – процесс, при котором теплопередача не происходит ни внутрь системы, ни наружу.
- Изохорический процесс – Процесс, при котором объем не изменяется и объем в системе остается неизменным.

- Изобарический процесс – Процесс, при котором не происходит изменения давления и давление в системе остается неизменным.
- Изотермический процесс – Процесс, при котором не происходит изменения температуры и объем в системе остается неизменным.
Четыре закона термодинамики
Термодинамика — это раздел физики, изучающий отношения между теплом, работой, температурой и энергией. Законы термодинамики описывают, как эти физические переменные ведут себя в различных обстоятельствах. Есть в основном четыре типа законов термодинамики.0007
- Нулевой закон термодинамики
- Первый закон термодинамики
- Второй закон термодинамики
- Третий закон термодинамики
Нулевой закон термодинамики
9000 5 Закон термодинамики Зерота гласит, что «Когда две системы в тепловом равновесии друг с другом, а также отдельно в тепловом равновесии с третьей системой, то говорят, что все три находятся в равновесии друг с другом».
Например: Предположим, что две системы А и В разделены адиабатической стенкой, при этом каждая система контактирует с третьей системой С с помощью проводящей стенки. Состояния систем (т. е. их физические переменные) будут изменяться до тех пор, пока А и В не придут к тепловому равновесию с С. После этого представьте, что адиабатическая стенка между А и В заменена проводящей стенкой, а С изолирована от А и В адиабатической стенкой. Можно проанализировать, что состояния A и B больше не меняются. Следовательно, они находятся в равновесии друг с другом.
Первый закон термодинамики
Первый закон термодинамики (обычно называемый законом сохранения энергии) гласит, что «Энергия не может быть ни создана, ни уничтожена, она может быть преобразована из одной формы в другую».
Внутренняя энергия (U) системы может быть изменена двумя способами передачи энергии: теплотой и работой.
Предположим, ∆Q – Тепло, поступающее в систему из окружающей среды
∆W — выполненная работа
∆U — изменение внутренней энергии
Итак, общий принцип сохранения энергии: ∆Q = ∆U + ∆W
Второй закон термодинамики
Второй закон термодинамики гласит, что «Любой самопроизвольный процесс всегда будет приводить к увеличению энтропии, которая измеряет хаотичность системы во Вселенной. Понятие энтропии связано со вторым законом термодинамики. Его можно представить как:
Понятие энтропии связано со вторым законом термодинамики. Его можно представить как:
ΔSuniv > 0
Где,
ΔSuniv — изменение энтропии
Третий закон термодинамики
Третий закон термодинамики гласит, что энтропия системы достигает постоянного значения, когда ее температура достигает абсолютного нуля (в градусах Кельвина). .
Определение, уравнение, применение и упражнение
Чарльз Лоу
Чарльз Лоу: Мы часто видели воздушный шар. Принцип работы воздушного шара чисто поверхностный и основан на законе Шарля. Воздушный шар состоит из сумки, корзины для перевозки пассажиров и источника топлива. При воспламенении топлива воздух внутри мешка нагревается. Этот горячий воздух расширяется по закону Шарля. Таким образом, согласно закону Шарля, когда температура воздуха увеличивается, объем воздуха также увеличивается, поэтому то же самое происходит и в воздушном шаре. Это делает сумку легче окружающего ее атмосферного воздуха, а выталкивающая сила толкает более легкую оболочку в воздух, и она летит.
Что такое Чарльз Лоу?
Эта концепция закона Шарля была названа в честь ученого Жака Шарля, эта концепция была сформулирована в 1780 году. Закон Шарля является одним из экспериментальных газовых законов, который описывает, как газы имеют тенденцию расширяться при нагревании. Согласно закону Шарля, «при постоянном давлении объем неподвижной массы прямо пропорционален температуре». Математически это можно записать как:
V ∝ T
V = kT
Уравнение и вывод закона Чарльза
Как мы знаем, при постоянном давлении объем фиксированной массы прямо пропорционален температуре. Таким образом, мы можем записать это как:
V∝T
V = kT
V/T = k = константа пропорциональности
Если температура увеличивается до T1, объем газа становится V1, это можно записать как:
V1/T1 = k ———————(1)
И далее температура увеличивается до T2, затем объем газа становится V2
V2/T2 = k ———————- (2)
Приравнивая (1) и (2) получаем,
V1/ T1 = V2/T2
ИЛИ,
V1T2 = V2T1
Где
V1 — объем идеального газа при температуре T1
T1 — температура газа
V2 Объем идеального газа при температуре T1
T2 – температура газа
k – константа пропорциональности
График закона Шарля (зависимость объем-температура)
Закон Шарля представляет собой зависимость объема от температуры, при повышении температуры объем газа увеличивается. График, построенный ниже, показывает, что с повышением температуры увеличивается и объем газа.
График, построенный ниже, показывает, что с повышением температуры увеличивается и объем газа.
Применение закона Чарльза
Некоторые из приложений закона Чарльза:
Легкие человека: Легкие человека представляют собой губчатые органы, наполненные воздухом, которые играют важную роль в дыхании. Воздух поступает в легкие, заставляя легкие расширяться и вытекать, когда они сокращаются. Зимой по мере снижения температуры воздуха. В результате снижается и температура тела. Согласно закону Шарля, объем прямо пропорционален температуре. Следовательно, уменьшение температуры также уменьшает объем. Это приводит к тому, что легкие сжимаются, а физические нагрузки, такие как бег трусцой, становятся трудными в морозные зимние дни.
Плавательный бассейн: В детстве мы все использовали плавательный бассейн во время занятий по плаванию. Поплавки для бассейнов наполнены воздухом, что делает их менее плотными, чем вода. Когда вода холоднее воздуха, воздух в поплавках сжимается из-за снижения температуры воздуха внутри поплавков. Это обратное явление происходит в жаркие летние дни, когда вода намного теплее.
Это обратное явление происходит в жаркие летние дни, когда вода намного теплее.
Выпечка: Мы можем испытать действие закона Шарля и на наших кухнях. Наши вкусные хлебобулочные изделия, такие как хлеб, пирожные и печенье, не были бы пористыми и мягкими без дрожжей. Дрожжи — это разрыхлитель, который превращает сахар в тесте в углекислый газ. Когда выпекаются хлеб и пирожные, конверсия ускоряется. Выделяющийся газ расширяется из-за повышения температуры в печи. Это расширение приводит к тому, что хлеб и пирожные приобретают губчатый вид.
Упражнение, основанное на законе Чарльза
Упражнение, основанное на законе Чарльза:
Вопрос 1: На корабле, плывущем в Индийском океане при температуре 23,4 °C, воздушный шар наполнен 2 л воздуха. Каков будет объем воздушного шара, когда корабль достигнет Тихого океана, где температура 26,1°С?
Решение: Согласно вопросу V1 = 2L
T1 = (23,4 + 273) = 296.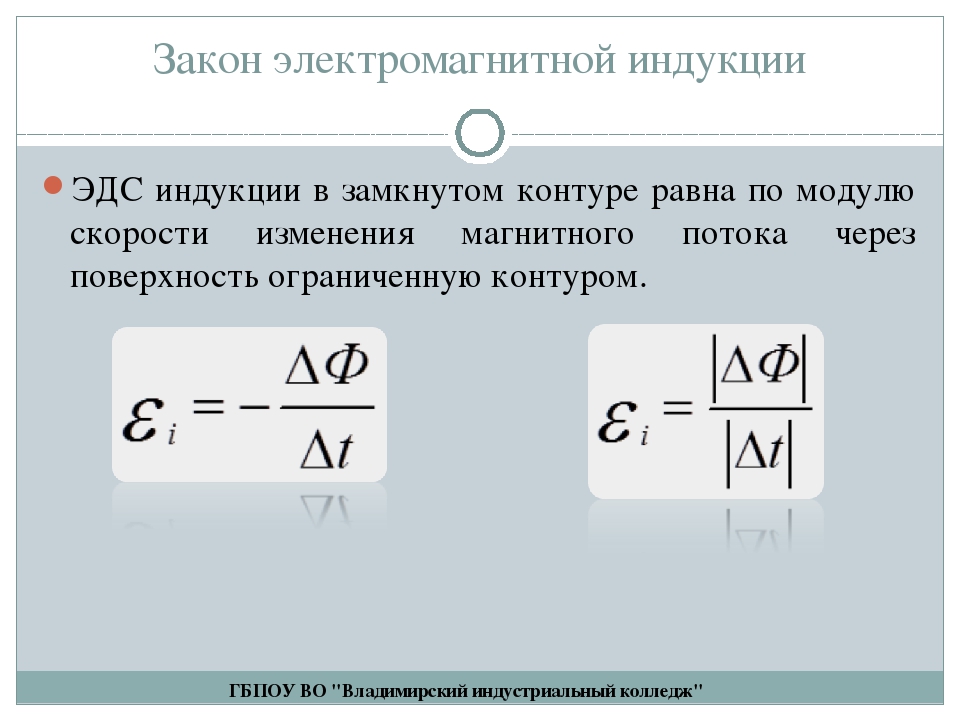

 Изолированный сосуд является примером изолированной системы.
Изолированный сосуд является примером изолированной системы.