Что такое понятие равномерного движения в физике?
Оглавление
Время чтения: 4 минуты
684
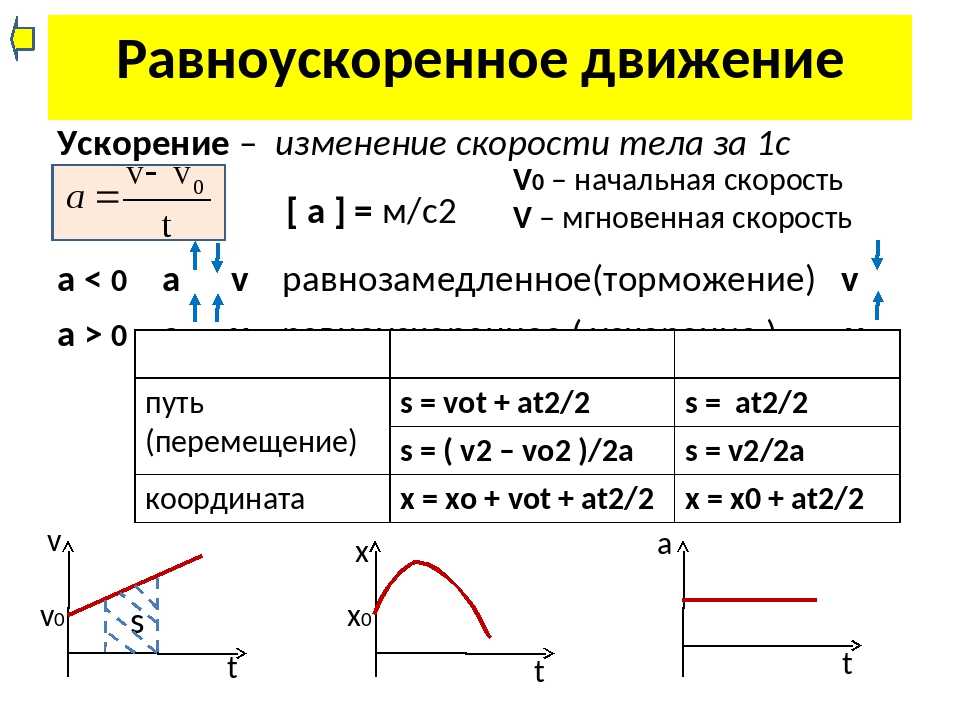
Понятие равномерного движения
В физике понятие равномерное движение тела – это движение в одном направлении (и по модулю, и по направлению) с равномерной скоростью. Если тело движется с равномерной скоростью, то отрезки, которое оно преодолеет за некоторый промежуток времени, будут равными. Это значит, что за каждые 20, 30, или 50 минут перемещение будет происходить на одинаковые расстояния.
Если рассматривать процесс равномерное движение по окружности или по прямой, можно сказать, что создать условия, при которых перемещение будет происходить на равные расстояния за одинаковые промежутки времени, практически невозможно. Можно постараться максимально приблизиться к этому.
Чтобы наглядно представить этот процесс, стоит расположить ось OY вокруг траектории ее движения. Чтобы определить, в каком направлении будет двигаться тело, в случае, если движение будет прямолинейным и равномерным, достаточно отследить координату Y.
{1}}\]
График равномерного движения по прямой можно изобразить следующим образом:
В данном случае координата y2 будет идентична координате x, а координата y1 будет соответствовать x0.
В зависимости от того, в каком направлении осуществляется движение и как расположена ось, ∆s может принимать и отрицательное, и положительное значение. Если равномерное движение и прямолинейное, модуль траектории перемещения идентичен проделанному пути.
Формула
Скорость движения тела, если тело движется по прямой равномерно, формула равномерного движения будет выглядеть так:
\[z=\frac{\Delta x}{\Delta y}=\frac{y 2-y 1}{t 2-t 1}\]
В том случае, если z будет иметь значение больше нуля, тело будет двигаться вокруг оси в положительном направлении, в противном случае равномерное прямолинейное движение будет осуществляться в отрицательном направлении.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Математическая характеристика равномерного движения по окружности
Закон перемещения тела при прямом, равномерном движении выражается посредством алгебраического тождества.
Уравнение равномерного движения выглядит следующим образом:
\[\boldsymbol{y(t)=y 0+z t}\\\boldsymbol{\mathrm{z}=\text { const }}\]
y0 – точка расположения объекта в момент времени t=0.
Скорость равномерного прямолинейного движения
Скорость равномерного прямолинейного движения это величина, которая показывает, как быстро меняются координаты движения тела. Следовательно, можно сказать, что если каждую минуту или секунду тело преодолевает равные промежутки пути, оно движется равномерно, или равноускоренно. Такой вид пути можно изобразить схематически следующим образом:
При таком движении важны следующие показатели:
- Время, затраченное на преодоление пути.
- Скорость.
- Перемещение.
Это соотношение можно вывести в следующую формулу: \[\boldsymbol{s=v \times t}\].
В данном уравнении движении s – это отрезок пути, или модуль перемещения;
v – модуль скорости;
t – время, на протяжении которого происходило движение.
Отсюда можно вывести еще одну формулу для определения скорости: \[v=\frac{s}{t}\].
Не стоит забывать о том, что скорость при прямолинейном равномерном движении – величина постоянная.
Оценить статью (85 оценок):
Поделиться
Перемещение и копирование формулы – Служба поддержки Майкрософт
Excel
Формулы и функции
Формулы
Формулы
Перемещение и копирование формулы
Excel для Microsoft 365 Excel для Интернета Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Еще…Меньше
Важно помнить о возможностях изменения относительной ссылки на ячейку при переходе или копировании формулы.
Перемещение формулы
-
В группе Буфер обмена на вкладке Главная нажмите кнопку Вырезать.
Формулы можно скопировать и путем перетаскивания границы выделенной ячейки в левую верхнюю ячейку области вставки. При этом будут заменяться все существующие данные.
-
Выполните одно из указанных ниже действий.
Чтобы вировать формулу иформатирование: в группе Буфер обмена на вкладке Главная нажмите кнопку В виде вкладки.
-
Чтобы вировать только формулу:в группе Буфер обмена на вкладке Главная нажмите кнопку В
org/ListItem”>
Выделите ячейку с формулой, которую необходимо переместить.
Копирование формулы
-
Вы выберите ячейку, содержащую формулу, которую нужно скопировать.
-
В группе Буфер обмена
-
Выполните одно из указанных ниже действий.
-
Чтобы вировать формулу и любое форматирование, в группе Буфер обмена на вкладке Главная нажмите кнопку В виде вкладки.
-
Чтобы вировать только формулу, в группе Буфер обмена на вкладке Главная нажмите кнопку Вировать ,выберите специальная ветвь ,а затем щелкните Формулы.
Примечание: В нее можно вклеить только результаты формулы. В группе Буфер обмена на вкладке Главная нажмите кнопку Вировать, выберите специальная ветвь ,а затем щелкните Значения.
-
-
Убедитесь, что ссылки на ячейки в формуле дают нужный результат. При необходимости переключить тип ссылки можно следующим образом:
-
-
Выделите ячейку с формулой.
-
В строке формул строка формул выделите ссылку, которую нужно изменить.
org/ListItem”>
Для переключения между сочетаниями нажмите F4.
В таблице подводится информация об обновлении типа ссылки при копировании формулы, содержащей ссылку, на две ячейки вниз и на две ячейки вправо.
-
|
Копируемая формула |
Первоначальная ссылка |
|
|---|---|---|
|
|
$A$1 (абсолютный столбец и абсолютная строка) |
$A$1 |
|
A$1 (относительный столбец и абсолютная строка) |
C$1 |
|
|
$A1 (абсолютный столбец и относительная строка) |
$A3 |
|
|
A1 (относительный столбец и относительная строка) |
C3 |
Примечание: Формулы также можно копировать в смежные ячейки с помощью маркер заполнения .
После проверки на то, что ссылки на ячейки в формуле дают нужный результат в шаге 4, вы выберите ячейку со скопированной формулой и перетащите его по диапазону, который вы хотите заполнить.
Перемещение формул очень похоже на перемещение данных в ячейках. Единственное, что нужно знать, — ссылки на ячейки, используемые в формуле, остаются нужными после перемещения.
-
Вы выберите ячейку с формулой, которую вы хотите переместить.
-
Щелкните Главная > вырезать (или нажмите CTRL+X).
-
Убедитесь, что ссылки на ячейки остаются нужными.
Совет: Вы также можете щелкнуть ячейки правой кнопкой мыши, чтобы вырезать и врезать формулу.
Выйдите из ячейки, в которая должна вться формула, и нажмите кнопку Вировать (или нажмите CTRL+V).
Совет: Формулу также можно скопировать и вкопировать в другую ячейку или на другой таблицу.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Копирование и вставка формулы в другую ячейку или на другой лист
Изменение типа ссылки: относительная, абсолютная, смешанная
Положение, длина пути и перемещения
Длина пути, пройденного автомобилем, движущимся из одной точки в другую, называется расстоянием, а пройденное расстояние также называется длиной пути. Однако, если он выбирает кратчайший путь, он становится перемещением. Можно также сказать, что разница между начальным и конечным положением автомобиля и есть его водоизмещение.
Но прежде чем мы двинемся дальше, дайте нам знать, что такое движение. Если мы посмотрим вокруг, то везде сможем увидеть движущиеся объекты. Дети играют, птицы летают, животные передвигаются в поисках пищи, люди ходят или бегают, транспортные средства бегают по дорогам, реки текут и т. д. В общем, мы можем найти движение повсюду во Вселенной. Но что подразумевается под движением?
Если вы заметили вышеупомянутые экземпляры, все они перемещаются из одного места в другое и меняют свое место. Следовательно, движение есть не что иное, как изменение положения тела во времени. Если тело покоится, это означает, что тело не движется, а просто означает, что оно описывается относительно системы отсчета.
Положение – Понимание на примере
Чтобы описать движение объекта, вы должны знать и уметь описывать его положение.
Давайте разберем это на примере, допустим, Рам переместился из точки R в S. Это означает, что начальное/предыдущее положение Рама было R, откуда он через какое-то время переместился в S. Теперь вопрос в том, как мы можем представить исходное положение Рама?
В физике мы задаем положение с помощью точки отсчета и набора трех взаимно перпендикулярных осей или прямоугольных систем координат. Это оси X, Y и Z. Контрольная точка известна как происхождение; это пересечение вышеупомянутых трех осей (X, Y и Z). Итак, мы берем точку R в качестве точки отсчета или начала координат с координатами (0, 0, 0), а S представлена набором координат по трем осям (X, Y, Z).
Поскольку мы знаем, что движение — это изменение положения во времени, мы устанавливаем в этой системе часы. Система координат вместе с часами является системой отсчета. Система отсчета — это произвольный набор осей, от которых описывается положение и движение объекта. Таким образом, если одна или несколько координат тела изменяются со временем, говорят, что тело находится в движении.
Длина пути
Длина пути — это фактическая длина пути, пройденного телом между Начальным и Конечным положениями.
Смещение – Понимание на примере
Это кратчайшая длина, т.е. расстояние по прямой линии между начальным и конечным положениями. Перемещение является векторной величиной.
(Изображение скоро будет обновлено)
Формула смещения:
Если s i – начальное положение объекта, а s f – конечное положение, то смещение этого объекта:
с = s i – s f
Здесь s – переменная, называемая смещением.
Поскольку смещение имеет величину и направление, оно является векторной величиной, а путь является скалярным, поскольку имеет только направление и не имеет его.
Объяснение с примерами
Правильно понимать положение, длину пути и смещение, а также разницу между ними. Ниже приведены некоторые примеры с пояснениями:
Возьмем три примера. В первом Рам начинает движение из точки R квадратного пути РГТУ с RS = 1 км. Он проходит через S, T, U и возвращается в R через 20 минут. Пройденный им путь равен 4 х 1 км = 4 км. Но если вы видите изменение его положения от начала до конца пути, оно равно нулю (в нем нет изменений). Рам начал в точке R и вернулся в R.
(Изображение скоро будет обновлено)
Во втором примере
Баран перемещается из точки R в точку S по прямой за 60 минут. Пройденный им путь равен 5 км. И общее расстояние от начальной до конечной точки, пройденное Рамом, также равно 5 км.
(Изображение скоро будет обновлено)
Теперь в третьем примере Рам путешествует по треугольному пути. Он стартует из точки R и достигает T через точку S за 120 минут. Пройденный им путь равен 3 км + 4 км = 7 км. Но если мы посмотрим, как далеко он находится от точки, откуда он начал свой путь, то это 5 км.
(Изображение скоро будет обновлено)
Если вы заметили приведенные выше примеры, пройденное расстояние и изменение положения могут совпадать, а могут и не совпадать.
Расстояние, пройденное телом, называется длиной пути. Тогда как изменение положения, то есть разница между начальным и конечным положениями тела, называется его перемещением.
Следовательно, длина пути равна 4 км, а смещение равно 0 в первом случае. Длина пути такая же, как и перемещение – 5 км во втором примере и в третьем примере длина пути 7 км, но перемещение равно 5 км.
Из приведенного выше текста мы понимаем, что положение объекта описывает точку, в которой объект находится в данный момент. Изменение положения описывает, что объект приводится в движение, и это пройденное расстояние является длиной пути. Кроме того, если объект выбирает кратчайший путь, это смещение.
Расстояние и смещение
Расстояние и смещение — две величины, которые могут казаться одним и тем же, но имеют совершенно разные определения и значения.
- Расстояние — это скалярная величина, которая относится к тому, «сколько земли преодолел объект» во время своего движения.
- Смещение — это векторная величина, которая указывает на то, «насколько далеко находится объект от места»; это общее изменение положения объекта.
Чтобы проверить свое понимание этого различия, рассмотрите движение, изображенное на диаграмме ниже. Учитель физики проходит 4 метра на восток, 2 метра на юг, 4 метра на запад и, наконец, 2 метра на север.
Несмотря на то, что учительница физики прошла в общей сложности 12 метров, ее перемещение равно 0 метрам. За время своего движения она «преодолела 12 метров земли» (расстояние = 12 м). Тем не менее, когда она заканчивает идти, она не находится «не на своем месте», т. Е. Для ее движения нет смещения (смещение = 0 м). Смещение, будучи векторной величиной, должно учитывать направление. 4 метра на восток отменяет 4 метра на запад; и 2 метра на юг отменяет 2 метра на север. Векторные величины, такие как смещение, равны известно направление . Скалярные величины, такие как расстояние, не знают направления. При определении общего расстояния, пройденного учителями физики, можно не учитывать различные направления движения.
Теперь рассмотрим другой пример. На приведенной ниже диаграмме показано положение лыжника в разное время. В каждый из указанных моментов времени лыжник поворачивается и меняет направление движения. Другими словами, лыжник перемещается из пункта А в пункт В, затем в пункт С и затем в пункт D.
С помощью диаграммы определите результирующее перемещение и расстояние, пройденное лыжником за эти три минуты. Затем нажмите кнопку, чтобы увидеть ответ.
В качестве последнего примера рассмотрим футбольного тренера, расхаживающего взад-вперед вдоль боковой линии. На приведенной ниже диаграмме показаны несколько позиций тренера в разное время. В каждой отмеченной позиции тренер делает «разворот» и движется в обратном направлении. Другими словами, тренер перемещается из позиции A в B, затем в C и затем в D.
Каково результирующее перемещение и расстояние между вагонами? Нажмите кнопку, чтобы увидеть ответ.
Чтобы понять различие между расстоянием и смещением, вы должны знать определения. Вы также должны знать, что векторная величина, такая как смещение, учитывает направление , а скалярная величина, такая как расстояние, не знает направления . Когда объект меняет направление движения, смещение учитывает это изменение направления; движение в противоположном направлении фактически начинается с отменить любое смещение, которое когда-то было.
Проверьте свое понимание
1. Каково перемещение команды по кроссу, если они начинают в школе, пробегают 10 миль и заканчивают обратно в школе?
2.