Перемещение при прямолинейном равномерном движении – формула
4.7
Средняя оценка: 4.7
Всего получено оценок: 144.
4.7
Средняя оценка: 4.7
Всего получено оценок: 144.
Наиболее простым видом движения является прямолинейное равномерное движение. Рассмотрим перемещение при таком движении.
Формула перемещения
Прямолинейное равномерное движение – это движение с постоянной скоростью $v$, без ускорения ($a=0$).
Рис. 1. Прямолинейное равномерное движение.Модуль вектора перемещения у такого движения прямо пропорционален времени движения $t$:
$$s=vt$$
А по определению, вектор перемещения равен разнице между начальной и текущей координатами материальной точки:
$$s=x-x_0$$
Подставляя значение вектора перемещения из одной формулы в другую, можно получить зависимость, описывающую текущую координату материальной точки в зависимости от времени:
$$x-x_0=vt$$
Окончательно имеем:
$$x=x_0+vt$$
Это и есть формула перемещения при прямолинейном равномерном движении.
Эту формулу можно представить и в векторном виде:
$$\overrightarrow x=\overrightarrow {x_0}+\overrightarrow v t$$
Движение на плоскости или в пространстве
При движении по плоскости или в трехмерном пространстве следует использовать векторную форму представленной формулы. Векторы проецируются на оси координат, и дальше проводятся расчеты для каждой координаты вектора перемещения.
Например, если начальная координата на плоскости задана точкой $(1,2)$, скорость задана вектором $(3,4)$, то после проекции на оси абсцисс и ординат получаем две формулы:
- По оси абсцисс: $$x=1+3t$$
- По оси ординат: $$x=2+4t$$
Теперь, подставив время (например, 5с) в эти формулы, получим точку $(16,22)$, которая будет координатами точки перемещения в указанный момент.
График перемещения
Во многих случаях движение тел удобно представлять в виде графика. По оси абсцисс в этом случае откладывается время в пути, а по оси ординат – значение координаты. Для построения графика используется полученная формула.
Для построения графика используется полученная формула.
Исходя из вида формулы, а также построив несколько различных графиков, можно отметить важные особенности графика перемещения при равномерном прямолинейном движении:
- График представляет собой прямую.
- График пересекает ось ординат в точке $(0,x_0)$.
- График пересекает ось абсцисс в точке $(-{x_0\over v},0)$.
- График пройдет через начало координат, если $x_0=0$.
График перемещения и траектория движения – это не одно и то же! График показывает зависимость координаты от времени по одной из осей. Траектория движения же показывает путь, который прошла точка вдоль прямой, на плоскости или в пространстве. Таким образом, если материальная точка движется на плоскости – для описания ее перемещения требуется два графика, а если в пространстве – то три, по количеству координатных осей.
График скорости
Вид графика скорости при равномерном прямолинейном движении можно построить, учитывая, что для равномерного движения $v=const$.
Из этого же графика ясно, что значение перемещения при данной скорости равно площади прямоугольника под прямой. Высота прямоугольника равна модулю скорости. Ширина прямоугольника равна времени пути.
Что мы узнали?
Координата перемещения при прямолинейном равномерном движении описывается формулой $x=x_0+vt$. Если движение происходит на плоскости или в пространстве – необходимо использовать векторный вид формулы и проецировать вектора на оси координат. График перемещения при равномерном движении представляет собой прямую.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
Валера Исхаков
10/10
Елизавета Фомичёва
10/10
Андрей Коробкин
10/10
Оценка доклада
4. 7
7
Средняя оценка: 4.7
Всего получено оценок: 144.
А какая ваша оценка?
Перемещение при прямолинейном равномерном движении
Содержание
На прошлом уроке мы научились находить координаты движущегося тела в определенный момент времени. Для этого мы использовали вектор перемещения, а точнее — его проекцию: $s_x = x_2 \space − \space x_1$. Итак, зная проекцию вектора перемещения и начальную координату тела, мы находили интересующую нас координату $x_2$, которую тело имеет по прошествии какого-то времени: $x_2 = x_1 \space + \space s_x$.
Но что делать, если вектор перемещения изначально не задан? На данном уроке вы узнаете, как его определить в самом простом случае — при прямолинейном и равномерном движении тела. А также вам предстоит знакомство с графиками зависимости модуля скорости и ее проекции от времени (они помогут нам в нахождении модуля и проекции перемещения) и уравнением движения тела.
Формулы скорости и перемещения в векторной форме
Для начала вспомним определение прямолинейного равномерного движения (рисунок 1).
Рисунок 1. Равномерное прямолинейное движениеПрямолинейное равномерное движение — это движение, при котором тело движется по прямолинейной траектории и проходит за любые равные промежутки времени одинаковые пути.
При таком движении перемещение тела с течением времени увеличивается. Быстроту этого увеличения характеризует скорость.
Что называется скоростью равномерного прямолинейного движения?
Скорость равномерного прямолинейного движения — это постоянная векторная величина, равная отношению перемещения тела за любой промежуток времени к значению этого промежутка:
$\vec \upsilon = \frac{\vec s}{t}$.
Скорость — это векторная величина: она имеет как направление, так и численное значение (ее модуль). Обратите внимание, что скорость при равномерном прямолинейном движении постоянна: не изменяется ни ее модуль, ни ее направление.
Теперь давайте выразим из формулы скорости искомое перемещение:
$\vec s = \vec \upsilon t$.
Хорошо, теперь у нас есть формула для перемещения. Но она в векторной форме. С одной стороны, это дает нам возможность судить о том, как скорость и перемещение направлены относительно друг друга. Из наших формул видно, что при прямолинейном равномерном движении эти величины сонаправлены друг другу.
С другой стороны, в таком виде мы не сможем использовать формулу перемещения для расчетов. Теперь нам нужно получить формулу для проекции вектора перемещения.
{"questions":[{"content":"Скорость при равномерном прямолинейном движении[[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["постоянна по модулю и направлению","постоянна только по модулю","постоянна только по направлению","непостоянна ни по модулю, ни по направлению"],"answer":[0]}}}]}Формула перемещения для практического использования
Итак, при решении задач нам понадобится формула, в которую будут входить проекции векторов на ось.
Как найти проекцию вектора перемещения тела, движущегося прямолинейно и равномерно, если известны проекция вектора скорости и время движения?
$s_x = \upsilon_x t$.
Обратите внимание, что проекции $s_x$ и $\upsilon_x$ могут иметь знак «минус». Это будет означать, что соответствующий проекции вектор направлен противоположно выбранной оси.
Например, если вектор скорости $\vec \upsilon_1$ сонаправлен оси OX (рисунок 2), то проекция скорости будет больше нуля: $\upsilon_{1x} > 0$. Если же скорость $\vec \upsilon_2$ направлена против оси OX, то проекция этого вектора будет отрицательной: $\upsilon_{2x} < 0$.
Рисунок 2. Знак проекции скорости в зависимости от ее направленияМы не изображаем на рисунках и схемах проекцию вектора скорости подобно проекции вектора перемещения (мы рассчитываем проекцию вектора скорости по вышеприведенной формуле). Нам достаточно знать, что при равномерном прямолинейном движении вектор скорости всегда сонаправлен с вектором перемещения. Так, если тело двигалось противоположно направлению координатной оси, то проекция вектора перемещения будет отрицательной. Используя формулу $\upsilon_x = \frac{s_x}{t}$, мы получим отрицательную проекцию вектора скорости.
Так, если тело двигалось противоположно направлению координатной оси, то проекция вектора перемещения будет отрицательной. Используя формулу $\upsilon_x = \frac{s_x}{t}$, мы получим отрицательную проекцию вектора скорости.
{"questions":[{"content":"Проекцию вектора перемещения можно рассчитать по формуле:[[choice-5]]","widgets":{"choice-5":{"type":"choice","options":["$s_x = \\upsilon_x t$","$\\vec s = \\vec \\upsilon t$","$s_x = \\vec \\upsilon t$","$s_x = \\frac{\\upsilon_x}{t}$"],"answer":[0]}}}]}Модуль вектора перемещения и путь
Иногда мы можем встретить задачи, при решении которых нам будет неважно направление векторов перемещения и скорости. Тогда мы можем использовать уже знакомую вам формулу, в которой фигурируют модули величин:
$s = \upsilon t$.
Используя эту формулу ранее, мы называли величину $s$ пройденным путем, а теперь называем ее перемещением. Ошибки здесь нет — это частный случай, когда путь равен модулю перемещения (рисунок 3).
При каком условии модуль вектора перемещения, совершенного телом за некоторый промежуток времени, равен пути, пройденному телом за тот же промежуток времени?
При движении в одном направлении модуль вектора перемещения, совершенного телом за некоторый промежуток времени, равен пути, пройденному этим телом за тот же промежуток времени.
Взгляните на рисунок 4, подтверждающий этот факт.
Рисунок 4. Движение тела по различным траекториямЕсли тело (автомобиль на рисунке 4) движется в одном направлении (например, из точки $O$ в точку $A$ или из точки $O$ в точку $C$), модуль вектора перемещения равен пройденному пути. Если же направление движения тела изменяется (например, при движении из точки $O$ в точку $B$ и обратно в точку $O$ или при движении по криволинейной траектории из точки $O$ в точку $D$), то путь, пройденный телом, будет больше модуля его перемещения.
{"questions":[{"content":"Модуль вектора перемещения равен пути, пройденному телом, в случае, если тело двигалось[[choice-11]]","widgets":{"choice-11":{"type":"choice","options":["прямолинейно","криволинейно","равномерно","равноускоренно"],"answer":[0]}}}]}График зависимости модуля вектора скорости от времени
Рассмотрим график зависимости модуля вектора скорости $\upsilon$ от времени $t$. Тело при этом движется равномерно и прямолинейно (рисунок 5).
Тело при этом движется равномерно и прямолинейно (рисунок 5).
Модуль вектора перемещения $s$ в данном случае мы можем рассчитать по формуле:
$s = \upsilon_1 t_1$.
А теперь взгляните на закрашенный зеленым цветом прямоугольник на рисунке 5. Его площадь $S$ по определению будет равна произведению его смежных сторон — $\upsilon_1$ (длины отрезка $O \upsilon_1$) и $t_1$ (длины отрезка $O t_1$).
При прямолинейном равномерном движении тела модуль вектора его перемещения численно равен площади прямоугольника (площади под графиком скорости), заключенного между графиком скорости, осью Ot и перпендикулярами к этой оси, восстановленными из точек, соответствующих моментам начала и конца наблюдения (в данном случае из точек $O$ и $t_1$).
{"questions":[{"content":"Площадь под графиком модуля скорости в зависимости от времени равна[[choice-15]]","widgets":{"choice-15":{"type":"choice","options":["модулю вектора перемещения","вектору перемещения","средней скорости движения","времени движения"],"answer":[0]}}}]}График зависимости проекции вектора скорости от времени
И все-таки, чаще мы будем иметь дело с задачами, при решении которых нам понадобится использовать проекции векторов.
Например, обратимся к задаче с катерами из прошлого урока. Два катера двигаются в противоположных направлениях (рисунок 6). Один из них проходит $60 \space км$, а другой — $50 \space км$. Пусть эти перемещения совершены за время $t_1$, равное $2 \space ч$.
Рисунок 6. Иллюстрация к задачеВ этом случае векторы скорости и перемещения первого катера будут сонаправлены друг другу, как и векторы скорости и перемещения второго катера. Их проекции: для первого катера они будут положительными, а для второго — отрицательными.
Проекция скорости первого катера:
$s_{1x} = \upsilon_{1x} t_1$,
$\upsilon_{1x} = \frac{s_{1x}}{t_1}$,
$\upsilon_{1x} = \frac{60 \space км}{2 \space ч} = 30 \frac{км}{ч}$.
Проекция скорости второго катера:
$\upsilon_{2x} = \frac{s_{2x}}{t_1}$,
$\upsilon_{2x} = \frac{−50 \space км}{2 \space ч} = −25 \frac{км}{ч}$.
А теперь взгляните на графики зависимости проекций векторов скорости от времени (рисунок 7).
Рисунок 7.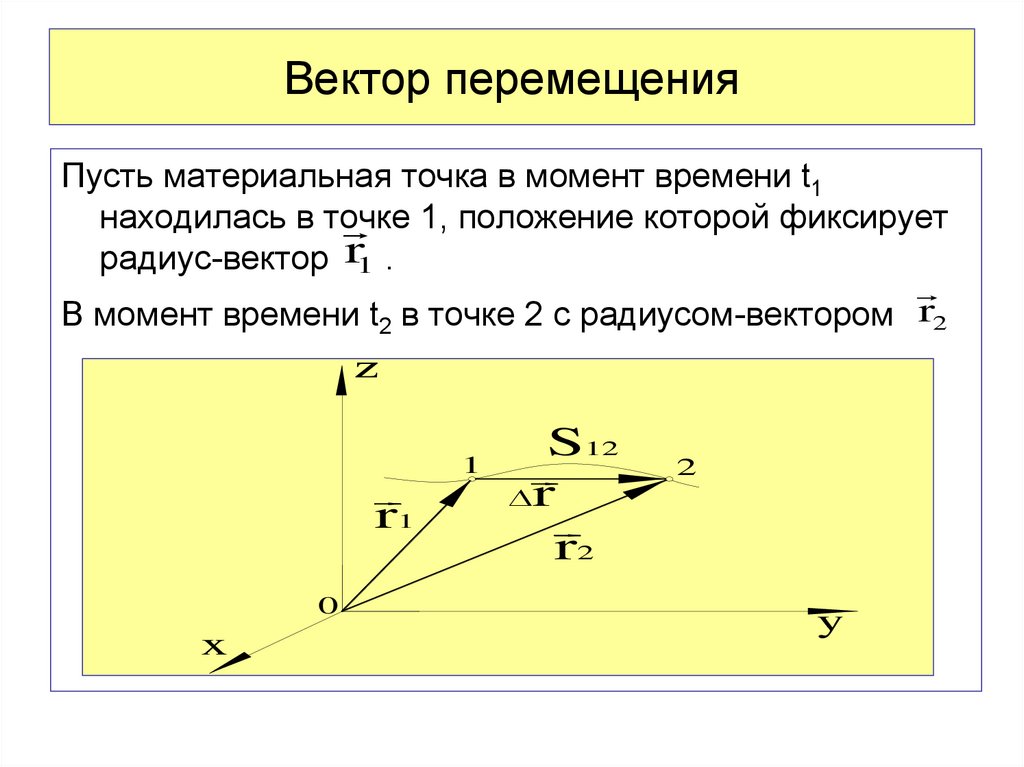 Графики зависимости проекций векторов скорости от времени движения
Графики зависимости проекций векторов скорости от времени движенияКакую информацию о движении двух тел можно получить по графикам, изображенным на рисунке 7?
Здесь мы видим и числовые значения проекций векторов скорости, и их знаки, а также знаки проекций перемещений, которые совершили катера за время $t_1$. Проекции этих перемещений численно равны площадям под графиками:
- проекция вектора перемещения $s_{1x}$ больше нуля и численно равна площади оранжевого прямоугольника;
- проекция вектора перемещения $s_{2x}$ меньше нуля и численно равна площади голубого прямоугольника.
{"questions":[{"content":"По графику зависимости проекции скорости равномерного прямолинейного движения от времени можно определить[[choice-19]]","widgets":{"choice-19":{"type":"choice","options":["проекцию вектора перемещения за данное время","вектор перемещения","среднюю скорость движения"],"answer":[0]}}}]}Уравнение движения
Теперь получим формулу для определения координаты тела при неизвестном векторе перемещения.
Рассмотрим автомобиль, который двигается равномерно и прямолинейно по какому-то участку дороги (рисунок 8). За тело отсчета возьмем светофор и направим ось OX в сторону движения автомобиля.
Рисунок 8. Прямолинейное равномерное движение автомобиляЧему будет равна проекция перемещения автомобиля из точки с координатой $x_0$ в точку с координатой $x$?
По определению проекции:
$s_x = x \space − \space x_0$.
По определению проекции скорости:
$s_x = \upsilon_x t$.
Приравняем правые части этих уравнений друг к другу:
$\upsilon_x t = x \space − \space x_0$.
Теперь выразим отсюда искомую координату $x$ и получим кинематический закон движения или уравнение движения.
Для определения координаты движущегося тела в любой момент времени достаточно знать его начальную координату и проекцию скорости движения на ось:
$x = x_0 \space + \space \upsilon_x t$.
{"questions":[{"content":"Уравнение прямолинейного и равномерного движения имеет вид:[[choice-22]]","widgets":{"choice-22":{"type":"choice","options":["$x = x_0 \\space + \\space \\upsilon_x t$","$x = \\upsilon_x t$","$x = x_0 \\space + \\space s_x t$","$s_x = \\upsilon_x t$"],"answer":[0]}}}]}Упражнения
Упражнение №1
Может ли график зависимости модуля вектора скорости от времени располагаться под осью Ot (то есть в области отрицательных значений оси скорости)?
Посмотреть ответ
Скрыть
Ответ:
График зависимости модуля вектора скорости от времени (рисунок 5) не может располагаться под осью Ot. Причина этому — само определение модуля какой-либо величины. Модуль — это всегда положительная величина.
Причина этому — само определение модуля какой-либо величины. Модуль — это всегда положительная величина.
Упражнение №2
Постройте графики зависимости проекций векторов скорости от времени для трех автомобилей, движущихся прямолинейно и равномерно, если два из них едут в одном направлении, а третий — навстречу им. Скорость первого автомобиля равна $60 \frac{км}{ч}$, второго — $80 \frac{км}{ч}$, а третьего — $90 \frac{км}{ч}$.
Посмотреть ответ
Скрыть
Ответ:
Графики зависимости проекций векторов скорости от времени для трех автомобилей показаны на рисунке 9.
Рисунок 9. Графики зависимости проекций векторов скорости от времени для трех автомобилейАвтомобили движутся равномерно. Значит, скорость не изменяется с течением времени — графики представляют собой прямые, параллельные оси времени Ot.
Первые два автомобиля движутся в одном направлении — мы примем его за направление оси OX. Поэтому проекции векторов скорости $\upsilon_{1x}$ и $\upsilon_{2x}$ будут положительными. Третий автомобиль двигается в противоположную сторону. Значит, проекция его вектора скорости $\upsilon_{3x}$ будет отрицательной.
Третий автомобиль двигается в противоположную сторону. Значит, проекция его вектора скорости $\upsilon_{3x}$ будет отрицательной.
Объяснение урока: Работа, совершаемая силой, выраженная в векторном представлении действуя на тело по вектору смещения с помощью скалярного произведения.
Работу, совершаемую силой над телом, можно определить следующим образом.
Определение: работа, совершаемая силой над телом
Работа, совершаемая силой над телом, зависит от силы, действующей на тело, и расстояние, на которое тело перемещается в направлении действия этой силы по формуле 𝑊=𝐹⋅𝑑(𝜃), потому что где 𝐹 — величина силы, 𝑑 — величина перемещение тела под действием силы, а 𝜃 – угол между направлениями 𝐹 и 𝑑.
Альтернативным способом представления работы, совершаемой силой над телом, является представление сила и перемещение как векторы, а не как величины векторов.
Произведение двух векторов ⃑𝑎 и
⃑𝑏 может быть скалярным произведением векторов, которое определяется как
следует.
Определение: скалярное произведение двух векторов
Скалярное произведение двух векторов определяется выражением ⃑𝑎⋅⃑𝑏=‖‖⃑𝑎‖‖‖‖⃑𝑏‖‖(𝜃), cos где 𝜃 — угол между ⃑𝑎 и ⃑𝑏. Угол берется против часовой стрелки от от ⃑𝑎 до ⃑𝑏, как показано следующий рисунок.
Работа, совершаемая силой с величиной 𝐹 при перемещении с величина 𝑑 равна ⃑𝐹⋅⃑𝑑⃑𝐹⋅⃑𝑑=‖‖⃑𝐹‖‖‖‖⃑𝑑‖‖(𝜃).cos
Графическое представление ⃑𝐹 и ⃑𝑑 показывает, что произведение величины ⃑𝐹 и величина компонента ⃑𝑑 в направлении ⃑𝐹 есть равно ‖‖⃑𝐹‖‖‖‖⃑𝑑‖‖(𝜃)cos.
Скалярное произведение двух векторов, выраженных в компонентной форме, может быть определено без речь идет об угле между векторами.
Предположим теперь, что векторы ⃑𝐹 и ⃑𝑑 перпендикулярны, как показано на следующем рисунке.
Произведение определяется как ⃑𝐹⋅⃑𝑑=(4,−3)⋅(3,4)⃑𝐹⋅⃑𝑑=(4×3)+(−3×4)=12−12=0.
Скалярное произведение двух перпендикулярных векторов равно нулю.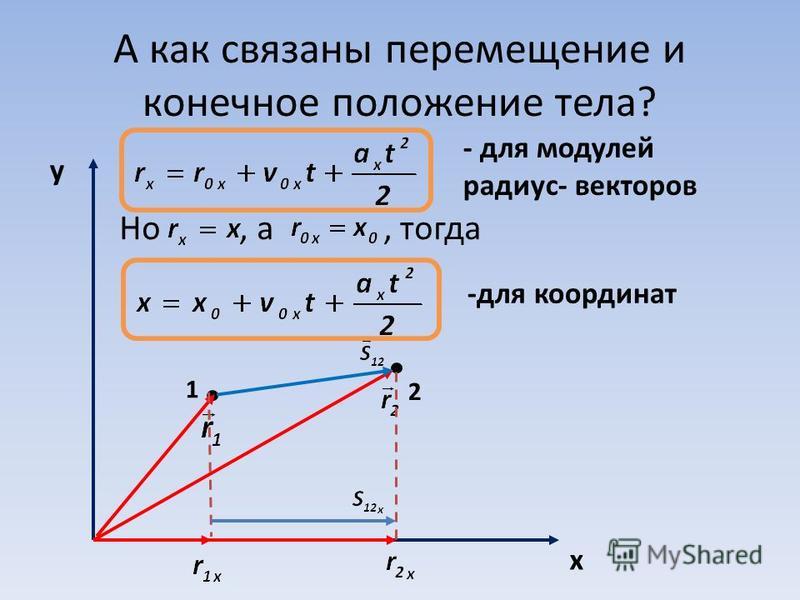 На тело не действуют никакие силы
направление перемещения, поэтому сила не действует на тело.
На тело не действуют никакие силы
направление перемещения, поэтому сила не действует на тело.
Давайте рассмотрим пример использования векторной записи для определения работы силы.
Пример 1. Расчет работы силы, действующей на частицу, где сила и положение даны в виде векторов
Частица движется в плоскости, в которой ⃑𝑖 и ⃑𝑗 — перпендикулярные единичные векторы. Сила ⃑𝐹=9⃑𝑖+⃑𝑗N действует на частицу. Частица движется из начала координат в точку с вектором положения −9⃑𝑖+6⃑𝑗 м. Найдите работу, совершенную силой.
Ответ
Работа силы равна скалярному произведению вектора силы и вектора смещения частицы. Вопрос не дает вектор смещения, однако он дает вектор положения. В вопросе также указано
что частица движется
в указанное положение от начала координат, поэтому вектор смещения частицы определяется выражением
⃑𝑑=(−9−0)⃑𝑖+(6−0)⃑𝑗,м
который равен заданному вектору положения.
Работа силы 𝑊 определяется скалярным произведением векторов что определяется как 𝑊=(9,1)⋅(−9,6)𝑊=(9×−9)+(1×6)=−81+6=−75.
Таким образом, выполненная работа определяется выражением 𝑊=−75.J
Проделанная работа отрицательна. Если энергия частицы сохраняется, то кинетическая энергия частицы должна уменьшаться. Если энергия частицы не сохраняется, вместо этого проделанная работа может увеличить потенциальную энергию частицы.
Теперь давайте рассмотрим пример, когда на тело действуют несколько сил, вызывающих перемещение.
Пример 2. Нахождение работы равнодействующей двух сил, действующих на тело
Тело движется в плоскости, в которой ⃑𝑖 и
⃑𝑗 — перпендикулярные единичные векторы. Две силы ⃑𝐹=9⃑𝑖−2⃑𝑗N и
⃑𝐹=9⃑𝑖−7⃑𝑗N
действовать на тело. Частица движется
из точки с вектором положения
−6⃑𝑖+2⃑𝑗 м
к точке
2⃑𝑖+3⃑𝑗 м. Найдите работу равнодействующей сил.
Найдите работу равнодействующей сил.
Ответ
На тело действуют две силы. Силы являются векторами, и равнодействующая векторов может определяется суммированием компонент векторов. 𝑥-составляющая результирующей силы определяется выражением ⃑𝐹=9⃑𝑖+9⃑𝑖=18⃑𝑖,R а 𝑦-компонента равнодействующей силы определяется выражением ⃑𝐹=−2⃑𝑗−7⃑𝑗=−9⃑𝑗.R
Следовательно, результирующая сила, действующая на тело, равна ⃑𝐹=18⃑𝑖−9⃑𝑗.RN
Конечный вектор положения тела равен 2⃑𝑖+3⃑𝑗, а вектор начального положения тела равен −6⃑𝑖+2⃑𝑗.
Таким образом, вектор смещения из начального положения в конечное положение равен ⃑𝑑=2⃑𝑖+3⃑𝑗−−6⃑𝑖+2⃑𝑗⃑𝑑=2−(−6)⃑𝑖+(3−2)⃑𝑗=8⃑𝑖+⃑𝑗.mm
.mm
.mm , у нас есть это
𝑊=⃑𝐹⋅⃑𝑑,R
что дает нам
𝑊=(18,−9)⋅(8,1)𝑊=(18×8)+(−9×1)=144−9=135.J Теперь рассмотрим пример, в котором ни одна из компонент ни вектор силы, ни компоненты вектора смещения не заданы напрямую.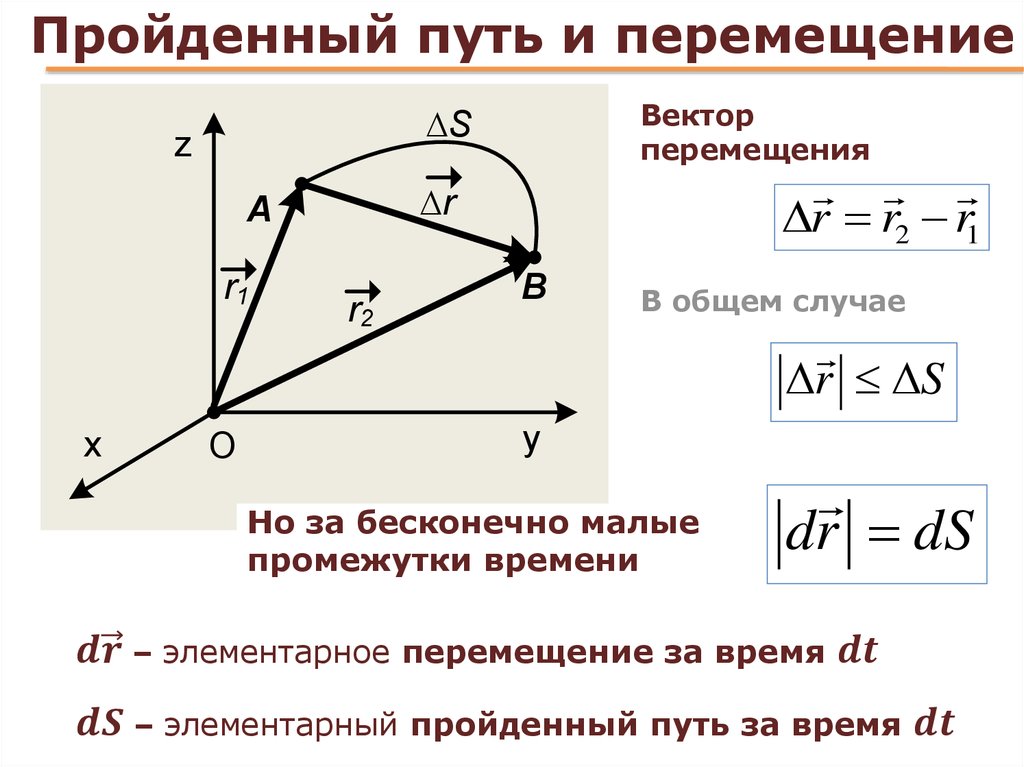
Пример 3. Использование векторов для нахождения работы силы с направлением и величиной, заданными отдельно
Частица переместилась из точки 𝐴(7,−3) в точку
𝐵(−9,2) по прямой под действием
силы ⃑𝐹 величины
8√10 Н
действует в том же направлении, что и вектор
⃑𝑐=−3⃑𝑖−⃑𝑗. Рассчитать работу
совершается силой, учитывая, что величина смещения
измеряется в метрах.
Ответ
Мы можем назвать вектор смещения 𝐴𝐵, ⃑𝑑. Вектор ⃑𝑑 показан с вектором ⃑𝑐 на следующем рисунке.
Вектор ⃑𝑑 задается
⃑𝑑=(−9−7)⃑𝑖+(2−(−3))⃑𝑗=−16⃑𝑖+5⃑𝑗.m
Скалярное произведение ⃑𝑑 и ⃑𝑐
не равно скалярному произведению ⃑𝑑 и ⃑𝐹.
Величина ⃑𝐹 дана, но использовать ⃑𝐹 через точку
расчет продукта, необходимо определить компоненты ⃑𝑖 и ⃑𝑗 ⃑𝐹.
Поскольку ⃑𝐹 действует по линии ⃑𝑐,
⃑𝑖 компонент ⃑𝐹
должна иметь величину, которая
в три раза больше величины ⃑𝑗 компонента ⃑𝐹. Эти отношения
можно выразить как
𝐹=3𝐹.
Эти отношения
можно выразить как
𝐹=3𝐹.
𝐹 и 𝐹 две стороны прямоугольного треугольника
с гипотенузой длиной 8√10. Поэтому это
в случае, когда
И снова, так как 𝐹=3𝐹,𝐹=24.
Зная компоненты ⃑𝐹, можно выразить ⃑𝐹
как ⃑𝐹=−24⃑𝑖−8⃑𝑗.N
Таким образом, выполненная работа 𝑊
𝑊=(−24,−8)⋅(−16,5)𝑊=(−24×−16)+(−8×5)=384−40=344.J
Теперь давайте рассмотрим другой пример, где ни компоненты
вектора силы, ни компоненты вектора смещения не заданы напрямую.
Пример 4. Нахождение работы векторной силы, действующей на тело, движущееся между двумя точками
Частица переместилась из точки 𝐴(−2,−2) в точку
𝐵(6,10) по прямой под действием
сила ⃑𝐹=𝑘⃑𝑖−6⃑𝑗
действующий в направлении, противоположном перемещению 𝐴𝐵. Найдите работу силы ⃑𝐹.
Ответ
Вектор смещения ⃑𝑑 — это вектор, хвост которого находится в точке ⃑𝐴
и его голова в ⃑𝐵. Вектор ⃑𝑑 задается выражением
⃑𝑑=(6−(−2))⃑𝑖+(10−(−2))⃑𝑗=8𝑖+12⃑𝑗.m
Вектор ⃑𝑑 задается выражением
⃑𝑑=(6−(−2))⃑𝑖+(10−(−2))⃑𝑗=8𝑖+12⃑𝑗.m
Направление ⃑𝑑 𝐴𝐵. Направление, в котором ⃑𝐹
действует противоположно 𝐴𝐵, поэтому ⃑𝐹
должен действовать вдоль прямой 𝐵𝐴𝐵𝐴=−8⃑𝑖−12⃑𝑗
Δ𝑦Δ𝑥=−12−8=32.
Чтобы ⃑𝐹 имел то же направление, что и
𝐵𝐴,
доля 𝑦-компоненты над
его 𝑥-компонента должна быть равна
𝐵𝐴. Следовательно, мы имеем это
Δ𝑦Δ𝑥=−6𝑘=32.
Перестановка, чтобы сделать 𝑘 предмет уравнения дает
3𝑘=−6×2𝑘=−4.
Теперь мы можем выразить ⃑𝐹 как
⃑𝐹=−4⃑𝑖−6⃑𝑗.N
Таким образом, выполненная работа 𝑊 равна
𝑊=(−4,−6)⋅(8,12)𝑊=(−4×8)+(−6×12)=−32−72=−104.J
Неудивительно, что проделанная работа отрицательна, поскольку сила действует в направлении, противоположном перемещению.
Когда энергия частицы, на которую действует сила, сохраняется, путь, который проходит частица, чтобы сместить ее, когда на нее действует сила, не влияет на работу, совершаемую этой силой над частицей.
Теперь рассмотрим пример, в котором рассматривается работа, совершаемая силой за интервал времени.
Пример 5. Определение работы силы при задании смещения во времени
Частица движется в плоскости, в которой ⃑𝑖 и
⃑𝑗 — перпендикулярные единичные векторы. Его водоизмещение
от источника в момент времени 𝑡 секунд
определяется выражением ⃑𝑟=2𝑡+7⃑𝑖+(𝑡+7)⃑𝑗m и на него действует
силой ⃑𝐹=6⃑𝑖+3⃑𝑗Н. Какую работу совершает сила между 𝑡=2с и
𝑡=3s?
Ответ
Включение в этот пример не требует решения его способом, который сильно отличается от предыдущих примеров, так как скалярные произведения векторов используются таким же образом. Единственная новая особенность, обнаруженная в этом примере, заключается в том, что мы должны найти
перемещения, которые соответствуют двум разным временам.
Смещение частицы при 𝑡=3 с и
𝑡=2с
должны быть определены. Это делается путем замены
3 и 2 как значения 𝑡, чтобы дать
⃑𝑑 и ⃑𝑑,
соответственно, что дает нам
⃑𝑑=2×3+7⃑𝑖+(3+7)⃑𝑗=25⃑𝑖+10⃑𝑗,⃑𝑑=2×2+7⃑𝑖+(2+7)⃑𝑑 15⃑𝑖+9⃑𝑗.мм
Это делается путем замены
3 и 2 как значения 𝑡, чтобы дать
⃑𝑑 и ⃑𝑑,
соответственно, что дает нам
⃑𝑑=2×3+7⃑𝑖+(3+7)⃑𝑗=25⃑𝑖+10⃑𝑗,⃑𝑑=2×2+7⃑𝑖+(2+7)⃑𝑑 15⃑𝑖+9⃑𝑗.мм
Смещение частицы между 𝑡=3 с и
𝑡=2s равно ⃑𝑑
минус ⃑𝑑, заданный
⃑𝑑−⃑𝑑=Δ𝑑=25⃑𝑖+10⃑𝑗−15⃑𝑖+9⃑𝑗=10⃑𝑖+⃑𝑗.m
Скалярное произведение ⃐
и Δ𝑑 дает нам выполненную работу, 𝑊,
между 𝑡=3s и
𝑡=2с. С
⃑𝐹=6⃑𝑖+3⃑𝑗,N
это дано
𝑊=(6,3)⋅(10,1)𝑊=(6×10)+(1×3)=63.J
Ключевые точки
- Работа, совершаемая постоянной силой ⃑𝐹 при перемещении
⃑𝑑 равно скалярному произведению
⃑𝐹 и ⃑𝑑,
𝑊=⃑𝐹⋅⃑𝑑,
или 𝑊=‖‖⃑𝐹‖‖‖‖⃑𝑑‖‖(𝜃), cos
где 𝜃 — угол между ⃑𝐹 и ⃑𝑑.
- Скалярное произведение ⃑𝐹 и ⃑𝑑 можно определить без использования угла 𝜃
выражая ⃑𝐹 и ⃑𝑑 в компонентной форме.
- Если компоненты ⃑𝐹 и ⃑𝑑
находятся в перпендикулярных направлениях ⃑𝑖 и
⃑𝑗, то
⃑𝐹⋅⃑𝑑=𝐹,𝐹⋅𝑑,𝑑=(𝐹𝑑)+𝐹𝑑.

Векторы положения и смещения Векторы позволяют нам описывать величины, которые имеют как направление, так и величину. Например, скорость и положение. Эти величины полезны при описании движения и положения частицы, движущейся по плоскости. Все векторы подчиняются законам сложения параллелограмма и закону треугольника. Эти законы позволяют нам выполнять арифметические действия над векторами. Положение и изменение положения (обозначаемое смещением) — это сущности, которые используют эти понятия для описания движения частицы. Давайте разберемся в них подробно.
Скаляры и векторы
В физике величины классифицируются с точки зрения векторов и скаляров. Разница между ними состоит в том, что величины, которые имеют направление и связанную с ними величину, называются векторами. Скалярная величина — это просто величина. В случае скалярных величин арифметические операции, такие как сложение, вычитание или умножение, выполняются так же, как и с действительными числами. Например, сумма двух скалярных величин со значениями 0,1 и 0,3 равна 0,4. Эти правила не применяются к векторным величинам. Их сложение и вычитание не так просты, как скалярные величины.
Например, сумма двух скалярных величин со значениями 0,1 и 0,3 равна 0,4. Эти правила не применяются к векторным величинам. Их сложение и вычитание не так просты, как скалярные величины.
В приведенной ниже таблице показаны некоторые примеры скалярных и векторных величин.
Scalar Quantities Vector Quantities Length Velocity Speed Force Mass Weight Density Pressure Энергия Ускорение
Законы сложения и вычитания векторов Два вектора нельзя сложить обычными арифметическими действиями, так как векторы содержат направления. Эти векторы можно сложить, используя законы сложения векторов. Для двух векторов P и Q их сложение определяется вектором R,
Если угол между двумя векторами равен θ, то величина результирующего вектора определяется как
R 2 = |P| 2 + |Q| 2 + 2|P||Q|cos(θ)
Угол, который результирующий вектор образует с вектором P, определяется выражением константа
Умножение вектора на константу не меняет своего направления, вместо этого этот вид умножения служит для масштабирования вектора Если константа, умноженная на вектор, больше 1, вектор увеличивается в своей длине, а уменьшается по длине, когда константа меньше 1,
Движение на плоскости
Когда объект движется на плоскости, он меняет свое положение, и важно определить величины, которые можно использовать для описания положения объекта на плоскости. Движение также требует направления. Например, предположим, что объект движется, как показано на рисунке ниже. Теперь для описания положения объекта требуются две вещи — направление и расстояние от начала координат. Просто сказать, что объект находится на расстоянии 5 м от начала координат, недостаточно.
Движение также требует направления. Например, предположим, что объект движется, как показано на рисунке ниже. Теперь для описания положения объекта требуются две вещи — направление и расстояние от начала координат. Просто сказать, что объект находится на расстоянии 5 м от начала координат, недостаточно.
Этот объект будет описан как 5 м в северо-восточном направлении. Таким образом, для обозначения положения объекта требуется вектор. Этот вектор называется вектором положения . На приведенной ниже диаграмме показана траектория движения объекта в плоскости. Пусть P и P’ будут положениями объекта в моменты времени « t » и « t’ ». На приведенном ниже рисунке показано положение P и P’ относительно начала координат.
Когда точки P и P’ соединены прямой линией с началом O. Отрезки OP и OP’ обозначают векторы положения. Вектор OP обозначается r, а OP’ обозначается r’. Если объект перемещается из P в P’ за время «t». Тогда смещение определяется изменением вектора положения. Вектор, обозначающий изменение вектора положения, также называется вектором смещения.
Тогда смещение определяется изменением вектора положения. Вектор, обозначающий изменение вектора положения, также называется вектором смещения.
Примечание: Вектор смещения зависит только от векторов начального и конечного положения. Если объект проходит путь и возвращается в то же начальное положение, в этом случае смещение считается равным нулю. На рисунке выше показан объект, путешествующий по большому пути и возвращающийся в ту же точку. В этом случае смещение равно нулю.
Величина вектора смещения меньше или равна расстоянию, пройденному частицей между ее начальным и конечным положениями.
Предположим, что частица движется из точки A в точку B по пройденному пути, как показано на рисунке выше. В этом случае смещение задается линией, соединяющей две точки. Таким образом, можно сказать, что смещение между двумя точками является кратчайшим расстоянием между этими точками.
Примеры задач
Вопрос 1. Допустим, A = 4i + 3j и B = 5i + 4j. Найдите результирующий вектор от сложения этих двух векторов.
Допустим, A = 4i + 3j и B = 5i + 4j. Найдите результирующий вектор от сложения этих двух векторов.
Ответ:
Дано:
A = 4i + 3j
B = 5i + 4j.
Результат этих двух векторов равен
Подставив векторы в это уравнение,
Вопрос 2. Допустим, A = 5i + 5j и B = 3i + 3j. Найдите результирующий вектор от сложения этих двух векторов.
Ответ:
Дано:
A = 5i + 5j
B = 3i + 3j.
Результирующая этих двух векторов определяется как
Подставляя векторы в это уравнение,
Вопрос 3. Допустим, есть два вектора A и B, где |A| = 3 и |В| = 4, а угол между ними равен 60°. Найдите величину и направление результирующего вектора.
Ответ:
Дано:
|A| = 3
|В| = 4,
θ = 60°
Результант этих двух векторов определяется выражением
Ч 2 = |А| 2 + |В| 2 + 2|A||B|cos(θ)
Угол определяется выражением θ = tan -1 (
Подставляя векторы в эти уравнения,
R 2 = |A| 2 + |B| 2 + 2|A||B|cos(θ)
⇒ R 2 = 3 2 + 4 2 + 2(3)(4)cos(60 )
⇒ R 2 = 25 + 12
⇒ R 2 = 37
⇒ R = √37
θ = tan -1 (
⇒ θ = tan -1 (
⇒ θ = 53°
Вопрос 4. Допустим, есть два вектора, где |A и B|
Допустим, есть два вектора, где |A и B|
Ответ:
Дано:
|A| = 24
|B | = 10,
θ = 90°
Результат этих двух векторов определяется выражением
Ч 2 = |А| 2 + |В| 2 + 2|A||B|cos(θ)
Угол определяется выражением θ = tan -1 (
Подставляя векторы в эти уравнения,
R 2 = |A| 2 + |B| 2 + 2|A||B|cos(θ)
⇒ R 2 = 24 2 + 10 2 + 2(24)(910)cos )
⇒ R 2 = 576 + 100
⇒ R 2 = 676
⇒ R = 26
θ = tan -1 (
⇒ θ = tan -1 (
Вопрос 5: Вектор положения частицы, движущейся в плоскости, определяется формулой 2 i + 3tj
Найдите смещение между t = 1 и t = 4 секунды
Ответ:
Смещение зависит только от начального и конечного положения частицы.

 Эти отношения
можно выразить как
𝐹=3𝐹.
Эти отношения
можно выразить как
𝐹=3𝐹. Вектор ⃑𝑑 задается выражением
⃑𝑑=(6−(−2))⃑𝑖+(10−(−2))⃑𝑗=8𝑖+12⃑𝑗.m
Вектор ⃑𝑑 задается выражением
⃑𝑑=(6−(−2))⃑𝑖+(10−(−2))⃑𝑗=8𝑖+12⃑𝑗.m
 Это делается путем замены
3 и 2 как значения 𝑡, чтобы дать
⃑𝑑 и ⃑𝑑,
соответственно, что дает нам
⃑𝑑=2×3+7⃑𝑖+(3+7)⃑𝑗=25⃑𝑖+10⃑𝑗,⃑𝑑=2×2+7⃑𝑖+(2+7)⃑𝑑 15⃑𝑖+9⃑𝑗.мм
Это делается путем замены
3 и 2 как значения 𝑡, чтобы дать
⃑𝑑 и ⃑𝑑,
соответственно, что дает нам
⃑𝑑=2×3+7⃑𝑖+(3+7)⃑𝑗=25⃑𝑖+10⃑𝑗,⃑𝑑=2×2+7⃑𝑖+(2+7)⃑𝑑 15⃑𝑖+9⃑𝑗.мм
 Например, сумма двух скалярных величин со значениями 0,1 и 0,3 равна 0,4. Эти правила не применяются к векторным величинам. Их сложение и вычитание не так просты, как скалярные величины.
Например, сумма двух скалярных величин со значениями 0,1 и 0,3 равна 0,4. Эти правила не применяются к векторным величинам. Их сложение и вычитание не так просты, как скалярные величины. Движение также требует направления. Например, предположим, что объект движется, как показано на рисунке ниже. Теперь для описания положения объекта требуются две вещи — направление и расстояние от начала координат. Просто сказать, что объект находится на расстоянии 5 м от начала координат, недостаточно.
Движение также требует направления. Например, предположим, что объект движется, как показано на рисунке ниже. Теперь для описания положения объекта требуются две вещи — направление и расстояние от начала координат. Просто сказать, что объект находится на расстоянии 5 м от начала координат, недостаточно. Тогда смещение определяется изменением вектора положения. Вектор, обозначающий изменение вектора положения, также называется вектором смещения.
Тогда смещение определяется изменением вектора положения. Вектор, обозначающий изменение вектора положения, также называется вектором смещения.Примечание: Вектор смещения зависит только от векторов начального и конечного положения. Если объект проходит путь и возвращается в то же начальное положение, в этом случае смещение считается равным нулю. На рисунке выше показан объект, путешествующий по большому пути и возвращающийся в ту же точку. В этом случае смещение равно нулю.
 Допустим, A = 4i + 3j и B = 5i + 4j. Найдите результирующий вектор от сложения этих двух векторов.
Допустим, A = 4i + 3j и B = 5i + 4j. Найдите результирующий вектор от сложения этих двух векторов. Дано:
A = 4i + 3j
B = 5i + 4j.
Результат этих двух векторов равен
Подставив векторы в это уравнение,
Дано:
A = 5i + 5j
B = 3i + 3j.
Результирующая этих двух векторов определяется как
Подставляя векторы в это уравнение,
Дано:
|A| = 3
|В| = 4,
θ = 60°
Результант этих двух векторов определяется выражением
Ч 2 = |А| 2 + |В| 2 + 2|A||B|cos(θ)
Угол определяется выражением θ = tan -1 (
Подставляя векторы в эти уравнения,
R 2 = |A| 2 + |B| 2 + 2|A||B|cos(θ)
⇒ R 2 = 3 2 + 4 2 + 2(3)(4)cos(60 )
⇒ R 2 = 25 + 12
⇒ R 2 = 37
⇒ R = √37
θ = tan -1 (
⇒ θ = tan -1 (
⇒ θ = 53°
 Допустим, есть два вектора, где |A и B|
Допустим, есть два вектора, где |A и B| Дано:
|A| = 24
|B | = 10,
θ = 90°
Результат этих двух векторов определяется выражением
Ч 2 = |А| 2 + |В| 2 + 2|A||B|cos(θ)
Угол определяется выражением θ = tan -1 (
Подставляя векторы в эти уравнения,
R 2 = |A| 2 + |B| 2 + 2|A||B|cos(θ)
⇒ R 2 = 24 2 + 10 2 + 2(24)(910)cos )
⇒ R 2 = 576 + 100
⇒ R 2 = 676
⇒ R = 26
θ = tan -1 (
⇒ θ = tan -1 (
Смещение зависит только от начального и конечного положения частицы.
