Главная
Формула период в физике: Формула периода колебаний пружинного маятника в физике

Формула период в физике: Формула периода колебаний пружинного маятника в физике

Содержание

Период колебаний нитяного и пружинного маятников

Цель урока: рассмотреть процесс колебаний на примере нитяного  и пружинного маятников, выяснить зависимость периода колебаний от различных физический величин: длины нити, ускорения свободного падения, коэффициента жесткости и массы.

1. Проверка домашнего задания. (работа по формуле “Скажи ты…)

– Что называется амплитудой колебания; периодом колебания; частотой колебания;    циклической частотой?

– Какой буквой обозначается циклическая частота?

– Какая математическая зависимость существует между периодом и частотой колебания?

Учащиеся в парах проверяют домашнюю работу:   упражнение №24.

2. Объяснение нового материала. Работа по теме урока.

Учитель. Как вы думаете, от каких величин может завесить период колебаний нитяного маятника?

Ученики.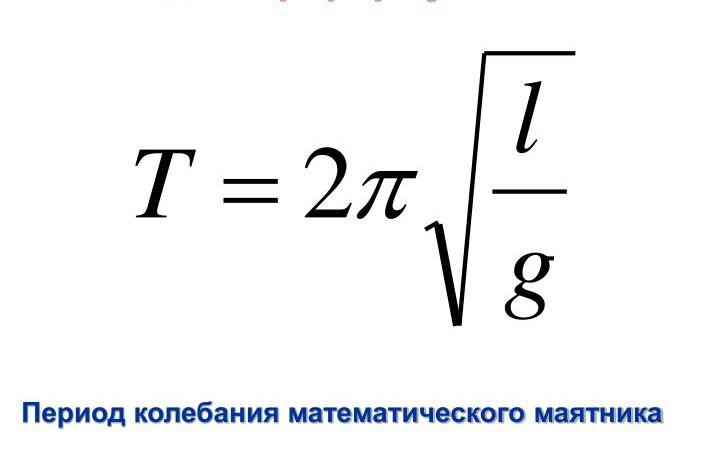

От длины нити и массы груза.

Учитель. Начнем с длины нити. Поставим опыт с двумя маятниками, имеющими разную длину нити, но одинаковую массу (эксперимент).

Ученики. С увеличением длины нити период колебаний увеличивается.

Учитель. А теперь посмотрим как зависит период колебаний от массы груза (эксперимент: маятники имеют одинаковую длину нити и разный вес грузов).

Учащиеся. Период не зависит от массы груза.

Учитель. Но период колебания нитяного маятника зависит еще от одной физической величины. Это ускорение свободного падения. Проведем эксперимент и “поможем “ силе тяжести положив магнит. Теперь при той же массе груза возвращающая сила будет больше.

Ученики. Период уменьшился, а частота увеличилась.

Учитель. А теперь выведем формулу для расчета периода колебания нитяного маятника.

формула Гюйгенса:

l – длина.

g – ускорение свободного падения.

Это очень важная формула и ее надо запомнить.

Учитель. От чего может зависеть период пружинного маятника?

Ученики. От жесткости  пружины, массы груза.

Учитель. Сначала на опыте посмотрим зависимость периода колебаний и жесткости пружины.(эксперимент : две пружины разной жесткости, но одинаковой длины и одинаковой массой груза)

Ученики. Период меньше там, где жесткость больше.

Учитель. А как вы думаете как зависит период от массы груза(эксперимент).

Ученики. Чем больше масса , тем больше и период.

Учитель.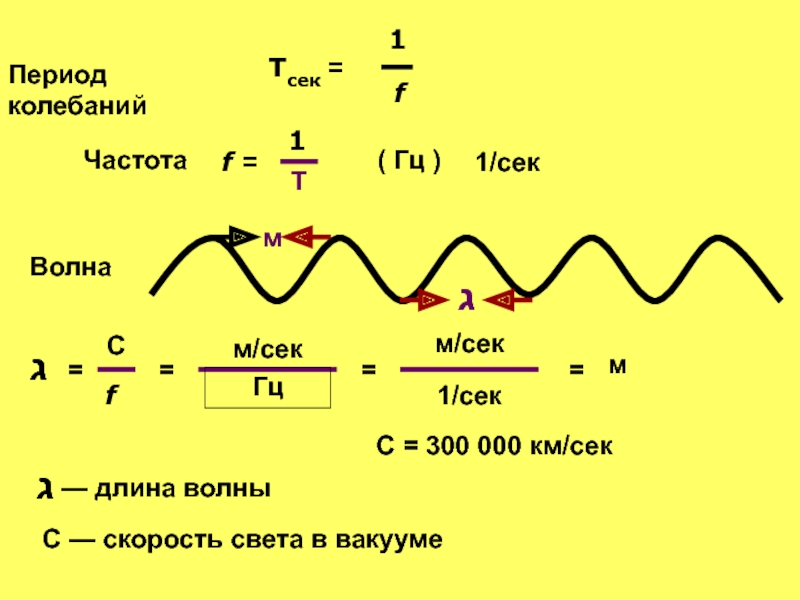 А теперь выведем формулу для расчета периода колебания пружинного маятника.

– возвращающая сила системы

– собственная частота системы.

Эту формулу так же запишите на обложку тетради и постарайтесь ее запомнить.

3. Закрепление материала

Решение задач Лукашик В.И.№ 873, 876.879

4.Домашнее задание. Лукашик В.И.№ 875, 877.880.

Список литературы:

1.Л.Э.Генденштейн,В.А.Орлов,Г.Г.Никифоров “Как научить решать задачи по физике (основная школа ). Подготовка к ГИА.

2. С.Е.Полянский “Поурочные разработки по физике”.

3. Лукашик В.И. “Сборник задач по физике”.

4. Учебник физики Перышкин А.В. Физика 9

Период колебаний – это… Что такое Период колебаний?

Период колеба́ний — наименьший промежуток времени, за который осциллятор совершает одно полное колебание (то есть возвращается в то же состояние[1], в котором он находился в первоначальный момент, выбранный произвольно).

В принципе совпадает с математическим понятием периода функции, но имея ввиду под функцией зависимость физической величины, совершающей колебания, от времени.

Это понятие в таком виде применимо как к гармоническим, так и к ангармоническим строго периодическими колебаниям (а приближенно – с тем или иным успехом – и непериодическим колебаниям, по крайней мере к близким к периодичности).

В случае, когда речь идет о колебаниях гармонического осциллятора с затуханием, под периодом понимается период его осциллирующей составляющей (игнорируя затухание), который совпадает с удвоенным временным промежутком между ближайшими прохождениями колеблющейся величины через ноль. В принципе, это определение может быть с большей или меньшей точностью и пользой распространено в некотором обобщении и на затухающие колебания с другими свойствами.

Обозначения: обычное стандартное обозначение периода колебаний: (хотя могут применяться и другие, наиболее часто это , иногда и т. д.).

Единицы измерения: секунда

Период колебаний связан соотношением взаимной обратности с частотой:

Для волновых процессов период связан кроме того очевидным образом с длиной волны

где – скорость распространения волны (точнее[2] – фазовая скорость).

В квантовой физике период колебаний прямо связан с энергией (поскольку в квантовой физике энергия объекта – например, частицы – есть частота[3] колебаний его волновой функции).

Теоретическое нахождение периода колебаний той или иной физической системы сводится, как правило, к нахождению решения динамических уравнений (уравнения), описывающего эту систему. Для категории линейных систем (а приближенно – и для линеаризуемых систем в линейном приближении, которое зачастую является очень хорошим) существуют стандартные сравнительно простые математические методы, позволяющие это сделать (если известны сами физические уравнения, описывающие систему).

Для экспериментального определения периода используются часы, секундомеры, частотомеры, стробоскопы, строботахометры, осциллографы. Также применяются биения, метод гетеродинирования в разных видах, используется принцип резонанса. Для волн можно померить период косвенно – через длину волны, для чего применяются интерферометры, дифракционные решетки итп. Иногда требуются и изощренные методы, специально разработанные для конкретного трудного случая (трудность могут представлять как само измерение времени, особенно если речь идет о предельно малых или наоборот очень больших временах, так и трудности наблюдения колеблющейся величины).

Периоды колебаний в природе

Представление о периодах колебаний различных физических процессов дает статья Частотные интервалы (учитывая то, что период в секундах есть обратная величина частоты в герцах).

Некоторое представление о величинах периодов различных физических процессов также может дать шкала частот элетромагнитных колебаний (см. Электромагнитный спектр) .

Периоды колебаний слышимого человеком звука находятся в диапазоне

от 5·10-5с до 0,2с

(четкие границы его несколько условны).

Периоды электромагнитных колебаний, соответствующих разным цветам видимого света – в диапазоне

от 1,1·10-15с до 2,3·10-15с.

Поскольку при экстремально больших и экстремально маленьких периодах колебаний методы измерения имеют тенденцию становятся всё более косвенными (вплоть до плавного перетекая в теоретические экстраполяции), трудно назвать четкую верхнюю и нижнюю границы для периода колебаний, измеренного непосредственно. Какую-то оценку для верхней границы может дать время существования современной науки (сотни лет), а для нижней – период колебаний волновой функции самой тяжелой из известных сейчас частиц ().

В любом случае границей снизу может служить планковское время, которое столь мало, что по современным представлениям не только вряд ли может быть вообще как-то физически измерено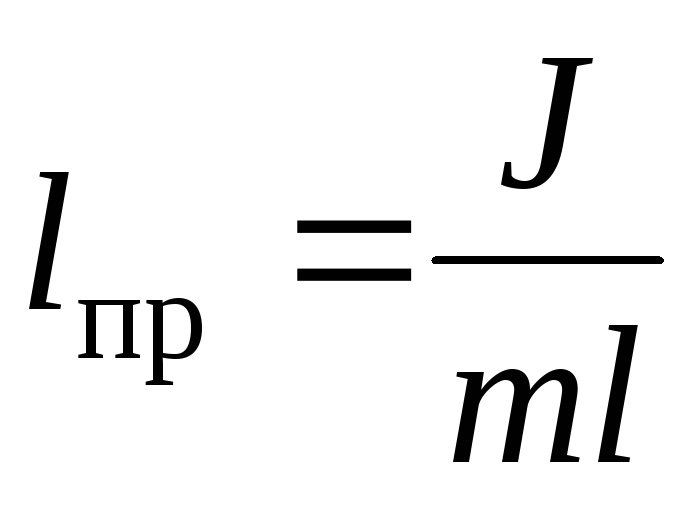

[4], но и вряд ли в более-менее обозримом будущем представляется возможность приблизиться к измерению величин даже на много порядков меньших. а границей сверху – время существования Вселенной – более десяти миллиардов лет.

Периоды колебаний простейших физических систем

Пружинный маятник

Период колебаний пружинного маятника может быть вычислен по следующей формуле:

,

где  — масса груза,  — жёсткость пружины.

Математический маятник

Период колебаний математического маятника:

где  — длина подвеса (к примеру нити),  — ускорение свободного падения.

Период колебаний (на Земле) математического маятника длиной 1 метр с хорошей точностью

[5] равен 2 секундам.

Физический маятник

Период колебаний физического маятника:

где — момент инерции маятника относительно оси вращения, — масса маятника, — расстояние от оси вращения до центра масс.

Крутильный маятник

Период колебаний крутильного маятника:

где  — момент инерции тела, а  — вращательный коэффициент жёсткости маятника.

Электрический колебательный (LC) контур

Период колебаний электрического колебательного контура:

,

где — индуктивность катушки, — ёмкость конденсатора.

Эту формулу вывел в 1853 году английский физик У. Томсон.

Примечания

  1. ↑ Состояние механической системы характеризуется положениями и скоростями всех ее материальных точек (строже говоря – координатами и скоростями, соответствующими всем степеням свободы данной системы), для немеханической – их формальными аналогами (которые также можно назвать координатами и скоростями в смысле абстрактного описания динамической системы – в количестве, также равном количеству ее степеней свободы).
  2. ↑ Для монохроматических волн это уточнение самоочевидно, для близких к монохроматическим – интуитивно очевидно по аналогии со строго монохроматическими, для существенно немонохроматических – наиболее ясный случай сводится к тому, что фазовые скорости всех монохроматических компонент совпадают друг с другом, поэтому комментируемое утверждение ьакже верно.
  3. ↑ С точностью до единиц измерения: в традиционных (обычных) системах физических единиц частота и энергия измеряются в разных единицах (поскольку до появления квантовой теории совпадение энергии и частоты было неизвестно, и, естественно, для каждой из величин была выбрана своя независимая единица измерения), поэтому при измерении их в обычных (разных) единицах, например, джоулях и герцах требуется переводной коэффициент (так называемая константа Планка). Однако можно выбрать систему единиц измерения так, чтобы в ней константа Планка стала равной 1 и пропала из формул; в такой системе единиц энергия любой частицы просто равна частоте колебания ее волновой функции (а значит обрата периоду этого колебания).
  4. ↑ Имеется в виду, конечно же, невозможность экспериментального измерения времен конкретных процессов или периодов колебаний такого порядка, а не просто вычисление некоторого числа.
  5. ↑ Лучше, чем 0,5%, если взять метрологическое или принятое техническое значение ускорения свободного падения; И с разбросом ~0.53% для максимального и минимального значений ускорения свободного падения, наблюдаемых на земле.

Ссылки

Как вычислить жесткость пружины из формулы для периода колебаний пружинного маятника?

Железо массой 1,5 кг опущено в 3 кг воды, где остывает от 100 градусов до 25 градусов. Вычислите, на сколько градусов нагреется вода.

Жук рухаючись з положення координатою х нульове дорівнює 10 м положення с координата x дорівнює 20 м знайдіть його швидкість якщо на подорож він витра … тив 20 секунд

Дано:R1= 16 Ом,R2= 12 Ом, R3= 24 Ом,R4= 28 Ом,R5= 12 Ом,U= 120 В.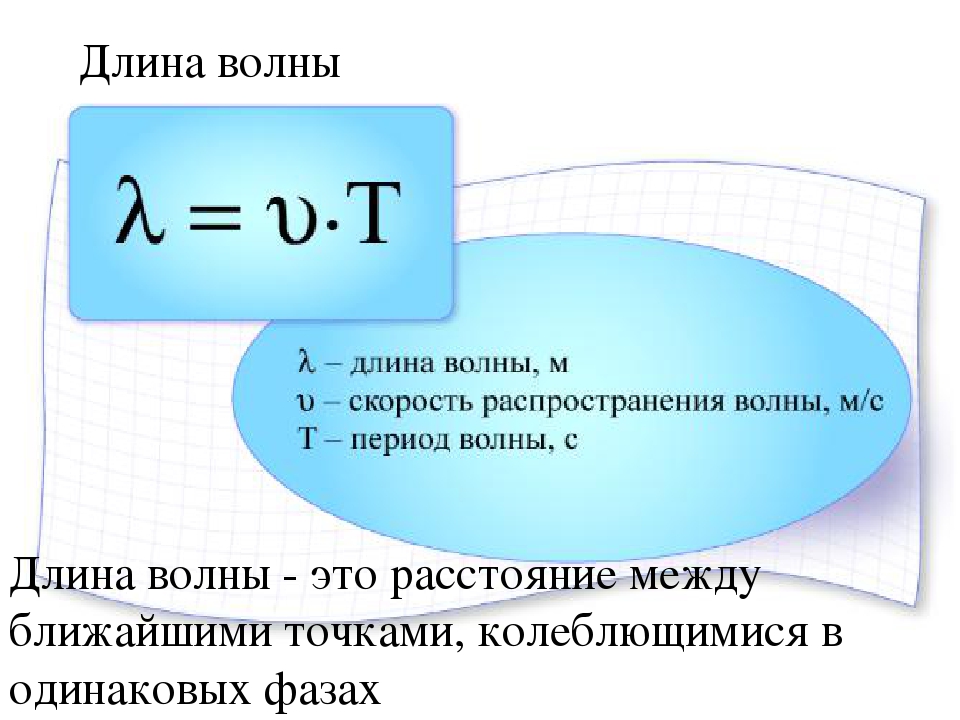 Найти токи всех ветвей и напряжения на каждомрезисторе​

1. Какое количество теплоты требуется для нагревания кирпича массой 3,08 кг от 11 до 89 ºС?( удельная теплоемкость кирпича взять 512 Дж/кг)2. Какое ко … личество теплоты отдал окружающей среде кипяток массой 4,9 кг при остывании до 13,5 ºС?( удельная теплоемкость кипятка взять за 4011 Дж/кг)3. Сколько энергии выделится при полном сгорании 2,03 т каменного угля?( удельная теплота сгорания торфа взять за 1,04*107)4.Воду какой массы можно нагреть от 1 до 77 ºС, сообщив ей количество теплоты 359,3 кДж?8 класс, решите СРОЧНО!! прошу контрольную по физике

определите проекцию скорости точки если при равномерном движении вдоль оси ox ее координата за время t=6 с изменилась от x1=1м до x2=-5м

Прямий провідник завдовжки 20 см, по якому проходе струм 0,25 А, розміщений в магнітному полі перпендикулярно до силових ліній. Визначте індукцію магн … ітного поля, якщо воно діє на провідник із силою 2,25 мН.

Провідний стрижень довжиною 50 см і масою 350 г лежить перпендикулярно до горизонтальних рейок. Уздовж рейок діє однорідне магнітне поле індукцією 20 … мТл, а по стрижню пропускають струм силою 12 А. З якою силою стрижень тисне на рейки, якщо струм в провіднику пропускають в такому напрямку, щоб сила Ампера була напрямлена вгору? Зробіть пояснювальний рисунок.

У діоді електрон підливає до анода, маючи швидкість 9мм/с . Яка мінімальна прискорюючи анода напруга. Напишіть з дано, будь ласка

Першу половину шляху автомобіль проїхав зі швидкістю 120 км/год, другу половину – зі швидкістю 60 км/год. Визначте середню швидкість руху автомобіля н … а всьому шляху

рассчитайте общую силу в цепи​

формула расчета, как найти для физического маятника

Что такое колебательный процесс 

Колебания — это движения или процессы, которые повторяются с определенным интервалом времени.

Систему, совершающую колебания, называют колебательной системой или осциллятором.

Исходя из физической природы, колебательные процессы бывают механического, электромагнитного и других видов.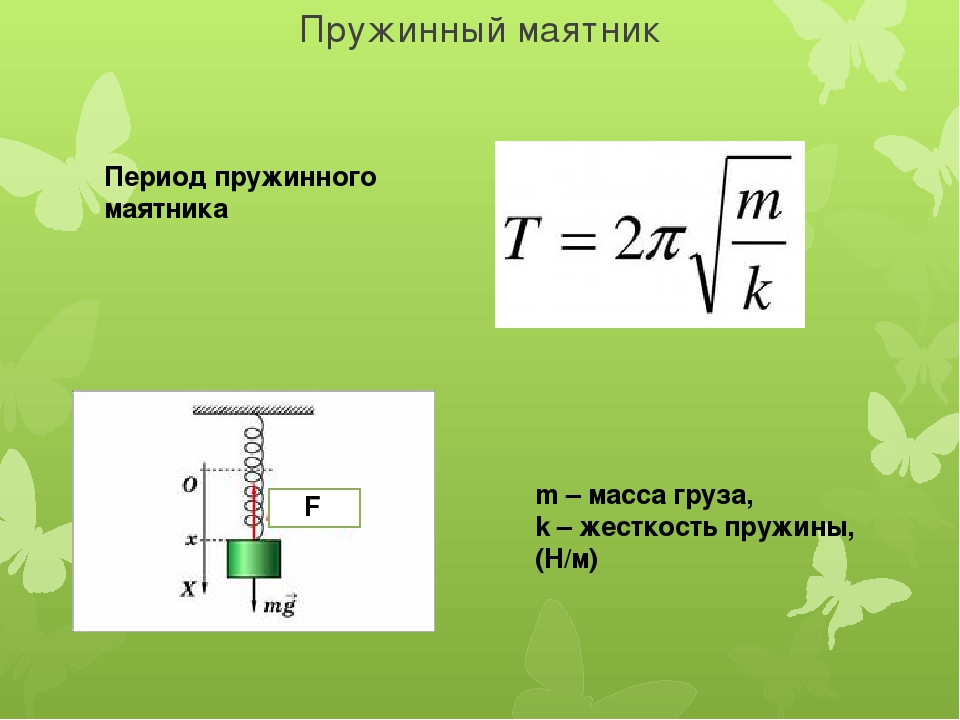

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Свободные или собственные колебания — колебания, которые наблюдают в системе, предоставленной себе после выведения из равновесного состояния.

Вынужденными колебаниями называют колебания, происходящие под действием внешней силы, изменяющейся периодически.

При механических колебаниях, которые относят к категории вынужденных:

\(F=F_{0}\cos \cot\)

Гармоническими колебаниями называют колебания, определяемые физической величиной, которая изменяется, согласно закону синуса или косинуса.

Разные периодические процессы, повторяющиеся в течение равных временных интервалов, могут быть записаны в виде суммы или суперпозиции гармонических колебаний.

Определение периода колебаний, формула

Колебательный процесс можно представить в виде уравнения.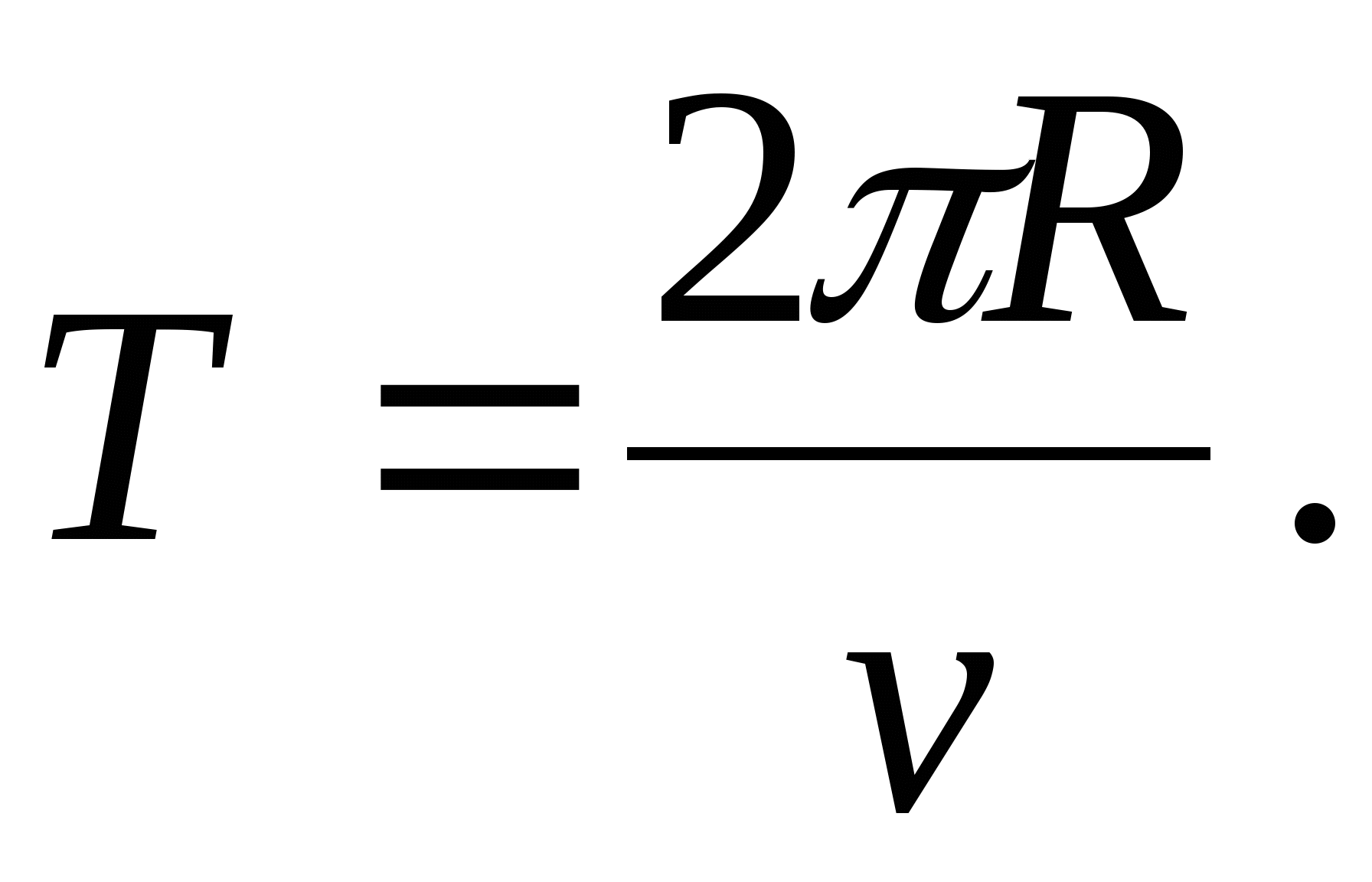 Тогда гармоническое колебание значения х будет представлено следующей формулой:

\(x(t)=A\times \cos \left(\omega _{0}t+\phi _{0} \right)\)

Где \(x(t)\) является отклонением колеблющейся физической величины от равновесного значения;

А представляет собой амплитуду гармонических колебаний;

\(\omega _{0}\) равно циклической или круговой частоте колебаний;

\(\phi _{0}\) является начальной фазой колебаний, характерной для момента времени t=0, что можно определить с помощью выбора начала отсчета времени;

\(cp(t)=(co_{0}t+cp_{0})\) описывает фазу колебаний в момент времени t, определяется в радианах, соответствует значению колеблющейся величины в данное время.

В случае, когда имеется какая-либо материальная точка с массой m, характеристика х будет соответствовать смещению тела из равновесного положения. Следует заметить, что амплитуда и частота гармонических колебаний обладают постоянными значениями. Исходя из того, что cos меняет значение в интервале от +1 до -1, параметр х будет изменяться от +А до –А. Так как:

\(\cos \left(\alpha +2\pi \right)=\cos \alpha,\)

то х остается без изменений при фазе колебаний, получающей приращение в $$2\pi$$

Период колебаний Т представляет собой минимальный временной интервал, в течение которого колебательная система возвращается в то состояние, в котором она находилась в начальный момент времени, определенный произвольно.

В этом случае фаза будет увеличена на \(2\pi:\)

\(\omega _{0}(t+T)+\phi _{0}=\left(\omega _{0}t+\phi _{0} \right)+2\pi\)

Из данного равенства можно вычислить период колебаний:

\(T=\frac{2\pi }{\omega _{0}}\)

Частота колебаний v является величиной, которая обратна периоду колебаний. Это количество полных колебаний, выполняемых за единицу времени:

\(v=\frac{\omega _{0}}{2\pi}\)

 

На графике изображены гармонические колебания, где а — зависимость смещения х от времени /, б — зависимость скорости vx от времени С, в — зависимость ускорения ах от времени t. {2}x(t)=0\)

Таким образом, получается, что формула циклической частоты пружинного маятника имеет следующий вид:

\(\omega =\sqrt{\frac{mgl}{J}}\)

В таком случае для расчета периода колебаний математического маятника будет использоваться формула:

\(T =\frac{2\pi }{\omega }=2\pi \sqrt{\frac{J}{mgl}}\)

Исходя из расчетов, можно сделать следующие выводы:

  1. Период пружинного маятника \(T =2\pi \sqrt{\frac{m}{k}}\)
  2. Период математического маятника \(T =2\pi \sqrt{\frac{L}{g}}\)
  3. Период крутильного маятника \(T =2\pi \sqrt{\frac{I}{K}}\)

В приведенных формулах:

  • T — период физического маятника;
  • J — момент силы маятника относительно оси вращения;
  • l — расстояние от оси вращения до центра масс;
  • m — масса маятника;
  • g=9.8 — ускорение свободного падения.

Примеры решений

Задача № 1

Шариком, привязанным к нити, совершено 60 колебаний в течение 2 минут. Необходимо определить, каковы период и частота колебаний шарика.

Решение

\(T =\frac{t}{N}=\frac{120}{60}=2\)

\(V=\frac{1}{T}=\frac{1}{2}=0.5\)

Ответ: период колебаний маятника равен 2 секундам, а частота составляет 0,5 Гц.

Задача № 2

Согласно изображенного графика зависимости координаты от времени, необходимо рассчитать характеристики колебательного движения тела.

 

Решение

А = 20

Т = 0,8

\(V=\frac{1}{T}=\frac{1}{0,8}=1,25\)

\(x(t)=A\sin 2\pi Vt=0.2\sin 2\pi \times 1.25t=0.2\sin 2.5\pi t\)

Ответ: амплитуда колебаний маятника составляет 0,2 метра, период колебаний соответствует 0,8 с, частота колебаний равна 1,25 Гц, уравнение координаты будет записано в следующем виде: \(x(t)=0.2\sin 2.5\pi t\)

Задача № 3

Необходимо определить, какой длиной обладает математический маятник, который совершает гармонические колебания при частоте 0,5 Гц на поверхности Луны. Ускорение свободного падения в данном случае составляет 1,6 м/с2. {2}}\approx 0.16\)

Ответ: длина математического маятника примерно составляет 0,16 метра.

Формула частоты период время частота цикл в секунду Гц амплитуда длительность периодический период времени до угловой частоты формула длина волны акустическое уравнение соотношение длина волны Гц миллисекунда мс расчет вычислить калькулятор t = 1 / f Гц герц до мс Рабочий лист от T до f

Формула частоты период время частота цикл в секунду герц Гц амплитуда длительность периодический период времени до угловой частоты формуляр длина волны акустическое уравнение соотношение длина волны Гц миллисекунда расчет мс расчет калькулятор t = 1 / f Гц герц в мс Рабочий лист от T к f – sengpielaudio Sengpiel Berlin


Заполните серое поле выше и щелкните мышью на панели вычислений в соответствующем столбце.

Частота означает колебания (циклы) в секунду в Гц = герц = 1 / с.
1 секунда = 1 с = 1000 мс | 1 мс = 0,001 с | 1 мкс = 0,000001 с
cps = циклов в секунду


Чтобы использовать калькулятор, просто введите значение.
Калькулятор работает в обоих направлениях знака ↔ .

Осиллоскоп: Ввод ящиков (разд.) и временной разверткой (Y) задают частоту.

Формула для периода (продолжительность цикла) T

Физическая величина символ шт. сокращение формула
Продолжительность цикла T = 1 / f второй с T = λ / c
Частота f = 1 / T герц Гц = 1 / с f = c / λ
Длина волны λ метр м λ = п / ш
Скорость волны в метр в секунду м / с c = λ × f

Преобразование времени – с течением времени на

Формулы и уравнения для частоты и длины волны

Формула для частоты: f (частота) = 1/ T (период).
f = c / λ = скорость волны c (м / с) / длина волны λ (м).
Формула для времени: T (период) = 1/ f (частота).
Формула для длины волны: λ (м) = c / f
λ = c / f = скорость волны c (м / с) / частота f (Гц).

Единица герц (Гц) когда-то называлась cps = количество циклов в секунду.


c = λ × f λ = c / f = c × T f = c / λ
Определите скорость среды:
Скорость звука или скорость света
Выберите: Скорость звука в воздухе при температуре 20 ° C: c = 343 м / с
или скорость радиоволн и света в вакууме: c = 299 792 458 м / с.

Скорость распространения электрических сигналов по оптоволокну составляет около 9/10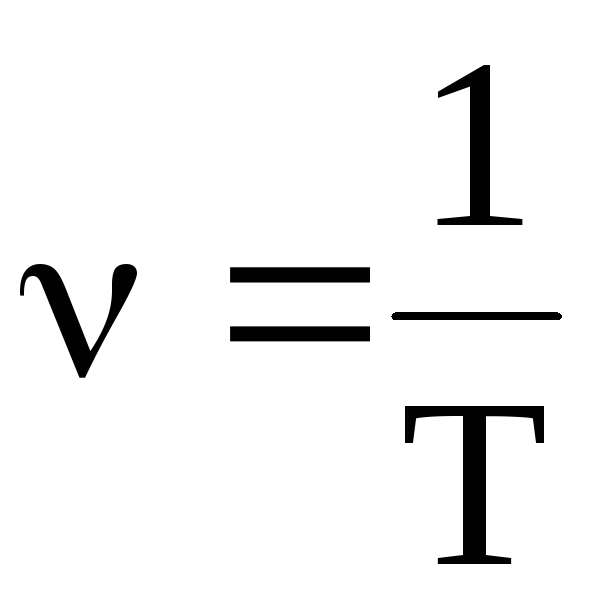
. скорость света ≈ 270 000 км / с.
Скорость распространения электрических сигналов по медным кабелям составляет около 2/3
. скорость света ≈ 200000 км / с.

Скорость звука c = 343 м / с также равняется 1235 км / h, 767 миль / ч, 1125 фут / с.

Волна состоит из четырех частей:
длина волны, период, частота и амплитуда
Изменение частоты (герц, Гц) никогда не изменяет амплитуду и наоборот

Угловая частота составляет ω = 2 π × f

Дано уравнение: y = 50 sin (5000 t)
Определите частоту и амплитуду.
Ответ: Амплитуда 50 и ω = 5000.
Итак, частота f = 1/ T = ω /2 π = 795,77 Гц.

Чтобы использовать калькулятор, просто введите значение.
Калькулятор работает в обоих направлениях знака ↔ .

Преобразование: частота в длину волны и наоборот


Синусоида или синусоида и период T
В физике и электротехнике для синусоидального процесса часто используется
угловая частота ω вместо частоты f .Скорость или частота вращения
– размер при вращательных движениях, предпочтительно механических, с указанием частоты
революций. Например, это важная функция для двигателей. Будет отдано в
1 / мин, в оборотах в минуту или в оборотах в минуту.


По оси y показано звуковое давление p (амплитуда звукового давления).
Если на графике по оси x показано время t , мы увидим период T = 1/ f .
Если на графике по оси x показано расстояние d , мы видим длину волны λ .
Наибольшее отклонение или удлинение обозначается как амплитуда a .


Амплитуда абсолютно не связана с частотой …
тоже ничего с длиной волны.

● Волновые графики ●
Волны можно изобразить как функцию времени или расстояния.Одночастотный
волна будет отображаться как синусоида (синосоида) в любом случае. С расстояния
На графике длина волны может быть определена. На временном графике период
и частота может быть получена. В обоих случаях скорость волны может составлять
. определенный. Источник:
http://hyperphysics.phy-astr.gsu.edu/hbase/sound/wavplt.html


В акустике выражение для синусоидальной волны записывается в виде
y = A sin (2 π f T + φ ).Где ω = 2 π f и A – амплитуда и
где f – частота волны, измеренная в герцах.
Сравнение математической формы y = A sin ( B T + φ ):
С этой акустической формой мы видим, что | B | = 2 π f . Следовательно, мы имеем
частота f = | B | / 2 π и период T = 2 π / | B | = 1/ f .


SI, кратные герцам (Гц)
Значение Обозначение Имя Значение Обозначение Имя
10 -1 Гц Гц децигерц 10 1 Гц даГц декагерц
10 −2 Гц кГц сантигерц 10 2 Гц Гц гектогерц
10 −3 Гц мГц миллигерц 10 3 Гц кГц килогерц
10 −6 Гц мкГц микрогерц 10 6 Гц МГц мегагерц
10 −9 Гц нГц наногерц 10 9 Гц ГГц гигагерц
10 −12 Гц пГц пикогерц 10 12 Гц ТГц терагерц
10 −15 Гц кГц фемтогерц 10 15 Гц PHz петагерц
10 −18 Гц Гц аттогерц 10 18 Гц Гц эксагерц
10 −21 Гц Гц зептогерц 10 21 Гц Гц зеттахерц
10 −24 Гц ггц йоктогерц 10 24 Гц Ягц йоттахерц
Обычные единицы с префиксом выделены жирным шрифтом.

Типичный вопрос: какова связь между длиной волны, температурой и частотой?

Объясните взаимосвязь между расстоянием, временем и частотой при определении
длина волны или: Каково уравнение с частотой, расстоянием и временем?

Скорость = расстояние / время
Скорость = длина волны × частота
следовательно
Длина волны × частота = расстояние / время
следовательно
Длина волны = расстояние / (время × частота)

Калькулятор Masterclock (тактовая частота)

Чтобы использовать калькулятор, просто введите значение.
Калькулятор работает в обоих направлениях знака ↔ .

Вычислитель с опорной частотой

Для настройки вниз можно изменить опорную частоту и настройку фортепиано.

100 центов эквивалентно полутону (полутону).

Названия нот: сравнение английской и немецкой систем

Расчет гармоник от основной частоты

Simple Harmonic Oscillator – Summary – The Physics Hypertextbook

Simple Harmonic Oscillator – Summary – The Physics Hypertextbook

Сводка

  • Колебательное движение повторяется и колеблется между двумя местоположениями.
    • Для одномерного движения максимальное смещение колебательной системы из положения равновесия называется ее амплитудой.
      • Обозначение амплитуды: A (курсивная заглавная буква a).
      • Единицей измерения амплитуды в системе СИ является метр [м], но могут использоваться и другие единицы длины.
  • Периодическое движение повторяет цикл движения с характерным временем.
    • Период – это время для завершения одного цикла периодического движения.
      • Обозначение периода – T (курсивная заглавная буква t).
      • Единицей измерения периода в системе СИ является секунда [с].
      • Время ( t ), количество циклов ( n ) и период ( T ) связаны следующим уравнением…
    • Частота – это количество циклов, которые проходят за единицу времени.
      • Обозначение частоты – f (длинное f или курсив в нижнем регистре f).
      • Единицей измерения частоты в системе СИ является герц [Гц], который равен обратной секунде.


        		 Гц = 1 = с -1 ⎤

        с
      • Число ( n ), время ( t ) и частота ( f ) связаны следующим уравнением…
    • Частота и период – обратные величины.
      f = 1 ⇔ т = 1
      т f
    • Фаза, фазовый угол или фазовый сдвиг – это состояние развития периодической системы.
      • Фаза обозначается символом φ (строчная фи).
      • Единицей измерения фазы в системе СИ является радиан [рад], но также могут использоваться градусы (°).
      • Фаза также может быть описана как часть цикла или периода.
      • Один полный цикл соответствует 2π радиан.
    • Угловая частота – это скорость изменения фазы во времени.
      • Обозначение угловой частоты – ω (строчная омега).
      • В системе СИ единицей угловой частоты является радиан в секунду [рад / с].
      • Угловая частота преобразует время в радианы для использования в уравнениях, содержащих синус и косинус.
      • Угловая частота и частота связаны следующим уравнением…

        ω = 2π f

    • Непериодическое колебательное движение называется апериодическим.
  • Простой гармонический осциллятор (сокращенно шо) – это любая механическая система, в которой результирующая сила, действующая на систему…
    • прямо пропорционален смещению системы из положения равновесия
    • – возвращающая сила (действует в направлении, противоположном смещению)

      ∑ F = – kx

  • Простое гармоническое движение (сокращенно ШМ)…
    • – это то, что делает простой гармонический осциллятор, когда он отклоняется от положения равновесия.

Нет постоянных условий.

  1. Механика
    1. Кинематика
      1. Движение
      2. Расстояние и перемещение
      3. Скорость и скорость
      4. Разгон
      5. Уравнения движения
      6. Свободное падение
      7. Графики движения
      8. Кинематика и расчет
      9. Кинематика в двух измерениях
      10. Снаряды
      11. Параметрические уравнения
    2. Dynamics I: Force
      1. Силы
      2. Сила и масса
      3. Действие-реакция
      4. Вес
      5. Динамика
      6. Статика
      7. Трение
      8. Силы в двух измерениях
      9. Центростремительная сила
      10. Кодовые ссылки
    3. Энергия
      1. Работа
      2. Энергия
      3. Кинетическая энергия
      4. Потенциальная энергия
      5. Сохранение энергии
      6. Мощность
      7. Простые машины
    4. Dynamics II: Импульс
      1. Импульс и импульс
      2. Сохранение импульса
      3. Импульс и энергия
      4. Импульс в двух измерениях
    5. Вращательное движение
      1. Кинематика вращения
      2. Инерция вращения
      3. Вращательная динамика
      4. Вращательная статика
      5. Угловой момент
      6. Энергия вращения
      7. Прокат
      8. Вращение в двух измерениях
      9. Сила Кориолиса
    6. планетарное движение
      1. Геоцентризм
      2. Гелиоцентризм
      3. Вселенская гравитация
      4. Орбитальная механика I
      5. Гравитационная потенциальная энергия
      6. Орбитальная механика II
      7. Гравитация вытянутых тел
    7. Периодическое движение
      1. Пружины
      2. Генератор простых гармоник
      3. Маятники
      4. Резонанс
      5. Эластичность
    8. Жидкости
      1. Плотность
      2. Давление
      3. Плавучесть
      4. Расход жидкости
      5. Вязкость
      6. Аэродинамическое сопротивление
      7. Режимы потока
  2. Теплофизика
    1. Тепло и температура
      1. Температура
      2. Тепловое расширение
      3. Атомная природа материи
      4. Закон о газе
      5. Кинетико-молекулярная теория
      6. Фазы
    2. Калориметрия
      1. Явное тепло
      2. Скрытое тепло
      3. Химическая потенциальная энергия
    3. Теплопередача
      1. Проводимость
      2. Конвекция
      3. Радиация
    4. Термодинамика
      1. Тепло и работа
      2. Диаграммы давление-объем
      3. Двигатели
      4. Холодильники
      5. Энергия и энтропия
      6. Абсолютный ноль
  3. Волны и оптика
    1. Волновые явления
      1. Природа волн
      2. Периодические волны
      3. Интерференция и суперпозиция
      4. Интерфейсы и барьеры
    2. Звук
      1. Природа звука
      2. Интенсивность
      3. Эффект Доплера (звук)
      4. Ударные волны
      5. Дифракция и интерференция (звук)
      6. Стоячие волны
      7. ударов
      8. Музыка и шум
    3. Физическая оптика
      1. Природа света
      2. Поляризация
      3. Эффект Доплера (светлый)
      4. Черенковское излучение
      5. Дифракция и интерференция (свет)
      6. Тонкопленочная интерференция
      7. Цвет
    4. Геометрическая оптика
      1. Отражение
      2. Преломление
      3. Зеркала сферические
      4. Сферические линзы
      5. Аберрация
  4. Электричество и магнетизм
    1. Электростатика
      1. Электрический заряд
      2. Закон Кулона
      3. Электрическое поле
      4. Электрический потенциал
      5. Закон Гаусса
      6. Проводники
    2. Электростатические приложения
      1. Конденсаторы
      2. Диэлектрики
      3. Аккумуляторы
    3. Электрический ток
      1. Электрический ток
      2. Электрическое сопротивление
      3. Электроэнергия
    4. Цепи постоянного тока
      1. Резисторы в цепях
      2. Батареи в цепях
      3. Конденсаторы в цепях
      4. Правила Кирхгофа
    5. Магнитостатика
      1. Магнетизм
      2. Электромагнетизм
      3. Закон Ампера
      4. Электромагнитная сила
    6. Магнитодинамика
      1. Электромагнитная индукция
      2. Закон Фарадея
      3. Закон Ленца
      4. Индуктивность
    7. Цепи переменного тока
      1. Переменный ток
      2. RC-цепи
      3. Цепи RL
      4. Цепи LC
    8. Электромагнитные волны
      1. Уравнения Максвелла
      2. Электромагнитные волны
      3. Электромагнитный спектр
  5. Современная физика
    1. Относительность
      1. Пространство-время
      2. Масса-энергия
      3. Общая теория относительности
    2. Quanta
      1. Излучение черного тела
      2. Фотоэлектрический эффект
      3. Рентгеновские лучи
      4. Антиматерия
    3. Волновая механика
      1. Волны материи
      2. Атомарные модели
      3. Полупроводники
      4. Конденсированное вещество
    4. Ядерная физика
      1. Изотопы
      2. Радиоактивный распад
      3. Период полураспада
      4. Энергия связи
      5. Деление
      6. Fusion
      7. Нуклеосинтез
      8. Ядерное оружие
      9. Радиобиология
    5. Физика элементарных частиц
      1. Квантовая электродинамика
      2. Квантовая хромодинамика
      3. Квантовая динамика вкусов
      4. Стандартная модель
      5. Помимо стандартной модели
  6. Фонды
    1. Шт.
      1. Международная система единиц
      2. Гауссова система единиц
      3. Англо-американская система единиц
      4. Единицы разного назначения
      5. Время
      6. Преобразование единиц
    2. Измерение
      1. Значащие цифры
      2. По порядку величины
    3. Графики
      1. Графическое представление данных
      2. Линейная регрессия
      3. Подгонка по кривой
      4. Исчисление
    4. Векторы
      1. Тригонометрия
      2. Сложение и вычитание векторов
      3. Векторное разрешение и компоненты
      4. Умножение векторов
    5. ссылку
      1. Специальные символы
      2. Часто используемые уравнения
      3. Физические константы
      4. Астрономические данные
      5. Периодическая таблица элементов
      6. Люди в физике
  7. Назад дело
    1. Предисловие
      1. Об этой книге
    2. Связаться с автором
      1. гленнелерт.нас
      2. Behance
      3. Instagram
      4. Твиттер
      5. YouTube
    3. Аффилированные сайты
      1. hypertextbook.com
      2. midwoodscience.org

Частота и период времени – Характеристики волн – GCSE Physics (Single Science) Revision

Частоту волны можно вычислить с помощью следующего уравнения:

\ [frequency = \ frac {1} {time ~ period} \]

\ [f = \ frac {1} {T} \]

где:

f – количество волн, производимых источником в секунду, измеряется в герцах (Гц).

T – время, необходимое для одного полного колебания, измеряется в секундах.

Все волны, включая звуковые и электромагнитные волны, подчиняются этому уравнению. Например, волна с периодом времени 2 секунды имеет частоту 1 ÷ 2 = 0,5 Гц.

Вопрос

Звуковая волна имеет период времени 0,0001 секунды. Какая у него частота?

Показать ответ

f = 1 ÷ T

f = 1 ÷ 0.0001 с

f = 10000 Гц

Вопрос

Радиоволна имеет период времени 0,0000003333333 секунды. Какая у него частота?

Показать ответ

f = 1 ÷ T

f = 1 ÷ 0,0000003333333 с

f = 3000 000 Гц

9016 число циклов формулы 9 единица времени.«Циклы» могут быть движениями чего-либо с периодическим движением, например пружины, маятника, чего-то вращения или волны. Частота равна 1, деленному на период, который представляет собой время, необходимое для одного цикла.

Производной единицей измерения частоты в системе СИ является герц, названный в честь Генриха Рудольфа Герца (символ hz). Один Гц – это один цикл в секунду.

f = частота, количество циклов в единицу времени

T = период, время, необходимое для одного цикла

N = количество циклов

t = количество времени

Частотная формула Вопросы:

1) Длинный маятник занимает 5.00 с для завершения одного цикла возвратно-поступательного движения. Какая частота движения маятника?

Ответ: Для завершения одного цикла маятнику требуется 5,00 с , поэтому это его период T. Частоту можно найти с помощью уравнения:

f = 0,20 цикла / с

частота маятника 0,20 цикл / с . Единицы циклов / с часто обозначаются как «Герцы» с символом «Гц». Таким образом, частота этого маятника также может быть обозначена как 0.20 Гц.

2) Тахометр в автомобиле измеряет количество оборотов шин в минуту (обороты и циклы – это одно и то же). Автомобиль движется с постоянной скоростью, а тахометр показывает 2400 оборотов в минуту. Какова частота пробуксовки шин, измеренная в циклах в секунду? Какой период в секундах?

Ответ: Рассматриваемое количество циклов (оборотов) составляет 2400 . Это количество циклов, которые происходят за одну минуту, что равно 60 секундам.Итак, частоту можно найти с помощью уравнения:

f = 40 циклов / с

Частота вращения шин составляет 40 циклов / с , что также можно записать как 40 Гц. Чтобы найти период из этого, измените уравнение, которое связывает период и частоту:

T = 0,025 с

Период вращения шин составляет 0,025 секунд.

Разница между периодом и частотой

Колебания и колебания механических систем остаются одной из важнейших областей изучения физики.Практически каждая система свободно колеблется или вибрирует самыми разными способами.

Что общего у океанского буйка, гитары, ребенка на качелях или биения сердца? Все они колеблются, то есть перемещаются между двумя точками. Само человеческое тело – это сокровищница вибрационных явлений. Даже атомы в нашем теле вибрируют. У каждой колеблющейся системы есть что-то общее. Это включает в себя силу и энергию. Вы начинаете движение, толкая ребенка на качелях, или можете увеличить энергию атомов, колеблющихся в кристалле, с помощью тепла.Итак, колебания создают волны.

Что общего между колебаниями или волнами? Особенность, связывающая такие явления, – периодичность. Ясно, что небольшое количество основополагающих принципов описывает все явления, что доказывает их обычность, чем вы могли представить. Вы заметите определенную закономерность или движение в каждом явлении, которое повторяется снова и снова. Периодическое движение – это движение, которое повторяется снова и снова через равные промежутки времени, например, движение гитарной струны или движение ребенка вперед и назад на качелях.Время, необходимое для завершения одного цикла вибрации или колебания, называется периодом волны. Частота просто относится к числу циклов колебания, происходящих в секунду.

Что такое частота?

Частота волны означает просто количество полных циклов или колебаний, которые происходят за одну секунду. Он измеряется в циклах в секунду или в герцах (Гц). Цикл – это одно полное колебание, а вибрация может быть одним или несколькими событиями, тогда как колебания в основном повторяются в течение нескольких циклов.Обычно обозначается буквой «f» и выражается как:

f = 1 / T, где ‘T’ представляет период времени, а ‘f’ – частота.

Что такое период?

Период является обратной величиной частоты и определяется как время, необходимое для одного полного обхода вибрации или колебания. Это просто относится ко времени, в течение которого что-то должно происходить периодически, и оно измеряется в секундах за цикл. Период времени обратно пропорционален частоте, что означает, что обе величины обратно пропорциональны друг другу.В форме уравнения период выражается как:

T = 1 / f, где «f» – частота, а «T» – период времени.

Разница между периодом и частотой

  1. Определение периода и частоты

И термины «период», и «частота» связаны между собой, потому что они демонстрируют определенный образец движения, но при этом совершенно разные. Оба относятся к периодическим явлениям и часто путают друг с другом. Период – это количество времени, которое требуется волне для завершения одного полного цикла колебаний или вибрации.Частота, напротив, относится к количеству полных циклов или колебаний, происходящих в секунду. Период – это величина, связанная со временем, а частота связана со скоростью. Период просто означает время, когда что-то должно происходить периодически, тогда как частота означает, как часто это происходит.

  1. Соотношение периода и частоты

Обе величины обратно пропорциональны друг другу. Частота выражается в циклах в секунду, колебаниях в секунду, вибрациях в секунду и т. Д.и обычно обозначается буквой «f». Период выражается в секундах на цикл. Единица измерения частоты – герц (Гц), а «Т» представляет период времени одного полного колебания. С математической точки зрения, обе величины обратны друг другу. В форме уравнения частота и период выражаются как:

f = 1 / T, где f – частота, а T – период.

Его также можно выразить как:

T = 1 / f

  1. Пример периода и частоты

Допустим, волна колеблется вверх и вниз за одну секунду, что означает, что период волны составляет 1 секунду.Частота и период обратно пропорциональны друг другу. Поскольку в секунду происходит только один цикл, частота волны будет 1 цикл в секунду. И если бы волна колебалась за полсекунды, период этой волны был бы 0,5 секунды, а частота была бы 1 / 0,5 = 2, то есть 2 периода в секунду. Таким образом, чем больше период времени, тем ниже частота и наоборот.

Период и частота: сравнительная таблица

Сводка периода по сравнению сЧастота

Как частота, так и период времени являются фундаментальными параметрами волн, связанными друг с другом, но они явно различаются по количеству. Частота волны связана с величиной скорости, тогда как период волны связан с величиной времени. Под периодом времени понимается время, за которое волна совершает один полный цикл колебания или вибрации, который обратно пропорционален частоте. Частота относится к количеству вибраций, которые происходят за одну секунду, что является обратной величиной периода времени.Частота обычно измеряется в герцах (Гц), а период измеряется в секундах. Оба они обратно пропорциональны друг другу, что означает, что чем выше частота, тем ниже период, и наоборот. Частота обозначается буквой «f», а период обозначается буквой «T».

Сагар Хиллар – плодовитый автор контента / статей / блогов, работающий старшим разработчиком / писателем контента в известной фирме по обслуживанию клиентов, базирующейся в Индии. У него есть желание исследовать разноплановые темы и разрабатывать высококачественный контент, чтобы его можно было лучше всего читать.Благодаря его страсти к писательству, он имеет более 7 лет профессионального опыта в написании и редактировании услуг на самых разных печатных и электронных платформах.

Вне своей профессиональной жизни Сагар любит общаться с людьми из разных культур и происхождения. Можно сказать, что он любопытен по натуре. Он считает, что каждый – это опыт обучения, и это приносит определенное волнение, своего рода любопытство, чтобы продолжать работать. Поначалу это может показаться глупым, но через некоторое время это расслабляет и облегчает начало разговора с совершенно незнакомыми людьми – вот что он сказал.”

Последние сообщения от Sagar Khillar (посмотреть все)

: Если вам понравилась эта статья или наш сайт. Пожалуйста, расскажите об этом. Поделитесь им с друзьями / семьей.

Cite
APA 7
Хиллар, С. (21 августа 2018 г.). Разница между периодом и частотой. Разница между похожими терминами и объектами. http://www.differencebetween.net/science/mat Mathematics-statistics/difference-between-period-and-frequency/.
MLA 8
Хиллар, Сагар.«Разница между периодом и частотой». Разница между похожими терминами и объектами, 21 августа 2018 г., http://www.differencebetween.net/science/mat Mathematics-statistics/difference-between-period-and-frequency/.

Что такое формула периода? – Mvorganizing.org

Какова формула периода?

Мы также можем вычислить период, используя формулу, полученную из основных уравнений синуса и косинуса. Период для функции y = A sin (Bx + C) и y = A cos (Bx + C) равен 2π / | B | радианы.Обратный период функции = частота. Частота определяется как количество циклов, завершенных за одну секунду.

Что такое период в звуковых волнах?

Период времени (обозначается «T») – это время, необходимое для прохождения одного полного цикла вибрации через заданную точку. По мере увеличения частоты волны временной период волны уменьшается. Частота и период времени находятся во взаимной зависимости, которую математически можно выразить как: T = 1 / f или как: f = 1 / T.

Каковы 4 свойства звука?

Мы используем четыре свойства звука: высоту, динамику (громкость или мягкость), тембр (цвет тона) и продолжительность.

Каковы 7 свойств звука?

Rammdustries LLC получает компенсацию за направление трафика и бизнеса этим компаниям.

  • 7 Характеристики звука и почему их нужно знать.
  • Частота.
  • Амплитуда.
  • Тембр.
  • Конверт.
  • Скорость.
  • Длина волны.
  • Фаза.

Каковы три основных компонента звука?

В звуковом брендинговом бизнесе принято считать, что существует три различных типа или элементов звука.Это голос, атмосфера (или эффекты) и музыка.

Какие пять источников звука?

Акустические инструменты, Электрические инструменты, Живые существа, такие как животные и птицы, использующие свои голосовые связки, Искусственные источники, такие как машины, любая вибрация, вызванная ветром, – это пять источников звука.

Какие 12 элементов музыки?

  • ЭЛЕМЕНТ. Основные связанные термины.
  • Ритм: (доля, метр, темп, синкопа)
  • Динамика: (форте, фортепиано и др.],
  • Мелодия: (высота, тема, соединение, разъединение)
  • Гармония: (аккорд, прогрессия, созвучие, диссонанс,
  • Цвет тона: (регистр, диапазон, аппаратура)
  • Текстура: (однотонная, омофоническая, полифоническая,
  • Форма:

Какие 7 элементов музыки?

В рамках этого класса мы будем обращаться к СЕМЬ элементам музыки: ритм, мелодия, гармония, тембр, динамика, текстура и форма.

Каковы 5 основных элементов музыки?

Хотя существует много разных подходов к описанию строительных блоков музыки, мы часто разбиваем музыку на пять основных элементов: мелодия, текстура, ритм, форма и гармония.

Омофоничны ли мелодия и аккомпанемент?

Самая распространенная фактура в западной музыке: мелодия и сопровождение. Несколько голосов, из которых один, мелодия, заметно выделяется, а другие образуют фон гармонического сопровождения. Если все партии имеют примерно одинаковый ритм, гомофонную текстуру также можно описать как гоморитмическую.

Какие 8 музыкальных элементов?

Восемь элементов музыки в алфавитном порядке: динамика, форма, гармония, мелодия, ритм, текстура, тембр и тональность.

Какие 10 элементов музыки?

Основные музыкальные элементы

  • Звук (обертон, тембр, высота, амплитуда, длительность)
  • Мелодия.
  • Гармония.
  • Ритм.
  • Текстура.
  • Структура / форма.
  • Выражение (динамика, темп, артикуляция)

Каковы шесть основных элементов музыки?

В этой серии представлены шесть ключевых элементов музыки, включая ритм, текстуру, динамику, высоту звука, форму и тембр.Дети получат знания об основных музыкальных приемах с помощью набора забавных заданий, основанных на каждом элементе, и на этом пути у них вырастут уверенность в себе и навыки сотрудничества.

Какие 13 элементов ритма?

  • Элементы ритма. Бить. Темп. Рубато.
  • Время.
  • Метр. Ритмический метр. Полифонический метр.
  • Органический ритм. Прозаические ритмы и равнина. Ритм, мелодия и гармония. Ритм, структура и стиль.

Какие бывают 4 типа ритма?

Мы можем использовать пять типов ритма:

  • Случайный ритм.
  • Обычный ритм.
  • Чередующийся ритм.
  • Плавный ритм.
  • Прогрессивный ритм.

Какой знак ритма?

Ритмические символы состоят из частей, каждая из которых имеет название: овальная часть ноты называется ЗАГОЛОВОК НОТЫ. Вертикальная линия, восходящая (или нисходящая) от всех нот, имеющих меньшую ценность, чем целая нота, называется STEM.

Как вы овладеваете ритмом в музыке?

Давайте рассмотрим несколько полезных советов, как улучшить свой ритм и ритм при воспроизведении музыки…Постарайтесь сразу включить одно или несколько в свою обычную практику, а затем со временем добавляйте другие.

  1. Подсчет и медленный темп.
  2. Запись и воспроизведение.
  3. Divide the Beat.
  4. Практикуйте ритм и ритм на разных инструментах.

Как ты успеваешь вовремя с музыкой?

1. Запишите себя

  1. Начни просто. Выберите песню, которую вы действительно хорошо знаете (подумайте: «У Мэри был ягненок»), а затем выберите медленный темп.
  2. Запишите, как вы играете (или поете, если ваш инструмент – это голос) в одиночку, без метронома или какой-либо резервной копии.
  3. Прослушайте запись.
  4. Постучите или хлопните вместе с записью.

Как вы читаете музыкальное время?

Посмотрев на размер, вы увидите два числа, расположенные вертикально. Верхнее число представляет количество ударов в такте, а нижнее число – какое значение ноты получает долю. Например, 4/4 означает, что в такте 4 доли, а четвертная нота (1/4) получает долю; четыре четвертных ноты в такте.

Как вы чувствуете ритм в музыке?

Практика ведет к совершенству В конце концов, вы сможете услышать бит, как только начнется песня. И когда вы научитесь стучать пальцем, вы также должны постукивать ногой и в конечном итоге задействовать все свое тело, пока не почувствуете, что двигаетесь или танцуете в такт песне!

Как мне найти свой ритм?

Слушая, закройте глаза и постарайтесь услышать постоянный ритм песни. Когда будете готовы, нажимайте пальцем на пульс, который вы чувствуете, или слегка хлопайте в ладоши на каждом ударе.Если вам удобны ритмы, попробуйте найти, где приходится первая доля каждого такта, и определите долю.

В чем разница между ритмом и долей?

Разница между ритмом и битом: Проще говоря, бит – это устойчивый пульс, лежащий в основе музыки на всем протяжении. Ритм – это то, как идут слова.

Насколько важен бит в музыке?

Почему бит важен? Бит – ключевой компонент музыки. Без такта невозможно определить, как быстро играть песню.Часто бит устанавливается на лету одним из музыкантов, который может просто отсчитать «1-2-3-4», чтобы все музыканты знали, на какой скорости играть.

Как узнать, сильные или слабые удары?

Сильные и слабые доли: основы Наиболее распространенное мнение о сильных и слабых долях (в интервале 4/4) звучит следующим образом: первая доля такта является самой сильной (это «мрачная доля»). Третья доля такта тоже сильная, но не такая сильная, как первая. Вторая и четвертая доли слабые.

Как долго длится бит?

Удар – обычно приемлемая скорость счета, где-то от 40 до 200 ударов в минуту (другими словами, от менее одного удара в секунду до более двух ударов в секунду) – см. Маркировку метронома.

Что такое базовый ритм?

В музыке и теории музыки ритм – это основная единица времени, пульс (регулярно повторяющееся событие) на уровне измерения (или уровне ударов). В популярном использовании ритм может относиться к множеству связанных понятий, включая пульс, темп, метр, определенные ритмы и грув.

Какая связь между частотой и периодом времени?

Звук | Вопросы с краткими / длинными ответами Частота выполнения цикла – это количество раз за секунду. Время, необходимое для выполнения одной вибрации, называется периодом времени. Частота и период времени обратно пропорциональны, количество колебаний в секунду – это частота.

Какая связь между частотой и длиной волны?

Длина волны и частота света тесно связаны. Чем выше частота, тем короче длина волны.Поскольку все световые волны движутся через вакуум с одинаковой скоростью, количество гребней волны, проходящих через данную точку за одну секунду, зависит от длины волны.

Как вы рассчитываете частоту?

Чтобы вычислить частоту, разделите количество раз, когда событие происходит, на промежуток времени. Пример: Анна делит количество переходов по веб-сайту (236) на продолжительность (один час или 60 минут).

Как рассчитать время по частоте?

Частота выражается в Гц (частота = циклы / секунды).Чтобы вычислить временной интервал известной частоты, просто разделите 1 на частоту (например, частота 100 Гц имеет временной интервал 1 / (100 Гц) = 0,01 секунды; 500 Гц = 1 / (500 Гц) = 0,002 секунды, и т. д.)

Какая частота волн?

герц

Как найти частоту в статистике?

Подсчитайте итоговые отметки, чтобы определить частоту каждого класса. Относительная частота класса данных – это процент элементов данных в этом классе. Относительную частоту можно рассчитать по формуле fi = fn f i = f n, где f – абсолютная частота, а n – сумма всех частот.

По какой формуле найти амплитуду?

Амплитуда – это расстояние между центральной линией функции и верхом или низом функции, а период – это расстояние между двумя пиками графика или расстояние, необходимое для повторения всего графика. Используя это уравнение: Амплитуда = AP Период = 2πB Горизонтальный сдвиг влево = C Вертикальный сдвиг = D.

Какая связь между частотой и амплитудой?

Связь между амплитудой и частотой. Когда высота больше, мы можем сказать, что это амплитуда мгновенного удара.Точно так же, когда вы и ваш партнер продолжаете бросать струну, чем больше будет совершенных волн, т. Е. Гребня и впадины, тем выше будет частота.

Как определить амплитуду по частоте и времени?

Формула для частоты: f (частота) = 1 / T (период). f = c / λ = скорость волны c (м / с) / длина волны λ (м). Формула для времени: T (период) = 1 / f (частота). λ = c / f = волновая скорость c (м / с) / частота f (Гц).

Частота прямо пропорциональна амплитуде?

Частота обратно пропорциональна амплитуде.

Что такое длина волны, частота и амплитуда?

АМПЛИТУДА И ДЛИНА ВОЛНЫ Длина волны означает длину волны от одного пика до другого. Амплитуда или высота волны измеряется от пика до впадины. Длина волны измеряется от пика к пику. Длина волны напрямую связана с частотой данной формы волны.

Что такое амплитуда и частота?

Краткое содержание урока. Давайте рассмотрим. Амплитуда – важный параметр волн и максимальное смещение точек на волне.Другими словами, амплитуда – это расстояние по вертикали между пиком или впадиной и точкой равновесия. Частота – это количество волновых циклов, проходящих через точку за единицу времени.

Что такое время и амплитуда длины волны?

Время, необходимое для пересечения фиксированной контрольной точки двумя последовательными сжатиями или разрежениями, называется периодом времени (T) волны. Амплитуда: величина максимального возмущения в среде по обе стороны от среднего значения называется амплитудой волны.

В чем разница между частотой и амплитудой?

Разница между частотой и амплитудой заключается в том, что частота – это количество циклов в секунду, а амплитуда – это размер волны. Амплитуда представляет собой энергию волны. Наиболее важные термины, относящиеся к этим волнам, – это длина волны, частота и амплитуда.

Чем выше амплитуда, тем выше частота?

Энергосодержание: амплитуда и частота Волна с высокой амплитудой – это волна с высокой энергией, а волна с низкой амплитудой – это волна с низкой энергией.Таким образом, волна определенной амплитуды будет передавать больше энергии в секунду, если она имеет более высокую частоту, просто потому, что за определенный период времени проходит больше волн.

Влияет ли амплитуда на частоту?

Амплитуда соответствует громкости звука. [BL] [OL] Поскольку звук на всех частотах имеет одинаковую скорость в воздухе, изменение частоты означает изменение длины волны. Амплитуда X полностью не зависит от скорости распространения vw и зависит только от количества энергии в волне.

Почему на частоту не влияет амплитуда?

1 Ответ. Вы предполагаете, что максимальная скорость останется прежней; не будет. Если у вас более высокая амплитуда, но та же частота, тогда все будет двигаться быстрее в крайних точках, чтобы поддерживать частоту.

Влияет ли амплитуда на частоту ШМ?

Одна особенность состоит в том, что период T и частота f простого гармонического осциллятора не зависят от амплитуды. Струна гитары, например, будет колебаться с одной и той же частотой независимо от того, мягко она или сильно щипает.Два важных фактора действительно влияют на период простого гармонического осциллятора.

Влияет ли изменение амплитуды на длину волны?

Как изменение амплитуды влияет на длину волны? Амплитуда не влияет на длину волны. Это также не влияет на скорость волны. Амплитуда – это энергия волны, измеренная от положения покоя до вершины гребня.

Что происходит с амплитудой при увеличении высоты тона?

Мы воспринимаем увеличение частоты как увеличение высоты звука, которое вы описали.По мере увеличения частоты (высоты тона) длина волны становится короче в соответствии с универсальным волновым уравнением (v = fλ). Амплитуда или интенсивность волны воспринимается нашими ушами как громкость (подумайте об «усилителе»).

Влияет ли изменение частоты на длину волны?

По мере увеличения длины волны ее частота и энергия (E) уменьшаются. Из этих уравнений вы можете понять, что с увеличением частоты длина волны становится короче. По мере уменьшения частоты длина волны увеличивается.

Что происходит при увеличении амплитуды?

Звук воспринимается громче, если амплитуда увеличивается, и тише, если амплитуда уменьшается. По мере увеличения амплитуды звуковой волны интенсивность звука увеличивается. Звуки с большей интенсивностью воспринимаются громче. Относительная сила звука часто выражается в единицах, называемых децибелами (дБ).

Simple Harmonic Motion (SHM) – частота, ускорение, смещение, скорость, графики SHM, период времени, система масса-пружина, маятник, энергия

Щелкните здесь, чтобы получить ответы на вопросы и домашнее задание по SHM.

Щелкните – для ответов SHM.

Объекты могут колебаться по-разному, но действительно важной формой колебаний является SHM или простое гармоническое движение.

Объект совершает простое гармоническое движение (SHM) if;

  1. ускорение объекта прямо пропорционально его смещению от его положения равновесия.
  2. , ускорение всегда направлено к положению равновесия.

Частота (f) колебания измеряется в герцах (Гц), это количество колебаний в секунду.Время одного колебания называется периодом (Т), оно измеряется в секундах.

Acceleration – мы можем рассчитать ускорение объекта в любой точке его колебания, используя приведенное ниже уравнение.

В этом уравнении; a = ускорение в мс -2 , f = частота в Гц, x = смещение от центрального положения в м.

Displacement – При использовании приведенного ниже уравнения калькулятор должен быть в радианах, а не в градусах! мы можем рассчитать смещение объекта в любой точке его колебания, используя приведенное ниже уравнение.

Члены в этом уравнении такие же, как и в приведенных выше уравнениях. Дополнительные члены в этом уравнении: A = амплитуда (максимальное смещение) в м, t = время с момента начала колебания в с.

Скорость – мы можем рассчитать скорость объекта в любой точке его колебания, используя приведенное ниже уравнение.

Члены в этом уравнении такие же, как и в приведенных выше уравнениях. Дополнительный член в этом уравнении: v = скорость в мс -1 .

Графики SHM

Когда мы строим график перемещения, скорости и ускорения во время SHM в зависимости от времени, мы получаем графики ниже.

Уравнение скорости упрощается до приведенного ниже уравнения, когда мы просто хотим знать максимальную скорость.

Уравнение ускорения упрощается до приведенного ниже уравнения, когда мы просто хотим знать максимальное ускорение.

Временной период системы масса-пружина

Период времени маятника

SHM и Энергетика

Для маятника, при котором энергия SHM передается вперед и назад между кинетической и потенциальной энергией.

Оставить комментарий