Закон всемирного тяготения Ньютона – Телеканал “Наука”
Все тела во Вселенной притягиваются друг к другу. Вот почему вас так тянет к холодильнику!
Признайтесь, вы тоже не до конца поняли, что такое закон всемирного тяготения Ньютона, когда учились в школе? Это неудивительно: человечество, за исключением нескольких астрономов и физиков, даже не подозревало о нем до 1687 года, да и потом еще лет 200 ученые трудились над строгим обоснованием гениальной теории Ньютона. Так что нет ничего стыдного даже для взрослого человека в том, чтобы освежить свои знания о неведомой силе, которая притягивает все тела во Вселенной, определяет траектории движения планет Солнечной системы, создает приливы и отливы и запускает течение рек на Земле, а однажды подсказала ученым сам факт существования планеты Нептун.
Как был открыт закон всемирного тяготения?По легенде, теория гравитации родилась в голове Ньютона благодаря упавшему на него яблоку, и это не пустой миф.
Близкие знакомые ученого оставили свидетельства о разговоре с ним и о самом «яблочном инциденте», который, по-видимому, случился в 1666 году, когда молодой Исаак пережидал эпидемию бубонной чумы в поместье своей матери. Находясь в самоизоляции, 23-летний юноша размышлял о том, почему яблоко падает перпендикулярно к земной поверхности, а не вбок или вверх, и пришел к выводу о том, что яблоко притягивает Землю так же, как Земля притягивает яблоко.
Пока чума косила англичан, погубив пятую часть населения Лондона, научная мысль Ньютона шагала за пределы нашей планеты и он спрашивал себя: как далеко простирается эта незримая сила (гравитация) и не она ли удерживает Луну вблизи Земли, не давая ей улететь? История с падением яблока стала популярна благодаря Вольтеру, описавшему инцидент со слов племянницы Ньютона, и биографу Уильяму Стьюкли, который изложил ее в книге «Воспоминания о жизни Ньютона», выпущенной в 1752 году.
На формулировку закона всемирного тяготения у гениального британского ученого ушло два десятка лет: впервые он оповестил мир о нем в 1687 году — в своем фундаментальном труде «Математические начала натуральной философии».
Так наконец удалось дать объяснение траектории движения планет вокруг Солнца, обосновать открытия немецкого астронома Кеплера, сформулированные в начале XVII века, ответив на главный вопрос: почему планеты движутся не по кругу, а по эллиптической орбите? Закон всемирного тяготения Ньютона и сама идея гравитации помогли объяснить феномены, о которых эмпирическим путем уже догадывались самые наблюдательные ученые. Большинство же людей верили в божий промысел, считали Землю центром Вселенной и даже не подозревали о том, что на яблоко и Луну влияют одни и те же физические законы.
Если все тела во Вселенной притягиваются, то почему мы чувствуем притяжение только к Земле, а не к холодильнику или друг к другу? Все дело в массе и расстоянии: до тех пор, пока масса предмета мала, а расстояние велико, мы не чувствуем никакого притяжения. И лишь когда речь идет о такой махине, как Земля, мы сполна ощущаем силу тяжести — одну из самых заметных проявлений силы всемирного тяготения.
Закон всемирного тяготения гласит: два любых тела притягиваются друг к другу с силой, прямо пропорциональной массе каждого из них и обратно пропорциональной квадрату расстояния между ними
Для подсчета используется формула: F = G ∙ (m1 ∙ m2) / R², где m — масса, R — расстояние между телами, G — гравитационная постоянная, значение которой было определено экспериментально. Эта постоянная G очень мала (6,67 ∙ 10–11 м³ / (кг ∙ с²)) — именно поэтому сила, с которой притягиваются тела небольшой массы, нами совершенно не ощущается.
Был ли Ньютон первооткрывателем?С момента публикации «Начал» многим ученым не нравилось, что Ньютон не объяснил физическую природу гравитации, не назвал ее источник, не привел доказательства. Некоторые ученые считали, что ученый промышляет плагиатом: мысль о том, что движение планет объясняется действием силы, которая притягивает каждую планету к Солнцу, уже высказывалась ранее, в том числе английским физиком Робертом Гуком — он даже сформулировал, что эта сила убывает обратно пропорционально квадрату расстояния от Солнца.
Свою теорию Гук изложил в том самом 1666 году, когда на Исаака упало яблоко, а в 1679 году посылал Ньютону письмо, где предлагал сотрудничать по решению этой задачи, но получил отказ и заверения о том, что эта тема давно не занимает адресата. В дальнейшем Гук требовал указывать его имя как первого автора закона тяготения и открыто обвинял Ньютона в плагиате. Ученые конфликтовали до конца жизни Гука, а спор о том, кто был первым, продолжался даже в XX веке.
«К сожалению, нам неизвестны детали того логического пути, которым Ньютон пришел к закону всемирного тяготения», — писали американские ученые в книге «Физика» в 1960 году.
«Если связать в одно все предположения и мысли Гука о движении планет и тяготении, высказанные им в течение почти 20 лет, то мы встретим почти все главные выводы “Начал” Ньютона, только высказанные в неуверенной и мало доказательной форме. Не решая задачи, Гук нашел ее ответ», — писал советский ученый Сергей Вавилов. Ньютон был блестящим математиком и смог решить поставленную Гуком задачу.
Лишь после того, как ньютоновская теория стала основой небесной механики в XVIII веке, физики приняли ее более благосклонно. Закон всемирного тяготения Ньютона стал подарком для астрономов, так как математически объяснил почти все, что происходит во Вселенной. Но, пожалуй, главным вкладом Ньютона в астрономию стало открытие в 1846 году Нептуна — самой дальней от Земли планеты и первой, обнаруженной путем математических расчетов.
Этому знаменательному событию предшествовало открытие Урана в 1781 году английским астрономом Уильямом Гершелем. Наблюдавшие за ее движением астрономы многие годы народились в затруднении: реальная орбита Урана не совпадала с вычисленной. Это недоразумение заставляло думать о том, что за Ураном прячется еще одна планета, которая влияет на нее своим притяжением. Французский математик Урбен Леверье провел расчеты с помощью ньютоновой механики и указал астрономам, где именно нужно искать восьмую планету.
Однако даже в начале XX века оставалось несколько загадок, которые не находили объяснения с помощью закона тяготения Ньютона. Как именно сила притяжения простирается через пространство Вселенной и где ее источник? Почему она действует мгновенно и на любом расстоянии? Как объяснить так называемый гравитационный парадокс? Почему наблюдается расхождение теоретического и наблюдаемого смещения движения перигелия Меркурия? Многие космологические проблемы помогла решить общая теория относительности, которую предложил Альберт Эйнштейн в 1915 году. Но это, как говорится, уже совсем другая история.
На сайте могут быть использованы материалы интернет-ресурсов Facebook и Instagram, владельцем которых является компания Meta Platforms Inc., запрещённая на территории Российской Федерации
Расскажите друзьям
- Космическая гонка
В горных породах Марса найдены признаки прошлой жизни
- Что было раньше
- Что было раньше
Обнаружена самая большая в Центральной Азии коллекция каменных украшений
- Околонаука
Алгоритм сплетников и запор у скорпионов: объявлены победители Шнобелевской премии
- Внеземное
Похоже, ученые наконец разгадали тайну колец Сатурна
- Физика всего
Обнаружены новые фазовые состояния воды
NASA, ESA, CSA, and STScI
Опубликована первая научная полноцветная фотография с телескопа «Джеймс Уэбб»
Shutterstock
Ученые выяснили, почему «королевы» муравьев живут в 5 раз дольше обычных рабочих
Современный карликовый крокодил
Shutterstock
Обнаружены еще два вида вымерших крокодилов, которые охотились на предков человека
Shutterstock
Ученые нашли простую физиологическую основу для различий в восприятии времени
Хомо футурис. Каким будет человек будущего?
Хотите быть в курсе последних событий в науке?
Оставьте ваш email и подпишитесь на нашу рассылку
Ваш e-mail
Нажимая на кнопку «Подписаться», вы соглашаетесь на обработку персональных данных
формулы, соотношения и формулировка, математическая запись и векторная форма
Физика
12.
11.21
10 мин.
Основным соотношением, которое используется в задачах по физике и механике на движение или взаимодействие тел, является второй закон Ньютона. Его формула связывает массу и ускорение. Однако перед ее применением на практике рекомендуется рассмотреть определения, основные понятия о физических величинах и ее составляющих.
Оглавление:
- Первоначальная запись закона
- Элементы и их зависимость
- Алгоритм перевода значений
Общие сведения
Впервые учащиеся знакомятся с тремя правилами Ньютона в классах, когда необходимо находить параметры в задачах на движение тел. Формула для 2 закона Ньютона выражается в таком виде: a=F/m. Последнюю можно сформулировать следующим образом: в любой инерциальной системе ускорение физического тела (a) — векторная величина, которая имеет прямо пропорциональную зависимость от силы F и обратно пропорциональную от массы физического тела(m).
Первоначальная запись закона
Однако вышеописанная формула — следствие или частный случай. Математическая запись в высших учебных заведениях сильно отличается от исходной формулы. Она имеет такой вид: F=d(p)/d(t). Последнее соотношение — второй закон Ньютона, формулировка которого имеет следующий вид: при воздействии силы F на тело в пространстве наблюдается прямо пропорциональная зависимость от дифференциала импульса d(p), сообщаемого ей за мгновенный промежуток времени t.
На основании второго закона Ньютона, формулировка которого описывается соотношением F=d(p)/d(t), а потом выводится выражение общего вида, математическая запись для импульса “p” имеет такой вид: p=mv, где m и v — масса и скорость соответственно. Затем нужно подставить в F=d(p)/d(t) значение р, т. е. F=d(mv)/d(t)=md(v)/d(t)=ma. Масса является константой, которая выносится за знак дифференциала md(v). Соотношение d(v)/d(t) эквивалентно величине ускорения «а», поскольку из курса физики известно, что a=v/t.
Для полного понимания второго утверждения Ньютона нужно рассмотреть элементы, из которых оно состоит, разобрать физический смысл и основные факторы их зависимости.
Элементы и их зависимость
Первым компонентом выражения F=ma является сила. Это параметр, имеющий направление (векторная) и воздействующий на материальную точку со стороны других тел. Он бывает двух типов — простым и составным. К первому относится только единичное воздействие, например, сила тяжести. Второй состоит из нескольких элементов и является результирующим (элементами могут быть другие F). Для силы справедливы следующие утверждения:
- имеет вектор направленности;
- приложена только к некоторой точке, а не ко всему телу;
- может состоять из нескольких элементов;
- применимы операции с векторами (сложение и вычитание).
Результирующая эквивалентна равнодействующей.
2. Она кратко записывается в такой форме: 1Н=1кг*1м/с 2 .
Следующий элемент — масса. Она является количественной характеристикой инертности вещества, которая показывает реакцию тела в результате действия на нее сторонних сил. Кроме того, у нее существуют и другие важные параметры:
- скорость перемещения в пространстве не влияет на изменение массы;
- алгебраическая сумма всех атомов эквивалентна общей массе тела;
- константа;
- не имеет направления (невекторная величина).
Ее единицей измерения является килограмм (кг). Однако в литературе существуют и производные единицы, образованные посредством соответствующих приставок, например, т (тонна), г (грамм).
Последний компонент соотношения — ускорение. Оно всегда обозначается литерой «а» и показывает изменение v за некоторое время. То есть v постоянно растет. Это можно увидеть из следующей формулы: v=v0+at, где v0 — нулевое значение скорости.
2)(c)= м/с+м/с=м/с.
Задача решена правильно. Однако процесс нахождения искомой величины возможно существенно сократить, выполнив подстановку: v=v0+(F/m)*t. Из последнего выражения понятно, что два пункта (2 и 3) можно не выполнять. Если произвести вычисления, то результат получится таким же, как и в первом случае.
II закон Ньютона следует применять при решении заданий по физике и механики на движение и взаимодействие, а также знать основные алгоритмы перевода единиц измерений.
Конспект урока ” Силы. Первый закон Ньютона”
Учитель физики МБОУ «Кустовская СОШ» Топоркова О.М.
Модуль: «Законы Ньютона».
Уважаемый ученик!
Предлагаю для ознакомления занятие №1
Урок№1 Тема: Силы. Первый закон Ньютона.
Цель. Изучение закона и закрепление знаний по теме урока.
Задачи урока :
Образовательные: отработать практические навыки применения первого закона Ньютона.
Развивающие: развивать умения учащихся работать с текстом.
Воспитательные: воспитать любознательность, внимательность, усидчивость.
Ход занятия.
План.
1.Биография Ньютона. Смотри на сайте http://fizportal.ru/physics-book-18
2. Сила.
Силой в механике называют величину, являющуюся мерой взаимодействия тел. Мы постоянно встречаемся с различными случаями взаимодействия тел друг на друга.
Просто говорят, что на тело действует сила, или к нему приложена сила. Следовательно, силу можно рассматривать как причину изменения скорости движения.
Одно тело может действовать на другое как непосредственным контактом (давление, трение), так и посредством создаваемых телами полей (гравитационное поле, электромагнитное поле).
Сила является векторной величиной, и имеет не только численное значение, но и направление. Обозначается буквой , модуль силы – F. Прямая, вдоль которой направлена сила, называется линией действия силы.
Говоря о силе, действующей на тело, важно указать, к какой точке тела она приложена.
На чертеже силу изображают в виде отрезка прямой со стрелкой на конце. Точка приложения силы – начало отрезка (точка А). Длина отрезка в определенном масштабе обозначает модуль силы. Если речь об абсолютно твердом (недеформируемом) теле, то считается, что сила приложена к любой точке на линии ее действия.
Иное дело – деформируемые тела. Если пальцем надавить на кусок пластилина или ластик, он изменит свою форму (деформируется).
Или другой пример –
доска, лежащая на опорах. Доска прогнется, если на нее положить груз, то есть середина доски переместится на большее расстояние, чем ее края.
Итак, результат действия силы на тело зависит от ее модуля, направления и точки приложения. Иными словами, сила – векторная величина, которая характеризуется численным значением, направлением в пространстве и точкой приложения.
3. Первый закон Ньютона.
Единицей силы в СИ принят ньютон (Н). Один ньютон (1 Н) – это сила, которая за 1 с изменяет скорость тела массой 1 кг на 1 м/с. Часто на практике применяются килоньютоны (1 кН = 1000 Н) и миллиньютоны (1 мН = 0,001 Н).
Ньютон сформулировал закон инерции, включив его в основу механики в качестве первого из трех законов. Поэтому этот закон называют первым законом Ньютона.
Первый закон механики, или закон инерции был сформулирован Ньютоном следующим образом:
Любое тело удерживается в состоянии покоя или равномерного прямолинейного движения, пока под действием приложенных сил не изменяет это состояние.
В окружении любого тела, покоится оно или движется, есть другие тела, некоторые из которых или все как-то действуют на тело, влияют на состояние его движения. Чтобы выяснить влияние окружающих тел, надо исследовать каждый отдельный случай.
ОПЫТ.
Рассмотрим какое-либо покоящееся тело, не обладающее ускорением, а скорость постоянна и равна нулю.
Допустим, это будет шарик, подвешенный на резиновом шнуре. Он находится в покое относительно Земли. Около шарика множество различных тел: шнур, на котором он висит, множество предметов в комнате и других помещениях и, конечно, Земля.
Однако, действие всех этих тел на шарик не одинаково. Если, например, убрать мебель в комнате, это не окажет какого-либо влияния на шарик. Но если перерезать шнур, шарик под влиянием Земли начнет падать вниз с ускорением. Но пока шнур не был перерезан, шарик находился в покое.
Этот простой опыт показывает, что из всех тел, окружающих шарик, только два заметно влияют на него: резиновый шнур и Земля. Их совместное влияние и обеспечивает состояние покоя шарика. Стоило устранить одно из этих тел — шнур, и состояние покоя нарушилось. Если бы возможно было убрать Землю, это тоже нарушило бы покой шарика: он стал бы двигаться в противоположном направлении.
Отсюда приходим к выводу, что действия на шарик двух тел — шнура и Земли, компенсируют (уравновешивают) друг друга. Когда говорят, что
действия двух или нескольких тел компенсируют друг друга, то это значит, что результат их совместного действия такой же, как если бы этих тел вовсе не было.
Рассмотренный пример, как и другие подобные примеры, позволяют сделать следующий вывод: если действия тел компенсируют друг друга, то тело под влиянием этих тел находится в состоянии покоя.
Однако, как выяснилось со временем, первый закон Ньютона выполняется только в инерциальных системах отсчета. Поэтому с точки зрения современных представлений закон Ньютона формулируют следующим образом:
Системы отсчета, относительно которых свободное тело при компенсации внешних воздействий движется равномерно и прямолинейно, называют инерциальными системами отсчета.
Свободным телом в этом случае называют тело, на которое другие тела не оказывают воздействия.
Необходимо помнить, что в первом законе Ньютона рассматриваются тела, которые могут быть представлены в качестве материальных точек.
4.Практика. Рассмотрим задачи на первый закон Ньютона.
Задача №1.
Как объяснить, что бегущий человек, споткнувшись, падает в направлении своего движения, а поскользнувшись, падает в направлении, противоположном направлению своего движения?
Решение: Это явление легко объясняется на основании первого закона Ньютона. Бегущий человек. Споткнувшись, падает в направлении своего движения. Потому что при этом ноги человека замедляют движение. А туловище сохраняет по инерции прежнее состояние движения. В то время как ноги начинают скользить вперед быстрее, потому человек падает назад.
Задача №2.
Парашютист падает с постоянной по модулю скоростью. Чему равен модуль силы сопротивления воздуха при этом движении?
Решение: Движение парашютиста равномерное и прямолинейное, поэтому, на основании 1 закона Ньютона, все силы, действующие на парашютиста, компенсируются. Так как парашютист движется под действием силы тяжести, то сила сопротивления воздуха по модулю равна силе тяжести парашютиста и противоположно направлена.
Задача №3.
Как направленно ускорение самолета, если на него действует 4 силы: по вертикали – сила тяжести = 200кН и подъемная сила 210кН. По горизонтали: сила тяжести мотора 20 кН и сила лобового сопротивления воздуха 10 кН. Чему равна равнодействующая всех сил?
Дано: F1 = 2*10 5 H F2 = 2, 1*10 5 H F3 = 2*10 4 H F4 =10 4 H R-? | Решение: R1 = F2 – F1, (по вертикали) R1 = 2, 1*105 – 2*105 = 104Н R1 = F3 – F4, (по горизонтали) R1 = 2*10 4 -10 4 =10 4 H Найдем равнодействующую всех сил, пользуясь правилом параллелограмма: = + Модуль силы R вычислим с помощью теоремы Пифагора: R= R = =1, 4*10 4 Н Ответ: Равнодействующая всех сил направлена под углом под углом 45°к горизонту и равна 1,4*104Н. |
5.Тесты. ПРОВЕРЬ СЕБЯ!
1. Равнодействующая всех сил, действующих на тело, равна нулю. Движется ли это тело или находится в состоянии покоя?
А. Тело движется равномерно и прямолинейно или находится в состоянии покоя.
Б. Тело движется равномерно или прямолинейно.
В. Тело находится в состоянии покоя.
2.Какая формулировка I закона Ньютона принята в настоящее время?
А. Тело движется равномерно и прямолинейно, если на него не действуют другие тела или действие их скомпенсировано.
Б. Сохранение скорости движения тела неизменной при отсутствии внешних воздействий называется инерцией.
В. Существуют такие системы отсчета, называемые инерциальными, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной (или покоится), если на него не действуют другие тела (или действие других тел скомпенсировано).
3. I закон Ньютона можно объяснить формулой:
А. F = mg
Б. F = m(v-vo)/t
В. S = vt
Ответы: А, В, Б.
Литература.
http://www.afportal.ru/physics/test/easy/5
http://www.calc.ru/Sila-V-Dinamike.html
http://festival.1september.ru/articles/581944/
5.2 Первый закон Ньютона. Общая физика с использованием исчисления I
5 Законы движения Ньютона
Цели обучения
К концу раздела вы сможете:
- Описывать первый закон движения Ньютона
- Распознать трение как внешнюю силу
- Определить инерцию
- Определить инерциальные системы отсчета
- Рассчитать равновесие для системы
Опыт показывает, что покоящийся объект остается в покое, если его оставить в покое, и что движущийся объект имеет тенденцию замедляться и останавливаться, если не предпринимать никаких усилий для поддержания его движения.
Однако Первый закон Ньютона дает более глубокое объяснение этому наблюдению.
Первый закон движения Ньютона
Тело в состоянии покоя остается в покое или, если оно находится в движении, остается в движении с постоянной скоростью, если на него не действует результирующая внешняя сила.
Обратите внимание на повторное использование глагола «остается». Мы можем думать об этом законе как о сохранении статус-кво движения. Также обратите внимание на выражение «постоянная скорость». это означает, что объект сохраняет путь по прямой линии, поскольку ни величина, ни направление вектора скорости не меняются. Мы можем использовать рисунок, чтобы рассмотреть две части первого закона Ньютона.
Рис. 5.7 (а) Хоккейная шайба показана в состоянии покоя; он остается в покое до тех пор, пока внешняя сила, такая как хоккейная клюшка, не изменит его состояние покоя; б) изображена хоккейная шайба в движении; он продолжает движение по прямой линии до тех пор, пока внешняя сила не заставит его изменить свое состояние движения.
Несмотря на то, что поверхность льда гладкая, она создает некоторое трение, которое замедляет движение шайбы.Вместо того, чтобы противоречить нашему опыту, первый закон Ньютона говорит, что должна быть причина для любого изменения скорости (изменение либо величины, либо направления). Эта причина является чистой внешней силой, которую мы определили ранее в этой главе. Объект, скользящий по столу или полу, замедляется из-за суммарной силы трения, действующей на объект. Если трение исчезнет, будет ли объект по-прежнему замедляться?
Представление о причине и следствии имеет решающее значение для точного описания того, что происходит в различных ситуациях. Например, рассмотрим, что происходит с объектом, скользящим по шероховатой горизонтальной поверхности. Объект быстро останавливается. Если мы посыпаем поверхность тальком, чтобы сделать поверхность более гладкой, объект будет скользить дальше. Если мы сделаем поверхность еще более гладкой, нанеся на нее смазочное масло, объект будет скользить еще дальше.
Экстраполируя на поверхность без трения и пренебрегая сопротивлением воздуха, мы можем представить объект, бесконечно скользящий по прямой. Таким образом, трение является причиной замедления (в соответствии с первым законом Ньютона). Объект не замедлился бы, если бы трение было устранено.
Рассмотрим стол для аэрохоккея (рисунок). Когда воздух отключен, шайба скользит только на короткое расстояние, прежде чем трение замедляет ее до остановки. Однако, когда воздух включен, создается поверхность, практически лишенная трения, и шайба скользит на большие расстояния, не замедляясь. Кроме того, если мы достаточно знаем о трении, мы можем точно предсказать, насколько быстро объект замедляется.
Рисунок 5.8 Таблица аэрохоккея полезна для иллюстрации законов Ньютона. Когда воздух выключен, трение быстро замедляет шайбу; но когда воздух включен, он сводит к минимуму контакт между шайбой и хоккейным столом, и шайба скользит далеко по столу. Первый закон Ньютона является общим и может быть применен ко всему: от предмета, скользящего по столу, до спутника на орбите и до крови, перекачиваемой из сердца.
Эксперименты подтвердили, что любое изменение скорости (скорости или направления) должно быть вызвано внешней силой. Идея общеприменимых или универсальных законов важна — это основная черта всех законов физики. Выявление этих законов похоже на распознавание закономерностей в природе, из которых можно обнаружить дальнейшие закономерности. Гениальность Галилея, впервые разработавшего идею первого закона движения, и Ньютона, разъяснившего его, заключалась в том, чтобы задать фундаментальный вопрос: «Что есть причина?» Мышление в терминах причины и следствия в корне отличается от типичного древнегреческого подхода, когда такие вопросы, как «Почему у тигра полосы?» ответили бы в аристотелевской манере, например: «Такова природа зверя». Способность мыслить в категориях причины и следствия — это способность установить связь между наблюдаемым поведением и окружающим миром.
Гравитация и инерция
Независимо от масштаба объекта, будь то молекула или субатомная частица, два свойства остаются действительными и поэтому представляют интерес для физики: гравитация и инерция.
Оба связаны с массой. Грубо говоря, масса — это мера количества материи в чем-то. Гравитация — это притяжение одной массы к другой, например притяжение между вами и Землей, удерживающее ваши ноги на полу. Величина этого притяжения — ваш вес, и это сила.
Масса также связана с инерцией , способностью объекта сопротивляться изменениям в его движении, другими словами, сопротивляться ускорению. Первый закон Ньютона часто называют законом инерции . Как мы знаем из опыта, одни объекты обладают большей инерцией, чем другие. Изменить движение большого валуна сложнее, чем, например, баскетбольного мяча, потому что валун имеет большую массу, чем баскетбольный мяч. Другими словами, инерция объекта измеряется его массой. Отношения между массой и весом исследуются далее в этой главе.
Инерциальные системы отсчета
Ранее мы сформулировали первый закон Ньютона следующим образом: «Тело в состоянии покоя остается в покое или, если оно находится в движении, остается в движении с постоянной скоростью, если на него не действует результирующая внешняя сила».
Его также можно сформулировать так: «Каждое тело остается в состоянии равномерного прямолинейного движения, если оно не вынуждено изменить это состояние под действием действующих на него сил». Для Ньютона «равномерное прямолинейное движение» означало постоянную скорость, включая случай нулевой скорости или покоя. Следовательно, первый закон гласит, что скорость объекта остается постоянной, если результирующая сила, действующая на него, равна нулю.
Первый закон Ньютона обычно считается утверждением о системах отсчета. Он предоставляет метод для идентификации специального типа системы отсчета: инерциальной системы отсчета . В принципе, мы можем сделать результирующую силу, действующую на тело, равной нулю. Если его скорость относительно данной системы отсчета постоянна, то эта система называется инерциальной. Итак, по определению, инерциальная система отсчета — это система отсчета, в которой действует первый закон Ньютона. Первый закон Ньютона применим к объектам с постоянной скоростью.
{2}[/латекс]). Таким образом, если не указано иное, мы считаем системы отсчета, закрепленные на Земле, инерциальными.
Наконец, ни одна инерциальная система отсчета не является более особенной, чем любая другая. Что касается законов природы, то все инерциальные системы эквивалентны. При анализе проблемы мы предпочитаем одну инерциальную систему отсчета просто из соображений удобства.
Первый закон Ньютона и равновесие
Первый закон Ньютона говорит нам о равновесии системы, то есть о состоянии, в котором силы, действующие на систему, уравновешены. Возвращаясь к силам и фигуристам на рисунке, мы знаем, что силы [латекс]{\mathbf{\overset{\to }{F}}}_{1}[/латекс] и [латекс]{\mathbf{\ overset{\to}{F}}}_{2}[/latex] объединяются, чтобы сформировать результирующую силу или результирующую внешнюю силу: [latex]{\mathbf{\overset{\to}}{F}}}_ {\ text {R}} = {\ mathbf {\ overset {\ to} {F}}} _ {\ text {net}} = {\ mathbf {\ overset {\ to} {F}}} _ {1 }+{\mathbf{\overset{\to }{F}}}_{2}.
[/latex] Чтобы создать равновесие, нам нужна уравновешивающая сила, которая будет производить чистую силу, равную нулю. Эта сила должна быть равна по величине, но противоположна по направлению [латекс] {\ mathbf {\ overset {\ to} {F}}} _ {\ текст {R}}, [/ латекс], что означает, что вектор должен быть [ латекс]\текст{−}{\mathbf{\overset{\to }{F}}}_{\text{R}}.[/latex] Имеются в виду фигуристы, для которых мы нашли [латекс]{\ mathbf{\overset{\to}}{F}}}_{\text{R}}[/latex] равно [латекс]30,0\mathbf{\шляпа{i}}+40,0\mathbf{\шляпа{j} }\,\text{N}[/latex], мы можем определить уравновешивающую силу, просто найдя [латекс]\text{−}{\mathbf{\overset{\to }{F}}}_{\text{ R}}=-30,0\mathbf{\hat{i}}-40,0\mathbf{\hat{j}}\,\text{N}.[/latex] См. диаграмму свободного тела на рисунке (b).
Мы можем представить первый закон Ньютона в векторной форме: F}}}_{\text{net}}=\mathbf{\overset{\to }{0}}\,\text{N}.[/latex]
Это уравнение говорит, что чистая сила, равная нулю, подразумевает что скорость [латекс]\mathbf{\overset{\to}}{v}}[/латекс] объекта постоянна.
(Слово «постоянная» может означать нулевую скорость.)
Первый закон Ньютона обманчиво прост. Если автомобиль находится в состоянии покоя, то единственными силами, действующими на автомобиль, являются вес и контактная сила дорожного покрытия, воздействующая на автомобиль (рисунок). Легко понять, что для изменения состояния движения автомобиля требуется ненулевая результирующая сила. Однако, если автомобиль движется с постоянной скоростью, распространенное заблуждение состоит в том, что сила двигателя, толкающая автомобиль вперед, больше по величине, чем сила трения, препятствующая движению вперед. На самом деле обе силы имеют одинаковую величину.
Рисунок 5.9 Автомобиль показан (а) припаркованным и (б) движущимся с постоянной скоростью. Как законы Ньютона применимы к припаркованному автомобилю? Что знание того, что автомобиль движется с постоянной скоростью, говорит нам о чистой горизонтальной силе, действующей на автомобиль?Пример
Когда первый закон Ньютона применим к вашему автомобилю?
Законы Ньютона применимы ко всем физическим процессам, связанным с силой и движением, включая такие обыденные вещи, как вождение автомобиля.
(a) Ваш автомобиль припаркован возле вашего дома. Применим ли в данном случае первый закон Ньютона? Почему или почему нет?
(b) Ваша машина движется с постоянной скоростью по улице. Применим ли в данном случае первый закон Ньютона? Почему или почему нет?
Стратегия
В (а) мы рассматриваем первую часть первого закона Ньютона, касающуюся покоящегося тела; в (b) мы рассматриваем вторую часть первого закона Ньютона для движущегося тела.
Решение
- Когда ваш автомобиль припаркован, все силы, действующие на автомобиль, должны быть уравновешены; сумма векторов равна 0 Н. Таким образом, результирующая сила равна нулю, и действует первый закон Ньютона. Ускорение автомобиля равно нулю, и в этом случае скорость также равна нулю.
- Когда ваш автомобиль движется с постоянной скоростью по улице, результирующая сила также должна быть равна нулю в соответствии с первым законом Ньютона. Двигатель автомобиля создает поступательное усилие; трение, сила между дорогой и шинами автомобиля, противодействующая движению вперед, имеет точно такую же величину, что и сила двигателя, поэтому результирующая сила равна нулю.
Тело остается в состоянии постоянной скорости до тех пор, пока результирующая сила не станет отличной от нуля. Поймите, что чистая сила, равная нулю, означает, что объект либо покоится, либо движется с постоянной скоростью, то есть не ускоряется. Как вы думаете, что происходит, когда машина ускоряется? Мы исследуем эту идею в следующем разделе.
Тело остается в состоянии постоянной скорости до тех пор, пока результирующая сила не станет отличной от нуля. Поймите, что чистая сила, равная нулю, означает, что объект либо покоится, либо движется с постоянной скоростью, то есть не ускоряется. Как вы думаете, что происходит, когда машина ускоряется? Мы исследуем эту идею в следующем разделе.Значение
Как показывает этот пример, существует два вида равновесия. В (а) автомобиль находится в состоянии покоя; мы говорим, что он находится в статическом равновесии . В (b) силы, действующие на автомобиль, уравновешены, но автомобиль движется; мы говорим, что он находится в динамическом равновесии . (Мы рассматриваем эту идею более подробно в разделе «Статическое равновесие и эластичность».) Опять же, две (или более) силы могут воздействовать на объект, но при этом объект будет двигаться. Кроме того, чистая сила, равная нулю, не может создавать ускорение.
Проверьте свое понимание
Парашютист раскрывает парашют и вскоре после этого движется с постоянной скоростью.
а) Какие силы действуют на него? б) Какая сила больше?
а. Его вес действует вниз, а сила сопротивления воздуха с парашютом действует вверх. б. ни один; силы равны по модулю
Используйте эту симуляцию, чтобы качественно предсказать, как внешняя сила повлияет на скорость и направление движения объекта. Объясните эффекты с помощью диаграммы свободного тела. Используйте диаграммы свободного тела для построения графиков положения, скорости, ускорения и силы и наоборот. Объясните, как графики соотносятся друг с другом. Учитывая сценарий или график, нарисуйте все четыре графика.
Резюме
- Согласно первому закону Ньютона, для любого изменения скорости (изменения величины или направления) должна существовать причина. Этот закон также известен как закон инерции.
- Трение — это внешняя сила, которая заставляет объект замедляться.
- Инерция — это тенденция объекта оставаться в покое или оставаться в движении. Инерция связана с массой объекта.
- Если скорость объекта относительно данной системы отсчета постоянна, то система инерциальна. Это означает, что для инерциальной системы отсчета справедлив первый закон Ньютона.
- Равновесие достигается, когда силы в системе уравновешены.
- Нулевая результирующая сила означает, что объект либо покоится, либо движется с постоянной скоростью; то есть не ускоряется.
Концептуальные вопросы
Принимая систему отсчета, связанную с Землей, как инерциальную, к каким из следующих объектов не может быть присоединена инерциальная система отсчета, и какие из них являются инерциальными системами отсчета?
(a) Автомобиль, движущийся с постоянной скоростью
(b) Автомобиль, ускоряющийся
(c) Лифт в свободном падении
(d) Космическая капсула на орбите Земли
(e) Лифт, спускающийся равномерно
Женщина везла открытую коробку с кексами на школьную вечеринку. Машина перед ней внезапно остановилась; она немедленно затормозила.
Она была пристегнута ремнем безопасности и не получила никакого физического вреда (просто сильное смущение), но кексы полетели в приборную панель и превратились в «смушкейки». Объясните, что произошло.
Скорость кекса перед торможением была такой же, как и у автомобиля. Таким образом, кексы были неограниченными телами в движении, и когда машина внезапно останавливалась, кексы продолжали двигаться вперед в соответствии с первым законом Ньютона.
Задачи
Две силы [латекса] {\ mathbf {\ overset {\ to} {F}}} _ {1} = \ frac {75.0} {\ sqrt {2}} (\ mathbf {\ hat {i }}-\mathbf{\шляпа{j}})\,\text{N}[/латекс] и [латекс]{\mathbf{\overset{\to}}{F}}}_{2}=\frac {150.0}{\sqrt{2}}(\mathbf{\hat{i}}-\mathbf{\hat{j}})\,\text{N}[/latex] действуют на объект. Найдите третью силу [латекс]{\mathbf{\overset{\to}}{F}}}_{3}[/латекс], которая необходима для уравновешивания первых двух сил. 9\circ[/latex] к востоку от севера с магнитудой 180,0 Н. (a) Найдите результирующую силу в компонентной форме.
б) Найдите модуль и направление равнодействующей силы. (c) Если соседи по дому Андреа и Дженнифер, Дэвид и Стефани, не согласны с переездом и хотят предотвратить его перемещение, с помощью какой совместной силы [латекс] {\ mathbf {\ overset {\ to} {F}}} _ {\ text {DS}}[/latex] должны ли они толкать, чтобы диван не двигался?
а. [латекс] {\ mathbf {\ overset {\ to} {F}}} _ {\ text {net}} = 95,0 \ mathbf {\ hat {i}} + 283 \ mathbf {\ hat {j}} \ text {N}[/латекс]; б. 29\circ[/latex] к северу от востока; в. [латекс] {\ mathbf {\ overset {\ to} {F}}} _ {\ text {DS}} = \ text {−} (95,0 \ mathbf {\ hat {i}} + 283 \ mathbf {\ hat {j}})\,\text{N}[/латекс]
Глоссарий
- инерция
- способность объекта сопротивляться изменениям в его движении
- инерциальная система отсчета
- система отсчета, движущаяся с постоянной скоростью относительно инерциальной системы отсчета, также является инерциальной; система отсчета, ускоряющаяся относительно инерциальной системы отсчета, не является инерциальной
- закон инерции
- см. первый закон движения Ньютона
первый закон движения Ньютона- Первый закон Ньютона
- тело в состоянии покоя остается в покое или, если оно находится в движении, остается в движении с постоянной скоростью, если на него не действует результирующая внешняя сила; также известный как закон инерции
Inertia – College Physics: OpenStax
Глава 4 Динамика: сила и законы движения Ньютона
Резюме
- Дайте определение массе и инерции.
- Поймите первый закон движения Ньютона.
Опыт подсказывает, что покоящийся объект останется в покое, если его оставить в покое, и что движущийся объект имеет тенденцию замедляться и останавливаться, если не предпринимать никаких усилий для поддержания его движения. Однако первый закон движения Ньютона утверждает следующее:
ПЕРВЫЙ ЗАКОН НЬЮТОНА ДВИЖЕНИЯ
Тело в состоянии покоя остается в покое или, если оно находится в движении, остается в движении с постоянной скоростью, если на него не действует результирующая внешняя сила.
Обратите внимание на повторное использование глагола «остается». Мы можем думать об этом законе как о сохранении статус-кво движения.
Вместо того, чтобы противоречить нашему опыту, Первый закон движения Ньютона утверждает, что должна быть причина (которая является чистой внешней силой) для любого изменения скорости (либо изменения величины, либо направления) . Мы определим чистую внешнюю силу в следующем разделе. Объект, скользящий по столу или полу, замедляется из-за суммарной силы трения, действующей на объект. Если трение исчезнет, будет ли объект по-прежнему замедляться?
Представление о причине и следствии имеет решающее значение для точного описания того, что происходит в различных ситуациях. Например, рассмотрим, что происходит с объектом, скользящим по шероховатой горизонтальной поверхности. Объект быстро останавливается. Если мы посыпаем поверхность тальком, чтобы сделать поверхность более гладкой, объект будет скользить дальше.
Если мы сделаем поверхность еще более гладкой, нанеся на нее смазочное масло, объект будет скользить еще дальше. Экстраполируя на поверхность без трения, мы можем представить объект, бесконечно скользящий по прямой линии. Таким образом, трение — это вызывают замедления (в соответствии с первым законом Ньютона). Объект вообще не замедлился бы, если бы трение было полностью устранено. Рассмотрим стол для аэрохоккея. Когда воздух отключен, шайба скользит только на короткое расстояние, прежде чем трение замедляет ее до остановки. Однако, когда воздух включен, создается поверхность, практически лишенная трения, и шайба скользит на большие расстояния, не замедляясь. Кроме того, если мы достаточно знаем о трении, мы можем точно предсказать, как быстро объект замедлится. Трение — это внешняя сила.
Первый закон Ньютона является полностью общим и может быть применен ко всему: от предмета, скользящего по столу, до спутника на орбите и до крови, перекачиваемой из сердца. Эксперименты полностью подтвердили, что любое изменение скорости (скорости или направления) должно быть вызвано внешней силой.
Идея общеприменимых или универсальных законов важна не только здесь — это основная черта всех законов физики. Выявление этих законов похоже на распознавание закономерностей в природе, из которых можно обнаружить дальнейшие закономерности. Гениальность Галилея, впервые разработавшего идею первого закона, и Ньютона, разъяснившего его, заключалась в том, чтобы задать фундаментальный вопрос: «Что есть причина?» Мышление в терминах причины и следствия — это мировоззрение, в корне отличное от типичного древнегреческого подхода, когда такие вопросы, как «Почему у тигра полосы?» ответили бы в аристотелевской манере: «Такова природа зверя». Возможно, это правда, но не полезное понимание.
Свойство тела оставаться в покое или оставаться в движении с постоянной скоростью называется инерцией . Первый закон Ньютона часто называют законом инерции . Как мы знаем из опыта, одни объекты обладают большей инерцией, чем другие. Очевидно, что изменить движение большого валуна сложнее, чем, например, баскетбольного мяча.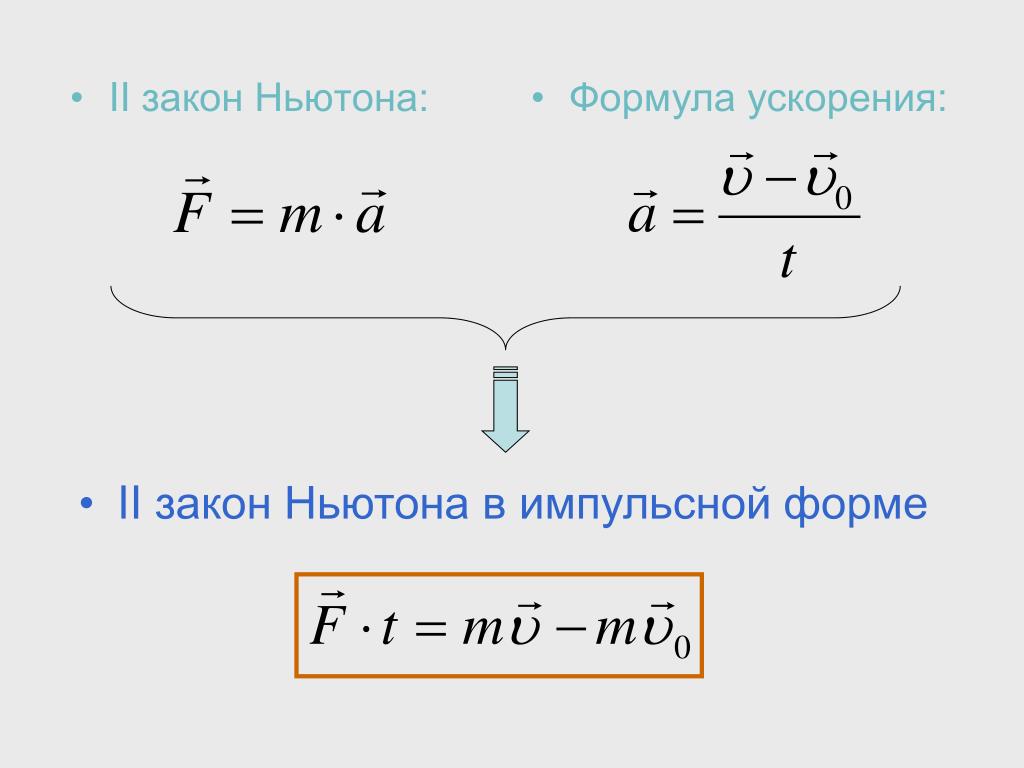
Инерция объекта измеряется его массой . Грубо говоря, масса — это мера количества «вещества» (или материи) в чем-либо. Количество или количество материи в объекте определяется количеством содержащихся в нем атомов и молекул различных типов. В отличие от веса, масса не зависит от местоположения. Масса объекта одинакова на Земле, на орбите или на поверхности Луны. На практике очень сложно сосчитать и идентифицировать все атомы и молекулы в объекте, поэтому массы не часто определяются таким образом. Оперативно массы предметов определяются путем сравнения с эталонным килограммом.
- Первый закон движения Ньютона гласит, что тело, находящееся в состоянии покоя, остается в покое или, если оно находится в движении, остается в движении с постоянной скоростью, если на него не действует результирующая внешняя сила. Это также известно как закон инерции .
- Инерция — это тенденция объекта оставаться в покое или оставаться в движении. Инерция связана с массой объекта.
- Масса – количество вещества в веществе.
Инерция связана с массой объекта.- инерция
- склонность объекта оставаться в покое или двигаться
- закон инерции
- см. первый закон движения Ньютона
- масса
- количество вещества в веществе; измеряется в килограммах
- Первый закон Ньютона
- покоящееся тело остается в покое или, если оно находится в движении, остается в движении с постоянной скоростью, если на него не действует чистая внешняя сила; также известный как закон инерции 9{#1}\!/_{\!#2}}
\ newcommand {\ convert} [2] {\ times \ left (\ frac {# 1} {# 2} \ right)}
\newcommand{\deq}{\displaystyle}
\newcommand{\ihat}{\шляпа я}
\ новая команда {\ jhat} {\ шляпа j}
\newcommand{\хат}{\шляпа к}
\newcommand{\vect}[3]{#1 \ihat #2 \jhat #3 \khat}
\newcommand{\KE}{\mbox{KE}}
\newcommand{\PE}{\mbox{PE}}
\newcommand{\E}{\mbox{E}}
\newtheorem[S]{предложение}[теорема]{Соединение}
\newtheorem[S]{понимание}[теорема]{понимание}
\newtheorem[S]{предупреждение}[теорема]{предупреждение}
\newtheorem[S]{наблюдение}[теорема]{наблюдение}
\newtheorem[S]{примечание}[теорема]{интерпретация}
\newtheorem[M]{замечание}[теорема]{пояснение}
\newtheorem[M]{конвенция}[теорема]{конвенция}
\newtheorem[L]{пример}[теорема]{пример}
\newtheorem[L]{упражнение}[теорема]{упражнение}
\newtheorem[L]{эвристика}[теорема]{перевод}
\newtheorem[L]{исследование}[теорема]{исследование}
\newtheorem[L]{исследование}[теорема]{исследование}
\newtheorem[L]{деятельность}[теорема]{деятельность}
\ newcommand {\ magdir} [7] {\ begin {массив} {lccl}
\text{Величина:} \amp \displaystyle #3 = \amp \displaystyle \sqrt{\left(#1\right)^2+\left(#2\right)^2} \amp = \displaystyle #4 \ \[6pt]
\text{Направление:} \amp \displaystyle #5 = \amp \displaystyle \tan^{-1}\left( \frac{#2}{#1} \right) \amp = \displaystyle #6 \mbox{ #7}
\конец{массив}}
\newcounter{piclen}
\newcounter{picwid}
\newcounter{boxlen}
\newcounter{boxwid}
\newcounter{FBDlen}
\newcounter{FBDwid}
\newcounter{centx}
\newcounter{цент}
\ новый счетчик {lblx}
\newcounter{lbly}
\ новая команда {\ drawbox} [4] {
\setcounter{boxlen}{#1}\addtocounter{boxlen}{#3}
\setcounter{boxwid}{#2}\addtocounter{boxwid}{#4}
\ положить (# 1, # 2) {\ строка (1,0) {# 3}}
\ положить (# 1, # 2) {\ строка (0,1) {# 4}}
\ поставить (\ theboxlen, \ theboxwid) {\ строка (-1,0) {# 3}}
\ поставить (\ theboxlen, \ theboxwid) {\ строка (0,-1) {# 4}}}
\newenvironment{FBD}[5]
{\ setcounter {centx} {# 3} \ addtocounter {centx} {# 1}
\setcounter{centy}{#4}\addtocounter{centy}{#2}
\setcounter{piclen}{\thecentx}\addtocounter{piclen}{\thecentx}
\setcounter{picwid}{\thecenty}\addtocounter{picwid}{\thecenty}
\setcounter{FBDlen}{#1}\addtocounter{FBDlen}{#1}
\setcounter{FBDwid}{#2}\addtocounter{FBDwid}{#2}
\setcounter{lbly}{#4}\addtocounter{lbly}{#2}\addtocounter{lbly}{#2}\addtocounter{lbly}{5}
\begin{центр}\begin{картинка}(\thepiclen,\thepicwid)
\put(#3,\thelbly){\setvlabel{$\scriptsize #5$}}
\drawbox{#3}{#4}{\theFBDlen}{\theFBDwid}}
{\конец{картинка}\конец{центр}}
\ новая команда {\ oneup} [3] {
\addtocounter{центы}{2}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{3}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{#1}\addtocounter{lbly}{-5}
\ поставить (\ thecentx, \ thecenty) {\ цвет {# 3} \ вектор (0,1) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 3} \ крошечный # 2}
\addtocounter{центы}{-2}}
\ новая команда {\ onedo} [3] {
\addtocounter{центы}{-2}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{3}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{-#1}\addtocounter{lbly}{3}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 3} \ вектор (0,-1) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 3} \ крошечный # 2}
\addtocounter{центы}{2}}
\newcommand{\oneri}[3]{
\addtocounter{centx}{2}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{#1}\addtocounter{lblx}{-5}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{4}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 3} \ вектор (1,0) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 3} \ крошечный # 2}
\addtocounter{centx}{-2}}
\newcommand{\onele}[3]{
\addtocounter{centx}{-2}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{-#1}\addtocounter{lblx}{3}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{4}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 3} \ вектор (-1,0) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 3} \ крошечный # 2}
\addtocounter{centx}{2}}
\newcommand{\twoup}[6]{
\addtocounter{центы}{2}
\ поставить (\ thecentx, \ thecenty) {\ круг * {1}}
\addtocounter{centx}{-5}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{-10}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{#1}\addtocounter{lbly}{-5}
\ поставить (\ thecentx, \ thecenty) {\ цвет {# 3} \ вектор (0,1) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 3} \ крошечный # 2}
\addtocounter{centx}{5}
\addtocounter{centx}{5}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{3}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{#4}\addtocounter{lbly}{-5}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 6} \ вектор (0,1) {# 4}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 6} \ крошечный # 5}
\addtocounter{centx}{-5}
\addtocounter{центы}{-2}}
\newcommand{\twodo}[6]{
\addtocounter{центы}{-2}
\ поставить (\ thecentx, \ thecenty) {\ круг * {1}}
\addtocounter{centx}{-5}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{-10}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{-#1}\addtocounter{lbly}{3}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 3} \ вектор (0,-1) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 3} \ крошечный # 2}
\addtocounter{centx}{5}
\addtocounter{centx}{5}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{3}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{-#4}\addtocounter{lbly}{3}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 6} \ вектор (0,-1) {# 4}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 6} \ крошечный # 5}
\addtocounter{centx}{-5}
\addtocounter{центы}{2}}
\ новая команда {\ twori} [6] {
\addtocounter{centx}{2}
\ поставить (\ thecentx, \ thecenty) {\ круг * {1}}
\addtocounter{центы}{5}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{#1}\addtocounter{lblx}{-5}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{4}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 3} \ вектор (1,0) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 3} \ крошечный # 2}
\addtocounter{центы}{-5}
\addtocounter{центы}{-5}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{#1}\addtocounter{lblx}{-5}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{-10}
\ поставить (\ thecentx, \ thecenty) {\ цвет {# 6} \ вектор (1,0) {# 4}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 6} \ крошечный # 5}
\addtocounter{центы}{5}
\addtocounter{centx}{-2}}
\ новая команда {\ twole} [6] {
\addtocounter{centx}{-2}
\ поставить (\ thecentx, \ thecenty) {\ круг * {1}}
\addtocounter{центы}{5}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{-#1}\addtocounter{lblx}{3}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{4}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 3} \ вектор (-1,0) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 3} \ крошечный # 2}
\addtocounter{центы}{-5}
\addtocounter{центы}{-5}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{-#1}\addtocounter{lblx}{3}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{-10}
\ поставить (\ thecentx, \ thecenty) {\ цвет {# 6} \ вектор (-1,0) {# 4}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 6} \ крошечный # 5}
\addtocounter{центы}{5}
\addtocounter{centx}{2}}
\newcommand{\oneur}[6]{
\addtocounter{centx}{#3}
\addtocounter{центы}{#4}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{#1}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{#2}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 6} \ вектор (# 3, # 4) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 6} \ крошечный # 5}
\addtocounter{centx}{-#3}
\addtocounter{центы}{-#4}}
\newcommand{\oneul}[6]{
\addtocounter{centx}{#3}
\addtocounter{центы}{#4}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{-#1}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{#2}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 6} \ вектор (# 3, # 4) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 6} \ крошечный # 5}
\addtocounter{centx}{-#3}
\addtocounter{центы}{-#4}}
\ новая команда {\ onedl} [6] {
\addtocounter{centx}{#3}
\addtocounter{центы}{#4}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{-#1}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{-#2}\addtocounter{lbly}{#4}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 6} \ вектор (# 3, # 4) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 6} \ крошечный # 5}
\addtocounter{centx}{-#3}
\addtocounter{центы}{-#4}}
\newcommand{\onedr}[6]{
\addtocounter{centx}{#3}
\addtocounter{центы}{#4}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{#1}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{-#2}\addtocounter{lbly}{#4}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 6} \ вектор (# 3, # 4) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 6} \ крошечный # 5}
\addtocounter{centx}{-#3}
\addtocounter{центы}{-#4}}
\newcommand{\studentA}{Абдул} \newcommand{\massA}{\mbox{85,0$\единица{кг}$}}
\newcommand{\studentB}{Бет} \newcommand{\massB}{\mbox{75,0$\единица{кг}$}}
\newcommand{\studentC}{Карл} \newcommand{\massC}{\mbox{$90. 0\единица{кг}$}}
\newcommand{\studentD}{Диана} \newcommand{\massD}{\mbox{80,0$\единица{кг}$}}
\newcommand{\studentE}{Эрик} \newcommand{\massE}{\mbox{95,0$\единица{кг}$}}
\newcommand{\studentF}{Фрэнсис} \newcommand{\massF}{\mbox{85,0$\единица{кг}$}}
\newcommand{\studentX}{Ксеркс} \newcommand{\massX}{\mbox{62,5$\единица{кг}$}}
\newcommand{\studentZ}{Zambert} \newcommand{\massZ}{\mbox{$95,0\unit{kg}$}}
\newcommand{\heA}{он}\newcommand{\himA}{его}\newcommand{\hisA}{его} \newcommand{\himselfA}{сам}
\newcommand{\HeA}{He}\newcommand{\HimA}{Him}\newcommand{\HisA}{His}
\newcommand{\heC}{он}\newcommand{\himC}{его}\newcommand{\hisC}{его} \newcommand{\himselfC}{сам}
\newcommand{\HeC}{He}\newcommand{\HimC}{Him}\newcommand{\HisC}{His}
\newcommand{\heE}{он}\newcommand{\himE}{его}\newcommand{\hisE}{его} \newcommand{\himselfE}{сам}
\newcommand{\HeE}{He}\newcommand{\HimE}{Him}\newcommand{\HisE}{His}
\newcommand{\heZ}{он}\newcommand{\himZ}{его}\newcommand{\hisZ}{его} \newcommand{\himselfZ}{сам}
\newcommand{\HeZ}{He}\newcommand{\HimZ}{Him}\newcommand{\HisZ}{His}
\ newcommand {\ heB} {она} \ newcommand {\ himB} {ее} \ newcommand {\ hisB} {ее} \ newcommand {\ himselfB} {она}
\newcommand{\HeB}{She}\newcommand{\HimB}{Her}\newcommand{\HisB}{Her}
\newcommand{\heD}{она}\newcommand{\himD}{ее} \newcommand{\hisD}{ее} \ newcommand{\himselfD}{ее себя}
\newcommand{\HeD}{She}\newcommand{\HimD}{Her}\newcommand{\HisD}{Her}
\ newcommand {\ heF} {она} \ newcommand {\ himF} {ее} \ newcommand {\ hisF} {ее} \ newcommand {\ himselfF} {herself}
\newcommand{\HeF}{She}\newcommand{\HimF}{Her}\newcommand{\HisF}{Her}
\newcommand{\heX}{\studentX}\newcommand{\himX}{\studentX}\newcommand{\hisX}{\studentX’s}\newcommand{\himselfX}{лицо \studentX}
\newcommand{\HeX}{\studentX}\newcommand{\HimX}{\studentX}\newcommand{\HisX}{\studentX’s}
\новая команда{\lt}{<}
\новая команда{\gt}{>}
\newcommand{\amp}{&}
\)
3.2.2 Translating Newton’s Second Law: The Equation Law”>
Подраздел II.3.2.2. Перевод второго закона Ньютона: закон уравнений ¶Результаты учащихсяПеревод второго закона Ньютона: закон уравнений
После успешного изучения данного подраздела учащиеся должны уметь …
изложите второй закон Ньютона своими словами
соответствуют результатам учащихся по подразделам II.3.2.2.1, II.3.2.2.2, II.3.2.2.3, II.3.2.2.4 и II.3.2.2.5.
Подраздел, на который ссылается
Подраздел I.3.4.2.2, как описывать силы, первый закон Ньютона, обсуждение падающих предметов, обсуждение простой части сложной ситуации
Второй закон Ньютона
Если смотреть из инерциальной системы отсчета, векторная сумма всех сил, действующих на объект, заставит этот объект ускоряться пропорционально его массе: \(\vec F_\mathrm{net} = m \vec a\text{ .}\)
Пробный камень (инерциальные рамки)
Вы также можете вспомнить обсуждение в подразделе II.
1.6.1.Давайте разберем это и соединим с вашим повседневным опытом. Как и в случае с первым законом Ньютона, неинерциальная вращающаяся система отсчета поверхности Земли представляет собой достаточно небольшой эффект, поэтому, пока мы не измеряем наш мир слишком близко, мы можем притворяться, что смотрим на него, по существу, с высоты птичьего полета. инерциальная система отсчета.
Пробный камень (в основном правда)
Вспомните эффективные теории. Нахождение на поверхности Земли обеспечивает по существу инерциальную систему отсчета.
Пробный камень (векторное уравнение)
Напомним подраздел I.3.4.2.2.
Перевод II.3.2.8История \(\vec F_\mathrm{net} =m \vec a\)
Ссылка на
Упражнение II.3.2.16
Это уравнение описывает, что происходит с конкретным объектом \(m\text{.}\) Если объект \(m\text{,}\) ускоряется в определенном направлении, \(\vec a\text{,}\), то это потому, что комбинация сил, \(\vec F_\mathrm{net}\text{,}\) не полностью компенсирует друг друга.
Это также можно выразить следующим образом: если комбинация сил \(\vec F_\mathrm{net}\text{,}\) не полностью компенсирует друг друга, то наш друг \(m\) должен ускоряться, \(\vec a\text{,}\) в определенном направлении. Кроме того, результирующее направление чистой силы определяет направление ускорения. Соединение английского языка и математики:\(\deq \vec F_\mathrm{net} \) \(= \) \(\дэкв м\) \(\deq \vec a \) \(\overbrace{\hspace{5em}}\) \(\overbrace{\hspace{4em}}\) \(\overbrace{\hspace{5em}}\) \(\overbrace{\hspace{5em}}\)
комбинация
всех сил
действующих на \(m\)вызывает что
объектна
изменить
его
скоростьConnectionII.3.2.9Оглядываясь назад
Следует помнить, что направление ускорения не определяет направление движения , а определяет направление изменения движения.
ConnectionII.3.2.10Заглядывая вперед
Эта идея будет важна, когда мы будем обсуждать, как напряжение действует как центростремительная сила, связь между скоростью и ускорением в пружине, которая колеблется, и объекты, которые движутся через гравитационное или электрическое поле.
Подподраздел II.3.2.2.1 Единицы силы
¶Результаты учащихсяЕдиницы силы
После успешного изучения этого подраздела учащиеся должны уметь …
использовать размерный анализ, чтобы определить, представляет ли величина силу
преобразовать силы, выраженные в различных единицах измерения, в ньютоны
оценить величину сил, которые они испытывают в жизни
Ссылка на 92}\text{.}\) Эта величина настолько распространена, что мы хотели бы иметь для нее сокращение. Кроме того, сэр Исаак Ньютон проделал такую новаторскую работу над этой концепцией, что в 1948 году было принято решение
4 Согласно: Международному бюро мер и весов (1977), Международная система единиц (330-331) (3-е изд. .), Министерство торговли США, Национальное бюро стандартов, с. 17, которая ссылается на 7-ю резолюцию (март 2017 г.) 9-й сессии ГКМВ (март 2017 г.). назвать единицу Ньютон, так что 92}\) Задание: Добавьте сюда несколько примеров.Добавьте пример, чтобы определить, является ли число силой или импульсом.
Добавить пример для «перевода» камней, фунтов, килограммов в ньютоны
Добавьте исследование, чтобы оценить размер различных сил, с которыми люди могут столкнуться в своей жизни
Подподраздел II.3.2.2.2 Расчет чистой силы
¶Результаты учащихсяРасчет чистой силы
После успешного изучения данного подраздела учащиеся должны уметь …
Подподраздел, на который ссылается
Обсуждение первого закона Ньютона Смысл здесь в том, что везде, где есть несколько сил, действующих на один объект, мы должны объединить их в виде векторов следующим образом:Этимология (нетто)
Хотя думать о сети как о «всем, что собрано с помощью сети» полезно, согласно etymonline.
Задание: Может быть, они должны быть рядом с рисунком над примером? com (март 2017 г.), на самом деле это происходит от старофранцузского net для «аккуратных» или «чистых», имеющих ощущение отделки и элегантности.ExampleII.3.2.12Сетевая сила, добавление вектора сил в одном направлении
Пример, на который ссылается
Пример II.3.2.18, Равновесие, Пример II.3.2.28, Пример II.3.2.25, обсуждение \ref*{se-FBD-AB}
Если есть \(5.0 \unit{N} \) сила вправо и \(4,0 \единица{N}\) сила вправо, то результирующая сила равна \(9.0 \unit{N}\) вправо.
Что нужно сделать: сделайте из этого предмета письменный стол, чтобы Абдул и Бет могли помочь вам переставить комнату в общежитии.Решение
\begin{уравнение*} \vec F_\mathrm{net} = \vec F_1 + \vec F_2 = \left( 5.0\unit{N} \ihat\right) + \left( 4.0 \unit{N} \ihat\right) = +9.0\ unit{N} \ihat \end{уравнение*}
ExampleII.
3.2.13Совокупная сила, добавление вектора сил в противоположном направленииПример, на который ссылается
Пример II.3.2.21, Равновесие
Если есть сила \(5,0 \unit{N}\) слева и сила \(4,0 \unit{N}\) справа, то результирующая сила равна \(1,0 \unit{N} \) Слева.
Решение
\begin{уравнение*} \vec F_\mathrm{net} = \vec F_1 + \vec F_2 = \left(-5.0\unit{N} \ihat\right) + \left( 4.0 \unit{N} \ihat\right) = -1.0 \unit{N} \ihat \end{уравнение*}
ExampleII.3.2.14Совокупная сила, добавление вектора равных по величине сил противоположного направления
Пример, на который ссылается
Равновесие, обсуждение \ref*{se-equi}
Если есть сила \(3,0 \unit{N}\) справа и сила \(3,0 \unit{N}\) слева, тогда результирующая сила равна \(0,0 \unit{N}\text{.}\)
В этом случае говорят, что объект находится «в равновесии».
Решение
\begin{уравнение*} \vec F_\mathrm{net} = \vec F_1 + \vec F_2 = \left( 3.
0\unit{N} \ihat\right) + \left(-3.0 \unit{N} \ihat\right) = 0.0\ unit{N} \ihat
\end{уравнение*}ConnectionII.3.2.15Заглядывая вперед
Изображения, включенные в эти примеры, в конечном итоге будут называться «диаграммами свободного тела», но пока вы можете просто считать их изображениями сил, действующих на тела.
Далее мы должны сделать пару примеров, которые показывают математику для ситуаций с силами в двух измерениях. В первом, упражнении II.3.2.16, одна сила действует в направлении \(x\), а другая – в направлении \(y\). Во втором, Упражнении II.3.2.17, одна сила действует в направлении \(x\), а другая – во втором квадранте.
Упражнение II.3.2.16 Объект толкают перпендикулярные силы
Упражнение, на которое ссылается
обсуждение результирующей силы, упражнение II.3.2.17 unit{N}\text{.}\) Какова результирующая сила?
Решение
Поскольку на массу действует несколько сил, вызывающих ускорение, должно быть ясно (вспомним историю), что нам нужно использовать второй закон Ньютона и найти результирующую силу, чтобы вычислить ускорение.
Мы, как обычно, начнем с диаграммы свободного тела (справа).Этот пример упрощен, потому что силы оказываются под прямым углом, поэтому найти их компоненты \(x\) и \(y\) несложно. Добавляя \(x\)-компоненты и отдельно добавляя \(y\)-компоненты, мы нашли компоненты чистой силы.
\(х\)-комп \(у\)-комп. \(F_1\) \(0 \единица N\) \(+5 \ед.Н\) \(F_2\) \(+4 \ед.Н\) 9\circ\textrm{S of W}\text{,}\) и на восток с \(4.0 \unit{N}\text{.}\) Какова чистая сила? Решение
Это следует той же логике, что и упражнение II.3.2.16, которое я не буду повторять здесь.
Этот пример немного сложнее, потому что силы должны быть разделены на компоненты \(x\) и \(y\). Добавляя \(x\)-компоненты и отдельно добавляя \(y\)-компоненты, мы нашли компоненты чистой силы.
\(х\)-комп.9\circ\textrm{W of N}\text{. }\)) В упражнении II.3.2.20 этот расчет будет использоваться для определения ускорения.Подподраздел II.3.2.2.3 Использование чистой силы для расчета других величин
¶Результаты учащихсяИспользование чистой силы для расчета других величин
После успешного изучения этого подраздела учащиеся должны уметь …
Как правило, цель нахождения результирующей силы заключается в том, что она заставляет объект изменять свою скорость. Давайте также рассмотрим несколько простых примеров этого расчета.
Пример II.3.2.18 Ускорение ящика, испытывающего результирующую силу
Пример, на который ссылается
нахождение \(m\) из \(F=ma\), пример II.3.2.28, пример II.3.2.25, обсуждение \ref*{se-FBD-AB}, пример II.4.1.6, Ответ II.4.1.6.1, пример II.4.3.2, пример II.4.4.7
Если силы из примера II.3.2.12 приложены к объекту массой \(2,0\unit{kg}\text{ ,}\) то он ускорится со скоростью
\begin{уравнение*} \vec a =\frac{\vec F_\mathrm{net}}{m} = \frac{+(92})(1,6\единица{с}) = 7,2 \единица гидроразрыва{м}{с} \end{уравнение*} Что нужно сделать: Как и прежде, сделайте этот объект письменным столом, чтобы Абдул и Бет могли помочь вам переставить вашу комнату в общежитии. 2} \jhat
\end{уравнение*}
9\circ\) N of W. (Осталось найти ускорение.)Подсказка2
Можно найти (вектор) ускорение из (вектора) чистой силы, используя либо \(x\ )- и \(y\)-компоненты, или , используя величину и направление.
Solution1
Зная массу и компоненты чистой силы, мы можем рассчитать ускорение.
\begin{уравнение*} \ vec a = \ frac {\ vec F_ \ mathrm {net}} {m} = \ frac {3,8 \ unit {N} \ ihat + 2,2 \ unit {N} \ jhat} {2,0 \ unit {kg}} = 1,92}\text{,}\) тогда какова масса объекта?
Решение
Наивно можно предположить, что \(\deq m = \frac{\vec F_\mathrm{net}}{\vec a}\text{,}\), но деление векторов не имеет математического смысла. В этом случае вы должны учитывать величины силы и ускорения, зная, что их направления совпадают. (Мы , а не «отменяем» указания.)
\begin{уравнение*} m =\frac{F_\mathrm{net}}{a} = \frac{9.
2 \cdot m} \ = \ 2.8 \unit{kg}
\end{уравнение*}ConnectionII.3.2.22Заглядывая вперед
Еще один пример использования этого уравнения можно увидеть во многих ванных комнатах. Весы, на которых стоят люди, используют пружину (представленную в подразделе II.4.3.1 и подробно обсуждаемую в разделе II.4.6), чтобы регулировать прилагаемую силу до тех пор, пока ваше ускорение не станет равным нулю (приводя вас в равновесие), а затем сообщают вам силу это необходимо, чтобы сбалансировать свой вес.
Эти идеи будет легче визуализировать, когда мы представим инструмент диаграммы свободного тела в подразделе II.3.2.3.1.
Подподраздел II.3.2.2.4 Равновесие
¶Результаты учащихсяРавновесие
После успешного изучения этого подраздела учащиеся должны уметь …
Подподраздел, на который ссылается
Пример II.3.2.14, первый закон Ньютона, обсуждение падающих предметов пара весов, как на весах , такие как те, что изображены на изображениях астрономического созвездия Весов.
Когда весы равны, они находятся в равновесии. Поскольку второй закон требует от нас вычислить сумму сил, действующих на объект, один из основных вопросов — определить, уравновешивают ли эти силы друг друга. В примере II.3.2.12 и примере II.3.2.13 силы не уравновешены, объект «не находится в равновесии» и будет ускоряться в определенном направлении. В примере II.3.2.14 силы уравновешены, объект «находится в равновесии», и он будет не изменить свою скорость (в соответствии с первым законом).ОпределениеII.3.2.23равновесие
Объект в равновесии имеет \(\vec F_\mathrm{net} = 0\unit N\) и \(\vec a =0\text{.}\)
Подподраздел II.3.2.2.5 Как законы работают вместе
¶Результаты учащихсяКак законы работают вместе
После успешного изучения этого подраздела учащиеся должны уметь …
Что нужно сделать: я должен переработать этот раздел. Создайте фокус.Ссылка на
Подраздел II.
3.2.1.2Когда на объект действуют силы, применяется второй закон Ньютона, поэтому мы обычно начинаем со второго закона. Если эти силы объединяются, чтобы дать результирующую силу, равную нулю, так что объект находится в равновесии, то применяется первый закон Ньютона. Если мы также заботимся о человеке или предмете, который толкает, то действует и третий закон.
Чтобы лучше понять, как работают вместе первый и второй законы, в разделе “Исследование II.3.3.2” предлагаются некоторые действия, которые вы можете выполнить или обдумать, чтобы подумать о шаблонах, которые вы можете увидеть, когда вы толкаете или не толкаете объекты. Исследование II.3.2.2 поможет вам обдумать некоторые следствия первого и второго закона. Когда вы будете готовы решить некоторые задачи, вы можете перейти к разделу II.3.3, но некоторые из этих примеров также будут ссылаться на третий закон Ньютона.
Разведка II.3.2.2 Без газа
Разведка, на которую ссылается
Subsubsection II.
3.2.2.5Во время долгой поездки с вашей подругой Бет ваша машина начинает глохнуть из-за того, что в ней заканчивается бензин незадолго до прибытия в новый город. Вы видите вдалеке знак заправочной станции и должны решить, что делать. Вы с Бет можете придумать три варианта.
- План А
Притормози, припаркуй машину, дойди до заправки, купи канистру с бензином, наполни ее, отнеси обратно в машину и вперед! Если вы следуете этому плану, прочитайте ответ 1.
- План Б
Оставьте машину в движении, продолжайте удерживать педаль газа до тех пор, пока бензина не станет совсем, и надейтесь вопреки всем надеждам, что вы довезете машину до заправочной станции, чтобы никому не пришлось таскать с собой тяжелую канистру с бензином. Если вы следуете этому плану, прочитайте Ответ 2.
- План С
Разогнаться чуть выше разрешенной скорости, поставить машину на нейтраль, включить мигающие огни опасности, ехать так далеко, как только возможно, и надеяться вопреки всем надеждам, что вы довезете машину до заправочной станции, чтобы никому не нужно носить с собой тяжелый газовый баллон.
Если вы следуете этому плану, прочитайте ответ 3.
Answer1
Как и планировалось, ты останавливаешься и паркуешь машину. Бет предлагает одному из вас остаться с машиной, возможно, потому что у нее домашняя работа по физике. Если вы решите разделиться, прочитайте ответ 5. Если вы решите путешествовать вместе, прочитайте ответ 7.
Ответ 2
Как только вы решите это сделать, бензин закончится. Думая, что сможешь доехать до заправки, ты убираешь ногу с педали газа. Вы довольно быстро замедляетесь и начинаете нервничать, что вас могут задеть сзади. Вы включаете аварийные огни. Примерно через минуту вы едете \(30 \unit{mph}\) и коротаете время, выполняя Упражнение 1. Люди сигналят вам, пытаясь пройти. Бет поворачивается к вам и спрашивает, почему вы так медленно едете. Если вы начинаете обсуждение Первого закона Ньютона, перейдите к ответу 4. Если вы смутитесь и решите остановиться, прочитайте ответ 6.
Answer3
Вы разгоняетесь до \(60 \unit{mph}\) до того, как кончится бензин, а затем быстро переводите машину в нейтраль. Вы постепенно снижаете скорость и, пытаясь не попасть сзади, ловко включаете аварийную сигнализацию. Примерно через минуту вы путешествуете \(52 \unit{mph}\) и коротаете время, выполняя Упражнение II.1.3.2). После \(2\unit{min}\text{,}\) вы едете \(43 \unit{миль/час}\), и люди теряют терпение, пытаясь пройти. После \(2,79\unit{min}\text{,}\) вы триумфально въезжаете на заправку на комфортной скорости \(36,7\unit{миль/ч}\text{.}\) Бет так счастлива, что покупает у вас полный бак бензина, и вы двое начинаете дискуссию о Первом законе Ньютона, закачивая бензин. Пожалуйста, прочтите ответ 8.
Answer4
После некоторого обсуждения вы с Бет понимаете, что когда машина находится в движении, трансмиссия (часть автомобиля, которая преобразует скорость вращения двигателя в скорость вращения оси и -wheels-turn) связан с осью, а это значит, что катящиеся колеса пытаются провернуть как детали двигателя, так и сами колеса.
В деталях двигателя есть смазка и масло, но для их вращения требуется много энергии. Это вызывает трение, которое рассеивает энергию и, что более важно, оказывает обратную силу на вращающиеся колеса. Ваш автомобиль не описывается Первым законом Ньютона, который требует, чтобы сила не применялась. Вместо этого ваша машина описывается вторым законом Ньютона, и сила изменяет скорость, заставляя вас двигаться медленнее. Автомобиль останавливается всего \(2,2\единица{мин}\), а до заправки еще нужно идти пешком. Бет сокрушается: «Если бы только был способ уменьшить усилие на оси…». Если вам приходит в голову мысль поставить машину на нейтраль, когда закончился бензин, то представьте, что вы читаете Ответ 3. Если вы перестанете говорить и пойдете пешком заправочной станции, затем прочитайте ответ 10.Answer5
Вы оставляете Бет в машине и идете пешком 45 минут до заправочной станции. Вы покупаете газовый баллон, заправляете его и начинаете нести обратно в машину.
Он очень тяжелый, и вы замечаете, как над ним кружат стервятники. Ты надеешься, что переживешь это. Возможно, было бы лучше взять с собой Бет, чтобы разделить это бремя. Ты спотыкаешься один раз, а потом снова. Вы клянетесь быть осторожнее в оценке потребления газа. Пройдя, кажется, несколько часов и, спотыкаясь, вернувшись к машине, вы обнаруживаете, что Бет очень взволнована. Она заявляет, что изобрела машину времени, чтобы вы могли вернуться к приключениям и начать заново, чтобы узнать кое-что о Первом законе Ньютона!Answer6
Вы остановились и припарковали машину. Бет предлагает одному из вас остаться с машиной, возможно, потому что у нее домашняя работа по физике. Если вы решите разделиться, прочитайте ответ 9. Если вы решите путешествовать вместе, прочитайте ответ 7.
Ответ7
Все идет по плану. Вы уезжаете в закат, к сожалению, не зная физики, которую вы, возможно, выучили. Конец!
Ответ8
Во время обсуждения вы с Бет понимаете, что вращающиеся колеса и вращающаяся ось все еще связаны с невращающейся рамой автомобиля.
Хотя это вызывает меньшее трение, чем если бы автомобиль находился в движении, некоторое трение все же остается, что рассеивает энергию и, что более важно, оказывает обратную силу на вращающиеся колеса. Ваш автомобиль не описывается Первым законом Ньютона, который требует, чтобы сила не применялась. Вместо этого ваша машина описывается вторым законом Ньютона, и сила изменяет скорость, заставляя вас двигаться медленнее. Вы заканчиваете заправляться и отправляетесь во множество счастливых приключений. Конец! Answer9
Вы оставляете Бет в машине и идете пешком 31 минуту до заправочной станции. Вы покупаете газовый баллон, заправляете его и начинаете нести обратно в машину. Он очень тяжелый, и вы замечаете, как над ним кружат стервятники. Ты надеешься, что переживешь это. Возможно, было бы лучше взять с собой Бет, чтобы разделить это бремя. Ты спотыкаешься один раз, а потом снова. Вы клянетесь быть осторожнее в оценке потребления газа.
Пройдя, кажется, несколько часов и, спотыкаясь, вернувшись к машине, вы обнаруживаете, что Бет очень взволнована. Она заявляет, что изобрела машину времени, чтобы вы могли вернуться к приключениям и начать заново, чтобы узнать кое-что о Первом законе Ньютона!Answer10
Вы и Бет счастливо идете пешком 25 минут до заправочной станции, всю дорогу обсуждая и решая физические задачи. Вы покупаете газовый баллончик, заправляете его и разделяете бремя переноски тяжелого газового баллончика. Вы возвращаетесь к машине, добавляете газ и едете навстречу множеству счастливых приключений. Конец!
Первый закон Ньютона. Определения физики
Этот веб-сайт поддерживается читателями. Я могу получить партнерскую комиссию бесплатно для вас, если вы сделаете покупку по ссылкам ниже. (подробнее)
Первый закон движения Ньютона можно резюмировать следующим образом: :
Каждое тело сохраняется в своем состоянии покоя или равномерного прямолинейного движения, если оно не вынуждено изменить это состояние под действием приложенных к нему сил.
Первый закон часто называют «законом инерция », где инерция — это тенденция чего-то не двигаться или изменять свое движение. Другой способ сформулировать первый закон таков: когда результирующая сила, действующая на объект, равна нулю, его движение не меняется . Конечно, это определение имеет мало смысла, если уже не имеется определения «силы», которое определено во втором законе Ньютона . Первый и второй законы, вероятно, лучше описать как определений или аксиом, а не как законы, поскольку они опираются как друг на друга, так и на понятие массы.
Из двух ситуаций, указанных в этой аксиоме, «тело в покое» легче всего наблюдать в повседневной жизни. Проще говоря, в отсутствие других сил неподвижное тело не будет двигаться без приложения к нему результирующей силы. Конечно, гравитация всегда действует на любой объект на поверхности Земли, но ей часто противодействует нормальная сила земли или того, на чем покоится объект, так что результирующая сила равна нулю, где результирующая сила есть сумма всех сил, действующих на тело:
Получите мой настенный календарь Аляски на 2023 год!
Если немного забежать вперед и учесть второй закон Ньютона и определение силы как производной движения по времени (или, проще говоря, массы, умноженной на ускорение):
(1)
Вы можете помочь поддержать меня и этот сайт! Поддержка на Patreon Подписаться на рассылку новостей становится очевидным, что объект с массой и нулевой результирующей силой не имеет ускорения.
Объект, который не ускоряется, находится в постоянном движении.Вторую ситуацию наблюдать сложнее: объект, находящийся в равномерном движении, останется в одном и том же равномерном движении (направление и скорость), если на него не действует сила, потому что почти все, что мы наблюдаем, подвержено влиянию сил трения или сопротивления воздуха. Однако эту концепцию можно визуализировать, представив действительно фрикционную поверхность или объект, движущийся в идеальном вакууме. Если к такому объекту не будет приложена какая-либо сила, он будет бесконечно двигаться по тому же пути и с той же скоростью.
Тело, движущееся (или не движущееся) любым способом, часто называют свободным телом .
Первый и второй законы приводят к теореме сохранения для линейного импульса частицы, которая утверждает, что если полная сила, действующая на частицу, равна нулю, то производная импульса по времени равна нулю, а линейный импульс частицы равен законсервированный.
Инерциальная система отсчета
Первый закон Ньютона действителен только в инерциальной системе отсчета (и в значительной степени, когда примерно в инерциальной системе отсчета), также известной как Система Галилея . Это представляет собой еще одно рекурсивное определение, поскольку инерциальная система отсчета — это система отсчета, в которой действует Первый закон Ньютона .
Пока для рабочего определения достаточно простого примера. Допустим, наша система отсчета — это система координат, построенная на вагоне поезда. Если вагон поезда (и наша система координат) стоит на месте или движется с постоянной скоростью, можно сказать, что мы смотрим в инерциальную систему отсчета. Законы Ньютона будут выполняться для объекта, измеренного внутри вагона поезда. Однако предположим, что вагон поезда и наша система отсчета начинают ускоряться. Теперь свободный объект внутри автомобиля будет двигаться против направления ускорения, казалось бы, без приложения силы.
Такая система отсчета называется неинерциальная система отсчета .Ссылки и дополнительная литература
Goldstein, H. (1959). Классическая механика . Чтение, Массачусетс: Аддисон-Уэсли. (стр. 2-5
Марион, Дж. Б., и Торнтон, С. Т. (1995). Классическая динамика частиц и систем . Форт-Уэрт: Saunders College Pub. (стр. 50-51)
Янг, Х. Д., Фридман, Р. А. , Ford, A.L., Zemansky, M.W., и Sears, F.W. (2003) Sears and Zemansky’s University Physics with Modern Physics . Сан-Франциско [Калифорния: Pearson Addison-Wesley. (стр. 124-127)
Я также на Patreon Законы движения – EWT
Фон
Движение можно определить как процесс или действие перемещения или изменения места или положения. А когда что-то движется, изменение его положения можно точно рассчитать с помощью законов физики. Именно сэр Исаак Ньютон установил некоторые из этих законов, известных как законы движения, приравнивая движение к силам.
Скорость
Определение скорости – это скорость чего-либо в заданном направлении ( показано на рисунке ниже). Скорость измеряется как изменение положения во времени, например, 25 миль в час или 5 футов в секунду. Если скорость постоянна, это количество времени, которое требуется для прохождения расстояния.
Авторы и права: GCSE Additional Science
Ньютон сформулировал важный закон скорости в 17 веке, утверждая, что объект в состоянии покоя (без скорости) остается в состоянии покоя, если к нему не приложена сила. Скорость и сила связаны между собой в Первый закон движения Ньютона . Первый закон также гласит, что движущийся объект будет оставаться в движении с той же скоростью и в том же направлении (то есть скоростью), если к нему не будет приложена сила. Это означает, что объект может изменить свое положение, даже если на него не действует сила. Это привело ко второму закону Ньютона, объясняющему изменение скорости во времени, то есть ускорение.
Ускорение
Ускорение — это скорость изменения скорости во времени. Например, нажмите на педаль газа, чтобы разогнать автомобиль, и он изменит скорость (скорость в заданном направлении). Нажмите на тормоз, и он замедлится и уменьшит скорость. Если автомобиль сталкивается с другим объектом и замедляется, сила удара зависит от ускорения или замедления, а не от скорости автомобиля. Второй закон Ньютона гласит, что сумма всех сил (F) равна массе (m), умноженной на ускорение (a), или F=ma . Таким образом, ускорение и сила тесно связаны с этим законом.
Авторы и права: Mathopenref
«Скорость — это изменение положения во времени. Ускорение — это изменение скорости во времени».
Объяснение
Скорость и первый закон движения Ньютона
Первый закон движения гласит, что тело будет оставаться в состоянии покоя или двигаться с постоянной скоростью, если к нему не будет приложена сила.
По существу, скорость в этом законе всегда постоянна. В состоянии покоя скорость остается равной нулю. Во время движения скорость остается неизменной до тех пор, пока не будет приложена сила. В состоянии покоя ускорение частицы или тела (а) равно нулю, а скорость (v) равна нулю. На рисунке ниже описана частица, которая имеет ядро частицы с одним или несколькими волновыми центрами, структуру стоячей волны, которая простирается до радиуса частицы, и сферические продольные бегущие волны за пределами этого радиуса. Стоячие волны генерируются входными волнами, которые, отражаясь, становятся внешними волнами. В покое длина стоячих волн (λ свинец ) соответствует длине волны внутренних волн (λ l ). Между частицей и окружающей средой нет разницы в длине волны/частоте. Частица покоится и останется в покое.Примечание: Бегущая волна представляет собой сферическую продольную волну. На рисунке выше показана простая синусоида, поскольку эта волна связана с трудностями описания трехмерной волны в двухмерном изображении.
Движущаяся частица имеет скорость больше нуля. Без ускорения (a=0) скорость остается постоянной в соответствии с первым законом движения Ньютона. Для наблюдателя длина волны на переднем фронте (λ опережает ) частицы сжата в направлении движения по отношению к продольным бегущим внутрь волнам (λ l ). Существует разница в длине волны или частоте с внешней средой, которая, как показано, подчиняется уравнениям Доплера. Эта разность частот является основой расчета скорости, как это будет показано математически. Это также причина, по которой частицы (и, следовательно, объекты, построенные на частицах) испытывают замедление времени и сокращение длины в направлении движения.
На рисунке ниже показана частица в движении без ускорения. Амплитуда волны постоянна и одинакова со всех сторон частицы. Частица будет поддерживать свою частоту стоячей волны как на переднем, так и на заднем фронте структуры стоячей волны, хотя она отличается от внешней среды.
Длина волны на переднем фронте меньше длины волны входящей волны (λ отведения < λ l ) и останется постоянной. Чем меньше длина волны переднего фронта, тем больше скорость. Если ядро частицы достигает края своего радиуса стоячей волны, длина волны переднего края близка к нулю, а ее скорость близка к скорости света.Скорость приводит к разнице длин волн. Эффект Доплера виден на изображении движущейся частицы выше и является основой для вывода уравнения скорости. Отношение основной длины волны к длине волны переднего края частицы определяется как:
Поскольку скорость света (c) и основная длина волны (λ l ) являются константами, скорость ( v) пропорциональна длине волны переднего фронта (λ ведет ). Оно будет описано ниже на этой странице как уравнение для скорости.
Ускорение и второй закон Ньютона
В первом законе движения, описанном в терминах волн, длина волны может различаться, но амплитуда волны постоянна.
Во втором законе амплитуда волны непостоянна и является причиной силы и ускорения. Частицы движутся, чтобы минимизировать амплитуду, один из законов теории энергетических волн. На рисунке ниже показана частица, первоначально находящаяся в покое (v i =0), теперь ускоренное (а>0). Частица будет двигаться в направлении минимальной амплитуды, поэтому передний фронт в уравнениях ускорения и скорости всегда относится к направлению движения, где амплитуда волны меньше, чем амплитуда в любом другом направлении, окружающем частицу. Точно так же амплитуда в направлении движения описывается с использованием тех же обозначений (A отведение ). Эта разность амплитуд приводит к силе, действующей на объект, и он ускоряется. Ядро частицы переместится из положения покоя на новую частоту.Следующий рисунок описывает изменение положения ядра частицы из-за ускорения, вызванного разностью амплитуд. Ускорение — это изменение положения ядра частицы, влияющее на длину волны и частоту.
Меньшее значение ускорения перемещает ядро частицы медленнее к краю, а большее значение ускорения перемещает ядро частицы быстрее к краю. Это требует измерения времени, чтобы определить медленнее или быстрее . Время основано на циклах длины волны (то есть частоте), таким образом, ускорение — это движение ядра частицы к краю радиуса, основанное на количестве циклов длины волны. Это видно из уравнения ускорения в следующем разделе этой страницы.«Первый закон движения Ньютона основан на длине волны. Второй закон основан на амплитуде волны».
Уравнение
Ускорение
Хотя существует множество искусственных сил, влияющих на движение и ускорение объекта (например, разгоняющегося автомобиля), существуют естественные силы, вызывающие ускорение объектов, которые можно рассчитать, например гравитационные силы. Например, у Земли есть естественное ускорение для тел у поверхности, известное как поверхностная гравитация (у Земли 9,81 м/с 2 ).
Уравнение для ускорения получено из уравнения гравитационной силы, показанного в статье Forces.Поверхностная гравитация (ускорение)
Подробные шаги по выводу уравнений можно найти в документе Forces .
Доказательство
Доказательством объяснения движения частиц энергетическими волнами являются выводы и расчеты:
- Второй закон Ньютона
- Рассчитано 11 гравитаций на поверхности планеты (ускорение) – см. пример расчета ниже
Поверхностная гравитация Земли (ускорение) – Расчет
Переменные:
- Q 1 = Q Земля = 3,570E51 ( из расчета партии для Земля ) 900E51 ( из Партия.
- Q 2 = 1 ( одна частица – все частицы ускоряются с одинаковой скоростью )
- r = r земля = 6 375 223 м ( средний радиус Земли )
Уравнение: Уравнение силы тяжести (ускорения) на поверхности – сверху
Результат: 9,81 м/с 2
Значения измеренной поверхности Земли: 900,020На этом сайте можно найти сводку различных расчетов ускорения; более подробные расчеты с инструкциями по воспроизведению этих расчетов можно найти в документе Forces .
Предыдущая: Слабая сила
Следующая: Уравнения силы
Физика лифта: Законы Ньютона | Nationwide Lifts
Вы когда-нибудь задумывались, почему мяч катится так далеко, когда вы его толкаете, а стена вашего дома не двигается, как бы вы на нее ни давили? Или, может быть, вы задавались вопросом, почему перо падает медленно, а книга падает прямо на землю? На эти вопросы есть ответы, и они начинаются с человека по имени Исаак Ньютон. Сэр Исаак Ньютон был математиком и ученым 17 века. В 1687 году он опубликовал Philosophiae Naturalis Principia Mathematica . Хотя прошло более 300 лет, книга Ньютона до сих пор считается одной из самых важных научных работ, когда-либо опубликованных. В нем он описывает три основных принципа, объясняющих, как силы воздействуют на объекты. Эти принципы в совокупности стали известны как законы движения Ньютона.
Первый закон Ньютона
Первый закон движения Ньютона гласит: «Объект в состоянии покоя остается в покое, а объект в движении остается в движении, если на него не действует внешняя сила».
Самый простой способ понять этот закон — представить себе мяч, стоящий на столе. Мяч сидит на столе без движения, пока вы не приложите к нему силу, например, не ударите по нему. После удара мяч будет катиться до тех пор, пока другая сила не заставит его остановиться или изменить направление.- Первый закон движения
- Первый закон Ньютона: инерция
- Описание Вселенной Ньютоном
- Инерция и первый закон движения Ньютона
Второй закон Ньютона
Второй закон движения Ньютона гласит: «Сила, действующая на объект, равна произведению массы этого объекта на его ускорение». Второй закон Ньютона выражается уравнением F = ma, где «F» — сила, действующая на объект, «m» — масса объекта, а «a» — ускорение объекта. Представьте, что мяч, лежащий на столе, — это баскетбольный или футбольный мяч. Толкать мяч, чтобы заставить его катиться, должно быть легко, так как он не имеет большой массы. Теперь представьте, что вы пытаетесь толкнуть шар для боулинга.
Вам нужно будет приложить больше силы, потому что шар для боулинга имеет большую массу. Второй закон Ньютона говорит нам нечто очень важное об отношениях между объектом и его движением: сила, действующая на объект, заставляет его ускоряться, и чем больше масса объекта, тем больше силы необходимо, чтобы замедлить объект, ускорить его. вверх или заставить его повернуться.- Что такое второй закон движения Ньютона?
- Второй закон движения Ньютона (видео)
- Законы Ньютона: заблуждения, определение ускорения и отдельные силы
Третий закон Ньютона
Третий закон Ньютона гласит: «Каждому действию есть равное и противоположное противодействие». Когда мы толкаем мяч, он катится, но мяч также немного давит на вашу руку. Однако, хотя величина силы в обоих направлениях одинакова, у вас намного больше массы, чем у мяча, поэтому мяч движется больше, чем ваша рука. А теперь представьте, что вы толкаетесь о стену вашего дома.
Будем надеяться, что стена не двигается, но ваша рука может прижаться к ней в зависимости от того, насколько сильно вы на нее надавите. Это происходит потому, что пока вы давите на стену, стена тоже давит на вас.- Законы Ньютона и причины движения
- Третий закон Ньютона: действие и противодействие
- Третий закон Ньютона и космические путешествия
Что происходит в лифте?
Когда вы входите в лифт, вам кажется, что вы имеете тот же вес, что и во время ожидания в коридоре. Когда вы поднимаетесь в лифте, вы чувствуете себя немного тяжелее, а когда спускаетесь, вы чувствуете себя немного легче, хотя бы на несколько секунд. Если бы вы встали на весы в лифте, показания вашего веса немного отличались бы при подъеме, нахождении в неподвижном состоянии и при опускании. Когда вы неподвижны, ваше ускорение равно 0, поэтому весы будут показывать только ваш кажущийся вес. Однако когда лифт поднимается, вы ускоряетесь, что увеличивает силу весов и увеличивает ваш кажущийся вес.
0\единица{кг}$}}
\newcommand{\studentD}{Диана} \newcommand{\massD}{\mbox{80,0$\единица{кг}$}}
\newcommand{\studentE}{Эрик} \newcommand{\massE}{\mbox{95,0$\единица{кг}$}}
\newcommand{\studentF}{Фрэнсис} \newcommand{\massF}{\mbox{85,0$\единица{кг}$}}
\newcommand{\studentX}{Ксеркс} \newcommand{\massX}{\mbox{62,5$\единица{кг}$}}
\newcommand{\studentZ}{Zambert} \newcommand{\massZ}{\mbox{$95,0\unit{kg}$}}
\newcommand{\heA}{он}\newcommand{\himA}{его}\newcommand{\hisA}{его} \newcommand{\himselfA}{сам}
\newcommand{\HeA}{He}\newcommand{\HimA}{Him}\newcommand{\HisA}{His}
\newcommand{\heC}{он}\newcommand{\himC}{его}\newcommand{\hisC}{его} \newcommand{\himselfC}{сам}
\newcommand{\HeC}{He}\newcommand{\HimC}{Him}\newcommand{\HisC}{His}
\newcommand{\heE}{он}\newcommand{\himE}{его}\newcommand{\hisE}{его} \newcommand{\himselfE}{сам}
\newcommand{\HeE}{He}\newcommand{\HimE}{Him}\newcommand{\HisE}{His}
\newcommand{\heZ}{он}\newcommand{\himZ}{его}\newcommand{\hisZ}{его} \newcommand{\himselfZ}{сам}
\newcommand{\HeZ}{He}\newcommand{\HimZ}{Him}\newcommand{\HisZ}{His}
\ newcommand {\ heB} {она} \ newcommand {\ himB} {ее} \ newcommand {\ hisB} {ее} \ newcommand {\ himselfB} {она}
\newcommand{\HeB}{She}\newcommand{\HimB}{Her}\newcommand{\HisB}{Her}
\newcommand{\heD}{она}\newcommand{\himD}{ее} \newcommand{\hisD}{ее} \ newcommand{\himselfD}{ее себя}
\newcommand{\HeD}{She}\newcommand{\HimD}{Her}\newcommand{\HisD}{Her}
\ newcommand {\ heF} {она} \ newcommand {\ himF} {ее} \ newcommand {\ hisF} {ее} \ newcommand {\ himselfF} {herself}
\newcommand{\HeF}{She}\newcommand{\HimF}{Her}\newcommand{\HisF}{Her}
\newcommand{\heX}{\studentX}\newcommand{\himX}{\studentX}\newcommand{\hisX}{\studentX’s}\newcommand{\himselfX}{лицо \studentX}
\newcommand{\HeX}{\studentX}\newcommand{\HimX}{\studentX}\newcommand{\HisX}{\studentX’s}
\новая команда{\lt}{<}
\новая команда{\gt}{>}
\newcommand{\amp}{&}
\)
1.6.1.
Это также можно выразить следующим образом: если комбинация сил \(\vec F_\mathrm{net}\text{,}\) не полностью компенсирует друг друга, то наш друг \(m\) должен ускоряться, \(\vec a\text{,}\) в определенном направлении. Кроме того, результирующее направление чистой силы определяет направление ускорения. Соединение английского языка и математики:
.), Министерство торговли США, Национальное бюро стандартов, с. 17, которая ссылается на 7-ю резолюцию (март 2017 г.) 9-й сессии ГКМВ (март 2017 г.). назвать единицу Ньютон, так что 92}\) Задание: Добавьте сюда несколько примеров.
com (март 2017 г.), на самом деле это происходит от старофранцузского net для «аккуратных» или «чистых», имеющих ощущение отделки и элегантности.
3.2.13Совокупная сила, добавление вектора сил в противоположном направлении
0\unit{N} \ihat\right) + \left(-3.0 \unit{N} \ihat\right) = 0.0\ unit{N} \ihat
\end{уравнение*}
Мы, как обычно, начнем с диаграммы свободного тела (справа).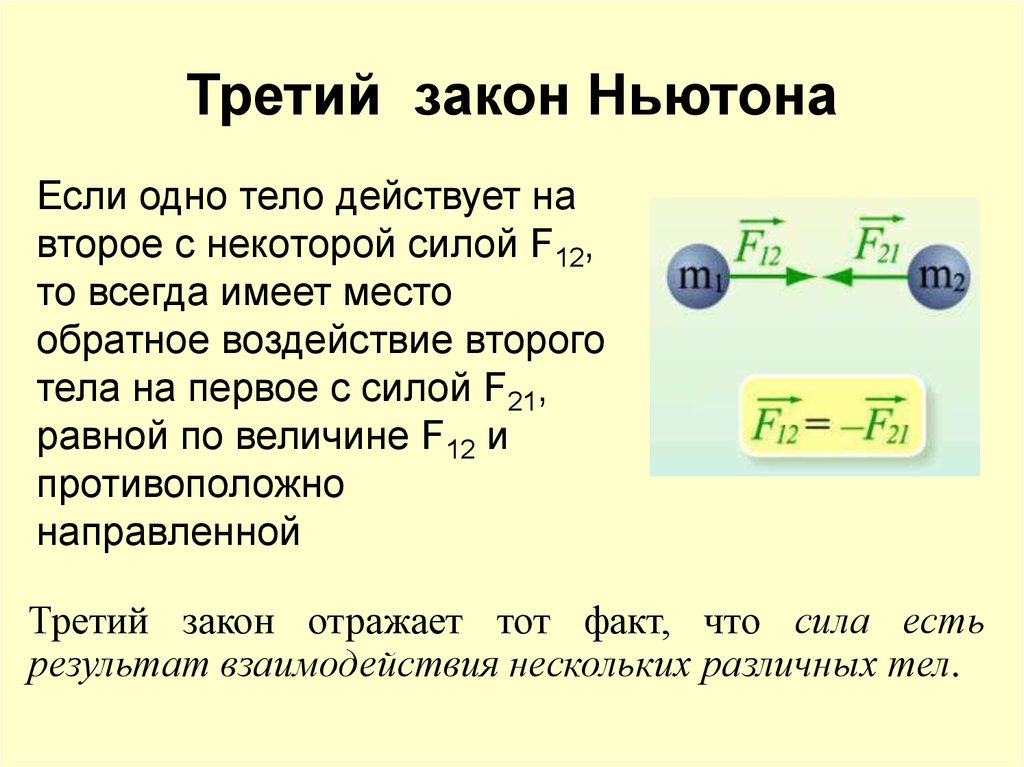
}\)) В упражнении II.3.2.20 этот расчет будет использоваться для определения ускорения.
2} \jhat
\end{уравнение*}
9\circ\) N of W. (Осталось найти ускорение.)
2 \cdot m} \ = \ 2.8 \unit{kg}
\end{уравнение*}
Когда весы равны, они находятся в равновесии. Поскольку второй закон требует от нас вычислить сумму сил, действующих на объект, один из основных вопросов — определить, уравновешивают ли эти силы друг друга. В примере II.3.2.12 и примере II.3.2.13 силы не уравновешены, объект «не находится в равновесии» и будет ускоряться в определенном направлении. В примере II.3.2.14 силы уравновешены, объект «находится в равновесии», и он будет не изменить свою скорость (в соответствии с первым законом).
3.2.1.2
3.2.2.5
Если вы следуете этому плану, прочитайте ответ 3.
В деталях двигателя есть смазка и масло, но для их вращения требуется много энергии. Это вызывает трение, которое рассеивает энергию и, что более важно, оказывает обратную силу на вращающиеся колеса. Ваш автомобиль не описывается Первым законом Ньютона, который требует, чтобы сила не применялась. Вместо этого ваша машина описывается вторым законом Ньютона, и сила изменяет скорость, заставляя вас двигаться медленнее. Автомобиль останавливается всего \(2,2\единица{мин}\), а до заправки еще нужно идти пешком. Бет сокрушается: «Если бы только был способ уменьшить усилие на оси…». Если вам приходит в голову мысль поставить машину на нейтраль, когда закончился бензин, то представьте, что вы читаете Ответ 3. Если вы перестанете говорить и пойдете пешком заправочной станции, затем прочитайте ответ 10.
Он очень тяжелый, и вы замечаете, как над ним кружат стервятники. Ты надеешься, что переживешь это. Возможно, было бы лучше взять с собой Бет, чтобы разделить это бремя. Ты спотыкаешься один раз, а потом снова. Вы клянетесь быть осторожнее в оценке потребления газа. Пройдя, кажется, несколько часов и, спотыкаясь, вернувшись к машине, вы обнаруживаете, что Бет очень взволнована. Она заявляет, что изобрела машину времени, чтобы вы могли вернуться к приключениям и начать заново, чтобы узнать кое-что о Первом законе Ньютона!
Хотя это вызывает меньшее трение, чем если бы автомобиль находился в движении, некоторое трение все же остается, что рассеивает энергию и, что более важно, оказывает обратную силу на вращающиеся колеса. Ваш автомобиль не описывается Первым законом Ньютона, который требует, чтобы сила не применялась. Вместо этого ваша машина описывается вторым законом Ньютона, и сила изменяет скорость, заставляя вас двигаться медленнее. Вы заканчиваете заправляться и отправляетесь во множество счастливых приключений. Конец!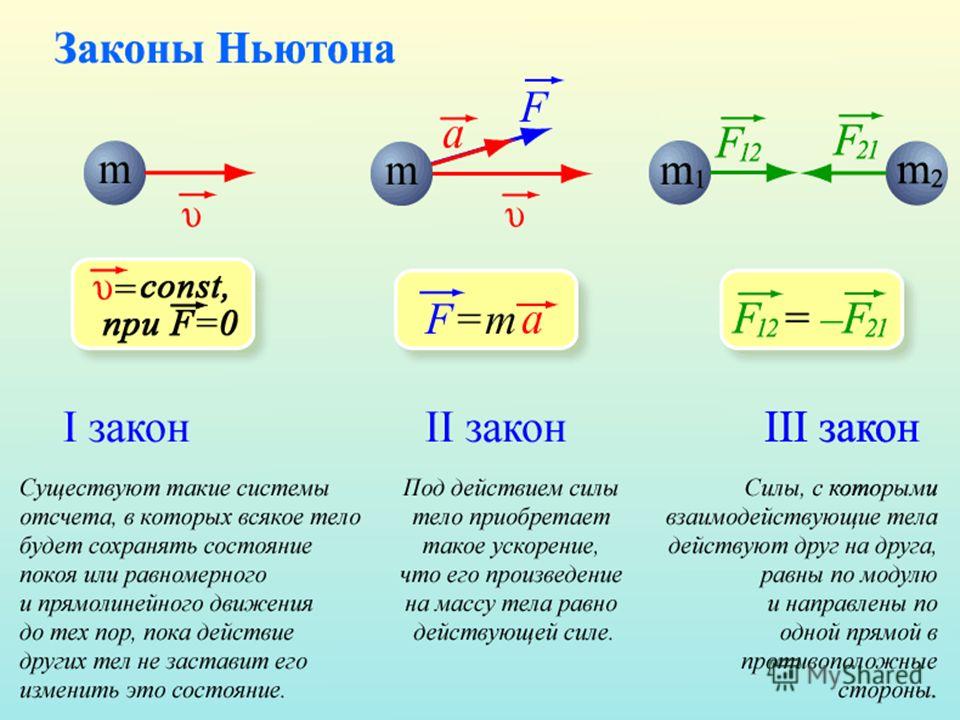 
Пройдя, кажется, несколько часов и, спотыкаясь, вернувшись к машине, вы обнаруживаете, что Бет очень взволнована. Она заявляет, что изобрела машину времени, чтобы вы могли вернуться к приключениям и начать заново, чтобы узнать кое-что о Первом законе Ньютона!
Объект, который не ускоряется, находится в постоянном движении.
Такая система отсчета называется неинерциальная система отсчета .
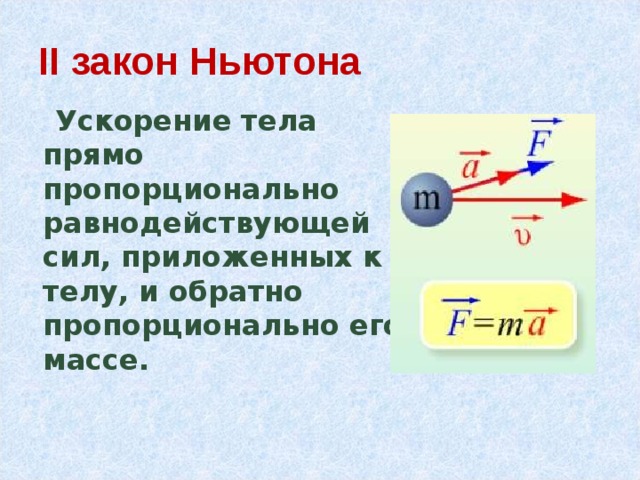
По существу, скорость в этом законе всегда постоянна. В состоянии покоя скорость остается равной нулю. Во время движения скорость остается неизменной до тех пор, пока не будет приложена сила. В состоянии покоя ускорение частицы или тела (а) равно нулю, а скорость (v) равна нулю. На рисунке ниже описана частица, которая имеет ядро частицы с одним или несколькими волновыми центрами, структуру стоячей волны, которая простирается до радиуса частицы, и сферические продольные бегущие волны за пределами этого радиуса. Стоячие волны генерируются входными волнами, которые, отражаясь, становятся внешними волнами. В покое длина стоячих волн (λ свинец ) соответствует длине волны внутренних волн (λ l ). Между частицей и окружающей средой нет разницы в длине волны/частоте. Частица покоится и останется в покое.
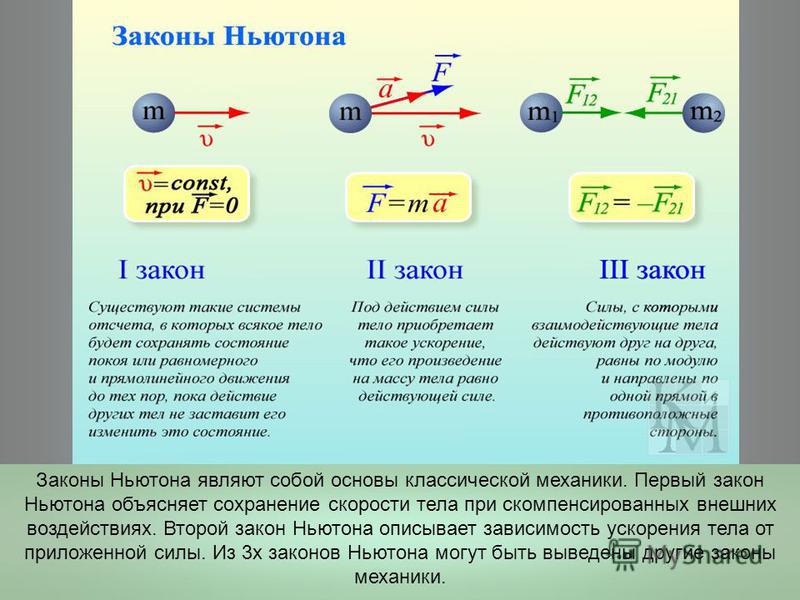Длина волны на переднем фронте меньше длины волны входящей волны (λ отведения < λ l ) и останется постоянной. Чем меньше длина волны переднего фронта, тем больше скорость. Если ядро частицы достигает края своего радиуса стоячей волны, длина волны переднего края близка к нулю, а ее скорость близка к скорости света.
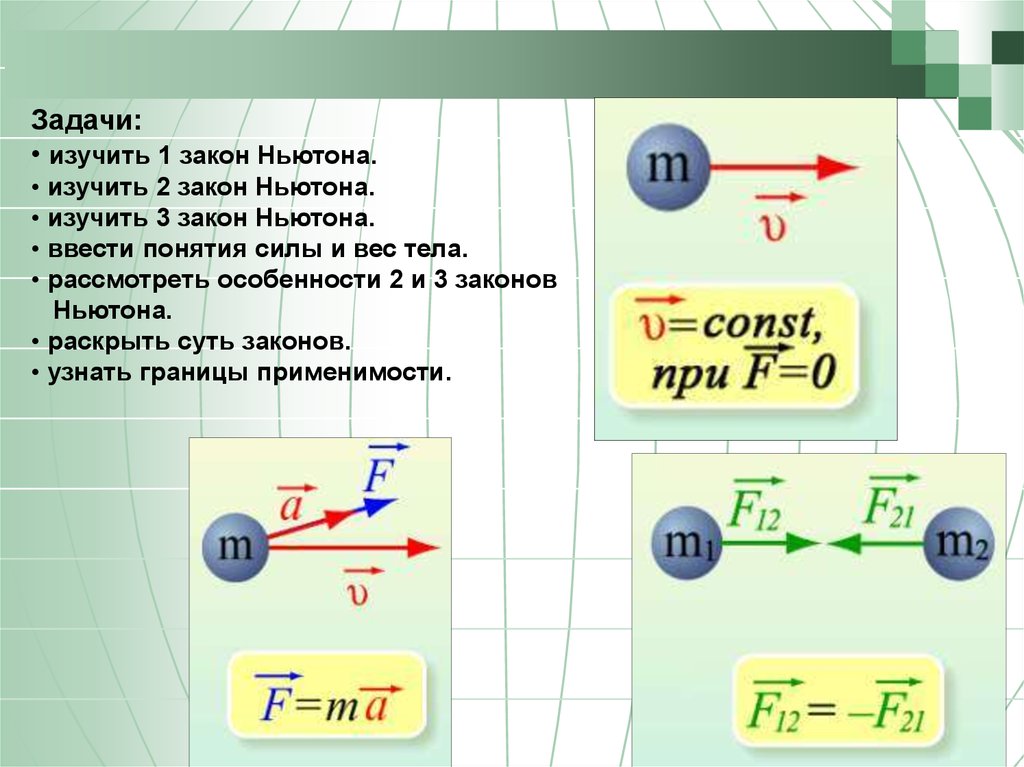Во втором законе амплитуда волны непостоянна и является причиной силы и ускорения. Частицы движутся, чтобы минимизировать амплитуду, один из законов теории энергетических волн. На рисунке ниже показана частица, первоначально находящаяся в покое (v i =0), теперь ускоренное (а>0). Частица будет двигаться в направлении минимальной амплитуды, поэтому передний фронт в уравнениях ускорения и скорости всегда относится к направлению движения, где амплитуда волны меньше, чем амплитуда в любом другом направлении, окружающем частицу. Точно так же амплитуда в направлении движения описывается с использованием тех же обозначений (A отведение ). Эта разность амплитуд приводит к силе, действующей на объект, и он ускоряется. Ядро частицы переместится из положения покоя на новую частоту.
Меньшее значение ускорения перемещает ядро частицы медленнее к краю, а большее значение ускорения перемещает ядро частицы быстрее к краю. Это требует измерения времени, чтобы определить медленнее или быстрее . Время основано на циклах длины волны (то есть частоте), таким образом, ускорение — это движение ядра частицы к краю радиуса, основанное на количестве циклов длины волны. Это видно из уравнения ускорения в следующем разделе этой страницы.
Уравнение для ускорения получено из уравнения гравитационной силы, показанного в статье Forces.
Самый простой способ понять этот закон — представить себе мяч, стоящий на столе. Мяч сидит на столе без движения, пока вы не приложите к нему силу, например, не ударите по нему. После удара мяч будет катиться до тех пор, пока другая сила не заставит его остановиться или изменить направление.
Вам нужно будет приложить больше силы, потому что шар для боулинга имеет большую массу. Второй закон Ньютона говорит нам нечто очень важное об отношениях между объектом и его движением: сила, действующая на объект, заставляет его ускоряться, и чем больше масса объекта, тем больше силы необходимо, чтобы замедлить объект, ускорить его. вверх или заставить его повернуться.
Будем надеяться, что стена не двигается, но ваша рука может прижаться к ней в зависимости от того, насколько сильно вы на нее надавите. Это происходит потому, что пока вы давите на стену, стена тоже давит на вас.