Онлайн калькулятор: Гидростатическое давление
Калькулятор ниже предназначен для расчета неизвестной величины по заданным, используя формулу давления столба жидкости.
Сама формула:
Калькулятор позволяет найти
- давление столба жидкости по известным плотности жидкости, высоте столба жидкости и ускорению свободного падения
- высоту столба жидкости по известным давлению жидкости, плотности жидкости и ускорению свободного падения
- плотность жидкости по известным давлению жидкости, высоте столба жидкости и ускорению свободного падения
- ускорение свободного падения по известным давлению жидкости, плотности жидкости и высоте столба жидкости
Вывод формул для всех случаев тривиален. Для плотности по умолчанию используется значение плотности воды, для ускорения свободного падения – земное ускорение, и для давления – величина равная давлению в одну атмосферу. Немного теории, как водится, под калькулятором.
Гидростатическое давление
Найтидавлениеплотностьвысотаускорение свободного паденияТочность вычисленияДавление в жидкости, Па
Высота столба жидкости, м
Плотность жидкости, кг/м3
Ускорение свободного падения, м/с2
content_copy Ссылка save Сохранить extension Виджет
Гидростатическое давление — давление столба воды над условным уровнем.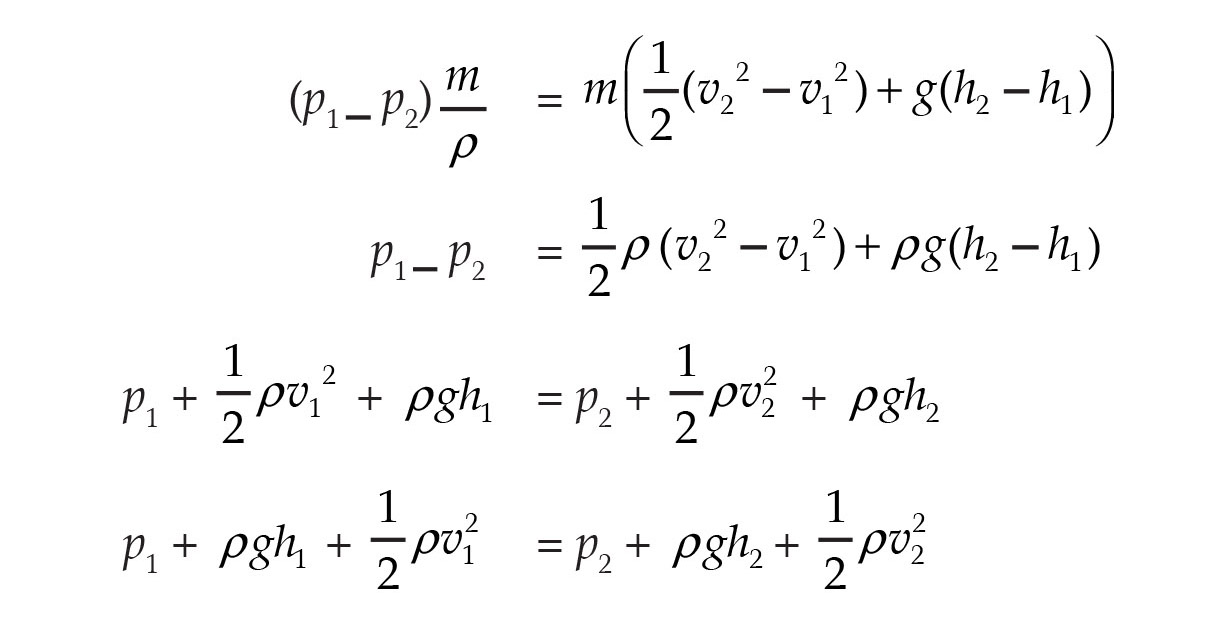
Формула гидростатического давления выводится достаточно просто
Из этой формулы видно, что давление не зависит от площади сосуда или его формы. Оно зависит только от плотности и высоты столба конкретной жидкости. Из чего следует, что, увеличив высоту сосуда, мы можем при небольшом объеме создать довольно высокое давление.
Также это приводит к такому явлению как гидростатический парадокс.
Гидростатический парадокс — явление, при котором сила весового давления налитой в сосуд жидкости на дно сосуда может отличаться от веса налитой жидкости. В сосудах с увеличивающимся кверху поперечным сечением сила давления на дно сосуда меньше веса жидкости, в сосудах с уменьшающимся кверху поперечным сечением сила давления на дно сосуда больше веса жидкости.
На картинке вверху давление на дно сосуда по всех случаях одинакова и не зависит от веса налитой жидкости, а только от ее уровня. Причина гидростатического парадокса состоит в том, что жидкость давит не только на дно, но и на стенки сосуда. Давление жидкости на наклонные стенки имеет вертикальную составляющую. В расширяющемся кверху сосуде она направлена вниз, в сужающемся кверху сосуде она направлена вверх. Вес жидкости в сосуде будет равен сумме вертикальных составляющих давления жидкости по всей внутренней площади сосуда
Источники в википедии: Гидростатическое давление Гидростатический парадокс
Расчёт давления жидкости на дно и стенки сосуда
Конспект по физике для 7 класса «Расчёт давления жидкости на дно и стенки сосуда». ВЫ УЗНАЕТЕ: Что такое гидростатическое давление. Как рассчитать давление жидкости на дно сосуда. Как рассчитать давление жидкости на стенки сосуда.
ВСПОМНИТЕ: Как формулируется закон Паскаля? Как определить давление твёрдого тела на опору? Как зависит масса тела от его плотности? Что такое вес тела? Как вес тела зависит от его массы?
Конспекты по физике Учебник физики Тесты по физике
Расчёт давления жидкости на дно и стенки сосуда
Жидкость, находящаяся в сосуде, оказывает давление как на дно сосуда, так и на его стенки. Поверхность жидкости, которая не соприкасается со стенками сосуда, называют свободной поверхностью жидкости. Давление, оказываемое покоящейся жидкостью, называют гидростатическим.
РАСЧЁТ ДАВЛЕНИЯ ЖИДКОСТИ НА ДНО СОСУДА
Вычислим давление жидкости на дно сосуда площадью S, если высота столба жидкости в этом сосуде равна h. Как известно, давление определяется по формуле p = F/S.
В нашем случае сила F, с которой жидкость действует на дно сосуда, равна её весу.
Вес жидкости определяется по формуле Р = mg. (1)
Следовательно, для определения веса жидкости необходимо найти её массу. Для этого воспользуемся формулой m = pV, где р — плотность жидкости, а V — объём жидкости. Для определения объёма необходимо найти произведение площади дна сосуда и высоты столба жидкости: V = Sh.
Следовательно, масса жидкости в сосуде определяется по формуле m = рSh. (2)
Подставим это выражение в формулу (1) и получим Р = gpSh. (3)
Теперь для нахождения давления необходимо вес жидкости разделить на площадь сосуда: P = gpSh/S
Сократив в полученном выражении S в числителе и знаменателе, получим формулу для расчёта давления жидкости на дно сосуда: p = pgh.
(4)
Давление жидкости на дно сосуда рассчитывают по формуле p = pgh.
РАСЧЁТ ДАВЛЕНИЯ ЖИДКОСТИ НА СТЕНКИ СОСУДА
Так как по закону Паскаля давление внутри жидкости на одном и том же уровне одинаково по всем направлениям, то по формуле (4) можно находить давление жидкости на стенки сосуда на любой глубине.
Из формулы (4) видно, что давление жидкости на дно и стенки сосуда прямо пропорционально высоте столба жидкости и зависит по только от высоты столба жидкости, но и от плотности жидкости р. Чем больше плотность жидкости, тем большее давление она оказывает при условии, что высота столба жидкости остаётся постоянной.
Даже при использовании дыхательных трубок, выступающих над водой, глубина погружения человека не может превышать 1,5 м, так как из-за давления воды у него не хватает сил увеличив объём грудной клетки и вдохнуть воздух. В 1943 г французами Ж. Кусто и Э. Ганьяном был изобретён акваланг специальный аппарат со сжатым воздухом, предназначенный для дыхания под водой и позволяющий находиться под водой от нескольких минут (на глубине около 40 м) до часа и более.
В соответствии с формулой (4) давление жидкости также зависит от ускорения свободного падения g. Значит, если представить себе один и тот же сосуд с жидкостью, помещенный на разные планеты, то давление на дно и стенки сосуда в нем будет различно в зависимости от значения g на планете.
ГИДРОСТАТИЧЕСКИЙ ПАРАДОКС
Из формулы (4) видно, что давление жидкости на дно и стенки сосуда зависит только от плотности и высоты столба жидкости и не зависит от формы сосуда.
Приведённая схема опыта показывает, что сила, с которой жидкость оказывает давление на дно сосудов различной формы, но с одинаковой площадью дна и одинаковой высотой столба жидкости в них, будет одной и той же. Каждый из сосудов снабжён съемным дном, и динамометры показывают именно 3 силу воздействия воды на дно сосудов, но не вес жидкости.
Очевидно, что вес жидкости в сосудах будет различным, так как объёмы жидкости в сосудах неодинаковы.
По закону Паскаля давление столба жидкости высотой h равномерно передаётся в любую точку дна каждого из сосудов. Именно поэтому сила, с которой жидкость оказывает давление на дно, больше веса жидкости в сосуде В, но меньше веса жидкости в сосуде С. Несмотря на кажущееся противоречие, ничего парадоксального в этих опытах нет.
ОПЫТ ПАСКАЛЯ
Даже небольшим количеством воды можно создать очень большое давление. В 1648 г. этот факт очень убедительно продемонстрировал В. Паскаль, поразив своих современников. В прочную, наполненную водой и закрытую со всех сторон бочку площадью поверхности 2 м2 была вставлена тоненькая трубочка площадью сечения 1 см2 и высотой 5 м. Затем Паскаль поднялся на балкон второго этажа и влил в эту трубочку всего кружку воды. Из-за малого диаметра трубки вода поднялась до большой высоты, и давление на стенки бочки так возросло, что планки (клёпки) бочки разошлись и вода стала вытекать из бочки.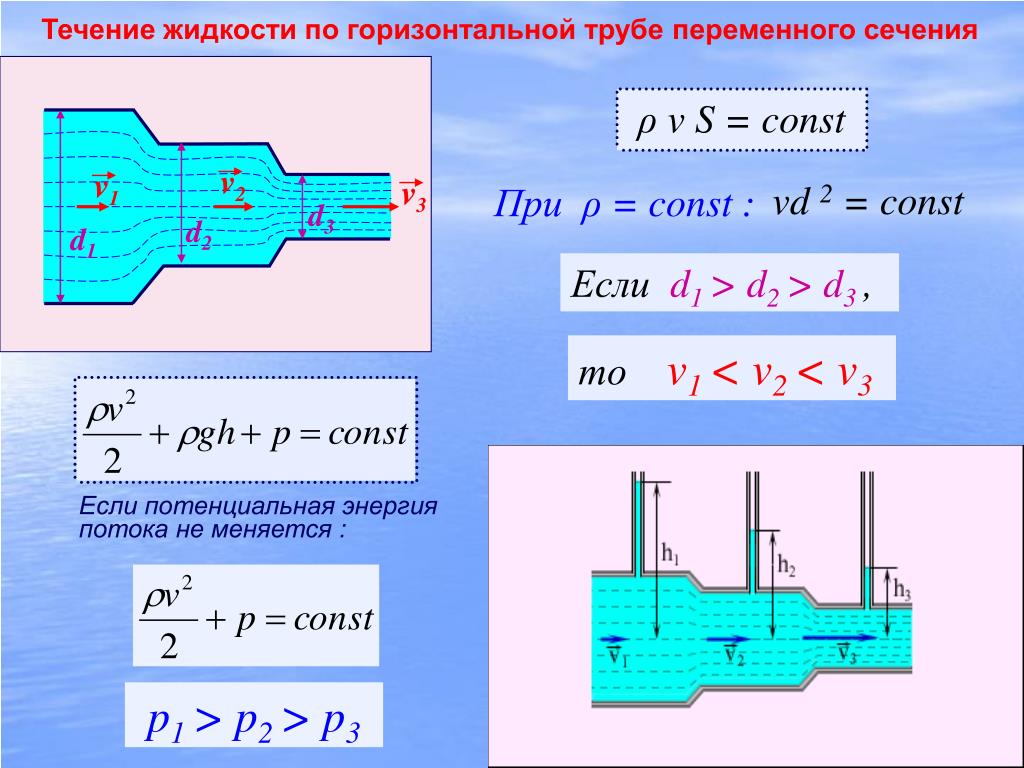
Вы смотрели Конспект по физике для 7 класса «Расчёт давления жидкости на дно и стенки сосуда»: Что такое гидростатическое давление. Как рассчитать давление жидкости на дно сосуда. Как рассчитать давление жидкости на стенки сосуда.
Вернуться к Списку конспектов по физике (В оглавление).
Формула давления
ОПРЕДЕЛЕНИЕДавление столба жидкости (гидростатическое давление) равно плотности этой жидкости, умноженной на высоту столба жидкости и ускорение свободного падения.
Здесь – давление, – плотность жидкости, – ускорение свободного падения ( м/с), – высота столба жидкости (глубина, на которой находится сдавливаемое тело).
Единица измерения давления – Па (паскаль).
Это векторная величина. В каждой точке жидкости давление одинаково во всех направлениях. Чаще всего в задачах требуется найти давление столба воды.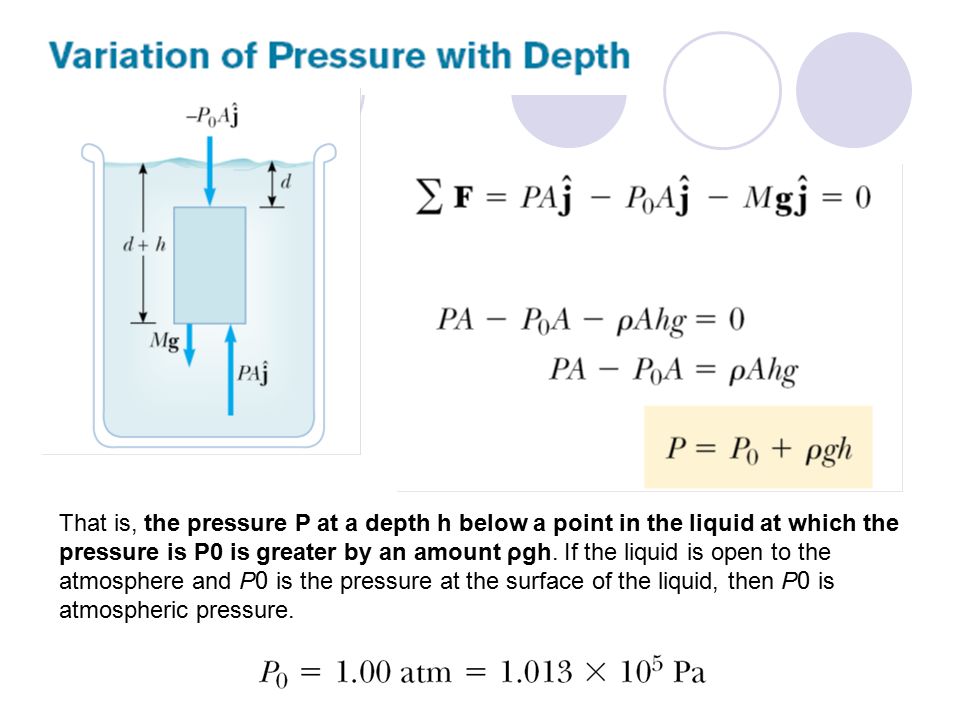
Её плотность – 1000 кг/м. Формула верна не только для жидкости, но и для идеального газа. Есть ещё одна формула давления:
Где – сила тяжести, действующая на жидкость (её вес), – площадь поверхности, на которую оказывается давление.
Примеры решения задач по теме «Давление»
ПРИМЕР 1| Задание | Высота воды в аквариуме 1 м. Найти давление на дно аквариума. |
| Решение | Напоминаем, плотность воды кг/м, а м/с. Таким образом:
(Па) |
| Ответ | Давление воды составляет 9800 Паскаль. |
| Задание | Закрытый сосуд устроен так, что его крышка подвижна (см. рисунок). Сосуд наполнен жидкостью, плотность которой известна. На крышку сосуда действует сила . Найти давление на дно сосуда, если известны площадь дна и крышки и объём жидкости в сосуде. |
| Решение | Пусть:
– площадь крышки – площадь дна – объём жидкости – плотность жидкости Крышка подвижна, значит она давит на жидкость с той силой, с которой внешние силы давят на неё сверху. Очевидно: Попробуем найти давление жидкости: Соберём всё вместе: |
| Ответ |
Все формулы по физике
Формула силы выталкивания
Формула напряжённости магнитного поля
Формула силы Ампера
Формула ЭДС
Формула длины волны
Формула давления воздуха, пара, жидкости или твердого тела. Как находить давление (формула)?
Давление – это физическая величина, которая играет особую роль в природе и жизни человека. Это незаметное глазу явление не только влияет на состояние окружающей среды, но и очень хорошо ощущается всеми. Давайте разберемся, что это такое, какие виды его существуют и как находить давление (формула) в разных средах.
Что называется давлением в физике и химии
Данным термином именуется важная термодинамическая величина, которая выражается в соотношении перпендикулярно оказываемой силы давления на площадь поверхности, на которую она воздействует.
Это явление не зависит от размера системы, в которой действует, поэтому относится к интенсивным величинам.
В состоянии равновесия, по закону Паскаля, давление одинаково для всех точек системы.
В физике и химии оное обозначается с помощью буквы «Р», что является сокращением от латинского названия термина – pressūra.
Если речь идет об осмотическом давлении жидкости (равновесие между давлением внутри и снаружи клетки), используется буква «П».
Единицы давления
Согласно стандартам Международной системы СИ, рассматриваемое физическое явление измеряется в паскалях (кириллицей – Па, латиницей – Ра).
Исходя из формулы давления получается, что один Па равен одному Н (ньютон – единица измерения силы) разделенному на один квадратный метр (единица измерения площади).
Однако на практике применять паскали довольно сложно, поскольку эта единица очень мала. В связи с этим, помимо стандартов системы СИ, данная величина может измеряться по-другому.
Ниже приведены наиболее известные ее аналоги.
Большинство из них широко используется на просторах бывшего СССР.
- Бары. Один бар равен 105 Па.
- Торры, или миллиметры ртутного столба. Приблизительно один торр соответствует 133, 3223684 Па.
- Миллиметры водяного столба.
- Метры водяного столба.
- Технические атмосферы.
- Физические атмосферы. Одна атм равна 101 325 Па и 1,033233 ат.
- Килограмм-силы на квадратный сантиметр. Также выделяются тонна-сила и грамм-сила. Помимо этого, есть аналог фунт-сила на квадратный дюйм.
Общая формула давления (физика 7-го класса)
Из определения данной физической величины можно определить способ ее нахождения. Выглядит он таким образом, как на фото ниже.
В нем F – это сила, а S – площадь. Иными словами, формула нахождения давления – это его сила, разделенная на площадь поверхности, на которую оно воздействует.
Также она может быть записана так: Р = mg / S или Р = pVg / S.
Таким образом, эта физическая величина оказывается связанной с другими термодинамическими переменными: объемом и массой.
Для давления действует следующий принцип: чем меньше пространство, на которое влияет сила – тем большее количество давящей силы на него приходится. Если, же площадь увеличивается (при той же силе) – искомая величина уменьшается.
Формула гидростатического давления
Разные агрегатные состояния веществ, предусматривают наличие у них отличных друг от друга свойств. Исходя из этого, способы определения Р в них тоже будут другими.
К примеру, формула давления воды (гидростатического) выглядит вот так: Р = pgh. Также она применима и к газам. При этом ее нельзя использовать для вычисления атмосферного давления, из-за разности высот и плотностей воздуха.
В данной формуле р – плотность, g – ускорение свободного падения, а h – высота. Исходя из этого, чем глубже погружается предмет или объект, тем выше оказываемое на него давление внутри жидкости (газа).
Рассматриваемый вариант является адаптацией классической примера Р = F / S.
Если вспомнить, что сила равна производной массы на скорость свободного падения (F= mg), а масса жидкости – это производная объема на плотность (m = pV), то формулу давление можно записать как P = pVg / S. При этом объем – это площад, умноженная на высоту (V = Sh).
Если вставить эти данные, получится, что площадь в числителе и знаменателе можно сократить и на выходе – вышеупомянутая формула: Р = pgh.
Рассматривая давление в жидкостях, стоит помнить, что, в отличие от твердых тел, в них часто возможно искривление поверхностного слоя. А это, в свою очередь, способствует образованию дополнительного давления.
Для подобных ситуаций применяется несколько другая формула давления: Р = Р0 + 2QH. В данном случае Р0 – давление не искривленного слоя, а Q – поверхность натяжения жидкости. Н – это средняя кривизна поверхности, которую определяют по Закону Лапласа: Н = ½ (1/R1+ 1/R2).
Составляющие R1 и R2 – это радиусы главной кривизны.
Парциальное давление и его формула
Хотя способ Р = pgh применим как для жидкостей, так и для газов, давление в последних лучше вычислять несколько другим путем.
Дело в том, что в природе, как правило, не очень часто встречаются абсолютно чистые вещества, ведь в ней преобладают смеси. И это касается не только жидкостей, но и газов. А как известно, каждый из таких компонентов осуществляет разное давление, называемое парциальным.
Определить его довольно просто. Оно равно сумме давления каждого компонента рассматриваемой смеси (идеальный газ).
Из этого следует, что формула парциального давления выглядит таким образом: Р = Р1+ Р2+ Р3… и так далее, согласно количеству составляющих компонентов.
Нередки случаи, когда необходимо определить давление воздуха. Однако некоторые по ошибке проводят вычисления только с кислородом по схеме Р = pgh. Вот только воздух – это смесь из разных газов.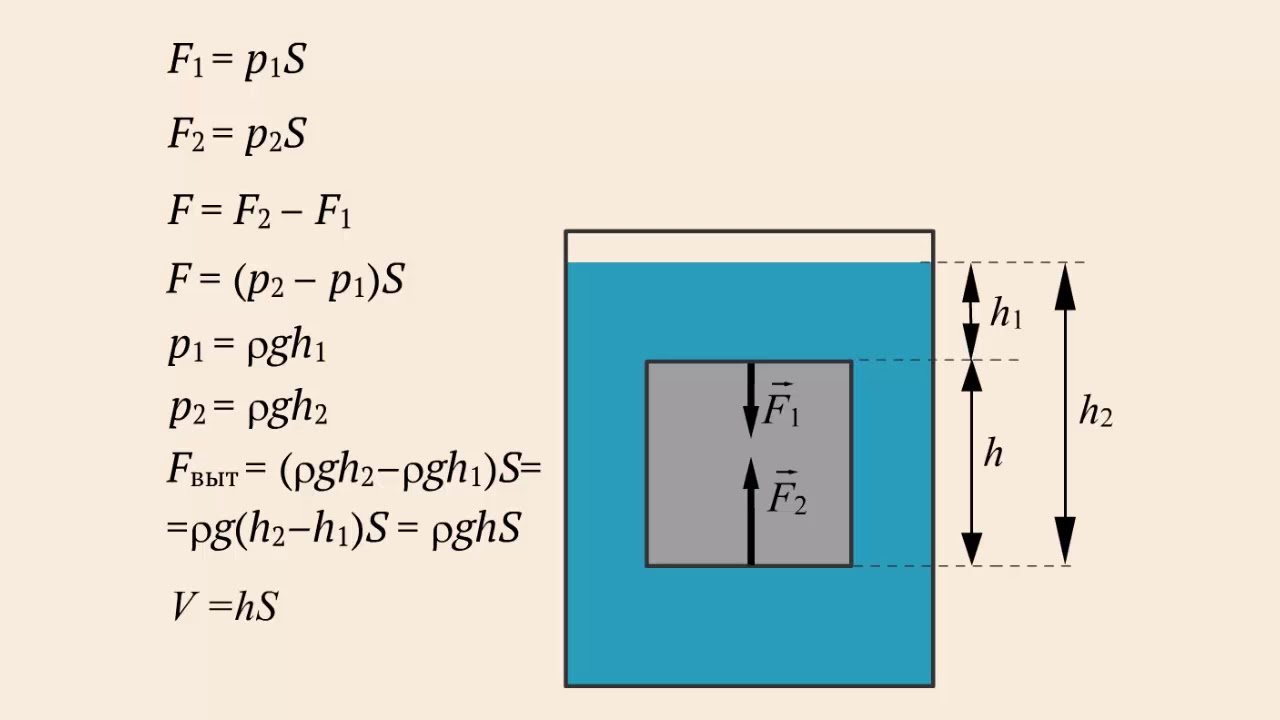
В нем встречаются азот, аргон, кислород и другие вещества. Исходя из сложившейся ситуации, формула давления воздуха – это сумма давлений всех его составляющих. А значит, следует приметь вышеупомянутую Р = Р1+ Р2+ Р3…
Наиболее распространенные приборы для измерения давления
Несмотря на то что высчитать рассматриваемую термодинамическую величину по вышеупомянутым формулам не сложно, проводить вычисление иногда попросту нет времени. Ведь нужно всегда учитывать многочисленные нюансы. Поэтому для удобства за несколько столетий был разработан ряд приборов, делающих это вместо людей.
Фактически почти все аппараты такого рода являются разновидностями манометра (помогает определять давление в газах и жидкостях). При этом они отличаются по конструкции, точности и сфере применения.
- Атмосферное давление измеряется с помощью манометра, именуемого барометром. Если необходимо определить разряжение (то есть давление ниже атмосферного) – применяются другая его разновидность, вакуумметр.
- Для того чтобы узнать артериальное давление у человека, в ход идет сфигмоманометр. Большинству он более известен под именем неинвазивного тонометра. Таких аппаратов существуют немало разновидностей: от ртутных механических до полностью автоматических цифровых. Их точность зависит от материалов, из которых они изготавливаются и места измерения.
- Перепады давления в окружающей среде (по-английски – pressure drop) определяются с помощью дифференциальных манометров или дифнамометров (не путать с динамометрами).
Виды давления
Рассматривая давление, формулу его нахождения и ее вариации для разных веществ, стоит узнать о разновидностях этой величины. Их пять.
- Абсолютное.
- Барометрическое
- Избыточное.
- Вакуумметрическое.
- Дифференциальное.
Абсолютное
Так называется полное давление, под которым находится вещество или объект, без учета влияния других газообразных составляющих атмосферы.
Измеряется оно в паскалях и являет собою сумму избыточного и атмосферного давлений. Также он является разностью барометрического и вакуумметрического видов.
Вычисляется оно по формуле Р = Р2 + Р3 или Р = Р2 – Р4.
За начало отсчета для абсолютного давления в условиях планеты Земля, берется давление внутри емкости, из которой удален воздух (то есть классический вакуум).
Только такой вид давления используется в большинстве термодинамических формул.
Барометрическое
Этим термином именуется давление атмосферы (гравитации) на все предметы и объекты, находящие в ней, включая непосредственно поверхность Земли. Большинству оно также известно под именем атмосферного.
Его причисляют к термодинамическим параметрам, а его величина меняется относительно места и времени измерения, а также погодных условий и нахождения над/ниже уровня моря .
Величина барометрического давления равна модулю силы атмосферы на площади единицу по нормали к ней.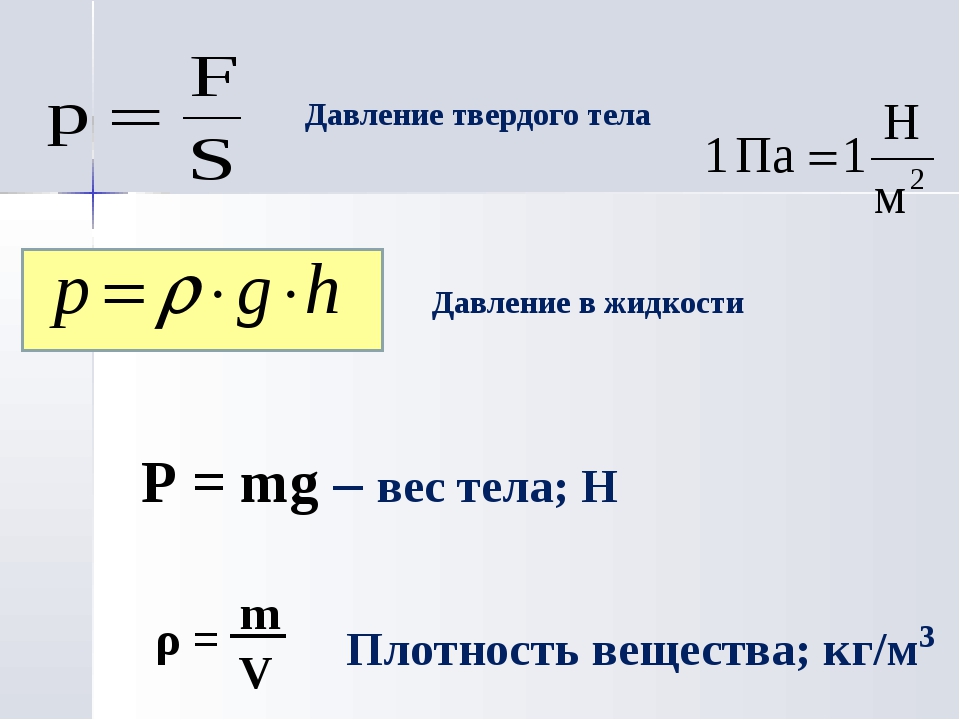
В стабильной атмосфере величина данного физического явления равна весу столпа воздуха на основание с площадью, равной единице.
Норма барометрического давления – 101 325 Па (760 мм рт. ст. при 0 градусов Цельсия). При этом чем выше объект оказывается от поверхности Земли, тем более низким становится давление на него воздуха. Через каждый 8 км оно снижается на 100 Па.
Благодаря этому свойству в горах вода в чайниках закивает намного быстрее, чем дома на плите. Дело в том, что давление влияет на температуру кипения: с его снижением последняя уменьшается. И наоборот. На этом свойстве построена работа таких кухонных приборов , как скороварка и автоклав. Повышение давления внутри их способствуют формированию в посудинах более высоких температур, нежели в обычных кастрюлях на плите.
Используется для вычисления атмосферного давления формула барометрической высоты. Выглядит она таким образом, как на фото ниже.
Р – это искомая величина на высоте, Р0 – плотность воздуха возле поверхности, g – свободного падения ускорение, h – высота над Землей, м – молярная масса газа, т – температура системы, r – универсальная газовая постоянная 8,3144598 Дж⁄(моль х К), а е – это число Эйклера, равное 2.
71828.
Часто в представленной выше формуле давления атмосферного вместо R используется К – постоянная Больцмана. Через ее произведение на число Авогадро нередко выражается универсальная газовая постоянная. Она более удобна для расчетов, когда число частиц задано в молях.
При проведении вычислений всегда стоит брать во внимание возможность изменения температуры воздуха из-за смены метеорологической ситуации или при наборе высоты над уровнем моря, а также географическую широту.
Избыточное и вакуумметрическое
Разницу между атмосферным и измеренным давлением окружающей среды называют избыточным давлением. В зависимости от результата, меняется название величины.
Если она положительная, ее называют манометрическим давлением.
Если же полученный результат со знаком минус – его именуют вакуумметрическим. Стоит помнить, что он не может быть больше барометрического.
Дифференциальное
Данная величина является разницей давлений в различных точках измерения.
Как правило, ее используют для определения падения давления на каком-либо оборудовании. Особенно это актуально в нефтедобывающей промышленности.
Разобравшись с тем, что за термодинамическая величина называется давлением и с помощью каких формул ее находят, можно сделать вывод, что это явление весьма важно, а потому знания о нем никогда не будут лишними.
Пластовое давление и температура — Мегаобучалка
Нефть и газ, заполняя пустоты продуктивного пласта, залегающего на больших глубинах в земной коре, находятся под действием пластовых давлений и температур.
Пластовое давление. Под пластовым понимают давление при котором нефть, газ и вода находятся в пустотах коллектора в естественных условиях залегания. Природа и величина этого давления обусловлены тем, что продуктивная часть пласта связана или была связана ранее с выходом пласта на поверхность, через который происходило питание его водой. Разность уровней между областью питания на поверхности и глубиной залегания пласта и определила наличие в поровом пространстве избыточного давления, называемого пластовым.
От величины пластового давления зависят запас пластовой энергии и свойства жидкостей и газов в пластовых условиях. Пластовое давление определяет запасы нефтяной и газовой залежи, дебиты скважин и условия эксплуатации залежей.
Пластовое давление измеряют в скважинах с помощью скважинных манометров или рассчитывают по положению уровня жидкости в скважине с высокой степенью достоверности. Так как за счет веса столба жидкости давление у подошвы пласта выше, чем у кровли, то определение пластового давления принято проводить в точке, соответствующей середине продуктивного пласта.
Пластовое давление и уровень жидкости измеряют в неработающих или специально для этого остановленных скважинах. Это позволяет избежать ошибок, связанных с процессом перераспределения давления при движении жидкости по пласту и в скважине.
Если уровень жидкости в скважине расположен ниже ее устья, о чем можно судить по отсутствию избыточного давления на устье скважины, то пластовое давление можно рассчитать по формуле:
Pn,=P-g-H (3.
(3.4)
где 7, и Ту – соответственно абсолютные температуры на забое и устье скважины.
Расчет по формуле (3.3) обеспечивает достаточную точность лишь для чисто газовых скважин. Наличие жидкости на забое скважины исключает применение данного метода.
Начальное пластовое давление, измеряемое до начала разработки залежи, кроме глубины залегания пласта зависит от процесса формирования залежи, особенно от переуплотнения коллектора, наличия гидродинамической связи с другими водонасыщенными пластами.
Пластовое давление можно выразить через высоту столба жидкости h, уравновешивающую его, по формуле:
h=Pn„/(p-g) (3.5)
сравнивая величину h, называемую гидростатическим напором, с глубиной залегания пласта Ндл, судят о пластовом давлении. Если гидростатический напор, обусловленный начальным пластовым давлением, составляет (0,8-1,3) Н„л, то давление считают нормальным. В противном случае говорят об аномально высоком и аномально низком пластовых давлениях.
Пластовая температура. В связи с наличием потока тепла от ядра Земли к поверхности с глубиной возрастает и температура с увеличением глубины на каждые 100 м, называется геотермическим градиентом. Для различных районов в зависимости от теплофизических свойств пород, толщины осадочного слоя пород и наличия
циркуляции подземных вод он может изменяться от 1 до 12 К на 100 м. Наиболее часто встречающее его значение ЗКна 100м.
По известному геотермическому градиенту легко оценить пластовую температуру, которую можно ожидать на данной глубине:
(3.
6)
где tg – температура нейтрального слоя; Г – геотермический градиент; Н – глубина, на которой определяется температура t; ho – глубина нейтрального слоя. Под нейтральным слоем подрузамевают слой земли, ниже которого не сказываются сезонные колебания температуры. Для большинства районов страны он находится на глубине 3-5 м. Температура в этом слое может быть принята равной среднегодовой температуре воздуха в данном районе.
Пластовые давление и температура несут информацию об энергетическом состоянии залежи. От них зависит большинство физических характеристик пород и насыщающих жидкостей и газов, фазовое состояние углеводородов в залежи.
что находится по формуле …=pgh (ро, ж, аш) в физике????
что находится по формуле …=pgh (ро, ж, аш) в физике????
0
2 K
больше 3лет назад
0 комментариев
Войдите что бы оставлять комментарии
Ответы (10)
давление жидкости
0
ответ написан больше 3лет назад
0 комментариев
Войдите что бы оставлять комментарии
Давление на глубине h в жидкости с плотностью ро)
0
ответ написан больше 3лет назад
0 комментариев
Войдите что бы оставлять комментарии
по-моему это формула на давление
0
ответ написан больше 3лет назад
0 комментариев
Войдите что бы оставлять комментарии
Давление жидкости на дно и стенки сосуда: P=pgh(где p-плотность жидкости, h-высота (глубина) жидкости
0
ответ написан больше 3лет назад
0 комментариев
Войдите что бы оставлять комментарии
густота, притяжение, высота
0
ответ написан больше 3лет назад
0 комментариев
Войдите что бы оставлять комментарии
Давление на дно! Однажды очень помогла эта формула на олимпиаде
0
ответ написан больше 3лет назад
0 комментариев
Войдите что бы оставлять комментарии
Так же это может оказаться давление твёрдого тела.
Поскольку p=F:S, где F-сила, S-площадь. F=mg, m=p(ро) V(объём) V=Sh. Получается что p=Spgh6:S. S и S сокращаются, получается p=pgh
0
ответ написан больше 3лет назад
0 комментариев
Войдите что бы оставлять комментарии
Это формула силы Архимеда (Fа) Ро-это плотность жидкости в которую погружено тело ж-это ускорение свободного падения= 9.8 (Иногда округляют до 10) аш-Это высота
0
ответ написан больше 3лет назад
0 комментариев
Войдите что бы оставлять комментарии
Смотря, что такое p, g и h. Если удельная теплоёмкость, масса и разница температур, то это количество тепла для нагревания тела. А если масса, ускорение и путь, то это работа силы, действующей на тело. Если же это электрический заряд, магнитная индукция и скорость заряженной частицы, то это сила Лоренца. Источник: ответы выше неверны
0
ответ написан больше 3лет назад
0 комментариев
Войдите что бы оставлять комментарии
Это нахождение гидростатического давления
0
ответ написан больше 3лет назад
0 комментариев
Войдите что бы оставлять комментарии
Оставить ответ
Войдите, чтобы написать ответ
Расчет давления жидкости на дно и стенки сосуда.
Формула давления воздуха, пара, жидкости или твердого телаДавление – это физическая величина, которая играет особую роль в природе и жизни человека. Это незаметное глазу явление не только влияет на состояние окружающей среды, но и очень хорошо ощущается всеми. Давайте разберемся, что это такое, какие виды его существуют и как находить давление (формула) в разных средах.
Что называется давлением в физике и химии
Данным термином именуется важная термодинамическая величина, которая выражается в соотношении перпендикулярно оказываемой силы давления на площадь поверхности, на которую она воздействует. Это явление не зависит от размера системы, в которой действует, поэтому относится к интенсивным величинам.
В состоянии равновесия, по давление одинаково для всех точек системы.
В физике и химии оное обозначается с помощью буквы «Р», что является сокращением от латинского названия термина – pressūra.
Если речь идет об осмотическом давлении жидкости (равновесие между давлением внутри и снаружи клетки), используется буква «П».
Единицы давления
Согласно стандартам Международной системы СИ, рассматриваемое физическое явление измеряется в паскалях (кириллицей – Па, латиницей – Ра).
Исходя из формулы давления получается, что один Па равен одному Н (ньютон – разделенному на один квадратный метр (единица измерения площади).
Однако на практике применять паскали довольно сложно, поскольку эта единица очень мала. В связи с этим, помимо стандартов системы СИ, данная величина может измеряться по-другому.
Ниже приведены наиболее известные ее аналоги. Большинство из них широко используется на просторах бывшего СССР.
- Бары . Один бар равен 105 Па.
- Торры, или миллиметры ртутного столба. Приблизительно один торр соответствует 133, 3223684 Па.
- Миллиметры водяного столба.
- Метры водяного столба.
- Технические атмосферы.
- Физические атмосферы. Одна атм равна 101 325 Па и 1,033233 ат.
- Килограмм-силы на квадратный сантиметр. Также выделяются тонна-сила и грамм-сила. Помимо этого, есть аналог фунт-сила на квадратный дюйм.
Также выделяются тонна-сила и грамм-сила. Помимо этого, есть аналог фунт-сила на квадратный дюйм.Общая формула давления (физика 7-го класса)
Из определения данной физической величины можно определить способ ее нахождения. Выглядит он таким образом, как на фото ниже.
В нем F – это сила, а S – площадь. Иными словами, формула нахождения давления – это его сила, разделенная на площадь поверхности, на которую оно воздействует.
Также она может быть записана так: Р = mg / S или Р = pVg / S. Таким образом, эта физическая величина оказывается связанной с другими термодинамическими переменными: объемом и массой.
Для давления действует следующий принцип: чем меньше пространство, на которое влияет сила – тем большее количество давящей силы на него приходится. Если, же площадь увеличивается (при той же силе) – искомая величина уменьшается.
Формула гидростатического давления
Разные агрегатные состояния веществ, предусматривают наличие у них отличных друг от друга свойств.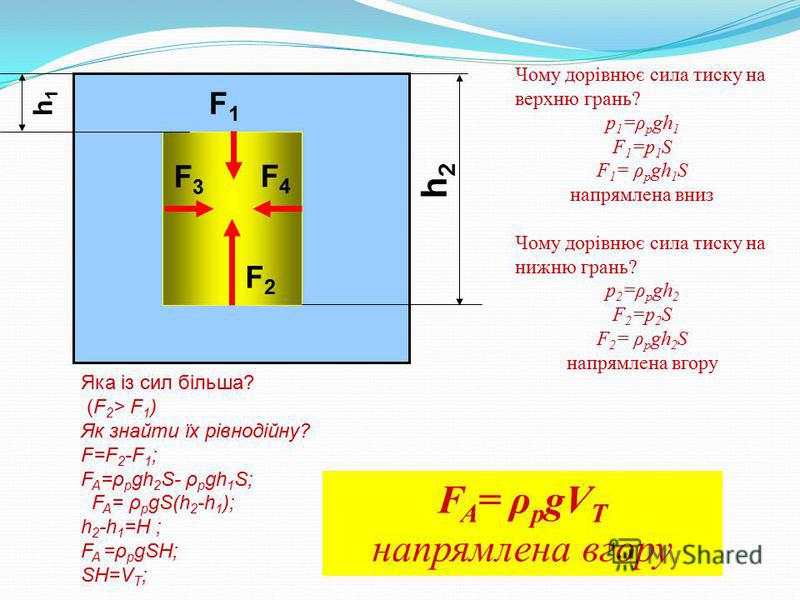
Исходя из этого, способы определения Р в них тоже будут другими.
К примеру, формула давления воды (гидростатического) выглядит вот так: Р = pgh. Также она применима и к газам. При этом ее нельзя использовать для вычисления атмосферного давления, из-за разности высот и плотностей воздуха.
В данной формуле р – плотность, g – ускорение свободного падения, а h – высота. Исходя из этого, чем глубже погружается предмет или объект, тем выше оказываемое на него давление внутри жидкости (газа).
Рассматриваемый вариант является адаптацией классической примера Р = F / S.
Если вспомнить, что сила равна производной массы на скорость свободного падения (F= mg), а масса жидкости – это производная объема на плотность (m = pV), то формулу давление можно записать как P = pVg / S. При этом объем – это площад, умноженная на высоту (V = Sh).
Если вставить эти данные, получится, что площадь в числителе и знаменателе можно сократить и на выходе – вышеупомянутая формула: Р = pgh.
Рассматривая давление в жидкостях, стоит помнить, что, в отличие от твердых тел, в них часто возможно искривление поверхностного слоя. А это, в свою очередь, способствует образованию дополнительного давления.
Для подобных ситуаций применяется несколько другая формула давления: Р = Р 0 + 2QH. В данном случае Р 0 – давление не искривленного слоя, а Q – поверхность натяжения жидкости. Н – это средняя кривизна поверхности, которую определяют по Закону Лапласа: Н = ½ (1/R 1 + 1/R 2). Составляющие R 1 и R 2 – это радиусы главной кривизны.
Парциальное давление и его формула
Хотя способ Р = pgh применим как для жидкостей, так и для газов, давление в последних лучше вычислять несколько другим путем.
Дело в том, что в природе, как правило, не очень часто встречаются абсолютно чистые вещества, ведь в ней преобладают смеси. И это касается не только жидкостей, но и газов. А как известно, каждый из таких компонентов осуществляет разное давление, называемое парциальным.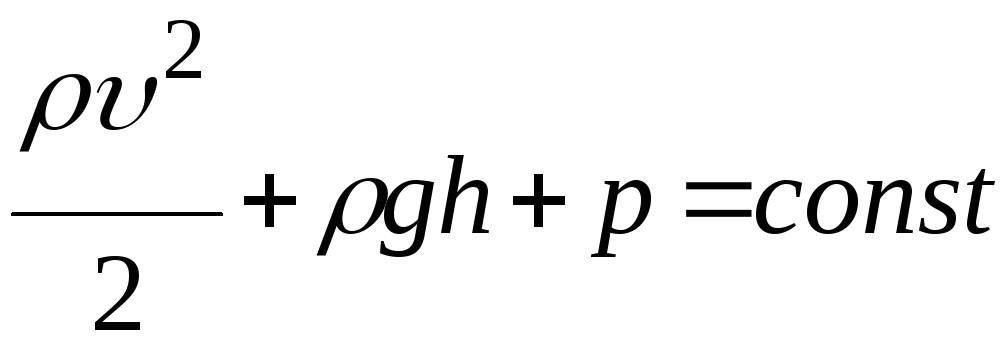
Определить его довольно просто. Оно равно сумме давления каждого компонента рассматриваемой смеси (идеальный газ).
Из этого следует, что формула парциального давления выглядит таким образом: Р = Р 1 + Р 2 + Р 3 … и так далее, согласно количеству составляющих компонентов.
Нередки случаи, когда необходимо определить давление воздуха. Однако некоторые по ошибке проводят вычисления только с кислородом по схеме Р = pgh. Вот только воздух – это смесь из разных газов. В нем встречаются азот, аргон, кислород и другие вещества. Исходя из сложившейся ситуации, формула давления воздуха – это сумма давлений всех его составляющих. А значит, следует приметь вышеупомянутую Р = Р 1 + Р 2 + Р 3 …
Наиболее распространенные приборы для измерения давления
Несмотря на то что высчитать рассматриваемую термодинамическую величину по вышеупомянутым формулам не сложно, проводить вычисление иногда попросту нет времени. Ведь нужно всегда учитывать многочисленные нюансы. Поэтому для удобства за несколько столетий был разработан ряд приборов, делающих это вместо людей.
Фактически почти все аппараты такого рода являются разновидностями манометра (помогает определять давление в газах и жидкостях). При этом они отличаются по конструкции, точности и сфере применения.
- Атмосферное давление измеряется с помощью манометра, именуемого барометром. Если необходимо определить разряжение (то есть давление ниже атмосферного) – применяются другая его разновидность, вакуумметр.
- Для того чтобы узнать артериальное давление у человека, в ход идет сфигмоманометр. Большинству он более известен под именем неинвазивного тонометра. Таких аппаратов существуют немало разновидностей: от ртутных механических до полностью автоматических цифровых. Их точность зависит от материалов, из которых они изготавливаются и места измерения.
- Перепады давления в окружающей среде (по-английски – pressure drop) определяются с помощью или дифнамометров (не путать с динамометрами).
Виды давления
Рассматривая давление, формулу его нахождения и ее вариации для разных веществ, стоит узнать о разновидностях этой величины.
Их пять.
- Абсолютное.
- Барометрическое
- Избыточное.
- Вакуумметрическое.
- Дифференциальное.
Абсолютное
Так называется полное давление, под которым находится вещество или объект, без учета влияния других газообразных составляющих атмосферы.
Измеряется оно в паскалях и являет собою сумму избыточного и атмосферного давлений. Также он является разностью барометрического и вакуумметрического видов.
Вычисляется оно по формуле Р = Р 2 + Р 3 или Р = Р 2 – Р 4 .
За начало отсчета для абсолютного давления в условиях планеты Земля, берется давление внутри емкости, из которой удален воздух (то есть классический вакуум).
Только такой вид давления используется в большинстве термодинамических формул.
Барометрическое
Этим термином именуется давление атмосферы (гравитации) на все предметы и объекты, находящие в ней, включая непосредственно поверхность Земли. Большинству оно также известно под именем атмосферного.
Его причисляют к а его величина меняется относительно места и времени измерения, а также погодных условий и нахождения над/ниже уровня моря.
Величина барометрического давления равна модулю силы атмосферы на площади единицу по нормали к ней.
В стабильной атмосфере величина данного физического явления равна весу столпа воздуха на основание с площадью, равной единице.
Норма барометрического давления – 101 325 Па (760 мм рт. ст. при 0 градусов Цельсия). При этом чем выше объект оказывается от поверхности Земли, тем более низким становится давление на него воздуха. Через каждый 8 км оно снижается на 100 Па.
Благодаря этому свойству в горах вода в чайниках закивает намного быстрее, чем дома на плите. Дело в том, что давление влияет на температуру кипения: с его снижением последняя уменьшается. И наоборот. На этом свойстве построена работа таких кухонных приборов, как скороварка и автоклав. Повышение давления внутри их способствуют формированию в посудинах более высоких температур, нежели в обычных кастрюлях на плите.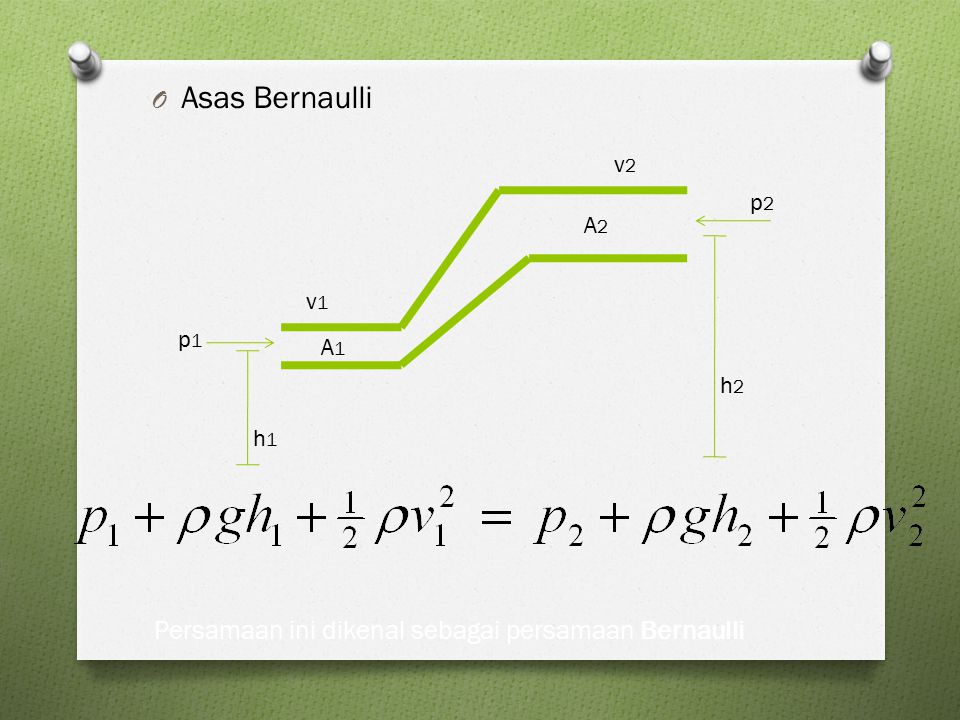
Используется для вычисления атмосферного давления формула барометрической высоты. Выглядит она таким образом, как на фото ниже.
Р – это искомая величина на высоте, Р 0 – плотность воздуха возле поверхности, g – свободного падения ускорение, h – высота над Землей, м – молярная масса газа, т – температура системы, r – универсальная газовая постоянная 8,3144598 Дж⁄(моль х К), а е – это число Эйклера, равное 2.71828.
Часто в представленной выше формуле давления атмосферного вместо R используется К – постоянная Больцмана. Через ее произведение на число Авогадро нередко выражается универсальная газовая постоянная. Она более удобна для расчетов, когда число частиц задано в молях.
При проведении вычислений всегда стоит брать во внимание возможность изменения температуры воздуха из-за смены метеорологической ситуации или при наборе высоты над уровнем моря, а также географическую широту.
Избыточное и вакуумметрическое
Разницу между атмосферным и измеренным давлением окружающей среды называют избыточным давлением.
В зависимости от результата, меняется название величины.
Если она положительная, ее называют манометрическим давлением.
Если же полученный результат со знаком минус – его именуют вакуумметрическим. Стоит помнить, что он не может быть больше барометрического.
Дифференциальное
Данная величина является разницей давлений в различных точках измерения. Как правило, ее используют для определения падения давления на каком-либо оборудовании. Особенно это актуально в нефтедобывающей промышленности.
Разобравшись с тем, что за термодинамическая величина называется давлением и с помощью каких формул ее находят, можно сделать вывод, что это явление весьма важно, а потому знания о нем никогда не будут лишними.
Рассмотрим, как можно рассчитать давление жидкости на дно и стенки сосуда. Решим сначала задачу с числовыми данными. Прямоугольный бак наполнен водой (рис. 96). Площадь дна бака 16 м2, высота его 5 м. Определим давление воды на дно бака.
Сила, с которой вода давит на дно сосуда, равна весу столба воды высотой 5 м и площадью основания 16 м2, иначе говоря, эта сила равна весу всей воды в баке.
Чтобы найти вес воды, надо знать ее массу. Массу воды можно вычислить по объему и плотности. Найдем объем воды в баке, умножив площадь дна бака на его высоту: V= 16 м2*5 м=80 м3. Теперь определим массу воды, для этого умножим ее плотность p = 1000 кг/м3 на объем: m = 1000 кг/м3 * 80 м3 = 80 000 кг. Мы знаем, что для определения веса тела надо его массу умножить на 9,8 Н/кг, так как тело массой 1 кг весит 9,8 Н.
Следовательно, вес воды в баке равен P = 9,8 Н/кг * 80 000 кг ≈ 800 000 Н. С такой силой вода давит на дно бака.
Разделив вес воды на площадь дна бака, найдем давление p:
p = 800000 H/16 м2 = 50 000 Па = 50 кПа.
Давление жидкости на дно сосуда можно рассчитать, пользуясь формулой, что значительно проще. Чтобы вывести эту формулу, вернемся к задаче, но только решим ее в общем виде.
Обозначим высоту столба жидкости в сосуде буквой h, а площадь дна сосуда S.
Объем столба жидкости V= Sh.
Масса жидкости т = pV,или m = pSh.
Вес этой жидкости P = gm, или P = gpSh.
Так как вес столба жидкости равен силе, с которой жидкость давит на дно сосуда, то, разделив вес P на площадь S, получим давление р:
p = P/S, или p = gpSh/S
p = gph.
Мы получили формулу для расчета давления жидкости на дно сосуда. Из этой формулы видно, что давление жидкости на дно сосуда прямо пропорционально плотности и высоте столба жидкости.
По этой формуле можно вычислять и давление на стенки, сосуда, а также давление внутри жидкости, в том числе давление снизу вверх, так как давление на одной и той же глубине одинаково по всем направлениям.
При расчете давления по формуле:
p = gph
надо плотность p выражать в килограммах на кубический метр (кг/м3), а высоту столба жидкости h – в метрах (м), g = 9,8 Н/кг, тогда давление будет выражено в, паскалях (Па).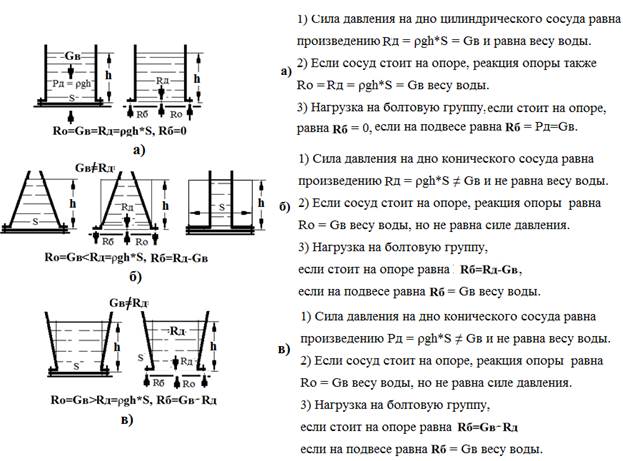
Пример. Определить давление нефти на дно цистерны, если высота столба нефти 10 м, а плотность ее 800 кг/м3.
Вопросы. 1. От каких величин зависит давление жидкости на дно сосуда? 2. Как зависит давление жидкости на дно сосуда от высоты столба жидкости? 3. Как зависит давление жидкости на дно сосуда от плотности жидкости? 4. Какие величины надо знать, чтобы рассчитать давление жидкости на стенки сосуда? 5. По какой формуле рассчитывают давление жидкости на дно и стенки сосуда?
Упражнения. 1. Определите давление на глубине 0,6 м в воде, керосине, ртути. 2. Вычислите давление воды на дно одной из глубочайших морских впадин, глубина, которой 10 900 м, Плотность морской воды 1030 кг/м3. 3. На рисунке 97 изображена футбольная камера, соединенная с вертикально расположенной стеклянной трубкой. В камере и трубке находится вода. На камеру положена дощечка, а на нее – гиря массой 5 кг. Высота столба воды в трубке 1 м. Определите площадь соприкосновения дощечки с камерой.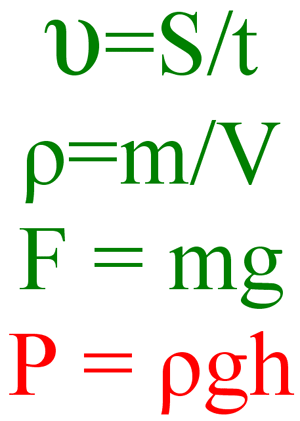
Задания. 1. Возьмите высокий сосуд. В боковой поверхности его по прямой, на разной высоте от дна сделайте три небольших отверстия. Закройте отверстия спичками и налейте в сосуд до верха воды. Откройте отверстия и проследите за струйками вытекающей воды (рис. 98). Ответьте на вопросы: почему вода вытекает из отверстий? Из чего следует, что давление увеличивается с глубиной? 2. Прочтите в конце учебника параграфы «Гидростатический парадокс. Опыт Паскаля», «Давление на дне морей и океанов. Исследование морских глубин».
Жидкости и газы передают по всем направлениям не только оказываемое на них внешнее давление, но и то давление, которое существует внутри их благодаря весу собственных частей. Верхние слои жидкости давят на средние, те – на нижние, а последние – на дно.
Давление, оказываемое покоящейся жидкостью, называется гидростатическим .
Получим формулу для расчета гидростатического давления жидкости на произвольной глубине h
(в окрестности точки А
на рисунке 98).
Сила давления, действующая в этом месте со стороны вышележащего узкого вертикального столба жидкости, может быть выражена двумя способами:
во-первых, как произведение давления в основании этого столба на площадь его сечения:
F = pS ;
во-вторых, как вес того же столба жидкости, т. е. произведение массы жидкости (которая может быть найдена по формуле m = ρV , где объем V = Sh ) на ускорение свободного падения g :
F = mg = ρShg .
Приравняем оба выражения для силы давления:
pS = ρShg .
Разделив обе части этого равенства на площадь S, найдем давление жидкости на глубине h :
p = ρgh . (37.1)
Мы получили формулу гидростатического давления . Гидростатическое давление на любой глубине внутри жидкости не зависит от формы сосуда, в котором находится жидкость, и равно произведению плотности жидкости, ускорения свободного падения и глубины, на которой рассматривается давление.
Одно и то же количество воды, находясь в разных сосудах, может оказывать разное давление на дно.
Поскольку это давление зависит от высоты столба жидкости, то в узких сосудах оно будет больше, чем в широких. Благодаря этому даже небольшим количеством воды можно создать очень большое давление. В 1648 г. это очень убедительно продемонстрировал Б. Паскаль. Он вставил в закрытую бочку, наполненную водой, узкую трубку и, поднявшись на балкон второго этажа дома, вылил в эту трубку кружку воды. Из-за малой толщины трубки вода в ней поднялась до большой высоты, и давление в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула (рис. 99).
Полученные нами результаты справедливы не только для жидкостей, но и для газов. Их слои также давят друг на друга, и потому в них тоже существует гидростатическое давление.
1. Какое давление называют гидростатическим? 2. От каких величин зависит это давление? 3. Выведите формулу гидростатического давления на произвольном глубине. 4. Каким образом с помощью небольшого количества воды можно создать большое давление? Расскажите об опыте Паскаля.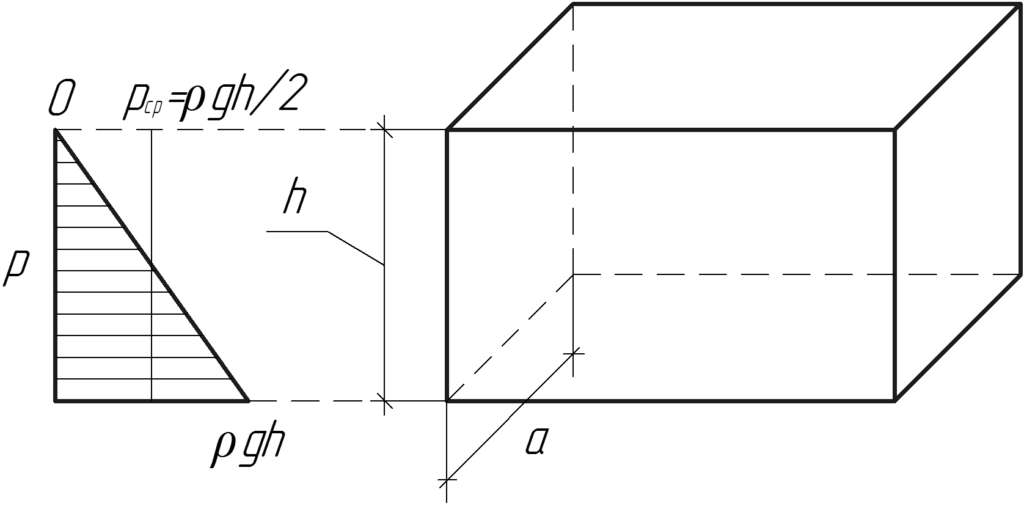
Экспериментальное задание.
Возьмите высокий сосуд и сделайте в его стенке три небольших отверстия на разной высоте. Закройте отверстия пластилином и наполните сосуд водой. Откройте отверстия и проследите за струями вытекающей воды (рис. 100). Почему вода вытекает из отверстий? Из чего следует, что давление воды увеличивается с глубиной?
В ходе этого урока с помощью математических преобразований и логических умозаключений будет получена формула для расчета давления жидкости на дно и стенки сосуда.
Тема: Давление твердых тел, жидкостей и газов
Урок: Расчет давления жидкости на дно и стенки сосуда
Для того чтобы упростить вывод формулы для расчета давления на дно и стенки сосуда, удобнее всего использовать сосуд в форме прямоугольного параллелепипеда (Рис. 1).
Рис. 1. Сосуд для расчета давления жидкости
Площадь дна этого сосуда – S , его высота – h . Предположим, что сосуд наполнен жидкостью на всю высоту h .
Чтобы определить давление на дно, нужно силу, действующую на дно, разделить на площадь дна. В нашем случае сила – это вес жидкости P , находящейся в сосуде
Поскольку жидкость в сосуде неподвижна, ее вес равен силе тяжести, которую можно вычислить, если известна масса жидкости m
Напомним, что символом g обозначено ускорение свободного падения.
Для того чтобы найти массу жидкости, необходимо знать ее плотность ρ и объем V
Объем жидкости в сосуде мы получим, умножив площадь дна на высоту сосуда
Эти величины изначально известны. Если их по очереди подставить в приведенные выше формулы, то для вычисления давления получим следующее выражение:
В этом выражении числитель и знаменатель содержат одну и ту же величину S – площадь дна сосуда. Если на нее сократить, получится искомая формула для расчета давления жидкости на дно сосуда:
Итак, для нахождения давления необходимо умножить плотность жидкости на величину ускорения свободного падения и высоту столба жидкости.
Полученная выше формула называется формулой гидростатического давления. Она позволяет найти давление на дно сосуда. А как рассчитать давление на боковые стенки сосуда? Чтобы ответить на этот вопрос, вспомним, что на прошлом уроке мы установили, что давление на одном и том же уровне одинаково во всех направлениях. Это значит, давление в любой точке жидкости на заданной глубине h может быть найдено по той же формуле.
Рассмотрим несколько примеров.
Возьмем два сосуда. В одном из них находится вода, а в другом – подсолнечное масло. Уровень жидкости в обоих сосудах одинаков. Одинаковым ли будет давление этих жидкостей на дно сосудов? Безусловно, нет. В формулу для расчета гидростатического давления входит плотность жидкости. Поскольку плотность подсолнечного масла меньше, чем плотность воды, а высота столба жидкостей одинакова, то масло будет оказывать на дно меньшее давление, чем вода (Рис. 2).
Рис. 2. Жидкости с различной плотностью при одной высоте столба оказывают на дно различные давления
Еще один пример. Имеются три различных по форме сосуда. В них до одного уровня налита одна и та же жидкость. Будет ли одинаковым давление на дно сосудов? Ведь масса, а значит, и вес жидкостей в сосудах различен. Да, давление будет одинаковым (Рис. 3). Ведь в формуле гидростатического давления нет никакого упоминания о форме сосуда, площади его дна и весе налитой в него жидкости. Давление определяется исключительно плотностью жидкости и высотой ее столба.
Рис. 3. Давление жидкости не зависит от формы сосуда
Мы получили формулу для нахождения давления жидкости на дно и стенки сосуда. Этой формулой можно пользоваться и для расчета давления в объеме жидкости на заданной глубине. Она может быть использована для определения глубины погружения аквалангиста, при расчете конструкции батискафов, подводных лодок, для решения множества других научных и инженерных задач.
Список литературы
- Перышкин А. В. Физика. 7 кл. – 14-е изд., стереотип. – М.: Дрофа, 2010.
- Перышкин А. В. Сборник задач по физике, 7-9 кл.: 5-е изд., стереотип. – М: Издательство «Экзамен», 2010.
- Лукашик В. И., Иванова Е. В. Сборник задач по физике для 7-9 классов общеобразовательных учреждений. – 17-е изд. – М.: Просвещение, 2004.
- Единая коллекция цифровых образовательных ресурсов ().
Домашнее задание
- Лукашик В. И., Иванова Е. В. Сборник задач по физике для 7-9 классов №504-513.
Жидкости и газы передают по всем направлениям приложенное к ним давление. Об этом гласит закон Паскаля и практический опыт.
Но существует еще и собственный вес, который тоже должен влиять на давление, существующее в жидкостях и газах. Вес собственных частей или слоев. Верхние слои жидкости давят на средние, средние на нижние, а последние – на дно. То есть мы можем говорить о существовании давления столба покоящейся жидкости на дно.
Формула давления столба жидкости
Формула для расчета давления столба жидкости высотой h имеет следующий вид:
где ρ – плотность жидкости,
g – ускорение свободного падения,
h – высота столба жидкости.
Это формула так называемого гидростатического давления жидкости.
Давление столба жидкости и газа
Гидростатическое давление, то есть, давление, оказываемое покоящейся жидкостью, на любой глубине не зависит от формы сосуда, в котором находится жидкость. Одно и то же количество воды, находясь в разных сосудах, будет оказывать разное давление на дно. Благодаря этому можно создать огромное давление даже небольшим количеством воды.
Это очень убедительно продемонстрировал Паскаль в семнадцатом веке. В закрытую бочку, полную воды, он вставил очень длинную узкую трубку. Поднявшись на второй этаж, он вылил в эту трубку всего лишь одну кружку воды. Бочка лопнула. Вода в трубке из-за малой толщины поднялась до очень большой высоты, и давление выросло до таких значений, что бочка не выдержала. То же самое справедливо и для газов. Однако, масса газов обычно намного меньше массы жидкостей, поэтому давление в газах, обусловленное собственным весом можно часто не учитывать на практике. Но в ряде случаев приходится считаться с этим. Например, атмосферное давление, которое давит на все находящиеся на Земле предметы, имеет большое значение в некоторых производственных процессах.
Благодаря гидростатическому давлению воды могут плавать и не тонуть корабли, которые весят зачастую не сотни, а тысячи килограмм, так как вода давит на них, как бы выталкивая наружу. Но именно по причине того же гидростатического давления на большой глубине у нас закладывает уши, а на очень большую глубину нельзя спуститься без специальных приспособлений – водолазного костюма или батискафа. Лишь немногие морские и океанические обитатели приспособились жить в условиях сильного давления на большой глубине, но по той же причине они не могут существовать в верхних слоях воды и могут погибнуть, если попадут на небольшую глубину.
Гидростатическое давление
Гидростатическое давление в жидкости можно рассчитать как
p = ρ gh (1)
, где
p = давление в жидкости (Н / м 2 , Па, фунт f / фут 2 , фунт / фут)
ρ = плотность жидкости (кг / м 3 , снаряды / фут 3 )
g = ускорение свободного падения (9,81 м / с 2 , 32.17405 фут / с 2 )
h = высота столба жидкости – или глубина в жидкости, где измеряется давление (м, футы)
Гидростатическое давление в водяной столб – или глубина ( плотность воды 1000 кг / м 3 ):
| Высота водяного столба | Давление | ||||
|---|---|---|---|---|---|
| (м) | (фут) | (кПа) | (бар) | (атм) | (фунт / кв. Дюйм) |
| 1 | 3.28 | 9,81 | 0,098 | 0,097 | 1,42 |
| 2 | 6,56 | 19,6 | 0,196 | 0,194 | 2,85 |
| 3 | 9,84 | 29,4 | 0,294 900 900 | 4,27 | |
| 4 | 13,1 | 39,2 | 0,392 | 0,387 | 5,69 |
| 5 | 16.4 | 49,1 | 0,491 | 0,484 | 7,11 |
| 6 | 19,7 | 58,9 | 0,589 | 0,581 | 8,54 |
| 7 | 23,0 | 68,7 | 0,687 | 0,6 | 10,0 |
| 8 | 26,2 | 78,5 | 0,785 | 0,775 | 11,4 |
| 9 | 29.5 | 88,3 | 0,883 | 0,871 | 12,8 |
| 10 | 32,8 | 98,1 | 0,981 | 0,968 | 14,2 |
| 12 | 39,4 | 118 | 1,18 | 1,16 | 17,1 |
| 14 | 45,9 | 137 | 1,37 | 1,36 | 19,9 |
| 16 | 52.5 | 157 | 1,57 | 1,55 | 22,8 |
| 18 | 59,0 | 177 | 1,77 | 1,74 | 25,6 |
| 20 | 65,6 | 196 | 1,96 | 1,96 | 28,5 |
| 25 | 82,0 | 245 | 2,45 | 2,42 | 35,6 |
| 30 | 98,4 | 294 | 2.94 | 2,90 | 42,7 |
| 35 | 115 | 343 | 3,43 | 3,39 | 49,8 |
| 40 | 131 | 392 | 3,92 | 3,87 | 56,9 |
| 50 | 164 | 491 | 4,91 | 4,84 | 71,1 |
| 60 | 197 | 589 | 5,89 | 5.81 | 85,4 |
| 70 | 230 | 687 | 6,87 | 6,78 | 100 |
| 80 | 262 | 785 | 7,85 | 7,75 | |
| 295 | 883 | 8,83 | 8,71 | 128 | |
| 100 | 328 | 981 | 9,81 | 9,68 | 142 |
Пример – Давление, действующее на глубине 1 м
Плотность воды при 4 o C составляет 1000 кг / м 3 .Давление, действующее в воде на высоте 1 м , можно рассчитать как
p = ρ gh
= ( 1000 кг / м 3 ) ( 9,81 м / с 2 ) (1 м)
= 9810 Па
Пример – Давление, действующее в воде на глубине
3 футаПлотность воды при 32 o F составляет 1,940 снарядов / фут 3 .Давление, действующее в воде на высоте 3 фута , можно рассчитать как
p = ρ gh
= ( 1,940 снарядов / фут 3 ) ( 32,17405 фут / с 2 ) (3 фута)
= 187,3 фунта f / фут 2 (psf)
= 9001 9001 9001 9001 2 (фунт / кв. Дюйм)
Давление в океане – глубина и широта
Давление в океане зависит от глубины и положения (широты) на Земле.
| Давление океана (МПа) | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Глубина (м) | Широта (градусы) | ||||||||||||||||||
| 0 | 15 | 30 | 45 | 60 | 75 | 90 | |||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||||
| 1000 | 10.080 | 10,083 | 10,093 | 10,106 | 10,120 | 10,130 | 10,133 | ||||||||||||
| 2000 | 20,208 | 20,215 | 20,234 | 20,261 | 20,308 | ||||||||||||||
| 30,383 | 30,394 | 30,424 | 30,464 | 30,505 | 30,535 | 30,545 | |||||||||||||
| 4000 | 40.606 | 40.620 | 40.660 | 40.714 | 40.768 | 40.808 | 40.823 | ||||||||||||
| 5000 | 50.874 | 50.892 | 50.942 | 51.010 | 51.079 | 51.129 | 61,188 | 61,210 | 61,270 | 61,352 | 61,434 | 61,495 | 61,517 | ||||||
| 7000 | 71.547 | 71,572 | 71,643 | 71,739 | 71,835 | 71,906 | 71,932 | ||||||||||||
| 8000 | 81,949 | 81,979 | 82,059 | 82,170 | 82,280 | 82,170 | 82,280 | 82,280 | 92,395 | 92,428 | 92,519 | 92,644 | 92,769 | 92,861 | 92,894 | ||||
| 10000 | 102.880 | 102,917 | 103,019 | 103,157 | 103,296 | 103,398 | 103,436 | ||||||||||||
- 1 Па = 10 -6 МПа = 10 -3 кПа 17 = 10 Н / мм 2 = 10 -5 бар = 0,1020 кп / м 2 = 1,020×10 -4 м H 2 O при 4 ° C / 39 ° F = 9,869×10 -6 атм = 0,004 дюйма H 2 O = 1,450×10 -4 фунтов на кв. Дюйм (фунт-сила / дюйм 2 ) = 0.02089 фунт-сила / фут 2 (фунт-сила на фут)
Жидкости и твердые вещества – Обзор MCAT
|
Гидростатическое давление: определение, уравнение и расчеты – видео и стенограмма урока
Давление в жидкости
Частицы газа не очень дружелюбны.Они расходятся, чтобы заполнить все пространство своего контейнера, наслаждаясь своим личным пространством и свободой. Но когда частицы газа летают, они иногда сталкиваются друг с другом, а также со стенками контейнера. Эти взаимодействия создают давление в контейнере, и в газе это давление одинаково для всей жидкости.
Но вы можете ясно видеть, что это не относится к жидкостям, потому что они не заполняют весь свой контейнер, как это делают газы. Это происходит из-за связей между молекулами жидкости, которые удерживают их вместе.Когда вы наливаете жидкость в емкость, она заполняет дно, потому что сила тяжести тянет ее вниз. Эта сила, вызванная гравитацией, такая же, как и на ваших весах – это вес жидкости, и именно она создает давление в этой жидкости.
Давление в жидкости также увеличивается с глубиной из-за силы тяжести. Жидкость внизу должна выдерживать вес всей жидкости над ней, а также всего воздуха над ней! Вы не замечаете веса воздуха вокруг вас, потому что ваше тело находится под таким же давлением, как и атмосфера, но любая жидкость под этой атмосферой определенно ощущает это.
Вы можете почувствовать это изменение давления, когда плывете на дно бассейна. По мере того, как вы погружаетесь глубже под воду, вы чувствуете, как давление увеличивается, потому что на вас ложится все больше и больше веса. Но давление не просто на вас накапливается. Поскольку вы находитесь в жидкости, вы почувствуете, что давление вокруг вас увеличивается.
Расчет давления жидкости
Когда жидкость находится в состоянии покоя, что означает, что она не течет, мы можем определить ее давление на заданной глубине, известной как гидростатическое давление .Мы определяем это с помощью уравнения: P = rho * g * d , где P – давление, rho – плотность жидкости, g – сила тяжести и d – глубина.
Вы также можете увидеть уравнение гидростатики, записанное как P = rho * g * h , где h обозначает высоту. Это можно использовать, потому что иногда мы хотим рассчитать давление жидкости, когда она заполняет столбец (например, при измерении барометрического давления), поэтому нам нужно знать высоту жидкости.Это все равно, что взять глубину и перевернуть ее вверх дном. Если вы используете соответствующее измерение, можно использовать любую букву, но может быть полезно придерживаться той буквы, которая лучше всего представляет то, что вы измеряете – глубину или высоту. 3.2, если вы знаете две другие переменные, вы можете легко вычислить третью. Все, что требуется, – это небольшая перестановка с последующим быстрым вычислением.
Резюме урока
В жидкости давление воздействует не только на емкость, в которой находится жидкость, но и на все части самой жидкости. Давление в жидкости вызывается весом жидкости, который представляет собой силу тяжести. По мере увеличения глубины увеличивается и давление, потому что сверху исходит больше веса (или силы).2) и d – глубина (или высота) жидкости.
Используя это уравнение, мы можем определить давление на любой заданной глубине в жидкости, если нам известна ее плотность. Мы также можем найти плотность или глубину жидкости, если мы знаем другие переменные и соответствующим образом изменим уравнение.
Результаты обучения
Когда вы дойдете до конца этого урока, вы сможете:
- Определить гидростатическое давление
- Понимать характеристики давления в жидкости
- Рассчитайте давление любой жидкости с помощью уравнения гидростатики
Калькулятор гидростатического давления
Этот калькулятор гидростатического давления определяет давление, возникающее на определенной глубине жидкости.Вы когда-нибудь задумывались, каков уровень давления в воде по сравнению с атмосферным давлением? Что определяет давление? Продолжайте читать, если хотите узнать, как можно оценить давление жидкости с помощью уравнения гидростатического давления. Вы также можете проверить наше атмосферное давление на калькуляторе высоты, если вы хотите идти не глубже, а выше.
Давление жидкости
Каждая частица жидкости подвергается действию гравитационной силы, направленной к Земле. Чем глубже мы находимся, тем больше таких частиц находится над нами и тем выше давление жидкости (потому что действующая сила больше – см. Наш калькулятор давления).Если жидкость находится в состоянии покоя, мы называем это гидростатическим давлением. Интересным фактом является то, что величина гидростатического давления не зависит от размера и формы резервуара, а только от глубины. Удивительно, но одинаковое гидростатическое давление будет присутствовать в огромном бассейне и тонкой трубе, если они имеют одинаковую высоту.
Уравнение гидростатического давления
В нашем калькуляторе гидростатического давления используется следующая формула гидростатического давления:
p = ρ * g * h + p0
где
-
p– гидростатическое давление, -
ρ– плотность жидкости, -
g– ускорение свободного падения (среднее значение для Землиg = 9.80655 м / с²), -
чглубина, -
p0– внешнее давление (обычно атмосферное давлениеp0 = 1 атм = 1013,25 гПа).
Приведенная выше формула для гидростатического давления позволяет определить силу плавучести, которая была впервые обнаружена древним изобретателем – Архимедом. В расширенном режиме нашего калькулятора гидростатического давления вы можете изменить как ускорение свободного падения g , так и внешнее давление p0 .
Самое глубокое место на Земле
Самая глубокая часть мирового океана – Марианская впадина, расположенная в Тихом океане. Достигает самой высокой известной глубины 10,994 м . Давайте воспользуемся нашим калькулятором гидростатического давления, чтобы оценить давление на дне Марианской впадины (не забудьте выбрать соленую воду с ρ = 1022 кг / м³ ). Поразительно, но давление здесь более чем в 1000 раз превышает атмосферное!
Жидкости
Принцип Паскаля
Изменение давления, приложенного к замкнутой жидкости, передается в неизменном виде всем частям жидкости и стенкам ее контейнера.Например, на диаграмме ниже, когда вы прикладываете дополнительное давление к поршню слева, это дополнительное давление передается жидкости справа, которая толкает поршень справа вверх. Именно так работает гидравлическая система.
На диаграмме ниже F 1 / A 1 = F 2 / A 2
Статическое давление и глубина
Поместите жидкость в контейнер, например цилиндр,
V = Ah
, где V – объем жидкости, A – площадь поперечного сечения цилиндра, а h – высота цилиндра.Давление на дно емкости P
P = F / A = pgh
Где F – вес жидкости в емкости, p – плотность жидкости, g – сила тяжести.
Давайте посмотрим, почему:
F = mg, где m – масса жидкости, а
m = pV, поэтому
F = pVg = pAhg (поскольку V = Ah)
Итак
P = F / A = pAhg / A = phg = pgh
Обратите внимание, что это уравнение также может быть получено из уравнения Бернулли.
Также обратите внимание, что разное давление жидкости на разных глубинах не противоречит принципу Паскаля.Принцип Паскаля заключается в изменении давления, и изменение давления будет равномерно передаваться повсюду. Это не говорит о том, что давление жидкости везде одинаково. Изменение давления будет добавлено к давлениям на разных глубинах.
Принцип Архимеда
Выталкивающая сила : восходящая сила, создаваемая жидкостью, которая противодействует весу погруженного объекта.
Принцип Архимеда : Выталкивающая сила, действующая на тело, погруженное в жидкость, равна весу жидкости, которую тело вытесняет.
Также следует отметить, что погруженный объект вытесняет объем жидкости, равный его собственному объему .
Например: объект весом 5 Н в воздухе помещается в воду и весит 4,5 Н. Тогда мы знаем, что разница в весе 0,5 Н будет весом вытесненной воды.
Расход
Когда топливо течет в одном направлении в трубе, скорость потока (Q) определяется как объем жидкости, вытекающей из трубы каждую секунду:
Q = vtA / t = vA, где v – скорость потока, а A – площадь поперечного сечения трубы.
Уравнение непрерывности
Если поток ламинарный, то уравнение неразрывности утверждает, что скорость потока Q будет постоянной, т. Е. Одинаковой в разных местах трубы. Следовательно, с уменьшением площади поперечного сечения скорость потока должна увеличиваться:
v 1 A 1 = v 2 A 2
Уравнение Бернулли
На диаграмме ниже мы смотрим на поток на 2 разных уровнях h2 и h3.Давление, скорость, площадь поперечного сечения (трубы) потока на 2 различных уровнях: P1 и P2, v1 и v2 и A1 и A2. Предположим, что p – плотность жидкости.
Обратите внимание, что на диаграмме p1 и p2 не совпадают, так как они находятся на разных уровнях. Но когда вы добавляете дополнительное давление к p1, это дополнительное давление будет добавлено и к p2.
Уравнение Буэрнулли имеет вид:
P 1 + pgh 1 + 1/2 pv 1 2 = P 2 + pgh 2 + 1/2 pv 2 2
Докажем:
Мы знаем проделанную работу ΔW = FΔd.В случае потока жидкости имеем F 1 на уровне 1 = P 1 A 1 , F 2 на уровне 2 = P 2 A 2 Расстояние Δd 1 на уровне 1 = v 1 t и расстояние Δd 2 на уровне 2 = v 2 t
Следовательно ΔW = P 1 A 1 v 1 t – P 2 A 2 v 2 t
Поскольку Avt – это в основном объем жидкости, Avt = V, который равен m / p, v = m / p, где m – масса жидкости, а p – плотность жидкости, мы имеем
1.ΔW = P 1 A 1 v 1 t – P 2 A 2 v 2 t = P 1 m / p – P 2 m / p
Когда жидкость перемещается с уровня 1 на уровень 2, изменение потенциальной энергии
2. ΔPE = mgh 2 – mgh 1
И изменение кинетической энергии
3. ΔKE = 1/2 мВ 2 2 – 1/2 мВ 1 2
Суммируя 2 и 3 выше, мы получим то же ΔW, что и в 1.
4. P 1 м / п – P 2 м / п = ΔPE + ΔKE = mgh 2 – mgh 1 + 1/2 мв 2 2 – 1/2 мв 1 2
Следовательно, имеем:
5. P 1 + pgh 1 + 1/2 pv 1 2 = P 2 + pgh 2 + 1/2 pv 2 2
Жидкость в покое
Применяя уравнение Буэрнулли к , удаляя предметы со скоростью v (так как v = 0), получаем:
ΔP = P 2 – P 1 = pgΔh = pg (h 1 -h 2 )
Это означает, что разница в давлении прямо пропорциональна разнице в уровнях заполнения.
Жидкость выходит через маленькое отверстие
Когда отверстие открывается, все PE = pgh на отверстии будет преобразовано в KE = 1/2 pv 2 . Итак, у нас есть
1/2 pv 2 = pgh, исключая p, получаем
1/2 v 2 = gh
По мере того, как жидкость вытекает, h станет меньше, и, следовательно, v также станет медленнее.
В отверстии расход R = vA, из которого можно определить соотношение между расходом R и высотой h.
Жидкость движется горизонтально
Применяя уравнение Буэрнулли, h 1 = h 2 , мы можем исключить члены pgh:
P 1 + 1/2 pv 1 2 = P 2 + 1/2 pv 2 2
P 1 – P 2 = (1/2) p (v 2 2 – v 1 2 )
По мере увеличения скорости движущейся жидкости ее статическое давление уменьшается.
Онлайн-калькулятор: Гидростатическое давление
Этот онлайн-калькулятор может решать задачи гидростатического давления, находя неизвестные значения в уравнении гидростатики.
Уравнение выглядит следующим образом:
В нем говорится, что разность давлений между двумя отметками в жидкости является продуктом изменения высоты, силы тяжести и плотности.
Калькулятор может решить это уравнение
- для давления с использованием известных значений плотности, высоты и силы тяжести
- для плотности с использованием известных значений давления, высоты и силы тяжести
- для высоты с использованием известных значений давления, плотности и силы тяжести
- для силы тяжести с использованием известных значений давления, высоты и плотности
Все формулы тривиальны.Значения по умолчанию для входа следующие:
- плотность – плотность воды
- гравитация – это сила тяжести на Земле
- давление 1 атм.
Вы также можете найти немного теории под калькулятором.
Гидростатическое давление
Решение для давления, плотности, высоты, гравитации, Точность вычисления,Цифры после десятичной точки: 2
content_copy Ссылка сохранить Сохранить , расширение Виджет
Гидростатическое давление – перепад давления между двумя отметками.
Упрощенная формула, которая не учитывает, например, сжатие жидкости, но дает хорошие оценки, может быть получена следующим образом:
Формула зависит только от высоты жидкостной камеры, а не от ее ширины или длины. При достаточно большой высоте можно добиться любого давления. Считается, что это впервые было продемонстрировано Паскалем в его эксперименте с бочкой.
Ствол Паскаля – это название гидростатического эксперимента, предположительно проведенного Блезом Паскалем в 1646 году.Во время эксперимента Паскаль вставил вертикальную трубку длиной 10 м (32,8 фута) в бочку, наполненную водой. Когда вода была налита в вертикальную трубу, Паскаль обнаружил, что увеличение гидростатического давления привело к разрыву ствола.
Эта особенность гидростатики получила название гидростатического парадокса. По выражению В. Х. Безанта,
- Любое количество жидкости, даже небольшое, может выдерживать любой вес, даже большой.
На рисунке выше показано, что статическое давление жидкости на заданной глубине не зависит от общей массы, площади поверхности или геометрии контейнера.Это зависит только от высоты жидкости. Это связано с тем, что давление на наклонные стенки имеет вертикальную часть, и в левом сосуде оно указывает вверх, в то время как в среднем сосуде оно указывает вниз, таким образом, добавляя или удаляя дополнительное давление к нижнему давлению, поэтому оно пропорционально только до высоты жидкости.
Источники:
Калькулятор глубины / уровня жидкости до гидростатического давления
Нажмите, чтобы перезагрузить страницу с уникальным веб-адресом для добавления в закладки или обмена текущими настройками
✕ очистить настройки
К сожалению, здесь не удалось отобразить графику, потому что ваш браузер не поддерживает холст HTML5.Приборы для измерения уровня гидростатических жидкостей
Запросите информацию о продуктах для измерения уровня гидростатических жидкостей для вашего приложения.
Сопутствующие инструменты
Руководство пользователя
Этот калькулятор и шкала преобразования будут преобразовывать высоту или глубину жидкости в любых единицах измерения в измерение гидростатического напора и отображать список преобразованных значений выше и ниже введенного уровня жидкости.
Формулы
Формулы расчета, используемые для этого инструмента:
P = L x ρ x г
ρ = ρ 0 x SG
Символы
- P = Давление
- L = Высота жидкости
- г = местная сила тяжести (например,грамм. стандартный = 9,80665 мс -2 )
- ρ = плотность жидкости
- ρ 0 = Плотность пресной воды (1000 кгм -3 при 4 ° C)
- SG = Удельный вес жидкости (например, пресная вода = 1)
Высота столба жидкости
Введите измеренную глубину жидкости до или высоту жидкости от точки, в которой должно быть вычислено гидростатическое давление.
Удельный вес (SG)
Введите здесь отношение плотности жидкости к плотности пресной воды (1000 кг / м 3 ).Значение по умолчанию установлено на удельный вес 1,00, что соответствует температуре пресной воды 4 градуса Цельсия.
Местная сила тяжести (г)
Введите ускорение свободного падения для вашего географического местоположения в метрах в секунду в секунду (мс -2 ). Местная сила тяжести зависит от нескольких факторов, таких как широта, высота над уровнем моря, местная геологическая плотность и т. Д. См. Данные вашей национальной геологической разведки для вашего местоположения или воспользуйтесь этим калькулятором местной силы тяжести, чтобы определить точное приближение.По умолчанию установлено значение 9,80665 мс -2 , что соответствует стандартной силе тяжести.
Гидростатическое давление
Это расчетное давление напора, ожидаемое на основе введенных значений уровня жидкости, удельного веса и местного веса. Расчет определяет разницу в давлении между дном столба жидкости и поверхностью жидкости, поэтому он исключает влияние давления воздуха или газа на поверхности.
Приложения
- Напор
- Испытания на водонепроницаемость
- Гидравлический напор
Справка
Давление, создаваемое баком дизельного топлива высотой 40 футов
Как определить диапазон давления, необходимый для измерения резервуара для хранения дизельного топлива глубиной 40 футов?
Чтобы определить давление, создаваемое 40-футовым дизельным топливом, вам необходимо знать удельный вес (S.ГРАММ.). Плотность дизельного топлива варьируется в зависимости от температуры и типа дизеля, но 0,95 – это максимум, который часто указывается многими ресурсами. Используя этот калькулятор, 40-футовая колонна дизельного топлива преобразовалась бы в 16,474 фунта на квадратный дюйм.
Эта шкала преобразования показывает значения преобразования в диапазоне от 0 до 40 футов:
Давление на дне круглого резервуара
По какой формуле рассчитывается давление жидкости на дне круглого резервуара?
Давление напрямую связано с высотой жидкости и не зависит от формы резервуара, поэтому вы должны использовать приведенную выше формулу.
Площадь и диаметр резервуара
Почему при преобразовании уровня жидкости в давление не учитывается площадь или диаметр резервуара?
Уровень жидкости прямо пропорционален гидростатическому давлению, поэтому нет других параметров, которые необходимо учитывать при преобразовании уровня жидкости в давление. Площадь или диаметр не влияют на уровень жидкости, но они влияют на ее содержание и измерение объема, например, в резервуаре с горизонтальным цилиндром.
Приборы для измерения уровня гидростатических жидкостей
Запросите информацию о продуктах для измерения уровня гидростатических жидкостей для вашего приложения.
.