Как рассчитывается линейная скорость?
Оглавление
Время чтения: 4 минуты
570
Интуитивное понятие о скорости мы получаем ещё с детства. Например, глядя в окно или находясь на улице отмечаем про себя, что некоторые из людей идут быстрее, чем другие, а машины на проезжей части движутся быстрее, чем любой из пешеходов. Однако для физики, как науки, такого, бытового понимания о скорости недостаточно, поэтому вводится её точное определение.
Понятие скорости
Скоростью материальной точки (тела) при равномерном движении называется физическая величина, показывающая, какой путь точка (тело), проходит за единицу времени.
Подчеркнём, что речь идёт именно о пути, а не о перемещении. Перемещением называется вектор, соединяющий точку начала и точку конца движения. Его величина равна расстоянию между этими точками. Путь представляет собой длину траектории, по которой происходило движение. Наглядно это можно показать на рисунке.
Равномерным движением называют движение, при котором за одинаковые промежутки времени тело проходит одно и то же расстояние. Направление движения при этом может изменяться. В качестве примера можно привести равномерное перемещение точки по окружности.
Формула понятия скорости следующая:
\[\overline{\mathrm{v}}=s / t\]
Чёрточка над \[\overline{\mathrm{v}}\] свидетельство того, что скорость является векторной, т.е. имеющей направление, величиной. Путь s и время t являются скалярными величинами, такими, которые направления в пространстве не имеют.
Чёрточка над \[\overline{\mathrm{v}}\] свидетельство того, что скорость является векторной, т.е. имеющей направление, величиной. Путь s и время t являются скалярными величинами, такими, которые направления в пространстве не имеют.
Из приведённой формулы очень легко найти размерность скорости. Т. к.
Существует ещё так называемая средняя скорость – скалярная величина, равная скорости, с которой бы тело перемещалось, если бы преодолевало путь, двигаясь равномерно.
Примеры
Поезд длиной 300 метров, двигаясь равномерно, проезжает тоннель длиной 420 метров за 3 минуты. Найти скорость поезда.
Решение:
Длину поезда обозначим через l, а длину тоннеля через L.
\[S = I + L = 300 + 420 = 720 м/с.\]
Скорость поезда – это скорость любой из его точек. Для простоты будем считать, что это скорость кабины машиниста.

Переводим минуты в секунды: 3 * 60 = 180с.
Скорость получаем, разделив перемещение на время: 720/180 = 4 м/с.
Ответ: Скорость поезда равна 4 м/с.
Машина 3 часа едет со скоростью 4 км/ч, затем 4 часа со скоростью 61,2 км/ч. Требуется найти среднюю скорость движения машины на всем её пути.
Решение:
Обозначим время движения машины со скоростью 4 км/ч, как \[t_{1}\], а время движения машины со скоростью 61,2 км/ч, как \[t_{2}\].
Находим общий путь, который проехала машина. Обозначим его, как S. Общий равен сумме путей, которые ехала машина со скоростью 58,4 км/ч и 61,2 км/ч. Первый из них обозначим как \[S_{1}\], он равен \[S_{1}\] = 3*58,4 = 175,2 км
Второй из них обозначим как S2, он равен: \[S_{2} = 4*61,2 = 244,8 км\]
Складываем эти расстояния и получаем: S = 175,2 + 244,8 = 420 км
Общее время t, которое она потратила будет \[t = t_{1} + t_{2} =3 + 4 = 7 ч\]
Чтобы узнать среднюю скорость, делим общее расстояние на общее время v = S/t = 420/7 = 60 км/ч.

Ответ: Средняя скорость машины равна 60 км/ч.
Обращать время в секунды, а скорость в метры в секунду здесь смысла не имеет, можно и так получить нужное решение.
Линейная скорость
Линейной скоростью именуют величину равную пути, проходимым телом за единицу времени. Движение тела при этом может быть как прямолинейным так и совершаться по криволинейной траектории, например, окружности. Отметим, что линейная скорость всегда направлена по касательной к траектории.
Формул для расчета линейной скорости существует множество, но общей можно назвать:
\[v=S / t\]
S – путь, который прошло тело, t – время, которое оно на это потратило.
Если тело вращается по окружности, то путь, проходимый им, равен её длине. Как известно из геометрии, указанная величина равна 2πR, где R – радиус окружности. Отсюда легко сообразить, что линейная скорость тела при равномерном движении по окружности будет \[\boldsymbol{v=2 \pi R / T}\].
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
О связи между линейной и угловой скоростями
Угловой скоростью называется векторная величина, показывающая, насколько быстро и в каком направлении вращается материальная точка или тело относительно центра вращения.
Угловая скоростьОбозначается она буквой ω. Формула нахождения угловой скорости следующая:
\[\overline{\omega}=\phi / t\],
где ϕ – угловое перемещение, t – время.
Измеряется угловая скорость в радианах в секунду рад/с.
Теперь о связи между линейной и угловой скоростью. Из формулы\[\boldsymbol{v=2 \pi R / T}\] следует, что v также будет равно v = 2πRν, где ν – частота вращения точки. Отсюда легко понять, что v = ωR.
Линейная скорость и ускорение при движении по окружности
Центростремительное ускорение движущейся равномерно по окружности точки вычисляется по формуле:
\[a=v^{2} / R\]
Оно связывает линейную скорость и ускорение.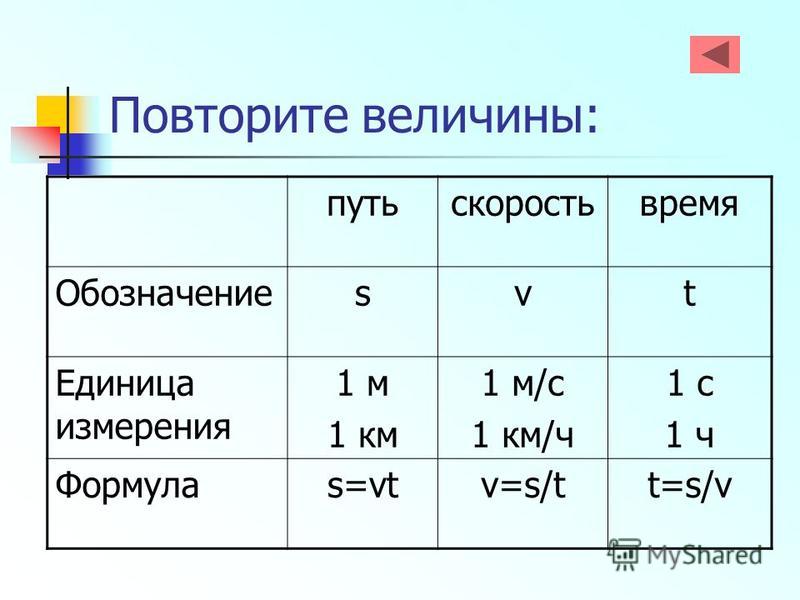 {2} R\]
{2} R\]
Оценить статью (39 оценок):
Поделиться
§17. РАСЧЁТ ПУТИ И ВРЕМЕНИ ДВИЖЕНИЯ. Помогите ответь на вопросы. Перышкин физика 7 класс – Рамблер/класс
§17. РАСЧЁТ ПУТИ И ВРЕМЕНИ ДВИЖЕНИЯ. Помогите ответь на вопросы. Перышкин физика 7 класс – Рамблер/классИнтересные вопросы
Школа
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания “Останкино”?
1. Как определить путь: а) при равномерном движении тела; б) при неравномерном движении тела?
Как определить путь: а) при равномерном движении тела; б) при неравномерном движении тела?
2. Как определить время: а) при равномерном движении тела; б) при неравномерном движении тела?
ответы
записывай ответы
§17. РАСЧЁТ ПУТИ И ВРЕМЕНИ ДВИЖЕНИЯ
№1
Чтобы определить путь, пройденный телом при равномерном движении, надо скорость тела умножить на время его движения: S=Vt. Если тело движется неравномерно, то, зная его среднюю скорость движения и время, за которое происходит это движения, находят путь: S=Vсрt.
№2
Теперь, зная, что S=Vt, можно найти время, при равномерном движении, в течение которого двигалось тело: t=S/V.
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Экскурсии
Мякишев Г. Я.
Я.
Досуг
Химия
похожие вопросы 3
Привет. Выручайте с ответом по физике…
Поплавок со свинцовым грузилом внизу опускают
сначала в воду, потом в масло. В обоих (Подробнее…)
ГДЗФизикаПерышкин А.В.Школа7 класс
ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.
Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)
ГДЗФизикаПерышкин А.В.Школа7 класс
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
(Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Уравнения в физике: значение и расчет
Какая польза от уравнений в реальном мире? Почему физики описывают физику на языке математических уравнений? Что такого особенного в математике, что мы можем использовать ее в окружающем нас мире? Какие есть примеры физических уравнений, что они нам говорят и как мы их решаем? Узнайте об этом в этой статье!
Определение уравнения в физике
Существует определение уравнения (будь то в физике или нет), но оно очень техническое и совсем не информативное. что мы может сказать об уравнениях физики то, что они делают . Уравнения в физике описывают отношения между физическими величинами. Уравнение всегда содержит знак «равно», \(=\).
В физике существует уравнение, описывающее зависимость между вашей скоростью, продолжительностью вашего путешествия и пройденным расстоянием. Чем больше ваша скорость, тем большее расстояние вы преодолеваете за то же время. Уравнение будет выглядеть так: \(\text{пройденное расстояние}=\text{скорость}\times \text{длительность поездки}}\). Мы видим, что удвоение времени в пути означает удвоение пройденного расстояния, если скорость остается неизменной, и что удвоение скорости означает удвоение пройденного расстояния, если время в пути остается прежним.
Уравнение будет выглядеть так: \(\text{пройденное расстояние}=\text{скорость}\times \text{длительность поездки}}\). Мы видим, что удвоение времени в пути означает удвоение пройденного расстояния, если скорость остается неизменной, и что удвоение скорости означает удвоение пройденного расстояния, если время в пути остается прежним.
Уравнение физики, которое мы ввели выше, выглядит немного неясным: букв так много, что отношения (знаки умножения и равенства) отходят на второй план. Однако отношения очень важны в физике. Вот почему люди присваивают символы количествам. Важно объяснить другим людям, что означают ваши символы, и удобно использовать стандартные символы для вещей, которые имеют стандартные символы.
Чтобы уравнение выглядело яснее, мы можем дать названия величинам, участвующим в задаче. Предположим, что пройденное расстояние равно \(d\) (для расстояния), наша скорость равна \(v\) (для скорости), а продолжительность нашего путешествия равна \(t\) (для времени). Уравнение теперь \(d=vt\).
Уравнение теперь \(d=vt\).
Мы опустили крестик умножения, потому что ясно, что это две разные вещи. Ничего не помещая между двумя величинами, мы умножаем их. Это уравнение выглядит намного яснее, и нетрудно сразу же вспомнить, например, что \(d\) означает расстояние. Это хорошо, мы только что записали уравнение физики!
Рис. 1: Всегда верное уравнение (также называемое тавтологией).
Типы физических уравнений
У вас может сложиться впечатление, что существует много разных типов физических уравнений, потому что все они выглядят по-разному. Хотя верно, что во многих областях физики есть свои собственные уравнения, каждое уравнение в физике имеет одну и ту же цель, а именно описание отношения между величинами. Однако мы можем провести различие между уравнениями, основываясь на том, как представляются величины в уравнении, как показывают следующие примеры. 92/2\).
У нас также есть дифференциальные уравнения (содержащие производные величин), тензорные уравнения (содержащие величины с несколькими входными данными, как векторы) и многие другие способы, которыми величины могут появляться в уравнениях.
Примеры уравнений физики
Рис. 2: Уравнения Эйнштейна о гравитации.
Соотношение между силой \(F\), которую вы прикладываете к объекту, массой \(m\) объекта и скоростью, с которой объект будет ускоряться (описывается ускорением \(a\)) как результат силы, которую вы прикладываете, определяется уравнением 92=4.\]
Мы видим, что энергия действительно увеличивается в четыре раза, если скорость удваивается. Это основная причина того, почему автомобиль разгоняется медленнее на высоких скоростях, чем на низких: ему нужно добавить больше энергии, чтобы получить ту же скорость из-за квадрата в уравнении выше!
Мы видели большое количество физических уравнений, но теперь пришло время поработать с ними и решить их.
Решение уравнений в физике
Рис. 3: Эдвард Виттен пишет уравнения теории струн на доске.
Решение уравнений в физике очень похоже на решение уравнений в математике, за исключением двух основных отличий.
- В физике всегда есть контекст, поэтому физическое уравнение следует из небольшой истории.
 Мы должны распаковать историю и преобразовать ее в разрешимое уравнение.
Мы должны распаковать историю и преобразовать ее в разрешимое уравнение. - Мы должны быть осторожны с юнитами. В общем, мы включаем единицы в все расчеты .
Давайте посмотрим, как это работает на примере задачи.
В: Джон всегда ходит со скоростью \(3\,\,\mathrm{mi/h}\)( миль в час). В прошлое воскресенье он гулял по городу и в итоге проехал в общей сложности \(9 \,\,\mathrm{ миль}\). Сколько времени у него ушло?
A: Первый шаг — преобразовать эту историю в разрешимое уравнение. Начнем с присвоения имен нужным нам величинам. Мы называем скорость ходьбы Джона \(v\), пройденное им расстояние \(d\) и время, затраченное им на это \(t\). Тот факт, что это было воскресенье и что он гулял по городу, не имеет значения для вопроса. Из рассказа мы знаем, что \(v=3\,\,\mathrm{mi/h}\) и что \(d=9\,\,\mathrm{mi}\). Теперь нам нужно найти уравнение, связывающее \(t\) с \(v\) и \(d\). К счастью, мы знаем, что \(d=vt\). Как и в случае с математическими уравнениями, мы изолируем \(t\), разделив обе части на \(v\), и у нас остается уравнение \(t=d/v\). Мы знаем \(d\) и \(v\), так что это разрешимое уравнение, так что шаг 1 выполнен! Давайте решим ее, соблюдая осторожность с единицами измерения. Заполняем:
Мы знаем \(d\) и \(v\), так что это разрешимое уравнение, так что шаг 1 выполнен! Давайте решим ее, соблюдая осторожность с единицами измерения. Заполняем:
\[t=\dfrac{9\,\,\mathrm{mi}}{3\,\,\mathrm{mi/h}}=\dfrac{9}{3}\dfrac{ \mathrm{mi}}{\frac{\mathrm{mi}}{\mathrm{h}}}=3\,\,\mathrm{h}.\]
Теперь давайте обязательно ответим на вопрос полностью. Джону потребовалось 3 часа (чтобы прогуляться по городу в прошлое воскресенье).
В приведенном выше примере у нас не было проблем с единицами измерения, потому что информация, предоставленная нам, была в единицах, которые «хорошо сочетаются». Если это не так, нам придется использовать наши знания о преобразованиях единиц измерения, как показано в примере ниже.
В: Анна хочет толкнуть машину, о которой мы можем предположить, что она не имеет трения и не находится ни на каком уклоне. Она толкает с силой \(500\,\,\mathrm{N}\), масса автомобиля равна \(4000\,\,\mathrm{lbs}\), а масса Анны равна \(170\ ,\,\mathrm{фунты}\). 2}}\\ =&0,276\,\,\dfrac{\mathrm{m}}{\mathrm{s}}\end{выровнено }.\] 92}\).
2}}\\ =&0,276\,\,\dfrac{\mathrm{m}}{\mathrm{s}}\end{выровнено }.\] 92}\).
Надеюсь, эти примеры прояснили, как язык математических уравнений полезен в реальном (физическом) мире.
Резюме: шаг за шагом
- Читая вопрос, дайте названия указанным величинам и запишите их значения (с указанием единиц).
- Определите, какую величину вам нужно знать, чтобы ответить на вопрос, и запишите уравнение физики, связывающее эту величину с записанными вами величинами.
- Решите уравнение (будьте осторожны с единицами измерения) и ответьте на вопрос полным предложением и с правильными единицами измерения.
Уравнения движения в физике
Рис. 4: Уравнение Шредингера, описывающее квантовую механику.
В конце концов, все, к чему стремится физика, — это предсказывать движение объектов. Следовательно, мы можем утверждать, что все уравнения в физике в некотором роде являются уравнениями движения. Однако некоторые уравнения описывают только движение объектов, а не причины движения.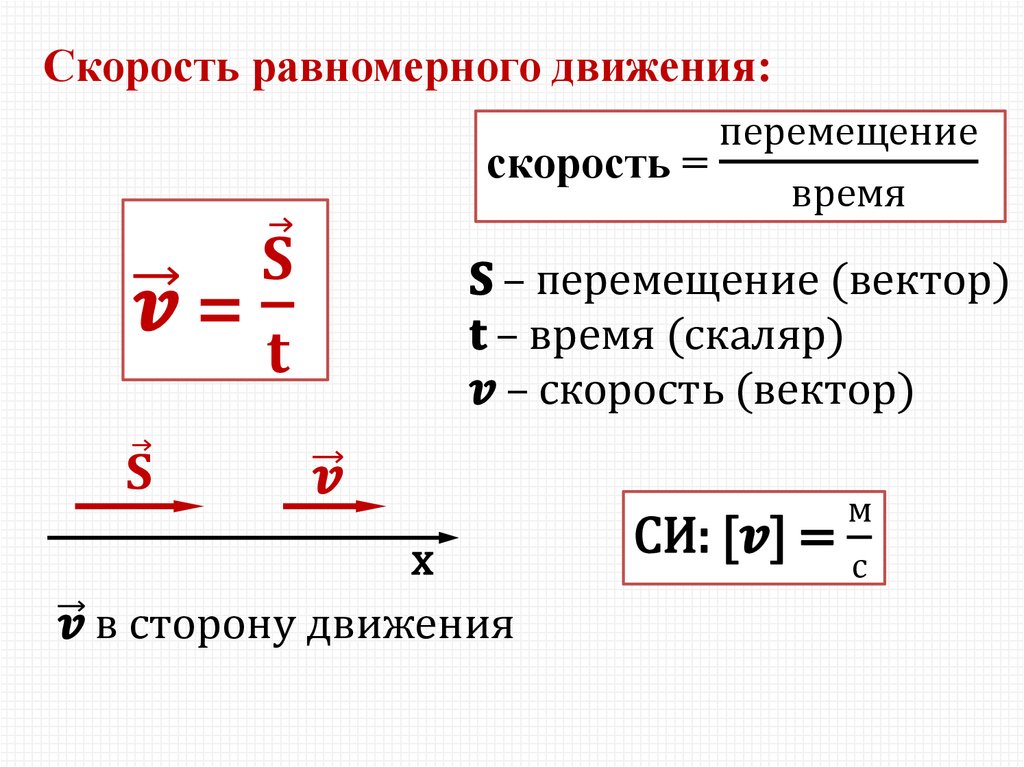 Давайте посмотрим на эти уравнения.
Давайте посмотрим на эти уравнения.
Сначала рассмотрим уравнение, описывающее движение с постоянной скоростью. Для начальной точки \(x_0\), скорости \(v\) и продолжительности движения \(t\) местоположение \(x\) объекта определяется как
\[x=x_0+vt .\]
Ранее мы знали, что пройденное расстояние равно \(d=vt\), так что это логично: местоположение объекта равно его начальному местоположению плюс пройденное расстояние.
Объект также может ускоряться. Для постоянного ускорения \(a\), начальной скорости \(v_0\), начальной точки \(x_0\) и продолжительности пути \(t\) задано местоположение\(x\) объекта к 92,\]
и мы приходим к приведенному выше уравнению! Обратите внимание, что для нулевого ускорения мы снова приходим к уравнению для постоянной скорости, что и ожидаем найти.
Уравнения в физике – основные выводы
- Уравнение в физике описывает отношение между физическими величинами.
- Уравнение всегда содержит знак равенства, \(=\).
 2\).
2\).
Уравнения времени гравитации для объектов, спроецированных вверх Рон Куртус
SfC Home > Physics > Gravity >
Рон Куртус
Когда вы проецируете объект вверх и отпускаете его с некоторой скоростью, он перемещается, пока не достигнет максимальной высоты или смещения, после чего падает на землю.
Начальная скорость имеет отрицательное значение, скорость отрицательна при движении вверх и положительна при движении вниз, а смещение отрицательно выше начальной точки и положительно ниже начальной точки. Скорость и перемещение являются векторами, а время — скалярной величиной, которая всегда положительна.
Примечание : В некоторых учебниках верх считается положительным, а низ – отрицательным. Вы должны знать, какое соглашение используется при работе с книгой.
( Для получения дополнительной информации см. Соглашение о направлении в уравнениях гравитации.
)
Вы можете использовать производные уравнения , чтобы найти время , необходимое для достижения заданной скорости, а также время, необходимое для достижения заданного смещения, как выше, так и ниже начальной точки.
У вас могут возникнуть следующие вопросы:
- Сколько времени зависит от скорости?
- Каково время перемещений над начальной точкой?
- Каково время перемещений ниже начальной точки?
Этот урок ответит на эти вопросы. Полезный инструмент: Преобразование единиц измерения
Время по отношению к скорости
Общее уравнение для времени, необходимого объекту для достижения заданной скорости:
t = (v − v i )/г
где
- t время в секундах (с)
- v — вертикальная скорость в метрах/секунду (м/с) или футах/секунду (фут/с)
- v i — вертикальная начальная скорость в м/с или футах/с
- г ускорение свободного падения (9,8 м/с 2 или 32 фут/с 2 )
( Для получения дополнительной информации см.
Вывод уравнений скорости и силы тяжести во времени.
)
Когда вы проецируете объект вверх, он движется в направлении, противоположном силе тяжести, и начальная скорость, когда вы его отпускаете, отрицательна или меньше нуля
( v i < 0).
На пути вверх
На пути вверх v отрицательно ( v < 0), и его абсолютное значение меньше, чем у в и :
|в| < |v я |
, где |v| и |v и | — абсолютные или положительные значения. Таким образом, (v − v i ) имеет положительное значение.
Время достижения максимального смещения
При максимальном смещении v = 0 и уравнение времени принимает вид:
т м = -v i /г
где т м время достижения максимального водоизмещения.
Примечание : Поскольку начальная скорость отрицательна, −v i является положительным числом.
На пути вниз
На пути вниз, v > 0 и v < |v i | . Таким образом, (v − v i ) имеет положительное значение.
Пример времени достижения различных скоростей
Если v i = −128 фут/с, найдите t для различных скоростей.
Решение
Поскольку v i выражено в футах/с, вы используете г = 32 фута/с 2 . Подставьте значения v i и g в уравнение:
t = (v − v i )/г
t = [( v фут/с) − (−128 фут/с)]/(32 фут/с 2 )
Отмена единиц приводит к формуле:
t = ( v + 128)/32 с
Замените на разными значениями, чтобы получить различные прошедшие периоды времени:
v = −128 фут/с т = 0 с Старт с начальной скоростью v = −64 фут/с т = 2 с Движение вверх v = 0 фут/с т м = 4 с При максимальном водоизмещении v = 32 фут/с т = 5 с Движение вниз v = 128 фут/с т = 8 с Вниз в начальной точке v = 160 фут/с т = 9 с Ниже начальной точки
Время для различных скоростей объекта, спроецированного вверх
Время смещения, движущегося вверх
Общее уравнение гравитации для прошедшего времени относительно смещения:
t = [−v i ± √(v i 2 + 2gy)]/g
где
- ± означает плюс или минус
- √(v i 2 + 2gy) – квадратный корень из числа (v i 2 + 2yg)
- y вертикальное смещение в метрах или футах
( Для получения дополнительной информации см.
Вывод уравнений гравитации во времени смещения. )
Для объекта, направленного вверх, −v i — положительное число. Для того, чтобы объект начал с t = 0, когда y = 0, уравнение для времени, которое требуется объекту, чтобы двигаться вверх к максимальному смещению, имеет отрицательную (-) версию:
t = [−v i − √(v i 2 + 2gy)]/г
Время достижения максимального смещения
Уравнение для времени достижения максимального смещения относительно начальной скорости уже было сформулировано:
т м = -v i /г
Уравнение для максимального смещения относительно начальной скорости:
г м = −v i 2 /2г
( Для получения дополнительной информации см. Уравнения смещения для объектов, проецируемых вверх.
)
Эти два уравнения позволяют легко определить время и максимальное перемещение. Однако вы можете захотеть увидеть взаимосвязь между факторами.
Решить y m = −v i 2 /2g для v i 2 :
v i 2 = −2gy м
Квадрат т м = -v i /г :
т м 2 = v i 2 /г 2
Замена в v i 2 = −2gy м :
т м 2 = −2gy м /г 2
т м 2 = −2y м /г
Извлечение положительного квадратного корня:
t м = √(−2y м /г)
Пример различных перемещений вверх
Если v i = −98 м/с, найти время различных перемещений при движении объекта вверх до максимального смещения.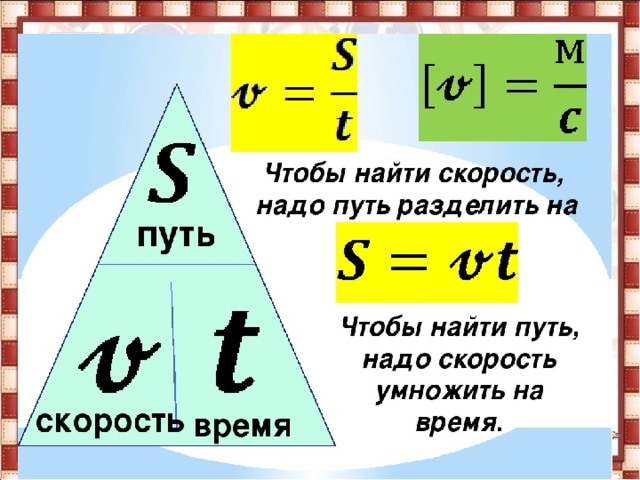
Решение
Поскольку v i в м/с, г = 9,8 м/с 2 . Кроме того, поскольку смещения находятся выше начальной точки, значения 90 157 и 90 158 будут отрицательными числами.
Вы можете легко определить время максимального смещения:
т м = -v i /г
т м = 98/9,8 с
т м = 10 с
Также:
г м = −v i 2 /2г
г м = − 98 2 / 2*9,8 м
г м = − 980 / 2 м
г м = − 490 м
Вы можете проверить правильность этих двух значений, подставив:
t м = √(−2y м /г)
10 = √( − 2*[ − 490]/9,8 )
10 = √( 100 )
10 = 10
Чтобы найти различные значения t по отношению к y , подставьте v i и g в уравнение:
t = [−v i − √(v i 2 + 2gy)]/г
Вы можете самостоятельно проверить правильность единиц и что t в секундах.
t = [ −(−98) − √ (−98 2 + 2*9,8 *y ) ]/ (9,8) секунд
Один из способов упростить уравнение — разбить дробь.
t = 98/9,8 − [√ (9604 + 19,6 y ) ]/ (9,8) с
t = 10 − [√( 9604 + 19,6 г )]/ 9,8 с
Уравнение все еще не очень простое, но вполне работоспособное. Простой случай, когда
у = 0:
t = 10 − [√( 9604 )]/ 9,8 с
t = 10 − 98/9,8 с
т = 0 с
Следующие результаты показывают время для различных перемещений выше и в начальной точке:
г = 0 м т = 0 с В начальной точке г = -49 м t = 0,5 с Перемещение вверх и выше начальной точки г = -98 м t = 1,1 с Движение вверх г = -196 м т = 2,25 с Движение вверх г м = −490 м т м = 10 с При максимальном водоизмещении
Время различных перемещений вверх
Время смещения вниз
После того, как объект достигает максимального смещения и начинает опускаться, уравнение меняется на:
t = [−v i + √(v i 2 + 2gy)]/г
Пока объект находится выше начальной точки, y имеет отрицательное значение. Когда он достигает начальной точки, y = 0. Затем, когда он ниже начальной точки, y становится положительным числом.
Когда он достигает начальной точки, y = 0. Затем, когда он ниже начальной точки, y становится положительным числом.
Пример для различных перемещений вниз
Как и в предыдущем примере, если v i = −98 м/с. Найдите времена различных перемещений при движении тела вниз.
Решение
Вы уже знаете максимальное перемещение и время:
г м = − 490 м
т м = 10 с
Используйте уравнение:
t = [−v i + √(v i 2 + 2gy)]/г
Замените и упростите:
t = 10 + [√( 9604 + 19,6 г )]/ 9,8 с
Следующие результаты показывают время для различных смещений при падении объекта с максимального смещения:
г м = −490 м т м = 10 с При максимальном водоизмещении г = -196 м т = 17,75 Падение г = -98 м т = 18,9 с Падение, но выше начальной точки г = -49 м т = 19,5 с Приближается к начальной точке на пути вниз г = 0 м т = 20 с В начальной точке спуска г = 196 м т = 21,8 с Ниже начальной точки
Время различных перемещений в направлении вниз
Резюме
Объект, брошенный вверх против силы тяжести, замедляется до тех пор, пока не достигнет максимального смещения, после чего его скорость увеличивается при падении на землю. Производные уравнения позволяют рассчитать время, которое требуется объекту, спроецированному вверх, чтобы достичь заданной скорости или заданного смещения от начальной точки.
Производные уравнения позволяют рассчитать время, которое требуется объекту, спроецированному вверх, чтобы достичь заданной скорости или заданного смещения от начальной точки.
Время относительно скорости:
t = (v − v i )/г
t м = −v i /g (время достижения максимального водоизмещения)
Время относительно смещения:
t = [−v i − √(v i 2 + 2gy)]/g (движение вверх)
t м = √(−2y м /g) (время достижения максимального водоизмещения)
t = [−v i + √(v i 2 + 2gy)]/g (движение вниз)
Be methodical in your calculations
Resources and references
Ron Kurtus’ Credentials
Websites
Gravity Resources
Gravity Calculations – Earth – Calculator
Books
(Notice: The Школа чемпионов может получать комиссионные от покупки книг)
Книги с самым высоким рейтингом по Simple Gravity Science
Книги с самым высоким рейтингом по Advanced Gravity Physics
Вопросы и комментарии
У вас есть вопросы, комментарии или мнения на эту тему? Если это так, отправьте электронное письмо с вашим отзывом.

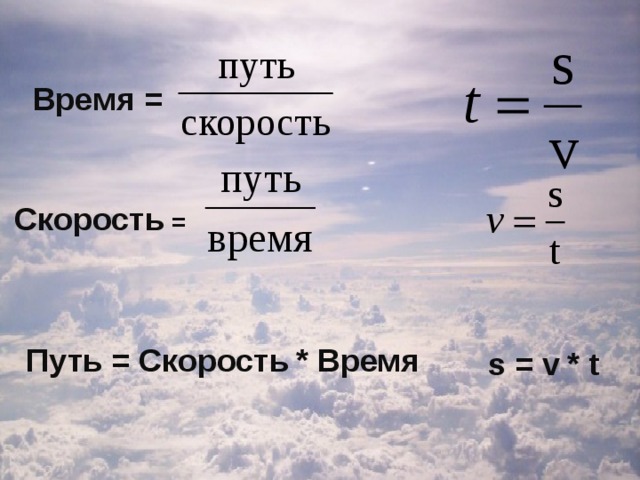 Мы должны распаковать историю и преобразовать ее в разрешимое уравнение.
Мы должны распаковать историю и преобразовать ее в разрешимое уравнение. 2\).
2\).
 Вывод уравнений скорости и силы тяжести во времени.
Вывод уравнений скорости и силы тяжести во времени.  Вывод уравнений гравитации во времени смещения. )
Вывод уравнений гравитации во времени смещения. )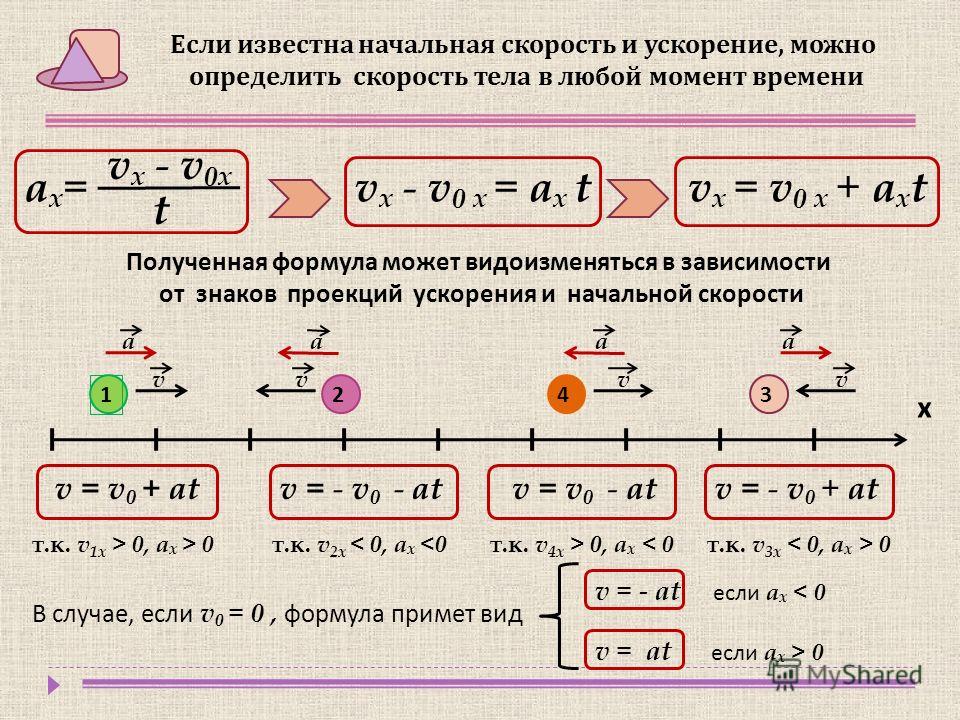 )
)