Формула полного ускорения: § 1.4 Полное ускорение материальной токи. Нормальное и тангенциальное ускорение.

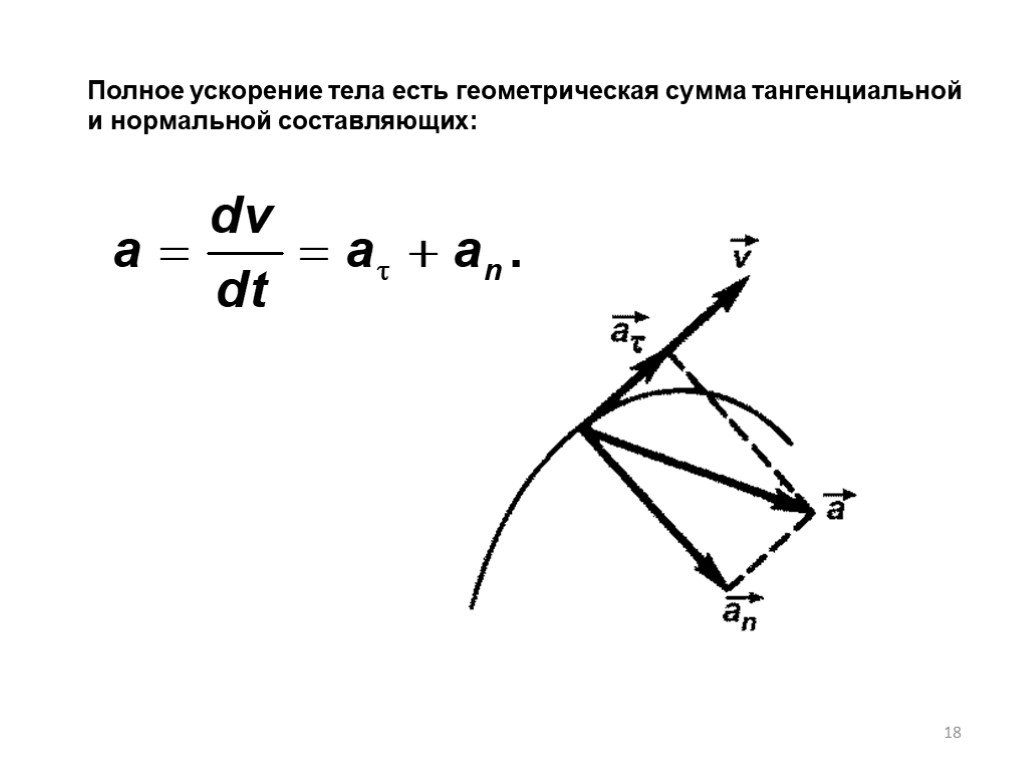
§ 1.4 Полное ускорение материальной токи. Нормальное и тангенциальное ускорение.

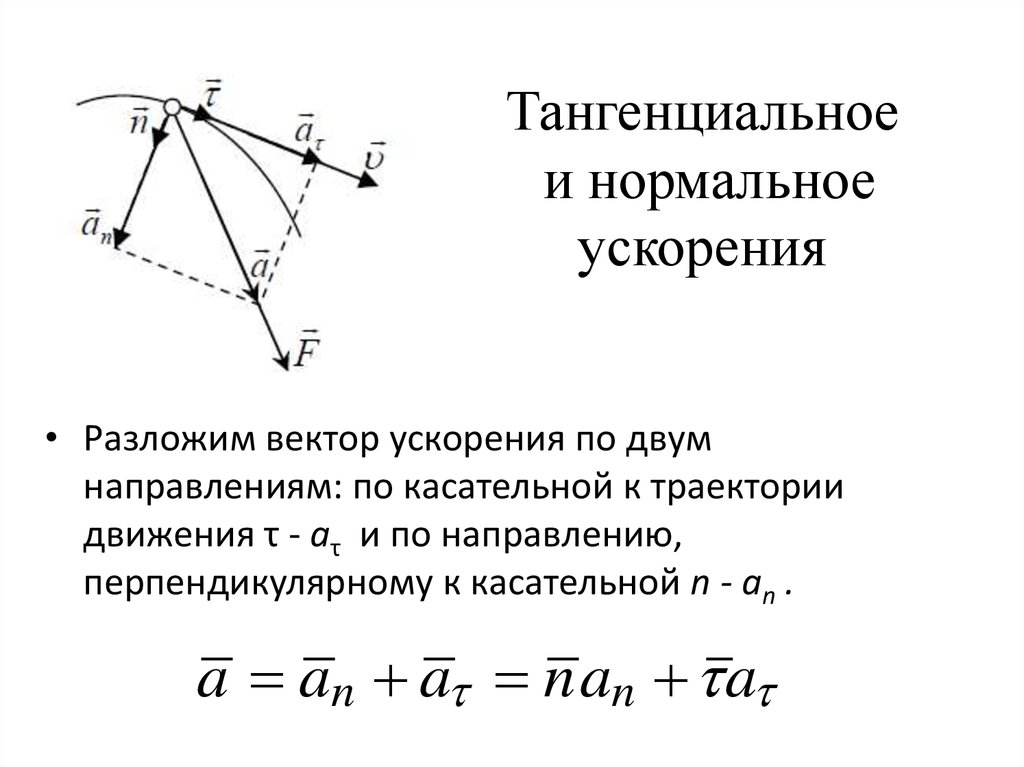
Вектор ∆υ можно разложить на две составляющие: – вдоль касательной, – вдоль нормали рис.1.4). Из рисунка видно, что – определяет изменение скорости по модулю, вторая составляющая, характеризует изменение скорости по направлению за промежуток времени Δt

(1.14)

Т

Рис.1.4

аким образом, полное ускорение имеет две взаимно-перпендикулярные составляющие: а_τ — тангенциальное, а_n — нормальное или центростремительное (рис. 1.5).

Тангенциальное ускорение а_τ, направленное по касательной к траектории, определяет быстроту изменения модуля скорости. Модуль тангенциального ускорения равен производной модуля скорости по времени:

(1. 15)

Нормальное ускорение

а_n, характеризует изменение скорости по направлению и совпадает с нормалью к траектории к центру ее кривизны. Модуль нормального ускорения

(1.16)

[R — радиус кривизны траектории].

Окончательно для вектора ускорения запишем

(1.17)

а его модуль равен

(1.18)

В заключении рассмотрим несколько случаев:

а) а_τ =0, а

_n =0. Так как а_n =0, то из (1.16) следует, что R→ ∞, т.е. траектория движения – прямая линия. Так как а_τ =0, то из (1.15) имеем υ = const, что соответствует равномерному прямолинейному движению;

б) а_τ = const, а_n =0. Движение прямолинейное (а_n =0). Скорость изменяется пропорционально времени (). При а_τ >0 движение равноускоренное, при а_τ < 0- равнозамедленное;

в) а_τ = 0, а_n = const. Движение равномерное (а_τ =0), υ = const. Из (1.16) следует, что при а_n = const R= const. Траекторией движения является окружность. В этом случае ускорение иногда называют центростремительным.

г) а_τ = const, а_n = const. Из первого соотношение следует, что скорость изменяется пропорционально квадрату времени, а означает, что R изменяется пропорционально квадрату времени. Траектория движения будет спираль.

тела вокруг неподвижной оси.

Абсолютно твёрдым телом называют систему материальных точек, расстояния между которыми остаются неизменными. Это понятие соответствует некоторой модели, в действительности абсолютно твёрдых тел нет, так как любое тело способно к деформации.

Вращательное движение – это такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения. Почти любое криволинейное движение можно представить как последовательность движений, проходящих по дугам окружностей.

Наиболее простой случай вращательного движения абсолютно твёрдого тела – вращение относительно неподвижной оси. Пусть радиус окружности, описываемой некоторой точкой, равен r, а ее линейное перемещение – dS. Тогда угловое перемещение dφ (угол поворота радиуса-вектора)

или dS = r dφ (1.19)

Кинематическими характеристиками вращательного движения кроме угла поворота являются угловая скорость ω и угловое ускорение β.

Если за промежуток времени Δt тело поворачивается на угол Δφ, то быстрота его вращения характеризуется угловой скоростью.

Угловая скорость равна первой производной от угла поворота тела по времени:

(1.20)

Вектор ω направлен вдоль оси вращения, его направление можно определить, пользуясь правилом правого винта (рис. 1.5). Если направление вращения винта совпадает с вращением тела, то конец винта укажет направление вектора ω.

Если ω = соnst, то вращательное движение называют равномерным.

Время одного полного поворота тела вокруг оси вращения называют

периодом обращения Т, а величину ν, обратную периоду, — частотой:

(1.21)

За один период угол поворота радиуса-вектора точки равен 2π рад, поэтому 2π = ω Т, или

(1. 22)

Быстрота изменения угловой скорости характеризуется угловым ускорением. Если за промежуток времени Δt угловая скорость получает приращение Δω.

Угловое ускорение равно первой производной от угловой скорости по времени или второй производной от угла поворота радиуса-вектора по времени:

(1.23)

Угловое ускорение также является векторной величиной. При ускоренном вращении β совпадает с вектором ω, при замедленном вращении β противоположно ω.

Если угловое перемещение всех точек абсолютно твердого тела одинаково, то все точки тела имеют одинаковую угловую скорость и одинаковое угловое ускорение в данный момент времени.

Линейные характеристики — перемещение, скорость, ускорение — различны для разных точек твердого тела. Связь между линейными и угловыми характеристиками движущейся точки можно получить, используя равенство 1.

19.

Дифференцируя это равенство по времени, получаем

или r (1.24)

Дифференцируя это равенство по времени дважды, получаем соотношение между тангенциальным и угловым ускорениями:

или a = r·β (1.25)

Связь между линейными и угловыми величинами выражается следующими формулами:

S= rφ; υ=r·ω; a_τ = r·β a_n = r·ω² . (1.26)

Формулы кинематики вращательного движения твердого тела вокруг неподвижной оси:

(1.27)

(1.28)

(1.

29)

Полное ускорение и его компоненты. Ускорение тангенциальное и нормальное ускорение. Формулы и пример решения задачи

От Masterweb

13.12.2018 19:00

В кинематике для однозначного определения характеристик движения тела в любой точке траектории необходимо знать его скорость и ускорение. Зависимость от времени этих величин предоставляет всю необходимую информацию для вычисления пройденного телом пути. Рассмотрим подробнее в статье, что такое ускорение тангенциальное и нормальное ускорение.

В физике

Прежде чем рассматривать для механического движения ускорение нормальное и тангенциальное ускорение, познакомимся с самим физическим понятием. Определение ускорения является достаточно простым. В физике под ним понимают характеристику изменения скорости. Последняя является векторной величиной, определяющей быстроту изменения координат движущегося объекта в пространстве. Скорость измеряется в метрах в секунду (расстояние, пройденное за единицу времени). Если ее обозначить символом v¯, тогда математическое определение ускорения a¯ будет выглядеть так:

a¯ = dv¯/dt

Это равенство определяет так называемое полное мгновенное ускорение. Мгновенным оно называется потому, что характеризует изменение скорости лишь в данный момент времени.

Если движение является равноускоренным, то есть в течение длительного времени ускорение не меняет своего модуля и направления, тогда можно записать следующую формулу для его определения:

a¯ = Δv¯/Δt

Где Δt>>dt. Величина a¯ здесь называется средним ускорением, которое в общем случае отличается от мгновенного.

Ускорение измеряется в системе СИ в метрах в квадратную секунду (м/с2).

Траектория движения и компоненты полного ускорения

Чаще всего тела в природе движутся по кривым траекториям. Примерами такого перемещения являются: вращение по своим орбитам планет, параболическое падение камня на землю, поворот автомобиля. В случае криволинейной траектории в любой момент времени скорость направлена по касательной к рассматриваемой точке траектории. Как при этом направлено ускорение?

Чтобы ответить на поставленный выше вопрос, запишем скорость тела в следующей форме:

v¯ = v*ut¯

Здесь ut¯ – вектор скорости единичный, индекс t означает, что он направлен по касательной к траектории (тангенциальная компонента). Символом v обозначен модуль скорости v¯.

Теперь, следуя определению ускорения, можно провести дифференцирование скорости по времени, имеем:

a¯ = dv¯/dt = dv/dt*ut¯ + v*d(ut¯)/dt

Таким образом, полное ускорение a¯ представляет собой векторную сумму двух компонент. Первое и второе слагаемое называются нормальным и тангенциальным ускорением точки. Подробнее рассмотрим каждую из этих компонент.

Ускорение тангенциальное

Запишем еще раз формулу для этой компоненты полного ускорения:

at¯ = dv/dt*ut¯

Это выражение позволяет описать свойства величины at¯:

• Она направлена точно так же, как и сама скорость или противоположно ей, то есть по касательной к траектории. Об этом свидетельствует элементарный вектор ut¯.
• Она характеризует изменение скорости по абсолютной величине, что отражает множитель dv/dt.

Эти свойства позволяют сделать важный вывод: для прямолинейного движения полное и тангенциальное ускорения – это одна и та же величина. В случае криволинейного перемещения полное ускорение всегда больше по модулю, чем тангенциальное. Когда рассматривают физические задачи на прямолинейное равноускоренное движение, то ведут речь именно об этой компоненте ускорения.

Ускорение нормальное

Рассматривая тему скорости, ускорения тангенциального и ускорения нормального, дадим характеристику последней величине. Запишем формулу для нее:

an¯ = v*d(ut¯)/dt = v*d(ut¯)/dL*dL/dt

Чтобы записать явно правую часть равенства, воспользуемся следующими соотношениями:

dL/dt = v;d(ut¯)/dL = 1/r

Здесь dL – это пройденный телом путь за промежуток времени dt, r – радиус кривизны траектории. Первое выражение соответствует определению скорости, второе равенство следует из геометрических соображений. Пользуясь этими формулами, получаем конечное выражение для нормального ускорения:

an¯ = v2/r

То есть величина an¯ не зависит от изменения скорости, как тангенциальная компонента, а определяется исключительно ее модулем. Нормальное ускорение вдоль нормали к данному участку траектории направлено, то есть к центру кривизны. Например, во время движения по окружности вектор an¯ направлен к ее центру, поэтому нормальное ускорение называют часто центростремительным.

Если за изменение абсолютной величины скорости ответственно ускорение тангенциальное, то нормальная компонента ответственна за изменение вектора скорости, то есть она определяет траекторию перемещения тела.

Ускорение полное, нормальное и тангенциальное

Разобравшись с понятием ускорения и с его компонентами, приведем теперь формулу, которая позволяет определить полное ускорение. Поскольку рассмотренные компоненты направлены под углом 90 o друг к другу, то для определения абсолютной величины их векторной суммы можно использовать теорему Пифагора. Формула для полного ускорения имеет вид:

a = √(at2 + an2)

Направление величины a¯ можно определить по отношению к вектору любой из компонент. Например, угол между a¯ и an¯ вычисляется так:

θ = arctg(at/an)

Учитывая приведенную выше формулу для модуля a¯, можно сделать вывод: при равномерном движении по окружности полное ускорение совпадает с центростремительным.

Решение задачи

Пусть тело движется по окружности радиусом 1 метр. Известно, что его скорость изменяется по следующему закону:

v = 2*t2 + 3*t

Необходимо определить ускорение тангенциальное и нормальное ускорение в момент t = 4 секунды.

Для тангенциального имеем:

at = dv/dt = 4*t + 3 = 19 м/с2

Для того чтобы найти модуль ускорения нормального, сначала следует вычислить значение скорости в заданный момент времени.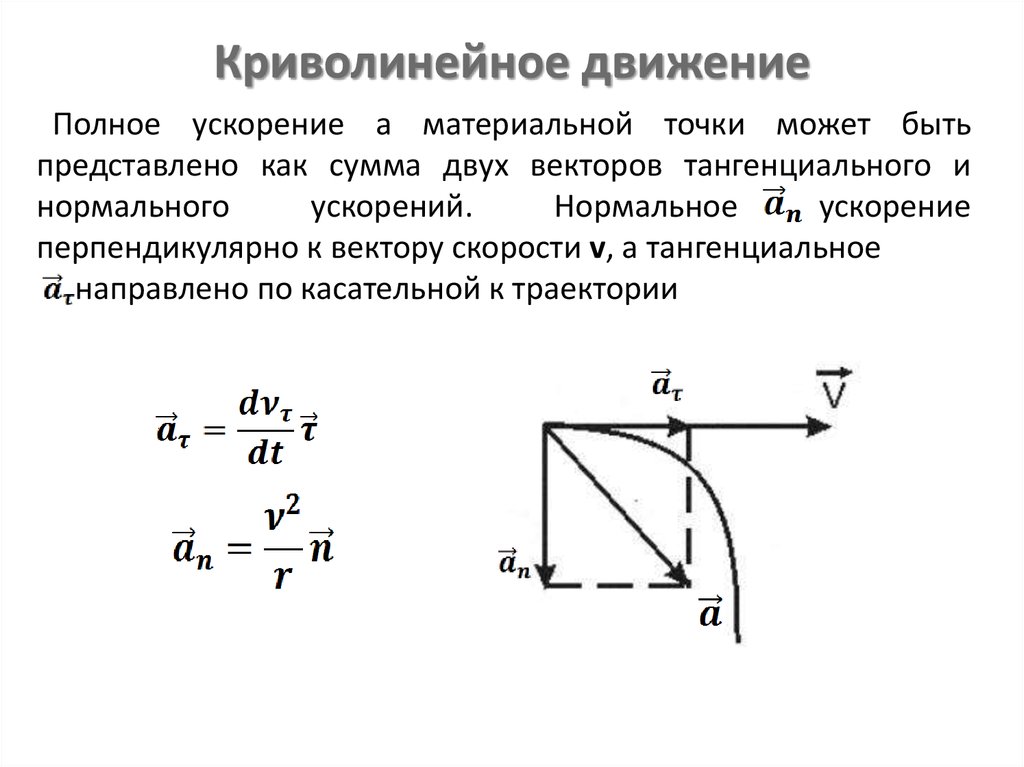 Имеем:

v = 2*42 + 3*4 = 44 м/с

Теперь можно воспользоваться формулой для an:

an = v2/r = 442/1 = 1936 м/с2

Таким образом, мы определили все величины, которые требовалось найти для решения задачи.

Тангенциальное ускорение – определение, формула, примеры решения

Тангенциальное ускорение – это скорость изменения тангенциальной скорости при вращательном движении любого объекта. Он действует в направлении касательной в точке движения объекта. Тангенциальная скорость также действует в том же направлении для объекта, совершающего круговое движение. Тангенциальное ускорение существует только тогда, когда объект движется по круговой траектории. Она положительна, если тело вращается с большей скоростью, отрицательна, когда тело замедляется, и равна нулю, когда тело движется равномерно по орбите.

 

Тангенциальное ускорение

Тангенциальное ускорение аналогично линейному ускорению, но только в одном направлении. Это как-то связано с круговым движением. Таким образом, тангенциальное ускорение — это скорость изменения тангенциальной скорости частицы на круговой орбите. Он всегда указывает на касательную траектории тела.

Тангенциальное ускорение работает, когда объект движется по круговой траектории. Тангенциальное ускорение похоже на линейное ускорение, но не то же самое, что прямолинейное линейное ускорение. Если предмет движется прямолинейно, он линейно ускоряется.

 

Например, машина, мчащаяся по повороту дороги. Автомобиль ускоряется по касательной к повороту дорожки.

Читайте также: Что такое ускорение?

Формула тангенциального ускорения

Тангенциальное ускорение обозначается символом a _t . Его единица измерения такая же, как и линейное ускорение, то есть метры в секунду в квадрате (м/с ² ). Его размерная формула дается выражением [M ⁰ L ¹ T ^-2 ]. Его формула определяется произведением радиуса окружности на угловое ускорение вращающегося объекта.

a _t = r α

где,

• a _t — тангенциальное ускорение,
• r — угловое ускорение 9.

Приведенное выше выражение дает связь между тангенциальным ускорением и угловым ускорением.

Теперь, с точки зрения угловой скорости и времени, формула имеет вид

ω — угловая скорость,

t — время.

Формула для углового перемещения и времени имеет вид0045

a _t — тангенциальное ускорение,

θ — угловое смещение или угол поворота,

t — затраченное время.

Ниже приведены различные случаи, возможные для различных значений тангенциального ускорения:

1. Когда _t больше нуля: Объект движется с ускорением, и величина скорости будет увеличиваться со временем.
2. Когда _t меньше нуля: Объект имеет замедленное или замедленное движение, и величина скорости будет уменьшаться со временем.
3. Когда _t равно нулю: Объект имеет равномерное движение, и величина скорости останется постоянной.

Подробнее: Равноускоренное движение

Решенные примеры по тангенциальному ускорению

Пример 1. Расчет тангенциального ускорения, если объект совершает круговое движение для радиуса 5 м и углового ускорения 2 рад0027 2 .

Решение:

Мы имеем,

R = 5

α = 2

Используем формулу, которую мы получаем,

A _T = R α

= 5 (2)

= R α

= 5 (2)

= st 10 м/с ²

Пример 2. Рассчитайте тангенциальное ускорение, если объект совершает круговое движение с радиусом 12 м и угловым ускорением 0,5 рад/с ² .

Решение:

У нас есть

R = 12

α = 0,5

с использованием формулы, которую мы получаем,

A _T = R α

= 12 (0,5)

= 6 м/с

= 12 (0,5)

= 6 м/с

= 2

Пример 3: Рассчитайте угловое ускорение, если объект совершает круговое движение с радиусом 20 м и тангенциальным ускорением 40 м/с ² .

Решение:

Имеем,

r = 20

A _T = 40

с использованием формулы, которую мы получаем,

A _T = R α

α = A _T /R

= 40/20

= 2 RAD/S ^{. 2}

Пример 4: Рассчитайте угловое ускорение, если объект совершает круговое движение с радиусом 2 м и тангенциальным ускорением 20 м/с ² .

Решение:

Имеем,

r = 2

a _t = 20

Using the formula we get,

a _t = r α

 α = a _t /r

= 20/2

= 10 rad/s ²

Пример 5: Рассчитать радиус, если объект совершает круговое движение с угловым ускорением 4 рад/с ² и тангенциальным ускорением 20 м/с ² .

Решение:

Имеем,

α = 4

A _T = 20

с использованием формулы, которую мы получаем,

A _T = R α

R = A _T /α

= 20/4

= 5 м

= 20/4

= 5 м 9000 3

555555559

= 5 м

= 20/40003

= 5 м

= 20/40003 = 5 м 9003

Часто задаваемые вопросы о тангенциальном ускорении

Вопрос 1: Каковы значения радиального и тангенциального ускорения при равномерном ускорении движения частицы?

Ответ:

Несмотря на отсутствие тангенциального ускорения, центростремительное ускорение должно присутствовать, чтобы всегда изменять направление скорости, а центростремительное ускорение в данном случае является результирующим ускорением. Это пример равномерного кругового движения.

Таким образом, если _r и _t представляют радиальное и тангенциальное ускорение, тогда _r ≠ 0 и _t = 0.

Вопрос 2: Что такое касательное ускорение?

Ответ:

Тангенциальное ускорение — это скорость изменения тангенциальной скорости при вращательном движении любого объекта. Он действует в направлении касательной в точке движения объекта.

Вопрос 3: Каково значение тангенциального ускорения при равномерном круговом движении?

Ответ:

Тангенциальное ускорение равно нулю при равномерном круговом движении. При равномерном круговом движении угловая скорость остается постоянной, поэтому тангенциальное ускорение = 0,

Подробнее: Равномерное круговое движение

Вопрос 4: Что такое единица СИ для тангенциального ускорения?

Ответ:

Единицей тангенциального ускорения в системе СИ является м/с ² .

Вопрос 5: Какая связь между тангенциальным ускорением и угловым ускорением?

Ответ:

Формула тангенциального ускорения определяется произведением радиуса окружности на угловое ускорение вращающегося объекта.

a _t = r α

где,

• a _t – тангенциальное ускорение,
• r — радиус окружности,
• α — угловое ускорение.

Ускорение | Определение, факты и единицы измерения

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• В этот день в истории
• Викторины
• Подкасты
• Словарь
• Биографии
• Резюме
• Популярные вопросы
• Обзор недели
• Инфографика
• Демистификация
• Списки
• #WTFact
• Товарищи
• Галереи изображений
• Прожектор
• Форум
• Один хороший факт

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Britannica объясняет
  В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
• Britannica Classics
  Посмотрите эти ретро-видео из архивов Encyclopedia Britannica.
• Demystified Videos
  В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.
• #WTFact Видео
  В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти.
• На этот раз в истории
  В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.

• Студенческий портал
  Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д.
• Портал COVID-19
  Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня.
• 100 женщин
  Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.