Формула производной деления: Производные сложной функции

Как осуществить деление производных? :: SYL.ru

Ребенок не слушается. Стоит ли ставить малыша в угол и на какое время

Челка-шторка и другие тенденции красоты, которые нужно оставить в уходящем году

Овощи, приготовленные на пару: шесть советов, как снизить потребление углеводов

Котлеты из брокколи и картошки – любимое блюдо пакистанцев (рецепт)

Эффект отросших волос – хит 2023: как создать образ и не выглядеть неряшливо

Капуста и грибы. Готовим полезную и оригинальную закуску

Сон на одной кровати: что должны избегать мамы, воспитывая мальчика-подростка

Как сочетать вязаную юбку и создавать с ней комфортные зимние наряды в 2023 году

Модные цвета для дам за 70: что можно и чего нельзя, чтобы выглядеть моложе

Французская коса: праздничные прически, которые легко сделать дома

Автор Алексей Рулев February 8, 2017

При работе с функциями часто приходится учитывать их специфику, производя сложение, умножение или деление производных.

Последнее из действий чаще всего вызывает вопросы у обучающегося, поэтому этот аспект стоит рассмотреть подробнее.

Производная частного

Когда выполняется деление производных, формула для преобразования выглядит как разность производной числителя, помноженного на знаменатель, и производной знаменателя, умноженного на числитель, и поделённое на квадрат знаменателя. При этом необходимо учитывать, что значение в нижней части дроби должно быть не равным нулю. При решении первых примеров преобразование производной частного нередко возникает проблема, поэтому лучше всего иметь перед глазами эту формулу:

Благодаря этой формуле удаётся привести пример в более простую форму, которую можно разделить на табличные функции производных, после чего решить данную задачу не составит большого труда.

Пример решения

В качестве примера, демонстрирующего ход решения, где выполняется деление производных, стоит рассмотреть следующий:

Согласно заданию, необходимо найти производную данного выражения. Воспользовавшись формулой, упрощающей деление производных, преобразуем исходный пример к следующему виду:

В результате в числителе оказалось две производные табличного вида, значения которых можно вычислить без дополнительных преобразований. В первом случае результатом будет единица, во втором – двойка. Подставив вычисленные данные в пример, получим дробь, в которой останется лишь произвести несложные вычисления в числителе, получив итоговый результат:

Маленькие хитрости

Перед применением формулы стоит внимательно посмотреть на деление производных. В некоторых случаях дробь можно упростить, благодаря чему приведенная в начале формула может оказаться ненужной или станет более простой. Упрощение дроби можно выполнить несколькими способами, включая деление числителя на знаменатель с целью определения целой части, а также домножением обеих частей дроби на одно и то же ненулевое число – этот приём часто применяется при наличии иррациональности под знаком производной.

Стоит отметить, что перед вначале необходимо проверить пример на наличие решения.

Для этого нужно найти область допустимых значений (ОДЗ), и если она будет существовать, не создавая неопределённостей различного вида, можно приступать к вычислениям.

Похожие статьи

• Основные типы дифференциальных уравнений первого порядка
• Деление на ноль. Увлекательная математика
• Эмбриональный период развития. Этапы и стадии эмбрионального периода
• Что такое интеграл? Интегралы с подробным решением. Таблица интегралов
• Как лечить миому матки без операции: способы, методы, отзывы
• Многочлены. Разложение многочлена на множители: способы, примеры
• Метод конечных элементов и его применение

Также читайте

Правила дифференцирования производной функций: формулы

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel. ru Математика Алгебра Производная функции: правила и формулы дифференцирования

В данной публикации мы рассмотрим правила и формулы дифференцирования производной функций, а также, разберем примеры для закрепления изученного материала.

Допустим, даны две функции f (x) и u (x), которые имеют производные в точке x. Тогда для них справедливы следующие формулы:

• 1. Константа в производной
• 2. Производная суммы/разности
• 3. Производная произведения
• 4. Производная частного
• 5. Производная сложной функции

1. Константа в производной

(c ⋅ f(x))‘ = c ⋅ f ‘(x), где c – константа

Т.е. константу можно вынести за знак производной.

Например: (5x³)‘ = 5 ⋅ (x³)‘

2.

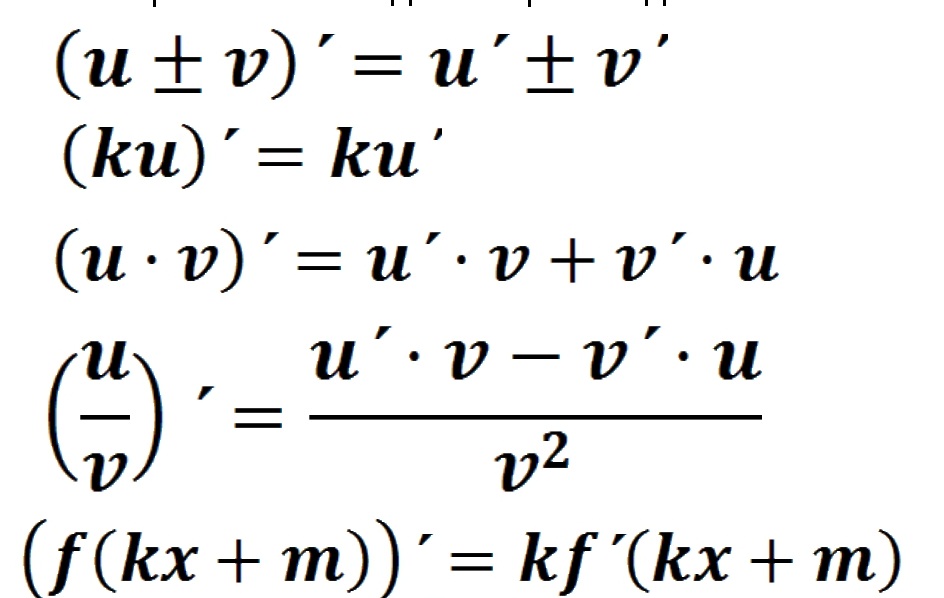Производная суммы/разности

(f(x) ± u(x))‘ = f ‘(x) ± u ‘(x)

Производная суммы/разности двух функций равняется сумме/разности, в которой слагаемыми выступают производные данных функций.

Например: (6x + x²)‘ = (6x)‘ + (x²)‘

3. Производная произведения

(f(x) ⋅ u(x))‘ = f ‘(x) ⋅ u(x) + f(x) ⋅ u ‘(x)

Производная произведения двух функций равняется сумме, в которой:

• первое слагаемое – это произведение производной первой функции на вторую;
• второе слагаемое – все наоборот.

Например: (ln x ⋅ x³)‘ = (ln x)‘ ⋅ x³

+ ln x ⋅ (x³)‘

4. Производная частного

Производная деления одной функции на другую находится по следующей формуле:

Например:

5.

Производная сложной функции

Допустим, производная функции y = y(f) находится в точке f₀ = f(x₀), а функции f = f(x) – в точке x₀.

Производная сложной функции в таком случае равняется:

[y(f(x))]‘ = y ‘(f) ⋅ f ‘(x)

• множимое – это производная данной функции по промежуточному аргументу f;
• множитель – производная промежуточного аргумента f по основному аргументу x.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

2}$$ $$\dfrac{г(х)}{ч(х)}$$ ?

Если вы смогли вывести правило деления, проверьте, совпадает ли оно с правилом, которое мы представляем ниже:

делитель минус делимое, умноженное на производную от делителя и деленное на квадрат делителя.

2(х)}$$$ 92}$$$

Похожие темы

• Производная линейной функции
• Производная постоянной функции
• Производная тригонометрических функций

Решенные задачи производной от деления двух функций

Посмотреть проблемы

Теория математики в твоем мобильном

Загрузите его бесплатно.

Частное правило — вывод, объяснение и пример Этот метод наиболее полезен при нахождении производной рационального выражения или функции, которая может быть выражена как отношение двух более простых выражений.

Правило частного помогает нам различать функции, выражения которых содержат числитель и знаменатель. Они будут использовать выражения числителя и знаменателя и их соответствующие производные.

Освоение этого конкретного правила или техники потребует постоянной практики. В этой статье вы узнаете, как:

• Описать правило частных своими словами.

• Узнайте, как применить это к различным функциям.

• Узнайте, как мы можем использовать другие производные правила наряду с частными правилами.

Не забудьте сохранить свой список производных правил, чтобы помочь вам догнать другие производные правила, которые нам, возможно, потребуется применить, чтобы полностью дифференцировать наши примеры. А пока, почему бы нам не пойти дальше и не понять наизусть процесс вычисления правила частного?

Что такое т он частное правило ?

Факторное правило утверждает, что производная функции $h(x) = \dfrac{f(x)}{g(x)}$ равна произведению знаменателя на производную числитель минус произведение числителя и производной знаменателя . В результате получится выражение, равное , деленное на квадрат знаменателя.

Бывают случаи, когда функция, с которой мы работаем, является рациональным выражением. Когда это происходит, полезно, если вы знаете правило отношения для производных. Это означает, что частное правило равно наиболее полезен, когда мы работаем с функциями, представляющими собой отношения двух выражений .

Когда нам дана функция рационального выражения (это означает, что она содержит выражения в числителе и знаменателе), мы можем использовать правило частного, чтобы найти ее производную.

Теперь, когда мы знаем, как работает частное правило, давайте разберемся с формулой частного правила и узнаем, как его вывести. 2$.

Мы можем использовать эту формулу для различных типов рациональных выражений, и любая функция переписывается как отношение двух более простых выражений. Убедитесь, что вы знаете этот процесс наизусть после этого обсуждения. Не волнуйся; мы подготовили мнемонические подсказки, вывод формул и примеры, чтобы помочь вам.

Доказательство частного правила для производных

Если вы относитесь к тем, кто легко запоминает формулу, узнав, как она выводится, мы покажем вам доказательство частного правила, аналогичное выводу формулы правила произведения.

Начнем с формального определения производных и запишем $\dfrac{d}{dx} \left[\dfrac{f(x)}{g(x)}\right]$ в этой форме.

\begin{align} h'(x) &= \dfrac{d}{dx} \left[\dfrac{f(x)}{g(x)}\right]\\&= \lim_{h \rightarrow 0} \dfrac{\dfrac{f(x +h)}{g(x+h)} – \dfrac{f(x)}{g(x)}}{h}\\&= \lim_ {h \rightarrow 0}\dfrac{1}{h}\left[\dfrac{f(x +h)}{g(x+h)} – \dfrac{f(x)}{g(x)} \right] \end{aligned}

Мы можем манипулировать этим выражением и получить выражения, показанные ниже:

\begin{align} h'(x) &= \lim_{h \rightarrow 0}\dfrac{1}{h}\left[\dfrac{f(x +h)g(x)}{g( x)g(x+h)} – \dfrac{f(x)g(x +h)}{g(x)g(x+h)}\right]\\&= \lim_{h \rightarrow 0 } \ dfrac {1} {h} \ left [\ dfrac {f (x + h) g (x) -f (x) g (x + h)} {g (x) g (x + h)} \ вправо]\\&= \lim_{h \rightarrow 0}\dfrac{1}{h}\left[\dfrac{f(x +h)g(x){\color{green}-f(x)g (x)} + f (x) g (x + h) {\ color {green} + f (x) g (x)}} {g (x) g (x + h)} \ right] \\ & = \lim_{h \rightarrow 0}\dfrac{1}{h}\left[\dfrac{g(x)[f(x+h) -f(x)]-f(x)[g(x+ h) -g(x)]}{g(x)g(x+h)}\right] \end{aligned}

Перепишем это выражение, чтобы оно имело формальные выражения для $f’(x)$ и $g’(x)$. 2} \end{aligned}

Используйте этот раздел в качестве руководства при выводе правила доказательства частного. Это также показывает, насколько полезно это правило, поскольку нам больше не нужно повторять этот процесс каждый раз, когда мы находим производную от $h(x) = \dfrac{f(x)}{g(x)}$.

Когда использовать правило отношения и как использовать мнемонику для формулы ?

Частное наиболее полезно, когда нам даны выражения, которые являются рациональными выражениями или могут быть переписаны как рациональные выражения. Вот несколько примеров функций, которые выиграют от правила отношения: 92}$. Сначала формула может показаться пугающей, но вот несколько мнемоник, которые помогут вам ознакомиться с правилом отношения:

• Попробуйте произнести правило отношения вслух и назначьте полезные ключевые термины, которые помогут вам, например: «$g$ $f$ простое число минус $f$ $g$ простое число в $g$ в квадрате.

• Вот еще: «Младшая производная от высокого минус высокая производная от низкого по всем младшим в квадрате». В этом случае «низкий» означает более низкое выражение (т. е. знаменатель), а «высокий» означает более высокое выражение (или числитель).

• Для этого тоже есть сокращенная фраза: «минимум $d$ максимума минус максимум $d$ минимума на всем низком минимуме».

Это лишь некоторые из многих мнемонических руководств, которые помогут вам. На самом деле, вы тоже можете придумать оригинальный для себя!

Конечно, лучший способ усвоить это правило — многократно находить производные различных функций.

Пример 1

Найдите производную от $h(x) = \dfrac{2x- 1}{x + 3}$, используя правило частных.

Решение

Мы видим, что $h(x)$ действительно является рациональным выражением, поэтому лучший способ дифференцировать $h(x)$ — использовать правило частных. Сначала представим $h(x)$ как отношения двух выражений, $\dfrac{f(x)}{g(x)}$, затем возьмем их соответствующие производные.

Функция	Производная
\ begin {выровнен} f (x) и = 2x-1 \ end {Aligned}	9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 {Aligned} F (x) и = 2x-10008	\begin{align}f'(x) &= \dfrac{d}{x} (2x-1)\\&= 2 \cdot \dfrac{d}{dx}x -1, \phantom{ x}\color{green}\text{Постоянное множественное правило}\\&= 2 \cdot (1) -0, \phantom{x}\color{green}\text{Постоянное правило}\\&= 2 \end {выровнено}
\begin{выровнено}g(x) &= x+3 \end{выровнено}	\begin{выровнено}g'(x) &= \dfrac{d}{ x} (x+3)\\&= 1 \cdot \dfrac{d}{dx}x +3, \phantom{x}\color{green}\text{Постоянное множественное правило}\\&= 1 \cdot (1) + 0, \phantom{x}\color{green}\text{Постоянное правило}\\&= 1 \end{align} 92}$. Оставить комментарий Отменить ответ Для отправки комментария вам необходимо авторизоваться. Меню Поиск: