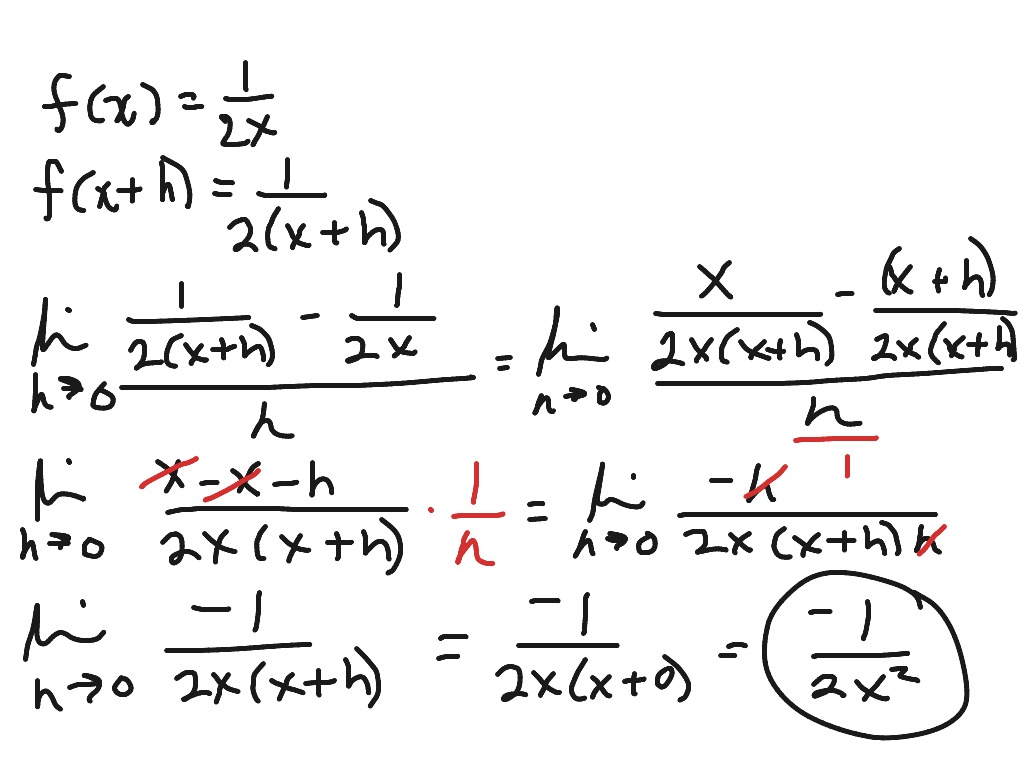Формула производной дроби: Производная дроби, формула и примеры

Справочник по высшей математике

Выгодский М.Я. Справочник по высшей математике. Изд-во “Наука”. М. 1977 г. Справочник включает весь материал, входящий в программу основного курса математики высших учебных заведений. Детальная рубрикация и подробный предметный указатель позволяют быстро получать необходимую информацию. Книга окажет неоценимую помощь студентам, инженерам и научным работникам. Оглавление ПРЕДИСЛОВИЕ АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ § 1. Понятие о предмете аналитической геометрии § 2. Координаты § 3. Прямоугольная система координат § 4. Прямоугольные координаты § 5. Координатные углы § 6. Косоугольная система координат § 7. Уравнение линии § 8. Взаимное расположение линии и точки § 9. Взаимное расположение двух линий § 10. Расстояние между двумя точками § 11. Деление отрезка в данном отношении § 11а. Деление отрезка пополам § 12. Определитель второго порядка § 13. Площадь треугольника § 14. Прямая линия; уравнение, разрешенное относительно ординаты (с угловым коэффициентом) § 15. Прямая, параллельная оси § 16. Общее уравнение прямой § 17. Построение прямой по ее уравнению § 18. Условие параллельности прямых § 19. Пересечение прямых § 20. Условие перпендикулярности двух прямых § 21. Угол между двумя прямыми § 22. Условие, при котором три точки лежат на одной прямой § 23. Уравнение прямой, проходящей через две точки § 24. Пучок прямых § 25. Уравнение прямой, проходящей через данную точку параллельно данной прямой § 26. Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой § 27. Взаимное расположение прямой и пары точек § 28. Расстояние от точки до прямой § 29. Полярные параметры прямой § 30. 2+bx+c § 51. Директрисы эллипса и гиперболы § 52. Общее определение эллипса, гиперболы и параболы § 53. Конические сечения § 54. Диаметры конического сечения § 55. Диаметры эллипса § 56. Диаметры гиперболы § 57. Диаметры параболы § 58. Линии второго порядка § 59. Запись общего уравнения второй степени § 60. Упрощение уравнения второй степени; общие замечания § 61. Предварительное преобразование уравнения второй степени § 62. Завершающее преобразование уравнения второй степени § 63. О приемах, облегчающих упрощение уравнения второй степени § 64. Признак распадения линий второго порядка § 65. Нахождение прямых, составляющих распадающуюся линию второго порядка § 66. Инварианты уравнения второй степени § 67. Три типа линий второго порядка § 68. Центральные и нецентральные линии второго порядка § 69. Нахождение центра центральной линии второго порядка § 70. Упрощение уравнения центральной линии второго порядка § 71. Равносторонняя гипербола как график уравнения y=k/x § 72. Равносторонняя гипербола как график уравнения y=(mx+n)/(px+q) § 73. Полярные координаты § 74. Связь между полярными и прямоугольными координатами § 75. Архимедова спираль § 76. Полярное уравнение прямой § 77. Полярное уравнение конического сечения АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ § 78. Понятие о векторах и скалярах § 79. Вектор в геометрии § 80. Векторная алгебра § 81. Коллинеарные векторы § 82. Нуль-вектор § 83. Равенство векторов § 84. Приведение векторов к общему началу § 85. Противоположные векторы § 86. Сложение векторов § 87. Сумма нескольких векторов § 88. Вычитание векторов § 89. Умножение и деление вектора на число § 90. Взаимная связь коллинеарных векторов (деление вектора на вектор) § 91. Проекция точки на ось § 92. Проекция вектора на ось § 93. Основные теоремы о проекциях вектора § 94. Прямоугольная система координат в пространстве § 95. Координаты точки § 96. Координаты вектора § 97. Выражения вектора через компоненты и через координаты § 98. Действия над векторами, заданными своими координатами § 99. Выражение вектора через радиусы-векторы его начала и конца § 100. Длина вектора. Расстояние между двумя точками § 101. Угол между осью координат и вектором § 102. Признак коллинеарности (параллельности) векторов § 103. Деление отрезка в данном отношении § 104. Скалярное произведение двух векторов § 104а. Физический смысл скалярного произведения § 105. Свойства скалярного произведения § 106. Скалярные произведения основных векторов § 107. Выражение скалярного произведения через координаты сомножителей § 108. Условие перпендикулярности векторов § 109. Угол между векторами § 110. Правая и левая системы трех векторов § 111. Векторное произведение двух векторов § 112. Свойства векторного произведения § 113. Векторные произведения основных векторов § 114. Выражение векторного произведения через координаты сомножителей § 115. Компланарные векторы § 116. Смешанное произведение § 117. Свойства смешанного произведения § 118. Определитель третьего порядка § 119. Выражение смешанного произведения через координаты сомножителей § 120. Признак компланарности в координатной форме § 121. Объем параллелепипеда § 122. Двойное векторное произведение § 123. Уравнение плоскости § 124. Особые случаи положения плоскости относительно системы координат § 125. Условие параллельности плоскостей § 126. Условие перпендикулярности плоскостей § 127. Угол между двумя плоскостями § 128. Плоскость, проходящая через данную точку параллельно данной плоскости § 129. Плоскость, проходящая через три точки § 130. Отрезки на осях § 131. Уравнение плоскости в отрезках § 132. Плоскость, проходящая через две точки перпендикулярно данной плоскости § 133. Плоскость, проходящая через данную точку перпендикулярно двум плоскостям § 134. Точка пересечения трех плоскостей § 135. Взаимное расположение плоскости и пары точек § 136. Расстояние от точки до плоскости § 137. Полярные параметры плоскости § 138. Нормальное уравнение плоскости § 139. Приведение уравнения плоскости к нормальному виду § 140. Уравнения прямой в пространстве § 141. Условие, при котором два уравнения первой степени представляют прямую § 142. Пересечение прямой с плоскостью § 143. Направляющий вектор § 144. Углы между прямой и осями координат § 145. Угол между двумя прямыми § 146. Угол между прямой и плоскостью § 147. Условия параллельности и перпендикулярности прямой и плоскости § 148. Пучок плоскостей § 149. Проекции прямой на координатные плоскости § 150. Симметричные уравнения прямой § 151. Приведение уравнений прямой к симметричному виду § 152. Параметрические уравнения прямой § 153. Пересечение плоскости с прямой, заданной параметрически § 154. Уравнения прямой, проходящей через две данные точки § 155. Уравнение плоскости, проходящей через данную точку перпендикулярно данной прямой § 156. Уравнения прямой, проходящей через данную точку перпендикулярно данной плоскости § 157. Уравнение плоскости, проходящей через данную точку и данную прямую § 158. Уравнение плоскости, проходящей через данную точку и параллельной двум данным прямым § 159. Уравнение плоскости, проходящей через данную прямую и параллельной другой данной прямой § 160. Уравнение плоскости, проходящей через данную прямую и перпендикулярной данной плоскости § 161. Уравнения перпендикуляра, опущенного из данной точки на данную прямую § 162. Длина перпендикуляра, опущенного из данной точки на данную прямую § 163. Условие, при котором две прямые пересекаются или лежат в одной плоскости § 164. Уравнения общего перпендикуляра к двум данным прямым § 165. Кратчайшее расстояние между двумя прямыми § 165а. Правые и левые пары прямых § 166. Преобразование координат § 167. Уравнение поверхности § 168. Цилиндрические поверхности, у которых образующие параллельны одной из осей координат § 169. Уравнения линии § 170. Проекция линии на координатную плоскость § 171. Алгебраические поверхности и их порядок § 172. Сфера § 173. Эллипсоид § 174. Однополостный гиперболоид § 175. Двуполостный гиперболоид § 176. Конус второго порядка § 177. Эллиптический параболоид § 178. Гиперболический параболоид § 179. Перечень поверхностей второго порядка § 180. Прямолинейные образующие поверхностей второго порядка § 181. Поверхности вращения § 182. Определители второго и третьего порядков § 183. Определители высших порядков § 184. Свойства определителей § 185. Практический прием вычисления определителей § 186. Применение определителей к исследованию и решению системы уравнений § 187. Два уравнения с двумя неизвестными § 188. Два уравнения с двумя неизвестными § 189. Однородная система двух уравнений с тремя неизвестными § 190. Два уравнения с двумя неизвестными § 190а. Система n уравнений с n неизвестными ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОГО АНАЛИЗА § 192. Рациональные числа § 193. Действительные (вещественные) числа § 194. Числовая ось § 195. Переменные и постоянные величины § 196. Функция § 197. Способы задания функции § 198. Область определения функции § 199. Промежуток § 200. Классификация функций § 201. Основные элементарные функции § 202. Обозначение функции § 203. Предел последовательности § 204. Предел функции § 205. Определение предела функции § 206. Предел постоянной величины § 207. Бесконечно малая величина § 208. Бесконечно большая величина § 209. Связь между бесконечно большими и бесконечно малыми величинами § 210. Ограниченные величины § 211. Расширение понятия предепа § 212. Основные свойства бесконечно малых величин § 213. Основные теоремы о пределах § 214. Число е § 215. Предел sinx/x при x стремящемся к 0 § 216. Эквивалентные бесконечно малые величины § 217. Сравнение бесконечно малых величин § 217а. Приращение переменной величины § 218. Непрерывность функции в точке § 219. Свойства функций, непрерывных в точке § 219а. Односторонний предел; скачок функции § 220. Непрерывность функции на замкнутом промежутке § 221. Свойства функций, непрерывных на замкнутом промежутке ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ § 223. Скорость § 224. Определение производной функции § 225. Касательная § 226. Производные некоторых простейших функций § 227. Свойства производной § 228. Дифференциал § 229. Механический смысл дифференциала § 230. Геометрический смысл дифференциала § 231. Дифференцируемые функции § 232. Дифференциалы некоторых простейших функций § 233. Свойства дифференциала § 234. Инвариантность выражения f'(x)dx § 235. Выражение производной через дифференциалы § 236. Функция от функции (сложная функция) § 237. Дифференциал сложной функции § 238. 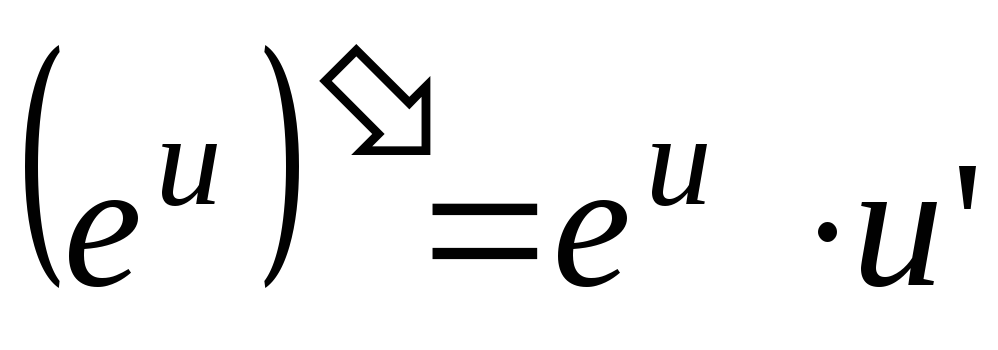Производная сложной функции § 239. Дифференцирование произведения § 240. Дифференцирование частного (дроби) § 241. Обратная функция § 242. Натуральные логарифмы § 243. Дифференцирование логарифмической функции § 244. Логарифмическое дифференцирование § 245. Дифференцирование показательной функции § 246. Дифференцирование тригонометрических функций § 247. Дифференцирование обратных тригонометрических функций § 247а. Некоторые поучительные примеры § 248. Дифференциал в приближенных вычислениях § 249. Применение дифференциала к оценке погрешности формул § 250. Дифференцирование неявных функций § 251. Параметрическое задание линии § 252. Параметрическое задание функции § 253. Циклоида § 254. Уравнение касательной к плоской линии § 254а. Касательные к кривым второго порядка § 255. Уравнение нормали § 256. Производные высших порядков § 257. Механический смысл второй производной § 258. Дифференциалы высших порядков § 259. Выражение высших производных через дифференциалы § 260. Высшие производные функций, заданных параметрически § 261. Высшие производные неявных функций § 262. Правило Лейбница § 263. Теорема Ролля § 264. Теорема Лагранжа о среднем значении § 265. Формула конечных приращений § 266. Обобщенная теорема о среднем значении (Коши) § 267. Раскрытие неопределенности вида 0/0 § 268. Раскрытие неопределенности вида бесконесность на бесконечность § 269. Неопределенные выражения других видов § 270. Исторические сведения о формуле Тейлора § 271. Формула Тейлора § 272. Применение формулы Тейлора к вычислению значений функции § 273. Возрастание и убывание функции § 274. Признаки возрастания и убывания функции в точке § 274а. Признаки возрастания и убывания функции в промежутке § 275. Максимум и минимум § 276. Необходимое условие максимума и минимума § 277. Первое достаточное условие максимума и минимума § 278. Правило нахождения максимумов и минимумов § 279. Второе достаточное условие максимума и минимума § 280. Нахождение наибольшего и наименьшего значений функции § 281. Выпуклость плоских кривых; точка перегиба § 282. Сторона вогнутости § 283. Правило для нахождения точек перегиба § 284. Асимптоты § 285. Нахождение асимптот, параллельных координатным осям § 286. Нахождение асимптот, не параллельных оси ординат § 287. Приемы построения графиков § 288. Решение уравнений. Общие замечания § 289. Решение уравнений. Способ хорд § 290. Решение уравнений. Способ касательных § 291. Комбинированный метод хорд и касательных ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ § 293. Первообразная функция § 294. Неопределенный интеграл § 295. Геометрический смысл интегрирования § 296. Вычисление постоянной интегрирования по начальным данным § 297. Свойства неопределенного интеграла § 298. Таблица интегралов § 299. Непосредственное интегрирование § 300. Способ подстановки (интегрирование через вспомогательную переменную) § 301. Интегрирование по частям § 302. Интегрирование некоторых тригонометрических выражений § 303. Тригонометрические подстановки § 304. Рациональные функции § 304а. Исключение целой части § 305. О приемах интегрирования рациональных дробей § 306. Интегрирование простейших рациональных дробей § 307. Интегрирование рациональных функций (общий метод) § 308. О разложении многочлена на множители § 309. Об интегрируемости в элементарных функциях § 310. Некоторые интегралы, зависящие от радикалов § 311. Интеграл от биномиального дифференциала § 312. Интегралы вида … § 313. Интегралы вида S R(sinx, cosx)dx § 314. Определенный интеграл § 315. Свойства определенного интеграла § 316. Геометрический смысл определенного интеграла § 317. Механический смысл определенного интеграла § 318. Оценка определенного интеграла § 318а. Неравенство Буняковского § 319. Теорема о среднем интегрального исчисления § 320. Определенный интеграл как функция верхнего предела § 321. Дифференциал интеграла § 322. Интеграл дифференциала. Формула Ньютона — Лейбница § 323. Вычисление определенного интеграла с помощью неопределенного § 324. Определенное интегрирование по частям § 325. Способ подстановки в определенном интеграле § 326. О несобственных интегралах § 327. Интегралы с бесконечными пределами § 328. Интеграл функции, имеющей разрыв § 329. О приближенном вычислении интеграла § 330. Формулы прямоугольников § 331. Формула трапеций § 332. Формула Симпсона (параболических трапеций) § 333. Площади фигур, отнесенных к прямоугольным координатам § 334. Схема применения определенного интеграла § 335. Площади фигур, отнесенных к полярным координатам § 336. Объем тела по поперечным сечениям § 337. Объем тела вращения § 338. Длина дуги плоской линии § 339. Дифференциал дуги § 340. Длина дуги и ее дифференциал в полярных координатах § 341. Площадь поверхности вращения ОСНОВНЫЕ СВЕДЕНИЯ О ПЛОСКИХ И ПРОСТРАНСТВЕННЫХ ЛИНИЯХ § 342. Кривизна § 343. Центр, радиус и круг кривизны плоской линии § 344. Формулы для кривизны, радиуса и центра кривизны плоской линии § 345. Эволюта плоской линии § 346. Свойства эволюты плоской линии § 347. Развертка (эвольвента) плоской линии § 348. Параметрическое задание пространственной линии § 349. Винтовая линия § 350. Длина дуги пространственной линии § 351. Касательная к пространственной линии § 352. Нормальная плоскость § 353. Вектор-функция скалярного аргумента § 354. Предел вектор-функции § 355. Производная вектор-функции § 356. Дифференциал вектор-функции § 357. Свойства производной и дифференциала вектор-функции § 358. Соприкасающаяся плоскость § 359. Главная нормаль. Сопутствующий трехгранник § 360. Взаимное расположение линии и плоскости § 361. Основные векторы сопутствующего трехгранника § 362. Центр, ось и радиус кривизны пространственной линии § 363. Формулы для кривизны, радиуса и центра кривизны пространственной линии § 364. О знаке кривизны § 365. Кручение РЯДЫ § 367. Определение ряда § 368. Сходящиеся и расходящиеся ряды § 369. Необходимое условие сходимости ряда § 370. Остаток ряда § 371. Простейшие действия над рядами § 372. Положительные ряды § 373. Сравнение положительных рядов § 374. Признак Даламбера для положительного ряда § 375. Интегральный признак сходимости § 376. Знакопеременный ряд. Признак Лейбница § 377. Абсолютная и условная сходимость § 378. Признак Даламбера для произвольного ряда § 379. Перестановка членов ряда § 380. Группировка членов ряда § 381. Умножение рядов § 382. Деление рядов § 383. Функциональный ряд § 384. Область сходимости функционального ряда § 385. О равномерной и неравномерной сходимости § 386. Определение равномерной и неравномерной сходимости § 387. Геометрический смысл равномерной и неравномерной сходимости § 388. Признак равномерной сходимости; правильные ряды § 389. Непрерывность суммы ряда § 390. Интегрирование рядов § 391. Дифференцирование рядов § 392. Степенной ряд § 393. Промежуток и радиус сходимости степенного ряда § 394. Нахождение радиуса сходимости § 395. Область сходимости ряда, расположенного по степеням х – х0 § 396. Теорема Абеля § 397. Действия со степенными рядами § 398. Дифференцирование и интегрирование степенного ряда § 399. Ряд Тейлора § 400. Разложение функции в степенной ряд § 401. Разложение элементарных функций в степенные ряды § 402. Применение рядов к вычислению интегралов § 403. Гиперболические функции § 404. Обратные гиперболические функции § 405. Происхождение наименований гиперболических функций § 406. О комплексных числах § 407. Комплексная функция действительного аргумента § 408. Производная комплексной функции § 409. Возведение положительного числа в комплексную степень § 410. Формула Эйлера § 411. Тригонометрический ряд § 412. Исторические сведения о тригонометрических рядах § 413. Ортогональность системы функций cos nx, sin nx § 414. Формулы Эйлера-Фурье § 415. Ряд Фурье § 416. Ряд Фурье для непрерывной функции § 417. Ряд Фурье для четной и нечетной функции § 418. Ряд Фурье для разрывной функции ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ АРГУМЕНТОВ § 420. Функция трех и большего числа аргументов § 421. Способы задания функций нескольких аргументов § 422. Предел функции нескольких аргументов § 424. Непрерывность функции нескольких аргументов § 425. Частные производные § 426. Геометрический смысл частных производных для случая двух аргументов § 427. Полное и частное приращения § 428. Частный дифференциал § 429. О выражении частной производной через дифференциал § 430. Полный дифференциал § 431. Геометрический смысл полного дифференциала (случай двух аргументов) § 432. Инвариантность выражения … полного дифференциала § 433. Техника дифференцирования § 434. Дифференцируемые функции § 435. Касательная плоскость и нормаль к поверхности § 436. Уравнение касательной плоскости § 437. Уравнения нормали § 438. Дифференцирование сложной функции § 439. Замена прямоугольных координат полярными § 440. Формулы для производных сложной функции § 441. Полная производная § 442. Дифференцирование неявной функции нескольких переменных § 443. Частные производные высших порядков § 444. Полные дифференциалы высших порядков § 445. Техника повторного дифференцирования § 446. Условное обозначение дифференциалов § 447. Формула Тейлора для функции нескольких аргументов § 448. Экстремум (максимум и минимум) функции нескольких аргументов § 449. Правило нахождения экстремума § 450. Достаточные условия экстремума (случай двух аргументов) § 451. Двойной интеграл § 452. Геометрический смысл двойного интеграла § 453. Свойства двойного интеграла § 454. Оценка двойного интеграла § 455. Вычисление двойного интеграла (простейший случай) § 456. Вычисление двойного интеграла (общий случай) § 457. Функция точки § 458. Выражение двойного интеграла через полярные координаты § 459. Площадь куска поверхности § 460. Тройной интеграл § 461. Вычисление тройного интеграла (простейший случай) § 462. Вычисление тройного интеграла (общий случай) § 463. Цилиндрические координаты § 464. Выражение тройного интеграла через цилиндрические координаты § 465. Сферические координаты § 466. Выражение тройного интеграла через сферические координаты § 467. Схема применения двойного и тройного интегралов § 468. Момент инерции § 471. Криволинейный интеграл § 472. Механический смысл криволинейного интеграла § 473. Вычисление криволинейного интеграла § 474. Формула Грина § 475. Условие, при котором криволинейный интеграл не зависит от пути § 476. Другая форма условия предыдущего параграфа ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ § 478. Уравнение первого порядка § 479. Геометрический смысл уравнения первого порядка § 480. Изоклины § 481. Частное и общее решения уравнения первого порядка § 482. Уравнения с разделенными переменными § 483. Разделение переменных. Особое решение § 484. Уравнение в полных дифференциалах § 484а. Интегрирующий множитель § 485. Однородное уравнение § 486. Линейное уравнение первого порядка § 487. Уравнение Клеро § 488. Огибающая § 489. Об интегрируемости дифференциальных уравнений § 490. Приближенное интегрирование уравнений первого порядка по методу Эйлера § 491. Интегрирование дифференциальных уравнений с помощью рядов § 492. О составлении дифференциальных уравнений § 493. Уравнение второго порядка § 494. Уравнение n-го порядка § 495. Случаи понижения порядка § 496. Линейное уравнение второго порядка § 497. Линейное уравнение второго порядка с постоянными коэффициентами § 498. Линейное уравнение второго порядка с постоянными коэффициентами без правой части § 498а. Связь между случаями 1 и 3 § 498 § 499. Линейное уравнение второго порядка с постоянными коэффициентами с правой частью § 500. Линейные уравнения любого порядка § 501. Метод вариации постоянных § 502. Системы дифференциальных уравнений. Линейные системы НЕКОТОРЫЕ ЗАМЕЧАТЕЛЬНЫЕ КРИВЫЕ § 503. Строфоида § 504. Циссоида Диокла § 505. Декартов лист § 506. Верзьера Аньези § 507. Конхоида Никомеда § 508. Улитка Паскаля; кардиоида § 509. Линия Кассини § 510. Лемниската Бернулли § 511. Архимедова спираль § 512. Эвольвента (развертка) круга § 513. Логарифмическая спираль § 514. Циклоиды § 515. Эпициклоиды и гипоциклоиды § 516. Трактриса § 517. Цепная линия

Производная 2 4. Производная косинуса: (cos x)′

Операция отыскания производной называется дифференцированием.

В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).

Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.

Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного – в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.

Пример 1. Найти производную функции

Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т.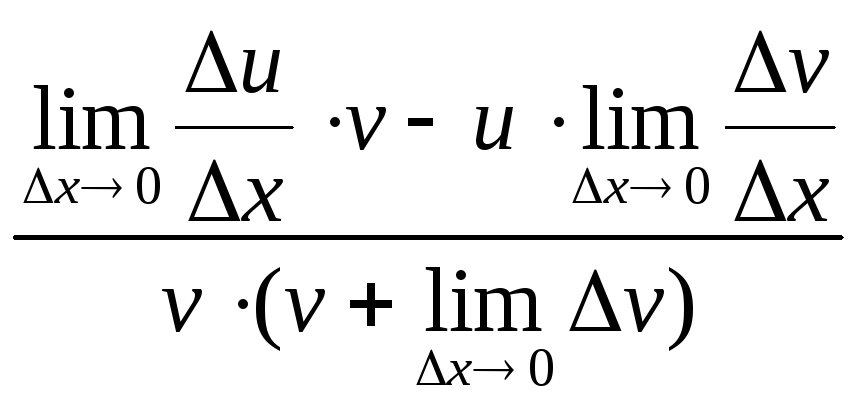 е.

Из таблицы производных выясняем, что производная “икса” равна единице, а производная синуса – косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:

Пример 2. Найти производную функции

Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:

Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.

Таблица производных простых функций

1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто
2. Производная независимой переменной. Чаще всего “икса”. Всегда равна единице. Это тоже важно запомнить надолго
3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни.
4. Производная переменной в степени -1
5. Производная квадратного корня
6. Производная синуса
7. Производная косинуса
8. Производная тангенса
9. Производная котангенса
10. Производная арксинуса
11. Производная арккосинуса
12. Производная арктангенса
13. Производная арккотангенса
14. Производная натурального логарифма
15. Производная логарифмической функции
16. Производная экспоненты
17. Производная показательной функции

Правила дифференцирования

1. Производная суммы или разности
2. Производная произведения
2a. Производная выражения, умноженного на постоянный множитель
3. Производная частного
4. Производная сложной функции

Правило 1. Если функции

дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции

причём

т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.

Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.

Правило 2. Если функции

дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение

причём

т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.

Следствие 1. Постоянный множитель можно выносить за знак производной :

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.

Например, для трёх множителей:

Правило 3. Если функции

дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём

т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.

Где что искать на других страницах

При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные – в статье “Производная произведения и частного функций ” .

Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.

А если при дифференцировании произведения или частного у вас появилось слагаемое u “v , в котором u – число, например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё слагаемое будет равно нулю (такой случай разобран в примере 10).

Другая частая ошибка – механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.

По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .

Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие “Производная суммы дробей со степенями и корнями “.

Если же перед Вами задача вроде , то Вам на занятие “Производные простых тригонометрических функций”.

Пошаговые примеры – как найти производную

Пример 3. Найти производную функции

Решение. Определяем части выражения функции: всё выражение представляет произведение, а его сомножители – суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:

Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, “икс” у нас превращается в единицу, а минус 5 – в ноль. Во втором выражении “икс” умножен на 2, так что двойку умножаем на ту же единицу как производную “икса”. Получаем следующие значения производных:

Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:

Пример 4. Найти производную функции

Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного: производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:

Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:

Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие “Производная суммы дробей со степенями и корнями” .

Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок “Производные простых тригонометрических функций” .

Пример 5. Найти производную функции

Решение. В данной функции видим произведение, один из сомножителей которых – квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:

Пример 6. Найти производную функции

Решение. В данной функции видим частное, делимое которого – квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:

Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .

Вычисление производной – одна из самых важных операций в дифференциальном исчислении. Ниже приводится таблица нахождения производных простых функций. Более сложные правила дифференцирования смотрите в других уроках:

• Таблица производных экспоненциальных и логарифмических функций

Приведенные формулы используйте как справочные значения. Они помогут в решении дифференциальных уравнений и задач. На картинке, в таблице производных простых функций, приведена “шпаргалка” основных случаев нахождения производной в понятном для применения виде, рядом с ним даны пояснения для каждого случая.

Производные простых функций

1. Производная от числа равна нулю
с´ = 0
Пример:
5´ = 0

Пояснение :
Производная показывает скорость изменения значения функции при изменении аргумента. Поскольку число никак не меняется ни при каких условиях – скорость его изменения всегда равна нулю.

2. Производная переменной равна единице
x´ = 1

Пояснение :
При каждом приращении аргумента (х) на единицу значение функции (результата вычислений) увеличивается на эту же самую величину. Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.

3. Производная переменной и множителя равна этому множителю
сx´ = с
Пример:
(3x)´ = 3
(2x)´ = 2
Пояснение :
В данном случае, при каждом изменении аргумента функции (х ) ее значение (y) растет в с раз. Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с .

Откуда следует, что
(cx + b)” = c
то есть дифференциал линейной функции y=kx+b равен угловому коэффициенту наклона прямой (k).

4. Производная переменной по модулю равна частному этой переменной к ее модулю
|x|” = x / |x| при условии, что х ≠ 0
Пояснение :
Поскольку производная переменной (см. формулу 2) равна единице, то производная модуля отличается лишь тем, что значение скорости изменения функции меняется на противоположное при пересечении точки начала координат (попробуйте нарисовать график функции y = |x| и убедитесь в этом сами.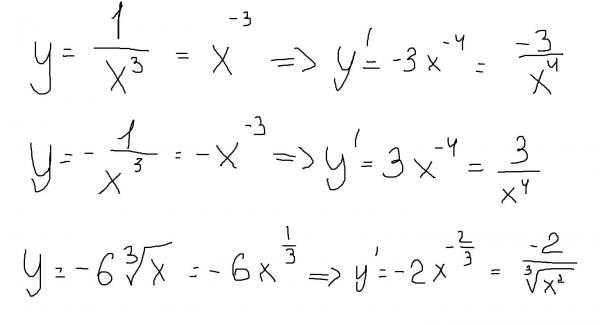 Именно такое значение и возвращает выражение x / |x| . Когда x 0 – единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных – наоборот, возрастает, но точно на такое же значение.

5. Производная переменной в степени равна произведению числа этой степени и переменной в степени, уменьшенной на единицу
(x c)”= cx c-1 , при условии, что x c и сx c-1 ,определены а с ≠ 0
Пример:
(x 2)” = 2x
(x 3)” = 3x 2
Для запоминания формулы :
Снесите степень переменной “вниз” как множитель, а потом уменьшите саму степень на единицу. Например, для x 2 – двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х. То же самое произошло для x 3 – тройку “спускаем вниз”, уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x 2 . Немного “не научно”, но очень просто запомнить.

6. Производная дроби 1/х
(1/х)” = – 1 / x 2
Пример:
Поскольку дробь можно представить как возведение в отрицательную степень
(1/x)” = (x -1)” , тогда можно применить формулу из правила 5 таблицы производных
(x -1)” = -1x -2 = – 1 / х 2

7.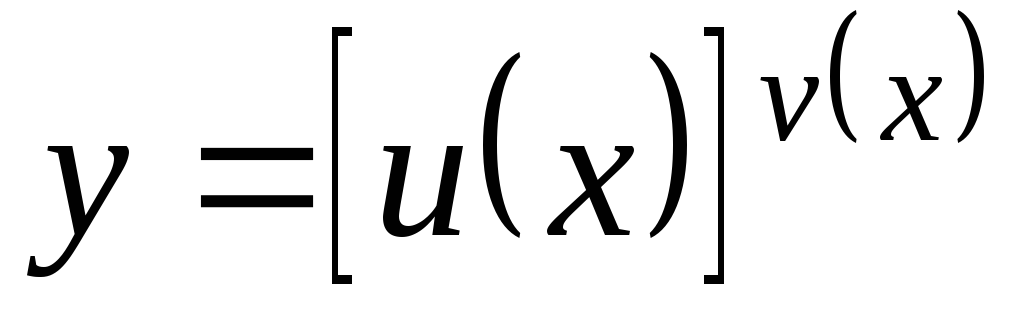 Производная дроби с переменной произвольной степени в знаменателе
(1 / x c)” = – c / x c+1
Пример:
(1 / x 2)” = – 2 / x 3

8. Производная корня (производная переменной под квадратным корнем)
(√x)” = 1 / (2√x) или 1/2 х -1/2
Пример:
(√x)” = (х 1/2)” значит можно применить формулу из правила 5
(х 1/2)” = 1/2 х -1/2 = 1 / (2√х)

9. Производная переменной под корнем произвольной степени
(n √x)” = 1 / (n n √x n-1)

Задача нахождения производной от заданной функции является одной из основных в курсе математики старшей школы и в высших учебных заведениях. Невозможно полноценно исследовать функцию, построить ее график без взятия ее производной. Производную функции легко можно найти, зная основные правила дифференцирования, а также таблицу производных основных функций. Давайте разберемся, как найти производную функции.

Производной функции называют предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

Понять это определение достаточно сложно, так как понятие предела в полной мере не изучается в школе. Но для того, чтобы находить производные различных функций, понимать определение не обязательно, оставим его специалистам математикам и перейдем сразу к нахождению производной.

Процесс нахождения производной называется дифференцированием. При дифференцировании функции мы будем получать новую функцию.

Для их обозначения будем использовать латинские буквы f, g и др.

Существует много всевозможных обозначений производных. Мы будем использовать штрих. Например запись g” означает, что мы будем находить производную функции g.

Таблица производных

Для того чтобы дать ответ на вопрос как найти производную, необходимо привести таблицу производных основных функций. Для вычисления производных элементарных функций не обязательно производить сложные вычисления. Достаточно просто посмотреть ее значение в таблице производных.

1. (sin x)”=cos x
2. (cos x)”= –sin x
3. (x n)”=n x n-1
4. (e x)”=e x
5. (ln x)”=1/x
6. (a x)”=a x ln a
7. (log a x)”=1/x ln a
8. (tg x)”=1/cos 2 x
9. (ctg x)”= – 1/sin 2 x
10. (arcsin x)”= 1/√(1-x 2)
11. (arccos x)”= – 1/√(1-x 2)
12. (arctg x)”= 1/(1+x 2)
13. (arcctg x)”= – 1/(1+x 2)

Пример 1.

Найдите производную функции y=500.

Мы видим, что это константа. По таблице производных известно, что производная константы, равна нулю (формула 1).

Пример 2. Найдите производную функции y=x 100 .

Это степенная функция в показателе которой 100 и чтобы найти ее производную нужно умножить функцию на показатель и понизить на 1 (формула 3).

(x 100)”=100 x 99

Пример 3. Найдите производную функции y=5 x

Это показательная функция, вычислим ее производную по формуле 4.

Пример 4. Найдите производную функции y= log 4 x

Производную логарифма найдем по формуле 7.

(log 4 x)”=1/x ln 4

Правила дифференцирования

Давайте теперь разберемся, как находить производную функции, если ее нет в таблице. Большинство исследуемых функций, не являются элементарными, а представляют собой комбинации элементарных функций с помощью простейших операций (сложение, вычитание, умножение, деление, а также умножение на число). Для нахождения их производных необходимо знать правила дифференцирования. Далее буквами f и g обозначены функции, а С – константа.

1. Постоянный коэффициент можно выносить за знак производной

Пример 5. Найдите производную функции y= 6*x 8

Выносим постоянный коэффициент 6 и дифференцируем только x 4 . Это степенная функция, производную которой находим по формуле 3 таблицы производных.

(6*x 8)” = 6*(x 8)”=6*8*x 7 =48* x 7

2. Производная суммы равна сумме производных

(f + g)”=f” + g”

Пример 6. Найдите производную функции y= x 100 +sin x

Функция представляет собой сумму двух функций, производные которых мы можем найти по таблице. Так как (x 100)”=100 x 99 и (sin x)”=cos x. Производная суммы будет равна сумме данных производных:

(x 100 +sin x)”= 100 x 99 +cos x

3. Производная разности равна разности производных

(f – g)”=f” – g”

Пример 7. Найдите производную функции y= x 100 – cos x

Эта функция представляет собой разность двух функции, производные которых мы также можем найти по таблице. Тогда производная разности равна разности производных и не забудем поменять знак, так как (cos x)”= – sin x.

(x 100 – cos x)”= 100 x 99 + sin x

Пример 8. Найдите производную функции y=e x +tg x– x 2 .

В этой функции есть и сумма и разность, найдем производные от каждого слагаемого:

(e x)”=e x , (tg x)”=1/cos 2 x, (x 2)”=2 x. Тогда производная исходной функции равна:

(e x +tg x– x 2)”= e x +1/cos 2 x –2 x

4. Производная произведения

(f * g)”=f” * g + f * g”

Пример 9. Найдите производную функции y= cos x *e x

Для этого сначала найдем производного каждого множителя (cos x)”=–sin x и (e x)”=e x . Теперь подставим все в формулу произведения. Производную первой функции умножим на вторую и прибавим произведение первой функции на производную второй.

(cos x* e x)”= e x cos x – e x *sin x

5. Производная частного

(f / g)”= f” * g – f * g”/ g 2

Пример 10. Найдите производную функции y= x 50 /sin x

Чтобы найти производную частного, сначала найдем производную числителя и знаменателя отдельно: (x 50)”=50 x 49 и (sin x)”= cos x. Подставив в формулу производной частного получим:

(x 50 /sin x)”= 50x 49 *sin x – x 50 *cos x/sin 2 x

Производная сложной функции

Сложная функция – это функция, представленная композицией нескольких функций. Для нахождения производной сложной функции также существует правило:

(u (v))”=u”(v)*v”

Давайте разберемся как находить производную такой функции. Пусть y= u(v(x)) – сложная функция. Функцию u назовем внешней, а v – внутренней.

Например:

y=sin (x 3) – сложная функция.

Тогда y=sin(t) – внешняя функция

t=x 3 – внутренняя.

Давайте попробуем вычислить производную этой функции. По формуле необходимо перемножить производные внутренней и внешней функции.

(sin t)”=cos (t) – производная внешней функции (где t=x 3)

(x 3)”=3x 2 – производная внутренней функции

Тогда (sin (x 3))”= cos (x 3)* 3x 2 – производная сложной функции.

Доказательство и вывод формул производной экспоненты (e в степени x) и показательной функции (a в степени x). nx. Формулы производных высших порядков.

Производная экспоненты равна самой экспоненте (производная e в степени x равна e в степени x):
(1) (e x )′ = e x .

Производная показательной функции с основанием степени a равна самой функции, умноженной на натуральный логарифм от a :
(2) .

Вывод формулы производной экспоненты, e в степени x

Экспонента – это показательная функция, у которой основание степени равно числу e , которое является следующим пределом:
.
Здесь может быть как натуральным, так и действительным числом. Далее мы выводим формулу (1) производной экспоненты.

Вывод формулы производной экспоненты

Рассмотрим экспоненту, e в степени x :
y = e x .
Эта функция определена для всех . Найдем ее производную по переменной x . По определению, производная является следующим пределом:
(3) .

Преобразуем это выражение, чтобы свести его к известным математическим свойствам и правилам.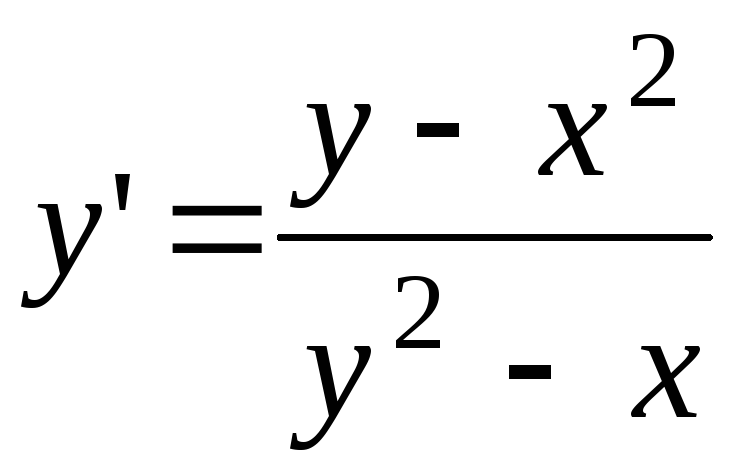 Для этого нам понадобятся следующие факты:
А) Свойство экспоненты :
(4) ;
Б) Свойство логарифма :
(5) ;
В) Непрерывность логарифма и свойство пределов для непрерывной функции:
(6) .
Здесь – некоторая функция, у которой существует предел и этот предел положителен.
Г) Значение второго замечательного предела:
(7) .

Применяем эти факты к нашему пределу (3). Используем свойство (4):
;
.

Сделаем подстановку . Тогда ; .
В силу непрерывности экспоненты,
.
Поэтому при , . В результате получаем:
.

Сделаем подстановку . Тогда . При , . И мы имеем:
.

Применим свойство логарифма (5):
. Тогда
.

Применим свойство (6). Поскольку существует положительный предел и логарифм непрерывен, то:
.
Здесь мы также воспользовались вторым замечательным пределом (7). Тогда
.

Тем самым мы получили формулу (1) производной экспоненты.

Вывод формулы производной показательной функции

Теперь выведем формулу (2) производной показательной функции с основанием степени a . Мы считаем, что и . Тогда показательная функция
(8)
Определена для всех .

Преобразуем формулу (8). Для этого воспользуемся свойствами показательной функции и логарифма .
;
.
Итак, мы преобразовали формулу (8) к следующему виду:
.

Производные высших порядков от e в степени x

Теперь найдем производные высших порядков. Сначала рассмотрим экспоненту:
(14) .
(1) .

Мы видим, что производная от функции (14) равна самой функции (14). Дифференцируя (1), получаем производные второго и третьего порядка:
;
.

Отсюда видно, что производная n-го порядка также равна исходной функции:
.

Производные высших порядков показательной функции

Теперь рассмотрим показательную функцию с основанием степени a :
.
Мы нашли ее производную первого порядка:
(15) .

Дифференцируя (15), получаем производные второго и третьего порядка:
;
.

Мы видим, что каждое дифференцирование приводит к умножению исходной функции на . Поэтому производная n-го порядка имеет следующий вид:
.

1.26: Решение дробных уравнений — Математика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

48329

Уравнение дробей — это уравнение, содержащее дроби, в знаменателе одного или нескольких членов которого есть неизвестное.

Пример 24.1

Ниже приведены примеры дробных уравнений:

a) \(\frac{3}{x}=\frac{9}{20}\)

b) \(\frac{x-2 }{x+2}=\frac{3}{5}\)

c) ​​\(\frac{3}{x-3}=\frac{4}{x-5}\)

d) \(\frac{3}{4}-\frac{1}{8 x}=0\)

e) \(\frac{x}{6}-\frac{2}{3 x}=\ frac{2}{3}\)

Свойство перекрестного произведения можно использовать для решения дробных уравнений.

Свойство перекрестного произведения

Если \(\frac{A}{B}=\frac{C}{D}\), то \(A \cdot D=B \cdot C\).

Используя это свойство, мы можем преобразовать дробные уравнения в не дробные. Мы должны соблюдать осторожность при применении этого свойства и использовать его только тогда, когда в каждой части уравнения есть одна дробь. Итак, дробные уравнения можно разделить на две категории.

I. Отдельные дроби с каждой стороны уравнения

Уравнения a), b) и c) в примере 24.1 попадают в эту категорию. Мы решаем эти уравнения здесь.

а) Решите \(\frac{3}{x}=\frac{9}{20}\)

\[\begin{array}{ll} \text{Cross-Product} & 3 \cdot 20=9 \cdot x \\ \text{Линейное уравнение} & 60=9 x \\ \text{Разделить на 9 обе стороны} & \frac{60}{9}=x \end{массив}\nonumber\]

Решение: \(x=\frac{60}{9}=\frac{20}{3}\ ).

b) \(\frac{x-2}{x+2}=\frac{3}{5}\)

\[\begin{array}{ll} \text{Cross-Product} & 5 \cdot(x-2)=3 \cdot(x+2) \\ \text{Удалить скобки} & 5 x-10=3 x+6 \\ \text{Линейное уравнение: изолировать переменную} & 5 x- 3 x=10+6 \\ & 2 x=16 \\ \text{Разделить на 2 с обеих сторон} & \frac{2 x}{2}=\frac{16}{2}\end{array}\nonumber \]

решение \(x=8\).

c) ​​\(\frac{3}{x-3}=\frac{4}{x-5}\)

\[\begin{array}{ll} \text{Cross-Product} & 3 \cdot(x-5)=4 \cdot(x-3) \\ \text{Удалить скобки} & 3 x-15=4 x-12 \\ \text{Линейное уравнение: изолировать переменную} & 3 x- 4 x=15-12 \\ & -x=3 \\ \text{Разделить на 2 обе стороны} & \frac{-x}{-1}=\frac{3}{-1}\end{array} \nonumber\]

Решение: \(x=-3\)

Примечание: Если у вас есть дробное уравнение и один из членов не является дробью, вы всегда можете учесть это, поставив 1 в знаменатель. Например:

Решить

\[\frac{3}{x}=15\nonnumber\]

Перепишем уравнение так, чтобы все члены были дробями.

\[\frac{3}{x}=\frac{15}{1}\nonumber\]

\[\begin{array}{ll} \text{Cross-Product} & 3 \cdot 1= 15 \cdot x \\ \text{Линейное уравнение: изолировать переменную} & 3=15 x \\ \text{Разделить на 15 обе стороны} & \frac{3}{15}=\frac{15 x}{15 } \end{array}\nonumber\]

Решение: \(x=\frac{3}{15}=\frac{3 \cdot 1}{3 \cdot 5}=\frac{1}{5 }\).

II. Множественные дроби по обе стороны уравнения

Уравнения d) и e) в примере 24.1 попадают в эту категорию. Мы решаем эти уравнения здесь.

Мы используем метод объединения рациональных выражений, который мы изучили в главе 23, чтобы свести нашу задачу к задаче с одной дробью в каждой части уравнения.

d) Решите \(\frac{3}{4}-\frac{1}{8 x}=0\)

Сначала мы понимаем, что в левой части уравнения есть две дроби, и поэтому мы не можем использовать свойство Cross-Product немедленно. Чтобы объединить LHS в одну фракцию, мы делаем следующее:

\[\begin{array}{ll} \text{Найдите НОК знаменателей} & 8 x \\ \text{Перепишите каждую дробь, используя НОК} & \frac{3 \cdot 2 x}{8 x }-\frac{1}{8 x}=0 \\ \text{Объедините в одну дробь} & \frac{6 x-1}{8 x}=0 \\ \text{Перепишите уравнение так, чтобы все термины дробные} & \frac{6 x-1}{8 x}=\frac{0}{1} \\ \text{Cross-Product} & (6 x-1) \cdot 1=8 x \ cdot 0 \\ \text{Удалить скобки} & 6 x-1=0 \\\text{Линейное уравнение: изолировать переменную} & 6 x=1 \\ \text{Разделить на 6 обе стороны} & \frac{6 x}{6}=\frac{1}{6} \end{массив}\nonumber\] 9{2}-4 x+4\right)=0 \\ & 3(x-2)(x-2)=0 \\ \text{Разделить на 3 обе стороны} & \frac{3(x-2) (x-2)}{3}=\frac{0}{3} \\ & (x-2)(x-2)=0 \\ \text{Квадратное уравнение: свойство нулевого произведения} & (x- 2)=0 \text { или }(x-2)=0 \end{array}\nonumber\]

Поскольку оба множителя одинаковы, то \(x-2=0\) дает \(x=2 \). Решение: \(x=2\)

Примечание: Существует еще один метод решения уравнений, в каждой из сторон которых есть несколько дробей. Он использует НОК всех знаменателей в уравнении. Мы демонстрируем это здесь, чтобы решить следующее уравнение: \(\frac{3}{2}-\frac{9}{2 x}=\frac{3}{5}\)

\[\begin{array} \text{Найдите НОК всех знаменателей в уравнении} & 10x \\ \text{Умножьте каждую дробь (оба LHS и RHS) по LCM} & 10 x \cdot \frac{3}{2}-10 x \cdot \frac{9}{2 x}=10 x \cdot \frac{3}{5} \\ & \frac{10 x \cdot 3}{2}-\frac{10 x \cdot 9}{2 x}=\frac{10 x \cdot 3}{5} \\ \text{Упростить каждую дробь} & \frac{5 x \cdot 3}{1}-\frac{5 \cdot 9}{1}=\frac{2 x \cdot 3}{1} \\ \text{Посмотрите, все знаменатели теперь равны 1, поэтому им можно пренебречь} & 5 x \cdot 3-5 \cdot 9=2 x \cdot 3 \\ \text{Решите, как любое другое уравнение} & 15 x-45=6 x \\ \text{Линейное уравнение: выделение переменной} & 15 x-6 x=45 \\ & 9 x=45 \\ & x=\frac{45}{9} \\ & x=5 \end{array} \nonumber\]

Решение \(x=5\)

Выход из задачи

Решите: \(\frac{2}{x}+\frac{1}{3}=\frac{1}{2}\)

---

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Версия лицензии

   4,0

   Показать страницу TOC

   нет

2. Теги

   На этой странице нет тегов.

Формула дробей – Что такое формула дробей? Примеры

Формула дробей помогает удобно выполнять многочисленные операции над дробями. По сравнению с обычными целыми числами основные арифметические операции с дробями выполняются по другим правилам. Формулы дробей помогают нам легко выполнять основные операции с дробями. Основная арифметическая операция сложения или вычитания требует, чтобы знаменатели дробей были равны. А при делении одной дроби на другую, деление преобразуется в умножение, путем взятия обратной 2-й дроби. Давайте узнаем больше о формуле дроби и решим несколько примеров в этом разделе.

Что такое формула дробей?

Дроби — один из важнейших аспектов арифметики, который мы используем в повседневной жизни. Дроби представляют числовое значение, которое является частью целого значения, и оно представлено с помощью этого символа / (называемого дробной линией), например, a/b. Формулы дробей помогают формировать правила, которым необходимо следовать, когда мы выполняем четыре основных арифметических действия, то есть сложение, вычитание, умножение и деление. Ниже приведены формулы дробей:

Формула 1

Смешанная дробь имеет целое число и связанную с ним дробь. Смешанная дробь преобразуется в неправильную дробь путем умножения знаменателя на целое число и добавления его к числителю, чтобы получить числитель неправильной дроби.

\( A\dfrac{b}{c}  = \dfrac{Ac + b}{c} \)

Формула 2

с тем же знаменателем для ответа. Знаменатель данных дробей равен знаменателю окончательного ответа.

\( \frac{a}{b}  +\frac{c}{b} = \frac{a + c}{b}\)

Формула 3

Для сложения разнородных дробей , каждая дробь умножается на подходящие константы, чтобы знаменатели двух дробей были равны. Цель состоит в том, чтобы получить равные знаменатели дробей, прежде чем выполнять процесс сложения.

\(\frac{a}{b}  +\frac{c}{d} =\frac{a .d}{b. d}  +\frac{c .b}{d .b} = \ frac{ad + bc}{bd}\)

Формула 4

Умножение дробей возможно путем умножения числителей, а затем знаменателей обеих дробей и записи их в виде одной дроби.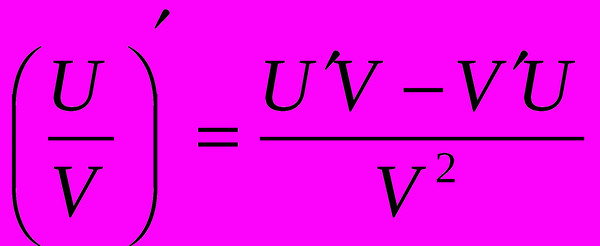 Далее этот продукт упрощается и сокращается для получения окончательного ответа.

\( \frac{a}{b} \times\frac{c}{d} = \frac{ac}{bd}\)

Формула 5

Деление дробей превращается в умножение дробей, сначала инвертируя дробь в знаменателе, а затем умножая ее на дробь в числителе.

\(\dfrac{(a/b)}{(c/d)} = \frac{a}{b} \times \frac{d}{c}\)

Формулы дробей

Другие важные формулы, которые мы используем, перечислены ниже:

Правило перекрестного умножения для проверки эквивалентности двух дробей: если a/b = c/d , тогда ad = bc /b — дробь, тогда b/a — ее обратная величина.

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.

Записаться на бесплатный пробный урок

Примеры использования формулы дробей

Пример 1.  Найти сумму дробей \(\frac{4}{11} \) и  \( \frac{5}{8} \) используя формулу дробей.

Решение:

\(\begin{align} \frac{4}{11}  +   \frac{5}{8} &=\frac{4 \times 8}{11 \times 8}  + \frac{5 \times 11}{8 \times 11} \\ &= \frac{32}{88}  +   \frac{55}{88} \\ &= \frac{32 + 55}{88} \ \ &= \frac{87}{88} \end{align} \)

Следовательно, сумма дробей равна \(\frac{87}{88}\).

Пример 2. Найдите значение \(\frac{24}{36} \div \frac{96}{288} \).

Решение:

\( \begin{align} \frac{24}{36} \div \frac{96}{288} & = \dfrac{\frac{24}{36}}{ \ frac{96}{288} } \\ &= \frac{24}{36} \times \frac{288}{96} \\ &=  \frac{24}{36} \times \frac{36 \times 8}{24 \times 4} \\ &= 2\end{align} \)

Следовательно, окончательное значение равно 2 по формуле дробей.

Пример 3. Молоко продается по цене 16 долларов США за галлон. Найдите стоимость \(6\dfrac{2}{5}\) галлонов молока.

Решение:

Стоимость одного галлона молока = 16 долл.  США

Следовательно, стоимость \(6\dfrac{2}{5}\) галлонов, т.е. = $102,4

Следовательно, стоимость галлонов молока составляет $102,4

Часто задаваемые вопросы о формулах дробей

Что такое формула дробей?

Формула дробей помогает удобно выполнять многочисленные операции над дробями. По сравнению с обычными целыми числами основные арифметические операции с дробями выполняются по другим правилам. Формулы дробей помогают нам легко выполнять основные операции с дробями. Основная арифметическая операция сложения или вычитания требует, чтобы знаменатели дробей были равны. А для деления одной дроби на другую деление преобразуется в умножение путем взятия обратной дроби.

Какая формула сложения используется для решения дробей?

При решении задач на дроби используются три разные формулы сложения:

Формула 1

Смешанная дробь имеет целое число и связанную с ним дробь. Смешанная дробь преобразуется в неправильную дробь путем умножения знаменателя на целое число и добавления его к числителю, чтобы получить числитель неправильной дроби.

\(A\dfrac{b}{c}  = \dfrac{Ac + b}{c} \)

Формула 2

Сложение одинаковых дробей возможно простым сложением числителей и наличием одного и того же знаменателя для ответа. Знаменатель данных дробей равен знаменателю окончательного ответа.

\(\frac{a}{b}  +\frac{c}{b} = \frac{a + c}{b} \)

Формула 3

Для сложения разнородных дробей каждая из дроби умножаются на подходящие константы, чтобы сделать знаменатели двух дробей равными. Цель состоит в том, чтобы получить равные знаменатели дробей, прежде чем выполнять процесс сложения.

\( \frac{a}{b}  +\frac{c}{d} =\frac{a .d}{b. d}  +\frac{c .b}{d .b} = \frac {ad + bc}{bd} \)

Что такое формула умножения, используемая для решения дробей?

Чтобы умножить две дроби, умножьте числители, умножьте знаменатели. Умножение дробей возможно путем умножения числителей, а затем знаменателей обеих дробей, а затем записи его в виде одной дроби. Далее этот продукт упрощается и сокращается для получения окончательного ответа.