Формула пути без ускорения: Страница не найдена – формулки.ру

Формула для пути с исключенным временем: .

14. Уравнение (закон) изменения скорости при равнопеременном движении: , или в координатной форме:

15. Формула для средней скорости при равнопеременном движении: .

16. П

    Рис.2

    реобразования Галилея, формула сложения скоростей: Пусть имеются две системы отсчета, К и К^’, причем К^’ движется вдоль положительного направления X с постоянной скоростью и в начальный момент времени начала координат совпадали, тогда очевидно , – это и есть преобразования координат, времени Галилея. Продифференцировав преобразования Галилея по времени, получим классическую формулу сложения скоростей . Скорость МТ относительно условно неподвижной системы отсчета равна векторной сумме скоростей, относительно подвижной СО и подвижной СО относительно неподвижной.

Основные определения кинематики вращательного движения:

18. Период – это значение интервала времени, за который тело совершает полный оборот по циклической траектории. Частота – величина обратная периоду, , . Число оборотов в секунду равно частоте, но обозначается n, .

19. Угловая скорость – скалярная величина, равная первой производной угла поворота по времени, . Далее мы введем угол и угловую скорость как векторные величины. При равномерном движении .

20. Ускорение при криволинейном движении – имеет две составляющие: тангенциальную, отвечающую за изменение скорости по величине и нормальную, или центростремительную, отвечающую за искривление траектории

С учетом выражения

окончательно получаем: , , где -единичный вектор, направленный к центру кривизны, – единичный вектор вдоль касательной к траектории. Более компактный вывод выглядит так: , следовательно, и .

Типичные задачи кинематики:

Задача №2. Чему равна скорость точек A,B,C,D на диске, рис.4, катящемся по плоскости без проскальзывания (чистое качение). Изобразите геометрическое место точек диска, у которых скорость по модулю равна скорости поступательного движения диска.

Задача № 3. Два автомобиля едут в попутном направлении с заданной скоростью. На какой минимальной дистанции необходимо держаться второму автомобилю, чтобы обезопасить себя от попадания камней, вырывающихся из-под колес первого автомобиля. Под каким углом к горизонту в системе отсчета, связанной с землей вылетают самые опасные камни? Сопротивлением воздуха пренебречь.

Ответ: , – вперед по ходу движения.

Задача № 4. Критическое для тела человека кратковременное ускорение (при котором есть шанс избежать серьезных травм) равно .

Каким должен быть минимальный тормозной путь, если начальная скорость автомобиля равнялась 100км/ч?

Задача № 5. (№1.23 из сборника задач [5]). Точка движется, замедляясь, по прямой с ускорением, модуль которого зависит от ее скорости по закону , где – положительная постоянная. В начальный момент скорость точки равна . Какой путь она пройдет до остановки? За какое время этот путь будет пройден?

Решение: записывая выражение для модуля ускорения и, разделяя переменные, получим: . Интегрируя с учетом начального условия , получим: . Остановке соответствует момент времени .

Интегрируя выражение для скорости, получаем . Ответ: .

Задача №6 (№ 1.39 из сборника задач [5]). Точка движется по дуге окружности радиуса R. Ее скорость зависит от пройденного пути S по закону , где – постоянная. Найти угол между вектором полного ускорения и вектором скорости в зависимости от S.

Решение: . Разделив переменные и проинтегрировав, получим: ; ; ; ; .

• Можно ли утверждать, что каждая частица покоится в собственной системе отсчета?

• Можно ли утверждать, что ускорение автомобиля равно нулю, если спидометр все время показывает одно и тоже значение?

• В какой точке траектории снаряд имеет наименьшую скорость?

• В чем ошибочность утверждения, что равнопеременное движение – это движение с постоянным по величине ускорением?

• Как вы себе представляете синхронизацию часов, находящихся в разных частях пространства?

• Можно ли по уравнению траектории восстановить уравнение движения тела?

• Могут ли вектора скорости и ускорения составлять между собой тупой угол?

• Как связаны между собой линейная и угловая скорость? Тангенциальное и угловое ускорения?

• В каких системах отсчета выполняется классическое правило сложения скоростей?

• В чем суть преобразований Галилея?

Прямолинейное равнопеременное движение – формулы и определения с примерами решения задач

Содержание:

1. Прямолинейное равнопеременное движение
2. Средняя скорость неравномерного движения
3. Мгновенная скорость
4. Ускорение
5. Единица ускорения
6. Равноускоренное движение
7. Скорость равноускоренного движения
8. График скорости равноускоренного движения
9. Графический способ вывода формулы пути равноускоренного движения
10. Средняя скорость равноускоренного движения
11. Уравнения равноускоренного движения
12. Пути, проходимые в равноускоренном движении за равные последовательные промежутки времени
13. Свободное падение тел
14. Равнозамедленное движение
15. Движение тела, брошенного вертикально вверх

Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.

Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Равнопеременное прямолинейное движение. Равнопеременным прямолинейным движением называется дви–жение, при котором за любые равные промежутки времени скорость те-ла изменяется на одинаковую величину и траектория – прямая линия.

Средняя скорость неравномерного движения

Большинство движений, наблюдаемых нами в природе и технике,— движения переменные, то есть неравномерные. Таковы, например, движения автомобиля, трактора, поезда, людей, животных и др.

Для характеристики неравномерного движения на каком-нибудь участке пути вводится понятие средней скорости движения.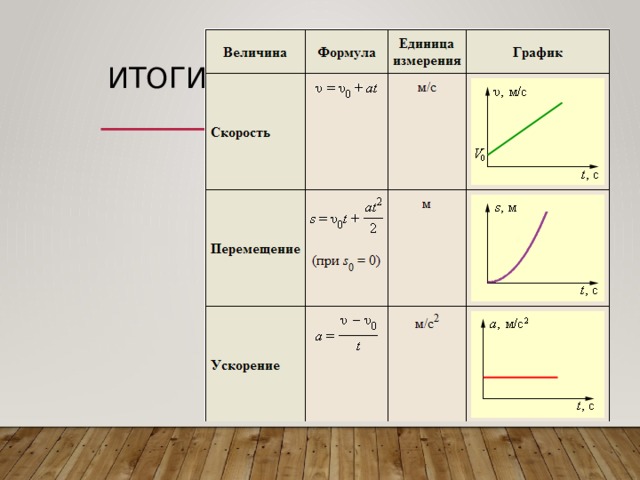

Рассмотрим пример. Допустим, что расстояние от Москвы до Горького (440 км) поезд прошёл за 11 час. Движение поезда на всём пути было явно неравномерное: он то ускорял движение, то замедлял и даже останавливался на промежуточных станциях. Но если бы путь в 440 км поезд прошёл за 11 час., двигаясь равномерно, то его скорость была бы: Скорость 40 является средней скоростью неравномерного движения на участке Москва — Горький.

Средняя скорость неравномерного движения на данном участке пути измеряется отношением длины участка пути к промежутку времени, в течение которого этот путь пройден

Но так же рассчитывается и скорость равномерного движения. Следовательно, можно сказать, что средняя скорость неравномерного движения равна скорости такого равномерного движения, при котором тело проходит тот же путь и за такой же промежуток времени, как и при данном неравномерном движении.

Если известны время и средняя скорость неравномерного движения на некотором участке пути, то длину этого участка пути можно рассчитать по формуле:

Мгновенная скорость

В каждый момент времени тело движется с определённой скоростью, и каждому моменту времени соответствует определённая точка на траектории.

Рис. 32. К понятию мгновенной скорости.

Скорость, которую имеет тело в данный момент времени или в данной точке траектории, называется мгновенной скоростью.

При равномерном движении тела его скорость во всех точках траектории одинакова. Это и будет его мгновенная скорость. Сложнее дело обстоит е случае неравномерного движения.

Допустим, что тело, двигаясь неравномерно-прямолинейно, за t сек. прошло путь АВ — s (рис. 32). Средняя скорость этого движения Эта скорость, вообще говоря, не характеризует движения в какой-нибудь точке пути С и не-определяет величину скорости в этой точке. Чтобы определить скорость в точке С, поступим следующим образом.

Разобьём весь наш путь АВ на отдельные участки и определим среднюю скорость на участке пути меньшем АВ; затем на участке меньшем и т. д., всё ближе и ближе подходя к точке С. По мере уменьшения участка пути, включающего точку С, а следовательно, и по мере уменьшения промежутка времени, за который этот участок проходится, изменение скорости на нём будет всё меньше и меньше. Движение за такие малые промежутки времени практически будет равномерным; скорость этого движения и можно принять за мгновенную скорость неравномерного движения в заданной точке траектории.

Подобные рассуждения можно провести относительно любой точки, взятой на траектории АВ.

Подкрепим теперь наши общие.рассуждения о мгновенной скорости числовыми данными. Допустим, что четыре наблюдателя определяют скорость автомобиля в момент его прохождения мимо какого-нибудь предмета у дороги. С момента прохождения автомобиля мимо этого предмета все наблюдатели одновременно измеряют пути, пройденные автомобилем от этого предмета за различные промежутки времени. Результаты их наблюдений следующие:
Какая же из полученных величин скорости ближе к мгновенной скорости, которую имел автомобиль, проезжая мимо указанного выше предмета?

Рис. 33. Определение мгновенной скорости на опыте.

Такой скоростью, очевидно, будет скорость, вычисленная из результата измерений четвёртого наблюдателя, так как за 3 сек.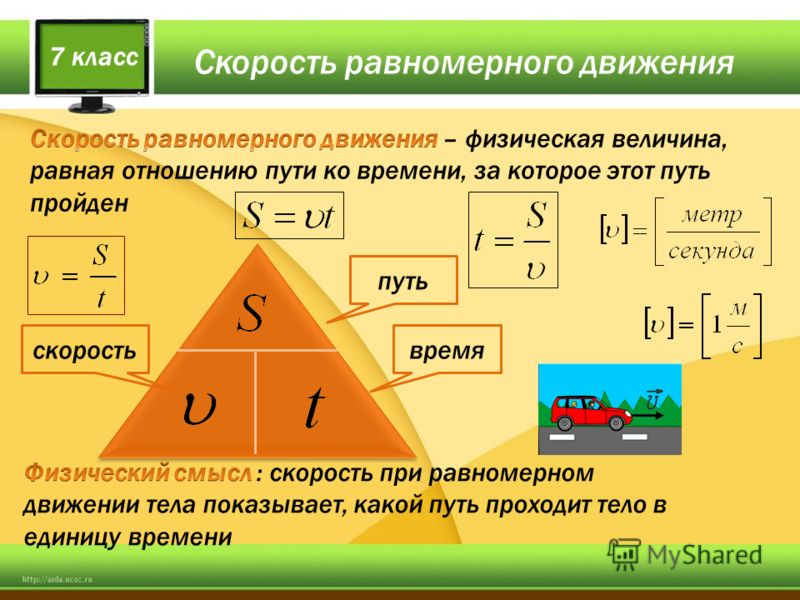 автомобиль меньше всего изменил свою скорость. Итак, чем меньше взять промежуток времени, тем точнее можно определить искомую скорость тела в заданный момент времени.

Мгновенную скорость можно определить на опыте. Обратимся к рисунку 33. С наклонной плоскости скатывается тележка с капельницей. По отметкам, оставляемым капельницей, легко установить, что тележка движется неравномерно. Допустим, нам нужно определить мгновенную скорость тележки в какой-либо точке наклонной плоскости, например у её основания С. Для этого к наклонной плоскости в точке С присоединим горизонтальный жёлоб СВ,

Пользуясь капельницей; так же как в опыте, описанном на странице 13, легко установить, что когда тележка проходит точку С, то дальше она на небольшом отрезке пути отточки С движется равномерно. Следовательно, скорость в точке Сбудет такой же, как на всём дальнейшем пути равномерного движения. Отмечая время равномерного движения какой-либо точки на тележке и измеряя пройденный ею путь, можно определить скорость равномерного движения; она и будет искомой мгновенной скоростью в точке С.

Для определения мгновенной скорости в какой-либо другой точке А нужно только поднять горизонтальную часть плоскости СВ на уровень точки А и произвести такие же измерения, как и для точки С.

Мгновенные скорости движения автомобиля отмечаются стрелкой на шкале спидометра.

Ускорение

Среди разнообразных переменных движений встречаются движения, в которых скорость непрерывно возрастает. Такие движения называются ускоренными.

Ускоренно, например, движется поезд, отходящий от станции и постепенно увеличивающий свою скорость, поднимающийся в воздух самолёт, пуля в канале ружья и т. д. В сущности начало всякого движения является движением ускоренным, так как всякое тело, начиная двигаться, не мгновенно „набирает“ свою скорость.

В разных ускоренных движениях скорость изменяется по-разному—в одних быстрее, в других медленнее. Сравним, например, движение поезда при отходе со станции с движением снаряда в стволе орудия при выстреле. Оба эти движения ускоренные. Но в то время как скорость поезда возрастает медленно, скорость снаряда за какие-нибудь сотые доли секунды увеличивается от нуля до сотен метров в секунду.

Таким образом, ускоренные движения отличаются одно от другого быстротой изменёния скорости.

Характеристикой быстроты изменения скорости является особая величина, называемая ускорением. Чем быстрее изменяется скорость движения, тем больше величина ускорения.

Обозначим начальную скорость переменного движения тела а скорость его через t сек. тогда изменение скорости за этот промежуток времени равно Допустим, что скорость движения изменяется равномерно; тогда изменение скорости за одну секунду будет равно: 

Величина, измеряемая отношением изменения скорости к тому промежутку времени, за которое это изменение произошло, называется ускорением.

Обозначив ускорение буквой а, мы можем написать:

Пусть, например, в некоторый момент времени скорость пули в стволе винтовки была 100 , а через 0,0014 сек. стала 800 . Значит, за 0,0014 сек. скорость пули изменилась на 

800  —100  = 700 . 

Ускорение движения пули внутри ствола винтовки будет равно:

 или за секунду.

Мы узнали, что ускорение движения пули внутри ствола за секунду. Как это надо представлять себе? Это надо представлять так, что при равномерном нарастании скорость пули за 1 сек. увеличилась бы на . Конечно, это не значит, что пуля внутри ствола на самом деле будет двигаться 1 сек.

Единица ускорения

Установим теперь единицу ускорения. Положив ед. скорости и t=1 ед. времени в формуле получим а = 1 ед. ускорения.

Это значит, что единицей ускорения является ускорение такого движения, при котором за единицу времени скорость изменяется на единицу скорости.

Если измерять скорость в  а время в секундах, то единицей ускорения будет ускорение такого движения, в котором за 1 сек. скорость изменяется на Наименование такой единицы ускорения:

Приняв за единицу скорости а за единицу времени 1 сек. , мы получим единицу ускорения

Этими двумя единицами чаще всего и измеряют ускорение, но, вообще говоря, за единицу ускорения можно принимать и т.д.

Численное значение ускорения, как и любой другой физической величины, зависит от выбора единиц измерения.

П р и м е р. Ускорение некоторого движения равно  Выразить это ускорение в

Равноускоренное движение

Познакомимся с ускоренным движением на опыте.

Рис. 34. Положения шарика через равные промежутки времени при его движении по наклонному жёлобу (отмечены флажками).

Установим наклонно жёлоб и предоставим шарику скатываться по нему. Определим пройденные шариком пути за одну, две, три и т. д. секунды. На рисунке 34 положения шарика на жёлобе в конце каждой из этих секунд обозначены флажками и помечены буквами Расстояние есть путь, пройденный шариком в течение первой секунды, —путь, пройденный шариком в течение второй секунды, —в течение третьей секунды и — в течение четвёртой секунды.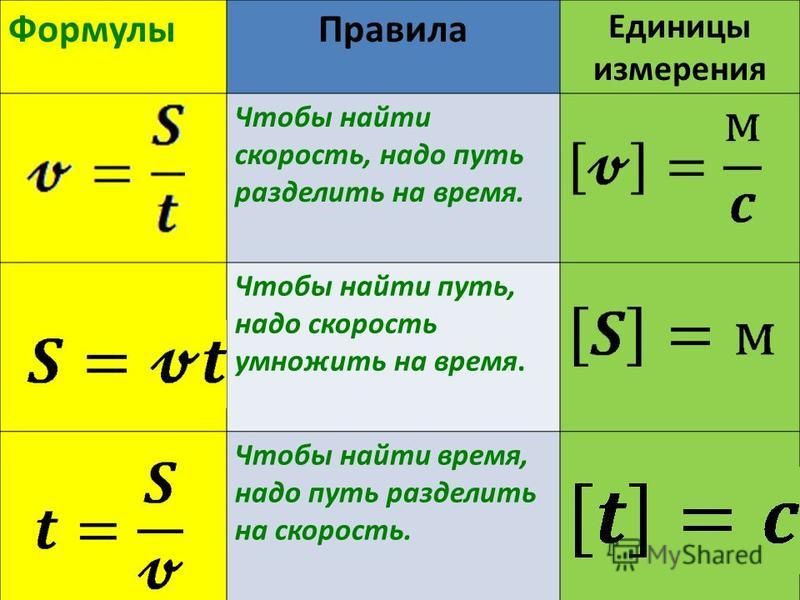 Эти расстояния личиваются, следовательно, скорость шарика его движения по наклонному жёлобу возрастала.

Чтобы установить закон возрастания скорости, измерим мгновенные скорости, которые будет иметь центр шарика в конце первой,второй, третьей и т. д. секунды.

Рис. 35. К установлению закона изменения скорости при движении шарика по наклонному жёлобу.

Для этого от нижнего конца наклонного жёлоба вверх по нему (рис. 35) отложим расстояния и проходимые шариком за одну, две, три секунды, и будем скатывать шарик сначала от затем от  и, наконец, от

Скатившись с наклонного жёлоба, шарик будет двигаться с разными скоростями, причём во всех случаях на некотором отрезке горизонтального пути движение шарика будет равномерным.

Измерив в каждом случае путь, пройденный шариком по горизонтальной плоскости за 1 сек., мы найдём скорость шарика на участке равномерного движения, т. е. его мгновенную скорость в точке о.

В одном из опытов были получены следующие численные значения мгновенных скоростей шарика:

В этом опыте скорость движения шарика по наклонному жёлобу увеличивалась за 1 сек.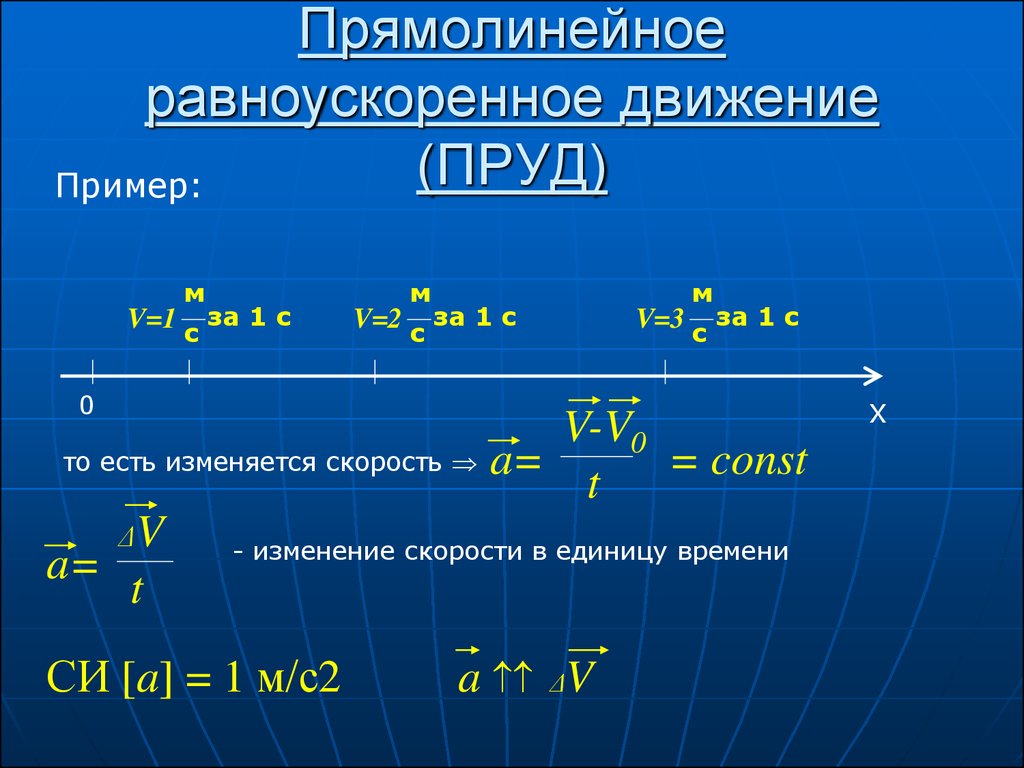 на одну и ту же величину (на 20 ), т. е. шарик двигался с ускорением 20 

Движение, при котором в любые равные промежутки времени скорость увеличивается на одну и ту же величину, называется равноускоренным.

Движение шарика по наклонному жёлобу есть равноускоренное движение.

Равноускоренное движение является одним из простейших видов ускоренных движений. Для равноускоренного движения, как мы увидим, зависимость скорости и пути от времени можно выразить простыми математическими формулами.

Скорость равноускоренного движения

В равноускоренном движении ускорение на всём протяжении пути не меняется, поэтому равноускоренное движение есть движение с постоянным ускорением.

Скорость в равноускоренном движении каждую секунду увеличивается на одну и ту же величину, численно равную ускорению.

Рассмотрим, как можно рассчитать скорость равноускоренного движения в конце какого-нибудь промежутка времени, если известны начальная скорость и ускорение.

Пусть в начале наблюдения скорость тела, например поезда, равна и поезд движется с ускорением 

Чему будет равна скорость поезда через t секунд?

Нам уже известно, что ускорение равноускоренного движения показывает, на сколько возрастает скорость за каждую секунду.

В нашем примере ускорение равно Значит, скорость поезда ежесекундно возрастает на в течение t секунд скорость возрастёт на величину, в t раз большую, т. е. на

Так как в начале наблюдения скорость поезда была равна  и через t сек она возросла на то в конце промежутка времени t она будет равна

Если обозначить скорость тела в конце промежутка времени t через то можно написать:

Что изменится, если начальная скорость будет равной, например,  и ускорение  или соответственно  и

Рассуждая по-прежнему, мы получим:

или 

Таким образом, алгебраическое выражение для конечной скорости остаётся без изменения. Изменяется только наименование скорости.

Следовательно, конечная скорость равноускоренного движения может быть рассчитана по формуле:

В этой формуле —начальная скорость, а — ускорение и t—время.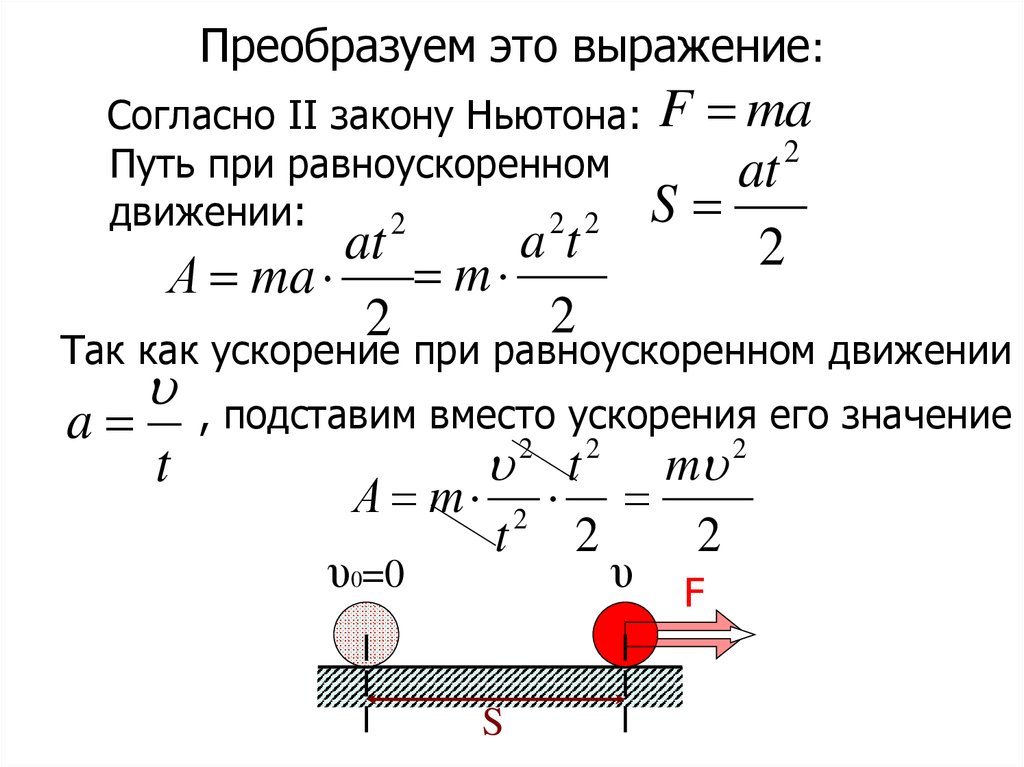

Тот же результат можем получить алгебраически из формулы: 

о которой говорится в параграфе 19.

Эта формула представляет собой уравнение первой степени. Решим его относительно 

 отсюда

Для равноускоренного движения, которое начинается из состояния покоя, поэтому из формулы (1) получим:

Значит, если начальная скорость равна нулю, то мгновенная скорость равноускоренного движения пропорциональна времени.

Пользуясь формулой (3), можно значение вычисленных в опыте § 21 скоростей представить в виде следующей таблицы:

Из этой таблицы видно, что скорость движения шарика по наклонному жёлобу в любой момент времени может быть рассчитана но формуле:

График скорости равноускоренного движения

Рис. 36. Оси координат (ось времён и ось скоростей).

Зависимость скорости равноускоренного движения от времени можно выразить не только алгебраически, но и графически. Для этого возьмём две взаимно перпендикулярные оси координат (рис. 36). Одну из них Ov назовём осью скоростей, а другую Ot— осью времён. Перпендикуляр, опущенный из любой какой-нибудь точки А на ось времён, отсекает на ней отрезок ОВ, численно равный (в выбранном масштабе) некоторому промежутку времени t, а перпендикуляр, опущенный из той же точки на ось скоростей, отсекает отрезок ОС, рав
ный по величине скорости в конце этого промежутка времени.

Из построения видно, что расстояние АВ определяет величину скорости в момент времени t.

Построим сначала график движения без начальной скорости. Пусть, например, ускорение По формуле рассчитаем скорость в конце первой секунды от начала движения, второй, третьей и т. д. и результаты запишем в таблицу.

Начертим оси координат Ov и Ot (рис. 37). На оси времён отложим равные отрезки 0—1. 1—2, 2—3 и т. д., каждый из которых соответствует 1 секунде.

Из концов этих отрезков по данным нашей таблицы (в масштабе 1 см—) отложим мгновенные скорости в конце первой секунды, второй и т. д. Верхние концы A, В, С полученных отрезков соединим. Получим прямую, проходящую через начало координат и наклонённую к осям. Эта прямая и будет представлять собой график скорости равноускоренного движения.

График скорости равноускоренного движения имеет такой же вид, как и полученный нами ранее график пути равномерного движения (рис. 37).

Рис. 37. График скорости равноускоренного движения с начальной скоростью, равной нулю.

Рис. 38. График скорости равноускоренного движения с начальной скоростью, не равной нулю.

В обоих случаях график представляет собой прямую, проходящую через начало координат. Эго не случайное совпадение. Дело в том, что пройденный путь при равномерном движении и скорость при равноускоренном движении изменяются по одному и тому же закону—прямо пропорционально времени. Закон же прямой пропорциональности, как это доказывается в математике, графически изображается прямой линией.

Построим теперь график для случая, когда начальная скорость не равна нулю, например и  Так же, как и в первом случае, но теперь по формуле  рассчитаем скорость в конце первой секунды от начального момента отсчёта, в конце второй, третьей и т. д. Результаты запишем в таблицу.

Отмечая соответствующие точки на графике и соединяя их между собой линией, получим график скорости равноускоренного движения с начальной скоростью (рис. 38). Так как скорость увеличивается в каждую секунду на одну и ту же величину, то линия, соединяющая точки А, В, С, D,—прямая, но она не проходит через точку пересечения осей, так как в момент t = 0 скорость тела не равняется нулю.

Графический способ вывода формулы пути равноускоренного движения

В равномерном движении пройденный путь графически изображался площадью прямоугольника, построенного на графике скорости (§ 11).

Рис. 40. К выводу формулы пути, пройденного при равноускоренном движении.

В равноускоренном же движении с начальной скоростью пройденный путь изображается площадью трапеции. Это мы используем для вывода формулы пути равноускоренного движения.

 На рисунке 40 график скорости равноускоренного движения изображён прямой АС. Путь, пройденный за время t, на том же рисунке изображается площадью ОАСВ; он численно равен площади ОАСВ. Эта площадь ограничена отрезком прямой АС, представляющим собой график скорости, отрезками

Из рисунка 40 видно, что если к площади прямоугольника ОАМВ прибавить площадь треугольника АСМ, то мы получим площадь S фигуры ОАСВ. Таким образом,

Но OB = AM = t, Отсюда для пройденного пути получим формулу:

или

Для движения без начальной скорости пройденный путь выразится формулой: 

По формуле  рассчитаем пройденные пути при равноускоренном движении за 1, 2, 3 и т. д. секунды для случая, когда ускорение равно  и полученные данные запишем в таблицу.

Из этой таблицы видно, что за две секунды тело пройдёт путь, в 4 раза больший, чем за первую секунду, за три секунды—в 9 раз больший и т. д., т.е. при равноускоренном движении без начальной скорости пройденный путь пропорционален квадрату времени.

Из формулы и из приведенной таблицы следует, что путь, проходимый телом в первую секунду, численно равен половине ускорения.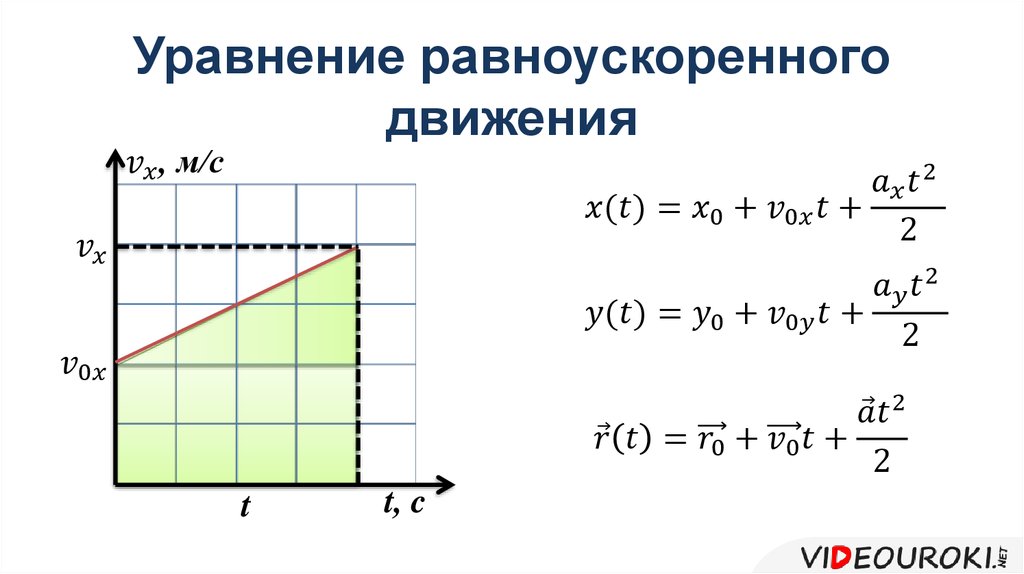 Если, например, поезд, двигаясь от станции, в первую секунду прошёл путь 1,5 м, то ускорение движения его 

Средняя скорость равноускоренного движения

Из формулы пути равноускоренного движения легко вывести формулу средней скорости.

Из определения средней скорости следует (см. § 17), что или разделив каждое слагаемое числителя на t, получим:

а преобразуя правую часть написанного равенства, будем иметь: 
или  

Так как то получим:

Итак, средняя скорость равноускоренного движения за некоторый промежуток времени равна полусумме начальной и конечной скоростей.

Для случая, когда

В равноускоренном движении скорость движения изменяется равномерно от до Поэтому средняя скорость такого движения равна среднему арифметическому начальной и конечной скоростей:

Уравнения равноускоренного движения

Формулы

называются уравнениями равноускоренного движения; они выражают зависимость скорости или пути в этом движении от времени.

Этих формул вполне достаточно для решения любой задачи на равноускоренное движение. Однако для упрощения расчётов в задачах, где не дано времени движения, целесообразно пользоваться ещё одной формулой.

Из формулы ускорения (§ 19) время Подставив его формулу получим:

Заменяя её значением  и преобразуя полученное выражение, придём к формуле:

откуда

или

Если начальная скорость равна нулю: то полученная формула (4) примет вид:

или

Формулами (4) и (5) часто пользуются для решения задач, когда не дано времени движения.

Пути, проходимые в равноускоренном движении за равные последовательные промежутки времени

Воспользуемся таблицей пройденных путей, приведённой на странице 43, и определим пути, проходимые телом в равноускоренном движении без начальной скорости за каждую отдельную секунду.

Пройденный путь за первую секунду от начала движения равен Обозначим его

Чтобы вычислить путь за вторую секунду, надо из пути, пройденного за две секунды, вычесть путь, пройденный за первую секунду:

Пройденный путь  за третью секунду найдём, вычитая из пути, пройденного за три секунды, путь, пройденный за две секунды:

Таким же образом найдём, что пути пройденные за четвёртую и пятую секунды, будут равны:

Составим отношение из числовых значений пройденных путей:

Преобразуя правую часть равенства, получим:

Из полученного нами равенства видно, что пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечётных чисел.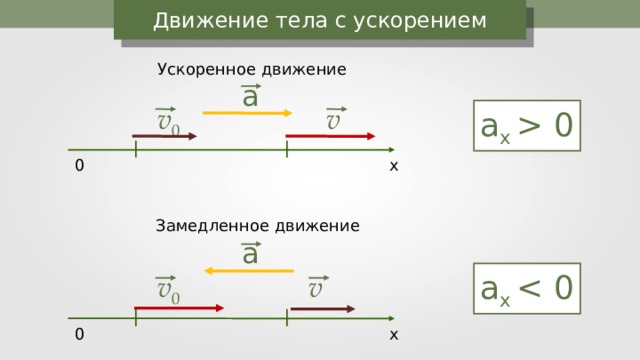

Свободное падение тел

Одним из интересных и важных видов движения является движение падающих тел. Изучим это движение на опыте.

Рис. 43. Тело, подвешенное на нити, натягивает нить по вертикали.

Рис. 44.

Подвесим на нити какое-нибудь тяжёлое тело (рис. 43), нить натянется вдоль определённого направления. Это направление, как известно, называется вертикальным или отвесным, а нить с грузом—отвесом.

Если пережечь нить, тело будет падать по вертикальному направлению.

Выпустим из рук с одинаковой высоты одновременно плашмя металлический кружок и такого же диаметра лёгкий картонный кружок. Мы увидим, что скорее упадёт металлический кружок. Почему? Не является ли причиной этого различие в весе падающих тел?

Такой вывод легко опровергается следующим опытом. Возьмём два одинаковых листа бумаги и, скомкав один из них, уроним оба листа с одинаковой высоты. Мы увидим, что скомканный лист упадёт быстрее. Следовательно, причиной различной скорости падения тел является не только различие в весе тел.

Положим картонный кружок на металлический и выпустим их из рук. Оба кружка упадут в одно и то же время. Этот опыт отличается от первого тем, что условия падения кружков здесь неодинаковы. Металлический кружок, падая, встречает сопротивление воздуха, между тем как для картонного кружка этого препятствия нет: оно устраняется металлическим кружком, падающим впереди картонного. Следовательно, на скорость падения тел влияет сопротивление воздуха.

Рассмотрим теперь, как будут падать тела в отсутствие сопротивления воздуха, в безвоздушном пространстве.

Возьмём стеклянную трубку длиной примерно 1,5 м с одним закрытым концом и с краном на другом конце (рис. 44). В трубку вложены: монета, птичье пёрышко, кусочек пробки, дробинка, т. е. тела разной формы и разного веса. Пока в трубке имеется воздух, упомянутые тела при перевёртывании трубки движутся с разными скоростями. Но стоит только откачать воздух из трубки, и те же тела будут двигаться с одинаковыми скоростями.

Падение тел в безвоздушном пространстве называется свободным падением.

Галилео Галилей (1564— 1642)—великий итальянский учёный, основатель опытной физики.

Галилей открыл законы падения тел и качания маятника, ему принадлежит идея закона инерции, включённого Ньютоном в число основных законов механики. Галилей изобрёл термометр, первый применил телескоп для астрономических исследований, открыл спутников Юпитера, солнечные пятна и фазы Венеры.

Галилей был ревностным пропагандистом взглядов Коперника, за что был судим судом папской инквизиции и под угрозой пыток вынужден был подписать отказ от своих убеждений. Однако на деле он остался верен им и до конца жизни продолжал развивать учение о гелиоцентрической системе мира.

Падение тел опытным путём впервые изучал в конце XVI в. Галилей, роняя тяжёлые тела с башни (рис. 45). Эти опыты показали, что все тела, независимо от их веса, достигали поверхности земли почти в одно и то же время.

Рис. 45. Наклонная башня, которой пользовался Галилей для изучения законов падения тел.

Законы падения Галилей открыл, изучая движение шарика по наклонному жёлобу. Это движение является тоже падением, только протекающим медленнее, чем падение по вертикали.

Исследования Галилея показали, что свободное падение есть движение равноускоренное.

Особенностью свободного падения является то, что все тела в данном месте падают с одинаковым ускорением. Это ускорение называется ускорением свободного падения,

Ускорение свободного падения обозначается буквой (первая буква латинского слова гравитас, что значит тяжесть).

Так как движение свободно падающего тела есть равноускоренное движение без начальной скорости, то расчёты пути и скорости в этом движении производятся по формулам, выведенным в § 22 и 24.

Так, если тело падает с высоты h в течение времени t, то

При этом тело достигает скорости

v = gt или

Величину g можно определить опытным путём, например заставляя стальной шарик падать с определённой высоты и измеряя время падения. Сопротивление воздуха, которое испытывает при этом шарик, незначительно.

При проведении одного такого опыта в пролёте школьной лестницы с высоты 17,6 м падал стальной шарик. Секундомер показал время падения 1,9 сек. По формуле нашли, что

Существуют, конечно, способы, позволяющие определить величину g значительно точнее, чем мы это делали в школе.

Численное значение g на разных широтах земного шара различно и колеблется между  на полюсах и  на экваторе; для Москвы

Ускорение свободного падения называют нормальным.

Причины, вызывающие различие в ускорениях свободного падения тел, будут рассмотрены далее.

В расчётах, если не требуется особой точности, пользуются значением g, равным или  или даже

Равнозамедленное движение

На рисунке 47 изображено движение шарика от толчка вверх по наклонному жёлобу.

Рис. 47. Движение шарика вверх по наклонному жёлобу.

Флажками отмечены положения шарика через одну, две, три секунды от начала движения. Расстояние между флажками, а следовательно, и пути, проходимые шариком за равные промежутки времени, уменьшаются. Значит, движение шарика замедленное.

Простейшим видом замедленного движения является движение равнозамедленное.

В равнозамедленном движении скорость за любые равные промежутки времени уменьшается на одну и ту же величину.

При этом ускорение, вычисляемое по формуле:

окажется отрицательной величиной, так как  меньше Пусть, например, скорость поезда при равнозамедленном движении за t= 10 сек. уменьшилась с  до  в таком случае ускорение

Равнозамедленное движение есть движение с постоянным отрицательным ускорением.

Чтобы получить формулы скорости и пути для равнозамедленного движения, достаточно в аналогичных формулах равноускоренного движения заменить а на — а.

Тогда формула скорости будет:

для пройденного же пути получим:

Равноускоренное и равнозамедленное движения часто называют равнопеременными движениями, так как в обоих этих движениях скорость изменяется равномерно.

Многие движения весьма близки к равнопеременным и при различных расчётах могут быть приняты за равнопеременные. Так, движения поездов и автомобилей при отходе их от остановки и при торможении, движение пули внутри ствола и многие другие могут рассматриваться как равнопеременные.

Движение тела, брошенного вертикально вверх

Примером замедленного движения (очень близкого к равнозамедленному) может служить движение тела, брошенного вертикально вверх.

Действительно всякое тело свободно падает с ускорением g, направленным вертикально вниз. Вследствие этого при движении тела вертикально вверх его скорость ежесекундно уменьшается на величину, численно равную ускорению свободного падения. Брошенное вертикально вверх тело движется равнозамедленно до тех пор, пока скорость его не станет равной нулю. В этот момент тело достигает наибольшей высоты и с этой высоты начинает свободно падать, двигаясь обратно вниз.

Формулы для подсчёта скорости и пути движения тела, брошенного вертикально вверх, для любого момента времени будут:

где h—высота, на которую поднимается тело за время t.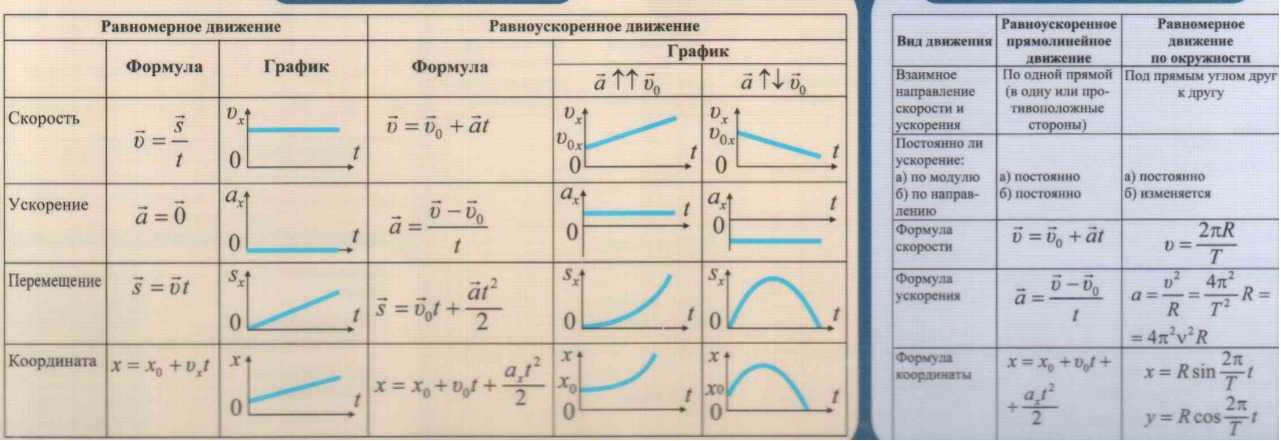

Формулу для расчёта высоты h можно также получить, рассматривая движение тела, брошенного вертикально вверх, как сложное движение, состоящее из двух движений: из движения равномерного, направленного вертикально вверх с некоторой начальной скоростью, и из свободного падения. Оба движения происходят по одной прямой; поэтому пройденный телом путь за некоторый промежуток времени будет равен алгебраической сумме путей, пройденных в каждом отдельном движении.

Обозначим скорость, с которой тело брошено вертикально вверх, через  Двигаясь только с этой скоростью равномерно, тело за t сек. могло бы подняться на высоту Но оно одновременно, свободно падая, в течение того же времени t опускается вниз на расстояние Действительная высота h, на которую поднимается тело вверх за t сек., будет равна или:

Рассмотрим следующий пример. Пусть тело брошено вертикально вверх со скоростью Для упрощения расчётов положим Определим, на какой высоте будет находиться тело через 3 сек. от начала движения.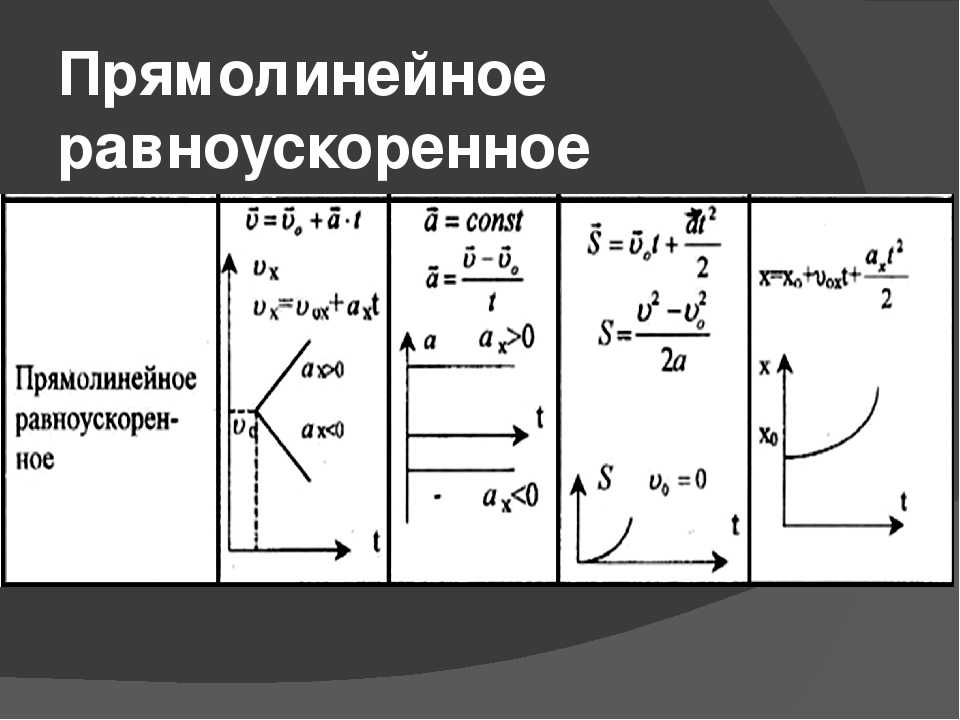 По формуле (2):

Так как в момент времени, когда тело достигает наибольшей высоты, то время полёта определится из уравнения (1):

отсюда

Чтобы определить наибольшую высоту, на которую поднимается тело, подставим найденную величину t в уравнение (2), определяющее h:

Найдём теперь, с какой скоростью тело, падая с этой высоты, вернётся к начальному своему положению. Так как тело, падая, будет двигаться равноускоренно без начальной скорости и пройдёт расстояние h, то скорость его будет равна:

т. е. скорость, с которой тело вернётся в то же место, откуда оно было брошено, равна первоначальной скорости (если не учитывать сопротивления воздуха).

Услуги по физике:

1. Заказать физику
2. Заказать контрольную работу по физике
3. Помощь по физике

Лекции по физике:

1. Физические величины и их измерение
2. Основные законы механики
3. Прямолинейное равномерное движение
4. Сила
5. Масса
6. Взаимодействия тел
7. Механическая энергия
8. Импульс
9. Вращение твердого тела
10. Криволинейное движение тел
11. Колебания
12. Колебания и волны
13. Механические колебания и волны
14. Бегущая волна
15. Стоячие волны
16. Акустика
17. Звук
18. Звук и ультразвук
19. Движение жидкости и газа
20. Молекулярно-кинетическая теория
21. Молекулярно-кинетическая теория строения вещества
22. Молекулярно – кинетическая теория газообразного состояния вещества
23. Теплота и работа
24. Температура и теплота
25. Термодинамические процессы
26. Идеальный газ
27. Уравнение состояния идеального газа
28. Изменение внутренней энергии
29. Переход вещества из жидкого состояния в газообразное и обратно
30. Кипение, свойства паров, критическое состояние вещества
31. Водяной пар в атмосфере
32. Плавление и кристаллизация
33. Тепловое расширение тел
34. Энтропия
35. Процессы перехода из одного агрегатного состояния в другое
36. Тепловое расширение твердых и жидких тел
37. Свойства газов
38. Свойства жидкостей
39. Свойства твёрдых тел
40. Изменение агрегатного состояния вещества
41. Тепловые двигатели
42. Электрическое поле
43. Постоянный ток
44. Переменный ток
45. Магнитное поле
46. Электромагнитное поле
47. Электромагнитное излучение
48. Электрический заряд (Закон Кулона)
49. Электрический ток в металлах
50. Электрический ток в электролитах
51. Электрический ток в газах и в вакууме
52. Электрический ток в полупроводниках
53. Электромагнитная индукция
54. Работа, мощность и тепловое действие электрического тока
55. Термоэлектрические явления
56. Распространение электромагнитных волн
57. Интерференционные явления
58. Рассеяние
59. Дифракция рентгеновских лучей на кристалле
60. Двойное лучепреломление
61. Магнитное поле и электромагнитная индукция
62. Электромагнитные колебания и волны
63. Природа света
64. Распространение света
65. Отражение и преломление света
66. Оптические приборы и зрение
67. Волновые свойства света
68. Действия света
69. Линзы и получение изображений с помощью линз
70. Оптические приборы и глаз
71. Фотометрия
72. Излучение и спектры
73. Квантовые свойства излучения
74. Специальная теория относительности в физике
75. Теория относительности
76. Квантовая теория и природа поля
77. Строение и свойства вещества
78. Физика атомного ядра
79. Строение атома

Понятие о равноускоренном движении.

Формулы перемещения и скорости. Равноускоренное вращение

Движение с ускорением различных объектов окружает нас каждый день. Достаточно лишь вспомнить автомобили, самолеты, велосипеды, вращающиеся колеса и валы, чтобы понять всю важность ускоренного перемещения тел в жизни человека. Для описания этого движения в физике существует специальный раздел, он называется кинематикой. В данной статье рассмотрим, какими формулами описывается перемещение при равноускоренном движении.

Понятие об ускорении, скорости и пути

Прежде чем записывать формулы перемещения при равноускоренном движении, следует дать понятие основным величинам, которые в них фигурируют.

Начнем с пути. Под этой величиной понимают расстояние, которое проходит тело за интервал времени, двигаясь по известной траектории. Чем за более короткое время тело проходит некоторый путь L, тем больше его скорость. Таким образом, скоростью тела является быстрота преодоления им расстояний в пространстве. В данный момент времени расчет скорости выполняют по такой формуле:

v¯ = dL/dt

Скорость – это вектор, а путь – скаляр. Скорость направлена вдоль касательной, восстановленной к данной точке траектории.

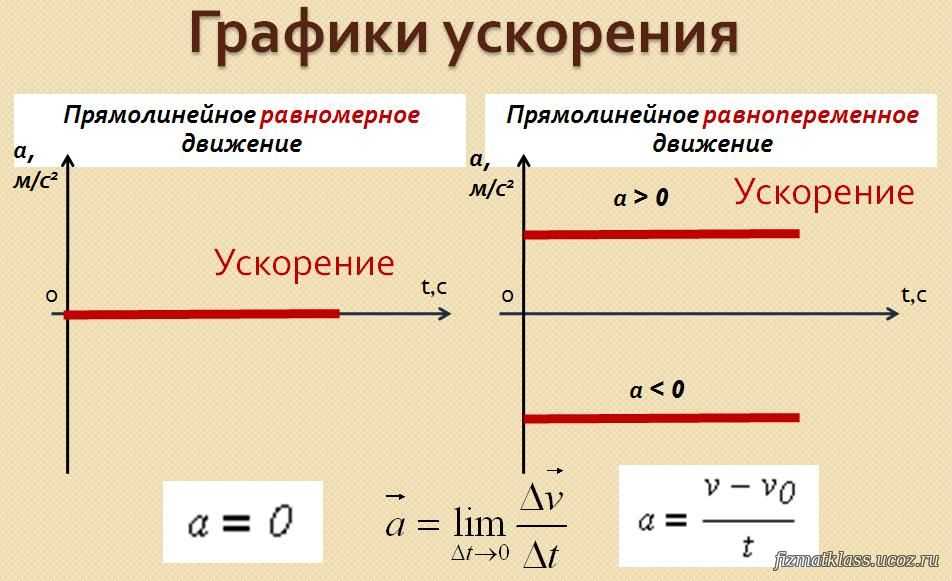
Если наблюдать за телом, движущимся вдоль траектории некоторое время, и в каждой точке траектории измерять его скорость, то окажется, что она постоянно меняется. Изменение скорости характеризуют ускорением. В соответствии с определением ускорения оно вычисляется так:

a¯ = dv¯/dt

Ускорение также является величиной векторной, только с направлением скорости оно не имеет ничего общего. Вектор ускорения повернут в сторону изменения скорости за данное время или, что одно и то же, в сторону действующей на тело силы.

Равноускоренное движение в физике

Чтобы понять, что такое равноускоренное перемещение, приведем следующий пример: предположим, что автомобиль находился в покое. Затем он начал движение, постоянно увеличивая свою скорость. Если за равные промежутки времени прирост модуля скорости автомобиля был одинаковым, то можно говорить о равноускоренном движении тела. Иными словами, во время рассматриваемого вида перемещения ускорение является величиной постоянной (a = const).

Не стоит думать, что движение с постоянным ускорением может только увеличивать скорость. В результате такого перемещения скорость тела может также уменьшаться до полной его остановки. Такая ситуация возникает, когда транспортное средство осуществляет процесс торможения. В этом случае ускорение будет направлено против вектора скорости.

В природе распространенным движением с постоянным ускорением является падение тел. До определенных скоростей, когда сопротивлением воздуха можно пренебречь, свободное падения является равноускоренным, причем величина ускорения равна 9,81 м/с².

Изменение скорости при движении с постоянным ускорением

В отличие от ускорения, скорость при равноускоренном движении постоянной величиной не является. Рассмотрим для простоты перемещение по прямой линии. В случае если вектора величин a¯ и v¯ совпадают, имеет место следующая формула для скорости:

v = v₀ + a*t

Это выражение предполагает, что до появления ускорения тело уже обладало некоторой скоростью v₀.

Данная формула показывает, что скорость линейно возрастает с течением времени. График функции v(t) представляет собой прямую линию, которая пересекает ось y на расстоянии v₀ от начала координат.

При равноускоренном движении скорость также может уменьшаться линейно. Для этого необходимо, чтобы вектора ускорения и скорости были противоположными (торможение автомобиля, свободный взлет тела в высоту). Для этого случая можно записать такое выражение:

v = v₀ – a*t

Как и в предыдущем случае, графиком равенства является прямая, только коэффициент ее наклона к оси x будет не положительным, а отрицательным.

Перемещение при равноускоренном движении

Формула пути однозначно получается, если взять интеграл по времени от скорости. В случае когда скорость тела увеличивается, для пути можно записать следующее выражение:

L = v₀*t + a*t²/2

Видно, что графиком функции L(t) является парабола (ее правая ветвь). То есть пройденный путь с течением времени быстро увеличивается.

Если ускорение приводит к уменьшению скорости, тогда формула перемещения при равноускоренном движении примет вид:

L = v₀*t – a*t²/2

Графиком для этого уравнения тоже будет парабола, однако ее ветвь постепенно приближается к некоторому постоянному значению. Последнее соответствует пройденному пути до остановки движущегося тела.

Движение с постоянным ускорением по окружности

Чтобы полнее охарактеризовать тему, следует также привести формулы перемещения при равноускоренном движении по окружности. В отличие от прямолинейного движения, этот вид перемещения описывается угловыми величинами. Тем не менее угловые величины являются полными аналогами соответствующих линейных характеристик.

Для скорости при равноускоренном движении вращения справедлива формула:

ω = ω₀ + α*t

Здесь ω – скорость угловая, которая измеряется в радианах в секунду (рад/с), α – ускорение угловое, оно измеряется в рад/с².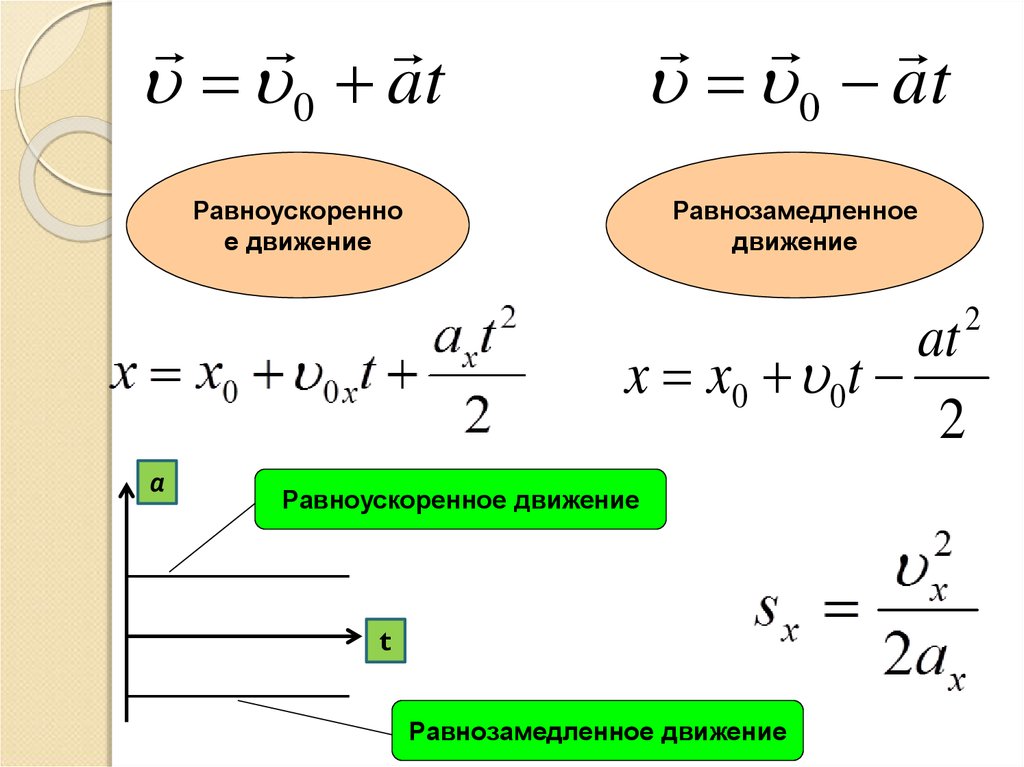

Аналогом пути для вращения является угол поворота θ. Для него справедлива формула:

θ = ω₀*t + α*t²/2

Таким образом, при равноускоренном вращении формулы кинематики сохраняют свой вид, но в них стоят уже угловые физические величины.

фактов, проблем, примеров — Lambda Geeks

В этой статье мы собираемся обсудить, как найти конечную скорость без ускорения, а также некоторые примеры и факты.

Конечная скорость объекта основана на его начальной скорости, связанной с ней энергии, положении, силе, действующей на объект, и продолжительности перемещения.

Скорость

Скорость определяется как отношение смещения объекта за интервал времени, определяемый соотношением

Скорость=Перемещение/Время

Скорость объекта можно рассчитать путем измерения полного смещения объекта за определенный интервал времени.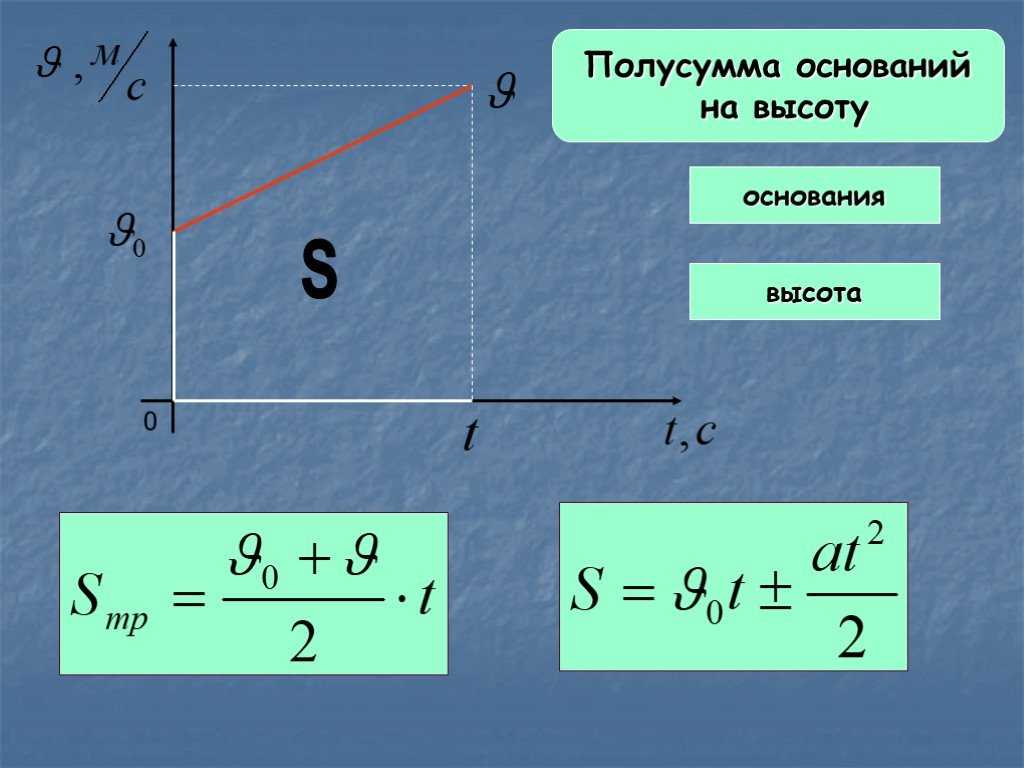

Конечная скорость

Конечная скорость появляется, когда тело достигает максимального ускорения за определенный период времени. Ускорение – это разница между конечной и начальной скоростью тела за время.

На основе движения тела, будь то плоское движение, равномерное круговое движение или движение снаряда, можно рассчитать конечную скорость, достигаемую объектом.

Конечная скорость объекта в линейном движении

Объект, движущийся по плоскости, подвергается воздействию различных внешних сил, поэтому скорость объекта может не быть постоянной каждый раз. Конечная скорость тела зависит от начальной скорости и от того, насколько скорость меняется со временем.

Рассчитайте конечную скорость объекта в линейном движении

Рассмотрим график зависимости скорости от времени объекта, ускоряющегося в равномерном линейном движении с начальной скоростью ‘u’ и преследующего конечную скорость ‘ в’.

График зависимости скорости от времени

Равномерно ускоряющийся объект, начальная скорость объекта в момент времени t=0 равна ‘u’. В момент времени t скорость объекта увеличивается до «v», следовательно, ускорение объекта равно (v-u).

Чтобы измерить площадь участка на приведенном выше рисунке, общая площадь равна сумме площадей треугольника (∆ABC) и четырехугольника (□ACDO).

Поскольку,

v=x/t

x=vt

x = Ar(∆ABC) + Ar(□ACDO)

=1/2 bh+lb

=1/2 t * (v-u)+ut

Поскольку нас интересует скорость без учета члена ускорения, который равен (v-u)

x=1/2 vt -1/2 ut+ut

x=1/2 vt+1/2 ut

2x=(v+u)t

2x/t=(v+u)

Следовательно, конечная скорость объекта is

v=2x/t-u

Зная перемещение объекта, время, затраченное на перемещение, и его начальную скорость, мы можем узнать конечную скорость, набранную объектом.

Проиллюстрируем это на простом примере. Рассмотрим автомобиль, движущийся со скоростью 20 км/ч из точки А в точку Б. Автомобиль проезжает расстояние 60 км за 2 часа. Какой должна быть конечная скорость автомобиля?

Автомобиль, едущий из точки А в точку В

Мы знаем начальную скорость автомобиля u=20 км/ч,

Продолжительность = 2 часа = 120 секунд

Расстояние = 60 км

Используя формулу, полученную выше 2x/t-u=2*60/2-20=60-20=40км/ч

Следовательно, конечная скорость автомобиля будет 40 км/ч.

Движение снаряда

Объект в движении снаряда будет двигаться по параболе. Начальная и конечная скорость объекта будут различаться, но энергия в процессе сохраняется. Изначально, когда объект находится на земле, у него больше потенциальной энергии, которая при полете преобразуется в кинетическую энергию.

Достигнув определенной высоты, где вся его потенциальная энергия преобразуется в кинетическую энергию, он свободно падает на землю, превращая эту кинетическую энергию в потенциальную. Следовательно, энергия сохраняется при метательном движении объекта. то есть сумма кинетической и потенциальной энергии объекта до достижения максимальной высоты равна полной энергии после полета.

Если «u» — начальная скорость, а «v» — конечная скорость объекта массы «m», а h ₀ — начальная высота объекта над землей, а h — максимальная достигнутая высота объектом в воздухе, затем

K.E _{начальный} +P.E _{начальный} =K.E _{окончательный} +P.E _{окончательный}

1/2 MU ² +MGH ₀ = 1/2 MV ² +MGH ₁

Решение этого уравнения.

V ² = U ² +2G (H ₀ -H ₁ )

V ² = U ² -2G (H ₁ -H _{0 -2G (H 1 -H} 0 -2)

Следовательно, конечная скорость объекта в движении снаряда до того, как он достигнет земли, равна

v=√u ² -2g(h ₁ -h ₀ )

Изменение скорости тела при движении снаряда равно Δ v=v-u.

Подумайте о вертолете, сбрасывающем посылки с едой людям в пострадавшем от наводнения районе. Какова будет скорость продуктовых наборов, сброшенных с вертолета, летящего сверху на высоте 600 м?

Конечно, начальная скорость посылки будет равна нулю до того, как она будет сброшена с вертолета, т.е. u=0, а высота вертолета над землей дана h=600м. Пусть v — конечная скорость посылки с едой, когда ее выпускают из вертолета.

Подстановка в приведенное ниже уравнение v=√12000=109,54 м/с

Следовательно, t=600/109,54=5,47 секунды – это время, необходимое для того, чтобы посылка с едой упала на землю после того, как она сброшена с вертолета.

Узнайте больше о движении снаряда.

Скорость тела при круговом движении

На тело, движущееся по кругу, действуют центробежная и центростремительная силы, которые равны и противоположны по направлению и определяются соотношением

F _c =mv ² /r

Скорость объекта всегда перпендикулярна обеим этим силам, направленным наружу от круговой траектории. В силу чего скорость есть изменение смещения во времени.

Если начальная скорость объекта массы «m», ускоряющегося по круговой траектории радиуса «r», равна «u», а «v» — конечная скорость объекта, то результирующая сила, действующая на объект, равна

Ф=Ф ₂ +Ф ₂

=mv ² /r+mu ² /r

=m/r ( v ² +u ² ) 2 F

u ²

v ² =u ² +r/m F

Следовательно, конечная скорость объекта, ускоряющегося по круговой траектории, равна

v=√ u ² +r0/m F0/m 0/m

Подробнее о мгновенной скорости и скорости: сравнительный анализ.

Часто задаваемые вопросы

Q1.

Какова конечная скорость мяча, ускоряющегося вниз при подъеме на высоту 5 м над землей, если масса мяча 500 грамм? Предположим, что начальная скорость мяча равна 3 м/с.

Дано: m=500 грамм

h ₀ =5m

h ₁ =0

движения, конечная скорость мяча

v=√ u ² -2g(h ₁ -h ₀ )

v=√{3 ² -2*10* (0-5)

v=√10{9+ }

v=√109

v=10,44 м/с

Очевидно, что скорость мяча, ускоряющегося вниз по земле, увеличивается из-за гравитационного притяжения Земли к окружающим его объектам.

Q2.

Если объект, движущийся с начальной скоростью 3 м/с, внезапно ускоряется и приобретает скорость 10 м/с. Какое расстояние пройдет объект за 5 минут?

Начальная скорость объекта u=3 м/с

Конечная скорость объекта v=10 м/с

Продолжительность t= 5 минут= 5* 60=300 секунд

v=2x/t-u

10=2x/300-3

13*300=2x

2x=3900

Следовательно, x=1950 м

  x=1,95 км

В течение 5 минут объект преодолеет расстояние 1,95 км.

Q3.

Расстояние от дома Ратан до ее школы 800 метров. Она выходит из дома и идет в школу в 7:45 с начальной скоростью 0,8 м/с. Она должна быть в школе за 5 минут до 8 часов, поэтому она спешит в школу и приходит вовремя. Какова была ее конечная скорость ходьбы?

Дано: d=800 м,

t=10 мин = 10*60 =600 секунд

Начальная скорость ходьбы u=0,8 м/с

Отсюда, /600-0,8

v=8/3-0,8

v=8-2,4/3=5,6/3=1,87 м/с

Следовательно, конечная скорость ходьбы Ратана составила 1,87 м/с.

Q4.

Какова будет скорость тела массой 30 кг, движущегося с начальной скоростью 3 м/с и ускоряющегося со скоростью 4 м/с при приложении силы 15 Н?

Конечная скорость объекта равна сумме начальной скорости и ускорения во времени.

Отсюда конечная скорость объекта V _{начальная} +V _{ускоряющая} = 3м/с+4м/с=7м/с

Горизонтальное и вертикальное перемещение снаряда

Предыдущие диаграммы, таблицы , и обсуждение относится к тому, как горизонтальная и вертикальная составляющие вектора скорости меняются со временем по ходу траектории снаряда. Теперь мы исследуем, как изменяются со временем горизонтальная и вертикальная составляющие смещения снаряда. Как уже говорилось, вертикальное смещение (обозначаемое символом y ​​ в обсуждении ниже) снаряда зависит только от ускорения свободного падения и не зависит от горизонтальной скорости. Таким образом, вертикальное смещение ( y ​​ ) снаряда можно предсказать, используя то же уравнение, которое используется для нахождения смещения свободно падающего объекта, совершающего одномерное движение. Это уравнение обсуждалось в Разделе 1 физического класса. Уравнение можно записать следующим образом.

 

y = 0,5 • g • t ² (уравнение для вертикального перемещения снаряда, запущенного горизонтально)

где g равно -9,8 м/с/с, а t — время в секундах. Приведенное выше уравнение относится к снаряду без начальной вертикальной скорости и, таким образом, предсказывает расстояние по вертикали, на которое падает снаряд, если он падает из состояния покоя. Ранее также обсуждалось, что сила тяжести не влияет на горизонтальное движение снаряда. Горизонтальное смещение снаряда зависит только от скорости, с которой он движется горизонтально ( v _ix ) и количество времени ( t ), в течение которого он перемещался по горизонтали. Таким образом, если горизонтальное перемещение ( x ) снаряда было представлено уравнением, то это уравнение было бы записано как снаряд (красный), путь снаряда, выпущенного из состояния покоя без горизонтальной скорости (синий) и путь того же объекта при выключенной гравитации (зеленый). Положение объекта показано с интервалом в 1 секунду. В этом примере начальная горизонтальная скорость равна 20 м/с, а начальная вертикальная скорость отсутствует (т. е. случай горизонтально запущенного снаряда).

Как видно на диаграмме выше, вертикальное расстояние падения из состояния покоя в течение каждой последующей секунды увеличивается (т. е. имеет место вертикальное ускорение). Также можно увидеть, что вертикальное смещение подчиняется приведенному выше уравнению (y = 0,5 • g • t ² ). Кроме того, поскольку отсутствует горизонтальное ускорение, горизонтальное расстояние, проходимое снарядом за каждую секунду, является постоянной величиной – снаряд проходит горизонтальное расстояние 20 метров за каждую секунду. Это согласуется с начальной горизонтальной скоростью 20 м/с. Таким образом, горизонтальное смещение составляет 20 м за 1 секунду, 40 метров за 2 секунды, 60 метров за 3 секунды и т. д. Эта информация сведена в таблицу ниже.

Время	Горизонтальный Рабочий объем	Вертикальный Рабочий объем
0 с	0 м	0 м
1 с	20 м	-4,9 м
2 с	40 м	-19,6 м
3 с	60 м	-44,1 м
4 с	80м	-78,4 м
5 с	100 м	-122,5 м

 

Теперь рассмотрим значения смещения для снаряда, запущенного под углом к ​​горизонтали (т. е. снаряда, запущенного не горизонтально). Как повлияет на значения смещения наличие начальной вертикальной составляющей скорости? На приведенной ниже схеме показано положение снаряда, запущенного под углом к ​​горизонту. Снаряд по-прежнему падает на 4,9 м, 19,6 м, 44,1 м и 78,4 м ниже прямолинейного пути без гравитации. Эти расстояния указаны на схеме ниже. 92. Однако траектория без гравитации больше не является горизонтальной линией, поскольку снаряд не запускается горизонтально. В отсутствие силы тяжести снаряд поднялся бы на расстояние по вертикали, равное времени, умноженному на вертикальную составляющую начальной скорости (v _iy • t). При наличии силы тяжести он упадет на расстояние 0,5 • g • t ² . Объединение этих двух влияний на вертикальное смещение дает следующее уравнение .

y = v _iy • t + 0,5 • g • t ²

(уравнение для вертикального смещения снаряда, запускаемого под углом)

где v _iy — начальная вертикальная скорость в м/с, t — время в секундах, g = -9,8 м/с/с (приблизительное значение ускорения свободного падения) . Если снаряд запущен с начальной вертикальной скоростью 19,6 м/с и начальной горизонтальной скоростью 33,9м/с, то перемещения снаряда по осям x и y можно рассчитать с помощью приведенных выше уравнений. Пример расчета показан ниже.

Расчеты для t = 1 секунда y = v iy * t + 0,5*g*t 2 где v iy = 19,6 м/с y = (19,6 м/с) * (1 с) + 0,5*(-9,8 м/с/с)*(1 с) 2 г = 19,6 м + (-4,9 м) г = 14,7 м (приблизительно) х = v ix * т где v ix = 33,9 м/с х = (33,9 м/с) * (1 с) х = 33,9 м

 

В следующей таблице приведены результаты таких расчетов для первых четырех секунд движения снаряда.

Время	Горизонтальный Рабочий объем	Вертикальный Рабочий объем
0 с	0 м	0 м
1 с	33,9 м	14,7 м
2 с	67,8 м	19,6 м
3 с	101,7 м	14,7 м
4 с	135,6 м	0 м

Данные в таблице выше показывают симметричный характер траектории снаряда.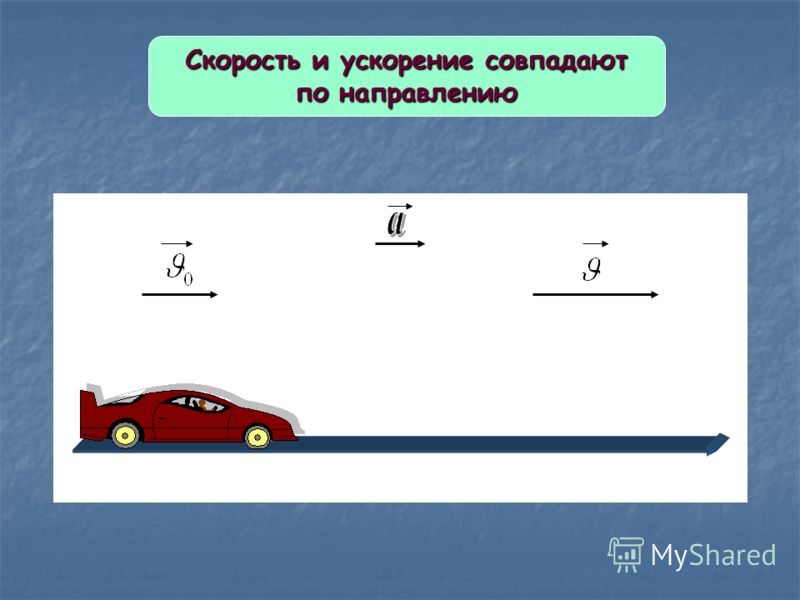 Вертикальное перемещение снаряда t за секунд до достижения пика равно вертикальному перемещению снаряда t за секунд после достижения пика. Например, снаряд достигает пика за 2 секунды; вертикальное смещение такое же через 1 секунду (1 с до достижения пика) такое же, как и через 3 секунды (1 с после достижения пика). Кроме того, время достижения пика (2 секунды) такое же, как и время падения с пика (2 секунды).

 

 

Мы хотели бы предложить …

Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего симулятора движения снарядов. Вы можете найти его в разделе Physics Interactives на нашем сайте. Симулятор позволяет исследовать концепции движения снаряда в интерактивном режиме. Измените высоту, измените угол, измените скорость и запустите снаряд.

Посетите: Симулятор движения снаряда

Проверьте свое понимание

Используйте свое понимание снарядов, чтобы ответить на следующие вопросы. Затем нажмите кнопку, чтобы просмотреть ответы.

1. Анна Литикаль сбрасывает мяч с вершины скалы высотой 78,4 метра. Через какое время мяч достигнет земли и на какой высоте будет находиться мяч после каждой секунды движения?

Щелкните здесь, чтобы увидеть схему ситуации.

 

2. Пушечное ядро ​​запускается горизонтально с вершины утеса высотой 78,4 метра. Через какое время мяч достигнет земли и на какой высоте он будет находиться после каждой секунды пути?

Щелкните здесь, чтобы увидеть схему ситуации.

 

3. Заполните приведенную ниже таблицу, указав значение горизонтальной и вертикальной составляющих скорости и ускорения снаряда.

 

 

 

 

4. На приведенной ниже диаграмме показана траектория снаряда, запущенного не горизонтально из возвышенного положения на вершине утеса. Начальные горизонтальная и вертикальная составляющие скорости равны 8 м/с и 19,6 м/с соответственно. Показаны положения объекта с интервалом в 1 секунду. Определите горизонтальную и вертикальную скорости в каждый момент времени, показанный на диаграмме.

 

 

 

 

Следующая диаграмма относится к вопросам № 1 и № 2 выше. Используется шкала, где 1 см = 5 метрам. (Обратите внимание, что 1 см может быть разным расстоянием для разных компьютерных мониторов, поэтому на диаграмме указана сантиметровая линейка.)

Вернуться к вопросу №1.

Вернуться к вопросу №2.

Следующий раздел:

Перейти к следующему уроку:

4.

3 Движение снаряда | University Physics Volume 1

Цели обучения

К концу этого раздела вы сможете:

• Использовать одномерное движение в перпендикулярных направлениях для анализа движения снаряда.
• Рассчитайте дальность, время полета и максимальную высоту снаряда, который запускается и поражает плоскую горизонтальную поверхность.
• Найдите время полета и скорость удара снаряда, который приземлился на высоте, отличной от высоты старта.
• Рассчитать траекторию снаряда.

Снарядное движение — это движение объекта, брошенного или отброшенного в воздух, с ускорением только под действием силы тяжести. Применения движения снаряда в физике и технике многочисленны. Некоторые примеры включают метеоры, когда они входят в атмосферу Земли, фейерверки и движение любого мяча в спорте. Такие объекты называются снарядами , а их путь называется траекторией . Движение падающих объектов, описанное в разделе «Движение по прямой линии», представляет собой простой одномерный тип движения снаряда, в котором нет горизонтального движения.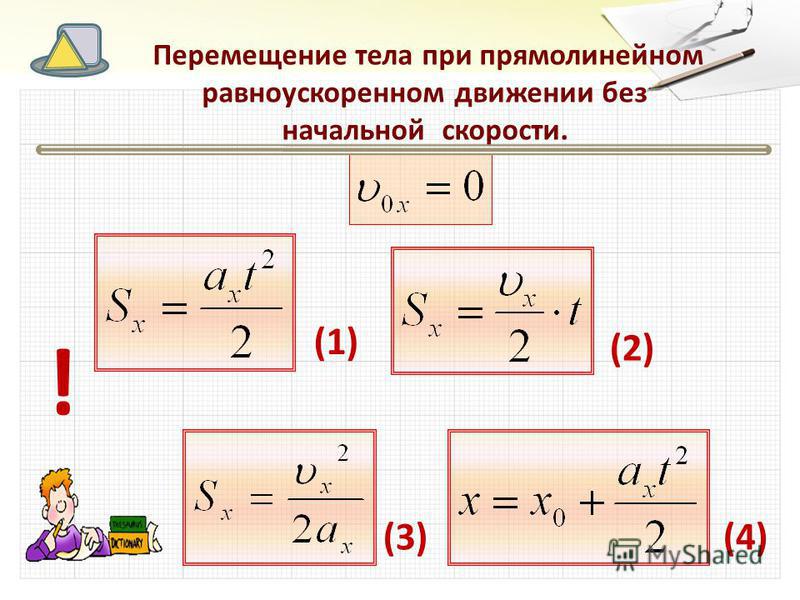 В этом разделе мы рассматриваем двумерное движение снаряда и не учитываем влияние сопротивления воздуха.

Наиболее важным фактом, который следует помнить, является то, что движения вдоль перпендикулярных осей являются независимыми и поэтому могут быть проанализированы отдельно. Мы обсуждали этот факт в разделе «Векторы смещения и скорости», где увидели, что вертикальное и горизонтальное движения независимы. Ключом к анализу двумерного движения снаряда является разбиение его на два движения: одно по горизонтальной оси, а другое по вертикальной. (Этот выбор осей является наиболее разумным, потому что ускорение, вызванное силой тяжести, является вертикальным; таким образом, нет никакого ускорения вдоль горизонтальной оси, когда сопротивление воздуха незначительно.) Как обычно, мы называем горизонтальную ось x – ось и вертикальная ось y ​​ – ось. Мы не обязаны использовать этот выбор осей; это просто удобно в случае гравитационного ускорения. В других случаях мы можем выбрать другой набор осей. (Рисунок) иллюстрирует обозначение смещения, где мы определяем [латекс] \overset{\to }{s} [/latex] как общее смещение, а [латекс] \overset{\to }{x} [/latex ] и [latex] \overset{\to }{y} [/latex] — его вектора-компоненты вдоль горизонтальной и вертикальной осей соответственно. Величины этих векторов равны s , x и y ​​ .

Рисунок 4.11 Полное перемещение s футбольного мяча в точке на его пути. Вектор [latex] \overset{\to }{s} [/latex] имеет компоненты [latex] \overset{\to }{x} [/latex] и [latex] \overset{\to }{y} [ /latex] по горизонтальной и вертикальной осям. Его величина равна s, и он составляет угол θ с горизонтом.

Чтобы полностью описать движение снаряда , мы должны включить скорость и ускорение, а также перемещение. Мы должны найти их компоненты вдоль 9{2}). [/latex]

Поскольку гравитация вертикальна, [латекс] {a}_{x}=0. [/latex] Если [latex] {a}_{x}=0, [/latex] это означает, что начальная скорость в направлении x равна конечной скорости в направлении x , или [latex] {v}_{x}={v}_{0x}.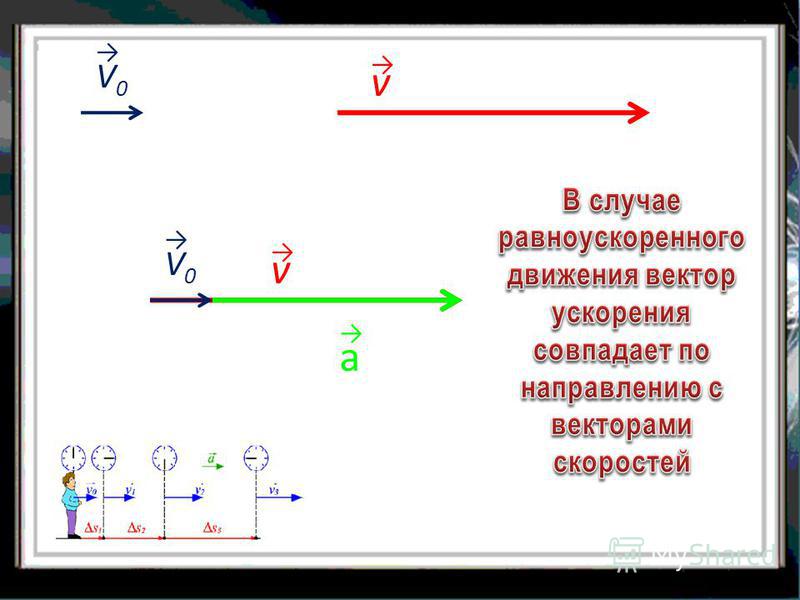 [/latex] С этими условиями на ускорение и скорость мы можем записать кинематическое (уравнение) через (уравнение) для движения в однородном гравитационном поле, включая остальные кинематические уравнения для постоянного ускорения из движения с постоянным ускорением. Кинематические уравнения для движения в однородном гравитационном поле становятся кинематическими уравнениями с [латекс] {а}_{у}=\текст{−}г,\енспейс{а}_{х}=0: [/латекс] 9{2}-2g(y-{y}_{0}) [/latex]

Используя этот набор уравнений, мы можем проанализировать движение снаряда, учитывая некоторые важные моменты.

Стратегия решения задач: Движение снаряда

1. Разложите движение на горизонтальную и вертикальную составляющие вдоль осей x и y ​​. Величины составляющих смещения [латекс] \перемещения{с} [/латекс] по этим осям равны х и y. Величины компонентов скорости [латекс] \overset{\to }{v} [/латекс] равны [латекс] {v}_{x}=v\text{cos}\,\theta \,\text {и}\,{v}_{y}=v\text{sin}\,\theta , [/latex], где v — величина скорости, а θ — ее направление относительно горизонтали, как показано на (рис. ).
2. Рассматривайте движение как два независимых одномерных движения: одно по горизонтали, а другое по вертикали. Используйте кинематические уравнения для горизонтального и вертикального движения, представленные ранее.
3. Найдите неизвестные в двух отдельных движениях: горизонтальном и вертикальном. Обратите внимание, что единственной общей переменной между движениями является время t 9{2}}, [/латекс]

   , где θ — направление смещения [латекс] \overset{\to }{s}. [/латекс]

Рис. 4.12 (a) Мы анализируем двумерное движение снаряда, разбивая его на два независимых одномерных движения вдоль вертикальной и горизонтальной осей. (b) Горизонтальное движение простое, потому что [латекс] {а}_{х}=0 [/латекс] и [латекс] {v}_{х} [/латекс] — константа. (в) Скорость в вертикальном направлении начинает уменьшаться по мере подъема объекта. В высшей точке вертикальная скорость равна нулю. Когда объект снова падает на Землю, вертикальная скорость снова увеличивается по величине, но указывает направление, противоположное начальной вертикальной скорости. (d) Движения x и y рекомбинируются, чтобы получить общую скорость в любой заданной точке траектории.

Пример

Снаряд фейерверка взрывается высоко и далеко

Во время фейерверка в воздух выстреливается снаряд с начальной скоростью 70,0 м/с под углом [латекс] 75,0\text{°} [/ латекс] над горизонталью, как показано на (рис.). Взрыватель рассчитан на воспламенение снаряда, когда он достигает своей высшей точки над землей. а) Вычислите высоту взрыва снаряда. б) Сколько времени проходит между запуском снаряда и взрывом? в) Чему равно горизонтальное перемещение снаряда при взрыве? г) Чему равно полное перемещение от точки запуска до высшей точки?

Рисунок 4.13 Траектория снаряда фейерверка. Взрыватель предназначен для подрыва снаряда в высшей точке его траектории, которая находится на высоте 233 м и на расстоянии 125 м по горизонтали.

Стратегия

Движение можно разбить на горизонтальное и вертикальное, в которых [латекс] {a}_{x}=0 [/латекс] и [латекс] {a}_{y}=\text{−} грамм. [/latex] Затем мы можем определить [latex] {x}_{0} [/latex] и [latex] {y}_{0} [/latex] равными нулю и найти нужные количества. 9{2}}{2g}. [/latex]

Теперь мы должны найти [latex] {v}_{0y}, [/latex] составляющую начальной скорости в направлении y ​​. Он задается как [латекс] {v}_{0y}={v}_{0}\text{sin}{\theta }_{0}, [/latex], где [латекс] {v}_{0 } [/latex] — начальная скорость 70,0 м/с, а [latex] {\theta }_{0}=75\text{°} [/latex] — начальный угол. Таким образом,

[латекс] {v}_{0y}={v}_{0}\text{sin}\,\theta =(70.0\,\text{m}\text{/}\text{s })\text{sin}\,75\text{°}=67,6\,\text{m}\text{/}\text{s} [/latex] 9{2})}. [/latex]

Таким образом, мы имеем

[латекс] y=233\,\text{m}\text{.} [/latex]

Обратите внимание, что поскольку значение up положительно, начальная вертикальная скорость положительна, как и максимальная высота, но ускорение в результате силы тяжести отрицательно. Отметим также, что максимальная высота зависит только от вертикальной составляющей начальной скорости, так что любой снаряд с начальной вертикальной составляющей скорости 67,6 м/с достигает максимальной высоты 233 м (без учета сопротивления воздуха).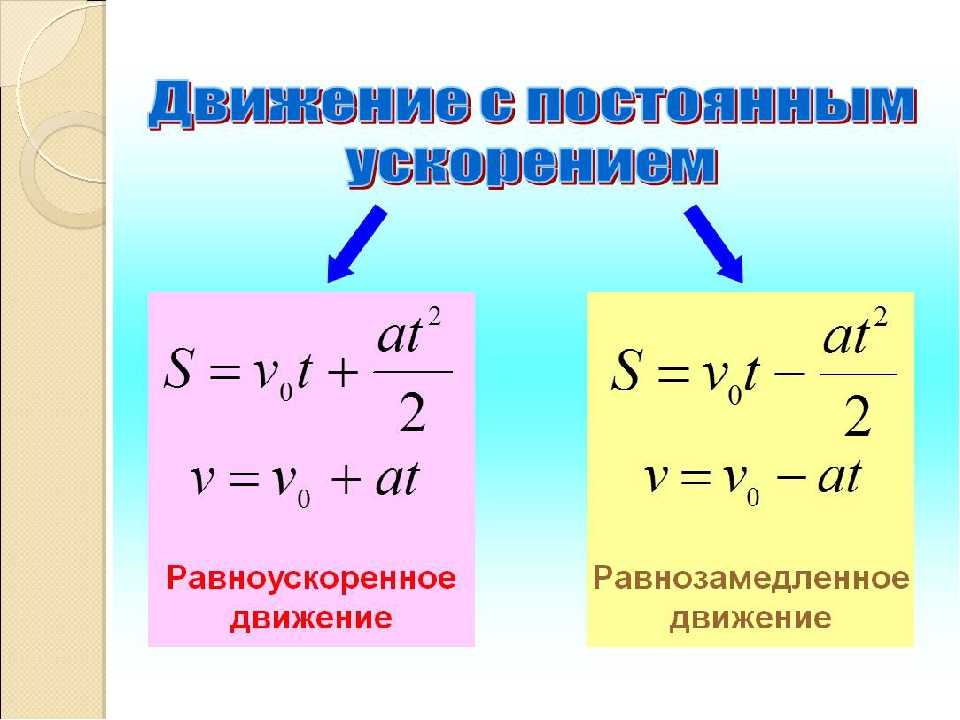 Числа в этом примере разумны для больших фейерверков, снаряды которых действительно достигают такой высоты перед взрывом. На практике сопротивлением воздуха нельзя полностью пренебречь, поэтому начальная скорость должна быть несколько больше заданной, чтобы достичь той же высоты. 9{2}}=6.90\text{s}\text{.} [/latex]

Это время подходит и для больших фейерверков. Если вы можете увидеть запуск фейерверка, обратите внимание, что проходит несколько секунд, прежде чем снаряд взорвется. Другой способ найти время — использовать [латекс] y\,\text{=}\,{y}_{0}+\frac{1}{2}({v}_{0y}+{v} _{у})т. [/latex] Это остается вам в качестве упражнения.

(c) Поскольку сопротивлением воздуха можно пренебречь, [латекс] {а}_{х}=0 [/латекс], а горизонтальная скорость постоянна, как обсуждалось ранее. Горизонтальное смещение — это горизонтальная скорость, умноженная на время по формуле [латекс] x={x}_{0}+{v}_{x}t, [/latex], где [латекс] {x}_{0} [/latex] равно нулю. Таким образом,

[latex] x={v}_{x}t, [/latex]

, где [latex] {v}_{x} [/latex] — x -компонент скорости, который задано

[латекс] {v}_{x}={v}_{0}\text{cos}\,\theta =(70.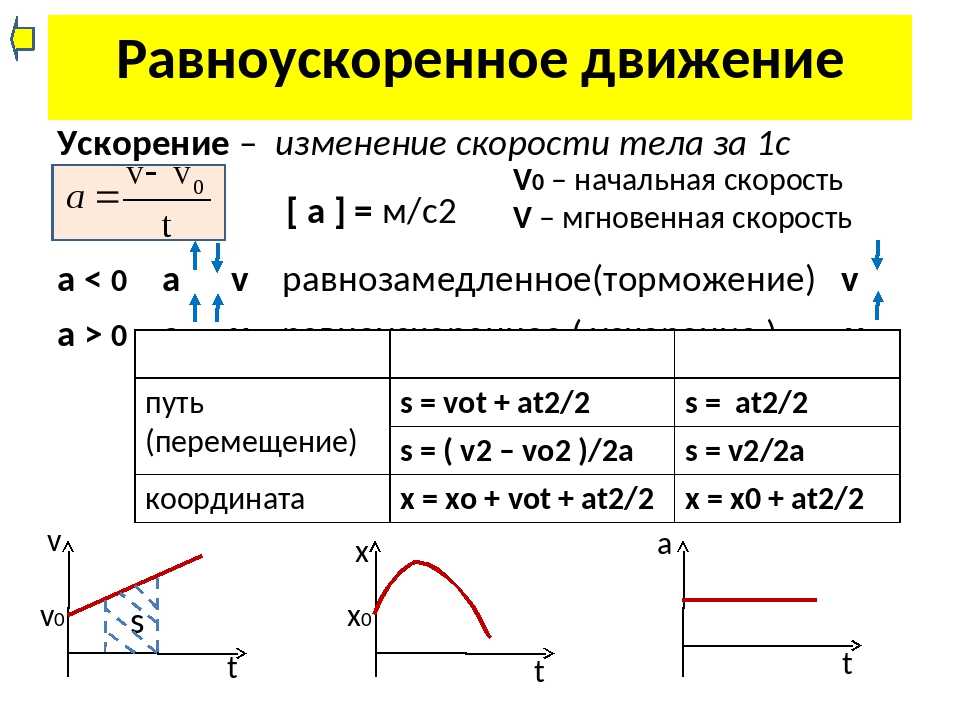 0\,\text{m}\text{/}\text{s })\text{cos}75\text{°}=18.1\,\text{m}\text{/}\text{s}. [/latex]

Time t для обоих движений одинаково, поэтому x равно

[latex] x=(18.1\,\text{m}\text{/}\text{s})6,90 \,\text{s}=125\,\text{m}\text{.} [/latex]

Горизонтальное движение – это постоянная скорость при отсутствии сопротивления воздуха. Найденное здесь горизонтальное смещение может быть полезно для предотвращения падения фрагментов фейерверка на зрителей. Когда снаряд взрывается, большое влияние оказывает сопротивление воздуха, и многие осколки приземляются прямо под ним. 9{-1}(\frac{233}{125})=61,8\text{°}. [/latex]

Обратите внимание, что угол для вектора смещения меньше, чем начальный угол запуска. Чтобы понять, почему это так, просмотрите (рисунок), на котором показана кривизна траектории по направлению к уровню земли.

При решении (Рисунок)(а) выражение, которое мы нашли для y ​​, справедливо для любого движения снаряда, когда сопротивлением воздуха можно пренебречь. {2}}{2g}. [/латекс]

Это уравнение определяет максимальную высоту снаряда над точкой старта и зависит только от вертикальной составляющей начальной скорости.

Проверьте свое понимание

Камень брошен горизонтально со скалы [латекс] высотой 100,0\,\text{м} [/латекс] со скоростью 15,0 м/с. (a) Определите начало системы координат. б) Какое уравнение описывает горизонтальное движение? в) Какие уравнения описывают вертикальное движение? г) Какова скорость камня в момент удара?

Показать решение

Пример

Расчет движения снаряда: теннисист

Теннисист выигрывает матч на стадионе имени Артура Эша и бьет мячом по трибунам со скоростью 30 м/с и под углом [латекс] 45\text{°} [/ латекс] над горизонталью ((Рисунок)). На пути вниз мяч ловится зрителем на высоте 10 м над точкой удара по мячу. а) Вычислите время, за которое теннисный мяч достигнет зрителя. б) Каковы модуль и направление скорости мяча в момент удара?

Рисунок 4. 14 Траектория удара теннисного мяча о трибуны.

Стратегия

Опять же, разложение этого двумерного движения на два независимых одномерных движения позволяет нам найти нужные величины. Время нахождения снаряда в воздухе определяется только его вертикальным движением. Таким образом, мы сначала решим для t . Пока мяч поднимается и падает вертикально, горизонтальное движение продолжается с постоянной скоростью. В этом примере запрашивается конечная скорость. Таким образом, мы рекомбинируем вертикальные и горизонтальные результаты, чтобы получить [латекс] \overset{\to }{v} [/латекс] в конечное время 9{2}. [/latex]

Если принять начальную позицию [latex] {y}_{0} [/latex] равной нулю, то конечная позиция будет y ​​ = 10 м. Начальная вертикальная скорость представляет собой вертикальную составляющую начальной скорости:

[латекс] {v}_{0y}={v}_{0}\text{sin}\,{\theta}_{0}=( 30,0\,\text{m}\text{/}\text{s})\text{sin}\,45\text{°}=21,2\,\text{m}\text{/}\text{s }. [/latex]

Подстановка y ​​ в (Рисунок) дает нам

[латекс] 10,0\,\text{m}=(21,2\,\text{м/с})t-(4,9{2}-(21,2\,\текст{м/с})t+10,0\,\текст{м}=0. [/latex]

Использование квадратичной формулы дает t = 3,79 с и t = 0,54 с. Поскольку мяч находится на высоте 10 м два раза на протяжении своей траектории — один раз по пути вверх и один раз по пути вниз — мы принимаем более длинное решение для времени, которое требуется мячу, чтобы достичь зрителя:

[латекс ] t=3.79\,\text{s}\text{.} [/latex]

Время движения снаряда полностью определяется вертикальным движением. Таким образом, любой снаряд, имеющий начальную вертикальную скорость 21,2 м/с и приземлившийся на 10,0 м ниже начальной высоты, тратит 3,79с в воздухе.

(b) Мы можем найти конечные горизонтальную и вертикальную скорости [latex] {v}_{x} [/latex] и [latex] {v}_{y} [/latex] с использованием результата из (а). Затем мы можем объединить их, чтобы найти величину вектора полной скорости [латекс] \overset{\to }{v} [/латекс] и угол [латекс] \тета [/латекс], который он образует с горизонтом. Поскольку [латекс] {v}_{x} [/латекс] является постоянным, мы можем найти его в любом горизонтальном положении. Мы выбираем начальную точку, потому что знаем и начальную скорость, и начальный угол. Следовательно, 9{-1}(\frac{21.2}{-15.9})=-53.1\text{°}. [/latex]

Значение

(a) Как упоминалось ранее, время движения снаряда полностью определяется вертикальным движением. Таким образом, любой снаряд, имеющий начальную вертикальную скорость 21,2 м/с и приземлившийся на 10,0 м ниже начальной высоты, находится в воздухе 3,79 с. (b) Отрицательный угол означает, что скорость [latex] 53,1\text{°} [/latex] ниже горизонтали в точке удара. Этот результат согласуется с тем фактом, что мяч ударяется в точку по другую сторону от вершины траектории и, следовательно, имеет отрицательное значение 9.0364 y ​​ составляющая скорости. Величина скорости меньше, чем величина начальной скорости, которую мы ожидаем, поскольку она воздействует на высоту 10,0 м над уровнем запуска.

Время полета, траектория и дальность полета

Интерес представляют время полета, траектория и дальность полета снаряда, запущенного на плоской горизонтальной поверхности и упавшего на ту же поверхность.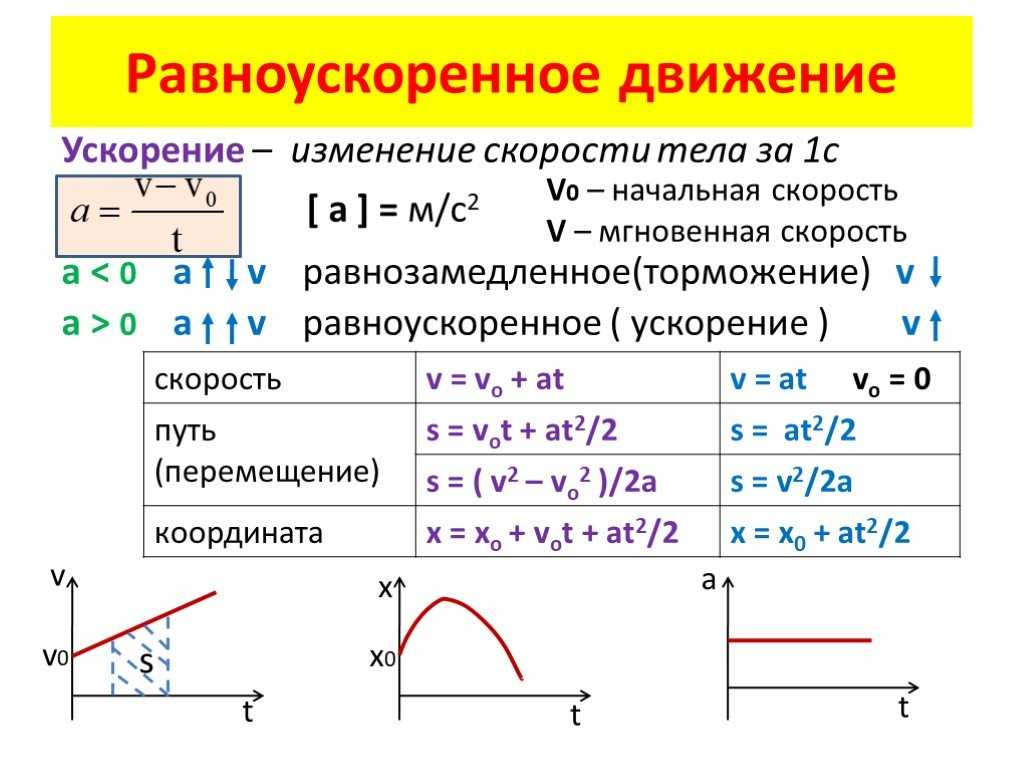 В этом случае кинематические уравнения дают полезные выражения для этих величин, которые выводятся в следующих разделах. 9{2}=0. [/latex]

Факторинг, мы имеем

[латекс] t({v}_{0}\text{sin}{\theta }_{0}-\frac{gt}{2})=0. [/latex]

Решение для t дает нам

[латекс] {T} _ {\ text {tof}} = \ frac {2 ({v} _ {0} \ text {sin} {\ theta }_{0})}{г}. [/latex]

Это время полета для снаряда, выпущенного и ударившегося о плоскую горизонтальную поверхность. (Рисунок) не применяется, когда снаряд приземляется на другой высоте, чем он был запущен, как мы видели на (Рисунок) теннисиста, ударяющего мячом по трибунам. Другое решение t = 0, соответствует времени запуска. Время полета линейно пропорционально начальной скорости в направлении y ​​ и обратно пропорционально g . Таким образом, на Луне, где гравитация составляет одну шестую от земной, снаряд, запущенный с той же скоростью, что и на Земле, будет находиться в воздухе в шесть раз дольше.

Траектория

Траектория снаряда может быть найдена путем исключения временной переменной t из кинематических уравнений для произвольного 9{2}\text{sin}2{\theta}_{0}}{g}. [/latex]

Обратите особое внимание на то, что (Рисунок) действителен только для запуска и удара о горизонтальную поверхность. Мы видим, что диапазон прямо пропорционален квадрату начальной скорости [latex] {v}_{0} [/latex] и [latex] \text{sin}2{\theta}_{0} [/latex] , и оно обратно пропорционально ускорению свободного падения. Таким образом, на Луне дальность была бы в шесть раз больше, чем на Земле, при той же начальной скорости. Кроме того, из коэффициента [латекс] \text{sin}2{\theta}_{0} [/latex] мы видим, что диапазон максимален при [латексе] 45\текст{°}. [/latex] Эти результаты показаны на (Рисунок). В (а) мы видим, что чем больше начальная скорость, тем больше радиус действия. В (b) мы видим, что диапазон максимален при [latex] 45\text{°}. [/latex] Это справедливо только для условий, в которых сопротивление воздуха не учитывается. Если учитывать сопротивление воздуха, максимальный угол несколько меньше. Интересно, что один и тот же диапазон найден для двух начальных углов запуска, которые в сумме составляют [латекс] 90\текст{°}. [/latex] Снаряд, выпущенный с меньшим углом, имеет более низкую вершину, чем больший угол, но оба они имеют одинаковую дальность.

Рисунок 4.15 Траектории снарядов на ровной местности. (a) Чем больше начальная скорость [латекс] {v}_{0}, [/латекс], тем больше диапазон для данного начального угла. (b) Влияние начального угла [латекс] {\ тета }_{0} [/латекс] на дальность полета снаряда с заданной начальной скоростью. Обратите внимание, что диапазон одинаковый для начальных углов [латекс] 15\текст{°} [/латекс] и [латекс] 75\текст{°}, [/латекс], хотя максимальная высота этих путей различна.

Пример

Сравнение ударов в гольфе

Игрок в гольф оказывается в двух разных ситуациях на разных лунках. На второй лунке он находится в 120 м от грина и хочет отбить мяч на 90 м и дать ему вылететь на грин. Он направляет бросок низко к земле под углом [latex] 30\text{°} [/latex] к горизонтали, чтобы мяч мог катиться после удара. На четвертой лунке он находится в 90 м от грина и хочет, чтобы мяч упал с минимальным количеством качения после удара. Здесь он направляет выстрел под углом [latex] 70\text{°} [/latex] к горизонтали, чтобы свести к минимуму скатывание после удара. Оба выстрела попали в ровную поверхность.

а) Какова начальная скорость мяча у второй лунки?

(b) Какова начальная скорость мяча у четвертой лунки?

(c) Напишите уравнение траектории для обоих случаев.

(d) Нарисуйте траектории.

Стратегия

Мы видим, что уравнение дальности имеет начальную скорость и угол, поэтому мы можем найти начальную скорость как для (a), так и для (b). Когда у нас есть начальная скорость, мы можем использовать это значение для записи уравнения траектории. 9{2}\hfill \end{array} [/latex]

(d) Используя графическую утилиту, мы можем сравнить две траектории, показанные на (рис. ).

Рисунок 4.16 Две траектории мяча для гольфа с дальностью 90 м. Точки удара обоих находятся на том же уровне, что и точка запуска.

Значение

Начальная скорость выстрела в [латекс] 70\text{°} [/латекс] больше, чем начальная скорость выстрела в [латекс] 30\текст{°}. [/latex] Обратите внимание на (Рисунок), что два снаряда, запущенные с одинаковой скоростью, но под разными углами, имеют одинаковую дальность, если углы запуска складываются в [латекс] 90\текст{°}. [/latex] Углы запуска в этом примере складываются, чтобы получить число больше, чем [latex] 90\text{°}. [/latex] Таким образом, выстрел в [latex] 70\text{°} [/latex] должен иметь большую стартовую скорость, чтобы достичь 90 м, иначе он приземлился бы на более коротком расстоянии.

Проверьте свое понимание

Если бы два удара в гольф на (рис.) были произведены с одинаковой скоростью, какой удар имел бы наибольшую дальность?

Показать решение

Когда мы говорим о дальности полета снаряда на ровной поверхности, мы предполагаем R очень мал по сравнению с окружностью Земли. Однако, если диапазон большой, Земля изгибается ниже снаряда, и ускорение, возникающее в результате силы тяжести, меняет направление вдоль траектории. Дальность больше, чем предсказано уравнением дальности, приведенным ранее, потому что снаряд должен упасть дальше, чем если бы он упал на ровную поверхность, как показано на (Рисунок), который основан на рисунке в «Началах » Ньютона. Если начальная скорость достаточно велика, снаряд выходит на орбиту. Поверхность Земли опускается на 5 м каждые 8000 м. За 1 с тело без сопротивления воздуха падает с высоты 5 м. Таким образом, если объекту задана горизонтальная скорость [латекс] 8000\,\текст{м}\текст{/}\текст{с} [/латекс] (или [латекс] 18000\текст{ми}\текст{ /}\text{hr}) [/latex] возле поверхности Земли, он выйдет на орбиту вокруг планеты, потому что поверхность непрерывно отклоняется от объекта. Это примерно скорость космического корабля “Шаттл” на низкой околоземной орбите, когда он работал, или любого спутника на низкой околоземной орбите. Эти и другие аспекты орбитального движения, такие как вращение Земли, более подробно рассматриваются в «Гравитации».

Рисунок 4.17 Снаряд в спутник. В каждом показанном здесь случае снаряд запускается с очень высокой башни, чтобы избежать сопротивления воздуха. С увеличением начальной скорости диапазон увеличивается и становится длиннее, чем он был бы на ровной поверхности, потому что Земля изгибается под его траекторией. При скорости 8000 м/с достигается орбита.

В PhET Explorations: Projectile Motion узнайте о движении снаряда с точки зрения угла запуска и начальной скорости.

Резюме

• Снарядное движение – это движение объекта, подверженное только ускорению свободного падения, где ускорение постоянно, как вблизи поверхности Земли.
• Для решения задач движения снаряда анализируем движение снаряда в горизонтальном и вертикальном направлениях, используя одномерные кинематические уравнения для x и y ​​ .
• Время полета снаряда, запущенного с начальной вертикальной скоростью [латекс] {v}_{0y} [/латекс] по ровной поверхности, определяется выражением

  [латекс] {T}_{tof}=\frac{2({v}_{0}\text{sin}\,\theta)}{g}. [/латекс]

  Это уравнение справедливо только тогда, когда снаряд приземляется на той же высоте, с которой он был запущен.

• Максимальное горизонтальное расстояние, пройденное снарядом, называется дальностью полета. Опять же, уравнение для дальности справедливо только тогда, когда снаряд приземляется на той же высоте, с которой он был запущен.

Концептуальные вопросы

Ответьте на следующие вопросы о движении снаряда на ровной поверхности, предполагая незначительное сопротивление воздуха, с начальным углом, не равным ни [латексу] 0\текст{°} [/латексу], ни [латексу] 90\text{°}: [/latex] (a) Всегда ли скорость равна нулю? б) Когда скорость минимальна? Максимум? в) Может ли скорость когда-либо быть такой же, как начальная скорость, в любой другой момент времени, кроме t = 0? (d) Может ли скорость когда-либо быть такой же, как начальная скорость, в момент времени, отличный от t = 0?

Показать решение

Ответьте на следующие вопросы о движении снаряда по ровной поверхности при пренебрежимо малом сопротивлении воздуха, когда начальный угол не равен ни [латексу] 0\text{°} [/латексу], ни [латексу] 90\text{°}: [/latex] (a) Всегда ли ускорение равно нулю? (b) Всегда ли ускорение направлено в том же направлении, что и составляющая скорости? в) Всегда ли ускорение противоположно направлению составляющей скорости?

Десятицентовик кладут на край стола так, что он слегка свисает. Четвертак скользит горизонтально по поверхности стола перпендикулярно краю и ударяется о монетку. Какая монета первой упадет на землю?

Показать решение

Задачи

Пуля выпущена горизонтально с высоты плеча (1,5 м) с начальной скоростью 200 м/с. а) Через какое время пуля упадет на землю? б) Какое расстояние пролетит пуля по горизонтали?

Показать решение

Мрамор скатывается со столешницы высотой 1,0 м и падает на пол в точке на расстоянии 3,0 м от края стола в горизонтальном направлении. а) Сколько времени шарик находится в воздухе? б) Какова скорость шарика, когда он оторвется от края стола? в) Какова его скорость в момент удара об пол?

Дротик брошен горизонтально со скоростью 10 м/с в мишень мишени для дротиков на расстоянии 2,4 м, как показано на следующем рисунке. а) На сколько ниже намеченной цели дротик попадает? (b) Что ваш ответ говорит вам о том, как опытные игроки в дартс бросают свои дротики?

Показать решение

Самолет, летящий горизонтально со скоростью 500 км/ч на высоте 800 м, сбрасывает ящик с припасами (см. следующий рисунок). Если парашют не раскроется, как далеко перед точкой выпуска ящик упадет на землю?

Предположим, что самолет в предыдущей задаче выпускает снаряд горизонтально в направлении своего движения со скоростью 300 м/с относительно самолета. а) На каком расстоянии от точки выброса пуля упадет на землю? б) Какова его скорость в момент удара о землю?

Показать решение

Питчер в фастболе может бросить бейсбольный мяч со скоростью 40 м/с (90 миль/ч). (a) Предполагая, что питчер может выпустить мяч на расстоянии 16,7 м от «домашней» пластины, так что мяч движется горизонтально, сколько времени потребуется мячу, чтобы достичь «домашней» пластины? (b) Как далеко мяч падает между рукой питчера и домашней пластиной?

Снаряд запущен под углом [латекс] 30\текст{°} [/латекс] и через 20 с приземляется на той же высоте, на которой был запущен. а) Чему равна начальная скорость снаряда? б) Какова максимальная высота? в) Каков диапазон? (d) Рассчитайте перемещение от точки запуска до положения на его траектории за 15 с.

Показать решение

Баскетболист бьет по корзине на расстоянии 6,1 м и на высоте 3,0 м над полом. Если мяч выпущен на высоте 1,8 м над полом под углом [latex] 60\text{°} [/latex] над горизонтом, какой должна быть начальная скорость, чтобы он прошел через корзину?

В данный момент воздушный шар находится в воздухе на высоте 100 м и снижается с постоянной скоростью 2,0 м/с. Именно в этот момент девочка бросает мяч горизонтально относительно себя с начальной скоростью 20 м/с. Когда она приземлится, где она найдет мяч? Не учитывать сопротивление воздуха.

Показать решение

Человек на мотоцикле, движущийся с постоянной скоростью 10 м/с, бросает пустую банку прямо вверх относительно себя с начальной скоростью 3,0 м/с. Найдите уравнение траектории, как ее видит сотрудник полиции на обочине дороги. Предположим, что начальное положение банки — это точка, в которую она была брошена. Не учитывать сопротивление воздуха.

Спортсмен может прыгнуть на 8,0 м в длину. На какое максимальное расстояние может прыгнуть спортсмен на Луне, где ускорение свободного падения составляет одну шестую земного?

Показать решение

Максимальное горизонтальное расстояние, на которое мальчик может бросить мяч, составляет 50 м. Предположим, что он может бросать с одинаковой начальной скоростью под любым углом. На какую высоту он подбрасывает мяч, когда бросает его прямо вверх?

Камень брошен со скалы под углом [латекс] 53\текст{°} [/латекс] к горизонту. Скала высотой 100 м. Начальная скорость камня 30 м/с. а) На какую высоту над краем утеса возвышается скала? б) Какое расстояние он переместил по горизонтали, когда находился на максимальной высоте? в) Через какое время после выброса он упадет на землю? г) Каков радиус скалы? д) Каково горизонтальное и вертикальное положение скалы относительно края обрыва в точке 9?0364 t = 2,0 с, t = 4,0 с и t = 6,0 с?

Показать решение

Пытаясь уйти от преследователей, секретный агент съезжает на лыжах со склона, наклоненного на [latex] 30\text{°} [/latex] ниже горизонта со скоростью 60 км/ч.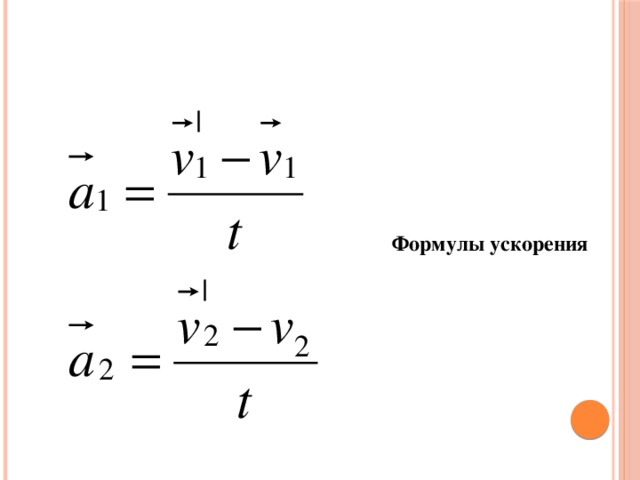 Чтобы выжить и приземлиться на снег на 100 м ниже, он должен расчистить ущелье шириной 60 м. Он это делает? Не учитывать сопротивление воздуха.

Игрок в гольф на фервее находится в 70 м от грина, который расположен ниже уровня фервея на 20 м. Если игрок в гольф ударит по мячу под углом [latex] 40\text{°} [/latex] с начальной скоростью 20 м/с, насколько близко он подлетит к грину?

Показать решение

Снаряд выпущен по холму, основание которого находится на расстоянии 300 м. Снаряд выпущен на [latex] 60\text{°} [/latex] над горизонтом с начальной скоростью 75 м/с. Холм может быть аппроксимирован плоскостью, наклоненной под углом [latex] 20\text{°} [/latex] к горизонтали. Относительно системы координат, показанной на следующем рисунке, уравнение этой прямой имеет вид [латекс] y=(\text{tan}20\text{°})x-109. [/latex] Где на холме приземляется снаряд?

Астронавт на Марсе пинает футбольный мяч под углом [латекс] 45\текст{°} [/латекс] с начальной скоростью 15 м/с.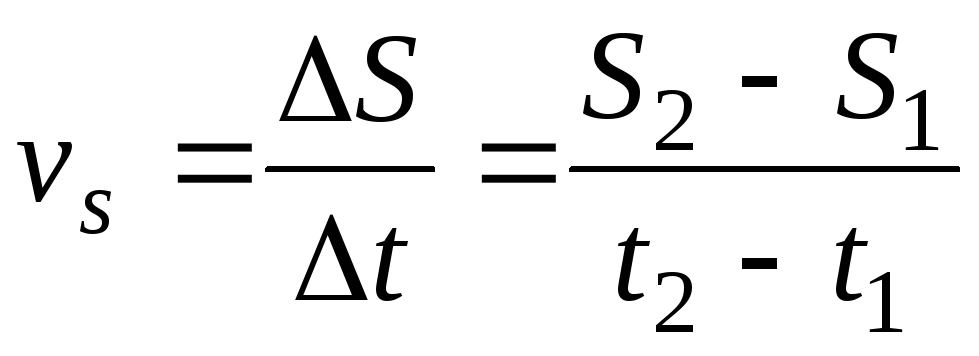 Если ускорение свободного падения на Марсе равно 3,7 м/с, а) какова дальность футбольного удара по плоской поверхности? (b) Какова будет дальность такого же толчка на Луне, где гравитация составляет одну шестую от земной?

Показать решение

Майку Пауэллу принадлежит рекорд по прыжкам в длину 8,95 м, установленный в 1991 году. Если он оторвался от земли под углом [latex] 15\text{°}, [/latex] какой была его начальная скорость?

Робот-гепард Массачусетского технологического института может перепрыгивать препятствия высотой 46 см и развивать скорость 12,0 км/ч. (a) Если робот стартует под углом [латекс] 60\текст{°} [/латекс] на этой скорости, какова его максимальная высота? б) Каким должен быть угол запуска, чтобы достичь высоты 46 см?

Показать решение

Гора Асама, Япония, является действующим вулканом. В 2009 году извержение выбросило твердые вулканические породы, которые упали на 1 км по горизонтали от кратера. Если бы вулканические породы были запущены под углом [латекс] 40\текст{°} [/латекс] к горизонту и приземлились на 900 м ниже кратера, (а) какова будет их начальная скорость и (б) каково время их полета?

Дрю Бриз из команды New Orleans Saints может бросить футбольный мяч со скоростью 23,0 м/с (50 миль в час). Если он направит бросок под углом [latex] 10\text{°} [/latex] от горизонтали, на какое расстояние он пролетит, если его нужно поймать на той же высоте, на которой он был брошен?

Показать решение

Лунный вездеход, использовавшийся в последних миссиях NASA Apollo , достиг неофициальной наземной лунной скорости 5,0 м/с благодаря астронавту Юджину Сернану. Если бы марсоход двигался с такой скоростью по плоской лунной поверхности и наткнулся на небольшой выступ, который отбросил его от поверхности под углом [latex] 20\text{°}, [/latex], как долго он находился бы «в воздухе» на Луне?

Футбольные ворота высотой 2,44 метра.
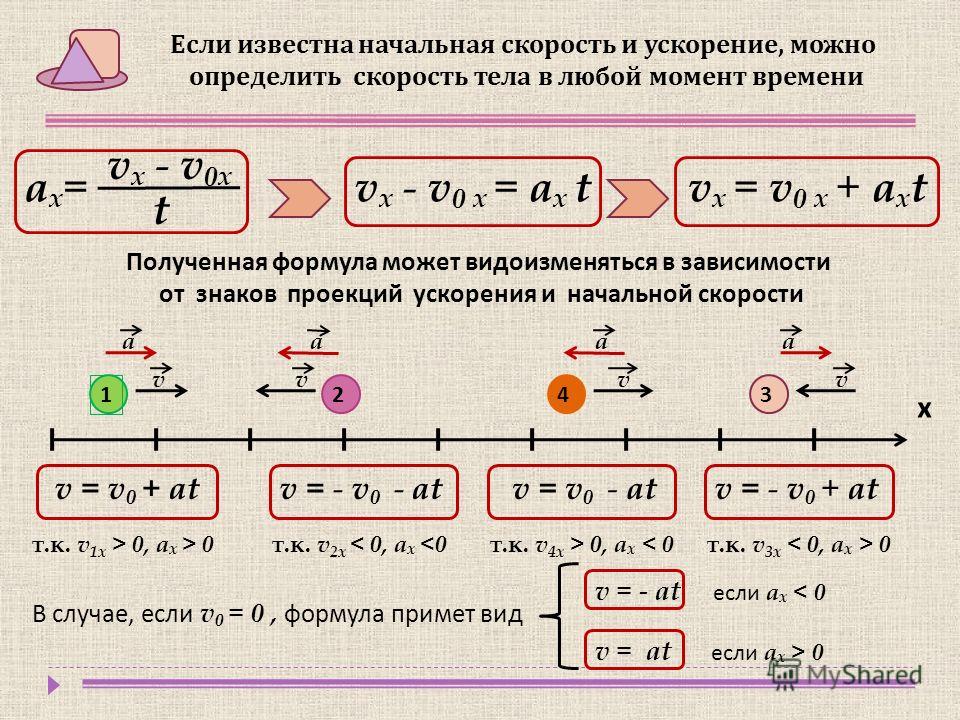