Как найти путь в физике?
Прочее › Чем отличается › Чем отличается путь от перемещения физика?
Пройдённым путём S называется длина линии, которую описывает тело при движении. При движении тела с постоянным ускорением а, путь тела S определяется формулой: S = V0 * t + a * t2 / 2, где V0 — начальная скорость движения тела, t — время движения тела.
- Как найти путь в физике формула?
- Как можно определить путь?
- Как измеряется путь в физике?
- Как найти путь в физике 7 класс формула?
- Что такое путь в физике?
- Как найти V?
- Как пишется путь в физике?
- Как найти время путь?
- Как найти путь через силу?
- Как найти L формула?
- Как найти путь в физике по графику?
- В чем измеряется путь?
- Чему равна V в физике?
- Что такое путь Физика 8 класс?
- Как найти путь в физике без скорости?
- Как определить длину пути?
- Что такое путь в физике 7 класс?
- Что означает буква L в физике?
- Что пройденный путь?
- Как найти V0 формула?
- Чему равна h в физике?
- Как рассчитать путь s при равномерном движении?
- Как найти h?
- Как найти путь зная только скорость?
Как найти путь в физике формула?
Если известны скорость и время движения, то можно найти расстояние.
Оно равно скорости, умноженной на время: s = v × t.
Как можно определить путь?
Чтобы определить путь, пройденный телом при равномерном движении, надо скорость тела умножить на время его движения: S=Vt Если тело движется неравномерно, то, зная его среднюю скорость движения и время, за которое происходит это движения, находят путь: S=Vсрt.
Как измеряется путь в физике?
Чем больше скорость, тем больший путь проходит тело за единицу времени. Если путь измеряется в метрах (м), а время движения в секундах (с), то скорость тела измеряется в (м/с). Метр в секунду (м/с) — единица скорости в международной системе единиц.
Как найти путь в физике 7 класс формула?
Чтобы определить путь, пройденный телом при равномерном движении, нужно скорость тела умножить на время его движения. Выразим время: t = S υ t = \frac{S}{\upsilon} t=υS. Чтобы рассчитать время при равномерном движении, нужно путь, пройденный телом, разделить на скорость его движения.
Что такое путь в физике?
Путь — скалярная физическая величина, равная длине траектории, описываемой телом за рассматриваемый промежуток времени.
Чаще всего обозначается как S, и в системе СИ измеряется в метрах. Траектория — непрерывная линия, вдоль которой движется материальная точка в заданной системе отсчета.
Как найти V?
Следствие. Объём прямоугольного параллелепипеда равен произведению площади основания на высоту. V = S (основания) ⋅ h.
Как пишется путь в физике?
Если необходимо решить математическую задачу, где даны расстояние (или путь), скорость и время, то расстояние (путь) обозначается буквой S (так же, как и в физике, например).
Как найти время путь?
Чтобы узнать расстояние, нужно скорость умножить на время. Чтобы найти время, нужно расстояние разделить на скорость.
Как найти путь через силу?
A = (F — k * m * g) / m. Найдем пройденный телом путь: S = a * t2 / 2 = (F — k * m * g) * t2 / (2 * m). Ответ: ускорение тела будет равно a = (F — k * m * g) / m, пройденный телом путь будет равен S = (F — k * m * g) * t2 / (2 * m).
Как найти L формула?
Длину той или иной окружности можно определить по следующей формуле: l = 2πr, где l — это длина самой окружности, а r — это её радиус.
2): 2.
Как определить длину пути?
Ответы1. Формула для вычисления расстояния: S = v * t. v — это скорость, t — время.
Что такое путь в физике 7 класс?
Путь — расстояние, пройденное телом вдоль траектории движения (единица измерения — [\(м\)]). Отрезок прямой, который соединяет начальную точку траектории тела с её конечной точкой, называют перемещением тела. Перемещение — минимальное расстояние, которое соединяет две выбранные точки траектории движения.
Что означает буква L в физике?
В физике — обозначение катушки индуктивности и величины, с этим связанной, а также длину или лагранжиан. В римской системе счисления означает 50. В технике, особенно в теплотехнике и термодинамике, а также в химии — обозначение удельной теплоты парообразования.
Что пройденный путь?
Пройденным путем называется длина траектории движения тела. Траектория движения это линия, которую описывает тело при движении. В зависимости от траектории движение может быть прямолинейным и криволинейным.
2)/2.
Чему равна h в физике?
H = 4,135 667 669… × 10−15 эВ·c. Это значение является составной частью определения Международной системы единиц. В ряде естественных систем единиц является единицей измерения действия.
Как рассчитать путь s при равномерном движении?
Пройдённым путём S называется длина линии, которую описывает тело при движении. При движении тела с постоянным ускорением а, путь тела S определяется формулой: S = V0 * t + a * t2 / 2, где V0 — начальная скорость движения тела, t — время движения тела.
Как найти h?
Чтобы определить высоту столба некоторой жидкости, необходимо воспользоваться следующей формулой: P = ro * g * h, отсюда находим, что: h = P / (ro * g) = P / (10 * ro). Ответ: высоту столба жидкости можно определить по формуле: h = P / (10 * ro).
Как найти путь зная только скорость?
Итак, чтобы найти расстояние, нужно скорость умножить на время.
Механика (Зубов В.Г.)
Механика (Зубов В.Г.)
ОглавлениеПРЕДИСЛОВИЕВВЕДЕНИЕ I. ОСНОВНЫЕ ПОНЯТИЯ КИНЕМАТИКИ § 1. Основные опыты и наблюдения. Что такое механическое движение? § 2. Относительность движений. Система отсчета § 3. Как определить положение тел друг относительно друга? Радиус-вектор § 4. Главное свойство радиус-вектора. Что такое вектор? § 6°. Как связан радиус-вектор с декартовыми координатами? § 7. Как определить конечный результат движения? Вектор перемещения § 8. Как связан вектор перемещения с приращением радиус-вектора? § 9°.  Определение вектора перемещения по координатам§ 10. Через какие точки проходило тело во время движения? Траектория § 11. Как связана траектория движения с векторами перемещения? § 12. Как определить положение тела на траектории? Длина пути § 14. Первые итоги. Примеры § 15. Как определить состояние движения в данной точке? Скорость § 16. Определение направления и модуля скорости § 17°. Определение скорости по изменению координат тела § 18. Две основные задачи кинематики § 19. Формула закона равномерного движения § 20. Порядок действий при решении задач кинематики § 21. Некоторые особенности практических транспортных задач § 22. Как количественно определить изменения скорости? Ускорение § 23. Изменение модуля скорости. Тангенциальное ускорение § 24. Изменение направления скорости. Нормальное ускорение § 25. Формула скорости равнопеременного движения § 27.  Различные случаи равнопеременных движений§ 28. Свободное падение тел. Закон Галилея § 29. Два примера свободного падения тел § 30. Принцип независимого сложения движений § 31°. Расчет криволинейного движения по координатам § 32. Правила перехода от одной системы отсчета к другой. Преобразования Галилея § 33. Поступательное и вращательное движения твердого тела § 34. Некоторые вопросы измерений. Системы единиц § 35°. Кинематика движения тел с большими скоростями § 36. Краткие сведения из истории II. ОСНОВНЫЕ ПОНЯТИЯ И ЗАКОНЫ ДИНАМИКИ § 38. Особенности действия окружающих тел § 39. Влияние собственных свойств тела на его ускорение § 40°. Влияние скорости движения тела на его ускорение § 41. Двусторонний характер действия тел § 42°. Взаимодействия тел и невозможность создания вечного двигателя § 43. Итоги основных опытов и наблюдений § 44.  Как количественно определить действия тел друг на друга? Сила§ 45. Измерение сил § 46. Сила — вектор. Принцип независимого действия сил § 47. Разложение сил на составляющие § 48. Связь между силой и ускорением § 50. Зависимость ускорения от массы тела § 51. Второй закон Ньютона § 52. Третий закон Ньютона § 53. Полная система законов динамики § 54. Две основные задачи динамики § 55. Порядок действий при решении задач на применение законов Ньютона § 56. Пример решения сложной задачи § 57. Краткие сведения из истории III. МЕХАНИЧЕСКИЕ СВОЙСТВА ТЕЛ. ИСПОЛЬЗОВАНИЕ ИХ В РЕШЕНИИ ПРАКТИЧЕСКИХ ЗАДАЧ § 58. Как ведут себя тела в свободном состоянии? Способность тел сохранять свою форму и объем § 59. Определение результата движения частей тела. Деформации § 60. Силы, возникающие при деформациях. Упругие и пластические деформации § 62. Упругие свойства твердых тел.  Закон Гука§ 63. Упругие пружины. Динамометры § 64. Упругие свойства жидкостей § 65. Упругие свойства газов. Закон Бойля — Мариотта § 66. Трение в жидкостях и газах § 67. Прыжок с парашютом § 68. Сухое трение § 69. Всемирное тяготение § 70. Пример применения закона всемирного тяготения. Первая космическая скорость § 71. Вес и невесомость § 72. Общий обзор механических свойств тел § 73. Принцип относительности механических явлений § 74°. Основные положения теории относительности § 75. Почему нужно искать новые формы законов Ньютона? § 76. Преобразование второго закона Ньютона § 77. Упругий удар шара о стенку § 78. Расчет силы давления струи воды на препятствие § 79. Гидромонитор § 80. Турбина § 81. Системы тел § 82. Новая форма третьего закона Ньютона. Закон сохранения количества движения § 83. Порядок действий при решении задач на применение закона сохранения количества движения § 84.  Реактивная сила тяги§ 85. Ракетные и реактивные двигатели § 87°. Уравнение движения тел с большими скоростями V. РАБОТА. ЭНЕРГИЯ. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ § 88. Еще один путь преобразования законов Ньютона § 89. Работа постоянной силы § 90. Работа переменной силы § 91. Кинетическая энергия тела § 92. Еще одна форма второго закона Ньютона § 93. Примеры применения разных форм второго закона Ньютона § 94. Работа силы тяжести § 95. Графический способ расчета работы. Работа упругой силы § 96°. Работа сил всемирного тяготения § 97. Работа силы трения § 98. Потенциальная энергия системы тел § 99°. Потенциальная энергия сил всемирного тяготения. Космические скорости § 101. Полная энергия системы тел. Закон сохранения энергии § 102. Значение закона сохранения энергии § 103. Примеры применения закона сохранения энергии § 104.  Мощность двигателей§ 105. Краткие сведения из истории VI. ВРАЩЕНИЕ ТЕЛ § 106. Угловое перемещение тела § 107. Угловая скорость тела § 108. Угловое ускорение тела § 109. Динамика вращения тел. Основные опыты и наблюдения § 110. Момент силы § 111°. Момент инерции тела § 112°. Уравнение моментов § 113°. Независимое сложение моментов сил § 115°. Кинетическая энергия вращающегося тела § 116. Сводка основных понятий и законов динамики вращения § 117. Общие условия равновесия тел § 118. Пример расчета простых механизмов ЗАКЛЮЧЕНИЕ |
Г. Механика. М.: Наука, 1978. – 352 с. (серия “Начала физики”)
Движение снаряда
Движение снарядаМы изучили кинематические уравнения для одномерный движение с постоянным ускорением в модуле 1.
Проблема обзора:Мяч брошен прямо вниз с начальной скоростью 8 м/с из высота 30 м. Через какой промежуток времени мяч ударится о землю?
Решение:
Для движения в трех измерениях с
постоянный
ускорение кинематические уравнения
Х-компонента ускорения изменяет только х-компоненту скорости, y-компонента ускорения изменяет только y-компоненту скорость и т. д.
Скорость как функция времени равна.
v x = v 0x + ∆v x = v 0x + a x ∆t,
v y = v 0y + a y ∆t,
в я = v 0z ∆t + a z ∆t,
или v = v 0 + и ∆t.
Примечание: если направления v 0 и разные, направление против отличается от направления v 0 .
При постоянном ускорении движения вдоль перпендикулярных осей
декартовой системы координат независимы и могут быть
анализируются отдельно.
Положение частицы в момент времени t определяется как
x = x 0 + v 0x ∆t + ½a x ∆t 2 ,
y = y 0 + v 0y ∆t + ½a г ∆t 2 ,
z = z 0 + v 0z ∆t + ½a z ∆t 2 ,
или р = r 0 + v 0 ∆t + ½ a ∆t 2 .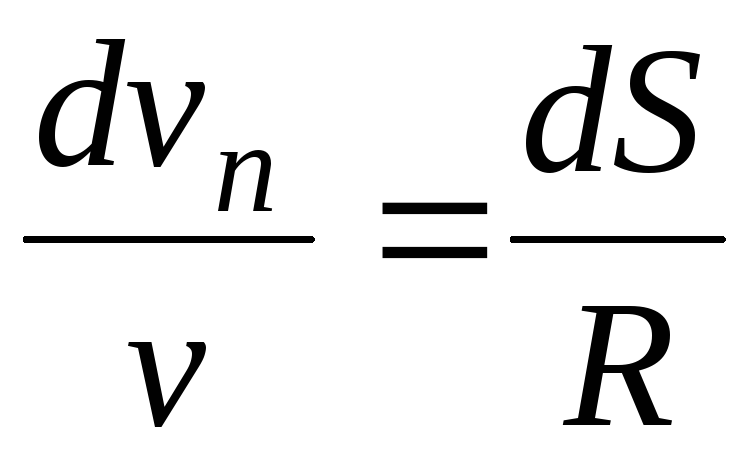
Примечание: Направления r 0 , v 0 , и и r могут быть разными. Если a постоянно, то x, y и z-координируются как функция времени можно найти самостоятельно.
Определим движение снаряда как движение частица через область трехмерного пространства, где она подвергается постоянное ускорение.
Например, объект, движущийся по воздуху вблизи поверхности земли, подвергается постоянному ускорению свободного падения g , направленному вниз. Если на объект не действуют никакие другие силы, т. е. если объект не имеет двигательной установки и сопротивлением воздуха пренебрегаем, то движение объекта – это движение снаряда. (Это причина движение с постоянным ускорением называется движением снаряда.)
Предположим, что мы хотим описать
движение такого объекта, начиная с момента времени t = 0. Сориентируем наш
система координат такая, что одна из осей, скажем, ось Y, указывает
вверх.
a x = a z = 0, a y = -g. Мы можем
вращать нашу систему координат вокруг оси y до тех пор, пока вектор скорости
объекта при t = 0 лежит в плоскости x-y, и мы можем выбрать
начало нашей системы координат должно быть в положении объекта в t
= 0,
При соответствующей ориентации координатных осей мы
can может рассматривать движение снаряда как движение в двух измерениях с
v x = v 0x , x = x 0 + v 0x t, v y = v 0y + a y t, y = y 0 + v 0y t
+ ½ на 2 .
Выбрав удобную ориентацию нашей системы координат, мы имеем упростил математику, связанную с решением задачи о движении снаряда.
Если y = -g, то
v x = v 0x , x = x 0 + v 0x t, v y = v 0y – gt, y = y 0 + v 0y t – ½gt 2 .
Пусть a y = -g. Если начальная скорость v 0 составляет угол θ 0 с осью x, затем
v 0x = v 0 cosθ 0 и v 0y = v 0 sinθ 0 .
v x = v 0 cosθ 0 =
постоянная, x = x 0 + v 0 cosθ 0 t,
v y = v 0 sinθ 0 – gt, y = y 0 + v 0 sinθ 0 t – ½gt 2 .
Мы можем решить x – x 0 = v 0 cosθ 0 t для t через x
– х 0 ,
t = (x – x 0 )/(v 0 cosθ 0 )
и подставить это выражение вместо
т в
y = y 0 + v 0 sinθ 0 t – ½gt 2 .
Получаем
y = y 0 + (x – x 0 )tan(θ 0 )
– g(x – x 0 ) 2 /(2v 0 2 cos 2 (θ 0 )),
уравнение пути или траектория объекта.
Это уравнение имеет вид y = y 0 + a(x – x 0 ) – b(x
– х 0 ) 2 ,
что является уравнением параболы. Если х 0 = у 0 = 0 проходит парабола
через происхождение.
Траектория движения снаряда – парабола.
Пример:
Предположим, что снаряд запущен с x 0 = y 0 = 0, v 0x = 4 м/с, v 0y = 3 м/с.
У нас есть
tanθ 0 = v 0y /v 0x = 3/4, θ 0 =
30,87 о , v 0 2 = v 0x 2 + v 0г 2 ,
v 0 = 5 м/с.
Снаряд движется по параболе до тех пор, пока не
воздействует на землю. Его координаты как функция времени:
x = (4 м/с)t, y = (3 м/с)t – (4,9м/с 2 )t 2 .
Компоненты его скорости v x = 4 м/с, v y = (3 м/с) – (9,8 м/с 2 )t 2 .
| т | х(т) | г(т) | в х (т) | в г (т) |
|---|---|---|---|---|
| 0 | 0 | 0 | 4 | 3 |
| 0,05 | 0,2 | 0,13775 | 4 | 2,51 |
| 0,1 | 0,4 | 0,251 | 4 | 2,02 |
| 0,15 | 0,6 | 0,33975 | 4 | 1,53 |
| 0,2 | 0,8 | 0,404 | 4 | 1,04 |
| 0,25 | 1 | 0,44375 | 4 | 0,55 |
| 0,3 | 1,2 | 0,459 | 4 | 0,06 |
| 0,35 | 1,4 | 0,44975 | 4 | -0,43 |
| 0,4 | 1,6 | 0,416 | 4 | -0,92 |
| 0,45 | 1,8 | 0,35775 | 4 | -1,41 |
| 0,5 | 2 | 0,275 | 4 | -1,9 |
| 0,55 | 2,2 | 0,16775 | 4 | -2,39 |
| 0,6 | 2,4 | 0,036 | 4 | -2,88 |
Как видно из приведенных ниже графиков, попадание снаряда
землю примерно через 0,6 секунды.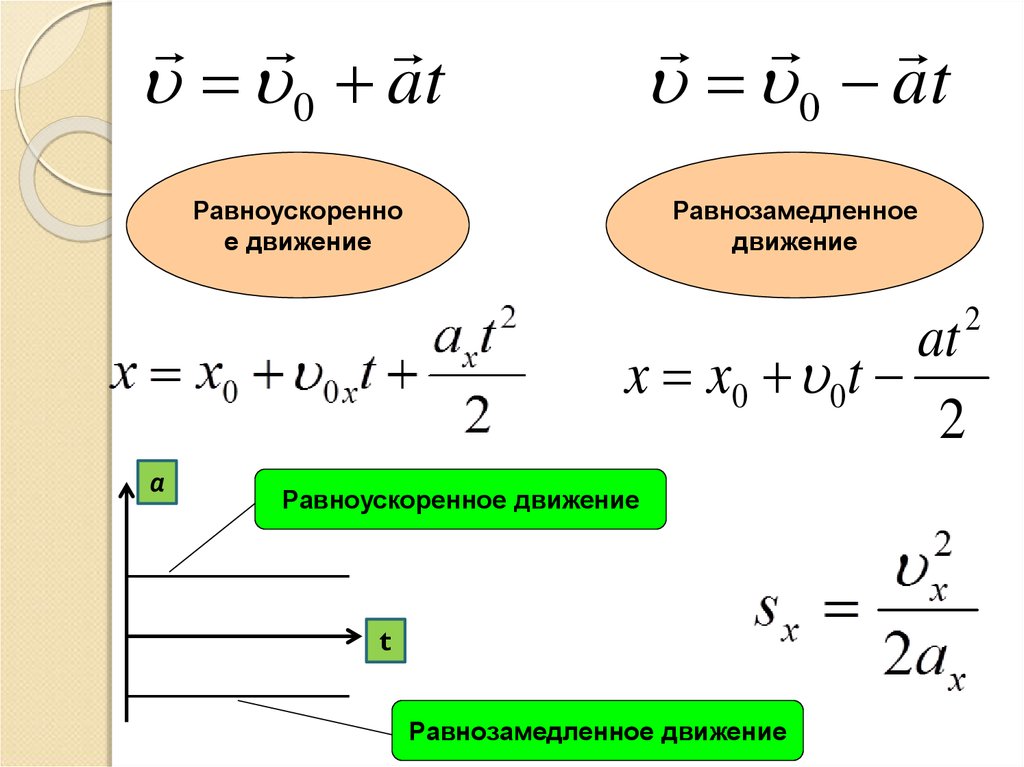
Он достигает своего максимума
высота примерно через 0,3 секунды. Его диапазон составляет примерно 2,4
метров. Примерно за 0,3 секунды он покрыл половину своего
диапазон.
Траектория движения снаряда симметрична относительно точки
максимальная высота. Снаряд накрывает
такое же горизонтальное расстояние, достигающее максимальной высоты, как и при падении
с максимальной высоты обратно на землю. Он принимает снаряд
достигает максимальной высоты столько же времени, сколько требуется, чтобы упасть с
максимальная высота до земли. Когда снаряд достигает цели
максимальной высоты примерно через 0,3 с
вертикальная составляющая его скорости равна нулю.
Мы можем найти время, когда снаряд достигает максимальной высоты, установив v y = v y0 – gt = 0 и решение для t. Находим
t max_height = v y0 /g = v 0 sinθ 0 /g.
Теперь мы можем найти диапазон R, подставив t = 2t max_height в
уравнение для x(t).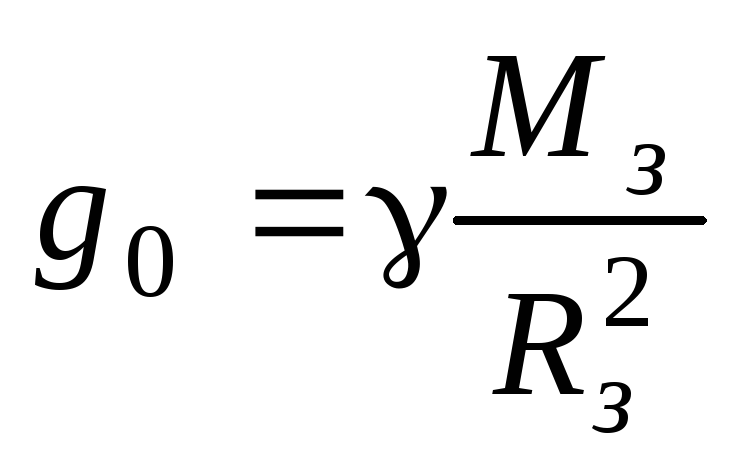
R = v 0 cosθ 0 2t max_height = (2v 0 2 cosθ 0 sinθ 0 )/g =
(v 0 2 sin2θ 0 )/г.
Аналогично находим
максимальной высоты h, подставив t max_height в
уравнение для y(t).
h max = v 0 sinθ 0 t max_height – ½gt 2 макс_высота = (v 0 2 грех 2 θ 0 )/2г.
Посмотрите на выражение для диапазона, R = (v 0 2 sin2θ 0 )/g. Для данного v 0 ,
R как функция угла запуска θ 0 имеет максимальное значение
когда sin2θ 0 имеет максимальное значение 1. Это происходит, когда 2θ 0 = 90 o или θ 0 = 45 o .
R max = v 0 2 /g — максимальный диапазон снаряда, запущенного со скоростью v 0 .
Внешняя ссылка: Максимальный диапазон
Проблема:
Одна из стратегий игры в снежки — бросить снежок под большим углом над
уровень земли. Пока ваш противник наблюдает за первым, вы бросаете второй
снежок под малым углом, приуроченный к прибытию раньше или одновременно с первым
один. Предположим, что оба снежка брошены со скоростью 25 м/с. Первый брошен под углом 70 или в отношении
горизонтальный.
а) Под каким углом следует бросить второй снежок, чтобы попасть в тот же
точка как первая?
(b) Через сколько секунд следует бросить второй снежок после первого
прийти одновременно?
Решение:
Проблема:
Астронавт на чужой планете обнаруживает, что может прыгать максимум горизонтальное расстояние 15 м, если ее начальная скорость 3 м/с. Что ускорение свободного падения на планете?
Решение:
- Рассуждение:
У нас есть движение с постоянным ускорением в двух измерениях, или снаряд движение.
Дальность полета снаряда над ровной поверхностью R = (v 0 2 sin2θ 0 )/g.
Чтобы иметь максимальную дальность для заданной начальной скорости, ее угол запуска должен быть 0 = 45 или . - Детали расчета:
Дальность полета космонавта R = (v 0 2 sin2θ 0 )/г’ = v 0 2 sin90 o /g’ = v 0 2 /g’.
Имеем g’ = v 0 2 /R = 0,6 м/с 2 .
Проблема:
Сова несет мышь к птенцам в своем гнезде. Его
положение при t = 0 находится в 4,0 м к западу (x 0 = -4,0 м) и 12,0 м над уровнем моря.
центр гнезда диаметром 30,0 см (y 0 = 12,0 м). Сова
летит на восток со скоростью 3,5 м/с под углом 30 o ниже горизонтали, т.е. v x0 = (3,5 м/с)cos(30 o ), v y0 = -(3,5 м/с)sin(30 o ), когда мышь случайно падает.
Достаточно ли повезло сове, что мышь попала в гнездо?
Рассчитайте горизонтальное положение мыши, когда она упала на 12,0 м.
Решение:
- Рассуждение:
У нас есть движение с постоянным ускорением в двух измерениях, или снаряд движение.
Дано: x 0 , y 0 , v x0 = v 0 cosθ 0 , v y0 = v 0 sinθ 0 , θ 0 = -30 o , а у = -г.
Использовать v x = v 0 cosθ 0 = постоянная, x = x 0 + v 0 cosθ 0 t, v y = v 0 sinθ 0 – gt, у = у 0 + v 0 sinθ 0 т – ½ гт 2 .
Решить y – y 0 = v 0 sinθ 0 t – ½gt 2 для t, чтобы найти время, за которое мышь упадет с высоты 12 м.
За это время горизонтальное положение мыши изменится на x = x 0 + v 0 cosθ 0 t. - Детали расчета:
(-12 м) = (-3,5 м/с)*0,5*t – 0,5*(9,8 м/с 2 )*t 2 .
t 2 + (0,357 с)*t – 2,45 с 2 = 0,
t = [-0,178 + (0,031 + 2,45) 1/2 ] с = 1,4 с.
За это время горизонтальное положение мыши изменится на x = x 0 + v 0 cosθ 0 t,
x = -4 м * (3,5 м/с) * 0,866 * (1,4 с) = 0,23 м = 23 см.
Центр гнезда находится в точке x = 0, а гнездо имеет радиус 15 см. мышь не попадает в гнездо.
Одновременное движение
Некоторые задачи связаны с движением двух частиц. Часто эти проблемы требуют, чтобы две частицы встретились в одном и том же месте в одно и то же время. Ан часто упоминаемая проблема – это проблема обезьяны.
Обезьяна висит на ветке дерева на определенной высоте h над уровнем моря.
земля. Работник зоопарка стоит на расстоянии d от дерева с бананом в руках.
его рука. Смотритель зоопарка знает, что обезьяна всегда отпускает ветку.
так же, как банан брошен к нему. В каком направлении должен смотритель зоопарка
бросить банан, чтобы обезьяна могла его поймать?
Анализ задачи:
Положение снаряда как функция времени определяется как r = v 0 т
+ ½ г т 2 .
Мы можем рассматривать движение снаряда как суперпозицию двух движений, движение с
постоянная скорость v 0 в начальном направлении и движение вниз с
постоянное ускорение, подобное движению свободно падающей частицы.
Если снаряд направлен
по цели и выстрелил при t = 0, затем движение с постоянной скоростью v 0 приведет снаряд в начальное положение цели через некоторое время t.
В
интервал времени между 0 и t движение вниз с постоянным ускорением несет
снаряд вниз на величину ½gt 2 . Наложение двух движений
приведет снаряд в момент времени t в положение свободно падающей цели в момент времени
t, независимо от величины v 0 .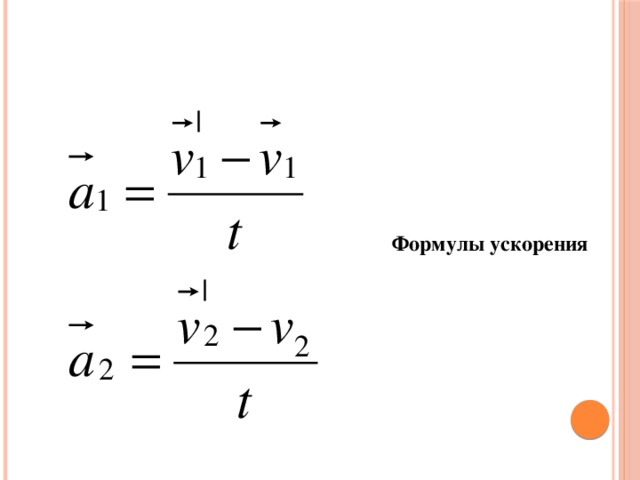
В промежутке времени между
0 и t свободно падающая цель перемещается вниз на величину ½gt 2 .
Демонстрации:
Баллистическая тележка
(Ютуб)
Мяч и тележка имеют одинаковую константу v x . Мяч и
горизонтальные движения тележки одинаковы. Вертикальное движение мяча равно
не зависит от его горизонтального движения и не влияет на его горизонтальное
движение.
Стреляй в цель
(Ютуб)
Без гравитации стрела попала бы в исходное положение цели.
Под действием силы тяжести стрела и цель ускоряются вниз с одинаковой скоростью. (Ютуб)
Внешняя ссылка: Движение снаряда
Для получения дополнительной информации о движении снаряда пожалуйста, изучите этот материал из “Кабинета физики”.
- Что такое снаряд?
- Характеристики траектории снаряда
- Описание снарядов с помощью чисел
- Горизонтальная и вертикальная составляющие скорости
- Горизонтальная и вертикальная составляющие смещения
- Начальные компоненты скорости
- Горизонтально запускаемые снаряды — Решение проблем
- Негоризонтально запущенные снаряды — Решение проблем
Линейное движение
Переход к погоне
Обсуждение
Эти уравнения движения
действительны только тогда, когда ускорение постоянно и движение ограничено прямой линией.
В реальном мире это нереальное понятие. Ни один объект никогда не двигался по прямой линии с постоянным ускорением где-либо во Вселенной в любое время. Однако было бы неправильно полностью игнорировать этот раздел или считать его бесполезным.
Во многих случаях полезно
предположить, что объект двигался или будет двигаться по пути,
по существу прямой и с почти постоянным ускорением.
То есть любое отклонение от идеального движения можно по существу игнорировать.
Движение по криволинейной траектории также может быть эффективно одномерным.
если есть только одна степень свободы для вовлеченных объектов. Например, дорога может извиваться и поворачивать и исследовать всевозможные
направлений, но движущиеся по нему автомобили имеют только одну степень
свобода: свобода движения в одном направлении или в противоположном
направление. (Вы не можете ехать по дороге по диагонали и надеяться остаться
на нем очень долго.) В этом отношении он мало чем отличается от ограниченного движения
к прямой линии.
Аппроксимация реальных ситуаций с помощью моделей, основанных на
в идеальных ситуациях обманом не считается. Так обстоят дела
сделать по физике. Это такая полезная техника, которую мы будем использовать
это снова и снова.
Наша цель в этом разделе — вывести уравнения, которые можно использовать для
описать движение объекта с точки зрения его трех кинематических
переменные: скорость, перемещение и время. Есть три способа
чтобы соединить их в пары: скорость-время, перемещение-время и скорость-перемещение.
В этом порядке их также часто называют первым, вторым и
третье уравнение движения, но нет веских причин учить
эти имена. Поскольку мы имеем дело с прямолинейным движением,
символ x будет использоваться для смещения. Направление движения будет указано знаком (положительное
величины указывают в направлении +x, в то время как отрицательные величины указывают
в направлении -х). Определить, какое направление является положительным, а
что отрицательное совершенно произвольно.
Законы физики изотропны; то есть они не зависят от ориентации системы координат.
Пока вы последовательны, это не имеет значения. Некоторые проблемы
легче понять и решить, однако, когда выбрано одно направление
положительный по сравнению с другим.
Скорость-Время
Связь между скоростью и временем проста во время постоянного ускоренное, прямолинейное движение. Постоянное ускорение подразумевает равномерная скорость изменения скорости. Чем дольше ускорение, тем больше изменение скорости. Если через некоторое время скорость увеличивается на определенную сумму, после удвоения этого времени она должна увеличиться на вдвое больше этой суммы. Изменение скорости прямо пропорционально времени , когда ускорение постоянно. Если объект уже запущен с определенным скорость, то его новая скорость будет равна старой скорости плюс эта изменение. Вы должны уметь видеть уравнение мысленным взором уже.
Это простейшее из трех уравнений для формального вывода.
Начать с
определение ускорения, раскройте член Δ v и найдите v как функцию t .
Поскольку ускорение также является первой производной скорости по ко времени это уравнение также может быть получено с помощью исчисления. Просто наоборот действие определения. Вместо дифференцирования скорости чтобы найти ускорение, интегрируйте ускорение, чтобы найти скорость. С ускорение считается постоянным, это довольно просто.
Символ v 0 (v ноль) называется начальной скоростью. Во многих текстах ему также присваивается символ u . Начальная скорость – это скорость, с которой движущийся объект
имеет, когда это впервые становится важным в проблеме. Например, метеор
был замечен глубоко в космосе, и проблема заключалась в том, чтобы определить его траекторию,
тогда начальная скорость будет равна скорости в момент
наблюдаемый. Но если бы задача состояла в том, чтобы определить его скорость при ударе,
тогда его начальная скорость, скорее всего, была бы скоростью, которую он имел
при входе в атмосферу Земли.
В этом случае ответ
на “Какова начальная скорость?” это “это зависит”. Оказывается, это ответ на многие вопросы.
Символ v означает скорость через некоторое время Δ t после того, как начальная скорость часто называется конечной скоростью. То, что принимается за конечную скорость, зависит от задачи, которую вы решаете. Нет жесткого и быстрого правила.
Последняя часть этого уравнения a Δ t представляет собой изменение скорости от начального значения. Напомним, что a — это скорость изменения скорости, а Δ t — это интервал времени с момента, когда объект имел начальную скорость v 0 . Ставка, умноженная на время, равна изменению. Таким образом, если бы объект ускорялся
в 10 мс -2 через 5 с он будет двигаться на 50 мс -1 быстрее, чем изначально. Если бы он стартовал со скоростью 15 мс -1 , его скорость после 5 с ускорения составила бы 65 мс -1 .
Displacement-Time
Смещение движущегося объекта прямо пропорционально скорости и время. Ускорение усугубляет эту простую ситуацию. Теперь скорость также прямо пропорциональна времени. Попробуйте сказать это в слова и звучит смешно. «Перемещение прямо пропорционально времени и прямо пропорционально скорость, которая прямо пропорциональна времени». время. Автомобиль, ускоряющийся в течение двух секунд, проедет в четыре раза больше расстояние автомобиля, ускоряющегося всего за одну секунду (2 2 = 4). Автомобиль, ускоряющийся в течение трех секунд, преодолеет в девять раз большее расстояние. (3 2 = 9).
Если бы это было так просто. Этот пример работает только тогда, когда начальная скорость
равен нулю. Изменение смещения на пропорционально квадрату на , когда ускорение постоянно, а начальная скорость равна нулю. Настоящий генерал
утверждение должно было бы учитывать любую начальную скорость и
как менялась скорость.
Это приводит к ужасно беспорядочной пропорциональности
утверждение. Изменение в 9Смещение 0927 прямо пропорционально , умноженному на , и пропорционально квадрату , умноженному на , когда ускорение постоянно. Функция, которая является одновременно линейной и квадратичной
называется квадратичным, что позволяет нам значительно сжать предыдущее утверждение. Изменение
в перемещение является квадратичной функцией времени при постоянном ускорении
Заявления о пропорциональности полезны, но не так кратки, как уравнения. Мы до сих пор не знаю, каковы константы пропорциональности для этого проблема. Единственный способ ответить на этот вопрос — с помощью алгебры.
Начните с определения скорости, расширьте Δ x и решите его для перемещения.
[a]
Чтобы продолжить, нам нужно прибегнуть к небольшому трюку, впервые опубликованному в Четырнадцатом
Century в Мертон-колледже в Оксфорде (иногда называемом Мертон-колледжем).
Правило). При постоянном ускорении скорость будет изменяться равномерно от
его начальное значение к его конечному значению, а среднее значение будет лежать на полпути
между крайностями. Таким образом, средняя скорость — это просто арифметическое
среднее значение начальной и конечной скоростей. Средняя скорость – это средняя
конечной и начальной скоростей при постоянном ускорении.
Подставляем первое уравнение движения [1] в это уравнение (4) и упрощаем с целью устранения против .
[b]
Наконец, подставьте [b] в [a] и найдите x как функцию t.
[2]
Поскольку скорость также является первой производной смещения по ко времени это уравнение также может быть получено с помощью исчисления. По факту, это намного проще, чем использовать алгебру. Просто отмените действие определение. Вместо того, чтобы дифференцировать перемещение, чтобы найти скорость, интегрируйте скорость [1], чтобы найти перемещение.
[a]
Символ x 0 (ex ноль) – это начальное смещение.
Много раз это значение равно нулю, и если это не так, мы можем сделать это так. если ты
спросите меня: “Когда мы должны это сделать?” Я бы сказал: «Это зависит от проблемы» и предоставил бы вам решать. Нет правила, которое вы можете запомнить, это
этот случай. Вы должны понять, что говорит уравнение, а затем
научиться применять его в конкретной ситуации. Точно так же x часто называют конечным смещением, но это не делает его «последним смещением», а скорее смещением в конце временного интервала, в течение которого
ускорение было постоянным.
Следует также отметить сходство между уравнениями [2] и [a]. Когда ускорение равно нулю, наше второе уравнение движения принимает вид к переставленному уравнению постоянной скорости. Как и предполагалось, смещение частично прямо пропорциональна времени, а частично прямо пропорциональна ко времени в квадрате.
[2]
[a]
Хотя символы скоростей в двух уравнениях могут выглядеть по-разному, они
действительно представляют одно и то же количество.
Если нет ускорения,
то скорость постоянна, значит, начальная скорость
такая же, как и конечная скорость, такая же, как и средняя скорость.
Термин ускорения в конце является корректировкой постоянной
уравнение скорости для учета того факта, что скорость
меняется. Положительное ускорение увеличило бы перемещение
и отрицательное ускорение уменьшит его. Это именно то, что
можно было бы ожидать. Если бы скорость объекта увеличивалась, он
двигаться дальше, чем если бы он оставался с постоянной скоростью. Так же,
если бы скорость объекта уменьшалась, его перемещение было бы меньше
чем если бы его скорость была постоянной. Приятно видеть, что уравнения
вести себя реалистично. Иначе вся эта математика была бы
пустая трата времени.
Скорость-Перемещение
Мы только что видели, что скорость прямо пропорциональна времени и перемещению
пропорциональна квадрату времени. Немного подумав,
новое заявление о пропорциональности должно быть очевидным. Изменение смещения пропорционально изменению квадрата скорости , когда ускорение постоянно.
Это утверждение особенно важно
для безопасности вождения. Когда вы удваиваете скорость автомобиля, требуется
в четыре раза большее расстояние, чтобы остановить его. Утройте скорость, и вам понадобится
в девять раз больше расстояния. Как и предыдущие отношения, это также
зависит от начальной скорости. К сожалению, определение эффекта
использовать только рассуждения – настоящая рутинная работа. Вместо этого займитесь алгеброй.
Последние два уравнения описывают одну кинематическую переменную как функцию
времени. Было бы неплохо, если бы у нас также было уравнение, которое было бы независимым
времени. То есть мы хотим ответить на вопрос: «Какова связь между скоростью и перемещением?» Способ сделать это должен быть очевиден. Мы должны объединить
наши первые два уравнения движения вместе таким образом, что
исключить время как переменную. Самый простой способ сделать это – решить
одно уравнение для времени, а затем подставить его в другое.
второе уравнение движения является квадратным и решает его относительно времени
внесло бы много гадостей в алгебру.