Формула pv в физике: Ответы: PV=vRT формула чего?…

Уравнение состояния идеального газа ❤️

1. Закон Авогадро

Из уравнения Клапейрона (см. предыдущий параграф) следует, что в процессах, происходящих с данной массой газа, произведение давления газа p на его объем V, деленное на абсолютную температуру T газа, постоянно: (pV)/T = const.

Однако если масса газа в процессе изменилось, то значение выражения (pV)/T тоже изменится! Это очень легко проверить.

Поставим опыт Надуйте щеки (рис. 40.1). При этом одновременно увеличились и давление воздуха во рту, и его объем, а температура этого воздуха осталась практически неизменной (равной температуре

тела).

Следовательно, значение выражения (pV)/T увеличилось. Причина, конечно, в том, что при надувании щек увеличивается масса воздуха во рту.

От чего же зависит значение отношения (pV)/T? Может, только от массы газа?

Оказывается, что это не так: опыт показывает, что если для различных газов сделать одинаковым значение отношения (pV)/T, то массы газов могут сильно различаться. На рисунке 40.2 схематически изображены воздушные шарики одинакового объема, наполненные водородом, гелием, кислородом и радоном при одинаковых температуре и давлении. (Из дальнейшего вы догадаетесь,

почему масса водорода взята равной 2 г.)

Ответ на вопрос, от чего зависит значение выражения (pV)/T, оказался на удивление простым. Его нашел в начале 19-го века итальянский ученый Амедео Авогадро.

Исследуя химические реакции между газами, он открыл закон, который называют сегодня законом Авогадро:

В равных объемах различных газов при одинаковых температурах и давлениях содержится одинаковое число молекул.

Отсюда следует, что значение выражения (pV)/T для данной массы газа пропорционально только числу молекул:

(pV)/T = kN,

Где k — коэффициент пропорциональности, одинаковый для всех газов. Его назвали настоянной Больцмана в честь австрийского физика Людвига Больцмана.

Измерения показали, что

K = 1,38 * 10-23 Дж/К.

Из закона Авогадро следует, что главной характеристикой газа является число молекул.

2. Единица количества вещества

Число молекул в образце вещества характеризуют физической величиной, которую называют количеством вещества и обозначают греческой буквой ν (произносится «ню»). (Это исторически сложившееся название может ввести в заблуждение, потому что его легко спутать с массой образца. Количество вещества надо понимать именно как характеристику числа молекул!)

Единицу количества вещества называют моль.

Один моль — это такое количество вещества, которое содержит столько же молекул, сколько атомов в 12 г углерода.

? 1. Во сколько раз число молекул в шести молях водорода больше, чем в двух молях кислорода?

? 2. Сколько молей водорода и кислорода нужно для того, чтобы в результате реакции между ними образовалось 2 моль воды? Подсказка. Вспомните химическую формулу воды.

Скоро мы поймем, почему ученые выбрали «произвольное» на первый взгляд определение моля.

Атомная единица массы

Массы атомов и молекул можно выражать в граммах: например, масса самого легкого атома (водорода) равна 1,67 * 10-24 г.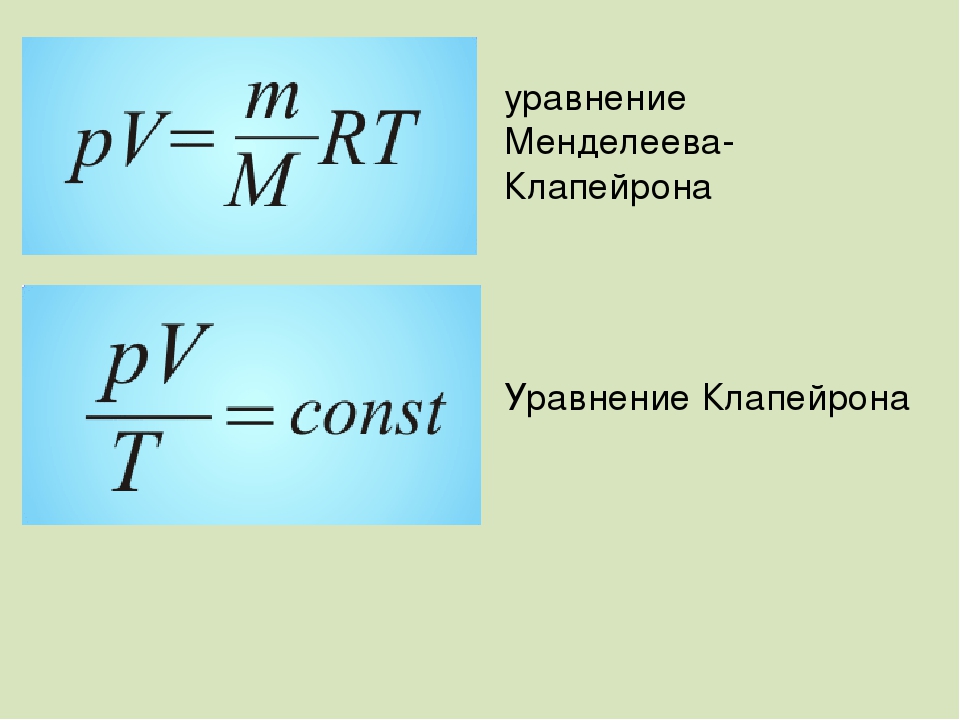 Но это неудобно: получаются громоздкие числа.

В качестве атомной единицы массы (сокращенно а. е. м.) взяли величину, близкую к массе атома водорода, а именно 1/12 массы атома углерода:

Такой выбор атомной единицы массы был обусловлен соображениями удобства при расчетах: во-первых, углерод входит в очень большое число химических соединений, во-вторых, при таком выборе атомной единицы массы значения масс многих атомов оказываются близкими к целым числам.

Сколько молекул а одном моле?

По определению в одном моле любого вещества содержится столько же молекул, сколько атомов в 12 г углерода. Значит, чтобы найти число молекул в одном моле, надо разделить 12 г, то есть массу одного моля углерода, на массу одного атома углерода, равную 12 а. е. м. В результате получим: Число молекул в одном моле называют постоянной Авогадро (обозначают NA) и записывают в виде

NA = 6 * 1023 моль-1. (2)

Сколько молекул в образце вещества, содержащем ν молей? В каждом моле NA молекул.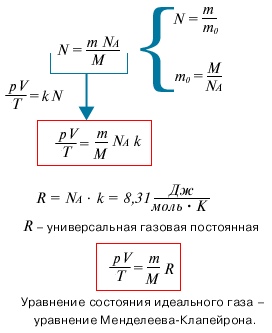 Следовательно, число N молекул в образце, содержащем ν молей, выражается формулой

N = νNA. (3)

? 3. Сколько молекул содержится: а) в 2 моль воды? б) в 5 моль кислорода? в) в 0,33 моль углекислого газа?

Есть ли в условии лишние данные?

? 4. Сколько молей в образце вещества, число молекул в котором равно: а) 6 * 1024; б) 3 * 1022; в) З, З * 1022; г) 6 * 1020?

Относительная атомная и молекулярная масса

Массу атома, выраженную в атомных единицах массы, называют относительной атомной массой.

Относительные массы всех атомов измерены. Вы можете найти их в Периодической системе химических элементов (таблице Менделеева, стр. 238-239).

Приведенное в ней значение часто округляют до целого числа.

Например, относительная атомная масса водорода равна 1, гелия — 4, а кислорода — 16.

Аналогично относительной атомной массе определяют и относительную молекулярную массу: она равна массе молекулы, выраженной в атомных единицах массы.

Чтобы найти относительную молекулярную массу молекулы данного вещества, надо знать: — химическую формулу этого вещества, то есть из каких атомов состоит молекула вещества, — относительные атомные массы этих атомов.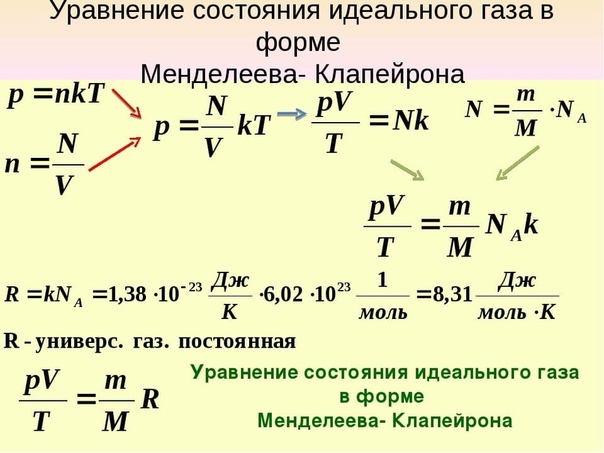

Например, относительная молекулярная масса воды равна 18, потому что молекула воды состоит из одного атома кислорода и двух атомов водорода.

? 5. Чему равна относительная молекулярная масса: а) водорода? б) гелия? в) кислорода?

г) углекислого газа?

3. Молярная масса

Массу одного моля вещества называют малярной массой и обозначают M.

Найдем молярную массу воды. Для этого массу m0 молекулы воды (18 а. е. м.) умножим на число молекул в одном моле, то есть на постоянную Авогадро NA. Согласно формуле (1) значение постоянной Авогадро равно отношению 1 г к 1 а. е. м., поэтому для молярной массы воды получаем:

Следовательно, полстакана воды (примерно 100 г) — это около 5,5 моль воды (рис. 40.3).

Обратите внимание: масса одного моля, выраженная в граммах, численно равна относительной молекулярной массе.

Это справедливо как для воды, так и для любого вещества, потому что для него можно провести точно такой же расчет молярной массы.

Равенство численного значения массы одного моля вещества (в граммах) и относительной молекулярной массы этого вещества не случайно: оно обусловлено тем, что в одном моле столько молекул, сколько атомных единиц массы в одном грамме. Это оказалось очень удобным для расчетов при проведении опытов, потому что массу образцов веществ измеряют часто в граммах.

В СИ молярную массу измеряют в кг/моль. Переводя граммы в килограммы, получаем для молярной массы воды:

Mh3O = 18 * 10-3 кг * моль-1.

? 6. Чему равна молярная масса: а) водорода? б) кислорода? в) углекислого газа?

Воздух представляет собой смесь различных газов, главным образом — азота и кислорода. При решении задач воздух часто считают газом с молярной массой

Mвозд = 29 * 10-3 кг * моль-1.

? 7. Объясните, почему масса образца вещества m, его молярная масса M и число молей ν в данном образце связаны соотношением

Ν = m/M. (4)

? 8. Сколько молей: а) в одном литре воды? б) в 1 кг поваренной соли? в) в воздухе, занимающем объем классной комнаты шириной 5 м, длиной 10 м и высотой 4 м? Плотность воздуха при комнатной температуре и атмосферном давлении равна 1,2 кг/м3.

? 9. Объясните, почему массу m0 молекулы вещества можно выразить через его молярную массу M формулой

M0 = M/NA. (5)

? 10. Чему равна масса одной молекулы воды?

? 11. Объясните, почему число N молекул в образце вещества массой m можно найти с помощью соотношений

N = νNA = (m/M)NA.

? 12.Оцените число молекул в капельке воды радиусом 1 мм. Сравните найденное число молекул с числом звезд в галактике, содержащей сто миллиардов звезд (рис. 40.4).

? 13. Почему изображенные на рисунке 40.2 шарики имеют равные объемы при одинаковых температурах и давлениях?

4. Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона)

Вернемся теперь к соотношению (pV)/T = kN.

? 14. Объясните, почему справедлива формула

(pV)/T = (m/M)kNA. (6)

Произведение постоянной Больцмана k на постоянную Авогадро NA называют универсальной газовой постоянной и обозначают R:

R = kNA = 8,31 Дж/(моль * К).

Используя универсальную газовую постоянную, уравнение (6) можно переписать в виде

PV = (m/M)RT. (7)

Это соотношение называют уравнением состояния идеального газа.

Дело в том, что модель идеального газа (которую мы рассмотрим в следующем параграфе) хорошо описывает уже известные нам свойства всех достаточно разреженных газов, например окружающего нас воздуха.

Уравнение идеального газа в виде формулы (7) предложил русский ученый Дмитрий Иванович Менделеев, поэтому его называют также уравнением Менделеева-Клапейрона.

Какие же задачи можно решать с помощью уравнения состояния идеального газа?

Плотность газа. Напомним, что плотность ρ = m/V.

? 15. Объясните, почему уравнение состояния идеального газа можно записать в виде

P = (ρ/M)RT.

Во многих задачах используют понятие нормальных условий для газа. По определению такими условиями называют давление 105 Па и температуру 0 ºС = 273 К.

? 16. Чему равна плотность воздуха: а) при нормальных условиях? б) при давлении 105 Па и комнатной температуре (20 ºС)?

Концентрация молекул газа. Концентрацией молекул и называют число молекул в единице объема. Ее можно выразить через число молекул N в данной массе газа и объем газа V:

N = N/V.

Концентрация молекул измеряется в 1/м3. Зная концентрацию молекул и объем газа, можно найти число молекул в нем.

? 17. Объясните, почему уравнение состояния идеального газ» можно записать в виде

P = nkT.

? 18. Рассмотрим газ при нормальных условиях. а) Чему равна при этом концентрация молекул? б) Различаются ли концентрации молекул различных газов при нормальных условиях? Обоснуйте свой ответ.

в) Сколько молекул воздуха вы вдыхаете при глубоком вдохе при 0 ºС, если объем легких увеличивается при этом на 2 л? Давление в легких считайте равным атмосферному.

Изменение массы газа. Из уравнения состояния идеального газа следует, что для одного и того же газа значение выражения (pV)/T пропорционально массе газа.

? 19. Гелий в баллоне с неплотно закрытым краном нагрели от 0 ºС до 20 ºС. При этом давление газа увеличилось от 2,2 * 105 Па до 2,3 * 105 Па.

Объем баллона 100 л. а) Во сколько раз увеличилась абсолютная температура газа? б) Во сколько раз увеличилось давление газа? в) Осталось ли неизменным значение выражения (pV)/T? г) На сколько уменьшилось число молей газа?

д) Насколько уменьшилась масса газа?

Изменение числа молекул вследствие изменения состава молекулы. Значение выражения (pV)/T пропорционально числу молекул, поэтому оно изменяется, если масса газа остается неизменной, но изменяется число молекул.

? 20. При нагревании водорода от 300 К до 1350 К все молекулы распались на атомы. Начальное давление равно атмосферному. Объем сосуда не изменился. а) Во сколько раз увеличилась абсолютная температура газа?

б) Во сколько раз увеличилось число молекул газа? в) Каким стало давление газа?

Дополнительные вопросы и задания

21. Сколько молей вещества: а) в ванне воды (200 л)? б) в баллоне, содержащем 100 г кислорода? в) в кубическом кристалле поваренной соли с длиной ребра 3 см?

Плотность поваренной соли 2,2 * 102 кг/м3.

22. Сколько молекул: а) в литре воды? б) в баллоне, содержащем 100 г углекислого газа (CO2)? в) в чайной ложке поваренной соли (6 г)?

23. Чему равна масса: а) 6 * 1023 молекул водорода? б) 3 * 1024 молекул воды? в) 4,2 * 1022 атомов кислорода?

24. В 1 г некоторого двухатомного газа содержится 2,14 * 1022 молекул. а) Чему равна молярная масса газа? б) Какой это газ?

25. Какой высоты слой воды покрыл бы земной шар, если бы на него вылили столько же чайных ложек воды (по 5 мл), сколько молекул воды содержится в одной чайной ложке? Площадь поверхности земного шара примите равной 500 млн км2.

26. Имеются алюминиевый и медный кубики. В каком из них больше атомов, и во сколько раз больше, если у них: а) равные массы? б) равные объемы? Примите, что плотность алюминия составляет 0,3 от плотности меди.

27. Полный стакан воды (200 мл) полностью испарился за 10 дней. Сколько молекул воды покидало стакан ежесекундно? Сравните это число с населением Земли.

28. В бассейн глубиной 2 м, длиной 50 м и шириной 10 м бросили один кристаллик поваренной соли массой 0,1 г. Спустя очень длительное время из бассейна зачерпнули стакан воды. Сколько ионов натрия окажется в атом стакане?

29. Одинакова ли концентрация молекул газов, содержащихся в шариках, изображенных на рисунке 40.2 (с. 22)? Чему она равна при нормальных условиях?

30. В цилиндре под постоянным давлением находился озон (трехатомный кислород O3) при температуре 727 ºС. Когда температуру понизили до 127 ºС, весь озон превратился в кислород O2. Как изменился объем газа?

31. В расположенном вертикально цилиндрическом сосуде с площадью поперечного сечения 10 см2 под поршнем с грузом общей массой 40 кг находится 0,05 молей газа. Температура газа 27 ºС, давление атмосферы 105 Па. а) Чему равно давление газа?

б) На какой высоте от дна сосуда находится поршень?

32. Цилиндрический сосуд разделен тонким подвижным поршнем на две части. В одной части сосуда находится 1 г водорода, а в другой — 1 г кислорода. Давление и температура газов одинаковы.

Какую часть сосуда занимает водород?

Постоянная клапейрона. Уравнение Менделеева-Клапейрона – О’Пять пО физике

1. Идеальным газом называется газ, в котором отсутствуют силы межмолекулярного взаимодействия. С достаточной степенью точности газы можно считать идеальными в тех случаях, когда рассматриваются их состояния, далекие от областей фазовых превращений.
2. Для идеальных газов справедливы следующие законы:

а) Закон Бойля – Mаpuomma: при неизменных температуре и массе произведение численных значений давления и объема газа постоянно:
pV = const

Графически этот закон в координатах РV изображается линией, называемой изотермой (рис.1).

б) Закон Гей-Люссака: при постоянном давлении объем данной массы газа прямо пропорционален его абсолютной температуре:
V = V0(1 + at)

где V – объем газа при температуре t, °С; V0 – его объем при 0°С. Величина a называется температурным коэффициентом объемного расширения. Для всех газов a = (1/273°С-1). Следовательно,

V = V0(1 +(1/273)t)

Графически зависимость объема от температуры изображается прямой линией – изобарой (рис. 2). При очень низких температурах (близких к -273°С) закон Гей-Люссака не выполняется, поэтому сплошная линия на графике заменена пунктиром.

в) Закон Шарля: при постоянном объеме давление данной массы газа прямо пропорционально его абсолютной температуре:
p = p0(1+gt)

где р0 – давление газа при температуре t = 273,15 К.
Величина g называется температурным коэффициентом давления. Ее значение не зависит от природы газа; для всех газов = 1/273 °С-1. Таким образом,
p = p0(1 +(1/273)t)

Графическая зависимость давления от температуры изображается прямой линией – изохорой (Рис. 3).

г) Закон Авогадро: при одинаковых давлениях и одинаковых температурах и равных объемах различных идеальных газов содержится одинаковое число молекул; или, что то же самое: при одинаковых давлениях и одинаковых температурах грамм-молекулы различных идеальных газов занимают одинаковые объемы.
Так, например, при нормальных условиях (t = 0°C и p = 1 атм = 760 мм рт. ст.) грамм-молекулы всех идеальных газов занимают объем Vm = 22,414 л.· Число молекул, находящихся в 1 см3 идеального газа при нормальных условиях, называется числом Лошмидта; оно равно 2,687*1019> 1/см3
3. Уравнение состояния идеального газа имеет вид:

pVm = RT

где р, Vm и Т – давление, молярный объем и абсолютная температура газа, а R – универсальная газовая постоянная, численно равная работе, совершаемой 1 молем идеального газа при изобарном нагревании на один градус:
R = 8.31*103 Дж/(кмоль*град)

Для произвольной массы M газа объем составит V = (M/m)*Vm и уравнение состояния имеет вид:
pV = (M/m) RT

Это уравнение называется уравнением Менделеева – Клапейрона.
4. Из уравнения Менделеева – Клапейрона следует, чти число n0 молекул, содержащихся в единице объема идеального газа, равно
n0 = NA/Vm = p*NA /(R*T) = p/(kT)

где k = R/NA = 1/38*1023 Дж/град – постоянная Больцмана, NA – число Авогадро.

Идеальный газ, уравнение состояния идеального газа, его температура и давление, объем… список параметров и определений, которыми оперируют в соответствующем разделе физики, можно продолжать достаточно долго. Сегодня мы поговорим как раз на эту тему.

Что рассматривается в молекулярной физике?

Основным объектом, который рассматривается в этом разделе, является идеальный газ. идеального газа было получено с учетом нормальных условий окружающей среды, и об этом мы поговорим немного позднее. Сейчас давайте подойдем к этой “проблеме” издалека.

Допустим, у нас есть некоторая масса газа. Ее состояние можно определить при помощи трех характера. Это, конечно же, давление, объем и температура. Уравнением состояния системы в этом случае будет формула связи между соответствующими параметрами. Она выглядит таким образом: F (p, V, T) = 0.

Вот здесь мы впервые потихоньку подбираемся к появлению такого понятия, как идеальный газ. Им называется газ, в котором взаимодействия между молекулами пренебрежимо малы. Вообще в природе такого не существует. Однако любой сильно близок к нему. От идеального мало чем отличаются азот, кислород и воздух, находящиеся в нормальных условиях. Чтобы записать уравнение состояния идеального газа, мы можем использовать объединенный Получим: pV/T = const.

Связанное понятие № 1: закон Авогадро

Он может рассказать нам о том, что если мы возьмем одинаковое количество молей абсолютно любого случайного газа и поставим их в одинаковые условия, среди которых температура и давление, то газы займут одинаковый объем. В частности, опыт проводился при нормальных условиях. Это означает, что температура была равна 273,15 Кельвинам, давление – одной атмосфере (760 миллиметров ртутного столба или же 101325 Паскалей). При таких параметрах газ занял объем равный 22,4 литра. Следовательно, мы можем говорить о том, что для одного моля любого газа соотношение числовых параметров будет величиной постоянной. Именно поэтому было принято решение этой цифре дать обозначение буквой R и назвать ее универсальной газовой постоянной. Таким образом, она равняется 8,31. Размерность Дж/моль*К.

Идеальный газ. Уравнение состояния идеального газа и манипуляции с ним

Давайте попробуем переписать формулу. Для этого запишем его в таком виде: pV = RT. Далее совершим нехитрое действие, умножим обе части уравнения на произвольное количество молей. Получим pVu = uRT. Примем во внимание тот факт, что произведение молярного объема на количество вещества есть просто объем. Но ведь количество молей одновременно будет равняться частному массы и молярной массы. Именно так выглядит Оно дает четкое понятие о том, какую систему образует идеальный газ. Уравнение состояния идеального газа примет вид: pV = mRT/M.

Выведем формулу для давления

Давайте проведем еще некоторые манипуляции с полученными выражениями. Для этого правую часть уравнения Менделеева-Клапейрона умножим и разделим на число Авогадро. Теперь внимательно смотрим на произведение количества вещества на Это есть не что иное, как общее число молекул в газе. -1 и носит название “коэффициент объемного расширения”. Мы можем подставить температуру как по шкале Цельсия, так и по шкале Кельвина. В последнем случае получим формулу V = Voat.

Постоянным остается объем

Это второй закон Гей-Люссака, более часто называемый законом Шарля. Выглядит он так: p/T = const. Есть и другая формулировка: p = po (1 + at). Преобразования могут быть проведены в соответствии с предыдущим примером. Как можно видеть, законы идеального газа иногда бывают достаточно похожими друг на друга.

Постоянным остается температура

Если температура идеального газа остается величиной постоянной, то мы можем получить закон Бойля-Мариотта. Он может быть записан таким образом: pV = const.

Связанное понятие № 2: парциальное давление

Допустим, у нас имеется сосуд с газами. Это будет смесь. Система находится в состоянии теплового равновесия, а сами газы между собой не реагируют. Здесь N будет обозначать общее количество молекул. N1, N2 и так далее, соответственно, количество молекул в каждом из компонентов имеющейся смеси. Возьмем формулу давления p = nkT = NkT/V. Ее можно раскрыть для конкретного случая. Для двухкомпонентной смеси формула примет вид: p = (N1 + N2) kT/V. Но тогда получится, что общее давление будет суммироваться из частных давлений каждой смеси. А значит, оно будет иметь вид p1 + p2 и так далее. Это и будут парциальные давления.

Для чего это нужно?

Полученная нами формула указывает на то, что давление в системе оказывается со стороны каждой группы молекул. Оно, кстати, не зависит от других. Этим воспользовался Дальтон при формулировании закона, названного впоследствии в его честь: в смеси, где газы не реагируют между собой химически, общее давление будет равно сумме парциальных давлений.

Как уже указывалось, состояние некоторой массы определяется тремя термодинамическими параметрами: давлением р, объемом V и температурой Т. Между этими параметрами существует определенная связь, называемая уравнением состояния .

Французский физик Б.Клапейрон вывел уравнение состояния идеального газа, объединив законы Бойля-Мариотта и Гей-Люссака.

1) изотермического (изотерма 1-1¢),

2) изохорного (изохора 1¢-2).

В соответствии с законами Бойля-Мариотта (1.1) и Гей-Люссака (1.4) запишем:

Исключив из уравнений (1.5) и (1.6) p 1 ” , получим

Так как состояния 1 и 2 были выбраны произвольно, то для данной массы газа величина остается постоянной, т.е.

. (1.7)
Выражение (1.7) является уравнением Клапейрона, в котором В – газовая постоянная, различная для разных газов.

Русский ученый Д.И.Менделеев объединил уравнение Клапейрона с законом Авогадро, отнеся уравнение (1.7) к одному молю, использовав молярный объем V m . Согласно закону Авогадро, при одинаковых р и Т моли всех газов занимают одинаковый молярный объем V m , поэтому постоянная В будет одинакова для всех газов. Эта общая для всех газов постоянная обозначается R и называется молярной газовой постоянной . Уравнению

удовлетворяет лишь идеальный газ, и оно является

уравнением состояния идеального газа , называемым также уравнением Менделеева-Клапейрона .

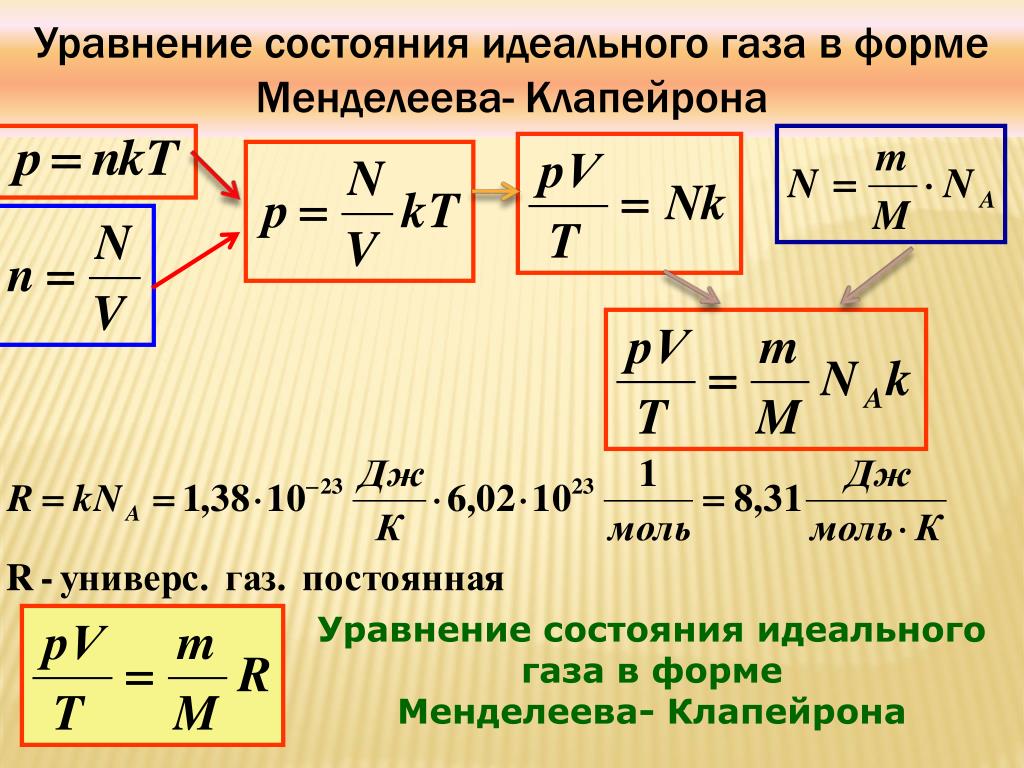
Числовое значение молярной газовой постоянной определим из формулы (1.8), полагая, что моль газа находится при нормальных условиях (р 0 =1,013×10 5 Па, Т 0 =273,15 К, V m =22,41×10 -3 м 3 /моль): R=8,31 Дж/(моль К).

От уравнения (1.8) для моля газа можно перейти к уравнению Клапейрона-Менделеева для произвольной массы газа. Если при некотором заданном давлении и температуре один моль газа занимает объем V m , то при тех же условиях масса m газа займет объем , где М – молярная масса (масса одного моля вещества). Единица молярной массы – килограмм на моль (кг/моль). Уравнение Клапейрона-Менделеева для массы m газа

где – количество вещества.

Часто пользуются несколько иной формой уравнения состояния идеального газа, вводя постоянную Больцмана :

Исходя из этого, уравнение состояния (1.8) запишем в виде

где – концентрация молекул (число молекул в единице объема). Таким образом, из уравнения

р=nkT (1.10)
следует, что давление идеального газа при данной температуре прямо пропор-ционально концентрации его молекул (или плотности газа). При одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул. Число молекул, содержащихся в 1 м 3 газа при нормальных условиях, называется

числом Лошмидта :

Основное уравнение молекулярно-кинетической

Теории идеальных газов

Для вывода основного уравнения молекулярно-кинетической теории рассмотрим одноатомный идеальный газ. Предположим, что молекулы газа движутся хаотически, число взаимных столкновений между ними пренебрежимо мало по сравнению с числом ударов о стенки сосуда, а соударения молекул со стенками сосуда абсолютно упругие. Выделим на стенке сосуда некоторую элементарную площадку DS (рис.50) и вычислим давление, оказываемое на эту площадку.

За время Dt площадки DS достигнут только те молекулы, которые заключены в объеме цилиндра с основанием DS и высотой Dt (рис. 50).

Число этих молекул равно nDSDt (n-концентрация молекул). Необходимо, однако, учитывать, что реально молекулы движутся к площадке DS под разными углами и имеют различные скорости, причем скорость молекул при каждом соударении меняется. Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных направлений, так что в любой момент времени вдоль каждого из них движется 1/3 молекул, причем половина (1/6) движется вдоль данного направления в одну сторону, половина- в противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку DS будет 1/6nDS Dt. При столкновении с площадкой эти молекулы передадут ей импульс

Уравнение Менделеева-Клапейрона – уравнение состояния для идеального газа, отнесенное к 1 молю газа. В 1874 г. Д. И. Менделеев на основе уравнения Клапейрона объединив его с законом Авогадро, используя молярный объем V m и отнеся его к 1 молю, вывел уравнение состояния для 1 моля идеального газа:

pV = RT , где R – универсальная газовая постоянная,

R = 8,31 Дж/(моль. К)

Уравнение Клапейрона-Менделеева показывает, что для данной массы газа возможно одновременно изменение трех параметров, характеризующих состояние идеального газа.

Для произвольной массы газа М, молярная масса которого m: pV = (М/m) . RT . или pV = N А kT ,

где N А – число Авогадро, k – постоянная Больцмана.

Вывод уравнения:

С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса газа и один из параметров – давление, объем или температура – остается постоянным, а изменяются только остальные два и получить теоретически газовые законы для этих условий изменения состояния газа.

Такие процессы называют изопроцессами. Законы, описывающие изопроцессы, были открыты задолго до теоретического вывода уравнения состояния идеального газа.

Изотермический процесс

– процесс изменения состояния системы при постоянной температуре. Для данной массы газа произведение давления газа на его объем постоянно, если температура газа не меняется . Это закон Бойля – Мариотта.

Для того, чтобы температура газа оставалась в процессе неизменной, необходимо, чтобы газ мог обмениваться теплотой с внешней большой системой – термостатом. Роль термостата может играть внешняя среда (воздух атмосферы). Согласно закону Бойля-Мариотта, давление газа обратно пропорционально его объему: P 1 V 1 =P 2 V 2 =const. Графическая зависимость давления газа от объема изображается в виде кривой (гиперболы), которая носит название изотермы. Разным температурам соответствуют разные изотермы.

Изобарный процесс – процесс изменения состояния системы при постоянном давлении. Для газа данной массы отношение объема газа к его температуре остается постоянным, если давление газа не меняется . Это закон Гей-Люссака. Согласно закону Гей-Люссака, объем газа прямо пропорционален его температуре: V/T=const. Графически эта зависимость в координатах V-T изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изобарой. Разным давлениям соответствуют разные изобары. Закон Гей-Люссака не соблюдается в области низких температур, близких к температуре сжижения (конденсации) газов.

Изохорный процесс – процесс изменения состояния системы при постоянном объеме. Для данной массы газа отношение давления газа к его температуре остается постоянным, если объем газа не меняется. Этот газовый закон Шарля. Согласно закону Шарля, давление газа прямо пропорционально его температуре: P/T=const. Графически эта зависимость в координатах P-Т изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изохорой. Разным объемам соответствуют разные изохоры. Закон Шарля не соблюдается в области низких температур, близких и температуре сжижения (конденсации) газов.

Законы Бойля – Мариотта, Гей-Люссака и Шарля являются частными случаями объединенного газового закона: Отношение произведения давления газа и объема к температуре для данной массы газа – величина постоянная: PV/T=const.

Итак, из закона pV = (М/m) . RT выводятся следующие законы:

T = const => PV = const – закон Бойля – Мариотта.

p = const => V/T = const – закон Гей – Люссака .

V= const => p/T = const – закон Шарля

Если идеальный газ является смесью нескольких газов, то согласно закону Дальтона, давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов. Парциальное давление – это такое давление, которое производил бы газ, если бы он один занимал весь объем, равный объему смеси.

Некоторых, возможно, интересует вопрос, каким образом удалось определить постоянную Авогадро N A = 6,02·10 23 ? Значение числа Авогадро было экспериментально установлено только в конце XIX – начале XX века. Опишем один из таких экспериментов.

В откачанный до глубокого вакуума сосуд объемом V = 30 мл поместили навеску элемента радия массой 0,5 г и выдержали там в течение одного года. Было известно, что за секунду 1 г радия испускает 3,7·10 10 альфа-частиц. Эти частицы представляют собой ядра гелия, которые тут же принимают электроны из стенок сосуда и превращаются в атомы гелия. За год давление в сосуде выросло до 7,95·10 -4 атм (при температуре 27 о С). Изменением массы радия за год можно пренебречь. Итак, чему равна N A ?

Сначала найдем, сколько альфа-частиц (то есть атомов гелия) образовалось за один год. Обозначим это число как N атомов:

N = 3,7·10 10 · 0,5 г · 60 сек · 60 мин · 24 час · 365 дней = 5,83·10 17 атомов.

Запишем уравнение Клапейрона-Менделеева PV = n RT и заметим, что число молей гелия n = N/N A . Отсюда:

N A = NRT = 5,83 . 10 17 . 0,0821 . 300 = 6,02 . 10 23

PV 7,95 . 10 -4 . 3 . 10 -2

В начале XX века этот способ определения постоянной Авогадро был самым точным. Но почему так долго (в течение года) длился эксперимент? Дело в том, что радий добывается очень трудно. При его малом количестве (0,5 г) радиоактивный распад этого элемента дает очень мало гелия. А чем меньше газа в замкнутом сосуде, тем меньшее он создаст давление и тем большей будет ошибка измерения. Понятно, что ощутимое количество гелия может образоваться из радия только за достаточно долгое время.

Давление газа.Ур-е состояния ид. газа.Изопроцессы

Давление газа возникает в результате столкновений молекул со стенками сосуда ( и на помещенное в газ тело ), в котором находится беспорядочно движущиеся молекулы  газа. Чем чаше удары, тем они сильнее – тем выше давление. Если масса и объем газа неизменны, то его давление в закрытом сосуде всецело зависит от температуры. Давление зависит и от скорости поступательно движущихся газовых молекул. Единица измерения давления — паскаль p(Па). Измеряют давление газа манометром (жидкостным, металлическим и электрическим).

Идеальный газ – это модель реального газа. За идеальный газ принимают газ в сосуде, когда молекула, пролетая от стенки до стенки сосуда не испытывает столкновения с другими молекулами. Точнее, Идеальный газ – это газ, взаимодействие между молекулами которого пренебрежимо мало ⇒ E_к >> E_р .

Основное уравнение МКТ связывает макроскопические параметры (давление p, объём V, температура T, масса m) газовой системы с микроскопическими параметрами (масса молекулы , средняя скорость их движения):       

, где n— концентрация, 1/м³; m — масса молекулы, кг;  — средняя квадратичная скорость молекул, м/с.

Уравнение состояния идеального газа  — формула, устанавливающая зависимость между давлением, объёмом и абсолютной температурой идеального газа, характеризующее состояние данной системы газа. — уравнение Менделеева — Клапейрона (для произвольной массы газа).             R = 8,31 Дж/моль·К  — универсальная газовая постоянная.           pV = RT – (для 1 моля).

Часто необходимо исследовать ситуацию, когда меняется состояние газа при его неизменном количестве (m=const) и в отсутствие химических реакций (M=const). Это означает, что количество вещества ν=const. Тогда:

Для постоянной массы идеального газа отношение произве­дения давления на объем к абсолютной  температуре в данном состоянии есть величина постоянная:   — уравнение Клапейрона. 

Термодинамический процесс (или просто процесс) — это изменение состояния газа с течением времени. В ходе термодинамического процесса меняются значения макроскопических параметров — давления, объёма и температуры. Особый интерес представляют изопроцессы — термодинамические процессы, в которых значение одного из макроскопических параметров остаётся неизменным. Поочерёдно фиксируя каждый из трёх параметров, мы получим три вида изопроцессов.

Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака. Эти законы называют законами для изопроцессов:

Изопроцессы – это процессы, которые совершаются при одинаковом параметре или Т-температуре, или V-объеме, или р-давлении.

Изотермический процесс — — закон Бойля — Мариотта  (при постоянной температуре и данной массы газа произведение давления на объем есть величина постоянная)

 

Изобарный процесс —  — закон Гей-Люссака (при постоянном давлении для данной массы газа отношение объема к температуре есть величина постоянная)

Изохорный процесс — — закон Шарля (при постоянном объеме для данной массы газа отношение давления к температуре есть величина постоянная.

Вывели газовые законы из уравнения Менделеева — Клапейрона. Но исторически всё было наоборот: газовые законы были установлены экспериментально, и намного раньше. Уравнение состояния появилось впоследствии как их обобщение.

 

 

Уравнение Менделеева-Клапейрона | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Тема:

Уравнения состояния

Из уравнения состояния идеального газа p₁V₁ / T₁ = p₂V₂ / T₂можно сделать вывод, что

для данной массы газа отношение произведения давле­ния газа на его объем к абсолютной тем­пературе газа является величиной постоянной:

pV / T = const.

Установлено, что для 1 моля газа эта константа равняется 8,31 Дж / (моль • К). Она называется универсальной газовой постоянной и обозначается буквой R. Следовательно, урав­нение состояния идеального газа для 1 моля газа можно записать в виде:

pV_M = RT,

где V_M — объем 1 моля газа, или молярный объем.

Это уравнение состояния иде­ального газа называется урав­нением Клапейрона в честь французского физика, который впервые его вывел.

Известный русский ученый Д. И. Менделеев вывел уравнение состояния для произволь­ного количества газа. Учитывая, что объем произвольной массы газа V = vV_M = (m / M) • V_M, где v — количество вещества, m — масса газа, M — его молярная масса, уравнение состоя­ния идеального газа можно записать в более общем виде:

pV = (m / M) • RT.

В таком виде оно называется уравнением Менделеева-Клапейрона. Все газовые зако­ны, открытые экспериментальным путем, можно вывести из этого уравнения как следствие, считая постоянным один из мак­ропараметров. Материал с сайта http://worldofschool.ru

Если учесть, что плотность газа ρ = m / V, то уравнение Менделеева-Клапейрона будет иметь вид:

p = (ρ / M) • RT.

Уравнение Менделеева-Кла­пейрона является общим урав­нением состояния идеального газа для произвольной его массы.

На этой странице материал по темам:

• Закон клапейрона-менделеева формулировка

• Закон клапейрона формулировка

• Закон менделеева клапейрона формулировка

• Закон клапейрона менделеева формулировка

• Формула клапейрона менделеева задачи

Вопросы по этому материалу:

• Зависимость между какими физическими величинами устанав­ливает уравнение состояния идеального газа?

• Какое значение имеет универсальная газовая постоянная?

• Что такое молярный объем?

• Чем отличается уравнение состояния идеального газа от урав­нения Менделеева-Клапейрона?

Диаграммы давление-объем – Гиперучебник по физике

Обсуждение

математика, математика, математика

Вспомните предыдущий раздел…

∆ U  =  Q  +  W

Система

Q  > 0	поглощает тепло из окружающей среды
Q  < 0	система выделяет тепло в окружающую среду
Вт  > 0	работа, проделанная над системой средой
Вт  < 0	работа системы над окружающей средой

Систему можно описать тремя термодинамическими переменными — давлением, объемом и температурой.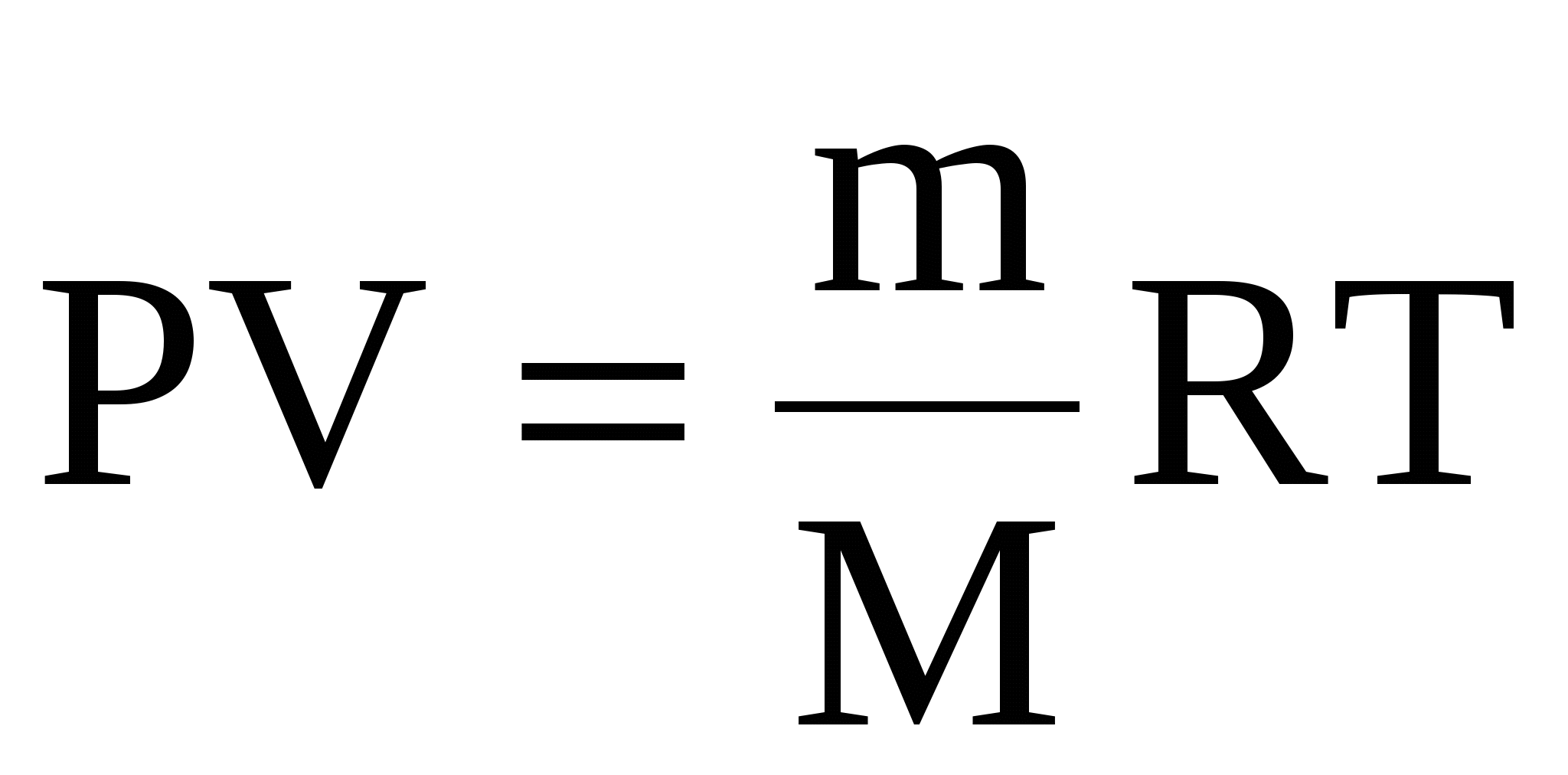 Ну, может быть, это только две переменные. Поскольку все связано законом идеального газа, одна переменная всегда может быть описана как зависящая от двух других.

		⎧ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎩	P  =	НРТ
				В
PV  =  нРТ	⇒		В  =	НРТ
				П
			Т  =	ПВ
				нР

Температура зависит от давления и объема на графике давление-объем (график PV).

Функция состояния

∆ U  =  ³ ₂ nR ∆ T

Функция Пути: Работа

W  = ∫  F  ·  d s  = ∫  P   dV

W  = −  область на графике PV

Функция Пути: Тепло

Q  = ∆ U  +  W  =  н. з. ∆ T

c P  =	удельная теплоемкость при постоянном давлении
с В  =	удельная теплоемкость при постоянном объеме

кривые

• изобарический
  • постоянное давление
  • «бар» происходит от греческого слова «тяжелый»: βαρύς [ меняет ]
  • примеры: утяжеленный поршень, гибкий контейнер в земной атмосфере, воздушный шар
  • График PV представляет собой горизонтальную линию

  Вт  = – П ∆ В

  ⇒

  ∆ U  =  Q  −  P ∆ В

• изохорный
  • постоянный объем
  • «хор» происходит от греческого слова «объем»: χώρος [ хорос ]
  • примеры: закрытый жесткий контейнер, термометр постоянного объема
  • График PV представляет собой вертикальную линию

  Вт  = 0

  ⇒

  ∆ U  =  Q

• изотермический
  • постоянная температура
  • «терм» происходит от греческого слова «тепло»: θερμότητα [ thermotita ]
  • примеры: «медленные» процессы, выдох через широко открытый рот
  • График PV представляет собой прямоугольную гиперболу

  ∆ U  =  0

  ⇒

  Q  = − Вт

• адиабатический
  • без теплообмена с окружающей средой
  • адиабатический имеет сложное греческое происхождение, означающее «не+через+пройти»: α + ∆ια + βατός [ a  +  dia  +  vatos ]
  • примеры: «быстрые» процессы, вытеснение воздуха через сжатые губы, насос для велосипедных шин
  • Диаграмма PV представляет собой «крутую гиперболу»

  Q  = 0

  ⇒

  ∆ U  =  Вт

  PV ^γ  =  константа

  γ =	с Р	=	α + 1
  	с В		α

  3/2 + 1	=	5	одноатомный
  3/2		3
  5/2 + 1	=	7	двухатомный
  5/2		5

Супермен спасает положение благодаря адиабатическому охлаждению. Быстрое расширение газа, выброшенного из легких Супермена, охладило перегретый грузовик, предотвратив попытку злого генерала Зода взорвать его топливный бак. Спасибо, Супермен.

… и остальные

жидкости

твердые вещества

Идеальные газы и закон идеального газа: pV = nRT

Температура, Т

Температура должна быть в кельвинах. Не забудьте добавить 273, если вам дана температура в градусах Цельсия.

Использование уравнения идеального газа

Расчеты по уравнению идеального газа включены в мою книгу расчетов (см. ссылку в самом низу страницы), и я не могу их повторить здесь. Однако есть пара вычислений, которые я не сделал в книге, которые дают разумное представление о том, как работает уравнение идеального газа.

Молярный объем при ст.

Если вы производили простые расчеты по уравнениям, вы, вероятно, использовали молярный объем газа.

1 моль любого газа занимает 22,4 дм ³ при ст. ст. (стандартные температура и давление, принятые за 0°С и давление в 1 атмосферу). Возможно, вы также использовали значение 24,0 дм ³ при комнатной температуре и давлении (примерно 20°C и 1 атмосфера).

Эти цифры на самом деле верны только для идеального газа, и мы посмотрим, откуда они взялись.

Мы можем использовать уравнение идеального газа для расчета объема 1 моля идеального газа при 0°C и давлении 1 атмосфера.

Во-первых, мы должны правильно подобрать единицы измерения.

0°C составляет 273 K. T = 273 K

1 атмосфера = 101325 Па p = 101325 Па

Мы знаем, что n = 1, потому что пытаемся вычислить объем 1 моля газа.

И, наконец, R = 8,31441 Дж К ^-1 моль ^-1 .

Вписывая все это в уравнение идеального газа, а затем переставляя его, мы получаем:

И, наконец, поскольку нас интересует объем в кубических дециметрах, вам нужно не забыть умножить его на 1000, чтобы перевести кубические метры в кубические дециметры.

Таким образом, молярный объем идеального газа равен 22,4 дм ³ при ст.

И, конечно же, вы можете переделать это вычисление, чтобы найти объем 1 моля идеального газа при комнатной температуре и давлении — или при любой другой температуре и давлении.

Нахождение относительной формулы массы газа по его плотности

Это так же сложно, как и при использовании уравнения идеального газа.

Плотность этана равна 1.264 г дм ^-3 при 20°С и 1 атмосфере. Рассчитайте относительную формульную массу этана.

Значение плотности означает, что 1 дм ³ этана весит 1,264 г.

Опять же, прежде чем делать что-либо еще, разберитесь с неудобными юнитами.

Давление в 1 атмосферу равно 101325 Па.

Объем 1 дм ³ нужно перевести в кубические метры, разделив на 1000. У нас есть объем 0,001 м ³ .

Температура 293 К.

Теперь поместите все числа в форму уравнения идеального газа, которое позволяет вам работать с массами, и измените его так, чтобы вычислить массу 1 моля.

Масса 1 моля чего-либо — это просто относительная формула массы в граммах.

Таким образом, относительная формула массы этана равна 30,4, т. е. 3 сиг.

Теперь, если вы сложите относительную формулу массы этана, C ₂ H ₆ , используя точные значения относительных атомных масс, вы получите ответ 30.07 до 4 значащих цифр. Что отличается от нашего ответа – так что не так?

Есть две возможности.

• Возможно, я использовал неверное значение плотности. Я снова подсчитал сумму, используя немного другое значение, указанное при другой температуре из другого источника. На этот раз я получил ответ 30,3. Таким образом, значения плотности могут быть не совсем точными, но оба они дают практически одинаковый ответ.

• Этан не идеальный газ.Ну, конечно же, это не идеальный газ — такого не бывает! Однако, если предположить, что значения плотности близки к правильным, ошибка находится в пределах 1% от ожидаемой. Таким образом, хотя этан и не ведет себя как идеальный газ, он не за горами.

Если вам нужно узнать о реальных газах, самое время прочитать о них.

Изохорный процесс – уравнение идеального газа – pV Diagram

Изохорный процесс – это термодинамический процесс, в котором объем замкнутой системы остается постоянным (V = const).Он описывает поведение газа внутри контейнера, который нельзя деформировать.

Поскольку объем остается постоянным, теплопередача в систему или из нее не влияет на работу p∆V , а только изменяет внутреннюю энергию системы (температуру). Случай n ➝ ∞   соответствует изохорному (постоянному объему) процессу для идеального газа и политропному процессу .

См. также: Что такое идеальный газ.

Предположим, что изохорный подвод тепла в идеальном газе.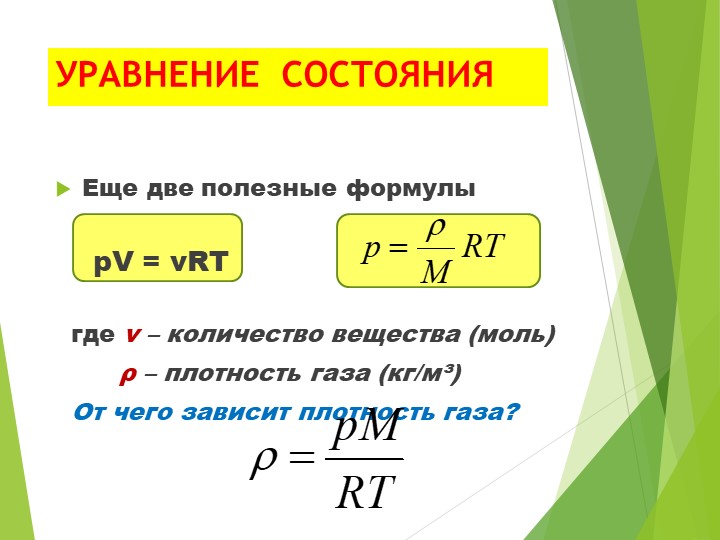 В идеальном газе молекулы не имеют объема и не взаимодействуют. Согласно закону идеального газа давление изменяется линейно с температурой и количеством и обратно пропорционально объему.

PV = NRT PV = NRT

где:

P – это абсолютное давление газа

N – это количество вещества

T – абсолютная температура

V это объем

R  это идеальная или универсальная газовая постоянная, равная произведению постоянной Больцмана и постоянной Авогадро,

В этом уравнении символ R представляет собой универсальную газовую постоянную , которая имеет одинаковое значение для всех газов, а именно, R = 8.31 Дж/моль К.

Изохорный процесс может быть выражен по закону идеального газа как:

или

.

Давление-объем работы по замкнутой системе определяется как:

Согласно идеальной газ модели, внутренняя энергия может быть рассчитана на:

ΔU = MC _V ΔT

, где свойство C _V (J / MOL K) упоминается как удельная теплоемкость (или теплоемкость ) при постоянном объеме, потому что при определенных особых условиях (постоянный объем) оно связывает изменение температуры системы с количеством энергии, добавленной в результате теплопередачи.

Поскольку система не совершает никакой работы, первый закон термодинамики диктует ∆U = ∆Q. Следовательно:

Q =   м c _v ∆T

См. также: Удельная теплоемкость при постоянном объеме и постоянном давлении.

См. также: Формула МайераИзохорный процесс – основные характеристикиДавление прямо пропорционально температуре Кельвина для фиксированной массы газа при постоянном объеме.

 

Литература:

Ядерная и реакторная физика:

1. J.Р. Ламарш, Введение в теорию ядерных реакторов, 2-е изд., Аддисон-Уэсли, Рединг, Массачусетс (1983).
2. Дж. Р. Ламарш, А. Дж. Баратта, Введение в ядерную технику, 3-е изд., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
3. WM Stacey, Физика ядерных реакторов, John Wiley & Sons, 2001, ISBN: 0-471-39127-1.
4. Гласстоун, Сезонске. Разработка ядерных реакторов: разработка реакторных систем, Springer; 4-е издание, 1994 г. , ISBN: 978-0412985317
5. WSC. Уильямс.Ядерная физика и физика элементарных частиц. Кларендон Пресс; 1 издание, 1991 г., ISBN: 978-0198520467
6. Кеннет С. Крейн. Введение в ядерную физику, 3-е издание, Wiley, 1987, ISBN: 978-0471805533
7. Г. Р. Кипин. Физика ядерной кинетики. Паб Эддисон-Уэсли. Ко; 1-е издание, 1965 г.
8. Роберт Рид Берн, Введение в работу ядерных реакторов, 1988 г.
9. Министерство энергетики, ядерной физики и теории реакторов США. Справочник по основам Министерства энергетики, том 1 и 2, январь 1993 г.

Advanced Reactor Physics:

1. К. О. Отт, В. А. Безелла, Введение в статистику ядерных реакторов, Американское ядерное общество, исправленное издание (1989 г.), 1989 г., ISBN: 0-894-48033-2.
2. К. О. Отт, Р. Дж. Нойхольд, Введение в динамику ядерных реакторов, Американское ядерное общество, 1985, ISBN: 0-894-48029-4.
3. Д. Л. Хетрик, Динамика ядерных реакторов, Американское ядерное общество, 1993, ISBN: 0-894-48453-2.
4. Э. Э. Льюис, В. Ф.Миллер, Вычислительные методы переноса нейтронов, Американское ядерное общество, 1993, ISBN: 0-894-48452-4.

См. выше:

Изохорический процесс

Physlet Physics Кристиана и Беллони: Исследование 20.5

Исследование 20.5: Диаграммы PV и работа

Дождитесь полной загрузки анимации.

Существует временная задержка, поскольку система должна быть в равновесии, прежде чем произойдет изменение состояния.

Закон идеального газа: PV = nRT. В этой анимации N = nR (т. е. k _B = 1). Это, таким образом, дает закон идеального газа как PV = NT. Работа, совершаемая во время термодинамического процесса, зависит от типа процесса (и может быть положительной, отрицательной или нулевой). Начать сначала. Работа определяется уравнением

 Вт = ∫ P дВ,

, так что на диаграмме давление-объем площадь под кривой равна работе , выполненной газом при расширении. Для аналитического решения работы необходимо знать, как давление зависит от объема (постоянно ли давление, изменяется ли линейно с объемом и т. д.).?). Как давление зависит от объема, зависит от типа процесса (изотермический, изобарический, изохорный, адиабатический).

Три анимации показывают три разных процесса, которые начинаются при одной и той же температуре и заканчиваются при одной температуре.

1. Каково изменение внутренней энергии (ΔU) для этих процессов (помните, что ΔU = (3/2)nRΔT = (3/2)NΔT для идеального одноатомного газа)?
2. Оцените площадь под кривой (сосчитайте блоки на графике) при переходе системы от одной температуры к другой (от одной изотермы на графике к другой).Это значение проделанной работы, поскольку работа равна W = ∫ PdV. Какой процесс работает положительно? Какой процесс работает отрицательно? В каком процессе работает ноль?
3. Первый закон термодинамики ΔU = Q – W, записанный как Q = W + ΔU, говорит, что тепло, поступающее в систему, может быть использовано для совершения работы и/или увеличения внутренней энергии. Следовательно, какой процесс требует больше всего тепла?
4. Сравните площадь под кривой, которую вы оценили в (b), со значением, которое вы рассчитали, используя приведенные ниже уравнения (найденные с помощью исчисления и решения интеграла):
   • Постоянное давление: W = P(V _f – V _i )
   • Адиабатическая: W = (P _f V _f – P _i V _i )/(1 – γ), где γ (отношение C _P /C _V , удельная теплоемкость при постоянное давление, деленное на удельную теплоемкость при постоянном объеме) для идеального одноатомного газа составляет 5/3.

Когда вы получите красивый график, щелкните его правой кнопкой мыши, чтобы клонировать график и изменить его размер для лучшего просмотра.

Исследование, автором которого является Энн Дж. Кокс.

Physlets были разработаны в колледже Дэвидсона и преобразованы из Java в JavaScript с использованием системы SwingJS, разработанной в колледже Святого Олафа.

Закон идеального газа

Термодинамика , начавшаяся как попытка повысить эффективность паровых двигателей в начале 1800-х годов, может рассматриваться как исследование взаимосвязи между теплом, передаваемым к объекту или от него, и работой, совершаемой над объектом или объектом. .И теплота, и работа связаны с передачей энергии, но теплота связана с передачей энергии из-за разницы температур.

Нулевой закон термодинамики (не обессудьте, я его не назвал!) гласит, что если объект А находится в тепловом равновесии с объектом В, а объект В находится в тепловом равновесии с объектом С, то объекты А и С должны находиться в тепловом равновесии друг с другом. Этот закон настолько интуитивен, что его почти не нужно формулировать, но, определяя доказательства 1-го и 2-го законов термодинамики, ученые поняли, что им нужно конкретно сформулировать этот закон, чтобы завершить свои доказательства.

первый закон термодинамики на самом деле является переформулировкой закона сохранения энергии. В частности, в нем говорится, что изменение внутренней энергии замкнутой системы равно теплоте, переданной системе, плюс работа, совершенная над системой, и записывается как:

.

 

В этом уравнении важно соблюдать правила знаков, где положительное значение для тепла, Q, представляет тепло, добавленное в систему, а положительное значение для работы, W, указывает на работу, совершенную с газом.Если бы энергия вытягивалась из системы, как в случае теплоты, отбираемой из системы, или работы, совершаемой системой, эти величины были бы отрицательными.

В большинстве случаев вы будете использовать первый закон термодинамики для анализа поведения идеальных газов, который можно упростить, проанализировав определение работы над газом.

 

Если работа — это сила, умноженная на перемещение, а давление — это сила, действующая на площадь, то силу можно заменить давлением, умноженным на площадь.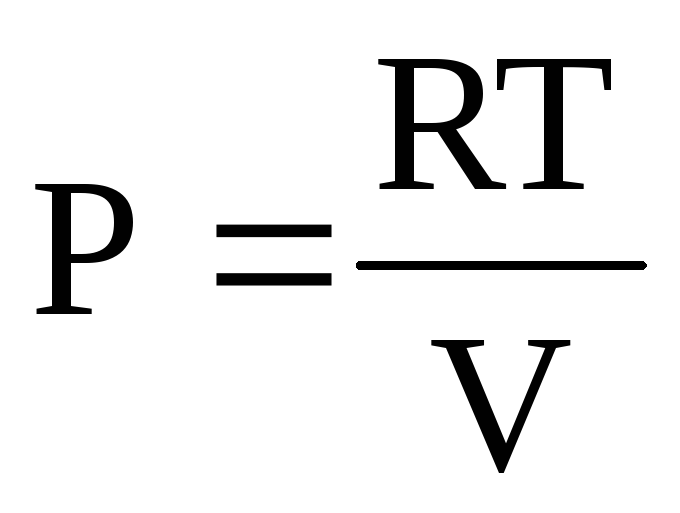 Площадь, умноженная на смещение, дает изменение объема газа. Из-за соглашения о знаках, согласно которому работа, совершаемая над газом, положительна (соответствует уменьшению объема), вы можете записать работу как W = -PΔV.

 

Вопрос: Пять тысяч джоулей тепла добавляется в замкнутую систему, которая затем совершает работу в 3000 джоулей. Каково чистое изменение внутренней энергии системы?

Ответ:

 

 

Вопрос: Жидкость превращается в газ при атмосферном давлении (101 325 Па).Объем жидкости составил 5×10 ^-6 м ³ . Объем газа 5×10 ^-3 м ³ . Сколько работы было проделано в процессе?

Ответ:

 

 

Диаграммы давления-объема

(диаграммы PV) являются полезными инструментами для визуализации термодинамических процессов газов. Эти диаграммы показывают давление по оси ординат и объем по оси абсцисс и используются для описания изменений, которые претерпевает заданное количество газа.Поскольку количество газа остается постоянным, диаграмма PV не только показывает давление и объем, но также может использоваться для определения температуры газа в сочетании с законом идеального газа. Пример диаграммы PV показан ниже, показывая два состояния газа, состояние A и состояние B.

 

При переходе из состояния А в состояние В объем газа увеличивается, а давление газа уменьшается. При переходе из состояния В в состояние А объем газа уменьшается, а давление увеличивается.Поскольку работа, проделанная над газом, определяется как W=-PΔV, вы можете найти работу, проделанную над газом, графически из диаграммы PV, взяв площадь под кривой. Из-за соглашения о положительных/отрицательных знаках, когда объем газа расширяется, газ совершает работу (W отрицательное значение), а когда газ сжимается, над газом совершается работа (W положительное значение).

 

Вопрос: Используя диаграмму PV справа, найдите объем работы, необходимый для перехода из состояния A в состояние B, а затем объем работы, необходимый для перехода из состояния B в состояние C.

Ответ: Объем работы при переходе из состояния A в B равен площади под графиком для этого перехода. Так как под прямой нет площади, то работа не совершалась. Работу при переходе из состояния В в состояние С можно найти, взяв площадь под линией на PV-диаграмме.

Обратите внимание, что работа отрицательна, что указывает на то, что газ совершил работу, что коррелирует с расширением газа.

 

При изучении изменений состояния идеального газа существует ряд изменений состояния, при которых одна из характеристик газа или процесса остается постоянной, что показано на диаграмме PV ниже.

Типы процессов включают:

• Адиабатический — Теплота (Q) не передается в систему или из нее
• Изобарический — Давление (P) остается постоянным
• Изохорный — Объем (V) остается постоянным
• Изотермический — Температура (T) остается постоянной

В адиабатическом процессе тепловой поток (Q) равен нулю. Применяя первый закон термодинамики, если ΔU=Q+W, а Q равно 0, изменение внутренней энергии газа должно быть равно работе, совершенной над газом (ΔU=W).

В изобарическом процессе давление газа остается постоянным. Поскольку давление постоянно, на диаграмме PV для изобарического процесса показана горизонтальная линия. Далее, применив это к закону идеального газа, вы обнаружите, что V/T должно оставаться постоянным для процесса.

В изохорном процессе объем газа остается постоянным.Диаграмма PV для изохорного процесса представляет собой вертикальную линию. Поскольку W=-PΔV, а ΔV=0, работа над газом равна нулю. Это также отражено графически на диаграмме PV. Работу можно найти, взяв площадь под графиком PV, но площадь под вертикальной линией равна нулю. Применяя это к закону идеального газа, вы обнаружите, что P/T должно оставаться постоянным для изохорного процесса.

В изотермическом процессе температура газа остается постоянной. Поэтому линии на PV-диаграмме, описывающие любой процесс, происходящий при постоянной температуре, называются изотермами.В изотермическом процессе произведение давления на объем газа остается постоянным. Далее, поскольку температура постоянна, внутренняя энергия газа должна оставаться постоянной.

 

Вопрос: Идеальный газ совершает адиабатическое расширение, совершая работу в 2000 Дж. На сколько изменилась внутренняя энергия газа?

Ответ: Поскольку процесс адиабатический, Q=0, следовательно:

 

 

Вопрос: Теплота отводится от идеального газа при снижении его давления с 200 кПа до 100 кПа.Затем газ расширяется от объема 0,05 м ³ до 0,1 м ³ , как показано на диаграмме PV ниже. Если кривая АС представляет собой изотерму, найти работу, совершенную газом, и теплоту, переданную газу.

Ответ: Работа, совершаемая газом при перемещении из А в В, равна нулю, так как площадь под графиком равна нулю. Однако при движении из В в С работу, совершаемую газом, можно найти, взяв площадь под графиком.

Знак минус указывает на то, что газ совершил работу в 5000 джоулей.Поскольку АС находится на изотерме, температура газа должна оставаться постоянной, поэтому внутренняя энергия газа должна оставаться постоянной. Зная, что ΔU=Q+W, если ΔU=0, то Q должно быть равно -W, следовательно, к газу должно быть добавлено 5000 джоулей.

 

Второй закон термодинамики можно сформулировать по-разному. В одном из утверждений этого закона говорится, что тепло естественным образом перетекает от более теплого объекта к более холодному и не может течь от более холодного объекта к более теплому без совершения работы над системой.Это можно довольно легко наблюдать в повседневных обстоятельствах. Например, контакт холодной ложки с горячим супом никогда не приведет к тому, что суп станет горячее, а ложка — холоднее.

Второй закон термодинамики также ограничивает эффективность любой тепловой машины и доказывает, что невозможно создать тепловую машину со 100-процентным КПД, даже если полностью устранить трение.

Другая формулировка этого закона гласит, что уровень энтропии , или беспорядка, в замкнутой системе может только возрастать или оставаться прежним.Это означает, что ваш рабочий стол никогда не станет более организованным без работы. Это также означает, что вы не можете бросить горсть пластиковых строительных блоков и наблюдать, как они самопроизвольно приземляются на впечатляющую модель средневекового замка. К сожалению, это даже означает, что независимо от того, сколько раз Шалтай-Болтай падает со стены, все его фигуры на земле никогда не окажутся более организованными после того, как он упадет на землю, по сравнению с тем, как он потерял равновесие.

Последний закон термодинамики, третий закон термодинамики , также известный как Теорема Нернста в честь ее первооткрывателя Вальтера Нернста, утверждает, что ни один материал никогда не может быть охлажден до абсолютного нуля (хотя материалы могут быть очень близки!)

 

Диаграмма P-V | bartleby

Объяснение

Важно отметить, что, измеряя изменения объема термодинамической системы при постоянном давлении, можно измерить проделанную работу, а знак термина «PdV» может облегчить нахождение работы, проделанной системы на окружение или окружением на систему.

Математически,

W=PdV

Чтобы понять ситуацию, совершается ли работа системой или над системой, мы рассматриваем сжатие или расширение объема как параметр для понимания.

Важное преимущество диаграмм P-V или, точнее, поскольку индикаторная диаграмма облегчает нам измерение количества тепла, отводимого или поглощаемого в виде работы, причина в том, что кривая площади или PV представляет собой чистую выполненную работу.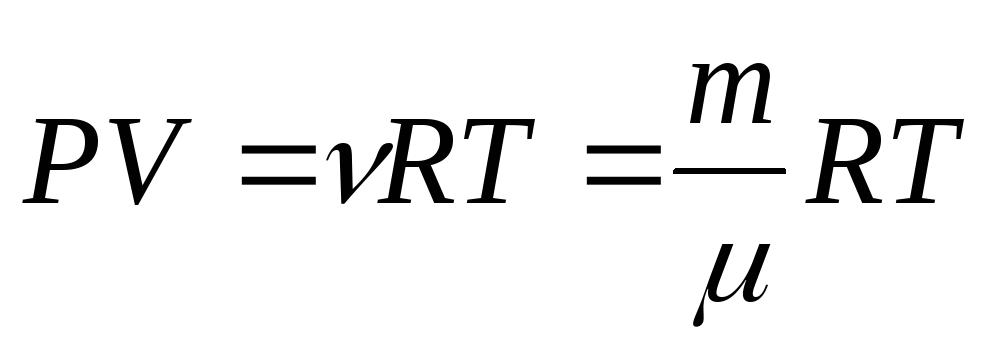 Так как диаграмма PV представлена ​​циклическим процессом в той или иной форме, то и вся кривая проходит через процесс таким образом, что представляет собой комбинацию теплоты, отводимой системой, и теплоты, поглощаемой системой.

См. рис. 2 ниже, где ясно показано, что для пути ABC индикаторная диаграмма PV будет давать выходную работу, а CDA дает энергию, необходимую для входной работы, необходимой для достижения начального состояния системы, которое завершает весь цикл .

Можно отметить, что, хотя каждая система подчиняется закону сохранения энергии, как эмпирическому правилу, в термодинамике это сохранение энергии также включает потерю энергии в виде тепла в окружающую среду.

Рассмотрим контейнер, состоящий из жидкости до уровня V, и подвижный поршень используется для изменения его объема за счет сжатия или расширения жидкости.

Здесь возникают следующие два случая.

• Если поршень вытолкнуть вверх, то уровень жидкости увеличится, значит, система (жидкость) совершила работу над окружающей средой (пустой областью), и ее конечный объемный уровень больше начального. Это означает, что выполненная работа является отрицательной величиной.

Следовательно, если система совершает работу над окружающей средой, то она является отрицательной величиной.

• Если поршень опустить, т.е. давление на жидкость увеличивается, то объем жидкости уменьшается, значит, окружающая среда (пустая область) совершила работу над системой (жидкость), и конечный объем меньше чем первоначальный объем жидкости. Это означает, что выполненная работа является положительной величиной.

Следовательно, если работа над системой совершается окружением, то это положительная величина.   

Теперь, чтобы понять диаграмму PV на практике, давайте визуализируем ее особенности, изучая кривую PV.

Как показано на рис. 2, по оси x отложено изменение объема, а по оси y — изменение давления в системе.

Можно ясно представить, что:

1. для пути AB существует постоянное давление, а объем изменяется или увеличивается, поэтому выполненная работа отрицательна для пути AB, пройденного системой;
2. для пути BC давление меняется, а объем остается постоянным, поэтому работа равна нулю;
3. для пути CD, Давление является постоянной величиной, а объем изменяется или уменьшается, поэтому выполненная работа положительна для пути CD, пройденного системой;
4. для пути DA давление меняется, а объем остается постоянным, поэтому работа равна нулю.

Теперь практичность этого уравнения заключается в том, что с помощью этой диаграммы мы можем найти температуру, теплообмен, внутреннюю энергию системы и совершенную работу.

Используя первый закон термодинамики

ΔU=Q−Wгде ΔU=изменение внутренней энергииQ= теплота, подводимая к системе

dU=nCVdT=nCV(T2−T1)W=PdV=P(V2−V1)

Здесь C _V — удельная теплоемкость при постоянном объеме.

Теперь воспользуемся вторым законом термодинамики, согласно которому изменение энтропии системы (то есть случайность системы) является постоянным для обратимого процесса и изменение энтропии системы больше нуля

Математически, если

 S _f = энтропия системы в начальном состоянии газа

 S _i = энтропия системы в конечном состоянии газа

Для обратимой системы

Sf −Si=0

Для необратимой системы

Sf−Si>0

Следовательно, первый закон термодинамики

dU=TdS−PdV

Теперь давайте обсудим различные системы одну за другой и проанализируем, как изменяются законы термодинамики. .

Приведенная стоимость (PV)

Деньги сейчас более ценны, чем деньги позже .

Почему? Потому что вы можете использовать деньги, чтобы заработать больше денег!

Вы можете заняться бизнесом, или купить что-то сейчас, а потом продать дороже, или просто положить деньги в банк, чтобы получать проценты.

Пример: Вы можете получить 10% годовых на свои деньги.

Итак, 1000 долларов сейчас могут заработать 1000 долларов x 10% = 100 долларов в год.

Ваша 1000 долларов сейчас может стать 1100 долларов через год .

Текущая стоимость

Итак, 1000 долларов сейчас — это то же самое , что и 1100 долларов в следующем году (под 10% годовых).

Мы говорим, что Текущая стоимость 1100 долларов в следующем году составит 1000 долларов

Потому что мы могли бы превратить 1000 долларов в 1100 долларов (если бы мы могли заработать 10% годовых).

Теперь давайте расширим эту идею в будущем…

Как рассчитать будущие платежи

Давайте останемся с процентной ставкой 10%. Это означает, что деньги растут на 10% каждый год, вот так:

Итак:

• 1100 долларов в следующем году то же самое, что и 1000 долларов сейчас .
• И 1210 долларов через 2 года это то же самое, что и 1000 долларов сейчас .
• и т. д.

На самом деле все эти суммы равны (учитывая когда они появляются и 10% годовых).

Упрощенный расчет

Но вместо того, чтобы «прибавлять 10%» к каждому году, проще умножить на 1,10 (объяснено в разделе «Сложные проценты»):

Итак, мы получаем это (тот же результат, что и выше):

Будущее Назад в настоящее

И чтобы увидеть, сколько денег в будущем стоит сейчас , вернитесь назад (делите на 1,10 каждый год вместо умножения):

Пример: Сэм обещает вам

500 долларов в следующем году , какова текущая стоимость?

Чтобы перевести будущий платеж на один год назад разделить на 1. 10

Итак, 500 долларов в следующем году равно 500 долларов ÷ 1,10 = 454,55 долларов сейчас (с точностью до цента).

Текущая стоимость $454,55

 

Пример: Алекс обещает вам

900 долларов через 3 года , какова текущая стоимость?

Взять будущий платеж на три года назад разделить на 1,10 трижды

Итак, 900 долларов за 3 года это:

$900 ÷ 1.10 ÷ 1,10 ÷ 1,10

900 $ ÷ (1,10 × 1,10 × 1,10)

$900 ÷ 1,331

$676,18 теперь (с точностью до цента).

Лучше с экспонентами

Но вместо $900 ÷ (1,10 × 1,10 × 1,10) лучше использовать показатели степени (показатель степени говорит , сколько раз использовать число при умножении).

Пример: (продолжение)

Приведенная стоимость 900 долларов через 3 года (за один раз):

$900 ÷ 1.10 ³ = 676,18 долларов теперь (с точностью до цента).

Как формула это:

PV = FV / (1+r) ⁿ

• PV Текущая стоимость
• FV является будущей стоимостью
• r процентная ставка (в десятичном виде, т.е. 0,10, а не 10%)
• n число лет

Пример: (продолжение)

Используйте формулу для расчета приведенной стоимости 900 долларов через 3 года :

PV = FV / (1+r) ⁿ

PV = 900 долларов США / (1 + 0.10) ³ = 900 долл. США / 1,10 ³ = 676,18 долл. США (с точностью до цента).

 

Экспоненты проще использовать, особенно с калькулятором. Например, 1,10 6 быстрее, чем 1,10 × 1,10 × 1,10 × 1,10 × 1,10 × 1,10

Используем формулу еще немного:

Пример: Сколько сейчас стоит 570 долларов в следующем году при процентной ставке 10%?

PV = 570 долларов США / (1+0.