Механическая работа. Физика 7 класс
Похожие презентации:
Механическая работа
Механическая работа
Механическая работа
Механическая работа
Механическая работа. Условия, при которых совершается механическая работа
Механическая работа. Сила упругости
Механическая работа, мощность. 7 класс
Механическая работа. 7 класс
Механическая работа. Работа силы, действующей по направлению движения тела
Механическая работа. Единицы работы. Мощность. Единицы мощности
1. Механическая работа
Урок физики в 7 классеКессова Екатерина Васильевна,
учитель физики МБОУ СОШ №111
г. Минеральные Воды
900igr.net
2. Объяснить пословицы и поговорки
Работа не волк, в лес не убежит.С печи сыт не будешь. Не печь кормит, а руки.
С горы вскачь, а в гору хоть плачь.
Сверху легко бросать, попробуй-ка снизу.
В гору семеро тащат, а с горы и один толкает.
Без труда не выловишь и рыбку из пруда.

Берись дружно, не будет грузно.
Встать пораньше да шагнуть подальше.
3. Актуализация знаний учащихся
Что такое сила?Сила – мера взаимодействия тел.
От чего зависит результат действия силы на тела?
Результат действия силы на тело зависит от ее
модуля, направления, точки приложения.
Какие типы сил Вам известны?
Сила упругости F упр; Тяжести F тяж; Вес тела
Р; Сила трения Fтр.
4. Сила упругости
возникают при деформации;одновременно у двух тел;
перпендикулярны поверхности;
противоположны смещению;
при малых деформациях выполняется
закон Гука F упр = -к х
5. Сила тяжести
сила, с которой Земля притягивает ксебе тело;
формула для нахождения силы тяжести
Fт =mg;
направлена по радиусу к центру Земли;
не зависит от массы тела;
относится к гравитационным силам
6. Сила трения покоя
Сила трения покоя – сила, действующаяна тело со стороны соприкасающегося с
ним другого тела вдоль поверхности
соприкосновения тел, если тела покоятся
относительно друг друга.

7. Сила трения скольжения
Сила трения скольжения – сила трения,возникающая при относительном движении
соприкасающихся тел и направленная
против скорости их относительного
движения.
Fтр.=µN
8. Сила трения качения
Сила трения качения возникает приусловии, когда одно тело катится по
поверхности другого.
Fтр. качения<< Fтр.
скольжения
9. Механическая работа
Термин «Работа» ввел французскийученый Ж. Понселе.
Работа – это деятельность человека.
10. Примеры механической работы
Поезд движется под действием силы тяги.Санки движутся под действием силы мускул.
При полете сила давления сгорающих газов
перемещает ракету.
Подъёмная сила действует на воздушный
шар.
F
Опыт 1 Под действием силы тело перемещается на 0,5 м,
затем на 1 метр.
Вывод: Работа зависит от расстояния. Чем оно больше , тем
больше и работа
Опыт 2.Нагруженная тележка перемещается на 1 м.
Увеличиваем нагрузку и повторяем опыт.

Вывод: Чем больше сила, тем больше совершенная работа.
13. Механическая работа
14. Формула для расчета работы
A~FЗапишем:
A~s
где F – сила, приложенная к телу;
s – путь, проделанный телом.
A=F∙s
За единицу работы принимают работу,
совершенную силой в 1 ньютон
на пути в 1 метр.
1Н м 1Дж (Джоуль)
1 кДж = 1000 Дж
1 МДж = 1000 кДж = 1000000 Дж
1 мДж = 0,001Дж
F=1 Н
1м
15. Джоуль Джеймс Прескотт (1818—1889)
Обосновал на опытахзакон сохранения
энергии. Установил
закон, определяющий
тепловое действие
электрического тока.
Вычислил скорость
движения молекул
газа и установил ее
зависимость от
температуры.
Формула для расчета работы
A= F∙s
A
F
s
A
s
F
17. Формула для расчета работы
18. Когда работа совершается?
Шайба скользит по льдуv=const
s
19. Когда работа совершается?
Шайба скользит по льдуСила тяжести действует на шайбу
перпендикулярно направлению
движения
Влияет ли сила тяжести на движение шайбы?
v=const
s
если F v, то А=0
Fтяж
20.
 Когда работа совершается?
Когда работа совершается?Толкаем тяжелый груз,
прикладываем силу, груз не
двигается.
Совершается ли работа?
НЕТ
Почему?
Груз не сдвинулся с места, проделанный путь равен 0
если s=0, то А=F·0=0
Значит, работа не совершается!
21. Работа может быть как положительной, так и отрицательной
FсЕсли сила и направление движения
совпадают, то А>0
Если сила и направление перемещения
противоположны, то А<0
А=Fтяж·h
А= – Fc·h
Fтяж
Работа силы тяжести.
а) если тело движется вверх, то А<0.
б) если тело движется вниз, то А>0.
23. Работа может быть как положительной, так и отрицательной
Если сила и направление движениясовпадают, то А>0
А = F тяги ·s
Если сила и направление перемещения
противоположны, то А<0
А = – Fтр ·s
v=const
Fтяги
Fтр
Fтяж
24. Условия, при которых работа не равна нулю
для совершения работы необходимовыполнение трех условий:
1.
 к телу должна быть приложена
к телу должна быть приложенакакая-то сила,
2. тело должно двигаться;
3. направление движения не должно
быть перпендикулярным по
отношению к направлению
действия силы.
Если хотя бы одно из этих условий
не будет выполнено, то работа
будет равна нулю.
Если тело, к которому приложена
сила, продолжает оставаться в
покое, то механическая работа при
этом не совершается.
v
F
Fт
25. Закрепление материала
Положительнаяработа А=F∙S
Отрицательная работа
А= — Fтp• S
27. Задача: В каком случае совершается механическая работа?
1v=0
2
v
Fт
1. Брусок покоится
2. Брусок движется по гладкому стеклу
3. Брусок перемещается под действием силы F
3
v
F
28. 1. В каком из перечисленных случаев совершается механическая работа?
2.Одинаковую ли работу совершают мальчики при равномерномперемещении на одном и том же пути?
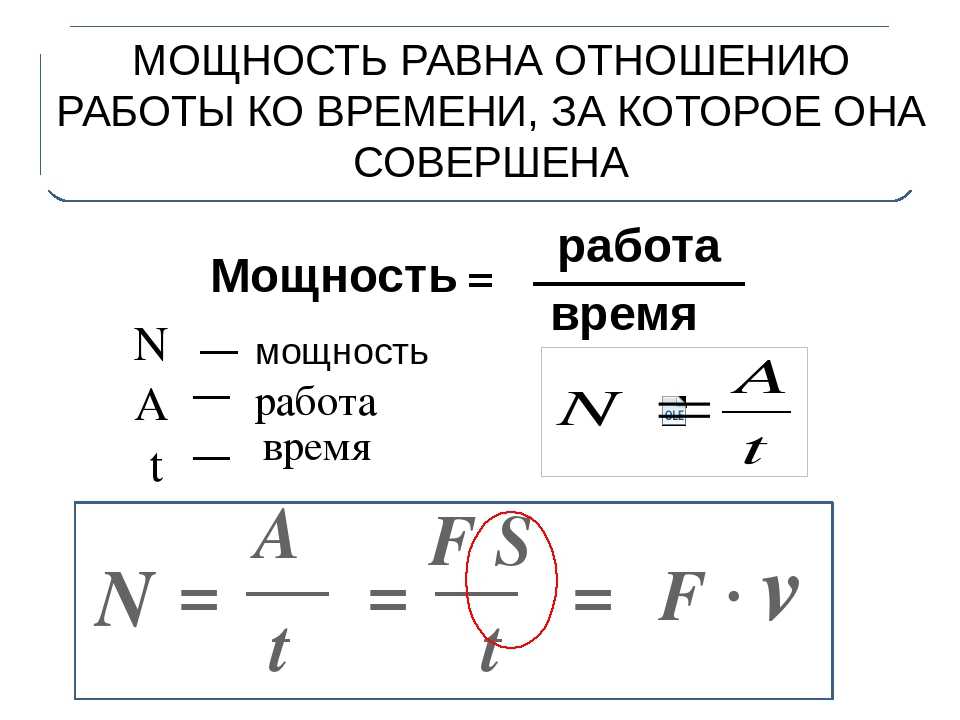
3.Определите механическую работу по перемещению
бруска.
29. Физическая пауза
«Гимнастика для глаз»Зажмурьте глаза, а потом откройте их. Повторите 5
раз.
Делайте круговые движения глазами: налево вверх – направо – вниз – направо – вверх – налево вниз. Повторите 10 раз.
Вытяните вперёд руку. Следите взглядом за ногтем
пальца, медленно приближая его к носу, а потом
медленно отодвиньте обратно. Повторите 5 раз.
Посмотрите в окно вдаль 1 минуту.
Проверка
1. Какую работу изучают в физике?
А.труд рабочего; Б. труд инженера; В.механическую работу
2. Дополните предложение “Механическая работа совершается только тогда, когда
А. … на тело действует сила.
Б. … тело движется.
В. … на тело действует сила и оно движется под
действием этой силы.
3. В каком из перечисленных случаев совершается механическая работа?
А. Шарик катится по гладкому горизонтальному столу равномерно.
Б. Автопогрузчик поднимает груз
В. Кирпич лежит на земле
4. Как обозначается механическая работа?
А.
 F Б. S. В. A.
F Б. S. В. A.5 Для того, чтобы вычислить механическую работу, надо…
А. силу умножить на путь. Б. сложить силу и путь В. путь поделить на силу.
6. В каких единицах измеряется механическая работа?
А) Н Б) Па.
В) Дж
7. В каком случае сила совершает положительную работу?
А) Если направление действия силы совпадает с направлением движения тела.
Б) Если направление
действия силы противоположно направлению движения тела В) Работа всегда имеет положительное
значение.
8. Может ли сила совершать отрицательную работу?
А) Не может. Б) Может, если направление силы, действующей на тело, противоположно направлению
движения. В) Может, если тело не двигается
9. Может ли механическая работа равняться нулю?
А) Не может Б) Может, если направление силы, действующей на тело, противоположно направлению
движения.
В) Может, если направление силы, действующей на тело, перпендикулярно направлению движения
10. Вычислите работу, которая совершается при перемещении тела на 4 м под
действием силы 12 Н
А) 16 Н.

Б 48 Н
В) 4 Н
1. В
2. В
3. Б
4. В
5. А
6. В
7. А
8. Б
9. В
10.Б
31. Домашнее задание
§ 53 упр. 28 (1, 3, 4.) Ответить навопросы в конце параграфа. Определить
работу силы тяжести при подъёме
портфеля.
Подготовить высказывания, пословицы,
поговорки о работе, труде.
32. Рефлексия
33. Литература:
А.В. Перышкин. Учебник физики 7 класс.А.В. Перышкин. Сборник задач по физике 7-9 класс.
Марон А.Е., Е.А Марон Дидактический материал 7 класс.
Марон А.Е., Е.А Марон Сборник качественных задач по
физике. 7-9 класс.
В.И. Лукашик Сборник задач по физике 7-9 класс.
Интернет – ресурсы:
http://mymark.narod.ru/kab/ssosud.jpg;
http://sc.uriit.ru/dlrstore/47802304-57bc-4fdb-ae78d1c481245954/7_189.swf;
http://www.spb-guide.ru/foto_8633.htm
http://www.ilovepetersburg.ru/content/petergofpetrodvorets-fontany-fotogalereya-4-mb
34. Используемые ресурсы ЕКЦОР:
http://schoolcollection. edu.ru/catalog/res/85292ef2-631e-4ebf8469-a838920777da/?
edu.ru/catalog/res/85292ef2-631e-4ebf8469-a838920777da/?http://schoolcollection.edu.ru/catalog/res/59b11a0d-7bf6-482db76789649b68782f/?interface=pupil&class=49&subject
=30
http://school-collection.edu.ru/catalog/res/f1ce32150914-4c91-af8e-91e11f41f04b/?
http://schoolcollection.edu.ru/catalog/res/172203a3-f7bf-467085cd-a4c37739528a/?
English Русский Правила
Урок физики в 7-м классе “Механическая работа”
Работа – это главное в жизни. От всех неприятностей, от всех бед можно найти только одно избавление – в работе.
Эрнест Хемингуэй
Оборудование: компьютер, проектор, электронные учебные пособия “Физика 7 класс”. УМК “Сферы”. Москва. Просвещение, 2009., Библиотека наглядных пособий Физика 7-11 классы. ООО “Дрофа”, 2004 г.
1. Организационный момент.
Учитель зачитывает высказывания великих людей о работе (слайд 2).
Вопрос: Ребята, что вы понимаете под словом работа?
Ответ: Процесс получения какого-либо продукта.
Ответ: В обыденной жизни под словом “работа” мы понимаем различные действия человека, механизма.
А какая из физических величин необходима человеку для совершения работы?
Ответ: Сила.
Итак, ребята, сегодня на уроке вы узнаете:
- Что такое механическая работа;
- Как рассчитать механическую работу;
- Когда механическая работа положительна, когда отрицательна и когда равна нулю.
Сегодня на уроке вы вспомните:
- Что такое сила;
- От чего зависит результат действия силы;
- Какие силы бывают и как они направлены (слайд 3).

2. Актуализация знаний
Ребята, а какие силы были изучены нами в этом учебном году?
Ответ: сила тяжести, сила упругости, вес тела, сила трения. Давайте вспомним понятие “силы” и виды сил, о которых мы узнали в 7 классе.
Вопрос: Что такое сила? От чего зависит результат действия силы?
Ответ: Сила – векторная физическая величина и результат её действия зависит от трёх характеристик: направления, точки приложения, модуля (слайд 4).
Рис. 1
Сила трения.
Одна из самых любимых детских сказок – сказка “Репка”. Сегодня мы рассмотрим её с научной точки зрения и увидим, что для того чтобы объяснить некоторые события в сказках нужно знать физику.
Ученик: Посадил дед репку. Выросла репка
большая-пребольшая, тяжёлая-претяжёлая,
разрослась она во все стороны, грунт потеснила.
Вопрос: Какая сила мешала дедушке самостоятельно вытянуть репку?
Ответ: Сила трения покоя.
Вопрос: Какие ещё силы трения вам известны? Когда они возникают? Куда направлены?
Ответ: Сила трения скольжения, сила трения качения. Направлены в сторону противоположную движению, против внешней силы (слайд 5).
Вопрос: Какая ещё сила действовала на всех героев сказки “Репка”?
Ответ: Сила тяжести.
Сила тяжести
Ребята, давайте посмотрим фрагмент мультфильма
и ответим на вопросы к нему.
(Слайд 6: фрагмент из мультфильма Незнайка).
Вопрос: Может ли такое случиться в земных условиях? Если нет, то почему?
Ответ: Нет, так как на земле существует сила тяжести, которая действует на любой предмет и притягивает его к Земле.
Вопрос: Куда направлена сила тяжести?
Ответ: Всегда к Земле.
Вопрос: Что предлагал найти Незнайка?
Ответ: Вес.
Вопрос: Что такое вес?
Ответ: Вес-это сила, которая вследствие притяжения к Земле действует на опору или подвес со стороны тела?
Вопрос: А в земных условиях человек не может пребывать в невесомости?
Ответ: Может, при полёте вниз, но при этом на
него действует сила тяжести, он не будет парить, а
будет притягиваться к Земле (слайд 7).
Рис. 2
Вопрос: Почему капли дождя падают на Землю? (Слайд 8)
Рис. 3
Ответ: На них действует сила тяжести.
Сила упругости.
Посмотрим следующий фрагмент и ответим на вопрос: какая сила возникает в этом случае? (Слайд 9: фрагмент из мультфильма “Добрыня Никитич”)
Ответ: сила упругости, возникает при деформациях тел, т.е. при изменении формы и объёма тела.
Вопрос: Как направлена сила упругости?
Ответ: Всегда в сторону, противоположную деформации.
Под действием силы тяжести многие тела падают на землю. Но, всё же, действие силы тяжести не всегда приводит к движению тела. Например, кирпич лежит на опоре и не падает.
Почему?
Ответ: На кирпич со стороны опоры действует
сила упругости, которая равна по модулю силе
тяжести, направлена в противоположную сторону и
уравновешивает её (слайд 10).
Рис. 4
Вывод: Одновременно на одно и то же тело может действовать несколько сил (слайд 11).
Рис.5
Работа с опорным конспектом (ОК) (слайд 12)
Один учащийся располагает силы на доске, остальные в рабочих тетрадях.
Рис. 6
3. Изучение нового материала.
3.1.Объяснение нового материала.
Мы вспомнили все силы неслучайно. Тема нашего урока “Механическая работа”. Как мы выяснили в начале урока, без силы никакая работа совершаться не может.
Под работой человек понимает различные
действия, приводящие к получению “продукта”.
Например, мы говорим: работает учитель, работает
компьютер, работает трактор, холодильник. Мы
понимает, что речь идёт о разных вещах, и не
стремимся сравнивать работу грузчика с работой
компьютера.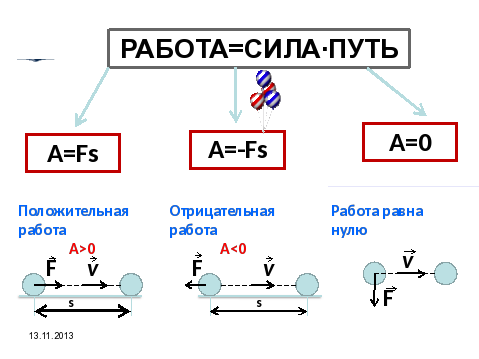
Итак, в физике механическая работа – это величина, которую можно измерить. Под механической работой понимают связь между силой, действующей на тело и его перемещением или движением тела под действием силы.
Считается, что механическая работа совершается, когда тело движется под действием силы.
Таким образом, в физике понятие работы напрямую связано с силой (нет силы, нет работы). Поэтому принято говорить о работе некоторой силы.
Нетрудно понять, что чем большая сила действует на тело и чем длиннее путь, который проходит тело под действием этой силы, тем большая совершается работа.
Механическая работа прямо пропорциональна
приложенной силе и прямо пропорциональна
пройденному пути.
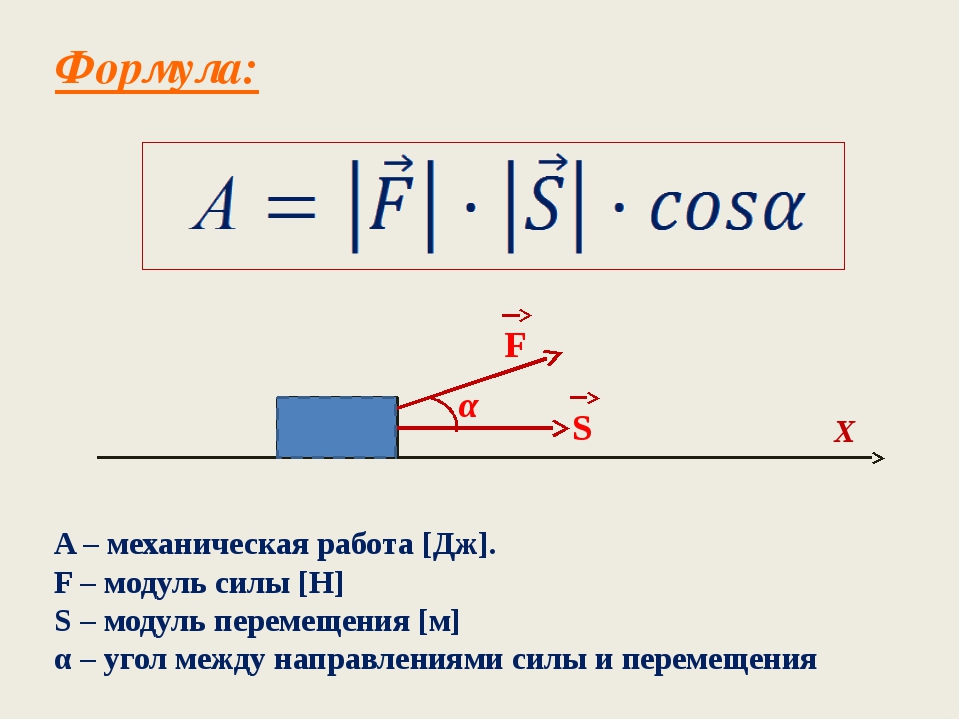
Формула работы (слайд 14).
Рис. 7
Работа – физическая величина и, следовательно, у неё есть единица измерения (слайды 15-16).
Рис. 8
1Н*м = 1 Дж – единица измерения работы названа в честь английского физика Джеймса Прескотта Джоуля.
За единицу работы принимают работу, совершаемую силой в 1 Н на пути 1 м.
1 кДж=1000 Дж
3.2. Рефлексия
Наступило время проверить как вы усвоили понятие механической работы.
Совершается ли механическая работа в следующих случаях? (Примеры совершения и не совершения механической работы слайды 17-22).
Если мы пытаемся сдвинуть с места тяжёлый
предмет, но сила, с которой мы на него действуем
меньше силы трения покоя, то предмет остаётся на
месте. В этом случае, несмотря на нашу усталость,
мы не совершаем механической работы, так как нет
перемещения тела. Как бы не было тяжело
мифологическому герою Атланту удерживать на
плечах небесный свод, Атлант не совершает
механической работы, так как небесный свод в этом
случае не двигался.
Как бы не было тяжело
мифологическому герою Атланту удерживать на
плечах небесный свод, Атлант не совершает
механической работы, так как небесный свод в этом
случае не двигался.
Механическая работа равна нулю в случае, когда равны нулю либо силы, действующие на тело, либо под действием сил тело не перемещается.
Рис. 9
(Заполнение опорного конспекта урока, слайд 23)
3.3. Расширение знаний о физической величине
Знак работы.
Мы выяснили, что работа может быть равной нулю.
(Приведу примеры из жизни: не выучил урок –
работа равна нулю; выучил урок – выполнил
полезную работу; набросал на пол фантики от
конфет – совершил работу отрицательную).
Оказывается, механическая работа, может быть
отрицательной и положительной. Рассмотрим, в
каких случаях и какая по знаку работа
совершается (анимация “Положительная,
отрицательная работы и работа, равная нулю”, слайд
24).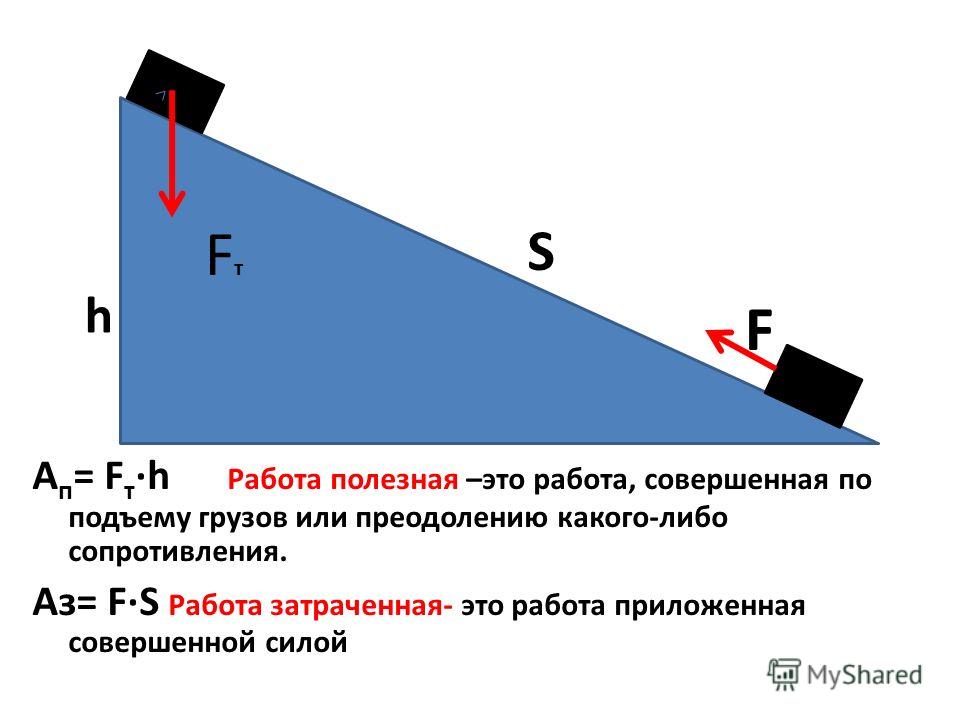
Рис. 10
Вопрос: Какая из известных вам сил, всегда совершает отрицательную работу?
Ответ: Сила трения.
(Показываю движение деревянного бруска по плоскости и выясняем, что сила тяги совершает положительную работу, сила трения – отрицательную. Задаю вопросы: Совершает ли работу сила тяжести? Как направлена сила тяжести по отношению к перемещению бруска? Делаем вывод, что работа силы равна нулю, если она направлена перпендикулярно перемещению).
Дополним ОК.
Рис. 11
Проверим, как вы усвоили понятия положительной и отрицательной работы.
1. Какой знак работы силы тяжести в каждом случае?
Рис. 12
2. Какую работу совершают сила трения и внешняя сила?
Рис. 13
4. Закрепление изученного
Закрепление изученного
Тест по теме “Механическая работа”
- Что такое механическая работа?
- К неподвижному массивному телу массой 100 кг приложена сила 200 Н. При этом положение тела не изменилось. Чему равна работа силы?
- Какая из перечисленных ниже единиц принята за единицу работы?
- Тело под действием силы 40 Н переместилось на 2 метра. Чему равна работа?
- Какую работу совершает сила трения при попытке человека сдвинуть с места тяжёлый шкаф?
З) Произведение силы на скорость тела
Е) Отношение пути ко времени движения тела
Р) Произведение силы на путь, пройденный по направлению силы
Г) 20000 Дж
Е) 0 Дж
Ж) 20 Дж
П) Ньютон
Н) Метр
Ш) Джоуль
И) 80 Дж
К) 20 Н
Л) 0 Дж
И) Равную нулю
К) Положительную
Л) Отрицательную
Если результатом является слово “решил”, то ты молодец!
6. Подведение итогов урока. Постановка
домашнего задания.
Подведение итогов урока. Постановка
домашнего задания.
Дома: п. 53, задание 17 (1) – экспериментальное.
Задача: Бочка заполнена водой. Пользуясь ведром, половину воды из бочки вычерпала девочка. Оставшуюся часть воды – мальчик. Одинаковую ли работу совершили девочка и мальчик? Ответ обоснуйте.
Тест (Приложение)
AP Physics – Unit 3
Мы познакомились с законами движения Ньютона и с тем, как мы можем использовать диаграммы свободного тела с F net = ma для решения некоторых интересных задач. В этом разделе мы продолжим наши исследования, используя концепцию Силы, приложенной к массе, когда она перемещается на некоторое расстояние (расстояние в направлении).
Начнем!
- Определение работы
- Скалярный продукт
- Работа, совершаемая переменной силой
- Теорема работы-энергии
- Определение силы
Работа — это количество, которое полезно при описании того, как объекты взаимодействуют с другими объектами.
Работа , совершаемая агентом, прилагающим постоянную силу к объекту, является произведением составляющей силы, направленной в направлении смещения, и величины смещения объекта.
Обратите внимание, что слово «работа» используется во многих смыслах, которые не соответствуют «физической работе»:
- “Сегодня мне нужно на работу.”
- “Завершение этой лаборатории требует много работы.”
- “Я займусь этим позже, когда у меня будет больше времени.”
«Физическая работа» возникает при соблюдении условий, описанных выше: когда к объекту прикладывается Сила в направлении, которое движется с некоторым смещением. Давайте посмотрим на некоторые примеры этого.
Постоянная горизонтальная сила 100 Н используется для протаскивания 20-килограммового ящика на расстояние 2,0 м по столу без трения. Какую работу совершает ящик в каждой из следующих ситуаций?
- Какую работу совершает горизонтальная сила?
- Какую работу совершает сила, действующая вниз под действием силы тяжести?
- Какую работу совершает нормальная сила, поднимающаяся со стола?
Решение:
Начните, , конечно, , нарисовав диаграмму ситуации в свободном теле, потому что мы смотрим на работу, совершаемую определенной силой, и поэтому нам нужно определить эту силу. Не все проблемы с работой и энергией сосредоточены на силе, но по мере того, как мы развиваем эти идеи, мы хотим хорошо продемонстрировать процесс.
Не все проблемы с работой и энергией сосредоточены на силе, но по мере того, как мы развиваем эти идеи, мы хотим хорошо продемонстрировать процесс.
Самый простой способ решить эту задачу — использовать формулу «Работа равна силе, умноженной на расстояние», где приложенная сила равна 100 Н, а расстояние, пройденное по этой силовой линии, равно 2 метрам.
Использование этой формулы предполагает , что Сила и пройденное расстояние имеют одно и то же направление.
Важно знать, что формула Работы на самом деле основана на векторах, поэтому на самом деле мы используем направление Силы и направление перемещения. В этом случае эти два вектора имеют одинаковое направление, т.е. между ними угол θ, равный 0 градусов. Применение более формального анализа дает тот же результат:
.Решение:
Хотя сила земного притяжения притягивает ящик с силой мг = 196 ньютонов, смещения в этом направлении нет.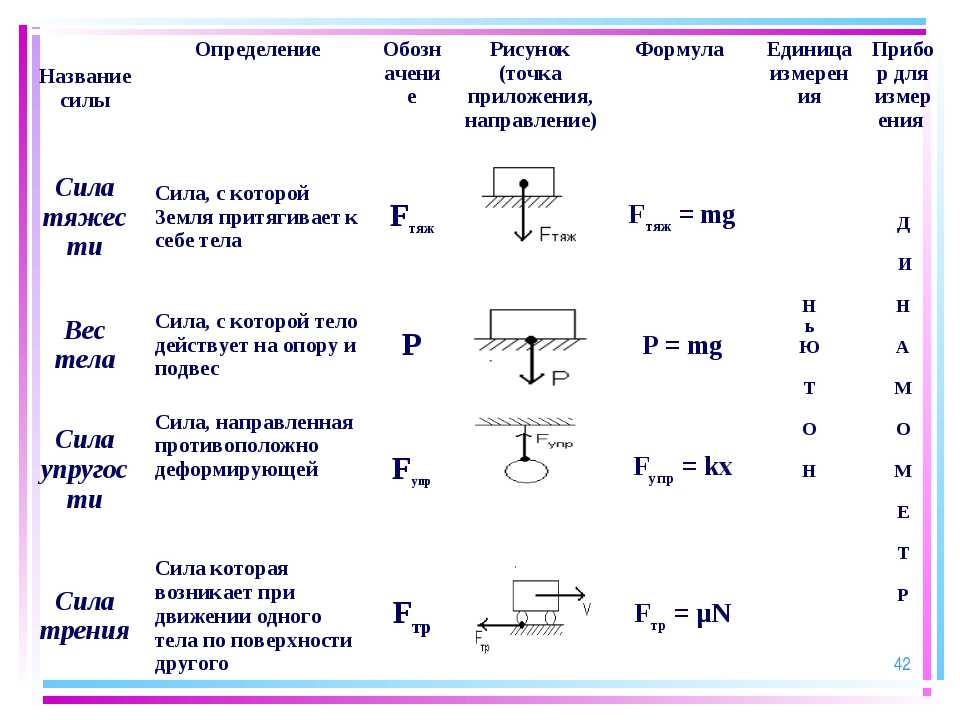 Следовательно, сила тяжести не действует на ящик.
Следовательно, сила тяжести не действует на ящик.
Мы можем продемонстрировать это более формально, написав:
Решение:
Используя те же рассуждения, что и выше, мы можем определить, что Работа, совершаемая Нормальной силой из таблицы, равна 0 Джоулей.
Та же постоянная горизонтальная сила 100 Н используется для того, чтобы протащить 20-килограммовый ящик на расстояние 2,0 м по шероховатой поверхности с постоянной скоростью.
Сколько работы совершает приложенная сила сейчас? Какую работу совершает сила трения?
Решение:
Если приложенная сила и перемещение остаются неизменными, то работа, совершаемая приложенной силой, остается той же: 200 Дж.
Чтобы рассчитать работу, совершаемую трением, рассмотрите силу трения, действующую в направлении 180 градусов, и перемещение блока вдоль стола в положительном направлении x, 0 градусов.
θ между этими двумя векторами составляет 180 градусов, и это то, что мы используем для расчета работы, совершаемой трением, тогда:
Важно понимать, что, хотя работа вычисляется с использованием векторных величин, она сама является скаляром количество: у него нет направления.
Силы, действующие на движущийся объект, могут «совершать над объектом положительную работу», и в этом случае (мы скоро увидим) сила увеличивает энергию объекта. Сила также может «совершать отрицательную работу над объектом», и в этом случае сила уменьшает энергию объекта.
Вычисленные положительные и отрицательные значения работы относятся к энергии, добавленной к объекту или удаленной от него, а не к «направлению работы».
Работа — это скалярная величина, не имеющая направления.
Постоянная сила 100 Н прикладывается под углом 30° над горизонталью и используется для протаскивания 20-килограммового ящика на расстояние 2,0 м по поверхности без трения.
Какую работу совершает приложенная сила?
Решение:
Есть несколько способов решить эту проблему. Один из способов — посмотреть на смещение в положительном направлении x и убедиться, что вы используете только тот компонент прилагаемой Силы, который совпадает с этим смещением. Это F x , что мы можем видеть на диаграмме F cos θ . В этом случае:
Один из способов — посмотреть на смещение в положительном направлении x и убедиться, что вы используете только тот компонент прилагаемой Силы, который совпадает с этим смещением. Это F x , что мы можем видеть на диаграмме F cos θ . В этом случае:
Использование другого определения работы, где θ указывает угол между двумя векторами, приводит к тому же результату:
100-N применяется на 30° над горизонталью и используется для перетаскивания 20 кг ящик 2,0 м по шероховатой поверхности (μ = 0,15).
Какую работу совершает трение?
Решение:
Опять же, сила трения и перемещение направлены в противоположные стороны, поэтому можно ожидать, что работа силы трения будет отрицательной. Но как на самом деле рассчитать силу трения?
Если бы мы знали, что коробку тянут с постоянной скоростью, мы бы знали, что F прикладное и F трение были одинаковыми. Но нам не предоставили эту информацию. Однако мы можем рассчитать трение, используя μ и нормальную силу.
Однако мы можем рассчитать трение, используя μ и нормальную силу.
Только убедитесь, что правильно рассчитали Нормальную силу. С силой, приложенной к ящику, нормальная сила больше не равна мг !
Нет. В некоторых случаях трение работает положительно.
Рассмотрим случай, когда официант несет поднос с напитком. Поскольку сервировочный поднос движется с боковым ускорением (вправо на приведенной здесь диаграмме), между подносом и стаканом возникает сила статического трения. Сила трения между этими двумя объектами показана парами сил: сила на напитке от подноса и пара третьего закона, сила на подносе от напитка. Инерция напитка такова, что он «хочет» оставаться в покое, но сила трения о поднос (вправо) и перемещение напитка (вправо) направлены в одну сторону.
В этой ситуации сила трения совершает положительную работу, F трение x .
Чтобы проанализировать эти проблемы, необходимо нарисовать хорошие диаграммы свободного тела!
- Я поднимаю яблоко массой 0,306 кг (3,00 Ньютона) на высоту 50 см с постоянной скоростью — какую работу я совершил?
- Какую работу совершила земная гравитация в предыдущей задаче?
- Какую работу я совершаю, опуская яблоко массой 3,00 Н на 50 см?
- Какую работу я совершаю, удерживая неподвижно в воздухе яблоко массой 3,00 Н?
- Какую работу я совершаю, перенося яблоко массой 3,00 Н на расстояние 50 см с постоянной скоростью?
Решение:
- Яблоко движется с постоянной скоростью вверх, поэтому результирующая сила, действующая на него, равна 0.
 Следовательно, прилагаемая мной сила равна силе тяжести, или 3,0 Н. Сила, которую я применяю, и перемещение направлены в одном направлении, поэтому:
Следовательно, прилагаемая мной сила равна силе тяжести, или 3,0 Н. Сила, которую я применяю, и перемещение направлены в одном направлении, поэтому: - Сила земного притяжения тянет в направлении, противоположном смещению, поэтому мы ожидаем, что Работа будет отрицательной, и так оно и есть:
- Это интересная проблема. Я опускаю яблоко с постоянной скоростью, которая включает в себя уравновешенные силы — земное притяжение тянет вниз с силой 3,0 Н, а я толкаю вверх с силой 3,0 Н — по мере того, как мяч движется вниз. Поскольку я поднимаю вверх на , а яблоко движется на вниз на , сила и перемещение действуют в противоположных направлениях. Основываясь на предыдущих расчетах, я совершаю над яблоком работу -1,5 Дж.
- Хотя я прикладываю силу 3,0 Н вверх, если нет смещения в направлении Силы, работа не совершается.
- Это действительно интересно: есть Сила вверх от моей руки, поддерживающей яблоко, но яблоко имеет боковое смещение.
 Работа, проделанная мной в этих условиях, равна:
Работа, проделанная мной в этих условиях, равна: Отличный вопрос, который можно задать: «Подожди, ты не прикладываешь немного силы, чтобы сдвинуть яблоко вбок?» И это правда, если бы яблоко с самого начала не двигалось, а мы хотели, чтобы оно двигалось боком, нам пришлось бы приложить результирующую силу вбок, чтобы заставить его двигаться. За этот короткий промежуток времени мы — это , выполняющие Работу над яблоком, но как только оно движется вбок, его инерция увлекает его за собой. Единственная сила, которую мы должны продолжать прикладывать, направлена вверх против гравитации, и эта направленная вверх сила, как мы определили, не совершает работы над яблоком.
Понятие -вектора встречается, конечно, в физике, но оно существует и в математике, и в информатике. Применение векторов в каждой области немного различается, но принципы одинаковы.
Мы собираемся расширить наше определение Работы, включив в него математическое определение одного из видов векторного умножения, называемого скалярным произведением.
7.2.1. Определение скалярного произведения
Мы уже видели, как скалярная величина, умноженная на вектор, дает новый вектор, указывающий в том же направлении, но с величиной, измененной на величину скаляра. 3 i , например, является единичным вектором i , но с величиной 3.
Если вместо скаляра и вектора у вас есть два вектора, есть два полезных способа перемножить их вместе, и мы мы будем использовать оба из них в этом курсе. Первый способ умножить два вектора — использовать скалярное произведение:
“Скалярный продукт”, обозначенный точкой достаточно точно, является мерой того, насколько параллельны два вектора, и легко рассчитывается следующим образом (используя в качестве примера двумерные x-y векторов):
It можно показать (хотя мы этого здесь не делаем), что скалярное произведение равно ABcosθ … это формула, которую мы используем для вычисления Work! Следовательно:
Если вам нужно рассчитать выполненную работу, а F и x были даны вам в i, j , вы можете использовать скалярное произведение, чтобы легко решить эту проблему.
Если вектор A = 3 i + 5 j и вектор B = -1 i + 2 j :
- 9 :
- 9001 начало координат, (0, 0).
- Что такое скалярное произведение A • B ?
- Чему равен угол между векторами А и В ?
Решение:
На объект действует сила 4 i + -3 j Ньютонов, которая перемещает его на 10 i + 3 j метров. Какую работу совершила сила без объекта?
Решение:
Для такой теоретической задачи достаточно просто применить процесс скалярного произведения для вычисления проделанной работы.
Помните, что скалярное произведение дает скалярный результат — результат не связан с направлением, даже если в процессе мы перемножаем векторы.
До этого момента мы рассматривали работу, совершаемую постоянной силой, Силой, приложенной , или силой земного притяжения . Существует множество ситуаций, в которых сила изменяется в зависимости от положения: резиновая лента, например, тем сильнее тянет назад, чем больше вы ее растягиваете.
Существует множество ситуаций, в которых сила изменяется в зависимости от положения: резиновая лента, например, тем сильнее тянет назад, чем больше вы ее растягиваете.
Если вы пытаетесь найти работу, совершаемую «средней силой, равной некоторому числу ньютонов…», простое уравнение работает нормально. Если Сила меняется в зависимости от положения, вам нужно будет произвести расчет.
Небольшое количество Работы, выполненной Силой, приложенной к небольшому перемещению:
Общее количество Работы, выполненной Силой, которая изменяется в зависимости от смещения:
7.3.1. Два способа определения работы, выполняемой переменной силой
Если сила переменная, у нас есть две общие стратегии для определения того, сколько работы совершается при некотором перемещении:
- Используйте график зависимости силы от смещения для определения области под кривой
Здесь ширина каждой колонны составляет 1 метр, а количество Работы, проделанной Силой во время этого смещения, равно просто высоте колонны (F), умноженной на ширину колонны (1 метр).
 Общая проделанная работа — это, конечно же, общая площадь под кривой.
Общая проделанная работа — это, конечно же, общая площадь под кривой. - Использовать заданную функцию F(x) и интегрировать относительно x .
Если у вас есть функция силы F как функция положения, вы можете выполнить интегрирование по интервалу x начальный до x окончательный для определения общего объема выполненной работы.
Давайте посмотрим, как использовать каждую из этих стратегий.
Используя приведенный выше график, определите общую работу, выполненную силой при перемещении массы от 0 до 10 м по оси x.
Решение:
Сложите квадраты площади под кривой от 0 до 10 м, чтобы получить общую работу 22,5 Дж.
7.3.2. Закон Гука
Как упоминалось выше, резиновая лента или пружина являются хорошим примером устройства, которое прикладывает различное усилие в зависимости от того, насколько сильно оно растянуто. Идеальная пружина соответствует «закону Гука».
Идеальная пружина соответствует «закону Гука».
Закон Гука описывает поведение некоторых пружин в ограниченном диапазоне условий, в которых сила, приложенная пружиной (растянутой или сжатой), линейно пропорциональна ее смещению и направлена в противоположную сторону.
Значение k называется «постоянной пружины» и описывает силу на метр, необходимую для сжатия или растяжения пружины.
Груз массой 100 грамм прикрепляют к одному концу висящей пружины и медленно отпускают, так что она останавливается, растягивая пружину на 50 сантиметров. Рассчитайте жесткость пружины.
Решение:
После того, как масса была прикреплена и помещена в положение, в котором она находится в состоянии покоя, сила земного притяжения, притягивающая массу, и сила пружины, тянущая ее вверх, равны друг другу. . Зная Силу, которую прикладывает пружина и растяжение x пружины мы можем вычислить:
7.3.3. Интегрирование F(x) с системой масса-пружина
По мере развития некоторых из этих идей мы будем использовать эту ситуацию в качестве нашего контекста: масса, покоящаяся на гладкой (без трения) горизонтальной поверхности, с одним концом прикрепленной пружины к якорю на одном конце.
Определения:
- положение равновесия – положение x 0 , при котором на массу не действует результирующая сила
- х мин – положение, при котором пружина максимально сжата, на расстоянии А от положения равновесия
- x max – положение, при котором пружина максимально растянута, на расстоянии А от положения равновесия
Брусок массой m прикреплен к пружине с жесткостью k и расположен горизонтально на поверхности без трения, причем пружина закреплена на одном конце. Пружина сжимается от положения равновесия на расстояние x , а затем выпущен. Какую работу совершит пружина, чтобы вернуть брусок в положение равновесия?
Решение:
Это важное решение, которое вы должны хорошо понимать, прежде чем двигаться дальше.
Возьмем определение интеграла работы и подставим – kx из закона Гука, а затем оценим интеграл, интегрируя по отношению к x .
Это количество работы, которую совершает пружина, возвращая массу в положение равновесия.
Продолжая задачу выше, если бы мы сжали пружину вдвое сильнее (2 x ), какую работу совершила бы пружина (по сравнению с предыдущим ответом), чтобы вернуть массу в положение равновесия?
Решение:
Учитывая, что x 2 член в предыдущем результате, мы можем ожидать, что проделанная работа увеличится в 2 2 , что даст нам «четырехкратное увеличение работы» в качестве ответа. Решите задачу еще раз с пределами 0 и 2 x , чтобы убедиться, что это правильно. 🙂
Если сила F меняется в задаче, мы не можем использовать нашу кинематику с постоянным ускорением для анализа движения… но мы можем использовать концепцию Работы.
Взгляните на этот важный вывод, в котором используются два важных уравнения — второй закон движения Ньютона и рабочий интеграл — для получения новой зависимости.
Давайте начнем с определения Работы и 2-го закона Ньютона:
Здесь у нас небольшая проблема: м постоянно, но ускорение и меняется, поэтому нам нужно интегрировать. .. но мы не можем интегрировать и по отношению к x . Давайте воспользуемся цепным правилом, чтобы преобразовать в во что-то другое:
.. но мы не можем интегрировать и по отношению к x . Давайте воспользуемся цепным правилом, чтобы преобразовать в во что-то другое:
Подставив обратно в интеграл…
Здесь у нас есть пара dx выражений. Мы интегрируем по x , а также дифференцируем по x . Эти две операции обратны друг другу, поэтому они эффективно компенсируют друг друга.
Так как теперь мы интегрируем по скорости v , мы должны изменить наши ограничения. В позиции x i у нас есть скорость v i , а в конечном x у нас было окончательное v . Наконец, вычислите интеграл.
Это уравнение показывает, что сила, совершающая работу над движущейся массой, изменит скорость этой массы.
7.4.1. Определение кинетической энергии
Вы можете узнать выражение . Это выражение так часто встречается в наших расчетах, что у него есть собственная «быстрая» переменная, К .
Выражение называется «кинетической энергией массы» и представлено переменной K .
Три полоски в знаке «равно» означают, что выражение «K» определено как . Эти два выражения эквивалентны друг другу.
Таким образом, работа, вызывающая изменение кинетической энергии, может быть записана несколькими способами:
Напомним, что выполненная работа может быть положительной или отрицательной. Положительная работа увеличивает кинетическую энергию объекта, а отрицательная работа уменьшает кинетическую энергию объекта.
7.4.2. Решение некоторых задач работы-энергии
Массу 6,00 кг, находящуюся в состоянии покоя, тянут с постоянной горизонтальной силой 12,0 Н на расстояние 3,00 м, ускоряя массу по поверхности без трения. Найдите конечную скорость блока, используя две разные стратегии.
- Стратегия 1: Рассчитайте ускорение массы, а затем используйте кинематику, чтобы найти конечную скорость блока после того, как он пройдет 3,00 м.

- Стратегия 2: Рассчитайте работу, совершаемую массой блока, а затем используйте теорему о работе и энергии, чтобы найти конечную скорость блока.
Решение:
Решение:
Какая стратегия кажется вам более удобной при решении этой проблемы? Какая стратегия лучше адаптируется к различным ситуациям?
Дротик загружается в винтовку Nerf с пружинным приводом, вдавливая пружину на расстояние d . Для следующего нагружения пружина сжимается на расстояние 2 d . Насколько быстрее второй дротик вылетит из ружья по сравнению с первым?
Решение:
Стратегия: найти работу, которую пружина совершает над дротиком, чтобы изменить его кинетическую энергию.
Таким образом, двойное сжатие x подразумевает, что скорость дротика, вылетающего из пистолета, будет в два раза больше исходной скорости.
Мощность в физике означает скорость выполнения Работы. Если сила выполняет некоторую Работу, то чем быстрее выполняется работа, тем больше Энергии необходимо для выполнения этой Работы.
Если сила выполняет некоторую Работу, то чем быстрее выполняется работа, тем больше Энергии необходимо для выполнения этой Работы.
Если сила совершает работу в течение некоторого периода времени, мы можем рассчитать среднюю мощность, необходимую для выполнения этой работы. Если у нас есть функция, основанная на времени, для выполняемой Работы, мы также можем рассчитать мгновенную Силу, используемую для выполнения этой работы.
Единицы мощности: Вт , где 1 Вт = 1 Джоуль/1 секунда.
Интересным результатом этого является то, что мы можем вычислить мгновенную мощность, используемую силой, если мы знаем силу и скорость движущегося объекта.
На свадебном торжестве жених сидит в кресле, а его друзья поднимаются против силы тяжести, используя силу 800 ньютонов, чтобы поднять его на 2,0 метра в воздух. Им потребовалось около 4 секунд, чтобы поднять его.
- Сколько Работы потребовалось, чтобы поднять жениха и стул в воздух?
- Сколько средней мощности было использовано при подъеме?
Решение:
- Мы можем рассчитать работу, проделанную друзьями, как простой расчет сила-время-расстояние.
 Верно, что друзьям приходится ускорять стул, когда они только начинают подниматься, но затем они замедляют его в конце, когда жених достигает верхней высоты — таким образом, результирующая сила, прилагаемая ими во время подъема, составляет 800 Н, а Суммарная работа во время подъема составляет:
Верно, что друзьям приходится ускорять стул, когда они только начинают подниматься, но затем они замедляют его в конце, когда жених достигает верхней высоты — таким образом, результирующая сила, прилагаемая ими во время подъема, составляет 800 Н, а Суммарная работа во время подъема составляет: - Чтобы рассчитать среднюю мощность, используйте заданное время вместе с только что рассчитанной работой:
На том же свадебном торжестве тот же жених сидит на том же стуле, и его друзья поднимаются против силы тяжести, используя силу 800 ньютонов, чтобы поднять его на 2,0 метра в воздух. Друзьям требуется всего 1 секунда, чтобы поднять его.
- Сколько Работы потребовалось, чтобы на этот раз поднять жениха и стул в воздух?
- Сколько средней мощности было использовано при подъеме?
Решение:
- Хотя на этот раз Работа выполняется быстрее, фактический объем Работы такой же, как и раньше:
- Однако, поскольку работа была выполнена в четыре раза быстрее, мы ожидаем, что используемая Сила будет в четыре раза больше, и это оказывается правдой:
Лифт массой 1000 кг несет груз массой 800 кг. Сила трения 4000 Н задерживает движение лифта вверх по мере его движения вверх
Сила трения 4000 Н задерживает движение лифта вверх по мере его движения вверх
- Найдите минимальную мощность, необходимую для подъема лифта с постоянной скоростью 3,00 м/с.
- Если двигатель должен иметь коэффициент безопасности 3:1, какой должна быть номинальная мощность двигателя в лошадиных силах? (746 Вт = 1 л.с.)
- Какую мощность должен развивать двигатель в любой момент (в зависимости от v ), если он предназначен для обеспечения ускорения 1,00 м/с 2 ?
Решение:
- Как мы видели, есть два способа рассчитать мощность. В этом случае удобнее формула P = Fv .
- Коэффициент безопасности три к одному означает, что нам нужен двигатель в три раза мощнее, чем мы думаем.
- Мощность как функция против ? Поскольку P = Fv , они на самом деле просто просят нас рассчитать F Натяжение в этих новых условиях.

формула проделанной работы, определение, расчет, примеры
(1) Введение в Work Done
- В повседневной жизни мы используем такие термины, как работа и энергия.
- Термин «работа» обычно используется в контексте любого вида деятельности, требующей физических или умственных усилий.
- Но это не то, как мы определяем работу в физике.
- Когда мы толкаем или тянем тяжелый груз или поднимаем его над полом, мы выполняем работу, но человек, несущий тяжелый груз и стоящий на месте, не выполняет никакой работы согласно научному определению работы.
- Еще один термин, который мы часто используем, — энергия. Энергия обычно ассоциируется с проделанной работой в том смысле, что человек, чувствующий себя очень энергичным, способен выполнять много работы.
- Таким образом, энергия определяется как способность совершать работу.
- Существует множество форм энергии, таких как химическая энергия, механическая энергия, электрическая энергия, тепловая энергия и т.
 д. Эти формы энергии можно использовать по-разному.
д. Эти формы энергии можно использовать по-разному. - Одна форма энергии может быть преобразована в другую форму энергии.
- В этой главе мы будем изучать работу, связь между работой и энергией, сохранение энергии и т. д.
(2) Выполненная работа Определение и формула
- Мы уже знаем, что работа считается выполненной, когда Сила производит движение.
- Выполненная работа определяется таким образом, что она включает в себя как силу, приложенную к телу, так и перемещение тела.
- Рассмотрим блок, размещенный на горизонтальном полу без трения. На этот блок действует постоянная сила F . Действие этой силы заключается в перемещении тела на расстояние d по прямой линии в направлении действия силы.
- Теперь работа, совершаемая этой силой, равна произведению величины приложенной силы на расстояние, на которое перемещается тело. Математически выполненная формула работы будет иметь вид 9.
 0597 $W=Fd$ —-(1)
0597 $W=Fd$ —-(1)
где, F=| Ф | - Рассмотрим приведенный ниже рисунок
- В этом случае сила, действующая на блок, постоянна, но направление силы и направление смещения, вызванного этой силой, различны. Здесь сила F действует под углом θ к перемещению d
- Действующая составляющая силы вдоль направления перемещения Fcosθ и эта составляющая силы отвечает за перемещение блока в заданном направлении.
- Таким образом, работа силы F in при перемещении тела на перемещение d равна
W=(| F |cosθ)| д | (2)
В уравнении 2 выполненная работа определяется как произведение величины смещения d и составляющей силы в направлении смещения. - Мы знаем, что скалярное произведение двух векторов A и B , где A образует угол θ с B определяется как
A . Б =| А | | B |cosθ
- Сравнивая уравнение 2 с определением скалярных произведений, формулу выполненной работы можно записать как
W= F . d (3)
d (3) - Теперь рассмотрим два частных случая:-
(i) Когда угол θ=0, т. е. сила направлена в том же направлении, что и перемещение, тогда из уравнения (2)
W=| Ф | | д |
это тот же результат, что и в уравнении 1
(ii), когда угол θ=90, т.е. направление силы перпендикулярно направлению смещения, тогда из уравнения (2)
W=(| F |cos90)| d |=0
то есть приложенная сила не имеет составляющей вдоль смещения и, следовательно, сила не совершает никакой работы над телом. - Работа, совершаемая силой над телом, может быть положительной, отрицательной и равной нулю, т. е.
(а) Совершенная работа положительна: сила направлена в том же направлении, что и перемещение, например, работа, совершаемая силой при толкании блока массы м
(b) Совершенная работа отрицательна:- Сила противоположна смещению, например, когда тело скользит по горизонтальной поверхности, работа, совершаемая силами трения на теле, отрицательна, так как сила трения всегда действует противоположно смещению тела.
(c) Совершенная работа равна нулю:- Сила направлена под прямым углом к перемещению, например работа центростремительной силы на тело, движущееся по окружности. - Единица выполненной работы в любой системе единиц равна единице силы, умноженной на единицу расстояния. В системе СИ единицей работы является 1 Нм, и она называется Джоуль (Дж). Таким образом,
1Дж=1Нм
В системе СГС единицей измерения является эрг
1эрг=1 дин-см
и 1 эрг=10 -7 Дж - Если на тело действует более одной силы, то необходимо рассчитать работу, совершенную каждой силой отдельно и сложены вместе.
$W=W_1 + W_2 + W_3 $
Решено Примеры расчета выполненной работы
NCERT Упражнение 2.15 | Единицы и измерения Класс 11 Физика
Пример-1Сила 10 Н действует на расстоянии 10 м в направлении действия силы. Вычислите работу, совершаемую силой?
Решение
Здесь сила и перемещение происходят в одном и том же направлении.
 Таким образом, используя формулу для выполненной работы, работа, выполненная силой, рассчитывается как
Таким образом, используя формулу для выполненной работы, работа, выполненная силой, рассчитывается как Пример-2
Ящик тянут по полу за веревку, которая образует с горизонтом угол 30°. Сила, приложенная к веревке, равна 100 Н, а ящик протащили на 10 м. Вычислите работу, совершенную этой силой?
Решение
Здесь Сила и перемещение находятся под углом 60°. Итак, работа, совершенная силой
$W= F \times d cos \theta = 100 \times 10 \times .5 = 500 J$
Пример-3
Мальчик толкает машинку из состояния покоя на гладком горизонтальном полу с направленной силой 10 Н под углом 60° от горизонтали. Масса игрушечной машинки 5 кг. Определите работу, которую совершил мальчик за 5 с?
Решение
Прежде всего, мы можем разделить силу на горизонтальную и вертикальную составляющие
Горизонтальная составляющая =10 * cos 60 =5 Н
Вертикальная составляющая =10 * sin 60 =8,66 Н 92 = 12,5 м$
Таким образом, работа выполнена по формуле работы
$ W = F \times d = 5 \times 12,5 = 62,5 J $

 Следовательно, прилагаемая мной сила равна силе тяжести, или 3,0 Н. Сила, которую я применяю, и перемещение направлены в одном направлении, поэтому:
Следовательно, прилагаемая мной сила равна силе тяжести, или 3,0 Н. Сила, которую я применяю, и перемещение направлены в одном направлении, поэтому:  Работа, проделанная мной в этих условиях, равна:
Работа, проделанная мной в этих условиях, равна:  Общая проделанная работа — это, конечно же, общая площадь под кривой.
Общая проделанная работа — это, конечно же, общая площадь под кривой.
 Верно, что друзьям приходится ускорять стул, когда они только начинают подниматься, но затем они замедляют его в конце, когда жених достигает верхней высоты — таким образом, результирующая сила, прилагаемая ими во время подъема, составляет 800 Н, а Суммарная работа во время подъема составляет:
Верно, что друзьям приходится ускорять стул, когда они только начинают подниматься, но затем они замедляют его в конце, когда жених достигает верхней высоты — таким образом, результирующая сила, прилагаемая ими во время подъема, составляет 800 Н, а Суммарная работа во время подъема составляет:
 д. Эти формы энергии можно использовать по-разному.
д. Эти формы энергии можно использовать по-разному.  0597 $W=Fd$ —-(1)
0597 $W=Fd$ —-(1)  d (3)
d (3) 