Электротехника: Резонансная частота.
Резонансная частота.
Параллельный колебательный контур (рисунок 1) или последовательный колебательный контур (рисунок 2) могут использоваться в генераторах синусоидальных колебаний. Если в одной из этих схем зарядить конденсатор то он будет разряжаться заряжая катушку индуктивности, катушка разряжаясь будет заряжать конденсатор, этот процесс будет повторяться с определённым периодом T. Период это время одного колебания. Частота колебаний это величина обратная периоду. Разделив единицу на численное значение периода получим численное значение частоты.
Рисунок 1 – Параллельный колебательный контур
Рисунок 2 – Последовательный колебательный контур
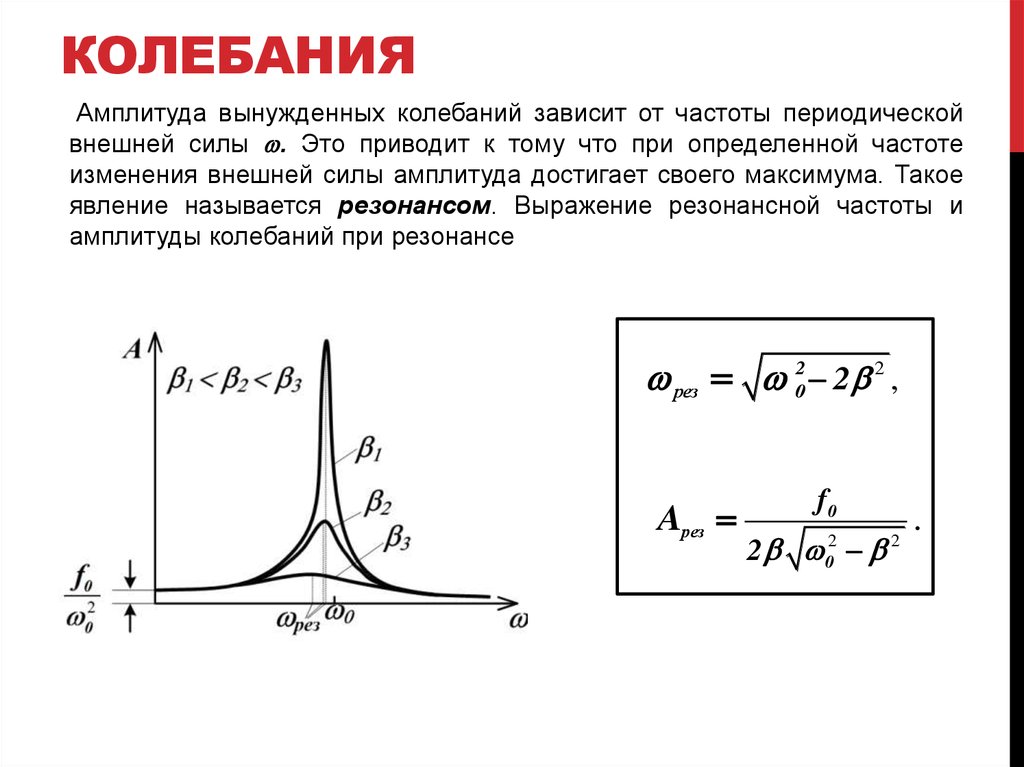
Частота возникших колебаний называется собственной частотой колебаний контура для контуров изображённых на рисунках выше эта частота равна резонансной частоте этих контуров.
Резонансная частота контура зависит от индуктивности L и ёмкости C её элементов, для колебательного контура (последовательного или параллельного) её можно найти по формуле:
Где L-индуктивность катушки контура, C-ёмкость конденсатора контура.
Если на параллельный или последовательный колебательный контур подавать переменное синусоидальное напряжение и изменять его частоту то будут меняться реактивные сопротивления элементов контура, если частота увеличивается то сопротивление конденсатора уменьшается а сопротивление катушки увеличивается и наоборот: если частота уменьшается то сопротивление конденсатора увеличивается а сопротивление катушки уменьшается, очевидно что есть такая частота при которой сопротивление катушки и конденсатора равны эта частота и есть резонансная. Сопротивление параллельного колебательного контура при этой частоте будет наибольшим (по сравнению с сопротивлениями этого контура при других частотах) а сопротивление последовательного колебательного контура при такой частоте будет наименьшим.
Для расчёта резонансной частоты и периода колебаний колебательного контура с катушкой и конденсатором можно воспользоваться программой:
Индуктивность L=ГнмГнмкГннГн
Резонансная частота f=ГцкГцМГц
Период колебаний T=смсмкс
Следующее Предыдущее Главная страница
Подписаться на: Комментарии к сообщению (Atom)
Последовательный колебательный контур – Резонанс напряжений
Последовательный колебательный контур обозначение на схеме
Последовательный колебательный контур — это цепь, состоящая их катушки индуктивности и конденсатора, которые соединяются последовательно.
Идеальный последовательный колебательный контур
На схемах идеальный последовательный колебательный контур обозначается вот так:
где
L — индуктивность, Гн
С — емкость, Ф
Реальный последовательный колебательный контур
Реальный колебательный контур имеет сопротивление потерь катушки и конденсатора.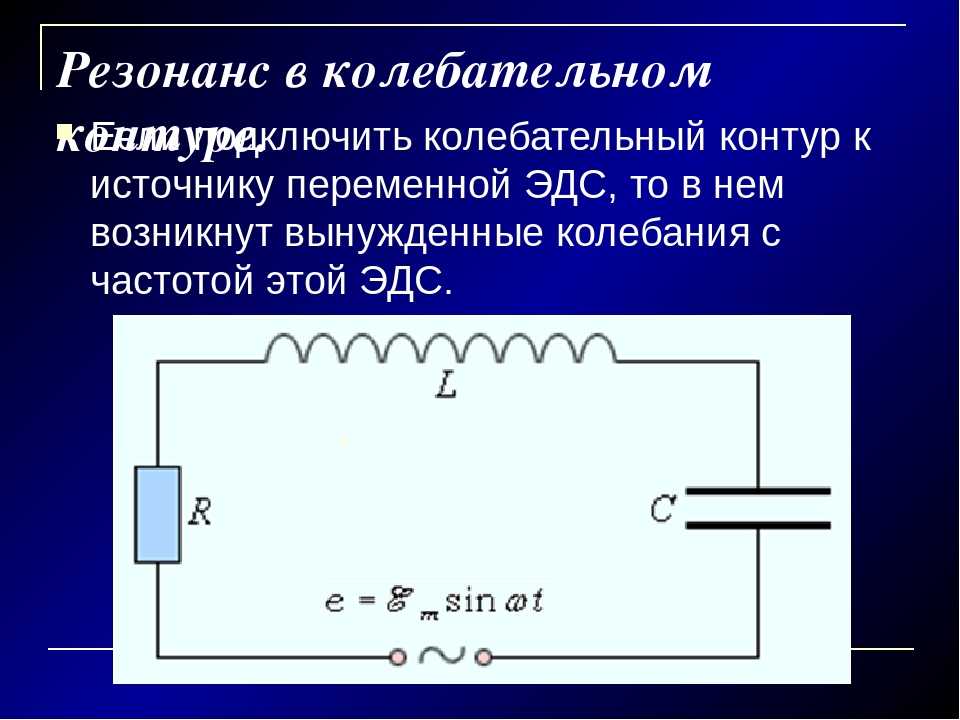
Это суммарное суммарное сопротивление потерь обозначается буквой R. В результате, реальный последовательный колебательный контур будет иметь такой вид:
R — это суммарное сопротивление потерь катушки и конденсатора
L — собственно сама индуктивность катушки
С — собственно сама емкость конденсатора
Принцип работы последовательного колебательного контура
Генератор частоты и последовательный колебательный контур
Давайте проведем классический эксперимент, который есть в каждом учебнике по электронике. Для этого соберем вот такую схему:
Генератор (Ген)у нас будет выдавать синус.
Для того, чтобы снять осциллограмму силы тока через последовательный колебательный контур, мы подключим в схему шунтовый резистор с малым сопротивлением в 0,5 Ом и с него уже будем снимать напряжение. То есть в данном случае мы шунт используем для наблюдения силы тока в цепи.
А вот и сама схема в реальности:
Слева-направо: шунтовый резистор, катушка индуктивности и конденсатор.
Как вы уже поняли, сопротивление R — это суммарное сопротивление потерь катушки и конденсатора, так как нет идеальных радиоэлементов. Оно «прячется» внутри катушки и конденсатора, поэтому в реальной схеме отдельным радиоэлементом мы его не увидим.
Теперь нам осталось подцепить эту схему к генератору частоты и осциллографу, и прогнать по некоторым частотам, снимая осциллограмму с шунта Uш , а также снимая осциллограмму с самого генератора UГЕН.
С шунта мы будем снимать напряжение, которое у нас отображает поведение силы тока в цепи, а с генератора собственно сам сигнал генератора. Давайте прогоним нашу схемку по некоторым частотам и глянем что есть что.
Влияние частоты генератора на сопротивление колебательного контура
В схеме я взял конденсатор на 1мкФ и катушку индуктивности на 1 мГн. На генераторе настраиваю синус размахом в 4 Вольта. Вспоминаем правило: если в цепи соединение радиоэлементов идет последовательно друг за другом, значит, через них течет одинаковая сила тока.
Красная осциллограмма — это напряжение с генератора частоты, а желтая осциллограмма — отображение силы тока через напряжение на шунтовом резисторе.
Частота 200 Герц с копейками:
Как мы видим, при такой частоте ток в этой цепи есть, но очень слабый
Добавляем частоту. 600 Герц с копейками
Здесь мы уже отчетливо видим, что сила тока возросла, а также видим, что осциллограмма силы тока опережает напряжение. Попахивает реактивным сопротивлением конденсатора.
Добавляем частоту. 2 Килогерца
Сила тока стала еще больше.
3 Килогерца
Сила тока увеличилась. Заметьте также, что сдвиг фаз стал уменьшаться.
4,25 Килогерц
Осциллограммы почти уже сливаются в одну. Сдвиг фаз между напряжением и силой тока становится почти незаметным.
И вот на какой-то частоте у нас сила тока стала максимальной, а сдвиг фаз стал равен нулю. Запомните этот момент. Для нас он будет очень важен.
Ну а давайте далее будем увеличивать частоту.
Смотрим, что получается в итоге.
Еще совсем недавно ток опережал напряжение, а сейчас уже стал запаздывать после того, как выровнялся с ним по фазе. Так как ток уже отстает от напряжения, здесь уже попахивает реактивным сопротивлением катушки индуктивности.
Увеличиваем частоту еще больше
Сила тока начинает падать, а сдвиг фаз увеличивается.
22 Килогерца
74 Килогерца
Как вы видите, с увеличением частоты, сдвиг приближается к 90 градусов, а сила тока становится все меньше и меньше.
Резонанс последовательного колебательного контура
Давайте подробнее рассмотрим тот самый момент, когда сдвиг фаз был равен нулю и сила тока, проходящая через последовательный колебательный, контур была максимальна:
Это явление носит название резонанса.
Не будем углубляться в теорию высшей математики и комплексных чисел. Дело в том, что в этот самый момент реактивное сопротивление катушки и конденсатора становятся равными, но противоположными по знаку.
Поэтому, эти реактивные сопротивления как-бы вычитаются друг из друга, что в сумме дает ноль, и в цепи остается только активная составляющая сопротивления, то есть то самое паразитное сопротивление катушки и конденсатора, или иначе, сопротивление потерь R.
Как вы помните, если у нас сопротивление становится малым, а в данном случае сопротивления потерь катушки и конденсатора очень маленькие, то в цепи начинает течь большая сила тока согласно закону Ома: I=U/R. Если генератор мощный, то напряжение на нем не меняется, а сопротивление становится пренебрежимо малым и вуаля! Ток растет как грибы после дождя, что мы и увидели, посмотрев на желтую осциллограмму при резонансе.
Формула Томсона (резонанса) для последовательного колебательного контура
Если при резонансе у нас реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора XL=XC , то можно уравнять их реактивные сопротивления и уже отсюда вычислить частоту, на которой произошел резонанс.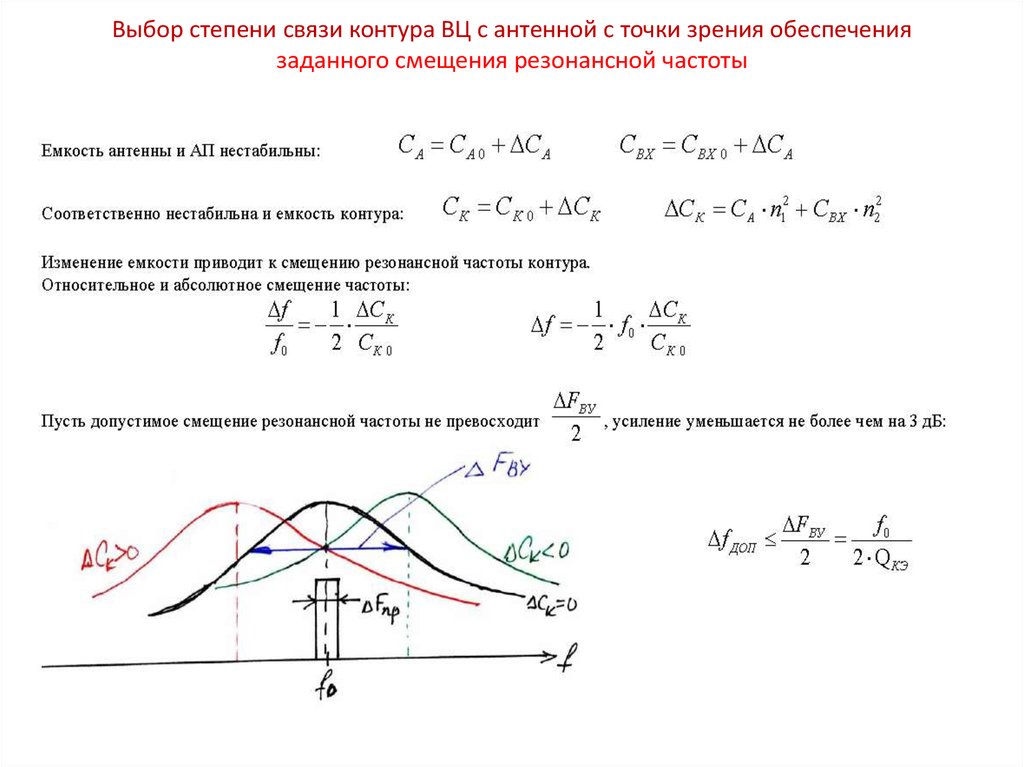
Итак, реактивное сопротивление катушки у нас выражается формулой:
Реактивное сопротивление конденсатора вычисляется по формуле:
Приравниваем обе части и вычисляем отсюда F:
В данном случае мы получили формулу резонансной частоты. Это формула по другому называется формулой Томсона, как вы поняли, в честь ученого, который ее вывел.
Давайте по формуле Томсона посчитаем резонансную частоту нашего последовательного колебательного контура. Для этого я буду использовать свой RLC-транзисторметр.
Замеряем индуктивность катушки:
И замеряем нашу емкость:
Высчитываем по формуле нашу резонансную частоту:
У меня получилось 5, 09 Килогерц.
С помощью регулировки частоты и осциллографа я поймал резонанс на частоте 4,78 Килогерц (написано в нижнем левом углу)
Спишем погрешность в 200 с копейками Герц на погрешность измерений приборов.
Как вы видите, формула Томпсона работает.
Резонанс напряжений
Давайте возьмем другие параметры катушки и конденсатора и посмотрим, что у нас происходит на самих радиоэлементах. Нам ведь надо досконально все выяснить ;-). Беру катушку индуктивности с индуктивностью в 22 микрогенри:
и конденсатор в 1000 пФ
Из них собираю последовательный колебательный контур. Итак, чтобы поймать резонанс, я не буду в схему добавлять резистор. Поступлю более хитрее.
Так как мой генератор частоты китайский и маломощный, то при резонансе у нас в цепи остается только активное сопротивление потерь R. В сумме получается все равно маленькое значение сопротивления, поэтому ток при резонансе достигает максимальных значений. В результате этого, на внутреннем сопротивлении генератора частоты падает приличное напряжение и выдаваемая амплитуда частоты генератора падает. Я буду ловить минимальное значение этой амплитуды. Следовательно это и будет резонанс колебательного контура.
Перегружать генератор — это не есть хорошо, но что не сделаешь ради науки!
Ну что же, приступим ;-). Давайте сначала посчитаем резонансную частоту по формуле Томсона. Для этого я открываю онлайн калькулятор на просторах интернета и быстренько высчитываю эту частоту. У меня получилось 1,073 Мегагерц.
Ловлю резонанс на генераторе частоты по его минимальным значениям амплитуды. Получилось как-то вот так:
Размах амплитуды 4 Вольта
Хотя на генераторе частоты размах более 17 Вольт! Вот так вот сильно просело напряжение. И как видите, резонансная частота получилась чуток другая, чем расчетная: 1,109 Мегагерц.
Теперь небольшой прикол 😉
Вот этот сигнал мы подаем на наш последовательный колебательный контур:
Как видите, мой генератор не в силах выдать большую силу тока в колебательный контур на резонансной частоте, поэтому сигнал получился даже чуть искаженным на пиках.
Ну а теперь самое интересное. Давайте замеряем падение напряжения на конденсаторе и катушке на резонансной частоте.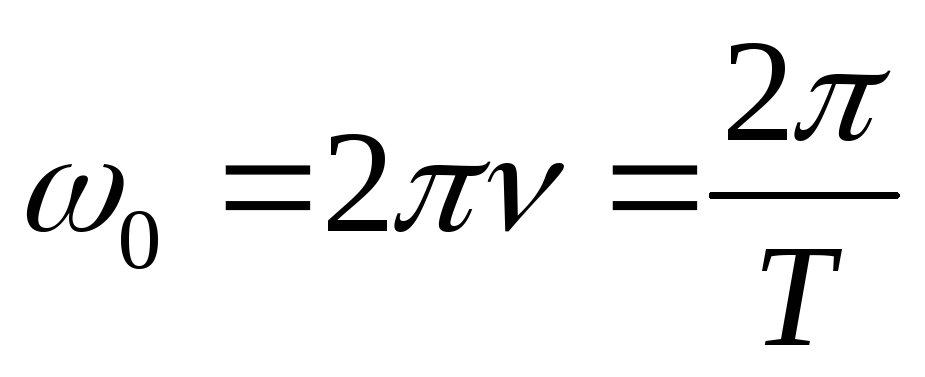
То есть это будет выглядеть вот так:
Смотрим напряжение на конденсаторе:
Размах амплитуды 20 Вольт (5х4)! Откуда? Ведь подавали мы на колебательный контур синус с частотой в 2 Вольта!
Ладно, может с осциллографом что-то произошло?. Давайте замеряем напряжение на катушке:
Народ! Халява!!! Подали 2 Вольта с генератора, а получили 20 Вольт и на катушке и на конденсаторе! Выигрыш энергии в 10 раз! Успевай только снимать энергию с конденсатора или с катушки!
Ну ладно раз такое дело… беру лампочку от мопеда на 12 Вольт и цепляю ее к конденсатору или катушке. Лампочке ведь вроде как по-барабану на какой частоте работать и какой ток кушать. Выставляю амплитуду, чтобы на катушке или конденсаторе было где то Вольт 20 так как среднеквадратичное напряжение будет где-то Вольт 14, и цепляю поочередно к ним лампочку:
Как видите — полный ноль. Лампочка гореть не собирается, так что побрейтесь фанаты халявной энергии).
Вы ведь не забыли, что мощность определяется произведением силы тока на напряжение? Напряжения вроде как-бы хватает, а вот силы тока — увы! Поэтому, последовательный колебательный контур носит также название узкополосного (резонансного) усилителя напряжения, а не мощности!
Объяснение резонанса напряжения
При резонансе напряжение на катушке и на конденсаторе оказались намного больше, чем то, которое мы подавали на колебательный контур. В данном случае у нас получилось в 10 раз больше. Почему же напряжение на катушке при резонансе равняется напряжению на конденсаторе. Это легко объясняется. Так как в последовательном колебательном контуре катушка и кондер идут друг за другом, следовательно, в цепи протекает одна и та же сила тока.
При резонансе реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора. Получаем по правилу шунта, что на катушке у нас падает напряжение UL = IXL , а на конденсаторе UC = IXC .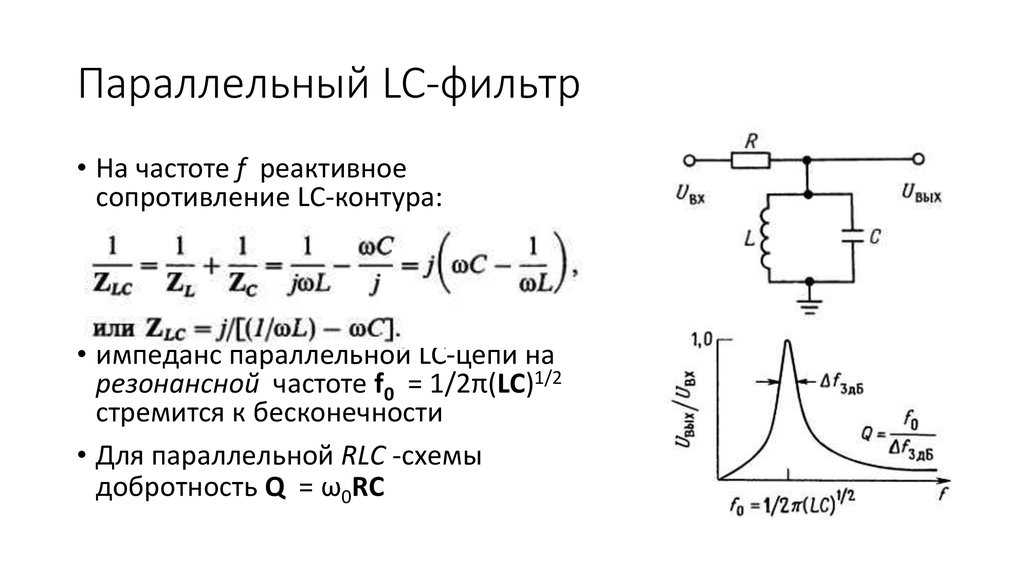
А так как при резонансе у нас XL = XC , то получаем что UL = UC , ток ведь в цепи один и тот же ;-). Поэтому резонанс в последовательном колебательном контуре называют также резонансом напряжений, так как напряжение на катушке на резонансной частоте равняется напряжению на конденсаторе.
Добротность последовательного колебательного контура
Ну раз уж мы начали задвигать тему колебательных контуров, поэтому мы не можем обойти стороной такой параметр, как добротность колебательного контура. Так как мы уже провели некоторые опыты, то нам будет проще определить добротность, исходя из амплитуды напряжений. Добротность обозначается буквой Q и вычисляется по первой простой формуле:
Давайте посчитаем добротность в нашем случае.
Так как цена деления одного квадратика по вертикали 2 Вольта, следовательно, амплитуда сигнала генератора частоты 2 Вольта.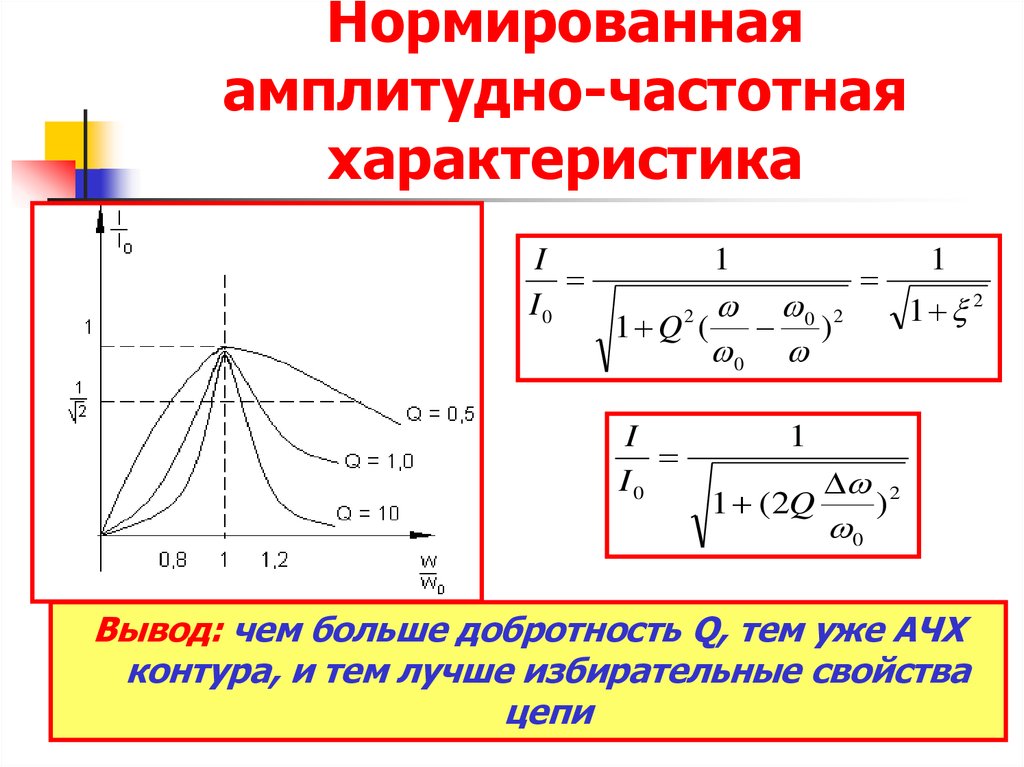
А это то, что мы имеем на зажимах конденсатора или катушки. Здесь цена деления одного квадратика по вертикали 5 Вольт. Считаем квадратики и умножаем. 5х4=20 Вольт.
Считаем по формуле добротности:
Q=20/2=10. В принципе немного и не мало. Пойдет. Вот так вот на практике можно найти добротность.
Есть также вторая формула для вычисления добротности.
где
R — сопротивление потерь в контуре, Ом
L — индуктивность, Генри
С — емкость, Фарад
Зная добротность, можно легко найти сопротивление потерь R последовательного колебательного контура.
Также хочу добавить пару слов о добротности. Добротность контура — это качественный показатель колебательного контура. В основном его стараются всегда увеличить различными всевозможными способами. Если взглянуть на формулу выше, то можно понять, для того, чтобы увеличить добротность, нам надо как-то уменьшить сопротивление потерь колебательного контура.
Львиная доля потерь относится к катушке индуктивности, так как она уже конструктивно имеет большие потери. Она намотана из провода и в большинстве случаев имеет сердечник. На высоких частотах в проводе начинает проявляться скин-эффект, который еще больше вносит потери в контур.
Видео на тему «Как работает колебательный контур. Резонанс»:
Резюме
Последовательный колебательный контур состоит из катушки индуктивности и конденсатора, соединенных последовательно.
Катушка и конденсатор имеют паразитные омические потери, так как не являются идеальными радиоэлементами. Сумма этих потерь называется сопротивлением потерь R последовательного колебательного контура.
На какой-то частоте реактивное сопротивление катушки становится равным реактивному сопротивлению конденсатора и в цепи последовательного колебательного контура наступает такое явление, как резонанс.
При резонансе реактивные сопротивления катушки и конденсатора хоть и равны по модулю, но противоположны по знаку, поэтому они вычитается и в сумме дают ноль. В цепи остается только активное сопротивление потерь R.
При резонансе сила тока в цепи становится максимальной, так как сопротивление потерь катушки и конденсатора R в сумме дают малое значение.
При резонансе напряжение на катушке равняется напряжению на конденсаторе и превышает напряжение на генераторе.
Коэффициент, показывающий во сколько раз напряжение на катушке либо на конденсаторе превышает напряжение на генераторе, называется добротностью Q последовательного колебательного контура и показывает качественную оценку колебательного контура. В основном стараются сделать Q как можно больше.
На низких частотах колебательный контур имеет емкостную составляющую тока до резонанса, а после резонанса — индуктивную составляющую тока.
Формула резонансной частоты – GeeksforGeeks
Резонансная частота определяется как частота контура, когда значения емкостного импеданса и индуктивного импеданса становятся равными.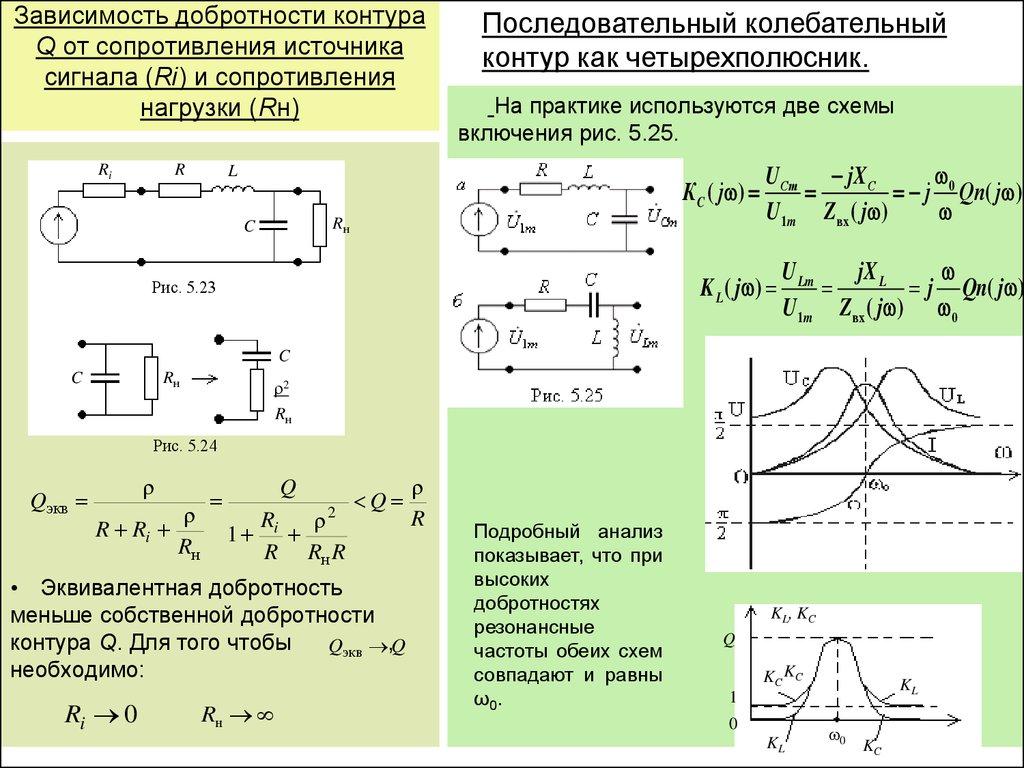
Она определяется как частота, при которой тело или система достигает наивысшей степени колебаний. Резонансный контур состоит из параллельно соединенных конденсатора и катушки индуктивности. Он в основном используется для создания заданной частоты или для учета определенной частоты в сложной цепи. Резонансная частота существует только тогда, когда цепь является чисто резистивной.
Формула
Формула резонансной частоты представляет собой обратную величину произведения удвоенного числа пи и квадратного корня из произведения индуктивности и емкости. Он представлен символом f или . Его стандартной единицей измерения являются герцы или секунды (Гц или с -1 ), а его размерная формула определяется как [M 0 L 0 T -1 ].
f или = 1/2π√(LC)
где,
f o – резонансная частота,
L – индуктивность цепи,
C – емкость цепи.
Вывод
Проблемы с образцамиПредположим, у нас есть цепь, в которой резистор, катушка индуктивности и конденсатор соединены последовательно под источником переменного тока.
Значение сопротивления, индуктивности и емкости равно R, L и C.
Теперь известно, что импеданс цепи Z определяется выражением0002 Z = R + jωL – j/ωC
Z =R + j (ωL – 1/ωC)
Для выполнения условия резонанса цепь должна быть чисто резистивной. Следовательно, мнимая часть импеданса равна нулю.
ωl – 1/ωc = 0
ωl = 1/ωc
ω 2 = 1/lc
Положение ω = 1/2πf O , мы получаем
(1/2πf O ), мы получаем
(1/2πf ). 2 = 1/LC
f o = 1/2π√(LC)
Отсюда выводится формула для резонансной частоты.
Задача 1. Рассчитайте резонансную частоту для схемы индуктивности 5 ч и емкости 3 F.
Решение:
. 3
Используя формулу, которую мы имеем,
f о = 1/2π√(LC)
= 1/ (2 × 3,14 × √(5 × 3))
= 1/24,32
90,0042 = 1/24,321 Гц
Задача 2. Вычислить резонансную частоту для цепи с индуктивностью 3 Гн и емкостью 1 Ф.
Решение:
Мы имеем,
L = 3
C = 1
Используем формулу, которую мы имеем,
F O = 1/2πлья (2 × 3,14 × √(3 × 1))
= 1/10,86
= 0,092 Гц
Задача 3. Вычислить резонансную частоту цепи с индуктивностью 4 Гн и емкостью 2,5 Ф. Решение:
Имеем,
L = 4
C = 2,5
Используя формулу, которую мы имеем,
f o = 1/2π√(LC)
= 1/(2 × 3,14 × √(4 × 2,5))
= 1/60,38
= 0,159 Гц
Задача 4.
Рассчитайте индуктивность цепи, если емкость равна 4 Ф, а резонансная частота равна 0,5 Гц.
Решение:
Имеем,
f o = 0,5
C = 4
Используя формулу f
3
o = 1/2π√(LC)=> L = 1/4π 2 Cf o 2
= 1/ (4 × 3,14 × 3,14 × 900,3 0,5 0,5) = 1/39,43
= 0,025 Гн
Задача 5. Вычислить индуктивность цепи, если емкость равна 3 Ф, а резонансная частота равна 0,023 Гц.
Решение:
Имеем,
f o = 0,023
C = 3
Используя формулу имеем,
F O = 1/2π√ (LC)
=> L = 1/4π 2 CF O 2
= 1/(4 × 3,14 × 3.14 × 3 × 0,023 × 0,023 )
= 1/0,0199
= 50,25 Гн
Задача 6. Вычислить емкость цепи, если индуктивность равна 1 Гн, а резонансная частота равна 0,3 Гц.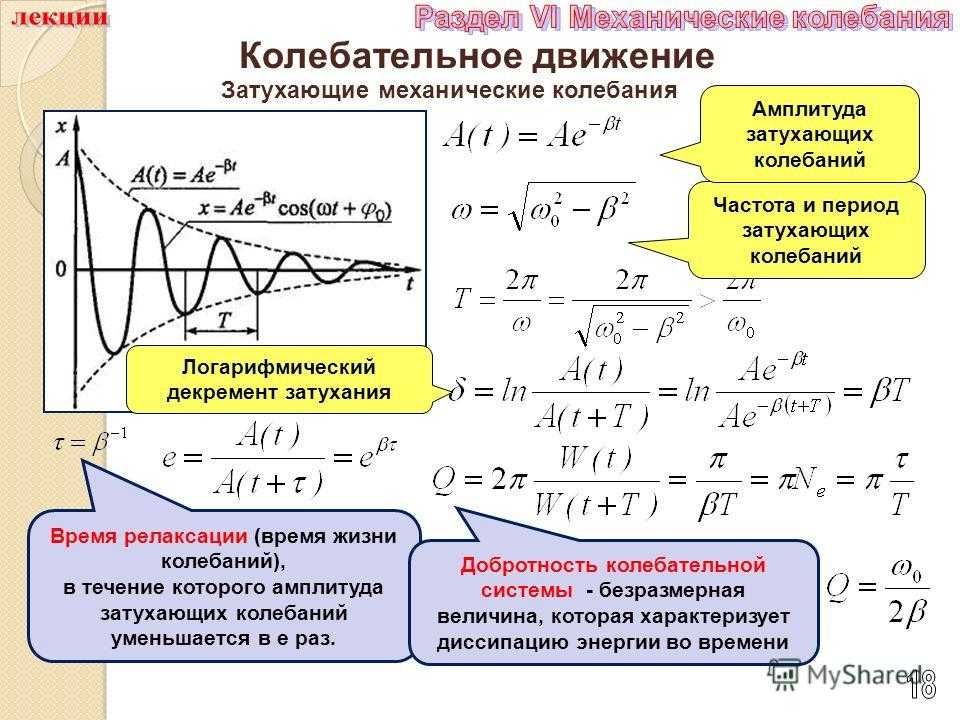
Решение:
Имеем,
f o = 0,3
L = 1
Используя формулу имеем,
f o = 1/2π√(LC)
=> C = 1/4π 2 Lf o 2
х 3 х 3 х 3,0 х 3,14 )= 1/3,54
= 0,282 Ф
Задача 7. Вычислить емкость цепи, если индуктивность равна 0,1 Гн, а резонансная частота равна 0,25 Гц.
Решение:
Имеем,
f o = 0,25
L = 0,1
Используя формулу имеем,
F O = 1/2π√ (LC)
=> C = 1/4π 2 LF O 2
= 1/(4 × 3,14 × 3.14 × 0,25 × 0,25 )
= 1/0,246
= 4,06 F
Цепи переменного тока серии RLC | Физика
Цели обучения
К концу этого раздела вы сможете:
- Вычислять импеданс, фазовый угол, резонансную частоту, мощность, коэффициент мощности, напряжение и/или ток в последовательной цепи RLC.
- Нарисуйте принципиальную схему последовательной цепи RLC.
- Объясните значение резонансной частоты.
Полное сопротивление
В цепи переменного тока катушки индуктивности, конденсаторы и резисторы препятствуют току. Как они ведут себя, когда все три встречаются вместе? Интересно, что их индивидуальные сопротивления в омах не просто складываются. Поскольку катушки индуктивности и конденсаторы ведут себя противоположным образом, они частично или полностью компенсируют эффект друг друга. На рис. 1 показана цифра 9.0339 Цепь серии RLC с источником переменного напряжения, поведение которой рассматривается в этом разделе. Суть анализа цепи RLC состоит в частотной зависимости X L и X C и их влиянии на фазу зависимости напряжения от тока (установлено в предыдущий раздел). Это приводит к частотной зависимости схемы с важными «резонансными» свойствами, которые лежат в основе многих приложений, таких как радиотюнеры.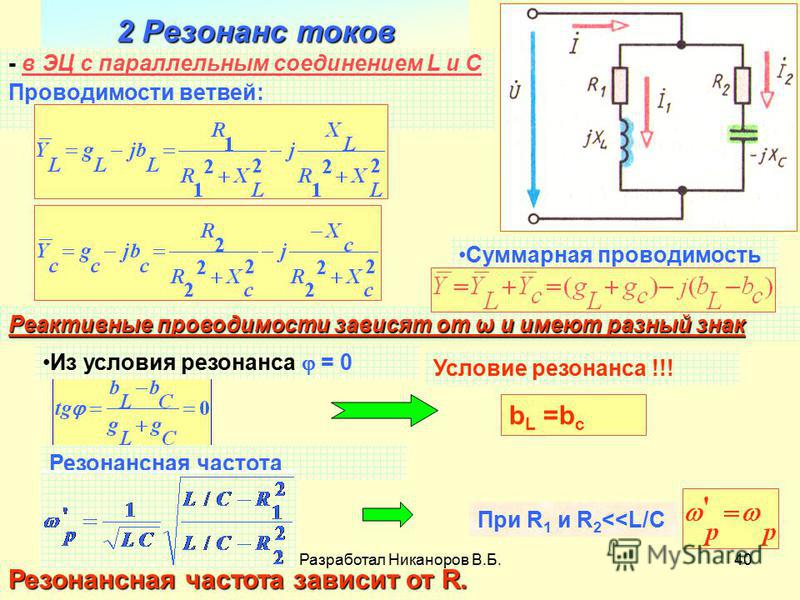
Рис. 1. Цепь серии RLC с источником переменного напряжения.
Комбинированный эффект сопротивления R , индуктивная реактивность x L , и емкостная реактивность x C – до C – до 9000 C . . Ток, напряжение и импеданс в цепи RLC связаны версией закона Ома для переменного тока:
[латекс]{I}_{0}=\frac{{V}_{0}}{Z}\ text{ или }{I}_{\text{rms}}=\frac{{V}_{\text{rms}}}{Z}\\[/latex].
Здесь I 0 — пиковое значение тока, В 0 — пиковое напряжение источника, а Z — полное сопротивление цепи. Единицами импеданса являются омы, и его влияние на цепь, как и следовало ожидать: чем больше импеданс, тем меньше ток. Чтобы получить выражение для Z через R , X L и X C , мы теперь рассмотрим, как различные компоненты связаны с напряжением на источнике.
Напряжение. Эти напряжения обозначены цифрой 9.0339 V R , V L и V C , и V C на рис. так что мы можем сказать, что токи в R , L и C равны и находятся в фазе. Но из предыдущего раздела мы знаем, что напряжение на катушке В L опережает ток на одну четвертую периода, напряжение на конденсаторе В С соответствует току на одну четвертую цикла, а напряжение на резисторе В R точно совпадает по фазе с током. Figure 2 shows these relationships in one graph, as well as showing the total voltage around the circuit V = V R + V L + V C , где все четыре напряжения являются мгновенными значениями. Согласно петлевому правилу Кирхгофа, общее напряжение в цепи равно В это тоже напряжение источника.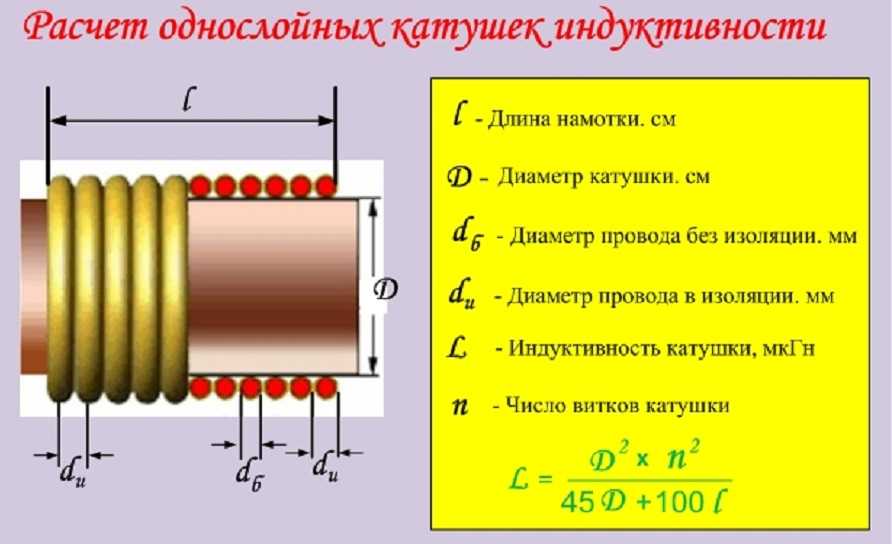
Из рисунка 2 видно, что V R находится в фазе с током, V L опережает на 90°, а V следует за ним. Таким образом, V L и V C сдвинуты по фазе на 180º (гребень к впадине) и имеют тенденцию сокращаться, хотя и не полностью, если они не имеют одинаковую величину. Поскольку пиковые напряжения не выровнены (не по фазе), пиковое напряжение 9{2}}} \\ [/latex],
, где V 0 R , V 0 L и V 0 0
, который представляет собой импеданс цепи переменного тока серии RLC .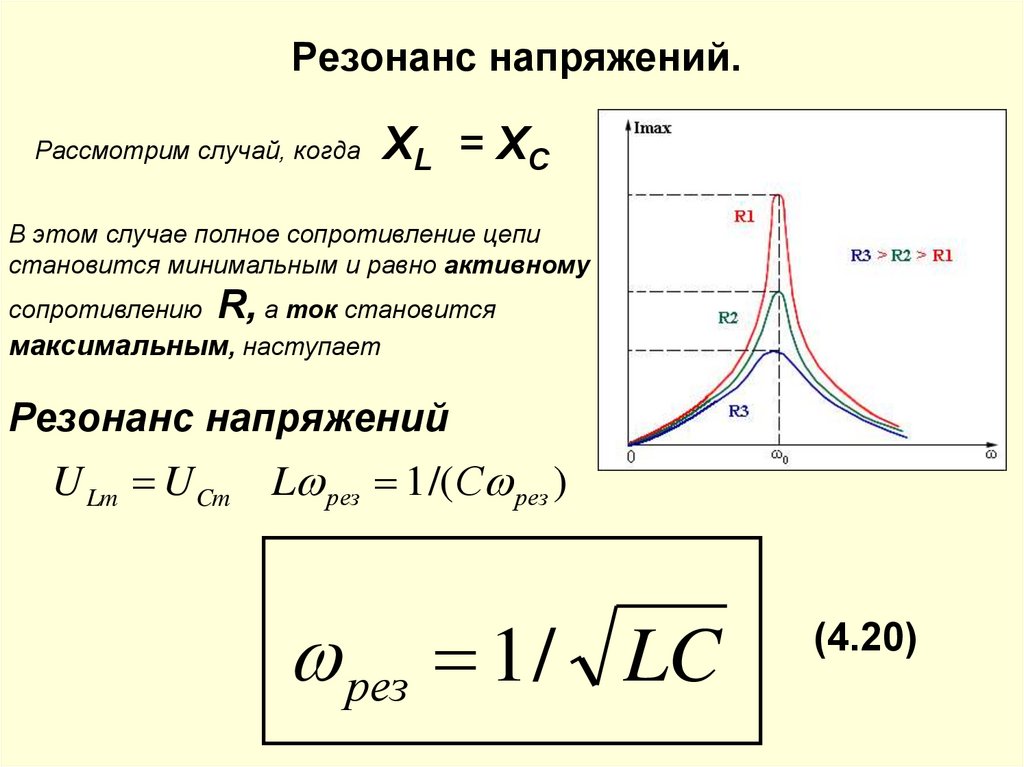
Для цепей без резистора принять R = 0; для тех, у кого нет индуктора, принять X L = 0; а для тех, у кого нет конденсатора, возьмите X C = 0,
Рисунок 2. На этом графике показано отношение напряжения в цепи RLC к току. Напряжения на элементах схемы складываются, чтобы равняться напряжению источника, которое, как видно, не совпадает по фазе с током.
Пример 1. Расчет импеданса и тока
Схема серии RLC имеет резистор 40,0 Ом, катушку индуктивности 3,00 мГн и конденсатор 5,00 мкФ. (a) Найдите импеданс цепи при 60,0 Гц и 10,0 кГц, отметив, что эти частоты и значения для L и C такие же, как в Примере 1 и Примере 2 из Реактивного, Индуктивного и Емкостного. (b) Если источник напряжения имеет В среднеквадратичное значение = 120 В, чему равно I {2}}\\[/latex] , чтобы найти импеданс, а затем закон Ома, чтобы найти ток.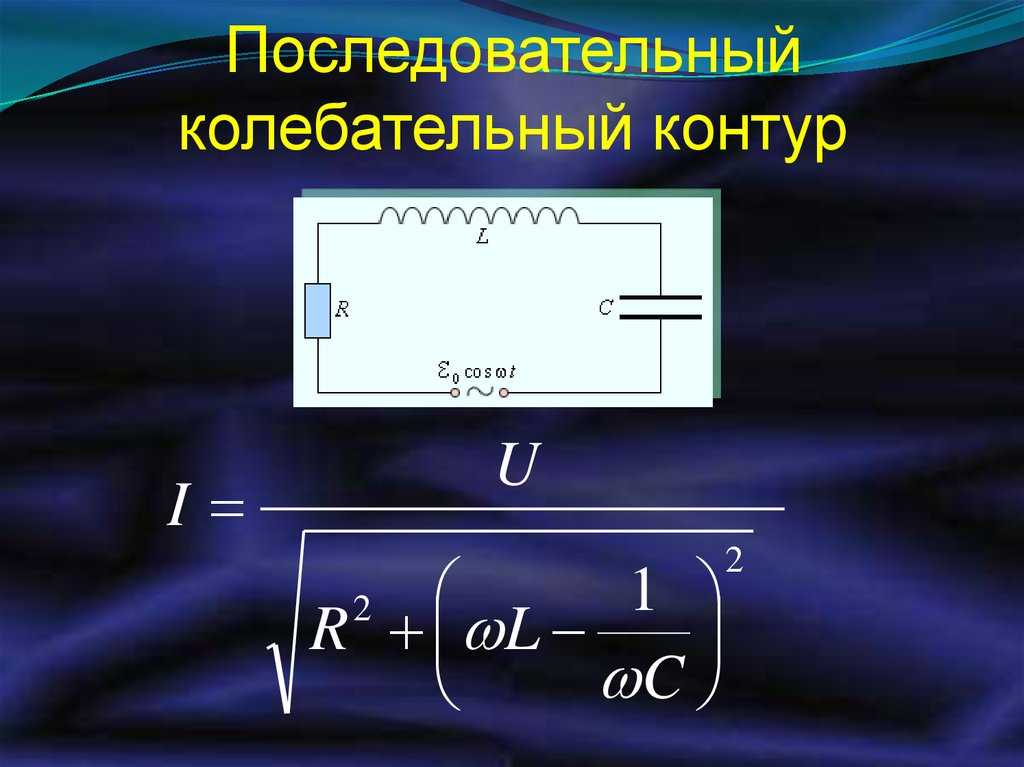
{2 }}\\[/латекс] дает 9{2}}\\ & =& 190\text{ }\Omega\text{ at }10.0\text{ kHz}\end{array}\\[/latex]
In В обоих случаях результат почти совпадает с наибольшим значением, а импеданс определенно не является суммой отдельных значений. Видно, что на высокой частоте доминирует X L , а на низкой частоте X C .
Раствор для (б)Текущий I среднеквадратичное значение можно найти, используя версию закона Ома для переменного тока в уравнении rms}}=\frac{{V}_{\text{rms}}}{Z}=\frac{120\text{V}}{531\text{}\Omega}=0,226\text{A}\ \[/латекс] при 60,0 Гц
Наконец, при 10,0 кГц мы находим
[латекс]{I}_{\text{rms}}=\frac{{V}_{\text{rms}}} {Z}=\frac{120\text{ V}}{190\text{ }\Omega}=0,633\text{ A}\\[/latex] на частоте 10,0 кГц
Обсуждение для (a) Ток при частоте 60,0 Гц такой же (с точностью до трех цифр), что и для конденсатора в примере 2 из Reactance, Inductive and Capacitive.
Конденсатор доминирует на низких частотах. Ток на частоте 10,0 кГц лишь немного отличается от тока, найденного только для индуктора в примере 1 из Reactance, Inductive, and Capacitive. Индуктор доминирует на высоких частотах.
Резонанс в цепях переменного тока серии
RLC 9{2}}}\\[/latex]Реактивные сопротивления зависят от частоты: X L большие на высоких частотах и X C большие на низких частотах, как мы видели в трех предыдущих примерах. На некоторой промежуточной частоте f 0 реактивные сопротивления будут равны и сокращаются, что дает Z = R — это минимальное значение импеданса и максимальное значение для I среднеквадратичное значение результатов. Мы можем получить выражение для f 0 , взяв:
Подстановка определений X L и X C ,
[latex]2\pi f_{0}L=\frac }C}\\[/латекс].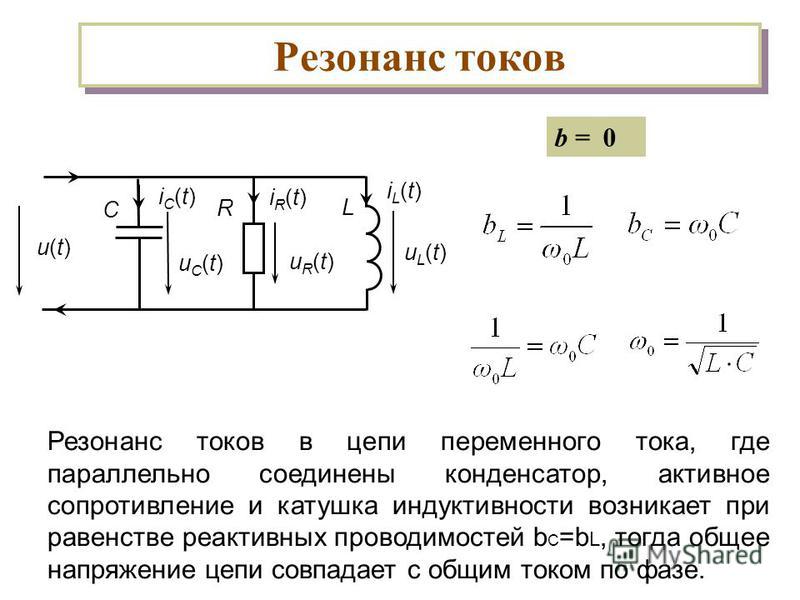
Решение этого выражения для f 0 дает
[латекс]{f}_{0}=\frac{1}{2\pi \sqrt{LC}}\\[/latex],
, где f 0 — резонансная частота цепи серии RLC . Это также 90 339 собственная частота 90 340, при которой цепь будет колебаться, если она не управляется источником напряжения. При f 0 эффекты катушки индуктивности и конденсатора компенсируются, так что Z = R , а I среднеквадратичное значение является максимальным.
Резонанс в цепях переменного тока аналогичен механическому резонансу, где резонанс определяется как вынужденные колебания (в данном случае вызванные источником напряжения) на собственной частоте системы. Приемник в радио – это Цепь RLC , лучше всего генерирующая f 0 . Переменный конденсатор часто используется для настройки f 0 для получения нужной частоты и отклонения других.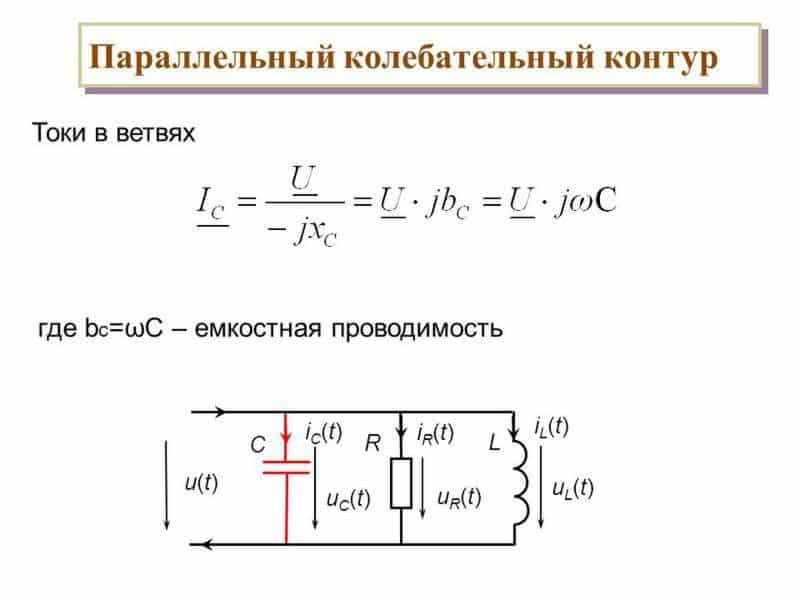
На рисунке 3 представлен график зависимости тока от частоты, иллюстрирующий резонансный пик в I среднеквадратичное значение при f 0 . Две кривые относятся к двум разным цепям, которые отличаются только величиной сопротивления в них. Пик ниже и шире для схемы с более высоким сопротивлением. Таким образом, цепь с более высоким сопротивлением не резонирует так сильно и не будет такой избирательной, например, в радиоприемнике.
Рис. 3. График зависимости тока от частоты для двух цепей серии RLC, отличающихся только величиной сопротивления. Оба имеют резонанс при f 0 , но при более высоком сопротивлении он ниже и шире. Источник управляющего переменного напряжения имеет фиксированную амплитуду В 0 .
Пример 2. Расчет резонансной частоты и тока
Для той же цепи серии RLC , имеющей резистор 40,0 Ом, катушку индуктивности 3,00 мГн и конденсатор 5,00 мкФ: (a) Найдите резонансную частоту.
(б) Вычислить I действующее значение при резонансе, если В действующее значение составляет 120 В. 1}{2\pi\sqrt{LC}}\\[/латекс]. Ток на этой частоте такой же, как если бы в цепи был только резистор.
Решение для (a)
Ввод заданных значений для L и C в выражение, данное для f 9{-6}\text{ F}\right)}}=1.30\text{ кГц}\end{array}\\[/latex]
Обсуждение для (a)Мы видим, что резонансная частота равна между 60,0 Гц и 10,0 кГц, двумя частотами, выбранными в предыдущих примерах. Этого и следовало ожидать, поскольку на низкой частоте преобладал конденсатор, а на высокой частоте — катушка индуктивности. Их эффекты одинаковы на этой промежуточной частоте.
Решение для (b)Ток определяется законом Ома. В резонансе два реактивных сопротивления равны и компенсируются, так что импеданс равен одному сопротивлению. Таким образом,
[латекс] {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} = \ frac {120 \ text {V}} {40,0 \ text { }\Omega}=3.
00\text{ A}\\[/latex].
При резонансе ток больше, чем на более высоких и более низких частотах, рассмотренных для той же цепи в предыдущем примере.
Мощность в цепях переменного тока серии
RLCЕсли ток в цепи RLC зависит от частоты, то подводимая к ней мощность также зависит от частоты. Но средняя мощность — это не просто ток, умноженный на напряжение, как в чисто резистивных цепях. Как видно на рисунке 2, напряжение и ток не совпадают по фазе в Цепь RLC . Существует фазовый угол ϕ между напряжением источника В и током I , который можно найти из
[латекс]\cos\varphi =\frac{R}{Z}\\[ /latex]
Например, на резонансной частоте или в чисто резистивной цепи Z = R , так что [latex]\text{cos}\varphi =1\\[/latex]. Это означает, что ϕ = 0º и что напряжение и ток совпадают по фазе, как и ожидается для резисторов.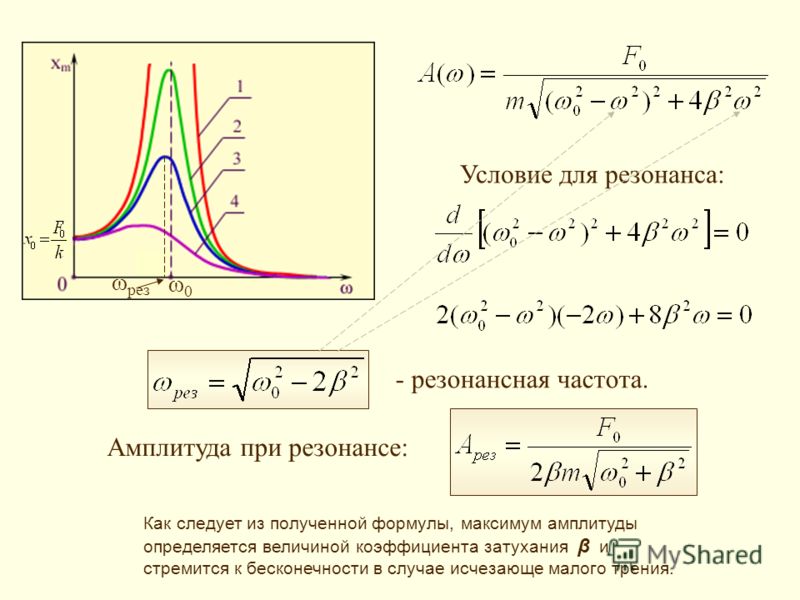
На других частотах средняя мощность меньше, чем на резонансе. Это происходит как из-за того, что напряжение и ток не совпадают по фазе, так и из-за того, что I среднеквадратичное значение ниже. Тот факт, что напряжение и ток источника не совпадают по фазе, влияет на мощность, подаваемую в цепь. Можно показать, что средняя мощность равна
[латекс] {P} _ {\ text {ave}} = {I} _ {\ text {rms}} {V} _ {\ text {rms }}\cos\varphi\\[/latex],
Таким образом, cos ϕ называется коэффициентом мощности , который может принимать значения от 0 до 1. Коэффициенты мощности, близкие к 1, желательны при проектировании эффективного двигателя, например . На резонансной частоте cos ϕ = 1.
Пример 3. Расчет коэффициента мощности и мощности
Для той же цепи серии RLC , имеющей резистор 40,0 Ом, катушку индуктивности 3,00 мГн, конденсатор 5,00 мкФ и источник напряжения с V rms для 120 В: (a) Рассчитайте коэффициент мощности и фазовый угол для f = 60,0 Гц.
{-1} 0,0753=\текст{85,7º}\текст{ при }60,0\текст{Гц}\\[/латекс].
Фазовый угол близок к 90º, что согласуется с тем фактом, что конденсатор доминирует в цепи на этой низкой частоте (чистая цепь RC имеет напряжение и ток, сдвинутые по фазе на 90º) .
Стратегия и решение для (B)Средняя мощность при 60,0 Гц составляет
P Ave = I Орчины V RMS 10101010101010 V RM10101010101010101010 0 V . I Среднеквадратичное значение оказалось равным 0,226 А в Пример 1: Расчет импеданса и тока . Ввод известных значений дает P ср = (0,226 А)(120 В)(0,0753) = 2,04 Вт при 60,0 Гц. На резонансной частоте мы знаем, что cos ϕ = 1, и I среднеквадратичное значение равно 6,00 А в . Мощность, подаваемая в цепь переменного тока RLC серии , рассеивается только за счет сопротивления. Катушка индуктивности и конденсатор имеют входную и выходную энергию, но не рассеивают ее из цепи. Скорее они передают энергию туда и обратно друг другу, при этом резистор рассеивает именно то, что источник напряжения помещает в цепь. Это предполагает отсутствие значительного электромагнитного излучения от катушки индуктивности и конденсатора, такого как радиоволны. Такое излучение может происходить и может быть даже желательным, как мы увидим в следующей главе об электромагнитном излучении, но его также можно подавить, как в случае с этой главой. Схема аналогична колесу автомобиля, движущегося по неровной дороге, как показано на рис. 4. Равномерно расположенные неровности на дороге аналогичны источнику напряжения, приводящему в движение колесо вверх и вниз. Рис. 4. Принудительное, но демпфированное движение колеса на рессоре автомобиля аналогично цепи переменного тока RLC серии . Амортизатор гасит движение и рассеивает энергию, аналогично сопротивлению в цепи RLC . Масса и пружина определяют резонансную частоту. Чистая цепь LC с незначительным сопротивлением колеблется на частоте f 0 , той же резонансной частоте, что и цепь RLC . Он может служить эталоном частоты или тактовой схемой, например, в цифровых наручных часах. Рис. 5. LC-контур аналогичен массе, колеблющейся на пружине без трения и движущей силы. Энергия движется вперед и назад между катушкой индуктивности и конденсатором точно так же, как она движется от кинетической к потенциальной в системе масса-пружина. Создавайте схемы с конденсаторами, катушками индуктивности, резисторами и источниками переменного или постоянного напряжения и проверяйте их с помощью лабораторных приборов, таких как вольтметры и амперметры. Нажмите, чтобы загрузить симуляцию. Запуск с использованием Java. [латекс] {I}_{0}=\frac{{V}_{0}}{Z}\text{ или }{I}_{\text{rms}}=\frac{{V}_ {\text{rms}}}{Z}\\[/латекс], , где I o — пиковое значение тока, а V o — пиковое напряжение источника. [латекс]{f}_{0}=\frac{1}{2\pi \sqrt{LC}}\\[/latex] [латекс]\text{cos}\varphi =\frac{R}{Z}\\[/латекс], [латекс] {P} _ {\ text {ave}} = {I} _ {\ text {rms}} {V} _ {\ text {rms}} \ cos \ varphi \\ [/latex], cos ϕ называется коэффициентом мощности, который принимает значения от 0 до 1. 1. Зависит ли резонансная частота цепи переменного тока от пикового напряжения источника переменного тока? Объясните, почему да или почему нет. 2. Предположим, у вас есть двигатель с коэффициентом мощности, значительно меньшим 1. Объясните, почему было бы лучше улучшить коэффициент мощности в качестве метода улучшения выходной мощности двигателя, а не увеличивать входное напряжение. 1. Схема RL состоит из резистора 40,0 Ом и катушки индуктивности 3,00 мГн. (а) Найдите его импеданс 2. Цепь RC состоит из резистора 40,0 Ом и конденсатора 5,00 мкФ. (а) Найдите его импеданс на частотах 60,0 Гц и 10,0 кГц. (b) Сравните эти значения Z со значениями, найденными в Пример 1: Расчет импеданса и тока , в котором также была катушка индуктивности. 3. Схема LC состоит из катушки индуктивности 3,00 мГн и конденсатора 5,00 мкФ. (а) Найдите его импеданс на частотах 60,0 Гц и 10,0 кГц.
. Таким образом, P ср = (3,00 А)(120 В)(1) = 360 Вт при резонансе (1,30 кГц) большей мощности, чем на более высоких и более низких частотах.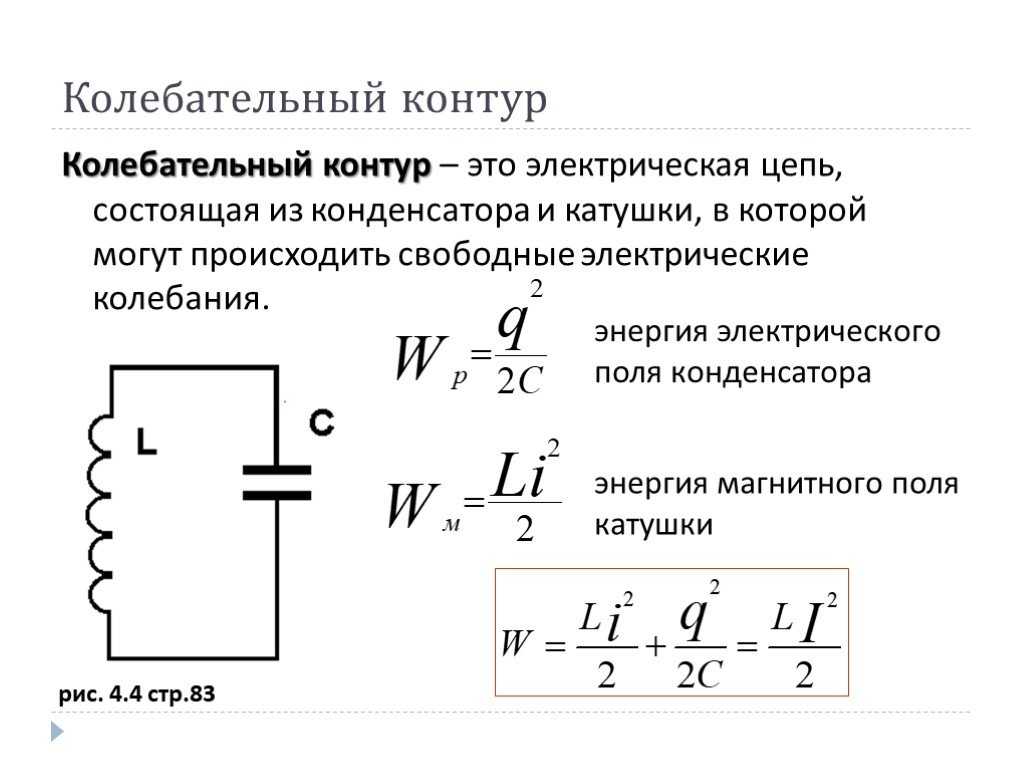
Амортизатор аналогичен сопротивлению, демпфирующему и ограничивающему амплитуду колебаний. Энергия в системе переходит туда и обратно между кинетической (аналогично максимальному току и энергии, хранящейся в индукторе) и потенциальной энергией, запасенной в автомобильной пружине (аналогично отсутствию тока и энергии, запасенной в электрическом поле конденсатора). Амплитуда движения колес максимальна, если удары о неровности дороги происходят на резонансной частоте.
При очень малом сопротивлении для поддержания колебаний требуется лишь очень небольшая затрата энергии. Схема аналогична автомобилю без амортизаторов. Как только он начинает колебаться, он некоторое время продолжает работать на своей собственной частоте. На рис. 5 показана аналогия между LC схема и масса на пружине. Резюме раздела
9{2}}\\[/латекс]. Концептуальные вопросы
Задачи и упражнения
4. Какова резонансная частота катушки индуктивности 0,500 мГн, подключенной к конденсатору емкостью 40,0 мкФ?
5. Для приема AM-радио вам понадобится схема RLC , которую можно заставить резонировать на любой частоте от 500 до 1650 кГц. Это достигается с помощью фиксированной катушки индуктивности 1,00 мкГн, соединенной с переменным конденсатором. Какой диапазон емкости нужен?
6. Предположим, у вас есть запас катушек индуктивности в диапазоне от 1,00 нГн до 10,0 Гн и конденсаторов в диапазоне от 1,00 пФ до 0,100 Ф. Каков диапазон резонансных частот, который может быть получен при комбинации одной катушки индуктивности и одного конденсатора ?
7. Какая емкость необходима для получения резонансной частоты 1,00 ГГц при использовании катушки индуктивности 8,00 нГн?
8. Какая индуктивность необходима для получения резонансной частоты 60,0 Гц при использовании конденсатора 2,00 мкФ?
9.
Самая низкая частота в диапазоне FM-радио составляет 88,0 МГц. а) Какая индуктивность необходима для получения этой резонансной частоты, если он подключен к конденсатору емкостью 2,50 пФ? (b) Конденсатор переменный, что позволяет регулировать резонансную частоту до 108 МГц. Какая должна быть емкость на этой частоте?
10. Цепь RLC серии имеет резистор 2,50 Ом, катушку индуктивности 100 мкГн и конденсатор 80,0 мкФ. (a) Найдите полное сопротивление цепи при частоте 120 Гц. (b) Найдите полное сопротивление цепи на частоте 5,00 кГц. (c) Если источник напряжения имеет В СКЗ = 5,60 В, чему равно I СКЗ на каждой частоте? г) Какова резонансная частота цепи? (e) Чему равно I среднеквадратичное значение при резонансе?
11. Цепь RLC серии имеет резистор 1,00 кОм, катушку индуктивности 150 мкГн и конденсатор 25,0 нФ. а) Найдите полное сопротивление цепи на частоте 500 Гц. (b) Найдите полное сопротивление цепи на частоте 7,50 кГц.
12. Цепь RLC серии имеет резистор 2,50 Ом, катушку индуктивности 100 мкГн и конденсатор 80,0 мкФ. (а) Найдите коэффициент мощности при 90 339 f 90 340 = 120 Гц. (b) Каков фазовый угол на частоте 120 Гц? в) Какова средняя мощность на частоте 120 Гц? г) Найдите среднюю мощность на резонансной частоте контура.
13. Схема серии RLC имеет резистор 1,00 кОм, катушку индуктивности 150 мкГн и конденсатор 25,0 нФ. (а) Найдите коэффициент мощности при 90 339 f 90 340 = 7,50 Гц. б) Каков фазовый угол на этой частоте? в) Какова средняя мощность на этой частоте? г) Найдите среднюю мощность на резонансной частоте контура.
14. Цепь серии RLC имеет резистор 200 Ом и катушку индуктивности 25,0 мГн.
При 8000 Гц фазовый угол составляет 45,0º. а) Чему равно сопротивление? б) Найдите емкость цепи. (в) Если 9{2}}\\[/латекс]
- резонансная частота:
- частота, при которой импеданс в цепи минимален, а также частота, при которой цепь колебалась бы, если бы она не приводилась в действие источником напряжения; рассчитано по формуле [латекс]{f}_{0}=\frac{1}{2\pi \sqrt{\text{LC}}}\\[/latex]
- фазовый угол:
- обозначается как ϕ , величина, на которую напряжение и ток не совпадают по фазе друг с другом в цепи
- коэффициент мощности:
- величина, на которую мощность, подаваемая в цепь, меньше теоретического максимума цепи из-за несовпадения фаз напряжения и тока; рассчитывается по cos ϕ
Избранные решения задач и упражнений
1. (a) 40,02 Ом при 60,0 Гц, 193 Ом при 10,0 кГц (b) При 60 Гц, с конденсатором Z = 531 Ом, что более чем в 13 раз выше, чем без конденсатора.