Физика для лириков и не только – Запоминалки
«Бац!»- взмахнул кнутом пастух.
«Пора вставать!» – пропел петух.
Если слово «бац» запомнишь,
Формулу объёма вспомнишь: V = abc
Чтобы в скорость жизнь вдохнуть,
Раздели на время путь: v = S / t
Плотность тела так найдём:
Делим массу на объём: ρ = m / v
Нам без силы и пути век работы не найти.
Путь на силу ты перемножь…
Догадайся, что найдёшь? A = F S
Чтобы давление нам получить,
Силу на площадь надо делить: P = F/ S
Не лезьте в воду глубоко –
В воде давленье велико.
Надавит сверху РО-ЖЕ-АШ-
И вдруг концы свои отдашь?
Волк сказал : «АМ!» –
И зайчик побежал с ускорением: F = am
Как для слушателей лектор,
Как приёмнику детектор,
Так для силы нужен вектор.
Как сложить две силы вместе?
Отвечаем честь по чести:
Стройте параллелограмм.
Векторы по сторонам начертить придётся вам.
Для него диагонали суммой векторною стали
Силы, что мы с вами взяли.
Ну а прочие детали
Разберёшь в задачах сам.. F = F1+F2
Шагал ишак, кричал: «ИА» ([I] = А).
Он РОМ ([R]= Ом) в подарок вёз,
Прошёл тяжёлый перевал,
Вздохнул, как паровоз: «УВ!» ([U]=В).
Но ты, конечно, не осёл, всё делаешь легко.
И букву I, и букву U запомнишь хорошо! U = I∙R
Радиотехники главный закон
Давным-давно вывел Георг Симонс Ом.
Чтобы найти силу тока в цепи
U на R ты раздели: I = U /R
Бабочка летела в синий лес,
Вот тебе и ЭДС: ε = B l v sinα
Ничего для нас нет проще, чем
делить длину на площадь.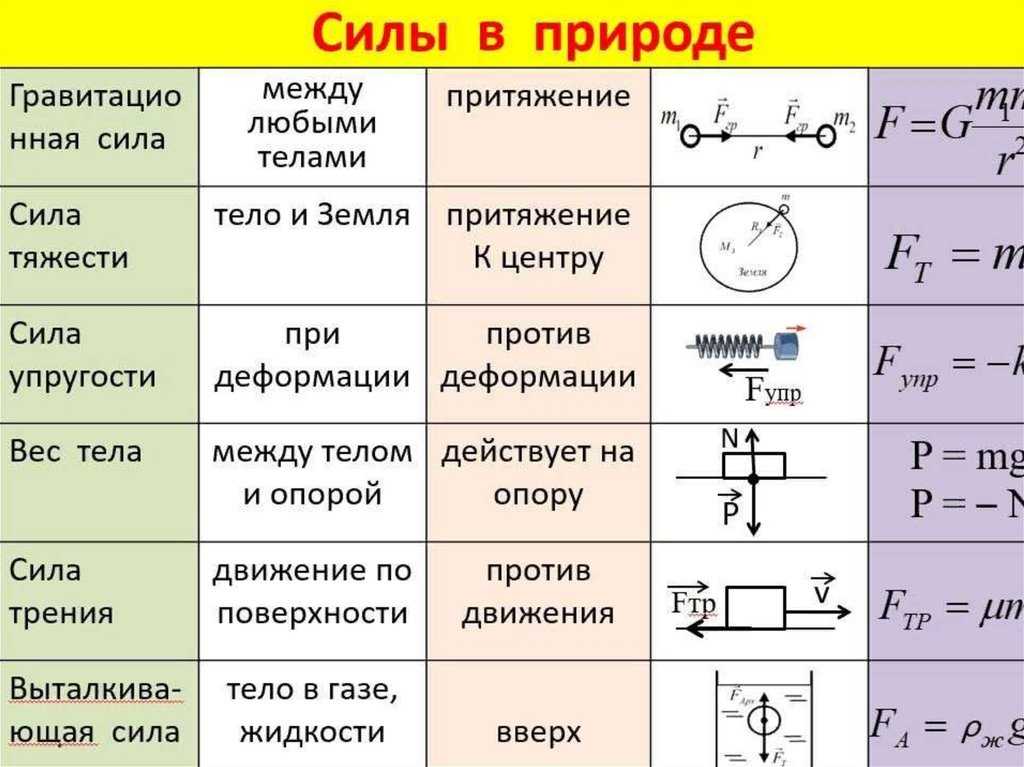
Может нам деление дать сопротивление.
Не учли мы здесь пока материал проводника,
А учесть его мы можем, если всё на «ρ» умножим:
R = ρ l / S
Друг за другом расположим
Все резисторы в цепи,
И сопротивления мы сложим
Что получим? – посмотри: R = R1 + R2
При разветвлении – всем надо знать –
Сопротивления трудно считать:
Ведь величины, обратные им,
Складывать нужно самим: 1/R = 1/R1 +1/R2
Знает каждый инженер: v = ω R
Согласен я со всеми, период – это время,
Время оборот, когда вращалось что-то:
T = t / N
Для каждой ситуации в упругой деформации
Закон везде один:
Все силы, как и водится, в пропорции находятся
К увеличенью
длин.
А если при решении у длин есть уменьшение
Закон и тут закон:
Пропорции упрямые прямые (те же самые)
Но знак у них сменён.
И что это за мука закон запомнить Гука!
Но мы пойдём на риск
Напишем слева силу, а справа чтобы было
Знак «минус», «k» и «х»: Fупр= – kx
Мой знакомый Амонтон
Предложил простой закон.
«Сила тренья такова:
μ на N – и все дела!»: Fтр = μ N
Знаменитый Ампер был великим левшой:
Он B I l очень сильно, но левой рукой:
3/2 КоТа в мешке
Мечтали съесть по серой мышке.
А вам советую найти
Эту формулу в серьезной книжке: Е = 3/2 kT
что это такое, чему равно, история, как округлить
Даже если вы давно закончили школу и из всего курса математики помните только таблицу умножения, мы уверены: про число пи вы знаете.
Скажете сходу, чему оно равно? Помните, для чего нужно число пи и как его посчитать? Если нет, читайте наш урок
Мария Макулова
Редактор раздела «Образование»
Вячеслав Смольняков
Учитель математики и информатики высшей квалификационной категории, эксперт ОГЭ и ЕГЭ Региональной предметной комиссии по математике и информатике
Ирина Ходакова
Учитель математики
Представляете, мы живем в эпоху технологического прорыва, но до сих пор не можем точно рассчитать площадь съеденного круглого торта? Все потому, что в формуле вычисления площади круга используется число π.
От автомобильного колеса до орбиты спутника, от часового механизма до электромагнитных и звуковых волн. В любой научной области есть расчеты, и практически в любом расчете не обойтись без числа пи. Даже там, где, казалось бы, окружности нет места, например в статистике.
Что такое число пи
Число пи — это отношение длины окружности к ее диаметру.
Обозначается оно буквой греческого алфавита π. Если записать это отношение математическими символами, то выглядит оно так: π = C/d, где C — это длина окружности, а d — диаметр окружности. То есть π — это результат деления длины окружности на ее диаметр. Но само по себе число пи не является каким-то параметром окружности. Это математическая постоянная, или константа (то есть неизменная), которая нужна для расчета определенных данных. Например, число пи необходимо, чтобы посчитать площадь круга.
Число пи — это результат деления длины окружности на ее диаметр
Чему равно число пи
Число пи не имеет точного значения. Это легко проверить. Возьмите круг любого размера, разделите его окружность на диаметр — у вас получится десятичная дробь с множеством цифр после запятой. Математики называют такие числа иррациональными. Результат, который вы увидите, будет равен 3 целых и сколько-то десятых, сотых, тысячных — и далее насколько хватит дисплея калькулятора.
У числа пи бесконечное количество знаков после запятой. Но для удобства в расчетах используют округленные значения.
Число π примерно равно 3,14, или, если точнее, 3,1415926535. Именно значение с десятью знаками после запятой принято использовать. Но все дело в округлении. Там, где не нужны максимально точные расчеты, за число пи часто берут 3. А вот для точных расчетов в науке ученые используют число пи с 38-ю знаками десятичного разложения (после запятой в десятичной дроби). Итак:
π = 3,14
или
π = 3,1415926535
Как посчитать число пи самостоятельно
Возьмите несколько круглых предметов разного размера, например тарелку, блюдце и крышку от кастрюли. Измерьте окружность каждого. Для этого используйте сантиметровую ленту. Или можно обернуть их по окружности ниткой или веревкой, а потом полученную длину нитки или веревки измерить линейкой. С помощью сантиметровой ленты или линейки измерьте и диаметр каждого предмета.
Длина окружности и диаметры у каждого будут разные, ведь предметы разные по размеру. Теперь для каждого предмета разделите его длину окружности на диаметр. Вы увидите, что во всех случаях, какого бы размера ни был круглый предмет, полученное значение будет 3 целых и далее десятые и сотые доли. Оно необязательно соответствует принятому значению в 3,14, но всегда будет около него.
Какого бы размера ни был круглый предмет, при делении длины его окружности на диаметр получится 3 целых и далее десятые и сотые доли — приблизительно 3,14
Практическое применение числа пи
В школе нас учат использовать число пи для вычисления площади круга. Рассчитывается она по следующей формуле: S = πr², где S — площадь, π — число пи, r² — радиус в квадрате. Можно использовать эту формулу: S = d²/4*π, где d² — диаметр.
Зная число пи и диаметр, можно посчитать длину окружности. Для этого вспомним школьные уравнения.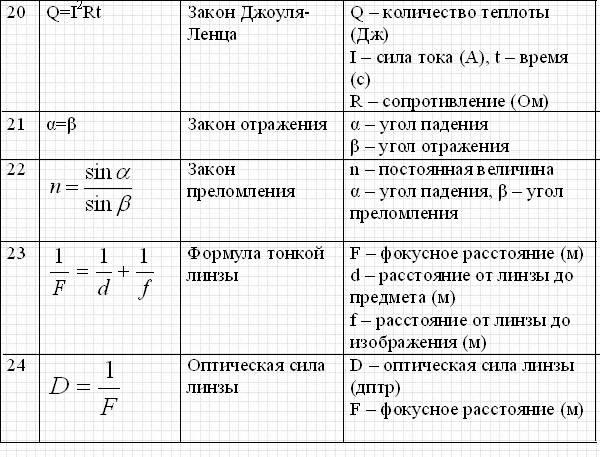
Если π = C/d, то C (длина окружности) высчитывается по формуле C = π*d.
Но применение числа пи в науке гораздо шире. Оно используется практически для любых расчетов в любой области, будь то архитектура, авиация и даже статистика. Например, число π нужно для расчета времени полета самолета и расстояния, которое он должен преодолеть. А в статистике с помощью числа пи рассчитывают значения ниже так называемой кривой нормального распределения. Это нужно для того чтобы, например, выяснить, как распределялись голоса респондентов при опросе.
S (площадь круга) = πr²
История числа пи
Считается, что первым обозначать число пи буквой греческого алфавита π (pi) стал британский математик Уильям Джонс в 1706 году, а популяризировал обозначение его швейцарский коллега Леонард Эйлер в 1737 году. Есть версия, что эта буква выбрана не случайно, а как начальная в греческом слове perijereia, что означает «окружность», «периферия».
Как и на многие явления, известные науке сегодня, на существование некой постоянной, с помощью которой можно посчитать площадь круга, обратили внимание еще в Древнем мире. Но ученые того времени приходили к разному мнению относительно значения этой постоянной: одни использовали значение 3,125, другие — 3,16, третьи — 3,139. Но всегда это значение было 3 с небольшим.
На точное вычисление числа пи ушли тысячелетия. Первым, кто определил более-менее приблизительное значение π, был древнегреческий ученый Архимед. По его расчетам пи равно 3,142857142857143. Как мы знаем сейчас, верными оказались только первые два десятичных числа.
Точнее оказались расчеты китайского математика 480-х годов нашей эры — 3,1415927. Именно это значение числа пи считалось самым верным до 1420-х годов, пока ученые не расширили этот ряд до 16 цифр после запятой, затем до 20-ти, 32-х и так далее.
В XX веке с приходом компьютерных систем и вычислительной техники дело пошло быстрее: теперь уже точные десятичные значения высчитывали машины.
С помощью специальных алгоритмов математики во всем мире продолжают определять новые, более точные значения числа пи, устанавливая рекорды по количеству цифр десятичного разложения (после запятой в десятичной дроби).
В ТЕМУ
Популярные вопросы и ответы
Как округлить число пи?
Чтобы не запоминать число пи с большим количеством десятичных значений, его принято округлять. В математике все округления проводятся по строгим правилам. Для округления значения числа пи применяют метод округления к ближайшему целому. Если перед округляемым числом стоит число 5 и большее, то число округляется в большую сторону. Например, 12,513. Другой пример: 12,5812,613.
Если перед округляемым числом стоит число менее 5, то число округляется в меньшую сторону. Например, 12,412. Или: 12,3412,312.
Итак, возьмем π – 3,1415. Округление начинают с последнего значения, в данном случае это 5.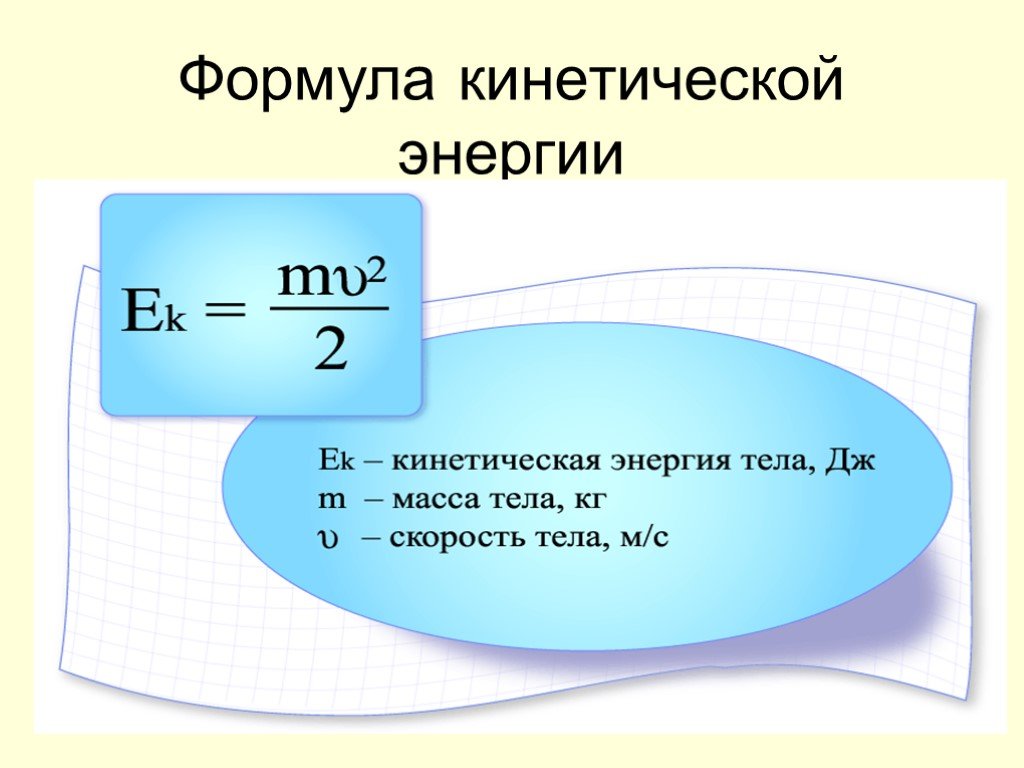
Значит, следующая за ним единица округляется до двух: 3,14153,142. Последнее число 2 меньше пяти, значит, последующее 4 остается неизменным: 3,1423,14. Вот мы и пришли к общепринятому значению числа пи.
По тому же принципу давайте продолжим округление до целого числа: 3,143,23. И вот у нас получилось значение числа пи 3.
Как запомнить число пи?
Вячеслав Смольняков, учитель математики и информатики высшей квалификационной категории, эксперт ОГЭ и ЕГЭ Региональной предметной комиссии по математике и информатике:
На практике мы часто используем округление числа пи до сотых — 3,14. Чуть реже нам нужна большая точность, и мы уже берем значение 3,14159. Чтобы запомнить дробную часть, можно воспользоваться нехитрым приемом: выучить одну фразу «Это я знаю и помню прекрасно». Количество букв в словах соответствует первым цифрам числа пи: «это» — 3, «я» — 1, «знаю» — 4 и так далее.
Для запоминания большего количества цифр есть специальные стихотворения, это называется мнемонический метод запоминания.
Ирина Ходакова, учитель математики:
Чтобы запомнить значение числа π используют один из самых популярных способов — запомнить фразу, в которой количество букв в каждом слове совпадает с цифрами числа π.
Например, «Что(3) я(1) знаю(4) о(1) круге(5)?»
Чтобы запомнить больше знаков числа π, пользуются различными приемами мнемотехники (совокупность приемов, облегчающих запоминание информации). Например, существует стихотворение С. Боброва «Волшебный двурог» для запоминания числа π, которое совсем не сложно выучить:
«Чтобы нам не ошибаться,
Надо правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Ну и дальше надо знать,
Если мы вас спросим —
Это будет пять, три, пять,
Восемь, девять, восемь»
Где используется число пи?
Вячеслав Смольняков:
В школе ученики впервые знакомятся с числом пи в 6 классе, и я обычно привожу разные примеры того, где это можно использовать в реальной жизни.
Например, девочки на уроках технологии часто шьют круглые изделия, и число пи поможет им рассчитать, какое количество тесьмы необходимо для того, чтобы обшить по краю круглую салфетку. Мальчикам часто бывает интересно, как рассчитать, какое расстояние они преодолели на уроке физкультуры, бегая по кругу в спортзале. А еще все любят подарки… Сколько нужно упаковочной бумаги, чтобы обернуть подарок, который находится в коробке цилиндрической формы? Для всего этого нужно знать про число пи. В более старших классах мы используем знание о числе пи уже для решения геометрических задач (однако оно используется не только в геометрии).
В науке число пи используется в множестве геометрических формул, прежде всего для нахождения объемов тел, площадей фигур, которые содержат круг. В тригонометрии это число является одним из основных. Также мы можем его встретить при расчете интегралов в высшей математике, встречается оно и в формулах математической статистики и физики.
Если же рассказывать про то, откуда человечество вообще заинтересовалось данной темой, то стоит переместиться в древность.
Получение знаний в ту эпоху, как и сейчас, носило практический характер. Сколько нужно каменных блоков, чтобы построить круглую башню? Вопросы, подобные этому, интересовали и Архимеда, и древних правителей, которым нужно было рассчитать ресурсы для обороны собственных владений.
В XX веке при помощи компьютеров человечество смогло рассчитать уже несколько десятков триллионов знаков после запятой, причем, как и в древности, это имеет практическое значение — при помощи данного расчета можно оценить производительность компьютерных систем.
Ирина Ходакова:
Изначально число π было необходимо для применения в строительстве. Ведь порой из-за погрешности в значении числа π падали башни и рушились целые дворцы. Сейчас π используется в различных сферах нашей жизни.
Мы уже выяснили, что число π позволяет нам рассчитывать и создавать окружности. Если колеса на вашем автомобиле будут немного отличаться друг от друга, то поездки для вас станут как минимум не очень удобными.
Но применение числа π этим не ограничивается. Например, без числа π нельзя было бы обеспечить качественную работу телевизоров, радио и телефонов, так как инженеры используют π для расчета и оптимизации звуковых волн. Также π играет важную роль в расчете времени и расстояния путешествия на самолете, так как на большие расстояния самолеты летят по округлой дуге. Не было бы даже многих игр, таких как футбол, баскетбол, теннис, ведь мячи должны быть абсолютно круглыми.
Что вы знаете про число пи?
Посмотрим, насколько хорошо вы разобрались в теме. Потренируйтесь в несложных расчетах и ответьте на простые вопросы для самопроверки.
| Пройти тест |
Примерно 3,14
У числа пи нет точного значения. Но для расчетов принято округленное значение до сотых. Это 3,14.
Ровно 3
У числа пи нет точного значения. Но для расчетов принято округленное значение до сотых.
Это 3,14.
Около 3
У числа пи нет точного значения. Но для расчетов принято округленное значение до сотых. Это 3,14.
| Дальше |
| Проверить |
| Узнать результат |
Это сумма длины окружности и диаметра окружности
Число пи — это отношение длины окружности к ее диаметру. Обозначается оно буквой греческого алфавита π. То есть π — это результат деления длины окружности на ее диаметр.
Это отношение длины окружности к диаметру окружности
Число пи — это отношение длины окружности к ее диаметру. Обозначается оно буквой греческого алфавита π. То есть π — это результат деления длины окружности на ее диаметр.
Это произведение радиуса окружности и длины окружности
Число пи — это отношение длины окружности к ее диаметру.
Обозначается оно буквой греческого алфавита π. То есть π — это результат деления длины окружности на ее диаметр.
| Дальше |
| Проверить |
| Узнать результат |
3,1415927
Один из методов запоминания числа пи — это подсчет количество букв в каждом слове предложения. В нашем предложении «Это я знаю и помню прекрасно» в каждом слове такое количество букв: 3, 1, 4, 1, 5, 9. То есть по предложению мы запоминаем, что число пи равно 3,14159.
3,1415
Один из методов запоминания числа пи — это подсчет количество букв в каждом слове предложения. В нашем предложении «Это я знаю и помню прекрасно» в каждом слове такое количество букв: 3, 1, 4, 1, 5, 9. То есть по предложению мы запоминаем, что число пи равно 3,14159.
3,14159
Один из методов запоминания числа пи — это подсчет количество букв в каждом слове предложения.
В нашем предложении «Это я знаю и помню прекрасно» в каждом слове такое количество букв: 3, 1, 4, 1, 5, 9. То есть по предложению мы запоминаем, что число пи равно 3,14159.
| Дальше |
| Проверить |
| Узнать результат |
14 см
Вычисляем площадь круга по формуле S = πr². Нам известно, что радиус равен 2 см. 2 в квадрате — это 4. Теперь 4 умножаем на число пи — 3,14. Получаем 12,56 см — это площадь нашего круга.
12,56 см
Вычисляем площадь круга по формуле S = πr². Нам известно, что радиус равен 2 см. 2 в квадрате — это 4. Теперь 4 умножаем на число пи — 3,14. Получаем 12,56 см — это площадь нашего круга.
16,09 см
Вычисляем площадь круга по формуле S = πr². Нам известно, что радиус равен 2 см.
2 в квадрате — это 4. Теперь 4 умножаем на число пи — 3,14. Получаем 12,56 см — это площадь нашего круга.
| Дальше |
| Проверить |
| Узнать результат |
8,87 см
Используем формулу С = πd, где С — длина окружности, а d — диаметр. Мы знаем, что он равен 6 см. Число пи нам тоже известно — 3,14. Умножаем 6 на 3,14 — получаем 18,84 см.
12,48 см
Используем формулу С = πd, где С — длина окружности, а d — диаметр. Мы знаем, что он равен 6 см. Число пи нам тоже известно — 3,14. Умножаем 6 на 3,14 — получаем 18,84 см.
18,84 см
Используем формулу С = πd, где С — длина окружности, а d — диаметр. Мы знаем, что он равен 6 см. Число пи нам тоже известно — 3,14. Умножаем 6 на 3,14 — получаем 18,84 см.
| Дальше |
| Проверить |
| Узнать результат |
5,73 см
Для расчетов нам поможет та же формула С = πd.
Только в этом случае нам известна длина окружности (С) и число пи. Чтобы по этим данным вычислить диаметр, немного изменим нашу формулу — d = С/π, то есть 18 делим на 3,14. Это равно 5.73248408. Далее используем метод округления к ближайшему целому — округляем до сотых. Получаем 5,73.
6,05 см
Для расчетов нам поможет та же формула С = πd. Только в этом случае нам известна длина окружности (С) и число пи. Чтобы по этим данным вычислить диаметр, немного изменим нашу формулу — d = С/π, то есть 18 делим на 3,14. Это равно 5.73248408. Далее используем метод округления к ближайшему целому — округляем до сотых. Получаем 5,73.
5,13 см
Для расчетов нам поможет та же формула С = πd. Только в этом случае нам известна длина окружности (С) и число пи. Чтобы по этим данным вычислить диаметр, немного изменим нашу формулу — d = С/π, то есть 18 делим на 3,14. Это равно 5.73248408. Далее используем метод округления к ближайшему целому — округляем до сотых.
Получаем 5,73.
| Дальше |
| Проверить |
| Узнать результат |
21,13 см
Для этого расчета вспомним, чему равен диаметр: d = 2r. То есть диаметр равен радиусу, умноженному на два. В нашей задаче радиус окружности — 7 см. Значит, диаметр — 14 см. Далее используем уже знакомую формулу С = πd. Считаем. 3,14 умножаем на 14, получаем 43,96 см.
43,96 см
Для этого расчета вспомним, чему равен диаметр: d = 2r. То есть диаметр равен радиусу, умноженному на два. В нашей задаче радиус окружности — 7 см. Значит, диаметр — 14 см. Далее используем уже знакомую формулу С = πd. Считаем. 3,14 умножаем на 14, получаем 43,96 см.
35,56 см
Для этого расчета вспомним, чему равен диаметр: d = 2r. То есть диаметр равен радиусу, умноженному на два.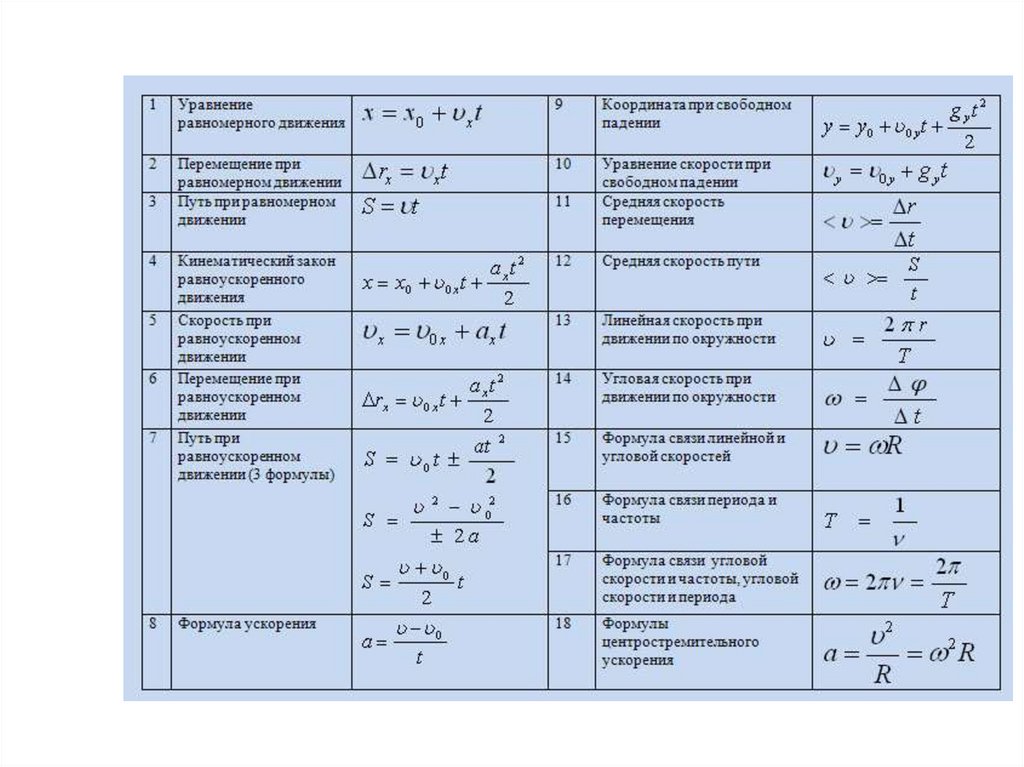
В нашей задаче радиус окружности — 7 см. Значит, диаметр — 14 см. Далее используем уже знакомую формулу С = πd. Считаем. 3,14 умножаем на 14, получаем 43,96 см.
| Дальше |
| Проверить |
| Узнать результат |
Прочитайте статью еще раз и пройдите тест повторно.
| Пройти еще раз |
Прочитайте статью еще раз и пройдите тест повторно.
| Пройти еще раз |
Прочитайте статью еще раз и пройдите тест повторно.
| Пройти еще раз |
Вы хорошо разобрались в материале, но ошибки еще есть.
| Пройти еще раз |
Вы хорошо разобрались в материале, но ошибки еще есть.
| Пройти еще раз |
Вы изучили правило и умеете его применять.
| Пройти еще раз |
Фото на обложке: shutterstock.com
Уравнения поля: физика бейсбола
Наконец-то настал день открытия. Как и в каждом новом сезоне, этот приходит с множеством вопросов высшей лиги: могут ли Филлис повторить? Смогут ли расточительные янки преодолеть засуху в Мировой серии? Это год, когда легкая атлетика восстанавливает свое свободное волшебство? Но ответы на все эти важные вопросы, в конечном счете, возникнут в результате бесчисленного множества мелких взаимодействий, как человеческих (питчер лицом вниз к отбивающему, бегун с базы бросает вызов руке кетчера, хитрый двойной переключатель тренера), так и физических (мяч попадает в золотую середину летучей мыши). , острый ползунок, рассекающий воздух, поп-муха, описывающая параболическую дугу в небе).
Алан Натан, профессор физики Иллинойсского университета в Урбана-Шампейне, натренировал свой экспертный взгляд на те вопросы физики, которые составляют кванты игры.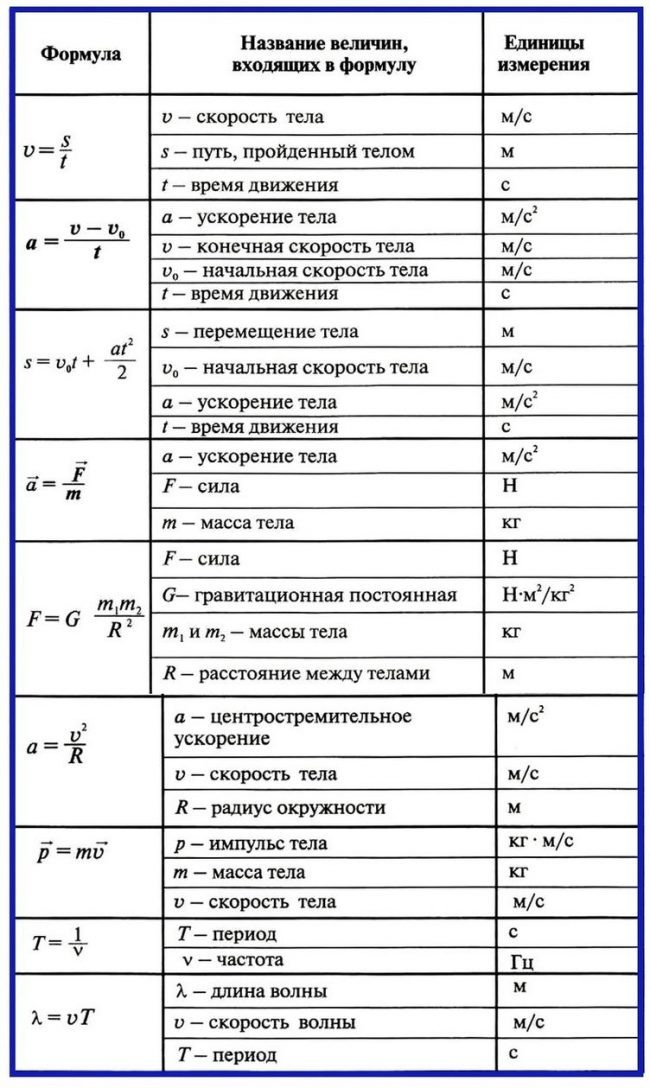
Натан поддерживает онлайн-репозиторий по физике бейсбола, опираясь на свои собственные работы и работы других ученых, интересующихся бейсболом. Мы поговорили с ним о закрытых летучих мышах, таинственном «гиробаре» и о том, хватит ли у его любимой команды рабочей силы, чтобы провести еще один чемпионский сезон.
[ Далее следует отредактированная стенограмма интервью. ]
Как вы заинтересовались этой темой?
Все началось достаточно безобидно. У нас есть такие информационно-просветительские программы, предназначенные в основном для школьников, изучающих естественные науки, и мы по очереди выступаем с докладами, обычно о наших собственных исследованиях. Вот эта книга, Физика бейсбола, Роберта Адэра, которая лежала у меня на полке семь или восемь лет и ни разу не открывалась — это было в далёком 1997 году — и я подумал: «Ну, позвольте мне согласиться на расскажи об этом, и это заставит меня прочитать это». Так я и сделал, и это было бы разовым делом, если бы не тот факт, что в аудитории был репортер местной газеты.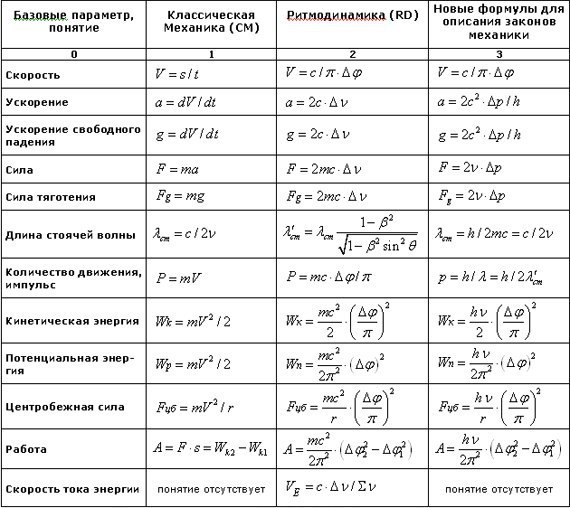
На вашей веб-странице
Абсолютно. Например, это один из определяющих факторов того, как далеко улетит мяч. Как правило, если вы хотите ударить по летящему мячу, вам нужно придать этому мячу обратное вращение. Так называемая сила Магнуса, действующая на вращающийся бейсбольный мяч, будет направлена вверх для мяча с обратным вращением, и в основном она противостоит гравитации.
С другой стороны, если вы сделаете обратное — если ударите по верхней части мяча — мяч, как правило, упадет вниз, так что он будет приземляться, и у него будет верхнее вращение. Но сам топ-спин может привести к интересным вещам. Иногда отбивающий может попасть в тонущую леску; опять же, это еще одна ударная стратегия. В этом случае удар по мячу больше похож на линейный удар, но он немного увенчан, поэтому мяч имеет верхнее вращение. Верхнее вращение заставляет мяч падать быстрее, и это то, что вы можете сделать для линейного драйва, чтобы он упал перед аутфилдером. Таким образом, есть всевозможные стратегии ударов, которые могут использовать отбивающие, и я подозреваю, что, хотя они не думают об этом, может быть, в таких терминах, они действительно понимают, о чем идет речь.
Раз уж мы заговорили о стратегиях нанесения ударов, я вижу, вы поработали над плюсами и минусами закрытых летучих мышей. Не могли бы вы провести нас через это?
Идея укупоривания биты заключается в том, что вы просверливаете отверстие в стволе летучей мыши — может быть, глубиной в фут, может быть, около дюйма в диаметре — и забиваете его пробкой. Сама пробка не делает ничего, кроме как скрывает тот факт, что вы совершили это незаконное действие. Идея заключается в следующем: с меньшим весом биты в голове биты, в стволе, вы можете быстрее замахнуться битой. Но это компромисс. Поскольку рабочий конец биты имеет меньший вес, вы можете махать ею быстрее, но она менее эффективна при передаче энергии мячу. И поэтому есть что-то вроде противоречия относительно того, является ли чистый результат положительным или отрицательным с точки зрения отбивающего. Мой вывод с точки зрения получения максимальной скорости отбитого мяча, а это то, что вам нужно, если вы хотите отбить самый длинный летающий мяч, заключается в том, что это чистая потеря для отбивающего.
Другими словами, то, что вы получаете в скорости замаха, не вполне компенсирует то, что вы теряете в эффективности передачи энергии.Тогда вы можете спросить, а почему отбивающие делают это? На самом деле есть веская причина, по которой они могут это сделать. Дело не в том, чтобы получить максимальную скорость мяча, а в том, чтобы иметь лучший контроль над битой. Таким образом, с меньшим весом биты в стволе вам гораздо легче манипулировать битой, чтобы быстрее доставить биту в зону удара. Отбивающие проводят различие между скоростью биты (насколько быстро летучая мышь на самом деле движется, когда она ударяет по мячу) и быстротой летучей мыши, которая больше связана с ускорением, способностью отбивающего перевести биту из того места, где она первоначально находилась на его плече. зону удара как можно быстрее. А это означает, что вы можете даже изменить свой замах в середине замаха, что происходит, когда вы получаете больше информации о том, где мяч в конечном итоге окажется.
Таким образом, несмотря на то, что закупоривание биты, скорее всего, не позволит вам совершать более длинные хоум-раны, это может позволить вам чаще устанавливать хороший контакт.
Так что даже если вы жертвуете своей скоростью отбитого мяча и, возможно, своей репутацией, если вы Сэмми Соса, у вас есть некоторые преимущества.
Ага. И я думаю, что этот вид компромисса очень похож на тот компромисс, который делают игроки на уровне старшей школы и колледжа. Применяются те же вещи, за исключением того, что они не используют деревянные биты. На самом деле они могут легально уменьшить вес ствола биты, выбрав биту, которая не такая тяжелая. С недеревянными битами вы можете легче изменить момент инерции биты, что в основном связано с тем, насколько она тяжелая в стволе, почти не зависит от общего веса биты, и вы можете сделать это на законных основаниях. Таким образом, интересно то, что большинство университетских игроков, похоже, предпочитают биты с меньшим весом в стволе, в некотором смысле жертвуя самой высокой скоростью мяча в пользу большего контроля над битой и возможности чаще наносить ствол биты на мяч. .
Что касается физики качки, то два года назад все слышали о “гироболе”.
Видели ли мы что-то подобное в Высшей бейсбольной лиге или это миф?
Я не зайду так далеко, чтобы сказать, что это миф. Я не думаю, что это миф. Но это, конечно, редко используется. Как вы сказали, два года назад, когда Дайсуке Мацудзака впервые попал в Высшую бейсбольную лигу из японского бейсбола, именно тогда все разговоры велись о гироболе. Гиробар — это мяч, брошенный с тем, что можно назвать вращением пули, что-то вроде спирали для футбольного мяча. Таким образом, ось вращения более или менее совпадает с направлением движения. То, как сила Магнуса действует на вращающийся бейсбольный мяч, заключается в том, что сила наибольшая, когда ось вращения перпендикулярна направлению движения. Когда они в одном направлении, силы Магнуса нет. Таким образом, мяч может вращаться, но это вращение не приводит к отклонению мяча. И поэтому казалось бы, что это бесполезная подача. Но когда я проанализировал его, я пришел к выводу, что при разумном использовании это не бесполезная подача.
И причина этого в том, что большинство подаваемых мячей вращаются. Если отбивающий видит, что из руки вылетает мяч, который выглядит как фастбол с четырьмя швами, что является своего рода самой прямой подачей и подачей, которая меньше всего падает, потому что у нее много обратного вращения, отбивающий ожидает, что подача придет. более или менее на определенной высоте. Если вместо этого это на самом деле гиробол — ради аргумента скажем, что его бросают так же сильно, как фастбол — тогда на него не действует восходящая сила Магнуса. Он свободно падает под действием силы тяжести, поэтому в итоге он падает больше, чем обычный фастбол с четырьмя швами, и это совершенно полезная подача, если отбивающий ожидает, что он сделает что-то еще.
Старая пословица, как сказал великий левша Уоррен Спан, гласит, что «отбивание мяча — это время, а подача — это нарушение времени». Вам не нужно бросать самый быстрый мяч, чтобы вывести людей из игры — все, что вам нужно сделать, это бросить то, чего они не ожидают.
Действительно хорошие питчеры знают, как это сделать.
Свидетель Джейми Мойер, например.
Грег Мэддакс — еще один прекрасный пример того, кто сделал карьеру, не обязательно всегда выбрасывая свои лучшие вещи, но всегда смешивая вещи таким образом, что отбивающий этого не ожидает.
Теперь, когда я посмотрел на подачу Мацудзаки в сезоне 2007 года, я пришел к выводу, что если он и бросал подачу, то не так часто. Может быть, один или два раза за игру максимум. Существует система отслеживания подачи под названием Pitch f/x, которая установлена на каждом стадионе высшей лиги, и все данные совершенно бесплатны для всего мира. Ну, вы должны знать, где его найти и как его интерпретировать. Отличительной чертой гироскопа будет мяч, который не разбивается, не имеет ни горизонтального, ни вертикального разрыва. Итак, я искал такие предложения от Мацудзаки, и вы время от времени видите несколько таких, которые выглядят так, как будто они могут соответствовать требованиям. Если он бросает его, это не та подача, на которой вы хотели бы давать людям постоянную диету, потому что, как только они это поймут и поймут, по этой подаче будет легко попасть. Так что вы должны бросить его обдуманно, и если он бросит его — никто не знает наверняка, — он определенно бросит его рассудительно.
Переходя к товарищу Мацудзаки по команде Тиму Уэйкфилду, не могли бы вы рассказать нам о его фирменной подаче, наклболе?
Ну, я должен признать, что я понимаю, что меньше всего.
Думаю, это верно для всех.
Ключ к пониманию наклбола заключается в том, что если бы мяч был идеально гладким, воздух обтекал бы его достаточно плавно. Но швы на мяче нарушают поток воздуха, в результате чего мяч ломается. Это совсем не то же самое, что эффект от вращающегося бейсбольного мяча — он совсем другой. Таким образом, ключ к броску наклбола заключается в том, что если вы бросаете вращающийся мяч, один из способов думать об этом состоит в том, что вращающийся бейсбольный мяч усредняется по разным ориентациям швов, поэтому нет никакого чистого эффекта из-за взаимодействия воздуха со швами. Но если вы бросаете мяч почти без вращения — может быть, он совершает пол-оборота или даже четверть оборота на пути к исходной пластине — тогда когда воздух движется над мячом, это взаимодействие воздуха с этими швами. это меняет характер воздушного потока, превращая его из приятного плавного потока в своего рода турбулентный поток. Это вызывает локальные колебания давления, из-за которых шар ломается, причем ломается более или менее непредсказуемо.
Если вы используете эту систему Pitch f/x, чтобы посмотреть на любой другой кувшин, и вы нанесете каждый шаг на своего рода диаграмму x-y, где x — излом в горизонтальном направлении, а y — излом в вертикальном направлении, то высоты тона попадают в красивые, аккуратные маленькие кластеры. У вас есть симпатичный небольшой кластер, показывающий фастбол с четырьмя швами, крученый мяч, каттер. Но вы посмотрите на Уэйкфилд, и это повсюду. Нет красивого, аккуратного кластера, а это значит, что у мяча нет того, что можно было бы назвать характерным разрывом. Это действительно буквально непредсказуемо. Все знают, что это произойдет, но все, что вам нужно сделать, это посмотреть на то, что делает кетчер, чтобы понять, что никто не знает, куда он идет — я имею в виду, что кетчеру тоже приходится иметь дело с этим. [ Примечание редактора: в 2006 году «Ред Сокс» вновь приобрели кэтчера Дуга Мирабелли специально за его способность ловить наклбол Уэйкфилда. ] Это сложная подача. С Уэйкфилдом действительно смешно; он ближе всего к биполярному питчеру, которого я когда-либо видел. Он попадает на насыпь, и либо она у него в тот день, либо нет. Когда он на ходу, он совершенно неуязвим. А когда он не работает, они бьют его. Иногда этот мяч действительно танцует, а иногда нет. А потом бывают времена, когда он танцует так сильно, что он не может это контролировать, а потом он гуляет с людьми, и у него плохой день. Он почти 0,500 карьерных питчеров; он выигрывает половину игр, которые проводит. Это просто отражает тот факт, что иногда он включен, а иногда нет.