закон простыми словами, формула, в чем измеряется, от чего зависит, как был открыт
Вместе с преподавателем физики разбираемся, в чем измеряется и от чего зависит сила Архимеда. А в конце статьи вспомним известную легенду о том, как был открыт закон Архимеда, и узнаем, действует ли он в условиях невесомости
Сила Архимеда. Фото: pexels.comБорис Михеев Автор КП Николай Герасимов Старший преподаватель физики
Содержание
- Определение закона
- Формула
- В чем измеряется
- Вопросы и ответы
Как объяснить, почему плавают огромные корабли из стали, которая тяжелее воды? Да еще и перевозят тонны грузов.
История сохранила нам немного имен ученых-практиков, чьи изобретения изменили мир. Навсегда забыт гений, который придумал колесо. Но любой современный школьник назовет Архимеда, даже если знает о нем только легенду про мокрого голого философа, бежавшего по улице Сиракуз с криком: «Эврика!», то есть «Нашел!». А ведь ученый заслужил вечную благодарную память человечества благодаря многим изобретениям и открытиям:
- Теория рычага и способы его расчета. На этой основе построены боевые машины для метания тяжелых камней и «коготь Архимеда» — машина для переворачивания римских трирем;
- Шкив и многоступенчатый блок, полиспаст;
- Червячная передача;
- Архимедов винт и насосы, работающие на его принципе;
- Одометр, машина для измерения пройденного пути;
- «Архимедово число»: отношение длины окружности к ее диаметру
- Фокусировка световых лучей при помощи зеркал.
 По легенде, так были сожжены римские корабли, осаждавшие Сиракузы. Недавно энтузиасты провели экспериментальную проверку и удалось поджечь деревянный баркас.
По легенде, так были сожжены римские корабли, осаждавшие Сиракузы. Недавно энтузиасты провели экспериментальную проверку и удалось поджечь деревянный баркас.
Однако самое знаменитое открытие — закон Архимеда, основа гидростатики. Удивительно, что он был почти забыт, пока корабли строили из дерева. И только когда они стали железными, а потом стальными, инженеры осознали важность силы Архимеда и стали применять ее формулу при расчетах водных и воздушных судов.
Определение закона Архимеда простыми словами
На тело, погруженное в жидкость или газ, действует подъемная, она же выталкивающая сила (сила Архимеда), равная весу вытесненного объема жидкости или газа.
Вектор силы Архимеда направлен против направления действия силы тяжести. Следствия закона Архимеда:
- В невесомости закон Архимеда не действует.
- Если сила Архимеда меньше силы тяжести, то тело утонет.
- Если силы одинаковы по величине, тело «повисает» в окружающей среде.

- Если сила Архимеда больше силы тяжести, то тело всплывает, пока они не уравновесятся. В воде этот момент наступит на поверхности.
Формула силы Архимеда
Предыдущая формулировка годится только для участка цепи, где отсутствует сам источник электродвижущей силы. В реальности ток течет по замкнутому контуру, где обязательно есть батарея или генератор, имеющий собственное внутреннее сопротивление. Поэтому формула закона Ома для полной цепи выглядит несколько сложнее
Где: FA — сила Архимеда;
ρ — плотность жидкости или газа, в которое погружают тело;
g — ускорение свободного падения, которое зависит от того, на какой планете или спутнике мы находимся. Для поверхности Земли, например, ускорение примерно равно 9,8 м/с2;
V — объем погруженной в среду части тела.
это интересно
Закон Паскаля
Объяснение закона простыми словами и его формула
подробнее
В чем измеряется сила Архимеда
Единица измерения силы Архимеда в системе СИ — ньютон (Н).
1Н = 1 кг·м/с2
Архимед и наше время
В перечне военных трофеев, взятых римлянами в Сиракузах, есть некий «Планетарий Архимеда» — механическая модель движения планет. Он не сохранился, но есть подозрение, что загадочное устройство, случайно обнаруженное в затонувшем корабле у острова Антикитера, тоже сделано золотыми руками Архимеда. Прямых доказательств этого факта нет, но уже выяснено, что время изготовления приблизительно соответствует годам жизни гениального инженера.
Популярные вопросы и ответы
Отвечает Николай Герасимов, старший преподаватель по физике Домашней школы «ИнтернетУрок».
От чего зависит сила Архимеда?
Например, для определения выталкивающей силы, действующей на камень, лежащий на дне озера, нужно брать весь его объем. Если же определяем силу Архимеда, действующую на мяч, плавающий по этому озеру, то нужно брать лишь объем той части, которая находится под водой.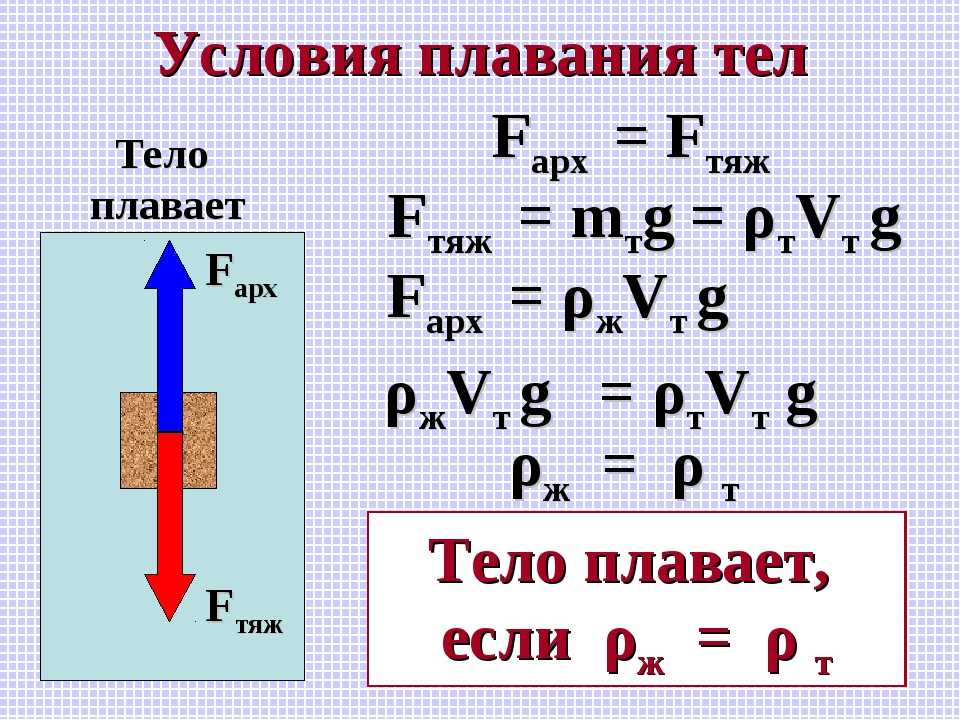 Зависимость выталкивающей силы от ускорения свободного падения позволяет сделать интересный вывод о том, что в невесомости силы Архимеда нет.
Зависимость выталкивающей силы от ускорения свободного падения позволяет сделать интересный вывод о том, что в невесомости силы Архимеда нет.
Зная, что сила Архимеда зависит от плотности жидкости, можно объяснить следующее явление: куриное яйцо, помещенное в обычную воду, утонет и будет лежать на дне банки. Но стоит добавить в эту банку насыщенный раствор поваренной соли и тем самым изменить плотность воды — и яйцо начинает всплывать.
Как был открыт закон Архимеда?
Открытие закона Архимеда связано с интересной легендой. Древнегреческий царь Герон II приказал ювелирам изготовить золотую корону, что и было вскоре выполнено. Царь заподозрил, что ювелиры его обманули и сделали корону из электрона, сплава золота и серебра. Отличить подделку на глаз не удалось. Для проверки пригласили ученого из Сиракуз по имени Архимед. Достаточно было сравнить объем короны с объемом куска золота такой же массы.
Сложность состояла в определении объема короны, так как она была сложной формы, и вычислить объем по математическим формулам было невозможно.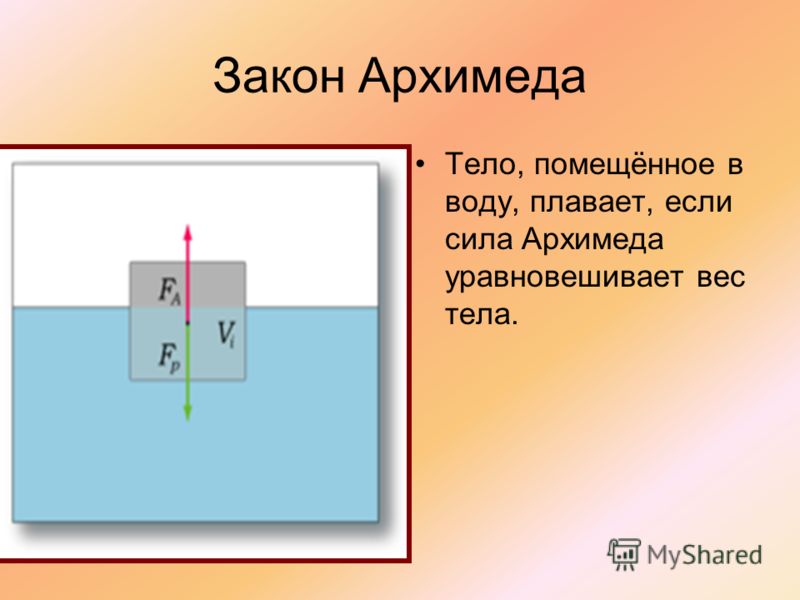 Долгие размышления не увенчались успехом, и Архимед решил сходить отдохнуть в баню. Именно там ученому пришла гениальная идея: погружаясь в воду, тело вытесняет ее в объеме, который равен объему погруженной части тела. «Эврика!» («Нашел!») — закричал Архимед и побежал к царю.
Долгие размышления не увенчались успехом, и Архимед решил сходить отдохнуть в баню. Именно там ученому пришла гениальная идея: погружаясь в воду, тело вытесняет ее в объеме, который равен объему погруженной части тела. «Эврика!» («Нашел!») — закричал Архимед и побежал к царю.
Сравнив объемы воды, вытесненной короной и куском золота такой же массы, он уличил ювелиров в нечестности и алчности. Так Архимедом был открыт закон, который позволяет нам объяснить, почему ходят по морям и океанам огромные корабли, изготовленные из железа, а маленькая металлическая гайка тонет.
Какой буквой обозначают силу Архимеда?
Как и большинство сил, сила Архимеда обозначается буквой F. Это первая буква английского слова force – сила. В индексе пишут букву А или В, которые позволяют отличить силу Архимеда FA или выталкивающую силу FВ от других сил в природе.
формула, чему равна, от чего зависит, единица измерения, примеры
Содержание:
- История открытия
- Формула закона Архимеда
Содержание
- История открытия
- Формула закона Архимеда
- Применение архимедовой силы
История открытия
Сила Архимеда названа по имени ученого, который и сформулировал закон.
Решение было найдено, когда ученый обнаружил интересную зависимость: если опустить предмет в воду, то объем выплеснутой воды будет равен объему предмета. Таким образом Архимед смог сравнить величину золотой короны и исходного куска золота. Мастера уличили в нечестности, а древнегреческий философ обосновал закон о силе, которая выталкивает тела из воды.
Архимедова сила — сила, направленная противоположно силе земного притяжения, когда тело находится в жидкости или газе.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Формула закона Архимеда
Закон определяет связь между весом тела, погруженного в жидкость или газ, и силой, которая его выталкивает. Согласно ему, подъемная сила зависит от веса погруженного тела или силы тяжести, действующей на него.
Силу Архимеда следует рассчитывать по формуле: FА = pжgVт
Расшифровка формулы:
P — плотность жидкости
g — ускорение свободного падения
V — объем тела
Выталкивающая сила (FА) всегда действует противоположно силе притяжения (Fт). Поэтому тело выплывает из воды или газа на поверхность. Нахождение тела в жидкости зависит от нескольких параметров. Чем больше плотность жидкости, тем сильнее она вытесняет тело. То же самое касается и объема — меньшее тело утонет гораздо быстрее, чем тело большего объема. Пример: железный гвоздь утонет, а большое судно плавает на поверхности воды.
Примечание
V — обозначение объема только погруженной части тела.
Если сила тяжести равна силе Архимеда, тело плавает на поверхности. Если притяжение будет превосходить архимедову силу, тело утонет. Единицей измерения при расчете подъемной силы является ньютон.
Применение архимедовой силы
Человек чувствует силу Архимеда в действии, когда занимается плаванием. Все предметы в воде становятся легче, так как на них действует архимедова сила.
Закон Архимеда широко применяется на практике в ряде систем. В первую очередь открытие позволило конструировать корабли, не опасаясь того, что они утонут. Проведя необходимые вычисления, инженеры строят суда таким образом, чтобы они вытесняли массу воды, равную или превосходящую вес корабля. Для этого объем погружающейся части корабля делают таким, что на него будет действовать выталкивающая сила, большая по величине или равная весу судна.
Другая область применения подъемной силы — воздухоплавание. Гелий, которым заполняются воздушные шары, имеет низкую плотность, по сравнению с кислородом. Сам шар вытесняет определенное количество воздуха из атмосферы. Начинает действовать выталкивающая сила, поднимающая шар высоко в небо.
Гелий, которым заполняются воздушные шары, имеет низкую плотность, по сравнению с кислородом. Сам шар вытесняет определенное количество воздуха из атмосферы. Начинает действовать выталкивающая сила, поднимающая шар высоко в небо.
Примечание
Уменьшить плотность воздуха можно с помощью увеличения его температуры. Поэтому многие воздушные шары оборудованы специальными горелками. Чтобы поднять такой шар, нужно постоянно нагревать воздух внутри него.
Насколько полезной была для вас статья?
Рейтинг: 2.63 (Голосов: 8)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
11.7 Принцип Архимеда – Колледж по физике, главы 1-17
11 Статистика жидкости
Резюме
- Определение выталкивающей силы.
- Государственный закон Архимеда.

- Поймите, почему объекты плавают или тонут.
- Понять взаимосвязь между плотностью и законом Архимеда.
Когда вы встаете после принятия теплой ванны, ваши руки кажутся странно тяжелыми. Это потому, что у вас больше нет плавучей поддержки воды. Откуда берется эта выталкивающая сила? Почему одни вещи плавают, а другие нет? Получают ли объекты, которые тонут, какую-либо поддержку от жидкости? Ваше тело поддерживается атмосферой или это касается только гелиевых шаров? (См. рис. 1.)
Ответы на все эти и многие другие вопросы основаны на том факте, что давление в жидкости увеличивается с глубиной. Это означает, что восходящая сила на нижней части объекта в жидкости больше, чем направленная вниз сила на верхней части объекта. Есть сетка наверху, или выталкивающая сила на любой предмет в любой жидкости. (См. рис. 2.) Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и всплывет. Если выталкивающая сила меньше веса тела, то оно утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится в жидкости.
Это означает, что восходящая сила на нижней части объекта в жидкости больше, чем направленная вниз сила на верхней части объекта. Есть сетка наверху, или выталкивающая сила на любой предмет в любой жидкости. (См. рис. 2.) Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и всплывет. Если выталкивающая сила меньше веса тела, то оно утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится в жидкости.
ВЫПУТНАЯ СИЛА
Выталкивающая сила – это результирующая восходящая сила, действующая на любой объект в любой жидкости.
Рис. 2. Давление из-за веса жидкости увеличивается с глубиной, так как P=hρg . Это давление и связанная с ним восходящая сила на дне цилиндра больше, чем направленная вниз сила на верхней части цилиндра. Их отличие – выталкивающая сила F B .
 (Горизонтальные силы компенсируются.)
(Горизонтальные силы компенсируются.)Насколько велика эта выталкивающая сила? Чтобы ответить на этот вопрос, подумайте о том, что происходит, когда погруженный объект вынимают из жидкости, как показано на рис. 3.9.0005 Рис. 3. (a) На объект, погруженный в жидкость, действует выталкивающая сила F B . Если F B больше веса объекта, объект поднимется. Если F B меньше веса объекта, объект утонет. (b) Если объект удаляется, он заменяется жидкостью, имеющей вес w fl . Поскольку этот вес поддерживается окружающей жидкостью, выталкивающая сила должна равняться весу вытесненной жидкости. то есть F B = w fl , формулировка закона Архимеда.
Пространство, которое он занимает, заполнено жидкостью, имеющей вес[латекс]\boldsymbol{w _{\textbf{fl}}}. [/latex]Этот вес поддерживается окружающей жидкостью, поэтому выталкивающая сила должна быть равна[латексу] ]\boldsymbol{w_{\textbf{fl}}},[/latex]вес жидкости, вытесненной объектом. Это дань уважения гению греческого математика и изобретателя Архимеда (ок. 287–212 до н. э.), который сформулировал этот принцип задолго до того, как понятия силы были прочно установлены. Говоря словами, принцип Архимеда выглядит следующим образом: выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости. В форме уравнения принцип Архимеда равен
[/latex]Этот вес поддерживается окружающей жидкостью, поэтому выталкивающая сила должна быть равна[латексу] ]\boldsymbol{w_{\textbf{fl}}},[/latex]вес жидкости, вытесненной объектом. Это дань уважения гению греческого математика и изобретателя Архимеда (ок. 287–212 до н. э.), который сформулировал этот принцип задолго до того, как понятия силы были прочно установлены. Говоря словами, принцип Архимеда выглядит следующим образом: выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости. В форме уравнения принцип Архимеда равен
[латекс]\boldsymbol{F_{\textbf{B}}=w_{\textbf{fl}}},[/латекс]
, где [латекс]\boldsymbol{F_{\textbf{B}}}[/latex]является выталкивающей силой, а[латекс]\boldsymbol{w_{\textbf{fl}}}[/latex]является весом жидкость, вытесненная объектом. Принцип Архимеда действителен в целом для любого объекта в любой жидкости, полностью или частично погруженного в воду.
ПРИНЦИП АРХИМЕДА
В соответствии с этим принципом выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости.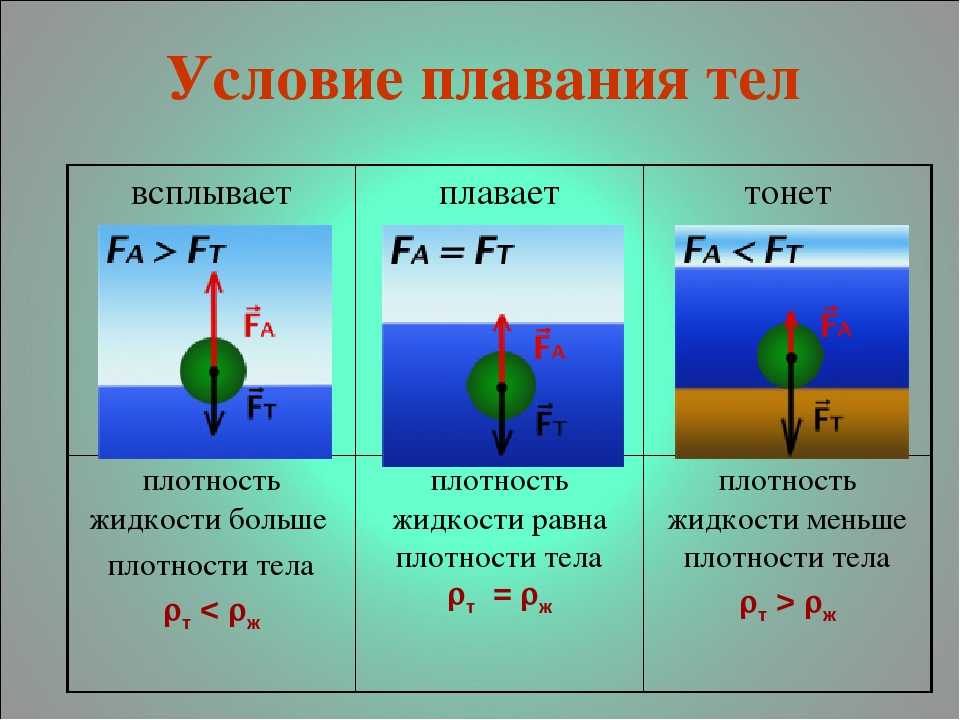 В форме уравнения принцип Архимеда равен
В форме уравнения принцип Архимеда равен
[латекс]\boldsymbol{F_{\textbf{B}}=w_{\textbf{fl}}},[/latex]
, где[латекс]\boldsymbol{F_{\textbf{B}}}[ /latex] – выталкивающая сила, а [latex]\boldsymbol{w _{\textbf{fl}}}[/latex] – вес жидкости, вытесненной объектом.
Humm … Высокотехнологичные купальники для тела были представлены в 2008 году в рамках подготовки к Олимпийским играм в Пекине. Одна проблема (и международное правило) заключалась в том, что эти костюмы не должны давать никакого преимущества в плавучести. Как вы думаете, можно ли проверить это правило?
ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ: ИССЛЕДОВАНИЕ НА ДОМУ
Плотность алюминиевой фольги в 2,7 раза больше плотности воды. Возьмите кусок фольги, скатайте его в шар и бросьте в воду. Он тонет? Почему или почему нет? Можете ли вы заставить его утонуть?
Бросьте кусок глины в воду. Он утонет. Затем слепите кусок глины в форме лодки, и она будет плавать. Из-за своей формы лодка вытесняет больше воды, чем глыба, и испытывает большую выталкивающую силу.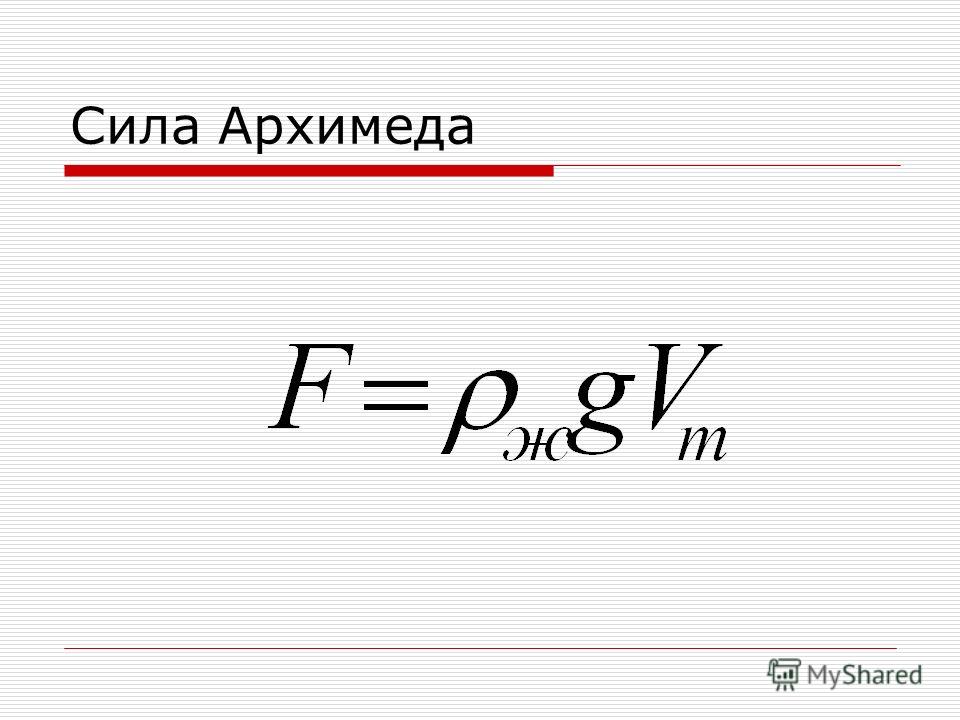 То же самое и со стальными кораблями. 93}[/latex]воды?
То же самое и со стальными кораблями. 93}[/latex]воды?
Стратегия для (a)
Чтобы найти выталкивающую силу, мы должны найти вес вытесненной воды. Мы можем сделать это, используя плотности воды и стали, приведенные в таблице 1. Заметим, что, поскольку сталь полностью погружена в воду, ее объем и объем воды одинаковы. Зная объем воды, мы можем найти ее массу и вес.
Решение для (a)
Сначала мы используем определение плотности [латекс]\boldsymbol{\rho=\frac{m}{V}}[/латекс], чтобы найти объем стали, а затем мы замените значения массы и плотности. Это дает 97\textbf{ N}},[/latex]что намного больше, чем выталкивающая сила, поэтому сталь останется погруженной. Обратите внимание, что выталкивающая сила округляется до двух цифр, потому что плотность стали выражается только двумя цифрами.
Стратегия для (b)
Здесь нам дан максимальный объем воды, который может вытеснить стальная лодка. Выталкивающая сила равна весу этого объема воды.
Решение для (b)
Масса вытесненной воды определяется по ее отношению к плотности и объему, оба из которых известны. то есть 98\textbf{ N.}} \end{array}[/latex]
Обсуждение
Максимальная выталкивающая сила в десять раз превышает вес стали, а это означает, что корабль может нести груз, в девять раз превышающий его собственный вес, без тонет.
ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ: ИССЛЕДОВАНИЕ НА ДОМУ
Кусок бытовой алюминиевой фольги толщиной 0,016 мм. Возьмите кусок фольги размером 10 на 15 см. а) Какова масса этого куска фольги? (b) Если фольгу сложить так, чтобы получились четыре стороны, и добавить к этой «лодке» скрепки или шайбы, то какая форма лодки позволит вместить больше всего «груза» при погружении в воду? Проверьте свой прогноз.
Плотность играет решающую роль в законе Архимеда. Средняя плотность объекта — это то, что в конечном итоге определяет, плавает ли он. Если его средняя плотность меньше плотности окружающей жидкости, он будет плавать. Это связано с тем, что жидкость, имеющая более высокую плотность, содержит большую массу и, следовательно, больший вес в том же объеме. Таким образом, выталкивающая сила, равная весу вытесненной жидкости, больше веса объекта. Точно так же объект, более плотный, чем жидкость, утонет.
Это связано с тем, что жидкость, имеющая более высокую плотность, содержит большую массу и, следовательно, больший вес в том же объеме. Таким образом, выталкивающая сила, равная весу вытесненной жидкости, больше веса объекта. Точно так же объект, более плотный, чем жидкость, утонет.
Степень погружения плавучего объекта зависит от того, как плотность объекта связана с плотностью жидкости. На рисунке 4, например, незагруженный корабль имеет меньшую плотность и меньше погружено в воду по сравнению с тем же загруженным кораблем. Мы можем получить количественное выражение для фракции, погруженной в воду, учитывая плотность. Погруженная доля представляет собой отношение погруженного объема к объему объекта, или
[латекс]\boldsymbol{\textbf{фракция погружена}\:=}[/латекс][латекс]\boldsymbol{\frac{V _{\textbf{sub}}}{V _{\textbf{obj}}}} [/latex][latex]\boldsymbol{=}[/latex][latex]\boldsymbol{\frac{V _{\textbf{fl}}}{V _{\textbf{obj}}}}.[/latex]
Погруженный объем равен объему вытесненной жидкости, который мы называем [латекс]\boldsymbol{V_{\textbf{fl}}}. [/latex]Теперь мы можем получить соотношение между плотностями, подставив [латекс]\жирныйсимвол {\rho=\frac{m}{V}}[/latex]в выражение. Это дает
[/latex]Теперь мы можем получить соотношение между плотностями, подставив [латекс]\жирныйсимвол {\rho=\frac{m}{V}}[/latex]в выражение. Это дает
[латекс]\boldsymbol{\frac{V _{\textbf{fl}}}{V_{\textbf{obj}}}}[/latex][латекс]\boldsymbol{=}[/latex][латекс]\ жирный символ {\ гидроразрыва {m _ {\ textbf {fl}}/\ rho _ {\ textbf {fl}}} {m _ {\ textbf {obj}}/\ bar {\ rho} _ {\ textbf {obj}}}} ,[/латекс]
, где [латекс]\boldsymbol{\bar{\rho}_{\textbf{obj}}}[/latex] — средняя плотность объекта, а [латекс]\boldsymbol{\rho _{\textbf{fl}} }[/latex] — плотность жидкости. Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, в результате чего остается
[латекс]\boldsymbol{\textbf{фракция погружена}\:=}[/латекс][латекс]\boldsymbol{\frac{\bar{\rho}_{\textbf{obj}}}{\rho _{\ textbf{fl}}}}.[/latex]
Рисунок 4. Незагруженное судно (а) плавает выше в воде, чем загруженное судно (б). Мы используем это последнее соотношение для измерения плотности. Это делается путем измерения доли погруженного плавучего объекта, например, с помощью ареометра. Полезно определить отношение плотности объекта к жидкости (обычно воде) как удельный вес :
Это делается путем измерения доли погруженного плавучего объекта, например, с помощью ареометра. Полезно определить отношение плотности объекта к жидкости (обычно воде) как удельный вес :
[латекс]\boldsymbol{\textbf{удельный вес}\:=}[/латекс][латекс]\boldsymbol{\frac{\bar{\rho}}{\rho _{\textbf{w}}}}, [/латекс]
, где[латекс]\boldsymbol{\bar{\rho}}[/латекс]является средней плотностью объекта или вещества, а[латекс]\boldsymbol{\rho _{\textbf{w}}}[/латекс]является плотность воды при 4,00°С. Удельный вес безразмерен, независимо от того, какие единицы измерения используются для [латекс]\жирныйсимвол{\ро}.[/латекс]Если объект плавает, его удельный вес меньше единицы. Если он тонет, его удельный вес больше единицы. Более того, доля плавучего объекта, находящегося под водой, равна его удельному весу. Если удельный вес объекта точно равен 1, то он останется в жидкости во взвешенном состоянии, не тонет и не плавает. Аквалангисты пытаются получить это состояние, чтобы они могли парить в воде. Мы измеряем удельный вес жидкостей, таких как аккумуляторная кислота, радиаторная жидкость и моча, как показатель их состояния. Одно из устройств для измерения удельного веса показано на рис. 5.9.0005
Мы измеряем удельный вес жидкостей, таких как аккумуляторная кислота, радиаторная жидкость и моча, как показатель их состояния. Одно из устройств для измерения удельного веса показано на рис. 5.9.0005
УДЕЛЬНЫЙ ВЕС
Удельный вес — это отношение плотности объекта к жидкости (обычно воде).
Рисунок 5. Этот ареометр плавает в жидкости с удельным весом 0,87. Стеклянный ареометр наполнен воздухом и утяжелен свинцом на дне. Он лучше всего всплывает в самых плотных жидкостях и был откалиброван и промаркирован таким образом, чтобы по нему можно было напрямую считывать удельный вес.
Пример 2: расчет средней плотности: плавающая женщина
Предположим, что женщина весом 60,0 кг плавает в пресной воде, и [латекс]\жирныйсимвол{97,0\%}[/латекс] ее объема находится под водой, когда ее легкие наполнены воздухом. Какая у нее средняя плотность?
Стратегия
Мы можем найти плотность тела женщины, решив уравнение {\rho}_{\textbf{obj}}}{\rho_{\textbf{fl}}}}[/latex]
для плотности объекта.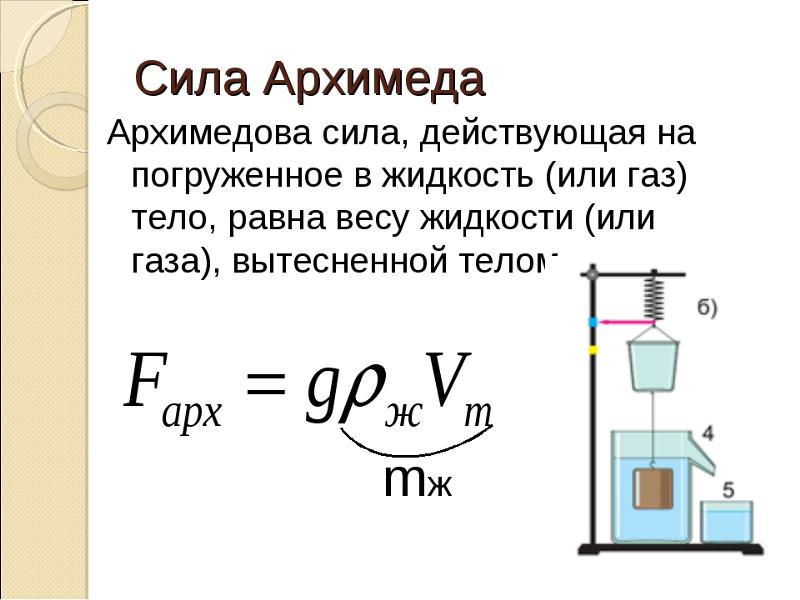 3}}[/латекс][латекс ])[/латекс][латекс]\boldsymbol{=\:93}}.[/latex]
3}}[/латекс][латекс ])[/латекс][латекс]\boldsymbol{=\:93}}.[/latex]
Обсуждение
Ее плотность меньше плотности жидкости. Мы ожидаем этого, потому что она плавает. Плотность тела — один из показателей процентного содержания жира в организме человека, представляющий интерес для медицинской диагностики и спортивных тренировок. (См. рис. 6.)
Рисунок 6. Субъект в «резервуаре для жира», где его взвешивают, когда он полностью погружен в воду, что является частью определения плотности тела. Субъект должен полностью опорожнить легкие и удерживать металлический груз, чтобы утонуть. Делаются поправки на остаточный воздух в его легких (измеряемый отдельно) и вес металла. Его скорректированный вес в погруженном состоянии, его вес в воздухе и щипковые тесты стратегических жировых областей используются для расчета его процентного содержания жира в организме.
Существует много очевидных примеров объектов или веществ с более низкой плотностью, плавающих в жидкостях с более высокой плотностью: масло на воде, воздушный шар, кусочек пробки в вине, айсберг и горячий воск в «лавовой лампе». назвать несколько. Менее очевидные примеры включают лаву, поднимающуюся из вулкана, и горные хребты, плавающие на более плотной коре и мантии под ними. Даже кажущаяся твердой Земля обладает жидкими характеристиками.
назвать несколько. Менее очевидные примеры включают лаву, поднимающуюся из вулкана, и горные хребты, плавающие на более плотной коре и мантии под ними. Даже кажущаяся твердой Земля обладает жидкими характеристиками.
Один из наиболее распространенных методов определения плотности показан на рис. 7.
Рис. 7. (а) Монета взвешивается в воздухе. (b) Определяется кажущийся вес монеты, когда она полностью погружена в жидкость известной плотности. Эти два измерения используются для расчета плотности монеты.Предмет, в данном случае монета, взвешивается в воздухе, а затем снова взвешивается при погружении в жидкость. Плотность монеты, показатель ее подлинности, можно рассчитать, если известна плотность жидкости. Этот же метод можно использовать и для определения плотности жидкости, если известна плотность монеты. Все эти расчеты основаны на законе Архимеда.
Принцип Архимеда гласит, что выталкивающая сила, действующая на объект, равна весу вытесненной жидкости. Это, в свою очередь, означает, что объект кажется весящим меньше в погруженном состоянии; мы называем это измерение кажущимся весом объекта . Объект испытывает кажущуюся потерю веса , равную весу вытесненной жидкости. В качестве альтернативы, на весах, измеряющих массу, объект испытывает кажущуюся потерю массы , равную массе вытесненной жидкости. это
Это, в свою очередь, означает, что объект кажется весящим меньше в погруженном состоянии; мы называем это измерение кажущимся весом объекта . Объект испытывает кажущуюся потерю веса , равную весу вытесненной жидкости. В качестве альтернативы, на весах, измеряющих массу, объект испытывает кажущуюся потерю массы , равную массе вытесненной жидкости. это
[латекс]\boldsymbol{\textbf{очевидная потеря веса}=\textbf{вес вытесненной жидкости}}[/латекс]
или
[латекс]\boldsymbol{\textbf{кажущаяся потеря массы}=\textbf{масса вытесненной жидкости.}}[/латекс]
Следующий пример иллюстрирует использование этой техники.
Пример 3. Расчет плотности: является ли монета подлинной?
Масса древнегреческой монеты определена на воздухе как 8,630 г. Когда монета погружена в воду, как показано на рисунке 7, ее кажущаяся масса составляет 7800 г. Вычислите его плотность, учитывая, что плотность воды составляет[латекс]\boldsymbol{1,000\textbf{ г/см}^3}[/латекс]и что эффекты, вызванные проволокой, подвешивающей монету, незначительны. 3}.[/latex]Это также объем монеты, так как она полностью погружена в воду. Теперь мы можем найти плотность монеты, используя определение плотности: 93}.[/latex]
3}.[/latex]Это также объем монеты, так как она полностью погружена в воду. Теперь мы можем найти плотность монеты, используя определение плотности: 93}.[/latex]
Обсуждение
Из Таблицы 1 видно, что эта плотность очень близка к плотности чистого серебра, подходящего для этого типа древних монет. Большинство современных подделок не являются чистым серебром.
Это возвращает нас к принципу Архимеда и тому, как он возник. Как гласит история, царь Сиракуз поручил Архимеду определить, поставляет ли королевский коронщик корону из чистого золота. Чистоту золота трудно определить по цвету (оно может быть разбавлено другими металлами и все равно выглядеть таким же желтым, как чистое золото), а другие аналитические методы еще не были придуманы. Однако даже древние люди понимали, что плотность золота больше, чем у любого другого известного тогда вещества. Архимед якобы мучился над своей задачей и однажды получил вдохновение в общественных банях, размышляя о поддержке, которую вода оказала его телу. Он придумал свой ныне знаменитый принцип, увидел, как применять его для определения плотности, и голышом побежал по улицам Сиракуз с криком «Эврика!» (по-гречески «я нашел»). Подобное поведение время от времени можно наблюдать и у современных физиков!
Он придумал свой ныне знаменитый принцип, увидел, как применять его для определения плотности, и голышом побежал по улицам Сиракуз с криком «Эврика!» (по-гречески «я нашел»). Подобное поведение время от времени можно наблюдать и у современных физиков!
ИССЛЕДОВАНИЯ PHET: ПЛАВУЧОСТЬ
Когда объекты всплывут и когда они утонут? Узнайте, как плавучесть работает с блоками. Стрелки показывают приложенные силы, и вы можете изменять свойства блоков и жидкости.
Рис. 8. Плавучесть- Выталкивающая сила — это результирующая восходящая сила, действующая на любой объект в любой жидкости. Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и всплывет. Если выталкивающая сила меньше веса тела, то оно утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится в жидкости. 93}?[/latex]
2: Иногда бревна плавают вертикально в озере, потому что один конец стал заболоченным и более плотным, чем другой.
 Какова средняя плотность бревна одинакового диаметра, которое [латекс]\boldsymbol{20,0\%}[/латекс]длины плавает над водой?
Какова средняя плотность бревна одинакового диаметра, которое [латекс]\boldsymbol{20,0\%}[/латекс]длины плавает над водой?3: Найдите плотность жидкости, в которой плавает ареометр с плотностью [латекс]\boldsymbol{0,750\textbf{ г/мл}}[/латекс]с [латексом]\boldsymbol{92,0\% }[/latex] его объема погружено.
93}?[/latex]5: В костях птиц есть воздушные карманы, чтобы уменьшить их вес — это также дает им среднюю плотность, значительно меньшую, чем у костей других животных. Предположим, орнитолог взвешивает птичью кость в воздухе и в воде и обнаруживает, что ее масса равна[latex]\boldsymbol{45.0\textbf{g}}[/latex], а видимая масса в погруженном состоянии составляет[latex]\boldsymbol{3.60\textbf {g}}[/latex](кость водонепроницаема). а) Какая масса воды вытесняется? б) Каков объем кости? в) Какова его средняя плотность?
6: Камень массой 540 г в воздухе имеет кажущуюся массу 342 г при погружении в воду. а) Какая масса воды вытесняется? б) Каков объем камня? в) Какова его средняя плотность? Соответствует ли это стоимости гранита?
7: Принцип Архимеда можно использовать для расчета плотности как жидкости, так и твердого тела.
 Предположим, что кусок железа массой 390,0 г в воздухе имеет кажущуюся массу 350,5 г, когда он полностью погружен в неизвестную жидкость. а) Какую массу жидкости вытесняет железо? (b) Каков объем железа, используя его плотность, как указано в таблице 1 (c) Рассчитайте плотность жидкости и определите ее.
Предположим, что кусок железа массой 390,0 г в воздухе имеет кажущуюся массу 350,5 г, когда он полностью погружен в неизвестную жидкость. а) Какую массу жидкости вытесняет железо? (b) Каков объем железа, используя его плотность, как указано в таблице 1 (c) Рассчитайте плотность жидкости и определите ее.8: При иммерсионном измерении плотности женщины установлено, что ее масса в воздухе составляет 62,0 кг, а кажущаяся масса 0,0850 кг при полном погружении с пустыми легкими. а) Какую массу воды она вытесняет? б) Каков ее объем? (c) Рассчитайте ее плотность. (d) Если объем ее легких составляет 1,75 л, может ли она плавать, не топчась на месте, с легкими, наполненными воздухом?
9: Плотность некоторых рыб немного меньше плотности воды, и они должны прилагать усилия (плавать), чтобы оставаться под водой. Какую силу должен приложить морской окунь массой 85,0 кг, чтобы оставаться погруженным в соленую воду, если плотность его тела составляет[latex]\boldsymbol{1015\textbf{ кг/м}^3}?[/latex]
10: (a) Рассчитайте выталкивающую силу 2-литрового гелиевого баллона.
 (b) Учитывая, что масса резины в воздушном шаре составляет 1,50 г, какова результирующая вертикальная сила, действующая на воздушный шар, если его отпустить? Можно пренебречь объемом резины.
(b) Учитывая, что масса резины в воздушном шаре составляет 1,50 г, какова результирующая вертикальная сила, действующая на воздушный шар, если его отпустить? Можно пренебречь объемом резины.11: (a) Какова плотность женщины, плавающей в пресной воде с [латексом]\boldsymbol{4,00\%}[/латекс] ее объема над поверхностью? Это можно измерить, поместив ее в резервуар с отметками на боку, чтобы измерить, сколько воды она вытесняет, когда плавает и удерживается под водой (кратковременно). б) Сколько процентов ее объема находится над поверхностью, когда она плавает в морской воде? 93}[/latex](за исключением воздуха в легких). а) Вычислите его объем. б) Найдите выталкивающую силу воздуха, действующую на него. в) Каково отношение выталкивающей силы к его весу?
13: Простой компас можно сделать, поместив небольшой стержневой магнит на плавающую в воде пробку. а) Какая часть простой пробки окажется под водой, когда она будет плавать в воде? б) Если пробка массой 10,0 г поместить на нее магнит массой 20,0 г, какая часть пробки окажется под водой? в) Будут ли стержневой магнит и пробка плавать в этиловом спирте?
14: Какую часть веса железного якоря будет поддерживать выталкивающая сила при погружении в соленую воду?
15: Известны случаи, когда подлые мошенники выдавали позолоченные вольфрамовые слитки за чистое золото и продавали их жадным по ценам намного ниже стоимости золота, но заслуженно намного выше стоимости вольфрама.
 С какой точностью вы должны быть в состоянии измерить массу такого слитка в воде и вне воды, чтобы сказать, что это почти чистый вольфрам, а не чистое золото?
С какой точностью вы должны быть в состоянии измерить массу такого слитка в воде и вне воды, чтобы сказать, что это почти чистый вольфрам, а не чистое золото?16: Двуспальный надувной матрас для кемпинга имеет размеры 100 см на 200 см на 15 см в надутом состоянии. Вес матраса 2 кг. Насколько тяжелый человек может выдержать надувной матрас, если его поместить в пресную воду?
17: По рисунку 3 докажите, что выталкивающая сила, действующая на цилиндр, равна весу вытесненной жидкости (принцип Архимеда). Вы можете предположить, что выталкивающая сила равна[латекс]\boldsymbol{F_2-F_1}[/latex]и что концы цилиндра имеют одинаковую площадь[латекс]\boldsymbol{A}.[/latex]Обратите внимание, что объем цилиндр (и вытесняемая им жидкость) равен [латекс]\boldsymbol{(h_2-h_1)A}.[/latex]
18: (a) Человек массой 75,0 кг плавает в пресной воде, [latex]\boldsymbol{3,00\%}[/latex] его объема над водой, когда его легкие пусты, и[latex]\boldsymbol{ 5,00\%}[/latex] его объема над водой, когда его легкие полны.
 Вычислите объем вдыхаемого им воздуха, который называется емкостью легких, в литрах. (b) Кажется ли этот объем легких приемлемым?
Вычислите объем вдыхаемого им воздуха, который называется емкостью легких, в литрах. (b) Кажется ли этот объем легких приемлемым?- Закон Архимеда
- выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости
- выталкивающая сила
- результирующая восходящая сила, действующая на любой объект в любой жидкости
- удельный вес
- отношение плотности объекта к жидкости (обычно воде)
Принцип Архимеда: определение и применение
Когда-то человеку по имени Архимед поручили выяснить, как определить, сделана корона из золота или подделка, не испортив ее. Из-за странной формы короны он не знал ее объема, чтобы сказать, насколько она плотная. Однажды Архимед принял ванну и заметил, что вода поднимается в зависимости от того, какая часть его тела находится в воде. Объем погруженной части его тела был таким же объемом, как и вода, поднявшаяся с пути — или, другими словами, вытесненная.
 Он понял, что таким образом может определить объем короны и сравнить ее вес с таким же объемом чистого золота, чтобы убедиться, что они весят одинаково. Эта мысль так поразила его, что он голышом побежал по городу с криком: «Эврика!» Этот момент лампочки привел к принципу Архимеда.
Он понял, что таким образом может определить объем короны и сравнить ее вес с таким же объемом чистого золота, чтобы убедиться, что они весят одинаково. Эта мысль так поразила его, что он голышом побежал по городу с криком: «Эврика!» Этот момент лампочки привел к принципу Архимеда.Определение принципа Архимеда
Вопрос о том, произошла ли описанная выше история так или нет, является спорным. Независимо от того, как возникла эта идея, нам нужно точно определить, что мы подразумеваем под принципом Архимеда, прежде чем мы сможем углубиться в него.
Принцип Архимеда гласит, что направленная вверх выталкивающая сила на полностью или частично погруженный объект равна весу жидкости вытесняемого объектом.
Мы обсудим, почему это верно как интуитивно, так и математически.
Интуитивное объяснение
Если мы погрузим куб из невесомого пластика, наполненный водой, такой как куб слева на изображении ниже, он будет плавать в равновесии с окружающей водой, потому что вся вода имеет одинаковую плотность.
 Силы, действующие на куб, — это сила тяжести, направленная вниз, и выталкивающая сила, направленная вверх. Поскольку куб не ускоряется, согласно второму закону Ньютона \(\sum F = ma\), сумма этих сил равна нулю. Это означает, что выталкивающая сила равна весу воды в кубе.
Силы, действующие на куб, — это сила тяжести, направленная вниз, и выталкивающая сила, направленная вверх. Поскольку куб не ускоряется, согласно второму закону Ньютона \(\sum F = ma\), сумма этих сил равна нулю. Это означает, что выталкивающая сила равна весу воды в кубе.Что, если мы заменим куб на металлический куб того же размера, как на крайнем правом изображении выше? Вода вокруг куба не знала бы, что он чем-то отличается от наполненного водой куба, поэтому выталкивающая сила, действующая на куб, равнялась бы весу воды, который может содержать куб. Но теперь вес куба больше, поэтому он упадет на дно стакана. Если вы поднимете куб со дна, он будет казаться легче, чем он есть на самом деле, из-за выталкивающей силы, толкающей его вверх.
Математическое объяснение
Когда мы погружаем объект в жидкость, жидкость оказывает давление на объект со всех сторон. На изображении ниже мы погружаем куб в воду.
Мы упростили силы из-за давления воды в одну нисходящую силу и одну восходящую силу.
 Горизонтальные давления, действующие на куб, равны и противоположны друг другу, поэтому в сумме они равны нулю, и мы исключаем их из изображения.
Горизонтальные давления, действующие на куб, равны и противоположны друг другу, поэтому в сумме они равны нулю, и мы исключаем их из изображения.Давление равно силе на единицу площади, или
$$P=\frac{F}{A}.$$
Мы также знаем, что давление в точке в жидкости равно плотности жидкости, умноженной на ускорение свободного падения и высоту жидкости над точкой:
$$P=\rho_\text{f} gh.$$
Вот почему сила, действующая на нижнюю часть куба, больше, чем сила на верхнюю, потому что давление увеличивается с глубиной увеличивается. Объединив эти два уравнения, уравнение для силы, действующей на вершину куба, будет выглядеть следующим образом:
$$F_1=\rho_\text{f} gh_1 A,$$
и сила, действующая на дно куба, будет равна:
$$F_2=\rho_\text{f} g h_2 A. $$
Чтобы найти выталкивающую силу, мы хотим найти разницу между силой, действующей сверху, и силой, действующей снизу:
$$F_2 – F_1 = \rho_\text{f} g (h_2 – h_1)A.$$
Обратите внимание, что \(h_2-h_1\) — это просто высота куба, и, умножив ее на грань куба, \(A\), мы получим объем куба, вернее, объем воды, вытесненный кубом.
 Теперь мы получаем следующее уравнение для выталкивающей силы:
Теперь мы получаем следующее уравнение для выталкивающей силы:$$F_\text{b} = \rho_\text{f} V_\text{f} g$$
Масса равна произведению плотности на объем,
$$m=\rho V,$$ поэтому мы можем заменить массу жидкости на плотность и объем жидкости:
$$F_b=m_\text{f} g$$
Поскольку вес равен произведению массы на силу тяжести, этот результат означает, что плавучесть сила равна весу вытесненной жидкости, как сказал Архимед.
Давление увеличивается по мере увеличения глубины в жидкости, но это не означает, что увеличивается выталкивающая сила. Высота объекта остается неизменной, поэтому разница давлений между верхом и низом объекта остается постоянной независимо от того, насколько глубоко объект находится в жидкости. Выталкивающая сила зависит только от веса вытесненной жидкости и ускорения свободного падения, а не от глубины объекта.
Принцип Архимеда – Формула/Уравнение
Как было только что доказано выше, принцип Архимеда приводит к следующей формуле для плавучести :
$$F_\text{b}=m_\text{f} g.
 $ $
$ $Вы также можете использовать следующее уравнение, заменив массу на плотность, умноженную на объем, как мы описали выше:
$$F_b=\rho V g.$$
Оба этих уравнения означают одно и то же; тот, который вы используете, зависит от того, какая информация у вас есть. Одним из важных моментов является то, что вы использовать массу, плотность или объем жидкости, а не объекта .
Это самое важное, что нужно помнить о плавучести и о том, где происходит большинство ошибок. Объем жидкости не всегда совпадает с объемом объекта.
Принцип Архимеда и закон плавучести
Что, если наш куб всплывет? Если мы знаем, что объект полностью погружен в воду, то мы знаем, что объем жидкости, которую вытесняет объект, равен объему объекта. Но если он плавает, это не так. Вот почему важно помнить, что используемый вами объем — это объем жидкости, вытесненной жидкостью, а не объем объекта.
Когда объект плавает в жидкости, единственными силами, действующими на него, являются выталкивающая и гравитационная силы.
 На изображении выше мы можем видеть две силы, действующие на плавающий куб. Поскольку плавающий объект не ускоряется, согласно второму закону Ньютона сумма двух сил равна нулю. Это означает, что для плавающих объектов выталкивающая сила (вес вытесненной жидкости) равна силе тяжести (или весу) объекта. Мы называем это 92}) \\&= 157\,\mathrm{N}\end{align}
На изображении выше мы можем видеть две силы, действующие на плавающий куб. Поскольку плавающий объект не ускоряется, согласно второму закону Ньютона сумма двух сил равна нулю. Это означает, что для плавающих объектов выталкивающая сила (вес вытесненной жидкости) равна силе тяжести (или весу) объекта. Мы называем это 92}) \\&= 157\,\mathrm{N}\end{align}Поскольку гравитационная сила больше выталкивающей силы, куб полностью погружен в воду, что говорит о том, что мы использовали правильный объем.
Далее рассмотрим плавающий куб.
Допустим, наш тот же куб из примера выше весит \(13\,\mathrm{kg}\) вместо \(16\,\mathrm{kg}\). Это заставляет куб плавать, но мы не знаем, какая его часть торчит из воды. Какой процент куба находится под водой?
Мы можем написать уравнение выталкивающей силы, которое мы использовали выше, но на этот раз мы не можем использовать тот же объем куба, так как мы не знаем, насколько глубоко погружен куб.
 Мы разделим объем на площадь основания куба, \(A\), которую мы знаем, умноженную на нашу неизвестную высоту, \(h\):
Мы разделим объем на площадь основания куба, \(A\), которую мы знаем, умноженную на нашу неизвестную высоту, \(h\):$$F_\text{b} = \rho (Ah) g$$
Мы также можем установить выталкивающую силу равной весу объекта (масса объекта, \(m_\mathrm{o}\), умноженная на ускорение свободного падения):
92}\end{align}Теперь у нас есть высота погруженного куба:
$$h=0,208\,\mathrm{m}$$
Чтобы узнать, какая часть куба погружена, мы можно создать соотношение между объемом под водой и общим объемом. Мы будем использовать нижний индекс \(\mathrm{w}\) для переменной в воде, и мы будем использовать нижний индекс \(\mathrm{t}\) для всех переменных куба:
$$ \frac{V_\mathrm{w}}{V_\mathrm{t}}=\frac{Ah_\mathrm{w}}{Ah_\mathrm{t}}$$
Площади сокращаются, поскольку они одинаковы, поэтому мы можем подставить значения высот:
\begin{align}\frac{V_\mathrm{w}}{V_\mathrm{t}} &= \ frac{0.208\,\mathrm{m}}{0.25\,\mathrm{m}} =0.83.\end{align}
Куб на 83% погружен в воду.

Принцип Архимеда Применение
Принцип Архимеда играет важную роль во многих технических проектах. Вот некоторые приложения принципа Архимеда.
- Понимание принципа Архимеда позволяет инженерам проектировать плавучие корабли, даже если они сделаны из тяжелых материалов.
- Ареометры используют принцип Архимеда для определения плотности жидкостей.
- Подводные лодки используют принцип Архимеда, чтобы управлять тем, как они всплывают и погружаются в воду.
- Принцип Архимеда позволяет инженерам создавать спасательные жилеты, способные удерживать тело человека на плаву.
Принцип Архимеда Заключение
Принцип Архимеда является интуитивно понятным и полезным инструментом при решении физических задач, связанных с плавучестью. Кроме того, это позволяет нам найти объем, который в противном случае было бы очень трудно проанализировать. Зная объем и массу, мы можем затем получить плотность объектов, а также проанализировать их материальные свойства.


 По легенде, так были сожжены римские корабли, осаждавшие Сиракузы. Недавно энтузиасты провели экспериментальную проверку и удалось поджечь деревянный баркас.
По легенде, так были сожжены римские корабли, осаждавшие Сиракузы. Недавно энтузиасты провели экспериментальную проверку и удалось поджечь деревянный баркас.

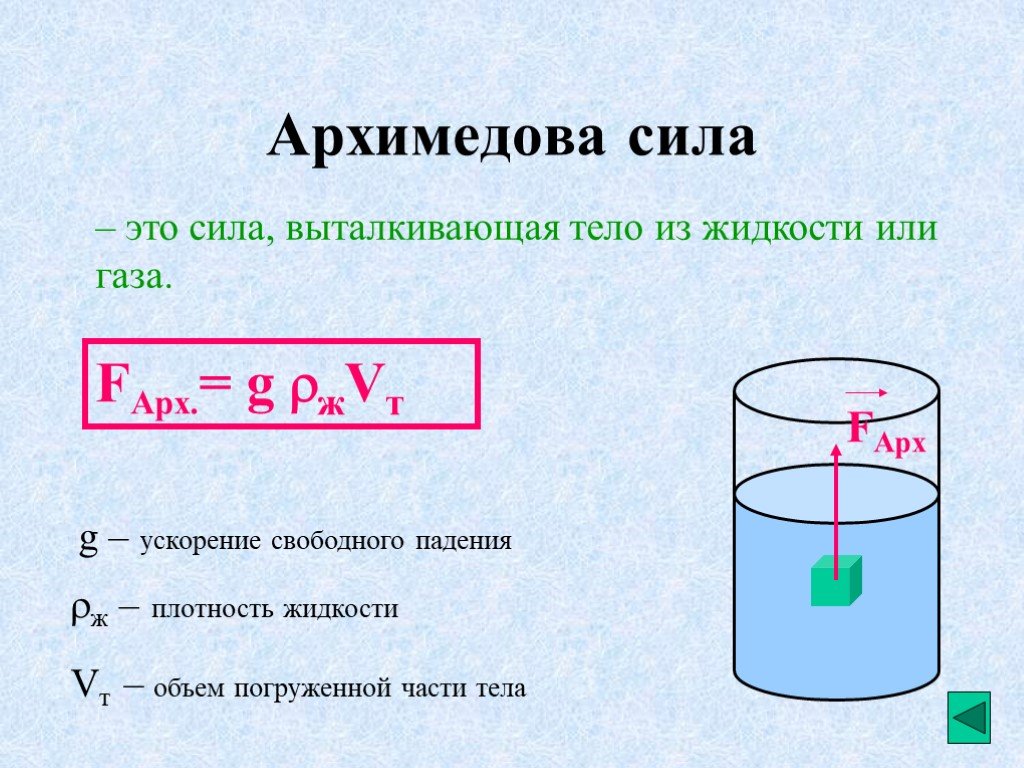 Какова средняя плотность бревна одинакового диаметра, которое [латекс]\boldsymbol{20,0\%}[/латекс]длины плавает над водой?
Какова средняя плотность бревна одинакового диаметра, которое [латекс]\boldsymbol{20,0\%}[/латекс]длины плавает над водой? Предположим, что кусок железа массой 390,0 г в воздухе имеет кажущуюся массу 350,5 г, когда он полностью погружен в неизвестную жидкость. а) Какую массу жидкости вытесняет железо? (b) Каков объем железа, используя его плотность, как указано в таблице 1 (c) Рассчитайте плотность жидкости и определите ее.
Предположим, что кусок железа массой 390,0 г в воздухе имеет кажущуюся массу 350,5 г, когда он полностью погружен в неизвестную жидкость. а) Какую массу жидкости вытесняет железо? (b) Каков объем железа, используя его плотность, как указано в таблице 1 (c) Рассчитайте плотность жидкости и определите ее. (b) Учитывая, что масса резины в воздушном шаре составляет 1,50 г, какова результирующая вертикальная сила, действующая на воздушный шар, если его отпустить? Можно пренебречь объемом резины.
(b) Учитывая, что масса резины в воздушном шаре составляет 1,50 г, какова результирующая вертикальная сила, действующая на воздушный шар, если его отпустить? Можно пренебречь объемом резины. С какой точностью вы должны быть в состоянии измерить массу такого слитка в воде и вне воды, чтобы сказать, что это почти чистый вольфрам, а не чистое золото?
С какой точностью вы должны быть в состоянии измерить массу такого слитка в воде и вне воды, чтобы сказать, что это почти чистый вольфрам, а не чистое золото? Вычислите объем вдыхаемого им воздуха, который называется емкостью легких, в литрах. (b) Кажется ли этот объем легких приемлемым?
Вычислите объем вдыхаемого им воздуха, который называется емкостью легких, в литрах. (b) Кажется ли этот объем легких приемлемым? Он понял, что таким образом может определить объем короны и сравнить ее вес с таким же объемом чистого золота, чтобы убедиться, что они весят одинаково. Эта мысль так поразила его, что он голышом побежал по городу с криком: «Эврика!» Этот момент лампочки привел к принципу Архимеда.
Он понял, что таким образом может определить объем короны и сравнить ее вес с таким же объемом чистого золота, чтобы убедиться, что они весят одинаково. Эта мысль так поразила его, что он голышом побежал по городу с криком: «Эврика!» Этот момент лампочки привел к принципу Архимеда. Силы, действующие на куб, — это сила тяжести, направленная вниз, и выталкивающая сила, направленная вверх. Поскольку куб не ускоряется, согласно второму закону Ньютона \(\sum F = ma\), сумма этих сил равна нулю. Это означает, что выталкивающая сила равна весу воды в кубе.
Силы, действующие на куб, — это сила тяжести, направленная вниз, и выталкивающая сила, направленная вверх. Поскольку куб не ускоряется, согласно второму закону Ньютона \(\sum F = ma\), сумма этих сил равна нулю. Это означает, что выталкивающая сила равна весу воды в кубе. Горизонтальные давления, действующие на куб, равны и противоположны друг другу, поэтому в сумме они равны нулю, и мы исключаем их из изображения.
Горизонтальные давления, действующие на куб, равны и противоположны друг другу, поэтому в сумме они равны нулю, и мы исключаем их из изображения. Теперь мы получаем следующее уравнение для выталкивающей силы:
Теперь мы получаем следующее уравнение для выталкивающей силы: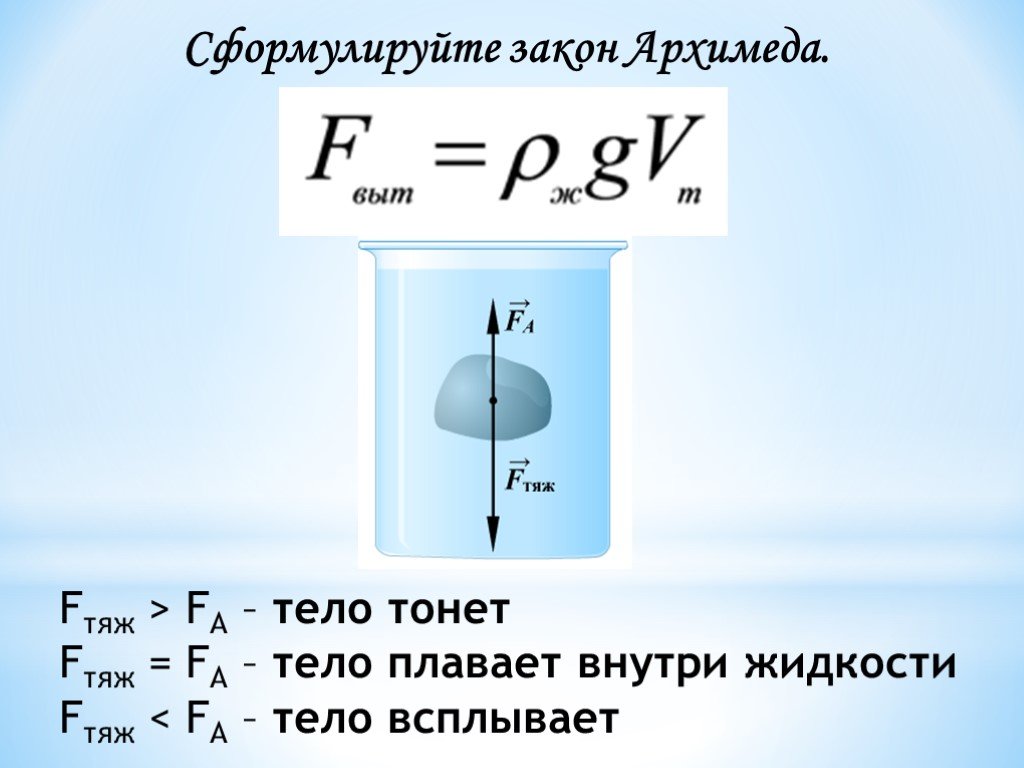 $ $
$ $ На изображении выше мы можем видеть две силы, действующие на плавающий куб. Поскольку плавающий объект не ускоряется, согласно второму закону Ньютона сумма двух сил равна нулю. Это означает, что для плавающих объектов выталкивающая сила (вес вытесненной жидкости) равна силе тяжести (или весу) объекта. Мы называем это 92}) \\&= 157\,\mathrm{N}\end{align}
На изображении выше мы можем видеть две силы, действующие на плавающий куб. Поскольку плавающий объект не ускоряется, согласно второму закону Ньютона сумма двух сил равна нулю. Это означает, что для плавающих объектов выталкивающая сила (вес вытесненной жидкости) равна силе тяжести (или весу) объекта. Мы называем это 92}) \\&= 157\,\mathrm{N}\end{align} Мы разделим объем на площадь основания куба, \(A\), которую мы знаем, умноженную на нашу неизвестную высоту, \(h\):
Мы разделим объем на площадь основания куба, \(A\), которую мы знаем, умноженную на нашу неизвестную высоту, \(h\):
