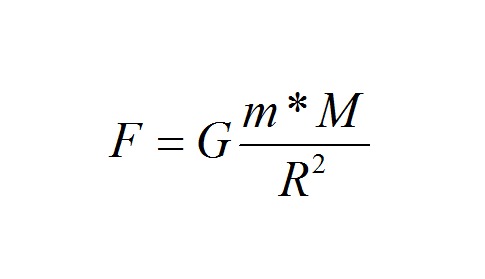Вы спросили: Как рассчитать силу притяжения между Землей и Луной?
Сила гравитации между Землей и Луной составляет около 2,0 х 1020 4,4 Н. Сила тяготения между Солнцем и Луной составляет примерно 10 х 20 2,2 Н. Следовательно, Сила Солнца-Луны = XNUMX х Сила Земли-Луна. Так почему же Луна вращается вокруг Земли?
Для этого мы используем старую формулу P = m. g, где m — масса объекта, а g — ускорение свободного падения, значение которого примерно равно 10 м/с2.
Так называемая перегрузка — это единица ускорения, соответствующая ускорению силы тяжести на Земле. Стоит помнить, что это не равно G (заглавная буква), которая представляет гравитационную постоянную Ньютона. Поскольку на нее влияет гравитация, сила g может сильно различаться в зависимости от планеты, на которой вы находитесь.
Сила гравитации. Хотя Солнце намного больше Луны, оно меньше влияет на приливы и отливы из-за своего большого расстояния от Земли. … То есть сила притяжения Солнца к Земле почти в 200 раз больше, чем у Луны.
Из-за гравитации Луны она оказывает прямое влияние на Землю. Гравитационная сила спутника способна перемещать большие массы воды согласно чередованию ее фаз.
Совет для расчета силы веса какого-либо объекта на Земле заключается в том, что мы можем приблизить гравитацию к значению 10 м/с2. Таким образом, просто умножьте массу на 10, чтобы получить силу веса. Например, на человека массой 80 кг действует сила веса 800 Н.
Будучи силой притяжения между двумя телами, модуль (численное значение), с которым частица 1 притягивается к частице 2, такой же, как частица 2 притягивается к частице 1.
Эта величина определяется следующим уравнением: Центростремительное ускорение получается из отношения квадрата скорости (V) тела к радиусу (R) пройденного кругового пути.
F относится к гравитационной силе, вектору, который мы в конечном итоге хотим вычислить и передать в функцию applyForce(). … G — универсальная гравитационная постоянная, которая в нашем мире равна 6,67428 х 10^-11 метров в кубе на килограмм на секунду в квадрате.
Гравитация отвечает за определение веса объектов и заставляет их падать на землю после того, как их отпустили. Она является одной из четырех фундаментальных сил природы, остальные — электромагнетизм, слабая сила и сильная сила.
Сила притяжения между двумя объектами равна произведению их масс, деленной на квадрат расстояния между ними. То есть, чем больше масса объекта и чем он ближе, тем больше сила его притяжения к другому объекту. Это объясняет, почему мы не просто уплываем к Солнцу.
Гравитация — это сила притяжения, существующая между всеми массовыми частицами во Вселенной. Гравитация отвечает за прикрепление объектов к поверхности планет и, согласно законам движения Ньютона, отвечает за удержание объектов на орбитах друг вокруг друга.
Ньютон сделал вывод о существовании силы взаимного притяжения между всеми телами, которая будет зависеть от их массы.
…
Планета Гравитация.
Универсальное тяготение — это закон, описанный Ньютоном, который касается отношений притяжения между Солнцем и планетами Солнечной системы.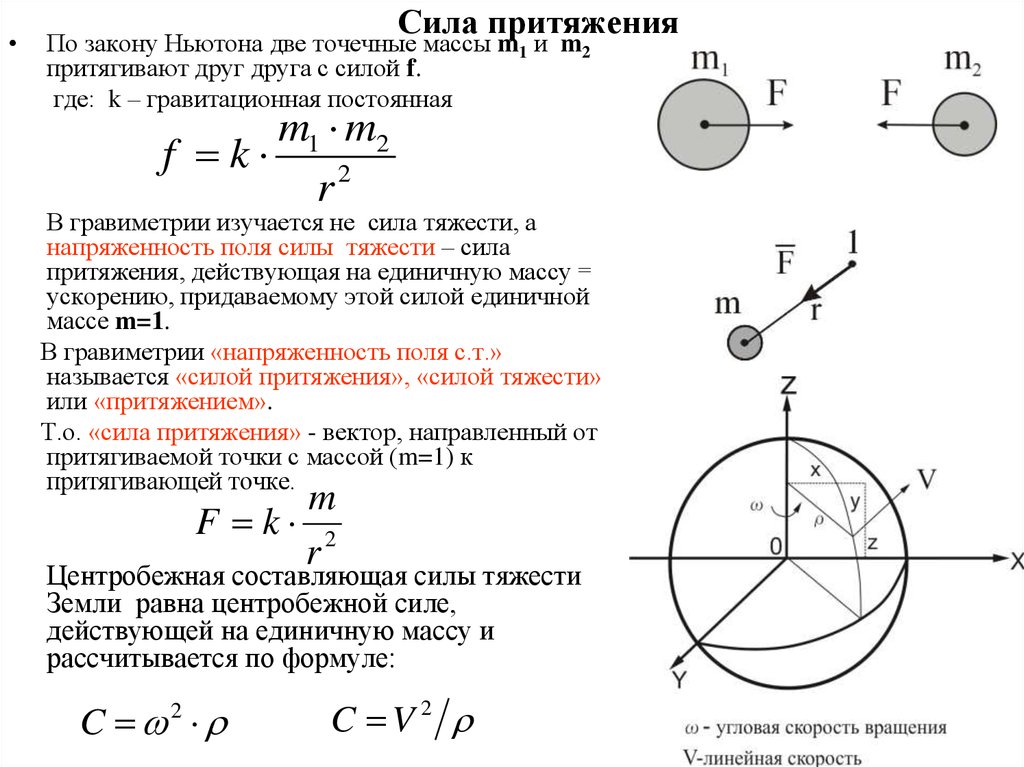
… Сила пропорциональна массе планеты и массе Солнца; • Сила обратно пропорциональна квадрату расстояния, разделяющего эти два небесных тела.
Гравитационная сила – это сила притяжения, возникающая между всеми телами, имеющими массу. Планета Земля, например, способна притягивать тела вокруг себя к своему центру из-за своего гравитационного поля.
Гравитационное взаимодействие. Закон всемирного тяготения 10 класс онлайн-подготовка на Ростелеком Лицей
Введение
Из законов динамики нам хорошо известно, что для того, чтобы тело двигалось ускоренно, на него должна действовать сила, как в данном примере с автомобилем на рис. 1. Равнодействующая направлена таким образом, что машина ускоряется.
Рис. 1. Иллюстрация действий сил на тело
В то же время мы хорошо знаем, что земля сообщает одинаковое ускорение любым падающим на нее телам. Эту силу, с которой действует земля на падающие тела, мы традиционно называем сила тяжести. На рис. 2 проиллюстрировано действие силы тяжести.
Рис. 2. Иллюстрация действия силы тяжести
В конце XVII века Исаак Ньютон, которому на тот момент было всего 22 года, предположил, что свойство притягивать тела характерно не только для земли, но и для любых тел, обладающих массами (рисунок 3). Такую силу он назвалсилой всемирного тяготения,а взаимодействие, ответственное за появление этой силы, было названо гравитационным (от латинского gravitas – «тяжесть»).
Рис. 3. Взаимодействие двух тел обладающих массой
Формулировка закона
Закон всемирного тяготения позволяет описывать не только падение тел на землю, но и движение планет, звезд, приливы, отливы и множество других универсальных явлений, которые протекают в природе. Попробуем восстановить ход рассуждений Ньютона, а он получил математическую формулу, описывая движение Луны вокруг Земли, и тоже получить закон всемирного тяготения.
Если Земля сообщает любому телу, находящемуся на ее поверхности, ускорение свободного падения g, которое, как мы знаем, по модулю равно g = 9,8 , то Луне притяжение Земли сообщает центростремительное ускорение.
Запишем некоторые характеристики.
Радиус Земли (он нам понадобится в расчетах) R3 = 6370 км, орбиты Луны RЛ = 384000 км, период обращения Луны вокруг Земли, так называемый лунный месяц Т = 27,3 суток.
Воспользуемся этими данными и рассуждениями для дальнейших выводов.
Ньютон предположил, что сила, с которой Земля притягивает те или иные объекты, зависит от расстояния между объектом и центром Земли. Известно, что расстояние от Луны до центра Земли примерно в 60 раз больше чем радиус Земли, т. е. расстояние от любого тела находящегося на поверхности Земли.
А во сколько же раз отличается ускорение, приобретаемое телами в результате такого притяжения? Для начала рассчитаем ускорение, которое приобретает Луна в результате своего притяжения Землей. Ускорение, которым обладает любое тело, находящееся на поверхности Земли, вы и так хорошо знаете, это ускорение свободного падения.
Переходим к расчетам.Центростремительное ускорение Луны, вызванное притяжением Земли, может быть рассчитано по формуле:
Угловая скорость нам не известна, но мы прекрасно знаем, что угловая скорость связана с периодом вращения таким соотношением:
Получим:
Само по себе это значение может ничего нам не говорить, но сравним его с величиной ускорения свободного падения g = 9,8 и тоже вызванной земным притяжением.
Итак, находим отношение:
Почему выделяем именно 602? Дело в том, что Луна по отношению к поверхности Земли расположена как раз на расстоянии приблизительно в 60 раз больше, чем сам радиус Земли.
На тот момент из исследований Галилео Галилея было хорошо известно, что ускорение, приобретаемое телами в результате притяжения Землей, не зависит от их массы, т. е. если яблоко у поверхности Земли обладает ускорением 9,8, вызванным земным притяжением:
то, помещенное на орбиту Луны, оно будет обладать точно таким же ускорением, как и Луна, т. е. в 3600 раз меньшим, чем ускорение свободного падения у поверхности Земли:
Исходя из наших расчетов, мы с вами получаем, что сила, с которой Земля притягивает Луну, обратно пропорциональна квадрату расстояния между центрами этих объектов:
Кроме этого, из второго закона Ньютона мы знаем, что сила прямо пропорциональна массе объекта. Т. е. в данном случае сила прямо пропорциональна массе Луны или другого небесного тела:
Из третьего закона Ньютона мы знаем, что сила действия вызывает аналогичное противодействие, направленное в противоположную сторону, значит, сила взаимодействия между Землей и Луной будет пропорциональна не только массе Луны, но и массе Земли тоже:
Объединяя все это в одну пропорциональность, мы можем получить, что сила, с которой взаимодействуют Земля и Луна, пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними:
А если обобщать и говорить не только о Земле и Луне, то запишем аналогичную пропорциональность, но уже для двух произвольных масс.
Если же перейти к строгому равенству, то мы получаем ту самую формулировку, которая впервые появилась в знаменитом труде Ньютона «Математические начала натуральной философии» (1687) и носит название закона всемирного тяготения.
Формулировка
Закон всемирного тяготения: тела притягиваются друг к другу с силой, модуль которой пропорционален произведению их масс и обратно пропорционален квадрату расстояния между ними. Сила направлена вдоль прямой, соединяющей центры тел.
Математическая запись этой формулы
Как Луна влияет на Землю
Несмотря на то, что Луна расположена от Земли достаточно далеко, расстояние составляет порядка 400 000 км, ее влияние на Землю все-таки весьма ощутимо.
Итак, поговорим о том, как Луна влияет на вес тел, находящихся на Земле. Сразу оговоримся: мы не будем учитывать влияние Солнца и других небесных тел, так как оно по сравнению с влиянием Луны значительно меньше.
Мы не будем сейчас вдаваться в детальные подробности того, как мы получили те данные, о которых сейчас поговорим, а остановимся лишь на результате. Если подсчитать, воспользовавшись законом всемирного тяготения, влияние Луны на вес тел на Земле, то окажется что в наиболее близкой к Луне и в наиболее удаленной от Луны точках земной поверхности вес тела несколько уменьшается, а в точке, лежащей на средней линии, вес тела немного увеличивается. При этом изменение веса, показанное на рисунке 4 красным цветом, в два раза меньше, чем изменение веса, показанное на рисунке 5 также красным цветом, для точек наиболее близкой и наиболее удаленной.
| Рис. 4. Изменение веса в зависимости от расстояния до Луны | Рис. 5. Изменение веса в зависимости от расстояния до Луны |
Если бы Луны вообще не было на земной орбите, то вес тела уменьшился бы совершенно незначительно. Если перейти от ньютонов к единицам ускорения , то эта величина составляла бы всего лишь 0,0001 . По сравнению, например, с ускорением свободного падения 10 (мы здесь его округлили от 9,8 до 10), вы видите, что разница составляет порядка одной стомиллионной доли. Немного? Да, немного, но если сравнивать с радиусом Земли те изменения, которые привносит такое небольшое измерение ускорения в результате отсутствия Луны, то мы получим, что Rз = 6400 км. И эти стомиллионные доли изменения приводят к тому, что высота уровня воды в точках, показанных на рис. 4, поднимается на 54 см, в точках, показанных на рис. 5, она падает на 27 см (см. рис. 3).
Речь идет о явлении приливов и отливов. Именно Луна определяет наличие приливов и отливов на Земле.
Благодаря вращению Земли места подъемов и опусканий уровня воды постоянно перемещаются.
Еще одно интересное влияние Луны на Землю – в результате приливов и отливов, волна, которая бежит вдоль земли трется о поверхность земли и, значит, несколько замедляет вращение Земли. Интересно, что тот факт, что мы всегда видим Луну повернутой к нам одним боком, тоже предопределил теперь уже влияние Земли на Луну.
Границы применимости
А сейчас поговорим об ограничениях, о границах применимости той формулировки закона всемирного тяготения, которую мы записали. В каких случаях он справедлив? К примеру, есть два тела А и В. Они, согласно закону всемирного тяготения, притягиваются друг к другу. Если эти тела притягиваются и, например, находятся на расстоянии, показанном на рисунке 6, то какую величину брать в качестве r (расстояния между ними) – либо самое маленькое между ними, либо расстояние между наиболее дальними краями, или же расстояние между серединками? А где взять эту серединку? Итак, возникает вопрос: применима ли формула закона всемирного тяготения для тел неправильной формы, находящихся на таком расстоянии друг от друга?
Рис.
6. Положение тел А и В
Ответ мы можем получить, для этого увеличим расстояние между телами. Когда мы их разнесли достаточно далеко друг от друга, нужно ли учитывать их размеры? Нет, ведь их размеры по сравнению с расстоянием между ними очень малы, поэтому в данном случаи мы их можем полагать материальными точками. Итак, первое ограничение:
1. Закон всемирного тяготения применим для тел, размеры которых несущественны по сравнению с расстоянием между ними. Такие тела мы называем материальными точками. Это первое условие.
Однако есть ситуации, когда можно рассматривать тела, обладающие реальными размерами и находящиеся на небольшом расстоянии друг от друга. Это тела примерно такой формы, как показано на рисунке 7.
Рис. 7. Положение тел сферической формы
Представьте себе, что это идеальные сферы. Если тела, обладающие сферической формой, или, говорят, сферической симметрией, находятся даже на небольшом расстоянии друг от друга, мы можем пользоваться формулой закона всемирного тяготения в качестве расстояния r.
В этом случае мы берем расстояние между центрами тел, именно в такой форме мы пользуемся законом всемирного тяготения, когда рассматриваем наше притяжение к центру Земли.
Второе условие, при котором можно применять закон всемирного тяготения в той форме, которую мы записали:
2. Тела должны обладать сферической симметрией.
Гравитационная постоянная
Поняв, в каких случаях можно применять формулу для закона всемирного тяготения, вернемся к величине G (коэффициенту пропорциональности):
Эта величина носит название гравитационной постоянной. Выясним какой смысл у гравитационной постоянной G. Запишем еще раз закон всемирного тяготения:
Отсюда несложно получить, что гравитационная постоянная G может быть вычислена по формуле:
Итак, отсюда мы получаем физический смысл гравитационной постоянной. В самом деле, если мы возьмем две материальные точки, расположенные на расстоянии 1 м друг от друга, а масса этих материальных точек равна 1 кг, то гравитационная постоянная будет численно равна силе, с которой притягиваются эти две точки.
Физический смысл гравитационной постоянной: она численно равна силе, с которой мысленно притягиваются две материальные точки массами по 1 кг, расположенные в вакууме на расстоянии 1 м друг от друга.
Поговорим о том, как вычислить гравитационную постоянную. Из курса физики 9 класса вы знаете, что эта же формула для гравитационной постоянной для закона всемирного тяготения в случае притяжения к Земле может быть заменена формулой для силы тяжести:
Где м – это масса тела, а g – ускорение свободного падения. Отсюда несложно получить фомулу для гравитационной постоянной:
Можно оценить гравитационную постоянную. Получилось следующее значение гравитационной постоянной:
Эта величина и носит название гравитационной постоянной и является так называемой универсальной физической постоянной, т. е. одинаковой в любой точке Вселенной.
Модельное представление опыта Кавендиша
Величину гравитационного взаимодействия определяет величина гравитационной постоянной, одной из фундаментальных физических констант.
Она составляет:
Как видите, это сравнительно небольшая, даже маленькая величина. Как же ее измерить? Впервые она была измерена несколько сотен лет назад английским ученым Генри Кавендишем. Если говорить об этом человеке, то он был нетипичным ученым, он задолго до Кулона определил закон взаимодействия электрических зарядов, первым в истории науки определил среднюю плотность Земли с достаточно большой точностью. Однако он практически не занимался публикацией своих открытий, они стали известны уже после его смерти.
Для определения гравитационной постоянной Кавендиш сконструировал так называемые крутильные весы, принципиальная схема которых показана на рисунке 8.
Рис. 8. Принципиальная схема крутильных весов
Обратите внимание: на деревянном коромысле подвешены сравнительно небольшие свинцовые шары одинаковой массы. Само деревянное коромысло подвешено на тончайшей посеребренной медной проволочке длиной порядка 1 м. Если к этим шарам подносить массивные также свинцовые шары, то вследствие гравитационного притяжения нить будет немного закручиваться и шарики массы m будут притягиваться к шарикам массы М.
В какой-то момент сила гравитационного взаимодействия уравновесится с силой упругости закрученной нити и система придет в равновесие. Сравнивая эти две силы, Кавендиш и определял гравитационную постоянную.
Вы понимаете, что значение гравитационной постоянной очень мало, поэтому углы на которые отклонялась нить также очень малы, он их регистрировал при помощи сложных оптических приборов. Также для того, чтобы избежать конвекционных потоков, т. е. влияния потоков воздуха, вся система была помещена в воздушный колпак, показанный на рисунке 9.
Рис. 9. Воздушный колпак
Интересно, что Кавендиш в своих опытах не измерял напрямую значение гравитационной постоянной, он ставил своей целью как раз определить значение средней плотности Земли, и он определили его как:
Тогда эта величина была неизвестна, и он сказал, что плотность Земли в 5,48 раз больше, чем плотность воды. Современное значение плотности, измеренное более точными приборами, составляет:
Отличие всего в 0,04, менее чем в 1 %.
Настолько точно несколько сотен лет назад ученому удалось поставить эксперимент. Какой вывод сделал Кавендиш из значения, которое он получил? Дело в том, что средняя плотность поверхностных слоев Земли составляет порядка:
Отсюда вывод: раз средняя плотность значительно выше, значит где-то в глубине Земли, глубоко, находятся плотные породы, например железо или какие-то другие плотные металлы.
Сама гравитационная постоянная, по всей видимости, впервые в науку была введена французским ученым Пуассоном в трактате по механике в 1811 году, и вычислил он ее как раз из результатов опыта Генри Кавендиша.
Выводы
Подводим итоги.
- Взаимодействие, свойственное всем телам во Вселенной и проявляющееся в их взаимном притяжении друг к другу, называют гравитационным, а само явление – всемирным тяготением или гравитацией.
- Закон всемирного тяготения имеет следующий вид:
Сила взаимодействия между двумя телами массами , находящимися на расстоянии друг от друга, прямо пропорционально произведению масс этих тел и обратно пропорционально квадрату расстояния между ними.
Направление силы вдоль прямой, соединяющей центры тел, представлено на рисунке 10.
Рис. 10. Направление силы вдоль прямой, соединяющей центры тел
3. Справедлив этот закон в таком виде для:
- если тела можно положить материальными точками, т. е. их размерами можно пренебречь по сравнению с расстоянием между телами;
- если тела обладают сферической симметрией.
Напомним, что мы с вами записали и поняли, чему равна гравитационная постоянная и обсудили ее универсальный характер:
Именно гравитационное взаимодействие как одно из четырех универсальных физических взаимодействий является наиболее ответственным за движение крупных небесных тел – планет, звезд, целых галактик.
Законы движение небесных тел (законы Кеплера)
Вам хорошо известно, что к появлению законов всемирного тяготения привело наблюдение за телами космических масштабов, за планетами, за солнцем, за кометами, за метеоритами и т.
Первый закон Кеплера: все планеты Солнечной системы движутся по эллиптическим орбитам, в одном из фокусов эллипса находится Солнце.
Эллипс – это одна из геометрических фигур, условно его можно представить ка вытянутую окружность. Обратите внимание на иллюстрацию (рис. 10) первого закона Кеплера. В одном из фокусов эллипса находится Солнце, обратите внимание на расположение нашей планеты, наиболее ближняя к солнцу точка называется перигелий, она обозначена буквой Р, наиболее далекая точка называется афелий, это точка А.
Расстояние a, показанное на рисунке 11, называется полуось.
Рис. 11. Иллюстрация первого закона Кеплера
Возможно, вам сложно представить, что такое эллипс или его фокус, вас должен успокаивать тот факт, что в реальности орбиты, по которым вращаются планеты вокруг Солнца, практически неотличимы от круговых, круг – это частный случай эллипса. Единственная планета, у которой эллипсоидальная траектория, – это Плутон, но совсем недавно Плутон был вынесен из списка планет, и он является, по современной астрономической классификации, небесным телом. Итак, траектория движения практически всех планет Солнечной системы – это окружность.
Второй закон Кеплера: радиус-вектор планеты, планета движется по траектории (внешняя окружность) которая показана на рисунке 12, и за одинаковые промежутки времени описывает одинаковые площадки, т. е. площадь, заштрихованная горизонтально (рис. 12), равна площади заштрихованной вертикально (рис. 12), если время движения планет в эти два отрезка одинаковое.
Рис. 12. Иллюстрация второго закона Кеплера
Третий закон Кеплера:
T – это период вращения планеты вокруг Солнца (на рис. 13 эта область закрашена), a – это половина или большая полуось, т. е. квадраты периодов вращения планет относятся как кубы больших полуосей.
Рис. 13. Иллюстрация третьего закона Кеплера
Несмотря на то что законы Кеплера практически полностью описывали движение небесных тел (а следует сказать, что по современным воззрениям точность действия законов Кеплера составляет практически порядка одного процента, это очень хорошая точность, т. е. на 99 % они правильно описывают движение небесных объектов) они остаются лишь обобщением некоторых эмпирических наблюдений, которые проводили астрономы. Фундамент под эти законы как раз и подвел Исаак Ньютон, выведя закон всемирного тяготения. Тем не менее отдадим должное трудам астрономов того времени: Тихо Праге, Иоганна Кеплера и других, ведь им было неизмеримо сложнее, чем современным астрономам, с точки зрения техники, которая у них была, и с точки зрения математического аппарата и устройств для обработки наблюдений.
Кроме этого, гравитационное взаимодействие обуславливает наличие приливов, отливов, а также множества других физических явлений.
Закон всемирного тяготения Ньютона в 2007 г. был проверен и на расстояниях, меньших одного сантиметра (от 55 мкм до 9,35 мм). С учетом погрешностей эксперимента в исследованном диапазоне расстояний отклонений от закона Ньютона не обнаружено.
А как формула для закона всемирного тяготения превращается в формулу для силы тяжести, которую вы уже хорошо знаете, мы обсудим на следующем уроке.
Список литературы
- Касьянов В. А. Физика 10 класс. – М.: Дрофа, 2010.
- А. В. Перышкин, Е. М. Гутник. Физика 9. – М. Дрофа 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «All-Физика» (Источник)
- Интернет-портал «emto.com.ua» (Источник)
Домашнее задание
- Что такое гравитационная постоянная и каков физический смысл этой постоянной?
- Сформулируйте закон всемирного тяготения.
- Как и во сколько раз изменится сила тяготения, если при неизменном расстоянии массы тел возрастут вдвое?
Как рассчитать силу гравитации
Обновлено 22 декабря 2020 г.
Кевин Бек
Гравитация повсюду — как в буквальном смысле, так и в повседневных сознательных действиях людей по всей планете. Трудно или невозможно представить себе жизнь в мире, свободном от его эффектов, или даже в таком, где эффекты были изменены на «небольшую» величину — скажем, «всего» примерно на 25 процентов. Что ж, представьте, что вы переходите от неспособности прыгнуть достаточно высоко, чтобы коснуться баскетбольного кольца высотой 10 футов, к способности с легкостью бросать данки; это примерно то, что 25-процентное увеличение способности прыгать благодаря уменьшению гравитации дало бы огромному количеству людей!
Гравитация, одна из четырех фундаментальных физических сил, влияет на все инженерные предприятия, которые когда-либо предпринимали люди, особенно в сфере экономики.
Умение вычислять силу гравитации и решать связанные с ней задачи является базовым и важным навыком на вводных курсах по физике.
Сила гравитации
Никто не может точно сказать, что такое гравитация, но ее можно описать математически и в терминах других физических величин и свойств. Гравитация — одна из четырех фундаментальных сил в природе, остальные — сильное и слабое ядерное взаимодействие (действующие на внутриатомном уровне) и электромагнитное взаимодействие. Гравитация — самая слабая из четырех, но она оказывает огромное влияние на то, как устроена сама Вселенная. 92}
, где G — только что определенная константа, M — масса объекта, а d — расстояние между объектом и точкой, в которой измеряется поле. Глядя на выражение для F грав , вы можете увидеть, что г имеет единицы силы, деленные на массу, поскольку уравнение для г по сути является уравнением силы тяжести (уравнение для F грав ) без учета массы меньшего объекта.
Таким образом, переменная g имеет единицы измерения ускорения. Вблизи поверхности Земли ускорение, обусловленное силой земного притяжения, составляет 9,8 метра в секунду за секунду, или 9,8 м/с 2 . Если вы решите продвинуться далеко в физике, вы увидите эту цифру больше раз, чем сможете сосчитать.
Формула силы тяжести
Объединение формул в двух предыдущих разделах дает соотношение
F=мг
где г = 9,8 м/с 2 на Земле. Это частный случай второго закона Ньютона, который равен
F=ma
. Формула ускорения свободного падения может использоваться обычным образом с так называемыми ньютоновскими уравнениями движения, которые связывают массу ( m ), скорость ( v ), линейное положение ( x ), вертикальное положение ( y ), ускорение ( a ) и время ( t ). То есть так же, как d = (1/2) at 2 , расстояние, которое объект пройдет за время t по прямой под действием данного ускорения, расстояние y объект упадет под действием силы тяжести за время t получается из выражения d = (1/2) gt 2 , или 4,9 t 2 для объектов, падающих под действием земного притяжения.
В вводной физике, когда вас просят решить задачи гравитации, включая свободное падение, вас просят игнорировать эффекты сопротивления воздуха. На практике эти эффекты значительны, как вы узнаете, если будете заниматься инженерным делом или аналогичной областью.
Учебное пособие по гравитации и космической скорости
Гравитация — это сила, которая придает структуру большинству крупных объектов во Вселенной. Он удерживает Землю вместе и на ее орбите вокруг Солнца. Он удерживает Солнце вместе и на его орбите вокруг Млечного Пути. Он даже скрепляет саму Вселенную.
Гравитация также вызывает многие астрономические явления, такие как приливы и отливы. Поскольку это, пожалуй, самая важная сила для больших объектов, нам необходимо понять ее основные свойства.
- Каждый объект оказывает гравитационное притяжение на любой другой объект.
- Гравитационная сила между двумя объектами зависит от их масс , которые на больше для больших масс.
- Гравитационная сила между двумя объектами зависит от их расстояния , будучи слабее чем дальше друг от друга находятся объекты.
Ньютон открыл математическое выражение для силы тяжести и показал, что оно имеет следующий вид.
Сила тяжести = постоянная x мм/об 2 , Где M и m – массы, а r – их расстояние. Постоянная называется универсальной гравитационной постоянной, и ее значение зависит от используемых единиц измерения.
Если массы выражены в килограммах (кг), а расстояние измеряется в метрах, а сила в метрических единицах называется ньютонами, то G = 6,67×10 -11 . ньютон-м 2 -кг -2 .
Ньютон является единицей силы и определяется так, что сила в 1 ньютон производит ускорение 1 метр в секунду 2 на массу 1 килограмм.
Небольшая возня затем показывает, что Ньютон также может быть выражен в более
основные единицы, так что единицы ньютон = килограмм-метр-сек -2 = кг-м-сек -2 .
Таким образом, единицы G могут быть выражены в метрах 3 -кг -1 -сек -2 .
Критические идеи для понимания просты.
- Чем больше масса, тем больше сила
- Чем больше разделение, тем меньше сила.
Обратите внимание, что удвоение расстояния не уменьшает силу в 2 раза. Она уменьшает ее на 90 150 квадратов 90 151 расстояния, или, в данном случае, в 4 раза.
Например, предположим, что Земля была в 3 раза дальше от Солнца, чем сейчас. Как изменится сила притяжения между ними? Ответ: Было бы 3 2 = в 9 раз слабее.
1. Предположим, что Луна была в пять раз ближе к Земле, чем сейчас. Как изменится сила притяжения между ними?
| А)..Было бы в 5 раз слабее. B).. Было бы в пять раз сильнее. С).. Было бы в 10 раз сильнее. D).. Было бы в 25 раз сильнее. E).. Было бы в 125 раз сильнее. |
2.
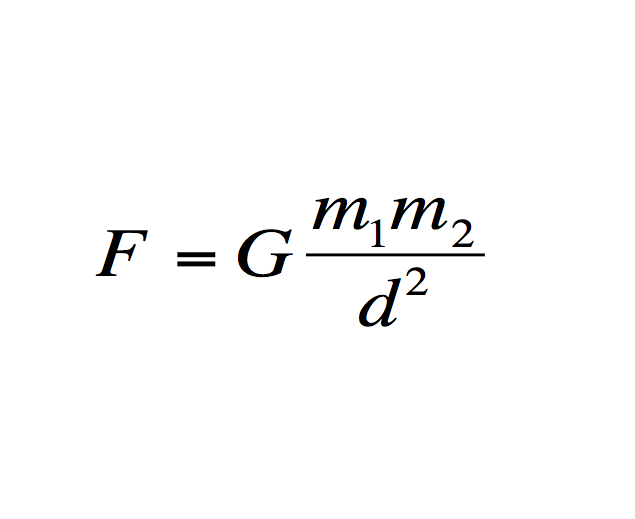Предположим, что две звезды обращаются друг вокруг друга. Если одна звезда взорвется и потеряет половину своей массы, что произойдет с силой притяжения между парой?
| A) …Он станет вдвое сильнее. B)… Он станет в четыре раза сильнее. C)…Он будет вдвое слабее. D)… Он будет на четверть меньше. E)… Не изменится. |
Сила гравитации влияет на многие аспекты астрономических объектов. В частности, in определяет скорость, с которой что-то движется, чтобы избежать гравитации объекта. Эта скорость называется скоростью убегания .
Формула скорости убегания от сферического объекта, такого как луна, планета или звезда, выглядит следующим образом:
V = (2GM/R)
где G — гравитационная постоянная, M — масса объекта, R — его радиус.
Обратите внимание, что для заданной массы по мере того, как R становится меньше, V будет увеличиваться .
Заметьте также, что формула скорости убегания очень похожа на закон всемирного тяготения, как и следовало ожидать. В конце концов, большая сила гравитационного притяжения затруднит уклонение от объекта, и поэтому вы должны двигаться быстрее, чтобы вырваться на свободу.
Предположим, у нас есть две планеты A и B. Они имеют одинаковый радиус, но планета A более массивна, чем планета B.
3. Что имеет большую скорость убегания?
| A)… A B)… B C)… Масса не влияет на скорость убегания. |
4. Предположим, что в приведенной выше задаче масса A в 9 раз больше массы B. Как скорость убегания из А по сравнению с В?
| А)… В 9 раз меньше. Б)… Он в 9 раз больше. С)… Он в 3 раза меньше. D) . Он в 3 раза больше. E)… Они одинаковые. |
Теперь давайте фактически рассчитаем скорость убегания V для объекта, для
например, Солнце.
Масса Солнца составляет примерно 2×10 30 кг, а его
радиус примерно 7×10 8 метров. Учитывая, что G = 6,67×10 -11 , что такое V? Обратите внимание, что при решении этой задачи ваш ответ будет в метрах/сек.
Подставляя приведенные выше числа в формулу, находим V = (2GM/R) = (2×6,67×10 -11 x2x10 30 /7×10 8 ) = (2×6,67x2x10 -11+30 /7×10 8 ) = (4×10 11 ) = 6,3×10 5 м/сек.
Этот ответ может быть легче интерпретировать, если мы выразим его в километрах в секунду, а не метры/сек. Чтобы сделать это преобразование, вспомните, что километр равен 1000 (=10 3 )метров. Таким образом, 6,3×10 5 м/с = 6,3×10 5 м/с/10 3 м/км = 6,3×10 2 км/сек = 630 км/сек.
5. Повторите приведенный выше расчет, чтобы найти скорость убегания от Земли. Масса Земли составляет 5,97×10 24 кг, а радиус 6,38×10 6 метров.
Сделайте такой же перевод из м/сек в км/сек в конце.
| А)… 125 км/сек. B)… 11,2 км/сек C)…1,12 км/сек D)… 12 500 км/сек. Е)… 1120 км/сек. |
Ученые часто считают удобным 9Расчеты в масштабе 0150 , такие как тот, который мы только что сделали, чтобы не нужно было переделывать математику, если мы хотим применить расчеты на другую планету или объект. Например, предположим, что у нас есть планета того же радиуса, что и Земля, но в 25 раз массивнее. Поскольку скорость убегания зависит от квадратного корня из массы, чтобы найти скорость убегания для этой более массивной планеты, мы просто умножаем скорость убегания Земли на квадратный корень из 25 (=5), чтобы найти, что ее скорость убегания составляет около 56 км/сек.
Точно так же, если планета имеет ту же массу, но другой радиус, мы снова можем масштабировать скорость убегания. На этот раз мы делим на квадратный корень из коэффициента, на который радиус больше.
Если и масса, и радиус отличаются от земных (а они, конечно, обычно будет), примените оба коэффициента масштабирования . Например, Уран примерно в 15 раз массивнее Земли, а его радиус примерно в 4 раза больше земного. Какова его скорость убегания?
Масса в 15 раз больше, значит, V равно 15 = 3,87. раз больше. Радиус в 4 раза больше означает, что V в 4 = 2 раза меньше. Комбинация коэффициентов масштабирования дает нам, что V в 3,87/2 = 1,94 раза больше или V = 1,94×11,2 км/сек = 21,7 км/сек.
6. Какова скорость убегания от Юпитера, если его масса в 300 раз больше массы Земли, а радиус в 10 раз больше. Подсказка Используйте приведенные выше принципы масштабирования.
| А)… 6,13 км/сек. B)… 333,2 км/сек C)…1,12 км/сек D)… 61,3 км/сек. Е)… 33,3 км/сек. |
Хотя гравитация удерживает вместе большинство астрономических объектов, она также может и разрывать их на части.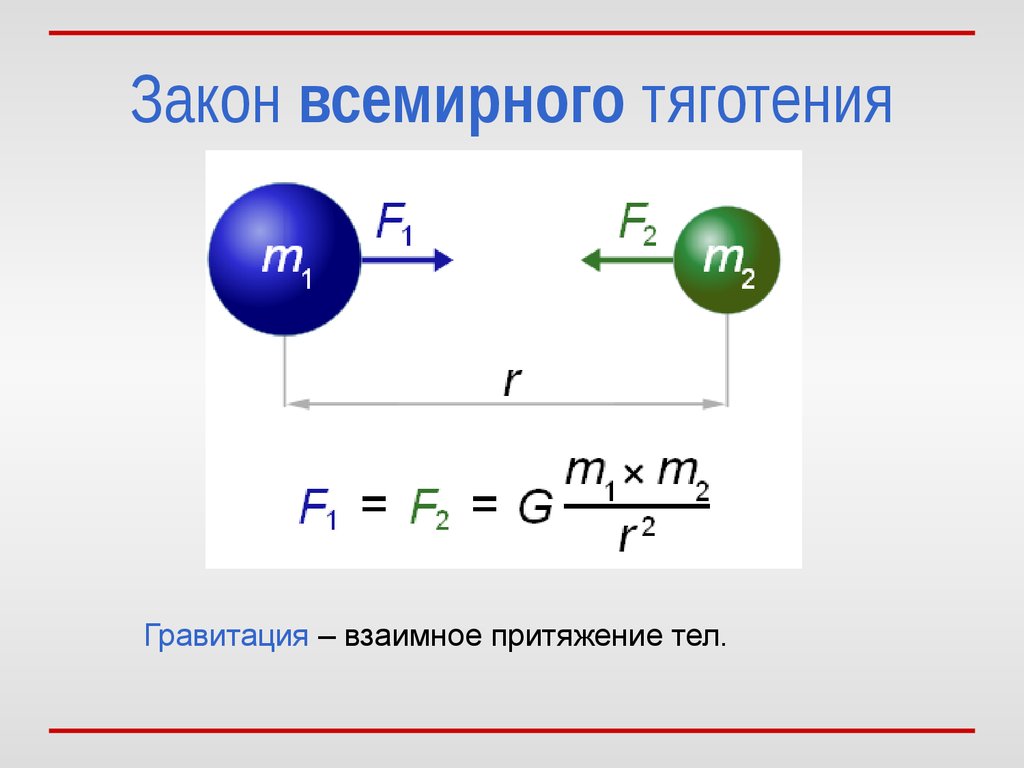
Например, если бы вы могли прыгнуть в черную дыру массой примерно в 1 солнечную массу, вы бы растянулись на 90 150 и разорвались на атомы ее гравитацией.
Менее драматическим примером растягивающей силы гравитации являются приливы и отливы. Океанские приливы на Земле возникают из-за гравитационного притяжения Луны к Земле (с некоторой помощью Солнца). Подробное обсуждение приливов будет позже. Здесь мы просто рассмотрим общий случай гравитационного растяжения объекта.
Предположим, мы поместили две маленькие массы, A и B, на одну линию с третьей, большей массой, C (см. рисунок). Для простоты давайте проигнорируем гравитационное притяжение маленьких объектов и предположим, что ни один из трех не движется.
7. Что будет с более мелкими?
| А)… Они останутся там, где они есть. B)… Они почувствуют гравитационную силу от C и будут двигаться к ней. C)…Они будут ощущать гравитационную силу от C, но их инерция будет удерживать их от движения.  |