Переменный ток | Формулы по физике
Электродвижущая сила переменного тока
Найти
Известно, что:
εBSω =
Вычислить ‘ε’Электродвижущая сила переменного тока
Найти
Известно, что:
eε_msinωt =
Вычислить ‘e’Максимальная сила переменного тока
Найти
Известно, что:
I_mε_mR =
Вычислить ‘I_m’Действующее (эффективное) значение силы переменного тока
Известно, что:
I_efI_m =
Вычислить ‘I_ef’Средняя мощность переменного тока
Найти
Известно, что:
p_средI_mR =
Вычислить ‘p_сред’Действующее (эффективное) значение напряжения переменного тока
Найти
Известно, что:
U_efU_m =
Вычислить ‘U_ef’Напряжение переменного тока
Найти
Известно, что:
UU_mcosωt =
Вычислить ‘U’Максимальная сила переменного тока
Найти
Известно, что:
I_mU_mCω =
Вычислить ‘I_m’Ёмкостное сопротивление
Найти
Известно, что:
X_cCω =
Вычислить ‘X_c’Сила и ёмкостное сопротивление переменного тока
Найти
Известно, что:
IUX_c =
Вычислить ‘I’Сила и индуктивное сопротивление переменного тока
Найти
Известно, что:
IUX_L =
Вычислить ‘I’Индуктивное сопротивление
Найти
Известно, что:
X_LωL =
Вычислить ‘X_L’Закон Ома для цепи переменного тока
Найти
Известно, что:
XRX_LX_C =
Закон Ома для цепи переменного тока
Найти
Известно, что:
XRωLC =
Вычислить ‘X’Сдвиг фаз между током и напряжением переменного тока
Найти
Известно, что:
φX_LX_CR =
Вычислить ‘φ’Резонанс в цепи переменного тока
Известно, что:
UILC =
Вычислить ‘U’Первая формула трансформатора: напряжение
Найти
Известно, что:
U1U2N1N2 =
Вычислить ‘U1’Вторая формула трансформатора: сила тока
Найти
Известно, что:
I1I2N2N1 =
физические формулы, использующие мощность и напряжение
При выборе какого-либо электрического оборудования одним из важных параметров, на который обращается внимание, является мощность изделия. Этот параметр неразрывно связан с силой тока и напряжением. Чтобы рассчитать силу тока, напряжение или мощность в электрической цепи, используются несложные формулы. Но чтобы осмысленно проводить такие вычисления, желательно понимать физическую природу возникновения этих величин.
Этот параметр неразрывно связан с силой тока и напряжением. Чтобы рассчитать силу тока, напряжение или мощность в электрической цепи, используются несложные формулы. Но чтобы осмысленно проводить такие вычисления, желательно понимать физическую природу возникновения этих величин.
- Физическое понятие величин
- Сила тока
- Разность потенциалов
- Электрическая мощность
- Закон Ома для цепи
- Практический расчёт
Физическое понятие величин
Это понятие было введено ещё в 1600 году английским физиком Уильямом Гилбертом, изучающим магнитные и электрические явления. Исследуя магнетизм в природе, учёный установил, что некоторые тела при трении начинают обладать силой притяжения по отношению к другим предметам, в частности, к янтарю.
Продолжая его исследования, немецкий физик Отто фон Герике в 1663 году изобрёл электрическую машину, которая представляла собой металлический стержень с одетым на него серным шаром. В результате он выяснил, что материалы могут не только притягивать вещества, но и отталкивать. Но только через восемьдесят лет американец Бенджамин Франклин создал теорию электричества, введя такие термины, как отрицательный и положительный заряд.
Дальнейшее развитие электричество получило после опытов Шарля Кулона и открытия им закона взаимодействия зарядов. Заключался он в следующем: сила влияния двух точечных зарядов друг на друга в вакууме прямо пропорциональна их произведению и обратно пропорциональна расстоянию между ними в квадрате. После этого благодаря экспериментам таких учёных, как Джоуль, Ленц, Ом, Ампер, Фарадей, Максвелл были введены понятия ток, напряжение и электромагнетизм.
Так, в 1897 году англичанин Джозеф Томсон установил, что носителями зарядов являются электроны. Ранее, в 1880 году, электротехник из России Дмитрий Лачинов сформулировал необходимые условия для передачи электричества на расстояния.
После этих открытий были выработаны фундаментальные определения электричества. Сегодня под ним понимаются свойства материалов образовывать вокруг себя электрическое поле, оказывающее воздействие на располагающиеся рядом другие заряженные частицы. Заряды условно принято разделять на положительные и отрицательные. При их перемещении возникает магнитное поле, при этом одинакового знака заряды притягиваются, а разного — отталкиваются.
Сила тока
Ток — это упорядоченное движение носителей заряда, происходящее под влиянием электрического поля. В качестве положительно заряженных частиц выступают электроны, а отрицательных — дырки. Математически это явление описывается с помощью формулы I = Q*T, где I — ток проводимости (А), Q — заряд частицы (Кл), T — время ©.
То есть электрическим током называется количество зарядов, прошедших через поперечное сечение вещества. Но эта формулировка верна только для тока постоянной величины, в то время как для изменяемого во времени она будет выглядеть I (T) = dQ/dT.
Плотность движения носителей заряда в материале, то есть количество электричества, проходящего за условно принятое время, называется силой тока. Согласно Международной системе (СИ) его единицей измерения является ампер. Один ампер равен перемещению электрического заряда, равного одному кулону, через поперечное сечение за одну секунду.
Носители заряда могут двигаться как упорядоченно, так и хаотично. При их движении возникает электрическое поле, обозначаемое латинской буквой E. Значение, определяющееся отношением тока к поперечному сечению проводника, называется плотностью тока. За единицу её измерения принимается А/мм2.
По своему виду ток различают на следующие типы:
- Переноса.
 Характеризуется движением зарядов, осуществляемым в свободном пространстве. Этот тип характерен для газоразрядных приборов.
Характеризуется движением зарядов, осуществляемым в свободном пространстве. Этот тип характерен для газоразрядных приборов. - Смещения. Возникает в диэлектриках и определяется упорядоченным перемещением связанных заряженных частиц.
- Полный. Определяется суммарным значением тока: проводимости, переноса и смещения.
- Постоянный. Это такой вид, который может изменять величину, но не изменяет направление движения, то есть свой знак.
- Переменный. Такого вида ток может изменяться как по величине, так и по направлению (знаку).
Переменный вид разделяется по форме и может быть синусоидальным и несинусоидальным. Для расчёта силы тока синусоидальной формы используется формула Is = Ia*sin ωt, где Ia — максимальное значение тока (A), ω — угловая скорость, равная 2πf (Гц).
Физические тела, в которых возможно протекание тока, называют проводниками, а в тех, где возникают препятствия его прохождению — диэлектриками.
Промежуточное состояние между ними занимают полупроводники.
Разность потенциалов
Напряжением принято называть физическую величину, характеризующую электрическое поле. Она показывает, какую работу понадобится совершить полю для того, чтобы переместить единичный заряд из одной точки в другую. При этом принимается, что этот перенос не влияет на распределение зарядов в источнике поля. Согласно Международной системе единиц напряжение измеряется в вольтах.
Работа по переносу складывается из двух величин — электрических и сторонних. Если сторонние силы не действуют, то напряжение на участке цепи равно разности потенциалов и вычисляется по формуле U = φ1-φ2. При этом потенциал определяется отношением напряжённости электрического поля к заряду. Для его расчёта используют формулу φ = W/q.
Другими словами, это характеристика поля в определённой точке, не зависящей от величины заряда, находящегося в нём. То есть напряжение в общем случае определяется работой электростатического поля, возникающего при движении заряда вдоль его силовых линий.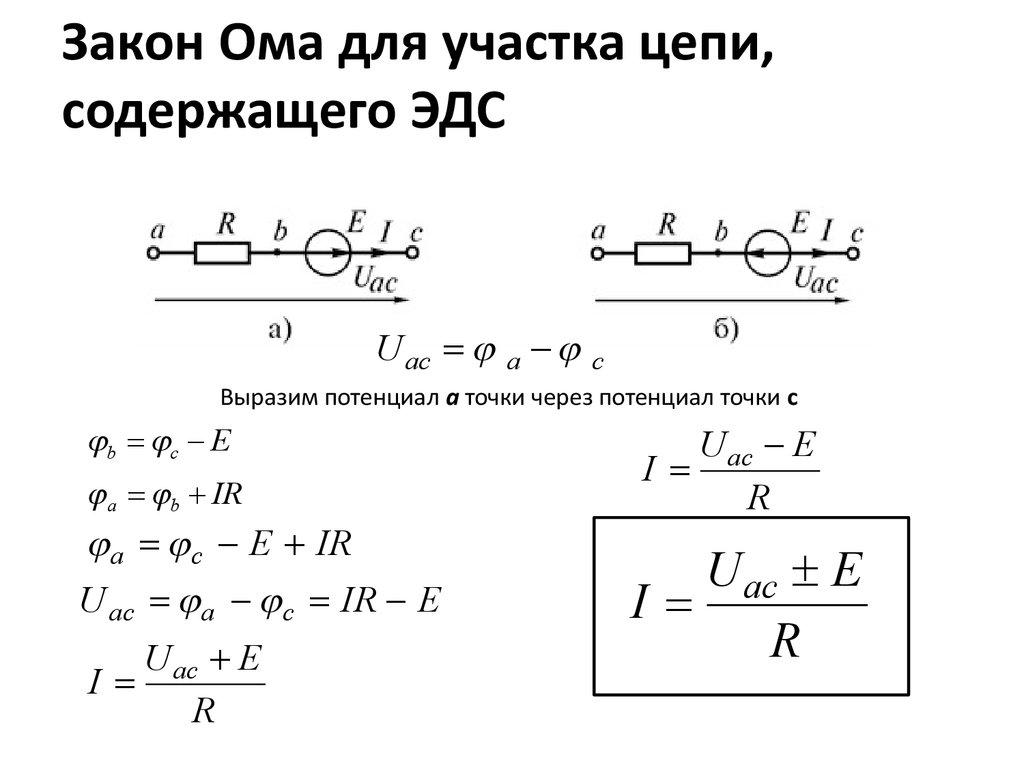 Математически его можно рассчитать по формуле U = A/q, где А — совершаемая работа по перемещению (Дж), q — энергия заряда (Кл).
Математически его можно рассчитать по формуле U = A/q, где А — совершаемая работа по перемещению (Дж), q — энергия заряда (Кл).
Применительно к сети переменного тока для напряжения используются следующие понятия:
- Мгновенное. Это значение физической величины, измеренное в конкретный момент времени: U = U (t). Для синусоидального сигнала мгновенное напряжение находится с помощью выражения U (t) = Ua sin (ὤt + φ).
- Амплитудное. Характеризуется наибольшей величиной мгновенного значения без учёта знака: Ua = max (U (t)).
- Среднее. Определяется за полный период сигнала по формуле Us = 1/T ʃ U (t)*dt. Для синусоидальной формы это значение равно нулю.
Проводя расчёт напряжения, редко используется понятие электрического потенциала. Связано это с тем, что условно принято за одну из точек потенциала принимать землю.
Это значение берётся равным нулю, а все остальные потенциалы считаются относительно неё. Говоря, что напряжение в определённой точке составляет 300 вольт, имеется в виду разность потенциалов между этой точкой и землёй, равная этому значению.
Электрическая мощность
Электрическая мощность характеризует скорость передачи электрической энергии или её преобразование. Единицей её измерения является ватт. Для того чтобы посчитать мощность на определённом участке цепи, необходимо перемножить значение напряжения и силы тока на этом участке. Исходя из определения электрического напряжения, можно сказать, что заряд при движении совершает работу, численно равную ей на участке цепи. Если же умножить работу на количество зарядов, то можно найти общее значение работы, которую совершили заряды на этом участке.
Исходя из физического определения, что мощность — это работа за единицу времени, получается выражение P = A/Δt, где A — работа, совершаемая зарядом при перемещении от начальной точки к конечной (Дж), Δt — время, затраченное на полное перемещение заряда ©.
Для всех зарядов в цепи мощность можно найти благодаря формуле P = (U/ Δt) * Q, где Q — общее число зарядов.
Так как ток представляет собой заряд, протекающий в единицу времени (I = Q/ Δt), то получается, что мощность равна произведению тока на напряжение, то есть P = U*I (Вт).
В цепи с постоянным током его сила и напряжение всегда имеют постоянное значение в определённой точке, поэтому для любого момента времени мощность можно вычислить по формуле P = I*U = I2*R = U2/R, где R — сопротивление прохождению тока в электрической цепи (Ом). Если же в этой сети находится источник электродвижущей силы, то мощность находится как P = I*E+ I2*r, где Е — электродвижущая сила или ЭДС (В), r — внутреннее сопротивление источника ЭДС (Ом).
Для цепи, в которой её параметры изменяются по какому-то циклу, мощность в определённой точке интегрируется по времени. При этом существуют следующие виды мощности:
- Активная.
 Для её нахождения используется расчёт, учитывающий угол сдвига фаз φ. Находится согласно формуле P = U*I*cos φ.
Для её нахождения используется расчёт, учитывающий угол сдвига фаз φ. Находится согласно формуле P = U*I*cos φ. - Реактивная. Характеризуется нагрузками, создаваемыми электрическими устройствами в виде колебаний энергии электромагнитного поля. Её вычисление осуществляется по формуле P = U*I*sin φ.
- Полная. Определяется произведением действующих значений тока и напряжения, связана с другими видами мощности выражением S= √(P 2 +Q 2).
Закон Ома для цепи
Проводя расчёты мощности по напряжению и току на практике, часто используют закон Ома. Он устанавливает связь между током, сопротивлением и напряжением. Этот закон был открыт путём проведения Симоном Омом ряда экспериментов и сформулирован им в 1826 году. Он выяснил, что величина тока на участке цепи прямо пропорциональна разности потенциалов и обратно пропорциональна сопротивлению этого участка.
youtube.com/embed/dwaSF3W4TxU”>Закон Ома можно записать в следующем виде: I = U/R, где I — значение силы тока (А), U — разность потенциалов (В), R — сопротивление цепи прохождению тока (Ом).
Для полной же цепи эту формулу можно записать так: I = E/(R+ r0), где E — ЭДС источника питания (В), r0 — внутреннее сопротивление источника напряжения (Ом).
Таким образом, для участка цепи будет справедливо выражение P = U2/R = I2R, а для полной цепи — P = (E/(R+ R0))2*R. Именно эти две формулы и используются чаще всего для расчётов электрических сетей или мощности необходимого оборудования.
Различные компоненты электрической сети в определённый момент времени потребляют разную величину тока. Поэтому очень важно правильно рассчитать, какое количество энергии подводится в тот или иной момент в определённое место цепи, чтобы не допустить перегрузок на линии и возникновения аварийных ситуаций.
Этим и занимаются разработчики схем, упрощая их до состояния, когда можно рассчитать необходимую мощность, используя закон Ома.
Практический расчёт
Например, пусть понадобится узнать, на какой ток необходимо приобрести устанавливаемый на участок цепи автоматический выключатель. При этом известно, что в линию, на которой он будет установлен, одновременно будут включаться холодильник с максимальной мощностью потребления энергии один киловатт, бойлер (два киловатта) и люстра, потребляющая 90 ватт. В месте установки используется однофазная сеть, рассчитанная на рабочее напряжение 220 вольт.
На первом этапе расчёта понадобится суммировать всю мощность подключаемых к линии электроприборов. Так, P общ. = 1000 + 2000 + 90 +220 = 3310 Вт. Используя формулу P = I*U, находится необходимое значение тока: I = P/U = 3310/220 = 15,04 А.
Из стандартного ряда выключателей наиболее близкое значение имеет автомат на 16 А. Поскольку необходимо покупать устройство защиты с небольшим запасом, то для рассматриваемого примера подойдёт выключатель, рассчитанный на 20 ампер.
Благодаря таким вычислениям можно рассчитать любой параметр электрической цепи, но это при учёте достаточного количества вводных данных.
формулы и порядок расчета при разных известных показателях
Сила тока — это движение заряженных частиц, являющееся одной из ключевых характеристик в цепи электричества. Данная величина измеряется Амперами. Силой электрического тока измеряется нагрузка на проводящих ток проводах, шинах и дорожках плат.
Благодаря этой величине можно понять, сколько энергии протекает в проводнике за определённое количество времени. Вычислить значение можно разными способами, которые зависят от имеющихся в наличии данных.
Из-за того, что варианты решения и известные значения могут быть разными, можно встретиться с проблемами в расчетах. Далее рассмотрим, как правильно можно определить силу тока с помощью разных значений.
С помощью мощности и напряжения
В случае если из всех известных данных у вас есть только значение мощности потребления и напряжение, нужно воспользоваться простой формулой, не включающей в себя сопротивление: P = IU
При этом из этой же формулы можно получить следующую: I = P/U
Данная формула подходит для цепи с постоянным током.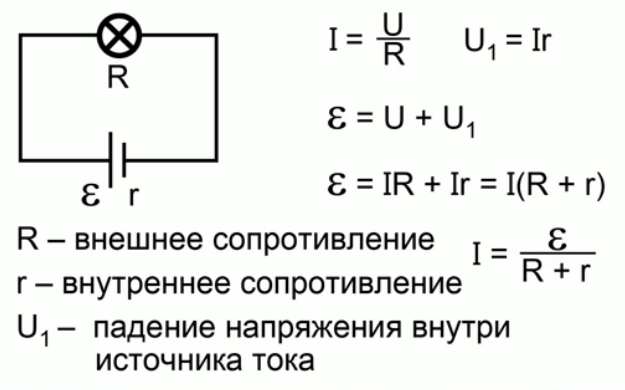 А для расчетов силы тока в цепях с переменным током (такая формула может понадобиться Вам, если Вы хотите вычислить силу тока в электрическом двигателе) нужно учитывать ещё и коэффициент мощности (его же иначе называют «косинус фи»).
А для расчетов силы тока в цепях с переменным током (такая формула может понадобиться Вам, если Вы хотите вычислить силу тока в электрическом двигателе) нужно учитывать ещё и коэффициент мощности (его же иначе называют «косинус фи»).
В этом случае для электродвигателя с тремя фазами действует нужно построить расчет немного иначе.
Найдите P, учитывая при этом коэффициент полезного действия: Р1 = Р2/η
В этой формуле P 2 является активной полезной мощностью на вале, а η является коэффициентом полезного действия. Эти значения обычно можно найти на самом двигателе.
После этого нужно найти полную мощность с учётом коэффициента мощности (он же cos φ, его значение указано на двигателе): S = P1/cosφ
Далее определите ток потребления: Iном = S/(1,73·U)
1.73 является корнем из трёх, это значение нужно для расчёта цепи на три фазы. Значение напряжение будет зависеть от способа включения электродвигателя (треугольником или звездой) и Вольт, чаще всего встречается 380.
С помощью напряжения или мощности и сопротивления
Бывает и так, что для расчета силы электрического тока нужно задействовать напряжение с определённого участка или величину нагрузки. Тогда проще всего применить закон Ома, который знает каждый, кто немного разбирается в физике.
Если же напряжение Вам неизвестно, но вы знаете значение мощности и сопротивления, проводите расчет по следующей формуле: P=UI
Снова применяя закон Ома, можно получить следующее: U=IR
В таком случае: P=I2*R
Получаем следующую формулу: I2=P/R
Кроме того, можно применить следующий расчет, исходя из этих же формул и значений: I=(P/R)1/2
С помощью электродвижущей силы, внутреннего сопротивления и нагрузки
В некоторых студенческих учебниках встречаются так называемые задачки с подвохом. К ним относятся и те, где есть электродвижущая сила и значение внутреннего сопротивления.
Вспоминая закон Ома, силу электрического тока можно получить следующим образом: I=E/(R+r)
Здесь Е будет электродвижущей силой, а r будет внутренним сопротивлением. R представляет собой нагрузку.
R представляет собой нагрузку.
С помощью закона Джоуля-Ленца
Некоторые затрудняются определять силу тока, если есть:
- Время;
- Значение сопротивления;
- Кол-во выделяемого тепла от проводника.
С помощью решения задачи, нужно воспользоваться законом Джоуля-Ленца: Q=I2Rt
Исходя из этой формулы, расчет нужно построить так: I2=QRt
Либо так: I=(Q/Rt)1/2
Практические примеры
Чтобы правильно понять все приведённые выше формулы, предлагаем Вам рассмотреть несколько примеров, которые могут встретиться в учебниках по физике.
Первый пример: рассчитаем силу тока из 2-х резисторов, при этом в цели есть последовательное и параллельное соединение. В источнике питания двенадцать Вольт.
Исходя из условий задачи, нужно получить два значения: одно для последовательного, а другое для параллельного соединения.
Для получения значения последовательного соединения, нужно сложить сопротивления, чтобы вывести общее: R1+R2=1+2=3 Ома
Далее определить силу тока можно через закон Ома: I=U/R=12/3=4 Ампера
Для параллельного соединения расчёт будет следующим: Rобщ=(R1*R2)/(R1+R2)=1*2/3=2/3=0,67
С применением закона Ома результат будет таким: I=12*0,67=18А
Второй пример: нужно найти ток при соединении разных элементов цепи. На выход питание составляет 24 Вольта, на резисторы от первого к третьему 1, 2 и 3 Ома соответственно.
В этом случае воспользовавшись формулой, которую мы определили выше, видим следующий расчет: Rприв=(R2*R3)/(R2+R3)=(3*3)|(3+3)=9/6=3/2=1,5 Ома
С этой формулой схема будет выглядеть так:
Теперь определяем силу тока: I=U/(R1+Rприв)=24/(1+1,5)=24/2,5=9,6 Ампер
Это все способы определения силы. Потренируйтесь использовать эти расчеты для типовых задач, и Вы сможете лучше понять принцип вычисления силы тока в электрической цепи!
Потренируйтесь использовать эти расчеты для типовых задач, и Вы сможете лучше понять принцип вычисления силы тока в электрической цепи!
Лекция 15, 11 октября 2000 г.
Лекция 15, 11 октября 2000 г.индекс курса
Вспомнить с последней лекции:
- Создание магнитных полей:
- Длинный прямой провод: B = m 0 I / 2p r
- Соленоид: B = m 0 n I
- Сила магнитного поля:
- Движущийся заряд: F = q v B sinq
- Провод: F = B I l sinq
- Крутящий момент в токовой петле: t = B I A sinq
- Усилие между двумя проводами: F / l = m 0 I 1 I 2 / 2p d
- привлекательный, когда токи одного направления
- отталкивающий, когда токи противоположны по направлению
Мы видели, что магнитное поле воздействует на провод, по которому течет ток, и что провод, по которому течет ток, создает магнитное поле. Токи создаются электрическими полями, так что, похоже, между электричеством и магнетизмом существует какая-то связь.
В этой главе мы установим эту связь, увидев, как магнитное поле может создавать разность потенциалов.
Магнитный поток будет играть важную роль на протяжении всей этой главы.
Токи создаются электрическими полями, так что, похоже, между электричеством и магнетизмом существует какая-то связь.
В этой главе мы установим эту связь, увидев, как магнитное поле может создавать разность потенциалов.
Магнитный поток будет играть важную роль на протяжении всей этой главы.
20.1 ЭДС индукции и магнитный поток
Эксперименты 19 века показали, что изменяющееся магнитное поле может производить ЭДС. Мы количественно определяем изменение с точки зрения магнитного потока. Магнитный поток определяется аналогично электрическому потоку. Для проволочной петли площадью A в магнитном поле B магнитный поток F определяется выражением:
F = B perp A = B A cosq
где q — угол между перпендикуляром к плоскости петли и магнитным полем B. Единицы магнитного потока в системе СИ — Тм². Другой способ взглянуть на поток — думать о нем как о подсчете силовых линий магнитного поля, проходящих через петлю.
Если петля ориентирована перпендикулярно полю (q=0), то поток будет большим. Если петля ориентирована параллельно полю (q = 90°), силовые линии магнитного поля не проходят через петлю, и поток равен нулю.
Если петля ориентирована параллельно полю (q = 90°), силовые линии магнитного поля не проходят через петлю, и поток равен нулю.
Пример: P20.2
Квадратная петля со стороной 2,00 м помещена в магнитное поле напряженностью 0,300 Тл. Если поле образует угол 50,0° с нормалью к плоскости петли, как на рис. 20.2, определите магнитный поток через петлю.
Из того, что нам дано, мы используем
F = B A cosq = (0,300T)(2,00m)²cos50,0° = 0,386 Tm²
20.2 Закон индукции Фарадея
Закон индукции Фарадея связывает изменение магнитного потока с ЭДС индукции:
ЭДС = -N (DF/Dt)
где N — число витков в катушке, в которых индуцируется ЭДС, а DF — изменение потока, происходящее за время Dt. Это один из случаев, когда термин ЭДС несколько отличается от напряжения, и поэтому я буду использовать его.ЭДС индукции пропорциональна изменению магнитного потока, F = BAcosq. Существует три способа изменения потока:
- изменение величины магнитного поля, В,
- изменение угла между контуром и магнитным полем, q, или
- изменение площади петли, А.

Знак минус напоминает вам, что полярность ЭДС индукции препятствует изменению потока. Это точно указано в законе Ленца:
Полярность ЭДС индукции такова, что она создает ток, магнитное поле которого противодействует изменению магнитного потока через контур. То есть индуцированный ток имеет тенденцию поддерживать первоначальный поток через цепь.
Пример: P20.13
Проволочная петля радиусом 0,30 м расположена так, что внешнее магнитное поле напряженностью +0,30 Тл перпендикулярно петле. Поле меняется на -0,20 Тл за 1,5 с. (Здесь знаки плюс и минус относятся к противоположным направлениям цикла.) Найти величину средней ЭДС индукции в контуре за это время.
Петля всегда перпендикулярна полю, поэтому нормаль к петле параллельна полю, поэтому q = 0, а cosq = 1.
Таким образом, поток через контур равен F = BA = Bpr².
Первоначально поток равен
F i = (0,30T)p(0,30m) 2 = 0,085Tm²
, а после изменения поля поток равен
F f = (-0,20T)p(0,30m) 2 = -0,057Tm²
Величина средней ЭДС индукции: с = 0,095В = 95мВ.
Пример: P20.10
Гибкая петля на рисунке P20.10 имеет радиус 12 см и находится в магнитном поле силой 0,15 Тл. Петлю захватывают в точках А и В и растягивают до закрытия. Если для замыкания контура требуется 0,20 с, найти величину средней ЭДС индукции в нем за это время.
Это тот случай, когда изменение потока вызвано изменением площади контура.
И магнитное поле, и угол q остаются постоянными.
Когда петля растянута так, что ее площадь равна нулю, поток через петлю равен нулю.
Таким образом, изменение потока равно его первоначальному значению,
F i = B A cosq = (0,15T)p(0,12m)² = 6,8×10 -3 Tm²
Таким образом, средняя ЭДС индукции равна:
ЭДС = N (DF / Dt) = (6,8×10 -3 Тм²)/(0,20 с) = 3,4×10 -2 В = 34 мВ.
20.3 ЭДС движения
Интересным применением закона Фарадея является создание ЭДС посредством движения проводника.
В качестве простого примера рассмотрим проводящий стержень, движущийся перпендикулярно однородному магнитному полю с постоянной скоростью v. На первый взгляд у нас есть просто стержень, а не полная проводящая петля, и мы рассмотрим, что происходит, используя только силу, действующую на движущийся заряд, F = qvBsinq.
Эта сила будет действовать на свободные заряды в проводнике.
Он будет иметь тенденцию перемещать отрицательный заряд к одному концу и оставлять другой конец стержня с чистым положительным зарядом.
На первый взгляд у нас есть просто стержень, а не полная проводящая петля, и мы рассмотрим, что происходит, используя только силу, действующую на движущийся заряд, F = qvBsinq.
Эта сила будет действовать на свободные заряды в проводнике.
Он будет иметь тенденцию перемещать отрицательный заряд к одному концу и оставлять другой конец стержня с чистым положительным зарядом.
Разделенные заряды создадут электрическое поле, которое будет стремиться сблизить заряды. Когда существует равновесие, магнитная сила F=qvB будет уравновешивать электрическую силу F=qE, так что свободный заряд в стержне не будет ощущать результирующей силы. Таким образом, в равновесии E = vB. Разность потенциалов на концах стержня определяется как DV = E l, или
ДВ = Э л = Б л в
Эта разность потенциалов существует из-за избытка заряда на концах проводника, создаваемого движением через магнитное поле. Если направление движения меняется на противоположное, меняется и полярность разности потенциалов.
Теперь давайте рассмотрим, что произойдет, если мы добавим токопроводящие шины для верхней и нижней части стержня, чтобы они соприкасались, и резистор между ними, чтобы замкнуть контур. Мы можем применить закон Фарадея к полной петле. Изменение потока через петлю пропорционально изменению площади от движения стержня:
DF = B DA = B l Dx.
Используя закон Фарадея, мы находим величину ЭДС равной (N = 1):ЭДС = DF/Dt = B l Dx/Dt = B l v
где я использовал соотношение v = Dx/Dt. Это тот же результат, который мы получили, рассматривая проводящий стержень сам по себе.Если проводящая цепь имеет полное сопротивление, R, то ток равен
I = ЭДС / R = B l v / R
Пример: P20.18
Над областью, где вертикальная составляющая магнитного поля Земли составляет 40,0 мкТл и направлена вниз, провод длиной 5,00 м удерживается в направлении восток-запад и перемещается горизонтально на север со скоростью 10,0 м/с.
Рассчитайте разность потенциалов между концами провода и определите, какой конец положительный.
Вертикальная составляющая магнитного поля перпендикулярна проводу и его движению, так что это то, что нам нужно. Использование выражения, полученного для DV, дает:
DV = B l v = (40,0 мкТл)(5,00 м)(10,0 м/с) = 2,00 мВ
Чтобы определить, какой конец положительный, рассмотрим положительный заряд, движущийся на север через нисходящее магнитное поле. Правило правой руки дает силу, направленную на запад. Таким образом, западный конец провода будет иметь чистый положительный заряд и более положительный потенциал.
© Роберт Харр, 2000 г.ЭДС движения | Физика
Цель обучения
К концу этого раздела вы сможете:
- Рассчитать ЭДС, силу, магнитное поле и работу, связанную с движением объекта в магнитном поле.
Как мы видели, любое изменение магнитного потока индуцирует противодействующую этому изменению ЭДС — процесс, известный как индукция. Движение является одной из основных причин индукции. Например, магнит, перемещаемый по направлению к катушке, создает ЭДС, а катушка, перемещаемая по направлению к магниту, создает аналогичную ЭДС. В этом разделе мы сконцентрируемся на движении в магнитном поле, стационарном относительно Земли, производя то, что условно называется ЭДС движения . Одна ситуация, когда возникает ЭДС движения, известна как эффект Холла и уже исследовалась. На заряды, движущиеся в магнитном поле, действует магнитная сила F = qvB sin θ , которая перемещает противоположные заряды в противоположных направлениях и создает ЭДС f = Bℓv . Мы видели, что эффект Холла имеет приложения, включая измерения B и v . Теперь мы увидим, что эффект Холла является одним из аспектов более широкого явления индукции, и обнаружим, что ЭДС движения можно использовать в качестве источника энергии. Рассмотрим ситуацию, показанную на рис. 1. Стержень движется со скоростью v по паре проводящих рельсов, разделенных расстоянием ℓ в однородном магнитном поле B .
Например, магнит, перемещаемый по направлению к катушке, создает ЭДС, а катушка, перемещаемая по направлению к магниту, создает аналогичную ЭДС. В этом разделе мы сконцентрируемся на движении в магнитном поле, стационарном относительно Земли, производя то, что условно называется ЭДС движения . Одна ситуация, когда возникает ЭДС движения, известна как эффект Холла и уже исследовалась. На заряды, движущиеся в магнитном поле, действует магнитная сила F = qvB sin θ , которая перемещает противоположные заряды в противоположных направлениях и создает ЭДС f = Bℓv . Мы видели, что эффект Холла имеет приложения, включая измерения B и v . Теперь мы увидим, что эффект Холла является одним из аспектов более широкого явления индукции, и обнаружим, что ЭДС движения можно использовать в качестве источника энергии. Рассмотрим ситуацию, показанную на рис. 1. Стержень движется со скоростью v по паре проводящих рельсов, разделенных расстоянием ℓ в однородном магнитном поле B . Рельсы неподвижны относительно B и соединены с неподвижным резистором R . Резистор может быть любым, от лампочки до вольтметра. Рассмотрим область, окруженную движущимся стержнем, рельсами и резистором. B перпендикулярен этой области, и площадь увеличивается по мере движения стержня. Таким образом, магнитный поток, заключенный между рельсами, стержнем и резистором, увеличивается. При изменении потока индуцируется ЭДС в соответствии с законом индукции Фарадея.
Рельсы неподвижны относительно B и соединены с неподвижным резистором R . Резистор может быть любым, от лампочки до вольтметра. Рассмотрим область, окруженную движущимся стержнем, рельсами и резистором. B перпендикулярен этой области, и площадь увеличивается по мере движения стержня. Таким образом, магнитный поток, заключенный между рельсами, стержнем и резистором, увеличивается. При изменении потока индуцируется ЭДС в соответствии с законом индукции Фарадея.
Рис. 1. (а) ЭДС движения = B ℓ v индуцируется между рельсами, когда этот стержень движется вправо в однородном магнитном поле. Магнитное поле B направлено внутрь страницы, перпендикулярно движущимся стержню и рельсам и, следовательно, ограниченной ими области. (b) Закон Ленца дает направления индуцированного поля и тока, а также полярность индуцированной ЭДС. Поскольку поток увеличивается, индуцированное поле направлено в противоположном направлении или выходит за пределы страницы. RHR-2 дает показанное направление тока, и полярность стержня будет управлять таким током. RHR-1 также указывает на ту же полярность стержня. (Обратите внимание, что буквенный символ E, используемый в эквивалентной схеме в нижней части части (b), представляет ЭДС.)
RHR-2 дает показанное направление тока, и полярность стержня будет управлять таким током. RHR-1 также указывает на ту же полярность стержня. (Обратите внимание, что буквенный символ E, используемый в эквивалентной схеме в нижней части части (b), представляет ЭДС.)
Чтобы найти величину ЭДС, индуцированной вдоль движущегося стержня, воспользуемся законом индукции Фарадея без знака:
[латекс]\текст{ЭДС} = \text{N}\frac{\Delta\Phi}{\ Дельта т}\\[/латекс].
Здесь и далее под «ЭДС» подразумевается величина ЭДС. В этом уравнении N = 1 и поток Φ = BA cos θ . У нас есть θ = 0º и cos θ = 1, так как B перпендикулярно A . Теперь Δ Φ = Δ( BA ) = B Δ A , так как B является однородным. Обратите внимание, что площадь, заметаемая стержнем, составляет Δ A = ℓ Δ x . Ввод этих величин в выражение для ЭДС дает
[латекс]\text{ЭДС}=\frac{B\Delta A}{\Delta t}=B\frac{\ell\Delta x}{\Delta t}\ \[/латекс].
Наконец, обратите внимание, что Δ x / Δ t = v , скорость стержня. Ввод этого в последнее выражение показывает, что
ЭДС = Bℓv ( B ,ℓ и v перпендикулярно)
— ЭДС движения. Это то же самое выражение, которое было дано ранее для эффекта Холла.
Установление связей: объединение силМежду электрической и магнитной силами существует много связей. Тот факт, что движущееся электрическое поле создает магнитное поле и, наоборот, движущееся магнитное поле создает электрическое поле, является частью того, почему электрические и магнитные силы теперь считаются разными проявлениями одной и той же силы. Это классическое объединение электрических и магнитных сил в то, что называется электромагнитной силой, является источником вдохновения для современных усилий по объединению других основных сил.
Чтобы найти направление индуцируемого поля, направление тока и полярность индуктируемой ЭДС, мы применяем закон Ленца, как описано в Законе Фарадея об индукции: закон Ленца. (См. рис. 1(b).) Поток увеличивается, так как увеличивается закрытая площадь. Таким образом, индуцированное поле должно противостоять существующему и быть за пределами страницы. Таким образом, RHR-2 требует, чтобы I было направлено против часовой стрелки, что, в свою очередь, означает, что вершина стержня положительна, как показано на рисунке.
(См. рис. 1(b).) Поток увеличивается, так как увеличивается закрытая площадь. Таким образом, индуцированное поле должно противостоять существующему и быть за пределами страницы. Таким образом, RHR-2 требует, чтобы I было направлено против часовой стрелки, что, в свою очередь, означает, что вершина стержня положительна, как показано на рисунке.
ЭДС движения также возникает, если магнитное поле движется, а стержень (или другой объект) неподвижен относительно Земли (или какого-либо наблюдателя). Мы видели пример этого в ситуации, когда движущийся магнит индуцирует ЭДС в неподвижной катушке. Важно относительное движение. В этих наблюдениях проявляется связь между магнитными и электрическими полями. Движущееся магнитное поле создает электрическое поле за счет ЭДС индукции. Мы уже видели, что движущееся электрическое поле создает магнитное поле — движущийся заряд подразумевает движущееся электрическое поле, а движущийся заряд создает магнитное поле.
ЭДС движения в слабом магнитном поле Земли обычно не очень велики, иначе мы заметили бы напряжение вдоль металлических стержней, таких как отвертка, при обычных движениях. Например, простой расчет ЭДС движения стержня длиной 1 м, движущегося со скоростью 3,0 м/с перпендикулярно полю Земли, дает ЭДС = Бℓv = (5,0 × 10 −5 Тл)(1,0 м)(3,0 м /с) = 150 мкВ. Это небольшое значение соответствует опыту. Однако есть эффектное исключение. В 1992 и 1996 годах с помощью космического корабля “Шаттл” были предприняты попытки создать большие ЭДС движения. Привязанный спутник должен был быть выпущен по проводу длиной 20 км, как показано на рисунке 2, для создания ЭДС 5 кВ за счет движения с орбитальной скоростью через поле Земли. Эту ЭДС можно было бы использовать для преобразования части кинетической и потенциальной энергии шаттла в электрическую энергию, если бы удалось создать полную цепь. Чтобы завершить цепь, неподвижная ионосфера должна была обеспечить обратный путь для протекания тока. (Ионосфера — это разреженная и частично ионизированная атмосфера на орбитальных высотах. Она проводит из-за ионизации. Ионосфера выполняет ту же функцию, что и стационарные рельсы и соединительный резистор на рисунке 1, без которых не было бы полной цепи.
Например, простой расчет ЭДС движения стержня длиной 1 м, движущегося со скоростью 3,0 м/с перпендикулярно полю Земли, дает ЭДС = Бℓv = (5,0 × 10 −5 Тл)(1,0 м)(3,0 м /с) = 150 мкВ. Это небольшое значение соответствует опыту. Однако есть эффектное исключение. В 1992 и 1996 годах с помощью космического корабля “Шаттл” были предприняты попытки создать большие ЭДС движения. Привязанный спутник должен был быть выпущен по проводу длиной 20 км, как показано на рисунке 2, для создания ЭДС 5 кВ за счет движения с орбитальной скоростью через поле Земли. Эту ЭДС можно было бы использовать для преобразования части кинетической и потенциальной энергии шаттла в электрическую энергию, если бы удалось создать полную цепь. Чтобы завершить цепь, неподвижная ионосфера должна была обеспечить обратный путь для протекания тока. (Ионосфера — это разреженная и частично ионизированная атмосфера на орбитальных высотах. Она проводит из-за ионизации. Ионосфера выполняет ту же функцию, что и стационарные рельсы и соединительный резистор на рисунке 1, без которых не было бы полной цепи. ) на ток в кабеле за счет магнитной силы F = IℓB sin θ выполняет работу, которая уменьшает кинетическую и потенциальную энергию шаттла и позволяет преобразовать ее в электрическую энергию. Оба испытания оказались неудачными. В первом кабель болтался и его можно было протянуть только на пару сотен метров; во втором трос оборвался при почти полном вытягивании. Следующий пример указывает на принципиальную осуществимость.
) на ток в кабеле за счет магнитной силы F = IℓB sin θ выполняет работу, которая уменьшает кинетическую и потенциальную энергию шаттла и позволяет преобразовать ее в электрическую энергию. Оба испытания оказались неудачными. В первом кабель болтался и его можно было протянуть только на пару сотен метров; во втором трос оборвался при почти полном вытягивании. Следующий пример указывает на принципиальную осуществимость.
Пример 1. Расчет большой ЭДС движения объекта на орбите
Рис. 2. ЭДС движения как преобразование электроэнергии для космического челнока является мотивацией для эксперимента с привязанным спутником. Было предсказано, что ЭДС 5 кВ будет индуцироваться в тросе длиной 20 км при движении с орбитальной скоростью в магнитном поле Земли. Цепь завершается обратным путем через стационарную ионосферу.
Рассчитайте ЭДС движения, индуцированную вдоль проводника длиной 20,0 км, движущегося с орбитальной скоростью 7,80 км/с перпендикулярно магнитному полю Земли 5,00 × 10 −5 Тл. {3}\text{ V}\end{массив}\\[/latex].
{3}\text{ V}\end{массив}\\[/latex].
Полученное значение превышает измеренное напряжение 5 кВ для эксперимента с челноком, поскольку фактическое орбитальное движение троса не перпендикулярно полю Земли. Значение 7,80 кВ — это максимальная ЭДС, полученная при θ = 90º и sin θ = 1.
- ЭДС, индуцированная движением относительно магнитного поля B , называется ЭДС движения
ЭДС = Bℓv ( B ,ℓ и против перпендикулярно)
, где ℓ — длина объекта, движущегося со скоростью v относительно поля.
Концептуальные вопросы
- Почему часть цепи должна двигаться относительно других частей, чтобы иметь полезную ЭДС движения? Рассмотрим, например, что рельсы на рисунке 1 неподвижны относительно магнитного поля, а стержень движется.
- Мощную индукционную пушку можно сделать, поместив металлический цилиндр внутрь катушки соленоида.
 Цилиндр принудительно выталкивается при быстром включении соленоидного тока. Используйте законы Фарадея и Ленца, чтобы объяснить, как это работает. Почему цилиндр может стать активным/горячим при выстреле из пушки?
Цилиндр принудительно выталкивается при быстром включении соленоидного тока. Используйте законы Фарадея и Ленца, чтобы объяснить, как это работает. Почему цилиндр может стать активным/горячим при выстреле из пушки? - Индукционная плита нагревает кастрюлю с катушкой переменного тока, расположенной под кастрюлей (и без горячей поверхности). Может ли поверхность печи быть проводником? Почему не работает катушка с постоянным током?
- Объясните, как можно оттаять замерзшую водопроводную трубу, обернув вокруг нее катушку с переменным током. Имеет ли значение, является ли труба проводником? Объяснять.
Задачи и упражнения
1. Используйте закон Фарадея, закон Ленца и RHR-1, чтобы показать, что магнитная сила, действующая на ток в движущемся стержне на рисунке 1, направлена в направлении, противоположном его скорости.
2. Если в спутниковом тросе, показанном на рис. 2, течет ток, используйте закон Фарадея, закон Ленца и RHR-1, чтобы показать, что на трос действует магнитная сила в направлении, противоположном его скорости.
3. (a) Реактивный самолет с размахом крыла 75,0 м летит со скоростью 280 м/с. Какая ЭДС индуцируется между законцовками крыльев, если вертикальная составляющая поля Земли равна 3,00 × 10 −5 Тл? б) Может ли ЭДС такой величины иметь какие-либо последствия? Объяснять.
4. (a) Отвертка из цветного металла используется в магнитном поле 2,00 Тл. Какая максимальная ЭДС может быть наведена на его длине 12,0 см при движении со скоростью 6,00 м/с? (б) Вероятно ли, что эта ЭДС будет иметь какие-либо последствия или даже будет замечена?
5. С какой скоростью должен двигаться скользящий стержень на рисунке 1, чтобы создать ЭДС 1,00 В в поле 1,50 Тл, если длина стержня составляет 30,0 см?
6. Стержень длиной 12,0 см на рисунке 1 движется со скоростью 4,00 м/с. Какова напряженность магнитного поля, если индуцируется ЭДС 95,0 В?
7. Докажите, что когда B , ℓ и v не взаимно перпендикулярны, ЭДС движения определяется выражением ЭДС = Bℓv sin θ . Если v перпендикулярно B , тогда θ – это угол между ℓ и B . Если ℓ перпендикулярно B , то θ является углом между v и B .
Если v перпендикулярно B , тогда θ – это угол между ℓ и B . Если ℓ перпендикулярно B , то θ является углом между v и B .
8. Во время полета космического корабля “Шаттл” в августе 1992 года можно было выпустить только 250 м троса, рассмотренного в примере 1 (выше). ЭДС движения 40,0 В создавалась в поле Земли 5,00 × 10 −5 Тл при движении со скоростью 7,80 × 10 3 м/с. Каков угол между скоростью шаттла и полем Земли, если предположить, что проводник перпендикулярен полю?
9. Комплексные концепции Выведите выражение для тока в системе, подобной показанной на рис. 1, при следующих условиях. Сопротивление между рельсами Р , рельсы и подвижный стержень одинаковы по поперечному сечению А и имеют одинаковое удельное сопротивление ρ . Расстояние между рельсами равно l, и стержень движется с постоянной скоростью v перпендикулярно однородному полю B . В нулевой момент времени подвижный стержень находится рядом с сопротивлением Р .
В нулевой момент времени подвижный стержень находится рядом с сопротивлением Р .
10. Интегрированные концепции Привязной спутник на рис. 2 имеет массу 525 кг и находится на конце троса длиной 20,0 км и диаметром 2,50 мм с прочностью на растяжение стали. а) На сколько растянется трос, если к спутнику приложить силу 100 Н? (Предположим, что спутник и шаттл находятся на одной высоте над Землей.) (b) Какова эффективная силовая постоянная троса? в) Сколько энергии запасается в нем при растяжении силой 100 Н?
11. Интегрированные концепции Привязанный спутник, обсуждаемый в этом модуле, вырабатывает 5,00 кВ и течет ток 10,0 А. а) Какую силу магнитного сопротивления это создает, если система движется со скоростью 7,80 км/с? б) Сколько кинетической энергии отводится от системы за 1,00 ч, если пренебречь изменением высоты или скорости за это время? в) Как изменится скорость, если масса системы равна 100 000 кг? (d) Обсудите долгосрочные последствия (скажем, недельный полет) на орбите космического корабля “Шаттл”, отметив, какое влияние оказывает снижение скорости, и оценив величину этого эффекта.
Избранные решения задач и упражнений
1. (а) 0,630 В (б) Нет, это очень маленькая ЭДС.
5. 2,22 м/с
11.(а) 10,0 Н (б) 2,81 × 10 8 Дж (в) 0,36 м/с (г) Для недельного полета (168 часов) изменение по скорости будет 60 м/с, или примерно 1%. В общем, уменьшение скорости приведет к тому, что орбита начнет двигаться по спирали внутрь, потому что скорости больше не будет достаточно для поддержания круговой орбиты. Долгосрочные последствия заключаются в том, что шаттлу потребуется немного больше топлива для поддержания желаемой скорости, иначе орбита будет немного спиральной внутрь.
Объяснение урока: Цепи переменного тока
В этом объяснении мы научимся определять значения электрических величин в цепях, питаемых переменным напряжением.
Направление условного тока в цепи от положительного полюса к отрицательному полюсу элемента, как показано на рис. диаграмма ниже.
Если мы перевернем батарею в этой цепи, направление тока также изменится на противоположное, как на диаграмме ниже.
Когда ток течет в одном направлении, это называется постоянным током или постоянным током. Многие электрические системы, включая электричество в домах используйте не постоянный, а переменный ток.
Переменный ток представляет собой переменный ток и отличается тем, что он не направлен в одном направлении, а меняет свое направление. Давайте смотреть при постоянном токе для двух разных цепей на графике ниже.
Для обеих цепей, представленных синей и зеленой линиями, ток непостоянен, а всегда положителен или отрицательный. Это означает, что его направление всегда одинаково.
Тот же тип графика для переменного тока показывает, что ток колеблется между положительным и отрицательным значением, как показано ниже.
Переменный ток вырабатывается с помощью генераторов переменного тока, состоящих из проволочных петель, вращающихся с постоянной скоростью через магнитные поля.
Типичная конструкция генератора переменного тока состоит из проволочной петли, свободно вращающейся вокруг одной оси. Однородное магнитное поле B перпендикулярно
к проводу, как на схеме ниже.
Однородное магнитное поле B перпендикулярно
к проводу, как на схеме ниже.
Это вращение в магнитном поле индуцирует электродвижущую силу, ЭДС, в контуре. Эта ЭДС создает переменный ток, сначала в одном направлении, затем переключаясь на другое направление по мере вращения. Если бы петля стояла на месте, ЭДС не было бы индуцированный – он должен двигаться.
Чтобы найти эту ЭДС индукции, давайте сначала посмотрим на ЭДС, индуцированную на простом прямом проводе длиной 𝐿 в однородном магнитном поле. Чтобы в таком проводе возникла ЭДС, этот провод должен двигаться. На схеме ниже показан провод длины 𝐿, обозначенной синей линией, движущейся со скоростью 𝑣, обозначенной желтым линия. Он движется под углом 𝜃 к направлению однородного магнитного поля с напряженностью 𝐵, обозначены зелеными линиями.
Уравнение, описывающее ЭДС индукции 𝜀 в этом проводе, имеет вид
𝜀=𝐵𝐿𝑣(𝜃),грех
где 𝐵 — напряженность магнитного поля, 𝐿 — длина провода, 𝑣 —
скорость провода при прохождении через магнитное поле, а 𝜃 — угол наклона провода. скорость соответствует направлению магнитного поля.
скорость соответствует направлению магнитного поля.
Прямой провод, движущийся с постоянной скоростью, не является способом, которым генераторы переменного тока используют движение для создания ЭДС. У них есть провод петли внутри них быстро вращаются, а это означает, что вместо того, чтобы выражать движение со скоростью 𝑣, это выражается как угловая частота 𝜔, которая измеряется в радиан в секунду. Преобразование скорости 𝑣 и угловая частота 𝜔 могут быть выполнены с помощью уравнения 𝑣=𝜔𝑟, где 𝑟 — расстояние от оси вращения до провода.
На приведенном ниже рисунке показан провод, вращающийся по кругу на расстоянии 𝑟 от оси вращения.
Это делает уравнение для ЭДС индукции в одиночном прямом вращающемся проводе 𝜀=𝐵𝐿𝜔𝑟(𝜃),грех но теперь угол между скоростью провода и направлением магнитного поля быстро меняется в проводе как он вращается.
Из-за связи уравнения с углом 𝜃 ЭДС индукции имеет максимальное значение, когда
провод движется перпендикулярно направлению магнитного поля, и его минимум равен 0, когда он движется параллельно
направление магнитного поля. На приведенной ниже диаграмме показана проволока, вращающаяся с постоянной угловой скоростью в однородном магнитном поле.
поле в различных точках.
На приведенной ниже диаграмме показана проволока, вращающаяся с постоянной угловой скоростью в однородном магнитном поле.
поле в различных точках.
Когда угол 𝜃 равен 90 или 270 градусов (𝜋2 или 3𝜋2 в радиан), ЭДС индукции максимальна. Когда угол 0 или 180 градусов (0 или 𝜋 в радиан), ЭДС индукции равна 0.
Если посмотреть на витки проволоки в генераторе переменного тока, то только две из них будут учитывать ЭДС индукции: те, что сверху и снизу, так как боковые провода в петле не будут иметь ЭДС индукции независимо от угла. Обратите внимание на местоположение верхней и нижней проволоки петли на диаграмме ниже, которая показывает полный оборот.
Это означает, что для катушки индуцируется двойная ЭДС по сравнению с прямым проводом, так как имеется два провода, а не
только один. Это создает коэффициент 2 в уравнении для ЭДС индукции при использовании катушки.
𝜀=2𝐵𝐿𝜔𝑟(𝜃),грех
но это только для одного цикла. При наличии нескольких петель конечная ЭДС индукции умножается на 𝑛,
где 𝑛 – количество петель, что дает уравнение
𝜀=2𝑛𝐵𝐿𝜔𝑟(𝜃).sin
При наличии нескольких петель конечная ЭДС индукции умножается на 𝑛,
где 𝑛 – количество петель, что дает уравнение
𝜀=2𝑛𝐵𝐿𝜔𝑟(𝜃).sin
Однако это уравнение можно упростить, заметив, что площадь квадратной петли 𝐴 является произведением двух его сторон. Поскольку ось вращения проходит через центр проводов, длина одной стороны равна 𝐿, а другой 2𝑟. Это означает, что площадь катушки 𝐴 равна 𝐴=2𝑟𝐿, что упрощает уравнение до 𝜀=𝑛𝐴𝐵𝜔(𝜃).sin
Последний шаг можно сделать для дальнейшего упрощения этого уравнения, связав 𝜃 с угловой частотой. Проволочная петля вращается с постоянной угловой частотой 𝜔, которая находится в единицах радиан в секунду. Точный угол 𝜃 может можно найти, просто умножив угловую частоту на время, прошедшее 𝜃=𝜔𝑡, который затем можно заменить на 𝜃 в синусоидальном члене, чтобы получить окончательное уравнение.
Определение: ЭДС индукции, вызванная вращением проводящей катушки в однородном магнитном поле
ЭДС индукции 𝜀 вращающегося контура в однородном магнитном поле равна
𝜀=𝑛𝐴𝐵𝜔(𝜔𝑡),грех
где 𝑛 — количество витков в витке, 𝐴 — площадь витка, 𝐵
— напряженность магнитного поля, 𝜔 — угловая частота, а 𝑡 — время.
Давайте рассмотрим пример с использованием этого уравнения.
Пример 1: ЭДС индукции в генераторе переменного тока
Генератор переменного тока содержит 5 прямоугольных петель проводящего провода с длинами сторон 15 см и 25 см, концы которых образуют клеммы. Стороны петель с одинаковой длиной друг с другом параллельны друг другу. Петли вращаются со скоростью 15 оборотов в секунду в течение 620 мТ однородное магнитное поле. Какова максимальная разность потенциалов на клеммах? Дайте ответ с точностью до двух знаков после запятой.
Ответ
Вспомните уравнение для ЭДС индукции при вращении проводящей катушки: 𝜀=𝑛𝐴𝐵𝜔(𝜔𝑡).sin
Мы хотим найти пиковую разность потенциалов, где ЭДС абсолютно максимальна. Максимум возникает, когда sin(𝜔𝑡)=1, поэтому мы можем просто заменить весь этот член на 1 в уравнении для ЭДС: 𝜀=𝑛𝐴𝐵𝜔(1)𝜀=𝑛𝐴𝐵𝜔.
Теперь нам нужно найти остальные значения. Дано количество петель 𝑛, 5, как и магнитное поле,
620 мТл, но мы хотим его в обычном
тесла.
Дано количество петель 𝑛, 5, как и магнитное поле,
620 мТл, но мы хотим его в обычном
тесла.
1 000 миллитесла в 1 тесла: 11000, ТМТ и мы можем преобразовать 620 мТл в тесла, умножив его на это соотношение: 11000×620=0,62.TmTmTT
Таким образом, значение 𝐵 равно 0,62 T.
Далее нам нужно вычислить площадь петель, 𝐴. Нам говорят, что эти петли прямоугольные, с длинами сторон 15 см и 25 см, и стороны одинаковой длины параллельны друг другу. Это означает, что петля выглядит так.
Прежде чем идти дальше, давайте преобразуем эти длины сторон в метров от сантиметры. Есть 100 сантиметров в 1 метр: 1100,мкм Итак, получение длин сторон в метрах означает умножение на это соотношение: 1100×15=0,15, 1100×25=0,25.мкмммммсмсм
В метрах, 15 см 0,15 м и 25 см 0,25 м.
Площадь прямоугольника равна произведению двух его непараллельных сторон. Итак, мы умножаем эти длины сторон вместе, чтобы получить площадь: 𝐴=0,15×0,25𝐴=0,0375,ммм
Площадь этого прямоугольника 0,0375 м 2 .
Наконец, нам нужна угловая частота 𝜔. Это должно быть в единицах радиан в секунду, поэтому мы должны преобразовать из заданного значения оборотов в секунду.
Полный оборот по кругу равен 2𝜋. Итак, если представить угловую частоту в терминах радианов, мы должны умножить оборотов в секунду на 2𝜋: 𝜔=15×2𝜋𝜔=30𝜋.ss
Итак, 𝜔 движется через 30 𝜋 в секунду. Теперь у нас есть все члены, необходимые для завершения уравнения 𝜀=𝑛𝐴𝐵𝜔.
Теперь мы можем подставить значения. 𝑛 — 5 петель, 𝐴 — 0,0375 м 2 , 𝐵 есть 0,62 Тл, а 𝜔 равно 30𝜋: 𝜀=(5)0,0375(0,62)30𝜋.mTs
Мы можем расширить единицу измерения тесла. 1 тесла 1 вольт-секунда на квадратный метр: ТВсм=×, поэтому использование этого в уравнении дает 𝜀=(5)0,03570,62×30 𝜋.мВсмс
Умножение угловой частоты и напряженности магнитного поля отменяет единицы
секунды:
𝜀=(5)0,035718,6𝜋, мВм
и умножение последних трех слагаемых вместе аннулирует единицы
квадратный метр,
оставляя позади вольты:
(5)0,035718,6𝜋=10,956. мВмВ
мВмВ
Округлив до двух знаков после запятой, пиковая разность потенциалов на клеммах равна 10,96 вольт.
На приведенном ниже графике показано изменение ЭДС индукции во времени.
Мы видим, что в разные моменты времени она бывает как положительной, так и отрицательной, причем самая высокая и самая низкая точки имеют величину 𝑛𝐴𝐵𝜔.
Поскольку этот график продолжается бесконечно во времени, участки, когда он положителен, полностью отменяются участками, где он положительный отрицательный. Это означает, что средняя ЭДС будет просто равна нулю: 𝜀=0.avg
Это ничего не говорит нам о цепи, поскольку означает, что каждая отдельная цепь переменного тока будет иметь в среднем 0 ЭДС, независимо от
количества петель, площади или напряженности магнитного поля. Вместо этого мы можем посмотреть на это, используя среднеквадратичное значение. А
Среднеквадратичное значение (среднеквадратичное значение) находится путем возведения в квадрат каждого возможного числа в каждой точке графика, а затем нахождения среднего
из всех этих чисел, а затем извлечь из него квадратный корень.
При возведении в квадрат отрицательного значения оно становится положительным, поэтому все значения в квадрате положительные. Это меняет график на вид как на следующей схеме.
Затем все эти значения складываются и делятся на общее количество значений, чтобы найти среднее значение: sumofallvaluesnumberofvalues.
Затем извлекается квадратный корень из среднего: rmssumofallvaluesnumberofvalues=.
Когда этот квадратный корень извлекается из любого синусоидального графика, конечное среднеквадратичное значение всегда равно 1√2 пиковое значение: среднеквадратичное пиковое значение синусоидального графика = 1√2×.
Среднеквадратичное значение ЭДС в 1√2 раза превышает максимальное возможное значение ЭДС, называемое пиковой ЭДС. Это означает, что среднеквадратичное значение ЭДС переменного тока равно 𝜀=1√2𝜀.rmspeak
Давайте рассмотрим пример.
Пример 2: Среднеквадратичное значение ЭДС в генераторе переменного тока
Генератор переменного тока содержит 50 прямоугольных витков проводящего провода с длиной стороны
55 см и 35 см,
концы которых образуют клеммы. Стороны петель с одинаковой длиной друг с другом параллельны друг другу. Петли вращаются в однородном магнитном поле с
18 оборотов в секунду в течение
Однородное магнитное поле 360 мТл. Что такое среднеквадратичное напряжение
через терминалы? Дайте ответ ближайшему
вольт.
Стороны петель с одинаковой длиной друг с другом параллельны друг другу. Петли вращаются в однородном магнитном поле с
18 оборотов в секунду в течение
Однородное магнитное поле 360 мТл. Что такое среднеквадратичное напряжение
через терминалы? Дайте ответ ближайшему
вольт.
Ответ
Вспомните уравнение для ЭДС индукции при вращении проводящей катушки: 𝜀=𝑛𝐴𝐵𝜔(𝜔𝑡).sin
Чтобы найти среднеквадратичное значение напряжения, нам сначала нужно найти пиковую разность потенциалов, где ЭДС максимальна. Этот максимум происходит когда sin(𝜔𝑡)=1, поэтому мы можем просто заменить весь этот член на 1 в уравнении для ЭДС: 𝜀=𝑛𝐴𝐵𝜔(1)𝜀=𝑛𝐴𝐵𝜔.
Теперь нам нужно найти другие термины. Преобразуем магнитное поле от 360 мТ до Тесла. Есть 1 000 миллитесла в 1 тесла: 11000, ТМТ а умножение 360 мТл на это соотношение даст ответ в тесла: 11000×360=0,36.TmTmTT
Итак, значение 𝐵 равно 0,36 T.
Далее нам нужно вычислить площадь петель, 𝐴. Нам говорят, что эти петли прямоугольные, со стороной длина 55 см и 35 см. Преобразуем эти длины сторон в метров от сантиметры. Есть 100 сантиметров в 1 метр: 1100,мкм и умножение длин сторон на это соотношение дает 1100×55=0,55, 1100×35=0,35.mcmcmmmcmcmm
Таким образом, 55 см равно 0,55 м, а 35 см это 0,35 м.
Площадь этих прямоугольных петель равна произведению этих длин сторон: 𝐴=0,55×35𝐴=0,1925, ммм поэтому площадь этого прямоугольника равна 0,1925 м 2 .
Теперь нам нужно найти угловую частоту 𝜔 в радиан в секунду. Каждый революция это 2𝜋: 𝜔=18×2𝜋𝜔=36𝜋.ss
Угловая частота 𝜔 составляет 36𝜋 в секунду. Теперь у нас есть все необходимые термины завершить уравнение 𝜀=𝑛𝐴𝐵𝜔.
Теперь мы можем подставить значения. 𝑛 — 50 петель, 𝐴 —
0,1925 м 2 , 𝐵 есть
0,36 Тл, а 𝜔
36𝜋s:
𝜀=(50)0,1925(0,36)36𝜋. mTs
mTs
Давайте расширим единицу тесла в уравнение. 1 тесла 1 вольт-секунда на квадратный метр: TVsmmVsms=×,𝜀=(50)0,19250,36×36𝜋.
Умножение напряженности магнитного поля и угловой частоты вместе отменяет единицы измерения секунды: 𝜀=(50)0,192512,96𝜋, мВм и умножение последних трех слагаемых вместе аннулирует единицы квадратных метров, выходит вольт как единственная единица: 𝜀=(50)0,192512,96𝜋=391,88.мВмВ
Таким образом, пиковое значение разности потенциалов равно 391,88 В. Затем возьмем это значение и умножить его на 1√2: 𝜀=1√2𝜀1√2(391,88)=277,1.rmspeakVV
Округлено до ближайшего вольта, среднеквадратичное напряжение, таким образом, составляет 277 вольт.
Это соотношение 1√2 справедливо для любого среднеквадратичного значения, основанного на синусоидальной функции. Если ЭДС
является синусоидальным, то таким же является и последующий ток цепи, а это означает, что он следует тому же соотношению для
среднеквадратичное.
Переменный ток 𝐼 может быть представлен синусоидально. Это означает, что средний ток равен 0, так как позитивы сокращаются с негативами в каждой точке. Это продемонстрировано на графике ниже.
Мы можем найти среднеквадратичное значение, используя то же отношение 1√2, что и ЭДС, поскольку они оба синусоидальны: rmsofsinusoidalgraphpeakvalue=1√2×, это означает, что среднеквадратичное значение тока 𝐼 составляет 1√2 пикового значения: 𝐼=1√2𝐼.rmspeak
Давайте рассмотрим несколько примеров.
Пример 3: Среднеквадратичное значение тока
Переменный ток имеет пиковое значение 1,35 А. Что такое среднеквадратичное значение тока? Дайте ответ с точностью до трех знаков после запятой.
Ответ
Вспомните уравнение для определения среднеквадратичного значения тока: 𝐼=1√2𝐼.rmspeak
Нам дано пиковое значение тока 1,35 А. Подставив это
значение в уравнение, мы получаем
𝐼 = 1 √ 2 (1,35), среднеквадратичное значение A
и последующее умножение членов дает
1√2(1,35)=0,9546.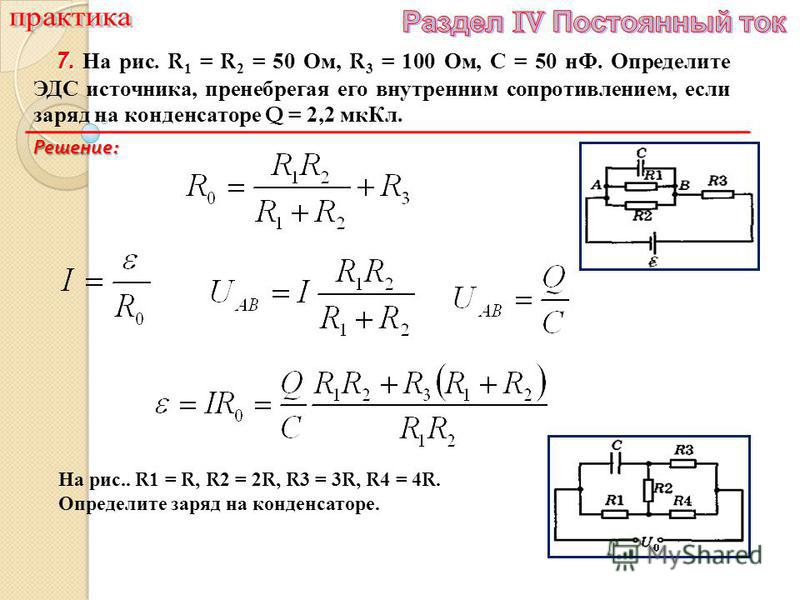 AA
AA
С точностью до трех знаков после запятой среднеквадратичное значение этого тока равно 0,955 ампер.
Пример 4: Графическое представление среднеквадратичного значения тока
Красная линия представляет изменение мгновенного значения переменного тока, протекающего по проводнику. Какая из линий правильно представляет среднеквадратичное значение тока?
- Черная линия
- Зеленая линия
- Фиолетовая линия
- Оранжевая линия
- Синяя линия
Ответ
Линия, которая лучше всего представляет среднеквадратичное значение тока, ближе всего к значению 1√2 пика. Красная линия представляет собой переменный ток, поэтому его пики будут абсолютное максимальное значение.
Представим 1√2 в десятичной форме: 1√2=0,707.
Таким образом, среднеквадратичное значение тока будет максимально умножено на 0,707, или около 70% от максимального значения.
Итак, мы ищем линию примерно на 70% вверх по графику. Черная линия чуть выше
50%, поэтому линии под ним, зеленая и желтая, не могут быть им.
Черная линия чуть выше
50%, поэтому линии под ним, зеленая и желтая, не могут быть им.
Фиолетовая линия составляет около 80 %, поэтому наилучшей линией, вероятно, будет та, что находится чуть ниже нее, синяя линия, которая ближе всего к 70%.
Итак, ответ Е: синяя линия.
Мощность в цепи связана с током уравнением 𝑃=𝐼𝑅, где 𝑃 — мощность цепи, 𝐼 — ток в цепи, а 𝑅 это сопротивление цепи.
Поскольку это уравнение содержит ток 𝐼, а ток в цепи переменного тока синусоидальный, мощность равна также синусоидальный. Максимальная мощность в цепи достигается, когда 𝐼 находится на пике: 𝑃=𝐼𝑅,maxpeak но средняя мощность не равна 0, как в случаях тока или ЭДС. Сила не может быть отрицательной, как и у вас не может быть отрицательной энергии. В среднем выглядит так 𝑃=12𝐼𝑅.avgpeak
Чтобы выразить это в терминах среднеквадратичных значений, мы можем привести 12 к квадрату значения тока, чтобы получить
𝑃=1√2𝐼𝑅,средн.пик
и поскольку 𝐼=1√2𝐼rmspeak, мы можем подставить его в уравнение, чтобы получить
𝑃=1√2√21𝐼𝑅.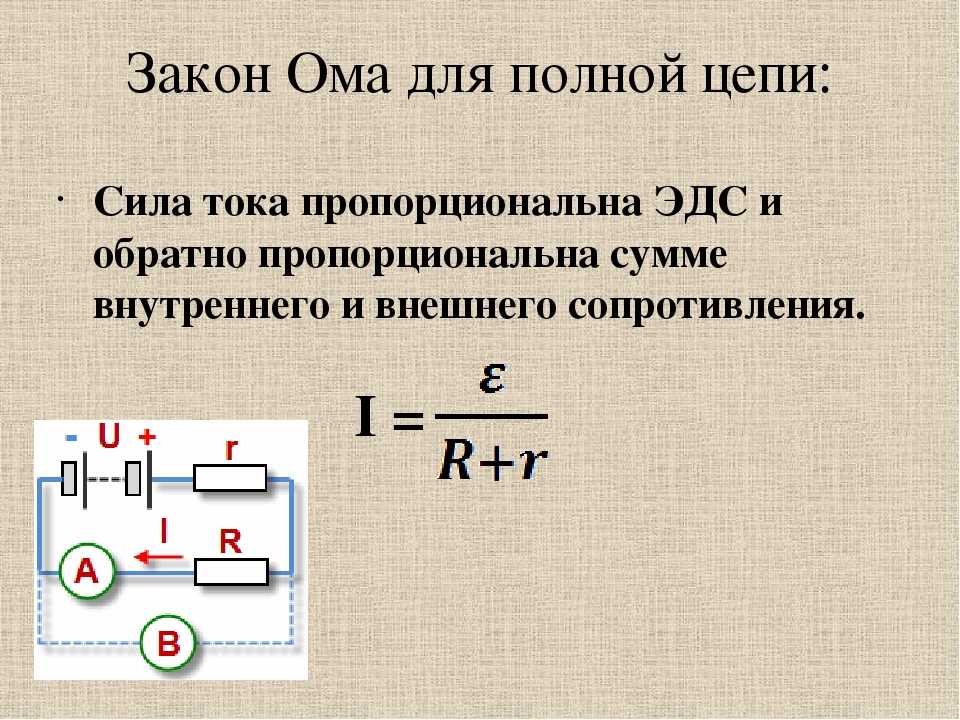 avgrms
avgrms
Затем квадратные корни из 2 сокращаются при умножении, оставляя после себя только среднеквадратичное значение 𝐼: 𝑃=(𝐼)𝑅.avgrms
Давайте рассмотрим пример.
Пример 5: Рассеивание энергии в переменном токе
Переменный ток имеет пиковое значение 1,75 А через Резистор 148 Ом. Какова энергия, рассеиваемая током в время 365 с? Дайте свой ответ в килоджоулей с точностью до одного десятичного знака.
Ответ
Вспомните общее уравнение мощности, 𝑃: 𝑃=𝑊Δ𝑡, где 𝑊 — работа, а Δ𝑡 — изменение во времени.
Чтобы найти энергию, рассеиваемую за определенный период времени для переменного тока, мы хотим вместо этого использовать среднюю мощность, 𝑃среднее: 𝑃=𝑊Δ𝑡.avg
Мы хотим найти работу, выполненную контуром, чтобы найти его энергию, поскольку работа — это энергия, рассеиваемая контуром.
Чтобы изолировать работу в уравнении, мы умножим обе части на 𝛿𝑡:
𝑃×Δ𝑡=𝑊Δ𝑡×Δ𝑡, среднее
в результате чего члены Δ𝑡 отменяются с правой стороны, оставляя работу:
Δ𝑡𝑃=𝑊. avg
avg
Изменение времени, Δ𝑡, составляет 365 секунд, но мы не знаем среднюю мощность. Чтобы найти его, вспомните уравнение, связывающее среднюю мощность со среднеквадратичными значениями тока и сопротивления: 𝑃=(𝐼)𝑅.среднеквадратичное
Нам дано значение сопротивления в цепи, но только пиковое значение тока, а не среднеквадратичное значение.
Действующее значение тока равно пиковому значению тока, умноженному на 1√2: 𝐼=1√2𝐼, rmspeak а пиковое значение тока равно 1,75 А, поэтому подставив это в уравнение дает 1√21,75=1,237.AA
Теперь у нас есть все необходимые значения, которые нужно подставить в уравнение средней мощности. Действующее значение тока 1,237 А и сопротивление 148 Ом: 𝑃=(𝐼)𝑅𝑃=(1,237)(148),avgrmsavgAΩ и единицы ампер, умноженные на омы становятся Вт, что дает среднюю мощность (1,237)(148)=226,625.AΩW
Теперь подставим эти значения в уравнение для нахождения работы. Подставляя значения
226,625 Вт для средней мощности и
365 секунд на изменение времени,
Δ𝑡𝑃=𝑊(365)(226,625)=𝑊,среднееW
и ватты, умноженные на
секунды становятся
джоуль, единица энергии в системе СИ. Это делает энергию, рассеиваемую цепью:
(365)(226.625)=82718.sWJ
Это делает энергию, рассеиваемую цепью:
(365)(226.625)=82718.sWJ
Теперь нам нужно выразить этот ответ в килоджоулях. Есть 1 000 Дж в 1 кДж: 11000,кДжДж поэтому, чтобы преобразовать 82 718 джоулей в килоджоулей, нам нужно умножить на эту пропорцию: 11000×82718;кДжДжДж джоули отменяются, оставляя позади килоджоулей дать =82,7.кДж
Это делает энергию, рассеиваемую этой схемой за 365 секунд. около 82,7 кДж.
Теперь, когда мы знаем отношения между действующими значениями ЭДС, тока и мощности, давайте рассмотрим индуктивную, емкостную и резистивные цепи.
Резистивная цепь — это цепь, содержащая резистор, как показано на схеме ниже.
Ток в такой цепи находится полностью в фазе с ЭДС, так как они пропорциональны друг другу, как показывает уравнение
𝑉=𝐼𝑅. На приведенной ниже диаграмме показано изменение разности потенциалов с течением времени, представленное желтой линией.
по сравнению с изменением тока во времени, представленным синим цветом.
Символ слева от схемы с волной представляет собой генератор переменного тока, который генерирует переменный ток в схема.
Цепь переменного тока может также содержать конденсатор, который на принципиальных схемах изображается двумя близкими линиями. Такая схема называется емкостной цепью и показана на диаграмме ниже.
Соотношение между током и разностью потенциалов в емкостной цепи переменного тока отличается от резистивной. Заряд не может проходить через конденсатор. Вместо этого заряд накапливается по бокам зарядных пластин. Ток, вызывающий это накопление заряда пропорционально изменению разности потенциалов на пластинах со временем: 𝐼∝Δ𝜀Δ𝑡.
Это означает, что ток будет максимальным, когда изменение разности потенциалов будет максимальным. Изменение в
разность потенциалов максимальна (она имеет самый крутой наклон), когда сама разность потенциалов равна 0. Когда разность потенциалов
находится на максимуме, его наклон равен нулю, что означает, что его ток равен нулю, поскольку разность потенциалов в этой точке не меняется. На рисунке ниже показана зависимость между током и разностью потенциалов в емкостной цепи переменного тока.
На рисунке ниже показана зависимость между током и разностью потенциалов в емкостной цепи переменного тока.
Поскольку разность потенциалов от генератора переменного тока увеличивается и уменьшается, она аналогичным образом изменяет разность потенциалов на пластины конденсатора. Разность потенциалов на этих пластинах постепенно меняет сторону по мере того, как разность потенциалов на генератор переменного тока аналогичным образом меняет направление.
Вместо тока, точно следующего за разностью потенциалов, как в резистивной цепи, ток опережает потенциал разница. Это происходит из-за постоянной зарядки и разрядки пластин конденсатора.
В емкостных цепях переменного тока разность потенциалов на конденсаторе и ток накопления заряда не совпадают по фазе друг с другом. Изменение разности потенциалов опережает изменение тока на 90 градусов или на 𝜋2 рад, как показано на рисунке ниже.
Цепь переменного тока может также содержать катушку индуктивности, которая на принципиальных схемах изображается изогнутой линией. На рисунке ниже показан индуктор
в цепи переменного тока.
На рисунке ниже показан индуктор
в цепи переменного тока.
Когда индуктор имеет переменный ток в катушках, он индуцирует аналогично изменяющееся магнитное поле. Это магнитное поле затем создает разность потенциалов на индукторе, которая создает ток, противоположный первоначальному направлению тока. Изменение магнитного поля, а также результирующая разность потенциалов пропорциональны изменению тока со временем: 𝜀∝Δ𝐼Δ𝑡.
Разность потенциалов будет максимальной при максимальном изменении тока. Изменение тока максимальное (у него самый крутой наклон), когда сам ток равен 0. Когда ток максимален, его наклон равен нулю, что означает его потенциал разница равна нулю, так как ток в этой точке не меняется. На рисунке ниже показано соотношение между текущим и разность потенциалов в индуктивной цепи переменного тока.
Индуктивные цепи переменного тока не имеют той же разности фаз, что и емкостные цепи переменного тока: изменение разности потенциалов
опережает изменение тока, а не опережает ток.
Это связано с тем, что разность потенциалов, индуцированная в катушках индуктора, препятствует изменению тока при переключении, заставляя разность потенциалов опережать ток. Это показано на диаграмме ниже.
В индуктивных цепях переменного тока изменение разности потенциалов составляет 90 градусов, или 𝜋2 рад, за изменением тока.
Теперь посмотрим на график, представляющий токи резистивной, емкостной и индуктивной цепи с источником переменного тока. Три цветные линии представляют собой изменение тока в цепи во времени в зависимости от свойств цепи.
Линия, которая соответствует только резистивной цепи, будет линией, которая соответствует кривым ЭДС, поскольку они прямо пропорциональны друг другу. Это только синяя линия.
Мы ожидаем, что линия, представляющая емкостную цепь, будет иметь угол 90 градусов, или 𝜋2 впереди ЭДС. Это описание наиболее точно соответствует оранжевой линии, так как ее вершины находятся позади э.д.с.
ЭДС опережает линию, представляющую ток индуктивной цепи, на
90 градусов,
или 𝜋2.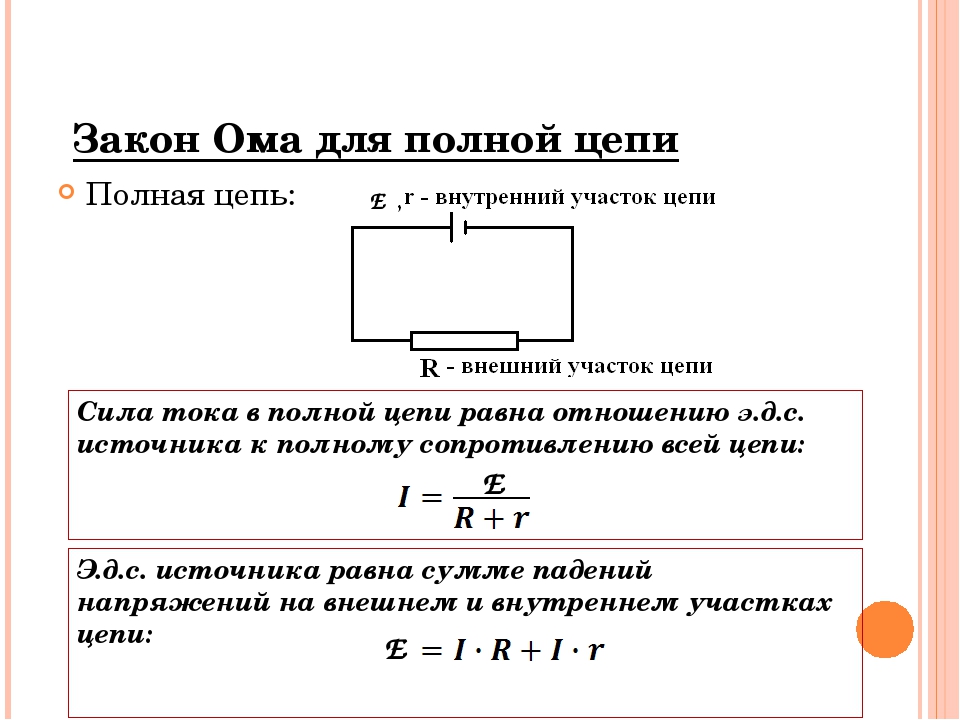

 Характеризуется движением зарядов, осуществляемым в свободном пространстве. Этот тип характерен для газоразрядных приборов.
Характеризуется движением зарядов, осуществляемым в свободном пространстве. Этот тип характерен для газоразрядных приборов. Промежуточное состояние между ними занимают полупроводники.
Промежуточное состояние между ними занимают полупроводники.
 Для её нахождения используется расчёт, учитывающий угол сдвига фаз φ. Находится согласно формуле P = U*I*cos φ.
Для её нахождения используется расчёт, учитывающий угол сдвига фаз φ. Находится согласно формуле P = U*I*cos φ.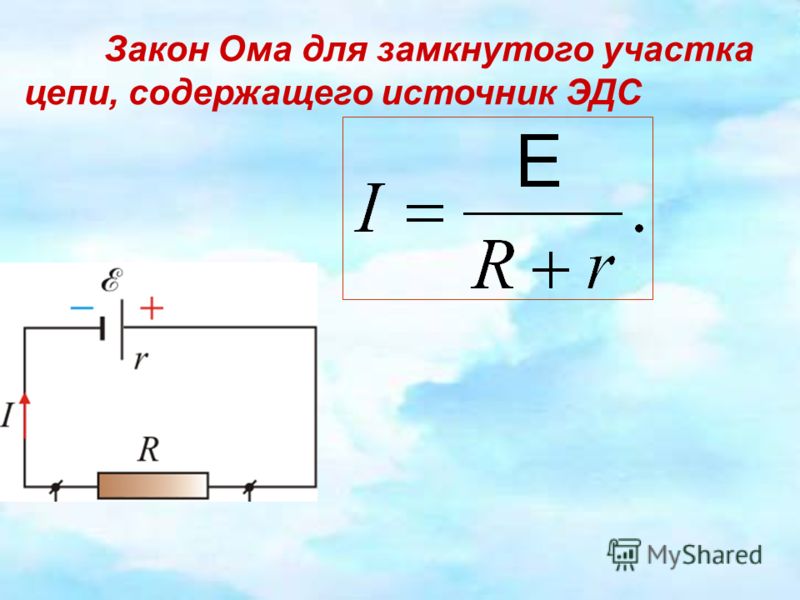


 Цилиндр принудительно выталкивается при быстром включении соленоидного тока. Используйте законы Фарадея и Ленца, чтобы объяснить, как это работает. Почему цилиндр может стать активным/горячим при выстреле из пушки?
Цилиндр принудительно выталкивается при быстром включении соленоидного тока. Используйте законы Фарадея и Ленца, чтобы объяснить, как это работает. Почему цилиндр может стать активным/горячим при выстреле из пушки?