Формула силы Архимеда в физике
Формула силы Архимеда в физикеОпределение и формула силы Архимеда
Эмпирически еще в древней Греции было получено, что тело, погруженное в жидкость, весит меньше, чем находящееся в воздухе. На тело в жидкости со всех сторон она оказывает давление. Силы давления направлены перпендикулярно поверхности тела в каждой его точке. В том случае, если все силы, действующие на тело, были бы равны по модулю, то это тело испытывало только всестороннее сжатие. Мы знаем, что при увеличении глубины гидростатическое давление увеличивается, следовательно, силы давления, которые приложены к нижним частям тела больше, чем силы, которые действуют на тело вверху.
Если заменить все силы давления, которые приложены к телу, находящемуся в жидкости, одной результирующей силой, то эта сила будет направлена вверх. В этой связи ее назвали выталкивающей силой. По-другому ее называют силой Архимеда (${\overline{F}}_A$). Именно Архимед отметил факт ее существования и определил, как ее вычислить.
Сила Архимеда оказывает свое действие на тела не только в жидкостях, но и газах, там, где существует гиростатическое давление.
Величина силы Архимеда
Сила Архимеда, оказывающая действие на тело, погруженное в жидкость (или газ), равна весу жидкости (или газа), в объеме вытесненной (вытесненным) этим телом.
Рассмотрим тело в виде прямоугольного параллелепипеда полностью находящееся в жидкости рис.1. Предположим, что верхнее и нижнее основания располагаются параллельно горизонту.
Силы давления, действующие на боковые грани параллелепипеда, попарно уравновешены (например, ${\overline{F}}_{12}$=$-{\overline{F}}_{21}$). Они только сжимают параллелепипед. Силы, которые действуют на верхнюю и нижнюю грани параллелепипеда не равны между собой. Сила ($F_1$), действия столба жидкости на верхнюю грань, будет равна:
\[F_1=p_1S=(\rho gh_1+p_0)S\ \left(1\right),\]
где $\rho $ – плотность жидкости; $S$ – площадь основания; $h_1$ – высота столба жидкости над верхним основанием параллелепипеда.
Сила давления жидкости на нижнее основание параллелепипеда:
\[F_2=p_2S=(\rho gh_2+p_0)S\ \left(2\right),\]
где $h_2$ – высота столба жидкости над нижним основанием. Так как $h_2>h_1$, значит $F_2>F_1$. Модуль результирующей силы, действующей на тело со стороны жидкости:
\[F_A=F_2-F_1=\rho g{S(h}_2-h_1)\ (3).\ \]
Если обозначить высоту параллелепипеда как $h=h_2-h_1$, получим:
\[F_A=\rho gSh=\rho gV\ \left(4\right),\]
где $V$ – объем параллелепипеда. При нахождении тела в жидкости (газе) частично, то под V понимают объем погруженный в вещество (жидкость, газ). Правую часть выражения (4) еще называют весом жидкости, которую вытесняет тело, погруженное в нее.
На тело, находящееся в жидкости или газе, действует сила Архимеда, величина которой равна весу вещества (жидкости или газа) в объеме погруженной части тела. Сила Архимеда направлена вертикально вверх.
Сила Архимеда направлена вертикально вверх.
Закон Архимеда (4) выполняется для тел любой формы.
Сила Архимеда дает возможность плавать разного рода кораблям, несмотря на то, что плотность материала, из которого изготовлен корпус транспортного средства в несколько раз больше, чем плотность воды. Необходимо только чтобы вес воды, которую вытесняет подводная часть судна, был равен силе тяжести, которая действует на судно. Средняя же плотность корабля меньше плотности воды.
Сила Архимеда действует на тела находящиеся в воздухе. Но так как плотность воздуха мала, действием этой силы часто пренебрегают. В состоянии невесомости сила Архимеда равна нулю. В состоянии невесомости нет гидростатического давления.
Следует учесть, рассуждая о действии силы Архимеда, мы имеем в виду, что тело окружено жидкостью (газом), может быть за исключением своей верхней части. Если тело примыкаем ко дну сосуда или его стенке, то равнодействующая сил гидростатического давления станет прижимать тело ко дну или стенке.
Пример 2
Задание. Чему равна сила натяжения каната (N), при помощи которого из пресного водоема равномерно двигая, поднимают тело плотностью $\rho $ и объемом V? Плотность воды считайте известной (${\rho }_g$). Движение рассмотрите в жидкости.
Решение. Рассмотрим силы, действующие на тело, поднимаемое из воды (рис.2).
В соответствии со вторым законом Ньютона равнодействующая всех сил, приложенных к телу равна нулю, так как тело поднимают равномерно:
В проекции на ось Y инерциальной системы отсчета, которую мы связали с Землей, уравнение (2.1) даст нам следующее скалярное выражение:
\[N-mg+F_A=0\ \left(2.2\right).\]
Масса поднимаемого тела может быть найдена как:
\[m=\rho V\ \left(2.3\right). \]
\]
Силу Архимеда определим как:
\[F_A={\rho }_gVg\ \left(2.4\right).\]
Подставим правые части выражений (2.3) и (2.4) в формулу (2.2) вместо соответствующих величин, выразим силу натяжения каната:
\[N=\rho Vg-{\rho }_gVg=\left(\rho -{\rho }_g\right)Vg.\]
Ответ. $N=\left(\rho -{\rho }_g\right)Vg$
Читать дальше: формула скорости волны.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Формула закона Архимеда в физике
Формула закона Архимеда в физикеОпределение и формула закона Архимеда
Силу, которая действует на тело, находящееся в жидкости или газе называют выталкивающей силой. Существование этой силы обосновал и рассчитал ее величину ученый из древней Греции Архимед. Направлена эта сила вертикально вверх.
Силу давления воды на верхнюю поверхность цилиндра вычислим как:
\[F_1={\rho }_ggh_1S\ \left(2\right).\]
Над нижней поверхностью тела высота столба жидкости равна $h_2$, значит, сила давления воды на нее составляет величину:
\[F_2={\rho }_ggh_2S\ \left(3\right).\]
Очевидно, что $F_2>F_1$. Разница между силами $F_2и{\ F}_1$ составляет силу выталкивания:
\[F_A=F_2-F_1={\rho }_ggS\ \left(h_2-h_1\right)={\rho }_ggSH={\rho }_ggV\ .\]
Мы получили, что сила Архимеда равна:
Выражение (4) можно назвать формулой закона Архимеда. Если тело частично погружено в жидкость, то V – часть тела, находящаяся в жидкости. Сила Архимеда оказывает свое действие на тела не только в жидкостях, но и газах, там, где существует гиростатическое давление.
Если обозначить массу жидкости, которая занимает объем, равный объему тела как $m_g={\rho }_gV$, то выражение (4) преобразуем к виду:
\[F_A=m_gg=P_g\ \left(5\right),\]
где $P_g$ – вес жидкости, которая занимает объем, равный объему тела находящийся в ней.
Закон Архимеда в современной формулировке: На любое тело, которое погружено в жидкость (газ), находящуюся в состоянии равновесия, действует со стороны жидкости (газа) сила выталкивания, равная произведению плотности вещества в котором находится тело, на ускорение свободного падения и на объем погруженной части тела.
Если погрузить в жидкость тело, то величина силы Архимеда не зависит от положения тела в жидкости. Сила выталкивания не зависит от вещества, из которого сделано, погруженное в жидкость тело, ни от глубины погружения тела (при полном погружении тела).
Из-за выталкивающей силы вес каждого тела в жидкости меньше, чем в воздухе. Уменьшение веса тела произойдет, если перенести тело из вакуума в любой газ. Если вес тела в вакууме равен $P$, то его вес в жидкости или газе равен:
\[P’=P-F_A\left(6\right).\]
Примеры задач на закона Архимеда
Пример 1
Задание. Чему равен объем тела, полностью погруженного в воду, если на него действует сила Архимеда, равная 100 Н?
Решение.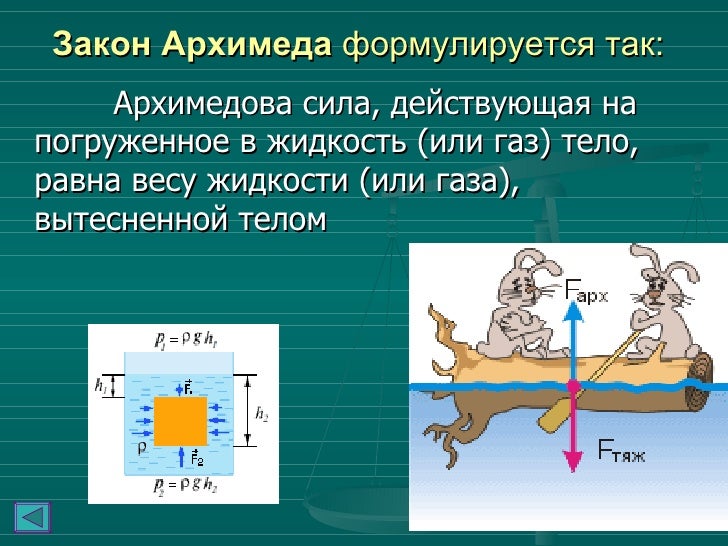 3$
3$
Пример 2
Задание. Чему равна плотность жидкости, в которую погружают тело, если его вес в воде составляет $P$, а в неизвестной жидкости $P_1$? Масса данного тела $m,\ $плотность воды ${\rho }_v$.
Решение. Сделаем рисунок.
Из закона Архимеда мы знаем, что тело теряет в своем весе величину, равную модулю силы Архимеда, то есть:
\[mg-P_1=F_A\left(2.1\right),\]
где $P=mg$ – вес тела в воздухе.
Сила Архимеда равна:
\[F_A={\rho }_gVg\ \left(2.2\right).\]
Значит, изменения веса тела при погружении его в воду запишем как:
\[mg-P_1={\rho }_{g1}Vg\left(2.3\right).\]
При погружении того же тела в неизвестную жидкость получим:
\[mg-P_2={\rho }_{g2}Vg\left(2.4\right).\]
Из формулы (2.4) выразим плотность жидкости:
\[{\rho }_{g2}=\frac{mg-P_2}{gV}\left(2. 5\right).\]
5\right).\]
Нам следует найти объем тела, мы его выразим из (2.3), получим:
\[V=\frac{mg-P_1}{g{\rho }_{g1}}\left(2.6\right).\]
Подставим результат (2.6)в выражение для плотности неизвестной жидкости (2.5):
\[{\rho }_{g2}={\rho }_{g1}\cdot \frac{mg-P_2}{mg-P_1}=\frac{mg-P_2}{mg-P_1}{\rho }_v.\]
Ответ. ${\rho }_{g2}=\frac{mg-P_2}{mg-P_1}{\rho }_v$
Читать дальше: формула коэффициента полезного действия.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
закон простыми словами, формула, в чем измеряется, от чего зависит, как был открыт
Вместе с преподавателем физики разбираемся, в чем измеряется и от чего зависит сила Архимеда. А в конце статьи вспомним известную легенду о том, как был открыт закон Архимеда, и узнаем, действует ли он в условиях невесомости
Борис Михеев
Автор КП
Николай Герасимов
Старший преподаватель физики в
Домашней школе «ИнтернетУрок»
Как объяснить, почему плавают огромные корабли из стали, которая тяжелее воды? Да еще и перевозят тонны грузов. Это происходит благодаря открытию, сделанному за два с лишним столетия до нашей эры изобретателем и ученым Архимедом.
Это происходит благодаря открытию, сделанному за два с лишним столетия до нашей эры изобретателем и ученым Архимедом.
История сохранила нам немного имен ученых-практиков, чьи изобретения изменили мир. Навсегда забыт гений, который придумал колесо. Но любой современный школьник назовет Архимеда, даже если знает о нем только легенду про мокрого голого философа, бежавшего по улице Сиракуз с криком: «Эврика!», то есть «Нашел!». А ведь ученый заслужил вечную благодарную память человечества благодаря многим изобретениям и открытиям:
- Теория рычага и способы его расчета. На этой основе построены боевые машины для метания тяжелых камней и «коготь Архимеда» — машина для переворачивания римских трирем;
- Шкив и многоступенчатый блок, полиспаст;
- Червячная передача;
- Архимедов винт и насосы, работающие на его принципе;
- Одометр, машина для измерения пройденного пути;
- «Архимедово число»: отношение длины окружности к ее диаметру
- Фокусировка световых лучей при помощи зеркал.
 По легенде, так были сожжены римские корабли, осаждавшие Сиракузы. Недавно энтузиасты провели экспериментальную проверку и удалось поджечь деревянный баркас.
По легенде, так были сожжены римские корабли, осаждавшие Сиракузы. Недавно энтузиасты провели экспериментальную проверку и удалось поджечь деревянный баркас.
Однако самое знаменитое открытие — закон Архимеда, основа гидростатики. Удивительно, что он был почти забыт, пока корабли строили из дерева. И только когда они стали железными, а потом стальными, инженеры осознали важность силы Архимеда и стали применять ее формулу при расчетах водных и воздушных судов.
Определение закона Архимеда простыми словами
На тело, погруженное в жидкость или газ, действует подъемная, она же выталкивающая сила (сила Архимеда), равная весу вытесненного объема жидкости или газа.
Вектор силы Архимеда направлен против направления действия силы тяжести. Следствия закона Архимеда:
- В невесомости закон Архимеда не действует.

- Если сила Архимеда меньше силы тяжести, то тело утонет.
- Если силы одинаковы по величине, тело «повисает» в окружающей среде.
- Если сила Архимеда больше силы тяжести, то тело всплывает, пока они не уравновесятся. В воде этот момент наступит на поверхности.
Принцип Архимеда. Фото: shutterstock.com
Формула силы Архимеда
Предыдущая формулировка годится только для участка цепи, где отсутствует сам источник электродвижущей силы. В реальности ток течет по замкнутому контуру, где обязательно есть батарея или генератор, имеющий собственное внутреннее сопротивление. Поэтому формула закона Ома для полной цепи выглядит несколько сложнее
Где: FA — сила Архимеда;
ρ — плотность жидкости или газа, в которое погружают тело;
g — ускорение свободного падения, которое зависит от того, на какой планете или спутнике мы находимся. Для поверхности Земли, например, ускорение примерно равно 9,8 м/с2;
V — объем погруженной в среду части тела.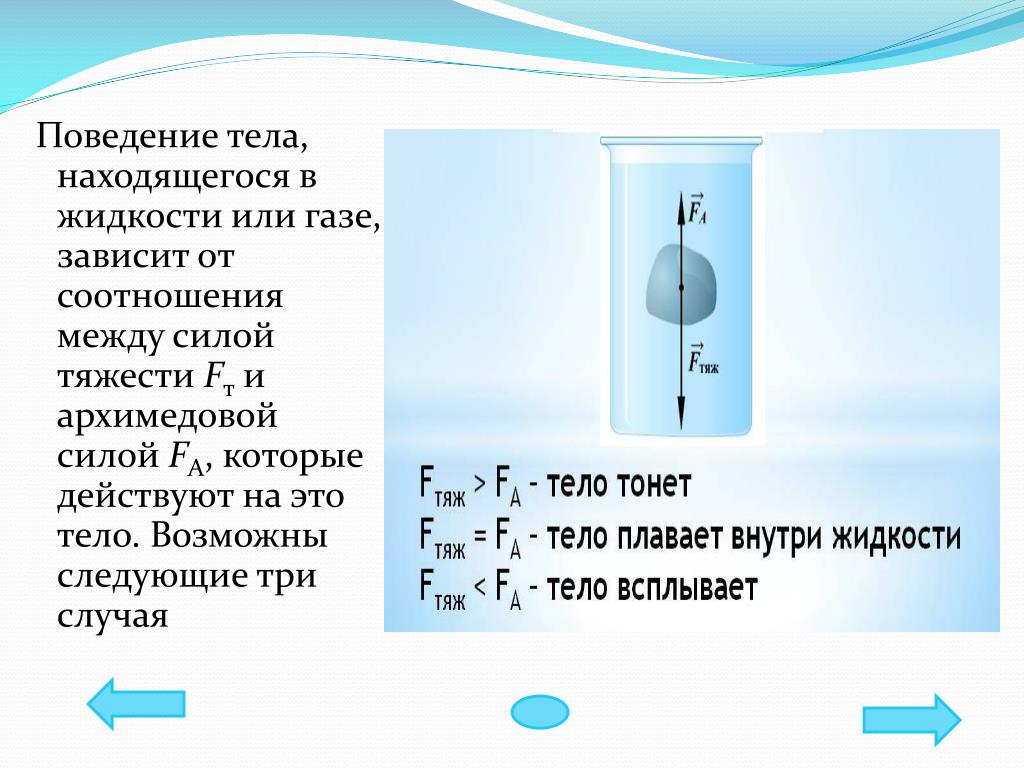
В чем измеряется сила Архимеда
Единица измерения силы Архимеда в системе СИ — ньютон (Н). 1Н = 1 кг·м/с2
Архимед и наше время
В перечне военных трофеев, взятых римлянами в Сиракузах, есть некий «Планетарий Архимеда» — механическая модель движения планет. Он не сохранился, но есть подозрение, что загадочное устройство, случайно обнаруженное в затонувшем корабле у острова Антикитера, тоже сделано золотыми руками Архимеда. Прямых доказательств этого факта нет, но уже выяснено, что время изготовления приблизительно соответствует годам жизни гениального инженера.
Популярные вопросы и ответы
Николай Герасимов, старший преподаватель по физике Домашней школы «ИнтернетУрок»:
— Сила Архимеда, она же выталкивающая сила, действует на любое тело, погруженное в жидкость или газ.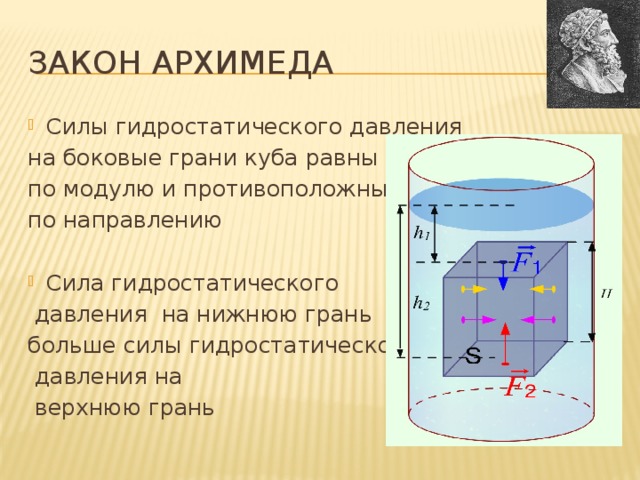 Эта сила всегда пытается вытолкнуть инородное тело из жидкости или газа.
Эта сила всегда пытается вытолкнуть инородное тело из жидкости или газа.
От чего зависит сила Архимеда?
— Так, например, для определения выталкивающей силы, действующей на камень, лежащий на дне озера, нужно брать весь его объем. Если же определяем силу Архимеда, действующую на мяч, плавающий по этому озеру, то нужно брать лишь объем той части, которая находится под водой. Зависимость выталкивающей силы от ускорения свободного падения позволяет сделать интересный вывод о том, что в невесомости силы Архимеда нет.
Зная, что сила Архимеда зависит от плотности жидкости, можно объяснить следующее явление: куриное яйцо, помещенное в обычную воду, утонет и будет лежать на дне банки. Но стоит добавить в эту банку насыщенный раствор поваренной соли и тем самым изменить плотность воды — и яйцо начинает всплывать.
Как был открыт закон Архимеда?
— Открытие закона Архимеда связано с интересной легендой. Древнегреческий царь Герон II приказал ювелирам изготовить золотую корону, что и было вскоре выполнено. Царь заподозрил, что ювелиры его обманули и сделали корону из электрона, сплава золота и серебра. Отличить подделку на глаз не удалось. Для проверки пригласили ученого из Сиракуз по имени Архимед. Достаточно было сравнить объем короны с объемом куска золота такой же массы.
Древнегреческий царь Герон II приказал ювелирам изготовить золотую корону, что и было вскоре выполнено. Царь заподозрил, что ювелиры его обманули и сделали корону из электрона, сплава золота и серебра. Отличить подделку на глаз не удалось. Для проверки пригласили ученого из Сиракуз по имени Архимед. Достаточно было сравнить объем короны с объемом куска золота такой же массы.
Сложность состояла в определении объема короны, так как она была сложной формы, и вычислить объем по математическим формулам было невозможно. Долгие размышления не увенчались успехом, и Архимед решил сходить отдохнуть в баню. Именно там ученому пришла гениальная идея: погружаясь в воду, тело вытесняет ее в объеме, который равен объему погруженной части тела. «Эврика!» («Нашел!») — закричал Архимед и побежал к царю.
Сравнив объемы воды, вытесненной короной и куском золота такой же массы, он уличил ювелиров в нечестности и алчности. Так Архимедом был открыт закон, который позволяет нам объяснить, почему ходят по морям и океанам огромные корабли, изготовленные из железа, а маленькая металлическая гайка тонет.
Какой буквой обозначают силу Архимеда?
— Как и большинство сил, сила Архимеда обозначается буквой F. Это первая буква английского слова force – сила. В индексе пишут букву А или В, которые позволяют отличить силу Архимеда FA или выталкивающую силу FВ от других сил в природе.
Фото на обложке: pexels.com
формулировка закона, от чего зависит, единица измерения
Автор na5club На чтение 8 мин. Опубликовано
Пожалуй, одной из самых интересных, но и не очень простых, тем в физике является архимедова сила. Формула, описывающая её, была получена в III веке до нашей эры. В гидростатике и аэростатике закон часто ещё называют гидростатическим. Его особенность в том, что он справедлив для физической среды, в которой присутствует сила тяжести. Поэтому в невесомости правило не действует.
Содержание
- Общие сведения
- Опыт на исследование силы
- Физическая природа
- Решение задач
Общие сведения
В третьем веке до нашей эры в Сиракузах жил и трудился учёный-теоретик Архимед. Его работы послужили основами механики, гидростатики, геометрии. По одной из легенд царь Гиерон заказал для себя корону из чистого золота. Но получив её от ювелиров, засомневался в чистоте материала. Вызвав к себе Архимеда, он поручил ему узнать, содержит ли изделие примеси других металлов.
Его работы послужили основами механики, гидростатики, геометрии. По одной из легенд царь Гиерон заказал для себя корону из чистого золота. Но получив её от ювелиров, засомневался в чистоте материала. Вызвав к себе Архимеда, он поручил ему узнать, содержит ли изделие примеси других металлов.
Как это сделать учёный на то время не знал. По преданиям размышляя о поставленной задаче, Архимед направился в баню. Погружаясь в ванную с водой, он обратил внимание, что жидкость поднялась на определённый уровень.
Это позволило изобретателю догадаться, что вытеснение происходит на объём равный опускаемому в неё телу. Так, получив по слитку золота и серебра, равных массе короны, сиракузец провёл эксперимент. Учёный замерил вытесненный объём воды изделием и слитками, определив разницу.
Впоследствии открытие Архимеда было сформулировано так: если тело погрузить в жидкость, то на него начнёт действовать выталкивающая сила, равная её массе в объёме погружённой части тела. Как показали исследования, это правило оказалось справедливым и для газов.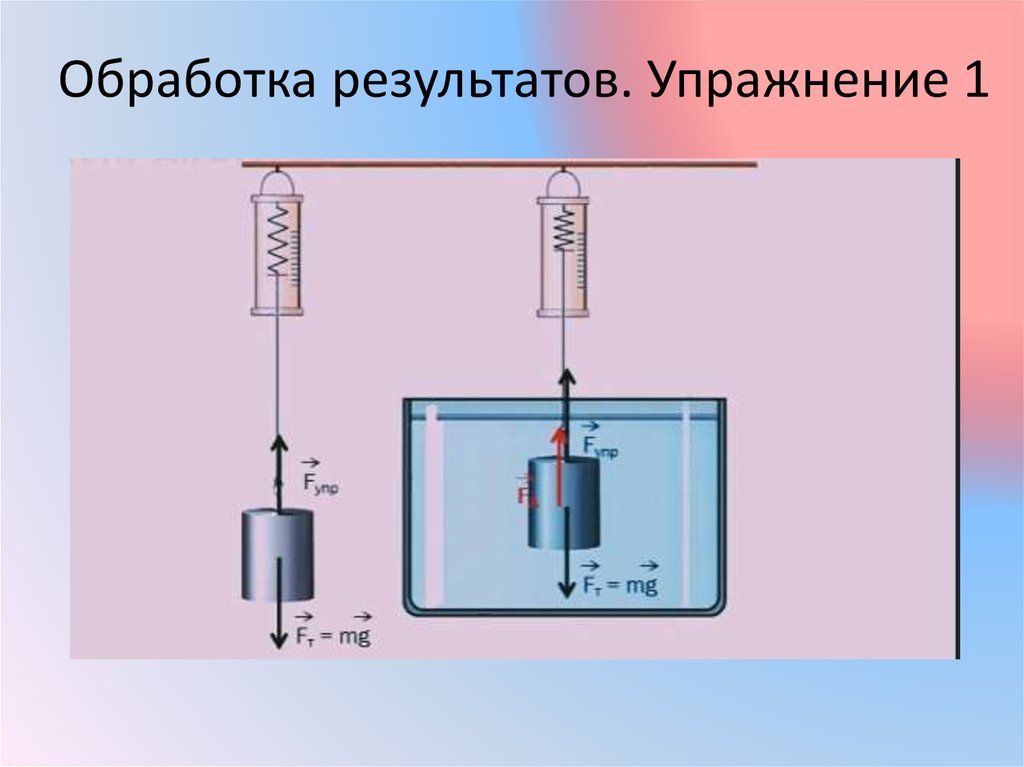 Оно стало основой гидростатики и получило название — закон Архимеда.
Оно стало основой гидростатики и получило название — закон Архимеда.
На основании своего утверждения исследователь сформулировал ещё следствия. Звучали они так:
- Тела, имеющие вес, равный жидкости, будучи в неё, опущены, погружаются таким образом, что никакая их часть не выступает над поверхностью воды, но при этом они и не тонут.
- Вещество, которое легче, чем жидкость, будучи погружено в неё, не сможет опуститься целиком, некоторая часть остаётся над поверхностью. При этом объём жидкости, соответствующий погруженной части тела, будет равным массе всего тела.
- На лёгкие тела, помещённые в жидкость, действует выталкивающая сила равная по величине весу, на который жидкая среда тяжелее этого вещества.
- Если масса тела тяжелее, чем жидкость, то при погружении оно будет опускаться до тех пор, пока не дойдёт до самого низа.
Для доказательства гипотезы Архимеда служат гидростатические весы. Это измерительное устройство, позволяющее измерять вес тел, погружённых в любую жидкость.
Самый яркий пример использования закона в технике — подводная лодка. Её средняя плотность изменяется количеством воды в специальных боксах суднах: если они наполняются водой, то она погружается, а когда воду вытесняют сжатым воздухом — лодка всплывает.
Опыт на исследование силы
Можно провести простой эксперимент. Пусть есть брусок, который имеет определённый вес. Измерить его проще всего на пружинных весах — динамометре. По сути, вес — это сила, с которой тело действует на подвес и опору. Подвесив предмет к динамометру, можно определить его массу. Пусть измерительное устройство покажет силу в один ньютон. Это значит, что сила упругости (F) пружины тоже будет такого же значения. Подвешенное тело находится в равновесии. Значит, обратной силе упругости будет тяжесть (Fg). Это воздействие приложено к центру масс тела и направлено вниз. При этом: F = Fg = 1 Н.
Теперь можно взять стакан с водой и погрузить в него измеренный брусок. В тот момент, когда произойдёт только соприкосновение твёрдой и жидкой поверхности, по динамометру можно будет наблюдать за уменьшением сил. Когда же всё тело погрузится в воду, показания значительно уменьшатся. Так, во втором случае: F = 0,2 Н.
Из опыта можно сделать вывод, что так как при погружении сила тяжести не изменяется, то возникает новое воздействие. При этом оно происходит со стороны воды и направлено противоположно Fg. Называется такая сила архимедовой, или выталкивающей (Fa). В этом случае уравнение равновесия примет вид: F + Fa = Fg. Отсюда сила Архимеда равняется: Fa = Fg — F.
Этот опыт выполняют преподаватели в седьмом классе. Он помогает объяснить закон Архимеда простыми словами и наглядно его продемонстрировать. Причём можно экспериментально установить, чему будет равна силы выталкивания для того или иного случая. Например, подставив значения, полученные в опыте с бруском и водой, получится: Fa = 1 Н — 0,2 Н = 0,8 Н.
Как оказалось, на тело, погружённое в газ, действует выталкивающая сила. В воздухоплавании её называют подъёмной. Причём направлена она тоже вертикально вверх. Считается, что летательный аппарат сможет подняться лишь тогда, когда выталкивание превысит силу тяжести. Вычисляется подъёмная сила по тем же формулам, что и для жидкости. Поэтому формулировка закона и следствия подходят как для одной, так и другой среды. Просто жидкость рассматривать удобней.
Физическая природа
Итак, пусть имеется жидкость, в которую полностью погружён физический объект. Известно, что в глубине жидкость сжата. Это давление называется гидростатическим. Оно зависит от глубины и плотности. Помещённое тело занимает в пространстве какой-то объём. При этом верхняя часть предмета находится на меньшей глубине. Значит, гидростатическое давление наверху будет меньше чем внизу.
С рассмотренным процессом связана сила. Чтобы её определить нужно давление умножить на площадь. Так как сверху воздействие меньше чем снизу, а площади одинаковые, то и действующие силы будут разными. Значит, справедливо записать: Fн > Fв. Для того чтобы найти равнодействующую, нужно учесть следующие факторы:
- сила Fв давит сверху вниз;
- снизу вверх тело выталкивает Fн;
- высота положений граней тела, считая от поверхности жидкости, соотносится как h3 > h2.
Итак, равнодействующую силу можно найти как F = Fн — Fв. Так как Fн по своему значению больше чем Fв, то она будет совпадать по направлению с ней. Эта и есть сила, которую называют — архимедовой.
Особенность же выталкивающей силы заключается в том, что с ростом глубины давление жидкости (газа) увеличивается. Например, воздушный шарик, он стремится вверх из-за того, что давление внизу больше чем вверху.
Пусть тело будет частично погружено в жидкость. Площадь основания можно обозначить как S, а глубину затопления — h. Сверху на предмет действует атмосферное давление P1. Поскольку нижняя часть тела находится на глубине h, воздействие будет больше и равно P2. Атмосферное давление действует и на жидкость. Если бы его не было, то гидростатическое воздействие вычислялось как p = ρ * g * h. Но оно есть, поэтому P2 = Pат + ρ * g * h.
Площадь основания можно обозначить как S, а глубину затопления — h. Сверху на предмет действует атмосферное давление P1. Поскольку нижняя часть тела находится на глубине h, воздействие будет больше и равно P2. Атмосферное давление действует и на жидкость. Если бы его не было, то гидростатическое воздействие вычислялось как p = ρ * g * h. Но оно есть, поэтому P2 = Pат + ρ * g * h.
Зная давление, можно найти равнодействующую, которая и будет архимедовой силой: F =(Pат + ρ * g * h) * S — Paт * S = Paт * S + ρ * g * h * S — Paт * S = ρ * g * h * S, где:
- ρ — плотность среды;
- g — ускорение свободного падения;
- h — высота погружения;
- S — площадь поперечного сечения тела.
Произведение h * S является не чем иным, как объёмом той части тела, которое погружено в жидкость. Именно его и смог определить в своё время изобретатель. Отсюда формулу для силы Архимеда можно записать так: F = ρ * g * V. В качестве единицы её измерения был принят ньютон (Н).
Решение задач
Для успешного решения задач по теме нужно, прежде всего знать определение закона Архимеда. Он гласит, что на тело, погружённое в жидкость или газ, действует сила, направленная вертикально вверх и равная весу жидкости, вытесненной этим предметом. При этом её можно вычислить, умножив плотность на ускорение свободного падения и объём погружённой части. Следует отметить, что для удобства рекомендуется условие задачи не только записывать в краткой форме, но и изображать на рисунке, указывая все действующие силы.
Вот некоторые задача рассчитанные на самостоятельную проработку учениками в рамках школьной программы по физике:
- К динамометру подвесили тело весом 4 Н и объёмом 200 см3. Определить, какую F покажет измерительное устройство, если тело полностью опустится в воду. Для рассматриваемого случая условие равновесия будет выглядеть так: Fтяж = F + Fарх.
 Отсюда искомая величина равняется разности сил тяжести и Архимеда. Так как предмет не движется, то Fтяж = P, а Fарх = ρ * g * V. Для того чтобы полученная сила измерялась в ньютонах, нужно все значения подставить в единицах СИ. Значит, F = P — ρ * g * V = 4 Н — 1000 кг / м3 * 10 Н / кг * 200 * 10-6 м3 = 2 Н.
Отсюда искомая величина равняется разности сил тяжести и Архимеда. Так как предмет не движется, то Fтяж = P, а Fарх = ρ * g * V. Для того чтобы полученная сила измерялась в ньютонах, нужно все значения подставить в единицах СИ. Значит, F = P — ρ * g * V = 4 Н — 1000 кг / м3 * 10 Н / кг * 200 * 10-6 м3 = 2 Н. - Что покажет динамометр, если цилиндрический предмет, выполненный из стали массой 312 гр опустить в стакан с водой наполовину. Из справочника взять значения для плотности стали и воды. Сила Архимеда окажется приложенной к центру тяжести вытесенной жидкости, то есть погружённой части тела. Вверх будет направлена искомая сила F, а вниз тяжести. Значит: F = Fg — Fарх = mg — ρgV. По условию погружено ½ V цилиндра, отсюда V = m / 2*ρ ст. Подставив равенства в формулу Архимеда и упростив выражение итоговое равенство примет вид: F = mg (1 — ρ / 2ρст) = 0,312 / 10 * (1 — (1 / 2 * 7,8)) = 2,92 Н.
- В стакане с водой лежит камень. Изменится ли архимедова сила, если ёмкость переместить под колокол вакуумного насоса и откачать воздух? Рассуждать нужно следующим образом.
 Так как сила выталкивания не зависит от атмосферного давления, то никакого изменения не произойдёт.
Так как сила выталкивания не зависит от атмосферного давления, то никакого изменения не произойдёт.
При решении задач нужно не только знать закон и формулу Архимеда, но и уметь анализировать условие. Но, кроме этого, важным этапом является перевод единиц измерения.
Закон архимеда вывод формулы. Основные теоретические сведения. Открытие силы Архимеда
Закон Архимеда – закон статики жидкостей и газов, согласно которому на погруженное в жидкость (или газ) тело действует выталкивающая сила, равная весу жидкости в объеме тела.
История вопроса
«Эврика!» («Нашел!») – именно этот возглас, согласно легенде, издал древнегреческий ученый и философ Архимед, открыв принцип вытеснения. Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, из чистого ли золота сделана его корона, не причиняя вреда самому царскому венцу. Взвесить корону Архимеду труда не составило, но этого было мало – нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото. Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну – и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну – и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Однако, что правда – то правда: именно Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Давление, которое ранее действовало на вытесненную жидкость, теперь будет действовать на твердое тело, вытеснившее ее. И, если действующая вертикально вверх выталкивающая сила окажется больше силы тяжести, тянущей тело вертикально вниз, тело будет всплывать; в противном случае оно пойдет ко дну (утонет).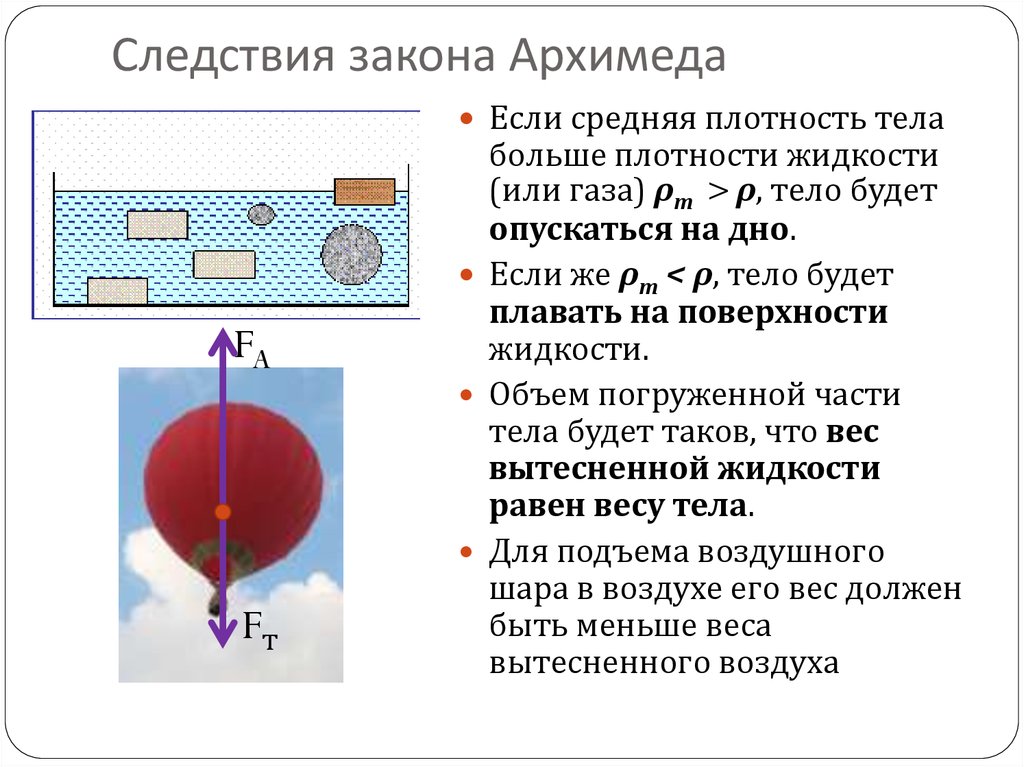 Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.
Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.
Закон Архимеда и молекулярно-кинетическая теория
В покоящейся жидкости давление производится посредством ударов движущихся молекул. Когда некий объем жидкости вымещается твердым телом, направленный вверх импульс ударов молекул будет приходиться не на вытесненные телом молекулы жидкости, а на само тело, чем и объясняется давление, оказываемое на него снизу и выталкивающее его в направлении поверхности жидкости. Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Такая картина выталкивания объясняет, почему судно, сделанное из стали, которая значительно плотнее воды, остается на плаву. Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, – и корабль плывет.
Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, – и корабль плывет.
Формулировка и пояснения
Тот факт, что на погруженное в воду тело действует некая сила, всем хорошо известен: тяжелые тела как бы становятся более легкими – например, наше собственное тело при погружении в ванну. Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается поднять на суше. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился.
Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился.
Существование гидростатического давления приводит к тому, что на любое тело, находящееся в жидкости или газе, действует выталкивающая сила. Впервые значение этой силы в жидкостях определил на опыте Архимед. Закон Архимеда формулируется так: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу того количества жидкости или газа, которое вытеснено погруженной частью тела.
Формула
Сила Архимеда, действующая на погруженное в жидкость тело, может быть рассчитана по формуле: F А = ρ ж gV пт,
где ρж – плотность жидкости,
g – ускорение свободного падения,
Vпт – объем погруженной в жидкость части тела.
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести Fт и архимедовой силы FA, которые действуют на это тело. Возможны следующие три случая:
1) Fт > FA – тело тонет;
2) Fт = FA – тело плавает в жидкости или газе;
3) Fт
Цели урока: убедиться в существовании выталкивающей силы, осознать причины её возникновения и вывести правила для её вычисления, содействовать формированию мировоззренческой идеи познаваемости явлений и свойств окружающего мира.
Задачи урока: Работать над формированием умений анализировать свойства и явления на основе знаний, выделять главную причину, влияющую на результат. Развивать коммуникативные умения. На этапе выдвижения гипотез развивать устную речь. Проверить уровень самостоятельности мышления школьника по применению учащимися знаний в различных ситуациях.
Архимед – выдающийся ученый Древней
Греции, родился в 287 году до н. э. в портовом и
судостроительном г. Сиракузы на острове Сицилия.
Архимед получил блестящее образование у своего
отца, астронома и математика Фидия, родственника
сиракузского тирана Гиерона,
покровительствовавшего Архимеду. В юности
провёл несколько лет в крупнейшем культурном
центре в Александрии, где у него сложились
дружеские отношения с астрономом Кононом и
географом-математиком Эратосфеном. Это
послужило толчком к развитию его выдающихся
способностей. В Сицилию вернулся уже зрелым
ученым. Он прославился многочисленными научными
трудами главным образом в области физики и
геометрии.
э. в портовом и
судостроительном г. Сиракузы на острове Сицилия.
Архимед получил блестящее образование у своего
отца, астронома и математика Фидия, родственника
сиракузского тирана Гиерона,
покровительствовавшего Архимеду. В юности
провёл несколько лет в крупнейшем культурном
центре в Александрии, где у него сложились
дружеские отношения с астрономом Кононом и
географом-математиком Эратосфеном. Это
послужило толчком к развитию его выдающихся
способностей. В Сицилию вернулся уже зрелым
ученым. Он прославился многочисленными научными
трудами главным образом в области физики и
геометрии.
Последние годы жизни Архимед был в
Сиракузах, осажденных римским флотом и войском.
Шла 2-я Пуническая война. И великий ученый, не
жалея сил, организовывает инженерную оборону
родного города. Он построил множество
удивительных боевых машин, топивших вражеские
корабли, разносивших их в щепы, уничтожавших
солдат. Однако слишком маленьким было войско
защитников города по сравнению с огромным
римским войском. И в 212 г. до н.э. Сиракузы были
взяты.
И в 212 г. до н.э. Сиракузы были
взяты.
Гений Архимеда вызывал восхищение у римлян и римский полководец Марцелл приказал сохранить ему жизнь. Но солдат, не знавший в лицо Архимеда, убил его.
Одним из важнейших его открытий стал закон, впоследствии названный законом Архимеда. Существует предание, что идея этого закона посетила Архимеда, когда он принимал ванну, с возгласом “Эврика!” он выскочил из ванны и нагим побежал записывать пришедшую к нему научную истину. Суть этой истины и предстоит выяснить, нужно убедиться в существовании выталкивающей силы, осознать причины её возникновения и вывести правила для её вычисления.
Давление в жидкости или газе зависит от глубины погружения тела и приводит к появлению выталкивающей силы, действующей на тело и направленной вертикально вверх.
Если тело опустить в жидкость или газ, то под
действием выталкивающей силы оно будет
всплывать из более глубоких слоев в менее
глубокие. Выведем формулу для определения силы
Архимеда для прямоугольного параллелепипеда.
Давление жидкости на верхнюю грань равно
где: h2 – высота столба жидкости над верхней гранью.
Сила давления на верхнюю грань равна
F1= р1*S = ж*g*h2*S,
Где: S – площадь верхней грани.
Давление жидкости на нижнюю грань равно
где: h3 – высота столба жидкости над нижней гранью.
Сила давления на нижнюю грань равна
F2= p2*S = ж*g*h3*S,
Где: S – площадь нижней грани куба.
Поскольку h3 > h2, то р2 > р1 и F2 > F1.
Разность между силами F2 и F1 равна:
F2 – F1 = ж*g*h3*S – ж*g*h2*S = ж*g*S* (h3 – h2).
Так как h3 – h2 = V – объему тела или части тела, погруженной в жидкость или газ, то F2 – F1 = ж*g*S*H = g* ж*V
Произведение плотности на объем есть масса жидкости или газа. Следовательно, разность сил равна весу вытесненной телом жидкости:
F2 – F1= mж*g = Pж = Fвыт.
Выталкивающая сила есть сила Архимеда, определяющая закон Архимеда
Равнодействующая сил, действующих на боковые
грани равна нулю, поэтому в расчетах не
участвует.
Таким образом, на тело, погруженное в жидкость или газ, действует выталкивающая сила равная весу вытесненной им жидкости или газа.
Закон Архимеда, впервые был упомянут Архимедом в трактате “О плавающих телах”. Архимед писал: “тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела”.
Рассмотрим, как зависит сила Архимеда и зависит ли от веса тела, объема тела, плотности тела и плотности жидкости.
Исходя из формулы силы Архимеда, она зависит от
плотности жидкости, в которую погружено тело, и
от объёма этого тела. Но она не зависит, например,
от плотности вещества тела, погружаемого в
жидкость, так как эта величина не входит в
полученную формулу.
Определим теперь вес тела, погружённого в
жидкость (или газ). Так как две силы, действующие
на тело в этом случае, направлены в
противоположные стороны (сила тяжести вниз, а
архимедова сила вверх), то вес тела в жидкости
будет меньше веса тела в вакууме на архимедову
силу:
P А = m т g – m ж g = g (m т – m ж)
Таким образам, если тело погружено в жидкость
(или газ), то оно теряет в своём весе столько,
сколько весит вытесненная им жидкость (или газ).
Следовательно:
Сила Архимеда зависит от плотности жидкости и объема тела или его погруженной части и не зависит от плотности тела, его веса и объема жидкости.
Определение силы Архимеда лабораторным методом.
Оборудование: стакан с чистой водой, стакан с соленой водой, цилиндр, динамометр.
Ход работы:
- определяем вес тела в воздухе;
- определяем вес тела в жидкости;
- находим разницу между весом тела в воздухе и весом тела в жидкости.
4. Результаты измерений:
Сделать вывод как зависит сила Архимеда от плотности жидкости.
Выталкивающая сила действует на тела любых геометрических форм. В технике наиболее распространены тела цилиндрической и сферической форм, тела с развитой поверхностью, полые тела в форме шара, прямоугольного параллелепипеда, цилиндра.
Гравитационная сила приложена к центру масс погруженного в жидкость тела и направлена перпендикулярно к поверхности жидкости.
Подъемная сила действует на тело со стороны
жидкости, направлена по вертикали вверх,
приложена к центру тяжести вытесненного объема
жидкости. Тело движется в направлении,
перпендикулярном к поверхности жидкости.
Тело движется в направлении,
перпендикулярном к поверхности жидкости.
Выясним условия плавания тел, которые основываются на законе Архимеда.
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести F т и силы Архимеда F A , которые действуют на это тело. Возможны следующие три случая:
- F т > F A – тело тонет;
- F т = F A – тело плавает в жидкости или газе;
- F т
Другая формулировка (где P t – плотность тела, P s – плотность среды, в которую оно погружено):
- P t > P s – тело тонет;
- P t = P s – тело плавает в жидкости или газе;
- P t
Плотность организмов живущих в воде почти не отличается от плотности воды, поэтому прочные скелеты им не нужны! Рыбы регулируют глубину погружения, меняя среднюю плотность своего тела. Для этого им необходимо лишь изменить объем плавательного пузыря, сокращая или расслабляя мышцы.
Если тело лежит на дне в жидкости или газе, то
сила Архимеда равна нулю.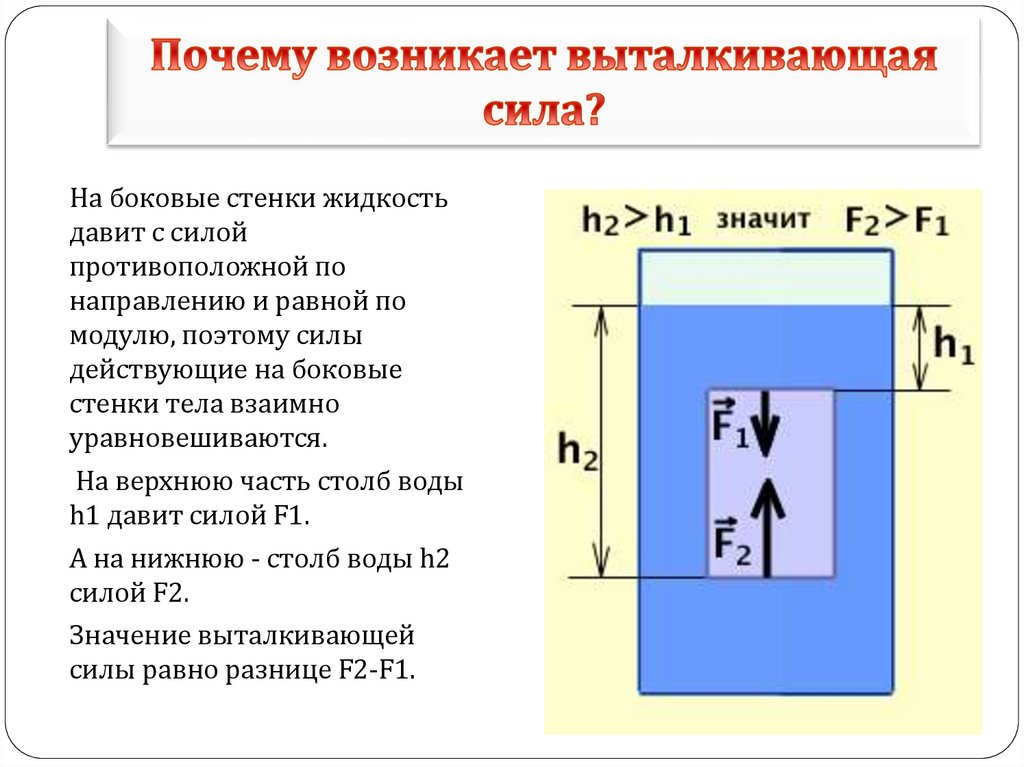
Закон Архимеда используется в судостроении и воздухоплавании.
Схема плавающего тела:
Линия действия силы тяжести тела G проходит через центр тяжести K (центр водоизмещения) вытесненного объема жидкости. В нормальном положении плавающего тела центр тяжести тела Т и центр водоизмещения K размещены по одной вертикали, называемой осью плаванья.
При качке центр водоизмещения К перемещается в точку К1, и сила тяжести тела и Архимедова сила FА образуют пару сил, которая стремится либо вернуть тело в исходное положение, либо увеличить крен.
В первом случае плавающее тело обладает статической устойчивостью, во втором случае устойчивость отсутствует. Устойчивость тела зависит от взаимного расположения центра тяжести тела Т и метацентра М (точки пересечения линии действия архимедовой силы при крене с осью плавания).
В 1783 году братья МОНГОЛЬФЬЕ изготовили
огромный бумажный шар, под которым поместили
чашку с горящим спиртом. Шар наполнился горячим
воздухом и начал подниматься, достигнув высоты
2000 метров.
В предыдущем параграфе мы назвали две формулы, при помощи которых силу Архимеда можно измерить. Теперь выведем формулу, при помощи которой силу Архимеда можно вычислить.
Закон Архимеда для жидкости выражается формулой (см. § 3-е):
Примем, что вес вытесненной жидкости равен действующей силе тяжести:
Wж = Fтяж = mжg
Масса вытесненной жидкости может быть найдена из формулы плотности:
r = m/V Ю mж = rжVж
Подставляя формулы друг в друга, получим равенство:
Fарх = Wж = Fтяж = mж g = rжVж g
Выпишем начало и конец этого равенства:
Fарх = rж gVж
Вспомним, что закон Архимеда справедлив для жидкостей и газов. Поэтому вместо обозначения «rж» более правильно использовать «rж/г». Также заметим, что объём жидкости, вытесненной телом, в точности равен объёму погруженной части тела: Vж = Vпчт. С учётом этих уточнений получим:
Итак, мы вывели частный случай закона Архимеда – формулу, выражающую способ вычисления силы Архимеда. Вы спросите: почему же эта формула – «частный случай», то есть менее общая?
Вы спросите: почему же эта формула – «частный случай», то есть менее общая?
Поясним примером. Вообразим, что мы проводим опыты в космическом корабле. Согласно формуле Fарх = Wж, архимедова сила равна нулю (так как вес жидкости равен нулю), согласно же формуле Fарх = rж/г gVпчт архимедова сила нулю не равна, так как ни одна из величин (r, g, V) в невесомости в ноль не обращается. Перейдя от воображаемых опытов к настоящим, мы убедимся, что справедлива именно общая формула.
Продолжим наши рассуждения и выведем ещё один частный случай закона Архимеда. Посмотрите на рисунок. Поскольку бревно находится в покое, следовательно, на него действуют уравновешенные силы – сила тяжести и сила Архимеда. Выразим это равенством:
Fарх = Fтяж
Или, подробнее:
rж gVпчт = mт g
Разделим левую и правую части равенства на коэффициент «g»:
rж Vпчт = mт
Вспомнив, что m = rV, получим равенство:
rж Vпчт = rт Vт
Преобразуем это равенство в пропорцию:
В левой части этой пропорции стоит дробь, показывающая долю, которую составляет объём погруженной части тела от объёма всего тела. Поэтому всю дробь называют погруженной долей тела:
Поэтому всю дробь называют погруженной долей тела:
Используя эту формулу, предскажем, чему должна быть равна погруженная доля бревна при его плавании в воде:
ПДТ (полена) » 500 кг/м 3: 1000 кг/м 3 = 0,5
Число 0,5 означает, что плавающее в воде бревно погружено наполовину. Так предсказывает теория, и это совпадает с практикой.
Итак, обе формулы в рамках являются менее общими, чем исходная, то есть имеют более узкие границы применимости . Почему же так произошло? Причина – применение нами формулы W = F тяж. Вспомним, что она не верна, если тело или его опора (подвес) движутся непрямолинейно (см. § 3-г). Упоминавшийся нами космический корабль именно так и движется – по круговой орбите вокруг Земли.
F A = ρ g V , {\displaystyle F_{A}=\rho gV,}
Описание
Выталкивающая или подъёмная сила по направлению противоположна силе тяжести , прикладывается к центру тяжести объёма, вытесняемого телом из жидкости или газа.
Обобщения
Некий аналог закона Архимеда справедлив также в любом поле сил, которое по-разному действуют на тело и на жидкость (газ), либо в неоднородном поле. Например, это относится к полю сил инерции (например, к полю центробежной силы) – на этом основано центрифугирование . Пример для поля немеханической природы: диамагнетик в вакууме вытесняется из области магнитного поля большей интенсивности в область с меньшей.
Вывод закона Архимеда для тела произвольной формы
Гидростатическое давление
p
{\displaystyle p}
на глубине
h
{\displaystyle h}
, оказываемое жидкостью плотностью
ρ
{\displaystyle \rho }
на тело, есть
p
=
ρ
g
h
{\displaystyle p=\rho gh}
. Пусть плотность жидкости (
ρ
{\displaystyle \rho }
) и напряжённость гравитационного поля (
g
{\displaystyle g}
) – постоянные величины, а
h
{\displaystyle h}
– параметр. Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат
O
x
y
z
{\displaystyle Oxyz}
, причём выберем направление оси z совпадающим с направлением вектора
g
→
{\displaystyle {\vec {g}}}
. {**}grad(h)=\nabla h={\vec {e}}_{z}.}
{**}grad(h)=\nabla h={\vec {e}}_{z}.}
Получаем, что модуль силы Архимеда равен ρ g V {\displaystyle \rho gV} , и направлена сила Архимеда в сторону, противоположную направлению вектора напряжённости гравитационного поля.
Замечание . Закон Архимеда можно также вывести из закона сохранения энергии. Работа силы, действующей со стороны погруженного тела на жидкость, приводит к изменению ее потенциальной энергии:
A = F Δ h = m ж g Δ h = Δ E p {\displaystyle \ A=F\Delta h=m_{\text{ж}}g\Delta h=\Delta E_{p}}
где m ж − {\displaystyle m_{\text{ж}}-} масса вытесненной части жидкости, Δ h {\displaystyle \Delta h} – перемещение ее центра масс. Отсюда модуль вытесняющей силы:
F = m ж g {\displaystyle \ F=m_{\text{ж}}g}
И статики газов.
Энциклопедичный YouTube
1 / 5
Закон Архимеда формулируется следующим образом : на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу жидкости (или газа) в объёме погруженной части тела .
F A = ρ g V , {\displaystyle {F}_{A}=\rho {g}V,} Сила называется силой Архимеда :
Сила называется силой Архимеда :где ρ {\displaystyle \rho } – плотность жидкости (газа), g {\displaystyle {g}} – ускорение свободного падения , а V {\displaystyle V} – объём погружённой части тела (или часть объёма тела, находящаяся ниже поверхности). Если тело плавает на поверхности (равномерно движется вверх или вниз), то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.
Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.
Что касается тела, которое находится в газе, например в воздухе, то для нахождения подъёмной силы нужно заменить плотность жидкости на плотность газа.
 Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.
Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.Закон Архимеда можно объяснить при помощи разности гидростатических давлений на примере прямоугольного тела.
P B − P A = ρ g h {\displaystyle P_{B}-P_{A}=\rho gh} F B − F A = ρ g h S = ρ g V , {\displaystyle F_{B}-F_{A}=\rho ghS=\rho gV,}где P A , P B – давления в точках A и B , ρ – плотность жидкости, h – разница уровней между точками A и B , S – площадь горизонтального поперечного сечения тела, V – объём погружённой части тела.
В теоретической физике также применяют закон Архимеда в интегральной форме:
F A = ∬ S p d S {\displaystyle {F}_{A}=\iint \limits _{S}{p{dS}}} ,где S {\displaystyle S} – площадь поверхности, p {\displaystyle p} – давление в произвольной точке, интегрирование производится по всей поверхности тела.
В отсутствие гравитационного поля, то есть в состоянии невесомости , закон Архимеда не работает.
 Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции , поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами .
Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции , поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами .Обобщения
Некий аналог закона Архимеда справедлив также в любом поле сил, которое по-разному действуют на тело и на жидкость (газ), либо в неоднородном поле. Например, это относится к полю сил инерции (например, центробежной силы) – на этом основано центрифугирование . Пример для поля немеханической природы: диамагнетик в вакууме вытесняется из области магнитного поля большей интенсивности в область с меньшей.
Вывод закона Архимеда для тела произвольной формы
Гидростатическое давление жидкости на глубине h {\displaystyle h} есть p = ρ g h {\displaystyle p=\rho gh} . При этом считаем ρ {\displaystyle \rho } жидкости и напряжённость гравитационного поля постоянными величинами, а h {\displaystyle h} – параметром.
 Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат
O
x
y
z
{\displaystyle Oxyz}
, причём выберем направление оси z совпадающим с направлением вектора
g
→
{\displaystyle {\vec {g}}}
. Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку
d
S
{\displaystyle dS}
. На неё будет действовать сила давления жидкости направленная внутрь тела,
d
F
→
A
=
−
p
d
S
→
{\displaystyle d{\vec {F}}_{A}=-pd{\vec {S}}}
. Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности:
Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат
O
x
y
z
{\displaystyle Oxyz}
, причём выберем направление оси z совпадающим с направлением вектора
g
→
{\displaystyle {\vec {g}}}
. Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку
d
S
{\displaystyle dS}
. На неё будет действовать сила давления жидкости направленная внутрь тела,
d
F
→
A
=
−
p
d
S
→
{\displaystyle d{\vec {F}}_{A}=-pd{\vec {S}}}
. Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности:F → A = − ∫ S p d S → = − ∫ S ρ g h d S → = − ρ g ∫ S h d S → = ∗ − ρ g ∫ V g r a d (h) d V = ∗ ∗ − ρ g ∫ V e → z d V = − ρ g e → z ∫ V d V = (ρ g V) (− e → z) {\displaystyle {\vec {F}}_{A}=-\int \limits _{S}{p\,d{\vec {S}}}=-\int \limits _{S}{\rho gh\,d{\vec {S}}}=-\rho g\int \limits _{S}{h\,d{\vec {S}}}=^{*}-\rho g\int \limits _{V}{grad(h)\,dV}=^{**}-\rho g\int \limits _{V}{{\vec {e}}_{z}dV}=-\rho g{\vec {e}}_{z}\int \limits _{V}{dV}=(\rho gV)(-{\vec {e}}_{z})}
При переходе от интеграла по поверхности к интегралу по объёму пользуемся обобщённой теоремой Остроградского-Гаусса .
 {**}grad(h)=\nabla h={\vec {e}}_{z}}
{**}grad(h)=\nabla h={\vec {e}}_{z}}Получаем, что модуль силы Архимеда равен ρ g V {\displaystyle \rho gV} , а направлена она в сторону, противоположную направлению вектора напряжённости гравитационного поля.
Другая формулировка (где ρ t {\displaystyle \rho _{t}} – плотность тела, ρ s {\displaystyle \rho _{s}} – плотность среды, в которую оно погружено).
Выталкивающая сила называется. Закон Архимеда: определение и формула
Почему мы можем лежать на поверхности моря, не опускаясь на дно? Почему плавают на поверхности воды тяжелые корабли?
Наверное, существует какая-то сила, которая выталкивает людей и кораблики, то есть, все тела из воды и позволяет плавать на поверхности.
Зависимость давления в жидкости или газе от глубины погружения тела приводит к появлению выталкивающей силы,или иначе силы Архимеда, действующей на любое тело, погруженное в жидкость или газ. Рассмотрим силу Архимеда подробнее на примере.
Все мы пускали кораблики по лужам. А какой кораблик без капитана? Что мы наблюдали? Кораблик под весом капитана погружается глубже. А если мы мы размещали на нашем кораблике пять или восемь капитанов? Наш кораблик опускался на дно.
А какой кораблик без капитана? Что мы наблюдали? Кораблик под весом капитана погружается глубже. А если мы мы размещали на нашем кораблике пять или восемь капитанов? Наш кораблик опускался на дно.
Что же мы можем извлечь полезного из данного опыта? Когда увеличивался вес кораблика, то мы видели, что кораблик ниже опускался в воду. То есть, вес тела увеличивал давление на воду, а выталкивающая сила оставалась прежней.
Когда же вес тела превысил величину выталкивающей силы, то кораблик под действием этой силы опустился на дно. То есть, существует выталкивающая сила, одинаковая для конкретного тела, но разная для различных тел.
Выталкивающая сила, она же сила Архимеда, действующая на тело, погружённое в жидкость, равна весу жидкости, вытесненной этим телом.
Кирпич, как всем известно, пойдет на дно в любом случае, а вот деревянная дверь не только будет плавать на поверхности, но и может еще удержать пару пассажиров. Сила эта и называется архимедовой силой и выражается формулой:
Fвыт = g*m ж = g* ρ ж * V ж = P ж,
где m ж – это масса жидкости,
а P ж – вес вытесненной телом жидкости.
А так как масса у нас равна: m ж = ρ ж * V ж, то из формулы архимедовой силы мы видим, что она не зависит от плотности погруженного тела, а только от объема и плотности вытесненной телом жидкости.
Архимедова сила – это векторная величина. Причина существования выталкивающей силы – разница в давлении на верхнюю и нижнюю часть тела.Указанное на рисунке давление P 2 > P 1 из-за большей глубины. Для возникновения силы Архимеда достаточно того, чтобы тело было погружено в жидкость хотя бы частично.
Так, если тело плывёт по поверхности жидкости, значит выталкивающая сила, действующая на погружённую в жидкость часть этого тела равна силе тяжести всего тела. Если плотность тела больше плотности жидкости, то тело тонет, если меньше – то всплывает.
Тело же, погруженное в жидкость, теряет в своем весе ровно столько, сколько весит вытесненная им вода. Поэтому, естественно предположить, что если вес тела меньше веса воды такого же объема, то оно будет плавать на поверхности, а если больше – то утонет.
Если же вес тела и воды будет равен, то тело может замечательно плавать в толще воды, как и поступают все водные обитатели. Плотность оганизмов, живущих в воде почти не отличается от плотности воды, поэтому прочные скелеты им не нужны!
Рыбы регулируют глубину погружения, меняя среднюю плотность своего тела. Для этого им необходимо лишь изменить объем плавательного пузыря, сокращая или расслабляя мышцы.
У берегов Египта, водится удивительная рыба фагак. Приближение опасности заставляет фагака быстро заглатывать воду. При этом в пищеводе рыбы происходит бурное разложение продуктов питания с выделением значительного количества газов. Газы заполняют не только действующую полость пищевода, но и имеющийся при ней слепой вырост. В результате тело фагака сильно раздувается, и, в соответствии с законом Архимеда, он быстро всплывает на поверхность водоема. Здесь он плавает, повиснув вверх брюхом, пока выделившиеся в его организме газы не улетучатся. После этого сила тяжести опускает его на дно водоема, где он укрывается среди придонных водорослей.
На поверхность твердого тела, погруженного в жидкость, действуют, как мы знаем, силы давления. Так как давление увеличивается с глубиной погружения, то силы давления, действующие на нижнюю часть тела и направленные вверх, больше, чем силы, действующие на верхнюю его часть и направленные вниз, и мы можем ожидать, что равнодействующая сил давления будет направлена вверх. Опыт подтверждает это предположение.
Рис. 258. Если груз погружен в воду, показание динамометра уменьшается
Рис. 259. Пробка, погруженная в воду, натягивает нитку
Если, например, гирю, подвешенную к крючку динамометра, опустить в воду, то показание динамометра уменьшится (рис. 258).
Равнодействующая
сил давления на тело, погруженное в жидкость, называется выталкивающей силой. Выталкивающая
сила может быть больше силы тяжести, действующей на тело; например, кусок
пробки, привязанный к дну сосуда, наполненного водой, стремясь всплыть,
натягивает нитку (рис. 259). Выталкивающая сила возникает и в случае частичного
погружения тела. Кусок дерева, плавающий на поверхности воды, не тонет именно
благодаря наличию выталкивающей силы, направленной вверх.
Кусок дерева, плавающий на поверхности воды, не тонет именно
благодаря наличию выталкивающей силы, направленной вверх.
Если тело, погруженное в жидкость, предоставить самому себе, то оно тонет, остается в равновесии или всплывает на поверхность жидкости в зависимости от того, меньше ли выталкивающая сила силы тяжести, действующей на тело, равна ей или больше ее. Выталкивающая сила зависит от рода жидкости, в которую, погружено тело. Например, кусок железа тонет в воде, но плавает в ртути; значит, в воде выталкивающая сила, действующая на этот кусок меньше, а в ртути – больше силы тяжести.
Найдем выталкивающую силу, действующую на твердое тело, погруженное в жидкость.
Рис. 260. а) Тело находится в жидкости, б) Тело заменено жидкостью
Выталкивающая
сила, действующая на тело (рис. 260 а), есть равнодействующая сил давления
жидкости на его поверхность. Представим себе, что тело удалено и его место
занято той же жидкостью (рис. 260, б). Давление на поверхность такого мысленно
выделенного объёма будет таким же, каким было давление на поверхность самого тела. Значит, и равнодействующая сила давления на тело (выталкивающая сила) равна
равнодействующей сил давления на выделенный объем жидкости. Но выделенный объем
жидкости находится в равновесии. Силы, действующие на него, – это сила тяжести и выталкивающая
сила (рис.
261, а). Значит, выталкивающая сила равна по модулю силе тяжести, действующей
на выделенный объем жидкости, и направлена вверх. Точкой приложения этой силы
должен быть центр тяжести выделенного объема. В противном случае равновесие
нарушилось бы, так как сила тяжести и выталкивающая сила образовали бы пару сил
(рис. 261, б). Но, как уже сказано, выталкивающая сила для выделенного объема
совпадает с выталкивающей силой тела. Мы приходим, таким образом, к закону
Архимеда:
Значит, и равнодействующая сила давления на тело (выталкивающая сила) равна
равнодействующей сил давления на выделенный объем жидкости. Но выделенный объем
жидкости находится в равновесии. Силы, действующие на него, – это сила тяжести и выталкивающая
сила (рис.
261, а). Значит, выталкивающая сила равна по модулю силе тяжести, действующей
на выделенный объем жидкости, и направлена вверх. Точкой приложения этой силы
должен быть центр тяжести выделенного объема. В противном случае равновесие
нарушилось бы, так как сила тяжести и выталкивающая сила образовали бы пару сил
(рис. 261, б). Но, как уже сказано, выталкивающая сила для выделенного объема
совпадает с выталкивающей силой тела. Мы приходим, таким образом, к закону
Архимеда:
Выталкивающая
сила, действующая на тело, погруженное в жидкость, равна по модулю силе
тяжести, действующей на жидкость в объеме, занимаемом телом (вытесненный
объем), направлена вертикально вверх и приложена в центре тяжести этого объема.
Центр тяжести вытесненного объема называют центром давления.
Рис. 261. а) Равнодействующая сил давления на поверхность погруженного тела равна силе тяжести, действующей на жидкость, объем которой равен объему тела, б) Если бы точка приложения равнодействующей силы не совпадала с центром тяжести вытесненного объема жидкости, то получилась бы пара сил и равновесие этого объема было бы невозможным
Для тела, имеющего простую форму, можно вычислить выталкивающую силу, рассмотрев силы давления на его поверхность. Пусть, например, тело, погруженное в жидкость, имеет форму прямого параллелепипеда и расположено так, что две его противолежащие грани горизонтальны (рис. 262). Площадь его основания обозначим через , высоту – через , а расстояние от поверхности до верхней грани – через .
Равнодействующая
сил давления жидкости составляется из сил давления на боковую поверхность
параллелепипеда и на его основания. Силы действующие на боковые грани, взаимно
уничтожаются, так как для противолежащих граней силы давления равны по модулю и
противоположны по направлению. Давление на верхнее основание равно , на нижнее
основание равно . Следовательно, силы давления на
верхнее и на нижнее основания равны соответственно
Давление на верхнее основание равно , на нижнее
основание равно . Следовательно, силы давления на
верхнее и на нижнее основания равны соответственно
причем сила направлена вниз, а сила – вверх. Таким образом, равнодействующая всех сил давления на поверхность параллелепипеда (выталкивающая сила) равна разности модулей сил и :
и направлена вертикально вверх. Но – это объем параллелепипеда, а – масса вытесненной телом жидкости. Значит, выталкивающая сила действительно равна по модулю силе тяжести, действующей на вытесненный объем жидкости.
Рис. 262. К вычислению выталкивающей силы
Рис. 263. Опытная проверка закона Архимеда при помощи «ведерка Архимеда»
Если
тело, подвешенное к чашке весов, погрузить в жидкость, то весы показывают
разность между весом тела и выталкивающей силой, т. е. весом вытесненной
жидкости. Поэтому закону Архимеда придают иногда следующую формулировку: тело,
погруженное в жидкость, теряет в своем весе столько, сколько весит вытесненная
им жидкость.
Для иллюстрации справедливости этого вывода сделаем следующий опыт (рис. 263): пустое ведерко («ведерко Архимеда») и сплошной цилиндр , имеющий объем, в точности равный вместимости ведерка, подвесим к динамометру. Затем, подставив сосуд с водой, погрузим цилиндр в воду; равновесие нарушится, и растяжение динамометра уменьшится. Если теперь наполнить ведерко водой, то динамометр снова растянется до прежней длины. Потеря в весе цилиндра как раз равна весу воды в объеме цилиндра.
По
закону равенства действия и противодействия выталкивающей силе, с которой жидкость
действует на погруженное тело, соответствует сила, с которой тело действует на
жидкость. Эта сила направлена вертикально вниз и равна весу жидкости,
вытесненной телом. Следующий опыт демонстрирует сказанное (рис. 264). Неполный
стакан с водой уравновешивают на весах. Затем в стакан погружают тело,
подвешенное на штативе; при этом чашка со стаканом опускается, и для
восстановления равновесия приходится добавить на другую чашку гирю, вес которой
равен весу воды, вытесненной телом.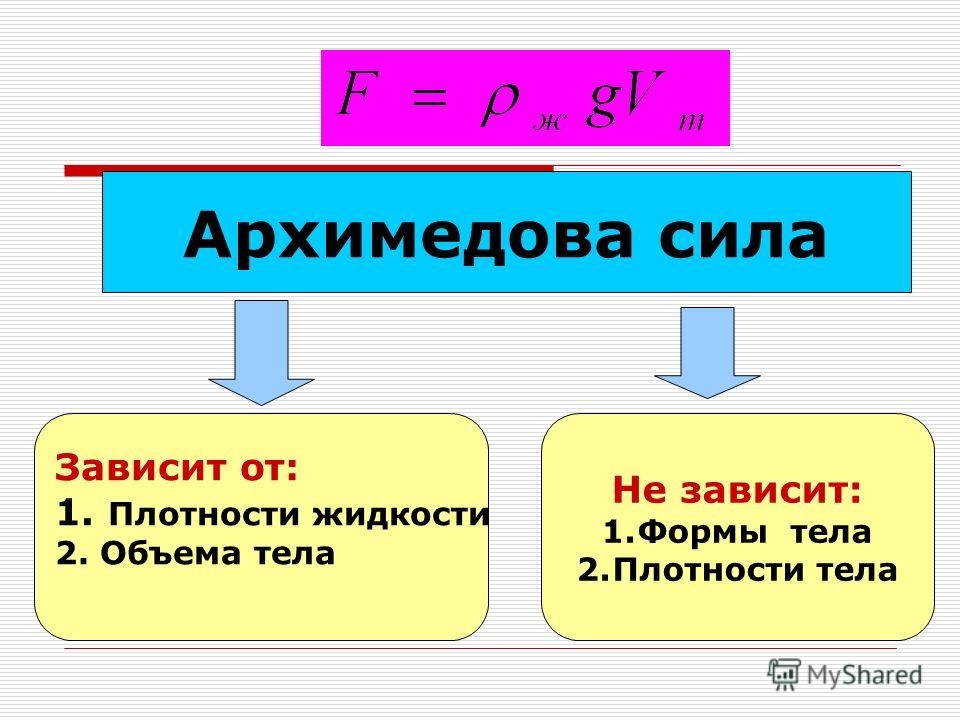
Рис. 264. Вес гири, которую нужно положить на левую чашку весов, равен весу воды, вытесненной телом
160.1. Найдите выталкивающую силу, действующую на погруженный в воду камень массы 3 кг, если его плотность равна .
160.2. Куб с ребром 100 мм погружен в сосуд, наполненный водой, поверх которой налит керосин так, что линия раздела обеих жидкостей проходит посередине ребра куба. Найдите выталкивающую силу, действующую на куб. Плотность керосина равна .
160.3 . Кусок пробки массы 10 г, обмотанный медной проволокой с поперечным сечением , остается в равновесии в воде, не погружаясь и не всплывая (табл. 1). Найдите длину проволоки.
160.4. Что произойдет с весами, находящимися в равновесии, если в стакане с водой, стоящий на чашке весов, погрузить палец, не прикасаясь пальцем ни к дну, ни к стенкам стакана?
160.5. К чашкам весов подвешены на нитках кусок меди и кусок железа массы 500 г
каждый (табл. 1). Нарушится ли равновесие, если медь погрузить в воду, а железо
– в керосин плотности . Гирю какой массы и на какую чашку
весов нужно поставить, чтобы восстановить равновесие?
Гирю какой массы и на какую чашку
весов нужно поставить, чтобы восстановить равновесие?
Цели урока: убедиться в существовании выталкивающей силы, осознать причины её возникновения и вывести правила для её вычисления, содействовать формированию мировоззренческой идеи познаваемости явлений и свойств окружающего мира.
Задачи урока: Работать над формированием умений анализировать свойства и явления на основе знаний, выделять главную причину, влияющую на результат. Развивать коммуникативные умения. На этапе выдвижения гипотез развивать устную речь. Проверить уровень самостоятельности мышления школьника по применению учащимися знаний в различных ситуациях.
Архимед – выдающийся ученый Древней
Греции, родился в 287 году до н.э. в портовом и
судостроительном г. Сиракузы на острове Сицилия.
Архимед получил блестящее образование у своего
отца, астронома и математика Фидия, родственника
сиракузского тирана Гиерона,
покровительствовавшего Архимеду. В юности
провёл несколько лет в крупнейшем культурном
центре в Александрии, где у него сложились
дружеские отношения с астрономом Кононом и
географом-математиком Эратосфеном. Это
послужило толчком к развитию его выдающихся
способностей. В Сицилию вернулся уже зрелым
ученым. Он прославился многочисленными научными
трудами главным образом в области физики и
геометрии.
Это
послужило толчком к развитию его выдающихся
способностей. В Сицилию вернулся уже зрелым
ученым. Он прославился многочисленными научными
трудами главным образом в области физики и
геометрии.
Последние годы жизни Архимед был в Сиракузах, осажденных римским флотом и войском. Шла 2-я Пуническая война. И великий ученый, не жалея сил, организовывает инженерную оборону родного города. Он построил множество удивительных боевых машин, топивших вражеские корабли, разносивших их в щепы, уничтожавших солдат. Однако слишком маленьким было войско защитников города по сравнению с огромным римским войском. И в 212 г. до н.э. Сиракузы были взяты.
Гений Архимеда вызывал восхищение у римлян и римский полководец Марцелл приказал сохранить ему жизнь. Но солдат, не знавший в лицо Архимеда, убил его.
Одним из важнейших его открытий стал
закон, впоследствии названный законом Архимеда.
Существует предание, что идея этого закона
посетила Архимеда, когда он принимал ванну, с
возгласом “Эврика!” он выскочил из ванны и нагим
побежал записывать пришедшую к нему научную
истину. Суть этой истины и предстоит выяснить,
нужно убедиться в существовании выталкивающей
силы, осознать причины её возникновения и
вывести правила для её вычисления.
Суть этой истины и предстоит выяснить,
нужно убедиться в существовании выталкивающей
силы, осознать причины её возникновения и
вывести правила для её вычисления.
Давление в жидкости или газе зависит от глубины погружения тела и приводит к появлению выталкивающей силы, действующей на тело и направленной вертикально вверх.
Если тело опустить в жидкость или газ, то под действием выталкивающей силы оно будет всплывать из более глубоких слоев в менее глубокие. Выведем формулу для определения силы Архимеда для прямоугольного параллелепипеда.
Давление жидкости на верхнюю грань равно
где: h2 – высота столба жидкости над верхней гранью.
Сила давления на верхнюю грань равна
F1= р1*S = ж*g*h2*S,
Где: S – площадь верхней грани.
Давление жидкости на нижнюю грань равно
где: h3 – высота столба жидкости над нижней гранью.
Сила давления на нижнюю грань равна
F2= p2*S = ж*g*h3*S,
Где: S – площадь нижней грани куба.
Поскольку h3 > h2, то р2 > р1 и F2 > F1.
Разность между силами F2 и F1 равна:
F2 – F1 = ж*g*h3*S – ж*g*h2*S = ж*g*S* (h3 – h2).
Так как h3 – h2 = V – объему тела или части тела, погруженной в жидкость или газ, то F2 – F1 = ж*g*S*H = g* ж*V
Произведение плотности на объем есть масса жидкости или газа. Следовательно, разность сил равна весу вытесненной телом жидкости:
F2 – F1= mж*g = Pж = Fвыт.
Выталкивающая сила есть сила Архимеда, определяющая закон Архимеда
Равнодействующая сил, действующих на боковые грани равна нулю, поэтому в расчетах не участвует.
Таким образом, на тело, погруженное в жидкость или газ, действует выталкивающая сила равная весу вытесненной им жидкости или газа.
Закон Архимеда, впервые был упомянут Архимедом
в трактате “О плавающих телах”. Архимед
писал: “тела более тяжелые, чем жидкость,
опущенные в эту жидкость, будут опускаться пока
не дойдут до самого низа, и в жидкости станут
легче на величину веса жидкости в объеме, равном
объему погруженного тела”.
Рассмотрим, как зависит сила Архимеда и зависит ли от веса тела, объема тела, плотности тела и плотности жидкости.
Исходя из формулы силы Архимеда, она зависит от
плотности жидкости, в которую погружено тело, и
от объёма этого тела. Но она не зависит, например,
от плотности вещества тела, погружаемого в
жидкость, так как эта величина не входит в
полученную формулу.
Определим теперь вес тела, погружённого в
жидкость (или газ). Так как две силы, действующие
на тело в этом случае, направлены в
противоположные стороны (сила тяжести вниз, а
архимедова сила вверх), то вес тела в жидкости
будет меньше веса тела в вакууме на архимедову
силу:
P А = m т g – m ж g = g (m т – m ж)
Таким образам, если тело погружено в жидкость (или газ), то оно теряет в своём весе столько, сколько весит вытесненная им жидкость (или газ).
Следовательно:
Сила Архимеда зависит от плотности жидкости и
объема тела или его погруженной части и не
зависит от плотности тела, его веса и объема
жидкости.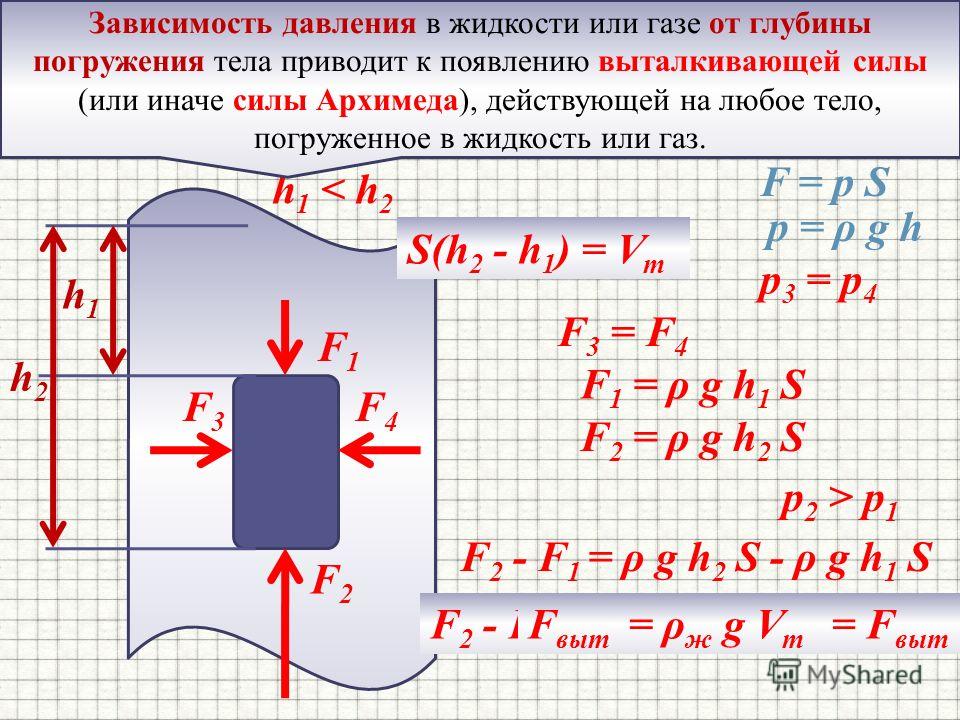
Определение силы Архимеда лабораторным методом.
Оборудование: стакан с чистой водой, стакан с соленой водой, цилиндр, динамометр.
Ход работы:
- определяем вес тела в воздухе;
- определяем вес тела в жидкости;
- находим разницу между весом тела в воздухе и весом тела в жидкости.
4. Результаты измерений:
Сделать вывод как зависит сила Архимеда от плотности жидкости.
Выталкивающая сила действует на тела любых геометрических форм. В технике наиболее распространены тела цилиндрической и сферической форм, тела с развитой поверхностью, полые тела в форме шара, прямоугольного параллелепипеда, цилиндра.
Гравитационная сила приложена к центру масс погруженного в жидкость тела и направлена перпендикулярно к поверхности жидкости.
Подъемная сила действует на тело со стороны
жидкости, направлена по вертикали вверх,
приложена к центру тяжести вытесненного объема
жидкости. Тело движется в направлении,
перпендикулярном к поверхности жидкости.
Выясним условия плавания тел, которые основываются на законе Архимеда.
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести F т и силы Архимеда F A , которые действуют на это тело. Возможны следующие три случая:
- F т > F A – тело тонет;
- F т = F A – тело плавает в жидкости или газе;
- F т
Другая формулировка (где P t – плотность тела, P s – плотность среды, в которую оно погружено):
- P t > P s – тело тонет;
- P t = P s – тело плавает в жидкости или газе;
- P t
Плотность организмов живущих в воде почти не отличается от плотности воды, поэтому прочные скелеты им не нужны! Рыбы регулируют глубину погружения, меняя среднюю плотность своего тела. Для этого им необходимо лишь изменить объем плавательного пузыря, сокращая или расслабляя мышцы.
Если тело лежит на дне в жидкости или газе, то сила Архимеда равна нулю.
Закон Архимеда используется в судостроении и
воздухоплавании.
Схема плавающего тела:
Линия действия силы тяжести тела G проходит через центр тяжести K (центр водоизмещения) вытесненного объема жидкости. В нормальном положении плавающего тела центр тяжести тела Т и центр водоизмещения K размещены по одной вертикали, называемой осью плаванья.
При качке центр водоизмещения К перемещается в точку К1, и сила тяжести тела и Архимедова сила FА образуют пару сил, которая стремится либо вернуть тело в исходное положение, либо увеличить крен.
В первом случае плавающее тело обладает статической устойчивостью, во втором случае устойчивость отсутствует. Устойчивость тела зависит от взаимного расположения центра тяжести тела Т и метацентра М (точки пересечения линии действия архимедовой силы при крене с осью плавания).
В 1783 году братья МОНГОЛЬФЬЕ изготовили огромный бумажный шар, под которым поместили чашку с горящим спиртом. Шар наполнился горячим воздухом и начал подниматься, достигнув высоты 2000 метров.
Из–за разности давлений в жидкости на разных уровнях возникает выталкивающая или Архимедова сила, которая вычисляется по формуле:
где: V – объем вытесненной телом жидкости, или же объем погружённой в жидкость части тела, ρ – плотность жидкости в которую погружено тело, и следовательно, ρV – масса вытесненной жидкости.
Архимедова сила, действующая на погруженное в жидкость (или газ) тело, равна весу жидкости (или газа), вытесненной телом. Это утверждение, называемоезаконом Архимеда , справедливо для тел любой формы.
При этом вес тела (т.е. сила с которой тело действует на опору или подвес) погруженного в жидкость уменьшается. Если принять, что вес покоящегося тела в воздухе равен mg , а именно так мы и будем поступать в большинстве задач (хотя вообще говоря на тело в воздухе также действует очень маленькая сила Архимеда со стороны атмосферы, ведь тело погружено в газ из атмосферы), то для веса тела в жидкости можно легко вывести следующую важную формулу:
Эта формула может быть использована при решении большого количества задач. Ее можно запомнить. При помощи закона Архимеда осуществляется не только мореплавание, но и воздухоплавание. Из закона Архимеда вытекает, что если средняя плотность тела ρ т больше плотности жидкости (или газа) ρ (или по–другому mg > F A), тело будет опускаться на дно. Если же ρ т ρ
(или по–другому mg F
A), тело будет плавать на поверхности жидкости. Объем погруженной части тела будет таков, что вес вытесненной жидкости равен весу тела. Для подъема воздушного шара в воздухе его вес должен быть меньше веса вытесненного воздуха. Поэтому воздушные шары заполняют легкими газами (водородом, гелием) или нагретым воздухом.
Если же ρ т ρ
(или по–другому mg F
A), тело будет плавать на поверхности жидкости. Объем погруженной части тела будет таков, что вес вытесненной жидкости равен весу тела. Для подъема воздушного шара в воздухе его вес должен быть меньше веса вытесненного воздуха. Поэтому воздушные шары заполняют легкими газами (водородом, гелием) или нагретым воздухом.
Плавание тел
Если тело находится на поверхности жидкости (плавает), то на него действует всего две силы (Архимеда вверх и тяжести вниз), которые уравновешивают друг друга. Если тело погружено только в одну жидкость, то записав второй закон Ньютона для такого случая и выполнив простые математические операции можем получить следующее выражение связывающее объемы и плотности:
где: V погр – объем погруженной части тела, V – полный объем тела. При помощи этого соотношения легко решается большинство задач на плавание тел.
Основные теоретические сведения
Импульс тела
Импульсом (количеством движения) тела называют физическую векторную величину, являющуюся количественной характеристикой поступательного движения тел.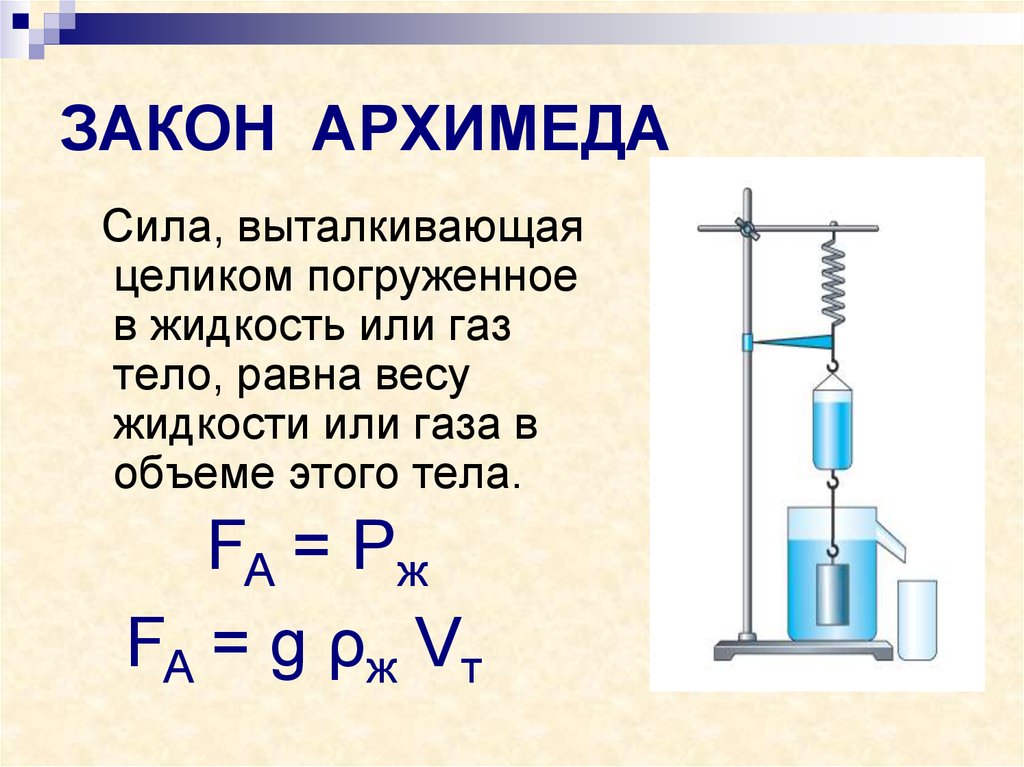 Импульс обозначается р . Импульс тела равен произведению массы тела на его скорость, т.е. он рассчитывается по формуле:
Импульс обозначается р . Импульс тела равен произведению массы тела на его скорость, т.е. он рассчитывается по формуле:
Направление вектора импульса совпадает с направлением вектора скорости тела (направлен по касательной к траектории). Единица измерения импульса – кг∙м/с.
Общий импульс системы тел равен векторной сумме импульсов всех тел системы:
Изменение импульса одного тела находится по формуле (обратите внимание, что разность конечного и начального импульсов векторная):
где: p н – импульс тела в начальный момент времени, p к – в конечный. Главное не путать два последних понятия.
Абсолютно упругий удар – абстрактная модель соударения, при которой не учитываются потери энергии на трение, деформацию, и т.п. Никакие другие взаимодействия, кроме непосредственного контакта, не учитываются. При абсолютно упругом ударе о закрепленную поверхность скорость объекта после удара по модулю равна скорости объекта до удара, то есть величина импульса не меняется. Может поменяться только его направление. При этом угол падения равен углу отражения.
Может поменяться только его направление. При этом угол падения равен углу отражения.
Абсолютно неупругий удар – удар, в результате которого тела соединяются и продолжают дальнейшее своё движение как единое тело. Например, пластилиновый шарик при падении на любую поверхность полностью прекращает свое движение, при столкновении двух вагонов срабатывает автосцепка и они так же продолжают двигаться дальше вместе.
Закон сохранения импульса
При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, такая система называется замкнутой .
В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой. Этот фундаментальный закон природы называетсязаконом сохранения импульса (ЗСИ) . Следствием его являются законы Ньютона. Второй закон Ньютона в импульсной форме может быть записан следующим образом:
Как следует из данной формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Аналогично можно рассуждать для равенства нулю проекции силы на выбранную ось. Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:
Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:
Аналогичные записи можно составить и для остальных координатных осей. Так или иначе, нужно понимать, что при этом сами импульсы могут меняться, но именно их сумма остается постоянной. Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны.
Казалось бы, нет ничего проще, чем закон Архимеда. Но когда-то сам Архимед здорово поломал голову над его открытием. Как это было?
С открытием основного закона гидростатики связана интересная история.
Интересные факты и легенды из жизни и смерти Архимеда
Помимо такого гигантского прорыва, как открытие собственно закона Архимеда, ученый имеет еще целый список заслуг и достижений. Вообще, он был гением, трудившимся в областях механики, астрономии, математики. Им написаны такие труды, как трактат «о плавающих телах», «о шаре и цилиндре», «о спиралях», «о коноидах и сфероидах» и даже «о песчинках». В последнем труде была предпринята попытка измерить количество песчинок, необходимых для того, чтобы заполнить Вселенную.
В последнем труде была предпринята попытка измерить количество песчинок, необходимых для того, чтобы заполнить Вселенную.
Роль Архимеда в осаде Сиракуз
В 212 году до нашей эры Сиракузы были осаждены римлянами. 75-летний Архимед сконструировал мощные катапульты и легкие метательные машины ближнего действия, а также так называемые “когти Архимеда”. С их помощью можно было буквально переворачивать вражеские корабли. Столкнувшись со столь мощным и технологичным сопротивлением, римляне не смогли взять город штурмом и вынуждены были начать осаду. По другой легенде Архимед при помощи зеркал сумел поджечь римский флот, фокусируя солнечные лучи на кораблях. Правдивость данной легенды представляется сомнительной, т.к. ни у одного из историков того времени упоминаний об этом нет.
Смерть Архимеда
Согласно многим свидетельствам, Архимед был убит римлянами, когда те все-таки взяли Сиракузы. Вот одна из возможных версий гибели великого инженера.
На крыльце своего дома ученый размышлял над схемами, которые чертил рукой прямо на песке. Проходящий мимо солдат наступил на рисунок, а Архимед, погруженный в раздумья, закричал: «Прочь от моих чертежей». В ответ на это спешивший куда-то солдат просто пронзил старика мечом.
Проходящий мимо солдат наступил на рисунок, а Архимед, погруженный в раздумья, закричал: «Прочь от моих чертежей». В ответ на это спешивший куда-то солдат просто пронзил старика мечом.
Ну а теперь о наболевшем: о законе и силе Архимеда…
Как был открыт закон Архимеда и происхождение знаменитой “Эврика!”
Античность. Третий век до нашей эры. Сицилия, на которой еще и подавно нет мафии, но есть древние греки.
Изобретатель, инженер и ученый-теоретик из Сиракуз (греческая колония на Сицилии) Архимед служил у царя Гиерона второго. Однажды ювелиры изготовили для царя золотую корону. Царь, как человек подозрительный, вызвал ученого к себе и поручил узнать, не содержит ли корона примесей серебра. Тут нужно сказать, что в то далекое время никто не решал подобных вопросов и случай был беспрецедентным.
Архимед долго размышлял, ничего не придумал и однажды решил сходить в баню. Там, садясь в тазик с водой, ученый и нашел решение вопроса. Архимед обратил внимание на совершенно очевидную вещь: тело, погружаясь в воду, вытесняет объем воды, равный собственному объему тела. Именно тогда, даже не потрудившийся одеться, Архимед выскочил из бани и кричал свое знаменитое «эврика», что означает «нашел». Явившись к царю, Архимед попросил выдать ему слитки серебра и золота, равные по массе короне. Измеряя и сравнивая объем воды, вытясняемой короной и слитками, Архимед обнаружил, что корона изготовлена не из чистого золота, а имеет примеси серебра. Это и есть история открытия закона Архимеда.
Именно тогда, даже не потрудившийся одеться, Архимед выскочил из бани и кричал свое знаменитое «эврика», что означает «нашел». Явившись к царю, Архимед попросил выдать ему слитки серебра и золота, равные по массе короне. Измеряя и сравнивая объем воды, вытясняемой короной и слитками, Архимед обнаружил, что корона изготовлена не из чистого золота, а имеет примеси серебра. Это и есть история открытия закона Архимеда.
Суть закона Архимеда
Если Вы спрашиваете себя, как понять закон Архимеда, мы ответим. Просто сесть, подумать, и понимание придет. Собственно, этот закон гласит:
На тело, погруженное в газ или жидкость действует выталкивающая сила, равная весу жидкости (газа) в объеме погруженной части тела. Эта сила называется силой Архимеда.
Как видим, сила Архимеда действует не только на тела, погруженные в воду, но и на тела в атмосфере. Сила, которая заставляет воздушный шар подниматься вверх – та же сила Архимеда. Высчитывается Архимедова сила по формуле:
Здесь первый член – плотность жидкости (газа), второй – ускорение свободного падения, третий – объем тела. Если сила тяжести равна силе Архимеда, тело плавает, если больше – тонет, а если меньше – всплывает до тех пор, пока не начнет плавать.
Если сила тяжести равна силе Архимеда, тело плавает, если больше – тонет, а если меньше – всплывает до тех пор, пока не начнет плавать.
В данной статье мы рассмотрели закон Архимеда для чайников. Если Вы хотите узнать, как как решать задачи, где есть закон Архимеда, обращайтесь к . Лучшие авторы с удовольствием поделятся знаниями и разложат решение самой сложной задачи «по полочкам».
Калькулятор принципа Архимеда
Автор Purnima Singh, PhD
Отзыв Стивена Вудинга
Последнее обновление: 29 апреля 2022 г.
Содержание:- Что такое закон Архимеда? – Определение принципа Архимеда
- Формула принципа Архимеда
- Плавучесть и закон плавучести
- Пример расчета силы плавучести
- Как пользоваться калькулятором принципа Архимеда
- Часто задаваемые вопросы
Принципиальный калькулятор Архимеда Омни поможет вам понять концепцию плавучести . Вы также можете использовать его для определения плотностей и изменений массы и веса объектов, когда они погружены в жидкость.
Вы когда-нибудь задумывались почему одни предметы плавают, а другие тонут ? Если у вас есть, вы пришли в нужное место.
Продолжайте читать эту статью, чтобы узнать о принципе Архимеда и его формуле . Вы также найдете примеры расчетов выталкивающей силы и некоторые интересные приложения принципа Архимеда.
Начнем сначала с изучения принципа Архимеда.
Что такое закон Архимеда? – Определение принципа Архимеда
Когда мы погружаем объект в любую жидкость, на объект действует направленная вверх сила. Эта восходящая сила называется выталкивающей силой или выталкивающей силой .
Происхождение выталкивающей силы заключается в том, что давление увеличивается с увеличением глубины жидкости (вспомните уравнение гидростатического давления). Следовательно, восходящая сила, приложенная жидкостью к нижней части объекта, больше, чем направленная вниз сила, приложенная к верхней части объекта. Воспользуйтесь нашим специальным инструментом, чтобы узнать больше о плавучести и провести эксперименты с плавучестью дома.
Воспользуйтесь нашим специальным инструментом, чтобы узнать больше о плавучести и провести эксперименты с плавучестью дома.
Согласно закону Архимеда, когда объект частично или полностью погружен в жидкость, он вытесняет часть жидкости. Выталкивающая сила, действующая на предмет, равна весу вытесненной им жидкости .
Чтобы понять, что означает принцип, попробуем вывести формулу закона Архимеда.
Принципиальная формула Архимеда
Рассмотрим объект высотой h−xh-xh−x и массой MMM, погруженный в жидкость плотностью ρ\rhoρ (см. рис. 1). Если aaa — площадь поперечного сечения его верхней и нижней граней, мы можем записать выражения для вертикально направленной вниз (F1F_1F1) и восходящей силы (F2F_2F2) на объект как:
Рис. 1: Давление на объект, погруженный в жидкости увеличивается с глубиной.F1=p1a=xρgaF2=p2a=hρga\маленький \начать{выравнивать*} F_1 &= p_1 a = x \rho g a\\ F_2 &= p_2 a = h \rho g a \end{align*}F1F2=p1a=xρga=p2a=hρga
где:
- p1=xρgp_1 = x \rho gp1=xρg – Давление на верхнюю грань объект;
- p2=hρgp_2 = h \rho gp2=hρg – Давление на нижнюю грань объекта;
- xxx – глубина верхней поверхности объекта в жидкости; и
- hhh – Глубина нижней поверхности объекта в жидкости.

Поскольку h>xh>xh>x, заметим, что F2>F1F_2 > F_1F2>F1. Чистая восходящая сила или выталкивающая сила, действующая на объект, равна:
FB=F2−F1=(h−x)ρga=[(h−x)×a]ρg=Vρg\small \начать{выравнивать*} F_B & = F_2 – F_1\\ & = (h – x) \rho g a\\ & = [(h-x)\times a]\rho g\\ & = V\rho g \end{align*}FB=F2−F1=(h−x)ρga=[(h−x)×a]ρg=Vρg
Где VVV — объем объекта, а равен объему вытесненной жидкости VflV_{fl}Vfl.
Если mmm — масса вытесненной жидкости, мы можем переписать вышеприведенное уравнение как:
FB=Vflρg=mg\small \начать{выравнивать*} F_B & = V_{fl} \rho g \\ & = м г \конец{выравнивание*} FB=Vflρg=mg
Другими словами, выталкивающая сила, действующая на объект, равна весу жидкости, вытесненной объектом.
Плавучесть и закон плавучести
Поскольку истинный вес объекта равен Wobj=MgW_{obj} = M g Wobj=Mg, а сила, действующая на него вверх, равна FB=mgF_B= m gFB=mg, наблюдаемый вес объекта в жидкости составляет (см. рис. 2):
рис. 2):
Wobs=Wobj-FB=Mg-mg\маленький \начать{выравнивать*} W_{obs} &= W_{obj} – F_B\\ &= Мг – м г \end{align*}Wobs=Wobj-FB=Mg-mg
Это означает, что когда объект погружен в жидкость, его наблюдаемый вес становится меньше его истинного веса на величину, равную весу жидкости, вытесняемой объектом.
Теперь, , если вес жидкости, вытесненной погруженным телом, больше или равен весу тела, тело будет плавать. В противном случае он утонет 96\ \rm{N} \\ \end{align*}FB=Mh3O×g=3,70×105 кг×9,8 м/с2=3,63×106 N
- Вы также можете использовать наш принципиальный калькулятор Архимеда, чтобы решить ту же задачу с всего несколько кликов.
Как пользоваться калькулятором Архимеда
В этом разделе мы попытаемся определить плотность неизвестного объекта с помощью нашего калькулятора Архимеда. Пусть истинная масса (масса в воздухе) и кажущаяся масса (при погружении в воду) камня равны 540 г и 340 г соответственно. Рассчитаем среднюю плотность этой породы следующим образом:
Рассчитаем среднюю плотность этой породы следующим образом:
Введите истинную массу и кажущуюся массу породы как 540 г и 340 г в соответствующих полях.
В раскрывающемся меню выберите тип жидкости в качестве воды. Поле плотности заполнится автоматически. Вы также можете ввести плотность жидкости вручную.
Принципиальный калькулятор Архимеда покажет плотность горной породы как 2,70 г/см 3 и объем скалы 200 см 3 . Он также покажет выталкивающую силу , действующую на камень как 1,96 Н, и сообщение, будет ли камень всплывать или тонет.
Рассмотрим другой пример, когда мы бросаем камень массой 5 кг в цилиндрический контейнер с площадью основания 700 см 2 . Если высота воды внутри сосуда изменится на 2,86 см, мы можем рассчитать выталкивающую силу как:
Нажмите на
Расширенный режимкнопку под калькулятором и введите изменение высоты жидкости (2,9 см) и площади поверхности жидкости (700 см 2 ).
Введите истинную массу объекта (5 кг).
Калькулятор отобразит объем вытесненной жидкости (2030 см 3 ) и выталкивающую силу (19,89 Н).
Примечание. Вы можете ввести любые известные вам переменные, а калькулятор рассчитает остальные.
Часто задаваемые вопросы
Как рассчитать плотность по закону Архимеда?
Чтобы рассчитать плотность объекта по закону Архимеда, следуйте приведенным инструкциям:
Измерьте массу объекта в воздухе (m a ) и когда он полностью погружен в воду (m w ).
Рассчитать потерю массы (м a – m w ), что также является массой вытесненной воды.
Определите объем вытесненной воды путем деления массы вытесненной воды на плотность воды, т.
 е. 1000 кг/м 3 . Это значение также является объемом объекта.
е. 1000 кг/м 3 . Это значение также является объемом объекта.Найдите плотность объекта , разделив его массу на объем.
Какова выталкивающая сила монеты, погруженной в воду, если она вытесняет 200 г жидкости?
1,96 Н . Выталкивающая сила, действующая на монету, равна весу вытесненной ею воды. Вес 200 г (0,2 кг) воды равен W = 0,2 кг × 9,8 м/с 2 = 1,96 Н. Следовательно, выталкивающая сила также равна 1,96 Н.
По какой формуле вычисляется выталкивающая сила?
Формула для расчета выталкивающей силы F B на тело, погруженное в жидкость:
F B = V × g × d
где:
- V – Объем жидкости, вытесняемой погруженным телом;
- г – ускорение свободного падения; и
- d – Плотность жидкости.
Каково применение принципа Архимеда?
Некоторые области применения принципа Архимеда:
- Проектирование кораблей и подводных лодок;
- Ареометры для определения удельного веса или плотности жидкостей;
- Геология для определения плотности и, следовательно, чистоты неизвестных объектов; и
- Воздушные шары.

Как плавучесть объясняется законом Архимеда?
Согласно закону Архимеда, будет ли объект плавать или тонуть в жидкости, зависит от следующих критериев:
Если истинный вес тела, погруженного в жидкость, больше выталкивающей силы , действующей на него, то тело опустится на дно жидкости.
Если истинный вес меньше чем выталкивающая сила , тело будет плавать .
Purnima Singh, PhD
🤔 Введите значение двух или более известных переменных, и калькулятор рассчитает остальные.
Свойства объекта
Истинная масса объекта
Плотность объекта
Объем объекта
Истинный вес объекта
Кажущаяся масса объекта
Кажущий вес объекта
Свойства жидкости
Жидкости типа
Плотность жидкости
объема вытесненной жидкости
Масса жидкости смещена
РЕЗУЛЬТАТ
Сила BUOYANCY
. Проверка 403
Проверка 403
. похожие калькуляторы гидромеханики 💧
гравитация в градусах APIБаллистический коэффициент уравнение Бернулли… еще 37
Принцип Архимеда | Физика
Цели обучения
К концу этого раздела вы сможете:
- Определение выталкивающей силы.
- Государственный закон Архимеда.
- Поймите, почему объекты плавают или тонут.
- Понять взаимосвязь между плотностью и законом Архимеда.
Когда вы встаете после принятия теплой ванны, ваши руки кажутся странно тяжелыми. Это потому, что у вас больше нет плавучей поддержки воды. Откуда берется эта выталкивающая сила? Почему одни вещи плавают, а другие нет? Получают ли объекты, которые тонут, какую-либо поддержку от жидкости? Ваше тело поддерживается атмосферой или это касается только гелиевых шаров? (См. рис. 1.)
Рис. 1. (a) Даже объекты, которые тонут, например этот якорь, частично поддерживаются водой при погружении. (b) Подводные лодки имеют регулируемую плотность (балластные цистерны), так что они могут плавать или тонуть по желанию. (Фото: Allied Navy) (c) Наполненные гелием воздушные шары тянут вверх свои нити, демонстрируя плавучесть воздуха. (кредит: Crystl)
(Фото: Allied Navy) (c) Наполненные гелием воздушные шары тянут вверх свои нити, демонстрируя плавучесть воздуха. (кредит: Crystl)
Ответы на все эти и многие другие вопросы основаны на том факте, что давление в жидкости увеличивается с глубиной. Это означает, что восходящая сила на нижней части объекта в жидкости больше, чем направленная вниз сила на верхней части объекта. Есть сетка наверху, или выталкивающая сила на любой объект в любой жидкости. (См. рис. 2.) Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и всплывет. Если выталкивающая сила меньше веса тела, то оно утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится в жидкости.
Выталкивающая силаВыталкивающая сила — это чистая направленная вверх сила, действующая на любой объект в любой жидкости.
Рис.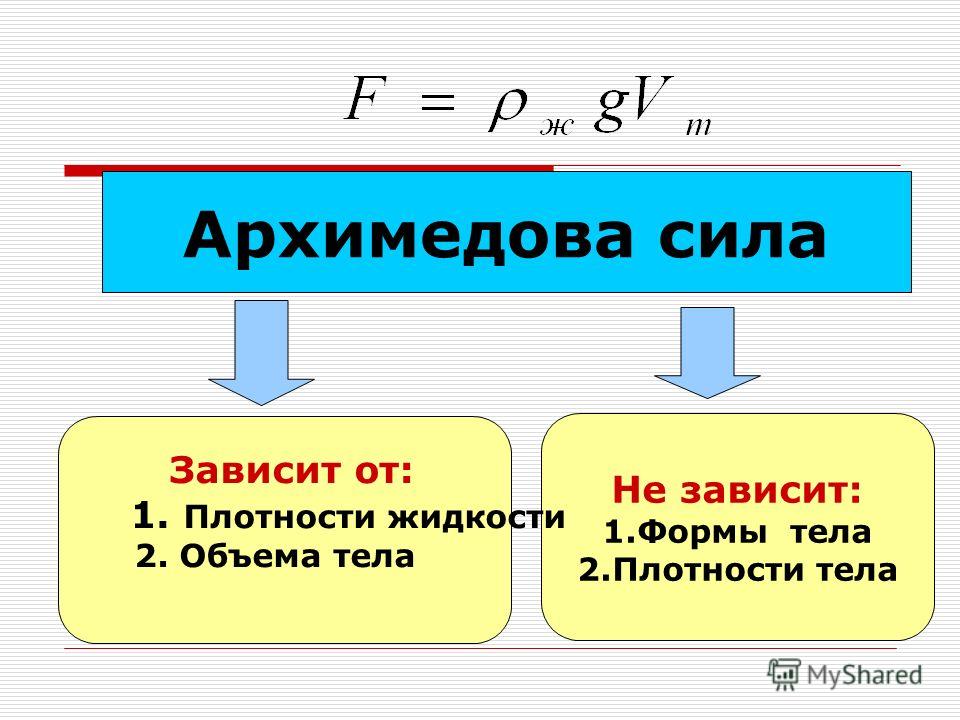 2. Давление из-за веса жидкости увеличивается с глубиной, начиная с P = hρg . Это давление и связанная с ним восходящая сила на дне цилиндра больше, чем направленная вниз сила на верхней части цилиндра. Их отличие – выталкивающая сила F B . (Горизонтальные силы компенсируются.)
2. Давление из-за веса жидкости увеличивается с глубиной, начиная с P = hρg . Это давление и связанная с ним восходящая сила на дне цилиндра больше, чем направленная вниз сила на верхней части цилиндра. Их отличие – выталкивающая сила F B . (Горизонтальные силы компенсируются.)
Насколько велика эта выталкивающая сила? Чтобы ответить на этот вопрос, подумайте о том, что происходит, когда погруженный объект вынимают из жидкости, как показано на рис. 3.9.0003
Рис. 3. (a) На объект, погруженный в жидкость, действует выталкивающая сила F B . Если F B больше веса объекта, объект поднимется. Если F B меньше веса объекта, объект утонет. (b) Если объект удаляется, он заменяется жидкостью, имеющей вес w fl . Поскольку этот вес поддерживается окружающей жидкостью, выталкивающая сила должна равняться весу вытесненной жидкости. то есть F B = w fl , формулировка закона Архимеда.
Пространство, которое он занимает, заполнено жидкостью, имеющей вес w fl . Этот вес поддерживается окружающей жидкостью, поэтому выталкивающая сила должна равняться w fl , весу жидкости, вытесненной объектом. Это дань уважения гению греческого математика и изобретателя Архимеда (ок. 287–212 до н. э.), который сформулировал этот принцип задолго до того, как понятия силы были прочно установлены. Прописью Закон Архимеда заключается в следующем: выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости. In equation form, Archimedes’ principle is
F B = w fl ,
where F B is the buoyant force and w fl is the weight of the fluid смещается объектом. Принцип Архимеда действителен в целом для любого объекта в любой жидкости, полностью или частично погруженного в воду.
Закон Архимеда Согласно этому принципу выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости. In equation form, Archimedes’ principle is
In equation form, Archimedes’ principle is
F B = w fl ,
where F B is the buoyant force and w fl is the weight of the fluid смещается объектом.
Humm … Высокотехнологичные купальники для тела были представлены в 2008 году в рамках подготовки к Олимпийским играм в Пекине. Одна проблема (и международное правило) заключалась в том, что эти костюмы не должны давать никакого преимущества в плавучести. Как вы думаете, можно ли проверить это правило?
Установление связей: домашнее исследованиеПлотность алюминиевой фольги в 2,7 раза больше плотности воды. Возьмите кусок фольги, скатайте его в шар и бросьте в воду. Он тонет? Почему или почему нет? Можете ли вы заставить его утонуть?
Плавающий и тонущий
Бросьте в воду кусок глины. Он утонет. Затем слепите кусок глины в форме лодки, и она будет плавать. Из-за своей формы лодка вытесняет больше воды, чем глыба, и испытывает большую выталкивающую силу. То же самое и со стальными кораблями. 9{3}\text{или}\text{г/мл}\справа)\\[/латекс]
Из-за своей формы лодка вытесняет больше воды, чем глыба, и испытывает большую выталкивающую силу. То же самое и со стальными кораблями. 9{3}\text{или}\text{г/мл}\справа)\\[/латекс]
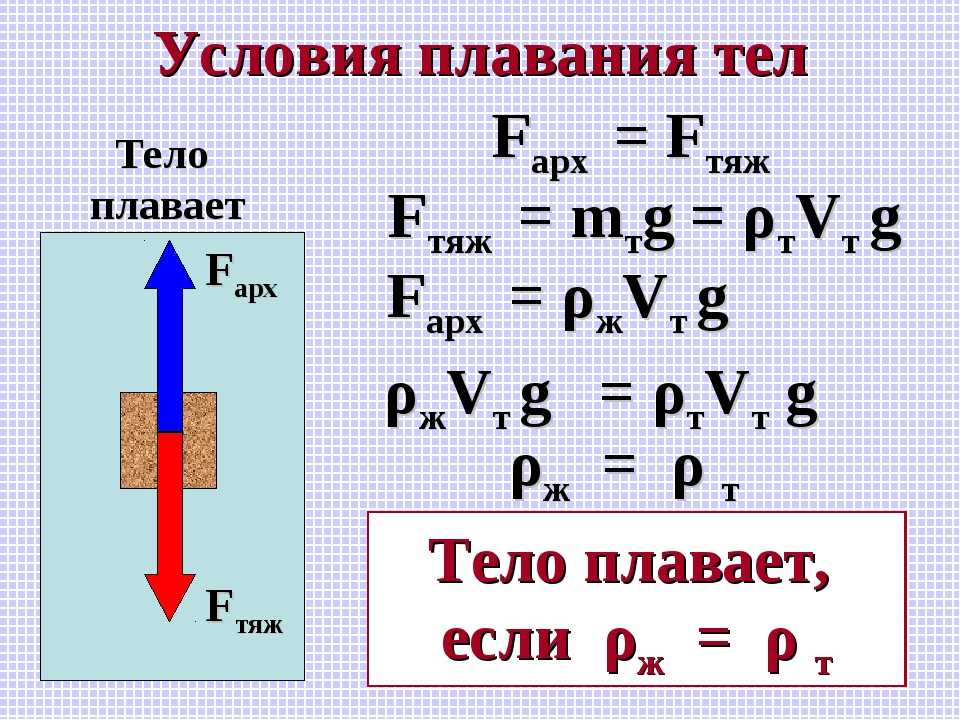 30
30Пример 1. Расчет выталкивающей силы: зависимость от формы. вес стали. б) Какова максимальная выталкивающая сила, которую вода могла бы воздействовать на ту же сталь, если бы из нее сделали лодку, способную переместить 1,00 × 10
5 м 3 воды? Стратегия для (a) Чтобы найти выталкивающую силу, мы должны найти вес вытесненной воды.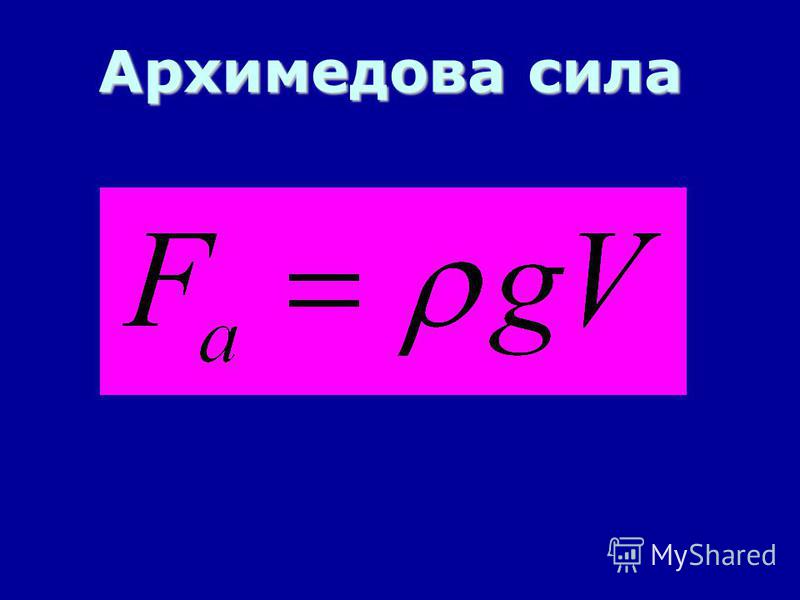 Мы можем сделать это, используя плотности воды и стали, приведенные в таблице 1. Заметим, что, поскольку сталь полностью погружена в воду, ее объем и объем воды одинаковы. Зная объем воды, мы можем найти ее массу и вес.
Мы можем сделать это, используя плотности воды и стали, приведенные в таблице 1. Заметим, что, поскольку сталь полностью погружена в воду, ее объем и объем воды одинаковы. Зная объем воды, мы можем найти ее массу и вес.
Сначала мы используем определение плотности [латекс]\rho =\frac{m}{V}\\[/латекс] , чтобы найти объем стали, а затем подставляем значения по массе и плотности. Это дает 9{7}\text{N}\\[/latex], что намного больше выталкивающей силы, поэтому сталь останется погруженной. Обратите внимание, что выталкивающая сила округляется до двух цифр, потому что плотность стали выражается только двумя цифрами.
Стратегия для (b)Здесь нам дан максимальный объем воды, который может вытеснить стальная лодка. Выталкивающая сила равна весу этого объема воды.
Решение для (b) Масса вытесненной воды определяется по ее отношению к плотности и объему, оба из которых известны. то есть 9{8}\text{N}\end{массив}\\[/latex].
то есть 9{8}\text{N}\end{массив}\\[/latex].
Максимальная выталкивающая сила в десять раз превышает вес стали, а это означает, что корабль может нести груз, в девять раз превышающий его собственный вес, и не утонуть.
Соединения: домашнее исследованиеКусок бытовой алюминиевой фольги толщиной 0,016 мм. Возьмите кусок фольги размером 10 на 15 см. а) Какова масса этого куска фольги? (b) Если фольгу сложить так, чтобы получились четыре стороны, и добавить к этой «лодке» скрепки или шайбы, то какая форма лодки позволит вместить больше всего «груза» при погружении в воду? Проверьте свой прогноз.
Плотность и принцип Архимеда
Плотность играет решающую роль в принципе Архимеда. Средняя плотность объекта — это то, что в конечном итоге определяет, плавает ли он. Если его средняя плотность меньше плотности окружающей жидкости, он будет плавать. Это связано с тем, что жидкость, имеющая более высокую плотность, содержит большую массу и, следовательно, больший вес в том же объеме. Таким образом, выталкивающая сила, равная весу вытесненной жидкости, больше веса объекта. Точно так же объект, более плотный, чем жидкость, утонет. Степень погружения плавучего объекта зависит от того, как плотность объекта связана с плотностью жидкости. На рисунке 4, например, незагруженный корабль имеет меньшую плотность и меньше погружено в воду по сравнению с тем же загруженным кораблем. Мы можем получить количественное выражение для фракции, погруженной в воду, учитывая плотность. Погруженная доля представляет собой отношение погруженного объема к объему объекта, или
Таким образом, выталкивающая сила, равная весу вытесненной жидкости, больше веса объекта. Точно так же объект, более плотный, чем жидкость, утонет. Степень погружения плавучего объекта зависит от того, как плотность объекта связана с плотностью жидкости. На рисунке 4, например, незагруженный корабль имеет меньшую плотность и меньше погружено в воду по сравнению с тем же загруженным кораблем. Мы можем получить количественное выражение для фракции, погруженной в воду, учитывая плотность. Погруженная доля представляет собой отношение погруженного объема к объему объекта, или
[латекс] \ text {фракция погружена =} \ frac {{V} _ {\ text {sub}}} {{V} _ {\ text {obj}}} = \ frac {{V} _ {\ text{fl}}}{{V}_{\text{obj}}}\\[/latex].
Погруженный объем равен объему вытесненной жидкости, который мы называем V fl . Теперь мы можем получить соотношение между плотностями, подставив [латекс]\ро =\фрак{м}{В}\\[/латекс] в выражение. Это дает
[латекс]\frac{{V}_{\text{fl}}}{{V}_{\text{obj}}}=\frac{{m}_{\text{fl}} /{\rho}_{\text{fl}}}{{m}_{\text{obj}}/{\overline{\rho}}_{\text{obj}}}[/latex],
, где [латекс]{\overline{\rho}}_{\text{obj}}\\[/латекс] – средняя плотность объекта, а ρ fl – плотность жидкости. Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они сокращаются в уравнении, оставляя
Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они сокращаются в уравнении, оставляя
[латекс]\текст{фракция под водой}=\фракция{{\overline{\rho}}_{ \text{obj}}}{{\rho }_{\text{fl}}}\\[/latex].
Рис. 4. Незагруженное судно (а) плавает выше в воде, чем загруженное судно (б).
Мы используем это последнее соотношение для измерения плотности. Это делается путем измерения доли погруженного плавучего объекта, например, с помощью ареометра. Полезно определить отношение плотности объекта к жидкости (обычно воде) как удельный вес :
[латекс]\text{удельный вес}=\frac{\overline{\rho}}{{ \rho }_{\text{w}}}\\[/latex],
, где [latex]\overline{\rho }\\[/latex] – средняя плотность объекта или вещества, а ρ w – плотность воды при 4,00°C. Удельный вес безразмерен и не зависит от того, какие единицы измерения используются для ρ . Если объект плавает, его удельный вес меньше единицы. Если он тонет, его удельный вес больше единицы. Более того, доля плавучего объекта, находящегося под водой, равна его удельному весу. Если удельный вес объекта точно равен 1, то он останется в жидкости во взвешенном состоянии, не тонет и не плавает. Аквалангисты пытаются получить это состояние, чтобы они могли парить в воде. Мы измеряем удельный вес жидкостей, таких как аккумуляторная кислота, радиаторная жидкость и моча, как показатель их состояния. Одно из устройств для измерения удельного веса показано на рис. 5.9.0003
Более того, доля плавучего объекта, находящегося под водой, равна его удельному весу. Если удельный вес объекта точно равен 1, то он останется в жидкости во взвешенном состоянии, не тонет и не плавает. Аквалангисты пытаются получить это состояние, чтобы они могли парить в воде. Мы измеряем удельный вес жидкостей, таких как аккумуляторная кислота, радиаторная жидкость и моча, как показатель их состояния. Одно из устройств для измерения удельного веса показано на рис. 5.9.0003
Удельный вес — это отношение плотности объекта к жидкости (обычно воде).
Рис. 5. Этот ареометр плавает в жидкости с удельным весом 0,87. Стеклянный ареометр наполнен воздухом и утяжелен свинцом на дне. Он лучше всего всплывает в самых плотных жидкостях и был откалиброван и промаркирован таким образом, чтобы по нему можно было напрямую считывать удельный вес.
Пример 2. Расчет средней плотности: плавающая женщина
Предположим, что женщина весом 60,0 кг плавает в пресной воде, при этом 97,0% ее объема погружено под воду, когда ее легкие наполнены воздухом. Какая у нее средняя плотность?
Какая у нее средняя плотность?
Плотность тела женщины можно найти, решив уравнение {\rho}_{\text{fl}}}\\[/latex]
для плотности объекта. Это дает
[латекс] {\ overline {\ rho}} _ {\ text {obj}} = {\ overline {\ rho}} _ {\ text {person}} = \ left (\ text {фракция погружена} \right)\cdot {\rho}_{\text{fl}}\\[/latex]. 9{3}}\\[/латекс].
ОбсуждениеЕе плотность меньше плотности жидкости. Мы ожидаем этого, потому что она плавает. Плотность тела — один из показателей процентного содержания жира в организме человека, представляющий интерес для медицинской диагностики и спортивных тренировок. (См. рис. 6.)
Рис. 6. Субъект в «резервуаре для жира», где его взвешивают, когда он полностью погружен в воду, в рамках определения плотности тела. Субъект должен полностью опорожнить легкие и удерживать металлический груз, чтобы утонуть. Делаются поправки на остаточный воздух в его легких (измеряемый отдельно) и вес металла. Его скорректированный вес в погруженном состоянии, его вес в воздухе и щипковые тесты стратегических жировых областей используются для расчета его процентного содержания жира в организме.
Его скорректированный вес в погруженном состоянии, его вес в воздухе и щипковые тесты стратегических жировых областей используются для расчета его процентного содержания жира в организме.
Существует много очевидных примеров объектов или веществ с более низкой плотностью, плавающих в жидкостях с более высокой плотностью: масло на воде, воздушный шар, кусочек пробки в вине, айсберг и горячий воск в «лавовой лампе», ” назвать несколько. Менее очевидные примеры включают лаву, поднимающуюся из вулкана, и горные хребты, плавающие на более плотной коре и мантии под ними. Даже кажущаяся твердой Земля обладает жидкими характеристиками.
Дополнительные измерения плотности
Один из наиболее распространенных методов определения плотности показан на рис. 7.
Рис. 7. (a) Монета взвешивается в воздухе. (b) Определяется кажущийся вес монеты, когда она полностью погружена в жидкость известной плотности. Эти два измерения используются для расчета плотности монеты.
Предмет, в данном случае монета, взвешивается в воздухе, а затем снова взвешивается при погружении в жидкость. Плотность монеты, показатель ее подлинности, можно рассчитать, если известна плотность жидкости. Этот же метод можно использовать и для определения плотности жидкости, если известна плотность монеты. Все эти расчеты основаны на законе Архимеда. Принцип Архимеда гласит, что выталкивающая сила, действующая на объект, равна весу вытесненной жидкости. Это, в свою очередь, означает, что объект выглядит как , весит меньше в погруженном состоянии; мы называем это измерение кажущимся весом объекта . Объект испытывает кажущуюся потерю веса , равную весу вытесненной жидкости. В качестве альтернативы, на весах, измеряющих массу, объект испытывает кажущуюся потерю массы , равную массе вытесненной жидкости. То есть
кажущаяся потеря массы = масса вытесненной жидкости
или
кажущаяся потеря массы = масса вытесненной жидкости.
Следующий пример иллюстрирует использование этой техники.
Пример 3. Расчет плотности: является ли монета подлинной?
Масса древнегреческой монеты определена на воздухе как 8,630 г. Когда монета погружена в воду, как показано на рисунке 7, ее кажущаяся масса составляет 7800 г. Рассчитайте ее плотность, учитывая, что плотность воды составляет 1000 г/см 3 и что эффекты, вызванные проволокой, подвешивающей монету, пренебрежимо малы.
СтратегияЧтобы рассчитать плотность монеты, нам нужны ее масса (которая задана) и объем. Объем монеты равен объему вытесненной воды. Объем вытесненной воды V w можно найти, решив уравнение для плотности [латекс]\rho =\frac{m}{V}\\[/latex] для V .
Раствор Объем воды [латекс] {V} _ {\ text {w}} = \ frac {{m} _ {\ text {w}}} {{\ rho } _ {\ text{w}}}\\[/latex] где м w — масса вытесненной воды. Как уже отмечалось, масса вытесненной воды равна кажущейся потере массы, которая составляет 9{3}\\[/латекс].
Как уже отмечалось, масса вытесненной воды равна кажущейся потере массы, которая составляет 9{3}\\[/латекс].
Из Таблицы 1 видно, что эта плотность очень близка к плотности чистого серебра, подходящего для этого типа древних монет. Большинство современных подделок не являются чистым серебром.
Это возвращает нас к принципу Архимеда и тому, как он возник. Как гласит история, царь Сиракуз поручил Архимеду определить, поставляет ли королевский коронщик корону из чистого золота. Чистоту золота трудно определить по цвету (оно может быть разбавлено другими металлами и все равно выглядеть таким же желтым, как чистое золото), а другие аналитические методы еще не были придуманы. Однако даже древние люди понимали, что плотность золота больше, чем у любого другого известного тогда вещества. Архимед якобы мучился над своей задачей и однажды получил вдохновение в общественных банях, размышляя о поддержке, которую вода оказала его телу. Он придумал свой ныне знаменитый принцип, увидел, как применять его для определения плотности, и голышом побежал по улицам Сиракуз с криком «Эврика!» (по-гречески «я нашел»).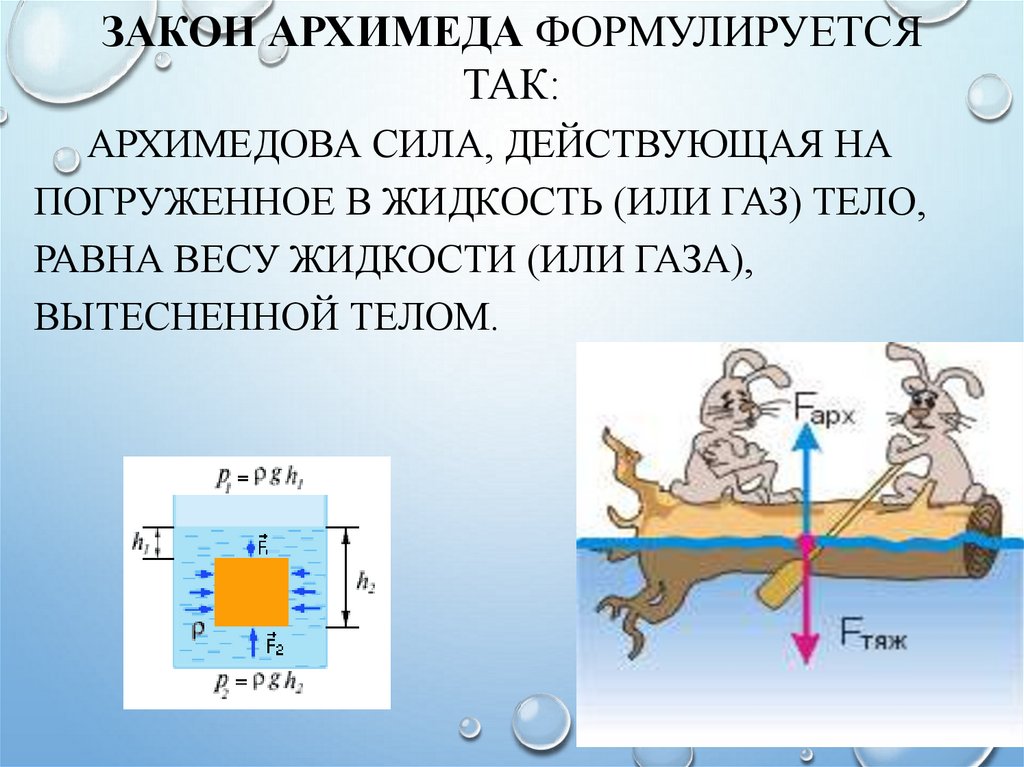 Подобное поведение время от времени можно наблюдать и у современных физиков!
Подобное поведение время от времени можно наблюдать и у современных физиков!
Когда объекты всплывут и когда они утонут? Узнайте, как плавучесть работает с блоками. Стрелки показывают приложенные силы, и вы можете изменять свойства блоков и жидкости.
Нажмите, чтобы запустить симуляцию.
Резюме раздела
- Выталкивающая сила — это чистая направленная вверх сила, действующая на любой объект в любой жидкости. Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и всплывет. Если выталкивающая сила меньше веса тела, то оно утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится в жидкости.
- Принцип Архимеда гласит, что выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости.
- Удельный вес — это отношение плотности объекта к жидкости (обычно воде).

Концептуальные вопросы
1. Чтобы вытащить пробку в полной ванне, требуется большее усилие, чем когда она пуста. Противоречит ли это принципу Архимеда? Поясните свой ответ.
2. Создают ли жидкости выталкивающую силу в «невесомой» среде, например, в космическом корабле? Поясните свой ответ.
3. Будет ли один и тот же корабль плавать выше в соленой воде, чем в пресной? Поясните свой ответ.
4. Шарики упали в частично заполненную раковину ванны на дно. Часть их веса приходится на выталкивающую силу, но сила, действующая на дно ванны, увеличивается точно на вес шариков. Объяснить, почему.
Задача и упражнения
1. Какая часть льда находится под водой, когда он плавает в пресной воде, если плотность воды при 0°С очень близка к 1000 кг/м 3 ?
2. Бревна иногда плавают вертикально в озере, потому что один конец стал заболоченным и более плотным, чем другой. Какова средняя плотность бревна одинакового диаметра, которое плавает на 20,0 % своей длины над водой?
3. Найдите плотность жидкости, в которой плавает ареометр плотностью 0,750 г/мл, погруженный на 92,0% своего объема.
Найдите плотность жидкости, в которой плавает ареометр плотностью 0,750 г/мл, погруженный на 92,0% своего объема.
4. Если ваше тело имеет плотность 995 кг/м 3 , какая часть вашего тела будет погружена при плавном плавании в: (a) пресной воде? (b) Соленая вода плотностью 1027 кг/м 3 ?
5. В костях птиц есть воздушные карманы, чтобы уменьшить их вес — это также дает им среднюю плотность, значительно меньшую, чем у костей других животных. Предположим, орнитолог взвешивает птичью кость в воздухе и в воде и обнаруживает, что ее масса составляет 45,0 г , а ее кажущаяся масса в погруженном состоянии составляет 3,60 г (кость водонепроницаема). а) Какая масса воды вытесняется? б) Каков объем кости? в) Какова его средняя плотность?
6. Камень массой 540 г в воздухе имеет кажущуюся массу 342 г при погружении в воду. а) Какая масса воды вытесняется? б) Каков объем камня? в) Какова его средняя плотность? Соответствует ли это стоимости гранита?
7. Принцип Архимеда можно использовать для расчета плотности жидкости и твердого тела. Предположим, что кусок железа массой 390,0 г в воздухе имеет кажущуюся массу 350,5 г, когда он полностью погружен в неизвестную жидкость. а) Какую массу жидкости вытесняет железо? (b) Каков объем железа, используя его плотность, указанную в таблице 1. (c) Рассчитайте плотность жидкости и определите ее.
Принцип Архимеда можно использовать для расчета плотности жидкости и твердого тела. Предположим, что кусок железа массой 390,0 г в воздухе имеет кажущуюся массу 350,5 г, когда он полностью погружен в неизвестную жидкость. а) Какую массу жидкости вытесняет железо? (b) Каков объем железа, используя его плотность, указанную в таблице 1. (c) Рассчитайте плотность жидкости и определите ее.
8. При иммерсионном измерении плотности тела женщины установлено, что ее масса в воздухе составляет 62,0 кг, а кажущаяся масса – 0,0850 кг при полном погружении с пустыми легкими. а) Какую массу воды она вытесняет? б) Каков ее объем? (c) Рассчитайте ее плотность. (d) Если объем ее легких составляет 1,75 л, может ли она плавать, не топчась на месте, с легкими, наполненными воздухом?
9. Плотность некоторых рыб немного меньше плотности воды, и они должны прилагать усилия (плавать), чтобы оставаться под водой. Какую силу должен приложить групер массой 85,0 кг, чтобы оставаться погруженным в соленую воду, если плотность его тела равна 1015 кг/м 3 ?
10. (a) Рассчитайте выталкивающую силу 2-литрового гелиевого баллона. (b) Учитывая, что масса резины в воздушном шаре составляет 1,50 г, какова результирующая вертикальная сила, действующая на воздушный шар, если его отпустить? Можно пренебречь объемом резины.
(a) Рассчитайте выталкивающую силу 2-литрового гелиевого баллона. (b) Учитывая, что масса резины в воздушном шаре составляет 1,50 г, какова результирующая вертикальная сила, действующая на воздушный шар, если его отпустить? Можно пренебречь объемом резины.
11. (a) Какова плотность женщины, плавающей в пресной воде с 4,00% своего объема над поверхностью? Это можно измерить, поместив ее в резервуар с отметками на боку, чтобы измерить, сколько воды она вытесняет, когда плавает и удерживается под водой (кратковременно). б) Сколько процентов ее объема находится над поверхностью, когда она плавает в морской воде?
12. Некий человек имеет массу 80 кг и плотность 955 кг/м 3 (без учета воздуха в легких). а) Вычислите его объем. б) Найдите выталкивающую силу воздуха, действующую на него. в) Каково отношение выталкивающей силы к его весу?
13. Можно сделать простой компас, поместив небольшой стержневой магнит на плавающую в воде пробку. а) Какая часть простой пробки окажется под водой, когда она будет плавать в воде? б) Если пробка массой 10,0 г поместить на нее магнит массой 20,0 г, какая часть пробки окажется под водой? в) Будут ли стержневой магнит и пробка плавать в этиловом спирте?
14. Какая часть веса железного якоря будет поддерживаться выталкивающей силой при погружении в соленую воду?
Какая часть веса железного якоря будет поддерживаться выталкивающей силой при погружении в соленую воду?
15. Известны случаи, когда подлые мошенники выдавали позолоченные вольфрамовые слитки за чистое золото и продавали их жадным по ценам намного ниже стоимости золота, но заслуженно намного выше стоимости вольфрама. С какой точностью вы должны быть в состоянии измерить массу такого слитка в воде и вне воды, чтобы сказать, что это почти чистый вольфрам, а не чистое золото?
16. Двуспальный надувной матрас, используемый для кемпинга, имеет размеры 100 см на 200 см на 15 см в надутом состоянии. Вес матраса 2 кг. Насколько тяжелый человек может выдержать надувной матрас, если его поместить в пресную воду?
17. По рисунку 3 докажите, что выталкивающая сила, действующая на цилиндр, равна весу вытесненной жидкости (принцип Архимеда). Можно считать, что выталкивающая сила равна F 1 – F 2 и что торцы цилиндра имеют равные площади А . Обратите внимание, что объем цилиндра (и объем вытесняемой им жидкости) )A равен ( ч 2 – ч 1 ) A .
Обратите внимание, что объем цилиндра (и объем вытесняемой им жидкости) )A равен ( ч 2 – ч 1 ) A .
Рис. 3. (a) На объект, погруженный в жидкость, действует выталкивающая сила F B . Если F B больше веса объекта, объект поднимется. Если F B меньше веса объекта, объект утонет. (b) Если объект удаляется, он заменяется жидкостью весом ш фл . Поскольку этот вес поддерживается окружающей жидкостью, выталкивающая сила должна равняться весу вытесненной жидкости. То есть F B = w fl , формулировка закона Архимеда.
18. (a) Человек массой 75,0 кг плавает в пресной воде, при этом 3,00 % его объема над водой, когда его легкие пусты, и 5,00 % его объема над водой, когда его легкие полны. Вычислите объем вдыхаемого им воздуха, который называется емкостью легких, в литрах. (b) Кажется ли этот объем легких приемлемым?
Глоссарий
- Закон Архимеда:
- выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости
- выталкивающая сила:
- результирующая восходящая сила, действующая на любой объект в любой жидкости
- удельный вес:
- отношение плотности объекта к жидкости (обычно воде)
Избранные решения задач и упражнений
1.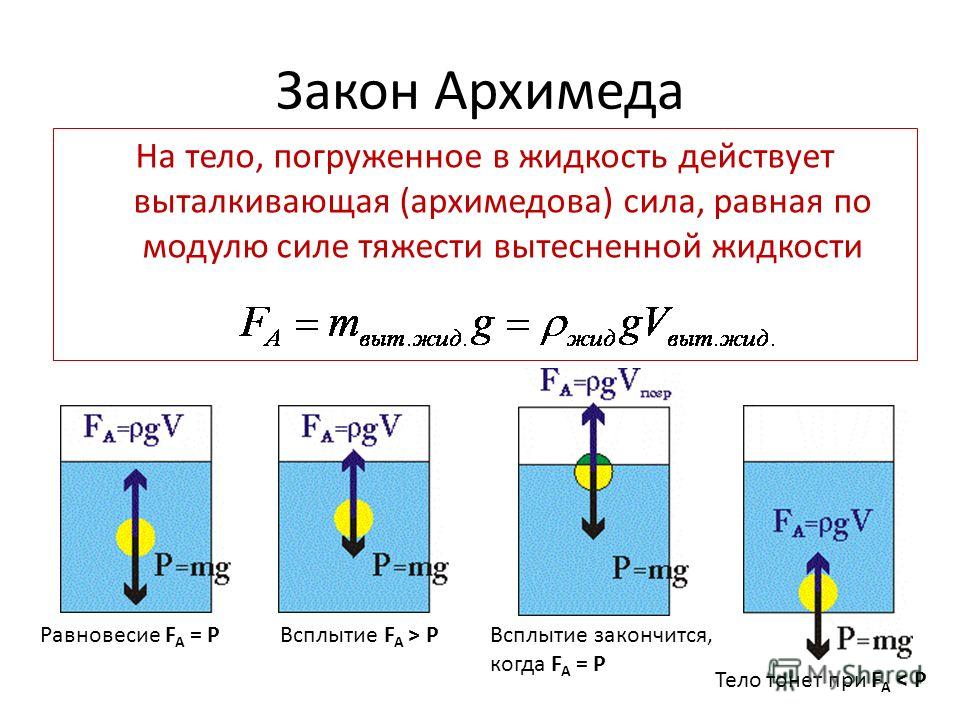 91,7%
91,7%
3. 815 кг/м 3 9{3}\right)\\[/latex]
15. Разница составляет 0,006%.
17. [латекс]{F}_{\text{net}}={F}_{2}-{F}_{1}={P}_{2}A-{P}_{1 }A=\left({P}_{2}-{P}_{1}\right)A\\[/latex]
[латекс]=\left({h}_{2}{\rho }_{\text{fl}}g-{h}_{1}{\rho}_{\text{fl}}g\right)A\\[/latex]
[латекс]=\left( {h}_{2}-{h}_{1}\right){\rho}_{\text{fl}}\text{gA}\\[/latex]
, где [латекс]{\rho }_{\text{fl}}\\[/latex] = плотность жидкости. Следовательно,
[латекс] {F} _ {\ text {net}} = \ left ({h} _ {2} – {h} _ {1} \ right) {\ mathrm {A \ rho}}_ {\ text {fl}} g = {V} _ {\ text {fl}} {\ rho} _ {\ text {fl}} g = {m} _ {\ text {fl}} g = {w} _{\text{фл}}\\[/латекс]
где [latex]{w}_{\text{fl}}\\[/latex] вес вытесненной жидкости.
Закон Архимеда
Цель
•
Связать слова Закона Архимеда с реальным поведением подводных объектов.•
исследовать причину плавучести; то есть изменение давления с глубиной в жидкости.
•
Использовать закон Архимеда для определения плотности неизвестного материала.
Оборудование
- Аппарат виртуальной плавучести
- Карандаш
Моделирование и инструменты
Откройте симуляцию аппарата плавучести, чтобы выполнить эту лабораторную работу.
Изучение аппарата
В этой лабораторной работе мы будем использовать плавучий аппарат. Вы можете получить быстрый доступ к справке, наведя указатель мыши на большинство объектов на экране.
Рисунок 1 : Плавучий аппарат
Чтобы исследовать выталкивающие силы, нам нужно измерить вес и объем объектов, а также их погруженный вес при полном или частичном погружении в жидкость. Мы будем использовать воду в качестве жидкости в этой лаборатории. Нам также необходимо измерить массу и объем вытесненной жидкости. Для измерения веса наших объектов доступны подвесные весы и цифровые весы. Перелив воды из бака выливается в градуированный цилиндр. Объем этой вытесненной воды можно считать по мерному цилиндру, а вес воды можно определить, взвесив мерный цилиндр до и после перелива. Для изучения доступны два простых и два составных объекта. Они состоят из пробки, алюминия и неизвестного материала. Эти объекты можно взвешивать в воздухе, а также при частичном или полном погружении. Подвесные весы поднимаются и опускаются путем перетаскивания поддерживающего их металлического рычага. Как подвесную шкалу, так и градуированный цилиндр можно более точно прочитать, увеличив масштаб. Мерный цилиндр опорожняется, перетащив и отпустив его над резервуаром. Вы обнаружите, что некоторые действия, которые можно было бы сделать с реальным оборудованием, запрещены. Например, если вы удалите пробку и алюминиевый предмет с подвесных весов, а затем прикрепите к ним новый предмет, вы обнаружите, что дальнейшее переполнение невозможно без предварительного опорожнения цилиндра.
Нам также необходимо измерить массу и объем вытесненной жидкости. Для измерения веса наших объектов доступны подвесные весы и цифровые весы. Перелив воды из бака выливается в градуированный цилиндр. Объем этой вытесненной воды можно считать по мерному цилиндру, а вес воды можно определить, взвесив мерный цилиндр до и после перелива. Для изучения доступны два простых и два составных объекта. Они состоят из пробки, алюминия и неизвестного материала. Эти объекты можно взвешивать в воздухе, а также при частичном или полном погружении. Подвесные весы поднимаются и опускаются путем перетаскивания поддерживающего их металлического рычага. Как подвесную шкалу, так и градуированный цилиндр можно более точно прочитать, увеличив масштаб. Мерный цилиндр опорожняется, перетащив и отпустив его над резервуаром. Вы обнаружите, что некоторые действия, которые можно было бы сделать с реальным оборудованием, запрещены. Например, если вы удалите пробку и алюминиевый предмет с подвесных весов, а затем прикрепите к ним новый предмет, вы обнаружите, что дальнейшее переполнение невозможно без предварительного опорожнения цилиндра. Точно так же вы не можете взвешивать более одного предмета на цифровых весах за раз, и вы не можете устроить беспорядок, опуская предмет в воду, пока цилиндр находится на цифровых весах. Еще одна вещь, которая в значительной степени запрещена, — это перетаскивание экрана при увеличении. Когда вы пытаетесь переместить объект на экране, а он ведет себя не так, как ожидалось, это означает, что сначала нужно сделать что-то еще. Есть не так много вариантов.
Точно так же вы не можете взвешивать более одного предмета на цифровых весах за раз, и вы не можете устроить беспорядок, опуская предмет в воду, пока цилиндр находится на цифровых весах. Еще одна вещь, которая в значительной степени запрещена, — это перетаскивание экрана при увеличении. Когда вы пытаетесь переместить объект на экране, а он ведет себя не так, как ожидалось, это означает, что сначала нужно сделать что-то еще. Есть не так много вариантов.
Закон Архимеда:
На тело, полностью или частично погруженное в жидкость, действует выталкивающая сила, равная весу вытесненной жидкости.
Эта и многие другие фразы, которые вы услышите при изучении плавучести, по большей части бессмысленны без непосредственного опыта. Таким образом, наше исследование устройства будет в основном сосредоточено на различных ситуациях, с которыми вы столкнетесь, и соответствующей терминологии. Пока мы здесь, наше использование погружает в одних случаях и погружает в других не означает, что это два разных явления. Оба относятся к объекту, полностью или частично находящемуся в жидкости.
Пока мы здесь, наше использование погружает в одних случаях и погружает в других не означает, что это два разных явления. Оба относятся к объекту, полностью или частично находящемуся в жидкости.
1. Что такое «выталкивающая сила» и что ее создает?
Давайте попробуем это с системой на Рисунке 1. Щелкните правой кнопкой мыши (или Ctrl) и увеличьте масштаб висячей шкалы. Кажется, что изначально он читается как ноль. Такая шкала не очень точна. Наше моделирование отражает этот уровень точности. (Уменьшите масштаб.) Теперь перетащите предмет из пробки и алюминиевого сплава и бросьте его куда-нибудь под вешалку. Он должен стать прикрепленным к вешалке. (Если он отказывается прикрепляться, вероятно, вы уже немного опустили шкалу или в градуированном цилиндре может быть немного воды.) Вы должны обнаружить, что он весит около 4,4 Н. Увеличив масштаб и оценив цифру, мы можем получить 4,41 Н. Перетащите его на цифровую шкалу, и вы получите более точный ответ около 4,41 Н. Какую шкалу следует использовать? Мы всегда будем использовать значение подвесной шкалы, в данном случае 4,41 Н, если только нам не нужно использовать цифровую шкалу для измерения. Это произойдет только тогда, когда нам нужно взвесить градуированный цилиндр. Теперь о «(погруженном) весе при полном или частичном погружении в воду». Перетащите объект обратно на подвесную шкалу. Медленно перетащите опорный рычаг над шкалой вниз, пока алюминиевый диск не погрузится примерно наполовину. Шкала может показывать около 3,73 Н. Это условный вызов, поскольку положение средней точки неизвестно. Давайте использовать это значение в следующем обсуждении. Это «погруженный вес». Мы будем использовать термин
Какую шкалу следует использовать? Мы всегда будем использовать значение подвесной шкалы, в данном случае 4,41 Н, если только нам не нужно использовать цифровую шкалу для измерения. Это произойдет только тогда, когда нам нужно взвесить градуированный цилиндр. Теперь о «(погруженном) весе при полном или частичном погружении в воду». Перетащите объект обратно на подвесную шкалу. Медленно перетащите опорный рычаг над шкалой вниз, пока алюминиевый диск не погрузится примерно наполовину. Шкала может показывать около 3,73 Н. Это условный вызов, поскольку положение средней точки неизвестно. Давайте использовать это значение в следующем обсуждении. Это «погруженный вес». Мы будем использовать термин
W’
(“ W простое число”) для обозначения веса в погруженном состоянии. Итак, его фактический вес составляет 4,41 Н, а при частичном погружении он кажется легче, может быть, 3,73 Н. Он не потерял в весе. Вода оказывает восходящую силу на дно диска. Итак, мы бы сказали, что объект с силой 4,41 Н был поднят силой F b , так что кажется, что он весит или имеет вес в погруженном состоянии 3,73 Н. Поскольку он находится в вертикальном равновесии, мы можем сказать
Итак, мы бы сказали, что объект с силой 4,41 Н был поднят силой F b , так что кажется, что он весит или имеет вес в погруженном состоянии 3,73 Н. Поскольку он находится в вертикальном равновесии, мы можем сказать
| F | |
90,23 Давайте посмотрим на силы и нарисуем векторные стрелки для представления каждой силы. Мы знаем, что объект имеет реальный вес, направленную вниз силу, Вт . Мы измеряем эту силу с помощью нашей шкалы, находя направленную вверх силу, которая ее уравновешивает. Но вес, W , является направленной вниз силой. Когда объект немного погружен в воду, шкала оказывает меньшее вверх сила, Вт’ . Поскольку пара дисков все еще находится в равновесии, некоторая дополнительная направленная вверх сила должна компенсировать разницу.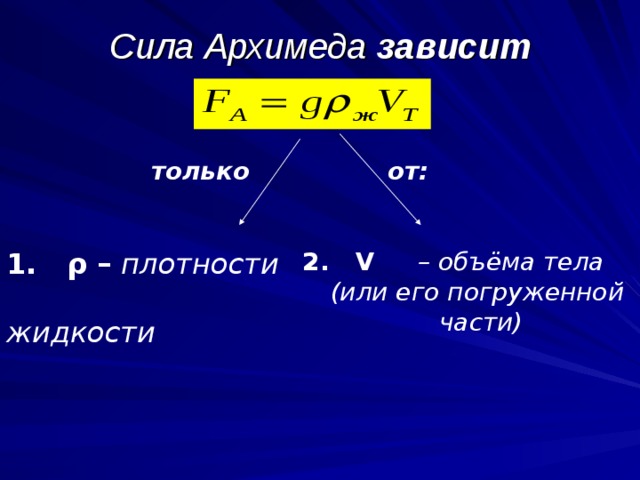 Это выталкивающая сила, F b .
Это выталкивающая сила, F b .
Рисунок 2
Поскольку объект все еще находится в равновесии, три векторные стрелки, показанные на рисунке 2а, должны векторно складываться до нуля. Это показано двумя способами на рисунках 2b и 2c. Рисунок 2c представляет собой диаграмму свободного тела, FBD, где векторы исходят от точки, представляющей объект, на который действуют силы. Мы будем использовать FBD на протяжении всей этой лабораторной работы, чтобы помочь нам изобразить силы, действующие на объект, и помочь нам составить уравнения, связывающие действующую силу. Наш FBD помогает нам сложить вместе три вектора силы, чтобы получить результирующую силу, равную нулю.
| = | Weight submerged + F b + Weight = 0 | ||||
| = | W + + F 9024 + + F 9024 + + F | 555 +55555552915595555552
Ш’ + Ф б – Ш = 0,
так
F b = W – W ′.
Возвращаясь к нашим измеренным значениям,
a
F b = W − W ′ = 4,41 Н − 3,73 Н = Н.
Это значение, 0,68 Н, является выталкивающей силой. Выталкивающая сила – это часть веса, которую весы больше не должны поддерживать, потому что присутствует новая восходящая сила. Это направленная вверх сила, вызванная давлением на нижнюю часть диска. Если вы опустите диск дальше, выталкивающая сила станет больше, а погруженный вес, Вт ′, уменьшается на равную величину. Попытайся.
Попытайся.
2. Что такое «вытесненная жидкость» и как ее вес связан с выталкивающей силой?
В предыдущем разделе вы сосредоточились на выталкивающей силе как на кажущемся уменьшении веса подводного объекта. Каков источник этой силы? С парой пробки и алюминиевого диска, прикрепленной к весу, опустите весы до упора. В цилиндр попадет много воды. Когда это будет сделано, снова поднимите весы. Теперь постепенно опускайте диски в воду. Обратите внимание на поведение воды. Ее уровень повышается, потому что диски «вытесняют» часть воды. То есть они занимают место воды. Таким образом, он поднимается, чтобы освободить место. Когда вода занимала это пространство, она поддерживалась водой под ней. Когда диски занимают одинаковое пространство, вода под ними создает точно такую же восходящую силу. Это выталкивающая сила. Он был там все время, но просто задерживал воду, пока не прибыли диски. Итак, «выталкивающая сила равна весу вытесненной жидкости!» Нам нужно выяснить, как определить этот вес. Заполните бак. Для этого просто перетащите мерный цилиндр куда-нибудь над резервуаром и отпустите его. Он опустеет и вернется на свой пост. Теперь постепенно опускайте диски в воду и следите за тем, что происходит с «вытесненной водой». Поскольку на этот раз наш резервуар изначально был полным, вытесненная вода перелилась в градуированный цилиндр. Мы сделали это, чтобы мы могли взвесить его или найти его объем. Давайте воспользуемся нашими предыдущими результатами, чтобы увидеть взаимосвязь между выталкивающей силой и весом вытесненной жидкости. Если ваш аппарат находится не в том месте, где вы его оставили в конце части 1, повторите часть 1, чтобы восстановить его. Обязательно увеличьте масштаб один раз для большей точности. Вставьте свое значение из 1a в следующий пробел.
Заполните бак. Для этого просто перетащите мерный цилиндр куда-нибудь над резервуаром и отпустите его. Он опустеет и вернется на свой пост. Теперь постепенно опускайте диски в воду и следите за тем, что происходит с «вытесненной водой». Поскольку на этот раз наш резервуар изначально был полным, вытесненная вода перелилась в градуированный цилиндр. Мы сделали это, чтобы мы могли взвесить его или найти его объем. Давайте воспользуемся нашими предыдущими результатами, чтобы увидеть взаимосвязь между выталкивающей силой и весом вытесненной жидкости. Если ваш аппарат находится не в том месте, где вы его оставили в конце части 1, повторите часть 1, чтобы восстановить его. Обязательно увеличьте масштаб один раз для большей точности. Вставьте свое значение из 1a в следующий пробел.
б
Вес вытесненной воды = выталкивающая сила на диске = N
с
Перетащите градуированный цилиндр на цифровую шкалу. Показание шкалы с цилиндром и водой = N
Показание шкалы с цилиндром и водой = N
Это вес жидкости плюс вес градуированного цилиндра. Итак, нам нужно найти вес градуированного цилиндра и вычесть его из общей суммы, чтобы найти вес воды. Опорожните цилиндр, как и раньше. Поместите цилиндр на цифровые весы.
д
Вес пустого мерного цилиндра, Вт c = Н
e
F b = масса вытесненной воды = Вт Пример: (1,69 – 0,98)Н = 0,71 Н
Понятно? Вскоре мы увидим, почему ваши значения для (b) и (e) были примерно одинаковыми. Но пока вы должны понимать, что мы подразумеваем под утверждением, что выталкивающая сила равна весу вытесненной жидкости .
3. Определение и использование объема вытесненной жидкости
Теперь предположим, что у нас не было ни одной из наших шкал.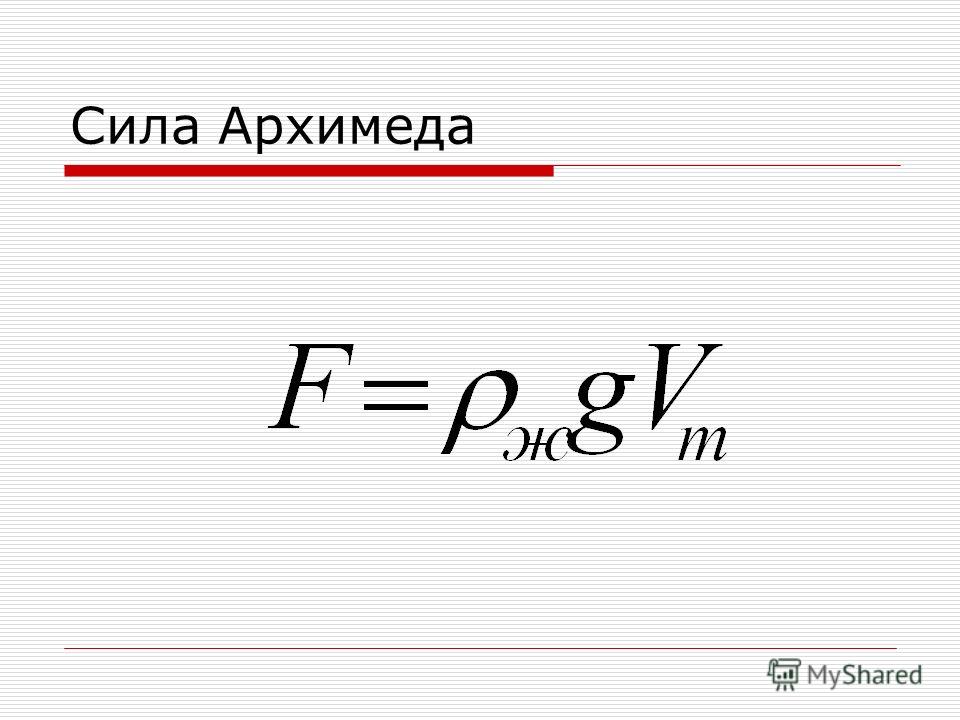 Не могли бы вы еще определить F b ? Мы знаем, что вес воды можно найти из Вт воды = м воды г = ρ воды г 9 В воды02:30 . Поскольку мы знаем, что плотность воды составляет 1000 кг/м 3 , мы могли бы вычислить вес воды, если бы знали ее объем. Вы можете увеличить цилиндр, чтобы прочитать показания объема, но есть функция «Увеличение цилиндра», которая сделает это за вас. Теперь вы можете прочитать объем в мл.
Не могли бы вы еще определить F b ? Мы знаем, что вес воды можно найти из Вт воды = м воды г = ρ воды г 9 В воды02:30 . Поскольку мы знаем, что плотность воды составляет 1000 кг/м 3 , мы могли бы вычислить вес воды, если бы знали ее объем. Вы можете увеличить цилиндр, чтобы прочитать показания объема, но есть функция «Увеличение цилиндра», которая сделает это за вас. Теперь вы можете прочитать объем в мл.
Примечание:
Мерный цилиндр измеряет объем в мл. Вам всегда нужно будет преобразовать его в m 3 . (1 мл = 1 см 3 = 10 –6 м 3 )
ф
Используйте приведенное ниже уравнение, чтобы найти F b .
F B = W ДЕЙСТВЕННАЯ ВОДА = ρ Вода GV Вода = 1000 кг/м 3 × 9,80 Н/кг × м 3 6666666666666666666666666666666666 гг. Пример:
Пример:
1000 кг/м 3 × 9,80 Н/кг × 72 × 10 −6 м 3 = 0,71 Н
А алюминиевый диск? Если бы вы взвесили его, а затем полностью погрузили в воду, вы могли бы измерить его объем, затем вычислить его плотность и убедить короля, что его диск не серебряный. Между прочим, мы пошли на дополнительные расходы, предоставив несмачиваемому полипропиленовому градуированному цилиндру в этом приборе, чтобы избежать необходимости учитывать мениск. Пожалуйста.
Теория
Закон Архимеда
Принцип Архимеда очень легко сформулировать словами, но чтобы научиться его использовать, нужно попрактиковаться в самых разных ситуациях. В этой лабораторной работе мы сначала исследуем буквальное значение этого принципа. Затем мы применим его в нескольких ситуациях. Вы будете использовать формулировку принципа для рисования диаграмм свободного тела (FBD) и создания уравнений, которые можно использовать для нахождения неизвестных величин, таких как объем, масса или плотность объекта или жидкости, в которую он погружен. Решение задач с использованием закона Архимеда может быть очень сложным. Самый важный шаг — использовать слова принципа для создания уравнения. Одним из важных инструментов, помогающих составить уравнение, является диаграмма свободного тела. Принцип Архимеда обычно предполагает, что объекты находятся в вертикальном равновесии. И условия, которые входят в
Решение задач с использованием закона Архимеда может быть очень сложным. Самый важный шаг — использовать слова принципа для создания уравнения. Одним из важных инструментов, помогающих составить уравнение, является диаграмма свободного тела. Принцип Архимеда обычно предполагает, что объекты находятся в вертикальном равновесии. И условия, которые входят в
| F | |
y 3
y 3
9029 y 33303. сила) и т.д. Если вы забыли…
Закон Архимеда:
На тело, полностью или частично погруженное в жидкость, действует выталкивающая сила, равная весу вытесненной жидкости.
Без дополнительной информации это не более чем магическое заклинание! Нам нужно копнуть немного глубже и узнать, что вызывает выталкивающую силу и почему эта сила меняется по мере того, как объекты постепенно погружаются в жидкость. Мы начнем с пары интерактивных анимаций, встроенных в лабораторный аппарат.
Мы начнем с пары интерактивных анимаций, встроенных в лабораторный аппарат.
Изменение давления в зависимости от глубины
Нажмите кнопку Давление , чтобы загрузить интерактивную симуляцию. По мере необходимости перемещайте маленький цилиндр вверх и вниз, чтобы воссоздать последующее обсуждение. На рис. 3а сплошной латунный цилиндр показан над баком, полностью заполненным водой. Атмосферное давление действует практически одинаково на все стороны цилиндра и на поверхность воды, что обозначено пятью P атм стрелки на рис. 3а. В любое время горизонтальное давление будет отменено. Поэтому нам нужно только исследовать вертикальное давление.
Рисунок 3
Постепенно опускайте цилиндр, пока он не будет погружен примерно на 1/4, как показано на рисунке 3b. (Вода, переливающаяся по бокам, не показана. Она также волшебным образом возвращается по мере необходимости. ) Обратите внимание на векторы, которые появляются и изменяются при перемещении цилиндра вверх и вниз. Черный вектор, P up , восходящее давление, оказываемое водой, показано в двух местах вместе с синим вектором ΔP .
) Обратите внимание на векторы, которые появляются и изменяются при перемещении цилиндра вверх и вниз. Черный вектор, P up , восходящее давление, оказываемое водой, показано в двух местах вместе с синим вектором ΔP .
1
Что происходит с восходящим давлением, P вверх и Δ P при опускании цилиндра? Пока не позволяйте цилиндру полностью погрузиться в воду.
На заданной глубине ч в сосуде с водой, подвергающемся воздействию атмосферы, существует давление, обусловленное весом водяного столба над этой точкой плюс вес атмосферы над поверхностью. Это давление является всенаправленным и определяется выражением
( 1 )
P = ρ w gh + P атм .
Нас интересует только давление вверху, P , внизу и внизу, P вверх , цилиндра. В более общем смысле мы будем называть их P 1 и P 2 соответственно. При частично погруженном цилиндре появляется только восходящее давление на дно цилиндра. (См. рис. 4а.) Как насчет Δ Р ? Δ P — разница давлений между верхом и низом цилиндра. В настоящее время в верхней части цилиндра действует давление P вниз = P атм атм. Давление, действующее на дно, равно P up , что равно P атм + ρ w gh 2 . Δ P , разница в этих двух давлениях составляет всего P вверх – P вниз = ρ w gh 2 . Это объясняет, почему Δ P всегда (до сих пор) равняется P до . Давайте изменим это.
В более общем смысле мы будем называть их P 1 и P 2 соответственно. При частично погруженном цилиндре появляется только восходящее давление на дно цилиндра. (См. рис. 4а.) Как насчет Δ Р ? Δ P — разница давлений между верхом и низом цилиндра. В настоящее время в верхней части цилиндра действует давление P вниз = P атм атм. Давление, действующее на дно, равно P up , что равно P атм + ρ w gh 2 . Δ P , разница в этих двух давлениях составляет всего P вверх – P вниз = ρ w gh 2 . Это объясняет, почему Δ P всегда (до сих пор) равняется P до . Давайте изменим это.
Рисунок 4
По мере того, как вы продолжаете тянуть цилиндр вниз, останутся только три вектора, и каждый из них будет продолжать увеличиваться в длину, но останется равным друг другу, пока не будет достигнута определенная точка.
2
Где находится вершина цилиндра, когда происходит этот переход?
Продолжайте опускать цилиндр, пока он не окажется примерно на полпути к дну резервуара, как показано на рисунке 4b. Теперь вы можете ясно видеть нисходящий вектор P вниз . Перетащите цилиндр вверх и вниз в этой средней части резервуара. При этом вектор ΔP ведет себя иначе, чем раньше.
3
Что происходит с Δ P , когда цилиндр опускается, будучи полностью погруженным в воду?
4
Что происходит с P вверх и P вниз , когда цилиндр опускается полностью погруженным в воду? Как это объясняет ваш ответ на предыдущий вопрос?
Таким образом, разница в давлении сверху вниз составляет всего
P 2 – P 1 = ρ г (h 2 – h 1 ).
В случае частично затопленного объекта
h 1 = 0,
, поэтому это уравнение будет работать как для частично, так и для полностью затопленного объекта.
Влияние перепада давления, Δ
P , на выталкивающую силуМы нашли простое уравнение, которое дает разницу давлений между верхом и низом нашего цилиндра, когда он частично или полностью погружен в воду. Как это связано с плавучестью?
Рисунок 5 : Обратите внимание, что 5a совпадает с 3b, а 5b совпадает с 4b.
Для цилиндра с площадью верхней и нижней поверхности A c общая сила, создаваемая давлением воды, будет
F Net Water = F 2 – F 1 = (P 2 – P 1 ) A C = ρ G (H 2 = H
 с .
с .Рассмотрим цилиндр высотой h c . In Figure 5a, with
h 2 = h c ,
ρ w g(h 2 − h 1 )
reduces to
ρ w g . Суммарная сила, F чистая вода , оказываемое давлением воды на цилиндр, будет
| F net water | = | ρ w g | ||
| = | ρ w gV c | |||
| = | вес воды, которая заняла бы объем цилиндра | |||
| F 2 | = | «вес вытесненной воды». |
Теперь рассмотрим полностью погруженный в воду цилиндр на рис. 5b. В этом случае
H 2 – H 1 = H C
, SO
ρ W G (H 2 – H 1 )
303633036330396330363303330396330333033303330.9633039633033303963303330.963303963303963303330. ρ w gh c. Суммарная сила, F чистая вода , оказываемая давлением воды на цилиндр будет
| F net water | = | ρ w gh c A c |
| = | ρ w gV c | |
| = | вес воды, которая заняла бы весь объем цилиндра | |
| F 2 | = | «вес вытесненной воды». |
Итак, какой бы объем цилиндра ни был погружен в воду, выталкивающая сила, действующая на него, равна весу такого же объема воды.
А разные формы? Как насчет конуса или сферы? Результат точно такой же, но доказательство не так просто. Мы не будем продолжать это дальше. Рассмотрим три случая: цилиндр из алюминия, цилиндр с жидкой водой и цилиндр из пробки. Цилиндр жидкой воды создать невозможно, но мы можем представить его заключенным в тонкую невесомую цилиндрическую оболочку.
5
Когда цилиндр из алюминия опускают в наш резервуар, когда выталкивающая сила F b начнет превышать вес цилиндра? (а) когда он частично погружен в воду; б) при полном погружении; (с) никогда
6
Почему это так?
7
Как только алюминиевый цилиндр полностью погрузится в воду, мы можем удержать его на месте, прикрепив что из следующего? а) пробковый блок; (б) блок алюминия; (c) блок воды; (г) нет необходимости
Нажмите кнопку Плавучесть . Выберите алюминиевый цилиндр. Используйте это, чтобы проверить свои рассуждения и исправить их, если необходимо.
Выберите алюминиевый цилиндр. Используйте это, чтобы проверить свои рассуждения и исправить их, если необходимо.
8
Когда цилиндр с водой опускают в наш бак, когда выталкивающая сила F b начнет превышать вес цилиндра? (а) когда он частично погружен в воду; б) при полном погружении; (с) никогда
9
Почему это так?
10
Как только цилиндр с водой полностью погрузится в воду, мы можем удержать его на месте, прикрепив что из следующего? а) пробковый блок; (б) блок алюминия; (c) блок воды; (г) нет необходимости
Выберите водяной цилиндр. Используйте это, чтобы проверить свои рассуждения и исправить их, если необходимо.
11
Как цилиндр пробка опускается в наш бак, когда будет действовать выталкивающая сила, F b , начинают превышать вес баллона? (а) когда он частично погружен в воду; б) при полном погружении; (с) никогда
12
Почему это так?
13
Как только цилиндр из пробки полностью погрузится в воду, мы можем удержать его на месте, прикрепив что из следующего? а) пробковый блок; (б) блок алюминия; (c) блок воды; (г) нет необходимости
Выберите пробковый цилиндр. Используйте это, чтобы проверить свои рассуждения и исправить их, если необходимо.
Используйте это, чтобы проверить свои рассуждения и исправить их, если необходимо.
14
Полезно оставить все три цилиндра полностью погруженными примерно на одинаковую глубину, а затем щелкать разные значки, чтобы переключаться между тремя материалами. Есть одна вещь, которая остается неизменной независимо от выбранного цилиндра. Что это? Почему?
Последнее предложение: снова откройте симуляцию Pressure . Опустите цилиндр до упора. Какие-нибудь мысли?
Принцип Архимеда с дополнительными приложенными силами
Большая часть нашей работы с принципом Архимеда включает в себя дополнительные силы, такие как предложенные в конце каждого из трех наборов вопросов выше. Типичные примеры включают:
•
Спасатель, вытаскивающий человека на причал, обнаружит, что человек становится тяжелее по мере того, как его поднимают из воды. Это приводит к стратегии старта с большим подтягиванием вверх, чтобы дать пловцу начальную скорость подъема, облегчая остальную часть подтягивания.
Это приводит к стратегии старта с большим подтягиванием вверх, чтобы дать пловцу начальную скорость подъема, облегчая остальную часть подтягивания.•
Буй в реке будет удерживаться на месте тяжелым грузом, лежащим на дне реки. В этом случае вступает в игру «последний вопрос», приведенный выше.•
Выталкивающая сила может использоваться для частичной или полной поддержки другого объекта. Например, спасательный жилет должен обеспечивать достаточную выталкивающую силу, чтобы выдерживать как собственный вес, так и вес человека, который его носит. Заболоченный спасательный жилет может продолжать обеспечивать ту же подъемную силу, но добавленная вода создаст дополнительную нежелательную нисходящую силу.
Анализ таких ситуаций обычно предполагает использование уравнений поступательного равновесия. То есть, если тело находится в равновесии, сумма сил в любом направлении будет равна нулю. Выталкивающая сила — это просто другая сила. Это немного сложнее, потому что оно меняется, когда объект погружается на разную глубину. Не менее важно и то, что тщательная диаграмма свободного тела, FBD, необходима для выяснения того, какие объекты и силы задействованы.
Выталкивающая сила — это просто другая сила. Это немного сложнее, потому что оно меняется, когда объект погружается на разную глубину. Не менее важно и то, что тщательная диаграмма свободного тела, FBD, необходима для выяснения того, какие объекты и силы задействованы.
Рисунок 6
Пример 1: Стальной анкер в воздухе весит 2000 Н. Какая сила потребуется, чтобы удержать его при полном погружении в воду? То есть, каков его кажущийся вес, Вт ′, в погруженном состоянии? W ′ — неизвестная направленная вверх опорная сила в данном случае. Помимо направленной вверх опорной силы Вт ′, имеется восходящая выталкивающая сила, F b , и направленная вниз сила тяжести, то есть его вес, Вт . Сумма этих сил равна нулю. Итак, (используя звездные величины)
F b + W ′ = W.
Другие соображения:
| F b | = | weight of fluid (water) displaced |
| = | ρ water gV water = ρ water gV anchor , |
так как якорь вытесняет равный объем воды.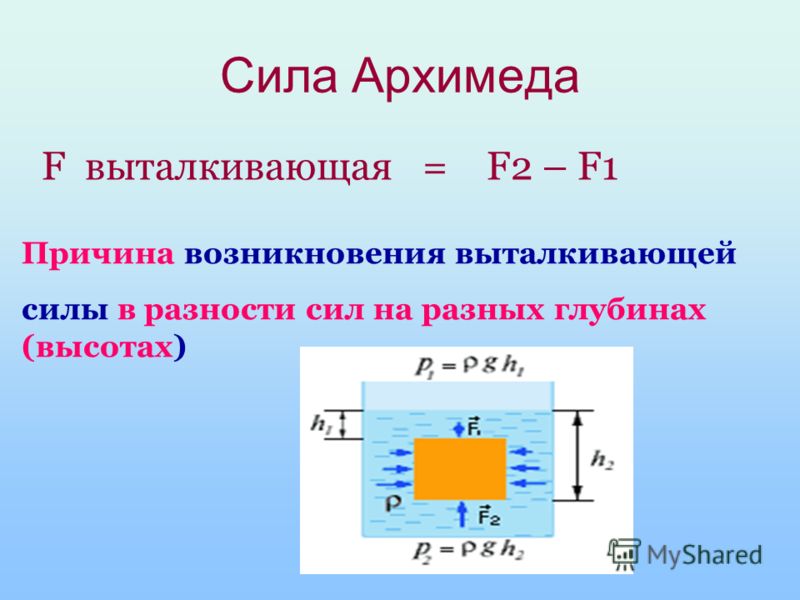 И, поскольку мы знаем вес и массу якоря, мы можем найти его объем, посмотрев его плотность и используя ρ сталь = m якорь V якорь . Что изменится, когда якорь сорвется с поверхности воды?
И, поскольку мы знаем вес и массу якоря, мы можем найти его объем, посмотрев его плотность и используя ρ сталь = m якорь V якорь . Что изменится, когда якорь сорвется с поверхности воды?
Процедура
Пожалуйста, распечатайте рабочий лист для этой лабораторной работы. Этот лист понадобится вам для записи ваших данных.
В следующих разделах вы соберете и проанализируете данные, чтобы исследовать принцип Архимеда в некоторых типичных ситуациях, таких как предложенная в примере 1. Вам не будут предоставлены пошаговые инструкции, но у вас будут пробелы. для данных, которые вам необходимо собрать. Этот метод используется, потому что проблемы с плавучестью всегда носят произвольный характер. Дело не в том, чтобы найти подходящее уравнение; скорее, вы попытаетесь найти способ, которым ваша информация вписывается в принцип Архимеда. Вы также получите руководство по разработке FBD, а также уравнения, описывающие ваши FBD. Обратите внимание, что уравнения имеют скалярную форму. То есть мы скажем «Сумма восходящих сил = сумма направленных вниз сил» (все положительные величины), а не «Сумма восходящих сил + сумма направленных вниз сил = 0» (все векторы). .
Вы также получите руководство по разработке FBD, а также уравнения, описывающие ваши FBD. Обратите внимание, что уравнения имеют скалярную форму. То есть мы скажем «Сумма восходящих сил = сумма направленных вниз сил» (все положительные величины), а не «Сумма восходящих сил + сумма направленных вниз сил = 0» (все векторы). .
I. Подтверждение принципа Архимеда для случая, когда
ρ объект > ρ жидкость Использование переполненияВ этом разделе мы непосредственно измерим выталкивающую силу и вес воды, вытесненной тонущим объектом. Затем мы подтвердим, что они равны. Нашим объектом будет алюминиевый диск. Если симуляция плавучести или давления все еще открыта, нажмите кнопку Закрыть .
Рисунок 7a и Рисунок 7b
Рисунок 7c и Рисунок 7d
ФБД 7е
Прямое измерение выталкивающей силы: взвешивание алюминиевого диска в воздухе (рис. 7а) дает нам Вт . Взвешивание в погруженном состоянии (7с) дает нам Вт ′. Из нашего FBD (7e) мы видим, что
7а) дает нам Вт . Взвешивание в погруженном состоянии (7с) дает нам Вт ′. Из нашего FBD (7e) мы видим, что
F b + W и ‘ = W и ,
так
( 2 )
F b = W al − W al ‘.
Измерение веса вытесненной воды: взвешивание пустого мерного цилиндра (7b) дает нам W cyl . Взвешивание цилиндра после получения переливной воды (7d) дает нам W cylw перемещений.
( 3 )
F b = W вытесненная вода = (W цилиндр смещен ) − W цилиндр
1
Соберите и запишите следующие данные: W al , W cyl , W al ′, W cylw .
2
Рассчитайте выталкивающую силу F b дважды, используя уравнение 2 и уравнение 3. Покажите свои расчеты F b для каждого метода и процентную разницу между ними.
Покажите свои расчеты F b для каждого метода и процентную разницу между ними.
II. Подтвердите принцип Архимеда для
ρ объекта ρ жидкости Используя переполнениеВ этом разделе мы непосредственно измерим выталкивающую силу и вес воды, вытесненной плавающим объектом, и убедимся, что они снова равны. Нашим объектом будет пробковый диск. На этот раз вы заполните все недостающие части. Используйте часть I в качестве модели. Соберите и запишите данные, необходимые ниже.
Также заполните недостающие части ниже, включая рисунки 8a, 8c, 8d и FBD 8e.
1
Отправьте свои ответы на рисунки 8a, 8c и 8d, загрузив скриншотов
каждого. Для 8a и 8c просто сделайте снимок шкалы. Для 8d сделайте снимок показания цифровой шкалы.
Рисунок 8a и Рисунок 8b
Рисунок 8с и Рисунок 8d
2
Взвешивание пробкового диска в воздухе (рис. 8а) дает нам Вт пробка . Взвешивание в частично погруженном состоянии (8с) дает нам W пробка ‘ . На этот раз он плывет. (Обратите внимание на провисшую струну.) Итак, W пробка ‘ = N.
8а) дает нам Вт пробка . Взвешивание в частично погруженном состоянии (8с) дает нам W пробка ‘ . На этот раз он плывет. (Обратите внимание на провисшую струну.) Итак, W пробка ‘ = N.
3
Нарисуйте FBD 8e слева от плавающей пробки. Должно быть два вектора силы. Также используйте инструмент Sketch .
создать эскиз экрана, добавив и пометив пару векторных стрелок слева от плавающей пробки в аппарате плавучести. Возьмите Скриншот FBD и пробки и загрузить как “Buoy_FBD8e.png”.
ФБД 8е
Используйте уравнения
2F b = W al − W al ‘.
и
3F b = W вытесненная вода = (W cylw, вытесненная ) − W cyl
в качестве ориентира при составлении уравнений 4 и 5.
4
Из FBD 8e мы можем сказать, что
( 4 )
F b = .
Взвешивание пустого мерного цилиндра (8b) дает нам W cyl . Взвешивание цилиндра после получения переливной воды (8d) дает нам
W cylw смещения.
( 5 )
F b =
5–8
Соберите и запишите следующие данные: W пробка , W цилиндр , W пробка ′, W цилиндр .
9–11
Рассчитайте выталкивающую силу F b дважды, используя уравнение 4 и уравнение 5. Покажите свои расчеты F b для каждого метода и разницу в процентах.
III. Определение плотности неизвестного материала
Мы подтвердили, что принцип Архимеда правильно описывает силы, действующие на тело, полностью или частично погруженное в воду. Это дает нам отправную точку для более сложных ситуаций, которые не так просты. Один из ваших вариантов объекта — это составной объект с пробкой наверху и стержнем незначительного объема, соединяющим его с большой девяткой.0023 черный неизвестный объект
Это дает нам отправную точку для более сложных ситуаций, которые не так просты. Один из ваших вариантов объекта — это составной объект с пробкой наверху и стержнем незначительного объема, соединяющим его с большой девяткой.0023 черный неизвестный объект
Плотность пробки
Вы уже знаете вес пробки из части II. По весу можно рассчитать массу. Что вам нужно, так это объем пробки. Вы можете найти это, используя другой составной объект — пробку с прикрепленным к ней алюминиевым диском. Он находится в середине левого столбца объектов.
1–7
Прикрепите предмет из пробки/алюминия к подвесным весам. Медленно опустите систему, наблюдая, как вода переливается в цилиндр. Продолжайте до тех пор, пока алюминиевый цилиндр полностью не погрузится в воду. Используйте «Cylinder Zoom», чтобы прочитать и записать объем воды, вытесненный алюминием. Пройдите немного дальше, чтобы убедиться, что шатун игнорируется, что не приводит к переполнению. Продолжайте и обратите внимание, что пробка полностью погрузилась в воду. Вы хотите узнать объем пробки. Запишите следующие данные, чтобы найти объем пробки, переведите его в m 3 и вычислить его плотность в кг/м 3 .
Продолжайте до тех пор, пока алюминиевый цилиндр полностью не погрузится в воду. Используйте «Cylinder Zoom», чтобы прочитать и записать объем воды, вытесненный алюминием. Пройдите немного дальше, чтобы убедиться, что шатун игнорируется, что не приводит к переполнению. Продолжайте и обратите внимание, что пробка полностью погрузилась в воду. Вы хотите узнать объем пробки. Запишите следующие данные, чтобы найти объем пробки, переведите его в m 3 и вычислить его плотность в кг/м 3 .
1
V все в мл
2
V алюминий + пробка в мл
3
V пробка в мл
4
V пробка в м 3
5
W пробка в N (из части II)
6
M пробка в кг
7
ρ пробка в кг/м 3
Покажите расчеты для V пробки (мл), V пробки (m 3 ) и ρ пробки .
Определение плотности неизвестного материала
Верните предмет из пробки/алюминия на место. Опорожните мерный цилиндр.
8
Прикрепите неизвестную систему № 2 (внизу слева) к подвесным весам. Постепенно опустите его как можно ниже. Чем эта составная система отличается от системы пробка/алюминий?
9
Нарисуйте FBD 9 слева от плавающей пробки-неизвестной системы. Также используйте инструмент Sketch для создания эскиза экрана, добавляя и маркируя векторные стрелки слева от плавающей пробки в аппарате плавучести. Возьмите Скриншот FBD и пробки и загрузить как “Buoy_FBD9.png”.
FBD 9
10
Из вашего FBD вы можете сказать, что
( 6 )
F b = .
11
Мы хотим знать плотность неизвестного материала, ρ u . Если бы мы могли найти его вес, мы могли бы использовать
Если бы мы могли найти его вес, мы могли бы использовать
W u = ρ u gV u ,
, так как мы знаем g и можем измерить V u с помощью нашей системы перелива. Итак, чтобы найти ρ u , нам просто нужно W u . Мы знаем W пробка , поэтому, если бы мы знали F b , мы могли бы найти ρ u с помощью уравнения 6. Из уравнений 4 и 5 вы знаете два разных способа нахождения F б . Итак, вы готовы идти. Таким образом, у нас есть два уравнения,
F B = W CORK + W U ,
и
W U = ρ U GV U .
Объедините два уравнения и найдите ρ u . Покажи свою алгебру.
12–16 лет
Определить общую выталкивающую силу F b любым из методов, предложенных выше. Покажите свои расчеты выталкивающей силы, F b , а неизвестная плотность ρ u .
17
Неизвестный материал – бетон. Проверьте онлайн, чтобы увидеть, является ли ваш результат разумным. Обратите внимание, что бетон различается по плотности в зависимости от его производства.
Принцип Архимеда: формула, вывод, применение
Принцип Архимеда, впервые сформулированный Архимедом, говорит нам о соотношении между кажущимся весом объекта, погруженного в воду, и весом вытесненной им воды. Он включает в себя такие факторы, как Выталкивающая сила , с помощью которой устанавливается эта связь. Принцип Архимеда также находит свое применение в некоторых случаях реальной жизни.
Подробнее: важные примечания о гравитации
Соглашение
 Закон Архимеда, Выталкивающая сила, Кажущийся вес, вес, Ареометры. Закон Архимеда, Выталкивающая сила, Кажущийся вес, вес, Ареометры.Принцип Архимеда: определение[Нажмите здесь, чтобы просмотреть примеры вопросов] Принцип Архимеда гласит, что когда объект полностью или частично погружен в воду, он испытывает восходящую выталкивающую силу, которая равна весу воды, вытесненной погруженным объектом. Принцип Архимеда Выталкивающая сила – это, по сути, направленная вверх сила, которая отвечает за кажущееся уменьшение веса погруженного объекта. Также уменьшение веса объекта равно вытесненной им воде. Bluyant Force Подробнее: Принцип архимеды: Формула и деривация[Click здесь для предыдущих лет] Формула для Archimedes ρ x g x V Fb = выталкивающая сила, g = ускорение свободного падения , p = плотность V = объем. ВыводМы знаем, что Вес = масса × сила тяжести (m × g) Следовательно, масса = плотность × объем (p × V) Таким образом, масса вытесненной жидкости = W = плотность × объем × сила тяжести W = p × V × g Из принципа Архимеда: Вес вытесненной жидкости = кажущийся вес объекта = выталкивающая сила b = выталкивающая сила, p = плотность жидкости, V= объем жидкости г = ускорение под действием силы тяжести . Кажущийся вес: Объяснение[Нажмите здесь, чтобы просмотреть примеры вопросов] Фактический вес объекта, помещенного на любую твердую поверхность, направлен вниз через центр тяжести. Когда этот объект погружается в воду, он испытывает восходящую силу, которая является выталкивающей силой. Кажущийся вес Эта выталкивающая сила в некоторой степени уменьшает силу опускания объекта, и объект кажется легче, что является кажущимся весом объекта. Чтобы рассчитать кажущийся вес, можно вычесть выталкивающую силу из фактического веса объекта. Эффекты закона Архимеда: плавание и опускание[Нажмите здесь, чтобы просмотреть вопросы прошлых лет] Когда объект погружен в воду, он либо всплывает, либо тонет в зависимости от плотности объекта и жидкости. Примем W 1 за действительный вес объекта и W 2 за выталкивающую силу.
Принцип Архимеда: Применение[Нажмите здесь, чтобы просмотреть примеры вопросов] Принцип Архимеда имеет несколько реальных применений.
Архимед Принципы применения
Применение принципа Архимеда
Применение принципа Архимеда
Применение Принципа Архимеда Интересные факты, основанные на Законе Архимеда:-
Подробнее: Что следует помнить[Нажмите здесь, чтобы просмотреть вопросы за предыдущие годы]
F B = буровая сила, G = удвоение. V = объем.
Примеры вопросовВопросы 1. Деревянный брусок имеет следующие размеры: 0,12 х 0,34 х 0,43 кубических метра. Он плывет по реке самой широкой стороной вниз. Древесина погружена на высоту 0,053 метра. Какова масса куска дерева? [3 балла] Ответ. Согласно закону Архимеда, вес вытесненной воды равен выталкивающей силе: W 1 = F b Чтобы удерживать дерево на плаву, выталкивающая сила должна иметь ту же величину, что и сила F b = масса дерева × г Объем вытесненной воды равен V вытесненной воды = 0,053 м x 0,34 м x 0,43 м 7 м 0,0Таким образом, масса смещенной воды составляет M WaterDispled = ρ Вода В . Ответ. Мы знаем, что, Если объект плавает, выталкивающая сила равна весу объекта. Том сферы:- 4/3πr 3 V = 4/3π (10 см) 3 V = 4000π/3 см 3 V = 4π/3 L Теперь умножьте. по плотности получаем: М = 4π/3 л × 0,70 кг/л = 2,93 кг. Масса вытесненной воды. Теперь V= m/p = 2,93 L Вопросы 3. Вы погружаете баскетбольный мяч в воду до тех пор, пока половина его объема не окажется под водой. Если радиус баскетбольного мяча равен 12 см, какова выталкивающая сила мяча из-за воды? [4 балла] Отв. Выталкивающая сила – это масса вытесненной воды, умноженная на ускорение свободного падения: F плавучесть = m вытесненная вода 9 Объем вытесненной воды составляет половину объема баскетбольного мяча: V вытесненной воды = ½ V баскетбольного мяча = 2/3πr 3 Здесь r = 12 см. Используя уравнение плотности, масса вытесненной воды равна м вытесненной воды = ρ воды V вытесненной воды Выталкивающая сила равна M (вытесненной воды) = P воды × V вытесненной воды 3 выталкивающая сила равнаF= M (вытесненная вода) =P воды × V вытесненной воды = 35 N Вопрос 4. Металлический шар радиусом 2 см полностью погружен в воду. Найдите силу плавучести при плотности воды 1000 кг на метр кубический. [2 балла] Ответ. Радиус сферы = 2 см = 0,02 м Объем твердой сферы = Выталкивающая сила = плотность воды x объем под водой x ускорение свободного падения F = 1000 x 9,8 x 33,5 x 10 F= 0,33 Н Вопросы 5. Что тяжелее: хлопок или железо? Ответ на основе закона Архимеда. [1 балл] Ответ. Кажущийся вес обоих материалов одинаков, но выталкивающая сила, которую испытывает хлопок, велика, поскольку объем хлопка больше, чем объем железа. Вопросы 6. В каком из следующих случаев корабль будет плавать выше: в пресной воде или в морской воде? Объяснять. [1 балл] Ответ. Выталкивающая сила равна весу вытесненной жидкости. Плотность соленой воды больше, чем пресной. Таким образом, требуется вытеснить меньше воды из-за высокой плотности, чтобы поддерживать плавучесть объекта. Таким образом, корабль будет плавать выше в соленой воде из-за ее высокой плотности. Подробнее: Принцип Архимеда | Описание и фактыЗакон Архимеда о плавучести Просмотреть все СМИ
Просмотреть весь связанный контент → Популярные вопросы Что привело Архимеда к открытию своего принципа? Король Сиракуз Хейрон II заказал корону из чистого золота, но подумал, что коронщик мог обмануть его и использовать немного серебра. Архимед Узнайте больше о жизни Архимеда.Что такое принцип Архимеда? На тело, покоящееся в жидкости, действует выталкивающая вверх сила, называемая выталкивающей силой, которая равна весу жидкости, вытесняемой телом. Если тело полностью погружено в воду, объем вытесненной жидкости равен объему тела. Если тело погружено лишь частично, объем вытесненной жидкости равен объему погруженной части тела. механика жидкости: принцип Архимеда Подробнее о принципе Архимеда читайте в статье о механике жидкости.Для чего используется закон Архимеда? Принцип Архимеда очень полезен для вычисления объема объекта, который не имеет правильной формы. Объект необычной формы можно погрузить под воду, а объем вытесненной жидкости равен объему объекта. Его также можно использовать для расчета плотности или удельного веса объекта. Например, для объекта более плотного, чем вода, объект можно взвесить в воздухе, а затем взвесить при погружении в воду. Когда объект находится под водой, он весит меньше из-за выталкивающей силы, толкающей вверх. Тогда удельный вес объекта равен весу объекта в воздухе, деленному на то, сколько веса объект теряет при помещении в воду. Но самое главное, принцип описывает поведение любого тела в любой жидкости, будь то корабль в воде или воздушный шар в воздухе. Корабль: Гидростатика Узнайте, как принцип Архимеда используется при проектировании кораблей. Какова формула выталкивающей силы? Выталкивающая сила ( B ) равна весу ( W ) жидкости, которую вытесняет тело в этой жидкости. Вес W можно записать через плотность ( D ) жидкости как W = DVg , где V — объем вытесненной жидкости, а g — это 9,8 метра в секунду за секунду, значение ускорения от земного притяжения. Принцип Архимеда , физический закон плавучести, открытый древнегреческим математиком и изобретателем Архимедом, согласно которому на любое тело, полностью или частично погруженное в покоящуюся жидкость (газ или жидкость), действует направленная вверх или выталкивающая сила , сила, величина которой равна весу жидкости, вытесняемой телом. Объем вытесненной жидкости эквивалентен объему объекта, полностью погруженного в жидкость, или той части объема, находящейся под поверхностью, для объекта, частично погруженного в жидкость. Вес вытесненной части жидкости эквивалентен величине выталкивающей силы. Узнайте, почему объект всплывает или тонет Посмотреть все видео к этой статье Если вес объекта меньше веса вытесненной жидкости, объект поднимается, как в случае с деревянным бруском, выпущенным под поверхность воды или наполненный гелием воздушный шар, выпущенный в воздух. Объект тяжелее, чем количество вытесненной им жидкости, хотя и тонет при освобождении, имеет кажущуюся потерю веса, равную весу вытесненной жидкости. Фактически, при некоторых точных взвешиваниях необходимо делать поправку, чтобы компенсировать эффект плавучести окружающего воздуха. Тест “Британника” Физика и законы природы Какая сила замедляет движение? Каждому действию есть равное и противоположное что? В этом викторине по физике нет ничего, что E = mc было бы квадратным. Выталкивающая сила, которая всегда противодействует гравитации, тем не менее вызывается гравитацией. Давление жидкости увеличивается с глубиной из-за (гравитационного) веса жидкости наверху. Это увеличивающееся давление прикладывает силу к погруженному объекту, которая увеличивается с глубиной. Результат – плавучесть. Редакторы Британской энциклопедии Эта статья была недавно отредактирована и дополнена Эриком Грегерсеном. 11.7 Принцип Архимеда – Колледж физикиГлава 11 Статика жидкости Резюме
Когда вы встаете после принятия теплой ванны, ваши руки кажутся странно тяжелыми. Это потому, что у вас больше нет плавучей поддержки воды. Откуда берется эта выталкивающая сила? Почему одни вещи плавают, а другие нет? Получают ли объекты, которые тонут, какую-либо поддержку от жидкости? Ваше тело поддерживается атмосферой или это касается только гелиевых шаров? (См. рис. 1.) Рис. 1. (а) Даже объекты, которые тонут, как этот якорь, частично поддерживаются водой, когда они погружены в воду. (b) Подводные лодки имеют регулируемую плотность (балластные цистерны), так что они могут плавать или тонуть по желанию. (Фото: Allied Navy) (c) Наполненные гелием воздушные шары тянут вверх свои нити, демонстрируя плавучесть воздуха. (кредит: Crystl) Ответы на все эти и многие другие вопросы основаны на том факте, что давление в жидкости увеличивается с глубиной. Это означает, что восходящая сила на нижней части объекта в жидкости больше, чем направленная вниз сила на верхней части объекта. ВЫПУТНАЯ СИЛАВыталкивающая сила – это чистая направленная вверх сила, действующая на любой объект в любой жидкости. Рисунок 2. Давление из-за веса жидкости увеличивается с глубиной, так как P=hρg . Это давление и связанная с ним восходящая сила на дне цилиндра больше, чем направленная вниз сила на верхней части цилиндра. Их отличие – выталкивающая сила F B . (Горизонтальные силы компенсируются.) Насколько велика эта выталкивающая сила? Чтобы ответить на этот вопрос, подумайте о том, что происходит, когда погруженный объект вынимают из жидкости, как показано на рис. Пространство, которое он занимает, заполнено жидкостью, имеющей вес [латекс]{w_{\text{fl}}}.[/латекс] Этот вес поддерживается окружающей жидкостью, поэтому выталкивающая сила должна быть равна [латексу]{ w_{\text{fl}}},[/latex] вес жидкости, вытесненной объектом. Это дань уважения гению греческого математика и изобретателя Архимеда (ок. 287–212 до н. э.), который сформулировал этот принцип задолго до того, как понятия силы были прочно установлены. [латекс] {F_{\text{B}}=w_{\text{fl}}},[/латекс] , где [латекс]{F_{\text{B}}}[/латекс] — выталкивающая сила, а [латекс]{w_{\текст{fl}}}[/латекс] — вес жидкости, вытесняемой объект. Принцип Архимеда действителен в целом для любого объекта в любой жидкости, полностью или частично погруженного в воду. ПРИНЦИП АРХИМЕДАСогласно этому принципу выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости. В форме уравнения принцип Архимеда равен [латекс] {F_{\text{B}}=w_{\text{fl}}},[/latex] , где [латекс]{F_{\text{B}}}[/latex] выталкивающая сила, а [latex]{w_{\text{fl}}}[/latex] – вес жидкости, вытесненной объектом. Humm … Высокотехнологичные купальники для тела были представлены в 2008 году в рамках подготовки к Олимпийским играм в Пекине. УСТАНОВЛЕНИЕ СОЕДИНЕНИЙ: ДОМАШНЕЕ РАССЛЕДОВАНИЕПлотность алюминиевой фольги в 2,7 раза больше плотности воды. Возьмите кусок фольги, скатайте его в шар и бросьте в воду. Он тонет? Почему или почему нет? Можете ли вы заставить его утонуть? Бросьте кусок глины в воду. Он утонет. Затем слепите кусок глины в форме лодки, и она будет плавать. Из-за своей формы лодка вытесняет больше воды, чем глыба, и испытывает большую выталкивающую силу. То же самое и со стальными кораблями. Пример 1: Расчет выталкивающей силы: зависимость от формы 93}[/латекс] воды?Стратегия для (a) Чтобы найти выталкивающую силу, мы должны найти вес вытесненной воды. Мы можем сделать это, используя плотности воды и стали, приведенные в таблице 1. Заметим, что, поскольку сталь полностью погружена в воду, ее объем и объем воды одинаковы. Решение для (a) Сначала мы используем определение плотности [латекс]{\rho=\frac{m}{V}}[/латекс], чтобы найти объем стали, а затем подставляем значения по массе и плотности. Это дает 97\text{ N}},[/latex], что намного больше выталкивающей силы, поэтому сталь останется погруженной. Обратите внимание, что выталкивающая сила округляется до двух цифр, потому что плотность стали выражается только двумя цифрами. Стратегия для (b) Здесь нам дан максимальный объем воды, который может вытеснить стальная лодка. Выталкивающая сила равна весу этого объема воды. Решение для (b) Масса вытесненной воды определяется по ее отношению к плотности и объему, которые известны. то есть 98\text{ N.}} \end{array}[/latex] Обсуждение Максимальная выталкивающая сила в десять раз превышает вес стали, а это означает, что корабль может нести груз, в девять раз превышающий его собственный вес, без тонет. ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ: ИССЛЕДОВАНИЕ НА ДОМУКусок бытовой алюминиевой фольги толщиной 0,016 мм. Возьмите кусок фольги размером 10 на 15 см. а) Какова масса этого куска фольги? (b) Если фольгу сложить так, чтобы получились четыре стороны, и добавить к этой «лодке» скрепки или шайбы, то какая форма лодки позволит вместить больше всего «груза» при погружении в воду? Проверьте свой прогноз. Плотность играет решающую роль в законе Архимеда. Средняя плотность объекта — это то, что в конечном итоге определяет, плавает ли он. Если его средняя плотность меньше плотности окружающей жидкости, он будет плавать. Это связано с тем, что жидкость, имеющая более высокую плотность, содержит большую массу и, следовательно, больший вес в том же объеме. Таким образом, выталкивающая сила, равная весу вытесненной жидкости, больше веса объекта. Точно так же объект, более плотный, чем жидкость, утонет. Степень погружения плавучего объекта зависит от того, как плотность объекта связана с плотностью жидкости. [латекс] {\ текст {фракция погружена} \: =} [/ латекс] [латекс] {\ гидроразрыва {V _ {\ текст {под}}} {V _ {\ текст {obj}}}} [/ латекс] [латекс] {=} [/латекс] [латекс] {\ гидроразрыва {V _ {\ текст {fl}}} {V _ {\ текст {obj}}}}. [/латекс] Погруженный объем равен объему вытесненной жидкости, который мы называем [латекс] {V _ {\ текст {fl}}}. [/латекс] Теперь мы можем получить соотношение между плотностями, подставив [латекс] {\ rho= \frac{m}{V}}[/latex] в выражение. Это дает [латекс] {\ гидроразрыва {V _ {\ текст {fl}}} {V _ {\ текст {obj}}}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {м_ {\text{fl}}/\rho_{\text{fl}}}{m_{\text{obj}}/\bar{\rho}_{\text{obj}}}},[/latex] , где [latex]{\bar{\rho}_{\text{obj}}}[/latex] — средняя плотность объекта, а [latex]{\rho _{\text{fl}}}[/latex ] – плотность жидкости. [латекс] {\ текст {фракция погружена} \: =} [/латекс] [латекс] {\ гидроразрыва {\ бар {\ rho} _ {\ текст {obj}}} {\ rho _ {\ текст {fl} }}}.[/латекс] Рисунок 4. Незагруженное судно (а) плавает выше в воде, чем загруженное судно (б).Мы используем это последнее соотношение для измерения плотности. Это делается путем измерения доли погруженного плавучего объекта, например, с помощью ареометра. Полезно определить отношение плотности объекта к жидкости (обычно воде) как удельный вес : [латекс] {\ текст {удельный вес} \: =} [/ латекс] [латекс] {\ гидроразрыва {\ бар {\ rho}} {\ rho _ {\ текст {ш}}}}, [/ латекс] , где [латекс]{\bar{\rho}}[/латекс] — средняя плотность объекта или вещества, а [латекс]{\rho_{\text{w}}}[/латекс] — плотность воды. при 4,00°С. Удельный вес безразмерен, независимо от того, какие единицы измерения используются для [латекса] {\ rho}. УДЕЛЬНЫЙ ВЕСУдельный вес — это отношение плотности объекта к жидкости (обычно воде). Рисунок 5. Этот ареометр плавает в жидкости с удельным весом 0,87. Стеклянный ареометр наполнен воздухом и утяжелен свинцом на дне. Он лучше всего всплывает в самых плотных жидкостях и был откалиброван и промаркирован таким образом, чтобы по нему можно было напрямую считывать удельный вес.  Пример 2: расчет средней плотности: плавающая женщинаПредположим, что женщина весом 60,0 кг плавает в пресной воде, при этом [латекс]{97,0\%}[/латекс] ее объема находится под водой, когда ее легкие наполнены воздухом. Какая у нее средняя плотность? Стратегия Плотность тела женщины можно найти, решив уравнение _{\text{obj}}}{\rho_{\text{fl}}}}[/latex] для плотности объекта. Это дает [латекс] {\ bar {\ rho} _ {\ text {obj}} = \ bar {\ rho} _ {\ text {person}} = \ text { (фракция погружена)} \ cdotp \: \rho_{\text{fl}}.}[/латекс] 93}}.[/latex] Обсуждение Ее плотность меньше плотности жидкости. Мы ожидаем этого, потому что она плавает. Плотность тела — один из показателей процентного содержания жира в организме человека, представляющий интерес для медицинской диагностики и спортивных тренировок. (См. рис. 6.)
Рисунок 6. Субъект в «резервуаре для жира», где его взвешивают, когда он полностью погружен в воду, что является частью определения плотности тела.  Субъект должен полностью опорожнить легкие и удерживать металлический груз, чтобы утонуть. Делаются поправки на остаточный воздух в его легких (измеряемый отдельно) и вес металла. Его скорректированный вес в погруженном состоянии, его вес в воздухе и щипковые тесты стратегических жировых областей используются для расчета его процентного содержания жира в организме. Субъект должен полностью опорожнить легкие и удерживать металлический груз, чтобы утонуть. Делаются поправки на остаточный воздух в его легких (измеряемый отдельно) и вес металла. Его скорректированный вес в погруженном состоянии, его вес в воздухе и щипковые тесты стратегических жировых областей используются для расчета его процентного содержания жира в организме.Существует много очевидных примеров объектов или веществ с более низкой плотностью, плавающих в жидкостях с более высокой плотностью: масло на воде, воздушный шар, кусочек пробки в вине, айсберг и горячий воск в «лавовой лампе». назвать несколько. Менее очевидные примеры включают лаву, поднимающуюся из вулкана, и горные хребты, плавающие на более плотной коре и мантии под ними. Даже кажущаяся твердой Земля обладает жидкими характеристиками. Один из наиболее распространенных методов определения плотности показан на рис. 7. Рис. 7. (а) Монета взвешивается в воздухе. (b) Определяется кажущийся вес монеты, когда она полностью погружена в жидкость известной плотности. Эти два измерения используются для расчета плотности монеты. Эти два измерения используются для расчета плотности монеты.Предмет, в данном случае монета, взвешивается в воздухе, а затем снова взвешивается при погружении в жидкость. Плотность монеты, показатель ее подлинности, можно рассчитать, если известна плотность жидкости. Этот же метод можно использовать и для определения плотности жидкости, если известна плотность монеты. Все эти расчеты основаны на законе Архимеда. Принцип Архимеда гласит, что выталкивающая сила, действующая на объект, равна весу вытесненной жидкости. Это, в свою очередь, означает, что объект кажется весящим меньше в погруженном состоянии; мы называем это измерение кажущимся весом объекта . Объект испытывает кажущуюся потерю веса , равную весу вытесненной жидкости. В качестве альтернативы, на весах, измеряющих массу, объект испытывает кажущуюся потерю массы , равную массе вытесненной жидкости. это [латекс] {\ текст {очевидная потеря веса} = \ текст {вес вытесненной жидкости}} [/ латекс] или [латекс] {\ текст {кажущаяся потеря массы} = \ текст {масса вытесненной жидкости. Обсуждение Из таблицы 1 видно, что эта плотность очень близка к плотности чистого серебра, подходящего для этого типа древних монет. Большинство современных подделок не являются чистым серебром. Это возвращает нас к принципу Архимеда и тому, как он возник. Как гласит история, царь Сиракуз поручил Архимеду определить, поставляет ли королевский коронщик корону из чистого золота. Чистоту золота трудно определить по цвету (оно может быть разбавлено другими металлами и все равно выглядеть таким же желтым, как чистое золото), а другие аналитические методы еще не были придуманы. Однако даже древние люди понимали, что плотность золота больше, чем у любого другого известного тогда вещества. Архимед якобы мучился над своей задачей и однажды получил вдохновение в общественных банях, размышляя о поддержке, которую вода оказала его телу. ИССЛЕДОВАНИЯ PHET: ПЛАВУЧОСТЬКогда объекты всплывут и когда они утонут? Узнайте, как плавучесть работает с блоками. Стрелки показывают приложенные силы, и вы можете изменять свойства блоков и жидкости. Рис. 8. Плавучесть
|

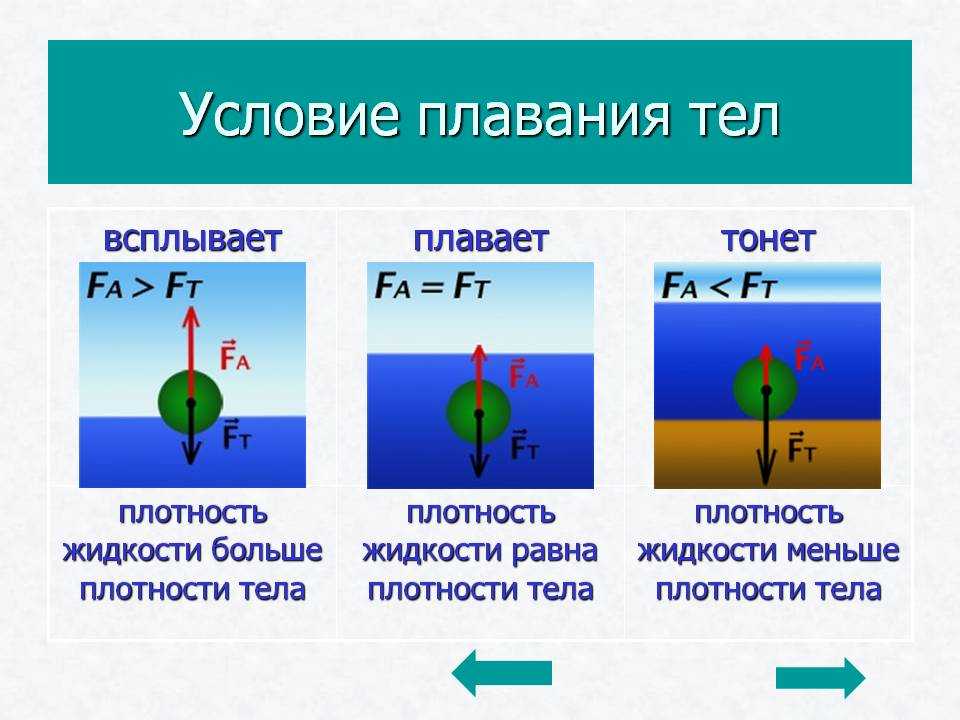 По легенде, так были сожжены римские корабли, осаждавшие Сиракузы. Недавно энтузиасты провели экспериментальную проверку и удалось поджечь деревянный баркас.
По легенде, так были сожжены римские корабли, осаждавшие Сиракузы. Недавно энтузиасты провели экспериментальную проверку и удалось поджечь деревянный баркас.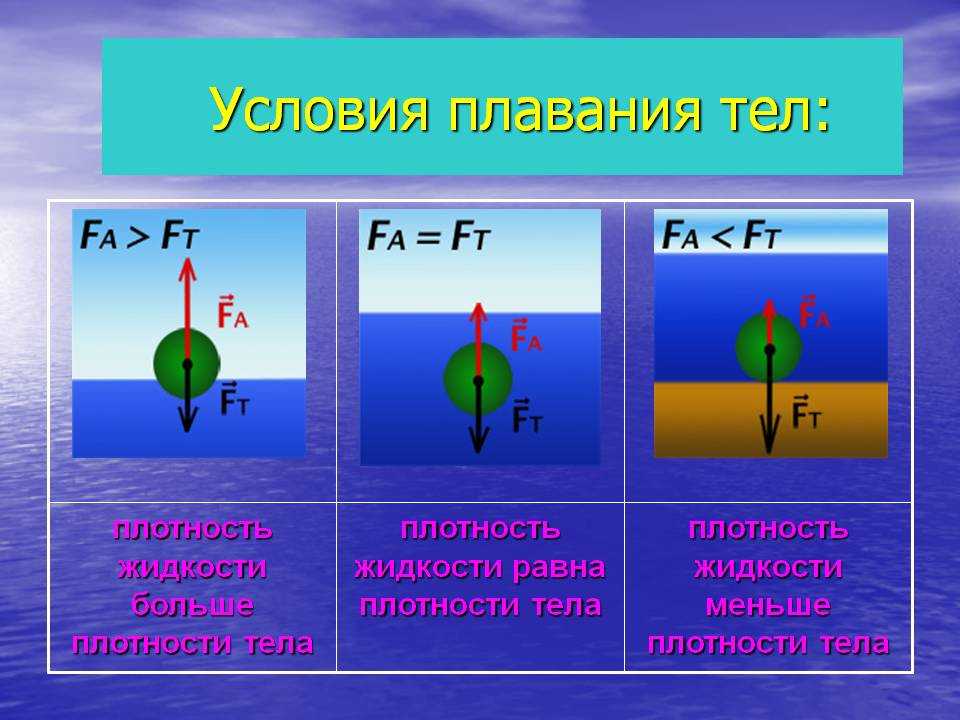
 Самый яркий пример использования закона в технике — подводная лодка. Её средняя плотность изменяется количеством воды в специальных боксах суднах: если они наполняются водой, то она погружается, а когда воду вытесняют сжатым воздухом — лодка всплывает.
Самый яркий пример использования закона в технике — подводная лодка. Её средняя плотность изменяется количеством воды в специальных боксах суднах: если они наполняются водой, то она погружается, а когда воду вытесняют сжатым воздухом — лодка всплывает.
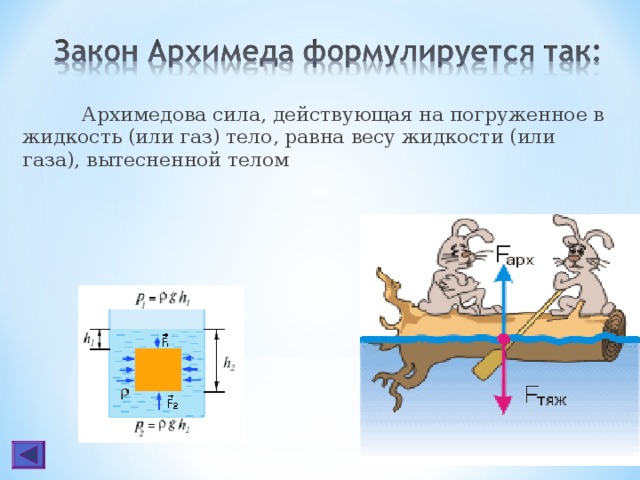 Отсюда искомая величина равняется разности сил тяжести и Архимеда. Так как предмет не движется, то Fтяж = P, а Fарх = ρ * g * V. Для того чтобы полученная сила измерялась в ньютонах, нужно все значения подставить в единицах СИ. Значит, F = P — ρ * g * V = 4 Н — 1000 кг / м3 * 10 Н / кг * 200 * 10-6 м3 = 2 Н.
Отсюда искомая величина равняется разности сил тяжести и Архимеда. Так как предмет не движется, то Fтяж = P, а Fарх = ρ * g * V. Для того чтобы полученная сила измерялась в ньютонах, нужно все значения подставить в единицах СИ. Значит, F = P — ρ * g * V = 4 Н — 1000 кг / м3 * 10 Н / кг * 200 * 10-6 м3 = 2 Н.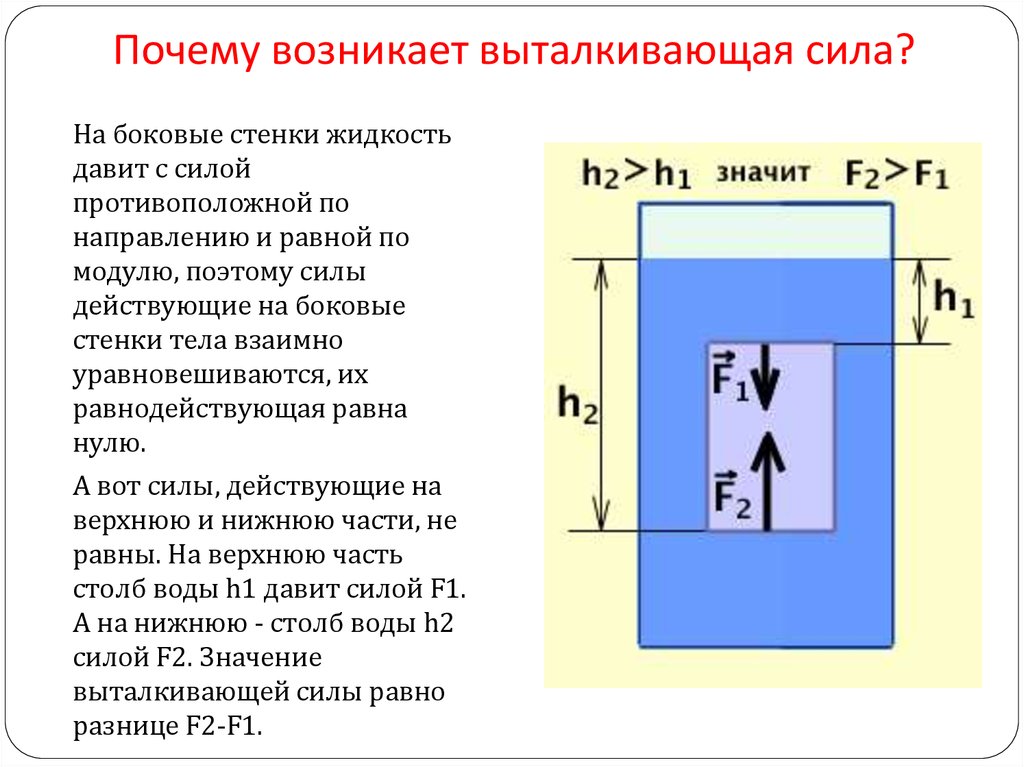 Так как сила выталкивания не зависит от атмосферного давления, то никакого изменения не произойдёт.
Так как сила выталкивания не зависит от атмосферного давления, то никакого изменения не произойдёт.
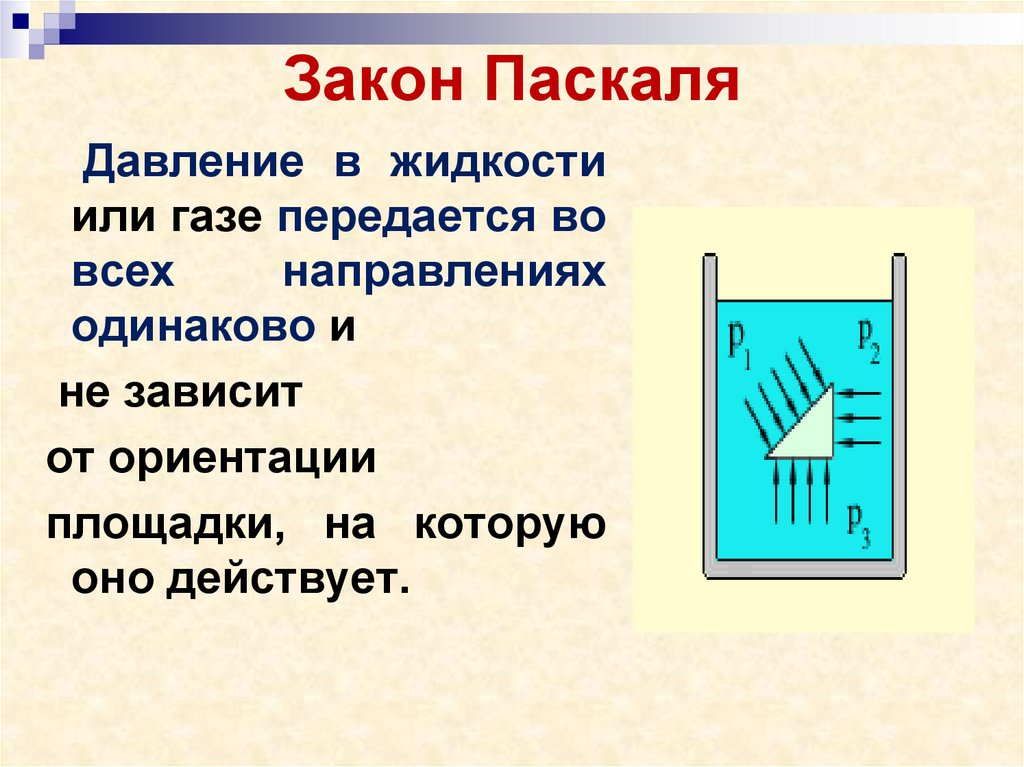 Сила называется силой Архимеда :
Сила называется силой Архимеда : Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.
Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции , поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами .
Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции , поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами . Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат
O
x
y
z
{\displaystyle Oxyz}
, причём выберем направление оси z совпадающим с направлением вектора
g
→
{\displaystyle {\vec {g}}}
. Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку
d
S
{\displaystyle dS}
. На неё будет действовать сила давления жидкости направленная внутрь тела,
d
F
→
A
=
−
p
d
S
→
{\displaystyle d{\vec {F}}_{A}=-pd{\vec {S}}}
. Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности:
Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат
O
x
y
z
{\displaystyle Oxyz}
, причём выберем направление оси z совпадающим с направлением вектора
g
→
{\displaystyle {\vec {g}}}
. Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку
d
S
{\displaystyle dS}
. На неё будет действовать сила давления жидкости направленная внутрь тела,
d
F
→
A
=
−
p
d
S
→
{\displaystyle d{\vec {F}}_{A}=-pd{\vec {S}}}
. Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности:

 е. 1000 кг/м 3 . Это значение также является объемом объекта.
е. 1000 кг/м 3 . Это значение также является объемом объекта.
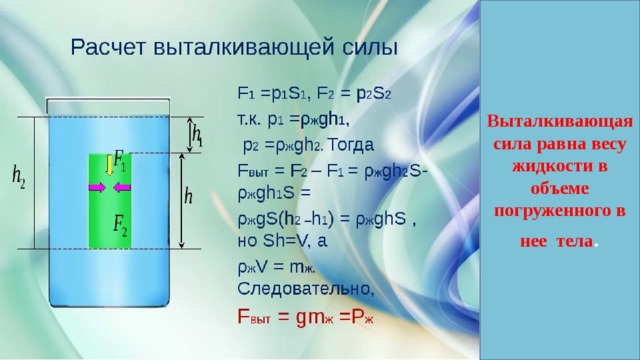

 Это приводит к стратегии старта с большим подтягиванием вверх, чтобы дать пловцу начальную скорость подъема, облегчая остальную часть подтягивания.
Это приводит к стратегии старта с большим подтягиванием вверх, чтобы дать пловцу начальную скорость подъема, облегчая остальную часть подтягивания.