Сила тока ?. Формула силы тока. Как обозначается ? единица измерения силы тока?
Автор Даниил Леонидович На чтение 5 мин. Просмотров 9k. Опубликовано Обновлено
Электрический ток — это направленный поток отрицательно заряженных частиц. Величину электрического тока определяют по числу электронов, протекающих сквозь проводник с неким поперечным сечением за определенную единицу времени.
Однако в полной мере охарактеризовать ток только движением электронов невозможно. Он также имеет другие параметры. Действительно, объем электричества, равного одному кулону способно проходить через металлический проводник в течение одной секунды или другого промежутка времени.
Если принять во внимание временной промежуток как характеристику, то можно увидеть, что интенсивность потоков в разных случаях будет не одинаковой.
Содержание
- Общее описание силы тока
- Способы измерения силы тока
- Отличие напряжения от силы тока
- Заключение
Общее описание силы тока
Сила тока является объемом электрических зарядов, проходящих сквозь поперечные профили проводников в интервале времени, равному одной секунде. Как уже было выше сказано, что за единиц силы тока принимают Ампер, которая и принадлежит к Международной СИ, используемой во всех странах мира.
Один ампер равен силе изменения потока электричества при прохождении по параллельным, парным линейным проводникам бесконечной длины, имеют ничтожно малую площадь кругового сечения. Эти материалы находятся в вакууме друг от друга на расстоянии одного метра. Он вызывает силу взаимного влияние равную 2*10-7. Единица исчисления силы тока Ампер соответствует одному кулону, пройденному за одну секунду через поперечный профиль материала проводника.
Эти материалы находятся в вакууме друг от друга на расстоянии одного метра. Он вызывает силу взаимного влияние равную 2*10-7. Единица исчисления силы тока Ампер соответствует одному кулону, пройденному за одну секунду через поперечный профиль материала проводника.
В математическом исчислении характеристика выглядит как 1 А = 1 кулон/1 секунда. Величина показателя относительно большая, поэтому для бытовых электроприборов и микросхем применяют дополнительные единицы: 1 мА и 1 мкА, которые равны одной тысячной и одной миллионной части ампера.
Если известна величина электрозаряда, прошедшего сквозь проводник с нужным сечением за требуемый промежуток времени, то параметр можно выразить следующей формулой: l=q/t.
В замкнутой сети без ответвлений за одну секунду времени проходит одинаковое количество электронов в любом участке проводника. Поскольку заряды не могут накапливаться исключительно в одном участке электрической цепи, то его интенсивность не зависит от толщины и сечения кабеля.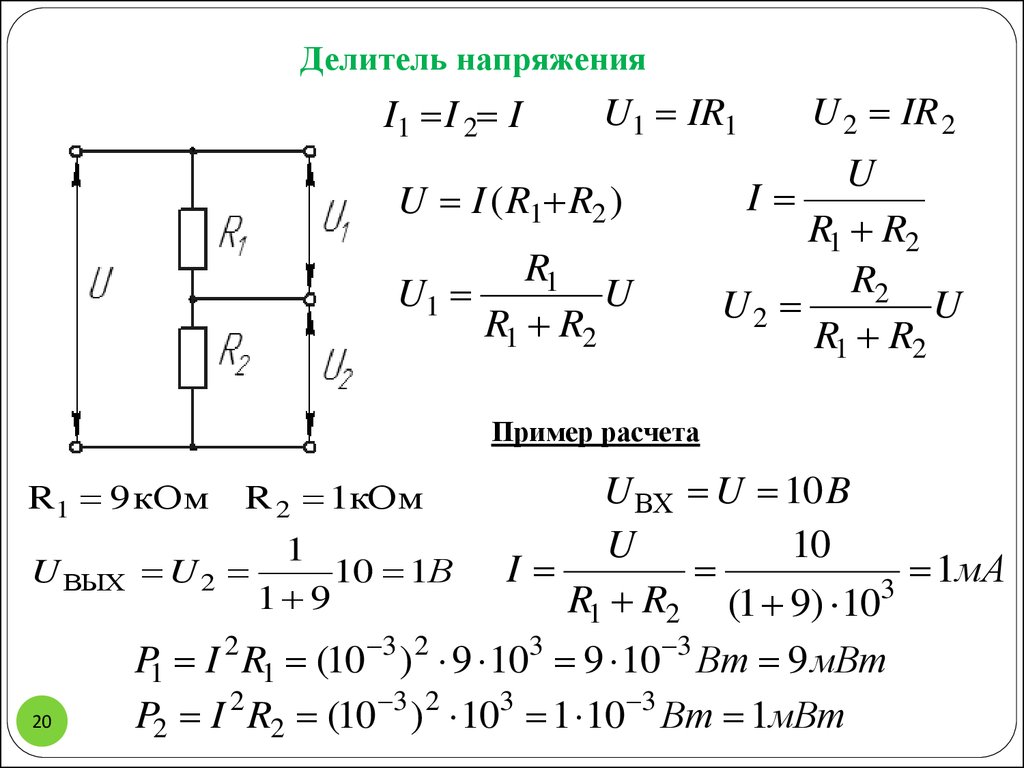
Для более сложных цепей с ответвлениями такое утверждение также остается истинным. Но такое определение действует только для отдельных участков схемы, которые следует рассматривать как элементарная сеть.
Способы измерения силы тока
Для того чтобы узнать силу тока на требуемом участке цепи, одних теоретических вычислений не достаточно. Да, можно использовать формулы и узнать величину, но она будет приблизительной. Поскольку приборостроение, электроника и электрика — науки точные и не терпят погрешностей, был изобретен индукционный, а позднее электронный прибор, который способен показывать точные величины.
Амперметр предназначен для измерений силы тока на отдельных участках электрической цепи. Но значения, равные 1 Амперу и более можно увидеть только в силовых установках и сетях. Для снятия показаний с них используют специальные понижающие трансформаторы. Из курсов физики многие знают от чего зависит интенсивность действий электрического тока. Инициатором движения электронов является магнитное поле.
Ток подается на основные катушки, в которых создается индукция. С ее помощью во второстепенной катушке генерируется электричество меньшей величины. Показатель зависит от числа витков обмоток. Они прямо пропорциональны. Поэтому даже на крупных предприятиях, где напряжение достигает нескольких тысяч вольт применяют микроамперметры или миллиамперметры. Это связано, прежде всего, с безопасностью обслуживающего персонала.
Довольно часто в обиходе можно услышать термин мультиметр. Его отличие от амперметра заключается в возможности измерять несколько характеристик одновременно, тогда как амперметр является узкоспециализированным прибором.
Включают устройство в разрыв электрической цепи. При таком способе замеров, ток протекает через измеритель к потребителю. Следовательно, соединять прибор нужно до или после элемента нагрузки, так как в простой схеме без ответвлений он будет всегда одинаковым.
Существует ошибочное убеждение, что ток до потребителя и после не одинаковый, так как часть электричества тратится на компонента. Такое утверждение ошибочно, поскольку в ток представляет собой электромагнитный процесс, выполняемый в теле металлического проводника. Результатом становится упорядоченное движение электронов вдоль всей длины проводника. Но саму энергию переносят не электроны, а магнитное поле, которое окружает тело проводника.
Такое утверждение ошибочно, поскольку в ток представляет собой электромагнитный процесс, выполняемый в теле металлического проводника. Результатом становится упорядоченное движение электронов вдоль всей длины проводника. Но саму энергию переносят не электроны, а магнитное поле, которое окружает тело проводника.
Важно!
Через любой поперечный профиль металла простых электрических цепей проходит одинаковое количество электрического заряда. Сколько электронов вышло из положительного полюса источника питания, столько заходит в отрицательный полюс, пройдя через элемент нагрузки. В ходе движения электроны не могут расходоваться, как другие частицы материала. Они составляют единое целое с проводником и их количество всегда одинаковое.
Отличие напряжения от силы тока
Электричество, как и любая другая материя, имеет собственные характеристики, используемые для определения эффективности работы и контроля заданных параметров. В физике существуют такие понятия как «напряжение» и «сила тока».
Такие различия заключены в принципе действия электричества. Под силой тока понимают объем потока электронов, способных пройти на расстояние одного метра за установленный интервал времени. Напряжение наоборот выражено в количестве потенциальной энергии. Оба понятия тесно связаны между собой. К внешним факторам влияния на них относят:
- материал, из которого изготовлен проводник;
- температура;
- магнитное поле;
- условия окружающей среды.
Отличия также заключаются в способах получения этих параметров. Когда на заряды проводника воздействует внешнее магнитное поле, формируется напряжение, которое генерирует поток между точками цепи. Так же специалисты выделяют отличия в энергопотреблении, называемым мощностью. Если напряжение характеризует параметры потенциальной энергии, то ток — кинетической.
” src=”https://www.youtube.com/embed/qx30dA0krB4?feature=oembed” frameborder=”0″ allow=”accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture” allowfullscreen=””>Заключение
Сила тока является одним из важных параметров, характеризующих электричество. Он показывает, какой объем электрического заряда проходит через поперечный профиль металлического проводника. Данная характеристика широко применяется в электронике и энергетике.
«Почему, чем выше напряжение, тем меньше ток? » — Яндекс Кью
ПопулярноеСообщества
Такой вопрос у меня возник при изучении ТОЭ. Ведь по закону Ома, сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению. I=U/R. Вот например, есть лампа (HL) и источник напряжения GB1 — GB3 — батарейки, S1 — выключатель.
Яркость лампочки будет зависеть от силы тока, чем она больше, тем ярче горит лампочка. А теперь, вместо одной батарейки мы вставили перемычку, уменьшив тем самым напряжение.
Будет интересно увидеть, почитать ваши рассуждения, ответы. Четкого, внятного ответа я не нашел.
ФизикаНаукаЭлектроника
Андрей Денисов
·
1,2 K
ОтветитьУточнитьValery Timin
Физика
189
физика математика · 29 мая
Вы правильно думаете:
“по закону Ома, сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению. I=U/R. “
I=U/R. “
Надо понимать, что это уравнение может быть применено либо к полной цепи – в Вашем случае, либо к участку цепи – это почти всегда. Даже в Вашем случае можно считать к случаю “участок цепи”, если учесть внутреннее сопротивление батареек – от 0.3 до 1-2 Ом. Автомобильный аккумулятор вообще 0,01 Ом. Это первое.
Второе. При параллельном включении одинаковых батареек общее напряжение не зависит от их количества. Но внутреннее (общее!!! или эквивалентное) сопротивление батареек обратно пропорционально их количеству. Поэтому при учете внутреннего сопротивления батареек при удалении одной ток чуть-чуть уменьшится. Но НИКОГДА НЕ ЗАКОРАЧИВАЙ БАТАРЕЙКИ! (и НЕ СТАВЬТЕ ПЕРЕМЫЧКУ ВМЕСТО БАТАРЕЙКИ – как у Вас написано: похоже, Вы и не ставили. Батарейки (все!) сдохнут через минуту или даже взорвутся!). Это то же самое, что и закорачивание фазы и нуля в розетке! (в детстве пробовал – так что можешь поверить). Формула для тока в Вашей цепи:
I = U/(R+Rвн/N),
где N – колич. батареек,
батареек,
Rвн – внутр.сопр.батарейки, которое зависит от степени ее зарядки. У поработавшей батареки внутреннее сопротивление увеличивается, поэтому ток (общий! см. формулу) уменьшается, а не потому, что напряжение батарейки уменьшается. У разряженной батарейки внутреннее сопротивление очень большое! А напряжение можешь проверить вольтметром – эксперимент достаточно интересный. И для некоторых очень неожиданный.
Третье – по загловку. Вашего вопроса: почему, чем выше напряжение, тем меньше ток? Это чушь. Так не бывает. А когда такое бывает – где-то в ответах уже есть намек на некоторые специфические особенности использования электричества от генераторов переменного тока с конечной мощностью.
Комментировать ответ…Комментировать…
Александр Наумов
Физика
283
Инженер. Электроника, программирование. · 29 мая
“Чем выше напряжение, тем меньше ток” – из вопроса, строго говоря, не понятно о какой ситуации идет речь. Ничего не проясняет и схема с закорачиванием батарейки.
Однако можно предположить, что автора интересует вопрос в контексте тока потребления современных бытовых и прочих приборов, имеющих в своем составе стабилизаторы вторичных напряжений и/или токов. Например… Читать далее
Ничего не проясняет и схема с закорачиванием батарейки.
Однако можно предположить, что автора интересует вопрос в контексте тока потребления современных бытовых и прочих приборов, имеющих в своем составе стабилизаторы вторичных напряжений и/или токов. Например… Читать далее
Андрей Денисов
30 мая
Благодарю за ответ! Именно так я и подразумевал вопрос. Ибо сейчас получаю высшее по автоматизации, имея уже… Читать дальше
Комментировать ответ…Комментировать…
N & O
Физика
1,5 K
Астрономия физика космология квантовая механика · 6 июл
Когда вы меняете количество элементов в источнике питания вы тем самым меняете ЭДС и внутреннее сопротивление источника питания. А применяете при этом ошибочно закон Ома для участка цепи. I=U/R. Он справедлив только на участке спирали лампочки. Для такого случая есть закон Ома для полной (замкнутой) цепи. I=З/(R+r)
Принцип “выше напряжение меньше ток” применяется при… Читать далее
I=З/(R+r)
Принцип “выше напряжение меньше ток” применяется при… Читать далее
Комментировать ответ…Комментировать…
Владимир Яшагин
Технологии
173
Инженер путей сообщения электромеханик. Электро и теплоэнергетика ,электрические машины. э… · 29 мая
Хороший вопрос. Первое утверждение не опровергает закон Ома , так как относится к другой области электротехники .Закон Ома пока не зыблем до сверх проводимости и не о том речь. Речь идёт о трансформаторе, Силовой трансформатор является одним из важнейших элементов каждой электрической сети. Передача эл. энергии на большие расстояния от места её производства до… Читать далее
Комментировать ответ…Комментировать…
Akilya Galimova
Технологии
61
Преподаватель технического университета, кандидат технических наук, проектировщик в. .. · 30 мая
.. · 30 мая
Если привести в Вашем вопросе схему и тестовую часть в соответствие с друг с другом (батарейки нужно включить в цепь последовательно, тогда и можно утверждать, что при закорачивании одной из батареек, напряжение снизиться), то можно ответить на вопрос. Световой поток зависит не только от тока, но и от напряжения. Если напряжение снизить, то световой поток тоже… Читать далее
Комментировать ответ…Комментировать…
Юрий Шимановский
3,3 K
🍀 Естествоиспытатель · 28 мая · shymanovsky.mooo.com
А откуда взялось первое утверждение? Если говорить о цепи постоянного тока (как на картинке) то такого не будет. Во первых, напряжение не изменится при если мы вынули одну батарейку при параллельном включении. Хотя возрастет сопротивление цепи, поскольку батарейки обладают сопротивлением. См. формулу расчета сопротивления для параллельного включения резисторов. То есть… Читать далее
То есть… Читать далее
1 эксперт согласен
Андрей Денисов
28 мая
Юрий благодарю за ответ. Пожалуй пример схемы не лучший взят. Но подразумевается, что источник имел в начале… Читать дальше
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
Закон Ома. Онлайн расчёт для постоянного и переменного тока.
Онлайн расчёт электрических величин напряжения, тока и мощности для участка цепи,
полной цепи, цепи
с резистивными, ёмкостными и индуктивными элементами.
Теория и практика для начинающих.
Начнём с терминологии.
Электрический ток – это направленное движение заряженных частиц, при котором происходит перенос заряда из одной области
электрической цепи в другую.
Силой электрического тока (I) является величина, которая численно равна количеству заряда Δq, протекающего через заданное поперечное
сечение проводника S за единицу времени Δt: I = Δq/Δt.
Напряжение электрического тока между точками A и B электрической цепи – физическая величина, значение которой равно работе эффективного
электрического поля, совершаемой при переносе единичного пробного заряда из точки A в точку B.
Омическое (активное) сопротивление – это сопротивление цепи постоянному току, вызывающее безвозвратные потери энергии
постоянного тока.
Теперь можно переходить к закону Ома.
Закон Ома был установлен экспериментальным путём в 1826 году немецким физиком Георгом Омом и назван в его честь.
По большому счёту, Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях,
определяющих зависимость между электрическими величинами, такими как: напряжение, сопротивление и сила тока исключительно
для проводников, обладающих постоянным сопротивлением. При расчёте напряжений и токов в нелинейных цепях, к примеру, таких, которые содержат полупроводниковые или электровакуумные приборы,
этот закон в простейшем виде уже использоваться не может.
При расчёте напряжений и токов в нелинейных цепях, к примеру, таких, которые содержат полупроводниковые или электровакуумные приборы,
этот закон в простейшем виде уже использоваться не может.
Тем не менее, закон Ома был и остаётся основным законом электротехники, устанавливающим связь силы
электрического тока с сопротивлением и напряжением.
Формулировка закона Ома для участка цепи может быть представлена так: сила тока в проводнике прямо
пропорциональна напряжению (разности потенциалов) на его концах и обратно пропорциональна сопротивлению этого проводника
и записана в следующем виде:
I=U/R,
где
I – сила тока в проводнике, измеряемая в амперах [А];
U – электрическое напряжение (разность потенциалов), измеря- емая в вольтах [В];
R – электрическое сопротивление проводника, измеряемое в омах [Ом].
Производные от этой формулы приобретают такой же незамысловатый вид: R=U/I и U=R×I.
Зная любые два из трёх приведённых параметров можно произвести и расчёт величины мощности,
рассеиваемой на резисторе.
Мощность является функцией протекающего тока I(А) и приложенного напряжения U(В) и вычисляется по следующим формулам,
также являющимся производными от основной формулы закона Ома:
P(Вт) = U(В)×I(А) = I2(А)×R(Ом) =
U2(В)/R(Ом)
Формулы, описывающие закон Ома, настолько просты, что не стоят выеденного яйца и, возможно, вообще не заслуживают отдельной крупной статьи на страницах уважающего себя сайта.
Не заслуживают, так не заслуживают. Деревянные счёты Вам в помощь, уважаемые дамы и рыцари!
Считайте, учитывайте размерность, не стирайте из памяти, что:
Единицы измерения напряжения: 1В=1000мВ=1000000мкВ;
Единицы измерения силы тока:1А=1000мА=1000000мкА;
Единицы измерения сопротивления:1Ом=0.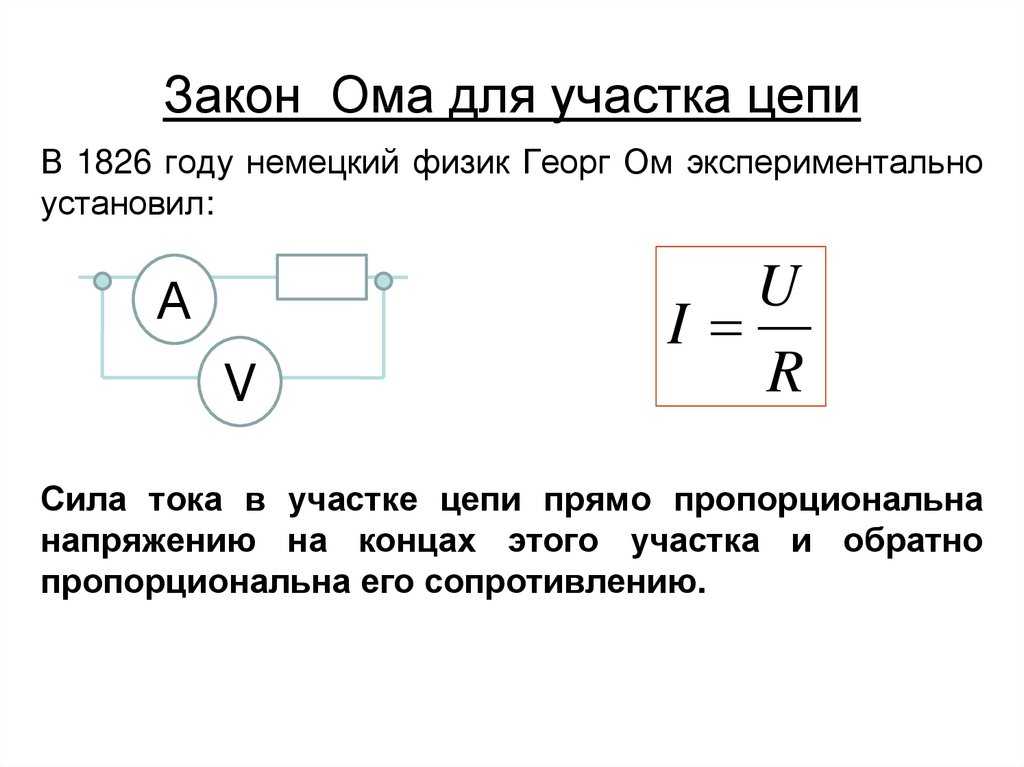 001кОм=0.000001МОм;
001кОм=0.000001МОм;
Единицы измерения мощности:1Вт=1000мВт=100000мкВт.
Ну и так, на всякий случай, чисто для проверки полученных результатов, приведём незамысловатую таблицу, позволяющую в онлайн режиме проверить расчёты, связанные со знанием формул закона Ома.
ТАБЛИЦА ДЛЯ ПРОВЕРКИ РЕЗУЛЬТАТОВ РАСЧЁТОВ ЗАКОНА ОМА.
Вводить в таблицу нужно только два имеющихся у Вас параметра, остальные посчитает таблица.
| Напряжение U | ВмВ мкВ | |
| Сопротивление R | ОмкОм МОм | |
| Сила тока I | АмА мкА | |
| Мощность Р | ВтмВт мкВт | |
Все наши расчёты проводились при условии, что значение внешнего сопротивления R значительно превышает внутреннее сопротивление источника напряжения rвнутр.

Если это условие не соблюдается, то под величиной R следует принять сумму внешнего и внутреннего сопротивлений: R = Rвнешн + rвнутр , после чего закон приобретает солидное название – закон Ома для полной цепи:
I=U/(R+r) .
Для многозвенных цепей возникает необходимость преобразования её к эквивалентному виду:
Значения последовательно соединённых резисторов просто суммируются, в то время как значения параллельно соединённых резисторов
определяются исходя из формулы:
1/Rll = 1/R4+1/R5.
А онлайн калькулятор для расчёта величин сопротивлений при параллельном соединении нескольких проводников можно найти на странице
ссылка на страницу.
Теперь, что касается закона Ома для переменного тока.
Если внешнее сопротивление у нас чисто активное (не содержит ёмкостей и индуктивностей), то формула, приведённая выше,
остаётся в силе.
Единственное, что надо иметь в виду для правильной интерпретации закона Ома для переменного тока – под значением U следует
понимать действующее (эффективное) значение амплитуды переменного сигнала.
А что такое действующее значение и как оно связано с амплитудой сигнала переменного тока?
Приведём диаграммы для нескольких различных форм сигнала.
Слева направо нарисованы диаграммы синусоидального сигнала, меандра (прямоугольный сигнал со скважностью, равной 2),
сигнала треугольной формы, сигнала пилообразной формы.
Глядя на рисунок можно осмыслить, что амплитудное значение приведённых сигналов – это максимальное значение, которого достигает
амплитуда в пределах положительной, или отрицательной (в наших случаях они равны) полуволны.
Рассчитываем действующее значение напряжение интересующей нас формы:
Для синуса U = Uд = Uа/√2;
для треугольника и пилы U = Uд = Uа/√3;
для меандра U = Uд = Uа.
С этим разобрались!
Теперь посмотрим, как будет выглядеть формула закона Ома при наличии индуктивности или ёмкости
в цепи переменного тока.
В общем случае смотреться это будет так:
А формула остаётся прежней, просто в качестве сопротивления R выступает полное сопротивление цепи Z,
состоящее из активного, ёмкостного и индуктивного сопротивлений.
Поскольку фазы протекающего через эти элементы тока не одинаковы, то простым арифметическим сложением сопротивлений этих
трёх элементов обойтись не удаётся, и формула приобретает вид:
Реактивные сопротивления конденсаторов и индуктивностей мы с Вами уже рассчитывали на странице
ссылка на страницу и знаем, что величины эти зависят от частоты, протекающего через них тока
и описываются формулами:
XC = 1/(2πƒС) , XL = 2πƒL .
Нарисуем таблицу для расчёта полного сопротивления цепи для переменного тока.
Количество вводимых элементов должно быть не менее одного, при наличии
индуктивного или емкостного элемента – необходимо указать значение частоты
f !
КАЛЬКУЛЯТОР ДЛЯ ОНЛАЙН РАСЧЁТА ПОЛНОГО СОПРОТИВЛЕНИЯ ЦЕПИ.
| Сопротивление R | ОмкОм МОм | |
| Индуктивность L | ГнмГн мкГн | |
| Ёмкость С | МкФ нФ пФ | |
| Частота f | Гц кГц МГц   | |
| Реактивное сопротивление XC | ||
| Реактивное сопротивление XL | ||
| Полное сопротивление цепи Z |
Теперь давайте рассмотрим практический пример применения закона Ома в цепях переменного тока и рассчитаем
простенький бестрансформаторный источник питания.
Токозадающими цепями в данной схеме являются элементы R1 и С1.
Допустим, нас интересует выходное напряжение Uвых = 12 вольт при токе нагрузки 100 мА.
Выбираем стабилитрон Д815Д с напряжением стабилизации 12В и максимально допустимым током стабилизации 1,4А.
Зададимся током через стабилитрон с некоторым запасом – 200мА.
С учётом падения напряжения на стабилитроне, напряжение на токозадающей цепи равно 220в – 12в = 208в.
Теперь рассчитаем сопротивление этой цепи Z для получения тока, равного 200мА: Z = 208в/200мА = 1,04кОм.
Резистор R1 является токоограничивающим и выбирается в пределах 10-100 Ом в зависимости от максимального тока
нагрузки.
Зададимся номиналами R1 – 30 Ом, С1 – 1 Мкф, частотой сети f – 50 Гц и подставим всё это хозяйство в таблицу.
Получили полное сопротивление цепи, равное 3,183кОм. Многовато будет – надо увеличивать ёмкость С1.
Поигрались туда-сюда, нашли нужное значение ёмкости – 3,18 Мкф, при котором Z = 1,04кОм.
Всё – закон Ома выполнил свою функцию, расчёт закончен, всем спать полчаса!
9.4: Удельное сопротивление и сопротивление – Physics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4402
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Различать сопротивление и удельное сопротивление
- Дайте определение термину проводимость
- Опишите электрический компонент, известный как резистор
- Укажите зависимость между сопротивлением резистора и его длиной, площадью поперечного сечения и удельным сопротивлением
- Укажите зависимость между удельным сопротивлением и температурой
Что движет током? Мы можем думать о различных устройствах, таких как батареи, генераторы, настенные розетки и т.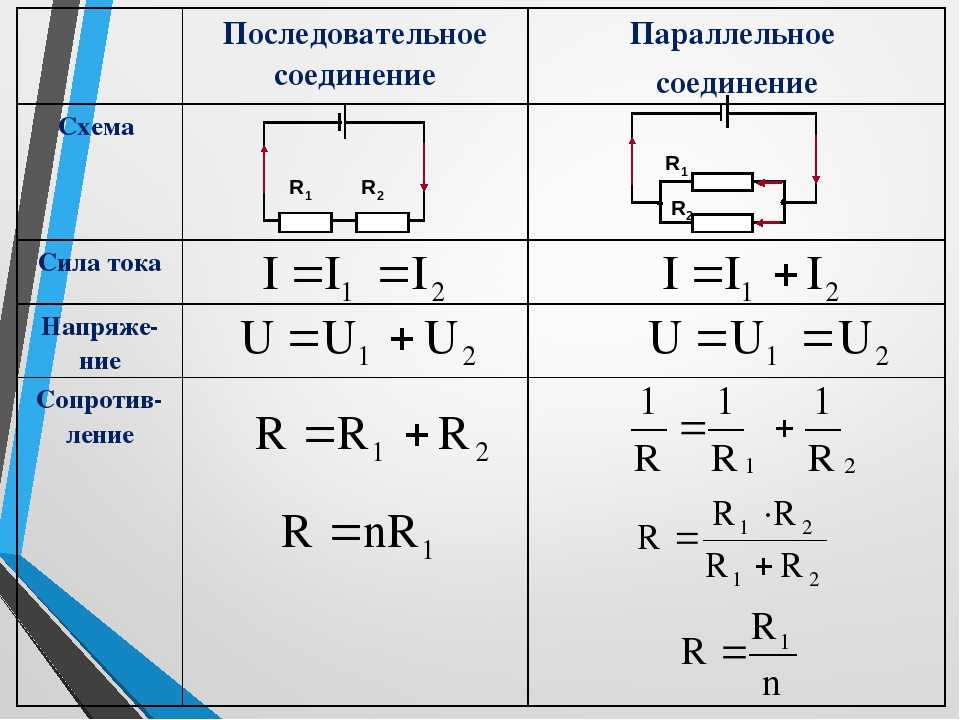 д., которые необходимы для поддержания тока. Все подобные устройства создают разность потенциалов и называются источниками напряжения. Когда источник напряжения подключен к проводнику, он создает разность потенциалов V , создающий электрическое поле. Электрическое поле, в свою очередь, воздействует на свободные заряды, вызывая ток. Величина тока зависит не только от величины напряжения, но и от характеристик материала, через который протекает ток. Материал может сопротивляться потоку зарядов, и мера того, насколько материал сопротивляется потоку зарядов, известна как удельное сопротивление . Это удельное сопротивление грубо аналогично трению между двумя материалами, которые сопротивляются движению.
д., которые необходимы для поддержания тока. Все подобные устройства создают разность потенциалов и называются источниками напряжения. Когда источник напряжения подключен к проводнику, он создает разность потенциалов V , создающий электрическое поле. Электрическое поле, в свою очередь, воздействует на свободные заряды, вызывая ток. Величина тока зависит не только от величины напряжения, но и от характеристик материала, через который протекает ток. Материал может сопротивляться потоку зарядов, и мера того, насколько материал сопротивляется потоку зарядов, известна как удельное сопротивление . Это удельное сопротивление грубо аналогично трению между двумя материалами, которые сопротивляются движению.
Удельное сопротивление
Когда к проводнику прикладывается напряжение, создается электрическое поле \(\vec{E}\), и заряды в проводнике испытывают силу, вызванную электрическим полем. Полученная плотность тока \(\vec{J}\) зависит от электрического поля и свойств материала. Эта зависимость может быть очень сложной. В некоторых материалах, в том числе и в металлах, при данной температуре плотность тока примерно пропорциональна напряженности электрического поля. В этих случаях плотность тока можно смоделировать как 9{-1}\).
Эта зависимость может быть очень сложной. В некоторых материалах, в том числе и в металлах, при данной температуре плотность тока примерно пропорциональна напряженности электрического поля. В этих случаях плотность тока можно смоделировать как 9{-1}\).
Электропроводность является неотъемлемым свойством материала. Другим внутренним свойством материала является удельное сопротивление, или электрическое сопротивление . Удельное сопротивление материала является мерой того, насколько сильно материал сопротивляется прохождению электрического тока. Символ удельного сопротивления — строчная греческая буква rho, \(\rho\), а удельное сопротивление — величина, обратная электропроводности:
\[\rho = \dfrac{1}{\sigma}.\]
Единица измерения Удельное сопротивление в единицах СИ представляет собой омметр \((\Omega \cdot m\). Мы можем определить удельное сопротивление через электрическое поле и плотность тока.
\[\rho = \dfrac{E}{J}.\]
Чем больше удельное сопротивление, тем большее поле необходимо для создания данной плотности тока. {-1}\)ConductorsSemiconductors [1]Insulators”>
{-1}\)ConductorsSemiconductors [1]Insulators”>
Материалы, перечисленные в таблице, разделены на категории проводников, полупроводников и изоляторов на основе широких групп удельного сопротивления. Проводники имеют наименьшее удельное сопротивление, а изоляторы – наибольшее; полупроводники имеют промежуточное удельное сопротивление. Проводники имеют разную, но большую плотность свободного заряда, в то время как большинство зарядов в изоляторах связаны с атомами и не могут свободно перемещаться. Полупроводники занимают промежуточное положение, имея гораздо меньше свободных зарядов, чем проводники, но обладая свойствами, из-за которых количество свободных зарядов сильно зависит от типа и количества примесей в полупроводнике. Эти уникальные свойства полупроводников используются в современной электронике, что мы и рассмотрим в последующих главах. 9{-5} \dfrac{V}{m}.\end{align*}\]
Значение
Из этих результатов неудивительно, что медь используется для проводов для передачи тока, потому что сопротивление довольно маленький. 2}\). Третьей важной характеристикой является пластичность. Пластичность — это мера способности материала втягиваться в провода и мера гибкости материала, а медь обладает высокой пластичностью. Подводя итог, можно сказать, что для того, чтобы проводник был подходящим кандидатом для изготовления проволоки, необходимо, по крайней мере, три важные характеристики: низкое удельное сопротивление, высокая прочность на растяжение и высокая пластичность. Какие еще материалы используются для электропроводки и в чем их преимущества и недостатки?
2}\). Третьей важной характеристикой является пластичность. Пластичность — это мера способности материала втягиваться в провода и мера гибкости материала, а медь обладает высокой пластичностью. Подводя итог, можно сказать, что для того, чтобы проводник был подходящим кандидатом для изготовления проволоки, необходимо, по крайней мере, три важные характеристики: низкое удельное сопротивление, высокая прочность на растяжение и высокая пластичность. Какие еще материалы используются для электропроводки и в чем их преимущества и недостатки?
- Ответить
Серебро, золото и алюминий используются для изготовления проводов. Все четыре материала имеют высокую проводимость, серебро имеет самую высокую. Все четыре легко вытягиваются в провода и обладают высокой прочностью на растяжение, хотя и не такой высокой, как у меди. Очевидным недостатком золота и серебра является стоимость, но серебряные и золотые провода используются для специальных применений, таких как провода для громкоговорителей.
 Золото не окисляется, что обеспечивает лучшее соединение между компонентами. У алюминиевых проводов есть свои недостатки. Алюминий имеет более высокое удельное сопротивление, чем медь, поэтому требуется больший диаметр, чтобы соответствовать сопротивлению на длину медных проводов, но алюминий дешевле меди, так что это не главный недостаток. Алюминиевые проволоки не обладают такой высокой пластичностью и прочностью на растяжение, как медь, но пластичность и прочность на растяжение находятся в пределах допустимых уровней. Есть несколько проблем, которые необходимо решить при использовании алюминия, и необходимо соблюдать осторожность при выполнении соединений. Алюминий имеет более высокую скорость теплового расширения, чем медь, что может привести к ослаблению соединений и возможной опасности возгорания. Окисление алюминия не проходит и может вызвать проблемы. При использовании алюминиевых проводов необходимо использовать специальные методы, а такие компоненты, как электрические розетки, должны быть рассчитаны на прием алюминиевых проводов.
Золото не окисляется, что обеспечивает лучшее соединение между компонентами. У алюминиевых проводов есть свои недостатки. Алюминий имеет более высокое удельное сопротивление, чем медь, поэтому требуется больший диаметр, чтобы соответствовать сопротивлению на длину медных проводов, но алюминий дешевле меди, так что это не главный недостаток. Алюминиевые проволоки не обладают такой высокой пластичностью и прочностью на растяжение, как медь, но пластичность и прочность на растяжение находятся в пределах допустимых уровней. Есть несколько проблем, которые необходимо решить при использовании алюминия, и необходимо соблюдать осторожность при выполнении соединений. Алюминий имеет более высокую скорость теплового расширения, чем медь, что может привести к ослаблению соединений и возможной опасности возгорания. Окисление алюминия не проходит и может вызвать проблемы. При использовании алюминиевых проводов необходимо использовать специальные методы, а такие компоненты, как электрические розетки, должны быть рассчитаны на прием алюминиевых проводов.
PhET
Просмотрите это интерактивное моделирование, чтобы узнать, как площадь поперечного сечения, длина и удельное сопротивление провода влияют на сопротивление проводника. Отрегулируйте переменные с помощью ползунков и посмотрите, станет ли сопротивление меньше или больше.
Температурная зависимость удельного сопротивления
Взглянув на таблицу \(\PageIndex{1}\), вы увидите столбец с пометкой «Температурный коэффициент». Удельное сопротивление некоторых материалов сильно зависит от температуры. В некоторых материалах, таких как медь, удельное сопротивление увеличивается с повышением температуры. На самом деле у большинства проводящих металлов удельное сопротивление увеличивается с повышением температуры. Повышение температуры вызывает усиление колебаний атомов в структуре решетки металлов, которые препятствуют движению электронов. В других материалах, таких как углерод, удельное сопротивление уменьшается с повышением температуры. Во многих материалах зависимость приблизительно линейна и может быть смоделирована линейным уравнением: 9оС\).
Также обратите внимание, что температурный коэффициент \(\alpha\) отрицателен для полупроводников, перечисленных в таблице \(\PageIndex{1}\), а это означает, что их удельное сопротивление уменьшается с повышением температуры. Они становятся лучшими проводниками при более высокой температуре, потому что повышенное тепловое возбуждение увеличивает количество свободных зарядов, доступных для переноса тока. Это свойство уменьшаться \(\rho\) с температурой также связано с типом и количеством примесей, присутствующих в полупроводниках.
Сопротивление
Теперь рассмотрим сопротивление провода или компонента. Сопротивление является мерой того, насколько сложно пропустить ток через провод или компонент. Сопротивление зависит от удельного сопротивления. Удельное сопротивление является характеристикой материала, используемого для изготовления провода или другого электрического компонента, тогда как сопротивление является характеристикой провода или компонента.
Для расчета сопротивления рассмотрим отрезок токопроводящего провода площадью поперечного сечения A , длина L и удельное сопротивление \(\rho\). Через проводник подключена батарея, создающая на нем разность потенциалов \(\Delta V\) (рис. \(\PageIndex{1}\)). Разность потенциалов создает электрическое поле, пропорциональное плотности тока, согласно \(\vec{E} = \rho \vec{J}\).
Через проводник подключена батарея, создающая на нем разность потенциалов \(\Delta V\) (рис. \(\PageIndex{1}\)). Разность потенциалов создает электрическое поле, пропорциональное плотности тока, согласно \(\vec{E} = \rho \vec{J}\).
Величина электрического поля на отрезке проводника равна напряжению, деленному на длину, \(E = V/L), а величина плотности тока равна силе тока, деленной на сечение. площадь сечения, \(J = I/A\). Используя эту информацию и вспомнив, что электрическое поле пропорционально удельному сопротивлению и плотности тока, мы можем увидеть, что напряжение пропорционально току:
\[\begin{align*} E &= \rho J \\[4pt] \dfrac{V}{L} &= \rho \dfrac{I}{A} \\[4pt] V &= \ left(\rho \dfrac{L}{A}\right) I. \end{align*}\]
Определение: Сопротивление
Отношение напряжения к току определяется как сопротивление \(R \):
\[R \equiv \dfrac{V}{I}. \]
\]
Сопротивление цилиндрического сегмента проводника равно удельному сопротивлению материала, умноженному на длину, деленную на площадь:
\[R \equiv \dfrac{V}{I} = \rho \dfrac{L}{A}.\]
Единицей сопротивления является ом, \(\Омега\). Для данного напряжения, чем выше сопротивление, тем меньше ток.
Резисторы
Обычным компонентом электронных схем является резистор. Резистор можно использовать для уменьшения протекающего тока или обеспечения падения напряжения. На рисунке \(\PageIndex{2}\) показаны символы, используемые для обозначения резистора на принципиальных схемах цепи. Два широко используемых стандарта для принципиальных схем предоставлены Американским национальным институтом стандартов (ANSI, произносится как «AN-see») и Международной электротехнической комиссией (IEC). Обе системы широко используются. В этом тексте мы используем стандарт ANSI для его визуального распознавания, но мы отмечаем, что для более крупных и сложных схем стандарт IEC может иметь более четкое представление, что облегчает его чтение.
Зависимость сопротивления от материала и формы
Резистор можно смоделировать в виде цилиндра с площадью поперечного сечения A и длиной L , изготовленного из материала с удельным сопротивлением \(\rho\) (рисунок \( \PageIndex{3}\)). Сопротивление резистора равно \(R = \rho \dfrac{L}{A}\)
. Рисунок \(\PageIndex{3}\): Модель резистора в виде однородного цилиндра длиной L и площадь поперечного сечения A . Его сопротивление потоку тока аналогично сопротивлению трубы потоку жидкости. Чем длиннее цилиндр, тем больше его сопротивление. Чем больше его площадь поперечного сечения А , тем меньше его сопротивление. Наиболее распространенным материалом для изготовления резисторов является углерод. Углеродная дорожка намотана на керамический сердечник, и к нему присоединены два медных вывода. Второй тип резистора — это металлопленочный резистор, который также имеет керамический сердечник. Дорожка изготовлена из оксида металла, обладающего полупроводниковыми свойствами, подобными углероду. Снова в концы резистора вставлены медные выводы. Затем резистор окрашивается и маркируется для идентификации. Резистор имеет четыре цветные полосы, как показано на рисунке \(\PageIndex{4}\). 9{-5} \, \Омега\), а сверхпроводники вообще не имеют сопротивления при низких температурах. Как мы видели, сопротивление связано с формой объекта и материалом, из которого он состоит.
Второй тип резистора — это металлопленочный резистор, который также имеет керамический сердечник. Дорожка изготовлена из оксида металла, обладающего полупроводниковыми свойствами, подобными углероду. Снова в концы резистора вставлены медные выводы. Затем резистор окрашивается и маркируется для идентификации. Резистор имеет четыре цветные полосы, как показано на рисунке \(\PageIndex{4}\). 9{-5} \, \Омега\), а сверхпроводники вообще не имеют сопротивления при низких температурах. Как мы видели, сопротивление связано с формой объекта и материалом, из которого он состоит.
Сопротивление объекта также зависит от температуры, так как \(R_0\) прямо пропорционально \(\rho\). Для цилиндра мы знаем \(R = \rho \dfrac{L}{A}\), поэтому, если L и A не сильно меняются с температурой, R имеет ту же температурную зависимость, что и \( \ро\). (Изучение коэффициентов линейного расширения показывает, что они примерно на два порядка меньше типичных температурных коэффициентов удельного сопротивления, поэтому влияние температуры на 9оС\).
Многие термометры основаны на влиянии температуры на сопротивление (рис. \(\PageIndex{5}\)). Один из наиболее распространенных термометров основан на термисторе, полупроводниковом кристалле с сильной температурной зависимостью, сопротивление которого измеряется для получения его температуры. Устройство маленькое, поэтому быстро приходит в тепловое равновесие с той частью человека, к которой прикасается.
Рисунок \(\PageIndex{5}\): Эти известные термометры основаны на автоматизированном измерении сопротивления термистора в зависимости от температуры. 9oC)\right) \\[5pt] &= 4.8 \, \Omega \end{align*} \]Значимость
Обратите внимание, что сопротивление изменяется более чем в 10 раз по мере того, как нить нагревается до высокая температура и ток через нить накала зависит от сопротивления нити и приложенного напряжения. Если нить используется в лампе накаливания, начальный ток через нить при первом включении лампы будет выше, чем ток после того, как нить достигнет рабочей температуры.
Упражнение \(\PageIndex{2}\)
Тензорезистор — это электрическое устройство для измерения деформации, как показано ниже. Он состоит из гибкой изолирующей подложки, поддерживающей узор из проводящей фольги. Сопротивление фольги изменяется по мере растяжения подложки. Как изменится сопротивление тензорезистора? Влияет ли на тензодатчик изменение температуры?
- Ответить
Рисунок из фольги растягивается по мере растяжения подложки, а дорожки из фольги становятся длиннее и тоньше. Поскольку сопротивление рассчитывается как \(R = \rho \dfrac{L}{A}\), сопротивление увеличивается по мере растяжения дорожек из фольги. При изменении температуры изменяется и удельное сопротивление дорожек фольги, изменяя сопротивление. Одним из способов борьбы с этим является использование двух тензодатчиков, один из которых используется в качестве эталона, а другой используется для измерения деформации. Два тензодатчика поддерживают постоянную температуру
Сопротивление коаксиального кабеля
Длинные кабели иногда могут действовать как антенны, улавливая электронные шумы, то есть сигналы от другого оборудования и приборов. Коаксиальные кабели используются во многих приложениях, требующих устранения этого шума. Например, их можно найти дома в соединениях кабельного телевидения или других аудиовизуальных соединениях. Коаксиальные кабели состоят из внутреннего проводника радиуса \(r_i\), окруженного вторым, внешним концентрическим проводником радиусом \(r_0\) (рисунок \(\PageIndex{6}\)). Пространство между ними обычно заполнено изолятором, например, полиэтиленом. Между двумя проводниками возникает небольшой радиальный ток утечки. Определить сопротивление коаксиального кабеля длиной 9 см.0048 л .
Коаксиальные кабели используются во многих приложениях, требующих устранения этого шума. Например, их можно найти дома в соединениях кабельного телевидения или других аудиовизуальных соединениях. Коаксиальные кабели состоят из внутреннего проводника радиуса \(r_i\), окруженного вторым, внешним концентрическим проводником радиусом \(r_0\) (рисунок \(\PageIndex{6}\)). Пространство между ними обычно заполнено изолятором, например, полиэтиленом. Между двумя проводниками возникает небольшой радиальный ток утечки. Определить сопротивление коаксиального кабеля длиной 9 см.0048 л .
Стратегия
Мы не можем использовать уравнение \(R = \rho \dfrac{L}{A}\) напрямую. Вместо этого мы смотрим на концентрические цилиндрические оболочки толщиной dr и интегрируем.
Решение
Сначала находим выражение для \(dR\), а затем интегрируем от \(r_i\) до \(r_0\), 9{r_0} \dfrac{1}{r} dr \\[5pt] &= \dfrac{\rho}{2\pi L} \ln \dfrac{r_0}{r_i}.\end{align*}\]
Значение
Сопротивление коаксиального кабеля зависит от его длины, внутреннего и внешнего радиусов и удельного сопротивления материала, разделяющего два проводника. Поскольку это сопротивление не бесконечно, между двумя проводниками возникает небольшой ток утечки. Этот ток утечки приводит к затуханию (или ослаблению) сигнала, передаваемого по кабелю.
Упражнение \(\PageIndex{3}\)
Сопротивление между двумя проводниками коаксиального кабеля зависит от удельного сопротивления материала, разделяющего два проводника, длины кабеля и внутреннего и внешнего радиусов двух проводников. проводник. Если вы проектируете коаксиальный кабель, как сопротивление между двумя проводниками зависит от этих переменных?
- Ответить
Чем больше длина, тем меньше сопротивление.
 Чем больше удельное сопротивление, тем выше сопротивление. Чем больше разница между внешним радиусом и внутренним радиусом, то есть чем больше отношение между ними, тем больше сопротивление. Если вы пытаетесь максимизировать сопротивление, выбор значений этих переменных будет зависеть от приложения. Например, если кабель должен быть гибким, выбор материалов может быть ограничен.
Чем больше удельное сопротивление, тем выше сопротивление. Чем больше разница между внешним радиусом и внутренним радиусом, то есть чем больше отношение между ними, тем больше сопротивление. Если вы пытаетесь максимизировать сопротивление, выбор значений этих переменных будет зависеть от приложения. Например, если кабель должен быть гибким, выбор материалов может быть ограничен.
Phet: Цепь батареи и резистора
Просмотрите эту симуляцию, чтобы увидеть, как приложенное напряжение и сопротивление материала, через который протекает ток, влияют на ток через материал. Вы можете визуализировать столкновения электронов и атомов материала, влияющие на температуру материала.
Эта страница под названием 9.4: Сопротивление и сопротивление распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.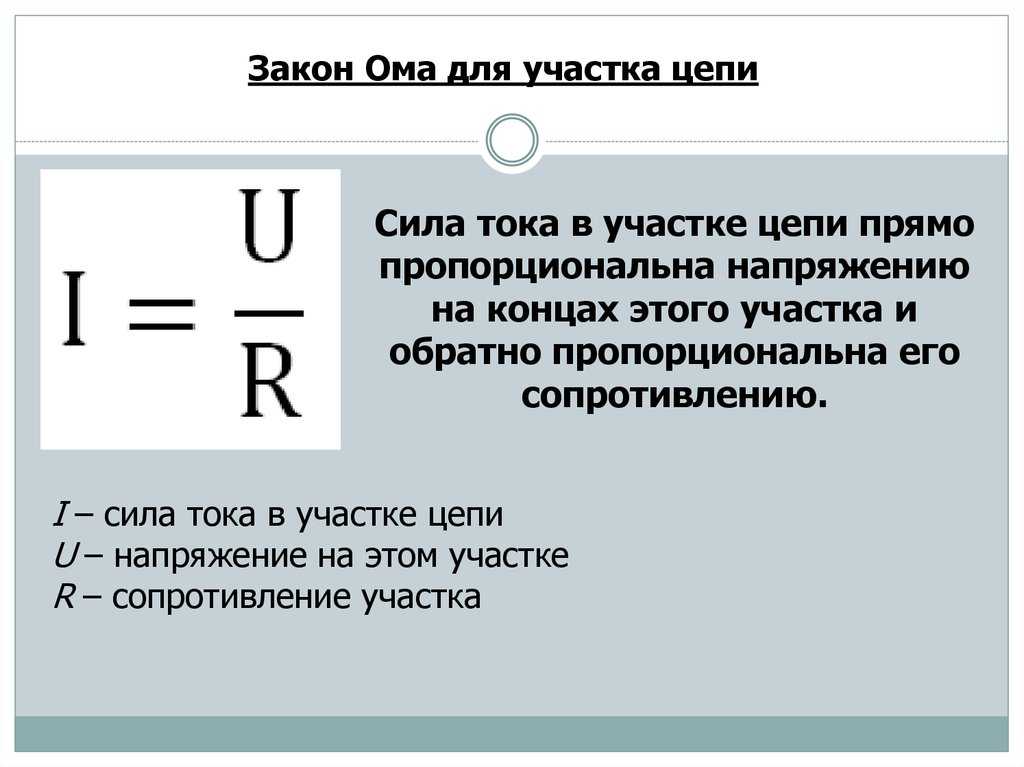
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- электропроводность
- Ом
- сопротивление
- удельное сопротивление
- источник@https://openstax.
 org/details/books/university-physics-volume-2
org/details/books/university-physics-volume-2
Мощность, рассеиваемая резистором? Надежность цепи и примеры расчетов
В электронике слово «рассеивание» довольно распространено, и те, кто работает в этой отрасли, слишком хорошо его знают или, по крайней мере, должны знать. Я говорю должен, потому что очевидно, что это не всегда так. Что ж, я подробнее остановлюсь на том, почему я сразу сказал «должен». Но пока давайте сосредоточимся на теме диссипации.
Возьмем, к примеру, полностью заряженный конденсатор, такой как конденсатор емкостью 3,0 фарад, используемый в аудиосистеме. В этом случае, если вы снимаете конденсатор для хранения, замены или проведения технического обслуживания системы, вы определенно хотите, чтобы конденсатор рассеивал свой заряд.
Это был момент, который не смог понять один джентльмен, даже после того, как предоставил ему подробные детали вместе с необходимыми шагами. Однако несоблюдение надлежащих протоколов разрядки плюс катание конденсатора в багажнике плюс WD-40 равняется событию, которое могло бы вдохновить одну из моих любимых групп (The Power Station) на написание одной из моих любимых песен (Some Like it Hot). Кроме шуток, в его багажнике горела жара, и по сей день его прозвище все еще «дым-дым-дым».
Однако несоблюдение надлежащих протоколов разрядки плюс катание конденсатора в багажнике плюс WD-40 равняется событию, которое могло бы вдохновить одну из моих любимых групп (The Power Station) на написание одной из моих любимых песен (Some Like it Hot). Кроме шуток, в его багажнике горела жара, и по сей день его прозвище все еще «дым-дым-дым».
Что такое рассеиваемая мощность?
Рассеяние мощности определяется как процесс, при котором электронное или электрическое устройство выделяет тепло (потери или потери энергии) как нежелательное производное от своего основного действия. Как и в случае с центральными процессорами, рассеивание мощности является основной проблемой в компьютерной архитектуре.
Кроме того, рассеивание мощности в резисторах считается естественным явлением. Факт остается фактом: все резисторы, являющиеся частью цепи и имеющие на ней падение напряжения, будут рассеивать электрическую мощность. Более того, эта электрическая мощность преобразуется в тепловую энергию, и поэтому все резисторы имеют номинальную мощность. Кроме того, номинальная мощность резистора — это классификация, которая характеризует максимальную мощность, которую он может рассеивать, прежде чем он достигнет критического отказа.
Кроме того, номинальная мощность резистора — это классификация, которая характеризует максимальную мощность, которую он может рассеивать, прежде чем он достигнет критического отказа.
Как вы, наверное, знаете, мощность выражается в ваттах (Вт), а формула мощности: P (мощность) = I (ток) x E (напряжение). Что касается законов физики, если есть увеличение напряжения (E), то ток (I) также будет увеличиваться, и, в свою очередь, будет увеличиваться рассеиваемая мощность резистора. Однако, если вы увеличите значение резистора, ток уменьшится, а также уменьшится рассеиваемая мощность резистора. Эта корреляция следует закону Ома, который устанавливает формулу тока как I (ток) = V (напряжение) ÷ R (сопротивление).
Расчет мощности, рассеиваемой резистором
В области электроники рассеиваемая мощность также является параметром измерения, который количественно определяет выделение тепла в цепи из-за неэффективности. Другими словами, рассеиваемая мощность является мерой того, сколько мощности (P = I x E) в цепи преобразуется в тепло. Как я упоминал ранее, у каждого резистора есть номинальная мощность, и с точки зрения конструкции это позволяет разработчикам оценить, будет ли конкретный резистор соответствовать их конструктивным требованиям в схеме. Итак, теперь давайте подробнее рассмотрим, как рассчитать этот критический параметр конструкции.
Как я упоминал ранее, у каждого резистора есть номинальная мощность, и с точки зрения конструкции это позволяет разработчикам оценить, будет ли конкретный резистор соответствовать их конструктивным требованиям в схеме. Итак, теперь давайте подробнее рассмотрим, как рассчитать этот критический параметр конструкции.
Во-первых, согласно закону Ома,
В (напряжение) = I (ток) × R (сопротивление)
I (ток) = V (напряжение) ÷ R (сопротивление)
P (мощность) = I (ток) × V (напряжение)
Следовательно, для расчета мощности, рассеиваемой резистором, формулы следующие:
P (рассеиваемая мощность) = I2 (ток) × R (сопротивление)
или
P (рассеиваемая мощность) = V2 (напряжение) ÷ R (сопротивление)
Итак, используя приведенную выше принципиальную схему в качестве справки, мы можем применить эти формулы для определения мощности, рассеиваемой резистором.
Напряжение = 9 В
Сопротивление = 100 Ом
I (ток) = 9 В ÷ 100 Ом или I (ток) = 90 мА
P (мощность) = 90 мА × 9 В или P (мощность) = 0,81 Вт или 810 мВт
P (рассеиваемая мощность) = V2 (напряжение) ÷ R (сопротивление)
или
P (рассеиваемая мощность) = 92 ÷ 100
или
P (рассеиваемая мощность) = 81 ÷ 100 или P (мощность рассеиваемая мощность) = 810 мВт
Рассеиваемая мощность: хорошо или плохо?
Вообще говоря, нет; тем не менее, есть некоторые случаи, когда рассеивание тепла является хорошей вещью. Возьмем, к примеру, электрические нагреватели, в которых используется резистивная проволока, такая как нихром. Нихром является уникальным нагревательным элементом благодаря своей экономичности, устойчивости к потоку электронов, прочности, гибкости, стойкости к окислению и стабильности при высоких температурах.
Кроме того, еще одним примером благоприятного рассеяния тепла являются лампы накаливания, которые используются в качестве экономичных обогревателей. В целом, при нормальных условиях рассеивание тепла нежелательно, но в тех редких случаях, когда оно имеет место, оно будет заключаться в усилиях по контролю рассеивания тепла, а не в его сдерживании.
Вот некоторые важные моменты, на которые следует обратить внимание при рассмотрении рассеиваемой мощности.
Убедитесь, что номинальная мощность резистора соответствует требованиям вашей схемы.
Обязательно перепроверьте, зависит ли рейтинг вашей микросхемы от использования радиаторов.
Если вы проектируете печатные платы, убедитесь, что ваши дорожки достаточно велики, чтобы поддерживать низкое сопротивление и избегать чрезмерного нагрева.

При проектировании схемы переключения убедитесь, что время переключения максимально короткое.
Чтобы сократить время переключения, сделайте скорость нарастания как можно более крутой, уменьшив емкость на линии. Кроме того, в области электроники скорость нарастания определяется как изменение тока, напряжения или других электрических величин в единицу времени.
Резисторы — это многогранные компоненты, доступные для ваших цепей.
Как дизайнеры, вы постоянно сталкиваетесь с постоянно возникающими проблемами при проектировании электронных схем. Одним из наиболее важных аспектов проектирования является поиск правильных компонентов, отвечающих потребностям вашей схемы. Кроме того, обнаружение этих компонентов также означает, что они должны безопасно функционировать в пределах заданных параметров напряжения, мощности и тока. Поэтому расчет таких параметров, как рассеиваемая мощность, имеет решающее значение для общей схемы.
Стратегии рассеивания мощности и использование резисторов в ваших цепях более чем эффективны с набором инструментов Cadence для проектирования и анализа. Решая любую задачу компоновки в Allegro PCB Designer, вы получаете быстрые, чистые и готовые к производству проекты.
Если вы хотите узнать больше о том, как у Cadence есть решение для вас, обратитесь к нам и нашей команде экспертов. Вы также можете посетить наш канал YouTube и посмотреть видеоролики о моделировании и системном анализе, а также узнать, что нового в нашем наборе инструментов для проектирования и анализа.
Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты. Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.
Подпишитесь на LinkedIn Посетить сайт Больше контента от Cadence PCB Solutions
УЧИТЬ БОЛЬШЕЗакон Ома: значение, формула и сопротивление
Закон Ома был сформулирован в 1827 году немецким физиком Георгом Симоном Омом на основе экспериментов, которые он проводил с простыми электрическими цепями, содержащими провода различной длины.
Закон Ома является одним из самых фундаментальных и важных принципов электрических цепей.
Закон Ома утверждает, что напряжение в двух точках электрической цепи прямо пропорционально 9004 текущий , проходящий между этими двумя точками. Константа пропорциональности равна сопротивлению .
Формула закона Ома:
Здесь V — напряжение на проводнике, I — ток, протекающий через проводник, а R — электрическое сопротивление проводника. Сопротивление в законе Ома всегда равно постоянному значению и может быть рассчитано путем проведения серии измерений напряжения и тока в подходящем диапазоне значений перед нанесением данных на прямолинейный график и вычислением его градиента.
Прежде чем продолжить объяснение закона Ома, мы должны рассмотреть некоторые основные понятия, касающиеся электрических цепей.
Закон Ома: электрические цепи
Электрическая цепь представляет собой набор электрических компонентов, соединенных проводниками, по которым может проходить электрический ток. Электрический ток состоит из движущихся электронов, которые обтекают провод под действием приложенного напряжения. Чтобы электрические компоненты могли пропускать электрический заряд, они должны быть изготовлены из электропроводящие материалы . Проводник представляет собой материал или электрический компонент, который способствует прохождению заряда (электрического тока) в одном или нескольких направлениях. Мы говорим, что такие материалы являются хорошими проводниками электричества.
Электрический ток состоит из движущихся электронов, которые обтекают провод под действием приложенного напряжения. Чтобы электрические компоненты могли пропускать электрический заряд, они должны быть изготовлены из электропроводящие материалы . Проводник представляет собой материал или электрический компонент, который способствует прохождению заряда (электрического тока) в одном или нескольких направлениях. Мы говорим, что такие материалы являются хорошими проводниками электричества.
Пример электрической цепи, адаптировано из изображения: MikeRun CC BY-SA 4.0
Металлы являются хорошими проводниками электричества, поэтому мы создаем электрические цепи, такие как те, которые используются в бытовой электронике, из меди , который обладает высокой проводимостью.
При изучении электрических цепей мы часто делаем различие между омическими проводниками и неомическими проводниками.
Омический проводник — это проводник, который подчиняется закону Ома.
График зависимости напряжения от тока омического проводника имеет линейную зависимость, чего нельзя сказать о неомических проводниках.
График зависимости напряжения от тока для омического и неомического материала, Iñaki Caparros-StudySmarter Originals
Неомический проводник не подчиняется закону Ома . Зависимость между напряжением и током для неомического проводника нелинейна.
Поведение неомических проводников не обязательно такое же, как показано на рисунке выше. Важной особенностью является то, что существует нелинейная зависимость между током и напряжением, что означает, что график зависимости напряжения от тока не является прямой линией. Некоторыми примерами неомических проводников являются нити накала лампы или некоторые полупроводники, такие как транзисторы или диоды.
Некоторые материалы плохо проводят электричество. Мы называем такие материалы или электрические компоненты, изготовленные из таких материалов, как изоляторы .
Изоляторы можно использовать для замедления или остановки потока заряда, а также они могут использоваться в различных реальных условиях, например, в качестве пластикового покрытия электрических проводов, которое защищает нас от удара электрическим током.
Закон Ома: напряжение
Напряжение также известно как разность потенциалов. Разность потенциалов между двумя точками проводника равна разнице электрических потенциалов между двумя точками. Разность потенциалов в электрической цепи создается элементами или батареями. В стандартных единицах мы выражаем разность потенциалов/напряжение в вольт (В).
В электрических цепях напряжение генерируется ячейкой или батареей, у которых есть положительная клемма с более высоким потенциалом и отрицательная клемма с более низким потенциалом.
Закон Ома: Ток
Ток – это скорость потока электрического заряда. Прибор, который мы используем для измерения силы тока в электрической цепи, называется амперметром .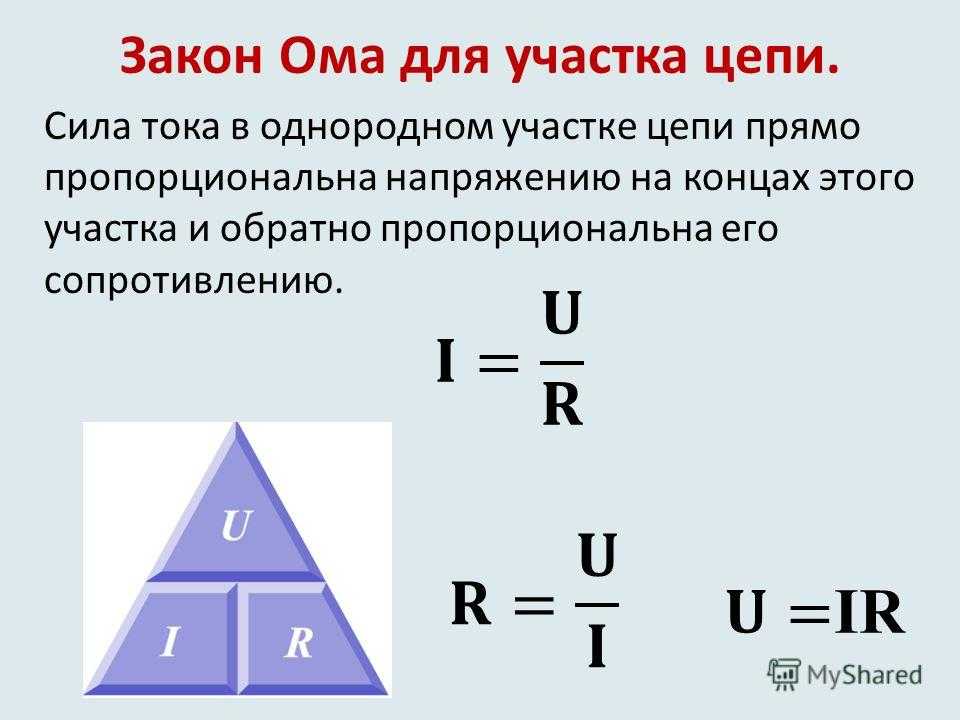 Стандартной единицей электрического тока является А мпер (А).
Стандартной единицей электрического тока является А мпер (А).
Закон Ома: сопротивление
Сопротивление — это мера сопротивления проводников потоку электричества. Стандартной единицей измерения сопротивления является O hm (Ом). Сопротивление электрического проводника увеличивается с длиной и уменьшается с толщиной. Сопротивление также зависит от типа материала, из которого он изготовлен.
Алюминиевый провод имеет более высокое сопротивление, чем медный провод той же длины и площади поперечного сечения, что означает, что медь является лучшим проводником электричества, чем алюминий. Но алюминиевый провод имеет меньшее сопротивление, чем медный провод, в четыре раза превышающий его длину.
Чтобы увеличить электрическое сопротивление электрической цепи, мы можем добавить компонент, называемый резистором . Фиксированный резистор подчиняется закону Ома, и разные постоянные резисторы имеют разные постоянные сопротивления для разных целей.
Примеры резисторов с различным сопротивлением в электрических цепях, wikipedia.org
Вывод закона Ома
Точного вывода формулы закона Ома не существует. Как упоминалось ранее, закон был сформулирован в 1827 году Георгом Симоном Омом, но это эмпирический закон, а это означает, что он изначально был основан на наблюдениях, а не выведен из первых принципов. Ом открыл закон, наблюдая за поведением омических проводников при подаче на них тока. Основываясь на полученных данных, Ом констатировал наличие линейной зависимости между током и силой тока, но теоретически закон не вывел.
Еще раз к формуле закона Ома
Теперь, когда мы выяснили, что означает каждый термин в законе Ома, давайте вспомним формулу:
Или, выражаясь словами: уравнение, что существует прямая зависимость между напряжением и силой тока. Мы говорим, что напряжение на проводнике прямо пропорционально протекающему по нему току. Это означает, что если мы увеличим ток, проходящий через проводник, в определенный раз, напряжение увеличится во столько же раз, и наоборот. Например, если мы удвоим разность потенциалов на проводе, ток, проходящий через него, также удвоится.
Например, если мы удвоим разность потенциалов на проводе, ток, проходящий через него, также удвоится.
Мы можем изменить формулу закона Ома, чтобы сделать сопротивление или ток предметом формулы. Если мы знаем значения любых двух переменных в законе Ома, мы можем вычислить значение оставшейся отсутствующей переменной. Например, если мы знаем ток, проходящий через компонент в электрической цепи, и мы также знаем разность потенциалов между двумя сторонами компонента, мы можем рассчитать сопротивление проводника по следующей формуле:
Это по-прежнему закон Ома, только измененный, чтобы сделать R предметом формулы. Точно так же, если мы знаем разность потенциалов на компоненте и его сопротивление, мы можем рассчитать ток I, проходящий через него: мы знаем значения двух других.
Треугольник закона Ома с напряжением (V), током (I) и сопротивлением (R), Iñáki Caparros-StudySmarter Originals
Этот треугольник называется треугольником закона Ома . Чтобы напомнить себе, как вычислять каждый из V, I и R, мы создали треугольник с V в верхнем сегменте и I и R в нижних сегментах. Чтобы вычислить значение любой из переменных в нижней части треугольника, мы просто делим значение V на значение другой оставшейся переменной в нижней части треугольника. V просто рассчитывается путем умножения значений двух переменных в нижнем сегменте треугольника, а именно I и R.
Чтобы напомнить себе, как вычислять каждый из V, I и R, мы создали треугольник с V в верхнем сегменте и I и R в нижних сегментах. Чтобы вычислить значение любой из переменных в нижней части треугольника, мы просто делим значение V на значение другой оставшейся переменной в нижней части треугольника. V просто рассчитывается путем умножения значений двух переменных в нижнем сегменте треугольника, а именно I и R.
Если вам сложно переставить уравнения, вы можете предпочесть вычислить V, I и R с помощью треугольника закона Ома. Только не забудьте нарисовать треугольник и разделить его на три части: верхняя часть содержит V, а две нижние части содержат I и R.
9-вольтовая батарея создает в проводе ток силой 3 А. Каково сопротивление провода?
Для решения этой задачи воспользуемся законом Ома. Используя наши знания о преобразовании уравнений или законе треугольника Ома, мы находим, что формула для вычисления сопротивления:
Чтобы найти одну из двух переменных нижнего уровня треугольника закона Ома, мы делим напряжение на другую переменную нижнего уровня. В этом случае делим V на I, чтобы найти R.
В этом случае делим V на I, чтобы найти R.
Следовательно, сопротивление провода в данном примере равно:
Определить напряжение электрической цепи с током 0,5 А и сопротивлением 20 Ом .
В этом случае нам нужно использовать первую форму закона Ома. Формулу закона Ома для напряжения находим по треугольнику закона Ома:
Теперь мы можем ввести данные для электрической цепи, приведенные в вопросе, подставив 0,5 А для тока и 20 Ом для сопротивления: переключатель замкнут.
Электрическая цепь с напряжением V= 30 В и сопротивлением R= 10 Ом, Iñaki Caparros-StudySmarter Originals
Как видно из рисунка выше, электрическая цепь имеет разность потенциалов 30 В на своих клеммах, и резистор имеет сопротивление 10 Ом. Мы должны изменить первоначальную форму формулы закона Ома. Если мы посмотрим на треугольник закона Ома, мы можем изменить формулу для расчета тока:
Используя значения переменных, представленных на рисунке, мы можем рассчитать ток следующим образом:
Закон Ома – основные выводы в двух точках электрической цепи пропорционально
току , проходящему через нее, а константой пропорциональности является сопротивление .


 Золото не окисляется, что обеспечивает лучшее соединение между компонентами. У алюминиевых проводов есть свои недостатки. Алюминий имеет более высокое удельное сопротивление, чем медь, поэтому требуется больший диаметр, чтобы соответствовать сопротивлению на длину медных проводов, но алюминий дешевле меди, так что это не главный недостаток. Алюминиевые проволоки не обладают такой высокой пластичностью и прочностью на растяжение, как медь, но пластичность и прочность на растяжение находятся в пределах допустимых уровней. Есть несколько проблем, которые необходимо решить при использовании алюминия, и необходимо соблюдать осторожность при выполнении соединений. Алюминий имеет более высокую скорость теплового расширения, чем медь, что может привести к ослаблению соединений и возможной опасности возгорания. Окисление алюминия не проходит и может вызвать проблемы. При использовании алюминиевых проводов необходимо использовать специальные методы, а такие компоненты, как электрические розетки, должны быть рассчитаны на прием алюминиевых проводов.
Золото не окисляется, что обеспечивает лучшее соединение между компонентами. У алюминиевых проводов есть свои недостатки. Алюминий имеет более высокое удельное сопротивление, чем медь, поэтому требуется больший диаметр, чтобы соответствовать сопротивлению на длину медных проводов, но алюминий дешевле меди, так что это не главный недостаток. Алюминиевые проволоки не обладают такой высокой пластичностью и прочностью на растяжение, как медь, но пластичность и прочность на растяжение находятся в пределах допустимых уровней. Есть несколько проблем, которые необходимо решить при использовании алюминия, и необходимо соблюдать осторожность при выполнении соединений. Алюминий имеет более высокую скорость теплового расширения, чем медь, что может привести к ослаблению соединений и возможной опасности возгорания. Окисление алюминия не проходит и может вызвать проблемы. При использовании алюминиевых проводов необходимо использовать специальные методы, а такие компоненты, как электрические розетки, должны быть рассчитаны на прием алюминиевых проводов.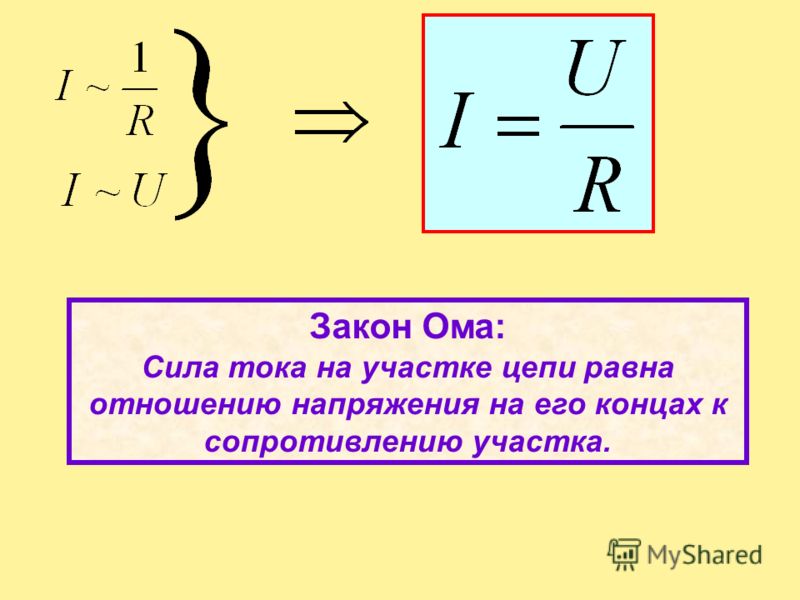
 Чем больше удельное сопротивление, тем выше сопротивление. Чем больше разница между внешним радиусом и внутренним радиусом, то есть чем больше отношение между ними, тем больше сопротивление. Если вы пытаетесь максимизировать сопротивление, выбор значений этих переменных будет зависеть от приложения. Например, если кабель должен быть гибким, выбор материалов может быть ограничен.
Чем больше удельное сопротивление, тем выше сопротивление. Чем больше разница между внешним радиусом и внутренним радиусом, то есть чем больше отношение между ними, тем больше сопротивление. Если вы пытаетесь максимизировать сопротивление, выбор значений этих переменных будет зависеть от приложения. Например, если кабель должен быть гибким, выбор материалов может быть ограничен. org/details/books/university-physics-volume-2
org/details/books/university-physics-volume-2