Формула силы тяготения: Закон всемирного тяготения — урок. Физика, 9 класс. - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Закон всемирного тяготения (формулировка, формула, условия применимости формулы). Сила тяжести. Вес

Похожие презентации:

Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов

Газовая хроматография

Геофизические исследования скважин

Искусственные алмазы

Трансформаторы тока и напряжения

Транзисторы

Воздушные и кабельные линии электропередач

Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса

Магнитные аномалии

Нанотехнологии

Вопрос № 7
Закон всемирного тяготения
(формулировка, формула,
условия применимости
формулы). Сила тяжести. Вес.
Попытки объяснить строение Солнечной системы занимали умы
многих великих людей.
После того, как Коперник
«поместил» Солнце в центр,
а все планеты «заставил»
обращаться вокруг него.
Особенно волновал вопрос:
что связывает планеты и
Солнце в единую систему?
Вспомним II ЗН

Ньютон связал силу с ускорением F=m*a.

Именно Солнце естественно считать причиной обращения вокруг
него Земли и планет.
Но не только П притягиваются к С
С притягивается к П
П притягиваются к П.
Все тала Вселенной, как небесные, так и находящиеся на
Земле, подвержены взаимному притяжению.
А мы наблюдаем это притяжение?
Почему?
Гравитационное взаимодействие – это взаимодействие,
свойственное всем телам Вселенной и проявляющееся в их
взаимном притяжении друг к другу.
Оно осуществляется с помощью особого вида материи –
гравитационного поля, существующего вокруг любого тела.
Особенность поля: всепроникающая способность
Гравитационный заряд характеризует взаимосвязь тел с

гравитационным полем.
Гравитационный заряд любого тела равен численно его
массе.
1642-1727
Исаак Ньютон
Получил выражение
для силы тяготения в
1666 году, когда было
ему 24 года.
По легенде, эта идея
ему пришла после
падения на него
яблока в саду.
Когда Ньютон открыл Закон всемирного
тяготения, он не знал ни одного числового
значения масс небесных тел, в том числе и точного
значения массы Земли.

Неизвестно ему было и значение гравитационной
постоянной G.
Неизвестным оно оставалось вплоть до 1798 года.
Малость G: хорошо или плохо?
Если бы G была
больше в 100 раз, то
время существования
Звезд, Солнца,
уменьшилось бы на
столько, что разумная
жизнь не успела бы
зародиться.
Два человека массой
по 60 кг, находящиеся
на расстоянии друг от
друга 1 метр
притягиваются с силой
F≈ 10-9 Н
Сила тяжести
Вспомним, при каких условиях справедлив Закон
Всемирного тяготения?
шар большого радиуса + материальная точка
Сила, с которой Земля притягивает находящиеся вблизи
тела, называется силой тяжести (Fт)
Гравитационное поле Земли принято называть полем
тяжести.
Вес тела –
это сила, с которой тело давит на опору
или растягивает подвес.
Р [P]=Н
Отличие силы тяжести от веса тела
Fт
1. Приложены к разным телам
к телу
к опоре, подвесу
2. Различная природа сил
гравитационная сила
сила упругости
3.

Fт = mg
для любого тела
Р
P = mg
для покоящегося тела
Перегрузка
– это состояние тела, при котором его вес превышает силу тяжести.
«Я почувствовал,— вспоминал Гагарин,—
какая-то непреоборимая сила все больше
и больше вдавливает меня в кресло. И хотя
оно было расположено так, чтобы до
предела сократить влияние огромной тяжести,
наваливающейся на мое тело, было трудно пошевелить рукой и ногой…»
При перегрузке все тело сильнее давит на опору и отдельные части тела
сильнее давят друг на друга.
Во время перегрузки у человека:
затрудняется дыхание,
ухудшается сердечная деятельность,
происходит перераспределение крови,
ее отлив или прилив к голове.
Поэтому переносить такие нагрузки сможет только натренированный и
опытный астронавт.
После включения ракетных двигателей и начала разгона, на астронавта
действуют две силы:
одна из них – сила тяжести (Fт= mg)
и сила реакции опоры (N=ma).
Так как ускорение ракеты a направлено вверх, то преобладающей
оказывается сила реакции опоры: N > mg.

Их равнодействующая F = N – mg по второму закону Ньютона равна
произведению массы на ускорение:
N – mg = ma, откуда
N = mg + ma.
Вес космонавта Р по третьему закону Ньютона равен по величине силе
реакции N, поэтому вес астронавта
P= m ( g + a ).
Это обозначает, что он получает нагрузку в несколько раз большую, чем
его масса.
Если космонавт испытывает n-кратную перегрузку, т.е. a=ng, то его вес
P=m(g + ng) = mg(n + 1).
Т. е. вес космонавта увеличился в (n+1) раз.
При n-кратной перегрузке вес космонавта увеличивается в (n+1) раз.
Чем меньше время действия перегрузки, тем большую ее

человек может перенести:
От 8g за 3с
до 5g за 12-15с (в вертикальном положении)
При мгновенном действии (0,1 с)
человек способен выдержать 20-кратные перегрузки.
После выключения двигателей, когда космический корабль
выходит на орбиту вокруг Земли, его ускорение, как мы знаем,
становится равным ускорению свободного падения: a = g.

Точно такое же ускорение будет и у космонавта,
находящегося внутри корабля. Это ускорение направлено
вниз, к центру Земли, и поэтому теперь из двух сил N и mg,
действующих на космонавта, преобладающей оказывается
сила тяжести. Их равнодействующая F = mg – N по второму
закону Ньютона равна произведению массы на ускорение
космонавта, т.е. mg. Поэтому
mg – N = mg, откуда
N = 0.
Это означает, что опора никак не реагирует на присутствие
космонавта. По третьему закону Ньютона такое возможно
лишь в том случае, если и сам космонавт не оказывает
никакого действия на свою опору, т. е. его вес равен нулю.
Невесомость – это состояние тела, при котором его вес равен
нулю.
Следует помнить, что невесомость
означает отсутствие веса, а не массы.
Масса тела, находящегося в состоянии
невесомости, остается такой же, какой и была.
В состоянии невесомости все тела и их отдельные части
перестают давить друг на друга. Космонавт при этом
перестает ощущать собственную тяжесть; предмет,
выпущенный из его пальцев, никуда не падает; маятник
замирает в отклоненном положении; исчезает различие
между полом и потолком.

Все эти явления объясняются тем,
что гравитационное поле сообщает всем телам в
космическом корабле одно и то же ускорение. Именно
поэтому выпущенный космонавтом предмет (без сообщения
ему скорости) никуда не падает: ведь он не может ни
«догнать» какую-нибудь стенку кабины, ни «отстать» от нее;
все они — и предметы и стены — движутся с одинаковым
ускорением.
Наряду с этим невесомость в условиях орбитального
полета играет роль специфического раздражителя,
действующего на организм человека. Она оказывает
существенное влияние на многие его функции: слабеют
мышцы и кости, организм обезвоживается и т. д. Однако все
эта изменения, вызванные невесомостью, обратимы. С
помощью лечебной физкультуры, а также лекарственных
препаратов нормальные функции организма могут быть
снова восстановлены.
В состоянии невесомости может находиться не только
космонавт в орбитальной космической станции, но и любое
свободно падающее (без вращения) тело.

Чтобы испытать
это состояние, достаточно совершить простой прыжок:
между моментом отрыва от Земли и моментом приземления
вы будете невесомы!

English Русский Правила

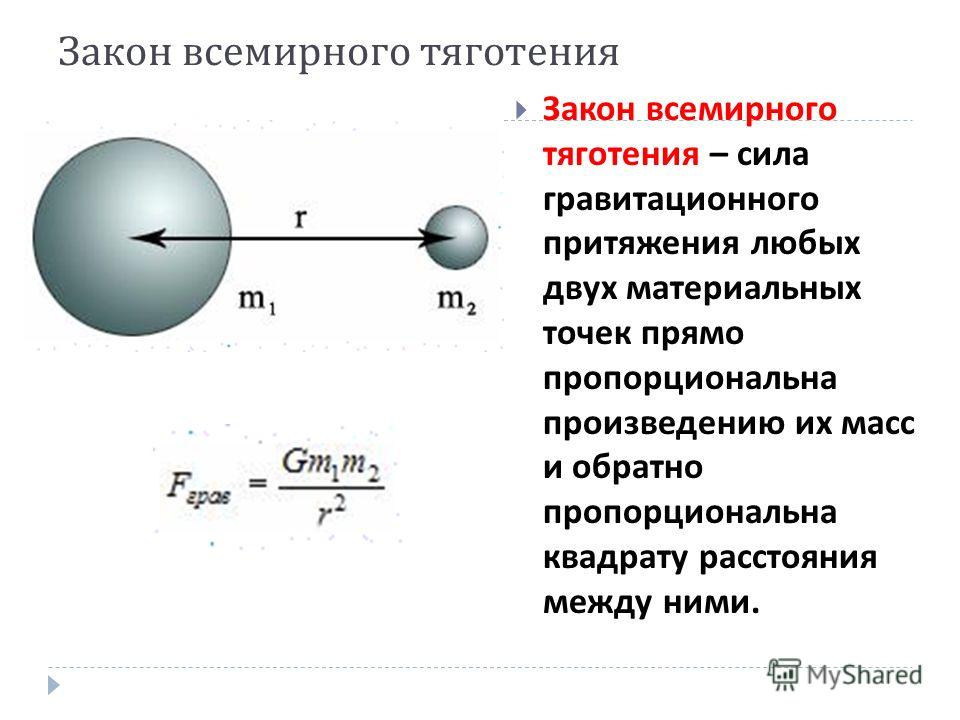
Формула закона всемирного тяготения для материальных точек

Если взаимодействующие между собой тела можно считать материальными точками или же если они имеют правильную сферическую форму, то формула закона всемирного тяготения имеет вид

F=Gm₁m²/r² (2.26)

где F – модуль силы тяготения; m₁ и m₂ – массы материальных точек; r – расстояние между ними; G – коэффициент пропорциональности, называемый

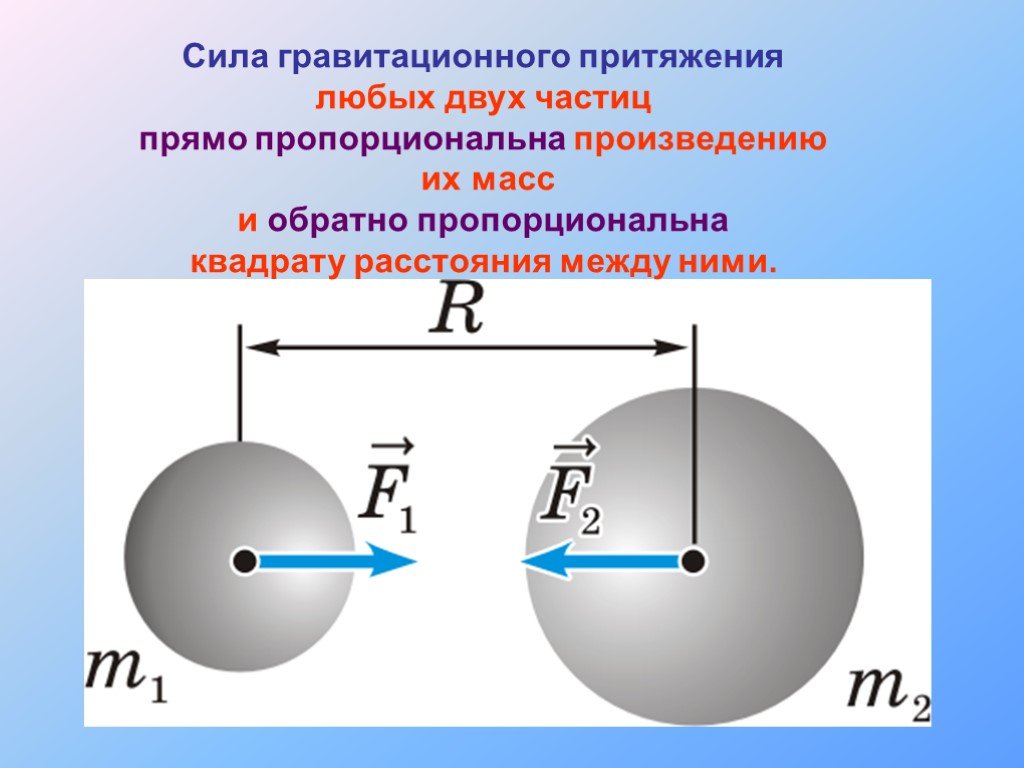
постоянной всемирного тяготения или гравитационной постоянной.

Силы, с которыми взаимно притягиваются тела по закону всемирного тяготения, являются центральными, т. е. они направлены вдоль прямой, соединяющей центры взаимодействующих тел.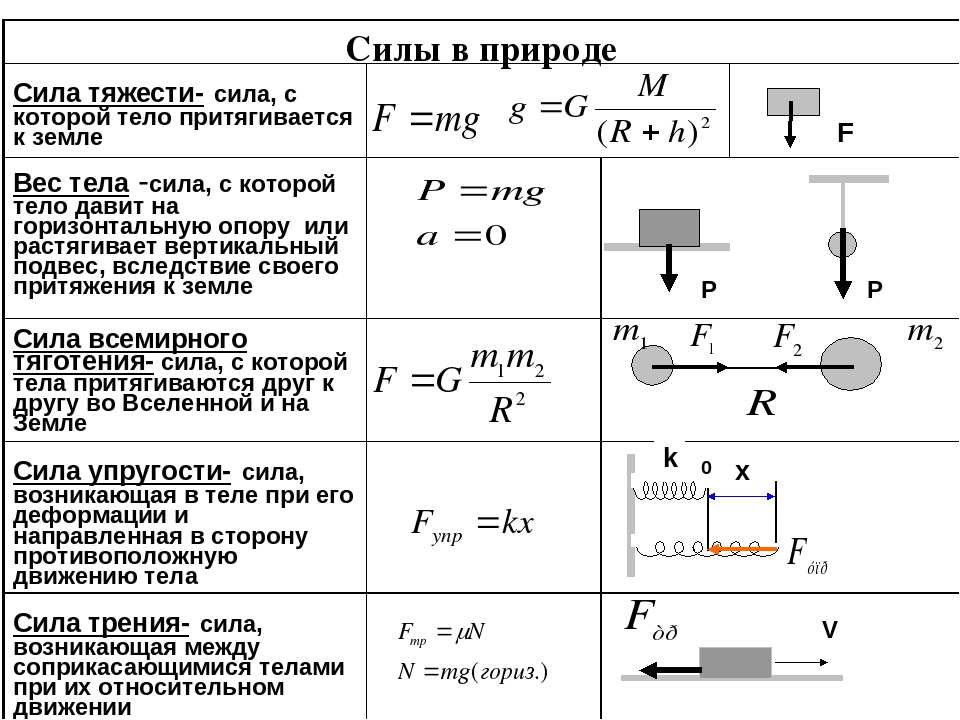

Гравитационная постоянная

Из (2.26) при m₁=m₂=m имеем

G=Fr²/m².

Из этой формулы видно, что гравитационная постоянная численно равна силе взаимного тяготения двух материальных точек, имеющих массы, равные единице массы, и находящихся друг от друга на расстоянии, равном единице длины.

Числовое значение гравитационной постоянной устанавливают экспериментально. Впервые это сделал английский ученый Кэвендиш с помощью крутильного динамометра (крутильных весов).

В СИ гравитационная постоянная имеет значение

G = 6,67·10^-11 Нм²/кг².

Следовательно, две материальные точки массой 1 кг каждая, находящиеся друг от друга на расстоянии 1 м, взаимно притягиваются гравитационной силой, равной 6,67·10^-11 Н.

Сила тяжести и ускорение свободного падения

Силу, с которой тело притягивается к Земле под действием поля тяготения Земли, называют силой тяжести. По закону всемирного тяготения на поверхности Земли (или вблизи этой поверхности) на тело массой m действует сила тяжести

F_т=GMm/R² (2.28)

где М – масса Земли; R – радиус Земли. Если на тело действует только сила тяжести, а все другие силы взаимно уравновешены, тело совершает свободное падение. Согласно второму закону Ньютона и формуле (2,28) модуль ускорения свободного падения g находят по формуле

g=F_т/m=GM/R². (2.29)

Из формулы (2.29) следует, что ускорение свободного падения не зависит от массы m падающего тела, т.е. для всех тел в данном месте Земли оно одинаково. Из формулы (2.29) следует, что Fт = mg. В векторном виде

F_т=mg (2.30)

В § 5 было отмечено, что поскольку Земля не шар, а эллипсоид вращения, ее полярный радиус меньше экваториального. Из формулы (2.28) видно, что по этой причине сила тяжести и вызываемое ею ускорение свободного падения на полюсе больше, чем на экваторе.

Сила тяжести действует на все тела, находящиеся в поле тяготения Земли, однако не все тела падают на Землю. Это объясняется тем, что движению многих тел препятствуют другие тела, например опоры, нити подвеса и т. п. Тела, ограничивающие движение других тел, называют связями. Под действием силы тяжести связи деформируются и сила реакции деформированной связи по третьему закону Ньютона уравновешивает силу тяжести.

В § 5 отмечалось также, что на ускорение свободного падения влияет вращение Земли. Это влияние объясняется так. Системы отсчета, связанные с поверхностью Земли (кроме двух, связанных с полюсами Земли), не являются, строго говоря, инерциальными системами отсчета – Земля вращается вокруг своей оси, а вместе с ней движутся по окружностям с центростремительным ускорением и такие системы отсчета. Эта неинерциальность систем отсчета проявляется, в частности, в том, что значение ускорения свободного падения оказывается различным в разных местах Земли и зависит от географической широты того места, где находится связанная с Землей система отсчета, относительно которой определяется ускорение свободного падения.

Измерения, проведенные на разных широтах, показали, что числовые значения ускорения свободного падения мало отличаются друг от друга. Поэтому при не очень точных расчетах можно пренебречь неинерциальностью систем отсчета, связанных с поверхностью Земли, а также отличием формы Земли от сферической, и считать, что ускорение свободного падения в любом месте Земли одинаково и равно 9,8 м/с².

Из закона всемирного тяготения следует, что сила тяжести и вызываемое ею ускорение свободного падения уменьшаются при увеличении расстояния от Земли. На высоте h от поверхности Земли модуль ускорения свободного падения определяют по формуле

g=GM/(R+h) 2. (2.31)

Установлено, что на высоте 300 км над поверхностью Земли ускорение свободного падения меньше, чем у поверхности Земли, на 1 м/с2. Следовательно, вблизи Земли (до высот нескольких километров) сила тяжести практически не изменяется, а потому свободное падение тел вблизи Земли является движением равноускоренным.

Закон Ньютона Калькулятор формул уравнений гравитации

Закон Ньютона Калькулятор формул уравнений гравитации – сила между объектами

Решение гравитационной силы, действующей между двумя объектами.

G -универсальная гравитационная константа
g = 6,6726 x 10 ^-11 N -M ² /кг ²

Входные данные:

. Конверсии:

Object 1 Mass (M ₁2)

)

) = 0

килограмм

Объект 2 Масса (M ₂)

= 0

килограмм

Расстояние между объектами (R)

= 0

метр

Раствор:

Гравитационная сила (F)

= не Calculated

Другие единицы измерения:

Изменить формулу
Выберите, чтобы найти другое неизвестное

Закон всемирного тяготения Ньютона

	гравитационная сила, действующая между двумя объектами
	mass of object 1
	mass of object 2
	distance between the objects

Kepler’s third law

	satellite orbit period
	средний радиус орбиты спутника
	масса планеты

гравитационное ускорение

	gravitational acceleration
	planet mass
	radius from the planet center

escape or critical speed

	escape or critical speed
	planet mass
	радиус планеты

Ссылки – Книги:
Типлер, Пол А. 1995. Физика для ученых и инженеров. Стоит Издатели. 3-е изд.

Графики роста младенцев — Процентили для младенцев Калькулятор оплаты сверхурочной работы Конвертер зарплаты в почасовую оплату – Вакансии Скидка в процентах – Калькулятор скидок при продаже Калькулятор повышения заработной платы Калькулятор линейной интерполяции Калькулятор возраста собаки Калькулятор закона идеального газа Калькуляторы полосовых сабвуферов Калькулятор уравнений гравитации Физика Уравнения Формулы Калькуляторы Уравнения силы Физический калькулятор Калькулятор уравнений удельного веса Второй закон Ньютона Калькулятор прогноза роста ребенка Калькулятор движения снаряда Калькулятор формул весовых уравнений Калькулятор формул потенциальной энергии Калькулятор формул кинетической энергии Калькулятор возраста кошки в человеческий возраст Калькулятор уравнений кругового движения Калькулятор теоремы Бернулли Буксировка: сцепное устройство для распределения веса Ипотечный калькулятор – Дополнительные платежи Калькулятор ставки капитализации Калькулятор кавитационного числа Наибольший общий делитель Евклид

Онлайн-веб-приложения, Богатые интернет-приложения, Технические инструменты, Спецификации, Практические руководства, Обучение, Приложения, Примеры, Учебники, Обзоры, Ответы, Ресурсы для просмотра тестов, Анализ, Решения для домашних заданий, Рабочие листы, Справка, Данные и информация для инженеров, Техники, преподаватели, репетиторы, исследователи, образование K-12, учащиеся колледжей и старших классов, проекты научной ярмарки и ученые

Джимми Рэймонд

Контакт: aj@ajdesigner. com

Политика конфиденциальности, отказ от ответственности и условия

Формула гравитации | Определения и примеры

Гравитация очень важна для нас. На Земле невозможно жить без гравитации. Гравитационная сила Солнца удерживает Землю на орбите вокруг него, удерживая нас вдали от солнца и тепла. Он содержит нашу атмосферу и воздух, которым мы должны дышать. Гравитация — это то, что удерживает нашу землю вместе.

На Земле гравитация меняется от места к месту. Гравитация немного сильнее в областях с избыточным весом, чем с недостаточным весом. НАСА использует два космических корабля для измерения этих различий в гравитационном притяжении Земли. Эти космические аппараты являются частью кампании «Земельная реформа и изменение климата» (GRACE).

Формула гравитации

Гравитация или Гравитация — это явление, которое дает представление о существовании силы между любыми двумя объектами, имеющими некоторую массу.