Формула скорости без ускорения: Скорость и путь при равноускоренном движении — урок. Физика, 9 класс.

Как найти скорость без времени: факты, задачи, примеры –

В этой статье мы собираемся изучить различные способы определения скорости без учета времени, а также примеры, некоторые факты и способы решения связанных проблем.

Исходя из этого, энергия объекта сохраняется; скорость объекта равна квадратному корню из удвоенного произведения его ускорения на расстояние, которое он проходит, также в зависимости от начальной скорости объекта.

Как найти конечную скорость без времени?

Ускоряющийся объект со временем меняет свою скорость.

Скорость, достигаемая объектом за период времени, пока он не перестанет ускоряться в течение этого времени, называется конечной скоростью объекта.

Давайте посмотрим, как найти конечную скорость без использования временного символа.

Рассмотрим график скорость-время, показывающий изменение скорости объекта при равномерном линейном движении во времени. Из графика видно, что время T = 0, скорость = u, а в момент времени T = t скорость = v.

График скорости-времени

Поскольку скорость – это отношение изменения положения с изменяющимся временем, смещение будет равно

х=vt — (1)

Приведенный выше график связан со смещением соотношением, показанным в уравнении (1).

Измерим площадь, покрытую объектом, общая площадь будет равна сумме площадей треугольника (∆ABC) и четырехугольника (□ ACDO).

х = Ar(∆ABC)+ Ar(∆ACDO)

=1/2 бч+фунт

=1/2 t*(vu)+ut—(3)

Поскольку ускорение равно изменению скорости со временем, т.е.

а=dv/dt — (4)

а=ву/т-0=ву/т

ву=ат—(5)

Подставляя уравнение (5) в уравнение (3)

х=1/2 t * at+ut

х=1/2 при²+ут—(6)

Таким образом,

Из уравнения (4) имеем

дв=адт

Интегрируя это уравнение, получаем

∫dv=∫dt

v = при + C

При t = 0 v = u, следовательно, C = u

Следовательно,

v=u+at —(7)

Теперь это уравнение является уравнением, зависящим от времени, а время t из приведенного выше соотношения равно

t=vu/a —(8)

Средняя скорость – это сумма всех скоростей, достигнутых объектом в разные промежутки времени, деленная на общее количество скоростей, суммированных вместе. Здесь у нас есть две скорости: начальная скорость u и конечная скорость v, поэтому средняя скорость равна

V_{средний}=V_{окончательный}+V_{начальный}/Общее количество скоростей

V_{средний}=(v+u)/2 — (9)

Используя уравнение (1), x=vt

Подставляя уравнения (8) и (9) в уравнение (1)

х=(v+u)/2 *(vu)/a

х=v²-u²/2а

2акс = v²-u²/2

v²=u²+2акс — (10)

Приведенное выше уравнение не зависит от времени и показывает связь между начальной скоростью объекта, постоянным ускорением и перемещением объекта.

Problem1: Мяч движется в прямолинейное движение с ускорением 2 м/с. Если начальная скорость мяча 4 м/с, то какой будет его скорость, когда он преодолеет расстояние 20 м?

Дано: a = 2 м / с

u = 4 м / с

d = 20 м

Используя уравнение (10),

v²=u²+2 оси

=4²+2*2*20

= 16 + 80 = 96 м / с

поэтому v=9. 8 м/с

Следовательно, когда мяч преодолеет расстояние 60 метров, скорость мяча составит 9.8 м / с.

Как определить скорость падающего объекта без учета времени?

Линейная скорость зависит от времени и представляет собой отношение изменения положения во времени.

Падение предмета сопровождается энергии внутри него, в форме кинетической энергии и потенциальной энергии, и энергия не может быть ни создана, ни исчезнуть. На основании этого факта мы можем рассчитать скорость объекта независимо от времени.

Когда объект поднимается на высота над землей приобретает некоторый потенциал энергия, которая затем преобразуется в кинетическую энергию и используется во время полета.

Рассмотрим объект массы m, который стоит на столе высотой h.₁, он испытывает внешнюю силу, набирает обороты и начинает ускоряться по направлению к земле. Поскольку объект покоится на столе, его начальная скорость u = 0 и, следовательно, кинетическая энергия также равна нулю. Объект на высоте h₁ имеет потенциальную энергию U₁ связанные с ним.

U₁= mgh₁

Начиная свой путь к земле, эта потенциальная энергия преобразуется в кинетическую энергию.

KE₂=1/2мВ²

После падения на землю потенциальная энергия тела U₂= mgh₀; так как ч₀=0, U_2=0.

Поскольку энергия объекта сохраняется, сумма кинетической энергии и потенциальной энергии до и после падения на землю будет равна.

KE₁+U₁=КЭ₂+U₂

U₁=КЭ₂

MGH₁=1/2мВ²

v²=2гх₁

v = √2gh₁-(Один)

Следовательно, скорость объекта, падающего на землю под действием силы тяжести, определяется уравнением (11).

Problem2: Мальчик играет с мячом. Он подбросил мяч высоко в воздух и наблюдает за его свободным падением. Какова будет скорость мяча при приближении к земле, если мяч поднимется на высоту 8 метров над поверхностью Земли?

Дано: Высота h = 8м,

g = 9. 8 м / с²

Используя уравнение (11),

v = √2gh₁

=√2*9.8*8

=√156.8=12.52 м/с

Следовательно, конечная скорость мяча, приближающегося к земле, будет равна 12.5 м / с.

Как найти горизонтальную скорость без времени?

Объект, движущийся в горизонтальном направлении независимо от ускорения свободного падения Земли и приложенной силы, называется горизонтальной скоростью.

Горизонтальная скорость в простоте равна отношению расстояния, пройденного объектом, и времени, затраченного на преодоление расстояния. Это,

Горизонтальная скорость V_H= пройденное расстояние/затраченное время

Для объекта, движущегося в движении снаряда, объект связан с двумя компонентами скорости: горизонтальной составляющей по оси x ‘V Cosθ’ в направлении движения и вертикальной составляющей по оси y ‘V Sinθ’, действующей вверх. при ускорении вверх, а затем вниз по отрицательной оси Y при ускорении по направлению к земле. График движения снаряда, показывающий постоянная горизонтальная скорость

Из приведенного выше графика, чтобы вычислить горизонтальную скорость, которая является постоянной и в направлении оси x, компонент косинуса по тригонометрии равен

Cosθ=соседний/гипотенуза=горизонтальная скорость/начальная скорость

Cosθ=V_H/V

V_H= V Cos θ — (12)

Вышеупомянутое соотношение показывает уравнение для определения горизонтальной скорости независимо от времени.

Пример: Мяч подбрасывается в воздух и движется по параболической траектории под углом 60 °.⁰ с поверхности Земли. Если начальная скорость мяча равна 5 м / с, найдите горизонтальную скорость мяча.

Дано: θ = 60⁰

Начальная скорость u = 5 м / с

Используя уравнение,

V_H=VCosθ

=5*Кос(60)

=5*1/2=2.5 м/с

Следовательно, горизонтальная скорость мяча составляет 2.5 м / с.

Дальность полета снаряда – это расстояние, которое объект преодолеет от своей начальной точки, которая находится в точке (0,0) на приведенном выше графике, в зависимости от горизонтальной скорости объекта и того, как долго объект находится в воздухе.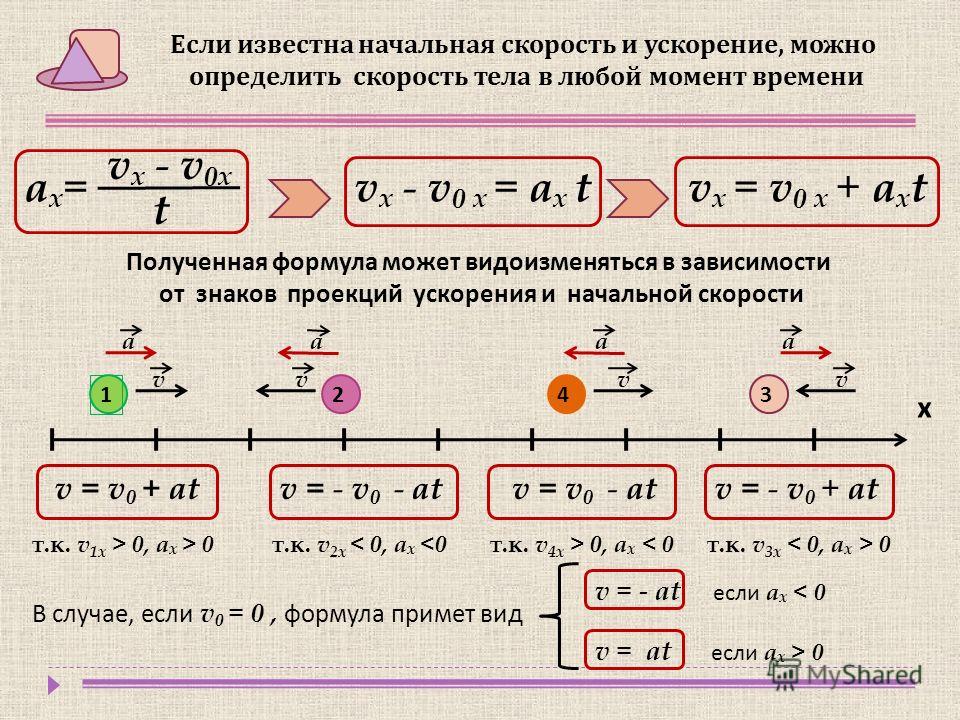

То есть,

Р=В_HT_f-(Один)

Где R – диапазон, В_H – горизонтальная скорость объекта, а T_f время полета.

Время, необходимое объекту во время движения снаряда, чтобы вернуться на землю при y = 0, упоминается как время полета.

Выведем уравнение для времени пролета, используя уравнение прямолинейного движения, приведенное ниже.

V=U+at—(14)

Начальная скорость объекта U=VSinθ

Конечная скорость V Cosθ =0

И a = -g, поскольку ускорение находится в отрицательной оси y.

Уравнение становится,

V= V Sinθ –gt

С момента финала скорость равна нулю,

0= VSinθ –gt

V Sinθ =gt

t=V Sinθ/g — (15)

Это время, необходимое объекту для достижения максимальной высоты во время полета.

Это означает, что время достижения максимальной высоты будет равно времени, необходимому объекту для покрытия оставшейся половины полета.

Значит, время для полета

T_f=2 В Sinθ/g — (16)

Подставляя уравнение (12) и уравнение (16) в уравнение (13),

R=V\ Cosθ*2V Sinθ/g

Р=В²/г* 2SinθCosθ

Р=В² Sin2θ/g — (17)

Следовательно, скорость движущегося снаряда объекта также равна

V=√Rg/Sin2θ — (18)

Скорость может быть рассчитана путем измерения дальности полета и угла, который объект составляет относительно земли.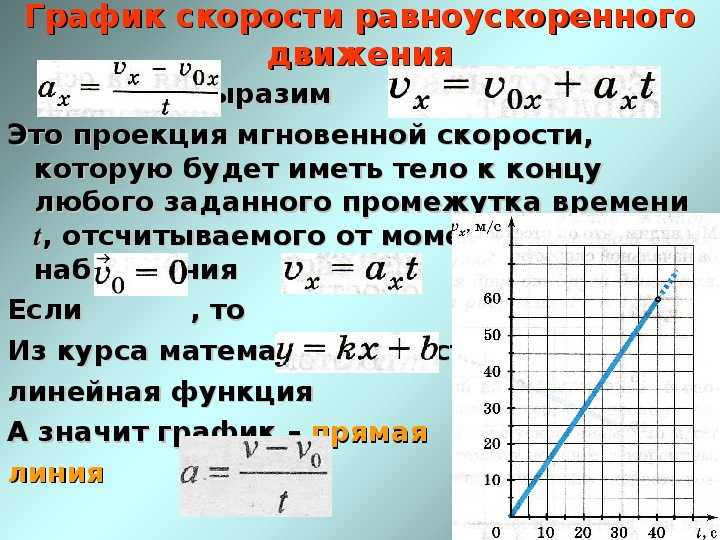

Подробнее о Снаряд Движение.

Как найти центростремительную скорость без учета времени?

Объект, движущийся по круговой траектории со временем, приобретает центростремительную скорость.

Направление скорости объекта по круговой траектории остается касательным к окружности и перпендикулярно центростремительной силе, направленной к центру.

Рассмотрим объект массы m, ускоряющийся по круговой траектории из-за внешней силы, приложенной к объекту. Центростремительная сила, действующая на объект, прямо пропорциональна квадрату, умноженному на скорость, достигаемую объектом, и обратно пропорциональна расстоянию от объекта до центра круга. Приложенная сила равна центростремительной силе, действующей на объект.

Ф=Ф_c

ма=мв²/r

а=в²/r

v²=ар

v=√ar—(19)

Скорость объекта при круговом движении равна квадратному корню из ускорения объекта и радиуса круговой траектории и не зависит от времени.

Пример: Представьте машину, движущуюся по круговой дорожке за пределами футбольной площадки с ускорением 40 км / ч. Диаметр земли 80 метров. Найдите скорость автомобиля.

Given: a=40km h=40*1000/60*60=11.1m/s

d=80м, r=80/2=40м

v=√ар

=√11.1 м/с*40 м

=√444

= 21.1 м / с²

=75.96 км/ч~ 76 км/ч

Следовательно, скорость автомобиля, разгоняющегося по круговой траектории, составляет 76 км / ч.

Подробнее о Как найти скорость с ускорением: разные подходы, проблемы, примеры.

Часто задаваемые вопросы

Q1. Две девушки играют в передачу с мячом; одна девушка бросает мяч высоко в воздух, образуя угол 45⁰ с направлением горизонтальной скорости передача мяча девушке, стоящей на расстоянии 10 м от нее. Какая скорость набирает мяч при броске?

Дано: θ = 45⁰

Дальность полета мяча на броске R = 10 метров

Р=В² без²θг

V=√Rg sin²θ

V=√10*9. 8/Sin(2*60)

V=√98/Sin(120)

V=√98/0.86

V=√113.95

V=10.67 м/с

Следовательно, скорость мяча во время полета составляет 10.67 м / с.

Какая средняя скорость?

Ускоряющийся объект меняет направление скорости и скорости вместе с определенной продолжительностью времени.

Сумма всех скоростей, изменяющихся во времени, деленная на общее количество изменений, называется средней скоростью.

Равноускоренное прямолинейное движение, ускорение, определение пути и перемещения по графику скорости

1. Равноускоренное движение
2. Ускорение
3. Уравнение скорости и график скорости при равноускоренном прямолинейном движении
4. Определение пути и перемещения по графику скорости
5. Задачи

п.1. Равноускоренное движение

Если тело начинает двигаться из состояния покоя, оно набирает скорость не мгновенно, а в течение некоторого времени. Аналогично происходит при торможении: тело останавливается не сразу, а теряя скорость постепенно.

Движение, во время которого скорость тела за любые равные промежутки времени увеличивается на одну и ту же величину, называют равноускоренным.

Примеры равноускоренного движения:

• скатывание велосипеда с горки, скатывание санок с горки;
• старт и торможение автомобиля, автобуса, трамвая, поезда;
• падение на землю камня, ракеты, метеорита.

Это интересно
Время разгона от 0 до 100 км/ч – одна из основных характеристик современных автомобилей.

Марка автомобиля		Время разгона, с
Nissan GTR Nismo		2,9
BMW M5 F90		2,8
Porsche 918 Spyder		2,6

п.2. Ускорение

Ускорение – это векторная величина, которая равна отношению изменения скорости тела к интервалу времени, за которое это изменение произошло: $$ \overrightarrow{a}=\frac{\overrightarrow{v}-\overrightarrow{v_0}} {t} $$ где \(\overrightarrow{v_0}\) – начальная скорость тела, \(\overrightarrow{v}\) – скорость тела в момент времени \(t\).

В системе СИ (см. §2 данного справочника) скорость измеряется в метрах в секунду, а время – в секундах. Поэтому:

Единицей ускорения в системе СИ является метр на секунду в квадрате (1 м/с²) – ускорение равноускоренного прямолинейного движения, при котором тело за 1 с увеличивает скорость на 1 м/с.

При описании прямолинейного движения мы переходим от векторов к проекциям на ось ОХ (см. §8 данного справочника).

При равноускоренном прямолинейном движении проекция ускорения равна: $$ a_x=\frac{v_x-v_{0x}}{t} $$ где \(v_{0x}\) – проекция начальной скорости, \(v_x\) – проекция скорости в момент времени \(t\).

п.3. Уравнение скорости и график скорости при равноускоренном прямолинейном движении

Для проекции скорости на ось ОХ в произвольный момент времени можем записать: $$ v_x(t)=v_{0x}+a_x t $$ Сравним полученное уравнение с уравнением прямой \(y(x)=kx+b \) (см. §38 справочника по алгебре для 7 класса).
В уравнении скорости роль углового коэффициента \(k\) играет проекция ускорения \(a_x\), а роль свободного члена \(b\) – начальная скорость \(v_{0x}\). 2},\ \ v_x(t)=20-5t $$ Проекция ускорения при торможении отрицательна. Скорость станет равна 0 через 4 с после начала торможения, автомобиль остановится.

Опишем полностью движение на всех участках: $$ v_x(t)= \begin{cases} 4t,\ \ 0\leq t\lt 5\\ 20,\ \ 5\leq t\lt 15\\ 20-5t,\ \ 15\leq t\leq 19 \end{cases} $$ И построим график:

Участок AB соответствует разгону автомобиля от 0 до 20 м/с, участок BC – равномерному движению со скоростью 20 м/с, участок CD – торможению от 20 м/с до 0.

п.4. Определение пути и перемещения по графику скорости

В §10 данного справочника мы рассматривали неравномерное прямолинейное движение, которое можно разбить на отдельные равномерные участки. Для такого движения путь равен сумме модулей площадей участков, определенных по графику скорости. А перемещение также равно сумме площадей, но уже с учетом знака.
Этот подход можно расширить на любое прямолинейное движение.

Пусть график скорости при прямолинейном движении разбит на \(n\) участков, площади которых легко определить (треугольники, прямоугольники, трапеции). Тогда:
Весь пройденный путь равен сумме модулей площадей всех участков: $$ s=|s_1|+|s_2|+…+|s_n| $$ Величина перемещения по оси ОХ равна сумме площадей всех участков с учетом знака: $$ \triangle x=s_1+s_2+…s_n $$ Конечная координата равна: \(x_к=x_0+\triangle x\)

Пример определения пути и перемещения по графику скорости
Для построенного выше графика скорости автомобиля получаем следующие участки:
1) ΔABE, его площадь равна $$ s_1=\frac12 AE\cdot BE=\frac12\cdot 5\cdot 20=50\ (м) $$ 2) прямоугольник EBCF, его площадь равна $$ s_2=EF\cdot BE=10\ cdot 20=200\ (м) $$ 3) ΔCFD, его площадь равна $$ s_2=\frac12 FD\cdot GF=\frac12\cdot 4\cdot20=40\ (м) $$ Весь пройденный путь: $$ s=s_1+s_2+s_3=50+200+40=290\ (м) $$ Скорость автомобиля все время оставалась положительной (направление движения не менялось), поэтому величина перемещения равна пройденному пути: $$ \triangle x=s=290\ (м) $$

п.5. Задачи

Задача 1. За 1 мин автобус увеличил скорость с 28,8 км/ч до 72 км/ч.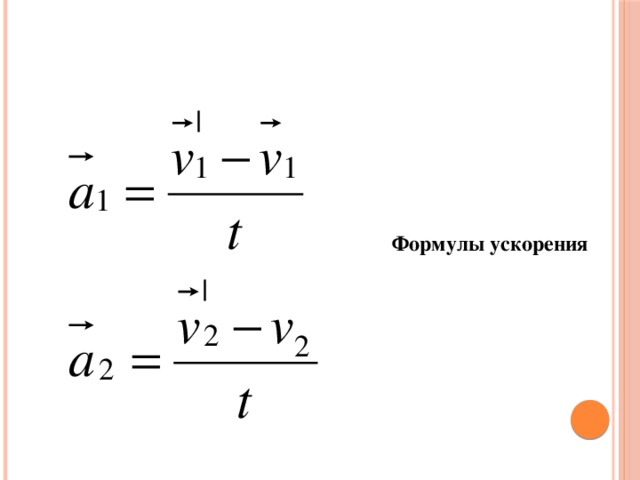 2}\right) $$ Уравнение зависимости скорости от времени: \begin{gather*} v(t)=v_0+at\\ v(t)=10+0,25t \end{gather*} График:

Скорость достигает значения \(v=20\ м/с\) в момент времени \(t=40\ с\).
Значит, время движения 40 с.

Путь по графику скорости равен площади четырехугольника ABCD. \begin{gather*} S_{ABCD}=S_{ABE}+S_{AECD}=\frac12 AE\cdot EB+AE\cdot AD=\frac12\cdot 40\cdot 10+40\cdot 10=200+400=600\ (м)\\ s=600\ м \end{gather*} Найденное значение пути совпадает с условием задачи. Все параметры движения найдены верно.
Ответ: 0,25 м/с²; 40 c

классическая механика – Расчет скорости без указания времени

спросил 6 лет, 3 месяца назад

Изменено 6 лет, 3 месяца назад

Просмотрено 26 тысяч раз

$\begingroup$

У меня вопрос “Яйцо падает из гнезда на высоте 3,70м над землей. Вычислите его скорость в момент удара о землю и время, необходимое для падения». 9-2$.

Однако время не указано, поэтому я не знаю, как рассчитать скорость яйца после того, как оно упадет на землю.

• классическая механика

$\endgroup$

2

$\begingroup$

Обратите внимание, что потенциальная энергия определяется как:

$$\text{E}_\text{pot}=\text{m}\cdot\text{g}\cdot\text{h}\tag1$$

А кинетическая энергия: 92}{2}\space\Longleftrightarrow\space\text{v}=\pm\sqrt{2\cdot\text{g}\cdot\text{h}}\tag3$$

Итак, для $\text {v}$ получим:

$$\text{v}\приблизительно\sqrt{2\cdot9.81\cdot3.70}=\sqrt{\frac{36297}{500}}\приблизительно8.520211265\ tag4$$

И время, которое потребуется:

$$t\приблизительно\frac{\sqrt{\frac{36297}{500}}}{9,81}=\sqrt{\frac{740}{981}} \приблизительно0.

868523065\tag5$$

$\endgroup$

0

9{-2}$ и $s=3,70 \text{ м}$.

Затем вы можете найти затраченное время, используя $v=u+at$, используя скорость, которую вы нашли в первой части.

$\endgroup$

Уравнения: скорость падающего объекта | Физика Фургон

Категория Выберите категориюО фургоне физикиЭлектричество и магнитыВсе остальноеСвет и звукДвижение вещейНовая и захватывающая физикаСостояния вещества и энергииКосмосПод водой и в воздухе

Подкатегория 92 * время, или V = gt. Знак минус просто означает, что объект движется вниз. Если бы он был положительным, то он двигался бы вверх. Для скорости, а не скорости, вы просто опускаете отрицательный знак.

Если у вас есть начальная скорость (если вы бросили мяч вверх или вниз вместо того, чтобы просто отпустить его), то вы также должны включить это в уравнение, что даст вам: V = Vo + gt, где Vo равно начальная скорость объекта. Это уравнение по-прежнему будет работать, если вы бросили мяч в сторону, а не прямо вверх или вниз, за ​​исключением того, что оно даст вам только скорость вверх-вниз, а не общую скорость. (И число, которое вы должны использовать для Vo, по-прежнему является просто скоростью вверх-вниз, с которой объект начинает движение.)

-Тамара

(опубликовано 22.10.2007)

Продолжение #1: Время падения?

Q:

Как определить время и скорость падения, если у вас есть только расстояние падения?
– Нед
Ботелл, Вашингтон, США

A:

Ну вам нужен еще один факт, ускорение. Если вы находитесь на поверхности земли, ускорение равно g = 32,2 фута/сек ² или 9,8 метра/сек ² . Однократное интегрирование ускорения дает V = V _o + g T , где V _o — начальная скорость, предположительно равная нулю, а T — время падения. Еще одно интегрирование дает d = V _o T + gT ²

/2. Итак, взяв V _o = 0, вы получите
T = sqrt(2d/g) и V=sqrt(2dg).

LeeH

То, что дает V Lee, является окончательным V. Если вам нужен средний V за осень, это вдвое меньше. Майк В.

(опубликовано 10.08.2009)

Дополнение №2: Сколько времени потребуется, чтобы упасть на Солнце?

Q:

Если бы Земля перестала вращаться вокруг Солнца и просто “упала” на Солнце, сколько времени потребовалось бы, чтобы “упасть” на Солнце и как это вычислить?
– Брэд (17 лет)
Канада

A:

Вы можете позаимствовать 3-й закон Кеплера, согласно которому период обращения пропорционален R

3/2 , где R – длинная ось эллипса орбиты. Падение на Солнце – это только половина орбиты, эллипс которой достигает Солнца, то есть половина R годовой орбиты Земли. Вся эта другая орбита, таким образом, заняла бы 2 ^-3/2 года, поэтому время падения составляет 2 ^-5/2 года, или ~65 дней. Майк В.

(опубликовано 25.