Гармоническое колебание, уравнения, графики движения. Изменение координаты, скорости, ускорения со временем. Примеры, тесты
Тестирование онлайн
Гармоническое колебание
Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.
График гармонического колебания
График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.
Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.
Уравнение гармонического колебания
Уравнение гармонического колебания устанавливает зависимость координаты тела от времени
График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой .
Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой .
Изменение скорости и ускорения при гармоническом колебании
Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия – достигает максимального значения.
Если колебание описывать по закону синуса
Максимальные значения скорости и ускорения
Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле
Определяются по формуле
Формулы зависимостей скорости от времени и ускорения от времени можно получить математически, зная зависимость координаты от времени. Аналогично равноускоренному движению, зависимость v(t) – это первая производная x(t). А зависимость a(t) – это вторая производная x(t).
При нахождении производной предполагаем, что переменной (то есть x в математике) является t, остальные физические величины воспринимаем как постоянные.
Находим производную сложной функции.
Основные формулы для решения задач по теме “Механические колебания и волны”.
Механические колебания
Основные формулы для решения задач.
Всякое колебательное движение, в том числе и гармоническое, характеризуется амплитудой , периодом колебаний , частотой , циклической (круговой) частотой и фазой колебаний .
Амплитудой называют наибольшее значение колеблющейся величины.
Число полных колебаний в единицу времени называют частотой:
.
Циклическая (круговая) частота – это число полных колебаний в течении с:
.
Периодом называю время, в течении которого совершается одно полное колебание:
.
Смещение, скорость и ускорение при гармоническом колебании определяются уравнениями
,
,
.
Здесь – фаза колебаний, а – начальная фаза.
Сила, действующая на тело при свободном гармоническом колебании (квазиупругая сила), всегда пропорциональна смещению и направлена в сторону, противоположную смещению:
где – коэффициент квазиупругой силы, измеряемый силой, вызывающей смещение , равное единице.
При отсутствии сопротивления среды циклическая частота свободных гармонических колебаний, называемых
,
Период колебания математического маятника длиной равен
.
Период колебаний физического маятника
,
где – момент инерции маятника относительно оси качаний, – расстояние от оси его до центра тяжести.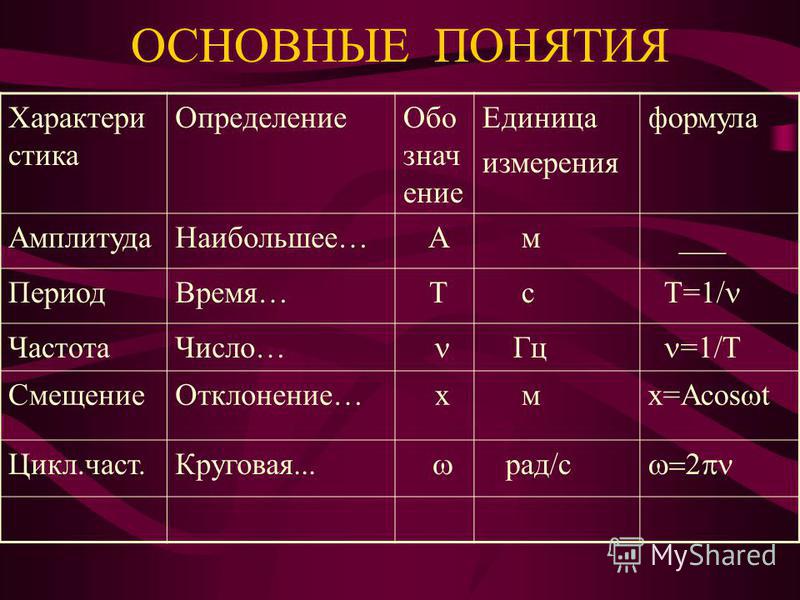
Полная энергия тела, совершающего гармонические колебания, постоянна и равна
.
Уравнение смещения в затухающих колебаниях при наличии силы сопротивления пропорциональной скорости (, где – коэффициент сопротивления) имеет вид:
.
Здесь – убывающая по времени амплитуда смещения; – коэффициент затухания; – циклическая частота; – начальные амплитуда и фаза, определяются из начальных условий.
Величины и выражаются через параметры системы формулами:
,
.
Логарифмический декремент затухания
,
где – амплитуды двух последовательных колебаний.
Амплитуда вынужденных колебаний
,
где – есть отношение амплитуды вынуждающей силы к массе тела; – собственная циклическая частота; – циклическая частота вынуждающей силы.
Резонансная циклическая частота равна
.
Гармонические колебания – Технарь
Гармонические колебания – колебания, совершаемые по законам синуса и косинуса.
Амплитуда колебаний
Амплитудой гармонического колебания называется наибольшее значение смещения тела от положения равновесия. Амплитуда может принимать различные значения. Она будет зависеть от того, насколько мы сместим тело в начальный момент времени от положения равновесия.
Амплитуда определяется начальными условиями, то есть энергией сообщаемой телу в начальный момент времени. Так как синус и косинус могут принимать значения в диапазоне от -1 до 1, то в уравнении должен присутствовать множитель Xm, выражающий амплитуду колебаний. Уравнение движения при гармонических колебаниях:
x = Xm*cos(ω0*t).
Период колебаний
Период колебаний – это время совершения одного полного колебания. Период колебания обозначается буквой Т. Единицы измерения периода соответствуют единицам времени. То есть в СИ — это секунды.
Частота колебаний – количество колебаний совершенных в единицу времени. Частота колебаний обозначается буквой ν. Частоту колебаний можно выразить через период колебания.
Частота колебаний обозначается буквой ν. Частоту колебаний можно выразить через период колебания.
ν = 1/Т.
Единицы измерения частоты в СИ 1/сек. Эта единица измерения получила название Герца. Число колебаний за время 2*pi секунд будет равняться:
ω0 = 2*pi* ν = 2*pi/T.
Частота колебаний
Данная величина называется циклической частотой колебаний. В некоторой литературе встречается название круговая частота. Собственная частота колебательной системы – частота свободных колебаний.
Частота собственных колебаний рассчитывается по формуле:
ω0 = √(k/m)
Частота собственных колебаний зависит от свойств материала и массы груза. Чем больше жесткость пружины, тем больше частота собственных колебаний. Чем больше масса груза, тем меньше частота собственных колебаний.
Эти два вывода очевидны. Чем более жесткая пружина, тем большее ускорение она сообщит телу, при выведении системы из равновесия.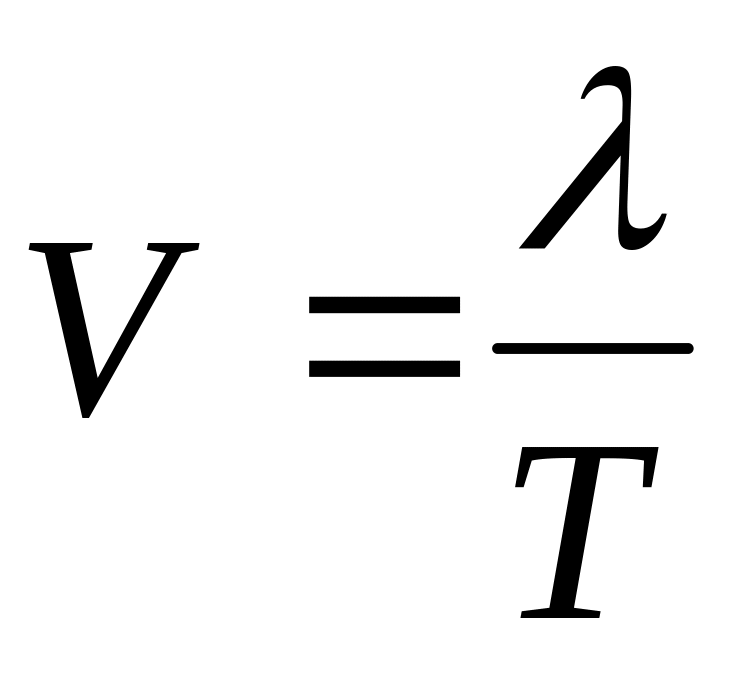
Период свободных колебаний:
T = 2*pi/ ω0 = 2*pi*√(m/k)
Примечателен тот факт, что при малых углах отклонения период колебания тела на пружине и период колебания маятника не будут зависеть от амплитуды колебаний.
Запишем формулы периода и частоты свободных колебаний для математического маятника:
ω0 = √(g/l),
тогда период будет равен:
T = 2*pi*√(l/g).
Данная формула будет справедлива лишь для малых углов отклонения. Из формулы видим, что период колебаний возрастает с увеличением длины нити маятника. Чем больше будет длина, тем медленнее тело будет колебаться.
От массы груза период колебаний совершенно не зависит. Зато зависит от ускорения свободного падения. При уменьшении g, период колебаний будет увеличиваться. Данное свойство широко используют на практике. Например, для измерения точного значения свободного ускорения.
Гармонические колебания. Амплитуда, период и частота колебательного движения
В рамках прошлой темы говорилось о новом виде механического движения – колебательном движении.
Механическое колебательное движение
Если колебания происходят в системе только под действием внутренних сил, то такие колебания называют свободными.
Колебательной системой называют такую физическую систему, в которой при отклонении от положения равновесия возникают и существуют колебания.
Маятник – это твердое тело, совершающее под действием приложенных сил колебания около неподвижной точки или вокруг оси.
В
рамках данной темы будет рассмотрен простейший вид колебательного движения —
гармонические колебания.
Гармонические колебания — это колебания, при которых смещение колеблющейся точки от положения равновесия изменяется с течением времени по закону синуса или косинуса.
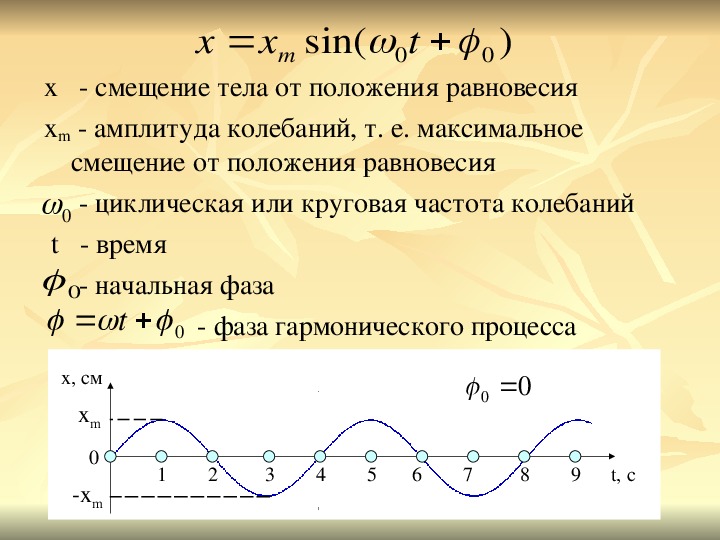
Смещение от положения равновесия при гармонических колебаниях описывается уравнениями вида:
Эти уравнения называют кинематическим законом гармонического движения.
Покажем, что гармонические колебания действительно подчиняются закону синуса или косинуса. Для этого рассмотрим следующую установку.
Возьмем нитяной маятник, а в качестве груза к нему выберем небольшой массивный сосуд с маленьким отверстием снизу и насыплем в него песок.А под полученную систему положим длинную бумажную ленту.
Если
ленту перемещать с постоянной скоростью в направлении, перпендикулярном
плоскости колебаний, то на ней останется волнообразная дорожка из песка, каждая
точка которой соответствует положению колеблющегося груза в тот момент, когда
он проходил над ней. Из опыта видно, что след, который оставляет песок на листе
бумаги, есть некая кривая.
Из опыта видно, что след, который оставляет песок на листе
бумаги, есть некая кривая.
Она называется синусоидой. Из курса математики старших классов вы узнаете о том, что аналогичные графики имеют функции типа
Значит, графически зависимость смещения колеблющейся точки от времени изображается синусоидой или косинусоидой.
Через точки, соответствующие положению равновесия маятника, проведена ось времени t, а перпендикулярно ей — ось смещения икс. График дает возможность приблизительно определить координату груза в любой момент времени.
Теперь разберемся с величинами, входящими в уравнение колебательного движения.
Смещение — величина, характеризующая положение колеблющейся точки в некоторый момент времени относительно положения равновесия и измеряемая расстоянием от положения равновесия до положения точки в данный момент времени.
Амплитуда
колебаний — максимальное смещение тела от положения равновесия.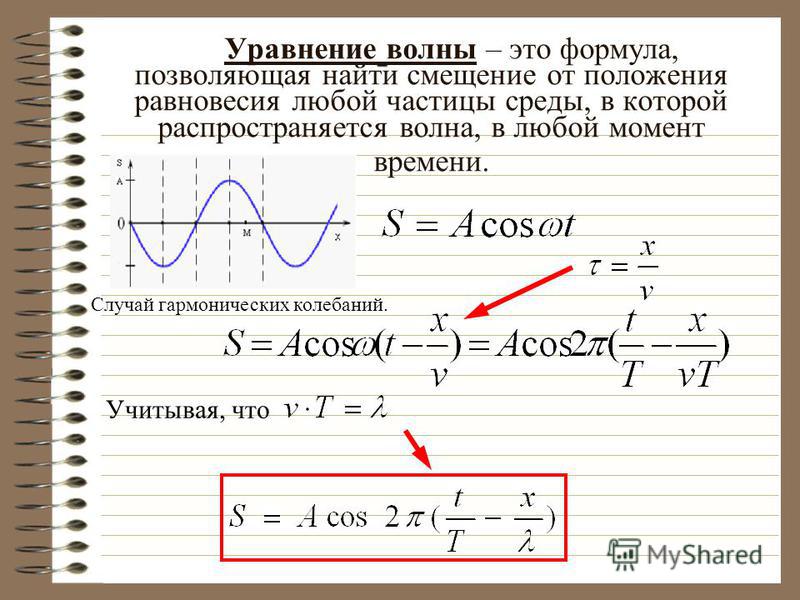
Циклическая, или круговая частота, показывающая, сколько колебаний совершает тело за 2p секунд.
j0 — это начальная фаза колебаний.
Фаза колебаний — это аргумент периодической функции, который при заданной амплитуде колебаний определяет состояние колебательной системы в любой момент времени.
Промежуток времени, в течение которого тело совершает одно полное колебание, называется периодом колебаний.
Период колебаний обычно обозначается буквой Т и в системе СИ измеряется в секундах.
Число колебаний в единицу времени называется частотой колебаний. Обозначается частота буквой ν. За единицу частоты принято одно колебание в секунду. Эта единица названа в честь немецкого ученого Генриха Герца.
Период колебания и частота колебаний связаны следующей зависимостью:
Т.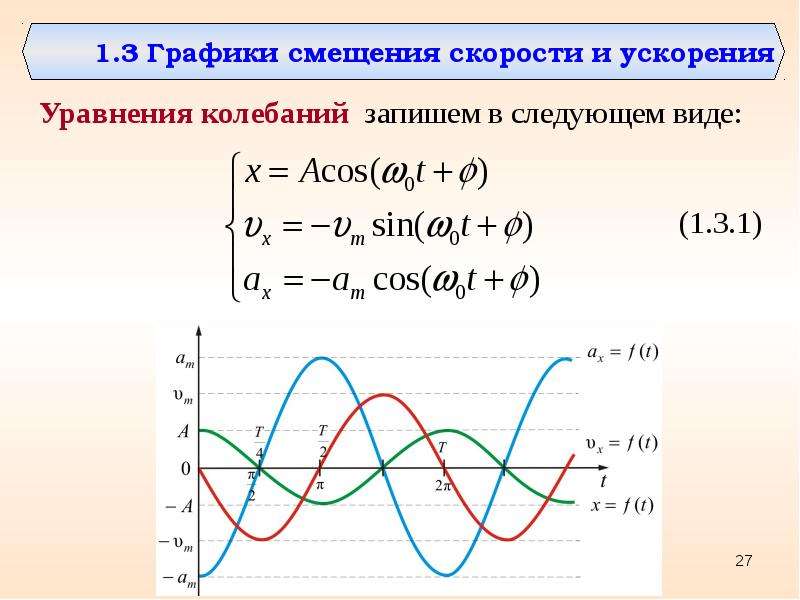 е.
частота — это величина обратная периоду и равная числу полных колебаний, совершаемых
за 1 секунду.
е.
частота — это величина обратная периоду и равная числу полных колебаний, совершаемых
за 1 секунду.
Циклическая частота также связана с периодом колебаний или частотой. Эту связь математически можно записать в следующем виде:
Таким образом, любое колебательное движение характеризуется амплитудой, частотой (или периодом) и фазой колебаний.
При совершении телом гармонических колебаний не только его координата, но и такие величины, как сила, ускорение, скорость, тоже изменяются по закону синуса или косинуса.
Это
следует из известных вам законов и формул, в которых указанные величины попарно
связаны прямо пропорциональной зависимостью, например законом Гука или вторым
законом Ньютона. Из этих формул видно, что сила и ускорение достигают
наибольших значений, когда колеблющееся тело находится в крайних положениях,
где смещение наиболее велико, и равны нулю, когда тело проходит через положение
равновесия.
Что же касается скорости, то она, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия достигает наибольшего значения.
Колебания, практически близкие к гармоническим, совершает тяжелый шарик, подвешенный на легкой и малорастяжимой нити, длина которой значительно больше диаметра шарика. Такую колебательную систему называют математическим маятником.
Математический маятник — это материальная точка, подвешенная на невесомой нерастяжимой нити, прикрепленной к подвесу и находящейся в поле силы тяжести.
Также гармонические колебания может совершать груз подвешенный на пружине, совершающий колебания в вертикальной плоскости. Такую колебательную систему называют пружинным маятником — это система, состоящая из материальной точки массой m и пружины.
Основные выводы:
– Гармонические колебания
— это колебания, при которых смещение колеблющейся точки от положения
равновесия изменяется с течением времени по закону синуса или косинуса.
– Любое колебательное движение характеризуется амплитудой, частотой (или периодом) и фазой колебаний.
– Амплитуда колебаний — максимальное смещение тела от положения равновесия.
– Промежуток времени, в течение которого тело совершает одно полное колебание, называется периодом колебаний.
– Число колебаний в единицу времени называется частотой колебаний.
– Фаза колебаний — это аргумент периодической функции, который при заданной амплитуде колебаний определяет состояние колебательной системы в любой момент времени.
– Математический и пружинный маятники — это простейшие идеализированные колебательные системы, подчиняющиеся закону синуса или косинуса.
– Математический маятник — это материальная точка, подвешенная на невесомой нерастяжимой нити, прикрепленной к подвесу и находящейся в поле силы тяжести.
– Пружинный маятник
— это система, состоящая из материальной точки массой m
и пружины, которая совершает колебания в вертикальной плоскости.
Задачи 12 класс. Колебания и волны
Методика решения задач по кинематике и динамике колебательного движения,
по волновым процессам
будет полезна как учащимся, так и абитуриентам
—————————————————————————————————-
Колебательные и волновые процессы изучают в одном разделе. Этим подчеркивается большое значение учения о колебаниях в современной науке и технике и то общее, что присуще этим движениям независимо от их природы.
Нужно сказать, что при решении задач этой темы учащимися и абитуриентами делается много ошибок, которые происходят из-за неверного толкования некоторых основных понятий.
В процессе решения задач можно научиться пользоваться соответствующими формулами, осознать те специфические отличия, которые имеет колебательное движение по сравнению с равномерным и равнопеременным.
В этих целях сначала решают задачи по кинематике колебательного движения материальной точки. Как частный, но важный случай этого движения рассматривают движение математического маятника.
Вопросы динамики колебательного движения и превращения энергии углубляют с помощью задач об упругих колебаниях и задач о математическом маятнике.
1. Колебательным движением называют движение, при котором происходит частичная или полная повторяемость состояния системы по времени.
Если значения физических величин, характеризующих данное колебательное движение, повторяются через равные промежутки времени, колебания называют периодическими.
Самым простым колебательным движением является гармоническое колебание материальной точки. Гармоническим называют колебание, в процессе которого величины, характеризующие движение (смещение, скорость, ускорение, сила и т.д.), изменяются с течением времени по закону синуса или косинуса (гармоническому закону).
Гармонические колебания являются простейшими, так что различные периодические процессы могут быть представлены как результат наложения нескольких гармонических колебаний.
рис. 1 (а, б, в)
Основные законы гармонических колебаний материальной точки можно установить из сопоставления равномерного кругового движения точки и движения ее проекции на диаметр окружности.
Если точка В, обладающая массой m, равномерно перемещается по окружности радиусом R с угловой скоростью ω (рис. 1а), то ее проекция на горизонтальный диаметр — точка С совершает гармонические колебания вдоль оси ОХ.
Смещение точки С от начала отсчета О движения — ее координата х в каждый момент, времени определяется уравнением
где t — время, прошедшее с начала колебаний; (φ+φ0) — фаза колебаний, характеризующая положение точки С в момент начала отсчета движения (на чертеже начальная фаза φ0 = 0), xm= R — амплитуда колебания (иногда ее обозначают буквой А).
Раскладывая вектор линейной скорости и вектор нормального ускорения по осям ОХ и OY рис. 1(б, в), для модулей составляющих и (скорости и ускорения точки С) получим:
Поскольку
уравнения скорости и ускорения точки, совершающей гармонические колебания, можно представить в виде:
Знак «минус» в последней формуле указывает на то, что ускорение при гармоническом колебании направлено в сторону, противоположную смещению.
Из полученных соотношений следует, что:
а) максимальные значения скорости и ускорения колеблющейся точки равны:
б) скорость и ускорение сдвинуты друг относительно друга на угол .
Там, где скорость наибольшая, ускорение равно нулю,
и наоборот.
в) Во всех точках траектории ускорение направлено к центру колебаний — точке О.
2. Учитывая формулу для ускорения, уравнение второго закона Ньютона для материальной точки, совершающей гармонические колебания, можно представить в виде
где F есть величина равнодействующей всех сил, приложенных к точке,
—
величина
возвращающей силы.
Величина возвращающей силы также изменяется по гармоническому закону.
Произведение mω2 стоящее в правой части этого уравнения, — величина постоянная, поэтому материальная точка может совершать гармонические колебания лишь при условии, что в процессе движения возвращающая сила изменяется пропорционально смещению и направлена к положению равновесия, т. е. F = − k·m.
Здесь k — постоянный для данной системы коэффициент, который в каждом конкретном случае может быть выражен дополнительной формулой через величины, характеризующие колебательную систему, и в то же время всегда равный mω2.
3. Кинетическая энергия гармонически колеблющейся точки равна:
В процессе гармонического колебания сила изменяется пропорционально смещению, поэтому в каждый момент времени потенциальная энергия точки равна:
Полная механическая энергия колеблющейся точки
При гармоническому закону происходит превращение энергии из одного вида в другой.
4. Другой пример получения уравнений гармонических колебаний. Тот факт, что движение вращающейся по окружности материальной точки происходит по синусоидальному закону, наглядно демонстрирует рис. 2. Здесь по оси абсцисс откладывается время колебания, а по оси ординат — значения проекции радиуса-вектора движущейся точки в соответсвующий момент времени.
рис. 2
В случае движения проекции точки по оси OY уравнение колебательного движения запишется так:
(1)
Отсчет времени и измерение y и ведется с момента прохождения тела через положение равновесия (при t = 0 х = 0).
При движения проекции точки по оси OX уравнение запишется в виде
(2).
отсчет времени ведется с момента наибольшего отклонения тела от положения равновесия, которое также принимают за начало отсчета (при t = 0 х = хm). Так, например, поступают, когда подсчитывают время и число колебаний маятника, поскольку трудно зафиксировать его положение в средней точке, где он имеет максимальную скорость.
Так, например, поступают, когда подсчитывают время и число колебаний маятника, поскольку трудно зафиксировать его положение в средней точке, где он имеет максимальную скорость.
Теперь, применив понятие производной функции, можно найти скорость тела.
Дифференцируя уравнение (1) по времени t (первая производная), получим выражение для скорости тела (материальной точки):
Дифференцируя полученное выражение еще раз по времени t (вторая производная), определим ускорение колеблющейся точки:
Как показывает практика, учащиеся трудно усваивают понятие о круговой частоте.
Из этого выражения следует, что круговая частота равна числу колебаний, совершаемых материальной точкой за секунд.
Нужно обратить внимание на то, что под знаком тригонометрической функции всегда
стоит фаза колебаний.
Фаза колебаний определяет величину смещения в момент времени t, начальная фаза определяет величину смещения в момент начала отсчета времени (t = 0).
Иногда абитуриенты, рассматривая колебания математического маятника, называют фазой угол отклонения нити от вертикали и тем самым делают ошибку. В самом деле, если представлять себе фазу как угол, то как, например, можно увидеть этот угол в случае гармонических колебаний груза на пружине?
Фаза колебаний — это угловая мера времени, прошедшего от начала колебаний. Любому значению времени, выраженному в долях периода, соответствует значение фазы, выраженное в угловых единицах. Ниже в таблице указано соответствие значения фазы φ значению времени t (считаем, что φ0 = 0).
Смещение х, скорость и ускорение а могут иметь одно и то же значение при разных углах или времени t, так как они выражаются циклическими функциями.
При решении задач, если это специально не оговаривается, за угол можно принимать его наименьшее значение.
5. Уравнения колебательного движения остаются одинаковыми для колебаний любой природы, и для электромагнитных колебаний в том числе.
В этом случае можно рассматривать, например, колебания величины заряда (qi), э.д.с. (ei), силы тока (i), напряжения (u), магнитного потока (Фi) и др. При этом в левой части уравнений стоят мгновенные значения указанных величин.
Частота и период электромагнитных колебаний колебаний (формула Томсона):
Волновым движением называется процесс распространения колебаний в среде. Частицы среды, в которой распространяется волна, не переносятся вместе с волной, а лишь совершают колебания около своего положения равновесия.
В поперечной волне они колеблются в направлениях, перпендикулярных к направлению распространения волны, в продольной — вдоль направления распространения волны.
Распространяясь в среде, волна переносит с собой энергию от источника колебаний.
Механические поперечные волны могут возникать только в твердой среде.
Возникновение продольных волн возможно в твердой, жидкой и газообразной средах.
Параметрами волн являются: энергия, длина волны λ (лямбда), частота ν (ню), период колебаний T, скорость υ.
1. Волнам присущи одинаковые свойства и явления: отражение от границы раздела двух сред, в которых распространяется волна, преломление — изменение направления волны при после ее прохождения границы раздела двух сред, интерференция — явление наложение волн, в результате которого происходит усиление или ослабление колебаний, дифракция — явление огибания волнами препятствий или отверстий.
Условием возникновения интерференции является когерентность волн — они должны иметь одинаковую частоту колебаний и постоянную разность фаз этих колебаний.
Условие максимумов (усиления волн):
Максимумы колебаний при интерференции возникает в тех точках среды, для которых в разности хода волн укладывается четное число полуволн.
Условие минимумов (ослабление волн):
Минимумы колебаний при интерференции возникает в тех точках среды, для которых в разности хода волн укладывается нечетное число полуволн.
—————————————————————————————————-
Решая приведенные ниже задачи, Вы сможете глубже понятьприроду колебательного и волнового движения
—————————————————————————————————-
Для решения задач Вам могут потребоваться таблицы
физических постоянных или кратных и дольных приставок к единицам физических величин
Гармонические колебания
1. Напишите уравнение гармонических колебаний, если частота равна 0,5 Гц, амплитуда 80 см. Начальная фаза колебаний равна нулю.
Напишите уравнение гармонических колебаний, если частота равна 0,5 Гц, амплитуда 80 см. Начальная фаза колебаний равна нулю.
Решение:
2. Период гармонических колебаний материальной точки равен 2,4 с, амплитуда 5 см, начальная фаза равна нулю. Определите смещение колеблющейся точки через 0,6 с после начала колебаний.
З. Напишите уравнение гармонических колебаний, если амплитуда равна 7 см и за 2 мин совершается 240 колебаний. Начальная фаза колебаний равна π /2 рад.
Решение:
4. Вычислите амплитуду гармонических колебаний, если для фазы π /4 рад смещение равно 6 см.
5. Напишите уравнение гармонических колебаний, если за 1 мин совершается 60 колебаний; амплитуда равна 8 см, а начальная фаза 3·π /2 рад.
6. Амплитуда колебаний равна 12 см, частота 50 Гц. Вычислите смещение колеблющейся точки через 0,4 с. Начальная фаза колебаний равна нулю.
Вычислите смещение колеблющейся точки через 0,4 с. Начальная фаза колебаний равна нулю.
7. Уравнение гармонических колебаний тела x = 0,2·cos(πt) в (СИ). Найдите амплитуду, период, частоту и циклическую частоту. Определите смещение тела через 4 с; 2 с.
Колебания математического маятника и груза на пружине
1. Математический маятник (см. рис.) совершает колебания с амплитудой 3 см. Определите смещение маятника за время, равное Т/2 и Т. Начальная фаза колебаний равна π рад. Решение: Ответ: Кинетическая энергия маятника увеличивается, потенциальная уменьшается. |
|
2. Груз на пружине (см. рис.) совершает колебания с амплитудой 4 см. Определите смещение груза за время, равное Т/2 и Т. Начальная фаза колебаний равна нулю. |
|
3. На вращающемся диске укреплен шарик. Какое движение совершает тень шарика на вертикальном экране? |
|
| |
5. Груз на пружине за Т/2 смещается на 6 см. С какой амплитудой колеблется груз? Начальная фаза колебаний равна π рад. |
|
6. По какой траектории будет двигаться шарик, если пережечь нить в момент прохождения маятником положения равновесия? | |
7. Первый маятник Фуко (1891, Париж) имел период колебаний 16 с Определите длину маятника. Примите g = 9,8 м/с2.
Первый маятник Фуко (1891, Париж) имел период колебаний 16 с Определите длину маятника. Примите g = 9,8 м/с2.
8. Два маятника, длины которых отличаются на 22 см, совершают в одном и том же месте Земли за некоторое время один 30 колебаний, другой 36 колебаний. Найдите длины маятников.
9. Груз массой 200 г совершает колебания на пружине с жесткостью 500 Н/м. Найдите частоту колебаний и наибольшую скорость движения груза, если амплитуда колебаний 8 см.
10. Определите ускорение свободного падения на Луне, если маятниковые часы идут на ее поверхности в 2,46 раза медленнее, чем на Земле.
11. Пружина под действием груза удлинилась на 1 см. Определите, с каким периодом начнет совершать колебания этот груз на пружине, если его вывести из положения равновесия.
12. Под действием подвешенного тела пружина удлинилась на .
Докажите, что период вертикальных колебаний этого груза равен
13. Груз висит на пружине и колеблется с периодом 0,5 с. На сколько укоротится пружина, если снять с нее груз?
Груз висит на пружине и колеблется с периодом 0,5 с. На сколько укоротится пружина, если снять с нее груз?
14. Пружина под действием прикрепленного к ней груза массой 5 кг, совершает 45 колебаний в минуту. Найдите коэффициент жесткости пружины.
15. На сколько уйдут часы за сутки, если их перенести с экватора на полюс?
(gэ= 978 см/с2, gп= 983 см/с2.)
16. Часы с маятником длиной 1 м за сутки отстают па 1 ч. Что надо сделать с длиной маятника, чтобы часы не отставали?
17. Для определения на опыте ускорения свободного падения заставили колебаться груз на нити, при этом он совершил 125 колебаний за 5 мин. Длина маятника равна 150 см. Чему равно g?
Электромагнитные колебания
Период, частота, напряжение, ЭДС, сила переменного электрического тока
1. |
|
2. По графику, изображенному на рисунке, определите амплитуду напряжения, период и значение напряжения для фазы рад. |
|
3. По графику, изображенному на рисунке, определите амплитуду силы тока, период и частоту. Напишите уравнение мгновенного значения силы переменного тока. |
|
4. Значение напряжения, измеренное в вольтах, задано уравнением , где t выражено в секундах. Чему равна амплитуда напряжения, период и частота?
Чему равна амплитуда напряжения, период и частота?
5. Мгновенное значение силы переменного тока частотой 50 Гц равно 2 А для фазы π/4 рад. Какова амплитуда силы тока? Найдите мгновенное значение силы тока через 0,015 с, считая от начала периода.
6. Мгновенное значение ЭДС переменного тока для фазы 60° равно 120 В. Какова амплитуда ЭДС? Чему равно мгновенное значение ЭДС через 0,25 с, считая от начала периода? Частота тока 50 Гц.
Механические и электромагнитные волны
1. Почему морские волны увеличивают свою высоту, приближаясь к берегу?
2. Определите длину волны по следующим данным: a) υ = 40 м/с, Т = 4 с; б) υ = 340 м/с, ν = 1 кГц.
3. Определите скорость распространения волны, если ее длина 150 м, а период 12 с. На каком расстоянии находятся ближайшие точки волны, колеблющиеся в противоположных фазах?
4. Какой частоте камертона соответствует звуковая волна в воздухе длиной 34 м? Скорость звука в воздухе равна 340 м/с.
5. На земле услышан гром через 6 с после наблюдения молнии. На каком расстоянии от наблюдателя возникла молния?
6. Радиопередатчик искусственного спутника Земли работает на частоте 20 МГц. Какова длина волны передатчика?
7. На какой частоте должен работать радиопередатчик корабля, передающий сигнал бедствия «SOS», если по международному соглашению этот сигнал передается на волне длиной 600 м?
| источники: | Балаш В.А. “Задачи по физике и методы их решения”. Пособие для учителей. М., “Просвещение”, 1974. |
7.7.Затухающие колебания – Лекции по физике
Все реальные колебательные системы являются диссипативными. Энергия механических колебаний такой системы постепенно расходуется на работу против сил трения, поэтому свободные колебания всегда затухают – их амплитуда постепенно уменьшается. Во многих случаях, когда отсутствует сухое трение, в первом приближении можно считать, что при небольших скоростях движения силы, вызывающие затухание механических колебаниях, пропорциональны скорости. Эти силы, независимо от их происхождения, называют силами сопротивления.
| (7.17) |
где r – коэффициент сопротивления, v – скорость движения. Запишем второй закон Ньютона для затухающих колебаний тела вдоль оси ОХ
или
| (7.18) |
Перепишем это уравнение в следующем виде:
и обозначим:
где представляет ту частоту, с которой совершались бы свободные колебания системы при отсутствии сопротивления среды, т. е. при r = 0. Эту частоту называют собственной частотой колебания системы; β – коэффициент затухания. Тогда
е. при r = 0. Эту частоту называют собственной частотой колебания системы; β – коэффициент затухания. Тогда
| (7.19) |
Будем искать решение уравнения (7.19) в виде
где U – некоторая функция от t.
Продифференцируем два раза это выражение по времени t и, подставив значения первой и второй производных в уравнение (7.19), получим
Решение этого, уравнения существенным образом зависит от знака коэффициента, стоящего при U. Рассмотрим случай, когда этот коэффициент положительный. Введем обозначение тогда С вещественным ω решением этого уравнения, как мы знаем, является функция
Таким образом, в случае малого сопротивления среды , решением уравнения (7.19) будет функция
| (7.20) |
График этой функции показан на рис. 7.8. Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки. Величину называют собственной циклической частотой колебаний диссипативной системы. Затухающие колебания представляют собой непериодические колебания, т.к, в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения. Величину обычно называют периодом затухающих колебаний, правильнее – условным периодом затухающих колебаний,
Величину называют собственной циклической частотой колебаний диссипативной системы. Затухающие колебания представляют собой непериодические колебания, т.к, в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения. Величину обычно называют периодом затухающих колебаний, правильнее – условным периодом затухающих колебаний,
Натуральный логарифм отношения амплитуд смещений, следующих друг за другом через промежуток времени, равный периоду Т, называют логарифмическим декрементом затухания.
Обозначим через τ промежуток времени, за который амплитуда колебаний уменьшается в е раз. Тогда
откуда
Следовательно, коэффициент затухания есть физическая величина, обратная промежутку времени τ, в течение которого амплитуда убывает в е раз. Величина τ называется временем релаксации.
Пусть N – число колебаний, после которых амплитуда уменьшается в е раз, Тогда
Следовательно, логарифмический декремент затухания δ есть физическая величина, обратная числу колебаний N, по истечению которого амплитуда убывает в е раз
Динамика колебательного движения.
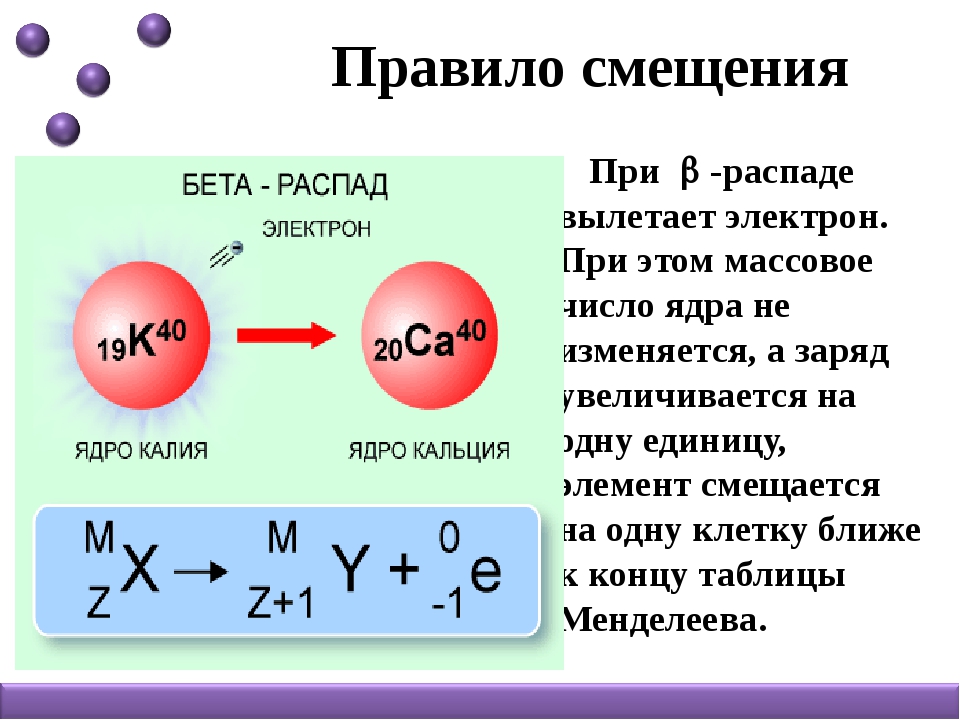 Уравнение движения маятника
Уравнение движения маятникаДинамика колебательного движения. Уравнение движения маятника
- Подробности
- Просмотров: 609
«Физика – 11 класс»
Колебания тела можно описать, используя законы Ньютона.
Уравнение движения тела, колеблющегося под действием силы упругости.
Согласно второму закону Ньютона произведение массы тела на ускорение его равно равнодействующей всех сил, приложенных к телу:
Запишем уравнение движения для шарика, движущегося прямолинейно вдоль горизонтали под действием силы упругости Fупр пружины.
Направим ось ОХ вправо. Пусть начало отсчета координат соответствует положению равновесия шарика.
В проекции на ось ОХ уравнение движения можно записать так:
mах = Fx упр
где
ах и Fx упр – проекции ускорения и силы упругости пружины на эту ось.
Согласно закону Гука проекция Fx ynp прямо пропорциональна смещению шарика из положения равновесия.
Смещение же равно координате х шарика, причем проекция силы и координата имеют противоположные знаки. Следовательно,
Fx yпp = -kх
Разделив левую и правую части уравнения на массу, получим уравнение, описывающее колебания тела под действием силы упругости:
Проекция ускорения тела прямо пропорциональна его координате, взятой с противоположным знаком.
Так как масса и жесткость пружины — постоянные величины, то их отношение также постоянная величина.
Уравнение движения математического маятника
При колебаниях маятника на нерастяжимой нити он все время движется по дуге окружности, радиус которой равен длине нити l.
Положение маятника в любой момент времени определяется одной величиной — углом альфа (α) отклонения нити от вертикали.
Пусть угол α>0, если маятник отклонен вправо от положения равновесия,
и α
Касательную к траектории будем считать направленной в сторону положительного отсчета углов.
Проекция силы тяжести на касательную к траектории маятника в момент, когда нить маятника отклонена от положения равновесия на угол α, равна:
Ft = -mg sin α
Знак «-» здесь стоит потому, что величины Ft и а имеют противоположные знаки.
При отклонении маятника вправо (α > 0) составляющая силы тяжести Ft направлена влево и ее проекция отрицательна: Ft < 0.
При отклонении маятника влево (α < 0) эта проекция положительна: F t > 0.
Проекция ускорения маятника на касательную к его траектории аt характеризует быстроту изменения модуля скорости маятника.
Поступая налогично выводу форулы для маятника, колеблющегося под действием силы упругости,
получим уравнение движения для математического маятника (нитяного маятника):
Проекция ускорения тела прямо пропорциональна его координате, взятой с противоположным знаком.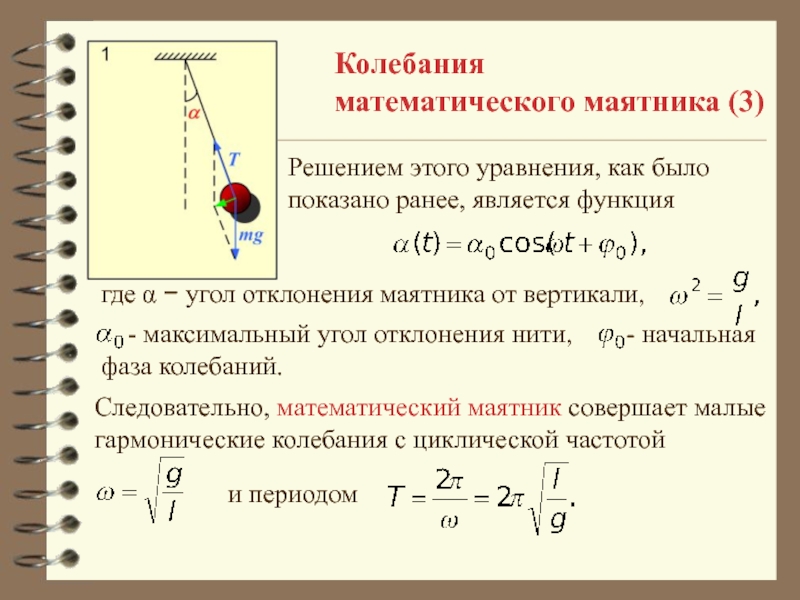
где
l – длина нити маятника,
g – ускорение свободного падения,
х – смещение маятника.
Вывод:
Движение маятника на пружине и колебания маятника на нити происходят одинаковым образом, хотя силы, вызывающие колебания, имеют различную физическую природу.
Ускорение прямо пропорционально координате (смещению от положения равновесия).
Колебания в этих двух случаях совершаются под действием сил, равнодействующая которых прямо пропорциональна смещению колеблющегося тела от положения равновесия и направлена в сторону, противоположную этому смещению.
Источник: «Физика – 11 класс», учебник Мякишев, Буховцев, Чаругин
Механические колебания. Физика, учебник для 11 класса – Класс!ная физика
Свободные, затухающие и вынужденные колебания —
Условия возникновения свободных колебаний. Математический маятник —
Динамика колебательного движения. Уравнение движения маятника —
Гармонические колебания —
Фаза колебаний —
Превращение энергии при гармонических колебаниях —
Вынужденные колебания. Резонанс —
Примеры решения задач —
Краткие итоги главы
Уравнение движения маятника —
Гармонические колебания —
Фаза колебаний —
Превращение энергии при гармонических колебаниях —
Вынужденные колебания. Резонанс —
Примеры решения задач —
Краткие итоги главы
Калькулятор смещения s = (1/2) (v + u) t
Использование калькулятора
Этот калькулятор смещения находит смещение (пройденное расстояние) объектом, используя его начальную и конечную скорости, а также пройденное время. Средняя скорость объекта умножается на пройденное время, чтобы найти смещение. Уравнение x = ½ (v + u) t можно манипулировать, как показано ниже, для нахождения любого из четырех значений, если остальные три известны.
Уравнений смещения для этих расчетов:
\ (s = \ dfrac {1} {2} (v + u) t \)
Где:
с = рабочий объем
v = конечная скорость
u = начальная скорость
t = время
В разных ресурсах используются несколько разные переменные, поэтому вы также можете столкнуться с этим же уравнением с v i или v 0 , представляющим начальную скорость (u), и v f , представляющим конечную скорость (v), например, в следующей форме:
\ (s = \ dfrac {1} {2} (v_f + v_i) t \)
Где:
с = рабочий объем
v f = конечная скорость
v i = начальная скорость
t = время
Расчет смещения, используемый в калькуляторе:
Решая различные переменные, мы можем использовать следующие формулы:
- Данные v, u и t решают относительно s
Заданная начальная скорость, конечная скорость и время вычисляют смещение.
- Даны s, t и u решают относительно v
По заданному смещению, времени и начальной скорости вычисляется конечная скорость. - Даны s, t и v решают относительно u
По заданному смещению, времени и конечной скорости вычисляется начальная скорость. - Даны v, u и t решают относительно s
Заданная начальная скорость, конечная скорость и время вычисляют смещение.
Задача перемещения 1:
Автомобиль ехал по дороге 45 секунд. Машина свернула на улицу со скоростью 20 м / с и к концу улицы двигалась со скоростью 23 м / с. Как долго длится улица?
Поскольку нам даны начальная скорость (20 м / с), конечная скорость (23 м / с) и время (45 секунд), уравнение может быть применено напрямую. s = ½ (20 + 23) * 45 = 967. 5 метров
5 метров
Задача смещения 2:
Когда кувшин бросает подачу из-под насыпи питчера, он находится примерно в 60 футах от своей тарелки. Если мяч покидает его руку со скоростью 132 фут / с и достигает домашней пластины со скоростью 110 фут / с, сколько времени потребуется мячу, чтобы пройти от насыпи до домашней пластины?
В этой задаче нам дается другой набор значений. Уравнение s = ½ (v + u) t может быть алгебраически преобразовано в t = 2s / (v + u).Водоизмещение составляет 60 футов, начальная скорость – 132 фут / с, а конечная скорость – 110 фут / с.
t = 2 (60 футов) / (132 + 110 фут / с) = 0,496 секунды
Формула смещения| Формула для нахождения смещения и деривации
Мы находим смещение, определяя начальное и конечное положение объекта. Формула смещения имеет следующий вид:
Δx = xf – xi… .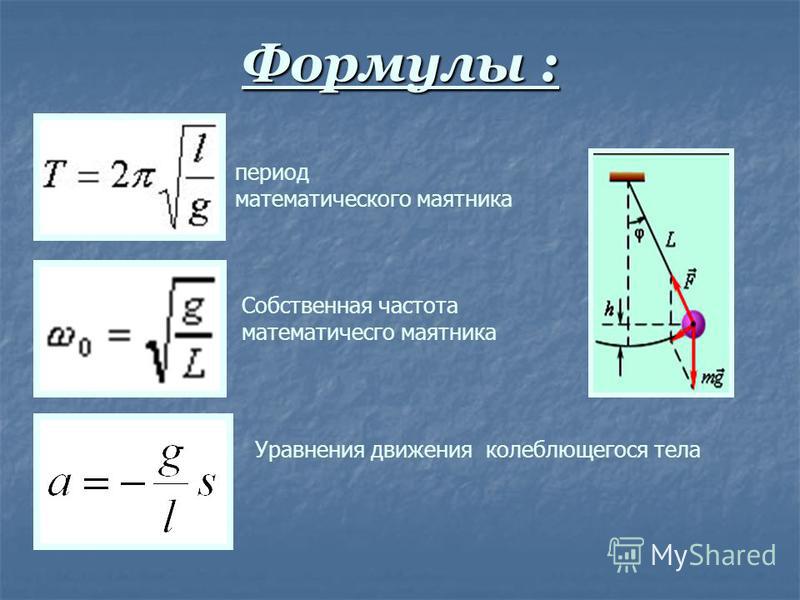 .eq (1)
.eq (1)
Где
xf – конечное положение, а
xi – начальное положение
Δx – изменение положения объект
Допустим, я держал мяч для гольфа в исходной точке или в точке 0, как показано на диаграмме A:
[Изображение будет загружено в ближайшее время]
Теперь я перемещаю мяч на 3 точки вправо, как показано на диаграмме B.Поскольку мяч переместился, что означает, что он совершил смещение, как мы видим, его начальное положение было 0 в точке A, а конечное – 3 метра в точке B, поэтому его смещение можно рассчитать с помощью уравнения 1, которое составляет:
Δx = xf – xi = 3 – 0 = + 3 м, т.е. вправо
Итак, мяч сместился на 3 метра из точки A в точку B.
Теперь мяч перемещается на – 4 очка или – 4 м до точки C, поэтому конечная позиция теперь становится начальной и конечной, xi = – 4 м. Таким образом, мы можем найти смещение AC, используя уравнение (1) как:
Δx = xf – xi = – 4 – (+ 3) = – 7 м, т. е.е., слева
е.е., слева
Однако мы должны помнить, что смещение не зависит от положения начала координат, как мы видели на диаграмме, оно зависит только от разницы между двумя положениями.
[Изображение будет загружено в ближайшее время]
Здесь
x1 = x-координата точки A, т. Е. Начальное положение объекта по оси x
x2 = x-координата точки B, т. Е. Конечная положение объекта по оси x
Расстояние по горизонтали, т.е., по оси x = (x2 – x1)
y1 = координата y точки A, т. е. начальное положение объекта по оси y
y2 = координата y точки B, т. е. конечное положение объекта по оси y
Расстояние по вертикали, то есть по оси y = (y2 – y1)
Мы знаем, что смещение – это кратчайшее расстояние между двумя точками; в двумерной системе формула расстояния может использоваться для нахождения кратчайшего расстояния между двумя точками, т. е. {2}} {2 \ times 4} \] = \ [\ frac {144-4} {8} \] = 17.{2}} \] = \ [\ sqrt {41} \] м ~ 6.44 м
{2}} {2 \ times 4} \] = \ [\ frac {144-4} {8} \] = 17.{2}} \] = \ [\ sqrt {41} \] м ~ 6.44 м
Вопрос 4: Митхила бросает мяч для крикета на 30 футов восточнее своего питомца. Ее питомец ловит мяч и уносит его мимо вас, а вы стоите в 38 футах к западу от того места, где находится Митхила. Что такое смещение мяча для крикета?
Решение: Начальное положение = 0 км, а конечное положение рассчитывается как 38 – 30 = – 8 км
Теперь, используя формулу, Δx = xf – xi = – 8 – 0 = – 8 м
D = 8 м от исходного положения Митхилы.
Калькулятор смещения
Смещение – это термин, который показывает, насколько перемещен объект.Теперь у вас может возникнуть сомнение, и вы спросите, не об этом ли говорит термин «расстояние»? Да, термины «расстояние» и «смещение» часто путают и используют как синонимы.
Вот подробное объяснение смещения и расстояния, их различий и того, как их легко вычислить.
Что такое смещение?
Рассмотрим схему, приведенную ниже.
Предположим, что частица перемещается из A в B через C, как показано здесь. Тогда чистое расстояние, которое он преодолел, составит 3 + 4, что составляет 7 метров.Но если вы внимательно посмотрите, то смещение, которое он претерпел от A к B, составляет 5 м, если бы он двигался по прямому пути между A и B, не проходя через C.
Таким образом, 7 метров – это общее «расстояние», которое прошла частица, а 5 метров – это полное «смещение», которое она претерпела в своем положении.
Итак, теперь ясно, что:
- Расстояние – это полная длина, пройденная частицей от исходного положения, а
- Смещение – это кратчайшая длина от начальной до конечной точки.
При внимательном наблюдении мы замечаем одну общность между этими двумя терминами – оба имеют одну и ту же «начальную точку» в качестве ссылки на их измерение.
Что еще нужно знать о расстоянии и смещении?
Расстояние всегда может быть положительным; при этом смещение может быть нулевым, положительным или отрицательным. Запутался как? Давайте посмотрим.
Запутался как? Давайте посмотрим.
Рассмотрим случай движения частиц в виде однородной волны. Каждая частица перемещается на определенное расстояние от среднего положения вверх и вниз или в положительном и отрицательном направлениях.Таким образом, после того, как частица завершит один полный цикл, чистое смещение частицы от среднего положения равно нулю. Но он прошел расстояние, равное одной длине волны.
Рассмотрим другой пример, как показано ниже:
Если частица стартовала из точки A, проходит через B, C и D по часовой стрелке и снова достигает точки A, то:
Общее пройденное расстояние составляет периметр прямоугольника, как показано, т. Е. 10 + 5 + 10 + 5 = 30 м
Полное смещение частицы от ее начального положения равно нулю, потому что она наконец достигла того места, откуда она стартовала.
Как насчет того, чтобы он двигался вверх до точки А на расстояние 5 м? Тогда его окончательное смещение будет -5м. да. Таким образом, смещение зависит от направления или векторной величины.
Как насчет расстояния в этом случае? Было бы 30 + 5 = 35м. Это означает, что расстояние не зависит от направления или является скалярной величиной. Это всего лишь сумма полных длин путей, по которым движется частица, независимо от направления.
Кратчайшее расстояние между двумя точками – прямая линия.- Архимед
Ключевые моменты о расстоянии и смещении- Расстояние – это фактическая длина, которую частица прошла от своей начальной точки.
- Смещение – это чистая длина, которую частица прошла между своей начальной и конечной точками.
- Смещение может быть равно расстоянию, больше или меньше.
- Чтобы рассчитать смещение, вам нужна точка отсчета. Поскольку это относится к этой точке, вычисляется смещение.Но для расчета расстояния никаких ориентиров не требуется.
- Дистанцию можно преодолеть, путешествуя по любому пути между двумя заданными точками. Но смещение – это только один уникальный путь между двумя заданными точками.

- Расстояние – это скалярная величина, обозначаемая буквой «d», а смещение – вектором, обозначаемым буквой «s».
- Численно, чтобы рассчитать расстояние, вы можете умножить скорость на затраченное время; в то время как для получения смещения вам нужно умножить скорость и время.
- Зная расстояние, вы можете иметь представление о пути, по которому двигалась частица. Но с помощью значения смещения вы никогда не сможете узнать путь, который прошла частица, чтобы достичь своей конечной точки.
Знаете ли вы?
Смещение в физике сокращенно обозначается как Δs. Что ж, за этим стоит интересный факт. В то время как Δ (дельта по-гречески) представляет собой изменение или разницу между двумя величинами, s представляет собой пройденное пространственное расстояние.То есть Δs представляет собой изменение пространственного расстояния, которое прошла частица. Следовательно, смещение причины представлено s или Δs, чтобы быть точным.
Время – это самое большое расстояние между двумя местами.
По какой формуле рассчитывается смещение?
Смещение частицы рассчитывается по формуле: s = ½ (v + u) xt,
Где s – смещение
V – конечная скорость в м / с
U – конечная скорость в м / с
T – время, необходимое для перехода от исходного положения к конечному, в секундах.
Как калькулятор смещения CalculatorHut помогает вам?
Студенты считают расчет смещения неотъемлемой частью своих заданий. Бесплатный онлайн-калькулятор смещения CalculatorHut поможет легко рассчитать смещение. Они также могут перекрестно проверять результаты, которые они сделали вручную.
CalculatorHut – это центр научных и ненаучных онлайн-калькуляторов, который бесплатно ответит на все ваши потребности в расчетах. Он имеет широкий спектр более 100 калькуляторов по различным темам – калькуляторы здоровья, финансовые калькуляторы, калькуляторы транспортных средств, физические калькуляторы, химические калькуляторы, математические калькуляторы и многие другие бесплатные научные онлайн-калькуляторы.
Чем CalculatorHut отличается от других бесплатных онлайн-калькуляторов? Вот как: если вам понравился наш огромный выбор калькуляторов и вы хотите, чтобы они были встроены в качестве виджетов на ваш веб-сайт, вы можете написать нам на [email protected]. Мы разработаем виджет абсолютно бесплатно для вас в соответствии с вашими настройками!
Мы ценим отзывы пользователей. Мы пропустили какой-нибудь бесплатный онлайн-калькулятор? Пожалуйста дай нам знать. Мы будем более чем рады удовлетворить ваши потребности в бесплатном онлайн-калькуляторе бесплатно в любое время!
Вот еще одна фантастическая новость! Вы можете бесплатно носить с собой в кармане наш широкий ассортимент онлайн-калькуляторов.Да! Приложение CalculatorHut доступно для бесплатной загрузки в Play Store, и это замечательное приложение станет вашим другом, который сделает любые вычисления проще и проще! Удачных расчетов с CalculatorHut!
Определение площади (и смещения)
Как было сказано в предыдущей части этого урока, график зависимости скорости от времени можно использовать для определения ускорения объекта (наклона).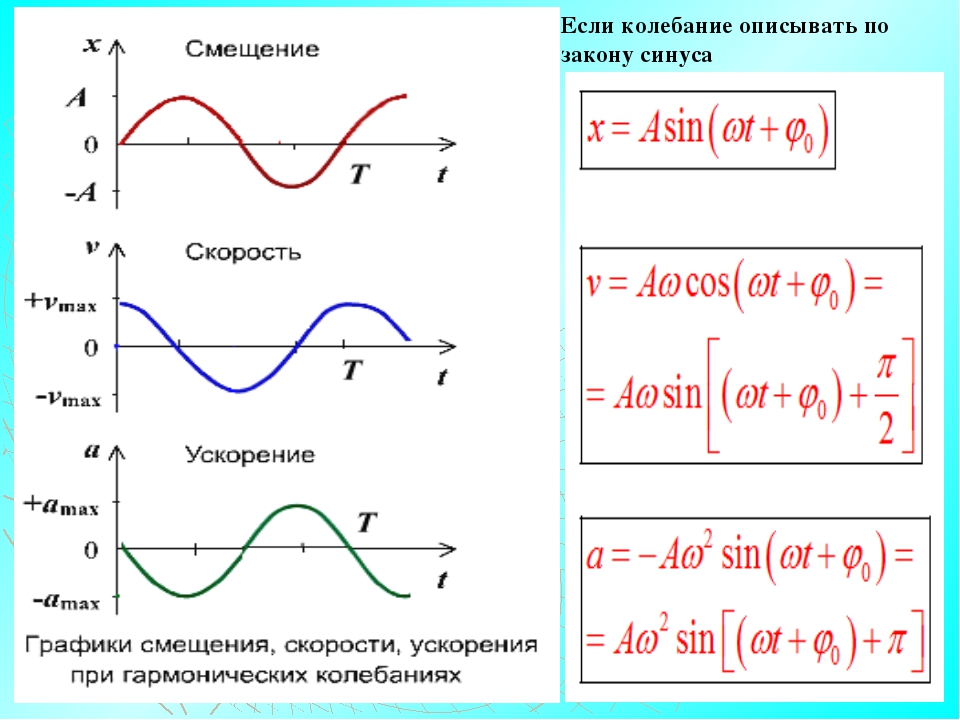 В этой части урока мы узнаем, как можно использовать график зависимости скорости от времени для определения смещения объекта.Для графиков зависимости скорости от времени область, ограниченная линией и осями, представляет смещение. На приведенной ниже диаграмме показаны три различных графика скорость-время; заштрихованные области между линией и осью времени представляют смещение в течение указанного временного интервала.
В этой части урока мы узнаем, как можно использовать график зависимости скорости от времени для определения смещения объекта.Для графиков зависимости скорости от времени область, ограниченная линией и осями, представляет смещение. На приведенной ниже диаграмме показаны три различных графика скорость-время; заштрихованные области между линией и осью времени представляют смещение в течение указанного временного интервала.
| Заштрихованная область представляет смещение в течение от 0 секунд до 6 секунд. Эта площадь, имеющая форму прямоугольника, может быть рассчитана с помощью соответствующего уравнения. | |
| Заштрихованная область представляет смещение в течение от 0 секунд до 4 секунд. Эту площадь, имеющую форму треугольника, можно рассчитать с помощью соответствующего уравнения. | |
Заштрихованная область представляет смещение в течение от 2 до 5 секунд. Эта площадь, имеющая форму трапеции, может быть рассчитана с помощью соответствующего уравнения. Эта площадь, имеющая форму трапеции, может быть рассчитана с помощью соответствующего уравнения. | |
Метод, используемый для нахождения площади под линией на графике скорость-время, зависит от того, является ли участок, ограниченный линией и осями, прямоугольником, треугольником или трапецией. Формулы площади для каждой формы приведены ниже.
| Прямоугольник | Треугольник | Трапеция |
| Площадь = b • h | Площадь = ½ • b • h | Площадь = ½ • b • (h 1 + h 2 ) |
Расчет площади прямоугольника
Теперь мы рассмотрим несколько примеров вычисления площади для каждой из вышеперечисленных геометрических фигур.Сначала рассмотрим расчет площади для нескольких прямоугольников. Решение для поиска области показано для первого примера ниже. Заштрихованный прямоугольник на графике скорость-время имеет основание 6 с и высоту 30 м / с. Поскольку площадь прямоугольника определяется по формуле A = b x h, площадь равна 180 м (6 s x 30 м / с). То есть за первые 6 секунд движения объект сместился на 180 метров.
Решение для поиска области показано для первого примера ниже. Заштрихованный прямоугольник на графике скорость-время имеет основание 6 с и высоту 30 м / с. Поскольку площадь прямоугольника определяется по формуле A = b x h, площадь равна 180 м (6 s x 30 м / с). То есть за первые 6 секунд движения объект сместился на 180 метров.
| Площадь = b * h Площадь = (6 с) * (30 м / с) Площадь = 180 м |
Теперь попробуйте следующие две практические задачи, чтобы проверить свое понимание.Определите смещение (т.е. площадь) объекта в течение первых 4 секунд (Практика A) и от 3 до 6 секунд (Практика B).
Расчет площади треугольника
Теперь мы рассмотрим несколько примеров вычисления площади для нескольких треугольников. Решение для поиска области показано для первого примера ниже. Заштрихованный треугольник на графике скорость-время имеет основание 4 секунды и высоту 40 м / с.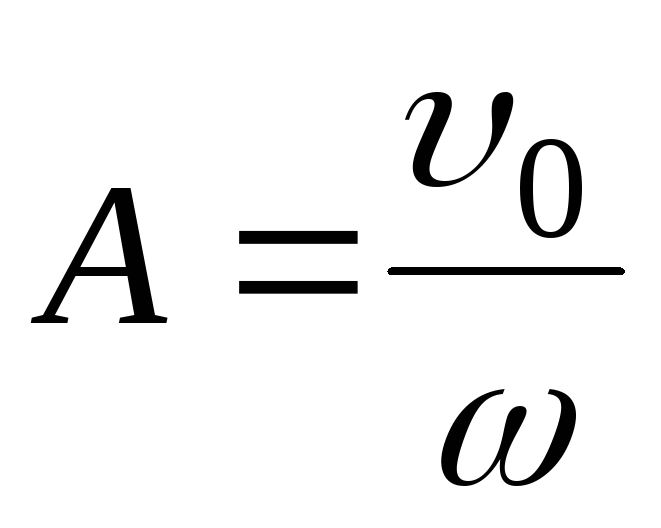 Так как площадь треугольника определяется по формуле A = ½ * b * h, площадь равна ½ * (4 с) * (40 м / с) = 80 м. То есть за четыре секунды движения объект сместился на 80 метров.
Так как площадь треугольника определяется по формуле A = ½ * b * h, площадь равна ½ * (4 с) * (40 м / с) = 80 м. То есть за четыре секунды движения объект сместился на 80 метров.
| Площадь = ½ * b * h Площадь = ½ * (4 с) * (40 м / с) Площадь = 80 м |
Теперь попробуйте следующие две практические задачи, чтобы проверить свое понимание. Определите смещение объекта в течение первой секунды (Практика A) и в течение первых 3 секунд (Практика B).
Расчет площади трапеции
Наконец, мы рассмотрим несколько примеров расчета площади для нескольких трапеций. Решение для поиска области показано для первого примера ниже. Заштрихованная трапеция на графике скорость-время имеет основание 2 секунды и высоту 10 м / с (слева) и 30 м / с (справа). Поскольку площадь трапеции определяется по формуле A = ½ * (b) * (h 1 + h 2 ), площадь составляет 40 м [½ * (2 с) * (10 м / с + 30 м / с)]. То есть объект сместился на 40 метров за промежуток времени от 1 секунды до 3 секунд.
То есть объект сместился на 40 метров за промежуток времени от 1 секунды до 3 секунд.
| Площадь = ½ * b * (h 1 + h 2 ) Площадь = ½ * (2 с) * (10 м / с + 30 м / с) Площадь = 40 м |
Теперь попробуйте следующие две практические задачи, чтобы проверить свое понимание. Определите смещение объекта в интервале времени от 2 до 3 секунд (Практика A) и в течение первых 2 секунд (Практика B).
Альтернативный метод для трапеций
Альтернативный способ определения площади трапеции включает разбиение трапеции на треугольник и прямоугольник. Площади треугольника и прямоугольника можно вычислить индивидуально; площадь трапеции равна сумме площадей треугольника и прямоугольника. Этот метод проиллюстрирован на рисунке ниже.
Треугольник: Площадь = ½ * (2 с) * (20 м / с) = 20 м
Прямоугольник: Площадь = (2 с) * (10 м / с) = 20 м
Общая площадь = 20 м + 20 м = 40 м
На этом уроке было усвоено, что область, ограниченная линией и осями графика скорость-время, равна перемещению объекта за этот конкретный период времени. Область может быть обозначена как прямоугольник, треугольник или трапеция. В дальнейшем площадь можно определить по соответствующей формуле. После расчета эта область представляет смещение объекта.
Область может быть обозначена как прямоугольник, треугольник или трапеция. В дальнейшем площадь можно определить по соответствующей формуле. После расчета эта область представляет смещение объекта.
Положение и перемещение
Положение и перемещениеПоложение и перемещение
Многие предметы, с которыми мы сталкиваемся в повседневной жизни, находятся в движении или состоят из частей. которые находятся в движении. Движение – это правило, а не исключение. Физические законы, управляющие движением этих объектов универсальны, т.е. все объекты движутся по одним и тем же правилам, и одна из целей этого класса – понять эти правила.
Когда объект движется, его позиция изменяется как функция времени.
Положение объекта
дано относительно некоторой согласованной точки отсчета. Недостаточно просто
укажите расстояние от
ориентир. Мы также должны указать направление . Расстояние – это скаляр количество, это число, заданное в каких-то единицах . Позиция – это вектор количество. У него тоже есть величина
как направление. Величина векторной величины – это число (в единицах измерения).
сообщая вам, сколько существует количества, и направление сообщает вам, какие
как он указывает. Единичный вектор – направление
показатель. Это безразмерный вектор с величиной 1, используемый для определения
направление. В тексте векторные величины обычно выделяются жирным шрифтом.
введите или со стрелкой над символом. Таким образом, хотя d = расстояние, d = смещение.
У него тоже есть величина
как направление. Величина векторной величины – это число (в единицах измерения).
сообщая вам, сколько существует количества, и направление сообщает вам, какие
как он указывает. Единичный вектор – направление
показатель. Это безразмерный вектор с величиной 1, используемый для определения
направление. В тексте векторные величины обычно выделяются жирным шрифтом.
введите или со стрелкой над символом. Таким образом, хотя d = расстояние, d = смещение.
Ссылки:
Скаляры и векторы (пожалуйста, исследуйте!)
Направление вектора
Позиция
Удобный способ указать положение объекта
с помощью системы координат .
Мы выбираем фиксированную точку, которая называется исходной точкой и три направленные линии, которые проходят через начало координат и являются
перпендикулярны друг другу. Эти линии называются осями координат .
трехмерной прямоугольной (декартовой) системы координат и помечены
оси x, y и z. Три числа с единицами измерения определяют положение
точка P. Эти числа представляют собой координаты x, y и z точки P.
Координаты точки P в
На диаграмме справа находятся (a, b, c).
Три числа с единицами измерения определяют положение
точка P. Эти числа представляют собой координаты x, y и z точки P.
Координаты точки P в
На диаграмме справа находятся (a, b, c).
Координаты точки P – это компонентов вектора положения. Единичный вектор указание в направлении x имеет x-компоненту 1 и y- и z- компоненты нуль. Обозначается он i . Аналогично единичный вектор указывающий в направлении y, обозначается j , а единичный вектор в направлении оси z обозначается k .Единичные векторы указатели поворота.
Компоненты любого вектора складываются, чтобы сформировать вектор. Вектор положения точки P с координатами (a, b, c) в терминах его компонентов может быть записано как r = a i + b j + c к .
Амплитуда вектора положения равна его длине r. Это зависит от выбора начала системы координат. Это расстояние по прямой от точки P до начала координат.
Ниже представлено трехмерное представление вектора положения. r = a i + b j + c k . Пожалуйста, нажмите
на изображении!
r = a i + b j + c k . Пожалуйста, нажмите
на изображении!
(Используйте современный браузер. 3D-приложения не работают в Internet Explorer.
или более старые браузеры.)
Чтобы получить наилучший вид, измените область просмотра, перетащив мышь и
увеличивайте или уменьшайте масштаб по мере необходимости.
Нажмите кнопки, чтобы выбрать другой вектор
или другая схема добавления составляющих векторов.
Пример:
Вектор положения здания Nielsen Physics Building на небольшой карте с левым нижним углом в качестве исходной точки.
Рабочий объем
Изменение положения называется смещением . На диаграмме ниже показан позиции P 1 и P 2 игрока в два разных момента времени.
Стрелка, указывающая от P 1 к P 2 , – это вектор смещения .
Его величина прямолинейная. расстояние между P 1 и P 2 .
Компоненты вектора смещения от P 1 до
P 2 – это (x 2 – x 1 ) по оси x, (y 2 –
y 1 ) по оси ординат.
Вектор смещения d от P 1 до P 2 может
можно записать как d = (x 2 – x 1 ) i + (y 2 – y 1 ) j .
Смещение d составляет (x 2 – x 1 ) единиц в
Направление x плюс (y 2 – y 1 ) единиц в направлении y.
Величина смещения равна d = ((x 2 – x 1 ) 2 + (y 2 – y 1 ) 2 ) ½ . Это следует из
Пифагорейский
теорема.
Расстояние между двумя точками P 1 с координатами (x 1 , y 1 ,
z 1 ) и P 2 с координатами (x 2 , y 2 , z 2 ) составляет
d = ((x 2 – x 1 ) 2 + (y 2 – y 1 ) 2 + (z 2 – z1) 2 ) ½ .
- Расстояние d – это величина вектора смещения d .
- г. направление вектора смещения d – это направленный отрезок прямой от P 1 к P 2 .
- Мы называем этот направленный отрезок геометрической или графической представление вектора d .
- Нарисуем острие стрелки на P 2 , чтобы обозначить что отрезок начинается в точке P 1 и заканчивается в точке P 2 .
Тройка действительных чисел d x = (x 2 – x 1 ), d y = (y 2 – y 1 ), d z = (z 2 – z 1 ) называются декартовыми компонентами d .
Ссылка: Расстояние и смещение (пожалуйста, исследуйте!)
Задача:
Футбольный защитник пробегает 15,0 м
прямо по игровому полю (в
положительное направление x) в 2.50 с.
Затем его ударили и толкнули на 3,00 м. прямо назад за 1,75 с. Он
ломает подкат и бежит прямо
вперед еще 21,0 м за 5,20 с.
Рассчитайте его вектор смещения и
общее пройденное расстояние.
прямо назад за 1,75 с. Он
ломает подкат и бежит прямо
вперед еще 21,0 м за 5,20 с.
Рассчитайте его вектор смещения и
общее пройденное расстояние.
Решение:
- Рассуждение:
Выберите систему координат, чтобы вы могли отслеживать игрока. - Детали расчета:
Выберите свою систему координат, чтобы игрок начинает с x = 0.После 2,5 с, он попадает на х = 15 м.
Затем он перемещается на 3 м назад и заканчивает вверх при x = 12 м еще через 1,75 с.
Он продвигается вперед на 21 метр в следующем 5,2 с и заканчивается на x = 12 м + 21 м. = 33 м.
Его смещение вектор d = (33 m) i , то есть 33 м вперед.
Его общее пройденное расстояние 15 м. + 3 м + 21 м = 39 м.
Примечание: общее пройденное расстояние НЕ ЯВЛЯЕТСЯ расстоянием по прямой. от начальной до конечной точки, если объект не движется по прямой линия без изменения направления.
Проблема:
Путешествуя по прямой автомагистрали между штатами, вы обратите внимание, что отметка мили показывает 260. Вы путешествуете, пока не достигнете отметки в 150 миль. маркер, а затем вернитесь к маркеру длиной 175 миль. Что величина вашего результирующего смещения от 260-мильной отметки?
Решение:
- Рассуждение:
Результирующее смещение – это вектор d , сумма двух векторов д 1 и d 2 , которые указывают в противоположных направлениях. - Детали расчета:
Результирующее смещение – это вектор d , сумма двух векторов д 1 и d 2 , которые указывают в противоположных направлениях.
Проблема:
Острие лопасти вертолета
5,00 м от центра вращения.
За один оборот лезвия
вычислить вектор смещения и
общее расстояние, пройденное наконечником
лезвия.
Решение:
- Рассуждение:
После одного оборота наконечник возвращается в исходное положение. Его вектор смещения d = 0. - Детали расчета:
Общее пройденное расстояние на кончике равна окружности окружности радиуса r = 5 м.
Окружность = 2πr = 31,42 м.
Общее расстояние, пройденное чаевые 31.42 мес.
Вектор смещения имеет одинаковую величину и направление, независимо от выбор начала координат системы координат. Величина и направление вектор смещения, однако, зависит от системы отсчета , в которой система координат закреплена и находится в состоянии покоя.
Пример:
Автомобиль двинулся вперед расстояние 6 м, при этом ребенок переместился с заднего сиденья вперед сиденье на расстоянии 1 м.
- Использование автомобиля в качестве системы отсчета и привязка системы координат
в машине смещение ребенка d (car) = (1 m) i .

- Использование дороги в качестве системы отсчета и привязка системы координат на дороге смещение ребенка составляет d (дорога) = (6 м) i + (1 м) i = (7 м) i .
Уравнения гравитационного смещения для падающих объектов Рона Куртуса
SfC Home> Физика> Гравитация>
Рон Куртус
Смещение объекта – это изменение положения от начальной точки в определенном направлении, которое может быть представлено как вектор.Он отличается от расстояния, на котором не указано направление.
Когда вы бросаете объект с некоторой высоты над землей, он имеет нулевую начальную скорость. Простые уравнения позволяют рассчитать смещение , на которое объект падает на , пока не достигнет заданной скорости или по истечении заданного периода времени. Уравнения предполагают, что сопротивление воздуха незначительно.
Примеры демонстрируют применение уравнений.
Вопросы, которые могут у вас возникнуть:
- Какое уравнение позволяет смещению достичь заданной скорости?
- Каково уравнение для смещения за данный момент времени?
- Какие примеры этих уравнений?
Этот урок ответит на эти вопросы.Полезный инструмент: Конвертация единиц
Смещение по скорости
Общее уравнение гравитации для смещения относительно скорости:
y = (v 2 – v i 2 ) / 2g
( Подробную информацию о выводе см. В разделе «Вывод уравнений силы тяжести смещения-скорости». )
Поскольку начальная скорость v i = 0 для падающего объекта, уравнение сводится к:
y = v 2 / 2g
где
- y – вертикальное смещение в метрах (м) или футах (футах)
- v – вертикальная скорость в м / с или фут / с
- g – ускорение свободного падения (9.
 8 м / с 2 или 32 фут / с 2 )
8 м / с 2 или 32 фут / с 2 )
Поскольку объект движется вниз от начальной точки, y и v являются положительными числами.
Смещение падающего объекта как функция скорости или времени
Смещение по времени
Общее уравнение силы тяжести для смещения относительно времени:
y = gt 2 /2 + v i t
( См. Раздел «Вывод уравнений силы тяжести смещения во времени») для получения подробной информации.)
Поскольку v i = 0 для упавшего объекта, уравнение сводится к:
y = gt 2 /2
, где t – время в секундах (с).
Примеры
Следующие примеры иллюстрируют применение уравнений.
Учитывая скорость
Если v = 75 футов / с, как далеко упал объект?
Решение
Поскольку v выражается в фут / с, g = 32 фут / с 2 . Подставьте значения в уравнение:
Подставьте значения в уравнение:
y = v 2 / 2g
y = (75 футов / с) * (75 футов / с) / 2 * (32 фут / с 2 )
y = (5625 футов 2 / с 2 ) / (64 футов / с 2 )
y = 87,89 футов
Учитывая прошедшее время
Если t = 4 секунды и g = 9,8 м / с 2 , найдите смещение, с которым упал объект.
Решение
Заменить значения в уравнении:
y = gt 2 /2
y = (9,8 м / с 2 ) * (16 с 2 ) / 2
y = 78,4 м
Сводка
Смещение – это изменение положения от начальной точки в определенном направлении. Следующие уравнения позволяют рассчитать смещение, с которым объект падает, пока не достигнет заданной скорости или по истечении заданного периода времени:
y = v 2 / 2g
y = gt 2 /2
Будьте уверены в себе
Ресурсы и ссылки
Полномочия Рона Куртуса
Сайты
Гравитационные ресурсы
Падающие тела – Гипертекст по физике
Уравнения падающего тела – Википедия
Расчет силы тяжести – Земля – Калькулятор
Кинематические уравнения и свободное падение – Физический класс
Книги
(Примечание: Школа чемпионов может получать комиссионные от покупки книг)
Книги по простой науке о гравитации с самым высоким рейтингом
Книги по углубленной физике гравитации с самым высоким рейтингом
Вопросы и комментарии
Есть ли у вас какие-либо вопросы, комментарии или мнения по этой теме? Если да, отправьте свой отзыв по электронной почте. Я постараюсь вернуться к вам как можно скорее.
Я постараюсь вернуться к вам как можно скорее.
Поделиться страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/science/
gravity_equations_falling_displacement.htm
Пожалуйста, включите его в качестве ссылки на свой веб-сайт или в качестве ссылки в своем отчете, документе или диссертации.
Авторские права © Ограничения
Где ты сейчас?
Школа чемпионов
Гравитационные темы
Уравнения гравитационного смещения для падающих предметов
Лекция 5: Смещения
Дельта-обозначение
Когда я спрашиваю вас, который час, я действительно прошу вас дать мне показания часов.
 Однако когда я спрашиваю, сколько времени занимает какое-то событие, я хочу знать интервал
времени.Мы используем время в двух смыслах. В физике мы обычно имеем в виду
временной интервал вместо показания часов. На самом деле время на часах действительно
промежуток времени с полуночи прошлой ночью. Чтобы математически различать
интервал и показания часов мы используем так называемую «дельта-нотацию». Давайте рассмотрим
два показания часов, например, показания в начале и в конце гонки. Использовать
буква t с индексами 1 и 2 для обозначения первого и второго чтения
соответственно.Временной интервал обозначается большой греческой дельтой Δ перед t , например
это:
Δ t = t 2 – t 1 Δ не означает «умножить на Δ». Это просто префикс, указывающий на изменение
в количестве тн . Для мирских событий, которые мы
нужно обсуждать, время всегда идет вперед и Δ t всегда положительно.
Однако когда я спрашиваю, сколько времени занимает какое-то событие, я хочу знать интервал
времени.Мы используем время в двух смыслах. В физике мы обычно имеем в виду
временной интервал вместо показания часов. На самом деле время на часах действительно
промежуток времени с полуночи прошлой ночью. Чтобы математически различать
интервал и показания часов мы используем так называемую «дельта-нотацию». Давайте рассмотрим
два показания часов, например, показания в начале и в конце гонки. Использовать
буква t с индексами 1 и 2 для обозначения первого и второго чтения
соответственно.Временной интервал обозначается большой греческой дельтой Δ перед t , например
это:
Δ t = t 2 – t 1 Δ не означает «умножить на Δ». Это просто префикс, указывающий на изменение
в количестве тн . Для мирских событий, которые мы
нужно обсуждать, время всегда идет вперед и Δ t всегда положительно. Дельта-запись может использоваться для любой изменяющейся величины. В частности, позиция может
изменение.И, в отличие от времени, он может меняться в обоих направлениях, поэтому Δ x может быть либо
положительным или отрицательным.
В частности, позиция может
изменение.И, в отличие от времени, он может меняться в обоих направлениях, поэтому Δ x может быть либо
положительным или отрицательным.
Справочная информация
Чтобы иметь возможность говорить о положении чего-либо, мы должны установить система координат, также известная как система отсчета. Ограничимся описанием что-то движется вперед и назад по одной линии. У нас будет достаточно проблем в одном измерения, прежде чем мы перейдем к двух- и трехмерному движению.Рабочий объем
Положение объекта – это место на числовой прямой.Когда объект перемещается в другое положение, его смещение – это второе положение минус первое положение. Δ x = x 2 – x 1 Слово смещение означает, что мы отслеживаем, в каком направлении происходит движение. В одном размер направление обозначается знаком: отрицательное, если налево, и положительное, если право.
 Слово расстояние означает, как далеко перемещается объект независимо от направления. это
всегда положительный и равен абсолютному значению или величине смещения.
Слово расстояние означает, как далеко перемещается объект независимо от направления. это
всегда положительный и равен абсолютному значению или величине смещения.Если следовать правилу всегда вычитать первую позицию из второй, знак всегда оказывается положительным, если смещение вправо, и отрицательным, если смещение влево. (Это предполагает систему отсчета с положительной стороной ось справа). Когда мы проиллюстрируем смещение, нарисовав стрелку с его хвост в первом положении и кончик стрелки во втором, он будет указывать вправо для положительного смещения и влево для отрицательного смещения.
Когда смещения происходят на отрицательной стороне оси, легко ошиблись с двойным минусом. Когда вы вычисляете смещения, вы сначала нужно нарисовать стрелку, затем вычислить значение и, наконец, проверить, что знак соответствует направлению стрелки.
Смещение и расстояние, в чем разница?
Мы очень точно определили смещение. В этом определении знак очень важно. Путешествие из позиции +3 в −3 – это смещение −6 мес.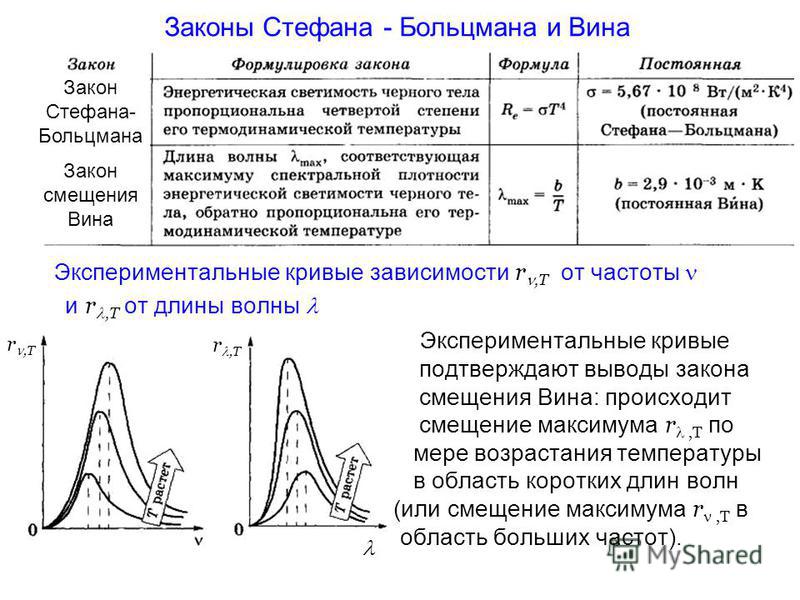 Обратный путь от −3 до +3 равен смещению +6 м. Общее смещение
для этой поездки получается добавлением
два смещения: (−6 м) + (+6 м) = 0 м.
Общее расстояние, пройденное за весь
поездка не нулевая, это 12 м.
Обратный путь от −3 до +3 равен смещению +6 м. Общее смещение
для этой поездки получается добавлением
два смещения: (−6 м) + (+6 м) = 0 м.
Общее расстояние, пройденное за весь
поездка не нулевая, это 12 м.Таким образом, слова расстояние и смещение имеют очень разные значения, поскольку мы используем их в физике.
Небольшие прогулки
Вот несколько примеров смещений: Здесь у нас есть положительное смещение, имеющее место на положительной стороне оси.В
начало и конец находятся на положительной стороне оси, начальная позиция меньше, чем
финиш. Следовательно, смещение положительное.
Когда отделка ближе к началу координат и оба находятся на положительной стороне оси, тогда смещение отрицательное. Стрелка указывает влево, смещение отрицательное. и все в порядке с миром.
Смещение к началу координат на отрицательной стороне оси положительное. Вычитание −4 из −1 дает положительный +3.
 Стрелка указывает вправо, значит, знак правильный.
Стрелка указывает вправо, значит, знак правильный. Переход влево должен дать отрицательное смещение даже на отрицательной стороне источник. Вычитание −2,5 из −4 оставляет −1,5. Хороший!
Вычисление смещений, пересекающих начало координат, может быть непростым делом. Но направление стрелка всегда подает правильный знак. Вот два последних примера.
Знак смещения не зависит от того, где происходит смещение, но только по его направлению.Фактически, если бы числовая линия была смещена влево или вправо, все измерения положения были бы другими, но смещения не изменились бы.
Графики положения в зависимости от времени
Движение, которое происходит взад и вперед по числовой прямой, можно представить в виде график положение-время. Горизонтальный размер графика представляет время с течением времени. течет слева направо. Числовая линия представлена вертикальным размером график с положительными положениями над временной осью и отрицательными положениями под ней.
Совершите небольшое путешествие …
Давайте совершим путешествие и покажем, как это будет выглядеть на графике положение-время. Я катаюсь на Ninja Kawasaki Power-Wheels с двумя передними скоростями и одной задним ходом. Я начинаю из положения -5 в верхнем положении, затем переключитесь на низкое и через несколько секунд с визгом остановитесь. Включив задний ход, я возвращаюсь примерно к исходной точке, останавливаюсь и выхожу. Вот что за может выглядеть графическое изображение этой поездки.В течение первых двух секунд я разгоняюсь до большой скорости.Скорость определяется как изменение положения, деленное на интервал времени, в течение которого произошло это изменение: Судя по графику, от второго до четвертого скорость довольно постоянна. второй. Между 2,5 и 3,5 с Δ x составляет около 2,57 м. Δ t – 1 с. Таким образом, v = 2,57 м / 1 с. = 2,57 м / с в области высоких скоростей.
Слово скорость обычно используется для обозначения абсолютного значения скорости. Скорость
может быть отрицательным при движении к отрицательной стороне оси.Скорость будет
положительный в этом случае. Другими словами, скорость – это пройденное расстояние, разделенное на время.
интервал.
Скорость
может быть отрицательным при движении к отрицательной стороне оси.Скорость будет
положительный в этом случае. Другими словами, скорость – это пройденное расстояние, разделенное на время.
интервал.
[Различие между скоростью и скоростью, расстоянием и смещение – полезный, но используемые слова произвольны. я попытаюсь используйте эти слова последовательно, как я определил их в этих лекциях. Ты Следует отметить, что иногда другие авторы могут быть не совсем так последовательный. В частности, первое издание PSSC Physics в нашей библиотеке использует скорость, в одномерном случае, означает смещение, деленное на время интервал, то есть наша скорость.Во втором и последующих изданиях используется термин так же, как и мы.]
После нажатия кнопки низкой скорости тележка замедляется или замедляется. Мы используем слово “ускорение” тоже для этого замедления. Когда тележка движется в положительном Направление, замедление технически будет называться отрицательным ускорением.
 Между t = 5,5 с и t = 8,5 с скорость относительно постоянна. Как видите, за 1
с интервалом в этом регионе тележка прошла 0.85 с. Таким образом, скорость здесь составляет 0,85 м / с.
Между t = 5,5 с и t = 8,5 с скорость относительно постоянна. Как видите, за 1
с интервалом в этом регионе тележка прошла 0.85 с. Таким образом, скорость здесь составляет 0,85 м / с.При остановке тележка снова отрицательно ускоряется. Другими словами, тележка теряет часть своей положительной скорости, пока не достигнет нуля. Нулевая скорость – горизонтальная линия на графике.
Когда она начинает движение назад, тележка снова имеет «отрицательное ускорение», но теперь оно набирает обороты.
скорость в отрицательном направлении. В период времени, когда скорость постоянна,
в обратном направлении график показывает смещение -0,85 м за одну секунду.
Таким образом, v = −0,85 м / с, отрицательная скорость. Это та же скорость, что и низкая скорость движения вперед,
но не с той же скоростью. Замедление до остановки приводит к потере отрицательной скорости,
что математически называется положительным ускорением.
Теперь этот график положение-время был полностью составлен.

 В положении равновесия маятник обладает максимальной кинетической энергией
В положении равновесия маятник обладает максимальной кинетической энергией 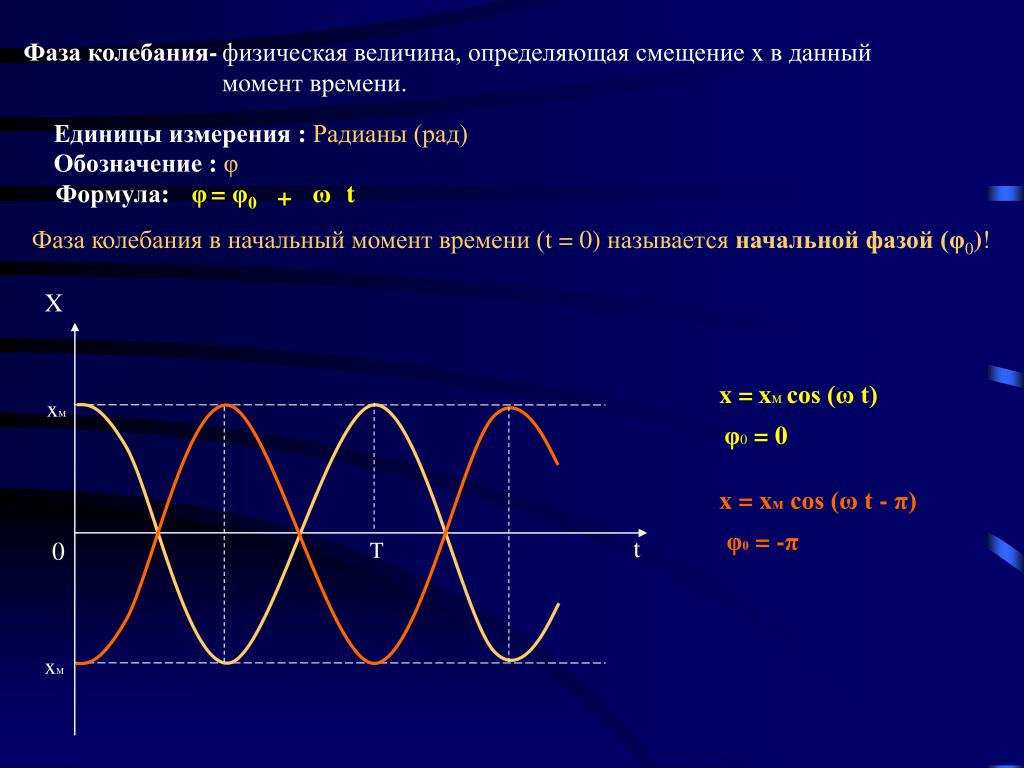
 По графику, изображенному на рисунке, определите амплитуду ЭДС, период тока и частоту.
Напишите уравнение ЭДС.
По графику, изображенному на рисунке, определите амплитуду ЭДС, период тока и частоту.
Напишите уравнение ЭДС.




 8 м / с 2 или 32 фут / с 2 )
8 м / с 2 или 32 фут / с 2 )