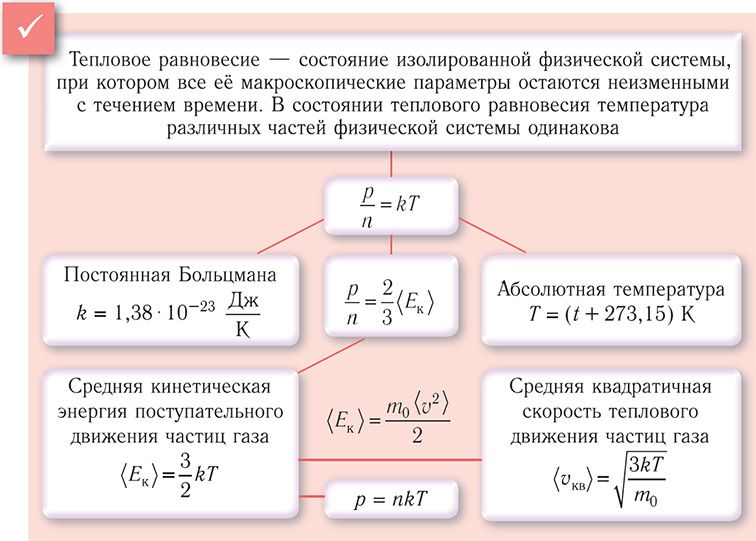
Температура как мера средней кинетической энергии молекул
Представляем формулу основного уравнения молекулярно-кинетической теории (МКТ) газов:
(где n=NV – это концентрация частиц в газе, N – это число частиц, V – это объем газа, 〈E〉 – это средняя кинетическая энергия поступательного движения молекул газа, υkv – это средняя квадратичная скорость, m0 – это масса молекулы) связывает давление – макропараметр, достаточно просто измеряющийся с такими микропараметрами, как средняя энергия движения отдельной молекулы (или в другом выражении), как масса частицы и ее скорость. Но находя только лишь давление, нельзя установить кинетические энергии частиц отдельно от концентрации. Поэтому для нахождения в полном объеме микропараметров нужно знать еще какую-то физическую величину, связанную с кинетической энергией частиц, составляющих газ. За данную величину можно взять термодинамическую температуру.
Газовая температура
Для определения газовой температуры нужно вспомнить важное свойство, которое сообщает о том, что в условиях равновесия средняя кинетическая энергия молекул в смеси газов одинаковая для различных компонентов данной смеси. Из данного свойства следует то, что если 2 газа в различных сосудах находятся в тепловом равновесии, тогда средние кинетические энергии молекул данных газов одинаковые. Это свойство мы и будем использовать. К тому же в ходе экспериментов доказано, что для любых газов (при неограниченном числе), которые находятся в состоянии теплового равновесия, справедливо следующее выражение:
Из данного свойства следует то, что если 2 газа в различных сосудах находятся в тепловом равновесии, тогда средние кинетические энергии молекул данных газов одинаковые. Это свойство мы и будем использовать. К тому же в ходе экспериментов доказано, что для любых газов (при неограниченном числе), которые находятся в состоянии теплового равновесия, справедливо следующее выражение:
С учетом вышесказанного, используем (1) и (2) и получаем:
Из уравнения (3) следует, что величина θ, которой мы обозначили температуру, вычисляется в Дж, в чем измеряется также и кинетическая энергия. В лабораторных работах температура в системе измерения вычисляется в кельвинах. Поэтому введем коэффициент, который уберет данное противоречие. Он обозначается k, измеряется в ДжК и равняется 1,38·10-23. Данный коэффициент называется постоянной Больцмана. Таким образом:
θ=kT (4), где T – это термодинамическая температура в кельвинах.
Связь термодинамической температуры и средней кинетической энергией теплового движения молекул газа выражается формулой:
E=32kT (5).
Из уравнения (5) видно, что средняя кинетическая энергия теплового движения молекул прямо пропорциональна температуре газа. Температура является абсолютной величиной. Физический смысл температуры заключается в том, что она, с одной стороны, определяется средней кинетической энергией, которая приходится на 1 молекулу. А с другой стороны, температура – это характеристика системы в целом. Таким образом, уравнение (5) показывает связь параметров макромира с параметрами микромира.
Известно, что температура – это мера средней кинетической энергии молекул.
Можно установить температуру системы, а затем рассчитать энергию молекул.
Абсолютный ноль температур
В условиях термодинамического равновесия все составляющие системы характеризуются одинаковой температурой.
Определение 3Температура, при которой средняя кинетическая энергия молекул равняется 0, давление идеального газа равняется 0, называется абсолютным нулем температур
 Абсолютная температура никогда не является отрицательной. Пример 1
Абсолютная температура никогда не является отрицательной. Пример 1Необходимо найти среднюю кинетическую энергию поступательного движения молекулы кислорода, если температура T=290 K. А также найти среднюю квадратичную скорость капельки воды диаметра d=10-7 м, взвешенной в воздухе.
Решение
Найдем среднюю кинетическую энергию движения молекулы кислорода по уравнению, связывающему энергию и температуру:
E=32kT (1.1).
Поскольку все величины заданы в системе измерения, проведем вычисления:
E=32·1,38·10-23·10-7=6·10-21 Дж.
Перейдем ко второй части задания. Положим, что капелька, взвешенная в воздухе, – это шар (рисунок 1). Значит, массу капельки можно рассчитать как:
m=ρ·V=ρ·πd36.
Рисунок 1
Найдем массу капельки воды. Согласно справочных материалов, плотность воды в нормальных условиях равняется ρ=1000 кгм3, тогда:
m=1000·3,14610-73=5,2·10-19 (кг).
Масса капельки чрезмерно маленькая, поэтому, сама капелька сравнима с молекулой газа, и тогда можно использовать при расчетах формулу средней квадратичной скорости капли:
E=mυkυ22 (1. 2),
2),
где 〈E〉 мы уже установили, а из (1.1) понятно, что энергия не зависит от разновидности газа, а зависит только лишь от температуры. Значит, мы можем применить полученную величину энергии. Найдем из (1.2) скорость:
υkυ=2Em=6·2Eπρd3=32kTπρd3 (1.3).
Рассчитаем:
υkυ=2·6·10-215,2·10-19=0,15 мс
Ответ: Средняя кинетическая энергия поступательного движения молекулы кислорода при заданной температуре равняется 6·10-21 Дж. Средняя квадратичная скорость капельки воды при заданных условиях равняется 0,15 м/с.
Пример 2Средняя энергия поступательного движения молекул идеального газа равняется 〈E〉, а давление газа p. Необходимо найти концентрацию частиц газа.
Решение
В основу решения задачи положим уравнение состояния идеального газа:
p=nkT (2.1).
Прибавим к уравнению (2.1) уравнение связи средней энергии поступательного движения молекул и температуры системы:
E=32kT (2.2).
Из (2.1) выражаем необходимую концентрацию:
n=pkT 2. 3.
3.
Из (2.2) выражаем kT:
kT=23E (2.4).
Подставляем (2.4) в (2.3) и получаем:
n=3p2E
Ответ: Концентрацию частиц можно найти по формуле n=3p2E.
Автор: Роман Адамчук
Преподаватель физики
формула, характеристики движения частиц газа, единицы измерения
Физика
12.11.21
13 мин.
Физическую величину, являющуюся мерой взаимодействия материи, то есть перехода из одного состояния в другое, называют энергией. Кинетическая средняя величина определяет перемещение материальной точки. Это понятие было введено Готфридом Вильгельмом Лейбницем, который и сформулировал закон сохранения силы. Фактически это работа движения, зависящая от направления и скорости. Важное значение здесь имеет выбранная система отсчёта.
Важное значение здесь имеет выбранная система отсчёта.
Оглавление:
- Общие сведения
- Движение частиц
- Температура и энергия
- Решение задач
Общие сведения
В природе есть два закона сохранения: импульса и момента. Они являются следствием свойств пространства. Другими словами, описываются однородностью какого-либо выделенного места и изотропностью. Все направления в пространстве считаются равноправными.
В седьмом классе изучают силу, характеризующуюся работой. Если на тело оказывается воздействие, приводящее к движению, то возникает действие. Например, пусть имеется спица, на которую нанизана бусинка. Она может свободно перемещаться по ней, если к телу приложена сила. Её направление по касательной к спице можно обозначить как F1. Угол, образованный между направлением силы и движения, пусть будет J1.
Чтобы бусинка двигалась по прямой, на неё должны действовать другие силы. Это воздействие определяется реакцией спицы. Представить её можно в виде упругости F2 и трения F3. Углы, которые образуются после перемещения S, можно обозначить так: между F2 и вектором — J2, S и F3 — J3.
Это воздействие определяется реакцией спицы. Представить её можно в виде упругости F2 и трения F3. Углы, которые образуются после перемещения S, можно обозначить так: между F2 и вектором — J2, S и F3 — J3.
Второй закон Ньютона в векторной форме записывается как F1 + F2 + F3 = m * a. Это уравнение можно рассмотреть в проекции вдоль спицы на ось икс. Она имеет следующий вид: F1 * cos (J1) + F2 * cos (J2) + F3 * cos (J3) = m * ax. Пусть силы будут постоянные по направлению и модулю. Справа и слева стоит постоянное число, следовательно, движение будет равноускоренным.
Проекцию вектора перемещения можно записать так: Sa = (Vx2- Vox2) / 2ax. Отсюда: ax = (Vx2- Vox2) / 2 Sx, где Vx — конечная скорость, V0 — начальная. Полученную формулу можно подставить во второй закон Ньютона. В результате получится: F1 * cos (J1) + F2 * cos (J2) + F3 * cos (J3) = m * (Vx2 — V02) / 2 Sx.
Проекция перемещения равна модулю. Левую и правую часть можно умножить на него.
В левой части есть три однотипных слагаемых F * S * cos (J). Эту физическую величину называют работой и обозначают буквой A. Но справедливо равенство только для постоянной силы. Измеряется она в ньютонах, умноженных на метр, или в джоулях. Справа стоит величина, которая является работой, связанной с движением тела. Следовательно, это какая-то средняя кинетическая энергия молекул, формула которой будет иметь вид Ech = mv
Движение частиц
Молекулы — это частицы, которые подчиняются законам классической механики. В системе они совершают беспорядочное движение. Отсюда следует, что число микросостояний будет определяться интенсивностью перемещений. Для определения этого значения было введено понятие термодинамическая вероятность — мера хаотичности движения молекул (энтропия). Если рассматривать твёрдые тела, то величина параметра будет небольшой. Это связано с тем, что скорости атомов невелики, а сами частицы имеют устойчивые связи.
Отсюда следует, что число микросостояний будет определяться интенсивностью перемещений. Для определения этого значения было введено понятие термодинамическая вероятность — мера хаотичности движения молекул (энтропия). Если рассматривать твёрдые тела, то величина параметра будет небольшой. Это связано с тем, что скорости атомов невелики, а сами частицы имеют устойчивые связи.
В газе же взаимодействие проявляется в короткие моменты при столкновении молекул. Этот процесс сопровождается резким изменением скорости. Все законы рассматривают для так называемой идеальной среды. Для неё предполагается, что расстояние между молекулами намного больше, чем радиус воздействия межмолекулярных сил.
Так, если размер частицы имеет примерное значение, равное d = 3·10-8 см, то для идеального газа физики считают, что число молекул в единице объёма не должно превышать 3·1022 см-3.
Для рассматриваемого состояния установлено три закона:
- произведение объёма на постоянную температуру определяется таким изменением давления, что выражение p * V будет постоянным значением;
- при определённом давлении величина объёма газа к его температуре является постоянной V / T = const;
- давление связано с температурой формулой pV = n RT, где R — газовая постоянная, n — число молей.

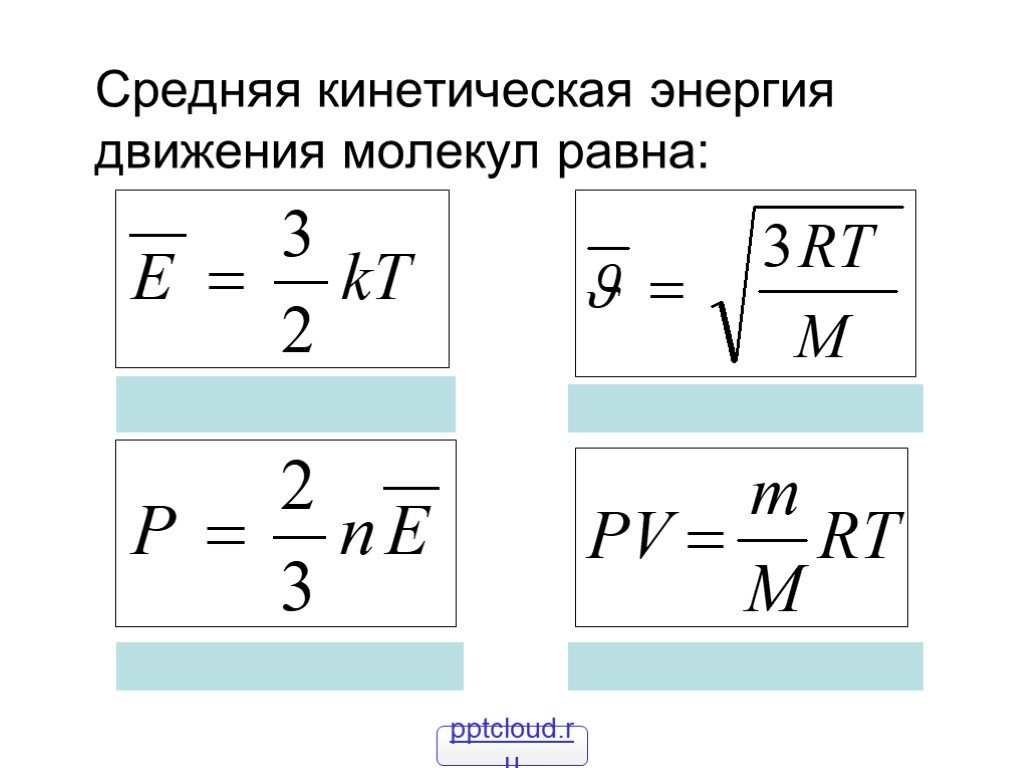
Последнее уравнение с учётом постоянной Больцмана (k = p / nT) является основой кинетической теории газов. Средняя величина давления находится как усреднённое значение квадрата скорости всех групп молекул: p = n * m (V2) / 3. Эта формула получена с учётом того, что каждая молекула имеет приблизительно одинаковую скорость. Её можно переписать так: p = (2 / 3) * n * Ek. Отсюда получается усреднённая кинетическая энергия молекул: Ek = 1 / 2 *(m * V2).
Поступательное движение атомов и молекул, взятое по большему числу хаотично перемещающихся частиц, является мерилом температуры. Если она измеряется в градусах Кельвина, то её связь c энергией описывается отношением Ek = (3 * k T) / 2.
Следует отметить, что выражение справедливо только при расчёте для одной частицы. Такой энергией обладает каждая молекула, так как она находится в тепловом хаотическом движении.
Температура и энергия
Если взять два тела с разной температурой и обеспечить между их поверхностями контакт, то через время произойдёт выравнивание температуры. Ранее считалось, что существует некая субстанция, которая, хаотично смешиваясь, уравновешивает показатели. Но на самом деле происходит просто изменение кинетической энергии. Именно она и определяет состояние равновесия.
Ранее считалось, что существует некая субстанция, которая, хаотично смешиваясь, уравновешивает показатели. Но на самом деле происходит просто изменение кинетической энергии. Именно она и определяет состояние равновесия.
Это свойство позволило связать энергию с температурой через коэффициент пропорциональности Больцмана: T = (2 * m 0 * V 2) / 3 * K * 2. Если при расчётах использовать это выражение, в ответе получится так называемая абсолютная температура. Её значение служит мерой кинетической энергии теплового движения молекул идеального газа. В качестве единиц измерения взят Кельвин.
Идеальный газ описывается уравнением Клайперона — Менделеева: p * V = (m * R * T) / µ. В то же время газовую постоянную можно определить как произведение постоянной Больцмана на число Авогадро (Na). Это значение равняется 6,02 * 1023. Измеряется в молях и показывает количество структурных частиц на один моль вещества. Формулу для хаотического движения молекул можно вывести следующим образом:
- Поскольку концентрация этих веществ определяется как (m * Na) / µ * V, выражение для давления легко представить в виде p = n * k * T.

- Подставив в формулу давления для одноатомного газа полученное равенство, можно получить p = (1 / 3) ∗ (n ∗ m ∗ v2c) = (n ∗ k ∗ T).
- После сокращения обеих частей на три вторых и концентрацию молекул получится равенство: m * V2 / 2 = (3 * k * T) / 2.
- В правой части стоит значение полной кинетической работы, поэтому формулу можно записать как Ek = (3 * k * T) / 2.
Таким образом, газовая температура зависит от среднекинетической энергии. Эти две величины связаны прямо пропорционально. Температура имеет абсолютное значение, поэтому её физический смысл заключается в определении средней кинетической энергии, приходящейся на молекулу. Но температура характеризует систему в целом. Значит, с помощью формулы можно установить связь параметров макромира и микромира.
Следует отметить, что средняя суммарная тепловая энергия перемещения молекул определяется только температурой газа. То есть кинетическая энергия поступательного хаотичного движения частиц не зависит от химического состава, массы, давления или занимаемого объёма.
Решение задач
Самостоятельное решение примеров позволяет закрепить теоретические знания. Существуют определённые типы заданий, с помощью которых можно проработать весь изученный материал и наглядно увидеть практическое применение знаний. Вот некоторые из них:
- Выяснить, какова средняя кинетическая энергия поступательного движения молекулы газа неона, если созданное давление при концентрации 2, 65 * 1025 м-3 составляет 98,8 кПа. Решение примера следует начать с записи уравнения для идеального газа: p = (m 0 * n * V2) / 3. Так как энергию молекулы можно вычислить из выражения E = (m 0 V2) / 2, то нужная формула примет вид p = (2 * n * E) / 3. Отсюда искомая величина равняется E = 3 p / 2 n. Теперь нужно подставить исходные данные и выполнить количественный расчёт: Ek = (3 * 98,8 * 103) / (2 * 2,65 * 1025) = 5,6 * 10-21 джоулей.
- Средняя энергия поступательного движения частицы гелия равняется 60 Дж, а давление составляет 2 * 105 Па.
 Необходимо найти концентрацию частиц газа. В основе решения лежит уравнение идеальной системы: p = n * k * T. Добавив к нему формулу связи движения и температуры E = (3 / 2) * kT, можно выразить искомую концентрацию: kT = (2 * E) / 3. Отсюда: n = 3p / 2E = 3 * 2 * 105 / 2 * 60 = 6 * 105 / 60 = 105 / 10 = 104 м-3.
Необходимо найти концентрацию частиц газа. В основе решения лежит уравнение идеальной системы: p = n * k * T. Добавив к нему формулу связи движения и температуры E = (3 / 2) * kT, можно выразить искомую концентрацию: kT = (2 * E) / 3. Отсюда: n = 3p / 2E = 3 * 2 * 105 / 2 * 60 = 6 * 105 / 60 = 105 / 10 = 104 м-3. - Найти работу, которая выполняется телом в течение трёх секунд после воздействия, если изменение энергии происходит по графику в виде параболы. Трем секундам соответствует энергия, равная 2 Дж, шести — 4 Дж. Для выяснения работы нужно воспользоваться определением кинетической энергии. Так как существует силовое взаимодействие, то А = ΔEk. В соответствии с графиком энергия изменяется от четырёх джоулей до двух. Значит, работа равна A = 2 — 4 = -2 Дж.
Решать задачи по исследованию кинетической работы несложно. Нужно лишь знать несколько формул и внимательно следить за размерностью величин при выполнении вычислений.
Руководство по движению для начинающих: температура воздуха и кинетическая энергия
Руководство по движению для начинающих: температура воздуха и кинетическая энергия — деятельность
| ||||||||||||||||||||||
Какое уравнение связывает среднюю кинетическую энергию с температурой в высокотемпературном пределе?
Короче говоря, наблюдаемая кинетическая энергия (такая, которую мы знаем из повседневной химии и физики) — которая совпадает со средним ансамблем кинетической энергии — для одноатомного идеальный газ , это:
#\mathbf(<< barE >> = U = K = 3/2 RT)#
, но средняя кинетическая энергия для одиночной системы одноатомных идеальных газов равна:
#color(blue)(<< E >> = 3/2 nRT)#
Итак, мы видим, что кинетическая энергия здесь зависит от числа #\mathbf(“моль”)# с газа .
Но, как мы должны знать, #”1 моль”# одноатомного газа равен #”1 моль”# любого другого одноатомного газа при определении в терминах #”моль”#с. Массы в #”g”# различаются на , хотя это не имеет значения, потому что это уравнение требует #”mol”#s газа, а не #”g”# газа.
Более того, #R#, универсальная газовая константа , никогда не меняется.
Таким образом, идентичность одноатомного идеального газа не имеет значения при определении его средней кинетической энергии. Только его температура.
Вы можете прочитать ниже интересный вывод.
ЕДИНАЯ СИСТЕМА ОДНОАТОМНЫХ ИДЕАЛЬНЫХ ГАЗОВ
У нас есть то, что называется одиночной системой газов, а затем у нас есть то, что называется ансамблем систем газов. Сейчас мы сосредоточены на системе с одним процессором . 9(-34) “J”*”s”#
#del# означает «частная производная», что является просто причудливым способом сказать: «давайте сосредоточимся только на этой функции при нахождении ее наклона во всех точках функции».
Если мы немного поработаем с первым уравнением, мы сможем понять, почему идентичность одноатомного идеального газа не имеет значения.
УПРОЩЕНИЕ ФУНКЦИИ, КОТОРАЯ БУДЕТ ДИФФЕРЕНЦИИРОВАНА 9(“не” бета)]#
#= -(-(3N)/(2бета))#
#= цвет (зеленый)(3/2 Nk_BT)#
Что-то интересное в том, что #Nk_B = nR#, где #n# — количество #”моль”#с, а #R# — универсальная газовая постоянная. Итак, мы действительно только что вывели:
#цвет(синий)(<< E >> = 3/2 нРТ)#
, который показывает, что средняя кинетическая энергия одиночной системы одноатомных идеальных газов зависит только от числа #”моль”#с (которое одинаково для всех одноатомных идеальных газов) и температуру (которую мы предполагали одинаковой для всех рассматриваемых систем).
ЭНЕРГИЯ, КОТОРУЮ МЫ ЗНАЕМ И ЛЮБИМ??
Хорошо, теперь мы можем перейти к ансамблю систем одноатомных идеальных газов.




 Необходимо найти концентрацию частиц газа. В основе решения лежит уравнение идеальной системы: p = n * k * T. Добавив к нему формулу связи движения и температуры E = (3 / 2) * kT, можно выразить искомую концентрацию: kT = (2 * E) / 3. Отсюда: n = 3p / 2E = 3 * 2 * 105 / 2 * 60 = 6 * 105 / 60 = 105 / 10 = 104 м-3.
Необходимо найти концентрацию частиц газа. В основе решения лежит уравнение идеальной системы: p = n * k * T. Добавив к нему формулу связи движения и температуры E = (3 / 2) * kT, можно выразить искомую концентрацию: kT = (2 * E) / 3. Отсюда: n = 3p / 2E = 3 * 2 * 105 / 2 * 60 = 6 * 105 / 60 = 105 / 10 = 104 м-3.
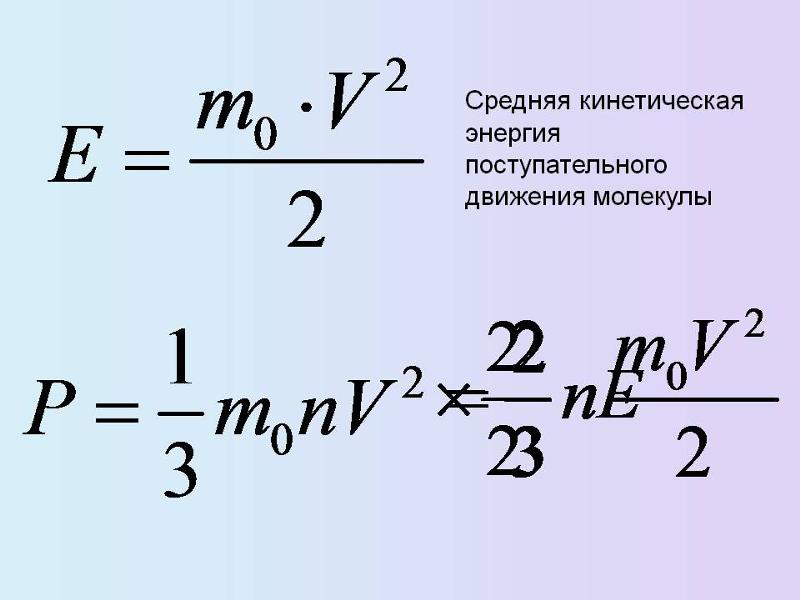 math.toronto.edu/mathnet/questionCorner/scinot.html). ]
math.toronto.edu/mathnet/questionCorner/scinot.html). ] 
 Что
формула для определения кинетической энергии?
Что
формула для определения кинетической энергии?  Используя формулу кинетической энергии вместе с вашим ответом на вопрос
8, рассчитайте кинетическую энергию водорода.
Используя формулу кинетической энергии вместе с вашим ответом на вопрос
8, рассчитайте кинетическую энергию водорода.