Формула температуры газа: 2.1. [ ] - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Абсолютная температура идеального газа

Давление газа определяют хаотические удары перемещающихся молекул. Это означает, что уменьшение давления при охлаждении газа можно объяснить уменьшением средней энергии поступательного движения молекул (). Давление газа достигнет нуля, когда в соответствии с основным законом молекулярно кинетической теории:

. Концентрация молекул газа n считается постоянной отличной от нуля.

Абсолютная температура идеального газа

Для охлаждения газа существует предел. Абсолютным нулем называют температуру, при которой прекращается поступательное движение молекул.

Идеальный газ (в отличие от реальных газов) остается в газообразном состоянии при любых температурах. Величину температуры, при которой прекратится поступательное движение молекул, можно найти из закона, который определил Ж. Шарль: температурный коэффициент давления идеального газа не зависит от рода газа и равен . При этом давление идеального газа при произвольной температуре равно:

где t – температура по шкале Цельсия; – давление при .

Приравняем давление в выражении (2) к нулю, выразим температуру, при которой молекулы идеального газа прекратят свое поступательное движение:

В. Кельвин предположил, что полученное значение абсолютного нуля будет соответствовать прекращению поступательного движения молекул любого вещества. Температуры ниже абсолютного нуля (T=0 К) природе не бывает. Так как при температуре абсолютного нуля нельзя отнимать энергию теплового движения молекул и уменьшать температуру тела, так как энергия теплового движения отрицательной быть не может. В лабораториях получена температура близкая к абсолютному нулю (около тысячной доли градуса).

Термодинамическая шкала температур

По термодинамической шкале температур (она же шкала Кельвина) началом отсчета считается абсолютный нуль температур. Температуру обозначают большой буквой T. Размер градуса совпадает с градусом по шкале Цельсия:

Одинаковыми будут производные, если брать их с использованием разных температурных кал:

При переходе от шкалы Кельвина к шкале Цельсия сохраняются определения термических коэффициентов объемного расширения и коэффициента давления.

В международной системе единиц (СИ) единица температуры является основной, ее называют кельвином (К). В системе СИ термодинамическая шкала температур используется для отсчета температуры.

В соответствии с международным соглашением размер кельвина определяют из таких условий: температуру тройной точки волы принимают равной 273,16 К. Тройной точке воды по Цельсию, соответствует 0,01 ^oС, температура таяния льда по кельвину равна 273,15 К.

Температура, измеряемая в кельвинах, называется абсолютной. Связью между абсолютной температурой и температурой по Цельсию отражает выражение:

Абсолютная температура, кинетическая энергия молекул и давление идеального газа

Величина средней энергии поступательного движения молекул прямо пропорциональна температуре газа:

где – постоянная Больцмана. Формула (6) означает, что средняя величина кинетической энергии поступательного движения молекул не зависит от рода идеального газа, а определено только его температурой.

Давление идеального газа определено только его температурой:

Примеры решения задач

Расчет температуры и давления газа: онлайн калькулятор

Комбинированный газовый закон — это формула, которая связывает основные параметры идеального газа и позволяет вычислять неизвестные в случаях, если заданы пять остальных величин.

Идеальный газ

Идеальный газ — это математическая модель с определенными допущениями, которая позволяет исследовать свойства газообразных веществ с достаточной точностью. К допущениям, которые используются в модели идеального газа, относятся:

пренебрежение размерами молекул;
силы молекулярного взаимодействия не учитываются;
соударение атомов и молекул абсолютно упруго;
газ находится в термодинамическом равновесии.

Благодаря этим допущениям ученые изучили основные свойства газообразных веществ и вывели основные законы, которым подчиняются любые газы. Комбинированный закон объединяет все перечисленные ниже зависимости.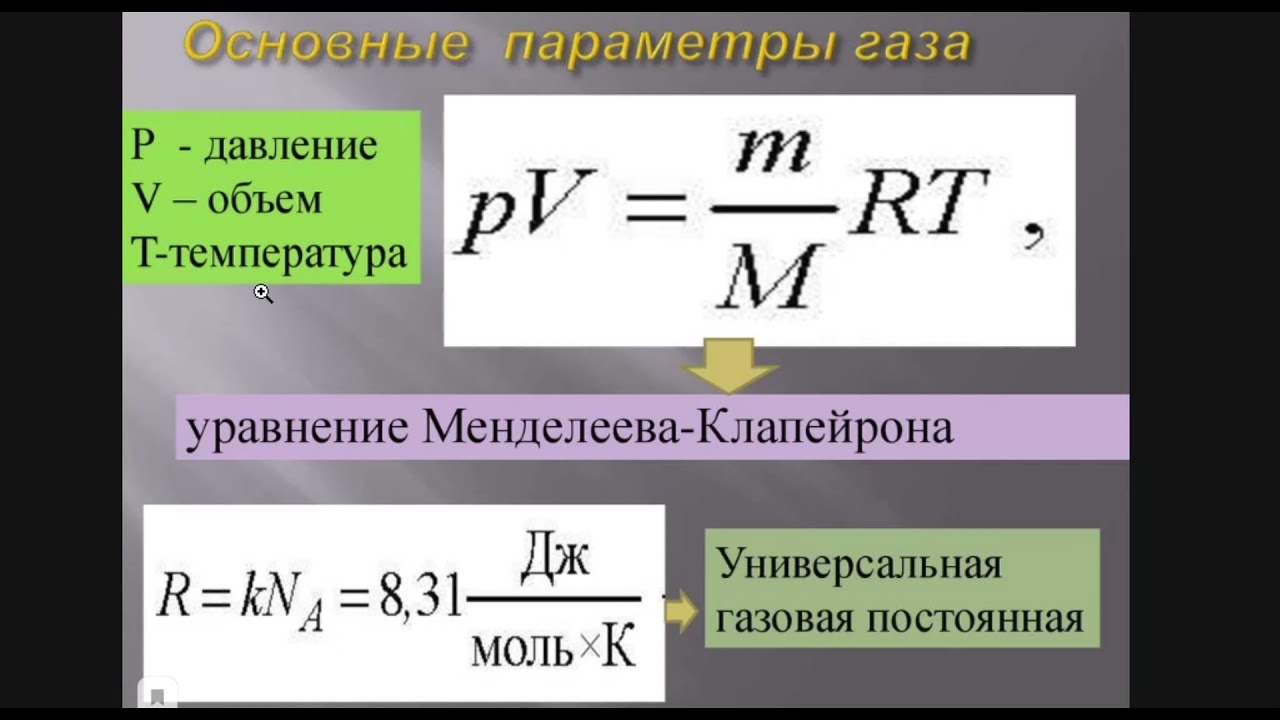

Газовые законы

Любое газообразное вещество характеризуется тремя простыми параметрами: объемом, давлением и температурой. Газ тем и хорош, что он заполняет весь предоставленный объем или может сжиматься до минимальных объемов, иногда переходя в состояние жидкости. Сжимать газ можно двумя способами:

при постоянном давлении уменьшить температуру;
при постоянной температуре увеличить давление.

Эти две простые формулировки отражают в себе два известных газовых закона: изобару и изотерму. В изобарном процессе изменение температуры приводит к прямо пропорциональному изменению объема. Вспомните жидкий азот: он занимает минимум места, при этом его температура составляет 63,29 К, что соответствует –209 градусам Цельсия. Если температуру азота поднять до 20 градусов Цельсия, то 1 литр жидкого азота превратится в 700 литров газа. Увеличивается температура, увеличивается объем и наоборот. Эти изменения обусловлены тем, что соотношение объема к температуре газа остается статичным.

В изотермическом процессе температура не изменяется и для сжатия газа придется увеличить давление. Это процесс проще для понимания, так как сдавливая газ мы уменьшаем его объем подобно тому, как утрамбовывание грунта или снега позволяет уложить их более плотно и с меньшим объемом. В этом изотермическом процессе изменение давления приводит к обратно пропорциональному изменению объема. Больше давление, меньше объем и наоборот. Такая динамика обусловлена тем, что произведение давления на объем — это всегда постоянная величина.

Если же объем газа не изменяется, то процесс называется изохорным и в этом процессе отображается взаимосвязь давления и температуры. Согласно закону, изменение одного параметра вызывает прямо пропорциональное изменение другого. Это означает, что увеличение давления в сосуде вызывает рост температуры находящегося там газа. Верно и обратное утверждение.

Комбинированный закон

Все перечисленные законы подчиняются общей формулировке: при постоянстве одного параметра, отношение двух других также постоянно. Обобщая эти законы в динамике получаем комбинированный газовый закон, который описывается формулой:

P1×V1/T1 = P2×V2/T2,

где P1, V1 и T1 — соответственно начальные давление, объем и температура, а P2, V2 и T2 — конечные.

Используя данную формулу легко определить динамику параметров во время нагрева газа или его сжатия.

Наша программа позволяет рассчитать соотношение параметров идеального газа при их изменении. Для использования калькулятора требуется задать пять известных величин, после чего программа определит последнее неизвестное. Рассмотрим небольшой пример.

Пример использования калькулятора

Представим баллон газа объемом 15 л под давлением 120 кПа и при температуре –20 градусов Цельсия. Определим температуру газа, если баллон будет заменен на емкость объемом 10 л и давлением 150 кПа. На первый взгляд у нас есть все параметры, однако в газовых законах температура обязательно указывается в кельвинах, а не градусах. Для перевода температуры в систему Си достаточно прибавить к значению величину 273. Получаем, что температура газа составляет 253 К. Теперь вводим данные в соответствующие ячейки и смотрим на результат: конечная температура теперь равна 210 К или –63 градуса Цельсия. Очевидно, что газ подчинился приведенным выше законам и при уменьшении объема его температура также уменьшилась.

Заключение

Газовые законы — серьезная тема школьного курса физики, которую более подробно разбирают на первом году обучения в вузах. Комбинированный закон газа прост на первый взгляд, но обилие параметров может запутать школьника, а выведение пропорций и вовсе способно превратить задачу в ад. Для упрощения расчетов используйте наш онлайн-калькулятор, не забывая переводить все заданные параметры в систему СИ.

Калькулятор закона состояния идеального газа (давление–объем–температура–количество) • Термодинамика — теплота • Онлайн-конвертеры единиц измерения

Калькулятор закона состояния идеального газа определяет одну из четырех величин, входящих в уравнение состояния (давление, объем, температура или количество), если известны три другие величины.

Пример: Рассчитать давление в паскалях в 70-литровом баке работающего на метане автомобиля, если в нем хранится 800 молей метана при 30 °С.

Еще несколько примеров решения задач о состоянии идеального газа под приводится калькулятором.

Выберите неизвестную величину для решения уравнения состояния идеального газа:

PVTn

Абсолютное давление

Pпаскаль (Па)мегапаскаль (МПа)килопаскаль (кПа)гектопаскаль (гПа)ньютон на кв. метр (Н/м²)бар (бар)килограмм-сила на кв. метр (кгс/м²)торр (торр)psi (psi)миллиметр ртутного столба (0°C) (мм рт.ст.)мм вод. столба (4°C) (мм вод. ст., мм H₂O)техническая атмосфера (ат)физическая атмосфера (атм)

Объем

Vкубический метр (м³)кубический дециметр (дм³)кубический сантиметр (см³)литр (л)миллилитр (мл)галлон американскийкварта СШАунция жидкая СШАунция жидкая британскаякубический фут (фут³)кубический дюйм (дюйм³)

Температура

Tградус Цельсия (°C)градус Фаренгейта (°F)градус Ранкина (°Ra)кельвин (К)

ИЛИ

Для расчета выберите неизвестную величину и введите три известные величины из четырех имеющихся в уравнении состояния газа (давление, объем, температура, количество). Четвертая величина будет рассчитана после нажатия на кнопку Рассчитать. Количество можно ввести в молях или указать молярную массу и массу газа. Для определения молярной массы любого газа можно использовать калькулятор молярной массы. Если нужно определить молярную массу смеси газов, например, сухого воздуха, нужно определить молярные массы каждого газа и умножить их на процентное содержание по массе каждого газа в воздухе.

Примеры решения задач по уравнению состояния идеального газа (уравнению Менделеева — Клапейрона)

Задача 1: Плотность воздуха при нормальных условиях (температура 0 °С и атмосферное абсолютное давление 100 кПа) составляет 1,28 кг/м³. Определить среднюю молярную массу воздуха.

Решение: Поскольку плотность воздуха задана, это означает, что в калькулятор можно ввести массу одного кубического метра воздуха, равную 1,28 кг. Введите в калькулятор данные:

Выберите n (Количество в молях) в селекторе Выберите неизвестную величину.
Введите абсолютное давление P = 100 кПа.
Введите объем V = 1 м³.
Введите температуру T = 0 °C.
Нажмите кнопку Рассчитать.
Калькулятор покажет количество молей в 1 м³ воздуха.
Введите массу воздуха m = 1,28 кг и нажмите кнопку Рассчитать.
Калькулятор рассчитает молярную массу воздуха M = 0,029 кг/моль

Задача 2: Молярная масса газа кислорода (O₂) M = 32 г/моль. Определить абсолютную температуру 128 г. кислорода, находящегося в 10-литровом сосуде под давлением P = 3 МПа.

Решение: Нажмите кнопку Reset и введите в калькулятор данные задачи:

Выберите T (Температура) в селекторе Выберите неизвестную величину.
Введите молярную массу кислорода N = 32 г/моль.
Введите массу кислорода m = 128 г.
Калькулятор рассчитает количество кислорода в молях.
Введите объем V = 4 л и давление P = 3 МПа.
Нажмите кнопку Рассчитать.
Считайте температуру в кельвинах.

Задача 3: В сосуде высокого давления находится газ под давлением P = 0.5 МПа при температуре T = 15 °С. Объем газа V = 5 л. Рассчитать объем этой массы газа при нормальных условиях (P = 100 кПа, T = 0 °С).

Решение: Нажмите кнопку Reset и введите в калькулятор данные задачи:

Выберите T (Температура) в селекторе Выберите неизвестную величину.
Введите давление P = 500 кПа.
Введите температуру T = 15 °C.
Введите объем V = 5 л.
Нажмите кнопку Рассчитать.
Калькулятор рассчитает количество в молях, которое будет использовано в следующем шаге.
Выберите Объем в селекторе Выберите неизвестную величину.
Введите температуру и давление P = 100 kPa, T = 0 °C (нормальные условия) и нажмите кнопку Рассчитать.
Калькулятор рассчитает новый объем газа V = 23.69 л при нормальных условиях.

Задача 4: Рассчитать давление в паскалях в 70-литровом баке работающего на метане автомобиля, если в нем хранится 12,8 кг метана (молярная масса 16 г/моль) при 30 °С.

Определения и формулы

Идеальный газ

Идеальный газ — теоретическая модель, в которой газ представляется в виде множества свободно движущихся частиц бесконечно малого размера, которые взаимодействуют друг с другом абсолютно упруго, то есть при столкновении двух частиц их кинетическая энергия не изменяется и не превращается ни в какую другую форму энергию, например, в потенциальную энергию или в тепло. Считается, что суммарный размер частиц настолько мал, что занимаемый ими объем в сосуде пренебрежимо мал. Эта теоретическая модель полезна, так как она упрощает многие расчеты, а также в связи с тем, что идеальный газ подчиняется законам классической механики. Идеальный газ можно представить себе в виде множества абсолютно твердых сфер, которые только сталкиваются друг с другом и больше никак не взаимодействуют.

В обычных условиях, например, при стандартных условиях (при температуре 273,15 К и давлении в 1 стандартную атмосферу) большинство реальных газов ведут себя как идеальный газ. В общем случае, газ ведет себя как идеальный при низком давлении и высокой температуре, когда расстояния между молекулами газа относительно велики. В этих условиях потенциальная энергия вследствие действия межмолекулярных сил намного меньше кинетической энергии частиц. Размер молекул также незначителен по сравнению с расстоянием между ними. Идеальная модель не работает при низких температурах и высоких давлениях, а также для тяжелых газов. При понижении температуры и повышении давления реальный газ может стать жидкостью или даже перейти в твердое состояние, то есть может произойти фазовый переход. В то же время, модель идеального газа не допускает жидкого или твердого состояния.

Закон идеального газа

Идеальный газ, как и любой другой газ, можно охарактеризовать четырьмя переменными и одной константой, а именно:

давление (P),
объем (V),
количество в молях (n),
температура (T), and
универсальная газовая постоянная (R)

Эти четыре переменные и одна константа объединены в приведенном ниже уравнении, которое называется уравнением состояния идеального газа:

Это уравнение также известно под названием закона идеального газа и уравнения Менделеева — Клапейрона или уравнения Клапейрона, так как уравнение было впервые выведено в 1834 г. французским инженером Эмилем Клапейроном (1799–1864). О вкладе Д. И. Менделеева — чуть ниже. В этом уравнении:

P — абсолютное давление, измеряемое в СИ в паскалях (Па),
V — объем, измеряемый в СИ в кубических метрах (м³),
n — количество вещества (газа) в молях (сокращение моль). Один моль любого вещества в граммах численно равен средней массы одной молекулы в соединении, выраженной в атомных единицах массы. Например, один моль кислорода с атомной массой 16 соответствует 16 граммам. Один моль идеального газа при стандартных условиях занимает 22,4 литра.
T — абсолютная температура.
R — универсальная газовая постоянная, являющаяся физическим коэффициентом пропорциональности уравнения состояния идеального газа.

Приведенное выше уравнение показывает, что при нулевой абсолютной температуре получается нулевой объем. Однако это не означает, что объем реального газа действительно исчезает. При очень низких температурах все газы становятся жидкостями и уравнение идеального газа к ним неприменимо.

Универсальная газовая постоянная соответствует работе, выполненной при расширении одного моля идеального газа при нагревании на 1 К при постоянном давлении. Размерность постоянной — работа на количество вещества на температуру. Постоянная в точности равна 8,31446261815324 Дж⋅К⁻¹⋅моль⁻¹. Универсальная газовая постоянная также определяется как произведение числа Авогадро N_A и постоянной Больцмана k:

Входящая в уравнение состояния идеального газа универсальная газовая постоянная была предложена и введена в уравнение Дмитрием Менделеевым в 1877 г. Поэтому уравнение состояния идеального газа в литературе на русском языке и ее переводах на другие языки, называется уравнением Менделеева — Клапейрона.

Количество газа в молях часто бывает удобно заменить массой газа. Количество газа в молях n, его масса m в граммах и молярная масса M в граммах на моль связаны формулой:

Заменяя в уравнении состояния идеального газа n на m/M, имеем:

Для определения молярной массы элемента, его относительная атомная масса умножается на коэффициент молярной массы в кг/моль

Например, молярная масса кислорода как элемента в единицах системы СИ

Если ввести в уравнение состояния идеального газа плотность ρ = m/V, мы получим:

Теперь введем понятие удельной газовой постоянной, которая представляет собой отношение универсальной газовой постоянной R к молярной массе M:

Например, удельная газовая постоянная сухого воздуха приблизительно равна 287 Дж·кг⁻¹·К⁻¹. Подставив удельную газовую постоянную в уравнение состояния идеального газа, получим:

Закон идеального газа объединяет четыре более простых эмпирических газовых закона, открытых в XVII–XIX вв. несколькими учеными, которые аккуратно измеряли свойства газа. Простые газовые законы можно также вывести из уравнения состояния идеального газа (PV=nRT). Поскольку в этом уравнении R является постоянной величиной, можно записать

Поскольку PV/NT — постоянная величина, можно записать это иначе:

Здесь индексы 1 и 2 показывают начальное и конечное состояние газа в системе. Мы будем использовать это уравнение ниже при описании четырех газовых законов.

Отметим, что исторически именно эмпирические законы поведения газа, описанные ниже, привели к открытию обобщенного закона состояния идеального газа. Эти законы были открыты несколькими учеными, которые проводили эксперименты, изменяя только две переменные состояния газа и оставляя две другие переменные постоянными.

Закон Бойля — Мариотта (

T=const, n=const)

Роберт Бойль

Изменим предыдущее уравнение с учетом, что количество газа в молях n и его температура Т остаются неизменными:

или

Эдм Мариотт

Это закон Бойля — Мариотта, описывающий зависимость объема V фиксированного количества газа в молях n от давления P при постоянной температуре T. Давление фиксированной массы газа при неизменной температуре обратно пропорционально его объему. Закон был сформулирован англо-ирландским химиком и физиком Робертом Бойлем в 1662 г. В России и континентальной Европе это закон называют законом Бойля — Мариотта с учетом вклада в открытие закона французского физика и священника Эдма Мариотта.

Закон Авогадро (

T=const, P=const)

Амедео Авогадро

Если температура и давление остаются неизменными, можно записать

Это закон Авогадро, указывающий, что при неизменных температуре и давлении равные объемы любых газов содержат одинаковое количество молекул. Это уравнение показывает, что, если количество газа увеличивается, объем газа пропорционально растет. Иными словами, количество атомов или молекул газа не зависит от их размеров или от молярной массы газа. Закон назван в честь итальянского ученого Амедео Авогадро, который опубликовал гипотезу об отношениях объема газа и его количества в молях в 1811 году. Число Авогадро также носит его имя.

Закон Гей-Люссака (

P=const, n=const)

Жак Шарль

При постоянном давлении объем фиксированного количества газа в молях пропорционален абсолютной температуре системы с газом.

В англоязычной литературе этот закон называется законом объемов и законом Шарля. Закон описывает как расширяется любой газ при увеличении его абсолютной температуры. Закон был сформулирован в неопубликованной работе французским ученым Жаком Шарлем в 80-х гг. XVIII в. Его соотечественник Жозеф Луи Гей-Люссак опубликовал этот закон в 1803 г. и указал, что приоритет открытия принадлежит Жаку Шарлю. Поэтому этот закон в литературе не на английском языке часто называют законом Гей-Люссака. В русскоязычной литературе закон носит имя Гей-Люссака. Итальянцы называют этот закон первым законом Гей-Люссака (ит. prima legge di Gay-Lussac).

Закон Шарля (или второй закон Гей-Люссака) (

V=const, n=const)

Жозеф Луи Гей-Люссак

Закон Шарля (называемый также вторым законом Гей-Люссака) гласит, что давление фиксированного количества газа в молях при его неизменном объеме прямо пропорционально абсолютной температуре газа:

Закон был сформулирован Гей-Люссаком в 1802 г. В литературе на других языках этот закон также называют законом Амонтона по имени французского ученого Гийома Амонтона, который на сто лет раньше обнаружил количественную зависимость объема газа от его температуры. Иногда закон называют вторым законом Гей-Люссака и законом Шарля, так как сам Гей-Люссак считал, что закон открыт Шарлем. Закон зависимости давления от температуры был также независимо открыт английским физиком Джоном Дальтоном в 1801 г. Итальянцы называют этот закон вторым законом Вольта–Гей-Люссака (ит. seconda legge di Volta – Gay-Lussac), потому что итальянец Алессандро Вольта независимо проводил исследования газов и получил аналогичные результаты.

При нагревании воздуха в оболочке воздушного шара его плотность уменьшается и становится меньше плотности окружающего воздуха; в результате шар приобретает положительную плавучесть

Автор статьи: Анатолий Золотков

Примеры решенных задач по физике

Ниже приведены условия и решения задач. Закачка решений в формате doc начнется автоматически через 10 секунд.

№ 514.

Определить молярную массу газа, если при температуре Т=300 К и давлении p=0,2 МПа он имеет плотность ρ=2,41 кг/м3.

Дано : T= 300 K

P= 2×105 Па

ρ=2,41 кг/м3

Найти:  Решение.

Для решения задачи воспользуемся уравнением Менделеева-Клапейрона, записанного в виде:

P= (1) , где ρ – плотность газа; R – молярная газовая постоянная (R =8. 31 Дж/(моль∙К)) ; T – температура газа ; P – давление газа ; μ – молярная масса газа.

Выражая из (1) молярную массу μ, получим :

= (3)

Подставляя, заданные числовые значения физических величин в формулу (3) и вычисляя, получим :

==0,03 кг/моль

Ответ : =0,03 кг/моль.

№ 524

Найти отношения теплоёмкостей Cp/Cv для газовой смеси, состоящей из 10 г гелия и 25 г водорода?

Дано: газ He

газ Н2

ν1= m1/M1 = 10/4 =2,5 моль

ν2= m2/M2 = 25/2 = 12,5 моль

Найти : Cp/Cv Решение.

Молярную теплоёмкость смеси Cv при постоянном объёме найдём следующим. Теплоты, необходимую для нагревания смеси на ΔТ, выразим двумя способами :

Q=Cv(ν1+ν2)ΔT (1)

Q=(Cv1ν1+Cv2ν2)ΔT (2)

где Cv1 – молярная теплоёмкость гелия ; Cv2 – молярная теплоёмкость кислорода.

Приравняв правые части (1) и (2) и разделив обе части полученного равенства на ΔТ, получим :

Cv(ν1+ν2)=Cv1ν1+Cv2ν2 , откуда

Cv=(Cv1ν1+Cv2ν2)/(ν1+ν2) (3)

Рассуждая так же, получим формулу для вычисления молярной теплоёмкости при постоянном давлении :

Cp=(Cp1ν1+Cp2ν2)/(ν1+ν2) (4)

Вычислим отношение формул (4) и (3), получим :

Cp/Cv=(Cp1ν1+Cp2ν2)/(Cv1ν1+Cv2ν2) (5)

Молярные теплоёмкости газа при постоянном объёме и давлении выражаются соответственно :

Cv=iR/2 ; Cp=(i+2)R/2 , где i – число степеней свободы молекулы газа.

Используя эти выражения запишем формулы для молярных теплоёмкостей гелия и кислорода.

Сv1=i1R/2 (6) ; Cp1=(i1+2)R/2 (7) ,где i1=3 (так как молекула гелия одноатомная).

Сv2=i2R/2 (8) ; Cp2=(i2+2)R/2 (9) , где i2=5 (так как молекула водорода двухатомная).

Подставляя, полученные выражения (6), (7), (8) и (9) в формулу (5), получим :

Cp/Cv=[(i1+2)ν1+(i2+2)ν2]/(i1ν1+i2ν2) (10)

Произведя вычисления, получим :

Cp/Cv=[(3+2)∙2,5+(5+2)∙12,5]/(3∙2,5+5∙12,5)= 1,4286 Дж/(К моль)

Ответ : Cp/Cv=1,4286 Дж/(К моль).

№534

Найти среднюю длину свободного пробега молекулы азота в сосуде объемом 6 л. Масса газа 0,5 г.

Дано : d=3×10-8 см=3×10-11 см

p=105 Па

T=273 K

Найти :

Решение.

Средняя длина свободного пробега молекул газа выражается формулой :

=1/πd2n (1)

где d – диаметр молекулы ; n – концентрация молекул.

Концентрация молекул связана с давлением и температурой газа выражением:

n=p/kT (2)

где к – постоянная Больцмана (к=1.38×10-23 Дж/К)

Из уравнения Менделеева-Клайперона можем записать:

(3)

, где V – объем газа, R – молярная газовая постоянная, m и M – масса и молярная масса газа соответственно.

Подставляя (3) в (2), а затем в выражение (1), получим:

= (4)

Вычисления по формуле (4) дают

== 1,9336×10-3 м

Ответ: =1,9336×10-3 м.

№ 546

Газ, для которого γ=Cp/Cv=4/3, находится под давлением P=2×105 Па и занимает объём V=3 дм3. В результате изобарического нагревания объём увеличился в 3 раза. Определить количество теплоты, переданное газу.

Дано : γ=Cp/Cv=4/3

P=2×105 Па

V=3 дм3=3×10-3 м3

V2/V=3

Найти : Q

Решение.

Количество теплоты, участвующее в изобарном процессе выражается формулой :

Q= (1) , где m – масса газа ; M – молярная масса газа ; Cp – молярная теплоёмкость при p=const ; ΔT – изменение температуры газа.

Изменение температуры газа :

ΔT=T2-T1 (2)

Начальную Т1 и конечную Т2 температуры газа найдём из уравнения Менделеева-Клапейрона :

T1= (3) ; T2= (4)

где V и V2 – объёмы газа до нагревания и после, соответственно.

С учётом выражений (3) и (4), формула (2) примет вид :

ΔT= (5)

Подставляя полученное выражение для ΔТ согласно (5) в уравнение (1), получим :

Q= (6)

С учётом уравнения : R=Cp-Cv выражение (6) примет вид :

Разделив числитель и знаменатель последнего выражения на Cv и, учитывая, что V2=3V, получим :

Q= (7)

Произведя вычисления по формуле (7), найдём количество теплоты, подведённое к газу :

Q==4800 Дж=4. 8 кДж

Ответ : Q=4.8 кДж.

№ 556

Во сколько раз необходимо увеличить объём ν=5 моль идеального газа при изотермическом расширении, если его энтропия увеличилась на ΔS=57.6 Дж/К?

Дано : ν=5 моль

T=const

ΔS=57.6 Дж/К

Найти : V2/V1

Решение.

Как известно, изменение энтропии выражается общей формулой :

ΔS=S2-S1= (1)

При вычислении по формуле (1) вынесем температуру Т за знак интеграла (при изотермическом процесс T=const). Вычислив интеграл, найдём :

ΔS= (2)

где Q – количество теплоты.

Количество теплоты при изотермическом процессе выражается формулой :

Q=νRTln(V2/V1) (3)

С учётом (2) уравнение (3) примет вид :

ΔS=

Отсюда изменение объёма газа :

V2/V1= (4)

Вычисления по формуле (4) дают :

V2/V1==4

Ответ : объём газа необходимо увеличить в 4 раза.

Абсолютная температура. Температура — мера средней кинетической энергии молекул

Подробности: Просмотров: 615

«Физика – 10 класс»

Абсолютная температура.

Вместо температуры Θ, выражаемой в энергетических единицах, введём температуру, выражаемую в привычных для нас градусах.

Будем считать величину Θ прямо пропорциональной температуре Т, измеряемой в градусах:

Θ = kТ, (9.12)

где k — коэффициент пропорциональности.

>Определяемая равенством (9.12) температура называется абсолютной.

Такое название, как мы сейчас увидим, имеет достаточные основания. Учитывая определение (9.12), получим

По этой формуле вводится температурная шкала (в градусах), не зависящая от вещества, используемого для измерения температуры.

Температура, определяемая формулой (9.13), очевидно, не может быть отрицательной, так как все величины, стоящие в левой части этой формулы, заведомо положительны. Следовательно, наименьшим возможным значением температуры Т является значение Т = 0, если давление р или объём V равны нулю.

Предельную температуру, при которой давление идеального газа обращается в нуль при фиксированном объёме или при которой объём идеального газа стремится к нулю при неизменном давлении, называют абсолютным нулём температуры.

Это самая низкая температура в природе, та «наибольшая или последняя степень холода», существование которой предсказывал Ломоносов.

Английский учёный У. Томсон (лорд Кельвин) (1824—1907) ввёл абсолютную шкалу температур. Нулевая температура по абсолютной шкале (её называют также шкалой Кельвина) соответствует абсолютному нулю, а каждая единица температуры по этой шкале равна градусу по шкале Цельсия.

Единица абсолютной температуры в СИ называется кельвином (обозначается буквой К).

Постоянная Больцмана.

Определим коэффициент k в формуле (9.13) так, чтобы изменение температуры на один кельвин (1 К) было равно изменению температуры на один градус по шкале Цельсия (1 °С).

Мы знаем значения величины Θ при 0 °С и 100 °С (см. формулы (9.9) и (9.11)). Обозначим абсолютную температуру при 0 °С через Т₁, а при 100 °С через Т₂. Тогда согласно формуле (9.12)

Θ₁₀₀ – Θ₀ = k(T₂ -T₁),

Θ₁₀₀ – Θ₀ = k • 100 K = (5,14 – 3,76) • 10^-21 Дж.

Отсюда

Коэффициент

k = 1,38 • 10^-23 Дж/К (9.14)

называется постоянной Больцмана в честь Л. Больцмана, одного из основателей молекулярно-кинетической теории газов.

Постоянная Больцмана связывает температуру Θ в энергетических единицах с температурой Т в кельвинах.

Это одна из наиболее важных постоянных в молекулярно-кинетической теории.

Зная постоянную Больцмана, можно найти значение абсолютного нуля по шкале Цельсия. Для этого найдём сначала значение абсолютной температуры, соответствующее 0 °С. Так как при 0 °С kT₁ = 3,76 • 10^-21 Дж, то

Один кельвин и один градус шкалы Цельсия совпадают. Поэтому любое значение абсолютной температуры Т будет на 273 градуса выше соответствующей температуры t по Цельсию:

Т (К) = (f + 273) (°С). (9.15)

Изменение абсолютной температуры ΔТ равно изменению температуры по шкале Цельсия Δt: ΔТ(К) = Δt (°С).

На рисунке 9.5 для сравнения изображены абсолютная шкала и шкала Цельсия. Абсолютному нулю соответствует температура t = -273 °С.

В США используется шкала Фаренгейта. Точка замерзания воды по этой шкале 32 °F, а точка кипения 212 °Е Пересчёт температуры из шкалы Фаренгейта в шкалу Цельсия производится по формуле t(°C) = 5/9 (t(°F) – 32).

Отметим важнейший факт: абсолютный нуль температуры недостижим!

Температура — мера средней кинетической энергии молекул.

Из основного уравнения молекулярно-кинетической теории (9.8) и определения температуры (9.13) вытекает важнейшее следствие:
абсолютная температура есть мера средней кинетической энергии движения молекул.

Докажем это.

Из уравнений (9.7) и (9.13) следует, что Отсюда вытекает связь между средней кинетической энергией поступательного движения молекулы и температурой:

Средняя кинетическая энергия хаотичного поступательного движения молекул газа пропорциональна абсолютной температуре.

Чем выше температура, тем быстрее движутся молекулы. Таким образом, выдвинутая ранее догадка о связи температуры со средней скоростью молекул получила надёжное обоснование. Соотношение (9.16) между температурой и средней кинетической энергией поступательного движения молекул установлено для идеальных газов.

Однако оно оказывается справедливым для любых веществ, у которых движение атомов или молекул подчиняется законам механики Ньютона. Оно верно для жидкостей, а также и для твёрдых тел, где атомы могут лишь колебаться возле положений равновесия в узлах кристаллической решётки.

При приближении температуры к абсолютному нулю энергия теплового движения молекул приближается к нулю, т. е. прекращается поступательное тепловое движение молекул.

Зависимость давления газа от концентрации его молекул и температуры. Учитывая, что из формулы (9.13) получим выражение, показывающее зависимость давления газа от концентрации молекул и температуры:

Из формулы (9.17) вытекает, что при одинаковых давлениях и температурах концентрация молекул у всех газов одна и та же.

Отсюда следует закон Авогадро, известный вам из курса химии.

Закон Авогадро:

В равных объёмах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.

Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Основные положения МКТ. Тепловые явления – Физика, учебник для 10 класса – Класс!ная физика

Почему тепловые явления изучаются в молекулярной физике — Основные положения молекулярно-кинетической теории. Размеры молекул — Примеры решения задач по теме «Основные положения МКТ» — Броуновское движение — Силы взаимодействия молекул. Строение газообразных, жидких и твёрдых тел — Идеальный газ в МКТ. Среднее значение квадрата скорости молекул — Основное уравнение молекулярно-кинетической теории газов — Примеры решения задач по теме «Основное уравнение молекулярно-кинетической теории» — Температура и тепловое равновесие — Определение температуры. Энергия теплового движения молекул — Абсолютная температура. Температура — мера средней кинетической энергии молекул — Измерение скоростей молекул газа — Примеры решения задач по теме «Энергия теплового движения молекул» — Уравнение состояния идеального газа — Примеры решения задач по теме «Уравнение состояния идеального газа» — Газовые законы — Примеры решения задач по теме «Газовые законы» — Примеры решения задач по теме «Определение параметров газа по графикам изопроцессов»

Уравнение Менделеева-Клапейрона – О’Пять пО физике!

Уравнение Менделеева-Клапейрона – уравнение состояния для идеального газа, отнесенное к 1 молю газа. В 1874 г. Д. И. Менделеев на основе уравнения Клапейрона объединив его с законом Авогадро, используя молярный объем V_m и отнеся его к 1 молю, вывел уравнение состояния для 1 моля идеального газа:

pV = RT, где R — универсальная газовая постоянная,

R = 8,31 Дж/(моль^.К)

Уравнение Клапейрона-Менделеева показывает, что для данной массы газа возможно одновременно изменение трех параметров, характеризующих состояние идеального газа. Для произвольной массы газа М, молярная масса которого m: pV = (М/m)^.RT. или pV = N_АkT,

где N_А — число Авогадро, k — постоянная Больцмана.

Вывод уравнения:

С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса газа и один из параметров – давление, объем или температура – остается постоянным, а изменяются только остальные два и получить теоретически газовые законы для этих условий изменения состояния газа.

Такие процессы называют изопроцессами. Законы, описывающие изопроцессы, были открыты задолго до теоретического вывода уравнения состояния идеального газа.

Изотермический процесс – процесс изменения состояния системы при постоянной температуре. Для данной массы газа произведение давления газа на его объем постоянно, если температура газа не меняется. Это закон Бойля – Мариотта.

Для того, чтобы температура газа оставалась в процессе неизменной, необходимо, чтобы газ мог обмениваться теплотой с внешней большой системой – термостатом. Роль термостата может играть внешняя среда (воздух атмосферы). Согласно закону Бойля-Мариотта, давление газа обратно пропорционально его объему: P₁V₁=P₂V₂=const. Графическая зависимость давления газа от объема изображается в виде кривой (гиперболы), которая носит название изотермы. Разным температурам соответствуют разные изотермы.

Изобарный процесс – процесс изменения состояния системы при постоянном давлении. Для газа данной массы отношение объема газа к его температуре остается постоянным, если давление газа не меняется. Это закон Гей-Люссака. Согласно закону Гей-Люссака, объем газа прямо пропорционален его температуре: V/T=const. Графически эта зависимость в координатах V-T изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изобарой. Разным давлениям соответствуют разные изобары. Закон Гей-Люссака не соблюдается в области низких температур, близких к температуре сжижения (конденсации) газов.

Изохорный процесс – процесс изменения состояния системы при постоянном объеме. Для данной массы газа отношение давления газа к его температуре остается постоянным, если объем газа не меняется. Этот газовый закон Шарля. Согласно закону Шарля, давление газа прямо пропорционально его температуре: P/T=const. Графически эта зависимость в координатах P-Т изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изохорой. Разным объемам соответствуют разные изохоры. Закон Шарля не соблюдается в области низких температур, близких и температуре сжижения (конденсации) газов.

Законы Бойля – Мариотта, Гей-Люссака и Шарля являются частными случаями объединенного газового закона: Отношение произведения давления газа и объема к температуре для данной массы газа – величина постоянная: PV/T=const.

Итак, из закона pV = (М/m)^.RT выводятся следующие законы:

T = const => PV = const — закон Бойля — Мариотта.

p = const => V/T = const — закон Гей-Люссака.

V= const => p/T = const — закон Шарля

Если идеальный газ является смесью нескольких газов, то согласно закону Дальтона, давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов. Парциальное давление – это такое давление, которое производил бы газ, если бы он один занимал весь объем, равный объему смеси.

Некоторых, возможно, интересует вопрос, каким образом удалось определить постоянную Авогадро N_A = 6,02·10²³ ? Значение числа Авогадро было экспериментально установлено только в конце XIX – начале XX века. Опишем один из таких экспериментов.

В откачанный до глубокого вакуума сосуд объемом V = 30 мл поместили навеску элемента радия массой 0,5 г и выдержали там в течение одного года. Было известно, что за секунду 1 г радия испускает 3,7·10¹⁰ альфа-частиц. Эти частицы представляют собой ядра гелия, которые тут же принимают электроны из стенок сосуда и превращаются в атомы гелия. За год давление в сосуде выросло до 7,95·10^-4 атм (при температуре 27 ^оС). Изменением массы радия за год можно пренебречь. Итак, чему равна N_A?

Сначала найдем, сколько альфа-частиц (то есть атомов гелия) образовалось за один год. Обозначим это число как N атомов:

N = 3,7·10¹⁰ · 0,5 г · 60 сек · 60 мин · 24 час · 365 дней = 5,83·10¹⁷ атомов.

Запишем уравнение Клапейрона-Менделеева PV = nRT и заметим, что число молей гелия n = N/N_A. Отсюда:

N_A = NRT = 5,83 ^.10^{17 .}0,0821^.300 = 6,02 ^.10²³

PV 7,95 ^.10^-4^. 3 ^. 10^-2

В начале XX века этот способ определения постоянной Авогадро был самым точным. Но почему так долго (в течение года) длился эксперимент? Дело в том, что радий добывается очень трудно. При его малом количестве (0,5 г) радиоактивный распад этого элемента дает очень мало гелия. А чем меньше газа в замкнутом сосуде, тем меньшее он создаст давление и тем большей будет ошибка измерения. Понятно, что ощутимое количество гелия может образоваться из радия только за достаточно долгое время.

законов о газе

Газовые законы

Нижеследующее содержание является сутью лекции 18. В этой лекции мы рассматриваем законы газа: законы Шарля, Бойля, Авагадро и Гей-Люссака, а также законы идеального и комбинированного газа.

Законы о свойствах газа

Есть 4 общих закона, которые связывают 4 основных характерных свойства газов друг с другом. Каждый закон назван его первооткрывателем. Хотя важно понимать отношения, охватываемые каждым законом, знание отправителя не так важно и будет лишним после введения закона о комбинированном газе.Так что сосредоточьтесь на понимании отношений, а не на запоминании имен.

Закон Чарльза – дает соотношение между объемом и температурой , если давление и количество газа поддерживаются постоянными :

1) Если температура газа по Кельвину увеличивается, объем газа увеличивается. (Постоянная P, n)
2) Если температура газа по Кельвину понижается, объем газа уменьшается. (Постоянная P, n)

Это означает, что объем газа прямо пропорционален его температуре Кельвина. Подумайте об этом так: если вы увеличиваете объем газа и должны поддерживать постоянное давление, единственный способ добиться этого – это также повысить температуру газа.

Расчеты с использованием закона Чарльза включают изменение температуры (T ₂) или объема (V ₂) от известного начального количества каждого из них (V ₁ и T ₁):

Закон Бойля – гласит, что объем заданного количества газа, удерживаемого при постоянной температуре, изменяется обратно пропорционально приложенному давлению, когда температура и масса постоянны.

Уменьшение объема газа означает, что молекулы ударяются о стенки чаще, увеличивая давление, и, наоборот, если объем увеличивается, расстояние, которое молекулы должны пройти, чтобы столкнуться со стенками, увеличивается, и они реже ударяются о стенки, тем самым уменьшая давление.

Как и закон Чарльза, закон Бойля можно использовать для определения текущего давления или объема газа, если известны начальные состояния и одно из изменений:

Закон Авагадро – Дает соотношение между объемом и количеством газа в молях, когда давление и температура поддерживаются постоянными.

Если количество газа в баллоне увеличивается, объем увеличивается. Если количество газа в баллоне уменьшается, объем уменьшается. Это, конечно, при условии, что контейнер имеет расширяемые стенки.

Отношение снова прямо пропорционально, поэтому уравнение для вычислений равно

Закон Гей-Люссака – гласит, что давление заданного количества газа, удерживаемого в постоянном объеме, прямо пропорционально температуре Кельвина.

Если вы нагреете газ, вы дадите молекулам больше энергии, и они будут двигаться быстрее. Это означает большее воздействие на стенки контейнера и увеличение давления. И наоборот, если вы охладите молекулы, они замедлятся, и давление снизится.

Для расчета изменения давления или температуры с использованием закона Гей-Люссака уравнение выглядит следующим образом:

Чтобы немного поиграть с отношениями, попробуйте эту симуляцию.

Закон об идеальном газе:

Комбинация представленных выше законов порождает Закон об идеальном газе:

Добавление константы пропорциональности, называемой идеальной или универсальной газовой постоянной (R), завершает уравнение.

Как видите, для константы возможно множество единиц. Единственная постоянная константы – это то, что шкала температуры во всем – KELVIN.

При использовании закона идеального газа для расчета любого свойства газа вы должны сопоставить единицы с газовой постоянной, которую вы выбираете для использования, и вы всегда должны указывать температуру в градусах Кельвина.

Чтобы использовать уравнение, вам просто нужно уметь определить, чего не хватает в вопросе, и изменить уравнение, чтобы решить его.

Типичный вопрос: 6,2 литра идеального газа содержится при 3,0 атм и температуре 37 ° C. Сколько молей этого газа присутствует?

Поскольку единицы газовой постоянной задаются в атмосфере, молях и градусах Кельвина, важно убедиться, что вы конвертируете значения, указанные в других шкалах температуры или давления.Для этой задачи преобразуйте температуру ° C в K с помощью уравнения:

Т = ° С + 273

Т = 37 ° С + 273
Т = 310 К

Теперь вы можете вставить значения. Решите относительно количества родинок

n = PV / RT

n = (3,0 атм x 6,2 л) / (0,08206 л атм / моль K x 310 K)
n = 0,75 моль

Вот некоторые практические проблемы с использованием Закона об идеальном газе: Практика

Закон о комбинированном газе

Я сказал выше, что запоминание всех уравнений для каждого из отдельных законов газа станет неактуальным после введения последующих законов. Закон, о котором я говорил, это Закон о комбинированном газе:

Закон комбинированного газа позволяет вывести любое из необходимых соотношений путем объединения всех изменяемых частей в законе идеального газа: а именно давления, температуры и объема. R и количество молей не фигурируют в уравнении, поскольку они обычно постоянны и поэтому сокращаются, поскольку они появляются в равных количествах с обеих сторон уравнения.

Как вы можете видеть выше, уравнение может быть решено для любого из входящих в него параметров.Но что еще более важно, вы можете исключить из уравнения все, что останется постоянным.

Например, если в вопросе говорится, что система с давлением 1 атм и объемом 2 литра претерпела изменение до 3,5 литров, вычислите новое давление, вы можете просто исключить температуру из уравнения и получить:

P ₂ = P ₁ V ₁ / V ₂ = (1 атм) (2 л) / 3,5 л) = 0,6 атм

Поскольку в вопросе никогда не упоминается температура, мы можем предположить, что она остается постоянной и поэтому будет отменена при вычислении.Вы также должны подумать над ответом, который вы получите с точки зрения того, что вы знаете о газах и о том, как они действуют. Мы увеличили объем, поэтому давление должно снизиться. Проверяя наш ответ, он кажется правильным, поскольку давление упало с 1 атм до 0,6 атм.

Итак, единственное уравнение, которое вам действительно нужно знать, – это закон комбинированного газа для расчета изменений свойств газа.

Вот некоторые практические проблемы с решениями: Практика

Вот некоторые проблемы для других газовых законов, которые вы можете вывести из закона о комбинированном газе: Практика и ПОЗ.

11.9: Закон идеального газа: давление, объем, температура и моль

Существует ряд химических реакций, для которых требуется аммиак. Чтобы провести реакцию эффективно, нам нужно знать, сколько аммиака у нас есть для стехиометрических целей. Используя законы газа, мы можем определить количество молей, присутствующих в резервуаре, если мы знаем объем, температуру и давление в системе.

Закон об идеальном газе

Закон комбинированного газа показывает, что давление газа обратно пропорционально объему и прямо пропорционально температуре.Закон Авогадро показывает, что объем или давление прямо пропорциональны количеству молей газа. Если сложить все вместе, получится следующее уравнение:

\ [\ dfrac {P_1 \ times V_1} {T_1 \ times n_1} = \ dfrac {P_2 \ times V_2} {T_2 \ times n_2} \]

Как и в случае с другими газовыми законами, мы также можем сказать, что \ (\ frac {\ left (P \ times V \ right)} {\ left (T \ times n \ right)} \) равно константе. Константу можно оценить при условии, что описываемый газ считается идеальным.

Закон об идеальном газе – это единое уравнение, которое связывает давление, объем, температуру и количество молей идеального газа. Если мы подставим константу в переменную \ (R \), уравнение станет:

\ [\ dfrac {P \ times V} {T \ times n} = R \]

Закон идеального газа удобно изменить так, чтобы он выглядел так, без знаков умножения:

\ [PV = nRT \]

Переменная \ (R \) в уравнении называется постоянной идеального газа .

Определение постоянной идеального газа

Значение \ (R \), постоянной идеального газа, зависит от единиц, выбранных для давления, температуры и объема в уравнении идеального газа. Для температуры необходимо использовать градусы Кельвина, а для объема принято использовать единицы СИ – литры. Однако давление обычно измеряется в одной из трех единиц: \ (\ text {kPa} \), \ (\ text {atm} \) или \ (\ text {mm} \: \ ce {Hg} \). Следовательно, \ (R \) может иметь три разных значения.

Мы покажем, как рассчитывается \ (R \), когда давление измеряется в \ (\ text {kPa} \).Объем \ (1.00 \: \ text {mol} \) любого газа на STP (стандартная температура, 273,15 K и давление, 1 атм) измеряется как \ (22.414 \: \ text {L} \). В уравнение идеального газа и решите относительно \ (R \).

\ [\ begin {align *} R & = \ frac {PV} {nT} \\ [4pt] & = \ frac {101.325 \: \ text {kPa} \ times 22.414 \: \ text {L}} { 1.000 \: \ text {mol} \ times 273.15 \: \ text {K}} \\ [4pt] & = 8.314 \: \ text {кПа} \ cdot \ text {L / K} \ cdot \ text {mol} \ end {align *} \]

Это значение \ (R \), которое должно использоваться в уравнении идеального газа, когда давление задано в \ (\ text {kPa} \). В таблице ниже приведены краткие сведения об этом и других возможных значениях \ (R \). Важно выбрать правильное значение \ (R \) для использования в данной задаче.

Таблица \ (\ PageIndex {1} \): значения постоянной идеального газа
Единица \ (P \)	Единица \ (В \)	Единица \ (n \)	Единица \ (Т \)	Стоимость и единица \ (R \)
\ (\ text {кПа} \)	\ (\ text {L} \)	\ (\ text {mol} \)	\ (\ text {K} \)	\ (8.314 \: \ text {J / K} \ cdot \ text {mol} \)
\ (\ text {atm} \)	\ (\ text {L} \)	\ (\ text {mol} \)	\ (\ text {K} \)	\ (0,08206 \: \ text {L} \ cdot \ text {atm / K} \ cdot \ text {mol} \)
\ (\ text {mm} \: \ ce {Hg} \)	\ (\ text {L} \)	\ (\ text {mol} \)	\ (\ text {K} \)	\ (62.36 \: \ text {L} \ cdot \ text {mm} \: \ ce {Hg} / \ text {K} \ cdot \ text {mol} \)

Обратите внимание, что единица измерения для \ (R \), когда давление находится в \ (\ text {kPa} \), была изменена на \ (\ text {J / K} \ cdot \ text {mol} \) . \ text {o} \ text {C} \)? Предположим, что кислород идеален.\ text {o} \ text {C} = 292 \: \ text {K} \)

Масса \ (\ ce {O_2} = 3.76 \: \ text {g} \)

Найти: V =? L

Перечислите другие известные количества.

\ (\ ce {O_2} = 32,00 \: \ text {г / моль} \)

\ (R = 8.314 \: \ text {J / K} \ cdot \ text {mol} \)

Спланируйте проблему.

Сначала определите количество молей O ₂ из заданной массы и молярной массы.
Затем измените уравнение алгебраически, чтобы найти V

\ [V = \ frac {nRT} {P} \ nonumber \]

Рассчитать.

\ [3.76 \: \ cancel {\ text {g}} \ times \ frac {1 \: \ text {mol} \: \ ce {O_2}} {32.00 \: \ cancel {\ text {g}} \ : \ ce {O_2}} = 0,1175 \: \ text {mol} \: \ ce {O_2} \ nonumber \]

2.Теперь подставьте известные величины в уравнение и решите.

\ [V = \ frac {nRT} {P} = \ frac {0.1175 \: \ cancel {\ text {mol}} \ times 8.314 \: \ cancel {\ text {J / K}} \ cdot \ cancel { \ text {mol}} \ times 292 \: \ cancel {\ text {K}}} {88.4 \: \ cancel {\ text {kPa}}} = 3.23 \: \ text {L} \: \ ce {O_2 } \ nonumber \]

Подумайте о своем результате. Количество молей кислорода намного меньше одного моля, поэтому объем должен быть довольно небольшим по сравнению с молярным объемом \ (\ left (22.4 \: \ text {L / mol} \ right) \), поскольку давление и температура достаточно близки к стандартным. Результат состоит из трех значащих цифр из-за значений для \ (T \) и \ (P \). Поскольку джоуль \ (\ left (\ text {J} \ right) = \ text {kPa} \ cdot \ text {L} \), единицы компенсируются правильно, оставляя объем в литрах.

Пример \ (\ PageIndex {2} \): газ аргон

Образец 4,22 моля Ar имеет давление 1,21 атм и температуру 34 ° C. Каков его объем?

Решение

Этапы решения проблем
Определите «данную» информацию и то, что проблема просит вас «найти».«	Дано: n = 4,22 моль P = 1,21 атм Т = 34 ° С Найти: V =? L
Перечислите другие известные количества.	нет
Спланируйте проблему.	1.Первый шаг – перевести температуру в Кельвин. 2. Затем измените уравнение алгебраически, чтобы найти V \ [V = \ frac {nRT} {P} \ nonumber \]
Рассчитать.	1. 34 + 273 = 307 К 2. Теперь подставьте известные величины в уравнение и решите. \ [\ begin {align } V = \ frac {(4.22 \, \ cancel {mol}) (0.08205 \ frac {L. \ cancel {atm}} {\ cancel {mol.K}}) (307 \, \ cancel {K)}} {1.21 \ cancel {atm} } \\ [4pt] & = 87.9 \, L \ end {align } \]
Подумайте о своем результате.	Количество молей Ar велико, поэтому ожидаемый объем также должен быть большим.

Упражнение \ (\ PageIndex {1} \)

Образец 0,0997 моль O ₂ имеет давление 0,692 атм и температуру 333 К.Каков его объем?

Ответ

3,94 л

Упражнение \ (\ PageIndex {2} \)

Для 0,00554 моль образца H ₂, P = 23,44 торр и T = 557 K. Каков его объем?

Ответ

8,21 л

Идеальное поведение газа – StatPearls

Введение

Закон идеального газа – это простое уравнение, демонстрирующее взаимосвязь между температурой, давлением и объемом для газов.Эти конкретные отношения вытекают из закона Шарля, закона Бойля и закона Гей-Люссака. Закон Чарльза определяет прямую пропорциональность между объемом и температурой при постоянном давлении, закон Бойля определяет обратную пропорциональность давления и объема при постоянной температуре, а закон Гей-Люссака определяет прямую пропорциональность давления и температуры при постоянном объеме. Вместе они образуют уравнение закона идеального газа: PV = NRT. P – давление, V – объем, N – количество молей газа, R – универсальная газовая постоянная, а T – абсолютная температура.

Универсальная газовая постоянная R – это число, которое удовлетворяет пропорциям зависимости давление-объем-температура. R имеет разные значения и единицы, которые зависят от давления, объема, молей и температуры пользователя. Различные значения R находятся в онлайн-базах данных, или пользователь может использовать анализ размеров для преобразования наблюдаемых единиц давления, объема, молей и температуры в соответствие с известным значением R. Если единицы согласованы, приемлем любой подход.Значение температуры в Законе идеального газа должно быть в абсолютных единицах (Ренкин [градусы R] или Кельвин [K]), чтобы правая часть не была равна нулю, что нарушает соотношение давления-объема-температуры. Преобразование в абсолютные единицы температуры является простым добавлением к температуре по Фаренгейту (F) или Цельсию (C): градусы R = F + 459,67 и K = C + 273,15.

Для того, чтобы газ был «идеальным», есть четыре основных допущения:

Частицы газа имеют незначительный объем.
Частицы газа одинакового размера и не имеют межмолекулярных сил (притяжения или отталкивания) с другими частицами газа.
Частицы газа движутся случайным образом в соответствии с законами движения Ньютона.
Частицы газа совершают идеальные упругие столкновения без потери энергии.

На самом деле идеальных газов не бывает. Любая частица газа обладает объемом в системе (незначительным, но тем не менее присутствующим), что нарушает первое предположение.Кроме того, частицы газа могут быть разного размера; например, газообразный водород значительно меньше газообразного ксенона. Газы в системе действительно имеют межмолекулярные силы с соседними частицами газа, особенно при низких температурах, когда частицы не движутся быстро и не взаимодействуют друг с другом. Несмотря на то, что частицы газа могут двигаться беспорядочно, они не имеют совершенных упругих столкновений из-за сохранения энергии и импульса внутри системы. [1] [2] [3]

Идеальные газы – это строго теоретическая концепция, но реальные газы могут вести себя идеально при определенных условиях.Системы с очень низким давлением или высокими температурами позволяют оценивать реальные газы как «идеальные». Низкое давление в системе позволяет частицам газа испытывать меньшие межмолекулярные силы с другими частицами газа. Точно так же высокотемпературные системы позволяют частицам газа быстро перемещаться внутри системы и проявлять меньшие межмолекулярные силы друг с другом. Следовательно, для целей расчетов реальные газы можно считать «идеальными» как для систем низкого давления, так и для высокотемпературных систем.

Закон идеального газа также верен для системы, содержащей несколько идеальных газов; это известно как идеальная газовая смесь. При наличии нескольких идеальных газов в системе предполагается, что эти частицы не имеют никаких межмолекулярных взаимодействий друг с другом. Идеальная газовая смесь разделяет общее давление системы на парциальные составляющие давления каждой из различных частиц газа. Это позволяет переписать предыдущее уравнение идеального газа: Pi · V = ni · R · T. В этом уравнении Pi – это парциальное давление компонентов i, а ni – моли компонентов i.В условиях низкого давления или высоких температур газовые смеси могут считаться идеальными газовыми смесями для простоты расчета.

Когда системы не работают при низком давлении или высоких температурах, частицы газа могут взаимодействовать друг с другом; эти взаимодействия сильно снижают точность закона идеального газа. Однако существуют и другие модели, такие как уравнение состояния Ван-дер-Ваальса, которые учитывают объем частиц газа и межмолекулярные взаимодействия. Обсуждение, выходящее за рамки закона об идеальном газе, выходит за рамки данной статьи.

Функция

Несмотря на другие более строгие модели для представления газов, закон идеального газа универсален для представления других фаз и смесей. Christensen et al. провели исследование по созданию калибровочных смесей кислорода, изофлурана, энфлурана и галотана. Эти газы обычно используются в анестетиках, которые требуют точных измерений для обеспечения безопасности пациента. В этом исследовании Christensen et al. сравнил использование предположения об идеальном газе с более строгими моделями для определения парциальных давлений каждого из газов.Предположения об идеальном газе имели ошибку 0,03% для калибровочного эксперимента. Это исследование пришло к выводу, что ошибку из предположения об идеальном газе можно использовать для настройки калибровки анестетиков, но само отклонение не было значительным для предотвращения использования на пациентах. [4] [5] [6]

Помимо газовых смесей, закон идеального газа может моделировать поведение определенных плазм. В исследовании Oxtoby et al. Исследователи обнаружили, что пылевые частицы плазмы можно смоделировать с помощью поведения идеального газа.Исследование предполагает, что причина такого сходства связана с низкой степенью сжатия пылевой плазмы, обеспечивающей идеальное поведение газа. Хотя необходимо будет создать более сложные модели, плазменные фазы были точно представлены в соответствии с законом идеального газа.

Идеальные газы также внесли свой вклад в изучение поверхностного натяжения воды. Sega et al. доказал, что вклад идеального газа в поверхностное натяжение воды не тривиален, а весьма ограничен. Sega et al. создали новое выражение, которое лучше отражает вклад идеального газа в поверхностное натяжение.Это может позволить более точное представление границ раздела газ-жидкость в будущем.

Закон идеального газа и его поведение в первую очередь служат первым шагом к получению информации о системе. Доступны более сложные модели для точного описания системы; однако, если точность не является главным соображением, закон идеального газа обеспечивает простоту вычислений, обеспечивая при этом физическое понимание системы. [7] [8]

Проблемы, вызывающие озабоченность

Основная проблема Закона об идеальном газе заключается в том, что он не всегда точен, поскольку истинных идеальных газов не существует.Основные предположения Закона об идеальном газе являются теоретическими и не учитывают многие аспекты реальных газов. Например, закон идеального газа не учитывает химические реакции, происходящие в газовой фазе, которые могут изменить давление, объем или температуру системы. Это серьезная проблема, потому что давление может быстро возрасти в газовых реакциях и быстро стать угрозой безопасности. Другие зависимости, такие как уравнение состояния Ван-дер-Ваальса, более точны при моделировании реальных газовых систем.

Клиническая значимость

Закон идеального газа представляет собой простой расчет для определения физических свойств данной системы и служит в качестве исходного расчета. Как было исследовано Кристенсеном и др., Закон идеального газа можно использовать для калибровки смесей анестетиков с номинальной погрешностью. На большой высоте закон идеального газа будет более точным для контроля давления потока газа в пациента, чем на уровне моря. При значительных колебаниях температуры необходимо отрегулировать давление, необходимое для доставки кислорода пациенту; Закон идеального газа можно использовать в качестве приближения.В то время как более сложные вычисления обеспечивают в целом большую точность, закон идеального газа может развить интуицию врача при работе с реальными газами.

Улучшение результатов группы здравоохранения

Все члены межпрофессиональной группы здравоохранения, будь то клиницисты, медсестры, специалисты по анестезии или медсестры по анестезии, должны быть знакомы с Законом об идеальных газах и его применением в медицине. Простота использования формулы и ее применения может предотвратить врачебные ошибки и оптимизировать уход за пациентом в определенных ситуациях (например,g., анестезия), где это применимо. [Уровень 5]

Кинетическая температура, тепловая энергия

Статистические методы становятся более точным способом изучения природы при большом количестве частиц. Таким образом, мы ожидаем, что описание скоростей молекул в газе на самом деле будет наиболее вероятным распределением, поскольку мы имеем дело с числами частиц в диапазоне числа Авогадро. Но это наиболее вероятное распределение (распределение Максвелла-Больцмана) подчиняется ограничениям, а именно, что число частиц постоянно и что полная энергия постоянна (закон сохранения энергии).Максимизация вероятностного распределения с учетом этих ограничений в целом является сложной математической задачей (см., Например, Richtmyer и др.). Один из способов подойти к решению более интуитивно – это рассмотреть известный нам физический пример, а именно физику атмосферы под действием силы тяжести, отраженную в барометрической формуле. Следующее лечение следует за разработкой Rohlf.

В этом подходе мы используем тот факт, что средняя кинетическая энергия молекул может быть выражена через кинетическую температуру.Кроме того, мы знаем, что сохранение энергии в этом случае включает просто баланс кинетической энергии и гравитационной потенциальной энергии, если мы рассматриваем атмосферу как идеальный газ.

Из выражения для кинетической температуры

у нас есть экспериментально проверенное выражение для молекулярной кинетической энергии. В барометрической формуле:

у нас есть описание идеальной газовой системы, которое можно использовать, чтобы помочь разработать аргумент правдоподобия для распределения Максвелла по скоростям.Шаги в этом процессе следующие:

Для одного направления в пространстве этот процесс дает выражение:

, а когда включены все направления скорости, получается соотношение распределения скорости Максвелла:

Следует отметить, что хотя мы использовали физическую ситуацию, зависящую от гравитации, для получения распределения скоростей, гравитация не появляется в конечном результате. То есть полученный результат является общим, не содержащим g. Барометрическая формула использовалась просто как конструкция, чтобы связать распределение скоростей с ограничениями по энергии и количеству частиц.

Как сделать P V T давление объем температура формула расчетов газа Закон Бойля Закон Чарльза Закон Гей-Люссака Идеальное поведение газа Примеры пересмотра Графики GCSE химия физика KS4 наука A Level igcse revision notes

Док Брауна Химия KS4 science GCSE / IGCSE / AS Chemistry Revision Notes

Часть 2 Подробнее продвинутые темы об идеальном газе законы, расчеты, теория кинетических моделей частиц (разделы 4a – 4b)

Более продвинутые идеи, вовлекающие газы расчет газового закона с использованием закона Бойля, закона Чарльза, закона Гей-Люссака, P1V1 / T1 = P2V2 / T2.Газовые законы, касающиеся давления, объема и температура очень важна как для GCSE, так и для A level Chemistry

Основная теория частиц и свойства газов, жидкости и твердые тела, изменения состояния и решения описаны на Заметки GCSE / IGCSE по моделям частиц газов, жидкостей и твердых тел, описание и объяснение их свойств, и продвинутые студенты должны быть знакомы со ВСЕМ его содержанием перед изучением этой страницы ….

Субиндекс для части 2: Раздел 4 Поведение идеального газа и законы газа: Введение кинетическая теория частиц идеального газа * Температурная шкала Кельвина * 4а Закон Бойля * 4b.Закон Чарльза и Гей-Люссака и уравнение комбинированного закона газа * 4c. Уравнение идеального газа PV = nRT * 4d. Закон Дальтона о парциальных давлениях * 4e. Закон диффузии Грэма * 5а. Отклонения газов от идеального поведение и их причины * 5b. Уравнение состояния Ван-дер-Ваальса * 5c Коэффициенты сжимаемости * 5d В Критическая точка Критическая температура и критическое давление *

Для других расчетов см. страница “Индекс расчетов” включая определение родинки и Константа Авогадро

И молярный объем газа и объемные соотношения реагирующих газов.

Максвелл Больцмановское распределение кинетических энергий частиц обсуждается в КИНЕТИКА страницы.

Док Брауна Заметки о пересмотре химии: химия в основной школе, химия GCSE, химия IGCSE, уровень O & ~ Школьные курсы естественных наук для 8, 9 и 10 классов в США или их эквиваленты для детей от 14 до 16 лет студенты естественных наук на государственном экзамене по химии

4.Идеальное поведение газа и газовые законы

Введение в кинетическую модель частиц идеального газа

(продвинутый) кинетический Теория газов основана на следующих шести фундаментальных постулатах:
1. Газы состоят из мельчайшие дискретные частицы (обычно молекулы).
2. Частицы находятся в непрерывное хаотическое движение, движущееся по прямым линиям между очень частыми столкновениями с друг друга и стороны контейнера (примерно 10 ⁹ / с).
3. Обстрел стенки контейнера частицами вызывают явление, которое мы называем давлением (т.е. сила удара на единицу площади). Чем больше сила столкновения и чем чаще происходят столкновения, тем больше давление газа на поверхность контейнера.
4. Столкновения идеально эластичный, т.е. без потерь энергии при столкновении из-за трения.
5. На относительно низком уровне давления среднее расстояние между частицами велико по сравнению с диаметр частиц и, следовательно, межмолекулярные силы между частиц можно пренебречь.
6. Средняя кинетическая энергия частиц прямо пропорциональна их абсолютной температуре по шкале Кельвина (K), т.е. KE (J) Т (К)
  - Это означает, что если вы нагреете газ, средняя кинетическая энергия частиц увеличивается, поэтому средняя скорость тоже увеличивается.
  - Температурная шкала Кельвина объяснено ниже.
Когда ведет себя газ согласно этой модели, законы газа, описанные в разделах 4a – 4e, являются повиновался.
Однако в реальных газах все не так просто, и это неидеальное поведение обсуждается в разделе 5.

Температурная шкала Кельвина

В прошлом было проведено много измерений. сделано, чтобы исследовать, как (i) давление и объем данной массы изменяются при постоянная температура и как (ii) давление и объем газа фиксированной массы газ меняется в зависимости от температуры (см. два графика слева и справа).Это привело в формулировке законов газов, описанных в следующем разделе 4а. вместе как использовать их в расчетах и решении задач.

Однако перед этим, если вы посмотрите на эти два графика поведения газа при изменении давления или объема в зависимости от температуры, одна вещь становится ясной, когда линии графика экстраполируются обратно на x по оси они дают значение 273 ^o C. Это породило идею, что была минимально возможная температура 273 ^o ° C и дальнейшие эксперименты подтверждали это снова и снова.При 273 ^o ° C все вещества твердые и с точки зрения кинетической теории частиц материи, при 273 ^o C частицы практически не двигаются т.е. ~ нет колебания атомов в твердом теле.

Следовательно, как и , установлен Шкала Цельсия (шкала Цельсия), новая шкала температуры была предложена в наименьшее значение которого было 0 (известное как абсолютный ноль ), а не 273. Это называется шкалой Кельвина для температуры или абсолютной температуры. Температурная шкала , обозначается единицей К .Между прочим, вы не говорите градусы Кельвина, как вы говорите градусы Цельсия, вы просто говорит Кельвин. Температурная шкала Кельвина также была разработана таким образом, чтобы 1 K изменение температуры или интервал, точно равно 1 ^o C Изменение по Цельсию или интервал. Таким образом, вы можете легко переключаться между двумя шкалами температур. простым расчетом

K = ^o C + 273 и ^o C = K 273 и это температура в К, которую вы должны использовать в расчетах по закону газа (4b.)

Некоторые примеры разработаны ниже и потренируйтесь в чтении термометра Цельсия, который вы используете в школе или колледж лаборатория!

7 ^o С

7 + 273 = 267 К

36 ^o С

36 + 273 = 309 К

77 ^o С

77 + 273 = 350 К

101.5 ^o С

101,5 + 273,0 = 374,5 К

132 ^o С

132 + 273 = 405 К

206 ^o С

206 + 273 = 479 К

Некоторые знакомые температуры указаны ниже. связь двух температурных шкал

	абсолютное ноль	Замораживание точка воды	Кузов температура	Кипячение точка воды
Цельсия шкала	273 ^o С	0 ^o С	37 ^o С	100 ^o С
Кельвин шкала	0 К	273 К	310 К	373 К

Кажется немного странным сказать, что ваше тело температура 310, поэтому всегда важно указывать и единицы измерения!

НАЧАЛО СТРАНИЦЫ

5.Модель частиц газа – движение и давление газа

Все частицы имеют массу , и их движение дает им кинетическую энергию и импульс.
Частицы в газе находятся в постоянном случайное движение – случайное направление, различные скорости и кинетические энергии.
Когда быстро движутся частицы газа сталкиваются с поверхностью, их миллионы ударов создают силу, которую мы измерить как давление газа – суммарную силу ударов на единицу площади.
Частицы сталкиваются с контейнером поверхность полностью случайна и ударяется под любым углом, НО, эффект создать чистую силу под прямым углом к поверхности – давление газа!
Чем больше количество столкновений на единицу площади поверхности, тем выше давление, если объем газа и температура остаются постоянными.
Если температура поддерживается постоянной и объем увеличился, удары стали более распространенными и менее частыми за единицу площади, поэтому давление газа снижается.
- И наоборот, если газ сжатие в меньший объем при постоянной температуре, число ударов на единицу площади увеличивается, поэтому давление увеличивается.
- Из измерений объемов и давление газов при постоянном давлении, числовой обратный закон может можно сформулировать – закон Бойля .
- давление x объем = постоянная (при постоянной температуре)
- pV = постоянная
- p = давление в паскалях (Па), V = объем (м ³)
- Вы можете подключить два давления и два объема по простому уравнению
- p ₁ x V ₁ = p ₂ x V ₂
- , где 1 представляет оригинал условия, и 2 конечная ситуация, если принудительное изменение p ₁ или V ₁.
- Примеры простого газа расчеты

Подробнее о расчетах давления и объема газа

4а. Закон Бойля для объема и газа давление

Теория частиц давления газа было объяснено в Части 1 поэтому в этом разделе основное внимание уделяется закону газа расчеты давления и объема .
Закон Бойля гласит, что для данной массы газа при постоянной температуре (^o C или K) произведение давления, умноженное на объем постоянный.
p x V = константа
Следовательно, для начального значения p ₁ и V ₁, которые изменяются до конечных значений p ₂ и V ₂, следующие уравнение применимо…
p ₁ x V ₁ = p ₂ x V ₂ (для фиксированного количества газа при постоянной температура)
или п ₂ = p ₁ x V ₁ / V ₂ _{или V ₂ = p ₁ x V ₁ / p ₂}
График показывает, как давление и объем изменяются согласно закону Бойлса при двух разных температурах.
При более низких температурах объем и давление значения ниже (см. следующий раздел).
Вы можете использовать любой объем или единицы давления, которые вам нравятся, пока и , и p, и V имеют то же шт. .
Использование теории частиц и Простые арифметические значения объясняют закон Бойлса .
- Если газ сжат до половины Исходный объем: концентрация или плотность газа увеличивается вдвое.Следовательно будет вдвое больше столкновений с поверхностью, что приведет к удвоению ударный эффект, т.е. удвоение давления.
- Если объем газа увеличивается в три раза, концентрация уменьшается в том же размере. фактор, поэтому вероятность столкновения частиц со стенками контейнера составляет аналогично уменьшается, поэтому давление уменьшается в три раза.
Газы e.грамм. кислород для больниц, может быть хранятся под высоким давлением, что обеспечивает достаточно эффективное хранение. Потому что внутреннее давление в цилиндре намного больше, чем внешнее давление, при установке клапана большой объем газа может быть выпущен в поток медленно в контролируемых условиях для дыхания пациента.
Примеры расчетов по закону Бойля (предполагается постоянная температура)
Бывший.4 кв. 1
- 240см ³ воздуха при давлении 100кПа в велосипедном насосе сжимается до объема 150см ³.
- Какое давление сжатый воздух в насосе?
- p ₁ x V ₁ = p ₂ x V ₂, перекомпоновка для масштабирования под новый повышенное давление
- п. ₂ = p ₁ x V ₁ / V ₂ = 100 x 240/150 = 160 кПа
Бывший.Q4a 2
- 10 м ³ бутана газ под давлением 1,2 атм требовалось хранить при давлении 6 атм. На какой объем должен ли газ быть сжат до необходимого давления хранения?
- p ₁ x V ₁ = p ₂ x V ₂, переставляем в уменьшенное для нового нижний объем
- В ₂ = p ₁ x V ₁ / p ₂ = 1.2 x 10/6 = 2,0 м ³
Бывший. Q4a 3
- A 100 см ³ газовый шприц содержащий 80 см ³ газа, сжатого до 60 см ³. Если атмосферное давление составляет 101325 Па, а температура остается постоянной, какое давление газа в шприце после сжатия.
- p x V = постоянная
- p ₁ x V ₁ = p ₂ х В ₂
- п. ₂ = p ₁ x V ₁ / V ₂
- п. ₂ = 101325 x 80/60 = 135100 Па
Бывший.4 квартал
- В стационаре давление газа в 100 дм ³ Баллон с кислородом составляет 5,52 атм (5-кратное атмосферное давление). Какой объем газ может медленно выделяться пациенту при выпуске его в атмосферное давление 1,01?
- p x V = постоянная
- В ₂ = p ₁ x V ₁ / p ₂
- В ₂ = p ₁ x V ₁ / p ₂ = 5.52 x 100 / 1,01 = 546,5 дм ³

НАЧАЛО СТРАНИЦЫ

Расчеты 4б. Закон Чарльза / Закон Гей-Люссака для давления / объема и температура

и комбинированные уравнение закона газа

Теория частиц давления газа было объяснено в части 1 , поэтому в этом разделе основное внимание уделяется закону газа. расчеты, включающие давление и объем и их изменение с температура.
Закон Чарльза / Гей-Люссака гласит, что для фиксированной массы газа …
- (i) объем газа напрямую пропорциональна абсолютной температуре (K) при постоянном давлении
  - V = постоянная x T (правый график) или
  - В / Т = постоянная , или
  - В ₁ / В ₂ = T ₁ / T ₂ для условий, изменяющихся с 1 (начальное) до 2 (финал),
  - или В ₁ / T ₁ = V ₂ / T ₂ для постоянного давления
  - V ₁ x T ₂ = V ₂ х Т ₁
  - В ₂ = В ₁ x Т ₂ / Т ₁
  - или T ₂ = Т ₁ x В ₂ / В ₁
  - Кинетические рассуждения о частицах – увеличение температура увеличивает кинетическую энергию молекул, давая более сильные столкновения, которые выталкивают (расширяют) газ при постоянном давление.
  - Обратите внимание, что графики экстраполируют назад к 0K (абсолютный ноль, шкала Кельвина) или -273 ^o C (Шкала Цельсия).
- OR (ii) давление газа прямо пропорционально абсолютной температуре (K) при постоянном объеме ,
  - p = константа x T (правый график), или
  - p / T = постоянная , или
  - п. ₁ / п ₂ = T ₁ / T2 для условий, изменяющихся с 1 (начального) до 2 (финал),
  - или p ₁ / T ₁ = p ₂ / T ₂ для постоянного объема
  - п ₁ x Т ₂ = Т ₁ x п ₂
  - p ₂ = p ₁ x Т ₂ / Т ₁
  - или T ₂ = T ₁ x p ₂ / p ₁
  - Кинетические рассуждения о частицах – увеличение температура увеличивает кинетическую энергию молекул, давая более сильные столкновения, которые увеличивают давление, если объем стесненный (постоянный).
  - Отметим еще раз, что графики экстраполировать обратно к 0K (абсолютный ноль, шкала Кельвина) или -273 ^o C (Шкала Цельсия).
Во всех расчетах абсолютная температура или шкала Кельвина должны использоваться для T ( K = ^o C + 273 ).
Если все законы описаны в 4a и 4b объединены, вы получите следующее общее выражение
p x V / T = постоянная (для заданная масса газа).
Это может быть выражено в обобщенная форма для расчетов на основе начальный набор из условий ₁ (1) изменение на новый и окончательный набор условий ₂ (2) для данной массы газа, что дает уравнение для расчета комбинированного давления, объема, температуры газа …
p ₁ x V ₁ p ₂ x V ₂
=
Т ₁ Т ₂
Сокращенно ‘: p ₁ V ₁ / T ₁ = p ₂ V ₂ / T ₂
поэтому три перестановки для решения проблем с участием всех трех переменных:
- p ₂ = p ₁ V ₁ T ₂ / В ₂ Т ₁
- В ₂ = p ₁ V ₁ T ₂ / p ₂ T ₁
- Т ₂ = p ₂ V ₂ T ₁ / p ₁ V ₁
Если одна переменная постоянна, перестановки для двух других переменных:
- p ₂ = p ₁ V ₁ / V ₂ (при постоянном температура)
- В ₂ = В ₁ Т ₂ / Т ₁ (при постоянном давлении)
- Т ₂ = p ₂ T ₁ / p ₁ (при постоянном объеме)
Примечание :
- Если температура постоянная, вы получите Закон.
- Если p или V постоянны, вы получить закон Чарльза / Гей-Люссака.
- Вы можете использовать любой объем или единицы давления, которые вам нравятся, пока и p, или , оба V имеют то же шт. .
- Графики p или V зависимости от температуры становятся недействительными после того, как газ конденсируется в жидкость, НО при экстраполяции назад все строки кажутся происходящими из y = 0 (для p или V), x = 273 ^o C (для T).
- Это было частью научных доказательств. это привело к убеждению, что 273 ^o C было минимально возможным температура, хотя теоретического верхнего предела нет вообще.
- Это привело к созданию нового термодинамического абсолюта. температурная шкала или шкала Кельвина, которая начинается с ОК.
Примеры расчета PVT
Бывший.4b 1 квартал
- Давление, оказываемое газ в герметичном контейнере составляет 100 кПа при 17 ^o C. Было обнаружено, что контейнер может протечь, если внутреннее давление превысит 120 кПа. Предполагая постоянный объем, при какой температуре в ^o C будет контейнер начать течь?
- 17 ^o C + 273 = 290 К
- п. ₁ / т. ₁ = P ₂ / T ₂
- переставляем по размеру до более высокого температура
- T ₂ = T ₁ x p ₂ / p ₁
- T ₂ = 290 x 120/100 = 348 K или 348 273 = 75 ^o C когда контейнер может протечь
Бывший.4b 2 квартал
- Баллон пропана газ при 20 ^o ° C оказывал давление 8,5 атмосфер. При воздействии на солнце она прогревается до 28 ^o С. Какое давление оказывает контейнерная сторона теперь опыт?
- 20 ^o С = 273 + 20 = 293K, 28 ^o C = 273 + 28 = 301K
- p ₂ = p ₁ x Т ₂ / Т ₁
- p ₂ = 8.5 x 301/293 = 8,73 атм
Бывший. 4b 3 квартал
- Студент был исследование скорости реакции между гранулами известняка и различными концентрации соляной кислоты. Однако после выполнения целой серии экспериментов с разными концентрациями кислоты, не было времени заниматься последний запланированный эксперимент. Объем углекислого газа, собранный через 5 минут в 100 см ³ газовый шприц использовали для определения скорости реакции.Все эксперименты проводились за одно занятие при температуре 22 ^o ° C кроме последнего. Это было сделано на следующем уроке, давая углеродный объем диоксида 47,0 см ³ через 5 минут, но при более высоком температура 27 ^o C (в градусах Кельвина назовите это T ₁ , а другая температура T ₂ ).
- Сделать данные справедливый анализ, в идеале все объемы газа должны измеряться в одном и том же температура, но можно внести поправку для последнего эксперимента.
- (а) Рассчитайте объем объем 47.0 см ³ газа при 27 ^o C, будет занимать при 22 ^o C.
  - В ₁ / В ₂ = Т ₁ / Т ₂ поэтому V ₂ = V ₁ x Т ₂ / Т ₁
  - В ₁ = 47.0 см ³, T ₁ = 273 + 27 = 300K, T ₂ = 273 + 22 = 295 КБ
  - В ₂ = 47,0 x 295/300 = 46,2 см ³
- (б) Если температура было проигнорировано, каков% погрешности измерения скорости реакции?
  - Ошибка объема = 47.0 46,2 = +0,8 см ³, следовательно ….
  - Ошибка
    % = 0,8 x 100/47 = + 1,7% (так что вы бы переоценили скорость реакции без этой поправки)
  - % ошибки в объем будет таким же, как рассчитанный для ставки, например в см ³ / мин.
- (c) Если Расчетное значение для 22 ^o C должно использоваться при расчете скорости анализ? и это еще один источник ошибок?
  - г. теоретический расчетный объем газа для 22 ^o ° C следует использовать для вычисляя скорость, это немного повысит точность, НО есть другая проблема!
  - Если реакция была к сожалению, выполняется при более высокой температуре (т.е.е. 27 ^o C) есть второй источник ошибок. При более высокой температуре реакция быстрее, поэтому вы обязательно получите больший объем газа, образованный за пять минут. Поэтому вы рассчитаете более высокую скорость реакции, например, в см ³ газа в минуту при 27 ^o C, что могло бы произойти / было бы измерено при 22 ^o C и поэтому несправедливое сравнение со всеми остальными результатами предыдущего урок.
  - Итак, хотя можно достаточно хорошо исправить ошибку объема из-за «расширенного» объема газа при при более высокой температуре объем газа все равно будет слишком большим из-за более высокая скорость реакции при 27 ^o C , и вас не так много может исправить эту ошибку, за исключением того, что повторить эксперимент при 22 ^o ° C, что в любом случае лучше всего делать !
    - Обратите внимание, что если температура эксперимента скорости была слишком низкой по сравнению со всеми другими экспериментов, “двойная ошибка” повторится снова, но на этот раз измеренный объем газа и расчетная скорость / скорость реакции будут ниже чем ожидалось.
- (d) Вам нужно сделать какая поправка на объем кислоты, добавленной в известняк? Объясни свой решение.
  - Коррекция не требуется для этого у всех . Хотя жидкости расширяются / сжимаются при нагревании / охлаждении, объем изменения намного меньше по сравнению с изменениями объема газа при той же температуре изменение. Это связано с относительно сильными межмолекулярными силами между жидкими молекулы, которые практически отсутствуют в газах.
Бывший. 4b 4 квартал
- 25 см ³ газа при 1.01 атм. при 25 ^o C был сжат до 15 см ³ при 35 ^o C.
- Рассчитать финал давление газа.
- p ₁ = 1,01 атм, p ₂ =?, V ₁ = 25 см ³, V ₂ = 15 см ³,
- Т1 = 25 + 273 = 298 К, Т2 = 35 + 273 = 308 К
- (p ₁ x V ₁) / T ₁ = (p ₂ x V ₂) / T ₂
- p ₂ = (p ₁ x V ₁ x Т ₂) / (В ₂ x Т ₁)
- p ₂ = (1.01 x 25 x 308) / (15 x 298) = 1,74 атм
Бывший. 4b 5 квартал
Бывший. 4b Q6
- Топливные и воздушные газы в цилиндрах двигателя автомобиля 1200 см ³ перейти от 25 ^o C до сгорание и повышение до пиковой температуры 2100 ^o C после горение. Если нормальное атмосферное давление составляет 101 кПа, рассчитайте пиковое давление, достигнутое после сгорания.Хотя движение поршня изменяет громкость, (i) ради аргумента предположим, что громкость постоянный.
- Т ₁ = 25 + 273 = 298 К, Т ₂ = 2100 + 273 = 2373 К, P1 = 101 кПа
- p / T = константа
- п. ₁ / п. ₂ = Т ₁ / Т2
- p ₂ = p ₁ x Т ₂ / Т ₁
- p ₂ = 101 x 2373/298 = 804 кПа
  - (ii) Для большей реалистичности предположим, что начальный объем паров топлива и воздуха составлял 400 см3, теперь пересчитайте конечное давление.
  - Теперь вам нужно использовать полный PVT выражение.
  - (p ₁ x V ₁) / T ₁ = (p ₂ x V ₂) / T ₂
  - p ₂ = (p ₁ x V ₁ x Т ₂) / (В ₂ x Т ₁)
  - p ₂ = (101 x 400 x 2373) / (1200 x 298) = 268 кПа
Пр.Q7

Закон комбинированного газа уравнение (только для продвинутых студентов)

Существует уравнение, объединяющее оба Закон Бойля и закон Чарльза плюс моль газа.
Уравнение, известное как уравнение идеального газа , дается как:
pV = nRT
p = давление в паскали (единица измерения Па )
V = объем в кубических метров ( м ³ )
n = моль газа ( моль = масса в г / молекулярная масса газа M _r)
R = постоянная идеального газа = 8.314 джоулей на кельвин на моль ( Дж · К ^-1 моль ^-1 )
T = температура в кельвинах ( K )
Вы должны преобразовать в эти единицы для правильного расчета с использованием pV = nRT
Подробнее о pV = nRT расчеты – химия более сложная страница

НАЧАЛО СТРАНИЦЫ

ДРУГИЕ ПОЛЕЗНЫЕ СТРАНИЦЫ

Передовой примечания к расчетам газового закона, кинетические модельная теория ИДЕАЛЬНОГО ГАЗА и неидеальных газов

См. Также расчеты по газу

Моли и молярный объем газа, закон Авогадро

Объем реагирующего газа отношения, закон Авогадро Вычисления по закону Гей-Люссака

Все остальные страницы расчетов

Что такое относительная атомная масса ?, относительная изотопная масса и расчет относительной атомной массы
Расчет относительной формула / молекулярная масса соединения или молекулы элемента
Закон сохранения массы и простые вычисления реагирующей массы
Состав по процентной массе элементов в комплексе
Эмпирическая формула и формула массы соединения из реагирующих масс (легкий старт, без родинок)
Расчет соотношения реагирующих масс реагентов и продуктов из уравнений (Не используя моль) и краткое упоминание фактического процентного выхода и теоретического выхода, атомная экономика и определение массы по формуле
Представляем родинки: связь между молями, массой и формульной массой основа расчета мольного отношения реагирующих веществ (относящиеся к реагирующим массам и формуле масса)
С использованием моль, чтобы вычислить эмпирическую формулу и вывести молекулярную формулу соединения / молекулы (исходя из реагирующих масс или% состава)
Моли и молярный объем газа, закон Авогадро
Объем реагирующего газа отношения, закон Авогадро и закон Гей-Люссака (соотношение газообразных продукты)
Молярность, объемы и раствор концентрации (и схемы аппаратов)
Как выполнить расчет объемного титрования e.грамм. кислотнощелочное титрование (и схемы аппаратов)
Расчет продуктов электролиза (отрицательный катод и положительный анод)
Прочие расчеты например % чистоты,% процентного содержания и теоретический выход, объемное титрование аппарат, разведение растворов (и схемы аппаратов), кристаллизационная вода, количество реагентов требуется, атом эконом
Передача энергии при физических / химических изменениях, экзотермические / эндотермические реакции
Расчеты по газу с учетом отношений PVT, Лоулз Бойля и Чарльза (эта страница)
Расчет радиоактивности и периода полураспада, включая датирующие материалы

НАЧАЛО СТРАНИЦЫ

Законы о газе

Опыт показал, что несколько свойств газа могут быть связаны друг с другом при определенных условиях.Свойства: давление ( P ), объем ( V ), температура ( T , в кельвинах) и количество материала, выраженное в молях ( n ). Мы обнаружили, что образец газа не может иметь случайных значений для этих свойств. Вместо этого будут иметь место только определенные значения, продиктованные некоторыми простыми математическими соотношениями.

Закон Бойля

Первое простое соотношение, называемое законом газа: Простая математическая формула, связывающая два или более свойств газа., находится между давлением газа и его объемом. Если количество газа в образце и его температура поддерживаются постоянными, то по мере увеличения давления газа объем газа пропорционально уменьшается. Математически это записывается как

P∝1V

, где символ «∝» означает «пропорционально». Это одна из форм закона Бойля – закона газа, который связывает давление и объем, который связывает давление газа с его объемом.

Более полезная форма закона Бойля связана с изменением условий газа.Для заданного количества газа при постоянной температуре, если мы знаем начальное давление и объем пробы газа, а также изменения давления или объема, мы можем вычислить, каким будет новый объем или давление. Эта форма закона Бойля записана

P _i V _i = P _f V _f

, где нижний индекс i относится к начальным условиям, а нижний индекс f относится к конечным условиям.

Чтобы использовать P _i V _i = P _f V _f, вам необходимо знать любые три переменные, чтобы вы могли алгебраически вычислить четвертую переменную. Кроме того, величины давления должны иметь те же единицы измерения, что и две величины объема. Если две одинаковые переменные не имеют одинаковых переменных, одно значение необходимо преобразовать в единицу измерения другого значения.

Пример 4

Что произойдет с объемом газа, если его давление увеличится? Предположим, что все остальные условия остаются неизменными.

Решение

Если давление газа увеличивается, объем в ответ уменьшается.

Упражнение по развитию навыков

Что произойдет с давлением газа, если его объем увеличится? Предположим, что все остальные условия остаются неизменными.

Пример 5

Если образец газа имеет начальное давление 1.56 атм и начальный объем 7,02 л, каков конечный объем при снижении давления до 0,987 атм? Предположим, что количество и температура газа остаются постоянными.

Решение

Ключ к решению подобных проблем – уметь определять, какие величины представляют какие переменные из соответствующего уравнения. По формулировке вопроса можно сказать, что 1,56 атм – это P _i, 7,02 L – V _i и 0.987 атм – это P _f. Мы ищем окончательный объем – V _f. Следовательно, подставляя эти значения в P _i V _i = P _f V _f:

(1,56 атм) (7,02 л) = (0,987 атм) × В _f

В выражении есть атмосферы с обеих сторон уравнения, поэтому они сокращаются алгебраически:

(1.56) (7,02 л) = (0,987) × В _f

Теперь разделим обе части выражения на 0,987, чтобы выделить V _f, искомую величину:

(1,56) (7,02 л) 0,987 = Vf

Произведя умножение и деление, получаем значение V _f, что составляет 11,1 л. Объем увеличивается. Это должно иметь смысл, потому что давление уменьшается, поэтому давление и объем обратно пропорциональны.

Упражнение по развитию навыков

Если образец газа имеет начальное давление 3.66 атм и начальный объем 11,8 л, каково конечное давление, если объем уменьшится до 5,09 л? Предположим, что количество и температура газа остаются постоянными.

Если единицы аналогичных количеств не совпадают, одна из них должна быть преобразована в единицы другой величины, чтобы расчет работал правильно. Не имеет значения, какое количество преобразовано в другую единицу; единственное, что имеет значение, это то, что преобразование и последующая алгебра выполняются правильно.Следующий пример иллюстрирует этот процесс.

Пример 6

Если образец газа имеет начальное давление 1,56 атм и начальный объем 7,02 л, каков будет конечный объем, если давление будет изменено на 1775 торр? Имеет ли ответ смысл? Предположим, что количество и температура газа остаются постоянными.

Решение

Этот пример аналогичен примеру 5, за исключением того, что теперь конечное давление выражается в торр.Чтобы математика работала правильно, одно из значений давления должно быть преобразовано в другую единицу. Изменим начальное давление на торр:

1,56 атм × 760 торр 1 атм = 1190 торр

Теперь мы можем использовать закон Бойля:

(1190 торр) (7,02 л) = (1775 торр) × В _f

Торр алгебраически сокращается с обеих сторон уравнения, оставляя

(1190) (7,02 л) = (1775) × В _f

Теперь разделим обе части уравнения на 1,775, чтобы выделить V _f с одной стороны.Решая для окончательного объема,

Vf = (1190) (7,02 л) 1775 = 4,71 л

Поскольку давление увеличивается, имеет смысл уменьшить объем.

Примечание

Ответ для окончательного объема по существу будет таким же, если мы переведем 1775 торр в атмосферы: 1775 торр × 1 атм. 760 торр = 2.336 атм. Используя закон Бойля: (1,56 атм) (7,02 л) = (2,335 атм) × В _f; Vf = (1,56 атм) (7,02 л) 2,336 атм = 4.69 л.

Упражнение по развитию навыков

Если образец газа имеет начальное давление 375 торр и начальный объем 7,02 л, каково конечное давление, если объем будет изменен на 4577 мл? Имеет ли ответ смысл? Предположим, что количество и температура газа остаются постоянными.

Для вашего здоровья: дыхание

Дыхание, безусловно, является важным вкладом в ваше здоровье! Без дыхания мы не смогли бы выжить.Любопытно, что сам процесс дыхания – не более чем применение закона Бойля.

Легкие – это серия постоянно сужающихся трубок, которые заканчиваются множеством крошечных мешочков, называемых альвеолами. Именно в альвеолах кислород из воздуха передается в кровоток, а углекислый газ из кровотока передается в легкие для выдоха. Чтобы воздух мог входить и выходить из легких, давление внутри легких должно измениться, заставляя легкие изменять объем – как и предсказывает закон Бойля.

Изменение давления вызывается диафрагмой, мышцей, покрывающей нижнюю часть легких. Когда диафрагма опускается, она увеличивает размер наших легких. Когда это происходит, давление воздуха в наших легких немного снижается. Это заставляет влетать новый воздух, и мы вдыхаем. Снижение давления небольшое – всего 3 торр, или около 0,4% атмосферы. Мы вдыхаем только 0,5–1,0 л воздуха на нормальный вдох.

Для выдоха воздуха необходимо расслабить диафрагму, которая давит на легкие и немного уменьшает объем легких.Это немного увеличивает давление воздуха в легких, и воздух вытесняется наружу; мы выдыхаем. Для выдоха требуется всего 1-2 торр дополнительного давления. Итак, с каждым вдохом наши тела проводят экспериментальную проверку закона Бойля.

Закон Чарльза

Другой простой газовый закон связывает объем газа с его температурой. Эксперименты показывают, что при повышении температуры пробы газа ее объем увеличивается до тех пор, пока давление и количество газа остаются постоянными.Математически это можно записать как

. V ∝ T

Здесь необходимо уточнить понятие температуры. Хотя шкала Кельвина является предпочтительной шкалой температуры, шкала Цельсия также является обычной шкалой температур, используемой в науке. Шкала Цельсия основана на точках плавления и кипения воды и на самом деле является общей температурной шкалой, используемой в большинстве стран по всему миру (за исключением США, где до сих пор используется шкала Фаренгейта). Значение температуры по Цельсию напрямую связано с ее значением по Кельвину простым выражением:

Температура Кельвина = Температура Цельсия + 273

Таким образом, легко перейти с одной температурной шкалы на другую.

Примечание

Шкалу Кельвина иногда называют абсолютной шкалой, потому что нулевая точка на шкале Кельвина находится в абсолютном нуле, самой низкой из возможных температур. На других температурных шкалах абсолютный ноль составляет -260 ° C или -459 ° F.

Выражение, связывающее объем газа с его температурой, порождает следующий вопрос: с какой температурной шкалой связан объем газа? Ответ заключается в том, что объемы газа напрямую связаны с температурой Кельвина .Следовательно, температуру пробы газа всегда следует выражать в градусах Кельвина (или переводить в них).

Пример 7

Что происходит с объемом газа, если его температура понижается? Предположим, что все остальные условия остаются постоянными.

Решение

Если температура пробы газа понижается, объем также уменьшается.

Упражнение по развитию навыков

Что произойдет с температурой газа, если его объем увеличится? Предположим, что все остальные условия остаются постоянными.

Как и в случае с законом Бойля, взаимосвязь между объемом и температурой может быть выражена в терминах начальных и конечных значений объема и температуры следующим образом:

ViTi = VfTf

, где V _i и T _i – начальный объем и температура, а V _f и T _f – конечный объем и температура.Это закон Чарльза – газовый закон, который связывает объем и абсолютную температуру. Ограничение на его использование состоит в том, что давление газа и количество газа должны оставаться постоянными. (Закон Шарля иногда называют законом Гей-Люссака в честь ученого, который продвигал работу Шарля.)

Пример 8

Проба газа при 20 ° C имеет начальный объем 20,0 л. Каков ее объем, если температура изменяется на 60 ° C? Имеет ли ответ смысл? Предположим, что давление и количество газа остаются постоянными.

Решение

Хотя температуры даны в градусах Цельсия, мы должны преобразовать их в кельвины, прежде чем мы сможем использовать закон Чарльза. Таким образом,

20 ° C + 273 = 293 K = T _i 60 ° C + 273 = 333 K = T _f

Теперь мы можем подставить эти значения в закон Чарльза вместе с начальным объемом 20,0 л:

20,0 L293 K = Vf333 K

Умножая 333 K на другую часть уравнения, мы видим, что наши единицы измерения температуры будут сокращаться:

(333 К) (20.0 L) 293 K = Vf

Решение для окончательного объема, V _f = 22,7 л. Таким образом, при повышении температуры объем увеличивается. Это имеет смысл, потому что объем прямо пропорционален абсолютной температуре (пока давление и количество остаются постоянными).

Упражнение по развитию навыков

Проба газа при 35 ° C имеет начальный объем 5.06 л. Каков его объем при изменении температуры до −35 ° C? Имеет ли ответ смысл? Предположим, что давление и количество газа остаются постоянными.

Закон о комбинированном газе

Можно построить и другие газовые законы, но мы остановимся только на двух. Комбинированный газовый закон Газовый закон, который связывает давление, объем и абсолютную температуру. объединяет законы Бойля и Чарльза, чтобы связать изменения давления, объема и температуры пробы газа:

PiViTi = PfVfTf

Чтобы применить этот газовый закон, количество газа должно оставаться постоянным.Как и в случае с другими законами о газе, температура должна быть выражена в кельвинах, а единицы измерения аналогичных величин должны быть одинаковыми. Из-за зависимости от трех величин одновременно, трудно предсказать заранее, что произойдет с одним свойством пробы газа при изменении двух других свойств. Лучший способ узнать это – вычислить это математически.

Пример 9

Образец газа имеет P _i = 1,50 атм, V _i = 10.5 л и T _i = 300 K. Каков конечный объем, если P _f = 0,750 атм и T _f = 350 K?

Решение

Используя закон комбинированного газа, замените пять величин:

(1,50 атм) (10,5 л) 300 К = (0,750 атм) (Vf) 350 К

Мы алгебраически изменим это выражение, чтобы выделить V _f на одной стороне уравнения:

Vf = (1.50 атм) (10,5 л) (350 К) (300 К) (0,750 атм) = 24,5 л

Обратите внимание, как отменяются все единицы, кроме единицы объема.

Упражнение по развитию навыков

Образец газа имеет P _i = 0,768 атм, V _i = 10,5 л и T _i = 300 K. Каково конечное давление, если V _f = 7,85 л и т _ф = 250 К?

Пример 10

Баллон с пробой газа имеет температуру 22 ° C и давление 1.09 атм в аэропорту Кливленда. Баллон имеет объем 1070 мл. Воздушный шар доставляется самолетом в Денвер, где температура составляет 11 ° C, а давление – 655 торр. Каков новый объем воздушного шара?

Решение

Первая задача – преобразовать все количества в правильные и согласованные единицы. Температура должна быть выражена в кельвинах, а единицы измерения давления различны, поэтому необходимо преобразовать одну из величин. Переведем атмосферы в торр:

22 ° C + 273 = 295 K = T _i 11 ° C + 273 = 284 K = T _f 1.09 атм × 760 торр1 атм = 828 торр = Pi

Теперь мы можем подставить величины в комбинированный закон:

(828 торр) (1070 мл) 295 K = (655 торр) × Vf284 K

Чтобы найти V _f, мы умножаем 284 K в знаменателе правой части на числитель слева и делим 655 торр в числителе правой части на знаменатель слева:

(828 торр) (1070 мл) (284 K) (295 K) (655 торр) = Vf

Обратите внимание, что торр и кельвин сокращаются, поскольку они находятся как в числителе, так и в знаменателе.Единственная единица, которая остается, – это миллилитры, то есть единица объема. Итак, V _f = 1300 мл. Общее изменение заключается в том, что объем баллона увеличился на 230 мл.

Упражнение по развитию навыков

Воздушный шар, используемый для подъема метеорологических приборов в атмосферу, содержит газ объемом 1150 л на земле, где давление составляет 0,977 атм, а температура составляет 18 ° C.В воздухе этот газ имеет давление 6,88 торр и температуру -15 ° C. Какой новый объем газа?

Закон об идеальном газе

До сих пор используемые нами законы газа были сосредоточены на изменении одного или нескольких свойств газа, таких как его объем, давление или температура. Есть один газовый закон, который связывает все независимые свойства газа при любых конкретных условиях, а не изменение условий.Этот газовый закон называется законом идеального газа. Газовый закон, который связывает объем, давление, температуру и количество газа. Формула этого закона выглядит следующим образом:

PV = nRT

В этом уравнении P – давление, V – объем, n – количество молей и T – температура. R называется постоянной закона идеального газа Константа появляется в законе идеального газа. и представляет собой константу пропорциональности, которая связывает значения давления, объема, количества и температуры пробы газа.Переменные в этом уравнении не имеют индексов i и f , чтобы указать начальное и конечное состояние. Закон идеального газа связывает четыре независимых свойства газа при любых условиях.

Значение R зависит от того, какие единицы используются для выражения других величин. Если объем выражен в литрах, а давление в атмосферах, то правильное значение R будет следующим:

R = 0.08205 L⋅atmmol⋅K

Это может показаться странным модулем, но это то, что требуется для того, чтобы единицы работали алгебраически.

Пример 11

Какой объем в литрах 1,45 моль газа N ₂ при 298 К и 3,995 атм?

Решение

Используя закон идеального газа, где P = 3,995 атм, n = 1,45 и T = 298,

(3,995 атм) × V = (1.45 моль) (0,08205 л⋅атммоль⋅К) (298 К)

С правой стороны кроты и кельвины сокращаются. Кроме того, поскольку атмосферы появляются в числителе по обе стороны уравнения, они также сокращаются. Единственная оставшаяся единица – литры, единица объема. Итак

3,995 × В = (1,45) (0,08205) (298) л

Разделив обе части уравнения на 3,995 и оценив, мы получим В, = 8,87 л. Обратите внимание, что условия газа не меняются. Скорее, закон идеального газа позволяет нам определить, каким должно быть четвертое свойство газа (здесь объем) , если известны три других свойства (здесь количество, давление и температура).

Упражнение по развитию навыков

Каково давление пробы газа CO ₂, если 0,557 моль содержится в емкости объемом 20,0 л при температуре 451 К?

Для удобства ученые выбрали 273 К (0 ° C) и давление 1,00 атм в качестве набора стандартных условий для газов. Такое сочетание условий называется стандартной температурой и давлением (STP) 273 K (0 ° C) и 1.Давление 00 атм. В этих условиях 1 моль любого газа имеет примерно такой же объем. Мы можем использовать закон идеального газа для определения объема 1 моль газа на STP:

(1,00 атм) × V = (1,00 моль) (0,08205 л⋅атммоль⋅К) (273 К)

Этот объем равен 22,4 л. Поскольку этот объем не зависит от типа газа, идея о том, что 1 моль газа имеет объем 22,4 л при стандартном давлении, дает удобный коэффициент преобразования:

1 моль газа = 22,4 л (при СТП)

Пример 12

Циклопропан (C ₃ H ₆) – газ, который ранее использовался в качестве анестетика.Сколько молей газа содержится в пробе объемом 100,0 л, если газ находится на уровне STP?

Решение

Мы можем настроить простое одностадийное преобразование, которое связывает моли и литры:

100,0 л C3H6 × 1 моль 22,4 л = 4,46 моль C3H6

В 100,0 л содержится почти 4,5 моль газа.

Примечание

Из-за своей горючести циклопропан больше не используется в качестве анестезирующего газа.

Упражнение по развитию навыков

Фреон – это торговое название серии фтор- и хлорсодержащих газов, которые ранее использовались в холодильных системах.Какой объем у 8,75 моль фреона на СТП?

Примечание

Многие газы, известные как фреон, больше не используются, потому что их присутствие в атмосфере разрушает озоновый слой, который защищает нас от ультрафиолетового излучения солнца.

Карьера: респираторный терапевт

Определенные заболевания, такие как эмфизема, рак легких и тяжелая астма, в первую очередь поражают легкие.Респираторные терапевты помогают пациентам с проблемами дыхания. Они могут оценить, помочь диагностировать и лечить нарушения дыхания и даже помочь оказать неотложную помощь при остром заболевании, когда дыхание затруднено.

Большинство респираторных терапевтов должны закончить как минимум два года колледжа и получить степень младшего специалиста, хотя терапевты могут взять на себя больше ответственности, если у них есть высшее образование. Терапевты также должны сдать государственные или национальные сертификационные экзамены.После получения сертификата респираторные терапевты могут работать в больницах, кабинетах врачей, домах престарелых или на дому у пациентов. Терапевты работают с таким оборудованием, как кислородные баллоны и респираторы, иногда могут выписывать лекарства для облегчения дыхания, проводить тесты и обучать пациентов дыхательным упражнениям и другой терапии.

Поскольку респираторные терапевты работают напрямую с пациентами, умение хорошо работать с другими является обязательным условием для этой карьеры. Это важная работа, потому что она связана с одной из важнейших функций организма.

Упражнения по обзору концепции

Какие свойства помогают нам предсказать законы газа?
Чем закон идеального газа отличается от других законов газа?

ответов

Газовые законы связывают четыре свойства: давление, объем, температуру и количество молей.
Закон идеального газа не требует изменения свойств газа.

Ключевые вынос

Физические свойства газов можно предсказать с помощью математических формул, известных как законы газа.

Упражнения

Какие условия пробы газа должны оставаться постоянными, чтобы можно было использовать закон Бойля?
Какие условия пробы газа должны оставаться постоянными, чтобы можно было использовать закон Чарльза?
Имеет ли значение идентичность газа при использовании закона Бойля? Почему или почему нет?
Имеет ли значение принадлежность газа при использовании закона Чарльза? Почему или почему нет?
Проба газообразного азота помещается в баллон объемом 1 штука.88 л и давление 1,334 атм. Каким будет объем баллона, если давление изменить на 0,662 атм? Предположим, что температура и количество газа остаются постоянными.
Образец газообразного гелия в поршне имеет объем 86,4 мл под давлением 447 торр. Каким будет объем гелия, если давление на поршень увеличится до 1240 торр? Предположим, что температура и количество газа остаются постоянными.
Если газ имеет начальное давление 24 650 Па и начальный объем 376 мл, каков будет конечный объем, если давление газа изменится на 775 торр? Предположим, что количество и температура газа остаются постоянными.
Проба газа имеет начальный объем 0.9550 л и начальное давление 564,5 торр. Каким будет конечное давление газа при изменении объема до 587,0 мл? Предположим, что количество и температура газа остаются постоянными.
Человек делает нормальный вдох объемом около 1,00 л. Если исходная температура воздуха составляет 18 ° C, а воздух нагревается до 37 ° C, каков новый объем воздуха? Предположим, что давление и количество газа остаются постоянными.
Человек делает нормальный вдох объемом около 1,00 л. Если исходная температура воздуха составляет -10 ° C, а воздух нагревается до 37 ° C, каков новый объем воздуха? Предположим, что давление и количество газа остаются постоянными.
Смесь паров воздуха и газа в автомобильном баллоне имеет начальную температуру 450 К и объем 12.7 см ³. Газовая смесь нагревается до 565 ° C. Если давление и количество остаются постоянными, каков конечный объем газа в кубических сантиметрах?
При следующих условиях для газа: V _i = 0,665 л, T _i = 23,6 ° C, V _f = 1,034 л. Что такое T _f в градусах Цельсия и Кельвина?
Предполагая, что количество останется прежним, каким должен быть конечный объем газа, который имеет начальный объем 387 мл, начальное давление 456 торр, начальную температуру 65.0 ° C, конечное давление 1,00 атм и конечная температура 300 K?
При нажатии на сопло баллончика 0,15 мл газа расширяется до 0,44 мл, а его давление падает с 788 торр до 1,00 атм. Если начальная температура газа составляет 22,0 ° C, какова конечная температура газа?
Используйте закон идеального газа, чтобы показать, что 1 моль газа на STP имеет объем около 22.4 л.
Используйте стандартный коэффициент преобразования, чтобы определить значение постоянной закона идеального газа R , которая имеет единицы измерения л · торр / моль · К.
Сколько молей газа содержится в образце объемом 27,6 л при 298 К и давлении 1,44 атм?
Сколько молей газа содержится в 0.066 л образца при 298 К и давлении 0,154 атм?
Образец газообразного диоксида углерода 0,334 моль ограничен объемом 20,0 л и имеет давление 0,555 атм. Какова температура углекислого газа в кельвинах и градусах Цельсия?
Что должно быть V для пробы газа, если n = 4.55 моль, P = 7,32 атм, T = 285 K?
Каково давление 0,0456 моль газообразного Ne в объеме 7,50 л при 29 ° C?
Каково давление 1,00 моль газообразного аргона, имеющего объем 843,0 мл и температуру -86?0 ° С?

ответов

температура и количество газа
Идентичность не имеет значения, потому что переменные закона Бойля не идентифицируют газ.
Закон идеального газа подтверждает, что 22.4 л равняется 1 моль.

Ideal Gas Law Chemistry Tutorial

Пожалуйста, не блокируйте рекламу на этом сайте.
Без рекламы = для нас нет денег = для вас нет бесплатных вещей!

Вывод уравнения идеального газа

Для постоянного количества газа:

Закон Бойля говорит нам, что объем газа (V) обратно пропорционален его давлению (P):
Закон Чарльза говорит нам, что объем газа (V) прямо пропорционален его температуре в Кельвинах (T):
и уравнение комбинированного газа говорят нам, что объем газа (V) прямо пропорционален его температуре в Кельвинах (T) и обратно пропорционален его давлению (P):

Но что, если у нас нет постоянного количества газа? Что, если бы мы добавили еще газа или убрали немного газа? Что тогда будет с объемом газа?

Принцип Авогадро говорит нам, что для газа при постоянной температуре и давлении объем газа (V) прямо пропорционален количеству молекул газа (N):

В ∝ N

и поскольку моль эквивалентен количеству молекул Авогадро, мы можем сказать, что объем газа (V) прямо пропорционален молям газа (n).

V n

Помните, что мы объединили закон Бойля и закон Чарльза, чтобы получить уравнение комбинированного газа:

Итак, теперь мы можем также включить V ∝ n, чтобы дать новое соотношение между количеством газа (n), его объемом (V), давлением (P) и температурой (T):

Мы можем превратить это соотношение в уравнение, используя коэффициент пропорциональности R:

Если мы изменим это уравнение, мы обнаружим, что

Если нам известны значения P, V, n и T, то мы можем найти значение константы R.

Объем (V) различных количеств газа (n) был измерен при постоянном давлении 101,3 кПа (1 атм) и 298 K (25 ° C).
Эти значения затем использовались для вычисления значения константы R, как показано в таблице ниже:

Эксперимент

Давление
(кПа)

Объем
(л)

Моль
(моль)

Температура
(К)

101.3

24,5

1,00

298

101,3 × 24,5
1 × 298

R = 8,3

101,3

48,9

2,00

298

101.3 × 48,9
2 × 298

R = 8,3

101,3

73,4

3,00

298

101,3 × 73,4
3 × 298

R = 8,3

101.3

97,8

4,00

298

101,3 × 97,8
4 × 298

R = 8,3

101,3

122

5,00

298

101.3 × 122
5 × 298

R = 8,3

Если мы измеряем давление в килопаскалях (кПа), объем в литрах (л), температуру в Кельвинах (К) и количество газа в молях (моль), то мы находим, что R = 8,314, и он имеет единицы измерения кПа LK ^-1 моль ^-1.
Давление, оказываемое газом в этом объеме, на самом деле является мерой энергии частиц газа, поэтому единицы этой газовой постоянной R чаще всего выражаются в Джоулях на Кельвин на моль, JK ^-1 моль ^-1.
R = 8,314 Дж · К ^-1 моль ^-1

Газовая постоянная R является особой, потому что ее значение не зависит от природы используемого газа.
Если описанный выше эксперимент проводится с использованием:

углекислый газ, CO _{2 (г)}, тогда R = 8,314 Дж K ^-1 моль ^-1
газообразный азот, N _{2 (г)}, тогда R = 8,314 Дж K ^-1 моль ^-1
газообразный гелий, He _(г), тогда R = 8.314 Дж К ^-1 моль ^-1

Итак, R называется газовой постоянной, а уравнение PV = nRT известно как уравнение идеального газа или, как закон идеального газа.

Так как R зависит только от количества присутствующего газа и не зависит от того, из чего состоят молекулы газа, то молекулы газа не должны взаимодействовать друг с другом, поскольку в противном случае значение R было бы ожидается, что они изменятся и отразят влияние этих взаимодействий на величину давления (например).

Путем преобразования закона идеального газа (уравнение идеального газа) PV = nRT его можно использовать для расчета давления (P), объема (V), температуры (T) или количества (n) газа:

Для расчета давления газа:	п =	nRT В
Для расчета объема газа:	В =	nRT P
Для расчета температуры газа:	Т =	PV nR
Для расчета количества газа:	п =	PV RT

Обратите внимание, что закон идеального газа поддерживается кинетической теорией газов:

Закон идеального газа гласит, что при постоянной температуре (T) и объеме (V) давление газа (P) прямо пропорционально количеству газа (n).
Номер детали
То есть увеличиваются моли молекул газа и давление возрастает.
Уменьшите количество молей молекул газа и давление упадет.
Кинетическая теория газов говорит нам, что давление создается молекулами газа, сталкивающимися со стенками контейнера, другими словами, для данного объема газа (при постоянном давлении):
P ∝ количество молекул газа
Итак, поскольку количество молекул газа связано с количеством газа в молях, Закон идеального газа поддерживается кинетической теорией газов.
Закон об идеальном газе гласит, что объем газа (V) зависит от количества газа (n), его температуры (T) и его объема (V).
Обратите внимание, что объем газа не зависит от размера или объема молекул газа.
Объем газа зависит от количества газа, а НЕ от каких-либо других свойств газа.
Кинетическая теория газов говорит нам, что газ состоит из огромного количества газовых частиц, которые настолько малы, что их размеры пренебрежимо малы по сравнению со средним расстоянием между ними, то есть объем молекул газа незначителен по сравнению с объем пространства, занимаемого газом.

Абсолютная температура идеального газа

Абсолютная температура идеального газа

Термодинамическая шкала температур

Абсолютная температура, кинетическая энергия молекул и давление идеального газа

Примеры решения задач

Расчет температуры и давления газа: онлайн калькулятор

Идеальный газ

Газовые законы

Комбинированный закон

Пример использования калькулятора

Заключение

Калькулятор закона состояния идеального газа (давление–объем–температура–количество) • Термодинамика — теплота • Онлайн-конвертеры единиц измерения

Примеры решения задач по уравнению состояния идеального газа (уравнению Менделеева — Клапейрона)

Определения и формулы

Идеальный газ

Закон идеального газа

Закон Бойля — Мариотта (

Закон Авогадро (

Закон Гей-Люссака (

Закон Шарля (или второй закон Гей-Люссака) (

Примеры решенных задач по физике

Абсолютная температура. Температура — мера средней кинетической энергии молекул

Абсолютная температура. Температура — мера средней кинетической энергии молекул

Уравнение Менделеева-Клапейрона – О’Пять пО физике!

законов о газе

Газовые законы

Законы о свойствах газа

Закон об идеальном газе:

Закон о комбинированном газе

11.9: Закон идеального газа: давление, объем, температура и моль

Закон об идеальном газе

Определение постоянной идеального газа

Идеальное поведение газа – StatPearls

Введение

Функция

Проблемы, вызывающие озабоченность

Клиническая значимость

Улучшение результатов группы здравоохранения

Кинетическая температура, тепловая энергия

Законы о газе

Закон Бойля

Пример 4

Упражнение по развитию навыков

Пример 5

Упражнение по развитию навыков

Пример 6

Примечание

Упражнение по развитию навыков

Для вашего здоровья: дыхание

Закон Чарльза

Примечание

Пример 7

Упражнение по развитию навыков

Пример 8

Упражнение по развитию навыков

Закон о комбинированном газе

Пример 9

Упражнение по развитию навыков

Пример 10

Упражнение по развитию навыков

Закон об идеальном газе

Пример 11

Упражнение по развитию навыков

Пример 12

Примечание

Упражнение по развитию навыков

Примечание

Карьера: респираторный терапевт

Упражнения по обзору концепции

ответов

Ключевые вынос

Упражнения

ответов

Ideal Gas Law Chemistry Tutorial

Вывод уравнения идеального газа

Оставить комментарий Отменить ответ