Формула умножение матриц 3х3: Умножение матриц онлайн

Транспонирование и умножение матриц

Эти операции над матрицами не относятся к числу линейных.

ОПРЕДЕЛЕНИЕ. Транспонированной матрицей для матрицыразмераназывается матрица размера, полученная иззаменой всех ее строк столбцами с теми же порядковыми номерами.

То есть, если =, то,=1,2,…,,=1,2,…,.

ПРИМЕР.

=; ==

3х2 2х3 3х3 3х3

ОПРЕДЕЛЕНИЕ. Если =, то матрицаА называется симметрической.

Все диагональные матрицы симметрические, так как равны их элементы, симметричные относительно главной диагонали.

Очевидно, справедливы следующие свойства операции транспонирования:

ОПРЕДЕЛЕНИЕ. Пусть =– матрица размера,=– матрица размера.

Произведение этих матриц– матрица=размера, элементы которой вычисляются по формуле:

, =1,2,…,,=1,2,…,,

то есть элемент -й строки и-го столбца матрицыравен сумме произведений соответствующих элементов-й строки матрицыи-го столбца матрицы.

ПРИМЕР.

= , =

2х3 3х1 2х3 3х1 2х1

Произведение – не существует.

3х1 2х3

CВОЙСТВА ОПЕРАЦИИ УМНОЖЕНИЯ МАТРИЦ

1. , даже если оба произведения определены.

ПРИМЕР. ,, хотя

ОПРЕДЕЛЕНИЕ. Матрицы иназываютсяперестановочными, если , в противном случаеиназываютсянеперестановочными.

Из определения следует, что перестановочными могут быть лишь квадратные матрицы одного размера.

ПРИМЕР.

матрицы иперестановочные.

, то есть ,

значит, и– перестановочные матрицы.

Вообще единичная матрица перестановочна с любой квадратной матрицей того же порядка, и для любой матрицы . Это свойство матрицыобъясняет, почему именно она называется единичной: при умножении чисел таким свойством обладает число 1.

Если соответствующие произведения определены, то:

2.

3. ,

4.

5.

ПРИМЕР.

,

2х2 2х1 2х1 1х2

1х2 2х2 1х2

ЗАМЕЧАНИЕ. Элементами матрицы могут быть не только числа, но и функции. Такая матрица называется функциональной.

ПРИМЕР.

Каждой квадратной матрице можно по определенным правилам поставить в соответствие некоторое число, которое называется ее определителем.

Рассмотрим квадратную матрицу второго порядка:

Её определителем называется число, которое записывается и вычисляется так:

(1.1)

Такой определитель называется

определителем второго порядка и может

обозначаться по-другому: или.

Определителем третьего порядка называется число, соответствующее квадратной матрице , которое вычисляется по правилу:

(1.2)

Это правило вычисления определителя третьего порядка называется правилом треугольников и схематически его можно представить так:

ПРИМЕР. ;

Если справа от определителя приписать первый, а затем второй столбец, то правило треугольников можно модифицировать:

Сначала умножаются числа на главной диагонали и двух ей параллельных диагоналях, затем – числа на другой (побочной) диагонали и ей параллельных.

Из суммы первых трех произведений вычитается сумма остальных.

Группируя слагаемые в (1.2) и используя (1.1), заметим, что

(1.3)

То есть при вычислении определителя третьего порядка используются определители второго порядка, причем – определитель матрицы, полученный извычеркиванием элемента(точнее, первой строки и первого столбца, на пересечении которых стоит),– вычеркиванием элемента,– элемента.

ОПРЕДЕЛЕНИЕ. Дополнительным минором элементаквадратной матрицыназывается определитель матрицы, получаемой извычеркиванием-ой строки и-го столбца.

ПРИМЕР.

и так далее: матрица третьего порядка имеет 9 дополнительных миноров.

ОПРЕДЕЛЕНИЕ. Алгебраическим дополнением элемента квадратной матрицыназывается число.

ПРИМЕР.

Для матрицы :

Для матрицы :и так далее.

Итак, с учетом сформулированных определений (1.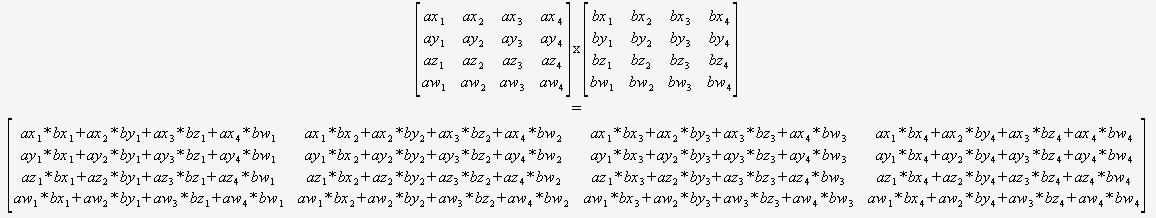 3) можно переписать в виде: .

Перейдем теперь к общему случаю.

ОПРЕДЕЛЕНИЕ. Определителем

квадратной матрицы порядканазывается число, которое записывается и вычисляется следующим образом:

(1.4)

Равенство (1.4) называется разложением определителя по элементам первой строки. В этой формуле алгебраические дополнения вычисляются как определители -го порядка. Таким образом, при вычислении определителя 4-го порядка по формуле (1.4) надо, вообще говоря, вычислить 4 определителя 3-го порядка; при вычислении определителя 5-го порядка – 5 определителей 4-го порядка и т.д. Однако если, к примеру, в определителе 4-го порядка первая строка содержит 3 нулевых элемента, то в формуле (1.4) останется лишь одно ненулевое слагаемое.

ПРИМЕР.

Рассмотрим (без доказательства) свойства определителей:

1. Определитель можно разложить по элементам первого столбца:

(1. 5)

ПРИМЕР.

ЗАМЕЧАНИЕ. Рассмотренные примеры позволяют сделать вывод: определитель треугольной матрицы равен произведению элементов главной диагонали.

2. При транспонировании матрицы величина ее определителя не меняется: .

Отсюда следует, что строки и столбцы определителя равноправны.

3. Если в определителе поменять местами две строки (два столбца), то определитель изменит свой знак, не изменившись по абсолютной величине.

4. Определитель, имеющий две равные строки (столбца), равен нулю.

5. Если все элементы некоторой строки (столбца) определителя умножить на число , то величина определителя умножится на это число.

Отсюда, в частности, следует, что общий множитель любой строки (столбца) можно выносить за знак определителя.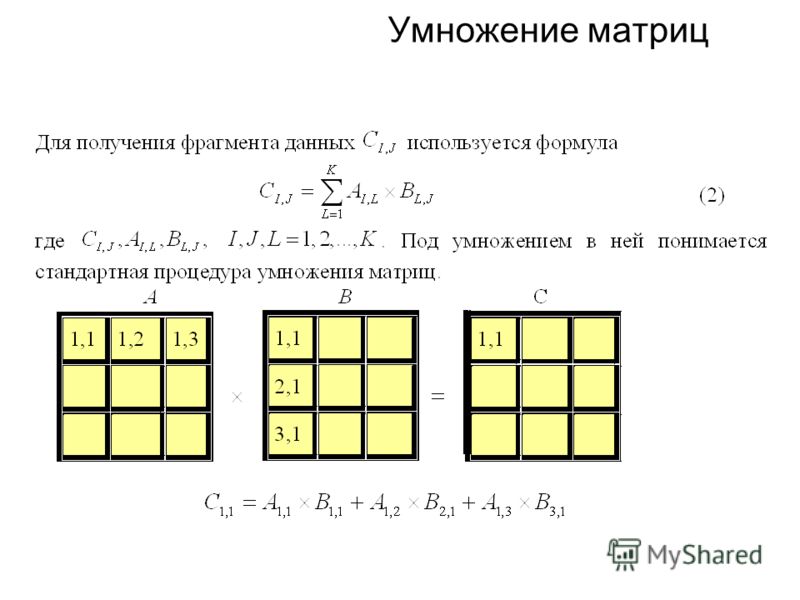

Кроме того, определитель, имеющий нулевую строку или нулевой столбец, равен нулю.

6. Определитель, имеющий пропорциональные строки (столбцы), равен нулю.

7. Определитель можно разложить по элементам любой строки (любого столбца): (1.6)

или

(1.7)

Равенство (1.6) называется разложением определителя по элементам -й строки.

Равенство (1.7) называется разложением определителя по элементам -го столбца.

8. Сумма произведений всех элементов некоторой строки (столбца) на

алгебраические дополнения соответствующих элементов другой строки

(столбца) равна нулю, то есть при ипри.

9. Определитель не изменится от прибавления ко всем элементам некоторой строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число.

10. Определитель произведения двух матриц одного порядка равен произведению определителей этих матриц: (– квадратные матрицы одного порядка).

ПРИМЕР. , так как элементы первой и второй строк этого определителя соответственно пропорциональны (свойство 6).

Особенно часто при вычислении определителей используется свойство 9, так как оно позволяет в любом определителе получать строку или столбец, где все элементы, кроме одного, равны нулю.

ПРИМЕР.

Как умножить матрицу 3х3 на 2х3. Математика для чайников. Матрицы и основные действия над ними. Умножение матрицы на вектор

Прежде всего, ЧТО должно получиться в результате умножения трёх матриц ? Кошка не родит мышку. Если матричное умножение осуществимо, то в итоге тоже получится матрица. М-да, хорошо мой преподаватель по алгебре не видит, как я объясняю замкнутость алгебраической структуры относительно её элементов =)

Произведение трёх матриц можно вычислить двумя способами:

1) найти , а затем домножить на матрицу «цэ»: ;

2) либо сначала найти , потом выполнить умножение .

Результаты обязательно совпадут, и в теории данное свойство называют ассоциативностью матричного умножения :

Пример 6

Перемножить матрицы двумя способами

Алгоритм решения двухшаговый: находим произведение двух матриц, затем снова находим произведение двух матриц.

1) Используем формулу

Действие первое:

Действие второе:

2) Используем формулу

Действие первое:

Действие второе:

Ответ :

Более привычен и стандартен, конечно же, первый способ решения, там «как бы всё по порядку». Кстати, по поводу порядка. В рассматриваемом задании часто возникает иллюзия, что речь идёт о каких-то перестановках матриц. Их здесь нет. Снова напоминаю, что в общем случае ПЕРЕСТАВЛЯТЬ МАТРИЦЫ НЕЛЬЗЯ . Так, во втором пункте на втором шаге выполняем умножение , но ни в коем случае не . С обычными числами такой бы номер прошёл, а с матрицами – нет.

Свойство ассоциативности умножения справедливо не только для квадратных, но и для произвольных матриц – лишь бы они умножались:

Пример 7

Найти произведение трёх матриц

Это пример для самостоятельного решения. В образце решения вычисления проведены двумя способами, проанализируйте, какой путь выгоднее и короче.

Свойство ассоциативности матричного умножения имеет место быть и для бОльшего количества множителей.

Теперь самое время вернуться к степеням матриц. Квадрат матрицы рассмотрен в самом начале и на повестке дня вопрос.

Определение. Произведением двух матриц А и В называется матрица С , элемент которой, находящийся на пересечении i -й строки и j -го столбца, равен сумме произведений элементов i -й строки матрицы А на соответствующие (по порядку) элементы j -го столбца матрицы В .

Из этого определения следует формула элемента матрицы C :

Произведение матрицы А на матрицу В обозначается АВ .

Пример 1. Найти произведение двух матриц А и B , если

,

.

Решение. Удобно нахождение произведения двух матриц А и В записывать так, как на рис. 2:

На схеме серые стрелки показывают, элементы какой строки матрицы А на элементы какого столбца матрицы В нужно перемножить для получения элементов матрицы С , а линиями цвета элемента матрицы C соединены соответствующие элементы матриц A и B , произведения которых складываются для получения элемента матрицы C .

В результате получаем элементы произведения матриц:

Теперь у нас есть всё, чтобы записать произведение двух матриц:

.

Произведение двух матриц АВ имеет смысл только в том случае, когда число столбцов матрицы А совпадает с числом строк матрицы В .

Эту важную особенность будет легче запомнить, если почаще пользоваться следующими памятками:

Имеет место ещё одна важная особенность произведения матриц относительно числа строк и столбцов:

В произведении матриц АВ число строк равно числу строк матрицы А , а число столбцов равно числу столбцов матрицы В .

Пример 2. Найти число строк и столбцов матрицы C , которая является произведением двух матриц A и B следующих размерностей:

а) 2 Х 10 и 10 Х 5;

б) 10 Х 2 и 2 Х 5;

Пример 3. Найти произведение матриц A и B , если:

.

A B – 2. Следовательно, размерность матрицы C = AB – 2 X 2.

Вычисляем элементы матрицы C = AB .

Найденное произведение матриц: .

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн .

Пример 5. Найти произведение матриц A и B , если:

.

Решение. Число строк в матрице A – 2, число столбцов в матрице B C = AB – 2 X 1.

Вычисляем элементы матрицы C = AB .

Произведение матриц запишется в виде матрицы-столбца: .

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн .

Пример 6. Найти произведение матриц A и B , если:

.

Решение. Число строк в матрице A – 3, число столбцов в матрице B – 3. Следовательно, размерность матрицы C = AB – 3 X 3.

Вычисляем элементы матрицы C = AB .

Найденное произведение матриц: .

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн .

Пример 7. Найти произведение матриц A и B , если:

.

Решение. Число строк в матрице A – 1, число столбцов в матрице B – 1. Следовательно, размерность матрицы C = AB – 1 X 1.

Вычисляем элемент матрицы C = AB .

Произведение матриц является матрицей из одного элемента: .

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн .

Программная реализация произведения двух матриц на С++ разобрана в соответствующей статье в блоке “Компьютеры и программирование”.

Возведение матрицы в степень

Возведение матрицы в степень определяется как умножение матрицы на ту же самую матрицу. Так как произведение матриц существует только тогда, когда число столбцов первой матрицы совпадает с числом строк второй матрицы, то возводить в степень можно только квадратные матрицы. n -ая степень матрицы путём умножения матрицы на саму себя n раз:

Пример 8. Дана матрица . Найти A ² и A ³ .

Найти произведение матриц самостоятельно, а затем посмотреть решение

Пример 9. Дана матрица

Найти произведение данной матрицы и транспонированной матрицы , произведение транспонированной матрицы и данной матрицы.

Свойства произведения двух матриц

Свойство 1. Произведение любой матрицы А на единичную матрицу Е соответствующего порядка как справа, так и слева, совпадает с матрицей А, т.е. АЕ = ЕА = А.

Иными словами, роль единичной матрицы при умножении матриц такая же, как и единицы при умножении чисел.

Пример 10. Убедиться в справедливости свойства 1, найдя произведения матрицы

на единичную матрицу справа и слева.

Решение. Так как матрица А содержит три столбца, то требуется найти произведение АЕ , где

–
единичная матрица третьего порядка. Найдём элементы произведения С = АЕ :

Получается, что АЕ = А .

Теперь найдём произведение ЕА , где Е – единичная матрица второго порядка, так как матрица А содержит две строки. Найдём элементы произведения С = ЕА :

За неколько секунд сервер выдаст точное решение. Умножением матриц онлайн будет являться матрица , каждый элемент которой вычисляется как скалярное произведение строк первой матрицы на соответствующие столбцы второй матрицы по правилу умножения матриц . При умножении матриц онлайн , каждый элемент полученной матрицы будет результатом умножения строк одной матрицы на столбцы другой матрицы согласно правилу произведения матриц . Найти онлайн произведение двух матриц допустимых размерностей сводится к нахождению матрицы соответствующей им размерности. Операция умножения онлайн двух матриц размерностей NxK и KxM сводится к нахождению матрицы размерности MxN. Элементы этой матрицы составляют скалярное произведение умножаемых матриц , это результат умножения матриц онлайн . Задача по нахождению произведения матриц онлайн или операция умножения матриц онлайн заключается в умножении строк на столбцы матриц согласно правилу умножения матриц . www.сайт находит произведение матриц заданных размерностей в режиме онлайн . Умножение матриц онлайн заданной размерности – это нахождение соответствующей размерности матрицы, элементами которой будут скалярные произведения соответствующих строк и столбцов умножаемых матриц . Нахождение произведения матриц онлайн широко распространено в теории матриц , а так же линейной алгебры. Произведение матриц онлайн используется для определения результирующей матрицы от умножения заданных матриц . Для того, чтобы вычислить произведение матриц или определить умножение матриц онлайн , необходимо затратить не мало времени, в то время как наш сервер в считанные секунды найдет произведение матриц онлайн от умножения двух заданных матриц онлайн . При этом ответ по нахождению произведения матриц будет правильным и с достаточной точностью, даже если числа при умножении матриц онлайн будут иррациональными. На сайте www.сайт допускаются символьные записи в элементах матриц , то есть произведение матриц онлайн может быть представлено в общем символьном виде при умножении матриц онлайн . Полезно проверить ответ, полученный при решении задачи на умножение матриц онлайн , используя сайт www. сайт . При совершении операции умножения матриц онлайн необходимо быть внимательным и предельно сосредоточенным при решении задачи. В свою очередь наш сайт поможет Вам проверить своё решение на тему умножение матриц онлайн . Если у Вас нет времени на долгие проверки решенных задач, то www.сайт безусловно будет являться удобным инструментом для проверки умножения матриц онлайн .

Умножать две матрицы можно только при условии, что в первой из них ровно такое же количество столбцов, сколько строк во второй. Сами же значения при этом могут быть не только целыми, но и дробными. Получив расшифровку вычисления этой задачи, вы сможете понять, как происходит перемножение. Это сэкономит ваше время и поможет лучше разобраться в вычислительных тонкостях.

Допустим, у вас имеется две матрицы, и вам предстоит найти их произведение. Сделать это оперативно и с наивысшей точностью вам поможет данный онлайн-калькулятор. Он не просто умножит две матрицы без затруднений за пару минут, но и позволит вам детальнее разобраться в самом алгоритме этих расчётов. Таким образом, применение онлайн-калькулятора способствует закреплению пройденного в теории материала. Можно также сначала производить вычисления вручную, а затем проверять их здесь, это превосходная тренировка для мозга.

Инструкция пользования данным онлайн-калькулятором не представляет сложности. Чтобы умножить матрицы онлайн для начала укажите количество имеющихся столбцов и строк в первой матрице посредством нажатия на иконки «+» или «-» слева от матрицы и под ней. Затем введите числа. Повторите те же операции для второй матрицы. Далее остаётся лишь кликнуть кнопку «Вычислить» – и перед вами откроется искомое значение вместе с детальным алгоритмом вычислений.

Данное методическое пособие поможет Вам научиться выполнять действия с матрицами : сложение (вычитание) матриц, транспонирование матрицы, умножение матриц, нахождение обратной матрицы. Весь материал изложен в простой и доступной форме, приведены соответствующие примеры, таким образом, даже неподготовленный человек сможет научиться выполнять действия с матрицами. Для самоконтроля и самопроверки Вы можете бесплатно скачать матричный калькулятор >>> .

Я буду стараться минимизировать теоретические выкладки, кое-где возможны объяснения «на пальцах» и использование ненаучных терминов. Любители основательной теории, пожалуйста, не занимайтесь критикой, наша задача – научиться выполнять действия с матрицами .

Для СВЕРХБЫСТРОЙ подготовки по теме (у кого «горит») есть интенсивный pdf-курс Матрица, определитель и зачёт!

Матрица – это прямоугольная таблица каких-либо элементов . В качестве элементов мы будем рассматривать числа, то есть числовые матрицы. ЭЛЕМЕНТ – это термин. Термин желательно запомнить, он будет часто встречаться, не случайно я использовал для его выделения жирный шрифт.

Обозначение: матрицы обычно обозначают прописными латинскими буквами

Пример: рассмотрим матрицу «два на три»:

Данная матрица состоит из шести элементов :

Все числа (элементы) внутри матрицы существуют сами по себе, то есть ни о каком вычитании речи не идет:

Это просто таблица (набор) чисел!

Также договоримся не переставлять числа, если иного не сказано в объяснениях. У каждого числа свое местоположение, и перетасовывать их нельзя!

Рассматриваемая матрица имеет две строки:

и три столбца:

СТАНДАРТ : когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали по косточкам матрицу «два на три».

Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной , например: – матрица «три на три».

Если в матрице один столбец или одна строка , то такие матрицы также называют векторами .

На самом деле понятие матрицы мы знаем еще со школы, рассмотрим, например точку с координатами «икс» и «игрек»: . По существу, координаты точки записаны в матрицу «один на два». Кстати, вот Вам и пример, почему порядок чисел имеет значение: и – это две совершенно разные точки плоскости.

Теперь переходим непосредственно к изучению действий с матрицами :

1) Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу) .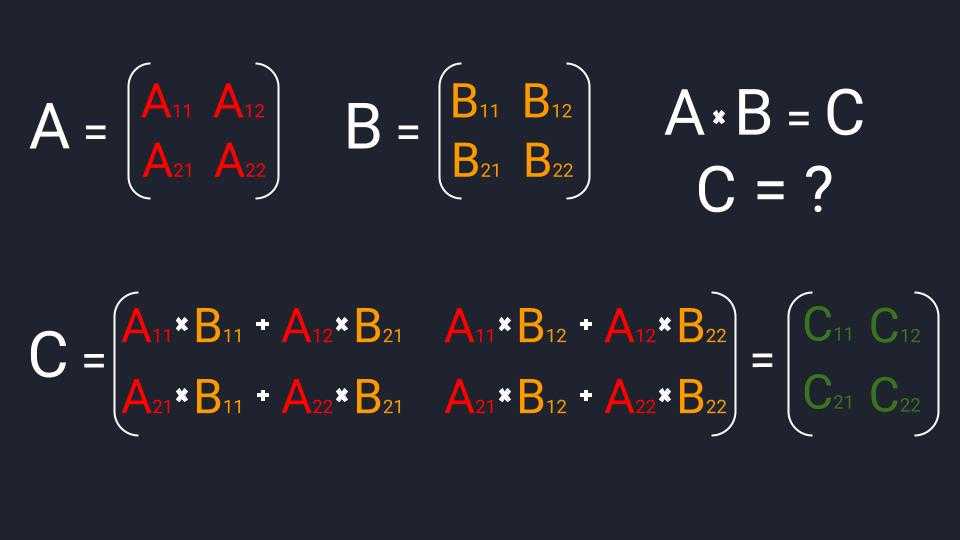

Вернемся к нашей матрице . Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит.

Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак :

У нуля, как Вы понимаете, знак не меняется, ноль – он и в Африке ноль.

Обратный пример: . Выглядит безобразно.

Внесем минус в матрицу, сменив у КАЖДОГО элемента матрицы знак :

Ну вот, гораздо симпатичнее получилось. И, самое главное, выполнять какие-либо действия с матрицей будет ПРОЩЕ. Потому что есть такая математическая народная примета: чем больше минусов – тем больше путаницы и ошибок .

2) Действие второе. Умножение матрицы на число .

Пример:

Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число.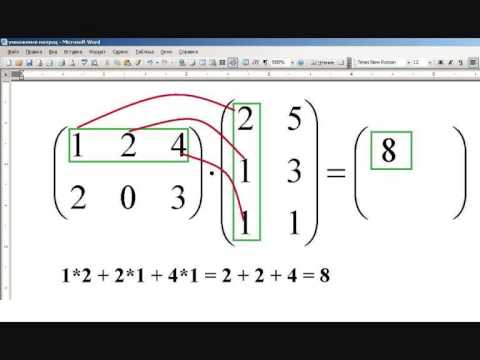 В данном случае – на тройку.

Еще один полезный пример:

– умножение матрицы на дробь

Сначала рассмотрим то, чего делать НЕ НАДО :

Вносить дробь в матрицу НЕ НУЖНО, во-первых, это только затрудняет дальнейшие действия с матрицей, во-вторых, затрудняет проверку решения преподавателем (особенно, если – окончательный ответ задания).

И, тем более, НЕ НАДО делить каждый элемент матрицы на минус семь:

Из статьи Математика для чайников или с чего начать , мы помним, что десятичных дробей с запятой в высшей математике стараются всячески избегать.

Единственное, что желательно сделать в этом примере – это внести минус в матрицу:

А вот если бы ВСЕ элементы матрицы делились на 7 без остатка , то тогда можно (и нужно!) было бы поделить.

Пример:

В этом случае можно и НУЖНО умножить все элементы матрицы на , так как все числа матрицы делятся на 2 без остатка .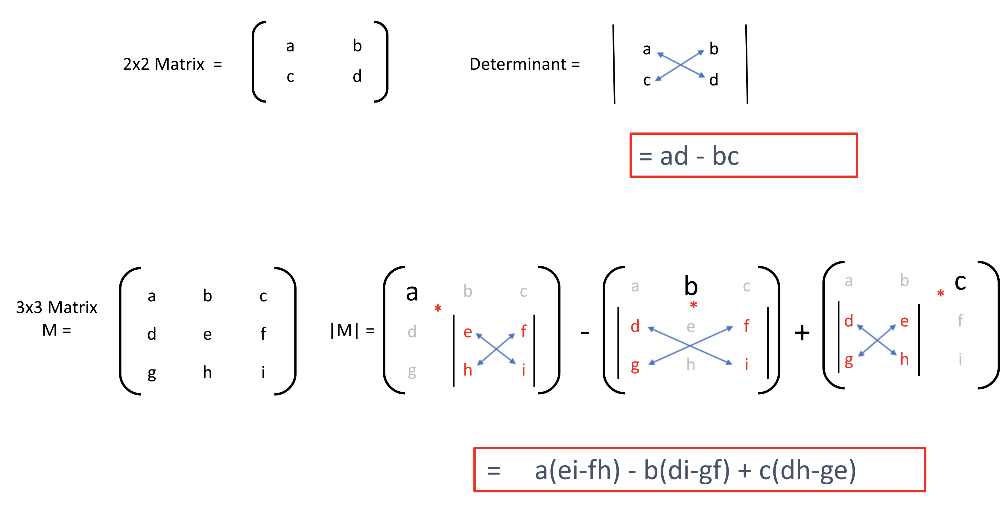

Примечание: в теории высшей математики школьного понятия «деление» нет. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». То есть, деление – это частный случай умножения.

3) Действие третье. Транспонирование матрицы .

Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.

Пример:

Транспонировать матрицу

Строка здесь всего одна и, согласно правилу, её нужно записать в столбец:

– транспонированная матрица.

Транспонированная матрица обычно обозначается надстрочным индексом или штрихом справа вверху.

Пошаговый пример:

Транспонировать матрицу

Сначала переписываем первую строку в первый столбец:

Потом переписываем вторую строку во второй столбец:

И, наконец, переписываем третью строку в третий столбец:

Готово. Грубо говоря, транспонировать – это значит повернуть матрицу набок.

4) Действие четвертое. Сумма (разность) матриц .

Сумма матриц действие несложное.
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.

Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой!

Пример:

Сложить матрицы и

Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы :

Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов .

Пример:

Найти разность матриц ,

А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу :

Примечание: в теории высшей математики школьного понятия «вычитание» нет. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.

5) Действие пятое. Умножение матриц .

Какие матрицы можно умножать?

Чтобы матрицу можно было умножить на матрицу нужно, чтобы число столбцов матрицы равнялось числу строк матрицы .

Пример:
Можно ли умножить матрицу на матрицу ?

Значит, умножать данные матрицы можно.

А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!

Следовательно, выполнить умножение невозможно:

Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно.

Следует отметить, что в ряде случаев можно умножать матрицы и так, и так.
Например, для матриц, и возможно как умножение , так и умножение

Как сделать умножение матриц и обратное в MS Excel « Microsoft Office :: WonderHowTo

• org/Person”> Автор Шон Конати
• 03.05.10 5:18

Это видео об умножении, определении и обращении матрицы в Excel. Сначала мы должны взять две матрицы в Excel. Если взять две матрицы 3х3 и перемножить их, то в результате получится матрица 3х3. Сначала мы должны выбрать ячейки 3×3 в Excel и затем дать формулу = mmult (а затем выбрать первую матрицу, она автоматически примет номера строк и ячеек, затем выберите вторую матрицу). Тогда он даст ответ. Затем, если вы хотите найти определитель матрицы A, введите формулу = mdeterm (выберите матрицу A). Гнездо нажмите Enter. Вы получите определитель A. Затем, если вы хотите найти обратную A, введите формулу = minverse (выберите матрицу A) и нажмите cntl+shft+enter. Вы получите обратное. Если вы хотите умножить три матрицы за раз, вы должны указать эту формулу. То есть =mmult(выберите матрицу A, выберите матрицу B). Это умножит AxB. Затем дайте формулу =mmult(mmult(matrix A selection, B selection), (matrix c selection) ). Тогда вы получите AxBxC. У вас есть возможность выбрать матрицу AxB, а затем матрицу C, чтобы получить матрицу AxBxC. Итак, это формула для создания матрицы в Excel.

Хотите освоить Microsoft Excel и поднять перспективы работы на дому на новый уровень? Начните свою карьеру с нашего учебного комплекта Microsoft Excel Premium от А до Я в новом магазине Gadget Hacks Shop и получите пожизненный доступ к более чем 40 часам базовых и продвинутых инструкций по функциям, формулам, инструментам и многому другому.

Купить сейчас (скидка 97%) >

Другие выгодные предложения:

• Скидка 97 % на The Ultimate White Hat Hacker Certification Bundle 2021
• Скидка 98 % на комплект Accounting Mastery Bootcamp 2021
• Скидка 99 % на The All-in-One Data Scientist Mega Bundle 2021
• Скидка 59 %: XSplit Lifetime Подписка (Windows)
• Скидка 98 % на пакет сертификации Premium Learn To Code 2021
• Скидка 62 % Программное обеспечение MindMaster Mind Mapping: бессрочная лицензия
• Скидка 41 %0006

• Горячий
• Последние

Скалярное произведение матрицы Объяснение

Данные собираются в различных форматах: от чисел до изображений, категорий и звуковых волн. Однако нам нужны числовые данные, чтобы анализировать их на компьютерах. Модели машинного обучения и глубокого обучения требуют больших объемов данных. Их производительность сильно зависит от объема данных. Таким образом, мы стремимся собрать как можно больше данных, чтобы построить надежную и точную модель. По мере увеличения объема данных операции, выполняемые со скалярами, становятся неэффективными. Нам нужны векторизованные или матричные операции для эффективного выполнения вычислений. Вот где на помощь приходит линейная алгебра.

Что такое скалярное произведение матрицы?

Скалярное произведение матрицы — это базовое вычисление линейной алгебры, используемое в моделях глубокого обучения для более эффективного выполнения операций с большими объемами данных. Это результат умножения двух матриц с совпадающими строками и столбцами, таких как матрица 3×2 и матрица 2×3. Его также можно рассчитать в NumPy с помощью операции np.dot.

Линейная алгебра — одна из самых важных тем в области науки о данных. В этом посте мы рассмотрим две основные, но очень важные операции линейной алгебры: скалярное произведение и умножение матриц. Эти основные операции являются строительными блоками сложных моделей машинного обучения и глубокого обучения, поэтому важно понимать их.

 

Как найти скалярное произведение

Скалярное произведение двух векторов представляет собой сумму произведений элементов относительно положения. Первый элемент первого вектора умножается на первый элемент второго вектора и так далее. Сумма этих продуктов представляет собой точечный продукт, который можно сделать с помощью функции np.dot().

Давайте сначала создадим два простых вектора в виде массивов NumPy и посчитаем скалярное произведение.

Два пустых массива. | Изображение: Soner Yildirim

Скалярное произведение этих двух векторов представляет собой сумму произведений элементов в каждой позиции. В этом случае скалярный продукт равен (1*2)+(2*4)+(3*6) .

Скалярный продукт для двух массивов NumPy. | Изображение: Soner Yildirim

Поскольку мы умножаем элементы в одних и тех же позициях, два вектора должны иметь одинаковую длину, чтобы получить скалярное произведение.

Учебное пособие по основам скалярного произведения. | Видео 3Blue1Brown.

Подробнее о науке о данных: пошаговое объяснение анализа главных компонентов

 

Как рассчитать матрицу скалярного произведения

В науке о данных мы в основном имеем дело с матрицами. Матрица — это набор векторов строк и столбцов, объединенных структурированным образом. Таким образом, умножение двух матриц включает множество операций скалярного произведения векторов. Будет понятнее, когда мы рассмотрим несколько примеров. Давайте сначала создадим две матрицы 2×2 с помощью NumPy.

Два массива 2×2 Num{y. | Изображение: Soner YildirimДва массива 2×2. | Изображение: Soner Yildirim

Матрица 2×2 состоит из двух строк и двух столбцов. Индекс строк и столбцов начинается с нуля. Например, первая строка A (строка с нулевым индексом) — это массив [4,2]. Первый столбец A — это массив [4,0]. Элемент первой строки и первого столбца равен четырем. Мы можем получить доступ к отдельным строкам, столбцам или элементам с помощью следующего синтаксиса NumPy.

Синтаксис NumPy для доступа к первому столбцу и строке массивов. | Изображение: Сонер Йилдирим

Это важные понятия, которые необходимо понять, чтобы понять умножение матриц.

Умножение двух матриц включает скалярное произведение между первой строкой матрицы и столбцами второй матрицы. Первым шагом является скалярное произведение между первой строкой A и первым столбцом B. Результатом этого скалярного произведения является элемент результирующей матрицы в позиции [0,0] (т. е. первая строка, первый столбец).

Нахождение скалярного произведения двух матриц. | Изображение: Сонер Йилдирим

Таким образом, результирующая матрица C будет иметь (4*4) + (2*1) в первой строке и первом столбце. С[0,0] = 18 .

Следующим шагом является скалярное произведение первой строки A и второго столбца B.

Нахождение скалярного произведения первой строки A и второго столбца B. | Изображение: Soner Yildirim

C будет иметь (4*0) + (2*4) в первой строке и втором столбце. С[0,1] = 8 .

Первый ряд A готов, поэтому мы начинаем со второго ряда A и повторяем те же шаги.

Продолжение процесса скалярного произведения, умножение второй строки A и первого столбца B. | Изображение: Soner Yildirim

C будет иметь (0*4) + (3*1) во второй строке и первом столбце. С[1,0] = 3 .

Последний шаг — скалярное произведение между второй строкой A и вторым столбцом B.

Заключительный шаг в процессе скалярного произведения, умножение второй строки A на вторую строку B. | Изображение: Soner Yildirim

C будет иметь (0*0) + (3*4) во второй строке и втором столбце. С[1,1] = 12 .

Теперь мы видели, как это делается шаг за шагом. Все эти операции также можно выполнить с помощью операции np. dot :

Нахождение матрицы скалярного произведения с помощью операции np.dot. | Изображение: Soner Yildirim

Как вы помните из векторного скалярного произведения, два вектора должны иметь одинаковую длину, чтобы получить скалярное произведение. Каждая операция скалярного произведения в матричном умножении должна следовать этому правилу. Скалярные произведения выполняются между строками первой матрицы и столбцами второй матрицы. Таким образом, строки первой матрицы и столбцы второй матрицы должны иметь одинаковую длину.

Здесь я хочу подчеркнуть важный момент: длина строки равна количеству столбцов. Точно так же длина столбца равна количеству строк.

Рассмотрим следующую матрицу D:

Пример матрицы 3×2. | Изображение: Soner Yildirim

D имеет три строки и два столбца, поэтому это матрица 3×2. Длина строки равна двум, что является количеством столбцов, а длина столбца равно трем, что является количеством строк.

Длина строки и столбца для матрицы D. | Изображение: Сонер Йилдирим

Это длинное объяснение, но суть в том, что для выполнения матричного умножения количество столбцов в первой матрице должно быть равно количеству строк во второй матрице.

Еще о науке о данных: 4 способа добавления столбца в Pandas

Например, мы можем умножить матрицу 3×2 на матрицу 2×3.

Умножение матриц 3×2 и 2×3 для получения матрицы скалярного произведения 3×3. | Изображение: Soner Yildirim

Форма результирующей матрицы будет 3×3, потому что мы выполняем три операции скалярного произведения для каждой строки A, а A имеет три строки. Простой способ определить вид получившейся матрицы — взять количество строк из первой и количество столбцов из второй:

• Умножение 3×2 и 2×3 возвращает 3×3.
• Умножение 3×2 и 2×2 возвращает 3×2.
• Умножение 2×4 и 4×3 возвращает 2×3.

Если условия, которые мы обсуждали, не выполняются, умножение матриц невозможно. Рассмотрим следующие матрицы C и D. Обе они являются матрицами 3×2:

Попытка перемножить две матрицы 3×2.