Формула умножения матрицу на матрицу: Умножение матриц. - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Умножение матриц.

Определение.

Результатом умножения матриц A_m×n и B_n×k будет матрица C_m×k такая, что элемент матрицы C, стоящий в i-той строке и j-том столбце (c_ij), равен сумме произведений элементов i-той строки матрицы A на соответствующие элементы j-того столбца матрицы B:

c_ij = a_i1 · b_1j + a_i2 · b_2j + … + a_in · b_nj

Замечание.

Две матрицы можно перемножить между собой тогда и только тогда, когда количество столбцов первой матрицы равно количеству строк второй матрицы.

Пример 1.

Найти матрицу C равную произведению матриц A = 4290 и B = 31-34

Решение:

С = A · B = 4290· 31-34 = 612279

Элементы матрицы C вычисляются следующим образом:

c₁₁ = a₁₁·b₁₁ + a₁₂·b₂₁ = 4·3 + 2·(-3) = 12 – 6 = 6

c₁₂ = a

11·b₁₂ + a₁₂·b₂₂ = 4·1 + 2·4 = 4 + 8 = 12

c₂₁ = a₂₁·b₁₁ + a₂₂·b₂₁ = 9·3 + 0·(-3) = 27 + 0 = 27

c₂₂ = a₂₁·b₁₂ + a₂₂·b₂₂ = 9·1 + 0·4 = 9 + 0 = 9

Пример 2

Найти матрицу C равную произведению матриц A = 21-304-1 и B = 5-16-307.

Решение:

C = A · B = 21-304-1· 5-16-307 = 7-219-153-1823-417

Элементы матрицы C вычисляются следующим образом:

c₁₁ = a₁₁·b₁₁ + a₁₂·b₂₁ = 2·5 + 1·(-3) = 10 – 3 = 7

c₁₂ = a₁₁·b₁₂ + a₁₂·b₂₂ = 2·(-1) + 1·0 = -2 + 0 = -2

c₁₃ = a₁₁·b₁₃ + a₁₂·b₂₃ = 2·6 + 1·7 = 12 + 7 = 19

c₂₁ = a₂₁·b₁₁ + a₂₂·b₂₁ = (-3)·5 + 0·(-3) = -15 + 0 = -15

c₂₂ = a₂₁·b₁₂ + a₂₂·b₂₂ = (-3)·(-1) + 0·0 = 3 + 0 = 3

c₂₃ = a₂₁·b₁₃ + a₂₂·b₂₃ = (-3)·6 + 0·7 = -18 + 0 = -18

c₃₁ = a₃₁·b₁₁ + a₃₂·b₂₁ = 4·5 + (-1)·(-3) = 20 + 3 = 23

c₃₂ = a₃₁·b₁₂ + a₃₂·b₂₂ = (4)·(-1) + (-1)·0 = -4 + 0 = -4

c₃₃ = a₃₁·b₁₃ + a₃₂·b₂₃ = 4·6 + (-1)·7 = 24 – 7 = 17

Как перемножать матрицы в экселе

Одной из частых операций, которую выполняют при работе с матрицами, является перемножение одной из них на другую. Программа Excel является мощным табличным процессором, который предназначен, в том числе и для работы над матрицами. Поэтому у него имеются инструменты, которые позволяют перемножить их между собой. Давайте узнаем, как это можно выполнить различными способами.

Процедура перемножения матриц

Сразу нужно сказать, что перемножить между собой можно далеко не все матрицы, а только те, которые соответствуют определенному условию: число столбцов одной матрицы должно быть равным числу строк другой и наоборот. Кроме того, исключается наличие в составе матриц пустых элементов. В этом случае тоже выполнить требуемую операцию не получится.

Способов перемножить матрицы в Экселе все-таки не так уж и много — всего два. И оба они связаны с применением встроенных функций Excel. Разберем в деталях каждый из данных вариантов.

Способ 1: функция МУМНОЖ

Наиболее простым и популярным вариантом среди пользователей является применение функции МУМНОЖ. Оператор

МУМНОЖ относится к математической группе функций.

Как раз его непосредственной задачей и является нахождение произведения двух матричных массивов. Синтаксис МУМНОЖ имеет такой вид:

Таким образом этот оператор имеет два аргумента, которые представляют собой ссылки на диапазоны двух перемножаемых матриц.

Теперь давайте посмотрим, как используется функция МУМНОЖ на конкретном примере. Имеется две матрицы, число строк одной из которых, соответствует количеству столбцов в другой и наоборот. Нам нужно перемножить два этих элемента.

«Вставить функцию»

Активируется Мастер функций. Перемещаемся в блок «Математические», кликаем по наименованию «МУМНОЖ» и клацаем по кнопке «OK» в нижней части окна.

После того, как оба аргумента внесены, не спешим жать на кнопку «OK», так как мы имеем дело с функцией массива, а это значит, что для получения корректного результата обычный вариант завершения работы с оператором не подойдет.

Данный оператор предназначен не для того, чтобы выводить результат в одну ячейку, так как выводит его в целый диапазон на листе. Итак, вместо нажатия кнопки «OK» жмем комбинацию кнопок Ctrl+Shift+Enter.

Как видим, после этого предварительно выделенный диапазон был заполнен данными. Это и есть результат умножения матричных массивов. Если взглянуть на строку формул, после выделения любого из элементов данного диапазона, то мы увидим, что сама формула обернута в фигурные скобки. Это и есть признак функции массива, который добавляется после нажатия сочетания клавиш Ctrl+Shift+Enter перед выводом результат на лист.

Способ 2: использование составной формулы

Кроме того, существует ещё один способ умножения двух матриц. Он более сложный, чем предыдущий, но тоже заслуживает упоминания, как альтернативный вариант. Данный способ предполагает использование составной формулы массива, которая будет состоять из функции

СУММПРОИЗВ и вложенного в неё в качестве аргумента оператора ТРАНСП.

«Вставить функцию»

Мастер функций запускается. Перемещаемся в блок операторов

«Математические», но на этот раз выбираем наименование СУММПРОИЗВ. Клацаем по кнопке «OK».

Происходит открытие окна аргументов вышеуказанной функции. Данный оператор предназначен для перемножения различных массивов между собой. Его синтаксис следующий:

В качестве аргументов из группы «Массив» используется ссылка на конкретный диапазон, который нужно перемножить. Всего может быть использовано от двух до 255 таких аргументов. Но в нашем случае, так как мы имеем дело с двумя матрицами, нам понадобится как раз два аргумента.

Ставим курсор в поле «Массив1». Тут нам нужно будет ввести адрес первой строки первой матрицы. Для этого, зажав левую кнопку мыши, нужно просто выделить её на листе курсором.

Тут же координаты данного диапазона будут отображены в соответствующем поле окна аргументов. После этого следует зафиксировать координаты полученной ссылки по столбцам, то есть, эти координаты нужно сделать абсолютными. Для этого перед буквами в выражении, которое вписано в поле, устанавливаем знак доллара ($). Перед координатами, отображенными в цифрах (строки), это делать не следует. Также, можно вместо этого выделить всё выражение в поле и трижды нажать на функциональную клавишу F4. В данном случае абсолютными тоже станут лишь координаты столбцов.

После этого устанавливаем курсор в поле «Массив2». С этим аргументом будет посложнее, так как по правилам умножения матриц, вторую матрицу нужно «перевернуть». Для этого используем вложенную функцию ТРАНСП.

Чтобы перейти к ней, клацаем по значку в виде треугольника, направленного острым углом вниз, который размещен слева от строки формул. Открывается список недавно используемых формул. Если вы в нем найдете наименование «ТРАНСП», то щелкайте по нему. Если же вы давно использовали данный оператор или вообще никогда не применяли его, то в этом списке указанное наименование вы не отыщите. В этом случае требуется нажать по пункту

«Другие функции…».

Открывается уже хорошо знакомое нам окно Мастера функций. На этот раз перемещаемся в категорию «Ссылки и массивы» и выбираем наименование «ТРАНСП». Щелкаем по кнопке «OK».

Производится запуск окна аргументов функции ТРАНСП. Данный оператор предназначен для транспонирования таблиц. То есть, попросту говоря, он меняет местами столбцы и строки. Это нам и нужно сделать для второго аргумента оператора СУММПРОИЗВ. Синтаксис функции ТРАНСП предельно простой:

То есть, единственным аргументом данного оператора является ссылка на тот массив, который следует «перевернуть». Вернее, в нашем случае даже не на весь массив, а только на его первый столбец.

Итак, устанавливаем курсор в поле «Массив» и выделяем первый столбец второй матрицы на листе с зажатой левой кнопкой мыши. Адрес отобразится в поле. Как и в предыдущем случае, тут тоже нужно сделать определенные координаты абсолютными, но на этот раз не координаты столбцов, а адреса строк. Поэтому ставим знак доллара перед цифрами в ссылке, которая отображается в поле. Можно также выделить всё выражение и дважды кликнуть по клавише F4. После того, как нужные элементы стали иметь абсолютные свойства, не жмем на кнопку «OK», а так же, как и в предыдущем способе, применяем нажатие комбинации клавиш Ctrl+Shift+Enter.

Но на этот раз у нас заполнился не массив, а только одна ячейка, которую мы ранее выделили при вызове Мастера функций.

Нам нужно заполнить данными такой же по размеру массив, как и в первом способе. Для этого следует скопировать формулу, полученную в ячейке, на равнозначный диапазон, который будет равен количеству строк первой матрицы и количеству столбцов второй. В конкретно нашем случае получается три строки и три столбца.

Для копирования прибегнем к использованию маркера заполнения. Наводим курсор на нижний правый угол ячейки, в которой расположена формула. Курсор преобразуется в черный крестик. Это и есть маркер заполнения. Зажимаем левую кнопку мыши и протягиваем курсор по всему вышеуказанному диапазону. Сама начальная ячейка с формулой должна стать левым верхним элементом данного массива.

Как видим, выделенный диапазон заполнен данными. Если их сравнить с тем результатом, который мы получили благодаря применению оператора МУМНОЖ, то увидим, что значения полностью идентичны. Это означает, что умножение двух матриц выполнено верно.

Как видим, несмотря на то, что был получен равнозначный результат, использовать функцию для умножения матриц МУМНОЖ значительно проще, чем применять для этих же целей составную формулу из операторов СУММПРОИЗВ и ТРАНСП. Но все-таки данный альтернативный вариант тоже нельзя оставить без внимания при изучении всех возможностей перемножения матриц в Microsoft Excel.

Отблагодарите автора, поделитесь статьей в социальных сетях.

Функционал программы Microsoft Excel позволяет рассчитывать сложные математические операции. В том числе и перемножение матриц. Сделать это можно произведя несколько шагов.

Как пример возьмёт матрицу :

Для начала элементы матриц запишем в ячейки и оставим курсор там где в конце должен появиться результат.

После этого выбираем в основном меню раздел “Формулы”, в нем нажимаем “Математические” и в списке кликаем на пункт “МУМНОЖ”.

Откроется специальное окно. В нём нужно ввести адреса ячеек наиболее удобным для себя способом в поля “Массив1” и “Массив 2”. В них нужно ввести координаты элементов матриц.

После подтверждения действия в рабочем окне можно увидеть результат в обычном матричном виде и выделяем два столбца и две строки.

Далее на клавиатуре нажимаем клавишу F2 и одновременно нажимаем комбинацию клавиш Ctrl+Shift+Enter. После этого будет показан полный результат перемножения матриц.

Программа Microsoft Office Excel позволяет выполнять операции с матрицами с помощью встроенных функций и формул. Рассмотрим основные операции над матрицами:

умножение и деление матрицы на число;
сложение, вычитание и умножение матриц;
транспонирование матрицы;
нахождение обратной матрицы;
вычисление определителя.

Введем условные обозначения. Матрица А размерностью i x j — это прямоугольная таблица чисел, состоящая из i строк и j столбцов, а_ij — элемент матрицы.

Умножение и деление матрицы на число в Excel

Способ 1

Рассмотрим матрицу А размерностью 3х4. Умножим эту матрицу на число k. При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k.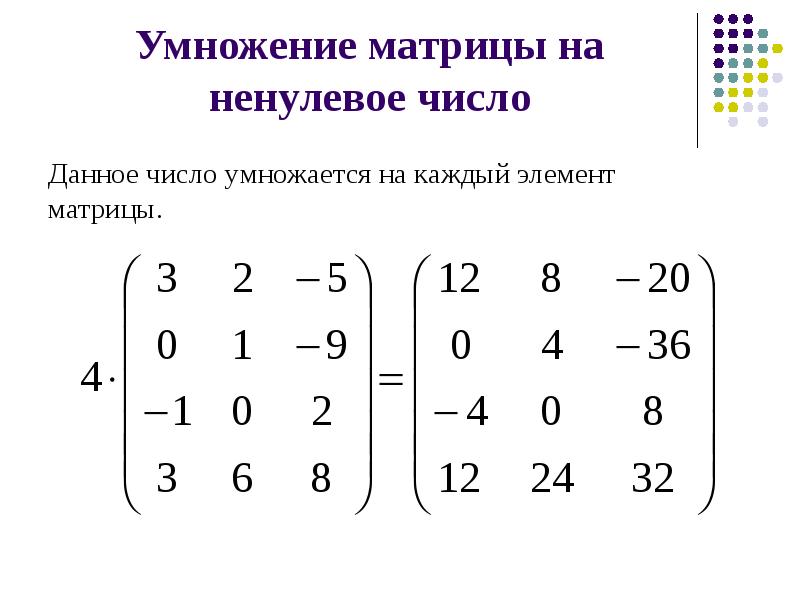

Введем элементы матрицы в диапазон В3:Е5, а число k — в ячейку Н4. В диапазоне К3:N5 вычислим матрицу В, полученную при умножении матрицы А на число k: В=А*k. Для этого введем формулу =B3*$H$4 в ячейку K3, где В3 — элемент а₁₁ матрицы А.

Примечание: адрес ячейки H4 вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась.

С помощью маркера автозаполнения копируем формулу ячейки К3 вниз и вправо на весь диапазон матрицы В.

Таким образом, мы умножили матрицу А в Excel и получим матрицу В.

Для деления матрицы А на число k в ячейку K3 введем формулу =B3/$H$4 и скопируем её на весь диапазон матрицы В.

Способ 2

Этот способ отличается тем, что результат умножения/деления матрицы на число сам является массивом. В этом случае нельзя удалить элемент массива.

Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий исходную матрицу А, нажимаем на клавиатуре знак умножить (*) и выделяем ячейку с числом k. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.

Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/h5, т.е. знак «*» меняем на «/».

Сложение и вычитание матриц в Excel

Способ 1

Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С будет равен сумме соответствующих элементов матриц А и В, т. е. с_ij = а_ij + b_ij.

Рассмотрим матрицы А и В размерностью 3х4. Вычислим сумму этих матриц. Для этого в ячейку N3 введем формулу =B3+h4, где B3 и h4 – первые элементы матриц А и В соответственно. При этом формула содержит относительные ссылки (В3 и H3), чтобы при копировании формулы на весь диапазон матрицы С они могли измениться.

С помощью маркера автозаполнения скопируем формулу из ячейки N3 вниз и вправо на весь диапазон матрицы С.

Для вычитания матрицы В из матрицы А (С=А – В) в ячейку N3 введем формулу =B3 — h4 и скопируем её на весь диапазон матрицы С.

Способ 2

Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива.

Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А, нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.

Умножение матриц в Excel

Следует отметить, что умножать матрицы можно только в том случае, если количество столбцов первой матрицы А равно количеству строк второй матрицы В.

Рассмотрим матрицы А размерностью 3х4 и В размерностью 4х2. При умножении этих матриц получится матрица С размерностью 3х2.

Вычислим произведение этих матриц С=А*В с помощью встроенной функции =МУМНОЖ(). Для этого выделим диапазон L3:M5 — в нём будут располагаться элементы матрицы С, полученной в результате умножения. На вкладке Формулы выберем Вставить функцию.

В диалоговом окне Вставка функции выберем Категория Математические — функция МУМНОЖ — ОК.

В диалоговом окне Аргументы функции выберем диапазоны, содержащие матрицы А и В. Для этого напротив массива1 щёлкнем по красной стрелке.

Выделим диапазон, содержащий элементы матрицы А (имя диапазона появится в строке аргументов), и щелкнем по красной стрелке.

Для массива2 выполним те же действия. Щёлкнем по стрелке напротив массива2.

Выделим диапазон, содержащий элементы матрицы В, и щелкнем по красной стрелке.

В диалоговом окне рядом со строками ввода диапазонов матриц появятся элементы матриц, а внизу — элементы матрицы С. После ввода значений нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.

ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы С.

Мы получим результат умножения матриц А и В.

Мы можем изменить значения ячеек матриц А и В, значения матрицы С поменяются автоматически.

Транспонирование матрицы в Excel

Транспонирование матрицы — операция над матрицей, при которой столбцы заменяются строками с соответствующими номерами. Обозначим транспонированную матрицу А Т .

Пусть дана матрица А размерностью 3х4, с помощью функции =ТРАНСП() вычислим транспонированную матрицу А Т , причем размерность этой матрицы будет 4х3.

Выделим диапазон Н3:J6, в который будут введены значения транспонированной матрицы.

На вкладке Формулы выберем Вставить функцию, выберем категорию Ссылки и массивы — функция ТРАНСП — ОК.

В диалоговом окне Аргументы функции указываем диапазон массива В3:Е5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.

ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А Т .

Нажмите для увеличения

Мы получили транспонированную матрицу.

Нахождение обратной матрицы в Excel

Матрица А -1 называется обратной для матрицы А, если АА -1 =А -1 А=Е, где Е — единичная матрица. Следует отметить, что обратную матрицу можно найти только для квадратной матрицы (одинаковое количество строк и столбцов).

Пусть дана матрица А размерностью 3х3, найдем для неё обратную матрицу с помощью функции =МОБР().

Для этого выделим диапазон G3:I5, который будет содержать элементы обратной матрицы, на вкладке Формулы выберем Вставить функцию.

В диалоговом окне Вставка функции выберем категорию Математические — функция МОБР — ОК.

В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.

ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А -1 .

Нажмите для увеличения

Мы получили обратную матрицу.

Нахождение определителя матрицы в Excel

Определитель матрицы — это число, которое является важной характеристикой квадратной матрицы.

Как найти определить матрицы в Excel

Пусть дана матрица А размерностью 3х3, вычислим для неё определитель с помощью функции =МОПРЕД().

Для этого выделим ячейку Н4, в ней будет вычислен определитель матрицы, на вкладке Формулы выберем Вставить функцию.

В диалоговом окне Вставка функции выберем категорию Математические — функция МОПРЕД — ОК.

В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем ОК.

Нажмите для увеличения

Мы вычислили определитель матрицы А.

В заключение обратим внимание на важный момент. Он касается тех операций над матрицами, для которых мы использовали встроенные в программу функции, а в результате получали новую матрицу (умножение матриц, нахождение обратной и транспонированной матриц). В матрице, которая получилась в результате операции, нельзя удалить часть элементов. Т.е. если мы выделим, например, один элемент матрицы и нажмём Del, то программа выдаст предупреждение: Нельзя изменять часть массива.

Нажмите для увеличения

Мы можем удалить только все элементы этой матрицы.

Видеоурок

Кратко об авторе:

Шамарина Татьяна Николаевна — учитель физики, информатики и ИКТ, МКОУ “СОШ”, с. Саволенка Юхновского района Калужской области. Автор и преподаватель дистанционных курсов по основам компьютерной грамотности, офисным программам. Автор статей, видеоуроков и разработок.

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.

Есть мнение?
Оставьте комментарий

Понравился материал?
Хотите прочитать позже?
Сохраните на своей стене и
поделитесь с друзьями

Вы можете разместить на своём сайте анонс статьи со ссылкой на её полный текст

Умножение матрицы на число в excel. Функции для работы с матрицами в Excel

В разделе на вопрос Как создать матрицу в Excel???? заданный автором Masha Kalganova лучший ответ это Что конкретно нужно сделать?
Документ эксель – безразмерная (всеразмерная) матрица, каждый элемент которой может быть числом, текстом или любым другим значением. Да хоть формулой.
Если напечатать 3 циферки в ряд, под ними еще 3 в ряд, под ними еще 3 в ряд, получим квадратную матрицу 3х3.
Вопрос в чем?
Умножение матрицы на число в Excel
Формулы написать?
В верхней левой клетке новой матрицы
=левая верхняя клетка старой матрицы * клетка с числом (ткнуть мышкой) , нажать F4 дабы стало $x$y, где x,y – координаты клетки. Это зафиксирует клетку при копировании. Далее жмем Enter и копируем содержимое клетки в 2 соседние клетки в ряд. Далее копируем эти 3 клетки в следующие 3 ряда и получаем тот же результат, что у меня на картинке. То есть умножение матрицы на число.
Блин, математику не знают, а в интернете лазают!

Решение систем линейных алгебраических уравнений в Excel Методы решения систем линейных алгебраических уравнений хорошо описаны в учебнике “Основы вычислительной математики. Демидович Б.П., Марон И.А. 1966”. Скачать – 11Мб

1. Метод обратной матрицы (решение в Excel)

Если дано уравнение:
A*X = B, где A – квадратная матрица, X,B – вектора;
причем B – известный вектор (т е столбец чисел), X – неизвестный вектор,
то решение X можно записать в виде:
X = A -1 *B, где A -1 – обратная от А матрица.
В MS Excel обратная матрица вычисляется функцией МОБР(), а перемножаются матрицы (или матрица на вектор) – функцией МУМНОЖ().

Имеются “тонкости” использования этих матричных действий в Excel. Так, чтобы вычислить обратную матрицу от матрицы А, нужно:

1. Мышкой выделить квадратную область клеток, где будет размещена обратная матрица. 2. Начать вписывать формулу =МОБР(3. Выделить мышкой матрицу А. При этом правее скобки впишется соответствующий диапазон клеток. 4. Закрыть скобку, нажать комбинацию клавиш: Ctrl-Shift-Enter 5. Должна вычислиться обратная матрица и заполнить предназначенную для неё область Чтобы умножить матрицу на вектор: 1. Мышкой выделить область клеток, где будет размещён результат умножения 2. Начать вписывать формулу =МУМНОЖ(3. Выделить мышкой матрицу – первый сомножитель. При этом правее скобки впишется соответствующий диапазон клеток. 4. С клавиатуры ввести разделитель; (точка с запятой) 5. Выделить мышкой вектор- второй сомножитель. При этом правее скобки впишется соответствующий диапазон клеток. 6. Закрыть скобку, нажать комбинацию клавиш: Ctrl-Shift-Enter 7. Должно вычислиться произведение и заполнить предназначенную для него область Есть и другой спососб, при котором используется кнопка построителя функции Excel. Пример СЛАУ 4-го порядка

Скачать документ Excel, в котором этот пример решён различными методами.

2. Метод Гаусса

Метод Гаусса подробно (по шагам) выполняется только в учебных целях, когда нужно показать, что Вы это умеете. А чтобы решить реальную СЛАУ, лучше применить в Excel метод обратной матрицы или воспользоваться специальными программами, например, этой

Краткое описание.

3. Метод Якоби (метод простых итераций)

Для применения метода Якоби (и метода Зейделя) необходимо, чтобы диагональные компоненты матрицы А были больше суммы остальных компонент той же строки. Заданная система не обладает таким свойством, поэтому выполняю предварительные преобразования.

(1)’ = (1) + 0,43*(2) – 0,18*(3) – 0,96*(4) (2)’ = (2) + 0,28*(1) – 1,73*(3) + 0,12*(4) (3)’ = (3) – 0,27*(1) – 0,75*(2) + 0,08*(4) (4)’ = (4) + 0,04*(1) – 6,50*(2) + 8,04*(3) Примечание: подбор коэффицентов выполнен на листе “Анализ”. Решаются системы уравнений, цель которых – обратить внедиагональные элементы в нуль. Коэффиценты – это округлённые результаты решения таких систем уравнений. Конечно, это не дело. В результате получаю систему уравнений:
Для применения метода Якоби систему уравнений нужно преобразовать к виду:
X = B2 + A2*X Преобразую:

Далее делю каждую строку на множитель левого столбца, то есть на 16, 7, 3, 70 соответственно. Тогда матрица А2 имеет вид:

А вектор В2:

Способ 1

Рассмотрим матрицу А размерностью 3х4 . Умножим эту матрицу на число k . При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k .

Введем элементы матрицы в диапазон В3:Е5 , а число k — в ячейку Н4 . В диапазоне К3: N 5 вычислим матрицу В , полученную при умножении матрицы А на число k : В=А* k . Для этого введем формулу =B3*$H$4 в ячейку K 3 , где В3 — элемент а 11 матрицы А .

Примечание: адрес ячейки H 4 вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась.

С помощью маркера автозаполнения копируем формулу ячейки К3 В .

Таким образом, мы умножили матрицу А в Excel и получим матрицу В .

Для деления матрицы А на число k в ячейку K 3 введем формулу =B3/$H$4 В .

Способ 2

Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/h5, т.е. знак «*» меняем на «/».

Сложение и вычитание матриц в Excel

Способ 1

Рассмотрим матрицы А и В размерностью 3х4 . Вычислим сумму этих матриц. Для этого в ячейку N 3 введем формулу =B3+h4 , где B3 и h4 – первые элементы матриц А и В соответственно. При этом формула содержит относительные ссылки (В3 и H 3 ), чтобы при копировании формулы на весь диапазон матрицы С они могли измениться.

С помощью маркера автозаполнения скопируем формулу из ячейки N 3 вниз и вправо на весь диапазон матрицы С .

Для вычитания матрицы В из матрицы А (С=А – В ) в ячейку N 3 введем формулу =B3 — h4 и скопируем её на весь диапазон матрицы С .

Способ 2

Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А , нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В . После ввода формулы нажимаем сочетание клавиш Ctrl+ Shift+ Enter , чтобы значениями заполнился весь диапазон.

Умножение матриц в Excel

Рассмотрим матрицы А размерностью 3х4 и В размерностью 4х2 . При умножении этих матриц получится матрица С размерностью 3х2.

Вычислим произведение этих матриц С=А*В с помощью встроенной функции =МУМНОЖ() . Для этого выделим диапазон L 3: M 5 — в нём будут располагаться элементы матрицы С , полученной в результате умножения. На вкладке Формулы выберем Вставить функцию .

В диалоговом окне Вставка функции выберем Категория Математические — функция МУМНОЖ — ОК .

В диалоговом окне Аргументы функции выберем диапазоны, содержащие матрицы А и В . Для этого напротив массива1 щёлкнем по красной стрелке.

А (имя диапазона появится в строке аргументов), и щелкнем по красной стрелке.

Для массива2 выполним те же действия. Щёлкнем по стрелке напротив массива2.

Выделим диапазон, содержащий элементы матрицы В , и щелкнем по красной стрелке.

В диалоговом окне рядом со строками ввода диапазонов матриц появятся элементы матриц, а внизу — элементы матрицы С . После ввода значений нажимаем на клавиатуре сочетание клавиш Shift + Ctrl ОК .

ВАЖНО. Если просто нажать ОК С .

Мы получим результат умножения матриц А и В .

Мы можем изменить значения ячеек матриц А и В , значения матрицы С поменяются автоматически.

Транспонирование матрицы в Excel

Пусть дана матрица А размерностью 3х4 , с помощью функции =ТРАНСП() вычислим транспонированную матрицу А Т , причем размерность этой матрицы будет 4х3 .

Выделим диапазон Н3: J 6 , в который будут введены значения транспонированной матрицы.

В диалоговом окне Аргументы функции указываем диапазон массива В3:Е5 А Shift + Ctrl и щелкаем левой кнопкой мыши по кнопке ОК .

ВАЖНО. Если просто нажать ОК , то программа вычислит значение только первой ячейки диапазона матрицы А Т .

Нажмите для увеличения

Мы получили транспонированную матрицу.

Нахождение обратной матрицы в Excel

Матрица А -1 называется обратной для матрицы А , если А А -1 =А -1 А=Е , где Е — единичная матрица. Следует отметить, что обратную матрицу можно найти только для квадратной матрицы (одинаковое количество строк и столбцов).

Пусть дана матрица А размерностью 3х3 , найдем для неё обратную матрицу с помощью функции =МОБР() .

Для этого выделим диапазон G 3: I 5 , который будет содержать элементы обратной матрицы, на вкладке Формулы выберем Вставить функцию .

В диалоговом окне Вставка функции выберем категорию Математические — функция МОБР — ОК .

В диалоговом окне Аргументы функции указываем диапазон массива В3: D 5 , содержащего элементы матрицы А . Нажимаем на клавиатуре сочетание клавиш Shift + Ctrl и щелкаем левой кнопкой мыши по кнопке ОК .

ВАЖНО. Если просто нажать ОК , то программа вычислит значение только первой ячейки диапазона матрицы А -1 .

Нажмите для увеличения

Мы получили обратную матрицу.

Нахождение определителя матрицы в Excel

Определитель матрицы — это число, которое является важной характеристикой квадратной матрицы.

Как найти определить матрицы в Excel

Пусть дана матрица А размерностью 3х3 , вычислим для неё определитель с помощью функции =МОПРЕД() .

Для этого выделим ячейку Н4 , в ней будет вычислен определитель матрицы, на вкладке Формулы выберем Вставить функцию .

В диалоговом окне Вставка функции выберем категорию Математические — функция МОПРЕД — ОК .

В диалоговом окне Аргументы функции указываем диапазон массива В3: D 5 , содержащего элементы матрицы А . Нажимаем ОК .

Нажмите для увеличения

Мы вычислили определитель матрицы А .

В заключение обратим внимание на важный момент. Он касается тех операций над матрицами, для которых мы использовали встроенные в программу функции, а в результате получали новую матрицу (умножение матриц, нахождение обратной и транспонированной матриц). В матрице, которая получилась в результате операции, нельзя удалить часть элементов. Т.е. если мы выделим, например, один элемент матрицы и нажмём Del , то программа выдаст предупреждение: Нельзя изменять часть массива .

Нажмите для увеличения

Мы можем удалить только все элементы этой матрицы.

Видеоурок

Учитель физики, информатики и ИКТ, МКОУ “СОШ”, с. Саволенка Юхновского района Калужской области. Автор и преподаватель дистанционных курсов по основам компьютерной грамотности, офисным программам. Автор статей, видеоуроков и разработок.

РХТУ им. Д.B. Менделеева Кафедра ИКМ Методическое пособие по изучению Excel

Операции с матрицами в Excel

Как и над числами, над матрицами можно проводить ряд операций, причем в случае с матрицами некоторые из операций являются специфическими.

Транспонирование .

Транспонированной называется матрица (A T), в которой столбцы исходной матрицы (А) заменяются строками с соответствующими номерами.

Пример . Пусть в диапазон ячеек А1:Е2 введена матрица размера 2×5. Необходимо получить транспонированную матрицу.

Выделить указателем мыши при нажатой левой кнопке блок ячеек, где будет находиться транспонированная матрица. В нашем примере блок размера 5 x2 в диапазоне А4:В8.

Стандартная  вставка функции.

Мастер функций в рабочем полеКатегория выбратьСсылки и массивы , а в рабочем полеФункция – имя функции ТРАСП (рис.1)

рис.1

Появившееся диалоговое окно ТРАСП мышью отодвинуть в сторону от исходной матрицы и ввести диапазон исходной матрицы А1:Е2 в рабочее поле Массив (указателем мыши при нажатой левой кнопке). После чего, не нажимая кнопку ОК, нажать сочетание клавишCTRL+SHIFT+ENTER(рис.2)

Если транспонированная матрица не появилась в заданном диапазоне А4:В8, то надо щелкнуть указателем мыши в строке формул и повторить нажатие клавиш CTRL+SHIFT+ENTER.

В результате в диапазоне А4:В8 появится транспонированная матрица.

Рис.2

Вычисление определителя матрицы

Пусть в диапазон А1:С3 введена матрица. Необходимо вычислить определитель матрицы

Табличный курсор поставить в ячейку, в которой требуется получить значение определителя, например. В А4.

Нажать на панели инструментов Стандартная кнопкуВставка функции

В появившемся диалоговом окне Мастер функций в рабочем полеКатегории выбратьМатематические, а в рабочем полеФункция – имя функции МОПРЕД. После этого нажать на кнопку ОК.

Появившееся диалоговое окно МОПРЕД мышью отодвинуть в сторону от исходной матрицы и ввести диапазон исходной матрицы А1:С3 в рабочее поле Массив (указателем мыши при нажатой левой кнопке). После чего нажать кнопку ОК.

В ячейке А4 появится значение определителя матрицы.

Нахождение обратной матрицы

Пусть в диапазон А1:С3 введена матрица. Необходимо в диапазоне А5:С7 получить обратную матрицу.

Выделить блок ячеек под обратную матрицу (в нашем примере А5:С7)

Нажать на панели инструментов Стандартная кнопкуВставка функции

В появившемся диалоговом окне Мастер функций в рабочем полеКатегории выбратьМатематические, а в рабочем полеФункция – имя функции МОБР. После этого нажать на кнопку ОК.

Появившееся диалоговое окно МОБР мышью отодвинуть в сторону от исходной матрицы и ввести диапазон исходной матрицы А1:С3 в рабочее поле Массив (указателем мыши при нажатой левой кнопке). После чего, не нажимая кнопку ОК, нажать сочетание клавишCTRL+SHIFT+ENTER

Если обратная матрица не появилась в заданном диапазоне А1:С3, то надо щелкнуть указателем мыши в строке формул и повторить нажатие клавиш CTRL+SHIFT+ENTER.

В результате в диапазоне А1:С3 появится обратная матрица.

Сложение и вычитание матриц, умножение и деление матрицы на число

Пример. Пусть матрица А введена в диапазон А1:С2, а матрица В – в диапазон А4:С5. Необходимо найти матрицу С, являющуюся их суммой, в диапазоне Е1:G2.

Табличный курсор установить в левый верхний угол результирующей матрицы – ячейку Е1.

Ввести формулу для вычисления первого элемента результирующей матрицы =А1+А4 (предварительно установить английскую раскладку клавиатуры)

Скопируйте введенную формулу в остальные ячейки результирующей матрицы.

В результате в ячейках E1:G2 появится матрица, равная сумме исходных матриц.

Подобным образом вычисляется разность матриц, только в формуле вместо знака +, ставится знак -.

Если необходимо умножить (разделить) матрицу А на число k, то формула будет иметь вид =А1*k.

Рис.3

Умножение матриц

Произведение двух матриц определено, если число столбцов первой матрицы произведения равно числу строк второй матрицы произведения.

Пример . Пусть матрица введена в диапазонA1:D3, а матрица В – в диапазон А4:В7. Необходимо найти произведение этих матриц С=Аx В.

Выделить блок ячеек указателем мыши при нажатой левой кнопке под результирующую матрицу. Если матрица А имеет размерность 3 x 4, а матрица В имеет размерность 4 x 3, то результирующая матрица С имеет размерность 3 x 3. Поэтому следует внимательно следить, чтобы размерность матрицы С в точности соответствовала определению произведения двух матриц. Пусть матрица С будет размещаться в диапазонеF1:G3.

Нажать на панели инструментов Стандартная кнопкуВставка функции

В появившемся диалоговом окне Мастер функций в рабочем полеКатегории выбратьМатематические, а в рабочем полеФункция – имя функции МУМНОЖ. После этого нажать на кнопку ОК.

Появившееся диалоговое окно МУМНОЖ мышью отодвинуть в сторону от исходной матрицы и ввести диапазон первой матрицы А1:D3 в рабочее полеМассив1 (указателем мыши при нажатой левой кнопке), а диапазон матрицы В – А4:В7 ввести в рабочее полеМассив2 . После чего, не нажимая кнопку ОК, нажать сочетание клавишCTRL+SHIFT+ENTER(рис.3)

Рис.4

Если произведение матриц не появилось в заданном диапазоне А1:С3, то надо щелкнуть указателем мыши в строке формул и повторить нажатие клавиш CTRL+SHIFT+ENTER.

В результате в диапазоне F1:G3 появится обратная матрица.

Вычислим определитель (детерминант) матрицы с помощью функции МОПРЕД() или англ. MDETERM, разложением по строке/столбцу (для 3 х 3) и по определению (до 6 порядка).

Определитель матрицы (det) можно вычислить только для квадратных матриц, т.е. у которых количество строк равно количеству столбцов.

Для вычисления определителя в MS EXCEL есть специальная функция МОПРЕД() . В аргументе функции необходимо указать ссылку на диапазон ячеек (массив), содержащий элементы матрицы (см. файл примера ).

Массив может быть задан не только как интервал ячеек, например A7:B8 , но и как , например =МОПРЕД({5;4:3;2}) . Запись с использованием массива констант позволяет не указывать элементы в отдельных ячейках, а разместить их в ячейке вместе с функцией. Массив в этом случае указывается по строкам: например, сначала первая строка 5;4, затем через двоеточие записывается следующая строка 3;2. Элементы отделяются точкой с запятой.

Для матриц порядка 2 можно определитель можно вычислить без использования функции МОПРЕД() . Например, для вышеуказанной матрицы выражение =A7*B8-B7*A8 вернет тот же результат.

Для матрицы порядка 3, например размещенной в диапазоне A16:C18 , выражение усложняется =A16*(B17*C18-C17*B18)-B16*(A17*C18-C17*A18)+C16*(A17*B18-B17*A18) (разложение по строке).

В файле примера для матрицы 3 х 3 определитель также вычислен через разложение по столбцу и по правилу Саррюса.

Свойства определителя

Теперь о некоторых свойствах определителя (см. файл примера ):

Определитель равен определителю исходной матрицы
Если в матрице все элементы хотя бы одной из строк (или столбцов) нулевые, определитель такой матрицы равен нулю
Если переставить местами две любые строки (столбца), то определитель полученной матрицы будет противоположен исходному (то есть, изменится знак)
Если все элементы одной из строк (столбца) умножить на одно и тоже число k, то определитель полученной матрицы будет равен определителю исходной матрицы, умноженному на k
Если матрица содержит строки (столбцы), являющиеся линейной комбинацией других строк (столбцов), то определитель =0
det(А)=1/det(А -1), где А -1 – матрице А (А – квадратная невырожденная матрица).

Вычисление определителя матрицы по определению (до 6 порядка включительно)

СОВЕТ : Этот раздел стоит читать только продвинутым пользователям MS EXCEL. Кроме того материал представляет только академический интерес, т.к. есть функция МОПРЕД() .

Как было показано выше для вычисления матриц порядка 2 и 3 существуют достаточно простые формулы и правила. Для вычисления определителя матриц более высокого порядка (без использования функции МОПРЕД() ) придется вспомнить определение:

Определителем квадратной матрицы порядка n х n является сумма, содержащая n! слагаемых (=ФАКТР(n) ). Каждое слагаемое представляет собой произведение n элементов матрицы, причем в каждом произведении содержится элемент из каждой строки и из каждого столбца матрицы А . Перед k-ым слагаемым появляется коэффициент (-1) , если элементы матрицы А в произведении упорядочены по номеру строки, а количество инверсий в k-ой перестановке множества номеров столбцов нечетно.

где (α 1 ,α 2 ,…,α n ) – перестановка чисел от 1 до n , N(α 1 ,α 2 ,…,α n ) – число , суммирование идёт по всем возможным перестановкам порядка n .

Попытаемся разобраться в этом непростом определении на примере матрицы 3х3.

Для матрицы 3 х 3, согласно определения, число слагаемых равно 3!=6, а каждое слагаемое состоит из произведения 3-х элементов матрицы. Ниже приведены все 6 слагаемых, необходимых для вычисления определителя матрицы 3х3:

а21*а12*а33
а21*а32*а13
а11*а32*а23
а11*а22*а33
а31*а22*а13
а31*а12*а23

а21, а12 и т.д. – это элементы матрицы. Теперь поясним, как были сформированы индексы у элементов, т.е. почему, например, есть слагаемое а11*а22*а33, а нет а11*а22*а13.

Посмотрим на формулу выше (см. определение). Предположим, что второй индекс у каждого элемента матрицы (от 1 до n) соответствует номеру столбца матрицы (хотя это может быть номер строки (это не важно т.к. определители матрицы и ее равны). Таким образом, второй индекс у первого элемента в произведении всегда равен 1, у второго – 2, у третьего 3. Тогда первые индексы у элементов соответствуют номеру строки и, в соответствии с определением, должны определяться из перестановок чисел от 1 до 3, т.е. из перестановок множества (1, 2, 3).

Теперь понятно, почему среди слагаемых нет а11*а22*а13, т.к. согласно определения (в каждом произведении содержится элемент из каждой строки и из каждого столбца матрицы А ), а в нашем слагаемом нет элемента из строки 3.

Примечание : Перестановкой из n чисел множества (без повторов) называется любое упорядочивание данного множества, отличающиеся друг от друга лишь порядком входящих в них элементов. Например, дано множество их 3-х чисел: 1, 2, 3. Из этих чисел можно составить 6 разных перестановок: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 1, 2), (3, 2, 1). См. статью

Число перестановок множества из 3-х чисел =3!=6 (что, конечно, равно числу слагаемых в выражении для расчета определителя, т.к. каждому слагаемому соответствует своя перестановка). Для матрицы 3х3 все перестановки приведены в примечании выше. Можно убедиться, что в каждом слагаемом первые индексы у элементов равны соответствующим числам в перестановке. Например, для слагаемого а21*а12*а33 использована перестановка (2, 1, 3).

СОВЕТ : Для матрицы 4 порядка существует 4! перестановок, т.е. 26, что соответствует 26 слагаемым, каждое из которых является произведением различных 4-х элементов матрицы. Все 26 перестановок можно найти в статье .

Теперь, когда разобрались со слагаемыми, определим множитель перед каждым слагаемым (он может быть +1 или -1). Множитель определяется через четность числа инверсий соответствующей перестановки.

Примечание : Об инверсиях перестановок (и четности числа инверсий) можно почитать, например, в статье

Например, первому слагаемому соответствует перестановка (2, 1, 3), у которой 1 инверсия (нечетное число) и, соответственно, -1 в степени 1 равно -1. Второму слагаемому соответствует перестановка (2, 3, 1), у которой 2 инверсии (четное число) и, соответственно, -1 в степени 2 равно 1 и т.д.

Сложив все слагаемые: (-1)*(а21*а12*а33)+(+1)*(а21*а32*а13)+(-1)*(а11*а32*а23)+(+1)*(а11*а22*а33)+(-1)*(а31*а22*а13)+(+1)*(а31*а12*а23) получим значение определителя.

В файле примера на листе 4+, и зменяя порядок матрицы с помощью , можно вычислить определитель матрицы до 6 порядка включительно.

Следует учитывать, что при вычислении матрицы 6-го порядка в выражении используется уже 720 слагаемых (6!). Для 7-го порядка пришлось бы сделать таблицу для 5040 перестановок и, соответственно, вычислить 5040 слагаемых! Т.е. без использования МОПРЕД() не обойтись (ну, или можно вычислить определитель вручную методом Гаусса).

Facebook

Twitter

Вконтакте

Одноклассники

Google+

Действия с матрицами

Матрицы и действия с ними, определители

Сложение матриц

Сложение определено для матриц одного типа, т.е. для матриц, у которых число строк и столбцов совпадает. Сумма матриц $A=\{A_{ik}\}$ и $B=\{B_{ik}\}$, матрица $A+B$, определяется следующим образом: $(A+B)_{ik}=A_{ik}+B_{ik}$, $1 \leq i \leq m, 1 \leq k \leq n$. Иными словами: складываются элементы матриц $A$ и $B$, стоящие на одинаковом месте (т.е. на пересечении одинаковых строк и столбцов) и записываются в то же место.

Пример. Пусть \[ A=\left( \begin{array}{ccc} 1 &4 & -1 \\ 3 & -6 & 7 \end{array} \right) , \] \[ B=\left( \begin{array}{ccc} 2 &1 & 0 \\ 1 & 3 & 4 \end{array} \right) , \] тогда \[ A+B=\left( \begin{array}{ccc} 3 & 5 & -1 \\ 4 & -3 & 11 \end{array} \right) . \]

Умножение матрицы на число

Пусть $A=\{a_{ik}\}$ – матрица типа $(m,n)$, $\lambda$ – произвольное число. Тогда матрица $\{\lambda a_{ik}\}$ называется произведением числа $\lambda $ на матрицу $A$ и обозначается $\lambda \cdot A$.

Пример. Пусть \[ A=\left( \begin{array}{ccc} 1 &4 & -1 \\ 7 & 5 & 2 \\ 3 & -6 & 7 \end{array} \right) , \] тогда \[ 5A=\left( \begin{array}{ccc} 5 &20 & -5 \\ 35 & 25 & 10 \\ 15 & -30 & 35 \end{array} \right) . \]

Замечание.

Как и в обычной, в матричной арифметике знак умножения иногда не указывают, так что выражения $c\cdot A$ и $cA$ равноправны.

Пусть \[ A=\left( \begin{array}{cc} 2 & 3 \\ 4 & 5 \end{array} \right), B=\left( \begin{array}{cc} 1 & -2 \\ 3 & 4 \end{array} \right). \]

Вычислить $3A-2B$.

Проверить ответ

\[3A-2B=\left( \begin{array}{cc} 4 & 13 \\ 6 & 7 \end{array} \right)\]

Транспонирование матриц

Если для заданной матрицы $A$ ее строки записать как столбцы, получим новую матрицу, которая называется транспонированной исходной, и обозначается $A^T$.T\) (это выражение занимает меньше места).

Элементарные свойства операций с матрицами

Введенные операции обладают многими естественными арифметическими свойствами. Перечислим ряд из них.

1. Для любых матриц $A,B,C$ одного типа $(A+B)+C=A+(B+C)$(ассоциативность сложения).

2. Для любых матриц $A,B$ одного типа $A+B=B+A$ (коммутативность сложения).

3. Пусть $(m,n)$-матрица $O$ состоит из нулей. Такая матрица играет роль нуля при сложении матриц типа $(m,n)$, $A+O=A$, $0\cdot A=O$ для любой матрицы $A$ того же типа.

4. Для любых чисел $c_1,c_2$ и любой матрицы $A$ верно $(c_1+c_2)A=c_1A+c_2A$.

5. Для любых матриц $A,B$ одного типа и любого числа $c$ верно $c(A+B)=cA+cB$.

6. Для любых чисел $c_1,c_2$ и любой матрицы $A$ верно $(c_1c_2)A=c_1(c_2A)$.

7. Для любой матрицы $A$ верно $1\cdot A=A$.

8. Для любых матриц $A,B$ одного типа $(A+B)^T=A^T+B^T$.na_{im}b_{mk}. \] Таким образом следует вычислить все $mp$ элементов матрицы $C$. Еще раз подчеркнем, что для того, чтобы можно было перемножать матрицы $A$ и $B$, их типы должны быть согласованы!

Пример. Пусть \[ A=\left( \begin{array}{ccc} 1 &4 & -1 \\ 3 & -6 & 7 \end{array} \right) , B=\left( \begin{array}{cc} 2 &1 \\ 1 & 3 \\ -3 &5 \end{array} \right) . \]

В данном случае матрица $A$ имеет тип (2,3), матрица $B$ имеет тип (3,2), так что типы матриц согласнованы и в результате умножения $A$ на $B$ получим матрицу типа $(2,2)$. Получаем: \[ AB=\left ( \begin{array}{cc} 1\cdot 2 +4 \cdot 1+(-1)\cdot (-3) & 1\cdot 1 +4 \cdot 3+(-1)\cdot 5\\ 3\cdot 2 +(-6) \cdot 1+7\cdot (-3) &3\cdot 1 +(-6) \cdot 3+7\cdot 5 \end{array} \right )= \left( \begin{array}{cc} 9 & 8\\ -21 & 20 \end{array} \right).T\).

6. Для квадратных матриц $A,B$ одного типа $det(AB)=detA \cdot detB$.

7. Рассмотрим квадратную матрицу порядка $n$, $E=diag\{1,1,1,…,1\}$. Такая матрица играет выделенную роль в умножении матриц: для любых матриц $A,B$ имеем $EA=A$, $BE=B$. Матрица $E$ называется единичной матрицей порядка $n$. Согласно описанным выше результатам, $detE=1$.

1. Умножить матрицы:

а) \[ \left( \begin{array}{cc} 2 & 1 \\ 3 & 4 \end{array} \right)\cdot \left( \begin{array}{cc} 1 & -1 \\ 2 & 1 \end{array} \right). \]

б) \[ \left( \begin{array}{ccc} 3 & 1 & 1 \\ 2 & 1 & 2 \\ 1 & 2 & 1 \end{array} \right)\cdot \left( \begin{array}{ccc} 1 &1 & -1 \\ 2 & -1 & 1 \\ -1 & 2 & 1 \end{array} \right). \]

2. Вычислить \[ \left( \begin{array}{cc} 3 & 2 \\ -4 & -2 \end{array} \right)^5.{-1}=\frac{1}{ad-bc}\left( \begin{array}{cc} d & -b \\ -c & a \end{array} \right). \]

Таким образом, для матрицы порядка 2 формулы для обратной матрицы достаточно простые. Для больших порядков формулы становятся существенно более громоздкими.

Найти обратную матрицу для матрицы

1. \[ A=\left( \begin{array}{ccc} 2 &2 & 3 \\ 1 & -1 & 0 \\ -1 & 2 & 1 \end{array} \right). \]

2. \[ A=\left( \begin{array}{ccc} 2 &-1 & 0 \\ 0 & 2 & -1 \\ -1 & -1 & 1 \end{array} \right). \]

3. \[ A=\left( \begin{array}{ccc} 1 &1 & 1 \\ 1 & 2 & 2 \\ 2 & 3 & 4 \end{array} \right). \]

Матричные уравнения

Матричными уравнениями называются уравнения вида \[ AX=G, \quad \quad(12)\] \[ XB=G, \quad \quad(13)\] \[ AXB=G, \quad \quad(14)\] где матрицы $A,B,G$ заданы и требуется построить матрицу $X$.{-1}. \]

1. Найти решение матричного уравнения (12), если \[ A=\left( \begin{array}{cc} 2 & 6 \\ -9 & 3 \end{array} \right) , G=\left( \begin{array}{cc} -26 & -50 \\ 27 & -15 \end{array} \right) . \]

2. Найти решение матричного уравнения (12), если \[ A=\left( \begin{array}{cc} 8 & -7 \\ -5 & 4 \end{array} \right) , G=\left( \begin{array}{cc} 25 & -34 \\ -16 & 22 \end{array} \right) . \]

3. Найти решение матричного уравнения (13), если \[ B=\left( \begin{array}{cc} -8 & -5 \\ -9 & 5 \end{array} \right) , G=\left( \begin{array}{cc} -20 & 30 \\ -19 & 20 \end{array} \right) . \]

4. Найти решение матричного уравнения (13), если \[ B=\left( \begin{array}{cc} 9 & 8 \\ -3 & 7 \end{array} \right) , G=\left( \begin{array}{cc} -72 & 23 \\ 0 & 58 \end{array} \right) . \]

5. Найти решение матричного уравнения (14), если \[ A=\left( \begin{array}{cc} 4 & 2 \\ 3 & -4 \end{array} \right) , B=\left( \begin{array}{cc} -1 & 2 \\ -2 & -1 \end{array} \right) , G=\left( \begin{array}{cc} 20 & -50 \\ 26 & 23 \end{array} \right) . \]

6. Найти решение матричного уравнения (14), если \[ A=\left( \begin{array}{cc} -4 & -2 \\ -3 & 3 \end{array} \right) , B=\left( \begin{array}{cc} 3 & 4 \\ 4 & 3 \end{array} \right) , G=\left( \begin{array}{cc} 132 & 134 \\ 18 & 24 \end{array} \right) . \]

формула, решения, свойства. Сложение и вычитание матриц

Данное методическое пособие поможет Вам научиться выполнять действия с матрицами : сложение (вычитание) матриц, транспонирование матрицы, умножение матриц, нахождение обратной матрицы. Весь материал изложен в простой и доступной форме, приведены соответствующие примеры, таким образом, даже неподготовленный человек сможет научиться выполнять действия с матрицами. Для самоконтроля и самопроверки Вы можете бесплатно скачать матричный калькулятор >>> .

Я буду стараться минимизировать теоретические выкладки, кое-где возможны объяснения «на пальцах» и использование ненаучных терминов. Любители основательной теории, пожалуйста, не занимайтесь критикой, наша задача – научиться выполнять действия с матрицами .

Для СВЕРХБЫСТРОЙ подготовки по теме (у кого «горит») есть интенсивный pdf-курс Матрица, определитель и зачёт!

Матрица – это прямоугольная таблица каких-либо элементов . В качестве элементов мы будем рассматривать числа, то есть числовые матрицы. ЭЛЕМЕНТ – это термин. Термин желательно запомнить, он будет часто встречаться, не случайно я использовал для его выделения жирный шрифт.

Обозначение: матрицы обычно обозначают прописными латинскими буквами

Пример: рассмотрим матрицу «два на три»:

Данная матрица состоит из шести элементов :

Все числа (элементы) внутри матрицы существуют сами по себе, то есть ни о каком вычитании речи не идет:

Это просто таблица (набор) чисел!

Также договоримся не переставлять числа, если иного не сказано в объяснениях. У каждого числа свое местоположение, и перетасовывать их нельзя!

Рассматриваемая матрица имеет две строки:

и три столбца:

СТАНДАРТ : когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали по косточкам матрицу «два на три».

Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной , например: – матрица «три на три».

Если в матрице один столбец или одна строка , то такие матрицы также называют векторами .

На самом деле понятие матрицы мы знаем еще со школы, рассмотрим, например точку с координатами «икс» и «игрек»: . По существу, координаты точки записаны в матрицу «один на два». Кстати, вот Вам и пример, почему порядок чисел имеет значение: и – это две совершенно разные точки плоскости.

Теперь переходим непосредственно к изучению действий с матрицами :

1) Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу) .

Вернемся к нашей матрице . Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит.

Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак :

У нуля, как Вы понимаете, знак не меняется, ноль – он и в Африке ноль.

Обратный пример: . Выглядит безобразно.

Внесем минус в матрицу, сменив у КАЖДОГО элемента матрицы знак :

Ну вот, гораздо симпатичнее получилось. И, самое главное, выполнять какие-либо действия с матрицей будет ПРОЩЕ. Потому что есть такая математическая народная примета: чем больше минусов – тем больше путаницы и ошибок .

2) Действие второе. Умножение матрицы на число .

Пример:

Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.

Еще один полезный пример:

– умножение матрицы на дробь

Сначала рассмотрим то, чего делать НЕ НАДО :

Вносить дробь в матрицу НЕ НУЖНО, во-первых, это только затрудняет дальнейшие действия с матрицей, во-вторых, затрудняет проверку решения преподавателем (особенно, если – окончательный ответ задания).

И, тем более, НЕ НАДО делить каждый элемент матрицы на минус семь:

Из статьи Математика для чайников или с чего начать , мы помним, что десятичных дробей с запятой в высшей математике стараются всячески избегать.

Единственное, что желательно сделать в этом примере – это внести минус в матрицу:

А вот если бы ВСЕ элементы матрицы делились на 7 без остатка , то тогда можно (и нужно!) было бы поделить.

Пример:

В этом случае можно и НУЖНО умножить все элементы матрицы на , так как все числа матрицы делятся на 2 без остатка .

Примечание: в теории высшей математики школьного понятия «деление» нет. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». То есть, деление – это частный случай умножения.

3) Действие третье. Транспонирование матрицы .

Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.

Пример:

Транспонировать матрицу

Строка здесь всего одна и, согласно правилу, её нужно записать в столбец:

– транспонированная матрица.

Транспонированная матрица обычно обозначается надстрочным индексом или штрихом справа вверху.

Пошаговый пример:

Транспонировать матрицу

Сначала переписываем первую строку в первый столбец:

Потом переписываем вторую строку во второй столбец:

И, наконец, переписываем третью строку в третий столбец:

Готово. Грубо говоря, транспонировать – это значит повернуть матрицу набок.

4) Действие четвертое. Сумма (разность) матриц .

Сумма матриц действие несложное.
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.

Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой!

Пример:

Сложить матрицы и

Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы :

Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов .

Пример:

Найти разность матриц ,

А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу :

Примечание: в теории высшей математики школьного понятия «вычитание» нет. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.

5) Действие пятое. Умножение матриц .

Какие матрицы можно умножать?

Чтобы матрицу можно было умножить на матрицу нужно, чтобы число столбцов матрицы равнялось числу строк матрицы .

Пример:
Можно ли умножить матрицу на матрицу ?

Значит, умножать данные матрицы можно.

А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!

Следовательно, выполнить умножение невозможно:

Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно.

Следует отметить, что в ряде случаев можно умножать матрицы и так, и так.
Например, для матриц, и возможно как умножение , так и умножение

Сложение матриц:

Вычитание и сложение матриц сводится к соответствующим операциям над их элементами. Операция сложения матриц вводится только для матриц одинакового размера, т. е. для матриц , у которых число строк и столбцов соответственно равно. Суммой матриц А и В, называется матрица С, элементы которой равны сумме соответствующих элементов. С = А + В c ij = a ij + b ij Аналогично определяется разность матриц .

Умножение матрицы на число:

Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число. Произведением матрицы А на число k называется матрица В, такая что

b ij = k × a ij . В = k × A b ij = k × a ij . Матрица – А = (-1) × А называется противоположной матрице А.

Свойства сложения матриц и умножения матрицы на число:

Операции сложения матриц и умножения матрицы на число обладают следующими свойствами: 1. А + В = В + А; 2. А + (В + С) = (А + В) + С; 3. А + 0 = А; 4. А – А = 0; 5. 1 × А = А; 6. α × (А + В) = αА + αВ; 7. (α + β) × А = αА + βА; 8. α × (βА) = (αβ) × А; , где А, В и С – матрицы, α и β – числа.

Умножение матриц (Произведение матриц):

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы . Произведением матрицы А m×n на матрицу В n×p , называется матрица С m×p такая, что с ik = a i1 × b 1k + a i2 × b 2k + … + a in × b nk , т. е. находиться сумма произведений элементов i – ой строки матрицы А на соответствующие элементы j – ого столбца матрицы В. Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко показать, что А × Е = Е × А = А, где А квадратная матрица , Е – единичная матрица того же размера.

Свойства умножения матриц:

Умножение матриц не коммутативно, т.е. АВ ≠ ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными. Самым характерным примером может служить единичная матрица , которая является перестановочной с любой другой матрицей того же размера. Перестановочными могут быть только квадратные матрицы одного и того же порядка. А × Е = Е × А = А

Умножение матриц обладает следующими свойствами: 1. А × (В × С) = (А × В) × С; 2. А × (В + С) = АВ + АС; 3. (А + В) × С = АС + ВС; 4. α × (АВ) = (αА) × В; 5. А × 0 = 0; 0 × А = 0; 6. (АВ) Т = В Т А Т; 7. (АВС) Т = С Т В Т А Т; 8. (А + В) Т = А Т + В Т;

2. Определители 2-го и 3-го порядков. Свойства определителей.

Определителем матрицы второго порядка, или определителем второго порядка, называется число, которое вычисляется по формуле:

Определителем матрицы третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:

Это число представляет алгебраическую сумму, состоящую из шести слагаемых. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы . Каждое слагаемое состоит из произведения трех сомножителей.

Знаки, с которыми члены определителя матрицы входят в формулу нахождения определителя матрицы третьего порядка можно определить, пользуясь приведенной схемой, которая называется правилом треугольников или правилом Сарруса. Первые три слагаемые берутся со знаком плюс и определяются из левого рисунка, а последующие три слагаемые берутся со знаком минус и определяются из правого рисунка.

Определить количество слагаемых, для нахождения определителя матрицы , в алгебраической сумме, можно вычислив факториал: 2! = 1 × 2 = 2 3! = 1 × 2 × 3 = 6

Свойства определителей матриц

Свойства определителей матриц:

Свойство № 1:

Определитель матрицы не изменится, если его строки заменить столбцами, причем каждую строку столбцом с тем же номером, и наоборот (Транспонирование). |А| = |А| Т

Следствие:

Столбцы и строки определителя матрицы равноправны, следовательно, свойства присущие строкам выполняются и для столбцов.

Свойство № 2:

При перестановке 2-х строк или столбцов определитель матрицы изменит знак на противоположный, сохраняя абсолютную величину, т.е.:

Свойство № 3:

Определитель матрицы , имеющий два одинаковых ряда, равен нулю.

Свойство № 4:

Общий множитель элементов какого-либо ряда определителя матрицы можно вынести за знак определителя .

Следствия из свойств № 3 и № 4:

Если все элементы некоторого ряда (строки или столбца) пропорциональны соответствующим элементам параллельного ряда, то такой определитель матрицы равен нулю.

Свойство № 5:

определителя матрицы равны нулю, то сам определитель матрицы равен нулю.

Свойство № 6:

Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель матрицы можно представить в виде суммы 2-х определителей по формуле:

Свойство № 7:

Если к какой–либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель матрицы не изменит своей величины.

Пример применения свойств для вычисления определителя матрицы :

Это одна из самых распространенных операций с матрицами. Матрица, которая получается после умножения, называется произведением матриц.

Произведением матрицы A m × n на матрицу B n × k будет матрица C m × k такая, что элемент матрицы C , находящийся в i -ой строке и j -ом столбце, то есть элемент c ij равен сумме произведений элементов i -ой строки матрицы A на соответствующие элементы j -ого столбца матрицы B .

Процесс умножения матриц возможен только в случае, когда число столбцов первой матрицы равно числу строк второй матрицы.

Пример:
Можно ли умножить матрицу на матрицу ?

m = n , значит, умножать данные матрицы можно.

Если же матрицы поменять местами, то, при таких матрицах, умножение уже не будет возможно.

m ≠ n , таким образом, выполнять умножение нельзя:

Довольно часто можно встретить задания с подвохом, когда ученику предлагается умножить матрицы , умножение которых заведомо невозможно.

Обратите внимание, что иногда можно умножать матрицы и так, и так. К примеру, для матриц, и возможно как умножение MN , так и умножение NM.

Это не очень сложное действие. Умножение матриц лучше понимать на конкретных примерах, т.к. только определение может сильно запутать.

Начнем с самого простого примера:

Необходимо умножить на . Первым делом приведем формулу для данного случая:

– здесь хорошо прослеживается закономерность.

Умножить на .

Формула для этого случая: .

Умножение матриц и результат:

В результате получена т.н. нулевая матрица.

Очень важно помнить, что здесь не работает «правило перестановки мест слагаемых» так как почти всегда MN ≠ NM . Поэтому, производя операцию умножения матриц их ни в коем случае нельзя менять местами.

Теперь рассмотрим примеры умножения матриц третьего порядка:

Умножить на .

Формула очень похожа на прошлые:

Решение матрицы: .

Это тоже самое умножение матриц, только вместо второй матрицы берется простое число. Как можно догадаться, такое умножение выполнять гораздо проще.

Пример умножения матрицы на число:

Тут все понятно – для того, чтобы умножить матрицу на число , необходимо каждый элемент матрицы последовательно умножить на указанное число. В данном случае – на 3.

Еще один полезный пример:

– умножение матрицы на дробное число.

Первым делом покажем то, чего делать не надо:

При умножении матрицы на дробное число не нужно вносить дробь в матрицу, так как это в первую очередь только затрудняет дальнейшие действия с матрицей, во-вторых, затрудняет проверку решения преподавателем.

И, тем более, не нужно делить каждый элемент матрицы на -7:

Что стоит сделать в данном случае – это внести минус в матрицу:

Если бы у вас был пример, когда все элементы матрицы делились бы на 7 без остатка, то тогда можно (и нужно!) было бы поделить.

В данном примере можно и нужно умножить все элементы матрицы на ½, т.к. каждый элемент матрицы делится на 2 без остатка.

Будем последовательно “исключать” неизвестные. Для этого первое уравнение системы оставим без изменений, а второе и третье преобразуем:

1) ко второму уравнению прибавим первое, умноженное на –2, и приведем его к виду –3x 2 –2x 3 = –2;

2) к третьему уравнению прибавим первое, умноженное на – 4, и приведем его к виду –3x 2 – 4x 3 = 2.

В результате из второго и третьего уравнений будет исключено неизвестное x 1 и система примет вид

Второе и третье уравнения системы умножим на –1, получим

Коэффициент 1 в первом уравнении при первом неизвестном х 1 называется ведущим элементом первого шага исключения.

На втором шаге первое и второе уравнения остаются без изменений, а к третьему уравнению применим тот же способ исключения переменной x 2 . Ведущим элементом второго шага является коэффициент 3. К третьему уравнению прибавим второе, умноженное на –1, тогда система преобразуется к виду

(1.2)

Процесс приведения системы (1.1) к виду (1.2) называются прямым ходом метода Гаусса.

Порядок действий решения системы (1.2) называется обратным ходом. Из последнего уравнения получим х 3 = –2. Подставляя это значение во второе уравнение, получим х 2 = 2. После этого первое уравнение дает х 1 = 1. Таким образом, – решение системы (1.1).

Понятие матрицы

Рассмотрим величины, входящие в систему (1.1). Набор из девяти числовых коэффициентов, стоящих в уравнениях перед неизвестными, образует таблицу чисел, которая называется матрицей :

Числа таблицы называются элементами матрицы. Элементы образуют строки и столбцы матрицы. Количество строк и количество столбцов образуют размерность матрицы. Матрица А имеет размерность 3´3 (“три на три”), причем первое число указывает количество строк, а второе – столбцов. Часто матрицу обозначают, указывая ее размерность А (3 ´ 3) . Так как число строк и столбцов в матрице А одинаково, матрица называется квадратной. Количество строк (и столбцов) в квадратной матрице называется ее порядком , поэтому А – матрица третьего порядка .

Правые части уравнений, также образуют таблицу чисел, т.е. матрицу:

Каждая строка этой матрицы образована единственным элементом, поэтому B (3 ´ 1) называется матрицей–столбцом , ее размерность 3´1. Набор неизвестных также можно представить как матрицу-столбец:

Умножение квадратной матрицы на матрицу-столбец

С матрицами можно производить различные операции, которые будут подробно рассмотрены в дальнейшем. Здесь же разберем только правило умножения квадратной матрицы на матрицу-столбец. По определению , результатом умножения матрицы А (3 ´ 3) на столбец В (3 ´ 1) является столбец D (3 ´ 1) , элементы которого равны суммам произведений элементов строк матрицы А на элементы столбца В :

2)второй элемент столбца D равен сумме произведений элементов второй строки матрицы А на элементы столбца В :

Из приведенных формул видно, что умножить матрицу на столбец В можно только в случае, если число столбцов матрицы А равно числу элементов в столбце В .

Рассмотрим еще два числовых примера умножения матрицы (3 ´3) на столбец (3 ´1) :

Пример 1.1

АВ = .

Пример 1.2

АВ = .

Определение. Произведением двух матриц А и В называется матрица С , элемент которой, находящийся на пересечении i -й строки и j -го столбца, равен сумме произведений элементов i -й строки матрицы А на соответствующие (по порядку) элементы j -го столбца матрицы В .

Из этого определения следует формула элемента матрицы C :

Произведение матрицы А на матрицу В обозначается АВ .

Пример 1. Найти произведение двух матриц А и B , если

Решение. Удобно нахождение произведения двух матриц А и В записывать так, как на рис.2:

На схеме серые стрелки показывают, элементы какой строки матрицы А на элементы какого столбца матрицы В нужно перемножить для получения элементов матрицы С , а линиями цвета элемента матрицы C соединены соответствующие элементы матриц A и B , произведения которых складываются для получения элемента матрицы C .

В результате получаем элементы произведения матриц:

Теперь у нас есть всё, чтобы записать произведение двух матриц:

Произведение двух матриц АВ имеет смысл только в том случае, когда число столбцов матрицы А совпадает с числом строк матрицы В .

Эту важную особенность будет легче запомнить, если почаще пользоваться следующими памятками:

Имеет место ещё одна важная особенность произведения матриц относительно числа строк и столбцов:

В произведении матриц АВ число строк равно числу строк матрицы А , а число столбцов равно числу столбцов матрицы В .

Пример 2. Найти число строк и столбцов матрицы C , которая является произведением двух матриц A и B следующих размерностей:

а) 2 Х 10 и 10 Х 5;

б) 10 Х 2 и 2 Х 5;

Пример 3. Найти произведение матриц A и B , если:

A B – 2. Следовательно, размерность матрицы C = AB – 2 X 2.

Вычисляем элементы матрицы C = AB .

Найденное произведение матриц: .

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн .

Пример 5. Найти произведение матриц A и B , если:

Решение. Число строк в матрице A – 2, число столбцов в матрице B C = AB – 2 X 1.

Вычисляем элементы матрицы C = AB .

Произведение матриц запишется в виде матрицы-столбца: .

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн .

Пример 6. Найти произведение матриц A и B , если:

Решение. Число строк в матрице A – 3, число столбцов в матрице B – 3. Следовательно, размерность матрицы C = AB – 3 X 3.

Вычисляем элементы матрицы C = AB .

Найденное произведение матриц: .

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн .

Пример 7. Найти произведение матриц A и B , если:

Решение. Число строк в матрице A – 1, число столбцов в матрице B – 1. Следовательно, размерность матрицы C = AB – 1 X 1.

Вычисляем элемент матрицы C = AB .

Произведение матриц является матрицей из одного элемента: .

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн .

Программная реализация произведения двух матриц на С++ разобрана в соответствующей статье в блоке “Компьютеры и программирование”.

Возведение матрицы в степень

Возведение матрицы в степень определяется как умножение матрицы на ту же самую матрицу. Так как произведение матриц существует только тогда, когда число столбцов первой матрицы совпадает с числом строк второй матрицы, то возводить в степень можно только квадратные матрицы. n -ая степень матрицы путём умножения матрицы на саму себя n раз:

Пример 8. Дана матрица . Найти A ² и A ³ .

Найти произведение матриц самостоятельно, а затем посмотреть решение

Пример 9. Дана матрица

Найти произведение данной матрицы и транспонированной матрицы , произведение транспонированной матрицы и данной матрицы.

Свойства произведения двух матриц

Свойство 1. Произведение любой матрицы А на единичную матрицу Е соответствующего порядка как справа, так и слева, совпадает с матрицей А, т.е. АЕ = ЕА = А.

Иными словами, роль единичной матрицы при умножении матриц такая же, как и единицы при умножении чисел.

Пример 10. Убедиться в справедливости свойства 1, найдя произведения матрицы

на единичную матрицу справа и слева.

Решение. Так как матрица А содержит три столбца, то требуется найти произведение АЕ , где

–
единичная матрица третьего порядка. Найдём элементы произведения С = АЕ :

Получается, что АЕ = А .

Теперь найдём произведение ЕА , где Е – единичная матрица второго порядка, так как матрица А содержит две строки. Найдём элементы произведения С = ЕА :

Функция МУМНОЖ

Функция МУМНОТ возвращает матричное произведение двух массивов. Результатом является массив с таким же числом строк, что и массив1, и с таким же числом столбцов, что и массив2.

Примечание: Если у вас установлена текущая версия Microsoft 365, можно просто ввести формулу в верхней левой ячейке диапазона вывода и нажать клавишу ВВОД, чтобы подтвердить использование формулы динамического массива. Иначе формулу необходимо вводить с использованием прежней версии массива, выбрав диапазон вывода, введя формулу в левой верхней ячейке диапазона и нажав клавиши CTRL+SHIFT+ВВОД для подтверждения. Excel автоматически вставляет фигурные скобки в начале и конце формулы. Дополнительные сведения о формулах массива см. в статье Использование формул массива: рекомендации и примеры.

Синтаксис

МУМНОЖ(массив1; массив2)

Аргументы функции МУМНОЖ описаны ниже.

Замечания

Число столбцов в массиве1 должно быть таким же, как число строк в массиве “массив2”, и оба массива должны содержать только числа.
Массив1 и массив2 могут быть заданы как диапазоны ячеев, константы массива или ссылки.
Функция МУМНОЖ возвращает значение ошибки #ЗНАЧ! в следующих случаях, указанных ниже.
- Если какая-либо ячейка пуста или содержит текст.
- Число столбцов в массиве1 отличается от числа строк в массиве “массив2”.
Массив a, который является произведением двух массивов b и c, определяется следующим образом:

где i — номер строки, а j — номер столбца.

Примеры

Пример 1

Пример 2

Чтобы указанные выше формулы вычислялись правильно, нужно вводить их в виде формул массивов. После ввода формулы нажмите ввод, если у вас есть текущая Microsoft 365 подписка. в противном случае нажмите CTRL+SHIFT+ВВОД. Если формула не будет введена как формула массива, возвращается единственный результат.

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

Произведение матриц – это… Что такое Произведение матриц?

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами.

Правила выполнения операций над матрицами сделаны такими, чтобы было удобно записывать системы линейных уравнений.

Обычно матрицу обозначают заглавной буквой латинского алфавита и выделяют круглыми скобками «(…)» (встречается также выделение квадратными скобками «[…]», двойными прямыми линиями «||…||»).

Числа, составляющие матрицу (элементы матрицы), часто обозначают той же буквой, что и саму матрицу, но строчной.

У каждого элемента матрицы есть 2 нижних индекса (a_ij) — первый «i» обозначает номер строки, в которой находится элемент, а второй «j» — номер столбца. Говорят «матрица размерности », подразумевая, что в матрице m строк и n столбцов.

История

Понятие матрицы впервые появилось в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу.

Матрица как запись коэффициентов системы линейных уравнений

Систему из m уравнений с n неизвестными

можно представить в матричном виде

и тогда всю систему можно записать так:

AX = B,

где A имеет смысл таблицы коэффициентов a_ij системы уравнений.

Если m = n и матрица A невырожденная, то решение этого уравнения состоит в нахождении обратной матрицы A ^{– 1}, поскольку умножив обе части уравнения на эту матрицу слева

A ^{– 1}AX = A ^{– 1}B

A ^{− 1}A — превращается в E (единичную матрицу). И это даёт возможность получить столбец корней уравнений

X = A ^{– 1}B.

Все правила, по которым проводятся операции над матрицами выводятся из операций над системами уравнений.

Операции над матрицами

Пусть a_ij — элементы матрицы A, а b_ij — элементы матрицы B.

Линейные операции:

Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен

b_ij = λa_ij

Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен

c_ij = a_ij + b_ij

Вычитание матриц A − B определяется аналогично сложению, это операция нахождения матрицы C, элементы которой

c_ij = a_ij – b_ij

Сложение и вычитание допускается только для матриц одинакового размера.

Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть

A + Θ = A

Все элементы нулевой матрицы равны нулю.

Нелинейные операции:

Умножение матриц (обозначение: AB, реже со знаком умножения ) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

В первом множителе должно быть столько же столбцов, сколько строк во втором. Если матрица A имеет размерность , B — , то размерность их произведения AB = C есть . Умножение матриц не коммутативно.

Умножение матриц ассоциативно. Возводить в степень можно только квадратные матрицы.

Транспонирование матрицы (обозначение: A^T) — операция, при которой матрица отражается относительно главной диагонали, то есть

Если A — матрица размера , то A^T — матрица размера

Квадратная матрица и смежные определения

Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.

Для квадратных матриц существует единичная матрица E (аналог единицы для операции умножения чисел) такая, что умножение любой матрицы на неё не влияет на результат, а именно

EA = AE = A

У единичной матрицы единицы стоят только по главной диагонали, остальные элементы равны нулю

Для некоторых квадратных матриц можно найти так называемую обратную матрицу. Обратная матрица A ^{– 1} такова, что если умножить матрицу на неё, то получится единичная матрица:

AA ^{− 1} = E

Обратная матрица существует не всегда. Матрицы, для которых обратная существует, называются невырожденными (или регулярными), а для которых нет — вырожденными (или сингулярными). Матрица невырождена, если все ее строки (столбцы) линейно независимы как векторы. Максимальное число линейно независимых строк (столбцов) называется рангом матрицы. Определителем (детерминантом) матрицы называется значение нормированной кососимметрической (антисимметрической) полилинейной формы валентности на столбцах матрицы. Квадратная матрица над числовым полем вырождена тогда и только тогда, когда ее определитель равен нулю.

Свойства матриц

A + (B + C) = (A + B) + C
A + B = B + A
A(BC) = (AB)C
A(B + C) = AB + AC
(B + C)A = BA + CA
(A^T)^T = A
(A * B)^T = B^T * A^T

Элементарные преобразования матриц

Элементарными преобразованиями строк матрицы называются следующие преобразования:

Умножение строки на число отличное от нуля
Прибавление одной строки к другой строке

Элементарные преобразование столбцов матрицы определяются аналогично.

Типы матриц

Матрица линейного оператора

Матрица линейного оператора — матрица, выражающая линейный оператор в некотором базисе. Для того, чтобы ее получить, необходимо подействовать оператором на векторы базиса и координаты полученных векторов (образов базисных векторов) записать в столбцы матрицы.

Матрица оператора аналогична координатам вектора. При этом действие оператора на вектор равносильно умножению матрицы на столбец координат этого вектора в том же базисе.

Выберем базис . Пусть — произвольный вектор. Тогда его можно разложить по этому базису:

где x^k — координаты вектора в выбранном базисе.

Здесь и далее предполагается суммирование по немым индексам.

Пусть — произвольный линейный оператор. Подействуем им на обе стороны предыдущего равенства, получим

Вектора также разложим в выбранном базисе, получим

где — j-я координата k-го вектора из .

Подставим разложение в предыдущую формулу, получим

Выражение , заключённое в скобки, есть ни что иное, как формула умножения матрицы на столбец, и, таким образом, матрица при умножении на столбец x^k даёт в результате координаты вектора , возникшего от действия оператора на вектор , что и требовалось получить.

См. также

Литература

Ссылки

Wikimedia Foundation. 2010.

{n} a_ {ik} b_ {kj} $, где $ i = 1, … m, j = 1, … p $

Вы говорите, что знаете, как умножать матрицы, поэтому обратите внимание на один конкретный элемент в произведении $ C = AB $, а именно на элемент в позиции $ (i, j) $, то есть в строке $ i $ th и $ j $ -й столбец.

Чтобы получить этот элемент, вы:

сначала перемножают все элементы $ i $ -й строки матрицы $ A $ попарно со всеми элементами $ j $ -го столбца матрицы $ B $;
, а затем добавьте этих продуктов $ n $.

Вы должны повторить эту процедуру для каждого элемента $ C $, но давайте сейчас увеличим масштаб этого конкретного (но произвольного) элемента в позиции $ (i, j) $:

$$ \ begin {pmatrix} а_ {11} & \ ldots & a_ {1n} \\ \ vdots & \ ddots & \ vdots \\ \ color {blue} {\ mathbf {a_ {i1}}} & \ color {blue} {\ rightarrow} & \ color {blue} {\ mathbf {a_ {in}}} \\ \ vdots & \ ddots & \ vdots \\ а_ {m1} & \ ldots & a_ {mn} \ end {pmatrix} \ cdot \ begin {pmatrix} b_ {11} & \ ldots & \ color {красный} {\ mathbf {b_ {1j}}} & \ ldots & b_ {1p} \\ \ vdots & \ ddots & \ color {красный} {\ downarrow} & \ ddots & \ vdots \\ b_ {n1} & \ ldots & \ color {красный} {\ mathbf {b_ {nj}}} & \ ldots & b_ {np} \ end {pmatrix} знак равно \ begin {pmatrix} c_ {11} & \ ldots & c_ {1j} & \ ldots & c_ {1p} \\ \ vdots & \ ddots & & & \ vdots \\ c_ {i1} & & \ color {фиолетовый} {\ mathbf {c_ {ij}}} & & c_ {ip} \\ \ vdots & & & \ ddots & \ vdots \\ c_ {m1} & \ ldots & c_ {mj} & \ ldots & c_ {mp} \ end {pmatrix} $$ с элементом $ \ color {purple} {\ mathbf {c_ {ij}}} $, равным: $$ \ mathbf {\ color {purple} {c_ {ij}} = \ color {blue} {a_ {i1}} \ color {red} {b_ {1j}} + \ color {blue} {a_ {i2} } \ color {красный} {b_ {2j}} + \ cdots + \ color {blue} {a_ {in}} \ color {red} {b_ {nj}}} $$ Теперь обратите внимание, что в приведенной выше сумме левый внешний индекс всегда равен $ i $ ($ i $ -я строка в $ A $), а правый внешний индекс всегда равен $ j $ ($ j $ -й столбец $ B $).{n} \ color {синий} {\ mathbf {a_ {ik}}} \ color {красный} {\ mathbf {b_ {kj}}} $$ Таким образом, приведенная выше формула дает вам элемент на позиции $ (i, j) $ в матрице продукта $ C = AB $ и, следовательно, полностью определяет $ C $, позволяя $ i = 1, …, m $ и $ j = 1, …, p $.

Может ли кто-нибудь объяснить, что это означает, на примере? И как мы получили эту формулу?

Иллюстрация выше должна дать вам представление об общей формуле, но вот конкретный пример, где я взял матрицы $ 3 \ times 3 $ для $ A $ и $ B $ и сосредоточился на элементе в позиции $ (2,3) $. :

$$ \ begin {pmatrix} а_ {11} и а_ {12} и а_ {13} \\ \ color {blue} {1} & \ color {blue} {2} & \ color {blue} {3} \\ а_ {31} и а_ {32} и а_ {33} \ end {pmatrix} \ cdot \ begin {pmatrix} b_ {11} & b_ {12} & \ color {красный} {6} \\ b_ {21} & b_ {22} & \ color {красный} {5} \\ b_ {31} & b_ {32} & \ color {красный} {4} \ end {pmatrix} знак равно \ begin {pmatrix} c_ {11} & c_ {12} & c_ {13} \\ c_ {21} & c_ {22} & \ color {фиолетовый} {\ mathbf {c_ {23}}} \\ c_ {31} и c_ {32} и c_ {33} \ end {pmatrix} $$ с элементом $ \ color {purple} {\ mathbf {c_ {23}}} $, равным: $$ \ begin {array} {rccccccc} \ color {purple} {c_ {23}} & = & \ color {синий} {a_ {21}} \ color {red} {b_ {13}} & + & \ color {blue} {a_ {22}} \ color {red} {b_ {23}} & + & \ color {синий} {a_ {23}} \ color {красный} {b_ {33}} & = & \ displaystyle \ sum_ {k = 1} ^ {3} \ color {blue} {a_ {2k}} \ color {red} {b_ {k3}} \\ & = & \ color {blue} {1} \ cdot \ color {red} {6} & + & \ color {blue} {2} \ cdot \ color {red} {5} & + & \ color {blue} {3} \ cdot \ color {красный} {4} \\ [8pt] & = & 6 & + & 10 & + & 12 & = & 28 \ end {array} $$

матриц – интуиция за умножением матриц

Короткий ответ: матрица соответствует линейному преобразованию .Для перемножить двух матриц – это то же самое, что составить соответствующие линейные преобразования (или линейные карты ).

В тексте по линейной алгебре (например, Хоффмана-Кунце) рассматривается следующее:

Это имеет смысл в контексте векторных пространств над полем. Вы можете говорить о векторных пространствах и (линейных) отображениях между ними, даже не упоминая основы. Когда вы выбираете базис, вы можете записать элементы вашего векторного пространства как сумму базовых элементов с коэффициентами в вашем базовом поле (то есть вы получаете явные координаты для своих векторов в терминах, например, реальных чисел).Если вы хотите что-то вычислить, вы обычно выбираете базы для своих векторных пространств. Затем вы можете представить свою линейную карту в виде матрицы по отношению к заданным базам с записями в вашем базовом поле (см., Например, вышеупомянутую книгу для получения подробной информации о том, как). Мы определяем умножение матриц таким образом, чтобы умножение матриц соответствовало композиции линейных отображений.

Добавлен ( Подробная информация о представлении линейной карты матрицей ). Пусть $ V $ и $ W $ – два векторных пространства с упорядоченными базами $ e_1, \ dots, e_n $ и $ f_1, \ dots, f_m $ соответственно, а $ L: V \ to W $ – линейное отображение.

Прежде всего отметим, что поскольку $ e_j $ генерирует $ V $, а $ L $ является линейным, $ L $ полностью определяется изображениями $ e_j $ в $ W $, то есть $ L (e_j) $. Явно обратите внимание, что по определению базиса любой $ v \ in V $ имеет уникальное выражение вида $ a_1e_1 + \ cdots + a_ne_n $, и $ L $, примененное к нему, выглядит как $ a_1L (e_1) + \ cdots + a_nL (e_n) $.

Теперь, поскольку $ L (e_j) $ находится в $ W $, оно имеет уникальное выражение вида $ b_1f_1 + \ dots + b_mf_m $, и ясно, что значение $ e_j $ в $ L $ однозначно определяется $ b_1, \ dots, b_m $, коэффициенты $ L (e_j) $ относительно заданного упорядоченного базиса для $ W $.2 = L \ circ L $ одного линейного преобразования $ L: V \ to V $, или, скажем, вычислить матрицу, соответствующую единичному преобразованию $ v \ mapsto v $.

линейная алгебра – Почему исторически мы умножаем матрицы именно так?

Вот ответ, прямо отражающий историческую перспективу из статьи Мемуары по теории матриц Автор Кейли, 1857 г. Эта статья доступна здесь.

Этой статье приписывают «первое абстрактное определение матрицы» и «матричную алгебру, определяющую сложение, умножение, скалярное умножение и обратное» (источник).

В статье использованы нестандартные обозначения. Постараюсь поместить его в более «современные» (но все же нестандартные) обозначения. Основная часть содержания этого поста будет со страниц 20-21.

Чтобы ввести обозначения, $$ (X, Y, Z) = \ left (\ begin {array} {ccc} а & b & c \\ а ‘& b’ & c ‘\\ a ” & b ” & c ” \ end {array} \ right) (x, y, z) $$

будет представлять набор линейных функций $ (ax + by + cz, a’z + b’y + c’z, a”z + b”y + c”z) $, которые затем называются $ ( X, Y, Z) $.

Кэли определяет сложение и скалярное умножение, а затем переходит к матричному умножению или «композиции». Он специально хочет заняться проблемой:

$$ (X, Y, Z) = \ left (\ begin {array} {ccc} а & b & c \\ а ‘& b’ & c ‘\\ a ” & b ” & c ” \ end {array} \ right) (x, y, z) \ quad \ text {где} \ quad (x, y, z) = \ left (\ begin {array } {ccc} \ альфа и \ бета и \ гамма \\ \ alpha ‘& \ beta’ & \ gamma ‘\\ \ alpha ” & \ beta ” & \ gamma ” \\ \ end {array} \ right) (\ xi, \ eta, \ zeta) $$

Теперь он хочет представить $ (X, Y, Z) $ в терминах $ (\ xi, \ eta, \ zeta) $.Он делает это, создавая другую матрицу, которая удовлетворяет уравнению:

$$ (X, Y, Z) = \ left (\ begin {array} {ccc} А & В & С \\ A ‘& B’ и C ‘\\ A ” & B ” & C ” \\ \ end {array} \ right) (\ xi, \ eta, \ zeta) $$

Он продолжает писать, что мы получаем значение:

$$ \ begin {align} \ left (\ begin {array} {ccc} А & В & С \\ A ‘& B’ и C ‘\\ A ” & B ” & C ” \\ \ end {array} \ right) & = \ left (\ begin {array} {ccc} а & b & c \\ а ‘& b’ & c ‘\\ a ” & b ” & c ” \ end {array} \ right) \ left (\ begin {array} {ccc} \ альфа и \ бета и \ гамма \\ \ alpha ‘& \ beta’ & \ gamma ‘\\ \ alpha ” & \ beta ” & \ gamma ” \\ \ end {array} \ right) \\ [.25см] & = \ left (\ begin {array} {ccc} a \ alpha + b \ alpha ‘+ c \ alpha’ ‘& a \ beta + b \ beta’ + c \ beta ” & a \ gamma + b \ gamma ‘+ c \ gamma’ ‘\\ a ‘\ alpha + b’ \ alpha ‘+ c’ \ alpha ” & a ‘\ beta + b’ \ beta ‘+ c’ \ beta ” & a ‘\ gamma + b’ \ gamma ‘+ c’ \ гамма ” \\ a ” \ alpha + b ” \ alpha ‘+ c’ ‘\ alpha’ ‘& a’ ‘\ beta + b’ ‘\ beta’ + c ” \ beta ” & a ” \ gamma + b ‘ ‘\ gamma’ + c ” \ gamma ” \ end {array} \ right) \ end {align} $$

Это стандартное определение умножения матриц. Я должен верить, что умножение матриц было определено для решения этой конкретной проблемы.В статье продолжается упоминание некоторых свойств матричного умножения, таких как некоммутативность, композиция с единицей и нулем и возведение в степень.

Вот письменное правило композиции:

Любая строка составной матрицы получается путем последовательного комбинирования соответствующей строки первой матрицы компонентов с несколькими столбцами второй матрицы (стр. 21)

Нахождение произведения двух матриц

Помимо умножения матрицы на скаляр, мы можем умножить две матрицы.Нахождение продукта двух матриц возможно только тогда, когда внутренние размеры одинаковы, что означает, что количество столбцов первой матрицы равно количеству строк второй матрицы. Если [latex] A [/ latex] представляет собой матрицу [latex] \ text {} m \ text {} \ times \ text {} r \ text {} [/ latex], а [latex] B [/ latex] является [latex] \ text {} r \ text {} \ times \ text {} n \ text {} [/ latex] матрица, тогда матрица продукта [latex] AB [/ latex] представляет собой [latex] \ text {} m \ text {} \ times \ text {} n \ text {} [/ latex] матрица.Например, продукт [latex] AB [/ latex] возможен, потому что количество столбцов в [latex] A [/ latex] такое же, как количество строк в [latex] B [/ latex]. Если внутренние размеры не совпадают, товар не определен.

Рисунок 1

Мы умножаем записи [latex] A [/ latex] на записи [latex] B [/ latex] в соответствии с определенным шаблоном, как описано ниже. Процесс умножения матрицы становится более понятным при работе с задачами с действительными числами.

Чтобы получить записи в строке [latex] i [/ latex] из [latex] AB, \ text {} [/ latex], мы умножаем записи в строке [latex] i [/ latex] из [latex] A [/ латекс] по столбцу [латекс] j [/ латекс] в [латекс] B [/ латекс] и доп. Например, для заданных матриц [латекс] A [/ latex] и [latex] B, \ text {} [/ latex], где размеры [latex] A [/ latex] равны [latex] 2 \ text {} \ times \ text {} 3 [/ latex], а размеры [latex] B [/ latex] равны [latex] 3 \ text {} \ times \ text {} 3, \ text {} [/ latex] продукт [ latex] AB [/ latex] будет матрицей [latex] 2 \ text {} \ times \ text {} 3 [/ latex].

[латекс] A = \ left [\ begin {array} {rrr} \ hfill {a} _ {11} & \ hfill {a} _ {12} & \ hfill {a} _ {13} \\ \ hfill {a} _ {21} & \ hfill {a} _ {22} & \ hfill {a} _ {23} \ end {array} \ right] \ text {и} B = \ left [\ begin {array} {rrr} \ hfill {b} _ {11} & \ hfill {b} _ {12} & \ hfill {b} _ {13} \\ \ hfill {b} _ {21} & \ hfill {b} _ {22} & \ hfill {b} _ {23} \\ \ hfill {b} _ {31} & \ hfill {b} _ {32} & \ hfill {b} _ {33} \ end {array} \ справа] [/ латекс]

Умножьте и сложите, как показано ниже, чтобы получить первую запись матрицы произведения [латекс] AB [/ латекс].

Чтобы получить запись в строке 1, столбце 1 [latex] AB, \ text {} [/ latex] умножьте первую строку в [latex] A [/ latex] на первый столбец в [latex] B [/ латекс], и доп.
[латекс] \ left [\ begin {array} {ccc} {a} _ {11} & {a} _ {12} & {a} _ {13} \ end {array} \ right] \ cdot \ left [\ begin {array} {c} {b} _ {11} \\ {b} _ {21} \\ {b} _ {31} \ end {array} \ right] = {a} _ {11} \ cdot {b} _ {11} + {a} _ {12} \ cdot {b} _ {21} + {a} _ {13} \ cdot {b} _ {31} [/ latex]
Чтобы получить запись в строке 1, столбце 2 [latex] AB, \ text {} [/ latex] умножьте первую строку [latex] A [/ latex] на второй столбец в [latex] B [/ latex ], и добавить.
[латекс] \ left [\ begin {array} {ccc} {a} _ {11} & {a} _ {12} & {a} _ {13} \ end {array} \ right] \ cdot \ left [\ begin {array} {c} {b} _ {12} \\ {b} _ {22} \\ {b} _ {32} \ end {array} \ right] = {a} _ {11} \ cdot {b} _ {12} + {a} _ {12} \ cdot {b} _ {22} + {a} _ {13} \ cdot {b} _ {32} [/ latex]
Чтобы получить запись в строке 1, столбце 3 [latex] AB, \ text {} [/ latex] умножьте первую строку [latex] A [/ latex] на третий столбец в [latex] B [/ latex ], и добавить.
[латекс] \ left [\ begin {array} {ccc} {a} _ {11} & {a} _ {12} & {a} _ {13} \ end {array} \ right] \ cdot \ left [\ begin {array} {c} {b} _ {13} \\ {b} _ {23} \\ {b} _ {33} \ end {array} \ right] = {a} _ {11} \ cdot {b} _ {13} + {a} _ {12} \ cdot {b} _ {23} + {a} _ {13} \ cdot {b} _ {33} [/ latex]

Так же поступаем и получаем второй ряд [латекс] АВ [/ латекс].Другими словами, строка 2 [латекса] A [/ latex] умножается на столбец 1 [latex] B [/ latex]; строка 2 [латекса] A [/ latex] умножена на столбец 2 [латекса] B [/ latex]; строка 2 [латекса] A [/ latex] умножается на столбец 3 [латекса] B [/ latex]. По завершении матрица продуктов будет

[латекс] AB = \ left [\ begin {array} {c} \ begin {array} {l} {a} _ {11} \ cdot {b} _ {11} + {a} _ {12} \ cdot {b} _ {21} + {a} _ {13} \ cdot {b} _ {31} \\ \ end {array} \\ {a} _ {21} \ cdot {b} _ {11} + {a} _ {22} \ cdot {b} _ {21} + {a} _ {23} \ cdot {b} _ {31} \ end {array} \ begin {array} {c} \ begin { массив} {l} {a} _ {11} \ cdot {b} _ {12} + {a} _ {12} \ cdot {b} _ {22} + {a} _ {13} \ cdot {b } _ {32} \\ \ end {array} \\ {a} _ {21} \ cdot {b} _ {12} + {a} _ {22} \ cdot {b} _ {22} + {a } _ {23} \ cdot {b} _ {32} \ end {array} \ begin {array} {c} \ begin {array} {l} {a} _ {11} \ cdot {b} _ {13 } + {a} _ {12} \ cdot {b} _ {23} + {a} _ {13} \ cdot {b} _ {33} \\ \ end {array} \\ {a} _ {21 } \ cdot {b} _ {13} + {a} _ {22} \ cdot {b} _ {23} + {a} _ {23} \ cdot {b} _ {33} \ end {array} \ справа] [/ латекс]

Общее примечание: свойства умножения матриц

Для матриц [latex] A, B, \ text {} [/ latex] и [latex] C [/ latex] выполняются следующие свойства.

Умножение матриц ассоциативно: [латекс] \ left (AB \ right) C = A \ left (BC \ right) [/ latex].
Умножение матриц является распределительным: [latex] \ begin {array} {l} \ begin {array} {l} \\ C \ left (A + B \ right) = CA + CB, \ end {array} \ hfill \ \ \ left (A + B \ right) C = AC + BC. \ hfill \ end {array} [/ latex]

Обратите внимание, что умножение матриц не коммутативно.

Пример 8: Умножение двух матриц

Умножить матрицу [латекс] A [/ латекс] и матрицу [латекс] B [/ латекс].

[латекс] A = \ left [\ begin {array} {cc} 1 & 2 \\ 3 & 4 \ end {array} \ right] \ text {and} B = \ left [\ begin {array} {cc} 5 & 6 \\ 7 & 8 \ end {array} \ right] [/ latex]

Решение

Сначала проверяем размеры матриц. Матрица [латекс] A [/ latex] имеет размеры [латекс] 2 \ times 2 [/ latex], а матрица [latex] B [/ latex] имеет размеры [латекс] 2 \ times 2 [/ latex]. Внутренние размеры такие же, поэтому мы можем выполнить умножение. Изделие будет иметь размеры [латекс] 2 \ умножить на 2 [/ латекс].

Выполняем описанные ранее операции.

Рисунок 2

Пример 9: Умножение двух матриц

Дано [латекс] A [/ латекс] и [латекс] B: [/ латекс]

Найдите [латекс] AB [/ латекс].
Найдите [латекс] BA [/ латекс].

[латекс] A = \ left [\ begin {array} {l} \ begin {array} {ccc} -1 & 2 & 3 \ end {array} \ hfill \\ \ begin {array} {ccc} 4 & 0 & 5 \ end {array} \ hfill \ end {array} \ right] \ text {and} B = \ left [\ begin {array} {c} 5 \\ -4 \\ 2 \ end {array} \ begin {array } {c} -1 \\ 0 \\ 3 \ end {array} \ right] [/ latex]

Решение

Размеры [латекса] A [/ latex] равны [latex] 2 \ text {} \ times \ text {} 3 [/ latex], а размеры [latex] B [/ latex] – [latex] 3 \ text {} \ times \ text {} 2, \ text {} [/ latex] эти матрицы можно перемножать, потому что количество столбцов в [latex] A [/ latex] совпадает с количеством строк в [latex] Б [/ латекс].В результате получится матрица [latex] 2 \ text {} \ times \ text {} 2 [/ latex], количество строк в [latex] A [/ latex] по количеству столбцов в [latex] B [/латекс].
[латекс] \ begin {array} {l} \ hfill \\ AB = \ left [\ begin {array} {rrr} \ hfill -1 & \ hfill 2 & \ hfill 3 \\ \ hfill 4 & \ hfill 0 & \ hfill 5 \ end {array} \ right] \ text {} \ left [\ begin {array} {rr} \ hfill 5 & \ hfill -1 \\ \ hfill -4 & \ hfill 0 \\ \ hfill 2 & \ hfill 3 \ end { массив} \ right] \ hfill \\ \ text {} = \ left [\ begin {array} {rr} \ hfill -1 \ left (5 \ right) +2 \ left (-4 \ right) +3 \ left (2 \ right) & \ hfill -1 \ left (-1 \ right) +2 \ left (0 \ right) +3 \ left (3 \ right) \\ \ hfill 4 \ left (5 \ right) +0 \ left (-4 \ right) +5 \ left (2 \ right) & \ hfill 4 \ left (-1 \ right) +0 \ left (0 \ right) +5 \ left (3 \ right) \ end { массив} \ right] \ hfill \\ \ text {} = \ left [\ begin {array} {rr} \ hfill -7 & \ hfill 10 \\ \ hfill 30 & \ hfill 11 \ end {array} \ right] \ hfill \ end {array} [/ latex]
Размеры [латекса] B [/ latex] равны [латексу] 3 \ times 2 [/ latex], а размеры [latex] A [/ latex] – [латекса] 2 \ times 3 [/ latex].Внутренние размеры совпадают, поэтому продукт определен и будет матрицей [латекс] 3 \ умножить на 3 [/ латекс].
[латекс] \ begin {array} {l} \ hfill \\ BA = \ left [\ begin {array} {rr} \ hfill 5 & \ hfill -1 \\ \ hfill -4 & \ hfill 0 \\ \ hfill 2 & \ hfill 3 \ end {array} \ right] \ text {} \ left [\ begin {array} {rrr} \ hfill -1 & \ hfill 2 & \ hfill 3 \\ \ hfill 4 & \ hfill 0 & \ hfill 5 \ end { массив} \ right] \ hfill \\ \ text {} = \ left [\ begin {array} {rrr} \ hfill 5 \ left (-1 \ right) + – 1 \ left (4 \ right) & \ hfill 5 \ left (2 \ right) + – 1 \ left (0 \ right) & \ hfill 5 \ left (3 \ right) + – 1 \ left (5 \ right) \\ \ hfill -4 \ left (-1 \ right) +0 \ left (4 \ right) & \ hfill -4 \ left (2 \ right) +0 \ left (0 \ right) & \ hfill -4 \ left (3 \ right) +0 \ left (5 \ right) \\ \ hfill 2 \ left (-1 \ right) +3 \ left (4 \ right) & \ hfill 2 \ left (2 \ right) +3 \ left (0 \ right) & \ hfill 2 \ left (3 \ right) +3 \ left (5 \ right) \ end {array} \ right] \ hfill \\ \ text {} = \ left [\ begin {array} {rrr} \ hfill -9 & \ hfill 10 & \ hfill 10 \\ \ hfill 4 & \ hfill -8 & \ hfill -12 \\ \ hfill 10 & \ hfill 4 & \ hfill 21 \ end {array} \ right] \ hfill \ end {array} [/ latex]

Анализ решения

Обратите внимание, что продукты [латекс] AB [/ латекс] и [латекс] BA [/ латекс] не равны.

[латекс] AB = \ left [\ begin {array} {cc} -7 & 10 \\ 30 & 11 \ end {array} \ right] \ ne \ left [\ begin {array} {ccc} -9 & 10 & 10 \ \ 4 & -8 & -12 \\ 10 & 4 & 21 \ end {array} \ right] = BA [/ latex]

Это иллюстрирует тот факт, что умножение матриц не коммутативно.

Вопросы и ответы

Возможно ли определение

AB , но не BA ?

Да, рассмотрим матрицу A с размерностью [латекс] 3 \ times 4 [/ latex] и матрицу B с размерностью [latex] 4 \ times 2 [/ latex].Для продукта AB внутренние измерения равны 4, и продукт определен, но для продукта BA внутренние измерения равны 2 и 3, поэтому продукт не определен.

Пример 10: Использование матриц в реальных задачах

Вернемся к задаче, представленной в начале этого раздела. В приведенной ниже таблице представлены потребности в оборудовании двух футбольных команд.

	Wildcats	Грязевые кошки
Голы	6	10
Шарики	30	24
Трикотажные изделия	14	20

У нас также указаны цены на оборудование, указанные в таблице ниже.

Цель	$ 300
Мяч	$ 10
Джерси	$ 30

Преобразуем данные в матрицы. Таким образом, матрица потребности в оборудовании записывается как

[латекс] E = \ left [\ begin {array} {c} 6 \\ 30 \\ 14 \ end {array} \ begin {array} {c} 10 \\ 24 \\ 20 \ end {array} \ справа] [/ латекс]

Матрица затрат записывается как

[латекс] C = \ left [\ begin {array} {ccc} 300 & 10 & 30 \ end {array} \ right] [/ latex]

Производим матричное умножение, чтобы получить стоимость оборудования.

[латекс] \ begin {массив} {l} \ hfill \\ \ hfill \\ CE = \ left [\ begin {array} {rrr} \ hfill 300 & \ hfill 10 & \ hfill 30 \ end {array} \ right] \ cdot \ left [\ begin {array} {rr} \ hfill 6 & \ hfill 10 \\ \ hfill 30 & \ hfill 24 \\ \ hfill 14 & \ hfill 20 \ end {array} \ right] \ hfill \\ \ text { } = \ left [\ begin {array} {rr} \ hfill 300 \ left (6 \ right) +10 \ left (30 \ right) +30 \ left (14 \ right) & \ hfill 300 \ left (10 \ вправо) +10 \ влево (24 \ вправо) +30 \ влево (20 \ вправо) \ end {array} \ right] \ hfill \\ \ text {} = \ left [\ begin {array} {rr} \ hfill 2,520 и \ hfill 3,840 \ end {array} \ right] \ hfill \ end {array} [/ latex]

Общая стоимость оборудования для Wildcats составляет 2520 долларов, а общая стоимость оборудования для Mud Cats составляет 3840 долларов.

Как: дана матричная операция, оцените ее с помощью калькулятора.

Сохраните каждую матрицу как матричную переменную [latex] \ left [A \ right], \ left [B \ right], \ left [C \ right], .. [/ latex].
Введите операцию в калькулятор, вызывая при необходимости каждую матричную переменную.
Если операция определена, калькулятор представит матрицу решения; если операция не определена, отобразится сообщение об ошибке.

Пример 11: Использование калькулятора для выполнения матричных операций

Найдите [латекс] AB-C [/ латекс] из

[латекс] A = \ left [\ begin {array} {rrr} \ hfill -15 & \ hfill 25 & \ hfill 32 \\ \ hfill 41 & \ hfill -7 & \ hfill -28 \\ \ hfill 10 & \ hfill 34 & \ hfill -2 \ end {array} \ right], B = \ left [\ begin {array} {rrr} \ hfill 45 & \ hfill 21 & \ hfill -37 \\ \ hfill -24 & \ hfill 52 & \ hfill 19 \\ \ hfill 6 & \ hfill -48 & \ hfill -31 \ end {array} \ right], \ text {и} C = \ left [\ begin {array} {rrr} \ hfill -100 & \ hfill -89 & \ hfill -98 \\ \ hfill 25 & \ hfill -56 & \ hfill 74 \\ \ hfill -67 & \ hfill 42 & \ hfill -75 \ end {array} \ right] [/ latex].

Решение

На странице матрицы калькулятора мы вводим матрицу [latex] A [/ latex] выше как матричную переменную [latex] \ left [A \ right] [/ latex], матрицу [latex] B [/ latex] выше как матричная переменная [latex] \ left [B \ right] [/ latex] и матрица [latex] C [/ latex] выше как матричная переменная [latex] \ left [C \ right] [/ latex].

На главном экране калькулятора мы вводим задачу и при необходимости вызываем каждую матричную переменную.

[латекс] \ влево [A \ вправо] \ раз \ влево [B \ вправо] – \ влево [C \ вправо] [/ латекс]

Калькулятор дает нам следующую матрицу.

[латекс] \ left [\ begin {array} {rrr} \ hfill -983 & \ hfill -462 & \ hfill 136 \\ \ hfill 1,820 & \ hfill 1,897 & \ hfill -856 \\ \ hfill -311 & \ hfill 2,032 & \ hfill 413 \ end {array} \ right] [/ latex]

Умножение матриц

Объективы

Разберитесь в композициях преобразований.
Понимать взаимосвязь между матричными продуктами и композициями матричных преобразований.
Научитесь комфортно заниматься базовой алгеброй с использованием матриц.
Рецепт: умножение матриц (два способа).
Фото: Композиция преобразований.
Словарный запас: Состав .

В этом разделе мы изучаем композиции преобразований. Как мы увидим, композиция – это способ объединения преобразований. Состав матричных преобразований соответствует понятию умножения двух матриц вместе. Мы также обсуждаем сложение и скалярное умножение преобразований и матриц.

Композиция в линейной алгебре означает то же самое, что и в исчислении. Вот определение.

Определение

Пусть T: Rn → Rm и U: Rp → Rn – преобразования. Их состав является преобразованием T◦U: Rp → Rm, определенным

(T◦U) (x) = T (U (x)).

Составление двух преобразований означает их объединение в цепочку: T◦U – это преобразование, которое сначала применяет U, а затем T (обратите внимание на порядок операций). Точнее, чтобы оценить T◦U по входному вектору x, сначала вы оцениваете U (x), затем вы берете этот выходной вектор U и используете его как входной вектор T: то есть (T◦U) (x ) = Т (U (х)).Конечно, это имеет смысл только тогда, когда выходы U являются действительными входами T, то есть когда диапазон U содержится в домене T.

RpxRnU (x) RmT◦U (x) UTT◦U

Вот изображение композиции T◦U как «машины», которая сначала запускает U, затем берет его выходные данные и передает их в T; аналогичная картина представлена в этом подразделе раздела 3.1.

T◦UUTRpxRmT◦U (x) U (x) Rn

Домен и содомен композиции

Чтобы определить T◦U, область значений U должна равняться области T.
Область T◦U – это область U.
Кодомен T◦U является кодоменом T.

Вспомните из этого определения в разделе 3.1, что тождественное преобразование – это преобразование IdRn: Rn → Rn, определенное как IdRn (x) = x для каждого вектора x.

Последнее свойство называется ассоциативностью . Развернув обе стороны, написано:

S◦ (T◦U) (x) = S (T◦U (x)) = S (T (U (x))) = S◦T (U (x)) = (S◦T) ◦U (Икс).

Другими словами, и S◦ (T◦U), и (S◦T) ◦U – это преобразование, определяемое сначала применением U, затем T, а затем S.

Состав преобразований , а не в целом. То есть, вообще говоря, T◦UB = U◦T, даже если обе композиции определены.

В этом пункте мы вводим, казалось бы, несвязанную операцию с матрицами, а именно умножение матриц. Как мы увидим в следующем подразделе, умножение матриц в точности соответствует композиции соответствующих линейных преобразований. Для начала нам понадобится некоторая терминология.

Обозначение

Пусть A – матрица размера m × n.Обычно мы будем писать aij для записи в i-й строке и j-м столбце. Он называется i, j записью матрицы.

a11 ··· a1j ··· a1n ……… ai1 ··· aij ··· ain ……… am1 ··· amj ··· amnEIIIGFJJJHjthcolumnithrow

Определение (умножение матриц)

Пусть A – матрица размера m × n, а B – матрица размера n × p. Обозначим столбцы B через v1, v2, …, vp:

B = C ||| v1v2 ··· vp ||| D.

Продукт AB представляет собой матрицу размера m × p со столбцами Av1, Av2, …, Avp:

AB = C ||| Av1Av2 ··· Avp ||| D.

Другими словами, матричное умножение определяется столбец за столбцом или «распределяется по столбцам B».

Для определения векторов Av1, Av2, …, Avp количество строк в B должно равняться количеству столбцов в A.

Размеры матриц в матричном произведении

Для определения AB количество строк B должно быть равно количеству столбцов A.
Произведение матрицы размера m × n и матрицы размера n × p является матрицей размера m × p.

Если B имеет только один столбец, то AB также имеет один столбец. Матрица с одним столбцом – это то же самое, что и вектор, поэтому определение матричного произведения обобщает определение произведения матрица-вектор из этого определения в разделе 2.3.

Если A – квадратная матрица, то мы можем умножить ее на себя; мы определяем его степеней как

A2 = AAA3 = AAA и т. Д.

Правило строки-столбца для умножения матриц

Вспомните определение в разделе 2.3 видно, что произведение вектора-строки и вектора-столбца является скаляром

Aa1a2 ··· anBEIIGx1x2 … xnFJJH = a1x1 + a2x2 + ··· + тревога.

Следующая процедура нахождения матричного произведения намного лучше приспособлена к вычислениям вручную; предыдущее определение больше подходит для доказательства теорем, таких как эта теорема ниже.

Рецепт: правило строки-столбца для умножения матриц

Пусть A – матрица размера m × n, пусть B – матрица размера n × p, и пусть C = AB. Тогда запись ij в C – это i-я строка A, умноженная на j-й столбец B:

cij = ai1b1j + ai2b2j + ··· + ainbnj.

Вот схема:

a11 ··· a1k ··· a1n ……… ai1 ··· aik ··· ain ……… am1 ··· amk ··· amnEIIIGFJJJHithrowb11 ··· b1j · ·· b1p ……… bk1 ··· bkj ··· bkp ……… bn1 ··· bnj ··· bnpEIIIIGFJJJJHjthcolumn = c11 ··· c1j ··· c1p. …….. ci1 ··· cij ··· cip ……… cm1 ··· cmj ··· cmpEIIIGFJJJHijentry

Правило строки-столбца для умножения матрицы на вектор в разделе 2.3 гласит, что если A имеет строки r1, r2, …, rm и x является вектором, то

Ax = EIIG — r1 —— r2 —…— rm — FJJHx = EIIGr1xr2x … rmxFJJH.

Определение умножения матриц:

AC ||| c1c2 ··· cp ||| D = C ||| Ac1Ac2 ··· Acp ||| D.

Отсюда следует, что

EIIG — r1 —— r2 —…— rm — FJJHC ||| c1c2 ··· cp ||| D = EIIGr1c1r1c2 ··· r1cpr2c1r2c2 ··· r2cp ……… rmc1rmc2 ··· rmcpFJJH.

Хотя умножение матриц удовлетворяет многим свойствам, которые можно было бы ожидать (см. Конец раздела), при выполнении арифметических операций с матрицами следует соблюдать осторожность, поскольку есть несколько свойств, которые в целом не выполняются.

Предостережения относительно умножения матриц

Хотя умножение матриц в общем случае не коммутативно, существуют примеры матриц A и B с AB = BA.Например, это всегда работает, когда A – нулевая матрица или когда A = B. Читателю предлагается найти другие примеры.

Цель этого пункта – показать, что умножение матриц соответствует композиции преобразований, то есть стандартная матрица для T◦U является произведением стандартных матриц для T и для U. Трудно поверить, что наша сложная матрица Формула умножения матриц на самом деле означает нечто интуитивно понятное, например, «соединение двух преобразований вместе»!

Теорема

Пусть T: Rn → Rm и U: Rp → Rn – линейные преобразования, и пусть A и B – их стандартные матрицы, соответственно, так что A – матрица m × n, а B – матрица n × p.Тогда T◦U: Rp → Rm – линейное преобразование, а его стандартная матрица – произведение AB.

Доказательство

Сначала проверим, что T◦U линейно. Пусть u, v векторы в Rp. Тогда

T◦U (u + v) = T (U (u + v)) = T (U (u) + U (v)) = T (U (u)) + T (U (v)) = T ◦U (u) + T◦U (v).

Если c – скаляр, то

T◦U (cv) = T (U (cv)) = T (cU (v)) = cT (U (v)) = cT◦U (v).

Поскольку T◦U удовлетворяет двум определяющим свойствам из раздела 3.3, это линейное преобразование.

Теперь, когда мы знаем, что T◦U линейно, имеет смысл вычислить его стандартную матрицу.Пусть C – стандартная матрица T◦U, поэтому T (x) = Ax, U (x) = Bx и T◦U (x) = Cx. По этой теореме из раздела 3.3 первый столбец C – это Ce1, а первый столбец B – это Be1. У нас

T◦U (e1) = T (U (e1)) = T (Be1) = A (Be1).

По определению, первый столбец продукта AB – это произведение A на первый столбец B, то есть Be1, поэтому

Ce1 = T◦U (e1) = A (Be1) = (AB) e1.

Отсюда следует, что C имеет тот же первый столбец, что и AB. Тот же аргумент, что и для i-го стандартного координатного вектора ei, показывает, что C и AB имеют один и тот же i-й столбец; поскольку у них одинаковые столбцы, это одна и та же матрица.

Теорема оправдывает наш выбор определения матричного произведения. Это единственная причина, по которой матричные произведения определяются таким образом. Перефразировать:

Продукты и композиции

Матрица композиции двух линейных преобразований является произведением матриц преобразований.

Вспомните из этого определения в разделе 3.3, что единичная матрица – это матрица размера n × n, столбцы которой являются стандартными векторами координат в Rn.Единичная матрица – это стандартная матрица тождественного преобразования: то есть x = IdRn (x) = Inx для всех векторов x в Rn. Для любого линейного преобразования T: Rn → Rm имеем

IRm◦T = T

и точно так же для любой матрицы A размера m × n мы имеем

ImA = A.

Аналогично T◦IRn = T и AIn = A.

В этом подразделе мы описываем еще две операции, которые можно выполнять с преобразованиями: сложение и скалярное умножение. Затем мы переводим эти операции на язык матриц.Это аналогично тому, что мы сделали для композиции линейных преобразований, но гораздо менее тонко.

Определение

Пусть T, U: Rn → Rm – два преобразования. Их сумма является преобразованием T + U: Rn → Rm, определяемым формулой
(Т + U) (х) = Т (х) + U (х).
Обратите внимание, что добавление преобразований определяется только в том случае, если оба преобразования имеют один и тот же домен и кодомен.
Пусть T: Rn → Rm – преобразование, а c – скаляр. Скалярное произведение c с T – это преобразование cT: Rn → Rm, определенное формулой
(cT) (x) = c · T (x).

Подчеркнем, что сумма двух преобразований T, U: Rn → Rm – это еще одно преобразование, называемое T + U; его значение на входном векторе x является суммой выходных сигналов T и U. Точно так же произведение T на скаляр c – это другое преобразование, называемое cT; его значение на входном векторе x – это вектор c · T (x).

В одном из вышеупомянутых свойств мы использовали 0 для обозначения преобразования Rn → Rm, которое равно нулю на каждом входном векторе: 0 (x) = 0 для всех x. Это называется преобразованием нуля .

Приведем аналогичные операции для матриц.

Определение

Факт

Пусть T, U: Rn → Rm – линейные преобразования со стандартными матрицами A, B соответственно, и пусть c – скаляр.

Стандартная матрица для T + U – A + B.
Стандартная матрица для cT – cA.

С учетом изложенного, следующие свойства являются следствием соответствующих свойств преобразований. Они также легко проверяются непосредственно из определений.

В одном из вышеупомянутых свойств мы использовали 0 для обозначения матрицы m × n, все элементы которой равны нулю. Это стандартная матрица нулевого преобразования, она называется нулевой матрицей .

Мы также можем комбинировать сложение и скалярное умножение матриц с умножением матриц. Поскольку матричное умножение соответствует композиции преобразований (теорема), следующие свойства являются следствием соответствующих свойств преобразований.

Большинство вышеперечисленных свойств легко проверить непосредственно из определений. Однако свойство ассоциативности (AB) C = A (BC) не является (попробуйте!). Это намного проще доказать, связав умножение матриц с композицией преобразований и используя тот очевидный факт, что композиция преобразований ассоциативна.

Операции с матрицами

Что касается линейной алгебры, две наиболее важные операции с векторами – это сложение векторов [сложение двух (или более) векторов] и скалярное умножение (умножение вектора на скаляр).Аналогичные операции определены для матриц.

Добавление матрицы . Если A и B являются матрицами одного размера , то их можно складывать. (Это похоже на ограничение на добавление векторов, а именно, могут быть добавлены только векторы из того же пространства R ⁿ; например, вы не можете добавить 2-вектор к 3-вектору.) Если A = [ a _ij] и B = [ b _ij] – обе матрицы m x n , тогда их сумма, C = A + B , также является матрицей m x n , и ее элементы задаются формулой

Таким образом, чтобы найти записи A + B , просто добавьте соответствующие записи A и B .

Пример 1 : Рассмотрим следующие матрицы:

Какие два можно добавить? Какова их сумма?

Поскольку можно складывать только матрицы одного размера, определяется только сумма F + H ( G не может быть добавлена ни к F , ни к H ). Сумма F и H составляет

.
Поскольку сложение действительных чисел коммутативно, отсюда следует, что сложение матриц (если оно определено) также коммутативно; то есть для любых матриц A, и B одинакового размера, A + B всегда будут равны B + A .
Пример 2 : Если какая-либо матрица A добавлена к нулевой матрице того же размера, результат явно будет равен A :
Это матричный аналог утверждения a + 0 = 0 + a = a , который выражает тот факт, что число 0 является аддитивным тождеством в наборе действительных чисел.
Пример 3 : Найдите матрицу B такую, что A + B = C , где
Если
, то матричное уравнение A + B = C становится
Поскольку две матрицы равны тогда и только тогда, когда они имеют одинаковый размер и их соответствующие элементы равны, из этого последнего уравнения следует
Следовательно,
Этот пример мотивирует определение вычитания матрицы : Если A и B являются матрицами одинакового размера, то записи A – B находятся простым вычитанием записей B из соответствующие записи A .Поскольку уравнение A + B = C эквивалентно B = C – A , использование вычитания матрицы выше даст тот же результат:
Скалярное умножение . Матрицу можно умножить на скаляр следующим образом. Если A = [ a _ij] – матрица, а k – скаляр, то
То есть матрица kA получается путем умножения каждой записи A на k .
Пример 4 : Если
, то скалярное кратное 2 A получается путем умножения каждой записи A на 2:
Пример 5 : Если A и B – матрицы одного размера, то A – B = A + (- B ), где – B – скалярное кратное (-1) В . Если
, затем
Это определение вычитания матрицы согласуется с определением, проиллюстрированным в Примере 8.
Пример 6 : Если
, затем
Умножение матриц . Безусловно, самая важная операция с матрицами – это умножение матриц , процесс умножения одной матрицы на другую. Первый шаг в определении умножения матриц – вспомнить определение скалярного произведения двух векторов. Пусть r и c будут двумя n ‐ векторами. Записывая r как матрицу строк 1 x n и c как матрицу столбца n x 1, скалярное произведение r и c равно
Обратите внимание, что для определения скалярного произведения r и c оба должны содержать одинаковое количество записей.Кроме того, здесь важен порядок, в котором эти матрицы записаны в этом продукте: вектор-строка идет первым, вектор-столбец – вторым.
Теперь последний шаг: как умножаются две общие матрицы? Во-первых, чтобы сформировать продукт AB, количество столбцов A должно соответствовать количеству строк B ; если это условие не выполняется, то продукт AB не определяется. Этот критерий следует из указанного выше ограничения для умножения матрицы строк r на матрицу столбцов c , а именно, что количество записей в r должно соответствовать количеству записей в c .Если A – это м x n и B – n x p , то определяется продукт AB , и размер матрицы продукта AB будет м x с. . Следующая диаграмма помогает определить, определен ли матричный продукт, и если да, то размеры продукта:
Представление матрицы m x n A как составной из векторов-строк r ₁, r ₂,…, r _m от R ⁿ и матрица n x p B , составленная из векторов-столбцов c ₁, c ₂,…, c _p из R ⁿ,
и
правило вычисления элементов матричного произведения AB : r _i · c _j = ( AB ) _ij, то есть
Пример 7 : Учитывая две матрицы
определяет, какой матричный продукт, AB или BA , определен, и оценивает его.
Поскольку A – 2 x 3, а B – 3 x 4, продукт AB в таком порядке определяется, и размер матрицы продукта AB будет 2 x 4. Продукт BA – это , а не , поскольку первый фактор ( B ) имеет 4 столбца, а второй фактор ( A ) имеет только 2 строки. Количество столбцов первой матрицы должно соответствовать количеству строк второй матрицы, чтобы их произведение было определено.
Если взять скалярное произведение строки 1 в A и столбца 1 в B , получим запись (1, 1) в AB . С
запись (1, 1) в AB – 1:
Скалярное произведение строки 1 в A и столбца 2 в B дает запись (1, 2) в AB ,
и скалярное произведение строки 1 в A и столбца 3 в B дает запись (1, 3) в AB :
Первая строка продукта завершается скалярным произведением строки 1 в A и столбца 4 в B , что дает запись (1, 4) в AB :
Теперь для второй строки AB : скалярное произведение строки 2 в A и столбца 1 в B дает запись (2, 1) в AB ,
и скалярное произведение строки 2 в A и столбца 2 в B дает запись (2, 2) в AB :
Наконец, взяв скалярное произведение строки 2 в A со столбцами 3 и 4 в B , получаем (соответственно) записи (2, 3) и (2, 4) в AB :
Следовательно,
Пример 8 : Если
и
вычисляет (3, 5) запись продукта CD .
Во-первых, обратите внимание, что, поскольку C составляет 4 x 5, а D составляет 5 x 6, произведение CD действительно определено, и его размер составляет 4 x 6. Однако нет необходимости вычислять все двадцать‐ четыре записи CD , если требуется только одна конкретная запись. Запись (3, 5) в CD является скалярным произведением строки 3 в C и столбца 5 в D :
Пример 9 : Если
убедитесь, что
но
В частности, обратите внимание, что хотя оба продукта AB и BA определены, AB не равно BA ; действительно, они даже не одного размера!
Предыдущий пример иллюстрирует, возможно, самое важное различие между умножением скаляров и умножением матриц.Для действительных чисел a и b всегда выполняется уравнение ab = ba , то есть умножение действительных чисел коммутативно; порядок, в котором написаны коэффициенты, не имеет значения. Однако категорически неверно, что умножение матриц коммутативно. Для матриц A, и B , приведенных в Примере 9, были определены оба продукта AB и BA , но они определенно не были идентичными. Фактически, матрица AB была 2 x 2, а матрица BA была 3 x 3.Вот еще одна иллюстрация некоммутативности умножения матриц: Рассмотрим матрицы
Поскольку C составляет 3 x 2, а D – 2 x 2, продукт CD определен, его размер составляет 3 x 2, и
Продукт DC , однако, не определен, поскольку количество столбцов D (которое равно 2) не равно количеству строк C (которое равно 3). Следовательно, CD ≠ DC , поскольку DC даже не существует.
Из-за чувствительности к порядку записи коэффициентов обычно не говорят просто: «Умножьте матрицы A, и B, ». Обычно важно указать, какая матрица идет первой, а какая – второй в продукте. По этой причине выражение «Умножить A справа на B » означает образовать произведение AB , а «Умножить A слева на B » означает образовать произведение BA . .
Пример 10 : Если
и x – это вектор (−2, 3), покажите, как A можно умножить справа на x и вычислить произведение.
Поскольку A равно 2 x 2, чтобы умножить A справа на матрицу, эта матрица должна иметь 2 строки. Следовательно, если x записано как 2 x 1 столбец , матрица
, то можно вычислить произведение A x , и в результате получится еще одна матрица столбца 2 x 1:
Пример 11 : Рассмотрим матрицы
Если A умножить справа на B , получится
, но если A умножить слева на B , то получится
Обратите внимание, что оба продукта определены и имеют одинаковый размер, но не равны.
Пример 12 : Если A и B являются квадратными матрицами, такими, что AB = BA , то говорят, что A и B перемещаются по на . Покажите, что любые две квадратные диагональные матрицы порядка 2 коммутируют.
Пусть
– две произвольные диагональные матрицы 2 x 2. Тогда
и
Начиная с a ₁₁ b ₁₁ = b ₁₁ a ₁₁ и a ₂₂ b ₂₂ = b ₂₂ a ₂₂, AB действительно равно BA , как и нужно.
Хотя матричное умножение обычно не коммутативно, оно иногда и коммутативно; например, если
, затем
Несмотря на такие примеры, как эти, необходимо указать, что в целом умножение матриц не является коммутативным .
Есть еще одно различие между умножением скаляров и умножением матриц. Если a и b являются действительными числами, то уравнение ab = 0 означает, что a = 0 или b = 0.То есть, единственный способ, при котором произведение действительных чисел может быть равным 0, – это если хотя бы один из множителей сам равен 0. Аналогичное утверждение для матриц, однако, неверно. Например, если
, затем
Обратите внимание, что даже если ни G , ни H не являются нулевой матрицей, произведение GH будет.
Еще одним отличием умножения скаляров от умножения матриц является отсутствие общего закона сокращения для умножения матриц.Если a, b и c являются действительными числами, причем a ≠ 0, то, отбрасывая множитель a , уравнение ab = ac подразумевает b = c . Для умножения матриц такого закона не существует; то есть утверждение AB = AC не означает , а не , подразумевает B = C , даже если A не равно нулю. Например, если
, затем оба
и
Таким образом, даже если AB = AC и A не является нулевой матрицей, B не равно C .

Пример 13 : Хотя умножение матриц не всегда коммутативно, всегда ассоциативно . То есть, если A, B и C являются любыми тремя матрицами, так что продукт (AB) C определен, то продукт A (BC) также определен, и

То есть, пока порядок факторов не меняется, то, как они сгруппированы, не имеет значения.

Проверить ассоциативный закон для матриц

Первый, с

продукт (AB) C –

Сейчас, с

продукт A (BC) это

Следовательно, (AB) C = A (BC) , как и ожидалось.Обратите внимание, что ассоциативный закон подразумевает, что произведение A, B и C (в таком порядке) может быть записано просто как ABC ; круглые скобки не нужны, чтобы разрешить двусмысленность, потому что нет двусмысленности.

Пример 14 : Для матриц

проверьте уравнение ( AB ) ^T = B ^T A ^T.

Первая,

означает

Сейчас, с

B ^T A ^T действительно равно ( AB ) ^T.Фактически, уравнение

справедливо для любых двух матриц, для которых определено произведение AB . Это говорит о том, что если продукт AB определен, то транспонирование продукта равно произведению перемещений в обратном порядке .

Матрицы идентичности . Нулевая матрица 0 _{m x n} играет роль аддитивной идентичности в наборе матриц m x n точно так же, как число 0 в наборе действительных чисел (вспомните пример 7).То есть, если A является матрицей m x n и 0 = 0 _{m x n} , то

Это матричный аналог утверждения, что для любого действительного числа a ,

Имея в руках аддитивную идентичность, вы можете спросить: «А как насчет мультипликативной идентичности ?» В наборе действительных чисел мультипликативным тождеством является число 1, так как

Есть ли матрица, которая играет роль и эту роль ? Рассмотрим матрицы

и убедитесь, что

Таким образом, AI = IA = A .Фактически, легко показать, что для этой матрицы I оба продукта AI и IA будут равны A, для любой матрицы 2 x 2 A . Следовательно,

– мультипликативная единица в наборе матриц 2 x 2. Аналогично матрица

– мультипликативная единица в наборе матриц 3 x 3 и так далее. (Обратите внимание, что I ₃ – это матрица [δ _ij] _{3 x 3}.В общем случае матрица I _n – диагональная матрица nxn с каждым диагональным элементом, равным 1 – называется единичной матрицей порядка n и служит мультипликативной единицей в наборе всех Матрицы nxn .

Есть ли мультипликативная идентичность в наборе всех матриц m x n , если m ≠ n ? Для любой матрицы A в M _mxn ( R ) матрица I _m является левым тождеством ( I _m A = A ) и I _n – это правый идентификатор ( AI _n = A ).Таким образом, в отличие от набора матриц n x n , набор неквадратных матриц m x n не обладает двухсторонней идентичностью qunique , поскольку I _m ≠ I _n , если m ≠ n .

Пример 15 : Если A – квадратная матрица, то A ² обозначает продукт AA, A ³ обозначает продукт AAA и т. Д. Если A – это матрица

показывают, что A ³ = – A .

Расчет

показывает, что A ² = – I . Умножение обеих частей этого уравнения на A дает A ³ = – A , как и нужно. [Техническое примечание: можно показать, что в определенном точном смысле набор матриц вида

, где a и b – действительные числа, структурно идентичен набору комплексных чисел a + bi .Поскольку матрица A, в этом примере имеет такую форму (с a = 0 и b = 1), A соответствует комплексному числу 0 + 1 i = i , а аналог матричное уравнение A ² = – I , полученное выше, равно i ² = -1, уравнение, которое определяет мнимую единицу, i .]

Пример 16 : Найдите недиагональную матрицу, которая коммутирует с

Проблема заключается в запросе недиагональной матрицы B , такой что AB = BA .Как и A , матрица B должна быть 2 x 2. Один из способов создать такую матрицу B – создать A ², поскольку, если B = A ², ассоциативность подразумевает

(Это уравнение доказывает, что A ² будет коммутировать с A на с любой квадратной матрицей A ; кроме того, оно предлагает, как можно доказать, что каждая интегральная степень квадратной матрицы A будет добираться до A .)

В данном случае

, который недиагонален. Эта матрица B действительно коммутирует с A , что подтверждается расчетами

.
и
Пример 17 : Если
доказывают, что
для каждого натурального числа n .
Несколько предварительных расчетов показывают, что данная формула действительно верна:
Однако, чтобы установить, что формула верна для всех натуральных чисел n , необходимо дать общее доказательство.Здесь это будет сделано с использованием принципа математической индукции , который читается следующим образом. Пусть P (n) обозначает предложение относительно положительного целого числа n . Если можно показать, что
и
, то оператор P (n) действителен для всех целых положительных чисел n . В данном случае утверждение P (n) является утверждением
Поскольку A ¹ = A , утверждение P (1) определенно верно, поскольку
Теперь, предполагая, что P (n) истинно, то есть предполагая, что
теперь необходимо установить срок действия выписки P ( n + 1), что составляет
Но это утверждение действительно верно, потому что
По принципу математической индукции доказательство завершено.
Инверсия матрицы . Пусть a будет заданным действительным числом. Поскольку 1 является мультипликативным тождеством в наборе действительных чисел, если существует число b такое, что
, затем b называется , обратным или мультипликативным обратным a и обозначается a ^-1 (или 1/ a ). Аналог этого утверждения для квадратных матриц выглядит следующим образом. Пусть A будет заданной матрицей n x n .Поскольку I = I _n является мультипликативным тождеством в наборе матриц n x n , если существует матрица B , такая что
, тогда B называется (мультипликативным) , обратным A и обозначается A ^-1 (читается « A обратный»).
Пример 18 : Если
, затем
с
и
Еще одно различие между умножением скаляров и умножением матриц заключается в существовании обратных.Хотя каждое ненулевое действительное число имеет обратное, существуют ненулевые матрицы, у которых нет обратного .
Пример 19 : Показать, что ненулевая матрица
не имеет обратного.
Если бы эта матрица имела инверсию, то
для некоторых значений a, b, c и d . Однако, поскольку вторая строка A является нулевой строкой, вы можете видеть, что вторая строка продукта также должна быть нулевой строкой:
(Когда звездочка, * появляется как запись в матрице, это означает, что фактическое значение этой записи не имеет отношения к настоящему обсуждению.) Поскольку (2, 2) элемент произведения не может равняться 1, произведение не может быть равным единичной матрице. Следовательно, невозможно построить матрицу, которая могла бы служить обратной для A .
Если матрица имеет инверсию, она называется обратимой . Матрица в примере 23 обратима, а матрица в примере 24 – нет. Позже вы узнаете различные критерии для определения обратимости данной квадратной матрицы.
Пример 20 : Пример 18 показал, что
Учитывая, что
проверьте уравнение ( AB ) ⁻¹ = B ⁻¹ A ⁻¹.
Сначала вычислите AB :
Затем вычисляем B ⁻¹ A ⁻¹:
Теперь, поскольку произведение AB и B ⁻¹ A ⁻¹ равно I ,
B ⁻¹ A ⁻¹ действительно является инверсией AB . Фактически, уравнение
справедливо для любых обратимых квадратных матриц того же размера.Это говорит о том, что если A и B являются обратимыми матрицами одинакового размера, то их произведение AB также является обратимым, и обратное произведение равно произведению обратных в обратном порядке . (Сравните это уравнение с уравнением с транспонированием в примере 14 выше.) Этот результат можно в общем доказать, применяя ассоциативный закон для матричного умножения. С
и
следует, что ( AB ) ^-1 = B ^-1 A ^-1, как требуется.
Пример 21 : Обратная матрица
это
Покажите, что обратное значение B ^T равно ( B ⁻¹) ^T.
Форма B ^T и ( B ^-1) ^T и умножьте:
Этот расчет показывает, что ( B ⁻¹) ^T является обратной величиной B ^T.[Строго говоря, это показывает только то, что ( B ^-1) ^T – это правый обратный B ^T, то есть когда он умножает B ^T справа, продукт – это личность. Также верно, что ( B ⁻¹) ^T B ^T = I , что означает ( B ⁻¹) ^T – это левый обратный из В ^Т.Однако нет необходимости явно проверять оба уравнения: если квадратная матрица имеет обратное, нет различия между левым обратным и правым обратным.] Таким образом,
уравнение, которое фактически справедливо для любой обратимой квадратной матрицы B . Это уравнение говорит, что если матрица обратима, то ее транспонирование также является обратным, а обратное транспонирование – это транспонирование обратного.
Пример 22 : Используйте свойство распределения для матричного умножения, A ( B ± C ) = AB ± AC , чтобы ответить на этот вопрос: если матрица 2 x 2 D удовлетворяет уравнение D ² – D – 6 I = 0 , каково выражение для D ⁻¹?
По указанному выше распределительному свойству D ² – D = D ² – DI = D (D – I) .Следовательно, из уравнения D ² – D – 6 I = 0 следует D (D – I) = 6 I . Умножение обеих частей этого уравнения на 1/6 дает
, что означает
В качестве иллюстрации этого результата матрица
удовлетворяет уравнению D ² – D – 6 I = 0 , как вы можете убедиться.С
и
матрица 1/6 ( D − I ) действительно равна D ⁻¹, как заявлено.
Пример 23 : Уравнение ( a + b ) ² = a ² + 2 ab + b ² является тождеством, если a и b настоящие числа. Однако покажите, что ( A + B ) ² = A ² + 2 AB + B ² – это , а не , если A и B – это матрицы 2 x 2.[Примечание: законы распределения для матричного умножения: A ( B ± C ) = AB ± AC , данные в Примере 22, и сопутствующий закон ( A ± B ) C = AC ± BC .]
Из законов распределения для умножения матриц следует
Поскольку матричное умножение не коммутативно, BA обычно не равно AB , поэтому сумма BA + AB не может быть записана как 2 AB .В общем, тогда ( A + B ) ² ≠ A ² + 2 AB + B ². [Любые матрицы A и B , которые не коммутируются (например, матрицы в Примере 16 выше), предоставят конкретный контрпример к утверждению ( A + B ) ² = A ² + 2 AB + B ², что также установило бы, что это не личность.]
Пример 24 : Предположим, что B обратимый. Если A коммутирует с B , покажите, что A также коммутирует с B ⁻¹.
Проба . Сказать « A курсирует с B » означает AB = BA . Умножьте это уравнение на B ⁻¹ слева и справа и используйте ассоциативность:
Пример 25 : Число 0 имеет только один квадратный корень: 0.Покажите, однако, что нулевая матрица (2 на 2) имеет бесконечно много квадратных корней, найдя все матрицы 2 x 2 A такие, что A ² = 0 .
Точно так же, как число a называется квадратным корнем из b , если a ² = b , матрица A называется квадратным корнем из B , если A ² = B . Пусть
– произвольная матрица 2 x 2.Возводя его в квадрат и устанавливая результат равным 0 , получаем
Записи (1, 2) в последнем уравнении означают, что b ( a + d ) = 0, что выполняется, если (Случай 1) b = 0 или (Случай 2) d = – а .
Случай 1. Если b = 0, то диагональные записи подразумевают, что a = 0 и d = 0, а записи (2, 1) означают, что c является произвольным. Таким образом, для любого значения c каждая матрица вида
– это квадратный корень из 0 _2×2.
Случай 2. Если d = – a , то оба недиагональных входа будут равны 0, а диагональные записи будут равны a ² + bc . Таким образом, если b и c выбраны так, что bc = – a ², A ² будет равно 0 .
Аналогичная цепочка рассуждений, начинающаяся с записей (2, 1), приводит либо к a = c = d = 0 (и b произвольно) или к такому же выводу, что и раньше: до тех пор, пока b и c выбираются так, что bc = – a ², матрица A ² будет равна 0 .
Все эти случаи можно резюмировать следующим образом. Любая матрица следующей формы будет иметь свойство, состоящее в том, что ее квадрат представляет собой нулевую матрицу 2 на 2:
Поскольку существует бесконечно много значений a, b и c , таких что bc = – a ², нулевая матрица 0 _2×2 имеет бесконечно много квадратных корней. Например, если выбрать a = 4, b = 2 и c = −8, получится ненулевая матрица
.
площадью
Основы линейной алгебры: скалярное произведение и умножение матриц | автор Soner Yıldırım
Разъяснено на примерах
Фото Маркуса Списке на Unsplash
Данные собираются во многих различных форматах, от чисел до изображений, от категорий до звуковых волн.Однако нам нужны данные, представленные числами, чтобы иметь возможность анализировать их на компьютерах. Модели машинного обучения и глубокого обучения требуют больших объемов данных. Их производительность сильно зависит от объема данных. Таким образом, мы стремимся собрать как можно больше данных, чтобы построить надежную и точную модель. По мере увеличения объема данных операции, выполняемые со скалярами, становятся неэффективными. Нам нужны векторизованные или матричные операции для эффективных вычислений. Вот где в игру вступает линейная алгебра .
Линейная алгебра – одна из самых важных тем в области науки о данных. В этом посте мы рассмотрим основные, но очень важные операции линейной алгебры: Точечное произведение и умножение матриц. Эти базовые операции являются строительными блоками сложных моделей машинного обучения и глубокого обучения, поэтому очень важно иметь полное представление о них.
Скалярное произведение двух векторов – это сумма произведений элементов относительно положения.Первый элемент первого вектора умножается на первый элемент второго вектора и так далее. Сумма этих произведений является скалярным произведением, которое можно сделать с помощью функции np.dot () .
Давайте сначала создадим два простых вектора в виде множества массивов и вычислим скалярное произведение.
Скалярное произведение этих двух векторов представляет собой сумму произведений элементов в каждой позиции. В этом случае скалярное произведение равно (1 * 2) + (2 * 4) + (3 * 6).
Поскольку мы умножаем элементы в одних и тех же позициях, два вектора должны иметь одинаковую длину, чтобы получить скалярное произведение.
В области науки о данных мы в основном имеем дело с матрицами. Матрица – это набор векторов строк и столбцов, объединенных структурированным образом. Таким образом, умножение двух матриц включает в себя множество операций скалярного произведения векторов. Это станет более ясным, когда мы рассмотрим несколько примеров. Давайте сначала создадим две матрицы 2×2 с помощью NumPy.
Матрица 2×2 имеет 2 строки и 2 столбца. Индексы строк и столбцов начинаются с 0. Например, первая строка A (строка с индексом 0) является массивом [4,2].Первый столбец A – это массив [4,0]. Элемент в первой строке и первом столбце равен 4. Мы можем получить доступ к отдельным строкам, столбцам или элементам с помощью следующего синтаксиса numpy.
Это важные концепции для понимания умножения матриц.
Умножение двух матриц включает скалярные произведения между строками первой матрицы и столбцами второй матрицы. Первый шаг – это скалярное произведение между первой строкой A и первым столбцом B. Результатом этого скалярного произведения является элемент результирующей матрицы в позиции [0,0] (т.е.е. первая строка, первый столбец).
Таким образом, итоговая матрица C будет иметь (4 * 4) + (2 * 1) в первой строке и первом столбце. C [0,0] = 18.
Следующий шаг – это скалярное произведение первой строки A и второго столбца B.
C будет иметь (4 * 0) + (2 * 4) в первой строке и втором столбце. C [0,1] = 8.
Первая строка A завершена, поэтому мы начинаем со второй строки A и выполняем те же шаги.
C будет иметь (0 * 4) + (3 * 1) во второй строке и первом столбце. C [1,0] = 3.
Последний шаг – это скалярное произведение между второй строкой A и вторым столбцом B.
C будет иметь (0 * 0) + (3 * 4) во второй строке и втором столбце. C [1,1] = 12.
Мы пошагово видели, как это делается. Все эти операции выполняются с помощью операции np.dot :
Как мы помним из векторного скалярного произведения, два вектора должны иметь одинаковую длину, чтобы получить скалярное произведение. Каждая операция скалярного произведения в матричном умножении должна соответствовать этому правилу.Точечные произведения выполняются между строками первой матрицы и столбцами второй матрицы. Таким образом, строки первой матрицы и столбцы второй матрицы должны иметь одинаковую длину.
Здесь я хочу подчеркнуть важный момент. Длина строки равна количеству столбцов. Точно так же длина столбца равна количеству строк.
Рассмотрим следующую матрицу D:
D имеет 3 строки и 2 столбца, поэтому это матрица 3×2. Длина строки равна 2, что соответствует количеству столбцов, а длина столбца – 3, что соответствует количеству строк.
Я долго объяснял, но хочу сказать, что для возможности выполнения умножения матриц количество столбцов первой матрицы должно быть равно количеству строк второй матрицы.
Требование для умножения матриц состоит в том, что количество столбцов первой матрицы должно быть равно количеству строк второй матрицы.
Например, мы можем умножить матрицу 3×2 на матрицу 2×3.
Форма результирующей матрицы будет 3×3, потому что мы выполняем 3 операции скалярного произведения для каждой строки A, а A имеет 3 строки.Простой способ определить форму результирующей матрицы – взять количество строк из первой и количество столбцов из второй:
Умножение 3×2 и 2×3 возвращает 3×3
3×2 и умножение 2×2 возвращает 3×2
Умножение 2×4 и 4×3 возвращает 2×3
Если условия, которые мы обсуждали, не выполняются, умножение матриц невозможно.