Формула уравнение бернулли: Ничего не найдено для %25D0%25Bc%25D0%25B5%25D1%2585%25D0%25B0%25D0%25Bd%25D0%25B8%25D0%25Ba%25D0%25B0 %25D1%2583%25D1%2580%25D0%25B0%25D0%25B2%25D0%25Bd%25D0%25B5%25D0%25Bd%25D0%25B8%25D0%25B5 %25D0%25B1%25D0%25B5%25D1%2580%25D0%25Bd%25D1%2583%25D0%25Bb%25D0%25Bb%25D0%25B8 - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Уравнение Бернулли – вывод формулы, физический смысл, примеры использования

Зависимость между скоростью жидкости, находящейся в неизменном состоянии, и давлением определяется уравнением Бернулли. Этот закон нашёл широкое применение в гидродинамике: при расчётах трубопроводов и измерениях расхода жидкостей. Практически все нормальные дроссельные расходомеры изготавливаются на основе исследований, выполненных швейцарским физиком и математиком.

Содержание

Исследования учёного
Условия действия
Количественная сторона
Применение в гидравлике
Подъёмная сила

Исследования учёного

Даниил Бернулли родился в Голландии в 1700 году. В 1725 году он начал работать на кафедре физиологии, где увлёкся основами теоретической физики. Через 25 лет он возглавил кафедру экспериментальной физики, которой и руководил до конца своих дней. Основным его трудом считается создание теории гидродинамической зависимости, известной как Закон Бернулли. Открытие учёного предвосхитило зарождение молекулярно-кинетического учения поведения газов.

Причиной открытия принципа стало изучение действия закона сохранения энергии в различных ситуациях. Бернулли установил, что давление жидкости в замкнутом пространстве зависит от сечения объекта, в котором она находится. Чем меньше сечение трубы, тем ниже будет созданное давление в пропускаемом через неё жидком веществе.

Этот факт был доказан экспериментально и описан математически.

Правило в математической формулировке имеет вид (pv²/ 2) + p * g * h + ρ = const, где:

p — количество жидкости на единицу объёма;
v — скорость движения потока;
h — уровень, на который поднят элемент жидкости;
ρ — сила, действующая на единицу площади;
g — ускорение, придаваемое жидкости под действием притяжения Земли.

Чтобы понять физический смысл уравнения Бернулли, нужно рассмотреть трубу переменного сечения, в которой существует точка А и Б. Первая располагается в широкой части, а вторая — в узкой. В соответствии с уравнением непрерывности скорость V1 в части трубы, имеющей большее сечение, будет меньше, чем скорость жидкости V2 в узком сечении. Если в жидкость поместить прибор для измерения давления, он покажет какое-то значение P1 в точке A и P2 в точке Б. При этом там, где скорость движения жидкости медленнее, давление будет больше.

Объясняется это следующим образом: если V1 больше V2, значит, при движении происходит изменение скорости течения. Представив, что в жидкости находится точка, можно утверждать о её движении с ускорением. Это означает, что на неё действуют силы.

Одна из них совпадает с направлением течения, тем самым ускоряя движение. Обусловлена эта сила разностью давления.

Так как движение происходит от точки А к Б, то и давление возле А будет больше, чем около Б. Эта разность давлений и приводит к ускорению.

Условия действия

Закон применим для условия, при котором соблюдается неразрывность струи воздуха или жидкости. В тех участках потока, где скорость течения больше, давление будет меньше и наоборот. Это утверждение и называется теоремой Бернулли. По сути, закон позволяет установить связь между давлением, скоростью, высотой.

Пусть имеется труба переменного сечения с изменяющейся высотой. Внизу она широкая, а затем сужается. По ней течёт жидкость. Площадь сечения можно обозначить как S1 и S2, а давление участков и скорость движения на них P1, P2, V1, V2. Высота внизу будет равняться S1, а вверху S2.

Выделив участок в трубе с жидкостью, можно сказать, что она движется слева направо и через некоторое время полностью сдвинется в область S2. Изменение положения слева будет равно расстоянию дельта L1, а справа — дельта L2.

Течение является:

ламинарным — находящаяся в трубке жидкость перемешивается слоями без хаотических изменений давления и скорости, турбулентность отсутствует;
стационарным — распределение скоростей не изменяется с течением времени;
скоростным — в движении принимает участие такой параметр, как ускорение;
идеальным с несжимаемой жидкостью.

Последнее обозначает, что нет вязкости. Поэтому на жидкость действует только сила упругости и тяжести, а силы трения нет. Система не является замкнутой, а значит закон сохранения энергии применительно к рассматриваемому участку использовать нельзя. Зато вполне можно применить теорему о кинетической энергии.

Для газов уравнение можно использовать лишь в том случае, если их плотность изменяется незначительно. Но касаемо аэродинамики учитывается и то, что изменение давления воздуха гораздо меньше атмосферного. Поэтому уравнение можно применять в аэродинамических расчётах.

Согласно ему, сумма действующих всех сил на тело (рассматриваемый кусок жидкости) равняется изменению кинетической энергии объекта: ΣAi = ΔEk. На нижний участок действует сила давления, выполняющая положительную работу, а на верхний — отрицательную. Кроме этого, действует и сила тяжести. Так как жидкость поднимается, она имеет тоже отрицательный знак. Сила бокового давления перпендикулярна любой точке в системе, поэтому никакого влияния она не оказывает.

Количественная сторона

Исходя из сил, действующих на тело, изменение кинетической энергии можно описать выражением: ΔEk = Ap1 +Ap2 +Ag. Чтобы найти работу, необходимо силу умножить на пройденное расстояние. Поэтому работа силы давления равна произведению самой силы F на модуль перемещения ΔL и косинусу угла между ними: Ap1 = F1* ΔL *1.

Чтобы найти силу, нужно давление умножить на площадь. Значит: Ap1 = p 1 * S1 * ΔL1 = p1V1. Таким же образом находится работа для второго состояния: Ap2 = F1* ΔL2 *(-1) = — p2 * S2 * ΔL2 = -p2 * V2. Жидкость несжимаемая, следовательно: V1=V2=V.

Работу силы тяжести можно вычислить исходя из того, что рассматриваемый кусок жидкости является относительным, то есть он, хотя и не статический, в любом месте будет подвергаться воздействию одинаковой силы тяжести. Верным будет выражение: Ag = — ΔEp = — (m2 * g * h3 — m1 * g * h2) = m1 * g * h2 — m2 * g * h3. Так как жидкость несжимаемая, её плотность не изменится. Отсюда можно утверждать: Ag = ρ * V * g * h2 — ρ * V * g * h3.

Зная количественные показатели всех трёх работ, можно найти изменение кинетической энергии. Из физики известно, что оно равно разнице конечной и начальной энергии. Течение стационарное, значит, скорость с течением времени не изменится. Следовательно, кинетическая энергия будет определяться разницей появившейся энергии в верхней части и ушедшей из нижней области: ΔEk = (m2 * v2²)/2 — (m1 * v1²) / 2.

Воспользовавшись тем, что масса равняется произведению плотности на объём, формулу можно привести к виду: ΔEk = (ρ * V * v2²)/2 — (ρ * V * v1²) / 2. Теперь найденные выражения для работ нужно подставить в теорему о кинетической энергии. Получится следующее равенство: p1V — p2V + ρ * V * g * h2 — ρ * V * g * h3 = (ρ * V * v2²) / 2 — (ρ * V * v1²) / 2. Разделив левую и правую часть на объём, выражение можно упростить до вида: p1 — p2 + ρ * g * h2 — ρ * g * h3 = (ρ * v2²)/2 — (ρ * v1²) / 2 .

То место, где давление p1, некая точка внутри трубки, пусть будет обозначено цифрой один, а там, где p2, — цифрой два. Всё что относится к единице можно записать в левой части, а к двойке — в правой: ρ1 * g * h2 + (ρ * v1²) / 2 = ρ * g * h3 + (ρ * v2²) / 2. Полученная формула показывает, что при переходе в пределе одной линии скорость, давление и высота изменяются. Поэтому в любой точке будет справедливым выражение: ρ1+ ρ * g * h + (ρ * v1) / 2 = const. Это и есть количественное описание уравнения Бернулли для идеальной жидкости.

Применение в гидравлике

Наиболее типичным примером использования уравнения является решение заданий по нахождению скорости вытекания жидкости из отверстия в широком сосуде. Такой ёмкостью называют систему, в которой диаметр сосуда значительно больше размера отверстия. Необходимо найти скорость вытекающей жидкости U1. Известно, что высота столба жидкости, на который действует сила тяжести g, равна h.

Пусть в жидкости, находящейся сверху, имеется точка один. Через некоторое время она окажется внизу в положении два. На верх жидкости давит атмосферное давление, поэтому p1=pатм. Высота в точке один равна h. Скорость U1 считают равной нулю. Давление p2 в точке два будет также равно атмосферному. Так как жидкость опустится на дно, то высота h3 станет нулевой.

Все эти величины следует подставить в уравнение Бернулли. Получится выражение: pатм + ρ * g * h + 0 = pатм + (ρ * U²) / 2 + 0. Атмосферное давление взаимно уничтожается: ρ * g * h = (ρ * U²) / 2. В левой и правой части стоит плотность, на которую можно сократить. Отсюда получается, что вид жидкости значения не имеет. Это может быть: вода, ртуть, расплавленный металл. Эффект от этого не поменяется. Из формулы можно выразить искомое U2. Оно будет равно: U2 = (2 * g * h)^½.

Интересным фактом является то, что полученный ответ при решении задачи называется формулой Торричелли. Она показывает, что скорость, с которой вытекает жидкость из широкого сосуда, равна скорости тела при свободном падении с той же высоты.

Используя уравнение, можно легко рассчитать давление жидкости на дно и стенки сосуда. В этом случае закон Бернулли является обобщением для формулы гидростатического давления. Пусть имеется сосуд с жидкостью высотой h. Точка, находящаяся наверху, характеризуется давлением p1 = pатм., высотой h2 равной h и скоростью U1. Для точки на дне параметры будут следующие: p2 = p, h3 = 0, U2 = 0. Скорости принимаются равными нулевому значению, так как рассматриваемая жидкость находится в состоянии покоя.

Данные следует подставить в уравнение. В итоге получится равенство: pатм + ρ * g * h + 0 = p + 0 + 0. Из него несложно найти неизвестное: p = pатм + ρ * g * h. Полученный ответ является формулой гидростатического давления и подтверждает закон Паскаля.

Аналогично уравнение Бернулли для потока реальной жидкости используется при расчёте расхода в карбюраторе, пульверизаторе, учёте статического и динамического давления.

Подъёмная сила

Самолёт летает благодаря тому, что набегающий на крыло напор воздуха создаёт подъёмную силу. Её можно рассчитать и оценить с помощью уравнения. Геометрически крыло можно представить в виде плоскости с углом a (угол атаки). На него действует поток воздуха со скоростью U. Частица воздуха ударяет в твёрдую поверхность и отражается от неё. Угол отражения равен углу атаки, а её скорость равняется U’. Нужно рассчитать подъёмную силу. Для этого необходимо выполнить три шага:

рассмотреть изменение скорости воздуха;
узнать импульс частиц;
используя закон Ньютона, определить силу.

В результате получится, что на крыло действует сила, состоящая из двух компонентов: подъёмной силы Fy и аэродинамического сопротивления Fx. Fy = Cy * p * U²* S, а Fx = Cx * p * U²* S. В формулах С является коэффициентом, а S — площадью крыла.

Для расчёта используется уравнение Бернулли. Выглядеть оно будет следующим образом: Pп. к + (ρ * Uп. к) * 2 / 2 + ρ * g * hп. к = Pн. к + (ρ * Uн. к) * 2 / 2 + ρ * g * hн. к, где: п. к — под крылом, а н. к — над крылом. Это уравнение можно упростить, приняв, что давления над и под крылом примерно одинаковые, поэтому плотность будет также одинаковая. Кроме того, высота крыла довольно маленькая. Исходя из этого, формулу можно упростить, и она примет вид: pп. к-pн.к = (ρ * (Uн.к + Uп. к) * (Uн.к — Uп. к)) / 2 = 2 * U1 * U2. Теперь можно найти подъёмную силу. Для этого разность давлений нужно умножить на площадь крыла: Fy = (pп.к-pн. к) * S.

Таким образом, используя метод, можно рассчитать подъёмную силу, обусловленную эффектом Бернулли. Например, пусть дано, что площадь крыла равна 50 м². Скорость потока воздуха над крылом и под ним соответственно равны: U1 = 320 м/с, U2 = 290 м/с. Найти грузоподъёмность. Для решения задания нужно знать дифференциальную плотность воздуха. Это справочная величина, равная 1,29 кг/м3.

Используя уравнение Бернулли, можно записать: pп. к-pн.к = ρ * (U2н.к — U2п. к). Подъёмная сила равна площади крыла, умноженной на разность давления. Подставив одно выражение в другое, получим рабочую формулу: Fy = ρ * (U2н.к — U2п. к) * S / 2. После выполнения расчёта получится ответ 590 кН. То есть грузоподъёмность самолёта составит порядка 59 тонн.

Реальные вычисления для таких задач довольно сложные, поэтому часто используют онлайн-калькуляторы.

ФизикаПлотность вещества – формулы и примеры вычислений величины

ФизикаЧто такое свет в физике – определение, свойства и природа света

Уравнение Бернулли

Характеристика уравнения Бернулли

Определение 1

Дифференциальное уравнение первого порядка, имеющее стандартный вид $y’+P\left(x\right)\cdot y=Q\left(x\right)\cdot y^{n}$, где $P\left(x\right)$ и $Q\left(x\right)$ — непрерывные функции, а $n$ — некоторое число, называется дифференциальным уравнением Якоба Бернулли.

При этом на число $n$ накладываются ограничения:

$n\ne 0$, так как при $n = 0$ дифференциальное уравнение представляет собой линейное неоднородное, и какой-то иной специальный метод решения в этом случае не нужен;
$n\ne 1$, так как если мы имеем в качестве $n$ единицу, дифференциальное уравнение представляет собой линейное однородное, метод решения которого также известен.

Кроме того, не рассматривается специально тривиальное решение дифференциального уравнения Бернулли $y=0$.

Не следует путать дифференциальное уравнение математика Якоба Бернулли с законом Бернулли, названным в честь дяди его племянника, известного как Даниил Бернулли.

Замечание 1

Даниил Бернулли — физик, наиболее известная найденная им закономерность состоит в описании взаимосвязи скорости потока жидкости и давления. Закон Бернулли также применим и для ламинарных течений газа. В целом он применяется в гидравлике и гидродинамике.

Решение уравнения Бернулли сведением к линейному неоднородному

Основной метод решения дифференциального уравнения Бернулли состоит в том, что посредством преобразований оно приводится к линейному неоднородному. {3} }{2} -4\cdot x\cdot \ln \left|x\right|+C\cdot x$.

Уравнение бернулли – справочник студента

Дифференциальным уравнением Бернулли называется уравнение вида

где m ≠ 0 и m ≠ 1.

Таким образом, дифференциальное уравнение Бернулли обязательно содержит функцию y в степени, отличной от нуля и единицы.

Дифференциальное уравнение Бернулли можно решить двумя методами.

Переходом с помощью подстановки к линейному уравнению.
Методом Бернулли.

Переход от уравнения Бернулли к линейному уравнению.

Уравнение делим на :

которое является линейным дифференциальным уравнение первого порядка. Его можно решить методом вариации константы Лагранжа или методом Бернулли.

Решение методом Бернулли.

Решение следует искать в виде произведения двух функций y = u ⋅ v. Подставив его в дифференциальное уравнение, получим уравнение

Из слагаемых, содержащих функцию u в первой степени, вынесем её за скобки:

Приравняв выражение в скобках нулю, то есть
,
получим дифференциальное уравнение с разделяющимися переменными для определения функции v.
Функцию u следует находить из дифференциального уравнения

которое также является уравнение с разделяющимися переменными.

Пример 1. Решить дифференциальное уравнение Бернулли

Решение. Решим дифференциальное уравнение двумя методами.

1. Переход от уравнения Бернулли к линейному уравнению. Данное уравнение умножим на y³:

.
Введём обозначение , тогда , и приходим к уравнению
или
.
Решим его методом Бернулли. В последнее уравнение подставим z = u ⋅ v, z’ = u’v + uv’:

Выражение в скобках приравняем нулю и решим полученное дифференциальное уравнение:
Полученную функцию v подставим в уравнение:
Тогда

2. Методом Бернулли. Ищем решение в виде произведения двух функций y = u ⋅ v. Подставив его и y’ = u’v + uv’ в данное дифференциальное уравнение, получим

Выражение в скобках приравняем нулю и определим функцию v:
Полученную функцию v подставим в уравнение и определим функцию u:
И, наконец, найдём решение данного дифференциального уравнения:

Пример 2.

Решить дифференциальное уравнение Бернулли

Решение. Это уравнение, в котором m = −1. Применив подстановку y = u ⋅ v, получим

Выражение в скобках приравняем нулю и определим функцию v:
Полученную функцию v подставим в уравнение и определим функцию u:
Таким образом, получаем решение данного дифференциального уравнения:
.

Пример 3. Решить дифференциальное уравнение Бернулли

Решение. Это уравнение можно решить, используя подстановку y = u ⋅ v. Получаем

Приравняем нулю выражение в скобках и решим полученное уравнение с разделяющимися переменными:
Подставляем v в данное уравнение и решаем полученное уравнение:
или
Разделим переменные:
и проинтегрируем обе части уравнения:
Далее используем подстановку
:
.
Введём обозначения:
Продолжаем:
Таким образом, получаем функцию u:
.
и решение данного дифференциального уравнения:

Нет времени вникать в решение? Можно заказать работу!

Пример 4. Решить задачу Коши для дифференциального уравнения
при условии .
Решение. Перепишем уравнение, перенося в левую сторону линейные слагаемые, а в правую — нелинейные:

.
Это уравнение Бернулли, которое можно решить, используя подстановку y = u ⋅ v, y’ = u’v + uv’:
Выражение в скобках приравняем нулю и решим дифференциальное уравнение с разделяющимися переменными:
Подставим функцию v в данное уравнение и решим полученное дифференциальное уравнение:
Вычислим каждый интеграл отдельно. Первый:
.
Второй интеграл интегрируем по частям. Введём обозначения:
Решаем:
Приравниваем друг другу найденные значения интегралов и находим функцию u:
Таким образом, общее решение данного дифференциального уравнения:
.
Используем начальное условие, чтобы определить значение константы:

Ищем частное решение, удовлетворяющее начальному условию:
В результате получаем следующее частное решение данного дифференциального уравнения:
.

И напоследок — пример с альтернативным обозначением производных — через дробь.

Пример 5. Решить дифференциальное уравнение Бернулли

Решение. Решим это уравнение первым из представленных в теоретической части методом — переходом к линейному уравнению. Разделив данное уравнение почленно на y³, получим

.
Введём новую функцию . Тогда

.
Подставляя эти значения в уравнение, полученное на первом шаге, получим линейное уравнение:
.
Найдём его общий интеграл:
,
.
Подставляя эти значение в полученное линейное уравнение, получаем
или
.
Приравниваем нулю выражение в скобках:
Для определения функции u получаем уравнение
.
Разделяем переменные:
Интегрируем по частям:
Таким образом, общий интеграл данного уравнения
или
.

Пройти тест по теме Дифференциальные уравнения

Всё по теме «Дифференциальные уравнения»

Порядок дифференциального уравнения и его решения, задача Коши Дифференциальные уравнения с разделяющимися переменными Однородные дифференциальные уравнения первого порядка Линейные дифференциальные уравнения первого порядка Дифференциальные уравнения в полных дифференциалах Дифференциальные уравнения второго порядка, допускающие понижение порядка

Поделиться с друзьями

Источник: https://function-x. ru/differential_equations9.html

Уравнение Бернулли

Уравнение Бернулли для реальной и идеальной жидкости

Ниже задача с решением уравнения Бернулли. Примеры уравнения Бернулли по формулам.

Уравнение Бернулли позволяет выполнить расчет водоснабжения и отопления: Подобрать диаметры и насосы. В этой статье будет расписан энергетический и геометрический смысл уравнения Бернулли.

Скачайте видео: Задача на расчет уравнения Бернулли
График Бернулли и уравнение Бернулли для идеальной жидкости:

График Бернулли и уравнение Бернулли для реальной жидкости:

где,

Смысл уравнения Бернулли

Смысл уравнения Бернули в том, чтобы показать, что внутри системы заполненной жидкостью (участка трубопровода) сохраняется общая энергия между разными точками. То есть на участке трубопровода необходимо выделить две точки, и эти две точки равны друг другу по значению полной энергии. Полная энергия состоит из потенциальной и кинетической энергии.

Назначение уравнения Бернули

Понять, как распределяется давление в системе трубопроводов. А также с помощью уравнения находить неизвестные параметры внутри системы. Например, найти давление в каждой течке пространства системы заполненной жидкостью.

Подробнее на видео: (для запуска видео кликните по окошку) На видео намного больше информации

Следующий урок

Решая задачу с уравнением Бернулли, Вы фактически занимаетесь гидравлическим расчетом. О том, как делать гидравлический расчет — написано тут: Конструктор водяного отопления

Задача. Пример решения уравнения Бернулли
По решению задачи необходимо найти давление в точке 2 при известных параметрах: давление и расход.

Как понять уравнение Бернулли?

Для расчета уравнения Бернулли необходимо выбрать две точки в пространстве
Например,
Точка 1 – это место где известно давление
Точка 2 – это место где нужно узнать давление

Поймите, что каждый кусок формулы измеряется давлением: м. в.ст. (метр водяного столба)

То есть для того, чтобы быстро считать гидравлику систем водоснабжения и отопления, необходимо меньше всего выражаться в Барах, Паскалях и тому подобное.

Проще выражать давление в единице измерения: м.в.ст. (метр водяного столба)

Вы этим самым упростите себе жизнь… просто другая единица это еще один процесс, который отнимает время.
Решение задачи
Сборка формулы уравнения Бернулли

Как избавится от минуса?

Как избавится от множителя (-1)?

Необходимо множитель (-1) помножить на каждый слагаемый член. Знак каждого слагаемого члена меняется на противоположный. То есть (+ на -) (- на +). Далее перестановка слагаемых.

Ответ:
Что такое идеальная жидкость?

Идеальная жидкость — это жидкость, не обладающая внутренним трением. То есть такая жидкость не создает гидравлическое сопротивление.

Реальная жидкость — это жидкость, которая обладает вязкостью. То есть внутренним сопротивлением.

Формула Бернулли для реальной жидкости
Коэффициент Кориолиса – это поправка кинетической энергии на реальную жидкость.
Потому что реальная жидкость движется не равномерно

У реальной жидкости серединная струйка воды движется быстрее остальных. При ламинарном режиме градиент: Чем ближе к стенке, тем медленнее движется поток воды.

Формула коэффициента Кориолиса
Что такое коэффициент Кориолиса?
Коэффициент Кориолиса характеризует отношение действительной кинетической энергии потока жидкости в данном сечении к той кинетической энергии потока, которую он имел бы, если бы все частицы двигались с одинаковой скоростью, равной средней скорости потока.
Чему равен коэффициент Кориолиса?

Нд.п. – Это динамические потери. Это потери вызванные движением воды.

Подробнее о формулах: Конструктор водяного отопления
Имеются дополнительные задачи с уравнением Бернули на реальную жидкость:
Задача1
Задача2
Задача3
Дополнительные задачи тут: Расчет водоснабжения и отопления своими руками
Посмотрите видеоурок по составлению уравнения Бернулли:

Посмотреть другие уроки: Расчет водоснабжения и отопления своими руками
Как сделать гидравлический расчет погружного насоса?
Посмотрите видео:

Подробнее о программе

Источник: http://infosantehnik. ru/str/91.html

Уравнение Бернулли — вывод формулы, физический смысл, примеры использования

Время на чтение: 14 минут

Исследования учёного

Даниил Бернулли родился в Голландии в 1700 году. В 1725 году он начал работать на кафедре физиологии, где увлёкся основами теоретической физики.

Через 25 лет он возглавил кафедру экспериментальной физики, которой и руководил до конца своих дней. Основным его трудом считается создание теории гидродинамической зависимости, известной как Закон Бернулли.

Открытие учёного предвосхитило зарождение молекулярно-кинетического учения поведения газов.

Этот факт был доказан экспериментально и описан математически.

Правило в математической формулировке имеет вид (pv2/ 2) + p * g * h + ρ = const, где:

p — количество жидкости на единицу объёма;
v — скорость движения потока;
h — уровень, на который поднят элемент жидкости;
ρ — сила, действующая на единицу площади;
g — ускорение, придаваемое жидкости под действием притяжения Земли.

В соответствии с уравнением непрерывности скорость V1 в части трубы, имеющей большее сечение, будет меньше, чем скорость жидкости V2 в узком сечении. Если в жидкость поместить прибор для измерения давления, он покажет какое-то значение P1 в точке A и P2 в точке Б.

При этом там, где скорость движения жидкости медленнее, давление будет больше.

Так как движение происходит от точки А к Б, то и давление возле А будет больше, чем около Б. Эта разность давлений и приводит к ускорению.

Условия действия

Течение является:

ламинарным — находящаяся в трубке жидкость перемешивается слоями без хаотических изменений давления и скорости, турбулентность отсутствует;
стационарным — распределение скоростей не изменяется с течением времени;
скоростным — в движении принимает участие такой параметр, как ускорение;
идеальным с несжимаемой жидкостью.

Согласно ему, сумма действующих всех сил на тело (рассматриваемый кусок жидкости) равняется изменению кинетической энергии объекта: ΣAi = ΔEk.

На нижний участок действует сила давления, выполняющая положительную работу, а на верхний — отрицательную. Кроме этого, действует и сила тяжести. Так как жидкость поднимается, она имеет тоже отрицательный знак.

Сила бокового давления перпендикулярна любой точке в системе, поэтому никакого влияния она не оказывает.

Количественная сторона

Верным будет выражение: Ag = — ΔEp = — (m2 * g * h3 — m1 * g * h2) = m1 * g * h2 — m2 * g * h3. Так как жидкость несжимаемая, её плотность не изменится. Отсюда можно утверждать: Ag = ρ * V * g * h2 — ρ * V * g * h3.

Зная количественные показатели всех трёх работ, можно найти изменение кинетической энергии. Из физики известно, что оно равно разнице конечной и начальной энергии.

Течение стационарное, значит, скорость с течением времени не изменится.

Следовательно, кинетическая энергия будет определяться разницей появившейся энергии в верхней части и ушедшей из нижней области: ΔEk = (m2 * v22)/2 — (m1 * v12) / 2.

Воспользовавшись тем, что масса равняется произведению плотности на объём, формулу можно привести к виду: ΔEk = (ρ * V * v22)/2 — (ρ * V * v12) / 2. Теперь найденные выражения для работ нужно подставить в теорему о кинетической энергии.

Получится следующее равенство: p1V — p2V + ρ * V * g * h2 — ρ * V * g * h3 = (ρ * V * v22) / 2 — (ρ * V * v12) / 2.

Разделив левую и правую часть на объём, выражение можно упростить до вида: p1 — p2 + ρ * g * h2 — ρ * g * h3 = (ρ * v22)/2 — (ρ * v12) / 2 .

Полученная формула показывает, что при переходе в пределе одной линии скорость, давление и высота изменяются. Поэтому в любой точке будет справедливым выражение: ρ1+ ρ * g * h + (ρ * v1) / 2 = const.

Это и есть количественное описание уравнения Бернулли для идеальной жидкости.

Применение в гидравлике

Все эти величины следует подставить в уравнение Бернулли. Получится выражение: pатм + ρ * g * h + 0 = pатм + (ρ * U2) / 2 + 0. Атмосферное давление взаимно уничтожается: ρ * g * h = (ρ * U2) / 2.

В левой и правой части стоит плотность, на которую можно сократить. Отсюда получается, что вид жидкости значения не имеет. Это может быть: вода, ртуть, расплавленный металл. Эффект от этого не поменяется.

Из формулы можно выразить искомое U2. Оно будет равно: U2 = (2 * g * h)½.

Точка, находящаяся наверху, характеризуется давлением p1 = pатм., высотой h2 равной h и скоростью U1. Для точки на дне параметры будут следующие: p2 = p, h3 = 0, U2 = 0.

Скорости принимаются равными нулевому значению, так как рассматриваемая жидкость находится в состоянии покоя.

Аналогично уравнение Бернулли для потока реальной жидкости используется при расчёте расхода в карбюраторе, пульверизаторе, учёте статического и динамического давления.

Подъёмная сила

На него действует поток воздуха со скоростью U. Частица воздуха ударяет в твёрдую поверхность и отражается от неё. Угол отражения равен углу атаки, а её скорость равняется U’. Нужно рассчитать подъёмную силу.

Для этого необходимо выполнить три шага:

рассмотреть изменение скорости воздуха;
узнать импульс частиц;
используя закон Ньютона, определить силу.

В результате получится, что на крыло действует сила, состоящая из двух компонентов: подъёмной силы Fy и аэродинамического сопротивления Fx. Fy = Cy * p * U2 * S, а Fx = Cx * p * U2 * S. В формулах С является коэффициентом, а S — площадью крыла.

Это уравнение можно упростить, приняв, что давления над и под крылом примерно одинаковые, поэтому плотность будет также одинаковая. Кроме того, высота крыла довольно маленькая. Исходя из этого, формулу можно упростить, и она примет вид: pп. к-pн.к = (ρ * (Uн.к + Uп. к) * (Uн.к — Uп. к)) / 2 = 2 * U1 * U2.

Теперь можно найти подъёмную силу. Для этого разность давлений нужно умножить на площадь крыла: Fy = (pп.к-pн. к) * S.

Реальные вычисления для таких задач довольно сложные, поэтому часто используют онлайн-калькуляторы.

Источник: https://nauka.club/fizika/uravneniye-bernulli.html

Основы гидравлики

Бернулли — вне всякого сомнения — имя, знакомое и специалистам, и обывателям, которые хоть немного интересуются науками.

Этот человек оставил ослепительный след в истории познавания человечеством окружающего мира, как физик, механик, гидравлик и просто общепризнанный гений, Даниил Бернулли навсегда останется в памяти благодарных потомков за свои идеи и выводы, которые долгое время существования человечества были покрыты мраком неизведанного. Открытия и законы, которыми Бернулли осветил путь к познанию истины, являются фундаментальными, и придали ощутимый импульс развитию многих естественных наук. К таковым относится и уравнение Бернулли в Гидравлике, которое он вывел почти три века назад. Данное уравнение является основополагающим законом этой сложной науки, объясняющим многие явления, описанные даже древними учеными, например, великим Архимедом.

Попробуем уяснить несложную суть закона Бернулли (чаще его называют уравнением Бернулли), описывающего поведение жидкости в той или иной ситуации.

Выделим в стационарно текущей идеальной жидкости трубку тока, которая ограничена сечениями S1 и S2, (рис. 1). (Понятие идеальной жидкости абстрактно, как и понятие всего идеального. Идеальной считается жидкость, в которой нет сил внутреннего трения, т. е.

трения между отдельными слоями и частицами подвижной жидкости). Пусть в месте сечения S1 скорость течения ν1, давление p1 и высота, на которой это сечение расположено, h2. Аналогично, в месте сечения S2 скорость течения ν2, давление p2 и высота сечения h3.

За бесконечно малый отрезок времени Δt жидкость переместится от сечения S1 к сечению S1′, от S2 к S1′.
По закону сохранения энергии, изменение полной энергии E2 — E1 идеальной несжимаемой жидкости равно работе А внешних сил по перемещению массы m жидкости:
E1 — E2 = A (1)
где E1 и E2 — полные энергии жидкости массой m в местах сечений S1 и S2 соответственно.

С другой стороны, А — это работа, которая совершается при перемещении всей жидкости, расположенной между сечениями S1 и S2, за рассматриваемый малый отрезок времени Δt.

Чтобы перенести массу m от S1 до S1′ жидкость должна переместиться на расстояние L1 = ν1Δt и от S2 до S1′ — на расстояние L2 = ν2Δt. Отметим, что L1 и L2 настолько малы, что всем точкам объемов, закрашенных на рис.

1, приписывают постоянные значения скорости ν, давления р и высоты h. Следовательно,

A = F1L1 + F2L2 (2)

где F1 = p1S1 и F2 = — p2S2 (сила отрицательна, так как направлена в сторону, противоположную течению жидкости; см. рис. 1).

Полные энергии E1 и E2 будут складываться из кинетической и потенциальной энергий массы m жидкости:
E1 = mv12/2 + mgh2 (3)
E2 = mv22/2 + mgh3 (4)
Подставляя (3) и (4) в (1) и приравнивая (1) и (2), получим
mv12/2 + mgh2+ p1S1v1Δt = mv22/2 + mgh3+ p2S2v2Δt. (5)

Согласно уравнению неразрывности для несжимаемой жидкости, объем, занимаемый жидкостью, всегда остается постоянным, т. е.

ΔV = S1v1Δt = S2v2Δt.
Разделив выражение (5) на ΔV, получим
ρv12/2 + ρgh2 +p1 = ρv22/2 + ρgh3 + p2,
где ρ — плотность жидкости.
После некоторых преобразований эту формулу можно представить в другом виде:
v12/2g + p1/ρg + z1 = v22/2g + p2/ρg + z2.
Поскольку сечения выбирались произвольно, то в общем случае можно записать:
ρv2/2 +ρgh +p = const (6).

Выражение (6) получено швейцарским физиком Д. Бернулли (опубликовано в 1738 г. ) и называется уравнением Бернулли.

Даниил Бернулли (Daniel Bernoulli, 1700 — 1782), швейцарский физик, механик и математик, один из создателей кинетической теории газов, гидродинамики и математической физики. Академик и иностранный почётный член (1733) Петербургской академии наук, член Академий: Болонской (1724), Берлинской (1747), Парижской (1748), Лондонского королевского общества (1750).

Уравнение Бернулли по своей сути является интерпретацией закона сохранения энергии применительно к установившемуся течению идеальной жидкости. Уравнение хорошо выполняется и для реальных жидкостей, для которых внутреннее трение не очень велико.

Величина р в формуле (6) называется статическим давлением (давление жидкости на поверхность обтекаемого ею тела), величина ρν2/2 — динамическим давлением, величина ρgh — гидростатическим давлением.

Статическое давление обусловлено взаимодействием поверхности жидкости с внешней средой и является составляющей внутренней энергии рассматриваемого элементарного объема жидкости (т. е.

характеризуется взаимодействием внутренних частиц жидкости, вызванных внешним возмущением — давлением), а гидростатическое – положением этого объема жидкости в пространстве (зависит от высоты над поверхностью Земли).

Динамическое давление характеризует кинематическую составляющую энергии этого объема, поскольку зависит от скорости потока, в котором движется рассматриваемый элементарный объем жидкости.

Для горизонтальной трубки тока изменение потенциальной составляющей ρgh будет равно нулю (поскольку h3 – h2 = 0), и выражение (6) примет упрощенный вид:
ρv2/2 + p = const (7).
Выражение p + ρν2/2 называется полным давлением.
Таким образом, содержание уравнения Бернулли для элементарной струйки при установившемся движении можно сформулировать так: удельная механическая энергия при установившемся движении элементарной струйки идеальной жидкости, представляющая собой сумму удельной потенциальной энергии положения и давления и удельной кинетической энергии, есть величина постоянная.

Все члены уравнения Бернулли измеряются в линейных единицах.

В гидравлике широко применяют термин напор, под которым подразумевают механическую энергию жидкости, отнесенную к единице ее веса (удельную энергию потока или неподвижной жидкости).

Величину v2/2g называют скоростным (кинетическим) напором, показывающим, на какую высоту может подняться движущаяся жидкость за счет ее кинетической энергии. Величину hп = p/ρg называют пьезометрическим напором, показывающим на какую высоту поднимается жидкость в пьезометре под действием оказываемого на нее давления.

Величину z называют геометрическим напором, характеризующим положение центра тяжести соответствующего сечения движущейся струйки над условно выбранной плоскостью сравнения.

Сумму геометрического и пьезометрического напоров называют потенциальным напором, а сумму потенциального и скоростного напора — полным напором.

На основании анализа уравнения Бернулли можно сделать вывод, что при прочих неизменных параметрах потока (жидкости или газа) величина давления в его сечениях обратно пропорциональна скорости, т. е. чем выше давление, тем меньше скорость, и наоборот.

Это явление используется во многих технических конструкциях и устройствах, например, в карбюраторе автомобильного двигателя (диффузор), в форме крыла самолета.

Увеличение скорости воздушного потока в диффузоре карбюратора приводит к созданию разрежения, всасывающего бензин из поплавковой камеры, а специальная форма сечения самолетного крыла позволяет создавать на его нижней стороне зону повышенного давления, способствующего появлению подъемной силы.

***

Геометрическая интерпретация уравнения Бернулли

Поскольку напор измеряется в линейных величинах, можно дать графическую (геометрическую) интерпретацию уравнению Бернулли и его составляющим.

На графике (рис. 2) представлена горизонтальная плоскость сравнения 0-0, относительно которой геометрический напор будет в каждом сечении равен вертикальной координате z центра тяжести сечения (линия геометрического напора проходит по оси струйки).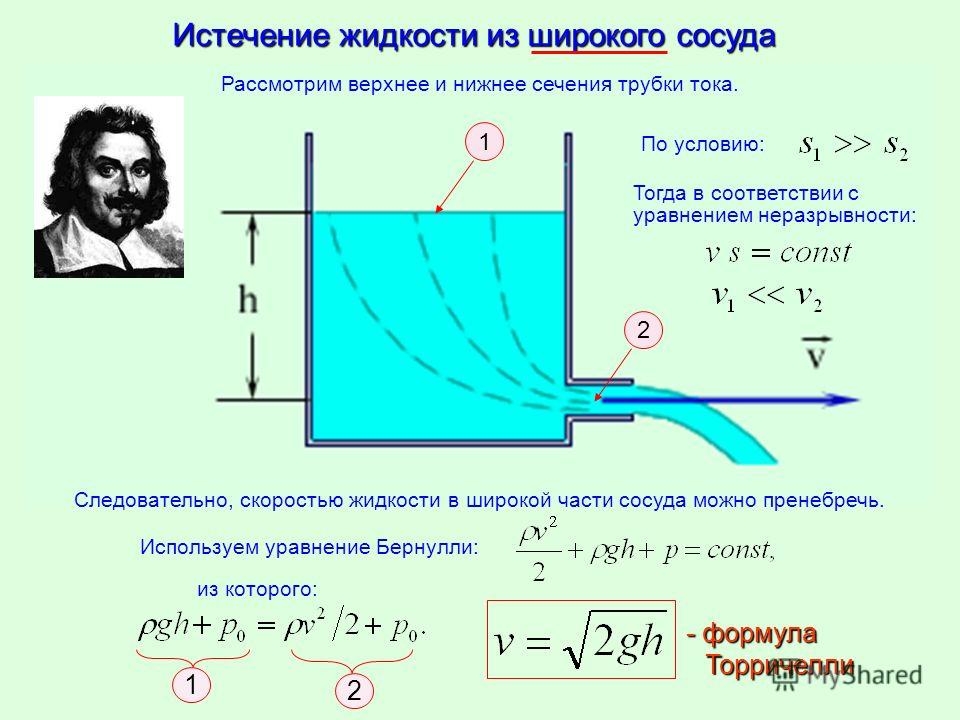 Линия К-К, характеризующая потенциальный напор струйки, получена сложением геометрического и пьезометрического напора в соответствующих сечениях (т. е. разница координат точек линии К-К и соответствующих точек оси струйки характеризует пьезометрический напор в данном сечении). Полный напор характеризуется линией MN, которая параллельна плоскости сравнения О-О, свидетельствуя о постоянстве полного напора H’e (удельной механической энергии) идеальной струйки в любом ее сечении.

При движении реальной жидкости, обладающей вязкостью, возникают силы трения между ограничивающими поток поверхностями и между слоями внутри самой жидкости.

Для преодоления этих сил трения расходуется энергия, которая превращается в теплоту и рассеивается в дальнейшем движущейся жидкостью. По этой причине графическое изображение уравнения Бернулли для идеальной жидкости будет отличаться от аналогичного графика для реальной жидкости.

Если обозначить hf потери напора (удельной энергии) струйки на участке длиной L, то уравнение Бернулли для реальной жидкости примет вид:

v12/2g + p1/ρg + z1 = v22/2g + p2/ρg + z 2 + hf.

Для реальной жидкости полный напор вдоль струйки не постоянен, а убывает по направлению течения жидкости, т. е. его графическая интерпретация имеет вид не прямой линии, а некоторой кривой МЕ (рис. 3). Заштрихованная область характеризует потери напора.

Падение напора на единице длины элементарной струйки, измеренной вдоль оси струйки, называют гидравлическим уклоном:
i = dHe/dL = — dhf/dL .
Гидравлический уклон положителен, если напорная линия снижается по течению жидкости, что всегда бывает при установившемся движении.
α1v12/2g + p1/ρg + z1 = α2v22/2g + p2/ρg + z 2 + hf,

Для практического применения уравнения Бернулли необходимо распространить его на поток реальной жидкости:

где α1,α2 — коэффициенты Кориолиса, учитывающие различие скоростей в разных точках сечения потока реальной жидкости. На практике обычно принимают α1 = α2 = α: для ламинарного режима течения жидкости в круглых трубах α = 2, для турбулентного режима α = 1,04…1,1.

***

Из уравнения Бернулли для горизонтальной трубки тока и уравнения неразрывности (S1v1Δt = S2v2Δt) видно, что при течении жидкости по горизонтальной трубе, которая имеет различные сечения, скорость жидкости больше в более узких местах (где площадь сечения S меньше), а статическое давление больше в более широких местах, т. е. там, где скорость меньше. Это можно увидеть, установив вдоль трубы ряд манометров.

Данный опыт показывает, что в манометрической трубке В, которая прикреплена к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С, которые прикреплены к широкой части трубы, что соответствует уравнению Бернулли.

Так как динамическое давление зависит от скорости движения жидкости (газа), то уравнение Бернулли можно использовать для измерения скорости потока жидкости. Принципиально это свойство жидкости для определения скорости потока реализовано в так называемой трубке Пито – Прандтля (обычно ее называют трубкой Пито).

Трубка Пито – Прандтля (см. рис. 2) состоит из двух тонких стеклянных трубок, одна из которых изогнута под прямым углом (Г-образно), а вторая — прямая. Одним из свободных концов каждая трубка присоединена к манометру.

Изогнутая трубка имеет открытый свободный конец, направленный против тока и принимающий напор потока жидкости, а вторая погружена в поток перпендикулярно току, и скорость потока на давление внутри трубки не влияет, т. е.

внутри этой трубки действует лишь статическая составляющая давления жидкости.

Разница между давлением в первой трубке (полное давление) и второй трубке (статическое давление), которую показывает манометр, является динамическим давлением, определяемым по формуле:
p = ρv2/2.
Определив с помощью трубки Пито — Прандтля динамическое давление в потоке жидкости, можно легко вычислить скорость этого потока:
v = √(2p0gh/ρ).

Уравнение Бернулли также используют для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жидкостью, с маленьким отверстием в боковой стенке на некоторой глубине ниже уровня жидкости.

Рассмотрим два сечения (на уровне h2 свободной поверхности жидкости в сосуде и на уровне h2 выхода ее из отверстия) и применим уравнение Бернулли:

ρv12/2 + ρgh2 + p1 = ρv22/2 + ρgh3 + p2,

Так как давления р1 и р2 в жидкости на уровнях первого и второго сечений равны атмосферному, т. е. р1 = р2, то уравнение будет иметь вид

v12/2 +gh2 = v22/2 +gh3.
Из уравнения неразрывности мы знаем, что ν1/ν2 = S2/S1, где S1 и S2 — площади поперечных сечений сосуда и отверстия. Если S1значительно превышает S2, то слагаемым ν12/2 можно пренебречь и тогда:
v2 = √2gh.

Это выражение получило название формулы Торричелли.

Формулу Торричелли можно использовать для подсчета объемного (или массового) расхода жидкости, истекающего из отверстия в сосуде с поддерживаемым постоянно уровнем под действием атмосферного давления.

При этом используется формула Q = vS (для определения массового расхода – m = ρvS), по которой определяется расход жидкости за единицу времени.

Если требуется узнать расход жидкости за определенный промежуток времени t, то его определяют, умножив расход за единицу времени на время t.
Следует отметить, что такая методика расчета расхода реальной жидкости через отверстие в стенке сосуда дает некоторые погрешности, обусловленные физическими свойствами реальных жидкостей, поэтому требует применения поправочных коэффициентов (коэффициентов расхода).
***

Пример решения задачи на определение расхода жидкости

Определить примерный объемный расход воды, истекающей из отверстия диаметром 10 мм, проделанном в вертикальной стенке широкого сосуда на высоте h = 1 м от верхнего, постоянно поддерживаемого, уровня воды за 10 секунд. Ускорение свободного падения принять равным g = 10 м/с2. Коэффициент расхода воды через отверстие — µs = 0,62.

Решение:
По формуле Торричелли определим скорость истечения воды из отверстия:
v = √2gh = √2×10×1 ≈ 4,5 м/с.
Определим расход воды Q за время t = 10 секунд:
Q = µsvSt = 0,62×4,5×3,14×0,012/4 × 10 ≈ 0,0022 м3 ≈ 2,2 литра.
***

На практике расход жидкости в трубопроводах измеряют расходомерами, например, расходомером Вентури. Расходомер Вентури (см рис.

2) представляет собой конструкцию из двух конических патрубков, соединенных цилиндрическим патрубком.

В сечениях основной трубы и цилиндрического патрубка устанавливают трубки-пьезометры, которые фиксируют уровень жидкости, обусловленный полным давлением в потоке.

При прохождении жидкости через сужающийся конический патрубок часть потенциальной энергии потока преобразуется в кинетическую, и, наоборот, – при прохождении потока по расширяющемуся коническому патрубку, кинетическая энергия уменьшается, а потенциальная растет.

Это сказывается на скорости движения жидкости по рассматриваемым участкам. Перепад высоты уровня жидкости в пьезометрах позволяет рассчитать среднюю скорость потока жидкости на рассматриваемых участках и вычислить объемный расход по внутреннему сечению трубы.

В расходомерах учитываются потери напора в самом приборе при помощи коэффициента расхода прибора φ.

***

Гидравлические сопротивления

Главная страница

Специальности

Учебные дисциплины

Олимпиады и тесты

Источник: http://k-a-t.ru/gidravlika/7_Bernulli/

Уравнение Бернулли — Всё для чайников

Подробности Категория: Гидравлика

Документальные учебные фильмы. Серия «Физика».

Даниил Бернулли (Daniel Bernoulli; 29 января (8 февраля) 1700 — 17 марта 1782), швейцарский физик-универсал, механик и математик, один из создателей кинетической теории газов, гидродинамики и математической физики. Академик и иностранный почётный член (1733) Петербургской академии наук, член Академий: Болонской (1724), Берлинской (1747), Парижской (1748), Лондонского королевского общества (1750). Сын Иоганна Бернулли.

Закон (уравнение) Бернулли является (в простейших случаях) следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

Здесь

— плотность жидкости, — скорость потока, — высота, на которой находится рассматриваемый элемент жидкости, — давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости, — ускорение свободного падения.

Уравнение Бернулли также может быть выведено как следствие уравнения Эйлера, выражающего баланс импульса для движущейся жидкости.
В научной литературе закон Бернулли, как правило, называется уравнением Бернулли(не следует путать с дифференциальным уравнением Бернулли), теоремой Бернулли или интегралом Бернулли.
Константа в правой части часто называется полным давлением и зависит, в общем случае, от линии тока.

Размерность всех слагаемых — единица энергии, приходящаяся на единицу объёма жидкости.

Первое и второе слагаемое в интеграле Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объёма жидкости.

Следует обратить внимание на то, что третье слагаемое по своему происхождению является работой сил давления и не представляет собой запаса какого-либо специального вида энергии («энергии давления»).

Соотношение, близкое к приведенному выше, было получено в 1738 г. Даниилом Бернулли, с именем которого обычно связывают интеграл Бернулли. В современном виде интеграл был получен Иоганном Бернулли около 1740 года.

Для горизонтальной трубы высота постоянна и уравнение Бернулли принимает вид: .

Эта форма уравнения Бернулли может быть получена путём интегрирования уравнения Эйлера для стационарного одномерного потока жидкости, при постоянной плотности : .

Согласно закону Бернулли, полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока.

Полное давление состоит из весового , статического и динамического давлений.

Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление падает. Это является основной причиной эффекта Магнуса. Закон Бернулли справедлив и для ламинарных потоков газа.

Явление понижения давления при увеличении скорости потока лежит в основе работы различного рода расходомеров (например труба Вентури), водо- и пароструйных насосов.

А последовательное применение закона Бернулли привело к появлению технической гидромеханической дисциплины — гидравлики.

Закон Бернулли справедлив в чистом виде только для жидкостей, вязкость которых равна нулю. Для приближённого описания течений реальных жидкостей в технической гидромеханике (гидравлике) используют интеграл Бернулли с добавлением слагаемых, учитывающих потери на местных и распределенных сопротивлениях.

Известны обобщения интеграла Бернулли для некоторых классов течений вязкой жидкости (например, для плоскопараллельных течений), в магнитной гидродинамике, феррогидродинамике.

В статье были спользованны материалы Wikipedia

Источник: https://forkettle.ru/vidioteka/estestvoznanie/47-fizika/gidravlika/109-uravnenie-bernulli

Дифференциальное уравнение Бернулли и методы его решения

Дано определение дифференциального уравнения Бернулли. Рассмотрены методы его решения: приведением к линейному уравнению и методом Бернулли. Дан пример подробного решения уравнения методом Бернулли.

Содержание

Решение дифференциального уравнения Бернулли приведением к линейному уравнению ⇓Решение методом Бернулли ⇓Пример решения дифференциального уравнения Бернулли ⇓ Дифференциальное уравнение Бернулли – это уравнение вида:, где n ≠ 0, n ≠ 1, p и q – функции от x.

Рассмотрим дифференциальное уравнение Бернулли: (1) , где n ≠ 0, n ≠ 1, p и q – функции от x. Разделим его на y n. При y ≠ 0 или n (2) . Это уравнение сводится к линейному с помощью замены переменной: . Покажем это.

По правилу дифференцирования сложной функции:

;

. Подставим в (2) и преобразуем: ; . Это – линейное, относительно z, дифференциальное уравнение. После его решения, при n > 0, следует рассмотреть случай y = 0. При n > 0, y = 0 также является решением уравнения (1) и должно входить в ответ.

Решение методом Бернулли

Рассматриваемое уравнение (1) также можно решить методом Бернулли. Для этого ищем решение исходного уравнения в виде произведения двух функций: y = u·v, где u и v – функции от x. Дифференцируем по x: y′ = u′ v + u v′.

Подставляем в исходное уравнение (1): ; (3) . В качестве v возьмем любое, отличное от нуля, решение уравнения: (4) . Уравнение (4) – это уравнение с разделяющимися переменными. Решаем его и находим частное решение v = v(x).

Подставляем частное решение в (3). Поскольку оно удовлетворяет уравнению (4), то выражение в круглых скобках обращается в нуль. Получаем: ; . Здесь v – уже известная функция от x. Это уравнение с разделяющимися переменными.

Находим его общее решение, а вместе с ним и решение исходного уравнения y = uv.

Пример решения дифференциального уравнения Бернулли

Решить уравнение

Решение

На первый взгляд, кажется, что это дифференциальное уравнение не похоже на уравнение Бернулли. Если считать x независимой переменной, а y – зависимой (то есть если y – это функция от x), то это так. Но если считать y независимой переменной, а x – зависимой, то легко увидеть, что это – уравнение Бернулли.

Итак, считаем что x является функцией от y. Подставим и умножим на : ; ; (П.1) . Это – уравнение Бернулли с n = 2. Оно отличается от рассмотренного выше, уравнения (1), только обозначением переменных (xвместо y). Решаем методом Бернулли.

Делаем подстановку: x = u v, где u и v – функции от y. Дифференцируем по y: . Подставим в (П.1): ; (П.2) . Ищем любую, отличную от нуля функцию v(y), удовлетворяющую уравнению: (П.3) . Разделяем переменные: ; ; .

Положим C = 0, поскольку нам нужно любое решение уравнения (П.3). ; . Подставим в (П.2) учитывая, что выражение в скобках равно нулю (ввиду (П.3)): ; ; . Разделяем переменные. При u ≠ 0 имеем: ; (П.4) ; . Во втором интеграле делаем подстановку : ; .

Интегрируем по частям: . Подставляем в (П.4): . Возвращаемся к переменной x: ; ; .

Ответ

Источник: https://1cov-edu.ru/differentsialnye-uravneniya/bernulli/

Уравнение Бернулли

В 1700-х гг. Даниэль Бернулли исследовал силы, действующие в движущемся жидкость. На этом слайде показана одна из многих форм Бернулли. уравнение . Уравнение появляется во многих физиках, гидромеханика и учебники по самолетам. Уравнение утверждает, что статическое давление пс в потоке плюс динамическое давление, половина плотности r умножить на скорость V в квадрате, равна постоянной на всем протяжении поток. Назовем эту константу полным давлением pt потока.

Как обсуждалось на свойства газа page, есть два способа взглянуть на жидкость; из большого, макро масштаб свойства жидкости, которые мы можем измерить, и из малого, микромасштаба молекулярного движения и взаимодействия. На этой странице мы рассмотрим уравнение Бернулли с обеих точек зрения.

Вывод макромасштаба

Термодинамика это отрасль науки, которая описывает свойства макромасштаба жидкости. Один из основных результатов изучения термодинамика – это сохранение энергии; внутри системы энергия не создается и не уничтожается, но может быть преобразована из одной формы в другую. Мы выведем уравнение Бернулли, начав с уравнение сохранения энергии. Наиболее общая форма сохранения энергии дана на Уравнение Навье-Стокса страница. Эта формула включает эффекты нестационарных течений и вязкий взаимодействия. Предполагая постоянный невязкий поток мы имеем упрощенную уравнение сохранения энергии в терминах энтальпия жидкости:

ht2 – ht1 = q – шш

где ht — полная энтальпия жидкости, q – это теплопередача в жидкость, а wsh – это полезная работа, совершаемая жидкостью.

При отсутствии теплопередачи в жидкость и без работы, совершаемой жидкостью 92)1 = константа = pt

Это простейшая форма уравнения Бернулли, наиболее часто используемая. цитируется в учебниках. Если мы делаем разные предположения при выводе, мы можем вывести другие формы уравнения.

Важно при применении любого известного вам уравнения ограничения на его использование; ограничения обычно возникают в вывод уравнения при некоторых упрощающих предположениях о характер проблемы. Если вы игнорируете ограничения, вы часто можете получить неверный «ответ» из уравнения. За Например, эта форма уравнения была получена при предположении, что течение было несжимаемым, а значит что скорость потока намного меньше скорости звука. Если вы используете эту форму для сверхзвукового потока, ответ будет неправильный.

Расчет на молекулярном уровне

Мы можем сделать другую интерпретацию уравнения принимая во внимание движение молекул газа. Молекулы внутри жидкости находятся в постоянном хаотическом движении и сталкиваются друг с другом другим и со стенками объекта в жидкости. Движение молекулы придает молекулам линейный импульс и давление жидкости является мерой этого импульса. Если газ покоится, то все движение молекул является случайным, и давление, которое мы обнаруживаем, является полное давление газа. Если газ приводится в движение или потоки, некоторые из случайных составляющих скорости изменяются в пользу направленного движения. Направленное движение мы называем упорядоченным, т.к. в отличие от неупорядоченного случайного движения.

Мы можем связать «давление» с импульсом заказанного движение газа. Мы называем это давление динамическое давление. Оставшееся беспорядочное движение молекул по-прежнему производит давление называется статическое давление . На молекулярном уровне, нет различия между случайным и упорядоченным движением. Каждый молекула имеет скорость в каком-либо направлении до тех пор, пока не столкнется с другую молекулу, и скорость меняется. Но если суммировать все скорости всех молекул вы обнаружите упорядоченный движение. Из закона сохранения энергии и импульса статический давление плюс динамическое давление равно первоначальному общему давление в потоке (при условии, что мы не прибавляем и не убавляем энергию в поток). Форма динамического давления – это плотность, умноженная на квадрат скорости разделить на два.

Применение уравнения Бернулли

Проблема жидкостей, показанная на этом слайде, представляет собой низкоскоростной поток через трубка с изменяющейся площадью поперечного сечения. Для обтекания вдоль центр трубы, скорость уменьшается от первой до второй станции. Уравнение Бернулли описывает соотношение между скоростью, плотность и давление для этой задачи потока. Так как плотность постоянна для задачи с низкой скоростью уравнение в нижней части слайда связывает давление и скорость на станции два с условиями на станции номер один.

На небольшой скорости аэродинамический профиль, поток несжимаем и плотность остается равной постоянный. Тогда уравнение Бернулли сводится к простому соотношению между скоростью и статическим давлением. Поверхность аэродинамического профиля представляет собой упорядочить. Так как скорость меняется вдоль линии тока уравнение Бернулли можно использовать для вычисления изменения под давлением. Статическое давление, интегрированное по всей поверхности аэродинамического профиля дает полную аэродинамическую усилие на фольге. Эту силу можно разложить на подъемная сила и сопротивление аэродинамического профиля. 9М

Экскурсии с гидом
Основные уравнения гидродинамики:
Статическая трубка Пито:
Навигация . .

Домашняя страница руководства для начинающих

12.2: Уравнение Бернулли – Физика LibreTexts

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 1572

OpenStax
OpenStax

Цели обучения

К концу этого раздела вы сможете:

Объясните члены уравнения Бернулли.
Объясните, как уравнение Бернулли связано с сохранением энергии.
Объясните, как вывести принцип Бернулли из уравнения Бернулли.
Рассчитайте по принципу Бернулли.
Перечислите некоторые применения принципа Бернулли.

Когда жидкость течет в более узкий канал, ее скорость увеличивается. Это означает, что его кинетическая энергия также увеличивается. Откуда берется это изменение кинетической энергии? Увеличенная кинетическая энергия возникает из-за чистой работы, совершаемой над жидкостью, чтобы протолкнуть ее в канал, и работы, совершаемой над жидкостью силой тяжести, если жидкость меняет вертикальное положение. Вспомните теорему о работе и энергии, 92.\]

Существует разница давлений при сужении канала. Эта разница давлений приводит к результирующей силе, действующей на жидкость: вспомните, что давление, умноженное на площадь, равно силе. Совершенная чистая работа увеличивает кинетическую энергию жидкости. В результате давление в быстро движущейся жидкости будет падать, независимо от того, находится ли жидкость в трубе или нет.

Существует ряд типичных примеров падения давления в быстро движущихся жидкостях. Занавески для душа имеют неприятную привычку выпирать в душевую кабину, когда душ включен. Высокоскоростной поток воды и воздуха создает внутри душа область пониженного давления, а с другой стороны – нормальное атмосферное давление. Разница давлений приводит к тому, что результирующая сила вдавливает штору внутрь. Возможно, вы также заметили, что при обгоне грузовика на шоссе ваш автомобиль имеет тенденцию сворачивать в его сторону. Причина та же — высокая скорость воздуха между автомобилем и грузовиком создает область более низкого давления, и автомобили сталкиваются друг с другом за счет большего давления снаружи (Рисунок $\PageIndex{1}$) эффект наблюдался еще в середине 1800-х годов, когда было обнаружено, что поезда, идущие в противоположных направлениях, ненадежно наклоняются друг к другу.

Рисунок $\PageIndex{1}$: автомобиль, проезжающий мимо грузовика по шоссе, вид сверху. Воздух, проходящий между автомобилями, течет по более узкому каналу и должен увеличивать свою скорость ($v_2$ больше, чем $vv_1$), в результате чего давление между ними падает ($P_1$ меньше, чем $P_0 $).

Большее внешнее давление сталкивает автомобиль и грузовик.

Установление связей: Возьмите домой Исследование с листом бумаги:

Держите короткий край листа бумаги параллельно рту одной рукой по обеим сторонам рта. Страница должна наклоняться вниз над вашими руками. Удар над верхней частью страницы. Опишите, что происходит, и объясните причину такого поведения. 92 + \rho gh = константа \label{eq1}\]

где $P$ – абсолютное давление, $\rho$ – плотность жидкости, $v$ – скорость жидкости, $h$ — высота над некоторой точкой отсчета, а $g$ — ускорение свободного падения. Если мы проследим за небольшим объемом жидкости на его пути, различные величины в сумме могут измениться, но общее количество останется постоянным. Пусть индексы 1 и 2 относятся к любым двум точкам на пути, по которому следует кусочек жидкости; Уравнение Бернулли принимает вид: 93\), или энергии на единицу объема. Уравнение Бернулли на самом деле является просто удобной формулировкой сохранения энергии для несжимаемой жидкости в отсутствие трения .

Создание соединений: сохранение энергии

Сохранение энергии, приложенной к потоку жидкости, дает уравнение Бернулли. Чистая работа, выполняемая давлением жидкости, приводит к изменениям $KE$ и $PE_g$ жидкости на единицу объема. Если в потоке жидкости участвуют другие формы энергии, уравнение Бернулли можно изменить, чтобы учесть эти формы. К таким формам энергии относится тепловая энергия, рассеиваемая из-за вязкости жидкости.

Общая форма уравнения Бернулли состоит из трех членов (уравнение \ref{eq1}) и широко применима. Чтобы лучше понять его, мы рассмотрим ряд конкретных ситуаций, которые упрощают и иллюстрируют его использование и значение.

Уравнение Бернулли для статических жидкостей

Давайте сначала рассмотрим очень простую ситуацию, когда жидкость статична, то есть $v_1 = v_2 = 0$. Уравнение Бернулли в этом случае имеет вид

\[P_1 + \rho gh_1 = P_2 + \rho gh_2.\]

Мы можем еще больше упростить уравнение, приняв $h_2 = 0$ (мы всегда можем выбрать некоторую высоту равной нулю, как мы часто делали для других ситуаций, связанных с гравитационной силой, и считать все остальные высоты относительными к этому). В этом случае мы получаем

\[P_2 = P_1 + \rho gh_1.\]

Это уравнение говорит нам, что в статических жидкостях давление увеличивается с глубиной. Когда мы идем от точки 1 к точке 2 в жидкости, глубина увеличивается на $h_1$, и, следовательно, $P_2$ больше, чем $P_1$ на величину $\rho gh_1$. В самом простом случае $P_1$ равен нулю в верхней части жидкости, и мы получаем знакомое соотношение $P = \rho gh$. (Напомним, что $P = \rho gh$ и $\Delta PE_g = mgh$.) Уравнение Бернулли включает тот факт, что давление, обусловленное весом жидкости, равно $\rho gh$. Хотя мы вводим уравнение Бернулли для потока жидкости, оно включает многое из того, что мы изучали для статических жидкостей в предыдущей главе. 92.\]

Ситуации, в которых жидкость течет на постоянной глубине, настолько важны, что это уравнение часто называют принципом Бернулли. Это уравнение Бернулли для жидкостей на постоянной глубине. (Обратите внимание еще раз, что это относится к небольшому объему жидкости, когда мы следуем за ней вдоль ее пути. ) Как мы только что обсуждали, давление падает по мере увеличения скорости движущейся жидкости. Мы можем видеть это из принципа Бернулли. Например, если в уравнении $v_2$ больше $v_1$, то $P_2$ должно быть меньше $P_1$, чтобы выполнялось равенство. 92.\end{align*}\]

Обсуждение

Это абсолютное давление в шланге больше, чем в сопле, как и ожидалось, поскольку $v$ больше в сопле. Давление $P_2$ в сопле должно быть атмосферным, так как оно выходит в атмосферу без других изменений условий.

Применение принципа Бернулли

Существует ряд устройств и ситуаций, в которых жидкость течет на постоянной высоте и, таким образом, может быть проанализирована с помощью принципа Бернулли.

Применение: Унос

Люди уже давно применяют принцип Бернулли, используя пониженное давление в высокоскоростных жидкостях для перемещения предметов. При более высоком внешнем давлении высокоскоростная жидкость выталкивает другие жидкости в поток. Этот процесс называется уносом . Вовлекающие устройства использовались с древних времен, в частности, в качестве насосов для подъема воды на небольшие высоты, например, при осушении болот, полей или других низменных местностей. Некоторые другие устройства, использующие концепцию уноса, показаны на рисунке $\PageIndex{2}$.

Рисунок $\PageIndex{2}$: Примеры устройств захвата, использующих повышенную скорость жидкости для создания низкого давления, которое затем захватывает одну жидкость другой. (а) Горелка Бунзена использует регулируемое газовое сопло, увлекающее воздух для правильного сгорания. (b) В распылителе используется выжимная груша для создания струи воздуха, увлекающей за собой капли духов. Распылители краски и карбюраторы используют очень похожие методы для перемещения соответствующих жидкостей. (c) Обычный аспиратор использует высокоскоростной поток воды для создания области более низкого давления. Аспираторы могут использоваться в качестве отсасывающих насосов в стоматологических и хирургических ситуациях или для осушения затопленного подвала или создания пониженного давления в сосуде.

(d) Дымоход водонагревателя предназначен для захвата воздуха в трубу, проходящую через потолок.

Применение: крылья и паруса

Крыло самолета — прекрасный пример действия принципа Бернулли. На рисунке $\PageIndex{1a}$ показана характерная форма крыла. Крыло наклонено вверх под небольшим углом, а верхняя поверхность длиннее, благодаря чему воздух обтекает его быстрее. Таким образом, давление на верхнюю часть крыла уменьшается, создавая результирующую восходящую силу или подъемную силу. (Крылья также могут набирать подъемную силу, толкая воздух вниз, используя принцип сохранения количества движения. Отклоняющиеся молекулы воздуха создают восходящую силу, действующую на крыло — третий закон Ньютона.) Паруса также имеют характерную форму крыла. (См. рисунок $\PageIndex{1b}$.) Давление на переднюю сторону паруса, $P_{front}$, ниже, чем давление на заднюю часть паруса, $P_{back} $. Это приводит к поступательной силе и даже позволяет вам плыть против ветра.

Рисунок $\PageIndex{3}$ (a) Принцип Бернулли помогает объяснить подъемную силу, создаваемую крылом.

(b) Паруса используют ту же технику для создания части своей тяги.

Установление связей: возьмите домой исследование с двумя полосками бумаги

Для хорошей иллюстрации принципа Бернулли сделайте две полоски бумаги, каждая длиной около 15 см и шириной 4 см. Поднесите узкий конец одной полоски к губам и накиньте ее на палец. Удар по бумаге. Что случается? Теперь поднесите к губам две полоски бумаги, разделенные пальцами. Подуй между полосками. Что случается?

Применение: измерение скорости

На рисунке $\PageIndex{4}$ показаны два устройства, которые измеряют скорость жидкости на основе принципа Бернулли. Манометр на рисунке $\PageIndex{1a}$ подключен к двум трубкам, которые достаточно малы, чтобы не нарушать поток. Трубка, обращенная к набегающей жидкости, создает мертвую зону с нулевой скоростью ($v_1 = 0$) перед собой, а жидкость, проходящая через другую трубку, имеет скорость $v_2$. Это означает, что принцип Бернулли, сформулированный в 92.\]

(Напомним, что символ $\propto$ означает «пропорционально». 2 \), (b) Этот тип устройства для измерения скорости представляет собой трубку Прандтля, также известную как трубка Пито. 92.\]

Принцип Бернулли имеет множество применений, включая увлечение, крылья и паруса, а также измерение скорости.

Глоссарий

Уравнение Бернулли: уравнение, полученное в результате применения закона сохранения энергии к несжимаемой жидкости без трения: P + 1/2 pv ² + pgh = постоянная, через жидкость

Принцип Бернулли: Уравнение Бернулли, применяемое на постоянной глубине: P ₁ + 1/2 PV ₁ ² = P ₂ + 10355 P ₂ + 1/13555 P ₂ + 10355 P ₂ + 10355 P ₂ + 10355.

Эта страница под названием 12.2: Уравнение Бернулли распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или страница
Автор
ОпенСтакс
Лицензия
СС BY
Версия лицензии
4,0
Программа OER или Publisher
ОпенСтакс
Показать оглавление
нет
Метки
1. Уравнение Бернулли
2. Принцип Бернулли
3. Унос

Уравнение Бернулли | Инженерная библиотека

На этой странице представлена глава об уравнении Бернулли из «Справочника DOE по основам: термодинамика, теплопередача и поток жидкости», DOE-HDBK-1012/3-9. 2, Министерство энергетики США, июнь 1992 г.

Другие связанные главы из «Справочника по основам Министерства энергетики: термодинамика, теплопередача и поток жидкости» можно увидеть справа.

Уравнение Бернулли является частным случаем общего уравнения энергии, которое, вероятно, является наиболее широко используемым инструментом для решения задач о течении жидкости. Он обеспечивает простой способ соотнесения напора по высоте, скоростного напора и напора жидкости. Можно изменить уравнение Бернулли таким образом, чтобы он учитывал потери напора и работу насоса.

Общее уравнение энергии

Принцип сохранения энергии гласит, что энергия не может быть ни создана, ни уничтожена. Это эквивалентно Первому закону термодинамики, который был использован для построения общего уравнения энергии в модуле по термодинамике. Уравнение 3-8 представляет собой формулировку общего уравнения энергии для открытой системы.

В + (U + PE + KE + PV) _в = W + (U + PE + KE + PV) _из + (U + PE + KE + PV) _{хранится}

(3-8)

куда:

Упрощенное уравнение Бернулли

Уравнение Бернулли является результатом применения общего уравнения энергии и первого закона термодинамики к стационарной системе, в которой не совершается никакой работы над жидкостью или ею, тепло не передается к жидкости или от жидкости и не происходит никаких изменений в внутренней энергии (т. е. без изменения температуры) жидкости. В этих условиях общее уравнение энергии упрощается до уравнения 3-9.2 \over 2 g_c} + P_2 V_2 $$

(3-10)

где:

м	=	масса (фунт)
с	=	высота над эталоном (футы)
против	=	средняя скорость (фут/сек)
г	=	ускорение свободного падения (32,17 фут/сек ² )
г _с	=	гравитационная постоянная, (32,17 ft-lbm/lbf-sec ² )

Примечание. Коэффициент g _c требуется только в том случае, если используется английская система измерения и масса измеряется в фунтах. По сути, это коэффициент преобразования, необходимый для прямого вывода единиц измерения. Никакой фактор не требуется, если масса измеряется в порциях или если используется метрическая система измерения.

Каждый член в уравнении 3-10 представляет форму энергии, которой обладает движущаяся жидкость (потенциальная, кинетическая энергия и энергия, связанная с давлением). По сути, уравнение физически представляет собой баланс энергий KE, PE, PV, так что если одна форма энергии увеличивается, одна или несколько других уменьшаются, чтобы компенсировать это, и наоборот. 92 \над 2 г} + P_2 \nu_2 {г_с \над г} $$

(3-11)

куда:

с	=	высота над контрольным уровнем (футы)
против	=	средняя скорость жидкости (фут/сек)
Р	=	давление жидкости (фунт-сила/фут ² )
ν	=	удельный объем жидкости (фут ³ /фунт)
г	=	ускорение свободного падения (фут/сек ² )
г _с	=	гравитационная постоянная, (32,17 ft-lbm/lbf-sec ² )

Головка

Поскольку единицы для всех различных форм энергии в уравнении 3-11 измеряются в единицах расстояния, эти термины иногда называют «напором» (напорный напор, скоростной напор и подъемный напор). Срок 9Головка 0032 используется инженерами по отношению к давлению. Это ссылка на высоту, обычно в футах, столба воды, который будет поддерживать данное давление. Каждая из энергий, которыми обладает жидкость, может быть выражена в терминах напора. Высота напора представляет собой потенциальную энергию жидкости из-за ее подъема над опорным уровнем. Скоростной напор представляет собой кинетическую энергию жидкости. Это высота в футах, на которую текущая жидкость поднялась бы в столбе, если бы вся ее кинетическая энергия была преобразована в потенциальную энергию. Напор представляет собой энергию потока столба жидкости, вес которого эквивалентен давлению жидкости.

Сумма подъемного, скоростного и напорного напора жидкости называется полным напором. Таким образом, уравнение Бернулли утверждает, что общий напор жидкости постоянен.

PDH Classroom предлагает курс повышения квалификации, основанный на этой справочной странице уравнения Бернулли. Этот курс можно использовать для выполнения кредитных требований PDH для поддержания вашей лицензии PE.

Теперь, когда вы прочитали эту справочную страницу, заработайте за это признание!

Просмотреть курс сейчас:

Просмотреть курс

Преобразование энергии в жидкостных системах

Уравнение Бернулли позволяет легко исследовать, как происходит передача энергии между подъемным напором, скоростным напором и напором. Можно исследовать отдельные компоненты трубопроводных систем и определить, какие свойства жидкости изменяются и как это влияет на энергетический баланс.

Если труба, содержащая идеальную жидкость, подвергается постепенному расширению в диаметре, уравнение неразрывности говорит нам, что по мере увеличения диаметра и проходного сечения скорость потока должна уменьшаться, чтобы поддерживать тот же массовый расход. Поскольку скорость на выходе меньше скорости на входе, скоростной напор потока должен уменьшаться от входа к выходу. Если труба расположена горизонтально, напор не меняется; следовательно, уменьшение скоростного напора должно компенсироваться увеличением напора. Поскольку мы рассматриваем идеальную несжимаемую жидкость, удельный объем жидкости не изменится. Единственный способ увеличения напора несжимаемой жидкости — это увеличение давления. Таким образом, уравнение Бернулли показывает, что уменьшение скорости потока в горизонтальной трубе приведет к увеличению давления.

Если труба постоянного диаметра, содержащая идеальную жидкость, подвергается уменьшению высоты, возникает тот же чистый эффект, но по другим причинам. В этом случае скорость потока и скоростной напор должны быть постоянными, чтобы удовлетворять уравнению неразрывности массы.

Таким образом, уменьшение высоты подъема может быть компенсировано только увеличением напора. Опять же, жидкость несжимаема, поэтому увеличение напора должно привести к увеличению давления.

Хотя на уравнение Бернулли наложено несколько ограничений, оно применяется во многих задачах с физическими жидкостями. Как и в случае сохранения массы, уравнение Бернулли может быть применено к задачам, в которых более чем один поток может входить или выходить из системы одновременно. 2 } $$ $$ v_1 = 40 ~{\text{ft} \over \text{sec}} $$ 92} }\справа) } \номер \\ &=& 39.3 ~\text{ft} \end{эквнаррай} $$

Ограничения на упрощенное уравнение Бернулли

Практическое применение упрощенного уравнения Бернулли к реальным трубопроводным системам невозможно из-за двух ограничений. Одним из серьезных ограничений уравнения Бернулли в его нынешнем виде является то, что при решении задач о трубопроводах не допускается жидкостное трение. Следовательно, уравнение 3-10 применимо только к идеальным жидкостям. Однако в действительности полный напор, которым обладает жидкость, не может быть полностью перенесен из одной точки в другую из-за трения. Учет этих потерь напора дал бы гораздо более точное описание того, что происходит физически. Это особенно верно, потому что одной из целей насоса в жидкостной системе является преодоление потерь давления из-за трения в трубах.

Второе ограничение уравнения Бернулли состоит в том, что жидкость не может совершать работу над жидкостью. Это ограничение предотвращает анализ двух точек в потоке жидкости, если между двумя точками есть насос. Поскольку большинство проточных систем включают насосы, это является существенным ограничением. К счастью, упрощенное уравнение Бернулли можно изменить так, чтобы оно удовлетворительно учитывало как потери напора, так и работу насоса.

Расширенный Бернулли

Уравнение Бернулли можно изменить, чтобы учесть прирост и потерю напора. Полученное уравнение, называемое расширенным уравнением Бернулли, очень полезно при решении большинства задач о течении жидкости. На самом деле расширенное уравнение Бернулли, вероятно, используется чаще, чем любое другое уравнение течения жидкости. Уравнение 3-12 является одной из форм расширенного уравнения Бернулли. 92 \более 2 г} + P_2 \nu_2 {g_c \более g} + H_f $$

(3-12)

куда:

с	=	высота над контрольным уровнем (футы)
против	=	средняя скорость жидкости (фут/сек)
Р	=	давление жидкости (фунт-сила/фут ² )
ν	=	удельный объем жидкости (фут ³ /фунт)
Н _р	=	напор добавлен насосом (ft)
Н _f	=	потеря напора из-за жидкостного трения (футы)
г	=	ускорение свободного падения (фут/сек ² )
г _с	=	гравитационная постоянная, (32,17 ft-lbm/lbf-sec ² )

Потеря напора из-за жидкостного трения (H _f ) представляет собой энергию, используемую для преодоления трения, вызванного стенками трубы. Хотя это представляет собой потерю энергии с точки зрения потока жидкости, обычно это не представляет собой значительную потерю общей энергии жидкости. Это также не нарушает закон сохранения энергии, поскольку потеря напора из-за трения приводит к эквивалентному увеличению внутренней энергии (u) жидкости. Эти потери максимальны, когда жидкость протекает через входы, выходы, насосы, клапаны, фитинги и любые другие трубопроводы с шероховатой внутренней поверхностью.

Большинство методов оценки потери напора из-за трения являются эмпирическими (основаны почти исключительно на экспериментальных данных) и основаны на константе пропорциональности, называемой коэффициентом трения (f), которая будет обсуждаться в следующем разделе.

Пример: Расширенный Бернулли

Вода перекачивается из большого резервуара в точку на 65 футов выше резервуара. Сколько футов напора должен добавить насос, если через 6-дюймовую трубу протекает 8000 фунтов/ч, а потеря напора на трение составляет 2 фута? Плотность жидкости составляет 62,4 фунта/фут 9 . 0359 3 , а площадь поперечного сечения 6-дюймовой трубы составляет 0,2006 фута ² .

Решение:

Для использования модифицированной формы уравнения Бернулли опорные точки выбирают на поверхности резервуара (точка 1) и на выходе из трубы (точка 2). Давление на поверхности резервуара такое же, как давление на выходе из трубы, т. е. атмосферное давление. Скорость в точке 1 будет практически нулевой.

Используя уравнение для массового расхода, определить скорость в точке 2: 92} }\right) } + 0 ~\text{ft} + 2 ~\text{ft} \nonumber \\ H_p &=& 67 ~\text{ft} \end{эквнаррай} $$

Студент должен отметить, что решение этой примерной задачи имеет числовое значение, которое «имеет смысл» из данных, приведенных в задаче. Общее увеличение напора на 67 футов связано в первую очередь с увеличением оценки на 65 футов и на 2 фута фрикционного напора.

Применение уравнения Бернулли к трубке Вентури

Многие компоненты установки, такие как трубка Вентури, могут быть проанализированы с использованием уравнения Бернулли и уравнения неразрывности. Вентури представляет собой устройство для измерения расхода, состоящее из постепенного сжатия, за которым следует постепенное расширение. Пример трубки Вентури показан на рисунке 6. Путем измерения перепада давления между входом трубки Вентури (точка 1) и горловиной трубки Вентури (точка 2) можно определить скорость потока и массовый расход на основе формулы Бернулли. уравнение. 92 \над 2 г} + P_2 \nu_2 {г_с \над г} $$

(3-13)

Применение уравнения неразрывности к точкам 1 и 2 позволяет нам выразить скорость потока в точке 1 как функцию скорости потока в точке 2 и отношения двух площадей потока.

$$ \rho_1 A_1 v_1 = \rho_2 A_2 v_2 $$ $$ v_1 = { \rho_2 A_2 v_2 \над \rho_1 A_1 } $$ $$ v_1 = v_2 ~{A_2 \over A_1} $$

Используя алгебру для преобразования уравнения 3-13 и подстановки приведенного выше результата вместо v _{1 92 } $$}

Следовательно, скорость потока в горловине трубки Вентури и объемный расход прямо пропорциональны квадратному корню из дифференциального давления.

Уравнение Бернулли – вывод формулы, физический смысл, примеры использования

Исследования учёного

Условия действия

Количественная сторона

Применение в гидравлике

Подъёмная сила

Уравнение Бернулли

Характеристика уравнения Бернулли

Решение уравнения Бернулли сведением к линейному неоднородному

Уравнение бернулли – справочник студента

Уравнение Бернулли

Уравнение Бернулли — вывод формулы, физический смысл, примеры использования

Исследования учёного

Условия действия

Количественная сторона

Применение в гидравлике

Подъёмная сила

Основы гидравлики

Геометрическая интерпретация уравнения Бернулли

Пример решения задачи на определение расхода жидкости

Главная страница

Специальности

Учебные дисциплины

Олимпиады и тесты

Уравнение Бернулли — Всё для чайников

Дифференциальное уравнение Бернулли и методы его решения

Решение методом Бернулли

Пример решения дифференциального уравнения Бернулли

Уравнение Бернулли

12.2: Уравнение Бернулли – Физика LibreTexts

Уравнение Бернулли для статических жидкостей

Применение принципа Бернулли

Применение: Унос

Применение: крылья и паруса

Применение: измерение скорости

Глоссарий

Уравнение Бернулли | Инженерная библиотека

Общее уравнение энергии

Упрощенное уравнение Бернулли

Головка

Преобразование энергии в жидкостных системах

Ограничения на упрощенное уравнение Бернулли

Расширенный Бернулли

Применение уравнения Бернулли к трубке Вентури

Оставить комментарий Отменить ответ