Формула ускорение движения: Ускорение (видео) | Прямолинейное движение

Ускорение Формула Уравнение Наука Скорость, сила и движение, угол, текст, прямоугольник png

Ускорение Формула Уравнение Наука Скорость, сила и движение, угол, текст, прямоугольник png

теги

• угол,
• текст,
• прямоугольник,
• логотип,
• черный,
• номер,
• параллель,
• образование Наука,
• физика,
• количество,
• черно-белый,
• скаляр,
• скорость,
• символ,
• площадь,
• бренд,
• одномерное пространство,
• уравнения движения,
• сила,
• смещение,
• линия,
• диаграмма,
• круг,
• кинематика,
• ускорение,
• формула,
• уравнение,
• наука,
• движение,
• png,
• прозрачный,
• бесплатная загрузка

Об этом PNG

Размер изображения

1244x803px

Размер файла

7.24KB

MIME тип

Image/png

Скачать PNG ( 7. 24KB )

изменить размер PNG

ширина(px)

высота(px)

Лицензия

Некоммерческое использование, DMCA Contact Us

• Математика геометрия формула евклидово уравнение, математические заметки, угол, текст, треугольник png 6354x6354px 911.07KB
• Физика Скоростная формула Ускорение, линия, угол, текст, логотип png 1161x861px 9.11KB
• математические уравнения, математические формулы, математические обозначения, cdr, угол, текст png 1080x763px 356.8KB
• Геометрия круга света, наука и техника, синий механический, синий, угол, электроника png 800x800px 299. 43KB
• Формула Математика Евклидова, математическая формула, угол, текст, монохромный png 3500x3313px 875.77KB
• Квадратичное уравнение Квадратичная формула Квадратичная функция Математика, формула, угол, текст, прямоугольник png 1500x673px 7.22KB
• Момент инерции Маятник Формула движения Колебания, математическое уравнение, угол, белый, текст png 1507x663px 9.78KB
• Движение Физика Кинематика Eenparig Rechtlijnige Уравнение Бевинга, Кааба, угол, текст, логотип png 969x1031px 6.8KB
• Класс Начальная школа Студент Образование, школа, угол, белый, текст png 556x453px 82. 99KB
• Бренд Пойнт Паттерн, FaceTime, угол, белый, текст png 422x750px 18.4KB
• синий логотип, круг логотип шрифт, шаблоны, синий, угол, текст png 5618x5506px 822.62KB
• Химическое уравнение Химия Формула Физика, наука, угол, текст, химический png 768x827px 172.39KB
• Математические уравнения, Формула Математика Функция Евклида, Оси математических функций, синий, угол, текст png 800x800px 366.32KB
• круглый красный логотип, круг рисунок, подсветка, угол, текст, форма png 800x800px 49.88KB
• org/ImageObject”> Движение снаряда Atış hareketi Скорость, скорость движения, угол, текст, прямоугольник png 640x453px 12.95KB
• Черно-белый прямоугольник круг монохромный, точки, угол, белый, текст png 1600x1600px 26.41KB
• MathML Массово-энергетическая эквивалентность Формула Математика Википедия, e = mc2, угол, текст, товарный знак png 1280x427px 18.1KB
• оранжевый, синий и черный логотип, технология Logo Circle, круг, синий, текст, информационные технологии png 1488x1483px 68.44KB
• комиксов чат головы иллюстрации, рисунок круга, подчеркивание, угол, карандаш, текст png 800x780px 33KB
• org/ImageObject”> социальные медиа логотип, социальные медиа логотип компьютер иконки, социальные, угол, белый, текст png 600x564px 22.72KB
• желтый, красный и зеленый иллюстрации ассорти-формы, геометрическая форма Геометрия Плоский дизайн, круг, угол, текст, прямоугольник png 1994x2155px 115.07KB
• Эквивалентность массы – энергии уравнения поля Эйнштейна Теория формулы относительности, Математика, угол, текст, число png 735x861px 210.86KB
• Центростремительная сила Круговое вращение Круговое движение, сила и движение, угол, текст, рука png 792x508px 79.33KB
• Траектория движения Дифференциальное уравнение Физика Физическое тело, траектория полета, синий, угол, текст png 1280x529px 23. 13KB
• две черно-бирюзовые границы, веб-камера Twitch Streaming Media, стример, синий, угол, белый png 1600x850px 102.81KB
• школьные принадлежности, школьный фон, угол, текст, рюкзак png 712x712px 122.99KB
• химическая тематика иллюстрации, химическая лаборатория рисования науки, каракули, угол, текст, фреска png 1640x1064px 2.32MB
• Цифровая подпись Цифровые данные, другие, разное, угол, белый png 1404x556px 76.85KB
• Круг Круговое движение Круговая орбита, круг, угол, белый, треугольник png 1276x842px 81.42KB
• org/ImageObject”> Теорема Пифагора Угол Числовая линия, Угол, угол, текст, прямоугольник png 2400x2384px 40.82KB
• Квадратичное уравнение Квадратичная функция Квадратичная формула Завершая квадрат, формула, угол, текст, прямоугольник png 2000x617px 30.38KB
• Квадратичное уравнение Квадратичная формула Алгебра Квадратичная функция, формула функции, угол, текст, прямоугольник png 1280x395px 13.9KB
• Математика евклидова формула бумаги, математические различные формулы, угол, текст, монохромный png 4050x4050px 627.53KB
• Физика Наука Химия Символ, музыкальные элементы, угол, текст, лаборатория png 600x564px 20.93KB
• org/ImageObject”> Круговое движение Круг Скорость Центростремительная сила Положение, круг, угол, текст, треугольник png 1717x1244px 71.79KB
• Компьютерные иконки Атом Физика Наука, наука, логотип, атом, символ png 512x512px 16.72KB
• иллюстрация закрученной стрелки, эскиз чертежа стрелки, эскиз стрелки, угол, карандаш, текст png 1047x1245px 40.58KB
• Круг, тонкий, угол, белый, симметрия png 770x770px 12.87KB
• Шрифт номера символа круга, 1, текст, черный, номер png 1181x1181px 34.8KB
• черно-фиолетовая текстовая иллюстрация, Бумажная математическая формула науки, Фиолетовые математические заметки, угол, текст, симметрия png 4050x4050px 788. 52KB
• круглые контейнеры разных цветов, инфографическая карта Flyer Circle, классификация Circle, шаблон, текст, круг Рамка png 626x626px 256.35KB
• Технологии евклидова, синяя граница, синие линии, граница, рамка, синий png 591x472px 6.57KB
• серая и синяя спиральная графика, математическая евклидова формула, креативная тяга синего пространства бесплатно, синий, угол, свободный Шаблон дизайна логотипа png 5314x3543px 12.85MB
• Золотая спираль Золотое сечение число Фибоначчи Золотой прямоугольник, евклидов, угол, белый, текст png 1600x1012px 42.47KB
• Диаграмма Компьютерный файл, элемент PPT, шаги 1, 2, 3 и 4, иллюстрация, инфографика, шаблон, метка png 2315x3004px 1. 08MB
• Угловой номер линии, WhatsApp, белый, текст, число png 600x600px 46KB
• Стрелка, Стрелка, угол, текст, прямоугольник png 1600x1600px 48.84KB
• Круг Площадь Символ Угол Марка, PPT, текст, улыбка, красный png 500x500px 15.46KB
• математические уравнения, математическое уравнение евклидовой формулы, математический набросок материала, угол, текст, цифровой png 918x670px 147.15KB
• буква M, черно-белая монохромная линия art, буква m, угол, белый, текст png 1000x1000px 23.61KB

Нахождение формулы измерения ускорения

Физические величины используются для количественной оценки свойств системы. Чтобы придать смысл этим физическим величинам, численное значение и общепринятая единица объединяются. Например, чтобы измерить длину балки, мы говорим, что балка равна 6 [числовая величина] + метры [единица измерения].

Размерные формулы представляют собой важный способ выражения этих систем в легком для понимания формате.

Физические величины

Чтобы полностью понять концепцию размерных формул, нам нужно понять классы физических величин. Как правило, существует два класса физических величин: фундаментальные или основные величины и производные величины.

Фундаментальные или основные величины – это те величины, которые не определяются с помощью других физических величин. Вместо этого они образуют основу, для которой определяются другие величины, называемые производными. Основные величины и их единицы СИ включают: длину (метр (м)), массу (килограмм (кг)), время (секунда (с)), температуру (Кельвин (К)), электрический ток (Ампер (А)), световой поток. интенсивность (кандела (кд)) и количество вещества (моль (моль)). В этой статье мы сосредоточимся на длине, массе и времени.

Применение размерных формул

Применение размерных формул для определения производных единиц измерения имеет несколько преимуществ

• Оно демонстрирует, как другие физические величины могут быть представлены в терминах их основных единиц.
• Используется для проверки размерной правильности формулы производной величины.
•  Уменьшает количество ошибок, возникающих при преобразовании из одной единицы измерения в другую в разных системах (например, из единиц СИ в британские единицы).

Когда физическую величину записывают в виде ее размерной формулы, мы получаем размерное уравнение.

Чтобы выразить размерные формулы, используя длину, массу и время, мы присваиваем базовые значения: [L] для длины, [M] для массы и [T] для времени.

Предпосылки для формулы измерения ускорения

Чтобы вывести формулу измерения для ускорения , мы должны получить формулы для смещения и скорости , двух величин, от которых зависит ускорение.

Размерная формула для смещения

Смещение [d] — это изменение положения или движения. Длина представляет смещение.

[d] = [L]

Это также записывается как:

[d] = [M0 L1 T0]

Это означает, что перемещение имеет одно измерение длины и не имеет измерения массы и времени. .

Размерная формула для смещения:  [л] .

Размерная формула скорости

Скорость [v] определяется как смещение относительно времени. Это представлено как:

v = Перемещение/Время

Поскольку перемещение [d] задано как [L], мы имеем:

[v] = [L]/[T]

Это может быть далее в упрощенном виде:

[v] = [L][T-1] или  [LT-1]

Далее это можно выразить следующим образом:

[v] = [M0 L1 T-1 ]

Уравнение размеров, приведенное выше, похоже на формулу измерения смещения. Скорость имеет одно измерение длины, минус одно (-1) измерение времени и не имеет измерения массы.

Размерная формула для ускорения

Ускорение [a] можно определить как скорость изменения скорости во времени. Это может быть представлено как:

[a] = Изменение скорости/Изменение во времени

Ранее мы получили скорость как [LT-1], поэтому ускорение задается как:

[a] = [LT -1]/[T]

Это может быть дополнительно упрощено как:

[a] = [L][T-2] или [LT-2]

Это может быть дополнительно выражено как:

[a] = [M0 L1 T-2]

Правая часть приведенного выше уравнения показывает размерную формулу для ускорения. Согласно этому размерному уравнению, ускорение имеет одно измерение длины, минус два (-2) измерения времени и не имеет измерения массы.

Из приведенных выше примеров легко прикрепить единицы к различным количествам. Например, ускорение может быть выражено в метрах в секунду в квадрате (м.с-2) или футах в секунду в квадрате (фт.с-2), а скорость может быть выражена в метрах в секунду (м. с-1) или километрах в час (км). .ч-1). Какую бы единицу вы ни выбрали, вы можете проверить ее согласованность с помощью размерной формулы.

Чтобы лучше проиллюстрировать, давайте выведем формулу измерения силы.

Размерная формула силы

Сила [f] определяется как удар, который заставляет объект определенной массы ускоряться. Это можно выразить просто как

[f] = масса * ускорение

Используя размерную формулу для ускорения, мы имеем:

[f] = [M] * [M0 L1 T-2]

Это можно объединить, чтобы получить:

[f] = [M1 L1 T-2]

Сила имеет одно измерение по массе, одно измерение по длине и менее двух (-2) измерений по времени. Сила выражается в ньютонах, килограмм-метр в секунду в квадрате (кг.м.с-2).

Другие размерные формулы

Как уже отмечалось, одним из преимуществ размерных формул является возможность проверки размерной правильности в формулах. Это означает, что эти концепции можно применять ко все более и более сложным формулам. Другие полезные размерные формулы и их уравнения включают:

Мощность [P] = [M1 L2 T-3]

Плотность [D] = [M1 L3 T0]

Давление [P] = [M1 L-1 T-2]

Энергия [E] = [M1 L2 T-2]

Ограничения размерных формул

Однако использование размерных формул имеет некоторые ограничения.

• Сложно определить функции, когда они подчиняются логарифмическим или экспоненциальным функциям.
• Размерные формулы нельзя использовать для расчета констант пропорциональности.
• Для более сложных физических величин может потребоваться знание формул других измерений.
• Нет уникальных букв, используемых для различения физических величин. Например, Мощность [P] и Давление [P]

Как правило, чтобы представить размерную формулу для физической величины, основные величины (масса, длина, время и т. д.) должны быть объединены с их соответствующими степенями (0, 1, 2 и т. д.). Физические величины не обязательно должны иметь все основные величины.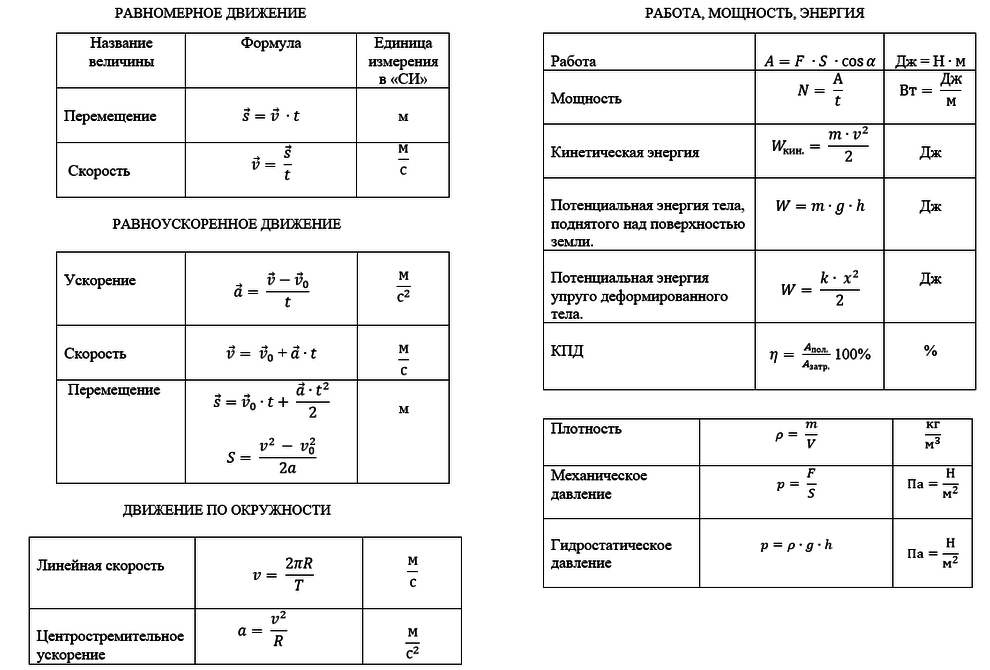 Перемещение [L], скорость [LT-1] и ускорение [LT-2] — хорошие примеры таких физических величин.

Будьте первым, кто оставит комментарий ниже.

исчисление – дифференциальное уравнение второго порядка для ускорения

спросил 8 лет, 11 месяцев назад

Изменено 6 лет, 8 месяцев назад

Просмотрено 10 тысяч раз

$\begingroup$

Можете ли вы помочь мне понять и решить этот вопрос:

Пуля выпущена вертикально вверх с начальной скоростью $u$. Составьте дифференциальное уравнение второго порядка для ускорения и путем двойного интегрирования найдите уравнение для смещения $s$, пройденного пулей, через время $t$ с момента выстрела.

Я не могу уложить это в голове. Я не сделал никакой работы, даже не знаю, как начать. Все, что я знаю, это то, что $v(t)=u-gt$, где $v(t)$ — скорость в момент времени $t$, $u$ — начальная скорость, $-g$ — ускорение Земли. Отсюда следует, что при $t = 0$ скорость $v(t)$ будет равна начальной скорости $u$; и в некоторый момент времени скорость $v(t)$ будет равна нулю. Нужно ли дифференцировать уравнение $v(t)=u-gt$, чтобы получить уравнение для ускорения? А затем дважды проинтегрировать уравнение ускорения? Я даже не уверен, что $v(t)=u-gt$ — правильное уравнение скорости.

Большое спасибо!

• исчисление
• физика

$\endgroup$

$\begingroup$

Предположим, что наша вертикальная ось направлена ​​вверх. Второй закон Ньютона говорит нам, что $$m\ddot y=F.$$ Закон тяготения (опять же благодаря Ньютону) скажет в нашем случае, что $F=-mg$, что приводит нас к дифференциальному уравнению $$\ddot y=-g. $$ Предположим также, что начальная координата вашей пули равна $y_0$, а начальная скорость равна $\dot y(0)=v_0$. Суммарная задача (это так называемая задача Коши) пишет $$\begin{случаи} \дточка у=-г\\ \точка у(0)=v_0\\ у (0) = у_0 \end{case}$$ 9\прайм(т) = а(т) $$ В вашем случае $a(t) = -g$ является константой. Уравнение $v(t)=u-gt$, которое вы записали, есть не что иное, как интеграл от последнего уравнения с начальным условием $v(0) = u$. Вам нужно еще раз проинтегрировать это по отношению к $t$ и начальному условию = «высота конца пистолета над полом», чтобы получить $s$.

$\endgroup$

$\begingroup$

Пусть $t=0$ будет моментом выстрела пули. Тогда скорость как функция времени равна $v(t)=u-gt$, если предположить, что положительное значение означает, что она направлена ​​вверх.

Ускорение определяется выражением $a(t)=\dfrac{d}{dt}v(t)=-g$.

Перемещение является интегралом скорости или вторым интегралом ускорения.