Формула средней скорости при равноускоренном прямолинейном движении
Из первого уравнения системы (1) имеем:
\[a_x=\frac{v_x-v_{0x}}{t}\left(7\right).\]
Величину ускорения из уравнения (7) подставим в формулу (5) получим, что перемещение по оси X равно:
\[\Delta x=\frac{v_x+v_{0x}}{2}t\left(8\right).\]
Найдем проекцию средней скорости на ось X из определения средней скорости движения:
\[{\left\langle v\right\rangle }_x=\frac{\Delta x}{t}\left(9\right).\]
Разделим правую и левую части выражения (8) на время движения тела. Получим, что средняя скорость при рассматриваемом движении равна:
\[\frac{\Delta x}{t}=\frac{v_x+v_{0x}}{2}={\left\langle v\right\rangle }_x\left(10\right).\]
Примеры задач с решением
Пример 1
Задание. 2}$
2}$
Читать дальше: формулы свободного падения.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Ускорение при равноускоренном прямолинейном движении
теория по физике 🧲 кинематика
- Равноускоренное прямолинейное движение — движение по прямой линии с постоянным ускорением (a=const).
- Ускорение — векторная физическая величина, показывающая изменение скорости тела за 1 с. Обозначается как a.
- Единица измерения ускорения — метр в секунду в квадрате (м/с2).
- Акселерометр — прибор для измерения ускорения.
v — скорость тела в данный момент времени, v0 — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость
Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.
Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.
Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.
Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:
Проекция ускорения
Проекция ускорения на ось ОХvx — проекция скорости тела в данный момент времени, v0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость
Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:
- Если вектор ускорения направлен в сторону оси ОХ, то его проекция положительна.
- Если вектор ускорения направлен в сторону, противоположную направлению оси ОХ, его проекция отрицательная.

При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.
Направление вектора ускорения
Направление вектора ускорения не всегда совпадает с направлением вектора скорости!
Равноускоренным движением называют такое движение, при котором скорость за
Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу (а↑↓v).
Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.
График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (ax=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.
Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:
- Если график лежит выше оси времени, движение равноускоренное (направление вектора ускорения совпадает с направлением оси ОХ). На рисунке выше тело 1 движется равноускорено.
- Если график лежит ниже оси времени, движение равнозамедленное (вектор ускорения направлен противоположно оси ОХ).
 На рисунке выше тело 2 движется равнозамедлено.
На рисунке выше тело 2 движется равнозамедлено.
Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.
Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.
Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t1 = 1 и t2 = 3 с.
В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).
Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.
В момент времени t1 = 1с ускорение a = 2 м/с2. В момент времени t2 = 3 ускорение a = 0 м/с2.
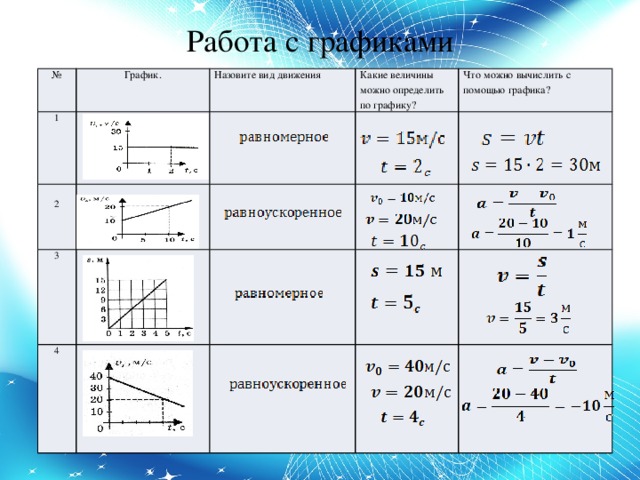
Задание EF18774На рисунке показан график зависимости координаты x тела, движущегося вдоль оси
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.
Алгоритм решения
- Определить, какому типу движения соответствует график зависимости координаты тела от времени.
- Определить величины, которые характеризуют такое движение.
- Определить характер изменения величин, характеризующих это движение.
- Установить соответствие между графиками А и Б и величинами, характеризующими движение.
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
- перемещение и путь;
- скорость;
- ускорение.
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
Ответ: 24pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17992 Начальная скорость автомобиля, движущегося прямолинейно и равноускоренно, равна 5 м/с. После прохождения расстояния 40 м его скорость оказалась равной 15 м/c. Чему равно ускорение автомобиля?
После прохождения расстояния 40 м его скорость оказалась равной 15 м/c. Чему равно ускорение автомобиля?Алгоритм решения
- Записать исходные данные.
- Записать формулу, связывающую известные из условия задачи величины.
- Выразить из формулы искомую величину.
- Вычислить искомую величину, подставив в формулу исходные данные.
Решение
Запишем исходные данные:
- Начальная скорость v0 = 5 м/с.
- Конечная скорость v = 15 м/с.
- Пройденный путь s = 40 м.
Формула, которая связывает ускорение тела с пройденным путем:
Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».
Выразим из формулы ускорение:
Подставим известные данные и вычислим ускорение автомобиля:
Ответ: 2,5pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18202Внимательно прочитайте текст задания и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела vx от времени.
На рисунке приведён график зависимости проекции скорости тела vx от времени.
Алгоритм решения
- Охарактеризовать движение тела на участке графика, обозначенном в условии задачи.
- Вычислить ускорение движение тела на этом участке.
- Выбрать график, который соответствует графику зависимости от времени проекции ускорения тела.
Решение
Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.
Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:
- t1 = 6 с.
 Этой точке соответствует скорость v1 = 0 м/с.
Этой точке соответствует скорость v1 = 0 м/с. - t2 = 10 с. Этой точке соответствует скорость v2 = –10 м/с.
Используем для вычислений следующую формулу:
Подставим в нее известные данные и сделаем вычисления:
Этому значению соответствует график «г».
Ответ: гpазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18027 На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси х. Определите модуль ускорения тела.Алгоритм решения
- Записать формулу ускорения.
- Записать формулу для вычисления модуля ускорения.
- Выбрать любые 2 точки графика.
- Определить для этих точек значения времени и проекции скорости (получить исходные данные).
- Подставить данные формулу и вычислить ускорение.

Решение
Записываем формулу ускорения:
По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:
Выбираем любые 2 точки графика. Пусть это будут:
- t1 = 1 с. Этой точке соответствует скорость v1 = 15 м/с.
- t2 = 2 с. Этой точке соответствует скорость v2 = 5 м/с.
Подставляем данные формулу и вычисляем модуль ускорения:
Ответ: 10pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 11.4k | Оценить:
3.S: Движение по прямой (краткое содержание)
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 5369
- OpenStax
- OpenStax
Ключевые термины
| ускорение свободного падения | ускорение объекта под действием силы тяжести |
| среднее ускорение | скорость изменения скорости; изменение скорости во времени |
| средняя скорость | общее пройденное расстояние, деленное на прошедшее время |
| средняя скорость | перемещение, деленное на время, в течение которого происходит перемещение |
| смещение | изменение положения объекта |
| пройденное расстояние | общая длина пути, пройденного между двумя позициями |
| истекшее время | разница между временем окончания и временем начала |
| свободное падение | состояние движения, которое является результатом только гравитационной силы |
| мгновенное ускорение | ускорение в определенный момент времени |
| мгновенная скорость | абсолютное значение мгновенной скорости |
| мгновенная скорость | скорость в определенный момент или момент времени |
| кинематика | описание движения через такие свойства, как положение, время, скорость и ускорение |
| позиция | местоположение объекта в определенное время |
| полный водоизмещение | сумма индивидуальных перемещений за заданный период времени |
| задача преследования двух тел | задача кинематики, в которой неизвестные вычисляются путем одновременного решения кинематических уравнений для двух движущихся объектов |
Ключевые уравнения
| Рабочий объем | $$\Delta x = x_{f} – x_{i}$$ |
| Полный водоизмещение | $$\Delta x_{Total} = \sum \Delta x_{i}$$ |
| Средняя скорость | $$\bar{v} = \frac{\Delta x}{\Delta t} = \frac{x_{2} – x_{1}}{t_{2} – t_{1}}$$ |
| Мгновенная скорость | $$v(t) = \frac{dx(t)}{dt}$$ |
| Средняя скорость | $$\bar{s} = \frac{Total\; расстояние}{Прошло\; время}$$ |
| Мгновенная скорость | $$Мгновенно\; скорость = |v(t)|$$ |
| Среднее ускорение | $$\bar{a} = \frac{\Delta v}{\Delta t} = \frac{v_{f} – x_{0}}{t_{f} – t_{0}}$$ |
| Мгновенное ускорение | $$a(t) = \frac{dv(t)}{dt}$$ |
| Позиция по средней скорости | $$x = x_{0} + \bar{v} t$$ |
| Средняя скорость | $$\bar{v} = \frac{v_{0} + v}{2}$$ 9{2} – 2 г(г – г_{0})$$ |
| Скорость от ускорения | $$v(t) = \int a(t)dt + C_{1}$$ |
| Позиция по скорости | $$x(t) = \int v(t)dt + C_{2}$$ |
Резюме
3.
 1 Положение, перемещение и средняя скорость
1 Положение, перемещение и средняя скорость- Кинематика — это описание движения без учета его причин. В этой главе оно ограничивается движением по прямой линии, называемым одномерным движением.
- Смещение — это изменение положения объекта. Единицей перемещения в СИ является метр. Смещение имеет направление, а также величину.
- Пройденное расстояние — это общая длина пути, пройденного между двумя позициями.
- Время измеряется изменениями. Время между двумя точками положения x 1 и x 2 равно \(\Delta\)t = t 2 − t 1 . Прошедшее время для события равно \(\Delta\)t = t f – t 0 , где t f — конечное время, а t 0 — начальное время. Начальное время часто принимается равным нулю.
- Средняя скорость \(\bar{v}\) определяется как смещение, деленное на прошедшее время. Если x 1 , t 1 и x 2 , t 2 являются двумя точками времени положения, средняя скорость между этими точками равна
\[\bar{v} = \frac{\Delta x}{\Delta t} = \frac{x_{2} – x_{1}}{t_{2} – t_{1}} \ldotp\ ]
3.
 2 Мгновенная скорость и скорость
2 Мгновенная скорость и скорость- Мгновенная скорость является непрерывной функцией времени и дает скорость в любой момент времени во время движения частицы. Мы можем рассчитать мгновенную скорость в определенный момент времени, взяв производную функции положения, которая дает нам функциональную форму мгновенной скорости v(t).
- Мгновенная скорость является вектором и может быть отрицательным.
- Мгновенная скорость находится путем взятия абсолютного значения мгновенной скорости, и оно всегда положительное.
- Средняя скорость равна общему пройденному расстоянию, деленному на прошедшее время.
- Наклон графика зависимости положения от времени в определенный момент времени дает мгновенную скорость в этот момент времени.
3.3 Среднее и мгновенное ускорение
- Ускорение — это скорость изменения скорости. Ускорение — это вектор; оно имеет как величину, так и направление. Единицей ускорения в системе СИ является метр в секунду в квадрате.

- Ускорение может быть вызвано изменением величины или направления скорости, или и тем, и другим.
- Мгновенное ускорение a(t) является непрерывной функцией времени и дает ускорение в любой конкретный момент времени во время движения. Он рассчитывается из производной функции скорости. Мгновенное ускорение — это наклон графика зависимости скорости от времени.
- Отрицательное ускорение (иногда называемое замедлением) — это ускорение в отрицательном направлении в выбранной системе координат.
3.4 Движение с постоянным ускорением
- При анализе одномерного движения с постоянным ускорением определите известные величины и выберите соответствующие уравнения для решения неизвестных. Для решения неизвестных необходимо одно или два кинематических уравнения, в зависимости от известных и неизвестных величин.
- Задачи преследования двух тел всегда требуют одновременного решения двух уравнений для неизвестных.
3.
 5 Свободное падение
5 Свободное падение- Объект в свободном падении испытывает постоянное ускорение, если сопротивлением воздуха можно пренебречь.
- На Земле все свободно падающие объекты имеют ускорение g из-за силы тяжести, которое в среднем составляет g = 9,81 м/с 2 .
- Для объектов в свободном падении направление вверх обычно считается положительным для смещения, скорости и ускорения.
3.6 Нахождение скорости и перемещения по ускорению
- Интегральное исчисление дает нам более полную формулировку кинематики.
- Если ускорение a(t) известно, мы можем использовать интегральное исчисление для получения выражений для скорости v(t) и положения x(t).
- Если ускорение постоянно, интегральные уравнения сводятся к уравнению 3.12 и уравнению 3.13 для движения с постоянным ускорением.
Авторы и ссылки
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойолы Мэримаунт) и Билл Моебс со многими сотрудничающими авторами.
 Эта работа находится под лицензией OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Эта работа находится под лицензией OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Эта страница под названием 3.S: Движение по прямой линии (краткое описание) распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- source@https://openstax.
 org/details/books/university-physics-volume-1
org/details/books/university-physics-volume-1
- source@https://openstax.
2. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
2. ПРЯМОЛИнейНОЕ ДВИЖЕНИЕ- ДВИЖЕНИЕ ПО ПРЯМОЙ ЛИНИИ
- 2.1. Должность
- 2.2. Скорость
- 2.3. Ускорение
- 2.4. Постоянное ускорение
- 2.5. Гравитационное ускорение
В механике нас интересует попытка понять движение объектов. В этой главе будет обсуждаться движение объектов в 1 измерении. Движение в 1 измерении — это движение по прямой линии.
Положение объекта на прямой линии можно однозначно определить по его расстояние от (выбранного пользователем) источника. (см. рис. 2.1). Примечание : позиция полностью определяется 1 координатой (поэтому это 1-мерное проблема).
Рисунок 2.1. Одномерное положение.
Рисунок 2. 2. графики зависимости x от t для различных скоростей.
2. графики зависимости x от t для различных скоростей.
Для данной задачи начало может быть выбрано в любой точке. удобный. Например, положение объекта в момент времени t = 0 часто выбран в качестве источника. Положение объекта в общем случае будет функцией времени: x(t). Рисунок 2.2. показывает положение в зависимости от времени для объект в состоянии покоя, а также для объектов, движущихся влево и вправо.
Наклон кривой на графике зависимости положения от времени зависит от скорость объекта. См., например, рисунок 2.3. Через 10 секунд гепард преодолел расстояние 310 метров, человек 100 метров, а свинья 50 метров. Очевидно, что гепард имеет наибольшую скорость. Похожий вывод получается, когда мы рассматриваем время, необходимое для покрытия фиксированного расстояние. Гепард преодолевает 300 метров за 10 с, человек за 30 с, а свинья требуется 60 с. Ясно, что более крутой наклон кривой зависимости x от t график соответствует более высокой скорости.
Рисунок 2.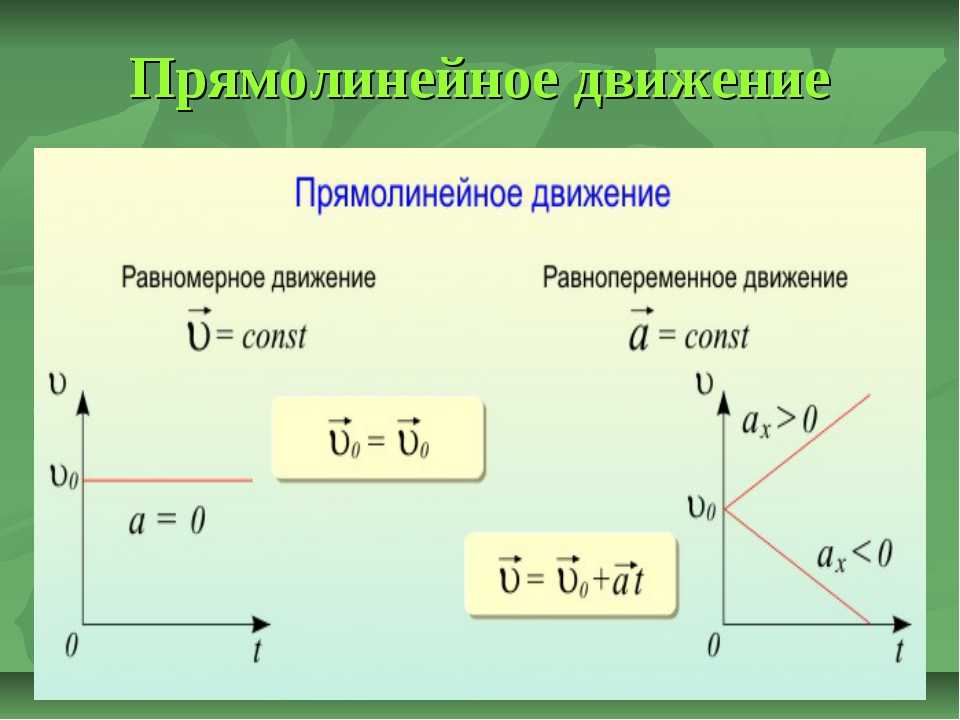 3. графики x и t для различных существ.
3. графики x и t для различных существ.
Объект, который меняет свое положение, имеет ненулевую скорость. В среднем скорость объекта в течение заданного интервала времени определяется как:
Если объект движется вправо, средняя скорость положительна. Ан объект, движущийся влево, имеет отрицательную среднюю скорость. Это ясно из определение средней скорости, которая зависит только от положения объекта в момент времени t = t 1 и в время t = t 2 . Это хорошо показано в задаче 2-1 из примера . и 2-2 .
Пример задачи 2-1
Вы едете на потрепанном пикапе по прямой дороге 5,2 мили со скоростью 43 мили в час, в этот момент у вас закончилось топливо. Вы идете на 2 мили дальше, до ближайшего АЗС, за 27 мин (= 0,450 ч). Какова ваша средняя скорость от время, когда вы завели свой грузовик, до того, как вы прибыли на станцию?
Пикап первоначально преодолевает расстояние 5,2 мили со скоростью
43 мили/час. Это занимает 7,3 минуты. После того, как у пикапа закончился
газа, вам потребуется 27 минут, чтобы дойти до ближайшей заправки, что составляет 1,2
миль вниз по дороге. Когда вы приедете на заправку, вы покрыли (5.2
+ 1,2) = 6,4 мили за период (7,3 + 27) = 34,3 минуты. Ваш средний
скорость до этой точки:
Это занимает 7,3 минуты. После того, как у пикапа закончился
газа, вам потребуется 27 минут, чтобы дойти до ближайшей заправки, что составляет 1,2
миль вниз по дороге. Когда вы приедете на заправку, вы покрыли (5.2
+ 1,2) = 6,4 мили за период (7,3 + 27) = 34,3 минуты. Ваш средний
скорость до этой точки:
Пример задачи 2-2
Предположим, вы затем везете топливо обратно в грузовик, делая туда и обратно за 35 мин. Какова ваша средняя скорость на всем пути от начало вашего движения к вам возвращение к грузовику с топливом ?
Вам потребуется еще 35 минут, чтобы вернуться к своей машине. Когда вы достигнете своего грузовик, вы снова находитесь в 5,2 милях от исходной точки и путешествовали уже (34,4 + 35) = 69,4 минуты. В этот момент ваша средняя скорость равна:
После этого эпизода вы возвращаетесь домой. Вы преодолеваете 5,2 мили
снова за 7,3 минуты (скорость 43 мили/час).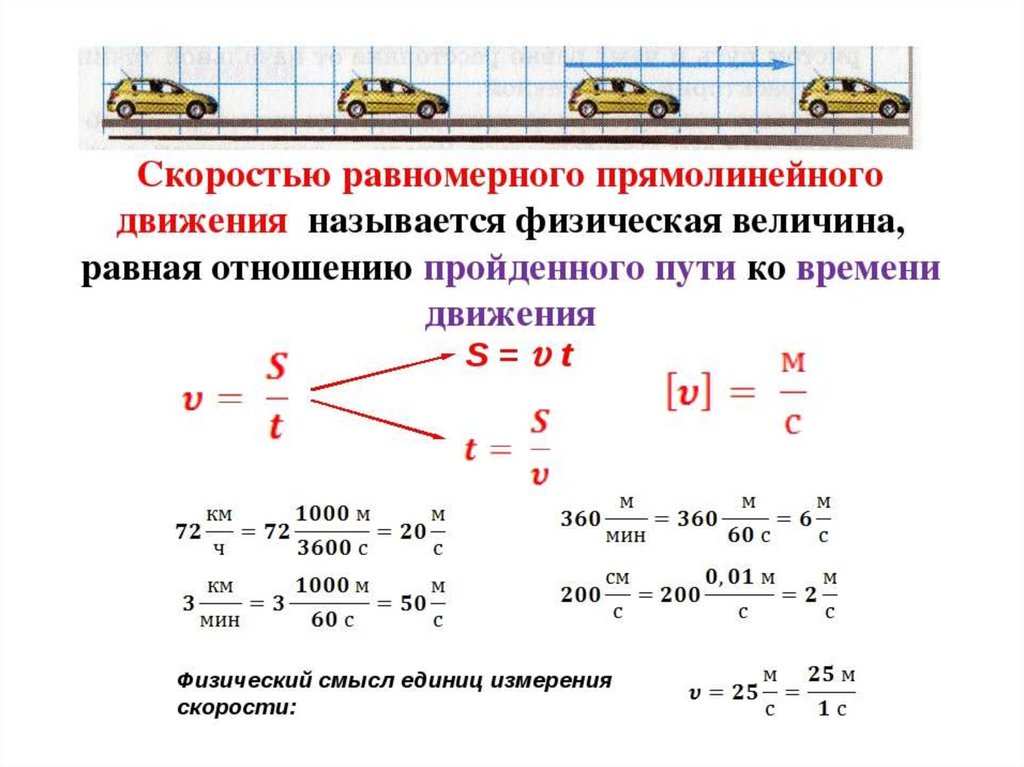 Когда ты приедешь домой,
вы находитесь в 0 милях от исходной точки, и, очевидно, ваша средняя скорость равна:
Когда ты приедешь домой,
вы находитесь в 0 милях от исходной точки, и, очевидно, ваша средняя скорость равна:
Средняя скорость пикапа, оставленного в гараже также 0 миль/час. Поскольку средняя скорость тела зависит только от его начальное и конечное положение и время, а не движение объекта в между, это вообще не полезный параметр. Более полезное количество мгновенная скорость объекта при данной мгновенный. Мгновенная скорость – это значение, при котором средняя скорость приближается по мере приближения временного интервала, в течение которого он измеряется, к нулю:
Например: см. пример задачи 2-5 .
Теперь можно рассчитать скорость объекта при t = 3,5 с:
Скорость объекта определяется с точки зрения изменения
положение этого объекта во времени. Величина, используемая для описания изменения
скорость тела во времени есть ускорение а. среднее ускорение за интервал времени между
t 1 и t 2 определяется как:
Величина, используемая для описания изменения
скорость тела во времени есть ускорение а. среднее ускорение за интервал времени между
t 1 и t 2 определяется как:
Обратите внимание на сходство между определением средней скорости и определение среднего ускорения. мгновенный ускорение a определяется как:
Из определения ускорения видно, что ускорение имеет следующие единицы измерения:
Положительное ускорение обычно интерпретируется как означающее увеличение скорости. Однако это неверно. Из определения ускорение, можно сделать вывод, что ускорение положительное, если
Это, очевидно, верно, если скорости положительны, а скорость
увеличивается со временем. Однако это верно и для отрицательных скоростей, если
скорость становится менее отрицательной с течением времени.
Объекты, падающие под действием силы тяжести, являются одним из примеров объектов движется с постоянным ускорением. Постоянное ускорение означает, что ускорение не зависит от времени:
Интегрируя это уравнение, скорость объекта может быть получено:
где v 0 — скорость объекта в момент времени t = 0. Из скорость, положение объекта как функцию времени можно рассчитано:
где x 0 — положение объекта в момент времени t = 0,
Примечание 1 : проверить эти отношения, интегрируя формулы для положение и скорость.
Примечание 2 : уравнения движения лежат в основе большинства задач (см. пример задачи 7).
Пример задачи 2-8
Заметив полицейскую машину, вы тормозите Porsche с 75 км/ч до 45 км/ч.
на дистанции 88 м. а) Чему равно ускорение, если считать его постоянным?
б) Сколько времени прошло? c) Если вы продолжаете замедляться с
ускорение, рассчитанное в (а) выше, сколько времени пройдет, чтобы привести
машина отдыхает с 75 км/ч? d) В (c) выше, какое расстояние будет
покрытый ? д) Предположим, что при втором испытании с рассчитанным ускорением
в (а) выше и с другой начальной скоростью, вы останавливаете свой автомобиль после
прохождение 200 м. Каково было общее время торможения?
Каково было общее время торможения?
а) Нашими отправными точками являются уравнения движения:
(1)
(2)
Предоставляется следующая информация:
* v(t = 0) = v 0 = 75 км/ч = 20,8 м/с
* v(t 1 ) = 45 км/ч = 12,5 м/с
* x(t = 0) = x 0 = 0 м (Примечание: начало координат определяется как положение Porsche при t = 0 с)
* х(т 1 ) = 88 м
* а = константа
Из уравнения (1) получаем:
(3)
Замените (3) в (2):
(4)
Из уравнения (4) мы можем получить ускорение a:
(5)
б) Подставьте уравнение (5) в уравнение (3):
(6)
в) Автомобиль находится в состоянии покоя в момент времени t 2 :
(7)
Подставив ускорение, рассчитанное с использованием уравнения (5), в уравнение (3):
(8)
d) Подставьте t 2 (из уравнения (8)) и a (из уравнения (5)) в уравнение (2):
(9)
д) Предоставляется следующая информация:
* v(t 3 ) = 0 м/с (Примечание: Porsche в состоянии покоя при t = t 3 )
* x(t = 0) = x 0 = 0 м (Примечание: начало координат определяется как положение Porsche при t = 0)
* х(т 3 ) = 200 м
* a = постоянная = – 1,6 м/с 2
Уравнение (1) говорит нам:
(10)
Подставьте уравнение (10) в уравнение (2):
(11)
Время t 3 теперь можно легко вычислить:
(12)
Частным случаем постоянного ускорения является свободное падение (падение в
вакуум). В задачах о свободном падении направление свободного падения
определяется вдоль оси Y, и положительное положение вдоль оси Y
соответствует восходящему движению. Ускорение свободного падения (g) равно 9,8.
м/с 2 (по отрицательной оси ординат). Уравнения движения на свободе
fall очень похожи на рассмотренные ранее для постоянных
ускорение:
В задачах о свободном падении направление свободного падения
определяется вдоль оси Y, и положительное положение вдоль оси Y
соответствует восходящему движению. Ускорение свободного падения (g) равно 9,8.
м/с 2 (по отрицательной оси ординат). Уравнения движения на свободе
fall очень похожи на рассмотренные ранее для постоянных
ускорение:
где y 0 и v 0 – положение и скорость объекта в момент времени t = 0,
Пример
Питчер подбрасывает бейсбольный мяч вертикально вверх с начальной скоростью 25 м/с. (а) Сколько времени нужно, чтобы достичь высшей точки? б) на какой высоте находится мяч подняться выше точки его выброса? в) Через какое время мяч достигнет точка на 25 м выше точки его выброса.
Рисунок 2.4. Вертикальное положение бейсбольного мяча как функция времени.
а) Нашими отправными точками являются уравнения движения:
Начальные условия:
* v(t = 0) = v 0 = 25 м/с (движение вверх)
* y(t = 0) = y 0 = 0 м (Примечание: начало координат определяется как положение мяча в т = 0)
* г = 90,8 м/с 2
Высшая точка получена в момент времени t = t 1 . В этот момент скорость равна нулю:
Мяч достигает высшей точки через 2,6 с (см. рис. 2.4).
б) Положение шара в момент t 1 = 2,6 с легко определить. рассчитано:
c) Уравнение для y(t) можно легко переписать как:
где у — высота мяча в момент времени t. Это уравнение может быть легко решается для t:
Используя начальные условия, указанные в (а), это уравнение можно использовать для расчета времени достижения мячом высоты 25 м (y = 25 м):
t = 1,4 с
t = 3,7 с
Рис.

 На рисунке выше тело 2 движется равнозамедлено.
На рисунке выше тело 2 движется равнозамедлено. Этой точке соответствует скорость v1 = 0 м/с.
Этой точке соответствует скорость v1 = 0 м/с.

 Эта работа находится под лицензией OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Эта работа находится под лицензией OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0). org/details/books/university-physics-volume-1
org/details/books/university-physics-volume-1