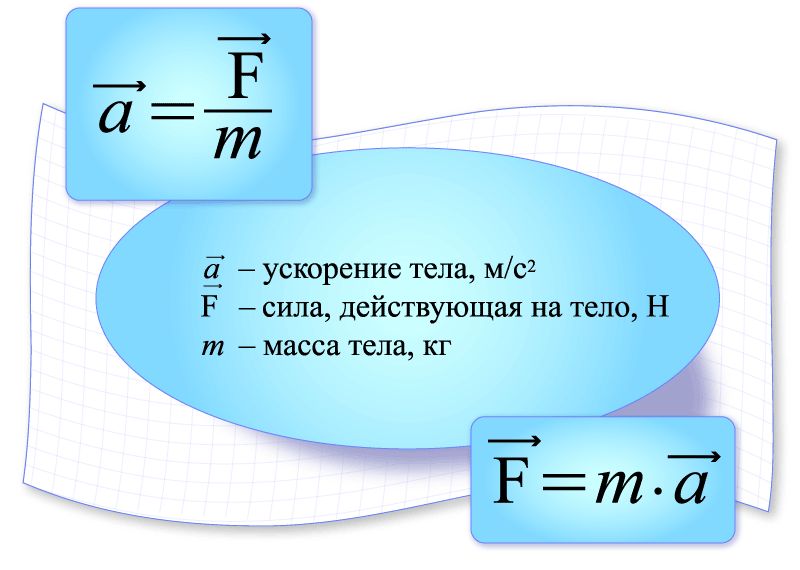
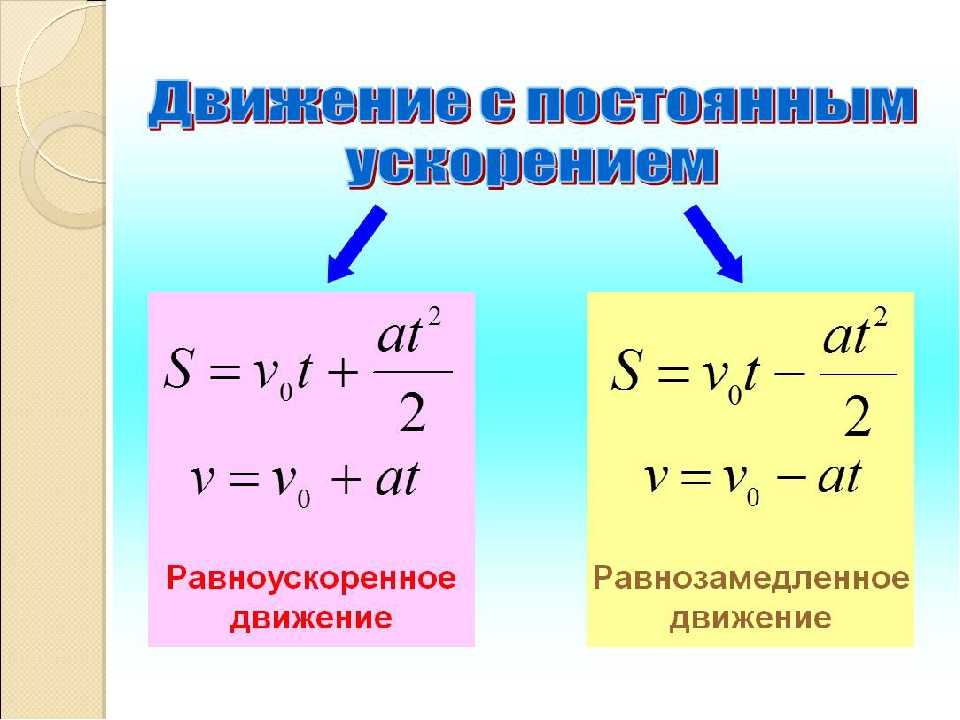
Формула ускорение в физике: Ускорение – формула, определение, закон кратко (физика 9 класс) - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

2$).

Движение с ускорением, вектор которого не меняется по модулю и направлению, называется равноускоренным.

Определить ускорение при равноускоренном прямолинейном движении можно по формуле:

Где $v_1, v_0$ — скорости в начале и в конце рассматриваемого периода времени длительностью $t$.

Отношение изменения скорости к промежутку времени, за который произошло это изменение, называют средним ускорением:

В отличие от равноускоренного, здесь имеют значение направления векторов.

Если начальная скорость больше конечной, происходит замедление, которое в физике также принято называть ускорением, но выраженным с отрицательным знаком.

Мгновенное ускорение — ускорение, развиваемое за очень малый промежуток времени (его длительность стремится к нулю):

Содержание

Ускорение при движении по окружности

Поскольку ускорение — векторная величина, при движении отличном от прямолинейного оно не остается неизменным даже если модуль скорости не изменяется. В связи с этим ускорение вычисляется из начальной и конечной скоростей по правилам векторной математики, т. е. с учетом изменения направления.

Тело, движущееся по окружности, удобно рассматривать как обладающее двумя ускорениями: тангенциальным ($a_$), направленным по касательной к траектории, и центростремительным, направленным к центру ($a_n$). При равномерном движении по окружности тангенциальное ускорение, отражающее мгновенную скорость тела, может быть равно нулю, но центростремительное имеет место даже в этом случае. Поэтому любое движение по криволинейной траектории является движением с ускорением.

Готовые работы на аналогичную тему

Центростремительное ускорение называется также нормальным, тангенциальное — касательным.

Касательное ускорение определяется как мгновенное при движении на очень малое угловое расстояние, когда длина дуги и длина хорды между начальной и конечной точками малоразличимы (сравниваются мгновенные скорости в этих точках).

Формула для определения центростремительного ускорения:

Где $v$ — мгновенная скорость, $R$ — радиус траектории.

При движении по искривленной траектории величину результирующего ускорения получают из тангенциального и нормального исходя из теоремы Пифагора:

Такое ускорение называется полным.

Найти ускорение тела, разгоняющегося за 10 с от 5 до 100 км/ч.

Под действием различных физических сил тела ускоряют или замедляют свое движение.

Spravochnick. ru

24.04.2017 4:12:57

2017-04-24 04:12:57

Источники:

Https://spravochnick. ru/fizika/formuly_uskoreniya_v_fizike/

Ускорение – формула, определение, закон кратко (физика 9 класс) » /> » /> .keyword { color: red; }

Ускорение по физике

Из курса физики 9 класса известно, что движение бывает равномерным и неравномерным. При неравномерном движении за равные промежутки времени материальная точка проходит разные расстояния, мгновенная скорость её движения также изменяется. Мера быстроты изменения скорости называется ускорением. Поговорим на эту тему, дадим определение ускорения, приведём его формулу.

Ускорение движения

Большинство движений в природе неравномерны. Если рассмотреть такое движение, то расстояния, проходимые за одинаковые промежутки времени будут разными. Следовательно, и скорость (она равна отношению пройденного расстояния ко времени прохождения) тоже будет разной.

Рис. 1. Пример неравномерного движения.

Более того, для разных движений изменение скорости за одинаковые промежутки времени также будет неодинаково. К примеру, рассмотрим разгон мяча и автомобиля. К концу разгона и тот и другой могут достичь мгновенной скорости 50 метров в секунду. Однако автомобиль достигает такой скорости за десять секунд, а мяч — в сто раз быстрее, за одну десятую секунды. Как охарактеризовать такое различие?

Физическая величина, характеризующая быстроту изменения скорости, называется ускорением.

Формулу ускорения легко получить, если учесть, что скорость — это быстрота изменения координаты, а ускорение — это быстрота изменения скорости:

Фактически ускорение — это «скорость изменения скорости». Поэтому формула ускорения аналогична формуле скорости, только в числителе вместо координаты стоит скорость.

Из приведённой формулы можно получить единицу измерения ускорения. Поскольку скорость в системе СИ измеряется в метрах в секунду, а время — в секундах, то ускорение получается в метрах в секунду в квадрате (иногда говорят метр в секунду за секунду).

Рис. 2. Ускорение в физике.

Равноускоренное движение

По аналогии со скоростью ускорение может быть средним и мгновенным. Мгновенное ускорение — это ускорение, для которого промежуток времени измерения стремится к нулю:

В противном случае ускорение получается средним за время $t$.

Движение, при котором мгновенное ускорение в любой момент времени остаётся постоянным и равным среднему ускорению за любой промежуток времени, называется равноускоренным. При равноускоренном движении скорость изменяется по линейному закону.

Примером равноускоренного движения является свободное падение тела в первые секунды, когда сопротивление воздуха ещё пренебрежительно мало.

Рис. 3. Свободное падение тела.

Что мы узнали?

Быстроту изменения скорости характеризует такая физическая величина, как ускорение. Единица измерения ускорения — метр в секунду за секунду. Движение, при котором мгновенное ускорение постоянно в любой момент времени, называется равноускоренным.

Рис. 1. Пример неравномерного движения.

Рис. 3. Свободное падение тела.

В противном случае ускорение получается средним за время t.

Obrazovaka. ru

23.09.2018 13:44:25

2018-09-23 13:44:25

Источники:

Https://obrazovaka. ru/fizika/uskoreniya-formula. html

Ускорение тела в физике, теория и онлайн калькуляторы » /> » /> .keyword { color: red; }

Ускорение по физике

Ускорением тела называют векторную величину показывающую быстроту изменения скорости движения тела. Обозначают ускорение как $\overline$.

Среднее ускорение тела

Допустим, что в моменты времени $t$ и $t+\Delta t$ скорости равны $\overline(t)$ и $\overline(t+\Delta t)$.

Получается, что за время $\Delta t$ скорость изменяется на величину:

\[\Delta \overline=\overline\left(t+\Delta t\right)-\overline\left(t\right)\left(1\right),\]

Тогда среднее ускорение тела равно:

Мгновенное ускорение тела

Устремим промежуток времени $\Delta t$ к нулю, тогда из уравнения (2) получим:

Формула (3) является определением мгновенного ускорения. Принимая во внимание, что в декартовой системе координат:

\[\overline=x\left(t\right)\overline+y\left(t\right)\overline+z\left(t\right)\overline\left(4\right),\ а\ \overline=\frac(5)\]

Из выражения (6) следует, что проекции ускорения на оси координат (X, Y,Z) равны:

При этом модуль ускорения найдем в соответствии с выражением:

Для выяснения вопроса о направлении ускорения движения тела Вектор скорости представим как:

Где $v$ — модуль скорости тела; $\overline$ — единичный вектор касательный к траектории движения материальной точки. Подставим выражение (8) в определение мгновенной скорости, получим:

Единичный касательный вектор $\overline$ определяется точкой траектории, которая в свою очередь характеризуется расстоянием ($s$) от начальной точки.

Значит вектор $\overline$ — это функция от $s$:

Параметр $s$ — функция от времени. Получаем:

Где вектор $\overline$ по модулю не изменяется. Это означает, что вектор $\frac$ перпендикулярен $\overline$. Вектор $\overline$ является касательным к траектории, $\frac$ перпендикулярен к этой касательной, то есть, направлен по нормали, которая называется главной. Единичный вектор в направлении главной нормали обозначим $\overline$.

Величина $\left|\frac>\right|=\frac$, где $R$ — радиус кривизны траектории.

И так мы получили:

Принимая во внимание, что $\frac=v$, из (9) можно записать следующее:

Выражение (13) показывает, что полное ускорение тела состоит из двух компонент, которые взаимно перпендикулярны. Тангенциального ускорения ($_$), направленного по касательной к траектории движения и равного:

Модуль полного ускорения равен:

Единицей измерения ускорения в Международной системе единиц (СИ) является метр на секунду в квадрате:

Прямолинейное движение тела

Если траекторией движения материальной точки является прямая, то вектор ускорения направлен вдоль той же прямой, что и вектор скорости. 2,$ чему равны ускорения этих двух точек в момент времени, когда равны их скорости, если $A$, B, C,D, E.F — постоянные большие нуля.

Решение: Найдем ускорение первой материальной точки:

У второй материальной точки ускорение будет равно:

Мы получили, что точки движутся с постоянными ускорениями, которые не зависят от времени, поэтому момент времени, в который скорости равны, искать не обязательно.

Ответ: $a_1=-2С\frac$, $a_2=2F\frac$

Задание: Движение материальной точки задано уравнением: $\overline\left(t\right)=A\left(\overline\ >\right),$ где $A$ и $\omega $ — постоянные величины. Начертите траекторию движения точки, изобразите на ней вектор ускорения этой точки. Каков модуль центростремительного ускорения ($a_n$) точки в этом случае?

Решение:

Рассмотрим уравнение движения нашей точки:

В координатной записи уравнению (2.1) соответствует система уравнений:

Возведем в квадрат каждое уравнение системы (2.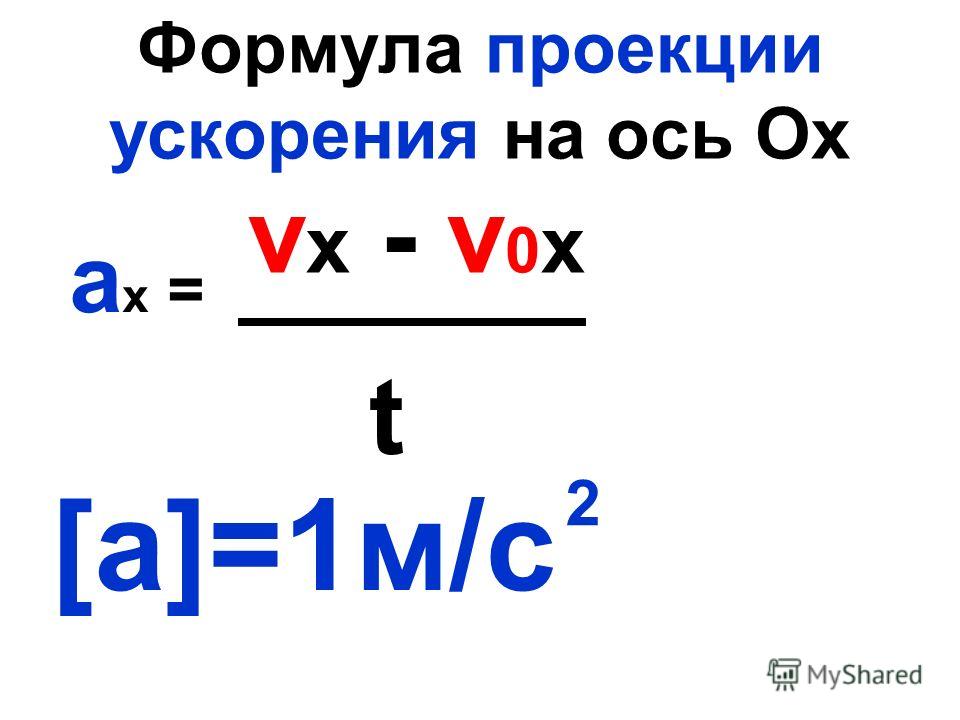 2) и сложим их:

Мы получили уравнение окружности радиуса $A$ (рис.1).

Величину центростремительного ускорения, учитывая, что радиус траектории равен А, найдем как:

Проекции скорости на оси координат равны:

Величина скорости равна:

Подставим результат (2.6) в (2.4), нормальное ускорение равно:

Легко показать, что движение точки в нашем случае является равномерным движением по окружности и полное ускорение точки равно центростремительному ускорению. Для этого можно взять производную от проекций скоростей (2.5) по времени и используя выражение:

Допустим, что в моменты времени $t$ и $t+\Delta t$ скорости равны $\overline(t)$ и $\overline(t+\Delta t)$. Получается, что за время $\Delta t$ скорость изменяется на величину:

\[\Delta \overline=\overline\left(t+\Delta t\right)-\overline\left(t\right)\left(1\right),\]

Тогда среднее ускорение тела равно:

Для этого можно взять производную от проекций скоростей 2.

Www. webmath. ru

30.11.2020 10:13:05

2020-11-30 10:13:05

Источники:

Https://www. webmath. ru/poleznoe/fizika_96_uskorenie_tela. php

что такое ускорение? ? по физике — Спрашивалка

МС

Мария Саркисян

ускорение

@……..

Ускоре́ние — производная скорости по времени, векторная величина, показывающая, на сколько изменяется вектор скорости точки (тела) при её (его) движении за единицу времени (то есть ускорение учитывает не только изменение величины скорости, но и её направления).

ЛА

Людмила Андрианова

Ускорение (в русскоязычной литературе обычно обозначается a) — векторная величина, характеризующая быстроту изменения скорости тела.

Например, вблизи Земли падающее на Землю тело, в случае, когда можно пренебречь сопротивлением воздуха, увеличивает свою скорость примерно на 9,8 м/с каждую секунду, то есть, его ускорение равно 9,8 м/с^2. 2, производная единица системы СГС

Aleksey Uljnkin

мне балл пожалуйста

Анна Гуреева

Это движение, которое совершается под воздействием силы. Когда к движущемуся предмету постоянно преложена сила, а другие силы не действуют или находятся в равновесии. Вы должны понять, что толчок – не преложенная сила. Сила должна как бы чувствоваться постоянно. Представьте, что вы хоть и двигаетесь, но вас толкают с одной и той же силой. Вы будете двигаться все быстрее и быстрее, пока сила не прекратится.

СИ

Серых Ирина

Нет, ребята! Ускорение-это не прибавка “скорости к скорости”! Ускорение-это энергия движения. Она есть и в постоянном движении и, даже, в замедляющемся движении. Что меняет, если начальная скорость больше конечной, или скорости равны? Есть одна, основная-СРЕДНЯЯ-скорость. ОТ неё надо “плясать”! Кстати, при свободном падении (на Земле) ускорение не 9,8,а 4,9 м/сек. сек. 9,8-это скорость в конце первой секунды падения. Есть v начальное, v-конечное, и средняя скорость-at. Если начальная скорость при свободном падении равна 0, то конечная скорость будет 2at. И формула будет s=2att/2 (площадь треугольника). Все расчёты по механике на мощность, разгон, КПД…. надо забыть. Пока за основу расчётов не будете брать СРЕДНЮЮ скорость при движении. Пример: какая мощность мотора Вашего автомобиля, если известна масса его и время разгона до 100 км/час? f=ma m=1170 кг. t=18 сек. v конеч. =27,7 м/сек. a=v/t v- СРЕДНЯЯ- =13,9 м. /сек. a=13,9:18=0,77 f=1170 х 0,77=903 кг. м. Это 12 л. с. А мотор ваших “Жигулей”-75 л. с. Это-5625 кг. м. КПД-16 % У всех машин!
Вот упрощенная формула для автомобилей: 12N=ma N-в “лошадиных силах” сразу, чтобы не переводить кг. м. в л. с. (Жигули….) 12*75=1170*a a=0,77 м/сек. сек Время разгона до сотни- 13,9:0,77=18 секунд. (проверь-те на своей машине… И КПД и мощность..)
Теперь можно узнать, какую мощность надо при езде по асфальту, грунтовке, или по бездорожью. .. И какой будет расход топлива!

Елена !

Чтобы было понятнее, скорость изменения скорости. Или функция скорости во времени.

ВБ

Владимир Белов

Величина, численно равная изменению скорости тела в единицу времени.

Сергей Коськин

мне бал тоже

Макс Ловягин

Ускорение-это физическая величена, определяющая быстрому изменения скорости тела, то есть первая производная от скорости по времени.

СР

Сергей Редькин

Ускорение – это величина, которая характиризует быстроту изменения скорости

АК

Анна Куляба

at-средняя скорость. Она=4,9..м/сек. 2at-конечная скорость. Она=9,8..м/с. V=at. V-средняя скорость. Расчёты надо вести из средней скорости: V=at. a=4,9 м/сс

NД

Neo Джаборов

для описания движения тел с изменяющейся скоростью необходима физическая величина характеризуюшая процесс изменения скорости с течением времени

ДК

Дашута Косенкова

Ускорение – это величина, которая характиризует быстроту изменения скорости . Единица ускорения – 1 м / с 2

ВБ

Владимир Бобков

В формуле Ньютона S=att/2 – ошибка! Площадь треугольника-(путь) -можно рассчитать: 9,8/2*t – (V/2*t)- но ускорение из 9,8… нельзя, т. к. это не средняя скорость.
Средняя скорость (at)-это равномерное движение, НАЧАЛЬНАЯ скорость=КОНЕЧНОЙ. Средняя скорость-(0+V конечная) /2=at. V конечная=2at. Формула будет: (0+2at)/2. V средняя=2at/2 т. е V=at
S=at*t (без /2). a=S/tt. (а было 2S/tt)
Ньютон пытался уравнять ускорения 2S/tt и F/m, но мешало /2…
“Если что-то двигается-значит оно имеет вес, и на него действует сила”…
S/tt и F/m Ньютон назвал “ускорением”. S/tt-это изменение скорости, а F/m-это сила, которая изменяет скорость движения. И они РАВНЫ !!!s/tt=F/m.
Путь, время, вес можно измерить. Силу-только рассчитать! Искать просто “а”- бессмысленно. А вот с помощью ускорения можно найти S,V,t,F,m,КПД….
Ошибочно считают, что ускорение-это “прибавка скорости к скорости”. Вовсе нет!
Это ЭНЕРГИЯ движения. (у машины-бензин). Если машина прошла путь S за время t, то НЕ имеет значения как она двигалась. ..скорость нарастала, или наоборот, или она равномерно прошла весь путь, рывками, с остановками…. СРЕДНЯЯ скорость будет одна: S/t=V (средней). А V ср. =at.
Для простоты расчётов удобнее всего брать “равномерное движение”,что и есть “средняя скорость”.При равномерном движении ускорение такое-же, как и с нарастанием скорости. (а что говорит 2-й Закон Ньютона ?)…
Формула, которую всю жизнь искал Ньютон: S/tt=F/m. Под эту формулу подходит любой пример движущегося тела….
Пример: камень весом …20 кг. передвинули на…. 15 м. за… 20 секунд. Какую приложили силу. Решение: (не надо и ускорение искать): 15:400=F:20. F=0,75 кг. м
Машина. S=…200 м. t=…25 секунд, m=…1650 кг. кпд двс=16% (у ВСЕХ 16%)
Решение: 200/625=F/1650. F=528 кг. м. Это (при 100% кпд) При 16%=3300 кг. м/с
3300:75=44 л. с. (мотор у такой машины может и 500 л. с., но ТРЕБУЕТСЯ всего 44)

ДР

Дмитрий Рушатов

V=at только в одном случае: когда это равномерное движение, и V нач. =V конечной. А это есть СРЕДНЯЯ скорость. V мгновенная-это тоже СРЕДНЯЯ скорость: нач. мгновения-конец мгновения: (v+V)/2=V ср. =at. Но сначала найди-те “время”….
У “яблока..” конеч. скорость 9,8…-это НЕ скорость at, по-скольку V нач. =0. Вот тут и кроется ошибка в поиске ускорения. S/t=V ср. =at. V кон. =2Vср=2at. S=(0+2at)/2*t. S=att !(без/2).
“График движения НЕ имеет значения ни для Средней, ни для Ускорения.”, по-скольку “а”-это ЭНЕРГИЯ движения, которая вызывает изменение скорости .
“Равномерного” движения НЕ бывает. Любая скорость движения: “разгон- накат”.При не равномерном движении “Накат” больше “разгона”-(скорость растёт), или “накат” меньше “разгона”0 -(скорость снижается).
…Бегун пробежал 100 м. за 10 сек. V ср. =10 м/с…. Фактически, он ни ОДНОГО метра не пробежал “равномерно”! Он сделал 50 прыжков ускоряясь -(разгон), и снижая скорость до 0-“накат”. ..
И машина 100 м. за 10 сек.: “рабочий” такт- “разгон”, остальные-“накат”.
Но путь при разгоне превышал путь наката. Скорость росла.
…Если v нач. больше 0, и движение “р. ускор., то формула такая:
S=(v+v+2at)/2*t. (2v+2at)/2*t. vt+att=S. Если v=0, то S=att !
Нельзя искать “а”: (V-v)/t. Правильно: (v+V)/2t, или (V+v)/2t. (“график движения НЕ имеет значения”..)
Основная задача Законов Ньютона- найти СИЛУ (F) !. S,t,v,m…можно измерить. “ключик”–“ускорение”!

Похожие вопросы

Задача для физиков. Тангенциальное ускорение

Как найти ускорение тела? физика. кинематика.

что такое ускорение в физике?

Что такое ускорение и для чего его нужно знать?

Задачка по физике. Ускорение

Физика. Ускорение свободного падения

Что такое ускорение? определение по физике

что токое ускорение. физика

что такое центростремическое ускорение и угол рефрикации. физика

Что такое капилляр (в физике)???

Ускорение свободного падения, равноускоренное движение

Авторы
Руководители
Файлы работы
Наградные документы

Ковелин Д. А. 1

1МАОУ СОШ №15 г. Челябинска

Васильева И.В. 1

1МАОУ СОШ №15 г. Челябинска

Автор работы награжден дипломом победителя III степени

Диплом школьникаСвидетельство руководителя

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

Введение

Путешествуя на машине, мы заметили, что во время спуска в гору стоит указатель угла спуска. И задумались: «Для чего нужны эти данные?». Как взаимосвязаны между собой угол наклона горы, скорость и время, за которое машина будет спускаться с него. Изучая данный вопрос, нами было замечено, что часто дорожные катастрофы на склонах происходят именно из-за того, что водители не могут рассчитать, на какой скорости им нужно съезжать, не учитывают вид движения при спуске, а как следствие, не могут предугадать свой тормозной путь. Если бы на уроках физики учителя демонстрировали на опытах и давали четкое представление, где применяется данные знания, то школьники задумались о серьезности и важности изучения равноускоренного движения. Таким образом, в будущем уменьшая дорожные катастрофы и аварии.

Джанколи и Савельев И.В. говорят о равнопеременном движении, в которое входит равноускоренное и равнозамедленное движение, дают сложное математическое определение ускорению, использую дифференциал скорости по времени. В курсе физике 9-10 классов авторами Кабардиным и Касьяновым рассматриваются основные виды равнопеременного движения и вводятся основные формулы для нахождения координаты, расстояния, скорости и ускорения.

Существует много разнообразных способов продемонстрировать равноускоренное движение, тем более, что, имея под рукой современный телефон мы можем без особого труда измерить время, но погрешность данного эксперимента будет огромной. Наш эксперимент поможет точно установить, за какой время скатится шарик и затем, по данной формуле, найти его скорость.

Таким образом, цель нашего исследования заключается в следующем: определение ускорения материальной точки в зависимости от угла наклонной поверхности.

Задачи:

Изучить характеристики равноускоренного движения, изучив литературу по данному вопросу.

Вывести формулы движения по наклонной плоскости.

Собрать экспериментальную модель, для точного замера времени скатывания шарика.

Провести эксперимент.

Гипотеза: скорость шарика прямо пропорциональна углу наклона плоскости.

Глава 1. Теоретическая часть

1.1. Ускорение при разных видах движения

Все на уроках физкультуры играют в баскетбол. Но никто не задумывается как мяч движется во время полета. Оказывается, что при подбрасывании вверх его движение равнозамедленное, а при падении − равноускоренное. Но какое движение называют равноускоренным, а какое равнозамедленным и вообще, что такое ускорение?

Ускорение − физическая векторная величина, которая характеризует быстроту изменения скорость движения.

Ускорение является важной кинематической характеристикой материальной точки. Ускорение характеризует быстроту изменения скорости.[3] Если, например, ускорение тела равно 5 м/с², то это означает, что за каждую секунду скорость тела изменяется на 5 м/с.

Обозначается:

Единица измерения: [a] = [м/с²][4]

В ходе нашего исследования мы сравнивали равномерное движение и равнопеременное, к которому относятся равноускоренное и равнозамедленное движение (Таблица 1)

Таблица 1

Сравнительная таблица основных видов движения

Характеристики	Равномерное движение	Равнопеременное движение
Характеристики	Равномерное движение	Равноускоренное движение	Равнозамедленное движение
Проекция скорости	Не изменяется t	Увеличивается	Уменьшается
Проекция ускорения	0	Положительное	Отрицательное
Пример	Движение Земли вокруг Солнца	Свободное падения тел	Мяч подбросили вверх

[2]

1. 2.Характеристики равноускоренного движения

При равноускоренном прямолинейном движении координата тела меняется с течением времени в соответствии с законом движения:

( 1.1)

где x₀– начальная координата материальной точки, _0x– проекция начальной скорости и a_x– проекция ускорения точки на ось 0X.

Проекция скорости материальной точки на ось 0х в этом случае меняется по следующему закону:

(1.2)

При этом проекции скорости и ускорения могут принимать различные значения, в том числе и отрицательные. При равноускоренном движении a_x > 0.[2]

Графики зависимости x(t) и (t) представляют собой соответственно прямую и параболу (Рис.1), причем, как и в алгебре, по коэффициентам в уравнениях прямой и параболы можно судить о расположении графика функции относительно координатных осей. Соответственно прямая (t) имеет отрицательный наклон (tg= a_x> 0).[5]

Рис.1. Графики для x(t),_x(t) в случае x₀> 0, ₀_x> 0, a_x > 0.[2]

1.3. Наклонная плоскость

Наклонная плоскость— это плоская поверхность, установленная под углом к горизонтали. Наклонная плоскость является одним из простых механизмов. Она позволяет поднимать груз вверх, прикладывая к нему усилие, заметно меньшее, чем сила тяжести, действующая на этот груз (Рис. 2). Примерами наклонных плоскостей служат пандусы и трапы. Принцип наклонной плоскости можно видеть также в таких колющих и режущих инструментах, как стамеска, топор, плуг, клин, винт.[1]

Введем ось Ох направив ее вдоль движения шарика вниз, за начало отсчета возьмем вершину наклонной плоскости т.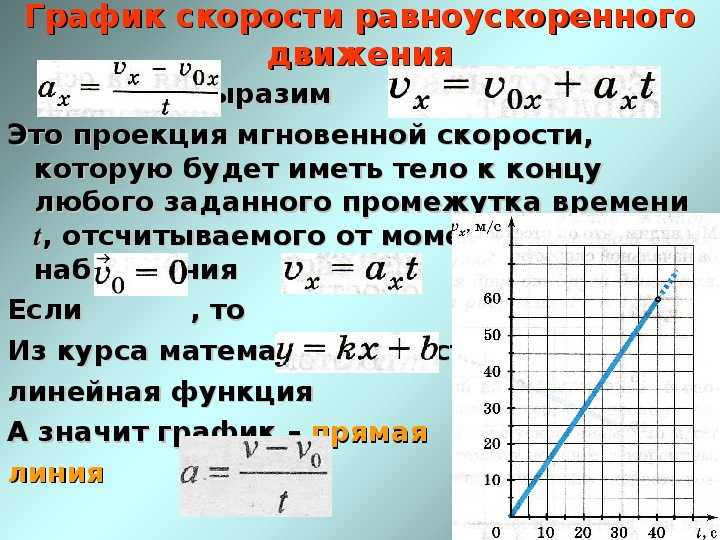 О. Тогда движение шарика будет являться равноускоренным видом движения, где начальная скорость равна нулю, т.е. м/с, [1,3]

Ох

Рис. 2. Наклонная плоскость

В формулы (1.1) и (1.2) подставим м/с,

(1.3)

Из формулы (1.3) можем без особого труда выразить ускорение:

(1.5)

А зная ускорение, всегда можно найти скорость по формуле (1.4), если знаешь время.[5]

Глава 2. Практическая часть

2.1. Описание экспериментальной установки

Наша установка (Рис.3) представляет из себя две деревянные плоскости, металлический шарик и секундомер.

2.2 Принцип работы установки

Используется закон равноускоренного движения, когда мяч скатывается вниз, набирая скорость. При этом его ускорение остается неизменным. Под разным углом наклона-разная скорость скатывания. На шарик действует сила тяжести, сопротивления качению, закон тяжести и упругости тела. Векторная (результирующая сила) сумма этих сил определяет ускорение тела.

Рис.3 Установка

Как будет проходить ход нашей работы.

Включаем секундомер кнопкой М.

Устанавливаем экспериментальную установку под углом 10°.

Фиксируем шарик у верхней черной полосы.

Отпускаем шарик.

Фиксируем время, за которое шарик скатился.

Сбрасываем секундомер кнопкой S.

Повторяем наш эксперимент с шариком под другими углами.

Записываем полученные результаты в таблицу.

2. 3.Лабораторная работа на тему: «Исследования ускорения материальной точки от угла наклона плоскости»

Лабораторная работа № 1

Тема: Определение ускорения движения тела.

Цель: определить ускорение движения тела. Найти зависимость ускорения от угла наклона поверхности.

Оборудование: поверхность, с изменяющемся углом относительно горизонта; секундомер.

Ход работы:

включите секундомер, нажав кнопку «M»;

установите определенный угол;

обнулите секундомер, нажав кнопку «S»;

зафиксируйте один из шариков возле красной линии;

отпустите шарик;

следите за включением и выключением секундомера;

вычислите по формуле (1. 6) ускорение шарика.

(1.6)

занесите полученные данные в таблицу 2;

измените угол наклона плоскости и проведите аналогичные измерения и вычисления.

Таблица 2

Исследование зависимости ускорения от угла наклона плоскости

Угол				60°
t,сек.	0,88	0,65	0,50	0,41
a,	1,47	2,69	4,56	6,78

Вывод: В данной лабораторной работе мы определили ускорение движения металлического шарика и определили зависимость ускорения от угла наклона поверхности

2. 4. Лабораторная работа на тему: «Определение скорости шарика в конце пути»

Лабораторная работа № 2

Тема: определения зависимости скорости шарика в конце пути по наклонной плоскости от угла наклона поверхности.

Цель: определить зависимости скорости шарика в конце пути по наклонной плоскости от угла наклона поверхности.

Оборудование: поверхность, с изменяющемся углом относительно горизонта; секундомер.

Ход работы:

найдите скорость в конце пути, используя формулу (1.4):

заполните таблицу 3, используя данные лабораторной работы 1

Таблица 3

Исследование зависимости скорости от ускорения и времени

				60°
	1,47	2,69	4,56	6,78
t,сек.	0,88	0,65	0,50	0,41
	1,29	1,74	2,28	2,77

Сделайте вывод на основе проведенного исследования.

Вывод: В данной лабораторной работе мы определили зависимость скорости шарика в конце пути по наклонной плоскости от угла наклона поверхности.

Заключение

В данной работе мы смогли изучить характеристики равноускоренного движения, собрать установку и провести эксперимент, записав полученные данные в таблицы. На основании этих измерений, можно будет по выведенной формуле сделать расчеты для транспортных средств, двигающихся со склона или в гору, чтобы предотвратить аварии и предугадать тормозной путь. Также это поможет школьникам в изучении темы по физике про равноускоренное движение и его измерение.

Список литературы

https://spravochnick.ru/fizika/statika/naklonnaya_ploskost/

Джанколи Д., Глава 2. Движение: кинематика в одном измерении / Д. Джанколи. // Физика. Т. I — М.: Мир, 1989. — С.32-64. — 656 с.

Кабардин О.Ф. Законы механического движения / О.Ф. Кабардин // Физика. 9 класс: учеб. для общеобразоват. организаций. — М.: Просвещение, 2014. — С.11-58. —176 с.

Касьянов В.А., Дмитриева В.Ф. Законы взаимодействия и движения тел / В.А. Касьянов. В.Ф. Дмитриева // Рабочая тетрадь по физике. 9 класс. К учебнику – Перышкина А.В. , Гутник Е.М —М.: Просвещение, 2013. — С.4-79. —208 с.

Савельев И.В. Механика, колебания и волны, молекулярная физика / И.В. Савельев // Курс общей физики. Т.I. — М.: Наука, 1970. —500 с.

Просмотров работы: 210

Ускорение и сила. Движение. Теплота

Ускорение и сила

Если на тело силы не действуют, то оно может двигаться только без ускорения. Напротив, действие на тело силы приводит к ускорению, и при этом ускорение тела будет тем большим, чем больше сила. Чем скорее мы хотим привести в движение тележку с грузом, тем больше придется напрягать свои мускулы. Как правило, на движущееся тело действуют две силы: ускоряющая – сила тяги, и тормозящая – сила трения или сопротивления воздуха.

Разность этих двух сил, так называемая результирующая сила, может быть направлена вдоль или против движения. В первом случае тело убыстряет движение, во втором – замедляет. Если эти две противоположно действующие силы равны одна другой (уравновешиваются), то тело движется равномерно, так, как если бы на него вообще не действовали силы.

Как же связаны сила и создаваемое ею ускорение? Ответ оказывается очень простым. Ускорение пропорционально силе:

(Знак означает «пропорционально».)

Но остается решить еще один вопрос: как влияют свойства тела на его способность ускорять движение под действием той или иной силы? Ведь ясно, что одна и та же сила, действуя на различные тела, придает им разные ускорения.

Ответ на поставленный вопрос мы найдем в том замечательном обстоятельстве, что все тела падают на Землю с одинаковым ускорением. Это ускорение обозначают буквой g. В районе Москвы ускорение g = 981 см/с².

Непосредственное наблюдение, на первый взгляд, не подтверждает одинаковости ускорения для всех тел. Дело в том, что при падении тел в обычных условиях, кроме силы тяжести, на них действует и «мешающая» сила – сопротивление воздуха. Различие в характере падения легких и тяжелых тел весьма смущало философов древности. Кусок железа падает быстро, пушинка парит в воздухе. Медленно опускается на Землю раскрытый лист бумаги, однако, свернутый в комок, этот же лист падает значительно быстрее. То, что воздух искажает «истинную» картину движения тела под действием Земли, понимали уже древние греки. Однако Демокрит думал, что, если даже удалить воздух, тяжелые тела будут всегда падать быстрее, чем легкие. А ведь сопротивление воздуха может привести и к обратному – скажем, листок алюминиевой фольги (широко развернутой) будет падать медленнее, чем шарик, скомканный из точно такого же кусочка фольги.

Кстати говоря, сейчас изготовляется металлическая проволока такой тонины (несколько микрон), что она парит в воздухе, как пушинка.

Аристотель считал, что в вакууме все тела должны падать одинаково. Однако из этого умозрительного заключения он делал следующий парадоксальный вывод: «падение разных тел с одинаковой скоростью настолько абсурдно, что ясна невозможность существования вакуума».

ИСААК НЬЮТОН (1643–1727) – гениальный английский физик и математик, один из величайших ученых в истории человечества. Ньютон сформулировал основные понятия и законы механики, открыл закон всемирного тяготения, создав тем самым физическую картину мира, остававшуюся неприкосновенной до начала XX века. Он разработал теорию движения небесных тел, объяснил важнейшие особенности движения Луны, дал объяснение приливов и отливов. В оптике Ньютону принадлежат замечательные открытия, способствовавшие бурному развитию этого раздела физики. Ньютон разработал могучий метод математического исследования природы: ему принадлежит честь создания дифференциального и интегрального исчисления. Это оказало громадное влияние на все последующее развитие физики, способствовало внедрению в нее математических методов исследования.

Никто из ученых древних и средних веков не догадался проверить на практике, с разными или одинаковыми ускорениями падают на Землю тела. Лишь Галилей своими замечательными опытами (он исследовал движение шаров по наклонной плоскости и падение тел, сбрасываемых с вершины наклонной Пизанской башни) показал, что все тела, вне зависимости от массы, падают в одном и том же месте земного шара с одинаковым ускорением. В настоящее время эти опыты весьма просто продемонстрировать при помощи длинной трубки, из которой выкачан воздух. Пушинка и камень падают в такой трубке совершенно одинаково: на тела действует лишь одна сила – вес, сопротивление воздуха сведено к нулю. При отсутствии сопротивления воздуха падение любых тел является равномерно-ускоренным движением.

Теперь вернемся к вопросу, поставленному выше. Как способность тела ускорять движение под действием заданной силы зависит от его свойств?

Закон Галилея говорит, что все тела, вне зависимости от их массы, падают с одним и тем же ускорением; значит, масса m кг под действием силы в m кГ движется с ускорением g.

Теперь предположим, что речь идет не о падении тел и на массу m кг действует сила в 1 кГ. Так как ускорение пропорционально силе, то оно будет в m раз меньше g.

Мы пришли к выводу, что ускорение тела a при заданной силе (в нашем примере в 1 кГ) обратно пропорционально массе.

Объединяя оба вывода, мы можем записать:

т.е. при неизменной массе ускорение пропорционально силе, а при неизменной силе обратно пропорционально массе.

Закон, связывающий ускорение с массой тела и действующей на него силой, был открыт великим английским ученым Исааком Ньютоном (1643–1727) и носит его имя*6.

Ускорение пропорционально действующей силе и обратно пропорционально массе тела и не зависит ни от каких других свойств тела. Из закона Ньютона следует, что именно масса является мерой «инертности» тела. При одинаковых силах труднее ускорить тело большей массы. Мы видим, что понятие массы, с которой мы ознакомились как со «скромной» величиной, определяемой взвешиванием на рычажных весах, приобрело новый глубокий смысл: масса характеризует динамические свойства тела.

Закон Ньютона мы можем записать так:

kF = mа,

где k – постоянный коэффициент. Этот коэффициент зависит от выбранных нами единиц.

Вместо того, чтобы пользоваться уже имевшейся у нас единицей силы (кГ), поступим иным образом. Как это часто стараются делать физики, подберем единицу силы так, чтобы коэффициент пропорциональности в законе Ньютона равнялся единице. Тогда закон Ньютона примет такой вид:

F = ma.

Как мы уже говорили, в физике принято измерять массу в граммах, путь – в сантиметрах и время – в секундах. Систему единиц, основанную на этих трех основных величинах, называют системой CGS (произносится «це-же-эс») или по-русски СГС.

Теперь подберем, пользуясь сформулированным выше принципом, единицу силы. Очевидно, сила равна единице в том случае, если она массе в 1 г придает ускорение, равное 1 см/с². Такая сила получила в этой системе название дины.

Согласно закону Ньютона, F = ma, сила выражается в динах, если m граммов будет умножено на a см/с². Поэтому пользуются такой записью:

Вес тела обозначается обычно буквой P. Сила P дает телу ускорение g, и, очевидно, в динах

P = mg.

Но у нас уже была единица силы – килограмм (кГ). Связь между новой и старой единицей находим сразу же из последней формулы:

1 килограмм (веса) = 981000 дин.

Дина – очень маленькая сила. Она равна примерно одному миллиграмму веса.

Мы упоминали уже о новой системе единиц (СИ), разработанной совсем недавно. Название для новой единицы силы ньютон (Н) вполне заслужено. При таком выборе единицы написание закона Ньютона будет наиболее простым, а определяют эту единицу так:

т.е. 1 ньютон – это сила, которая сообщает массе в 1 кг ускорение 1 м/с².

Нетрудно связать эту новую единицу с диной и с килограммом:

1 ньютон = 100000 дин = 1/9,8 кГ.

2. Центробежная сила

2. Центробежная сила Раскройте зонтик, уприте его концом в пол, закружите и бросьте внутрь мячик, скомканную бумагу, носовой платок – вообще какой-нибудь легкий и неломкий предмет. Вы убедитесь, что зонтик словно не желает принять подарка: мяч или бумажный ком сами

Сила = геометрия

Сила = геометрия Несмотря на постоянные болезни, Риман в конечном счете изменил бытующие представления о значении силы. Еще со времен Ньютона ученые считали силу мгновенным взаимодействием удаленных друг от друга тел. Физики называли ее «дальнодействием», это означало,

Самая загадочная сила природы

Самая загадочная сила природы Не говорю уже о том, как мало у нас надежды найти когда-нибудь вещество, непроницаемое для тяготения. Причина тяготения нам неизвестна: со времен Ньютона, открывшего эту силу, мы ни на шаг не приблизились к познанию ее внутренней сущности. Без

Глава 3 Гравитация — первая фундаментальная сила

Глава 3 Гравитация — первая фундаментальная сила С небес на землю и обратно В современной физике говорят о четырех фундаментальных силах. Первой открыли силу гравитации. Известный школьникам закон всемирного тяготения определяет силу притяжения F между любыми массами

Столкнувшись с неожиданным: ускорение Вселенной

Столкнувшись с неожиданным: ускорение Вселенной В начале 1990-х годов две разные группы ученых занялись измерением расстояния до сверхновых звезд (см. гл. 3) в надежде определить замедление Вселенной нахождением ее нынешней скорости расширения, которая, по их мнению, должна

73 Сила в сантиметрах, или Наглядно закон Гука

73 Сила в сантиметрах, или Наглядно закон Гука Для опыта нам потребуются: воздушный шарик, фломастер. В школе проходят закон Гука. Жил такой знаменитый ученый, который изучал сжимаемость предметов и веществ и вывел свой закон. Закон этот очень простой: чем сильнее мы

Сила – вектор

Сила – вектор Сила, так же как и скорость, есть векторная величина. Ведь она всегда действует в определенном направлении. Значит, и силы должны складываться по тем правилам, которые мы только что обсуждали.Мы часто наблюдаем в жизни примеры, иллюстрирующие векторное

Ускорение

Ускорение Для того чтобы охарактеризовать непостоянство скорости, физика пользуется понятием ускорения.Ускорением называют изменение скорости за единицу времени. Вместо того чтобы говорить: «скорость тела изменилась на величину a за 1 секунду», мы говорим короче:

Сила Кориолиса

Сила Кориолиса Своеобразие мира вращающихся систем не исчерпывается существованием радиальных сил тяжести. Познакомимся с еще одним интересным эффектом, теория которого была дана в 1835 году французом Кориолисом.Поставим перед собой такой вопрос: как выглядит

Сила и потенциальная энергия при колебании

Сила и потенциальная энергия при колебании При всяком колебании около положения равновесия на тело действует сила, «желающая» возвратить тело в положение равновесия. Когда точка удаляется от положения равновесия, сила замедляет движение, когда точка приближается к

Великая сила «пустяков»

Великая сила «пустяков» У Леночки Казаковой может оторваться пуговица от платья, но она от этого не перестанет быть Леночкой Казаковой. Законы науки, особенно законы физики, не допускают ни малейшего неряшества. Воспользовавшись аналогией, можно сказать, что законы

Лошадиная сила и работа лошади

Лошадиная сила и работа лошади Мы часто слышим выражение «лошадиная сила» и привыкли к нему. Поэтому мало кто отдает себе отчет в том, что это старинное наименование совершенно неправильно. «Лошадиная сила» – не сила, а мощность и притом даже не лошадиная. Мощность – это

Сила звука

Сила звука Как ослабевает звук с расстоянием? Физик ответит вам, что звук ослабевает «обратно пропорционально квадрату расстояния». Это означает следующее: чтобы звук колокольчика на тройном расстоянии был слышен так же громко, как на одинарном, нужно одновременно

Аномальное ускорение расширения Вселенной

Аномальное ускорение расширения Вселенной В 1998 году две исследовательские группы, независимо друг от друга, обнаружили поразительную аномалию расширения нашей Вселенной[75]. В 2011 году руководители групп (Сол Перлмуттер и Адам Рисс из Калифорнийского университета

Формула среднего ускорения с примерами и задачами

Механика

Формула ускорения

Это полное руководство, чтобы научиться находить ускорение в физике с помощью формулы ускорения.
Итак, если вы хотите извлечь пользу из этого руководства, вам понравятся практические советы в этом новом руководстве.
Это руководство включает:

Определение ускорения
Формула ускорения
Примеры из жизни
Типы
Подробнее

Давайте начнем.

Что такое ускорение?

В физике ускорение определяется как скорость изменения скорости тела во времени. Когда скорость тела изменяется, говорят, что оно ускоряется. Ускорения являются векторными величинами. Метр на секунду в квадрате ( м/с²) является единицей измерения ускорения. Положительное ускорение и отрицательное ускорение — это два типа ускорения.

Что такое формула ускорения?

Мы можем найти ускорение по следующей формуле и из второго закона Ньютона.

Принимая a за ускорение, начальную скорость за Vi, конечную скорость за Vf и t за интервал времени, единица ускорения в системе СИ метр в секунду за секунду мс ^-2

Ускорение по отношению к силе

С другой стороны, ньютоновская механика устанавливает для тела постоянной массы (m), рассматриваемого инерциальным наблюдателем, отношение пропорциональности по отношению к приложенной к объекту силе (F) и полученному ускорению (a), т. е. :
Ж = м. к
Это соотношение справедливо в любой инерциальной системе отсчета и позволяет вычислить ускорение по следующей формуле:
a = F / m
Эта формулировка подчиняется второму закону Ньютона.

Примеры ускорения

Некоторые примеры ускорения приведены в списке ниже:
1.- Когда вы нажимаете педаль акселератора в автомобиле, автомобиль движется все быстрее и быстрее. Это изменение скорости и есть ускорение.
2.- Если одна и та же сила используется для толкания грузовика и автомобиля, автомобиль будет иметь большее ускорение, чем грузовик, потому что автомобиль имеет меньшую массу.
3.- Пустую тележку легче толкать, чем полную, потому что полная тележка имеет большую массу, чем пустая.
4.- Объект двигался на север со скоростью 10 метров в секунду. Объект ускоряется и теперь движется на север со скоростью 15 метров в секунду. Объект был ускорен.
5.- При движении скейтборда ногой происходит изменение ускорения. Давай быстрее.

Что такое среднее ускорение в физике?

Среднее ускорение тела, указанное в приведенном выше уравнении, равно a за время t. Пусть время t разделено на множество меньших промежутков времени. Если скорость изменения скорости на протяжении всех этих интервалов остается постоянной, то и ускорение остается постоянным. Говорят, что такое тело обладает равномерным ускорением.

формула среднего ускорения

Равномерное ускорение в физике

«Тело имеет равномерное ускорение, если его скорость изменяется одинаково за равные промежутки времени, какими бы короткими они ни были».

Типы ускорения

Существует два типа ускорения:

Положительное ускорение
Отрицательное ускорение

Что такое положительное ускорение?

Ускорение тела положительно, если его скорость увеличивается со временем. Направление этого ускорения совпадает с направлением движения тела без изменения направления.

Примеры положительного ускорения

Когда поезд покидает станцию, его скорость увеличивается с увеличением времени, это пример положительного ускорения.
Когда мы запускаем транспортное средство, его скорость увеличивается со временем, это положительное ускорение.

Что такое отрицательное ускорение?

Ускорение тела отрицательно, если скорость тела уменьшается. Направление отрицательного ускорения противоположно направлению движения тела. Отрицательное ускорение также называют замедлением или запаздыванием.

Примеры отрицательного ускорения

Когда поезд достигает станции, его скорость со временем уменьшается, этот тип ускорения называется отрицательным ускорением.

аналогично:
Например, лифт, движущийся вверх (что мы принимаем за направление положительной скорости), может ускоряться вверх с положительным ускорением и двигаться быстрее или ускоряться вниз с отрицательным ускорением и двигаться медленнее.
Когда он движется вниз с отрицательной скоростью, он может ускоряться вниз с отрицательным ускорением и двигаться медленнее. Когда ускорение и скорость имеют положительные знаки, так что скорость (величина скорости) уменьшается, мы говорим о замедлении.
Как рассчитать ускорение свободного падения?
«Ускорение свободно падающих тел называется ускорением свободного падения». Бросьте объект с некоторой высоты и наблюдайте за его движением. Его скорость увеличивается, уменьшается или остается постоянной по мере приближения к земле? Галилей был первым ученым, заметившим, что все свободно падающие тела имеют одинаковое ускорение независимо от их массы.

Примеры расчета ускорения

Гоночный автомобиль увеличивает свою скорость с постоянной скоростью 18,5 м/с до 46,1 м/с за 2,47 секунды. Каким будет его среднее ускорение?

A = DV / DT = (V _F – V _I) / (T _F – T _I), где V _F = 46,1 м / с, V _I = 18. / с, t _f = 2,47 с, t _i = 0 с.
Итак: a = (46,1 – 18,5) / 2,47 = 11,17 м/с ²

Мотоциклист едет со скоростью 22,4 м/с и понимает, что ошибся с маршрутом. Нажмите на тормоз, и мотоцикл остановится через 2,55 с. Каково будет его замедление?

A = DV / DT = (V _F – V _I) / (T _F – T _I), где V _F = 0 M / S, V _I = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 22.4 = 224. м/с, t _f = 2,55 с, t _i = 0 с.
Итак: а = (0 – 22,4) / 2,55 = -8,78 м/с Каково будет ускорение толкаемого тела?

а = Ф/м, где Ф = 10 Н, м = 2 кг.
Таким образом:
a = 10/2 = 5 м/с ²

Кто-то тянет предмет мебели весом 400 кг в одну сторону с суммарной силой 150 ньютонов. Другой человек толкает его в том же направлении с силой 200 ньютонов, но в противоположном направлении дует ветер с силой 10 ньютонов. Каково будет ускорение мебели?

Мы знаем, что a = F / m, где чистая сила будет суммой сил в том же смысле минус противодействующая им: F = 150 Н (человек 1) + 200 Н (человек 2) – 10 Н (ветер), что дает 340 Н. Мы также знаем, что m = 400 кг.
Тогда: а = 340 Н / 400 кг = 0,85 м/с . В этот момент дует восточный ветер силой 100 Н. Каково будет новое ускорение самолета, сохраняющего курс?

Поскольку сила ветра перпендикулярна направлению движения самолета, она не окажет никакого влияния на его движение. Он продолжит двигаться с ускорением на север со скоростью 2 м/с ² .

Два мальчика, один слабый и один сильный, играют в перетягивание каната, каждый на одном конце веревки. Первая тяга влево делает это с силой 5 Н, а вторая тянет в противоположном направлении с силой 7 Н. Принимая во внимание, что 1 ньютон (Н) равен 1 килограмму-метру в секунду в квадрате. (кг-м/с2), какое ускорение приобретет тело самого слабого ребенка, когда другой будет тянуть его в противоположном направлении?

Из F = ma мы знаем, что a = F/m, но мы должны найти результирующую силу, которая будет равна 2 Н (7 Н для сильного ребенка – 5 Н для слабого).
Затем, мы должны найти массу, которая для целей расчета должна быть выведена из силы, которой противодействует слабый ребенок, а именно: 1 Н = 1кг.м/с ² , то есть это величина силы мобилизовать килограмм массы со скоростью один метр в секунду в квадрате.
Следовательно, 5N = 5кг.м/с ² . Следовательно, m = 5 кг.
И, наконец, мы знаем, что a = 2N (F) / 5kg (m) = 0,4 м/с ²

Пожарная машина увеличивает свою скорость с 0 до 21 м/с на восток, за 3,5 секунды . Каково его ускорение?

Мы знаем, что: V _i = 0 м/с, V _f = 21 м/с, t = 3,5 секунды. Поэтому применим формулу:
a = dv / dt = (v _f – v _i ) / (t _f – t _i ), то есть a = 21м/с/3,5 с = 6 м/с ²

Автомобиль снижает свою скорость с 21 м/с на восток до 7 м/с на восток за 3,5,0 секунды. Каково его ускорение?

Зная, что V _i = 21 м/с, V _f = 7 м/с, t = 3,5 секунды, и что a = dv / dt = (v _f – v _i )/(t _f – t _i), вычислить его просто. :
а = 7м/с – 21м/с / 3,5с = -4м/с ² , то есть отрицательное ускорение (замедление).

Похожие темы:

Механика в физике
Виды движения
Виды сил
Первый закон Ньютона
Второй закон Ньютона
Третий закон Ньютона
Ускорение по сравнению с скоростью
Velocity
Скорость
Разница между расстоянием и смещением
Разница между скоростью и ускорением
. .com/physics/acceleration-formula
http://www.physicsclassroom.com/class/1DKin/Lesson-1/Acceleration

Функции положения, скорость и ускорение — Krista King Math

Функция положения также указывает направление

Распространенным применением производных является взаимосвязь между скоростью, скоростью и ускорением. В этих задачах обычно дается уравнение положения в форме «???x=???» или «???s(t)=???», что говорит вам о расстоянии объекта от некоторой контрольной точки. Это уравнение также учитывает направление, поэтому расстояние может быть отрицательным, в зависимости от того, в каком направлении ваш объект удалился от контрольной точки.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Средняя скорость объекта

???\text{средняя скорость}=\frac{\text{расстояние}}{\text{время}}???

Средняя скорость объекта

???\frac{\text{изменение положения}}{\text{изменение во времени}}=\frac{s(b)-s(a)}{ba} ???

Чтобы найти скорость, возьмите производную от исходного уравнения положения. Скорость есть абсолютное значение скорости. Скорость определяет направление движения, поэтому она может быть отрицательной. Это как скорость, но в определенном направлении. Скорость, с другой стороны, никогда не может быть отрицательной, потому что она не учитывает направление, поэтому скорость является абсолютным значением скорости. Чтобы найти ускорение, возьмите производную скорости.

Использование функции положения для определения скорости и ускорения

Пройти курс

Хотите узнать больше об исчислении 1? У меня есть пошаговый курс для этого. 🙂

Учить больше

Как найти скорость и ускорение

Пример

Предположим, что частица движется вдоль оси ???x???, так что ее положение в момент времени ???t??? определяется формулой 9{\ гидроразрыва {1} {2}}???

???a(1)=-\frac{3}{2}???

Поскольку ускорение отрицательно при ???t=1???, скорость должна уменьшаться в этой точке.

Поскольку скорость положительна и уменьшается при ???t=1???, это означает, что скорость в этой точке также уменьшается.

Начав с положения, продифференцировать, чтобы найти скорость, затем снова продифференцировать, чтобы найти ускорение

Расчет мгновенной скорости

Мы используем термин «мгновенная скорость» для описания скорости объекта в конкретный момент времени. Учитывая уравнение, которое моделирует положение объекта во времени, ???s(t)???, мы можем взять его производную, чтобы получить скорость, ???s'(t)=v(t)???. Затем мы можем подставить конкретное значение времени для расчета мгновенной скорости. 92+2???

???v(25)=9,377???

Скорость при ???t=25??? ???9,377??? РС.

8:45 — это время, когда начинается движение, а это значит, что время соответствует ???t=0???. Вопрос касается скорости после ???6??? минут прошло, в 8:51 утра, но в нашем уравнении положения, ???t??? измеряется в секундах. Превратим минуты в секунды.

???t=(6\\text{min})\left(\frac{60\s}{1\\text{min}}\right)???

???t=360??? s

Теперь мы можем подключить ???t=360??? в ???v(t)???. 92+2???

???v(360)=1 944 002???

Скорость в 8:51 ???1 944 002??? РС.

Получить доступ к полному курсу исчисления 1

Начать

Изучение математикиКриста Кинг 9 марта 2019 г. математика, изучение онлайн, онлайн-курс, онлайн-математика, функции положения, скорость, ускорение, положение, скорость, направление, производные

0 лайков
Урок 10: Ускорение
Ускорение — это вектор, который измеряет изменение скорости объекта.
Не забывайте, что скорость — это вектор, поэтому она имеет величины и направления .
Это означает, что ускорение может быть любым из следующих трех…
изменение скорости, величины скорости (с 34 км/ч до 67 км/ч)
изменение направления (с востока на северо-восток)
изменение как скорости, так и направления (с 34 км/ч на восток до 12 км/ч на запад)
Ускорение является мерой скорости изменения скорости.
Поскольку скорость является мерой скорости изменения смещения и имеет уравнение…
уравнение ускорения должно быть похоже. ..
a = ускорение (м/с/с или просто м/с ² )
Δv = изменение скорости ( м/с )
Δt = интервал времени ( с )
Обратите внимание на единицы измерения ускорения.
Так как мы берем скорость и делим на время, мы получим (без всякого упрощения) м/с/с единиц.
На самом деле это означает, что за каждую прошедшую секунду скорость объекта будет изменяться на это количество метров в секунду.
Чтобы было немного легче читать, мы используем немного математики, чтобы получить м/с ² для единиц.
Пример 1: Автомобиль, движущийся со скоростью 50 км/ч, разгоняется до 60 км/ч за 7,0 секунд. Определить его ускорение.
Сначала нам нужно изменить скорость из км/ч в м/с:
50 км/ч = 14 м/с
*Примечание. оставьте фактическое 13,88888889, которое вы видите на своем калькуляторе, для ваших расчетов… никогда не округляйте до конца задачи!!!
60 км/ч = 17 м/с (то же самое, что и другая скорость)
Теперь воспользуемся формулой, имея в виду, что Δv = v _f – v _i
а = Δv / Δt = (v _f – v _i ) / t
= (17 – 14) / 7,0
а = 0,40 м/с ²
Если вы получили другой ответ, проверьте следующее…
Вы использовали округленные значения 17 м/с и 14 м/с, или вы использовали фактические значения , которые вы видели на своем калькуляторе?
Когда вы добрались до конца, вы использовали правила округления в соответствии с цифрами ?
В физике ускорение — это не только увеличение скорости, но и уменьшение скорости.
Хотя вы, возможно, слышали, как люди используют слово замедление для описания замедления объекта, на самом деле это неправильная физика.
Торможение может означать только одно.
Вместо этого мы называем уменьшение скорости отрицательным ускорением.
Это на самом деле помогает нам при выполнении вычислений, а также позволяет нам придать большее значение ускорению.
Пример 2: Вы идете по улице и видите, как огромный огурец весом 112 кг катится к вам со скоростью 12 м/с. Вы, конечно, удивлены огурчиком такого размера, не говоря уже о том, что он катится по улице. Вы прыгаете перед ним и начинаете толкать его, пока, наконец, не остановите его через 27,4 секунды. В этот момент вы арестованы за вмешательство в «самый большой в мире чемпионат по прокатке солений». Определить ускорение рассола.
В этом примере у вас есть объект, который сначала движется, а в конечном итоге находится в состоянии покоя. Если вы подумаете о Δv = v _f – v _i части формулы ускорения, вы заметите, что конечная скорость равна нулю (вы остановили ее) минус еще одно число дает вам отрицательное Δv. Поскольку время никогда не бывает отрицательным, ваше ускорение будет отрицательным.
а = Δv / Δt = (v _f – v _i ) / т
= (0 – 12) / 27,4
а = -0,44 м/с ²
В этом случае отрицательный знак означает, что вы «отнимали» скорость у объекта, который изначально двигался в положительном направлении. Объект замедлялся.
Пример 3: После того, как вас арестовали, официальные лица начинают катить рассол обратно к стартовой линии, чтобы Хаанс ван дер Винкль, действующий чемпион из Нидерландов, мог сделать вторую попытку. После толчка в течение 8,8 с огурец катится назад (к линии старта) со скоростью 4,31 м/с. Определить ускорение рассола.
В этом примере они заставляют объект ускоряться, но он движется в противоположном направлении. Поскольку скорость — это вектор, мы можем просто поставить знак минус перед ее скоростью и сказать, что она движется в отрицательном направлении.
а = Δv / Δt = (v _f – v _i ) / t
= (-4,31 – 0) / 8,8
а = -0,49 м/с ²
В этом случае означает ли отрицательное ускорение, что рассол замедлялся? Нисколько! было ускорение в отрицательном направлении . Отрицательное ускорение может означать…
1. Объект, движущийся в положительном направлении (с положительной скоростью), замедляется.
или
2. Объект, движущийся в отрицательном направлении (с отрицательной скоростью), ускоряется.
Так как же уследить за всеми этими типами ускорения. «Ускорение назад означает… я не знаю!»
Попробуйте это. Мне всегда помогало.
Обычно мы визуализируем ускорение как положительное, а замедление как отрицательное. Я поставил это в верхнем ряду.
Положительная скорость означает, что она движется в положительном направлении (например, вперед), а отрицательное направление — назад.
А теперь поиграйте в «Морской бой».
положительный X положительный = положительный
положительный X отрицательный = отрицательный
отрицательный X отрицательный = положительный
Итак, читая таблицу, объект движется назад (-v), то есть движется все быстрее и быстрее (ускоряется) означает, что он имеет отрицательное ускорение .
Быстро нарисуйте это (по памяти) на листке бумаги в начале экзамена, чтобы не забыть!
Ускорение как изменение направления можно почувствовать, если вы находитесь в машине, проходящей поворот.
Даже если скорость та же (например, 50 км/ч), направление меняется
Вы чувствуете это ускорение, когда чувствуете, что ваше тело «толкается» к внешней стороне кривой.
Ваше направление меняется каждую секунду!
Вот почему важно различать «скорость» и «скорость» и почему мы определяем ускорение как изменение скорости .
Ускорение, как и скорость, имеет направление.
Если мы изменим либо скорость, либо направление, либо и то, и другое, скорость изменится, и мы ускоримся.
Кинематика — ускорение
Кинематика — ускорение
[Глава 2 цели]
БХС -> Мистер Стэнбро -> Физика -> Механика -> Кинематика -> эта страница
Что такое ускорение:
Ускорение — это скорость, с которой изменения скорости. Другими словами, зная ускорение объекта говорит вам о том, насколько высока скорость объект меняется.
Поскольку скорость — это скорость изменения положения, а ускорение – это скорость изменения скорости, ускорение – это «ставка ставки».
При ускорении:
Очень важно отметить, что ускорение определяется в с точки зрения изменения скорости – не скорости . Это может показаться как незначительный момент, но это не так. Поскольку ускорение – это скорость изменения скорости,
Вы ускоряетесь всякий раз, когда вы:
ускорить – Это не трудно понять, так как это общая концепция ускорения.
помедленнее – Люди обычно называют это замедление, как если бы оно физически отличалось от “ускорение” дела – а физику все равно – если ваша скорость меняется, вы ускоряетесь.
изменить направление – Это может быть сложно понять. Поскольку скорость — это ваша скорость и направление, ваша скорость изменяется, если меняется ваше направление (даже если ваша скорость остается прежней). такой же). Поскольку вы ускоряетесь, если ваша скорость меняется, вы ускоряетесь, когда меняете направление – даже если ваша скорость останется прежней . Большинство людей ссылаются ускорение с изменением скорости (и увеличением скорости), поэтому они думают: «Хорошо, на тесте я должен сказать, что объект ускоряется, если меняет направление, но это действительно какой-то «фальшивое» ускорение в отличие от «настоящего» ускорения ускорение” Нет. Это ускорение так же реально, как и «ускоряющий» (и «замедляющий») вид ускорения.
Чем ускорение не является:
Так как ускорение связано с изменением скорости – когда скорость меняется, вы ускоряетесь, студенты часто получают ошибочное представление о том, что «ускорение есть изменение скорости». НЕТ!! Ускорение – это скорость, с которой скорость изменения – есть важная разница!
Сказать, что «ускорение есть изменение скорости», все равно, что сказать «скорость — это изменение положения» (это звучит глупо, не правда ли? Это?). Скорость говорит вам, как быстро меняется положение. Ускорение сообщает вам, насколько высока скорость меняется.
Ускорение — это , а не изменение скорости!
Расчет ускорений:
Предположим, что скорость спринтера изменилась с 0 м/с до 10 м/с за 2 секунд в начале гонки. Каково ее ускорение?
Обратите внимание на нечетные единицы измерения ускорения – расстояние (длину), деленное в 2 раза. Одна единица времени получается из скорости в числителе дробь, а другой исходит из знаменателя. Количество Например, 4 мили/час/сек — это ускорение (4 мили/час/сек означает, что скорость изменяется на 4 мили/ч каждую секунду).
Работа с ускорениями:
Пример:
Автомобиль трогается с места и разгоняется со скоростью 2 м/с/с в течение 5 секунд. Как быстро это будет происходить?
Решение:
Утверждение «автомобиль трогается с места» означает, что автомобиль стартует скорость 0 м/с. Ускорение 2 м/с/с означает, что автомобиль скорость изменяется на 2 м/с каждую секунду. Если скорость автомобиля начинается при скорости 0 м/с и изменении на 2 м/с в первую секунду она будет равна 2 м/с по истечении 1 секунды. В течение второй секунды (?!) его скорость увеличивается на 2 м/с – с 2 м/с до 4 м/с. Его скорость будет быть 6 м/с через 3 секунды, 8 м/с через 4 секунды и 10 м/с через 5 секунд. секунды.
В качестве альтернативы, если вы предпочитаете, есть более алгебраический подход. Если тогда , так . Если скорость начинается с 0 м/с и изменяется на 10 м/с, она заканчивается на 10 РС.
Указание направления ускорения:
Как и скорость, ускорения в одномерных движениях положительные, если они действуют в положительном направлении, и отрицательные, если они действовать в негативном направлении. Определить направление немного более абстрактно для ускорений, чем для скоростей, однако – по крайней мере пока не привыкнешь.
Нужно помнить 3 вещи:
Ускорение объекта есть изменение его скорости разделить на время.
Если объект движется в положительном направлении, его скорость положительный. Если он движется в отрицательном направлении, скорость отрицательная.
Изменение скорости равно конечной скорости минус начальная скорость.
Пример:
Скорость автомобиля изменяется с +2 м/с до +10 м/с за 4 секунды. какая его ускорение?
Решение:
Изменение скорости автомобиля = конечная скорость – начальная скорость = 10 м/с – 2 м/с = 8 м/с. Его ускорение = его изменение скорости разделить на затраченное время = (8 м/с)/(4 с) = 2 м/с/с.
Пример:
Скорость автомобиля изменяется с +10 м/с до +2 м/с за 4 секунды. какая его ускорение?
Решение:
Изменение скорости автомобиля = конечная скорость – начальная скорость = 2 м/с – 10 м/с = -8 м/с. Его ускорение = его изменение скорости разделить на затраченное время = (-8 м/с)/(4 с) = -2 м/с/с.
Пример:
Скорость автомобиля изменяется с -2 м/с до -10 м/с за 4 секунды. какая его ускорение?
Решение:
Изменение скорости автомобиля = конечная скорость – начальная скорость = -10 м/с – (-2 м/с) = -10 м/с + 2 м/с = -8 м/с. Его ускорение = его изменение скорости, деленное на затраченное время = (-8 м/с)/(4 с) = -2 м/с/с.
Пример:
Скорость автомобиля изменяется с -10 м/с до -2 м/с за 4 секунды. какая его ускорение?
Решение:
Изменение скорости автомобиля = конечная скорость – начальная скорость = -2 м/с – (-10 м/с) = -2 м/с + 10 м/с = 8 м/с. Его ускорение = его изменение скорости, деленное на затраченное время = (8 м/с)/(4 с) = 2 м/с/с.
Из этих примеров обратите внимание, что вы просто следуете (простому) правила, особенно помня, что изменение скорости является конечная скорость минус начальная скорость – НЕ большое число минус маленькое число!
Расчет ускорений при изменении только направления:
В примерах выше вы видели, что это довольно просто вычислить ускорение тела при изменении его скорости используя алгебру. Объект также ускоряется, когда его направление изменяется, но «нормальной» алгебры недостаточно, чтобы вычислить ускорение в этот случай – вам нужно использовать векторной алгебры и не будем заморачиваться с вычислением этих ускорений в этом курсе.
Практический тест на ускорение:
Вам понадобится браузер с поддержкой Java, чтобы пройти практический тест по Первому закону Ньютона.

[Глава 2 цели]

БХС -> Мистер Стэнбро -> Физика -> Механика -> Кинематика -> эта страница

последнее обновление 22 ноября 2005 г., JL Стэнбро
Одномерное движение: одномерное движение с постоянным ускорением
В предыдущем разделе о положении, скорости и ускорение мы нашли что движение с постоянным ускорением задается позиционными функциями форма:
x ( t ) = в ² + v ₀ t + x ₀
где a ускорение (постоянное), v ₀ скорость во времени t = 0, а x ₀ — положение в момент времени t = 0. Скорость и ускорение функции для такой функции положения задаются уравнениями
v ( t ) = at + v ₀ и a ( t ) = a .
Теперь мы будем использовать эти уравнения для решения некоторых физических задач, связанных с движением. в одном измерении с постоянным ускорением.
Свободное падение
Первое приложение, которое мы обсудим, — это объекты в свободном падении. В В общем случае ускорение объекта в гравитационном поле Земли не равно постоянный. Если объект находится далеко, он будет испытывать более слабое гравитационное воздействие. сила, чем если бы он был рядом. Однако у поверхности земли ускорение свободного падения приблизительно постоянно и равно независимо от массы объекта (т. е. при отсутствии трения от ветра сопротивление, перо и рояль падают с одинаковой скоростью). Это почему мы можем использовать наши уравнения для постоянного ускорения для описания объектов в свободное падение вблизи земной поверхности. Значение этого ускорения равно а = 9,8 м/с ² . Однако с этого момента мы будем обозначать это значение через 90 870 г 90 871 , где 90 870 г 90 871 равно понимается как константа 9,8 м/с ² . (Обратите внимание, что это недействительно при больших расстояниях от поверхности земли: Луна, например, , а не ускоряются к нам со скоростью 9,8 м/с ² .)
Уравнения, описывающие объект, движущийся перпендикулярно поверхности земля (т.е. вверх и вниз) теперь легко писать. Если мы найдем источник нашего координаты прямо на земной поверхности, а положительное направление обозначим как то, что указывает вверх, мы находим, что:
x ( t ) = – gt ² + v ₀ t + x ₀
Обратите внимание на знак -, который возникает из-за ускорения силы тяжести. вниз, , в то время как положительное положение-направление было выбрано вверх.
Как это относится к объекту в свободном падении? Ну, если ты стоишь на вершине башни высотой х и отпустили предмет, начальная скорость объект v ₀ = 0, а исходное положение x ₀ = ч . Подстановка этих значений в приведенное выше уравнение мы находим, что движение объекта, свободно падающего с высота h определяется по формуле:
х ( т ) = – гт ² + ч
Если мы хотим узнать, например, сколько времени требуется объекту, чтобы достичь земля, мы просто устанавливаем x ( t ) = 0 и решить для t . Мы находим, что при t = объект ударяется о землю (т.е. достигает положения 0).
Выстрел пулей прямо вверх
Уравнение
x ( T ) = – GT ² + V ₀ T + x _{0870 T + x _{0870 .
для объекта, движущегося вверх и вниз вблизи земной поверхности, можно использовать для более
чем просто описание падающего объекта. Мы также можем понять, что происходит с
пуля, выпущенная прямо вверх с поверхности земли с начальной скоростью v ₀ . Поскольку начальное положение пули примерно x ₀ = 0,
уравнение для этого движения имеет вид:}}
x ( т ) = – гт ² + v ₀ т
С какой скоростью будет лететь пуля, когда она вернется и попадет в земной шар? Чтобы ответить на этот вопрос, мы должны (i) найти время, через которое пуля удариться о землю, и (ii) найти функцию скорости, чтобы мы могли оценить ее в то время. Настройка x ( t ) = 0 снова и решая для t мы находим, что либо t = 0 или t = 2 v ₀ / g . Ну т =0 это как раз время когда пуля ушла из землю, поэтому время, в которое она вернется, упав сверху, должно быть т = 2 v ₀ / г . Используя наши знания из предыдущего раздела, v ( t ) = – gt + v ₀ . Если подставляем t = 2 v ₀ / g , находим, что скорость пули при возвращении вниз и ударяется о землю – г (2 v ₀ / г ) + v ₀ = – v ₀ . Другими словами, пуля движется с той же скоростью, что и в момент выстрела, только в противоположное направление.
Формула ускорения (уравнение) в физике: как ее использовать
Формула ускорения — это одно из основных уравнений в физике, которое вы обязательно должны изучить и применить на практике. В конце концов, ускорение является одним из строительных блоков физики.
«Движение называется равноускоренным, если, начиная с состояния покоя, оно приобретает за равные промежутки времени равные скорости». — Галилео Галилей, Две новые науки, 1638
Общая формула для среднего ускорения может быть выражена как:
ускорение = (v _{Окончательный} −v _{Начальный} )/(t _{Окончательный} −t _{Первоначальный} )
Где v обозначает скорость, а t обозначает время. В алгебраической записи формула может быть выражена как:
a=Δv/Δt
Ускорение можно определить как скорость изменения скорости во времени. Ускорение — одно из самых основных понятий современной физики, лежащее в основе практически любой физической теории, связанной с движением объектов.
Единицей ускорения в системе СИ является метр в секунду в секунду (м/с ² ). Несомненно, всем знакомо ощущение ускорения, когда вы нажимаете на педаль газа и откидываетесь на свое сиденье. На самом деле почти каждый наблюдаемый эффект движения возникает из-за ускорения из-за влияния сил. Ускорение, как и скорость, является векторной величиной, то есть имеет как величину, так и направление. Строго говоря, нет такого понятия, как «замедление», есть только ускорение в противоположном направлении.
Ускорение — один из основных параметров движения. Параметры перемещения (d), скорости (v) и ускорения (a) имеют тесную математическую зависимость. Информация об одном из параметров может быть использована для определения неизвестной информации о других параметрах. В общем, есть 4 основных уравнения, которые связывают эти 3 параметра друг с другом и со временем:
d = v _i t+(1/2)at ²
v _f = v _i +в
v _f = v _i +2ad
d = ((v _i + v _f )/2)t
Эти 4 уравнения можно использовать для предсказания неизвестной информации о движении объекта на основе известной информации о движении объекта. Итак, если известно ускорение объекта, пройденное им расстояние и его начальная скорость, можно определить конечную скорость объекта. Точно так же, если бы кто-то знал начальную скорость объекта, ускорение и прошедшее время, он мог бы определить, какое расстояние он преодолел. Рассмотрим несколько простых примеров, иллюстрирующих использование этих формул.
«Ускорение конечно, я думаю, в соответствии с некоторыми законами физики». — Терри Райли
Использование формул ускорения
(1)
Скажем, вы находитесь на парусной лодке, а именно на 16-футовом Hobie Cat. Сначала вы едете со скоростью 3 м/с. Вы ловите сильный порыв ветра и через 7 секунд движетесь со скоростью 10 м/с. Какое у вас было среднее ускорение?
Подставив наши значения в формулу для среднего ускорения, мы получим a=(10−3)/7=7/7=1 м/с ² . Среднее ускорение лодки составляло один метр в секунду за секунду. Другой способ прочитать это значение — сказать: за каждую секунду ваша скорость увеличивается на один метр в секунду.
(2)
Самолет из состояния покоя начинает разгоняться со скоростью 3 м/с ² по взлетно-посадочной полосе, прежде чем окончательно оторваться от земли через 32 секунды. Какое расстояние пролетел самолет по земле до взлета?
В этом вопросе нам дается три элемента информации: начальная скорость самолета (0 м/с), ускорение самолета (3 м/с ² ) и продолжительность движения (32 секунды). Подставив эти значения в первое из четырех уравнений, приведенных выше:
d = v _i t+(1/2)at ²
дает нам:
d = (0)(32)+(0,5)(3)(32) ² = 1536 метров.
То есть до взлета самолет пролетел всего 1536 метров.
«Гравитация и ускорение эквивалентны». — Альберт Эйнштейн
(3)
Перышко падает на поверхность Луны с высоты 8 метров. Ускорение свободного падения на Луне 1,5 м/с ² . Через какое время перо упадет на землю?
В этом случае нам даны начальная скорость (0 м/с), ускорение (1,5 м/с ² ) и общее пройденное расстояние (8 м). Подставив эти значения в первое уравнение
d = v _i t+(1/2)at ²
дает нам:
8=(0)t+(0,5)(1,5)t ²
8=(0,5)(1,5)t ²
8=0,75 т ²
10,66=t ²
3,26 = t
Таким образом, перышку потребуется всего 3,26 секунды, чтобы попасть на поверхность Луны.
(4)
Стартовав из состояния покоя, ракетный корабль разгоняется со скоростью 15 м/с ² на расстоянии 650 м. Какова конечная скорость ракетного корабля?
В этом случае мы знаем начальную скорость (0 м/с), пройденное расстояние (650 м) и скорость ускорения (15 м/с ² ). Подставив эти значения в третье уравнение:
v _f = v _i +2ad
дает нам:
v _f = 0+2(15)(650)
v _f = (30)(650)
v _f = 19 500 м/с
Конечная скорость ракетного корабля составляет 19 500 м/с.
Мгновенное ускорение
До сих пор мы рассматривали только случаи, когда имеем либо среднее ускорение, либо ускорение равномерное. Однако простое среднее ускорение объекта может упустить важную информацию о движении этого объекта. Имея только среднее ускорение в течение определенного периода времени, вы не можете сказать, изменилось ли ускорение объекта в течение этого периода времени. Возможно, он начал ускоряться очень медленно, а затем его ускорение со временем увеличилось.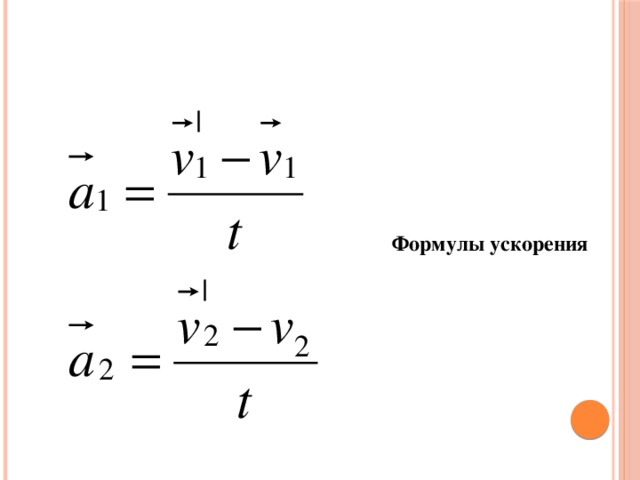 Что мы можем сделать, так это разделить эту продолжительность на более мелкие сегменты и рассчитать среднее ускорение для этих сегментов, что даст нам больше информации об объекте. Допустим, у нас есть некоторое расстояние от A до E. Мы можем разделить это расстояние на 4 сегмента AB, BC, CD и DE и вычислить среднее ускорение для каждого из этих интервалов.
Теперь представьте, что мы продолжаем делить это расстояние на более мелкие интервалы и вычислять среднее ускорение для этих интервалов до бесконечности. В конце концов, мы достигли бы точки, в которой у нас есть ускорение объекта в одной математической точке. Это также известно как его мгновенное ускорение — ускорение объекта в определенный момент времени. Мгновенное ускорение объекта можно рассматривать как среднее ускорение этого объекта за бесконечно малый интервал времени. Концепция мгновенного ускорения, возможно, является самой важной концепцией в физике и составляет основу практически всей ньютоновской физики. Можно определить мгновенное ускорение объекта, используя инструменты исчисления, чтобы найти вторую производную функции смещения объекта или первую производную функции скорости объекта.