Формула ускорения без пути: Скорость и путь при равноускоренном движении — урок. Физика, 9 класс.

Ускорение при равноускоренном прямолинейном движении

• Равноускоренное прямолинейное движение — движение по прямой линии с постоянным ускорением (a=const).
• Ускорение — векторная физическая величина, показывающая изменение скорости тела за 1 с. Обозначается как a.
• Единица измерения ускорения — метр в секунду в квадрате (м/с²).
• Акселерометр — прибор для измерения ускорения.

Формула ускорения

Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:

v — скорость тела в данный момент времени, v₀ — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость

Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.

Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе).

Получим 10 м/с.

Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:

Проекция ускорения

Проекция ускорения на ось ОХ

v_x — проекция скорости тела в данный момент времени, v_0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость

Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:

• Если вектор ускорения направлен в сторону оси ОХ, то его проекция положительна.
• Если вектор ускорения направлен в сторону, противоположную направлению оси ОХ, его проекция отрицательная.

При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.

Направление вектора ускорения

Направление вектора ускорения не всегда совпадает с направлением вектора скорости!

Равноускоренным движением

называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают (а↑↑v).

Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу (а↑↓v).

Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.

График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (a_x=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.

Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:

• Если график лежит выше оси времени, движение равноускоренное (направление вектора ускорения совпадает с направлением оси ОХ). На рисунке выше тело 1 движется равноускорено.
• Если график лежит ниже оси времени, движение равнозамедленное (вектор ускорения направлен противоположно оси ОХ). На рисунке выше тело 2 движется равнозамедлено.

Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.

Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее.

Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.

Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t₁ = 1 и t₂ = 3 с.

В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).

Чтобы найти ускорение в момент времени

t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.

В момент времени t₁ = 1с ускорение a = 2 м/с². В момент времени t₂ = 3 ускорение a = 0 м/с².

Задание EF18774

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси

Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

---

Алгоритм решения

1. Определить, какому типу движения соответствует график зависимости координаты тела от времени.
2. Определить величины, которые характеризуют такое движение.
3. Определить характер изменения величин, характеризующих это движение.
4. Установить соответствие между графиками А и Б и величинами, характеризующими движение.

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

• перемещение и путь;
• скорость;
• ускорение.

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

Ответ: 24

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17992 Начальная скорость автомобиля, движущегося прямолинейно и равноускоренно, равна 5 м/с. После прохождения расстояния 40 м его скорость оказалась равной 15 м/c. Чему равно ускорение автомобиля?

---

Алгоритм решения

1. Записать исходные данные.
2. Записать формулу, связывающую известные из условия задачи величины.
3. Выразить из формулы искомую величину.
4. Вычислить искомую величину, подставив в формулу исходные данные.

Решение

Запишем исходные данные:

• Начальная скорость v₀ = 5 м/с.
• Конечная скорость v = 15 м/с.
• Пройденный путь s = 40 м.

Формула, которая связывает ускорение тела с пройденным путем:

Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».

Выразим из формулы ускорение:

Подставим известные данные и вычислим ускорение автомобиля:

Ответ: 2,5

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18202

Внимательно прочитайте текст задания и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела v_x от времени.

Какой из указанных ниже графиков  совпадает с графиком зависимости от времени проекции ускорения этого тела a_x в интервале времени от 6 с до 10 с?

---

Алгоритм решения

1. Охарактеризовать движение тела на участке графика, обозначенном в условии задачи.
2. Вычислить ускорение движение тела на этом участке.
3. Выбрать график, который соответствует графику зависимости от времени проекции ускорения тела.

Решение

Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.

Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:

• t₁ = 6 с. Этой точке соответствует скорость v₁ = 0 м/с.
• t₂ = 10 с. Этой точке соответствует скорость v₂ = –10 м/с.

Используем для вычислений следующую формулу:

Подставим в нее известные данные и сделаем вычисления:

Этому значению соответствует график «г».

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18027 На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси х. Определите модуль ускорения тела.

---

Алгоритм решения

1. Записать формулу ускорения.
2. Записать формулу для вычисления модуля ускорения.
3. Выбрать любые 2 точки графика.
4. Определить для этих точек значения времени и проекции скорости (получить исходные данные).
5. Подставить данные формулу и вычислить ускорение.

Решение

Записываем формулу ускорения:

По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:

Выбираем любые 2 точки графика. Пусть это будут:

• t₁ = 1 с. Этой точке соответствует скорость v₁ = 15 м/с.
• t₂ = 2 с. Этой точке соответствует скорость v₂ = 5 м/с.

Подставляем данные формулу и вычисляем модуль ускорения:

Ответ: 10

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алиса Никитина | Просмотров: 13.2k

уравнение, формула ускорения и пройденного пути, график

Что такое равноускоренное движение: понятие в физике 

Равноускоренным называют неравномерное движение, при котором скорость объекта за одинаковые промежутки времени изменяется на одну и ту же величину.

При равноускоренном движении наблюдается зависимость скорости от времени. Выведем эту закономерность, которая поможет изучать и анализировать равноускоренное движение.

Закон зависимости времени от скорости можно вывести из определения ускорения:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

\(\vec a=\frac{\vec v-{\vec v}_0}t\)

Где \(\vec v\) — текущая или конечная скорость; \(\vec v_0\) — начальная скорость; t —  промежуток времени.

Найдем значение для\( \vec v\) из приведенного выше равенства:

\(\vec v=\vec v+\vec a\times t\) — векторное выражение закона зависимости скорости от времени при равноускоренном движении.

В проекции на ось х, закон будет иметь следующий вид:

\(v_x=v_{0x}+a_x\times t\)

Характеристики равноускоренного движения

Характеристиками равноускоренного движения являются:

• скорость;
• перемещение;
• ускорение.

Скоростью \((\vec v)\) называют векторную величину, характеризующую быстроту и направление движения.

Средняя скорость вычисляется по формуле:

\(\vec v=\frac{\Delta\vec r}{\Delta t}\)

Где \(\Delta\vec r\) — перемещение, которое осуществило тело, \(\Delta t\) — время, за которое случилось это перемещение.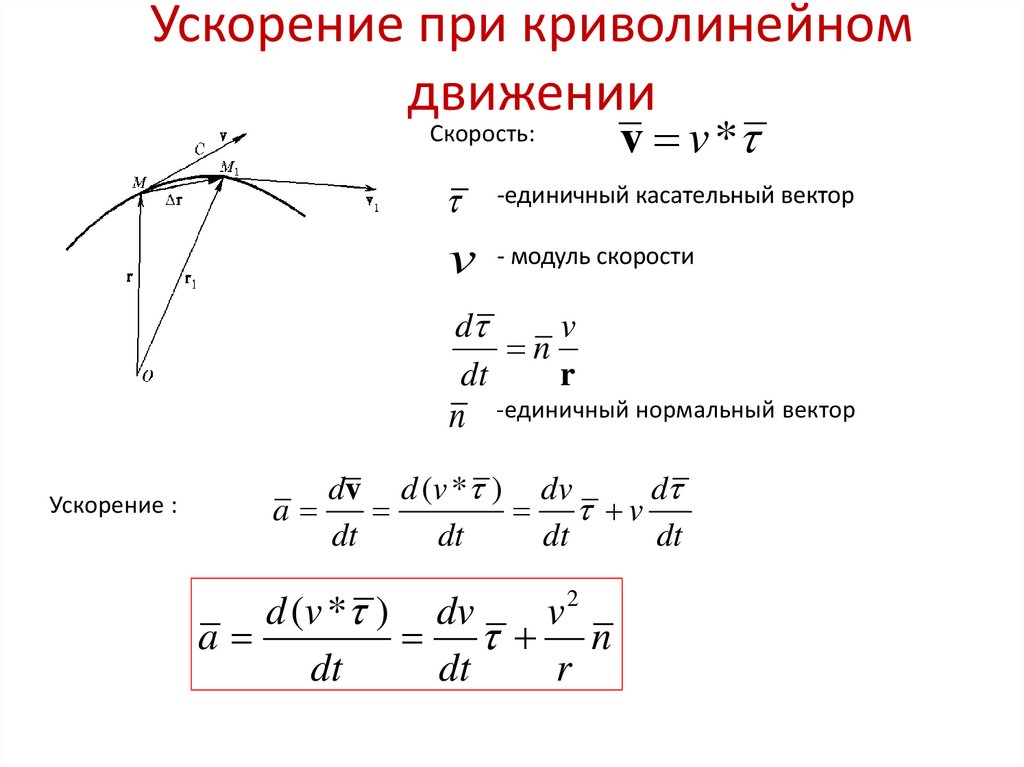

Мгновенную скорость можно вычислить тогда, когда \(\Delta t\) стремится к нулю, а вектор перемещения \((\vec r)\) совпадает с путем (расстоянием) перемещения \((\vec s)\):

\(v=\frac{ds}{dt}\)

Ускорением тела \((\vec a)\) называют величину, равную отношению изменения скорости к промежутку времени, за который это изменение скорости случилось.

Расчет величины производится по формуле:

\(a=\frac{\Delta V}{\Delta t}\)

Ускорение называется мгновенным при условии, что среднее ускорение за промежуток времени стремится к нулю:

\(a=\frac{dv}{dt}.\)

Полное ускорение и компоненты его разложения

Формулы равноускоренного движения

Для равноускоренного движения верны следующие уравнения для нахождения ускорения, скорости, времени и пути:

1. Ускорение движения может быть определено следующим способом: \(a=\frac vt\).
2. Время разгона рассчитывается по формуле:\( t=\frac va\). 2}2\).

Формула координаты тела при равноускоренном прямолинейном движении

Построение графика

math – Рассчитать положение ускоряющегося тела через определенное время

спросил 14 лет, 6 месяцев назад

Изменено 4 месяца назад

Просмотрено 58 тысяч раз

Как рассчитать положение ускоряющегося тела (например, автомобиля) через определенное время (например, 1 секунду)? 92 = 6m

Это уравнение получено путем аналитического интегрирования уравнений, утверждающих, что скорость есть скорость изменения положения, а ускорение есть скорость изменения скорости.

Обычно в ситуации программирования игры используется несколько иная формулировка: в каждом кадре переменные скорости и положения интегрируются не аналитически, а численно:

 s = s + u * dt;
и = и + а * dt;
 

, где dt — длина кадра (измеренная с помощью таймера: 1/60 секунды или около того). Этот метод имеет то преимущество, что ускорение может меняться во времени.

Редактировать Несколько человек заметили, что метод численного интегрирования Эйлера (как показано здесь), хотя и является самым простым для демонстрации, имеет довольно низкую точность. См. Velocity Verlet (часто используется в играх) и Runge Kutta 4-го порядка («стандартный» метод для научных приложений) для улучшения алгоритмов.

6

Ну, это зависит от того, постоянно ли ускорение. Если это просто 92

Если a непостоянно, необходимо численно проинтегрировать. Сейчас существует множество методов, и ни один из них не сравнится с выполнением этого вручную по точности, так как все они в конечном счете являются приблизительными решениями.

Самый простой и наименее точный метод Эйлера. Здесь вы делите время на дискретные фрагменты, называемые временными шагами, и выполняете

 v[n] = v[n-1] * t * a[t]
 

n — индекс, t — размер временного шага. Аналогично обновляется позиция. Это действительно хорошо только для тех случаев, когда точность не так важна. Специальная версия метода Эйлера даст точное решение для движения снаряда (см. вики), поэтому, хотя этот метод является грубым, он может быть идеальным для некоторых ситуаций.

Наиболее распространенным методом численного интегрирования, используемым в играх и некоторых химических симуляциях, является Velocity Verlet, который представляет собой особую форму более общего метода Verlet. Я бы порекомендовал этот, если Эйлер слишком груб.

1

В этой статье: http://www.ugrad.math.ubc.ca/coursedoc/math201/notes/applications/velocity.html (веб-архив) вы можете найти эту формулу:

р(т) = х(0) + v(0)*т + (1/2) 92

где

• p(t) = положение в момент времени t
• x (0) = позиция в нулевое время
• v(0) = скорость в нулевое время (если у вас нет скорости, вы можете игнорировать этот термин)
• а = ускорение
• t = ваш текущий товар

Предполагая, что вы имеете дело с постоянным ускорением, формула выглядит так:

расстояние = (начальная_скорость * время) + (ускорение * время * время) / 2

, где

расстояние пройденное расстояние

начальная_скорость начальная скорость (ноль, если тело изначально находится в состоянии покоя, поэтому в этом случае вы можете опустить этот термин)

время время

ускорение равно (постоянное) ускорение

Убедитесь, что при расчете используются правильные единицы измерения, т. е. метры, секунды и т. д.

Очень хорошая книга на эту тему — «Физика для разработчиков игр».

При постоянном ускорении и начальной скорости v0, 92) + (v0 * т)

Переменное ускорение: определение, график и уравнение

Переменное ускорение — это ситуация, когда существует разница в среднем ускорении в разных точках на пути движущегося объекта.

Различия могут быть как по величине, направлению, так и по величине и направлению. Переменное ускорение возникает, когда изменения скорости объекта неодинаковы через равные промежутки времени. Таким образом, она зависит как от скорости, так и от времени.

Вы также можете узнать о постоянном ускорении.

Примеры переменного ускорения

Представьте, что полицейский гонится за преступником и натыкается на толпу. Полицейскому придется снизить темп и, в конце концов, снова увеличить его, как только он доберется до менее занятого места. То же самое происходит, когда автомобиль ускоряется на шоссе и сталкивается с потоком машин. Автомобиль будет очень мало ускоряться в пробке, а когда дорога освобождается, его ускорение увеличивается.

Инструменты, необходимые для работы с переменным ускорением

Чтобы решать вопросы с переменным ускорением, вы должны иметь базовые знания в области исчисления. Это важно, потому что для того, чтобы получить скорость, когда задано смещение, вы должны дифференцировать смещение. Между тем, чтобы определить ваше перемещение с заданной скоростью, вы должны интегрировать скорость. Этот процесс повторяется между скоростью и ускорением и наоборот.

Круглый ящик для инструментов для решения задач с переменным ускорением, Нджоку – StudySmart Originals

Функция времени при переменном ускорении

Помните, что переменное ускорение зависит от времени, потому что изменение ускорения происходит в пределах временных интервалов. Однако мы начнем с решения примеров, выражающих скорость и перемещение как функции времени.

Смещение s частицы, движущейся по прямой из точки O в момент времени t секунд, определяется как: s=4t3-9t, где 0 Найти:

а. Водоизмещение при t = 3

б. Время, за которое частица возвращается в точку O.

Решение:

a. Чтобы найти смещение s, просто подставьте значение t = 3 в уравнение 81 метр.

б. Чтобы найти время, необходимое для возвращения в точку O, это означает, что смещение равно нулю, и его следует ввести в уравнение.

Таким образом:

0=4t3-9t

Факторизация

0=t(4t2-9)

Разложим 4t2-9 отдельно

4t2-9 = (2t – 3) (2t + 3)

Таким образом:

0 = t (2t – 3) ( 2t + 3)

t = 0, 2t – 3 = 0 или 2t + 3 = 0

t = 0, 3/2 или -3/2

Напомним, что 0

Это означает, что ответ равен 3 /2 секунды.

Движение игрушечной машинки по прямому пути было смоделировано по уравнению s=-t3+4t2. Если эта игрушка уходит в момент времени t = 0 и возвращается в начале пути, докажите ограничение 0 ≤ t ≤ 4.

Решение:

С начала движения,

с ≥ 0

Итак,

-t3+4t2≥0

4t2-t3≥0

0(05-9)t2 0002 т2 ≥0 и 4 – t ≥ 0

t2 ≥0 и 4 ≥ t

Так как время не может быть отрицательным. В этом случае можно рассматривать только t ≥ 0.

таким образом; t ≤ 4

t ≥ 0 и t ≤ 4

, что доказывает ограничение 0 ≤ t ≤ 4.

Связь между скоростью и временем тела, движущегося по прямой, определяется выражением:

v=2t2-16t+24 для t ≥ 0

Найти:

1. Начальная скорость.
2. Время, в течение которого объект мгновенно находится в покое.
3. Время, когда скорость равна 64 м/с.
4. Наибольшая скорость на интервале 0 ≤ t ≤ 5.

Решение

а. При начальной скорости время равно нулю, потому что движение только началось.

t = 0

подставьте значение t в уравнение, чтобы найти скорость

v=2(02)-16(0)+24

v = 24 м/с.

б. При мгновенной скорости в состоянии покоя v = 0

Подставьте это в уравнение, чтобы найти время.

0=2t2-16t+24

0=2(t2-8t+12)

Разделить обе части на 2

0=t2-8t+12

Разложить на множители

0 = (t – 0002 0 = (t – 8t+12) t – 2)

t = 6 или 2

Таким образом, объект мгновенно останавливается через 2 секунды и 6 секунд.

в. При скорости = 64 м/с время равно:

64=2t2-16t+24

64=2(t2-8t+12)

Разделить обе части на 2

32=t2-8t+12

0=t2-8t+12-35

2 0=t2-8t-20

Факторизация

0 = (t – 10) (t + 2)

t = 10 или -2

Таким образом, объект движется со скоростью 64 м/с через 10 секунд.

д. Наибольшая скорость между 0 ≤ t ≤ 5 — это максимальная скорость, достигнутая объектом в пределах t = 0 и t = 5.

Чтобы вывести это, можно построить график уравнения со значениями от 0 до 5, где v по оси y и t по оси x.

Первоначально значение для t = 0 было получено в ответе на вопрос а) как 24 м/с. Используйте тот же подход и заполните таблицу для значений от 1 до 5. 309 у=в=2т2 -16t+24 24 10 0 -6 -8 -6

График ниже показывает максимальную скорость Это видно из таблицы и подтверждается графиком, что наибольшая скорость составляет 24 м/с. Это получается в момент времени t = 0,

График зависимости скорости от времени, показывающий максимальную скорость, Njoku – StudySmarter Originals

Применение дифференцирования в переменном ускорении

Скорость определяется как изменение смещения во времени. Мы объяснили функцию времени в перемещении и скорости, таким образом, v=dsdt.

Аналогичным образом ускорение определяется как изменение скорости во времени. Если скорость завышена как функция t для получения ускорения, тогда a=dvdt=d2sdt2.

Знание дифференциального исчисления потребуется при определении скорости, если перемещение выражается как функция времени. Точно так же можно получить ускорение, если скорость выражается как функция времени. Давайте рассмотрим несколько примеров, чтобы было понятнее:

Трехколесный велосипед движется горизонтально. Смещение q из состояния покоя O в момент времени t определяется как:

q=t4-32t+12

а. Определите скорость трехколесного велосипеда, когда t равно 4 с.

б. Найдите момент, когда он достигнет мгновенной скорости.

в. Вычислите ускорение, когда t равно 1,5 секунды.

Решение:

а. q – это смещение, заданное как

q=t4-32t+12

Помните, что вы дифференцируете смещение, чтобы получить скорость.

v=dqdt=d(q=t4-32t+12)dt

v=4t3-32

Поскольку функция скорости t была получена, подставьте в уравнение значение t = 4.

v=4(43)-32

v = 256-32

v = 224

Следовательно, скорость трехколесного велосипеда равна 224 м/с

b. Чтобы найти время, в которое трехколесный велосипед приобретает мгновенную скорость, всегда помните, что в данный момент объект находится в покое. Это означает, что в этот момент скорость равна нулю.

Введите значение v = 0 в уравнение v=4t3-32, чтобы найти время t.

0=4t3-32

4t3=32

Разделить обе части на 4

t3=8

Найдите кубический корень из обеих сторон

t = 2

Следовательно, трехколесный велосипед приобретает мгновенную скорость через 2 с.

в. Не забудьте дифференцировать свою скорость при определении ускорения.

Поскольку v=4t3-32

a=dvdt=d(v=4t3-32)dt

a=12t2

Теперь вас просят найти ускорение. Просто подставьте значение t = 1,5 в уравнение ускорения.

a=12(1,52)a=27 мс-2

Следовательно, ускорение в момент времени t = 1,5 с равно 27 мс-2

Использование переменного ускорения в минимальном и максимальном случаях

Идея переменного ускорения также имеет полезное применение при нахождении минимального и максимального значений смещения, скорости и ускорения.

У женщины есть пружина, которая покидает ее руку в момент времени t = 0 секунд и движется вертикально по прямой линии, прежде чем вернуться обратно в ее руку. Расстояние y между пружиной и ее рукой через t секунд определяется как:

y=-0,2t3+0,4t2+0,6t, 0 ≤ t ≤ 3

а. Докажите ограничение 0 ≤ t ≤ 3.

b. Рассчитайте максимальное расстояние между рукой женщины и пружиной.

Решение:

а. y=-0,2t3+0,4t2+0,6t

факторизация

y=-0,2t(t2-2t-3)

дальнейшая факторизация

y = -0,2t (t – 3) (t + 1)

когда y = 0, тогда

-0,2t = 0, t – 3 = 0 или t + 1 = 0

t = 0, 3 или -1 0 или 3. Это оправдывает ограничение t, 0 ≤ t ≤ 3.

б. Помните, что когда частица достигает своего максимального смещения, она на мгновение становится покоящейся. Мы говорим, что его скорость мгновенно достигает состояния покоя, и v = 0,

Таким образом, чтобы найти максимальное перемещение, нам нужно знать время, за которое объект мгновенно становится неподвижным. Для этого нам нужно найти t-функцию v. v=-0,6t2+0,8t+0,6

Теперь у нас есть функция t нашей скорости в уравнении, давайте найдем t, когда v мгновенно покоится.

v = 0

0=-0,6t2+0,8t+0,6

Факторизация

0=-0,2(3t2-4t-3)

Разделить обе части на -0,2

-4 0=3

Используя формулу для квадратных уравнений -b±b2-4ac2a

Где a = 3, b = -4 и c = -3

После подстановки значений и решения уравнения

t = 1,8685 или -0,5351.

Помните, что отрицательное значение t недопустимо, поэтому t = 1,8685

Это означает, что расстояние y становится максимальным через 1,8685 секунды.

Подставьте значение t, чтобы найти ymax.

y=-0.2t3+0.4t2+0.6t

ymax=-0.2(1.86853)+0.4(1.86852)+0.6(1.8685)

ymax=1.2129

Максимальное расстояние между рукой женщины и 1,21 метра.

Использование интегрирования в задачах с переменным ускорением

Сначала мы увидели, как дифференцирование используется для нахождения скорости по заданному смещению по времени. Мы также видели, как этот процесс используется для нахождения ускорения, когда скорость дана как функция времени. Чтобы выполнить обращение этих ситуаций, таких как от скорости к смещению, а также от ускорения к скорости, используется интегрирование.

Вы знаете, что:

v=dsdt другое a=dvdt

Затем:

s=∫vdt другое v=∫adt

data-custom-editor=”chemistry” (t-5)ms-2 is ускорение баскетбольного мяча, отброшенного подростком. Мяч стартует со скоростью 8 м/с. Определить время (с), в течение которого баскетбольный мяч находится в состоянии покоя.

Решение:

Иллюстрация мгновенного покоя баскетбольного мяча Нджоку – StudySmarter Originals

a = t – 5

v=∫adt

v=∫(t-5)dt

v=t22-5t+c не забывайте добавлять константу c после каждого интегрирования.

Нам сказали, что мяч стартовал со скоростью 8 м/с, значит, в момент времени t = 0, v = 8

Таким образом, подставляем значения t и v в уравнение

8=022-5 (0)+c

c = 8

Это означает, что функция t скорости:

v=t22-5t+8.

Теперь у нас есть полное уравнение для скорости, мы можем определить время (с) мгновенного покоя мяча.

v = 0, потому что объект на мгновение находится в покое.

v=t22-5t+8

0=t22-5t+8

Умножьте уравнение на 2, чтобы избавиться от дроби (t – 2) = 0

t = 8 или 2

Таким образом, баскетбольный мяч мгновенно находится в состоянии покоя через 2 и 8 секунд.