Главная
Формула ускорения физика: Ускорение (видео) | Прямолинейное движение

Формула ускорения физика: Ускорение (видео) | Прямолинейное движение

Ускорение. Прямолинейное движение с постоянным ускорением

Физика – Поурочные планы к учебникам Г. Я. Мякишева, С. В. Громова и В. Л. Касьянова 10 класс

Ускорение. Прямолинейное движение с постоянным ускорением – ВВЕДЕНИЕ. ФИЗИКА В ПОЗНАНИИ ВЕЩЕСТВА, ПОЛЯ, ПРОСТРАНСТВА И ВРЕМЕНИ

Цель: сформулировать признаки движения тела с постоянным ускорением.

Ход урока

I. Проверка домашнего задания

1. Какое движение называется равномерным прямолинейным?

2. При равномерном прямолинейном движении мгновенная скорость совпадает со средней скоростью. Почему?

3. Почему при равномерном прямолинейном движении за любые равные промежутки времени тело перемещается на одно и то же расстояние.

4. Как по графику зависимости скорости от времени определяют перемещение тела при равномерном прямолинейном движении?

5. Как угол наклона графика равномерного прямолинейного движения зависит от скорости?

II. Изучение нового материала

При движении тел их скорости обычно меняются либо по модулю, либо по направлению, либо одновременно и по модулю, и по направлению.

Эксперимент 1

Взять в руки мяч и разжать пальцы. Как изменяется скорость? (При падении мяча скорость его быстро нарастает.)

Эксперимент 2

Приведем в движение легкую тележку, непродолжительным толчком. Как изменится скорость? (Скорость тележки, движущейся по столу, уменьшается с течением времени до полной остановки.)

Величину, характеризующую быстроту изменения скорости, называют ускорением. 

Простой случай неравномерного движения – это движение с постоянным ускорением, при котором модуль и направление не меняются со временем, оно может быть прямолинейным и криволинейным.  

Равноускоренное движение (тело разгоняется), если 

При замедленном движении (тело тормозит), если   Графики скорости будут отображать V(t)-зависимость скорости от времени (см. рис. 24).

По графику V(t) можно определить ускорение.

График ускорения: a(t) a = const.

Из утверждения, что величина перемещения тела численно равна площади под графиком зависимости скорости движения тела от времени, можно вывести:

 – закон равноускоренного прямолинейного движения.

Зависимость координаты от времени при прямолинейном равноускоренном движении.

Графики зависимости координат от времени при движении с постоянным ускорением (рис. 26).

Уравнение 

Уравнение 

V0 = 0.

Оба движения равноускоренные.

Построение графиков зависимости координаты от времени при а – const сводится к построению отрезков параболы (рис. 27). Для лучшего усвоения графиков полезно повторить соответствующий раздел математики.

III. Повторение. Беседа

1. Какое движение называют равноускоренным или равнопеременным?

2. Что называют ускорением?

3. Какая формула выражает смысл ускорения?

4. Чем отличается «ускоренное» прямолинейное движение от «замедленного»?

5. Постройте и объясните график скорости прямолинейного равноускоренного движения с начальной скоростью и без начальной скорости.

6. Как по графику скорости равноускоренного движения можно определить ускорение и путь, пройденный телом в этом движении?

IV. Решение задач

1. Велосипедист, едущий со скоростью 18 км/ч, начинает спускаться с горы.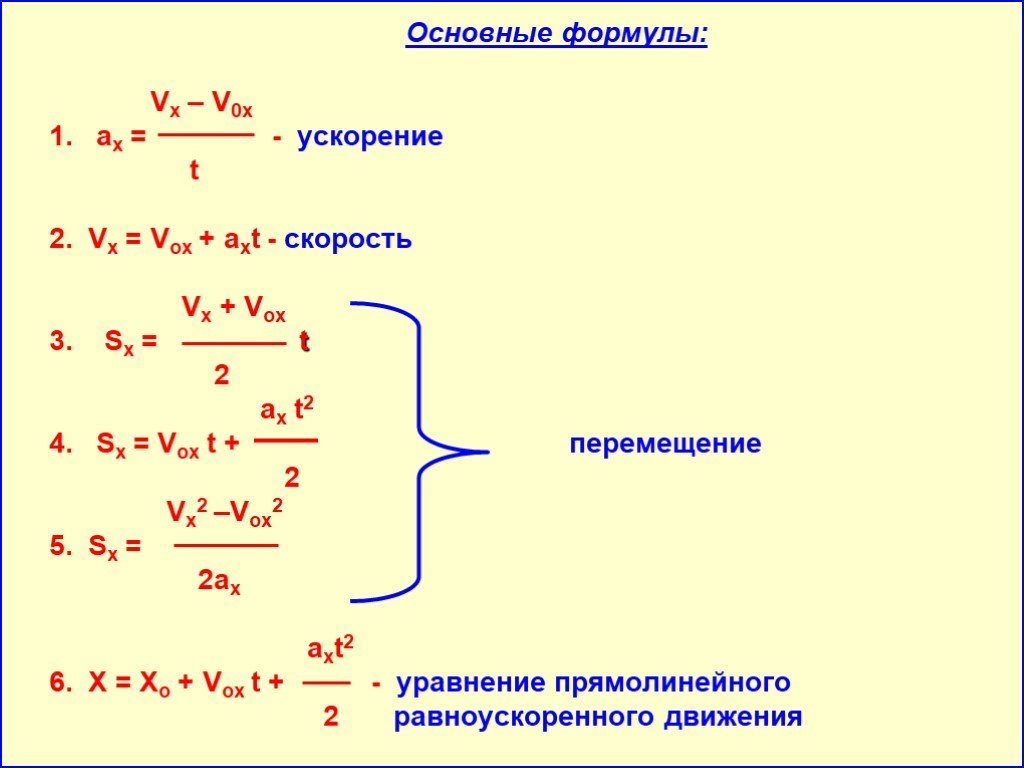 Определить скорость велосипедиста через 6 с, если ускорение равно 0,8 м/с2.

Дано:

Решение:

Движение велосипедиста равноускоренное, т. е. а 0. Ось Ох направим по направлению движения велосипедиста.

Скорость можно определить по формуле:   С учетом знаков проекций на ось Ох формула скорости примет вид: 

Проверим размерность (рис. 28):

Вычислим значение скорости: V = 5 + 0,8 · 6 = 9,8 м/с.

(Ответ: V = 9,8 м/с – конечная скорость велосипедиста.)

2. Поезд через 20 с после начала движения приобретает скорость 90,6 м/с. Через сколько времени от начала движения скорость поезда станет равна 3 м/с?

Дано:

Решение:

Движение поезда носит равноускоренный характер, скорость увеличивается, ускорение постоянно и положительно (а = const).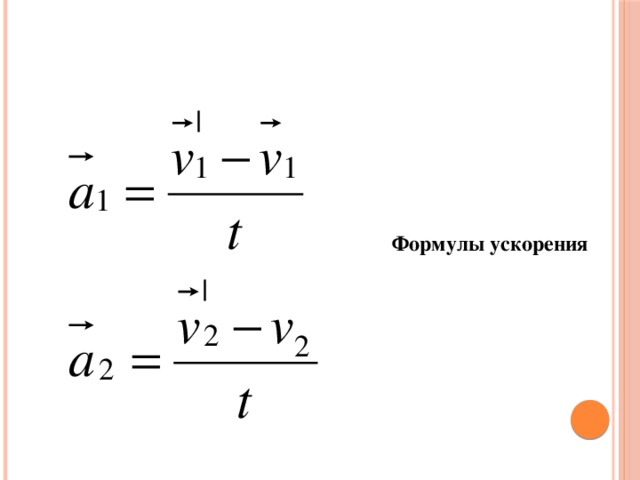

Найдем ускорение движения:   (проекция конечной скорости положительна), т. к. 

Пользуясь формулой ускорения, найдем промежуток времени:

(Ответ: t2 = 100 с.)

3. Скорость автомобиля за 10 с уменьшилась с 10 до 6 м/с. Написать формулу зависимости x(t) скорости от времени, построить график этой зависимости и по графику определить скорость через 20 с.

Решение: Скорость автомобиля уменьшается, следовательно, движение равнозамедленное, т. е. ах

Чтобы найти зависимость Vx(t) для данной задачи, необходимо определить ускорение автомобиля.

Знак *-* перед ах уже учли в уравнении (1). В данном случае находится модуль ускорения. Уравнение скорости движения: V = 10 – 0,4t.

Построим график зависимости (рис. 29).

Достаточно определить две точки, так как графиком скорости является прямая линия. Можно составить таблицу.

Т

0

5

V

10

8

Через t2 = 20 с скорость автомобиля будет равна V2 = 2 м/с.

Значение скорости можно проверить аналитически, если подставить в уравнение скорости вместо времени значение t2 = 20 с. Получим:

V2 = 10 — 0,4 · 20 = 10 — 8 = 2м/с.

(Ответ: V2 = 2 м/с; Vx(t) = 10 – 0,4t.)

4. Самолет летел со скоростью 216 км/ч и стал двигаться с ускорением 9 м/с2 в течение 20 секунд. Какое расстояние пролетел самолет за это время и какой скорости он достиг? (Ответ: S= 3000 м = 3 км; V = 240 м/с. )

5. Автомобиль при движении со скоростью 43,2 км/ч останавливается в течение 3 с. Какое расстояние проезжает он до остановки? (Ответ: 18 м.)

6. Поезд движется со скоростью 20 м/с. При торможении до полной остановки он прошел расстояние в 200 м. Определите время, в течение которого происходило торможение. (Ответ: 20 секунд)

7. Уравнение скорости движущегося тела V = 5 + 4t. Написать уравнение перемещения S(t) и описать характер движения, определить начальные условия. (Ответ: V0 = 5 м/с; а = 4 м/с2;S(t) = 5t + 2t2.)

8. Два пункта Ап В расположены на расстоянии l = 240 м друг от друга на склоне горы. От пункта А начинает равноускоренно спускаться к пункту В велосипедист с начальной скоростьюV01 = 8 м/с. Одновременно из пункта В к пункту А начинает равнозамедленно подниматься мотоциклист с начальной скоростью V02 = 16 м/с. Они встречаются через t1 = 10 с, к этому времени велосипедист проехал S1 = 130 м. С каким ускорением ехал каждый из них? (Ответ: а1 = 1 м/с2; а2 = 1 м/с2.)

9. Два велосипедиста едут навстречу друг другу Один, имея скорость 18 км/ч, движется равнозамедленно с ускорением 20 см/с2, другой, имея скорость 5,4 км/ч, движется равноускоренно с ускорением 0,2 м/с2. Через какое время велосипедисты встретятся и какое перемещение совершит каждый из них до встречи, если расстояние между ними в начальный момент времени 130 м? (Ответ: S1 = 60 м; S2 = 70 м; t1 = 20 с)

10. Условие движения тела дано в виде х = 15t + 0,4t2. Определить начальную скорость и ускорение движения тела, а также координату и скорость тела через 5 с. (Ответ: а = 0,8 м/с2;V0 = 15 м/с; х = 85 м; V = 19 м/с.)

11. Уравнение движения материальной точки имеет вид х = -3t2. Определить перемещение и скорость точки через 2 секунды. (Ответ: V = -12 м/с; S = -12 м.)

12. Пользуясь графиком (рис. 30), определите перемещение каждого тела через 4 с. Запишите формулу скорости для каждого движения.

Домашнее задание

П. 13-16, с. 36 задачи (1-2).

Формула ускорения с массой и силой

Автор ФизикаGoeasy / 10 мая 2020 г. 9 ноября 2021 г.

Источник изображения canva

Скаляры и векторы в физике

Включите JavaScript

Скаляры и векторы в физике

В этой статье мы рассмотрим формулу ускорения с массой и силой. Мы уже обсуждали формулу ускорения со скоростью и временем. В этой статье мы рассмотрим формулу ускорения с массой и силой. Мы используем формулу ускорения с массой и силой, когда нам ничего не известно о скорости движущегося тела и времени. В данном случае у нас есть информация только о

  • Сила (f), действующая на тело или объект и 
  • Масса (m) тела или объекта 

Согласно второму закону движения Ньютона, сила равна массе, умноженной на ускорение, мы можем использовать это соотношение, чтобы найти ускорение движущегося объекта. Конечно, нам нужно иметь действующую силу и массу.

Формула ускорения с массой и силой

Мы знаем, что формула силы в соответствии со вторым законом движения Ньютона равна \[f=m\times a\]. Теперь, если мы хотим найти ускорение из этой формулы силы, нам придется переформулировать приведенное выше уравнение. Таким образом, переставляя приведенное выше уравнение, мы получаем \[a=\frac{f}{m}\] Здесь, 92\)) 

  • масса \(m\) выражена в \(кг\) 

    • Мы также можем использовать треугольник формулы силы, чтобы найти третью величину, если даны любые две силы, массы и ускорения.

    Решенные вопросы на основе формулы ускорения с массой и силой

    Вопрос 1 Автомобиль массой 1000 кг движется со скоростью 10 м/с и на него действует поступательная сила 1000 Н от двигателя и тормозящая сила 500 Н из-за трения. Какова будет его скорость через 10 секунд? 9{-2}\)

    Дополнительная литература 

    • http://hyperphysics. phy-astr.gsu.edu/hbase/hframe.html

    сообщите об этом объявлении

    Искать на этом сайте

    Искать:

    сообщите об этом объявлении

    Категории

    Последние сообщения


    сообщите об этом объявлении сообщите об этом объявлении

    Расчет размерной формулы ускорения/углового ускорения

    Размерная формула ускорения:

    [ M 0 L 1 T -2 ]

    , где [T] [L] [L] [L] [L] [L] [L] [L] [L] [L] [L] [L] [L] [L] [L] . количества: Масса , Длина и Время .

    Из приведенной выше формулы мы можем получить измерений ускорения как (0, 1, -2) .

    Как рассчитать размерную формулу ускорения?

    Мы можем вывести эту формулу, используя определение ускорения.

    В физике мы можем определить ускорение как скорость изменения скорости. Таким образом, математически ускорение равно

    .
  Ускорение = скорость/время

    Мы знаем Скорость = расстояние/время . Подставив значение Скорость в приведенное выше уравнение, мы получим

      Ускорение = (расстояние/время)/время
  Ускорение = расстояние/время  2 
  Ускорение = расстояние  1  * время  -2

    Размерность, мы используем

    • [L]       для расстояния
    • [T] для времени 4
    • 90 становится 3 10 9014
    • 90 Ускорение = [L 1 ] * [T -2 ]

      Так как формула не включает основную величину Масса , мы можем использовать [M 0 ] , что равно 1 .

        Ускорение = [M  0  ] * [L  1  ] * [Т  -2  ]

      Следовательно, размерное уравнение ускорения имеет вид a = [ M 0 L 1 T -2 ]

      .

      Какова размерная формула углового ускорения?

      The dimensional formula of angular acceleration is

      [M 0 L 0 T -2 ]

      where [M] , [L], и [T] являются фундаментальными величинами: Масса , Длина и Время .

      Вычислите размерную формулу углового ускорения

      Мы можем определить угловое ускорение как скорость изменения угловой скорости. Итак, формула становится

       
      
  Угловое ускорение (α) = угловая скорость (ω) / время (t)

      Также мы можем определить Угловая скорость как скорость изменения угла θ . Следовательно,

        Угловая скорость (ω) = угол (θ) / время (t)

      Подставляя значение ω в первое уравнение, получаем

        Угловое ускорение (α) = (угол/время)/время
                         α = угол/время  2 
                         α = Угол * время  -2

      В физике Угол (θ) является безразмерной величиной, и мы используем [T] для представления Время

      . Следовательно, уравнение принимает вид

        α = [Т  -2  ]

      Поскольку формула не включает фундаментальные величины Масса и Длина , мы можем использовать [M 0 ] * [L 0 ] , что равно 1 .

        Угловое ускорение = [M  0  ] * [L  0  ] * [T  -2  ]

      Следовательно, размерное уравнение углового ускорения имеет вид α = [M 0 L 0 T -2 ] .

      2. Какова размерная формула ускорения свободного падения?

      The dimensional formula of acceleration due to gravity is

      [ M 0 L 1 T -2 ]

      where [M] , [L], и [T] являются фундаментальными величинами: Масса , Длина и Время .

      Вывод

      В физике мы можем определить ускорение под действием силы тяжести как ускорение свободно падающего тела под действием силы тяжести.

      Мы знаем формулу Силы,

        Сила = масса * ускорение свободного падения (g)
  г = сила / масса

      Размерная формула Силы равна [ M 1 L 1 T -2 ] , и мы представляем массу с [M] .

    Оставить комментарий