Путь, пройденный при равнопеременном движении
Ландсберг Г.С. 2010-03-23 20:26 (0)
Воспользуемся графическим способом нахождения пройденного пути для случая равноускоренного движения. Пусть график скорости равноускоренного движения изображен прямой (рис. 36). Путь, пройденный за время , численно равен площади трапеции :
Рис. 36. Графическое нахождение формулы пути, пройденного при равноускоренном движении
Но (начальная скорость), (скорость в момент при ускорении ). Значит,
| (22.1) |
Эта формула справедлива как для равноускоренного, так и для равнозамедленного движения; в первом случае и одинаковы по знаку, а во втором — противоположны.
Для движения с начальной скоростью, равной нулю, на графике вместо трапеции получается прямоугольный треугольник с катетами и , так что площадь, выражающая пройденный путь, оказывается равной
(22. 2) 2) |
Эту формулу можно было бы получить и непосредственно из предыдущей формулы, полагая .
На рис. 37 дан график пути равноускоренного движения с начальной скоростью, равной нулю. График построен по формуле (22.2) для значения . Он изображается кривой линией, поднимающейся вверх все круче и круче. Расстояния точек графика от оси времени пропорциональны квадратам расстояний от оси пути. Такая кривая называется параболой.
Рис. 37. График пути при равноускоренном движении
Из формулы (22.2) видно, что при начальной скорости, равной нулю, путь, пройденный при равноускоренном движении за первую секунду движения ( ) численно равен половине ускорения. Если известен путь, пройденный без начальной скорости за время , то ускорение можно найти по формуле
| (22.3) |
Если начальная скорость равна нулю, можно выразить путь , пройденный к моменту , через скорость и в этот момент или скорость — через пройденный путь. Действительно, в этом случае и . Исключая из этих выражений , найдем
Действительно, в этом случае и . Исключая из этих выражений , найдем
| (22.4) |
| (22.5) |
Наконец, зная пройденный путь и ускорение, можно, воспользовавшись формулой (22.2), найти время движения:
| (22.6) |
22.1. Напишите формулы, аналогичные (22.4) и (22.5), для случая начальной скорости \(v_0\), не равной нулю.
22.2. Покажите, пользуясь формулой (22.1), что для равноускоренного движения пути, проходимые точкой за любые равные промежутки времени, следующие друг за другом, получают одинаковое приращение.
22.3. Покажите, пользуясь формулой (22.2), что для равноускоренного движения без начальной скорости приращения пути за любые равные промежутки времени, следующие друг за другом, равны двойному пути, проходимому точкой за первый такой промежуток времени.
22.4. Электровоз подходит по горизонтальному пути к уклону, имея скорость 8 м/с, затем движется по уклону вниз с ускорением 0,2 м/с2. Определите длину уклона, если электровоз проходит его за 30 с.
22.5. Электровоз начинает двигаться равноускоренно в тот момент, когда с ним поравнялся мальчик, бегущий равномерно со скоростью 2 м/с. Определите скорость электровоза в тот момент, когда он догонит мальчика.
22.6. Автомобиль, пройдя с постоянным ускорением некоторое расстояние от остановки, достиг скорости 20 м/с. Какова была его скорость на половине этого расстояния?
22.7. Какой путь прошло тело за время, в течение которого скорость его увеличилась с 4 до 12 м/с, если ускорение равно 2 м/с2?
Видео
Физика воздуха. Сжимаемость воздуха.
2020-05-23
Что такое электричество? | ПРОСТО ФИЗИКА с Алексеем Иванченко
2020-05-23
Курс подготовки к ЕГЭ.
 Физика. Урок №1 Кинематика равномерного движения
Физика. Урок №1 Кинематика равномерного движения2018-12-22
Батавские слезки – опыты
2017-12-15
Тепловой рычаг – физические опыты
2017-12-15
Секрет ЖК-монитора – поляризационная пленка
2017-12-15
ЛАЗЕР В ВОДЕ – физические опыты
ЭЛЕКТРОХРОМНАЯ ПЛЕНКА с токопроводящим слоем и жидкокристаллической основой
2017-12-15
Урок из космоса.Физика невесомости
2017-12-12
Абсолютный ноль – погоня за абсолютным нулём
2017-12-12
Формула вывода Определение Концепция » ExamLimiT
Центростремительное ускорение является произведением квадрата угловой скорости и радиуса окружности. Вывод формулы, определение, единица измерения, размерность, понятие.
Определение: Частица, движущаяся по круговой траектории с постоянной скоростью, всегда имеет ускорение по направлению к центру окружности, которое называется радиальным ускорением, нормальным ускорением или центростремительным ускорением.

Если частица с угловой скоростью ω вращается по окружности радиуса r, то ее центростремительное ускорение равно
a c = ω 2 r = v 2 /r
Обратите внимание, что скорость частицы всегда направлена по касательной к окружности, но центростремительное ускорение всегда направлено к центру этой окружности . Таким образом, при равномерном круговом движении скорость и центростремительное ускорение перпендикулярны друг другу .
- Вывод центростремительного ускорения
- Центростремительное ускорение: единица измерения и размер
- Центростремительное ускорение: векторная форма:
- Центростремительное ускорение: решения проблем
- Несколько вопросов Ответы
- Оглянитесь на свои знания
Вывод центростремительного ускорения
Когда объект движется по круговой траектории, его направление постоянно меняется, и поэтому его линейная скорость не остается неизменной.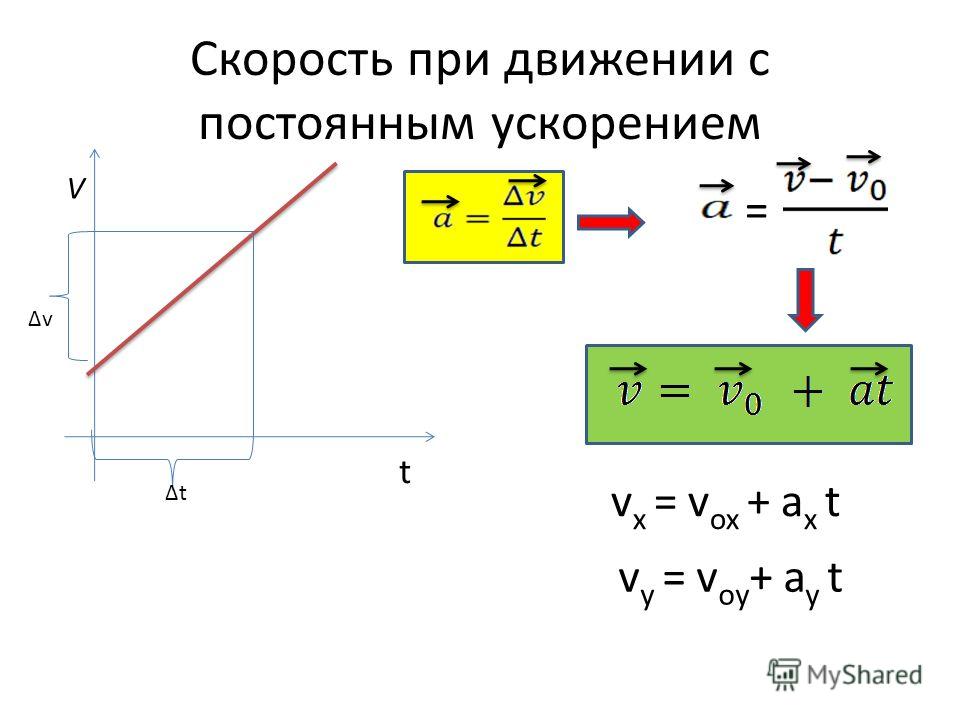 Это изменение скорости при круговом движении создает ускорение, которое всегда направлено к центру окружности. Это известно как центростремительное ускорение. Здесь математически мы выведем формулу центростремительного ускорения простым способом.
Это изменение скорости при круговом движении создает ускорение, которое всегда направлено к центру окружности. Это известно как центростремительное ускорение. Здесь математически мы выведем формулу центростремительного ускорения простым способом.
Рассмотрим частицу массой m
В точке A линейная скорость частицы равна v по касательной AP. Составляющая этой скорости по радиусу АО равна нулю, так как АО и АР взаимно перпендикулярны.
В точке B скорость частицы v вместе с BQ. На данный момент v можно разделить на две перпендикулярные составляющие.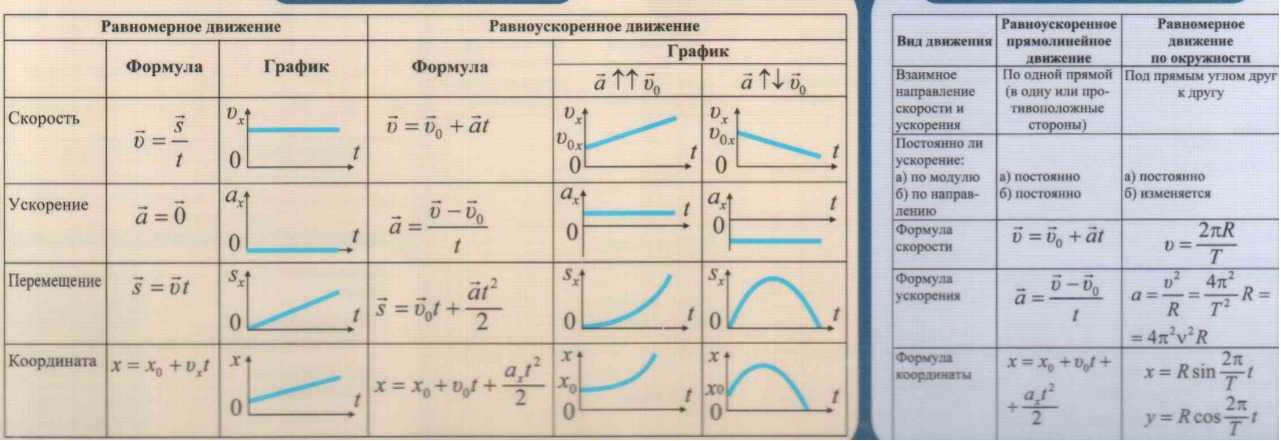
Если θ очень мало, так что θ → 0 , тогда мы можем рассматривать sinθ = θ и cosθ = 1 . Опять же, если угол ∠AOB очень мал, то можно считать, что BR и BS также перекрываются с AP и AO соответственно.
Итак, вдоль АВ начальная скорость частицы = v , а конечная скорость равна vcosθ = v . Это означает, что изменение скорости равно ( v – v ) = 0
или ускорение a t
То есть по направлению АР или по касательной к окружности ускорение частицы равно нулю.
Теперь по направлению АО начальная скорость частицы = 0, а конечная скорость = vsinθ = vθ.
или изменение скорости = ( vθ − 0) = vθ .
или, ускорение вдоль AP равно a c = vθ/t
или, a c = vω [как ω 9 908047]{2}r$$
- Где a c = центростремительное ускорение
- v = линейная скорость
- r = радиус окружности
- ω = угловая скорость.
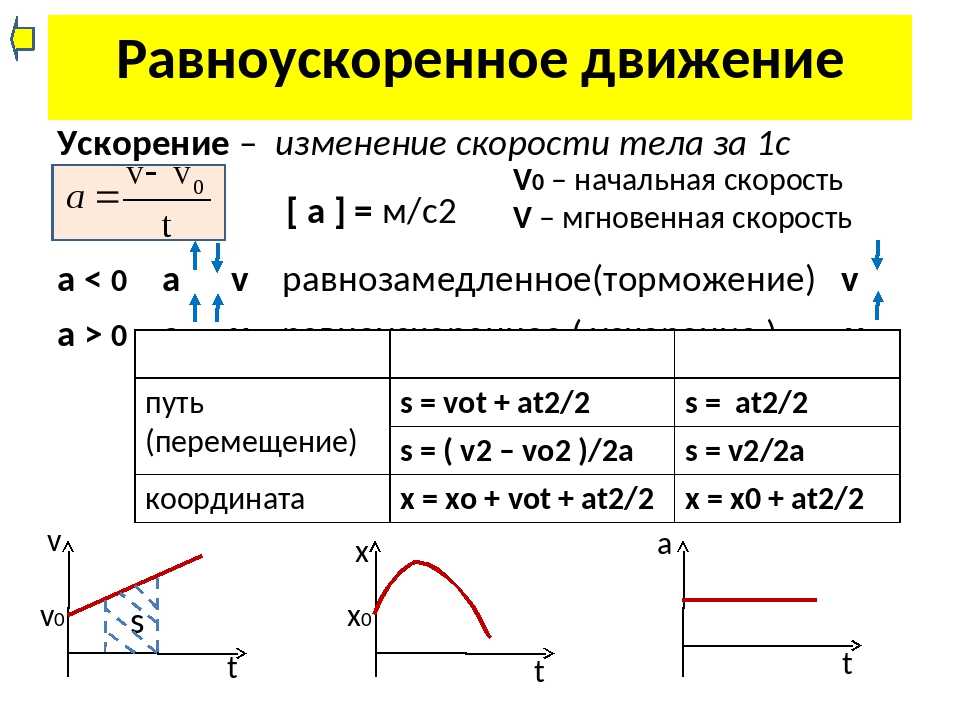
Подумайте об этом : Может ли частица иметь ускорение при движении с постоянной скоростью?
Центростремительное ускорение: единица измерения и размер
Единица центростремительного ускорения = (единица скорости) 2 / (единица радиуса)
= (м/с) 2 / м
= м/с 2
Размер центростремительного ускорения = [размер скорости] 2 / [размер радиуса)]
= [LT −1 ] 2 /[L]
= [LT −2 ]
| Блок Centripetal Centripetal Eccelere 2 | |
| FPS единица центростремительного ускорения | |
| Размер центрипета. Она имеет как величину, так и направление. Его направление всегда направлено к центру круга. Соотношение между линейной и угловой скоростью в векторной форме определяется формулой – $$\overrightarrow{v} = \overrightarrow{\omega} \times \overrightarrow{r}$$ Дифференцируя по времени t, получаем- $$\frac{d\overrightarrow{v}}{dt} = \omega \times \frac{d\overrightarrow{r}}{dt} + \overrightarrow{ r} \times \frac{d\overrightarrow{\omega} }{dt}\\ \overrightarrow{a} = \overrightarrow{\omega} \times \overrightarrow{v} + \overrightarrow{r} \times \overrightarrow{\alpha} \\ \overrightarrow{a} = \overrightarrow{a_{c}}+\overrightarrow{a_{t}}$$ Где α – угловое ускорение. Обратите внимание, что- $$\overrightarrow{a_{c}} = \overrightarrow{\omega} \times \overrightarrow{v} \\ или, \overrightarrow{a_{c}} = \overrightarrow{\omega} \times (\overrightarrow{\omega} \times \overrightarrow{r})$$ – это векторная форма центростремительного ускорения. форма вектора центростремительного ускоренияПодумайте о : Какая физическая величина остается неизменной при равномерном круговом движении? Центростремительное ускорение: решения проблемЧеловек вращает стержень длиной 10 м. Вычислите угловую скорость, необходимую для создания центростремительного ускорения, в 5 раз превышающего ускорение свободного падения. Ответ: Здесь в этой задаче даны данные: – r = 10м, Найти радиальное ускорение часовой стрелки настенных часов длиной 0,2 м. Ответ: Для часовой стрелки период времени T = 12 часов, а r = 0,2 м. От чего зависит центростремительное ускорение?Радиальное ускорение зависит от двух факторов: один из них — угловая скорость (или линейная скорость), а другой — радиус кругового пути. В принципе, центростремительное ускорение пропорционально квадрату угловой скорости. Каковы единица и размерность центростремительного ускорения? Единицей центростремительного ускорения является метр в секунду в квадрате в системе СИ. Оглянитесь на свои знанияКакая формула для центростремительного ускорения является правильной? V 2 /R В/R V 2 R VR [V2/R] Длиная бара центр с угловой скоростью 2 рад/с. Каким будет радиальное ускорение? 3 м/с 2 4 м/сек. 2 5 м/сек. 2 6 м/сек. скорость 4 см/с. каково его радиальное ускорение? 4 см/с 2 16 см/с 2 64 см/с 2 2 см/с 2 [4 см/с 2 ] [4 см/с 2 ] [4 см/с 2 ] не правильная формула центростремительного ускорения?V 2 /R ω 2 R ωV . Скачать PDF Центростремительное ускорение и центростремительная сила: определение Каждые четыре года мы наблюдаем, как лучшие спортсмены со всего мира собираются в одном городе для участия в Олимпийских играх. Спортсмены должны быть в отличной форме. Но знаете ли вы, что они также полагаются на науку для оптимизации своей работы? Например, спортсмены, соревнующиеся в метании молота, полагаются на физику, которая помогает им оптимизировать дистанцию броска, когда они размахивают семикилограммовым железным шаром, прикрепленным к стальной проволоке, прежде чем отпустить его. Каждый участник надеется, что его бросок преодолеет самое дальнее расстояние, что позволит ему забрать золотую медаль домой. Что делают эти спортсмены, отпуская молоток на 9-й минуте?0047 точный правильный момент, чтобы он мчался по прямой линии, является ярким примером как центростремительного ускорения, так и центростремительной силы. Метание молота: пример центростремительного ускорения и центростремительной силы Теперь, когда у нас есть представление о том, как центростремительное ускорение и сила проявляются в повседневной жизни, давайте углубимся в эти понятия. В этой статье будут представлены две составляющие вращательного и кругового движения: центростремительное ускорение и центростремительная сила. Мы определим центростремительное ускорение и центростремительную силу и приведем формулу для каждого из них. Затем мы обсудим, как эти понятия соотносятся друг с другом, прежде чем работать над некоторыми примерами. Определение центростремительного ускорения и центростремительной силы В дальнейшем мы определяем центростремительное ускорение и центростремительную силу. Центростремительное ускорение — это ускорение, направление которого всегда указывает радиально внутрь к центру кругового пути, по которому движется объект. Ускорение всегда является результатом действия силы, что приводит к следующему определению центростремительной силы: Центростремительная сила — это радиально направленная внутрь внешняя сила, приложенная к объекту, чтобы удерживать его в пределах круговой траектории. Имея в виду эти определения, мы теперь рассмотрим формулы для расчета центростремительного ускорения и центростремительной силы объекта, совершающего круговое движение. Формулы центростремительного ускорения и центростремительной силыДля расчета центростремительного ускорения мы используем формулу центростремительного ускорения ac=v2rac=v2r где скорость, измеренная в мс, равна радиусу кругового пути, измеренному в м. Мы можем получить формулу центростремительной силы, следуя формуле центростремительного ускорения. F=ма. На основании этого закона мы знаем, что сила, действующая на объект, является произведением массы и ускорения. Для центростремительной силы мы знаем, что связанное с ней ускорение также является центростремительным. Следовательно, мы должны подставить его формулу в приведенное выше уравнение, чтобы получить формулу для центростремительной силы. Подставив в это выражение формулу центростремительного ускорения, мы получим формулу центростремительной силы: Fc=mac=mv2r. Здесь – масса объекта, измеренная в кг, vis – скорость, измеренная в мс, а r – радиус, измеренный в м. Обратите внимание, что ускорение и сила являются векторными величинами с величиной и направлением. Приведенные выше формулы дают только величину векторных величин. Связь между центростремительной силой и центростремительным ускорением Выше мы только что видели, как центростремительная сила математически связана с центростремительным ускорением. Имеют ли центростремительное ускорение и центростремительная сила противоположные направления?Центростремительное ускорение и центростремительная сила не имеют противоположных направлений. Помните, что ускорение объекта всегда в том же направлении , что и результирующая сила, действующая на него! Круговое движение не является исключением из этого правила. Как для центростремительного ускорения, так и для центростремительной силы их направление всегда направлено внутрь к центру окружности. Вы можете легко запомнить это, поняв, что слово центростремительный означает поиск центра или тенденцию двигаться к центру. Поскольку ускорение и результирующая сила всегда указывают в одном и том же направлении, а мы знаем, что центростремительный означает направление к центру, теперь мы можем понять, почему не было необходимости записывать формулы из предыдущего раздела в векторной записи. Какие силы вызывают центростремительное ускорение?Центростремительные силы вызывают центростремительное ускорение. Натяжение, гравитация и трение являются типичными примерами центростремительных сил, ответственных за круговое движение. Например, если мы прикрепим объект к веревке и раскачаем ее горизонтально над головой, объект будет двигаться по кругу из-за натяжения. Натяжение нити удерживает объект на его круговой траектории и, следовательно, создает центростремительную силу. Натяжение: пример центростремительной силы Натяжение: пример центростремительной силы. Другой пример — обращение Луны вокруг Земли. Луна удерживается на своей орбите гравитацией, а гравитация обеспечивает центростремительную силу, приложенную к Луне. Гравитация: пример центростремительной силы Гравитация: пример центростремительной силы То же самое относится к трению. Трение: пример центростремительной силы Из приведенных выше примеров мы можем понять, что каждый раз, когда объект совершает круговое движение, он имеет центростремительное ускорение, потому что направление его скорости в любой точке пути постоянно меняется. Это ускорение вызвано центростремительной силой, ограничивающей движение объекта по окружности. Вывод центростремительного ускорения и силы В этом разделе мы приводим геометрический вывод центростремительного ускорения. Для точного вывода потребовалось бы исчисление, чтобы вывести уравнение для центростремительного ускорения. Однако это можно обойти, используя неофициальное визуальное доказательство. Начнем с рассмотрения частицы, движущейся по окружности с постоянной скоростью, и нарисуем вектор положения и соответствующий вектор скорости в разные моменты времени. Для объектов, совершающих круговое движение, вектор скорости всегда касается вектора положения. Когда объект совершает круговое движение, его вектор положения и вектор скорости постоянно изменяются. Вектор положения изменяется из-за вектора скорости. Следовательно, если частица движется со скоростью v по окружности радиусом r, мы можем определить время, которое требуется частице, чтобы совершить один полный оборот: v=dt→t=dv. Для круга мы знаем, что расстояние будет равно 2πr, что является длиной окружности. Следовательно, мы находим время по окружности этого первого круга через: t1=2πrv. Теперь мы также знаем, что направление скорости меняется из-за центростремительного ускорения. Для объектов, совершающих круговое движение, вектор ускорения всегда указывает на центр окружности Когда частица движется по зеленой окружности радиусом r, вектор скорости изменяется из-за вектора ускорения. Вспоминая, что ускорение — это скорость изменения положения, мы можем переставить векторы предыдущего рисунка, чтобы сформировать круг, аналогичный первому. Изменения вектора скорости описывают второй круг. Этот круг будет иметь радиус и требует столько же времени, сколько требуется частице, чтобы двигаться по круговой траектории радиуса r из первого изображения. Однако для этого второго круга мы знаем, что центростремительное ускорение отвечает за скорость частицы. Следовательно, если круг имеет радиус и скорость, то мы можем определить время, за которое частица совершает один полный оборот: t2=2πrскорость=2πвач. Обе окружности должны совершить полный оборот за одинаковое время, поскольку они описывают один и тот же случай кругового движения. Следовательно, если мы приравняем оба уравнения времени друг к другу, мы можем решить для центростремительного ускорения следующим образом: Умножение крестом, получается acr=v2 , что после деления обеих частей на r дает ac=v2r. Это уравнение для центростремительного ускорения, которое мы искали. Примеры центростремительного ускорения и центростремительной силыВ этом разделе мы проведем два расчета, используя примеры центростремительного ускорения и центростремительной силы. Прежде чем приступить к решению задачи, всегда помните, что сначала нужно прочитать и определить все предоставленные вам переменные, прежде чем применять необходимые формулы для ответа на вопрос. Груз массой 15 кг привязан к веревке длиной 3 минуты и раскачивается горизонтально над головой. Если масса имеет скорость 4 мс, определите центростремительное ускорение и центростремительную силу массы. Из предоставленной информации масса 15 кг, радиус 3 м, скорость 4 мс. Итак, у нас есть m=15kgr=3mv=4ms. Теперь мы можем рассчитать центростремительное ускорение и центростремительную силу для этой ситуации, используя соответствующие формулы. Центростремительное ускорение равно ac=v2r=(4мс)23м=16м2с23м=5,33мс2. |


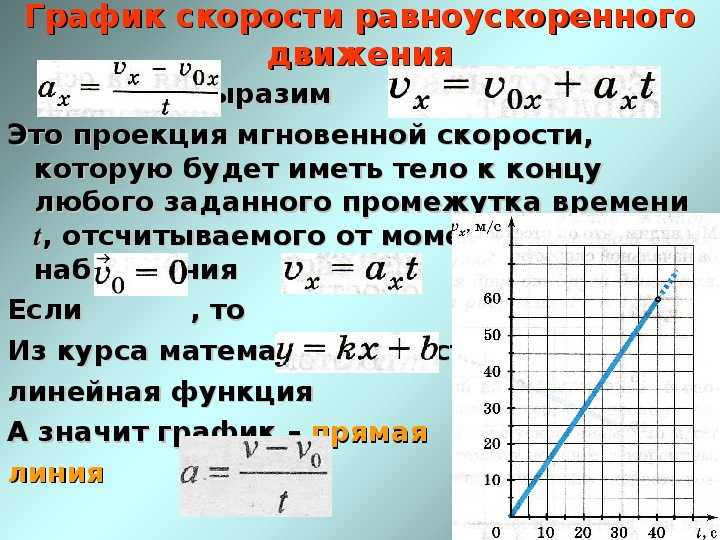
 Таким образом, мы можем видеть, что когда объект вращается по круговой траектории, она состоит из двух видов ускорений, 9{2}}$$
Таким образом, мы можем видеть, что когда объект вращается по круговой траектории, она состоит из двух видов ускорений, 9{2}}$$
 SENTER 7 7 7 7. Примечания
SENTER 7 7 7 7. Примечания  Почему? Атлеты входят в круг, начинают вращаться и, в конце концов, отпускают молоток примерно после четырех или пяти вращений. Каждое вращение означает, что спортсмен ускоряется, тем самым увеличивая скорость и оптимизируя расстояние, которое проходит молот. Впечатляет, правда? Кто бы мог подумать, что спортсмены используют физику?
Почему? Атлеты входят в круг, начинают вращаться и, в конце концов, отпускают молоток примерно после четырех или пяти вращений. Каждое вращение означает, что спортсмен ускоряется, тем самым увеличивая скорость и оптимизируя расстояние, которое проходит молот. Впечатляет, правда? Кто бы мог подумать, что спортсмены используют физику?
 Ускорение и сила связаны вторым законом движения Ньютона, который равен
Ускорение и сила связаны вторым законом движения Ньютона, который равен Зная последнее, достаточно умножить его на массу объекта, чтобы получить первое. Рассмотрим теперь более подробно концептуальную связь между центростремительным ускорением и центростремительной силой.
Зная последнее, достаточно умножить его на массу объекта, чтобы получить первое. Рассмотрим теперь более подробно концептуальную связь между центростремительным ускорением и центростремительной силой. И ac, и Fc явно заявляют, что векторная форма этих величин всегда указывает на центр кругового пути.
И ac, и Fc явно заявляют, что векторная форма этих величин всегда указывает на центр кругового пути. Если автомобиль движется по кривой с уклоном, трение действует как внешняя сила, заставляющая автомобиль оставаться на своем пути.
Если автомобиль движется по кривой с уклоном, трение действует как внешняя сила, заставляющая автомобиль оставаться на своем пути.
 Теперь, если мы перестроим эти векторы скорости и ускорения, сохраняя их перпендикулярными друг другу, мы получим следующее:0003
Теперь, если мы перестроим эти векторы скорости и ускорения, сохраняя их перпендикулярными друг другу, мы получим следующее:0003
