Вращательная кинематика – Физика 298
“Люди говорят об убийстве времени, а
время тихо их убивает
Дион Бусико London Assurance (1841)
- На сегодняшний день мы рассмотрели кинематика и динамика частиц, в том числе поступательная и круговое движение, а также поступательное движение системы частиц (в частности, твердых тел) с точки зрения движение центра масс системы (тела). В В последнем случае мы можем представить себе, что вся масса объект находится в центре масс до внешней речь идет о поступательных силах.
- Следующим шагом является рассмотрение вращения твердого тела вокруг
фиксированная ось вращения. Примечание
что, поскольку мы рассматриваем твердое тело, каждая частица в теле остается неподвижной относительно
остальным
 Этот
означает, что при таком вращательном движении каждая частица движется в
окружность, центр которой лежит на оси вращения. В
на диаграмме справа объект вращается вокруг оси z; в
две частицы образца движутся по кругу с радиусом r 1 и р 2 . Если мы можем
описывают круговое движение частицы без непосредственного
относительно его радиуса, то все частицы в системе будут
описывается одной и той же системой уравнений.
Хотя радиусы частиц различны, их
угловые повороты одинаковы. Поэтому
это
необходимо ввести угловые переменные.
Этот
означает, что при таком вращательном движении каждая частица движется в
окружность, центр которой лежит на оси вращения. В
на диаграмме справа объект вращается вокруг оси z; в
две частицы образца движутся по кругу с радиусом r 1 и р 2 . Если мы можем
описывают круговое движение частицы без непосредственного
относительно его радиуса, то все частицы в системе будут
описывается одной и той же системой уравнений.
Хотя радиусы частиц различны, их
угловые повороты одинаковы. Поэтому
это
необходимо ввести угловые переменные.
-
- Угловая скорость (скорость) и Угловое ускорение
Угловая скорость
и угловое ускорение определяются аналогично
скорость и ускорение. Там
средние и мгновенные значения каждого из них.
Там
средние и мгновенные значения каждого из них.
Угловой ускорение не то же самое как центростремительное ускорение. Центростремительное ускорение возникает из-за изменение в
Точно как и в поступательном случае, разница между угловыми скорость и угловая скорость – это направление. Угловой скорость должна включать направление вращения вокруг оси в вопрос. Для например, 10 рад/с по часовой стрелке примерно ось x – угловая скорость, 10 рад/с относительно оси абсцисс угловая скорость.
- Уравнения кинематики вращения
По прямой аналогии с поступательной кинематикой уравнений, круговое движение вокруг одной оси при постоянном угловое ускорение может быть описано следующими четырьмя уравнения,
где мы сделали замены,
Обратите внимание, что так же, как
+x определяется произвольно вправо, положительное значение
тета может быть определена как по часовой стрелке или против часовой стрелки.
- Связь между Angular и
Трансляционные переменные
Запуск от определение радианной меры путем дифференцирования с относительно времени, мы можем показать, что
где v тангенциальная скорость, а a — тангенциальная ускорение.
А частица, совершающая круговое движение с переменным углом скорость (неравномерное круговое движение), будет испытывать два компоненты ускорения, тангенциальная составляющая из-за изменение величины его скорости и радиальной (центростремительной) составляющая из-за изменения направления ее скорости
Сеть ускорение частицы есть векторная сумма этих двух компоненты, как указано ниже. для вашего телефона информация
Возможно одновременное вращение вокруг нескольких осей.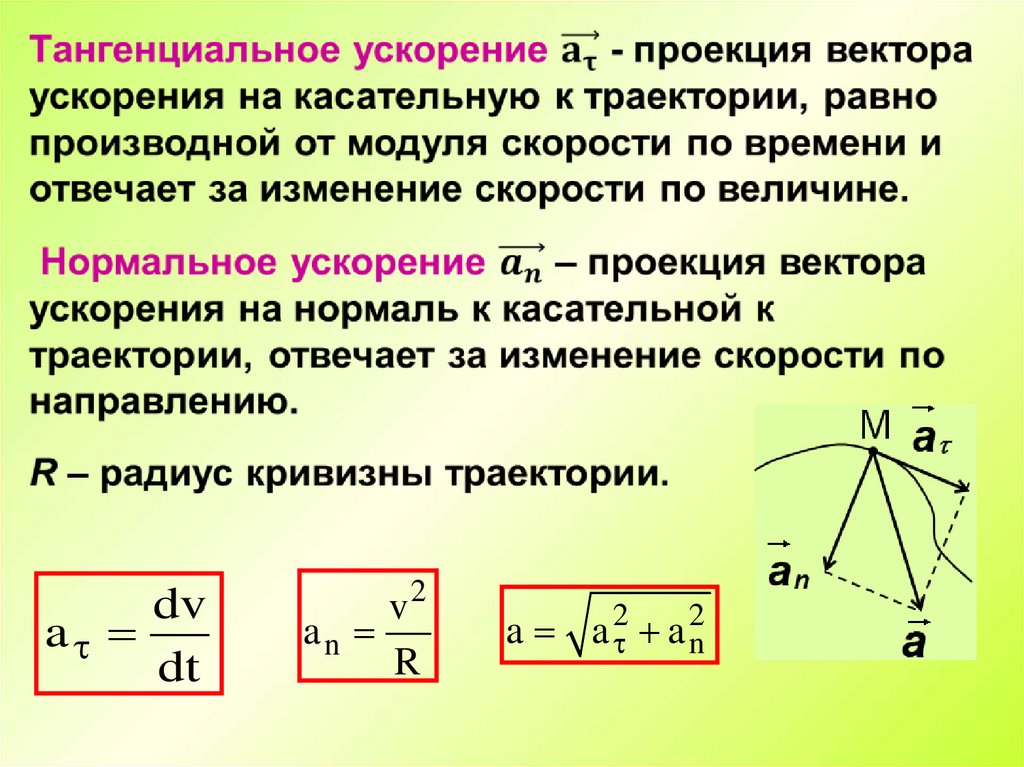

 Этот
означает, что при таком вращательном движении каждая частица движется в
окружность, центр которой лежит на оси вращения. В
на диаграмме справа объект вращается вокруг оси z; в
две частицы образца движутся по кругу с радиусом r 1 и р 2 . Если мы можем
описывают круговое движение частицы без непосредственного
относительно его радиуса, то все частицы в системе будут
описывается одной и той же системой уравнений.
Хотя радиусы частиц различны, их
угловые повороты одинаковы. Поэтому
это
необходимо ввести угловые переменные.
Этот
означает, что при таком вращательном движении каждая частица движется в
окружность, центр которой лежит на оси вращения. В
на диаграмме справа объект вращается вокруг оси z; в
две частицы образца движутся по кругу с радиусом r 1 и р 2 . Если мы можем
описывают круговое движение частицы без непосредственного
относительно его радиуса, то все частицы в системе будут
описывается одной и той же системой уравнений.
Хотя радиусы частиц различны, их
угловые повороты одинаковы. Поэтому
это
необходимо ввести угловые переменные.