Как правильно выводить формулы. Как выводить формулы по физике
В каждой задаче по физике требуется из формулы выразить неизвестную, следующим шагом подставить численные значения и получить ответ, в некоторых случаях необходимо только выразить неизвестную величину. Способов выведения неизвестной из формулы много. Если посмотреть страницы Интернета, то мы увидим множество рекомендаций по этому поводу. Это говорит о том, что единого подхода к решению этой проблемы научное сообщество еще не выработало, а те способы, которые используются, как показывает опыт работы в школе – все они малоэффективны. До 90% учащихся выпускных классов не умеют правильно выразить неизвестное. Те же, кто умеют это делать – выполняют громоздкие преобразования. Очень странно, но физики, математики, химики имеют разные подходы, объясняя методы переноса параметров через знак равенства (предлагают правила треугольника, креста или пропорций др.) Можно сказать, что имеют разную культуру работы с формулами. Можно представить, что происходит с большинством учеников, которые встречается с разными трактовками решения данной проблемы, последовательно посещая уроки этих предметов.
Научите выражать из формул величины. 10 класс, мне стыдно не знать, как из одной формулы делать другую.
Да не переживай – это проблема многих моих одноклассников, хоть я и в 9 кл. Учителя показывают это чаще всего методом треугольника, но мне кажется, что это неудобно, да и запутаться легко. Покажу наиболее простой способ, которым я пользуюсь…
Допустим, дана формула:
Ну более простая….тебе из этой формулы нужно найти время. Ты берешь и в эту формулу подставляешь числа только разные, исходя из алгебры. Допустим:
и тебе наверное хорошо видно, что чтобы найти время в алгебраическом выражении 5 нужно 45/9 т.е переходим к физике: t=s/v
У большинства учащихся формируется психологический блок. Часто учащиеся отмечают, что при чтении учебника трудности в первую очередь вызывают те фрагменты текста, в которых много формул, что «длинные выводы все равно не понять», но при этом возникает чувство неполноценности, неверия в свои силы.
Я, предлагаю следующее решение данной проблемы – большинство учащихся все – таки могут решать примеры и, следовательно, расставлять порядок действий. Используем это их умение.
1. В той части формулы, где содержится переменная, которую нужно выразить, надо расставь порядок действий, причем в одночленах, не содержащих искомую величину этого делать не будем.
2. Затем в обратной последовательности вычислений перенесите элементы формулы в другую часть формулы (через знак равенства) с противоположным действием (« минус» – «плюс», «разделить» – « умножить», « возведение в квадрат» – «извлечение корня квадратного»).
То есть найдем в выражении последнее действие и перенесем одночлен или многочлен, исполняющий это действие, через знак равенства первым, но уже с противоположным действием. Таким образом, последовательно, находя последнее действие в выражении, перенесите из одной части равенства в другую все известные величины. В заключение перепишем формулу так, чтобы неизвестная переменная стояла слева.
Получаем четкий алгоритм работы, точно знаем, сколько преобразований необходимо выполнить. Можем для тренировки использовать уже известные формулы, можем выдумывать свои. Для начала работы над усвоением данного алгоритма была создана презентация.
Опыт работы с учащимися показывает, что данный способ хорошо воспринимается ими. Реакция учителей на мое выступление на фестивале «Учитель профильной школы» также говорит о положительном зерне, заложенном в этой работе.
Чтобы вывести формулу сложного , нужно прежде всего путем анализа установить, из каких элементов состоит вещество и в каких весовых отношениях соединены друг с другом входящие в него элементы. Обычно состав сложного выражают в процентах, но он может быть выражен и в любых других числах, указывающих отношение между весовыми количествами элементов, образующих данное вещество. Например, состав окиси алюминия, содержащей 52,94% алюминия и 47,06% кислорода, будет вполне определен, если мы скажем, что и соединены в весовом отношении 9:8, т.
Зная весовой состав сложного и атомные веса образующих его элементов, нетрудно найти относительное число атомов каждого элемента в молекуле взятого вещества и таким образом установить его простейшую формулу.
Положим, например, что требуется вывести формулу хлористого кальция, содержащего 36% кальция и 64% хлора. Атомный вес кальция 40, хлора 35,5.
Обозначим число атомов кальция в молекуле хлористого кальция через х, а число атомов хлора через у. Так как атом кальция весит 40, а атом хлора 35,5 кислородных единиц, общий вес атомов кальция, входящих в состав молекулы хлористого кальция, будет равен 40
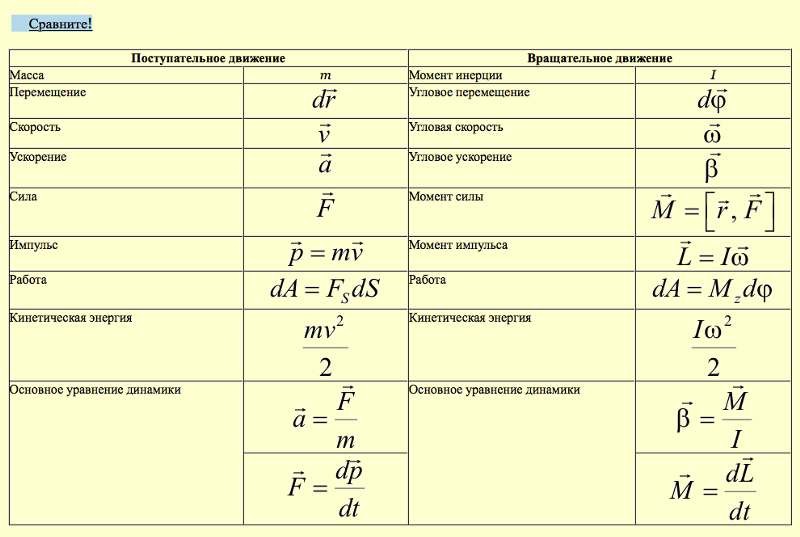 второго отношения на наименьший из них. Получаем
второго отношения на наименьший из них. Получаемх: у = 1:2
Следовательно, в молекуле хлористого кальция на один атом кальция приходятся два атома хлора. Этому условию удовлетворяет целый ряд формул: СаСl 2 , Са 2 Сl 4 , Са 3 Сl 6 и т. д. Так как у нас нет данных, чтобы судить, какая из написанных формул отвечает действительному атомному составу молекулы хлористого кальция, мы остановимся на простейшей из них СаСl 2 , указывающей наименьшее возможное число атомов в молекуле хлористого кальция.
Однако произвол в выборе формулы отпадает, если наряду с весовым составом вещества известен также его молекулярный вес. В этом случае нетрудно вывести формулу, выражающую истинный состав молекулы. Приведем пример.
Путем анализа установлено, что глюкоза содержит на 4,5 вес. ч. углерода 0,75 вес. ч. водорода и 6 вес. ч. кислорода. Молекулярный вес ее был найден равным 180. Требуется вывести формулу глюкозы.
Как и в предыдущем случае, находим сперва отношение между числом атомов углерода (атомный вес 12), водорода и кислорода в молекуле глюкозы.
2х :у: 16z = 4,5: 0,75: 6
откуда
Разделив все три члена второй половины равенства на 0,375, получаем:
х :у: z= 1: 2: 1
Следовательно, простейшая формула глюкозы будет СН 2 O. Но вычисленный по ней равнялся бы 30, тогда как в действительности глюкозы 180, т. е. в шесть раз больше. Очевидно, что для глюкозы нужно принять формулу C 6 H 12 O 6 .
Формулы, основанные, кроме данных анализа, также и на определении молекулярного веса и указывающие действительное число атомов в молекуле, называются истинными или молекулярнымиформулами; формулы же, выведенные только из данных анализа, называются простейшими или эмпирическими.
Познакомившись с выводом химических формул,» легко понять, как устанавливаются точные молекулярные веса. Как мы уже упоминали, существующие методы определения молекулярных весов в большинстве случаев не дают вполне точных результатов. Но, зная хотя бы приблизительный и процентный состав вещества, можно установить его формулу, выражающую атомный состав молекулы. Так как вес молекулы равняется сумме весов образующих ее атомов, сложив веса атомов, входящих в состав молекулы, мы определим ее вес в кислородных единицах, т. е. молекулярный вес вещества. Точность найденного молекулярного веса будет такой же, как и точность атомных весов.
Но, зная хотя бы приблизительный и процентный состав вещества, можно установить его формулу, выражающую атомный состав молекулы. Так как вес молекулы равняется сумме весов образующих ее атомов, сложив веса атомов, входящих в состав молекулы, мы определим ее вес в кислородных единицах, т. е. молекулярный вес вещества. Точность найденного молекулярного веса будет такой же, как и точность атомных весов.
Нахождение формулы химического соединения во многих случаях может быть значительно упрощено, если воспользоваться понятием овалентности элементов.
Напомним, что валентностью элемента называется свойство его атомов присоединять к себе или замещать определенное число атомов другого элемента.
Что такое валентностьэлемента определяется числом, показывающим, сколько атомов водорода (или другого одновалентного элемента) присоединяет или замещает атом данного элемента.
Понятие о валентности распространяется не только на отдельные атомы, но и на целые группы атомов, входящие в состав химических соединений и участвующие как одно целое в химических реакциях. Такие группы атомов получили название радикалов. В неорганической химии наиболее важными радикалами являются: 1) водный остаток, или гидроксил ОН; 2) кислотные остатки; 3) основные остатки.
Такие группы атомов получили название радикалов. В неорганической химии наиболее важными радикалами являются: 1) водный остаток, или гидроксил ОН; 2) кислотные остатки; 3) основные остатки.
Водный остаток, или гидроксил, получается, если отмолекулы воды отнять один атом водорода. В молекуле воды гидроксил связан с одним атомом водорода, следовательно, группа ОН одновалентна.
Кислотными остатками называются группы атомов (аиногда и один атом), «остающиеся» от молекул кислот, если мысленно отнять от них один или несколько атомов водорода, замещаемых металлом. этих групп определяется числом отнятых атомов водорода. Например, дает два кислотных остатка – один двухвалентный SO 4 и другой одновалентный HSO 4 , входящий в состав различных кислых солей. Фосфорная кислотаН 3 РО 4 может дать три кислотных остатка: трехвалентный РО 4 , двухвалентный НРО 4 и одновалентный
Н 2 РО 4 и т. д.
Основными остатками мы будем называть; атомы или группы атомов, «остающиеся» от молекул оснований, если мысленно отнять от них один или несколько гидроксилов. Например, последовательно отнимая от молекулы Fe(OH) 3 гидроксилы, получаем следующие основные остатки: Fe(OH) 2 ,
FeOH и Fe. их определяется числом отнятых гидроксильных групп:Fe(OH) 2
– одновалентен; Fe(OH)-двухвалентен; Fe – трехвалентен.
Например, последовательно отнимая от молекулы Fe(OH) 3 гидроксилы, получаем следующие основные остатки: Fe(OH) 2 ,
FeOH и Fe. их определяется числом отнятых гидроксильных групп:Fe(OH) 2
– одновалентен; Fe(OH)-двухвалентен; Fe – трехвалентен.
Основные остатки, содержащие гидроксильные группы, входят в состав так называемых основных солей. Последние можно рассматривать как основания, в которых часть гидроксилов замещенакислотными остатками. Так, при замещении двух гидроксилов вFe(OH)3 кислотным остатком SO 4 получается основная соль FeOHSO 4 , при замещении одного гидроксила в Bi(OH) 3
кислотным остатком NO 3 получается основная соль Bi(OH) 2 NO 3 и т.д.
Знание валентностей отдельных элементов и радикалов позволяет в простых случаях быстро составлять формулы очень многих химических соединений, что освобождает химика от необходимости механически их заучивать.
Химические формулыПример 1. Составить формулу гидрокарбоната кальция – кислой соли угольной кислоты.
В состав этой соли должны входить атомы кальция и одновалентные кислотные остатки НСО 3 . Так как двухвалентен, то на один атом кальция надо взять два кислотных остатка. Следовательно, формула соли будет Са(НСО 3)г.
Этот урок – полезное дополнение к предыдущей теме ” “.
Умение делать такие вещи – штука не просто полезная, она – необходимая . Во всех разделах математики, от школьной до высшей. Да и в физике тоже. Именно по этой причине задания подобного рода обязательно присутствуют и в ЕГЭ и в ОГЭ. Во всех уровнях – как базовом, так и профильном.
Собственно, вся теоретическая часть подобных заданий представляет собой одну единственную фразу. Универсальную и простую до безобразия.
Удивляемся, но запоминаем:
Любое равенство с буквами, любая формула – это ТОЖЕ УРАВНЕНИЕ!
А где уравнение, там автоматически и . Вот и применяем их в удобном нам порядке и – готово дело.) Читали предыдущий урок? Нет? Однако… Тогда эта ссылочка – для вас.
Ах, вы в курсе? Отлично! Тогда применяем теоретические знания на практике.
Начнём с простого.
Как выразить одну переменную через другую?
Такая задача постоянно возникает при решении систем уравнений. Например, имеется равенство:
3 x – 2 y = 5
Здесь две переменные – икс и игрек.
Допустим, нас просят выразить x через y .
Что означает это задание? Оно означает, что мы должны получить некоторое равенство, где слева стоит чистый икс. В гордом одиночестве, безо всяких соседей и коэффициентов. А справа – что уж получится.
И как же нам получить такое равенство? Очень просто! С помощью всё тех же старых добрых тождественных преобразований! Вот и применяем их в удобном нам порядке, шаг за шагом добираясь до чистого икса.
Анализируем левую часть уравнения:
3 x – 2 y = 5
Здесь нам мешаются тройка перед иксом и –2 y . Начнём с –2у , это попроще будет.
Начнём с –2у , это попроще будет.
Перекидываем –2у из левой части в правую. Меняя минус на плюс, разумеется. Т.е. применяем первое тождественное преобразование:
3 x = 5 + 2 y
Полдела сделано. Осталась тройка перед иксом. Как от неё избавиться? Разделить обе части на эту самую тройку! Т.е. задействовать второе тождественное преобразование.
Вот и делим:
Вот и всё. Мы выразили икс через игрек . Слева – чистый икс, а справа – что уж получилось в результате “очищения” икса.
Можно было бы сначала поделить обе части на тройку, а затем – переносить. Но это привело бы к появлению дробей в процессе преобразований, что не очень удобно. А так, дробь появилась лишь в самом конце.
Напоминаю, что порядок преобразований никакой роли не играет. Как нам удобно, так и делаем. Самое главное – не порядок применения тождественных преобразований, а их правильность!
А можно из этого же равенства
3 x – 2 y = 5
выразить y через x ?
А почему – нет? Можно! Всё то же самое, только на этот раз нас интересует слева чистый игрек. Вот и очищаем игрек от всего лишнего.
Вот и очищаем игрек от всего лишнего.
Первым делом избавляемся от выражения 3х . Перебрасываем его в правую часть:
–2 y = 5 – 3 x
Осталась двойка с минусом. Делим обе части на (-2):
И все дела.) Мы выразили y через х. Переходим к более серьёзным заданиям.
Как выразить переменную из формулы?
Не проблема! Точно так же! Если понимать, что любая формула – тоже уравнение .
Например, такое задание:
Из формулы
выразить переменную с.
Формула – тоже уравнение! Задание означает, что через преобразования из предложенной формулы нам надо получить какую-то новую формулу. В которой слева будет стоять чистая с , а справа – что уж получится, то и получится…
Однако… Как нам эту самую с вытаскивать-то?
Как-как… По шагам! Ясное дело, что выделить чистую с сразу невозможно: она в дроби сидит. А дробь умножается на r … Значит, первым делом очищаем выражение с буквой с , т.е. всю дробь целиком. Здесь можно поделить обе части формулы на r .
А дробь умножается на r … Значит, первым делом очищаем выражение с буквой с , т.е. всю дробь целиком. Здесь можно поделить обе части формулы на r .
Получим:
Следующим шагом надо вытащить с из числителя дроби. Как? Легко! Избавимся от дроби. Нету дроби – нету и числителя.) Умножаем обе части формулы на 2:
Осталась элементарщина. Обеспечим справа букве с гордое одиночество. Для этого переменные a и b переносим влево:
Вот и всё, можно сказать. Осталось переписать равенство в привычном виде, слева направо и – ответ готов:
Это было несложное задание. А теперь задание на основе реального варианта ЕГЭ:
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 749 МГц. Скорость погружения батискафа вычисляется по формуле
где с = 1500 м/с – скорость звука в воде,
f 0 – частота испускаемых импульсов (в МГц),
f – частота отражённого от дна сигнала, регистрируемая приёмником (в МГц).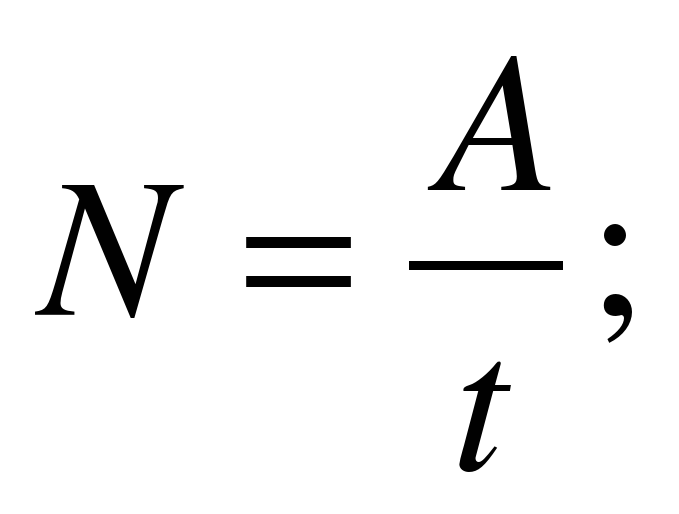
Определите частоту отражённого сигнала в МГц, если скорость погружения батискафа равна 2 м/с.
“Многа букафф”, да… Но буквы – это лирика, а общая суть всё равно та же самая . Первым делом надо выразить эту самую частоту отражённого сигнала (т.е. букву f ) из предложенной нам формулы. Вот этим и займёмся. Смотрим на формулу:
Напрямую, естественно, букву f никак не выдернешь, она снова в дробь запрятана. Причём и в числитель и в знаменатель. Поэтому самым логичным шагом будет избавиться от дроби. А там – видно будет. Для этого применяем второе преобразование – умножаем обе части на знаменатель.
Получим:
А вот тут – очередные грабли. Прошу обратить внимание на скобки обеих частях! Частенько именно в этих самых скобочках и кроются ошибки в подобных заданиях. Точнее, не в самих скобочках, а в их отсутствии.)
Скобки слева означают, что буква v умножается на весь знаменатель целиком . А не на его отдельные кусочки…
А не на его отдельные кусочки…
Справа же, после умножения, дробь исчезла и остался одинокий числитель. Который, опять же, весь целиком умножается на буковку с . Что и выражается скобками в правой части.)
А вот теперь скобки и раскрыть можно:
Отлично. Процесс идёт.) Теперь буковка f слева стала общим множителем . Выносим её за скобки:
Осталось всего ничего. Делим обе части на скобку (v – c ) и – дело в шляпе!
В принципе, всё готово. Переменная f уже выражена . Но можно дополнительно “причесать” полученное выражение – вынести f 0 за скобку в числителе и сократить всю дробь на (-1), тем самым избавившись от лишних минусов:
Вот такое выражение. А вот теперь и числовые данные подставить можно. Получим:
Ответ: 751 МГц
Вот и всё. Надеюсь, общая идея понятна.
Делаем элементарные тождественные преобразования с целью уединить интересующую нас переменную. Главное здесь – не последовательность действий (она может быть любой), а их правильность.
Главное здесь – не последовательность действий (она может быть любой), а их правильность.
В этих двух уроках рассматриваются лишь два базовых тождественных преобразования уравнений. Они работают всегда . На то они и базовые. Помимо этой парочки, существует ещё множество других преобразований, которые тоже будут тождественными, но не всегда, а лишь при определённых условиях.
Например, возведение обеих частей уравнения (или формулы) в квадрат (или наоборот, извлечение корня из обеих частей) будет тождественным преобразованием, если обе части уравнения заведомо неотрицательны .
Или, скажем, логарифмирование обеих частей уравнения будет тождественным преобразованием, если обе части заведомо положительны. И так далее…
Подобные преобразования будут рассматриваться в соответствующих темах.
А здесь и сейчас – примеры для тренировки по элементарным базовым преобразованиям.
Простенькая задачка:
Из формулы
выразить переменную а и найти её значение при S =300, V 0 =20, t =10.
Задачка посложнее:
Средняя скорость лыжника (в км/ч) на дистанции в два круга рассчитывается по формуле:
где V 1 и V 2 – средние скорости (в км/ч) на первом и втором кругах соответственно. Какова была средняя скорость лыжника на втором круге, если известно, что первый круг лыжник пробежал со скоростью 15 км/ч, а средняя скорость на всей дистанции оказалась равной 12 км/ч?
Задача на основе реального варианта ОГЭ:
Центростремительное ускорение при движении по окружности (в м/с 2) можно вычислить по формуле a =ω 2 R , где ω – угловая скорость (в с -1), а R – радиус окружности. Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 8,5 с -1 , а центростремительное ускорение равно 289 м/с 2 .
Задача на основе реального варианта профильного ЕГЭ:
К источнику с ЭДС ε=155 В и внутренним сопротивлением r =0,5 Ом хотят подключить нагрузку с сопротивлением R Ом. Напряжение на этой нагрузке, выражаемое в вольтах, даётся формулой:
Напряжение на этой нагрузке, выражаемое в вольтах, даётся формулой:
При каком сопротивлении нагрузки напряжение на ней будет 150 В? Ответ выразите в омах.
Ответы (в беспорядке): 4; 15; 2; 10.
А уж где числа, километры в час, метры, омы – это как-нибудь сами…)
Воспользовавшись записью первого начала термодинамики в дифференциальной форме (9.2), получим выражение для теплоёмкости произвольного процесса:
Представим полный дифференциал внутренней энергии через частные производные по параметрам и :
После чего формулу (9.6) перепишем в виде
Соотношение (9.7) имеет самостоятельное значение, поскольку определяет теплоёмкость в любом термодинамическом процессе и для любой макроскопической системы, если известны калорическое и термическое уравнения состояния.
Рассмотрим процесс при постоянном давлении и получим общее соотношение между и .
Исходя из полученной формулы, можно легко найти связь между теплоемкостями и в идеальном газе. Этим мы и займемся. Впрочем, ответ уже известен, мы его активно использовали в 7.5.
Этим мы и займемся. Впрочем, ответ уже известен, мы его активно использовали в 7.5.
Уравнение Роберта Майера
Выразим частные производные в правой части уравнения (9.8), с помощью термического и калорического уравнений, записанных для одного моля идеального газа. Внутренняя энергия идеального газа зависит только от температуры и не зависит от объёма газа, следовательно
Из термического уравнения легко получить
Подставим (9.9) и (9.10) в (9.8), тогда
Окончательно запишем
Вы, надеюсь, узнали (9.11). Да, конечно, это уравнение Майера. Еще раз напомним, что уравнение Майера справедливо только для идеального газа.
9.3. Политропические процессы в идеальном газе
Как отмечалось выше первое начало термодинамики можно использовать для вывода уравнений процессов, происходящих в газе. Большое практическое применение находит класс процессов, называемых политропическими. Политропическим называется процесс, проходящий при постоянной теплоемкости .
Уравнение процесса задается функциональной связью двух макроскопических параметров, описывающих систему. На соответствующей координатной плоскости уравнение процесса наглядно представляется в виде графика – кривой процесса. Кривая, изображающая политропический процесс, называется политропой. Уравнение политропического процесса для любого вещества может быть получено на основе первого начала термодинамики с использованием его термического и калорического уравнений состояния. Продемонстрируем, как это делается на примере вывода уравнения процесса для идеального газа.
Вывод уравнения политропического процесса в идеальном газе
Требование постоянства теплоёмкости в процессе позволяет записать первое начало термодинамики в виде
Используя уравнение Майера (9.11) и уравнение состояния идеального газа, получаем следующее выражение для
Разделив уравнение (9.12) на T и подставив в него (9.13) придем к выражению
Разделив () на , находим
Интегрированием (9. 15), получаем
15), получаем
Это уравнение политропы в переменных
Исключая из уравнения () , с помощью равенства получаем уравнение политропы в переменных
Параметр называется показателем политропы, который может принимать согласно () самые разные значения, положительные и отрицательные, целые и дробные. За формулой () скрывается множество процессов. Известные вам изобарный, изохорный и изотермический процессы являются частными случаями политропического.
К этому классу процессов относится также адиабатный или адиабатический процесс . Адиабатным называется процесс, проходящий без теплообмена (). Реализовать такой процесс можно двумя способами. Первый способ предполагает наличие у системы теплоизолирующей оболочки, способной изменять свой объем. Второй – заключается в осуществлении столь быстрого процесса, при котором система не успевает обмениваться количеством теплоты с окружающей средой. Процесс распространения звука в газе можно считать адиабатным благодаря его большой скорости.
Из определения теплоемкости следует, что в адиабатическом процессе . Согласно
где – показатель адиабаты.
В этом случае уравнение политропы принимает вид
Уравнение адиабатного процесса (9.20) называют также уравнением Пуассона, поэтому параметр часто именуют постоянной Пуассона. Постоянная является важной характеристикой газов. Из опыта следует, что ее значения для разных газов лежат в интервале 1,30 ÷ 1,67, поэтому на диаграмме процессов адиабата «падает» более круто, чем изотерма.
Графики политропических процессов для различных значений представлены на рис. 9.1.
На рис. 9.1 графики процессов пронумерованы в соответствии с табл. 9.1.
Скорость | Физика
Проделаем опыт. Установим на тележку капельницу (рис. 11). Из капельницы через одинаковые промежутки времени падают капли окрашенной жидкости. Если присоединить к тележке груз (как это показано на рисунке 11), то при определенной его величине расстояния между следами, оставленными каплями на бумаге (при движении тележки), могут оказаться равными.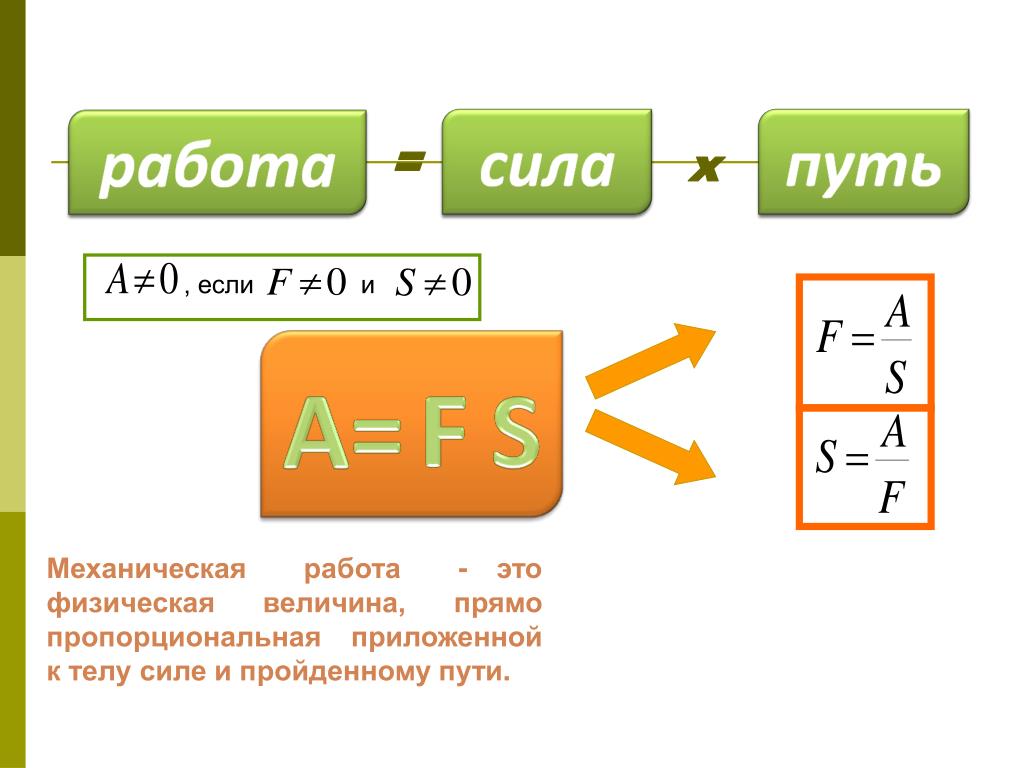 Это означает, что тележка за одинаковые промежутки времени проходит равные пути.Повернув кран капельницы так, чтобы капли падали чаще, повторим опыт. Следы капель и в этом случае оказываются на равных расстояниях друг от друга, хотя и меньших, чем в первом опыте. А это значит, что и за меньшие одинаковые промежутки времени тележка проходит одинаковые пути.
Это означает, что тележка за одинаковые промежутки времени проходит равные пути.Повернув кран капельницы так, чтобы капли падали чаще, повторим опыт. Следы капель и в этом случае оказываются на равных расстояниях друг от друга, хотя и меньших, чем в первом опыте. А это значит, что и за меньшие одинаковые промежутки времени тележка проходит одинаковые пути.
Если какое-нибудь тело за любые равные промежутки времени проходит одинаковые пути, то его движение называют равномерным.
Быстроту движения характеризуют физической величиной, называемой скоростью. Известно, что самолет движется быстрее автомобиля, а искусственный спутник Земли — быстрее самолета.
Скорость тела при равномерном движении показывает, какой путь проходит тело за единицу времени. Например, если за каждый час пешеход проходит 3 км, а самолет пролетает 900 км, то говорят, что скорость пешехода 3 км/ч, а скорость самолета 900 км/ч.
Если же известно, что тот же пешеход за каждые два часа проходит 6 км, то, для того чтобы узнать, какой путь он проходит за 1 ч, следует эти 6 км разделить на 2 ч. При этом мы снова получим 3 км/ч.
При этом мы снова получим 3 км/ч.
Итак, чтобы определить скорость тела при равномерном движении, надо пройденный телом путь разделить на время движения, т. е.
.
Обозначим все величины, входящие в это выражение, латинскими буквами:
s — путь, v — скорость, t — время.
Тогда формулу для нахождения скорости можно представить в следующем виде:
В СИ за единицу скорости принимают скорость такого равномерного движения, при котором движущееся тело за 1 с походит путь, равный 1 м. Эту единицу обозначают или 1 м/с (читается “метр в секунду”).
На практике часто применяют другую единицу скорости: 1 км/ч. Найдем связь между разными единицами скорости. Так как 1 км = 1000 м, а 1 ч = 60 мин = 3600 с, то мы можем записать:
.
Рассмотрим пример. Пусть требуется выразить скорость самолета, равную 720 км/ч, в метрах в секунду. Переводя километры в метры, а час в секунды, получаем
.
При равномерном движении числовое значение скорости не изменяется. Если, например, скорость тела равна 60 км/ч, то это значение будет оставаться таким же на протяжении всего времени движения.
Если, например, скорость тела равна 60 км/ч, то это значение будет оставаться таким же на протяжении всего времени движения.
Но, кроме своего числового значения, скорость имеет и свое направление. Поэтому на рисунках скорость тела изображают в виде стрелки (рис. 12). Стрелка указывает направление скорости (а следовательно, и движения) тела.
.
Величины, имеющие направление в пространстве, называют векторными величинами или просто векторами. Скорость — величина векторная. Векторной величиной, как мы увидим позже, является также сила. С другой стороны, такие величины, как масса, путь, объем, векторами не являются: они не имеют направления в пространстве и характеризуются лишь числовым значением.
В таблице 2 приведены значения некоторых скоростей, встречающихся в природе.
Таблица 2
Скорости движения, м/с
Не все указанные в таблице 2 движения являются равномерными. Лишь звук, свет и радиоволны при определенных условиях распространяются с постоянной скоростью. Скорости остальных тел меняются в процессе движения. Поэтому для них указаны средние или наибольшие значения, которые могут быть достигнуты этими телами.
Скорости остальных тел меняются в процессе движения. Поэтому для них указаны средние или наибольшие значения, которые могут быть достигнуты этими телами.
Движения, при которых скорость тела на разных участках траектории различна, называются неравномерными.
Неравномерные движения характеризуют средней скоростью. Средняя скорость неравномерного движения находится так же, как и скорость равномерного движения, т. е. пройденный телом путь делится на время движения:Только полученное при этом значение может не совпадать со скоростью движения тела на отдельных участках траектории. При неравномерном движении тело на одних участках имеет меньшую скорость, на других — большую. Например, поезд, отходящий от станции, начинает двигаться все быстрее и быстрее. Подъезжая к станции, он, наоборот, замедляет свое движение.
Лишь при равномерном движении скорость тела на протяжении всей траектории имеет неизменное числовое значение.
Зная скорость и время равномерного движения тела, можно вычислить пройденный телом путь. Из формулы (6.1) следует, что
Из формулы (6.1) следует, что
(6.2)
Итак, чтобы найти путь, пройденный при равномерном движении, надо скорость тела умножить на время движения.
Если же известны путь и скорость, то можно найти время движения. Из формулы (6.2) получаем
(6.3)
Итак, чтобы найти время движения, надо путь, пройденный телом, разделить на его скорость.
1. Какое движение называют равномерным? 2. Что показывает скорость равномерного движения? 3. Как определяется скорость при равномерном движении? 4. Как находится пройденный путь, если известны скорость и время движения? 5. Как находится время движения, если известны путь и скорость движения? 6. Какое движение называют неравномерным? 7. Как нужно изменить условия опыта, изображенного на рисунке 11, чтобы движение тележки стало неравномерным? Как при этом изменятся расстояния между следами, оставляемыми падающими каплями? 8. Как находится средняя скорость? 9. Какие величины называют векторными? Как их изображают на рисунках?
Экспериментальные задания. 1. Определите среднюю скорость, с которой вы пробегаете 100 м. 2. Если у вас дома есть игрушечный заводной автомобиль, то, сделав необходимые измерения, найдите среднюю скорость, с которой он перемещается. Результаты измерений и вычислений запишите в тетрадь.
1. Определите среднюю скорость, с которой вы пробегаете 100 м. 2. Если у вас дома есть игрушечный заводной автомобиль, то, сделав необходимые измерения, найдите среднюю скорость, с которой он перемещается. Результаты измерений и вычислений запишите в тетрадь.
Формула работы
- Евсиевич Нинель Валерьевна
Разделы: Начальная школа
Цели:
- сформировать представление о величине «производительность», выявить зависимость между величинами: объем выполненной работы (А), производительность (V) и время (t), построить формулу работы А = V * t, V = A : t, t = A : V.
- повторить и закрепить решение примеров на
порядок действий, соотношение между единицами
дины, времени, массы.

ХОД УРОКА
I.
– Кто из Вас знает, кем работают ваши родители и
на каком предприятии они трудятся?
– А кто из Вас знает пословицы о труде?
- Работа силушку копит, а лень ее топит.
- Под лежачий камень вода не течет.
- Трудолюбив, как муравей.
- Не спеши языком, торопись делом.
- Кто мало говорит, тот много делает.
- Без труда не вытащишь рыбку из пруда.
- Рабочие руки не знают скуки.
- Дело мастера боится.
- Всякое умение трудом дается.
- Без труда нет добра.
- Без труда день годом станет.
- Горька работа, да сладок мед.
II. Актуализация знаний
(На доске таблица и формулы. Дети придумывают задачи и решают устно)
| S | V | t |
| ? км | 60 км/ч | 4 ч |
| 720 км | ? км/ч | 6 ч |
| 57 км | 19 км/ч | ? ч |
– Найдите среди формул те, которые показывают,
как найти неизвестные значения пути, скорости и
времени. (Формулы выставляются на доске и
комментируются)
(Формулы выставляются на доске и
комментируются)
– А зачем вообще нужны формулы? (Показывают,
как решать похожие между собой задачи).
– Подберите формулы для решения первой задачи.
(S = V * t)
– Придумайте по этой формуле задачу, аналогичную
первой задачи.
– Запишите формулу, подходящую к задаче: «Один
всадник проскакал 70 км за 2 ч, а второй – 90 км за 3
ч. Какой из них скакал быстрее?» (V = S: t)
– Решите эту задачу, пользуясь формулой.
(1. 70 : 2 = 35 (км/ч) – скорость первого всадника.
2. 90 : 3 = 30 (км/ч) – скорость второго всадника.
3. 35 км/ч > 30 км/ч => 1 всадник скакал быстрее)
III. Постановка проблемы
– Подберите формулу к задаче: «Один мастер
сделал 2 детали за 4 часа, а второй – 21 деталь
за 3 часа. Кто из них работал быстрее?» (Подходящей
формулы среди данных нет)
– Сформулируйте цель урока –
установить, какие величины описывают процесс
выполнения работы, и установить взаимосвязь
между ними.
– Тема урока – Формула работы.
IV. «Открытие» детьми нового знания.
– О каких величинах идет речь в последней
задаче – о площади, объеме, пройденном пути? (Нет.
В задаче говориться о количестве деталей,
сделанных рабочими, о скорости и времени их
работы).
– Как найти скорость работы мастеров? (Надо
количество сделанных деталей разделить на время
работы).
– Скорость работы называют производительностью
и обозначают (V), всю выполненную работу – А, время
работы – t.
– Попробуйте установить взаимосвязь между этими
величинами. (А = V * t, V = A : t, t = A : V)
– Теперь, зная формулу работы, давайте решим
задачу.
V = A : t
1. 24 : 4 = 6 (дет./ч) – производительность первого
мастера.
2. 21 : 3 = 7 (дет./ч) – производительность второго
мастера.
3. Второй мастер работал быстрее.
Практическая работа на производительность
– Решите устно в течение 2 минут следующие уравнения.
9 + х = 12 х – 27 = 8 5 * х = 25
8 * х = 480 52 : х = 13 420 : х = 7
40 – х = 12 х : 19 = 4 800 + х = 823
90 : х = 5 34 – х = 17 х – 36 = 15
х * 50 = 250 18 + х = 110 х – 25 = 118
– Давайте проверим количество правильных
ответов и вычислим производительность каждого
из вас.
– Как это сделать? (Количество верных ответов
разделить на 2).
– А какая у вас производительность за урок? (То
что получилось умножить на 45 минут).
Закрепление понятия «производительность»
- С. 44, №1
V. Первичное закрепление
- С.44, №2
- С. 44, №3
- С.44, №4 (а)
VI. Самостоятельная работа с самопроверкой по эталону
- С.44, №4 (б).
VII. Закрепление пройденного
- С.45, №10 (а)
VIII. Итог
– Что сегодня на уроке было самым интересным?
– Что сегодня на уроке было главным?
– Где нам могут пригодиться эти знания?
– Какую поговорку выберем своим девизом?
IX. Домашнее задание
- С.44, №5 и №7
Приложение 1
Формула T Score: Расчет в простых шагах
Содержание:
T Score в статистике.
Что такое формула Т-показателя?
Пример формулы T-счета
T-баллы в психометрии
T-баллы в статистике
Посмотрите видео с обзором формулы:
Пример формулы T-балла
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Что такое формула Т-показателя?
Показатель t — это одна из форм стандартизированной тестовой статистики (другой вариант, с которым вы столкнетесь в элементарной статистике, — это показатель z). Формула оценки t позволяет вам взять индивидуальную оценку и преобразовать ее в стандартизированную форму, которая поможет вам сравнивать оценки.
Вы захотите использовать формулу t-показателя, если вам неизвестно стандартное отклонение генеральной совокупности и у вас есть небольшая выборка (менее 30).
Формула t-показателя:
Где
x̄ = среднее значение выборки
μ 0 = среднее значение генеральной совокупности
s = стандартное отклонение выборки
n = размер выборки
Если у вас есть только один элемент в вашей выборке, квадратный корень в знаменателе становится равным √1. Это означает, что формула принимает следующий вид:
Это означает, что формула принимает следующий вид:
Проще говоря, чем больше показатель t, тем больше разница между группами, которые вы тестируете. На него влияют многие факторы, в том числе:
Для чего используется формула Т-показателя?
Традиционно вы ищете t-счет в t-таблице. Количество элементов в вашей выборке минус один — это ваши степени свободы. Например, если в вашей выборке 20 элементов, то df = 19.. Вы используете степени свободы вместе с уровнем достоверности, который вы готовы принять, чтобы решить, поддерживать или отвергать нулевую гипотезу.
Формула t-показателя также может использоваться для решения вопросов вероятности. У вас не будет альфа-уровня, но вы можете использовать результат формулы вместе с калькулятором, таким как TI-83, для нахождения вероятностей.
В следующем примере показано, как рассчитать формулу t-показателя для одной выборки. Парные выборки и независимые выборки используют разные формулы.
- Если у вас есть парные образцы, следуйте инструкциям в t-тесте для парных образцов .

- Для независимых выборок см.: независимых выборок t-критерий .
Пример формулы T Score
Нужна помощь с домашним заданием? Посетите нашу обучающую страницу!
Пример вопроса:
Юридическая школа утверждает, что ее выпускники зарабатывают в среднем 300 долларов в час. Выбирается выборка из 15 выпускников, и выясняется, что их средняя заработная плата составляет 280 долларов США при стандартном отклонении выборки 50 долларов США. Если предположить, что заявление школы верно, какова вероятность того, что средняя зарплата выпускников будет не выше 280 долларов?
Шаг 1: Подставьте информацию в формулу и решите:
x̄ = среднее значение выборки = 280
μ 0 = среднее значение генеральной совокупности = 300
s = стандартное отклонение выборки = 50
n = размер выборки = 15
t = (280 – 300)/(50/√15) = -20/12,
5 = -1,549. Шаг 2: Вычтите 1 из размера выборки, чтобы получить степени свободы:
15 – 1 = 14. Степени свободы позволяют вам узнать, какую форму распределения t использовать (их много, но вы можете решить эти проблемы, не зная этого факта!).
Степени свободы позволяют вам узнать, какую форму распределения t использовать (их много, но вы можете решить эти проблемы, не зная этого факта!).
Шаг 3: Используйте калькулятор, чтобы найти вероятность, используя ваши степени свободы (8). У вас есть несколько вариантов, включая TI-83 (см. Как найти распределение t на TI 83). Вот результат онлайн-калькулятора, который я нашел несколько лет назад (ныне несуществующего). Обратите внимание, что я выбрал переключатель под левым хвостом, так как мы ищем результат не более 280 долларов:
Вероятность 0,0718, или 7,18%.
Наверх.
Показатель t в психометрическом (психологическом) тестировании — это специальный термин, равный — это не то же самое, что t-показатель, который вы получаете из t-теста.
Т-показатели в t-критериях могут быть положительными или отрицательными. Т-показатели в психометрическом тестировании всегда положительны , со средним значением 50.
Разница в 10 (положительная или отрицательная) от среднего представляет собой разницу в одно стандартное отклонение. Например, 70 баллов — это два стандартных отклонения выше среднего, а 0 баллов — это одно стандартное отклонение ниже среднего.
Например, 70 баллов — это два стандартных отклонения выше среднего, а 0 баллов — это одно стандартное отклонение ниже среднего.
Показатель t аналогичен показателю z — он равен количество стандартных отклонений от среднего . В то время как z-оценка возвращает значения в диапазоне от -5 до 5 (большинство оценок находится в диапазоне от -3 до 3) стандартных отклонений от среднего значения, t-оценка имеет большее значение и возвращает результаты от 0 до 100 (большинство оценок находится в диапазоне от 0 до 100). 20 и 80). Многие люди предпочитают t-показатели, потому что отсутствие отрицательных чисел означает, что с ними легче работать, и существует более широкий диапазон, поэтому десятичные дроби почти исключены. В этой таблице показаны z-показатели и их эквивалентные t-показатели.
Преобразование T-показателя в психометрии
Посмотрите видео для примера:
Как преобразовать t-показатель из z-показателя (психометрия)
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Вычисление t-показателя на самом деле просто преобразование из z-показателя в t-показатель, очень похожее на преобразование градусов Цельсия в градусы Фаренгейта. Формула для преобразования z-показателя в t-показатель:
T = (Z x 10) + 50.
Пример вопроса: Кандидат на работу проходит письменный тест, средний балл которого равен 1026, а стандартное отклонение равно 209. Кандидат набирает 1100 баллов. Рассчитайте t-балл для этого кандидата.
Примечание. Если вы получили z-показатель для вопроса, перейдите к шагу 2.
Шаг 1: Рассчитайте z-показатель. (См.: Как рассчитать z-оценку). Z-показатель для данных в этом примере вопроса равен 0,354.
Шаг 2: Умножьте значение z из шага 1 на 10:
10 * 0,354 = 3,54.
Шаг 3: Добавьте 50 к результату из Шага 2:
3,54 + 50 = 53,54.
Вот и все!
Советы :
- z-показатели и t-показатели представляют собой стандартные отклонения от среднего, но в то время как «0» по z-показателю соответствует 0 стандартным отклонениям от среднего, «50» по t-показателю представляет тоже самое.
 Это связано с тем, что для t-показателей используется среднее значение 50, а для z-показателей используется среднее значение 0, .
Это связано с тем, что для t-показателей используется среднее значение 50, а для z-показателей используется среднее значение 0, . - Показатель выше 50 выше среднего; ниже 50 ниже среднего. Как правило, показатель t выше 60 означает, что показатель находится в верхней одной шестой распределения; выше 63, верхняя одна десятая. Оценка
ниже 40 указывает самую низкую позицию в одну шестую; ниже 37, нижняя одна десятая.
Наверх.
Ссылки
Левин, Д. (2014). Даже вы можете изучить статистику и аналитику: простое для понимания руководство по статистике и аналитике, 3-е издание. Pearson FT Press
УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Формула T-счета: расчет в простых шагах» От StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/probability-and-statistics/t-distribution/t-score-formula/
————————————————– ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
Численность, математика и статистика – Набор академических навыков
Уравнения движения (Механика)
ContentsToggle Главное меню 1 Уравнения движения 2 Проверьте себя 3 Внешние ресурсы
Уравнения движения
Уравнения движения, также известные как уравнения SUVAT, используются при ускорении постоянно. Они известны как уравнения СУВАТ, потому что содержат следующие переменные: $s$ – расстояние, $u$ – начальная скорость, $v$ – скорость в момент времени $t$, $a$ – ускорение и $t$ – время. Однако каждое уравнение SUVAT не содержит всех переменных, поэтому для ответа на некоторые вопросы может потребоваться использование одной или нескольких из них. Уравнения следующие: 92. \end{align*}
Величины $s$, $u$, $v$ и $a$ являются векторными величинами, поэтому их знак указывает направление движения. {-1} }$, когда прекращает ускорение. 9{-1} }$. С какой скоростью он двигался, когда вышел из самолета?
{-1} }$, когда прекращает ускорение. 9{-1} }$. С какой скоростью он двигался, когда вышел из самолета?
Решение
Из вопроса мы знаем, что \begin{align} s &= ?\\ u &= ?\\ v &= 40\\ a &= 9.8\\ t &= 4.05 \end{align} Мы хотите найти $u$, начальную скорость, из значений, которые у нас есть. Уравнение, которое у нас есть, которое включает $u$, $v$, $a$ и $t$, имеет вид \[v = u + at.\]. Однако его нужно изменить, чтобы сделать $u$ объектом уравнения. Это дает \[u = v – at.\] При подстановке известных нам значений мы получаем \begin{align} u &= v – at,\\ &= 40 – \left(9{-1} }$, каково расстояние в $\mathrm{m}$ от $A$ до $B$?
Решение
Из вопроса мы знаем значения некоторых переменных. Лучше всего записать то, что мы знаем, в виде списка \begin{align} s &= ?\\ u &= 5\\ v &= 10\\ a &= ?\\ t &= 6 \end{align} Из списка значений, которые мы знаем, нам нужно использовать уравнение $s = \left(\frac{u+v}{2}\right)t$, чтобы найти $s$. При подстановке получаем: \begin{align} s& = \left(\frac{u+v}{2}\right)t,\\ &= \left(\frac{5 + 10}{2}\right) \times 6,\\ &=45 \mathrm{m}. \end{align} Расстояние от $A$ до $B$ равно $45 \mathrm{m}$. 9{-1} }. \end{align} Для $t$ имеем \begin{align} \frac{2}{3} \mathrm{minute} & = \frac{2}{3} \times 60\mathrm{s}, \\ & = 40\mathrm{s}. \end{align} Теперь мы можем записать то, что мы знаем, в список \begin{align} s &= ?\\ u &= 0\\ v &= \frac{50}{3} \\ a &= ? \\ t &= 40 \end{align} Обратите внимание, что $u=0$, потому что автомобиль начинает движение в состоянии покоя. Из списка значений, которые мы знаем, нам нужно использовать уравнение $s = \left(\frac{u+v}{2}\right)t$, чтобы найти $s$. При подстановке получаем: \begin{align} s& = \left(\frac{u+v}{2}\right)t,\\ &= \left(\frac{0 + 5/3}{2}\ справа) \times 40,\\ &=\frac{100}{3} \mathrm{m}. \end{align} Расстояние от $A$ до $B$ равно $\frac{100}{3}\mathrm{m}$. 9{-1} }$ при внезапном торможении. Автомобиль проходит $40\mathrm{m}$ при торможении, а затем останавливается. Каково было ускорение автомобиля при торможении?
\end{align} Расстояние от $A$ до $B$ равно $45 \mathrm{m}$. 9{-1} }. \end{align} Для $t$ имеем \begin{align} \frac{2}{3} \mathrm{minute} & = \frac{2}{3} \times 60\mathrm{s}, \\ & = 40\mathrm{s}. \end{align} Теперь мы можем записать то, что мы знаем, в список \begin{align} s &= ?\\ u &= 0\\ v &= \frac{50}{3} \\ a &= ? \\ t &= 40 \end{align} Обратите внимание, что $u=0$, потому что автомобиль начинает движение в состоянии покоя. Из списка значений, которые мы знаем, нам нужно использовать уравнение $s = \left(\frac{u+v}{2}\right)t$, чтобы найти $s$. При подстановке получаем: \begin{align} s& = \left(\frac{u+v}{2}\right)t,\\ &= \left(\frac{0 + 5/3}{2}\ справа) \times 40,\\ &=\frac{100}{3} \mathrm{m}. \end{align} Расстояние от $A$ до $B$ равно $\frac{100}{3}\mathrm{m}$. 9{-1} }$ при внезапном торможении. Автомобиль проходит $40\mathrm{m}$ при торможении, а затем останавливается. Каково было ускорение автомобиля при торможении?
Решение
Как и в случае с предыдущими вопросами, лучше сначала перечислить, что мы знаем \begin{align} s &= 40\\ u &= 22\\ v &= 0\\ a &= ?\\ t &= ? \end{align} Мы знаем, что конечная скорость должна быть $v=0$, так как в вопросе говорится, что машина останавливается. {-1} } $ в обратном направлении, от $B$ до $A$. 9{-2} }$.
{-1} } $ в обратном направлении, от $B$ до $A$. 9{-2} }$.
Проверьте себя
Попробуйте наш тест Numbas по уравнениям движения: Equations of Motion
Внешние ресурсы
- BBC Bitesize: Higher Physics
- BBC Bitesize: GCSE Physics
Учебные пособия и практические занятия доктора Юэ-Линг Вонг по естественнонаучному образованию
Учебные пособия и практические занятия по естественнонаучному образованию доктора Юэ-Линг Вонг| Учебники и практические упражнения для естественнонаучного образования | |||||||||||||||||||||||||||||||||||||||||||||||||
| Общая физика :: Движение снаряда :: Как рассчитать #1 Задача №1: найти
где приземлится пушечное ядро, учитывая начальную скорость ( v 0 ) и угол выстрела ( θ 0 ) Решение Пошаговое руководство:
[произошла ошибка при обработке этой директивы] | ||||||||||||||||||||||||||||||||||||||||||||||||
| Формула теста | |||||||||||||||||||||||||||||||||||||||||||||||||
t — Easy Guides — Wiki
- определение t-критерия
- Формула t-теста для одной выборки
- Независимый двухвыборочный t-критерий
- Что такое независимый t-критерий?
- Независимая формула t-теста
- Парный выборочный t-критерий
- Что такое парный t-критерий?
- Формула парного t-теста
- Онлайн-калькулятор t-теста
- Информация
t-критерий Стьюдента равен статистический тест , который широко используется для сравнения среднего значения двух групп выборок. Следовательно, необходимо оценить, отличаются ли средние значения двух наборов данных статистически значимо друг от друга.
Существует множество типов t-критерия :
- Одновыборочный t-критерий , используемый для сравнения среднего значения генеральной совокупности с теоретическим значением.
- Стьюдентный критерий для двух непарных выборок , используемый для сравнения среднего значения двух независимые образцы .
- Парный t-критерий , используемый для сравнения средних между двумя связанными группами выборок.
Целью этой статьи является описание различных формул теста t . Критерий Стьюдента является параметрическим критерием , поскольку формула зависит от среднего и стандартного отклонения сравниваемых данных.
Обратите внимание, что онлайн-калькулятор t-теста доступен здесь для вычисления статистики t-теста без какой-либо установки.
Связанная книга:
Практическая статистика в R для сравнения групп: числовые переменные
Как упоминалось выше, одновыборочный t-критерий используется для сравнения среднего значения генеральной совокупности с указанным теоретическим средним значением (\(\mu\)).
Пусть X представляет собой набор значений размера n, где означает м, а стандартное отклонение S. Сравнение наблюдаемых средних значений (m) населения с теоретическим значением \(\mu\) выполняется по следующей формуле:
\[ t = \frac{m-\mu}{s/\sqrt{n}} \]
Чтобы оценить, является ли различие статистически значимым, вы должны сначала прочитать в t проверочную таблицу критическое значение t-распределения Стьюдента , соответствующее выбранному вами уровню значимости альфа (5%). степени свободы (df), используемые в этом тесте:
степени свободы (df), используемые в этом тесте:
\[ df = n – 1 \]
Если абсолютное значение статистики t-теста (|t|) больше критического значения, то разница имеет большое значение. В противном случае это не так. Уровень значимости или ( p-значение ) соответствует риску, указанному таблицей t-теста для рассчитанного |t| ценность.
Тест t можно использовать только при нормальном распределении данных.
Что такое независимый t-тест?
Независимый (или две непарные выборки) t-тест используется для сравнения средних значений двух несвязанных групп выборок.
Например, у нас есть когорта из 100 человек (50 женщин и 50 мужчин). Вопрос состоит в том, чтобы проверить, значительно ли средний вес женщин отличается от веса мужчин?
В этом случае у нас есть две независимые группы выборок, и непарный t-критерий можно использовать для проверки различия средних. 92}}{n_A+n_B-2}
\]
92}}{n_A+n_B-2}
\]
После определения статистического значения t-критерия вы должны прочитать в таблице t-теста критическое значение распределения Стьюдента , соответствующее уровню значимости альфа по вашему выбору (5%). . степени свободы (df), используемые в этом тесте:
\[ df = n_A + n_B -2 \]
критическое значение, то разница значительна. В противном случае это не так. уровень значимости или ( p-значение ) соответствует риску, указанному таблицей t-теста для рассчитанного |t| ценность.
Этот тест можно использовать только тогда, когда две сравниваемые группы выборок (A и B) подчиняются двумерному нормальному распределению с равными дисперсиями .
Если дисперсии двух сравниваемых групп различны, можно использовать t-критерий Велча .
Что такое парный t-критерий?
Парный критерий Стьюдента используется для сравнения средних значений двух связанных выборок. Это когда у вас есть два значения (пара значений) для одних и тех же выборок.
Это когда у вас есть два значения (пара значений) для одних и тех же выборок.
Например, 20 мышей получали лечение X в течение 3 месяцев. Вопрос состоит в том, чтобы проверить, влияет ли лечение X на вес мышей в конце 3-месячного лечения. Вес 20 мышей измеряли до и после лечения. Это дает нам 20 наборов значений до лечения и 20 наборов значений после лечения при двойном измерении веса одних и тех же мышей.
В этом случае можно использовать парный t-критерий , поскольку два сравниваемых набора значений связаны. У нас есть пара значений для каждой мыши (одно до и другое после лечения).
Формула парного t-критерия
Чтобы сравнить средние значения двух парных наборов данных, сначала должны быть рассчитаны различия между всеми парами.
Пусть d представляет разность между всеми парами. Среднее значение разницы d сравнивается с 0. Если между двумя парами выборок имеется какое-либо существенное различие, то ожидается, что среднее значение d будет далеко от 0,9. 0011
0011
t Статистическое значение теста можно рассчитать следующим образом:
\[ t = \frac{m}{s/\sqrt{n}} \]
m и s являются средним и стандартным отклонением разности (d) соответственно. n размер d.
Как только значение t определено, вы должны прочитать в таблице t-теста критическое значение распределения t Стьюдента , соответствующее уровню значимости альфа на ваш выбор (5%). степеней свободы (df), используемых в этом тесте:
\[ df = n – 1 \]
значения, то разница существенна. В противном случае это не так. Уровень значимости или ( p-значение ) соответствует риску, указанному таблицей t-теста для рассчитанного |t| ценность.
Критерий можно использовать только тогда, когда разность d имеет нормальное распределение.
Вам больше не нужны SPSS или Excel для выполнения t-теста .
Онлайн-калькулятор t-критерия доступен здесь для выполнения t-критерия Стьюдента без какой-либо установки.
В зависимости от типов t-критерия Стьюдента , которые вы хотите выполнить, щелкните следующие ссылки:
- Одновыборочный t-критерий
- Стьюдентный критерий независимой выборки
- Парные образцы t-критерий
Понравилась эта статья? Я был бы очень признателен, если бы вы помогли его распространению, отправив его по электронной почте другу или поделившись им в Twitter, Facebook или Linked In.
Подарите мне немного любви с помощью кнопок «Мне нравится» ниже… Спасибо и, пожалуйста, не забудьте поделиться и прокомментировать ниже!!
Avez vous aimé c этой статьей? Je vous serais très reconnaissant si vous aidiez à sa диффузия en l’envoyant par courriel à un ami ou en le partageant sur Twitter, Facebook или Linked In.
Montrez-moi un peu d’amour avec les like ci-dessous … Merci et n’oubliez pas, s’il vous plaît, de partager et de commenter ci-dessous!
кинематических уравнений | PASCO
Что такое кинематические уравнения?
Кинематические уравнения представляют собой набор уравнений, описывающих движение объекта с постоянным ускорением. Уравнения кинематики требуют знания производных, скорости изменения и интегралов. Чтобы сосредоточиться на школьной физике, мы не будем рассматривать интегралы.
Когда мы используем кинематические уравнения, мы используем специальные обозначения для обозначения начальных и конечных измерений.
Например, когда у нас есть начальное значение скорости, оно записывается как $ \Large\mathcal{v}_{\normalsize0} $.
Когда мы пишем конечную скорость, мы просто пишем $\Large\mathcal{v}$ без нижнего индекса.
Следовательно, изменение скорости объекта представляется уравнением $\Delta\Large\mathcal{v} = \mathcal{v} – \mathcal{v}_{\normalsize0} $. Это обозначение также применимо к смещению и времени.
Это означает, что $ {\large x}_0 $ — это начальное положение, $ {\large x} $ — это конечное положение, $ {\large t}_0 $ — начальное время, а $ \large t $ — конечное время. .
Важно помнить, что начальное время, $ {\large t}_0 $, будет равно нулю для уравнений кинематики.
Поскольку временной интервал равен $ \Delta\mathcal{t} $ и $ {\mathcal{t}}_0 = 0{\normalsize{s}} $, мы знаем, что $ \Delta\mathcal{t} = \mathcal{ т} $.
Это обозначение также применимо к смещению и времени.
Это означает, что $ {\large x}_0 $ — это начальное положение, $ {\large x} $ — это конечное положение, $ {\large t}_0 $ — начальное время, а $ \large t $ — конечное время. .
Важно помнить, что начальное время, $ {\large t}_0 $, будет равно нулю для уравнений кинематики.
Поскольку временной интервал равен $ \Delta\mathcal{t} $ и $ {\mathcal{t}}_0 = 0{\normalsize{s}} $, мы знаем, что $ \Delta\mathcal{t} = \mathcal{ т} $.
Как выбрать правильное уравнение?
Кинематические уравнения могут применяться к множеству задач размерного движения, рассматривающих движение объекта с постоянным ускорением.
При решении задач формула, которую мы выбираем, должна включать неизвестную переменную, а также три известные переменные.
В каждом из уравнений отсутствует одна переменная.
Это позволяет вам определить, какая переменная не задана или не запрошена в вашей задаче, прежде чем выбрать уравнение, в котором также отсутствует эта переменная. Давайте посмотрим поближе.
Давайте посмотрим поближе.
Не хватает смещения? В этой формуле отсутствует $ \Delta{\large x} $, и ее следует использовать для задач, которые не включают или не требуют смещения.
$ \Large v = v_0 + \Large {at} $
Не хватает ускорения? Эта формула идеальна для задач, которые не включают или не требуют ускорение. Однако важно помнить, что иногда ускорение косвенно упоминается, например, когда объект находится в свободном падении (см. ниже).
$ \Большой\Дельта\большой х = \Большой (\фракция {v + v_0}{2}) \большой т $ 92 + \Large 2a\Delta{\large x} $
Скорость, ускорение и сопротивление воздуха
Когда мы используем уравнения кинематики, мы можем сделать некоторые математические предположения.
Когда движущийся объект движется по воздуху, сопротивление воздуха замедляет скорость объекта.
К счастью, когда мы используем уравнения движения, мы предполагаем, что сопротивление воздуха достаточно незначительно, чтобы им можно было пренебречь.
Второе предположение, которое мы можем сделать при использовании этих уравнений, касается ускорения. Мы уже знаем, что ускорение для задач кинематики постоянно, а значит, среднее ускорение равно этому значению. Объекты в свободном падении или снаряды испытывают одинаковое ускорение, независимо от их массы. Это означает, что всякий раз, когда объект брошен, брошен или падает, он движется с постоянным нисходящим ускорением в 9 долларов.2$.
Поскольку уравнения кинематики используются, когда ускорение объекта постоянно, мы можем использовать простое уравнение для определения средней скорости объекта. Чтобы найти среднюю скорость, просто прибавьте начальную скорость к конечной скорости и разделите на 2.
$ \LARGE v_{ \textrm {среднее}} = \bar{v} = \frac {v_1 + v_2}{2} $ Это уравнение можно использовать только при постоянном ускорении
Когда объект движется прямолинейно вдоль оси x, мы можем использовать смещение объекта и временной интервал для определения средней скорости. Это уравнение учитывает начальное положение, конечное положение и временной интервал.
Это уравнение учитывает начальное положение, конечное положение и временной интервал.
$ \LARGE v_{ \textrm {среднее}} = \bar{v} = \frac {x_2 – x_1}{t_2 – t_1} = \frac {\Delta x}{\Delta t} $
Вы можете использовать наклон линии, касательной к излечению положение-время, чтобы определить скорость объекта. Скорость объекта в определенный момент времени называется мгновенной скоростью. Построение графика положение-время может помочь вам определить как мгновенную скорость, так и среднюю скорость. Точно так же построение графика зависимости скорости от времени может помочь вам определить мгновенное ускорение и среднее ускорение объекта, поскольку ускорение — это скорость изменения скорости. Однако, когда мы применяем это к уравнениям кинематики, которые имеют постоянное ускорение, мгновенное ускорение объекта будет равно его среднему ускорению.
Как вывести уравнения кинематики
Первое уравнение: $ \large v = v_0 + at $
1.) Чтобы начать вывод первого кинематического уравнения, мы должны сначала рассмотреть определение ускорения. $ \Large a = \frac {\Delta v}{\Delta t} $
$ \Large a = \frac {\Delta v}{\Delta t} $
2.) Мы знаем, что $ \Large \Delta v = v – v\normalsize{_0} $ , и когда мы это подставим, мы получим $ \Large a = \frac {v – v_0}{\Delta t} $
3.) Если мы решим для $\Large v $, уравнение станет $\Large v = v_0 + \Large a \Delta t $
4.) Мы можем обозначить интервал времени как для генерации первого кинематического уравнения.
$ \НАИБОЛЬШИЙ v = v_0 + в $
Второе уравнение: $ \Delta x = (\frac {v + v_{\normalsize0}}{2}) t $
Чтобы вывести это уравнение, рассмотрим график зависимости скорости от времени с постоянным ускорением. Наклон графика скорости можно интерпретировать как ускорение, а площадь под графиком равна смещению объекта $ \Delta x $ .
Здесь высота синего прямоугольника равна $\large v_0 $, а ширина $\large t $, поэтому площадь равна $\large v_0 t $.
Основание красного треугольника равно $ \large t $, а высота равна $ \large v – v_0 $, поэтому площадь красного треугольника равна $ \large \ frac {1}{2} t (v – v_0) $ . 2 $
92 $
2 $
92 $
Мы можем получить третье кинематическое уравнение, подставив первую кинематическую формулу во вторую формулу.
1.) Начните со второго кинематического уравнения. $ \large \frac {\Delta x}{t} = (\frac {\Large v + v_{\normalsize0}}{2}) $
2.) Подставляем первую кинематическую формулу вместо $\large v$. $ \Large v = v\normalsize{_0} + \Large в $
3.) После подстановки уравнение становится $ \large \frac {\Delta x}{t} = \frac {\Large (v_0 + at) + v_0}{2} $ 92 + 2а \Дельта х $
Четвертое кинематическое уравнение может быть получено с использованием первого и второго кинематических уравнений.
1.) Начните со второй кинематической формулы. $ \large \Delta x = (\frac {v + v_{\normalsize0}}{2}) t $
2.) Мы можем использовать первую кинематическую формулу, $ \Large \mathcal{v} = \mathcal{v}\normalsize{_0} + \large at $, чтобы найти время. $ \large t = \frac {\Large v – v _{\normalsize0}}{a} $
3.) Мы можем подставить наше выражение для времени во вторую кинематическую формулу. $ \large \Delta x = (\frac {\Large v + v_{\normalsize0}}{2}) (\frac {\Large v – v_{\normalsize0}}{\Large a}) $
92 + 2а \Дельта х $
$ \large \Delta x = (\frac {\Large v + v_{\normalsize0}}{2}) (\frac {\Large v – v_{\normalsize0}}{\Large a}) $
92 + 2а \Дельта х $
Решение задач для кинематических уравнений
При решении задач кинематики есть шаги, которым вы можете следовать, чтобы структурировать свой мыслительный процесс. Прочитав задачу, начертите схему и отметьте известные и неизвестные. Определите, что вас просят найти. Затем определите переменные, которые предоставляет проблема. Затем определите, какие уравнения связывают ваши известные переменные с неизвестной переменной. Затем можно приступать к решению.
Свободное падение 92)} = \large 5.1 \textrm m $
Беспроводная фотоворота и заборчик
Беспроводной фотозатвор совершенствует конструкцию традиционных фотозатворов, чтобы предоставить учащимся данные о скорости в реальном времени и расширенные функции для большего количества приложений. Беспроводные интеллектуальные ворота позволяют учащимся собирать высокоточные данные о движении различных объектов — от исследований свободного падения и движения снарядов до маятников и столкновений тележек.
2.) Вы и ваш партнер расходитесь во мнениях относительно того, сможете ли вы заставить штакетник упасть на землю ровно за 1,0 с. Ваш напарник считает, что забор слишком легкий, чтобы его так быстро опустить, но вы убеждены, что это возможно. Предполагая, что ускорение является постоянным, а сопротивление воздуха пренебрежимо мало, с какой высоты вам нужно бросить штакетник, чтобы «умные ворота» зафиксировали его удар о землю ровно через 1,0 с? 92 = 4,9 \textrm м $
Линейное движение в одном измерении
1.) Ваш класс использует датчик движения и MatchGraph! изучать движение. Ваш партнер надевает коньки и удаляется от датчика движения со скоростью 5 м/с. Он останавливается через 23 м. Если торможение вашего партнера было постоянным, сколько времени ему потребовалось, чтобы остановиться?
Каковы заданные значения? $ \large v_0 = 5 \textrm {м/с} $ $ \large v_0 = 0 \textrm {м/с} $ $ \большой x – x_0 = 23 \textrm m $
Мы можем изменить формулу второй кинематики $ \Delta x = (\frac {v + v_{\normalsize0}}{2}) t $
Подставим наше уравнение вместо $\Delta x $ и перестроим уравнение. $ х – х_0 = \ гидроразрыва {1} {2} (v_0 + v) t $
$ х – х_0 = \ гидроразрыва {1} {2} (v_0 + v) t $
Подготовьте уравнение для решения $\large t$ и подставьте известные значения для решения.
$ \Large t = 2 (\frac {x – x_0}{v_0 + v}) = 2 (\frac {23 \textrm m}{5 \textrm {м/с} + 0 \textrm {м/с}} ) = \large 11.6 \textrm s $
Тележка и гусеничная система Dynamics
Dynamics Cart and Track Systems — это многоцелевые наборы оборудования, которые позволяют преподавателям демонстрировать и преподавать различные сложные темы физики в области кинематики и динамики.
С момента своего изобретения динамические системы PASCO стали незаменимыми инструментами в физических лабораториях по всему миру.
Наши динамические системы представляют собой комплексные решения для экспериментов, которые позволяют учащимся наблюдать, измерять и анализировать движение посредством практических экспериментов.
Независимо от того, являетесь ли вы новичком в динамических системах или хотите расширить возможности своих существующих систем, мы предлагаем ряд настраиваемых динамических систем в соответствии с вашим бюджетом и потребностями. 92 $
92 $
Линейное движение во втором измерении
Задачи, включающие наклонную плоскость, пандус или снаряд, потребуют от нас разделения движения на векторные компоненты $\small\overrightarrow{\normalsize x} $ и $\small \overrightarrow{\normalsize y} $.
Рассмотрим реактивный самолет с двумя перпендикулярными двигателями, которые двигают его вдоль осей x и y.
Когда работает только вертикальный двигатель, реактивный самолет движется вдоль оси y.
Точно так же, когда работает только горизонтально ориентированный двигатель, реактивный самолет движется вдоль оси x.
Когда оба двигателя включены, движение струи происходит как в направлении x, так и в направлении y, но ни x, ни y не влияют друг на друга.
По этой причине мы можем анализировать компоненты $\small\overrightarrow{\normalsize x} $ и $\small \overrightarrow{\normalsize y} $ для каждого вектора отдельно, признавая при этом, что они
связаны общей стоимостью $\large t$.
Направления компонентов можно передать, назначив каждому знак плюс или минус. 92 + 2a_yy $
92 + 2a_yy $
Мы можем представить векторные компоненты $\small\overrightarrow{\normalsize x} $ и $\small \overrightarrow{\normalsize y} $ с помощью диаграмм свободного тела — метод, обычно используемый для решения задач, связанных с законами Ньютона. Мы углубимся в это, когда будем изучать динамику. На данный момент важно понимать, что некоторые проблемы должны быть разбиты на компоненты x и y. Например, когда тележка спускается по пандусу, она испытывает движение в направлениях x и y. Его движение зависит от чистого ускорения в направлении x вдоль рампы. Поскольку есть компонент ускорения силы тяжести, который ускоряет тележку вниз по склону, часть ускорения силы тяжести является вертикальной. Ниже вы найдете векторную диаграмму Smart Cart, которая разбивает свое движение на компоненты x и y.
Величины составляющих смещения по осям равны x и y. Величины компонент скорости $ \large v $ равны
$ \large v_x = v\cos \Theta $ и $ \large v_y = v\sin \Theta $, где $ \large v $ — величина скорости, а theta — ее направление.
1.) Тележка Smart Cart высвобождается из состояния покоя на вершине 45-градусного пандуса длиной 5,0 м. Какова конечная скорость умной тележки, если ускорение постоянно, а трение пренебрежимо мало? 9{\circ})] (5,0 \textrm м) = 8,3 \textrm {м/с} $
Беспроводная умная тележка
Wireless Smart Cart — это динамическая тележка следующего поколения со встроенными датчиками, которые измеряют ее положение, скорость, ускорение, силу и вращение.
Полностью функциональная тележка Wireless Smart Cart с треком или без него предоставляет учащимся данные о движении в режиме реального времени, интерактивные графики и интуитивно понятные функции анализа на любом устройстве с подключением Bluetooth и программным обеспечением PASCO.
От вводных экспериментов с линейным и вращательным движением до законов Ньютона и столкновений нескольких тележек — Wireless Smart Cart расширяет возможности классических экспериментов и позволяет учащимся исследовать новый мир экспериментальных возможностей.
Векторный дисплей Smart Cart
Векторный дисплей Smart Cart дает новую жизнь векторным демонстрациям с живыми векторными дисплеями для скорости, ускорения и силы Smart Cart в движении. По мере движения тележки на векторном дисплее загораются стрелки, указывающие направление и величину движения тележки. Этот инновационный дизайн позволяет учащимся наблюдать за векторами скорости, силы и ускорения в режиме реального времени, когда тележка катится по склону, свободно падает, вращается или сталкивается с другой тележкой.
Узнайте больше о правильной настройке динамической тележки и направляющей системы для вашего класса.
Движение снаряда
Снарядное движение возникает, когда единственное ускорение, испытываемое объектом в полете, вызвано гравитацией, которая тянет его вниз.
Объект в движении называется снарядом, а его путь известен как его траектория.
Горизонтальное расстояние, пройденное снарядом, называется его дальностью.
Конечное положение за вычетом начального положения снаряда называется его перемещением, с. В двумерных задачах движения снаряда часто предполагается, что сопротивление воздуха и трение пренебрежимо малы.
Поскольку движения вдоль перпендикулярной оси независимы, мы можем анализировать их отдельно, разбивая их на компоненты x и y.
Когда мы применяем кинематические уравнения для каждого компонента, мы используем нижние индексы x и y для обозначения отношения каждой переменной к осям x или y.
Для компонентов x и y ускорение постоянно, что позволяет нам использовать кинематические уравнения.
92 $
В двумерных задачах движения снаряда часто предполагается, что сопротивление воздуха и трение пренебрежимо малы.
Поскольку движения вдоль перпендикулярной оси независимы, мы можем анализировать их отдельно, разбивая их на компоненты x и y.
Когда мы применяем кинематические уравнения для каждого компонента, мы используем нижние индексы x и y для обозначения отношения каждой переменной к осям x или y.
Для компонентов x и y ускорение постоянно, что позволяет нам использовать кинематические уравнения.
92 $
Визуальное представление полного смещения, $\Large s $, летящего мяча в точке на его пути показано выше. Вектор $\Large s$, имеет вдоль осей компоненты $\Large x$ и $\Large y$. Его величина составляет угол $\Theta$ с горизонтом. Обратите внимание, что $\Large s $ и $\Large x $ могут обозначать смещение. Здесь мы используем $\Large s $, чтобы упростить идентификацию каждого вектора. Мы можем использовать ряд шагов для анализа движения снаряда.
Шаг 1: Разбейте движение на горизонтальные и вертикальные компоненты по осям x и y.
$ \large A_x = A\cos\Theta $$ \large A_y = A\sin\Theta $
Величины составляющих смещения по осям равны $\large x$ и $\large y$. Величины составляющих скорости, $\Large v $, являются $\Large v_x = v \normalsize \cos\Theta $ и $\Large v_y = v \normalsize \sin\Theta $, где $\Large v $ — величина скорости, а theta равна его направление. 9{-1} (v_y/v_x) $
Когда мы рассматриваем горизонтальную и вертикальную составляющие движения, мы находим горизонтальное движение простым, потому что $\large a_x = \normalsize 0 $ и $\large v_x $ является постоянным. Скорость в вертикальном направлении начинает уменьшаться по мере подъема объекта. На его высоте вертикальная скорость объекта равна нулю. Когда он падает обратно, вертикальная скорость увеличивается по величине, но в направлении, противоположном его первоначальному пути. X- и y-движения рекомбинируются, чтобы найти полную скорость в любой заданной точке во время траектории снаряда.
Метательные установки
Продемонстрируйте независимость x- и y-движения, помогая учащимся развивать практические знания кинематических уравнений с помощью высокоточной и воспроизводимой мини-пусковой установки для снарядов PASCO. Мини-пусковая установка запускает снаряды с высокой повторяемостью, что позволяет учащимся исследовать движение снаряда, сравнивая влияние различных углов запуска и скорости на дальность полета снаряда.
Мини-пусковая установка запускает снаряды с высокой повторяемостью, что позволяет учащимся исследовать движение снаряда, сравнивая влияние различных углов запуска и скорости на дальность полета снаряда.1.) Предположим, вы используете гранатомет для запуска шарика горизонтально со стола со скоростью . Если стол имеет высоту 3,0 м, как далеко пролетит шарик, прежде чем Smart Gate замерит его удар о землю? 92} = 7,8 \textrm м $
2.) Умная тележка, оснащенная аксессуаром для баллистической тележки, движется по горизонтальной дорожке. Тележка запускает мяч с дорожки на уровне земли и ловит его на расстоянии 15 м. Горизонтальная составляющая скорости запуска равна $ \large v_{0x} = \normalsize +3.0 \textrm {м/с} $. Если предположить, что сопротивление воздуха или трение отсутствуют, какова вертикальная составляющая $ \large v_{0y} $ начальной скорости запуска?
Мы ищем $ \Large v_{0y} $ и наши известные значения: $ \Large v_{0x} = \normalsize +3. 0 \textrm {м/с} $ и $ \Large x = \normalsize 15 \textrm m $
92)(5,0 \textrm с) = 25,0 \textrm {м/с} $
0 \textrm {м/с} $ и $ \Large x = \normalsize 15 \textrm m $
92)(5,0 \textrm с) = 25,0 \textrm {м/с} $
Предлагаемые связанные темы
Вращательное движение
Кинематика вращательного движения описывает отношения между угловой скоростью, углом поворота, угловым ускорением и временем. Каждая из кинематических переменных для линейного движения имеет аналог вращательного движения. Подобно уравнениям линейной кинематики, уравнения вращательного движения используют нижние индексы для обозначения начальных значений и исключают нижние индексы для обозначения конечных значений. Ниже вы найдете уравнения вращательного движения и их уравнения поступательного, линейного движения. 92+2ах$
Прямолинейное движение заряженных частиц в магнитных полях
Первый закон движения Ньютона гласит, что если на объект не действует результирующая сила, то его скорость постоянна.
Когда скорость заряженной частицы параллельна магнитному полю, она не испытывает результирующей силы и движется в пространстве прямолинейно.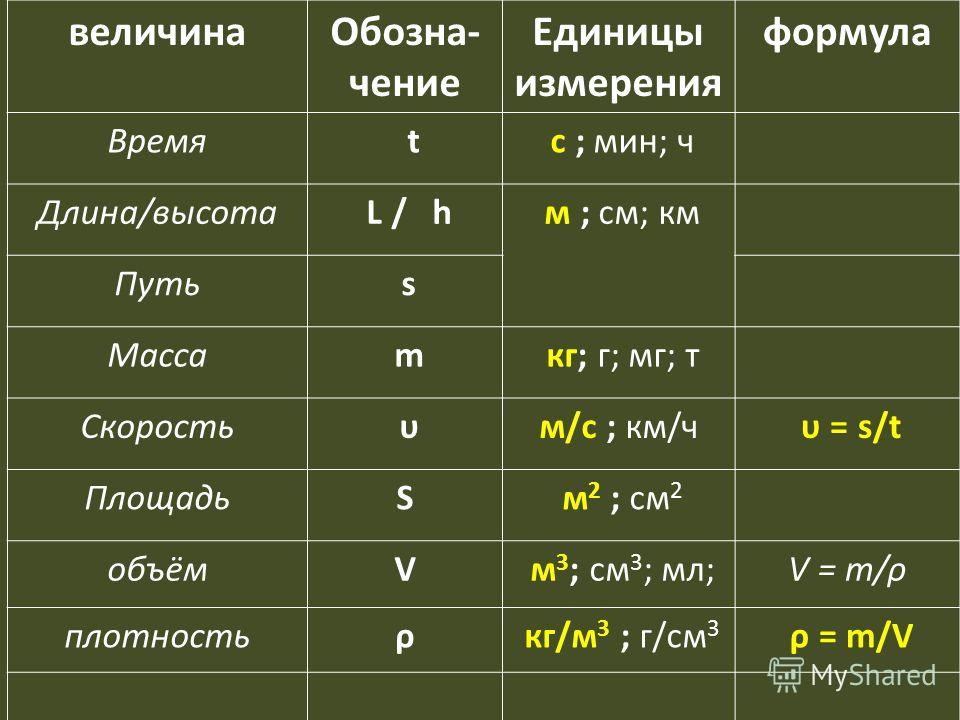 Это называется прямолинейным движением.
Если вектор скорости не параллелен и не перпендикулярен магнитному полю, составляющая скорости, параллельная полю, останется постоянной.
Это называется прямолинейным движением.
Если вектор скорости не параллелен и не перпендикулярен магнитному полю, составляющая скорости, параллельная полю, останется постоянной.
Катящиеся объекты с различными моментами инерции
В одном классическом школьном вопросе по физике участвуют два цилиндра. Вопрос гласит: у вас есть два цилиндра, один полый и один сплошной, с одинаковыми массами и диаметрами. Если их обоих скатить вниз по склону, какой из цилиндров первым достигнет дна?
Когда мы катим объект, его кинетическая энергия принимает две формы: поступательную (прямолинейное движение) и вращательную (вращение). Поступательная энергия с постоянным ускорением
можно описать с помощью кинематических уравнений, но чтобы ответить на наш вопрос, мы должны сосредоточиться на инерции вращения. Вращательная инерция зависит не только от массы и вращательного
скорость объекта, но и от того, как масса распределяется вокруг оси вращения. Это означает, что обруч будет иметь большую инерцию вращения, чем цилиндр такой же массы при
та же угловая скорость, потому что масса в обруче движется быстрее из-за большего удаления его от оси вращения. 92$, где $I$ равен моменту инерции, $\large m$
равно массе объекта, а $ \large r $ равно радиусу. Если два цилиндра имеют разные диаметры, но равные массы, то цилиндр большего диаметра будет иметь
больший момент инерции. Теперь рассмотрим наш первоначальный вопрос. Полый цилиндр имеет ту же массу и диаметр, что и сплошной цилиндр, но его масса более «размазана», что
заставляет его иметь больший момент инерции. Итак, определяет ли величина момента инерции объекта, достигнет ли он дна первым? Не обязательно.
На самом деле, если вы катите два цилиндра вниз по склону, твердый цилиндр каждый раз будет достигать дна первым. Это может показаться нелогичным, потому что полый цилиндр имеет большую
момента инерции, но сплошной цилиндр или сфера всегда достигают дна раньше полого предмета, независимо от диаметра.
92$, где $I$ равен моменту инерции, $\large m$
равно массе объекта, а $ \large r $ равно радиусу. Если два цилиндра имеют разные диаметры, но равные массы, то цилиндр большего диаметра будет иметь
больший момент инерции. Теперь рассмотрим наш первоначальный вопрос. Полый цилиндр имеет ту же массу и диаметр, что и сплошной цилиндр, но его масса более «размазана», что
заставляет его иметь больший момент инерции. Итак, определяет ли величина момента инерции объекта, достигнет ли он дна первым? Не обязательно.
На самом деле, если вы катите два цилиндра вниз по склону, твердый цилиндр каждый раз будет достигать дна первым. Это может показаться нелогичным, потому что полый цилиндр имеет большую
момента инерции, но сплошной цилиндр или сфера всегда достигают дна раньше полого предмета, независимо от диаметра.
Планетарные орбиты (законы Кеплера)
В 16 веке немецкий астроном Иоганн Кеплер объявил свои три закона движения планет.
Законы гласят:
(1) Все планеты движутся вокруг Солнца по эллиптическим орбитам с Солнцем в одном из фокусов. (2) Радиус-вектор, соединяющий любую планету с Солнцем, заметает равные площади за равные промежутки времени.
(3) Квадраты сидерических периодов обращения планет прямо пропорциональны кубам их средних расстояний от Солнца.
(2) Радиус-вектор, соединяющий любую планету с Солнцем, заметает равные площади за равные промежутки времени.
(3) Квадраты сидерических периодов обращения планет прямо пропорциональны кубам их средних расстояний от Солнца.
Эти законы в конечном итоге помогли развитию законов Ньютона, когда он сформулировал закон всемирного тяготения, в котором он описал гравитацию между Землей и Луной, а также Солнцем и планетами. Ньютон пришел к выводу, что движение тел, подверженных действию центральной гравитационной силы, не всегда следует одним и тем же эллиптическим орбитам, заявленным первым законом Кеплера. Вместо этого их пути определяются общей энергией тела, что позволяет этим телам двигаться по гиперболическим или даже параболическим орбитам. Возможно, наиболее интересным аспектом законов Кеплера является то, что они также применимы ко всем другим силам обратных квадратов, включая электромагнитные силы внутри атома (с учетом релятивистских и квантовых эффектов).
Скорость убегания
Скорость убегания — это скорость, с которой должен двигаться объект, чтобы вырваться из гравитационного колодца планеты или луны и покинуть его без дальнейшего движения. Например, объект на Луне должен развить скорость 2,38 км/с, чтобы избежать гравитационного поля Луны.
Для сравнения, объекту на Солнце нужна скорость убегания 618 км/сек!
Например, объект на Луне должен развить скорость 2,38 км/с, чтобы избежать гравитационного поля Луны.
Для сравнения, объекту на Солнце нужна скорость убегания 618 км/сек!
Спутниковые орбиты
Спутники удерживаются в пределах трех типов околоземных орбит в космосе. Высокая околоземная орбита наиболее удалена от поверхности Земли и является местом расположения многих метеорологических спутников и спутников связи. Средняя или средняя околоземная орбита включает в себя навигационные и большинство специальных спутников, а низкая околоземная орбита — это место, где вращается большинство научных спутников. Расстояние между спутником и поверхностью Земли, также известное как высота орбиты, определяет орбитальную скорость спутника. Чем выше орбита спутника, тем медленнее он будет двигаться. Другие факторы, влияющие на орбиту спутника, включают эксцентриситет и наклонение.
Уравнения времени гравитации для падающих объектов Рон Куртус
SfC Home > Physics > Gravity >
Рон Куртус
Когда вы бросаете объект с некоторой высоты над землей, его начальная скорость равна нулю. Простые уравнения позволяют рассчитать время падающего объекта для достижения заданной скорости и время, необходимое для достижения заданного смещения. В уравнениях предполагается, что сопротивлением воздуха можно пренебречь.
Простые уравнения позволяют рассчитать время падающего объекта для достижения заданной скорости и время, необходимое для достижения заданного смещения. В уравнениях предполагается, что сопротивлением воздуха можно пренебречь.
Примеры демонстрируют применение уравнений.
У вас могут возникнуть следующие вопросы:
- Какое уравнение определяет время достижения заданной скорости?
- Какое уравнение определяет время достижения заданного смещения?
- Какие примеры этих уравнений?
Этот урок ответит на эти вопросы. Полезный инструмент: Преобразование единиц
Время по отношению к скорости
Общее уравнение гравитации для прошедшего времени относительно скорости:
t = (v − v i )/г
( Подробности о выводе см. в разделе Вывод уравнений скорости и силы тяжести. )
Поскольку начальная скорость v i = 0 для объекта, который просто падает, уравнение сводится к:
т = об/г
где
- t время в секундах
- v — вертикальная скорость в метрах/секунду (м/с) или футах/секунду (фут/с)
- g ускорение свободного падения (9,8 м/с 2 или 32 фут/с 2 )
Поскольку объект движется в направлении силы тяжести, v — положительное число.
Прошедшее время падения объекта как функция скорости или смещения
Время по отношению к смещению
Общее уравнение силы тяжести для прошедшего времени по отношению к смещению:
t = [−v i ± √(v i 2 + 2gy)]/г
где
- ± означает плюс-минус
- √(v i 2 + 2gy) — квадратный корень из числа (v i 2 + 2gy)
- y вертикальное смещение в метрах (м) или футах (футах)
( Подробную информацию о выводе см. в разделе Вывод уравнений гравитации смещения во времени. )
Когда объект просто брошен, начальная скорость равна нулю ( v i = 0), и уравнение для прошедшего времени принимает вид:
t = ± √(2gy)/г
Поскольку время t всегда положительное, уравнение выглядит так:
t = √(2gy)/г
Замените g на √(g 2 ) и упростите уравнение:
t = √(2gy)/√(g 2 )
Таким образом, получается уравнение времени:
t = √(2г/г)
Примеры
Следующие примеры иллюстрируют применение уравнений.
При заданной скорости
Через какое время падающий объект достигнет скорости 224 фута/с?
Решение
Так как v выражено в фут/с, г = 32 фут/с 2 . Подставьте значения в уравнение:
т = об/г
t = (224 фут/с)/(32 фут/с 2 )
t = 7 секунд
При заданном смещении
Через какое время объект упадет с высоты 200 метров?
Решение
Поскольку перемещение выражено в метрах, г = 9,8 м/с 2 . Подставьте значения в уравнение:
t = √(2г/г)
t = √ [2*(200 м)/(9,8 м/с 2 )]
t = √ (40,8 с 2 )
т = 6,39 с
Резюме
Существуют простые уравнения для падающих объектов, которые позволяют рассчитать время, необходимое для достижения заданной скорости или перемещения. Вот эти уравнения:
Вот эти уравнения:
т = об/г
t = √(2г/г)
Проверьте свои номера
Ресурсы и ссылки
Рон Куртус.
Гравитационные расчеты – Земля – Калькулятор
Кинематические уравнения и свободное падение — Класс физики
Книги
(Примечание: Школа чемпионов может получать комиссионные от покупки книг)
Книги с самым высоким рейтингом по Simple Gravity Science
355
рейтинг книг по Advanced Gravity PhysicsВопросы и комментарии
У вас есть какие-либо вопросы, комментарии или мнения по этому вопросу? Если это так, отправьте электронное письмо с вашим отзывом. Я постараюсь вернуться к вам как можно скорее.
Поделиться этой страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.

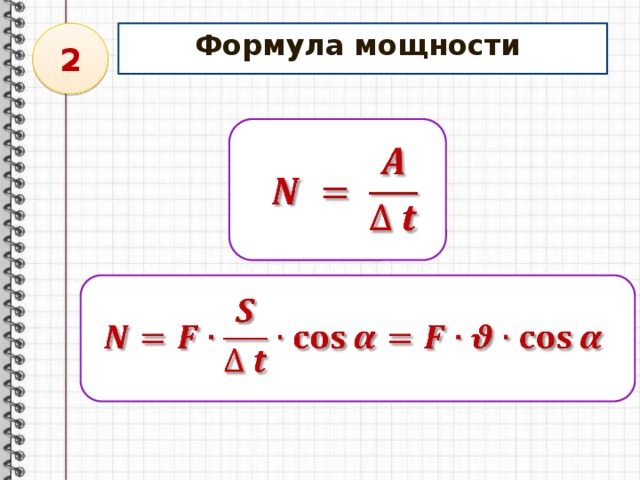

 Это связано с тем, что для t-показателей используется среднее значение 50, а для z-показателей используется среднее значение 0,
Это связано с тем, что для t-показателей используется среднее значение 50, а для z-показателей используется среднее значение 0, Основное направление решения задачи: попытаться вывести уравнения
которые используют эти параметры с известными значениями.)
Основное направление решения задачи: попытаться вывести уравнения
которые используют эти параметры с известными значениями.)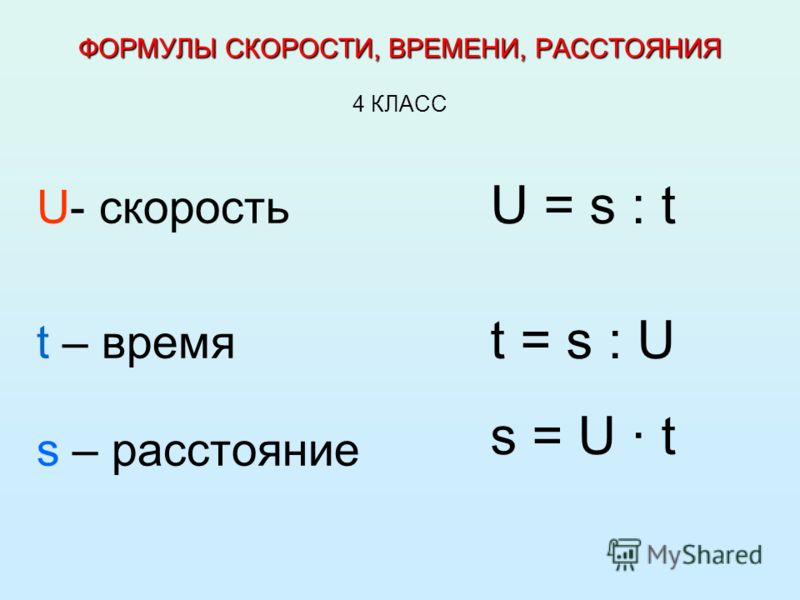 × потому что
(градус) = 6,928 м/сек.
× потому что
(градус) = 6,928 м/сек.
 После этого момента он начнет падать.
После этого момента он начнет падать.
 ×
сек. = 5,653 м
×
сек. = 5,653 м