Молекулярная кинетика | Формулы по физике
Количество вещества (моль)
Найти
Известно, что:
νNN_A =
Вычислить ‘ν’Мольная масса
Найти
Известно, что:
Mmν =
Вычислить ‘M’Масса молекулы
Найти
Известно, что:
m0mN =
Вычислить ‘m0’Мольная масса
Найти
Известно, что:
Mm0N_A =
Вычислить ‘M’Число молекул
Найти
Известно, что:
NmN_AM =
Вычислить ‘N’Основное уравнение молекулярно-кинетической теории
Найти
Известно, что:
pnm0v =
Вычислить ‘p’Внутренняя энергия молекул
Найти
Известно, что:
Emv =
Вычислить ‘E’Давление идеального газа
Найти
Известно, что:
pnE =
Вычислить ‘p’Концентрация молекул
Найти
Известно, что:
Газ: давление, объем, средняя кинетическая энергия
Найти
Известно, что:
pVNE =
Вычислить ‘p’Газ: давление, объем, температура
Найти
Известно, что:
pVNkT =
Вычислить ‘p’Средняя кинетическая энергия
Найти
Известно, что:
EkT =
Вычислить ‘E’Газ: давление, концентрация, температура
Найти
Известно, что:
pnkT =
Вычислить ‘p’Газ: количество вещества, громкость
Найти
νVV_M =
Вычислить ‘ν’Уравнение среднеквадратичной скорости молекулы
Найти
Известно, что:
vkTm0 =
Вычислить ‘v’Уравнение состояния идеального газа (уравнение Менделеева – Клапейрона)
Найти
Известно, что:
pVmRTM =
Уравнение состояния идеального газа (уравнение Менделеева – Клапейрона)
Найти
Известно, что:
pVTνR =
Вычислить ‘p’Закон бойля-мариотта (изотермический процесс)
Найти
Известно, что:
p1V1p2V2 =
Вычислить ‘p1’Закон гей-люссака (изобарный процесс)
Известно, что:
V1T1V2T2 =
Вычислить ‘V1’Тепловое расширение газа
Найти
Известно, что:
VV0αT =
Вычислить ‘V’Закон Шарля (изохорный процесс)
Найти
Известно, что:
Температурная зависимость давления газа
Найти
Известно, что:
pp0γT =
Вычислить ‘p’Формулы для вычисления массы тел различной формы
Это странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т. е. следующая статья будет называться «Масса полой детали»).
е. следующая статья будет называться «Масса полой детали»).
Тут самое время вспомнить, что масса тела — это его объем , умноженный на плотность его материала (см. таблицы плотностей):
Объем сплошной детали — это… ее объем и больше ничего.
Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр.
Буквой обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.
Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).
1. Масса параллелепипеда (бруска)
Объем параллелепипеда: , где — длина, — ширина, — высота.
Тогда масса:
2. Масса цилиндра
Объем цилиндра: , где — диаметр основания, — высота цилиндра.
Тогда масса:
3. Масса шара
Объем шара: , где — диаметр шара.
Тогда масса:
4.
 Масса сегмента шара
Масса сегмента шараОбъем сегмента шара: , где — диаметр основания сегмента, — высота сегмента.
Тогда масса:
5. Масса конуса
Объем любого конуса: , где — площадь основания, — высота конуса.
Для круглого конуса: , где — диаметр основания, — высота конуса.
Масса круглого конуса:
6. Масса усеченного конуса
Поскольку невозможно объять необъятное, рассмотрим только круглый усеченный конус. Его объем — это разность объемов двух вложенных конусов: с основаниями и : , где , . После никому не интересных алгебраических преобразований получаем:
, где — диаметр большего основания, — диаметр меньшего основания, — высота усеченного конуса.
Отсюда масса:
7. Масса пирамиды
Объем любой пирамиды равен одной трети произведения площади ее основания на высоту (то же самое, что и для конусов (часто мы не замечаем, насколько мироздание к нам благосклонно)): , где — площадь основания, — высота пирамиды.
Для пирамиды с прямоугольным основанием: , где — ширина, — длина, — высота пирамиды.
Тогда масса пирамиды:
8. Масса усеченной пирамиды
Рассмотрим усеченную пирамиду с прямоугольным основанием. Ее объем — это разность объемов двух подобных пирамид с основаниями и : , где , .
Исчеркав половину тетрадного листа, получаем: , где , — ширина и длина большего основания, , — ширина и длина меньшего основания, — высота пирамиды.
И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот. В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим: .
Тогда масса усеченной прямоугольной пирамиды:
или
Для пирамиды с квадратным основанием (, ) формула выглядит проще:
вычисление массы
Physics (Impulse) —
Impulse — очень важное уравнение, которое необходимо понимать для оптимизации производительности. Само уравнение получено из уравнения силы (F = MA)
Шаги для получения уравнения импульса следующие:
F=MA
Шаг 1 : Разложите формулу ускорения из уравнения силы на его скоростные куски.
F= M*(Vf-Vi)/время
Шаг 2 : Переместите «время» под изменением скорости в сторону силы уравнения, умножив каждую сторону на время. Умножая каждую часть на «время», «время» в правой части уравнения будет сокращено. (не меняется) мы можем использовать приведенное выше уравнение, однако, если масса изменяется, вы можете просто умножить массу на скорость, так что это будет выглядеть ниже.
F(время) = MVf-MVi
Приведенная выше формула имеет некоторые преимущества с точки зрения анализа. MVf-MVi представляет собой изменение импульса. Импульс = масса * скорость.
давайте посмотрим на F(время) = масса (Vf-Vi)
Эта формула говорит нам, что мы можем использовать один из двух методов для изменения импульса (правая часть уравнения в этом примере неизменна). Мы можем либо увеличить силу, выраженную слева, либо увеличить время (слева), в течение которого сила выражается.
Давайте посмотрим, как это применимо на примере из реальной жизни. Пусть спортсмен, совершающий прыжки в глубину, весит 100 кг и при приземлении движется со скоростью 4 м/с. Итак, наш импульс непосредственно перед контактом с землей равен 100 кг * 4 м/с = 400 м/с/кг. Теперь, чтобы остановить этот импульс, мы можем использовать один из двух методов…
Пусть спортсмен, совершающий прыжки в глубину, весит 100 кг и при приземлении движется со скоростью 4 м/с. Итак, наш импульс непосредственно перед контактом с землей равен 100 кг * 4 м/с = 400 м/с/кг. Теперь, чтобы остановить этот импульс, мы можем использовать один из двух методов…
Сила * (Время) = 400 м/с/кг
Первый метод (большая сила )
800 кг * (0,5 секунды) = 400 м/с/кг
или
Метод 2 (большее время)
400 кг * (1 секунда) = 400 м/с/кг
В обоих случаях спортсмен соответствует требованиям, чтобы остановить свой импульс. Однако метод выполнения задачи был реализован двумя различными способами. В первом методе использовалось увеличение силы, а во втором — увеличение времени приложения меньшей силы. В зависимости от тренировочных целей вы можете предпочесть один метод другому.
Уравнение импульса можно использовать для определения изменения импульса, что означает, что оно может сказать вам, насколько объекты замедляются, а также ускоряются. На самом деле мы можем использовать уравнение импульса для определения высоты вертикального прыжка, высоты штанги и результатов практически любого движения.
На самом деле мы можем использовать уравнение импульса для определения высоты вертикального прыжка, высоты штанги и результатов практически любого движения.
Следующее видео в импульсе
Нравится:
Нравится Загрузка…
Единицы, конверсии и т. д.
Единицы, преобразования и т. д.Гидрология BC ENV 3025
Гидрологические величины
- основные измерения (например, скорость воды в потоке, масса воды в дождевание)
- производные количества (сброс в поток)
Единицы и размеры
 см
или мм или дюйм
см
или мм или дюйм- многие величины имеют размерность, представляющую собой некоторую комбинацию этих фундаментальных размеры
- в уравнениях размеры с обеих сторон должны совпадать
- Наиболее распространенная система единиц, используемая сегодня, — это СИ (Международная система д’Юнитес)
| Количество | Блок | |||
| Базовые блоки: | ||||
| длина | метр | |||
| масса | килограмм | |||
| температура | кельвин | |||
| время | второй | |||
| Производные единицы: | ||||
| район | квадратных метра | |||
| объем | куб.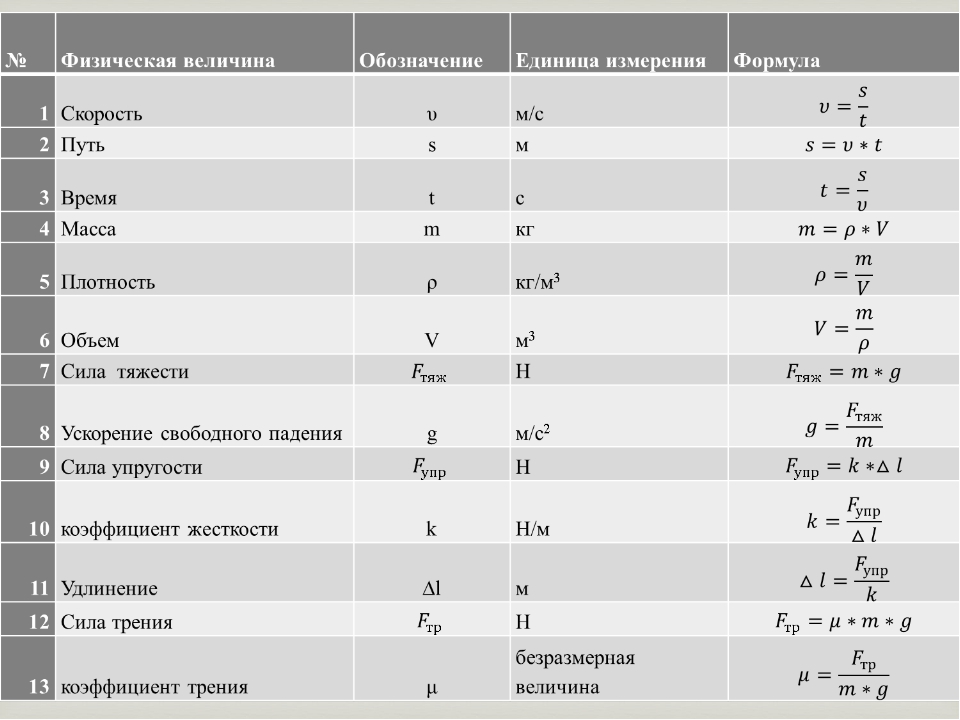 м. м. | |||
| скорость | метра в секунду | |||
| ускорение | метра в секунду в квадрате | |||
| плотность | килограмм на кубический метр | |||
| сила | ньютон | |||
| давление | паскаль | |||
| напряжение | паскаль | |||
| энергия | Дж | |||
| количество тепла | Дж | |||
| работа | джоуля | |||
| мощность | Вт | |||
| вязкость, динамическая | паскаль-секунда | |||
| вязкость, кинематическая | квадратных метра в секунду | |||
| удельная теплоемкость | джоуля на килограмм-кельвин |

 см
или мм или дюйм
см
или мм или дюйм