Формула в физике периода: Амплитуда, частота, период колебаний — урок. Физика, 9 класс.

Основные формулы по физике – колебания и волны. Связь между периодом и круговой частотой

При изучении этого раздела следует иметь в виду, что колебания различной физической природы описываются с единых математических позиций. Здесь надо четко уяснить такие понятия, как гармоническое колебание, фаза, разность фаз, амплитуда, частота, период колебани.

Надо иметь в виду, что во всякой реальной колебательной системе есть сопротивления среды, т.е. колебания будут затухающими. Для характеристики затухания колебаний вводится коэффициент затухания и логарифмический декремент затухани.

Если колебания совершаются под действием внешней, периодически изменяющейся силы, то такие колебания называют вынужденными. Они будут незатухающими. Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы. При приближении частоты вынужденных колебаний к частоте собственных колебаний амплитуда вынужденных колебаний резко возрастает. Это явление называется резонансом.

Переходя к изучению электромагнитных волн нужно четко представлять, что

электромагнитная волна – это распространяющееся в пространстве электромагнитное поле. Простейшей системой, излучающей электромагнитные волны, является электрический диполь. Если диполь совершает гармонические колебания, то он излучает монохроматическую волну.

Таблица формул: колебания и волны

Физические законы, формулы, переменные	Формулы колебания и волны
Уравнение гармонических колебаний: где х – смещение (отклонение) колеблющейся величины от положения равновесия; А – амплитуда; ω – круговая (циклическая) частота; α – начальная фаза; (ωt+α) – фаза.
Связь между периодом и круговой частотой:
Частота:
Связь круговой частоты с частотой:
Периоды собственных колебаний 1) пружинного маятника: где k – жесткость пружины; 2) математического маятника: где l – длина маятника, g – ускорение свободного падения; 3) колебательного контура: где L – индуктивность контура, С – емкость конденсатора.
Частота собственных колебаний:
Сложение колебаний одинаковой частоты и направления: 1) амплитуда результирующего колебания где А 1 и А 2 – амплитуды составляющих колебаний, α 1 и α 2 – начальные фазы составляющих колебаний; 2) начальная фаза результирующего колебания
Уравнение затухающих колебаний: е = 2,71… – основание натуральных логарифмов.
Амплитуда затухающих колебаний: где А 0 – амплитуда в начальный момент времени; β – коэффициент затухания;
Коэффициент затухания: колеблющегося тела где r – коэффициент сопротивления среды, m – масса тела; колебательного контура где R – активное сопротивление, L – индуктивность контура.
Частота затухающих колебаний ω:
Период затухающих колебаний Т:
Логарифмический декремент затухания:

(лат. amplitude — величина) — это наибольшее отклонение колеблющегося тела от положения равновесия.

Для маятника это максимальное расстояние, на которое удаляется ша-рик от своего положения равновесия (рисунок ниже). Для колебаний с малыми амплитудами за такое расстояние можно принимать как длину дуги 01 или 02, так и длины этих отрезков.

Амплитуда колебаний измеряется в единицах длины — метрах , санти-метрах и т. д. На графике колебаний амплитуда определяется как макси-мальная (по модулю) ордината синусоидальной кривой, (см. рис. ниже).

Период колебаний.

Период колебаний — это наименьший промежуток времени, через который система, соверша-ющая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент времени, выбранный произвольно.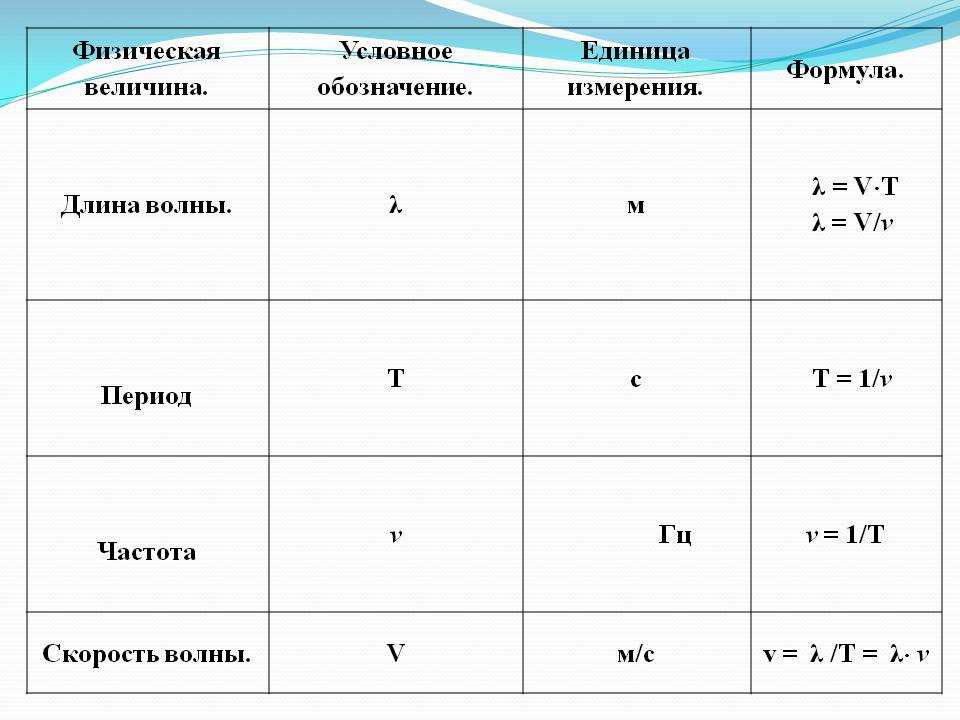

Другими словами, период колебаний (Т ) — это время, за которое совершается одно полное ко-лебание. Например, на рисунке ниже это время, за которое грузик маятника перемещается из крайней правой точки через точку равновесия О в крайнюю левую точку и обратно через точку О снова в крайнюю правую.

За полный период колебаний, таким образом, тело проходит путь, равный четы-рем амплитудам. Период колебаний измеряется в единицах времени — секундах , минутах и т. д. Период колебаний может быть определен по известному графику колебаний, (см. рис. ниже).

Понятие «период колебаний», строго говоря, справедливо, лишь когда значения колеблющей-ся величины точно повторяются через определенный промежуток времени, т. е. для гармоничес-ких колебаний. Однако это понятие применяется также и для случаев приблизительно повторяю-щихся величин, например, для затухающих колебаний .

Частота колебаний.

Частота колебаний — это число колебаний, совершаемых за единицу времени, например, за 1 с .

Единица частоты в СИ названа

герцем (Гц ) в честь немецкого физика Г. Герца (1857-1894). Если частота колебаний (v ) равна 1 Гц , то это значит, что за каждую секунду совершается одно колебание. Частота и период колебаний связаны соотношениями:

В теории колебаний пользуются также понятием циклической , или круговой частоты ω . Она связана с обычной частотой v и периодом колебаний Т соотношениями:

.

Циклическая частота — это число колебаний, совершаемых за 2π секунд.

Сила Кориолиса равна:

где – точечнаямасса ,-вектор угловой скорости вращающейся системы отсчёта,- вектор скорости движения точечной массы в этой системе отсчёта, квадратными скобками обозначена операция

векторного произведения .

Величина называется кориолисовым ускорением.

По физической природе

Механические (звук ,вибрация )

Электромагнитные (свет ,радиоволны , тепловые)

Смешанного типа – комбинации вышеперечисленных

По характеру взаимодействия с окружающей средой

Вынужденные – колебания, протекающие в системе под влиянием внешнего периодического воздействия. Примеры: листья на деревьях, поднятие и опускание руки. При вынужденных колебаниях может возникнуть явление

резонанса : резкое возрастание амплитуды колебаний при совпадениисобственной частоты осциллятора и частоты внешнего воздействия.

Свободные (или собственные) – это колебания в системе под действием внутренних сил, после того как система выведена из состояния равновесия (в реальных условиях свободные колебания всегдазатухающие ). Простейшими примерами свободных колебаний являются колебания груза, прикреплённого к пружине, или груза, подвешенного на нити.

Автоколебания – колебания, при которых система имеет запаспотенциальной энергии , расходующейся на совершение колебаний (пример такой системы –

механические часы ). Характерным отличием автоколебаний от вынужденных колебаний является то, что их амплитуда определяется свойствами самой системы, а не начальными условиями.

Параметрические – колебания, возникающие при изменении какого-либо параметра колебательной системы в результате внешнего воздействия.

Случайные – колебания, при которых внешняя или параметрическая нагрузка является случайным процессом.

Гармонические колебания

где х А ω

Обобщенное гармоническое колебание в дифференциальном виде

(Любое нетривиальное

Скорость и ускорение при гармонических колебаниях.

Согласно определению скорости, скорость – это производная от координаты по времени

Таким образом, мы видим, что скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на p/2.

Величина – максимальная скорость колебательного движения (амплитуда колебаний скорости).

Следовательно, для скорости при гармоническом колебании имеем: ,

а для случая нулевой начальной фазы (см. график).

Согласно определению ускорения, ускорение – это производная от скорости по времени:

–

вторая производная от координаты по времени.

Тогда: .

Ускорение при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на p/2 и колебания смещения наp(говорят, что колебания происходятв противофазе) .

Величина

Максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем: ,

а для случая нулевой начальной фазы: (см. график).

Из анализа процесса колебательного движения, графиков и соответствующих математических выражений видно, что при прохождении колеблющимся телом положения равновесия (смещение равно нулю) ускорение равно нулю, а скорость тела максимальна (тело проходит положение равновесия по инерции), а при достижении амплитудного значения смещения – скорость равна нулю, а ускорение максимально по модулю (тело меняет направление своего движения).

Гармонические колебания – колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид

где х – смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t;А – амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия;ω – циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд;- полная фаза колебаний,- начальная фаза колебаний.

Обобщенное гармоническое колебание в дифференциальном виде

(Любое нетривиальное решение этого дифференциального уравнения – есть гармоническое колебание с циклической частотой)

До сих пор мы рассматривали собственные колебания, т. е. колебания, происходящие в отсутствие внешних воздействий. Внешнее воздействие было нужно лишь для того, чтобы вывести систему из состояния равновесия, после чего она предоставлялась самой себе. Дифференциальное уравнение собственных колебаний вообще не содержит следов внешнего воздействия на систему: это воздействие отражается лишь в начальных условиях.

Установление колебаний. Но очень часто приходится сталкиваться с колебаниями, которые происходят при постоянно присутствующем внешнем воздействии. Особенно важен и в то же время достаточно прост для изучения случай, когда внешняя сила имеет периодический характер. Общей чертой вынужденных колебаний, происходящих под действием периодической внешней силы, является то, что спустя некоторое время после начала действия внешней силы система полностью «забывает» свое начальное состояние, колебания приобретают стационарный характер и не зависят от начальных условий. Начальные условия проявляются только в период установления колебаний, который обычно называют переходным процессом.

Синусоидальное воздействие. Рассмотрим вначале наиболее простой случай вынужденных колебаний осциллятора под действием внешней силы, изменяющейся по синусоидальному закону:

Рис. 178. Возбуждение вынужденных колебаний маятника

Такое внешнее воздействие на систему можно осуществить различными способами. Например, можно взять маятник в виде шарика на длинном стержне и длинную пружину с малой жесткостью и прикрепить ее к стержню маятника недалеко от точки подвеса, как показано на рис. 178. Другой конец горизонтально расположенной пружины следует заставить двигаться по закону ? с помощью кривошипно-шатунного механизма, приводимого в движение электромотором. Действующая

на маятник со стороны пружины вынуждающая сила будет практически синусоидальна, если размах движения левого конца пружины В будет много больше амплитуды колебаний стержня маятника в точке закрепления пружины С.

Уравнение движения. Уравнение движения для этой и других подобных систем, в которых наряду с возвращающей силой и силой сопротивления на осциллятор действует вынуждающая внешняя сила, синусоидально изменяющаяся со временем, можно записать в виде

Здесь левая часть в соответствии со вторым законом Ньютона, является произведением массы на ускорение. Первый член в правой части представляет собой возвращающую силу, пропорциональную смещению из положения равновесия. Для подвешенного на пружине груза это упругая сила, а во всех других случаях, когда ее физическая природа иная, эту силу называют квазиупругой. Второе слагаемое есть сила трения, пропорциональная скорости, например сила сопротивления воздуха или сила трения в оси. Амплитуду и частоту со раскачивающей систему вынуждающей силы будем считать постоянными.

Разделим обе части уравнения (2) на массу и введем обозначения

Теперь уравнение (2) принимает вид

В отсутствие вынуждающей силы правая часть уравнения (4) обращается в нуль и оно, как и следовало ожидать, сводится к уравнению собственных затухающих колебаний.

Опыт показывает, что во всех системах под действием синусоидальной внешней силы в конце концов устанавливаются колебания, которые также происходят по синусоидальному закону с частотой вынуждающей силы со и с постоянной амплитудой а, но с некоторым сдвигом по фазе относительно вынуждающей силы. Такие колебания называются установившимися вынужденными колебаниями.

Установившиеся колебания. Рассмотрим вначале именно установившиеся вынужденные колебания, причем для простоты пренебрежем трением. В этом случае в уравнении (4) не будет члена, содержащего скорость:

Попробуем искать решение соответствующее установившимся вынужденным колебаниям, в виде

Вычислим вторую производную и подставим ее вместе с в уравнение (5):

Чтобы это равенство было справедливо в любой момент времени, коэффициенты при слева и справа должны быть одинаковы. Из этого условия находим амплитуду колебаний а:

Исследуем зависимость амплитуды а от частоты вынуждающей силы. График этой зависимости показан на рис. 179. При формула (8) дает Подставив сюда значения видим, что постоянная во времени сила просто смещает осциллятор в новое положение равновесия, сдвинутое от старого на Из (6) следует, что при смещение

как, очевидно, и должно быть.

Рис. 179. График зависимости

Фазовые соотношения. По мере роста частоты вынуждающей силы от 0 до установившиеся колебания происходят в фазе с вынуждающей силой а их амплитуда постоянно увеличивается, сначала медленно, а по мере приближения со к – все быстрее и быстрее: при амплитуда колебаний неограниченно возрастает

При значениях со, превосходящих частоту собственных колебаний формула (8) дает для а отрицательное значение (рис. 179). Из формулы (6) ясно, что при колебания происходят в противофазе с вынуждающей силой: когда сила действует в одну сторону, осциллятор смещен в противоположную. При неограниченном увеличении частоты вынуждающей силы амплитуда колебаний стремится к нулю.

Амплитуду колебаний во всех случаях удобно считать положительной, чего легко добиться, вводя сдвиг фаз между вынуждающей

силой и смещением:

Здесь а по-прежнему дается формулой (8), а сдвиг фазы равен нулю при и равен при Графики зависимости от частоты вынуждающей силы показаны на рис. 180.

Рис. 180. Амплитуда и фаза вынужденных колебаний

Резонанс. Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы имеет немонотонный характер. Резкое увеличение амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте осциллятора называется резонансом.

Формула (8) дает выражение для амплитуды вынужденных колебаний в пренебрежении трением. Именно с этим пренебрежением связано обращение амплитуды колебаний в бесконечность при точном совпадении частот Реально амплитуда колебаний в бесконечность, конечно же, обращаться не может.

Это означает, что при описании вынужденных колебаний вблизи резонанса учет трения принципиально необходим. При учете трения амплитуда вынужденных колебаний при резонансе получается конечной. Она будет тем меньше, чем больше трение в системе. Вдали от резонанса формулой (8) можно пользоваться для нахождения амплитуды колебаний и при наличии трения, если оно не слишком сильное, т. е. Более того, эта формула, полученная без учета трения, имеет физический смысл только тогда, когда трение все же есть. Дело в том, что само понятие установившихся вынужденных колебаний применимо только к системам, в которых есть трение.

Если бы трения совсем не было, то процесс установления колебаний продолжался бы бесконечно долго. Реально это означает, что полученное без учета трения выражение (8) для амплитуды вынужденных колебаний будет правильно описывать колебания в системе только спустя достаточно большой промежуток времени после начала действия вынуждающей силы. Слова «достаточно большой промежуток времени» означают здесь, что уже закончился переходный процесс, длительность которого совпадает с характерным временем затухания собственных колебаний в системе.

При малом трении установившиеся вынужденные колебания происходят в фазе с вынуждающей силой при и в противофазе при как и в отсутствие трения. Однако вблизи резонанса фаза меняется не скачком, а непрерывно, причем при точном совпадении частот смещение отстает по фазе от вынуждающей силы на (на четверть периода). Скорость изменяется при этом в фазе с вынуждающей силой, что обеспечивает наиболее благоприятные условия для передачи энергии от источника внешней вынуждающей силы к осциллятору.

Какой физический смысл имеет каждый из членов в уравнении (4), описывающем вынужденные колебания осциллятора?

Что такое установившиеся вынужденные колебания?

При каких условиях можно использовать формулу (8) для амплитуды установившихся вынужденных колебаний, полученную без учета трения?

Что такое резонанс? Приведите известные вам примеры проявления и использования явления резонанса.

Опишите сдвиг по фазе между вынуждающей силой и смещением при разных соотношениях между частотой со в вынуждающей силы и собственной частотой осциллятора.

Чем определяется длительность процесса установления вынужденных колебаний? Дайте обоснование ответа.

Векторные диаграммы. Убедиться в справедливости приведенных выше утверждений можно, если получить решение уравнения (4), описывающее установившиеся вынужденные колебания при наличии трения. Поскольку установившиеся колебания происходят с частотой вынуждающей силы со и некоторым сдвигом по фазе то решение уравнения (4), соответствующее таким колебаниям, следует искать в виде

При этом скорость и ускорение, очевидно, тоже будут изменяться со временем по гармоническому закону:

Амплитуду а установившихся вынужденных колебаний и сдвиг фазы удобно определять с помощью векторных диаграмм. Воспользуемся тем обстоятельством, что мгновенное значение любой изменяющейся по гармоническому закону величины можно представить как проекцию вектора на некоторое заранее выбранное направление, причем сам вектор равномерно вращается в плоскости с частотой со, а его неизменная длина равна

амплитудному значению этой осциллирующей величины.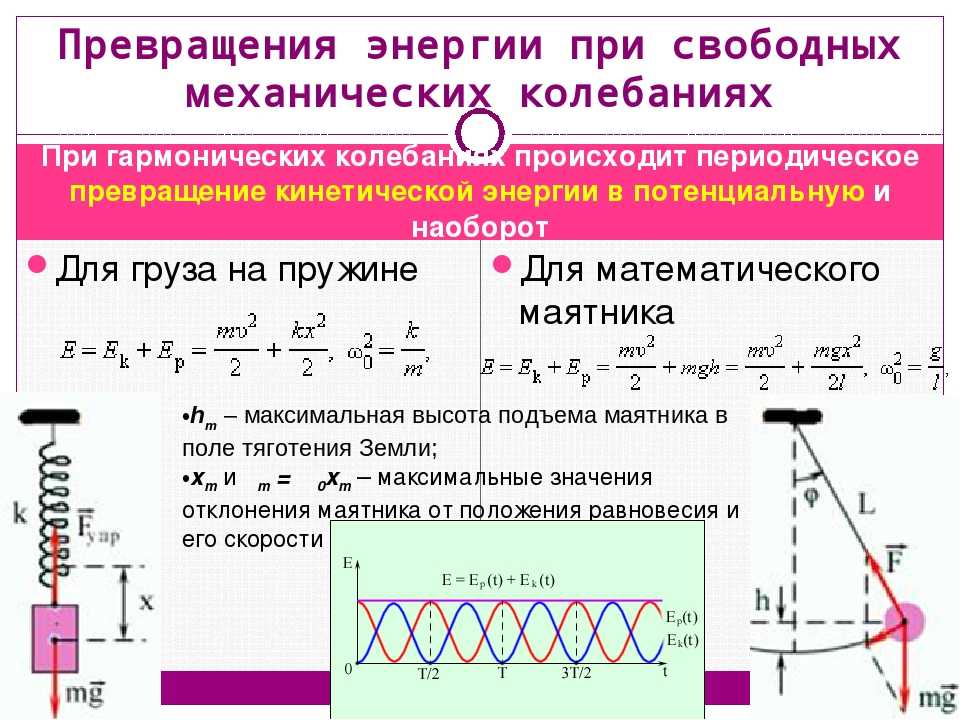 В соответствии с этим сопоставим каждому члену уравнения (4) вращающийся с угловой скоростью вектор, длина которого равна амплитудному значению этого члена.

Поскольку проекция суммы нескольких векторов равна сумме проекций этих векторов, то уравнение (4) означает, что сумма векторов, сопоставляемых членам, стоящим в левой части, равна вектору, сопоставляемому величине стоящей в правой части. Чтобы построить эти векторы, выпишем мгновенные значения всех членов левой части уравнения (4), учитывая соотношения

Из формул (13) видно, что вектор длины сопоставляемый величине опережает на угол вектор сопоставляемый величине Вектор длины сопоставляемый члену х, опережает на вектор длины т. е. эти векторы направлены в противоположные стороны.

Взаимное расположение этих векторов для произвольного момента времени показано на рис. 181. Вся система векторов вращается как целое с угловой скоростью со против часовой стрелки вокруг точки О.

Рис. 181. Векторная диаграмма вынужденных колебаний

Рис. 182. Вектор сопоставляемый внешней силе

Мгновенные значения всех величин получаются проецированием соответствующих векторов на заранее выбранное направление Вектор, сопоставляемый правой части уравнения (4), равен сумме векторов, изображенных на рис. 181. Это сложение показано на рис. 182. Применяя теорему Пифагора, получаем

откуда находим амплитуду установившихся вынужденных колебаний а:

Сдвиг фазы между вынуждающей силой и смещением как видно из векторной диаграммы на рис. 182, отрицателен, так как вектор длины отстает от вектора Поэтому

Итак, установившиеся вынужденные колебания происходят по гармоническому закону (10), где а и определяются формулами (14) и (15).

Рис. 183. Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы

Резонансные кривые. Амплитуда установившихся вынужденных колебаний пропорциональна амплитуде вынуждающей силы Исследуем зависимость амплитуды колебаний от частоты вынуждающей силы. При малом затухании у эта зависимость имеет очень резкий характер. Если то при стремлении со к частоте свободных колебаний амплитуда вынужденных колебаний а стремится к бесконечности, что совпадает с полученным ранее результатом (8). При наличии затухания амплитуда колебаний в резонансе уже не обращается в бесконечность, хотя и значительно превышает амплитуду колебаний под действием внешней силы той же величины, но имеющей частоту, далекую от резонансной. Резонансные кривые при разных значениях постоянной затухания у приведены на рис. 183. Для нахождения частоты резонанса сорез, нужно найти, при каком со подкоренное выражение в формуле (14) имеет минимум. Приравнивая производную этого выражения по со нулю (или дополняя его до полного квадрата), убеждаемся, что максимум амплитуды вынужденных колебаний имеет место при

Резонансная частота оказывается меньше частоты свободных колебаний системы. При малых 7 резонансная частота практически совпадает с При стремлении частоты вынуждающей силы к бесконечности, т. е. при амплитуда а, как видно из (14), стремится к нулю. При т. е. при действии постоянной внешней силы, амплитуда Если подставить сюда и получим Это есть статическое смещение осциллятора из положения равновесия под действием постоянной силы и смещение осциллятора происходит в противофазе с вынуждающей силой. В резонансе, как видно из (15), смещение отстает по фазе от внешней силы на Вторая из формул (13) показывает, что при этом внешняя сила изменяется в фазе со скоростью т. е. все время действует в направлении движения. Что именно так и должно быть, ясно из интуитивных соображений.

Резонанс скорости. Из формулы (13) видно, что амплитуда колебаний скорости при установившихся вынужденных колебаниях равна . С помощью (14) получаем

Рис. 184. Амплитуда скорости при установившихся вынужденных колебаниях

Зависимость амплитуды скорости от частоты внешней силы показана на рис. 184. Резонансная кривая для скорости хотя и похожа на резонансную кривую для смещения, но отличается от нее в некоторых отношениях. Так, при т. е. при действии постоянной силы, осциллятор испытывает статическое смещение из положения равновесия и скорость его после того, как закончится переходный процесс, равна нулю. Из формулы (19) видно, что амплитуда скорости при обращается в нуль. Резонанс скорости имеет место при точном совпадении частоты внешней силы с частотой свободных колебаний

Как строятся векторные диаграммы для установившихся вынужденных колебаний при синусоидальном внешнем воздействии?

Чем определяется частота, амплитуда и фаза установившихся вынужденных гармонических колебаний?

Опишите различия резонансных кривых для амплитуды смещения и амплитуды скорости. Какими характеристиками колебательной системы определяется острота резонансных кривых?

Как связан характер резонансной кривой с параметрами системы, определяющими затухание ее собственных колебаний?

формулы, примеры вычислений с пояснениями / Справочник :: Бингоскул

Колебательное движение: формулы, примеры вычислений с пояснениями

добавить в закладки удалить из закладок

Содержание:

Физики классифицировали движения, наблюдаемые в природе и используемые человечеством в повседневной деятельности, по ряду критериев. Сегодня рассмотрим колебательное. Разберёмся, какие бывают колебания, где встречаются в природе. Каково обозначение частоты и периода колебаний, в чем измеряется их число.

Колебательным называется неравномерное (с изменяющейся во времени скоростью) движение, повторяющееся во времени. Если повторяется через одинаковые промежутки – относится к периодическим, через неравномерные – к непериодическим. Во время такого движения повторяются его основные состояния, например, углы отклонения, если речь идёт о маятнике или ему подобных системах.

Исходя из закона сохранения энергии, в реальных замкнутых системах движения будут затухающими – часть энергии уходит на преодоление сопротивления – трения, энергия внутри системы перетекает из одной формы в иную. Несмотря на природу, колебания объединяют общие закономерности, связанные с волнами.

Кроме материальных объектов: маятник, детские качели, поршень в двигателе, колебательные движения присущи и электромагнитным волнам.

Время, за которое система либо тело совершает одно полное колебание, называется его периодом. Для примера возьмём неупругую нитку длиной 20–40 см, привяжем к ней металлический предмет. Держим нитку за конец, чтобы тело висело на ней, и оттягиваем груз в сторону — в начальную точку, из которой она начнёт совершать колебательные движения. Отпускаем предмет.

Количество колебаний, которые система совершает за одну секунду, называется её частотой. Оттягиваем, затем отпускаем гайку, считаем, сколько циклов движений – количество раз вернётся в изначальную точку – совершит за, например, 5 секунд. Получившееся число делим на 5, получаем частоту движения системы.

Формулы колебательного движения  Период и частота перемещения тела взаимосвязаны, причем обратно пропорционально.

Формула количество колебаний:

 υ = 1 : T, где:

• υ – частота;
• T – период.

Период измеряется в секундах, частота – в герцах (Гц). Единица названа в честь немецкого учёного Генриха Р. Герца. 

Для определения периода колебаний следует разделить время его совершения на число колебаний:

T = t : n.

С t в формуле понятно – это время, что же такое n в физике колебания? Количество циклов движения, совершаемых системой за время наблюдения t.

Простейшая колебательная система, рассматриваемая на уроках физики, представлена пружинным маятником – прикрепленный к висящей на опоре пружине груз. Последний перемещается вверх-вниз благодаря силе упругости пружины.

​Период движения груза вычисляется по формуле:

, где:

• m – масса подвешенного тела;
• k – жесткость, упругость пружинного механизма.

Мироздание не существует без рассматриваемого движения: атомы колеблются у мест своей дислокации, электроны периодически вращаются вокруг ядра, а планеты – вокруг звёзд. Птицы совершают взмахи крыльями, а деревья колышутся под воздействием ветра.

Поделитесь в социальных сетях:

4 ноября 2021, 19:42

Физика

Could not load xLike class!

Использование уравнений маятника — физика средней школы

• Войти
• Биографии репетитора
• Подготовка к тесту

  СРЕДНЯЯ ШКОЛА

  • ACT Репетиторство
  • SAT Репетиторство
  • Репетиторство PSAT
  • ASPIRE Репетиторство
  • ШСАТ Репетиторство
  • Репетиторство STAAR

  ВЫСШАЯ ШКОЛА

  • Репетиторство MCAT
  • Репетиторство GRE
  • Репетиторство по LSAT
  • Репетиторство по GMAT

  К-8

  • Репетиторство AIMS
  • Репетиторство по HSPT
  • Репетиторство ISEE
  • Репетиторство ISAT
  • Репетиторство по SSAT
  • Репетиторство STAAR

  Поиск 50+ тестов

• Академическое обучение

  репетиторство по математике

  • Алгебра
  • Исчисление
  • Элементарная математика
  • Геометрия
  • Предварительный расчет
  • Статистика
  • Тригонометрия

  репетиторство по естественным наукам

  • Анатомия
  • Биология
  • Химия
  • Физика
  • Физиология

  иностранные языки

  • французский
  • немецкий
  • Латинский
  • Китайский мандарин
  • Испанский

  начальное обучение

  • Чтение
  • Акустика
  • Элементарная математика

  прочие

  • Бухгалтерия
  • Информатика
  • Экономика
  • Английский
  • Финансы
  • История
  • Письмо
  • Лето

  Поиск по 350+ темам

• О
  • Обзор видео
  • Процесс выбора наставника
  • Онлайн-репетиторство
  • Мобильное обучение
  • Мгновенное обучение
  • Как мы работаем
  • Наша гарантия
  • Влияние репетиторства
  • Обзоры и отзывы
  • Освещение в СМИ
  • О преподавателях университета

Звоните прямо сейчас, чтобы записаться на обучение:

(888) 888-0446

Все ресурсы по физике для старших классов

6 Диагностические тесты 233 практических теста Вопрос дня Карточки Learn by Concept

Справка по физике для старших классов » Движение и механика » Гармоничное движение » Использование уравнений маятника

Масса на маятнике падает из состояния покоя. Замечено, что период колебаний равен . Какова длина строки?

Возможные ответы:

Правильный ответ:

Пояснение:

Уравнение для периода маятника .

Масса маятника не имеет значения при расчете зависимости между периодом и длиной струны, поскольку единственными переменными в уравнении являются длина струны и сила тяжести.

Поскольку нам известны период и постоянная гравитации, мы можем найти длину струны.

Сообщить об ошибке

Груз на маятнике падает из состояния покоя. Если длина струны , каков период колебаний?

Возможные ответы:

Правильный ответ:

Объяснение:

Уравнение для периода маятника .

Масса маятника не имеет значения при расчете зависимости между периодом и длиной струны, поскольку единственными переменными в уравнении являются длина струны и сила тяжести.

Поскольку нам известны длина струны и постоянная силы тяжести, мы можем найти период.

Сообщить об ошибке

Маятник длиной прикреплен к массе . Когда он качается взад и вперед, каков период?

Возможные ответы:

Правильный ответ:

Объяснение:

Формула для периода маятника:

Нам известны длина нити и ускорение свободного падения. Нам также дана масса, но эта информация не имеет значения; период не зависит от массы.

Используйте данные значения для расчета периода.

Сообщить об ошибке.

Посмотреть репетиторов

Мэллори
Сертифицированный репетитор

Государственный университет Сан-Хосе, магистр искусств, образование.

Посмотреть репетиторов

Фелипе
Сертифицированный репетитор

Университет OCAD, Торонто, бакалавр искусств, промышленного и товарного дизайна.

Все ресурсы по физике для старших классов

6 диагностических тестов 233 практических теста Вопрос дня Карточки Learn by Concept

Период маятника: уравнения, коэффициенты и единицы измерения

Когда что-то свободно свисает с потолка, и вы толкаете его, оно начинает раскачиваться взад-вперед. Но как быстро он будет качаться и почему? Это то, на что мы действительно можем ответить, и есть довольно простая формула, чтобы понять это. Эти вопросы связаны со свойством, называемым периодом маятника.

Значение периода маятника

Чтобы понять, что такое период маятника, нам нужно знать значение двух вещей: периода и маятника.

Маятник представляет собой систему, состоящую из объекта определенной массы, подвешенного на стержне или шнуре к неподвижной оси. Висячий объект называется боб .

Маятник будет качаться вперед и назад, и максимальное значение, которое принимает угол θ шнура с вертикалью, называется амплитуда . Эта ситуация на самом деле довольно сложная, и в этой статье мы будем говорить только о простой версии маятника.

Простой маятник представляет собой маятник, в котором стержень или шнур не имеют массы, а ось вращения не имеет трения.

На рисунке ниже изображен простой маятник.

Простой маятник, адаптированный из изображения Chetvorno (Public Domain).

В этой статье всякий раз, когда мы говорим о маятнике, мы имеем в виду простой маятник с малой амплитудой. Теперь, когда мы понимаем, что мы подразумеваем под маятником, нам нужна еще одна информация, а именно, что мы подразумеваем под периодом.

период маятника – это продолжительность одного полного колебания боба.

Например, продолжительность времени между двумя последовательными ситуациями, в которых груз маятника находится полностью вправо, составляет один период маятника.

Влияние длины на период маятника

Длина шнура маятника влияет на период маятника. Это утверждение довольно убедительно, если мы просто посмотрим на несколько повседневных примеров.

Некоторые елочные игрушки являются довольно хорошими примерами маятника. Эти маленькие украшения имеют небольшую длину шнура в пару сантиметров и небольшие периоды менее полсекунды (быстро раскачиваются).

Качели для детской площадки являются примером маятника со шнуром длиной в несколько метров. Период этих колебаний часто превышает 3 секунды.

Набор качелей, из которых левые будут иметь более короткий период, чем правые, Wikimedia Commons (Public Domain).

Таким образом, чем длиннее шнур, тем больше период маятника.

Другие факторы, влияющие на период маятника

Есть два других фактора, влияющих на период маятника: ускорение свободного падения и амплитуда маятника. Поскольку мы говорим только о маятниках с малыми амплитудами, единственный другой фактор, который мы должны учитывать, — это гравитационное ускорение. С очень малым гравитационным ускорением мы можем представить, как вещи разыгрываются в замедленном темпе. Таким образом, мы ожидаем, что чем больше ускорение свободного падения, тем быстрее качается маятник и тем меньше период маятника.

Но подождите, почему масса шарика не влияет на период маятника? Это очень похоже на то, что масса объекта не влияет на скорость его падения: если масса удваивается, сила тяжести, действующая на него, тоже удваивается, но ускорение остается прежним: То же самое испытывает груз нашего маятника: сила, действующая на груз 1, который в два раза массивнее, чем на груз 2, в два раза больше, но и сам груз в два раза тяжелее, чем груз 2. Таким образом, груз 1 в два раза так же трудно переместить, как и боб 2, и поэтому ускорение обоих бобов будет одинаковым (опять же на). Следовательно, период маятника не зависит от массы груза.

Вы можете экспериментально проверить это, подойдя к качелям на детской площадке и измерив период качания, когда на них кто-то находится и когда на них никого нет. Два измеренных периода окажутся одинаковыми: масса шарика не влияет на период колебания.

Формула периода времени для маятника

Если длина шнура маятника и g ускорение свободного падения, формула для периода T маятника:

Мы видим, что были правы в своих предсказаниях. Большая длина шнура маятника и меньшее гравитационное ускорение вызывают больший период маятника, а масса груза вообще не влияет на период маятника.

Это хорошее короткое упражнение, чтобы проверить правильность единиц измерения в этом уравнении.

Схема простого маятника с малой амплитудой с указанием соответствующих величин, Арьян ван Дензен – StudySmarter.

Немного посчитав, мы можем вывести формулу для периода маятника. Нам нужно измерять углы в радианах, чтобы для малых углов мы имели примерно sin( θ ) = θ . Единственные результирующие силы, действующие на груз массой м , — это горизонтальные силы, а единственная горизонтальная сила, которую мы можем найти, — это горизонтальная часть натяжения шнура.

Общее натяжение шнура примерно равно вертикальной составляющей натяжения, поскольку амплитуда маятника мала. Эта вертикальная составляющая равна направленной вниз силе на груз (поскольку на груз нет чистой вертикальной силы), что составляет его вес мг .

Тогда горизонтальная часть напряжения равна – мг sin( θ ) (со знаком минус, потому что ускорение направлено в сторону, противоположную его положению, которое мы принимаем за положительное). Это примерно – мг θ из-за малой амплитуды маятника. Итак, ускорение боба равно.

Ускорение также измеряется как вторая производная по времени от горизонтального положения, что приблизительно. But постоянна, так что уравнение теперь, где мы должны решить для угла θ как функция времени t . Решение этого уравнения (как вы можете проверить) таково, где A — амплитуда маятника. Мы видим, что θ равно A в каждую единицу времени, поэтому период маятника определяется выражением. Этот вывод ясно показывает, откуда берутся все факторы, влияющие на период маятника.

Делаем вывод, что на Земле единственным фактором, влияющим на период маятника, является длина шнура маятника.

Примеры расчетов

Предположим, мы можем рассматривать детские качели как простой маятник. Каков период качелей, седло которых расположено на 4 м ниже оси вращения, если мы позволим им раскачиваться только плавно, т. е. с небольшой амплитудой?

Мы знаем, что г = 10 м/с ² и т.д. Тогда период T этого маятника вычисляется как:

.

Это действительно то, что мы знаем из собственного опыта.

Предположим, мы можем рассматривать серьгу как простой маятник. Если кто-то идет, он лишь немного толкает сережку, вызывая небольшую амплитуду. Каков срок службы такой серьги, если длина шнура 1 см?

Период этого маятника рассчитывается следующим образом:

.

Это также то, что мы знаем из опыта: маленький маятник качается очень быстро.

Частота маятника

Частота (часто обозначаемая как f ) системы всегда обратна периоду этой системы.

Следовательно, частота маятника определяется как:

.

Помните, что стандартной единицей измерения частоты является герц (Гц), который является обратным значением секунды.

Период маятника – основные выводы

• Маятник представляет собой систему, состоящую из объекта определенной массы, подвешенного на стержне или шнуре к неподвижной оси. Висячий объект называется бобом. Максимальный угол шнура с вертикалью называется амплитудой.

• Простой маятник — это маятник, в котором стержень или шнур не имеют массы, а ось не имеет трения.

• Период маятника – это продолжительность одного полного колебания боба.