Что такое время в физике и механике: понятие, формула, как обозначается
Попробуйте сходу дать точное определение: что такое время? Мысль вертится вокруг этого понятия, пытается ухватиться, но вот сформулировать однозначное определение сложно. Есть разные концепции и трактовки времени в философии, физике, метрологии.
В классической механике и теории относительности используются совершенно разные концепции времени. В первом случае время характеризует последовательность событий, происходящих в трехмерном пространстве. Во втором рассматривается еще и как четвертая координата.
Но обо всем по порядку. Давайте узнаем, как люди измеряли время, почему секунда – его мельчайшая принятая единица. Также определим понятие времени в физике, рассмотрим явления релятивистского и гравитационного замедления времени.
Что такое время?
Течение времени – совершенно естественное явление. Время идет, все вокруг меняется, происходят разные события.
Если бы вокруг ничего не происходило, понятие времени не имело бы традиционного смысла. Другими словами, без событий времени не существует. Итак:
Время – мера того, как меняется окружающий мир. Время определяет длительность существования объектов, изменение их состояний и процессы, протекающие в них.
В системе СИ время измеряется в секундах и обозначается буквой t.
Как люди измеряли время?
Для измерения времени нужны какие-либо повторяющиеся с одинаковым периодом события. Например, смена дня и ночи. Солнце каждый день встает на востоке и садится на западе, а Луна каждый синодический месяц проходит весь цикл фаз освещенности солнцем – от тоненького серпа полумесяца до полнолуния.

Древним людям ничего не оставалось, как привязать отсчет времени к движению небесных тел и событиям, связанным с ним. А именно – к смене дней, ночей и сезонов года.
В году 4 сезона и 12 месяцев. Именно столько раз за весну, лето, осень и зиму Луна меняет свои фазы.
По мере развития прогресса методы измерения времени совершенствовались, появились солнечные, водяные, песочные, огненные, механические, электронные и, наконец, молекулярные часы.
Часы FOCS 1Часы FOCS 1 в Швейцарии измеряют время с погрешностью хода около одной секунды за 30 миллионов лет. Это очень точные часы, но через 30 миллионов лет их все же придется “подвести”.Почему в часе 60 минут, в минуте – 60 секунд, а в сутках – 24 часа?
Сразу оговоримся, что изложенное ниже во многом является личными предположениями автора, сделанными на основе исторических сведений. Если у наших читателей появятся уточнения или вопросы, мы будем рады видеть их в обсуждениях.
Древним народам нужна была какая-то основа, чтобы строить свои системы счисления. В Вавилоне за такую основу было взято число 60.
Именно благодаря шестидесятеричной системе счисления, придуманной шумерами и позже распространившейся в Древнем Вавилоне, окружность содержит 360 градусов, градус – 60 минут, а минута – 60 секунд.Год можно представить в виде окружности, содержащей 360 градусов. Возможно, число 360 в данном контексте взялось оттого, что в году 365 дней, и эту цифру просто округлили до 360.
Когда-то самой короткой единицей измерения времени был
Но почему день делится на 12 часов? За это нужно сказать спасибо древним египтянам и их двенадцатиричной системе.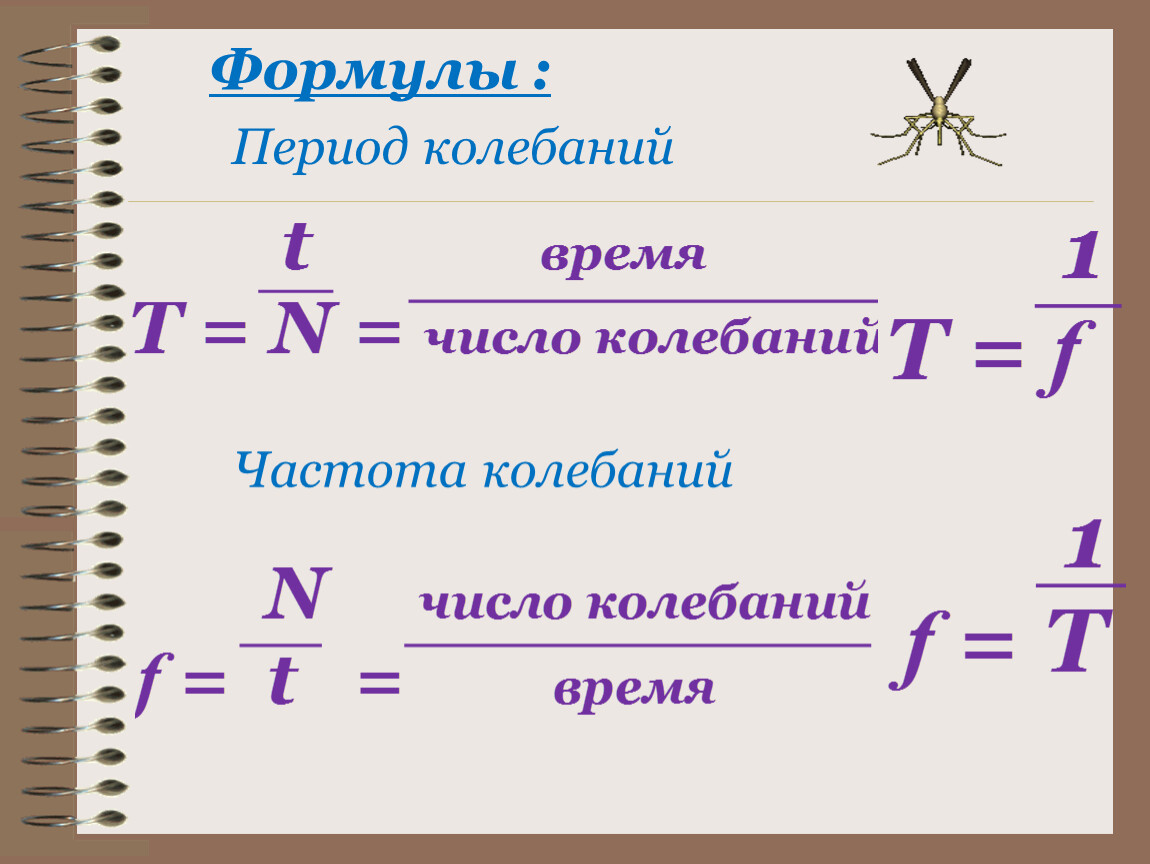 День и ночь делились на 12 раных частей, считаясь разными царствами бытия. Скорее всего, первоначально использование числа 12 связано с количеством оборотов Луны вокруг Земли за год.
День и ночь делились на 12 раных частей, считаясь разными царствами бытия. Скорее всего, первоначально использование числа 12 связано с количеством оборотов Луны вокруг Земли за год.
Самая большая единица измерения времени
Как в голову древним индуистам пришли такие цифры? Ответа на этот вопрос мы не знаем, но вся система как будто говорит нам, что тогда люди знали о Вселенной немного больше, чем мы.
Представление о времениКальпу в индуизме еще называют «днем Брахмы». День сменяется ночью, равной ему по продолжительности. 30 дней и ночей составляют месяц, а год состоит из 12 месяцев. Вся жизнь Брахмы – 100 лет, по прошествии которых мир погибает вместе с ним.
Если перевести сто лет Брахмы в наши традиционные годы, получится 
Вывод: если все это правда, то беспокоится не стоит – Вселенная будет существовать еще долгое время.
Кальпа – самая большая единица измерения времени согласно книге рекордов Гиннеса.Первые часы
Сначала было достаточно палочки, на которой каменным топором можно делать зарубки и тем самым отсчитывать прошедшие дни. Но это скорее был календарь, а не часы.
Первые и самые древние часы – солнечные. Их действие основано на изменении длины тени предметов по мере того, как солнце движется по небосводу. Такие часы представляли собой гномон – длинный шест, воткнутый в землю. Солнечные часы применялись в Древнем Египте и Китае. О них было доподлинно известно уже в
Затем появились водяные, песочные и огненные часы. Работа этих механизмов не была привязана к движению небесных светил. Долгое время водяные часы были главным инструментом для измерения времени.
Первые механические часы были изготовлены китайскими мастерами в 725 году нашей эры.
В средневековой Европе механические часы устанавливались в башнях соборов и имели только одну стрелку – часовую. Карманные часы появились только в 1675 году (изобретение запатентовал Гюйгенс), а наручные – намного позже.
Первые наручные часы были исключительно женским аксессуаром. Они представляли собой богато украшенные изделия, точность хода которых отличалась огромными погрешностями. У уважающего себя мужчины не могло быть и мысли о том, чтобы носить наручные часы.Современные часы
Сейчас механические или электронные часы есть у каждого. Они измеряют время с относительно небольшими погрешностями. Однако самыми точными часами в мире являются атомные часы. Их еще называют молекулярными или квантовыми.
Как мы помним, для определения единицы времени необходим какой-то периодический процесс. Когда-то самой короткой единицей был день. То есть единица измерения время была привязана к периодичности восхода и заката солнца. Потом минимальной единицей стал час, и так далее.
То есть единица измерения время была привязана к периодичности восхода и заката солнца. Потом минимальной единицей стал час, и так далее.
С 1967 года, согласно международной системе СИ, определение одной секунды привязано к периоду электромагнитного излучения, возникающего при переходе между сверхтонкими уровнями основного состояния атома
Время в физике
На данный момент не существует определенной и единой концепции определения времени в физике.
В классической механике время считается непрерывной, априорной и ничем не определяемой характеристикой мира.
Для измерения времени используется какая-либо периодическая последовательность событий. В классической физике время инвариантно относительно любой системы отсчета. То есть во всех системах события происходят одновременно.
Как найти время в физике? Простейшая формула, определяющая связь между пройденным путем, скоростью и временем, известна каждому школьнику и имеет вид:
Это формула времени для равномерного и прямолинейного движения. Здесь t – время, S – пройденное расстояние, v – cкорость.
Здесь t – время, S – пройденное расстояние, v – cкорость.
Более подробно об основах классической механики читайте в нашей отдельной статье.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Термодинамика говорит, что время необратимо. Необратимо по причине возрастания энтропии замкнутой системы. Кстати, в нашем тематическом материале читайте о том, что такое энтропия.
Но самое интересное начинается в релятивистской физике. Приведем цитату Стивена Хокинга, физика, написавшего краткую историю времени.
Нам приходится принять, что время не отделено полностью от пространства и не независимо от него, но вместе с ним образует единый объект, который называется пространством-временем
Также в релятивистской физике время перестает быть инвариантом и можно говорить об относительности времени. Другими словами, ход времени зависит от движения системы отсчета.
Это так называемое релятивистское замедление времени. Если часы находятся в неподвижной системе отсчета, то в движущемся теле все процессы происходят медленнее, чем в неподвижном. Именно поэтому космонавт, путешествующий в космосе на супер скоростном корабле, практически не постареет по сравнению со своим братом близнецом, оставшимся на Земле.
Релятивистское замедление времениПомимо релятивистского существует гравитационное замедление времени. Что это такое? Гравитационное замедление времени – изменение хода часов в гравитационном поле. Чем сильнее поле гравитации, тем сильнее замедление.
Вспомним о том, что секунда – это время, за которое атом изотопа цезия совершает 9 192 631 770 квантовых переходов. В зависимости от того, где находится атом (на земле, в космосе, вдали от любого объекта или у черной дыры) секунда будет иметь разные значения.
Поэтому и время процессов, связанных с данной системой отсчета, будет отличаться. Так, для наблюдателя у горизонта событий Шварцшильдовской черной дыры время практически остановится, а для наблюдателя на Земле все произойдет почти мгновенно.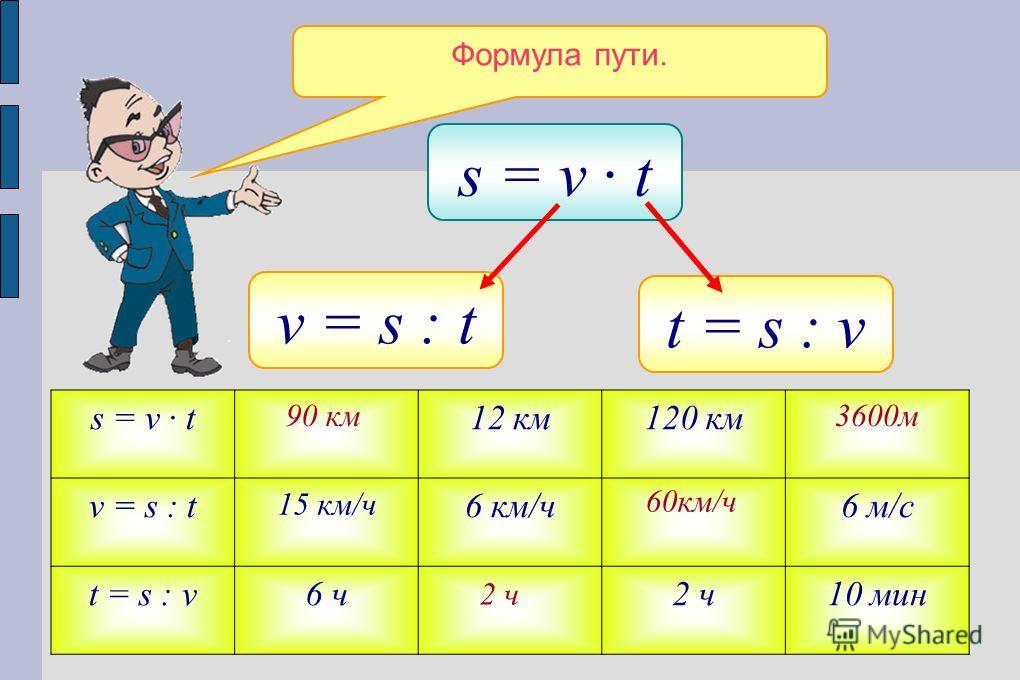
Людей всегда волновала тема путешествий во времени. Предлагаем вам посмотреть научно-популярный фильм на эту тему и напоминаем, что если у вас совершенно нет времени на учебные дела, наш студенческий сервис всегда поможет справится с актуальными задачами и проблемами.
Урок физики по теме “Расчет пути и времени движения”. 7-й класс
Ключевые слова: скорость, время, расстояние, расчет пути, расчет времени движения
(Презентация, слайд 1)
Цели урока: научить учеников вычислять путь, пройденный телом при равномерном движении и время движения; повышать интерес к физике, как науке об окружающем нас мире (слайд 2)
ХОД УРОКА
I. Повторение (слайд 3)
Повторение (слайд 3)
- Что называют движением?
- Какие виды движения вы знаете?
- Что понимают под скоростью?
- Как вычислить скорость?
- В каких величинах измеряется скорость?
Проверка упр.4(2,4).
– Ребята, а какие вы знаете пословицы о скорости?
Ответы учеников:
– Долго рассуждай, да скоро
делай!
– Семеро одного не ждут.
– Большой меньшого не дожидается.
– Под гору вскачь, а на гору хоть плачь.
– Тише едешь, дальше будешь.
– Делу – время, потехе – час.
II. Изучение
1. Прямолинейное равномерное движение (слайд
4). [4]
2. Так как V = S/t, то S = V · t, а также t = S/V (слайд
5).
3. Схема для запоминания формул расчета скорости,
времени, пути:
Рис. 1
1
4. Графики скорости и пути равномерного движения: (слайд 7)
Скорость – величина векторная (слайд 6) [4], поэтому она характеризуется не только модулем, но и направлением. В зависимости от выбранного положительным направления скорость может быть постоянной по величине, но положительной (если движение происходит по выбранному как положительное направлению) или отрицательной по знаку (если движение происходит противоположно выбранному направлению)
А) Графики скорости равномерного движения:
Рис. 2
Б) График пути равномерного движения:
Рис. 3
5. Вычисление пути и времени неравномерного движения: (слайд 8)
Vср = S / t, где S – весь пройденный телом путь, а t – все время движения.
Формулы для вычисления пути и времени будут
иметь тот же вид: S = Vср · t, а
также t = S / Vср, но в расчет берут
среднюю скорость движения.
Если в течение рассматриваемого промежутка времени направление движения не менялось, то средняя скорость перемещения равняется средней скорости в пути, в том случае, когда движение происходило в сторону возрастающих расстояний, или равняется отрицательно взятой средней скорости в пути, если движение совершалось в сторону убывающих расстояний.
III. Закрепление
1. Обсуждение вопросов к п.16.
2. Решение задач: (слайды 9-11)
1) Упр. 5(2):
На велосипеде без особого напряжения можно ехать со скоростью 3 м/c. На какое расстояние можно уехать за 1,5 часа?
| Дано V = 3 м/с t = 1,5 ч Найти: S |
СИ 5400с |
Решение S = V·t S = 3м/c· 5400 с = 16200 м = 16,2 км Ответ: 16,2 км |
2) Упр. 5(3):
5(3):
На рисунке 38 показан график зависимости пути равномерного движения от времени. Оs – ось пройденных путей, Оt – ось времени. По этому графику найдите, чему равен путь, пройденный телом за 2 часа. Затем рассчитайте скорость тела.
| Дано t = 2ч S = 200 км Найти: V |
Решение V = S/t V = 200 км/2 ч = 100 км/ч Ответ: 100 км/ч |
3) Упр. 5(4):
График зависимости скорости равномерного движения тела от времени представлен на рисунке 39. По этому графику определите скорость движения тела. Рассчитайте путь, который пройдет тело за 2ч, 4ч.
| Дано V=8 м/с t1 = 2ч t2 = 4ч Найти: S1 и S2 |
СИ 7200с |
Решение S = V·t S1 = 8м/с 7200с = 57500м = 57,6 км.  S2 = 8м/с 14400с = 115200м = 115,2 км Ответ: 57,6км и 115,2 км |
IV. Самостоятельное решение задач с последующим обсуждением полученных результатов (слайды 12-14).
а) Это интересно:
1. Самый быстрый зверь на Земле = гепард. Эта стройная пятнистая кошка на длиннющих ногах развивает скорость 110 км/ч. Но бежит недалеко. Если сразу не догонит жертву, тут же возвращается в засаду. Какое расстояние пробегает гепард за 5 секунд? (153 м). [2]
2. Несмотря на маленькие размеры колибри
способны пролететь значительные расстояния.
Например, рубиноголовая колибри весной и осенью
перелетают Мексиканский залив, преодолевая без
остановки примерно 900 км со скоростью 40 км/ч. При
порхающем полете крылья колибри движутся со
скоростью 3000-4800 взмахов в минуту. Определите
время перелета колибри через Мексиканский
залив. (81000с = 22ч.30мин). [2]
(81000с = 22ч.30мин). [2]
3. Самыми быстрокрылыми считаются ласточки и стрижи. Скорость их полета до 150 км/ч. Какое расстояние пролетают эти птицы за минуту? (2500м). [2]
б) Смешинки (слайды16-17):
1. Двигаясь равномерно и нигде не задерживаясь, мелкий отличник Олег добрался из дома до школы за 7 мин. Его соседка крупная троечница Оля тоже двигалась равномерно, также не задерживалась и добралась до школы за 57 мин. Чем отличался стремительный и целеустремленный бег в школу отличника Олега Хлопушина от тихой и печальной поступи троечницы Оли Ромашкиной? [3]
2. Печальный дядя Боря несет из магазина домой авоську с мелкими куриными яйцами. Через равные промежутки времени яйца из авоськи выпадают на землю и разбиваются. Можно ли сказать, что печальный дядя Боря движется равномерно, если коты, бегущие за ним, находят яйца на равных расстояниях одно за другим? [3]
V.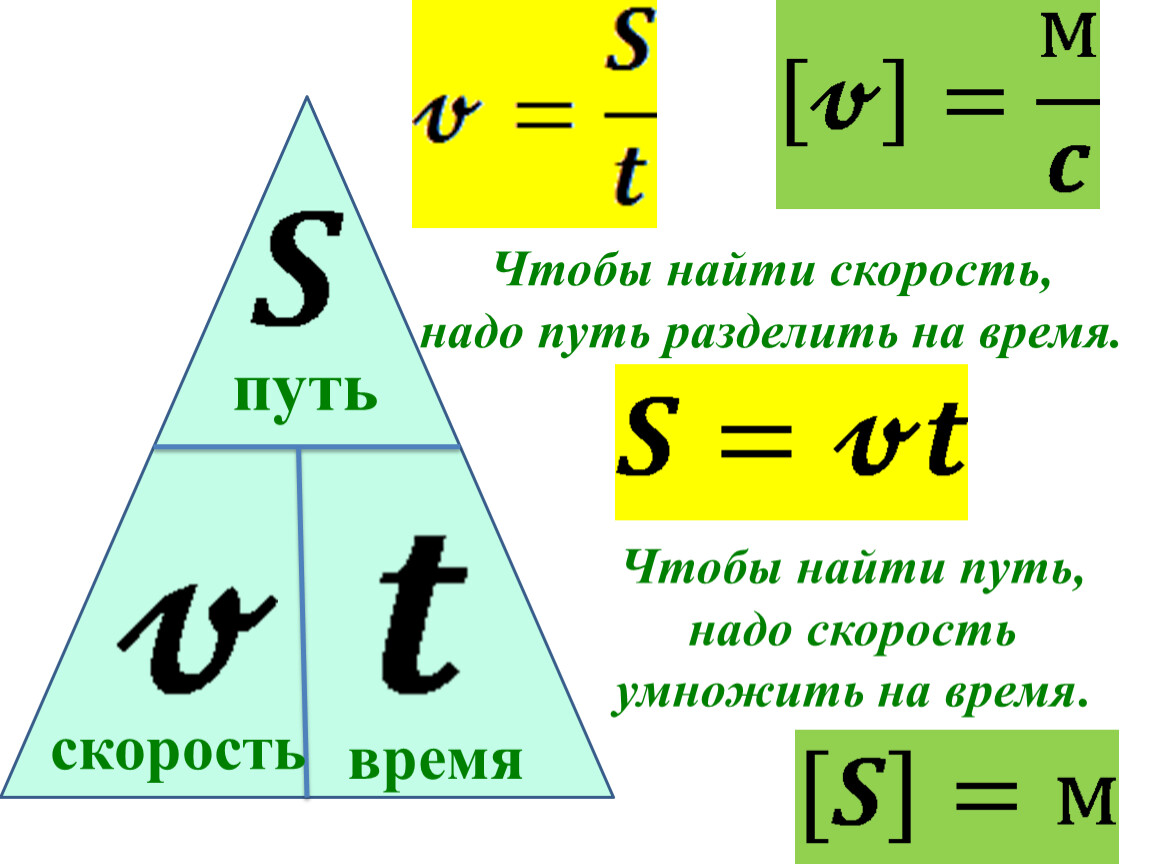 Подведение итогов урока, выставление
оценок
Подведение итогов урока, выставление
оценок
VI. Рефлексия
– Что нового вы сегодня узнали на уроке?
– Что вам больше всего понравилось?
VII. Домашнее задание (слайд 18)
П.16, упр.5(4,5), придумать и решить две задачи на расчет пути и времени равномерного движения. Постарайтесь сделать их оригинальными.
Использованные ресурсы:
- А.В.Перышкин. Физика – 7ласс «Дрофа», 2006год.
- А.М.Семке. «Физика. Занимательные материалы к урокам. 7 класс.» Москва, «НЦ ЭРФС» 2006г
- Г.Остер. Физика задачник, Москва, «Росмэн»,1995г
- Физика. Библиотека наглядных пособий. 7-11 кл. ООО «1С», 2004-2011, диск.
- Интернет ресурсы.
Math.ru
Артур Давидович ЧернинМ.: Наука, 1987. 224 с.
Тираж 150000 экз.
Серия Библиотечка «Квант», выпуск 59
| |||||||||||
Понятие времени – одно из самых фундаментальных в нашей системе знаний. В простой и наглядной форме, без использования математических формул книга рассказывает о развитии научных представлений о времени, об основных идеях современной физической концепции времени. Дается изложение важнейших вопросов физики, связанных с природой времени: однородность времени и закон сохранения энергии, относительность одновременности, световой конус и причинность, время вблизи черной дыры, прошлое и будущее Вселенной, время в микромире, стрела времени.Для школьников, студентов, преподавателей, лекторов.
Содержание
ПРЕДИСЛОВИЕ
Глава 1. ВРЕМЯ И МЫ
Чувство времени
Счетчик времени?
Альфа-ритм
Живые часы
От ощущения к понятию
Пространство
Пространство и время
Имена времени
Глава 2. В ПОИСКАХ СУЩНОСТИ ВРЕМЕНИ
В ПОИСКАХ СУЩНОСТИ ВРЕМЕНИ
Поток событий и законы природы
Великий год
Время и небо
Время и движение
Зенон
Ахиллес и черепаха
Мгновение и длительность
Окружность+прямая=спираль
Глава 3. ИСТОРИЯ ЧАСОВ
Солнечное время
“Время истекло”
Начало Нового времени
Часы на башне
Маятник Галилея
Автоколебания
Атомные часы
Модель Вселенной
Астрономические часы
Часы “Пульсар”
Глава 4. АБСОЛЮТНОЕ ВРЕМЯ
Галилей
Относительность
Инерция
Ньютон
Классическая механика
Инерциальные часы
Время классической механики
Время в “Началах”
Абсолютное время, абсолютное пространство
Глава 5. ВРЕМЯ И СВЕТ
ВРЕМЯ И СВЕТ
Эйнштейн
Система отсчета
Скорость света
Ни прибавить, ни убавить
Абсолютный рекорд
Одновременность
Относительность времени
Глава 6. СОБСТВЕННОЕ ВРЕМЯ
Время здесь и время там
Быстрые пионы
Красное, зеленое, голубое
Эффект Доплера
“Световые” часы
Разбегание галактик
Сверхсветовые скорости?
Глава 7. МИРОВАЯ ЛИНИЯ
4=3+1
Время-движение-пространство
События и лучи света
Прошлое, настоящее, будущее
Машина времени
Причина и следствие
Сегодня и вчера
Интервал
Бег времени
Глава 8. ВРЕМЯ И ТЯГОТЕНИЕ
Всемирное тяготение
Принцип эквивалентности
Лифт Эйнштейна
Тяготение и свет
Замедление времени
Измерение
Астрономический эксперимент
Черные дыры: время остановилось
Глава 9.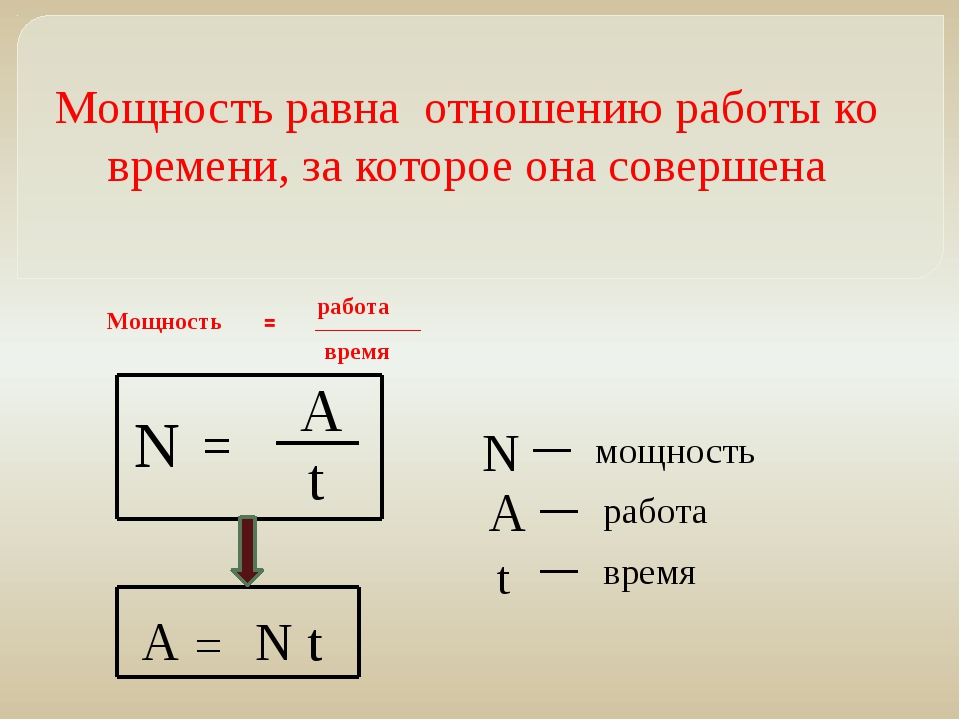 ПАРАДОКС ЧАСОВ
ПАРАДОКС ЧАСОВ
Снаряд Жюля Верна
Ускорение и перегрузки
Кто старше?
Из пушки … часами
Снова о четырехмерном
Кривизна
Глава 10. МИР ВО ВРЕМЕНИ И ПРОСТРАНСТВЕ
Глава 11. ВОЗРАСТ ВСЕЛЕННОЙ
Сингулярность
Нуль времени
Часы Вселенной
Одновременность
Срезы времени
Горизонт
Будущее
Пульсации и связь времен
Глава 12. ВРЕМЯ И ЭНЕРГИЯ
Симметрия времени
Вечный двигатель
Как быть с энергией тяготения?
Кванты, волны, частицы
Соотношение неопределенностей
Время против энергии
Не сохраняется, но …
Глава 13. ВОЛНЫ ВРЕМЕНИ
Тяготение и волны
Гравитон
Время среди квантов
Атом времени?
Время в самом начале
Из вакуума.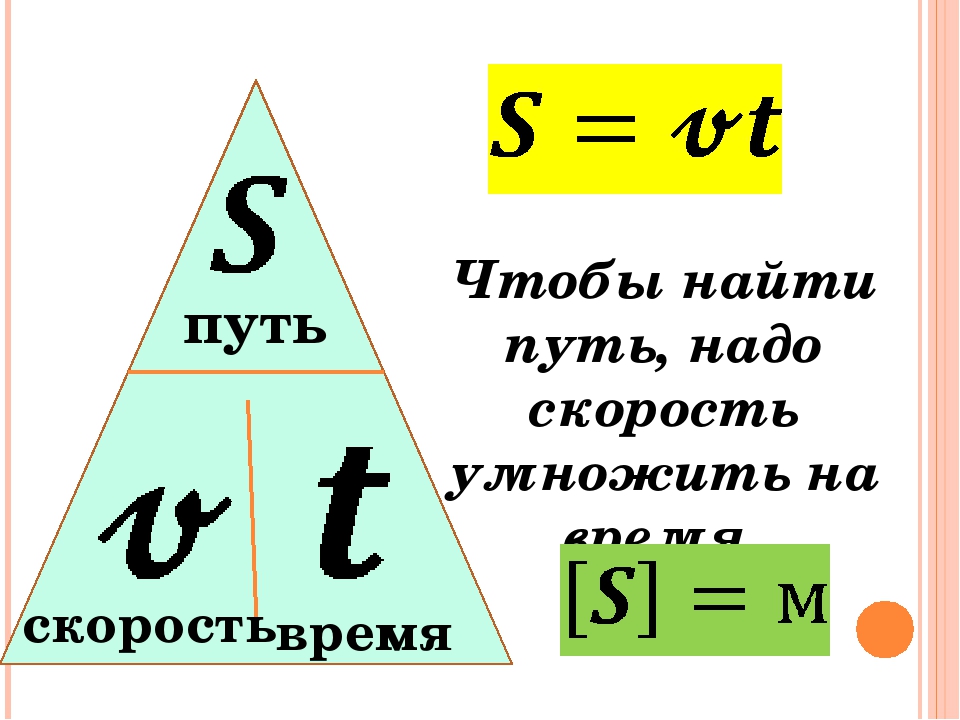 ..
..
Глава 14. СТРЕЛА ВРЕМЕНИ
Бег и направление
Гипотеза Больцмана
Обращение времени
Гипотеза Эддингтона
Т-инвариантность и “обширный ум”
От причины к следствию
Глава 15. ЧТО ТАКОЕ ВРЕМЯ?
Мир, время, мышление
Относительность
Кванты
Бег, необратимость, одномерность
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
| |||||||||||
| posted Oct 15, 2009, 1:24 AM by Дмитрий Белозёров
[
updated Dec 23, 2014, 6:24 AM
] |
Из курса физики седьмого класса мы помним, что механическое движение тела – это его перемещение во времени относительно других тел. Исходя из таких сведений, мы можем предположить необходимый набор инструментов для расчета движения тела. Во-первых, нам необходимо нечто, относительно чего мы будем производить наши расчеты. Далее, нам потребуется условиться, каким образом мы будем определять положение тела относительно этого «нечто». И наконец, нужно будет как-то фиксировать время. Таким образом, для того, чтобы рассчитать, где будет находиться в конкретный момент тело, нам понадобится система отсчета. Система отсчета в физикеСистемой отсчета в физике называют совокупность тела отсчета, системы координат, связанной с телом отсчета, и часы или иной прибор для отсчета времени. При этом всегда следует помнить, что всякая система отсчета условна и относительна. Всегда можно принять другую систему отсчета, относительно которой любое движение будет иметь совершенно другие характеристики. Относительность – это вообще немаловажный аспект, который следует учитывать практически при любых расчетах в физике. Например, во многих случаях мы далеко не в любой момент времени можем определить точные координаты движущегося тела. В частности, мы не можем расставить наблюдателей с часами на каждых ста метрах вдоль железнодорожного пути от Москвы до Владивостока. В таком случае мы рассчитываем скорость и местоположение тела приближенно в течение какого-то отрезка времени. Нам не важна точность до одного метра при определении местоположения поезда на пути в несколько сотен или тысяч километров. Для этого в физике существуют приближения. Одним из таких приближений является понятие «материальная точка». Материальная точка в физикеМатериальной точкой в физике обозначают тело, в случаях, когда его размерами и формой можно пренебречь. При этом считается, что материальная точка имеет массу исходного тела. Например, при расчете времени, которое понадобится самолету, чтобы долететь из Новосибирска до Новополоцка, нам не важны размеры и форма самолета. Практически всякое тело можно считать материальной точкой либо когда расстояние, преодолеваемое телом велико в сравнении с его размерами, либо когда все точки тела двигаются одинаково. Например, автомобиль, проехавший несколько метров от магазина до перекрестка, вполне сравним с этим расстоянием. Но даже в такой ситуации его можно считать материальной точкой, потому что все части автомобиля перемещались одинаково и на равное расстояние. А вот в случае, когда нам надо разместить тот же автомобиль в гараже, его уже никак не сочтешь материальной точкой. Придется учитывать его размеры и форму. Это тоже примеры, когда необходимо учитывать относительность, то есть относительно чего мы производим конкретные расчеты.
Для того, чтобы определить положение тела, которое совершило некоторое перемещение, можно графически приставить вектор перемещения к начальному положению тела. В этом случае вычисления будут производиться не с самим векторами, а с их проекциями на координатные оси и с их модулями. Эти величины которые будут представлять собой некоторые числа, положительные или отрицательные, но не будут иметь направления. Рассмотрим следующую задачу Необходимо определить координату движущегося тела, по известной начальной координате и известному вектору перемещения.
Определить координаты катеров по отношению к пристани и расстояние между ними. Построим координатную ось Ох, параллельно прямой вдоль которой двигаются катера. Спроецируем начала и концы векторов перемещений s1 и s2 на ось Ох, получим отрезки sx1 и sx2. Эти отрезки будут являться проекциями данных векторов. Проекция вектора на ось, будет положительной, если вектор сонаправлен с осью, и отрицательной, если вектор направлен в противоположную оси сторону. В нашем случае sx1 положительная проекция, а sx2 отрицательная проекция. Проекция вектора, будет равна разности координат конца и начала вектора. В нашем случае имеем: Теперь выразим из этих уравнений координаты x1 и x2. Расстояние между двумя катерами будет равно модулю разности их координат, Мы получили формулы для вычисления координат точек и расстояния между ними. Из условия задачи, катера встретились на расстоянии 100 км от пристани. х0 – точка встречи. Следовательно расстояние от х0 до пристани(начала координат) 100 км. х0=100 км. Так как мы выбрали ось Ох параллельно векторам перемещений катеров. По условию у нас даны числа 50 км и 60 км, это и есть модули векторов соответствующий перемещений.
В итоге получаем,
Ответ: х1=160 км, х2=50 км, l=110 км.
Довольно часто в физике приходится иметь дело с прямолинейным равномерным движением. Задача нахождения перемещения при равномерном прямолинейном движении довольно проста. По определению скорость равномерного прямолинейного движения – постоянная векторная величина, которая равна отношению перемещения тела за некий промежуток времени к величине этого промежутка: v(->) = s(->) /t, откуда следует,что перемещение s(->) = v(->) * t . где v(->) – скорость (векторная величина), s(->) – перемещение (векторная величина), t – время. При работе с векторными величинами для нахождения числовых значений величин применяют значения проекций конкретных величин на оси. В случае равномерного прямолинейного движения направления векторов скорости и перемещения совпадают, поэтому можно смело использовать в расчетах модульные значения. Тогда формула принимает вид: s = v*t Но такая формула известна уже давно, и в ней под буквой s понимали путь, пройденный телом. Так что же такое s – путь или модуль перемещения? Как характеризуется перемещение тела при прямолинейном равномерном движении?Дело в том, что при равномерном и прямолинейном движении модуль вектора перемещения за некий промежуток времени будет равен пройденному телом пути за тот же промежуток времени. Это утверждение можно подтвердить рисунком. Если изобразить векторно скорость движения тела в зависимости от времени, то модуль такого перемещения при равномерном прямолинейном движении будет в любой момент времени совпадать с путем, пройденным за это время телом. Если же направление тела будет меняться, то пройденный путь будет больше значения модуля перемещения. Поэтому принятое нами равенство справедливо только для случаев, когда тело двигается равномерно и прямолинейно. Можно изобразить данную ситуацию графически. Для этого проведем из точки 0 оси скорости и времени. (Рис. 1)Если применить проекции значений скорости и времени на оси, то тогда мы увидим, что скорость, как величина постоянная является прямой, проходящей параллельно оси времени. И если мы проведем перпендикуляры от временной оси в начальный и конечный моменты времени к линии скорости, то получим прямоугольник, площадь которого и будет равна перемещению за данный промежуток времени. Рис. 1 Стороны этого прямоугольника будут равны все тем же значениям v и t. Таким образом, мы видим, что и при построении проекций векторных величин, принятое нами выше равенство сохраняет свою справедливость. В случае же, когда мы имеем в расчетах дело с двумя телами, двигающимися равномерно и прямолинейно, при этом совпадают направления их движения, то расчеты также можно производить, применяя приведенную выше формулу. Если же два тела двигаются равномерно и прямолинейно, а направления их движения противоположны, но расположены вдоль одной оси, то можно по-прежнему использовать в расчетах значения их модулей. Но необходимо будет брать значение величин для одного тела со знаком минус в зависимости от того, направление какого из тел мы примем за положительное.
Хотите провести эксперимент? Да запросто. Возьмите длинную линейку, положите ее горизонтально и приподнимите один конец. У вас получится наклонная плоскость. А теперь возьмите монетку и положите на верхний конец линейки. Монетка начнет скользить вниз по линейке, проследите, как будет двигаться монетка с одинаковой скоростью или нет. Вы заметите, что скорость монетки будет постепенно возрастать. И изменение скорости будет напрямую зависеть от угла наклона линейки. Чем угол наклона круче, тем большую скорость будет набирать монетка к концу пути. Изменение скорости монеткиМожно попытаться узнать, как меняется скорость монетки за каждый одинаковый промежуток времени. Такое движение тела, когда его скорость за любые равные промежутки времени меняется одинаково, а тело при этом движется по прямой линии, называется в физике прямолинейным равноускоренным движением. Под скоростью в данном случае понимается скорость в каждый конкретный момент времени. Такая скорость называется мгновенной скоростью. Мгновенная скорость тела может меняться по-разному: быстрее, медленнее, может возрастать, а может уменьшаться. Для того чтобы охарактеризовать это изменение скорости, вводят величину, называемую ускорением. Понятие ускорения: формулаУскорение это физическая величина, показывающая, насколько изменилась скорость тела за каждый равный промежуток времени. Если скорость меняется одинаковым образом, то ускорение будет величиной постоянной. a = (v – v_0 )/ t, где a ускорение, v конечная скорость, v_0 начальная скорость, t время. Измеряется ускорение в метрах на секунду в квадрате (1 м/с2). Немного странная на первый взгляд единица очень легко объясняется: ускорение= скорость/время=(м/с)/с , откуда и выводится такая единица. Ускорение величина векторная. Оно может быть направлена либо в ту же сторону, что и скорость, если скорость возрастает, либо в противоположную сторону, если скорость уменьшается. Пример второго варианта это торможение. Если, например, автомобиль тормозит, то скорость его уменьшается. Тогда ускорение будет являться отрицательной величиной, и направлено оно будет не по ходу движения автомобиля, а в обратную сторону. В случаях, когда скорость у нас меняется от нуля до какой-либо величины, например, при старте ракеты, либо в случае, когда скорость наоборот уменьшается до нуля, например, при торможении поезда до полной остановки, можно использовать в расчетах только одно значение скорости.
Проекцию скорости на ось Ох при прямолинейном равноускоренном движении можно найти по следующей формуле: Выразим из этой формулы, формулу для проекции скорости которую имело лвижущееся тело к концу некоторого промежутка времени t. То есть, зная проекцию вектора начальной скорости V0x и проекцию вектора ускорения ax в любой момент времени можно вычислить проекцию вектора мгновенной скорости Vx, которую будет иметь тело в данной точке.
Графиком уравнения Vx=V0x+ax*t будет прямая линия. Расположение этой лини в системе координат будет определяться значениями ax b V0x. График проекции скорости тела при нулевой начальной скоростиНа следующем рисунке представлен график проекции вектора скорости движущегося тела, которое в начальный момент времени имел нулевую скорость, и двигалось равноускоренно и прямолинейно с ускорением ax=1,5 м/(с^2) в течение 40 секунд. Для построения такого графика, также достаточно взять несколько значений переменной t и посчитать в них значение проекции скорости Vx. А потом соединить их прямой линией. Как видите, график имеет начальную точку не в нуле, в значении, которое имеет начальная скорость. График проекции скорости тела при торможенииЕсли бы ускорение было отрицательным, то есть тело постепенно тормозило, то график составлял бы с положительным направлением оси Ох тупой угол. Ниже представлен график такой ситуации. Из графика видно, что тело начинало свое движение со скоростью 20 м/с, и постепенно замедляло её. За 10 секунд, оно полностью остановилось.
Попытаемся вывести формулу для нахождения проекции вектора перемещения тела, которое двигается прямолинейно и равноускоренно, за любой промежуток времени. Для этого обратимся к графику зависимости проекции скорости прямолинейного равноускоренного движения от времени. График зависимости проекции скорости прямолинейного равноускоренного движения от времениНиже на рисунке представлен график, для проекции скорости некоторого тела, которое движется с начальной скорость V0 и постоянным ускорением а. Если бы у нас было равномерное прямолинейное движение, то для вычисления проекции вектора перемещения, необходимо было бы посчитать площадь фигуры под графиком проекции вектора скорости. Теперь докажем, что и в случае равноускоренного прямолинейного движения проекция вектора перемещения Sx будет определяться таким же образом. То есть проекция вектора перемещения будет равняться площади фигуры под графиком проекции вектора скорости. Найдем площадь фигуры ограниченную осью оt, отрезками АО и ВС, а также отрезком АС.
Выделим на оси ot малый промежуток времени db. Проведем через эти точки перпендикуляры к оси времени, до их пересечения с графикос проекции скорости. Отметим точки пересечения a и c. За этот промежуток времени скорость тела поменяется от Vax до Vbx. Если взять этот промежуток достаточно малым, то можно считать что скорость остается практически неизменной, а следовательно мы будем иметь на этом промежутке дело с равномерным прямолинейным движением. За промежуток t3=3*t1, это тело совершит перемещение S3=9*S1 и т.д., для любого натурального n. Это конечно же будет выполняться, при условии, что время должно отсчитываться от одного и того же момента. На следующем рисунке хорошо представлена эта зависимость.
При увеличении промежутка времени, который отсчитывается от начал движения, в целое число раз по сравнению с t1, модули векторов перемещений будут возрастать как ряд квадратов последовательных натуральных чисел. Помимо этой закономерности, из представленного выше рисунка можно установить еще одну, следующую закономерность:
За последовательные равные промежутки времени, модули векторов перемещений, совершаемых телом, будут относиться между собой как ряд последовательных нечетных чисел. Стоит отметить, что такие закономерности будут верными только в равноускоренном движении.
Представьте себе электричку. Она едет тихонько по рельсам, развозя пассажиров по дачам. И вдруг сидящий в последнем вагоне хулиган и тунеядец Сидоров замечает, что на станции «Сады» в вагон входят контролеры. Билет, естественно, Сидоров не купил, а штраф платить ему хочется еще меньше. Относительность движения безбилетника в поездеИ вот, чтобы его не поймали, он быстренько совершает перемещение при прямолинейном равномерном движении в другой вагон. Контролеры, проверив билеты у всех пассажиров, движутся в том же направлении. Сидоров опять переходит в следующий вагон и так далее. И вот, когда он достигает первого вагона и идти дальше уже некуда, оказывается, что поезд как раз доехал до нужной ему станции «Огороды», и счастливый Сидоров выходит, радуясь тому, что проехал зайцем и не попался. Что мы можем извлечь из этой остросюжетной истории? Мы можем, без сомнения, порадоваться за Сидорова, а можем, кроме того, обнаружить еще один небезынтересный факт. В то время, как поезд за пять минут проехал пять километров от станции «Сады» до станции «Огороды», заяц Сидоров за это же время преодолел такое же расстояние плюс расстояние, равное длине поезда, в котором он ехал, то есть около пяти тысяч двухсот метров за те же пять минут. Получается, что Сидоров двигался быстрее электрички. Впрочем, такую же скорость развили и следующие за ним по пятам контролеры. Учитывая, что скорость поезда была около 60 км/ч впору выдать им всем несколько олимпийских медалей. Однако, конечно же, никто такой глупостью заниматься не будет, потому что все понимают, что невероятная скорость Сидорова была развита им только лишь относительно неподвижных станций, рельсов и огородов, и обусловлена эта скорость была передвижением поезда, а вовсе не невероятными способностями Сидорова. Относительно же поезда Сидоров двигался вовсе и не быстро и не дотягивает не то что до олимпийской медали, но даже до ленточки от нее. Вот тут-то мы и сталкиваемся с таким понятием как относительность движения. Понятие относительности движения: примерыОтносительность движения не имеет определения, так как не является физической величиной. Относительность механического движения проявляется в том, что некоторые характеристики движения, такие как скорость, путь, траектория и так далее, относительны, то есть зависят от наблюдателя. В различных системах отсчета эти характеристики будут различны. Кроме приведенного примера с гражданином Сидоровым в поезде, можно взять практически любое движение любого тела и показать, насколько оно относительно. Идя на работу, вы двигаетесь вперед относительно дома и в то же время передвигаетесь назад относительно автобуса, на который опоздали. Вы стоите на месте относительно плеера в кармане и несетесь с огромной скоростью относительно звезды по имени Солнце. В этом и заключается понятие относительности движения.
С древнейших времен движение материальных тел не переставало волновать умы ученых. Так, например, сам Аристотель считал, что если на тело не действуют никакие силы, то такое тело всегда будет находиться в покое. И лишь только спустя 2000 лет итальянский ученый Галилео Галилей смог исключить из формулировки Аристотеля слово «всегда». Галилей понял, что пребывание тела в состоянии покоя не является единственным следствием отсутствия внешних сил. Тогда Галилей заявил: тело, на которое не действуют никакие силы, будет либо находиться в покое, либо двигаться равномерно прямолинейно. То есть, движение с одинаковой скоростью по прямой траектории, с точки зрения физики, равнозначно состоянию покоя. Что есть состояние покоя?В жизни этот факт наблюдать очень сложно, поскольку всегда имеет место сила трения, которая не дает предметам и вещам покидать свои места. И в самом деле, на тело действую только две силы: сила тяжести и сила реакции опоры. Но расположены они на одной прямой и направлены друг против друга. Таким образом, по принципу суперпозиции, мы имеем, что общая сила, действующая на такое тело равна нулю. Однако это идеальный случай. В жизни сила трения проявляет себя почти во всех случаях. Галилей сделал важное открытие, приравняв состояние покоя и движение с постоянной скоростью по прямой линии. Но этого было недостаточно. Оказалось, что условие это выполняется не во всех случаях. Ясность в этот вопрос внес Исаак Ньютон, обобщивший исследования Галилея и, таким образом, сформулировавший Первый Закон Ньютона. Первый закон Ньютона: формулируем самиСуществуют две формулировки первого закона Ньютона современная и формулировка самого Исаака Ньютона. Современная формулировка звучит следующим образом: «Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго». Инерциальные системы отсчетаИнерциальными называют системы отсчета, в которых выполняется закон инерции. Закон же инерции заключается в том, что тела сохраняют свою скорость неизменной, если на них не действуют другие тела. Получается очень неудобоваримо, малопонятно и напоминает комичную ситуацию, когда на вопрос: “Где это «тут»?” отвечают: “Это здесь”, а на следующий логичный вопрос: “А где это «здесь»?” отвечают: “Это тут”. Формулировка самого Ньютона такова: «Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние». Однако на практике этот закон выполняется не всегда. Убедиться в этом можно элементарно. Когда человек стоит, не держась за поручни, в движущемся автобусе, и автобус резко тормозит, то человек начинает двигаться вперед относительно автобуса, хотя его не понуждает к этому ни одна видимая сила. То есть, относительно автобуса первый закон Ньютона в изначальной формулировке не выполняется. Очевидно, что он нуждается в уточнении. Уточнением и является введение инерциальных систем отсчета. То есть, таких систем отсчета, в которых первый закон Ньютона выполняется. Это не совсем понятно, поэтому попробуем перевести все это на человеческий язык. Инерциальные и неинерциальные системы отсчетаСвойство инерции любого тела таково, что до тех пор, пока тело остается изолированным от других тел, оно будет сохранять свое состояние покоя или равномерного прямолинейного движения. На практике это означает, что если в нашем примере за систему отсчета принять не автобус, а какую-то звезду на окраине Галактики, то первый закон Ньютона будет абсолютно точно выполняться для беспечного пассажира, не держащегося за поручни. При торможении автобуса он будет продолжать свое равномерное движение, пока на него не подействуют другие тела. Вот такие системы отсчета, которые никак не связаны с рассматриваемым телом, и которые никак не влияют на инертность тела, называются инерциальными. Для таких систем отсчета первый закон Ньютона в его исходной формулировке абсолютно справедлив. То есть закон можно сформулировать так: в системах отсчета, абсолютно никак не связанных с телом, скорость тела при отсутствии стороннего воздействия остается неизменной. В таком виде первый закон Ньютона легко доступен для понимания. Проблема заключается в том, что на практике очень сложно рассматривать движение конкретного тела относительно таких систем отсчета. Поэтому за такую систему отсчета условно часто принимают Землю, хотя она и связана с находящимися на ней телами и влияет на характеристики их движения. Но для многих расчетов такое приближение оказывается достаточным. Поэтому примерами инерциальных систем отсчета можно считать Землю для расположенных на ней тел, Солнечную систему для ее планет и так далее. Первый закон Ньютона не описывается какой-либо физической формулой, однако с помощью него выводятся другие понятия и определения. По сути, этот закон постулирует инертность тел. И таким образом выходит, что для инерциальных систем отсчета закон инерции и есть первый закон Ньютона. Еще примеры инерциальных систем и первого закона НьютонаТак, например, если тележка с шаром будет ехать сначала по ровной поверхности, с постоянной скоростью, а потом заедет на песчаную поверхность, то шар внутри тележки начнет ускоренное движение, хотя никакие силы на него не действуют (на самом деле, действуют, но их сумма равна нулю). Происходит это от того, что система отсчета (в данном случае, тележка) в момент попадания на песчаную поверхность, становится неинерциальной, то есть перестает двигаться с постоянной скоростью. Первый Закон Ньютона вносит важное разграничение между инерциальными и неинерциальными системами отсчета. Также важным следствием этого закона является тот факт, что ускорение, в некотором смысле, важнее скорости тела. Поскольку движение с постоянной скоростью по прямой линии суть нахождение в состоянии покоя. Тогда как движение с ускорением явно свидетельствуют о том, что либо сумма сил, приложенных к телу, не равно нулю, либо сама система отсчета, в которой находится тело, является неинерциальной, то есть движется с ускорением. Причем ускорение может быть как положительным (тело ускоряется), так и отрицательным (тело замедляется).
Второй закон Ньютона связывает вместе три, на первый взгляд, совершенно не связанные друг с другом величины: ускорение, массу и силу. Элементарный опыт по второму закону НьютонаНачнем с практической части. Нагрузите чем-нибудь две сумки или два пакета. Один чуть-чуть, а второй очень сильно. Только пакеты берите покрепче. А теперь примерно с одинаковой силой по очереди резко поднимите оба пакета вверх. Вы увидите, что легкий пакет практически взлетит, а вот тяжелый перемещаться будет намного медленнее. А теперь другой опыт положите на землю футбольный мячик и пните его пару раз. Один раз легонько, а второй раз со всей силы. Понаблюдайте, как изменится скорость мяча после пинка. В первом случае он потихоньку откатится на небольшое расстояние, во втором улетит далеко и на весьма приличной скорости. Ну вот и все, с практической частью закончили. Теперь немного порассуждаем. Действие равнодействующей силыМы знаем, что скорость тела изменяется под действием приложенной к нему силы. То есть, фактически, все случаи приложения различных сил в конкретный момент времени можно свести к действию одной равнодействующей силы. Таким образом, чтобы найти, как изменилась скорость тела, нам надо знать, какая сила действует на тело. Какое ускорение получает тело?В зависимости от величины и направления силы тело получит то или иное ускорение. Это четко видно в опыте с мячом. Когда мы подействовали на тело небольшой силой, мяч ускорился не очень сильно. Когда же сила воздействия увеличилась, то мяч приобрел гораздо большее ускорение. То есть, ускорение связано с приложенной силой прямо пропорционально. Чем больше сила воздействия, тем большее ускорение приобретает тело. От чего еще зависит ускорение, полученное телом в результате воздействия на него? Вспомним первую часть нашего опыта. То есть, второй вывод это то, что масса тела напрямую связана с ускорением, приобретаемым телом в результате воздействия силы. При этом, масса тела обратно пропорциональна полученному ускорению. Чем больше масса, тем меньше будет величина ускорения. Второй Закон Ньютона: формула и определениеИсходя из всего вышесказанного, приходим к тому, что можно записать второй закон Ньютона в виде следующей формулы: a =F / m , где a ускорение, F сила воздействия, m масса тела. Соответственно, второму закону Ньютона можно дать такое определение: ускорение, приобретаемое телом в результате воздействия на него, прямо пропорционально силе или равнодействующей сил этого воздействия и обратно пропорционально массе тела.
В первом законе Ньютона говорится о поведении тела, изолированного от воздействия других тел. Второй закон говорит о прямо противоположной ситуации. В нем рассматриваются случаи, когда тело или несколько тел воздействуют на данное. Оба эти закона описывают поведение одного конкретного тела. Но во взаимодействии всегда участвуют минимум два тела. Что будет происходить с обоими этими телами? Как описать их взаимодействие? Анализом этой ситуации и занялся Ньютон после формулировки своих первых двух законов. Займемся и мы такими же изысканиями. Взаимодействие двух телМы знаем, что при взаимодействии воздействуют друг на друга оба тела. Не бывает такого, чтобы одно тело толкнуло другое, а второе в ответ никак не отреагировало бы. Такое может происходить среди по-разному воспитанных людей, но никак не в природе. Мы знаем, что если мы пинаем мяч, то мяч в ответ пинает нас. Другое дело, что мяч имеет намного меньшую массу, чем тело человека, и потому его воздействие практически не ощутимо. Однако, если вы попробуете пнуть тяжелый железный мяч, то живо ощутите это ответное воздействие. Фактически, мы каждый день по многу раз пинаем очень и очень тяжелый мяч нашу планету. Мы толкаем ее каждым своим шагом, только при этом отлетает не она, а мы. А все потому, что планета в миллионы раз превосходит нас по массе. Соотношение сил во взаимодействии между теламиТак что из этих рассуждений видно, что при взаимодействии двух тел, не только первое действует на второе с некоторой силой, но и второе в ответ действует на первое также с некоторой силой. Возникает вопрос: а как соотносятся эти силы? Какая из них больше, какая меньше? Для этого необходимо проделать некоторые измерения. Потребуются два динамометра, но в домашних условиях их вполне могу заменить два безмена. Они измеряют вес, а вес это тоже сила, только выраженная в единицах массы в случае безмена. Поэтому, если у вас есть два безмена, то проделайте следующее. Один из них оденьте колечком на что-то неподвижное, например, на гвоздь в стене, а второй соедините с первым крючками. И хотя мы тянем только за один из них, окажется, что показания обоих, как на очной ставке, будут совпадать. Получается, что сила, с которой мы воздействуем вторым безменом на первый, равна силе, с которой первый безмен воздействует на второй. Третий закон Ньютона: определение и формулаСила действия равна силе противодействия. В этом и состоит суть третьего закона Ньютона. Определение его таково: силы, с которыми два тела действуют друг на друга, равны по величине и противоположны по направлению. Третий закон Ньютона можно записать в виде формулы: F_1 = – F_2, Где F_1 и F_2 силы действия друг на друга соответственно первого и второго тела. Справедливость третьего закона Ньютона была подтверждена многочисленными экспериментами. Этот закон справедлив как для случая, когда одно тело тянет другое, так и для случая, когда тела отталкиваются.
Как вы думаете, одновременно ли долетят до земли, сброшенные с крыши перо, пластиковая бутылка и монета? Можно проделать такой опыт и убедиться, что монета приземлится первой, бутылка второй, а перо долго будет болтаться в воздухе и может вообще не долететь до земли, если его подхватит и унесет внезапный ветерок. Так ли свободно свободное падение тел?Соответственно, делаем вывод, что свободное падение тел не подчиняется какому-либо одному правилу, и все предметы падают на землю по-своему. Тут бы как говорится, и сказке конец, но некоторые физики на этом не успокоились и предположили, что на свободное падение тел может оказывать влияние сила сопротивления воздуха и, соответственно, такие результаты эксперимента нельзя считать окончательными. Они взяли длинную стеклянную трубку и поместили в нее перо, дробинку, деревянную пробку и монету. Потом они закупорили трубку, откачали из нее воздух и перевернули. где v конечная скорость, v_0 начальная скорость, s перемещение, t время, g ускорение свободного падения. Вывод, что свободное падение любых тел происходит одинаково, на первый взгляд кажется нелепым с точки зрения повседневного опыта. Но на самом деле все правильно и логично. Просто, незначительная на первый взгляд величина сопротивления воздуха для многих падающих тел оказывается довольно ощутимой, а потому очень сильно замедляет их падение.
Как нам уже известно, сила тяжести действует на все тела, которые находятся на поверхности Земли и вблизи неё. При этом не важно, находятся ли они в состоянии покоя или совершают движение. Если некоторое тело будет свободно падать на Землю, то при этом оно будет совершать равноускоренное движение, причем скорость будет возрастать постоянно, так как вектор скорости и вектор ускорения свободного падения будут сонаправлены между собой. Суть движения вертикально вверхЕсли же подбросить некоторое тело вертикально вверх, и при этом считать что сопротивление воздуха отсутствует, то можно считать что оно тоже совершает равноускоренное движение, с ускорением свободного падения, которое вызвано силой тяжести. Через некоторое время наступит момент, когда скорость станет равняться нулю. В этот момент тело достигнет своей максимальной высоты и на какой-то момент остановится. Очевидно, что, чем большую начальную скорость мы придадим телу, тем на большую высоту оно поднимется к моменту остановки.
Как решать задачиКогда вы столкнетесь с задачами на движение тела вверх, при котором не учитывается сопротивление воздуха и другие силы, а считается, что на тело действует только сила тяжести, то так как движение равноускоренное, то можно применять те же самые формулы, что и при прямолинейном равноускоренном движении с некоторой начальной скорость V0. Необходимо также учитывать, что при движении вверх вектор ускорения свободного падения направлен вниз, а вектор скорости вверх, то есть они разнонаправлены, а следовательно, их проекции будут иметь разные знаки. Например, если Ось Ох направить вверх, то проекция вектора скорости при движении вверх, будет положительна, а проекция ускорения свободного падения отрицательна. Это надо учитывать, подставляя значения в формулы, иначе получится совершенно неверный результат.
Все мы ходим по Земле потому, что она нас притягивает. Если бы Земля не притягивала все находящиеся на ее поверхности тела, то мы, оттолкнувшись от нее, улетели бы в космос. Но этого не происходит, и всем известно о существовании земного притяжения. Притягиваем ли мы Землю? Притягивает Луна!А притягиваем ли мы сами к себе Землю? Смешной вопрос, правда? Но давайте разберемся. Вы знаете, что такое приливы и отливы в морях и океанах? Каждый день вода уходит от берегов, неизвестно где шляется несколько часов, а потом, как ни в чем не бывало, возвращается обратно. Так вот вода в это время находится не неизвестно где, а примерно посредине океана. Там образуется что-то наподобие горы из воды. Невероятно, правда? Вода, которая имеет свойство растекаться, сама не просто стекается, а еще и образует горы. И в этих горах сосредоточена огромная масса воды. Просто прикиньте весь объем воды, который отходит от берегов во время отливов, и вы поймете, что речь идет о гигантских количествах. Но раз такое происходит, должна же быть какая-то причина. И причина есть. Причина кроется в том, что эту воду притягивает к себе Луна. Вращаясь вокруг Земли, Луна проходит над океанами и притягивает к себе океанические воды. Луна вращается вокруг Земли, потому что она притягивается Землей. Но, выходит, что она и сама при этом притягивает к себе Землю. Земля, правда, для нее великовата, но ее влияние оказывается достаточным для перемещения воды в океанах. Сила и закон всемирного тяготения: понятие и формулаА теперь пойдем дальше и подумаем: если два громадных тела, находясь неподалеку, оба притягивают друг друга, не логично ли предположить, что и тела поменьше тоже будут притягивать друг друга? Просто они намного меньше и сила их притяжения будет маленькой? Оказывается, что такое предположение абсолютно верно. Возвращаясь к нашему исходному вопросу: «притягиваем ли мы Землю?», мы можем с уверенностью ответить: «да». Согласно третьему закону Ньютона мы притягиваем Землю ровно с такой же силой, с какой Земля притягивает нас. Силу эту можно рассчитать из закона всемирного тяготения. А согласно второму закону Ньютона воздействие тел друг на друга какой-либо силой выражается в виде придаваемого ими друг другу ускорения. Но придаваемое ускорение зависит от массы тела. Масса Земли велика, и она придает нам ускорение свободного падения. А наша масса ничтожно мала по сравнению с Землей, и поэтому ускорение, которое мы придаем Земле, практически равно нулю. Именно поэтому мы притягиваемся к Земле и ходим по ней, а не наоборот.
Одним из частных случаев всемирного тяготения является тот факт, что все тела притягиваются к Земле. Для нас, жителей планеты Земля, сила тяжести имеет огромное значение. Сила, с которой тело некоторой массы m будет притягиваться к Земле, согласно закону всемирного тяготения будет вычисляться по следующей формуле: Где Мз – масса земли, Но значение этой силы будет отличаться от значения силы тяжести которую мы вычисляем по формуле Fт =m*g. Отсюда можно выразить значение g. Как видите масса тела сократилась, а следовательно масса тела никак не влияет на ускорение свободного падения тел, которые находятся на Земле или вблизи её поверхности. А будет зависеть только от радиуса Земли, а точнее от расстояния от центра Земли, до центра данного тела массы m. Если мы например поднимем тело на некоторую высоту h, то расстояние между центрами Земли и тела увеличится, а следовательно должно измениться ускорение свободного падения тела. Так как расстояние в таком случае будет (Rз+h), то ускорение свободного падения на высоте h от поверхности Земли можно вычислить по формуле: Чем больше мы поднимем тело над Землей, тем будет меньше ускорение свободного падения. Следовательно, будет уменьшатся и сила тяжести которая действует на это тело. Чаще всего этим увеличением пренебрегают, так как расстояние, на которое поднимается тело от поверхности Земли, по сравнению с радиусом Земли пренебрежимо мало. Например, если человек массой 80 кг поднялся на гору высотой 3 км, то действующая на него сила тяжести уменишилась всего на 0. Применение формулы для других небесных телФормула, которую мы записали выше, подходит также для вычисления ускорения свободного падения на любых небесных объектах. То есть вместо радиуса и массы Земли необходимо подставить радиус и массу данного небесного объекта.
Мы знаем, что все тела притягиваются друг к другу. В частности, Луна, например, притягивается к Земле. Но возникает вопрос: если Луна притягивается к Земле, почему она вращается вокруг нее, а не падает на Землю? Для того чтобы ответить на этот вопрос, необходимо рассмотреть виды движения тел. Мы уже знаем, что движение может быть равномерным и неравномерным, но существуют и другие характеристики движения. В частности, в зависимости от направления различают прямолинейное и криволинейное движение. Прямолинейное движениеИзвестно, что тело двигается под действием приложенной к нему силы. Привязывает шнур одним концом к опоре. На другом конце шнура закрепляем наш предмет. Теперь, если мы оттянем наш предмет на некоторое расстояние, а потом отпустим, то увидим, как он начнет двигаться в направлении опоры. Его движение обусловлено силой упругости шнура. Именно так Земля притягивает все тела на ее поверхности, а также летящие из космоса метеориты. Только вместо силы упругости выступает сила притяжения. А теперь возьмем наш предмет на резинке и толкнем его не в направлении к/от опоры, а вдоль нее. Если бы предмет не был закреплен, он бы просто улетел в сторону. Но так как его держит шнур, то шарик, двигаясь в сторону, слегка растягивает шнур, тот тянет его обратно, и шарик чуть меняет свое направление в сторону опоры. Криволинейное движение по окружностиТак происходит в каждый момент времени, в итоге шарик движется не по первоначальной траектории, но и не прямолинейно к опоре. Шарик будет двигаться вокруг опоры по окружности. Траектория его движения будет криволинейной. Именно так вокруг Земли двигается Луна, не падая на нее. Именно так притяжение Земли захватывает метеориты, которые летят близко от Земли, но не прямо на нее. Эти метеориты становятся спутниками Земли. При этом от того, каким был их первоначальный угол движения по отношению к Земле, зависит, как долго они пробудут на орбите. Если их движение было перпендикулярно Земле, то они могут находиться на орбите бесконечно долго. Если же угол был меньше 90˚, то они будут двигаться по снижающейся спирали, и постепенно все-таки упадут на землю. Движение по окружности с постоянной по модулю скоростьюЕще один момент, который следует отметить, это то, что скорость криволинейного движения по окружности меняется по направлению, но одинакова по значению. Так как направление движения меняется, значит, движение происходит с ускорением. А так как оно меняется одинаково в каждый момент времени, следовательно, движение будет равноускоренным. А сила притяжения является силой, которая обусловливает постоянное ускорение. Луна двигается вокруг Земли именно благодаря этому, но если вдруг когда-либо движение Луны изменится, например, в нее врежется очень крупный метеорит, то она вполне может сойти со своей орбиты и упасть на Землю. Нам остается лишь надеяться, что этот момент не наступит никогда.
Вы когда-нибудь соревновались, кто дальше кинет камень или снежок? Все мальчишки наверняка проходили через это. И все знают, что чтобы камень пролетел как можно дальше, надо кинуть его как можно сильнее. То есть нужно придать ему как можно большую скорость. Сила человеческой руки ограничена, и камень мы можем кинуть относительно недалеко. Бексонечно долгое вращение вокруг ЗемлиЕсли же пойти дальше и предположить, что мы можем придать телу намного большую скорость? Такую, что дуга, которую тело опишет, будет уже не упираться в землю, а проходить на некотором расстоянии вокруг всей Земли? Тогда получится, что мы получим тело, способное бесконечно долго вращаться вокруг Земли. Единственное, что будет мешать нам это сопротивление воздуха. Значит надо избавиться от него. Избавиться от сопротивления воздуха мы можем на большой высоте. На высоте свыше трехсот километров воздуха уже практически нет. Именно начиная с такой высоты, и запускают искусственные спутники Земли. Спутники вращаются вокруг Земли по различным орбитам, но все они не падают на Землю. Движение спутника – пример свободного паденияЭто происходит потому, что запущены они были со скоростью, достаточной для того, чтобы преодолеть земное притяжение. Происходит оно с ускорением, как и положено свободно падающему телу, только ускорение это не увеличивает скорость тела по модулю, а изменяет по направлению. Поэтому спутники и движутся по орбите. Первая и вторая космическая скоростьСкорость, необходимая для того, чтобы тело начало вращаться по орбите вокруг Земли не падая, называется первой космической скоростью. Она составляет от 7,9 км/с. Чем больше высота тела над землей, тем величина этой скорости меньше. На высоте, например, 500 км эта скорость составляет уже 7,6 км/с. Это объясняется тем, что гравитационные силы уменьшаются с увеличением расстояния между телами. Первой космической скоростью обусловлено движение искусственных спутников земли. А есть ли такая скорость, которая позволит совсем вырваться из оков земного притяжения? Такая скорость есть и называется она второй космической скоростью.
Проделаем несколько несложных преобразований с формулами. По второму закону Ньютона силу можно найти: F=m*a. Ускорение находится следующим образом: a=v⁄t . Таким образом получаем: F=m*v/t. Определение импульса тела: формулаВыходит, что сила характеризуется изменением произведения массы на скорость во времени. Если обозначить это произведение некой величиной, то мы получим изменение этой величины во времени как характеристику силы. Эту величину назвали импульсом тела. Импульс тела выражается формулой: p=m*v , где p импульс тела, m масса, v скорость. Импульс это векторная величина, при этом его направление всегда совпадает с направлением скорости. Что же такое импульс тела: как понять?Попробуем по-простому, «на пальцах» разобраться, что такое импульс тела. Если тело покоится, то его импульс равен нулю. Логично. Если скорость тела изменяется, то у тела появляется некий импульс, который характеризует величину приложенной к нему силы. Если воздействие на тело отсутствует, но оно движется с некоторой скоростью, то есть имеет некий импульс, то его импульс означает, какое воздействие способно оказать данное тело при взаимодействии с другим телом. В формулу импульса входит масса тела и его скорость. То есть чем большей массой и/или скоростью обладает тело, тем большее воздействие оно может оказать. Это понятно и из жизненного опыта. Чтобы сдвинуть тело небольшой массы, нужна небольшая сила. Чем больше масса тела, тем большее придется приложить усилие. То же самое касается и скорости, которую сообщают телу. В случае же воздействия самого тела на другое, импульс также показывает величину, с которой тело способно действовать на другие тела. Импульс при взаимодействии телВозникает еще один вопрос: что произойдет с импульсом тела при его взаимодействии с другим телом? Масса тела измениться не может, если оно остается целым, а вот скорость может измениться запросто. При этом скорость тела изменится в зависимости от его массы. В самом деле, понятно, что при столкновении тел с очень разными массами, скорость их изменится по-разному. Если летящий на большой скорости футбольный мяч врежется в неготового к этому человека, например зрителя, то зритель может упасть, то есть приобретет некоторую небольшую скорость, но точно не полетит как мячик. А все потому, что масса зрителя намного больше массы мяча. Но при этом сохранится неизменным общий импульс этих двух тел. Закон сохранения импульса: формулаВ этом и заключается закон сохранения импульса: при взаимодействии двух тел их общий импульс остается неизменным. Закон сохранения импульса действует только в замкнутой системе, то есть в такой системе, в которой нет воздействия внешних сил или их суммарное действие равно нулю. В реальности практически всегда на систему тел оказывается стороннее воздействие, но общий импульс, как и энергия, не пропадает в никуда и не возникает из ниоткуда, он распределяется между всеми участниками взаимодействия. Закон сохранения импульса для двух тел в виде формулы будет выглядеть следующим образом: (p_1′ ) +(p_2′ ) = (p_1 ) + (p_2 ), где левая часть уравнения это сумма импульсов тел после взаимодействия, а правая часть после взаимодействия. Уравнение говорит нам, что общий импульс (сумма импульсов) остается неизменнным.
Реактивное движение – это все же движение. А мы знаем, что чтобы происходило движение, необходимо воздействие некоторой силы. Тело либо само должно оттолкнуться от чего-нибудь, либо стороннее тело должно толкнуть данное. Это хорошо известно и понятно нам из жизненного опыта. От чего оттолкнуться в космосе?У поверхности Земли можно оттолкнуться от поверхности либо от находящихся на ней предметов. Человек создал двигатели на основе пропеллеров, которые во много раз увеличивают площадь контакта со средой за счет вращения и позволяют отталкиваться от воды и воздуха. А как быть в случае безвоздушного пространства? От чего отталкиваться в космосе? Там нет воздуха, там ничего нет. Как осуществлять полеты в космосе? Вот тут-то и приходит на помощь закон сохранения импульса и принцип реактивного движения. Разберем подробнее. Импульс и принцип реактивного движенияИмпульс это произведение массы тела на его скорость. Когда тело неподвижно, его скорость равна нулю. Однако тело обладает некоторой массой. При отсутствии сторонних воздействий, если часть массы отделится от тела с некоторой скоростью, то по закону сохранения импульса, остальная часть тела тоже должна приобрести некоторую скорость, чтобы суммарный импульс остался по-прежнему равным нулю. Причем скорость оставшейся основной части тела будет зависеть от того, с какой скоростью отделится меньшая часть. Чем эта скорость будет выше, тем выше будет и скорость основного тела. Это понятно, если вспомнить поведение тел на льду или в воде. Если два человека будут находиться рядом, а потом один из них толкнет другого, то он не только придаст тому ускорение, но и сам отлетит назад. И чем сильнее он толкнет кого-либо, тем с большей скоростью отлетит сам. Наверняка, вам приходилось бывать в подобной ситуации, и вы можете представить себе, как это происходит. Так вот, именно на этом и основано реактивное движение. Ракеты, в которых реализован этот принцип, выбрасывают некоторую часть своей массы на большой скорости, вследствие чего сами приобретают некоторое ускорение в противоположном направлении. Потоки раскаленных газов, возникающие в результате сгорания топлива, выбрасываются через узкие сопла для придания им максимально большой скорости. Принцип полета ракетыВ ракетах применяют многоступенчатую систему. Во время полета нижняя ступень, израсходовав весь свой запас топлива, отделяется от ракеты, чтобы уменьшить ее общую массу и облегчить полет. Количество ступеней уменьшается, пока не остается рабочая часть в виде спутника или иного космического аппарата. Топливо рассчитывают таким образом, чтобы его хватило как раз для выхода на орбиту. При посадках на космические тела рассчитывают количество топлива для посадки и на обратный путь, если он запланирован. |
Формула для вычисления времени полного испарения аэрозольных капель с учётом коэффициентов испарения и поверхностного натяжения Текст научной статьи по специальности «Физика»
УДК 533. 72
72
DOI: 10.18384-2310-7251-2017-3-68-75
ФОРМУЛА ДЛЯ ВЫЧИСЛЕНИЯ ВРЕМЕНИ ПОЛНОГО ИСПАРЕНИЯ АЭРОЗОЛЬНЫХ КАПЕЛЬ С УЧЁТОМ КОЭФФИЦИЕНТОВ ИСПАРЕНИЯ И ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ
Кузьмин МХ.1, Хасанов А.С.2
1 Московский государственный областной университет 105005, г. Москва, ул. Радио, д. 10А, Российская Федерация
2 Российский экономический университет им. Г.В. Плеханова 117997, г. Москва, Стремянный пер., д. 36, Российская Федерация
Аннотация. Авторами статьи получена приближённая формула для времени полного испарения аэрозольных капель воды в воздушную среду в виде функции от их начальных радиусов. Для мелких и крупных капель формула выведена на основе модели нестационарного процесса испарения, учитывающей коэффициент испарения, коэффициент поверхностного натяжения и теплоту фазового перехода вещества капли. Формула для капель с промежуточными размерами выведена на основе формул для крупных и мелких капель с использованием непрерывности, гладкости и монотонности времени полного испарения капель как функции от их начальных радиусов. Приведены соответствующие графики.
Формула для капель с промежуточными размерами выведена на основе формул для крупных и мелких капель с использованием непрерывности, гладкости и монотонности времени полного испарения капель как функции от их начальных радиусов. Приведены соответствующие графики.
Ключевые слова: аэрозольные капли, время полного испарения, нестационарный процесс испарения.
FORMULA FOR CALCULATING THE COMPLETE EVAPORATION TIME OF AEROSOL DROPS WITH ALLOWANCE FOR THE EVAPORATION AND SURFACE TENSION COEFFICIENTS
M. Kuzmin\ A. Khasanov2
1 Moscow Region State University
ul Radio 10A, 105005 Moscow, Russian Federation
2 Plekhanov Russian University of Economics
Stremyannyi pereulok 36,117997 Moscow, Russian Federation Abstract. An approximate formula for the time of complete evaporation of aerosol water drops into the atmosphere is obtained as a function of their initial radii. For small and large drops the formula is derived on the basis of the model of the unsteady evaporation process, taking into account the evaporation coefficient, the coefficient of surface tension and the specific heat of the phase transition. The formula for drops of intermediate size is obtained on the basis of the formulas for large and small drops with the use of continuity, smoothness and monotonicity
An approximate formula for the time of complete evaporation of aerosol water drops into the atmosphere is obtained as a function of their initial radii. For small and large drops the formula is derived on the basis of the model of the unsteady evaporation process, taking into account the evaporation coefficient, the coefficient of surface tension and the specific heat of the phase transition. The formula for drops of intermediate size is obtained on the basis of the formulas for large and small drops with the use of continuity, smoothness and monotonicity
© Кузьмин М.К., Хасанов А.С., 2017.
of the complete evaporation time of drops as a function of their initial radii. The corresponding graphs are presented.
Key words: aerosol drops, complete evaporation time, unsteady evaporation process.
Введение
Процесс испарения аэрозольной капли в атмосфере зависит от многих факторов. Этот процесс, в том числе и задача о времени существования (полного испарения) капель, рассматривался в ряде работ. Применялись как математические модели этого процесса [4; 6], так и экспериментальные [5] и численные [3] методы. В работе [7] рассмотрена модель нестационарного процесса испарения аэрозольной капли, взвешенной в однокомпонентном газе, с учётом теплоты фазового перехода вещества капли, коэффициента испарения, коэффициента
Этот процесс, в том числе и задача о времени существования (полного испарения) капель, рассматривался в ряде работ. Применялись как математические модели этого процесса [4; 6], так и экспериментальные [5] и численные [3] методы. В работе [7] рассмотрена модель нестационарного процесса испарения аэрозольной капли, взвешенной в однокомпонентном газе, с учётом теплоты фазового перехода вещества капли, коэффициента испарения, коэффициента
1 dR
поверхностного натяжения и получена формула для скорости изменения —
dt
радиуса капли R = R(t), который в нестационарном процессе зависит от времени t. Заметим, что воздух приближенно можно рассматривать как однокомпонент-ный газ, так как он преимущественно состоит из азота. Целью данной работы является дальнейшее развитие результатов работы [7]. Перед записью формулы dR
для величины —, полученной в этой работе, введём обозначения. dt
Пусть pi и w1 – плотность и масса молекул вещества капли, ni и n2 – численная концентрация молекул первого компонента (пара) и второго компонента (газа) внешней парогазовой смеси, n = n1 + n2, к и pe – коэффициент теплопроводности и плотность парогазовой смеси. Величина D определяется по формуле D = nwiDi2/pe, где Di2 – коэффициент взаимной диффузии компонентов парогазовой смеси.
Поле температуры T в парогазовой смеси в сферической системе координат с началом в центре неподвижной капли является функцией двух переменных r и t: T = T(r, t), причём limT(r,t) = lim T(r,t) = To, где To – постоянная. Это верно и
для поля концентрации ci = n1/n первого компонента (пара) парогазовой смеси: Ci = Ci (r,t), limCi (r,t)= lim Ci (r,t) = cw,
где Cio – постоянная., к?с = с150кчу.
Тогда формулу для величины — из работы [7] можно записать в виде:
йг
йЯ
— = (т1/ pi ) (, Я), (1)
йг
где Г(г, Я) – функция, удовлетворяющая двум условиям:
Нт Г (, Я ) = 1, (2)
г н0 4 ‘
Нт Г (, Я ) = Б к/[ Б к+ау(к+к?с)Я ] • (3)
Точное выражение для функции Г(г, Я) нам не понадобится, так как целью данной работы является получение, основыванное на уравнении (1) и условиях (2) и (3), приближенной формулы для зависимости времени полного испарения т аэрозольной капли воды в воздушную среду от её начального радиуса Я0, т. е. функции т = т(Я0).
Формула для времени полного испарения малых капель
Оценки показывают, что при Я0 < Яь где Я1 = 10-7, для получения приближенной формулы т = т(Я0) функцию Я) в дифференциальном уравнении (1) можно заменить на её предельное выражение Нт Г (, Я) = 1 из формулы (2)
(время полного испарения таких капель является достаточно малой величиной). В результате получим дифференциальное уравнение — = епт1 / р, с начальным
йг
условием Я(0) = Я0. Так как в = аv(сlо -Сш), а с150 = С1$0 (1 + кс / Я), то это дифференциальное уравнение является дифференциальным уравнением с разделяющимися переменными. После разделения переменных, интегрирования обеих частей уравнения от 0 до т и учёта условий Я(0) = Я0, Я(т) = 0, получим формулу:
т = ф! (х ) = и [ х — 1п (1 + 1х)/1 ], (4)
где и = р,Я1 / [ауит! ((0 — С10 )], х = Я0 / Яь I = ЬЯ1 / кс, Ь = 1 — сю / сш. В формуле (4) х принадлежит отрезку 0 < х < 1, так как Я0 < Я1.
Формула для времени полного испарения крупных капель
Время полного испарения крупной капли является величиной на порядок большей по сравнению со временем испарения малых капель. Поэтому для вывода приближенной формулы для капель, радиусы которых на порядок больше радиуса Я1 = 10-7 м, т. е. в случае Я0 > Я2, где Я2 = 10Я1 = 10-6, функ-
цию F(t, R) в дифференциальном уравнении (1) заменим на её предельное выражение lim F(t,R) = Dk/|dK+av(K+K?a)RJ из формулы (3). Так как
Kqa = C1s0kqу = C1s0 (l + ka /R)kqY, то в результате также получим дифференциальное уравнение с разделяющимися переменными. После разделения переменных интегрируем обе части уравнения также от 0 до т, считая, что вклад той части процесса испарения, когда радиус капли становится малым, в рассматриваемом случае не является существенным. – v f Л
RiD к
+
Dк K0fca av b
Ro +—ln
vbRo + yj
(5)
где Ко = к+кяYClsо, Ко = к+кяYClo•
При Ro > R2 оценки показывают, что в правой части формулы (5) от множиВ к к0ка Вк
теля—можно оставить только величину-, так как вклад величины
ау Ь ау
Koka л , ka 1 – мал, а от множителя R0 +–ln
b b
ybRo + kay
для приближенных вычислений
можно оставить только первое слагаемое R0.В к
Перейдя в формуле (6) к переменной х = R0/R1, получим формулу:
Х = ф2 (х ) = и (х + 0,5их2), (7)
где и = ко/(Вк). В формуле (7) безразмерный радиус х принадлежит промежутку 10 < х < +<х>, так как R0 > R2•
Формула для времени полного испарения капель с промежуточными радиусами
Перейдём к выводу формулы для времени полного испарения т в случае, когда радиус капли принадлежит промежутку Rl < Ro < R2, т. е. 1 < х < 10. Формулу для зависимости времени полного испарения аэрозольной капли т от её начального радиуса R0 будем искать в классе гладких возрастающих функций. Если перейти к безразмерному радиусу х = R0/R1, то функция т = ф1(х) на промежутке 0 < х < 1 и функция т = ф2(х) на промежутке 10 < х < +<х> являются гладкими возрастающими функциями. Построим гладкую возрастающую функцию т = фз(х), определённую на промежутке 1 < х < 10. Эту функцию построим на основе найденных формул (4) и (7). Зависимость т = ф3(х) на отрезке 1 < х < 10 будем искать в виде:
т = ф3 (x) = U d0 (x-l)3 + d1 (x-l)2 + d2 (x-1) + d3
(8)
где й0, й1, й2, й3 – неизвестные коэффициенты, которые определяются из двух условий непрерывности фз(1) = ф1(1), фз(10) = ф2(10) и двух условий гладкости ф3 (1) = ф1 (1), ф3 (10) = ф2 (10) искомой зависимости т от х на всем промежутке
0 < х < +<х>. Легко получить следующие формулы для неизвестных коэффициентов:
1
729
-10м —9—ln (I +1)
1 +1 l У ‘
(9)
1
27
6 1
20м+-+-ln (1 +1)
1 +1 l У ‘
(10)
d2 =
1+l
h = 1 – jln (1 +1).
(11)
(12)
Функция т = т(х), определенная на промежутке 0 < х < +<х>, должна быть не только непрерывной и гладкой, но и возрастающей. Функция т = фз(х) возрастает на промежутке 1 < х < 10. Действительно, найдём производную функции т = фз(х):
2
т’ = фз (x ) = U[3do (x -1) + 2d1 (x -1) + d2].
(13)
Правая часть формулы (13) является квадратным трехчленом. Легко доказать его положительность на промежутке 1 < х < 10. Следовательно, функция т = ф3(х) возрастает на этом промежутке.
Заключение
Построенная нами приближенная зависимость времени полного испарения т аэрозольной капли в воздушную среду от безразмерного начального радиуса капли х = Я0/Я1 имеет вид:
т =
U [ x – ln (1 + lx)/1 ], если 0 < x < 1,
U
d0 (x -1)3 +d1 (x -1)2 +d2 (x -1) + d3
, если 1 < x <10,
U(x + 0,5mx2), если 10 < x <+^.
(14)
Так как коэффициенты й0, й1, й2, йз зависят только от величин I и и, то для вычислений по формуле (14) достаточно знать три параметра:
и = р,Я1 /[ауит! ((0 — сю)], I = ЬЯ1 /кс, и = к0ауЯ1/(Бк). Рассмотрим про-
l
цесс нестационарного испарения одиночных капель воды в воздушную среду 50% влажности при двух значениях температуры Т = 293 К и Т = 323 К, когда давление среды Р = 0,1 МПа. При этом, основываясь на данных, приведённых в работе [1] для коэффициента испарения воды, полагаем, что а = 0,034 при Т = 293 К и а = 0,026 при Т = 323 К. Для других величин используем значения, приведённые в работе [2]. При Т = 293 К легко найти значения перечисленных выше трёх параметров: и = 2,3212 • 103, I = 4,6266 • 101, и = 6,8112 • 10-2. При Т=323 К получим следующие значения: и = 5,9500 • 104, I = 5,0499 • 101, и = 1,4223 • 10-1. На основе формулы (14) можно построить графики зависимости т от х при Т = 293 К и Т = 323 К (рис. 1).
1,2 1
0,8 0,6 0,4 0,2
x = ßo/(lO 7м)
0 1 20 1 40 1 60 -1 80
Рис. 1. График зависимости времени полного испарения т капли воды в воздушную среду от безразмерного начального радиуса капли x = Яо/(107 м), где Ro – начальный радиус капли
ЛИТЕРАТУРА
1. Амелин А.Г. Теоретические основы образования тумана при конденсации пара. Изд. 3-е, доп. и перераб. М.: Химия. 1972. 304 с.
2. Варгафтик Н.Б. Справочник по теплофизическим свойствам газов и жидкостей. 2-е изд., доп. и перераб. М.: Наука. 1972. 720 с.
3. Высокоморная О.В., Кузнецов Г.В., Стрижак П.А. Испарение капель воды в высокотемпературной газовой среде // Инженерно-физический журнал. Т. 89 2016. № 1. С. 133-142.
4. Высокоморная О.В., Кузнецов Г.В., Стрижак П.А. Прогностическое определение интегральных характеристик испарения капель воды в газовых средах с различной температурой // Инженерно-физический журнал. Т. 90. 2017. № 3. С. 648-657.
5. Захаревич А.В., Кузнецов Г.В., Стрижак П.А. Экспериментальное исследование изменения температуры в центре капли воды в процессе её испарения в разогретом воздухе // Инженерно-физический журнал. Т. 89. 2016. № 3. С. 537-541.
6. Кочурова Н.Н., Коротких О.П., Абдуллин Н.Г., Айрапетова Е.Р., Караев Р.Р., Petzold G. Влияние поверхностных явлений на испарение и конденсацию водных систем // Инженерно-физический журнал. Т. 89, 2016, № 1. С. 104-108.
7. Кузьмин М.К. Теория нестационарного процесса испарения сферической аэрозольной капли с учётом зависимости давления насыщенного пара от кривизны её поверхности // Вестник Московского государственного областного университета. Серия: Физика-математика. 2012. № 3. С. 39-49.
REFERENCES
1. Amelin A.G. Teoreticheskiye osnovy obrazovaniya tumana pri kondensatsii para [The theoretical basis for the formation of fog in the condensation of vapor]. Moscow, Chemistry Publ., 1972. 304 p.
2. Vargaftik N.B. Spravochnik po teplofizicheskim svoistvam gazov i zhidkostei [Handbook on thermophysical properties of gases and liquids]. Moscow, Nauka Publ., 1972. 720 p.
3. Vysokomornaya O.V., Kuznetsov G.V., Strizhak P.A. [Evaporation of water droplets in high temperature gas environment]. In: Inzhenerno-fizicheskii zhurnal [Journal of Engineering Physics and Thermophysics], vol. 89, 2016, no. 1, pp. 133-142.
4. Vysokomornaya O.V., Kuznetsov G.V., Strizhak P.A. [Prognostic determination of the integral characteristics of evaporation of water droplets in gaseous media at different temperatures]. In: Inzhenerno-fizicheskii zhurnal [Engineering and Physics Journal], vol. 90, 2017, no. 3, pp. 648-657.
5. Zakharevich A.V., Kuznetsov G.V., Strizhak P.A. [Experimental study of temperature change in the center of a water drop in the process of evaporation in a heated air]. In: Inzhenerno-fizicheskii zhurnal [Journal of Engineering Physics and Thermophysics], vol. 89, 2016, no. 3, pp. 537-541.
6. Kochurova N.N., Korotkikh O.P., Abdullin N.G., Airapetova E.R., Karaev R.R., Petzold G. [The influence of surface phenomena on the evaporation and condensation of water systems]. In: Inzhenerno-fizicheskii zhurnal [Journal of Engineering Physics and Thermophysics], vol. 89, 2016, no. 1, pp. 104-108.
7. Kuz’min M.K. [Theory of a nonstationary process of evaporation of a spherical aerosol droplet with allowance for the dependence of the vapor pressure on the curvature of its surface]. In: Vestnik Moskovskogo gosudarstvennogo oblastnogo universiteta. Seriya: Fizika-matematika [Bulletin of Moscow Region State University. Series: Physics and Mathematics], 2012, no. 3, pp. 39-49.
ИНФОРМАЦИЯ ОБ АВТОРАХ
Кузьмин Михаил Кузьмич – доктор физико-математических наук, профессор кафедры математического анализа и геометрии Московского государственного областного университета;
e-mail: [email protected]
Хасанов Анис Саляхович – доктор физико-математических наук, профессор кафедры высшей математики Российского экономического университета им. Г.В. Плеханова; e-mail: [email protected]
INFORMATION ABOUT THE AUTHORS
Mikhayil K. Kuzmin – Doctor in Physics and Mathematics, professor at the Department of Mathematical Analysis and Geometry, Moscow Region State University; e-mail: [email protected]
Anis S. Khasanov – Doctor in Physics and Mathematics, professor at the Department of Higher Mathematics, Plekhanov Russian University of Economics; e-mail: [email protected]
ПРАВИЛЬНАЯ ССЫЛКА НА СТАТЬЮ
Кузьмин М.К., Хасанов А.С. Формула для вычисления времени полного испарения аэрозольных капель с учётом коэффициентов испарения и поверхностного натяжения // Вестник Московского государственного областного университета. Серия: Физика-Математика. 2017. № 3. С. 68-75. БО!: 10.18384-2310-7251-2017-3-68-75
CORRECT REFERENCE TO THE ARTICLE
Kuzmin M.K., Khasanov A.S. Formula for Calculating the Complete Evaporation Time of Aerosol Drops with Allowance for the Evaporation and Surface Tension Coefficients. In: Bulletin of Moscow Region State University. Series: Physics and Mathematics, 2017, no. 3, pp. 68-75. DOI: 10.18384-2310-7251-2017-3-68-75
Физик построил математическую модель путешествий во времени | Futurist
28 апреля 2017, 11:45
Преподаватель физики и математики из Университета Британской Колумбии Бен Типпет опубликовал исследование, в котором объясняет возможность путешествий во времени с точки зрения математики.
«Люди думают, что путешествия во времени – фантастика. И мы привыкли так думать. Однако математически это возможно», – заявил Бен Типпет.
Опираясь на теорию Эйнштейна, исследователь вывел формулу, которая показывает теоретическую возможность путешествий во времени. Согласно формуле, разделять пространство на три измерения – неправильно. Типпет считает, что для путешествий во времени должны быть представлены четыре измерения. В них же связаны различные направления, как в пространственно-временном континууме.
Статья по теме
«Временные» кристаллы открыли новое состояние веществаМодель Типпета предполагает искривление времени и пространства и создание своеобразного круга, а не прямой линии. По его мнению, именно круговая траектория пространства и времени способна вернуть объект в прошлое.
Модель напоминает TARDIS из сериала «Доктор Кто». Исследователь описывает свою модель как пузырь пространственно-временной геометрии. Пузырь перемещается со скоростью, большей во много раз, чем скорость света, что позволяет ему двигаться назад во времени.
Исследователь полагает, что для искривления пространства и времени необходима «экзотическая материя». Однако ее пока нет.
Понравилась статья?
Поделись с друзьями!
Поделиться 0 Поделиться 0 Твитнуть 0Подпишись на еженедельную рассылку
Специальная теория относительности Эйнштейна
Специальная теория относительности объясняет, как пространство и время связаны между собой для объектов, которые движутся с постоянной скоростью по прямой. Один из самых известных его аспектов касается объектов, движущихся со скоростью света.
Проще говоря, когда объект приближается к скорости света, его масса становится бесконечной, и он не может двигаться быстрее света. Это космическое ограничение скорости было предметом многочисленных дискуссий в физике и даже в научной фантастике, поскольку люди думают о том, как путешествовать на огромные расстояния.
Специальная теория относительности была разработана Альбертом Эйнштейном в 1905 году и составляет часть основы современной физики. Закончив свою работу по специальной теории относительности, Эйнштейн десять лет размышлял о том, что произойдет, если ввести ускорение. Это легло в основу его общей теории относительности, опубликованной в 1915 году.
История
До Эйнштейна астрономы (по большей части) понимали Вселенную в терминах трех законов движения, представленных Исааком Ньютоном в 1686 году.Вот эти три закона:
(1) Объекты в движении (или в состоянии покоя) остаются в движении (или в состоянии покоя), если внешняя сила не вызывает изменения.
(2) Сила равна изменению количества движения за изменение времени. Для постоянной массы сила равна массе, умноженной на ускорение.
(3) Для каждого действия существует равная и противоположная реакция.
Но, согласно Британской энциклопедии, за десятилетия до появления Эйнштейна в теории были трещины. В 1865 году шотландский физик Джеймс Клерк Максвелл продемонстрировал, что свет – это волна, имеющая как электрические, так и магнитные компоненты, и установил скорость света (186 000 миль в секунду).Ученые предположили, что свет должен проходить через некую среду, которую они назвали эфиром. (Теперь мы знаем, что передающая среда не требуется, и что свет в космосе движется в вакууме.)
Двадцать лет спустя неожиданный результат поставил это под сомнение. Физик А.А. Майкельсон и химик Эдвард Морли (оба в то время американцы) вычислили, как движение Земли через этот «эфир» влияет на то, как измеряется скорость света, и обнаружили, что скорость света одинакова независимо от движения Земли.Это привело к дальнейшим размышлениям австрийского физика Эрнста Маха и французского математика Анри Пуанкаре о поведении света и его несоответствии с классической механикой.
Эйнштейн начал думать о поведении света, когда ему было всего 16 лет, в 1895 году. Он провел мысленный эксперимент, говорится в энциклопедии, где он ездил на одной световой волне и смотрел на другую световую волну, движущуюся параллельно ему.
Классическая физика должна сказать, что световая волна, на которую смотрел Эйнштейн, будет иметь относительную скорость, равную нулю, но это противоречило уравнениям Максвелла, которые показали, что свет всегда имеет одинаковую скорость: 186 000 миль в секунду.Другая проблема с относительными скоростями заключается в том, что они могут показать, что законы электромагнетизма меняются в зависимости от вашей точки обзора, что также противоречило классической физике (которая гласила, что законы физики одинаковы для всех). специальная теория относительности, которую он разбил на повседневный пример человека, стоящего у движущегося поезда и сравнивающего наблюдения с человеком внутри поезда. Он представил себе поезд, находящийся на пути между двумя деревьями.Если молния ударит по обоим деревьям одновременно из-за движения поезда, человек в поезде увидит, как молния поразит одно дерево раньше другого. Но человек рядом с трассой видел бы одновременные удары.
«Эйнштейн пришел к выводу, что одновременность относительна; события, одновременные для одного наблюдателя, могут не быть для другого», – говорится в энциклопедии. “Это привело его к парадоксальной идее о том, что время течет по-разному в зависимости от состояния движения, и к выводу, что расстояние также относительно.”
Известное уравнение
Работа Эйнштейна привела к некоторым поразительным результатам, которые сегодня все еще кажутся нелогичными на первый взгляд, несмотря на то, что его физика обычно вводится на уровне средней школы.
В 2015 году исполняется 100 лет со дня публикации книги Альберта Эйнштейна« Генерал ». Теория относительности. Изучите основы теории относительности Эйнштейна в нашей инфографике. (Изображение предоставлено Карлом Тейтом, художником по инфографике)Одно из самых известных уравнений в математике исходит из специальной теории относительности.Уравнение – E = mc 2 – означает «энергия равна массе, умноженной на квадрат скорости света». Это показывает, что энергия ( E ) и масса ( m ) взаимозаменяемы; это разные формы одного и того же. Если масса каким-то образом полностью преобразована в энергию, это также показывает, сколько энергии будет находиться внутри этой массы: довольно много. (Это уравнение является одной из демонстраций того, почему атомная бомба настолько мощна, если ее масса преобразована во взрыв.)
Это уравнение также показывает, что масса увеличивается со скоростью, что фактически ограничивает скорость движения объектов во Вселенной. Проще говоря, скорость света ( c ) – это самая высокая скорость, с которой объект может перемещаться в вакууме. По мере движения объекта его масса также увеличивается. Приближаясь к скорости света, масса настолько велика, что достигает бесконечности, и для ее перемещения потребуется бесконечная энергия, что ограничивает скорость движения объекта. Единственная причина, по которой свет движется с такой скоростью, заключается в том, что фотоны, квантовые частицы, из которых состоит свет, имеют нулевую массу.
Особая ситуация во вселенной малых, называемая «квантовой запутанностью», сбивает с толку, потому что она, кажется, включает квантовые частицы, взаимодействующие друг с другом на скоростях, превышающих скорость света. В частности, измерение свойства одной частицы может мгновенно сказать вам свойство другой частицы, независимо от того, как далеко они находятся. Об этом явлении написано много, но до сих пор оно не получило полного объяснения с точки зрения выводов Эйнштейна.
Другой странный вывод работы Эйнштейна связан с осознанием того, что время движется относительно наблюдателя.Движущийся объект испытывает замедление времени, что означает, что время движется медленнее, когда человек движется, чем когда он стоит на месте. Следовательно, движущийся человек стареет медленнее, чем человек в состоянии покоя. Так что да, когда астронавт Скотт Келли провел почти год на борту Международной космической станции в 2015-16 годах, его брат-близнец, астронавт Марк Келли, постарел немного быстрее, чем Скотт.
Это становится особенно очевидным при скоростях, приближающихся к скорости света. Представьте себе 15-летнего подростка, путешествующего в 99 лет.5 процентов скорости света в течение пяти лет (с точки зрения космонавта). По данным НАСА, когда 15-летний мальчик вернется на Землю, ему будет всего 20 лет. Его одноклассникам, однако, будет 65 лет.
Хотя на этот раз расширение времени звучит очень теоретически, у него есть и практическое применение. Если в вашем автомобиле есть приемник глобального позиционирования (GPS), он пытается найти сигналы как минимум от трех спутников для координации вашего местоположения. Спутники GPS отправляют синхронизированные радиосигналы, которые слушает приемник, триангулируя (или, точнее говоря, трилатерируя) свое положение на основе времени прохождения сигналов.Проблема в том, что атомные часы на GPS движутся и, следовательно, будут работать быстрее, чем атомные часы на Земле, что создает проблемы с синхронизацией. Таким образом, по словам Ричарда Погга, астронома из Университета штата Огайо, инженерам необходимо сделать часы на GPS медленнее.
Согласно Physics Central, часы в космосе тикают быстрее, потому что спутники GPS находятся над Землей и испытывают более слабую гравитацию. Таким образом, даже несмотря на то, что спутники GPS движутся и каждый день испытывают замедление на семь микросекунд из-за своего движения, в результате более слабой гравитации часы тикают примерно на 45 микросекунд быстрее, чем наземные часы.Если сложить эти два показателя, то спутниковые часы GPS будут тикать быстрее, чем наземные, примерно на 38 микросекунд в день.
Специальная теория относительности и квантовая механика
По мере того, как наши знания физики расширяются, ученые сталкиваются с более противоречивыми ситуациями. Один пытается согласовать общую теорию относительности, которая хорошо описывает то, что происходит с большими объектами, с квантовой механикой, которую лучше всего использовать для очень маленьких вещей (таких как распад атома урана).Эти две области, которые превосходно описывают свои отдельные области, несовместимы друг с другом, что расстроило Эйнштейна и поколения ученых после него.
«Теория относительности дает бессмысленные ответы, когда вы пытаетесь уменьшить ее до квантового размера, в конечном итоге опускаясь до бесконечных значений в описании гравитации. Точно так же квантовая механика сталкивается с серьезными проблемами, когда вы увеличиваете ее до космических размеров», – статья в The Guardian указала в 2015 году.
«Квантовые поля несут определенное количество энергии даже в кажущемся пустом пространстве, и количество энергии увеличивается по мере того, как поля становятся больше.Согласно Эйнштейну, энергия и масса эквивалентны (это сообщение E = mc 2 ), поэтому накопление энергии в точности похоже на накопление массы. Достаточно большой, и количество энергии в квантовых полях станет настолько большим, что создаст черную дыру, которая заставляет Вселенную складываться сама по себе. Упс. “
Есть несколько идей, чтобы преодолеть это (которые выходят за рамки этой статьи), но один из подходов – представить квантовую теорию гравитации, в которой безмассовая частица (называемая гравитоном) генерирует силу.Но, как отметил физик Дэйв Голдберг в io9 в 2013 году, с этим есть проблемы. В самых маленьких масштабах гравитоны имели бы бесконечную плотность энергии, создавая невообразимо мощное гравитационное поле. Потребуются дополнительные исследования, чтобы увидеть, возможно ли это.
замедления времени | Объяснение, примеры и парадокс близнецов
Узнайте о трех простых и трех сложных способах путешествия во времени
Узнайте о трех простых способах (ничего не делать, ходить и вставать) и трех сложных способах (вращать вселенную, строить бесконечный цилиндр и построить червоточину) для путешествия во времени.
© MinutePhysics (издательский партнер Britannica) См. Все видео для этой статьиЗамедление времени , в специальной теории относительности, «замедление» часов, определяемое наблюдателем, находящимся в относительном движении относительно к тем часам. В специальной теории относительности наблюдатель в инерционном (т. Е. Неускоряющемся) движении имеет четко определенные средства определения того, какие события происходят одновременно с данным событием. Второй инерционный наблюдатель, который движется относительно первого, однако, не согласится с первым наблюдателем относительно того, какие события одновременны с данным событием.(Ни один из наблюдателей не ошибается в этом определении; скорее, их разногласия просто отражают тот факт, что одновременность является зависимым от наблюдателя понятием в специальной теории относительности.) Понятие одновременности требуется для того, чтобы провести сравнение хода часов, переносимых два наблюдателя. Если использовать понятие одновременности первого наблюдателя, обнаруживается, что часы второго наблюдателя идут медленнее, чем часы первого наблюдателя, на коэффициент квадратного корня из √ (1 – v 2 / c 2 ), где v – относительная скорость наблюдателей, а c равна 299 792 км (186 282 мили) в секунду – i.е., скорость света. Точно так же, используя понятие одновременности второго наблюдателя, обнаруживается, что часы первого наблюдателя идут медленнее на тот же фактор. Таким образом, каждый инерционный наблюдатель определяет, что все часы, движущиеся относительно этого наблюдателя, идут медленнее, чем собственные часы этого наблюдателя.
Тесно родственное явление, предсказываемое специальной теорией относительности, – это так называемый парадокс близнецов. Предположим, что один из двух близнецов, несущих часы, отправляется на ракетном корабле от другого близнеца, инерциального наблюдателя, в определенное время, и они воссоединяются позже.В соответствии с эффектом замедления времени, истекшее время на часах двойника на ракетном корабле будет меньше, чем у инерциального двойника-наблюдателя, т. Е. Неинерциальный двойник будет старше, чем инерционный двойник-наблюдатель, когда они воссоединяются.
Понять концепцию замедления времени в специальной теории относительности, объясненную Альбертом Эйнштейном и Ричардом Фейнманом
Неформальный обзор замедления времени в специальной теории относительности, разъясненный Альбертом Эйнштейном и Ричардом Фейнманом.
© Открытый университет (партнер по изданию Britannica) Посмотреть все видео к этой статьеЭффект замедления времени, предсказанный специальной теорией относительности, был точно подтвержден наблюдениями за увеличенным временем жизни нестабильных элементарных частиц, движущихся почти со скоростью света. Эффект парадокса часов также был подтвержден экспериментами, сравнивающими прошедшее время атомных часов на Земле с временем атомных часов, летящих в самолете. Последние эксперименты, кроме того, подтвердили гравитационный вклад в замедление времени, как предсказывает общая теория относительности.
| Замедление времени – это реальная и измеримая величина. Расширенное время обозначается символом t ’. Уравнение для замедления времени задается следующим образом: Замедление времени является относительной величиной и для его расчета полагается на сравнение между системами отсчета. Для этого важно, чтобы вы могли определить системы координат, обсуждаемые в вопросе, и связать их с проводимыми измерениями. Пример 1: Ракета движется с Земли через космос со скоростью 2.7х108 мс-1. Пилот считает, что путешествие займет 240 минут. Как долго думает Центр управления полетами на Земле полет длился? Шаг 1: Определите системы отсчета. Поскольку управление миссией находится вне системы отсчета ракеты (внешний наблюдатель), измеренное время равно t ’. Время, измеренное внутри ракеты, находится в системе отсчета ракеты (внутренний наблюдатель), поэтому измеренное время равно t. Пример 2: Космический корабль, движущийся с постоянной скоростью 0.75c проходит мимо Земли. Астронавт на космическом корабле измеряет время, за которое Усэйн Болт пробежал 100 метров. Космонавт измеряет это время 14,65 с. Вычислите время Усэйна Болта по наблюдениям с Земли. Ракета находится за пределами системы отсчета бегуна. Это означает, что время, наблюдаемое с ракеты, равно t ‘, а время, наблюдаемое со 100-метровой траектории, равно t. Пример 3: Ракета проходит два маяка, которые неподвижны относительно Земли. Астронавт в ракете измеряет время, необходимое ракете, чтобы пройти от первого маяка до второго маяка, равным 10.0 с. Наблюдатель на Земле измеряет время, за которое ракета проходит от первого маяка до второго маяка, составляет 40,0 с. Вычислите скорость ракеты относительно Земли. В этом случае время, измеренное наблюдателем, находящимся в системе отсчета маяка, является внешним по отношению к ракете и, следовательно, имеет время t ‘. Наблюдатель на ракете имеет время t, поскольку он находится в системе отсчета. |
Специальная теория относительности (замедление времени) Калькулятор
- Цель использования
- В моей карьере в ВВС летал на старше 21 года, любопытно, насколько я на самом деле постарел.
[1] 18.04.2021 10:44 Мужчина / 50 лет / Инженер / Очень /
- Цель использования
- Я пытаюсь откалибровать свою временную капсулу. Я наконец добрался до века с примитивной версией Интернета, пожалуйста, кто-нибудь hel
[2] 2021/04/16 13:08 Мужской / 40-летний уровень / Другое / Полезно /
- Цель использования
- узнать об увеличении времени для развлечения
[3] 2021/04/10 12:51 Мужчина / 30-летний уровень / Офисный работник / Государственный служащий / Очень /
- Цель использования
- Подсчитайте замедление времени для Настойчивости на пути к Марсу.
[4] 2021/02/17 19:18 Мужчина / 30-летний уровень / Учитель / Исследователь / Полезно /
- Цель использования
- Расчет разницы во времени между человеком, живущим на экваторе, и полярным кругом.
[5] 2021.01.20 06:18 Мужчина / 30 лет / Другое / Немного /
- Цель использования
- для определения того, какая доля ка мюона должна пройти в ускорителе, чтобы получить скорость убывания порядка секунд относительно внешних наблюдателей
- Комментарий / запрос
- Этот калькулятор был бы бесконечно улучшен, если бы вы могли управлять единицами измерения, изменять параметры ввода / вывода, и если бы у него был ключ для допустимых входных данных или более широкий диапазон допустимых значений. входы, чтобы передать то же значение.Например, если можно ввести единицы, составляющие долю c, или другие единицы, кроме км / с и интервалов времени, отличных от секунд. Также мне нужно было найти приемлемую для вас нотацию ввода для научной записи по следам и ошибкам.
В остальном это было полезно и точно.
[6] 2020/12/14 03:07 Мужской / 20-летний уровень / Другие / Полезные /
- Цель использования
- Разработка юмористического объяснения того, как мне удалось разгадать субботний кроссворд примерно в 60% моего среднего времени.
[7] 2020/12/06 09:48 Мужчина / 60 лет и старше / Пенсионер / Полезный /
- Цель использования
- Интересно, как влияет наша текущая скорость замедления времени путешествовать по Земле, когда она движется вокруг своей оси, вокруг Солнца, вокруг галактики и через вселенную, в отличие от гипотетического стационарного наблюдателя.
[8] 2020/11/18 10:27 Мужчина / 50-летний уровень / Офисный работник / Государственный служащий / Полезный /
- Цель использования
- Общее любопытство и нежелание делать вычисления / сделать свой собственный калькулятор.
[9] 2020/11/16 14:56 Мужской / Моложе 20 лет / Самозанятые лица / Очень /
- Цель использования
- Чтобы вычислить, сколько лет тому, кто путешествует долгое время на релятивистских скоростях . Художественная литература.
[10] 2020/09/05 11:25 Мужчина / 60 лет и старше / – / Очень /
Уравнения времени гравитации для падающих объектов, Рон Куртус
SfC Home> Физика> Гравитация>
Рона Куртуса (от 5 января 2011 г.)
Когда вы бросаете объект с некоторой высоты над землей, он имеет нулевую начальную скорость.Простые уравнения позволяют вычислить время , которое требуется падающему объекту , чтобы достичь заданной скорости, и время, необходимое для достижения заданного смещения. Уравнения предполагают, что сопротивление воздуха незначительно.
Примеры демонстрируют применение уравнений.
Вопросы, которые могут у вас возникнуть:
- Какое уравнение определяет время, необходимое для достижения заданной скорости?
- Каково уравнение времени для достижения заданного смещения?
- Какие примеры этих уравнений?
Этот урок ответит на эти вопросы.Полезный инструмент: Конвертация единиц
Время относительно скорости
Общее уравнение гравитации для затраченного времени относительно скорости:
t = (v – v i ) / г
( Подробную информацию о выводе см. В разделе «Вывод уравнений скорости-времени для гравитации». )
Поскольку начальная скорость v i = 0 для объекта, который просто падает, уравнение сводится к:
t = об / г
где
- t – время в секундах
- v – вертикальная скорость в метрах в секунду (м / с) или футах в секунду (фут / с)
- g – ускорение свободного падения (9.8 м / с 2 или 32 фут / с 2 )
Поскольку объект движется в направлении силы тяжести, v является положительным числом.
Затраченное время падающего объекта как функция скорости или смещения
Время относительно вытеснения
Общее уравнение гравитации для затраченного времени относительно смещения:
t = [−v i ± √ (v i 2 + 2gy)] / g
где
- ± означает плюс-минус
- √ (v i 2 + 2gy) – квадратный корень из величины (v i 2 + 2gy)
- y – вертикальное смещение в метрах (м) или футах (футах)
( См. Раздел «Вывод уравнений силы тяжести смещения во времени» для получения подробной информации о выводе.)
Когда объект просто бросают, начальная скорость равна нулю ( v i = 0), и уравнение для истекшего времени принимает следующий вид:
t = ± √ (2gy) / г
Поскольку время t всегда положительно, уравнение имеет следующий вид:
t = √ (2gy) / г
Измените g на √ (g 2 ) и упростите уравнение:
t = √ (2gy) / √ (g 2 )
Таким образом, результирующее уравнение времени будет:
t = √ (2y / г)
Примеры
Следующие примеры иллюстрируют применение уравнений.
Учитывая скорость
Сколько времени требуется, чтобы падающий объект достиг скорости 224 фут / с?
Решение
Поскольку v выражается в фут / с, g = 32 фут / с 2 . Подставьте значения в уравнение:
t = об / г
t = (224 фут / с) / (32 фут / с 2 )
t = 7 секунд
Учитывая водоизмещение
Сколько времени нужно, чтобы объект упал на 200 метров?
Решение
Поскольку смещение выражено в метрах, г = 9.8 м / с 2 . Подставьте значения в уравнение:
t = √ (2y / г)
t = √ [2 * (200 м) / (9,8 м / с 2 )]
t = √ (40,8 с 2 )
t = 6,39 с
Сводка
Существуют простые уравнения для падающих объектов, которые позволяют рассчитать время, необходимое для достижения заданной скорости или смещения. Вот эти уравнения:
t = об / г
t = √ (2y / г)
Проверьте свои номера
Ресурсы и ссылки
Полномочия Рона Куртуса
Сайты
Гравитационные ресурсы
Падающие тела – Physics Hypertextbook
Уравнения падающего тела – Википедия
Расчет силы тяжести – Земля – Калькулятор
Кинематические уравнения и свободное падение – Физический класс
Книги
Книги с самым высоким рейтингом по простой науке о гравитации
Книги с самым высоким рейтингом по продвинутой физике гравитации
Вопросы и комментарии
Есть ли у вас какие-либо вопросы, комментарии или мнения по этой теме? Если да, отправьте свой отзыв по электронной почте.Я постараюсь вернуться к вам как можно скорее.
Поделиться страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/science/
gravity_equations_falling_time.htm
Пожалуйста, включите его в качестве ссылки на свой веб-сайт или в качестве ссылки в своем отчете, документе или тезисе.
Авторские права © Ограничения
Где ты сейчас?
Школа чемпионов
Гравитационные темы
Уравнения гравитации и времени для падающих предметов
КАЛЬКУЛЯТОР ВРЕМЕНИ И РАССТОЯНИЯ СКОРОСТИ
Приведенные выше 3 формулы используются для решения задач, касающихся расстояния, скорости и времени. Если вы знаете 2 из 3 переменных, третью можно вычислить.Как обычно, на сайте www.1728.com у нас есть калькулятор, который сделает всю работу за вас.
Этот калькулятор ultra отличается тем, что позволяет выбирать между большой выбор единиц (по 12 на категорию). В отличие от других калькуляторов, вы НЕ ограничивается вводом расстояния в футах, времени в минутах и т. д., что делает этот калькулятор довольно универсален. Посмотрим на несколько примеров.
1) Вы можете пробежать 100 ярдов за 12 секунд. Какова ваша скорость в милях в час?
Самый важный шаг в использовании этого калькулятора:
ПЕРВЫЙ ВЫБЕРИТЕ, ЧТО ВЫ РЕШАЕТЕ ДЛЯ
В этом случае мы решаем для СКОРОСТИ, поэтому нажмите эту кнопку.
Введите 12 в поле «время» и выберите секунды в его меню.
Введите 100 в поле «Расстояние» и выберите ярды из его меню.
Нажмите кнопку РАССЧИТАТЬ, и вы увидите, что это составляет 17.045 миль в час. ПЛЮС вы получите
см. ответ в 11 других единицах !!
2) Ледник движется со скоростью 0,0009513 мм в секунду. Сколько времени это занимает ледник переместится на 1 милю?
ПЕРВЫЙ ЩЕЛКНИТЕ НА ТО, ЧТО ВЫ РЕШАЕТЕ – ВРЕМЯ
Введите 0,0009513 в поле скорости и выберите миллиметры в секунду из его меню.
Введите 1 в поле расстояния и выберите мили в соответствующем меню.
Щелкните ВЫЧИСЛИТЬ, и ваш ответ – 53,6 года (а также 11 других единиц).
3) Вы смотрите автогонку «Индианаполис 500», и машина только что уехала.
50 секунд, чтобы пройти один «круг» трека со скоростью 180 миль в час. Какова длина гоночной трассы?
ПЕРВЫЙ ЩЕЛКНИТЕ НА ТО, ЧТО ВЫ РЕШАЕТЕ – РАССТОЯНИЕ
Введите 180 в поле скорости и выберите мили в час из его меню.
Введите 50 в поле времени и выберите секунды в его меню.
Щелкните ВЫЧИСЛИТЬ, и ваш ответ будет 2,5 мили (или 13 200 футов, или 158 400 дюймов и т. Д.)
Надеюсь, этот калькулятор поможет вам с математическими задачами.
*********************************************** **** Числа отображаются в экспоненциальном представлении с указанием количества значащих цифр. укажите в поле выше. Для удобства чтения числа от 0,001 до 1000 не будут отображаться. в экспоненциальном представлении, но с той же точностью.Internet Explorer и большинство других браузеров будут отображать ответы правильно, но есть несколько браузеров, которые вообще не выводят без вывода .Если да, введите ноль в поле выше. Это устраняет все форматирование, но это лучше, чем не видеть вывод вообще.
Относительность | Физика для идиотов
Скорость. Точнее вполне конкретная скорость. Точнее 299 792 458 м / с, скорость света. Эта волшебная таинственная скорость лежит в основе теории относительности. Именно размышления Эйнштейна об этой скорости привели к одним из самых удивительных физических идей, когда-либо существовавших. Относительность бывает двух форм: специальной и общей.Один физик однажды сказал, что если бы у кого-то было достаточно времени, он бы придумал специальную теорию относительности, а общая теория относительности была бы таким гениальным ходом, если бы не Эйнштейн, эта идея, возможно, никогда бы не возникла.
Краткий обзор
- Специальная теория относительности – это теория, согласно которой независимо от того, с какой постоянной скоростью вы движетесь, все законы физики одинаковы.
- Общая теория относительности утверждает, что состояние покоя в гравитационном поле и ускорение физически идентичны.
Вместе эти два показывают, что независимо от того, как вы двигаетесь, все законы физики работают одинаково, и поэтому вы можете относиться к себе так, как если бы вы отдыхали.
Специальная теория относительности является специальной, потому что она имеет дело только с простыми системами. Системы, в которых объекты движутся по красивым прямым линиям с хорошими постоянными скоростями. Нет силы. Никакого разгона. Эйнштейн разработал 2 постулата специальной теории относительности
- Все физические законы одинаковы, независимо от постоянной скорости, с которой вы движетесь с .
- Скорость света всегда одна и та же, независимо от движения наблюдателя или источника света
Это означает, что абсолютного движения нет.Если вы едете в машине со скоростью 50 миль в час, вы не сможете доказать, что даже двигаетесь. Это может быть земля и все, что на ней, кроме вас и машины, движется назад со скоростью 50 миль в час, и если вы хотите сказать, что это происходит, вы не ошиблись бы, законы физики подтвердили бы это. Все, что вы можете сказать, это то, что одна вещь движется ОТНОСИТЕЛЬНО к другой, и какую из них вы выберете в качестве стационарной системы отсчета, решать вам.
Из двух постулатов специальной теории относительности вытекают некоторые очень важные следствия.
- Расширение времени
- Сокращение длины
Давайте посмотрим, как это происходит.
Одно из приведенных выше следствий специальной теории относительности – замедление времени. Это означает, что скорость света неизменна, и все законы одинаковы для постоянных скоростей, время может замедляться. Оказывается, время не является постоянной величиной во всей Вселенной, а полностью относительным.
Представьте, что вы находитесь на космическом корабле, и в вашей руке у вас есть модные часы нового типа, которые вы изобрели.По сути, это два зеркала, между которыми отражается фотон, и вы настроили его так, что каждый раз, когда фотон попадает в одно из зеркал, вы слышите щелчок. Вы также настроили его так, чтобы знать, сколько щелчков вы услышите за одну секунду, поэтому, если вы умеете считать, вы можете очень точно измерять время с помощью этих часов.
Теперь предположим, что ваш космический корабль в настоящее время неподвижен. К счастью, одна сторона сделана из стекла, поэтому мы можем видеть, что происходит.
Фотон поднимался бы к верхнему зеркалу и вызвал «Щелчок», а затем отскочил бы к нижнему зеркалу и вызвал бы еще один «Щелчок».Затем он снова и снова подпрыгивал вверх и вниз, снова и снова. Просто и легко.
А теперь предположим, что вы решили покататься на космическом корабле. Итак, теперь вы двигаетесь с постоянной скоростью. Все законы, которые применялись раньше, действуют и сейчас, но, как вы можете видеть из изображения ниже, что-то изменилось.
Пока вы путешествуете, вместе с часами движутся часы, поэтому, когда протоны устремляются в верхнее зеркало, путь вверх уже не будет прямым. Он должен двигаться по диагонали, а это, как видите, гораздо более длинный путь.Таким образом, время между щелчками будет больше. Так что для наблюдателя время на корабле замедляется. ОДНАКО, с вашей точки зрения на корабль, это не диагональное путешествие, это просто прямое движение вверх и вниз, поэтому время идет нормально.
Значит есть несоответствие. Ваши часы на борту показывают время, отличное от времени, например, на Земле, и хотя они оба разные, они все равно правильные. И именно поэтому возможно путешествие во времени
Чем быстрее вы путешествуете, тем больше замедляется время.Если вы и ваш друг стартовали на Земле с двумя синхронизированными часами, а затем совершили путешествие на 99% скорости света в течение 1 дня, когда вы вернетесь, часы ваших друзей будут почти ровно на 6 дней впереди ваших. Фактически вы только что провели день в путешествии на неделю в будущее !!
Используя простую тригонометрию, вы можете вычислить уравнение того, насколько различается время, когда вы двигаетесь с постоянной скоростью. Если вы неподвижны, то на часах будет
.Ситуация, когда предполагается, что ничего не движется, называется кадром покоя.Время, которое вы измеряете между щелчками в кадре покоя, будет выражено (просто вычислением расстояния / скорости)
.(1)
Когда вы движетесь с постоянной скоростью, ситуация будет
Таким образом, время между нажатиями будет
(2)
Используя закон Пифагора для правых треугольников, мы можем вычислить расстояние. Высота треугольника будет равна, а длина по дну будет соответствовать тому, насколько далеко часы переместились за один щелчок, поэтому (скорость, умноженная на время, – это расстояние)
Мы можем подставить это выражение для в Уравнение 2, а затем переставить для, что дает
Если мы теперь заменим на (из уравнения 1), мы получим уравнение для замедления времени
(3)
Это уравнение показывает, насколько движущиеся часы () будут отличаться от часов покоя ().
Для большинства значений, к которым мы привыкли в повседневной жизни, это отношение крошечное, поэтому знаменатель уравнения 3 обычно настолько близок к 1, что мы не можем обнаружить никакой разницы, и поэтому мы находим, что =. Например; два человека синхронизируют часы, а затем один из них едет со скоростью 120 миль в час. Если неподвижный человек записывает время 30 секунд, то движущийся человек записывает время 29,99999999999952 секунды. Эта разница слишком мала для измерения даже с использованием лучших технологий, поэтому на низких скоростях по сравнению со скоростью света мы действительно не замечаем эффектов относительности.
Как уже говорилось, скорость света всегда одна и та же, но, как мы только что выяснили, время может замедляться, если вы двигаетесь достаточно быстро. Скорость рассчитывается делением пройденного расстояния на время, но если время может меняться, то и расстояние должно меняться, чтобы скорость света оставалась постоянной.
Если время увеличивается в установленный коэффициент, то расстояние должно уменьшаться в том же раз, чтобы скорость света оставалась неизменной для движущегося наблюдателя.

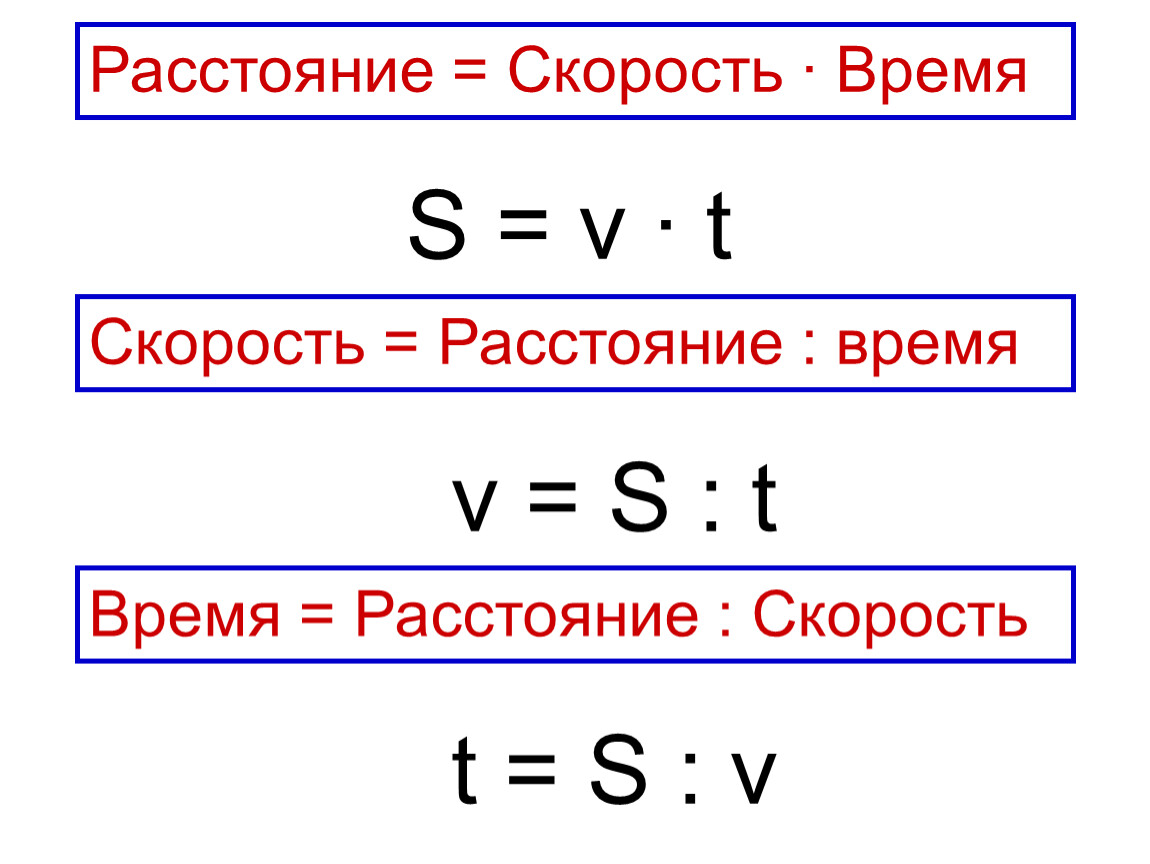 1)
1)
 Достаточно знать, какую скорость он развивает и расстояние между городами. В случае же, когда нам надо рассчитать сопротивление ветра на определенной высоте и при определенной скорости, то тут уж никак не обойтись без точного знания формы и размеров того же самолета.
Достаточно знать, какую скорость он развивает и расстояние между городами. В случае же, когда нам надо рассчитать сопротивление ветра на определенной высоте и при определенной скорости, то тут уж никак не обойтись без точного знания формы и размеров того же самолета. Но на практике часто встречаются задачи в которых необходимо вычислить положение тела, то есть записать его координаты в некоторой системе координат.
Но на практике часто встречаются задачи в которых необходимо вычислить положение тела, то есть записать его координаты в некоторой системе координат. Начало оси х=0 совместим с пристанью. За положительное направление примем направление на восток.
Начало оси х=0 совместим с пристанью. За положительное направление примем направление на восток. Длины отрезков sx1 и sx2 будут равны длинам векторов s1 и s2. Модуль каждой проекции будет равен модулю соответствующего ей вектора.
Длины отрезков sx1 и sx2 будут равны длинам векторов s1 и s2. Модуль каждой проекции будет равен модулю соответствующего ей вектора.


 В случае с линейкой и монеткой в домашних условиях это трудно проделать, но в условиях лаборатории можно зафиксировать, что при постоянном угле наклона скользящая монетка за каждую секунду изменяет свою скорость на одинаковую величину.
В случае с линейкой и монеткой в домашних условиях это трудно проделать, но в условиях лаборатории можно зафиксировать, что при постоянном угле наклона скользящая монетка за каждую секунду изменяет свою скорость на одинаковую величину. Так происходит в случае прямолинейного равноускоренного движения. Формула для ускорения выглядит следующим образом:
Так происходит в случае прямолинейного равноускоренного движения. Формула для ускорения выглядит следующим образом: Формула тогда примет вид: a =v /t для первого случая либо же: a = v_0 /t для второго.
Формула тогда примет вид: a =v /t для первого случая либо же: a = v_0 /t для второго. 2) в течение 4 секунд.
2) в течение 4 секунд.
 2=4*S1.
2=4*S1. То есть они являются как бы неким своеобразным признаком равноускоренного движения. Если необходимо проверить, является ли движение равноускоренным, то можно проверить эти закономерности, и если они будут выполняться, то движение будет равноускоренным.
То есть они являются как бы неким своеобразным признаком равноускоренного движения. Если необходимо проверить, является ли движение равноускоренным, то можно проверить эти закономерности, и если они будут выполняться, то движение будет равноускоренным.

 Каждый ваш шаг будет гигантским расстоянием для молекулы асфальта и ничтожным для планеты Земля. Любое движение, как и все его характеристики всегда имеют смысл только относительно чего-либо еще.
Каждый ваш шаг будет гигантским расстоянием для молекулы асфальта и ничтожным для планеты Земля. Любое движение, как и все его характеристики всегда имеют смысл только относительно чего-либо еще. Но если представить себе бесконечно длинный, абсолютно скользкий и гладкий каток, на котором стоит тело, то станет очевидно, что если придать телу импульс, то тело будет двигаться бесконечно долго и по одной прямой.
Но если представить себе бесконечно длинный, абсолютно скользкий и гладкий каток, на котором стоит тело, то станет очевидно, что если придать телу импульс, то тело будет двигаться бесконечно долго и по одной прямой. В исходном варианте первый закон Ньютона несколько неточен, а современный вариант в попытках исправить эту неточность оказался очень запутанным и потому неудачным. Ну а так как истина всегда где-то рядом, то попытаемся найти это «рядом» и разобраться, что же представляет собой данный закон.
В исходном варианте первый закон Ньютона несколько неточен, а современный вариант в попытках исправить эту неточность оказался очень запутанным и потому неудачным. Ну а так как истина всегда где-то рядом, то попытаемся найти это «рядом» и разобраться, что же представляет собой данный закон. Масло масляное. Замкнутый круг.
Масло масляное. Замкнутый круг. «Изолированным» – это значит никак не связанным, бесконечно удаленным от других тел.
«Изолированным» – это значит никак не связанным, бесконечно удаленным от других тел. Мы не можем переместиться на бесконечно далекую звезду и оттуда осуществлять какие-либо опыты на Земле.
Мы не можем переместиться на бесконечно далекую звезду и оттуда осуществлять какие-либо опыты на Земле.
 Хотите легко и быстро, на примерах понять, как это происходит? Запросто. Надо будет проделать пару элементарных опытов и немного порассуждать.
Хотите легко и быстро, на примерах понять, как это происходит? Запросто. Надо будет проделать пару элементарных опытов и немного порассуждать. Если на тело действуют несколько сил, то находят равнодействующую этих сил, то есть некую общую суммарную силу, обладающую определенным направлением и числовым значением.
Если на тело действуют несколько сил, то находят равнодействующую этих сил, то есть некую общую суммарную силу, обладающую определенным направлением и числовым значением. Ускорение двух грузов у нас было ощутимо разным, хотя силу мы старались прикладывать одинаковую. А вот масса грузов у нас отличалась. И в случае с большей массой ускорение тела было небольшим, а в случае меньшей массы намного большим.
Ускорение двух грузов у нас было ощутимо разным, хотя силу мы старались прикладывать одинаковую. А вот масса грузов у нас отличалась. И в случае с большей массой ускорение тела было небольшим, а в случае меньшей массы намного большим. Это и есть второй закон Ньютона.
Это и есть второй закон Ньютона.
 И потяните за колечко второго безмена. Проследите за показаниями обоих приборов. Каждый из них покажет силу, с которой на него воздействует другой безмен.
И потяните за колечко второго безмена. Проследите за показаниями обоих приборов. Каждый из них покажет силу, с которой на него воздействует другой безмен. Все тела во Вселенной взаимодействуют друг с другом, подчиняясь этому закону.
Все тела во Вселенной взаимодействуют друг с другом, подчиняясь этому закону. 2)/2 (если v_0 = 0), соответственно,
2)/2 (если v_0 = 0), соответственно, Только в этом случае, скорость, которую мы придали телу при броске, будет направлена вверх, а ускорение свободного падения направлено вниз, то есть они будут противоположно направлены друг к другу. Поэтому скорость будет постепенно уменьшаться.
Только в этом случае, скорость, которую мы придали телу при броске, будет направлена вверх, а ускорение свободного падения направлено вниз, то есть они будут противоположно направлены друг к другу. Поэтому скорость будет постепенно уменьшаться. 2)/2.
2)/2.
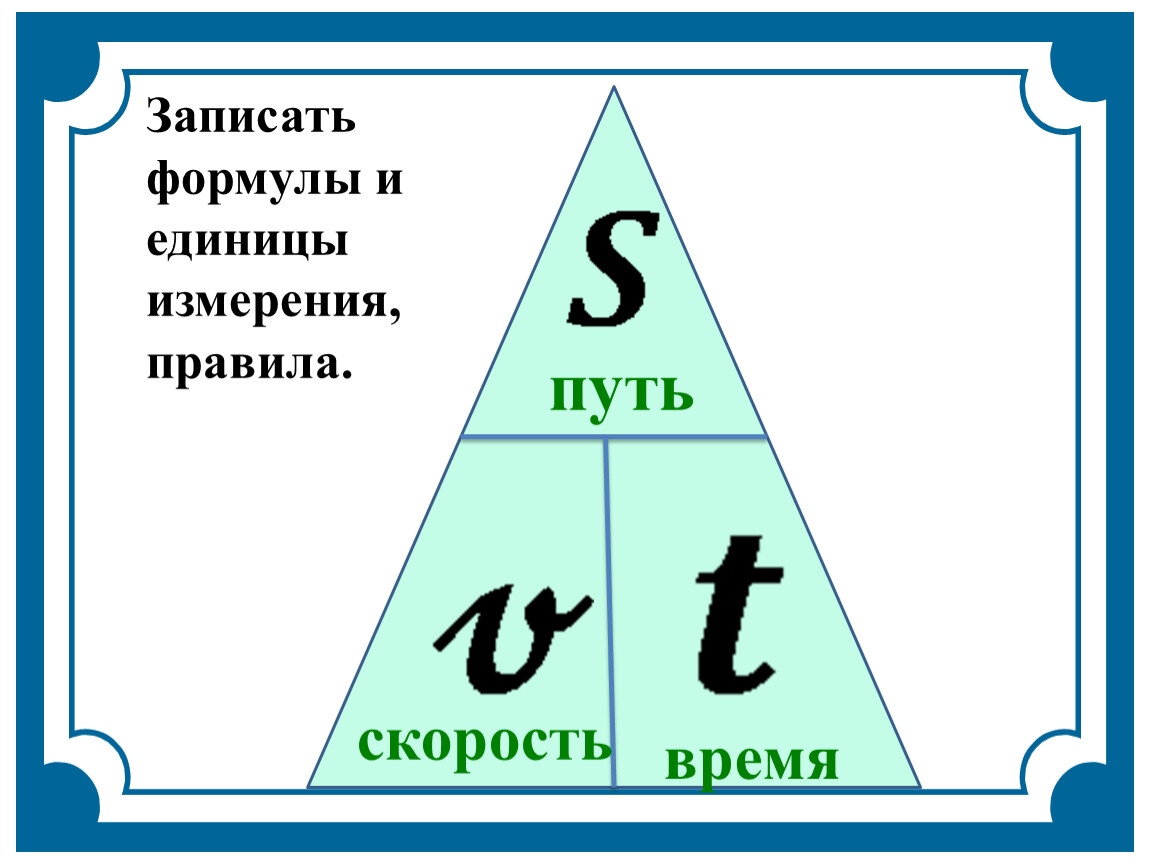 2 .
2 . 2).
2). 7 Н. Это очень мало, поэтому в таких случаях при расчетах берут вблизи поверхности земли значение ускорения свободного падения g=9,81.
7 Н. Это очень мало, поэтому в таких случаях при расчетах берут вблизи поверхности земли значение ускорения свободного падения g=9,81. Можно проделать несложный эксперимент, показывающий, как направление движения тела будет зависеть от направления приложенной к нему силы. Для этого потребуется произвольный предмет небольшого размера, резиновый шнур и горизонтальная или вертикальная опора.
Можно проделать несложный эксперимент, показывающий, как направление движения тела будет зависеть от направления приложенной к нему силы. Для этого потребуется произвольный предмет небольшого размера, резиновый шнур и горизонтальная или вертикальная опора.
 А это означает, что движение по окружности с постоянной по модулю скоростью происходит равноускорено.
А это означает, что движение по окружности с постоянной по модулю скоростью происходит равноускорено. Намного большую скорость телам могут придать различные артиллерийские орудия. Снаряды могут преодолевать несколько километров и даже десятков километров. Однако всегда траекторией всех этих летящих тел является дуга, концом упирающаяся в землю.
Намного большую скорость телам могут придать различные артиллерийские орудия. Снаряды могут преодолевать несколько километров и даже десятков километров. Однако всегда траекторией всех этих летящих тел является дуга, концом упирающаяся в землю. Как ни странно звучит, движение спутника вокруг Земли это пример свободного падения тела.
Как ни странно звучит, движение спутника вокруг Земли это пример свободного падения тела. Она составляет 11,2 км/с. При такой скорости тела описывают вокруг Земли не дугу, а эллипс, и тело удаляется на расстояние, достаточное для полного освобождения от земного притяжения. Такую скорость развивают ракеты, которые уходят в космическое пространство прочь от Земли.
Она составляет 11,2 км/с. При такой скорости тела описывают вокруг Земли не дугу, а эллипс, и тело удаляется на расстояние, достаточное для полного освобождения от земного притяжения. Такую скорость развивают ракеты, которые уходят в космическое пространство прочь от Земли. Единицей импульса является килограмм на метр в секунду (1 кг*м/с).
Единицей импульса является килограмм на метр в секунду (1 кг*м/с). Эта величина напрямую зависит от скорости и массы исходного тела.
Эта величина напрямую зависит от скорости и массы исходного тела.
 Для передвижения по поверхности используют ноги, колеса, гусеницы и так далее. В воде и воздухе можно отталкиваться от самих воды и воздуха, имеющих определенную плотность, и потому позволяющих взаимодействовать с ними. Природа для этого приспособила плавники и крылья.
Для передвижения по поверхности используют ноги, колеса, гусеницы и так далее. В воде и воздухе можно отталкиваться от самих воды и воздуха, имеющих определенную плотность, и потому позволяющих взаимодействовать с ними. Природа для этого приспособила плавники и крылья.
 При этом, на величину массы этих газов уменьшается масса ракеты, и она приобретает некую скорость. Таким образом реализован принцип реактивного движения в физике.
При этом, на величину массы этих газов уменьшается масса ракеты, и она приобретает некую скорость. Таким образом реализован принцип реактивного движения в физике.