Формула второго закона ньютона: Формула 2 закона ньютона – ответ на Uchi.ru

PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2.1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2.5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3.1 МКТ
  • 3. 2 Термодинамика
• 4 Электродинамика
  • 4.1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5.2 Волновая оптика
  • 5. 3 Фотометрия
  • 5.4 Квантовая оптика
  • 5.5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ – Репетитор по физике

Новые страницы

Запрос не дал результатов.

Изучение второго закона Ньютона с помощью машины Атвуда

Цель работы: проверить второй закон Ньютона.

Оборудование: машин Атвуда, перегрузки, электронный секундомер.

1. Краткая теория

Одним из основных законов всей физики является второй закон Ньютона.

Он гласит: ускорение, которое приобретает материальная точка под действием силы, прямо пропорционально величине этой силы, обратно пропорционально

массе материальной точки и направлено в сторону действия силы:

r

ar = F . (2.1)

m

Если на материальную точку действует несколько сил, то ускорение определяется геометрической сумой всех сил, называемой равнодействующей всех сил:

r           1  n     r

a =       ∑ Fi

m i =1

и направлено в сторону равнодействующей силы.

(2.2)

В том случае, когда силы действует не на материальную точку, а на массивное тело конечных размеров, второй закон Ньютона справедлив для центра масс этого тела. То есть ускорение центра масс тела прямо пропорционально  равнодействующей  всех   сил,   действующих  на   тело,   и обратно пропорционально массе всего тела. Однако обычно тела конечных размеров имеют достаточно малые размеры по сравнению с расстоянием, которое они проходят, поэтому их вполне можно считать материальными точками.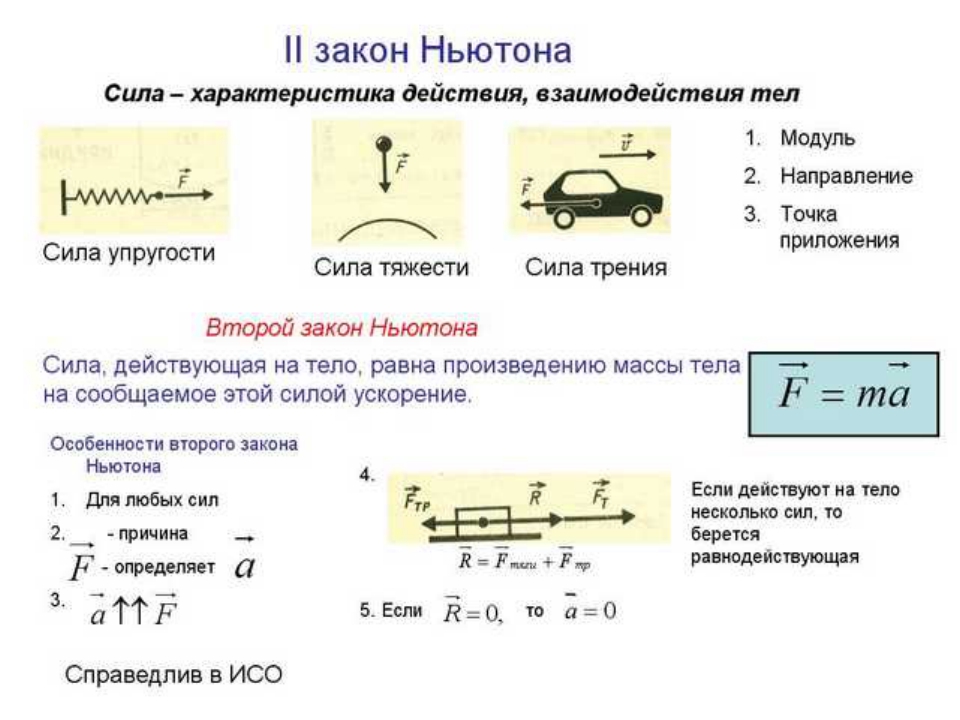

Для проверки второго закона Ньютона нужно, прежде всего, исследовать зависимость ускорения тела от действующей на него силы. Для этого нужно

менять  силу,  оставляя  постоянной  массу  тела.  Для  проверки  зависимости ускорения   от        массы            нужно менять            массу  тела     при      неизменной   силе,

действующей на тело.

Прежде чем приступать к рассмотрению экспериментальной установки рассмотрим вспомогательную задачу: через блок перекинута нить, к концам

которой прикреплены грузы, требуется найти ускорение, с которым движутся грузы.

Для решения задач динамики следует придерживаться следующей схемы:

1. Построить схематический рисунок по задаче, на котором изобразить все силы, действующие на каждое из тел, участвующих в движении.

2. Для каждого из тел, участвующих в движении, записать второй закон

Ньютона в векторной форме (2.2). Особо нужно отметить, что в правую часть формулы (2.2) все силы входят со знаком «+» как векторы.

3. Выбрать систему координат. Система координат может быть выбрана отдельно для каждого тела, участвующего в движении. Для оптимального выбора  системы  координат  оси   координат  следует  направлять  по   тому

направлению,            в          котором          направлено    большинство сил.     Это      позволит уменьшить количество ненулевых проекций сил. Если все силы, действующие на данное тело, параллельны одной прямой (линейная система сил), то систему координат можно выбрать только в виде одной оси, параллельной всем силам, действующим на данное тело. Если все силы, действующие на данное тело, параллельны  некоторой  плоскости  (плоская  система  сил),  то  достаточно выбрать только две оси, лежащие в плоскости, параллельной всем силам, действующим на данное тело. При этом опять оси координат должны быть взаимно перпендикулярны и направлены параллельно как можно большему числу сил. И, наконец, если система сил произвольная, то нужно определять все три оси координат.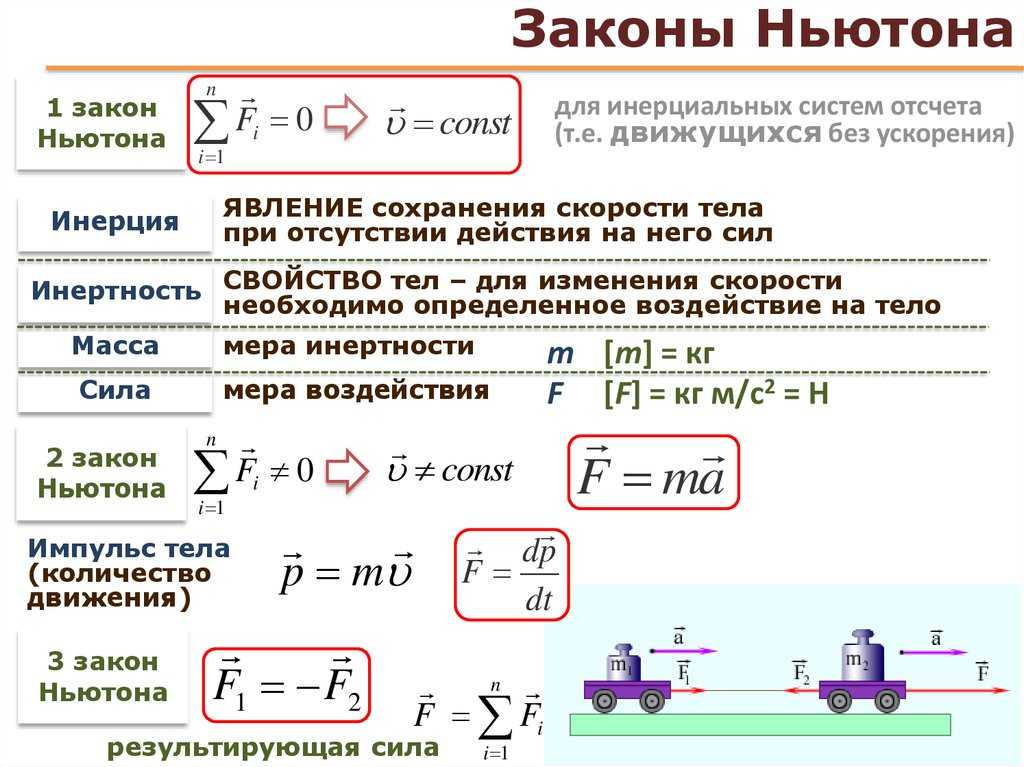

4. Спроецировать каждое векторное равенство, соответствующее второму закону Ньютона, на все оси координат. Сначала спроецировать векторное равенство формально, т.е. записать это равенство заново с теми же самыми знаками у слагаемых сил, только убрать символ вектора (стрелочку над обозначением данного вектора) и указать символ проекции (т.е. индекс оси, на которую выполняется проецирование, внизу  справа  около  обозначения вектора). После этого определить знаки проекций, т.е. выразить проекции через модули векторов с указанием конкретного знака проекции, если это возможно.

5.  В  результате  получится  несколько  алгебраических  уравнений,  в которых некоторые параметры оказываются неизвестными. Эти уравнения и

нужно решить как систему относительно неизвестных. Однако часто бывает,

что количество неизвестных больше, чем уравнений. В этом случае система оказывается неопределённой. Для её определения нужно добавить некоторые

уравнения. Эти уравнения могут быть получены из уравнений кинематики, связывающих между собой кинематические характеристики. В качестве добавочных  уравнений  могут  быть  уравнения,  полученные  из  некоторых

дополнительных условий. А именно, если тела связаны невесомыми связями (невесомые нити), то усилия на придание связям ускорения равны нулю. Это значит, что сила натяжения связи на её одном конце равна силе натяжения этой

связи на другом конце. Если связь нерастяжима, то перемещение одного её конца вдоль связи за некоторый промежуток времени равно перемещению её второго конца. Отсюда следует, что и скорость и ускорение концов связи вдоль

этой связи будут одинаковыми.

6. Решить систему полученных уравнений относительно требуемых неизвестных.

Применим эту схему к решению поставленной задачи.

1. Схема задачи представлена на рис. 2.1.

r            r T4     T3 r      r T2      T1

r           r

m2 g

m1 g

Рис.2.1.Силы, действующие на систему тел

На тела действует сила тяжести и сила натяжения нитей. На блок сила натяжения  нитей  и  сила  реакции  со  стороны  оси,  вокруг  которой  блок вращается (на рис. не показана).

2. В данном случае в движении участвуют три тела: два тела, подвешенные к нитям, и блок. Поэтому уравнений Ньютона будет три. Уравнение поступательного движения для первого тела:

r           r           r

для второго тела:

m1a1  = m1 g + T1 ,    (2.3)

r           r           r

m2 a2  = m2 g + T2 ,   (2.4)

и уравнение вращательного движения для блока:

r           r           r

где I  – момент инерции блока,

εr  – угловое ускорение,

Iε = M 3 + M 4 ,       (2.5)

r           r

M 3      M 4

– моменты сил натяжения нитей, действующих на блок.

3. Выберем систему координат. Для тел, подвешенных к нитям, достаточно выбрать одну ось. Направим её вертикально вниз и обозначим ox . Для блока нужно три оси, поскольку угловое ускорение направлено перпендикулярно к рисунку. Ось ox  направим вертикально вниз, oy  – вправо, а ось oz  перпендикулярно к рисунку в сторону наблюдателя.

4. Тогда проекции уравнений (2. 3)-(2.5) будут иметь вид

m1a1 x  = m1 g x  + T1 x ,      (2.6)

m2 a2 x  = m2 g x  + T2 x ,     (2.7)

Iε z  = M 3 z  + M 4 z .         (2.8)

Поскольку  направление  ускорения  тел  заранее  неизвестно  (оно  зависит  от соотношения масс тел), то конкретизировать их знаки не будем. Ускорение

свободного падения направлено вниз и совпадает по направлению с осью ox ,

значит, проекция его положительна. Силы  r       r

r

направлены вверх, значит, их

проекции       отрицательны.           Момент          силы

T4 относительно       оси      вращения

направлен к наблюдателю, т.е по оси oz , значит, его проекция положительна, а

r

момент  силы T3

направлен  от  наблюдателя,  против  оси oz ,  поэтому  его

проекции отрицательна. Так что уравнения (2.6)-(2.7) перепишутся по-другому:

m1a1 x  = m1 g − T1 ,	(2.9)
m2 a2 x  = m2 g − T2 ,	(2. 10)
Iε z  = −M 3 + M 4 .	(2.11)

В данных уравнениях мы выразили проекции векторов через их модули, о чём говорит тот факт, что обозначения величин не имеют ни символа вектора, ни символа проекции.

Моменты сил по модулю равны произведению модуля сил на плечо:

M 3  = T3 R,M 4  = T3 R ,      (2.12)

где R есть радиус блока.

Так что вместо третьего уравнения можно использовать уравнение:

Iε z  = T4 R − T3 R .           (2.13)

5. Неизвестными в этой системе уравнений являются следующие: ускорения трёх тел, участвующих в движении; величины сил натяжения нити в начале и в конце прямолинейного участка, таких неизвестных четыре. Всего получается 7 неизвестных, а уравнений только три. Так что требуется ещё 4 уравнения. Для отыскания этих уравнений воспользуемся прежде всего тем фактом, что нить невесома. Тогда силы натяжения на разных концах нитей будут равны:

T3  = T1 ,T4  = T2 ,     (2. 14)

Для отыскания ещё двух уравнений воспользуемся нерастяжимостью нити. Это приводит к равенству модулей ускорений тел. Однако, если одно из тел движется по направлению оси ox , другое – против направления этой оси. Так что их ускорения всегда противоположно направлены, поэтому:

a1 x  = −a2 x .           (2.15)

И последнее уравнение получим из условия отсутствия проскальзывания нити по блоку. Это приводит к тому, что тангенциальное ускорение точек обода блока равно по модулю ускорению нити. Что же касается знака ускорений, то из анализа направлений движения тел можно понять, что если первое тело движется вниз с ускорением, т.е. проекция его ускорения на ось ox положительна, то угловое ускорение блока направлено от наблюдателя, т.е против   оси   oz .   Так   что   проекции   ускорений   первого   тела   и   блока противоположны. Поэтому:

ε z R = −a1 x .         (2.16)

Это и есть недостающее уравнение системы. Выпишем теперь все уравнения:

⎧m1a1x  = m1 g − T1;

⎪m2 a2 x  = m2 g − T2 ;

⎪Iε z  = T4 R − T3 R;

⎨

⎪T3  = T1 ,T4  = T2 ;

(2. 17)

⎪   z R = −a1x ;

⎪

Из 4-го уравнения силы T3

и T4

⎪⎩a1x  = −a2 x .

подставим в третье:

⎧m1a1x  = m1g − T1;

⎪m2a 2 x  = m2g − T2 ;

⎨Iεz  = T2 R − T1R;

(2.18)

⎪ε R = −a   ;

⎪  z    1x

⎪⎩a1x  = −a 2 x .

Выразим теперь угловое ускорение из предпоследнего и подставим в третье:

⎧m1a1x  = m1 g − T1;

⎪m2 a2 x  = m2 g − T2 ;

⎨    − a1x

⎪I

⎪

= T2 R − T1R;

(2.19)

⎪⎩a1x  = −a2 x .

Теперь во втором уравнении заменим проекцию ускорения второго тела через

проекцию ускорения первого тела:

⎧m1a1x  = m1 g − T1;

⎪− m2 a1x  = m2 g − T2 ;

⎨    − a1x

⎪I

⎪

= T2 R − T1R;

(2.20)

⎪⎩a1x  = −a2 x .

Теперь из первого уравнения вычтем второе:

⎧(m1  + m2 )a1x  = (m1 − m2 ) g + T2 − T ;1

⎪

⎨

⎪⎩I

− a1x

R

= T2 R − T1R;

(2.21)

И, наконец, из последнего уравнения выразим разность сил натяжения нитей и подставим в первое:

( m1

+ m2

)a1 x

= ( m1

− m2

)g − I a1 x  .    (2.22)

R2

В результате получили одно уравнение, в котором только одно неизвестное –

ускорение первого тела. Найдём его:

a1 x

=  ( m1 − m2 )g

m  + m  +  I

1          2          R2

.           (2.23)

Проанализируем эту формулу. Из неё видно:

1.  Если  первое  тело  тяжелее  второго,  проекция  ускорения  первого  тела положительна, т.е. ускорение первого тела направлено вниз;

2. Если первое тело легче второго, его ускорение направлено вверх.

3. Если массы тел равны, то их ускорения равны нулю.

Таким  образом,  величина  ускорения  тел  определяется  разностью  масс  тел.

Поэтому величину

Fуск  = ( m1 − m2 )g

часто называют ускоряющей силой при решении подобных задач.

(2.24)

4. Если моментом инерции блока можно пренебречь, то формула ускорения упрощается:

a1x

= (m1 − m2 ) g .        (2.25)

m1 + m2

Из этой формулы видно, что ускорению тел способствует разность масс, а препятствует их сумма.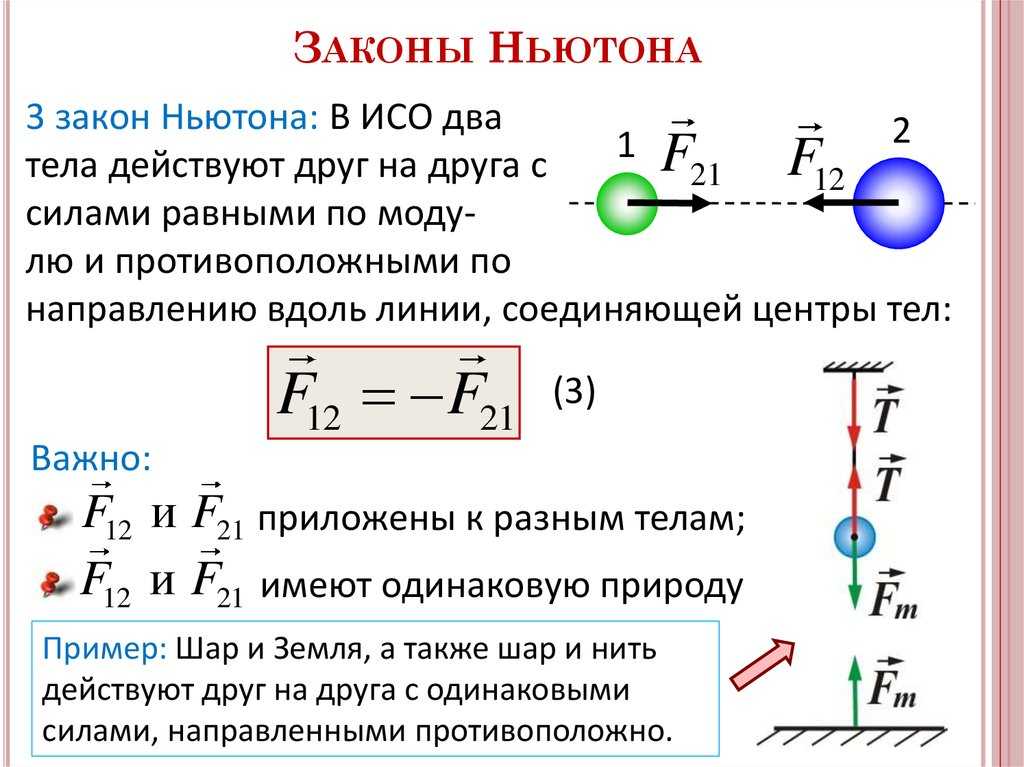

Этой формулой и пользуются в данной лабораторной работе, чтобы проверить второй закон Ньютона.

2. Экспериментальная установка

Экспериментальная установка представляет собой машину Атвуда, схема которой представлена на рис. 2.2.

К  нерастяжимой, невесомой,  гибкой  нити,  перекинутой  через  лёгкий блок, прикреплены платформы одинаковой массы (4). На эти платформы могут устанавливаться дополнительные перегрузки различных масс. Если масса одного из перегрузков больше, чем масса другого, обе платформы начинают

ускоренно двигаться. В работе эксперимент выполняется всегда таким образом, что масса правого перегрузка больше массы левого. Поэтому правая платформа движется          вниз,  а  левая  –  вверх.  Для  определения  ускорения  платформ

необходимо  измерить  время  прохождения  платформами  некоторого расстояния. С этой целью лабораторная работа снабжена электронным секундомером,   который    запускается   и    останавливается        по    команде

фотодатчиков 5 и 6. Когда правая платформа проходит мимо фотодатчика 6, секундомер запускается, когда платформа проходит мимо фотодатчика 5, секундомер  останавливается.  Таким   образом,   время,   которое   показывает

секундомер, есть время движения правой платформы от верхнего фотодатчика до нижнего. Расстояние между фотодатчиками измеряется с помощью мерной линейки 3, расположенной за установкой.

1

6

4          4

3

2

5

Рис. 2.2. Машина Атвуда

В исходном состоянии левая платформа касается магнита 2 и удерживается его магнитным полем. При выключении магнита обе платформы начинают   движение.   Для   определения   ускорения   платформ   необходимо

измерить:  1)  расстояние от  нижнего  конца  правой  платформы до  верхнего фотодатчика в исходном состоянии платформ, обозначим его s1 ; 2) расстояние

между фотодатчиками,         обозначим      его

платформы между фотодатчиками.

s2 ;       3)         время  движения       t           левой

Обозначим время движения платформы от начальной точки до первого

фотодатчика

t1 , время движения платформы до второго фотодатчика обозначим t2 .

Тогда можно записать следующие кинематические уравнения:

t 2

s  = a  1   , s

1          2          2

t 2

= a  2   .           (2.26)

2

В этих формулах три неизвестных:

t1 , t2 , g . При этом уравнений только

два. Однако можно использовать ещё тот факт, что разность времени полёта шарика до второго и первого фотодатчиков равна показаниям секундомера t :

t2  − t1  = t .  (2.27)

Выразим из первого уравнения системы (2.26) первое время из второго –

второе и подставим в (2.27):

t1 =

2s1 , t  =

a          2

2s2  .    (2.28)

a

2s2   −

a

2s1

a

= t .      (2.29)

В результате получаем одно уравнение с одним неизвестным. Из него легко найти ускорение платформ:

a = 2

( s  −

t 2

s  )2

.           (2.30)

3. Задания

1. Исследовать зависимость ускорения платформ от действующей силы.

Для      этого  согласно  формуле  (2. 25)  необходимо  изменять  разность  масс платформ, не меняя их сумму. Исследование состоит из двух экспериментов. В

первом эксперименте на платформы устанавливают перегрузки такие, чтобы масса правой платформы была или на немного (3-5 г) больше массы левой платформы.  Выполняют  эксперимент  по  измерению  ускорения  платформ.

Причём выполняется эксперимент три раза для увеличения точности. Данные заносят в табл.:

№	mл	mпр	s1	s2	t	a
1
2
3

По результатам последней колонки найти среднее значение ускорения и

погрешность.

Во       втором            эксперименте            оба      перегрузка     устанавливают          на        правую платформу. В этом случае ускоряющая сила становится больше, а общая масса

обеих  платформ       остаётся          неизменной.  Снова проводят        эксперимент  и заполняют таблицу, подобную предыдущей.

Проверяют отношение среднего значения ускорений во втором эксперименте к среднему значению ускорения в первом эксперименте. Оно должно быть равно в пределах погрешности отношению суммы масс перегрузков к разности их масс.

2. Исследовать зависимость ускорения платформ от их масс при одинаковой силе.  Для  этого  снова  выполняют два  эксперимента. В  первом

эксперименте на платформы устанавливают перегрузки такой массы, чтобы масса правой платформы была на немного (3-5 г) больше массы левой платформы.  Выполняют  эксперимент  с  заполнением  табл.  и  отысканием

среднего значения ускорения платформ.

Во втором эксперименте на каждую платформу добавляют по одинаковому перегрузку. Тем самым суммарная масса платформ возрастает, а

их разность остаётся неизменной. Снова выполняют эксперимент, заполняют таблицу и находят среднее значение ускорения.

Проверяют отношение ускорения в первом эксперименте к ускорению

платформ во втором эксперименте. Это отношение должно быть равно отношению массы платформ во втором эксперименте к массе платформ в первом  эксперименте.  При  этом  для  отыскания  отношения  масс  платформ нужно к массам перегрузков добавить массы самих платформ.

Равенство этих двух отношений должно быть верным в пределах погрешности эксперимента.

3. По результатам предыдущих заданий сделать вывод о справедливости второго закона Ньютона.

Вопросы для отчёта

1. Сформулировать законы механики Ньютона.

2. Что называется инерциальной системой отсчёта?

3. Как влияет на результаты эксперимента трение в блоке?

4. Вывести формулу натяжения нитей в эксперименте. Выяснить, от чего зависит натяжение нитей.

Материал взят из Методические указания к выполнению лабораторных работ по механике для студентов направления 010000 «Физико-математические науки» (А. С. Парахин)

Концепция системы – Колледж физики, главы 1-17

4 Динамика: сила и законы движения Ньютона

Резюме

• Определить результирующую силу, внешнюю силу и систему.
• Поймите второй закон движения Ньютона.
• Примените второй закон Ньютона для определения веса объекта.

Второй закон движения Ньютона тесно связан с первым законом движения Ньютона. Он математически устанавливает причинно-следственную связь между силой и изменениями в движении. Второй закон Ньютона носит более количественный характер и широко используется для расчета того, что происходит в ситуациях, связанных с силой. Прежде чем мы сможем записать второй закон Ньютона в виде простого уравнения, определяющего точное соотношение между силой, массой и ускорением, нам нужно уточнить некоторые уже упомянутые идеи.

Во-первых, что мы подразумеваем под изменением движения? Ответ заключается в том, что изменение движения эквивалентно изменению скорости. Изменение скорости по определению означает наличие ускорений . Первый закон Ньютона гласит, что результирующая внешняя сила вызывает изменение движения; таким образом, мы видим, что суммарная внешняя сила вызывает ускорение .

Сразу возникает другой вопрос. Что мы понимаем под внешней силой? Интуитивное представление о внешнем верно — внешняя сила действует снаружи системы интереса. Например, на рис. 1(а) интересующей нас системой является повозка плюс ребенок в ней. Две силы, действующие со стороны других детей, являются внешними силами. Между элементами системы действует внутренняя сила. Снова взглянув на рисунок 1 (а), сила, которую ребенок в тележке прилагает, чтобы повиснуть на тележке, является внутренней силой между элементами интересующей системы. Только внешние силы влияют на движение системы в соответствии с первым законом Ньютона. (Внутренние силы на самом деле компенсируются, как мы увидим в следующем разделе. ) Вы должны определить границы системы, прежде чем сможете определить, какие силы являются внешними . Иногда система очевидна, тогда как в других случаях определение границ системы является более тонким. Понятие системы является фундаментальным для многих областей физики, как и правильное применение законов Ньютона. К этой концепции мы будем возвращаться много раз в нашем путешествии по физике.

Рисунок 1. Различные силы, действующие на одну и ту же массу, вызывают различные ускорения. а) Двое детей толкают тележку с ребенком. Показаны стрелки, представляющие все внешние силы. Система интереса — это повозка и ее всадник. Вес w системы и опоры грунта N также показаны для полноты и считаются отменяемыми. Вектор f представляет трение, действующее на вагон, и он действует слева, противодействуя движению вагона. (b) Все внешние силы, действующие на систему, складываются вместе, образуя результирующую силу F ​​ _net . Диаграмма свободного тела показывает все силы, действующие на интересующую систему. Точка представляет собой центр масс системы. Каждый вектор силы простирается от этой точки. Поскольку справа действуют две силы, мы рисуем векторы коллинеарно. (c) Большая результирующая внешняя сила производит большее ускорение ( a’>a ), когда взрослый толкает ребенка.

Теперь кажется разумным, что ускорение должно быть прямо пропорционально и иметь то же направление, что и чистая (полная) внешняя сила, действующая на систему. Это предположение было подтверждено экспериментально и показано на рис. 1. В части (а) меньшая сила вызывает меньшее ускорение, чем большая сила, показанная в части (в). Для полноты показаны также вертикальные силы; предполагается, что они компенсируются, поскольку ускорение в вертикальном направлении отсутствует. Вертикальные силы — это вес[латекс]\textbf{w}[/латекс]и поддержка земли[латекс]\текстбф{N},[/латекс]и горизонтальная сила[латекс]\текстбф{ф}[ /латекс] представляет собой силу трения.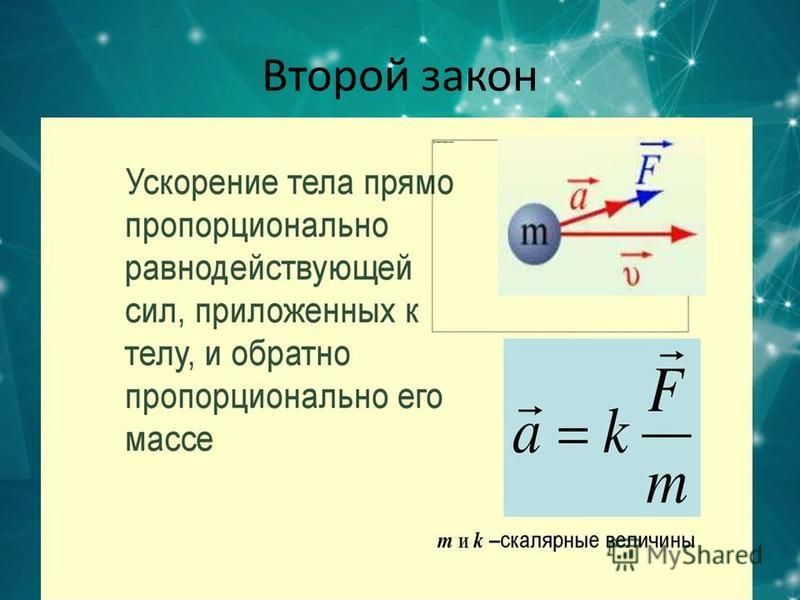 Они будут обсуждаться более подробно в последующих разделах. Сейчас мы определим трение как силу, противодействующую движению соприкасающихся объектов относительно друг друга. На рис. 1(b) показано, как векторы, представляющие внешние силы, складываются вместе, чтобы получить результирующую силу,[latex]\textbf{F}_{\textbf{net}}.[/latex]

Чтобы получить уравнение для второго закона Ньютона, мы сначала запишем отношение ускорения и чистой внешней силы в виде пропорциональности

[латекс]\boldsymbol{\textbf{a}\propto\textbf{F}_{\textbf{net}}},[/latex]

, где символ [латекс]\жирныйсимвол{\пропто}[/латекс]означает «пропорциональный», а[латекс]\текстбф{Ф}_{\текстбф{нет}}[/латекс]является чистой внешней силой. (Чистая внешняя сила представляет собой векторную сумму всех внешних сил и может быть определена графически, используя метод «голова к хвосту», или аналитически, используя компоненты. Методы такие же, как и для добавления других векторов, и рассматриваются в главе 3 «Двумерная кинематика». ) Эта пропорциональность выражает то, что мы сказали словами — ускорение прямо пропорционально чистой внешней силе . После выбора интересующей системы важно определить внешние силы и игнорировать внутренние. Не учитывать многочисленные внутренние силы, действующие между объектами внутри системы, такие как мышечные силы в теле ребенка, не говоря уже о бесчисленных силах между атомами в объектах, — это огромное упрощение, но, делая это, мы можем легко решить некоторые очень сложные задачи с минимальной ошибкой благодаря нашему упрощению

Теперь также кажется разумным, что ускорение должно быть обратно пропорционально массе системы. Другими словами, чем больше масса (инерция), тем меньше ускорение, создаваемое данной силой. И действительно, как показано на рис. 2, та же внешняя сила, приложенная к автомобилю, создает гораздо меньшее ускорение, чем при приложении к баскетбольному мячу. Пропорциональность записывается как

[латекс]\boldsymbol{\textbf{a}\:\propto}[/latex][латекс]\boldsymbol{\frac{1}{m}}[/latex]

, где[латекс]\boldsymbol{m}[/латекс] — масса системы. Эксперименты показали, что ускорение точно обратно пропорционально массе, точно так же, как оно точно линейно пропорционально суммарной внешней силе.

Рис. 2. Одна и та же сила, действующая на системы с разной массой, дает разные ускорения. а) Баскетболист толкает мяч, чтобы сделать передачу. (Влияние силы тяжести на мяч игнорируется.) (b) Тот же игрок прикладывает такую ​​же силу к заглохшему внедорожнику и создает гораздо меньшее ускорение (даже если трением можно пренебречь). (c) Диаграммы свободного тела идентичны, что позволяет проводить прямое сравнение двух ситуаций. Ряд паттернов для диаграммы свободного тела появится по мере того, как вы будете решать больше задач.

Было обнаружено, что ускорение объекта зависит только от чистой внешней силы и массы объекта. Объединение двух только что приведенных пропорций дает второй закон движения Ньютона.

ВТОРОЙ ЗАКОН НЬЮТОНА ДВИЖЕНИЯ

Ускорение системы прямо пропорционально внешней силе, действующей на систему, и направлено в том же направлении, что и обратно пропорционально ее массе.

В форме уравнения второй закон Ньютона равен

[латекс]\boldsymbol{\textbf{a}\:=}[/latex][латекс]\boldsymbol{\frac{\textbf{F}_{\textbf{net}}}{m}}.[ /latex]

Это часто записывается в более знакомой форме

[латекс]\boldsymbol{\textbf{F}_{\textbf{net}}=m}\textbf{a}.[/latex]

Когда учитываются только величина силы и ускорения, это уравнение выглядит просто как

[латекс]\boldsymbol{F _{\textbf{net}}=ma}.[/latex]

Хотя последние два уравнения на самом деле одинаковы, первое дает более полное представление о том, что означает второй закон Ньютона. Закон причинно-следственная связь между тремя величинами, которая не просто основана на их определениях. Справедливость второго закона полностью основана на экспериментальной проверке.

[латекс]\boldsymbol{\textbf{F}_{\textbf{net}}=m}\textbf{a}[/latex] используется для определения единиц силы с точки зрения трех основных единиц массы, длина и время. Единица силы СИ называется ньютон (сокращенно Н) и представляет собой силу, необходимую для ускорения системы массой 1 кг со скоростью[латекс]\boldsymbol{1\textbf{ м/с}^2}. [/латекс ] То есть [латекс]\boldsymbol{\textbf{F}_{\textbf{net}}=m}\textbf{a},[/latex] 92}.[/латекс]

В то время как почти во всем мире в качестве единицы силы используется ньютон, в Соединенных Штатах наиболее распространенной единицей силы является фунт (фунт), где 1 Н = 0,225 фунта.

Когда объект падает, он ускоряется к центру Земли. Второй закон Ньютона гласит, что результирующая сила, действующая на объект, отвечает за его ускорение. Если сопротивлением воздуха можно пренебречь, результирующая сила, действующая на падающий объект, представляет собой гравитационную силу, обычно называемую его весом [латекс]\textbf{w}.[/latex]Вес можно обозначить как вектор[латекс]\текстбф{ w}[/latex]потому что у него есть направление; вниз — это, по определению, направление силы тяжести, и, следовательно, вес — это направленная вниз сила. Величина веса обозначается как[latex]\boldsymbol{w}.[/latex]Галилей сыграл важную роль в демонстрации того, что в отсутствие сопротивления воздуха все объекты падают с одинаковым ускорением[latex]\boldsymbol{g}. [/latex]Используя результат Галилея и второй закон Ньютона, мы можем вывести уравнение для веса.

Рассмотрим объект с массой[латекс]\жирныйсимвол{м}[/латекс], падающий вниз к Земле. На него действует только нисходящая сила тяжести, которая имеет величину[latex]\boldsymbol{w}.[/latex]Второй закон Ньютона гласит, что величина чистой внешней силы, действующей на объект, равна[latex]\boldsymbol{F_{\ textbf{net}}=ma}.[/latex]

Поскольку на объект действует только направленная вниз сила тяжести,[латекс]\boldsymbol{F_{\textbf{net}}=w}.[/latex]Мы знаем, что ускорение объекта под действием силы тяжести равно[латекс]\ boldsymbol{g},[/latex]или[latex]\boldsymbol{a=g}.[/latex]Подстановка их во второй закон Ньютона дает

ВЕС

Это уравнение для веса —силы гравитации на массу[латекс]\boldsymbol{m}:[/latex]

[латекс]\boldsymbol{w=mg}.[/latex]

Поскольку[латекс]\boldsymbol{g=92)=9.8\textbf{ N}.}[/latex]

Напомним, что [latex]\boldsymbol{g}[/latex] может принимать положительное или отрицательное значение в зависимости от положительного направления в системе координат. Обязательно учитывайте это при решении задач с весом.

Когда чистая внешняя сила, действующая на объект, равна его весу, мы говорим, что он находится в свободном падении . То есть единственная сила, действующая на объект, — это сила тяжести. В реальном мире, когда объекты падают вниз к Земле, они никогда не находятся в состоянии свободного падения, потому что на объект всегда действует восходящая сила воздуха. 92}.[/latex] Таким образом, масса в 1,0 кг имеет вес 9,8 Н на Земле и всего около 1,7 Н на Луне.

Самое широкое определение веса в этом смысле состоит в том, что вес объекта есть гравитационная сила, действующая на него со стороны ближайшего крупного тела , такого как Земля, Луна, Солнце и так далее. Это наиболее распространенное и полезное определение веса в физике. Однако оно резко отличается от определения веса, используемого НАСА и популярными средствами массовой информации в связи с космическими путешествиями и исследованиями. Когда они говорят о «невесомости» и «микрогравитации», они на самом деле имеют в виду явление, которое в физике называется «свободным падением». Мы воспользуемся приведенным выше определением веса и проведем тщательное различие между свободным падением и фактической невесомостью.

Важно знать, что вес и масса — очень разные физические величины, хотя и тесно связанные между собой. Масса — это количество материи (сколько «вещества») и не меняется в классической физике, тогда как вес — это гравитационная сила, которая зависит от гравитации. Заманчиво приравнять их, поскольку большинство наших примеров происходят на Земле, где вес объекта лишь немного зависит от местоположения объекта. Кроме того, члены масса и веса используются взаимозаменяемо в повседневном языке; например, наши медицинские записи часто показывают наш «вес» в килограммах, но никогда в правильных единицах измерения — ньютонах.

РАСПРОСТРАНЕННЫЕ ЗАБЛУЖДЕНИЯ: МАССА ПРОТИВ. ВЕС

Масса и вес часто используются как синонимы в повседневном языке. Однако в науке эти термины резко отличаются друг от друга. Масса — это мера того, сколько материи содержится в объекте. Типичной мерой массы является килограмм (или «слаг» в английских единицах измерения). Вес, с другой стороны, является мерой силы тяжести, действующей на объект. Вес равен массе объекта ([latex]\boldsymbol{m}[/latex]), умноженной на ускорение свободного падения ([latex]\boldsymbol{g}[/latex]). Как и любая другая сила, вес измеряется в ньютонах (или фунтах в английских единицах измерения). 92}[/латекс]). Если вы измерите свой вес на Земле, а затем измерите свой вес на Луне, вы обнаружите, что «весите» намного меньше, даже если вы не выглядите стройнее. Это связано с тем, что на Луне сила гравитации слабее. На самом деле, когда люди говорят, что они «худеют», они на самом деле имеют в виду, что теряют «массу» (что, в свою очередь, заставляет их весить меньше).

ЭКСПЕРИМЕНТ НА ​​ДОМАШНИЙ КОНТРОЛЬ: МАССА И ВЕС

Что измеряют напольные весы? Когда вы встаете на напольные весы, что происходит с весами? Это слегка угнетает. Весы содержат пружины, которые сжимаются пропорционально вашему весу, подобно резиновым лентам, которые растягиваются при натяжении. Пружины обеспечивают меру вашего веса (для объекта, который не ускоряется). Это сила в ньютонах (или фунтах). В большинстве стран измерение делится на 9.80, чтобы дать показание в единицах массы килограммов. Весы измеряют вес, но откалиброваны для предоставления информации о массе. Стоя на весах в ванной, нажмите на стол рядом с вами. Что происходит с чтением? Почему? Измерят ли ваши весы ту же «массу» на Земле, что и на Луне?

 

Пример 1. Какое ускорение может создать человек, толкая газонокосилку?

Предположим, что чистая внешняя сила (толчок минус трение), действующая на газонокосилку, равна 51 Н (около 11 фунтов) параллельно земле. Масса косилки 24 кг. Каково его ускорение ?

Рис. 3. Чистая сила, действующая на газонокосилку, составляет 51 Н вправо. С какой скоростью газонокосилка ускоряется вправо?

Стратегия

Поскольку даны [латекс]\textbf{F}_{\textbf{net}}[/latex] и [латекс]\boldsymbol{m}[/latex], ускорение можно рассчитать непосредственно из Второй закон Ньютона, как указано в [latex]\boldsymbol{\textbf{F}_{\textbf{net}}=m\textbf{a}}. [/latex]

Решение

Величина ускорения [latex]\boldsymbol{a}[/latex]is[latex]\boldsymbol{a=\frac{F_{\textbf{net}}}{m}}.[/latex]Ввод известных значений дает 92.}[/latex]

Обсуждение

Направление ускорения совпадает с направлением чистой силы, которая параллельна земле. В этом примере нет информации об отдельных внешних силах, действующих на систему, но мы можем кое-что сказать об их относительных величинах. Например, сила, действующая на человека, толкающего косилку, должна быть больше, чем трение, противодействующее движению (поскольку мы знаем, что косилка движется вперед), а вертикальные силы должны уравновешиваться, если не должно быть ускорения в вертикальном направлении (ускорение в вертикальном направлении). косилка движется только горизонтально). Найденное ускорение достаточно мало, чтобы быть приемлемым для человека, толкающего косилку. Такое усилие не продлится слишком долго, потому что человек скоро достигнет максимальной скорости.

Пример 2: Какая реактивная тяга ускоряет эти сани?

До пилотируемых космических полетов ракетные салазки использовались для испытаний самолетов, ракетного оборудования и физиологических воздействий на людей на высоких скоростях. Они состояли из платформы, установленной на одном или двух рельсах и приводившейся в движение несколькими ракетами. Рассчитайте величину силы, действующей на каждую ракету, называемую ее тягой[latex]\textbf{T},[/latex]для четырехракетной силовой установки, показанной на рис. 4. Начальное ускорение саней равно[latex]\boldsymbol{492},[/latex]масса системы 2100 кг, а сила трения, противодействующая движению, известна как 650 Н.

Рис. 4. Сани испытывают реактивную тягу, которая ускоряет их вправо. Каждая ракета создает идентичную тягу Т . Как и в других ситуациях, когда есть только горизонтальное ускорение, вертикальные силы компенсируются. Земля воздействует на систему направленной вверх силой Н , равной по модулю и противоположной по направлению ее весу, w . Система здесь — это сани, их ракеты и всадник, поэтому никакие силы между этими объектами не учитываются. Стрелка, обозначающая трение ( f ), нарисована больше масштаба.

Стратегия

Хотя существуют силы, действующие вертикально и горизонтально, мы предполагаем, что вертикальные силы компенсируются, поскольку нет вертикального ускорения. Это оставляет нам только горизонтальные силы и более простую одномерную задачу. Направления обозначаются знаками плюс или минус, где право считается положительным направлением. См. диаграмму свободного тела на рисунке.

Решение

Поскольку ускорение, масса и сила трения известны, начнем со второго закона Ньютона и будем искать способы найти тягу двигателей. Поскольку мы определили направление силы и ускорения как действующие «вправо», нам нужно учитывать в расчетах только величины этих величин. Следовательно, мы начинаем с

[латекс]\boldsymbol{F_{\textbf{net}}=ma},[/latex]

, где[латекс]\boldsymbol{F_{\textbf{net}}}[/latex] net – чистая сила в горизонтальном направлении. Из рис. 4 видно, что тяга двигателя добавляется, а трение противодействует тяге. В форме уравнения чистая внешняя сила равна 94\textbf{ N}}.[/latex]

Обсуждение

Цифры довольно большие, поэтому результат может вас удивить. Подобные эксперименты проводились в начале 1960-х годов для проверки пределов человеческой выносливости и установки, предназначенной для защиты людей при аварийном катапультировании реактивного истребителя. Были получены скорости 1000 км/ч, с ускорениями 45 г с. (Напомним, что[latex]\boldsymbol{g},[/latex]ускорение свободного падения равно[latex]\boldsymbol{92}[/latex].) Хотя живые объекты больше не используются, на ракетных салазках была получена наземная скорость 10 000 км/ч. В этом примере, как и в предыдущем, интересующая система очевидна. В последующих примерах мы увидим, что выбор интересующей системы имеет решающее значение, и этот выбор не всегда очевиден.

Второй закон движения Ньютона — это больше, чем определение; это отношение между ускорением, силой и массой. Это может помочь нам делать прогнозы. Каждая из этих физических величин может быть определена независимо, поэтому второй закон говорит нам нечто основное и универсальное о природе. В следующем разделе представлен третий и последний закон движения.

 

Резюме раздела

 

Глоссарий

ускорение

скорость, с которой скорость объекта изменяется в течение определенного периода времени

свободное падение

ситуация, в которой единственной силой, действующей на объект, является сила тяжести

трение

сила, приложенная друг к другу соприкасающимися объектами; примеры включают шероховатые поверхности и сопротивление воздуха 90 266

чистая внешняя сила

векторная сумма всех внешних сил, действующих на объект или систему; заставляет массу ускоряться

Второй закон Ньютона

результирующая внешняя сила[латекс]\boldsymbol{F_{\textbf{net}}}[/latex]действующая на объекте с массой[латекс]\boldsymbol{m}[/latex] пропорциональна и действует в том же направлении, что и ускорение объекта,[latex]\textbf{a},[/latex]и обратно пропорциональное массе; определяется математически как [латекс]\boldsymbol{\textbf{a}=\frac{F_{\textbf{net}}}{m}}[/latex]

система

определяется границами объекта или набора наблюдаемых объектов; все силы, исходящие извне системы, считаются внешними силами

вес

сила[латекс]\textbf{w}[/латекс], обусловленная гравитацией, действующая на объект массы[латекс]\жирныйсимвол{м};[/латекс], определяемый математически как:[латекс]\жирныйсимвол{\текстбф{ w}=m\textbf{g}},[/latex]где[latex]\textbf{g}[/latex]является величиной и направлением ускорения свободного падения

 

Сила и масса – Гиперучебник по физике

[закрыть]

введение

Обсудить…

• разные силы на один и тот же объект (результат?)
• различных объектов с одинаковыми силами (результат?)
• разных объектов с одинаковым ускорением (как?)

Последствия…

Второй закон движения Ньютона гласит, что ускорение прямо пропорционально результирующей силе, когда масса постоянна…

и  ∝	∑ Ф

и что ускорение обратно пропорционально массе, когда результирующая сила постоянна…

и  ∝	1
	м

и что результирующая сила прямо пропорциональна массе при постоянном ускорении…

∑ Ф ∝	м

Более компактно это можно записать как уравнение, объединяющее эти отношения…

и  =	∑ Ф
	м

По разным причинам Второй закон Ньютона движения часто записывается с результирующей силой как предметом уравнения, подобного этому…

∑ F  =  м a

история

Лекс. II.		Закон II.
Пропорциональная мутация esse vi motrici impreſſæ, & fieri secundum lineaum rectam qua vis illa imprimitur.		Изменение движения всегда пропорционально приложенной движущей силе; и производится в направлении правой линии, по которой действует эта сила.
Si vis aliqua motum quemvis generet; dupla duplum, tripla triplum generabit, sive simul & semel, sive gradatim & succeſsive impreſsa fuerit. Ethic motus quoniam in eandem semper plagam cum vi generatrice determinatur, ſi corpus antea movebatur, motui ejus vel conspiranti additur, vel contrario subducitur, vel obliquo oblique adjicitur, & cum eo secundum utriusque Definitionem componitur.		Если какая-либо сила вызывает движение, то двойная сила вызовет двойное движение, тройная сила утроит движение, независимо от того, действует ли эта сила сразу и сразу или постепенно и последовательно. И так как это движение всегда направлено одним и тем же путем с порождающей силой, то, если тело двигалось раньше, оно прибавляется к прежнему движению или убавляется от него в зависимости от того, прямо совпадают ли они или прямо противоположны друг другу; или косо соединены, когда они наклонны, чтобы произвести новое движение, составленное из определения того и другого.

Ньютон также определил то, что он называл «количеством материи» и «количеством движения». Теперь мы называем их «массой» и «импульсом» соответственно.

Определение. И.		Определение I.
Quantitas materiæ est mensura ejusdem orta ex illius densitate et magnitudine conjunctim.		Количество материи есть ее мера, возникающая из ее плотности и объема одновременно.
Aer densitate duplicata, in spatio etiam duplicato, sit quadruplus; в трипликато секступлюс. Idem intelige de nive & pulveribus для сжатия и сжижения конденсата. Et par eft ratio corporum omnium, quae per caufas quascunque diversimode pendantur. Medii interea, si quod fuerit, interstitia partium libere pervadentis, hic nullam rationem habeo. Hanc autem quantitatem sub nomine corporis vel masse in sequentibus passim intelligo. Innotescit ea per corporis cujusque pondus: Nam ponderi пропорциональна esse reperi per Experimenta pendulorum accuratissime instituta, uti posthac docebitur.		Таким образом, воздух двойной плотности в двойном пространстве имеет учетверенное количество; в тройном пространстве, шестикратном количестве. То же самое следует понимать о снеге и тонкой пыли или порошках, которые сгущаются при сжатии или разжижении; и всех тел, которые чем-либо вызваны чем-либо, иначе сгущенным. В данном случае я не имею никакого отношения к медиуму, если таковой существует, который свободно проникает в промежутки между частями тела. Именно это количество я буду в дальнейшем подразумевать под названием тела или массы. И то же самое познается по весу каждого тела; ибо он пропорционален весу, как я обнаружил опытами на очень точно сделанных маятниках, что будет показано ниже.
Определение. II.		Определение II.
Quantitas motus est mensura ejusdem orta ex velocitate et quantite materiæ conjunctim.		Количество движения есть мера того же самого, возникающая из скорости и количества материи одновременно.
Motus totius est summa motuum in partibus singulis; ideoque in corpore duplo majore, æ quali cum velocitate, duplus est и dupla cum velocitate quadruplus.		Движение целого есть сумма движений всех частей; и поэтому в теле, удвоенном по количеству, с одинаковой скоростью движение двойное; с удвоенной скоростью – вчетверо.

Так что же такое масса?

1. выбрать объект, который будет стандартной единицей массы
2. толкать массу с воспроизводимой силой (или использовать принцип действия-противодействия)
3. измерить его ускорение
4. толкнуть неизвестную массу с той же силой
5. измерить новое ускорение
Масса
6. обратно пропорциональна ускорению

Масса …

• Масса является мерой сопротивления ускорению.
  (В более общем смысле масса является мерой сопротивления изменениям.)
• Масса — это скалярная величина, связанная с материей.
• Когда система состоит из нескольких объектов, важна их общая масса.
• Единицей массы в системе СИ является килограмм [кг].

Масса выбранных объектов

масса (кг)		объект
~10 53		наблюдаемая вселенная
~10 42		Млечный Путь
8	× 10 40	самая большая черная дыра (S5 0014+81)
6	× 10 32	самая массивная звезда (R136a1)
2	× 10 31	самая маленькая черная дыра (XTE J1650−500)
2,8~6	× 10 30	нейтронная звезда
1,99	× 10 30	Вс
1,90	× 10 27	Юпитер
5,97	× 10 24	Земля
6,42	× 10 23	Марс
7,35	× 10 22	Луна
1,31	× 10 22	Плутон
1,35	× 10  21	Гидросфера Земли
5. 14	× 10 18	Атмосфера Земли
1,84	× 10 15	Биосфера Земли
~150 000		синий кит
~5000		Африканский слон
~1750		легковой автомобиль
635		самый тяжелый человек в мире
100		автор
7,72		самая маленькая женщина в мире
3~7		шар для боулинга
0,16		бильярдный шар
~3	× 10 −6	снежинка
2,18	× 10 −8	Планковская масса
~10 −12		бактерия
~10 −15		вирус
3,9529264	× 10 −25	050788423 u”> уран 238 атом
3.0784789	× 10 −25	высший кварк
1,6749275	× 10 −27	нейтрон
1,6735328	× 10 −27	водород 1 атом
1.6726219	× 10 −27	протон
9.1093837	× 10 −31	нейтрино (верхний предел)
<1,8	× 10 −54	фотон (верхний предел)

Так что же такое сила?

Сила …

• Сила — это взаимодействие, вызывающее ускорение. В более общем смысле сила — это взаимодействие, вызывающее изменение.
• Сила — это векторная величина, связанная с взаимодействием.
• Когда на систему действует несколько сил, значение имеет чистая внешняя сила. Поскольку сила является векторной величиной, при объединении сил используйте геометрию вместо арифметики.
• Чтобы сила ускоряла объект, она должна исходить извне. Внешняя сила. Не могу подтягиваться за свои собственные бутсы. Любой, кто говорит, что вы можете, занимается гиперболой.
• Единицей силы в системе СИ является ньютон [Н = кг м/с ² ]. Эмпирическое правило: один ньютон примерно равен четверти фунта
.

Выбранные силы (от меньшего к большему)

усилие (Н)	устройство, событие, явление, процесс
10 −14	силы Ланжевена броуновского движения
10 −11	молекулярных моторов, потребляющих АТФ
10 −10	разрыв нековалентных связей (денатурация белков)
10 −09	разрыв ковалентных связей
10 −06	сила адгезии бактерий
0,032	порог осязания; указательный, средний, мизинец
0,044	порог осязания; безымянный палец
4,436–4,460	вес 1 фунт на Земле
4,448 22	вес 1 фунт в стандартной гравитации
9,780–9,832	вес 1 кг на Земле
9,806 65	вес 1 кг в стандартной гравитации
32	Поршень для френч-пресса
256	средний укус собаки
980	вес автора
2 200	пиковая сила стопы, человек 75 кг, бег
140 000	пиковое усилие стопы, азиатский слон весом 10 000 кг, бег

Концепция инерции существует во многих формах.