Формула высоты в физике: как найти высоту в физике (формула)

Все формулы по физике за 7 класс с пояснениями — таблица и шпаргалки

Шпаргалки по физике за 7 класс

В рамках одной статьи сложно охватить весь курс по физике, но мы осветили основные темы за 7 класс и этого достаточно, чтобы освежить знания в памяти. Скачайте и распечатайте обе шпаргалки — одна из них (подробная) пригодится для вдумчивой подготовки к ОГЭ и ЕГЭ, а вторая (краткая) послужит для решения задач.

Скачать PDF со всеми формулами и определениями по физике за 7 класс.

Скачать PDF со всеми формулами и определениями по физике за 7 класс (мелко на одной странице).

Для тех, кто находится на домашнем обучении или вынужден самостоятельно изучать материал ввиду пропусков по болезни, рекомендуем также учебник по физике А. В. Перышкина с формулами за 7 класс и легкими, доступными пояснениями по всем темам. Он был написан несколько десятилетий назад, но до сих пор очень популярен и востребован.

Измерение физических величин

Измерением называют определение с помощью инструментов и технических средств числового значения физической величины. Результат измерения сравнивают с неким эталоном, принятым за единицу. В итоге значением физической величины считается полученное число с указанием единиц измерения.

В курсе по физике за 7 класс изучают правила измерений с использованием приборов со шкалой. Если цена деления шкалы неизвестна, узнать ее можно с помощью следующей формулы:

ЦД = (max − min) / n, где ЦД — цена деления, max — максимальное значение шкалы, min — минимальное значение шкалы, n — количество делений между ними.

Вместо максимального и минимального можно взять любые другие значения шкалы, числовое выражение которых нам известно.

Выделяют прямое и косвенное измерение:

• при прямом измерении результат можно увидеть непосредственно на шкале инструмента;

• при косвенном измерении значение величины вычисляется через другую величину (например, среднюю скорость определяют на основе нескольких замеров скорости).

Для удобства и стандартизации измерений в 1963 году была принята Международная система единиц СИ. Она регламентирует, какие единицы измерения считать основными и использовать для формул. Обозначения этих единиц также учат в программе по физике за 7 класс.

Механическое движение: формулы за 7 класс

Механическое движение — перемещение тела в пространстве, в результате которого оно меняет свое положение относительно других тел. Закономерности такого движения изучают в рамках механики и конкретно ее раздела — кинематики.

Для того, чтобы описать движение, требуется тело отсчета, система координат, а также инструмент для измерения времени. Это составляющие системы отсчета.

Изучение механического движения в курсе по физике за 7 класс включает следующие термины:

• Перемещение тела — вектор, проведенный из начальной точки в конечную.

• Траектория движения — мысленная линия, вдоль которой перемещается тело.

• Путь — длина траектории тела от начальной до конечной точки.

• Скорость — быстрота перемещения тела или отношение пройденного им пути ко времени прохождения.

• Ускорение — быстрота изменения скорости, с которой движется тело.

Равномерное прямолинейное движение означает, что тело движется вдоль прямой с одинаковой скоростью. В таком случае перемещение тела и его путь будут равны.

Формула скорости равномерного прямолинейного движения:

V = S / t, где S — путь тела, t — время, за которое этот путь пройден.

Формула скорости равномерного криволинейного движения:

где S₁ и S₂ — отрезки пути, а t₁ и t₂ — время, за которое был пройден каждый из них.

Единица измерения скорости в СИ: метр в секунду (м/с).

Формула скорости равноускоренного движения:

V = V₀ + at, где V₀— начальная скорость, а — ускорение.

Единица измерения ускорения в СИ: м/с².

Сила тяжести, вес, масса, плотность

Формулы, понятия и определения, описывающие эти физические характеристики, изучают в 7 классе в рамках такого раздела физики, как динамика.

Вес тела или вещества — это векторная величина, которая характеризует, с какой силой оно действует на горизонтальную поверхность или вертикальный подвес. Не следует путать эту величину с массой, которая является скалярной величиной.

Вес тела измеряется в ньютонах, масса тела — в граммах и килограммах.

Формула веса:

P = mg, где m — масса тела, g — ускорение свободного падения.

Ускорение свободного падения возникает под действием силы тяжести, которой подвержены все находящиеся на нашей планете тела.

g = 9,806 65 м/с² или 9,8 Н/кг

Если тело находится в покое или в прямолинейном равномерном движении, его вес равен силе тяжести.

F_тяж = mg

Но эти понятия нельзя отождествлять: сила тяжести действует на тело ввиду наличия гравитации, в то время как вес — это сила, с которой само тело действует на поверхность.

Плотность тела или вещества – величина, указывающая на то, какую массу имеет данное вещество, занимая единицу объема. Плотность прямо пропорциональна массе и обратно пропорциональна объему.

Формула плотности:

ρ = m / V, где m — масса тела или вещества, V — занимаемый объем.

Единица измерения плотности в СИ: кг/м³.

Механический рычаг, момент силы

О механическом рычаге говорил еще Архимед, когда обещал перевернуть Землю, если только найдется подходящая точка опоры.

Это простой механизм, который помогает поднимать грузы, закрепленные на одном его конце, прилагая силу к другому концу. При этом вес груза намного превосходит прилагаемое усилие. В 7 классе физические формулы, описывающие этот процесс, изучаются в том же разделе динамики.

Рычаг — это некое твердое тело, способное вращаться вокруг неподвижной точки опоры, на один конец которого действует сила, а на другом находится груз. Перпендикуляр, проведенный от точки опоры до линии действия силы, называется плечом силы.

Рычаг находится в равновесии, если произведение силы на плечо с одной его стороны равно произведению силы на плечо с другой стороны.

Уравнение равновесия рычага:

F₁ × l₁ = F₂ × l₂

Из этого следует, что рычаг уравновешен, когда модули приложенных к его концам сил обратно пропорциональны плечам этих сил.

Момент силы — это векторная величина, числовую характеристику которой можно описать как произведение модуля силы на плечо.

Формула момента силы:

M = F × l, где F — модуль силы, l — длина плеча.

Единица измерения момента силы в СИ: ньютон-метр (Н·м).

Эта формула верна, если сила приложена перпендикулярно оси рычага. Если же она прилагается под углом, такой случай выходит за рамки курса физики за 7 класс и подробно изучается в 9 классе.

Правило моментов: рычаг уравновешен, если сумма всех моментов сил, которые поворачивают его по часовой стрелке, равна сумме всех моментов сил, которые поворачивают его в обратном направлении.

Можно сказать иначе: рычаг в равновесии, если сумма моментов всех приложенных к нему сил относительно любой оси равна нулю.

М₁ + М₂ + М_n + … = 0

Давление, сила давления

Прилагая одну и ту же силу к предмету, можно получить разный результат в зависимости от того, на какую площадь эта сила распределена. Объясняют этот феномен в программе 7 класса физические термины «давление» и «сила давления».

Давление — это величина, равная отношению силы, действующей на поверхность, к площади этой поверхности. Сила давления направлена перпендикулярно поверхности.

Формула давления:

p = F / S, где F — модуль силы, S — площадь поверхности.

Единица измерения давления в СИ: паскаль (Па).

1 Па = 1 Н/м²

Понятно, что при одной и той же силе воздействия более высокое давление испытает та поверхность, площадь которой меньше.

Формулу для расчета силы давления вывести несложно:

F = p × S

В задачах по физике за 7 класс сила давления, как правило, равна весу тела.

Давление газов и жидкостей

Жидкости и газы, заполняющие сосуд, давят на его стенки. Это давление зависит от высоты столба данного вещества и от его плотности.

Формула гидростатического давления:

р = ρ × g × h, где ρ — плотность вещества, g — сила тяжести, h — высота столба.

g = 9,8 м/с²

Единица измерения давления жидкости или газа в СИ: паскаль (Па).

Однородная жидкость или газ давит на стенки сосуда равномерно, поскольку это давление создают хаотично движущиеся молекулы. И внешнее давление, оказываемое на вещество, тоже равномерно распределяется по всему его объему.

Закон Паскаля: давление, производимое на поверхность жидкого или газообразного вещества, одинаково передается в любую его точку независимо от направления.

Внешнее давление, оказываемое на жидкость или газ, рассчитывается по формуле:

p = F / S, где F — модуль силы, S — площадь поверхности.

Сообщающиеся сосуды

Сообщающимися называются сосуды, которые имеют общее дно либо соединены трубкой. Уровень однородной жидкости в таких сосудах всегда одинаков, независимо от их формы и сечения.

Если ρ₁ = ρ₂, то h₁ = h₂ и ρ₁gh₁ = ρ₂gh₂, где:

p — плотность жидкости,

h — высота столба жидкости,

g = 9,8 м/с².

Если жидкость в сообщающихся сосудах неоднородна, т. е. имеет разную плотность, высота столба в сосуде с более плотной жидкостью будет пропорционально меньше.

Высоты столбов жидкостей с разной плотностью обратно пропорциональны плотностям.

Гидравлический пресс — это механизм, созданный на основе сообщающихся сосудов разных сечений, заполненных однородной жидкостью. Такое устройство позволяет получить выигрыш в силе для оказания статического давления на детали (сжатия, зажимания и т. д.).

Если под поршнем 1 образуется давление p₁ = f₁/s₁, а под поршнем 2 будет давление p₂ = f₂/s₂, то, согласно закону Паскаля, p₁ = p₂

Следовательно,

Силы, действующие на поршни гидравлического пресса F₁ и F₂, прямо пропорциональны площадям этих поршней S₁ и S₂.

Другими словами, сила поршня 1 больше силы поршня 2 во столько раз, во сколько его площадь больше площади поршня 2. Это позволяет уравновесить в гидравлической машине с помощью малой силы многократно бóльшую силу.

Закон Архимеда

Сила выталкивания тела, погруженного в жидкость или газ, равна весу данной жидкости или газа в таком же объеме, как у этого тела.

Формула архимедовой силы:

F_a = ρ × g × V, где ρ — плотность жидкости, V — объем жидкости, g — ускорение 9,8 м/с².

Закон Архимеда помогает рассчитать, как поведет себя тело при погружении в среды разной плотности. Верны следующие утверждения:

• если плотность тела выше плотности среды, оно уйдет на дно;

• если плотность тела ниже, оно всплывет на поверхность.

Другими словами, тело поднимется на поверхность, если архимедова сила больше силы тяжести.

Работа, энергия, мощность

Механическая работа — это скалярная величина, которая равна произведению перемещения тела на модуль силы, под действием которой было выполнено перемещение. Подразумевается, что перемещение произошло в том же направлении, в котором действует сила.

Формула работы в курсе физики за 7 класс:

A = F × S, где F — действующая сила, S — пройденный телом путь.

Единица измерения работы в СИ: джоуль (Дж).

Такое понятие, как мощность, описывает скорость выполнения механической работы. Оно говорит о том, какая работа была совершена в единицу времени.

Мощность — это скалярная величина, равная отношению работы к временному промежутку, потребовавшемуся для ее выполнения.

Формула мощности:

N = A / t, где A — работа, t — время ее совершения.

Также мощность можно вычислить, зная силу, воздействующую на тело, и среднюю скорость перемещения этого тела.

N = F × v, где F — сила, v — средняя скорость тела.

Единица измерения мощности в СИ: ватт (Вт).

Тело может совершить какую-либо работу, если оно обладает энергией — кинетической и/или потенциальной.

• Кинетической называют энергию движения тела. Она говорит о том, какую работу нужно совершить, чтобы придать телу определенную скорость.

• Потенциальной называется энергия взаимодействия тела с другими телами или взаимодействия между частями одного целого. Потенциальная энергия тела, поднятого над Землей, характеризует, какую работу должна совершить сила тяжести, чтобы опустить это тело снова на нулевой уровень.

Таблица с формулами по физике за 7 класс для вычисления кинетической и потенциальной энергии:

Кинетическая энергия	Пропорциональна массе тела и квадрату его скорости.	Ek = mv2/2
Потенциальная энергия	Равна произведению массы тела, поднятого над Землей, на ускорение свободного падения и высоту поднимания.	Ep= mgh
Полная механическая энергия	Складывается из кинетической и потенциальной энергии.	E = Ek+Ep
Сохранение и превращение энергии	Если механическая энергия не переходит в другие формы, то сумма потенциальной энергии и кинетической представляет собой константу.	Ek+ Ep= const

Для того, чтобы понять, какая часть совершенной работы была полезной, вычисляют коэффициент полезного действия или КПД. С его помощью определяется эффективность различных механизмов, инструментов и т. д.

Коэффициент полезного действия (КПД) отражает полезную часть выполненной работы. Также его можно выразить через отношение полезно использованной энергии к общему количеству полученной энергии.

Формула для расчета КПД:

где А_п— полезная работа, А_з— затраченная работа.

КПД выражается в процентах и составляет всегда меньше 100%, поскольку часть энергии затрачивается на трение, повышение температуры воздуха и окружающих тел, преодоление силы тяжести и т. д.

Удачи на экзаменах!

Физика обозначение букв и формулы. Обозначение: высота, ширина, длина

Построение чертежей – дело непростое, но без него в современном мире никак. Ведь чтобы изготовить даже самый обычный предмет (крошечный болт или гайку, полку для книг, дизайн нового платья и подобное), изначально нужно провести соответствующие вычисления и нарисовать чертеж будущего изделия. Однако часто составляет его один человек, а занимается изготовлением чего-либо по этой схеме другой.

Чтобы не возникло путаницы в понимании изображенного предмета и его параметров, во всем мире приняты условные обозначения длины, ширины, высоты и других величин, применяемых при проектировании. Каковы они? Давайте узнаем.

Величины

Площадь, высота и другие обозначения подобного характера являются не только физическими, но и математическими величинами.

Единое их буквенное обозначение (используемое всеми странами) было уставлено в середине ХХ века Международной системой единиц (СИ) и применяется по сей день. Именно по этой причине все подобные параметры обозначаются латинскими, а не кириллическими буквами или арабской вязью. Чтобы не создавать отдельных трудностей, при разработке стандартов конструкторской документации в большинстве современных стран решено было использовать практически те же условные обозначения, что применяются в физике или геометрии.

Любой выпускник школы помнит, что в зависимости от того, двухмерная или трехмерная фигура (изделие) изображена на чертеже, она обладает набором основных параметров.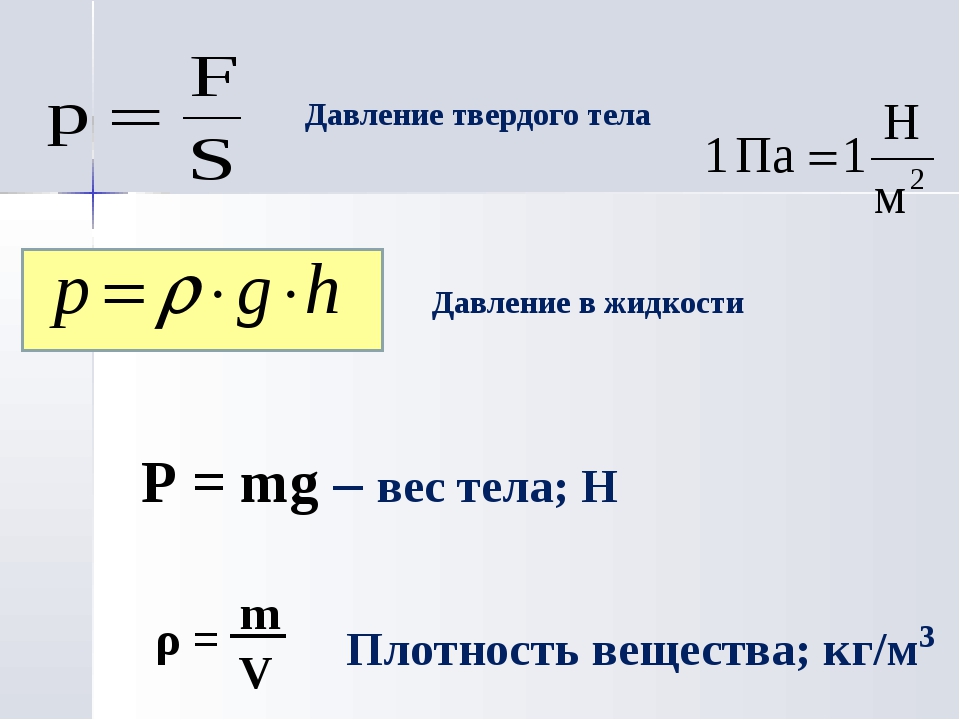 Если присутствуют два измерения – это ширина и длина, если их три – добавляется еще и высота.

Итак, для начала давайте выясним, как правильно длину, ширину, высоту обозначать на чертежах.

Ширина

Как было сказано выше, в математике рассматриваемая величина является одним из трех пространственных измерений любого объекта, при условии что его замеры производятся в поперечном направлении. Так чем знаменита ширина? Обозначение буквой «В» она имеет. Об этом известно во всём мире. Причем, согласно ГОСТу, допустимо применение как заглавной, так и строчной латинских литер. Часто возникает вопрос о том, почему именно такая буква выбрана. Ведь обычно сокращение производится по первой греческого или английского названия величины. При этом ширина на английском будет выглядеть как “width”.

Вероятно, здесь дело в том, что данный параметр наиболее широкое применение изначально имел в геометрии. В этой науке, описывая фигуры, часто длину, ширину, высоту обозначают буквами «а», «b», «с». Согласно этой традиции, при выборе литера «В» (или «b») была заимствована системой СИ (хотя для других двух измерений стали применять отличные от геометрических символы).

Большинство полагает, что это было сделано, дабы не путать ширину (обозначение буквой «B»/«b») с весом. Дело в том, что последний иногда именуется как «W» (сокращение от английского названия weight), хотя допустимо использование и других литер («G» и «Р»). Согласно международным нормам системы СИ, измеряется ширина в метрах или кратных (дольных) их единицах. Стоит отметить, что в геометрии иногда также допустимо использовать «w» для обозначения ширины, однако в физике и остальных точных науках такое обозначение, как правило, не применяется.

Длина

Как уже было указано, в математике длина, высота, ширина – это три пространственных измерения. При этом, если ширина является линейным размером в поперечном направлении, то длина – в продольном. Рассматривая ее как величину физики можно понять, что под этим словом подразумевается численная характеристика протяжности линий.

В английском языке этот термин именуется length. Именно из-за этого данная величина обозначается заглавной или строчной начальной литерой этого слова – «L». Как и ширина, длина измеряется в метрах или их кратных (дольных) единицах.

Высота

Наличие этой величины указывает на то, что приходится иметь дело с более сложным – трехмерным пространством. В отличие от длины и ширины, высота численно характеризует размер объекта в вертикальном направлении.

На английском она пишется как “height”. Поэтому, согласно международным нормам, ее обозначают латинской литерой «Н»/«h». Помимо высоты, в чертежах иногда эта буква выступает и как глубины обозначение. Высота, ширина и длина – все все эти параметры измеряются в метрах и их кратных и дольных единицах (километры, сантиметры, миллиметры и т. п.).

Радиус и диаметр

Помимо рассмотренных параметров, при составлении чертежей приходится иметь дело и с иными.

Например, при работе с окружностями возникает необходимость в определении их радиуса.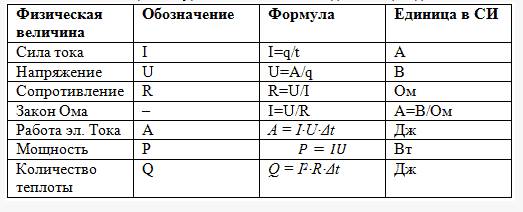 Так именуется отрезок, который соединяет две точки. Первая из них является центром. Вторая находится непосредственно на самой окружности. На латыни это слово выглядит как “radius”. Отсюда и строчная или заглавная «R»/«r».

Чертя окружности, помимо радиуса часто приходится сталкиваться с близким к нему явлением – диаметром. Он также является отрезком, соединяющим две точки на окружности. При этом он обязательно проходит через центр.

Численно диаметр равен двум радиусам. По-английски это слово пишется так: “diameter”. Отсюда и сокращение – большая или маленькая латинская буква «D»/«d». Часто диаметр на чертежах обозначают при помощи перечеркнутого круга – «Ø».

Хотя это распространенное сокращение, стоит иметь в виду, что ГОСТ предусматривает использование только латинской «D»/«d».

Толщина

Большинство из нас помнят школьные уроки математики. Ещё тогда учителя рассказывали, что, латинской литерой «s» принято обозначать такую величину, как площадь. Однако, согласно общепринятым нормам, на чертежах таким способом записывается совсем другой параметр – толщина.

Почему так? Известно, что в случае с высотой, шириной, длиной, обозначение буквами можно было объяснить их написанием или традицией. Вот только толщина по-английски выглядит как “thickness”, а в латинском варианте – “crassities”. Также непонятно, почему, в отличие от других величин, толщину можно обозначать только строчной литерой. Обозначение «s» также применяется при описании толщины страниц, стенок, ребер и так далее.

Периметр и площадь

В отличие от всех перечисленных выше величин, слово «периметр» пришло не из латыни или английского, а из греческого языка. Оно образовано от “περιμετρέο” («измерять окружность»). И сегодня этот термин сохранил свое значение (общая длина границ фигуры). Впоследствии слово попало в английский язык (“perimeter”) и закрепилось в системе СИ в виде сокращения буквой «Р».

Площадь – это величина, показывающая количественную характеристику геометрической фигуры, обладающей двумя измерениями (длиной и шириной). В отличие от всего перечисленного ранее, она измеряется в квадратных метрах (а также в дольных и кратных их единицах). Что касается буквенного обозначения площади, то в разных сферах оно отличается. Например, в математике это знакомая всем с детства латинская литера «S». Почему так – нет информации.

Некоторые по незнанию думают, что это связано с английским написанием слова “square”. Однако в нем математическая площадь – это “area”, а “square” – это площадь в архитектурном понимании. Кстати, стоит вспомнить, что “square” – название геометрической фигуры “квадрат”. Так что стоит быть внимательным при изучении чертежей на английском языке. Из-за перевода “area” в отдельных дисциплинах в качестве обозначения применяется литера «А». В редких случаях также используется «F», однако в физике данная буква означает величину под названием «сила» (“fortis”).

Другие распространенные сокращения

Обозначения высоты, ширины, длины, толщины, радиуса, диаметра являются наиболее употребляемыми при составлении чертежей. Однако есть и другие величины, которые тоже часто присутствуют в них. Например, строчное «t». В физике это означает «температуру», однако согласно ГОСТу Единой системы конструкторской документации, данная литера – это шаг (винтовых пружин, и подобного). При этом она не используется, когда речь идет о зубчатых зацеплениях и резьбе.

Заглавная и строчная буква «A»/«a» (согласно все тем же нормам) в чертежах применяется, чтобы обозначать не площадь, а межцентровое и межосевое расстояние. Помимо различных величин, в чертежах часто приходится обозначать углы разного размера. Для этого принято использовать строчные литеры греческого алфавита. Наиболее применяемые – «α», «β», «γ» и «δ». Однако допустимо использовать и другие.

Какой стандарт определяет буквенное обозначение длины, ширины, высоты, площади и других величин?

Как уже было сказано выше, чтобы не было недопонимания при прочтении чертежа, представителями разных народов приняты общие стандарты буквенного обозначения. Иными словами, если вы сомневаетесь в интерпретации того или иного сокращения, загляните в ГОСТы. Таким образом вы узнаете, как правильно обозначается высота, ширины, длина, диаметр, радиус и так далее.

Изучение физики в школе длится несколько лет. При этом ученики сталкиваются с проблемой, что одни и те же буквы обозначают совершенно разные величины. Чаще всего этот факт касается латинских букв. Как же тогда решать задачи?

Пугаться такого повтора не стоит. Ученые постарались ввести их в обозначение так, чтобы одинаковые буквы не встретились в одной формуле. Чаще всего ученики сталкиваются с латинской n. Она может быть строчной или прописной. Поэтому логично возникает вопрос о том, что такое n в физике, то есть в определенной встретившейся ученику формуле.

Что обозначает прописная буква N в физике?

Чаще всего в школьном курсе она встречается при изучении механики. Ведь там она может быть сразу в дух значениях – мощность и сила нормальной реакции опоры. Естественно, что эти понятия не пересекаются, ведь используются в разных разделах механики и измеряются в разных единицах. Поэтому всегда нужно точно определить, что такое n в физике.

Мощность — это скорость изменения энергии системы. Это скалярная величина, то есть просто число. Единицей ее измерения служит ватт (Вт).

Сила нормальной реакции опоры — сила, которая оказывает действие на тело со стороны опоры или подвеса. Кроме числового значения, она имеет направление, то есть это векторная величина. Причем она всегда перпендикулярна поверхности, на которую производится внешнее воздействие. Единицей измерения этой N является ньютон (Н).

Что такое N в физике, помимо уже указанных величин? Это может быть:

постоянная Авогадро;

увеличение оптического прибора;

концентрация вещества;

число Дебая;

полная мощность излучения.

Что может обозначать строчная буква n в физике?

Список наименований, которые могут за ней скрываться, достаточно обширен.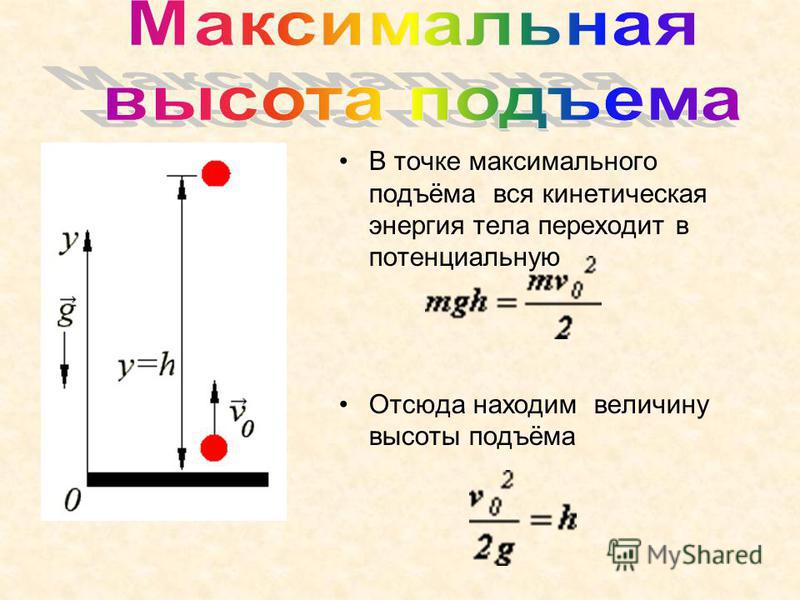 Обозначение n в физике используется для таких понятий:

показатель преломления, причем он может быть абсолютным или относительным;

нейтрон — нейтральная элементарная частица с массой незначительно большей, чем у протона;

частота вращения (используется для замены греческой буквы «ню», так как она очень похожа на латинскую «вэ») — число повторения оборотов за единицу времени, измеряется в герцах (Гц).

Что означает n в физике, кроме уже указанных величин? Оказывается, за ней скрываются основное квантовое число (квантовая физика), концентрация и постоянная Лошмидта (молекулярная физика). Кстати, при вычислении концентрации вещества требуется знать величину, которая также записывается латинской «эн». О ней будет идти речь ниже.

Какая физическая величина может быть обозначена n и N?

Ее название происходит от латинского слова numerus, в переводе оно звучит как «число», «количество». Поэтому ответ на вопрос о том, что значит n в физике, достаточно прост. Это количество любых предметов, тел, частиц — всего, о чем идет речь в определенной задаче.

Причем «количество» — одна из немногих физических величин, которые не имеют единицы измерения. Это просто число, без наименования. Например, если в задаче идет речь о 10 частицах, то n будет равно просто 10. Но если получается так, что строчная «эн» уже занята, то использовать приходится прописную букву.

Формулы, в которых фигурирует прописная N

Первая из них определяет мощность, которая равна отношению работы ко времени:

В молекулярной физике имеется такое понятие, как химическое количество вещества. Обозначается греческой буквой «ню». Чтобы его сосчитать, следует разделить количество частиц на число Авогадро :

Кстати, последняя величина тоже обозначается столь популярной буквой N. Только у нее всегда присутствует нижний индекс — А.

Чтобы определить электрический заряд, потребуется формула:

Еще одна формула с N в физике – частота колебаний. Чтобы ее сосчитать, нужно их число разделить на время:

Появляется буква «эн» в формуле для периода обращения:

Формулы, в которых встречается строчная n

В школьном курсе физики эта буква чаще всего ассоциируется с показателем преломления вещества. Поэтому важным оказывается знание формул с ее применением.

Так, для абсолютного показателя преломления формула записывается следующим образом:

Здесь с — скорость света в вакууме, v — его скорость в преломляющей среде.

Формула для относительного показателя преломления несколько сложнее:

n 21 = v 1: v 2 = n 2: n 1 ,

где n 1 и n 2 — абсолютные показатели преломления первой и второй среды, v 1 и v 2 — скорости световой волны в указанных веществах.

Как найти n в физике? В этом нам поможет формула, в которой требуется знать углы падения и преломления луча, то есть n 21 = sin α: sin γ.

Чему равно n в физике, если это показатель преломления?

Обычно в таблицах приводятся значения для абсолютных показателей преломления различных веществ.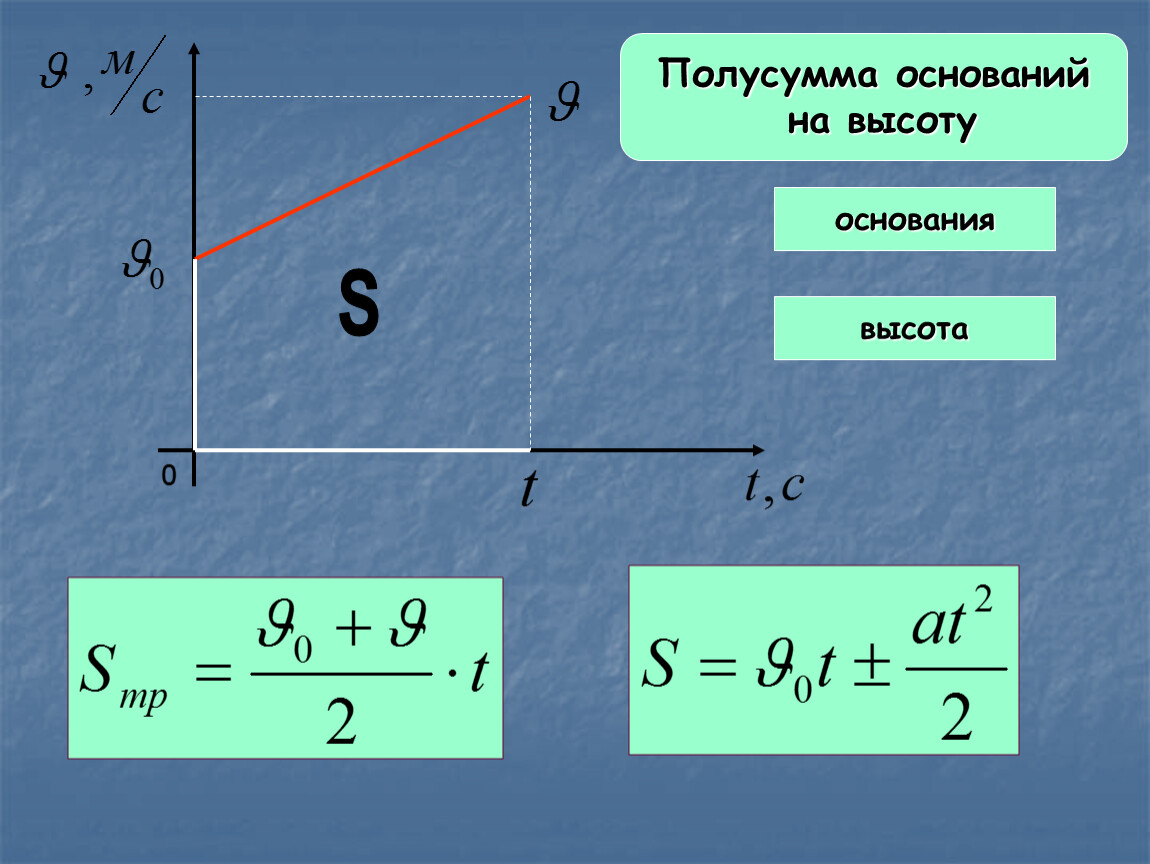 Не стоит забывать, что эта величина зависит не только от свойств среды, но и от длины волны. Табличные значения показателя преломления даются для оптического диапазона.

Итак, стало ясно, что такое n в физике. Чтобы не осталось каких-либо вопросов, стоит рассмотреть некоторые примеры.

Задача на мощность

№1. Во время пахоты трактор тянет плуг равномерно. При этом он прилагает силу 10 кН. При таком движении в течение 10 минут он преодолевает 1,2 км. Требуется определить развиваемую им мощность.

Перевод единиц в СИ. Начать можно с силы, 10 Н равны 10000 Н. Потом расстояние: 1,2 × 1000 = 1200 м. Осталось время — 10 × 60 = 600 с.

Выбор формул. Как уже было сказано выше, N = А: t. Но в задаче нет значения для работы. Для ее вычисления пригодится еще одна формула: А = F × S. Окончательный вид формулы для мощности выглядит так: N = (F × S) : t.

Решение. Вычислим сначала работу, а потом – мощность. Тогда в первом действии получится 10 000 × 1 200 = 12 000 000 Дж. Второе действие дает 12 000 000: 600 = 20 000 Вт.

Ответ. Мощность трактора равна 20 000 Вт.

Задачи на показатель преломления

№2. Абсолютный показатель преломления у стекла равен 1,5. Скорость распространения света в стекле меньше, чем в вакууме. Требуется определить, во сколько раз.

В СИ переводить данные не требуется.

При выборе формул остановиться нужно на этой: n = с: v.

Решение. Из указанной формулы видно, что v = с: n. Это значит, что скорость распространения света в стекле равна скорости света в вакууме, деленному на показатель преломления. То есть она уменьшается в полтора раза.

Ответ. Скорость распространения света в стекле меньше, чем в вакууме, в 1,5 раза.

№3. Имеются две прозрачные среды. Скорость света в первой из них равна 225 000 км/с, во второй — на 25 000 км/с меньше. Луч света идет из первой среды во вторую. Угол падения α равен 30º. Вычислить значение угла преломления.

Нужно ли переводить в СИ? Скорости даны во внесистемных единицах. Однако при подстановке в формулы они сократятся. Поэтому переводить скорости в м/с не нужно.

Выбор формул, необходимых для решения задачи. Потребуется использовать закон преломления света: n 21 = sin α: sin γ. А также: n = с: v.

Решение. В первой формуле n 21 — это отношение двух показателей преломления рассматриваемых веществ, то есть n 2 и n 1 . Если записать вторую указанную формулу для предложенных сред, то получатся такие: n 1 = с: v 1 и n 2 =с: v 2 . Если составить отношение двух последних выражений, получится, что n 21 = v 1: v 2 . Подставив его в формулу закона преломления, можно вывести такое выражение для синуса угла преломления: sin γ = sin α × (v 2: v 1).

Подставляем в формулу значения указанных скоростей и синуса 30º (равен 0,5), получается, что синус угла преломления равен 0,44. По таблице Брадиса получается, что угол γ равен 26º.

Ответ. Значение угла преломления — 26º.

Задачи на период обращения

№4. Лопасти ветряной мельницы вращаются с периодом, равным 5 секундам. Вычислите число оборотов этих лопастей за 1 час.

Переводить в единицы СИ нужно только время 1 час. Оно будет равно 3 600 секундам.

Подбор формул . Период вращения и число оборотов связаны формулой Т = t: N.

Решение. Из указанной формулы число оборотов определяется отношением времени к периоду. Таким образом, N = 3600: 5 = 720.

Ответ. Число оборотов лопастей мельницы равно 720.

№5. Винт самолета вращается с частотой 25 Гц. Какое время потребуется винту, чтобы совершить 3 000 оборотов?

Все данные приведены с СИ, поэтому переводить ничего не нужно.

Необходимая формула : частота ν = N: t. Из нее необходимо только вывести формулу для неизвестного времени. Оно является делителем, поэтому его полагается находить делением N на ν.

Решение. В результате деления 3 000 на 25 получается число 120. Оно будет измеряться в секундах.

Ответ. Винт самолета совершает 3000 оборотов за 120 с.

Подведем итоги

Когда ученику в задаче по физике встречается формула, содержащая n или N, ему нужно разобраться с двумя моментами. Первый — из какого раздела физики приведено равенство. Это может быть ясно из заголовка в учебнике, справочнике или слов учителя. Потом следует определиться с тем, что скрывается за многоликой «эн». Причем в этом помогает наименование единиц измерения, если, конечно, приведено ее значение. Также допускается еще один вариант: внимательно посмотрите на остальные буквы в формуле. Возможно, они окажутся знакомыми и дадут подсказку в решаемом вопросе.

Ни для кого не секрет, что существуют специальные обозначения для величин в любой науке. Буквенные обозначения в физике доказывают, что данная наука не является исключением в плане идентификации величин при помощи особых символов. Основных величин, а также их производных, достаточно много, каждая из которых имеет свой символ. Итак, буквенные обозначения в физике подробно рассматриваются в данной статье.

Физика и основные физические величины

Благодаря Аристотелю начало употребляться слово физика, так как именно он впервые употребил этот термин, который в ту пору считался синонимом термина философия. Это связано с общностью объекта изучения – законы Вселенной, конкретнее – то, как она функционирует. Как известно, в XVI-XVII веках произошла первая научная революция, именно благодаря ей физика была выделена в самостоятельную науку.

Михаил Васильевич Ломоносов ввел в русский язык слово физика посредством издания учебника в переводе с немецкого – первого в России учебника по физике.

Итак, физика представляет собой раздел естествознания, посвященный изучению общих законов природы, а также материи, ее движение и структуре. Основных физических величин не так много, как может показаться на первый взгляд – их всего 7:

• длина,
• масса,
• время,
• сила тока,
• температура,
• количество вещества,
• сила света.

Конечно, у них есть свои буквенные обозначения в физике. Например, для массы выбран символ m, а для температуры – Т. Также у всех величин есть своя единица измерения: у силы света – кандела (кд), а у количества вещества единицей измерения является моль.

Производные физические величины

Производных физических величин значительно больше, чем основных. Их насчитывается 26, причем часто некоторые из них приписывают к основным.

Итак, площадь является производной от длины, объем – также от длины, скорость – от времени, длины, а ускорение, в свою очередь, характеризует быстроту изменения скорости. Импульс выражается через массу и скорость, сила – произведение массы и ускорения, механическая работа зависит от силы и длины, энергия пропорциональна массе. Мощность, давление, плотность, поверхностная плотность, линейная плотность, количество теплоты, напряжение, электрическое сопротивление, магнитный поток, момент инерции, момент импульса, момент силы – все они зависят от массы. Частота, угловая скорость, угловое ускорение обратно пропорциональны времени, а электрический заряд имеет прямую зависимость от времени. Угол и телесный угол являются производными величинами из длины.

Какой буквой обозначается напряжение в физике? Напряжение, которое является скалярной величиной, обозначается буквой U. Для скорости обозначение имеет вид буквы v, для механической работы – А, а для энергии – Е. Электрический заряд принято обозначать буквой q, а магнитный поток – Ф.

СИ: общие сведения

Международная система единиц (СИ) представляет собой систему физических единиц, которая основана на Международной системе величин, включая наименования и обозначения физических величин. Она принята Генеральной конференцией по мерам и весам. Именно эта система регламентирует буквенные обозначения в физике, а также их размерность и единицы измерения. Для обозначения используются буквы латинского алфавита, в отдельных случаях – греческого. Также возможно в качестве обозначения использование специальных символов.

Заключение

Итак, в любой научной дисциплине есть особые обозначения для различного рода величин. Естественно, физика не является исключением. Буквенных обозначений достаточно много: сила, площадь, масса, ускорение, напряжение и т. д. Они имеют свои обозначения. Существует специальная система, которая называется Международная система единиц. Считается, что основные единицы не могут быть математически выведены из других. Производные же величины получают при помощи умножения и деления из основных.

Переходя к физическим приложениям производной, мы будем использовать несколько иные обозначения те, которые приняты в физике.

Во-первых, меняется обозначение функций. В самом деле, какие функции мы собираемся дифференцировать? Этими функциями служат физические величины, зависящие от времени. Например, координата тела x(t) и его скорость v(t) могут быть заданы формулами:

(читается ¾икс с точкой¿).

Имеется ещё одно обозначение производной, очень распространённое как в математике, так и в физике:

производная функции x(t) обозначается

(читается ¾дэ икс по дэ тэ¿).

Остановимся подробнее на смысле обозначения (1.16 ). Математик понимает его двояко либо как предел:

либо как дробь, в знаменателе которой стоит приращение времени dt, а в числителе так называемый дифференциал dx функции x(t). Понятие дифференциала не сложно, но мы не будем его сейчас обсуждать; оно ждёт вас на первом курсе.

Физик, не скованный требованиями математической строгости, понимает обозначение (1.16 ) более неформально. Пусть dx есть изменение координаты за время dt. Возьмём интервал dt настолько маленьким, что отношение dx=dt близко к своему пределу (1.17 ) с устраивающей нас точностью.

И тогда, скажет физик, производная координаты по времени есть попросту дробь, в числителе которой стоит достаточно малое изменение координаты dx, а в знаменателе достаточно малый промежуток времени dt, в течение которого это изменение координаты произошло.

Такое нестрогое понимание производной характерно для рассуждений в физике. Далее мы будем придерживаться именно этого физического уровня строгости.

Производная x(t) физической величины x(t) снова является функцией времени, и эту функцию снова можно продифференцировать найти производную производной, или вторую производную функции x(t). Вот одно обозначение второй производной:

вторая производная функции x(t) обозначаетсяx (t)

(читается ¾икс с двумя точками¿), а вот другое:

вторая производная функции x(t) обозначаетсяdt 2

(читается ¾дэ два икс по дэ тэ квадрат¿ или ¾дэ два икс по дэ тэ дважды¿).

Давайте вернёмся к исходному примеру (1.13 ) и посчитаем производную координаты, а заодно посмотрим на совместное использование обозначений (1.15 ) и (1.16 ):

x(t) = 1 + 12t 3t2 )

x(t) = dt d (1 + 12t 3t2 ) = 12 6t:

(Символ дифференцирования dt d перед скобкой это всё равно что штрих сверху за скобкой в прежних обозначениях.)

Обратите внимание, что производная координаты оказалась равна скорости (1.14 ). Это не случайное совпадение. Связь производной координаты со скоростью тела будет выяснена в следующем разделе ¾Механическое движение¿.

1.1.7 Предел векторной величины

Физические величины бывают не только скалярными, но и векторными. Соответственно, часто нас интересует скорость изменения векторной величины то есть, производная вектора. Однако прежде чем говорить о производной, нужно разобраться с понятием предела векторной величины.

Рассмотрим последовательность векторов ~u1 ; ~u2 ; ~u3 ; : : : Сделав, если необходимо, параллельный перенос, сведём их начала в одну точку O (рис. 1.5 ):

			Рис. 1.5. lim ~un = ~v
Концы векторов обозначим A1 ; A2 ; A3 ; : : : Таким образом, имеем:

Предположим, что последовательность точек A1 ; A2 ; A3 ; : : : ¾втекает¿2 в точку B:

lim An = B:

Обозначим ~v = OB. Мы скажем тогда, что последовательность синих векторов ~un стремится к красному вектору ~v, или что вектор ~v является пределом последовательности векторов ~un :

~v = lim ~un :

2 Вполне достаточно интуитивного понимания этого ¾втекания¿, но вас, быть может, интересует более строгое объяснение? Тогда вот оно.

Пусть дело происходит на плоскости. ¾Втекание¿ последовательности A1 ; A2 ; A3 ; : : : в точку B означает следующее: сколь бы малый круг с центром в точке B мы ни взяли, все точки последовательности, начиная с некоторой, попадут внутрь этого круга. Иными словами, вне любого круга с центром B имеется лишь конечное число точек нашей последовательности.

А если дело происходит в пространстве? Определение ¾втекания¿ модифицируется незначительно: нужно лишь заменить слово ¾круг¿ на слово ¾шар¿.

Предположим теперь, что концы синих векторов на рис. 1.5 пробегают не дискретный набор значений, а непрерывную кривую (например, указанную пунктирной линией). Таким образом, мы имеем дело не с последовательностью векторов ~un , а с вектором ~u(t), который меняется со временем. Это как раз то, что нам и нужно в физике!

Дальнейшее объяснение почти такое же. Пусть t стремится к некоторому значению t0 . Если

при этом концы векторов ~u(t) ¾втекают¿ в некоторую точку B, то мы говорим, что вектор

~v = OB является пределом векторной величины ~u(t):

t!t0

1.1.8 Дифференцирование векторов

Выяснив, что такое предел векторной величины, мы готовы сделать следующий шаг ввести понятие производной вектора.

Предположим, что имеется некоторый вектор ~u(t), зависящий от времени. Это означает, что длина данного вектора и его направление могут меняться с течением времени.

По аналогии с обычной (скалярной) функцией вводится понятие изменения (или приращения) вектора. Изменение вектора ~u за время t есть векторная величина:

~u = ~u(t + t) ~u(t):

Обратите внимание, что в правой части данного соотношения стоит разность векторов. Изменение вектора ~u показано на рис. 1.6 (напомним, что при вычитании векторов мы сводим их начала в одну точку, соединяем концы и ¾укалываем¿ стрелкой тот вектор, из которого производится вычитание).

~u(t) ~u

Рис. 1.6. Изменение вектора

Если промежуток времени t достаточно мал, то и вектор ~u за это время меняется мало (в физике, по крайней мере, так считается всегда). Соответственно, если при t ! 0 отношение~u= t стремится к некоторому пределу, то этот предел называется производной вектора ~u:

При обозначении производной вектора мы не будем использовать точку сверху (так как символ ~u_ не слишком хорошо смотрится) и ограничиваемся обозначением (1.18 ). Но для производной скаляра мы, разумеется, свободно используем оба обозначения.

Напомним, что d~u=dt это символ производной. Его можно понимать и как дробь, в числителе которой стоит дифференциал вектора ~u, соответствующий промежутку времени dt. Выше мы не стали обсуждать понятие дифференциала, так как в школе его не проходят; не будем обсуждать дифференциал и здесь.

Однако на физическом уровне строгости производную d~u=dt можно считать дробью, в знаменателе которой стоит очень малый интервал времени dt, а в числителе соответствующее малое изменение d~u вектора ~u. При достаточно малом dt величина данной дроби отличается от

предела в правой части (1.18 ) столь мало, что с учётом имеющейся точности измерений этим отличием можно пренебречь.

Этого (не вполне строгого) физического понимания производной нам окажется вполне достаточно.

Правила дифференцирования векторных выражений во многом аналогичны правилам дифференцирования скаляров. Нам понадобятся лишь самые простые правила.

1. Постоянный скалярный множитель выносится за знак производной: если c = const, то

d(c~u) = c d~u: dt dt

Мы используем это правило в разделе ¾Импульс¿, когда второй закон Ньютона

будет переписан в виде:

2. Постоянный векторный множитель выносится за знак производной: если ~c = const, то dt d (x(t)~c) = x(t)~c:

3. Производная суммы векторов равна сумме их производных:

dt d (~u + ~v) =d~u dt +d~v dt :

Последними двумя правилами мы будем пользоваться неоднократно. Посмотрим, как они работают в важнейшей ситуации дифференцирования вектора при наличии в пространстве прямоугольной системы координат OXY Z (рис. 1.7 ).

Рис. 1.7. Разложение вектора по базису

Как известно, любой вектор ~u единственным образом раскладывается по базису единичных

векторов ~ ,~ ,~ : i j k

~u = ux i + uy j + uz k:

Здесь ux , uy , uz проекции вектора ~u на координатные оси. Они же являются координатами вектора ~u в данном базисе.

Вектор ~u в нашем случае зависит от времени, а это значит, что его координаты ux , uy , uz являются функциями времени:

~u(t) = ux (t) i	Uy (t) j	Uz (t)k:

Дифференцируем это равенство.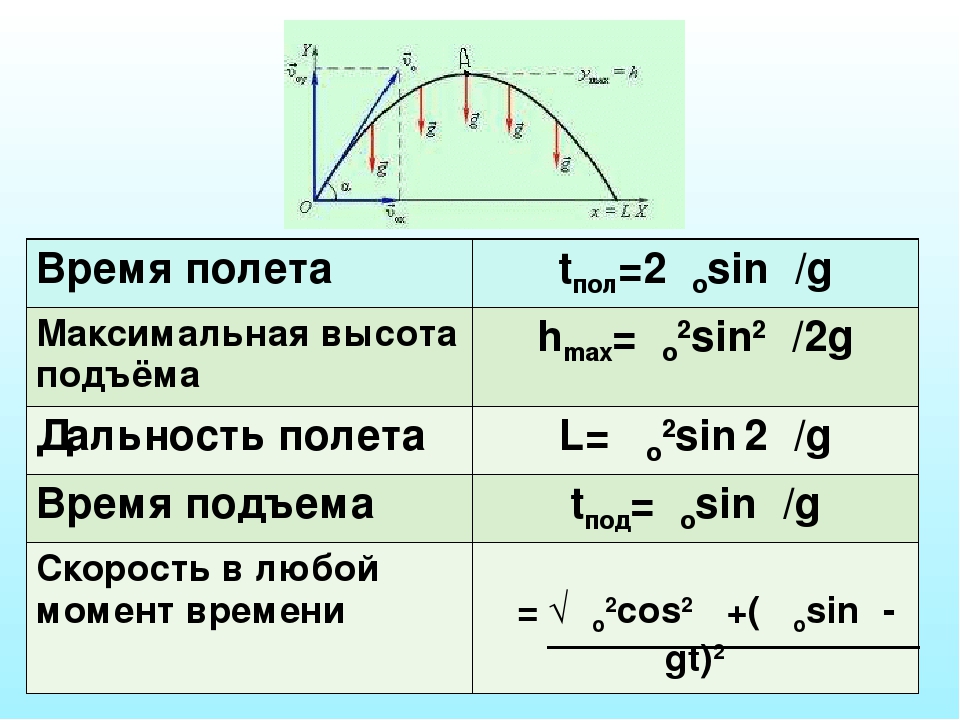 Сначала пользуемся правилом дифференцирования суммы:

ux (t)~ i +

uy (t)~ j

uz (t)~ k:

Затем выносим постоянные векторы за знак производной:

Ux (t)i + uy (t)j + uz (t)k:

Таким образом, если вектор ~u имеет координаты (ux ; uy ; uz ), то координаты производной d~u=dt являются производными координат вектора ~u, а именно (ux ; uy ; uz ).

Ввиду особой важности формулы (1.20 ) дадим более непосредственный её вывод. В момент времени t + t согласно (1.19 ) имеем:

~u(t + t) = ux (t + t) i + uy (t + t) j + uz (t + t)k:

Напишем изменение вектора ~u:

~u = ~u(t + t) ~u(t) =

Ux (t + t) i + uy (t + t) j + uz (t + t)k ux (t) i + uy (t) j + uz (t)k =

= (ux (t + t) ux (t)) i + (uy (t + t) uy (t)) j + (uz (t + t) uz (t)) k =
Ux i + uy j + uz k:
Делим обе части полученного равенства на t:
				T i +			t j +

В пределе при t ! 0 дроби ux = t, uy = t, uz = t переходят соответственно в производные ux , uy , uz , и мы снова получаем соотношение (1. 20 ):

Ux i + uy j + uz k.

Поделитесь статьей с друзьями:

Похожие статьи

Онлайн калькуляторы

Экзотические единицы длины

Следующий уникальный калькулятор служит для перевода экзотических единиц длины в…

Чей фунт тяжелее?

Следующий онлайн калькулятор о фунтах. Ранее он был очень популярен,…

Уровень жидкости в наклоненном цилиндрическом баке

Следующий онлайн калькулятор может вычислить уровень жидкости в цилиндрической таре…

Температурные шкалы

Следующий онлайн калькулятор переводит температуры между разными шкалами. Помните калькулятор…

Старинные русские деньги

Следующий калькулятор интересен тем, что он переводит древние российские денежные…

Соответствие размеров обуви

Следующий калькулятор будет очень полезен тем, кто решил купить или…

Системы измерения плоских углов

Следующий калькулятор работает очень просто, вам нужно ввести всего одно…

Рост в русской системе мер

Следующий онлайн калькулятор считает рост человека благодаря русской системе мер…

Размер экрана

Следующий онлайн калькулятор может вычислить габариты экрана телевизоров, компьютеров, проекторов,…

Размер снимка в пикселях и формат фотографии

Перед вами 2 калькулятора: один поможет вам подобрать формат снимков…

Перевод числа плиток в единицы площади и обратно

Следующие 2 калькуляторы переводят заданное число плиток в квадратные метры…

Перевод мер площади из метрической в английскую систему и обратно

Перед вами 2 онлайн-калькулятора. Они переводят меры площади из метрической…

Перевод мер длины из русской системы в метрическую и обратно

Следующий необычный калькулятор переводит меры длины из русской системы в…

Перевод мер длины из метрической в имперскую систему и обратно

Перед вами 2 калькулятора, которые предназначены для перевода мер длины…

Перевод кельвинов в градусы цельсия

Следующий простенький калькулятор переводит введенную вами toC из кельвинов в…

Перевод из фунтов в килограммы и обратно

Следующий калькулятор предназначен для перевода кг в фунты. Также есть…

Перевод из фунтов в дюймы

Следующий онлайн калькулятор переводит калибр древних артиллерийских орудий из фунтов…

Перевод из градусов Фаренгейта в градусы Цельсия

Давайте вспомним калькулятор, который переводит градусы Цельсия в градусы Фаренгейта:…

Перевод дробных чисел из одной системы счисления в другую

Как вы уже могли заметить на нашем сайте есть несколько…

Перевод градусов Цельсия в градусы Фаренгейта

Следующий уникальный калькулятор переводит градусы Цельсия в градусы Фаренгейта. Наверное,…

Перевод градусов минут и секунд в десятичные градусы и обратно

Следующий калькулятор умеет переводить значение угла, которое задано в градусах,…

Перевод градусов в радианы

Следующий калькулятор делает перевод единиц измерения углов из градусов, минут,…

Объем сегмента цилиндра

Следующий калькулятор делает расчет объема сегмента цилиндра. Давайте посмотрим каким…

Объем жидкости в наклоненном цилиндрическом баке

Следующий онлайн-калькулятор считает объем жидкости в бочке, которая имеет цилиндрическую…

Общее время наработки аппарата

 Следующий калькулятор служит для детального подсчета суммарной работы аппарата. Вам…

Сочетание цветов

Перед вами отличный помощник для IT специалистов. С помощью данного…

О римских цифрах

Следующий калькулятор переводит числа, записанные римскими цифрами в простые десятичные…

Метров в секунду и километров в час

Следующий калькулятор переводит скорость из м/с в км/час. Часто при…

Конвертер единиц давления

Начнем с истории. В 17 веке итальянским ученым Торричелли было…

Калькулятор горловины для цилиндрического бака

Следующий онлайн-калькулятор рассчитывает параметры горловины для цилиндрического бочки. Все работает…

Свободное падение. Примеры решения задач по физике. 9-10 класс

Свободное падение. Примеры решения задач по физике. 9-10 класс

Подробности

Просмотров: 1456

Задачи по физике – это просто!

Не забываем, что решать задачи надо всегда в системе СИ!

А теперь к задачам!

Элементарные задачи из курса школьной физики по кинематике.

Падение тела вниз. Бросок тела вертикально вверх.

Задача1

Шишка, висевшая на ели, оторвалась и за 2 секунды достигла земли.
На какой высоте висела шишка?
Какую скорость она имела у самой земли?

Помни!
1. В данной задаче начальная скорость тела равна нулю, и формулы становятся проще!
2. Будем грамотны! Рассчитываем проекцию вектора, но ответ должен быть в модулях! В последней записи перед ответом переходим от проекции к модулю.

Задача 2

С крыши дома высотой 25 метров падает кирпич. Определить время его падения на землю.

Помни!
1. В данной задаче начальная скорость тела равна нулю, формула упрощается!
2. Внимание, преобразование формулы! Делаем без ошибок!

Задача 3

Мяч брошен вертикально вверх с начальной скоростью 10м/с.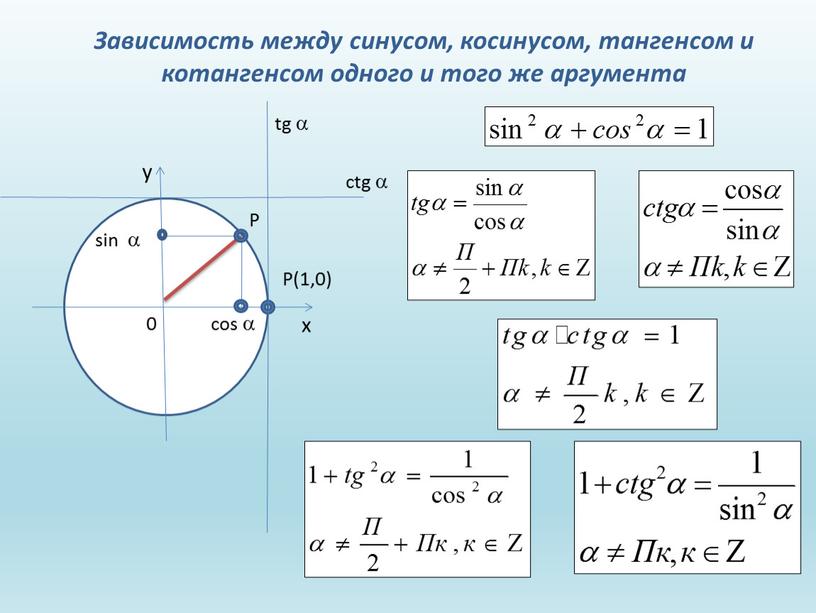 Определить время подъема мяча на максимальную высоту.

Гляди в оба!

Проекция вектора ускорения на ось отрицательна!
В расчете не забудьте о минусе!

Задача 4

Стрела пущена вертикально вверх со скоростью 30 м/с. Определить максимальную высоту подъема стрелы.

Помни!

1. Конечная скорость тела, брошенного вертикально вверх, (на максимальной высоте подъема) равна нулю! Без этой величины задачу не решить!
2. Проекция вектора ускорения на ось отрицательна, не забудьте подставить «минус»!

Задача 5

Определить через сколько времени упадет на землю мяч, запущенный вертикально вверх от земли с начальной скоростью 25 м/с.

Обрати внимание!
Движение тела состоит из двух частей: подъема и спуска.

Общее время движения: t = t_{подъема} + t_спуска

Интересно, что при таком движении тела время подъема и времени спуска одинаковы!
Убедимся в этом при расчете!

Выталкивающая сила в физике – виды, формулы и определения с примерами

Содержание:

Выталкивающая сила:

Наблюдение. Почему тяжело погрузить мяч в воду, и почему, как только мы его отпустим, он выпрыгивает из воды? Почему в море легче плавать, чем в озере? Почему в воде мы можем поднять камень, а в воздухе — нет?

Опыт 1. Подвесим к пружине тело (рис. 138). В связи с тем, что на тело действует сила тяжести

Газы во многом подобны жидкостям. На тела, помещённые в газ, также действует выталкивающая сила. Именно под действием этой силы воздушные шары, метеорологические зонды, детские шарики, наполненные водородом, поднимаются вверх.

А от чего зависит выталкивающая сила ?

Опыт 2. Два тела разного объёма, но одинаковой массы, погрузим полностью в одну и ту же жидкость (воду). Мы видим, что тело большего объёма выталкивается из жидкости (воды) с большей силой (рис. 139).

Выталкивающая сила зависит от объёма погружённого в жидкость тела. Чем больше объём тела, тем большая выталкивающая сила действует на него.

Опыт 3. Погрузим полностью два тела одинакового объёма и массы в разные жидкости, например воду и керосин (рис. 140). Нарушение равновесия в этом случае свидетельствует, что в воде на тело действует большая выталкивающая сила, это можно связать с тем, что плотность воды больше, чем плотность керосина.

Выталкивающая сила зависит от плотности жидкости, в которую погружено тело. Чем больше плотность жидкости, тем большая выталкивающая сила действует на погружённое в неё тело.

Обобщая результаты наблюдений и опытов можно сделать такой вывод.

На тело, погружённое в жидкость (газ), действует выталкивающая сила, равная по значению весу жидкости (газа), вытесненной этим телом.

Это утверждение называют законом Архимеда, древнегреческого учёного, который его открыл и, по легенде, успешно применил для решения практической задачи: определил, содержится ли в золотой короне царя Гиерона примесь серебра. Силу, которая выталкивает тело из жидкости или газа, называют еще архимедовой силой.

На основе закона Архимеда можно сразу написать формулу для определения выталкивающей силы, но чтобы лучше понять, вследствие чего она возникает, выполним простые расчёты. Для этого рассмотрим тело в форме прямоугольного бруска, погружённого в жидкость таким образом, чтобы его верхняя и нижняя фан и располагались параллельно поверхности жидкости (рис. 141).

Посмотрим, каким будет результат действия сил давления на поверхность этого тела.

Согласно закону Паскаля горизонтальные силы и  действующие на симметричные боковые грани бруска, попарно равны по значению и противоположно направлены. Они не выталкивают брусок вверх, а только сжимают его с боков. Рассмотрим силы гидростатического давления на верхнюю и нижнюю грани бруска.

Пусть верхняя грань площадью S расположена на глубине тогда сила давления , на неё будет равна: 

где — плотность жидкости.

Нижняя грань бруска площадью S расположена на большей глубине , поэтому сила давления на неё будет также больше, чем :  

Обе силы давления , и действуют вдоль вертикали, их равнодействующая и будет силой Архимеда , направленной вверх в сторону большей силы , а её значение будет равно разности сил

 и :  .

Поскольку разность является высотой бруска, то произведение  равно объёму тела , и мы окончательно получаем формулу,

являющуюся математическим выражением закона Архимеда:

Действительно, поскольку жидкость не сжимается, то объём вытесненной телом жидкости равен объёму этого тела, и произведение равно массе жидкости в объёме тела . В свою очередь, произведение  является весом этой жидкости.

Из приведённого расчета наглядно видно, что выталкивающая (архимедова) сила возникает вследствие того, что значения гидростатического давления на разных глубинах неодинаковы и возрастают с глубиной.

Архимедовую силу можно определить экспериментально.

Опыт 4. Подвесим тело к динамометру (рис. 142). На тело действует сила тяжести почти 10 Н. Погрузим тело в жидкость (рис. 143).

Динамометр показывает 6 Н. Определим разность показаний динамометра. Она равняется 4 Н.

Кстати:

Однажды у императора Цао-Цао, который правил в Китае свыше 2000 лет тому назад, возникла мысль взвесить слона. Как ни суетились сановники, никто из них не мог ничего придумать, ведь нигде не было таких гигантских весов, чтобы на них можно было взвесить слона. Когда все сановники признали свою беспомощность, пришёл человек по имени Чао Чун и сказал, что он может взвесить слона. Он попросил: «Прикажите поставить слона в большую лодку, после чего обозначьте уровень погружения лодки в воду. Снимите слона, а лодку загрузите камнями так, чтобы она погрузилась до отметки. Вес камней будет равен весу слона”. Талантливый самородок, на много лет опередивший великого Архимеда, получил за своё предложение «щедрое» вознаграждение – благосклонный кивок императора Цао-Цао.

Выталкивающая сила и закон Архимеда

При взаимодействии твердых неподвижных тел, действуя друг на друга, они только деформируются. И действие каждого из этих тел на другое характеризуется силой.

Как взаимодействуют твердое тело и жидкость

Если твердое тело взаимодействует с жидкостью, то оно проникает в жидкость. Что происходит в таком случае? Ответ на этот вопрос получим из опыта.

К резиновой нити прицепим груз и измерим длину нити, которая растягивается весом груза. Если же груз после этого опустить в воду, то станет заметным сокращение длины нити. Таким образом, вес тела в воде уменьшился. Это возможно только потому, что в жидкости на погруженное тело действует выталкивающая сила. Направление этой силы противоположно направлению действия силы тяжести.

Как рассчитать значение выталкивающей силы

Опыты показывают, что значение выталкивающей силы зависит как от характеристик погруженного тела, так и от свойств жидкости.

Возьмем металлический цилиндр и стакан, объем которого равен объему цилиндра. Прицепим их к крючку динамометра и определим вес цилиндра и стакана (рис. 110). Теперь полностью погрузим цилиндр в воду. Динамометр покажет уменьшение веса. Но если стакан полностью заполнить водой, то показания динамометра восстановятся. Таким образом, выталкивающая сила равна весу воды, объем которой равен объему тела. Если воду заменить насыщенным раствором соли в воде, то выталкивающая сила будет большей, так как большим будет вес воды, объем которой равен объему тела.

Если учесть, что вес жидкости   то для расчета выталкивающей силы можно использовать формулу

где – выталкивающая сила; – плотность жидкости; – объем погруженного в жидкость тела или его части.

Зависимость, выраженная формулой для выталкивающей силы, называется законом Архимеда, сама выталкивающая сила — силой Архимеда.

От чего зависит сила Архимеда

Почему действует сила Архимеда в жидкости? Представим себе, что в жидкость погружено тело в виде прямоугольного бруска (рис. 111).

На тело, погруженное в жидкость, действует выталкивающая сила, которая равна весу жидкости в объеме погруженного тела или его погруженной части.

В результате действия силы тяжести в жидкости существует давление, которое согласно закону Паскаля действует во всех направлениях. В связи с этим на верхнюю грань бруска будет действовать сила направленная вниз.

На нижнюю грань будет действовать сила направленная вверх. Так как , то и . Равнодействующая этих сил направлена вверх. Это и будет сила Архимеда.

Действует сила Архимеда и в газах, так как в них давление тоже изменяется с высотой.

Окончательно закон Архимеда можно сформулировать так: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу жидкости или газа в объеме погруженной части тела.

В газах сила Архимеда значительно меньше, чем в жидкостях, поскольку плотность газа намного меньше плотности жидкости.

Выталкивающая сила в жидкостях и газах

Почему мяч, если его погрузить в воду и отпустить, выпрыгивает над поверхностью воды? Почему тяжелый камень, который на суше нельзя сдвинуть с места, можно легко поднять под водой? Почему корабль, севший на мель, самостоятельно не может всплыть? Попробуем разобраться.

Существование выталкивающей силы:

Подвесим к коромыслу весов два одинаковых шара. Массы шаров равны, значит, весы будут уравновешены (рис. 27.1, а). Подставим под правый шар пустой сосуд (рис. 27.1, б). Затем нальем в сосуд воду и увидим, что равновесие весов нарушится (рис. 27.1, в), — некая сила пытается вытолкнуть шар из воды.

Откуда берется эта сила? Чтобы разобраться, рассмотрим погруженный в жидкость кубик. На него со всех сторон действуют силы гидростатического давления жидкости (рис. 27.2). Силы гидростатического давления действующие на боковые грани кубика, противоположны по направлению и равны по значению, так как площади боковых граней одинаковы и эти грани расположены на одинаковой глубине. Такие силы уравновешивают друг друга. А вот силы гидростатического давления , соответственно действующие на верхнюю и нижнюю грани кубика, друг друга не уравновешивают. На верхнюю грань кубика действует сила давления : где — гидростатическое давление жидкости; S — площадь грани. Аналогично на нижнюю грань кубика действует сила давления : Нижняя грань находится на большей глубине, чем верхняя поэтому сила давления больше силы давления

Равнодействующая этих сил равна разности значений сил и направлена в сторону действия большей силы, то есть вертикально вверх. По вертикали вверх на кубик, погруженный в жидкость, действует сила, обусловленная разностью давлений на его нижнюю и верхнюю грани, — выталкивающая сила: На тело, помещенное в газ, тоже действует выталкивающая сила, но она значительно меньше выталкивающей силы, действующей на то же тело в жидкости, поскольку плотность газа намного меньше плотности жидкости. Выталкивающую силу, которая действует на тело в жидкости или газе, называют также архимедовой силой (в честь древнегреческого ученого Архимеда (рис. 27.3), который первым указал на существование этой силы и вычислил ее значение).

Расчет и вычисление силы Архимеда

Вычислим значение архимедовой (выталкивающей) силы для кубика, погруженного в жидкость (см. рис. 27.2). Вы уже знаете, что архимедова сила равна разности сил давлений жидкости на нижнюю и верхнюю грани кубика: где — сила давления жидкости на верхнюю грань кубика; — сила давления жидкости на нижнюю грань кубика. Зная , найдем выталкивающую силу: Разность глубин , на которых находятся нижняя и верхняя грани кубика, — это высота h кубика, следовательно, . Произведение площади S основания кубика на его высоту h — это объем V кубика: V= Sh, значит, формула для расчета архимедовой силы: Здесь — это масса жидкости в объеме кубика, то есть масса жидкости, объем которой равен объему кубика. Так как , то Архимедова сила равна весу жидкости в объеме кубика:

Мы рассмотрели случай с кубиком, полностью погруженным в жидкость. Однако полученный результат выполняется для тела любой формы, а также в случаях, когда тело погружено в жидкость частично (для расчетов следует брать объем погруженной в жидкость части тела). Кроме того, результат справедлив и для газов. А теперь сформулируем закон Архимеда: На тело, погруженное в жидкость или газ, действует выталкивающая сила, которая равна весу жидкости или газа в объеме погруженной части тела: где — архимедова сила; — плотность жидкости или газа; — объем погруженной части тела. Архимедова сила приложена к центру погруженной части тела и направлена вертикально вверх (рис. 27.4).

Выясняем, всегда ли на тело, погруженное в жидкость, действует архимедова сила:

Подвесим к динамометру камешек на нити. Динамометр покажет вес камешка. Подставим стакан с водой так, чтобы камешек оказался полностью погруженным в воду. Показание динамометра уменьшится. Кажется, что камешек «потерял» часть своего веса. Но никакой потери веса тела в жидкости не происходит: вес перераспределяется между подвесом (нитью) и опорой (жидкостью). Даже если архимедова сила, действующая на тело, достаточна, чтобы его удержать, и подвес не будет растянут, тело все равно не находится в состоянии невесомости, ведь оно давит на опору — жидкость. Следует отметить: когда тело плавает, его вес распределяется на воду, окружающую всю поверхность тела. Поэтому во время плавания нам кажется, что мы потеряли вес. Такие комфортные условия поддержания тяжелого тела обусловили то, что в результате эволюции самые массивные существа на Земле живут в океане (рис. 27.5).

Именно архимедова сила помогает нам поднимать в воде тяжелые камни или другие предметы, ведь часть силы тяжести, действующей на эти тела, уравновешивается не силой наших рук, а выталкивающей силой.

Однако случается, что вода не помогает поднять тело, а наоборот — препятствует этому. Это происходит, если тело лежит на дне и плотно к нему прилегает. Вода не может попасть под нижнюю поверхность тела и помочь своим давлением поднять его. В таком случае, чтобы оторвать тело от дна, нужно преодолеть не только силу тяжести, действующую на тело, но и силу давления воды на верхнюю поверхность тела (рис. 27.6). Данное явление может стать причиной трагедии: если подводная лодка опустится на глинистое дно и вытеснит из­ под себя воду, всплыть сама она не сможет.

Пример №1

Однородный алюминиевый брусок массой 540 г полностью погружен в воду и не касается дна и стенок сосуда. Определите архимедову силу, действующую на брусок. Анализ физической проблемы. Для вычисления архимедовой силы нужно знать плотность воды и объем бруска. Объем бруска определим по его массе и плотности. Плотности воды и алюминия узнаем из таблиц плотностей (с. 249). Задачу будем решать в единицах СИ.

Дано:

,,,

Найти:

Решение:

По закону Архимеда: По определению плотности:

Подставим выражение для объема бруска в формулу для расчетов архимедовой силы:

Проверим единицу, найдем значение искомой величины:

Ответ:

Итоги:

На тело, находящееся в жидкости или газе, действует выталкивающая (архимедова) сила. Причина ее появления в том, что давление, которое оказывает жидкость или газ на верхнюю поверхность тела, отличается от давления, оказываемого на нижнюю поверхность тела. Закон Архимеда: на тело, погруженное в жидкость или газ, действует выталкивающая сила, которая направлена вертикально вверх и равна весу жидкости или газа в объеме погруженной части тела:

Условия плавания тел

При приготовлении раствора соли определенной плотности хозяйки погружают в него сырое яйцо: если плотность раствора недостаточна, яйцо тонет, если достаточна — всплывает. аналогично определяют плотность сахарного сиропа при консервации.

Вы наверняка можете привести множество примеров плавания тел. Плавают корабли и лодки, деревянные игрушки и воздушные шарики, плавают рыбы, дельфины, другие существа. А от чего зависит способность тела плавать? Проведем опыт. Возьмем небольшой сосуд с водой и несколько шариков, изготовленных из разных материалов. Будем поочередно погружать тела в воду, а потом отпускать их без начальной скорости. Далее в зависимости от плотности тела возможны разные варианты (см. таблицу).

Погружение

Тело начинает тонуть и в конце концов опускается на дно сосуда. Выясним, почему это происходит. На тело действуют две силы: 1) сила тяжести (поскольку ), направленная вертикально вниз; 2) выталкивающая сила направленная вертикально вверх. Тело погружается, а это значит, что сила, направленная вниз, больше: Поскольку . После сокращения на имеем:

тело тонет в жидкости или газе, если плотность тела больше, чем плотность жидкости или газа. Вариант 2. Плавание внутри жидкости. Тело не тонет и не всплывает, а остается плавать внутри жидкости. Попробуйте доказать, что в данном случае плотность тела равна плотности жидкости:

тело плавает внутри жидкости или газа, если плотность тела равна плотности жидкости или газа. Вариант 3. Всплытие. Тело начинает всплывать и в конце концов останавливается на поверхности жидкости, погрузившись в жидкость частично. Пока тело всплывает, архимедова сила больше силы тяжести: или: Остановка тела на поверхности жидкости означает, что архимедова сила и сила тяжести уравновешены: тело всплывает в жидкости или газе либо плавает на поверхности жидкости, если плотность тела меньше, чем плотность жидкости или газа.

Плавание тел в живой природе

Тела обитателей морей и рек содержат в своем составе много воды, поэтому их средняя плотность близка к плотности воды. Чтобы свободно двигаться в жидкости, они должны «управлять» средней плотностью своего тела. Приведем примеры. У рыб с плавательным пузырем такое управление происходит за счет изменения объема пузыря (рис. 28.1). Моллюск наутилус (рис. 28.2), обитающий в тропических морях, может быстро всплывать и снова опускаться на дно благодаря тому, что может менять объем внутренних полостей в организме (моллюск живет в закрученной спиралью раковине). Распространенный в Европе водяной паук (рис. 28.3) несет с собой в глубину воздушную оболочку на брюшке — именно она дает ему запас плавучести и помогает вернуться на поверхность.

Пример №2

Медный шар массой 445 г имеет внутри полость объемом 450 см3. Будет ли этот шар плавать в воде? Анализ физической проблемы. Чтобы ответить на вопрос, как поведет себя шар в воде, нужно плотность шара сравнить с плотностью воды Для вычисления плотности шара следует определить его объем и массу. Масса воздуха в шаре незначительна по сравнению с массой меди, поэтому Объем шара — это объем медной оболочки и объем полости Объем медной оболочки можно определить, зная массу и плотность меди. О плотностях меди и воды узнаем из таблиц плотностей (с. 249). Задачу целесообразно решать в представленных единицах.

Дано:

,,,

Найти:

Решение:

По определению плотности:

Объем шара: — объем медной оболочки.

Таким образом,

Решим задачу по действиям. 1. Определим объем шара:

2. Зная объем и массу шара, определим его плотность:

Анализ результата: плотность шара меньше плотности воды, поэтому шар будет плавать на поверхности воды.

Ответ: да, шар будет плавать на поверхности воды.

Итоги:

Тело тонет в жидкости или газе, если плотность тела больше, чем плотность жидкости или газа плавает внутри жидкости или газа, если плотность тела равна плотности жидкости или газа Тело всплывает в жидкости или газе либо плавает на поверхности жидкости, если плотность тела меньше плотности жидкости или газа

Судоходство и воздухоплавание

Стальной брусок в воде тонет, а стальные корабли плавают. Нейлоновая ткань падает в воздухе, а воздушные шары, изготовленные из этой ткани, поднимаются вверх сами и поднимают гондолы с пассажирами. Почему же стальные корабли плавают в воде, а воздушные шары называют аппаратами, которые легче воздуха? Получить ответы на эти вопросы вам помогут знания об основах судоходства и воздухоплавания.

Почему плавают суда

На первый взгляд, сталь непригодна для изготовления плавучего средства: плотность стали намного больше плотности воды, поэтому стальная пластинка в воде тонет. Но если из пластинки сделать кораблик и опустить его на поверхность воды, кораблик будет плавать (рис. 29.1). Почему? Дело в том, что погруженная в воду часть кораблика вытесняет воды достаточно, чтобы архимедова сила уравновесила силу тяжести, действующую на кораблик. Другими словами, средняя плотность кораблика за счет воздуха внутри него намного меньше плотности воды. Именно поэтому кораблик плавает на поверхности воды лишь немного в нее погружаясь.

Этот принцип лежит в основе конструкции всех судов. Средняя плотность судов намного меньше плотности воды, поэтому суда плавают на ее поверхности, погружаясь на относительно небольшую часть своего объема.

Характеристики судов:

Когда новое судно спускают на воду, оно начинает погружаться. Нижняя часть судна начинает вытеснять воду, вследствие чего возникает архимедова сила. Когда архимедова сила уравновешивает силу тяжести, действующую на судно, оно прекращает погружение. Глубину, на которую погружается судно, называют осадкой. Осадка судна изменяется в зависимости от загруженности судна и от того, в речной или морской воде оно находится. Разумеется, судно нельзя перегружать.

На корпус судна нанесена ватерлиния — линия, указывающая максимально допустимую осадку судна, при которой оно может безопасно плавать (рис. 29.2). Когда судно полностью нагружено, оно находится в воде вровень с ватерлинией.

Вес воды, которую вытесняет судно, погруженное в воду до ватерлинии, то есть архимедова сила, действующая на полностью нагруженное судно, называется полным водоизмещением судна. Напомним: поскольку нагруженное судно плавает на поверхности воды, то архимедова сила, которая действует на него, по значению равна силе тяжести, действующей на судно с грузом: Самые большие суда — танкеры для нефти — имеют полное водоизмещение до 5 млн кН, то есть их масса вместе с грузом достигает 500 000 т. Если из полного водоизмещения исключить вес самого судна, то получим максимальный вес груза, который может взять на борт данное судно, то есть определим грузоподъемность судна. грузоподъемность судна — максимальный вес груза, который судно может взять на борт, — это разность между полным водоизмещением судна и его весом. Украина — морское государство. В стране есть морской и речной флот, а также порты, имеющие большое экономическое значение: Одесский, Ильичевский, Южный, Николаевский, Херсонский, Бердянский, Мариупольский.

Как осуществилась мечта человека летать

Люди уже давно используют воздушные шары (аэростаты), поднимающиеся в воздух благодаря заполнению их оболочки горячим воздухом или легким газом. На воздушный шар в воздухе действует выталкивающая сила. Средняя плотность воздушного шара меньше плотности воздуха, поэтому выталкивающая сила больше силы тяжести и шар поднимается вверх. Разность между выталкивающей (архимедовой) силой и силой тяжести представляет собой подъемную силу воздушного шара. Сейчас воздушные шары используют для метеорологических и других исследований, соревнований, перевозок пассажиров, туристических и познавательных путешествий. Воздушные шары, наполненные легким газом (в основном гелием), называют шарльерами. В последнее время распространены воздушные шары, наполненные горячим воздухом, — современные монгольфьеры (рис. 29.3). Высокую температуру воздуха внутри шара поддерживают газовые горелки, установленные в его горловине. Поскольку плотность воздуха с высотой уменьшается, воздушные шары не могут подняться на какую угодно высоту. Воздушные шары поднимаются только до той высоты, где плотность воздуха равна средней плотности шара вместе с грузом.

Пример №3

В речном порту судно взяло на борт 100 т груза. В результате осадка судна увеличилась на 0,2 м и достигла максимально допустимой. Какова площадь сечения судна на уровне ватерлинии? Анализ физической проблемы. Когда на судно взяли груз, оно увеличило осадку и дополнительно вытеснило некоторый объем воды. По закону Архимеда, вес груза равен весу дополнительно вытесненной воды: Осадка судна увеличилась всего на 20 см, значит, площадь сечения судна на уровне поверхности воды изменилась незначительно. Поэтому объем дополнительно вытесненной воды равен где h — увеличение осадки; S — площадь сечения судна на уровне ватерлинии (по условию судно достигло максимальной осадки). Порт речной, поэтому плотность воды равна Задачу следует решать в единицах СИ.

Дано:

,,

Найти:

Решение:

1. Определим массу дополнительно вытесненной воды. По закону Архимеда:

поэтому

2. Определим объем дополнительно вытесненной воды:

3. Площадь S сечения судна на уровне ватерлинии найдем через объем вытесненной воды:

Ответ:

Мы решили задачу 1 по действиям. Решите эту задачу в общем виде (получите общую формулу, найдите значение искомой величины).

Пример №4

Объем воздушного шара равен Шар натягивает трос, которым прикреплен к причалу, с силой 800 Н. После освобождения троса шар смог подняться на некоторую высоту. Какова плотность воздуха на этой высоте, если плотность воздуха у причала

Анализ физической проблемы. Шар прекратил подъем потому, что на этой высоте его средняя плотность равна плотности воздуха . Чтобы определить среднюю плотность шара, следует найти его массу. Массу шара найдем по силе тяжести, действующей на шар. Для определения силы тяжести выполним пояснительный рисунок и покажем все силы, действовавшие на шар на причале: — сила тяжести; — архимедова сила, — сила натяжения троса. Шар на причале не двигался, поэтому силы, действовавшие на него, были скомпенсированы. Задачу будем решать по действиям в единицах СИ.

Дано:

,,,

Найти:

Решение:

Силы, действовавшие на прикрепленный к причалу шар, были скомпенсированы, следовательно:

1. Найдем архимедову силу, которая действовала на прикрепленный к причалу шар:

2. Найдем силу тяжести, действующую на шар:

3. Определим массу шара:

4. По известным массе и объему шара вычислим его среднюю плотность:

5. Плотность воздуха на высоте максимального подъема шара равна средней плотности шара, потому на этой высоте

Ответ:

Итоги:

Взаимодействие тел:

Вы узнали, что причиной изменения скорости движения тел и причиной изменения формы и объема тел является взаимодействие.

Вы ознакомились с разными силами в механике.

Вы продолжили знакомство с физическими телами и веществами и узнали о физических величинах, характеризующих тело, вещество, взаимодействие.

Вы узнали о давлении жидкостей и газов, ознакомились с законом Паскаля, законом Архимеда, доказали наличие атмосферного давления.

Калькулятор гравитационного потенциала

Использование калькулятора

Этот калькулятор GPE найдет недостающую переменную в уравнении физики для гравитационной потенциальной энергии, когда известны три переменные.

\ (PE_g = mgh \)

Где:

• PE _г или PE = потенциальная гравитационная энергия
• м = масса объекта
• g = ускорение свободного падения
• h = высота объекта

Что такое гравитационная потенциальная энергия (GPE)

Потенциальная энергия – это запасенная энергия объекта с учетом его положения относительно тела. Гравитационная потенциальная энергия – это один из видов потенциальной энергии, равный произведению массы объекта (м), ускорения силы тяжести (g) и высоты объекта (h) как расстояния от поверхности земли ( тело).

В этом примере масса 3 кг на высоте 5 метров под действием силы тяжести Земли будет иметь 147,15 Дж потенциальной энергии, ПЭ = 3 кг * 9.81 м / с ² * 5 м = 147,15 Дж.

9,81 метра в секунду в квадрате (или, точнее, 9,80665 м / с ² ) широко признано учеными в качестве рабочего среднего значения гравитационного притяжения Земли. Эта цифра основана на измерении силы тяжести на уровне моря на широте 45 °.

• На больших высотах сила тяжести немного уменьшается.
• Влияние широты на силу тяжести имеет значение, поскольку сила тяжести увеличивается с увеличением расстояния от экватора. На экваторе сила тяжести Земли составляет 9,780 м / с ² , а на полюсах – 9,832 м / с ² (источник: CRC Справочник по химии и физике ).

Ускорение свободного падения (до трех значащие цифры) для других планет и тел Солнечной системы выглядит следующим образом:

(источник таблицы: NASA)

* Стандартная плотность (g _n ).1.00g _n равно 9.80665 м / с ²

Ссылки / Дополнительная литература

Уравнений скорости тяжести для объектов, проецируемых вверх, Рон Куртус

SfC Home> Физика> Гравитация>

Рона Куртуса

Когда вы проецируете объект вверх и отпускаете его с начальной скоростью, он движется в направлении, противоположном силе тяжести . Таким образом, начальная скорость отрицательна. Скорость объекта также отрицательна на пути вверх, но положительна при спуске.

Примечание : Мы используем соглашение, согласно которому восходящие скорости отрицательны, а нисходящие скорости положительны. Кроме того, смещения выше начальной точки отрицательны, а смещения ниже начальной точки положительны.

В некоторых учебниках “вверх” положительно, а “вниз” – отрицательно. Вы должны знать, какое соглашение используется при работе с книгой.

( Для получения дополнительной информации см. Соглашение о направлении в уравнениях силы тяжести. )

По мере движения вверх объект замедляется, пока не достигнет максимальной высоты, при которой скорость равна нулю. Затем скорость увеличивается по мере того, как объект падает на землю.

Примечание : Если начальная скорость достаточно велика, объект может избежать силы тяжести. (См. Дополнительную информацию в разделе «Скорость гравитационного покидания». )

Полученные уравнения позволяют вычислить скорость объекта, проецируемого вверх, относительно времени, а также скорость при смещениях как выше, так и ниже начальной точки.

Вопросы, которые могут у вас возникнуть:

• Какая скорость относительно времени?
• Какова скорость смещения выше начальной точки?
• Какова скорость смещения ниже начальной точки?

Этот урок ответит на эти вопросы. Полезный инструмент: Конвертация единиц

---

---

Скорость относительно времени

Общее уравнение гравитации для скорости относительно времени:

v = GT + v _i

где

• v – вертикальная скорость в метрах в секунду (м / с) или футах в секунду (фут / с)
• г – ускорение свободного падения (9.8 м / с² или 32 фут / с²)
• t – время в секундах
• v _i – начальная вертикальная скорость вверх в м / с или фут / с

(Дополнительную информацию см. В разделе «Вывод уравнений силы тяжести со скоростью-временем»).

Когда вы проецируете объект вверх, начальная скорость при отпускании отрицательна или меньше нуля ( v _i < 0). Результирующие скорости будут отрицательными ( v < 0), когда объект движется вверх, нулевыми ( v = 0) при максимальном смещении или положительными ( v> 0), когда объект движется вниз, в зависимости от значение истекшего времени.

Время до максимального смещения

При определении скорости в разное время удобно знать время, необходимое для достижения максимального смещения, когда скорость составляет v = 0:

gt _m + v _i = 0

gt _m = −v _i

т _м = −v _i / г

где т _м – время до максимального водоизмещения.

Примечание : Поскольку v _i – отрицательное число, – v _i – положительное число.

Пример

Если начальная скорость объекта 19,6 м / с направлена ​​вверх, какова скорость в разное время?

Решение

v _i = −19,6 м / с и г = 9,8 м / с ² . Замените v _i и g в уравнении, чтобы получить формулу в виде t :

v = GT + v _i

v = (9.8 м / с ² ) ( т с) + (−19,6 м / с)

Упростить:

v = (9,8 т – 19,6) м / с

В таблице ниже показаны скорости для различных значений т :

т = 0 с	v = −19,6 м / с	Движение вверх от начальной точки
т = 1 с	v = −9.8 м / с	Объект движется вверх
т м = 2 с	v = 0 м / с	При пиковом или максимальном смещении
т = 3 с	v = 9,8 м / с	Объект движется вниз
т = 4 с	v = 19,6 м / с	Прохождение точки старта
т = 5 с	против = 29. 4 м / с	Продолжаем вниз

Скорости объекта, проецируемые вверх, в разное время

Скорость перемещения вверх

Общее уравнение гравитации для скорости объекта относительно смещения или движения от начальной точки:

v = ± √ (2gy + v _i ² )

где

• ± означает плюс-минус
• √ (2yg + v _i ² ) – квадратный корень из величины (2yg + v _i ² )
• y – вертикальное смещение в метрах или футах

(Дополнительную информацию см. В разделе «Вывод уравнений силы тяжести смещения и скорости».)

Поскольку скорость на пути вверх отрицательная ( v < 0), используется отрицательная ( – ) версия уравнения:

v = −√ (2gy + v _i ² )

Также обратите внимание, что смещение отрицательное ( y < 0) над начальной точкой.

Максимальное смещение относительно скорости

При максимальном смещении скорость v = 0.Таким образом:

−√ (2gy _м + v _i ² ) = 0

2gy _м + v _i ² = 0

2gy _м = −v _i ²

y _m = −v _i ² / 2g

, где y _м – максимальное смещение.

Если подставить значения для смещения, где y m _{, величина
(2gy + v i ² ) станет отрицательной, что приведет к значению √ (2gy + v i ² ) является воображаемым или невозможным.}

Пример

Если v _i = −64 ft / s, найдите значения v для различных перемещений y при движении вверх.

Решение

Поскольку g = 32 фут / с ² , замените g и v _i в уравнении, чтобы получить формулу в виде y :

v = −√ (2gy + v _i ² )

v = −√ [2 * (32 фут / с ² ) * ( y фут) + (−64 фут / с) ² ]

v = −√ (64 y футов ² / с ² + 4096 футов ² / с ² )

Поскольку √ (футы ² / с ² ) = фут / с, получаем:

v = −√ ( 64 y + 4096 ) фут / с

Подставьте значения для y в формулу, помня, что y отрицательное значение выше начальной точки:

y = 0 футов	v = −64 фут / с	Движение вверх от начальной точки
y = −32 футов	v = -45. 3 фут / с	Объект движется вверх
y м = −64 футов	v = 0 фут / с	При пиковом или максимальном смещении
y = −80 футов	–	v = −√ (- 1024 ) невозможно

Скорость перемещения вниз

Ниже максимального смещения значение v положительно, поскольку объект движется в направлении силы тяжести.Это означает, что используется положительная ( + ) версия общего уравнения:

v = √ (2gy + v _i ² )

Однако смещение отрицательно от максимального смещения до начальной точки, в которой время y = 0. С этого момента y имеет положительные значения.

Пример

Продолжая приведенный выше пример, где v _i = −64 ft / s, каковы скорости для различных смещений на пути вниз?

Решение

Положительная версия формулы:

v = √ ( 64 y + 4096 ) фут / с

Замещающие значения для и в формуле :

y м = −64 футов	v = 0 фут / с	При пиковом или максимальном смещении
y = −32 футов	v = 45. 3 фут / с	Объект движется вниз
y = 0 футов	v = 64 фут / с	Движение вниз в начальной точке
y = 32 фута	v = 78,4 фут / с	Движение вниз ниже начальной точки

Скорости перемещений объекта, спроецированного вверх

Сводка

Когда объект проецируется вверх, он движется в направлении, противоположном силе тяжести, и начальная скорость имеет отрицательное число.Скорость отрицательная, когда объект движется вверх, и положительная, когда он движется вниз. Смещение отрицательное выше начальной точки, положительное ниже начальной точки. Уравнения для скорости:

По времени

v = GT + v _i

По смещению

v = −√ (2gy + v _i ² ) растет

v _м = 0 (при максимальном смещении)

v = √ (2gy + v _i ² ) спускается

---

Думайте об успехе

---

Ресурсы и ссылки

Полномочия Рона Куртуса

Сайты

Гравитационные ресурсы

Расчет силы тяжести – Земля – Калькулятор

Книги

(Примечание: Школа чемпионов может получать комиссионные от покупки книг)

Книги с самым высоким рейтингом по простой науке о гравитации

Книги с самым высоким рейтингом по продвинутой физике гравитации

---

Вопросы и комментарии

Есть ли у вас какие-либо вопросы, комментарии или мнения по этой теме? Если да, отправьте свой отзыв по электронной почте. Я постараюсь вернуться к вам как можно скорее.

---

Поделиться страницей

Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:

---

Студенты и исследователи

Веб-адрес этой страницы:
www.school-for-champions.com/science/
gravity_equations_upward_velocity.htm

Пожалуйста, включите его в качестве ссылки на свой веб-сайт или в качестве ссылки в своем отчете, документе или диссертации.

Авторские права © Ограничения

---

Где ты сейчас?

Школа чемпионов

Гравитационные темы

Уравнения скорости силы тяжести для объектов, проецируемых вверх

---

Какова максимальная высота снаряда, класс 11, физика CBSE

Подсказка: сначала запишите вектор скорости, затем примените третье уравнение движения и введите значения различных величин в уравнение при максимальной высоте снаряда. Помните, что у снаряда на максимальной высоте скорость имеет только x-компоненту.

Полный пошаговый ответ:
Пусть снаряд движется с начальной скоростью u, которая составляет угол \ [\ text {} \! \! \ Theta \! \! \ Text {} \] с горизонталью.

Теперь вектор скорости после времени t определяется выражением

\ [\ overrightarrow {v} = {{v} _ {x}} \ widehat {i} + {{v} _ {y}} \ widehat {j } \] ——– (1)
\ [\ overrightarrow {v} = (u \ cos \ theta) \ widehat {i} + \ left (u \ sin \ theta -gt \ right) \ widehat {j} \]

Как мы знаем, у снаряда на максимальной высоте скорость имеет только x-компоненту.{2}} \ theta} {2g} \]

Дополнительная информация:
Движение снаряда – это движение объекта, брошенного или выброшенного в воздух, только под действием гравитационного ускорения. В механике существует множество применений движения снаряда. Такие объекты называются снарядами, а их путь – траекторией. Мы рассматриваем двумерное движение снаряда и пренебрегаем влиянием сопротивления воздуха.
Самый важный факт, о котором следует помнить, – это то, что движения по перпендикулярным осям независимы, и поэтому мы можем анализировать их отдельно.Метод анализа двумерного движения снаряда состоит в том, чтобы разбить его на два движения: одно по горизонтальной оси, а другое – по вертикальной оси.

Примечание: учащиеся должны избегать путаницы с концепцией, согласно которой единственная сила, действующая на движущийся вверх снаряд, – это сила тяжести. Их концепция движения побуждает их думать, что если объект движется вверх, тогда должна быть восходящая сила, а если объект движется вверх и вправо, должна быть и сила, направленная вверх и вправо.

Аппарат – 1: Скорость и высота – CCEA – GCSE Physics (Single Science) Revision – CCEA

Большой мрамор, регулируемая подставка, взлетно-посадочная полоса, маркер, линейка для метра, линейка 50 см, секундомер, защитные очки.

0.0.0.1:0.1.0.$0.$1.$2″> Метод

1. Установите устройство, как показано на схеме.
2. Отметьте маркером стартовую линию A в верхней части взлетно-посадочной полосы.
3. Аналогичным образом отметьте финишную линию B в нижней части взлетно-посадочной полосы.
4. Измерьте расстояние между точками A и B с помощью линейки.Запишите это расстояние в метрах в подходящую таблицу. Это расстояние останется неизменным на протяжении всего эксперимента.
5. Отрегулируйте опору так, чтобы взлетно-посадочная полоса имела высоту A по вертикали 5 см. Измерьте расстояние правилом 50 см и занесите в таблицу.
6. Поместите шарик в положение A. Освободите его и одновременно включите секундомер.
7. Остановите секундомер, когда шарик достигнет B. Запишите время в секундах в таблице.
8. Повторите еще два раза, а затем вычислите среднее время.Запишите в таблицу.
9. Рассчитайте среднюю скорость, используя уравнение: средняя скорость = \ (\ frac {пройденное расстояние} {среднее ~ время ~ занятое} \)
10. Повторите процедуру для 6 различных вертикальных высот, увеличивая высоту на 5 см каждый раз.
11. Постройте график зависимости средней скорости в м / с по оси y от высоты по вертикали в метрах по оси x.

Безопасность

• поставьте препятствие, например табурет, чтобы ноги не попали под взлетно-посадочную полосу, и убедитесь, что мрамор не упадет на чью-то ногу;
• убедитесь, что мрамор не упал на пол и не поскользнулся;
• закрепите взлетно-посадочную полосу зажимом в центре скамейки, чтобы она не упала на чью-то ногу;
• Наденьте защитные очки на случай, если мрамор попадет кому-нибудь в глаз.

Высота взлетно-посадочной полосы в см	Пройденное расстояние в м	Время в секундах (1)	Время в секундах (2)	Время в секундах (3)	Среднее затраченное время в с	Средняя скорость в м / с
5	1,75
10	1,75
15	1.75
20	1,75
25	1,75
30	1,75

График

Ошибка

Основной причиной ошибки в этом эксперименте является время реакции, когда человек запускает и останавливает секундомер.

Ошибка из-за времени реакции может быть сведена к минимуму:

• повторение времени для каждой высоты три раза и вычисление среднего времени, в течение которого шарик скатывается по взлетно-посадочной полосе;
• гарантирует, что время, необходимое для скатывания мрамора по взлетно-посадочной полосе, будет как можно большим. Это можно сделать:
• • сделав расстояние между A и B как можно большим;
  • сохраняя вертикальную высоту как можно меньше, чтобы мрамор не двигался слишком быстро.

Заключение

По мере увеличения высоты взлетно-посадочной полосы средняя скорость мрамора также увеличивается, что соответствует нашему прогнозу.

Однако мы можем сказать, что вертикальная высота не прямо пропорциональна средней скорости, поскольку линия наилучшего соответствия не является прямой линией, проходящей через начало координат.

с отличием Physics: Free Fall

Фон

Исследование свободно падающих тел восходит к временам Аристотеля.В то время Аристотель считал, что более массивные объекты будут падать быстрее, чем менее массивные. Он верил в это в значительной степени из-за того, что при рассмотрении камня и пера, падающего с одной и той же высоты, становится ясно, что камень первым ударяется о землю. При дальнейшем рассмотрении становится ясно, что Аристотель ошибался в своей гипотезе.

В качестве доказательства возьмите баскетбольный мяч и лист бумаги. Бросьте их одновременно с одной и той же высоты … приземляются ли они одновременно? Возможно нет.Теперь возьмите этот лист бумаги, скомкайте его в плотный клубок и повторите эксперимент. Что вы видите сейчас? Вы должны увидеть, что мяч и бумага приземляются одновременно. Таким образом, можно сделать вывод, что предсказания Аристотеля не учитывали влияние сопротивления воздуха. В рамках этого курса не принимаются во внимание силы сопротивления, такие как сопротивление воздуха.

В 17 веке Галилео Галилей начал новое исследование движения падающих тел.Галилей, осознавая, что сопротивление воздуха влияет на движение падающего тела, провел свой знаменитый мысленный эксперимент, в котором постоянно спрашивал, что произойдет, если будет устранен эффект сопротивления воздуха. Командир Аполлона-15 Дэвид Скотт провел этот эксперимент, находясь на Луне. Он одновременно уронил молот и перо и заметил, что они достигли земли одновременно.

Со времени экспериментов Галилея ученые пришли к лучшему пониманию того, как гравитационное притяжение Земли ускоряет свободно падающие тела.Путем экспериментов было определено, что местная напряженность гравитационного поля (g) на поверхности Земли составляет 9,8 Н / кг, что дополнительно указывает на то, что все объекты в свободном падении (без учета сопротивления воздуха) испытывают эквивалентное ускорение 9,8 м. / с ² к центру Земли.

(ПРИМЕЧАНИЕ: если вы оторветесь от поверхности Земли, местная напряженность гравитационного поля и, следовательно, ускорение свободного падения изменится.)

Вы можете смотреть на свободно падающие тела как на объекты, которые падают с некоторой высоты или отбрасывают вертикально вверх.В этом экзамене вы проанализируете движение каждого состояния.

Падающие предметы

Объекты, стартующие в состоянии покоя, имеют начальную скорость, равную нулю, что дает вам первую кинематическую величину, необходимую для решения проблемы. Кроме того, если вы назовете направление начального движения (вниз) положительным, объект будет иметь положительное ускорение и ускоряться при падении.

Важным первым шагом в анализе объектов в свободном падении является решение, какое направление по оси Y вы собираетесь называть положительным, а какое, следовательно, отрицательным.Хотя вы можете установить свое положительное направление любым удобным вам способом и получить правильный ответ, следование приведенным ниже советам может упростить вашу работу, чтобы постоянно находить правильный ответ.

1. Определите направление первоначального движения объекта и назначьте его положительным направлением. В случае падения объекта положительное направление оси Y будет направлено к нижней части бумаги.
2. Теперь, когда ось идентифицирована, вы можете идентифицировать и записывать данную кинематическую информацию.Не забывайте, что у падающего объекта начальная скорость равна нулю.
   • v ₀ = 0
   • v =?
   • Δy =?
   • a = 9,8 м / с ²
   • т =?
3. Обратите внимание на направление, в котором нарисованы векторные стрелки – если скорость и ускорение указывают в одном направлении, объект ускоряется. Если они указывают в противоположных направлениях, объект замедляется.

КЛЮЧЕВАЯ КОНЦЕПЦИЯ: Величина ускорения свободного падения (g) постоянна 9.81 м / с ² на поверхности Земли.

Вопрос: Какова скорость 2,5-килограммовой массы после того, как она свободно упала из состояния покоя на расстояние 12 метров?

Переменная	Значение
v 0	0
v	НАЙТИ
Δy	12 м
а	9.8 м / с 2
т	?

Ответ: Вертикальная проблема: Укажите положительное направление вниз. Это означает, что ускорение, которое также уменьшается, является положительной величиной.

Объекты, запущенные вверх

Изучение движения объекта, запущенного вертикально вверх, выполняется почти так же, как вы исследовали движение объекта, падающего из состояния покоя.Основное отличие состоит в том, что вы должны смотреть не на один, а на два сегмента его движения: вверх и вниз.

Прежде чем вы приступите к установлению системы отсчета и проработке количественного анализа, вы должны построить твердое концептуальное понимание того, что происходит, когда мяч находится в воздухе. Представьте, что мяч подбрасывается вертикально в воздух, как показано на рисунке.

Чтобы мяч двигался вверх, его начальная скорость должна быть больше нуля.Когда мяч поднимается, его скорость уменьшается, пока он не достигнет максимальной высоты, где он останавливается, а затем начинает падать. Когда мяч падает, его скорость увеличивается. Другими словами, мяч ускоряется все время, пока он находится в воздухе, как на пути вверх, в момент остановки в самой высокой точке, так и на пути вниз.

Причина ускорения мяча – сила тяжести. Все время, пока мяч находится в воздухе, его ускорение составляет 9,8 м / с ² вниз при условии, что это происходит на поверхности Земли.Обратите внимание, что ускорение может быть 9,8 м / с ² или -9,8 м / с ² . Знак ускорения зависит от направления, которое вы указали как положительное, но во всех случаях направление ускорения силы тяжести направлено вниз, к центру Земли.

Вы уже установили, что ускорение мяча за все время, пока он находится в воздухе, составляет 9,8 м / с. ² вниз. Это ускорение приводит к тому, что скорость мяча уменьшается с постоянной скоростью, пока он не достигнет максимальной высоты, после чего он разворачивается и начинает падать.Чтобы повернуться, скорость мяча должна пройти через ноль. Следовательно, на максимальной высоте скорость мяча должна быть равна нулю.

Вопрос: Мяч, брошенный вертикально вверх, достигает максимальной высоты 30 метров над поверхностью Земли. На максимальной высоте скорость мяча составляет:

Ответ: 0 м / с. Мгновенная скорость любого снаряда на максимальной высоте равна нулю.

Поскольку сила тяжести обеспечивает такое же ускорение мячу при движении вверх (замедляя его) и при спуске (ускоряя его), время достижения максимальной высоты совпадает с временем возврата в исходное положение.Подобным образом начальная скорость мяча на пути вверх будет равна скорости мяча в момент, когда он достигнет точки, из которой он был запущен на пути вниз. Другими словами, время подъема равно времени спуска, а начальная скорость подъема равна конечной скорости вниз (при условии, что объект начинается и заканчивается на одной и той же высоте над землей).

Теперь, когда концептуальное понимание движения мяча установлено, вы можете работать над количественным решением.Следуя ранее установленному эмпирическому правилу, вы можете начать с определения положительного направления движения мяча. Помните, что назначение положительных и отрицательных направлений совершенно произвольно. У вас есть свобода назначать их так, как вы считаете нужным. Однако, назначив их, не меняйте их.

Как только это положительное опорное направление установлено, все остальные скорости и смещения присваиваются соответствующим образом. Например, если вверх – положительное направление, ускорение свободного падения будет отрицательным, потому что ускорение силы тяжести направлено вниз, к центру Земли.В своей наивысшей точке шар будет иметь положительное смещение и нулевое смещение, когда он вернется в свою начальную точку. Если мяч не пойман, но продолжит движение к Земле мимо начальной точки, он будет иметь отрицательное смещение.

Уловка для решения задач свободного падения включает в себя симметрию. Время, необходимое объекту для достижения своей наивысшей точки, равно времени, необходимому для возврата в то же вертикальное положение. Скорость, с которой снаряд начинает свой путь вверх, равна скорости снаряда, когда он возвращается на ту же высоту (хотя, конечно, его скорость в противоположном направлении).Если вы хотите упростить задачу, по вертикали, в самой высокой точке, вертикальная скорость равна 0. Эта дополнительная информация может помочь вам в заполнении таблицы вертикальных перемещений. Если вы сократите движение объекта вдвое, вы можете упростить решение проблемы, но не забывайте, что если вы хотите, чтобы общее время в воздухе находилось в воздухе, вы должны удвоить время, необходимое для того, чтобы объект поднялся до своей наивысшей точки.

Вопрос: Баскетболист прыгнул прямо, чтобы отскочить.Если она была в воздухе 0,80 секунды, насколько высоко она прыгнула?

Переменная	Значение
v 0	?
v	0 м / с
Δy	НАЙТИ
а	-9,8 м / с 2
т	0.40 с

Ответ: Определите вверх как положительное направление оси Y. Обратите внимание, что если баскетболист находится в воздухе 0,80 секунды, он достигает своего максимального роста за 0,40 секунды, после чего его скорость равна нулю.

Невозможно найти Δx напрямую с данной информацией, поэтому сначала найдите v ₀ .

Теперь, когда известно v ₀ , решите для Δx.

Вопрос: Какой график лучше всего отображает взаимосвязь между ускорением объекта, свободно падающего у поверхности Земли, и временем, в которое он падает?

Ответ: (4) Ускорение свободного падения постоянное 9.8 м / с ² вниз по поверхности Земли.

Физика (потенциальная энергия и кинетическая энергия) –

Потенциальная энергия – это возможная энергия, которую объект имеет в зависимости от его положения.

Формула

Потенциальная энергия (PE) = масса * сила тяжести * высота

Как мы можем использовать эту формулу, чтобы лучше понимать движения? Давайте посмотрим на спортсменов, прыгающих с боксов и обратно…

Если мы смотрим на двух спортсменов, стоящих на одном прямоугольнике роста, мы сразу узнаем, что переменные Рост (высота прямоугольника) и Гравитация уравнения будут одинаковыми, но если вес (Масса) двух спортсменов разный, тогда должен сразу знать, что у более тяжелого будет больше ПЭ.

Аналогичный пример можно использовать для демонстрации различий в PE между двумя спортсменами одинаковой массы на разной высоте бокса. Опять же, поскольку сила тяжести такая же, как и вес (масса), мы можем сразу определить, что у спортсмена на более высоком ящике будет большая потенциальная энергия.

Тот же спортсмен в более высоком боксе будет иметь более высокий PE (больший рост) Тот же спортсмен в меньшем боксе будет иметь более низкий PE (меньший рост).

Кинетическая энергия (KE) – это количество энергии, которое объект получает от движения.2

PE = Масса * Плотность * Высота

Если мы посмотрим на PE, единственное, что мы действительно можем изменить, чтобы повлиять на PE, – это высота, на которой находится объект или спортсмен. Масса (вес спортсмена) не может быть изменена, как и сила тяжести. Однако мы всегда можем поместить спортсмена на более высокий или меньший ящик, из которого он спрыгнет.

Теперь, глядя на KE, какая часть формулы PE будет влиять на скоростной аспект формулы KE? ВЫСОТА.

Чем выше расположен объект, тем дальше он должен упасть и тем с большей скоростью будет объект при контакте.Другими словами, чем выше PE, тем больше у объекта потенциал для достижения более высокого KE. Ключевое слово – потенциал. Просто потому, что PE действительно высокий, не означает, что последующее действие приведет к чрезвычайно высокому KE, но это только в том случае, если один из аспектов уравнения KE уменьшается (обычно высота).

Например, если у вас есть спортсмен, перепрыгивающий из 6-футового бокса в 4-футовый бокс, атлет уменьшит свою потенциальную энергию, уменьшив рост на 2 фута, но у вас будет это снижение PE только за счет последующего развития KE. (падение с 6 до 4 футов).Даже несмотря на то, что потенциальная энергия с 6 до 4 футов снижена, у спортсмена все равно будет потенциальная энергия.

Приземление на бокс снизит KE при ударе за счет сохранения некоторой части PE (у спортсмена все еще есть PE, пока он находится на боксе) В верхней части прыжка PE спортсмена будет самым высоким, а KE будет самым низким

Потенциальная энергия спортсмена на высоте 6 футов:

Масса (200 фунтов) * Высота (6 футов) * Гравитация 9.8 м / с

Потенциальная энергия спортсмена на высоте 4 футов:

Масса (200 фунтов) * Высота (4 фута) * Плотность 9,8 м / с

Атлет должен был использовать кинетическую энергию, чтобы переместиться с 6 футов на 4 фута, что и позволило снизить PE.

Как только вы поймете концепции KE и PE, вы сможете разрабатывать обучающие программы, чтобы манипулировать аспектами их уравнений, увеличивая или уменьшая их величину.

ДОПОЛНИТЕЛЬНОЕ ВИДЕО

Нравится:

Нравится Загрузка…

Связанные

5.3 Движение снаряда | Texas Gateway

Свойства движения снаряда

Движение снаряда – это движение объекта, подбрасываемого (проецируемого) в воздух. После начальной силы, запускающей объект, он испытывает только силу тяжести. Объект называется снарядом, а его путь называется его траекторией. Когда объект движется по воздуху, он сталкивается с силой трения, которая замедляет его движение, называемое сопротивлением воздуха.Сопротивление воздуха значительно изменяет траекторию движения, но из-за сложности вычислений оно игнорируется во вводной физике.

Самая важная концепция движения снаряда состоит в том, что горизонтальных и вертикальных движения являются независимыми , что означает, что они не влияют друг на друга. На рис. 5.28 сравнивается пушечное ядро, падающее в свободном падении (синим цветом), и пушечное ядро, выпущенное горизонтально с метательным движением (красным). Вы можете видеть, что пушечное ядро ​​в свободном падении падает с той же скоростью, что и пушечное ядро ​​при движении снаряда.Имейте в виду, что если бы пушка запускала шар с любой вертикальной составляющей скорости, вертикальные смещения не совпадали бы идеально.

Поскольку вертикальные и горизонтальные движения независимы, мы можем анализировать их отдельно по перпендикулярным осям. Для этого мы разделяем движение снаряда на две составляющие его движения: одну по горизонтальной оси, а другую по вертикали.

Рис. 5.28 На диаграмме показано движение снаряда при выстреле пушечного ядра под горизонтальным углом по сравнению с выстрелом, сброшенным без горизонтальной скорости.Обратите внимание, что оба ядра со временем имеют одинаковое вертикальное положение.

Мы назовем горизонтальную ось x осью, а вертикальную ось y . Для обозначений d – это полное смещение, а x и y – его составляющие по горизонтальной и вертикальной осям. Величины этих векторов равны x и y , как показано на рисунке 5.29.

Рисунок 5.29 Мальчик пинает мяч под углом θ , и он перемещается по своей траектории на расстояние с .

Как обычно, мы используем скорость, ускорение и смещение для описания движения. Мы также должны найти компоненты этих переменных по осям x и y . Тогда компоненты ускорения очень просты: a _y = – g = –9,80 м / с ² . Обратите внимание, что это определение определяет направление вверх как положительное.Поскольку сила тяжести вертикальна, a _x = 0. Оба ускорения постоянны, поэтому мы можем использовать кинематические уравнения. Для обзора кинематические уравнения из предыдущей главы сведены в Таблицу 5.1.

x = x0 + vavgt x = x0 + vavgt (когда a = 0 a = 0)

vavg = v0 + v2 vavg = v0 + v2 (когда a = 0 a = 0)

v = v0 + atv = v0 + при

x = x0 + v0t + 12at2x = x0 + v0t + 12at2

v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0)

Таблица 5.