Первый закон термодинамики
Определение первого закона термодинамики (4 формулировки):
Энергия не может быть создана или уничтожена (закон сохранения энергии), она лишь переходит из одного вида в другой в различных физических процессах. Отсюда следует, что внутренняя энергия изолированной системы остается неизменной.
Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы против внешних сил.
Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданной системе и не зависит от способа, которым осуществляется этот переход.
Изменение внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты, переданной системе, и работой, совершенной системой над внешними силами.
Первый закон термодинамики в математическом виде:
\[ \Delta Q=\Delta U+A\ \qquad (1), \]
где \( \Delta Q \) – количество теплоты, которое получает термодинамическая система; \( \Delta U \) – изменение внутренней энергии рассматриваемой системы; A – работа, которую выполняет система над внешними телами (против внешних сил).
Первый закон термодинамики в дифференциальном виде:
\[ \delta Q=dU+\delta A\ \qquad (2), \]
где \( \delta Q \) – элемент количества теплоты, который получает система; \( \delta A \) – бесконечно малая работа, которую выполняет термодинамическая система; dU – элементарное изменение внутренней энергии, рассматриваемой системы. Следует обратить внимание на то, что в формуле (2) dU – элементарное изменение внутренней энергии является полным дифференциалом, в отличие от \( \delta Q \) и \( \delta A \).
Количество теплоты считают положительным, если система тепло получает и отрицательным, если тепло отводится от термодинамической системы. Работа будет больше нуля, если ее совершает система, и работа будет считаться отрицательной, если она совершается над системой внешними силами.
В то случае, если система вернулась в первоначальное состояние, то изменение ее внутренней энергии будет равно нулю:
\[\Delta U=0\ \qquad (3)\]
В таком случае в соответствии с первым законом термодинамики мы имеем:
\[\Delta Q=A\ \qquad (4)\]
Выражение (4) означает, что невозможен вечный двигатель первого рода.
То есть, принципиально нельзя создать периодически действующую систему (тепловой двигатель), совершающую работу, которая была бы больше, чем количество теплоты, полученное системой извне. Положение о невозможности вечного двигателя первого рода, также является одним из вариантов формулировки первого закона термодинамики.
Первый закон термодинами гласит, что энергия не может быть создана или уничтожена. Таким образом, энергия системы (замкнутой) – постоянна. Тем не менее, энергия может быть передана от одного элемента системы другому. Рассмотрим замкнутую систему, изолированную от остальных.
Передача энергии между различными подсистемами в ней может быть описана как :
E1 = E2
где: E1 = начальная энергия, E2 = конечная энергия
Внутрення энергия включает :
- Кинетическую энергию движения атомов
- Потенциальную энергию хранящуюся в химических связях
- Гравитационную энергию системы
Первый закон является основой для термодинамической науки и инженерного анализа.
Базируется на возможных типах обмена (энергии), ниже приведены 3 типа систем:
- пред – изолированные системы (isolated systems): отсутствует обмен элементами системы или энергией
- закрытые системы (closed systems): отсутствует обмен элементами системы, но присутствует некоторый обмен энергией
- открытые системы (open systems): возможен обмен как элементами системы, так и энергией
Первый закон термодинамики помогает использовать ключевые концепции внутренней энергии (internal energy), тепла (heat), и работы системы (system work)
- Внутренняя энергия ( Internal Energy) – Внутренняя энергия определяется как энергия случайных, находящихся в неупорядченном движении молекул. Энергия молекул находится в диапазоне от высокой, необходимой для движения, до заметной лишь с помощью микроскопа энергии на молекулярном или атомном уровне.
Например, у стакана с водой комнатной температы, стоящего на столе нет, на первый взгляд, никакой энергии: ни кинетической, ни потенциальной относительно стола. Но, с помощью микроскопа становится заметна “бурлящая” масса быстро двигающихся молекул. Если выплеснуть воду из стакана, эта микроскопическая энергия не обязательно заметно изменится, когда мы усредним добавленную кинетическую энергию на все молекулы воды. - Тепло – Тепло может быть определено, как энергия, передаваемая от объекта с более высокой температурой к объекту с менее высокой температурой. Сам по себе объект не обладает “теплом”; соответствующий термин для микроскопической энергии объекта – внутренняя энергия. Внутренняя энергия может увеличиваться путем переноса энергии к объекту от объекта, имеющего температуру выше – этот процесс называется нагревом.
- Работа
В случаях когда давление не является постоянным, работа может быть представлена интегральным образом, как площадь поверхности под кривой в координатах давление, объем, которые представляют происходящий процесс.
Например, у стакана с водой комнатной температы, стоящего на столе нет, на первый взгляд, никакой энергии: ни кинетической, ни потенциальной относительно стола. Но, с помощью микроскопа становится заметна “бурлящая” масса быстро двигающихся молекул. Если выплеснуть воду из стакана, эта микроскопическая энергия не обязательно заметно изменится, когда мы усредним добавленную кинетическую энергию на все молекулы воды.
Изменение внутренней энергии системы равно теплу (добавленному системе) минус работа, совершенная системой
dE = Q – W
где: dE – изменение внутренней энергии, Q – добавленное тепло, W – работа системы
1й закон не дает информации о характере процесса и не определяет конечного состояния равновесия. Интуитивно мы понимаем, что энергия переходит от объекта с более высокой температурой к объекту с менее высокой температурой. Таким образом, 2й закон нам нужен для получения информации о характере процесса.
Энтальпия
Энтальпия это термодинамический потенциал, используемый в химической термодинамике реакций и не циклических процессов, однозначная функция состояния термодинамической системы при независимых параметрах энтропии и давления, связана с внутренней энергией соотношением, приведенным ниже.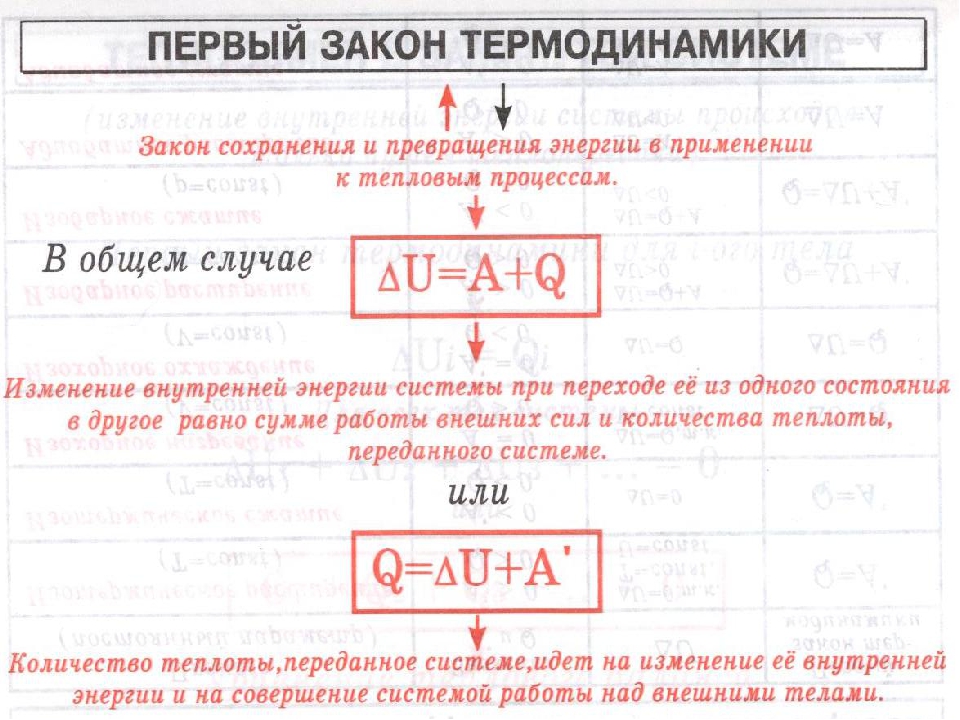
Энтальпия определяется как:
H = U + PV
где: H – энтальпия, U – внутренняя энергия, P – давление, V – объем системы
При постоянном давлении изменение энтальпии равно количеству теплоты, подведенной к системе, поэтому энтальпию часто называют тепловой функцией или теплосодержанием. В состоянии термодинамического равновесия энтальпия системы минимальна.
Энтальпия является точно измеряемым параметром, когда определены способы выражения трех других поддающихся точному определению параметров формулы выше.
Энтропия
Термин “энтропия” – величина, характеризующая степень неопределенности системы.
Однако, в термодинамике это понятие используется для определения связанной энергии системы. Энтропия определяет способность одной системы влиять на другую. Когда объекты пересекают нижнюю границу энергетического уровня необходимого для воздействия на окружающую среду, энтропия возрастает.
Энтропия связана со вторым законом термодинамики.
Энтропия (обычно обозначается S), функция состояния термодинамической системы, изменение которой dS в равновесном процессе равно отношению количества теплоты dQ, сообщенного системе или отведенного от нее, к термодинамической температуре Т системы.
в символьном виде записывается, как
dS=(dQ)/T
где: dS – изменение термодинамической системы, dQ – количество теплоты, сообщенное системе, T – термодинамическая температура системы
Неравновесные процессы в изолированной системе сопровождаются ростом энтропии, они приближают систему к состоянию равновесия, в котором S максимальна (закон неубывания энтропии).
Для вселенной в целом энтропия возрастает.
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Второй закон термодинамики
Определение второго закона термодинамики (2 формулировки):
Формулировка Кельвина и Планка Не существует циклического процесса, который извлекает количество теплоты из резервуара при определенной температуре и полностью превращает эту теплоту в работу.
(Невозможно построить периодически действующую машину, которая не производит ничего другого, кроме поднятия груза и охлаждения резервуара теплоты)
Формулировка Клаузиуса Не существует процесса, единственным результатом которого является передача количества теплоты от менее нагретого тела к более нагретому. (Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара)
Оба определения второго закона термодинамики опираются на первый закон термодинамики, утверждающий, что энергия убывает.
Второй закон связан с понятием энтропии (S).
Энтропия порождается всеми процессами, она связана с потерей системы способности совершать работу. Рост энтропии – стихийный процесс. Если объем и энергия системы постоянны, то любое измение в системе увеличивает энтропию. Если же объем или энергия системы меняются, энтропия системы уменьшается. Однако, энтропия вселенной при этом не уменьшается.
{(1)}_{(2)}{dS}}=S_1-S_2\le 0 \qquad (1),\]
где S – энтропия; L – путь по которому система переходит из одного состояния в другое.
В данной формулировке второго начала термодинамики следует обратить внимание на то, что рассматриваемая система должна быть замкнутой. В незамкнутой системе энтропия может вести себя как угодно (и убывать, и возрастать, и оставаться постоянной). Заметим, что энтропия не изменяется в замкнутой системе при обратимых процессах.
Рост энтропии в замкнутой системе при необратимых процессах — это переход термодинамической системы из состояний с меньшей вероятностью в состояния с большей вероятностью. Известная формула Больцмана дает статистическое толкование второго закона термодинамики:
\[S=kln\ w\ \qquad (2),\]
где k – постоянная Больцмана; w – термодинамическая вероятность (количество способов при помощи которых, может реализовываться рассматриваемое макросостояние системы).
Так, второй закон термодинамики является статистическим законом, который связан с описанием закономерностей теплового (хаотического) движения молекул, которые составляют термодинамическую систему.
Эффективность теплового двигателя
Эффективность теплового двигателя, действующего между двумя энергетическими уровнями , определена в пересчете на абсолютные температуры
\[ \eta = \dfrac{T_h – T_c}{T_h} = \frac{1 – T_c }{T_h} \]
где: η – эффективность, Th – верхняя граница температуры (K), Tc – нижняя граница температуры (K)
Для того, чтобы достичь максимальной эффективности Tc должна быть на столько низкой, на сколько это возможно. Чтобы эффект был 100% -м, Tc должна равнятся 0 по шкале Kельвина. Практически это невозможно, поэтому эффективность всегда меньше 1 (менее 100%).
- Изменение энтропии > 0 Необратимый процесс
- Изменение энтропии = 0 Двусторонний процесс (обратимый)
- Изменение энтропии < 0 Невозможный процесс (неосуществимый)
Энтропия определяет относительную способность одной системы влиять на другую. Когда энергия двигается к нижнему энергетическому уровню, где уменьшается возможность влияния на окружающую среду, энтропия увеличивается.
Определение энтропии
Энтропия определяется как :
\[ S = \dfrac{H}{T} \]
где: S = энтропия (кДж/кг*К), H – энтальпия> (кДж/кг), T = абсолютная температура (K)
Изменение энтропии системы вызвано изменением содержания темпла в ней. Изменение энтропии равно изменению темпла системы деленной на среднюю абсолютную температуру ( Ta):
\[ dS = \frac{dH}{T_a} \]
Сумма значений (H / T) для каждого полного цикла Карно равна 0.
Это происходит из-за того, что каждому положительному H противостоит отрицательное значение H.
Тепловой цикл Карно
Цикл Карно— идеальный термодинамический цикл.
В тепловом двигателе, газ (реверсивно) нагревается (reversibly heated), а затем охлаждается. Модель цика следующая:
Положение 1 — (изотермическое расширение) → Положение 2 — (адиабатическое расширение) → Положение 3 –(изотермическое сжатие) → Положение 4 –(адиабатическое сжатие) → Положение 1
Положение 1 – Положение 2: Изотермическое расширение Изотермическое расширение. В начале процесса рабочее тело имеет температуру Th , то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты QH. При этом объём рабочего тела увеличивается. QH=∫Tds=Th (S2-S1) =Th ΔS
Положение 2 – Положение 3: Адиабатическое расширение
Адиабатическое (изоэнтропическое) расширение.
Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника.
Положение 3 – Положение 4: Изотермическое сжатие Изотермическое сжатие. Рабочее тело, имеющее к тому времени температуру Tc, приводится в контакт с холодильником и начинает изотермически сжиматься, отдавая холодильнику количество теплоты Qc. Qc=Tc(S2-S1)=Tc ΔS
Положение 4 – Положение 1: Адиабатическое сжатие Адиабатическое (изоэнтропическое) сжатие. Рабочее тело отсоединяется от холодильника и сжимается без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя.
При изотермических процессах температура остаётся постоянной, при адиабатических отсутствует теплообмен, а значит, сохраняется энтропия.
Поэтому цикл Карно удобно представить в координатах T и S (температура и энтропия).
Законы термодинамики были определены эмперическим путем (эксперементально). Второй закон термодинамики – это обощение экспериментов, связанных с энтропией. Известно, что dS системы плюс dS окружающей среды равно или больше 0.
Энтропия адиабатически изолированной системы не меняется!
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!Больше интересного в телеграм @calcsbox
Первый закон термодинамики
Мы знаем, что внутреннюю энергию тел можно менять теплообменом – передавая или забирая некоторое количество теплоты (см. § 6-в). Но опыты Румфорда и Джоуля продемонстрировали, что внутреннюю энергию тел можно менять совершением работы (см. § 6-ж). То есть существуют два различных равноправных способа изменения внутренней энергии тел: теплопередача и работа (см. формулу).
” border=”0″ cellspacing=”0″ cellpadding=”0″>Q – полученное им количество теплоты, Дж
A – совершённая над телом работа, Дж
Эта формула гласит, что изменение внутренней энергии тела есть величина, равная сумме количества теплоты, полученной этим телом, и совершённой над ним работы. Это утверждение, отражающее закон сохранения и превращения энергии, называется первым законом термодинамики. Чтобы лучше его осознать, рассмотрим примеры.
Опыт «воздушное огниво». Возьмём толстостенный стеклянный цилиндр с поршнем. На дно цилиндра насыпем немного «серы» от спичек. Резко ударив по рукоятке, мы совершим механическую работу над воздухом: сожмём его. В результате воздух нагреется настолько сильно, что серный порошок в нём воспламенится без поджигания!
Объясним опыт.
Удар длился недолго, поэтому передачей теплоты из цилиндра наружу можно пренебречь. Извне теплота также не поступала. Следовательно, теплообмен отсутствовал, то есть Q = 0. Тогда формула первого закона термодинамики применительно к этому опыту запишется так: ΔU = 0 + A, то есть ΔU = A.
Последнюю формулу лучше писать наоборот: A = ΔU, что читается так: совершённая над телом работа идёт на изменение его внутренней энергии (если теплообмен отсутствует). То есть работа, совершённая над воздухом, привела к росту его внутренней энергии, и он нагрелся.
Опыт «туман в бутыли». Для него нам потребуются бутыль, пробка, шланг и насос (см. рисунок). Прежде чем вставить пробку, в бутыль наливают немного воды и несколько раз встряхивают, чтобы воздух внутри стал влажным. Удерживая пробку рукой, накачивают воздух. Когда нам становится трудно удерживать пробку, накачивание прекращают и ожидают 5–10 минут, чтобы воздух в бутыли охладился до комнатной температуры (так как при совершении над ним работы он нагрелся).
При отпускании пробки она вылетает, и в бутыли образуется туман!
Разделим объяснение результатов этого опыта на три этапа.
1-й этап. Накачивая воздух, мы совершаем над ним работу. По аналогии с опытом «воздушное огниво», запишем первый закон термодинамики так: ΔU = 0 + A. Поскольку А – положительная величина, значит, и ΔU положительна. То есть внутренняя энергия воздуха изменяется в большую сторону – возрастает.
2-й этап. Давая воздуху охладиться, работу не совершали: A = 0. Следовательно, первый закон термодинамики запишется: ΔU = –Q + 0. Знак «минус» означает, что воздух не получал теплоту, а отдавал её. Поскольку величина –Q является отрицательной, значит, и равная ей величина ΔU тоже отрицательна. Следовательно, внутренняя энергия воздуха изменяется в меньшую сторону – уменьшается.
3-й этап. Пробку отпускают, и она выталкивается струёй воздуха. Всё происходит быстро, поэтому теплообмен не успевает произойти: Q = 0.
Кроме того, работа совершается не над воздухом, а им самим, следовательно, первый закон термодинамики запишется: ΔU = –A. Поскольку величина –A является отрицательной, то и величина ΔU отрицательна. Значит, внутренняя энергия воздуха опять убывает. Он охлаждается, и в бутыли появляется туман.
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Физический справочник / / Физика для самых маленьких. Шпаргалки. Школа. / / Термодинамика. Внутренняя энергия. Работа. Количество теплоты. Тепловые явления. Первый закон термодинамики. Применение первого закона термодинамики к различным процессам. Уравнение теплового балланса. Второй закон термодинамики. Тепловые двигателиПоделиться:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если система (тело) получает энергию, то ΔQ системы > 0, если отдает энергию, то ΔQ системы < 0
При охлаждении – внутренняя энергия уменьшается за счет передачи тепла окружающей среде.
2.4. Второй закон термодинамики – Энергетика: история, настоящее и будущее
2.4. Второй закон термодинамики
Первый закон термодинамики, как уже сказано, характеризует процессы превращения энергии с количественной стороны. Второй закон термодинамики характеризует качественную сторону этих процессов. Первый закон термодинамики дает все необходимое для составления энергетического баланса какоголибо процесса.
Однако он не дает никаких указаний относительно возможности протекания того или иного процесса. Между тем далеко не все процессы реально осуществимы.
Следует подчеркнуть, что второй закон термодинамики, так же как и первый закон, сформулирован на основе опыта.
Проследим путь, приведший физиков к открытию этого закона.
Наиболее важные исследования теплоты в первой половине XIX века проводились с практической целью улучшить работу паровой машины. Английский изобретатель Джеймс Уатт (1736–1819) с предельной практичностью сформулировал задачу: сколько угля требуется, чтобы получить определенную работу, и какими способами при заданной величине работы можно свести к минимуму количество расходуемого горючего?
За исследование этой практической проблемы взялся молодой инженер Сади Карно.
Если исходить из первого закона термодинамики, то можно допустить протекание любого процесса, который не противоречит закону сохранения энергии. В частности, при теплообмене можно было бы предположить, что теплота может передаваться как от тела с большей температурой к телу с меньшей температурой, так и наоборот.
При этом согласно первому закону термодинамики накладывается только одно условие: чтобы количество теплоты, отданной одним телом, равнялось количеству теплоты, принятой другим телом.
Между тем из опыта известно, что теплота всегда самопроизвольно передается только от более нагретых тел к менее нагретым, т.е. самопроизвольный или естественный процесс теплообмена обладает свойством направленности в сторону тел с более низкой температурой, причем он прекращается при достижении равенства температур участвующих в теплообмене тел.
Возможен и обратный, не самопроизвольный (искусственный) процесс передачи теплоты от менее нагретых тел к более нагретым (например в холодильных установках), но для осуществления его требуется подвод энергии извне.
Констатация этой особенности теплоты, проявляющейся в процессе ее передачи, является одной из сторон сущности второго закона термодинамики.
«Проведав, что Природою дано
Стать силой движущей Огню,
Вошел в историю Карно,
Прославив молодость свою…»
(Э.
Г. Братута)
Сади Карно был сыном своего века. Его теоретические исследования отвечали на конкретный вопрос, поставленный развивающейся промышленностью: как сделать тепловой двигатель более экономичным. Результаты своих исследований он подытожил в работе, вышедшей в 1824 г., «Размышления о движущей силе огня и о машинах, способных развивать эту силу» (об этой работе уже упоминалось выше в 1.2). Появление этой небольшой работы стало началом нового этапа в истории физики не только благодаря полученным в ней результатам, но и благодаря примененному методу, который впоследствии использовался бесчисленное множество раз. В основу своего рассмотрения Карно положил невозможность осуществления вечного двигателя.
Свое исследование Карно начинает с восхваления паровых машин. Он констатирует, что теория этих машин развита очень слабо, и замечает, что для того, чтобы продвинуть ее, нужно несколько оторваться от чисто прикладного аспекта и рассмотреть движущую силу огня в общем виде.
Сади Карно (1796–1832) – французский физик и военный инженер – занимался изучением и усовершенствованием паровых машин, а также изучал теплоту как форму энергии.
Карно был первым ученым, начавшим количественное изучение взаимопревращения теплоты и работы, поэтому его с полным правом можно назвать отцом термодинамики. Он ввел важнейшее для термодинамики понятие обратимого процесса и заложил основы второго начала термодинамики. Позднее лорд Кельвин сказал о Карно, что «это был самый глубокий специалист по термодинамике в первой трети XIX века». Карно был очень практичным человеком и считал, что главная цель занятий наукой – приносить пользу людям.
С помощью мысленного эксперимента Карно доказал, что если исходить из невозможности вечного двигателя, то для получения работы необходимо иметь в машине два тела с различными температурами, причем теплород должен переходить от тела с более высокой температурой к телу с более низкой. Уподобляя теплород воде, а разность температур – разности уровней воды, Карно заключает, что как при падении воды работа измеряется произведением веса воды на разность уровней, так и в паровой машине работа независимо от природы рабочего вещества (вода, спирт и т.
д.) измеряется произведением количества теплорода на разность температур. В 1824 году Карно высказал гениальную мысль: для производства работы в тепловой машине необходима разность температур, необходимы два источника теплоты с различными температурами. Иными словами, отдача тепловой машины ограничена значениями температур нагревателя и холодильника. Как подчеркивает Карно, холодильник – столь же необходимый элемент, как и котел, причем если в машине не предусмотрен специальный охлаждающий элемент, то его роль играет окружающая среда. Все это и представляет собой суть «принципа Карно», или второго начала термодинамики, как он стал называться позже, после того как этому разделу физики было придано аксиоматическое построение.
Клаузиусу пришлось защищать принцип Карно (второе начало термодинамики) от многочисленных атак. Он вывел его из другого постулата, который представляется интуитивно более очевидным, чем принятый Карно. Новый постулат Клаузиуса гласит, что теплота не может самопроизвольно переходить от более холодного тела к более горячему без участия третьего тела.
Слово «самопроизвольно» стоит здесь, чтобы указать, что если иногда такой переход имеет место, как, скажем, в растворах, в холодильных машинах и т. п., то он в известном смысле «вынужденный», т. е. сопровождается другим, компенсирующим, явлением. Этому новому постулату Клаузиуса вскоре были даны другие эквивалентные формулировки: явления природы необратимы; явления происходят так, что энергия всегда вырождается, и т. п.
В наиболее общем виде второй закон термодинамики может быть сформулирован следующим образом: любой реальный самопроизвольный процесс является необратимым. Все прочие формулировки второго закона являются частными случаями этой наиболее общей формулировки.
У. Томсон (лорд Кельвин) предложил в 1851 году следующую формулировку второго закона термодинамики: невозможно при помощи неодушевленного материального агента получить от какой-либо массы вещества механическую работу путем охлаждения ее ниже температуры самого холодного из окружающих предметов.
Mакс Планк дал такую формулировку: невозможно построить периодически действующую машину, все действие которой сводилось бы к поднятию некоторого груза и охлаждению теплового источника.
Под периодически действующей машиной следует понимать двигатель, непрерывно (в циклическом процессе) превращающий тепло в работу. В самом деле, если бы удалось построить тепловой двигатель, который просто отбирал бы тепло от некоторого источника и непрерывно (циклично) превращал его в работу, то это противоречило бы сформулированному ранее положению о том, что работа может производиться системой только тогда, когда в этой системе отсутствует равновесие (в частности, применительно к тепловому двигателю, когда в системе имеется разность температур горячего и холодного источников).
Уильям Томсон (1824–1907) (в 1892 году за научные заслуги получил титул лорда Кельвина) – известный английский физик оставил после себя 25 книг, 660 научных статей и 70 изобретений в сфере термодинамики, теории электрических и магнитных явлений. Он предложил абсолютную шкалу температур (шкала Кельвина), экспериментально открыл ряд эффектов (в том числе эффект Джоуля–Томсона), установил зависимость периода колебаний контура от его емкости и индуктивности (формула Томсона), изобрел многие электроизмерительные приборы, разработал термодинамическую теорию термоэлектрических явлений, был активным участником осуществления телеграфной связи по трансатлантическому кабелю.
В возрасте 27 лет стал членом Лондонского королевского общества.
Если бы не существовало ограничений, накладываемых вторым законом термодинамики, то это означало бы, что можно построить тепловой двигатель при наличии одного лишь источника тепла. Такой двигатель мог бы действовать за счет охлаждения, например, воды в океане. Этот процесс мог бы продолжаться до тех пор, пока вся внутренняя энергия океана не была бы превращена в работу. Тепловую машину, которая действовала бы таким образом, немецкий физикохимик В. Ф. Оствальд (1853–1932) удачно назвал вечным двигателем второго рода (в отличие от вечного двигателя первого рода, работающего вопреки закону сохранения энергии). В соответствии со сказанным формулировка второго закона термодинамики, данная Планком, может быть видоизменена следующим образом: осуществление вечного двигателя второго рода невозможно. Следует заметить, что существование вечного двигателя второго рода не противоречит первому закону термодинамики; в самом деле, в этом двигателе работа производилась бы не из ничего, а за счет внутренней энергии, заключенной в тепловом источнике.
Подчеркнем важную особенность тепловых процессов. Механическую работу, электрическую работу, работу магнитных сил и т. д. можно без остатка, полностью, превратить в теплоту. Что же касается теплоты, то только часть ее может быть превращена в периодически повторяющемся процессе в механическую работу и иные виды работы; другая ее часть неизбежно должна быть передана холодному источнику. В этом суть второго закона термодинамики.
По одному из постулатов У. Томсона невозможно осуществление цикла теплового двигателя без переноса некоторого количества теплоты от источника тепла с более высокой температурой к источнику с более низкой температурой. Из постулата Томсона следует невозможность получения работы в тепловом двигателе, равной отнятому от горячего источника теплу Q 1, т. е. обязательно должно выполняться неравенство L<Q 1.
Но по закону сохранения энергии
L=Q 1 – Q 2,
где Q 2 – отводимое к холодному источнику тепло.
Поэтому в тепловых двигателях, какой бы конструкции они ни были, всегда должно быть Q 2 >0.
Отношение работы L к теплу Q 1 называют терми ческим коэффициентом полезного действия
η t =(L /Q 1)<1.
Таким образом, термический к. п. д. теплового двигателя всегда должен быть меньше единицы. Это положение впервые было доказано С. Карно (1824 г.) путем рассмотрения возможной работы идеального (обратимого) теплового
двигателя в условиях бесконечноёмких горячего и холодного источников тепла (T 1 =const и T 2 =const). С. Карно было доказано, что максимальный термический к. п. д. идеального теплового двигателя в условиях постоянства температур T 1 и T 2 составляет величину:
η t =1–(T 2 /T 1)<1.
Рис. 2.1. TS – диаграмма термодинамического кругового процесса
Анализируя выводы Карно, Клаузиус заметил, что для идеального теплового двигателя соблюдается соотношение
Q 1 /T 1 =Q 2 /T 2. Исходя из этого, Клаузиусом в конце XIX века была введена новая термодинамическая функция – энтропия, определяемая как отношение количества подведенной или отведенной теплоты к абсолютной температуре ее подвода или отвода:
Ѕ =Q/T.
Эта новая величина – энтропия (от греч. εν – в и τροπη – поворот, превращение) – математически строго определена, но физически мало наглядна. Клаузиус показал, что абсолютное значение энтропии остается неопределенным, определены лишь ее изменения в термически изолированных необратимых системах; в идеальном случае обратимых процессов энтропия остается постоянной.
Введению этой новой величины физики противодействовали весьма энергично, особенно изза ее таинственного характера, обусловленного главным образом тем, что она не действует на наши органы чувств. Поскольку ее изменение равно нулю для идеальных обратимых процессов и положительно для реальных обратимых процессов, то энтропия есть мера отклонения реального процесса от идеального. Этим объясняется данное Клаузиусом название этой величины, которое этимологически означает «изменение».
Введение этой величины позволило создать температурно-энтропийные, или так называемые TS- диаграммы (рис. 2.1), с помощью которых можно оценивать термодинамические процессы и определять эффективность тепловых двигателей.
На площади такой диаграммы точки отвечают определённому состоянию газообразного рабочего тела, поскольку для каждой из них известны две величины – параметры состояния, которые характеризуют газ. В данном случае ими будут T и S (т. е. температура и энтропия).
Если к некоторому количеству газа, состояние которого определено на рисунке точкой 1, подвести определённое количество теплоты dQ, то система перейдёт путём a в состояние, характеризуемое точкой 2, а затем вследствие отвода теплоты система путем b вернётся в первоначальное состояние (точка 1). Это означает, что система осуществила круговой процесс.
Для любого элементарного участка такого процесса существует зависимость
где dS – увеличение функции состояния системы – энтропии, кДж/К; dQ – количество подведённой теплоты, кДж; T – температура, при которой подводится теплота, К.
Поскольку dQ = TdS, то понятно, что количество подведенной теплоты в каком-либо процессе, в том числе в процессе, определяется на TS-диаграмме в определённом масштабе площадью, обозначаемой вертикальной штриховкой, а количество отведенного тепла – площадью с наклонной штриховкой.
Площадь, ограниченная кривыми1 – 2 и 2 – 1, является разницей между указанными площадями. Она характеризует количество теплоты, преобразованной, согласно закону сохранения энергии, в работу, выполненную 1 кг газа за цикл. Термодинамический к.п.д. цикла определяется как отношение этой площади к заштрихованной вертикальными линиями, которая соответствует подведенной энергии. Итак, из сказанного следует, что к.п.д. возрастает тем больше, чем выше расположена верхняя кривая и ниже – нижняя.
Рис. 2.2. Процессы в газах (изоэнтропы, изотермы, изохоры, изобары)
Если верхняя и нижняя температурные границы цикла жестко определены (на рис.2.1 они обозначены пунктиром), тогда к.п.д. тем выше, чем более близкой к прямоугольнику ABCD будет форма площади цикла1 – 2 и 2 – 1. Цикл, который на TS-диаграмме изображен прямоугольником ABCD, получил название цикла Карно. К.п.д. цикла Карно невозможно превысить никакими средствами, а его величина зависит только от температуры: наиболее высокой (изотермаАВ) и наиболее низкой (изотерма DC):
η K = В этом заключается суть второго закона термодинамики.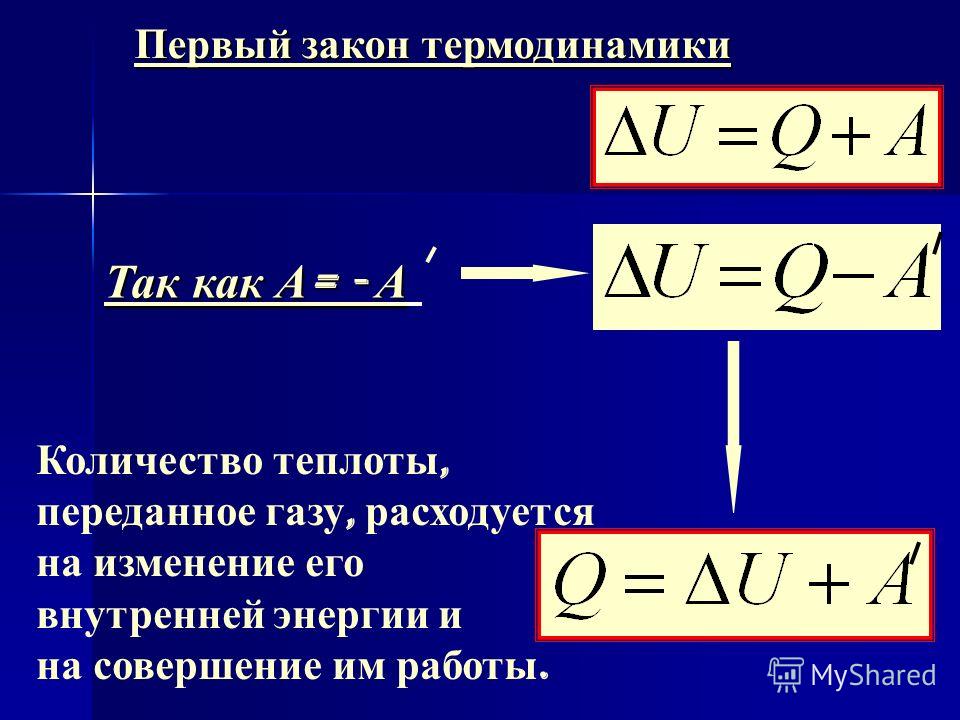
Из уравнения видно, что основным путем увеличения эффективности тепловых двигателей является повышение верхней температуры T 1 , при которой теплота подводится к рабочему телу, и понижение нижней T 2, при которой теплота отводится.
Теплота в конечном счете отводится к окружающей среде (в воздух или в воду). В связи с этим минимально возможная температура отвода теплоты близка к температуре этих сред.
Соотношение, справедливое и для обратимых (знак равенства), и для необратимых (знак >) процессов в любой системе, представляет собой аналитическое выражение второго закона термодинамики:
Относительно процессов, из которых составляется цикл Карно (см. рис. 2.1), не было выдвинуто условий их протекания, кроме того, что в процессе а теплота подводится, а в процессе b – отводится. На самом деле среди многочисленных возможных процессов часто выделяются четыре вида, условием осуществления которых есть постоянство одного из параметров состояния газа (рис. 2.2).
Изотермический процесс происходит при постоянной температуре; на TS -диаграмме изображается горизонтальными линиями.
Изоэнтропный процесс расширения или сжатия происходит без трения таким образом, что тепло к газу не подводится и не отводится (dQ =0). На TS -диаграмме этот процесс изображается вертикальными прямыми.
Изобарный процесс осуществляется при постоянном давлении p. Такие процессы очень широко представлены в природе и технике. На ТS диаграмме изобара изображена кривой линией.
Изохорные изменения состояния газа происходят, когда его нагревают или охлаждают при постоянном объеме. Изохора на TS- диаграмме изображена пунктирной кривой, более крутой, чем изобара.
Термодинамический цикл тепловых двигателей обычно состоит из ряда вышеназванных процессов. Для иллюстрации приведем в TS- диаграмме термодинамический цикл, по которому работает традиционная установка тепловой электрической станции, так называемый пароводяной цикл Ренкина (рис. 2.3).
Питательная вода, которая поступает в паровой котел, нагревается в нем (изобараа – в), испаряется (изотерма, которая совпадает с изобаройв – с), образовавшийся пар перегревается в пароперегревателе (изобарас – д) до температуры Т1.
Далее в турбине происходит изоэнтропное расширение пара (изоэнтроп аd – е), а в конденсаторе при Т 2 =const – его конденсация (изотерма е – f, которая совпадает с изобарой). Затем конденсат подается в котел насосом (изоэнтроп аf – а).
Рис. 2.3. Термодинамический цикл, по которому работает традиционная установка тепловой электрической станции (пароводяной цикл Ренкина)
Второе начало термодинамики • Джеймс Трефил, энциклопедия «Двести законов мироздания»
Природным процессам свойственна направленность и необратимость, однако в большинстве законов, описанных в этой книге, это не находит отражения — по крайней мере, явного. Разбить яйца и сделать яичницу не сложно, воссоздать же сырые яйца из готовой яичницы — невозможно. Запах из открытого флакона духов наполняет комнату — однако обратно во флакон его не соберешь. И причина такой необратимости процессов, происходящих во Вселенной, кроется во втором начале термодинамики, который, при всей его кажущейся простоте, является одним из самых трудных и часто неверно понимаемых законов классической физики.
Прежде всего, у этого закона имеется как минимум три равноправные формулировки, предложенные в разные годы физиками разных поколений. Может показаться, что между ними нет ничего общего, однако все они логически эквивалентны между собой. Из любой формулировки второго начала математически выводятся две другие.
Начнем с первой формулировки, принадлежащей немецкому физику Рудольфу Клаузиусу (см. Уравнение Клапейрона—Клаузиуса). Вот простая и наглядная иллюстрация этой формулировки: берем из холодильника кубик льда и кладем его в раковину. По прошествии некоторого времени кубик льда растает, потому что теплота от более теплого тела (воздуха) передастся более холодному (кубику льда). С точки зрения закона сохранения энергии, нет причин для того, чтобы тепловая энергия передавалась именно в таком направлении: даже если бы лед становился всё холоднее, а воздух всё теплее, закон сохранения энергии всё равно бы выполнялся. Тот факт, что этого не происходит, как раз и свидетельствует об уже упоминавшейся направленности физических процессов.
Почему именно так взаимодействуют лед и воздух, мы можем легко объяснить, рассматривая это взаимодействие на молекулярном уровне. Из молекулярно-кинетической теории мы знаем, что температура отражает скорость движения молекул тела — чем быстрее они движутся,тем выше температура тела. Значит, молекулы воздуха движутся быстрее молекул воды в кубике льда. При соударении молекулы воздуха с молекулой воды на поверхности льда, как подсказывает нам опыт, быстрые молекулы, в среднем, замедляются, а медленные ускоряются. Таким образом, молекулы воды начинают двигаться всё быстрее, или, что то же самое, температура льда повышается. Именно это мы имеем в виду, когда говорим, что тепло передается от воздуха ко льду. И в рамках этой модели первая формулировка второго начала термодинамики логически вытекает из поведения молекул.
При перемещении какого-либо тела на какое-либо расстояние под действием определенной силы совершается работа, и различные формы энергии как раз и выражают способность системы произвести определенную работу.
Поскольку теплота, отражающая кинетическую энергию молекул, представляет собой одну из форм энергии, она тоже может быть преобразована в работу. Но опять мы имеем дело с направленным процессом. Перевести работу в теплоту можно со стопроцентной эффективностью — вы делаете это каждый раз, когда нажимаете на педаль тормоза в своем автомобиле: вся кинетическая энергия движения вашего автомобиля плюс затраченная вами энергия силы нажатия на педаль через работу вашей ноги и гидравлической системы тормозов полностью превращается в теплоту, выделяющуюся в процессе трения колодок о тормозные диски. Вторая формулировка второго начала термодинамики утверждает, что обратный процесс невозможен. Сколько ни пытайтесь всю тепловую энергию превратить в работу — тепловые потери в окружающую среду неизбежны.
Проиллюстрировать вторую формулировку в действии несложно. Представьте себе цилиндр двигателя внутреннего сгорания вашего автомобиля. В него впрыскивается высокооктановая топливная смесь, которая сжимается поршнем до высокого давления, после чего она воспламеняется в малом зазоре между головкой блока цилиндров и плотно пригнанным к стенкам цилиндра свободно ходящим поршнем.
При взрывном сгорании смеси выделяется значительное количество теплоты в виде раскаленных и расширяющихся продуктов сгорания, давление которых толкает поршень вниз. В идеальном мире мы могли бы достичь КПД использования выделившейся тепловой энергии на уровне 100%, полностью переведя ее в механическую работу поршня.
В реальном мире никто и никогда не соберет такого идеального двигателя по двум причинам. Во-первых, стенки цилиндра неизбежно нагреваются в результате горения рабочей смеси, часть теплоты теряется вхолостую и отводится через систему охлаждения в окружающую среду. Во-вторых, часть работы неизбежно уходит на преодоление силы трения, в результате чего, опять же, нагреваются стенки цилиндров — еще одна тепловая потеря (даже при самом хорошем моторном масле). В-третьих, цилиндру нужно вернуться к исходной точке сжатия, а это также работа по преодолению трения с выделением теплоты, затраченная вхолостую. В итоге мы имеем то, что имеем, а именно: самые совершенные тепловые двигатели работают с КПД не более 50%.
Такая трактовка второго начала термодинамики заложена в принципе Карно, который назван так в честь французского военного инженера Сади Карно. Она сформулирована раньше других и оказала огромное влияние на развитие инженерной техники на многие поколения вперед, хотя и носит прикладной характер. Огромное значение она приобретает с точки зрения современной энергетики — важнейшей отрасли любой национальной экономики. Сегодня, сталкиваясь с дефицитом топливных ресурсов, человечество, тем не менее, вынуждено мириться с тем, что КПД, например, ТЭЦ, работающих на угле или мазуте, не превышает 30-35% — то есть, две трети топлива сжигается впустую, точнее расходуется на подогрев атмосферы — и это перед лицом угрозы глобального потепления. Вот почему современные ТЭЦ легко узнать по колоссальным башням-градирням — именно в них остужается вода, охлаждающая турбины электрогенераторов, и избытки тепловой энергии выбрасываются в окружающую среду. И столь низкая эффективность использования ресурсов — не вина, а беда современных инженеров-конструкторов: они и без того выжимают близко к максимуму того, что позволяет цикл Карно.
Те же, кто заявляет, что нашел решение, позволяющее резко сократить тепловые потери энергии (например, сконструировал вечный двигатель), утверждают тем самым, что они перехитрили второе начало термодинамики. С тем же успехом они могли бы утверждать, что знают, как сделать так, чтобы кубик льда в раковине не таял при комнатной температуре, а, наоборот, еще больше охлаждался, нагревая при этом воздух.
Третья формулировка второго начала термодинамики, приписываемая обычно австрийскому физику Людвигу Больцману (см. Постоянная Больцмана), пожалуй, наиболее известна. Энтропия — это показатель неупорядоченности системы. Чем выше энтропия — тем хаотичнее движение материальных частиц, составляющих систему. Больцману удалось разработать формулу для прямого математического описания степени упорядоченности системы. Давайте посмотрим, как она работает, на примере воды. В жидком состоянии вода представляет собой довольно неупорядоченную структуру, поскольку молекулы свободно перемещаются друг относительно друга, и пространственная ориентация у них может быть произвольной.
Другое дело лед — в нем молекулы воды упорядочены, будучи включенными в кристаллическую решетку. Формулировка второго начала термодинамики Больцмана, условно говоря, гласит, что лед, растаяв и превратившись в воду (процесс, сопровождающийся снижением степени упорядоченности и повышением энтропии) сам по себе никогда из воды не возродится. И снова мы видим пример необратимого природного физического явления.
Тут важно понимать, что речь не идет о том, что в этой формулировке второе начало термодинамики провозглашает, что энтропия не может снижаться нигде и никогда. В конце концов, растопленный лед можно поместить обратно в морозильную камеру и снова заморозить. Смысл в том, что энтропия не может уменьшаться в замкнутых системах — то есть, в системах, не получающих внешней энергетической подпитки. Работающий холодильник не является изолированной замкнутой системой, поскольку он подключен к сети электропитания и получает энергию извне — в конечном счете, от электростанций, ее производящих.
В данном случае замкнутой системой будет холодильник, плюс проводка, плюс местная трансформаторная подстанция, плюс единая сеть энергоснабжения, плюс электростанции. И поскольку рост энтропии в результате беспорядочного испарения из градирен электростанции многократно превышает снижение энтропии за счет кристаллизации льда в вашем холодильнике, второе начало термодинамики ни в коей мере не нарушается.
А это, я полагаю, приводит еще к одной формулировке второго начала: Холодильник не работает, если он не включен в розетку.
См. также:
Второй закон термодинамики – Термодинамика для чайников
Второе начало термодинамики задаёт ограничения на направление процессов, которые могут происходить в термодинамических системах, и исключает возможность создания вечного двигателя второго рода. Фактически к этому результату пришёл уже Сади Карно в сочинении «О движущей силе огня и о машинах, способных развивать эту силу»[5][6]. Однако Карно опирался на представления теории теплорода и не дал ясной формулировки второго начала термодинамики.
Это было сделано в 1850—1851 годах независимо Клаузиусом иКельвином. Имеется несколько различных, но в то же время эквивалентных формулировок этого закона.
Постулат Кельвина: «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счёт охлаждения теплового резервуара»[21]. Такой круговой процесс называется процессом Томсона-Планка, и постулируется, что такой процесс невозможен.
Постулат Клаузиуса: «Теплота не может самопроизвольно переходить от тела менее нагретого к телу более нагретому»[22]. Процесс, при котором не происходит никаких других изменений, кроме передачи теплоты от холодного тела к горячему, называется процессом Клаузиуса. Постулат утверждает, что такой процесс невозможен. Теплота может переходить самопроизвольно только в одном направлении, от более нагретого тела к менее нагретому, и такой процесс является необратимым.
Приняв за постулат невозможность процесса Томсона-Планка, можно доказать, что процесс Клаузиуса невозможен, и наоборот, из невозможности процесса Клаузиуса следует, что процесс Томсона-Планка также невозможен.
Следствие второго начала термодинамики, постулированного в указанных формулировках, позволяет ввести для термодинамических систем ещё одну функцию термодинамического состояния S, названную энтропией, такую, что её полный дифференциал для квазистатических процессов записывается как dS=δQ/T[23]. В совокупности с температурой и внутренней энергией, введёнными в нулевом и первом началах, энтропия составляет полный набор величин, необходимых для математического описания термодинамических процессов. Лишь две из упомянутых трёх величин, которыми термодинамика пополняет список используемых в физике переменных, являются независимыми.
законов термодинамики: определение, уравнения и примеры
Обновлено 28 декабря 2020 г.
Ли Джонсон
Вечный насос – один из многих вечных двигателей, которые разрабатывались годами с целью обеспечения непрерывного движения, и часто, как следствие, бесплатная энергия. Конструкция довольно проста: вода стекает с поднятой платформы по водяному колесу, которое прикреплено к шестерням, которые, в свою очередь, приводят в действие насос, который тянет воду с поверхности обратно на приподнятую платформу, где процесс начинается снова.
Когда вы впервые слышите о подобном дизайне, вы можете подумать, что это возможная и даже хорошая идея. И ученые того времени соглашались, пока не были открыты законы термодинамики и одним махом не разбили все надежды на вечное движение.
Законы термодинамики – одни из самых важных законов физики. Они стремятся описать энергию, в том числе то, как она передается и сохраняется, а также ключевую концепцию энтропии системы, которая убивает всякую надежду на вечное движение.Если вы изучаете физику или просто хотите понять многие термодинамические процессы, происходящие вокруг вас, изучение четырех законов термодинамики станет решающим шагом на вашем пути.
Что такое термодинамика?
Термодинамика – это раздел физики, изучающий тепловую энергию и внутреннюю энергию в термодинамических системах. Тепловая энергия – это энергия, передаваемая посредством теплопередачи, а внутреннюю энергию можно представить как сумму кинетической энергии и потенциальной энергии для всех частиц в системе.
Используя кинетическую теорию в качестве инструмента, который объясняет свойства тела материи путем изучения движений составляющих его частиц, физики смогли вывести многие важные взаимосвязи между важными величинами. Конечно, вычисление полной энергии миллиардов атомов было бы непрактичным, учитывая эффективную случайность их точных движений, поэтому процессы, используемые для вывода взаимосвязей, были построены на основе статистической механики и аналогичных подходов.
По сути, упрощение допущений и акцент на «среднее» поведение для большого числа молекул дали ученым инструменты для анализа системы в целом, не зацикливаясь на бесконечных вычислениях для одного из миллиардов атомов.
Важные количества
Чтобы понять законы термодинамики, вам необходимо убедиться, что вы понимаете некоторые из наиболее важных терминов. Температура – это мера средней кинетической энергии, приходящейся на молекулу вещества, т.
е.е. насколько молекулы движутся (в жидкости или газе) или колеблются на месте (в твердом теле). Единицей измерения температуры в системе СИ является Кельвин, где 0 Кельвин известен как «абсолютный ноль», который является самой низкой возможной температурой (в отличие от нулевой температуры в других системах), при которой прекращается любое движение молекул.
Внутренняя энергия – это полная энергия молекул в системе, то есть сумма их кинетической энергии и потенциальной энергии. Разница в температуре между двумя веществами позволяет теплу течь, то есть тепловая энергия , которая передается от одного к другому. Термодинамическая работа – это механическая работа, которая выполняется с использованием тепловой энергии, как в тепловом двигателе (иногда называемом двигателем Карно).
Энтропия – это понятие, которое трудно четко определить словами, но математически оно определяется как постоянная Больцмана ( k = 1,381 × 10 – 23 м 2 кг s – 1 K – 1 ), умноженное на натуральный логарифм количества микросостояний в системе.
На словах его часто называют мерой «беспорядка», но более точно его можно представить как степень, в которой состояние системы неотличимо от большого количества других состояний при рассмотрении на макроскопическом уровне.
Например, спутанный провод наушников имеет большое количество конкретных возможных конфигураций, но большинство из них выглядят так же «запутанными», как и другие, и поэтому имеют более высокую энтропию, чем состояние, в котором провод аккуратно свернут в спираль и не спутывается.
Нулевой закон термодинамики
Нулевой закон термодинамики получает свое число, потому что первый, второй и третий законы являются наиболее известными и широко преподаются, однако они не менее важны, когда дело доходит до понимания взаимодействия термодинамических систем.Нулевой закон гласит, что если тепловая система A находится в тепловом равновесии с тепловой системой B, а система B находится в тепловом равновесии с системой C, то система A должна быть в равновесии с системой C.
Это легко запомнить, если вы думаете о том, что значит для одной системы быть в равновесии с другой. Думая с точки зрения тепла и температуры: две системы находятся в равновесии друг с другом, когда тепло течет как таковое, чтобы довести их до одной и той же температуры, например, однородной теплой температуры, которую вы получаете через некоторое время после того, как налили кипяток в кувшин с более холодной водой. .
Когда они находятся в равновесии (то есть при одинаковой температуре), теплопередача либо не происходит, либо любое небольшое количество теплового потока быстро компенсируется потоком из другой системы.
Если подумать об этом, становится логичным, что если вы приведете третью систему в эту ситуацию, она сместится в сторону равновесия со второй системой, а если она находится в равновесии, она также будет в равновесии с первой системой.
Первый закон термодинамики
Первый закон термодинамики гласит, что изменение внутренней энергии для системы (∆ U ) равно теплу, передаваемому системе ( Q ) минус проделанная системой работа ( W ).
В символах это:
∆U = Q – W
По сути, это утверждение закона сохранения энергии. Система получает энергию, если ей передается тепло, и теряет ее, если работает в другой системе, а в противоположных ситуациях поток энергии меняется на противоположный. Помня, что тепло – это форма передачи энергии, а работа – это передача механической энергии, легко увидеть, что этот закон просто заново устанавливает закон сохранения энергии.
Второй закон термодинамики
Второй закон термодинамики утверждает, что полная энтропия замкнутой системы (т.е.е. изолированной системы) никогда не уменьшается, но может увеличиваться или (теоретически) оставаться неизменным.
Это часто интерпретируется как означающее, что «беспорядок» любой изолированной системы со временем нарастает, но, как обсуждалось выше, это не совсем точный способ взглянуть на концепцию, хотя в целом он верен. Второй закон термодинамики по существу гласит, что случайные процессы приводят к «беспорядку» в строгом математическом смысле этого слова.
Еще одним распространенным источником неправильного представления о втором законе термодинамики является значение термина «замкнутая система».Это следует рассматривать как систему, изолированную от внешнего мира, но без этой изоляции энтропия может уменьшиться. Например, грязная спальня, оставленная сама по себе, никогда не станет более опрятной, но она может, , переключиться в более организованное состояние с более низкой энтропией, если кто-то войдет в нее и будет работать над ней (то есть убирает ее).
Третий закон термодинамики
Третий закон термодинамики гласит, что когда температура системы приближается к абсолютному нулю, энтропия системы приближается к константе.Другими словами, второй закон оставляет открытой возможность того, что энтропия системы может оставаться постоянной, но третий закон поясняет, что это происходит только при абсолютном нуле .
Третий закон также подразумевает, что (и иногда его называют) невозможно снизить температуру системы до абсолютного нуля с помощью любого конечного числа операций.
Другими словами, фактически невозможно достичь абсолютного нуля, хотя можно подойти к нему очень близко и минимизировать увеличение энтропии для системы.
Когда система приближается к абсолютному нулю, это может привести к необычному поведению. Например, при приближении к абсолютному нулю многие материалы теряют всякое сопротивление потоку электрического тока, переходя в состояние, называемое сверхпроводимостью. Это связано с тем, что сопротивление току создается хаотическим движением ядер атомов в проводнике – близко к абсолютному нулю, они почти не двигаются, и поэтому сопротивление сводится к минимуму.
Вечный двигатель
Законы термодинамики и закон сохранения энергии объясняют, почему вечные двигатели невозможны.В соответствии со вторым законом термодинамики всегда будет образовываться некоторая «бесполезная» энергия, независимо от конструкции, которую вы выберете: энтропия системы будет увеличиваться.
Закон сохранения энергии показывает, что любая энергия в машине должна откуда-то поступать, а тенденция к энтропии показывает, почему машина не может идеально передавать энергию от одной формы к другой.
Используя пример водяного колеса и насоса из введения, водяное колесо должно иметь движущиеся части (например, ось и ее соединение с колесом, а также шестерни, которые передают энергию насосу), и они будут создавать трение, теряя часть энергии в виде тепла.
Это может показаться небольшой проблемой, но даже при небольшом падении выходной энергии насос не сможет вернуть все воды обратно на приподнятую поверхность, тем самым уменьшая энергию, доступную для следующая попытка. Тогда, в следующий раз, будет еще больше потраченной впустую энергии и больше воды, которую нельзя будет накачать, и так далее. Вдобавок к этому будут потери энергии от механизмов насоса.
Энтропия Вселенной и вы
Размышляя о втором законе термодинамики, вы можете задаться вопросом: если энтропия изолированной системы увеличивается, как могло случиться, что такая высоко «упорядоченная» система, как человек появился? Как мое тело принимает беспорядочный ввод в виде пищи и превращает ее в тщательно продуманные клетки и органы? Разве эти положения не противоречат второму закону термодинамики?
Оба эти аргумента совершают одну и ту же ошибку: люди не являются «закрытой системой» (т.
е. изолированная система) в строгом смысле слова, потому что вы взаимодействуете с окружающей вселенной и можете получать ее энергию.
Когда жизнь впервые появилась на Земле, хотя материя трансформировалась из состояния с более высокой энтропией в состояние с более низкой энтропией, в систему поступала энергия от Солнца, и эта энергия позволяет системе со временем становиться более низкой энтропией. Обратите внимание, что в термодинамике под «вселенной» часто понимают среду, окружающую состояние, а не всю космическую вселенную.
Для примера с человеческим телом, создающим порядок в процессе создания клеток, органов и даже других людей, ответ тот же: вы получаете энергию извне, и это позволяет вам делать некоторые вещи, которые кажутся противоречащими второй закон термодинамики.
Если бы вы были полностью отрезаны от других источников энергии и израсходовали бы всю запасенную энергию своего тела, то действительно было бы правдой, что вы не могли бы производить клетки или выполнять какие-либо действия, которые поддерживают ваше функционирование.
Если бы вы не нарушили второй закон термодинамики, вы бы умерли.
Второй закон термодинамики – обзор
1.7 Второй закон термодинамики – энтропия
Второй закон термодинамики , тщательно разработанный во многих современных учебниках по термодинамике, например, в Çengel and Boles (1994), Reynolds and Perkins ( 1977) и Роджерс и Мэйхью (1992), позволяют ввести понятие энтропии и определить идеальные термодинамические процессы.
Важное и полезное следствие второго закона термодинамики, известное как неравенство Клаузиуса , гласит, что для системы, проходящей через цикл, включающий теплообмен,
(1,22a) ∮ dQT≤0,
где d Q – элемент тепла, передаваемый системе при абсолютной температуре T . Если все процессы в цикле обратимы, то d Q = d Q R и равенство в ур. (1.22а), т.е.
(1.22b) ∮ dQRT = 0.
Свойство, называемое энтропией , для конечного изменения состояния затем определяется как
(1.
23a) S2 − S1 = ∫12dQRT.
Для постепенного изменения состояния
(1.23b) dS = mds = dQRT,
, где м – масса системы.
При устойчивом одномерном потоке через контрольный объем, в котором жидкость меняет состояние с условия 1 на входе на состояние 2 на выходе,
(1.24а) ∫12dQ.T≤m. (S2 − s1).
В качестве альтернативы это можно записать в терминах производства энтропии из-за необратимости, Δ S irv :
(1,24b) m. (S2 − s1) = ∫12dQ.T + ΔSirrev.
Если процесс адиабатический, dQ. = 0, то
(1,25) s2≥s1.
Если процесс также является обратимым , то
(1,26) s2 = s1.
Таким образом, для потока, претерпевающего адиабатический и обратимый процесс, энтропия останется неизменной (этот тип процесса называется изоэнтропическим ).Поскольку турбомашинное оборудование обычно является адиабатическим или близким к адиабатическому, изоэнтропическое сжатие или расширение представляет собой наилучший возможный процесс, который может быть достигнут.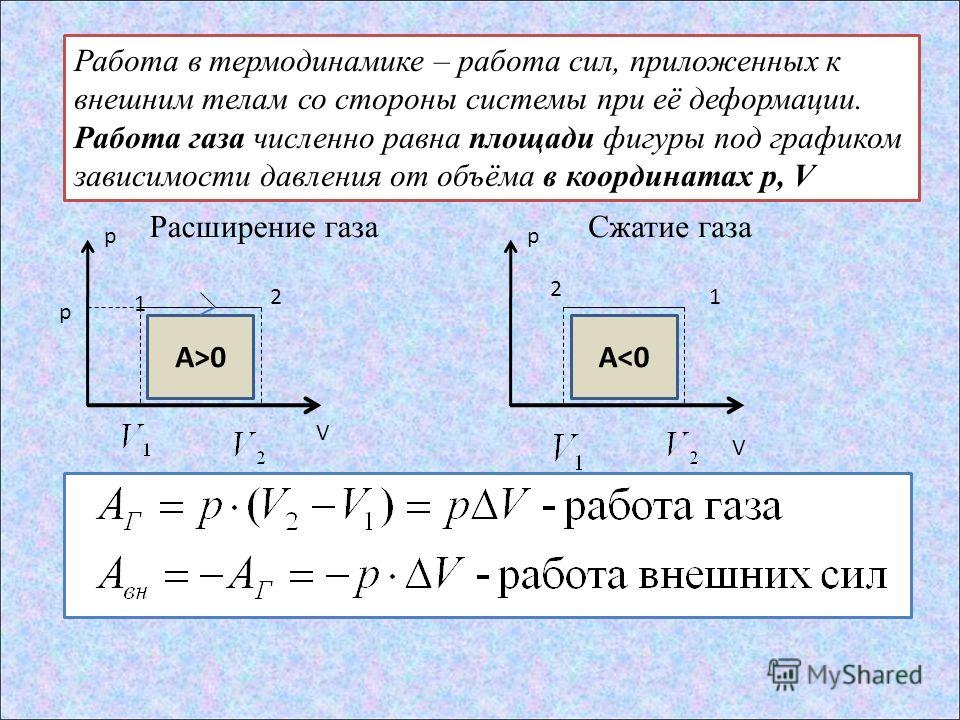
Чтобы максимизировать эффективность турбомашины, необходимо минимизировать необратимое производство энтропии Δ S ирв , и это основная цель любой конструкции.
Несколько важных выражений можно получить, используя предыдущее определение энтропии . Для системы массой м , претерпевающей обратимый процесс, d Q = d Q R = mT d s и d W = d W R = mp d v .В отсутствие движения, гравитации и других эффектов первый закон термодинамики, ур. (1.10b) становится
(1.27) Tds = du + pdv.
С h = u + pv , затем d h = d u + p d v + v d p и уравнение. Тогда (1.27) дает
(1.28) Tds = dh − vdp.
Уравнения (1.27) и (1.28) являются чрезвычайно полезными формами второго закона термодинамики, потому что уравнения записываются только в терминах свойств системы (нет членов, включающих Q или W ).
Следовательно, эти уравнения могут применяться к системе, в которой происходит любой процесс.
Энтропия – особенно полезное свойство для анализа турбомашин. Любое создание энтропии на пути потока машины можно приравнять к определенному количеству «потерянной работы» и, следовательно, к потере эффективности. Значение энтропии одинаково как в абсолютной, так и в относительной системе отсчета (см. Рисунок 1.7 ниже), и это означает, что его можно использовать для отслеживания источников неэффективности во всех вращающихся и неподвижных частях машины.Применение энтропии для учета потери производительности очень мощное средство и будет продемонстрировано в следующих разделах.
Что такое второй закон термодинамики? | Наука
Термодинамика – это изучение тепла и энергии. В его основе лежат законы, описывающие, как энергия движется внутри системы, будь то атом, ураган или черная дыра. Первый закон описывает, как энергия не может быть создана или уничтожена, а просто преобразована из одного вида в другой.
Однако второй закон, вероятно, более известен и даже более глубок, поскольку он описывает пределы того, что может делать Вселенная.Этот закон о неэффективности, вырождении и упадке. Он говорит нам, что все, что мы делаем, по своей сути расточительно и что во Вселенной происходят необратимые процессы. Он указывает нам стрелку на время и говорит о том, что наша вселенная неизбежно ждет мрачная и безрадостная судьба.
Несмотря на эти несколько обескураживающие идеи, идеи термодинамики были сформулированы во время большого технологического оптимизма – промышленной революции. В середине 19 века физики и инженеры создавали паровые машины для механизации работы и транспорта и пытались придумать, как сделать их более мощными и эффективными.
Многие ученые и инженеры, в том числе Рудольф Клаузиус, Джеймс Джоуль и лорд Кельвин, внесли свой вклад в развитие термодинамики, но отцом этой дисциплины был французский физик Сади Карно. В 1824 году он опубликовал книгу «Размышления о движущей силе огня» , в которой изложил основные принципы, почерпнутые из наблюдений за тем, как энергия перемещается вокруг двигателей и как связаны потраченное впустую тепло и полезная работа.
Второй закон можно выразить несколькими способами, самый простой из которых состоит в том, что тепло естественным образом перетекает от более горячего тела к более холодному.В ее основе лежит свойство термодинамических систем, называемое энтропией – в приведенных выше уравнениях она представлена буквой S – в общих чертах, мерой степени беспорядка в системе. Это можно представить по-разному, например, в расположении молекул – молекулы воды в кубике льда более упорядочены, чем те же самые молекулы после того, как они были нагреты до газа. В то время как молекулы воды находились в четко определенной решетке в кубике льда, они непредсказуемо плавают в газе.Следовательно, энтропия кубика льда ниже, чем у газа. Точно так же энтропия тарелки выше, когда она лежит кусками на полу, чем когда она находится в раковине целиком.
Более формальное определение энтропии при движении тепла вокруг системы дается в первом из уравнений. Бесконечно малое изменение энтропии системы (dS) рассчитывается путем измерения количества тепла, поступившего в замкнутую систему (δQ), деленного на общую температуру (T) в точке, где произошла теплопередача.
Второе уравнение – это способ выразить второй закон термодинамики через энтропию. Формула гласит, что энтропия изолированной природной системы всегда будет оставаться неизменной или увеличиваться – другими словами, энергия во Вселенной постепенно движется к беспорядку. Наше первоначальное утверждение второго закона вытекает из этого уравнения: тепло не может спонтанно течь от холодного объекта (низкая энтропия) к горячему объекту (высокая энтропия) в замкнутой системе, потому что это нарушило бы уравнение.(Холодильники, по-видимому, нарушают это правило, поскольку они могут замораживать предметы до гораздо более низких температур, чем окружающий их воздух. Но они не нарушают второй закон, потому что они не являются изолированными системами, требующими постоянного ввода электрической энергии для откачки тепла из их Холодильник нагревает комнату вокруг себя, и, если его отключить от сети, он естественным образом вернется к тепловому равновесию с комнатой.)
Эта формула также задает направление времени; в то время как любой другой известный нам физический закон будет работать одинаково независимо от того, идет ли время вперед или назад, это неверно для второго закона термодинамики.
Как бы долго вы ни стояли, кипящая вода вряд ли когда-нибудь превратится в глыбу льда. Разбитая пластина никогда не сможет собрать себя заново, поскольку это уменьшит энтропию системы в нарушение второго закона термодинамики. Некоторые процессы, как заметил Карно, необратимы.
Карно исследовал паровые машины, которые работают, сжигая топливо, нагревая цилиндр, содержащий пар, который расширяется и толкает поршень, чтобы затем сделать что-то полезное. Часть энергии топлива, которая извлекается и используется для чего-то полезного, называется работой, а оставшаяся часть – это потраченная впустую (и неупорядоченная) энергия, которую мы называем теплом.Карно показал, что теоретический максимальный КПД паровой машины можно предсказать, измерив разницу температур пара внутри цилиндра и воздуха вокруг него, известных в термодинамических терминах как горячий и холодный резервуары системы соответственно.
Тепловые двигатели работают, потому что тепло естественным образом перетекает из горячих мест в холодные. Если бы не было холодного резервуара, к которому он мог бы двигаться, не было бы теплового потока и двигатель не работал бы. Поскольку в холодном резервуаре всегда выше абсолютного нуля, ни один тепловой двигатель не может быть эффективным на 100%.
Поэтому двигатели с наилучшей конструкцией нагревают пар (или другой газ) до максимально возможной температуры, а затем выпускают выхлоп при минимально возможной температуре. Самые современные паровые двигатели могут достичь КПД около 60%, а дизельные двигатели автомобилей – около 50%. Бензиновые двигатели внутреннего сгорания расходуют гораздо больше энергии, чем их топливо.
Неэффективность заложена в любой системе, использующей энергию, и может быть описана термодинамически. Эта потраченная впустую энергия означает, что общий беспорядок во Вселенной – ее энтропия – со временем будет увеличиваться, но в какой-то момент достигнет максимума.В этот момент в невообразимо далеком будущем энергия во Вселенной будет равномерно распределена и поэтому для всех макроскопических целей будет бесполезна. Космологи называют это «тепловой смертью» Вселенной, неизбежным следствием неудержимого марша энтропии.
Общий вывод и количественная оценка третьего закона термодинамики
Физическая установка
Наша цель – предоставить окончательные количественные границы, применимые к любой процедуре охлаждения, а именно, мы хотим найти нижнюю границу температуры, которую может достичь система после любого процесса, который использует определенные ресурсы или длится определенное время t .Следовательно, мы должны допустить самые общие квантовые преобразования, то есть те, которые соблюдают сохранение полной энергии и являются микроскопически обратимыми (унитарными). Эта общая установка включает термодинамически необратимые протоколы, а также нереалистичные протоколы, в которых требуется полный контроль микроскопических степеней свободы ванны. Удивительно, но здесь мы обнаружим, как было обнаружено в случае второго закона 25,27,29,30 , что такая нереалистичная степень контроля, по-видимому, не дает преимущества перед очень грубым контролем.
Мы покажем, что плотность состояний резервуара, способствующая процессу охлаждения, оказывает важное влияние на скорость охлаждения системы. (Плотность состояний Ω ( E ) – это количество состояний с энергией E .) Мы видим, что чем быстрее растет Ω ( E ), тем ниже температура может быть достигнута с фиксированными ресурсами или в фиксированное количество времени. Более того: если Ω ( E ) растет экспоненциально или быстрее, то охлаждение до абсолютного нуля за конечное время в принципе возможно, с учетом нарушения третьего закона.Однако мы увидим, что экспоненциальную или сверхэкспоненциальную Ω ( E ) следует рассматривать как нефизическую. Это становится более интуитивным, когда выражается в терминах (микроканонической) теплоемкости C ( E ), связанной с S ( E ) = ln Ω ( E ) через
, где штрихи представляют дифференциалы. Если Ω ( E ) растет экспоненциально или быстрее, то C ( E ) бесконечно или отрицательно, что считается нефизическим.Если Ω ( E ) субэкспоненциально, то C ( E ) положительно. Причем, чем быстрее растет Ω ( E ), тем больше C ( E ). Только резервуар с бесконечномерным гильбертовым пространством может поддерживать рост S ( E ) для всех E . И действительно, бесконечные резервуары – это те, которые обеспечивают более быстрое охлаждение. Однако наши результаты являются общими и применимы также к конечномерному случаю.
Предположим, что мы хотим охладить квантовую систему с размерностью гильбертова пространства d и гамильтонианом H S с вырождением основного состояния g , щелью над основным состоянием Δ и максимальной энергией Дж .Какие ресурсы необходимы для этого?
Фундаментальные допущения
Давайте конкретизируем настройку и соберем допущения, которые мы примем (те, которые исходят из основных принципов):
(i) Мы считаем начало процесса, когда система еще не была контактировать с системой хранения работы (весом) или резервуаром, так что изначально общее состояние будет ρ S ⊗ ρ B ⊗ ρ W .Хотя может представлять интерес другой начальный сценарий, его рассмотрение выходит за рамки данной статьи.
(ii) Мы допускаем наиболее общее квантовое преобразование системы, ванны и веса, которое является обратимым (унитарным) и сохраняет полную энергию. Это может показаться ограничительным по сравнению с парадигмами, которые допускают произвольные условия взаимодействия, однако это не так, поскольку произвольные взаимодействия могут быть включены в модель, как показано в Приложении H ссылки. 27 и в исх.25, просто позволяя энергии рабочей системы колебаться. Во многих парадигмах это неявно обеспечивается за счет предположения, что вся недостающая энергия считается работой. Парадигмы, которые ослабляют это состояние, по существу игнорируют энергию, передаваемую другим системам, или рассматривают эти другие системы как классические. По сути, мы вводим энергосбережение, чтобы гарантировать, что мы должным образом учитываем все затраты энергии, связанные с взаимодействием, в то время как различные унитарные или условия взаимодействия просто передают или забирают энергию из веса для компенсации.Таким образом, процесс охлаждения представляет собой любое преобразование вида
, где U – глобальный унитарный показатель, удовлетворяющий
(iii) Затраченная на преобразование работа берется из веса. Поскольку нас интересуют предельные ограничения, мы рассматриваем идеализированный вес с гамильтонианом, имеющим непрерывный и неограниченный спектр. С помощью этой модели можно смоделировать любую другую рабочую систему 30 . Обозначим w max наихудшее значение затраченной работы, то есть
w max обычно будет намного больше, чем средняя работа 〈 W 〉.Ожидается, что любой физически разумный процесс, выполняемый за конечное время, будет конечным.
(iv) Мы также требуем, как в исх. 29 видно, что преобразование охлаждения коммутирует с переводами на вес. Другими словами, функционирование тепловой машины не зависит от источника энергии веса, так что это просто зависит от того, сколько работы передается от веса. Это можно понимать как определение того, что такое работа – это просто изменение энергии, которое мы можем вызвать в некоторой внешней системе.Это также гарантирует, что вес является только механизмом для доставки или сохранения работы, а не, например, дампом энтропии (см. Результат 1 в дополнительном обсуждении). Это также гарантирует, что процесс охлаждения всегда оставляет гирю в состоянии, которое можно использовать в следующем цикле или в процессе. Таким образом,
, где эрмитов оператор Π действует как для всех. Помимо этого, мы допускаем произвольное начальное состояние гири ρ W . В частности, он может быть когерентным, что дает преимущество 27 .
(v) Мы предполагаем, что ванна имеет объем V и находится в тепловом состоянии при заданной обратной температуре, с Z B статистической суммой ванны. Обозначим плотность свободной энергии ванны (в каноническом состоянии ρ B ) через.
(vi) Микроканоническая теплоемкость (2) неотрицательна C ( E ) для всех энергий E . Это означает, что S ( E ) сублинейен в E .Мы также доказываем в дополнительных методах, что если S ( E ) растет линейно или быстрее, то возможно идеальное охлаждение за конечное время.
С этими предположениями, мы показываем, что для идеального охлаждения системы до абсолютного нуля необходим хотя бы один из этих двух ресурсов, объем ванны V или наихудшее значение затраченной работы w max должно быть бесконечным. Кроме того, мы ограничили самую низкую достижимую температуру системы в терминах В и Вт макс .
Количественная оценка недостижимости из первых принципов
С допущениями (i) – (vi) мы рассматриваем два случая: один, когда начальное и конечное состояния являются тепловыми, и второй, когда мы допускаем произвольные начальное и конечное состояния. Наш первый результат относится к первому и заявляет, что в любом процессе, где вводимая работа наихудшего случая составляет w max , конечная температура системы не может быть ниже
в большом w max , В предел.Микроканоническая плотность свободной энергии при обратной температуре β 0 определяется как
, где E 0 является решением уравнения S ′ ( E 0 ) = β 0 . Напомним, что при большом объеме ванны V обычно бывает, что f mic ( β 0 ) = f банка ( β 0 ) и они не зависят от V .
Давайте проанализируем поведение уравнения (7) с точки зрения вложенных ресурсов. По мере роста w max , β 0 уменьшается, а f mic увеличивается, что приводит к более низкой конечной температуре. Поскольку вся зависимость от объема в уравнении (7) является явной, следовательно, большее значение V также переводится в более низкую конечную температуру.
Далее мы даем оценку для физически релевантного семейства энтропий
, где α > 0 и ν ∈ [1/2, 1) – две константы.Такая энтропия обширна, и если мы зададим ее, она описывает электромагнитное излучение (или любое безмассовое бозонное поле) в трехмерном ящике D объемом V . Обычно считается, что нет другого резервуара, плотность состояний которого растет быстрее с E , чем этот 36 , и, конечно же, нет такого резервуара, который имеет ν ≥1. Последний соответствует ванне с отрицательной теплоемкостью, о которой говорилось ранее, что обеспечивает охлаждение с конечной температурой Вт макс .В дополнительном обсуждении мы адаптируем оценку (7) к энтропии (9), получая
с точностью до главных членов. Теперь вся зависимость от V и w max очевидна. В частности, мы наблюдаем, что большие значения V и w max допускают более низкие температуры. А также более высокие значения ν , которые соответствуют более быстрому росту энтропии с учетом более низких температур.
Как упоминалось выше, процессы охлаждения, которые мы рассматриваем, являются очень общими.В частности, они могут изменять гамильтониан системы во время процесса, если конечный гамильтониан идентичен исходному H S . Это исключает неинтересный метод охлаждения, состоящий в изменении масштаба гамильтониана H S → 0. Однако наши оценки могут быть легко адаптированы к процессу, в котором конечный гамильтониан отличается от начального, как мы обсудим в заключении.
Давайте теперь рассмотрим более общий случай, когда ни начальное, ни конечное состояние не обязательно должны быть тепловыми, но вместо этого могут быть произвольными.Как уже хорошо известно 14,15,17,18,30 , недостижимость абсолютного нуля не является следствием того факта, что целевое состояние имеет низкую энергию, а, скорее, имеет низкую энтропию. Следовательно, это напрямую означает недостижимость какого-либо чистого состояния или, в более общем смысле, любого состояния с рангом g ниже, чем исходное состояние. Этот тип процессов обычно известен как стирание или очистка информации. Теперь мы анализируем ограничения любых процессов, которые принимают произвольное начальное состояние ρ S и преобразуют его в конечное состояние с поддержкой на проекторе g -rank P .Мы количественно оцениваем неточность преобразования ошибкой. Для ясности предположим, что система имеет тривиальный гамильтониан H S = 0 (общий случай рассматривается в дополнительном обсуждении), и обозначим через λ min и λ max. наименьшее и наибольшее собственные значения ρ S . В дополнительных методах мы показываем, что любой процесс ρ S → имеет ошибку
Результаты, представленные выше, а также другие более общие результаты, представленные в дополнительном обсуждении, количественно определяют нашу способность охлаждать систему (или, в более общем смысле, , перевести его в состояние с пониженным рангом) с точки зрения двух ресурсов: объема ванны V и колебания потребляемой работы в наихудшем случае w max .Таким образом, они представляют собой форму третьего закона в том смысле, что они накладывают ограничения на охлаждение при определенных ограниченных ресурсах. Теперь мы хотим перевести это во время, необходимое для охлаждения системы, и сделаем это, рассмотрев понятие тепловой машины и сделав два физически разумных предположения.
Тепловые машины
Напомним, что область вычислительной сложности основана на тезисе Черча-Тьюринга – идее о том, что мы рассматриваем компьютер как машину Тьюринга, а затем исследуем, как время вычислений масштабируется с размером проблема.Различные машины могут работать по-разному – головка компьютера может двигаться быстрее или медленнее по ленте памяти; информация может храниться в битах или в блоках памяти более высоких измерений, и головка может записывать в эту память с разными скоростями. Природа, кажется, не накладывает фундаментальных ограничений на размер блока памяти компьютера или скорость, с которой он может быть записан. Однако для любой физически разумной реализации компьютера и какой бы ни была скорость этих операций, она фиксирована и конечна, и только тогда мы исследуем масштабирование времени в зависимости от размера проблемы.И что важно, так это общее масштабирование времени с вводом (полиномиальным или экспоненциальным), а не какими-либо константами. Аналогично здесь мы рассмотрим стационарную тепловую машину и предположим, что она может передавать только конечное количество энергии в тепловую ванну за конечное время. Точно так же за конечное время он не может исследовать термальную ванну бесконечного размера. Тепловая машина, которая работала бы иначе, была бы физически нецелесообразной.
Мы можем рассматривать как V , так и w max как монотонные функции времени t .Чем дольше работает наша тепловая машина, тем больше работы она может выполнить в тепловую ванну и тем больший объем ванны она может исследовать. Для любой конкретной тепловой машины можно поставить конечную оценку, подставив эти функции в уравнение (10). В частности, если мы предположим, что взаимодействие опосредовано динамикой локального гамильтониана, то взаимодействие системы с ванной объемом V и пространственным размером d займет время
, где v пропорционально скорости звука в ванне (или скорости Либа-Робинсона 37 ), и V 1/ D линейного размера ванны.Реализация общих унитариев занимает гораздо больше времени, чем уравнение (12), но это служит нижней границей. Поскольку здесь нас интересует масштабирование температуры во времени, а не постоянные коэффициенты, нам не нужно беспокоиться о том, что практические тепловые машины работают с гораздо более медленными скоростями. Конечно, как и в случае с настоящими компьютерами, тепловые машины обычно имеют скорости значительно ниже границы Либа – Робинсона. Заметим, что, несмотря на конечность V , гильбертово пространство ванны может быть бесконечномерным.Если кто-то хочет иметь границу, которая не зависит от тепловой машины и скорости звука, которая является свойством ванны, то всегда можно принять v как скорость света. Хотя такое ограничение не было бы практически актуальным, оно было бы фундаментальным. Это похоже на границы вычислений, где для получения фундаментальной границы следует принять скорость гейта бесконечной (поскольку на это нет фундаментальных ограничений) и преобразовать количество битов, используемых в процессе, во время, умножив на скорость света.
Взаимосвязь между работой w max и временем t для наихудшего случая получается, если обратить внимание на следующее. В конечном t невозможно ввести в ванну бесконечный объем работы. Для простоты здесь мы предполагаем линейную зависимость
, где константа и будет зависеть от взаимодействия между системой и весом. Однако мы подчеркиваем, что если конкретная физическая установка неправильно моделируется соотношениями (12) и (13), то любая другая граница t ≥ h 1 ( w max ) и t ≥ ч 2 ( V ) тоже хорошо.Пока h 1 и h 2 являются строго монотонными функциями, принцип недостижимости будет сохраняться.
Ограничения при использовании термических машин
Теперь для любой конкретной термической машины мы можем вывести ограничения на температуру, которая может быть достигнута в данный момент времени t . Поскольку известная нам физическая система с самым быстрым ростом энтропии – это излучение, стоит посвятить следующий абзац случаю в уравнении (9), потому что это должно обеспечить границу, имеющую широкую применимость.Используя частные соотношения (12) и (13) и подставляя их в уравнение (10), для случая излучения получаем
в большом пределе t . Наша оценка (14) может быть легко адаптирована к любому другому отношению t ≥ h 1 ( w max ) и t ≥ h 2 ( V ). Интересно наблюдать в уравнении (14) взаимосвязь между характеристическим временем (сколько времени требуется для охлаждения до фиксированного значения) и размером системы V S .Используя обычное соотношение ln d ∝ V S , мы получаем сублинейное масштабирование
Что касается результата (11), то в пределе λ min → 0 граница становится тривиальной. Это может быть решено путем усечения начального состояния ρ S до подпространства, содержащего k наибольших собственных значений, и оптимизации результирующей границы как функции k . Кроме того, этот метод усечения позволяет распространить все наши результаты на бесконечномерные системы ( d = ∞).
примеров, вывод формул и проблемы в химии
Утверждение первого закона термодинамики
Первый закон термодинамики, также известный как «закон сохранения энергии».
[wp_ad_camp_1]
«Энергия не может быть создана или уничтожена, ее можно только изменить из одной формы в другую».
Или
«Общая энергия системы и ее окружения остается постоянной».
Математическая форма и вывод
Рассмотрим систему, начальная система которой ‘E 1 ‘, позволяя количеству тепла ‘q’ поглощаться системой из окружающей среды и выполнять некоторую работу ‘W’ с окружающей средой, в то время как внутренняя энергия изменить на
‘E 2 ‘.
Тогда изменение внутренней энергии определяется как
ΔE = E 1 – E 2
Согласно первому закону термодинамики
ΔE = q – W
Значение ΔE отрицательно, когда система теряет энергию и позитив, когда система набирает энергию.
Работа Давление-Объем
Рассмотрим газ, заключенный в цилиндр, снабженный поршнем без трения и невесомости. Пусть площадь поршня равна «A» внешнему давлению, действующему на поршень «P», то есть силе, оказываемой газом на поршень «F».
[wp_ad_camp_2]
Теперь, если система расширяется, и поршень движется против окружающей среды, путешествуя на расстояние ‘ΔI’. Тогда
Работа = Сила x Смещение
W = F x ΔI ———– 1
Так как,
P = F / A
Следовательно,
F = P x A ———— 2
Поместите значение ‘f’ в уравнение № 1, мы получим
W = P x A x ΔI ———— 3
Так как,
A x ΔL = ΔV
Итак, уравнение № 3 мы можем записать как
W = P x ΔV
Или
W = P ΔV
Согласно первому закону термодинамики
ΔE = q – w ———– 4
Положите значение ‘W’ в уравнении № 4 получаем
ΔE = q – P ΔV
Или
q = Δ E + p Δ V
[wp_ad_camp_3]
Применение первого закона термодинамики
Процесс при постоянном объеме
Согласно первому закону термодинамики
ΔE = q – P Δ V
ΔE = qv – P Δ V ————– 1
Где qv = тепло, поглощаемое при постоянном объеме, когда объем системы не изменяется
Δ V = 0
При этом условии работа не выполняется
P Δ V = px 0 = 0
Следовательно, уравнение № 1 принимает вид
Δ E = qv ————- 2
Это уравнение показывает, что при постоянном объеме выделяемое тепло равно изменению внутренней энергии, и никакой работы не происходит. Выполнено.
- Процесс при постоянном давлении
Когда в систему подается тепло при постоянном давлении, внутренняя энергия системы увеличивается, в результате чего система выполняет работу с окружающей средой:
[wp_ad_camp_4]
Таким образом,
qp = ΔE + PΔV ———- 1
где qp – тепло, поглощаемое при постоянном давлении
мы знаем, что
ΔE = E 1 – E 2
ΔV = V 1 – V 2
Тогда уравнение № 1 можно записать как:
= (E 2 – E 1 ) + P (V 2 – V 1 )
qp = (E 2 + PV 2 ) – (E 1 + PV 1 ) ———- 2
энтальпия ‘H’ математически определяется как:
H = E + PV
At исходное состояние
H 1 = E 1 + PV 1 900 03
В конечном состоянии
H 2 = E 2 + PV 2
Подставляя значение в уравнение 2, мы получаем
qp = H 2 – H 1 = Δ H
qp = ΔH ———– 3
Уравнение № 1 можно записать как:
ΔH = Δe + PΔV ———- 4
Уравнение № 3 показывает, что тепло, поглощаемое или выделяемое системой при постоянном давлении, равно изменение энтальпии системы.
Таким образом, изменение энтальпии – это тепло, поглощаемое или выделяемое системой при постоянном давлении.
Первый закон термодинамики для контрольных объемов – Термодинамика
В этом курсе мы рассматриваем три типа систем управления объемом – паровые силовые установки, системы охлаждения и авиационные реактивные двигатели. К счастью, мы сможем отдельно проанализировать каждый компонент системы независимо от всей системы, которая обычно представлена следующим образом:
В дополнение к потоку энергии через границу контрольного объема в виде тепла и работы, у нас также будет масса, текущая в контрольный объем и из него.Мы будем рассматривать только условия Steady Flow , в которых нет накопления энергии или массы в контрольном объеме, поэтому мы сочтем удобным вывести уравнение энергии в терминах мощности [кВт], а не энергии [кДж]. Кроме того, термин «Контрольный объем» указывает на то, что система не выполняет пограничной работы, и обычно у нас есть работа на валу, например, с турбиной, компрессором или насосом.
Рассмотрим элементарную массу d м, протекающую через впускное или выпускное отверстие контрольного объема, имеющую площадь A, объем d V, длину d x и среднюю постоянную скорость, как показано ниже.
Таким образом, массовый расход может быть определен следующим образом:
где: – массовый расход
– объемный расход
– плотность, – удельный объем
– скорость, это проходное сечение []
Масса жидкости течет через входные и выходные отверстия контрольного объема вместе с ее энергией. К ним относятся четыре типа энергии – внутренняя энергия ( u ), кинетическая энергия ( ke ), потенциальная энергия ( pe ) и работа потока ( w flow ).Чтобы оценить работу потока, рассмотрите следующую схему выходного порта, показывающую, как жидкость действует против окружающей среды через воображаемый поршень:
Интересно, что удельная работа потока просто определяется давлением P, умноженным на удельный объем v. В следующем разделе мы теперь можем разработать полное уравнение энергии для контрольного объема.
Рассмотрим контрольный объем, показанный на следующем рисунке.В условиях постоянного потока в контрольном объеме не происходит накопления массы или энергии, поэтому массовый расход применяется как к впускному, так и к выпускному отверстию. Кроме того, при постоянном массовом расходе удобнее разрабатывать уравнение энергии в терминах мощности [кВт], а не энергии [кДж], как это было сделано ранее.
Общая мощность, потребляемая за счет теплового и массового потока через впускной канал (1), должна равняться общей мощности за счет работы и массового расхода через выпускной порт (2), таким образом:
Удельная энергия e может включать кинетическую и потенциальную энергию, однако всегда будет включать комбинацию внутренней энергии ( и ) и работы потока ( Pv ), поэтому мы удобно комбинируем эти свойства с точки зрения энтальпии свойства (как было сделано в Глава 3a ) следующим образом:
Обратите внимание, что z – высота порта над некоторым опорным уровнем [м], а g – ускорение свободного падения [9.81]. Подставляя энергию e в приведенное выше уравнение энергии и упрощая, мы получаем окончательную форму уравнения энергии для регулируемого объема установившегося потока с одним входом и одним выходом следующим образом:
Обратите внимание, что энтальпия h является фундаментальной для уравнения энергии для контрольного объема.
При работе с закрытыми системами мы обнаружили, что создание схем T-v или P-v было значительным подспорьем в описании и понимании различных процессов.В системах с постоянным потоком мы обнаруживаем, что диаграммы давление-энтальпия ( P-h ) служат той же цели, и мы будем их широко использовать. В этом курсе мы рассматриваем три чистых жидкости – воду, хладагент R134a и диоксид углерода, и мы предоставили диаграммы P-h для всех трех в разделе «Таблицы свойств» в конце этой книги. Мы проиллюстрируем их использование на следующих примерах. Диаграмма P-h для воды показана ниже. Внимательно изучите его и постарайтесь понять значение отличительных форм кривых постоянной температуры в областях сжатой жидкости, насыщенной смеси (область качества) и перегретого пара.
Базовая паровая электростанция состоит из четырех взаимосвязанных компонентов, как правило, как показано на рисунке ниже. К ним относятся паровая турбина для выработки механической энергии на валу, конденсатор, который использует внешнюю охлаждающую воду для конденсации пара в жидкую воду, насос питательной воды для перекачивания жидкости до высокого давления и бойлер, который нагревается извне для кипячения воды до перегретый пар. Если не указано иное, мы предполагаем, что турбина и насос (а также все соединительные трубопроводы) являются адиабатическими и что конденсатор обменивает все свое тепло с охлаждающей водой.
Пример простой паровой электростанции – В этом примере мы хотим определить производительность этой базовой паровой электростанции в условиях, показанных на диаграмме, включая мощность турбины и насоса питательной воды, скорость теплопередачи котла и конденсатор и тепловой КПД системы.
В этом примере мы хотим оценить следующее:
- Выходная мощность турбины и мощность, необходимая для привода насоса питательной воды.
- Тепловая энергия, подаваемая в котел и сбрасываемая в конденсаторе в охлаждающую воду.
- Тепловой КПД электростанции η th , определяемый как чистая работа, выполненная системой, деленная на количество тепла, подаваемого в котел.
- Минимальный массовый расход охлаждающей воды в конденсаторе, необходимый для определенного повышения температуры.
Не пугайтесь сложности этой системы. Мы обнаружим, что можем решить каждый компонент этой системы отдельно и независимо от всех других компонентов, всегда используя один и тот же подход и одни и те же основные уравнения.Сначала мы используем информацию, представленную на приведенной выше схеме, чтобы построить четыре процесса (1) – (2) – (3) – (4) – (1) на диаграмме P-h . Обратите внимание, что жидкость, входящая и выходящая из котла, находится под высоким давлением 10 МПа, и аналогично, что входящая и выходящая из конденсатора жидкость находится под низким давлением 20 кПа. Состояние (1) задается пересечением 10 МПа и 500 ° C, а состояние (2) задается как 20 кПа при 90% качестве, состояние (3) задается пересечением 20 кПа и 40 ° C, и процесс перекачки питательной воды (3) – (4) следует линии постоянной температуры, так как T4 = T3 = 40 ° C.
Обратите внимание на диаграмму Ph , как мы можем получить мгновенное визуальное представление о производительности системы, в частности о тепловом КПД системы, сравнив разность энтальпии турбины (1) – (2) с энтальпией котла (4) – (1). Мы также заметили, что мощность, требуемая насосом питательной воды (3) – (4), ничтожна по сравнению с любым другим компонентом системы.
(Примечание: нам кажется странным, что единственный известный нам текст по термодинамике, который даже рассматривает использование диаграммы P-h для паровых электростанций, – это Engineering Thermodynamics – Jones and Dugan (1995).Он широко используется для холодильных систем, но не для паровых электростанций.)
Теперь мы рассматриваем каждый компонент как отдельный контрольный объем и применяем уравнение энергии, начиная с паровой турбины. Паровая турбина использует пар высокого давления – высокой температуры во входном отверстии (1) для выработки мощности на валу за счет расширения пара через лопатки турбины, в результате чего пар низкого давления – низкой температуры отклоняется в конденсатор на порт (2). Обратите внимание, что мы предположили, что изменение кинетической и потенциальной энергии жидкости незначительно, и что турбина является адиабатической.Фактически, любая потеря тепла в окружающую среду или увеличение кинетической энергии будет происходить за счет выходной мощности, поэтому практические системы спроектированы так, чтобы минимизировать эти эффекты потерь. Требуемые значения энтальпии для входного и выходного отверстий определяются из паровых таблиц.
Таким образом, мы видим, что в показанных условиях паровая турбина будет производить 8 МВт мощности.
Пар очень низкого давления из порта (2) теперь направляется в конденсатор, в котором тепло отбирается охлаждающей водой из близлежащей реки (или градирни), а пар конденсируется в область переохлажденной жидкости. Анализ конденсатора может потребовать определения массового расхода охлаждающей воды, необходимого для ограничения повышения температуры до определенной величины – в данном примере до 10 ° C. Это показано на следующей схеме конденсатора:
Обратите внимание, что наши паровые таблицы не включают область переохлажденной (или сжатой) жидкости, которую мы находим на выходе из конденсатора в порте (3).В этой области мы замечаем из диаграммы Ph , что в диапазоне чрезвычайно высоких давлений энтальпия жидкости равна энтальпии насыщенной жидкости при той же температуре, таким образом, с близким приближением h 3 = h f @ 40 ° C , независимо от давления.
Таким образом, мы видим, что в показанных условиях из пара в конденсаторе отбирается 17,6 МВт тепла.
Студенты часто спрашивали меня, почему мы должны отклонять такое большое количество тепла в конденсаторе, вызывающее такое большое снижение теплового КПД электростанции.Не вдаваясь в философские аспекты Второго закона (который мы рассмотрим позже, в главе 5 , мой лучший ответ дал мне Рэнди Шейдлер, старший инженер Гэвинской электростанции. Он заявил, что Четвертый закон термодинамики гласит: «Вы не можете качать пар!». , поэтому, пока мы не сконденсируем весь пар в жидкую воду, извлекая 17,6 МВт тепла, мы не сможем перекачать его до высокого давления, чтобы завершить цикл. (Рэнди не мог сказать. мне ссылку на источник этого удивительного наблюдения).
Чтобы определить изменение энтальпии Δh охлаждающей воды (или в насосе питательной воды, который следует далее), мы считаем воду несжимаемой жидкостью и оцениваем Δh следующим образом:
Энтальпия h определяется как:
В дифференциации:
Для несжимаемой жидкости: и
где – удельная теплоемкость жидкости
Таким образом:
Интегрирует:
Из таблиц пара находим, что удельная теплоемкость для жидкой воды C H 2 O = 4.18. Используя этот анализ, мы обнаружили на диаграмме конденсатора выше, что требуемый массовый расход охлаждающей воды составляет 421. Если этот расход не может поддерживаться близлежащей рекой, тогда градирня должна быть включена в проект электростанции.
Теперь рассмотрим насос питательной воды следующим образом:
Таким образом, как мы и подозревали на диаграмме выше P-h , требуемая мощность насоса чрезвычайно мала по сравнению с любым другим компонентом в системе и составляет всего 1% от выходной мощности турбины.
Последним компонентом, который мы рассматриваем, является котел, а именно:
Таким образом, мы видим, что в показанных условиях тепловая мощность, необходимая котлу, составляет 25,7 МВт. Обычно это обеспечивается сжиганием (или ядерной энергией). Теперь у нас есть вся информация, необходимая для определения теплового КПД паровой электростанции:
Тепловой КПД:
Обратите внимание, что работой насоса питательной воды обычно можно пренебречь.
Решенная проблема 4.1 – Паровая электростанция сверхкритического давления с подогревом для Афин, Огайо
В целях децентрализации национальной распределительной сети была предложена следующая сверхкритическая (25 МПа) угольная паровая электростанция (смоделированная по образцу Гэвинской электростанции в Чешире, штат Огайо) для обслуживания около 10 000 домашних хозяйств в Афинах, штат Огайо. Он будет размещен недалеко от очистных сооружений на восточной стороне Афин и будет охлаждаться водой из реки Хокинг. Сначала рассмотрим упрощенную систему, показанную ниже.Обратите внимание, что мы заменили «Котел» на «Парогенератор», поскольку при сверхкритических давлениях понятие кипящей воды не определено. Кроме того, мы специально разделили турбину на турбину высокого давления (HP) и турбину низкого давления (LP), поскольку мы обнаружим, что наличие одной турбины для расширения с 25 МПа до 10 кПа совершенно непрактично. Так, например, электростанция Гэвин имеет турбинный агрегат, состоящий из 6 турбин – турбины высокого давления, турбины промежуточного давления (повторного нагрева) и 4 больших турбин низкого давления, работающих параллельно.
Обратите внимание, что перед выполнением любого анализа мы всегда сначала набрасываем полный цикл на диаграмме P-h на основе представленных данных о давлении, температуре и качестве. Это приводит к следующей диаграмме:
При изучении графика диаграммы P-h мы замечаем, что система страдает двумя основными недостатками:
- Давление на выходе турбины низкого давления в канале (3) составляет 10 кПа, что значительно ниже атмосферного давления.Чрезвычайно низкое давление в конденсаторе приведет к попаданию воздуха в систему и, в конечном итоге, к ухудшению рабочих характеристик.
- Качество пара в порту (3) составляет 80%. Это неприемлемо. Конденсированная вода вызовет эрозию лопаток турбины, и мы всегда должны стараться поддерживать качество выше 90%. Один из примеров эффектов этой эрозии можно увидеть на концах лопаток последней ступени турбины Gavin LP. В течение 2000 года все четыре турбины низкого давления необходимо было заменить из-за снижения производительности в результате этой эрозии.(См .: Экскурсия по электростанции Гэвин – февраль 2000 г.)
Следующая измененная схема системы исправляет оба недостатка. Пар на выходе из турбины высокого давления (порт (2)) повторно нагревается до 550 ° C перед подачей в турбину низкого давления через порт (3). Также жидкий конденсат низкого давления в канале (5) перекачивается до давления 800 кПа и проходит через деаэратор перед тем, как перекачиваться насосом питательной воды до высокого давления 25 МПа.
Эта система упоминается как цикл повторного нагрева , и на основе приведенных выше данных отображается на диаграмме P-h следующим образом:
Таким образом, мы видим, что, несмотря на сложность системы, диаграмма P-h дает возможность интуитивного и качественного начального понимания системы.Используя методы, описанные ранее в этой главе для анализа каждого компонента, а также таблицы пара, определите следующее:
- Предполагая, что обе турбины адиабатические, и пренебрегая эффектами кинетической энергии, мы определяем общую выходную мощность обеих турбин [10,6 МВт].
- Предполагая, что и конденсатный насос, и насос питательной воды являются адиабатическими, определите мощность, необходимую для приведения в действие двух насосов [-204 кВт].
- Определите общую теплопередачу парогенератору, включая систему повторного нагрева [26.1 МВт].
- Определите общий тепловой КПД этой электростанции. (Тепловой КПД (η th ) определяется как общая проделанная работа (турбины, насосы), деленная на общее количество тепла, подаваемого извне в парогенератор и систему повторного нагрева) [40%].
- Определите количество тепла, отводимого охлаждающей воде в конденсаторе [-15,7 МВт].
- Предположим, что все тепло, отводимое в конденсаторе, поглощается охлаждающей водой из реки Хокинг. Во избежание теплового загрязнения охлаждающая вода не должна подниматься выше 10 ° C.Если пар выходит из конденсатора в виде насыщенной жидкости при 40 ° C, определите требуемый минимальный объемный расход охлаждающей воды [22,6 кубических метра / минуту].
- Обсудите, считаете ли вы, что предлагаемая система может быть охлаждена рекой Хокинг. Вам нужно будет провести некоторое исследование, чтобы определить минимальный сезонный сток в реке, чтобы подтвердить свое решение. (Подсказка – Google: Hocking River Flow)
(шаг 1 выше)
(шаг 2 выше)
(шаг 3 выше)
(шаг 6 выше)
Решенная проблема 4.2 – Открытый нагреватель питательной воды добавлен к паровой электростанции сверхкритического давления в Афинах, штат Огайо,
Спасибо Крису Дамбринку из Imtech.nl за то, что он ознакомил меня с этим альтернативным подходом к адаптации открытого подогревателя питательной воды к паровой электростанции (4 февраля 2010 г.).
Эта Решенная проблема является альтернативным расширением Решенной задачи 4.1, в которой мы удлиняем деаэратор, отбирая пар из выхода турбины высокого давления, и снижаем давление до 800 кПа с помощью дроссельного регулирующего клапана перед его подачей. в деаэратор.Это позволяет удобно преобразовать деаэратор в открытый нагреватель питательной воды , не требуя спускного крана из турбины низкого давления точно при давлении деаэратора, как показано на следующей диаграмме:
: массовая доля
= насос питательной воды
= насос конденсата
Обратите внимание, что перед выполнением любого анализа мы всегда сначала набрасываем полный цикл на диаграмме P-h на основе данных давления, температуры и качества, представленных на диаграмме системы.Это приводит к следующей диаграмме:
При рассмотрении графика диаграммы P-h мы замечаем следующее:
- Массовая доля пара y отбирается из выпускного отверстия турбины высокого давления (2) и проходит через дроссель, так что его давление снижается до давления деаэратора (9). Затем он смешивается с массовой долей (1-y) жидкой воды на станции (6). Массовая доля y выбирается таким образом, чтобы жидкость могла достичь насыщенного жидкого состояния на станции (7).
- Насос питательной воды затем перекачивает жидкость на станцию (8), тем самым экономя значительное количество тепла от парогенератора при нагревании жидкости от станции (8) до входа в турбину на станции (1). Верно, что при массовой доле (1-y) выходная мощность меньше из-за пониженного массового расхода в турбине низкого давления, однако конечным результатом обычно является повышение теплового КПД.
Таким образом, мы еще раз видим, что, несмотря на сложность системы, диаграмма P-h дает возможность интуитивного и качественного начального понимания системы.Используя методы, описанные ранее в этой главе для анализа каждого компонента, а также таблицы пара для оценки энтальпии на различных станциях (показаны красным) и пренебрегая кинетическими и потенциальными эффектами энергии, определите следующее:
- Предполагая, что открытый нагреватель питательной воды является адиабатическим, определите массовую долю пара y, которая требуется отводить из выпускного отверстия турбины высокого давления, который переведет текучую среду со станции (6) в состояние насыщенной жидкости в деаэраторе.[y = 0.20] Сначала нам нужно оценить энтальпию жидкости на станции (9) после прохождения через дроссельный регулирующий клапан:
Таким образом, мы находим, что для идеального дросселя энтальпия h9 = h3 не зависит от падения давления, что позволяет нам удобно изобразить процесс дросселирования в виде вертикальной линии на диаграмме P-h . Теперь определим массовую долю y, рассмотрев процесс смешивания в открытом нагревателе питательной воды следующим образом:
Обратите внимание, что мы можем оценить это значение y непосредственно из диаграммы P-h , просто измерив разность энтальпий (h7 – h6) и (h9 – h6) с помощью линейки.
- Предполагая, что и конденсатный насос, и насос питательной воды являются адиабатическими, определите мощность, необходимую для приведения в действие двух насосов [235 кВт]. Изучив схему системы выше, мы заметили кое-что очень странное в насосе питательной воды. До сих пор мы считали жидкую воду несжимаемой, поэтому перекачка ее до более высокого давления не приводила к повышению ее температуры. Однако во время недавнего посещения электростанции Гэвин мы обнаружили, что при давлении 25 МПа и температуре более 100 ° C вода перестает быть несжимаемой, а сжатие всегда приводит к повышению температуры.Мы не можем использовать простую формулу несжимаемой жидкости для определения работы насоса, однако необходимо оценить разницу энтальпии из таблиц для сжатой жидкой воды, что приведет к следующим результатам:
- Предполагая, что обе турбины адиабатические, определите новую (уменьшенную) суммарную выходную мощность обеих турбин.Вспомните из Решенной задачи 4.1, что выходная мощность турбин составила 10,6 МВт, если из турбины низкого давления не будет отбираться пар [8,98 МВт]
Таким образом, как и ожидалось, мы обнаруживаем, что полезная выходная мощность немного меньше, чем в предыдущей системе без крана турбины. Однако управление мощностью обычно осуществляется путем изменения скорости насоса питательной воды, и мы обычно находим резервуар для хранения жидкой воды, связанный с деаэратором, чтобы приспособиться к изменениям массового расхода воды.В нашем случае нам просто нужно увеличить массовый расход воды с 7 до 8,25, чтобы восстановить исходную выходную мощность.
- Определите общую теплопередачу парогенератору, включая систему повторного нагрева [21,4 МВт].
- Определите общий тепловой КПД этой электростанции.(Тепловой КПД (η th ) определяется как общая проделанная работа (турбины, насосы), деленная на общее количество тепла, подаваемого извне в парогенератор и систему повторного нагрева) [41%].
- Определите количество тепла, отводимого охлаждающей воде в конденсаторе [-12,6 МВт].
- Предположим, что все тепло, отводимое в конденсаторе, поглощается охлаждающей водой из реки Хокинг. Во избежание теплового загрязнения охлаждающая вода не должна подниматься выше 10 ° C.Если пар выходит из конденсатора в виде насыщенной жидкости при 40 ° C, определите требуемый минимальный объемный расход охлаждающей воды [18,1 кубических метров / минуту].
Обратите внимание, что всегда полезно проверять свои расчеты, оценивая тепловой КПД, используя только тепло, подаваемое в парогенератор и отбрасываемое конденсатором.
Обсуждение: Таким образом, мы обнаруживаем, что открытый нагреватель питательной воды действительно повысил КПД с 40% до 41%. Это может показаться незначительным, однако все основные компоненты уже были на месте, поскольку без деаэратора паросиловая установка выйдет из строя и выйдет из строя в течение очень короткого времени из-за утечки воздуха в систему. Кроме того, если снижение выходной мощности неприемлемо, его можно легко исправить, увеличив массовый расход в конструкции системы.Обратите внимание, что это надуманный пример, чтобы продемонстрировать, что независимо от того, насколько сложна система, мы можем легко построить всю систему на диаграмме P-h и сразу же получить интуитивное понимание и оценку производительности системы. Полезно проверить каждое значение энтальпии, считанное или оцененное из таблиц пара, и сравнить их со значениями на оси энтальпии на диаграмме P-h .
Введение и обсуждение
В первые дни холодильной техники обычно использовались два хладагента: аммиак и диоксид углерода.И то, и другое было проблематичным – аммиак токсичен, а диоксид углерода требует чрезвычайно высокого давления (от 30 до 200 атмосфер!) Для работы в холодильном цикле, а поскольку он работает в транскритическом цикле, температура на выходе компрессора чрезвычайно высока (около 160 ° C). ). Когда был открыт фреон 12 (дихлордифторметан), он полностью стал предпочтительным хладагентом. Это чрезвычайно устойчивая, нетоксичная жидкость, которая не взаимодействует со смазкой компрессора и работает при давлениях, всегда несколько превышающих атмосферное, так что в случае любой утечки воздух не попадет в систему, поэтому можно выполнить подзарядку без применить вакуум.
К сожалению, когда хладагент в конечном итоге протекает и попадает в озоновый слой, ультрафиолетовое излучение разрушает молекулу, высвобождая высокоактивные радикалы хлора, которые способствуют разрушению озонового слоя. С тех пор фреон 12 был запрещен к использованию в глобальном масштабе и был по существу заменен не содержащим хлора R134a (тетрафторэтан) – не таким стабильным, как фреон 12, однако он не обладает характеристиками разрушения озонового слоя.
Однако в последнее время международный научный консенсус состоит в том, что глобальное потепление вызывается деятельностью человека, связанной с энергией, и различные антропогенные вещества определяются на основе потенциала глобального потепления (ПГП) со ссылкой на двуокись углерода (ПГП = 1).Установлено, что R134a имеет GWP 1300, и в Европе в течение нескольких лет системам кондиционирования воздуха будет запрещено использовать R134a в качестве хладагента.
Новая горячая тема – возврат к двуокиси углерода (R744) в качестве хладагента (см., Например, веб-сайт: R744.com). Две предыдущие основные проблемы, связанные с высоким давлением и высокой температурой компрессора, оказались полезными. Очень высокое давление цикла приводит к высокой плотности жидкости на протяжении всего цикла, что позволяет миниатюризировать системы для тех же требований к мощности теплового насоса.Кроме того, высокая температура на выходе позволит мгновенно разморозить автомобильные лобовые стекла (нам не нужно ждать, пока двигатель автомобиля прогреется) и может использоваться для комбинированного отопления помещений и нагрева горячей воды в домашних условиях (см., Например: Norwegian IEA Heatpump Приложение к программе 28.
A Базовая парокомпрессионная холодильная установка с хладагентом R134a
В отличие от паровых электростанций, обычно проектирование и анализ систем охлаждения и тепловых насосов начинают с построения цикла на диаграмме P-h .
На следующей схеме показана базовая система охлаждения или теплового насоса с типичными характеристиками. Поскольку массовый расход хладагента не указан, весь анализ проводится с точки зрения удельных значений энергии. Обратите внимание, что одну и ту же систему можно использовать либо для холодильника, либо для кондиционера, в котором тепло, поглощаемое в испарителе (q , испаритель ), является желаемой мощностью, или для теплового насоса, в котором тепло отводится в конденсаторе ( q cond ) является желаемым выходом.
В этом примере мы хотим оценить следующее:
- Тепло, поглощаемое испарителем (q испаритель )
- Тепло, отводимое конденсатором (q cond )
- Выполненные работы для привода компрессора (w comp )
- Коэффициент полезного действия (COP) системы в качестве холодильника или теплового насоса.
Как и в случае с паровой электростанцией, мы обнаружили, что можем решить каждый компонент этой системы отдельно и независимо от всех других компонентов, всегда используя тот же подход и одни и те же основные уравнения.Сначала мы используем информацию, представленную на приведенной выше схеме, чтобы построить четыре процесса (1) – (2) – (3) – (4) – (1) на диаграмме P-h . Обратите внимание, что жидкость, входящая и выходящая из конденсатора (Состояние (2) – Состояние (3)), находится под высоким давлением 1 МПа. Жидкость входит в испаритель в состоянии (4) в виде насыщенной смеси при -20 ° C и выходит из испарителя в состоянии (1) в виде насыщенного пара. Состояние (2) определяется пересечением 1 МПа и 70 ° C в зоне перегрева. Видно, что состояние (3) находится в области переохлажденной жидкости при 30 ° C, поскольку температура насыщения при 1 МПа составляет около 40 ° C.Процесс (3) – (4) представляет собой вертикальную линию (h4 = h5), как обсуждается ниже.
В следующем разделе мы разработаем методы оценки решения этого примера с использованием таблиц хладагента R134a. Обратите внимание, что таблицы хладагентов не включают переохлажденную область, однако, поскольку линия постоянной температуры в этой области по существу вертикальна, мы используем значение энтальпии насыщенной жидкости при этой температуре.
Обратите внимание на диаграмму Ph , как мы можем получить мгновенную визуальную оценку производительности системы, в частности, коэффициента производительности системы, сравнив разность энтальпии компрессора (1) – (2) с разницей энтальпии компрессора (1) – (2) с разницей энтальпии компрессора (1) – (2) испаритель (4) – (1) в случае холодильника или конденсатор (2) – (3) в случае теплового насоса.
Теперь мы рассматриваем каждый компонент как отдельный контрольный объем и применяем уравнение энергии, начиная с компрессора. Обратите внимание, что мы предположили, что изменение кинетической и потенциальной энергии жидкости незначительно, и что компрессор является адиабатическим. Требуемые значения энтальпии для входного и выходного отверстий определены из таблиц хладагента R134a.
Перегретый хладагент под высоким давлением в канале (2) теперь направляется в конденсатор, в котором тепло отводится от хладагента, позволяя ему достичь области переохлажденной жидкости в канале (3).Это показано на следующей схеме конденсатора:
Дроссель – это просто расширительный клапан, который является адиабатическим и не работает, но позволяет значительно снизить температуру хладагента, как показано на следующей диаграмме:
Последним компонентом является испаритель, который отводит тепло из окружающей среды при низкой температуре, позволяя смеси жидкого хладагента и пара достичь состояния насыщенного пара на станции (1).
При определении коэффициента производительности – для холодильника или кондиционера желаемая мощность – это тепло, поглощаемое испарителем, а для теплового насоса желаемая мощность – это тепло, отводимое конденсатором, которое используется для обогрева дома. Требуемый ввод в обоих случаях – это работа, проделанная на компрессоре (то есть счет за электричество). Таким образом,
Обратите внимание, что для одной и той же системы мы всегда находим, что COP HP = COP R + 1.
Также обратите внимание, что значения COP обычно больше 1, поэтому они никогда не называются значениями «КПД», которые всегда имеют максимум 100%.
Таким образом, диаграмма P-h является широко используемым и очень полезным инструментом для приблизительной оценки системы холодильника или теплового насоса. Фактически, в официальном справочнике, предоставленном NCEES для использования на экзамене по основам инженерии, для R134a представлена только диаграмма P-h .Ожидается, что вы ответите на все вопросы по этому поводу, построив цикл на этой диаграмме, как показано выше.
Введение и описание
В связи с глобальным стремлением к энергоэффективности возобновился интерес к геотермальным тепловым насосам, которые использовались ограниченно более 60 лет. По сути, эта технология основана на том факте, что на несколько метров ниже поверхности земли температура остается относительно постоянной в течение всего года (около 13 ° C), теплее воздуха над ней зимой и прохладнее летом. .Это означает, что мы можем спроектировать тепловой насос, который может сочетать в себе горячую воду и отопление помещений зимой, когда в качестве источника тепла используется земля (а не наружный воздух) при значительном увеличении коэффициента полезного действия COP. Точно так же, с подходящей арматурой, мы можем использовать ту же систему летом для нагрева воды и кондиционирования воздуха, в которых земля используется как теплоотвод, а не наружный воздух. Это достигается за счет использования контура Ground для обеспечения теплопередачи с землей, как описано на веб-сайте USDOE: Geothermal Heat Pumps.Другое описание геотермальных тепловых насосов было предоставлено компанией David White Services из юго-восточного Огайо и включает видео на YouTube от WaterFurnace: GEOTHERMAL Как это работает.
Проблема
Мы хотим сделать предварительный термодинамический анализ следующей домашней геотермальной тепловой насосной системы, предназначенной для горячего водоснабжения и отопления помещений в зимний период. Обратите внимание, что с подходящей арматурой эту систему можно использовать как зимой для отопления помещений, так и летом для кондиционирования воздуха с подогревом горячей воды в течение всего года.
Обратите внимание, что секция конденсатора включает в себя как нагреватель горячей воды, так и нагреватель помещения, а станция (3) указана как находящаяся в области качества. Предположим, что 50 ° C – это разумная максимальная температура горячей воды для домашнего использования, таким образом, при высоком давлении 1,6 МПа максимальная мощность, доступная для нагрева горячей воды, будет иметь место, когда хладагент на станции (3) достигнет насыщенного жидкого состояния.( Quick Quiz: оправдывают это утверждение). Предположим также, что хладагент на станции (4) достигает температуры переохлажденной жидкости 20 ° C при нагревании воздуха.
1-й закон термодинамики
1-й закон термодинамики говорит нам, что энергия не создается и не разрушается, таким образом, энергия Вселенной – это постоянная . Однако энергия может быть передана из одной части Вселенной в другую. Чтобы решить термодинамические проблемы, нам нужно будет изолировать определенную часть Вселенной, систему, от остальной части Вселенной, окружающей среды.
Передача энергии между различными системами может быть выражена как:
E 1 = E 2 (1)
, где
E 1 = начальная энергия
2 = конечная энергия
Внутренняя энергия включает:
- Кинетическая энергия, связанная с движениями атомов
- Потенциальная энергия, запасенная в химических связях молекул
- Гравитационная энергия системы
Первый закон является отправной точкой для науки термодинамики и инженерного анализа.
Основываясь на типах обмена, которые могут иметь место, мы определим три типа систем:
- изолированные системы : без обмена материей или энергией
- закрытые системы: без обмена материей, но с некоторым обменом энергией
- открытые системы : обмен как веществом, так и энергией
Первый закон использует ключевые концепции внутренней энергии , тепла и работы системы .Он широко используется при обсуждении тепловых двигателей .
Внутренняя энергия Внутренняя энергия определяется как энергия, связанная со случайным, неупорядоченным движением молекул. Она отделена по масштабу от макроскопической упорядоченной энергии, связанной с движущимися объектами; это относится к невидимой микроскопической энергии на атомном и молекулярном уровне. Например, стакан воды комнатной температуры, стоящий на столе, не имеет видимой энергии, ни потенциальной, ни кинетической.Но в микроскопическом масштабе это бурлящая масса высокоскоростных молекул. Если бы воду перебросили через комнату, эта микроскопическая энергия не обязательно изменилась бы, когда мы наложим упорядоченное крупномасштабное движение на воду в целом. |
Тепло Тепло можно определить как энергию, передаваемую от высокотемпературного объекта к низкотемпературному объекту. Объект не обладает «теплом»; подходящим термином для микроскопической энергии в объекте является внутренняя энергия.Внутренняя энергия может быть увеличена путем передачи энергии объекту от объекта с более высокой температурой (более горячего) – это называется нагревом. |
Работа Когда работа выполняется термодинамической системой, обычно эту работу выполняет газ. Работа, совершаемая газом при постоянном давлении, равна W = p dV, где W – работа, p – давление, а dV – изменение объема. |
Тепловые двигатели Холодильники, тепловые насосы, цикл Карно, цикл Отто |
Изменение внутренней энергии системы равно напору, добавленному в систему за вычетом работы, выполненной система:
dE = Q – W (2)
, где
dE = изменение внутренней энергии
Q = тепло, добавленное к системе
W = работа, выполненная система
1 st закон не дает информации о направлении процессов и не определяет конечное состояние равновесия.Интуитивно мы знаем, что энергия течет от высокой температуры к низкой. Таким образом, закон 2 nd необходим для определения направления процессов .
Энтальпия – это «термодинамический потенциал», используемый в химической термодинамике реакций и нециклических процессов. Энтальпия определяется как
H = U + PV (3)
, где
H = энтальпия
U = внутренняя энергия
P = давление
объем
Энтальпия тогда является точно измеряемой переменной состояния, поскольку она определяется в терминах трех других точно определяемых переменных состояния.